Изобретение относится к области контроля и диагностирования систем автоматического управления и их элементов.
Известен способ контроля динамического блока в составе системы управления (Патент РФ №2136033, МКИ6 G05B 23/02, 1999), основанный на интегрировании выходного и входного сигналов блока с весом e-αt, где α - вещественная константа.
Недостатком этого способа является то, что его применение для контроля нескольких блоков системы управления произвольной структуры приводит к необходимости интегрирования входных и выходных сигналов каждого контролируемого блока.
Наиболее близким техническим решением (прототипом) является способ поиска неисправностей в динамических системах (Патент РФ №2199776, МКИ6 G05B 23/02, 2003).
Недостатком этого способа является то, что он предполагает определение функций чувствительности, что является достаточно трудоемкой задачей, связанной со значительными временными и аппаратными затратами.
Технической задачей, на решение которой направлено данное изобретение, является уменьшение аппаратных и временных затрат на диагностирование путем замены значений функций чувствительности на величины деформаций интегральных преобразований динамических характеристик системы, полученных в результате пробных отклонений параметров соответствующих блоков, а также обеспечение возможности сравнения результатов различных режимов диагностирования для выбора наилучшего в плане различимости дефектов путем применения нормированных диагностических признаков.
Поставленная задача достигается тем, что регистрируют реакцию заведомо исправной системы fjном(t), j=1, 2, …, k на интервале t∈[0, TK] в k контрольных точках и определяют интегральные оценки выходных сигналов Fjном(α), j=1, …, k, системы, для чего в момент подачи тестового сигнала на вход системы с номинальными характеристиками одновременно начинают интегрирование сигналов системы управления в каждой из k контрольных точек с весами e-αt, где 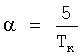 , путем подачи на первые входы k блоков перемножения сигналов системы управления, на вторые входы блоков перемножения подают экспоненциальный сигнал e-αt, выходные сигналы k блоков перемножения подают на входы k блоков интегрирования, интегрирование завершают в момент времени Tк, полученные в результате интегрирования оценки выходных сигналов Fjном(α), j=1, …, k регистрируют, определяют интегральные преобразования динамических характеристик модели для каждой из k контрольных точек, полученные в результате пробных отклонений параметров каждого из m блоков, для чего поочередно для каждого блока динамической системы вводят пробное отклонение параметра его передаточной функции и находят интегральные оценки выходных сигналов системы для параметра α и тестового сигнала x(t), полученные в результате интегрирования оценки выходных сигналов для каждой из k контрольных точек и каждого из m пробных отклонений Pji(α), j=1, …, k; i=1, …, m регистрируют, определяют деформации интегральных преобразований динамических характеристик модели, полученные в результате пробных отклонений параметров соответствующих блоков ΔPji(α)=Pji(α)-Fjном(α), j=1, …, k; i=1, …, m, определяют нормированные значения деформаций интегральных преобразований динамических характеристик модели, полученные в результате пробных отклонений параметров соответствующих блоков из соотношения
, путем подачи на первые входы k блоков перемножения сигналов системы управления, на вторые входы блоков перемножения подают экспоненциальный сигнал e-αt, выходные сигналы k блоков перемножения подают на входы k блоков интегрирования, интегрирование завершают в момент времени Tк, полученные в результате интегрирования оценки выходных сигналов Fjном(α), j=1, …, k регистрируют, определяют интегральные преобразования динамических характеристик модели для каждой из k контрольных точек, полученные в результате пробных отклонений параметров каждого из m блоков, для чего поочередно для каждого блока динамической системы вводят пробное отклонение параметра его передаточной функции и находят интегральные оценки выходных сигналов системы для параметра α и тестового сигнала x(t), полученные в результате интегрирования оценки выходных сигналов для каждой из k контрольных точек и каждого из m пробных отклонений Pji(α), j=1, …, k; i=1, …, m регистрируют, определяют деформации интегральных преобразований динамических характеристик модели, полученные в результате пробных отклонений параметров соответствующих блоков ΔPji(α)=Pji(α)-Fjном(α), j=1, …, k; i=1, …, m, определяют нормированные значения деформаций интегральных преобразований динамических характеристик модели, полученные в результате пробных отклонений параметров соответствующих блоков из соотношения 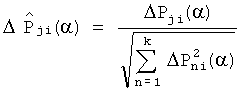 , замещают систему с номинальными характеристиками контролируемой, на вход системы подают аналогичный тестовый сигнал x(t), определяют интегральные преобразования динамических характеристик контролируемой системы для k контрольных точек Fj(α), j=1, …, k для параметра α, определяют отклонения интегральных преобразований динамических характеристик контролируемой системы для k контрольных точек от номинальных значении ΔFj(α)=Fj(α)-Fjном(α), j=1, …, k, определяют нормированные значения отклонений интегральных преобразований динамических характеристик контролируемой системы из соотношения
, замещают систему с номинальными характеристиками контролируемой, на вход системы подают аналогичный тестовый сигнал x(t), определяют интегральные преобразования динамических характеристик контролируемой системы для k контрольных точек Fj(α), j=1, …, k для параметра α, определяют отклонения интегральных преобразований динамических характеристик контролируемой системы для k контрольных точек от номинальных значении ΔFj(α)=Fj(α)-Fjном(α), j=1, …, k, определяют нормированные значения отклонений интегральных преобразований динамических характеристик контролируемой системы из соотношения 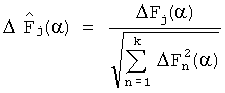 ,
,
определяют диагностические признаки из соотношения
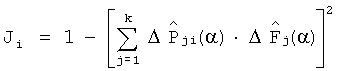 , i=1, …, m, по минимуму диагностического признака определяют неисправный блок.
, i=1, …, m, по минимуму диагностического признака определяют неисправный блок.
Сущность предлагаемого способа заключается в следующем.
Способ основан на использовании пробных отклонений параметров модели непрерывной динамической системы. Для получения диагностических признаков динамических элементов используются преобразования по Лапласу временных функций:
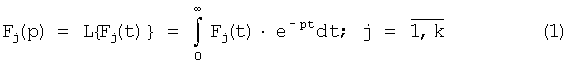
в области вещественных значений переменной Лапласа p=α, в интервале 0≤α≤∞. Использование преобразования Лапласа позволяет перейти от обработки временных функций к анализу численных значений их функционалов.
Интегральные преобразования находят на временном интервале Tk в k контрольных точках:
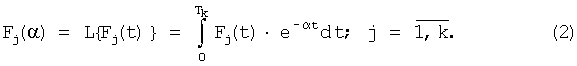
Прототип (Патент РФ №2199776, МКИ6 G05B 23/02, 2003) предполагает, что для каждого динамического элемента с номером i вычисляется диагностический признак по формуле:
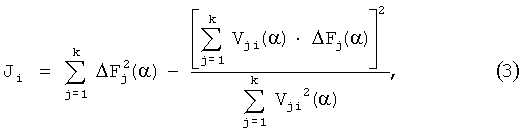
где ΔF(α)=(ΔFl(α), ΔF2(α), …, ΔFk(α))T - вектор изображений для вещественного значения переменной Лапласа α отклонений временных характеристик объекта в k контрольных точках;
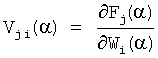 - структурная чувствительность для j-й контрольной точки, i-го динамического элемента и значения переменной Лапласа α.
- структурная чувствительность для j-й контрольной точки, i-го динамического элемента и значения переменной Лапласа α.
По минимуму значения диагностического признака (3) выносят решение о наличии дефекта в динамическом элементе.
Диагностические признаки одиночных структурных дефектов вида (3) принимают численные значения, которые зависят как от степени отклонения динамических характеристик, так и от свойств модели чувствительности и могут принимать в общем случае любые неотрицательные значения. Для практических целей удобно иметь диагностические признаки, область значений которых была бы ограничена, в частности, интервалом [0, 1], где крайние значения могли бы интерпретироваться как однозначное наличие (отсутствие) дефекта, а промежуточные значения - как вероятность наличия дефекта. Приведение диагностических признаков к единой шкале открывает возможности для сравнительного анализа условий и результатов диагностирования различных объектов диагностирования в терминах количественной различимости дефектов.
Возможность получения таких нормированных диагностических признаков дает векторная их интерпретация, рассмотренная ниже. Идея нормировки признака заключается в приведении векторов деформации динамических характеристик к единичной длине.
Произведем нормирование значений коэффициентов структурной чувствительности по всем контрольным точкам:
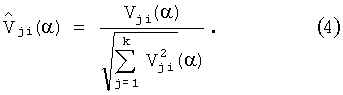
Подставляя эти значения в выражение (3), получим:
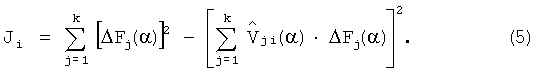
Коэффициенты структурной чувствительности (4) могут рассматриваться как координаты вектора 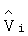 единичной длины в k-мерном пространстве:
единичной длины в k-мерном пространстве:
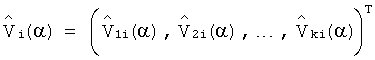 ,
,
а отклонение изображений реакций объекта - как вектор в пространстве той же размерности с координатами:

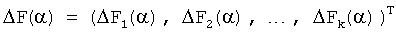 .
.
Тогда формула (5) с учетом введенных векторов запишется в виде:
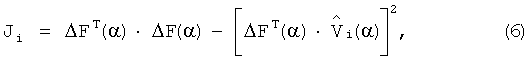
где 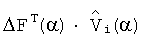 - скалярное произведение вектора отклонений динамической характеристики объекта на нормированный вектор структурной чувствительности по i-му динамическому элементу.
- скалярное произведение вектора отклонений динамической характеристики объекта на нормированный вектор структурной чувствительности по i-му динамическому элементу.
По определению скалярного произведения:
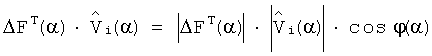 ,
,
где 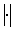 - означает длину вектора;
- означает длину вектора;
φ(α) - угол в k-мерном пространстве между этими векторами.
Если направление векторов ΔF(α) и 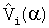 совпадают или противоположны, то cosφ(α)=±1 и
совпадают или противоположны, то cosφ(α)=±1 и 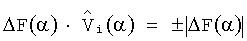 , подставляя эти значения в формулу (6), получим:
, подставляя эти значения в формулу (6), получим:
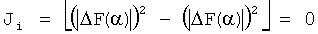 .
.
Таким образом, в терминах векторной интерпретации поиск одиночного структурного дефекта заключается в подборе такого индекса i, для которого нормированный вектор 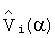 в k-мерном пространстве в наибольшей степени совпадает или противоположен с направлением соответствующего вектора ΔF(α) деформации динамических характеристик объекта.
в k-мерном пространстве в наибольшей степени совпадает или противоположен с направлением соответствующего вектора ΔF(α) деформации динамических характеристик объекта.
Сформируем нормированный диагностический признак путем деления каждого слагаемого выражения (5) на величину 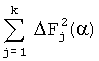 :
:
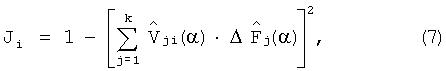
где 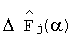 - элементы нормированного вектора деформации динамической характеристики объекта.
- элементы нормированного вектора деформации динамической характеристики объекта.
Используя векторную интерпретацию выражения (7), запишем его в следующем виде
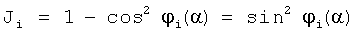
где 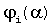 - угол между векторами единичной длины отклонений динамической характеристики объекта и структурной чувствительности для i-го динамического элемента и параметра интегрального преобразования α.
- угол между векторами единичной длины отклонений динамической характеристики объекта и структурной чувствительности для i-го динамического элемента и параметра интегрального преобразования α.
Таким образом, нормированный диагностический признак (7) представляет собой значение квадрата синуса угла, образованного в k-мерном пространстве нормированными векторами структурной чувствительности динамического элемента и деформации интегрального преобразования динамической характеристики объекта диагностирования.
Получение модели структурной чувствительности является отдельной, достаточно сложной задачей. Для уменьшения объема требуемых вычислений при получении диагностических признаков заменим в выражении (7) нормированные векторы 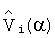 интегральных преобразований модели структурной чувствительности на нормированные векторы
интегральных преобразований модели структурной чувствительности на нормированные векторы 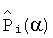 деформаций интегральных преобразований динамических характеристик модели, полученные в результате пробных отклонений параметров соответствующих блоков:
деформаций интегральных преобразований динамических характеристик модели, полученные в результате пробных отклонений параметров соответствующих блоков:
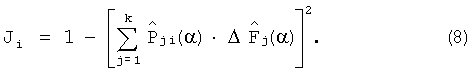
Выражение (8) позволяет получить значения нормированного диагностического признака, представляющего собой значение квадрата синуса угла, образованного вектором реальной деформации интегральной оценки динамической характеристики, обусловленной наличием дефекта в объекте, и вектором деформации интегральной оценки динамической характеристики, полученной в результате пробного отклонения параметров блока объекта. Пробное отклонение блока, минимизирующее значение диагностического признака (8), указывает на наличие дефекта в этом блоке. Область возможных значений признака лежит в интервале [0, 1].
Таким образом, предлагаемый способ поиска неисправностей сводится к выполнению следующих операций.
1. В качестве динамической системы рассматривают систему, состоящую из произвольно соединенных m динамических элементов.
2. Предварительно определяют время контроля ТК≥ТПП, где ТПП - время переходного процесса системы. Время переходного процесса оценивают для номинальных значений параметров динамической системы.
3. Определяют параметр интегрального преобразования сигналов из соотношения 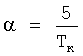 .
.
4. Фиксируют число контрольных точек k.
5. Предварительно определяют нормированные векторы 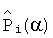 деформаций интегральных преобразований динамических характеристик модели, полученные в результате пробных отклонений параметров i-го блока каждого из m блоков для номинальных значений параметров передаточных функций блоков и определенного выше параметра α, для чего выполняют пункты 6-10.
деформаций интегральных преобразований динамических характеристик модели, полученные в результате пробных отклонений параметров i-го блока каждого из m блоков для номинальных значений параметров передаточных функций блоков и определенного выше параметра α, для чего выполняют пункты 6-10.
6. Подают тестовый сигнал x(t) (единичный ступенчатый, линейно возрастающий, прямоугольный импульсный и т.д.) на вход системы управления с номинальными характеристиками. Принципиальных ограничений на вид входного тестового воздействия предлагаемый способ не предусматривает.
7. Регистрируют реакцию системы fjном(t), j=1, 2, …, k на интервале t∈[0, TK] в k контрольных точках и определяют интегральные оценки выходных сигналов Fjном(α), j=1, …, k системы. Для этого в момент подачи тестового сигнала на вход системы управления с номинальными характеристиками одновременно начинают интегрирование сигналов системы управления в каждой из k контрольных точек с весами e-αt, где 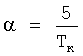 , для чего сигналы системы управления подают на первые входы к блоков перемножения, на вторые входы блоков перемножения подают экспоненциальный сигнал e-αt, выходные сигналы к блоков перемножения подают на входы k блоков интегрирования, интегрирование завершают в момент времени Тк, полученные в результате интегрирования оценки выходных сигналов Fjном(α), j=1, …, k регистрируют.
, для чего сигналы системы управления подают на первые входы к блоков перемножения, на вторые входы блоков перемножения подают экспоненциальный сигнал e-αt, выходные сигналы к блоков перемножения подают на входы k блоков интегрирования, интегрирование завершают в момент времени Тк, полученные в результате интегрирования оценки выходных сигналов Fjном(α), j=1, …, k регистрируют.
8. Определяют интегральные преобразования динамических характеристик модели для каждой из k контрольных точек, полученные в результате пробных отклонений параметров каждого из m блоков, для чего поочередно для каждого блока динамической системы вводят пробное отклонение параметра передаточной функции и выполняют пункты 6 и 7 для одного и того же тестового сигнала x(t). Полученные в результате интегрирования оценки выходных сигналов для каждой из k контрольных точек и каждого из m пробных отклонений Pji(α), j=1, …, k; i=1, …, m регистрируют.
9. Определяют деформации интегральных преобразований динамических характеристик модели, полученные в результате пробных отклонений параметров соответствующих блоков ΔPji(α)=Pji(α)-Fjном(α), j=1, …, k; i=1, …, m.
10. Определяют нормированные значения деформаций интегральных преобразований динамических характеристик модели, полученные в результате пробных отклонений параметров соответствующих блоков по формуле 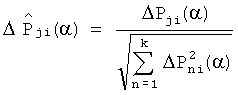 .
.
11. Замещают систему с номинальными характеристиками контролируемой. На вход системы подают аналогичный тестовый сигнал x(t).
12. Определяют интегральные преобразования динамических характеристик контролируемой системы для k контрольных точек Fj(α), j=1, …, k, осуществляя операции, описанные в пунктах 6 и 7 применительно к контролируемой системе.
13. Определяют отклонения интегральных преобразований динамических характеристик контролируемой системы для k контрольных точек от номинальных значений ΔFj(α)=Fjном(α), j=1, …, k.
14. Вычисляют нормированные значения отклонений интегральных преобразований динамических характеристик контролируемой системы по формуле 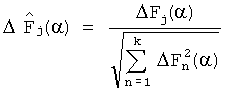 .
.
15. Вычисляют диагностические признаки наличия неисправного блока по формуле (8).
16. По минимуму значения диагностического признака определяют дефектный блок.
Поскольку диагностические признаки (8) имеют область возможных значений, ограниченную интервалом [0, 1], то разность между ближайшим к минимальному признаку и минимальным признаком (который указывает на дефектный блок) количественно характеризует различимость данного дефекта с учетом расположения блока на структурной схеме, вида и параметров передаточных функций блоков и всех условий диагностирования, при которых получены эти значения диагностических признаков (вид тестового сигнала, величина параметра α, количество и расположение контрольных точек, величина интервала Тк). Наилучшая различимость - когда указанная разность равна единице (в терминах векторной интерпретации нормированные векторы деформаций интегральных преобразований динамических характеристик этих блоков для пробных отклонений ортогональны). Наихудшая различимость - когда указанная разность равна нулю (в терминах векторной интерпретации нормированные векторы деформаций интегральных преобразований динамических характеристик этих блоков для пробных отклонений коллинеарные). Поэтому применение нормированных диагностических признаков позволяет сравнивать результаты диагностирования для выбора оптимальных режимов поиска дефектов.
Рассмотрим реализацию предлагаемого способа поиска одиночного дефекта для системы, структурная схема которой представлена на чертеже.
Передаточные функции блоков:
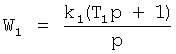 ;
;  :
: 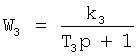 ,
,
номинальные значения параметров: T1=5 с; К1=1; К2=1; Т2=1 с; К3=1; Т3=5 с. При поиске одиночного дефекта в виде отклонения постоянной времени T1=4 с в первом звене путем подачи ступенчатого тестового входного сигнала единичной амплитуды и интегрального преобразования сигналов для параметра α=0.5 и Тк=10 с получены значения диагностических признаков по формуле (7) при использовании трех контрольных точек, расположенных на выходах блоков, и модели чувствительности: J1=0; J2=0.186; J3=0.018. Минимальное значение признака J1 однозначно указывает на наличие дефекта в первом блоке, а разность между третьим и первым признаками может количественно характеризовать фактическую различимость этого дефекта. Тот же дефект, найденный путем получения пробных отклонений на величину 5% и вычислений по формуле (8), дает следующие значения диагностических признаков: J1=0; J2=0.78; J3=0.074. Анализ значений диагностических признаков показывает, что значения второго и третьего признака, полученные при использовании пробных отклонений, больше, чем при использовании модели чувствительности. Это позволяет сделать вывод, что фактическая различимость дефекта первого блока выше при использовании заявляемого способа. Различимости дефектов второго и третьего блоков при поиске их с использованием пробных отклонений также не хуже, чем при использовании модели чувствительности.
Поиск неисправного блока согласно предлагаемому способу сводится к выполнению следующих операций.
1. Фиксируют число динамических элементов m=3.
2. Путем анализа графиков номинальных переходных характеристик определяем время переходного процесса системы. Для данного примера время переходного процесса составляет ТПП=8 с. Фиксируем время контроля Тk≥ТПП. Для данного примера фиксируем Тk=10 с.
3. Определяем параметр интегрального преобразования сигналов 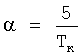 . Для данного примера α=0.5.
. Для данного примера α=0.5.
4. Фиксируем контрольные точки на выходах блоков: k=3.
5. Предварительно находим элементы векторов ΔP1(α), ΔP2(α), ΔP3(α) деформаций интегральных преобразований динамических характеристик модели, полученные в результате пробных отклонений параметров соответствующих блоков. Величину пробных отклонений выбираем равной 5%:
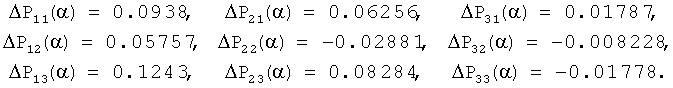
6. Находим нормированные векторы 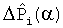 деформаций интегральных преобразований динамических характеристик модели, полученные в результате пробных отклонений параметров соответствующих блоков:
деформаций интегральных преобразований динамических характеристик модели, полученные в результате пробных отклонений параметров соответствующих блоков:
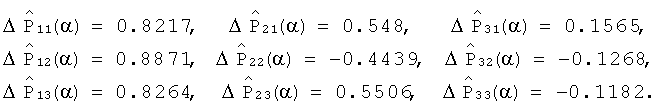
7. Замещаем систему с номинальными характеристиками контролируемой, в которой введено отклонение параметра Т1 первого блока от номинального на 20%. На вход системы подаем аналогичный тестовый сигнал x(t).
8. Определяем отклонения интегральных преобразований динамических характеристик контролируемой системы для трех контрольных точек от номинальных значений ΔFj(α)=F1(α)-Fjном(α), j=1, 2, 3
ΔF1(α)=0.4003, ΔF2(α)=0.2669, ΔF3(α)=0.07618.
9. Вычисляем нормированные значения отклонений интегральных преобразований динамических характеристик контролируемой системы 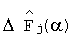
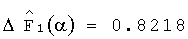
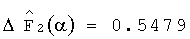
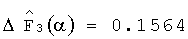
10. Вычисляем диагностические признаки наличия неисправного блока по формуле (8): J1=0, J2=0.7829, j3=0.07399.
11. По минимуму значения диагностического признака определяют дефектный блок (в данном случае - №1).
Моделирование процессов поиска дефектов во втором и третьем блоках для данного объекта диагностирования при том же параметре α и при единичном ступенчатом входном сигнале дает следующие значения диагностических признаков.
При наличии дефекта в блоке №2 (в виде уменьшения параметра Т2 на 20%): J1=0.7829, J2=0, J3=0.7462.
При наличии дефекта в блоке №3 (в виде уменьшения параметра Т3 на 20%): J1=0.07404, J2=0.7464, J3=0.
Минимальное значение диагностического признака в обоих случаях правильно указывает на дефектный блок.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ПОИСКА НЕИСПРАВНОГО БЛОКА В ДИНАМИЧЕСКОЙ СИСТЕМЕ | 2010 |
|
RU2439648C1 |
| СПОСОБ ПОИСКА НЕИСПРАВНОГО БЛОКА В НЕПРЕРЫВНОЙ ДИНАМИЧЕСКОЙ СИСТЕМЕ | 2013 |
|
RU2513504C1 |
| СПОСОБ ПОИСКА НЕИСПРАВНЫХ БЛОКОВ В НЕПРЕРЫВНОЙ ДИНАМИЧЕСКОЙ СИСТЕМЕ | 2012 |
|
RU2519435C1 |
| СПОСОБ ПОИСКА НЕИСПРАВНОГО БЛОКА В НЕПРЕРЫВНОЙ ДИНАМИЧЕСКОЙ СИСТЕМЕ | 2011 |
|
RU2439647C1 |
| Способ поиска неисправного блока в непрерывной динамической системе на основе введения пробных отклонений и анализа знаков передач | 2019 |
|
RU2711000C1 |
| СПОСОБ ПОИСКА НЕИСПРАВНОГО БЛОКА В ДИНАМИЧЕСКОЙ СИСТЕМЕ | 2011 |
|
RU2451319C1 |
| СПОСОБ ПОИСКА НЕИСПРАВНОГО БЛОКА В ДИСКРЕТНОЙ ДИНАМИЧЕСКОЙ СИСТЕМЕ | 2011 |
|
RU2444774C1 |
| СПОСОБ ПОИСКА НЕИСПРАВНЫХ БЛОКОВ В ДИНАМИЧЕСКОЙ СИСТЕМЕ | 2010 |
|
RU2453898C1 |
| СПОСОБ ПОИСКА НЕИСПРАВНЫХ БЛОКОВ В ДИСКРЕТНОЙ ДИНАМИЧЕСКОЙ СИСТЕМЕ | 2012 |
|
RU2473949C1 |
| СПОСОБ ПОИСКА НЕИСПРАВНОГО БЛОКА В ДИСКРЕТНОЙ ДИНАМИЧЕСКОЙ СИСТЕМЕ | 2012 |
|
RU2506623C1 |
Изобретение относится к области контроля и диагностирования систем автоматического управления и их элементов. Техническим результатом является уменьшение аппаратных и временных затрат на диагностирование. Способ заключается в том, что регистрируют реакцию заведомо исправной системы fjном(t), j=1, 2, …, k на интервале t∈[0, TK] в k контрольных точках, определяют интегральные оценки выходных сигналов Fjном(α), j=1, …, k системы, полученные в результате интегрирования оценки выходных сигналов Fjном(α), j=1, …, k регистрируют, определяют интегральные преобразования динамических характеристик модели для каждой из k контрольных точек, полученные в результате пробных отклонений параметров каждого из m блоков, определяют деформации интегральных преобразований динамических характеристик модели, определяют нормированные значения деформаций интегральных преобразований динамических характеристик модели, замещают систему с номинальными характеристиками контролируемой, на вход системы подают аналогичный тестовый сигнал x(t), определяют интегральные преобразования динамических характеристик контролируемой системы для k контрольных точек Fj(α), j=1, …, k для параметра α, определяют отклонения интегральных преобразований динамических характеристик контролируемой системы для k контрольных точек от номинальных значений ΔFj(α)=Fj(α)-Fjном(α), j=1, …, k, определяют нормированные значения отклонений интегральных преобразований динамических характеристик контролируемой системы, определяют диагностические признаки, по минимуму диагностического признака определяют неисправный блок. 1 ил.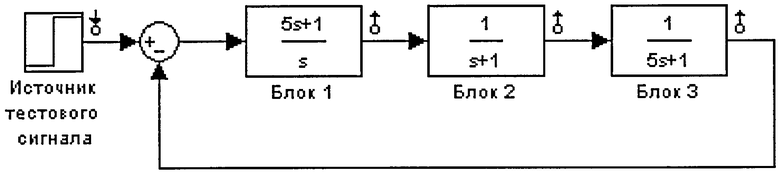
Способ поиска неисправного блока в динамической системе, основанный на том, что фиксируют число m динамических элементов, входящих в состав системы, определяют время контроля ТК>ТПП, определяют параметр интегрального преобразования сигналов из соотношения 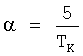 , используют тестовый сигнал на интервале t∈[0, ТК], в качестве динамических характеристик системы используют интегральные оценки, полученные для вещественных значений α переменной Лапласа, фиксируют число k контрольных точек системы, регистрируют реакцию объекта диагностирования и модели, определяют диагностический признак, по минимуму диагностического признака определяют неисправный блок, отличающийся тем, что регистрируют реакцию заведомо исправной системы Fjном(t), j=1, 2, …, k на интервале t∈[0, ТК] в k контрольных точках и определяют интегральные оценки выходных сигналов Fjном(α), j=1, …, k, для чего в момент подачи тестового сигнала на вход системы с номинальными характеристиками одновременно начинают интегрирование сигналов системы управления в каждой из k контрольных точек с весами e-αt, где
, используют тестовый сигнал на интервале t∈[0, ТК], в качестве динамических характеристик системы используют интегральные оценки, полученные для вещественных значений α переменной Лапласа, фиксируют число k контрольных точек системы, регистрируют реакцию объекта диагностирования и модели, определяют диагностический признак, по минимуму диагностического признака определяют неисправный блок, отличающийся тем, что регистрируют реакцию заведомо исправной системы Fjном(t), j=1, 2, …, k на интервале t∈[0, ТК] в k контрольных точках и определяют интегральные оценки выходных сигналов Fjном(α), j=1, …, k, для чего в момент подачи тестового сигнала на вход системы с номинальными характеристиками одновременно начинают интегрирование сигналов системы управления в каждой из k контрольных точек с весами e-αt, где 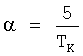 путем подачи на первые входы k блоков перемножения сигналов системы управления, на вторые входы блоков перемножения подают экспоненциальный сигнал e-αt, выходные сигналы k блоков перемножения подают на входы k блоков интегрирования, интегрирование завершают в момент времени ТК, полученные в результате интегрирования оценки выходных сигналов Fjном(α), j=1, …, k регистрируют, определяют интегральные преобразования динамических характеристик модели для каждой из k контрольных точек, полученные в результате пробных отклонений параметров каждого из m блоков, для чего поочередно для каждого блока динамической системы вводят пробное отклонение параметра его передаточной функции и находят интегральные оценки выходных сигналов системы для параметра α и тестового сигнала x(t), полученные в результате интегрирования оценки выходных сигналов для каждой из k контрольных точек и каждого из m пробных отклонений Pji(α), j=1, …, k; i=1, …, m, регистрируют, определяют деформации интегральных преобразований динамических характеристик модели, полученные в результате пробных отклонений параметров соответствующих блоков ΔPji(α)=Pji(α)-Fjном(α), j=1, …, k; i=1, …, m, определяют нормированные значения деформаций интегральных преобразований динамических характеристик модели, полученные в результате пробных отклонений параметров соответствующих блоков из соотношения
путем подачи на первые входы k блоков перемножения сигналов системы управления, на вторые входы блоков перемножения подают экспоненциальный сигнал e-αt, выходные сигналы k блоков перемножения подают на входы k блоков интегрирования, интегрирование завершают в момент времени ТК, полученные в результате интегрирования оценки выходных сигналов Fjном(α), j=1, …, k регистрируют, определяют интегральные преобразования динамических характеристик модели для каждой из k контрольных точек, полученные в результате пробных отклонений параметров каждого из m блоков, для чего поочередно для каждого блока динамической системы вводят пробное отклонение параметра его передаточной функции и находят интегральные оценки выходных сигналов системы для параметра α и тестового сигнала x(t), полученные в результате интегрирования оценки выходных сигналов для каждой из k контрольных точек и каждого из m пробных отклонений Pji(α), j=1, …, k; i=1, …, m, регистрируют, определяют деформации интегральных преобразований динамических характеристик модели, полученные в результате пробных отклонений параметров соответствующих блоков ΔPji(α)=Pji(α)-Fjном(α), j=1, …, k; i=1, …, m, определяют нормированные значения деформаций интегральных преобразований динамических характеристик модели, полученные в результате пробных отклонений параметров соответствующих блоков из соотношения 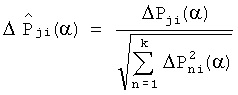 , замещают систему с номинальными характеристиками контролируемой, на вход системы подают аналогичный тестовый сигнал x(t), определяют интегральные преобразования динамических характеристик контролируемой системы для k контрольных точек Fj(α), j=1, …, k для параметра α, определяют отклонения интегральных преобразований динамических характеристик контролируемой системы для k контрольных точек от номинальных значений ΔFj(α)=Fj(α)-Fjном(α), j=1, …, k, определяют нормированные значения отклонений интегральных преобразований динамических характеристик контролируемой системы из соотношения
, замещают систему с номинальными характеристиками контролируемой, на вход системы подают аналогичный тестовый сигнал x(t), определяют интегральные преобразования динамических характеристик контролируемой системы для k контрольных точек Fj(α), j=1, …, k для параметра α, определяют отклонения интегральных преобразований динамических характеристик контролируемой системы для k контрольных точек от номинальных значений ΔFj(α)=Fj(α)-Fjном(α), j=1, …, k, определяют нормированные значения отклонений интегральных преобразований динамических характеристик контролируемой системы из соотношения 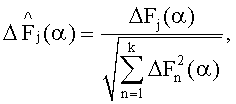
определяют диагностические признаки из соотношения 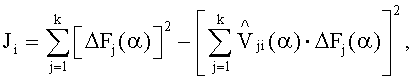 i=1, …, m, по минимуму диагностического признака определяют неисправный блок.
i=1, …, m, по минимуму диагностического признака определяют неисправный блок.
| СПОСОБ ПОИСКА НЕИСПРАВНОГО БЛОКА В ДИНАМИЧЕСКОЙ СИСТЕМЕ | 2001 |
|
RU2199776C2 |
| СПОСОБ ДИАГНОСТИРОВАНИЯ ДИНАМИЧЕСКОГО ОБЪЕКТА С ОБРАТНОЙ СВЯЗЬЮ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 1998 |
|
RU2138072C1 |
| JP 7098268 А, 11.04.1995 | |||
| US 4851985 А, 25.07.1989. | |||
Авторы
Даты
2011-11-27—Публикация
2009-06-23—Подача