Изобретение относится к области контрольно-измерительной техники, может быть использовано для определения амплитуд нановибраций объектов в диапазоне измеряемой величины от десятков до ста нанометров и может найти широкое применение в точном машиностроении и электронной технике.
Известен способ измерения амплитуд вибраций, сущностью которого является получение поля интерференции опорного и измерительного пучков когерентного излучения. Способ заключается в том, что после получения поля интерференции смещают частоту излучения одного из пучков относительно другого на величину, меньшую ω/2, где ω - частота вибрации контролируемого объекта, получают сигнал, пропорциональный яркости поля интерференции, производят фильтрацию сигнала и по его характеру судят об амплитуде вибрации. При фильтрации сигнала в нем оставляют гармонические составляющие с частотами, входящими в интервал nω±Δ, где n=1, 2, 3,..., a Δ<ω, измеряют размах сигнала до и после фильтрации и определяют по формуле амплитуду вибрации (см. патент на изобретение №2217707, МПК G01H 9/00).
Недостатками известного способа являются сложная техническая реализация, необходимость измерения яркости полей интерференции, необходимость изменять частоту излучения одного из световых пучков и контролировать ее.
Также известен способ определения амплитуды колебаний объекта по соотношению четных или нечетных гармоник спектрального ряда автодинного сигнала (Усанов Д.А., Скрипаль Ал.В., Скрипаль Ан.В. Физика полупроводниковых радиочастотных и оптических автодинов. Издательство Саратовского университета, Саратов, 2003 г., 312 с.).
Однако данный способ не применим для измерения амплитуд нановибраций, так как в спектре автодинного сигнала при нановибрациях четко различимы лишь одна или две гармоники.
Наиболее близким является способ определения амплитуды вибрации по двум гармоникам спектра автодинного сигнала (патент на изобретение №2300085). Способ заключается в облучении лазерным излучением объекта, преобразовании отраженного от него излучения в электрический сигнал, разложении сигнала в спектральный ряд и измерении амплитуды выбранных гармоник, в спектральном ряде выбирают две соседние гармоники, амплитуду вибрации объекта определяют из соотношения

где ξ - амплитуда вибраций объекта, λ - длина волны лазерного излучения, n - целое число, Jn - функция Бесселя n-го порядка, cn - спектральная составляющая ряда Фурье на частоте n⋅ν, ν - частота вибраций объекта (Патент на изобретение РФ №2300085. Способ определения амплитуды вибрации по двум гармоникам спектра автодинного сигнала /Усанов Д.А., Скрипаль А.В., Камышанский А.С. Опубл. 27.05.2007. Бюл. №15. Заявка №2005134749 от 9 ноября 2005 г. Патентообладатель - СГУ.).
Недостатком данного способа является высокая погрешность измерений.
Задача настоящего способа заключается в определении амплитуды нановибраций по спектру частотномодулированного полупроводникового лазерного автодина для повышения точности измерений.
Технический результат заключается в значительном повышении чувствительности и точности измерения амплитуды нановибраций объекта.
Поставленная задача решается за счет того, что освещают вибрирующий на частоте Ω объект лазерным излучением, преобразуют отраженное от объекта излучение в электрический автодинный сигнал, раскладывают сигнал в спектральный ряд, согласно решению лазерное излучение частотой ω0 модулируют с частотой Ω, равной частоте колебаний объекта, добиваются совпадения начальных фаз колебаний объекта и частотной модуляции лазера, измеряют амплитуду второй C2 и четвертой C4 гармоник спектра автодинного сигнала, по зависимости С2/С4(σ) вычисляют значение аргумента функции Бесселя первого рода σ, затем модулированным лазерным излучением освещают невибрирующий объект, измеряют значение амплитуд второй C2cal и четвертой C4cal гармоник спектра отраженного автодинного сигнала, по зависимости C2cal/C4cal(σM) вычисляют значение аргумента функции Бесселя первого рода σM, амлитуду нановибраций ξ находят по формуле
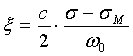 , где с - скорость света в вакууме.
, где с - скорость света в вакууме.
Изобретение поясняется чертежами. На фиг. 1, 2 представлены симулированный в математическом пакетме MathCad 14 частотномодулированный автодинный сигнал и его спектр при колебаниях отржателя с амптитудой  нм. В спектре автодинного сигнала, изображенном на фиг. 2, наблюдается четыре гармоники, амплитуды которых составляют
нм. В спектре автодинного сигнала, изображенном на фиг. 2, наблюдается четыре гармоники, амплитуды которых составляют  =6.44;
=6.44; 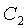 =0.14;
=0.14; 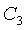 =0.31;
=0.31;  =0.11. На фиг. 3, 4 представлены симулированный в математическом пакетме MathCad 14 частотномодулированный автодинный сигнал и его спектр при неподвижном отражателе. В спектре автодинного сигнала на фиг. 4 наблюдается четыре гармоники, амплитуды которых составляют
=0.11. На фиг. 3, 4 представлены симулированный в математическом пакетме MathCad 14 частотномодулированный автодинный сигнал и его спектр при неподвижном отражателе. В спектре автодинного сигнала на фиг. 4 наблюдается четыре гармоники, амплитуды которых составляют  =5.74,
=5.74, 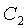 =0.27,
=0.27, 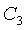 =0.18,
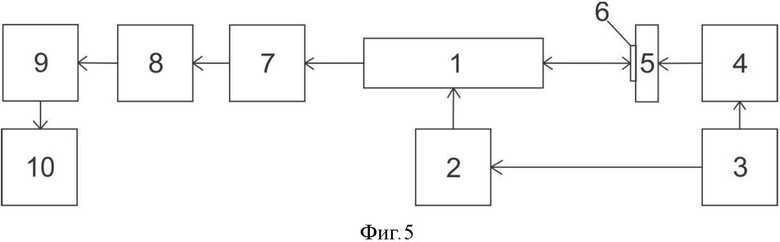
=0.18,  =0.03. На фиг. 5 представлена схема экспериментальной установки: 1 - полупроводниковый лазер, 2 - блок управления током питания, 3 - генератор сигналов на базе платформы NI ELVIS, 4 - усилитель сигнала, 5 - пьезокерамическая пластинка, 6 - объект, 7 - фотодетектор, 8 - фильтр переменного сигнала, 9 - АЦП, 10 - компьютер. На фиг. 6 представлен экспериментальный автодинный сигнал при колебаниях отражателя с амплитудой
=0.03. На фиг. 5 представлена схема экспериментальной установки: 1 - полупроводниковый лазер, 2 - блок управления током питания, 3 - генератор сигналов на базе платформы NI ELVIS, 4 - усилитель сигнала, 5 - пьезокерамическая пластинка, 6 - объект, 7 - фотодетектор, 8 - фильтр переменного сигнала, 9 - АЦП, 10 - компьютер. На фиг. 6 представлен экспериментальный автодинный сигнал при колебаниях отражателя с амплитудой  . На фиг. 7. представлен его спектр. На Фиг. 8 - экспериментальный частотномодулированный автодинный сигнал при колебниях отражателя с амплитудой
. На фиг. 7. представлен его спектр. На Фиг. 8 - экспериментальный частотномодулированный автодинный сигнал при колебниях отражателя с амплитудой  , на фиг. 9 - его спектр.
, на фиг. 9 - его спектр.
Теоретическое обоснование способа.
Для определения амплитуды нановибраций объекта по спектру частотномодулированного автодинного сигнала используют следующие теоретические предпосылки.
В атодинной системе в режиме стационарной генерации, когда изменения в системе происходят за времена, значительно превышающие период колебаний электромагнитного излучения, мощность излучения полупроводникового лазера может быть определена в результате использования малосигнального анализа скоростных уравнений (для комплексного электрического поля с запаздывающим аргументом и концентрации носителей заряда) и записана в виде зависимости от тока накачки (амплитудная составляющая) и фазового набега (фазовая составляющая) (Усанов Д.А., Скрипаль Ал.В., Скрипаль Ан.В. Физика полупроводниковых радиочастотных и оптических автодинов. - Саратов: Изд-во Сарат. ун-та, 2003. 312 с.):
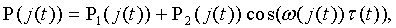
где 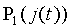 и
и 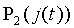 - амплитудные составляющие мощности излучения полупроводникового лазера,
- амплитудные составляющие мощности излучения полупроводникового лазера,  - фазовый набег в системе с внешним отражателем,
- фазовый набег в системе с внешним отражателем, 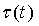 - время обхода лазерным излучением расстояния до внешнего отражателя,
- время обхода лазерным излучением расстояния до внешнего отражателя, 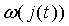 - частота излучения полупроводникового лазера, зависящая от плотности тока накачки
- частота излучения полупроводникового лазера, зависящая от плотности тока накачки 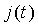 и уровня обратной связи. В предположении слабой обратной связи зависимость частоты излучения полупроводникового лазера с внешней оптической обратной связью от частоты уединенного лазера носит линейный характер.
и уровня обратной связи. В предположении слабой обратной связи зависимость частоты излучения полупроводникового лазера с внешней оптической обратной связью от частоты уединенного лазера носит линейный характер.
При использовании токовой модуляции частоты излучения полупроводникового лазера с частотой модуляции 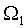 тока питания лазерного диода частота излучения полупроводникового лазера в автодинном режиме определится соотношением:
тока питания лазерного диода частота излучения полупроводникового лазера в автодинном режиме определится соотношением:
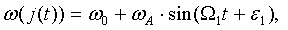
где 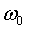 - частота излучения полупроводникового уединенного лазерного диода;
- частота излучения полупроводникового уединенного лазерного диода;  - амплитуда отклонения частоты излучения полупроводникового лазерного диода;
- амплитуда отклонения частоты излучения полупроводникового лазерного диода;  - частота модуляции тока питания лазерного диода;
- частота модуляции тока питания лазерного диода; 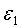 - начальная фаза.
- начальная фаза.
При движении отражателя по гармоническому закону время обхода лазерным излучением внешнего резонатора изменяется по закону:
 ,
,
где  - время обхода лазерным излучением внешнего резонатора с неподвижным отражателем,
- время обхода лазерным излучением внешнего резонатора с неподвижным отражателем, 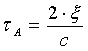 - амплитудное значение,
- амплитудное значение, 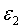 - начальная фаза,
- начальная фаза, 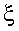 и
и  - амплитуда и частота колебаний отражателя лазерного излучения.
- амплитуда и частота колебаний отражателя лазерного излучения.
При использовании токовой модуляции частоты излучения полупроводникового лазера будут также изменяться амплитудные составляющие излучения полупроводникового лазера:
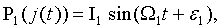
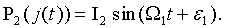
С учетом соотношений для амплитудной (4) и фазовой (2), (3) компонент при изменении тока питания лазера соотношение для мощности излучения полупроводникового лазера будет иметь вид:

Для получения аналитического выражения рассмотрим случай, когда частота модуляции лазерного излучения равна частоте колебаний отражателя  и начальные фазы в (5) равны
и начальные фазы в (5) равны  . Как будет показано ниже, эти условия легко реализуются в экспериментальной установке. Выражение (5) примет следующий вид:
. Как будет показано ниже, эти условия легко реализуются в экспериментальной установке. Выражение (5) примет следующий вид:

Обозначая за  величину
величину 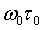 , а за
, а за 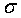 величину
величину 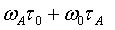 , выражение для
, выражение для 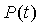 может быть представлено в виде разложения в ряд по функциям Бесселя (Усанов Д.А., Скрипаль А.В., Авдеев К.С. Определение расстояния до объекта с помощью частотномодулированного полупроводникового лазерного автодина //Письма в ЖТФ. 2007. Том 33. Вып. 21. С. 72-77.):
может быть представлено в виде разложения в ряд по функциям Бесселя (Усанов Д.А., Скрипаль А.В., Авдеев К.С. Определение расстояния до объекта с помощью частотномодулированного полупроводникового лазерного автодина //Письма в ЖТФ. 2007. Том 33. Вып. 21. С. 72-77.):
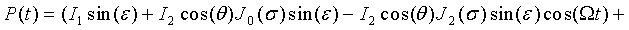

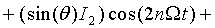

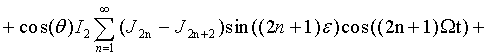
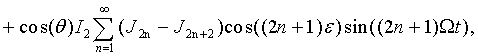
где 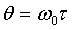 ,
,  ,
, 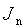 - функция Бесселя первого рода порядка
- функция Бесселя первого рода порядка  .
.
Используя разложение  в ряд Фурье:
в ряд Фурье:


можно получить следующие выражения для коэффициентов:
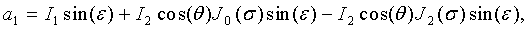
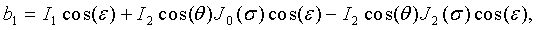

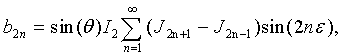

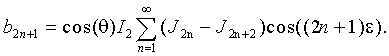
Вводя коэффициенты С1, С2, С3, С4, равные по модулю четным и нечетным спектральным составляющим сигнала и определяемые как:
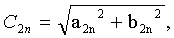
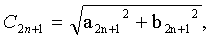
можно получить их значения в виде:

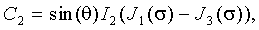
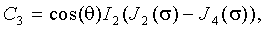
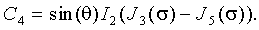
Соотношения (19) - (22) представляют собой связь спектральных составляющих частотномодулированного автодинного сигнала с функциями Бесселя первого рода.
Для определения амплитуды нановибраций 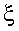 , входящей в параметр
, входящей в параметр  , используем отношение второй и четвертой гармоник:
, используем отношение второй и четвертой гармоник:
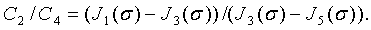
Решение полученного уравнения (23) относительно неизвестного параметра
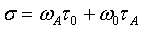
требует знания параметров токовой модуляции лазерного автодина, в частности амплитуды отклонения частоты 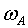 .
.
Численное моделирование с использованием предложенного метода применительно к частотномодулированному полупроводниковому лазерному автодину проводилось при следующих параметрах: длина волны лазерного излучения  нм, амплитуда отклонения частоты излучения полупроводникового лазерного диода
нм, амплитуда отклонения частоты излучения полупроводникового лазерного диода  рад/с, частота колебаний отражателя и частота модуляции тока питания лазерного диода
рад/с, частота колебаний отражателя и частота модуляции тока питания лазерного диода  Гц, амплитуда колебаний отражателя
Гц, амплитуда колебаний отражателя 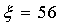 нм. С учетом параметров используемого в экспериментальной установке лазерного автодина выберем следующие значения отношения параметров
нм. С учетом параметров используемого в экспериментальной установке лазерного автодина выберем следующие значения отношения параметров 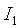 и
и 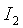 :
:  .
.
На фиг. 1 в качестве примера приведена зависимость мощности излучения частотномодулированного лазерного диода от времени, а на фиг. 2 - соответствующий ей спектр при колебаниях отражателя с амплитудой  нм.
нм.
Как следует из фиг. 2, в спектре автодинного сигнала наблюдается четыре гармоники, амплитуды которых составляют  =6.44;
=6.44; 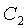 =0.14;
=0.14; 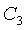 =0.31;
=0.31;  =0.11.
=0.11.
Для определения параметров токовой модуляции лазерного автодина по спектру автодинного сигнала из отношения второй и четвертой гармоник с использованием соотношений (23) вычисляется значение 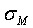 :
:
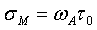
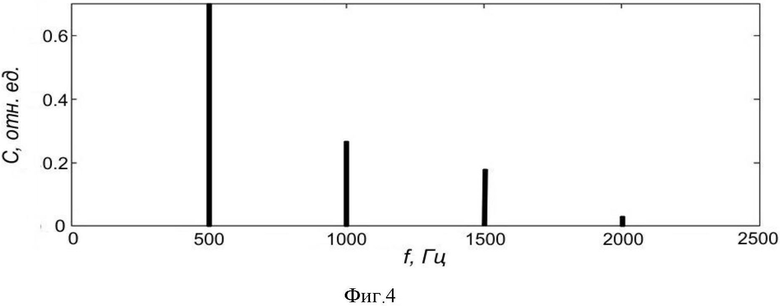
На фиг. 3 изображен калибровочный частотномодулированный автодинный сигнал при неподвижном отражателе. На фиг. 4 представлен его спектр.
В спектре автодинного сигнала (фиг. 4) наблюдается четыре гармоники, амплитуды которых составляют  =5.74,
=5.74, 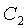 =0.27,
=0.27, 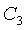 =0.18,
=0.18,  =0.03. Решение уравнения (23) позволяет определить значение калибровочной величины
=0.03. Решение уравнения (23) позволяет определить значение калибровочной величины 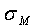 .
.
Для определения амплитуды нановибраций необходимо рассчитать аргумент функции Бесселя первого рода σ из соотношения (23), используя отношение второй к четвертой спектральных гармоник частотномодулированного автодинного сигнала при колебаниях отражателя.
Принимая во внимание, что 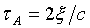 и
и 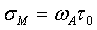 , получаем соотношение для определения амплитуды нановибраций:
, получаем соотношение для определения амплитуды нановибраций:

Для определения погрешности математического моделирования в исходный сигнал вводилась 10% случайная ошибка с помощью функции rnd в математическом пакете Mathcad 14. Вычисленная по формуле (25) величина амплитуды нановибрации совпала с заданным при постановке задачи значением. Погрешность определения амплитуды нановибраций составила 2,9%. При задании 5% случайной ошибки погрешность составила 1,6%.
Способ реализуется следующим образом.
Схема экспериментальной установки представлена на фиг. 5. Освещают объект 6, закрепленный на пьезокерамической пластинке 5, излучением от полупроводникового лазера 1, длина волны излучения лазера модулируется посредством гармонического изменения тока питания лазера с помощью встроенного в платформу NI ELVIS генератора сигналов 3, изменение тока питания лазерного диода осуществляется путем изменения напряжения питания, подаваемого на блок управления током питания 2, колебания пьезокерамической пластинки вобуждаются путем подачи на усилитель сигнала - 4 переменного напряжения с генератора - 3, частота и начальная фаза колебаний пьезокерамической пластинки синхронизируются с частотой и начальной фазой модуляции длины волны лазерного излучения, с помощью программного обеспечения к платформе NI ELVIS, преобразуют отраженное от вибрирующего объекта излучение в электрический сигнал с помощью фотодетектора 7, через фильтр переменного сигнала 8, аналого-цифровой преобразователь 9, подают сигнал на компьютер 10 и раскладывают в спектральный ряд, измеряют амплитуду второй C2 и четвертой C4 гармоник спектра автодинного сигнала, по зависимости С2/С4(σ) вычисляют значение аргумента функции Бесселя первого рода σ, затем модулированным лазерным излучением освещают невибрирующий объект, измеряют значение амплитуд второй C2cal и четвертой C4cal гармоник спектра отраженного автодинного сигнала, по зависимости C2cal/C4cal(σM) вычисляют значение аргумента функции Бесселя первого рода σM, амлитуду нановибраций ξ находят по формуле
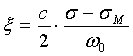 , где с - скорость света в вакууме.
, где с - скорость света в вакууме.
Практическая реализация способа осуществлялась следующим образом.
Длина волны излучения полупроводникового лазера модулировалась посредством гармонического изменения тока питания лазера с помощью встроенного в платформу NI ELVIS генератора сигналов. Эффективная модуляция тока питания лазерного диода наблюдалась при амплитуде модулирующего сигнала 20 мВ. Колебания пьезокерамической пластинки осуществлялись путем подачи на усилитель сигнала переменного напряжения с встроенного в платформу NI ELVIS генератора сигналов, амплитудой 20 мВ и 10 мВ, что соответствовало колебаниям пластинки с амплитудой около 60 нм и 30 нм, соответсвенно. Частота и начальная фаза колебаний пьезокерамической пластинки синхронизировались с частотой и начальной фазой модуляции длины волны лазерного излучения, с помощью программного обеспечения к платформе NI ELVIS. Предложенная схема колебаний пьезокерамической пластинки может быть использована для определения собственных частот и соответствующих им амплитуд колебаний исследуемой структуры.
При проведении измерений в пьезокерамической пластинке возбуждались с помощью генератора с частотой  Гц колебания с амплитудой, равной
Гц колебания с амплитудой, равной  , измеренной независимым методом.
, измеренной независимым методом.
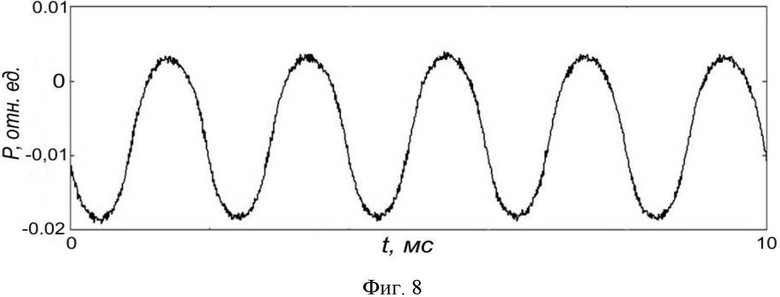
На фиг. 6, представлен автодинный сигнал без токовой модуляции при колебании отражателя с амплитудой  В спектре сигнала (фиг.7) присутствовала только первая и вторая гармоники, что не достаточно для измерения амплитуды вибрации без калибровки автодинного сигнала.
В спектре сигнала (фиг.7) присутствовала только первая и вторая гармоники, что не достаточно для измерения амплитуды вибрации без калибровки автодинного сигнала.
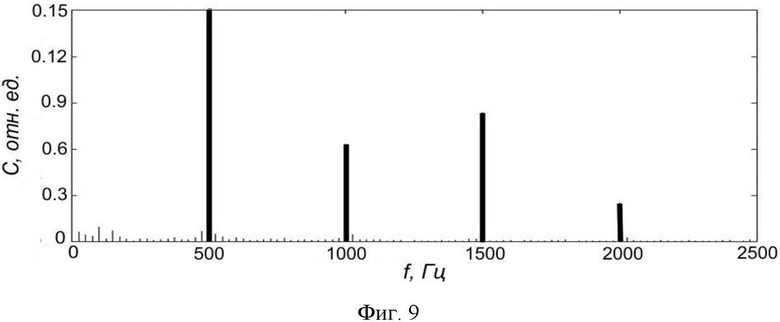
Для калибровки автодинного сигнала полупроводникового лазерного автодина подавалось модулирующее напряжение величиной 20 мВ и частотой 500 Гц. Измеренный автодинный сигнал и спектр частотномодулированного лазерного автодина приведены на фиг. 8 и фиг. 9 соответственно. Вычисленное значение по нескольким измерениям  при неподвижном отражателе составило
при неподвижном отражателе составило 
Зная величину σ и  , определяем амплитуду колебаний отражателя из соотношения
, определяем амплитуду колебаний отражателя из соотношения

Измеренное значение амплитуды колебаний отражателя в эксперименте составило  . Среднеквадратичное отклонение составило
. Среднеквадратичное отклонение составило  .
.
При проведении измерений амплитуды колебаний пьезокерамики с уменьшенной в 2 раза величиной подаваемого на нее напряжения измеренная величина амплитуды колебаний составила 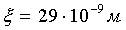 . Среднеквадратичное отклонение составило
. Среднеквадратичное отклонение составило 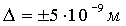 .
.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ОПРЕДЕЛЕНИЯ РАССТОЯНИЯ ДО ОБЪЕКТА | 2016 |
|
RU2629651C1 |
| СПОСОБ ИЗМЕРЕНИЯ НАНОПЕРЕМЕЩЕНИЙ | 2017 |
|
RU2658112C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ АМПЛИТУДЫ ВИБРАЦИИ ПО ДВУМ ГАРМОНИКАМ СПЕКТРА АВТОДИННОГО СИГНАЛА | 2005 |
|
RU2300085C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ АМПЛИТУДЫ НАНОВИБРАЦИЙ ПО СИГНАЛУ ЛАЗЕРНОГО АВТОДИНА | 2012 |
|
RU2507487C2 |
| СПОСОБ ИЗМЕРЕНИЯ СКОРОСТИ ДВИЖЕНИЯ ОБЪЕКТА | 2003 |
|
RU2247395C1 |
| СПОСОБ ИЗМЕРЕНИЯ АБСОЛЮТНОГО РАССТОЯНИЯ | 2020 |
|
RU2738876C1 |
| СПОСОБ ИЗМЕРЕНИЯ АМПЛИТУДЫ КОЛЕБАНИЙ БАРАБАННОЙ ПЕРЕПОНКИ | 2004 |
|
RU2258462C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ АМПЛИТУД ВИБРАЦИЙ | 2002 |
|
RU2208769C1 |
| СПОСОБ ДИСТАНЦИОННОГО КОНТРОЛЯ ФИЗИОЛОГИЧЕСКИХ ПАРАМЕТРОВ ЖИЗНЕДЕЯТЕЛЬНОСТИ ОРГАНИЗМА | 2005 |
|
RU2295911C1 |
| СПОСОБ БЕСКОНТАКТНОГО ИЗМЕРЕНИЯ НАНОВИБРАЦИЙ ПОВЕРХНОСТИ | 2011 |
|
RU2461803C1 |




Использование: для определения амплитуды нановибраций. Сущность изобретения заключается в том, что освещают вибрирующий на частоте Ω объект лазерным излучением, преобразуют отраженное от объекта излучение в электрический автодинный сигнал, раскладывают сигнал в спектральный ряд, при этом лазерное излучение частотой ω0 модулируют с частотой Ω, равной частоте колебаний объекта, добиваются совпадения начальных фаз колебаний объекта и частотной модуляции лазера, измеряют амплитуду второй C2 и четвертой C4 гармоник спектра автодинного сигнала, по зависимости С2/С4(σ) вычисляют значение аргумента функции Бесселя первого рода σ, затем модулированным лазерным излучением освещают невибрирующий объект, измеряют значение амплитуд второй C2cal и четвертой C4cal гармоник спектра отраженного автодинного сигнала, по зависимости C2cal/C4cal(σM) вычисляют значение аргумента функции Бесселя первого рода σM, амлитуду нановибраций ξ находят по определенному математическому выражению. Технический результат: повышение точности при определении амплитуды нановибраций. 9 ил.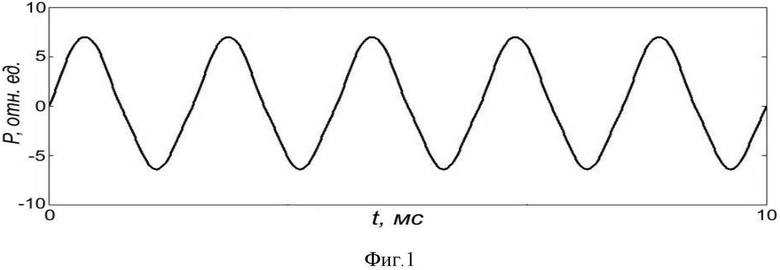
Способ измерения амплитуды нановибраций объекта, заключающийся в том, что освещают вибрирующий на частоте Ω объект лазерным излучением, преобразуют отраженное от объекта излучение в электрический автодинный сигнал, раскладывают сигнал в спектральный ряд, отличающийся тем, что лазерное излучение частотой ω0 модулируют с частотой Ω, равной частоте колебаний объекта, добиваются совпадения начальных фаз колебаний объекта и частотной модуляции лазера, измеряют амплитуду второй C2 и четвертой C4 гармоник спектра автодинного сигнала, по зависимости С2/С4(σ) вычисляют значение аргумента функции Бесселя первого рода σ, затем модулированным лазерным излучением освещают невибрирующий объект, измеряют значение амплитуд второй C2cal и четвертой C4cal гармоник спектра отраженного автодинного сигнала, по зависимости C2cal/C4cal(σM) вычисляют значение аргумента функции Бесселя первого рода σM, амлитуду нановибраций ξ находят по формуле
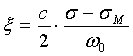 , где с - скорость света в вакууме.
, где с - скорость света в вакууме.
| СПОСОБ ОПРЕДЕЛЕНИЯ АМПЛИТУДЫ ВИБРАЦИИ ПО ДВУМ ГАРМОНИКАМ СПЕКТРА АВТОДИННОГО СИГНАЛА | 2005 |
|
RU2300085C1 |
| СПОСОБ ИЗМЕРЕНИЯ АМПЛИТУДЫ КОЛЕБАНИЙ БАРАБАННОЙ ПЕРЕПОНКИ | 2004 |
|
RU2258462C1 |
| СПОСОБ ИССЛЕДОВАНИЯ ПЕРИОДИЧЕСКИХ КОЛЕБАНИЙ | 1995 |
|
RU2098776C1 |
| СПОСОБ ИССЛЕДОВАНИЯ КОЛЕБАНИЙ | 1994 |
|
RU2097710C1 |
| JP 2010203860A, 16.09.2010 | |||
| JP 2010078393A, 08.04.2010 | |||
Авторы
Даты
2014-06-27—Публикация
2013-02-01—Подача