СПОСОБ ОПРЕДЕЛЕНИЯ ПЕРВИЧНЫХ И ОБОБЩЕННЫХ ВТОРИЧНЫХ ПАРАМЕТРОВ ОДНОРОДНОГО УЧАСТКА ТРЕХПРОВОДНОЙ ЛИНИИ ЭЛЕКТРОПЕРЕДАЧИ МЕТОДОМ ВОСЬМИПОЛЮСНИКА Российский патент 2014 года по МПК G01R27/02 

Изобретение относится к области систем обработки информации и может быть использовано при функциональном контроле и диагностировании трехфазных линий электропередачи (ЛЭП) трехпроводного исполнения на основании теории многополюсников.

Известен способ определения текущих первичных и вторичных параметров линии электропередачи для построения ее прямой Г-образной адаптивной модели [1], выбранный в качестве прототипа, заключающийся в том, что проводят измерения мгновенных значений сигналов напряжений и токов. Эти массивы отсчетов мгновенных значений тока и напряжения в начале и в конце ЛЭП, полученные в одни и те же моменты времени с определенным шагом дискретизации, передают с конца линии в ее начало по каналу связи. Далее по измеренным массивам отсчетов тока и напряжения сохраняют пары цифровых отсчетов токов и напряжений. Затем определяют потери активной мощности на активном сопротивлении продольной ветви ЛЭП, одновременно определяя действующее значение сигнала тока в ней и потери реактивной мощности на реактивном сопротивлении этой ветви. Далее определяют значения активного и реактивного сопротивлений продольной ветви ЛЭП. Затем определяют потери активной мощности на активном сопротивлении поперечной ветви ЛЭП, одновременно определяя действующие значения сигнала тока в ней и потери реактивной мощности на реактивном сопротивлении этой ветви. Далее определяют величины активного и реактивного сопротивлений поперечной ветви ЛЭП. Затем определяют численные значения коэффициентов затухания тока и напряжения и численные значения коэффициента сдвига фазы тока и сдвига фазы напряжения. Далее определяют численные значения активных и реактивных сопротивлений продольных и поперечных ветвей ЛЭП, а также коэффициентов затухания и сдвига фаз напряжений и токов на единицу длины линии электропередачи.

Достоверность полученных по этому патенту результатов возможна лишь при абсолютной синхронизации измерения мгновенных значений напряжений и токов в начале и в конце линии. Технически это трудно осуществимо.

Кроме того, представленный в прототипе алгоритм пригоден для определения вторичных параметров ЛЭП, представленных здесь лишь коэффициентами затухания и сдвига фаз, только в однопроводной линии электропередачи, где передача электрической энергии осуществляется лишь одной парой волн электромагнитного поля, или для симметричной многопроводной линии электропередачи, входящей в состав абсолютно симметричной электроэнергетической системы, где передача электрической энергии осуществляется несколькими равновеликими парами волн электромагнитного поля [2]. При нарушении симметрии напряжений и токов, а тем более самой многопроводной ЛЭП, передача электрической энергии будет осуществляться несколькими разновеликими (в трехпроводной - тремя) парами волн электромагнитного поля [3, 4]; в таком случае использование предлагаемого способа определения вторичных параметров ЛЭП без ряда допущений не корректно.

Представление однородного участка ЛЭП в виде четырехполюсника широко применяется в электротехнике и методики определения параметров ЛЭП через коэффициенты четырехполюсника [5]. Но это справедливо лишь для однопроводной ЛЭП.

Однородный участок трехпроводной ЛЭП, особенно при возможном нарушении его симметрии, а также при нарушении симметрии напряжений и токов, характеризующих электрическую энергию, передаваемую по этим ЛЭП, следует представлять в виде восьмиполюсников [6].

Задачей изобретения является формирование простого, информативного и достоверного способа определения первичных и обобщенных вторичных параметров однородного участка трехфазной линии электропередачи трехпроводного исполнения, а именно: обобщенных постоянной распространения волн электромагнитного поля, собственных и взаимных волновых сопротивлений, фазовой скорости и продольных параметров однородного участка трехпроводной ЛЭП.

Технический результат заключается в достоверном определении первичных и обобщенных вторичных параметров однородного участка трехпроводной линии электропередачи, а именно: активных сопротивлений и индуктивностей линейных проводов, активных проводимостей и емкостей между проводами, а также между проводами и «землей», в результате косвенных измерений входных и выходных фазных напряжений и линейных токов с последующим использованием теории восьмиполюсников.

Технический результат достигается тем, что однородный участок трехпроводной линии электропередачи замещается восьмиполюсником, экспериментальным определении его коэффициентов и в вычислении первичных и обобщенных вторичных параметров однородного участка, коэффициенты восьмиполюсника определяются в результате выполнения двух опытов холостого хода и двух опытов короткого замыкания в полнофазном и неполнофазном режимах и в результате аналитической обработки полученной таким образом информации определяются постоянная распространения результирующей волны электромагнитного поля, обобщенные собственные и взаимные волновые сопротивления, фазовая скорость, активные сопротивления, собственные и взаимные индуктивности линейных проводов.

Полученные таким образом численные значения первичных и обобщенных вторичных параметров однородного участка трехфазной ЛЭП трехпроводного исполнения являются ожидаемым результатом реализации этого изобретения.

Простота и достоверность предлагаемого способа достигается в результате непосредственного измерения электрических величин, позволяющих получить сведения об изображениях действующих значений входных и выходных напряжений и токов на комплексной плоскости, которые являются исходными данными для определения численных значений коэффициентов восьмиполюсника, замещающего исследуемый однородный участок трехфазной ЛЭП трехпроводного исполнения, а затем первичных и обобщенных вторичных параметров этого участка.

Предлагаемый способ является информативным за счет того, что при необходимости позволяет определить обобщенные вторичные и первичные параметры однородного участка трехпроводной ЛЭП на единицу длины линии.

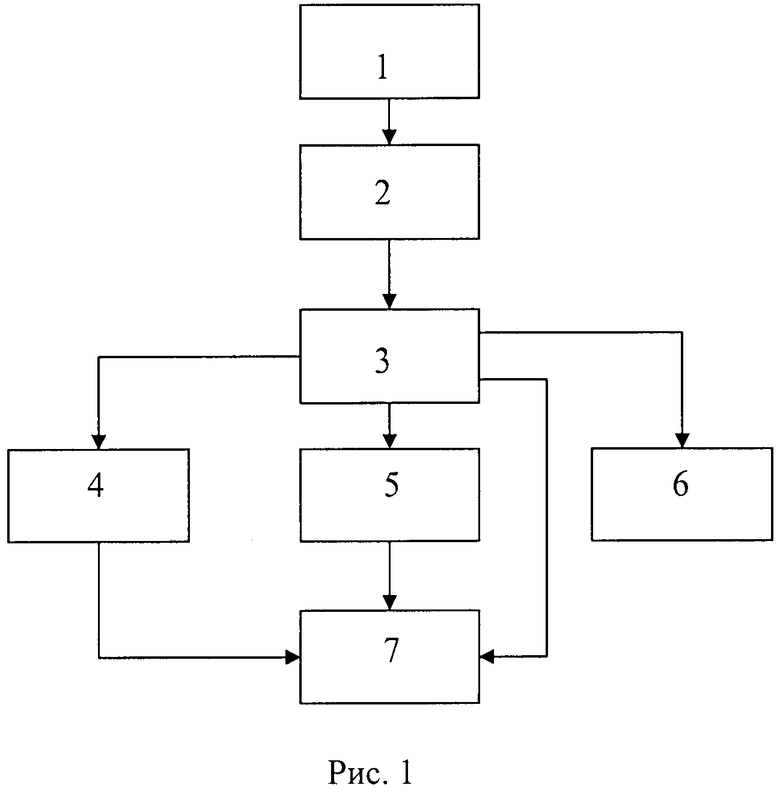
На рис.1 представлена структурная схема алгоритма способа определения первичных и обобщенных вторичных параметров однородного участка трехпроводной линии электропередачи методом восьмиполюсника.

На рис.2 иллюстрируется замещение однородного участка трехпроводной ЛЭП восьмиполюсником.

На рис.3 показана схема исполнения серии экспериментов по определению численных значений коэффициентов восьмиполюсника, замещающего однородный участок трехпроводной ЛЭП.

В блоке 1 (рис.1) выполняется выделение из реальной ЛЭП однородного участка протяженностью l, параметры которого неизменны на всем его протяжении. Этот участок можно представить в виде восьмиполюсника, как показано на рис.2.

Этот восьмиполюсник может быть описан уравнениями через А-параметры [4]:

$$\begin{array}{l}{\stackrel{.}{U}}_{1A}=A_a{\stackrel{.}{U}}_{2A}+B_a{\stackrel{.}{I}}_{2A}+N_a{\stackrel{.}{U}}_{2B}+O_a{\stackrel{.}{I}}_{2B}+P_a{\stackrel{.}{U}}_{2C}+Q_a{\stackrel{.}{I}}_{2C}\\ {\stackrel{.}{U}}_{1B}=A_b{\stackrel{.}{U}}_{2B}+B_b{\stackrel{.}{I}}_{2B}+N_b{\stackrel{.}{U}}_{2A}+O_b{\stackrel{.}{I}}_{2A}+P_b{\stackrel{.}{U}}_{2C}+Q_b{\stackrel{.}{I}}_{2C};\\ {\stackrel{.}{U}}_{1C}=A_c{\stackrel{.}{U}}_{2B}+B_c{\stackrel{.}{I}}_{2C}+N_C{\stackrel{.}{U}}_{2A}+O_c{\stackrel{.}{I}}_{2A}+P_c{\stackrel{.}{U}}_{2B}+Q_c{\stackrel{.}{I}}_{2B};\\ {\stackrel{.}{I}}_{1A}=C_a{\stackrel{.}{U}}_{2A}+D_a{\stackrel{.}{I}}_{2A}+E_a{\stackrel{.}{U}}_{2B}+F_a{\stackrel{.}{I}}_{2B}+G_a{\stackrel{.}{U}}_{2C}+H_a{\stackrel{.}{I}}_{2C};\\ {\stackrel{.}{I}}_{1B}=C_b{\stackrel{.}{U}}_{2B}+D_b{\stackrel{.}{I}}_{2B}+E_b{\stackrel{.}{U}}_{2A}+F_b{\stackrel{.}{I}}_{2A}+G_b{\stackrel{.}{U}}_{2C}+H_b{\stackrel{.}{I}}_{2C};\\ {\stackrel{.}{I}}_{1C}=C_c{\stackrel{.}{U}}_{2C}+D_c{\stackrel{.}{I}}_{2C}+E_c{\stackrel{.}{U}}_{2A}+F_c{\stackrel{.}{I}}_{2A}+G_c{\stackrel{.}{U}}_{2B}+H_c{\stackrel{.}{I}}_{2B};\end{array}\}(1)$$

где $${\stackrel{.}{U}}_{1A}$$ , $${\stackrel{.}{U}}_{1B}$$ , $${\stackrel{.}{U}}_{1C}$$ , $${\stackrel{.}{I}}_{1A}$$ , $${\stackrel{.}{I}}_{1B}$$ , $${\stackrel{.}{I}}_{1C}$$ и $${\stackrel{.}{U}}_{2A}$$ , $${\stackrel{.}{U}}_{2B}$$ , $${\stackrel{.}{U}}_{2C}$$ , $${\stackrel{.}{I}}_{1A}$$ , $${\stackrel{.}{I}}_{1B}$$ , $${\stackrel{.}{I}}_{1C}$$ , - изображения на комплексной плоскости действующих значений входных и выходных фазных напряжений и линейных токов; А_а, В_а, С_а, D_a, Е_а, F_a, G_a, Н_а, N_a, О_а, Р_а, Q_a, A_b, B_b, C_b, D_b, E_b, F_b, G_b, H_b, N_b, O_b, P_b, Q_b, A_c, В_с, С_с, D_c, Е_с, F_c, G_c, Н_с, N_c, О_с, Р_с и Q_c - пофазные коэффициенты восьмиполюсника.

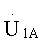
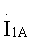
Коэффициенты восьмиполюсника могут быть определены так:

$$A_a=A_b=A_c=\frac{1}{3}{\displaystyle \sum _{i=1}^{3}ch{\gamma }_{i}l};(2)$$

$$\begin{array}{l}{B}_a=\frac{1}{3}{\displaystyle \sum _{i=1}^3{\underset{\_}{Z}}_{cAi}}sh{\gamma }_{i}l;\\ B_b=\frac{1}{3}{\displaystyle \sum _{i=1}^3{\underset{\_}{Z}}_{cBi}}sh{\gamma }_{i}l;\\ B_c=\frac{1}{3}{\displaystyle \sum _{i=1}^3{\underset{\_}{Z}}_{cCi}}sh{\gamma }_{i}l;\end{array}\}\text{ (3)}$$

$$\begin{array}{l}{C}_a=\frac{1}{3}{\displaystyle \sum _{i=1}^3\frac{sh{\gamma }_{1}l}{{\underset{\_}{Z}}_{cAi}}};\\ C_b=\frac{1}{3}{\displaystyle \sum _{i=1}^3\frac{sh{\gamma }_{1}l}{{\underset{\_}{Z}}_{cBi}}};\\ C_c=\frac{1}{3}{\displaystyle \sum _{i=1}^3\frac{sh{\gamma }_{1}l}{{\underset{\_}{Z}}_{cCi}}};\end{array}\}\text{ (4)}$$

$$D_a=D_b=D_c=\frac{1}{3}{\displaystyle \sum _{i=1}^{3}ch{\gamma }_{i}y};(5)$$

$$\begin{array}{l}{E}_a=\frac{1}{3}{\displaystyle \sum _{i=1}^3\frac{sh{\gamma }_{1}l}{{\underset{\_}{Z}}_{cABi}}};\\ E_b=\frac{1}{3}{\displaystyle \sum _{i=1}^3\frac{sh{\gamma }_{1}l}{{\underset{\_}{Z}}_{cABi}}};\\ E_c=\frac{1}{3}{\displaystyle \sum _{i=1}^3\frac{sh{\gamma }_{1}l}{{\underset{\_}{Z}}_{cCAi}}};\end{array}\}\text{ (6)}$$

$$\begin{array}{l}{F}_a=\frac{1}{3}{\displaystyle \sum _{i=1}^3\frac{{\underset{\_}{Z}}_{cBi}}{{\underset{\_}{Z}}_{cABi}}}ch{\gamma }_{i}l;\\ F_b=\frac{1}{3}{\displaystyle \sum _{i=1}^3\frac{{\underset{\_}{Z}}_{cAi}}{{\underset{\_}{Z}}_{cABi}}}ch{\gamma }_{i}l;\\ F_c=\frac{1}{3}{\displaystyle \sum _{i=1}^3\frac{{\underset{\_}{Z}}_{cAi}}{{\underset{\_}{Z}}_{cCAi}}ch{\gamma }_{i}l};\end{array}\}\text{ (7)}$$

$$\begin{array}{l}{G}_a=\frac{1}{3}{\displaystyle \sum _{i=1}^3\frac{sh{\gamma }_{1}l}{{\underset{\_}{Z}}_{cCAi}}};\\ G_b=\frac{1}{3}{\displaystyle \sum _{i=1}^3\frac{sh{\gamma }_{1}l}{{\underset{\_}{Z}}_{cBCi}}};\\ G_c=\frac{1}{3}{\displaystyle \sum _{i=1}^3\frac{sh{\gamma }_{1}l}{{\underset{\_}{Z}}_{cBCi}}};\end{array}\}\text{ (8)}$$

$$\begin{array}{l}{H}_a=\frac{1}{3}{\displaystyle \sum _{i=1}^3\frac{{\underset{\_}{Z}}_{cCi}}{{\underset{\_}{Z}}_{cCAi}}}ch{\gamma }_{i}l;\\ H_b=\frac{1}{3}{\displaystyle \sum _{i=1}^3\frac{{\underset{\_}{Z}}_{cCi}}{{\underset{\_}{Z}}_{cBCi}}}ch{\gamma }_{i}l;\\ H_c=\frac{1}{3}{\displaystyle \sum _{i=1}^3\frac{{\underset{\_}{Z}}_{cBi}}{{\underset{\_}{Z}}_{cBCi}}}ch{\gamma }_{i}l;\end{array}\}\text{ (9)}$$

$$\begin{array}{l}{N}_a=N_b=N_c=0;\\ O_a=O_b=O_c=0;\\ P_a=P_b=P_c=0;\\ Q_a=Q_b=Q_c=\mathrm{0,}\end{array}\}\text{ (10)}$$

где γ_i - постоянная распространения i-й пары волн электромагнитного поля; $${\underset{\_}{Z}}_{cAi}$$ , $${\underset{\_}{Z}}_{cBi}$$ , $${\underset{\_}{Z}}_{cCi}$$ и $${\underset{\_}{Z}}_{cABi}$$ , $${\underset{\_}{Z}}_{cBCi}$$ , $${\underset{\_}{Z}}_{cCAi}$$ - собственные и взаимные волновые сопротивления i-й пары волн электромагнитного поля.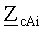

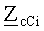
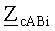
Из этих равенств очевидны следующие свойства коэффициентов восьмиполюсника, замещающего однородный участок трехпроводной ЛЭП:

$$\begin{array}{l}{A}_a=D_a;\\ A_a=D_a;\\ A_a=D_a;\end{array}\}(11)$$

$$\begin{array}{l}{A}_a{D}_a-B_a{C}_a=1;\\ A_b{D}_b-B_b{C}_b=1;\\ A_c{D}_c-B_c{C}_c=1.\end{array}\}\text{ (12)}$$

В блоке 2 (рис.1) экспериментально определяются численные значения этих коэффициентов. Для их определения достаточно выполнить серию экспериментов из четырех опытов. Опыты выполняются по схеме, изображенной на рис.3. В схеме участвуют: источник трехфазной ЭДС или три однофазных равных по величине синусоидальных ЭДС промышленной частоты, начальные фазы которых могут быть сдвинуты относительно друг друга на треть периода, желательно пониженного напряжения; шесть вольтметров и шесть амперметров, регистрирующие действующие значения напряжений и токов; шесть фазометров и двенадцать коммутирующих устройств, в качестве которых могут быть использованы обычные выключатели или рубильники.

Первый опыт может быть опытом холостого хода. Этот опыт предполагает отключение от исследуемой линии электропередачи электрической нагрузки Н. Для этого необходимо разомкнуть ключи S4, S5 и S6. Кроме того, должны быть разомкнуты ключи S7, S8, S9, S10, S11 и S12. Ключи S1, S2 и S3 должны быть замкнуты.

В качестве источника энергии в этом опыте может быть использован как автономный источник трехфазной ЭДС пониженного напряжения, так и действующая электроэнергетическая система. Нужно только подобрать соответствующие электроизмерительные приборы.

В этом случае вольтметры PV1, PV2 и PV3 покажут величины действующих фазных напряжений на входе восьмиполюсника соответственно U_lA1, U_lB1 и U_lC1. Амперметры РА1, РА2 и РА3 покажут величины линейных токов на входе восьмиполюсника соответственно I_1A1, I_1B1 и I_1С1. Фазометры Рφ1, Рφ2 и Рφ3 покажут углы сдвига фаз между соответствующими фазными напряжениями и линейными токами на входе анализируемого восьмиполюсника:

$$\begin{array}{l}{\varphi }_{11}={\varphi }_{1ua}-{\varphi }_{1ia1};\\ {\varphi }_{21}={\varphi }_{1ub}-{\varphi }_{1ib1};\\ {\varphi }_{31}={\varphi }_{1uс}-{\varphi }_{1iс1};\end{array}\}\text{ (13)}$$

где φ_1ua=0, φ_1ub=-120°, φ_1uc=120° - начальные фазы фазных напряжений на входе восьмиполюсника; φ_1ia1, φ_1ib1, φ_1ic1 - начальные фазы линейных токов на входе восьмиполюсника в первом опыте.

Из равенств (13) определятся численные значения начальных фаз токов на входе восьмиполюсника:

$$\begin{array}{l}{\phi }_{1ia1}={\phi }_{1ua}-{\phi }_{11};\\ {\phi }_{1ib1}={\phi }_{1ub}-{\phi }_{21};\\ {\phi }_{1ic1}={\phi }_{1uс}-{\phi }_{31}.\end{array}\}$$

Зная численные значения этих величин, входные напряжения и токи можно представить в виде:

$$\begin{array}{l}{\stackrel{\cdot }{U}}_{1A1}=U_{1A1}{e}^{{}^{j\phi }1ua};\\ {\stackrel{\cdot }{U}}_{1B1}=U_{1B1}{e}^{{}^{j\phi }1ub};\\ {\stackrel{\cdot }{U}}_{1C1}=U_{1C1}{e}^{{}^{j\phi }1uc};\\ {\stackrel{\cdot }{I}}_{1A1}=U_{1A1}{e}^{{}^{j\phi }1ia1};\\ {\stackrel{\cdot }{I}}_{1B1}=U_{1B1}{e}^{{}^{j\phi }1ib1};\\ {\stackrel{\cdot }{I}}_{1C1}=U_{1C1}{e}^{{}^{j\phi }1ic1}.\end{array}\}$$

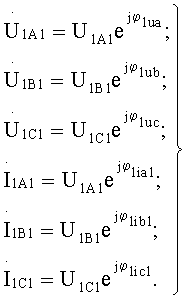
Токи на выходе анализируемого восьмиполюсника будут отсутствовать:

$${\stackrel{\cdot }{I}}_{2A1}={\stackrel{\cdot }{I}}_{2B1=}{\stackrel{\cdot }{I}}_{2C1}=0.\text{ (14)}$$

Этот факт подтверждается нулевыми значениями амперметров РА4, РА5 и РА6. Но показания вольтметров PV4, PV5 и PV6 отличны от нуля. Они покажут действующие значения фазных напряжений U_2Al, U_2B1 и U_2C1 на выходе восьмиполюсника.

Показания фазометров Рφ4, Рφ5 и Рφ6 в этом опыте отсутствуют.

Начальные фазы выходных фазных напряжений можно определить либо в результате прямых измерений специализированными приборами, либо в результате косвенных измерений, совмещенными с соответствующими расчетами. Исходными данными для таких расчетов могут быть, например, углы сдвига фаз между соответствующими выходными фазными напряжениями и входными линейными токами, которые могут зарегистрировать фазометры Рφ1, Рφ2 и Рφ3 при переключении входов на их измерительных обмотках напряжений с входных (рис.3) на выходные клеммы восьмиполюсника. Начальные фазы выходных фазных напряжений определятся так:

$$\begin{array}{l}{\varphi }_{2ua1}={\varphi }_{11}-{\varphi }_{1ia1};\\ {\varphi }_{2ub1}={\varphi }_{21}-{\varphi }_{1ib1};\\ {\varphi }_{2uc1}={\varphi }_{31}-{\varphi }_{1ic1};\end{array}\}$$

где φ₁₁, φ₂₁ и φ₃₁ - показания фазометров Рφ1, Рφ2 и Рφ3.

Такая операция позволит определить изображения выходных напряжений на комплексной плоскости:

$$\begin{array}{l}{\stackrel{\cdot }{U}}_{2A1}=U_{2A1}{e}^{{}^{j\varphi }2ua};\\ {\stackrel{\cdot }{U}}_{2B1}=U_{2B1}{e}^{{}^{j\varphi }2ub};\\ {\stackrel{\cdot }{U}}_{2C1}=U_{2C1}{e}^{{}^{j\varphi }2uc}.\end{array}\}$$

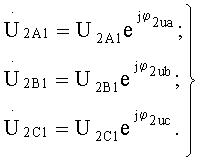
С учетом равенств (10) и (14) уравнения восьмиполюсника (1) перепишутся так:

$$\begin{array}{l}{\stackrel{\cdot }{U}}_{1A1}=A_a{\stackrel{\cdot }{U}}_{2A1};\\ {\stackrel{\cdot }{U}}_{1B1}=A_b{\stackrel{\cdot }{U}}_{2B1};\\ {\stackrel{\cdot }{U}}_{1C1}=A_c{\stackrel{\cdot }{U}}_{2C1};\\ {\stackrel{\cdot }{I}}_{1A1}=C_a{\stackrel{\cdot }{U}}_{2A1}+E_a{\stackrel{\cdot }{U}}_{2B1}+G_a{\stackrel{\cdot }{U}}_{2C1};\\ {\stackrel{\cdot }{I}}_{1B1}=C_b{\stackrel{\cdot }{U}}_{2B1}+E_b{\stackrel{\cdot }{U}}_{2A1}+G_b{\stackrel{\cdot }{U}}_{2C1};\\ {\stackrel{\cdot }{I}}_{1C1}=C_c{\stackrel{\cdot }{U}}_{2C1}+E_c{\stackrel{\cdot }{U}}_{2A1}+G_c{\stackrel{\cdot }{U}}_{2B1}.\end{array}\}\text{ (15)}$$

Из этих уравнений можно получить численные значения коэффициентов А_а, А_b и А_с:

$$\begin{array}{l}{A}_a=\frac{{\stackrel{\cdot }{U}}_{1A1}}{{\stackrel{\cdot }{U}}_{2A1}};\\ A_b=\frac{{\stackrel{\cdot }{U}}_{1B1}}{{\stackrel{\cdot }{U}}_{2B1}};\\ A_c=\frac{{\stackrel{\cdot }{U}}_{1C1}}{{\stackrel{\cdot }{U}}_{2C1}}.\end{array}\}$$

Из условий (11) следует, что по этим же уравнениям определяются и коэффициенты D_a, D_b и D_c:

$$\begin{array}{l}{D}_a=\frac{{\stackrel{\cdot }{U}}_{1A1}}{{\stackrel{\cdot }{U}}_{2A1}};\\ D_b=\frac{{\stackrel{\cdot }{U}}_{1B1}}{{\stackrel{\cdot }{U}}_{2B1}};\\ D_c=\frac{{\stackrel{\cdot }{U}}_{1C1}}{{\stackrel{\cdot }{U}}_{2C1}}.\end{array}\}$$

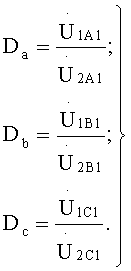
Вторым опытом может быть опыт короткого замыкания. Для этого опыта необходим автономный источник трехфазной ЭДС пониженного напряжения (≤4÷5% от U_iii) и чувствительный электроизмерительные приборы.

Опыт короткого замыкания выполняется замыканием ключей S10, S11 и S12. Кроме того, должны быть замкнуты ключи S1, S2 и S3. Ключи S4, S5, S6, S7, S8 и S9 должны быть разомкнуты.

Электроизмерительные приборы PV1, PV2, PV3 и РА1, РА2, РА3 при включении так, как показано на рис.3, в этом опыте будут регистрировать действующие значения фазных напряжений и линейных токов на входе восьмиполюсника, U_1A2, U_lB2, U_1C2 и I_1A2, I_1B2, I_1C2.

Фазометры Pφ1, Pφ2 и Рφ3 при включении так, как показано на рис.3, зарегистрируют углы сдвига начальных фаз входных фазных напряжений и линейных токов φ₁₂, φ₂₂ и φ₃₂.

На основании показаний этих приборов формируются изображения входных фазных напряжений и линейных токов на комплексной плоскости:

$$\begin{array}{l}{\stackrel{\cdot }{U}}_{1A2}=U_{1A2}{e}^{{}^{j\varphi }1ua};\\ {\stackrel{\cdot }{U}}_{1B2}=U_{1B2}{e}^{{}^{j\varphi }1ub};\\ {\stackrel{\cdot }{U}}_{1C2}=U_{1C2}{e}^{{}^{j\varphi }1uc};\\ {\stackrel{\cdot }{I}}_{1A2}=I_{1A2}{e}^{{}^{j\varphi }1ia2};\\ {\stackrel{\cdot }{I}}_{1B2}=I_{1B2}{e}^{{}^{j\varphi }1ib2};\\ {\stackrel{\cdot }{I}}_{1C2}=I_{1C2}{e}^{{}^{j\varphi }1ic2};\end{array}\}$$

где

$$\begin{array}{l}{\phi }_{lia2}={\phi }_{1ua}-{\phi }_{12};\\ {\phi }_{1ib2}={\phi }_{1ub}-{\phi }_{22};\\ {\phi }_{1ic2}={\phi }_{1uc}-{\phi }_{32}.\end{array}\}$$

Вольтметры PV4, PV5 и PV6 в этом опыте будут иметь нулевые значения, что свидетельствует об отсутствии выходных фазных напряжений:

$${\stackrel{\cdot }{U}}_{2A2}={\stackrel{\cdot }{U}}_{2B2}={\stackrel{\cdot }{U}}_{2C2}=0.\text{ (16)}$$

Но показания амперметров РА4, РА5 и РА6 будут отличны от нуля. Они позволят зарегистрировать действующие значения выходных линейных токов I_2А2, I_2В2 и I_2C2.

Если начала измерительных обмоток напряжения фазометров Рφ4, Рφ5 и Рφ6 переключить с выходных клемм восьмиполюсника (рис.3) на входные, то эти фазометры зарегистрируют углы сдвига фаз между соответствующими входными фазными напряжениями и выходными линейными токами:

$$\begin{array}{l}{\varphi }_{42}={\varphi }_{1ua}-{\varphi }_{2ia2};\\ {\varphi }_{52}={\varphi }_{1ua}-{\varphi }_{2ib2};\\ {\varphi }_{62}={\varphi }_{1ua}-{\varphi }_{2ic2}.\end{array}\}$$

Из этих равенств определяются начальные фазы выходных линейных токов:

$$\begin{array}{l}{\varphi }_{2ia2}={\varphi }_{1ua}-{\varphi }_{42};\\ {\varphi }_{2ib2}={\varphi }_{1ub}-{\varphi }_{52};\\ {\varphi }_{2ic2}={\varphi }_{1uc}-{\varphi }_{62}.\end{array}\}$$

Эта операция позволит определить изображения выходных линейных токов на комплексной плоскости:

$$\begin{array}{l}{\stackrel{\cdot }{I}}_{2A2}=I_{2A2}{e}^{{}^{j\phi }2ia2};\\ {\stackrel{\cdot }{I}}_{2B2}=I_{2B2}{e}^{{}^{j\phi }2ib2};\\ {\stackrel{\cdot }{I}}_{2C2}=I_{2C2}{e}^{{}^{j\phi }2ic2}.\end{array}\}$$

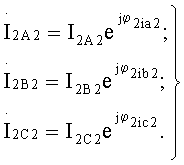
С учетом равенств (10) и (16) работа восьмиполюсника в режиме полнофазного короткого замыкания описывается уравнениями:

$$\begin{array}{l}{\stackrel{\cdot }{U}}_{1A2}=B_a{\stackrel{\cdot }{I}}_{2A2};\\ {\stackrel{\cdot }{U}}_{1B2}=B_b{\stackrel{\cdot }{I}}_{2B2};\\ {\stackrel{\cdot }{U}}_{1C2}=B_c{\stackrel{\cdot }{I}}_{2C2};\\ {\stackrel{\cdot }{I}}_{1A2}=D_a{\stackrel{\cdot }{I}}_{2A2}+F_a{\stackrel{\cdot }{I}}_{2B2}+H_a{\stackrel{\cdot }{I}}_{2C2};\\ {\stackrel{\cdot }{I}}_{1B2}=D_b{\stackrel{\cdot }{I}}_{2B2}+F_b{\stackrel{\cdot }{I}}_{2A2}+H_b{\stackrel{\cdot }{I}}_{2C2};\\ {\stackrel{\cdot }{I}}_{1C2}=D_c{\stackrel{\cdot }{I}}_{2C2}+F_c{\stackrel{\cdot }{I}}_{2A2}+H_c{\stackrel{\cdot }{I}}_{2B2}.\end{array}\}\text{ (17)}$$

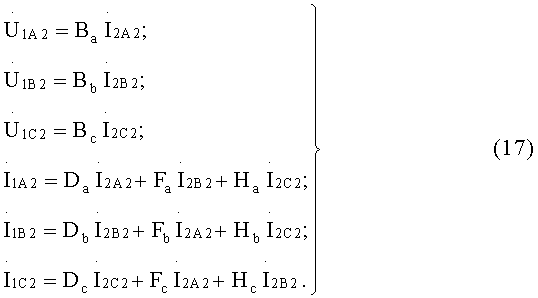
Из этих уравнений определяются коэффициенты В_а, В_b и В_c

$$\begin{array}{l}{B}_a=\frac{{\stackrel{\cdot }{U}}_{1A2}}{{\stackrel{\cdot }{I}}_{2A2}};\\ B_b=\frac{{\stackrel{\cdot }{U}}_{1B2}}{{\stackrel{\cdot }{I}}_{2B2}};\\ B_c=\frac{{\stackrel{\cdot }{U}}_{1C2}}{{\stackrel{\cdot }{I}}_{2C2}};\end{array}\}$$

Коэффициенты восьмиполюсника С_а, С_b и С_c определяются из условий (12):

$$\begin{array}{l}{C}_a=\frac{A_a{D}_a-1}{B_a};\\ C_b=\frac{A_b{D}_b-1}{B_b};\\ C_c=\frac{A_c{D}_c-1}{B_c}.\end{array}\}$$

Третий опыт, опыт неполнофазного холостого хода, выполняется при размыкании ключей S4, S5 и S6. Кроме того, должны быть разомкнуты ключи S2, S3, S7, S8, S9, S10, S11 и S12. Замкнут должен быть лишь ключ S1. Таким образом, к входу восьмиполюсника, замещающего однородный участок трехпроводной ЛЭП, оказывается подключенной лишь однофазная ЭДС $${\stackrel{\cdot }{E}}_A=E_A{e}^{j0}$$ . Энергия от других фаз трехфазного источника электрической энергии на вход восьмиполюсника не поступает. Это значит, что амперметры РА2 и РА3, а также фазометры Рφ2 и Рφ3 будут иметь нулевые значения. А вольтметр PV1, амперметр РА1 и фазометр Рφ1 будут иметь значения, отличные от нуля. Из-за наличия электромагнитных связей между токоведущими частями исследуемого однородного участка трехпроводной ЛЭП показания вольтметров PV2 и PV3 тоже будут отличны от нуля. Эти приборы должны обладать соответствующей чувствительностью. Показания перечисленных электроизмерительных приборов позволят сформулировать комплексные значения входных характеристик восьмиполюсника:

$$\begin{array}{l}{\stackrel{\cdot }{U}}_{1A3}=U_{1A3}{e}^{{}^{j0}};\\ {\stackrel{\cdot }{U}}_{1B3}=U_{1B3}{e}^{{}^{j0}};\\ {\stackrel{\cdot }{U}}_{1C3}=U_{1C3}{e}^{{}^{j0}};\\ {\stackrel{\cdot }{I}}_{1A3}=I_{1A3}{e}^{{}^{j{\phi }_{13}}}=I_{1A3}{e}^{j{\phi }_{1ia3}},\end{array}\}$$

где φ₁₃ - показание фазометра Рφ1.

Показания амперметров РА4, РА5, РА6 и фазометров Рφ4, Рφ5 и Рφ6, подключенных к выходным клеммам анализируемого восьмиполюсника, как показано на рис.3, имеют нулевые значения. То есть в этом случае справедливо равенство:

$${\stackrel{\cdot }{I}}_{2A3}={\stackrel{\cdot }{I}}_{2B3}={\stackrel{\cdot }{I}}_{2C3}=0.\text{ (18)}$$

Вольтметры PV4, PV5 и PV при исполнении этого опыта зарегистрируют выходные фазные напряжения U_2A3, U_2B3 и U_2С3. Переключение начала измерительных обмоток напряжения фазометров Pφ1, Pφ2 и Pφ1 с входных клемм восьмиполюсника на выходные позволит зарегистрировать этими приборами углы сдвига фаз между соответствующими выходными фазными напряжениями и входными линейными токами:

$$\begin{array}{l}{\phi }_{13}={\phi }_{2ua3}-{\phi }_{1ia3};\\ {\phi }_{23}={\phi }_{2ub3}-{\phi }_{1ib3}={\phi }_{2ub3};\\ {\phi }_{33}={\phi }_{2uc3}-{\phi }_{1ic3}={\phi }_{2uc3}.\end{array}\}$$

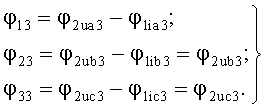
Эти равенства позволят определить начальные фазы выходных фазных напряжений φ_2ua3, φ_2ub3, φ_2uc3 и, в конечном счете, определить изображения этих напряжений на комплексной плоскости:

$$\begin{array}{l}{\stackrel{\cdot }{U}}_{2A3}=U_{2A3}{e}^{{}^{j\phi }2ua3};\\ {\stackrel{\cdot }{U}}_{2B3}=U_{2B3}{e}^{{}^{j\phi }2ub3};\\ {\stackrel{\cdot }{U}}_{2C3}=U_{2C3}{e}^{{}^{j\phi }2uc3}.\end{array}\}$$

С учетом равенств (10) и (18) работа восьмиполюсника в неполнофазном режиме холостого хода описывается уравнениями:

$$\begin{array}{l}{\stackrel{\cdot }{U}}_{1A3}=A_a{\stackrel{\cdot }{U}}_{2A3};\\ {\stackrel{\cdot }{U}}_{1B3}=A_b{\stackrel{\cdot }{U}}_{2B3};\\ {\stackrel{\cdot }{U}}_{1C3}=A_c{\stackrel{\cdot }{U}}_{2C3};\\ {\stackrel{\cdot }{I}}_{1A3}=C_a{\stackrel{\cdot }{U}}_{2A3}+E_a{\stackrel{\cdot }{U}}_{2B3}+G_a{\stackrel{\cdot }{U}}_{2C3};\\ 0=C_b{\stackrel{\cdot }{U}}_{2B3}+E_b{\stackrel{\cdot }{U}}_{2A3}+G_b{\stackrel{\cdot }{U}}_{2C3};\\ 0=C_c{\stackrel{\cdot }{U}}_{2C3}+E_c{\stackrel{\cdot }{U}}_{2A3}+G_c{\stackrel{\cdot }{U}}_{2B3}.\end{array}\}\text{ (19)}$$

В этих уравнениях известны численные значения коэффициентов А_а, А_b, А_с и С_а, С_b, С_с. Численные значения коэффициентов Е_а, Е_b, Е_с и G_a, G_b, G_c следует определить.

Численные значения коэффициентов Е_а и G_a могут быть определены из результатов совместного решения четвертого уравнения системы уравнений (15) и четвертого уравнения системы уравнений (19):

$$\begin{array}{l}{\stackrel{\cdot }{I}}_{1A1}=C_a{\stackrel{\cdot }{U}}_{2A1}+E_a{\stackrel{\cdot }{U}}_{2B1}+G_a{\stackrel{\cdot }{U}}_{2C1};\\ {\stackrel{\cdot }{I}}_{1A3}=C_a{\stackrel{\cdot }{U}}_{2A3}+E_a{\stackrel{\cdot }{U}}_{2B3}+G_a{\stackrel{\cdot }{U}}_{2C3}.\end{array}\}$$

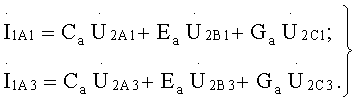
Из этих уравнений получается, что

$$E_a=\frac{C_a{\stackrel{\cdot }{U}}_{2A1}{\stackrel{\cdot }{U}}_{2C3}+{\stackrel{\cdot }{U}}_{2C1}{\stackrel{\cdot }{I}}_{1A3}-C_a{\stackrel{\cdot }{U}}_{2C1}{\stackrel{\cdot }{U}}_{2A3}+{\stackrel{\cdot }{U}}_{2C3}{\stackrel{\cdot }{I}}_{1A1}}{{\stackrel{\cdot }{U}}_{2С1}{\stackrel{\cdot }{U}}_{2B3}+{\stackrel{\cdot }{U}}_{2B1}{\stackrel{\cdot }{U}}_{2C3}};$$

$$G_a=\frac{{\stackrel{\cdot }{I}}_{1A3}-C_a{\stackrel{\cdot }{U}}_{2A3}-R_a{\stackrel{\cdot }{U}}_{2B3}}{{\stackrel{\cdot }{U}}_{2C3}}.$$

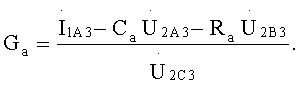
Из уравнений (6) следует, что Е_b=Е_а.

Тогда из решения пятого уравнения системы уравнений (19) получается, что

$$G_b=\frac{C_b{\stackrel{\cdot }{U}}_{2B3}-E_b{\stackrel{\cdot }{U}}_{2A3}}{{\stackrel{\cdot }{U}}_{2C3}}.$$

Уравнения (8) подтверждают равенство G_c=G_b.

Из последнего уравнения системы уравнений (19) следует, что

$$E_b=\frac{C_b{\stackrel{\cdot }{U}}_{2C3}-G_c{\stackrel{\cdot }{U}}_{2B3}}{{\stackrel{\cdot }{U}}_{2A3}};$$

Или проще: Е_с=G_a.

Четвертый опыт целесообразно выполнять как опыт короткого замыкания при неполнофазном питании восьмиполюсника.

В этом случае, как и в предыдущем, предлагается подключить лишь одну однофазную ЭДС. Пусть это будет $${\stackrel{\cdot }{E}}_A$$ . Для этого необходимо разомкнуть ключи S2 и S3 и замкнуть ключ S1. Кроме того, необходимо замкнуть ключи S10, S11 и S12, а также разомкнуть ключи S4, S5, S6, S7, S8 и S9.

В результате этих действий на входе анализируемого восьмиполюсника будут отсутствовать линейные токи 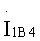$${\stackrel{\cdot }{I}}_{1B4}$$ и $${\stackrel{\cdot }{I}}_{1C4}$$ :

$${\stackrel{\cdot }{I}}_{1B4}={\stackrel{\cdot }{I}}_{1C4}=0.\text{ (20)}$$

Об этом будут свидетельствовать нулевые показания амперметров РА2 и РА3. А показания амперметра РА1 будут отличны от нуля: он покажет действующее значение линейного тока I_1А4. Вольтметры PV1, PV2 и PV3 позволят зарегистрировать входные фазные напряжения U_1A4, U_1B4 и U_1C4. Фазометр Pφ1 покажет угол сдвига фаз между входным напряжением U_1А4 и входным линейным током I_1A4:

φ₁₄=φ_1ua4-φ_1ia4.

Показания этих приборов позволят определить изображения входных характеристик электрической энергии на комплексной плоскости

$$\begin{array}{l}{\stackrel{\cdot }{U}}_{1A4}=U_{1A4}{e}^{{}^{j\varphi }1ua4};\\ {\stackrel{\cdot }{U}}_{1B4}=U_{1B4}{e}^{{}^{j\varphi }1ub4};\\ {\stackrel{\cdot }{U}}_{1C4}=U_{1C4}{e}^{{}^{j\varphi }1uc4};\\ {\stackrel{\cdot }{I}}_{1A4}=I_{1A4}{e}^{j{\varphi }_{1ia4}}.\end{array}\}$$

Численные значения выходных фазных напряжений в этом опыте будут отсутствовать:

$${\stackrel{\cdot }{U}}_{2A4}={\stackrel{\cdot }{U}}_{2B4}={\stackrel{\cdot }{U}}_{2C4}=0.\text{ (21)}$$

Об этом свидетельствуют нулевые показания вольтметров PV4, PV5 и PV6. А амперметры РА4, РА5 и РА6 покажут действующие значения выходных линейных токов I_2А4, I_2В4 и I_2С4.

Если начала измерительных обмоток напряжения фазометров Рφ4, Рφ5 и Рφ6 переключить с выходных клемм анализируемого восьмиполюсника на его входные клеммы, то эти приборы смогут зарегистрировать углы сдвига фаз между соответствующими входными фазными напряжениями и выходными линейными токами:

$$\begin{array}{l}{\varphi }_{44}={\varphi }_{1ua4}-{\varphi }_{2ia4};\\ {\varphi }_{54}={\varphi }_{1ub4}-{\varphi }_{2ib4};\\ {\varphi }_{64}={\varphi }_{1uc4}-{\varphi }_{2ic4}.\end{array}\}$$

Теперь можно сформулировать изображения выходных линейных токов на комплексной плоскости:

$$\begin{array}{l}{\stackrel{\cdot }{I}}_{2A4}=I_{2A4}{e}^{{}^{j\phi }2ia4};\\ {\stackrel{\cdot }{I}}_{2B4}=I_{2B4}{e}^{{}^{j\phi }2ib4};\\ {\stackrel{\cdot }{I}}_{2C4}=I_{2C4}{e}^{{}^{j\phi }2ic4}.\end{array}\}$$

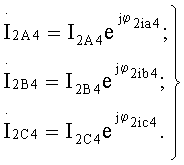
С учетом равенств (10), (20) и (21) работа восьмиполюсника в неполнофазном режиме короткого замыкания описывается уравнениями:

$$\begin{array}{l}{\stackrel{\cdot }{U}}_{1A4}=B_a{\stackrel{\cdot }{I}}_{2A4};\\ {\stackrel{\cdot }{U}}_{1B4}=B_b{\stackrel{\cdot }{I}}_{2B4};\\ {\stackrel{\cdot }{U}}_{1C4}=B_c{\stackrel{\cdot }{I}}_{2C4};\\ {\stackrel{\cdot }{I}}_{1A4}=D_a{\stackrel{\cdot }{I}}_{2A4}+F_a{\stackrel{\cdot }{I}}_{2B4}+H_a{\stackrel{\cdot }{I}}_{2C4};\\ 0=D_b{\stackrel{\cdot }{I}}_{2B4}+F_b{\stackrel{\cdot }{I}}_{2A4}+H_b{\stackrel{\cdot }{I}}_{2C4};\\ 0=D_c{\stackrel{\cdot }{I}}_{2C4}+F_c{\stackrel{\cdot }{I}}_{2A4}+H_c{\stackrel{\cdot }{I}}_{2B4}.\end{array}\}\text{ (22)}$$

В этих уравнениях известны численные значения коэффициентов В_а, В_b, В_с и D_a, D_b, D_c. Требуется определить численные значения коэффициентов F_a, F_b, F_c и Н_а, H_b, Н_с.

Численные значения коэффициентов F_a и Н_а можно определить в результате совместного решения четвертого уравнения системы уравнений (17) и четвертого уравнения системы уравнений (22):

$$\begin{array}{l}{\stackrel{\cdot }{I}}_{1A2}=D_a{\stackrel{\cdot }{I}}_{2A2}+F_a{\stackrel{\cdot }{I}}_{2B2}+H_a{\stackrel{\cdot }{I}}_{2C2};\\ {\stackrel{\cdot }{I}}_{1A4}=D_a{\stackrel{\cdot }{I}}_{2A4}+F_a{\stackrel{\cdot }{I}}_{2B4}+H_a{\stackrel{\cdot }{I}}_{2C4};\end{array}\}$$

В результате совместного решения этих уравнений получается, что

$$F_a=\frac{C_a{\stackrel{\cdot }{I}}_{2A2}{\stackrel{\cdot }{I}}_{2C4}+{\stackrel{\cdot }{I}}_{2C2}{\stackrel{\cdot }{I}}_{1A4}-D_a{\stackrel{\cdot }{I}}_{2C2}{\stackrel{\cdot }{I}}_{2A4}-{\stackrel{\cdot }{I}}_{1A2}{\stackrel{\cdot }{I}}_{2C4}}{{\stackrel{\cdot }{I}}_{2С2}{\stackrel{\cdot }{I}}_{2B4}+{\stackrel{\cdot }{I}}_{2B2}{\stackrel{\cdot }{I}}_{2C4}};$$

$$H_a=\frac{{\stackrel{\cdot }{I}}_{1A4}-D_a{\stackrel{\cdot }{I}}_{2A4}-F_a{\stackrel{\cdot }{I}}_{2B4}}{{\stackrel{\cdot }{I}}_{2C4}}.$$

Из совместного решения пятого уравнения системы уравнений (17) и пятого уравнения системы уравнений (22) можно определить коэффициенты F_b и Н_b.

Полученная таким образом система уравнений имеет вид:

$$\begin{array}{l}{\stackrel{\cdot }{I}}_{1B2}=D_b{\stackrel{\cdot }{I}}_{2B2}+F_b{\stackrel{\cdot }{I}}_{2A2}+H_b{\stackrel{\cdot }{I}}_{2C2};\\ 0=D_b{\stackrel{\cdot }{I}}_{2B4}+F_b{\stackrel{\cdot }{I}}_{2A4}+H_b{\stackrel{\cdot }{I}}_{2C4}.\end{array}\}$$

Результат совместного решения этих уравнений может быть представлен так:

$$F_b=\frac{D_b{\stackrel{\cdot }{I}}_{2B2}{\stackrel{\cdot }{I}}_{2C4}+D_b{\stackrel{\cdot }{I}}_{2C2}{\stackrel{\cdot }{I}}_{2B4}-{\stackrel{\cdot }{I}}_{1B2}{\stackrel{\cdot }{I}}_{2C4}}{{\stackrel{\cdot }{I}}_{2С2}{\stackrel{\cdot }{I}}_{2A4}-{\stackrel{\cdot }{I}}_{2A2}{\stackrel{\cdot }{I}}_{2C4}};$$

$$H_a=\frac{D_b{\stackrel{\cdot }{I}}_{1B4}+F_b{\stackrel{\cdot }{I}}_{2A4}}{{\stackrel{\cdot }{I}}_{2C4}}$$ .

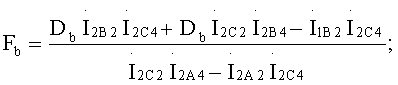
Для определения коэффициентов F_c и Н_с необходимо совместное решение последнего уравнения системы уравнений (17) и последнего уравнения системы уравнений (22).

Вновь полученная таким образом система уравнений имеет вид:

$$\begin{array}{l}{\stackrel{\cdot }{I}}_{1C2}=D_c{\stackrel{\cdot }{I}}_{2C2}+F_c{\stackrel{\cdot }{I}}_{2A2}+H_c{\stackrel{\cdot }{I}}_{2B2};\\ 0=D_c{\stackrel{\cdot }{I}}_{2C4}+F_c{\stackrel{\cdot }{I}}_{2A4}+H_c{\stackrel{\cdot }{I}}_{2B4}.\end{array}\}$$

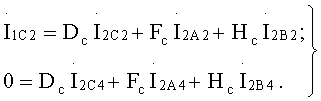
Результат совместного решения этих уравнений можно представить в виде:

$$F_c=\frac{D_c{\stackrel{\cdot }{I}}_{2C2}{\stackrel{\cdot }{I}}_{2B4}+D_c{\stackrel{\cdot }{I}}_{2B2}{\stackrel{\cdot }{I}}_{1C4}-{\stackrel{\cdot }{I}}_{2C2}-{\stackrel{\cdot }{I}}_{2B4}}{{\stackrel{\cdot }{I}}_{2B2}{\stackrel{\cdot }{I}}_{2A4}-{\stackrel{\cdot }{I}}_{2A2}{\stackrel{\cdot }{I}}_{2B4}};$$

$$H_c=\frac{D_c{\stackrel{\cdot }{I}}_{1C4}+F_c{\stackrel{\cdot }{I}}_{2A4}}{{\stackrel{\cdot }{I}}_{2B4}}$$ .

Таким образом определены численные значения всех коэффициентов восьмиполюсника, замещающего однородный участок трехфазной ЛЭП трехпроводного исполнения.

Численные значения коэффициентов восьмиполюсника, замещающего однородный участок трехфазной ЛЭП трехпроводного исполнения, позволят определить численные значения вторичных параметров этого участка. Для этого следует воспользоваться равенствами (2)-(9).

Эти равенства показывают, что коэффициенты восьмиполюсника, замещающего однородный участок трехпроводной ЛЭП, есть результат воздействия трех пар волн электромагнитного поля.

Электроизмерительные приборы, используемые в экспериментальном определении коэффициентов восьмиполюсника, регистрируют результат воздействия всех трех пар волн электромагнитного поля.

Определение результата действия каждой пары волн электромагнитного поля этими электроизмерительными приборами не представляется возможным. Невозможно и определение доли участия каждой пары волн электромагнитного поля в численном выражении каждого коэффициента восьмиполюсника. Именно поэтому не представляется возможным определение на основании полученных в предыдущем параграфе численных значений коэффициентов восьмиполюсника вторичных параметров однородного участка трехпроводной ЛЭП, замещенного этим восьмиполюсником, для каждой пары волн электромагнитного поля. Здесь оказывается невозможным определение постоянной распространения каждой пары волн электромагнитного поля, определение собственных и взаимных волновых сопротивлений для каждой пары волн электромагнитного поля.

Электроизмерительные приборы, используемые в опытах по определению численных значений коэффициентов анализируемого восьмиполюсника, регистрируют результирующее действие всех трех пар волн электромагнитного поля. Значит, и определенные таким образом коэффициенты восьмиполюсника характеризуют результирующее действие всех трех пар волн электромагнитного поля. Это означает, что здесь речь может идти лишь о результирующих, обобщенных вторичных параметрах: об обобщенной постоянной распространенной электромагнитного поля γ, об обобщенных собственных $${\underset{\_}{Z}}_{cA}$$ , $${\underset{\_}{Z}}_{cB}$$ , $${\underset{\_}{Z}}_{cC}$$ и взаимных $${\underset{\_}{Z}}_{cAB}$$ , $${\underset{\_}{Z}}_{cBC}$$ , $${\underset{\_}{Z}}_{cCA}$$ волновых сопротивлениях однородного участка трехфазной ЛЭП трехпровод-ного исполнения.

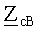
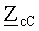
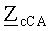
В блоке 3 (рис.1) с учетом равенства (2) обобщенная постоянная распространения волн электромагнитного поля по проводам исследуемой ЛЭП определится как обратная функция гиперболического косинуса, отнесенная к длине рассматриваемого участка линии электропередачи:

$$\gamma =\frac{arcch{A}_a}{l}=\frac{arcch{A}_b}{l}=\frac{arcch{A}_c}{l}.\text{ (23)}$$

Для определения обобщенной постоянной распространения электромагнитных волн в равенстве (23) можно использовать вместо коэффициентов А_а, А_b и А_с коэффициенты D_a, D_b и D_c.

В блоках 4 и 5 определяются обобщенные собственные и взаимные волновые сопротивления линейных проводов однородного участка трехфазной ЛЭП трехпроводного исполнения.

В блоке 4 из равенства (3) определяются обобщенные собственные волновые сопротивления линейных проводов однородного участка трехфазной ЛЭП трехпроводного исполнения протяженностью l:

$${\underset{\_}{Z}}_{cA}=\frac{B_a}{sh\gamma l};$$

$${\underset{\_}{Z}}_{cB}=\frac{B_b}{sh\gamma l};$$

$${\underset{\_}{Z}}_{cC}=\frac{B_c}{sh\gamma l}.$$

Обобщенные собственные волновые сопротивления однородного участка трехпроводной ЛЭП можно определить и из равенств (4):

$${\underset{\_}{Z}}_{cA}=\frac{sh\gamma l}{C_a};$$

$${\underset{\_}{Z}}_{cB}=\frac{sh\gamma l}{C_b};$$

$${\underset{\_}{Z}}_{cC}=\frac{sh\gamma l}{C_c}.$$

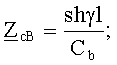
В блоке 5 определяются обобщенные взаимные волновые сопротивления.

Обобщенное взаимное волновое сопротивление между линейными проводами А и В можно определить из первого уравнения равенств (6),

$${\underset{\_}{Z}}_{cAB}=\frac{sh\gamma l}{E_a};$$

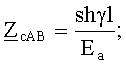
или из второго уравнения этих же равенств,

$${\underset{\_}{Z}}_{cAB}=\frac{sh\gamma l}{E_b}.$$

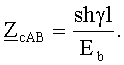
Возможно использование и иных формулировок, полученных из равенств (7):

$${\underset{\_}{Z}}_{cAB}=\frac{{\underset{\_}{Z}}_{cB}}{F_a}ch\gamma l$$

или

$${\underset{\_}{Z}}_{cAB}=\frac{{\underset{\_}{Z}}_{cA}}{F_b}ch\gamma l.$$

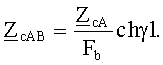
Но последнее действие возможно лишь после выполнения действий блока 4.

Обобщенное взаимное волновое сопротивление между линейными проводами В и С однородного участка трехфазной ЛЭП трехпроводного исполнения протяженностью l может быть найдено из (8):

$${\underset{\_}{Z}}_{cBC}=\frac{sh\gamma l}{G_b}$$

$${\underset{\_}{Z}}_{cBC}=\frac{sh\gamma l}{G_c}.$$

Иначе после выполнения действий блока 4 это сопротивление можно определить из равенств (9):

$${\underset{\_}{Z}}_{cBC}=\frac{{\underset{\_}{Z}}_{cC}}{H_b}ch\gamma l$$

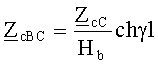
или

$${\underset{\_}{Z}}_{cBC}=\frac{{\underset{\_}{Z}}_{cB}}{H_c}ch\gamma l.$$

Обобщенное взаимное волновое сопротивление между линейными проводами С и А однородного участка трехпроводной ЛЭП может быть определено из третьего уравнения равенств (6)

$${\underset{\_}{Z}}_{cCA}=\frac{sh\gamma l}{E_c}$$ ,

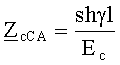
или из первого уравнения равенств (8)

$${\underset{\_}{Z}}_{cCA}=\frac{sh\gamma l}{G_a}.$$

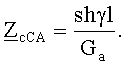
Иначе после выполнения действий блока 4 это сопротивление можно определить из третьего уравнения равенств (7)

$${\underset{\_}{Z}}_{cCA}=\frac{{\underset{\_}{Z}}_{cA}}{F_c}ch\gamma l$$ ,

или из первого уравнения равенств (9)

$${\underset{\_}{Z}}_{cCA}=\frac{{\underset{\_}{Z}}_{cC}}{H_a}ch\gamma l.$$

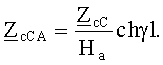
В блоке 6 (рис.1) определяется фазовая скорость результирующей волны электромагнитного поля, названной ранее обобщенной фазовой скоростью, по формуле:

$${\nu }_{\dot{0}}=\frac{2\pi f}{\mathrm{Im}(\gamma )},$$

где f - частота изменения мгновенного напряжения во времени.

Таким образом определены искомые вторичные параметры однородного участка трехпроводной ЛЭП.

В блоке 7 (рис.1) определяются означенные в задаче изобретения продольные параметры однородного участка трехпроводной ЛЭП, входящие в состав первичных параметров исследуемого участка линии электропередачи.

К продольным параметрам ЛЭП относятся собственные параметры линейных проводов: активные сопротивления R_A, R_B, R_С и собственные индуктивности L_A, L_B, L_С. Каждый линейный провод обладает и собственной емкостью. Но ее величина настолько мала, что практически не оказывает влияния на характер и интенсивность распространения электрической энергии по ЛЭП. Поэтому собственная емкость при анализе результатов передачи электрической энергии по ЛЭП обычно не учитывается.

На величину продольных параметров неизбежно оказывает влияние явление взаимной индукции между линейными проводами. Это явление обычно количественно учитывается взаимными индуктивностями М_АВ, М_ВС и М_СА.

Обобщенные величины собственных и взаимных волновых сопротивлений линейных проводов можно определить по формулам [4]:

$${\underset{\_}{Z}}_{cA}=\frac{\Delta }{\gamma ({\underset{\_}{Z}}_B{\underset{\_}{Z}}_C-{\underset{\_}{Z}}^2{}_{BC})};(24)$$

$${\underset{\_}{Z}}_{cB}=\frac{\Delta }{\gamma ({\underset{\_}{Z}}_A{\underset{\_}{Z}}_C-{\underset{\_}{Z}}^2{}_{CA})};(25)$$

$${\underset{\_}{Z}}_{cC}=\frac{\Delta }{\gamma ({\underset{\_}{Z}}_A{\underset{\_}{Z}}_B-{\underset{\_}{Z}}^2{}_{AB})};(26)$$

$${\underset{\_}{Z}}_{cAB}=\frac{\Delta }{\gamma ({\underset{\_}{Z}}_{AB}{\underset{\_}{Z}}_{BC}-{\underset{\_}{Z}}_C{Z}_{AB})};(27)$$

$${\underset{\_}{Z}}_{cBC}=\frac{\Delta }{\gamma ({\underset{\_}{Z}}_{AB}{\underset{\_}{Z}}_{CA}-{\underset{\_}{Z}}_A{Z}_{BC})};(28)$$

$${\underset{\_}{Z}}_{cCA}=\frac{\Delta }{\gamma ({\underset{\_}{Z}}_{AB}{\underset{\_}{Z}}_{BC}-{\underset{\_}{Z}}_B{Z}_{CA})},(29)$$

$$\Delta ={\underset{\_}{Z}}_A{\underset{\_}{Z}}_B{\underset{\_}{Z}}_C-{\underset{\_}{Z}}_A{\underset{\_}{Z}}^2{{}_B}_C-{\underset{\_}{Z}}_B{\underset{\_}{Z}}^2{}_{CA}-{\underset{\_}{Z}}_C{\underset{\_}{Z}}^2{}_{AB}+{\underset{\_}{2Z}}_{AB}{\underset{\_}{Z}}_{BC}{\underset{\_}{Z}}_{CA};$$

$${\underset{\_}{Z}}_A=R_A+j\omega L_A;$$

$${\underset{\_}{Z}}_B=R_B+j\omega L_B;$$

$${\underset{\_}{Z}}_C=R_C+j\omega L_C;$$

$${\underset{\_}{Z}}_{AB}=j\omega M_{AB};$$

$${\underset{\_}{Z}}_{BC}=j\omega M_{BC};$$

$${\underset{\_}{Z}}_{CA}=j\omega M_{CA};$$

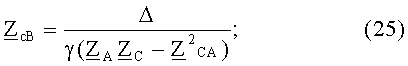
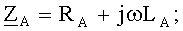
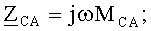
ω=2πf.

Совместное решение уравнений (24)-(29) позволит определить полные сопротивления $${\underset{\_}{Z}}_A$$ , $${\underset{\_}{Z}}_B$$ , $${\underset{\_}{Z}}_C$$ , $${\underset{\_}{Z}}_{AB}$$ , $${\underset{\_}{Z}}_{BC}$$ и $${\underset{\_}{Z}}_{CA}$$ . Для решения этих уравнений пришлось привлечь средства вычислительной техники с использованием специальных операционных систем.

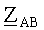
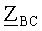
В частности, для решения указанных уравнений была использована операционная система MATLAB. Желаемый результат здесь оказался возможным при численном решении уравнений (24)-(29), которое свелось к уточнению начальных, в данном случае, справочных сведений о первичных параметрах ЛЭП.

Пусть продольные параметры ЛЭП ориентировочно определяются следующими величинами: активные сопротивления линейных проводов - R_A=R_B=R_C=0,13 Ом/км; собственные индуктивности - L_A=L_B=L_C=0,001 Гн/км.

Реактивные продольные сопротивления на частоте основной гармонической составляющей в таком случае определятся так:

Х_А=Х_В=Х_С=2πnL_A=2π·1·50·0,001=0,314 Ом/км.

Взаимная индуктивность между линейными проводами трехпроводной ЛЭП пусть определяется величиной М_АВ=М_ВС=М_СА - 0,0005 Гн/км. В таком случае полные взаимные сопротивления на частоте основной гармонической составляющей определяется так:

$${\underset{\_}{Z}}_{AB}={\underset{\_}{Z}}_{BC}={\underset{\_}{Z}}_{CA}=j2\pi nf{M}_{AB}=j2\pi \cdot 1\cdot 50\cdot \mathrm{0,0005}=0.157Ом/км.$$

Пусть по результатам серии экспериментов, выполненной по описанной ранее методике, оказалось, что обобщенная постоянная распространения волн электромагнитного поля на частоте основной гармонической составляющей равна (γ_n=-1,0632-j0,5083)км^-1.

Обобщенные собственные волновые сопротивления по результатам экспериментов и соответствующих расчетов на частоте основной гармонической пусть окажутся равными:

$${\underset{\_}{Z}}_{cA}=(\mathrm{185,36}-j\mathrm{152,8})Ом/км;$$

$${\underset{\_}{Z}}_{cB}=(\mathrm{230,2}-j\mathrm{189,76})Ом/км;$$

$${\underset{\_}{Z}}_{cС}=(\mathrm{205,44}-j\mathrm{189,76})Ом/км.$$

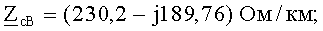
Обобщенные взаимные волновые сопротивления пусть окажутся такими:

$${\underset{\_}{Z}}_{cAB}=(\mathrm{52,04}-j\mathrm{483,68})Ом/км;$$

$${\underset{\_}{Z}}_{cBC}=(\mathrm{79,96}-j\mathrm{480,96})Ом/км;$$

$${\underset{\_}{Z}}_{cСA}=(\mathrm{20,64}-j\mathrm{479,16})Ом/км.$$

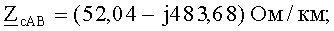
В операционной системе MATLAB система уравнений (24)-(29) в виде программного продукта помещается в файл funl(x,a), где х - массив параметров $${\underset{\_}{Z}}_A$$ , $${\underset{\_}{Z}}_B$$ , $${\underset{\_}{Z}}_C$$ , $${\underset{\_}{Z}}_{AB}$$ , $${\underset{\_}{Z}}_{BC}$$ и $${\underset{\_}{Z}}_{CA}$$ , требующие уточнения; a - массив уже определенных по изложенной ранее методике величин γ, $${\underset{\_}{Z}}_{cA}$$ , $${\underset{\_}{Z}}_{cB}$$ , $${\underset{\_}{Z}}_{cC}$$ , $${\underset{\_}{Z}}_{cAB}$$ , $${\underset{\_}{Z}}_{cBC}$$ и $${\underset{\_}{Z}}_{cCA}$$ .

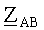
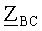
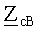
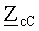
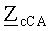
Начальные величины искомых параметров в операционной системе MATLAB задаются так:

>>х0=[0.13 0.314 0.13 0.314 0.13 0.314 0 0.157 0 0.157 0 0.157].

Ожидаемые результаты расчета имеют существенные ограничения: активные сопротивления, представленные в параметрах $${\underset{\_}{Z}}_A$$ , $${\underset{\_}{Z}}_B$$ и $${\underset{\_}{Z}}_C$$ , вещественной частью не могут быть отрицательными; а вещественная часть параметров $${\underset{\_}{Z}}_{AB},$$ $${\underset{\_}{Z}}_{BC}$$ и $${\underset{\_}{Z}}_{CA}$$ вообще отсутствует.

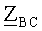
Первое ограничение реализуется в результате введения в программный продукт двух матриц:

>>А=diag ([-1 0-10-10-10-10-1 0]);

>>b=zeros (12,1).

Второе ограничение отдельно оговаривается в содержании файла funl(x,a).

Искомое решение получается после использования команды

>>[xfvar]=fmincon@fun1,x0,A,b).

В данном примере продольные параметры и взаимные сопротивления исследуемого однородного трехпроводного участка ЛЭП определяются в результате реализации описанного здесь алгоритма и оказываются равными:

$${\underset{\_}{Z}}_A=(\mathrm{0,1275}+j\mathrm{0,12712})Ом/км;$$

$${\underset{\_}{Z}}_B=(\mathrm{0,001}+j\mathrm{2,7478}\cdot {10}^{-6})Ом/км;$$

$${\underset{\_}{Z}}_{С}=(\mathrm{0,001}+j\mathrm{9,7479}\cdot {10}^{-6})Ом/км.$$

$${\underset{\_}{Z}}_{AB}=(0+j\mathrm{0,00099194})Ом/км;$$

$${\underset{\_}{Z}}_{BC}=(0-j\mathrm{2,0703}\cdot {10}^{-6})Ом/км;$$

$${\underset{\_}{Z}}_{СA}=(0-j\mathrm{0,0015})Ом/км.$$

Из полученных таким образом данных видна явная несимметрия исследуемой трехпроводной ЛЭП.

Активное сопротивление линии A (R_A=0,1275 Ом/км) несколько понизилось против ожидаемого (0,13 Ом/км). Зато активные сопротивления линий В и С снизилось почти до нуля (R_B=0,001 Ом/км; R_C=0,001 Ом/км).

Снизилось и индуктивное сопротивление линии А (Х_А=0,12712 Ом/км). Индуктивное сопротивление линий В и С снизилось практически до нуля (Х_B=2,7479·10^-6 Ом/км; Х_B=9,7479·10^-6 Ом/км). Такой результат вполне возможен, например, вследствие продольной реактивной мощности.

В таком случае собственная индуктивность линии А определится так:

$$L_A=\frac{X_A}{n\omega }=\frac{X_A}{2\pi nf}=\frac{\mathrm{0,12712}}{2\pi \cdot 1\cdot 50}=\mathrm{0,405}\cdot {10}^{-3}Гн/км$$

Индуктивность линий В и С оказывается ничтожно мала:

$$L_B=\frac{X_B}{n\omega }=\frac{X_B}{2\pi nf}=\frac{\mathrm{2,7478}\cdot {10}^{-6}}{2\pi \cdot 1\cdot 50}=9\cdot {10}^{-9}Гн/км$$

$$L_C=\frac{X_C}{n\omega }=\frac{X_C}{2\pi nf}=\frac{\mathrm{9,7479}\cdot {10}^{-6}}{2\pi \cdot 1\cdot 50}=\mathrm{3,1}\cdot {10}^{-8}Гн/км$$

Это обобщенные индуктивности с учетом возможных дополнительно включенных емкостных и иных элементов.

Полные взаимные сопротивления характеризуют электромагнитную связь между проводами и изначально считалось, что они имеют индуктивный характер. Но нередко емкостные связи между проводами перекрывают индуктивные. Так получилось между проводами В и С, С и А. С точки зрения явления взаимоиндукции эти пары проводов оказались включенными относительно друг друга встречно. Это означает, что в линии С изменилось условно положительное направление тока, что маловероятно. Целесообразнее говорить о преобладании емкостных связей или, в виду малости величин $${\underset{\_}{Z}}_{BCn}$$ и $${\underset{\_}{Z}}_{CAn},$$ с учетом 4%-й погрешности выполненных расчетов, считать их ничтожно малыми и впредь не учитывать.

Величина взаимной индуктивности между линейными проводами А и В определится по результатам выполненного расчета:

$$M_{AB}=\frac{\mathrm{Im}({\underset{\_}{Z}}_{ABn})}{2\pi nf}=\frac{\mathrm{0,00099194}}{2\pi \cdot 1\cdot 50}=\mathrm{3,157}\cdot {10}^{-6}Гн/км$$

С учетом вероятности «встречного» включения линейных проводов в исследуемой ЛЭП можно определить и взаимные индуктивности между проводами В и С, С и А:

$$M_{BC}=\frac{\mathrm{Im}({\underset{\_}{Z}}_{BCn})}{2\pi nf}=\frac{-\mathrm{2,0703}\cdot {10}^{-6}}{2\pi \cdot 1\cdot 50}=-7\cdot {10}^{-6}Гн/км$$

$$M_{CA}=\frac{\mathrm{Im}({\underset{\_}{Z}}_{CAn})}{2\pi nf}=\frac{-\mathrm{0,0015}}{2\pi \cdot 1\cdot 50}=-\mathrm{4,775}\cdot {10}^{-6}Гн/км$$

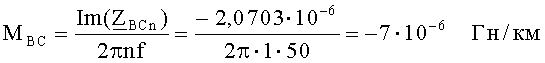
Знак «-» в численных значениях взаимных индуктивностях М_ВС и М_СА свидетельствует о «встречном» включении линейных проводов. Безусловно, это условное понятие.

Таким образом предлагается определять величины продольных параметров линейных проводов трехфазной трехпроводной ЛЭП и взаимных индуктивностей между линейными проводами этой же линии электропередачи.

Так реализуется способ определения первичных и обобщенных вторичных параметров однородного участка трехпроводной ЛЭП методом восьмиполюсника.

Источники информации

1. Способ определения текущих первичных и вторичных параметров линии электропередачи для построения ее прямой Г-образной адаптивной модели. / Д.В.Джумик, Е.И.Гольдштейн. - Патент №2334990, Россия. МКИ G01R 25/00. - Томский политехнический университет. №2007117275/28; 08.05.2007.

2. Большанин Г.А. Передача электрической энергии по однородному участку трехфазной ЛЭП трехпроводного исполнения, входящему в состав симметричной ЭЭС. /Г.А.Большанин, Л.Ю.Большанина, Е.Г.Марьясова. // Вестник Иркутского Государственного Технического Университета. 2011 - 10 (57). - C.179 - 186.

3. Костенко В.А. Волновые процессы и электрические помехи в многопроводных линиях высокого напряжения. / В.А.Костенко, Л.С.Перельман, Ю.П.Шкарин. - М.: Энергии, 1973. - 272 с.

4. Большанин Г. А. Распределение электрической энергии по участкам электроэнергетических систем. В 2-х кн. / Г.А.Большанин. - Братск: БрГУ, 2006. - 807 с.

5. Бессонов Л.А. Теоретические основы электротехники. / Л.А.Бессонов. - М.: Высшая школа, 1967. - 778 с.

6. Большанин Г.А. Использование теории восьмиполюсников и системы «МАТLАВ» при расчете результатов транспортировки электрической энергии. /Г.А.Большанин, Л.Ю.Большанина, Е.Г.Марьясова. // Системы. Методы. Технологии. - 2011. - №4(12). - С.76-83.