ОБЛАСТЬ ТЕХНИКИ
Настоящее изобретение относится к конструкции для обнаружения и/или определения местонахождения магнитного материала в области воздействия. Настоящее изобретение относится дополнительно к соответствующему способу и к компьютерной программе для управления конструкцией.
УРОВЕНЬ ТЕХНИКИ ИЗОБРЕТЕНИЯ
Конструкция такого рода известна из немецкой патентной заявки DE 10151778 A1. Важно, что в описанной в этой публикации конструкции пространственное распределение напряженности магнитного поля создается таким, что в зоне обследования формируется первая подзона, имеющая относительно низкую напряженность магнитного поля, и вторая подзона, имеющая относительно высокую напряженность магнитного поля. Положение в пространстве подзон в зоне обследования затем сдвигается так, что намагниченность частиц в зоне обследования локально изменяется. Регистрируются сигналы, которые зависят от намагниченности в зоне обследования, причем намагниченность оказывается под влиянием сдвига пространственного положения подзон, и информация относительно пространственного распределения магнитных частиц в зоне обследования извлекается из этих сигналов так, чтобы могло быть сформировано изображение зоны обследования. Такая конструкция имеет преимущество в том, что она может быть использована для исследования произвольных объектов обследования - например, человеческих тел - неразрушающим образом, и не приводя к каким-либо повреждениям, и с высоким пространственным разрешением, и близко к поверхности, и удаленно от поверхности обследуемого объекта.
Подобная конструкция и способ известны из В. Gleich и J. Weizenecker (2005), "Томографическая визуализация с использованием нелинейного отклика магнитных частиц" в Nature, vol.435, 30 June 2005, pp.1214-1217. Описанные в этой публикации конструкция и способ для визуализации магнитных частиц (MPI) используют преимущество кривой нелинейной намагниченности малых магнитных частиц.
MPI представляет собой способ для визуализации распределения магнитных наночастиц, который объединяет высокую чувствительность с возможностью быстрой динамической визуализации, что делает его перспективным для применений в медицинской визуализации. MPI применяет новый способ кодирования сигнала, основанный на динамическом смещении процесса локализованного возбуждения, и позволяет быструю объемную визуализацию. Однако в отличие от установившихся методов визуализации, таких как MRI и СТ, пока еще не подобрано простое математическое преобразование для восстановления изображения по полученным данным. Поэтому восстановление изображения MPI требует сведений о "системной функции", отесывающей отклик системы на данное пространственное распределение частиц, то есть отображения положения частицы в частотном отклике. Для решения проблемы восстановления системная функция должна быть инвертирована, что обычно требует некоторой конструкции регуляризации.
Системная функция может быть определена экспериментально измерением характеристики намагниченности точечного образца в большом числе пространственных положений, соответствующих числу пикселей или векселей изображения. Эта калибровочная процедура требует очень больших времен сбора данных и, кроме того, предоставляет системную функцию с содержанием шума. Из-за большого размера матрицы системной функции решение проблемы обратного восстановления также занимает достаточно много времени и требует большого объема машинной памяти.
СУЩНОСТЬ ИЗОБРЕТЕНИЯ
Цель настоящего изобретения заключается в предоставлении конструкции и способа для обнаружения и/или определения местонахождения магнитного материала в области воздействия, при которых требуется меньше времени для сбора данных о системной функции и/или для восстановления изображения и/или при которых требуется меньший объем памяти для сохранения данных о системной функции.
В первом объекте настоящего изобретения представлена конструкция, как определено в п.1 формулы, содержащая:
- средство выборки для создания выборочного магнитного поля, имеющего такую пространственную конфигурацию напряженности магнитного поля, что в области воздействия формируются первая подзона, имеющая низкую напряженность магнитного поля, и вторая подзона, имеющая более высокую напряженность магнитного поля,
- средство управления для изменения пространственного положения двух подзон в области воздействия посредством управляющего магнитного поля так, чтобы намагниченность магнитного материала изменилась локально,
- средство приема для получения сигналов обнаружения, причем сигналы обнаружения зависят от намагниченности в области воздействия, причем на намагниченность влияет изменение пространственного положения первой и второй подзон,
- средство сохранения для сохранения подмножества данных системной функции конструкции, причем упомянутая системная функция содержит множество данных системной функции, описывающих соотношение между пространственным положением магнитного материала и характеристикой системы для упомянутой конструкции и траектории, вдоль которой упомянутая первая подзона перемещается для сбора упомянутых данных системной функции, и
- средство восстановления для восстановления пространственного распределения магнитного материала в области воздействия по сигналам обнаружения и сохраненному подмножеству данных системной функции, используя дополнительные сведения о структуре системной функции, причем упомянутые средства восстановления приспособлены для создания сокращенного представления системной функции посредством применения преобразования Чебышева или косинусного типа вдоль пространственного измерения и решения задачи намного более разреженного восстановления, возникающей после преобразования.
В дополнительном объекте настоящего изобретения представлен соответствующий способ, как определено в п.11 формулы.
Еще в одном объекте настоящего изобретения представлена компьютерная программа, содержащая средство программного кода для того, чтобы компьютер управлял конструкцией, как заявлено в п.1 формулы, для выполнения этапов способа, как заявлено в п.11 формулы, когда упомянутая компьютерная программа выполняется на компьютере.
Предпочтительные варианты реализации изобретения определены в зависимых формулах. Следует понимать, что заявленный способ имеет подобные и/или идентичные предпочтительные варианты реализации, как и заявленное устройство, и как определено в зависимых формулах.
Настоящее изобретение основано на идее о том, что нет необходимости в получении и сохранении полной системной функции. Из теоретического понимания процесса кодирования сигнала возникло понимание структуры системной функции, что было использовано, чтобы ускорить получение системной функции и/или даже смоделировать ее части или всю системную функцию. Информация о матричной структуре также была использована, чтобы найти более компактные представления системной функции, помогая снизить требования к объему и конфигурации памяти и ускорить восстановление. Наконец, идентификация математического преобразования, ведущего к изображению из данных, может быть использована для ускорения процесса восстановления.
В соответствии с первым объектом настоящего изобретения эта общая идея используется, чтобы сократить область памяти для сохранения данных системной функции. В частности, сохраняется только подмножество данных системной функции, и только это подмножество сохраненных данных системной функции используется при восстановлении пространственного распределения магнитного материала в области воздействия, например, при восстановлении изображения по сигналам обнаружения, получаемым средством приема. Кроме того, сведения о структуре системной функции используются при восстановлении. Эти сведения могут содержать, как определено в предпочтительных вариантах реализации, простые пространственные симметрии, возникающие в частотных компонентах системной функции, представлениях пространственных зависимостей частотных компонент аналитическими функциями или информации о спектральной избыточности в пространственных компонентах. Эти сведения могут быть получены из аналитического анализа конструкции кодирования MPI или моделирования процесса кодирования, и для данной комбинации конструкции, то есть установки сканера, траектории движения первой подзоны, имеющей низкую напряженность магнитного поля (также обозначаемую как "точка, свободная от поля", FFP), и для данного магнитного материала.
Использование сведений о пространственных свойствах системной функции позволяют получить только пространственно сокращенную системную функцию, причем эти сведения используются в соответствии со вторым объектом настоящего изобретения. Тем самым может быть также ускорена калибровочная процедура.
Обычно использование сведений о спектральных свойствах системной функции позволяет сократить размер матрицы системной функции, тем самым ускоряя сбор данных, процесс обработки и восстановления.
В соответствии с предпочтительным вариантом реализации средство приема приспособлено для сбора только упомянутого подмножества данных системной функции конструкции посредством обнаружения сигналов, в то время как зонд упомянутого магнитного материала последовательно помещается во множество различных положений в упомянутой области воздействия. Этот вид сбора данных не очень отличается, в частности, относительно движения FFP через область воздействия, то есть относительно используемой траектории, от сбора сигналов от (реального) обследуемого объекта, например пациента, кроме того факта, что в соответствии с настоящим изобретением зонд не перемещается по всем положениям сетки, покрывающей область воздействия, но только по сокращенному множеству ее точек.
Много различных опций существует для положений, в которых зонд помещается для получения сигналов для сбора упомянутого подмножества данных системной функции. В соответствии с преимущественными вариантами реализации, множество положений располагается в квадранте или октанте упомянутой области воздействия или распределяется чередующимся образом по области воздействия.
Предпочтительно, средства восстановления приспособлены для первого восстановления полной системной функции по сохраненному подмножеству из множества данных системной функции и для последующего восстановления пространственного распределения магнитного материала по сигналам обнаружения, используя восстановленное множество данных полной системной функции. Полная системная функция может, после ее восстановления, также быть сохранена в средстве сохранения для использования в последующих восстановлениях.
Альтернативно, средства восстановления приспособлены для восстановления данных системной функции, которые требуются для восстановления пространственного распределения магнитного материала, но не содержатся в сохраняемом подмножестве множества данных системной функции, непрерывно, в течение восстановления пространственного распределения магнитного материала.
Хотя первый вариант реализации этих двух альтернатив имеет преимущество в том, что фактическое восстановление происходит быстрее, что особенно справедливо для последующих восстановлений, последний вариант реализации имеет преимущество потому, что требуется меньшая занимаемая область памяти.
Как рассмотрено выше, дополнительные сведения используются для восстановления полных данных системной функции (или, по меньшей мере, данных системной функции, требуемых для восстановления пространственного распределения магнитного материала). В предпочтительном варианте реализации используются пространственные симметрии, в частности пространственные зеркальные симметрии, имеющиеся в частотных компонентах системной функции. Такие зеркальные симметрии могут быть получены не только практическими измерениями, но также и из теоретических соображений, используя сведения о траектории (и ее симметрии), кривой намагниченности частиц и монтаже конструкции (и ее симметрии), в частности о ее средстве выборки, средстве управления и приемном средстве. Например, для траектории Лиссажу с частицами Ланжевена наблюдается пространственная зеркальная симметрия, которая имеет вполне определенную частотно-зависимую четность. Для случая 2D визуализации это означает, что только одна четверть полной системной функции должна быть измерена и сохранена.
В соответствии с другим вариантом реализации средство восстановления приспособлено для восстановления пространственного распределения магнитного материала в области воздействия, используя системную функцию с пониженным числом спектральных компонент, полученных из суммирования частотных компонент сохраненного подмножества данных системной функции с подобной пространственной информацией. Поскольку множественные частоты управляющего поля включены в движение свободной от поля точки, сигнал, создаваемый нелинейным откликом частиц, содержит суммы и разности этих частот. Соответственные частотные компоненты имеют одну и ту же пространственную конфигурацию и поэтому могут быть объединены без потери информации. Это приводит к уменьшенному числу строк в матрице системной функции, что означает, что только подмножество данных полной системной функции требуется и изначально сохраняется.
В соответствии с настоящим изобретением средства восстановления приспособлены для создания сокращенного представления системной функции, применяя математическое преобразование по пространственному измерению и решая задачу более разреженного восстановления, возникающую после преобразования. Тип операции преобразования основан на сведениях о функциональной форме пространственной конфигурации спектральных компонент в системной функции. Для траектории Лиссажу FFP спектральные компоненты тесно связаны с функциями Чебышева 2-го рода. Поэтому преобразование Чебышева адекватно для достижения разреженного представления матрицы системной функции и проблемы восстановления, которая сохраняет память и ускоряет восстановление. Иначе говоря, вследствие этого близкого соотношения каждая частотная компонента может быть аппроксимирована только несколькими коэффициентами соответствующего разложения. Альтернативно, может быть использовано преобразование косинусного типа.
Предпочтительно, упомянутое сокращенное представление системной функции создается преобразованием полной системной функции. В соответствии с практическим воплощением этого варианта реализации первыми получаются данные полной системной функции, и из них определяются коэффициенты сокращенного представления, например, функциональное описание с использованием полиномов. Это экономит область памяти и усилия при восстановлении. В соответствии с другим практическим воплощением этого варианта реализации первым получается только подмножество функциональных данных, из которого полные данные системной функции воспроизводятся для определения функционального описания. Альтернативно, функциональное описание, например полиномиальное, может быть приспособлено к полученному подмножеству, как рассматривается ниже.
Еще в одном варианте реализации средство приема приспособлено для непосредственного измерения упомянутого сокращенного представления системной функции в выбранных точках области воздействия, и средства восстановления приспособлены для определения коэффициентов упомянутых аналитических функций, которые используются для описания пространственной зависимости из упомянутого измеренного сокращенного представления системной функции. Точки подмножества выбираются так, что коэффициенты функционального описания могут быть определены по возможности просто.
Следует отметить, что изобретение реализуется не только в заявленных конструкциях, способах и компьютерных программах, но также и в средстве обработки, которое может быть реализовано в аппаратных средствах, программном обеспечении или их комбинации, которые действуют как средство восстановления в конструкции в соответствии с настоящим изобретением. Таким образом, изобретение также относится к средству обработки для восстановления пространственного распределения магнитного материала в области воздействия по сигналам обнаружения и сохраняемому подмножеству данных системной функции, используя дополнительные сведения о структуре системной функции. Дополнительно, настоящее изобретение относится также к соответствующему способу обработки и соответственной компьютерной программе для выполнения упомянутого способа.
КРАТКОЕ ОПИСАНИЕ ЧЕРТЕЖЕЙ
Эти и другие объекты изобретения будут очевидны из рассмотрения описываемого ниже варианта(ов) реализации. На нижеследующих чертежах:
Фиг.1 изображает конструкцию в соответствии с настоящим изобретением,
Фиг.2 - пример конфигурации линий поля, произведенной конструкцией в соответствии с настоящим изобретением,
Фиг.3 - увеличенный вид магнитной частицы, присутствующей в области воздействия,
Фиг.4а и 4b - характеристики намагниченности таких частиц,
Фиг.5 - блок-конструкция аппарата в соответствии с настоящим изобретением,
Фиг.6 - детектируемый временной сигнал s(t) и его спектр Sn,
Фиг.7 - характеристика M(t) намагниченности частиц, получаемый временной сигнал s(t), и значение спектральных компонент Sn для различных управляющих полей и кривых намагниченности частиц,
фиг.8 - диаграммы, иллюстрирующие соотношение между идеальным откликом частиц и смещением выборочного поля,
фиг.9 - диаграммы, иллюстрирующие пространственную зависимость спектральных компонент сигнала для гармонического управляющего поля в комбинации с постоянным градиентом выборочного поля,
фиг.10 - диаграммы, иллюстрирующие производную намагниченности идеальных частиц относительно компоненты поля Hz,
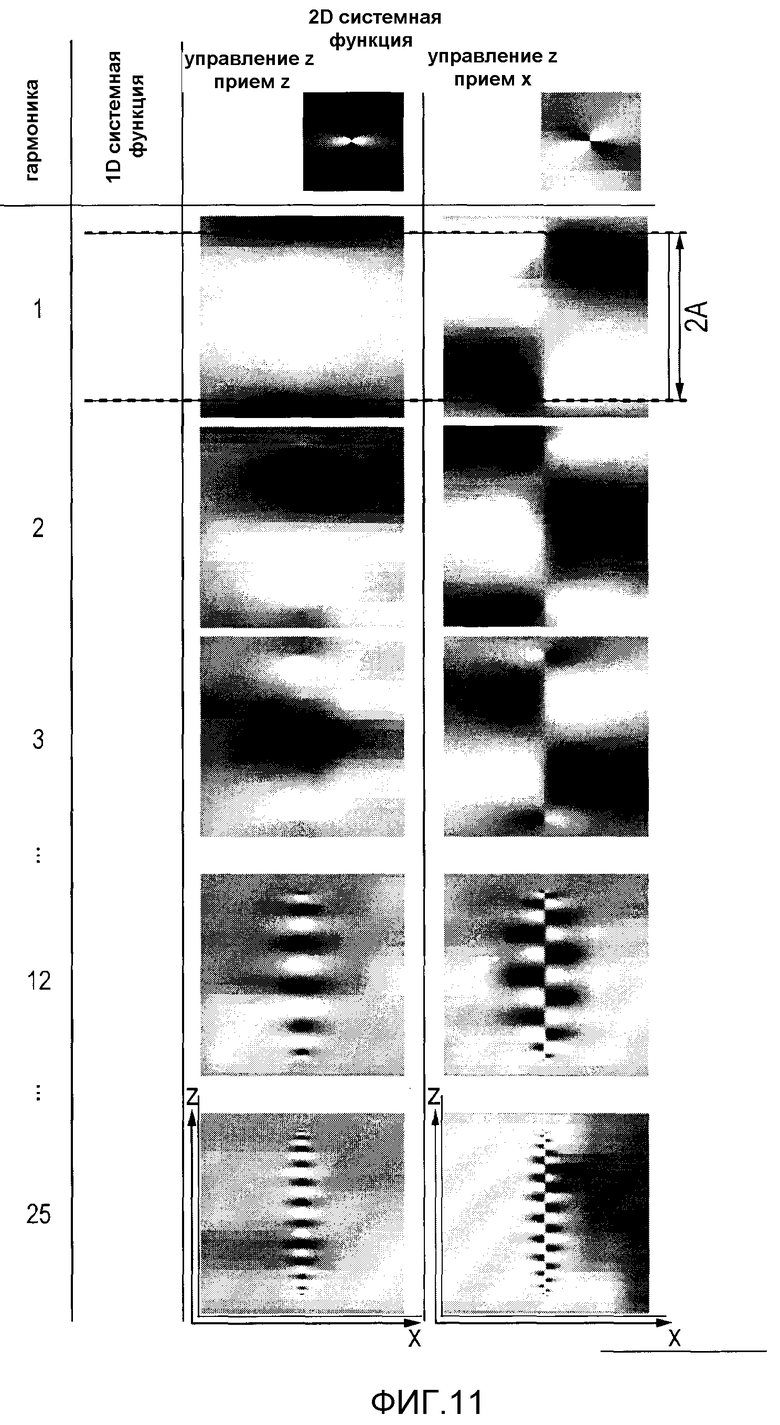
фиг.11 - диаграммы, иллюстрирующие системную функцию идеальных частиц при различных гармониках для 1D движения FFP по центральной линии в z направлении,
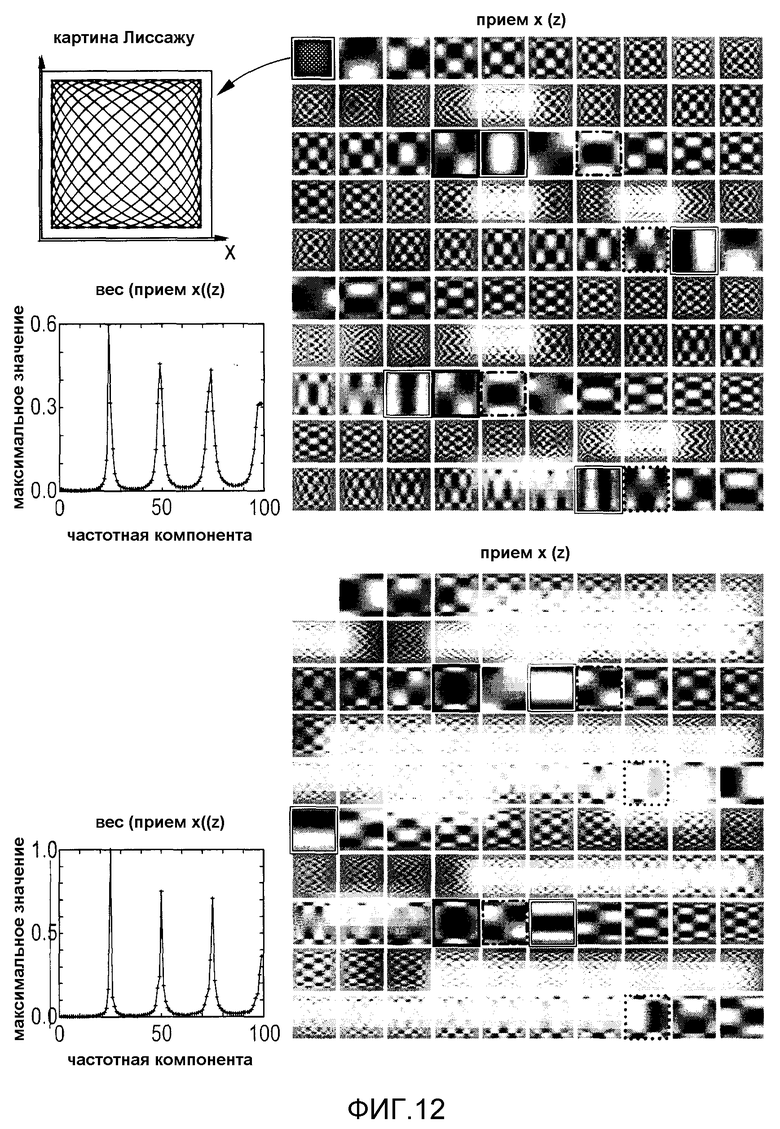
фиг.12 - диаграммы, иллюстрирующие последовательные частотные компоненты системной функции идеальных частиц для 2D Лиссажу FFP движения с отношением частот x/z, составляющим 24/25,
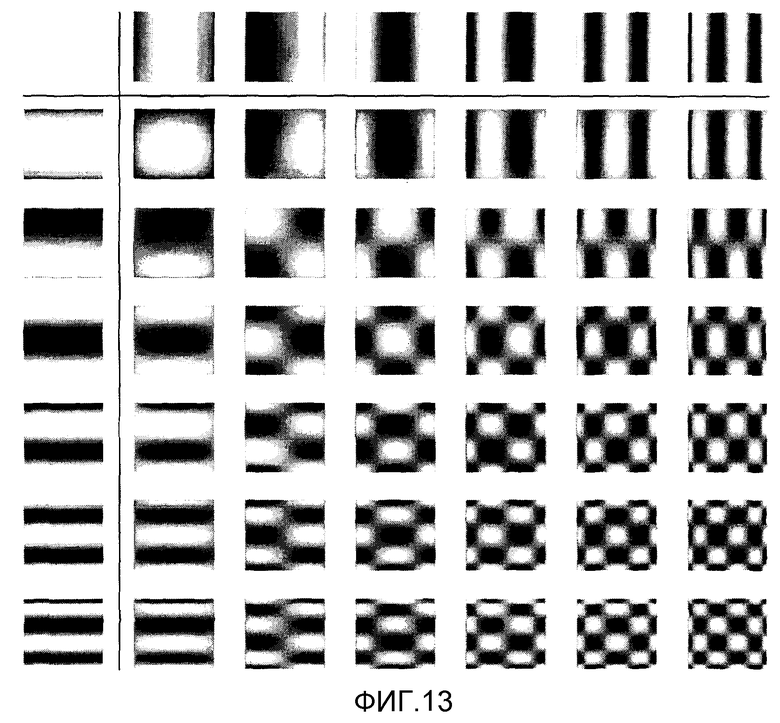
фиг.13 - графическая таблица 2D функций Чебышева,
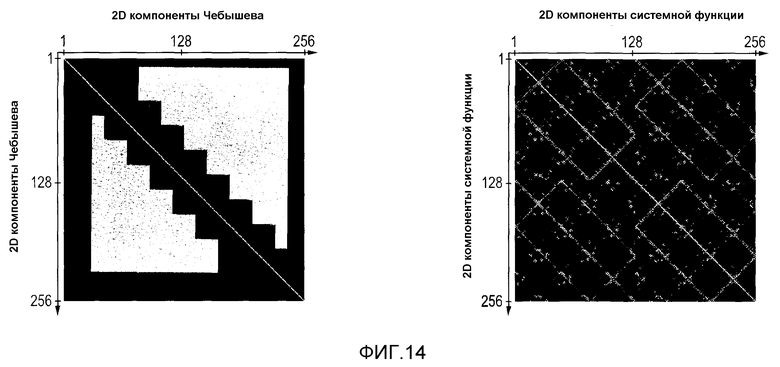
фиг.14 - графики ортогональности для первых 256 компонент базисного набора,
фиг.15 - образец изображения 64×64 и восстановление из разложения на компоненты Чебышева и системной функции, и
фиг.16-19 - использование матрицы системной функции или ее частей для восстановления в соответствии с известным способом и в соответствии с вариантами реализации изобретения.
ПОДРОБНОЕ ОПИСАНИЕ ИЗОБРЕТЕНИЯ
На фиг.1 показан произвольный объект, исследуемый посредством конструкции 10 в соответствии с настоящим изобретением. Номер 350 на фиг.1 обозначает объект, в данном случае человек или животное, размещаемые на столе для пациента, для которого показана только верхняя часть. До применения способа в соответствии с настоящим изобретением магнитные частицы 100 (не показаны на фиг.1) размещались в области воздействия 300 конструкции 10 по изобретению. В частности, перед терапевтической и/или диагностической обработкой, например, опухоли, магнитные частицы 100 помещаются в область воздействия 300, например, посредством жидкости (не показана), содержащей магнитные частицы 100, которая вводится в тело пациента 350.
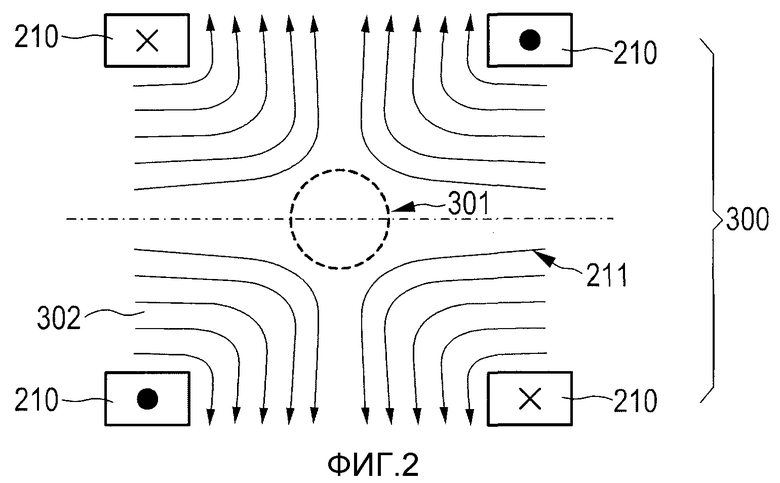
Как пример варианта реализации настоящего изобретения, на фиг.2 показана конструкция 10, содержащая множество катушек, формирующих средство 210 выборки, диапазон которого определяет область воздействия 300, которая также называется областью обработки 300. Например, средство 210 выборки, размещено выше и ниже пациента 350 или выше и ниже вершины стола. Например, средство 210 выборки содержит первую пару катушек 210′, 210′′, каждая из которых содержит две идентичных обмотки 210′ и 210′′, которые расположены коаксиально выше и ниже пациента 350 и по которым протекают равные токи, но в противоположных направлениях. Первая пара катушек 210′, 210′′, обе вместе, далее называются средством 210 выборки. Предпочтительно, в этом случае используются постоянные токи. Средство 210 выборки создает выборочное магнитное поле 211, которое в целом является градиентным магнитным полем, представленным на фиг.2 полевыми линиями. Оно имеет по существу постоянный градиент в направлении (например, вертикальном) оси пары катушки средства 210 выборки и достигает нулевого значения в точке на этой оси. Начиная с этой, свободной от поля точки (не показанной отдельно на фиг.2) напряженность выборочного магнитного поля 211 увеличивается во всех трех пространственных направлениях при увеличении расстояния от точки без поля. В первой подзоне 301, или области 301, которая обозначена пунктирной линией вокруг точки без поля, напряженность настолько мала, что намагниченность частиц 100, присутствующих в этой первой подзоне 301, не насыщается, тогда как намагниченность частиц 100, присутствующих во второй подзоне 302 (вне области 301), отвечает состоянию насыщения. Точка без поля, или первая подзона 301 области воздействия 300, предпочтительно является пространственно когерентной зоной; она может также быть точечной зоной, или линией, или плоской зоной. Во второй подзоне 302 (то есть в остающейся части области воздействия 300 с внешней стороны первой подзоны 301) напряженность магнитного поля достаточно велика, чтобы сохранить частицы 100 в состоянии насыщения. Изменяя положения двух подзон 301, 302 в пределах области воздействия 300, намагниченность (полная) в области воздействия 300 изменяется. Измеряя намагниченность в области воздействия 300, или физические параметры, связанные с намагниченностью, может быть получена информация о пространственном распределении магнитных частиц в области воздействия. Для изменения относительного пространственного положения двух подзон 301, 302 в области воздействия 300 дополнительное магнитное поле, так называемое магнитное поле 221 управления, накладывается на выборочное поле 211 в области воздействия 300 или, по меньшей мере, в части области воздействия 300.
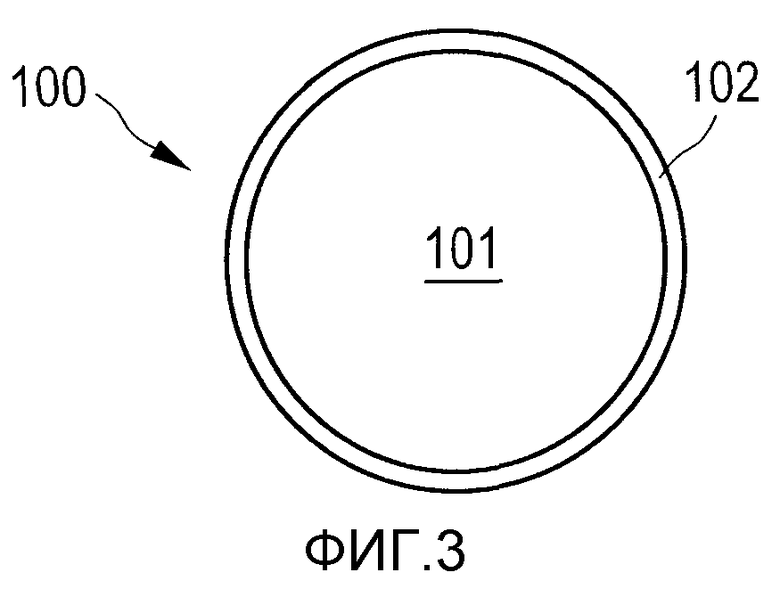
На фиг.3 показан пример магнитной частицы 100 такого рода, как используется вместе с конструкцией 10 настоящего изобретения. Она содержит, например, сферическую подложку 101, например, из стекла, на которой имеется мягкомагнитный слой 102 толщиной, например, 5 нм, и который состоит, например, из железоникелевого сплава (например, Пермаллоя). Этот слой может быть покрыт, например, покровным слоем 103, который защищает частицу 100 от химически и/или физически агрессивных сред, например кислот. Напряженность выборочного магнитного поля 211, требуемая для насыщения намагниченности таких частиц 100, зависит из различных параметров, например диаметра частиц 100, используемого магнитного материала для магнитного слоя 102, и от других параметров.
В случае, например, диаметра 10 мкм требуется магнитное поле приблизительно 800 А/м (соответствующее приблизительно плотности потока 1 мТ), тогда как в случае диаметра 100 мкм достаточно магнитного поля напряженностью 80 А/м. Еще меньшие значения получаются, когда выбирается покрытие 102 из материала, имеющего более низкую насыщенную намагниченность, или когда толщина слоя 102 уменьшена.
Для дополнительных особенностей предпочтительных магнитных частиц 100 соответствующие части патента DE 10151778, тем самым, включены здесь посредством ссылки, особенно параграфы 16-20 и параграфы 57-61 из патента ЕР 1304542 А2, заявляя приоритет относительно патента DE 10151778.
Размер первой подзоны 301 зависит, с одной стороны, от градиента напряженности выборочного магнитного поля 211 и, с другой стороны, от напряженности магнитного поля, требуемого для насыщения. Для достаточной насыщенности магнитных частиц 100 при напряженности магнитного поля 80 А/м и градиенте (в данном направлении пространства) напряженности выборочного магнитного поля 211, составляющем 160·103 А/м2, первая подзона 301, в которой намагниченность частиц 100 не насыщается, имеет размеры приблизительно 1 мм (в данном направлении пространства).
Когда дополнительное магнитное поле, далее называемое управляющим магнитным полем 221, накладывается на выборочное магнитное поле 210 (или градиентное магнитное поле 210) в области воздействия 300, первая подзона 301 сдвигается относительно второй подзоны 302 в направлении этого управляющего магнитного поля 221; степень этого сдвига увеличивается при увеличении напряженности управляющего магнитного поля 221. Когда наложенное управляющее магнитное поле 221 является переменным полем, положение первой подзоны 301 изменяется соответственно во времени и в пространстве. Выгодно принять или продетектировать сигналы от магнитных частиц 100, расположенных в первой подзоне 301, в другом диапазоне частот (сдвинутом к более высоким частотам), нежели диапазон частот изменения управляющего магнитного поля 221. Это возможно, поскольку частотные компоненты высших гармоник частоты управляющего магнитного поля 221 возникают вследствие изменения намагниченности магнитных частиц 100 в области воздействия 300 в результате нелинейности характеристик намагниченности.
Для создания этих магнитных управляющих полей 221 для любого данного направления в пространстве предоставляются три дополнительных пары катушек, а именно вторая пара 220′ катушек, третья пара 220′′ катушек и четвертая пара 220′′′ катушек, которые вместе далее называются средством 220 управления. Например, вторая пара 220′ катушек создает компоненту управляющего магнитного поля 221, которая ориентирована в направлении оси катушки первой пары 210′, 210′′ катушек, или средства 210 выборки, то есть, например, вертикально. С этой целью по обмоткам второй пары 220′ катушек протекают одинаковые токи в одном и том же направлении. Эффект, который может быть достигнут посредством второй пары катушки 220′, может быть в принципе также достигнут суперпозицией токов в том же самом направлении с противоположными, равными токами в первой паре 210′, 210′′ катушек так, чтобы ток уменьшался в одной катушке и увеличивался в другой катушке. Однако может быть выгодно, и особенно с целью интерпретации сигнала с большим отношением сигнала к шуму, когда постоянное во времени (или квазипостоянное) выборочное поле 211 (также называемое градиентным магнитным полем) и переменное во времени вертикальное управляющее магнитное поле создаются отдельными парами катушек средства 210 выборки и средства 220 управления.
Две дополнительные пары 220′′, 220′′′ катушек предоставляются для создания компонент управляющего магнитного поля 221, которые ориентированы в другом направлении в пространстве, например, горизонтально в продольном направлении области воздействия 300 (или пациента 350) и в перпендикулярном к нему направлении. Если бы третья и четвертая пары 220′′, 220′′′ катушек, типа катушек Гельмгольца (подобно парам катушек для средства 210 выборки и средства 220 управления), использовались с этой целью, то эти пары катушек должны были быть размещены слева и справа от области обработки, или спереди и позади этой области, соответственно. Это могло бы влиять на доступность области воздействия 300, или области обработки 300. Поэтому третья и/или четвертая пары магнитных катушек, или катушки 220′′, 220′′′, также размещаются выше и ниже области воздействия 300 и поэтому конфигурация их обмоток должна отличаться от таковой для второй пары к 220′ катушек. Катушки этого вида хорошо известны в магниторезонансных аппаратах с открытыми магнитами (открытое MRI), в которых пара радиочастотных (RF) катушек располагается выше и ниже области обработки, причем упомянутая пара RF катушек может создавать горизонтальное переменное магнитное поле. Поэтому конструкция таких катушек не нуждается в дополнительных пояснениях в данном случае.
Конструкция 10 в соответствии с настоящим изобретением дополнительно содержит средства 230 приема, которые только конструкциятично показаны на фиг.1. Средство 230 приема обычно содержит катушки, которые способны детектировать сигналы, индуцированные конфигурацией намагниченности магнитных частиц 100 в области воздействия 300. Катушки этого вида хорошо известны в магниторезонансных аппаратах, в которых, например, пара радиочастотных (RF) катушек располагается вокруг области воздействия 300, чтобы иметь настолько большое отношение сигнала к шуму, насколько это возможно. Поэтому конструкция таких катушек не нуждается в дополнительных пояснениях в данном случае.
В альтернативном варианте реализации для показанного на фиг.1 средства 210 выборки постоянные магниты (не показаны) могут быть использованы для создания градиентного выборочного магнитного поля 211. В пространстве между двумя полюсами таких (противоположных) постоянных магнитов (не показаны) формируется магнитное поле, которое подобно таковому на фиг.2, то есть когда противоположные полюса имеют одинаковую полярность. В другом альтернативном варианте реализации конструкции в соответствии с настоящим изобретением средство 210 выборки содержит и, по меньшей мере, один постоянный магнит, и, по меньшей мере, одну катушку 210′, 210′′, как изображено на фиг.2.
Частотные диапазоны, обычно используемые для или в различных компонентах средства 210 выборки, средства 220 управления и средства 230 приема примерно следующие: магнитное поле, создаваемое средством 210 выборки, или вовсе не изменяется во времени, или изменение сравнительно медленное, предпочтительно приблизительно от 1 Гц и приблизительно до 100 Гц. Магнитное поле, создаваемое средством 220 управления, изменяется предпочтительно приблизительно от 25 кГц и приблизительно до 100 кГц. Изменения магнитного поля, к которому должно быть чувствительно средство приема, находится предпочтительно в частотном диапазоне приблизительно от 50 кГц и приблизительно до 10 МГц.
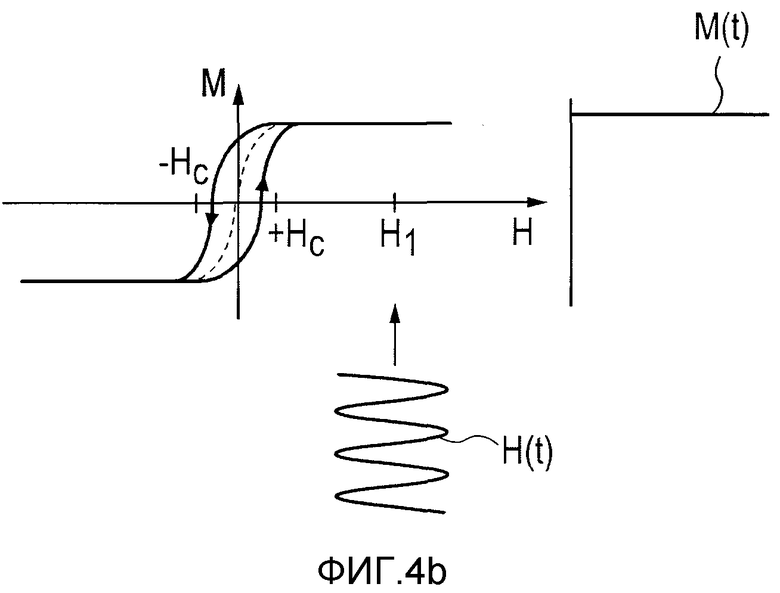
На фиг.4а и 4b показаны характеристики намагниченности, то есть изменение намагниченности М частицы 100 (не показана на фиг.4а и 4b) как функция напряженности Н поля в местоположении этой частицы 100, в дисперсной системе таких частиц. Видно, что намагниченность М не изменяется при напряженности поля более +Нс и при напряженности поля менее -Нс, что означает достижение насыщенной намагниченности. Намагниченность М не насыщается между значениями +Нс и -Нс.
На фиг.4а показано действие синусоидального магнитного поля H(t) в местоположении частицы 100, где абсолютные значения получающегося синусоидального магнитного поля H(t) (то есть "фиксируемые частицей 100") оказываются ниже напряженности магнитного поля, требуемого для магнитного насыщения частицы 100, то есть в случае, когда дополнительное магнитное поле не активно. Намагниченность частицы 100, или частиц 100, в этих условиях изменяется в пределах значений своего насыщения с частотой изменения магнитного поля H(t). Результирующее изменение намагниченности во времени отмечено обозначением M(t) справа на фиг.4а. Видно, что намагниченность также изменяется периодически и что намагниченность такой частицы периодически полностью обращается.
Пунктирная часть линии в центре кривой обозначает приблизительное среднее изменение намагниченности M(t) как функции напряженности синусоидального магнитного поля H(t). Как отклонение от этой центральной линии намагниченность простирается несколько вправо, когда магнитное поле Н увеличивается от -Нс до +Нс, и несколько влево, когда магнитное поле Н уменьшается от +Нс до -Нс. Этот известный эффект называется эффектом магнитного гистерезиса, который лежит в основе механизма для производства тепла. Площадь петли гистерезиса, которая сформирована между линиями кривой, форма и размер которой зависят от материала, является мерой для производства тепла при изменении намагниченности.
На фиг.4b показано действие синусоидального магнитного поля H(t), на которое наложено статическое магнитное поле H1. Поскольку намагниченность находится в насыщенном состоянии, она фактически не подвержена влиянию синусоидального магнитного поля H(t). Намагниченность M(t) остается постоянной во времени при этой площади. Следовательно, магнитное поле H(t) не вызывает изменения состояния намагниченности.
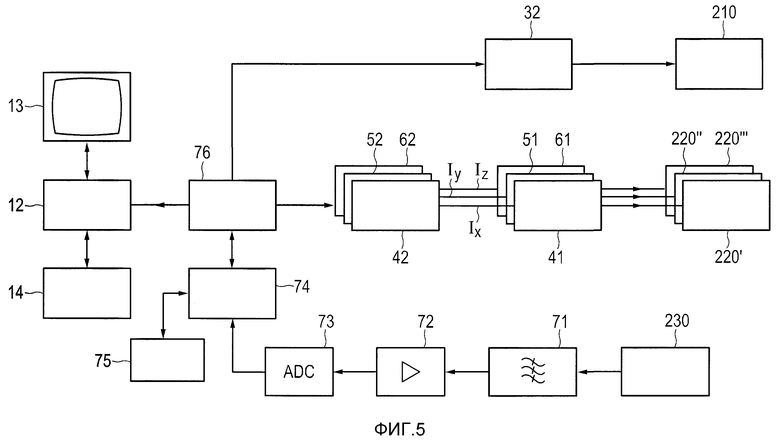
На фиг.5 показана блок-конструкция аппарата 10, показанного на фиг.1. Пара 210′, 210′′ катушек показана конструкциятично на фиг.5 и имеет для ясности обозначение 210. Пара (первое магнитное средство) 210 катушек питается постоянным током от управляемого источника 32 тока, причем упомянутый источник тока управляется блоком 76 управления. Блок 76 управления соединен с компьютером 12, который связан с монитором 13 для отображения распределения магнитных частиц в обследуемой области и с блоком 14 ввода, например с клавиатурой 14.
Пары (второе магнитное средство) 220′, 220′′, 220′′′ катушек соединены с усилителями 41, 51, 61 тока, от которого они получают питающий ток. Усилители 41, 51, 61 тока, в свою очередь, в каждом случае соединяются с источниками 42, 52, 62, переменного тока, который задает временное изменение усиливаемых токов Ix, Iy, Iz. Источники 42, 52, 62 переменного тока управляются блоком 76 управления.
Приемная катушка (средство приема) 230 также показана конструкциятично на фиг.5. Сигналы, индуцированные в приемной катушке 230, подаются на блок 71 фильтрации, посредством которого сигналы фильтруются. Цель этой фильтрации состоит в том, чтобы отделить измеренные значения, которые вызваны намагниченностью в обследуемой области, которая подвержена влиянию изменения положения этих двух частичных областей (301, 302), от других, мешающих сигналов. С этой целью блок 71 фильтрации может быть сконструирован, например, так, чтобы сигналы, которые имеют временные частоты, меньшие, чем временные частоты, на которых работают пары 220′, 220′′, 220′′′ катушек, или меньшие, чем вдвое этих временных частот, не проходили бы блок 71 фильтрации. Сигналы затем передаются через блок 72 усилителя на аналого-цифровой преобразователь 73 (ADC). Оцифрованные сигналы, произведенные аналого-цифровым преобразователем 73, подаются на блок 74 обработки изображения (также называемый средством восстановления), который восстанавливает пространственное распределение магнитных частиц из этих сигналов и соответственного положения, которое предполагалось для первой частичной области 301 первого магнитного поля в обследуемой области в течение приема соответственного сигнала и которое блок 74 обработки изображения получает из блока 76 управления. Восстановленное пространственное распределение магнитных частиц, наконец, передается через блок 76 управления на компьютер 12, который отображает его на мониторе 13.
Аппарат содержит также средство 75 сохранения, например жесткий диск или полупроводниковую память, связанную с блоком 74 обработки изображения, для сохранения получаемых сигналов обнаружения и данных системной функции аппарата 10. Средства 75 сохранения предоставляются для сохранения подмножества данных системной функции конструкции. Средства 74 восстановления (блок 74 обработки изображения) предоставляются для восстановления пространственного распределения магнитного материала 100 в области воздействия 300 по сигналам обнаружения и сохраненному подмножеству данных системной функции, используя дополнительные сведения о структуре системной функции.
Как рассмотрено выше, MPI использует новый способ кодирования сигнала, основанный на динамическом смещении процесса локализованного возбуждения, и позволяет быструю объемную визуализацию. Однако в отличие от установленных методов визуализации, подобных MRI и СТ, до сих пор не было простого математического преобразования для восстановления изображения из получаемых данных. Поэтому восстановление изображения MPI требует сведений о "системной функции", описывающей отклик системы для данного пространственного распределения частиц, то есть отображение положения частицы на частотной характеристике. Чтобы решить задачу восстановления, системная функция должна быть инвертирована, обычно при некоторой конструкции регуляризации.
До настоящего времени, системная функция определялась экспериментально измерением характеристики намагниченности точечного образца при большом числе пространственных положений, соответствующих числу пикселей или векселей изображения. Эта калибровочная процедура требует очень больших времен сбора данных и, кроме того, предоставляет системную функцию, которая содержит и шум. Из-за большого размера матрицы системной функции решение задачи обратного восстановления также занимает много времени и требует большого объема машинной памяти.
Из теоретического понимания процесса кодирования сигнала можно ожидать и лучшего понимания структуры системной функции. Это понимание может быть использовано для ускорения получения системной функции или даже моделирования частей, или всей системной функции. Информация о матричной структуре может, кроме того, помочь в нахождении более компактного представления системной функции, помогая снизить требования к объему и конфигурации памяти и ускорить восстановление. Наконец, идентификация математического преобразования, переводящего данные в изображение, могла бы существенно упростить процесс восстановления.
Далее рассматривается получение сигнала. Основной принцип получения сигнала в MPI заключается в нелинейном отклике намагниченности М(Н) ферромагнитных частиц на приложенное магнитное поле Н. Осциллирующее управляющее поле HD(t) достаточной амплитуды приводит к такой характеристике M(t) намагниченности частиц, которая имеет отличающийся спектр высших гармоник, нежели управляющее поле. Если, например, используется гармоническое управляющее поле, спектр управляющего поля содержит только основную частоту, тогда как отклик частиц содержит также частоты, кратные основной частоте. Информация, содержащаяся в этих высших гармониках, используется для MPI. Экспериментально, зависящее от времени изменение в намагниченности частиц измеряется посредством измерения напряжения, индуцированного в приемных катушках. Предполагая единственную приемную катушку с чувствительностью Sr(r), изменяющаяся намагниченность индуцирует напряжение

в соответствии с законом Фарадея. Причем µо - магнитная проницаемость вакуума. Чувствительность приемной катушки Sr(r)=Hr(r)/I0 понимается как поле Hr(r), которое катушка произведет при питании единичным током I0. Далее, чувствительность приемной катушки аппроксимируется, чтобы быть однородной по обследуемой области, то есть величина Sr(r) постоянна. Если Mx(r,t) представляет собой компоненту намагниченности, зафиксированную приемной катушкой в направлении х, то обнаруживаемый сигнал может быть записан как

Теперь рассмотрим сигнал s(r,t), создаваемый точечным распределением частиц. Интегрирование по объему может быть удалено, и намагниченность Mx(r,t) частиц определяется локальным полем H(r,t). В данном случае предполагается, что поле имеет только одну пространственную компоненту Hx(r,t), которая ориентирована в направлении приемной катушки. Сигнал (показанный на фиг.6а) может тогда быть записан как
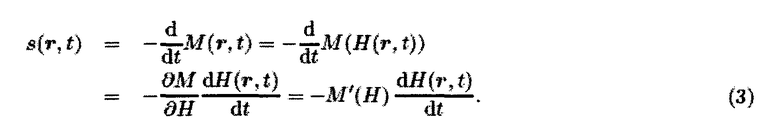
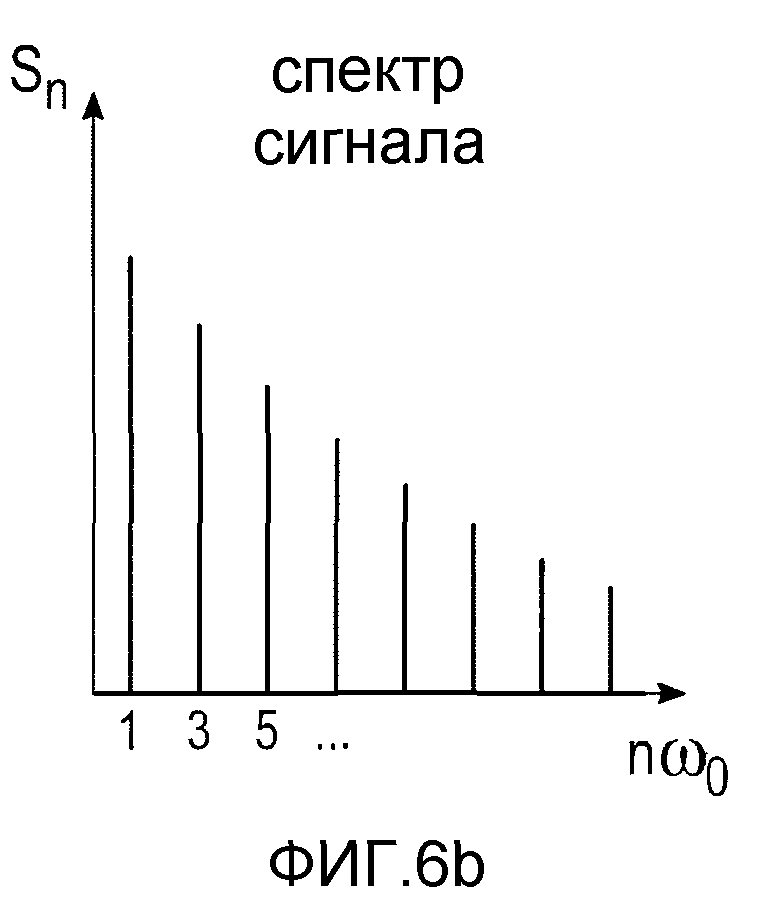
Поскольку это уравнение справедливо для всех ориентаций, когда поле ориентировано в направлении необходимой компоненты намагниченности, индекс х был опущен. Уравнение (3) показывает, что большой сигнал является следствием комбинации крутой кривой намагниченности с быстрыми изменениями поля. Фурье-разложение периодического сигнала s(t), создаваемого приложением однородного управляющего поля Н(r,t)=HD(t), приводит к такому спектру сигнала Sn, как показан на фиг.6b. Интенсивность и вес высших гармоник в спектре относятся к форме кривой намагниченности М(Н) и к форме колебаний и амплитуде управляющего поля HD(t). Чтобы показать их влияние на спектр, ряд представительных случаев показан на фиг.7.
Ступенчатая функция относится к непосредственному отклику частиц и создает спектр, богатый высшими гармониками. Спектральные компоненты имеют постоянную величину для нечетных кратных гармоник частоты управления. Четные гармоники отсутствуют вследствие синусоидальной формы временного сигнала s(t). Ступенчатая функция соответствует идеальному отклику частиц и отображает предельный случай для достижимого веса высших гармоник. Для этой кривой намагниченности треугольное и синусоидальное управляющие поля приводят к одинаковому результату.
Если отклик частиц на управляющее поле замедляется введением линейных пределов на кривой намагниченности, относительный вес высших гармоник уменьшается. Тем самым, гармоническое управляющее поле оказывается лучше, чем треугольное возбуждение, поскольку оно быстрее охватывает линейные пределы.
Последняя строка на фиг.7 показывает более реалистичную намагниченность частицы, задаваемую функцией Ланжевена

где ξ - отношение магнитной энергии частиц с магнитным моментом m во внешнем поле Н к тепловой энергии:

Более высокий магнитный момент приводит к более крутой кривой намагниченности и создает больше высших гармоник для данной амплитуды управляющего поля. Альтернативно, высшие гармоники могут быть образованы из пологой кривой, используя более быстрые изменения поля, например, индуцированные большей амплитудой управляющего поля. Следует отметить, что MPI использует ферромагнитные частицы, чтобы получить достаточно крутую кривую намагниченности. Для низких концентраций, однако, можно пренебречь их взаимными взаимовоздействиями, и они могут рассматриваться как газ парамагнитных частиц с чрезвычайно большим магнитным моментом - явление, известное также как "суперпарамагнетизм".
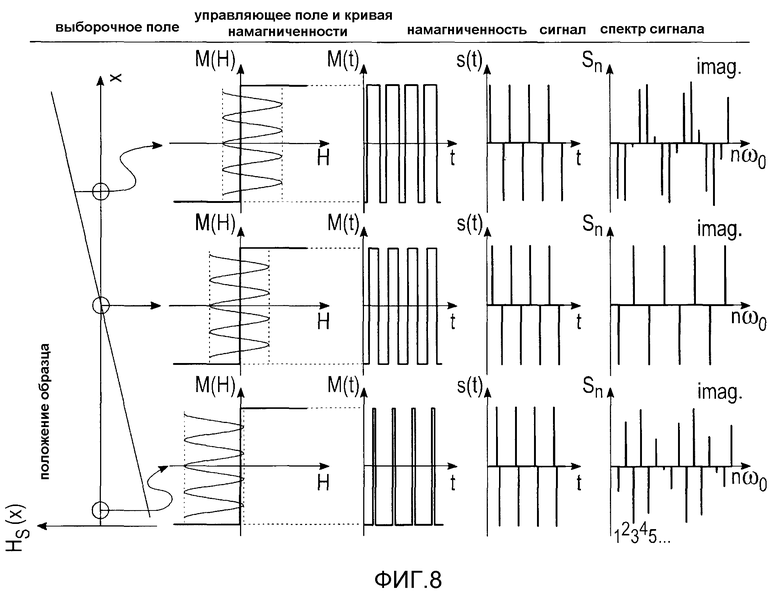
Далее рассматривается 1D пространственное кодирование. Чтобы закодировать пространственную информацию в сигнале, вводится статическое магнитное градиентное поле Hs(r), также называемое выборочным полем. Для 1D кодирования выборочное поле имеет ненулевой градиент только в направлении х, Gx=dHs/dx. Если градиент является ненулевым по полному FOV, выборочное поле может только быть нулем в единственной точке, "свободная от поля точка". В областях, далеких от FFP, намагниченность частиц приводится в насыщение выборочным полем.
Приложение пространственно однородного и периодического во времени управляющего поля HD(t), в дополнение к выборочному полю Hs(r), соответствует периодическому смещению FFP в направлении градиента. Частицы подвергаются действию локального поля

Знак "минус" был выбран, чтобы сделать последующие вычисления более удобными. Поскольку FFP проходит по каждому пространственному положению х в различные моменты времени, каждое положение может быть идентифицировано своим характерным спектральным откликом.
Далее подробно рассматриваются гармоническое управляющее поле и идеальные частицы. На фиг.8 показаны спектры в трех различных пространственных положениях, образованных идеальными частицами, подвергнутыми действию выборочного поля Hs с постоянным градиентом напряженности G и гармонического управляющего поля HD с частотой ωо и амплитудой А. Для n-ой гармоники, соответствующей n-ой компоненте разложения в ряд Фурье, находим следующую зависимость от положения х частицы:
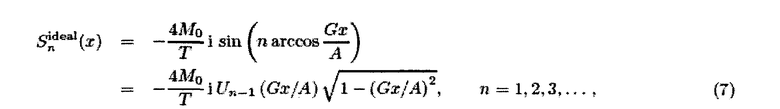
где Un(x) отображает полиномы Чебышева второго рода. Функции определены в пределах A/G<x<A/G. Косинусное управляющее поле использовано вместо синусного управляющего поля, чтобы получить более простое выражение. Пространственная зависимость для первых гармоник приведена в левой части графика на фиг.9. Видно увеличение числа колебаний с увеличением частотных компонент n. Это относится к тому факту, что полиномы Чебышева формируют полный ортогональный базисный набор так, что любое распределение С(х) частиц может быть разложено по этим функциям. Последовательные частотные компоненты имеют переменную пространственную четность относительно центра FOV (четная/нечетная).
Величина Sn(х) может рассматриваться как карта чувствительности, описывающая пространственный профиль чувствительности каждой частотной компоненты n. В эксперименте MPI распределение С(х) частиц образует спектральные компоненты сигнала

Таким образом, Sn(x) отображает системную функцию. Системная функция не только описывает пространственную зависимость сигнала, но также содержит и информацию о кривой намагниченности частиц, и о системных параметрах (например, об амплитуде А управляющего поля и частоте ω=2п/Т, о градиенте G выборочного поля).
Используя уравнение (7), спектральные компоненты (уравнение (8)) сигнала для идеальных частиц могут быть записаны как
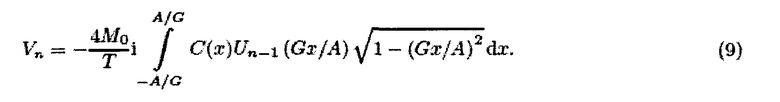
В этом обозначении Vn соответствуют коэффициентам ряда Чебышева. Из этого следует, что концентрация частиц может быть восстановлена выполнением преобразования Чебышева измеренных Vn, то есть оценивая ряд Чебышева
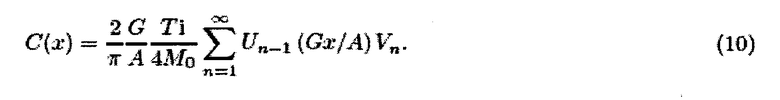
Следовательно, для идеальных частиц под влиянием гармонического управляющего поля и постоянного градиента выборочного поля восстановление пространственного распределения частиц просто соответствует вычислению суммы по измеренным гармоникам Vn, взвешенным с полиномами Чебышева второго рода. В выражениях системной функции 
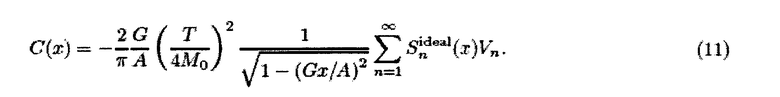
Далее рассматриваются особенности гармонического управляющего поля и частицы Ланжевена. Для более реалистичных частиц системная функция дается пространственной сверткой между производной кривой намагниченности, M′(Hs), и компонентами Чебышева:
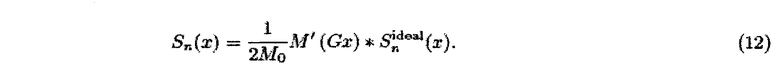
В зависимости от крутизны М(Н) функция Sn(x) будет размытой версией 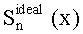
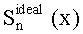
В процессе измерения, в соответствии с уравнением (8), FOV теперь относится к пределам, где функции Sn(х) имеют ненулевые значения. Достаточно крутая кривая намагниченности может предоставить ограничение для области, не намного большей, чем пределы, покрываемые FFP, то есть -A/G<x<A/G.
Поскольку компоненты системной функции не могут быть более острыми, чем ядро свертки, эксперимент MPI с частицами Ланжевена будет идти до пределов разрешения, коррелирующих с шириной М′(х). Однако, если кривая намагниченности известна, обращение свертки ядра М′(х) из изображения может быть использовано для восстановления полного разрешения. Поскольку производная кривой намагниченности представляет собой симметричную функцию, М′(х)=М′(-х), можно использовать уравнение (12), чтобы показать справедливость следующего
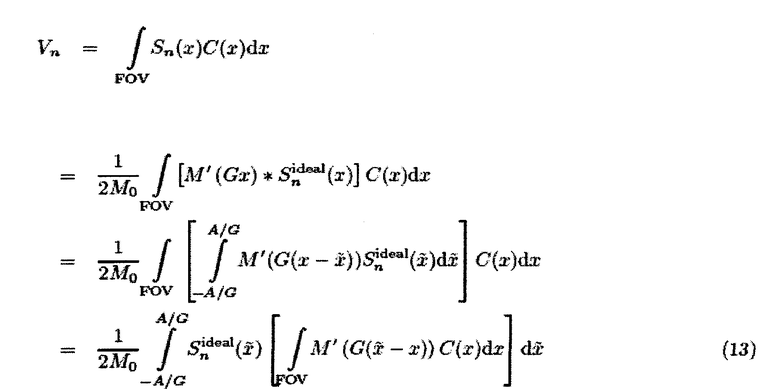

где С(x) соответствует выражению в квадратных скобках в уравнении (13). Поскольку уравнение (14) соответствует уравнению (9), восстановление для гармонического управляющего поля дается уравнением (11), то есть
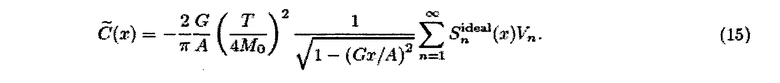
Это означает, что в интервале, где системная функция 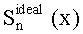

Таким образом, точное распределение С(х) концентрации может затем быть получено обращением свертки ядра М′(х) от С(х). Однако, как рассмотрено выше, восстановление с использованием уравнения (15) дает только С(х) на интервале -A/G<x<A/G, который покрывается движением FFP. Если концентрация частиц превышает эти пределы, обращение свертки требует дополнительных сведений о концентрации вне краев диапазона FFP.
С другой стороны, обращение свертки не обязательно. При условии, что кривая намагниченности частиц М(Н) является достаточно крутой, модифицированное распределение С(х) концентрации уже может удовлетворять требованиям к разрешающей способности для многих приложений.
Далее разъясняются особенности треугольного управляющего поля. Рассматривается случай применения треугольного управляющего поля вместо гармонического поля. Системная функция для идеальных частиц в этом случае имеет вид
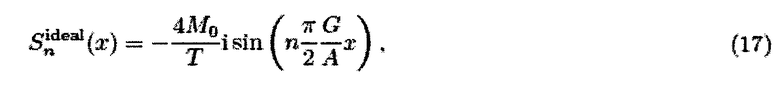
для движения FFP, покрывающего диапазон 0<x<2A/G. Теперь вместо ряда Чебышева для восстановления концентрации частиц может быть использован ряд Фурье:

Измеренные частотные компоненты Vn пропорциональны компонентам C(k) в k-пространстве, которые связаны с пространственным распределением C(х) преобразованием Фурье. В выражениях для системной функции уравнение (18) принимает вид

Для реалистичных частиц системная функция должна быть свернута с М′(Hs). Поскольку уравнения (12-14), полученные для возбуждения гармоническим управляющим полем, справедливы также и для треугольной системной функции, модифицированная/свернутая концентрация С(х) может быть восстановлена в диапазоне 0<x<2A/G.
Далее рассматривается матричная формулировка. Для восстановления изображения MPI непрерывное пространственное распределение частиц отображается на сетку, где каждая ячейка сетки представляет собой маленькую пространственную область. Кроме того, регистрируется только ограниченное число n частотных компонент. Если пространственные положения индексируются как m, частотные компоненты записываются как

или, в векторной/матричной записи,

Вычисление вектора концентрации тогда в основном соответствует инверсии матрицы S:

Это обозначение будет также использоваться для 2D или 3D визуализации, которая требует свертывания пространственных индексов в единственный индекс m. Таким образом, концентрация - всегда вектор, независимый от пространственной размерности.
Возвращаясь к случаю 1D для гармонического управляющего поля, введение скаляра

и диагональной матрицы
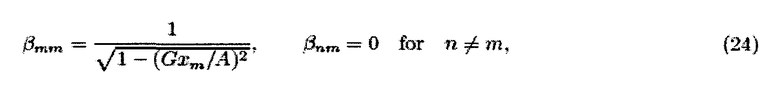
позволяет получить, посредством сравнения уравнения (22) с уравнением (11), следующее тождество:

Таким образом, в случае 1D визуализации идеальных частиц обратная матрица может быть просто получена умножением транспонированной матрицы на скаляр и диагональную матрицу.
Использование только ограниченного числа частотных компонент соответствует работе с усеченным рядом Чебышева. Теорема усечения Чебышева затем устанавливает, что ошибка в аппроксимации реального распределения концентрации ограничивается суммой абсолютных значений отброшенных коэффициентов. Еще более важно для разумно гладких распределений, что ошибка имеет порядок последнего сохраняемого коэффициента Чебышева.
Далее рассматриваются 2D и 3D пространственное кодирование.
Вначале рассматривается 1D управляющее поле. Первый этап при описании 2D и 3D визуализации заключается в рассмотрении 3D системной функции частиц в 3D выборочном поле Hs(r), объединенном с 1D управляющим полем HD(t). Используя гармоническое управляющее поле и выбирая установку катушек Максвелла, чтобы создать, таким образом, выборочное поле, полное поле может быть аппроксимировано в виде
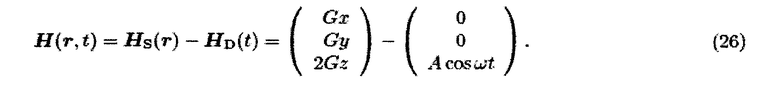
Системная функция может быть записана как свертка по z компоненте выборочного поля
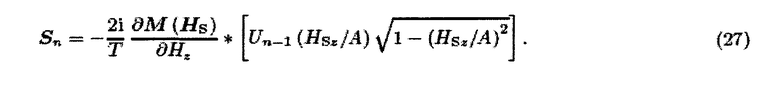
В этом векторе каждая компонента относится к сигналу, индуцированному соответственной x/y/z компонентой намагниченности. Обнаружение этих компонент требует трех ортогональных (набора) приемных катушек.
Для идеальных частиц точная пространственная зависимость принимает вид
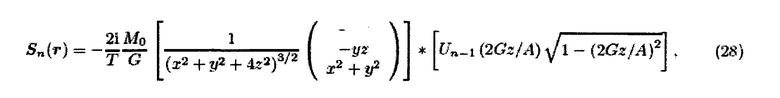
где звездочка обозначает свертку по z компоненте, то есть направлению движения FFP в результате действия управляющего поля. Таким образом, выражение, описывающее 3D пространственную зависимость соответствующей компоненты намагниченности, свертывается в направлении управляющего поля с набором 1D функций Чебышева.
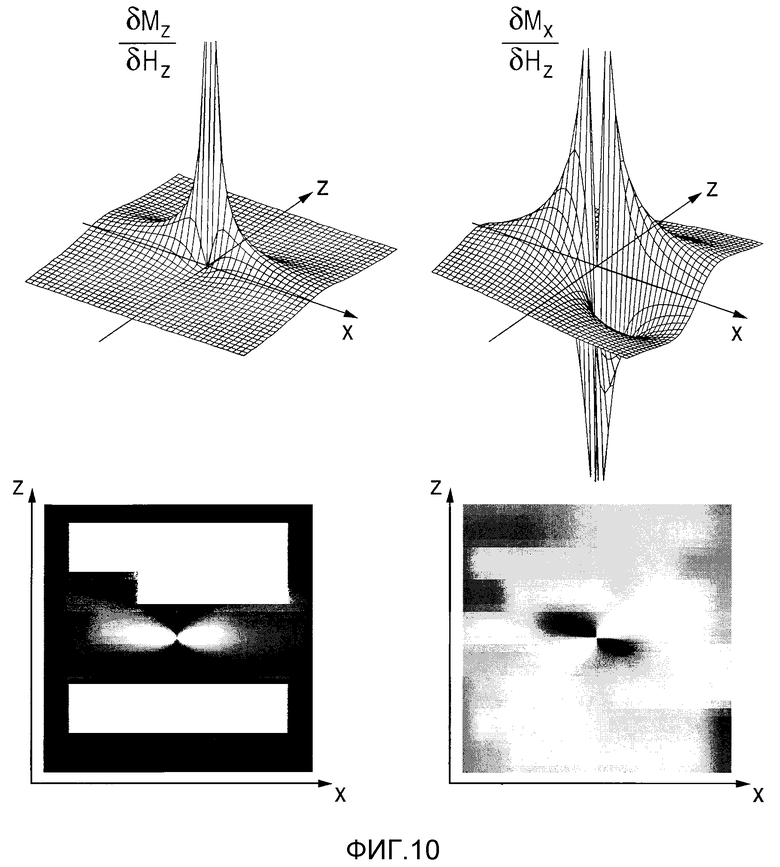
Форма ядра свертки определяется посредством ∂М/∂H, что описывает то, как намагниченность отвечает на изменение управляющего поля. Для идеальных частиц эта производная сингуляна в начале координат. На фиг.10 показана xz плоскость 3D ядра для компонент сигнала, обнаруживаемых в х и z направлении, Sn,x(r) и Sn,z(r), соответственно. Вдоль центральной линии в направлении управляющего поля ядро для намагниченности Mz соответствует дельта-распределению, как и в ситуации 1D. С увеличением расстояния от центральной линии ядро расширяется, и его амплитуда быстро уменьшается. Для Мх и по соображениям симметрии также и для My ядро нулевое на осях симметрии. Оно имеет большую амплитуду вблизи сингулярности в начале координат.
Чтобы сформировать 3D системную функцию идеальных частиц, 3D ядро свертывается по направлению управляющего поля с 1D полиномами Чебышева 1dупр3dсист.функ.
На фиг.11 показаны центральные 2D срезы, извлеченные из выбранных гармоник для вышеупомянутого случая 1D движения в z направлении под управляющим полем. Непосредственно на линии, покрываемой траекторией FFP, системная функция задается полиномами Чебышева и поэтому может кодировать произвольное распределение частиц, как рассмотрено для ситуации 1D. С увеличением расстояния до центральной линии размытие ядра свертки увеличивается так, что более тонкие структуры высших полиномов Чебышева усредняются до нулевых значений. Поэтому сигнал в высших компонентах системной функции конденсируется к линии траектории FFP (ср. гармоники 12 и 25 на фиг.11), где эффект размытия мал. Это можно объяснить тем, что только в близкой окрестности FFP изменение поля достаточно быстрое, чтобы стимулировать отклик частиц, который образует высокочастотные компоненты.
В эксперименте MPI может быть полезно использовать симметрии в системной функции, чтобы частично синтезировать системную функцию и, таким образом, ускорить ее получение и сократить требуемые объемы памяти. От 3D отклика до 1D движения FFP два основных правила могут быть получены для четности системной функции в пространственном направлении, индексированном как iε{х, y, z}.
1. "Основная" четность задается четностью ядра свертки, показанного на фиг.10. Оно четное, если приемное направление jε{x, y, z} ориентировано по направлению kε{x, y, z} управления. Это соответствует компоненте производной намагниченности ∂Mj/∂Hk для j=k. В другом случае четность ядра отрицательна:
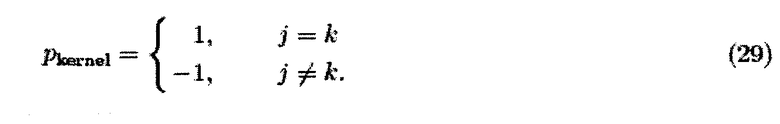
2. Если представляющее интерес пространственное направление является направлением управляющего поля, то есть i=k, то четность чередуется между последовательными гармониками h такой компоненты управляющего поля:

Причина заключается в переменной четности полиномов Чебышева в 1D системной функции. Четность, наблюдаемая для гармоники h в пространственном направлении i, в этом случае есть pi,j,k,h=pCheb·pkernel
Далее рассматривается 2D и 3D управляющее поле. Из фиг.11 ясно, что пространственное кодирование по полному расширению FOV не может быть достигнуто с использованием 1D движения FFP. Таким образом, для 2D или 3D пространственного кодирования управляющее поле должно быть добавлено для каждого кодируемого пространственного направления. Для простой реализации можно выбрать гармонические управляющие поля с небольшими различиями частот в различных пространственных направлениях, приводя к движению FFP по 2D или 3D картинам Лиссажу. Кроме того, на фиг.11 показано, что высокое разрешение получается только в близкой окрестности линии траектории FFP. Таким образом, картина Лиссажу должна быть достаточно плотной, чтобы достигнуть однородного разрешения.
На фиг.12 приведена 2D картина Лиссажу, образованная суперпозицией двух ортогональных гармонических управляющих полей с отношением частот ωx/ωz=24/25:

Используя 3D выборочное поле в соответствии с lD управлением, удвоенный градиент выборочного поля в z направлении требует, чтобы выполнялось Az=2Ax для покрытия квадратного FOV движением FFP. На фиг.12 показаны первые компоненты моделируемой 2D системной функции для идеальных частиц, подвергнутых суперпозиции 2D Лиссажу управляющего поля и 3D выборочного поля. Каждое приемное направление имеет свой собственный набор системных функций, обозначенных как «прием х» и «прием z. Компоненты, соответствующие высшим гармоникам соответствующей управляющей частоты обозначены рамками с двойной линией. На х канале они имеют интервал в 24 компоненты. В пространственном направлении х они очень похожи на 1D ряд Чебышева, тогда как в z направлении они не демонстрируют пространственной вариации. На z канале гармоники управляющей частоты демонстрируют интервал в 25 компонент с пространственной картиной, которая в основном повернута на 90 градусов относительно х компонент.
Хотя компоненты, соответствующие гармоникам частот управляющего поля позволяют только 1D кодирование в соответствующем направлении управляющего поля, компоненты, возникающие из смеси обеих управляющих частот, предоставляют пространственную вариацию в обоих направлениях в то же самое время. Например, движение налево от первой гармоники х управляющего поля на х канале (компонента 24) соответствует смеси частот mωx+n(ωx-ωz) с увеличением целого числа n и m=1. Для большего m начинают с высшей гармоники m. Движение направо соответствует отрицательному n. Таким образом, чистые гармоники управляющего поля и их окрестность относятся к низкой степени смешения, тогда как увеличение расстояния отвечает большему n и более высоким порядкам смешения.
Следует отметить, что компонента системной функции, наблюдаемая для mωx+n(ωх-ωz), появляется во второй раз на частоте mωx+n(ωx+ωz). Таким образом, каждая компонента, соответствующая смесям частот, появляется дважды. Примерами являются компоненты 23 и 73 (m=1, n=1, полужирные рамки) или 47 и 97 (m=2, n=1, пунктирные рамки), но также и 26 и 74 (m=1, n=-2, штриховые рамки) на х канале.
На фиг.12 также показаны графики максимальных интенсивностей (веса) образованных компонент системной функции. Самые высокие интенсивности найдены в высших гармониках частот управления, однако, с уменьшением к более высоким частотам. Компоненты, соответствующие смешанным частотам, имеют намного меньшую интенсивность, чем чистые гармоники.
Чем выше порядок компоненты системной функции, тем более тонкая у него пространственная структура. Это поведение и общие пространственные картины вполне напоминают 2D полиномы Чебышева, которые могут быть записаны как тензорное произведение 1D полиномов для каждого направления: Un(x)⊗Um(z). На фиг.13 приведены графики первых компонентов этих функций. 2D функции Чебышева удовлетворяют соотношению ортогональности. Графическое представление этого соотношения для первых 256 компонентов показано в левой части фиг.14. Внутреннее произведение между ортогональными функциями исчезает, и только произведение функции саму на себя является ненулевым, приводя к диагональной линии на фиг.14. В правой части показан соответствующий график 2D Лиссажу системной функции для идеальной частицы. Яркие пятна и линии диагонали указывают, что некоторые компоненты системной функции не ортогональны друг другу. Однако черные области преобладают, и можно заключить, что большая часть компонент ортогональна. Поэтому в системной функции имеется только небольшая избыточность.
Для демонстрации этого фантомное изображение (слева на фиг.15) расширено до равного числа 2D Чебышева и Лиссажу компонент системной функции, соответственно. Число компонент было выбрано как равное числу пикселей в изображении (64×64). Изображение, полученное из преобразования Чебышева, демонстрирует уменьшенное разрешение по сравнению с оригинальным изображением. Причина этого в том, что функции Чебышева предоставляют более высокое разрешение на краях FOV, но уменьшенное разрешение в центре. Чтобы сохранить высокое разрешение в центре изображения, высшие компоненты Чебышева должны были бы быть включены в разложение. Изображение, полученное из компонент системной функции, было восстановлено инверсией матрицы системной функции, используя минимальную регуляризацию для подавления шума. Половина компонент системной функции была взята из приема х системной функции, другая половина - из функции z (как показано на фиг.12). Разрешение изображения оказывается лучше, чем наблюдаемое для разложения Чебышева, но изображение имеет небольшие артефакты, из-за которых оно кажется менее однородным. Рассматривая тот факт, что некоторые компоненты системной функции не ортогональны и поэтому избыточны, качество изображения оказывается вполне хорошим. Восстановления только из х или z компонент дает значительно худшее качество изображения, указывая, что эти подмножества не достаточны для однородного отображения информации изображения.
Кодирование сигнала MPI может предоставить системную функцию, которая формирует удобный для анализа базисный набор, который может отобразить информацию изображения с высоким разрешением.
Для 1D гармонического возбуждения идеальных частиц системная функция соответствует ряду полиномов Чебышева второго рода. Поэтому быстрое и точное восстановление предоставляется преобразованием Чебышева.
Свойства реалистических частиц вводятся в системную функцию операцией типа свертки, приводящей к размытию компонентов с высоким разрешением. Это вводит предел разрешающей способности, который определяется крутизной кривой намагниченности частиц. Хотя, в принципе, изображение более высокого разрешения может быть восстановлено обращением свертки, разрешающая способность, предоставленная реалистическими частицами без обращения свертки, уже достаточно высока для многих практических приложений.
Системная функция для 2D визуализации определяется траекторией, используемой FFP, и ядром, представляющим область вокруг FFP, которая дает вклад в сигнал. Форма этого ядра FFP определяется топологией выборочного поля. Был показан простой случай постоянных градиентов выборочного поля во всех пространственных направлениях. Для идеальных частиц ядро имеет острые сингулярности, которые предоставляют высокое пространственное разрешение. Однако области вокруг этих острых пиков также дают вклад в сигнал. По-видимому, это причина для наблюдения того, что в 2D кодировании с использованием 2D картины Лиссажу, системная функция не отображается точно 2D функциями Чебышева. Поэтому восстановление не может быть выполнено с использованием преобразования Чебышева, как в 1D, но требует инверсии матрицы системной функции. Однако близкое соотношение между 2D системной функцией Лиссажу и 2D полиномами Чебышева очевидны. Это может быть использовано, чтобы преобразовать системную функцию в более разреженное представление, используя преобразование Чебышева, или преобразование косинусного типа, приводя к более низким требованиям к объему памяти и к более быстрому восстановлению.
Системная функция 2D Лиссажу не формирует полностью ортогональное множество, поскольку оно содержит избыточные компоненты. Тем не менее, это дает возможность кодирования информации изображения высокого разрешения, как показано на фиг.10. Возможные несоответствия между информационным содержанием получаемых данных и желаемым пиксельным разрешением могут быть сглажены с использованием конструкций регуляризации при восстановлении.
Чтобы ускорить трудоемкое экспериментальное получение системной функции, можно использовать правила четности, полученные для 2D системной функции. Теоретически они позволяют создавать полную системную функцию по измерению только одного квадранта в прямоугольнике фигуры Лиссажу. Для 3D фигуры Лиссажу одного октанта достаточно, чтобы ускорить в восемь раз получение системной функции. Экспериментально симметрия может быть нарушена несовершенным выравниванием катушек. Тем не менее, сведения об основных теоретических функциях и их четности могут помочь смоделировать системную функцию только по нескольким измеренным образцам.
В реальном эксперименте MPI обычно получают намного больше частотных компонент, чем желаемое число пикселей изображения. Поэтому имеется свобода в выборе компонент системной функции, чтобы составить более компактный базисный набор, обеспечивающий лучшую ортогональность. Например, дублирующие компоненты системной функции могут быть удалены после сбора данных, чтобы получить меньшую матрицу системной функции для ускорения восстановления изображения. Кроме того, выбор гармоник в соответствии с их весом может помочь уменьшить размер матрицы. Возможно также модифицировать вес определенных компонент для воздействия на разрешение изображения и соотношение сигнал/шум.
2D визуализация реалистических частиц не моделировалась в данной работе, но из 1D дифференцирования можно сделать заключение, что в зависимости от крутизны кривой намагниченности частицы произойдет размытие ядра FFP. Это может удалить сингулярности ядра, но также приведет и к некоторой потере разрешения, как рассмотрено для случая 1D.
3D визуализация не показана, но 2D результаты могут быть непосредственно экстраполированы на 3D введением дополнительного ортогонального управляющего поля, допускающего 3D траектории FFP. Для 3D траектории Лиссажу можно ожидать близкого подобия системной функции и произведений третьего порядка полиномов Чебышева.
Топология выборочного поля и траектории FFP, используемые в данной работе, были выбраны для их простой экспериментальной реализации. Однако возможны и многие альтернативные конфигурации поля. Для траектории FFP можно также использовать радиальные или спиральные конфигурации, или даже конфигурации, специально приспособленные к визуализируемой анатомии. Траектории могут быть приспособлены для предоставления варьирующегося разрешения изображения. Для выборочного поля топология, создающая линии, свободные от поля, вместо FFP, обещает более эффективное сканирование.
Из вышесказанного следует, что кодирование сигнала MPI, используя гармонические управляющие поля в комбинации с постоянными градиентами выборочного поля, предоставляют системную функцию, способную отображать информацию изображения с высоким разрешением в достаточно компактной форме. Соотношение, близкое к полиномам Чебышева второго рода, может быть использовано для ускорения получения системной функции, частично моделируя ее, или для сокращения требуемого объема памяти, применяя специально приспособленные преобразования разрежения, приводящие к меньшим временам восстановления.
Используемые в данном случае системные функции привязаны к конкретным конфигурациям поля и траекториям сканирования. Возможны многие другие конфигурации, обеспечивающие гибкость в приспособлении системных функции для удовлетворения определенных экспериментальных потребностей относительно скорости, разрешающей способности и чувствительности.
Некоторые главные варианты реализации способа, предложенного в соответствии с настоящим изобретением, по сравнению с известным способом, могут быть теперь показаны в виде простых блок-схем, иллюстрирующих соответствующее использование системной функции (или ее частей).
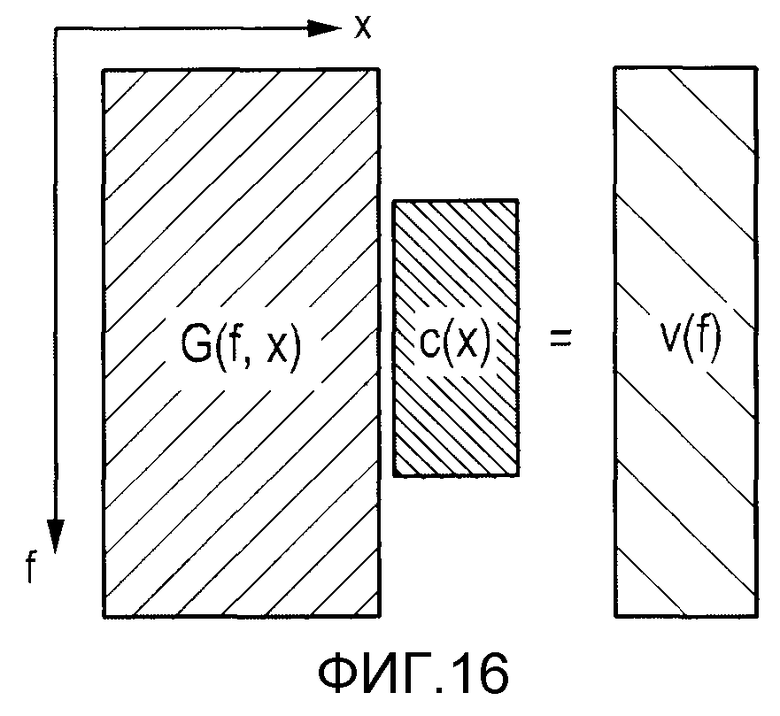
Известный способ для восстановления по существу требует следующих этапов (ср. с фиг.16, показывающей, какие части системной функции требуются/используются):
1. Однократное измерение полной "системной функции" для данной комбинации контрастного вещества, геометрии сканера и траектории:
а. Измерение временного отклика во всех пространственных положениях (пиксели/воксели).
b. Выполнение FFT временного сигнала, чтобы получить спектр частоты в каждом положении.
с. Сохранение результата в виде матрицы с компонентами частоты (строки) в связи с пространственными положениями (столбцы): "матрица системной функции", G(f, x).
2. Измерение представляющего интерес объекта:
а. Получение временного отклика.
b. Сохранение Фурье-преобразованного отклика: "вектор измерения", v(f).
3. Решение обратной задачи G(f, x)c(x)=v(f) или связанной регуляризованной задачи для получения распределения концентрации: "вектор изображения", c(х).
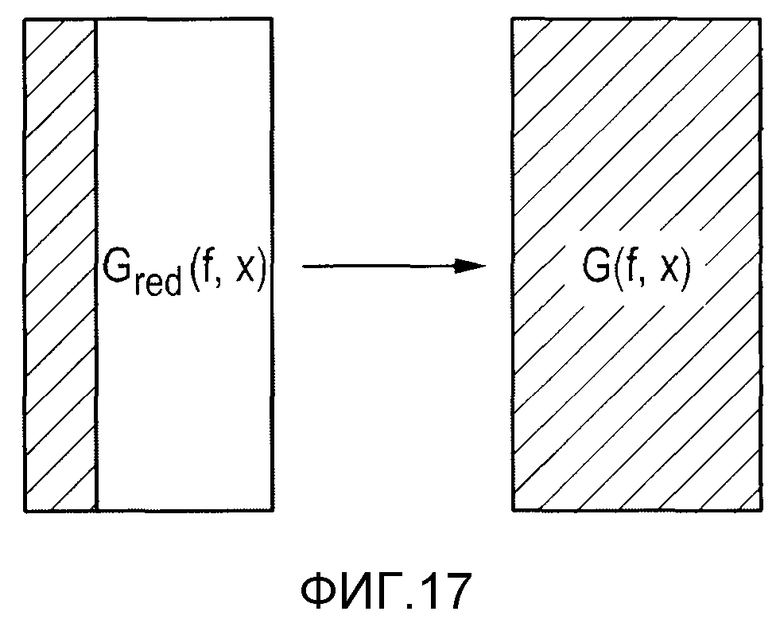
Первый вариант реализации в соответствии с настоящим изобретением, который использует пространственные симметрии (ср. фиг.17, 18), по существу требует следующих этапов для восстановления:
1. Использование очевидной зеркальной симметрии (ср. фиг.17):
а. Измерение сокращенной системной функции в выбранных положениях (например, один квадрант/октант или чередующиеся положения).
b. Создание полной матрицы системной функции операциями зеркальной симметрии.
c. Выполнение стандартного восстановления с полной матрицей.
2. Использование преобразования разрежения вдоль пространственных направлений (ср. фиг.18):
а. Измерение системной функции в выбранных положениях, чтобы получить коэффициенты для функционального множества, используемого для разложения пространственного распределения (например, коэффициенты Чебышева).
b. Поскольку пространственное распределение может быть аппроксимировано меньшим числом компонент в k-пространстве преобразования, системная функция представляется разреженной матрицей и, если истинное разрешении меньше, чем разрешение векселя, пространственный размер вектора меньше, чем в реальном пространстве х.
c. Решение разреженной обратной задачи в пространстве преобразования, чтобы получить c(k).
d. Использование обратного преобразования, чтобы получить изображение с(х).
Второй вариант реализации в соответствии с настоящим изобретением, который использует избыточные частотные компоненты (ср. фиг.19), по существу требует следующих этапов для восстановления:
1. Получение полной или пространственно сокращенной матрицы системной функции.
2. Идентификация частотных компонент (строки) с идентичной пространственной картиной (например, из теоретических соображений).
3. Суммирование этих компонент в матрице системной функции и векторе измерения.
4. Обратная сокращенная задача для получения изображения с(х).
Хотя изобретение было подробно рассмотрено на чертежах и предшествующем описании, эти демонстрация и описание следует считать иллюстративными или примерными и не ограничительными; изобретение не ограничивается раскрытыми вариантами реализации. Другие вариации раскрытых вариантов реализации могут быть поняты и осуществлены специалистами в данной области техники при осуществлении заявленного изобретения, из изучения чертежей, раскрытия и приложенной формулы.
В формуле слово "содержащий" не исключает других элементов или этапов, и единственное число не исключает множества. Единственный элемент или иной блок могут выполнить функции нескольких элементов, приведенных в формуле. То, что некоторые измерения приведены во взаимно различных зависимых пунктах формулы, не означает, что для получения преимуществ не может быть использована комбинация этих измерений.
Компьютерная программа может быть сохранена/распределена на подходящей среде, например оптическом носителе данных, или твердотельной среде, поставляемой вместе, или как часть других аппаратных средств, но может также быть распределена в других формах, например, через Интернет или другие проводные или беспроводные телекоммуникационные системы.
Любые обозначения в формуле не должны рассматриваться как ограничение объема притязаний изобретения.







Группа изобретений относится к медицине. В методике Визуализации Магнитных Частиц процесс восстановления требует сведений о так называемой системной функции. Эта функция описывает соотношение между пространственным положением и частотной характеристикой. Для разумных разрешений и данной области сканирования системная функция становится весьма большой, приводя к большим временам сбора для системной функции и к необходимости в большом объеме памяти во время восстановления. Настоящая группа изобретений позволяет сократить размер матрицы системной функции, используя структурные свойства матрицы. Такими свойствами являются, например, пространственные симметрии, сокращающие число столбцов, и идентичные характеристики на различных частотах, сокращающие число строк. В других вариантах реализации матрица может быть преобразована к разреженному представлению, используя соответствующие базовые функции. 2 н. и 9 з.п. ф-лы, 19 ил.
1. Конструкция (10) для обнаружения и/или определения местонахождения магнитного материала (100) в области воздействия (300), содержащая:
средство (210) выборки для создания выборочного магнитного поля (211), имеющего такую пространственную конфигурацию напряженности магнитного поля, что в области воздействия (300) формируются первая подзона (301), имеющая низкую напряженность магнитного поля, и вторая подзона (302), имеющая более высокую напряженность магнитного поля,
средство (220) управления для изменения пространственного положения двух подзон (301, 302) в области воздействия (300) посредством управляющего магнитного поля (221) так, чтобы намагниченность магнитного материала (100) изменялась локально,
средство (230) приема для получения сигналов обнаружения, причем сигналы обнаружения зависят от намагниченности в области воздействия (300), причем на намагниченность влияет изменение пространственного положения первой и второй подзоны (301, 302),
средство (75) сохранения для сохранения подмножества данных системной функции конструкции, причем упомянутая системная функция содержит множество данных системной функции, описывающее соотношение между пространственным положением магнитного материала и характеристикой системы для упомянутой конструкции и траектории, вдоль которой упомянутая первая подзона (301) перемещается для сбора упомянутых данных системной функции, и
средство (74) восстановления для восстановления пространственного распределения магнитного материала (100) в области воздействия (300) по сигналам обнаружения и сохраненному подмножеству данных системной функции, используя дополнительные сведения о структуре системной функции, причем упомянутые средства (74) восстановления приспособлены для создания сокращенного представления системной функции посредством применения преобразования Чебышева или преобразования косинусного типа в соответствии с пространственной размерностью и решения задачи намного более разреженного восстановления, возникающей после преобразования.
2. Конструкция (10) по п.1,
в которой упомянутое средство (230) приема приспособлено для сбора только упомянутого подмножества данных системной функции конструкции посредством обнаружения сигналов, в то время как зонд упомянутого магнитного материала последовательно помещается во множество различных положений в упомянутой области воздействия (300).
3. Конструкция (10) по п.2,
в которой упомянутое множество положений расположено в квадранте или октанте упомянутой области воздействия (300).
4. Конструкция (10) по п.2,
в которой упомянутое множество положений распределено чередующимся образом по области воздействия (300).
5. Конструкция (10) по п.1,
в которой упомянутые средства (74) восстановления приспособлены для первого восстановления полной системной функции из сохраненного подмножества в множестве данных системной функции и для последующего восстановления пространственного распределения магнитного материала по сигналам обнаружения, используя восстановленное множество данных полной системной функции.
6. Конструкция (10) по п.1,
в которой упомянутые средства (74) восстановления приспособлены для восстановления данных системной функции, которые требуются для восстановления пространственного распределения магнитного материала (100), но не содержатся в сохраненном подмножестве множества данных системной функции, непрерывно во время восстановления пространственного распределения магнитного материала (100).
7. Конструкция (10) по п.5 или 6,
в которой упомянутые средства (74) восстановления приспособлены для восстановления данных системной функции, используя пространственные симметрии, в частности пространственные зеркальные симметрии, существующие в частотных компонентах системной функции.
8. Конструкция (10) по п.1,
в которой упомянутое средство (74) восстановления приспособлено для восстановления пространственного распределения магнитного материала (100) в области воздействия (300), используя системную функцию с уменьшенным числом спектральных компонент, полученных из суммирования частотных компонент сохраненного подмножества данных системной функции с подобной пространственной информацией.
9. Конструкция (10) по п.1,
в которой упомянутые средства (74) восстановления приспособлены для создания сокращенного представления системной функции посредством преобразования полной системной функции.
10. Конструкция (10) по п.1,
в которой упомянутое средство (230) приема приспособлено для непосредственного измерения упомянутого сокращенного представления системной функции в выбранных точках области воздействия, и причем упомянутые средства (76) восстановления приспособлены для определения коэффициентов упомянутых аналитических функций, которые используются для описания пространственной зависимости, из упомянутого измеренного сокращенного представления системной функции.
11. Способ обнаружения и/или определения местонахождения магнитного материала (100) в области воздействия (300), содержащий этапы:
создания выборочного магнитного поля (211), имеющего такую пространственную конфигурацию напряженности магнитного поля, что в области воздействия (300) формируется первая подзона (301), имеющая низкую напряженность магнитного поля, и вторая подзона (302), имеющая более высокую напряженность магнитного поля,
изменения пространственного положения двух подзон (301, 302) в области воздействия (300) посредством управляющего магнитного поля (221) так, чтобы намагниченность магнитного материала (100) изменялась локально,
получения сигналов обнаружения, причем сигналы обнаружения зависят от намагниченности в области воздействия (300), причем на намагниченность влияет изменение пространственного положения первой и второй подзоны (301, 302),
сохранения подмножества данных системной функции конструкции (10), используемой для обнаружения и/или определения местонахождения магнитного материала (100) в области воздействия (300), причем упомянутая системная функция содержит множество данных системной функции, описывающее соотношение между пространственным положением магнитного материала и характеристикой системы для упомянутой конструкции и траектории, вдоль которой упомянутая первая подзона (301) перемещается для сбора упомянутых данных системной функции, и
восстановления пространственного распределения магнитного материала (100) в области воздействия (300) по сигналам обнаружения и сохраняемому подмножеству данных системной функции, используя дополнительные сведения о структуре системной функции, причем упомянутый этап восстановления включает в себя создание сокращенного представления системной функции посредством применения преобразования Чебышева или косинусного преобразования в соответствии с пространственной размерностью и решение задачи намного более разреженного восстановления, возникающей после преобразования.
| WO2006064405A1 (PHILIPS INTELLECTUAL PROPERTY), 22.06.2006 | |||
| WO2006064392A2 (PHILIPS INTELLECTUAL PROPERTY), 22.06.2006 | |||
| EP1304542A2 (PHILIPS CORP | |||
| INTELLECTUAL PROPERTY), 23.04.2003 | |||
| RU94019333A1 (Нюкомед Имагинг АС), 20.08.1996 |
Авторы
Даты
2014-08-20—Публикация
2009-11-27—Подача