СПОСОБ АНАЛИЗА ФОРМЫ КОМЛЯ ДЕРЕВА Российский патент 2014 года по МПК G01N33/46 A01G23/00 

Изобретение относится к дендрометрии при изучении роста и развития комля деревьев, преимущественно берез, и может быть использовано при фитоиндикации территорий и разработке мероприятий по защите земельных участков от водной эрозии, экологических и климатических технологий, а также в дендроэкологическом мониторинге за развитием овражной сети и рационализации землепользования с учетом изменений формы комля растущих, в частности, березовых деревьев.

Известен способ анализа комля древесного ствола по патенту №2254707, включающий разметку ствола на секции кратной или некратной длины в зависимости от расположения неровностей ствола с измерением соответствующих расстояний от корневой шейки, секции некратной длины размечают на неровностях комлевой части ствола, по крайней мере, дважды в трех точках неровности, а измерения вдоль и поперек ствола по секциям выполняют гибкой мерной лентой, причем поперек ствола измеряют гибкой мерной лентой периметр сечения ствола.

Недостатком является то, что измерения выполняют у деревьев выше корневой шейки ствола. Поэтому известный способ не позволяет учитывать влияние периметров комля ниже корневой шейки деревьев. Причем березы могут произрастать на склоне оврага, сильно изменяя высоту корневой шейки от точки склона по середине ствола.

Известен также способ анализа комля растущего дерева для определения поперечного профиля оврага по патенту №2416193 РФ, характеризующийся тем, что поперек оврага выбирают пробную полосу леса с расположенными вдоль нее деревьями, измеряют расстояния и общий угол склона в поперечном сечении оврага между серединами диаметров корневой шейки смежных вдоль пробной полосы деревьев.

Недостатком также является отсутствие измерений периметров комля дерева ниже корневой шейки, что не позволяет изучать влияние склона оврага или холма на комлевую часть, начиная на стволе от высоты 1,3 м над корневой шейкой до поверхности почвы на склоне. Кроме того, в дендрометрии до сих пор не выделены те лимитирующие факторы комля, которые влияют на параметры места произрастания дерева. Березы мало исследованы, хотя они являются великолепными растениями для климатических технологий.

Технический результат - расширение функциональных возможностей анализа формы комля деревьев, прежде всего берез, произрастающих на ровной местности или же на склоне оврага (холма), а также повышение точности измерений ниже корневой шейки, начиная от стандартной высоты ствола в 1,3 м над корневой шейкой дерева до поверхности почвы.

Этот технический результат достигается тем, что способ анализа формы комля дерева включает выбор пробной площади с учетными деревьями, измерение высоты кроны и полной высоты всех учетных деревьев, причем форму комля как симметричную геометрическую фигуру учитывают от поперечного сечения комля на пересечении с поверхностью почвы до стандартной высоты 1,3 м, при этом измерения периметров комля проводят не менее чем в трех поперечных сечениях комля каждого учетного дерева ниже корневой шейки ствола, а по измеренным данным, дополнительно с учетом периметров корневой шейки и сечения ствола на стандартной высоте 1,3 м, выявляют математическую закономерность симметричной формы комля по единой общей формуле, затем по параметрам выявленной единой математической закономерности формы комля выявляют рейтинг учетных деревьев для оценки качества формы комля, после чего выявляют закономерности с волновыми возмущениями влияния параметров учетных деревьев и их комлей на параметры в общем виде у математического уравнения формы комля, а затем для оценки качества места произрастания выделяют закономерности с волновыми возмущениями с сильной теснотой коррелятивной вариации для последующего выделения лимитирующих факторов комля и самого учетного дерева.

У учетных деревьев, произрастающих на склоне, ниже корневой шейки ствола измерения периметров комля проводят не менее чем в трех поперечных сечениях комля каждого учетного дерева, в частности: в первом сечении измеряют периметр комля березы на высоте между корневой шейкой и верхней точкой пересечения поверхности почвы с боковой линией комля, см; во втором сечении измеряют периметр комля дерева на верхней точке пересечения поверхности почвы с боковой линией комля; в третьем сечении измеряют полупериметр комля дерева в сечении в точке пересечения поверхности почвы с вертикальной осевой линией комля дерева.

При не нулевом угле местного склона дополнительно измеряют от корневой шейки ствола максимальную высоту комля на нижней стороне склона оврага, или холма, или террасы, или берега до нижней точки пересечения поверхности почвы с боковой линией комля учетного дерева.

Математическую закономерность симметричной формы комля выявляют по единой общей формуле:

$$P=a_1\exp \left(-a_{2}h\right)+a_3$$

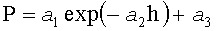
где P - переменный периметр поперечного сечения комля в данном месте измерения на разных высотах от корневой шейки;

h - высота от корневой шейки до поверхности почвы с отрицательными значениями не менее чем в трех поперечных сечениях комля каждого учетного дерева, а далее положительная стандартная высота 1,3 м, при этом корневая шейка получает значение высоты h=0;

a ₁, a ₂ и a ₃ - параметры статистической модели, причем:

a ₁ - начальное значение периметра комля дерева, физически представляемое как абсолютный выбег комля от ствола или сбег ствола учетного дерева от комля в точке пересечения продольной оси ствола с поверхностью почвы;

a ₂ - активность спада, то есть относительного сбега от крайних корней первого порядка до корневой шейки и дальше на стволе дерева до высоты 1,3 м, переменного периметра поперечного сечения комля учетного дерева по боковой линии симметричной формы;

a ₃ - постоянный периметр ствола по условному цилиндру на высотах от поверхности почвы до корневой шейки ствола учетного дерева и далее до высоты 1,3 м.

Рейтинг этих учетных деревьев для оценки качества формы комля выполняют по убыванию значений коэффициента корреляции по уравнению:

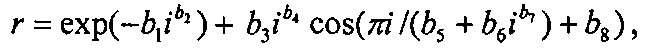
где r - коэффициент корреляции, мера тесноты связи между факторами,

i - номер места в рейтинге, занимаемого каждым учетным деревом,

b₁…b₈ - параметры вышеуказанной модели рангового распределения коэффициентов корреляции всех учетных деревьев на пробной площади.

Для обобщенной боковой линии формы комля по множеству учетных деревьев на пробной площади выявляют закономерности с волновыми возмущениями влияния параметров учетных деревьев на параметры уравнения формы комля в следующем общем виде:

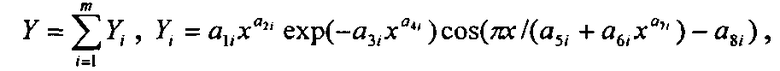
где Y - показатель, в нашем примере любой из трех параметров модели по единой общей формуле,

i - номер члена вышеуказанной формулы,

m - количество составляющих вышеуказанной формулы, шт.,

x - любой из влияющих переменных дерева и его комля,

a ₁…a ₈ - параметры одного члена вышеуказанной формулы, физически представляемого как асимметричный вейвлет-сигнал с переменными амплитудой и частотой колебательного возмущения всей совокупности или части популяции из множества учетных деревьев.

По измеренным данным выполняют полный факторный анализ взаимной зависимости между параметрами модели формы комля для оценки лимитирующих условий формирования абсолютной сбега комля у всех учетных на пробной площади деревьев в виде таблицы, в которой, с учетом принципа колебательной адаптации деревьев к условиям места произрастания, на первое место среди параметров деревьев встала максимальная высота комля, остальные шесть параметров остались в той же последовательности как и при детерминированном представлении развития и роста древесных растений.

Сущность технического решения заключается в том, что наиболее часто на склонах оврагов в лесостепной зоне России произрастают березы естественного происхождения. Они закрепляют овраги от водной эрозии, и происходит симбиоз между березняком и почвой на склоне оврага: березы своими корнями защищают почву от смыва, а почва наращивает свое плодородие, позволяя расти березам продуктивно без потери питательных веществ.

Сущность технического решения заключается также в том, что факторный анализ множества измеренных параметров комля у берез показал наибольшую тесноту связи изменения формы комля по боковой линии от поперечного сечения комля на поверхности почвы до стандартной высоты 1,3 м. При этом форма комля характеризуется уравнением экспоненциальной гибели (спада) с постоянным членом, а значения параметров математической модели зависят в основном от максимальной высоты комля на нижней стороне склона оврага или холма. Такая модель выявлена впервые.

Положительный эффект достигается тем, что выявление среднестатистической (математической) закономерности боковой линии формы комля по множеству произрастания деревьев на пробной площади, заложенной на склоне оврага или холма, а также на ровной местности, в зависимости от максимальной высоты комля, начиная от корневой шейки до самой нижней точки комля на нижней стороне березы по склону, позволяет проводить экологический мониторинг за состоянием и развитием самого оврага на участке с изучаемым березняком. Это позволит следить за укреплением склонов оврагов и холмов от водной эрозии в ходе роста и развития посаженных, например, берез. Такой мониторинг, по мере накопления опыта и данных измерений, дает возможность рекомендовать экологические и климатические технологии вначале на территориях лесостепной зоны России, а затем и в степной зоне. Это по опыту США (с 1960 года) и Китая (с 1970 года) значительно повысит урожайность зерновых культур на полях около оврагов и холмов, а также повысит продуктивность травяного покрова пойменных лугов на склонах оврагов со ставшими полноводными ручейками на их дне, а также на склонах холмов с родниками и берегов малых рек и их притоков.

Кроме того, положительный эффект достигается тем, что знание закономерности формы комля позволит прогнозировать рост и развитие деревьев на посадках при рекультивации земель на ровной или холмистой и овражистой местности. Модели формы комля позволят оценить густоту посадки деревьев саженцами или посева семенами при выполнении климатических и ландшафтно-экологических технологий.

Новизна технического решения заключается в том, что впервые измерения проводят ниже корневой шейки ствола растущего дерева по форме боковой линии при переходе от ствола к корням, что позволит в будущем подойти к поиску научно-технических решений и по изучению изменений формы корневой части дерева, а также к изучению несимметричных форм комлей различных видов деревьев. Кроме того, научная новизна заключается в том, что впервые получена математическая закономерность влияния максимальной высоты комля берез и других параметров растущих деревьев, при их измерении без разрушения самих деревьев, на изменение параметров типового уравнения боковой линии, симметричной относительно вертикальной оси ствола, поверхности комля произрастающих деревьев, причем, в частности, на месте произрастания каждой конкретной березы.

Предлагаемое техническое решение обладает существенными признаками, новизной и значительным положительным эффектом. Материалов, порочащих новизну технического решения, нами не обнаружено. Поэтому предлагаемое изобретение становится научно-техническим решением, полученным на основе выявления фундаментальной закономерности формы комля деревьев, но пока по боковой линии упрощенной до симметричной формы поверхности комлевой части лесных деревьев.

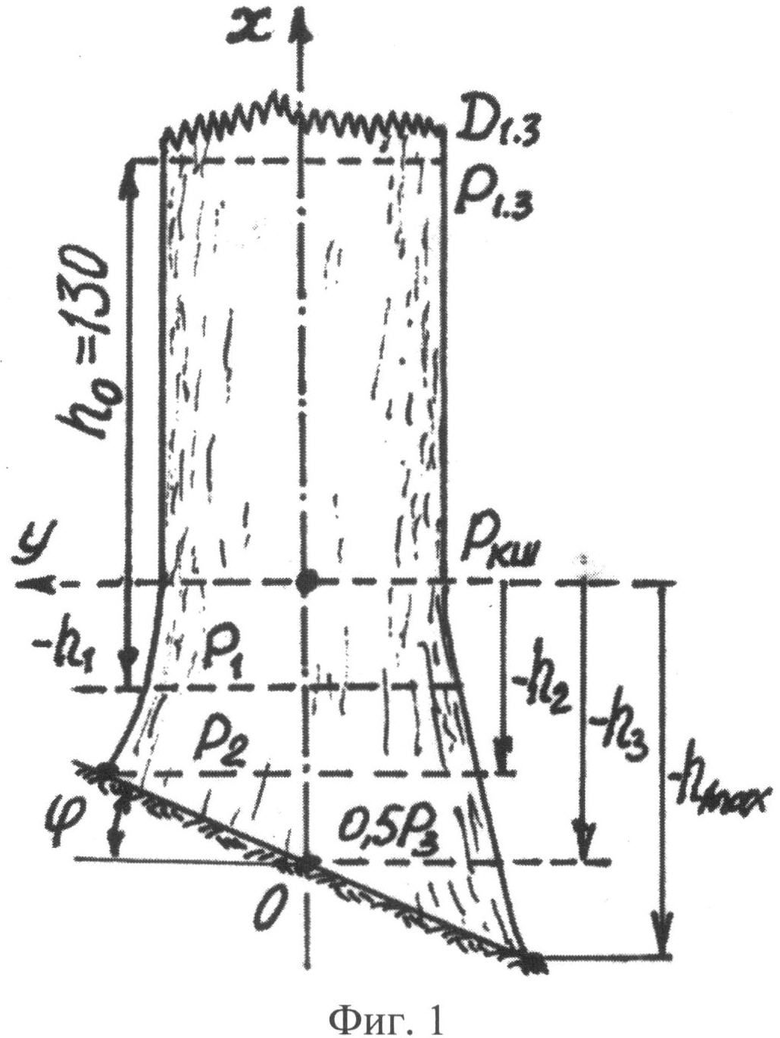
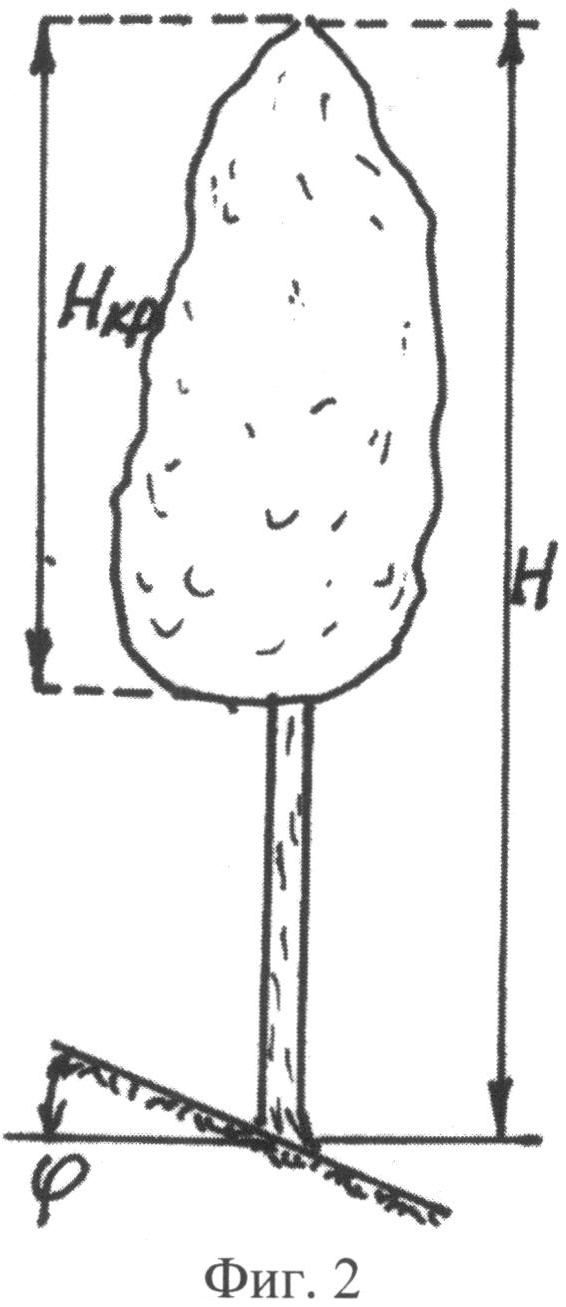
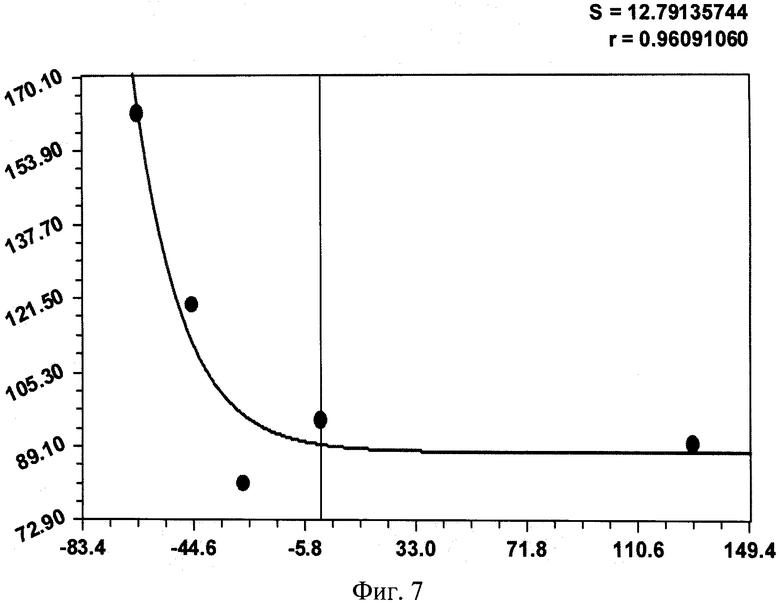
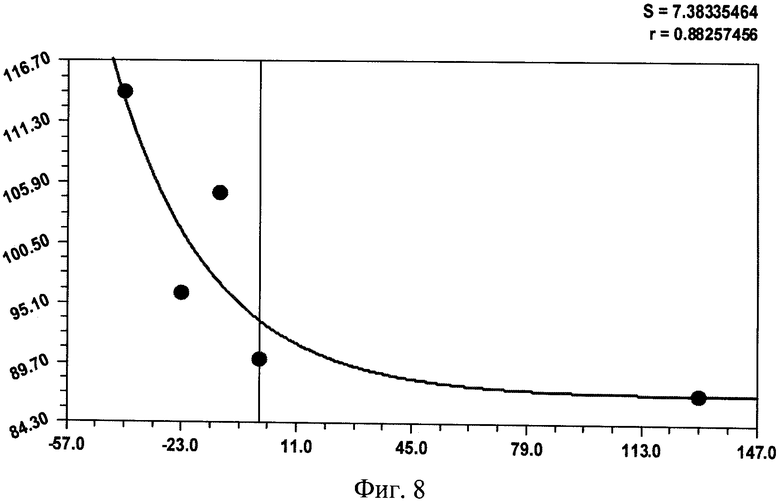
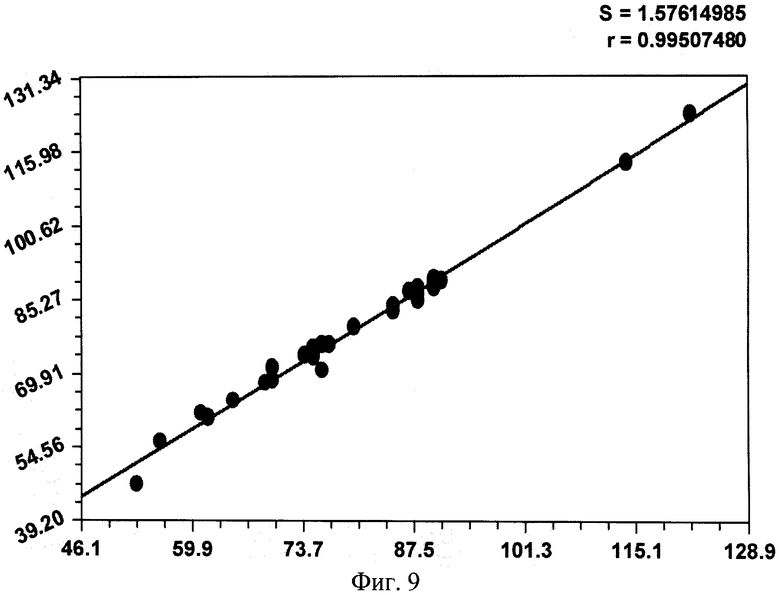
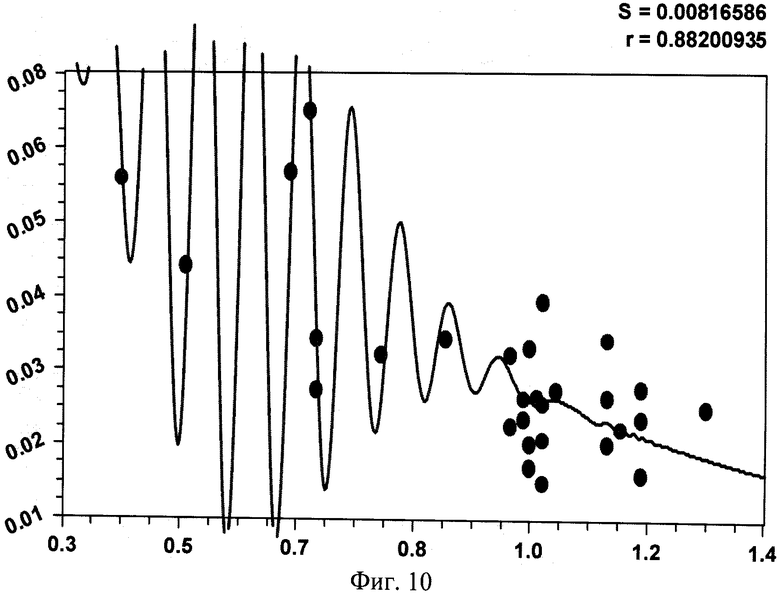
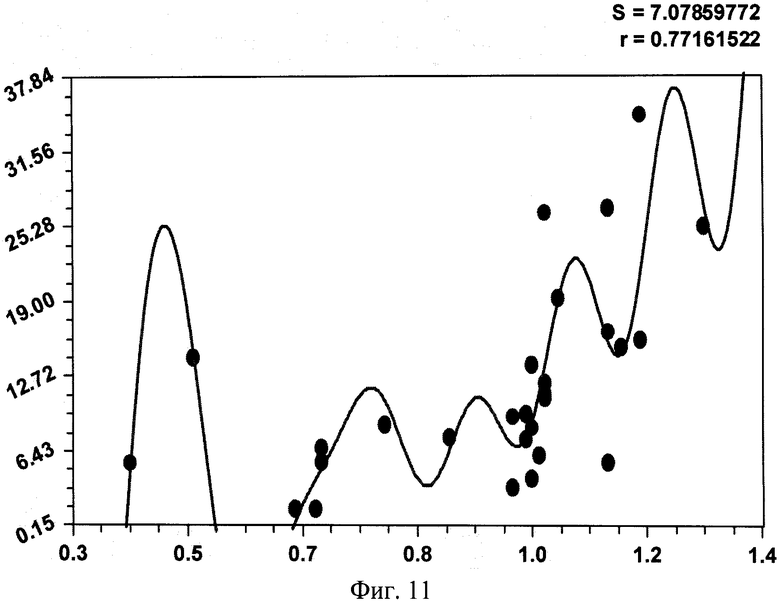
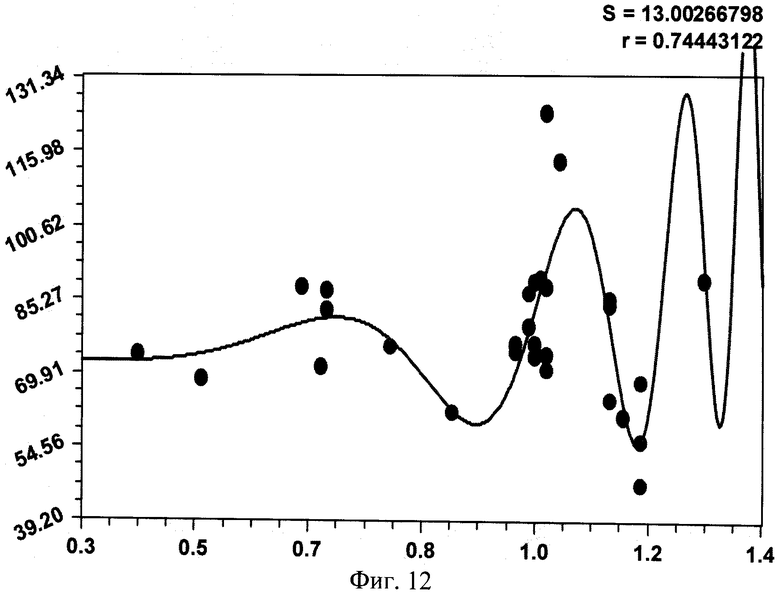
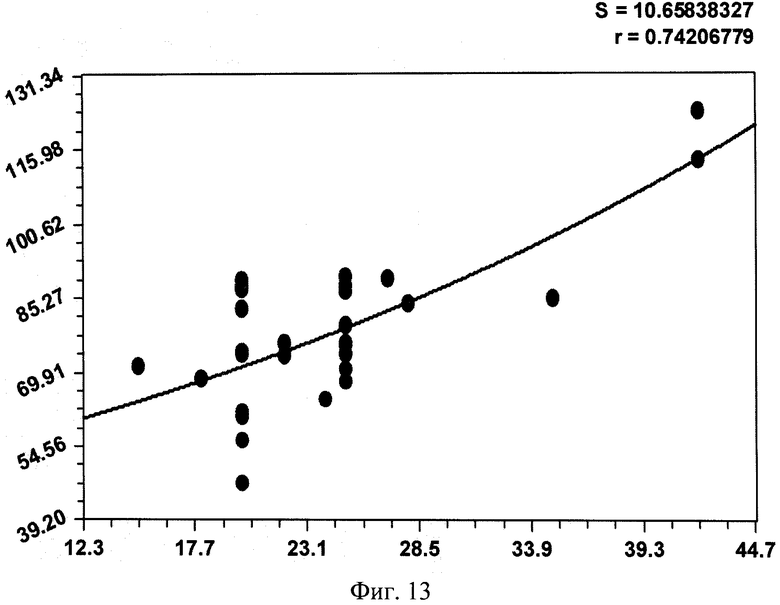
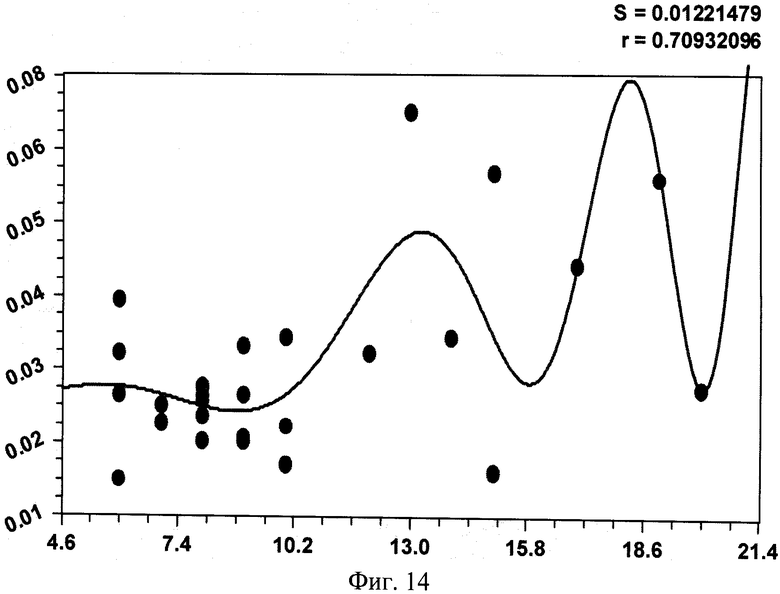
На фиг.1 приведена схема измерения параметров комля в прямоугольной системе координат с началом в середине корневой шейки, осью абсцисс вдоль продольной оси ствола вверх дерева и осью ординат в плоскости корневой шейки дерева; на фиг.2 - схема измерения высоты кроны и высоты всего учетного дерева; на фиг.3 показано фото части пробной площади с березами, из которых выбираются учетные деревья; на фиг.4 приведен график рейтингового распределения уравнений формы комля учетных берез по убыванию значений коэффициента корреляции; на фиг.5 - график боковой линии комля учетной березы №3 с самой математически правильной формой с максимальным коэффициентом корреляции 0,9995; на фиг.6 - то же, на фиг.5 два дерева №11 и №13 с одинаковым коэффициентом корреляции 0,9992, при этом форма комля по боковой линии у двух учетных берез различна; на фиг.7 - график боковой линии у предпоследнего в рейтинге учетного дерева березы №2 с волновым возмущением боковой линии; на фиг.8 - график боковой линии последнего в рейтинге учетного дерева №7 с коэффициентом корреляции 0,8826, где еще четче видно колебательное возмущение формы комля; на фиг.9 дан график влияния периметра ствола P_1.3 на параметр c с коэффициентом корреляции 0,9951; на фиг.10 - то же, на фиг.9 влияния высоты комля h_max на параметр b при коэффициенте корреляции 0,8820; на фиг. 11 - то же, на фиг.9 влияния высоты комля h_max на параметр а при коэффициенте корреляции 0,7716; на фиг.12 - то же, на фиг.9 влияния высоты комля h_max на параметр с при коэффициенте корреляции 0,7444; на фиг.13 - то же, на фиг.9 влияния диаметра ствола D_1.3 на параметр с при коэффициенте корреляции 0,7421: на фиг.14 - то же, на фиг.9 влияния высоты кроны H_кр на параметр b при коэффициент корреляции 0,7093.

На фиг.1 и фиг.2 приведены следующие условные обозначения:

φ - угол местного склона в месте произрастания дерева березы, град.;

D_1.3, P_1.3 диаметр и периметр ствола березы на стандартной высоте 1,3 м от корневой шейки;

P_кш - периметр сечения ствола на корневой шейке, см;

0,5 P₃ - половина периметра комля березы в сечении над точкой пересечения поверхности почвы с вертикальной осевой линией комля дерева, см;

h₁ - высота комля березы от корневой шейки до верхней точки пересечения поверхности почвы с боковой линией комля, см;

h₂ - высота комля березы от корневой шейки до верхней точки пересечения поверхности почвы с боковой линией комля, см;

h₃ - высота комля березы от корневой шейки до центральной точки пересечения поверхности почвы с вертикальной осевой линией комля, см;

h_max - максимальная высота комля березы от корневой шейки до нижней точки пересечения поверхности почвы с боковой линией комля, см;

H, H_кр - высоты дерева и кроны, м.

Способ анализа формы комля деревьев включает такие действия.

Вначале выбирают пробную площадь и на ней не менее 30 учетных деревьев одной породы, например березы. При этом пробная площадь может быть заложена на любой ровной или холмистой местности, а также на склонах оврагов или берегов водных объектов.

Форму комля принимают как симметричную геометрическую фигуру и ее учитывают от поперечного сечения комля на пересечении с поверхностью почвы до стандартной высоты 1,3 м. При этом измерения периметров комля проводят не менее чем в трех поперечных сечениях комля каждого учетного дерева ниже корневой шейки ствола, а по измеренным данным, дополнительно с учетом периметров корневой шейки и сечения ствола на стандартной высоте 1,3 м, выявляют математическую закономерность симметричной формы комля по единой общей формуле.

Затем по параметрам выявленной единой математической закономерности формы комля выявляют рейтинг учетных деревьев для оценки качества формы комля, после чего выявляют закономерности с волновыми возмущениями влияния параметров учетных деревьев и их комлей на параметры в общем виде у математического уравнения формы комля, а затем для оценки качества места произрастания выделяют закономерности с волновыми возмущениями с сильной теснотой коррелятивной вариации для последующего выделения лимитирующих факторов комля и самого учетного дерева.

У учетных деревьев, произрастающих на склоне, ниже корневой шейки ствола измерения периметров комля проводят не менее чем в трех поперечных сечениях комля каждого учетного дерева, в частности: в первом сечении измеряют периметр комля березы на высоте между корневой шейкой и верхней точкой пересечения поверхности почвы с боковой линией комля, см; во втором сечении измеряют периметр комля дерева на верхней точке пересечения поверхности почвы с боковой линией комля; в третьем сечении измеряют полупериметр комля дерева в сечении в точке пересечения поверхности почвы с вертикальной осевой линией комля дерева.

При не нулевом угле местного склона дополнительно измеряют от корневой шейки ствола максимальную высоту комля на нижней стороне склона оврага, или холма, или террасы, или берега до нижней точки пересечения поверхности почвы с боковой линией комля учетного дерева.

Математическую закономерность симметричной формы комля выявляют по единой общей формуле:

$$P=a_1\exp \left(-a_{2}h\right)+a_3$$ ,

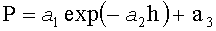
где P - переменный периметр поперечного сечения комля в данном месте измерения на разных высотах от корневой шейки;

h - высота от корневой шейки до поверхности почвы с отрицательными значениями не менее чем в трех поперечных сечениях комля каждого учетного дерева, а далее положительная стандартная высота 1,3 м, при этом корневая шейка получает значение высоты h=0;

a ₁, a ₂ и a ₃ - параметры статистической модели, причем:

a ₁ - начальное значение периметра комля дерева, физически представляемое как абсолютный выбег комля от ствола или сбег ствола учетного дерева от комля в точке пересечения продольной оси ствола с поверхностью почвы;

a ₂ - активность спада, то есть относительного сбега от крайних корней первого порядка до корневой шейки и дальше на стволе дерева до высоты 1,3 м, переменного периметра поперечного сечения комля учетного дерева по боковой линии симметричной формы;

a ₃ - постоянный периметр ствола по условному цилиндру на высотах от поверхности почвы до корневой шейки ствола учетного дерева и далее до высоты 1,3 м.

Рейтинг этих учетных деревьев для оценки качества формы комля выполняют по убыванию значений коэффициента корреляции по уравнению:

$$r=\exp \left(-b_1{i}^{b2}\right)+b_3{i}^{b4}\cos \left(\pi i/\left(b_s+b_6{i}^{b7}\right)+b_8\right)$$ ,

где r - коэффициент корреляции, мера тесноты связи между факторами,

i - номер места в рейтинге, занимаемого каждым учетным деревом,

b₁…b₈ - параметры вышеуказанной модели рангового распределения коэффициентов корреляции всех учетных деревьев на пробной площади.

Для обобщенной боковой линии формы комля по множеству учетных деревьев на пробной площади выявляют закономерности с волновыми возмущениями влияния параметров учетных деревьев на параметры уравнения формы комля в следующем общем виде:

$$Y={\displaystyle \sum _{i=1}^m{Y}_i,Y_i=a_{1i}{x}^{a_{2i}}\exp \left(-a_{3i}{x}^{a_{4i}}\right)\cos \left(\pi x/\left(a_{5i}+a_{6i}{x}^{a_{7i}}\right)-a_{8i}\right)}$$ ,

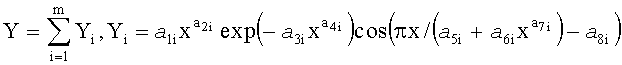
где Y - показатель, в нашем примере любой из трех параметров модели по единой общей формуле,

i - номер члена вышеуказанной формулы,

m - количество составляющих вышеуказанной формулы, шт.,

x - любой из влияющих переменных дерева и его комля,

a ₁…a ₈ - параметры одного члена вышеуказанной формулы, физически представляемого как асимметричный вейвлет-сигнал с переменными амплитудой и частотой колебательного возмущения всей совокупности или части популяции из множества учетных деревьев.

По измеренным данным выполняют полный факторный анализ взаимной зависимости между параметрами модели формы комля для оценки лимитирующих условий формирования абсолютной сбега комля у всех учетных на пробной площади деревьев в виде таблицы, в которой, с учетом принципа колебательной адаптации деревьев к условиям места произрастания, на первое место среди параметров деревьев встала максимальная высота комля, остальные шесть параметров остались в той же последовательности как и при детерминированном представлении развития и роста древесных растений.

Способ анализа комля деревьев, например берез на склоне оврага с ручейком и имеющего на склоне березняк естественного происхождения, реализуется следующим образом.

Для снижения линейной эрозии почвы оврагами применяют растения.

Методика измерения размеров осуществляется следующим образом. Сначала измеряем периметр корневой шейки ствола дерева, высоту, наклон склона. Цель - изучение растущих деревьев на склонах оврагов.

Выбирается участок оврага, на склонах которого растут деревья. На фиг.1 представлена модель формы дерева.

Форму комля принимают как симметричную геометрическую фигуру и ее учитывают от поперечного сечения комля на пересечении с поверхностью почвы до стандартной высоты 1,3 м. При этом измерения периметров комля проводят не менее чем в трех поперечных сечениях комля каждого учетного дерева ниже корневой шейки ствола, а по измеренным данным, дополнительно с учетом периметров корневой шейки и сечения ствола на стандартной высоте 1,3 м, выявляют математическую закономерность симметричной формы комля по единой общей формуле.

Затем по параметрам выявленной единой математической закономерности формы комля выявляют рейтинг учетных деревьев для оценки качества формы комля, после чего выявляют закономерности с волновыми возмущениями влияния параметров учетных деревьев и их комлей на параметры в общем виде у математического уравнения формы комля, а затем для оценки качества места произрастания выделяют закономерности с волновыми возмущениями с сильной теснотой коррелятивной вариации для последующего выделения лимитирующих факторов комля и самого учетного дерева.

У учетных деревьев, произрастающих на склоне, ниже корневой шейки ствола измерения периметров комля проводят не менее чем в трех поперечных сечениях комля каждого учетного дерева, в частности: в первом сечении измеряют периметр комля березы на высоте между корневой шейкой и верхней точкой пересечения поверхности почвы с боковой линией комля, см; во втором сечении измеряют периметр комля дерева на верхней точке пересечения поверхности почвы с боковой линией комля; в третьем сечении измеряют полупериметр комля дерева в сечении в точке пересечения поверхности почвы с вертикальной осевой линией комля дерева.

При не нулевом угле местного склона дополнительно измеряют от корневой шейки ствола максимальную высоту комля на нижней стороне склона оврага, или холма, или террасы, или берега до нижней точки пересечения поверхности почвы с боковой линией комля учетного дерева.

Математическую закономерность симметричной формы комля выявляют по единой общей формуле:

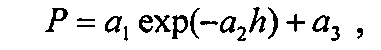
где P - переменный периметр поперечного сечения комля в данном месте измерения на разных высотах от корневой шейки;

h - высота от корневой шейки до поверхности почвы с отрицательными значениями не менее чем в трех поперечных сечениях комля каждого учетного дерева, а далее положительная стандартная высота 1,3 м, при этом корневая шейка получает значение высоты h=0;

a ₁, a ₂ и a ₃ - параметры статистической модели, причем:

a ₁ - начальное значение периметра комля дерева, физически представляемое как абсолютный выбег комля от ствола или сбег ствола учетного дерева от комля в точке пересечения продольной оси ствола с поверхностью почвы;

a ₂ - активность спада, то есть относительного сбега от крайних корней первого порядка до корневой шейки и дальше на стволе дерева до высоты 1,3 м, переменного периметра поперечного сечения комля учетного дерева по боковой линии симметричной формы;

a ₃ - постоянный периметр ствола по условному цилиндру на высотах от поверхности почвы до корневой шейки ствола учетного дерева и далее до высоты 1,3 м.

Рейтинг этих учетных деревьев для оценки качества формы комля выполняют по убыванию значений коэффициента корреляции по уравнению:

где r - коэффициент корреляции, мера тесноты связи между факторами,

i - номер места в рейтинге, занимаемого каждым учетным деревом,

b₁…b₈ - параметры вышеуказанной модели рангового распределения коэффициентов корреляции всех учетных деревьев на пробной площади.

Для обобщенной боковой линии формы комля по множеству учетных деревьев на пробной площади выявляют закономерности с волновыми возмущениями влияния параметров учетных деревьев на параметры уравнения формы комля в следующем общем виде:

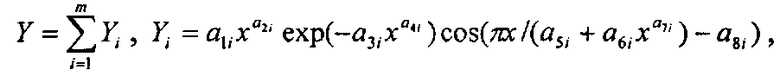
где Y - показатель, в нашем примере любой из трех параметров модели по единой общей формуле,

i - номер члена вышеуказанной формулы,

m - количество составляющих вышеуказанной формулы, шт.,

x - любой из влияющих переменных дерева и его комля,

a ₁…a ₈ - параметры одного члена вышеуказанной формулы, физически представляемого как асимметричный вейвлет-сигнал с переменными амплитудой и частотой колебательного возмущения всей совокупности или части популяции из множества учетных деревьев.

По измеренным данным выполняют полный факторный анализ взаимной зависимости между параметрами модели формы комля для оценки лимитирующих условий формирования абсолютной сбега комля у всех учетных на пробной площади деревьев в виде таблицы, в которой, с учетом принципа колебательной адаптации деревьев к условиям места произрастания, на первое место среди параметров деревьев встала максимальная высота комля, остальные шесть параметров остались в той же последовательности как и при детерминированном представлении развития и роста древесных растений.

После измерений и обработки данных подтвердили, что деревья, растущие на склоне оврага, поддерживают почву от смыва во время паводков из-за того, что они своими комлями управляют не только геометрией склона оврага, но и сами у себя формируют комли.

Пример. Для снижения линейной эрозии почвы оврагами применяют растения. Цель исследования - изучение формы комля деревьев, растущих в овраге, для выявления закономерностей взаимодействия между древесными растениями и склоном.

Объектами исследования были выбраны березы на склоне лесного оврага около деревни Ямолино Горномарийского района Республики Марий Эл. Эксперименты были проведены летом 2011 года (табл.1) на 30 березах.

Таблица 1 Периметры сечения комля на разных высотах, см № березы 1 2 3 4 5 7 8 9 10 11 12 13 14 15 Угол φ, град. 20 18 15 15 15 20 30 20 15 15 20 20 20 15 Диаметр D_1.3 20 20 15 18 20 20 25 20 35 20 24 20 20 27 Периметр сечения комля P_1.3 85 90 70 70 74 87 75 61 88 56 65 53 62 91 P_кш 87 95 75 80 79 90 85 71 110 72 67 81 75 110 P₁ 92 81 74 85 80 105 89 75 120 77 76 88 80 128 P₂ 106 120 80 104 85 96 98 79 125 84 80 90 85 135 P₃ 140 162 180 140 120 114 116 90 140 102 86 102 98 150 Высота сечения комля h₀ 130 130 130 130 130 130 130 130 130 130 130 130 130 130 h_кш 0 0 0 0 0 0 0 0 0 0 0 0 0 0 h₁ -19 -27 -15 -8 -6 -12 -17 -17 -12 -13 -18 -11 -13 -15 h₂ -40 -45 -24 -15 -10 -23 -30 -29 -20 -21 -28 -18 -20 -22 h₃ -81 -64 -60 -35 -36 -40 -48 -36 -40 -40 -41 -35 -45 -38 Высота h_max -70 -66 -69 -50 -40 -70 -80 -90 -115 -120 -115 -120 -117 -130

Продолжение таблицы 1 № березы 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 Угол φ, град. 20 20 20 20 15 15 20 15 15 15 15 15 20 15 15 Диаметр D_1.3 28 25 25 42 42 25 25 22 20 25 22 25 20 25 25 Периметр сечения комля P_1.3 85 69 76 122 114 88 90 77 75 88 75 80 90 75 76 P_кш 101 83 98 140 135 100 96 85 76 91 80 90 108 84 81 P₁ 105 90 101 147 145 106 98 89 81 100 85 95 105 88 84 P₂ 125 93 107 160 153 114 103 98 88 108 94 104 111 94 92 P₃ 134 106 116 188 176 126 112 108 102 122 100 118 128 108 110 Высота сечения комля h₀ 130 130 130 130 130 130 130 130 130 130 130 130 130 130 130 h_кш 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 h₁ -16 -13 -15 -16 -17 -22 -16 -22 -22 -25 -22 -22 -24 -20 -25 h₂ -31 -21 -28 -30 -30 -35 -28 -35 -40 -42 -38 -35 -40 -26 -38 h₃ -45 -40 -45 -40 -43 -50 -51 -60 -65 -71 -65 -55 -70 -62 -63 Высота h_max -115 -120 -105 -105 -107 -105 -104 -100 -100 -102 -103 -102 -103 -105 -103

Измерения формы комля (фиг.1) у дерева (фиг.2) в березняке (фиг.3) по боковой линии поверхности комля выполняется следующим образом.

Сначала определили участок оврага по методике, изложенной в патенте №2416193 РФ по прототипу, на склоне которого растут деревья. Выбрали учетные деревья для измерений в количестве 30 штук. Для измерений применяли гибкую мерную ленту и транспортир с отвесом. В ходе моделирования идентификацией устойчивых законов было выявлено, что дерево №6 имеет резко выделяющееся значение угла местного склона. В дальнейшем это наблюдение исключили из статистической выборки.

По принципу «от простого к сложному» можно предложить (табл.2) «кирпичики» для построения, по ходу структурно-параметрической идентификации биотехнического закона, любой статистической модели.

Таблица 2 Математические конструкты для построения статистической модели Фрагменты без предыстории изучаемого явления или процесса Фрагменты с предысторией изучаемого явления или процесса y=ax - закон линейного роста или спада (при отрицательном знаке перед правой стороной приведенной формулы) y=a - закон невлияния принятой переменной на показатель, который имеет предысторию значений y=ax^b - закон показательного роста (закон показательной гибели y=ax^-b не является устойчивым, из-за бесконечности при нулевом значении объясняющей переменной y=aexp(±cx) - закон Лапласа (Ципфа в биологии, Парето в экономике, Мандельброта в физике) экспоненциального роста или гибели, относительно которого создан метод операторных исчислений y=ax^bexp(-cx) - биотехнический закон в упрощенной форме y=aexp(±cx^d) - закон экспоненциального роста или гибели, - по автору статьи y=ax^bexp(-cx^d) - биотехнический закон, предложенный проф. П.М. Мазуркиным

В таблице 2 показаны все «нормальные» фрагменты, у которых впереди могут быть расположены оперативные константы, в виде знаков «+» или «-». Все шесть устойчивых законов распределения являются частными случаями биотехнического закона, показанного внизу таблицы 2.

Тогда формула (1) относится к математическому конструкту типа y=aexp(±cx) - закону Лапласа (Ципфа в биологии, Парето в экономике, Мандельброта в физике) экспоненциального роста или гибели (спада), относительно которого Лапласом был создан метод операторных исчислений.

Полученные данные из таблицы 1 обрабатывали в программной среде CurveExpert-1.3 по общей модели

где P - переменный периметр поперечного сечения комля в данном месте измерения на высотах от поверхности почвы до высоты 1,3 м, см; h - высота от поверхности почвы до корневой шейки (в таблице 1 отрицательные значения высоты), а далее до стандартной высоты 1,3 м, при этом корневая шейка получает значение высоты h=0; a ₁, a ₂ и a ₃ - параметры статистической модели (1), причем: a ₁ - начальное значение периметра комля дерева (абсолютный выбег комля в сечении в точке О на фиг.1 пересечения продольной оси ствола с поверхностью почвы); a ₂ - активность спада (относительного сбега от крайних корней первого порядка до корневой шейки и дальше на стволе дерева до высоты 1,3 м) периметра поперечного сечения комля по боковой линии симметричной формы комля; a ₃ - постоянный периметр ствола (по условному цилиндру) на высотах от поверхности почвы до нуля на уровне корневой шейки и далее до 1,3 м.

В таблице 3 даны результаты идентификации модели (1).

Таблица 3 Параметры модели формы комля березы на склоне лесного оврага № п/п Угол φ, град. D_1.3, см P_1.3, см Высота, м Параметры формы комля Коэффициент корреляции h₃ h_max H H_кр a b c 1 20 20 85 0.81 0.70 25 20 6.69037 0.026546 83.04457 0.9932 2 18 20 90 0.64 0.66 24 15 1.51942 0.060980 87.94076 0.9609 3 15 15 70 0.60 0.69 19 13 1.57073 0.070650 71.08551 0.9995 4 15 18 70 0.35 0.50 24 17 14.29537 0.046288 68.62046 0.9876 5 15 20 74 0.36 0.40 25 19 5.36991 0.059820 73.78199 0.9984 7 20 20 87 0.35 0.70 20 10 5.53268 0.034759 86.94283 0.8826 8 30 25 75 0.40 0.80 16 12 8.65897 0.032264 75.13772 0.9985 9 20 20 61 0.48 0.90 20 14 7.58516 0.034666 61.50150 0.9790 10 15 35 88 0.36 1.15 25 9 26.87762 0.018077 85.23958 0.9973 11 15 20 56 0.40 1.20 18 8 15.87560 0.026839 55.55888 0.9992 12 20 24 65 0.40 1.15 15 10 5.53349 0.034409 64.18781 0.9792 13 20 20 53 0.41 1.20 20 15 34.54058 0.013320 46.87999 0.9992 14 20 20 62 0.35 1.17 19 10 15.16259 0.020174 60.74845 0.9974 15 15 27 91 0.45 1.30 18 7 25.34656 0.023777 89.19265 0.9904 16 20 28 85 0.38 1.15 15 9 16.49362 0.025320 84.09267 0.9868 17 20 25 69 0.45 1.20 15 8 15.78504 0.022036 68.02200 0.9989 18 20 25 76 0.40 1.05 14 6 26.46798 0.011879 70.43326 0.9985 19 20 42 122 0.45 1.05 16 6 12.17655 0.040653 123.6581 0.9896 20 15 42 114 0.40 1.07 15 8 19.26593 0.026577 113.9366 0.9951 21 15 25 88 0.43 1.05 15 8 11.23616 0.024368 87.74433 0.9987 22 20 25 90 0.50 1.04 16 6 6.09201 0.025528 89.73489 0.9972 23 15 22 77 0.51 1.00 16 7 9.34285 0.020768 76.09297 0.9907 24 15 20 75 0.60 1.00 15 6 3.46519 0.032258 74.12755 0.9947 25 15 25 88 0.65 1.02 16 8 7.55135 0.022099 86.50699 0.9888 26 15 22 75 0.71 1.03 17 8 8.46063 0.018145 73.55011 0.9758

№ п/п Угол φ, град. D_1.3, см P_1.3, см Высота, м Параметры формы комля Коэффициент корреляции h₃ h_max H H_кр a b c 27 15 25 80 0.65 1.02 20 8 9.66769 0.025103 79.68765 0.9978 28 20 20 90 0.55 1.03 20 10 13.74723 0.014425 88.89935 0.9669 29 15 25 75 0.70 1.05 20 9 10.96744 0.018477 73.79080 0.9920 30 15 25 76 0.62 1.03 20 9 4.20086 0.033223 76.03804 0.9967

В таблицах 1 и 3 были приняты следующие условные обозначения:

φ - угол местного склона в месте произрастания дерева березы, град.;

D_1.3, P_1.3 - диаметр и периметр ствола березы на стандартной высоте 1,3 м от корневой шейки (фиг.1);

P_кш - периметр сечения ствола на корневой шейке, см;

P₁ - периметр комля березы на высоте между корневой шейкой и верхней точкой пересечения поверхности почвы с боковой линией комля, см;

P₂ - периметр комля березы над верхней точкой пересечения поверхности почвы с боковой линией комля, см;

P₃ - периметр комля березы в сечении над точкой пересечения поверхности почвы с вертикальной осевой линией комля дерева, см;

h₀ - стандартная высота 1,3 м (130 см);

h_кш - высота корневой шейки, равная нулю в принятой (относительно вертикальной осевой линии комля) системе координат, см;

h₁ - высота комля березы от корневой шейки до верхней точки пересечения поверхности почвы с боковой линией комля, см;

h₂ - высота комля березы от корневой шейки до верхней точки пересечения поверхности почвы с боковой линией комля, см;

h₃ - высота комля березы от корневой шейки до центральной точки пересечения поверхности почвы с вертикальной осевой линией комля дерева, см (в данных таблицы 3 для удобства сравнения с высотой дерева и высотой кроны дерева принят метр);

h_max - максимальная высота комля березы от корневой шейки до нижней точки пересечения поверхности почвы с боковой линией комля, см (в данных таблицы 3 для удобства сравнения принят метр);

H, H_кр - высоты дерева и кроны (фиг.2), м.

Из таблицы 3 видно, что адекватность модели (1) боковой линии нейлоидной формы комля очень высокая и по коэффициенту корреляции равна не меньше 0,8826. Максимальная теснота факторной связи равна 0,9995.

Далее примем правила отбора тех или иных бинарных факторных связей (1) для последующего математического и графического анализа.

В таблице 4 приведены интервалы изменения коэффициента корреляции при различных характеристиках связи между учтенными факторами.

Как известно из классической математической статистики, грубая классификация уровней коэффициента корреляции следующая:

а) до 0,3 - нет связи между факторами (то есть можно не учитывать эти связи, хотя они в других условиях проявления могут оказаться даже сильными по факторной связи);

б) от 0,3 до 0,7 - есть связь между двумя факторами, но она считается достаточно слабой, чтобы ее учитывать в практических выводах/однако дополнение волновыми возмущениями может перевести в сильные связи;

в) выше 0,7 - имеется сильная связь между переменными факторами даже при не волновых биотехнических закономерностях.

Таблица 4 Уровни факторных связей по коэффициенту корреляции Интервал коэффициента корреляции Характер тесноты связи между переменными факторами Существующая классификация Предлагаемая классификация Уточненная шкала для комля дерева 1 сильная связь однозначная однозначная 0,99…1,00 сильнейшая почти однозначная 0,95…0,99 сверхсильная 0,90…0,95 сильнейшая 0,7…0,9 сильная сильная 0,5…0,7 слабая связь средняя средняя 0,3…0,5 слабоватая слабоватая 0,1…0,3 нет связи слабая слабая 0,0…0,1 слабейшая слабейшая 0 нет связи нет связи

Однако такая шкала квантификации тесноты связи является очень грубой. Поэтому нами была предложена для технических экспериментов, в которых погрешность измерений не превышает 5%, другая шкала (третий столбец таблицы 4). Но для комля деревьев пришлось ввести еще два интервала, что нами было выполнено только при моделировании распределений рядов простых чисел. Это указывает на высокий уровень проявления закономерности (1) боковой линией комля березовых деревьев.

Тогда по значениям коэффициента корреляции из данных таблицы 3 получим четыре группы распределения формы комлей всех измеренных из части учетных (фиг.3) берез: I - 0,99-1,00; II - 0,95-0,99; III - 0,90-0,95; IV - 0,7-0,9. В первую группу попали 19 деревьев или 65,52%, во вторую группу - 9 деревьев или 31,03%, в третьей группе нет ни одного дерева, а в четвертой группе оказалось только одно дерево или 3,45% из общей численности 29 берез.

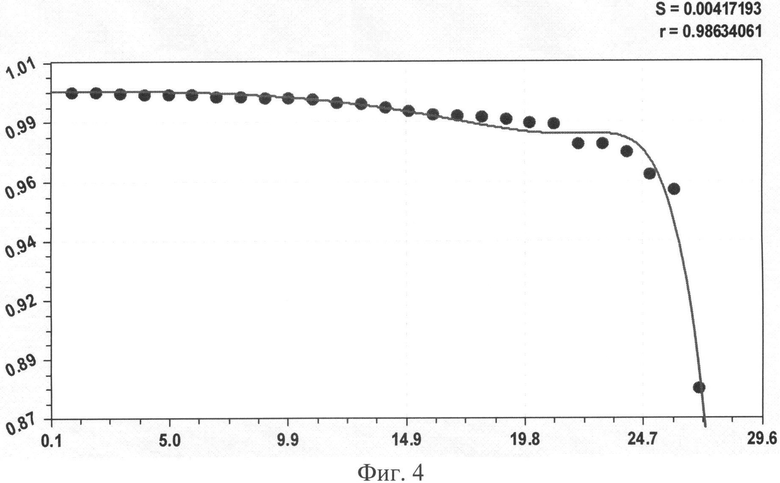
При этом в зависимости от рейтингового места i каждой березы из совокупности 29 деревьев коэффициент корреляции, по данным таблицы 3, получил (фиг.4) ранговое распределение в виде формулы

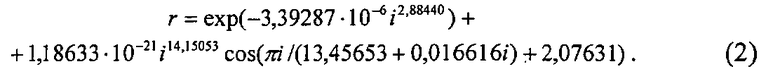
Формула (2) характеризует влияние экспериментатора на статистическую выборку. Первая составляющая является естественной составляющей, то есть коэффициент корреляции от наилучшей особи березы снижается по закону экспоненциальной гибели. Конечно же, этот закон зависит от отбора учетных берез в общей численности деревьев на пробной площади. Вторая составляющая, как правило, показывает антропогенное влияние. В данном примере оно характеризуется волновой закономерностью и график на фиг.4 показывает, что у последнего в рейтинге дерева комель резко отличается по своему качеству от остальных. Тогда следует ожидать, что при сплошном перечете деревьев по комлям формула (2) будет иметь более резкий спад по показателю тесноты факторной связи рангового распределения.

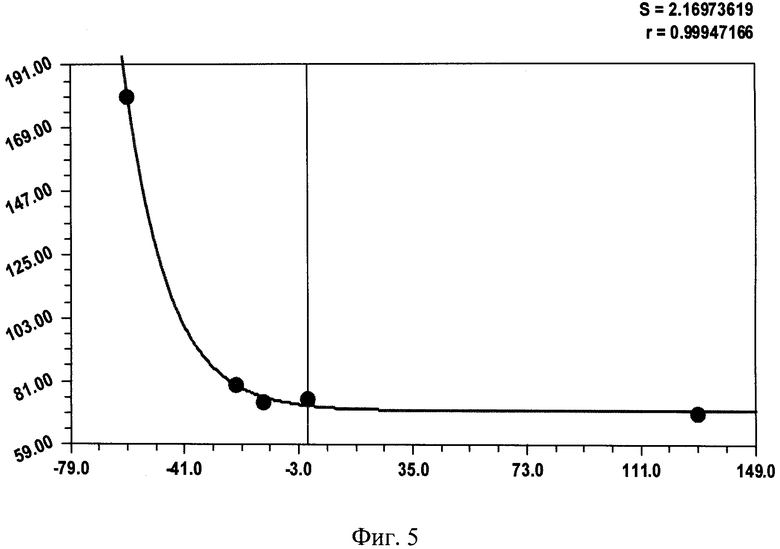
Береза №3 имеет самую математически правильную форму комля (фиг.5) с максимальным коэффициентом корреляции 0,9995.

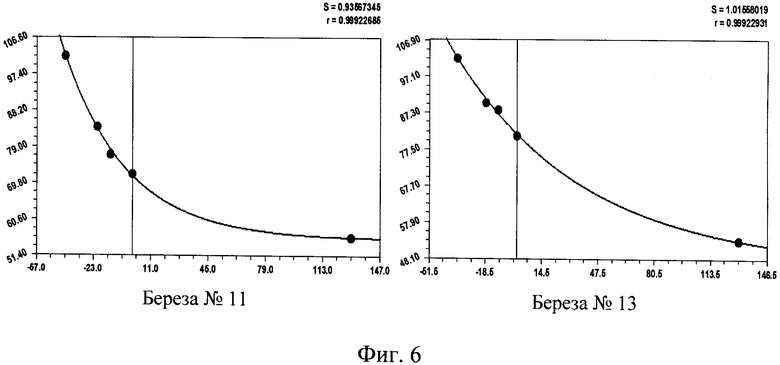
На фиг.6 показаны два дерева с одинаковым коэффициентом корреляции 0,9992. Как видно из сопоставления графиков, при этом форма комля по боковой линии различна.

Предпоследнее в рейтинге дерево березы №2 с коэффициентом корреляции формы показано на фиг.7, где имеется волновое возмущение боковой линии, а последнее дерево №7 с коэффициентом корреляции 0,8826 - на фиг.8. На последнем в рейтинге дереве березы еще четче видно колебательное возмущение боковой линии. Этот факт показывает, что этой особи пришлось труднее всех при колебательной адаптации комля к окружающей среде.

Параметры всех 29 моделей, по данным таблицы 4, изменяются в значительных пределах. Поэтому нами была выдвинута гипотеза о том, что комель дерева является своеобразным физическим «портретом» всего дерева и его места произрастания, поэтому значения параметров модели (1) сами должны зависеть от важнейших параметров растущего дерева.

Общее уравнение тренда (тенденции), то есть детерминированной закономерности без учета волновых возмущений, для всех 7×3=21 факторных отношений имеет вид

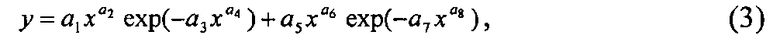
где y - показатель или зависимый количественный фактор, в нашем примере параметры формулы (1);

x - объясняющая переменная или влияющий фактор;

a ₁…a ₈ - параметры модели (3), получаемые идентификацией в программной среде CurveExpert1.38 или 1.40.

Эта двухчленная формула в каждом случае выявления закономерности была получена идентификацией устойчивых законов по таблице 2. При этом первая составляющая, как правило, показывает естественный процесс или явление, а вторая и последующие члены формулы (3) характеризуют, как правило, антропогенное влияние. Во многих случаев антропогенное влияние имеет характер колебательного возмущения.

В таблице 5 приведены результаты факторного влияния (по исходным данным из таблицы 3) на значения параметров модели (1).

На первом месте как влияющая переменная оказался диаметр на стандартной высоте, что указывает на правильность существующей в лесной таксации системы измерений лесных деревьев. Как зависимый показатель на первом месте находится первый параметр а формулы (1), то есть абсолютный сбег комля дерева.

Таблица 5 Факторный анализ влияния параметров берез на параметры модели (1) по детерминированным биотехническим закономерностям Параметры дерева (влияющий фактор x) Параметры формы комля Сумма коэфф. корр. Место I_x a b c Угол местного склона φ, град. 0,124 0,106 0,061 0,2910 7 Диаметр ствола D_1.3, см 0,367 0,652 0,7421 1,7611 1 Периметр ствола P_1.3, см 0,558 0,039 0,9951 1,5921 2 Высота при φ=0 комля h₃, м 0,474 0,009 0,081 0,5640 6 Высота при φ>0 комля h_max, м 0,662 0,7395 0,025 1,4265 3 Высота дерева березы H, м 0,068 0,364 0,133 0,5650 5 Высота кроны березы H_кр, м 0,162 0,487 0,349 0,9980 4 Сумма коэффициента корреляции 2,4150 2,3965 2,3862 7,1977 - Место I_y параметров модели 1 2 3 - 0,3427

Коэффициент коррелятивной вариации для всего множества влияния 7 влияющих переменных на три показателя равен 7,1977/21=0,3427.

Этот критерий (термин «коррелятивная вариация» по Ч. Дарвину) применяется при сравнении различных биологических объектов исследования, в данном случае группы из 29 берез, причем так можно сравнивать не только деревья и их группы в разных экологических условиях, но и растительные сообщества, находящие в разных местах произрастания.

Поэтому факторный анализ, проведенный по показателям одного и того же объекта исследования, имеет многогранное применение. Главное условие для факторного анализа это добротность и достоверность исходных данных. Тогда можно ожидать хороших результатов по выявлению биотехнических закономерностей между отдельными количественными факторами.

Из данных таблицы 5 видно, что наибольшую тесноту связи с коэффициентом корреляции 0,9951 имеет влияние периметра ствола P_1.3 на изменение третьего параметра модели (1), то есть на свободного члена, имеющего размерность и смысл теоретического периметра. Почти отсутствует факторная связь с наименьшим коэффициентом корреляции 0,009 влияния высоты комля вдоль продольной оси ствола на параметр b формулы (1), то есть на активность спада значений периметра или же на активность сбега боковой линии комля у берез.

Ранее нами была доказана волновая теория развития и роста деревьев. Поэтому проведена идентификация общей биотехнической закономерности

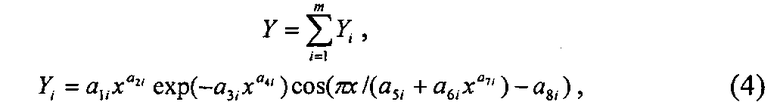
где Y - показатель, в нашем примере любой из трех параметров модели (1),

i - номер члена общей формулы,

m - количество составляющих общей формулы, шт.,

x - любой из семи влияющих переменных дерева и комля березы,

a ₁…a ₈ - параметры одного члена формулы (4), физически представляемого как асимметричный вейвлет-сигнал с переменными амплитудой и частотой колебательного возмущения совокупности (популяции) из 29 берез.

Данные идентификации модели (4) представлены в таблице 6. При этом волновыми оказались четыре закономерности или 400/21=19,05%. Их коэффициенты корреляции выделены крупным полужирным шрифтом.

.Таблица 6 Факторный анализ влияния параметров берез на параметры модели (1) по детерминированным и волновым биотехническим закономерностям Параметры дерева (влияющий фактор x) Параметры формы комля Сумма коэфф. корр. Место I_x a b c Угол местного склона φ, град. 0,124 0,106 0,061 0,291 1 Диаметр ствола D_1.3, см 0,367 0,652 0,7421 1,7611 2 Периметр ствола P_1.3, см 0,558 0,039 0,9951 1,5921 3 Высота при φ=0 комля h₃, м 0,474 0,009 0,081 0,56+4 6 Высота при φ>0 комля h_max, м 0,7716 0,8820 0,7444 2,398 1 Высота дерева березы H, м 0,068 0,364 0,133 0,565 5 Высота кроны березы H_кр, м 0,162 0,7093 0,349 1,2203 4 Сумма коэффициентов корреляции 2,5246 2,7613 3,1056 8,3915   Место I_y параметров модели 3 2 1 - 0,3996

С учетом принципа колебательной адаптации деревьев к условиям места своего произрастания на первое место среди параметров деревьев встала максимальная высота комля березы. Остальные шесть параметров остались в той же последовательности, что было при детерминированном представлении развития и роста древесных растений.

Коэффициент коррелятивной вариации, из-за волнового влияния максимальной высоты комля и высоты кроны дерева на формирование комля, повысился на 100×(0,3996-0,3427)/0,3427=16,55%.

Иерархия показателей a, b и c перевернулась и стала в новом рейтинге колебательного возмущения последовательностью c, b и a. В этом случае теоретический периметр поперечного сечения ствола на высоте 1,3 м оказывается наиболее значимым зависимым показателем. Это позволит в будущем обратить особое внимание на соотношение периметра к диаметру.

Таким образом, экологическая таксация деревьев коренным образом отличается от технической таксации стволов на древесину в виде кругляка. При этом модель (4) может быть доведена при моделировании по остаткам от предыдущих волновых составляющих даже ниже погрешности измерений.

Далее из таблицы 6 выделим закономерности с убывающими значениями коэффициента корреляции, то есть выполним ранжирование полученных биотехнических закономерностей по ухудшению их адекватности. В таблице 7 оставлены только сильные связи, то есть закономерности с коэффициентами корреляции свыше 0,7. В итоге доля сильных факторных связей оказалось равной 100×6/21=28,57%.

.Таблица 7 Сильные факторные связи влияния параметров берез на параметры модели (1) по детерминированным и волновым биотехническим закономерностям Параметры дерева (влияющий фактор x) Параметры формы комля a b c Угол местного склона φ, град.       Диаметр ствола D_1.3, см     0,7421 Периметр ствола P_1.3, см     0,9951 Высота при φ=0 комля h₃, м       Высота при φ<0 комля h_max, м 0,7716 0,8820 0,7444 Высота дерева березы H, м       Высота кроны березы H_кр, м   0,7093  

Из семи параметров деревьев березы три выпадают при уровне адекватности с коэффициентом корреляции выше 0,7. В итоге остаются только шесть закономерностей, которые приведем полностью в таблице 8 по убыванию их адекватности.

Таблица 8 Параметры общего уравнения (4) для сильных фауторов связей Номер i Вейвлет-сигнал $$Y_i=a_{1i}{x}^{a_{2i}}\exp \left(-a_{3i}{x}^{a_{4i}}\right)\cos \left(\pi x/\left(a_{5i}+a_{6i}{x}^{a_{7i}}\right)-a_{8i}\right)$$ амплитуда колебания полупериод колебания сдвиг a _1i a _2i a _3i a _4i a _5i a _6i a _7i a _8i Влияние периметра ствола P_1.3 на параметр с (фиг.9), коэффициент корреляции 0,9951 1 0,81164 1,04444 0 0 0 0 0 0 Влияние высоты комля h_max на параметр b (фиг.10), коэффициент корреляции 0,8820 1 0,12751 0 1,51799 1,19775 0 0 0 0 2 -2,83740е+9 15,61329 27,78498 1 0,038069 0,00014894 27,30161 2,39313 Влияние высоты комля h_max на параметр a (фиг.11), коэффициент корреляции 0,7716 1 0,010269 0 -7,05156 0,50604 0 0 0 0 2 -0,21501 0 -2,99769 1 -3,17374 3,24198 0,0024367 2,50904 3 240,27165 0 5,036881 1 0,11780 0,025113 1,95649 5,43455 Влияние высоты комля h_max на параметр с (фиг.12), коэффициент корреляции 0,7444 1 73,37379 0 -0,049923 0,40903 0 0 0 0 2 -4742,0259 2,57229 5,49302 0,0074645 0,66005 -0,29744 1,49662 -5,14666 Влияние диаметра ствола D_1.3 на параметр с (фиг.13), коэффициент корреляции 0,7421 1 46,33420 0 -0,021440 1 0 0 0 0 Влияние высоты кроны H_кр на параметр b (фиг.14), коэффициент корреляции 0,7093 1 0,013306 0 -0,17573 0,70463 0 0 0 0 2 0,0021097 0 -0,17164 0,91488 7,44397 -0,15644 1,06891 -4,50361

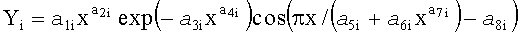
Высокий уровень адекватности формы комля у всех 29 берез позволяет повести дальше полный факторный анализ параметров модели (1). Для идентификации была применена общая формула (4).

Таким образом, предлагаемое техническое решение основано на результатах фундаментальных исследований влияния высоты поперечных сечений ствола и комля дерева на периметр этих сечений, а также влияния параметров комлевой части и высоты кроны лесных деревьев, произрастающих как единая популяция и как микрогеотехническая система десятилетиями на склоне оврага. Оказалось, что угол местного склона почти не влияет на изучаемые показатели.

При этом измерения по предлагаемому способу просты в исполнении и наглядны для школьников при изучении деревьев в экологических кружках.

Поэтому предлагаемый способ измерения и анализа комля растущих на ровной местности или же на склонах оврагов, холмов, террас и берегов водных объектов может быть применен в индикации не только рельефа, но и фитоиндикации отдельных мест произрастания древесных растений на пробных площадях. Минимальное количество учетных деревьев определяется возможностью идентификации биотехнических закономерностей с волновыми составляющими и должно быть не менее 30 особей одного вида.

Изобретение относится к дендрометрии при изучении роста и развития комля деревьев, преимущественно берез, и может быть использовано при фитоиндикации территорий и разработке мероприятий по защите земельных участков от водной эрозии, экологических и климатических технологий, а также в дендроэкологическом мониторинге за развитием овражной сети и рационализации землепользования с учетом изменений формы комля растущих, в частности, березовых деревьев. Cпособ включает выбор пробной площади с учетными деревьями, измерение высоты кроны и полной высоты всех учетных деревьев. Форму комля как симметричную геометрическую фигуру учитывают от поперечного сечения комля на пересечении с поверхность почвы до стандартной высоты 1,3 м. Проводят измерения периметров комля не менее чем в трех поперечных сечениях комля каждого учетного дерева ниже корневой шейки ствола, а по измеренным данным, дополнительно с учетом периметров корневой шейки и сечения ствола на стандартной высоте 1,3 м, выявляют математическую закономерность симметричной формы комля по единой общей формуле. По параметрам выявленной единой математической закономерности формы комля выявляют рейтинг учетных деревьев для оценки качества формы комля, после чего выявляют закономерности с волновыми возмущениями влияния параметров учетных деревьев и их комлей на параметры в общем виде у математического уравнения формы комля. Для оценки качества места произрастания выделяют закономерности с волновыми возмущениями с сильной теснотой коррелятивной вариации для последующего выделения лимитирующих факторов комля и самого учетного дерева. Способ обеспечивает расширение функциональных возможностей анализа формы комля деревьев, прежде всего берез, произрастающих на ровной местности или на склоне оврага, а также повышение точности измерений деревьев ниже корневой шейки, начиная от стандартной высоты ствола в 1,3 м над корневой шейкой дерева до поверхности почвы. 5 з.п. ф-лы, 14 ил., 8 табл., 1 пр.

1. Способ анализа формы комля дерева, включающий выбор пробной площади с учетными деревьями, измерение высоты кроны и полной высоты всех учетных деревьев, причем форму комля как симметричную геометрическую фигуру учитывают от поперечного сечения комля на пересечении с поверхностью почвы до стандартной высоты 1,3 м, при этом измерения периметров комля проводят не менее чем в трех поперечных сечениях комля каждого учетного дерева ниже корневой шейки ствола, а по измеренным данным, дополнительно с учетом периметров корневой шейки и сечения ствола на стандартной высоте 1,3 м, выявляют математическую закономерность симметричной формы комля по единой общей формуле, затем по параметрам выявленной единой математической закономерности формы комля выявляют рейтинг учетных деревьев для оценки качества формы комля, после чего выявляют закономерности с волновыми возмущениями влияния параметров учетных деревьев и их комлей на параметры в общем виде у математического уравнения формы комля, а затем для оценки качества места произрастания выделяют закономерности с волновыми возмущениями с сильной теснотой коррелятивной вариации для последующего выделения лимитирующих факторов комля и самого учетного дерева.

2. Способ анализа формы комля дерева по п.1, отличающийся тем, что у учетных деревьев, произрастающих на склоне, ниже корневой шейки ствола измерения периметров комля проводят не менее чем в трех поперечных сечениях комля каждого учетного дерева, в частности:
в первом сечении измеряют периметр на высоте между корневой шейкой и верхней точкой пересечения поверхности почвы с боковой линией комля;
во втором сечении измеряют периметр комля дерева на верхней точке пересечения поверхности почвы с боковой линией комля;
в третьем сечении измеряют полупериметр комля дерева в сечении в точке пересечения поверхности почвы с вертикальной осевой линией комля дерева.

3. Способ анализа формы комля дерева по п.1, отличающийся тем, что при не нулевом угле местного склона дополнительно измеряют от корневой шейки ствола максимальную высоту комля на нижней стороне склона оврага, или холма, или террасы, или берега до нижней точки пересечения поверхности почвы с боковой линией комля учетного дерева.

4. Способ анализа формы комля дерева по п.1, отличающийся тем, что математическую закономерность симметричной формы комля выявляют по единой общей формуле:
,
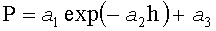где P - переменный периметр поперечного сечения комля в данном месте измерения на разных высотах от корневой шейки;
h - высота от корневой шейки до поверхности почвы с отрицательными значениями не менее чем в трех поперечных сечениях комля каждого учетного дерева, а далее положительная стандартная высота 1,3 м, при этом корневая шейка получает значение высоты h=0;
a ₁, a ₂ и a ₃ - параметры статистической модели, причем:
a ₁ - начальное значение периметра комля дерева, физически представляемое как абсолютный выбег комля от ствола или сбег ствола учетного дерева от комля в точке пересечения продольной оси ствола с поверхностью почвы;
a ₂ - активность спада, то есть относительного сбега от крайних корней первого порядка до корневой шейки и дальше на стволе дерева до высоты 1,3 м, переменного периметра поперечного сечения комля учетного дерева по боковой линии симметричной формы;
a ₃ - постоянный периметр ствола по условному цилиндру на высотах от поверхности почвы до корневой шейки ствола учетного дерева и далее до высоты 1,3 м.

5. Способ анализа формы комля дерева по п.1, отличающийся тем, что рейтинг этих учетных деревьев для оценки качества формы комля выполняют по убыванию значений коэффициента корреляции по уравнению:
,
где r - коэффициент корреляции, мера тесноты связи между факторами,
i - номер места в рейтинге, занимаемого каждым учетным деревом,
b₁…b₈ - параметры вышеуказанной модели рангового распределения коэффициентов корреляции всех учетных деревьев на пробной площади.

6. Способ анализа формы комля дерева по п.1, отличающийся тем, что для обобщенной боковой линии формы комля по множеству учетных деревьев на пробной площади выявляют закономерности с волновыми возмущениями влияния параметров учетных деревьев на параметры уравнения формы комля в следующем общем виде:
,
где Y - показатель, в нашем примере любой из трех параметров модели по единой общей формуле,
i - номер члена вышеуказанной формулы,
m - количество составляющих вышеуказанной формулы, шт.,
x - любой из влияющих переменных дерева и его комля,
a ₁…a ₈ - параметры одного члена вышеуказанной формулы, физически представляемого как асимметричный вейвлет-сигнал с переменными амплитудой и частотой колебательного возмущения всей совокупности или части популяции из множества учетных деревьев.