Изобретение относится к области электротехники, в частности к способу и устройству на его основе, в задачу которого входит определение некоторых параметров установившегося режима функционирования объекта электротехнического назначения системы переменного тока, например, промышленной частоты fc, когда из-за имеющих место в системе электроснабжения физических процессов аналоговые периодические электрические сигналы f(t) (токи, протекающие через элементы системы электроснабжения, напряжения на них) отличаются от синусоидальной формы, т.е. в общем случае являются аналоговыми периодическими несинусоидальными электрическими величинами f(t), которые представляют в виде суммы из k простых f(k)(t)=Am(k)sin(ωct+ψ(k)) гармонических электрических сигналов:
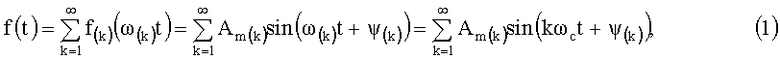
где k=1,2,3, … - целые числа, задающие как кратность частоты k-той гармоники, так и определяющие ее номер; Am(k) - амплитуда k-той гармоники; ψ(k) - начальная фаза колебания k-той гармоники; ω(k)=kωc - угловая частота k-той гармоники; ω(1)=ωс=2πfc - угловая частота основной первой гармоники (k=1), определяемой промышленной частотой f(1)=fc системы электроснабжения, при этом интересующий параметр функционирования объекта электротехнического назначения системы электроснабжения промышленной частоты связывают со значениями амплитуды Am(k=1) и начальной фазы колебания ψ(k=1) основной (k=1) гармоники f(1)(t)=Am(1)sin(ωct+ψ(1)), которая входит в структуру соответствующего электрического сигнала (1), т.е. либо мгновенного значения тока f(t)=i(t), либо мгновенного значения напряжения f(t)=u(t).
Наиболее близким по технической сущности является принятый за прототип способ по патенту «Патент №2442180 (RU), МПК G01R 29/00. Способ определения параметров гармоники несинусоидального электрического сигнала [Текст] / Мамаев В.А. (RU), Кононова Н.Н. (RU); заявитель и патентообладатель Северо-Кавказский государственный технический университет (RU). - №2010141291/28; заявл. 07.10.2010: опубл. №10.02.12. Бюл. №4». На основе способа по прототипу микропроцессорный информационный преобразователь МИП, из поданного на его вход аналогового несинусоидального периодического электрического сигнала f(t) (1) на своем выходе в цифровой форме генерирует информацию о параметрах входящей в состав аналогового электрического сигнала f(t) (1) k-той гармоники, а именно амплитуде Am(k) и начальной фазе колебания ψ(k) этой гармоники, при этом микропроцессорный информационный преобразователь МИП включает линейный (ЛП) и нелинейный (НП) преобразователи, причем линейный преобразователь ЛП переводит в цифровой формат fц(t) поданный на его вход аналоговый несинусоидальный периодический электрический сигнал f(t) (1), который с выхода линейного преобразователя ЛП подают на вход нелинейного преобразователя НП.
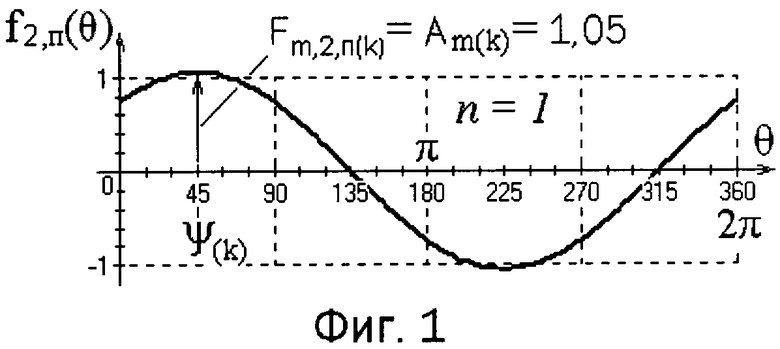
В прототипе приведены возможные алгоритмы, которые, будучи использованные в конкретном техническом устройстве, обеспечивают решение задачи по определению амплитуды Am(k) и начальной фазы колебания ψ(k) k-той гармоники. Среди предложенных в патенте RU №2442180 алгоритмов имеется относительно простой, в основе которого используют поиск координат максимума особым образом сформированной функции, у которой по прототипу в качестве аргумента используют вводимый в вычислительный процесс изменяемый угол θ, при этом сформированной функцией для k-той гармоники является функцией синуса, у которой максимальные значения имеют место при двух значениях изменяемого угла θ, один из которых однозначно интерпретируют как начальную фазу колебания ψ(k) k-той гармоники (фиг.1).
Недостатками простого алгоритма определения амплитуды Am(k) и начальной фазы колебания ψ(k) k-той гармоники по прототипу являются, во-первых, недостаточная точность определения конкретного значения начальной фазы колебания ψ(k) k-той гармоники, что обусловлено малой скоростью изменения производной у специально формируемой по патенту RU №2442180 функции синуса (2), аргументом которой является вводимый в вычислительный процесс изменяемый угол θ (фиг.1). Вторым недостатком является необходимость из двух значений аргумента 9 осуществить выбор истинного значения начальной фазы колебания ψ(k) k-той гармоники.
По выполняемым задачам НП можно условно рассматривать состоящим из функциональных нелинейных преобразователей ФНП, каждый из которых решает отдельную частную задачу.
Общими между прототипом и предлагаемым изобретением являются линейный преобразователь ЛП и входящие в структуру нелинейного преобразователя НП первый 1ФНП и второй 2ФНП функциональные нелинейные преобразователи (фиг.2). При этом линейный преобразователь ЛП поданный на его вход аналоговый электрический сигнал f(t) (1) преобразует в цифровой сигнал fц(t), который с выхода линейного преобразователя ЛП подают на первый вход первого функционального нелинейного преобразователя 1ФНП. Согласно прототипу (патент RU №2442180) на второй вход первого функционального нелинейного преобразователя 1ФНП подают изменяющуюся по закону синуса функцию со структурой 1·sin(ω(k)·t+θ), которая имеет единичную амплитуду и аргумент, который определяется через сумму двух слагаемых, причем первое слагаемое является произведением круговой частоты ω(k)=kωc k-той гармоники и времени t, а второе слагаемое согласно прототипу является вводимым дополнительным изменяемым (скользящим) фазовым углом колебания θ, при этом изменяющуюся по закону синуса функцию 1·sin(kωct+θ) специально генерирует нелинейный преобразователь НП. Первый функциональный нелинейный преобразователь 1ФНП перемножает поданные на его первый и второй входы сигналы и в результате на выходе первого функционального нелинейного преобразователя 1ФНП согласно принятым в описании предлагаемого изобретения обозначениям формирует первую функцию преобразования f1,п(t,θ):
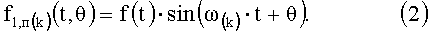
Первая функция преобразования f1,п(k)(t,θ) (2) согласно прототипу поступает на вход второго функционального нелинейного преобразователя 2ФНП. Этот преобразователь выполняет операцию определенного интегрирования по временному параметру первой функции преобразования f1,п(k)(t,θ) согласно выражению
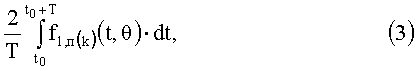
в котором Т=1/fc - период входящей в выражение (1) основной гармоники (k=1; f(1)=fc); t0 - момент запуска второго функционального нелинейного преобразователя 2ФНП на выполнение операции интегрирования.
В результате на своем выходе второй функциональный нелинейный преобразователь 2ФНП формирует вторую функцию преобразования f2,п(k)(θ) следующей структуры
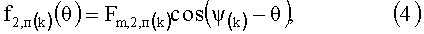
которая зависит только от вводимого дополнительного изменяемого (скользящего) фазового угла колебания θ и имеет амплитуду Fm,2,п(k), равную амплитуде Am(k) k-той гармоники, т.е. Am(k)=Fm,2,п(k).
По прототипу наиболее простой вариант определения значений Am(k) и ψ(k) основан на поиске параметров координат экстремумов функции (4) (фиг.1) на интервале интегрирования от t0 до t0+T, которые имеют место при двух значениях θ1,(k)=ψ(k) и θ2,(k)=ψ(k)±π k-той гармоники, одно из которых является истинным значением начальной фазы колебания ψ(k) k-той гармоники.
Положительный эффект от предлагаемого изобретения заключается в повышении точности определения начальной фазы колебания ψ(k) k-той гармоники и упрощении процедуры однозначного получения этого результата. Указанный положительный эффект достигают в результате того, что согласно изобретению формируют такую функциональную зависимость от изменяемого (скользящего) угла θ, которая на основе использования известных методов поиска параметров координат максимума функциональных зависимостей обеспечивает повышение точности определения такого значения угла θ=θ(k), при котором у формируемой согласно изобретению функциональной зависимости имеет место максимальное значение, причем полученное значение угла θ=θ(k) однозначно интерпретируют в качестве начальной фазы колебания θ(k)=ψ(k) k-той гармоники, которая входит в состав аналоговой периодической несинусоидальной электрической величины f(t) (1).
Возможность получения положительного эффекта от применения предлагаемого изобретения далее подтверждается соответствующими аналитическими выкладками. На их основе задают выполняемые функции вводимых согласно предлагаемому изобретению в структуру нелинейного преобразователя НП третьего, четвертого, пятого и шестого нелинейных функциональных преобразователей 3-6ФНП и через указанные связи между ними задают последовательность их действий (фиг.2).
С использованием выражения (2) в предлагаемом изобретении на основе выражения (5) посредством третьего нелинейного функционального преобразователя 3НФП формируют третью функцию преобразования f3,п(k)(θ):
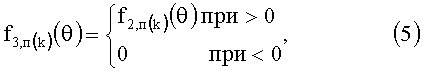
т.е. третий нелинейный функциональный преобразователь 3НФП из второй функции преобразования f2,п(θ) выделяет ее положительные значения, т.е. третья функции преобразования f3,п(k)(θ) состоит только из положительных однополярных импульсов функции косинуса (4), которые имеют амплитуды Fm,3,п(k), равные амплитуде k-той гармоники, т.е. Fm,3,п(k)=Fm,2,п(k)=Am(k).
Согласно предлагаемому изобретению третью функцию преобразования f3,п(k)(θ) умножают на вспомогательного коэффициента Квсп и формируют четвертую функцию преобразования f4,п(k)(θ)

причем на значение вспомогательного коэффициента Квсп накладывают условие, которое заключается в том, чтобы произведение (7) было больше единице во всем ожидаемом диапазоне изменения амплитуды k-той гармоники от Am(k),min до Am(k),max:
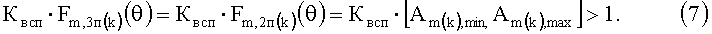
Преобразование (7) в предлагаемом изобретении осуществляет четвертый нелинейный функциональный преобразователь 4НФП.
Согласно предлагаемому изобретению четвертую функцию преобразования f4,п(k)(θ) (6) в возводят во вводимую в вычислительный процесс положительную степень n и получают пятую функцию преобразования f5,п(k)(θ) согласно следующему выражению
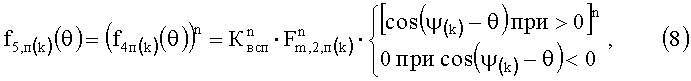
Преобразование (8) в предлагаемом изобретении осуществляет пятый нелинейный функциональный преобразователь 5НФП.
Пятая функция преобразования f5,п(k)(θ) (8) имеет единственный максимум при условии θ=ψ(k).
Согласно предлагаемому изобретению для получения значения начального фазового угла колебания ψ(k) k-той гармоники используют один из известных алгоритмов поиска координат экстремальных точек функции, который применяют для зависимости (8) на интервале изменения вводимого дополнительного фазового угла колебания θ.
В предлагаемом изобретении поиск значения начального фазового угла колебания ψ(k) k-той гармоники осуществляет шестой нелинейный функциональный преобразователь 6НФП, который на своем выходе в цифровой форме генерирует информацию о значении начального фазового угла колебания ψ(k) k-той гармоники.
В предлагаемом изобретении однозначность получения значения начального фазового угла колебания ψ(k) k-той гармоники обеспечена самой структурой третьей функции преобразования f3,п(k)(θ) (5).
Повышение точности получения значения начального фазового угла колебания ψ(k) k-той гармоники по предлагаемому изобретению обусловлено повышением скорости изменения производной пятой функции преобразования f5,п(k)(θ) (8), которую можно оценить на основе ее сопоставления с производной от второй функций преобразования f2,п(k)(θ) (4). Отношение производных в окрестностях значения начального фазового угла ψ(k) k-той гармоники примерно определяется выражением
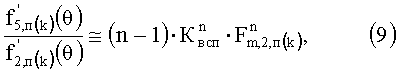
которое при соблюдении условия (7) будет больше единицы, причем чем бόльшее значение использовано для вспомогательного коэффициента Квсп, тем больше скорость изменения пятой функции преобразования f5,п(k)(θ) (8) в окрестности ее максимума, тем при выборе соответствующего алгоритма поиска координат максимума этой функции больше точность определения значения начального фазового угла ψ(k) k-той гармоники.
В выражении (6) значение используемого вспомогательного коэффициента Квсп в общем случае должно обеспечивать соблюдение требования условия (7). Для обеспечения этих требований можно, например, рекомендовать следующие возможные варианты.
Согласно первому простому варианту условие (7) можно соблюсти, если известно ожидаемое значение минимальной амплитуды Am(k),min k-той гармоники. Тогда значение вспомогательного коэффициента Квсп можно определить из условия
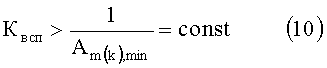
т.е. значение вспомогательного коэффициента Квсп не будет зависеть от амплитуды гармоники Am(k) k-той гармоники, у которой ее значение может быть больше Am(k),min.
По второму варианту вспомогательный коэффициент Квсп рассчитывают для каждого значения амплитуды Am(k) k-той гармоники непосредственно в процессе определения начального фазового угла колебания ψ(k) k-той гармоники, т.е. во втором варианте имеет место адаптивный процесс вычисления вспомогательного коэффициента Квсп.
Теоретической основой второго адаптивного варианта вычисления вспомогательного коэффициента Квсп являются следующие математические выражения. Непосредственное вычисление этого коэффициента осуществляется по следующему выражению
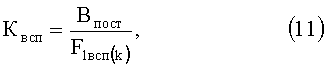
в котором текущее первое вспомогательное F1всп(k) числовое значение определяют по выражению (12) посредством выполнения операции определенного интегрирования выражения (5) на интервале от 0 до 2π:
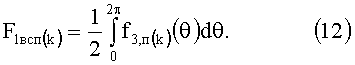
В выражении (11) Впост является вводимой в вычислительный процесс положительной числовой константой, которую предварительно определяют по выражению
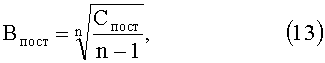
в котором числовой постоянный коэффициент Спост должен быть больше единицы, т.е. Спост>1.
Второй вариант определения вспомогательного коэффициента Квсп обеспечивает получение бόльшего единицы его постоянного значения, которое не зависит от текущего значения амплитуды Fm,2,п(k), однозначно связанного с амплитудой Am(k) k-той гармоники.
Учитывая наличие однозначной связи между Fm,2,п(k) и Am(k), при использовании второго адаптивного варианта вычисления вспомогательного коэффициента Квсп способ приобретает функцию, обеспечивающую определение амплитуды Am(k) k-той гармоники.
Из приведенных теоретических выкладок сущность предлагаемого способа определения начальной фазы колебания гармоники несинусоидального периодического электрического сигнала f(t) с периодом повторения Т, т.е. определение начальной фазы ψ(k) колебания входящей в структуру несинусоидального периодического электрического сигнала f(t) (1) k-той гармоники заключается в том, что способ определяет алгоритм функционирования микропроцессорного измерительного преобразователя МИП, который решает задачу определения начальной фазы колебания ψ(k) k-той гармоники, при этом микропроцессорный измерительный преобразователь МИП состоит из линейного ЛП и нелинейного НП преобразователей, причем линейный преобразователь ЛП поступающий на его вход несинусоидальный периодический электрический аналоговый сигнал f(t) преобразует в цифровой сигнал fц(t), который подают на вход нелинейного преобразователя НП, который в своей структуре содержит реализуемые согласно прототипу (патент RU №2442180) первый 1ФНП и второй 2ФНП функциональные нелинейные преобразователи, при этом на первый вход первого функционального нелинейного преобразователя 1ФНП подан цифровой сигнал fц(t), а на его второй вход подана синтезируемая средствами микропроцессора в цифровой форме синусоидальная функция 1·sin(ω(k)t+θ) с единичной амплитудой, у которой аргумент состоит из суммы двух слагаемых, причем первое слагаемое аргумента задано произведением циклической частоты ω(k) k-той гармоники и времени t, а второе слагаемое задано изменяемым (скользящим) фазовым углом θ, при этом первый функциональный нелинейный преобразователь 1ФНП перемножает поданные на его первый и второй входы функциональные зависимости и на своем выходе формирует первую функцию преобразования f1,п(k)(t,θ) (2), которая является как функцией времени t, так и изменяемого (скользящего) фазового угла θ, при этом первую функцию преобразования f1,п(k)(t,θ) подают на вход второго 2ФНП функционального нелинейного преобразователя, который выполняет операцию определенного интегрирования в пределах интервала времени, равного периоду Т первой функции преобразования f1,п(k)(t,θ) (3), причем результат преобразования в виде второй функции преобразования f2,п(k)(θ) (4) для k-той гармоники определяется гармонической функцией косинуса только от изменяемого (скользящего) фазового угла θ, отличается тем, что в структуру нелинейного преобразователя НП вводят третий, четвертый, пятый и шестой функциональные нелинейные преобразователи 3-6ФНП, при этом третий функциональный нелинейный преобразователь 3ФНП из поданной на его вход второй функции преобразования f2,п(k)(θ) путем выделения положительных ее значений на своем выходе формирует для k-той гармоники третью функцию преобразования f3,п(k)(θ) (5), которую подают на второй вход четвертого функционального нелинейного преобразователя 4ФНП, при этом на первый вход четвертого функционального нелинейного преобразователя 4ФНП подают бόльший единице вспомогательный коэффициент Квсп, причем четвертый функциональный нелинейный преобразователь 4ФНП перемножает поданные на его первый и второй входы сигналы и на своем выходе формирует четвертую функцию преобразования f4,п(k)(θ) (6), которую подают на первый вход пятого функционального преобразователя 5ФНП, при этом на его второй вход падают положительное больше единице число n, которое рассматривают как показатель степени, причем пятый функциональный преобразователь 5ФНП возводит в степень n поданную на его первый вход четвертую функцию преобразования f4,п(k)(θ) и на своем выходе формирует пятую функцию преобразования f5,п(k)(θ) (8), которую подают на вход шестого функционального преобразователя 6ФНП, который одним из известных методов осуществляет поиск такого аргумента пятой функции преобразования f5,п(k)(9) (8), при котором эта функция имеет максимальное значение, при этом удовлетворяющее этому условию значение аргумента θ является начальной фазой ψ(k) колебания k-той гармоники, причем подаваемый на первый вход четвертого функционального преобразователя 4ФНП вспомогательный коэффициент Квсп с соблюдением определенных требований принимают либо постоянным (10), либо аналитически рассчитывают (11) непосредственно в вычислительном процессе, связанным с определением начальной фазой ψ(k) колебания k-той гармоники.
Фиг.1, 2, 3 и 4 поясняют сущность предлагаемого изобретения.
График на фиг.1 соответствует случаю n=1, т.е. функциональной зависимости f2,п(k)(θ) (4), которая лежит в основе поиска начальной фазы колебания ψ(k) k-той гармоники по патенту RU №2442180. Амплитуда k-той гармоники принята равной 1,05 условных единиц, т.е. Fm,2,п(k)=Am(k)=1,05 у.е., начальная фаза колебания k-той гармоники принята равной ψ(k)=45°.
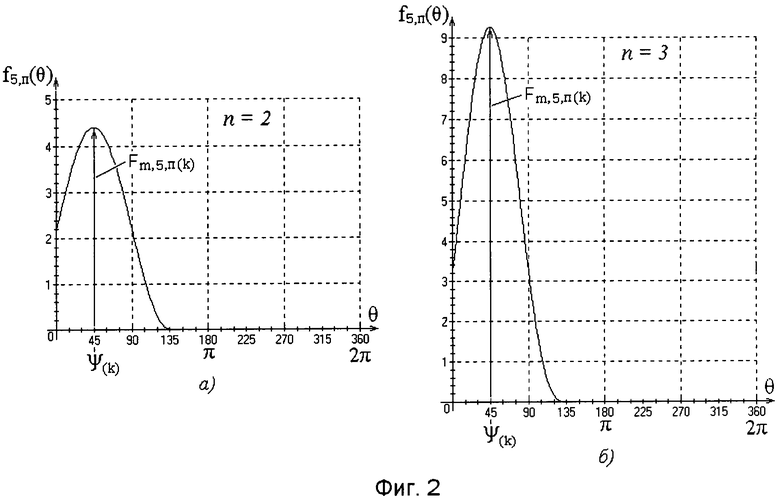
На фиг.2, а и 2, б для k-той гармоники с параметрами Am(k)=1,05 у.е. и ψ(k)=45° приведены построенные графики для пятой функции преобразования f5,п(k)(θ) (10), полученные в результате возведения в положительную бόльшую единице степень n (соответственно n=2 и n=3) четвертой функции преобразования f4,п(k)(θ) при использовании постоянного вспомогательного положительного коэффициента Квсп, равного двум.
Графические зависимости на фиг.2, а и 2, б иллюстрируют характер изменение пятой функции преобразования f5,п(k)(θ) (8) от используемых значений степеней, например n=2; 3. Сопоставление графиков на фиг.2 с графиком на фиг.1 подтверждают следуемые из предлагаемого изобретения преимущества в определении значения начальной фазы ψ(k) колебания k-той гармоники, которые обусловлены увеличением скорости изменения производной в окрестности максимума Fm,5,п(k) пятой функции преобразования f5,п(k)(θ) при использовании степени n>1.
На фиг.3 приведена упрощенная блок-схема микропроцессорного измерительного преобразователя МИП с указанием входящих в его структуру блоков и связей между ними. Пуск микропроцессорного измерительного преобразователя МИП на выполнение вычислительных процедур, связанных с определением начальной фазы колебания ψ(k) k-той гармоники, осуществляется командой ПУСК от измерительно-логического устройства, в состав которого, как вычислительный компонент, входит микропроцессорный измерительный преобразователь МИП.
Блок-схема (фиг.3) поясняет сущность алгоритма функционирования МИП, который состоит из двух основных преобразователей: линейного ЛП и нелинейного НП преобразователей. Преобразователь ЛП поступающий на его вход аналоговый несинусоидальный периодический электрический сигнал f(t) (1) переводит в цифровой вид fц(t). Преобразователь НП условно представлен в виде шести функциональных нелинейных преобразователей 1-6ФНП, при этом каждый из них решает свою частную задачу, причем преобразователи 1ФНП-2ФНП функционируют по приведенным в патенте RU №2442180 алгоритмам. Функциональный нелинейный преобразователь 1ФНП осуществляет перемножение поступающих соответственно на его первый вход сигнала fц(t) и на его второй вход генерируемого входящим в структуру МИП микропроцессором сигнала в форме синусоидальной функции 1·sin(ω(k)t+θ). Результатом действия функционального нелинейного преобразователя 1ФНП является преобразование сигнала fц(t), как функции только от времени t, в первую функцию преобразования f1,п(k)(t,θ) (3), которая является уже функцией двух переменных, а именно времени t и изменяемого (скользящего) фазового угла θ. Второй функциональный нелинейный преобразователь 2ФНП осуществляет математическую операцию определенного интегрирования (3) по времени t первой функции преобразования f1,п(k)(t,θ) (2) в пределах интервала времени, равном периоду повторения Т несинусоидального периодического электрического сигнала f(t) (1), при этом преобразователь 2ФНП на своем выходе выводит информацию в виде второй функции преобразования f2,п(k)(θ) (4), которая является только функцией изменяемого (скользящего) фазового угла θ и которая согласно прототипу (патент RU №2442180) имеет амплитуду Fm,2,п(k), равную амплитуде Am(k) k-той гармоники.
Для достижения положительного результата, связанного с повышением точности определения начальной фазы колебания ψ(k) k-той гармоники, согласно предлагаемому изобретению в структуру нелинейного преобразователя НП введены четыре функциональных нелинейных преобразователя 3ФНП-6ФНП. Указанные преобразователи реализуют вытекающую из приведенных в описании изобретения математических выкладок последовательность действий, при этом третий функциональный нелинейный преобразователь 3ФНП выделяет положительные мгновенные значения второй функции преобразования f2,п(k)(θ) (4) и формирует третью функцию преобразования f3,п(k)(θ) (5); четвертый функциональный нелинейный преобразователь 4ФНП имеет два входа и один выход и выполняет операцию перемножения (6) поступающего на его второй вход с выхода третьего функционального нелинейного преобразователя 3ФНП третьей функции преобразования f3,п(k)(θ) на поданный на его первый вход вспомогательного положительного коэффициента Квсп, при этом в результате выполнения математической операции умножения на выходе четвертого функционального нелинейного преобразователя 4ФНП формируют четвертую функцию преобразования f4,п(k)(θ) (6), которую подают на первый вход пятого функционального нелинейного преобразователя 5ФНП, при этом на его второй вход подают бόльшее единице положительное значение степени n, причем пятый функциональный нелинейный преобразователь 5ФНП осуществляет математическую операцию возведения в степень n четвертой функции преобразования f4,п(k)(θ) и на своем выходе формирует пятую функцию преобразования f5,п(k)(θ) (8), которую подают на вход шестого функционального преобразователя 6ФНП преобразования, который посредством поиска максимума у пятой функции преобразования f5,п(k)(θ) (8) на своем выходе в цифровой форме выдает однозначную информацию о значении начальной фазы колебания ψ(k) k-той гармоники, входящей в структуру несинусоидального периодического электрического сигнала f(t) (1).
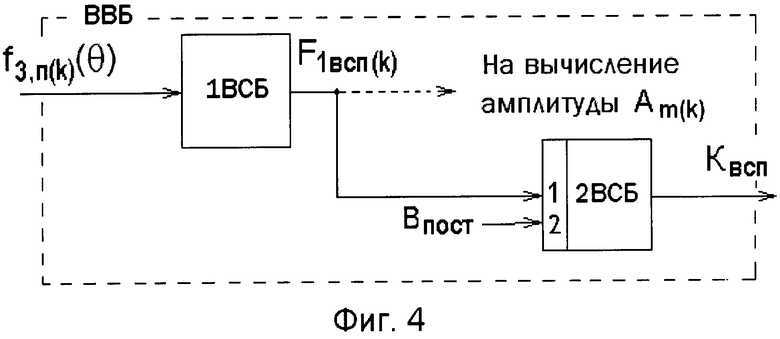
На фиг.4 приведен возможный вариант выполнения вспомогательного вычислительного блока ВВБ, который осуществляет адаптивное вычисление постоянного по величине и бόльшего единицы положительного значения вспомогательного коэффициента Квсп.
Вспомогательный вычислительный блока ВВБ включает первый 1 ВСБ и второй 2 ВСБ вычислительные субблоки. Первый вычислительный субблок 1 ВСБ на интервале от 0 до 2π согласно выражению (12) выполняет операцию определенного интегрирования поданной на его вход третьей функции преобразования f3,п(k)(θ) (5), при этом на своем выходе субблок 1 ВСБ формирует первое F1всп(k) вспомогательное числовое значение.
Первое вспомогательное числовое значение F1всп(k) подают на первый вход второго вычислительного субблока 2 ВСБ, а на его второй вход подают предварительно вычисленное по выражению (13) значение положительной числовой константы Впост.
Второй вспомогательный вычислительный субблок 2 ВСБ по выражению (11) вычисляет значение вспомогательного коэффициента Квсп, который подают на первый вход четвертого функционального нелинейного преобразователя 4ФНП (фиг.3).
Информация о значении первого вспомогательного числового значения F1всп(k) на выходе второго вычислительного субблока 2 ВСБ (фиг.4) может быть использована для вычисления амплитуды Am(k) k-той гармоники.
Предлагаемый способ определения начальной фазы колебания гармоники несинусоидального периодического электрического сигнала может быть реализован с использованием известных цифровых методов и средств обработки электрических сигналов и может быть использован как в самостоятельно функционирующем устройстве, предоставляющим информацию о начальной фазы колебания гармоники, так и в устройствах, измерения, автоматики и релейной защиты, связанных с обеспечением функционирования элементов системы электроснабжения промышленной частоты.
Изобретение относится к измерительной технике. Способ заключается в том, что для достижения положительного эффекта используют формируемую на основе электрического сигнала f(t) специальную функцию, значения которой определяются как временем t, так и вводимым изменяемым углом θ, при этом согласно предлагаемому изобретению указанную функцию возводят в положительную бόльшую единице степень n и для полученной таким образом функциональной зависимости в результате выполнения соответствующего вычислительного процесса выявляют такое значение угла θ, при котором эта функциональная зависимость имеет максимальное значение. Удовлетворяющий этому условию угол θ является искомым значением начальной фазы ψ(k) колебания k-той гармоники. Получаемая в процессе выполнения одной из вычислительных процедур информация может быть использована для определения значения амплитуды Am(k) k-той гармоники. Технический результат заключается в повышении точности определения начальной фазы ψ(k) колебания k-той гармоники, входящей в состав несинусоидального периодического электрического сигнала f(t). 4 ил.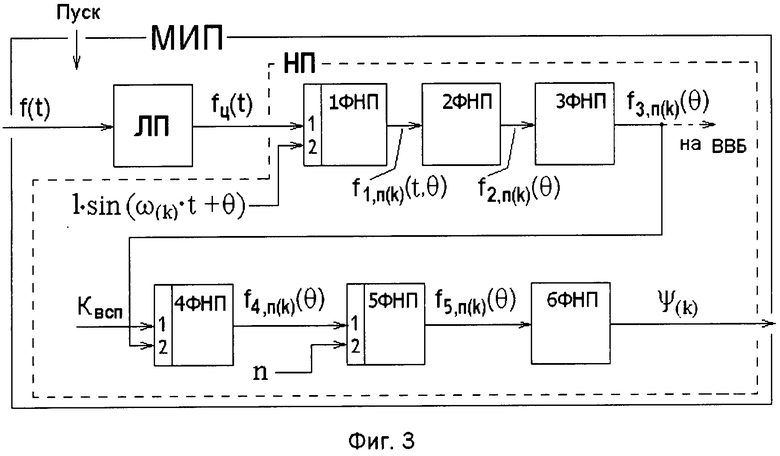
Способ определения начальной фазы колебания гармоники несинусоидального периодического электрического сигнала f(t) с периодом повторения Т, т.е. определение начальной фазы ψ(k) колебания входящей в структуру несинусоидального периодического электрического сигнала f(t) k-той гармоники, заключающийся в том, что способ определяет алгоритм функционирования микропроцессорного измерительного преобразователя (МИП), который решает задачу определения начальной фазы колебания ψ(k) k-той гармоники, при этом микропроцессорный измерительный преобразователь состоит из линейного и нелинейного преобразователей, причем линейный преобразователь поступающий на его вход несинусоидальный периодический электрический аналоговый сигнал f(t) преобразует в цифровой сигнал fц(t), который подают на вход нелинейного преобразователя, который в своей структуре содержит первый и второй функциональные нелинейные преобразователи, при этом на первый вход первого функционального нелинейного преобразователя подают цифровой сигнал fц(t), а на его второй вход подают синтезируемый средствами микропроцессора цифровой сигнал в форме синусоидальной функции 1·sin(ω(k)t+θ) с единичной амплитудой, у которой аргумент состоит из суммы двух слагаемых, причем первое слагаемое аргумента задано произведением циклической частоты ω(k) k-той гармоники и времени t, а второе слагаемое задано изменяемым (скользящим) фазовым углом θ, при этом первый функциональный нелинейный преобразователь перемножает поданные на его первый и второй входы сигналы и на своем выходе формирует первую функцию преобразования, которая является как функцией времени t, так и изменяемого (скользящего) фазового угла θ, при этом первую функцию преобразования подают на вход второго функционального нелинейного преобразователя, который выполняет операцию определенного интегрирования в пределах интервала времени, равном периоду Т первой функции преобразования, причем результат преобразования в виде второй функции преобразования для k-той гармоники определяется гармонической функцией косинуса только от изменяемого (скользящего) фазового угла θ, отличающийся тем, что в структуру нелинейного преобразователя вводят третий, четвертый, пятый, и шестой функциональные нелинейные преобразователи, при этом третий функциональный нелинейный преобразователь из поданной на его вход второй функции преобразования путем выделения положительных ее значений на своем выходе формирует для k-той гармоники третью функцию преобразования, которую подают на второй вход четвертого функционального нелинейного преобразователя, при этом на первый вход четвертого функционального нелинейного преобразователя подают бόльший единицы вспомогательный коэффициент, причем четвертый функциональный нелинейный преобразователь перемножает поданные на его первый и второй входы сигналы и на своем выходе формирует четвертую функцию преобразования, которую подают на первый вход пятого функционального преобразователя, при этом на его второй вход подают положительное больше единицы число n, которое рассматривают как показатель степени, причем пятый функциональный преобразователь возводит в степень n поданную на его первый вход четвертую функцию преобразования f4,п(k)(θ) и на своем выходе формирует пятую функцию преобразования, которую подают на вход шестого функционального преобразователя, который одним из известных методов осуществляет поиск такого аргумента пятой функции преобразования, при котором эта функция имеет максимальное значение, при этом удовлетворяющее этому условию значение аргумента θ является начальной фазой ψ(k) колебания k-той гармоники, причем подаваемый на первый вход четвертого функционального преобразователя вспомогательный коэффициент с соблюдением определенных требований принимают либо постоянным, либо аналитически рассчитывают непосредственно в вычислительном процессе, связанном с определением начальной фазы ψ(k) колебания k-той гармоники.
| СПОСОБ ОПРЕДЕЛЕНИЯ ПАРАМЕТРОВ ГАРМОНИКИ НЕСИНУСОИДАЛЬНОГО ЭЛЕКТРИЧЕСКОГО СИГНАЛА | 2010 |
|
RU2442180C1 |
| ИЗМЕРИТЕЛЬ ПАРАМЕТРОВ ГАРМОНИЧЕСКИХ ПРОЦЕССОВ | 2002 |
|
RU2229138C1 |
| ИЗМЕРИТЕЛЬ ПАРАМЕТРОВ ГАРМОНИЧЕСКОГО СИГНАЛА | 2008 |
|
RU2368909C1 |
| US 20070069766 A1 29.03.2007 | |||
| JP 0057114863 A 16.07.1982 | |||
Авторы
Даты
2014-11-27—Публикация
2013-02-21—Подача