Изобретение относится к области вакуумного машиностроения и компрессоростроения и может быть использовано в спиральных вакуумных насосах, воздушных и холодильных компрессорных машинах для улучшения удельных характеристик.
Задача повышения удельных характеристик вакуумных насосов и компрессоров актуальна и может быть решена путем снижения габаритных размеров и массы устройства при сохранении производительности.
Известные спиральные вакуумные насосы и компрессоры содержат цилиндрический корпус с размещенными внутри него спиральными элементами, один из которых неподвижен, а другой, за счет смещения оси подвижной спирали на величину эксцентриситета «е», совершает орбитальное движение относительно оси неподвижной спирали (Вакуумная техника: Справочник / К.Е. Демихов, Ю.В. Панфилов, Н.К. Никулин и др. под общ. ред. К.Е. Демихова, Ю.В. Панфилова. 3-е изд., перераб. и доп. М.: Машиностроение, 2009. С.330-338; Бесконтактные вакуумные насосы: учебное пособие / А.В. Бурмистров, С.И. Саликеев; Федер. Агенство по образованию. Казан. гос. технол. ун-т. - Казань: КГТУ, 2010. - С.39-51; Кочетова Г.С, Сакун И.А. Состояние и направление развития спиральных компрессоров. Обзорная информация. - М.: ЦИНТИ химнефтемаш, 1988. - 57 с.). Спирали в них имеют одинаковую длину, что не позволяет уменьшить диаметр корпуса при сохранении производительности.
Уменьшение диаметра корпуса при сохранении производительности может быть достигнуто, например, за счет сдвига центра торцевого диска подвижного спирального элемента относительно центра спирали при одновременном уменьшении его диаметра.
Например, известна спиральная машина, которая может работать как насос или компрессор, состоящая из цилиндрического корпуса и двух спиральных элементов: подвижного и неподвижного (патент US №4303379, F04C 18/00, 1981). Каждый спиральный элемент состоит из торцевого диска и собственно спирали. Спирали подвижного и неподвижного спиральных элементов имеют одинаковую длину, торцевой диск подвижного спирального элемента имеет диаметр 2R-e (где R - расстояние от центра до конца спирали, е - эксцентриситет), а центр торцевого диска подвижного спирального элемента смещен от центра подвижной спирали к внешнему концу подвижной спирали на е/2, чтобы тем самым уменьшить диаметр цилиндрического корпуса компрессора. Если дополнительно центр неподвижной спирали смещен от центра цилиндрического корпуса компрессора к внешнему концу неподвижной спирали на е/2, то диаметр цилиндрического корпуса компрессора может быть сведен, как минимум, к величине 2R+e.
Недостатком данного технического решения является то, что при минимальном диаметре цилиндрического корпуса неподвижная спираль периодически выходит из контакта с торцевым диском подвижного спирального элемента, что приводит к снижению производительности и степени сжатия за счет увеличения перетеканий и повреждения торцевого уплотнителя, размещенного на торце неподвижной спирали.
Наиболее близким техническим решением, выбранным в качестве прототипа, является спиральная машина, содержащая цилиндрический корпус с расположенными в нем двумя спиральными элементами, каждый из которых состоит из торцевого диска и эвольвентной спирали, причем спирали имеют одинаковые высоту, толщину и количество витков, один из спиральных элементов жестко закреплен в корпусе, другой вставлен в неподвижный спиральный элемент с возможностью совершения орбитального движения с эксцентриситетом относительно неподвижного спирального элемента, торцевой диск подвижного спирального элемента имеет минимальный диаметр d0=2R+e (R - расстояние от центра до конца спирали может быть выражено формулой R=2πrБn0+πrБ-е, где n0 - число витков спирали, rБ - радиус базовой окружности), и его центр смещен относительно центра подвижной спирали на е/2 к внешнему концу подвижной спирали, а центр корпуса смещен относительно центра неподвижной спирали на е/2 к внешнему концу неподвижной спирали (патент US №4304535, F04C 18/02, 1981).
При сохранении производительности минимальный диаметр корпуса машины, который удается достичь, составляет D0=2R+3e=d0+2e.
Задачей изобретения является уменьшение диаметра цилиндрического корпуса спиральной машины при сохранении производительности.
Техническое решение поставленной задачи достигается тем, что в спиральной машине, содержащей цилиндрический корпус с расположенными в нем двумя спиральными элементами, каждый состоит из торцевого диска и эвольвентной спирали, причем спирали имеют одинаковые высоту и толщину, один из спиральных элементов выполнен подвижным с возможностью движения с эксцентриситетом е относительно другого, выполненного неподвижным, центр торцевого диска подвижного спирального элемента смещен относительно центра спирали, центр цилиндрического корпуса смещен относительно центра спирали неподвижного спирального элемента и его диаметр имеет величину d+2e, где d - диаметр торцевого диска подвижного спирального элемента, согласно изобретению количество витков спирали подвижного спирального элемента на φ=0,2-0,45 витков больше количества витков спирали неподвижного спирального элемента, центр торцевого диска подвижного спирального элемента смещен от центра спирали на расстояние Δ и угол α, отсчитываемый от радиус-вектора конечной точки спирали по ходу раскручивания спирали, центр корпуса смещен относительно центра неподвижной спирали так, что при совмещении центров спиралей он совпадает с центром торцевого диска подвижного спирального элемента, причем при φ<(1+е/(πrБ,))/4 расстояние Δ=1/2Max[1.03e,z], угол 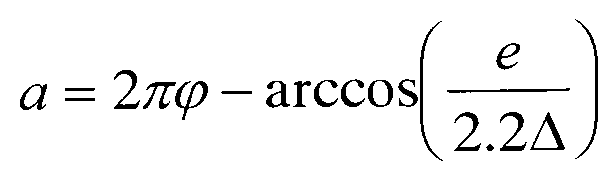 , диаметр торцевого диска подвижного спирального элемента d=πrБ(1-(φ+2n)-3e/2, при φ≥(1+е/(πrБ))/4 расстояние Δ=1/2Max[1.03rБ,z], угол
, диаметр торцевого диска подвижного спирального элемента d=πrБ(1-(φ+2n)-3e/2, при φ≥(1+е/(πrБ))/4 расстояние Δ=1/2Max[1.03rБ,z], угол 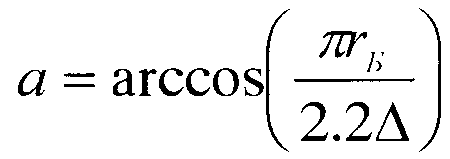 , диаметр торцевого диска подвижного спирального элемента d=π·rБ(4n+1+2φ)-2е, где
, диаметр торцевого диска подвижного спирального элемента d=π·rБ(4n+1+2φ)-2е, где 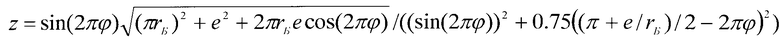 , е - эксцентриситет, rБ - радиус базовой окружности спиралей, n - число витков спирали неподвижного спирального элемента.
, е - эксцентриситет, rБ - радиус базовой окружности спиралей, n - число витков спирали неподвижного спирального элемента.
Решение поставленной задачи обеспечивает уменьшение диаметра цилиндрического корпуса машины по сравнению с прототипом на 2-8% при сохранении производительности.
Изобретение поясняется следующими чертежами:
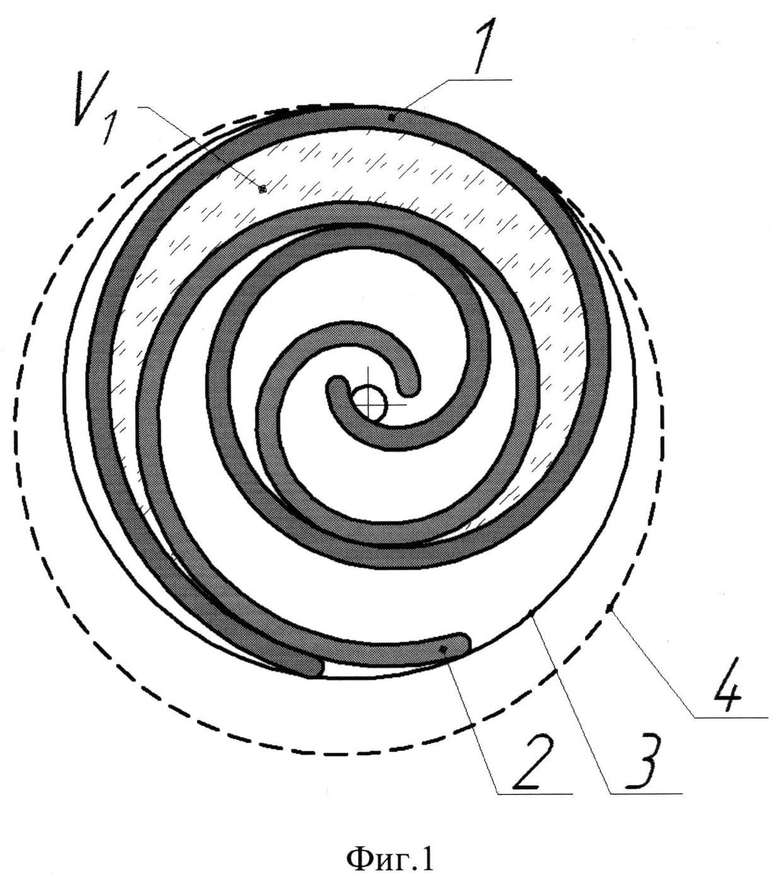
на фиг.1 показаны взаимные положения подвижной 1 и неподвижной 2 спиралей в предлагаемой машине при отсечении объема V1, 3 - торцевой диск подвижного спирального элемента, 4 - окружность корпуса;
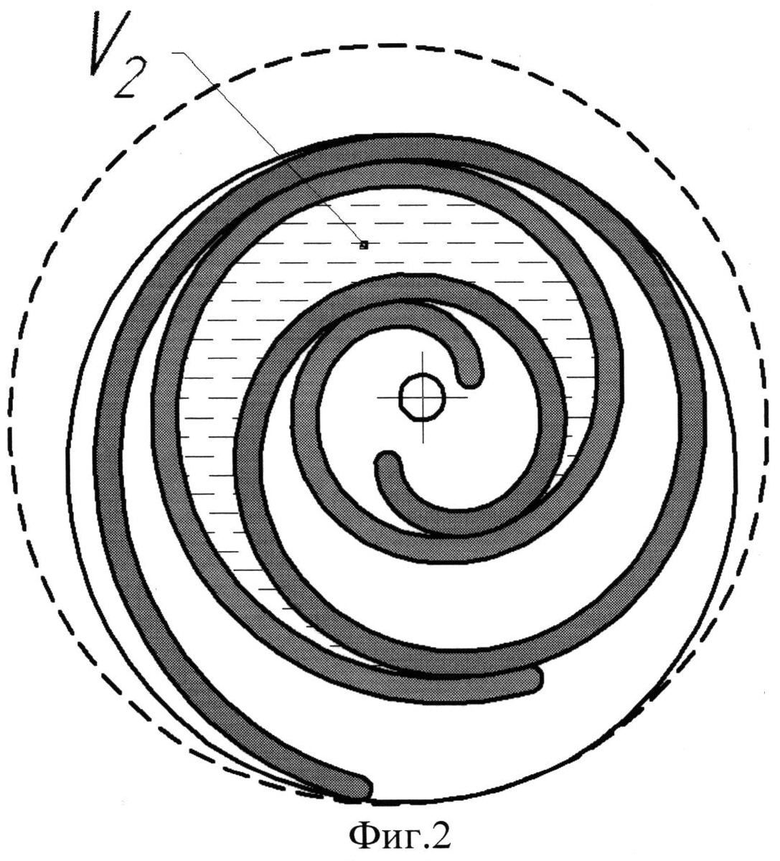
на фиг.2 показаны взаимные положения подвижной 1 и неподвижной 2 спиралей в предлагаемой машине при отсечении объема V2, 3 - торцевой диск подвижного спирального элемента, 4 - окружность корпуса;
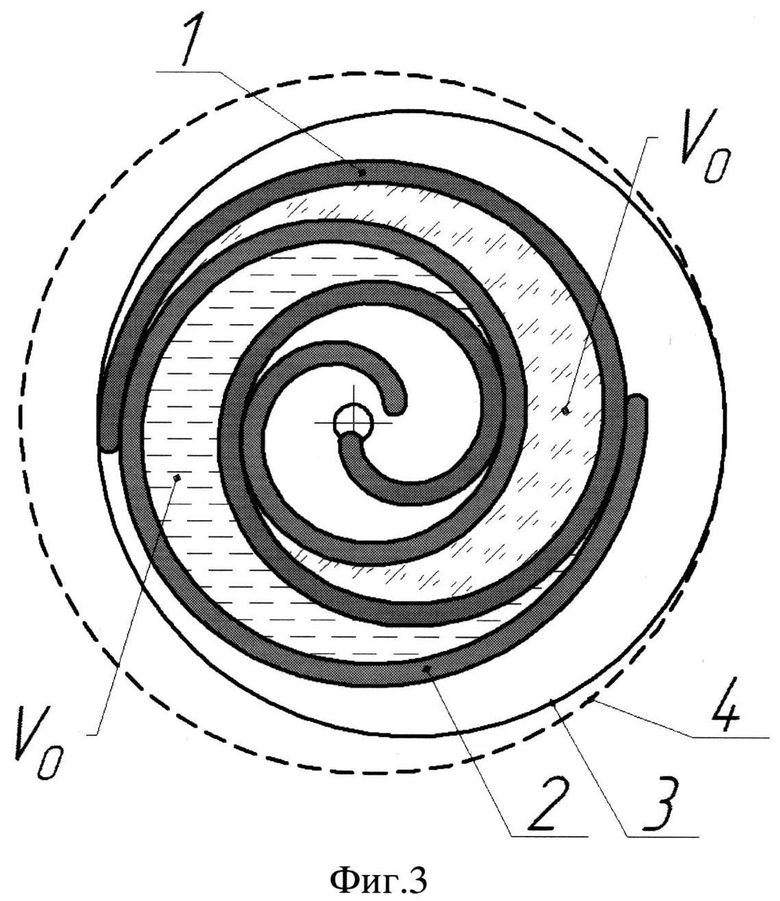
на фиг.3 показаны взаимные положения подвижной и неподвижной спиралей в прототипе в момент образования объемов V0;
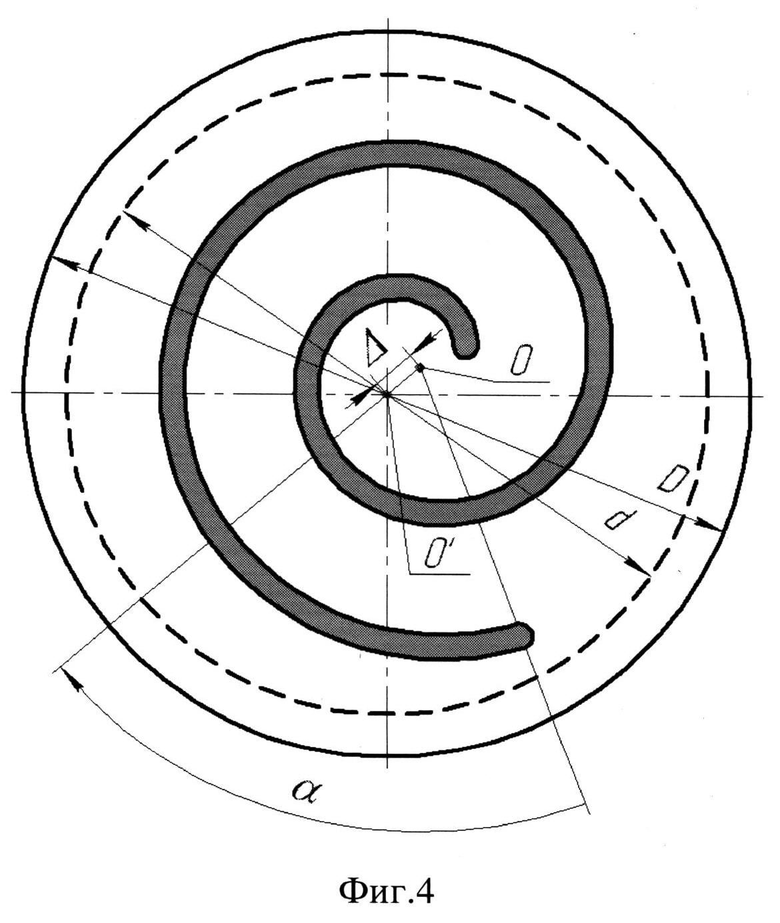
на фиг.4 показаны спиральные элементы при совмещении центров спиралей;
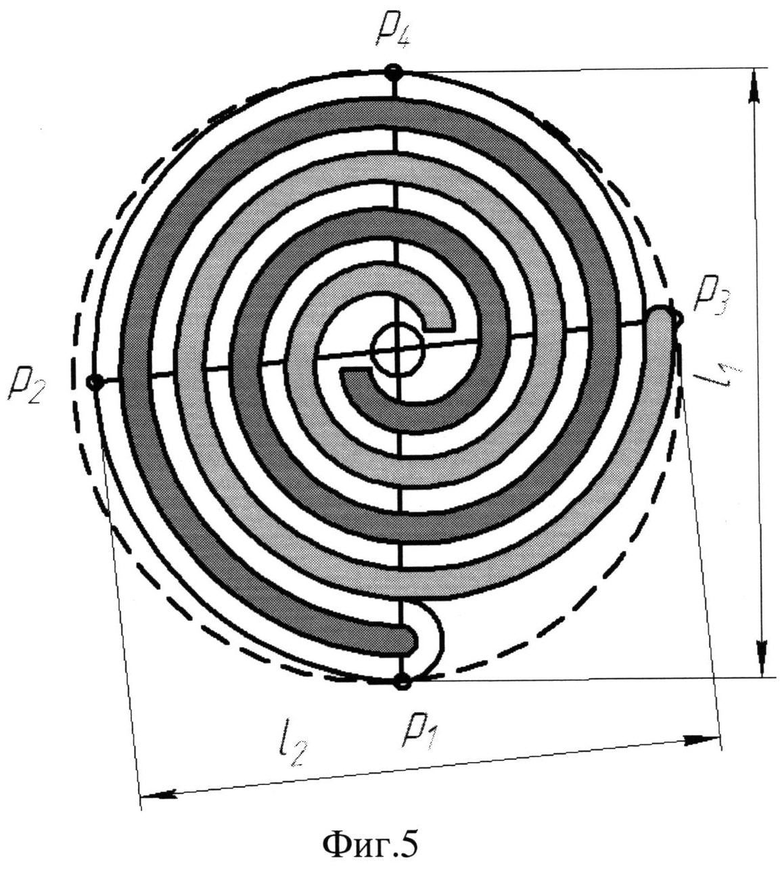
на фиг.5 показано построение основания подвижного спирального элемента;
на фиг.6 представлена схема предлагаемой спиральной машины;
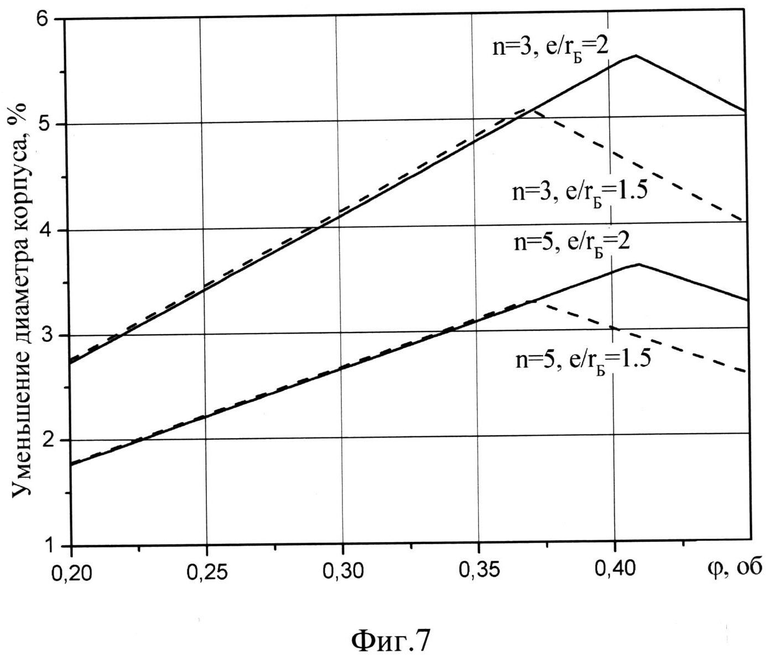
на фиг.7 приведена зависимость снижения диаметра корпуса в предлагаемой машине по сравнению с прототипом от удлинения подвижной спирали φ при различных отношениях е/rБ.
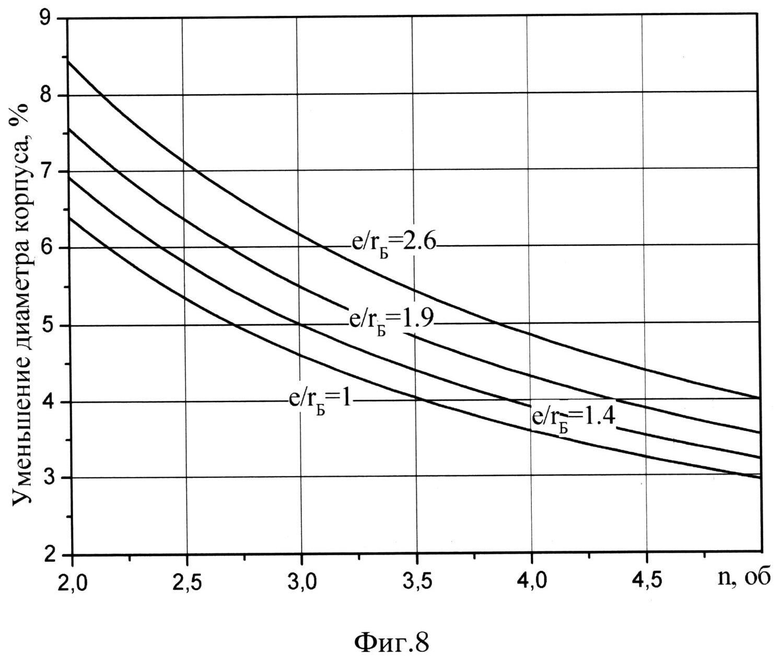
на фиг.8 приведена зависимость снижения диаметра корпуса в предлагаемой машине по сравнению с прототипом от числа витков неподвижной спирали n при различных отношениях е/rБ.
Сущность изобретения заключается в следующем.
В предлагаемой машине, в отличие от прототипа, спирали выполнены с разным количеством витков, причем количество витков подвижной спирали 1 на φ=0,2-0,45 витков больше количества витков неподвижной спирали 2 (фиг.1). При этом неподвижная спираль на φ/2 витков короче, чем в прототипе, и соответственно, подвижная спираль на φ/2 витков длиннее, чем в прототипе. Это приводит к тому, что образование отсечённых полостей происходит при разных углах поворота ротора и отсечённый объем V1 (фиг.1) больше отсечённого объема V2 (фиг.2). В прототипе длины спиралей равны и отсекаемые полости имеют одинаковый объем V0 (фиг.3). Так как отсечённый объем пропорционален количеству витков спирали, а суммарное количество витков подвижной и неподвижной спиралей в предлагаемой машине сохраняется равным суммарному количеству витков спиралей в прототипе, то и сумма отсеченных объемов V1 и V2 равна сумме отсеченных объемов 2V0, за счет этого производительность предлагаемой спиральной машины сохраняется. При φ>0,45 произойдет уменьшение производительности, а при φ<0,2 уменьшение диаметра корпуса будет незначительным.
Диаметр корпуса машины D связан с диаметром торцевого диска подвижного спирального элемента d соотношением D=d+2e. Уменьшение диаметра торцевого диска позволит уменьшить диаметр корпуса. Это достигается тем, что в предлагаемой спиральной машине у подвижного спирального элемента центр торцевого диска смещен относительно центра спирали на расстояние Δ и угол α (фиг.4), отсчитываемый от радиус-вектора конечной точки спирали по ходу раскручивания спирали, причем при φ<(1+е/(πrБ))/4 расстояние Δ=1/2Max[1.03<e,z], а угол 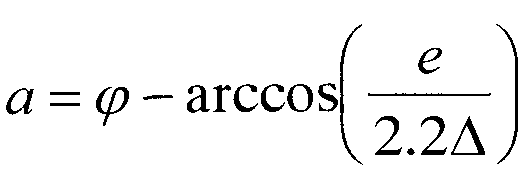 , диаметр торцевого диска подвижного спирального элемента d=2πrБ(1+2n)-е, при φ≥(1+e/(πrБ))/4 расстояние Δ=1/2Max[1.03rБ,z], а угол
, диаметр торцевого диска подвижного спирального элемента d=2πrБ(1+2n)-е, при φ≥(1+e/(πrБ))/4 расстояние Δ=1/2Max[1.03rБ,z], а угол 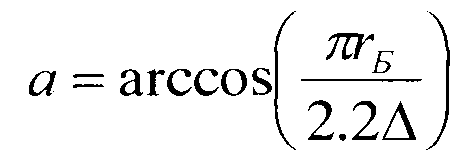 , диаметр торцевого диска подвижного спирального элемента d=4πrБ(1/4+n+φ)-2е, где
, диаметр торцевого диска подвижного спирального элемента d=4πrБ(1/4+n+φ)-2е, где 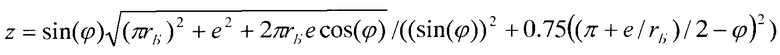 .
.
За счет сдвига центра торцевого диска подвижного спирального элемента и использования спиралей с разным количеством витков его диаметр d может быть уменьшен по сравнению с прототипом. В предлагаемой машине диаметр торцевого диска подвижного спирального элемента рассчитывают в зависимости от величины φ.
На фиг.5 показано построение основания подвижного спирального элемента. Минимально необходимое основание строится из условия отсутствия выхода неподвижной спирали за пределы этого основания при его движении. Для построения совмещаются центры спиралей подвижного и неподвижного спиральных элементов. При этом минимально необходимое основание подвижного спирального элемента представляет собой объединение площадей эквидистанты неподвижной спирали с радиусом, равным эксцентриситету подвижной спирали. По технологическим соображениям наилучшей формой торцевого диска является окружность, описанная вокруг минимально необходимого основания. Для нахождения ее диаметра проводятся отрезки ι1 и ι2, проходящие через центры и концы спиралей, до пересечения с минимально необходимым основанием (точки р1, р2, р3, Р4). Длину большего из этих отрезков с достаточной степенью точности можно принять равным диаметру описанной окружности, т.е. диаметру торцевого диска подвижного спирального элемента. Центр этой окружности находится в точке пересечения серединных нормалей к отрезкам ι1 и ι2.
При равенстве отрезков ι1 и ι2 достигается минимальный диаметр торцевого диска подвижного спирального элемента, а следовательно, и корпуса спиральной машины. Этот минимальный диаметр достигается при определенной величине φ, которая имеет конкретное значение для каждой спиральной машины и определяется по формуле φ=(1+е/(πrБ))/4. Это значение разбивает исходный интервал φ на подинтервалы 0,2≤φ<(1+е/(πrБ))/4 и (1+е/(πrБ))/4≤φ≤0,45. В зависимости от того, к какому подинтервалу относится выбранное из интервала 0,2-0,45 значение φ, используют разные выражения для вычисления расстояния Δ и угла α смещения центра торцевого диска подвижного спирального элемента от центра спирали.
При выводе формул расчета расстояния Δ и угла α использовали специально разработанную программу для ЭВМ. При выводе формул периферийные участки спиралей были заменены на дуги окружностей, что позволило получить аналитические выражения для указанных величин:
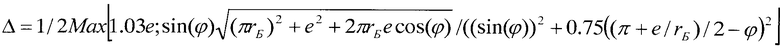 ,
,
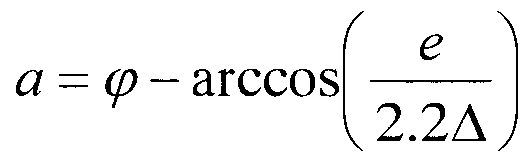 при 0,2≤φ<(1+е/(πrБ))/4 и
при 0,2≤φ<(1+е/(πrБ))/4 и
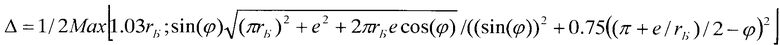 ,
,
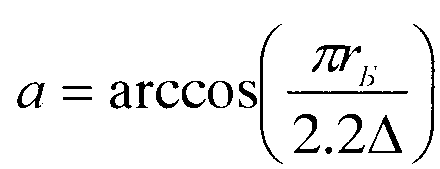 при (1+е/(πrБ))/4≤φ≤0,45.
при (1+е/(πrБ))/4≤φ≤0,45.
Для удобства выражение 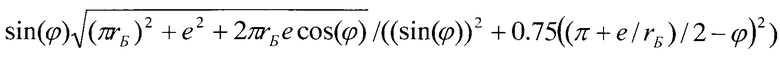 , входящее в формулы расчета Δ, обозначили буквой z, и формулы приобрели следующие вид Δ=1/2Max[1,03e,z] и Δ=1/2Max[1.03rБ,z].
, входящее в формулы расчета Δ, обозначили буквой z, и формулы приобрели следующие вид Δ=1/2Max[1,03e,z] и Δ=1/2Max[1.03rБ,z].
Используемая аппроксимация для замены периферийных участков спиралей на дуги окружностей имеет незначительную погрешность, из-за которой при некоторых значениях е и rБ возможен выход концов спиралей за пределы торцевого диска. Поэтому в формулах расчета Δ и α используются эмпирические коэффициенты 1.03 и 2.2 для компенсации этой погрешности.
При вычислении Δ из пар значений 1.03е и z или 1.03rБ и z выбирают максимальное, в противном случае произойдет выход концов спиралей за пределы торцевого диска.
Диаметр торцевого диска подвижного спирального элемента рассчитывают в зависимости от величины φ по формулам d=2πrБ(1+2n)-е при 0,2≤φ<(1+е/(πrБ))/4 и d=4πrБ(1/4+n+φ)-2e при (1+е/(πrБ))/4≤φ≤0,45.
Вокруг точек р1, р2, р3, Р4 должна быть описана такая окружность, чтобы все перечисленные точки находились внутри нее (фиг. 5). При этом существует четыре варианта построения такой окружности. Положение центра окружности торцевого диска для всех четырех случаев может быть задано расстоянием от центра спирали Δ и углом α, отсчитываемым от радиус-вектора конечной точки спирали по ходу раскручивания спирали, причем при 0,2≤φ<(1+е/(πrБ))/4 расстояние Δ=1/2Max[1.03e,z], а угол 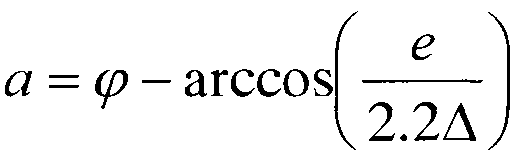 , при (1+е/(πrБ))/4≤φ≤0,45 расстояние Δ=1/2Max[1.03rБ,z], а угол
, при (1+е/(πrБ))/4≤φ≤0,45 расстояние Δ=1/2Max[1.03rБ,z], а угол 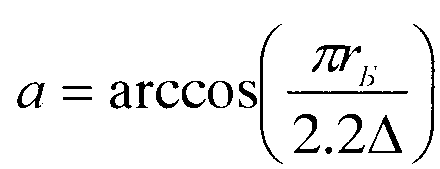 , где
, где 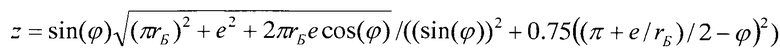 .
.
Ниже приведены варианты построения окружности, перечисленные в порядке возрастания φ:
1. Окружность строится по двум точкам р1 и р3, что происходит при 0,2≤φ<(1+е/(πrБ))/4 и z<1.03е. В этом случае центр окружности будет расположен на отрезке, соединяющем эти точки, и расстояние центра торцевого диска от центра спирали будет равно Δ=1/2Max[1.03e,z]=1/2·1,03e;
2. Окружность строится по трем точкам р1, р3 и р4. Это происходит при 0,2≤φ<(1+е/(πrБ))/4 и z>1.03e и расстояние от центра спирали будет равно Δ=1/2Max[1.03e,z]=1/2·z;
3. Окружность строится по трем точкам р1, р3 и р2. Это происходит при (1+е/(πrБ))/4≤φ≤0,45 и z>1.03rБ, и расстояние от центра спирали будет равно Δ=1/2Мах[1.03rБ,z]=z/2;
4. Окружность строится по двум точкам р2 и р3. Это происходит при (1+е/(πrБ))/4≤φ≤0,45 и z<1.03rБ, в этом случае центр окружности будет расположен на отрезке, соединяющем эти точки, и расстояние от центра спирали будет равно Δ=1/2Max[1,03rБ,z]=1/2·rБ.
Угол α рассчитывают по формуле 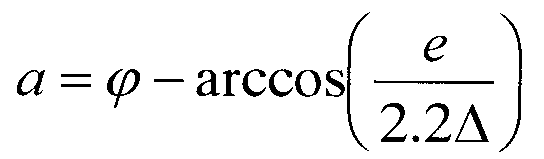 (варианты 1, 2) и по формуле
(варианты 1, 2) и по формуле 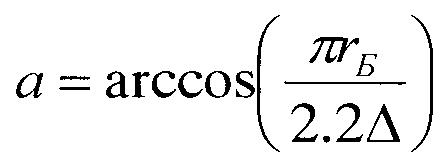 (варианты 3, 4).
(варианты 3, 4).
Для обеспечения возможности движения подвижного спирального элемента при одновременном уменьшении диаметра корпуса центр корпуса О′ (фиг.4) смещен от центра спирали неподвижного спирального элемента О так, что при совмещении центров спиралей он совпадает с центром торцевого диска подвижного спирального элемента.
При сохранении производительности минимальный диаметр цилиндрического корпуса предлагаемой машины достигается при φ=(1+е/(πrБ))/4 и диаметре торцевого диска d=2πrБ(1+2n)-2 в зависимости от величины е и rБ. Расчеты показывают, что минимальный диаметр корпуса предлагаемой машины в зависимости от числа витков неподвижной спирали и отношения е/rБ на 2-8% меньше диаметра корпуса прототипа.
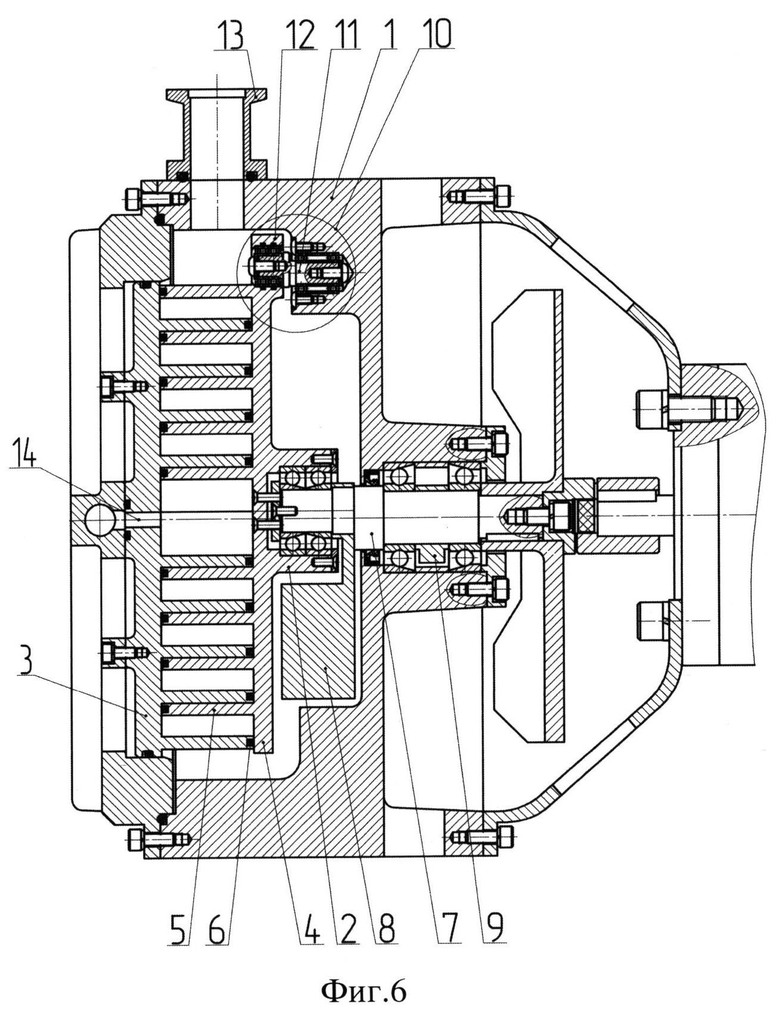
Заявляемая спиральная машина (фиг.6) содержит цилиндрический корпус 1 с размещенными внутри подвижным спиральным элементом 2 и неподвижным спиральным элементом 3, жестко закрепленным в корпусе. Спиральные элементы состоят из торцевых дисков 4 и 4′, спиралей 5 и 5′ и уплотнителей 6 и 6′, снижающих обратные перетекания через зазор между спиралью и ответным торцевым диском. В качестве базовой кривой спирали используется эвольвента. Спирали выполнены одинаковыми по высоте и толщине, но имеют разное количество витков. Свободными концами спирали вставлены одна в другую. В подвижный спиральный элемент 2 вставлен эксцентриковый механизм 7 с балансирами 8, 9, осуществляющий его вращение. В корпусе 1 со стороны подвижного спирального элемента 2 установлено противоповоротное устройство 10 для предотвращения поворота подвижного спирального элемента 2 относительно его геометрической оси. Противоповоротное устройство снабжено по меньшей мере одним поводком 11, размещенным в отверстии 12 с обратной стороны подвижного спирального элемента. В цилиндрической части корпуса в секторе между концами спиралей расположен всасывающий патрубок 13, а в центре торцевого диска неподвижной спирали - нагнетательное отверстие 14.
Спиральная машина работает следующим образом. Всасывание осуществляется через патрубок 13. При орбитальном движении подвижного спирального элемента 2 относительно неподвижного спирального элемента 3 образуются две замкнутые полости. Перемещение газа со стороны всасывания к стороне нагнетания и сжатие происходит благодаря уменьшению объемов замкнутых полостей. В определенный момент происходит соединение замкнутых полостей друг с другом и вытеснение сжимаемой среды в нагнетательное отверстие 14.
Для подтверждения достигаемого технического результата были произведены расчеты уменьшения диаметра корпуса предлагаемой машины относительно прототипа при различных значениях числа витков неподвижной спирали и отношениях е/rБ. Полученные данные свидетельствуют о том, что уменьшение диаметра корпуса предлагаемой машины по сравнению с прототипом происходит во всем указанном диапазоне φ (фиг. 7) при различных значениях е/rБ и количестве витков неподвижной спирали (фиг.8).
В качестве примера показан расчет параметров предлагаемой спиральной машины в сравнении с прототипом.
За основу принята спиральная машина, в которой число витков спиралей одинаково и равно n0=3, эксцентриситет е=3.85 мм, радиус базовой окружности rБ=2.5 мм.
Согласно полезной модели количество витков подвижной спирали на φ=0,2-0,45 витков больше количества витков в неподвижной спирали. Расчет приведен для φ=0.3.
Так как (1+е/(πrБ))/4=0.372, то выбранное значение φ входит в интервал 0,2≤φ<(1+е/(πrБ))/4.
Число витков неподвижной спирали n=n0-φ/2=2.85
Число витков подвижной спирали n′=n+φ=3.15
Для определения расположения центра торцевого диска подвижного спирального элемента относительно центра спирали вычисляют расстояние Δ и угол α.
Сначала определяют величину z по формуле
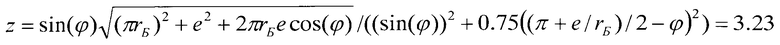
Так как z<1.03e=3.97 (вариант 2 построения окружности торцевого диска), то расстояние от центра спирали до центра торцевого диска подвижного спирального элемента рассчитывают по формуле Δ=1/2·1.03·е=1.98 мм.
Угол рассчитывают по формуле 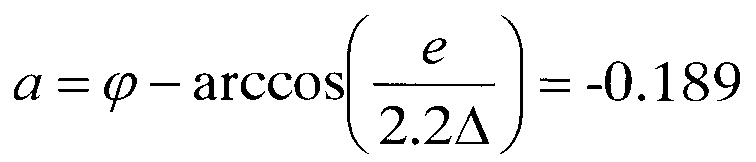 радиан.
радиан.
Расчет диаметра торцевого диска подвижного спирального элемента производят по формуле
d=2πrБ(1+2n)-е=101.393 мм.
Следовательно, диаметр корпуса составит D=d+2е=109.093 мм.
В прототипе минимальный диаметр корпуса при тех же исходных данных составит D0=2πrБ(2n0+1)+е=113.806 мм.
Уменьшение диаметра корпуса предлагаемой машины по сравнению с прототипом составляет 4.14 %.
Ниже приведен расчет для φ=0.4
Так как (1+е/(πrБ))/4=0.372, то выбранное значение φ входит в интервал (1+е/(πrБ))/4≤φ≤0,45.
Сначала определяют величину z по формуле
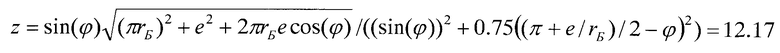
Так как z>1.03rБ=2.575 (вариант 4 построения окружности торцевого диска), то используют следующие формулы
Δ=1/2·z=6.08 мм
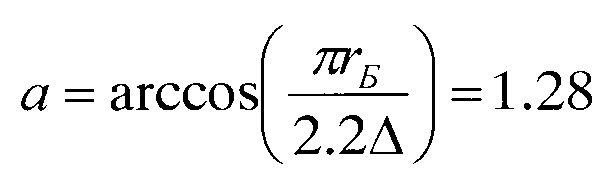 радиан
радиан
d=4πrБ(1/4+n+φ)-2е=100.685 мм
D=d+2e=108.385 мм.
Уменьшение диаметра корпуса предлагаемой машины по сравнению с прототипом составляет 4.76 %.
При указанных исходных параметрах минимальный достижимый диметр корпуса предлагаемой спиральной машины достигается при φ=(1+е/(πrБ))/4=0.373 и составляет 107.954 мм, что на 5.14% меньше диаметра корпуса прототипа.
Таким образом, при одинаковой производительности диаметр корпуса предлагаемой спиральной машины на 2-8 % меньше, чем в прототипе в зависимости от эксцентриситета, радиуса базовой окружности и количества витков спирали неподвижного спирального элемента, что обеспечивает повышение удельных характеристик машины.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПИРАЛЬНАЯ МАШИНА | 2014 |
|
RU2550225C1 |
| СПИРАЛЬНАЯ МАШИНА | 2015 |
|
RU2616894C2 |
| СПИРАЛЬНЫЙ КОМПРЕССОР | 2017 |
|
RU2655092C1 |
| БЕЗМАСЛЯНАЯ СПИРАЛЬНАЯ МАШИНА | 2014 |
|
RU2565342C1 |
| ЦЕНТРОБЕЖНЫЙ ПУЛЬПОВЫЙ НАСОС (ВАРИАНТЫ) | 2011 |
|
RU2484303C2 |
| БЕЗМАСЛЯНАЯ СПИРАЛЬНАЯ МАШИНА | 2014 |
|
RU2565344C1 |
| ОБОЮДНО ШНЕКОВЫЙ БЛОК ПОДВИЖНЫХ РАБОЧИХ КАМЕР МЕХАНИЧЕСКОГО СЖАТИЯ ИЛИ ИСПОЛЬЗОВАНИЯ ДАВЛЕНИЯ СЖАТОГО ЖИДКОГО И/ИЛИ ГАЗООБРАЗНОГО РАБОЧЕГО ТЕЛА, СПОСОБ ИЗГОТОВЛЕНИЯ СФЕРИЧЕСКОЙ СПИРАЛЬНОЙ СТЕНКИ СФЕРИЧЕСКОГО ШНЕКА ОБОЮДНО ШНЕКОВОГО БЛОКА | 2007 |
|
RU2373400C2 |
| Потенциометр | 1981 |
|
SU1010666A1 |
| РАБОЧИЕ ЭЛЕМЕНТЫ ОБЪЕМНОЙ МАШИНЫ С ОРБИТАЛЬНЫМ ДВИЖЕНИЕМ ПОДВИЖНОГО ЭЛЕМЕНТА И СПОСОБ ИЗГОТОВЛЕНИЯ РАБОЧИХ ЭЛЕМЕНТОВ ОБЪЕМНОЙ МАШИНЫ | 1999 |
|
RU2175082C2 |
| УСТРОЙСТВО ДЛЯ МОНИТОРИНГА СОСТОЯНИЯ БУКС КОЛЕСНЫХ ПАР ВАГОНОВ ДВИЖУЩЕГОСЯ ПОЕЗДА | 2008 |
|
RU2384444C1 |
Изобретение относится к области вакуумного машиностроения и компрессоростроения и может быть использовано в спиральных вакуумных насосах, воздушных и холодильных компрессорных машинах для улучшения удельных характеристик. Спиральная машина содержит цилиндрический корпус с расположенными в нем двумя спиральными элементами, каждый состоит из торцевого диска и эвольвентной спирали. Один из спиральных элементов жестко закреплен в корпусе, другой вставлен в неподвижный спиральный элемент с возможностью совершения орбитального движения с эксцентриситетом относительно неподвижного спирального элемента. При одинаковых высоте и толщине количество витков спирали подвижного спирального элемента больше количества витков спирали неподвижного спирального элемента. Центр торцевого диска подвижного спирального элемента смещен от центра спирали. Центр корпуса смещен относительно центра неподвижной спирали так, что при совмещении центров спиралей он совпадает с центром торцевого диска подвижного спирального элемента. Изобретение позволяет повысить удельные характеристики спиральной машины за счет уменьшения внутреннего диаметра корпуса при сохранении производительности и степени сжатия. 1 з.п. ф-лы, 8 ил.
1. Спиральная машина, содержащая цилиндрический корпус с расположенными в нем двумя спиральными элементами, каждый состоит из торцевого диска и эвольвентной спирали, причем спирали имеют одинаковые высоту и толщину, один из спиральных элементов выполнен подвижным с возможностью движения с эксцентриситетом е относительно другого, выполненного неподвижным, центр торцевого диска подвижного спирального элемента смещен относительно центра спирали, центр цилиндрического корпуса смещен относительно центра спирали неподвижного спирального элемента и его диаметр имеет величину d+2e, где d - диаметр торцевого диска подвижного спирального элемента, отличающаяся тем, что количество витков спирали подвижного спирального элемента на φ=0,2-0,45 витков больше количества витков спирали неподвижного спирального элемента, центр торцевого диска подвижного спирального элемента смещен от центра спирали на расстояние Δ и угол α, отсчитываемый от радиус-вектора конечной точки спирали по ходу раскручивания спирали, центр корпуса смещен относительно центра неподвижной спирали так, что при совмещении центров спиралей он совпадает с центром торцевого диска подвижного спирального элемента, причем при φ<(1+e/(πrБ))/4 расстояние Δ=1/2Max[1.03e,z], угол 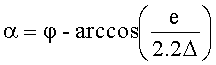 , диаметр торцевого диска подвижного спирального элемента d=2πrБ(1+2n)-e, при φ≥(1+e/(πrБ))/4 расстояние Δ=1/2Max[1.03rБ,z], угол
, диаметр торцевого диска подвижного спирального элемента d=2πrБ(1+2n)-e, при φ≥(1+e/(πrБ))/4 расстояние Δ=1/2Max[1.03rБ,z], угол 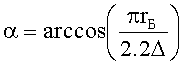 , диаметр торцевого диска подвижного спирального элемента d=4πrБ(1/4+n+φ)-2e, где
, диаметр торцевого диска подвижного спирального элемента d=4πrБ(1/4+n+φ)-2e, где 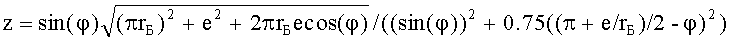 , е - эксцентриситет, rБ - радиус базовой окружности спиралей, n - число витков спирали неподвижного спирального элемента,.
, е - эксцентриситет, rБ - радиус базовой окружности спиралей, n - число витков спирали неподвижного спирального элемента,.
2. Спиральная машина по п.1, отличающаяся тем, что количество витков спирали подвижного спирального элемента на φ≥(1+e/(πrБ))/4 витков больше, чем количество витков спирали неподвижного спирального элемента.
| US 4304535 A,08.12.1981 | |||
| РАБОЧИЕ ЭЛЕМЕНТЫ СПИРАЛЬНОЙ МАШИНЫ | 1998 |
|
RU2149282C1 |
| Осветительное приспособление для микроскопа | 1926 |
|
SU10430A1 |
| US 6257851 B1, 10.07.2001 | |||
| US 5222883 A, 29.06.1993 | |||
| US 4477239 A, 16.10.1984 | |||
Авторы
Даты
2014-12-10—Публикация
2013-07-23—Подача