Изобретение относится к цифровому голографическому микроскопу (ЦГМ) и может быть использовано в качестве измерительной системы для неинвазивной экспресс-диагностики многокомпонентных биологических сред, содержащих исследуемый объект с целью определения вирусов, бактерий и других микроорганизмов в водоемах, на Земле и на других космических телах путем цифровой записи голограммы среды (в том числе жидкой) и цифрового восстановления ее изображения с сохранением амплитуды и фазы волны. ЦГМ (DIHM - Digital In-Line Holographic Microscope) позволяет также определить характеристики рассеяния интенсивности электромагнитного излучения на исследуемом объекте, его распределение по объему среды, определение глубины и его положение в 3- и 4-координатном пространстве, направление движения (трека), скорость, размер, осуществить накопление информации, сравнение объекта с тест-объектами и т.д.
ЦГМ относится к измерительным системам для автоматического контроля, технического диагностирования, системам распознавания образов (объектов) и передачи измерительной информации. Такие устройства используются на поверхности Земли, в скважинах или на разных глубинах водоемов для определения их биологических компонент. Система допускает полную автоматизацию.
Появлению устройств ЦГМ способствовало развитие современной элементной базы микроэлектроники - появление лазерных полупроводниковых и квазикогерентных светодиодов, матричных фотоприемников CCD (Charge-Coupled-Device), CMOS (Complementary Metal-Oxide-Semiconductor) и др. матриц (в дальнейшем - "матрицы"), а также реализация различных алгоритмов обработки изображений на стационарных и портативных ПК, позволяющих создать мобильные, автономные и портативные средства для осуществления сетевой дистанционной системы экспресс-анализа в различных точках и обрабатывать данные в реальном времени.
ЦГМ может восстанавливать изображение заданного объекта с объема биологической среды сложного состава.
Объектами могут служить рачки, бактерии и другие микроорганизмы, а также, к примеру, микрочастицы, следы ядерных заряженных частиц в облученной на ускорителях пузырьковой камере /1/ и т.д.
/1/ [Турухано Б.Г. Накопление информации на голограмме по глубине восстановленного изображения и загрузка пузырьковой камеры треками. ЖТФ, т.90, №1, с.181-187, т. 1970].
Устройство способно сохранить все данные в своей базе и осуществить их анализ в реальном времени или постфактум. Причем эти процессы и обработку данных можно осуществить в автоматическом режиме /2/.
/2/ [Консультативный центр МАТЛАБ компания SoftLine http://www.nsu.ru/matlab/MatLab_RU/default.asp.htm].
Для решения более широкого и полного круга задач и определения координат точечных объектов была выполнена и стала доступна и другая программа /3/.
/3/ [Программа для восстановления голографически записанных изображений и определения пространственного расположения точечных объектов "Digital Holography"». Свидет-во об официальной регистрации программы для ЭВМ №2009614972 от 11.09.2009].
Эти программы позволяют осуществить полный завершенный круг регистрации голограммы с помощью матрицы фотоприемников и вести обработку ее восстановленного изображения.
Устройство ЦГМ, в общем случае, состоит из двух частей: оптической, необходимой для создания голографической интерференционной картины (голограммы), и электронно-вычислительной для цифровой ее регистрации, считывания и обработки полученных данных в реальном времени или постфактум.
В общем случае при записи голограммы используется когерентный источник излучения, как правило, лазер, газовый/твердотельный (в стационарных системах) или твердотельный (в портативных устройствах), соосная двулучевая оптическая схема, в которой располагается объем (кювета) с изучаемым объектом, а также детектор голограммы в виде матрицы фотоприемников. Наилучшее разрешение исследуемого объекта достигнуто на уровне 225 nm /4/ с использованием ультрафиолетового излучения (λ=372 nm) и CMOS-матрицы с пикселем в 1,12 µm, при этом авторы осуществили математическую обработку данных для увеличения разрешения регистрирующих фотоприемников (пикселей).
/4/ [Aloon Greenbaum, Aydogan Ozkan. Increased space-bandwidth product in pixel super-resolved lensfree on-chip microscopy. Scientific Reports, published 24 April 2013].
Однако существующие в настоящее время системы и программы для ЦГМ дают лишь инструмент, позволяющий наилучшим и автоматическим образом определить характеристики изучаемого объекта при данной конфигурации конкретного ЦГМ, но не решают один из важных вопросов, а именно вопрос, связанный с повышением разрешающей способности системы на стадии записи голограммы. Поэтому с учетом имеющихся аппаратных, математических и компьютерных возможностей необходимо найти такие конструкции ЦГМ, которые позволили бы увеличить его разрешение и на уровне регистрации голограммы.
Известно ЦГМ /5/ состоящее из двух систем: оптической системы для записи голограммы и системы считывания информации с голограммы в реальном времени с использованием чипа GPU (устройство графической и цифровой обработки информации). GPU рассчитывает Френелевскую дифракцию света на исследуемом объекте, зарегистрированную на голограмме, и восстанавливает его изображение.
/5/ [Tomoyoshi Shimobaba, Nobuyuki Masuda and Tomoyoshi Ito. Multi-view and multi-resolution real-time digital holographic microscopy. Microscopy: Science, Technology, Application and Education, 1419-1425, 2010].
Оптическая система содержит источник когерентного излучения (лазер), кювету с исследуемыми объектами и с плоскими окнами и регистрирующую плоскую матрицу CCD-камеры. Изображение интерференционной картины (Габоровской голограммы /6/) записывается на матрице CCD-камеры, разрешение которой 1360×1024 пикселей при размере пикселя 4,65 мкм × 4,65 мкм.
/6/ [D. Gabor. A new microscopic principle. Nature 161, pp 777-778, 1948].
Устройство ЦГМ работает следующим образом.
Световая волна от лазера при входе в интерферометр разделяется на две части, проходя по двум его плечам.
Одна часть волны проходит через плечо, где находится исследуемый объект, дифрагируя на нем, после чего она на выходе из интерферометра встречается со второй частью волны, проходящей неискаженной через второе плечо, и интерферирует с ней. Из оптической системы устройства изображение переносится во вторую систему для восстановления, считывания и обработки информации с помощью GPU и PC.
Информация об исследуемом объекте представляет голограмму в виде Френелевской картины дифракции (интерференционные полосы различной формы и с различным расстоянием между ними), которая записывается на матрице CCD-камеры. Голограмма затем декодируется (восстанавливается) с помощью GPU и PC.
Недостатком устройства ЦГМ является запись на голограмме интерференционной картины в основном низкочастотного спектра, в результате чего система позволяет восстанавливать объекты с невысоким разрешением. Это связано с тем, что апертура матрицы записывающего устройства CCD-камеры небольшая и часть высокочастотного спектра интерференционной картины, расположенной на периферии голограммы, отсекается и теряется.
Другим недостатком можно считать Гауссово (колоколообразное) распределение интенсивности по сечению лазерного пучка, поэтому интерферограмма, записанная в плоскости матрицы CCD-камеры, различна по яркости по всей плоскости голограммы, что определяет качество записи, а при считывании приводит к различному соотношению сигнал/шум по полю матрицы и, как следствие, возможности увеличения случайных ошибок при восстановлении изображения и обработке полученных с голограммы данных.
Из известных устройств ЦГМ наиболее близким по технической сути является ЦГМ, описанный в работе /7/.
/7/ [S.K. Jericho, P. Klages, J. Nadeau, E.M. Dumas, M.H. Jericho, H.J. Kreuzer. In-line digital holographic microscopy for terrestrial and exobiological research. Planetary and Space Science 58, p.701-705, 2009].
Цифровой голографический микроскоп содержит источник излучения, обладающий оптической осью, направленной в сторону распространения луча, фокусирующий объектив, диафрагму и кювету с исследуемым объектом, которые расположены на оптической оси. Кювета имеет плоские - входное и выходное окна. Далее ЦГМ содержит плоскую матрицу CCD-камеры с фотоприемниками, электронно-вычислительную систему, включающую блок обработки данных, программное обеспечение, позволяющее восстанавливать изображение объекта и ПК.
Устройство работает следующим образом.
Луч от лазера фокусируется с помощью объектива в плоскости диафрагмы. После диафрагмы волна дифрагирует на объекте и рассеивается в виде сферических волн, которые интерферируют со световыми волнами, проходящими в этом же направлении без рассеяния, создавая интерференционную картину, которая фиксируется на матрице CCD-камеры.
Голограмма запоминается на плоской матрице CCD-камеры в виде 2-координатной интерференционной картины, на которой фиксируется одновременно амплитуда и фаза рассеянной объектом волны. Далее картина цифровым способом восстанавливается. Суть восстановления состоит в том, чтобы из 2-координатной голограммы получить полное 3-координатное изображение объекта, что возможно благодаря тому, что на голограмме фиксировались одновременно фаза и амплитуда волны, дифрагированной на объекте. Серия голограмм, снятых в разное время с определенной скоростью, позволяет восстанавливать 4-координатную траекторию объекта. Авторами получено разрешение около 2 мкм.
Недостатком устройства является запись на голограмме, в основном, низкочастотного спектра интерференционной картины, в результате чего система позволяет восстанавливать объекты с ограниченным разрешением. Это связано с тем, что апертура записывающей плоской матрицы CCD-камеры небольшая, и высокочастотная часть спектра интерференционной картины, расположенной на периферии голограммы, выпадает из общего контекста. Кроме этого, в силу Гауссового распределения лазерного пучка интерферограмма, записанная в плоскости матрицы CCD-камеры, не одинакова по яркости и контрастности.
Задачей предложенного изобретения является:
- сохранение одинаковой светосилы по сечению объема с исследуемыми объектами;
- увеличение разрешения ЦГМ;
- увеличение объема с исследуемыми объектами при сохранении его компактности.
Задача достигается тем, что в известном ЦГМ, содержащем источник излучения, обладающий оптической осью, направленной в сторону распространения пучка излучения, фокусирующий объектив, диафрагму и кювету для размещения исследуемого объекта, расположенные вдоль оптической оси, причем кювета имеет прозрачные входное и выходное окна, а входное окно плоское, матрицу фотоприемников, электронно-вычислительную систему, включающую блок обработки, программное обеспечение, позволяющее восстанавливать изображение объекта в статике и в движении, и ПК, новым является то, что дополнительно до кюветы введен фильтр для сглаживания Гауссового распределения и получения равномерного освещения по сечению пучка, выходное окно кюветы имеет форму полусферы с радиусом, равным расстоянию от входного до выходного окна, а матрица фотоприемников имеет форму полусферы, расположена параллельно выходному окну кюветы, повторяет его форму и жестко с ним связана.
Такая совокупность признаков в заявляемом ЦГМ позволяет:
1 - осуществить равномерное освещение по сечению пучка путем сглаживания Гауссового распределения источника излучения;
2 - повысить разрешение ЦГМ за счет увеличения апертуры матрицы фотоприемников и ее формы в виде полусферы, позволяющей зарегистрировать высокочастотные интерференционные полосы голограммы;
- увеличить объем с исследуемым объектом при сохранении компактности заявляемого устройства.
На Фиг.1 дана блок-схема ЦГМ. На Фиг.2 изображен конкретный пример конструктивного решения предлагаемого устройства ЦГМ. На Фиг.3 для сравнения дана одновременно картина интерференции пучков в случае использования устройства ЦГМ с полусферической матрицей и с плоской.
Устройство состоит из оптической и электронно-вычислительной систем. Оптическая схема содержит лазер 1, микрообъектив 2, диафрагму 3, фильтр 4, кювету с исследуемым объектом 5, матрицу 9, а электронно-вычислительная система содержит блок обработки данных 11 и ПК 12.
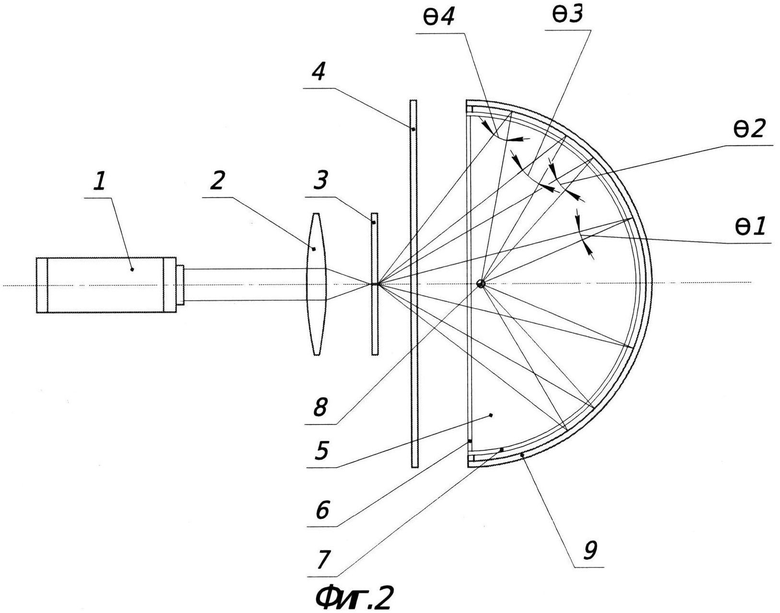
На Фиг.2 изображен конкретный пример конструктивного решения предлагаемого устройства ЦГМ для записи безлинзовой Френелевской голограммы с точечным источником вспомогательной волны, где 1 - источник излучения (лазер), 2 - микрообъектив, 3 - диафрагма, 4 - фильтр для сглаживания Гауссового распределения, 5 - кювета с исследуемым объектом, 6 - плоское входное окно кюветы, 7 - полусферическое выходное окно кюветы, 8 - исследуемый объект, 9 - полусферическая матрица, повторяющая форму выходного окна кюветы 7 и состоящая из фотоприемников, θ1, θ2, θ3, θ4 - углы между объектными и вспомогательными лучами, участвующими в создании голограммы на внутренней поверхности полусферической матрицы.
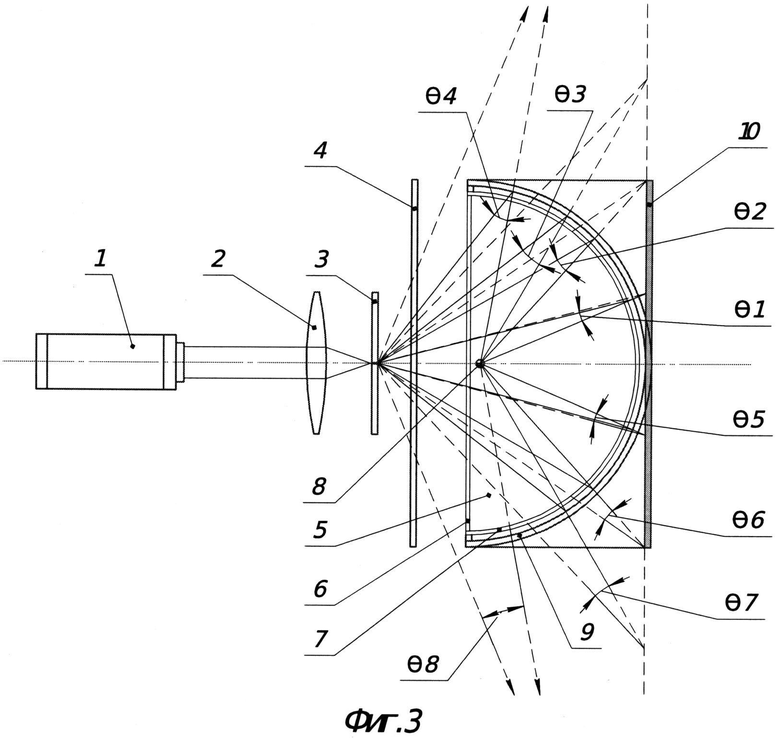
На Фиг.3. дано сравнение одновременно картин интерференции пучков в случае использования устройства ЦГМ с полусферической матрицей, предложенного в данной заявке (сплошные линии), и с плоской матрицей прототипа (линии пунктиром). Плоская матрица ЦГМ прототипа 10, а θ5, θ6, θ7, θ8, - углы между объектными и вспомогательными лучами, участвующими в создании голограммы на внутренней поверхности плоской матрицы прототипа.
Устройство работает следующим образом: пучок от источника излучения 1 (Фиг.1) попадает на микрообъектив 2, который фокусирует его. В фокусе микрообъектива установлена диафрагма 3, размером от нескольких единиц до долей мкм, отсекающая высокие частоты в фокусе микрообъектива с целью его очистки от когерентного шума, обусловленного дифракцией на дефектах объектива и на частицах, попадающихся на пути до исследуемого объекта. После этого пучок проходит через фильтр 4, сглаживающий его Гауссово распределение и превращающий его в равномерное по всему поперечному сечению. Далее пучок через плоское входное окно 6 поступает в кювету 5 с исследуемым объектом 8, дифрагируя на нем и направляясь сквозь прозрачное выходное окно в виде полусферы 7 в сторону полусферической матрицы 9. Кювета у своего основания (входного окна 6) имеет входное отверстие, позволяющее пропускать через него поток с исследуемыми объектами, и выходное отверстие для вывода этого потока. Как видно из Фиг.2, все рассеянные объектом лучи в пределах полусферы интерферируют с соответствующими вспомогательными (неискаженными) лучами под углами θ1, θ2, θ3, θ4 и попадают на полусферическую матрицу, создавая картину в виде интерференционных полос. На Фиг.3 пунктиром показаны дифрагированные объектом лучи, интерферирующие с референтными лучами под углами θ5, θ6, попадающими на плоскую матрицу, используемую в прототипе в качестве регистрирующей голограммы, и в этом же случае, θ7, θ8, которые не могут попасть на матрицу в силу ее ограниченного размера, будут отражаться из-за малого угла с плоской матрицей, не давая интерференцию. При существенном увеличении размеров плоского экрана, светосила периферийных лучей, попадающих на матрице, особенно под углами θ7, θ8, в силу их большой расходимости, наклонного падения и отдаленности от оси системы намного меньше по сравнению со светосилой лучей, которые регистрируются ближе к оси. В этом случае сложно записать на матрице голограмму, с которой можно получить изображение объекта с улучшенным разрешением. Для этого необходимо иметь очень большой динамический диапазон фоточувствительности фотоприемников, в то время как при записи на полусферической матрице сохраняется светосила лучей практически на всей поверхности матрицы из-за малого удаления от источника сферических волн - диафрагмы.
Из Фиг.3 видно, что углы θi(j) (i=1, 2, 3, 4 для полусферической матрицы; j=5, 6, 7, 8 для плоской матрицы) между дифрагирующими лучами на объекте и лучами референтной волны растут по мере удаления от оси системы и приближения к входному окну кюветы 6, т.е.:
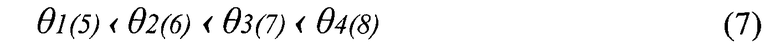
соответственно, и их синусы sinθi(j) также растут
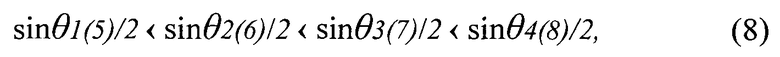
а согласно формуле

частота ν интерференционных полос, образованных в результате их интерференции, также растет. На Фиг.3 сплошными линиями сходятся интерферирующие лучи на внутренней поверхности полусферического экрана, а пунктирными линиями - плоского экрана ЦГМ. Т.о. в случае плоской матрицы, место пересечения лучей по мере удаления от оси также находится на большом расстоянии от нее, что требует намного больших габаритов плоских матриц.
Максимальный угол, образованный референтным и дифрагированным лучами, близкими к входному окну кюветы, дает пересечение у плоской матрицы, близкой к бесконечности, - а это требует существенного увеличения ее размера, что практически нереализуемо. С другой стороны, регистрация интерференции этих периферийных лучей необходима для повышения разрешения системы.
Такие большие размеры плоской матрицы, следовательно и системы в целом, неудобны не только для портативной, но даже для стационарной системы, т.к. в этом случае необходимо увеличить вибростойкость и термостабильность системы, которые влияют на качество (разрешение) голограммы. Особенно важно при регистрации на голограмме интерференционных полос высокой частоты и, соответственно, малых периодов, чтобы эти полосы точно сохраняли свое положение друг относительно друга в пространстве и во времени. Чем меньше период полос, регистрируемых голограммой, тем выше должно быть ее разрешение.
Разрешение голограммы
Разрешение голограммы R согласно критерию Rayleigh дается выражением:

где k - постоянный коэффициент, зависящий от формы матрицы,
λ - длина волны источника излучения, f - расстояние от объекта до регистрирующего экрана, D - апертура матрицы.
Разрешение ЦГМ, согласно выражению (1), зависит от следующих факторов:
а) λ - длина волны источника излучения
При создании голограммы с высоким разрешением в ЦГМ желательно использовать источник излучения, обладающий как можно более короткой длиной волны λ, что приводит к увеличению частоты интерференционных полос в плоскости регистрации голограммы, а впоследствии, при восстановлении голограммы, к более высокому разрешению восстановленного изображения объекта/ов и расширению частотного диапазона изображения объекта. Однако работать в УФ-й области и с λ<0,3 мкм - сложно, и в то же время, неоднозначно воздействие УФ-го излучения на исследуемые биологические объекты. Поэтому в существующие ЦГМ, при исследованиях биологических объектов, выбирают источники с малой λ в видимой области спектра с учетом их неразрушающего воздействия на исследуемый объект.
б) Апертура D (размер) матрицы ЦГМ
Апертура D (размер) матрицы линейно связана с разрешением ЦГМ.
Апертура регистрирующей матрицы, в существующих системах ЦГМ, зависит от ряда факторов: ограничения геометрических размеров и допустимого веса, определяемого конкретными задачами в каждом отдельном случае.
Небольшие габариты ЦГМ связаны с применением заявляемого устройства на земле, в космосе и под землей, с его погружением, к примеру, на большие глубины (до нескольких километров), где диаметр скважин или погружающихся аппаратов ограничен техническими и технологическими условиями, или при их поднятии в космос, где также имеет место сильное ограничение габаритов и веса летательных аппаратов;
ЦГМ, использующие схему Габоровской соосной (online) голографии, благодаря малой апертуре записывающих матриц, осуществляют регистрацию низких пространственных частот интерферирующих пучков, которые появляются в результате интерференции при малых углах между объектным и референтным пучками. Большие углы между этими пучками, ответственные за высокие пространственные частоты, определяющие высокое разрешение восстановленного изображения исследуемого объекта, расположены на периферии голограммы и выходят за пределы габаритов регистрирующей матрицы.
В случае применения схемы online записи голограммы с применением референтного соосного пучка в плоскости регистрации голограммы имеет место интерференция двух пучков с нарастающей пространственной частотой к периферии. Согласно определению передаточной функции, в оптической части ЦГМ передаточная функция A (νx, νy) представляет собой отношение выходного сигнала к входному в частотном представлении:
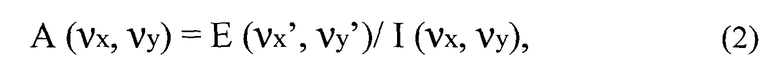
где E(νx′,νy′) и I(νx,νy) - соответственно распределение освещенности изображения (выходного сигнала) и яркости объекта (входного сигнала), νx′, νy′ - пространственные частоты изображения, νx, νy - пространственные частоты объекта. При этом пространственная частота в пространстве объекта ν и пространственная частота в пространстве изображения ν′ связаны линейной зависимостью:

где β - линейное увеличение системы.
Поэтому потеря высоких частот (на входе) при регистрации интерференционной картины на матрице ЦГМ, отвечающей за тонкую структуру объекта, напрямую и линейно будет связана с потерей этих же частот в пространстве восстановленного изображения (на выходе), что приводит к уменьшению передаточной функции A (νx, νy) и разрешения системы в целом. Таким образом, увеличение разрешения ЦГМ можно достигнуть путем линейного сохранения баланса всех частот объекта и его восстановленного изображения, благодаря регистрации высоких частот интерференционных полос, зарегистрированных на матрице при данной длине волны λ.
Известно, что пространственная частота интерференционных полос ν, в свою очередь, зависит от угла θ между интерферирующими лучами (дифрагированными на объекте и референтными) и от длины волны λ источника излучения, согласно выражению

Как видно из выражения (4), чем больше угол θ, тем больше частота интерференционных полос, регистрируемых на голограмме, и, соответственно, тем меньше расстояние между ними, а следовательно, тем выше должно быть разрешение для их пространственного разделения.
Raleigh предложил считать, что (в нашем случае) зарегистрированные на голограмме две интерференционные полосы равной интенсивности начинают разрешаться, когда главный максимум интенсивности одной полосы совпадает с первым минимумом другой полосы. При этом отношение интенсивностей в средней точке к интенсивности в максимуме равно 0,811.
Вблизи оптической оси голограммы - углы небольшие (Фиг.2 и 3), а их увеличение происходит по мере отдаления объектной волны от оптической оси, т.е. к периферии голограммы.
Необходимо отметить, что можно осуществить обработку данных с голограммы для достижения высокого разрешения изображения, но только в рамках тех частот, которые зарегистрировала плоская матрица. С целью регистрации матрицей высоких частот проводились работы по приближению объекта к матрице /8/ и с последующей цифровой обработкой данных.
/8/ [Ulf Schnars and W PO Juptner. Digital recording and numerical reconstruction of holograms. Meas. Sci. Technol., 13, R85-R101, 2002].
При регистрации плоской матрицей интерференционной картины, создаваемой референтными и объектными лучами, падающими на нее под малыми углами относительно ее плоскости, часть дифрагировнных объектом лучей регистрируется матрицей, а часть отражается от ее плоскости.
Известно, что закон отражения света справедлив не только для идеально отражающих поверхностей, но и для границы двух сред, частично отражающей свет, как в случае матрицы со светоприемниками, обладающими как плоскими, так и сферическими входными окнами - линзами (к примеру, матрицы КМОС), при этом закон не утверждает о соотношении отраженного и поглощенного света. Причем, начиная с определенного угла объектных лучей происходит их полное отражение, что приведет к тому, что соответствующие интерференционные полосы вообще не будут регистрироваться матрицей, тем самым, исключая крайнюю часть матрицы из общего процесса регистрации, и, соответственно, более высокие периферийные (крайние) частоты, которые должны были на ней регистрироваться.
В случае, когда расстояния от исследуемого объекта до плоской матрицы малы, Френелевское приближение уже недействительно и с целью получения высокого разрешения необходимо вести цифровую обработку с учетом характеристик пикселя (тип, плотность и площадь). Такая обработка нужна для повышения разрешения системы и увеличения отношения сигнал/шум для уменьшения вероятности появления ложных сигналов при восстановлении объекта и его характеристик. Кроме этого, при попытках приближения исследуемых объектов к матрице уменьшается рабочий объем кюветы, а время набора статистических данных увеличивается
в) f - расстояние от объекта до регистрирующего экрана
Разрешение системы растет с уменьшением величины f (см. (1). Из Фиг.3 видно, что ход лучей, распространяющихся от исследуемого объекта до полусферической матрицы - fсм (сплошные линии), всегда меньше длины хода лучей от исследуемого объекта до плоской матрицы (случай прототипа) - fплм (их продолжение указано пунктиром), т.е. fсфмАi<fплм (Ai+Bi) (Ai - отрезок луча до полусферической матрицы, Bi - отрезок луча до плоской матрицы, i - условное порядковое число луча, возрастающее по мере удаления от оптической оси). Исключение составляют только лучи, совпадающие с оптической осью (i=0):
fсфмАo<fплмBo, т.к. Ao=Bo.
Т.к. для данного объекта 8, изображенного на Фиг.3:
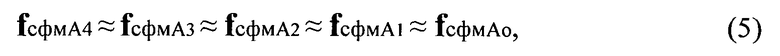
а соответствующие
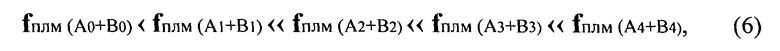
то очевидно, что разрешение у ЦГМ с полусферическим экраном будет выше в сравнении с плоским экраном, причем, как видно из выражения (1) и (6), в этом случае разрешение плоского экрана не только меньше, чем у полусферического экрана, но оно еще падает с удалением от оси, т.к. к периферии fплм существенно растет.
На увеличение разрешения ЦГМ влияет:
а) распределение интенсивности пучка излучения.
Сохранение одинаковой интенсивности по всему сечению пучка источника излучения, перпендикулярному оптической оси, с целью получения одинаковой интенсивности интерференционных полос на поверхности матрицы, которая регистрирует голограмму. Запись голограммы с разной интенсивностью интерференционных полос приведет к дополнительным проблемам при обработке, восстановленной с матрицы информации.
Интенсивность пучка когерентного источника излучения имеет Гауссово распределение (колокол), при котором центр яркий, а периферия слабее, поэтому в разных местах объема с исследуемыми объектами имеется разная светосила и поэтому эти объекты по-разному освещены, что и определяет различную амплитуду электрических сигналов, снятых с фотоприемников матрицы, а впоследствии характер и качество цифровой обработки изображения.
Преобразование Гауссового колоколообразного по сечению распределения интенсивности пучка в равномерное можно осуществить с помощью фильтра в виде амплитудно-фазовой маски, которая сглаживает распределение интенсивности, поднимая яркость на периферии, а также с помощью фильтра Гаусса, относящегося к числу сглаживающих фильтров.
Известны также фильтры типа "πShaper 12_12", конвертирующие Гауссовое распределение лазерного пучка в прямоугольное распределение в видимой, а также в УФ-й части спектра (в этом случае удобнее установить эти фильтры до расширяющей оптики).
Простейший прямоугольный сглаживающий фильтр Гаусса также усредняет интенсивность излучения по всему сечению пучка;
б) увеличение апертуры D матрицы, изготовленной в виде полусферы, благодаря которой осуществляется регистрация высокочастотной части голограммы.
Цель увеличения разрешения:
- разрешение наиболее близких интерференционных линий, образующихся в плоскости матрицы при регистрации голограммы, а также
- увеличение разрешения по всему исследуемому объему, благодаря созданию матрицы и кюветы полусферической формы для сохранения компактности ЦГМ.
Известно, что разрешающая способность голограммы пропорциональна ее размеру.
Полусферическая матрица (см. Фиг.3) обладает б′ольшим размером (площадь/периметр) (2πR2/πR), чем плоская квадратная матрица (площадь/ширина) (4R2/2R) в π/2=1,57 раз, а это, в свою очередь, позволяет увеличить кювету с исследуемым объемом, при сохранении габаритов системы, делая ЦГМ более эффективным и удобным (особенно портативный вариант).
Оценка величины разрешения ЦГМ со полусферической матрицей.
В связи с тем, что критерий Rayleygh определен эмпирическим путем для оптических устройств, с целью снятия зависимости от субъективности восприятия (две соседние точки разрешаются, если минимум интенсивности между ними достаточно мал, чтобы его разглядеть), то выражение разрешения согласно этому критерию (1) имеет различный вид. К примеру: коэффициент k может иметь разное значение в зависимости от размера и формы матрицы оптической системы, а именно, если форма круглая, то он равен 1,22, если квадратная - 1, если полусфера - 0,63, т.к. чем больше размер матрицы, тем выше разрешение при всех других равных условиях.
Поэтому можно определить разрешение для ЦГМ с полусферической матрицей по формуле (1).
Учитывая (см. Фиг.2), что k=0,63; λ=0,488 мкм (Ar лазер), f/D=0,312, то согласно выражению (1) R=kλf/D получаем следующее разрешение
R=0,63×0,488×0,312=0,095 мкм.
Таким образом, получено разрешение ЦГМ с полусферической матрицей 95 nm без использования специальной математической обработки.
Таким образом, в данной заявке предложены следующие конструктивные решения с использованием:
1) фильтра для сглаживания Гауссового распределения пучка источника излучения с целью увеличения светосилы периферийной картины интерференционных полос, регистрируемых на матрице;
2) полусферической матрицы, позволяющей:
- зарегистрировать высокочастотные интерференционные полосы голограммы, определяющие высокое разрешение восстановленного изображения;
- создать компактную систему ЦГМ;
- увеличить объем с исследуемым объектом.
ЛИТЕРАТУРА
1. Турухано Б.Г. Накопление информации на голограмме по глубине восстановленного изображения и загрузка пузырьковой камеры треками. ЖТФ, т.90, №1, с.181-187, т. 1970.
2. Консультативный центр МАТЛАБ компания SoftLine http://www.nose.ru/matlab/Mata_RU/default.asp.hum.
3. Программа для восстановления голографически записанных изображений и определения пространственного расположения точечных объектов "Digital Holography"». Патент РФ №2009614972 от 11.09.2009.
4. Aloon Greenbaum, Aydogan Ozkan. Increased space-bandwidth product in pixel super-resolved lensfree on-chip microscopy. Scientific Reports, published 24 April, 2013.
5. Tomoyoshi Shimobaba, Nobuyuki Masuda and Tomoyoshi Ito. Multi-view and multi-resolution real-time digital holographic microscopy. Microscopy: Science, Technology, Application and Education, pp.1419-1425, 2010.
6. D. Gabor. A new microscopic principle. Nature 161, pp.777-778, 1948.
7. S.K. Jericho, P. Klages, J. Nadeau, E.M. Dumas, M.H. Jericho, H.J. Kreuzer. In-line digital holographic microscopy for terrestrial and exobiological research. Planetary and Space Science 58, pp.701-705, 2009.
8. Ulf Schnars and W PO Juptner. Digital recording and numerical reconstruction of holograms. Meas. Sci. Technol., 13, R85-R101, 2002.
| название | год | авторы | номер документа |
|---|---|---|---|
| МЕТОД И УСТРОЙСТВО ДЛЯ РЕГИСТРАЦИИ СПЕКТРАЛЬНЫХ ЦИФРОВЫХ ГОЛОГРАФИЧЕСКИХ ИЗОБРАЖЕНИЙ ОПТИЧЕСКИ ПРОЗРАЧНЫХ МИКРООБЪЕКТОВ | 2015 |
|
RU2601729C1 |
| УСТРОЙСТВО ДЛЯ ИЗМЕРЕНИЯ ОТКЛОНЕНИЙ ОТ ПЛОСКОСТНОСТИ ПОВЕРХНОСТИ | 2004 |
|
RU2287776C2 |
| Устройство для записи голограммы объекта во встречных пучках | 1980 |
|
SU911450A1 |
| СПОСОБ ИЗМЕРЕНИЯ ВОЛНОВОГО ФРОНТА | 1988 |
|
RU1542281C |
| Устройство для измерения оптической разности хода | 1990 |
|
SU1787266A3 |
| Способ определения профиля показателя преломления оптических неоднородностей и устройство для его осуществления | 1990 |
|
SU1777053A1 |
| Способ определения частоты и амплитуды модуляции фазы волнового фронта, создаваемого колебаниями мембраны клетки | 2020 |
|
RU2743973C1 |
| ИНТЕРФЕРЕНЦИОННЫЙ МИКРОСКОП | 2013 |
|
RU2527316C1 |
| СОЛНЕЧНЫЙ ВЕКТОР-МАГНИТОГРАФ | 2009 |
|
RU2406982C1 |
| Способ экспресс-анализа величины динамического диапазона фотоотклика фазового голографического материала | 2020 |
|
RU2734093C1 |
Изобретение может быть использовано в качестве измерительной системы для неинвазивной экспресс-диагностики многокомпонентных биологических сред для определения вирусов, бактерий и других микроорганизмов. Микроскоп содержит источник излучения, фокусирующий объектив, диафрагму и кювету для размещения исследуемого объекта, расположенные вдоль оптической оси, матрицу фотоприемников, электронно-вычислительную систему, включающую блок обработки, программное обеспечение и ПК. Дополнительно до кюветы введен фильтр для сглаживания Гауссового распределения пучка излучения и получения равномерного освещения по сечению пучка. Кювета имеет прозрачное плоское входное окно. Выходное окно кюветы имеет форму полусферы с радиусом, равным расстоянию от входного до выходного окна кюветы. Матрица фотоприемников имеет форму полусферы, которая расположена параллельно выходному окну кюветы, повторяет его форму и жестко с ним связана. Технический результат - сохранение одинаковой светосилы по сечению кюветы и увеличение разрешения ЦГМ. 3 ил.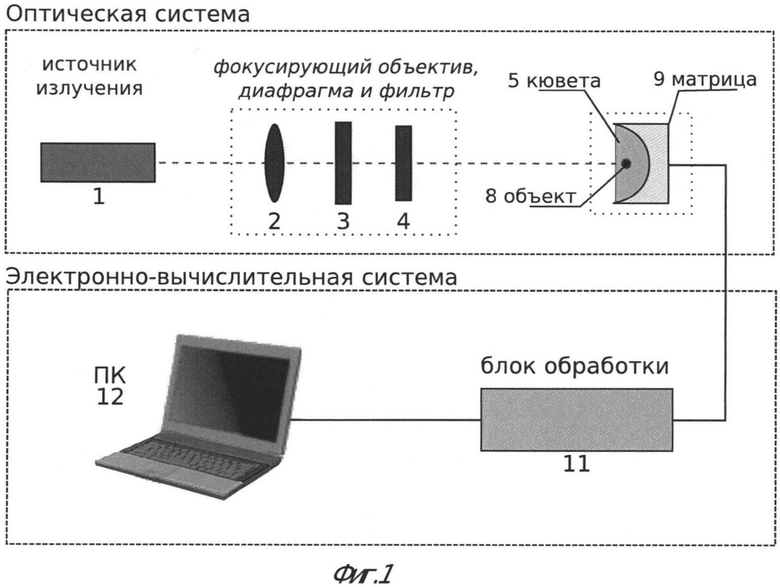
Цифровой голографический микроскоп, содержащий источник излучения, обладающий оптической осью, направленной в сторону распространения пучка излучения, фокусирующий объектив, диафрагму и кювету для размещения исследуемого объекта, расположенные вдоль оптической оси, причем кювета имеет прозрачные входное и выходное окна, а входное окно плоское, матрицу фотоприемников, электронно-вычислительную систему, включающую блок обработки, программное обеспечение и ПК, отличающийся тем, что дополнительно до кюветы введен фильтр для сглаживания Гауссового распределения пучка излучения и получения равномерного освещения по сечению пучка, выходное окно кюветы имеет форму полусферы с радиусом, равным расстоянию от входного до выходного окна кюветы, и матрица фотоприемников имеет форму полусферы, расположена параллельно выходному окну кюветы, повторяет ее форму и жестко с ним связана.
| S.K | |||
| Jericho, P | |||
| Klages, J | |||
| Nadeau, E.M | |||
| Dumas, M.H | |||
| Jericho, and H | |||
| J | |||
| Kreuzer, In-line digital holographic microscopy for terrestrial and exobiological research, Planetary and Space Science 58, 2009, 701-705, найдено в Интернет: http://4-deep.com/publications/ | |||
| US 2010060897 A1, 11.03.2010 | |||
| US 2009244667 A1, 01.10.2009 | |||
| US 2011157601 A1, 30.06.2011 | |||
| Голографический микроскоп | 1986 |
|
SU1314295A1 |
Авторы
Даты
2015-04-10—Публикация
2013-10-22—Подача