Перекрестная ссылка на родственную заявку
По этой заявке испрашивается приоритет предварительной заявки №61/469478 на патент США, поданной 30 марта 2011 года, под названием “Improving convergence rate of full wavefield inversion using spectral shaping” и предварительной заявки №61/508440 на патент США, поданной 15 июля 2011 года, под названием “Convergence rate of full wavefield inversion using spectral shaping”, которые полностью включены в эту заявку путем ссылки.
Область техники, к которой относится изобретение
В общем, это изобретение относится к области геофизической разведки, а более конкретно - к инверсии сейсмических данных, представляющей общий термин, используемый для обозначения процесса построения модели геологической среды на основании регистрируемых сейсмических данных. В частности, изобретение представляет собой способ повышения скорости сходимости инверсии полного волнового поля при использовании формирования спектра. Термин «инверсия полного волнового поля» (ИПВП) используется для обозначения способа инверсии, нацеленной на построение моделей геологической среды, по которым можно полностью интерпретировать регистрируемые сейсмические данные в точном количественном смысле: точное моделирование синтетических сейсмических данных на основании модели геологической среды, которая является результатом инверсии, близко соответствует реальным сейсмическим данным.
Предпосылки создания изобретения
При геофизической инверсии пытаются найти модель свойств геологической среды, по которой оптимально интерпретируют данные наблюдений и которая удовлетворяет геологическим и геофизическим ограничениям. Имеется большое количество хорошо известных способов геофизической инверсии. Эти хорошо известные способы делятся на две категории: итерационную инверсию и неитерационную инверсию. Ниже определяется, что обычно имеется в виду под каждой из двух категорий:
Неитерационная инверсия - инверсия, которую выполняют в предположении некоторой простой фоновой модели и обновлении модели на основании входных данных. В этом способе не используют обновленную модель в качестве входных данных на другом этапе инверсии. В случае сейсмических данных эти способы обычно называют построением изображения, миграцией, дифракционной томографией или инверсией Борна.
Итерационная инверсия - инверсия, включающая в себя повторения для улучшения модели свойств геологической среды, благодаря чему находят модель, которая удовлетворительно объясняет данные наблюдений. Если инверсия сходится, то конечная модель лучше объясняет данные наблюдений и более точно аппроксимирует реальные свойства геологической среды. Итерационной инверсией обычно получают более точную модель, чем неитерационной инверсией, но для нее требуются намного большие затраты на вычисления.
Наиболее распространенный способ итерационной инверсии, используемый в геофизике, представляет собой оптимизацию функции стоимости. Оптимизация функции стоимости включает в себя итерационную минимизацию или максимизацию значения с учетом модели М функции S(M) стоимости, которая является мерой несоответствия между данными вычислений и наблюдений (иногда также называемой целевой функцией), при этом данные вычислений моделируют с помощью компьютера, используя текущую модель геофизических свойств и физические основы прохождения сигнала источника в среде, представленной данной моделью геофизических свойств. Модельные вычисления можно выполнять любым из нескольких численных методов, включая, но без ограничения ими, метод конечных разностей, конечных элементов или трассирования лучей. Модельные вычисления можно выполнять в частотной или временной области.
Способы оптимизации функции стоимости являются локальными или глобальными. Глобальные способы включают в себя не что иное, как вычисление функции S(M) стоимости для совокупности моделей {M1,M2,M3,…} и выбор набора из одной или нескольких моделей из этой совокупности, по которым приближенно минимизируют S(M). Если желательно дальнейшее улучшение, то этот новый выбранный набор моделей можно использовать в качестве основы для построения новой совокупности моделей, которые, в свою очередь, могут быть проверены относительно функции S(M) стоимости. В случае глобальных способов каждую модель в проверяемой совокупности можно считать итерацией или на более высоком уровне каждый набор проверяемых совокупностей можно считать итерацией. Хорошо известные глобальные способы инверсии включают в себя метод Монте-Карло, имитации отжига, генетические и эволюционные алгоритмы.
К сожалению, способы глобальной оптимизации обычно сходятся очень медленно и поэтому в большинстве случаев геофизические инверсии основаны на локальной оптимизации функции стоимости. Алгоритмом 1 кратко излагается локальная оптимизация функции стоимости.
Алгоритм для выполнения локальной оптимизации функции стоимости
2. Вычисление градиента функции S(M) стоимости применительно к параметрам, которые описывают модель.
3. Поиск обновленной модели, то есть возмущение исходной модели в направлении отрицательного градиента, которым лучше объясняются данные наблюдений.
Эту процедуру повторяют, используя новую обновленную модель в качестве исходной модели для поиска другого градиента. Процесс продолжают до тех пор, пока не находят обновленную модель, которой удовлетворительно объясняются данные наблюдений. Обычно используемые локальные способы инверсии функции стоимости включают в себя метод градиентного поиска, сопряженных градиентов и Ньютона.
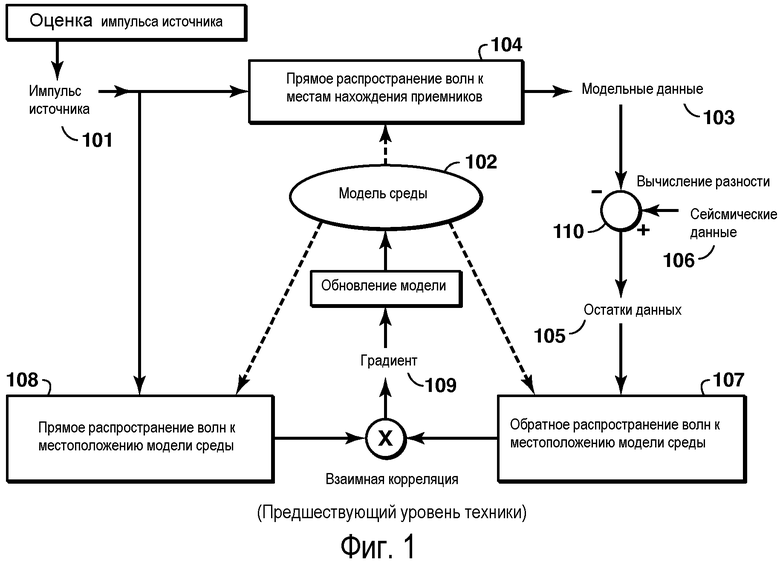
Очень общая функция стоимости представляет собой сумму разностей квадратов (с нормой L2) реальных и модельных сейсмических трасс. В таком случае, как показано на фигуре 1, последовательностью действий для типичной инверсии полного волнового поля градиент вычисляют через взаимную корреляцию двух волновых полей. Начав с оценивания сейсмического импульса (101) источника и исходной модели (102) геологической среды, образуют модельные сейсмические данные (103) в соответствии с распространением (104) волн вперед от источника к местам нахождения приемников. Остатки (105) данных образуют вычитанием (110) модельных данных из реальных сейсмических данных (106). Эти остатки затем распространяют обратно к модели (107) геологической среды и выполняют взаимную корреляцию с волновым полем источника, создаваемым при распространении (108) вперед от места нахождения источника до геологической среды. Результат этой взаимной корреляции представляет собой градиент (109), на основе которого обновляют модель геологической среды. Процесс повторяют с новой обновленной моделью до тех пор, пока разность между модельными и реальными сейсмическими данными не станет приемлемой.
Для других функций стоимости вычисление градиента может быть иным. Все-таки основные элементы последовательности действий из фиг.1 являются очень общими. Основные идеи настоящего изобретения могут быть тривиально преобразованы для случаев, когда используют вычисления альтернативных функций стоимости и градиентов.
В общем случае итерационная инверсия предпочтительна перед неитерационной инверсией, поскольку она дает более точные модели параметров геологической среды. К сожалению, для итерационной инверсии требуются настолько большие вычислительные ресурсы, что ее практически нецелесообразно применять ко многим, представляющим интерес задачам. Эти большие вычислительные ресурсы являются следствием того, что для всех способов инверсии требуются многочисленные моделирования с большим объемом вычислений. Время вычислений, затрачиваемое на любое индивидуальное моделирование, пропорционально количеству источников, подлежащих обращению, а обычно в геофизических данных имеется большое количество источников, при этом термин «источник», использованный ранее, относится к месту возбуждения источника. Задача усложняется при итерационной инверсии, поскольку количество моделирований, которые необходимо выполнять, пропорционально количеству итераций при инверсии, а количество необходимых итераций обычно составляет приблизительно от сотен до тысяч.
Снижение вычислительных затрат при инверсии полного волнового поля является основным требованием для того, чтобы способ стал практически применимым для трехмерных моделей месторождения, особенно в случае, когда необходимо высокое разрешение (например, при построении модели коллектора). Большое количество предложенных способов основано на идее одновременно моделируемых источников, кодированных (например, Krebs и соавторы, 2009; Ben-Hadj-Ali и соавторы, 2009; Moghaddam и Hermann, 2010) или когерентно суммируемых (например, Berkhout, 1992; Zhang и соавторы, 2005; Van Riel и Hendrik, 2005). Недостаток способов инверсии, основанных на кодированном одновременном моделировании, заключается в загрязнении результата инверсии переходным шумом, и они обычно ограничены конфигурацией регистрации данных (регистрация данных с помощью неподвижных приемников является необходимым условием для нескольких способов). Способы, основанные на когерентном суммировании, обычно приводят к потере информации. Тем не менее способы обоих видов могут быть очень полезными и являются предметом непрерывного исследования.
Другой способ снижения вычислительных затрат при инверсии полного волнового поля заключается в уменьшении количества итераций, необходимых для сходимости, и это является задачей настоящего изобретения. Способу не присущи типичные ограничения способов, упомянутых выше, хотя они не мешают их использованию. Фактически, его можно, в принципе, использовать в сочетании с любым из способов одновременно моделируемых источников, упомянутых выше, для возможного получения повышенной экономии вычислительных ресурсов.
Краткое изложение изобретения
Согласно одному осуществлению изобретением является реализуемый компьютером способ ускорения сходимости итерационной инверсии сейсмических данных для получения модели одного или нескольких физических параметров в области геологической среды, содержащий использование локальной оптимизации функции стоимости, в котором предполагаемую или текущую модель обновляют для уменьшения несоответствия между сейсмическими данными и модельно-имитированными данными, в котором частотный спектр обновленной модели регулируют при первой итерации и в дальнейшем до соответствия известному или расчетному частотному спектру для области геологической среды.
Краткое описание чертежей
Настоящее изобретение и его преимущества станут более понятными при обращении к нижеследующему подробному описанию и сопровождающим чертежам, на которых:
фиг.1 - блок-схема последовательности действий, показывающая основные этапы при инверсии полного волнового поля;
фиг.2 - схематическая иллюстрация результата применения формирующего фильтра согласно настоящему изобретению к сейсмическому импульсу источника и сейсмическим данным;
фиг.3 - блок-схема последовательности действий, показывающая основные этапы при осуществлении способа настоящего изобретения, включающего в себя применение формирующего спектр фильтра к входным данным и сейсмическому импульсу источника;
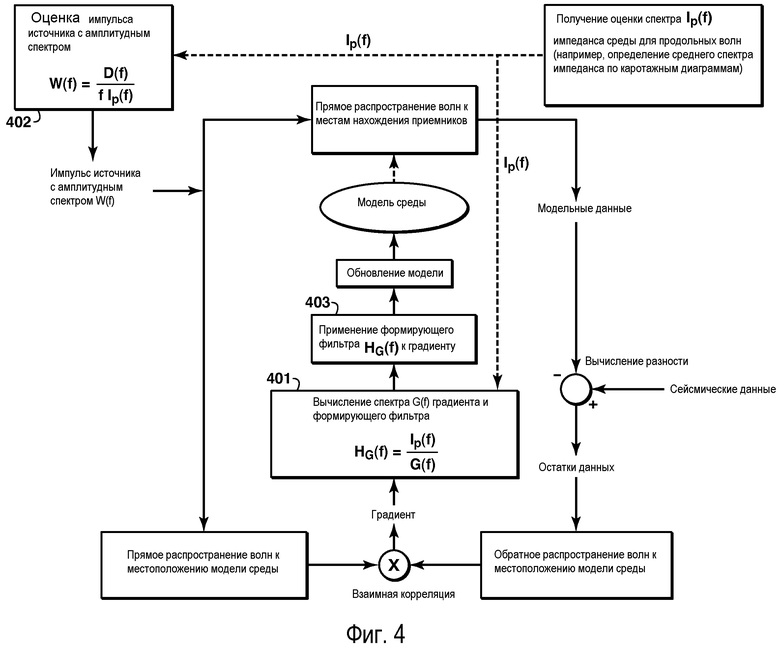
фиг.4 - блок-схема последовательности действий, показывающая основные этапы осуществления способа настоящего изобретения, включающего в себя применение формирующего спектр фильтра к градиенту функции стоимости;
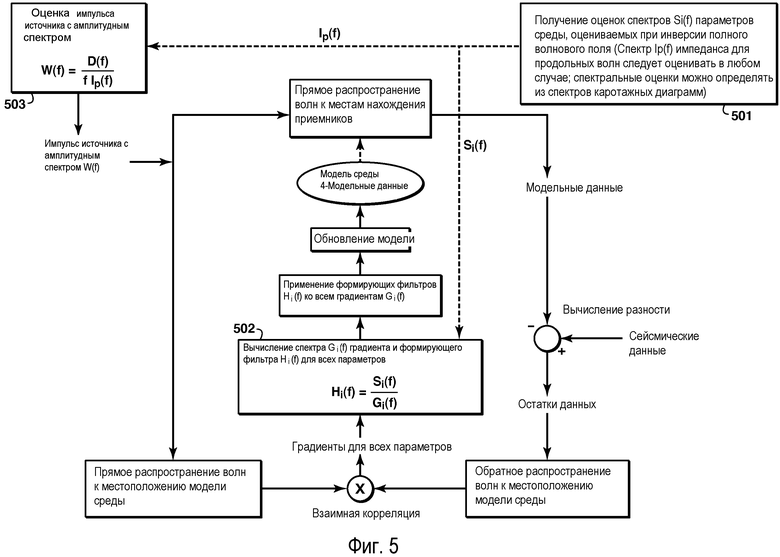
фиг.5 - блок-схема последовательности действий, показывающая основные этапы осуществления из фиг.4, распространенного на случай многопараметрической инверсии;
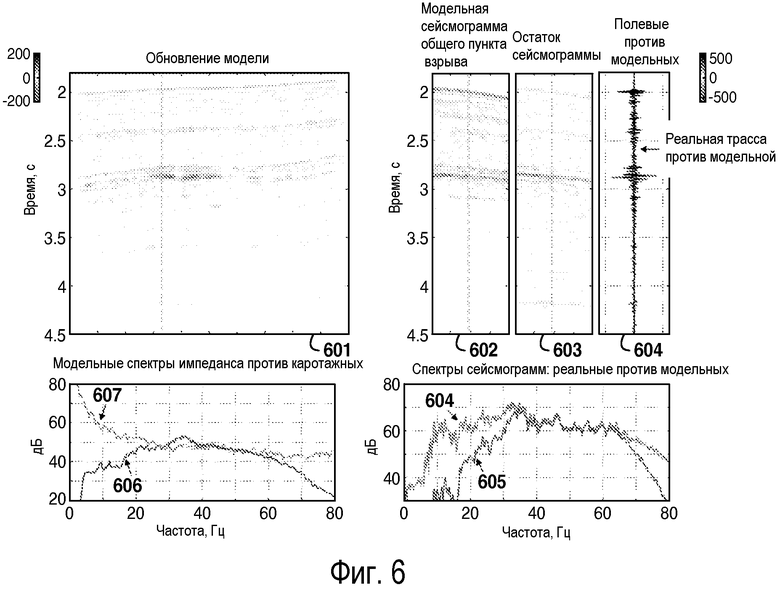
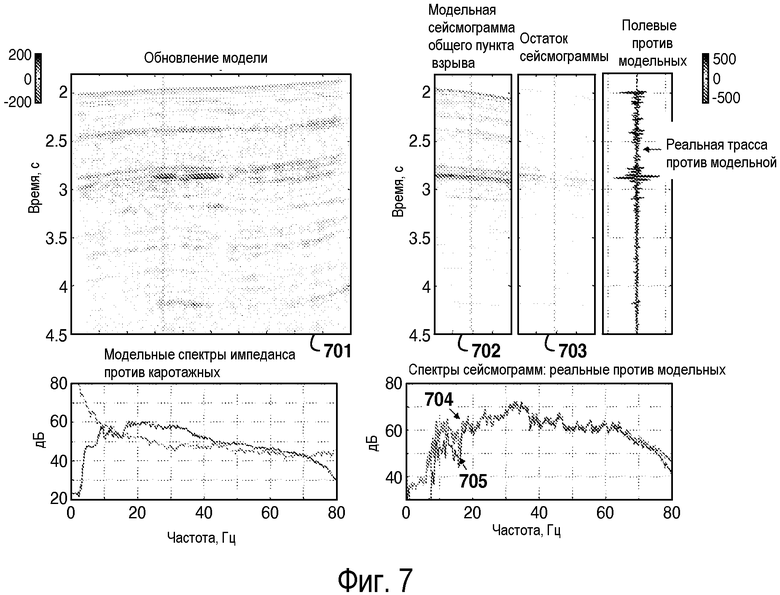
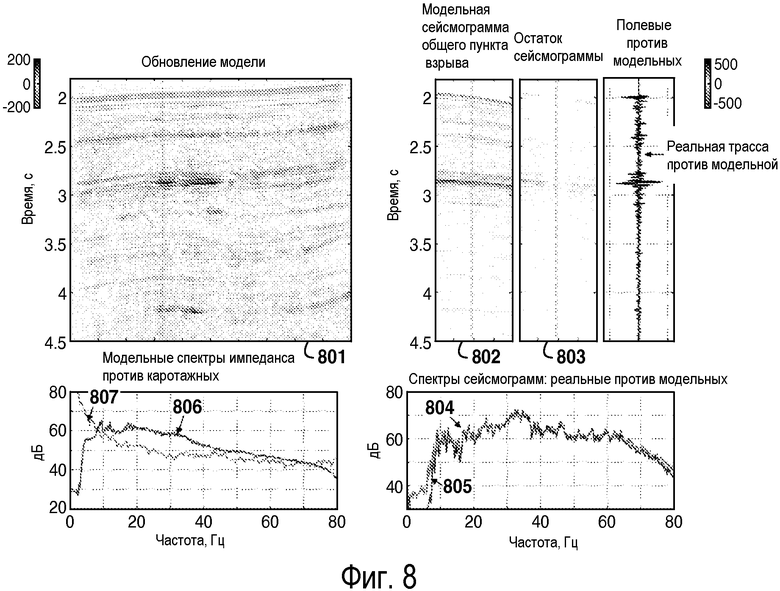
фиг. 6-8 - иллюстрация сходимости инверсии полного волнового поля (ИПВП) после 10 итераций (фиг.6), 50 итераций (фиг.7) и 100 итераций (фиг.8);
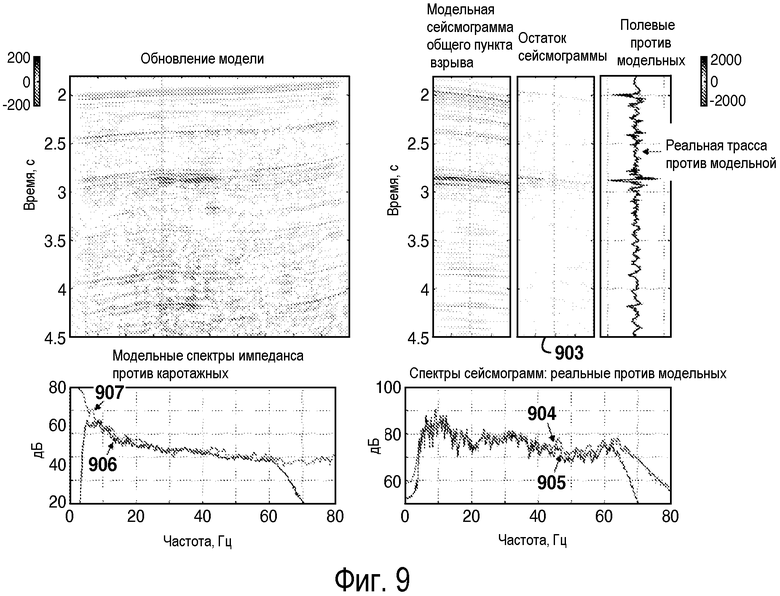
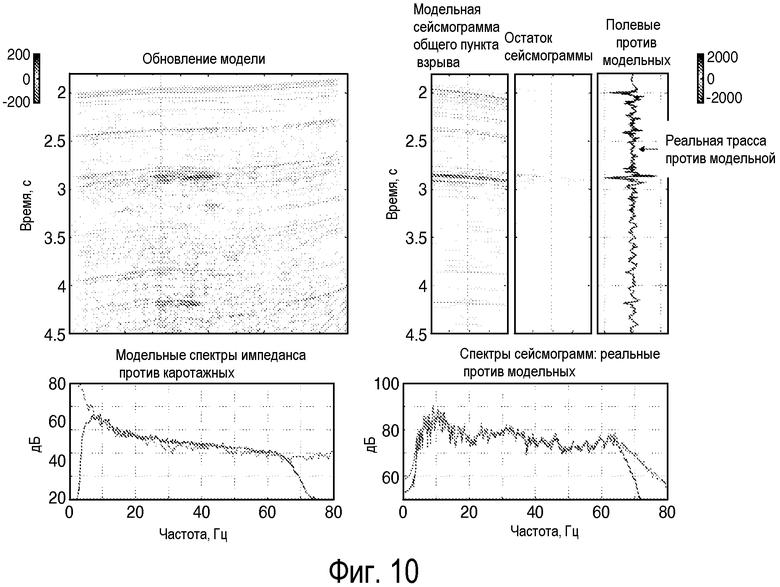
фиг. 9-10 - иллюстрация сходимости инверсии полного волнового поля после 1 итерации (фиг.9) и после 4 итераций (фиг.10) для случая применения формирующего фильтра настоящего изобретения к сейсмическим данным и сейсмическому импульсу источника из фигур 6-8;
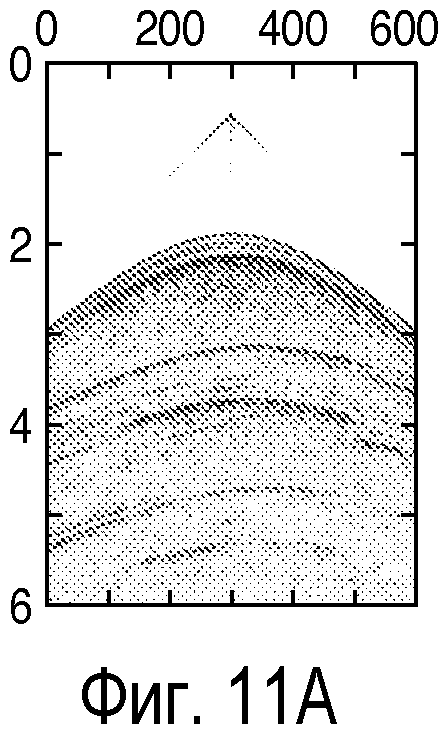
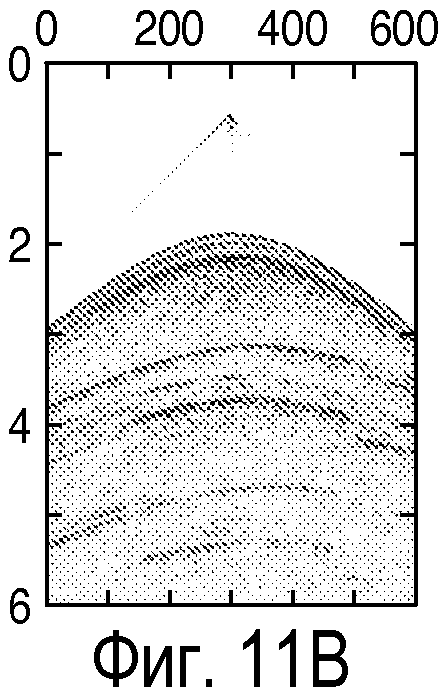
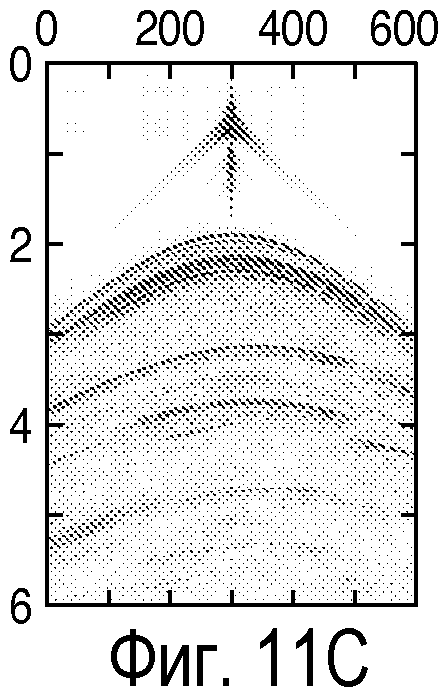
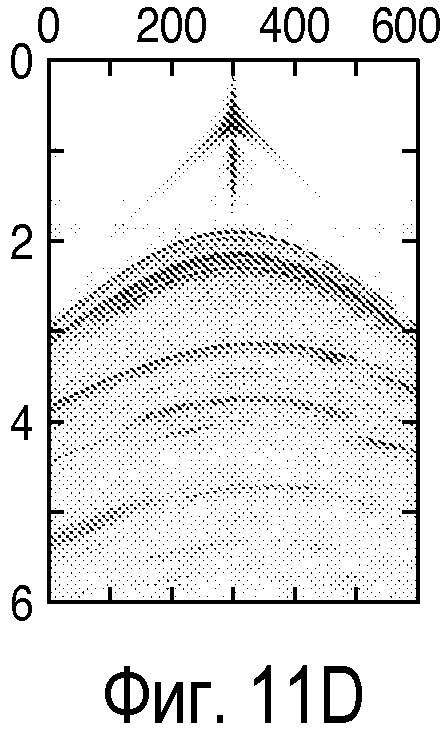
фиг. 11A-11D - иллюстрация синтетических примеров измеренной сейсмограммы общего пункта взрыва и модельной сейсмограммы общего пункта взрыва до и после формирования спектра в соответствии со способом настоящего изобретения; и
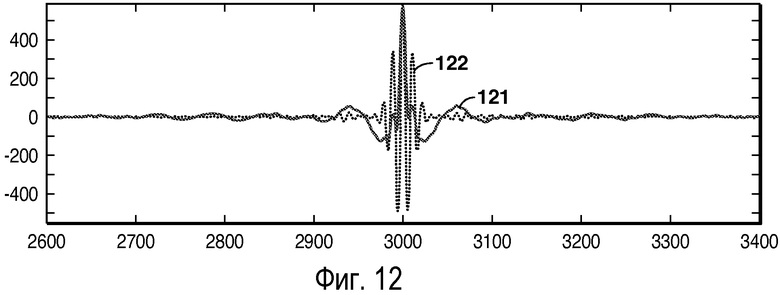
фиг.12 - иллюстрация влияния формирования спектра из фигур 11A-11D на функцию стоимости взаимной корреляции.
Изобретение будет описано применительно к примерам осуществлений. Однако в той степени, в какой нижеследующее подробное описание является специфическим для конкретного осуществления или конкретного использования изобретения, оно предназначено только для иллюстрации и не должно толковаться как ограничивающее объем изобретения. В противоположность этому оно предполагается охватывающим все варианты, модификации и эквиваленты, которые могут быть включены в объем изобретения, определяемый прилагаемой формулой изобретения. Специалисты в области техники, к которой относится изобретение, должны без труда осознать, что при практических применениях способа настоящего изобретения способ следует выполнять на компьютере, программируемом в соответствии с идеями, изложенными в этой заявке.
Подробное описание примеров осуществлений
Основная идея способа настоящего изобретения основана на предположении априорной известности правдоподобной оценки частотного спектра из геологической среды. В этом случае количество итераций, необходимых для сходимости, можно значительно уменьшить с гарантией, что инверсией будут создаваться модели геологической среды с требуемым частотным спектром в результате выполнения самой первой итерации. Интуитивно можно понять, что это означает отсутствие необходимости затрачивать вычислительные средства на итерации, при которых обычно модифицируется спектр в модели геологической среды, и, следовательно, инверсия сходится к конечному решению с большей скоростью.
Чтобы эта идея стала значимой и практически осуществимой, следует получить ответы на следующие вопросы.
(1) Можно ли обычно предполагать, что хорошие оценки частотного спектра доступны?
(2) Каким образом можно гарантировать, что в результате инверсии будет иметься требуемый частотный спектр, и, в частности, каким образом получать его после самой первой итерации?
Ответы на эти два вопроса даются в следующих двух разделах.
Оценка частотного спектра из моделей геологической среды
В статьях, посвященных неитерационной инверсии, Lancaster и Whitcombe (2000), Lazaratos (2006), Lazaratos и David (2008), а также Lazaratos и David (2009), выдвинули идею, что модель, образуемая при неитерационной инверсии, должна иметь частотный спектр, который в среднем аналогичен спектру из подземной геологической среды, измеряемому при скважинном каротаже. (Термины «амплитудный спектр» и «частотный спектр» в этой заявке могут использоваться на равных основаниях применительно к зависимости амплитуды от частоты.) Для любой данной области этот целевой спектр можно получать усреднением спектров из логарифмических кривых, регистрируемых в локальных скважинах. Теоретически, подходящей логарифмической кривой, подлежащей использованию применительно к данным метода отраженных волн при нормальном падении, является импеданс для продольных волн. На практике было обнаружено, что средние спектры для большей части логарифмических кривых в известной степени аналогичны. В действительности, типичные спектры скважинного каротажа в известной степени аналогичны для очень большого ряда географических мест, глубин и условий осадконакопления, так что общая форма целевых спектров из результатов инверсии является робастной и хорошо определенной. Вследствие стабильности и робастности спектров скважинного каротажа концепцию, изложенную в упомянутых выше публикациях, широко используют при неитерационной инверсии сейсмических данных, даже когда увязка с локальной скважиной отсутствует.
Регулирование частотного спектра из результатов инверсии
В общем случае имеются несколько параметров, характеризующих геологическую среду, которые можно оценивать с помощью сейсмической инверсии (например, импеданс для продольных волн, импеданс для поперечных волн, плотность, скорость продольных волн и т.д.). В принципе, частотные спектры для этих различных параметров могут быть различными. Следовательно, при обращении к частотному спектру из модели геологической среды упомянутые параметры необходимо точно определять. Сначала обратимся к случаю однопараметрической инверсии, когда модель геологической среды описывается только в значениях импеданса для продольных волн (Р) (импеданс является произведением скорости и плотности). Это является общим случаем применения инверсии, поскольку отражательная способность геологической среды большей частью зависит от вариаций импеданса для продольных волн. Затем будет описано, каким образом способ может быть распространен на многопараметрическую инверсию.
Частотный спектр из результатов инверсии связан с частотным спектром из сейсмических данных и частотным спектром сейсмического импульса источника. В частности, в случае сейсмических данных метода отраженных волн из сверточной модели следует, что сейсмический отклик данной геологической среды можно вычислять путем свертывания сейсмического импульса и отражательной способности среды. В предположении слабого рассеяния можно показать, что при нормальном падении функция отражательной способности может быть легко вычислена как производная импеданса для продольных волн. При наклонном падении для вычисления отражательной способности требуются дополнительные упругие параметры, но это не меняет существенно концепцию способа, представленного в этой заявке. В частотной области основная формула, описывающая сверточную модель, имеет вид:
D(f)=fIp(f)W(f), (1)
где f представляет частоту, D(f) представляет средний амплитудный спектр из сейсмических данных, W(f) представляет амплитудный спектр сейсмического импульса и Ip(f) представляет средний амплитудный спектр импеданса геологической среды для продольных волн. Вычисление производной импеданса для продольных волн во временной области соответствует умножению на i2πf в частотной области. Для упрощения настоящего рассмотрения множитель 2π опускается, поскольку он не влияет на результаты или реализацию способа. Множитель i также опускается, поскольку мы будем иметь дело только с амплитудным спектром.
Смысл того, что было сейчас обсуждено, заключается в том, что для того, чтобы конечным результатом инверсии был частотный спектр Ip(f), необходимо использовать сейсмический импульс, спектр W(f) которого связан со спектром D(f) из данных уравнением (1). Хотя теоретически уравнение (1) справедливо только в случае, когда амплитудный спектр в уравнении относится к конкретному параметру, импедансу для продольных волн, эмпирически было обнаружено, что спектры различных упругих параметров обычно полностью аналогичны. Далее будет описано, каким образом можно переформулировать задачу инверсии, чтобы при инверсии модель со спектром Ip(f) получалась в результате выполнения самой первой итерации.
Обновление для модели при инверсии полного волнового поля обычно вычисляют в виде масштабированной версии градиента целевой функции в зависимости от параметра (параметров) модели. В случае обычной (L2) целевой функции (наименьших квадратов) градиент можно определять путем взаимной корреляции распространяющегося вперед волнового поля источника и распространяющегося обратно остаточного волнового поля. Спектр распространяющегося вперед волнового поля источника пропорционален спектру W(f) входного сейсмического импульса. При условии, что типичные исходные модели инверсии являются очень гладкими и не создают отражений, для первой итерации остатки данных по существу такие же, как регистрируемые данные, и поэтому спектр из данных об обратно-распространяющемся остаточном волновом поле пропорционален D(f). Таким образом, спектр G(f) градиента равен произведению спектров двух взаимно коррелированных волновых полей, (W(f) и D(f)), дополнительно умноженному на частотно-зависимый множитель A(f), который зависит от особенностей решаемой задачи инверсии (например, двумерной в противоположность трехмерной, акустической инверсии в противоположность упругой инверсии, обновляемого упругого параметра и т.д.). Этот множитель может быть получен теоретически (например, для двумерных акустических инверсий при постоянной плотности A(f)=f1/2) или экспериментально с вычислением спектра градиента и сравнением его с произведением известных спектров W(f) и D(f). Поэтому можно записать:
G(f)=A(f)W(f)D(f). (2)
Допустим, что спектр Ip(f) импеданса геологической среды известен априори и что мы хотели бы иметь соотношение G(f)=Ip(f). В общем случае оно не будет справедливым. Все же можно надлежащим образом преобразовать исходную задачу инверсии в новую задачу инверсии путем применения формирующего фильтра H(f) к входному сейсмическому импульсу и данным. Новый, сформированный сейсмический импульс WS(f) и сформированные данные DS(f) связаны с исходным сейсмическим импульсом и спектрами из данных следующими соотношениями:
WS(f)=H(f)W(f),
DS(f)=H(f)D(f). (3)
Обращение модели, которое приводит в соответствие исходные данные D(f) при использовании сейсмического импульса W(f), эквивалентно обращению модели, которое приводит в соответствие сформированные данные DS(f) при использовании сформированного сейсмического импульса WS(f). Теперь по аналогии с уравнением (2) запишем для сформированного градиента GS(f):
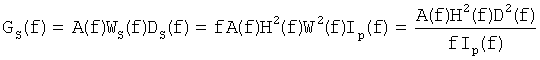
Теперь определим H(f) так, чтобы было
GS(f)=Ip(f), (5)
и используя уравнение (4), получим:
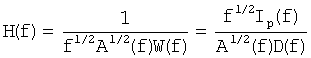
Используя последнее уравнение, получим следующие выражения для сформированного сейсмического импульса и спектров из данных:
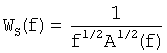
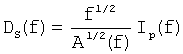
Результат от применения формирующего фильтра схематично показан на фиг.2, на которой частотный спектр формирующего фильтра представлен позицией 206. Исходная задача инверсии (сейсмический импульс W(f) (201) и данные D(f) (202)) преобразована в новую задачу инверсии (сейсмический импульс WS(f) (203) и данные DS(f) (204)), так что градиент (205) имеет требуемый спектр Ip(f).
Приведенное выше рассмотрение останется справедливым даже в случае, когда более широкий диапазон углов отражения (а не только нормальное падение) будет включен в инверсию. Произошла только концептуальная модификация уравнения (2), в котором теперь множителем A(f) учитывается влияние растяжения сейсмических сигналов после ввода кинематических поправок на сейсмический импульс (Dunkin и Levin, 1973).
Осуществления изобретения
Применение формирующего спектр фильтра к входным данным и сейсмическому импульсу источника
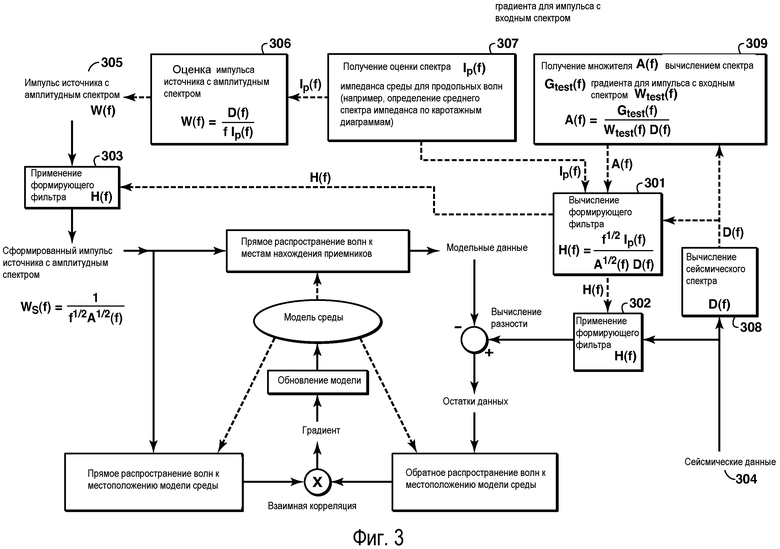
Как пояснялось в предшествующем разделе, способ может быть реализован применением подходящего формирующего спектр фильтра к сейсмическим данным и сейсмическому импульсу источника без модификации последовательности действий при выполнении инверсии, которая показана на фиг.1. На фиг.3 представлена блок-схема последовательности действий, описывающая осуществление способа. Формирующий фильтр H(f) (301) применяют (302 и 303) к сейсмическим данным (304) и сейсмическому импульсу (305) источника. Сейсмический импульс источника необходимо выбирать (306) так, чтобы его амплитудный спектр W(f), спектр D(f) из сейсмических данных и спектр Ip(f) из модели импеданса геологической среды для продольных волн были взаимосвязаны уравнением (1). Для определения формирующего фильтра, в дополнение к получению априорной оценки Ip(f) (307) спектра импеданса геологической среды, необходимо вычислить (308) спектр D(f) из сейсмических данных и множитель A(f) (309). Последний удобно получать вычислением спектра Gtest(f) градиента для данного входного сейсмического импульса Wtest(f) и затем приравниванием A(f) к отношению Gtest(f) и Wtest(f)D(f).
Применение формирующего спектр фильтра к градиенту
Вместо применения формирующего фильтра к сейсмическим данным и сейсмическому импульсу источника спектр градиента можно формировать так, чтобы он становился аналогичным априорной оценке Ip(f). Это схематично показано в виде последовательности действий на фиг.4. Теперь формирующий фильтр HG(f) применяют (403) непосредственно к градиенту. Фильтр HG(f) может быть получен (401) делением требуемого спектра Ip(f) на несформированный спектр G(f) градиента. Сейсмический импульс источника необходимо выбирать (402) так, чтобы его амплитудный спектр W(f), спектр D(f) из сейсмических данных и спектр Ip(f) из модели импеданса геологической среды для продольных волн были взаимосвязаны уравнением (1) из предшествующего раздела.
Это осуществление изобретения является особенно гибким, позволяющим легко применять изменяющийся во времени фильтр HG(f), при этом, поскольку спектр из сейсмических данных изменяется во времени, можно ожидать, что спектр G(f) градиента также будет изменяться; поэтому для формирования такого же целевого спектра Ip(f) фильтр HG(f) обязательно должен быть изменяющимся во времени. Хотя это можно легко осуществлять, когда формирующий фильтр применяют непосредственно к градиенту, это не так просто делать в первом осуществлении, описанном выше (когда формирующий фильтр применяли к данным и сейсмическому импульсу источника). С другой стороны, в первом осуществлении более целесообразно выполнять применение, когда данные содержат по существу волновые моды, а не однократные отражения.
Следует также отметить, что осуществление из фиг.4 можно применять для получения любого упругого параметра, а не только импеданса для продольных волн всего лишь заменой Ip(f) в формуле формирующего фильтра из этапа 401 амплитудным спектром, соответствующим другому упругому параметру. Это не справедливо для осуществления на фиг.3, которое действительно только применительно к импедансу для продольных волн.
Распространение на многопараметрическую инверсию
Способ можно распространить непосредственно на случай многопараметрической инверсии, когда в дополнение к импедансу для продольных волн оценивают несколько параметров геологической среды. Соответствующая последовательность действий показана на фиг.5. В предположении, что оценки Si(f) амплитудных спектров различных параметров геологической среды могут быть получены (501) (например, на основании средних спектров из каротажных диаграмм), спектры Gi(f) градиентов в зависимости от различных параметров можно формировать с использованием формирующих фильтров Hi(f), получаемых делением (502) требуемых спектров Si(f) на несформированные спектры Gi(f) градиентов.
И в этом случае заметим, что сейсмический импульс источника необходимо выбирать (503) так, чтобы амплитудный спектр W(f), спектр D(f) из сейсмических данных и спектр Ip(f) из модели импеданса геологической среды для продольных волн были взаимосвязаны уравнением (1). Вследствие этого априорная оценка Ip(f) необходима независимо от того, является или нет задачей инверсии получение оценки импеданса для продольных волн, за исключением осуществлений изобретения, в которых спектральные различия между различными упругими параметрами считают пренебрежимо малыми.
Сравнение со способами неитерационной инверсии
В способах неитерационной инверсии из приведенных выше источников (Lancaster и Whitcombe (2000), Lazaratos (2006), Lazaratos и David (2008), а также Lazaratos и David (2009)) прямое моделирование не выполняют, вследствие чего нет необходимости оценивать сейсмический импульс источника. Механизм регулирования конечного спектра в этих предшествующих способах заключается в формировании спектра таким образом, чтобы он соответствовал требуемому спектру. В способах неитерационной инверсии предполагается, что входные данные подвергают или будут подвергать миграции и суммированию и что после миграции и суммирования их можно будет моделировать с помощью сверточной модели (исходя из того, что сейсмический отклик можно находить свертыванием сейсмического импульса с отражательной способностью геологической среды, которая является производной импеданса). В предположении, что это справедливо, импеданс геологической среды можно получать путем применения формирующего фильтра к результату миграции и суммирования. Математический вывод относительно того, по какой причине этим формирующим фильтром должен обязательно извлекаться импеданс из данных, содержится в Lazaratos (2006) и в Lazaratos и David (2008). В последнем источнике указано, что формирующий фильтр лучше всего применять до миграции. Методология может быть распространена на инверсию других параметров, и это поясняется в работе Lazaratos (2006). Таким образом, традиционная неитерационная инверсия не является тем же самым, что и выполнение одного цикла процесса итерационной инверсии и затем прекращение процесса.
В случае итерационной инверсии с использованием способа настоящего изобретения механизм регулирования конечного спектра заключается в выборе спектра W(f) сейсмического импульса источника, который удовлетворяет уравнению (1). Но даже регулирование конечного спектра путем выбора сейсмического импульса W(f) не гарантирует регулирования спектра при каждой итерации, начиная с первой. Чтобы добиться этого, необходимо применить остальную часть способа изобретения, раскрытого в этой заявке, включая формирующий спектр фильтр. Пока это не произойдет, не будет общего снижения количества итераций и не будет повышения скорости вычислений, которое (то есть повышение скорости) является главным преимуществом настоящего изобретения при итерационной инверсии. Поэтому предпочтительно применять способ полностью до начала первой итерации.
В случае осуществления на фиг.3 формирующий фильтр применяют к сейсмическому импульсу и к данным один раз и нет необходимости в повторном применении. Осуществление на фиг.4 обеспечивает большую гибкость и, в принципе, может давать выигрыш от применения при каждой итерации. Формирующий фильтр на этом чертеже определен как отношение требуемого спектра к текущему G(f). Это отношение становится отличающимся от единицы при первой итерации, а при повторном применении формирующего фильтра, показанном на фиг.4, будет корректироваться до единицы. Если спектр обновления должен оставаться постоянным после этого, формирующий фильтр не будет давать эффекта, поскольку HG(f) становится тождественным оператором. Но если обновление G(f) отклоняется от цели (Ip(f) в случае импеданса для продольных волн), фильтр будет настроен на корректировку.
Примеры
Пример, иллюстрирующий, насколько процесс инверсии полного волнового поля может быть очень медленным применительно к сходимости, показан на фигурах 6, 7 и 8, иллюстрирующих поведение сходимости при решении небольшой двумерной задачи. Некоторые из графиков, имеющихся на всех трех фигурах, представляют собой кумулятивное обновление (601, 701, 801) модели, модельную сейсмограмму (602, 702, 802) общего пункта взрыва и остаток (603, 703, 803) данных для этой сейсмограммы, и сопоставление частотных спектров для реальных (604, 704, 804) и модельных (605, 705, 805) сейсмограмм общего пункта взрыва. После 10 итераций инверсии (фигура 6) все еще имеется значительное несоответствие между реальными и синтетическими данными, как это очевидно из рассмотрения остатков (603) данных и спектров (604, 605) сейсмограмм. Соответствие значительно повышается после 50 итераций (фигура 7), но рассмотрение спектров (704, 705) показывает, что все еще имеются различия на низких частотах. Требуется около 100 итераций (фигура 8) для достижения более полного соответствия и даже после этого все еще имеются различия в частотном диапазоне 5-8 Гц. Сопоставление (609) реальной и модельной трасс соответствует горизонтальному положению, показанному пунктирной вертикальной линией на 602 и 603 и аналогично на фигурах 7-10.
На фигурах 9 и 10 показан результат применения раскрытого изобретения к тому же примеру. Заметно, что в результате самой первой итерации (фиг.9) остатки (903) данных очень небольшие, синтетические (905) и реальные (904) спектры из данных очень похожи в пределах представляющей интерес ширины (5-60 Гц) полосы, и спектр обновления (906) модели очень похож на средний логарифмический спектр (907) импеданса. В противоположность этому на фигурах с 6 по 8 спектр (606) обновления модели начинается совсем иначе, чем средний логарифмический спектр (607) импеданса, и все еще до некоторой степени отличается даже после 100 итераций (806, 807). При использовании способа формирования спектра, описанного в этой заявке, инверсия по существу сходится за 4 итерации (фиг.10).
Целевую функцию взаимной корреляции обычно используют при сейсмической инверсии для приведения в соответствие фазы данных и ее часто считают робастной, хотя точные амплитуды могут не соответствовать физике моделирования. Несмотря на ее робастность по отношению к вариациям амплитуды, функция взаимной корреляции при ненулевом запаздывании обычно является осцилляционной по характеру и задача инверсии заключается в нахождении глобального максимума этой функции. Вследствие этого осцилляционного характера могут иметься трудности при нахождении максимумов с помощью алгоритма оптимизации. Задача усложняется, когда данные зашумлены. Если имеется механизм придания этой взаимной корреляции более резкого максимума, то он будет способствовать определению глобального максимума с помощью целевой функции и тем самым исключению застревания в локальных максимумах. Формирование спектра способствует достижению этой цели путем придания более резкого максимума функции корреляции, поскольку возрастает вес низкочастотной составляющей данных. Поэтому формирование не только улучшает сходимость инверсии полного волнового поля, но также придает форму целевой функции, что способствует лучшему определению местоположений максимумов с помощью алгоритма оптимизации. Кроме того, осцилляционный характер функции взаимной корреляции можно смягчить путем использования огибающей целевой функции взаимной корреляции при ненулевом запаздывании. Обычно огибающая имеет намного меньше осцилляций по сравнению с действительной функцией. Предпочтительным способом вычисления такой огибающей является преобразование Гильберта целевой функции взаимной корреляции при ненулевом запаздывании [Benitez и соавторы, 2001].
Типичная нормированная целевая функция взаимной корреляции имеет вид:
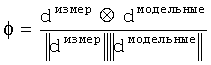
где dизмер представляет измеренные данные, dмодельные представляет модельные данные и ⊗ представляет оператор взаимной корреляции при ненулевом запаздывании. Операцию формирования можно считать свертыванием формирующей функции с данными наблюдений, а также прогнозируемыми данными. Сформированная нормированная целевая функция взаимной корреляции имеет вид:
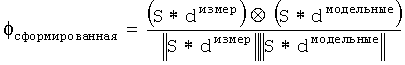
где S представляет формирующую функцию, которая имеет спектр, аналогичный спектрам импеданса (Lazaratos и соавторы, 2011).
Krebs и соавторы (в публикации международной заявки WO 2008/042081) показали, что скорость инверсии можно значительно повысить путем использования кодирования источников и одновременного обращения многочисленных источников в одной кодированной сейсмограмме. Согласно предпочтительному осуществлению, раскрытому в этой публикации, кодирование изменяют от одной итерации к следующей. Routh и соавторы показали, что целевая функция взаимной корреляции является особенно предпочтительной при одновременной инверсии данных кодированных источников, когда предположение о неподвижном приемнике не удовлетворяется (заявка №13/224005 на патент США).
Синтетический пример
Преимущества сформированной целевой функции взаимной корреляции можно показать на синтетическом примере. На фиг.12, полученной на основании наблюдений сейсмограммы общего пункта взрыва (фиг.11А) и спрогнозированной сейсмограммы общего пункта взрыва при сходимости (фиг.11В) до формирования, и тех же самых двух сейсмограмм после формирования (фигуры 11С и 11D), можно видеть, что после формирования функция взаимной корреляции имеет более резкий максимум и более слабый осцилляционный характер после формирования (121), чем до формирования (122). На фигуре 12 показана нормированная взаимная корреляция в зависимости от запаздывания, при этом нулевое запаздывание соответствует показателю 3000 по оси x. Смягчение осцилляционного характера потенциально может способствовать нахождению максимумов целевой функции с помощью алгоритмов оптимизации, которые являются глобальными по природе, такими как алгоритм имитации отжига, генетический алгоритм, эволюционные алгоритмы и т.д. Другой интересный аспект заключается в том, что можно работать с огибающей целевой функции взаимной корреляции как с параметром, подлежащим максимизации. Огибающая обычно имеет намного меньшую осцилляцию по сравнению с самой функцией.
Приведенное выше патентное описание обращено к конкретным осуществлениям настоящего изобретения и предназначено только для иллюстрации. Однако специалисту в данной области должно быть понятно, что возможны многочисленные модификации и варианты осуществлений, описанных в этой заявке. Все такие модификации и варианты предполагаются находящимися в объеме настоящего изобретения, определенном в прилагаемой формуле изобретения.
Список литературы
1. Ben-Hadj-Ali, H., Operto, S., and Virieux, J., "Three-dimensional frequency-domain inversion with phase encoding, Expanded Abstracts", 79th SEG Annual Meeting, Houston, 2288-2292 (2009).
2. Benitez, D., Gaydecki, P. A., Zaidi, A., and Fitzpatrick, A. P., "The use of the Hilbert transform in ECG signal analysis," Computers in Biology and Medicine, 399-406 (2001).
3. Berkhout, A. J., "Areal shot record technology," Journal of Seismic Exploration 1, 251-264 (1992).
4. Dunkin, J. W,, and Levin, F. K., "Effect of normal moveout on a seismic pulse," Geophysics 28, 635-642(1973).
5. Krebs et al., "Iterative inversion of data from simultaneous geophysical sources," PCT Patent Application Publication No. WO 2008/042081.
6. Krebs, J., Anderson, J., Hinkley, D., Neelamani, R., Lee, S., Baumstein, A., and Lacasse, M, "Full-wavefield seismic inversion using encoded sources," Geophysics 74, WCC177 - WCC188 (2009).
7. Lancaster, S., and Whitcombe, D., "Fast track "coloured" inversion," Expanded Abstracts, 70th SEG Annual Meeting, Calgary, 1572-1575 (2000).
8. Lazaratos, S., "Spectral Shaping Inversion for Elastic and Rock Property Estimation," Research Disclosure, Issue 511, (November 2006).
9. Lazaratos, S., and David, R. L., "Spectral shaping inversion and migration of seismic data," U.S. Publication No. 2010/0270026 (2008),
10. Lazaratos, S., and David, R. L., 2009, "Inversion by pre-migration spectral shaping," Expanded Abstracts, 79th SEG Annual Meeting, Houston.
11. Moghaddam, P., and Herrmann, F. J., "Randomized full-waveform inversion: a dimensionality-reduction approach," Expanded Abstracts, 80th SEG Annual Meeting, Denver, 978 - 982 (2010).
12. Routh et al., "Simultaneous source inversion for marine streamer data with cross-correlation objective function," U.S. Patent Application Serial No. 13/224,005 (2010).
13. Van Riel, P., and Hendrik, W. J. D., "Method of estimating elastic and compositional parameters from seismic and echo-acoustic data," U.S. Patent No. 6,876,928 (2005).
14. Zhang, Y., Sun, J., Notfors, C, Gray, S. Н., Cherris, L., Young, J., "Delayed-shot 3D depth migration," Geophysics 70, E21-28 (2005).
Изобретение относится к области геофизики и может быть использовано для обработки сейсмических данных. Предложен способ повышения скорости итерационной инверсии сейсмических данных для получения модели геологической среды с использованием локальной оптимизации функции стоимости. Частотный спектр обновленной модели при каждой итерации регулируют до соответствия известному или расчетному частотному спектру для области геологической среды, предпочтительно среднему амплитудному спектру импеданса геологической среды для продольных волн. Регулирование выполняют применением формирующего спектр фильтра к сейсмическому импульсу источника и к данным или применением фильтра, который можно изменять во времени, к градиенту функции стоимости. Технический результат - повышение точности получаемых данных. 2 н. и 21 з.п. ф-лы, 15 ил.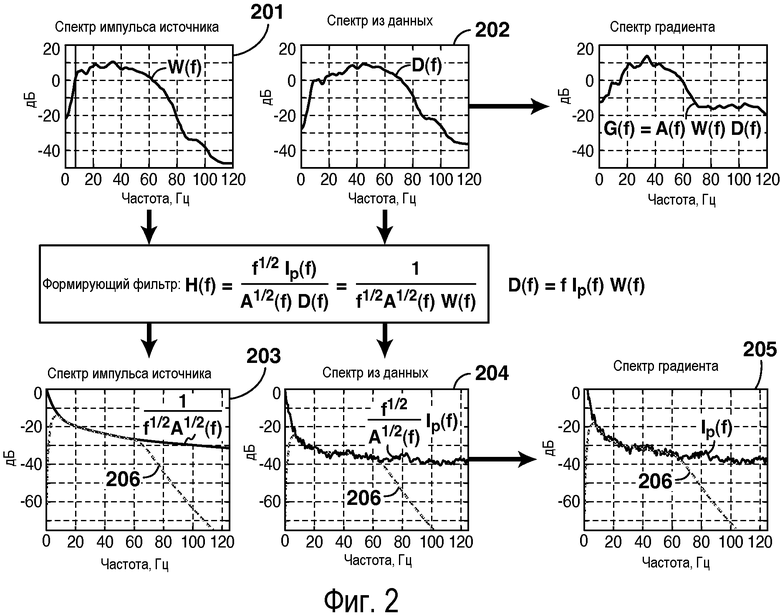
1. Реализуемый компьютером способ ускорения сходимости итерационной инверсии сейсмических данных для получения модели одного или нескольких физических параметров в области геологической среды, содержащий использование локальной оптимизации функции стоимости, в котором предполагаемую или текущую модель обновляют для уменьшения несоответствия между сейсмическими данными и модельно-имитированными данными, в котором частотный спектр обновленной модели регулируют при первой итерации и в дальнейшем до соответствия известному или расчетному частотному спектру для области геологической среды.
2. Способ по п. 1, в котором указанный один или несколько физических параметров представляет собой импеданс для продольных волн и в котором частотный спектр обновленной модели при каждой итерации регулируют до соответствия известному или расчетному частотному спектру, применяя формирующий спектр фильтр при первой итерации к сейсмическим данным и к сейсмическому импульсу источника, используемым для формирования модельно-имитированных данных, в котором сейсмический импульс источника до применения формирующего спектр фильтра выбирают так, чтобы получить частотный спектр W(f), который удовлетворяет D(f)≈fIp(f)W(f), где D(f) представляет средний частотный спектр из сейсмических данных, f представляет частоту и Ip(f) является средним частотным спектром импеданса для продольных волн в области геологической среды или аппроксимируется частотным спектром другого упругого параметра области геологической среды, и в котором указанный известный или расчетный частотный спектр для области геологической среды представляет собой Ip(f).
3. Способ по п. 2, в котором формирующий спектр фильтр удовлетворяет
H(f)={f1/2Ip(f)}/{A1/2(f)D(f)},
где A(f) представляет частотно-зависимый множитель, определенный так, что
G(f)=A(f)W(f)D(f),
где G(f) представляет частотный спектр градиента функции стоимости применительно к одному из одного или нескольких физических параметров.
4. Способ по п. 1, в котором обновление предполагаемой или текущей модели содержит вычисление градиента функции стоимости применительно к одному из одного или нескольких физических параметров и затем применение формирующего спектр фильтра к градиенту при по меньшей мере первой итерации; и в котором модельно-имитированные данные формируют, используя сейсмический импульс источника, имеющий частотный спектр W(f), который удовлетворяет D(f)≈fIp(f)W(f), где D(f) представляет средний частотный спектр из сейсмических данных, f представляет частоту и Ip(f) является средним частотным спектром импеданса для продольных волн в области геологической среды или аппроксимируется частотным спектром другого упругого параметра области геологической среды, и в котором указанный известный или расчетный частотный спектр представляет собой Ip(f).
5. Способ по п. 4, в котором формирующий спектр фильтр H(f) определяют делением известного или расчетного частотного спектра S(f) в области геологической среды для указанного одного из одного или нескольких физических параметров на спектр G(f) градиента до формирования.
6. Способ по п. 4, в котором формирующий спектр фильтр изменяют во времени.
7. Способ по п. 1, в котором известный или расчетный частотный спектр для области геологической среды получают, усредняя спектры каротажных диаграмм из области геологической среды.
8. Способ по п. 7, в котором модели по меньшей мере двух физических параметров получают одновременно, а известный или расчетный частотный спектр для каждого физического параметра получают, усредняя спектры каротажных диаграмм, определяющие этот физический параметр или соответствующие ему.
9. Способ по п. 1, в котором модели по меньшей мере двух физических параметров получают одновременно, а частотный спектр каждой обновленной модели при первой итерации и в дальнейшем регулируют до соответствия известному или расчетному частотному спектру соответствующего физического параметра в области геологической среды.
10. Способ по п. 9, в котором обновление предполагаемой или текущей модели конкретного физического параметра (обозначаемого индексом i) содержит вычисление градиента (∇i) функции стоимости применительно к этому конкретному физическому параметру и затем применение формирующего спектр фильтра к градиенту, в котором формирующий спектр фильтр подгоняют к конкретному физическому параметру и его известному или расчетному частотному спектру Si(f) из области геологической среды.
11. Способ по п. 10, в котором формирующий спектр фильтр определяют делением Si(f) на спектр градиента до формирования.
12. Способ по п. 10, в котором формирующий спектр фильтр изменяют во времени.
13. Способ по п. 2, в котором формирующий спектр фильтр получают в соответствии с критерием, заключающимся в том, что спектр градиента функции стоимости применительно к одному из одного или нескольких физических параметров, после применения формирующего спектр фильтра к сейсмическим данным и к сейсмическому импульсу источника, используемым для формирования модельно-имитированных данных, должен соответствовать известному или расчетному частотному спектру для области геологической среды.
14. Способ по п. 1, в котором один или несколько физических параметров выбирают из группы, состоящей из импеданса для продольных волн, импеданса для поперечных волн, плотности, скорости продольных волн и скорости поперечных волн.
15. Способ по п. 1, в котором модельно-имитированные данные формируют, используя сейсмический импульс источника, имеющий частотный спектр W(f), удовлетворяющий с точностью до коэффициента пропорциональности следующему уравнению:
D(f)=fIp(f)W(f),
где f представляет частоту, D(f) представляет средний частотный спектр из сейсмических данных и Ip(f) представляет средний частотный спектр импеданса продольных волн в области геологической среды или аппроксимацию его, основанную на частотном спектре другого упругого параметра.
16. Способ по п. 15, в котором D(f) и Ip(f) представляют средние спектры, что означает усредненные по области геологической среды.
17. Способ по п. 1, в котором функция стоимости представляет собой взаимную корреляцию между сейсмическими данными и модельно-имитированными данными, а оптимизация максимизирует функцию стоимости после того, как регулирование частотного спектра применяют к сейсмическим данным и модельно-имитированным данным.
18. Способ по п. 17, в котором кодирование источника используют относительно сейсмических данных и при имитации модели, а множество кодированных источников обращают одновременно.
19. Способ по п. 18, в котором кодирование изменяют для по меньшей мере одной итерации инверсии.
20. Способ по п. 1, в котором функция стоимости представляет собой функцию огибающей взаимной корреляции между сейсмическими данными и модельно-имитированными данными, а оптимизация максимизирует функцию стоимости.
21. Способ по п. 20, в котором кодирование источника используют относительно сейсмических данных и при имитации модели, а множество кодированных источников обращают одновременно.
22. Способ по п. 21, в котором кодирование изменяют для по меньшей мере одной итерации инверсии.
23. Используемый компьютером носитель, имеющий сохраненный на нем считываемый компьютером программный код, причем считываемый компьютером программный код предназначен для побуждения компьютера на осуществление способа инверсии сейсмических данных для получения модели одного или нескольких физических параметров в области геологической среды, при этом указанный способ содержит использование итерационной инверсии с локальной оптимизацией функции стоимости, в котором предполагаемую или текущую модель обновляют для уменьшения несоответствия между сейсмическими данными и модельными имитированными данными, в котором частотный спектр обновленной модели при каждой итерации регулируют до соответствия входному известному или расчетному частотному спектру для области геологической среды.
| US 20100270026 A1, 28.10.2010 | |||
| US 6999880 B2,14.02.2006 | |||
| US 6662147 B1, 09.12.2003 | |||
| Pratt, R | |||
| G., Shin, C., Hicks, G | |||
| J., 1998, Gauss-Newton and full Newton methods in frequency-space seismic waveform inversion, Geophys | |||
| J | |||
| Int., 133, 341-362 | |||
| US 7764572 B2, 27.07.2010. |
Авторы
Даты
2016-03-20—Публикация
2012-01-30—Подача