Перекрестная ссылка на родственные заявки
Данная заявка испрашивает приоритет по предварительной заявке на патент США 61/332, 463, поданной 7 мая 2010 года, озаглавленной «Снижение артефактов при итерационной инверсии геофизических данных», которая в своей полноте включена в состав данного документа посредством ссылки.
Область техники, к которой относится изобретение
В целом, изобретение относится к области геофизических исследований и, более конкретно, к обработке геофизических данных. В частности, изобретение относится к способу снижения артефактов при итерационной инверсии данных, возникающих в результате приближений, сделанных при инверсии.
Уровень техники
Геофизическая инверсия [1, 2] делает попытку определить модель свойств геологической среды, которая оптимально объясняет наблюдаемые данные и удовлетворяет геологическим и геофизическим ограничениям. Существует большое число хорошо известных методов геофизической инверсии. Эти хорошо известные методы попадают в одну из двух категорий: итерационная инверсия и неитерационная инверсия. Ниже даны определения того, что обычно подразумевается под каждой из двух категорий:
Неитерационная инверсия - это инверсия, которая выполняется исходя из предположения некоторой простой фоновой модели и обновления этой модели на основе входных данных. Этот метод не использует обновляемую модель в качестве входной для другого шага инверсии. Для случая сейсмических данных эти методы обычно упоминаются как формирующая изображение, миграционная, дифракционная томография или инверсия Борна.
Итерационная инверсия - это инверсия, включающая в себя повторяющееся улучшение модели свойств геологической среды, такое, что определяется модель, которая удовлетворительно объясняет наблюдаемые данные. Если инверсия сходится, то конечная модель будет лучше объяснять наблюдаемые данные и более точно аппроксимировать фактические свойства геологической среды. Итерационная инверсия обычно производит более точную модель, чем неитерационная инверсия, но она является более затратной для вычислений.
Два способа итерационной инверсии, обычно используемые в геофизике, это метод оптимизации функции стоимости и метод рядов. Оптимизация функции стоимости включает в себя итерационную минимизацию или максимизацию значения функции S(M) стоимости, относящуюся к модели M и являющуюся мерой несоответствия между вычисленными и наблюдаемыми данными (также иногда упоминается как целевая функция), в которой вычисленные данные моделируются с помощью компьютера, путем использования текущей модели геофизических свойств и физики, обуславливающей распространение сигнала источника в среде, представленной данной моделью геофизических свойств. Моделирующие вычисления могут быть выполнены с помощью любого из нескольких численных методов, включая, но не ограничиваясь, методами конечной разности, конечных элементов или построения лучей. Методы рядов включают в себя инверсию с использованием итерационных рядов при решении уравнения рассеяния (Weglein [3]). Решение записывается в форме рядов, где каждый член ряда соответствует более высоким порядкам рассеяния. Итерации в этом случае соответствуют добавлению к решению члена ряда более высокого порядка.
Методы оптимизации функции стоимости являются либо локальными, либо глобальными [4]. Глобальные методы просто включают в себя вычисление функции S(M) стоимости для совокупности моделей {M1, M2, M3,...} и выбор набора из одной или более моделей из этой совокупности, приблизительно минимизирующих S(M). Если требуется получить дополнительное улучшение, в этом случае этот новый выбранный набор моделей может использоваться как основа для формирования новой совокупности моделей, которая может быть снова протестирована в отношении функции S(M) стоимости. Для глобальных методов каждая модель в контрольной совокупности может считаться итерацией, или на более высоком уровне каждый набор из контрольных совокупностей может считаться итерацией. Хорошо известные глобальные методы инверсии включают в себя метод Монте-Карло, метод модельной «закалки», генетические и эволюционные алгоритмы.
Оптимизация локальной функции стоимости включает в себя:
1 - выбор начальной модели,
2 - вычисление градиента функции S(M) стоимости в отношении параметров, которые описывают модель,
3 - поиск обновленной модели, которая является возмущением начальной модели в направлении градиента и которая лучше объясняет наблюдаемые данные.
Эта процедура итерационно повторяется посредством использования новой обновленной модели в качестве начальной модели для другого градиентного поиска. Процесс продолжается до тех пор, пока не находится обновленная модель, которая удовлетворительно объясняет наблюдаемые данные. Обычно используемые локальные методы инверсии функции стоимости включают в себя градиентный поиск, сопряженные градиенты и метод Ньютона.
Как обсуждалось выше, итерационная инверсия является предпочтительной по сравнению с неитерационной инверсией, так как она выдает более точные параметрические модели геологической среды. К сожалению, итерационная инверсия настолько затратная по вычислениям, что непрактично применять ее во многих задачах, представляющих интерес. Эти высокие затраты на вычисления являются результатом того, что все методики инверсии требуют проведения большого числа трудоемких прямых и/или обратных модельных экспериментов. Прямое моделирование означает вычисление данных вперед по времени, а обратное моделирование означает вычисление данных, назад по времени.
Из-за своей высокой вычислительной стоимости, итерационная инверсия часто требует использования некоторых типов приближений, ускоряющих вычисления. К сожалению, в окончательной инверсной модели эти приближения обычно приводят к ошибкам, которые могут рассматриваться как артефакты приближений, использованных в инверсии.
Поэтому требуется общий способ итерационного инвертирования данных, который обеспечит возможность применения приближений без создания артефактов в результирующей инверсной модели. Настоящее изобретение удовлетворяет эту потребность.
Раскрытие изобретения
Модель физических свойств дает одно или более свойств геологической среды как функцию от местоположения в области. Сейсмическая волновая скорость является одним из таких физических свойств, но ими также являются (например) плотность, скорость p-волны, скорость поперечной (сдвиговой) волны, несколько параметров анизотропии, параметры затухания (q), пористость, проницаемость и сопротивление. Изобретение представляет собой способ снижения артефактов в модели физических свойств геологической среды, вызванных приближением, отличающимся от кодирования источников, в итерационном компьютеризированном процессе инверсии геофизических данных, причем упомянутый способ включает в себя варьирование приближений в ходе выполнения итераций. В одном конкретном варианте осуществления изобретение является компьютеризованным способом для осуществления инверсии измеренных геофизических данных с целью определения модели физических свойств для области геологической среды, включающий в себя:
(а) принятие модели физических свойств области геологической среды, причем упомянутая модель обеспечивает значения, по меньшей мере, одного физического свойства в местоположениях по всей области геологической среды;
b) выбор итерационного процесса инверсии данных, имеющего шаг, в котором производится вычисление обновления модели физических свойств, что делает ее более совместимой с измеренными геофизическими данными;
(c) выполнение приближения в упомянутом вычислении, которое либо ускоряет выбранный итерационный процесс инверсии данных, способом, отличающимся от кодирования источников, либо работает с компромиссной точностью;
(d) выполнение, используя компьютер, одного цикла выбранного итерационного процесса инверсии данных с упомянутым приближением и используя модель физических свойств;
(e) выполнение следующего итерационного цикла инверсии, в котором делается выбор менять какой-либо аспект приближения, или не менять;
(f) при необходимости, повторение (e), меняя приближение в нескольких или во всех итерационных циклах, вплоть до последней итерации, в которой удовлетворяется критерий сходимости или достигается другое условие остановки; и
g) загрузку обновленной модели физических свойств с последней итерации, или сохранение ее в памяти компьютера.
В некоторых вариантах осуществления изобретения, один или несколько типов артефактов идентифицируются в результатах инверсии как вызванные приближением, и тот аспект приближения, который изменяется в некоторых или во всех циклах итерации, выбирается для оказания влияния на артефакты одного или нескольких идентифицированных типов артефактов. Влияние на артефакты может быть таким, что артефакты от одного приближения могут не складываться арифметически с артефактами от другого итерационного цикла, использующего приближение с измененным аспектом.
Краткое описание чертежей
Настоящее изобретение и его преимущества будут более понятны со ссылкой на следующее подробное описание и прилагаемые чертежи, на которых:
Фиг. 1 представляет собой блок-схему основных этапов в общем способе, описанном в данном документе;
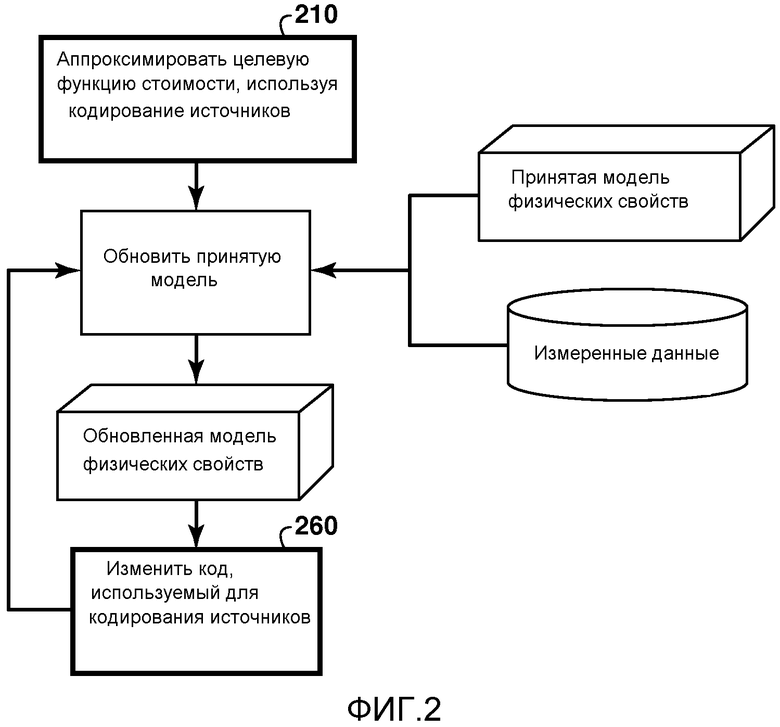
Фиг. 2 представляет собой блок-схему основных этапов в конкретном варианте осуществления способа на фиг. 1, где целевая функция аппроксимируется кодированием и суммированием источников;
Фиг. 3-5 относятся к примеру применения варианта осуществления изобретения по фиг. 2:
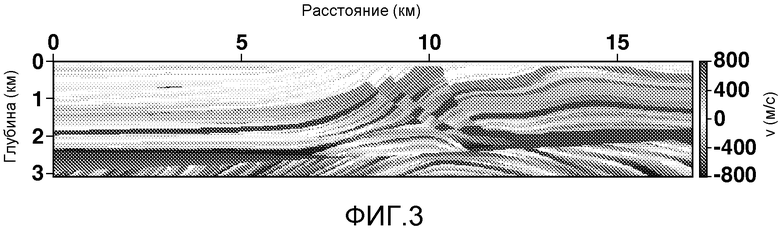
Фиг. 3 показывает скоростную сейсмическую модель, по которой в качестве примера были рассчитаны сейсмические данные;
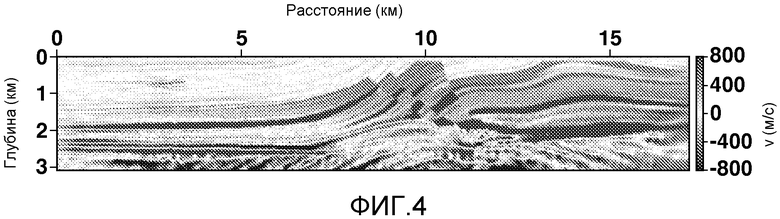
Фиг. 4 показывает инверсию данных скоростной сейсмической модели на фиг. 3, с использованием метода инверсии, приведенного на фиг. 2;
Фиг. 5 показывает инверсию данных скоростной сейсмической модели на фиг. 3, с использованием метода инверсии, приведенного на фиг. 2 без этапа, на котором код, используемый для кодирования источников, изменяется между итерациями;
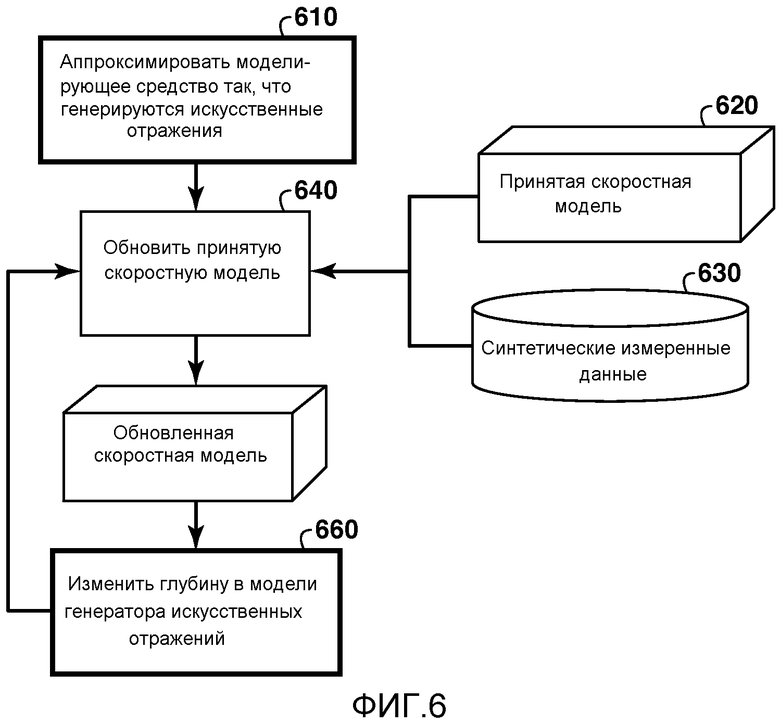
Фиг. 6 представляет собой блок-схему основных этапов в конкретном варианте осуществления способа на фиг. 1, в котором приближение является изменением размера ячеек сетки, применяемой в численной инверсии для того, чтобы использовать мелкую сетку только там, где это необходимо;
Фиг. 7-9 относятся к примеру применения варианта осуществления изобретения на фиг. 6:
Фиг. 7 представляет сейсмическую скоростную модель, по которой были рассчитаны сейсмические данные для этого примера;
Фиг. 8 показывает инверсию данных из скоростной сейсмической модели на фиг. 7, полученную с использованием метода инверсии, представленного на фиг. 6;
Фиг.9 представляет собой инверсию данных из скоростной сейсмической модели на фиг. 7 с использованием метода инверсии, представленного на фиг. 6 без этапа, на котором глубина генератора искусственных отражений меняется между итерациями;
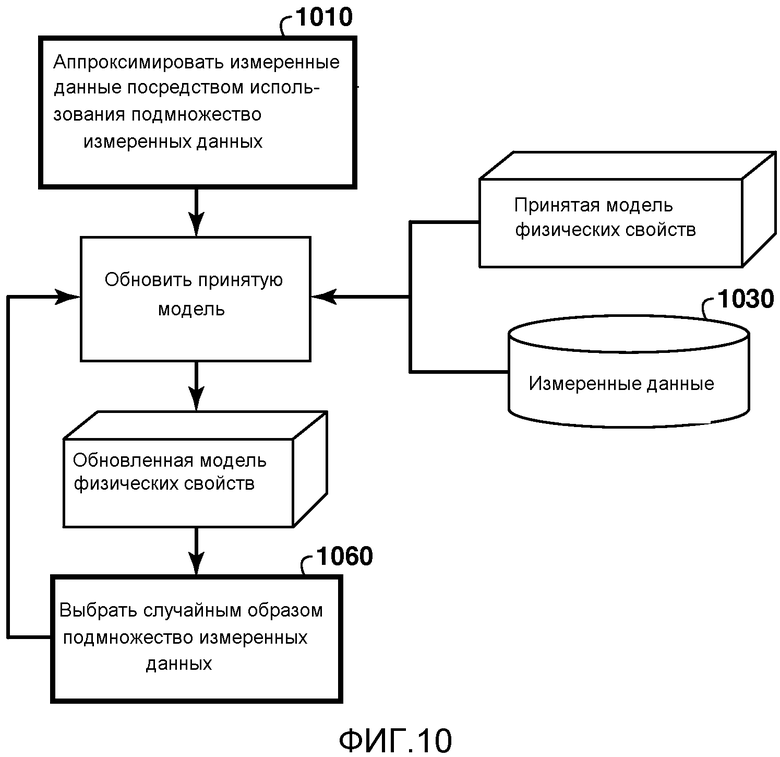
Фиг. 10 представляет собой блок-схему, показывающую основные этапы в конкретном варианте осуществления способа на фиг. 1, в котором приближение является использованием только подмножества измеренных данных;
Фиг. 11-13 относятся к примеру применения варианта осуществления изобретения на фиг. 10;
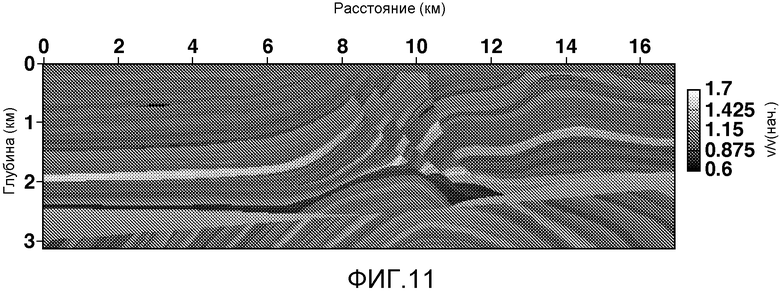
Фиг. 11 показывает модель сейсмических скоростей, по которой были рассчитаны сейсмические данные для этого примера;
Фиг. 12 показывает инверсию данных из модели сейсмической скорости на фиг. 11 с использованием метода инверсии, представленного на фиг. 10; и
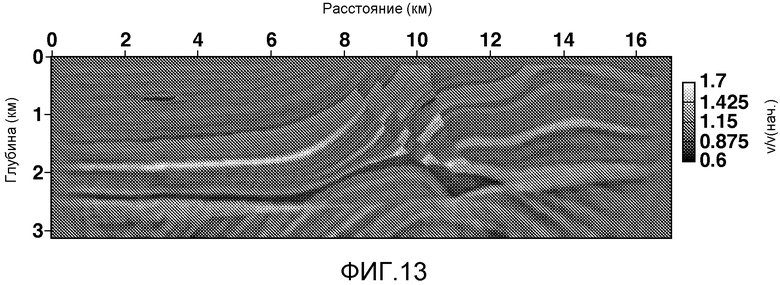
Фиг. 13 показывает инверсию данных из модели сейсмической скорости на фиг. 11 с использованием метода инверсии, представленного на фиг. 10, без этапа, на котором подмножество измеренных данных случайным образом меняется между итерациями.
В связи с патентными ограничениями, фиг. 3-5, 7-9 и 11-13 представляют собой преобразование цветных изображений в шкалу оттенков серого.
Изобретение будет описано в связи с предпочтительными вариантами осуществления. Тем не менее, в тех случаях, когда последующее подробное описание является специфичным применительно к конкретному варианту осуществления или конкретному использованию изобретения, оно предназначается только для иллюстрации и не должно рассматриваться как ограничивающее объем изобретения. Напротив, изобретение призвано охватывать все альтернативы, модификации и эквиваленты, которые могут быть включены в объем изобретения, определенного прилагаемой формулой изобретения.
Осуществление изобретения
Настоящее изобретение представляет собой способ снижения артефактов, вызванных применением приближений при итерационной инверсии геофизических данных. Геофизическая инверсия делает попытку определить модель геологических свойств, которая оптимально объясняет наблюдаемые геофизические данные. Чтобы проиллюстрировать способ изобретения, во всем документе используется пример сейсмических данных, но способ может быть успешно применен к любому способу геофизической разведки и любому типу геофизических данных. Инверсия данных наиболее точно осуществляется с помощью итерационных методов. К сожалению, итерационная инверсия часто является слишком затратной по вычислениям. Большая часть времени вычислений в итерационной инверсии тратится на выполнение затратных прямых и/или обратных модельных расчетов геофизических данных (здесь «прямой» означает вперед по времени, а «обратный» означает назад по времени). Высокая стоимость таких модельных расчетов отчасти связана с тем, что каждый геофизический источник во входных данных должен быть вычислен при отдельном запуске моделирующей программы. Таким образом, стоимость моделирования пропорциональна количеству источников в геофизических данных, обычно имеющему порядок от 1000 до 10000 источников в геофизическом исследовании. В обычной практике для снижения стоимости инверсии при осуществлении инверсии используются приближения. Эти приближения приводят к ошибкам, или артефактам, в инверсной модели. Данное изобретение уменьшает эти артефакты путем изменения некоторых аспектов приближения между итерациями инверсии так, что артефакт во время одной итерации не суммируется арифметически с артефактом в других итераций. Вследствие этого артефакт в инверсной модели снижается.
Некоторые общие приближения, выполняемые в ходе итерационной инверсии, следствием которых являются артефакты, включают в себя:
1. Обработка, примененная к измеренным данным
2. Неточные граничные условия при моделировании
3. Приближения при моделировании (например, низкий порядок аппроксимаций производных, используемых при моделировании, или размер ячеек сетки, используемый в расчете).
4. Приближения при параметризации модели (например, использование пространственной сетки параметров, являющейся слишком грубой для точного представления изменений в модели).
Два итерационных метода инверсии, которые обычно используются в геофизике - это метод оптимизации функции стоимости и метод рядов. Настоящее изобретение может быть применено к обоим этим методам. Краткая информация о каждом из этих методов приведена далее.
Итерационная оптимизация функции стоимости
Оптимизация функции стоимости осуществляется путем минимизации значения функции стоимости S (M) (иногда называемый целевой функцией), относящейся к модели M геологической среды и являющейся мерой несоответствия между наблюдаемыми (измеренными) геофизическими данными и соответствующими данными, рассчитанными при моделировании согласно принятой (предполагаемой) модели. Простая функция стоимости S, часто использующаяся в геофизической инверсии, определяется как:
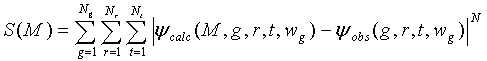
где
N = норма для функции стоимости (как правило, используется метод наименьших квадратов или L2-Норма, и в этом случае N=2),
M = модель геологической среды,
g = индекс сейсмограммы (для данных точечного источника он соответствует индивидуальному источнику),
Ng = число сейсмограмм,
r = индекс приемника в сейсмограмме,
Nr = число приемников в сейсмограмме,
t = индекс временной выборки в сейсмограмме,
Nt = количество временных выборок,
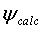
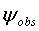
wg = форма импульса источника для сейсмограммы g, т. е. сигнал источника без влияния эффектов фильтрации земли.
Сейсмограммы в уравнении (1) могут быть любым типом сейсмограммы, которая может быть смоделирована при одном запуске программы прямого моделирования. Для сейсмических данных, сейсмограммы соответствует сейсмическому взрыву, хотя взрывы могут быть более общими, чем точечные источники [5]. Для точечных источников, индекс сейсмограммы g соответствует местоположению отдельных точечных источников. Для источников плоской волны g соответствует различным направлениям распространения плоских волн. Эти обобщенные исходные данные 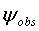
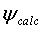
Одна из основных проблем итерационной инверсии заключается в том, что вычисление 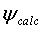
Инверсия итерационными рядами
Кроме оптимизации функции стоимости, геофизическая инверсия также может быть реализована с использованием методов итерационных рядов. Распространенным методом для этого является итерация уравнения Липпмана-Швингера [3]. Уравнение Липпмана-Швингера описывает рассеяние волн в среде, представленной целевой моделью физических свойств, в виде возмущения упрощенной модели. Уравнение является основой для разложения в ряд, который используется для определения рассеяния волн в целевой модели, с тем преимуществом, что для ряда требуется только, чтобы расчеты были выполнены для упрощенной модели. Этот ряд также может быть инвертирован для формирования итерационного ряда, что позволяет определить целевую модель из измеренных данных, и снова требуя только выполнения расчетов для упрощенной модели. Уравнение Липпмана-Швингера представляет собой общий формализм, который может быть применен ко всем типам геофизических данных и моделей, включая в себя сейсмические волны. Этот метод начинается с двух уравнений:
LG=-I (2)
L0G0=-I (3)
где L, L0 - это фактический и базовый дифференциальный оператор, соответственно, G и G0 - это фактический и базовый операторы Грина, соответственно, и I - это единичный оператор. Обратите внимание, что G представляет собой измеренные данные точечного источника, а G0 - смоделированные данные точечного источника по исходной модели. Уравнение Липпмана-Швингера для теории рассеяния записывается как:
G=G0+G0VG (4)
где V=L-L0, откуда может быть получена разница между истинной и исходной моделями.
Уравнение (4) решается итерационно относительно V, путем разложения его в ряд (в предположении, что G=G0 для первой аппроксимации G и т.д.) для получения:
G=G0+G0VG0+G0VG0VG0+ · (5)
Затем V раскладывается в ряд:
V=V(1)+V(2)+V(3)+ · (6)
где V(n) представляет собой часть V, имеющую n-ый порядок невязки данных (здесь невязкой данных является разница G-G0, измеренная на поверхности). Подстановка уравнения (6) в уравнение (5) и подбор членов одного и того же порядка, приводят к следующей системе уравнений для первых 3 порядков:
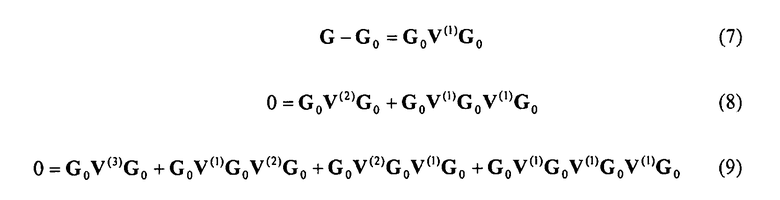
и аналогичных для более высоких порядков V. Эти уравнения могут быть решены итерационно путем решения уравнения (7) для V(1) путем инвертирования G0 с обеих сторон V(1), для получения:
V(1)=G0 -1 (G - G0)G0 -1 (10)
После чего V(1) из уравнения (10) подставляют в уравнение (8) и это уравнение решают относительно V2 как:
V(2)= - G0 -1 C0V(1)G0V(1)G0G0 -1 (11)
и так далее для более высоких порядков разложения V.
Уравнение (10) содержит сумму по источникам и частоте, которая может быть записана в явном виде как:
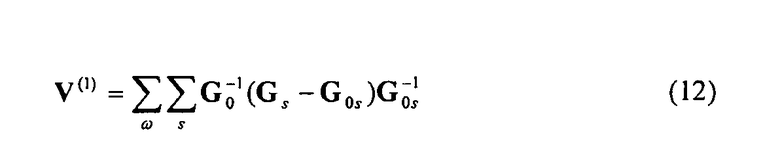
где Gs представляет собой измеренные данные для источника s, G0s - данные, полученные в результате моделирования для базовой модели источника s, а G0s -1 может интерпретироваться как форма импульса в источнике s, полученная при нисходящей аппроксимации. Уравнение (10), выполненное в частотной области, может интерпретироваться следующим образом: (1) Осуществить нисходящую аппроксимацию формы импульса в каждом источнике для базовой модели (член G0 -1), (2) Для каждого источника, осуществить нисходящую аппроксимацию приемников данных невязки для базовой модели (член G0 -1 (G - G0s)), (3) умножить эти два поля, затем просуммировать по всем источникам и частотам. Нисходящая аппроксимация для этого способа может быть выполнена, используя программное обеспечение для геофизического моделирования, например, используя метод конечных разностей.
Примерный вариант осуществления
Блок-схема на фиг. 1 показывает основные этапы в одном варианте осуществления настоящего способа изобретения. На этапе 110 выбирается приближение, которое улучшает некоторые аспекты процесса инверсии. Улучшение может быть скорее представлено в виде ускорения расчетов, чем повышения точности. Примеры таких приближений включают в себя использование приближенной целевой функции или использование приближения в моделирующем программном обеспечении. Эти приближения часто выбираются для снижения вычислительной стоимости инверсии. Однако вместо вычислительного ускорения, улучшение может касаться компромисса в точности, то есть приема большей неточности в одном из аспектов вычислений в обмен на большую точность в некотором другом аспекта. На этапе 140 на основе измеренных данных 130 производится обновление принятой модели 120 физических свойств. На этапе 140 приближение, выбранное на этапе 110, используется для выполнения обновления вычислений. Использование итерационной локальной оптимизации функции стоимости в качестве примера итерационной инверсии, и "обновления вычислений" в качестве термина, использующегося в данном документе, включают в себя, без ограничения, вычисление целевой функции (функции стоимости), градиента целевой функции, и всех процедур прямого моделирования, необходимых для выполнения рассмотренного выше. Этап 140 выдает обновленную модель 150 физических свойств, которые должны быть ближе к реальным свойствам геологической среды, чем те, которые были приняты моделью 120 физических свойств. Обычно, эта обновленная модель 150 физических свойств может дополнительно улучшаться путем подачи ее и измеренных данных 130 обратно в способ обновления на этапе 140 для получения дополнительно улучшенной модели физических свойств. Этот обычный итерационный метод инверсии имеет тот недостаток, что любые артефакты в инверсии, которые являются следствием приближения, выбранного на этапе 110, скорее всего, конструктивно усилятся в инверсии и «загрязнят» окончательный инвертированный результат.
Вместо того, чтобы напрямую возвращаться к этапу 140, в способ настоящего изобретения вставляется этап 160, на котором некоторые аспекты приближения, выбранные на этапе 110, изменяются таким образом, что артефакт, вызванный приближением изменяется, и поэтому не будет усилен за счет итераций на этапе 140. Посредством этого артефакт, являющийся следствием приближения, выбранного на этапе 110, будет снижен.
Примеры приближений и соответствующие артефакты
Следующая таблица содержит примеры этапа 110, то есть приближений, которые могут предпочтительно использоваться в инверсии данных, и которые являются подходящими (этап 160) для применения согласно настоящему изобретению. В первом столбце таблицы перечислены приближения, которые могут использоваться в настоящем изобретении. Во втором столбце перечислены артефакты, ассоциированные с каждым приближением. В последнем столбце перечислены признаки приближения, которые могут варьироваться между итерациями, чтобы вызывать изменения в артефакте между итерациями, что приведет к тому, что он будет некогерентно суммироваться в окончательной инверсной модели и, таким образом, снижен.
Приведенный выше перечень не является исчерпывающим. Список включает только примеры приближений, которые уменьшают время вычислений. Иногда предпочтительным является поступиться неточностью в одной области, чтобы получить больше точности в другой. Примером такого типа компромисса по точности приближения является использование менее точных граничных условий поглощающих границ при прямом моделирования с тем, чтобы сделать градиентные расчеты более точными. Условия поглощающих границ необходимы для решения дифференциального(ых) уравнения(ий), описывающего(их) распространение волн, например уравнения анизотропного распространения вязкоупругих волн (или некоторого его приближения) для случая сейсмических данных, или уравнений Максвелла для случая электромагнитных данных. В общем, компромисс по точности предполагает потерю точности в одном аспекте способа в обмен на повышение точности в другом аспекте.
Тестовый Пример 1 - Кодированная целевая функция
Фиг. 2-5 представляют собой синтетический пример выполнения инверсии, с использованием приближения для целевой функции, в котором сейсмические источники в измеренных данных кодируются, а затем суммируются; см. публикацию заявки США № 2010-0018718 на имя Джерома Кребса и др. Это приближение ускоряет инверсию, потому что закодированная целевая функция может быть оценена с помощью одного запуска программы моделирования, а не путем запуска ее всякий раз для каждого источника, как в случае обычной инверсии. Фиг. 2 - это не требующая разъяснений блок-схема, которая конкретизирует фиг. 1 для данного конкретного варианта осуществления, с этапом 210, показывающим приближение кодирования.
В данном примере модель геофизических свойств - это просто модель скорости акустической волны. На фиг. 3 показана базовая скоростная модель, т.е. «неизвестная» модель (которая будет инвертироваться и которая использовалась для генерации данных, которые будут инвертироваться) для этого примера. Изменение оттенков указывает скорость на каждой глубине и в каждом поперечном местоположении, как показано с помощью "цветового" линейки справа. На фиг. 4 показана инверсия, полученная в результате применения настоящего изобретения, как представлено на блок-схеме на фиг. 2. В этом примере источники кодируются случайным умножением их на плюс или на минус единицу. На этапе 260 кодирование источников меняется путем изменения начального числа при генерации случайных чисел, использующихся для генерации кодов, применяющихся для кодирования источников. Следует обратить внимание на хорошее соответствие с базовой моделью, показанное на фиг. 3.
На фиг. 5 показаны результаты применения метода инверсии, приведенные в блок-схеме на фиг. 2, но не включающие в себя новый признак этапа 260. Обратите внимание, что в инверсии на фиг. 5 преобладают перекрестные помехи (инверсия в виде пятен), в то время как артефакт перекрестных помех оказывается в основном невидимым при инверсии, получаемой в соответствии с настоящим изобретением (фиг. 4).
Кодирование одновременных источников описывалось ранее (и заявлялось) в публикации заявки США № 2010-0018718 вместе со способом изменения кодирования от одной итерации к другой; см. параграф 62 и п. 3 формулы в этой патентной публикации. Тем не менее публикация заявки США № 2010-0018718 не принимает во внимание и не раскрывает, что изобретение кодирования представляет собой конкретный пример общего изобретения, описанного в настоящем документе.
Тестовый Пример 2 - Приближение, создающее искусственные отражения
Фиг. 6-9 иллюстрируют синтетический пример выполнения инверсии с использованием приближения в моделирующем средстве, создающем искусственные отражения. Примером такого приближения является использование такого моделирующего средства конечных разностей, в котором размер ячеек в сетке меняется с изменением глубины от поверхности. Это приближение ускоряет инверсию, потому что сетка в моделирующем средстве может быть настроена для оптимизации ее путем изменения по глубине. Обычно для поверхностной части моделирующего средства конечных разностей необходимы меньшие ячейки сетки, чем требуются в более глубокой части модели. Артефакт, порожденный этим приближением - это искусственное отражение на границах между изменениями размера ячейки сетки.
На фиг. 6 представлена блок-схема для варианта осуществления настоящего изобретения, проиллюстрированного в данном примере. В данном примере моделирующего средства с переменной сеткой фактически не используется для формирования искусственного отражателя. Вместо этого (этап 610) искусственное отражение создается путем размещения фиктивного разрыва в модели плотности на глубине 500 метров. Такая модель разрыва плотности использовалась моделирующим средством для моделирования обновления, однако чтобы сгенерировать измеренные данных (630 на фиг. 6) использовалась модель постоянной плотности. В этом случае инверсия выполняется таким образом, что обновляется только скоростная модель (640), так что фиктивный разрыв плотности сохраняется на протяжении итераций инверсии.
Модель геофизических свойств в данном примере - это всего лишь модель (620) скорости звуковой волны. На фиг. 7 показана базовая скоростная модель (модель, которая будет инвертироваться и которая использовалась для генерации данных, которые будут инвертироваться) для этого примера. Изменение оттенков показывает скорость на каждой глубине. Фиг. 8 показывает инверсию, полученную в результате применения настоящего изобретения, как представлено на блок-схеме на фиг. 6. В этом примере на этапе 660 глубина фиктивных скачков плотности меняется случайным образом с использованием нормального распределения со средним, равным 500 метрам и дисперсией, равной 100 метрам. Обратите внимание на хорошее согласование с базовой моделью, показанное на фиг. 7. На фиг. 7-9 и 11-13, скорость нанесена на графике в виде безразмерной относительной скорости, равной инвертированной скорости, деленной на начальную скорость, причем последняя служит начальным предположением того, какой ожидается быть скоростная модель.
На фиг. 9 показан результат применения метода инверсии, описанного блок-схемой на фиг. 6, но не включающего в себя новый признак, представляющий собой этап 660. Следует отметить, что инверсия на фиг. 9 имеет отчетливо видные искусственные отражения 910 на глубине 500 метров, в то время как это искусственное отражение является в значительной степени невидимым при инверсии, которая использовала способ настоящего изобретения (фиг. 8).
Тестовый Пример 3 - случайные подмножества измеренных данных.
Фиг. 10-13 представляют собой синтетический пример выполнения инверсии с использованием приближения в измеренных данных. Примером такого приближения является использование подмножества измеренных данных (1010 на фиг. 10). Это приближение уменьшает количество измеренных данных, что ускоряет инверсию, поскольку вычислительное время инверсии прямо пропорционально количеству измеренных данных. В обычной инверсии для поддержания высокого горизонтального разрешения необходимы все измеренные данные, и таким образом, в обычной практике это приближение не используется. Артефакт, порожденный этим приближением, является «следами» в инверсных моделях и является следствием редких местоположений источника и ухудшения горизонтального разрешения. На рисунке 10 представлена блок-схема, которая конкретизирует этапы, показанные на фиг. 1, для варианта осуществления изобретения, который используется в данном примере. В данном примере для инверсии используется подмножество измеренных данных (1030 на фиг. 10), например, подмножество, состоящее из 5 данных, из общего числа 50 измеренных данных.
Модель геофизических свойств в данном примере - это просто модель скорости акустической волны. Фиг. 11 является базовой скоростной моделью (модель, которая будет инвертироваться, и которая использовалась для генерации данных, которые будут инвертироваться) для этого примера. Изменение оттенков показывает скорость на каждой глубине. Фиг. 12 показывает инверсию, полученную в результате применения настоящего изобретения, как представлено на блок-схеме на фиг.10. В этом примере, на этапе 1060, подмножество измеренных данных выбирается случайным образом по мере увеличения итерации инверсии. Это приводит к использованию различных подмножеств данных в каждом цикле итераций. Фиг. 12 показывает хорошее соответствие с базовой моделью, представленной на фиг. 11, при использовании десяти процентов измеренных данных.
На фиг. 13 показаны результаты применения метода инверсии, описанные в блок-схеме на фиг. 6, но не включающего в себя этап 1060 снижения артефакта. Можно отметить, что инверсия на фиг. 13 имеет искусственное следы в более глубоких частях, ниже 2000 метров, и коротковолновый шум по всей инверсной модели, в то время как эти следы шума подавлены в инверсии с использованием способа настоящего изобретения (фиг. 12), а коротковолновые шумы незаметны.
Следует иметь в виду, что блок-схемы на фиг. 2, 6 и 10 представляют собой примеры конкретных вариантов осуществления изобретения, описанного в более общем виде на фиг. 1.
Вышеизложенная патентная заявка направлена на конкретные варианты осуществления настоящего изобретения с целью иллюстрации. Однако специалистам в данной области должно быть очевидно, что в вариантах осуществления, описанных в данном документе, возможны многие модификации и изменения. Все такие модификации и изменения призваны быть в пределах объема настоящего изобретения, определяемого формулой изобретения. Специалисты в данной области техники легко поймут, что в практическом применении изобретения, по меньшей мере, некоторые из этапов в способе настоящего изобретения (как правило, этапы 140-160, а зачастую и генерация модели на этапе 120) выполняются на компьютере, т.е. изобретение может быть реализовано на компьютере. В таких случаях, результирующая обновленная физическая модель геологической среды может быть либо загружена или сохранена в память компьютера.
Источники информации
1. Tarantola, A., "Inversion of seismic reflection data in the acoustic approximation," Geophysics 49, 1259-1266 (1984).
2. Sirgue, L., and Pratt G. "Efficient waveform inversion and imaging: A strategy for selecting temporal frequencies," Geophysics 69, 231-248 (2004).
3. Weglein, A. B., Araujo, F. V., Carvalho, P. M., Stolt, R. FL, Matson, K. FL, Coates, R. T., Corrigan, D., Foster, D. J., Shaw, S. A., and Zhang, FL, "Inverse scattering series and seismic exploration," Inverse Problems 19, R27-R83 (2003).
4. Fallat, M. R., Dosso, S. E., "Geoacoustic inversion via local, global, and hybrid algorithms," Journal of the Acoustical Society of America 105, 3219-3230 (1999).
5. Berkhout, A. J., "Areal shot record technology," Journal of Seismic Exploration 1, 251-264 (1992).
6. Krebs, Jerome et al, "Iterative Inversion of Data from Simultaneous Geophysical Sources", U.S. Patent Application Publication No. 2010-0018718 (01-28-2010).
7. Clapp, R. G., "Reverse time migration with random boundaries," SEG International Exposition and Meeting (Houston), Expanded Abstracts, 2809-2813 (2009).
| название | год | авторы | номер документа |
|---|---|---|---|
| ИТЕРАТИВНАЯ ИНВЕРСИЯ ДАННЫХ ОТ ОДНОВРЕМЕННЫХ ГЕОФИЗИЧЕСКИХ ИСТОЧНИКОВ | 2007 |
|
RU2435215C2 |
| ИНВЕРСИЯ ОДНОВРЕМЕННЫХ ИСТОЧНИКОВ ДЛЯ ДАННЫХ СЕЙСМОПРИЕМНОЙ КОСЫ С ВЗАИМНОКОРРЕЛЯЦИОННОЙ ЦЕЛЕВОЙ ФУНКЦИЕЙ | 2011 |
|
RU2587498C2 |
| СКОРОСТЬ СХОДИМОСТИ ИНВЕРСИИ ПОЛНОГО ВОЛНОВОГО ПОЛЯ ПРИ ИСПОЛЬЗОВАНИИ ФОРМИРОВАНИЯ СПЕКТРА | 2012 |
|
RU2577387C2 |
| ПОЛНАЯ ИНВЕРСИЯ ВОЛНОВОГО ПОЛЯ ПРИ НАЛИЧИИ ПЛОЩАДНОГО И ТОЧЕЧНОГО ИСТОЧНИКОВ | 2017 |
|
RU2706831C1 |
| ГИБРИДНЫЙ СПОСОБ ДЛЯ ПОЛНОВОЛНОВОЙ ИНВЕРСИИ С ИСПОЛЬЗОВАНИЕМ СПОСОБА ОДНОВРЕМЕННЫХ И ПОСЛЕДОВАТЕЛЬНЫХ ИСТОЧНИКОВ | 2011 |
|
RU2570827C2 |
| ОРТОГОНАЛЬНОЕ КОДИРОВАНИЕ ИСТОЧНИКА И ПРИЕМНИКА | 2013 |
|
RU2612896C2 |
| КОДИРОВАНИЕ ОДНОВРЕМЕННЫХ ИСТОЧНИКОВ И РАЗДЕЛЕНИЕ ИСТОЧНИКОВ В КАЧЕСТВЕ ПРАКТИЧЕСКОГО РЕШЕНИЯ ПО ИНВЕРСИИ ПОЛНОГО ВОЛНОВОГО ПОЛЯ | 2011 |
|
RU2582480C2 |
| ПОЛНАЯ ИНВЕРСИЯ ВОЛНОВОГО ПОЛЯ С КОМПЕНСАЦИЕЙ ПОКАЗАТЕЛЯ КАЧЕСТВА | 2016 |
|
RU2693495C1 |
| СПОСОБЫ ОЦЕНИВАНИЯ ПАРАМЕТРОВ ГЕОЛОГИЧЕСКОЙ СРЕДЫ ПРИ ИНВЕРСИИ ПОЛНОГО ВОЛНОВОГО ПОЛЯ И ОБРАТНОЙ МИГРАЦИИ ВО ВРЕМЕННОЙ ОБЛАСТИ | 2011 |
|
RU2545487C2 |
| СПОСОБЫ ДЛЯ АППРОКСИМАЦИИ ОПЕРАЦИИ УМНОЖЕНИЯ ГЕССИАНА НА ВЕКТОР В ПОЛНОЙ ИНВЕРСИИ ВОЛНОВОГО ПОЛЯ | 2012 |
|
RU2613216C2 |





Изобретение относится к области геофизики и может быть использовано при обработке геофизических данных. Заявлен способ для снижения артефактов в модели (120) физических свойств геологической среды, получаемой посредством итерационной инверсии (140) геофизических данных (130), в котором артефакты ассоциированы с некоторым приближением (110), сделанным во время итерационной инверсии. В данном способе некоторый аспект приближения изменяется (160) по мере итерационного повторения инверсии таким образом, что артефакты не увеличиваются путем когерентного суммирования. Технический результат - повышение точности получаемых данных. 14 з.п. ф-лы, 13 ил.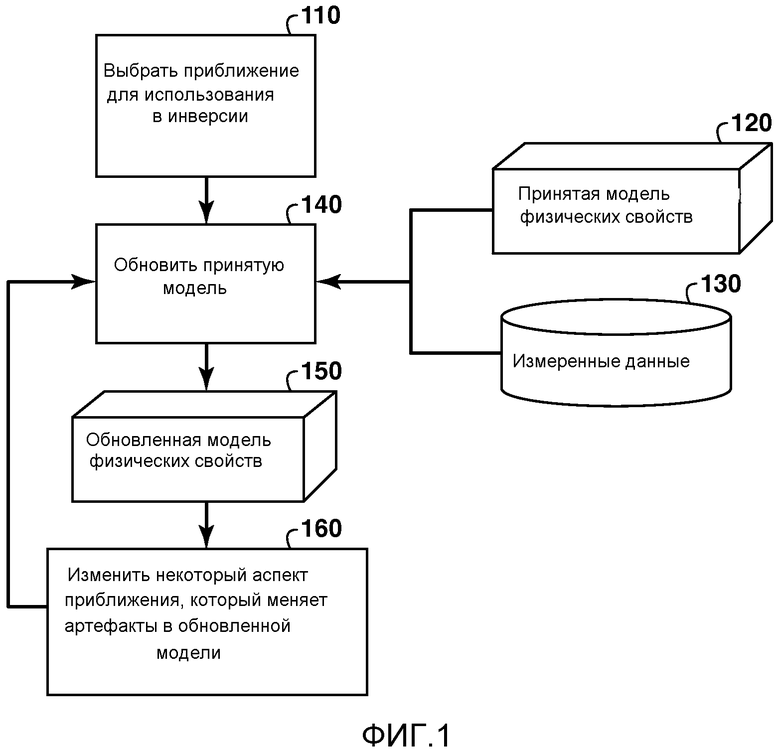
1. Способ снижения артефактов в модели физических свойств геологической среды, вызванных приближением, отличающимся от кодирования источников, в итерационном компьютеризированном процессе инверсии геофизических данных, причем упомянутый способ включает в себя варьирование приближения в ходе выполнения итераций.
2. Способ по п. 1, причем упомянутый способ включает в себя:
(a) принятие модели физических свойств геологической среды, причем упомянутая модель обеспечивает значения, по меньшей мере, одного физического свойства в местоположениях по всей области геологической среды;
(b) выбор итерационного процесса инверсии данных с шагом, в котором производится вычисление обновления модели физических свойств, что делает ее более совместимой с измеренными геофизическими данными, полученными в области геологической среды;
(c) выполнение в упомянутом вычислении приближения, которое либо ускоряет выбранный итерационный процесс инверсии данных, способом, отличающимся от кодирования источников, либо работает с компромиссной точностью;
(d) выполнение, используя компьютер, одного цикла выбранного итерационного процесса инверсии с упомянутым приближением и с использованием модели физических свойств;
(e) выполнение, используя компьютер, следующего итерационного цикла инверсии, в котором делается выбор того, менять какой-либо аспект приближения, или не менять;
(f) при необходимости, повторение (e), изменяя приближение в нескольких или во всех итерационных циклах, вплоть до последней итерации, в которой удовлетворяется критерий сходимости или достигается другое условие остановки; и
(g) загрузку обновленной модели физических свойств с последней итерации, или сохранение ее в памяти компьютера.
3. Способ по п. 2, в котором один или несколько типов артефактов в обновленной модели физических свойств геологической среды идентифицируются как вызванные приближением.
4. Способ по п. 3, в котором аспект приближения, изменяющийся в некоторых или во всех циклах итерации, выбирается для оказания влияния на артефакты одного или нескольких идентифицированных типов артефактов.
5. Способ по п. 4, в котором упомянутое влияние таково, что артефакты от одного приближения не складываются арифметически с артефактами от другого итерационного цикла, который использует приближение с измененным аспектом.
6. Способ по п. 2, в котором приближением является выбор подмножества измеренных геофизических данных для ввода в итерационный процесс инверсии, а измененным аспектом является другое выбранное подмножество.
7. Способ по п. 6, в котором каждое отличающееся подмножество выбирается случайным образом.
8. Способ по п. 1, в котором приближением являются несовершенные поглощающие границы в моделировании синтетических данных в процессе итерационной инверсии.
9. Способ по п. 1, в котором приближением являются отражающие границы в моделировании синтетических данных в процессе итерационной инверсии.
10. Способ по п. 1, в котором приближением являются случайные граничные условия в моделировании синтетических данных в процессе итерационной инверсии.
11. Способ по п. 1, в котором приближением является пространственное изменение в размере ячейки сетки в моделирующем средстве конечных разностей в процессе итерационной инверсии.
12. Способ по п. 1, в котором приближением является пространственное изменение в точности оператора моделирования в процессе итерационной инверсии.
13. Способ по п. 1, в котором приближением является использование размера ячейки сетки в моделировании синтетических данных в процессе итерационной инверсии, причем размер ячейки сетки является слишком грубым для точного представления изменений в модели.
14. Способ по п. 1, в котором приближением является использование большого шага по времени в моделирующем средстве временной области в итерационном процессе инверсии, где "большой" определяется относительно других используемых шагов по времени.
15. Способ по п. 1, в котором итерационный, компьютеризованный процесс инверсии геофизических данных содержит вычисление градиентов функции стоимости, а приближение содержит использование менее точных условий поглощающих границ, чтобы сделать градиентные расчеты более точными.
| WO 2009117174 A1, 24.09.2009 | |||
| US 20090006054 A1, 01.01.2009 | |||
| US 2008270028 A1, 30.10.2008 | |||
| US 20090319240 A1, 24.12.2009 | |||
| US 20100018718 A1, 28.01.2010. |
Авторы
Даты
2016-01-20—Публикация
2011-03-14—Подача