Изобретение относится к технике связи и может использоваться при проектировании новых и модернизации существующих систем передачи дискретной информации. Заявленный способ может быть использован для декодирования помехоустойчивых систематических блоковых кодов, обеспечивая высокую скорость и достоверность восстановления информации.
Заявленное техническое решение расширяет арсенал применения помехоустойчивых блоковых кодов за счет повышения кратности исправляемых кодом стираний.
Известен способ декодирования блоковых кодов (см. Дж. Кларк, мл., Дж Кейн «Кодирование с исправлением ошибок в системах цифровой связи». М.: Радио и связь, 1987, с. 96-128), в которых комбинации ошибок отыскиваются неалгебраическим методом. Недостатком подобного способа является сложность декодера, которая резко возрастает с ростом веса вектора ошибок, и поэтому подобный метод декодирования оказывается не эффективным при исправлении трех и более ошибок. Кроме того, вычислительная сложность процедуры отыскания ошибочных позиций в принятом кодовом векторе оказывается высокой.
Известен также способ декодирования блоковых кодов со стираниями элементов (см. патент РФ 2327297), в котором пространство кодовых комбинаций разбивается на кластеры и при правильном определении номера кластера декодирование осуществляется в подмножестве комбинаций (списке), принадлежащих выделенному кластеру с использованием метрики Евклида.
Недостатком данного способа является слабая защищенность номера кластера, при искажении которого декодер осуществляет поиск решения в подмножестве комбинаций (списке), отличном от истинного, что резко повышает вероятность ошибки декодирования.
Близким по технической сущности к заявленному способу является способ мягкого декодирования систематических блоковых кодов, в основе которого лежит процедура использования упорядоченных статистик индексов мягких решений (ИМР) (см. Р. Морелос-Сарагоса. Искусство помехоустойчивого кодирования. Методы, алгоритмы, применение. М., Техносфера, 2005, с. 213, …, 216). Недостатком этого способа является необходимость вычисления обратной матрицы относительно переставленной в соответствии с результатами сортировки ИМР исходной порождающей матрицы кода, приведения вновь образованной матрицы в систематическую форму и получения на этой основе эквивалентного кода, с помощью которого отыскивается в конечном счете образец ошибки. Достоинством способа является возможность исправления ошибок за пределами метрики Хэмминга.
Наиболее близким по технической сущности к заявленному способу является способ, представленный в патенте РФ 2444427, когда символы принятой кодовой комбинации V систематического (n, k)-кода по основному алгоритму упорядочиваются по убыванию их индексов мягких решений и на основании выполненных перестановок формируется вектор V′, который совместно с вектором V образуют двудольный граф для формирования матрицы перестановок Р, умножение на которую порождающей матрицы кода G приводит к получению новой матрицы G′, первые k столбцов которой проверяются на предмет линейной независимости, и в случае положительного исхода этой проверки матрица G′ приводится к систематической форме  , при этом первые k наиболее надежных элементов вектора V′ путем умножения на
, при этом первые k наиболее надежных элементов вектора V′ путем умножения на  образуют вектор эквивалентного кода Vэкв, который при поэлементном сложении по модулю два с вектором V′ формирует переставленный вектор ошибок Е′, и после умножения вектора Е′ на PT формируется вектор ошибок Е, действовавший в канале связи на вектор V, при этом в случае отрицательного результата проверки линейной независимости строк матрицы G′ осуществляется замена k-того столбца этой матрицы на (k+1)-й столбец и в случае необходимости на последующие столбцы до выполнения условия линейной независимости k первых столбцов матрицы G′, и при выполнении этого условия адекватно меняются местами элементы в V′ и столбцы Р, отличающийся тем, что для всех разрешенных кодовых комбинаций (n, k)-кода по их f старшим разрядам определяют номер кластера, при этом значение f выбирают в пределах 1<f≤k/2, и при формировании кодового вектора на передаче младший разряд комбинации (правый) выкалывается и заменяется на бит проверки четности f разрядов кластера, а приемник, приняв вектор V по градациям надежности и биту четности, оценивает правильность приема номера кластера и в случае положительного решения переходит к обработке (n-f, k-f)-кода по основному алгоритму, предварительно сформировав корректирующий вектор Wук путем умножения разрядов номера кластера на первые f строк порождающей матрицы G кода и последующего временного удаления из него разрядов кластера, после чего вектор Wук вычитается из вектора V, при этом разряды кластера вектора V также не учитываются, с присвоением младшему разряду вновь образованного вектора Vук наиболее низкой оценки градации надежности, после чего декодер работает по основному алгоритму, формируя вектора ошибок Е, который поразрядно складывается с векторами Wук, Vук, формируя переданный вектор V за счет возвращения на свои места старших разрядов номера кластера, при этом, если проверка на четность номера кластера не выполняется, декодер подвергает инверсии наиболее ненадежный бит из числа участвующих в проверке.
образуют вектор эквивалентного кода Vэкв, который при поэлементном сложении по модулю два с вектором V′ формирует переставленный вектор ошибок Е′, и после умножения вектора Е′ на PT формируется вектор ошибок Е, действовавший в канале связи на вектор V, при этом в случае отрицательного результата проверки линейной независимости строк матрицы G′ осуществляется замена k-того столбца этой матрицы на (k+1)-й столбец и в случае необходимости на последующие столбцы до выполнения условия линейной независимости k первых столбцов матрицы G′, и при выполнении этого условия адекватно меняются местами элементы в V′ и столбцы Р, отличающийся тем, что для всех разрешенных кодовых комбинаций (n, k)-кода по их f старшим разрядам определяют номер кластера, при этом значение f выбирают в пределах 1<f≤k/2, и при формировании кодового вектора на передаче младший разряд комбинации (правый) выкалывается и заменяется на бит проверки четности f разрядов кластера, а приемник, приняв вектор V по градациям надежности и биту четности, оценивает правильность приема номера кластера и в случае положительного решения переходит к обработке (n-f, k-f)-кода по основному алгоритму, предварительно сформировав корректирующий вектор Wук путем умножения разрядов номера кластера на первые f строк порождающей матрицы G кода и последующего временного удаления из него разрядов кластера, после чего вектор Wук вычитается из вектора V, при этом разряды кластера вектора V также не учитываются, с присвоением младшему разряду вновь образованного вектора Vук наиболее низкой оценки градации надежности, после чего декодер работает по основному алгоритму, формируя вектора ошибок Е, который поразрядно складывается с векторами Wук, Vук, формируя переданный вектор V за счет возвращения на свои места старших разрядов номера кластера, при этом, если проверка на четность номера кластера не выполняется, декодер подвергает инверсии наиболее ненадежный бит из числа участвующих в проверке.
Достоинством данного способа декодирования является возможность исправлять число ошибок, кратность которых превосходит число ошибок, определяемых метрикой Хэмминга и снижение вычислительной сложности процессора приемника, за счет снижения размерности порождающей матрицы эквивалентного кода.
Недостаток прототипа заключается в низкой скорости декодирования данных из-за необходимости для каждой кодовой комбинации в зависимости от конфигурации ИМР вычислять определитель матрицы размерности (k-f)×(k-f) при оценке свойства нелинейности строк переставленной матрицы G′. Таким образом, вычисление обратной матрицы в указанной процедуре обязательно. Кроме того, не используются все полезные свойства кластерного разбиения множества кодовых комбинаций. По сути в прототипе номер кластера применяется только для организации параметров укороченного кода, что ограничивает область применения способа использованием только систематических кодов.
Задачей изобретения является разработка способа декодирования кодовых комбинаций любых блоковых кодов, обеспечивающего получение технического результата, заключающегося в повышении скорости декодирования и достоверности принимаемой информации при исправлении ошибок.
Технический результат достигается тем, что для всех разрешенных кодовых комбинаций (n, k)-кода по их f старшим разрядам определяют номер кластера, при этом значение f выбирают в пределах 1<f≤k/2, и при формировании кодового вектора на передаче младший разряд комбинации (правый) выкалывается и заменяется на бит проверки четности f разрядов кластера, а приемник, приняв вектор Vпр по индексам мягких решений и биту четности оценивает правильность приема номера кластера и в случае положительного решения переходит к обработке символов (n-f, k-f)-кода по основному алгоритму ранжирования индексов мягких решений, предварительно сформировав корректирующий вектор Wук путем умножения разрядов номера кластера на первые f строк порождающей матрицы G кода и последующего временного удаления из него разрядов кластера, после чего вектор Wук вычитается из вектора Vпр, при этом разряды кластера вектора Vпр также не учитываются, с присвоением младшему разряду вновь образованного вектора Vук индекса мягкого решения равного нулю, после чего декодер работает по основному алгоритму, формируя вектора ошибок Ver, который поразрядно складывается с векторами Wук, Vук, формируя переданный вектор V за счет обратных перестановок символов и возвращения на свои места старших разрядов номера кластера, при этом, если проверка на четность номера кластера не выполняется, декодер подвергает инверсии наиболее ненадежный бит из числа участвующих в проверке. Особенностью является то, что любые f разрядов определяют номер кластера в двоичном представлении, а в совокупности все номера кластеров взятые по одному образуют полный набор элементов из поля GF(2f), при этом среди оставшихся n-f разрядов выбирают любые k-f разрядов так, чтобы в для всех комбинаций кластера на позициях этих разрядов оказался полный набор элементов из поля GF(2k-f), при этом кластер с номером ноль является базовым, а принятые комбинации любых других кластеров переводят в одну из комбинаций базового кластера путем сложения этих комбинаций с известной декодеру ключевой комбинацией Ki для кластера с номером i, признаком которой является наличие единичного элемента поля GF(2k-f) относительно операции сложения на позициях выделенных k-f разрядов, формируют далее вектор 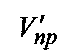 , в котором временно исключают разряды, указывающие на номер кластера, и путем лексикографической сортировки символов
, в котором временно исключают разряды, указывающие на номер кластера, и путем лексикографической сортировки символов 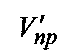 по признаку убывания соответствующих им индексов мягких решений образуют упорядоченный вектор
по признаку убывания соответствующих им индексов мягких решений образуют упорядоченный вектор 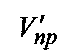 , формируя в соответствии с этим упорядочением матрицу перестановок Р, используя которую переставляют столбцы комбинаций базового кластера так, чтобы на позициях старших k-f разрядов этого кластера образовался полный набор элементов поля GF(2k-f), для чего в случае необходимости, одновременно корректируют Р и Vуп, а после отыскивают в кластере вектор с номером j, в котором на k-f позициях старших разрядов окажутся символы в точности равные битам на одноименных позициях вектора
, формируя в соответствии с этим упорядочением матрицу перестановок Р, используя которую переставляют столбцы комбинаций базового кластера так, чтобы на позициях старших k-f разрядов этого кластера образовался полный набор элементов поля GF(2k-f), для чего в случае необходимости, одновременно корректируют Р и Vуп, а после отыскивают в кластере вектор с номером j, в котором на k-f позициях старших разрядов окажутся символы в точности равные битам на одноименных позициях вектора  , при этом выделенный вектор после его упорядочения принимают за эталонный
, при этом выделенный вектор после его упорядочения принимают за эталонный 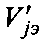 , после чего складывают этот вектор поразрядно с вектором
, после чего складывают этот вектор поразрядно с вектором  , получая упорядоченный вектор ошибок
, получая упорядоченный вектор ошибок 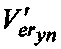 , при умножении которого на матрицу PT формируют истинный вектор ошибок Ver, по которому, возвращая разряды кластера, с учетом Vпр находят переданный вектор V, учитывая, что в ходе декодирования вектора Vпр при невыполнении условия четности для разрядов кластера их восстановление осуществляют путем известных итеративных преобразований символов, составляющих номер кластера и определенного для этого бита четности.
, при умножении которого на матрицу PT формируют истинный вектор ошибок Ver, по которому, возвращая разряды кластера, с учетом Vпр находят переданный вектор V, учитывая, что в ходе декодирования вектора Vпр при невыполнении условия четности для разрядов кластера их восстановление осуществляют путем известных итеративных преобразований символов, составляющих номер кластера и определенного для этого бита четности.
Способ, применимый к любому блоковому коду, осуществляют следующим образом. Код БЧХ (15, 5, 7) с порождающим полиномом g(x)=24678 имеет порождающую матрицу G вида
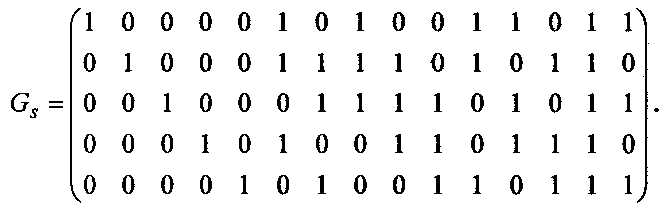
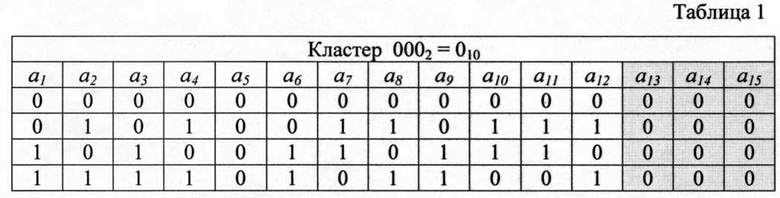
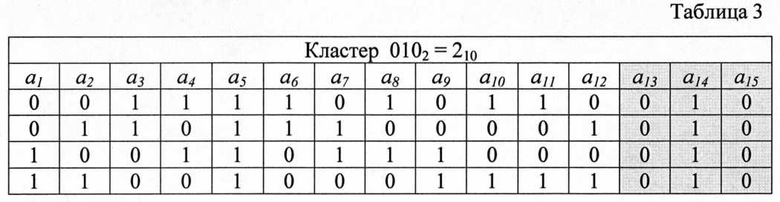
Множество кодовых комбинаций кода разбивается на кластеры путем выделения f любых разрядов, где 1<f≤k/2. Пусть f=3 и в качестве разрядов кластера в системе выделяются разряды a13, a14, a15 (см. таблицу 1). Все множество комбинаций кода разбитое на кластеры в соответствие с выбранным правилом представлено в таблицах 1-8, а номера всех кластеров образуют множество элементов поля GF(23). Анализ элементов столбцов кластеров показывает, что не все перестановки столбцов приводят к образованию полного набора элементов поля GF(2k-f). Подобное сочетание столбцов не может привести к образованию эквивалентного кода, и поэтому должно быть заменено на другое путем итеративных преобразований соседних столбцов. Например, столбец а, отдельно в сочетании со столбцами а3, а5, а6 и а9 не обеспечивает получение полного набора элементов поля GF(22) и поэтому в сочетании со столбцом а1 должны быть другие подходящие по значению ИМР столбцы. Число подобных неудачных сочетаний для всех столбцов составляет около 20% от общего возможного числа комбинаций столбцов, которые в подавляющем большинстве устраняются за одну итерацию, например, заменяя столбец, стоящий на второй позиции на третий столбец и так далее. Заметно, что столбец а5 всех кластеров при любом сочетании не обеспечивает получение желаемого результата, поэтому разряд а5 целесообразно отвести под бит проверки четности номера кластера, присваивая ему на приеме наиболее низкое значение ИМР. Для других кодов, исходя из указанного принципа, могут быть выбраны другие позиции кодовых комбинаций.




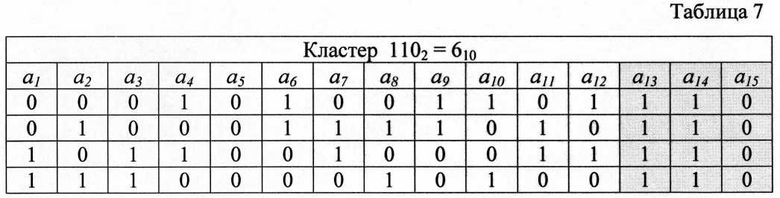
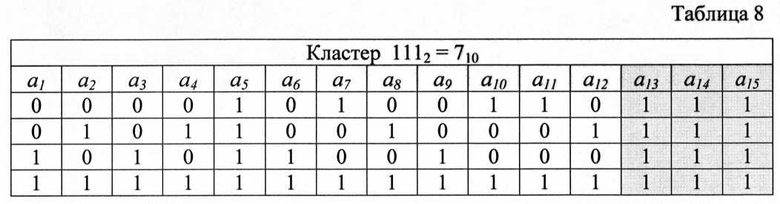
Пусть на выходе кодера образовался вектор вида
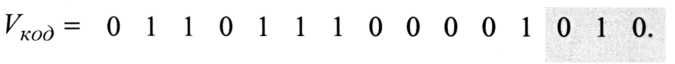
Для защиты номера кластера от ошибок передатчик заменяет бит а5 оставшейся части комбинации на бит проверки четность для символов, определяющих номер кластера 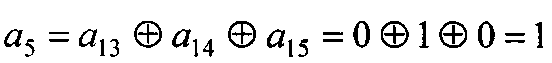 (в примере он остается без изменений). В канал связи будет передан вектор
(в примере он остается без изменений). В канал связи будет передан вектор

Приемник принимает вектор 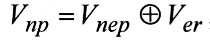 , устанавливая по какому-либо известному принципу индекс мягкого решения (ИМР) для каждого символа комбинации, где Ver - вектор мешающих факторов или вектор ошибок. Пусть соответствие символов и их целочисленных значений ИМР имеет вид
, устанавливая по какому-либо известному принципу индекс мягкого решения (ИМР) для каждого символа комбинации, где Ver - вектор мешающих факторов или вектор ошибок. Пусть соответствие символов и их целочисленных значений ИМР имеет вид
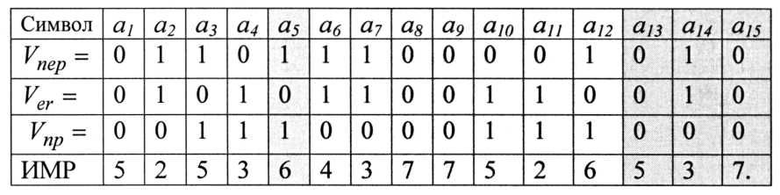
Следовательно, вектор ошибок представлен последовательностью вида

После приема вектора Vпр, декодер на первом шаге декодирования проверяет соответствие символов номера кластера (позиции а13, а14, a15) правилу четности. Если правило четности выполняется, декодер выполняет последующие шаги по восстановлению вектора Vпр. В противном случае, номер кластера восстанавливается с использованием арсенала итеративных преобразований в соответствии с правилом

где функция  возвращает знак своего аргумента; L(d1) - оценка надежности символа, участвующего в формировании проверочного бита; L(d2) - оценка надежности проверочного символа; µ - число исключенных из преобразований единичных символов при условии, что они имеют высокий показатель ИМР.
возвращает знак своего аргумента; L(d1) - оценка надежности символа, участвующего в формировании проверочного бита; L(d2) - оценка надежности проверочного символа; µ - число исключенных из преобразований единичных символов при условии, что они имеют высокий показатель ИМР.
Например, в полученной последовательности а5, а13, а14, а15 символ al5 является наиболее надежным. Ему соответствует информационное значение a15=0, поэтому µ=0. Последовательность, подлежащая коррекции, принимает вид:  В этой последовательности единицы представляются знаком +, а нули знаком -, вертикальная черта указывает на проверочный символ четности +6.
В этой последовательности единицы представляются знаком +, а нули знаком -, вертикальная черта указывает на проверочный символ четности +6.
На первом шаге итеративных преобразований получаем
L(d1)=[-3+0]+6·(-1)≈3 - новое значение апостериорной оценки для символа -5;
L(d2)=[-5+0]+6·(-1)≈5 - новое значение для символа -3.
Второй шаг итерации
L(d1)=[-3+5]+6·(-1)≈-2 - значение коррекции для символа -5;
L(d2)=[-5+3]+6·(-1)≈2 - значение коррекции для символа +4.
Третий шаг итерации
L(d1)=[-3+2]+6·(-1)≈1 - значение коррекции для символа -5;
L(d2)=[-5-2]+6·(-1)≈6 - значение коррекции для символа +4.
Итогом преобразований являются действия (-5+1=-4) и (-3+6)=+3.
В результате вместо искаженной последовательности 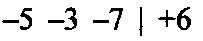 получают восстановленную последовательности символов
получают восстановленную последовательности символов  Следовательно, номер кластера, которому принадлежит комбинация, имеет номер 0102=210.
Следовательно, номер кластера, которому принадлежит комбинация, имеет номер 0102=210.
Разряды для оставшихся k-f символов подбираются так, чтобы комбинации бит этих разрядов в совокупности представляли полный набор элементов поля FG(2k-f). Например, подходящими кандидатами для всех кластеров являются символы а1 и а2 (см. таблицы 1-8), но, например, символы а4 и а8 этому требованию не отвечают. Пусть выбраны символы a1 и а2. Для любого кластера с номером i комбинация Ki, в которой a1=0 и а2=0 является ключевой, позволяющей перевести комбинацию из кластера с номером i в одну из комбинаций кластера с номером 0.
Для второго кластера такой комбинацией является комбинация вида
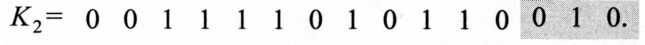
После удаления номера кластера получают
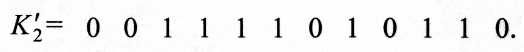
Штрих в значении векторов означает работу декодера без учета символов кластера. При использовании процедуры  получают вектор, в котором осуществляется ранжирование символов ai по убыванию значений их ИМР, так называемая лексикографическая сортировка массива данных. При этом символу проверки четности а5 искусственно присваивается наименьшее значение из возможных значений ИМР.
получают вектор, в котором осуществляется ранжирование символов ai по убыванию значений их ИМР, так называемая лексикографическая сортировка массива данных. При этом символу проверки четности а5 искусственно присваивается наименьшее значение из возможных значений ИМР.
Перевод вектора в нулевой кластер

Процедура сортировки с образованием матрицы перестановок Р.
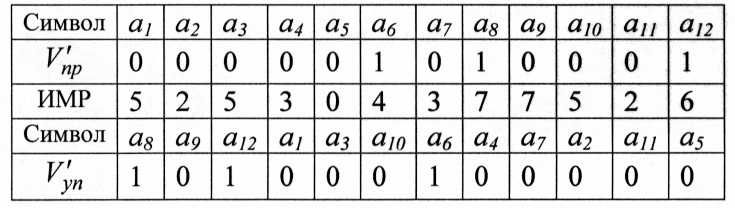
В новом формате на первых двух позициях оказываются символы, имеющие наиболее высокие значения ИМР, что отвечает требованиям перестановочного декодирования. Матрица Р принимает вид

Очевидно, что полной перестановки столбцов кластера K0 не требуется. Достаточно получить значения первых двух (трех) столбцов, чтобы выделить требуемый вектор из набора векторов кластера 
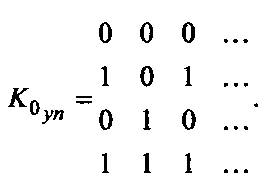
Первые два столбца в 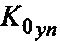 образуют полный набор элементов двоичного поля Галуа второй степени расширения, что говорит о возможности формирования эквивалентного кода. По совпадению элементов а8=1 и а9=0 в кластере
образуют полный набор элементов двоичного поля Галуа второй степени расширения, что говорит о возможности формирования эквивалентного кода. По совпадению элементов а8=1 и а9=0 в кластере  выделяется вторая строка
выделяется вторая строка  и осуществляется ранжирование ее элементов путем умножения
и осуществляется ранжирование ее элементов путем умножения 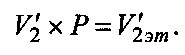 Это снижает сложность вычислительного процесса. Однако в случае образования пары a8 и а12 на позициях старших разрядов
Это снижает сложность вычислительного процесса. Однако в случае образования пары a8 и а12 на позициях старших разрядов  набор элементов поля GF(22) не является полным, следовательно, эквивалентный код образовать невозможно.
набор элементов поля GF(22) не является полным, следовательно, эквивалентный код образовать невозможно.

Далее выполнение операция 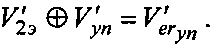
Выделение второй строки в кластере комбинаций по
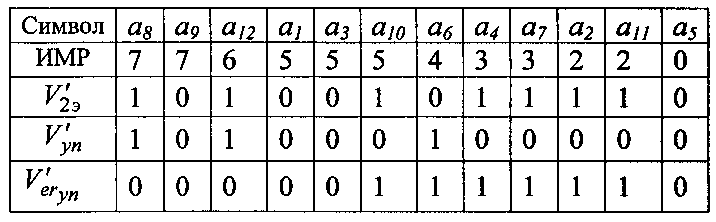
Обратные преобразования вида  обеспечивают получение образца ошибок, действовавших на вектор Vпep при передаче его по каналу связи.
обеспечивают получение образца ошибок, действовавших на вектор Vпep при передаче его по каналу связи.
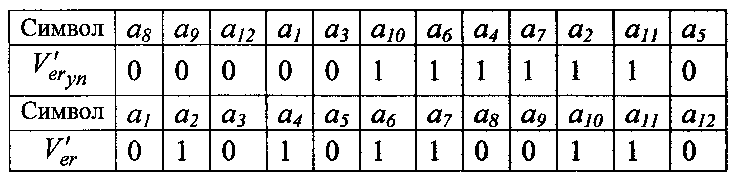
Возвращая номер кластера на свои позиции и применяя значение Ver к вектору Vпр, получают вектор Vпер.
Предложенный способ мягкого декодирования блоковых позволяет:
- в большинстве случаев исправлять стирания, кратность которых определяется соотношением n-k;
- по сравнению с аналогами существенно сократить время обработки кодовых комбинаций в декодере за счет исключения из вычислительного процесса процедуры поиска обратной матрицы для переставленной порождающей матрицы кода и последующего формирования на этой основе матрицы эквивалентного кода;
- применение способа для декодирования не только систематических блоковых кодов.
| название | год | авторы | номер документа |
|---|---|---|---|
| ДЕКОДЕР С ОБРАБОТКОЙ СПИСКА БАЗОВОГО КЛАСТЕРА | 2015 |
|
RU2605365C1 |
| СПОСОБ МЯГКОГО ДЕКОДИРОВАНИЯ СИСТЕМАТИЧЕСКИХ БЛОКОВЫХ КОДОВ | 2010 |
|
RU2444127C1 |
| ДЕКОДЕР С УПОРЯДОЧЕННОЙ СТАТИСТИКОЙ СИМВОЛОВ | 2012 |
|
RU2490804C1 |
| ПЕРЕСТАНОВОЧНЫЙ ДЕКОДЕР С СИСТЕМОЙ БЫСТРЫХ МАТРИЧНЫХ ПРЕОБРАЗОВАНИЙ | 2019 |
|
RU2718224C1 |
| ПЕРЕСТАНОВОЧНЫЙ ДЕКОДЕР С ПАМЯТЬЮ | 2017 |
|
RU2672300C2 |
| Перестановочный декодер с режимом обучения | 2017 |
|
RU2644507C1 |
| ПЕРЕСТАНОВОЧНЫЙ ДЕКОДЕР С ОБРАТНОЙ СВЯЗЬЮ | 2018 |
|
RU2704722C2 |
| ДЕКОДЕР С ИСПРАВЛЕНИЕМ СТИРАНИЙ | 2007 |
|
RU2344556C1 |
| СПОСОБ ДИНАМИЧЕСКОГО УПРАВЛЕНИЯ ПРОПУСКНОЙ СПОСОБНОСТЬЮ КАНАЛА СВЯЗИ НА БАЗЕ КЛАСТЕРНОГО ДЕКОДИРОВАНИЯ ПОЛЯРНЫХ КОДОВ | 2021 |
|
RU2779158C1 |
| МЯГКИЙ ДЕКОДЕР ПОСЛЕДОВАТЕЛЬНОГО ТУРБОКОДА | 2013 |
|
RU2538331C2 |
Изобретение относится к технике связи и может быть использовано в системах передачи дискретной информации. Техническим результатом является повышение скорости декодирования и достоверности принимаемой информации. Способ содержит этапы, на которых: для всех разрешенных кодовых комбинаций произвольного блокового (n, k)-кода по любым 1<f≤k/2 разрядам определяют номер кластера в двоичном представлении при условии, что в совокупности все образцы номеров кластеров образуют полный набор элементов из поля GF(2f). Среди оставшихся n-f разрядов выбирают k-f разрядов так, чтобы в совокупности для всех комбинаций кластера на позициях этих разрядов оказался полный набор элементов поля GF(2k-f). Кластер с номером ноль принимается за базовый. Любая комбинация из состава других кластеров может быть приведена к одной из комбинаций базового кластера после вычисления номера ее кластера i≠0 и сложения с известной приемнику ключевой комбинацией Ki. Признаком комбинации Ki в кластере является наличие единичного элемента поля GF(2k-f) относительно операции сложения на позициях k-f разрядов. Точное определение номера кластера обеспечивается выделением любого разряда не вошедшего в число выбранных ранее k-f разрядов для проверки четности разрядов номера кластера на передаче и их итеративных преобразований на основе индексов мягких решений (ИМР) на приеме. После вычисления номера кластера его разряды временно из процедуры декодирования исключаются. Оставшаяся часть принятого вектора 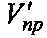 с использованием части Ki переводится в базовый кластер и упорядочивается по убыванию значений ИМР, формируя при этом вектор
с использованием части Ki переводится в базовый кластер и упорядочивается по убыванию значений ИМР, формируя при этом вектор 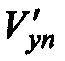 и матрицу перестановок Р. С использованием этой матрицы переставляются столбцы базового кластера, при этом обращают внимание на то, чтобы на позициях k-f старших разрядов образовался полный набор элементов из поля GF(2k-f). В случае необходимости одновременно переставляют ближайшие столбцы в кластере и в векторе
и матрицу перестановок Р. С использованием этой матрицы переставляются столбцы базового кластера, при этом обращают внимание на то, чтобы на позициях k-f старших разрядов образовался полный набор элементов из поля GF(2k-f). В случае необходимости одновременно переставляют ближайшие столбцы в кластере и в векторе 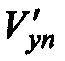 . Из полученного набора выбирают ту строку кластера, которая на позициях k-f разрядов совпадает с битами в
. Из полученного набора выбирают ту строку кластера, которая на позициях k-f разрядов совпадает с битами в 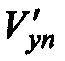 . Складывая этот вектор с
. Складывая этот вектор с 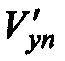 , получают упорядоченный образец ошибок
, получают упорядоченный образец ошибок 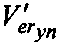 , который путем умножения на PT и возвращения разрядов номера кластера приводят к истинному вектору ошибок. 14 табл.
, который путем умножения на PT и возвращения разрядов номера кластера приводят к истинному вектору ошибок. 14 табл.
Способ мягкого декодирования блоковых кодов, заключающийся в том, что для всех разрешенных кодовых комбинаций (n, k)-кода по их f старшим разрядам определяют номер кластера, при этом значение f выбирают в пределах 1<f≤k/2, и при формировании кодового вектора на передаче младший разряд комбинации (правый) выкалывается и заменяется на бит проверки четности f разрядов кластера, а приемник, приняв вектор Vпр по индексам мягких решений и биту четности, оценивает правильность приема номера кластера и в случае положительного решения переходит к обработке символов (n-f, k-f)-кода по основному алгоритму ранжирования индексов мягких решений, предварительно сформировав корректирующий вектор Wук путем умножения разрядов номера кластера на первые f строк порождающей матрицы G кода и последующего временного удаления из него разрядов кластера, после чего вектор Wук вычитается из вектора Vпр, при этом разряды кластера вектора Vпр также не учитываются, с присвоением младшему разряду вновь образованного вектора Vук индекса мягкого решения равного нулю, после чего декодер работает по основному алгоритму, формируя вектора ошибок Ver, который поразрядно складывается с векторами Wук, Vук, формируя переданный вектор V за счет обратных перестановок символов и возвращения на свои места старших разрядов номера кластера, при этом, если проверка на четность номера кластера не выполняется, декодер подвергает инверсии наиболее ненадежный бит из числа участвующих в проверке, отличающийся тем, что любые f разрядов определяют номер кластера в двоичном представлении, а в совокупности все номера кластеров, взятые по одному, образуют полный набор элементов из поля GF(2f), при этом среди оставшихся n-f разрядов выбирают любые k-f разрядов так, чтобы для всех комбинаций кластера на позициях этих разрядов оказался полный набор элементов из поля GF(2k-f), при этом кластер с номером ноль является базовым, а принятые комбинации любых других кластеров переводят в одну из комбинаций базового кластера путем сложения этих комбинаций с известной декодеру ключевой комбинацией Ki для кластера с номером i, признаком которой является наличие единичного элемента поля GF(2k-f) относительно операции сложения на позициях выделенных k-f разрядов, формируют далее вектор 






| СПОСОБ МЯГКОГО ДЕКОДИРОВАНИЯ СИСТЕМАТИЧЕСКИХ БЛОКОВЫХ КОДОВ | 2010 |
|
RU2444127C1 |
| ДЕКОДЕР С ИСПРАВЛЕНИЕМ СТИРАНИЙ | 2007 |
|
RU2344556C1 |
| ДЕКОДЕР С ИСПРАВЛЕНИЕМ СТИРАНИЙ | 2008 |
|
RU2379841C1 |
| СПОСОБ КОДИРОВАНИЯ И ДЕКОДИРОВАНИЯ ДАННЫХ ДЛЯ СИСТЕМЫ РАДИОВЕЩАТЕЛЬНОЙ ПЕРЕДАЧИ ЦИФРОВЫХ СООБЩЕНИЙ | 1994 |
|
RU2110148C1 |
| US 6381726 B1, 30.04.2002 | |||
| US 2005210358 A1, 22.09.2005 | |||
| US 2004225940 A1, 11.11.2004. | |||
Авторы
Даты
2016-04-10—Публикация
2015-03-13—Подача