Изобретение относится к способам моделирования линий связи (ЛС), в частности к способам моделирования параметров и характеристик ЛС с распределенными параметрами, в том числе оптическим линиям связи (ОЛС). Способ может быть использован для расчета параметров ОЛС под заданные требования.
Известен способ моделирования ЛС с распределенными параметрами по книге Атабекова Г.И. «Основы теории цепей». М.: «Энергия», 1969 г. В известном способе изложен фундаментальный подход к моделированию ЛС с распределенными параметрами с точки зрения теории цепей. В качестве цепи с распределенными параметрами рассматривается однородная двухпроводная ЛС, т.е. такая ЛС, индуктивность, емкость, активное сопротивление и проводимость которой равномерно распределено вдоль всей длины ЛС. Эти параметры, отнесенные к единице длины линии, называются первичными параметрами линии, которые зависят от частоты и конструкции ЛС. Вычисление первичных параметров ЛС относят к задачам теории электромагнитного поля. Задачей моделирования является нахождение пространственно-временного распределения величины тока в линии и напряжения между проводами. Для этого выбирают положительное направление тока в ЛС, выделяют элементарный участок ЛС и представляют его, пользуясь первичными параметрами, в виде последовательно включенных сопротивления и индуктивности и параллельно включенных активной проводимости и емкости. Составляют дифференциальные уравнения ЛС для тока и напряжения, решение которых дает приближенное пространственно-временные зависимости тока и напряжения в ЛС при заданных начальных и граничных условия.
Недостатками известного способа являются: низкая точность отображения моделью реальных характеристик ЛС; пригодность модели только к низкочастотному диапазону; отсутствие возможности учета неоднородностей в ЛС при моделировании, что накладывает ограничения на область его применения, в частности невозможность моделирования ОЛС.
Известен способ моделирования ЛС с распределенными параметрами по книге Б.А. Машковцева, К.Н. Цибизова, Б.Ф. Емелина. «Теория волноводов». Л.: «Наука», 1966. В известном способе изложен фундаментальный подход к моделированию волноводных ЛС с распределенными параметрами с использованием динамических методов решения уравнений Максвелла. В качестве цепи с распределенными параметрами рассматривается однородная волноводная ЛС с неоднородностями в виде отверстий, щелей или углублений, которые в модели отображаются последовательным или параллельным контурами.
Недостатками известного способа являются: расчет элементов модели, составленной из отрезка ЛС, как системы с распределенными параметрами, и резонансных контуров как систем с сосредоточенными элементами, с использованием одной и той же переменной. Это приводит к снижению точности отображения моделью реальных характеристик ЛС в широком диапазоне частот (длин волн) и ограничивает область ее применения, в частности невозможность моделирования ОЛС.
Наиболее близким аналогом по технической сущности к заявленному является «Способ моделирования резонансной передающей линии с распределенными параметрами» по авторскому свидетельству СССР №364996 от 15 марта 1971 г. В способе-аналоге предварительно разделяют ЛС на равные отрезки с длинами l0, замещают каждый из отрезков l0 на четырехполюсник в виде фазового контура первого порядка (ФК1П) с волновым сопротивлением ρс, равным волновому сопротивлению ЛС, формируют эквивалентную схему моделируемой ЛС из каскадно-соединенных ФК1П, изменяют исходные параметры моделируемой ЛС, вычисляют характеристики ЛС с измененными параметрами и по результатам вычислений выбирают конструктивные параметры ЛС, соответствующие заданным требованиям.
Недостатком наиболее близкого аналога является узкая область применения способа, в частности он неприемлем для моделирования ОЛС, что обусловлено тем, что в прототипе не учитывается влияние явления полного внутреннего отражения (ПВО) на границе раздела оптически прозрачных сред, сердцевина/оболочка, на характеристики, что приводит к ошибочным вычислениям характеристик моделируемой ОЛС.
Целью заявленного технического решения является разработка способа моделирования ЛС, обеспечивающего расширение его области применения, в том числе для моделирования ОЛС, за счет учета влияния явления ПВО на границе раздела оптически прозрачных сред.
Поставленная цель достигается тем, что в известном способе моделирования ЛС с распределенными параметрами, заключающемся в том, что ЛС разделяют на равные отрезки с длинами l0, замещают каждый из отрезков l0 на четырехполюсник в виде ФК1П с волновым сопротивлением ρс, равным волновому сопротивлению ЛС, формируют эквивалентную схему моделируемой ЛС из каскадно-соединенных ФК1П, изменяют исходные параметры моделируемой ЛС, вычисляют характеристики ЛС с измененными параметрами и по результатам вычислений выбирают конструктивные параметры ЛС, соответствующие заданным требованиям. При моделировании ОЛС отрезки l0 выбирают из условия l0=p0sin(θ), где 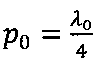 - длина отрезка вдоль траектории распространения оптического луча (ОЛ), Θ - угол падения ОЛ на поверхность оболочки ОЛС, a λ0 - средняя длина волны рабочего диапазона длин волн ОЛС, дополнительно на m-м участке ОЛС длиной L0, заключенном между смежными точками ПВО ОЛ, где m=1, 2,…, М, а М≥2, группируют вдоль продольной оси ОЛС по N отрезков с длинами l0, а в одну из последовательных ветвей первого и N-го ФК1П, принадлежащих каждому m-му участку моделируемой ОЛС, дополнительно включают ФК1П в режиме двухполюсника с холостым ходом и волновым сопротивлением ρр=ρоб/2, где ρоб - волновое сопротивление оболочки ОЛС. В качестве изменяемых параметров при моделировании ОЛС выбирают рабочую частоту f в исследуемом диапазоне частот, показатели преломления n1 и n2 соответственно сердцевины и оболочки ОЛС, а также диаметр d сердцевины и величину разницы (D-d), где D - внешний диаметр оболочки ОЛС. В качестве вычисляемых характеристик ОЛС выбирают частотные характеристики рабочего затухания α(f) и характеристического сопротивления R(f) в исследуемом диапазоне частот.
- длина отрезка вдоль траектории распространения оптического луча (ОЛ), Θ - угол падения ОЛ на поверхность оболочки ОЛС, a λ0 - средняя длина волны рабочего диапазона длин волн ОЛС, дополнительно на m-м участке ОЛС длиной L0, заключенном между смежными точками ПВО ОЛ, где m=1, 2,…, М, а М≥2, группируют вдоль продольной оси ОЛС по N отрезков с длинами l0, а в одну из последовательных ветвей первого и N-го ФК1П, принадлежащих каждому m-му участку моделируемой ОЛС, дополнительно включают ФК1П в режиме двухполюсника с холостым ходом и волновым сопротивлением ρр=ρоб/2, где ρоб - волновое сопротивление оболочки ОЛС. В качестве изменяемых параметров при моделировании ОЛС выбирают рабочую частоту f в исследуемом диапазоне частот, показатели преломления n1 и n2 соответственно сердцевины и оболочки ОЛС, а также диаметр d сердцевины и величину разницы (D-d), где D - внешний диаметр оболочки ОЛС. В качестве вычисляемых характеристик ОЛС выбирают частотные характеристики рабочего затухания α(f) и характеристического сопротивления R(f) в исследуемом диапазоне частот.
Благодаря новой совокупности существенных признаков в заявленном способе обеспечивается расширение его области применения, в том числе для моделирования ОЛС, за счет учета влияния явления ПВО ОЛ на границе раздела оптически прозрачных сред - сердцевина/оболочка. Причем учет влияния указанного явления обеспечивается путем моделирования его ФК1П в режиме двухполюсника с холостым ходом, включенным в одну из последовательных ветвей эквивалентной схемы моделируемой ОЛС, за счет чего обеспечивается корректное вычисление характеристик ОЛС, соответствующих заданным параметрам.
Заявленный способ поясняется чертежами, на которых показаны:
фиг. 1 - рисунок, поясняющий деление ОЛС на M участков по N отрезков;
фиг. 2 - рисунок, поясняющий определение отрезков длиной l0 на участке L0;
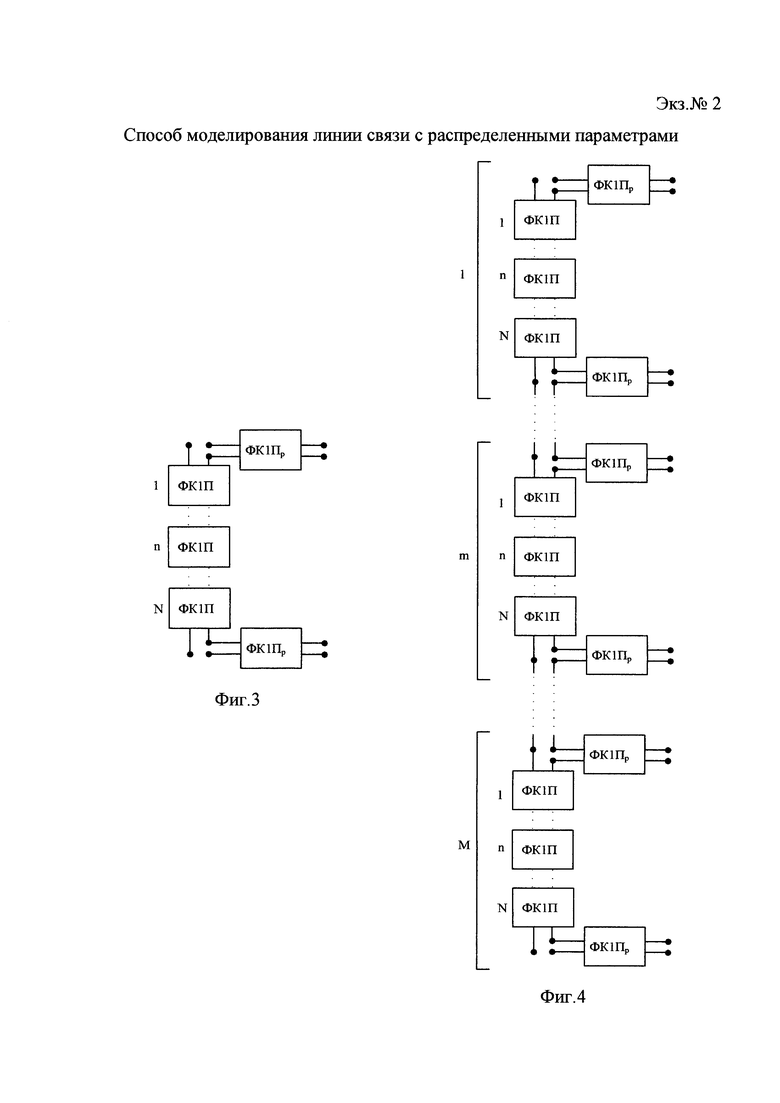
фиг. 3 - эквивалентная схема моделируемого участка L0;
фиг. 4 - эквивалентная схема моделируемой ОЛС;
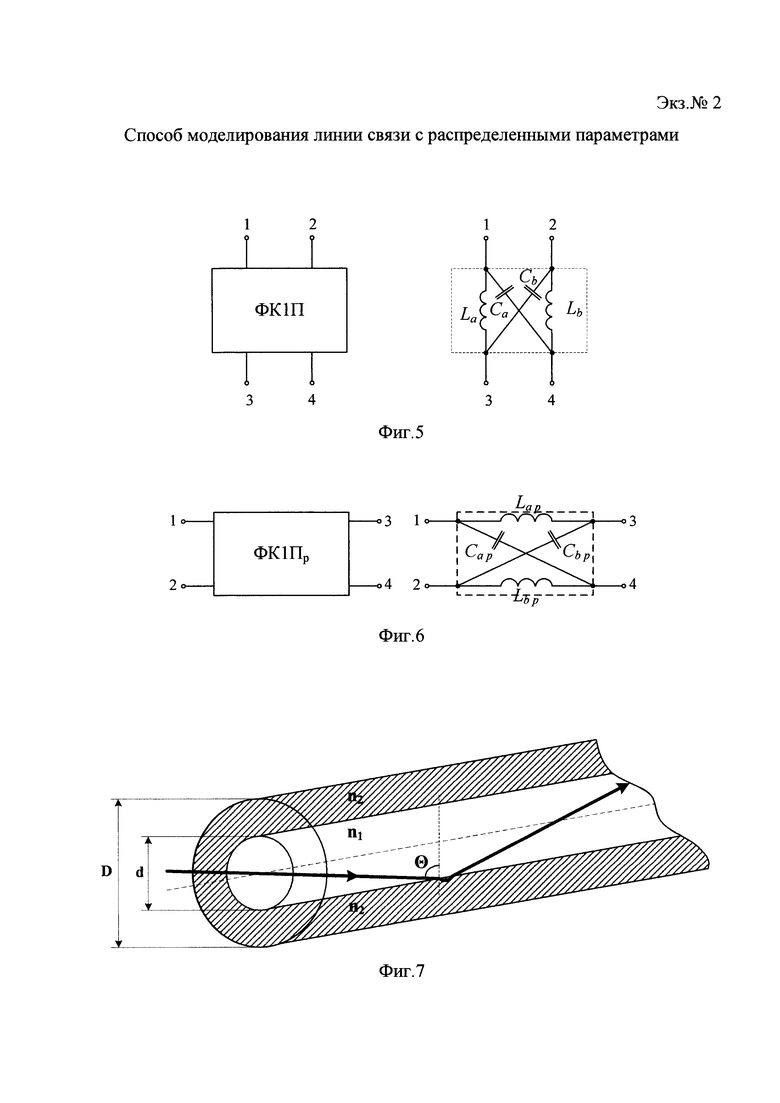
фиг. 5 - электрическая схема четырехполюсника в виде ФК1П;
фиг. 6 - электрическая схема четырехполюсника в виде ФК1Пр;
фиг. 7 - рисунок, поясняющий структуру ОЛС и механизм распространения в ней ОЛ;
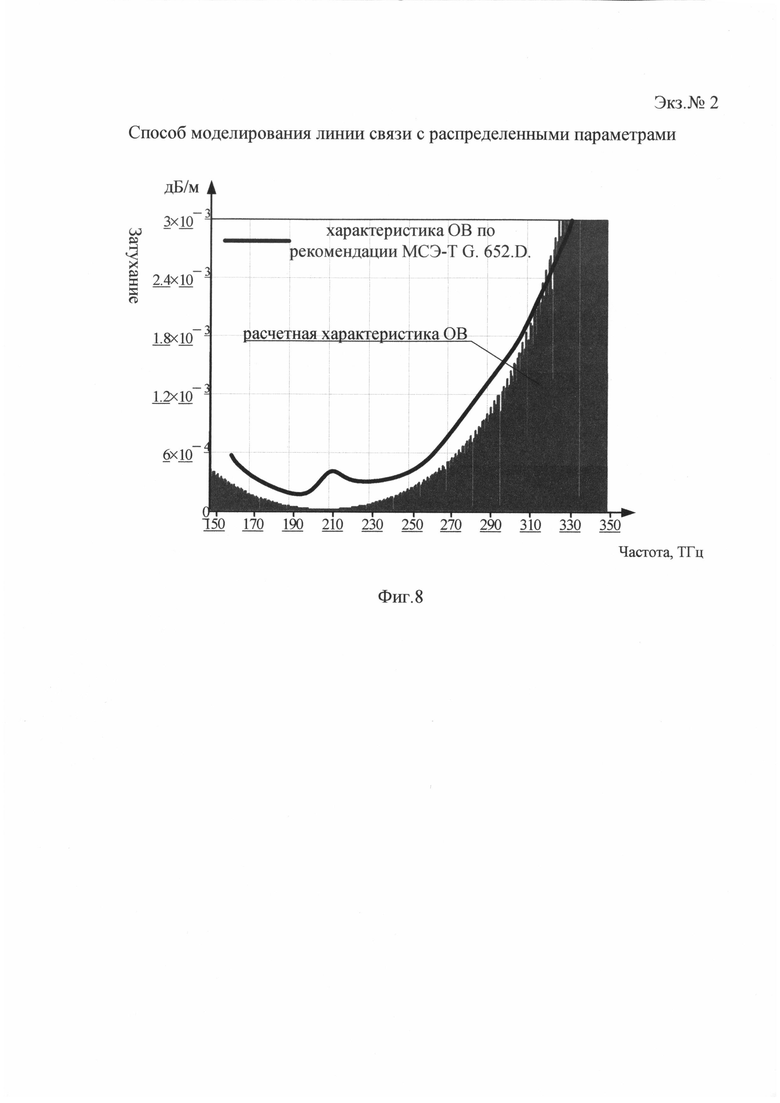
фиг. 8 - сравнение расчетной частотной характеристики рабочего затухания ОЛС со справочной характеристикой ОВ по рекомендации МСЭ-Т G. 654.D.
Реализация заявленного способа объясняется следующим образом.
В основе распространения ОЛ по ОЛС (оптическому волокну (ОВ)) лежит явление ПВО. При ПВО ОЛ проникает во вторую среду с показателем преломления n2, в которой проходит расстояние порядка длины волны распространяющегося ОЛ и возвращается в первую среду с показателем преломления n1 (Фиг. 7). Таким образом, возникает сдвиг точки выхода ОЛ относительно точки входа (Фиг. 2). Данное явление получило название эффекта Гуса-Хенхена. В результате по пути распространения ОЛ возникает гетероструктура, состоящая и чередующихся оптических элементов - сердцевины, где ОЛ распространяется от одной точки ПВО к следующей (для одномодового ОВ, при предельном угле ПВО - Θкп (Фиг. 7), ОЛ в сердцевине проходит расстояние около 11λ0), и оболочки, в которой ОЛ проходит расстояние лишь порядка длины волны. Поэтому структуру ОЛС относят к классу оптических гетероструктур (ОГС). ОГС - это направляющие системы, предназначенные для передачи сигналов оптического диапазона длин волн: инфракрасного, видимого, ультрафиолетового и рентгеновского. Гетероструктуры, как системы, составленные из чередующихся пар элементов с отличающимися значениями однотипных параметров, обладают спектральной избирательностью.
Наличие у ОЛС избирательности характеристики затухания на оси частот, подобной той, которая имеется у оптических фильтров (ОФ), дает основания поиска модели в виде ОФ, частотные характеристики которого полностью (или максимально приближенно) отображают частотные характеристики затухания ОЛС.
В настоящем способе теория и расчет ОЛС, как ОГС, основаны на общем подходе к структурам, как к цепям с распределенными параметрами, состоящими из отрезков передающих линий.
В соответствии с заданными требованиями к ОЛС выбирают среднюю длину волны рабочего диапазона длин волн ОЛС - λ0; показатели преломления n1 и n2, соответственно сердцевины и оболочки ОЛС; диаметр сердцевины d; внешний диаметр оболочки D, обеспечивающий минимально допустимое значение разности (D-d) (Фиг. 7).
ОЛС длиной один метр (в стандартах принято оценивать характеристики ОЛС на один метр линии) делят на М участков каждый длиной L0=d·tg(θ)(Фиг. 1), где L0 - линейная длина ОЛС между двумя соседними точками ПВО, при этом оптический путь (ОП), который проходит ОЛ на этом участке линии, делится на 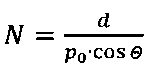 отрезков
отрезков 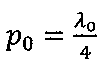 (Фиг. 2), которые соответствуют линейной длине ОЛС l0=p0sin (θ) - проекции отрезков с длинами р0, расположенными вдоль траектории ОЛ, на продольную ось ОЛС.
(Фиг. 2), которые соответствуют линейной длине ОЛС l0=p0sin (θ) - проекции отрезков с длинами р0, расположенными вдоль траектории ОЛ, на продольную ось ОЛС.
Каждый n-й отрезок длиной 10 замещают на четырехполюсник в виде ФК1П (Фиг. 5) с волновым сопротивлением ρс, равным волновому сопротивлению сердцевины ОЛС, и элементами схемы La, Са, Lb, Cb. Формируют эквивалентную схему участка линии L0 из каскадно-соединенных ФК1П, а в одну из последовательных ветвей первого (n=1) и N-го (n=N) ФК1П дополнительно включают ФК1П в режиме холостого хода, т.е. с разомкнутым выходом - ФК1Пр (Фиг. 6) с волновым сопротивлением ρр=ρоб/2, где ρоб - волновое сопротивление оболочки ОЛС, и элементами схемы Lap, Cap, Lbp, Cbp. В результате получено звено оптического фильтра шлейфного типа (ОМШФ) (Фиг. 3), состоящее из N каскадно-включенных ФК1П с волновым сопротивлением ρс и включенных по краям в одну из последовательных ветвей ФК1Пр в режиме холостого хода с волновым сопротивлением ρр. А М таких каскадно-включенных звеньев ОМШФ составляют эквивалентную схему моделируемой ОЛС, топология которой приведена на фиг. 4.
Схема, представленная на фиг. 3, является схемой звена ОМШФ. Вопросы синтеза ОМШФ и схемных элементов ФК1П в различных режимах работы и подключения подробно рассмотрены в книге Лапшина Б.А. «Оптические гетероструктуры. Новая теория и расчет». - СПб.: БХВ-Петербург, 2012. Таким образом схема ОМШФ, составленная из последовательно (каскадно) соединенной цепочки M звеньев ОМШФ является моделью ОЛС. На этом процесс формирования модели завершен.
Исходя из полученной топологии ОМШФ вычисляют частотные характеристики ОЛС: рабочее затухание α(f) и характеристическое сопротивление R(f). Оценивают полученные результаты в соответствии с требованиями. При соответствии полученных характеристик требуемым параметры ОЛС их оставляют неизменными; при неудовлетворительном решении исходные параметры изменяют (в реализуемых пределах) и проводят моделирование снова, до получения приемлемого результата.
В качестве примера, на фиг. 8 представлено сравнение расчетной частотной характеристики рабочего затухания α(f) ОЛС с показателями преломления n1=1,47 и n2=1,46, диаметром сердцевины d=9 мкм и оболочки D=125 мкм, со справочной характеристикой ОВ по рекомендации МСЭ-Т G. 652.D. Форма полученной характеристики соответствует справочной (Фиг. 9), для данного типа ОВ, что свидетельствует об адекватности заявленного способа.
Благодаря новой совокупности существенных признаков в заявленном способе обеспечивается расширение его области применения, в том числе для моделирования ОЛС, за счет учета влияния явления ПВО на границе раздела оптически прозрачных сред - сердцевина/оболочка.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ИЗМЕРЕНИЯ ЧАСТОТНОЙ ХАРАКТЕРИСТИКИ ПАССИВНОГО ЧЕТЫРЕХПОЛЮСНИКА В ВОЛНОВОДЕ | 1996 |
|
RU2125273C1 |
| КОАКСИАЛЬНЫЙ ВИБРАТОР И СИНФАЗНАЯ АНТЕННАЯ РЕШЕТКА ИЗ КОАКСИАЛЬНЫХ ВИБРАТОРОВ | 1998 |
|
RU2134923C1 |
| ФИКСИРОВАННЫЙ ФАЗОВРАЩАТЕЛЬ СВЧ | 2016 |
|
RU2621881C1 |
| МНОГОЭЛЕМЕНТНЫЙ ДИФФЕРЕНЦИАЛЬНЫЙ ФАЗОВРАЩАТЕЛЬ СВЧ | 2014 |
|
RU2574471C1 |
| Способ измерения параметров проходных сверхвысокочастотных элементов | 1977 |
|
SU713259A1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ОТНОСИТЕЛЬНОЙ ДИЭЛЕКТРИЧЕСКОЙ ПРОНИЦАЕМОСТИ И ТАНГЕНСА УГЛА ДИЭЛЕКТРИЧЕСКИХ ПОТЕРЬ ДИЭЛЕКТРИЧЕСКОЙ СТРУКТУРЫ | 2019 |
|
RU2716600C1 |
| УПРАВЛЯЕМЫЙ ПОЛОСКОВЫЙ ТРАНСФОРМАТОР ИМПЕДАНСОВ | 2018 |
|
RU2721482C2 |
| ФИКСИРОВАННЫЙ ФАЗОВРАЩАТЕЛЬ СВЧ | 2015 |
|
RU2619799C1 |
| КОАКСИАЛЬНЫЙ ВИБРАТОР | 1999 |
|
RU2144247C1 |
| ТРАНСФОРМАТОР СОПРОТИВЛЕНИЙ | 2015 |
|
RU2626296C2 |

Изобретение относится к способу моделирования линий связи, в частности к способу моделирования параметров и характеристик линий связи с распределенными параметрами, в том числе оптическим линиям связи (ОЛС). Способ может быть использован для расчета параметров ОЛС под заданные требования. Технический результат изобретения заключается в расширении его области применения, в том числе для моделирования ОЛС, за счет учета влияния явления полного внутреннего отражения на границе раздела оптически прозрачных сред. Линию связи разделяют на равные отрезки с длинами l0, замещают каждый из отрезков l0 на четырехполюсник в виде фазового контура первого порядка (ФК1П), формируют эквивалентную схему моделируемой линии связи из каскадно-соединенных ФК1П, изменяют исходные параметры моделируемой линии связи, вычисляют характеристики линии связи с измененными параметрами и по результатам вычислений выбирают конструктивные параметры линии связи, соответствующие заданным требованиям. При моделировании ОЛС дополнительно явление полного внутреннего отражения оптического луча моделируют ФК1П в режиме двухполюсника с холостым ходом, включенным в одну из последовательных ветвей эквивалентной схемы, моделируемой ОЛС. 2 з.п. ф-лы, 8 ил.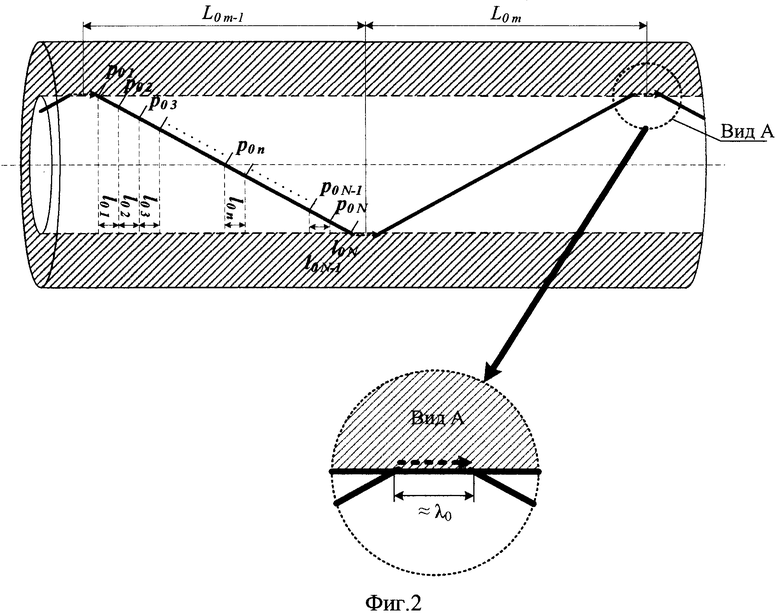
1. Способ моделирования линии связи с распределенными параметрами, заключающийся в том, что разделяют линию связи на равные отрезки с длинами l0, замещают каждый из отрезков l0 на четырехполюсник в виде фазового контура первого порядка с волновым сопротивлением ρс, равным волновому сопротивлению линии связи, формируют эквивалентную схему моделируемой линии связи из каскадно-соединенных фазовых контуров первого порядка, изменяют исходные параметры моделируемой линии связи, вычисляют характеристики линии связи с измененными параметрами и по результатам вычислений выбирают конструктивные параметры линии связи, соответствующие заданным требованиям, отличающийся тем, что при моделировании оптической линии связи отрезки l0 выбирают из условия l0=p0sin(Θ), где 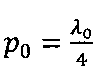 - длина отрезка вдоль траектории распространения оптического луча, Θ - угол падения оптического луча на поверхность оболочки оптической линии связи, а λ0 - средняя длина волны рабочего диапазона длин волн оптической линии связи, дополнительно на m-м участке оптической линии связи длиной L0, заключенном между смежными точками полного внутреннего отражения оптического луча, где m=1, 2, …, М, а М≥2, группируют вдоль продольной оси оптической линии связи по N отрезков с длинами l0, а в одну из последовательных ветвей первого и N-го фазовых контуров первого порядка, принадлежащих каждому m-му участку моделируемой оптической линии связи, дополнительно включают фазовый контур первого порядка в режиме двухполюсника с холостым ходом и волновым сопротивлением ρр=ρоб/2, где ρоб - волновое сопротивление оболочки оптической линии связи.
- длина отрезка вдоль траектории распространения оптического луча, Θ - угол падения оптического луча на поверхность оболочки оптической линии связи, а λ0 - средняя длина волны рабочего диапазона длин волн оптической линии связи, дополнительно на m-м участке оптической линии связи длиной L0, заключенном между смежными точками полного внутреннего отражения оптического луча, где m=1, 2, …, М, а М≥2, группируют вдоль продольной оси оптической линии связи по N отрезков с длинами l0, а в одну из последовательных ветвей первого и N-го фазовых контуров первого порядка, принадлежащих каждому m-му участку моделируемой оптической линии связи, дополнительно включают фазовый контур первого порядка в режиме двухполюсника с холостым ходом и волновым сопротивлением ρр=ρоб/2, где ρоб - волновое сопротивление оболочки оптической линии связи.
2. Способ по п. 1, отличающийся тем, что в качестве изменяемых параметров при моделировании оптической линии связи выбирают рабочую частоту ƒ в исследуемом диапазоне частот, показатели преломления n1 и n2 соответственно сердцевины и оболочки оптической линии связи, а также диаметр d сердцевины и величину разницы (D-d), где D - внешний диаметр оболочки оптической линии связи.
3. Способ по п. 1, отличающийся тем, что в качестве вычисляемых характеристик оптической линии связи выбирают частотные характеристики рабочего затухания α(ƒ) и характеристического сопротивления R(ƒ) в исследуемом диапазоне частот.
| СПОСОБ МОДЕЛИРОВАНИЯ РЕЗОНАНСНОЙ ПЕРЕДАЮЩЕЙ ЛИНИИ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ | 0 |
|
SU364996A1 |
| Аппарат для очищения воды при помощи химических реактивов | 1917 |
|
SU2A1 |
| Аппарат для очищения воды при помощи химических реактивов | 1917 |
|
SU2A1 |
| Пресс для выдавливания из деревянных дисков заготовок для ниточных катушек | 1923 |
|
SU2007A1 |
Авторы
Даты
2016-05-10—Публикация
2015-01-12—Подача