Изобретение относится к медицине, физической культуре и может быть использовано при мониторинге резервов физического здоровья и работоспособности детей, подростков, молодежи и взрослого населения.
Известен «СПОСОБ КОМПЛЕКСНОЙ ФУНКЦИОНАЛЬНОЙ ДИАГНОСТИКИ ФИЗИЧЕСКОГО СОСТОЯНИЯ ЧЕЛОВЕКА» RU 2036605 [1], путем регистрации функциональных показателей с последующей их балльной оценкой и определением индекса физического состояния (ИФС) и с вынесением суждения об ухудшении состояния по степени снижения ИФС, включающий измерение частоты сердечных сокращений, артериального давления, определение частоты массоростового показателя Катле, жизненного показателя по жизненной емкости легких, проведение пробы Штанге, пробы на быстроту зрительно-двигательной реакции с измерением расстояния, преодолеваемого падающим предметом от начала падения до его фиксации испытуемым, определение индекса Руфье, исследование гибкости позвоночника с измерением расстояния от пальцев рук до уровня стоп при максимально возможном наклоне вперед, регистрацию количества группировок из положения лежа на спине за 30 с, регистрацию количества отжиманий в упоре лежа за 30 с, проведение степ-теста, вычисляют индекс Скибинского и проводят пробу Серкина, определяя при этом и показатель Руфье, измеряют время, необходимое для восстановления частоты сердечных сокращений в покое, после чего проводят пробу на быстроту зрительно-двигательной реакции, степ-тест проводят по методике Астранда Римминга с определением показателя максимального потребления кислорода, после чего определяют ИФС по балльной формуле.
Недостатком известного способа является возможность оценки лишь отдельных характеристик физического состояния обследуемых, не давая общей картины состояния их здоровья. Естественно, что чем большее количество функциональных показателей подвергается оценке, тем достовернее интегральная характеристика физического и функционального состояния испытуемого.
Наиболее близким к заявляемому техническому решению является «СПОСОБ ОЦЕНКИ РЕЗЕРВОВ ФИЗИЧЕСКОГО ЗДОРОВЬЯ И РАБОТОСПОСОБНОСТИ НАСЕЛЕНИЯ» RU 2147208 [2], заключающийся в пассивной, активной и восстановительной фазах диагностики, при этом на фазе пассивной диагностики определяют пульс в покое, артериальное давление, жизненный показатель с помощью спирометра, в восстановительной фазе диагностики определяют восстанавливаемость пульса, на фазе активной диагностики оценивают гибкость позвоночника в тесте с наклоном вперед, силовую выносливость мышц рук и плечевого пояса за счет измерения количества отжиманий от пола, силовую выносливость мышц брюшного пресса, а оценку осуществляют путем получения обобщенного показателя в виде индекса физического состояния, общую работоспособность, при этом числовое выражение каждого отдельно измеренного показателя переводят в весовые коэффициенты относительно нормативных показателей для обследуемого различного возраста и пола, оценивающих состояние конкретной физиологической системы, производят суммирование весовых коэффициентов, к полученной сумме прибавляют весовые коэффициенты, характеризующие двигательную активность, по полученному индексу физического состояния оценивают физическое состояние и резервы здоровья путем его сравнения с показателями шкалы оценки индекса состояния здоровья организма человека.
Известный способ дает интегральную оценку здоровья обследуемого.
Недостатками известного способа являются: низкая точность, низкая релевантность и объективность оценки здоровья.
Техническим результатом предлагаемого изобретения является повышение точности, объективности и релевантности оценки здоровья человека.
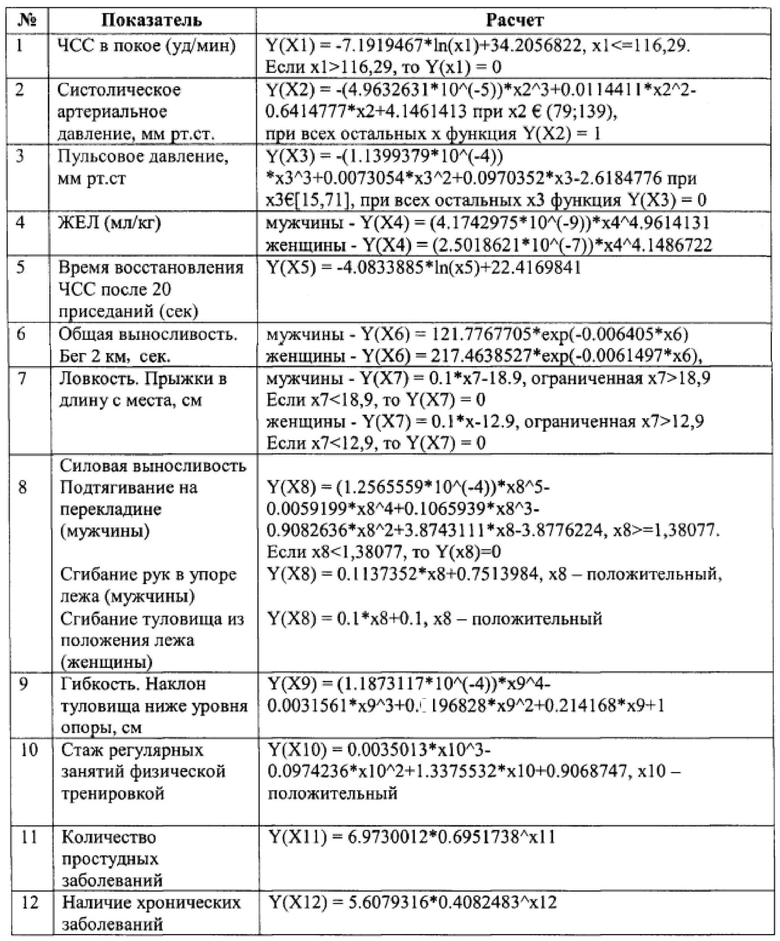
Технический результат достигается тем, что способ оценки резервов физического здоровья и работоспособности населения, заключающийся в пассивной, активной и восстановительной фазах диагностики, при этом на фазе пассивной диагностики определяют пульс в покое, артериальное давление, жизненный показатель с помощью спирометра, в восстановительной фазе диагностики определяют восстанавливаемость пульса, на фазе активной диагностики оценивают гибкость позвоночника в тесте с наклоном вперед, силовую выносливость мышц рук и плечевого пояса за счет измерения количества отжиманий от пола, силовую выносливость мышц брюшного пресса, а оценку резервов физического здоровья и работоспособности населения осуществляют путем определения индекса функционального состояния здоровья по суммированию баллов с учетом полученных числовых значений по каждому измеренному показателю и весовых коэффициентов относительно нормативных показателей для обследуемого пола и возраста, характеризуется тем, что дополнительно измеряют пульсовое давление в состоянии покоя, время восстановления ЧСС определяют после 20 приседаний, общую выносливость определяют по времени бега на 2 км, ловкость определяют по длине прыжком с места, силовую выносливость дополнительно измеряют путем подсчета количества подтягиваний на перекладине (для мужчин), гибкость позвоночника определяют путем измерения наклона туловища ниже опоры, определяют стаж регулярных занятий физической тренировкой, количество простудных заболеваний за год и количество хронических заболеваний, а баллы вычисляют следующим образом:
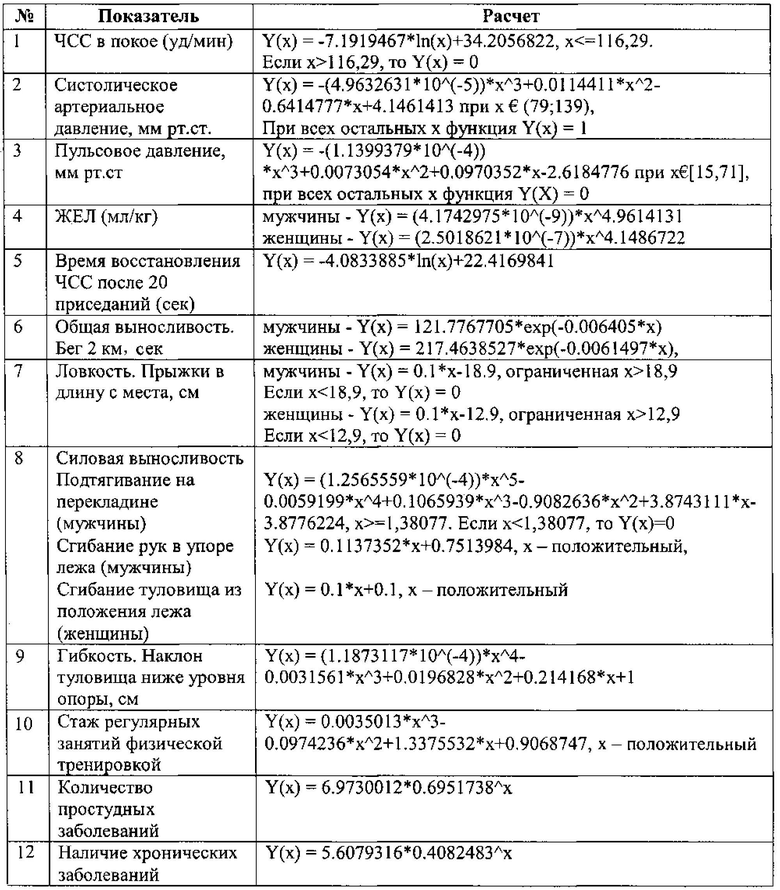
Полученные в результате расчетов баллы суммируют, если результат: более 60 - очень высокий индекс функционального состояния здоровья;
48-59 баллов - высокий индекс функционального состояния здоровья;
36-47 баллов - средний индекс функционального состояния здоровья;
24-35 баллов - низкий индекс функционального состояния здоровья;
ниже 24 баллов - очень низкий индекс функционального состояния здоровья.
Уровень физической активности можно вычислять по формуле:
N=(t+I+S)-(O+U+V),
где N - уровень нагрузки на отдельном занятии, в усл. ед.;
t - продолжительность нагрузки на одном занятии, в баллах;
I - интенсивность нагрузки, определяемая по частоте сердечных сокращений, в баллах;
S - систематичность выполнения нагрузки, в баллах;
О - физическая активность на работе и дома в дни занятий, в баллах;
U - индекс функционального состояния здоровья, в баллах (определяется по таблице выше);
V - возраст занимающегося, в баллах.
Данные параметры переводятся в баллы согласно представленной ниже таблице:

Если в результате получена +1 и больше, то физическая нагрузка превышает возможности организма; -1 и меньше - уровень нагрузки ниже возможности организма и может быть увеличен без опасности для здоровья; ±0,9 - нагрузка соответствует функциональному состоянию организма. При последнем диапазоне физической нагрузки создаются наиболее благоприятные условия для повышения уровня развития двигательных качеств с параллельным повышением индекса функционального состояния здоровья. Для женщин к оценке ФА прибавляется +1 балл.
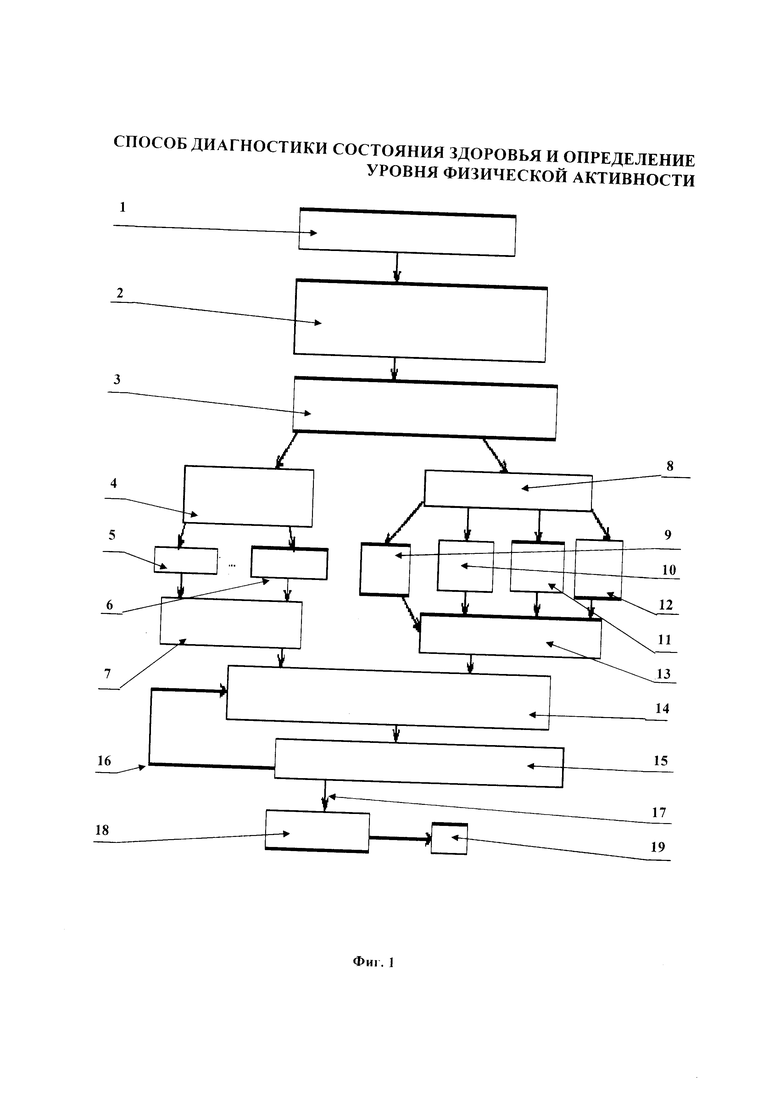
Для построения модели диагностики состояния здоровья выполнялась следующая последовательность действий (адаптационная модель построения системы диагностики состояния здоровья) (см. фиг. 1), где:
1 - задание n-точек (x,y) для построения модели;
2 - задание необходимой погрешности измерения и дополнительных вычислений, согласно условиям задачи (производится экспериментатором);
3 - построение функции регрессии для диагностики состояния здоровья (по методу наименьших квадратов);
4 - полиномиальные функции регрессии;
5 - 1 порядка;
6 - (n-1)-го порядка;
7 - определение отклонения от заданных точек;
8 - нелинейные функции регрессии;
9 - гиперболическая;
10 - логарифмическая;
11 - степенная;
12 - экспоненциальная;
13 - определение отклонения от заданных точек;
14 - выбор соответствующей оптимальной функции для дальнейшего построения (осуществляется по заданным критериям или вручную);
15 - построение модели, проверка достоверности и значимости;
16 - не соответствует условиям достоверности и значимости;
17 - соответствует условиям достоверности и значимости;
18 - выдача отчетов и результата расчета;
19 - выход.
Изначально задали параметры системы (n точек вида (x,y)), которые соответствуют определенному физическому состоянию организма. Затем экспериментатором вручную задается погрешность измерения и вычисления для дальнейшего построения модели. В дальнейшем строятся два вида функций регрессии, описывающих заданные изначально точки: полиномиальные функции до (n-1)-порядка включительно и нелинейные функции (степенная, логарифмическая, экспоненциальная, гиперболическая). Далее происходит расчет ошибок и отклонений данных функций от заданных изначально параметров. По данным оценкам экспериментатор производит выбор соответствующей функции для дальнейшего построения модели. Затем строится сама модель диагностики и вычисляется ее значимость и достоверность методами математической статистики. Если значимость и достоверность подтверждены, то модель считается построенной, если не подтверждены, то происходит повторный выбор уже другой из рассчитанных ранее функций.
На основе описанной адаптационной модели построения системы диагностики состояния здоровья был создан предлагаемый способ определения уровня здоровья и физической активности.
Нами обследовано 33 человека.
Были собраны следующие параметры функционального состояния организма.


Полученные данные занесены в таблицу 1.
Разработанная методика может быть сравнена с методикой определения уровня здоровья и физической активности В.И. Белова, которая уже прошла апробацию, имеет научное обоснование автора и доказательственную основу своей действенности. Коэффициент уровня здоровья, рассчитанный по методике В.И. Белова, занесен в таблицу 1 в столбце 4.
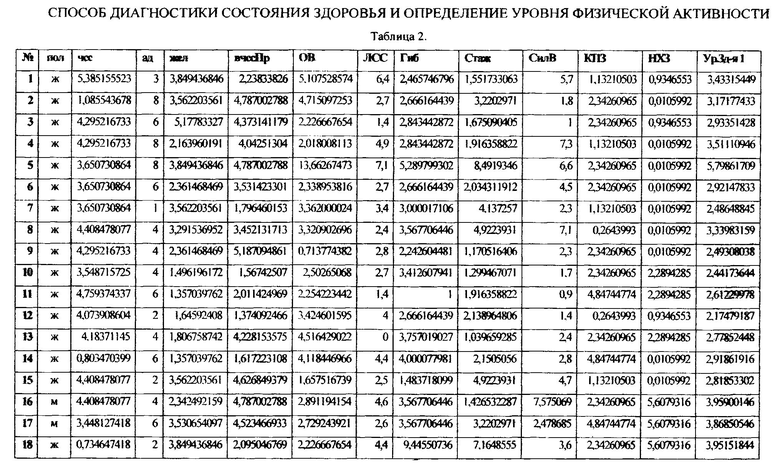
Обработаем данную таблицу 1 показателей функционального состояния организма с помощью предложенного алгоритма. Получим следующую таблицу данных (таблица 2).
Таким образом, 2 человека имеют очень высокий уровень здоровья, что составляет 6,1% испытуемых.
8 человек имеют низкий уровень здоровья, что составляет 24,2% испытуемых.
16 человек имеют средний уровень здоровья, что составляет 48,5% испытуемых.
7 человек имеют высокий уровень здоровья, что составляет 21,2% испытуемых.
Проведем статистическую обработку данных исследования.
Меры центральной тенденции - это величины, вокруг которых группируются остальные данные. Данные величины являются как бы обобщающими всю выборку показателями, что, во-первых, позволяет судить по ним обо всей выборке, а во-вторых, дает возможность сравнивать разные выборки, разные серии между собой. К мерам центральной тенденции в обработке результатов психологических исследований относятся: выборочное среднее, медиана, мода.
1. Выборочное среднее (М) - это результат деления суммы всех значений (X) на их количество (N).
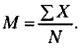
Рассчитанное М=3,44954072, таким образом, средний уровень здоровья в группе 3,45 баллов.
2. Медиана (Me) - это значение, выше и ниже которого количество отличающихся значений одинаково, т.е. это центральное значение в последовательном ряду данных. Медиана необязательно должна совпадать с конкретным значением. Совпадение происходит в случае нечетного числа значений (ответов), несовпадение - при четном их числе. В последнем случае медиана вычисляется как среднее арифметическое двух центральных значений в упорядоченном ряду.
Медиана = 3,33983159
3. Мода (Мо) - это значение, наиболее часто встречающееся в выборке, т.е. значение с наибольшей частотой. Если все значения в группе встречаются одинаково часто, то считается, что моды нет. Если два соседних значения имеют одинаковую частоту и больше частоты любого другого значения, мода есть среднее этих двух значений. Если то же самое относится к двум несмежным значениям, то существуют две моды, а группа оценок является бимодальной.
Мо=0
Отсутствие моды является положительным моментом, так как это говорит о том, что нет повторяющихся данных. Таким образом, нам удалось индивидуализировать процесс вычисления уровня здоровья. Значит, для каждого испытуемого соответствует свой индивидуальный и единственный в выборке уровень здоровья (что в других методиках нахождения уровня здоровья отсутствует).
Значения медианы и выборочного среднего очень близки, поэтому распределение наших статистических данных является нормальным (распределено по нормальному закону).
Меры разброса (изменчивости) - это статистические показатели, характеризующие различия между отдельными значениями выборки. Они позволяют судить о степени однородности полученного множества, его компактности, а косвенно и о надежности полученных данных и вытекающих из них результатов. Наиболее используемые в психологических исследованиях показатели: среднее отклонение, дисперсия, стандартное отклонение.
4. Размах (P) - это интервал между максимальным и минимальным значениями признака. Определяется легко и быстро, но чувствителен к случайностям, особенно при малом числе данных.
Размах нашего измерения Р=3,957624216
То есть разница между минимальным и максимальным значением уровня здоровья в нашей выборке составляет 3,96 баллов.
5. Среднее отклонение (МД) - это среднеарифметическое разницы (по абсолютной величине) между каждым значением в выборке и ее средним.
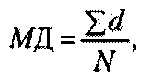
где 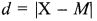 , М - среднее выборки, X - конкретное значение, N - число значений.
, М - среднее выборки, X - конкретное значение, N - число значений.
Множество всех конкретных отклонений от среднего характеризует изменчивость данных, но если не взять их по абсолютной величине, то их сумма будет равна нулю и мы не получим информации об их изменчивости. Среднее отклонение показывает степень скученности данных вокруг выборочного среднего.
В нашей выборке МД=0,672159114
Среднее отклонение небольшое, что говорит об относительной постоянности и скученности данных вокруг выборочного среднего. Данные исследования были проведены среди студентов, поэтому с учетом их социальной активности и условий образовательной среды, данный показатель является адекватным для наших исследований.
6. Дисперсия (D) характеризует отклонения от средней величины в данной выборке. Вычисление дисперсии позволяет избежать нулевой суммы конкретных разниц (d=Х-М) не через их абсолютные величины, а через их возведение в квадрат:
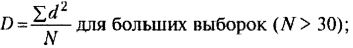
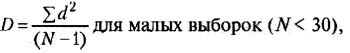
где 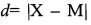 , М - среднее выборки, X - конкретное значение, N - число значений.
, М - среднее выборки, X - конкретное значение, N - число значений.
В нашей выборке D=0,807957747
Дисперсия также небольшая, то есть для данной группы испытуемых разброс данных вокруг средней арифметической небольшой.
7. Стандартное отклонение (5). Из-за возведения в квадрат отдельных отклонений d при вычислении дисперсии полученная величина оказывается далекой от первоначальных отклонений и потому не дает о них наглядного представления. Чтобы этого избежать и получить характеристику, сопоставимую со средним отклонением, проделывают обратную математическую операцию - из дисперсии извлекают квадратный корень. Его положительное значение и принимается за меру изменчивости, именуемую среднеквадратическим, или стандартным, отклонением:

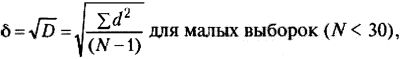
где 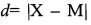 , М - среднее выборки, Х - конкретное значение, N - число значений.
, М - среднее выборки, Х - конкретное значение, N - число значений.
Стандартное отклонение нашей выборки δ=0,859347962
Мера изменчивости нашей выборки вокруг среднего арифметического равна 0,86 баллов.
8. Для порядковых данных в качестве меры изменчивости обычно берут полуквартильное отклонение (Q), именуемое еще полуквартильным коэффициентом. Вычисляется этот показатель следующим образом. Вся область распределения данных делится на четыре равные части. Если отсчитывать наблюдения начиная от минимальной величины на измерительной шкале, то первая четверть шкалы называется первым квартилем, а точка, отделяющая его от остальной части шкалы, обозначается символом 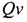 . Вторые 25% распределения - второй квартиль, а соответствующая точка на шкале - Q2. Между третьей и четвертой четвертями распределения расположена точка Q3. Полуквартильный коэффициент определяется как половина интервала между первым и третьим квартилями:
. Вторые 25% распределения - второй квартиль, а соответствующая точка на шкале - Q2. Между третьей и четвертой четвертями распределения расположена точка Q3. Полуквартильный коэффициент определяется как половина интервала между первым и третьим квартилями:
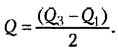
При симметричном распределении точка Q2 совпадет с медианой (а следовательно, и со средним), и тогда можно вычислить коэффициент Q для характеристики разброса данных относительно середины распределения. При несимметричном распределении этого недостаточно. Тогда дополнительно вычисляют коэффициенты для левого и правого участков:
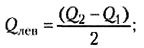
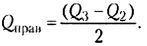
Наша выборка не симметрична, поэтому
Qлевое = 0,208511736
Qправое = 0,323340727
Таким образом, полуквартильное отклонение небольшое, что говорит о высокой статистической значимости полученных данных.
Вторичная статистическая обработка данных
Сравнивать нашу выборку можно с полученными данными уровня здоровья по методике В.И. Белова. Данные по методике В.И. Белова представлены в таблице 1.
К вторичным относят такие методы статистической обработки, с помощью которых на базе первичных данных выявляют скрытые в них статистические закономерности. Вторичные методы можно подразделить на способы оценки значимости различий и способы установления статистических взаимосвязей.
9. Способы оценки значимости различий. Для сравнения выборочных средних величин, принадлежащих к двум совокупностям данных, и для решения вопроса о том, отличаются ли средние значения статистически достоверно друг от друга, используют t-критерий Стьюдента. Его формула выглядит следующим образом:
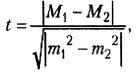
где M1, М2 - выборочные средние значения сравниваемых выборок, m1, m2 - интегрированные показатели отклонений частных значений из двух сравниваемых выборок, вычисляются по следующим формулам:
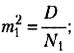
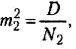
где D1, D2 - дисперсии первой и второй выборок, N1, N2 - число значений в первой и второй выборках. В нашей выборке число степеней свободы N=33+33-2=64, в качестве избранной вероятности допустимой ошибки выберем квантиль распределения α=0.001, Р=0.999 (99,9%).
Полученный нами Критерий Стьюдента = 8,785542754
Т табл = 3.496
Вычисленный критерий Стьюдента больше табличного, значит, сравниваемые средние значения двух выборок статистически достоверно различаются с вероятностью допустимой ошибки 0,999 (вероятностная погрешность), меньшей или равной ей.
10. Для сравнения дисперсий двух выборок используется F-критерий Фишера. Его формула выглядит следующим образом:
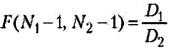
где D1, D2 - дисперсии первой и второй выборок соответственно, N1, N2 - число значений в первой и второй выборках.
Согласно представленным формулам, вычисленный критерий Фишера равен
F=1,045985766
Fтабл=1,804
Значения различаются, причем критерий Фишера, полученный по экспериментальным данным, меньше табличных данных, значит, наша математическая модель нахождения уровня здоровья описана адекватно, таким образом, полученные экспериментальные данные обработаны адекватно. Значит, предложенная математическая модель адекватно описывает эксперимент.
11. Определение количественной зависимости показателей уровня здоровья от значений его параметров и характеристик является задачей регрессионного анализа. Уровень здоровья в нашем алгоритме находится по обобщенной формуле, в которую входят все используемые параметры функционального состояния организма. Поэтому явным является факт взаимосвязи этих факторов с найденным уровнем здоровья, и проведение регрессионного анализа является лишним.
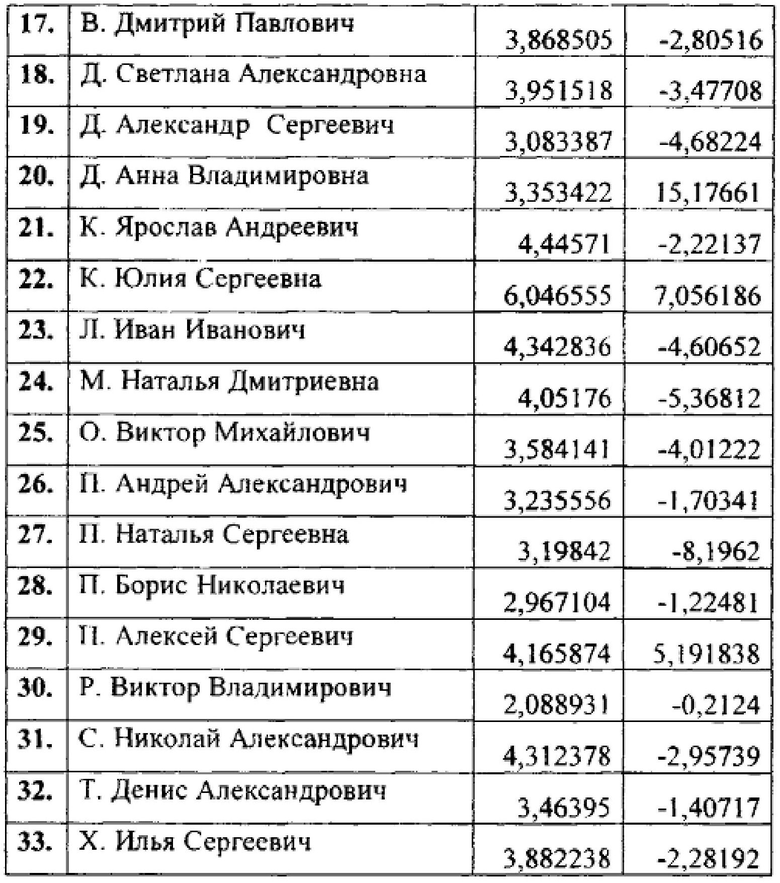
12. Найдем корреляцию между найденным уровнем здоровья и уровнем физической активности испытуемых.
Представим исходные данные в виде таблицы 3.
Построим точечный график функции для определения явной взаимосвязи между полученными данными. Аргументом данной функции является первый столбец, а значением - второй столбец. Таким образом строим функцию, состоящую из 33 точек вида (x,y). Как видно из графика зависимости уровня здоровья и физической активности, явной корреляции между данными не наблюдается.
Рассчитаем коэффициент корреляции, используя формулу Пирсона.
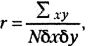
где x - отклонение отдельного значения X от среднего выборки (Мх), y - отклонение отдельного значения Y от среднего выборки (My), δх - стандартное отклонение для X, δy - стандартное отклонение для Y, N - число пар значений X и Y.
Вычисленный коэффициент корреляции r=0,13434. Коэффициент маленький, имеет прямую связь. Значит явной сильной зависимости между данными нет, она существует, но слабая.
Вычислим для него критерий Стьюдента согласно формуле, описанной выше:
Т-критерий Стьюдента = 0,754817
Табличный критерий для N-2 степеней свободы и с вероятностной погрешностью 0,01 равен 0.682756.
Вычисленный критерий Стьюдента больше табличного, значит, корреляция (зависимость) сравниваемых значений уровня здоровья и физической активности статистически значимы с вероятностью допустимой ошибки 0,999 (вероятностная погрешность), меньшей или равной ей.
Аналогичные статистические исследования проведем для выборки уровня физической активности испытуемых.
В результате получены следующие данные:


Таким образом, 7 человек имеют физические перенагрузки организма, что составляет 21,2% испытуемых. То есть организм работает на пределе человеческих возможностей.
6 человек имеют норму физической активности, что составляет 18,2% испытуемых.
16 человек имеют средний уровень здоровья, что составляет 48,5% испытуемых.
21 человек имеют недостаток физической активности, что составляет 63,6% испытуемых. Увеличение физической активности необходимо и не принесет вреда для здоровья.
Проведем статистическую обработку данных исследования.
Рассчитанное среднее арифметическое М=1,253651715, таким образом, средний уровень физической активности в группе 1,25 баллов.
Отсутствие моды является положительным моментом, так как это говорит о том, что нет повторяющихся данных. Таким образом, нам удалось индивидуализировать процесс вычисления уровня физической активности. Значит, для каждого испытуемого соответствует свой индивидуальный и единственный в выборке уровень физической активности (что в других методиках нахождения отсутствует).
Значения медианы и выборочного среднего очень близки, поэтому распределение наших статистических данных является нормальным (распределено по нормальному закону).
Размах нашего измерения Р=23,8.
То есть разница между минимальным и максимальным значением уровня физической активности в нашей выборке составляет 23,8 баллов.
В нашей выборке среднее отклонение = 2,652015452
В нашей выборке дисперсия D=17,6
Дисперсия большая, то есть для данной группы испытуемых разброс данных вокруг средней арифметической большой.
Стандартное отклонение нашей выборки δ=4,07
Мера изменчивости нашей выборки вокруг среднего арифметического равна 4,07 баллов.
Наша выборка не симметрична, поэтому полуквартильное отклонение
Qлевое = 0,627855501
Qправое = 0,498280675
Таким образом, полуквартильное отклонение небольшое, что говорит о высокой статистической значимости полученных нами данных.
Полученный нами Критерий Стьюдента = 8,698385786
Т табл = 3.496
Вычисленный критерий Стьюдента больше табличного, значит, сравниваемые средние значения двух выборок статистически достоверно различаются с вероятностью допустимой ошибки 0,999 (вероятностная погрешность), меньшей или равной ей.
Согласно представленным формулам, вычисленный критерий Фишера равен
F=1,062225051
Fтабл=1,804
Значения различаются, причем критерий Фишера, полученный по экспериментальным данным, меньше табличных данных, значит наша математическая модель нахождения уровня физической активности описана адекватно, таким образом, полученные экспериментальные данные обработаны адекватно. Значит, предложенная нами математическая модель адекватно описывает эксперимент.
Выводы
Проанализировав полученные данные, можно сделать следующие выводы:
1. Отсутствие моды в наших выборках говорит о том, что нет повторяющихся данных. Таким образом, нам удалось индивидуализировать процесс вычисления уровня здоровья и физической активности. Значит, для каждого испытуемого соответствует свой индивидуальный и единственный в выборке уровень физической активности (что в других методиках нахождения отсутствует).
2. Полуквартильное отклонение полученных данных говорит о высокой статистической значимости результатов.
3. При сравнении с данными, полученными по методике В.И. Белова, вычисленный критерий Стьюдента больше табличного, значит, сравниваемые средние значения выборок статистически достоверно различаются с вероятностью допустимой ошибки 0,999 (вероятностная погрешность), меньшей или равной ей.
4. При сравнении с данными, полученными по методике В.И. Белова, значения критерия Фишера, полученные по экспериментальным данным, меньше табличных данных, значит наша математическая модель нахождения уровня здоровья и физической активности описана адекватно, таким образом, полученные экспериментальные данные обработаны верно. Значит, предложенная математическая модель адекватно описывает эксперимент.
5. Рассчитанный коэффициент корреляции экспериментальных данных между уровнем здоровья и физической активностью r=0,13434. Существует слабая прямая корреляционная зависимость между этими данными.
Корреляция (зависимость) сравниваемых значений уровня здоровья и физической активности (согласно критерию Стьюдента) статистически значимы с вероятностью допустимой ошибки 0,999 (вероятностная погрешность), меньшей или равной ей.
Таким образом, разработанный нами метод нахождения уровня здоровья и физической активности является достоверным и статистически значимым.
Технический результат - повышение точности оценки здоровья человека достигается более полным и точным измерением исходных данных, а также использованием в расчетах уточненных физиологических и физических данных.
Технический результат - повышение объективности достигается тем, что результаты измерений и соответствующей математической обработки более точно соответствуют состоянию здоровья человека.
Технический результат - повышение релевантности достигается более полным сбором исходных данных и применением для их обработки статистически проверенных коэффициентов.
Промышленное применение
Изобретение может применяться для точной оценки физического состояния здоровья населения и определения допустимого уровня нагрузки человека.

| название | год | авторы | номер документа |
|---|---|---|---|
| Способ мониторинга состояния пациентов, перенесших острый ишемический инсульт (ОИИ), после курса когнитивной реабилитации | 2021 |
|
RU2771578C1 |
| СПОСОБ ДИАГНОСТИКИ УРОВНЯ ТРЕВОЖНОСТИ | 2009 |
|
RU2402268C1 |
| Способ выявления пациентов, нуждающихся в продолжении курсов когнитивных тренировок на фоне медикаментозной поддержки, после перенесенного острого ишемического инсульта | 2021 |
|
RU2767932C1 |
| Способ оценки уровня фитнес-здоровья | 2020 |
|
RU2754651C1 |
| Способ прогнозирования нарушений вегетативной регуляции у женщин в послеродовом периоде | 2016 |
|
RU2649508C1 |
| Способ диагностики у детей функционального расстройства центральной нервной системы, ассоциированного с сочетанным воздействием марганца, свинца, бензола, ксилола и стирола техногенного происхождения | 2016 |
|
RU2622010C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ СОСТОЯНИЯ ПЛОДА ЖЕНЩИН-МЕДИЦИНСКИХ РАБОТНИКОВ | 2003 |
|
RU2242930C1 |
| Способ оценки степени галитоза полости рта | 2020 |
|
RU2755170C1 |
| Способ оптимизации показателей качества жизни детей, пребывающих на дистанционном обучении, с помощью комплексной интеграционной программы | 2023 |
|
RU2836010C1 |
| СПОСОБ ОЦЕНКИ УСЛОВИЙ ТРУДА ЖЕНЩИН - МЕДИЦИНСКИХ РАБОТНИКОВ | 2004 |
|
RU2271152C1 |
Изобретение относится к медицине, физической культуре и может быть использовано при мониторинге резервов физического здоровья и работоспособности детей, подростков, молодежи и взрослого населения. Проводят диагностику состояния здоровья и определения уровня физической активности по трем фазам. На фазе пассивной диагностики определяют пульс в покое, артериальное давление, жизненный показатель с помощью спирометра. В восстановительной фазе диагностики определяют восстанавливаемость пульса. На фазе активной диагностики оценивают гибкость позвоночника в тесте с наклоном вперед, силовую выносливость мышц рук и плечевого пояса за счет измерения количества отжиманий от пола, силовую выносливость мышц брюшного пресса. Дополнительно измеряют пульсовое давление в состоянии покоя, время восстановления ЧСС определяют после 20 приседаний. Общую выносливость определяют по времени бега на 2 км, ловкость определяют по длине прыжком с места. Силовую выносливость дополнительно измеряют путем подсчета количества подтягиваний на перекладине (для мужчин). Гибкость позвоночника определяют путем измерения наклона туловища ниже опоры. Определяют стаж регулярных занятий физической тренировкой, количество простудных заболеваний за год и количество хронических заболеваний. Оценку резервов физического здоровья и работоспособности населения осуществляют путем определения индекса функционального состояния здоровья по суммированию баллов с учетом полученных числовых значений по каждому измеренному показателю и весовых коэффициентов относительно нормативных показателей для обследуемого пола и возраста. В зависимости от полученного значения индекс функционального состояния здоровья определяют как: очень высокий, высокий, средний, низкий или очень низкий. Способ позволяет повысить точность, объективность и релевантность оценки здоровья человека за счет определения уровня физической активности по показателям физических данных и работоспособности населения. 1 ил., 3 табл.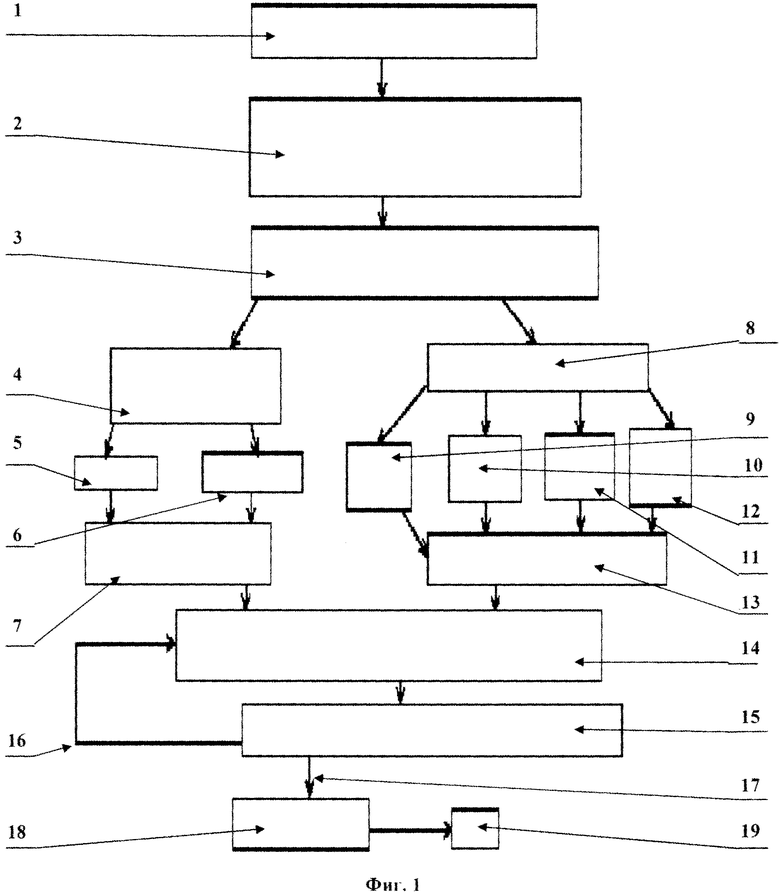
Способ оценки резервов физического здоровья и работоспособности населения, заключающийся в пассивной, активной и восстановительной фазах диагностики, при этом на фазе пассивной диагностики определяют пульс в покое, артериальное давление, жизненный показатель с помощью спирометра, в восстановительной фазе диагностики определяют восстанавливаемость пульса, на фазе активной диагностики оценивают гибкость позвоночника в тесте с наклоном вперед, силовую выносливость мышц рук и плечевого пояса за счет измерения количества отжиманий от пола, силовую выносливость мышц брюшного пресса, а оценку резервов физического здоровья и работоспособности населения осуществляют путем определения индекса функционального состояния здоровья по суммированию баллов с учетом полученных числовых значений по каждому измеренному показателю и весовых коэффициентов относительно нормативных показателей для обследуемого пола и возраста, отличающийся тем, что дополнительно измеряют пульсовое давление в состоянии покоя, время восстановления ЧСС определяют после 20 приседаний, общую выносливость определяют по времени бега на 2 км, ловкость определяют по длине прыжком с места, силовую выносливость дополнительно измеряют путем подсчета количества подтягиваний на перекладине (для мужчин), гибкость позвоночника определяют путем измерения наклона туловища ниже опоры, определяют стаж регулярных занятий физической тренировкой, количество простудных заболеваний за год и количество хронических заболеваний, а баллы вычисляют следующим образом:
а полученные в результате расчетов баллы суммируют, если результат:
более 60 - очень высокий индекс функционального состояния здоровья;
48-59 баллов - высокий индекс функционального состояния здоровья;
36-47 баллов - средний индекс функционального состояния здоровья;
24-35 баллов - низкий индекс функционального состояния здоровья;
ниже 24 баллов - очень низкий индекс функционального состояния здоровья.
| СПОСОБ ОЦЕНКИ РЕЗЕРВОВ ФИЗИЧЕСКОГО ЗДОРОВЬЯ И РАБОТОСПОСОБНОСТИ НАСЕЛЕНИЯ | 1999 |
|
RU2147208C1 |
| СПОСОБ ОЦЕНКИ РЕЗЕРВОВ ФИЗИЧЕСКОГО ЗДОРОВЬЯ И РАБОТОСПОСОБНОСТИ НАСЕЛЕНИЯ | 2010 |
|
RU2441580C1 |
| СОКОЛОВСКИЙ В | |||
| С | |||
| Донозологическая диагностика адаптационных резервов организма человека | |||
| Опыт применения и перспективы | |||
| ЛФК и массаж | |||
| Печь для непрерывного получения сернистого натрия | 1921 |
|
SU1A1 |
| Способ сопряжения брусьев в срубах | 1921 |
|
SU33A1 |
| ЯКОВЛЕВ М | |||
| Ю | |||
| Применение диагностического программного модуля мониторинга функциональных резервов организма для оценки эффективности | |||
Авторы
Даты
2016-05-27—Публикация
2014-08-26—Подача