Область техники, к которой относится изобретение
Настоящее изобретение относится к добыче нефти и газа с применением компьютерного моделирования нефтяного или газового коллектора (резервуара) и эксплуатационного оборудования.
Уровень техники
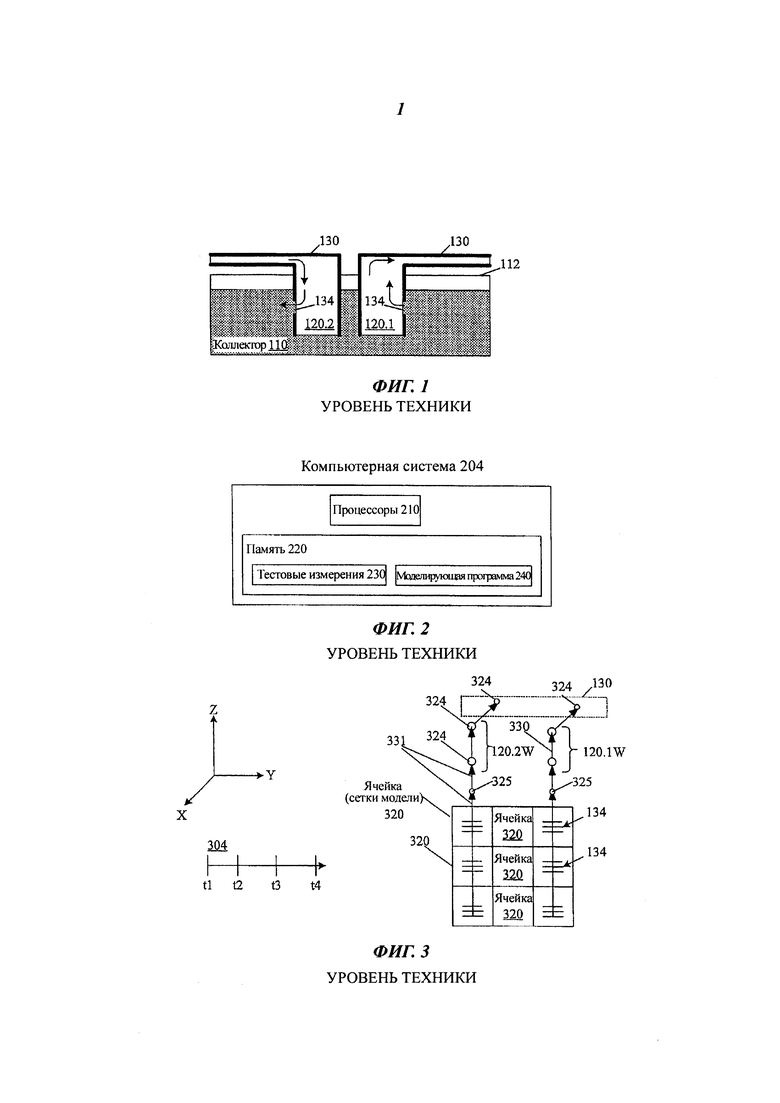
На фиг. 1 схематически показано эксплуатационное оборудование для извлечения нефти и/или газа из коллектора 110. Коллектор 110 состоит из подземных породных формаций ниже уровня поверхности 112 земли. В коллекторе был пробурен скважинный ствол 120.1 и соединен с поверхностным оборудованием 130 системой труб и насосов 130 для выкачивания из коллектора флюида (нефти или газа, возможно смешанных с водой или буровым раствором). В скважинный ствол 120.1 была вставлена обсадка, в которой были проделаны перфорации 134, позволяющие скважинному стволу сообщаться с коллектором. Другой скважинный ствол 120.2, присоединенный к поверхностной сети 130 и также имеющий перфорации 134, может опционально использоваться для нагнетания в коллектор воды, пара, углекислого газа или других химикатов для вытеснения нефти или газа по направлению к скважинному стволу 120.1 или для придания густой нефти большей подвижности.
Создание проекта эксплуатационного оборудования включает в себя выбор местоположения стволов скважин и химикатов для нагнетания, геометрических форм и размеров скважин, сетей трубопроводов и насосного оборудования, графиков бурения, графиков добычи и т.д. Оптимальный выбор этих и других параметров зависит от физических свойств коллектора 110, таких как давления, насыщения, пористости и, возможно, других параметров. Этот выбор облегчается компьютерным моделированием (симулированием), моделирующим добычу для существующего или гипотетического эксплуатационного оборудования и графиков добычи. Пригодная для этой цели компьютерная система 204 (фиг. 2) включает в себя один или более компьютерных процессоров 210, связанных с памятью 220. Обычно для того, чтобы определить те параметры, которые будут полезны, выполняются тестовые измерения в выбранных местоположениях в коллекторе 110 или в существующем эксплуатационном оборудовании. Тестовые данные могут включать в себя геологические данные по результатам сейсмического анализа, анализа образцов пород и каротажного исследования скважины. К этим данным могут относиться данные по пористости и проницаемости пород и другим свойствам, позволяющие определить полезные параметры, такие как давление или насыщение в некотором количестве местоположений. Тестовые измерения, изображенные как 230, сохраняются в памяти 220. Моделирующая программа 240, хранящаяся в памяти 220, исполняется процессорами, которые считывают тестовые данные 230 и выдают смоделированные результаты, которые можно сохранить в памяти 220 и/или вывести на принтер, монитор компьютера или другое устройство вывода, или передать другой компьютерной программе или другому компьютеру по сети или другим способом, для того чтобы ими могли воспользоваться инженеры-промысловики или другие работники.
Дискретная модель коллектора 110 и эксплуатационного оборудования создается компьютером 204 в памяти 220 для использования моделирующей программой 240, как показано на фиг. 3. В частности, на месторождение накладывается воображаемая сетка 320 ячеек (ячеек расчетной сетки) с данными, указывающими местоположение скважинных стволов 120 и перфораций 134. В каждой ячейке (обычно, но не обязательно, в ее центре) определен узел (не показан), и давление и возможно другие значения в ячейке моделируются как давление и возможно другие значения именно в этом узле. Участки скважинного ствола выше перфораций показаны как 120.1W, 120.2W, и далее по тесту будут называться просто «скважинами». В компьютерной модели определены узлы 324 вдоль по каждой скважине 120W (то есть 120.1W, 120.2W); эти узлы представляют собой точечные местоположения, в которых будут моделироваться давление или другие значения. Скважина может иметь один или более узлов 324. Соединения 330 представляют собой участки скважины между узлами 324. Аналогичные узлы и соединения (не показаны) могут представлять и поверхностную сеть 130. Могут быть определены другие узлы 325, которые представляют точечные местоположения в перфорированных участках стволов (ниже скважин). Соединения 331 представляют собой участки ствола между узлами 325 и между верхним узлом 325 ствола и первым узлом 324 скважины («устьевым узлом»). Поток материала между перфорационной ячейкой 320 (то есть ячейкой, перфорированной стволом) и стволом будет моделироваться как поток между перфорационной ячейкой и узлом 325, или как поток между ячейкой и соответствующим устьевым узлом 324.
Для определения различных местоположений выбирается система координат (XYZ). В компьютере 204 определяется временная ось 304 с моментами времени t1, t2, t3 ….
Для моделирования нефтяного или газового месторождения выбирают систему уравнений, в том числе уравнения гидравлического взаимодействия между узлами в скважинах, стволах скважин и в поверхностной сети; уравнения потоков, подчиняющихся и не подчиняющихся закону Дарси между ячейками 320; уравнения перфорации между ячейками 320 и узлами 325; уравнения баланса массы компонентов флюида для узлов и ячеек; ограничивающие уравнения и возможные другие. Смотри патент США №7,668,707 от 23 февраля 2010 года на имя Watts, III и др., включенный в настоящую заявку посредством ссылки. Уравнения могут включать в себя дифференциальные уравнения, которые дискретизируются с использованием известных способов. Уравнения символически могут быть записаны следующим образом:
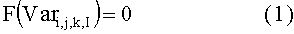
Где Vari,j,k,l представляет собой давления, расходы или другие переменные в узлах и соединениях в различные моменты времени. Нижний индекс «i» представляет собой момент времени ti на оси 304, а нижние индексы j, k, I представляют собой значения X, Y и Z соответственно. Значения Vari,j,k,l интерпретируются как независимые переменные.
Так как некоторые физические параметры можно выразить через другие, то имеется некоторая свобода в том, какие параметры выбирать в качестве независимых переменных (первичных переменных) в уравнениях (1). Кроме того, уравнения (1) зависят от способа дискретизации и, в частности, от того, где измеряется какое-либо конкретное значение Var - в ячейке 320, узлах 324 или 325 или в сегменте 330 или 331. Такой выбор повлияет на то, насколько эффективно компьютер сможет решать уравнения. Термин «эффективно» относится к минимальному использованию ресурсов компьютера, и в частности, ресурсов процессора и памяти. Обеспечивая решение, хорошо аппроксимирующее реальность, желательно уменьшить продолжительность вычисления и объем памяти, требуемый для решения уравнений.
Могут существовать миллионы разных местоположений и моментов времени, поэтому уравнение (1) может представлять миллионы или миллиарды скалярных уравнений. В типовом процессе уравнения (1) решаются для каждого из последовательных времен ti, то есть сначала для времени t1, затем для времени t2 и так далее. Решение для времени t1 зависит от тестовых измерений, хранящихся как показано поз. 230 на фиг. 2. Решение для каждого следующего времени ti находят, используя ранее найденные значения Var для времени ti-1, и, возможно, более ранних времен, и, возможно, с использованием тестовых измерений 230.
Уравнения (1) обычно являются нелинейными, и для каждого времени ti эти уравнения можно решить приближенно, используя метод Ньютона-Рафсона, проиллюстрированный на фиг. 4. Это итерационный метод, в котором на каждой итерации нелинейные уравнения (1) заменяются линейными. Для желаемого все большего и большего приближения к истинному решению, на последовательных итерациях используются различные линейные уравнения. Для упрощения обозначений, перепишем уравнения (1) следующим образом:
F(x)=0
Предположим, что хn является текущим итерационным решением в методе Ньютона-Рафсона. Тогда следующая итерация хn+1 получается так, так изложено ниже. Вычисляют якобиан JF(xn); он является матрицей частных производных F(x), оцененных на текущей итерации хn. Затем для хn+1 решают следующее линейное уравнение:
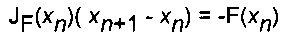
Это уравнение можно переписать в следующем другом виде:

или

где F'L=JF, и b является константой, равной правой части уравнения (3).
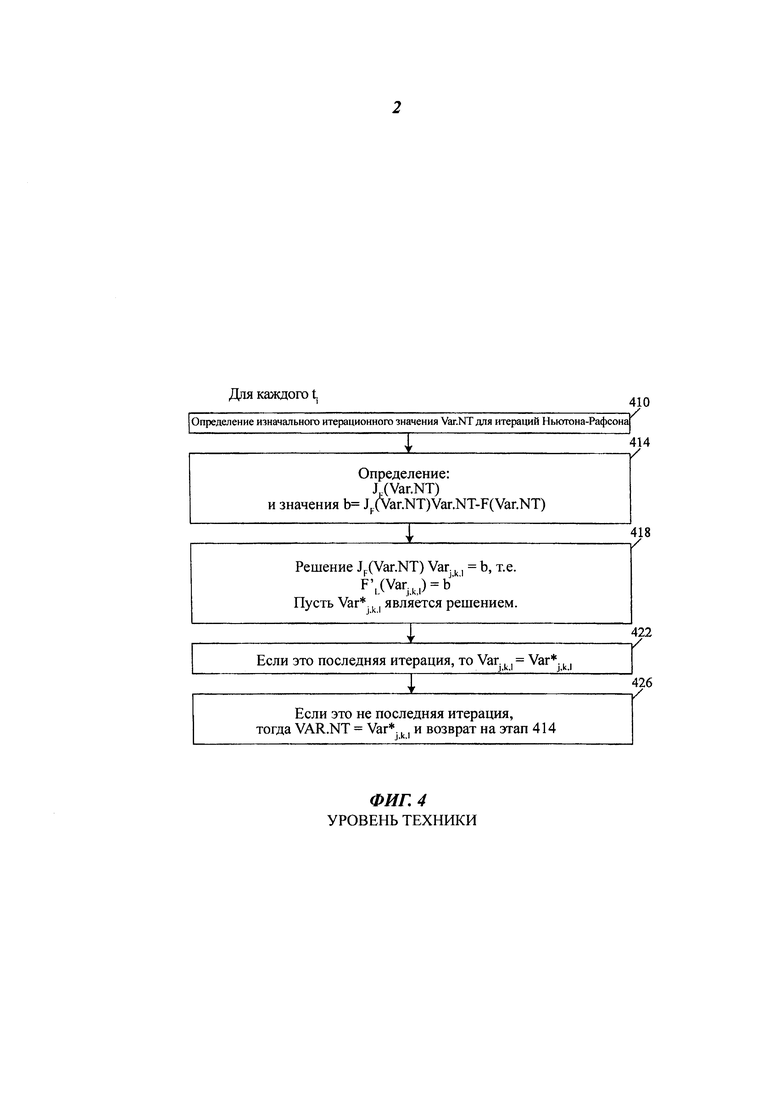
Этот процесс проиллюстрирован на фиг. 4. Символ Var.NT обозначает текущее приближение (аппроксимацию) хn. Так как ti неизменно, то Vari,j,k,l иногда можно записать просто как Varj,k,l. Значения Var.NT последней итерации берутся в качестве приближенного решения Vari,j,k,l уравнений (1) для времени ti.
На этапе 410 выбирают изначальные итерационные значения Var.NT, и это могут быть любые значения по желанию, например, значения Vari-1,j,k,l найденные на предыдущей итерации i-1 если i>1, или некоторые значения, полученные из изначальных измерений 230, если i=1.
На этапе 414, матрицу JF(Var.NT) и значение

определяют для уравнений (2)-(3). На этапе 418 эти уравнения решают, то есть решают следующее уравнение:

Обозначим решение как Var* j,k,l. Если это последняя итерация, то решение Var* j,k,l принимается за решение (1), и таким образом способ по фиг. 4 завершается для ti. Смотри этап 422. Если требуются другие итерации, то решение Var* j,k,l используется в качестве следующего значения Var.NT для следующей итерации (этап 426), и этапы 414-418 повторяются. Для получения все лучших и лучших приближений решения (1) может быть использовано любое количество итераций. Итерации могут быть прекращены, когда F(Var* j,k,l) близко к нулю в некотором смысле.
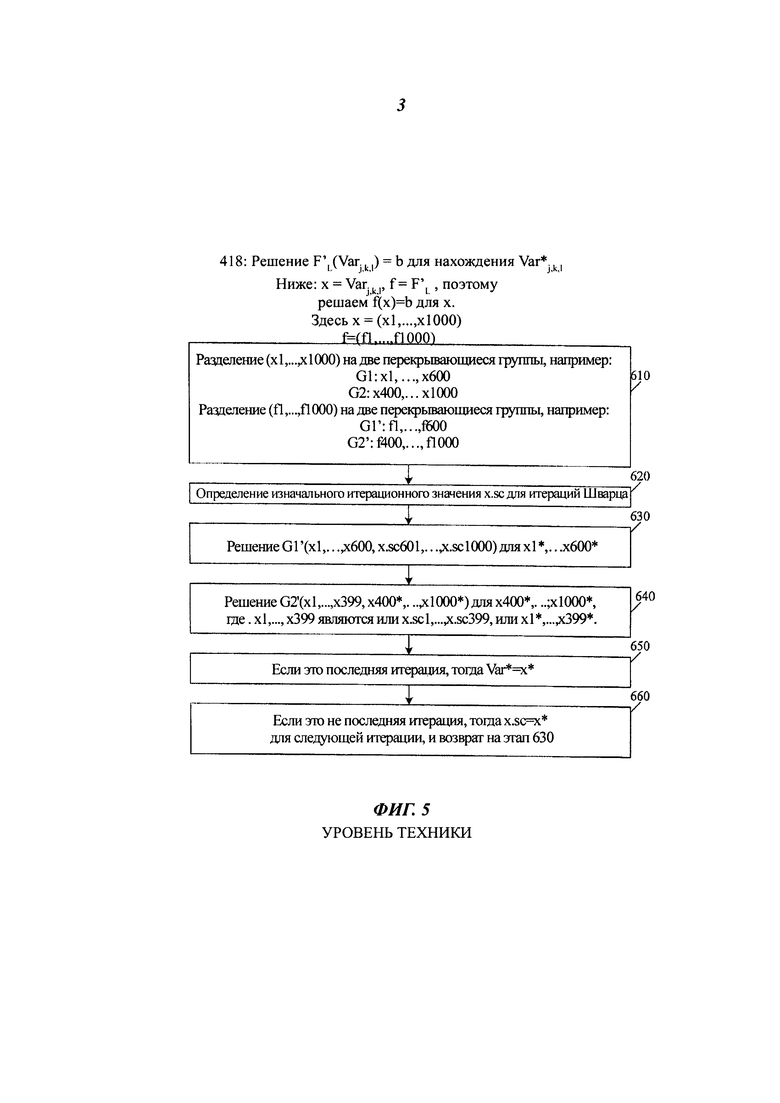
Уравнения (4) могут включать в себя миллиарды уравнений с миллиардами индивидуальных переменных, коллективно обозначенных как Varj,k,l. Поэтому компьютерная система 240 решает уравнения (4) приближенно. Примером приближенного метода является метод Шварца, проиллюстрированный на фиг. 5. В целях упрощения, функция F'L будет обозначаться просто как f, a Varj,k,l будет обозначаться как х. В этом случае, уравнение (4) можно записать следующим образом:

Функцией f представлены многие скалярные линейные функции, а переменной х представлено такое же количество скалярных компонентов. Метод Шварца будет проиллюстрирован на примере, в котором и х, и f имеют 1000 скалярных компонентов, обозначенных как х1, х2,…, x1000 для х, и обозначенных как f1, f2,…, f1000 для f.
На этапе 610 значения х1,…, х1000 разделяют на две перекрывающиеся группы значений (можно использовать более двух групп). В рассматриваемом ниже примере эти группы следующие:
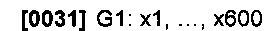
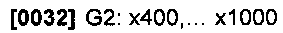
Также и скалярные функции f1,…,f1000 разделяют на две перекрывающиеся группы, причем в каждой группе столько же функций, сколько в G1, G2. Например, двумя группами функций могут быть следующие:
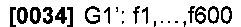
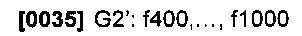
Мы используем запись G1'(x) для обозначения значений с f1(x) до f600(x); а запись G2'(x) будет обозначать значения с f400(x) до f1000(x).
Метод Шварца является итерационным методом, и итеративное решение будет обозначено как x.sc. Значение x.sc, выдаваемое методом Шварца, является решением х.
На этапе 620 любым подходящим способом определяется изначальное итерационное значение x.sc. Например, x.sc может быть присвоено значение Var.NT на этапе 418 текущей итерации метода Ньютона-Рафсона по фиг. 4.
На этапах 630-640 определяют следующее итеративное значение x.sc следующим образом.
На этапе 630 значениям х из G1\G2, то есть значениям от х601 до х1000, присваивают соответствующие значения текущего итерационного значения x.sc, и решают следующее уравнение для х1-х600:

где b1 является частью "b", соответствующей G1'. Другими словами, решают следующее уравнение:
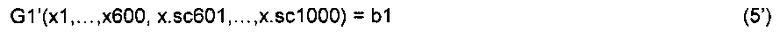
Решение обозначают как х1∗,…,х600∗.
Значения от х1* до х399* будут использованы в качестве соответствующих значений следующего итерационного значения x.sc как разъясняется ниже.
На этапе 640 следующее уравнение решают для х400* до х1000*:

где b2 является частью «b», соответствующей G2. В данном уравнении значения х1,…,х399 являются постоянными. В аддитивном методе Шварца этим значениям присваиваются соответствующие значения текущего итерационного значения x.sc. В мультипликативном методе Шварца этим значениям присваиваются соответствующие значения х1*,…,х399*, найденные на этапе 630. Решение (6) будет обозначено как х600*,…,х1000*. Значения от х1* до х1000* совместно будут обозначены как х*.
Если это последняя итерация, то х* может быть принято за решение (4'), то есть как значение Var* j,k,l на этапе 418. Смотри этап 650. Если требуются последующие итерации (этап 660), то решение х* используется как следующее итерационное значение x.sc, и этапы 630-640 повторяются. Для получения все более лучших и лучших приближений решения (4') может использоваться любое количество итераций.
В некоторых вариантах метода Шварца итерации, кроме первой, решаются для невязки b-f(x) а не для х. Невязку обновляют на каждой итерации. В частности, для обновления невязки для этапа 640 используются перекрывающиеся значения х400*,…,х600*, найденные на этапе 630.
Как вариант, компоненты х400*,…,х600* для х* получают для этапа 650 путем комбинирования соответствующих значений, полученных на этапах 630 и 640, то есть, комбинированием соответствующих компонентов решений уравнений (5) и (6) таким, чтобы минимизировать норму ||b-f(x*)|| невязки. Известным способом комбинирования этих компонентов является способ обобщенных минимальных невязок GMRES (Generalized Minimum Residual method).
Очевидно, что вычислительная сложность решения уравнений (1) зависит от выбора переменных Var и групп G1, G2, G1', G2'. В общем смысле коллекторы достаточно отличаются от скважин в части физических моделей, поэтому коллекторы и скважины обычно находятся в разных группах. В частности, каждая группа G1, G2 может быть определена ячейками 320 или узлами 324 или 325: каждая группа состоит из переменных, принадлежащих группе ячеек 320 или узлов 324 или 325 или соответствующих сегментов 330 или 331, а каждая группа G1', G2' функций состоит из уравнений для соответствующих ячеек и узлов. Таким образом, ячейки коллектора могут быть помещены в группу G1 (то есть, в группу узлов, определяющих G1), скважины - в группу G2, а перфорационные ячейки 320 (ячейки с перфорациями) и узлы 325 ствола могут входить в перекрытие между G1 и G2. Такая схема использована в программной системе моделирования месторождения NEXUS® Reservoir Simulation Software system, поставляемой компанией Halliburton, г. Хьюстон, Техас. В программе NEXUS®, переменными Var являются давления и составы компонентов в узлах 324 и 325, а также давления и массы компонентов в ячейках 320.
Дополнительная информация может быть найдена в указанных ниже публикациях, включенных в настоящую заявку посредством ссылки (при этом не заявляется о том, касаются ли данные публикации уровня техники, относящегося к настоящему раскрытию):
- Публикация заявки на патент США 2009/0294122 А1 (3 декабря 2009), авторы Hansen и др.
- Патент США №7,668,707 В2 (23 февраля 2010), авторы изобретения Watts III и др.
- Патент США №7,516,056 В2 (7 апреля 2009), авторы изобретения Wallis и др.
- Публикация заявки на патент США 2010/0286971 А1 (11 ноября 2010), авторы изобретения Middya и др.
- Заявка на патент Великобритании GB 2434235 А (18 июля 2007), заявитель Schlumberger Technology Corporation.
- Заявка на Европейский патент ЕР 2192507 А1 (2 июня 2010), заявитель Maersk Olie OG Gas A/S.
- Заявка PCT WO 2006/020952 A2 (23 февраля 2006), заявители Saudi Arabian Oil Company и ARAMCO Services Company.
- H. Kazemi, "Numerical Simulation of Water-Oil Flow in Naturally Fractured Reservoirs" (Численное моделирование потока вода-нефть в естественно-трещиноватых коллекторах), издание Society of Petroleum Engineers Journal, Декабрь 1976, страницы 317-326.
- Rafael Bru et al., "Overlapping additive and multiplicative Schwarz iterations for H-matrices" (Перекрывающиеся аддитивные и мультипликативные итерации Шварца для Н-матриц), издание Linear Algebra and its Applications, Elsevier, 2003.
Раскрытие изобретения
В данном разделе кратко излагаются некоторые признаки изобретения. Другие признаки могут быть раскрыты в последующих разделах. Изобретение определяется прилагаемой формулой изобретения, которая включена в настоящий раздел путем ссылки.
Авторами изобретения было обнаружено, что для достижения лучшей связи между коллектором и поверхностной сетью может быть желательным включение в перекрытие скважин 120W. В некоторых вариантах осуществления, тем не менее, из перекрытия удалены «перфорационные» ячейки 320 (то есть ячейки с перфорациями 134). Меньшее перекрытие сокращает сложность вычислений. В других вариантах осуществления перфорационные ячейки в перекрытие включены.
В соответствии с другим аспектом изобретения уравнения для узлов скважины и ствола обрабатываются для исключения некоторых не относящихся к давлению переменных. Поэтому, когда эти переменные рассматриваются непосредственно, то уменьшается ошибка, вызванная непосредственным рассмотрением, поэтому решение давления является более точным. Во многих случаях точность решения давления по коллектору и поверхностной сети определяет рабочие характеристики глобального линейного решателя для уравнений (4), то есть определяет способность получения точного решения для всех переменных при минимальных вычислительных затратах.
Изобретение не ограничено вышеперечисленными признаками и преимуществами, за исключением того, что определено приложенной формулой изобретения.
Краткое описание чертежей
На фиг. 1 показан вертикальный разрез нефтяного или газового месторождения с эксплуатационным оборудованием в соответствии с уровнем техники.
На фиг. 2 показана блок-схема компьютерной системы, которую можно использовать для моделирования нефтяных или газовых месторождений и эксплуатационного оборудования в соответствии с уровнем техники и некоторыми вариантами осуществления настоящего изобретения.
На фиг. 3 показана схема модели нефтяного или газового месторождения и поверхностной сети в соответствии с уровнем техники.
На фиг. 4 показана диаграмма метода Ньютона-Рафсона, применяемого для моделирования нефтяного или газового месторождения и эксплуатационного оборудования в соответствии с уровнем техники.
На фиг. 5 показана диаграмма метода Шварца, применяемого для моделирования нефтяного или газового месторождения и эксплуатационного оборудования в соответствии с уровнем техники.
На фиг. 6 показаны схемы тех моделей нефтяных или газовых месторождений и поверхностных сетей, которые используются для иллюстрации компьютерного моделирования в соответствии с некоторыми вариантами осуществления настоящего изобретения.
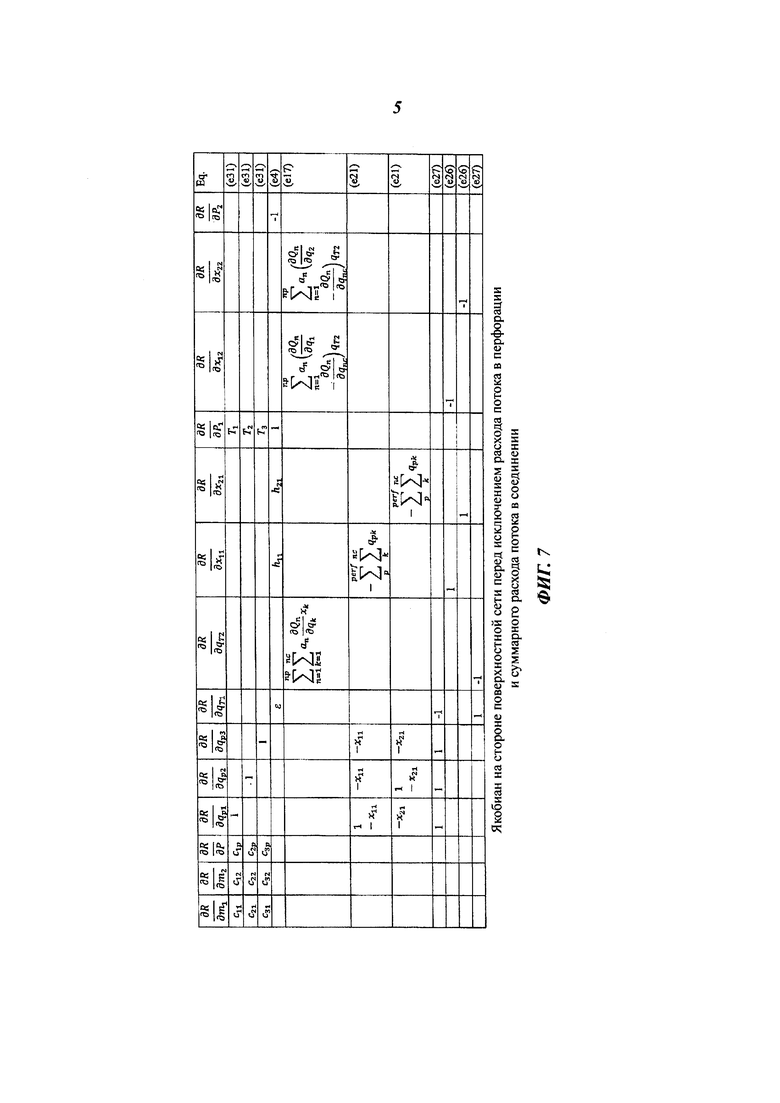
На фиг. 7 показан пример якобиана на стороне скважинного ствола и поверхностной сети перед исключением расходов потока в перфорациях и суммарных расходов потока в соединениях.
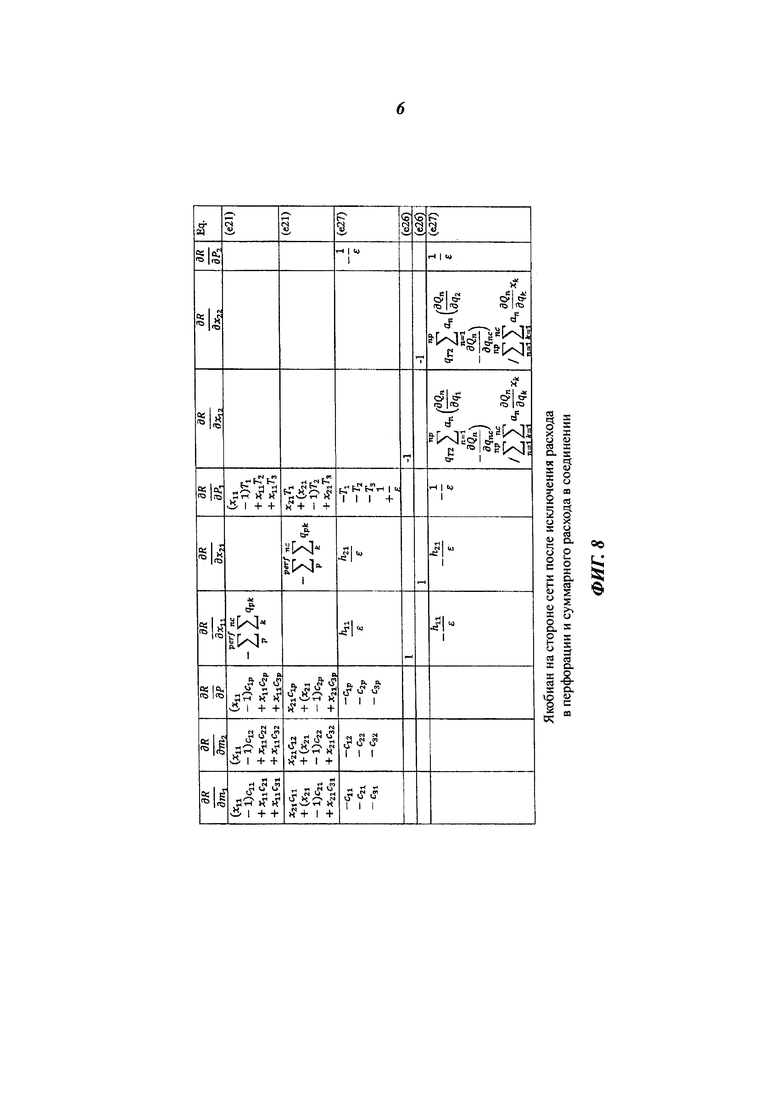
На фиг. 8 показан пример якобиана на стороне скважинного ствола и поверхностной сети после исключения расходов потока в перфорациях и суммарных расходов потока в соединениях.
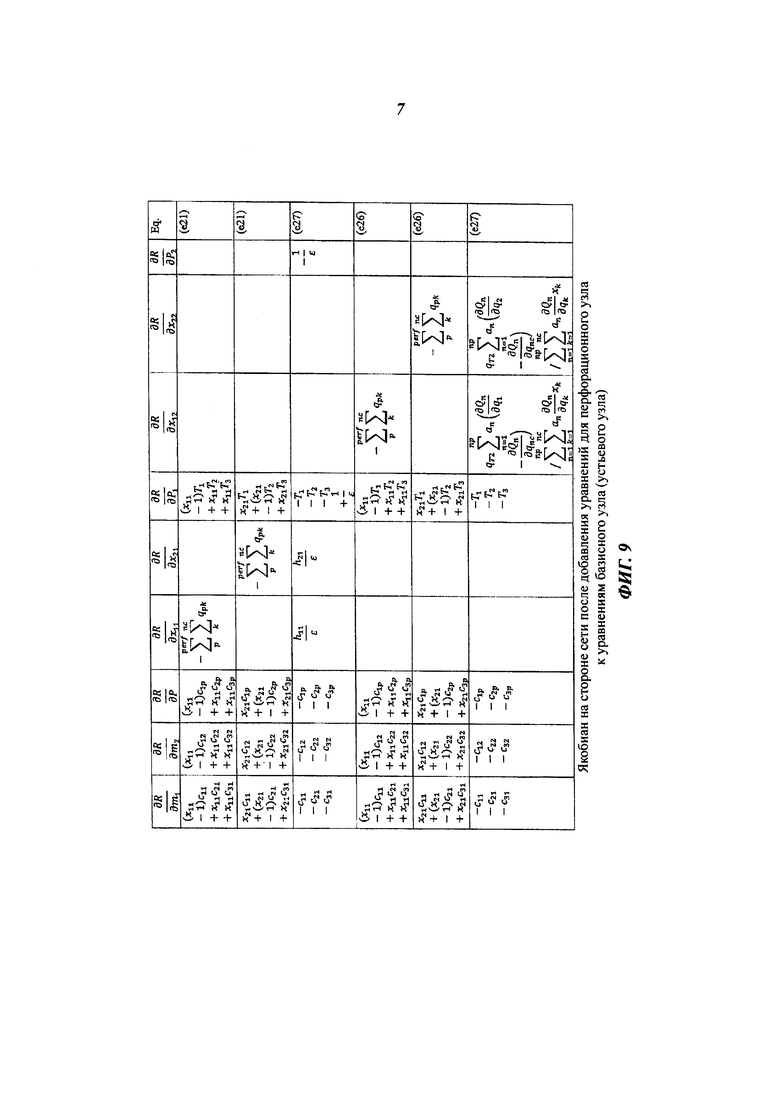
На фиг. 9 показан пример якобиана на стороне скважинного ствола и поверхностной сети после добавления уравнений для перфорационного узла (такого как 325) к уравнениями в устьевом узле, служащем базисным узлом.
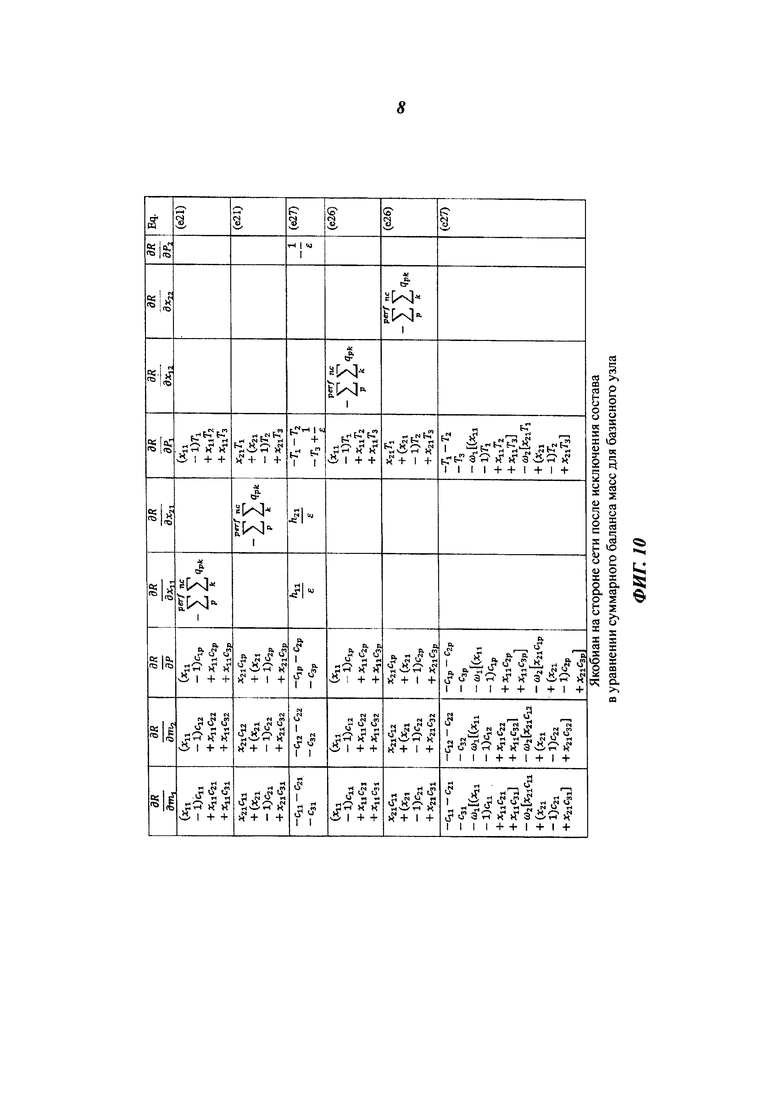
На фиг. 10 показан пример якобиана на стороне скважинного ствола и поверхностной сети после исключения составов в уравнении суммарного баланса массы для устьевого узла, служащего базисным узлом.
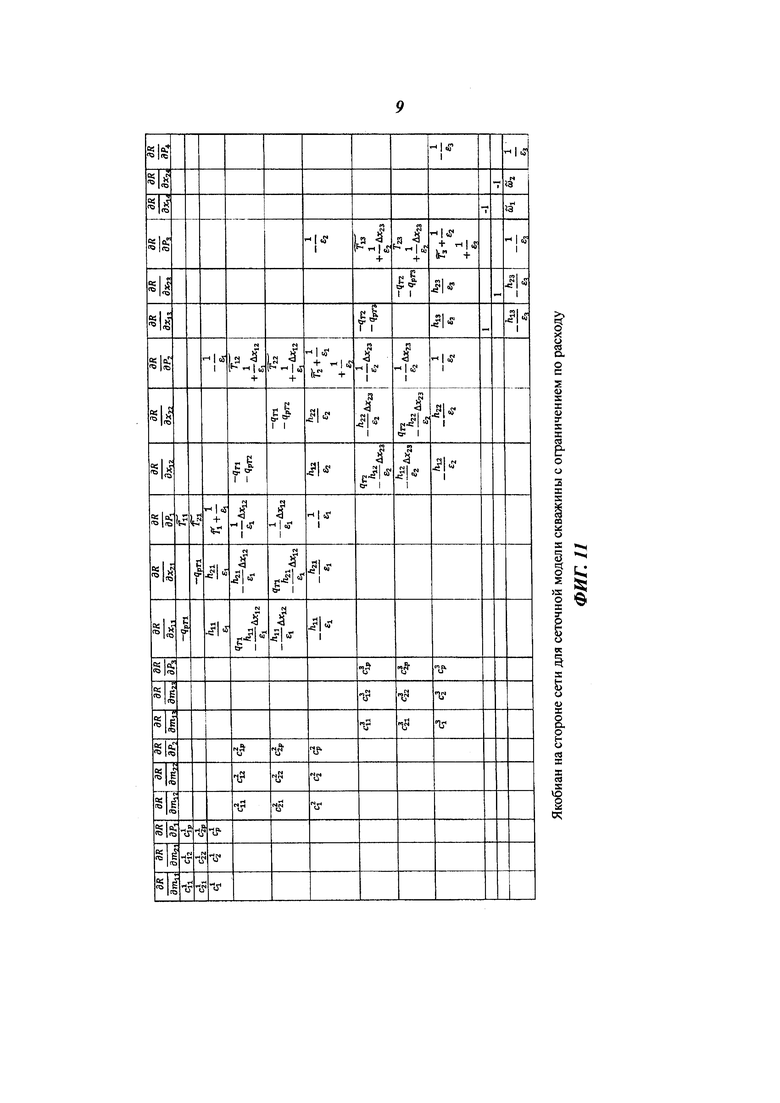
На фиг. 11 показан пример якобиана на стороне скважинного ствола и поверхностной сети для сеточной модели скважины с ограничением по расходу.
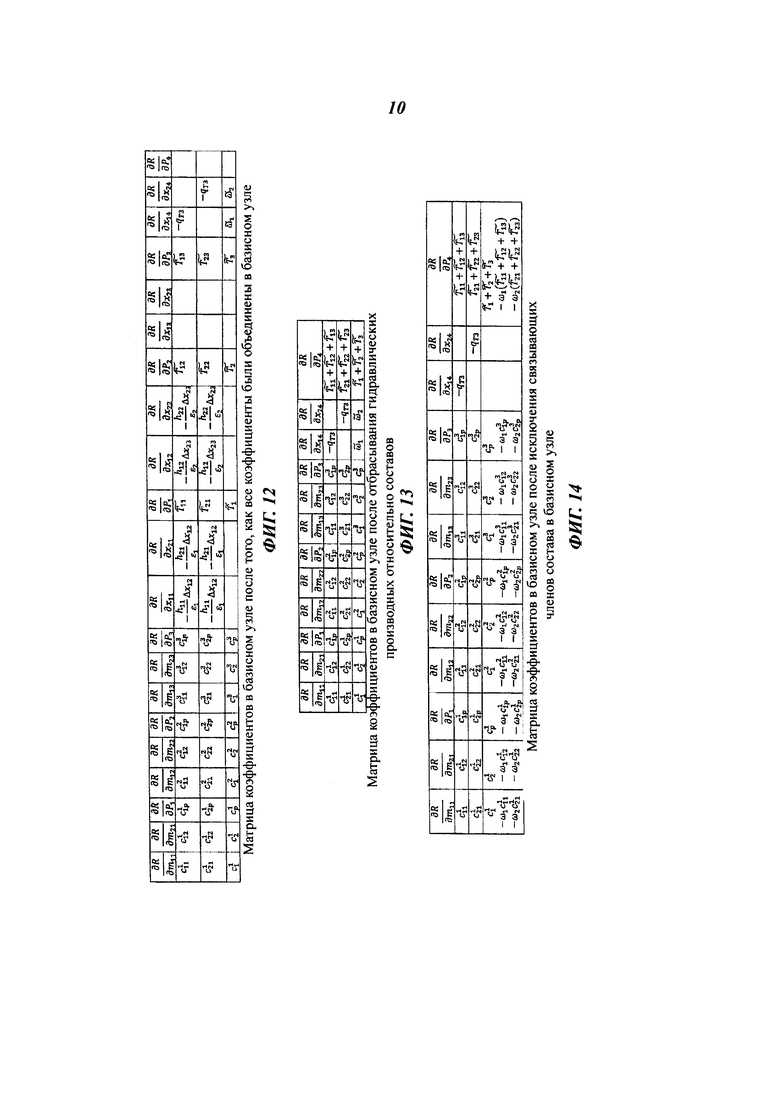
На фиг. 12 показан пример матрицы коэффициентов в базисном узле после того, как уравнения баланса массы для не являющихся базисными узлов были добавлены к базисному узлу.
На фиг. 13 показан пример матрицы коэффициентов в базисном узле после отбрасывания относящихся к гидравлике производных относительно составов.
На фиг. 14 показан пример матрицы коэффициентов в базисном узле после исключения связывающих членов состава в базисном узле.
На фиг. 15 показан пример глобальной матричной структуры для неявного построения с неявными скважинами и поверхностной сетью.
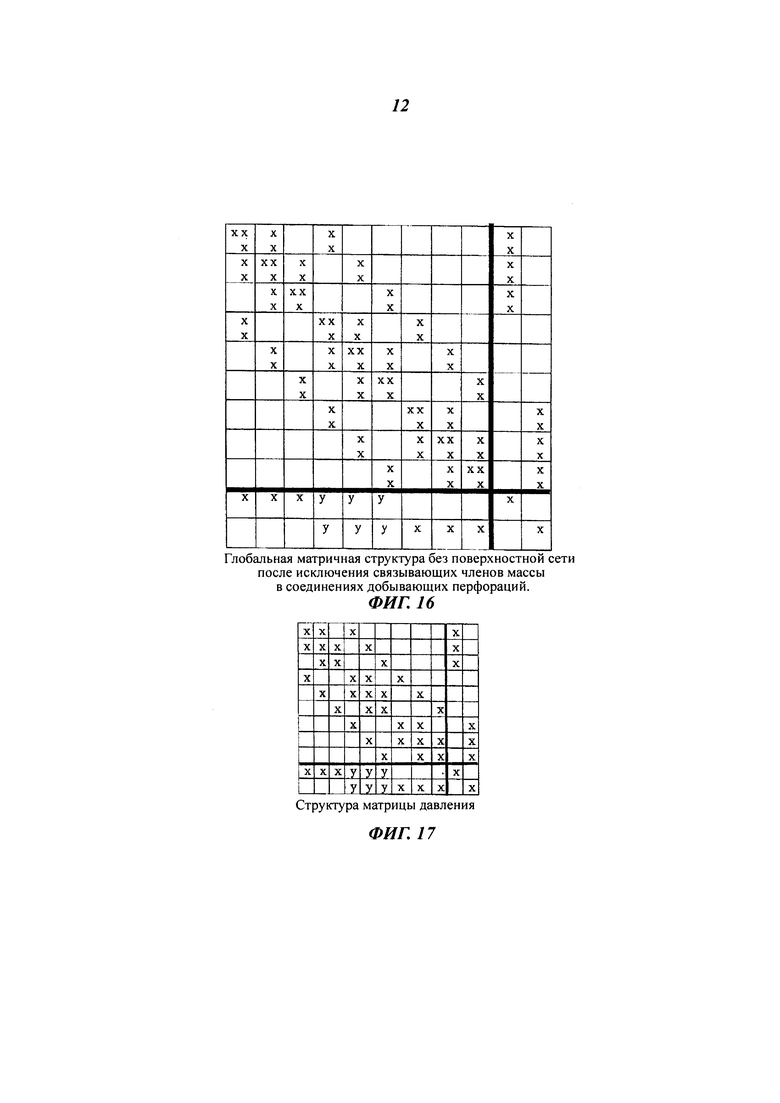
На фиг. 16 показан пример глобальной матричной структуры без поверхностной сети после исключения связывающих членов массы в соединениях добывающих перфораций.
Фиг. 17 иллюстрирует пример структуры матрицы давления.
На фиг. 18, 19 показаны диаграммы способов моделирования в соответствии с некоторыми вариантами осуществления настоящего изобретения.
Осуществление изобретения
Описанные в данном разделе варианты осуществления иллюстрируют, но не ограничивают изобретение. Изобретение определяется прилагаемой формулой изобретения.
Далее рассматриваются некоторые варианты осуществления настоящего изобретения на примере мультипликативного метода Шварца согласно фиг. 5. Тем не менее, изобретение включает в себя аддитивный метод Шварца, и может быть скомбинировано со многими существующими технологиями моделирования. Следует отметить, что методы Шварца являются частью класса методов, которые могут быть описаны следующим образом:
- Присвоение некоторым из переменных постоянных значений и решение некоторых или всех уравнений для остальных переменных;
- Последующее присвоение постоянных значений некоторым или всем из этих остальных переменных и нахождение решения для некоторых или всех переменных, которые были постоянными на предшествующем этапе.
В моделировании нефтяных и газовых систем одним из типов таких способов является способ IMPES (implicit pressure explicit saturation, неявное давление с явным насыщением): для решения уравнений (1) для каждого времени ti при имеющемся решении для времени ti-1 (где t0 означает изначальные значения), не относящимся к давлению переменным присваиваются значения при ti-1, и решаются уравнения для нахождения значений давления в моменты времени ti; затем давлениям присваиваются значения, которые были в моменты времени ti, и решаются уравнения для нахождения значений, не относящихся к давлению переменных для моментов времени ti. Некоторые из этих и других способов описаны в следующих публикациях, включенных в настоящую заявку посредством ссылки:
- Yuanlin Jiang, "Techniques for Modeling Complex Reservoirs and Advanced Wells" (Технологии моделирования сложных коллекторов и усовершенствованных скважин), Диссертация, Department of Energy Resources Engineering and the Committee on Graduate Studies, Университет Стэнфорд, Декабрь 2007.
- Wing Hong Felix Kwok, "Scalable Linear and Nonlinear Algorithms for Multiphase Flow in Porous Media" (Масштабируемые линейные и нелинейные алгоритмы для многофазного потока в пористой среде), Диссертация, Program in scientific computing and computational mathematics and the committee on graduate studies, Университет Стэнфорд, Декабрь 2007.
- Denis José Schiozer, "Simultaneous Simulation of Reservoir and Surface Facilities" (Одновременное моделирование коллекторного и наземного оборудования), Диссертация, Department of Petroleum Engineering and the committee on graduate studies, Университет Стэнфорд, Март 1994.
- Eero Vainikko, "Robust Additive Schwarz Methods - Parallel Implementations and Applications" (Устойчивые аддитивные методы Шварца - Параллельные реализации и применения), Диссертация на получение степени доктора наук, Department of Informatics, университет Бергена, Март 1997 года.
Другие подобные технологии включают использование предобуславливателя CPR (Constrained Pressure Residual - Ограниченная невязка давления).
Некоторые из вариантов осуществления совместимы с адаптивным неявным способом AIM (Adaptive Implicit Method) и с другими способами, описанными в документах, указанных в предшествующем параграфе. Некоторые варианты осуществления также совместимы с полностью неявным способом FIM (Fully Implicit method), то есть когда все переменные рассматриваются неявно (ни одну из них не заменяют константой), кроме метода Шварца на этапе по фиг. 5. Однако, как указано выше, изобретение включает производные от матрицы давления, которые не ограничиваются использованием метода Шварца.
Далее для моделей, показанных на фиг. 3 и фиг. 6 (описывается ниже) будут раскрыты некоторые варианты осуществления мультипликативного метода Шварца только с двумя группами переменных, G1 и G2. В некоторых из этих вариантов осуществления группа G1 соответствует коллекторным и перфорационным ячейкам 320, узлам 325 ствола и сегментам 331 и узлам 324 скважины и сегментам 330 скважин 120W. Группа G2 соответствует всем скважинам 120W, скважинным стволам, перфорационным ячейкам 320 и поверхностной сети 130. Перекрывающимися областями являются узлы 324 и сегменты 330 скважин 120W, узлы 325 ствола и сегменты 331, и перфорационные ячейки 320.
Глобальная линейная система (4) в матричном преставлении выглядит как:

Здесь нижние индексы r, w, f обозначают коллектор, скважину и поверхностную сеть 130 соответственно. Для нижнего индекса r, коллектор включает ячейки с перфорациями 134. Вектор [br, bw, bf] с правой стороны является тем же самым, что и b в уравнении (4). Вектор [хr, xw, xf] является те же самым, что и Varj,k,I.
В матрице с левой стороны строки с Аrr соответствуют коллекторной части уравнений (4), включая перфорационные ячейки 320. Строки с Awr соответствуют уравнениям скважины, которые включают уравнения потока от каждой перфорационной ячейки 320 в соответствующий узел 325 ствола. Строки Afw с соответствуют уравнениям эксплуатационного оборудования. Столбцы с Аrr соответствуют переменным коллектора (включая перфорационные ячейки 320). Столбцы с Аrw соответствуют переменным скважины. Столбцы с Аwf соответствуют переменным эксплуатационного оборудования. Пустые поля в матрице являются нулями.
Группа G1 состоит из переменных хr, xw, и уравнения G1' могут быть записаны как:

Эти уравнения получаются присвоением xf постоянных значений согласно вышеприведенному описанию. Значения bw в (8) не обязательно такие же, как в (7).
Группа G2 состоит из переменных xw, xf, и уравнения G2' могут быть записаны как:

Значения b в (9) не обязательно такие же, как в (7).
Система (9) не может существовать, если поверхностная сеть 130 отсутствует, или если ее не моделируют. Если в системе моделирования поверхностная сеть существует, то систему (9) можно решить известными способами, например, разреженным прямым решателем (sparse direct solver) или итерационным решателем типа ILU (Incomplete Lower/Upper). Мы обратим основное внимание на решение системы (8), которое является более сложным в некоторых вариантах осуществления.
Для FIM нам необходимо создать CPR уравнение для давления для коллектора. Для FIM и IMPES необходимо создание приближенной матрицы давления для узлов ствола, так как в обоих случаях используется неявное моделирование скважины.
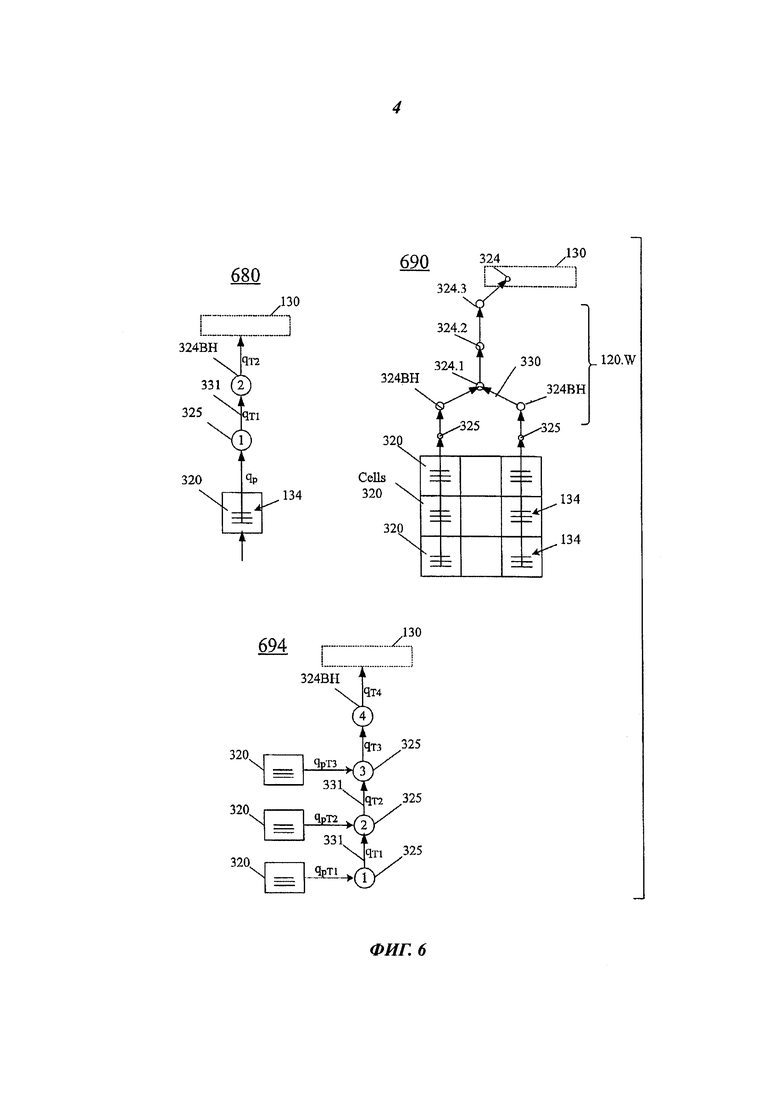
На фиг. 6 показаны примерные модели 680, 690, 694 скважин, которые будут использованы в дополнение к показанной на фиг. 3 модели для иллюстрирования некоторых вариантов осуществления настоящего изобретения. Показанные модели являются неограничивающими примерами. Все из этих моделей предназначены для добычных скважин (для выкачивания нефти или газа из коллектора), но аналогичные технологии применяются и для нагнетательных скважин (предназначенных для нагнетания воды или других веществ в коллектор). Модель 680 включает перфорационную ячейку 320, соединенную перфорацией 134 с узлом 325 ствола (также обозначенным как «узел 1»), «устьевой узел 2», также обозначенный как 324 ВН (первый узел скважины 120W ниже по потоку от перфорации), и поверхностную сеть 130. Переменные «q» обозначают массовый расход при передаче (масса за определенное время) в различных соединениях 330.
Модель 690 включает многосегментную скважину, разделяющуюся в узле 324.1 на два сегмента. В каждом сегменте соответствующий устьевой узел 324ВН соединен с соответствующим узлом 325 ствола, соединенным с перфорационными ячейками 320. Выше общего узла 324.1 имеются два других узла 324.2 и 324.3. Узел 324.3 соединен с поверхностной сетью 130. Показанные на фиг. 3 и фиг. 6 модели являются моделями «объединенной скважины» (lumped well model), то есть поток из перфорационных ячеек в каждом скважинном стволе моделируется как поток из этих ячеек в единый узел 325.
Модель 694 (сеточная модель скважины, то есть модель со множеством узлов 325) содержит три перфорационных узла 325, обозначенных снизу вверх как узлы 1, 2, 3. Узел 3 соединен с устьевым узлом 4 (обозначенным как 324ВН). Каждый из узлов 1, 2, 3 соединен с соответствующей перфорационной ячейкой 320. Узел 324ВН соединен с поверхностной сетью 130.
Глобальная матрица для неявного построения (FIM) модели 694 показана на фиг. 11. Далее мы рассмотрим то, как можно аппроксимировать решение давления на стороне скважины (уравнения (8)) простой моделью объединенной скважины.
Падение давления на соединении между верхним по потоку узлом и следующим нижним по потоку узлом (например от узла 1 до узла 2 в модели 680) может быть определено гидравлическим уравнением следующим образом:

Здесь нижние индексы up и dw обозначают нижние и верхние по потоку узлы (например, узлы 1 и 2 в модели 680) в соединении 330 или 331 по потоку;
- Рuр и Pdw являются давлениями в этих узлах;
- nс является количеством компонентов флюида, протекающего через соединение;
- для каждого компонента k, значение qk является массовым расходом потока этого компонента;
- f является функцией гидравлического уравнения (например, основанной на корреляции падения давления, табличном значении падении давления, законе Дарси или какой-либо другой модели).
Мы определяем состав компонента k как

где qT является суммарным массовым расходом потока через соединение (то есть суммой qk). (Обозначение х для составов не следует путать с символом х в уравнениях (7), (8) and (9)).
Следовательно:

где

Комбинирование уравнений (е6) и (е7) дает:

Дифференцирование уравнения (е6) дает:

Подстановка уравнений (е8) и (е9) в уравнение (е4) дает:
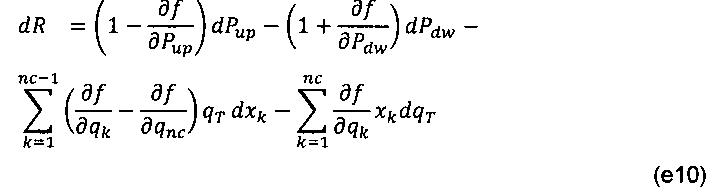
Таким образом, производные якобиана (частные производные) относительно первичных неизвестных будут выглядеть следующим образом:

Следует отметить, что буква R здесь соответствует F в уравнениях (1). Одинаковый символ R используется для различных скалярных уравнений (1).
На фиг. 7 приведен пример якобиана. Производные (е11)-(е14) показаны в четвертой строке, отмеченной "(е4)" в правом столбце (относящемся к уравнениям (е4)). Фиг. 7 предполагает, что производны е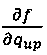 и
и 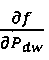 равны нулю. Это истинно, если f рассматривается явным образом (то есть заменяется значением с предыдущей итерации), но также может быть истинным при рассмотрении f неявным образом. Некоторые производные (е13), (е14) показаны символами h и ε.
равны нулю. Это истинно, если f рассматривается явным образом (то есть заменяется значением с предыдущей итерации), но также может быть истинным при рассмотрении f неявным образом. Некоторые производные (е13), (е14) показаны символами h и ε.
Для устьевого узла может быть применено ограничение давления:

где Pspec является предварительно заданной константой. В качестве альтернативы, на соединении может быть активировано ограничение по расходу потока фазы, то есть:

Здесь nр является количеством фаз (во многих задачах имеется три фазы: газ, нефть и вода). Для каждой фазы n, Qn является соответствующим объемным расходом потока; аn является соответствующей предварительно заданной константой. Qspec является максимально допустимым объемным расходом потока, который может протекать в соединении.
В альтернативном варианте может быть определено следующее ограничение:
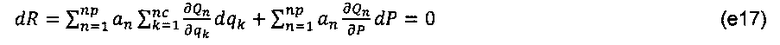
Подстановка уравнений (е8) и (е9) в уравнение (е17) дает:
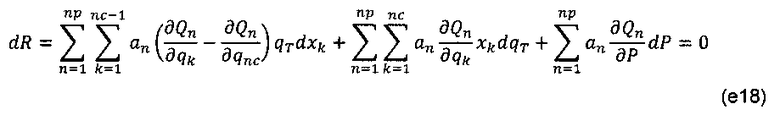
Обычно ограничение расхода задано для условий поверхности, поэтому член производной давления может быть опущен, хотя здесь он показан для более общего случая. Производные якобиана относительно первичных неизвестных получают следующим образом:

Приведенные выше уравнения получены рассмотрением потока через соединение 330.
Для каждого узла 324 и 325 используются уравнения баланса массы. В частности (см. для примера узлы 2 и 3 модели 694), для каждого узла ствола общий массовый расход потока каждого компонента в узел равен сумме массовых расходов потока этого же компонента из каждого входного соединения и каждой перфорации. Каждый из этих узлов может иметь или не иметь перфораций, и обозначим как perf количество перфораций во взятом для примера узле "r". Узел r может иметь множество входных соединений. Обозначим как "inc" количество входных соединений 330; обозначим как "out количество выходных соединений. Флюид втекает в узел через перфорации и соединения, поэтому общий массовый расход потока в узел будет:
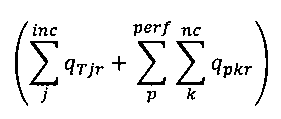
где qTjr является суммарным массовым расходом потока из соединения j в узел r, a qpkr является массовым расходом потока компонента к из перфорации р в узел.
Обозначим как xijr состав компонента i во входном потоке в узел r через соединение j; и обозначим как хir состав компонента i в суммарном входном потоке в узел r. Для компонента i массовый расход потока компонента из узла будет:
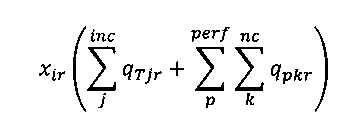
Входной массовый расход потока компонента i:
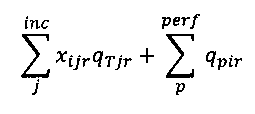
Уравнение баланса массы для компонента i тогда будет выглядеть как:
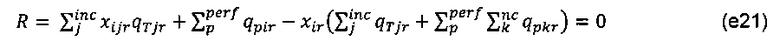
А соответствующие производные якобиана:
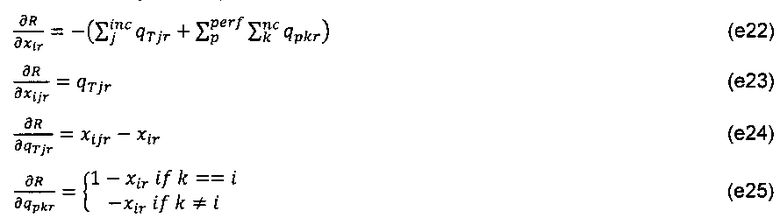
Уравнения (1) будут включать уравнения баланса массы для компонентов i=1,…nс-1.
Пример на фиг. 7 показывает якобиан для двух узлов, как в модели 680. Одним из узлов является узел 325, также показанный как узел 1, уравнения для которого соответствуют строкам, помеченным (е21), (е21), и (е27). Соответствующие переменные показаны в заглавной строке как qT1 (суммарный массовый расход потока от узла 1 к узлу 2), х11 (состав компонента 1 в узле 1), х21 (состав компонента 2 в узле 1).
Другим узлом является устьевой узел 2, соответствующий последним трем строкам. Соответствующими переменными являются qT2 (суммарный массовый расход потока из узла 2), х21 (состав компонента 1 в узле 2), х22 (состав компонента 2 в узле 2). Фиг. 7 в применимости не ограничена моделью 680.
Уравнение баланса массы может быть проще, если имеется только одно входное соединение и одно выходное соединение, и если узел не имеет перфораций; в этом случае уравнение примет вид:

где хup является составом компонента i в верхнем по потоку узле входного соединения в узел r, а xdw является составом компонента i в узле r. Например, см. строки, отмеченные (е26) в нижней части фиг. 7.
Уравнение суммарного баланса массы уравнивает входной массовый расход потока и выходной массовый расход потока в каждом узле r следующим образом:
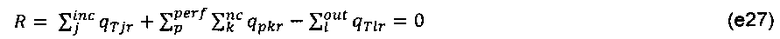
где qTIr является суммарным массовым расходом потока из узла r в выходное соединение I. Производные следующие:

Перенос массы между ячейкой 320 с перфорацией 134 и узлом 325 ствола описывается уравнением перфорации следующим образом (здесь мы предполагаем, что через перфорации идет добыча, а не нагнетание; индекс r обозначает коллекторную ячейку 320, ближайшую к перфорации):


Здесь qk является массовым расходом потока из перфорации р (ячейка 320) в узел 325; С является задаваемой пользователем константой; λnr является подвижностью фазы n в перфорационной ячейке 320, идентифицируемой индексом r, ρnr является плотностью фазы n в этой же ячейке; zknr является массовой долей компонента k в фазе n в ячейке; Рr является давлением в этой же ячейке; Pw является давлением в узле 325; Dr и Dw являются глубинами ячейки 320 и узла 325 соответственно; и γr является градиентом гидростатического давления, так что произведение γr(Dw-Dr) представляет разность в давлении за счет напора флюида.
Для первых трех строк фиг. 7, помеченных (е31), переменные в уравнении (е31) выражаются через первичные переменными: давление в перфорационной ячейке 320, и mi - масса компонента i в перфорационной ячейке 320.
Первичными переменными являются следующие:
1. В области сети (то есть в скважинах, а следовательно, в перекрытии между G1 и G2, и возможно в поверхностной сети, а следовательно, в группе G2):
- qT (суммарные потоки в разнообразных соединениях);
- xi (составы компонентов i в соединениях); и
- Р (давления).
2. В области коллектора (то есть, в коллекторных ячейках 320, а следовательно, в группе G1):
- mi, масса компонента i в перфорационной ячейке 320;
- Р (давления).
3. На границе между двумя областями (в перфорационных узлах 325, а следовательно, в группе G1):
- qpk (массовый расход потока компонента k через перфорацию р).
В уравнении (8):
- Строки Аwr соответствуют уравнениям (е10), (е15), (е16), (е17), (е18).
- Строки Аfw соответствуют некоторым из тех же самых уравнений, и возможно, другим уравнениям (не показаны) для поверхностной сети.
- Строки Аrr соответствуют уравнениям баланса массы для каждой ячейки, и уравнениям баланса объема для каждой ячейки (объем флюида = объем пор); эти уравнения могут быть хорошо известны и здесь не показаны.
В нижеследующем примере, иллюстрирующем решение уравнений (8) для модели 680 скважины, мы покажем, как исключить qT и qpk, и как упростить получающуюся в результате линейную систему, в которой первичными переменными являются хi, Р в области сети и mi, Р в области коллектора, до системы только давления. Данный пример включает в себя одну фазу с тремя компонентами. Якобиан Ньютона-Рафсона на стороне сети показан на фиг. 7 (фиг. 7 не ограничена моделью 680, но применима и для других моделей). Другими словами, на фиг. 7 показана часть 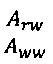 уравнения (8). В уравнении (е4) функция f рассматривается явным образом (ее значение является значением, полученным на предыдущей итерации, или является изначальным значением, если это первая итерация), поэтому ее производные равны нулю. Расходы qpk потока в перфорационных соединениях и суммарные расходы qTk потока во всех остальных соединениях сети исключаются, как показано на фиг. 8, и остаются только строки, изначально основанные на уравнениях баланса массы.
уравнения (8). В уравнении (е4) функция f рассматривается явным образом (ее значение является значением, полученным на предыдущей итерации, или является изначальным значением, если это первая итерация), поэтому ее производные равны нулю. Расходы qpk потока в перфорационных соединениях и суммарные расходы qTk потока во всех остальных соединениях сети исключаются, как показано на фиг. 8, и остаются только строки, изначально основанные на уравнениях баланса массы.
На фиг. 7 номер уравнения для каждой строки указан в правом столбце. На фиг. 8 - фиг. 9 строки были добавлены или вычтены согласно нижеследующему описанию, но в правом столбце указаны те же самые номера уравнений, как в соответствующих строках фиг. 7, что позволяет без труда идентифицировать строки. Предполагается, что ячейка 320 в модели 680 имеет одну перфорацию, а первые три строки фиг. 7 соответствуют уравнениям (е31). Первичные переменные указаны вверху рисунков, поэтому переменные в уравнениях (е31) выражаются в терминах первичных переменных, то есть масс m1 и m2 компонентов 1 и 2 в ячейке 320 и давления Р в ячейке. Значение Р1 на фиг. 7 является давлением в узле 1 ствола (Pw в уравнениях (е31)); Р2 является давлением в следующем узле 2 вверх по потоку по сважинному стволу.
Значения с в первых трех столбцах строк (е31) на фиг. 7 представляют собой соответствующие производные.
Значения, T1, T2, Т3 рассчитывают как:
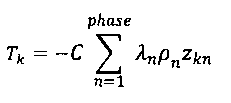
где k=1, 2, 3. См. уравнение (е31); индекс r опущен для простоты.
Переменная gT1 является массовым расходом потока в соединении между узлами 1 и 2 (то есть, узлами 320 и 324ВН) в модели 680. Переменная qT2 является массовым расходом потока из узла 2. Переменные хij являются составами в различных узлах; первый индекс, i, является номером компонента, а второй индекс является номером узла. То есть, х12 является составом компонента 1 в узле 2. Количество компонентов nс=3, и первичные переменные включают составы только для первых двух компонентов.
В строке для уравнения (е4), значения ε, h11, h21 зависят от функции f в уравнении. Подходящие для этой цели уравнения хорошо известны. Следует отметить, что функция f может рассматриваться явным или неявным образом.
Как указывалось выше, nр=1. Переменные Р1 и Р2 являются давлениями в узлах 1 и 2 соответственно.
В строке (е17) ограничивающее уравнение может быть для узла 2. В этом случае хk означает хk2, a dk даются уравнением (е6), то есть dk=хk2qТ2. Объемные расходы Qn потока представляют собой расходы в соединении от узла 2 до поверхностной сети. Как указывалось выше, применимость фиг. 7 - фиг. 10 не ограничивается моделью 680.
Следует отметить, что столбцы х12, х22 (составы узла 2) имеют нулевые значения в строках (е21), (е21), (е27) баланса массы для узла 1. Однако, столбцы х11, х21 (составы в узле 1) имеют несколько ненулевых значений в строках баланса массы (три последние строки (е26), (е26), (е27)) для узла 2. Желательно исключить эти ненулевые значения для того, чтобы построить матрицу давления из уравнений баланса массы.
На фиг. 8 суммарные массовые расходы qТ2 потока и расходы qpk потока в перфорационных соединениях были исключены. На фиг. 8 - фиг. 10 показаны только строки уравнения баланса массы для узлов 1 и 2. На фиг. 9 уравнения баланса массы в перфорационном узле 1 (первые три строки, помеченные соответственно как (е21), (е21), (е27)) были добавлены к соответствующим уравнениям базисного узла (устьевой узел 2 в этом случае), то есть строки 1, 2, 3 добавлены к соответствующим строкам 4, 5, 6 для устранения связывающих членов, относящихся к составу, между двумя этими узлами. Перед добавлением строки 4 и 5 умножили на 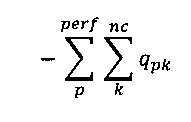 .
.
Теперь столбцы для составов х11, х21 узла 1 имеют нулевые значения для узла 2 (в трех последних строках). Столбцы для составов х12, х22 узла 2 сохраняют нулевые значения для узла 1 (в трех первых строках).
В базисном узле 2 (324ВН), члены состава остаются только в диагональном блоке, как показано ниже.
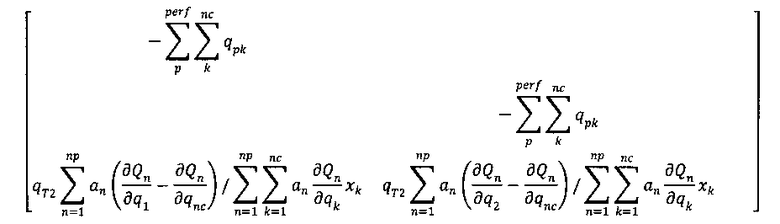
Мы можем исключить ненулевые члены состава в последней строке левым умножением последних трех строк на матрицу
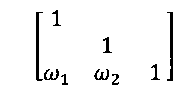
где:
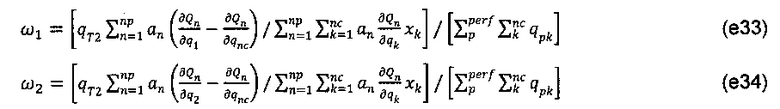
Это означает, что уравнения (26) баланса массы компонента для узла 2 добавляются к уравнению (27) суммарного баланса массы для узла 2 с соответствующими коэффициентами ω1 и ω2 для исключения членов хi2 и ω2 компонента узла 2 в уравнении суммарного баланса массы. Члены компонента узла 1 остаются нулевыми.
Получающаяся в результате матрица показана на фиг. 10. Следовательно, получена матрица давления на стороне скважины на основе базисного узла 2, как показано в последней строке фиг. 10. Другими словами, для узлов скважины остаются только переменные давления. В других вариантах осуществления аналогичные результаты получаются при использовании узла 1 в качестве базисного узла, и в частности, все члены компонента исключаются в уравнении суммарного потока массы для узла 1.
Что касается варианта осуществления по фиг. 10, так как

мы имеем:
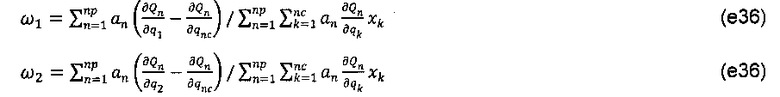
Далее объясним физическое значение этой матрицы давления. Для ограничения расхода нефти в системе тяжелой нефти:

Знаменатель в уравнениях (е36) и (е37) может быть переписан следующим образом:

а множители в уравнениях (е36) и (е37) могут быть упрощены как:

При подстановке уравнений (е39) и (е40) в последнюю строку на фиг. 10 коэффициент давления в базисном узле 2 (коэффициент Р1) может быть реорганизован следующим образом:
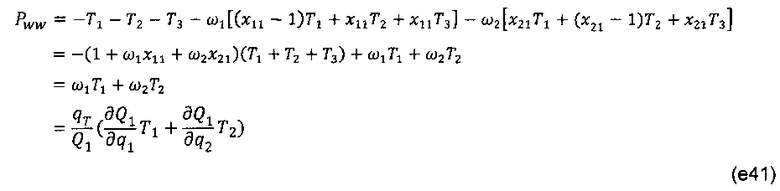
где:

См. уравнение (е31); индекс r опущен для простоты.
Очевидно, что коэффициент (коэффициент Р1) давления является суммой подвижностей каждого компонента, взятых с весом их вклада в общий расход потока нефтяной фазы, что не противоречит модели простой скважины. Единственным отличием является то, что матрица давления масштабирована на константу - 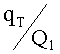
Связывающая матрица между коллектором и скважиной (левые три столбца в нижней строке фиг. 10) выглядит следующим образом:
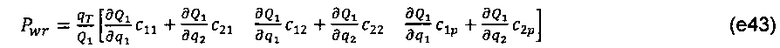
Как можно видеть по примерам на фиг. 7 и фиг. 8, связывающие члены хi1 состава во внедиагональной подматрице нижнего по потоку узла 2 являются отрицательными относительно связывающих членов состава в диагональной подматрице верхнего по потоку узла 1, когда f в гидравлическом уравнении (е4) рассматривается явным образом. (Здесь «внедиагональный» обозначает составы в одном узле в строках для другого узла; «диагональный» обозначает состав в узле в строках самого узла). Следует отметить, что строки 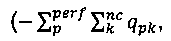 0) и (0,
0) и (0, 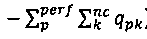 ) в строках (е21) фиг. 7 одинаковы с точностью до постоянного множителя, как строки (1, 0) и (0, 1) в строках (е26). Эти связывающие члены состава в первых nc-1 строках (уравнения баланса массы компонента) для каждого узла являются суммарным входным расходом потока в нижнем по потоку узле. Это должно быть истинно для всех узлов сеточной модели скважины, если не существует перекрестных потоков или ограничений, применяемых к этим узлам кроме устьевого узла. Мы покажем это на следующем примере.
) в строках (е21) фиг. 7 одинаковы с точностью до постоянного множителя, как строки (1, 0) и (0, 1) в строках (е26). Эти связывающие члены состава в первых nc-1 строках (уравнения баланса массы компонента) для каждого узла являются суммарным входным расходом потока в нижнем по потоку узле. Это должно быть истинно для всех узлов сеточной модели скважины, если не существует перекрестных потоков или ограничений, применяемых к этим узлам кроме устьевого узла. Мы покажем это на следующем примере.
На фиг. 11 показан якобиан на стороне скважинного ствола (часть 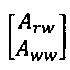 в уравнении (8)) после исключения суммарных расходов qTk потока и расходов qpTi потока (то есть на этапе фиг. 8) в перфорационных соединениях для модели 694 с ограничением по расходу, примененным к узлу 4. Первые три строки соответствуют уравнениям (21), (27) баланса массы для узла 1; следующие три строки соответствуют уравнениям (21), (27) баланса массы (MB) для узла 2; следующие три строки соответствуют уравнениям (21), (27) баланса массы (MB) для узла 3; последние три строки соответствуют уравнениям (21), (27) баланса массы для узла 4. Для каждого узла первые два уравнения баланса массы являются уравнениями для соответствующих компонентов 1 и 2; последнее уравнение баланса массы является уравнением для суммарного потока через узел.
в уравнении (8)) после исключения суммарных расходов qTk потока и расходов qpTi потока (то есть на этапе фиг. 8) в перфорационных соединениях для модели 694 с ограничением по расходу, примененным к узлу 4. Первые три строки соответствуют уравнениям (21), (27) баланса массы для узла 1; следующие три строки соответствуют уравнениям (21), (27) баланса массы (MB) для узла 2; следующие три строки соответствуют уравнениям (21), (27) баланса массы (MB) для узла 3; последние три строки соответствуют уравнениям (21), (27) баланса массы для узла 4. Для каждого узла первые два уравнения баланса массы являются уравнениями для соответствующих компонентов 1 и 2; последнее уравнение баланса массы является уравнением для суммарного потока через узел.
Столбцы P1, Р2, Р3 в левой половине обозначают давления в соответствующих перфорационных ячейках 320. Аналогичные символы в правой половине относятся к давлениям в соответствующих узлах 325.
На фиг. 12, 13, и 14 показан процесс построения матрицы давления. Фиг. 12 - фиг. 14 показывают только строки, соответствующие уравнениям баланса массы для узла 4 (последние три строки на фиг. 11). Для этих иллюстраций мы определяем:
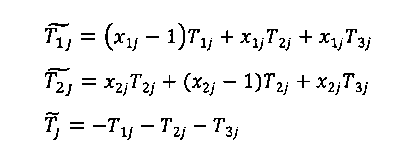
где j является индексом перфорации, а Т рассчитывается с использованием уравнения (е42).
На фиг. 12 уравнения баланса массы для узлов 1, 2, и 3 (первые девять строк) были добавлены к уравнениям в устьевом узле 4 (три последних строки) для получения показанной на фиг. 12 матрицы. В частности, первые уравнения (для компонента 1) для узлов 1, 2, 3 добавлены к первому уравнению для узла 4; вторые уравнения (для компонента 2) для узлов 1, 2, 3 добавлены ко второму уравнению для узла 4; а третьи уравнения (для суммарного потока) для узлов 1, 2, 3 добавлены к третьему уравнению для узла 4. В связывающих членах состава, соответствующих столбцам 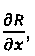 остаются члены
остаются члены 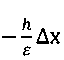 , сходные друг с другом. В этих членах значения h, ε являются гидравлическими производными относительно состава и суммарного расхода потока и рассчитываются с использованием уравнений (е13) и (е14), соответственно. Δх является разностью в массовом составе компонента между самим узлом и узлом, находящимся выше него по потоку. Как и в модели объединенной скважины, если градиент давления рассматривается явным образом, то есть функция f в уравнении (е4) вычисляется с использованием результатов предыдущей итерации, все эти производные равны нулю, так что все столбцы состава на фиг. 12 заполнены нулями. Затем все столбцы давления объединяют (добавляют) с последним столбцом, соответствующим давлению в устьевом узле, как показано на фиг. 13. И наконец, мы используем тот же способ, что и в модели 680 объединенной скважины для исключения диагональных членов состава, соответствующих последним трем столбцам на фиг. 13, а последняя строка на фиг. 14 берется в качестве коэффициентов давления для узла 4 скважины, у которого давление является единственным неизвестным для узла 4 на стороне скважины. Неизвестные давления отвязываются от других неизвестных на стороне скважины.
, сходные друг с другом. В этих членах значения h, ε являются гидравлическими производными относительно состава и суммарного расхода потока и рассчитываются с использованием уравнений (е13) и (е14), соответственно. Δх является разностью в массовом составе компонента между самим узлом и узлом, находящимся выше него по потоку. Как и в модели объединенной скважины, если градиент давления рассматривается явным образом, то есть функция f в уравнении (е4) вычисляется с использованием результатов предыдущей итерации, все эти производные равны нулю, так что все столбцы состава на фиг. 12 заполнены нулями. Затем все столбцы давления объединяют (добавляют) с последним столбцом, соответствующим давлению в устьевом узле, как показано на фиг. 13. И наконец, мы используем тот же способ, что и в модели 680 объединенной скважины для исключения диагональных членов состава, соответствующих последним трем столбцам на фиг. 13, а последняя строка на фиг. 14 берется в качестве коэффициентов давления для узла 4 скважины, у которого давление является единственным неизвестным для узла 4 на стороне скважины. Неизвестные давления отвязываются от других неизвестных на стороне скважины.
В предыдущих двух примерах, если функция f в гидравлическом уравнении (е4) рассматривается явным образом, или если градиент давления берется постоянным, то мы должны иметь:

и

где ref обозначает базисный узел. Мы можем применить тот же подход для связывающих членов от коллектора к стороне скважины и переместить эти члены 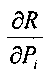 в столбец, соответствующий базисному узлу, как показано на фиг. 16. Отметим, что в этих связывающих членах для добывающих перфораций
в столбец, соответствующий базисному узлу, как показано на фиг. 16. Отметим, что в этих связывающих членах для добывающих перфораций 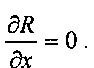 На стороне скважинного ствола связывающие члены
На стороне скважинного ствола связывающие члены 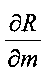 массы могут быть исключены с использованием упрощенных уравнений баланса массы на стороне коллектора, при введении новых связывающих членов между сетью и коллектором, как показано на фиг. 16.
массы могут быть исключены с использованием упрощенных уравнений баланса массы на стороне коллектора, при введении новых связывающих членов между сетью и коллектором, как показано на фиг. 16.
В частности, фиг. 15 показывает глобальную матричную структуру для неявного построения с неявными скважинами и поверхностной сетью. Толстые линии делят матрицу на девять блоков, которые соответствуют девяти блокам матрицы уравнения (7), то есть блокам Аrr, Аrw и т.д. Члены "х" указывают на возможные ненулевые элементы. Матрица на фиг. 15 имеет некоторое количество ячеек, некоторые из которых пустые (соответствуют нулевым элементам), а остальные имеют по четыре «х», указывающие на то, что ячейки могут иметь любую структуру.
На фиг. 16 показана матричная структура для показанного на фиг. 15 случая после исключения связывающих членов массы в соединениях добывающих перфораций. Показано только четыре блока, как и в матрице для уравнения (8), то есть блоки Аrr, Аrw, Аwr, Аww. В блоке Аww' давления являются единственными ненулевыми элементами. Члены "у" в блоке Awr означают «заполнители», то есть возможные ненулевые элементы, сгенерированные путем линейных комбинаций уравнений.
Матрица коэффициентов, получаемая из уравнений баланса массы, на стороне коллектора может быть упрощена до матрицы только давления, показанной на фиг. 17 и имеющей следующий вид:

где матрица Р продления и матрица R ограничения определяются следующим образом:

где
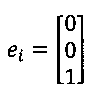
Матрица R ограничения является диагональной матрицей следующего вида:

где L является нижней матрицей LDU-факторизации диагональной подматрицы Arr, то есть:

В конце концов мы получаем глобальную линейную систему давления, включающую в себя коллектор и скважины, как показано на фиг. 17. В частности, мы получаем:

Ожидается, что благодаря вышеописанной обработке якобиана, ошибки аппроксимации в генерации приближенных решений методом Ньютона-Рафсона или другими методами уменьшаются, результатом чего может быть лучшее решение давления и, следовательно, лучшее общее решение уравнения (7).
В предыдущих двух примерах мы подразумевали наличие ограничения по расходу в скважинном соединении. При наличии ограничения по давлению, как показано в уравнении (е15), или если ограничений вообще не имеется (ограничение может быть наверху поверхностной сети), способ построения матрицы давления аналогичен и более прост. Множители, заданные в уравнениях (е33) и (е34) все равны нулю.
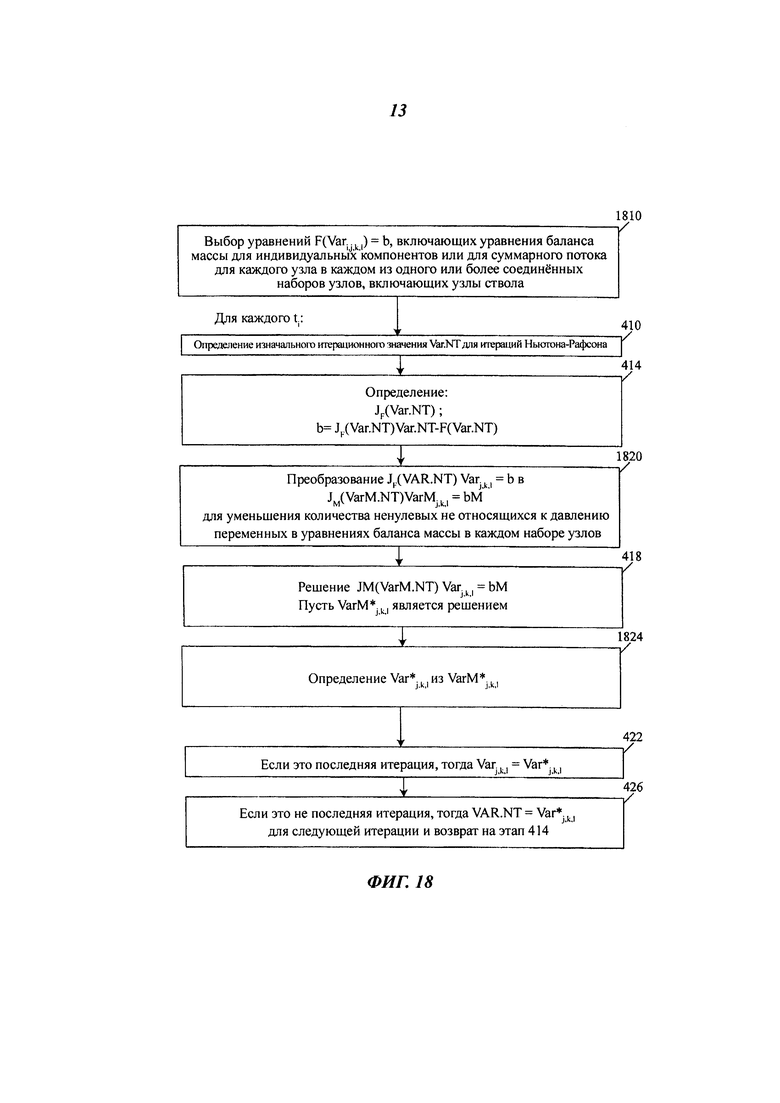
Вышеописанное обуславливание якобиана может быть использовано во многих схемах моделирования. Один пример проиллюстрирован на фиг. 18. На этапе 1810 выбирают уравнения (1), то есть F(Varj,j,k,l)=0, для включения уравнений баланса массы для выбранного набора узлов ствола (таких как узлы 1 и 2 в модели 680, или узлы 1-4 в модели 694). В некоторых осуществлениях эти узлы и соединения между ними образуют связный граф. В некоторых вариантах осуществления эти узлы являются последовательными узлами на траектории движения флюида. В некоторых вариантах осуществления набор узлов включает в себя узлы поверхностной сети 130 и/или коллекторные ячейки 320. В вышеприведенных примерах рассматривался только один набор узлов (таких как узлы 1 и 2), но может быть обеспечено множество наборов узлов. В каждом наборе выбирается базисный узел, и уравнения баланса массы других узлов добавляются к уравнению баланса массы базисного узла, а также для каждого набора выполняется другая обработка согласно приведенному выше описанию с целью исключения составов в уравнениях баланса массы базисного узла.
Уравнения баланса массы включают в себя, для каждого узла в наборе, уравнения для индивидуальных компонентов и/или уравнения для суммарного баланса массы. Также могут присутствовать уравнения перфораций.
Уравнения (1) затем решаются для каждого периода времени ti методом Ньютона-Рафсона согласно нижеследующему описанию. На этапе 410 (тот же, что на фиг. 4), выбирают изначальное итерационное значение Var.NT. На этапе 414 (тот же, что на фиг. 4), определяют якобиан при значении Var.NT, а член "b" правой стороны определяют для уравнения.

На этапе 1820 якобиан обрабатывают для исключения некоторых не относящихся к давлению коэффициентов путем комбинирования уравнений баланса массы в каждом наборе узлов, и, возможно, комбинируя разные столбцы, как проиллюстрировано выше со ссылкой на фиг. 7 - фиг. 17 и будет описано далее по тексту. Обозначим результирующий «модифицированный якобиан» как JM (то есть, JM может включать матрицу по фиг. 10 или фиг. 14), и обозначим соответствующие переменные как VarM (переменные могут меняться, так как могли быть добавлены столбцы давления; и некоторые столбцы могли быть отброшены; например, могли быть отброшены столбцы, соответствующие суммарным расходам потока в соединениях и расходам потока в перфорациях); и обозначим соответствующую правую сторону как bM. Уравнение (е50А) примет вид:

На этапе 418 (как на фиг. 4), компьютерная система решает уравнения (е50В), возможно (но не обязательно), используя метод Шварца, показанный на фиг. 5. Обозначим решение как VarM* j,k,l.
На этапе 1824 значения Var* j,k,l оригинальных переменных получают из VarM* j,k,l. Значения Var* j,k,l, следовательно, являются решением уравнения (е50А), и это решение используют в качестве следующего итерационного значения для Var.NT, после чего управление переходит к этапу 414, или же, альтернативно, выполнение метода Ньютона-Рафсона прекращают (этапы 422, 426 как на фиг. 4).
Возможны разнообразные варианты. Например, расчеты модифицированного якобиана этапов 414, 1820 могут выполняться в обобщенной форме без подстановки значения Var.NT, что фактически проиллюстрировано на фиг. 7 - фиг. 14. Затем, на каждой итерации значение Var.NT может быть подставлено в обобщенное выражение для модифицированного якобиана и модифицированной правой стороны для определения уравнения (е50В).
На фиг. 19 проиллюстрированы некоторые варианты осуществления обработки якобиана на этапе 1820. На этапе 1910 для каждого набора узлов выбирают базисный узел. В примерах, рассмотренных выше в отношении моделей 680 и 694, базисным узлом был устьевой узел, но вместо него может быть использован любой узел из набора. В некоторых вариантах осуществления базисный узел таков, что поток в базисный узел складывается из потоков из других узлов набора, или же таков, что поток из базисного узла складывается из потоков в другие узлы набора.
На этапе 1920, для соединений в пределах каждого набора исключают переменные qT суммарного массового расхода (как на фиг. 8). Из якобиана можно удалить некоторые строки.
На этапе 1930 в пределах каждого набора узлов уравнения баланса массы для не являющихся базисными узлов добавляют к соответствующим уравнениям баланса массы для базисного узла. В частности, уравнения баланса массы для каждого компонента к добавляют к уравнению баланса массы базисного узла для этого же компонента к; уравнения суммарного баланса массы (для полного потока через каждый не являющийся базисным узел) добавляют к уравнению суммарного баланса массы базисного узла. Перед добавлением может потребоваться умножение уравнений на некоторые коэффициенты. Коэффициенты зависят от уравнений (1) и от выбора первичных переменных. Добавление выполняют так, чтобы исключить недиагональные переменные массового потока (например, составы) в уравнениях баланса массы базисного узла.
На этапе 1940 уравнения баланса массы базисного узла комбинируют для исключения диагональных составов в уравнениях баланса массы базисного узла. Эта операция может быть выражена как левое умножение уравнений баланса массы базисного узла на матрицу L-1 где L является нижней матрицей в LU (lower-upper) факторизации квадратной матрицы, соответствующей диагональной части давления и состава уравнений баланса массы базисной матрицы. Пример матрицы L-1 описан выше в связи с уравнениями (е33), (е34), и выглядит как матрица:
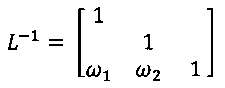
На этапе 1950 могут быть скомбинированы столбцы давления, как разъяснено выше в связи с уравнениями (е44), (е45).
В некоторых вариантах осуществления некоторые из этих операций опускаются. Например, можно опустить этап 1950 и/или 1940.
Как было отмечено выше, имеется много путей решения уравнения модифицированного якобиана на этапе 418, показанном на фиг. 18. В качестве примера можно привести способ с применением мультипликативного метода Шварца по фиг. 6, являющийся двухэтапным способом в предобусловливанием, выполняемым следующим образом: Уравнения (9) сети решают до выполнения итераций (для изначального итерационного значения x.sc, показанного на этапе 620 на фиг. 6), и в конце каждой итерации уравнения (9) решают снова для того, чтобы в расчете GMRES сохранять всегда нулевой сетевую невязку (невязку (9)). Процедура предобусловливания состоит из следующих этапов:
До выполнения итераций
1) Инициализация хr=0
2) Решение уравнения (9), то есть 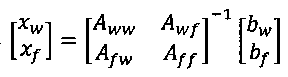 для определения xw и xf.
для определения xw и xf.
3) Обновление невязки в уравнении (8):
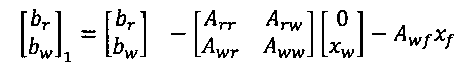
Выполнение итераций по методу Шварца, по к до достижения сходимости.
1) Решение уравнения (8) методом предобуславливателя CPR (Constraint Pressure Residual) с использованием матрицы (е46) давления согласно нижеследующему описанию:
2) Обновление невязки в уравнении (9):
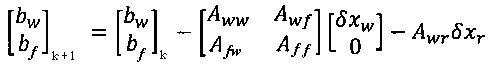
3) Решение уравнения (9), т.е. 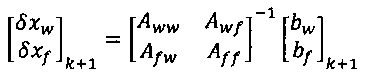
4) Обновление невязки в уравнении (8):
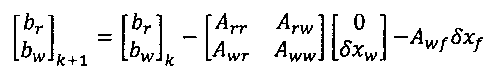
5) Расчет изменения δхr=δхr+Рδur решения, где Р как в (е47). Расчет изменения 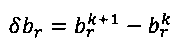 невязки. Передача δxr, δxw, δxf, δbr в GMRES для обновления решений xr, xw, xf.
невязки. Передача δxr, δxw, δxf, δbr в GMRES для обновления решений xr, xw, xf.
Этап 1) выше, решение уравнения (8) методом CPR:
1) Обновление невязки в уравнении (е50):
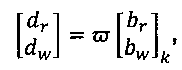 где ϖ - матрица ограничения, определенная ниже.
где ϖ - матрица ограничения, определенная ниже.
2) Решение уравнения (е50): 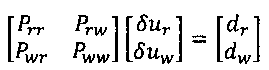
3) Отображение решения давления в полное решение:
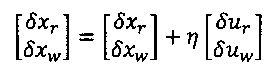
где η - матрица продления, определенная ниже.
4) Обновление невязки в уравнении (8):
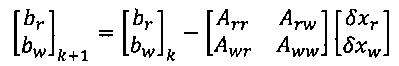
5) Решение уравнения (8):
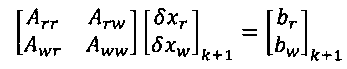
Матрицы ограничения и продления выглядят следующим образом:
ϖ - матрица ограничения

где Rr является матрицей ограничения в области коллектора и определяется в уравнении (е48). Rw является матрицей ограничения на стороне скважины и определяется следующим образом:

и wi=[ωx ω2 1 … ω1 ω2 1] где ω1 и ω2 определяют с использованием уравнений (е33) и (е34). Здесь nw является количеством скважин. Re является операционной матрицей, отвечающей за исключение связывающих членов массы, как показано на фиг. 14 и фиг. 16.
η - матрица продления.

Рr является матрицей продления на области коллектора, как определено в (е47). Pw является матрицей продления на стороне скважины:

где Ei для скважины i определено как:
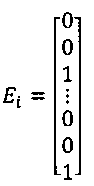
Здесь нули соответствуют столбцам с неизвестными состава, а единицы соответствуют столбцам с неизвестными давления.
Изобретение не ограничено вышеописанными вариантами осуществления. Изобретение включает в себя модифицированные методы Ньютона-Рафсона и Шварца. Например, в некоторых модификациях метода Ньютона-Рафсона для некоторого количества итераций используют один и тот же якобиан. Изобретение не ограничено конкретными переменными, и хотя в вышеприведенных примерах использовались составы из nс-1 компонентов составов и суммарные массовые расходы потока, вместо них можно использовать другие переменные, например, массовые расходы потока для всех компонентов. Кроме того, хотя вышеописанные примеры не используют уравнения объемного расхода потока (например, уравнения баланса объема) на стороне сети, другие варианты осуществления используют такие уравнения на стороне сети и используют объемные расходы потока и объемные составы (объемные доли индивидуальных компонентов) вместо массовых расходов или массовых составов (или совместно с ними). Члены объемного расхода потока исключают из уравнений баланса объема, используя способы, описанные выше для уравнений баланса массы.
Некоторые варианты осуществления обеспечивают способ определения множества значений (например, давлений, составов, расходов потока и т.д.) в промысловом объекте, реализуемый с использованием компьютера, при этом промысловый объект включает нефтяной и/или газовый коллектор и множество скважинных стволов, каждый из которых уже создан или подлежит созданию, причем каждый скважинный ствол обеспечивает один или более каналов для потока флюида в коллектор или потока флюида из коллектора. Способ включает:
получение компьютерной системой модели данных (например, моделей 680, 690, 694), представляющей коллектор и каждый скважинный ствол, причем модель содержит один или более узлов на указанном промысловом объекте, а узлы включают один или более наборов узлов, при этом каждый набор содержит единичный узел или множество соединенных друг с другом узлов, причем по меньшей мере один узел в каждом наборе находится в скважинном стволе. В некоторых вариантах осуществления набор содержит всего один узел, и диагональные члены состава исключаются как на этапе 1940; этап 1920 при этом может быть опущен. Разные наборы могут иметь, а могут и не иметь узлов в соответствующих разных скважинных стволах или сегментах скважинных стволов.
Способ также включает получение компьютерной системой системы линейных алгебраических уравнений, устанавливающих взаимосвязь между указанными значениями, представленными в уравнениях в качестве переменных, причем указанные значения включают давление для каждого узла в каждом наборе и включают значения расхода потока (например, массовые расходы потока или массовые составы или объемные расходы потока или составы), определенные расходами потока в узлы или из узлов, в каждом наборе, и для каждого узла уравнения содержат набор из одного или более уравнений со значениями в узле, при этом для по меньшей мере одного узла в каждом наборе узлов набор из одного или более уравнений содержит по меньшей мере одно уравнение с давлением в узле и с одним или более значениями расхода потока в узле;
выполнение компьютерной системой линейного преобразования системы уравнений, причем линейное преобразование включает линейное преобразование уравнений каждого набора уравнений для исключения по меньшей мере одного значения расхода потока из по меньшей мере одного уравнения в каждом наборе уравнений, и при этом линейное преобразование обеспечивает преобразованную систему уравнений; и
решение компьютерной системой преобразованной системы уравнений для указанных значений.
Некоторые варианты осуществления обеспечивают способ определения множества значений в промысловом объекте, реализуемый с использованием компьютера, при этом промысловый объект включает нефтяной и/или газовый коллектор и множество скважинных стволов, каждый из которых уже создан или подлежит созданию, причем каждый скважинный ствол обеспечивает один или более каналов для потока флюида в коллектор или потока флюида из коллектора, причем способ включает:
получение компьютерной системой модели данных, представляющей коллектор и каждый скважинный ствол, причем модель содержит один или более узлов на указанном промысловом объекте, а узлы включают набор из одного или более узлов скважины, каждый из которых является узлом в по меньшей мере одном скважинном стволе без перфораций по скважинному стволу между узлом и поверхностью земли;
получение компьютерной системой системы линейных алгебраических уравнений (например, на основе якобиана), устанавливающих взаимосвязь между указанными значениями, представленными в уравнениях в качестве переменных, при этом для каждого узла скважины указанные значения включают по меньшей мере одно значение в узле скважины;
решение компьютерной системой системы уравнений для указанных значений, причем решение системы включает:
решение компьютерной системой уравнений, полученных из первой подсистемы системы указанных уравнений (например, первой подсистемой могут быть уравнения (8)) с целью получения значений, включающих по меньшей мере одно значение в каждом узле скважины из указанного набора и по меньшей мере одно значение в коллекторе, или для получения разностей между такими значениями и их приближениями (например, разности могут быть δxr, δxw, δxf как указано выше);
решение компьютерной системой уравнений, полученных из второй подсистемы системы указанных уравнений (например, второй подсистемой могут быть уравнения (9)) с целью получения значений, включающих по меньшей мере одно значение в каждом узле скважины из указанного набора и по меньшей мере одно значение в коллекторе, или для получения разностей между такими значениями и их приближениями;
причем первая подсистема перекрывается со второй подсистемой, и по меньшей мере одно значение узла скважины из указанного набора или соответствующую разность между значением и его приближением величиной находят решением как первой подсистемы, так и второй подсистемы;
при этом способ дополнительно включает построение компьютерной системой решения системы уравнений по решениям первой и второй подсистем.
Изобретение включает компьютерные программы, обеспечивающие возможность выполнения компьютерной системой (такой как система, показанная на фиг. 2) любого из вышеописанных способов. Изобретение включает компьютерные программные продукты, например, машиночитаемые носители информации или компьютерные системы, содержащие компьютерную программу, обеспечивающую возможность выполнения компьютерной системой таких способов. Компьютерные программы могут быть сохранены на машиночитаемом носителе информации и могут быть переданы по компьютерной сети в компьютерную систему и загружены на такой носитель информации. Изобретение включает способы, содержащие передачу таких компьютерных программ по сети. Возможны другие осуществления и варианты в пределах объема изобретения, определенного в приложенной формуле изобретения.
Некоторая информация, относящаяся к вышеприведенному раскрытию, может быть получена из указанных ниже источников, включенных в настоящую заявку посредством ссылки (при этом не заявляется о том, касаются ли данные публикации уровня техники, относящегося к настоящему раскрытию):
- Публикация заявки на патент США 2012/0022841 А1 (26 января 2012), автор изобретения Appleyard.
- Martin J. Gander et al., "An optimal block iterative method and preconditioner for banded matrices with applications to PDEs on irregular domains" «Оптимальный блочный итерационный метод и предобусловливатель для ленточных матриц в применении к уравнениям в частных производных на нерегулярных областях», Report 10-05-21, страницы 1-27, май 2010, доступен в сети Интернет по адресу http://www.math.temple.edu/~szyld.
- РСТ публикация WO 2011/136861 А1 (3 ноября 2011), заявитель EXXONMOBIL Upstream Research Company.


Изобретение относится к добыче нефти и газа с применением компьютерного моделирования. Техническим результатом является повышение эксплуатации месторождения. Предложен способ определения множества значений в промысловом объекте, реализуемый с использованием компьютера, и включает этапы, на которых осуществляют: получение компьютерной системой модели данных, представляющей коллектор и каждый скважинный ствол, причем модель содержит один или более узлов на указанном промысловом объекте, а узлы включают один или более наборов узлов, при этом каждый набор содержит единичный узел или множество соединенных друг с другом узлов, причем по меньшей мере один узел в каждом наборе находится в скважинном стволе; получение компьютерной системой системы линейных алгебраических уравнений, устанавливающих взаимосвязь между указанными значениями, представленными в уравнениях в качестве переменных, причем указанные значения включают давление для каждого узла в каждом наборе и включают значения расхода потока, определенные расходами потока в узлы или из узлов, в каждом наборе, и для каждого узла уравнения содержат набор из одного или более уравнений со значениями в узле, при этом для по меньшей мере одного узла в каждом наборе узлов набор из одного или более уравнений содержит по меньшей мере одно уравнение с давлением в узле и с одним или более значениями расхода потока в узле; выполнение компьютерной системой линейного преобразования системы уравнений, причем линейное преобразование включает линейное преобразование уравнений каждого набора уравнений для исключения по меньшей мере одного значения расхода потока из по меньшей мере одного уравнения в каждом наборе уравнений и при этом линейное преобразование обеспечивает преобразованную систему уравнений; и решение компьютерной системой преобразованной системы уравнений для указанных значений. 10 н. и 10 з.п. ф-лы, 19 ил.
1. Способ определения множества значений в промысловом объекте, реализуемый с использованием компьютера, при этом промысловый объект включает нефтяной и/или газовый коллектор и множество скважинных стволов, каждый из которых уже создан или подлежит созданию, причем каждый скважинный ствол обеспечивает один или более каналов для потока флюида в коллектор или потока флюида из коллектора, причем способ включает:
получение компьютерной системой модели данных, представляющей коллектор и каждый скважинный ствол, причем модель содержит один или более узлов на указанном промысловом объекте, а узлы включают один или более наборов узлов, при этом каждый набор содержит единичный узел или множество соединенных друг с другом узлов, причем по меньшей мере один узел в каждом наборе находится в скважинном стволе;
получение компьютерной системой системы линейных алгебраических уравнений, устанавливающих взаимосвязь между указанными значениями, представленными в уравнениях в качестве переменных, причем указанные значения включают давление для каждого узла в каждом наборе и включают значения расхода потока, определенные расходами потока в узлы или из узлов, в каждом наборе, и для каждого узла уравнения содержат набор из одного или более уравнений со значениями в узле, при этом для по меньшей мере одного узла в каждом наборе узлов набор из одного или более уравнений содержит по меньшей мере одно уравнение с давлением в узле и с одним или более значениями расхода потока в узле;
выполнение компьютерной системой линейного преобразования системы уравнений, причем линейное преобразование включает линейное преобразование уравнений каждого набора уравнений для исключения по меньшей мере одного значения расхода потока из по меньшей мере одного уравнения в каждом наборе уравнений и при этом линейное преобразование обеспечивает преобразованную систему уравнений; и
решение компьютерной системой преобразованной системы уравнений для указанных значений.
2. Способ по п. 1, отличающийся тем, что значения расхода потока включают массовые составы всех компонентов кроме компонента в узлах набора и включают суммарные массовые расходы потока в каждый узел и/или из каждого узла каждого набора.
3. Способ по п. 1, отличающийся тем, что значения расхода потока включают массовые расходы потока всех компонентов в каждый узел и/или из каждого узла каждого набора.
4. Способ по п. 1, отличающийся тем, что для каждого набора узлов соответствующие одно или более уравнений включают по меньшей мере уравнение баланса для каждого узла в наборе, причем уравнение баланса является уравнением баланса массы или уравнением баланса объема и представляет баланс суммарного потока в узел и/или из узла или потока по меньшей мере одного, но не всех компонентов флюида в узел и/или из узла; а
выполнение линейного преобразования включает для каждого набора линейное комбинирование уравнений баланса для различных узлов, при этом в каждой линейной комбинации уравнений баланса для различных узлов одного и того же набора каждое из комбинируемых уравнений баланса представляет баланс суммарного потока, или каждое из комбинируемых уравнений баланса представляет баланс потока тех же одного или большего количества компонентов, что и каждое другое комбинируемое уравнение баланса.
5. Способ по п. 4, отличающийся тем, что в линейном преобразовании для каждого набора уравнений линейная комбинация уравнений баланса заменяет собой уравнение баланса для одного из узлов соответствующего набора узлов.
6. Способ по п. 5, отличающийся тем, что каждый набор узлов содержит базисный узел и каждый набор таков, что поток в базисный узел складывается из потоков из других узлов набора, или таков, что поток из базисного узла складывается из потоков в другие узлы набора; а в линейном преобразовании для каждого набора уравнений линейная комбинация заменяет собой соответствующее уравнение баланса для базисного узла.
7. Способ по п. 6, отличающийся тем, что для по меньшей мере одного набора узлов соответствующие одно или более уравнений включают множество уравнений баланса для по меньшей мере одного узла в наборе, причем множество уравнений баланса включает уравнение баланса, представляющее баланс суммарного потока в узел и/или из узла, и включает уравнение баланса, представляющее поток по меньшей мере одного или более, но не всех компонентов флюида в узел и/или из узла;
при этом выполнение линейного преобразования включает для по меньшей мере указанного по меньшей мере одного набора узлов линейное комбинирование друг с другом уравнений баланса для указанного по меньшей мере одного узла с целью исключения по меньшей мере одного значения расхода потока в уравнении баланса, представляющем баланс суммарного потока указанного по меньшей мере одного узла.
8. Способ по п. 1, отличающийся тем, что для по меньшей мере одного набора узлов соответствующие одно или более уравнений включают множество уравнений баланса для по меньшей мере одного узла в наборе, причем каждое уравнение баланса является уравнением баланса массы или уравнением баланса объема и представляет баланс суммарного потока в узел и/или из узла и/или потока по меньшей мере одного компонента флюида в узел и/или из узла;
при этом выполнение линейного преобразования включает для по меньшей мере указанного по меньшей мере одного набора узлов линейное комбинирование друг с другом уравнений баланса для указанного по меньшей мере одного узла с целью исключения по меньшей мере одного значения расхода потока в уравнении баланса, представляющего баланс суммарного потока в указанный по меньшей мере один узел или из указанного по меньшей мере одного узла.
9. Способ по любому из пп. 4-8, отличающийся тем, что каждое уравнение баланса является уравнением баланса массы, а значения расхода потока включают массовые составы всех компонентов кроме компонента в узлах набора и включают суммарные массовые расходы потока в каждый узел и/или из каждого узла каждого набора.
10. Способ по любому из пп. 4-8, отличающийся тем, что каждое уравнение баланса является уравнением баланса массы, а значения расходов потока включают массовые расходы потока всех компонентов в каждый узел и/или из каждого узла каждого набора.
11. Способ по любому из пп. 1-8, отличающийся тем, что один или более наборов узлов включают два набора узлов в соответствующих двух разных скважинных стволах.
12. Способ определения множества значений в промысловом объекте, реализуемый с использованием компьютера, при этом промысловый объект включает нефтяной и/или газовый коллектор и множество скважинных стволов, каждый из которых уже создан или подлежит созданию, причем каждый скважинный ствол обеспечивает один или более каналов для потока флюида в коллектор или потока флюида из коллектора, причем способ включает:
получение компьютерной системой модели данных, представляющей коллектор и каждый скважинный ствол, причем модель содержит один или более узлов на указанном промысловом объекте, а узлы включают набор из одного или более узлов скважины, каждый из которых является узлом в по меньшей мере одном скважинном стволе без перфораций по скважинному стволу между узлом и поверхностью земли;
получение компьютерной системой системы линейных алгебраических уравнений, устанавливающих взаимосвязь между указанными значениями, представленными в уравнениях в качестве переменных, при этом для каждого узла скважины указанные значения включают по меньшей мере одно значение в узле скважины;
решение компьютерной системой системы уравнений для указанных значений, причем решение системы включает:
решение компьютерной системой уравнений, полученных из первой подсистемы системы указанных уравнений с целью получения значений, включающих по меньшей мере одно значение в каждом узле скважины из указанного набора и по меньшей мере одно значение в коллекторе, или для получения разностей между такими значениями и их приближениями;
решение компьютерной системой уравнений, полученных из второй подсистемы системы указанных уравнений с целью получения значений, включающих по меньшей мере одно значение в каждом узле скважины из указанного набора и по меньшей мере одно значение в коллекторе, или для получения разностей между такими значениями и их приближениями; причем
первая подсистема перекрывается со второй подсистемой, и по меньшей мере одно значение узла скважины из указанного набора или соответствующую разность между значением и его приближением величиной находят решением как первой подсистемы, так и второй подсистемы; при этом способ дополнительно включает построение компьютерной системой решения системы уравнений по решениям первой и второй подсистем.
13. Машиночитаемый носитель или носители информации, содержащий компьютерную программу, обеспечивающую возможность выполнения компьютерной системой способа в соответствии с любым из пп. 1-8 и 12.
14. Машиночитаемый носитель или носители информации, содержащий компьютерную программу, обеспечивающую возможность выполнения компьютерной системой способа в соответствии с п. 9.
15. Машиночитаемый носитель или носители информации, содержащий компьютерную программу, обеспечивающую возможность выполнения компьютерной системой способа в соответствии с п. 10.
16. Машиночитаемый носитель или носители информации, содержащий компьютерную программу, обеспечивающую возможность выполнения компьютерной системой способа в соответствии с п. 11.
17. Компьютерная система, содержащая процессор и память, служащую для хранения компьютерной программы, при этом указанная программа при выполнении процессором обеспечивает возможность выполнения способа в соответствии с любым из пп. 1-8 и 12.
18. Компьютерная система, содержащая процессор и память, служащую для хранения компьютерной программы, при этом указанная программа при выполнении процессором обеспечивает возможность выполнения способа в соответствии с п. 9.
19. Компьютерная система, содержащая процессор и память, служащую для хранения компьютерной программы, при этом указанная программа при выполнении процессором обеспечивает возможность выполнения способа в соответствии с п. 10.
20. Компьютерная система, содержащая процессор и память, служащую для хранения компьютерной программы, при этом указанная программа при выполнении процессором обеспечивает возможность выполнения способа в соответствии с п. 11.
| US 20110040536 A1, 17.02.2011 | |||
| СПОСОБ ПОЛУЧЕНИЯ ЖИДКОСТИ ИЛИ/И ГАЗА ИЗ ПЛАСТОВОГО РЕЗЕРВУАРА | 2001 |
|
RU2281384C2 |
| ГЕНЕРАЦИЯ ПОСЛЕДОВАТЕЛЬНОСТИ ОПЕРАЦИЙ ПО КОМПЛЕКСНОМУ АНАЛИЗУ НА ОСНОВЕ ПРЕДСКАЗАТЕЛЬНОЙ МОДЕЛИ ОДИНОЧНОЙ СКВАЖИНЫ - МОДУЛЬНОГО ДИНАМИЧЕСКОГО ТЕСТЕРА (SWPM-MDT) | 2005 |
|
RU2336567C1 |
| US 20100252271 A1, 07.10.2010 | |||
| US 20060111882 A1, 25.05.2006 | |||
| US 20060080071 A1, 13.04.2006 | |||
| US 20070192071 A1, 16.08.2007. | |||
Авторы
Даты
2016-08-20—Публикация
2012-05-30—Подача