Предлагаемое изобретение относится к гидротехнике и может быть использовано для разрушения волновых пакетов (ударных волн, цунами) в различных системах защиты населения и береговой инфраструктуры и объектов от разрушения вследствие воздействия таких ударных волн.
Известны способы противодействия цунами (см., например, [1-5]). Рассмотренные методы противодействия цунами (борьбы с цунами) эффективны только тогда, когда противопоставляемые цунами устройства являются непреодолимым препятствием для названного волнового пакета (цунами). В случае если цунами, имеющая большую массу, амплитуду, скорость и, следовательно, импульс тела, имеет амплитуду и импульс тела больше (учитывая изменение амплитуды волны при взаимодействии с препятствием), чем противодействующая сила, импульс, препятствие, то фактически цунами не встречается с непреодолимым препятствием и при прохождении таких препятствий цунами не изменяет свою форму и скорость распространения.
Из известных наиболее близким по технической сущности и достигаемому результату является способ разрушения цунами, описанный в [5], заключающийся, в частности, в том, что на цунами оказывается механическое воздействие многими рядами водяных траншей. То есть этот способ противодействия цунами реализует препятствование распространению волны и эффективен только при незначительных значениях массы, амплитуды, скорости и, следовательно, импульса тела цунами. Данный метод не позволяет полностью решить поставленную задачу защиты от цунами.
Задачей предлагаемого технического решения является осуществление такого воздействия на цунами, при котором происходит ее разрушение.
Технический результат от использования предлагаемого решения - разрушение цунами.
Результат достигается тем, что в способе разрушения цунами, заключающемся в механическом воздействии на цунами, механическое воздействие производят путем модуляции цунами.
Модуляцию цунами проводят регулярным, периодическим механическим воздействием на подводную часть цунами.
Кроме того, модуляцию цунами можно проводить комплексом регулярных, периодических механических воздействий на подводную часть цунами.
В частности, регулярное механическое воздействие на подводную часть цунами производят периодически расположенными на пути прохождения цунами подводными препятствиями.
На дату подачи материалов заявки авторам не известны технические решения, совокупность существенных отличительных признаков которых совпадает с заявляемой.
Предлагаемый способ разрушения цунами поясняется чертежами:
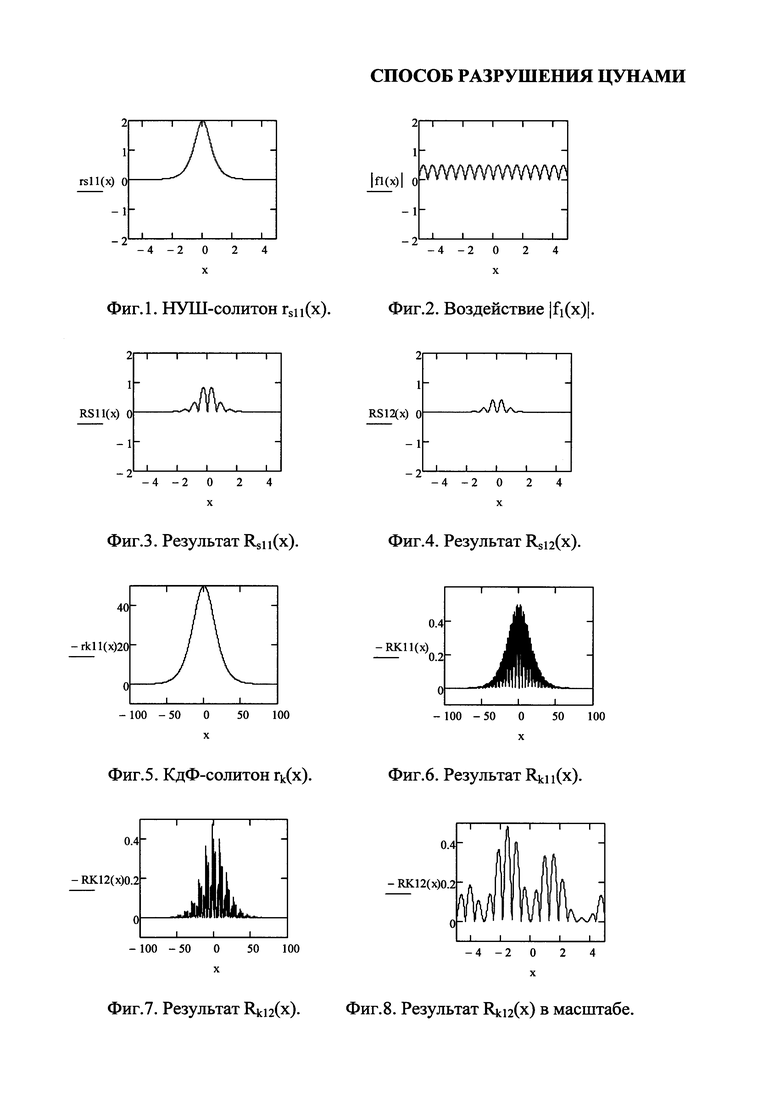
Фиг. 1 представляет НУШ-солитон rs11(x).
На фиг. 2 показано воздействие |f1(x)|, оказываемое на НУШ-солитон rs11(x).
На фиг. 3 приведен результат Rs11(x) модуляции НУШ-солитона.
На фиг. 4 приведен результат Rs12(x) модуляции НУШ-солитона.
Фиг. 5 представляет КдФ-солитон rk(x).
На фиг. 6 приведен результат Rk11(x) модуляции КдФ-солитона.
На фиг. 7 приведен результат Rk12(x) модуляции КдФ-солитона.
На фиг. 8 приведен результат Rk12(x) модуляции КдФ-солитона в масштабе.
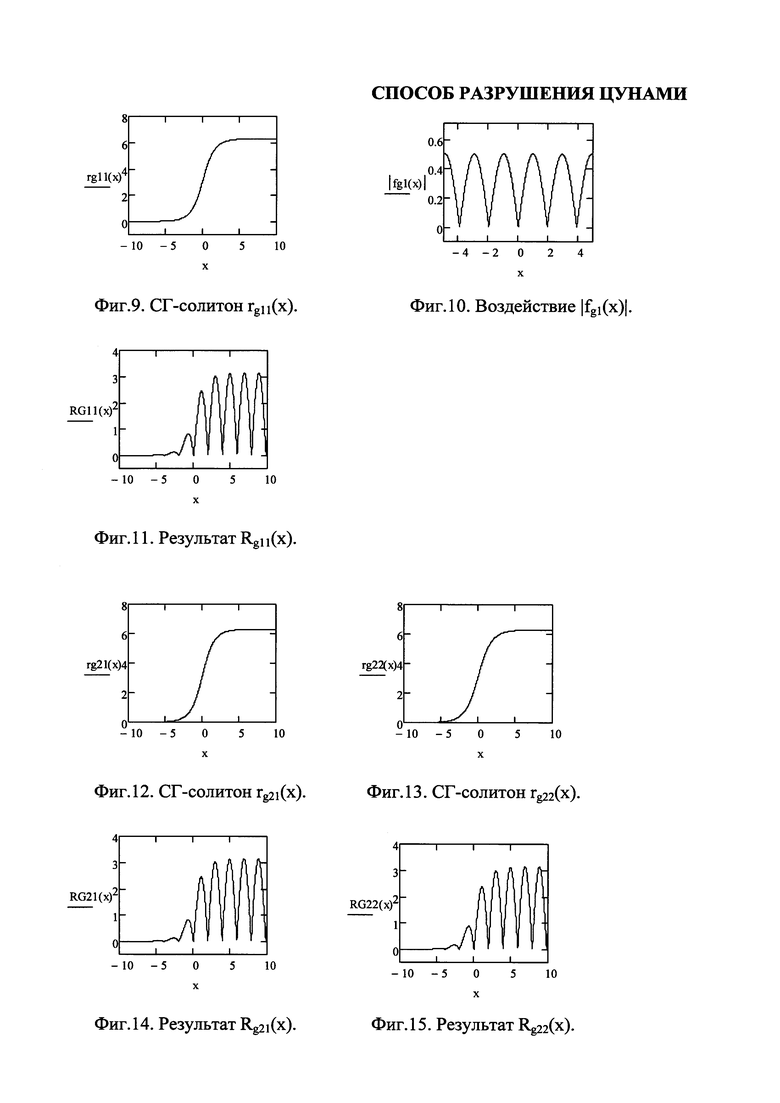
Фиг. 9 представляет СГ-солитон rg11(x).
На фиг. 10 показано воздействие |fg1(x)|, оказываемое на СГ-солитон rg11(x).
На фиг. 11 приведен результат Rg11(x) модуляции СГ-солитона.
Фиг. 12 представляет СГ-солитон rg21(x).
Фиг. 13 представляет СГ-солитон rg22(x).
На фиг. 14 приведен результат Rg21(x) модуляции СГ-солитона.
На фиг. 15 приведен результат Rg22(x) модуляции СГ-солитона.
Предлагаемое техническое решение описывается и реализуется, например, следующим образом.
Известно, что цунами является солитоном [6, с. 144, 220]. При этом солитон согласно общепринятым определениям - волновой пакет [7, с. 571] (обладающий аномально узким спектром), ударная волна [8, с. 214] и уединенная волна [9, 10], сохраняющая свою форму в течение всего срока жизни. То есть солитон обладает большей стабильностью и устойчивостью, чем любой другой волновой пакет, и менее подвержен деформациям, что, собственно, характеризует цунами. При этом цунами обладает поступательным движением. Так как цунами формируются вследствие смещения значительной массы воды, то такой волновой пакет имеет не только надводную часть, но и подводную часть [11, с. 110, 111].
Цунами (солитон) как волновой пакет на глубокой воде обычно описывается солитонным решением кубического нелинейного уравнения Шредингера (НУШ-солитон), хотя возможно использование солитонного решения уравнения Кортевега-де Фриза (КдФ-солитон). На мелкой воде, как правило, цунами описывается как КдФ-солитон. При этом известные формы цунами (ударной волны), вследствие поступательного движения, вблизи берега характеризуются опрокидыванием вершины (гребня), образование которой и опрокидывание связано с затормаживанием движения подводной части цунами вблизи берега - придонной массы воды (на мелкой воде) (расположенной под так называемой подошвой волны [1, с. 8; 12, с. 31]) при сохранении скорости гребня. Тем не менее, до опрокидывания гребня цунами как волна, наносящая удар, адекватно описывается солитонным решением нелинейного уравнения Кортевега-де Фриза (КдФ), а после опрокидывания - как КдФ-солитон с учетом уравнений движения.
Поднятый (например, вследствие сейсмических процессов) и распространяющийся слой жидкости (который в дальнейшем может быть оформлен как НУШ- или КдФ-солитон) описывается, как кинк, т.е. случай солитонного решения уравнения синус Гордона (СГ-солитон).
Известно, что наивысшей формой солитона является НУШ-солитон (солитонное решение кубического нелинейного уравнения Шредингера (НУШ)), вырождение которого приводит к КдФ-солитону, который, в свою очередь, может быть преобразован в СГ-солитон (солитонное решение уравнения синус Гордона, sin-Гордон, sine-Gordon, или, при вырождении - уравнения Клейна-Гордона) [9, 10].
То есть по сути задача разрушения цунами сводится к задаче разрушения солитона.
Солитоны являются резонансными образованиями и существуют только в резонансных системах, которые разрешают существование таких солитонов [9; 10; 13, с. 20]. Береговая линия (размеры бухт и т.п.) влияет на свойства резонансных систем.
В рамках существующей резонансной системы могут существовать только те солитоны, которые ею разрешены (в т.ч. которые имеют необходимые параметры и характеристики), в противном случае, солитоны дестабилизируются [9; 10; 13, с. 20]. К характеристикам солитона относится его частотный спектр. То есть значительное увеличение спектра волнового пакета влечет его разрушение. При этом любая модуляция солитона приводит к тому, что результирующий волновой пакет (результат модуляции солитона) будет иметь больший спектр, чем исходные импульс и колебание (и модулируемый, и модулирующий), что в данном случае изменяет условия существования солитона (с учетом его модуляции) в резонаторе и, как указано, приводит к его разрушению.
В отличие от прототипа и аналогов, в которых описывается изменение свойств резонансных систем, в предлагаемом техническом решении для достижения поставленной цели (разрушение цунами), следует механическим образом изменить свойства солитона, существующего и распространяющегося в данной системе. Указанное искусственное увеличение спектра солитона при его модуляции является требуемым изменением свойств солитона.
Увеличение спектра волнового пакета возможно при его модуляции (например, при перемножении с другим волновым пакетом или колебанием). Модуляция обеспечивается многократным (не одиночным) и регулярным механическим воздействием (или комплексом воздействий).
Модуляцию солитона проводят аналогично модуляции любого другого волнового пакета. Так как определение несущего колебания солитона проблематично (в отличие от определения несущей ординарных импульсов, что необходимо для модуляции импульсов по их несущей), то требуемую модуляцию волнового пакета следует проводить как воздействие на огибающую такого импульса (солитона). Модуляция солитона может носить избыточный характер, что приведет к разрушению соответствующего волнового пакета (что описано в литературе [14]). Аналитически это обосновывается как результат перемножения исходного импульса (солитона) с двумя колебаниями с некратными частотами. Спектр результирующего волнового пакета увеличен (сравнительно со спектром исходного импульса-солитона) за счет образования большого количества суммо-разностных и комбинационных частот, составляющих спектра, по которым распределяется энергия.
Аналитически и экспериментально (для критических и вырожденных условий и случаев) уже рассмотрено разрушение различных волновых пакетов (как электрических, так и механических импульсов на механическом маятнике) [15, 16].
Как указывалось, цунами на глубокой воде описывается НУШ-солитоном, определяемым по стандартному выражению [9; 10; 17, с.166; 18, с. 31; 19, с. 87]:
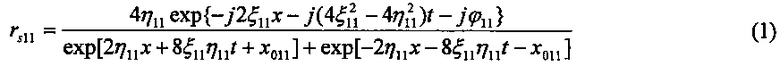
При значениях η11=1, ξ11=0, φ11=0, x011=0, при текущем значении t=0, форма солитона rs11(x) приводится на фиг. 1.
Как пример, воздействие осуществляется модулем обыкновенного гармонического колебания |f1(x)| (2) при параметрах A1=0,5, φ2=0 (фиг. 2).

Результаты различных видов модуляции Rs11(x) (3) и Rs12(x) (4) приведены на фиг. 3, фиг. 4 соответственно.


По сути, Rs12(x) (4) представляет разрушение НУШ-солитона вследствие его модуляции комплексом воздействий.
В результате модуляции исходный солитон преобразуется в модулированный сигнал, который представляет пакет обыкновенных волн (в отличие от исходного волнового пакета - НУШ-солитона). Такие модулированные сигналы не являются ударными волнами и не могут нанести ущерб, сопоставимый с воздействием цунами - НУШ-солитона.
Приведенная возможность разрушения более общей формы солитона (НУШ) показывает возможность разрушения и низших форм солитона (КдФ и СГ).
Как указывалось, цунами на мелкой воде и в некоторых случаях на глубокой воде описывается КдФ-солитоном, определяемым как [6, сс. 222, 281; 17, сс. 16, 18]:

Форма такого КдФ-солитона при параметре v=102 при текущем значении t=0 приведена на фиг. 5.
В случае если модуляция производится гармоническим колебанием fk1(x) (при параметрах B1=0,01, φ3=0) (6) и другими гармоническими колебаниями, варианты результата такой модуляции Rk11(x) (7) и Rk12(x) (8) приведены на фиг. 6, фиг. 7, соответственно. Кроме того, для наглядности результат модуляции Rk12(x) приведен в увеличенном масштабе на фиг. 8.


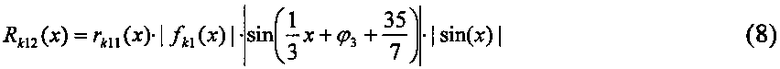
Как и в случае с разрушением НУШ-солитона регулярное, гармоническое воздействие на КдФ-солитон приводит к его разрушению (преобразованию из ударной волны) на группу обыкновенных волн разной амплитуды, которые не могут нанести ущерб аналогичный результату воздействия цунами - КдФ-солитона. При этом Rk12(x) (8) показывает разрушение КдФ-солитона комплексом регулярных, периодических воздействий.
Основное уравнение СГ-солитона rg11(x) (9) [17, с. 154] при текущем значении t=0 визуализуется при параметрах a=1, γ=1 как кинк (рис. 9).

Но даже в этом случае монолитный слой (кинк) может быть разрушен модуляцией (перемножением) обыкновенным синусоидальным колебанием (не говоря уже о более сложных колебаниях) - как указывалось, принципиально важным является то, чтобы воздействие носило регулярный, периодический характер.
Пример такого обыкновенного воздействия |fg1(x)| (10) при амплитуде C1=0,5 и фазе φ4=0 приведен на фиг. 10, а результат (Rg11(x) (11)) такого воздействия на кинк дается на фиг. 11.


Варианты описания и построения кинков rg21(x) (12) [6, с. 281] при параметрах ω0=0,1, v0=0,1, V1=0,1, и rg22(x) (13) [6, с. 281], при параметрах v2=1, α=0,9, а также результаты воздействия |fg1(x)| (10) на такие солитоны - Rg21(x) (14), Rg21(x) (15), приведены на фиг. 12, фиг. 13, фиг. 14, фиг. 15 соответственно.




Таким образом, показано, что при регулярном, периодическом воздействии (или комплексе таких воздействий) на солитоны основных видов (НУШ-солитон, КдФ-солитон, СГ-солитон), что фактически является модуляцией таких солитонов (практически, реализуемой за счет, например, перемножения солитона с гармоническим колебанием), исходные солитоны (как “монолитные” волновые пакеты - одиночные импульсы) разрушаются с образованием группы обыкновенных волн, хотя и с большой амплитудой. Образованные (вследствие рассмотренного воздействия) обыкновенные волны, конечно, опасны (за счет большой амплитуды и, возможно, большой частоты следования), но такая опасность не сравнима с опасностью от действия цунами.
Частота, амплитуда и фаза воздействия (каждого элемента комплекса воздействий) может быть определена с помощью моделирования, как приводящая к требуемому или приемлемому (в каждом конкретном случае) разрушению солитона (цунами). При выборе амплитуды воздействия необходимо учитывать, что воздействие с малой амплитудой может быть «проигнорировано» большой ударной волной, т.к. в этом случае технически затруднительно подвергнуть модуляции всю массу воды в цунами (подводную и надводную части цунами) слабым воздействием, что приводит к модуляции только сравнимой части модулируемого волнового пакета.
Требуется также учесть, что в случае широкого фронта волны рассмотренное воздействие (комплекс воздействий) должно иметь фронт больше чем несколько амплитуд разрушаемой волны. В противном случае разрушенный участок цунами будет восстановлен в порядке дифракции волны. Глубина защищаемой зоны определяется именно дифракцией ударной волны на зоне разрушения (с учетом полной ширины цунами или ее части и ширины воздействия по фронту цунами).
Из изложенного следует, что модуляция цунами (солитонов разных типов) за счет регулярного, периодического воздействия приводит к эффективному разрушению упомянутых волновых пакетов.
При этом модуляция цунами более сложными периодическими воздействиями, чем гармонические колебания (их модулем) с постоянной амплитудой и фазой приведут к более существенному разрушению соответствующих волновых пакетов.
Осуществление модуляции цунами может производиться регулярными (периодическими) механическими воздействиями на подводную часть соответствующего солитона.
Воздействие на подводную часть цунами влияет на весь солитон, т.к. цунами является не поперечной, а продольно-поперечной волной и представляет собой массу воды с поступательным движением. При этом поступательно перемещается и надводная часть солитона, и подводная часть волны, что и вызывает увеличение амплитуды солитона и его замедление (с увеличением амплитуды) при уменьшении глубины (при переходе на мелководье). Равным образом увеличение амплитуды происходит при сужении фронта распространяющегося солитона (например, при входе волны в бухту).
Возможным вариантом механического воздействия - модуляции цунами (волнового пакета, импульса, солитона) является «гребенка» (из подводных широких препятствий, барьеров, относительно близкорасположенных к поверхности - чтобы оказывать воздействие на подводную часть проходящей волны), проходя через которую солитон получает избыточную модуляцию и, следовательно, разрушается. Барьеры могут быть выполнены из цемента, бетона или железобетона в соответствии с [4].
Количество линий барьеров по глубине - не менее 3 линий, т.к. двух недостаточно для модуляции. Большее количество линий барьеров (более трех) может быть применено для воздействия на цунами с большим импульсом тела. То есть чем больше импульс тела, тем большее количество линий барьеров может потребоваться для модулирования такой волны. Количество линий (барьеров) и их характеристики (параметры), определяются, например, при моделировании, аналогичном приведенному, для конкретных, реальных случаев с выбранным априори разбросом значений импульса тела цунами (амплитудой, скоростью и массой).
Линии препятствий выполняются в виде широких (больше ширины защищаемой зоны не менее чем на длину подошвы волны с каждой стороны и общей шириной не менее трех длин подошвы волны) барьеров, трапецеидального или прямоугольного сечения. Сечение барьеров определяется только из соображений устойчивости при их подводном расположении и при воздействии на них большой массы воды. В данном случае под длиной подошвы принимается длина между наиболее низкими местами волны перед передним фронтом и после заднего фронта.
Уровень требуемого воздействия рассчитывается аналитически (по вышеприведенному алгоритму и аналитическим выражениям). Глубина расположения барьеров в «гребенке» (как и период их расположения - расстояние между ними) так же рассчитываются как обеспечивающие требуемый уровень разрушения цунами. Частота расположения барьеров соответствует частоте модулирующего колебания (или частотам комплекса воздействий). Иначе - расстояние между линиями барьеров соответствует или длине волны модулирующего колебания, или расстоянию между максимумами функции воздействия (см., например, фиг. 2, фиг. 10).
Требуемые расчеты могут быть выполнены моделированием механического воздействия «гребенки» на цунами (моделированием модуляции цунами) в соответствии с моделями, указанными выше.
При этом в выражениях солитонов учитывается связь скорости распространения цунами с его амплитудой. Уровень (амплитуда) требуемого воздействия на цунами (следовательно, и другие характеристики такого воздействия) определяют глубину модуляции.
Цунами, имеющая поступательное движение, проходя через такую «гребенку», будет не только модулирована, но и частично рассеяна на таких препятствиях. Количество линий барьеров не ограничивается.
Кроме того, принимается, что ширина разрушаемого участка цунами (по ширине препятствий) существенно меньше ширины фронта цунами.
Глубина защищаемой зоны определяется исходя из ширины барьеров в соответствии со стандартными положениями дифракции волн на краях препятствий и последующей интерференции волн.
Также механическое воздействие на цунами может быть осуществлено, например, восходящими потоками (в местах, в которых должны быть барьеры) или взрывами (с мощностью, определяемой требуемым уровнем модуляции для массы цунами), или иными методами.
Таким образом, модуляция цунами, в том числе выполняемая регулярным, периодическим механическим воздействием (или комплексом механических воздействий) на цунами (в данном случае на подводную часть цунами) решает поставленную задачу - разрушение цунами. Обеспечение соответствующей модуляции цунами позволяет разрушить такой волновой пакет, обладающий значительным импульсом тела.
Предлагаемое техническое решение обеспечивает достижение поставленной цели, разрушение цунами. В предлагаемом способе осуществляется именно противодействие цунами (разрушение волны, а не препятствование распространению в отличие от прототипа и других известных способов противодействия цунами [1-5], в которых противодействие цунами осуществляется за счет препятствования распространению волнового пакета) за счет механического воздействия на нее, приводящего к ее разрушению. То есть в прототипе и в других известных способах противодействия цунами [1-5] изменяют характеристики резонансной системы, в которой существует и распространяется цунами, тогда как в предлагаемом техническом решении изменяют характеристики (параметры) самой волны (цунами), что приводит к невозможности ее существования (в исходном виде) в такой резонансной системе с фиксированными характеристиками системы и, следовательно, к ее (цунами) разрушению.
ИСПОЛЬЗОВАННЫЕ ИСТОЧНИКИ
1. Воробьев Ю.Л. Цунами: предупреждение и защита / Ю.Л. Воробьев, В.А. Акимов, Ю.И. Соколов. М.: МЧС России, 2006, 264 с. / E-address: http://www.mchs.gov.ru/upload/site1/library/KH6MKDi8TG.pdf (извлечено 07.02.2015 г.).
2. Патент РФ №2489544, 2012. МПК E02B 3/04. Опубликовано 10.08.2013. Устройство для зашиты побережий от волн / Г.С. Хромов.
3. Патент РФ №2524814, 2013. МПК E02B 3/04. Опубликовано 10.08.2014. Цунами-гаситель / Н.В. Ясаков.
4. Патент РФ №2474643, 2011. МПК E02B 3/04. Опубликовано 10.02.2013. Способ и сооружение для ослабления разрушающих действий цунами / М.Я. Бикбау, У.М. Бикбау, Я.М. Бикбау, И. Элкинд, Г. Элкинд.
5. Патент РФ №2308058, 2005. МПК G01V 9/00. Опубликовано 10.10.2007. Способ борьбы с цунами / В.Ч. Цой.
6. Филиппов А.Т. Многоликий солитон / А.Т. Филиппов. М.: Наука, 1990, 288 с.
7. Физическая энциклопедия. Т. 4. Пойнтинга-Робертсона - Стримеры / Гл. ред. А.М. Прохоров. М.: Советская энциклопедия, 1994, 704 с.
8. Физическая энциклопедия. Т. 5. Стробоскопические приборы - Яркость / Гл. ред. А.М. Прохоров. М.: Большая Российская энциклопедия, 1998, 760 с.
9. Башкиров М. М. Парадокс Эйнштейна-Подольского-Розена, солитоны и дальнодействие / М.М. Башкиров, И.А. Володин, А.А. Конотоп, Г.П. Почанин, В.И. Сергеев, З.Н. Федорова // Вопросы радиоэлектроники. Сер. Общетехническая (ОТ). 2011, Вып. 2, С. 162-202.
10. Рухадзе А.А. Взаимосвязи солитонной теории и парадокса Эйнштейна-Подольского-Розена для проявления дальнодействия / А.А. Рухадзе, М.М. Башкиров, И.А. Володин, В.Г. Дмитриев, А.А. Конотоп, В.И. Сергеев, З.Н. Федорова, А.А. Чаплыгин // Нелинейный мир. 2010, Т. 8, №8, С. 475-488.
11. Кафтанова Ю.В. Специальные функции математической физики. Ч. 3. Моделирование аномальных и экстраординарных природных и техногенных процессов / Ю.В. Кафтанова. Харьков: ЧП Издательство «Новое слово», 2009, 596 с.
12. Самойлов К.И. Морской словарь. Т. 2 / К.И. Самойлов. М. - Л.: Государственное Военно-морское издательство НКВМФ Союза ССР, 1941, 168 с.
13. Сергеев В.И. Солитоны и дальнодействие проявления реакции материальных объектов (теория и эксперимент) / М.М. Башкиров, И.А. Володин, Г.П. Почанин, В.И. Сергеев. Саарбрюкен, ФРГ: Lambert Academic Publishing GmbH & CO. KG, 2012,390 с.
14. Дмитриев В.Г. О разрушении импульсов / В.Г. Дмитриев, А.А. Конотоп, Н.В. Косякин, Г.П. Почанин, В.И. Сергеев, З.Н. Федорова // Радиотехника. 2012, №4, С. 22-29.
15. Башкиров М.М. Об усилении и разрушении механических импульсов за счет дополнительной модуляции, при изменении параметров огибающего колебания / М.М. Башкиров, Н.В. Косякин, Г.П. Почанин, В.И. Сергеев, З.Н. Федорова // Радиопромышленность. 2011, Вып. 3, С. 167-176.
16. Почанин Г.П. Усиление КдФ-солитона за счет его дополнительной модуляции и усиления огибающей результирующего сигнала / Г.П. Почанин, В.П. Рубан, В.И. Сергеев, З.Н. Федорова // Радиопромышленность. 2013, Вып. 2, С. 153-170.
17. Лэм Дж. мл. Введение в теорию солитонов / Дж. Лэм. Могилев: Бибфизмат, 1997, 294 с.
18. Додд Р. Солитоны и нелинейные волновые уравнения / Р. Додд, Дж. Эйлбек, Дж. Гиббон, X. Моррис. М.: Мир, 1988, 694 с.
19. Захаров В. Е. Теория солитонов: Метод обратной задачи / В.Е. Захаров, С.В. Манаков, С.П. Новиков, Л.П. Питаевский / Под ред. С.П. Новикова. М.: Наука, 1980, 319 с.
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ понижения вязкости промодулированным ультразвуком в условиях резонансных частот жидкости | 2015 |
|
RU2657205C2 |
| АНТЕННА ЭЛЕКТРОМАГНИТНЫХ СОЛИТОНОВ | 2002 |
|
RU2208273C1 |
| СПОСОБ УСИЛЕНИЯ ИМПУЛЬСА | 2012 |
|
RU2509411C2 |
| СПОСОБ ПРОСТРАНСТВЕННО НЕОДНОРОДНОЙ МОДУЛЯЦИИ ФАЗЫ СВЕТА И ОПТИЧЕСКИЙ МОДУЛЯТОР ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2014 |
|
RU2561307C2 |
| Способ определения эффективной глубины заполненного флюидами разлома | 2019 |
|
RU2722971C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ПРЕДВЕСТНИКА ЦУНАМИ | 2005 |
|
RU2292569C1 |
| СПОСОБ ВОССТАНОВЛЕНИЯ ФОРМЫ РЕЛЬЕФА МОРСКОГО ДНА ПРИ ДИСКРЕТНЫХ ИЗМЕРЕНИЯХ ГЛУБИН ПОСРЕДСТВОМ ГИДРОАКУСТИЧЕСКИХ СРЕДСТВ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2006 |
|
RU2326408C1 |
| ЦУНАМИ-ГАСИТЕЛЬ | 2013 |
|
RU2524814C1 |
| СПОСОБ ОБНАРУЖЕНИЯ ВОЛН ЦУНАМИ, ПРИМЕНИМЫЙ ДЛЯ ВСЕХ ПРИЧИН ИХ ВОЗБУЖДЕНИЯ | 1999 |
|
RU2156988C1 |
| СПОСОБ ВОЗБУЖДЕНИЯ РЕАКЦИИ МАТЕРИАЛЬНОГО ОБЪЕКТА НА НЕОБРАЩЕННОЕ НА НЕГО ВНЕШНЕЕ ВОЗДЕЙСТВИЕ | 2004 |
|
RU2269770C1 |
Изобретение относится к области защиты от волн и может применяться для разрушения цунами. При осуществлении способа разрушения цунами на волну оказывают механическое воздействие. Механическое воздействие производят путем модуляции цунами. Модуляцию проводят регулярным периодическим воздействием на подводную часть цунами. Обеспечивается возможность разрушения цунами. 3 з.п. ф-лы. 15 ил.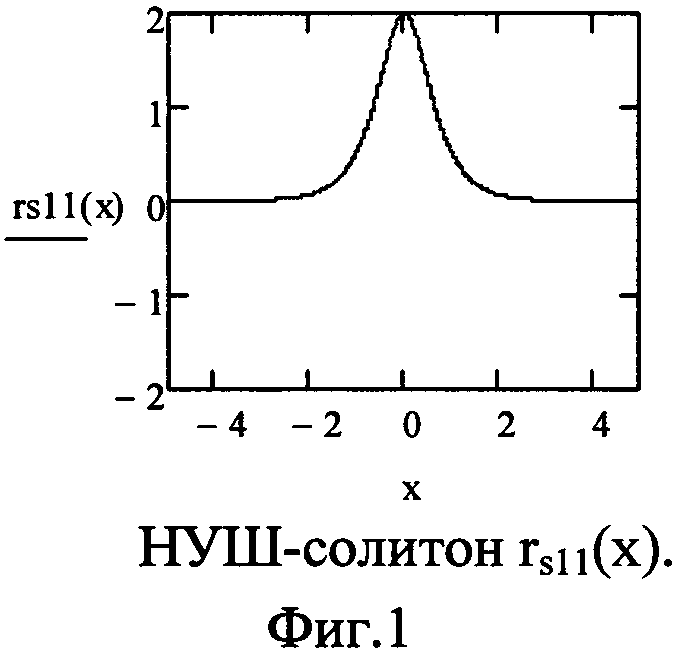
1. Способ разрушения цунами, заключающийся в механическом воздействии на цунами, отличающийся тем, что механическое воздействие производят путем модуляции цунами.
2. Способ по п. 1, отличающийся тем, что модуляцию цунами проводят регулярным, периодическим механическим воздействием на подводную часть цунами.
3. Способ по п. 1, отличающийся тем, что модуляцию цунами проводят комплексом регулярных, периодических механических воздействий на подводную часть цунами.
4. Способ по п. 2, отличающийся тем, что регулярное механическое воздействие на подводную часть цунами производят периодически расположенными на пути прохождения цунами подводными препятствиями.
| СПОСОБ БОРЬБЫ С ЦУНАМИ | 2005 |
|
RU2308058C2 |
| JPS 6389710 A, 20.04.1988 | |||
| JPH 1181269 A, 26.03.1999 | |||
| Многоступенчатая активно-реактивная турбина | 1924 |
|
SU2013A1 |
| СПОСОБ ГАШЕНИЯ ЭНЕРГИИ ВОЛН В ПРИБРЕЖНОЙ МОРСКОЙ ЗОНЕ | 1998 |
|
RU2130525C1 |
Авторы
Даты
2016-08-27—Публикация
2015-08-21—Подача