Область техники, к которой относится изобретение
Настоящее изобретение относится к связи, и, в конкретных вариантах своей реализации, к системам и способам для Множественного доступа с разреженным кодом.
Уровень техники
Множественный доступ с кодовым разделением каналов (CDMA) представляет собой технологию множественного доступа, в которой символы данных распределены по ортогональным или близким к ортогональным кодовым последовательностям. Традиционное CDMA-кодирование представляет собой двухэтапный процесс, в котором двоичный код отображается на символ квадратурной амплитудной модуляции (QAM) символ прежде, чем применяется расширяющая последовательность. Хотя традиционное CDMA-кодирование может обеспечить относительно высокие скорости кодирования, для удовлетворения постоянно растущих потребностей сетей беспроводной связи следующего поколения требуются новые технологии/механизмы для достижения даже еще более высоких скоростей кодирования.
Раскрытие изобретения
Благодаря вариантам реализации этого раскрываемого изобретения, которые описывают системы и способы для Множественного доступа с разреженным кодом, в большинстве случаев достигаются технические преимущества.
В соответствии с одним вариантом реализации изобретения, предлагается способ для мультиплексирования данных. В этом примере, способ включает в себя этапы, на которых: принимают некоторые первые двоичные данные, ассоциативно связанные с некоторым первым мультиплексируемым слоем, кодируют первые двоичные данные, выбирая некоторое первое кодовое слово из некоторой первой кодовой книги, и мультиплексируют первое кодовое слово, с, по меньшей мере, одним вторым кодовым словом из некоторой второй кодовой книги для того чтобы получить мультиплексированные кодовые слова. Первая кодовая книга назначена исключительно первому мультиплексируемому слою, а вторая кодовая книга назначена исключительно некоторому второму мультиплексируемому слою. Способ, кроме того, включает в себя этап, на котором передают мультиплексированные кодовые слова по совместно используемым ресурсам сети. Также предлагается устройство для выполнения этого способа.
В соответствии с другим вариантом реализации изобретения, предлагается способ для приема данных. В этом примере, способ включает в себя этап, на котором принимают сигнал, несущий мультиплексированные кодовые слова. Мультиплексированные кодовые слова включают в себя кодовые слова, принадлежащие множественным кодовым книгам, притом, что каждая кодовая книга назначена отличному от других мультиплексированному слою. Способ, кроме того, включает в себя этап, на котором идентифицируют некоторое первое кодовое слово в пределах мультиплексированных кодовых слов посредством приемника, связанного с некоторым первым мультиплексированным слоем. Первое кодовое слово принадлежит кодовой книге, которая назначена исключительно первому мультиплексированному слою. Способ, кроме того, включает в себя этап, на котором декодируют первое кодовое слово для того, чтобы получить некоторые первые двоичные данные. Также предлагается устройство для выполнения этого способа.
В соответствии с другим вариантом реализации изобретения, предлагается способ для проектирования кода Множественного доступа с разреженным кодом (SCMA-кода). В этом примере, способ включает в себя этапы, на которых генерируют множество кодовых книг многомерной модуляции, и генерируют из этого множества кодовых книг многомерной модуляции множество разреженных кодовых книг. Также предлагается способ для проектирования сигнатур низкой плотности (LDS-сигнатур).
Краткое описание чертежей
Для более полного понимания этого раскрываемого изобретения и его преимуществ обратимся теперь к нижеследующим описаниям, рассматриваемым в связи с прилагаемыми чертежами, в которых:
на Фиг. 1 проиллюстрирована схема традиционного CDMA-кодера;
на Фиг. 2 проиллюстрирована схема традиционной архитектуры CDMA-кодирования;
на Фиг. 3 проиллюстрирована схема варианта реализации SCMA-кодера;
на Фиг. 4 проиллюстрирована схема архитектуры SCMA-кодирования по варианту реализации изобретения;
на Фиг. 5 проиллюстрирована блок-схема алгоритма способа кодирования данных, соответствующего варианту реализации изобретения;
на Фиг. 6 проиллюстрирована блок-схема алгоритма способа декодирования данных, соответствующего варианту реализации изобретения;
на Фиг. 7 проиллюстрирована схема методологии, соответствующая варианту реализации изобретения, для разработки субоптимальной кодовой книги для SCMA-кодирования;
на Фиг. 8 проиллюстрирована схема методологии, соответствующая варианту реализации изобретения, для проектирования LDS-сигнатур;
на Фиг. 9 проиллюстрирована диаграмма, изображающая характеристику BLER (частоты блоков с ошибками);
на Фиг. 10 проиллюстрирована схема фактор-графового представления для SCMA-кода;
на Фиг. 11 проиллюстрирована схема другого фактор-графового представления для SCMA-кода;
на Фиг. 12 проиллюстрирована схема графа поворотов фазы;
на Фиг. 13 проиллюстрирована диаграмма, изображающая передаточную функцию для внешней информации, для вершин ресурса и слоя в LDS;
на Фиг. 14 проиллюстрирована диаграмма, изображающая выходную информацию слоя по отношению к входной внешней информации для вершин-ресурсов для LDS;
на Фиг. 15 проиллюстрирована диаграмма, изображающая передаточные функции для внешней информации, для LDS с сигнатурой S2;
на Фиг. 16 проиллюстрирована диаграмма, изображающая выходную информацию для LDS-сигнатуры S2;
на Фиг. 17 проиллюстрирована диаграмма, изображающая передаточную функцию для внешней информации, для четырех вершин-ресурсов для SCMA-кода без оптимизации фазы/сопряжения;
на Фиг. 18 проиллюстрирована диаграмма, изображающая передаточную функцию для внешней информации, для четырех вершин-ресурсов для SCMA-кода с оптимизацией фазы/сопряжения;
на Фиг. 19(а) проиллюстрирована диаграмма, изображающая влияние вариации мощности измерения многомерного "созвездия" на эффективность SCMA-кода;
на Фиг. 19(b) проиллюстрирована диаграмма, изображающая влияние вариации мощности измерения многомерного "созвездия" на эффективность другого SCMA-кода;
на Фиг. 20(а) проиллюстрирована диаграмма, изображающая влияние оператора перестановки на эффективность SCMA-кода;
на Фиг. 20(b) проиллюстрирована диаграмма, изображающая влияние оператора перестановки на эффективность другого SCMA-кода;
на Фиг. 21(а) проиллюстрирована диаграмма, изображающая влияние операторов фазы/сопряжения на эффективность SCMA-кода;
на Фиг. 21(b) проиллюстрирована диаграмма, изображающая влияние операторов фазы/сопряжения на эффективность другого SCMA-кода;
на Фиг. 22(а) проиллюстрирована диаграмма, изображающая сравнение двух различных критериев оптимизации для операторов фазы/сопряжения для SCMA-кода;
на Фиг. 22(b) проиллюстрирована диаграмма, изображающая сравнение двух различных критериев оптимизации для операторов фазы/сопряжения для другого SCMA-кода;
на Фиг. 23 проиллюстрирована диаграмма, изображающая влияние распределения операторов на эффективность SCMA-кода;
на Фиг. 24(а) проиллюстрирована диаграмма, изображающая влияние унитарного оператора в вещественной области на эффективность SCMA-кода;
на Фиг. 24(b) проиллюстрирована диаграмма, изображающая влияние унитарного оператора в вещественной области на эффективность другого SCMA-кода;
на Фиг. 25 проиллюстрирована диаграмма, изображающая полную полезную пропускную способность SCMA-кодов и влияние параметров проектирования;
на Фиг. 26 проиллюстрирована диаграмма, изображающая эффективность LDS-сигнатур с различным матрицами сигнатур;
на Фиг. 27(а) проиллюстрирована диаграмма, изображающая эффективность множества LDS-сигнатур;
на Фиг. 27(b) проиллюстрирована диаграмма, изображающая эффективность другого множества LDS-сигнатур;
на Фиг. 28(а) проиллюстрирована диаграмма, изображающая эффективность множества LDS-сигнатур с попарной оптимизацией операторов фазы;
на Фиг. 28(b) проиллюстрирована диаграмма, изображающая эффективность другого множества LDS-сигнатур с другой попарной оптимизацией операторов фазы;
на Фиг. 29 проиллюстрирована диаграмма, изображающая эффективность SCMA в сравнении с LDS-сигнатурами;
Фиг. 30 представляет собой структурную схему, на которой проиллюстрирована вычислительная платформа; и
на Фиг. 31 проиллюстрирована структурная схема устройства связи, соответствующего одному варианту реализации изобретения.
Соответствующие друг другу цифры и символы на различных фигурах обычно относятся к соответствующим друг другу частям, если не указано иное. Фигуры вычерчены таким образом, чтобы четко иллюстрировать соответствующие аспекты вариантов реализации изобретения, и не обязательно вычерчены в масштабе.
Осуществление изобретения
Ниже подробно рассматривается создание и использование раскрываемых вариантов реализации изобретения. Следует, однако, понимать, что настоящее раскрываемое изобретение предлагает много применимых изобретательских концепций, которые могут быть воплощены в широком разнообразии конкретных контекстов. Рассматриваемые конкретные варианты реализации изобретения представляют собой простую иллюстрацию конкретных способов создания и использования изобретения, и не ограничивают объем изобретения.
В данной заявке раскрывается технология кодирования "Множественный доступ с разреженным кодом" (SCMA), посредством которой потоки двоичных данных кодируются напрямую в многомерные кодовые слова. При прямом кодировании двоичных данных в многомерные кодовые слова, описываемые здесь технологии SCMA-кодирования обходятся без отображения на символы квадратурной амплитудной модуляции, достигая, таким образом, преимуществ в кодировании по отношению к традиционному CDMA-кодированию. Следует отметить, что описываемые здесь технологии SCMA-кодирования передают двоичные данные с использованием многомерного кодового слова, а не символа квадратурной амплитудной модуляции. Кроме того, технологии SCMA-кодирования по этому раскрываемому изобретения обеспечивают множественный доступ посредством назначения отличной от других кодовой книги для каждого мультиплексируемого слоя, в противоположность использованию уникальной расширяющей последовательности (например, LDS-сигнатуры и так далее), что является обычным в традиционном CDMA-кодировании. Кроме того, кодовые книги SCMA-кодирования содержат разреженные кодовые слова, так что приемники могут для обнаружения своих соответствующих кодовых слов среди мультиплексированных кодовых слов использовать алгоритмы передачи сообщений (МРА-алгоритмы), имеющие низкую сложность, что уменьшает сложность обработки основополосного сигнала на стороне приемника. В то время как большая часть этого раскрываемого изобретения может рассматриваться в контексте двоичных данных, аспекты этого раскрываемого изобретения в равной мере применимы и к другим видам данных, таким как М-ичные данные.
На Фиг. 1 проиллюстрирован традиционный CDMA-кодер 100 для кодирования данных. Как показано на фигуре, CDMA-кодер 100 отображает двоичные данные, полученные из FEC-кодера (кодера упреждающей коррекции ошибок), на символы квадратурной амплитудной модуляции (QAM-модуляции), и затем применяет расширяющие сигнатуры (s1, s2, s3, s4) для того, чтобы получить поток закодированных данных (qs1, qs2, qs3, qs4). Следует отметить, что расширяющие сигнатуры (s1, s2, s3, s4) представляют собой расширяющие последовательности CDMA-кодирования (например, LDS-сигнатуры и так далее), назначаемые различным мультиплексируемым слоям для достижения множественного доступа.
На Фиг. 2 проиллюстрирован пример архитектуры 200 традиционного CDMA-кодирования для передачи потоков 201-204 двоичных данных множеству пользователей 231-234 по сети 260, которая могла бы быть выполнена традиционным CDMA-кодером 100. Как показано на фигуре, каждый поток 201-204 двоичных данных отображается на символы 211-214 QAM-модуляции (символы квадратурной амплитудной модуляции) в соответствии с некоторым соотношением 270 "QAM - в - двоичные данные". В качестве примера, символ 211 QAM-модуляции ассоциативно связан с двоичным значением ′00′, символ 212 QAM-модуляции ассоциативно связан с двоичным значением ′01′, символ 213 QAM-модуляции ассоциативно связан с двоичным значением ′10′, а символ 214 QAM-модуляции ассоциативно связан с двоичным значением ′11′. Соответственно, символ 211 QAM-модуляции отображается на поток 201 двоичные данных, символ 212 QAM-модуляции отображается на потоки 202 и 204 двоичных данных, а символ 213 QAM-модуляции отображается на поток 203 двоичных данных.
Вслед за отображением "двоичные данные - QAM", символы 211-214 QAM-модуляции мультиплексируются вместе в соответствии с LDS-сигнатурами 221-224. Следует отметить, что каждая из LDS-сигнатур 221-224 отображается на различные мультиплексируемые слои, которые назначаются различным пользователям 231-234 для достижения множественного доступа. Следовательно, LDS-сигнатуры 221-224 остаются постоянными (то есть не изменяются на основе двоичных значений в потоках 201-204 двоичных данных). После этого, получаемые в результате одномерные кодовые слова 241-244 мультиплексируются вместе, образуя мультиплексированные кодовые слова 280, которые передаются по сети 260. При приеме, мультиплексированные кодовые слова 280 демультиплексируются в соответствии с LDS-сигнатурами 221-224 для того, чтобы получить символы 211-214 QAM-модуляции, которые используются для того, чтобы получить потоки 201-204 двоичных данных в соответствии с соотношением 270 "QAM - в - двоичные данные".
На Фиг. 3 проиллюстрирован SCMA-кодер 300 для кодирования данных в соответствии с аспектами этого раскрываемого изобретения. Как показано на фигуре, SCMA-кодер 300 отображает двоичные данные, принятые от FEC-кодера, напрямую в многомерные кодовые слова для того, получая поток (x1, х2, х3, x4) закодированных данных. Многомерные кодовые слова могут принадлежать различным многомерным кодовым книгам, при том что каждая кодовая книга ассоциативно связана с отличным от других мультиплексируемым слоем. Как здесь обсуждается, мультиплексируемые слои могут включать в себя любой слой, по которому множественные потоки данных могут быть переданы по совместно используемым ресурсам сети. Например, мультиплексируемые слои могут содержать пространственные слои множественного ввода - множественного вывода (MIMO), тоны Множественного доступа с ортогональным частотным разделением каналов (OFDMA), слои Множественного доступа с разделением по времени (TDMA), и другие.
На Фиг. 4 проиллюстрирован пример схемы 400 SCMA-мультиплексирования, предназначенной для кодирования данных в соответствии с аспектами этого раскрываемого изобретения. Как показано на Фигуре, в схеме 400 SCMA-мультиплексирования может использоваться множество кодовых книг 410, 420, 430, 440, 450 и 460, каждая из которых назначена отличному от других мультиплексируемому слою и включает в себя множество многомерных кодовых слов. Если описать это более конкретно, то кодовая книга 410 включает в себя кодовые слова 411-414, кодовая книга 420 включает в себя кодовые слова 421-424, кодовая книга 430 включает в себя кодовые слова 431-434, кодовая книга 440 включает в себя кодовые слова 441-444, кодовая книга 450 включает в себя кодовые слова 451-454, а кодовая книга 460 включает в себя кодовые слова 461-464. Каждое кодовое слово соответствующей кодовой книги шифров отображается на отличное от других двоичное значение. В этом примере, кодовые слова 411, 421, 431, 441, 451 и 461 отображаются на двоичное значение ′00′, кодовые слова 412, 422, 432, 442, 452 и 462 отображаются на двоичное значение ′01′, кодовые слова 413, 423, 433, 443, 453 и 463 отображаются на двоичное значение ′10′, а кодовые слова 414, 424, 434, 444, 454 и 464 отображаются на двоичное значение ′11′. Хотя кодовые книги, показанные на Фиг. 4, изображены как имеющие четыре кодовых слова на книгу, кодовые книги для SMAC могут иметь любое количество ключевых слов. Например, кодовые книги для SMAC могут иметь 9 кодовых слов (например, отображающихся на двоичные значения ′000′…′111′), 16 кодовых слов (например, отображающихся на двоичные значения ′0000′…′1111′), или больше.
Как показано на Фигуре, различные кодовые слова выбираются из разнообразных кодовых книг 410, 420, 430, 440, 450 и 460 в зависимости от двоичных данных, передаваемых в мультиплексируемом слое. В этом примере, из кодовой книги 410 выбирается кодовое слово 414, потому что в первом мультиплексируемом слое передается двоичное значение ′11′, из кодовой книги 420 выбирается кодовое слово 422, потому что во втором мультиплексируемом слое передается двоичное значение ′01′, из кодовой книги 430 выбирается кодовое слово 433, потому что в третьем мультиплексируемом слое передается двоичное значение ′10′, из кодовой книги 440 выбирается кодовое слово 442, потому что в четвертом мультиплексируемом слое передается двоичное значение ′01′, из кодовой книги 450 выбирается кодовое слово 452, потому что в пятом мультиплексируемом слое передается двоичное значение ′01′, а из кодовой книги 460 выбирается кодовое слово 464, потому что в шестом мультиплексируемом слое передается двоичное значение ′11′. После этого кодовые слова 414, 422, 433, 442, 452 и 464 мультиплексируются вместе для того, чтобы сформировать поток 480 мультиплексированных данных, который передан по совместно используемым ресурсам сети. Следует отметить, что кодовые слова 414, 422, 433, 442, 452 и 464 представляют собой разреженные кодовые слова 411, и, следовательно, могут быть идентифицированы при приеме потока 480 мультиплексированных данных с использованием МРА-алгоритмов.
На Фиг. 5 проиллюстрирован способ 500 для передачи данных по сети, соответствующий аспектам этого раскрываемого изобретения, который может выполняться передатчиком. Способ 500 начинается на этапе 510, на котором передатчик принимает входные данные, включающие в себя некоторые первые двоичные данные и некоторые вторые двоичные данные. После этого, способ 500 переходит на этап 520, на котором передатчик кодирует первый поток двоичных данных, выбирая некоторое первое кодовое слово из некоторой первой кодовой книги, назначенной некоторому первому мультиплексируемому слою. После этого, способ 500 переходит на этап 530, на котором передатчик кодирует второй поток двоичных данных, выбирая некоторое второе кодовое слово из некоторой второй кодовой книги, назначенной второму мультиплексируемому слою. Вслед за этим, способ 500 переходит на этап 540, на котором передатчик мультиплексирует первое кодовое слово со вторым кодовым словом для того, чтобы получить мультиплексированные кодовые слова. Наконец, способ 500 переходит на этап 550, на котором передатчик передает эти мультиплексированные кодовые слова по совместно используемым ресурсам сети.
На Фиг. 6 проиллюстрирован способ 600 для приема данных, мультиплексированных в соответствии с аспектами этого раскрываемого изобретения, который может выполняться приемником, ассоциативно связанным с первым мультиплексированным слоем. Способ 600 начинается на этапе 610, на котором приемник принимает сигнал, несущий мультиплексированные кодовые слова. Затем, способ 600 переходит на этап 620, на котором приемник идентифицирует некоторое первое кодовое слово из мультиплексированных кодовых слов. Первое кодовое слово - из некоторой первой кодовой книги, ассоциативно связанной с первым мультиплексированным слоем, и может быть идентифицировано приемником в соответствии с МРА-алгоритмом. После этого, способ 600 переходит на этап 630, на котором приемник декодирует первое кодовое слово в соответствии с первой кодовой книгой для того, чтобы получить некоторые первые двоичные данные.
Аспекты этого раскрываемого изобретения обеспечивают Множественный доступ с разреженным кодом (SCMA), имеющий нижеследующие характеристики: схема множественного доступа; эффективность кодирования и разреженные кодовые слова. На Фиг. 7 проиллюстрирована методология 700 для разработки субоптимальной кодовой книги 760 для SCMA-кодирования. Как показано на Фигуре, методология 700 включает в себя выбор параметров 710-755, которые включают в себя матрицу 710 отображения, вещественное многомерное "созвездие" (некоторую совокупность элементов) 720, вещественную унитарную матрицу 730, комплексное многомерное "созвездие" 740, оператор 750 перестановки и оператор 755 фазы и сопряжения. В некоторых вариантах реализации изобретения, для разработки кодовых книг для SCMA-кодирования могут быть использованы множественные материнские "созвездия". В дополнение к этому, методология 700 может включать в себя дополнительный этап распределения операторов сопряжения фазы входящим ветвям вершины-ресурса. Кодовую книгу 760 получают посредством объединения параметров 710-755 способом, изображенным на Фиг. 7.
В одном варианте реализации изобретения, LDS-сигнатура может рассматриваться как квазипроизводная при SCMA-кодировании. На Фиг. 8 проиллюстрирована методология 800 для проектирования LDS-сигнатур в соответствии с аспектами этого раскрываемого изобретения. В вариантах реализации этого раскрываемого изобретения, методология 800 для проектирования LDS-сигнатур может соответствовать упрощенному варианту проекта SCMA и может исключать этапы, относящиеся к проектированию материнского многомерного "созвездия" (которое, вообще говоря, может быть включено в проектирование SCMA). Например, материнское "созвездие" можно считать повторением одномерного "созвездия" QAM-модуляции (например, предполагая, что задано такое "созвездие" QAM-модуляции, как QPSK (квадратурная фазовая манипуляция)). В дополнение к этому, операторы могут быть ограничены операторами фазы, так что операторы сопряжения исключаются. Кроме того, методология 800 может включать в себя этап выделения операторов фазы вершины-ресурса ее входящим ветвям. Аспекты методологии 800 могут основываться на линейной матричной операции, которая специально разработана для проектирования LDS-сигнатуры. Такого рода линейной матричной операции не может быть применена при проектировании кодовых книг SCMA.
На Фиг. 9 проиллюстрирована диаграмма, изображающая характеристику BLER (частоты блоков с ошибками), которая показывает, как SCMA и множества LDS-сигнатур, раскрытые в этом описании, превосходят множества традиционных LDS-сигнатур. В Таблице 1 проиллюстрированы некоторые различия между SCMA и LDS.
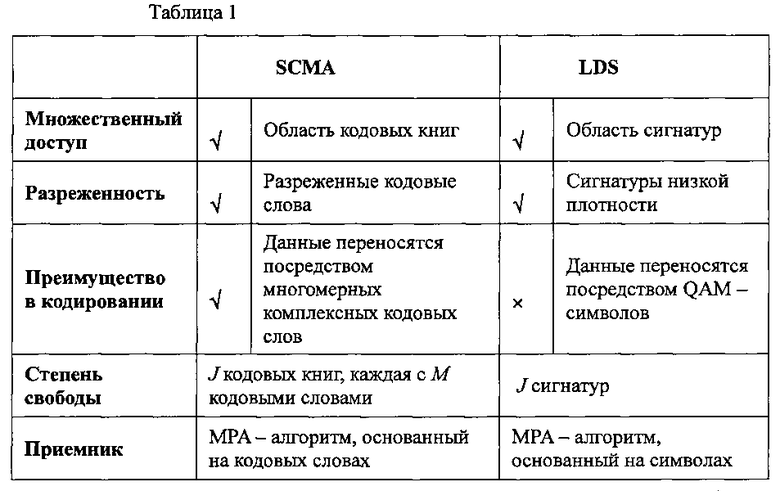
Аспекты этого раскрываемого изобретения представляют новый класс схемы множественного доступа, а именно Множественный доступ с разреженным кодом (SCMA). Аспекты этого раскрываемого изобретения предлагают определение Множественного доступа с разреженным кодом (SCMA), близкую к оптимальной многоступенчатую методологию проектирования для SCMA, методологию проектирования для LDS-сигнатур, алгоритм передачи сообщений, основанный на символе, для обнаружения SCMA. Аспекты этого раскрываемого изобретения предлагают многочисленные выгоды и/или преимущества, включающие в себя методологию оценки посредством EXIT диаграммы (Диаграммы передачи внешней информации), принятой для SCMA и LDS-структур, SCMA представляет собой новую схему множественного доступа, которая может быть использована как перспективная технология формы сигнала/доступа для стандарта 5G (Пятого поколения), SCMA имеет потенциальное преимущество превзойти LDS-сигнатуру, и SCMA, который имеет потенциал повысить пропускную способность сети беспроводной связи или сделать возможной передачу данных с меньшим предоставлением ресурса UL (линии связи с пользователем), DL (линии связи с устройством), D2D (линии связи устройства с устройством) или М2М (линии связи машины с машиной). Преимущества, получаемые из этого раскрываемого изобретения могут быть значительными, вследствие стремительно растущего количества базовых станций и оконечных устройств в сети.
Множественный доступ с разреженным кодом: Множественный доступ с разреженным кодом (SCMA) представляет собой предлагаемую схему множественного доступа/кодирования с нижеследующими свойствами: (i) Данные из области двоичных значений напрямую кодируются в кодовые слова многомерной комплексной области; (ii) Множественный доступ достигается посредством генерирования множественных кодовых книг, по одной для каждого слоя; и (iii) Кодовые слова этих кодовых книг являются разреженными, так что для обнаружения мультиплексированных кодовых слов может быть применена МРА-технология обнаружения множественных пользователей, имеющая умеренную сложность.
В этом раскрываемом изобретении используются нижеследующие обозначения и переменные. Множества двоичных, натуральных, целых, вещественных и комплексных чисел обозначены как В, N, Z, R и С, соответственно. Символы 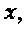 х и X, и представляют, соответственно, скаляры, векторы и матрицы, n-й элемент
х и X, и представляют, соответственно, скаляры, векторы и матрицы, n-й элемент 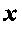 обозначается как xn или (x)n, а
обозначается как xn или (x)n, а 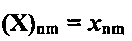 - представляет собой элемент n-й строки и m-го столбца матрицы X. Кроме того, хm представляет собой m-й столбец матрицы X. Транспонирование x представляет собой xT, a diag(x) представляет собой диагональную матрицу, в которой ее n-й диагональный элемент представляет собой (x)n. Аналогичным образом, diag(X) представляет собой вектор диагональных элементов матрицы X. Эрмитова матрица обозначена как ХH. Переменные и функции перечислены в Таблице 2.
- представляет собой элемент n-й строки и m-го столбца матрицы X. Кроме того, хm представляет собой m-й столбец матрицы X. Транспонирование x представляет собой xT, a diag(x) представляет собой диагональную матрицу, в которой ее n-й диагональный элемент представляет собой (x)n. Аналогичным образом, diag(X) представляет собой вектор диагональных элементов матрицы X. Эрмитова матрица обозначена как ХH. Переменные и функции перечислены в Таблице 2.

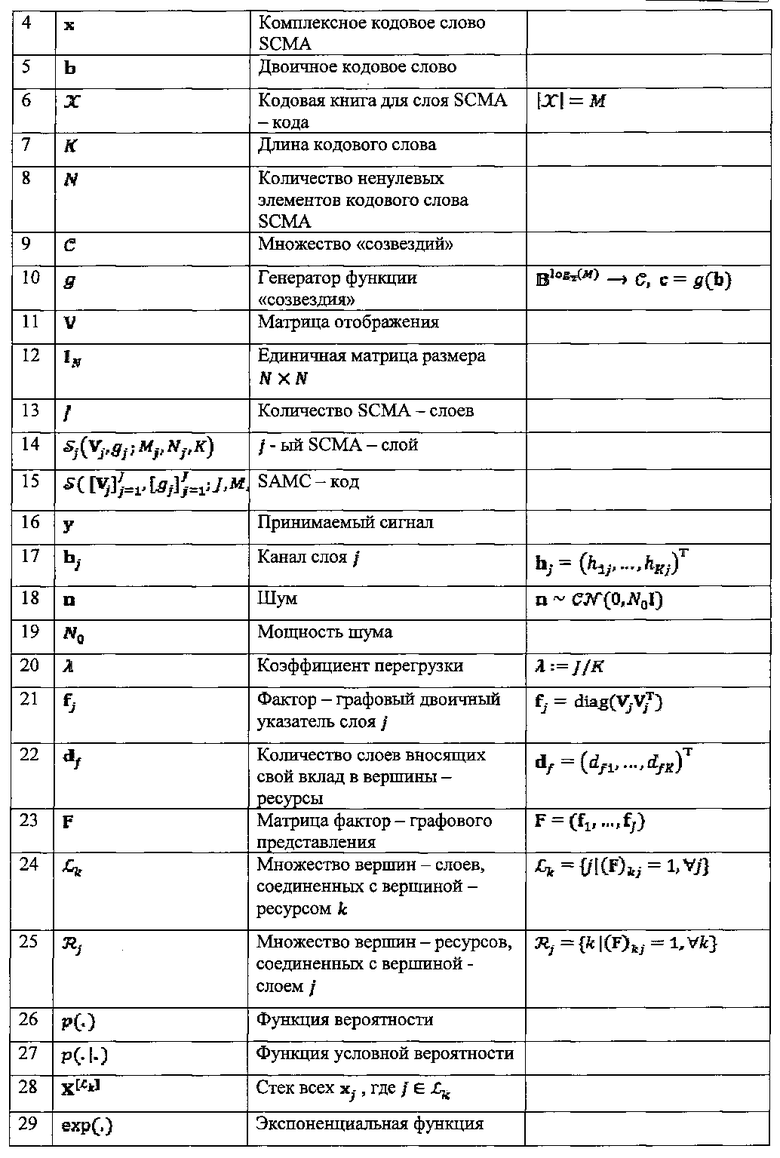
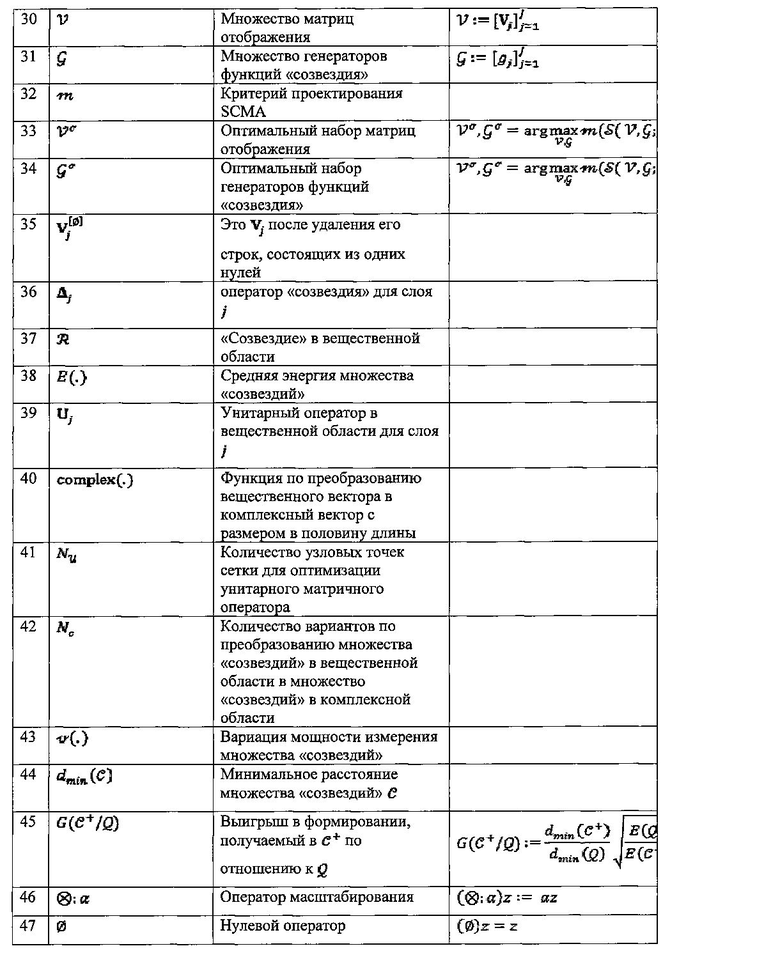

Приводимое ниже раскрытие включает в себя описания структуры SCMA-кода, технологий и механизмов для МРА-обнаружения для SCMA, рассмотрение задач/проблем оптимизации для проектирования SCMA-кода, и процедур проектирования многоступенчатого близкого к оптимальному SCMA-кода. Дополнительные раскрываемые вопросы описывают то, каким образом можно оценивать SCMA-коды, основываясь на методологиях оценки на уровне звена и посредством EXIT-диаграммы.
SCMA-кодер может быть определен следующим образом: 
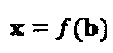 где
где 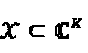 с кардинальным числом
с кардинальным числом 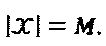 K - мерное комплексное кодовое слово x представляет собой разреженный вектор с N<K ненулевыми компонентами. Пусть с обозначает точку N - мерного комплексного "созвездия", определенную во множестве
K - мерное комплексное кодовое слово x представляет собой разреженный вектор с N<K ненулевыми компонентами. Пусть с обозначает точку N - мерного комплексного "созвездия", определенную во множестве 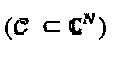 "созвездий", так что:
"созвездий", так что: 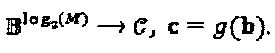 SCMA-кодер может быть переопределен как
SCMA-кодер может быть переопределен как 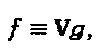 где матрица двоичного отображения
где матрица двоичного отображения 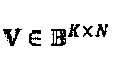 просто отображает N измерений точки "созвездия" в K-мерное кодовое слово SCMA. Отметим, что V содержит K-N строк, состоящих из одних нулей. Убрав из V строки, состоящие из одних нулей, остальное может быть представлено единичной матрицей IN, что означает то, что двоичный отображатель во время процесса отображения не переставляет измерения подпространства
просто отображает N измерений точки "созвездия" в K-мерное кодовое слово SCMA. Отметим, что V содержит K-N строк, состоящих из одних нулей. Убрав из V строки, состоящие из одних нулей, остальное может быть представлено единичной матрицей IN, что означает то, что двоичный отображатель во время процесса отображения не переставляет измерения подпространства 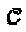 .
.
SCMA-кодер содержит l отдельных слоев, каждый из которых определен как 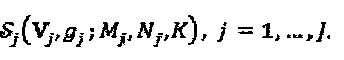 Функция gi "созвездия" генерирует множество
Функция gi "созвездия" генерирует множество 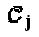 "созвездий" с Mj алфавитами длиной Nj. Матрица Vj отображения отображает точки Nj-мерных "созвездий" на кодовые слова SCMA для того, чтобы сформировать множество
"созвездий" с Mj алфавитами длиной Nj. Матрица Vj отображения отображает точки Nj-мерных "созвездий" на кодовые слова SCMA для того, чтобы сформировать множество 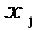 кодовых слов. Без потери общности можно предположить, что все слои имеют один и тот же или сходный размер и длину "созвездия", то есть
кодовых слов. Без потери общности можно предположить, что все слои имеют один и тот же или сходный размер и длину "созвездия", то есть 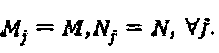 Подводя итог отметим, что SCMA-код может быть представлен как
Подводя итог отметим, что SCMA-код может быть представлен как 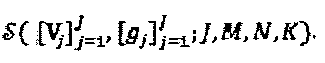 Кодовые слова SCMA мультиплексируются на К совместно используемых ортогональных (или близких к ортогональным) ресурсах (например, тонах OFDMA (Множественного доступа с ортогональным частотным разделением каналов) или пространственным слоям MIMO (Множественного ввода - множественного вывода)). Принятый сигнал после синхронного мультиплексирования слоев может быть выражен как:
Кодовые слова SCMA мультиплексируются на К совместно используемых ортогональных (или близких к ортогональным) ресурсах (например, тонах OFDMA (Множественного доступа с ортогональным частотным разделением каналов) или пространственным слоям MIMO (Множественного ввода - множественного вывода)). Принятый сигнал после синхронного мультиплексирования слоев может быть выражен как: 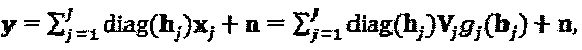 где
где 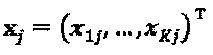 представляет собой кодовое слово SCMA для слоя j,
представляет собой кодовое слово SCMA для слоя j, 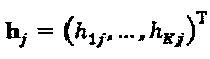 представляет собой вектор канала слоя j, и n ~
представляет собой вектор канала слоя j, и n ~ 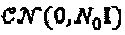 представляет собой фоновый шум. В случае, при котором все слои передаются из одной и той же точки передачи, все каналы идентичны hj=h, ∀j, и, следовательно, вышеупомянутое уравнению сводится к
представляет собой фоновый шум. В случае, при котором все слои передаются из одной и той же точки передачи, все каналы идентичны hj=h, ∀j, и, следовательно, вышеупомянутое уравнению сводится к 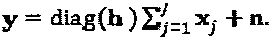 При мультиплексировании J слоев на К ресурсах коэффициент перегрузки кода определяется как λ:=J/К.
При мультиплексировании J слоев на К ресурсах коэффициент перегрузки кода определяется как λ:=J/К.
Сигнал, принимаемый на ресурсе k, может быть представлен как 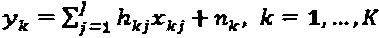 . Поскольку кодовые слова хj являются разреженными, то только некоторые из них конфликтуют за ресурс k. Множество ресурсов, занимаемых слоем j, зависит от матрицы отображения, и это множество определено индексом ненулевых элементов двоичного вектора-указателя
. Поскольку кодовые слова хj являются разреженными, то только некоторые из них конфликтуют за ресурс k. Множество ресурсов, занимаемых слоем j, зависит от матрицы отображения, и это множество определено индексом ненулевых элементов двоичного вектора-указателя 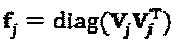 . Общее количество слоев, поступающих на ресурсы, определено как
. Общее количество слоев, поступающих на ресурсы, определено как 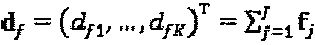 . Полная структура SCMA-кода S может быть представлена матрицей фактор-графов, определенной как F=(f1,…, fJ). Слой j и ресурс k соединяются в том случае, если и только в том случае, если (F)kf=1. Множество вершин-слоев, соединенных с вершиной-ресурсом k, определяется как
. Полная структура SCMA-кода S может быть представлена матрицей фактор-графов, определенной как F=(f1,…, fJ). Слой j и ресурс k соединяются в том случае, если и только в том случае, если (F)kf=1. Множество вершин-слоев, соединенных с вершиной-ресурсом k, определяется как  для ∀k. В качестве альтернативы, множество вершин-ресурсов, соединенных с вершиной-слоем j, представляет собой
для ∀k. В качестве альтернативы, множество вершин-ресурсов, соединенных с вершиной-слоем j, представляет собой 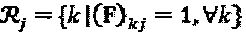 для ∀j. Основываясь на определении фактор-графа, принимаемый сигнал в ресурсе k можно перезаписать следующим образом:
для ∀j. Основываясь на определении фактор-графа, принимаемый сигнал в ресурсе k можно перезаписать следующим образом: 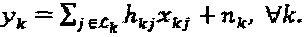 Следует отметить, что относящиеся к фактор-графу параметры F,
Следует отметить, что относящиеся к фактор-графу параметры F, 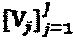 ,
, 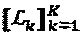 , и
, и 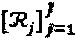 могут все представлять одну и ту же информацию, но в различных форматах.
могут все представлять одну и ту же информацию, но в различных форматах.
Нижеследующее описывает обнаружение посредством MAP-алгоритма, которое может быть выполнено SCMA-приемником, и рассматривается в работе: Reza Hoshyar (Реза Хошиар), Ferry P. Wathan (Ферри П. Вэзэн), Rahim Tafazolli (Рахим Тафазолли), "Novel Low-Density Signature for Synchronous CDMA Systems Over AWGN Channel ("Новая сигнатура низкой плотности для синхронных CDMA-систем в каналах с аддитивным белым гауссовым шумом"), IEEE trans, on signal processing, vol. 56, No. 4, pp. 1616, Apr. 2008 (труды Института инженеров по электротехнике и электронике (США) по обработке сигналов, том 56, Номер 4, стр. 1616, апрель 2008 г.), которая включена в данную заявку посредством ссылки так, как если бы она была воспроизведена здесь во всей своей полноте. Имея принимаемый сигнал у и знание 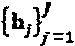 канала объединенное оптимальное MAP-обнаружение кодовых слов
канала объединенное оптимальное MAP-обнаружение кодовых слов 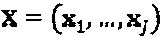 слоев может быть выражено как:
слоев может быть выражено как: 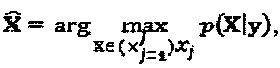 где
где  . Переданное кодовое слово слоя j может быть оценочно определено посредством максимизации предельного значения объединенной вероятности, что может быть задано как
. Переданное кодовое слово слоя j может быть оценочно определено посредством максимизации предельного значения объединенной вероятности, что может быть задано как 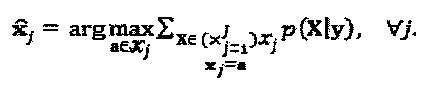
В соответствии с правилом Бэйза (Bays), вышеупомянутая условная вероятность выше может быть перезаписана как 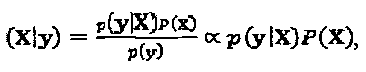 где
где 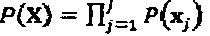 представляет собой объединенную априорную информацию всех статистически независимых слоев. Принимая, что в слоях - некоррелированные данные,
представляет собой объединенную априорную информацию всех статистически независимых слоев. Принимая, что в слоях - некоррелированные данные, 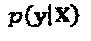 может быть разложена на множители как
может быть разложена на множители как 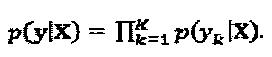 Вследствие разреженных кодовых слов, уk зависит только от слоев, которые соединены с вершиной-ресурсом k. Следовательно,
Вследствие разреженных кодовых слов, уk зависит только от слоев, которые соединены с вершиной-ресурсом k. Следовательно, 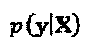 может быть далее сведена к:
может быть далее сведена к: 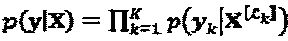 , где
, где 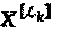 представляет собой стек всех хj с
представляет собой стек всех хj с 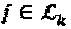 . Если все вершины-слои интерферируют на ресурсе k, или, что эквивалентно,
. Если все вершины-слои интерферируют на ресурсе k, или, что эквивалентно, 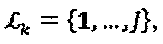 то
то 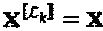 . Комбинируя вышеприведенные формулы и учитывая тот факт, что слой j зависит только от вершин-ресурсов, принадлежащих
. Комбинируя вышеприведенные формулы и учитывая тот факт, что слой j зависит только от вершин-ресурсов, принадлежащих 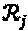 , оценку слоя j можно описать как:
, оценку слоя j можно описать как: 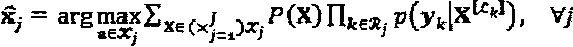 , где
, где 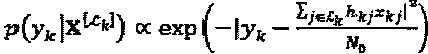 .
.
Вышеприведенное уравнение превращает исходную задачу совместного MAP-обнаружения в задачу маргинализации произведения функций (задачу MPF), которую намного более просто разрешить.
Задача MPF может не иметь "лобового" решения умеренной сложности, но близкое к оптимальному решение задачи может быть найдено итерационно посредством применения алгоритма передачи сообщений (МРА-алгоритма) по лежащему в его основе фактор-графу.
Обновление сообщения на вершине-ресурсе: Пусть 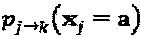 обозначает сообщение, переданное от вершины - слоя j на вершину - ресурс k о надежности взятого в слое j кодового слова
обозначает сообщение, переданное от вершины - слоя j на вершину - ресурс k о надежности взятого в слое j кодового слова 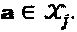 Обычно, ветвь, которая соединяет вершину-слой j и вершину-ресурс k, несет
Обычно, ветвь, которая соединяет вершину-слой j и вершину-ресурс k, несет 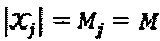 значений надежности для каждого возможного кодового слова, принадлежащего
значений надежности для каждого возможного кодового слова, принадлежащего 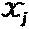 . Вершина-ресурс k обновляет и возвращает значения надежности следующим образом:
. Вершина-ресурс k обновляет и возвращает значения надежности следующим образом:
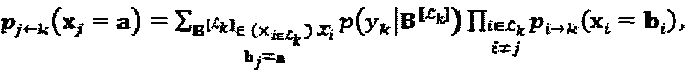 I
I 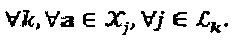
Сложность приемника, главным образом, зависит от количества сочетаний в вышеприведенном уравнении. Количество сочетаний на вершине-ресурсе k составляет  которое экспоненциально растет вместе с размером "созвездия" и количеством интерферирующих слоев. Внешняя информация
которое экспоненциально растет вместе с размером "созвездия" и количеством интерферирующих слоев. Внешняя информация 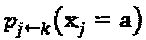 должна быть нормирована прежде, чем быть переданной от вершины-ресурса в соединенную с ней вершину-слой, например,
должна быть нормирована прежде, чем быть переданной от вершины-ресурса в соединенную с ней вершину-слой, например, 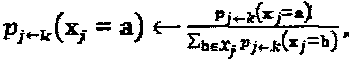
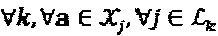 .
.
Обновление сообщения в вершине-слое. Пусть априорная информация о кодовых словах слоя j будет представлена как 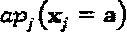 ,
,  Информацию ветви обновляют в вершине-слое j, основываясь на нижеследующей формуле,
Информацию ветви обновляют в вершине-слое j, основываясь на нижеследующей формуле, 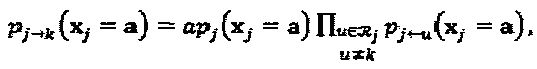
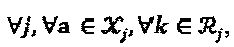 которая нормируется как:
которая нормируется как: 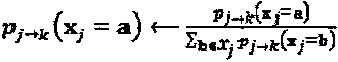 ,
, 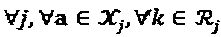 .
.
Вероятность вывода кодовых слов: Сообщения передаются итерационно между вершинами слоя и ресурса и после схождения внешние вероятности кодовых слов каждого слоя вычисляются следующим образом: 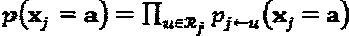 ,
, 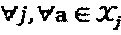 . Это уравнение может быть нормировано как
. Это уравнение может быть нормировано как 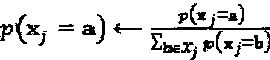 ,
, 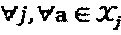 .
.
Задача проектирования SCMA-кода с заданной структурой 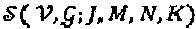 , где
, где 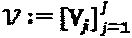 и
и 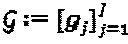 могут быть заданы как
могут быть заданы как  , где m представляет собой некоторый заданный критерий проектирования. Поскольку решение этой многомерной задачи не является прямым, то для получения субоптимального решения для этой задачи предлагается подход многоступенчатой оптимизации.
, где m представляет собой некоторый заданный критерий проектирования. Поскольку решение этой многомерной задачи не является прямым, то для получения субоптимального решения для этой задачи предлагается подход многоступенчатой оптимизации.
В качестве общей многоступенчатой методологии проектирования, разреженная кодовая книга генерируется следующим образом: Сначала генерируются многомерное модуляционное "созвездие" (многомерные модуляционные "созвездия"); и затем "созвездие" ("созвездия") передается (передаются) во множественные разреженные кодовые книги. Следуя вышеупомянутым двум большим этапам, ниже приводится подробное описание методологии проектирования для SCMA:
Как было описано ранее, множество матриц 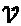 отображения может определять количество слоев, интерферирующих в каждой вершине-ресурсе, которые, в свою очередь, определяет сложность МРА-обнаружения. Чем более разреженными являются кодовые слова, тем менее сложным является МРА-обнаружение. Правила проектирования матриц отображения могут быть определены следующим образом: (1)
отображения может определять количество слоев, интерферирующих в каждой вершине-ресурсе, которые, в свою очередь, определяет сложность МРА-обнаружения. Чем более разреженными являются кодовые слова, тем менее сложным является МРА-обнаружение. Правила проектирования матриц отображения могут быть определены следующим образом: (1) 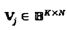 , (2)
, (2) 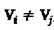 ,
, 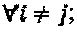 и (3)
и (3) 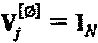 , где
, где 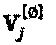 представляет собой Vj
после удаления ее строк, содержащих одни нули.
представляет собой Vj
после удаления ее строк, содержащих одни нули.
Единственное решение 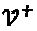 вышеупомянутой задачи определяется просто введением К-N векторов-строк, содержащих одни нули, в строки IN. Свойства этого решения могут быть нижеследующими: (1)
вышеупомянутой задачи определяется просто введением К-N векторов-строк, содержащих одни нули, в строки IN. Свойства этого решения могут быть нижеследующими: (1) 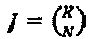 ; 2)
; 2) 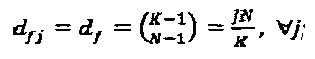 (3)
(3) 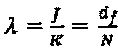 и (4)
и (4) 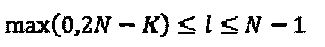 , где l представляет собой количество перекрывающихся элементов любых двух отличных друг от друга fj векторов.
, где l представляет собой количество перекрывающихся элементов любых двух отличных друг от друга fj векторов.
В качестве примера, при рассмотрении сложности, N должно быть достаточно малым по сравнению с K, для того, чтобы сохранять разумный уровень разреженности. В частности, если N=2, точки двумерных "созвездий" могут отображаться на K>2 ресурсов, создавая кодовые слова SCMA с минимумом интерферирующих вершин-слоев. Свойства отображения являются нижеследующими: (1) 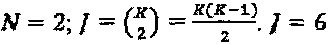 для К=4; (2)
для К=4; (2) 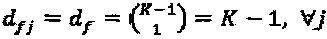 df=3 для К=4; (3)
df=3 для К=4; (3) 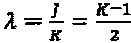 . λ=1.5 для К=4; и (4)
. λ=1.5 для К=4; и (4) 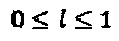 если К=4, что означает, что кодовые слова являются либо полностью ортогональными без перекрытий или они сталкиваются только на одном ненулевом элементе.
если К=4, что означает, что кодовые слова являются либо полностью ортогональными без перекрытий или они сталкиваются только на одном ненулевом элементе.
 для К=4
для К=4
На Фиг. 10 проиллюстрирован фактор-граф 1000, представляющий F по отношению к точкам "созвездий". При наличии отображающего множества 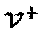 задача оптимизации SCMA-кода сводится к
задача оптимизации SCMA-кода сводится к 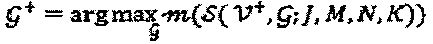
Одна задача может заключаться в том, чтобы определить j различных N-мерных "созвездий", каждое из которых содержит М точек. Для упрощения задачи оптимизации точки "созвездий", относящиеся к слоям, моделируются на основе материнского "созвездия" и операторов, специфических для слоев, то есть gj≡(Δj)g, ∀j, где Δj обозначает оператора "созвездия". В соответствии с этой моделью, оптимизация SCMA кода превращается в 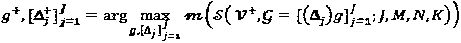 .
.
Вообще, вместо одного могли бы иметься множественные материнские "созвездия": 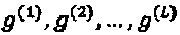 , и "созвездие" для слоя могло бы создаваться на одном из имеющихся материнских "созвездий", то есть
, и "созвездие" для слоя могло бы создаваться на одном из имеющихся материнских "созвездий", то есть  и
и 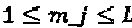 . В нижеследующем, мы предполагаем, что существует только одно материнское "созвездие". Нетрудно распространить эту методологию проектирования на случай, при котором существуют множественные материнские "созвездия". В качестве субоптимального подхода к вышеупомянутой задаче, материнское "созвездие" и операторы можно определять по-отдельности.
. В нижеследующем, мы предполагаем, что существует только одно материнское "созвездие". Нетрудно распространить эту методологию проектирования на случай, при котором существуют множественные материнские "созвездия". В качестве субоптимального подхода к вышеупомянутой задаче, материнское "созвездие" и операторы можно определять по-отдельности.
Для материнского многомерного "созвездия", проектирование "созвездия" в вещественной области может быть описано следующим образом. Цель может заключаться в том, чтобы спроектировать многомерное компактное "созвездие", которое минимизирует среднюю энергию алфавита для некоторого заданного минимального Евклидова расстояния между точками "созвездия". Мы сначала рассматриваем 2N-мерный вещественнозначный канал с аддитивным белым гауссовым шумом. С четным значением, составляющим 2N, результаты можно легко перенести на N-мерный комплекснозначный канал с аддитивным белым гауссовым шумом. Для некоторой заданной пары (2N, М), цель заключается в том, чтобы обнаружить "созвездие", имеющее минимальную энергию, 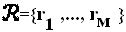 , где
, где  для m=1,…, М, сохраняя при этом Евклидово расстояние между различными точками (алфавитами) большим или равным некоторому пороговому значению
для m=1,…, М, сохраняя при этом Евклидово расстояние между различными точками (алфавитами) большим или равным некоторому пороговому значению  . "Созвездие"
. "Созвездие" 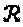 представляет собой точку в пространстве
представляет собой точку в пространстве 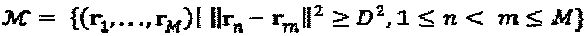 . Следуя этому подходу, нам следует определить функцию качества:
. Следуя этому подходу, нам следует определить функцию качества:
 и
и 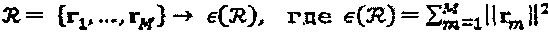 .
.
Ясно, что 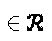 пропорциональна средней энергии
пропорциональна средней энергии 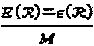 символа. Создание оптимальной кодовой книги
символа. Создание оптимальной кодовой книги 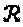 соответствует решению задачи оптимизации
соответствует решению задачи оптимизации 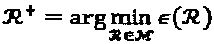 .
.
Допускаются произвольные вещественные значения символов r1, …, rм. Задача, определенная выше, представляет собой задачу невыпуклой оптимизации, поскольку все ограничения в множестве 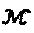 являются невыпуклыми. Более точно, она принадлежит к классу задач невыпуклого, квадратично ограниченного квадратичного программирования (QCQP-программирования). Невыпуклое QCQP-программирование представляет собой известную в литературе по оптимизации задачу со многими применениями. Невыпуклое QCQP-программирование является NP-трудной задачей. Следовательно, обычно трудно решить QCQP даже для небольшого количества ограничений.
являются невыпуклыми. Более точно, она принадлежит к классу задач невыпуклого, квадратично ограниченного квадратичного программирования (QCQP-программирования). Невыпуклое QCQP-программирование представляет собой известную в литературе по оптимизации задачу со многими применениями. Невыпуклое QCQP-программирование является NP-трудной задачей. Следовательно, обычно трудно решить QCQP даже для небольшого количества ограничений.
Субоптимальное решение предлагается в работе: Marko Веко (Марко Беко) и Rui Dinis (Руй Динис), "Designing Good Multi-Dimensional Constellations" (Проектирование хороших многомерных "созвездий"), IEEE wireless communications letters, vol. 1, No. 3, pp. 221-224, June 2012, (Записки Института инженеров по электротехнике и электронике (США) по беспроводной связи, том 1, Номер 3, страницы 221-224, июнь 2012 г.), которая включена в данную заявку посредством ссылки так, как если бы она была воспроизведена здесь во всей своей полноте). Субоптимальное решение, предложенное вышеупомянутой работе, на которую дана ссылка, основано на способах, основанных на переформулировании/линеаризации, также известных как выпукло-вогнутая процедура (ССР-процедура). Сформулированную задачу невыпуклой оптимизации пытаются решить, решая последовательность задач выпуклой оптимизации, где осуществляется минимизация выпуклой квадратичной целевой функции, ограниченную множеством линейных неравенств.
Что касается одноместных операций над "созвездиями" в вещественной области, то как только известно материнское вещественное "созвездие", одноместные операции можно для создания SCMA-кода напрямую применять к материнскому "созвездию". Задача проектирования выражается следующим образом: 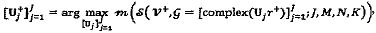 где r+ представляет собой функцию
где r+ представляет собой функцию 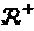 , Uj, представляет собой унитарную матрицу 2N×2N, a complex(·) представляет собой функцию, объединяющую каждые два следующих друг за другом измерения для того, чтобы сформировать комплексное измерение. Каждая унитарная матрица имеет
, Uj, представляет собой унитарную матрицу 2N×2N, a complex(·) представляет собой функцию, объединяющую каждые два следующих друг за другом измерения для того, чтобы сформировать комплексное измерение. Каждая унитарная матрица имеет 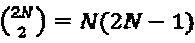 степеней свободы. Если унитарная матрица представлена заданными матрицами поворота, то унитарные параметры равномерно распределены в интервале [-π.π). На основе вышеупомянутой задачи оптимизации, имеются N(2N-1)J-1 независимые переменные, подлежащие оптимизации. Если каждая переменная выбирается из сетки с Nu точками на интервале [-π.π), то подход методом полного перебора требует
степеней свободы. Если унитарная матрица представлена заданными матрицами поворота, то унитарные параметры равномерно распределены в интервале [-π.π). На основе вышеупомянутой задачи оптимизации, имеются N(2N-1)J-1 независимые переменные, подлежащие оптимизации. Если каждая переменная выбирается из сетки с Nu точками на интервале [-π.π), то подход методом полного перебора требует 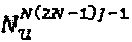 попыток. В качестве относительно простого примера: для N=2, J=6 и Nu=100 общее количество попыток методом полного перебора составляет 1070. Если предположить, что процессор может обрабатывать 1010 попыток в секунду (очень совершенный процессор), то для того, чтобы проверить каждую возможную гипотезу и определить оптимальную гипотезу, требуется более чем 3е52 лет! Эта задача является даже еще более сложной в случае, когда больший SCMA-код.
попыток. В качестве относительно простого примера: для N=2, J=6 и Nu=100 общее количество попыток методом полного перебора составляет 1070. Если предположить, что процессор может обрабатывать 1010 попыток в секунду (очень совершенный процессор), то для того, чтобы проверить каждую возможную гипотезу и определить оптимальную гипотезу, требуется более чем 3е52 лет! Эта задача является даже еще более сложной в случае, когда больший SCMA-код.
Остальная часть проектирования SCMA-кода может быть посвящена субоптимальному подходу, который является практически доступным и, в то же самое время, он не так уж далек от неизвестного оптимального решения. Основная идея решения, близкого к оптимальному, заключается в следующем: (1) основываясь на некотором заданном критерии "созвездие" в вещественной области переводят в комплексную область. Это "созвездие" в комплексной области используется в качестве материнского "созвездия"; и (2) основываясь на некоторых последовательно конкатенированных операторах, применяемых к этому материнскому "созвездию", создают "созвездия" для каждого слоя.
"Созвездие" в комплексной области: Вещественное "созвездие" 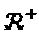 может быть с легкостью преобразовано в комплексное "созвездие"
может быть с легкостью преобразовано в комплексное "созвездие" 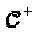 посредством объединения в пару любых двух вещественных измерений для того, чтобы сформировать комплексное измерение. 2N вещественных измерений могут быть объединены в пары посредством
посредством объединения в пару любых двух вещественных измерений для того, чтобы сформировать комплексное измерение. 2N вещественных измерений могут быть объединены в пары посредством 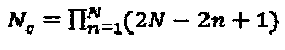 различных способов. Среди имеющихся возможных вариантов формирования пар выбирается вариант с максимальной вариацией мощности между комплексными измерениями, например, с использованием:
различных способов. Среди имеющихся возможных вариантов формирования пар выбирается вариант с максимальной вариацией мощности между комплексными измерениями, например, с использованием: 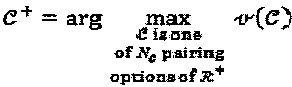 . где
. где 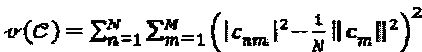 . Вариация мощности между измерениями "созвездия" помогает SIC-свойству МРА-обнаружителя лучше удалять отличающиеся по мощности интерферирующие сигналы, прибывающие из других "сталкивающихся" слоев в вершину-ресурс. Обоснование этого критерия оптимизации дополнительно описывается ниже. Отметим, что комплексное преобразование из
. Вариация мощности между измерениями "созвездия" помогает SIC-свойству МРА-обнаружителя лучше удалять отличающиеся по мощности интерферирующие сигналы, прибывающие из других "сталкивающихся" слоев в вершину-ресурс. Обоснование этого критерия оптимизации дополнительно описывается ниже. Отметим, что комплексное преобразование из 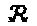 в
в 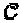 не изменяет свойства "созвездия", то есть
не изменяет свойства "созвездия", то есть 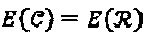 и
и 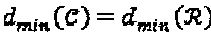 .
.
Например, пусть N=2 и М=4. Вещественное 2N=4-мерное решение определяется следующим образом:
 с
с 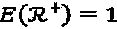 и
и
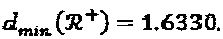 4 вещественных измерения могут быть скомбинированы 3 различными способами. В смысле
4 вещественных измерения могут быть скомбинированы 3 различными способами. В смысле 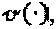 лучшее 2-мерное комплексное решение определяется следующим образом:
лучшее 2-мерное комплексное решение определяется следующим образом:
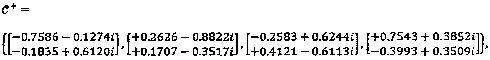 с
с 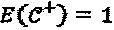 и
и 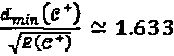 . Вариация мощности измерения количественно определена как
. Вариация мощности измерения количественно определена как 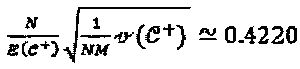 . Если алфавиты "созвездий" строятся на "созвездии" QPSK (Квадратурной фазовой манипуляции), традиционной для CDMA способом (Здесь, расширяющая последовательность в CDMA представляет собой просто
. Если алфавиты "созвездий" строятся на "созвездии" QPSK (Квадратурной фазовой манипуляции), традиционной для CDMA способом (Здесь, расширяющая последовательность в CDMA представляет собой просто 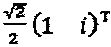 , и множество QPSK-созвездий представляет собой
, и множество QPSK-созвездий представляет собой 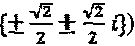 , то можно предложить нижеследующий типичный пример:
, то можно предложить нижеследующий типичный пример:
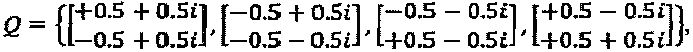 в котором
в котором 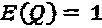 ,
, 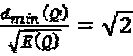 , и
, и 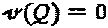 . Выигрыш при оптимизации многомерного "созвездия" определен как
. Выигрыш при оптимизации многомерного "созвездия" определен как 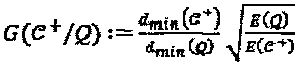 , что составляет приблизительно 1,25 децибела для этого конкретного примера. Выигрыш по минимальному Евклидову расстоянию может быть потенциально преобразован в выигрыши по отношению "сигнал-шум" (SNR) и разнесению, имеющие место для характеристики BLER (частоты блоков с ошибками) SCMA-кода. В то же время, вариация мощности измерения для
, что составляет приблизительно 1,25 децибела для этого конкретного примера. Выигрыш по минимальному Евклидову расстоянию может быть потенциально преобразован в выигрыши по отношению "сигнал-шум" (SNR) и разнесению, имеющие место для характеристики BLER (частоты блоков с ошибками) SCMA-кода. В то же время, вариация мощности измерения для 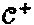 представляет собой преимущество для
представляет собой преимущество для 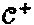 . Дополнительные подробности влияния вариации мощности измерения приводятся ниже.
. Дополнительные подробности влияния вариации мощности измерения приводятся ниже.
После оптимизации множества 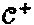 "созвездий", определяется соответствующая функция g+ "созвездия" для того, чтобы задать правило отображения между двоичными словами и точками алфавита "созвездий". Например, следуя правилу отображения Gray, двоичные слова любых двух ближайших точек "созвездия" могут иметь расстояние Хемминга, составляющее 1. В качестве альтернативы, после создания кодовых книг для всех слоев, правило двоичного отображения для каждой из кодовых книг слоя может быть задано отдельно.
"созвездий", определяется соответствующая функция g+ "созвездия" для того, чтобы задать правило отображения между двоичными словами и точками алфавита "созвездий". Например, следуя правилу отображения Gray, двоичные слова любых двух ближайших точек "созвездия" могут иметь расстояние Хемминга, составляющее 1. В качестве альтернативы, после создания кодовых книг для всех слоев, правило двоичного отображения для каждой из кодовых книг слоя может быть задано отдельно.
Операторы функции "созвездия": при наличии решения для материнского "созвездия" (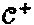 или, что эквивалентно, g+), исходная задача оптимизации SCMA далее сводится к
или, что эквивалентно, g+), исходная задача оптимизации SCMA далее сводится к 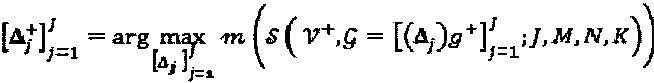 . Ниже описываются определение операторов и стратегия их оптимизации.
. Ниже описываются определение операторов и стратегия их оптимизации.
Что касается операторов "созвездия", то пусть δ обозначают оператора, примененного к 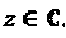 Эта операция обозначается как (δ)z. Три типичных оператора представляют собой масштабирование, комплексное сопряжение и поворот фазы. Оператор масштабирования ⊗:π выражается как (⊗:α)z-:=αz. Нулевой оператор представлен как (⌀)z=z. Оператор комплексного сопряжения определен так, как указано ниже:
Эта операция обозначается как (δ)z. Три типичных оператора представляют собой масштабирование, комплексное сопряжение и поворот фазы. Оператор масштабирования ⊗:π выражается как (⊗:α)z-:=αz. Нулевой оператор представлен как (⌀)z=z. Оператор комплексного сопряжения определен так, как указано ниже: 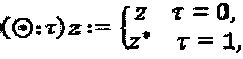 , и также оператор фазы определен как
, и также оператор фазы определен как 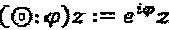 . Скалярный оператор может быть расширен до векторного оператора. Пусть Δ=(δ1, … δN)Т применяется к
. Скалярный оператор может быть расширен до векторного оператора. Пусть Δ=(δ1, … δN)Т применяется к 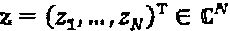 . По определению, (Δ)z=((δ1)z1, …, (δN)zN)Т. Аналогичным образом, матричный оператор Y=[γnm] может быть определен как (Y)z=r, где
. По определению, (Δ)z=((δ1)z1, …, (δN)zN)Т. Аналогичным образом, матричный оператор Y=[γnm] может быть определен как (Y)z=r, где 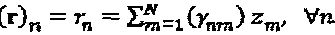 .
.
Векторная перестановка представляет собой пример матричного оператора, который может быть просто определен как 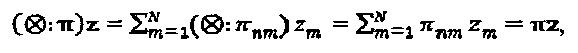 где π представляет собой матрицу перестановок. Множественные операторы могут быть последовательно конкатенированы. Например
где π представляет собой матрицу перестановок. Множественные операторы могут быть последовательно конкатенированы. Например 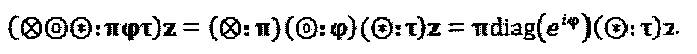 Операторы могут быть применены к генератору функции "созвездия"
Операторы могут быть применены к генератору функции "созвездия" 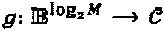 , где c=g(b). Функция (Δ)g определена как
, где c=g(b). Функция (Δ)g определена как 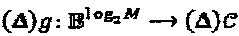 c
c  , где
, где 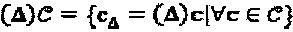 . В процессе проектирования SCMA-кода нам требуются те типы операторов "созвездия", которые не изменяют основные свойства множества "созвездий". Легко можно показать, что операторы перестановки, поворота фазы и сопряжения сохраняют первоначальные свойства "созвездия". Другими словами,
. В процессе проектирования SCMA-кода нам требуются те типы операторов "созвездия", которые не изменяют основные свойства множества "созвездий". Легко можно показать, что операторы перестановки, поворота фазы и сопряжения сохраняют первоначальные свойства "созвездия". Другими словами, 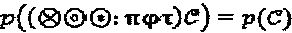 для
для 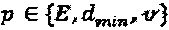 .
.
Как было упомянуто выше, "созвездия" для различных слоев SCMA создаются на основе материнского "созвездия" g и оператора Δj, специфического по слою и предназначенного для слоя j. Специфический по слою оператор определяется как  .
.
Что касается оптимизации операторов "созвездия", то при моделировании операторов "созвездия" так, как показано выше, задача оптимизации SCMA-кода может быть перезаписана следующим образом
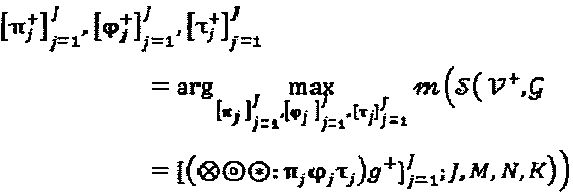 .
.
Пусть 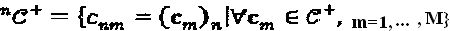 ,
, 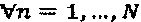 обозначает n-е измерение материнского "созвездия". Также предположим, что
обозначает n-е измерение материнского "созвездия". Также предположим, что
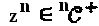 . Некоторый произвольный алфавит материнского кодового слова может быть представлен как z=(z, z2, …, zn)T. Пусть на этот момент оператор "созвездия" для слоя j ограничен матрицей перестановок πj. В соответствии с этими предположениями, кодовое слово SCMA для слоя j выражается как хj=qj(z)=Vjπjz. При рассмотрении канала AWGN (канала с аддитивным белым гауссовым шумом), групповой принимаемый сигнал представляет собой
. Некоторый произвольный алфавит материнского кодового слова может быть представлен как z=(z, z2, …, zn)T. Пусть на этот момент оператор "созвездия" для слоя j ограничен матрицей перестановок πj. В соответствии с этими предположениями, кодовое слово SCMA для слоя j выражается как хj=qj(z)=Vjπjz. При рассмотрении канала AWGN (канала с аддитивным белым гауссовым шумом), групповой принимаемый сигнал представляет собой 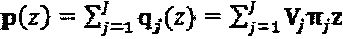 , где
, где  представляет собой вектор К×1, в котором элемент
представляет собой вектор К×1, в котором элемент 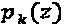 представляет интерферирующий многочлен для вершины-ресурса k. Интерферирующий многочлен может быть смоделирован как
представляет интерферирующий многочлен для вершины-ресурса k. Интерферирующий многочлен может быть смоделирован как 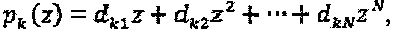 где
где 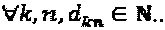 Поскольку количество интерферирующих слоев, приходящихся на вершину-ресурс, составляет df, то можно сделать заключение о том, что
Поскольку количество интерферирующих слоев, приходящихся на вершину-ресурс, составляет df, то можно сделать заключение о том, что 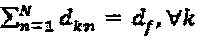 . В качестве примера, для N=2 и
. В качестве примера, для N=2 и 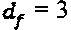 интерферирующий многочлен слоя 1 может представлять собой
интерферирующий многочлен слоя 1 может представлять собой 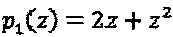 , означающее то, что первая вершина-ресурс берет 3 интерферирующих слоя, где два из них - из первого измерения материнского "созвездия", а третий элемент выбран из второго измерения материнского созвездия. Вообще, для некоторого заданного множества матриц отображения ν, структура
, означающее то, что первая вершина-ресурс берет 3 интерферирующих слоя, где два из них - из первого измерения материнского "созвездия", а третий элемент выбран из второго измерения материнского созвездия. Вообще, для некоторого заданного множества матриц отображения ν, структура 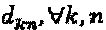 зависит от множества перестановок
зависит от множества перестановок 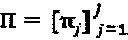 . Между p(z) и П имеется взаимно-однозначное отображение, но существует шанс, что два различных множества перестановок приводят к идентичным интерферирующим многочленам для любых двух вершин-ресурсов. Общее количество вариантов перестановки "созвездия" составляет
. Между p(z) и П имеется взаимно-однозначное отображение, но существует шанс, что два различных множества перестановок приводят к идентичным интерферирующим многочленам для любых двух вершин-ресурсов. Общее количество вариантов перестановки "созвездия" составляет 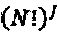 , в то время как общее количество отличных друг от друга интерферирующих многочленов ограничено только
, в то время как общее количество отличных друг от друга интерферирующих многочленов ограничено только 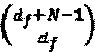 .
.
При взгляде на интерферирующий многочлен p(z) (k пропущен ради простоты) видно, что различные измерения материнского "созвездия" могли бы интерферировать в вершине-ресурсе. Задача МРА-обнаружителя заключается в том, чтобы итерационным способом отделить интерферирующие символы. В качестве основного правила: интерферирующие символы отделяются более легко, если их уровень мощности является более различающимся. Интуитивно понятно, что самый сильный символ обнаруживается (или его соответствующее значение надежности сходится) первым, и затем это помогает обнаруживать остальные символы, последовательно удаляя следующие самые сильные символы.
Исходя из этого рассуждения, материнское "созвездие" должно иметь различающийся уровень средней мощности по измерениям "созвездия", то есть, когда создаются пары измерений 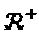 для формирования "созвездия" в комплексной области
для формирования "созвездия" в комплексной области  должна быть максимизирована. Это - правило, которое обсуждается ниже, для проектирования материнского комплексного "созвездия". Предполагая, что уровень мощности измерения материнского "созвездия" является в достаточной мере различающимся, необходимо выбирать множество перестановок таким образом, чтобы оно фиксировало как можно более сильное различие мощности по интерферирующим слоям. Вариацию мощности по слоям интерферирующего многочлена можно определить количественно и оптимизировать, следуя одному из двух подходов, описываемых следующим образом: Для некоторого данного интерферирующего многочлена p(z), простым показателем вариации мощности по интерферирующим слоям служит количество ненулевых коэффициентов. Например, если N=2 и
должна быть максимизирована. Это - правило, которое обсуждается ниже, для проектирования материнского комплексного "созвездия". Предполагая, что уровень мощности измерения материнского "созвездия" является в достаточной мере различающимся, необходимо выбирать множество перестановок таким образом, чтобы оно фиксировало как можно более сильное различие мощности по интерферирующим слоям. Вариацию мощности по слоям интерферирующего многочлена можно определить количественно и оптимизировать, следуя одному из двух подходов, описываемых следующим образом: Для некоторого данного интерферирующего многочлена p(z), простым показателем вариации мощности по интерферирующим слоям служит количество ненулевых коэффициентов. Например, если N=2 и 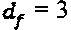 , мы предпочитаем
, мы предпочитаем 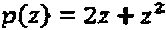 или
или 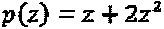 , а не
, а не 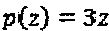 или
или 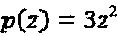 . В последних случаях, все три символа - из одного и того же измерения, следовательно, их вариация мощности является фактически нулевой. Пусть
. В последних случаях, все три символа - из одного и того же измерения, следовательно, их вариация мощности является фактически нулевой. Пусть 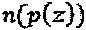 обозначает количество ненулевых коэффициентов (или, что эквивалентно, количество одночленов) в p(z).
обозначает количество ненулевых коэффициентов (или, что эквивалентно, количество одночленов) в p(z).
Критерий проектирования множества перестановок определяется следующим образом: 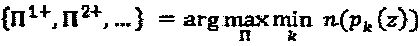 . Как показано выше, для вышеописанной задачи оптимизации могло бы иметься больше чем одно решение. Более точно, фактическая вариация мощности для
. Как показано выше, для вышеописанной задачи оптимизации могло бы иметься больше чем одно решение. Более точно, фактическая вариация мощности для 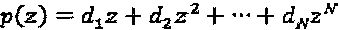 может быть количественно определена следующим образом:
может быть количественно определена следующим образом: 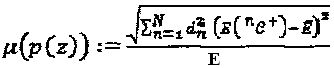 , где
, где 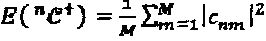 , и
, и 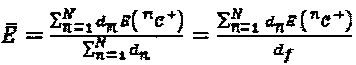 . Задача проектирования описывается, как:
. Задача проектирования описывается, как: 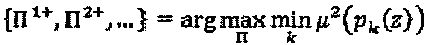 . Предположим, что
. Предположим, что 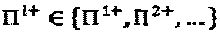 представляет собой решение - кандидат для оператора перестановки, приводящего к p(z) с коэффициентами
представляет собой решение - кандидат для оператора перестановки, приводящего к p(z) с коэффициентами 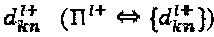 . Если к материнскому "созвездию" применяются операторы фаза и сопряжения, то интерферирующий многочлен может быть перезаписан как:
. Если к материнскому "созвездию" применяются операторы фаза и сопряжения, то интерферирующий многочлен может быть перезаписан как: 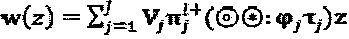 . Типичный многочлен, интерферирующий на ресурсе, может быть смоделирован как:
. Типичный многочлен, интерферирующий на ресурсе, может быть смоделирован как: 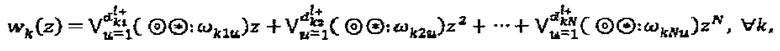 где
где 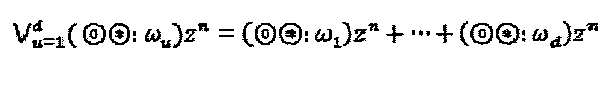 и
и 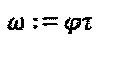 представляет собой параметр оператора фазы/сопряжения.
представляет собой параметр оператора фазы/сопряжения.
Физическая интерпретация вышеописанной модели заключается в том, что 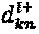 из
из 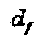 интерферирующих ветвей вершины-ресурса идут от измерения n материнского "созвездия", и каждая из этих
интерферирующих ветвей вершины-ресурса идут от измерения n материнского "созвездия", и каждая из этих 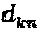 ветвей уникальным образом преобразовываются в соответствии с их оператором
ветвей уникальным образом преобразовываются в соответствии с их оператором  фазы/сопряжения. Как было упомянуто выше, множество
фазы/сопряжения. Как было упомянуто выше, множество 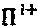 матриц перестановок максимизирует вариацию уровня мощности для
матриц перестановок максимизирует вариацию уровня мощности для 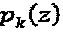 либо в смысле
либо в смысле 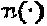 , либо в смысле
, либо в смысле 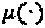 . Операторы
. Операторы 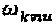 фазы/сопряжения не изменяют меры вариации мощности
фазы/сопряжения не изменяют меры вариации мощности 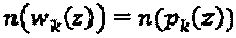 или
или 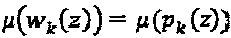 . Однако операторы ветви помогают увеличивать минимальное Евклидово расстояние между интерферирующими измерениями. Расстояние между любыми двумя множествами измерений с любыми произвольными операторами определяется как:
. Однако операторы ветви помогают увеличивать минимальное Евклидово расстояние между интерферирующими измерениями. Расстояние между любыми двумя множествами измерений с любыми произвольными операторами определяется как: 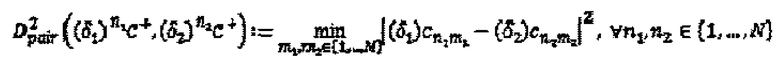 . Следовательно, для некоторого данного множества
. Следовательно, для некоторого данного множества 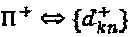 перестановок, операторы фазы/сопряжения каждой вершины-ресурса k оптимизируются следующим образом:
перестановок, операторы фазы/сопряжения каждой вершины-ресурса k оптимизируются следующим образом:
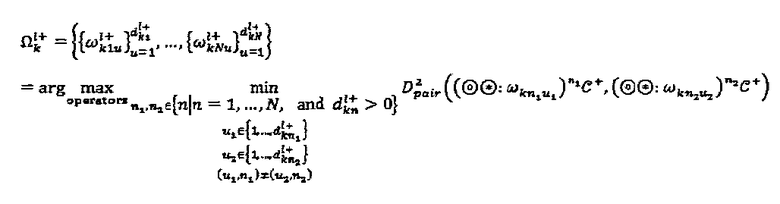
Решение вышеприведенной задачи находится методом полного перебора по всем возможным комбинациям операторов.  представляет решение для операторов вершины-ресурса k для данного кандидата
представляет решение для операторов вершины-ресурса k для данного кандидата 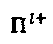 перестановки. Оптимальное попарное минимальное расстояние для
перестановки. Оптимальное попарное минимальное расстояние для 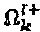 обозначается как
обозначается как 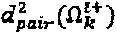 . Разреженная структура SCMA-кода помогает понизить сложность вышеописанной оптимизации, поскольку общее количество операторов ограничено до
. Разреженная структура SCMA-кода помогает понизить сложность вышеописанной оптимизации, поскольку общее количество операторов ограничено до 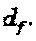 Анализ сложности оптимизации методом полного перебора дает следующее: (i) Количество операторов, подлежащих оптимизации:
Анализ сложности оптимизации методом полного перебора дает следующее: (i) Количество операторов, подлежащих оптимизации: 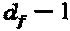 . Один оператор может быть нулевым; (ii) Количество пар во множестве измерений:
. Один оператор может быть нулевым; (ii) Количество пар во множестве измерений: 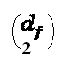 ; (iii) Количество вычислений расстояния в
; (iii) Количество вычислений расстояния в 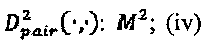 Количество операций суммирования/умножения вещественных чисел для вычисления расстояния: 7 суммирований + 10 умножений. Если стоимость умножения вещественных чисел в
Количество операций суммирования/умножения вещественных чисел для вычисления расстояния: 7 суммирований + 10 умножений. Если стоимость умножения вещественных чисел в 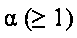 раз больше, чем сложения вещественных чисел, то общая стоимость вычисления расстояния составляет
раз больше, чем сложения вещественных чисел, то общая стоимость вычисления расстояния составляет 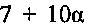 ; (v) Количество вариантов выбора для оператора фазы/сопряжения:
; (v) Количество вариантов выбора для оператора фазы/сопряжения: 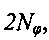 где
где 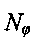 представляет собой количество узловых точек на сетке в фазовом интервале
представляет собой количество узловых точек на сетке в фазовом интервале 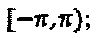 (vi) Максимальное количество интерферирующих многочленов:
(vi) Максимальное количество интерферирующих многочленов: 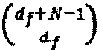 . Это сценарий самого плохого случая, при котором являющееся кандидатом множество
. Это сценарий самого плохого случая, при котором являющееся кандидатом множество 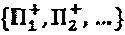 перестановок покрывает все возможности интерферирующих многочленов.
перестановок покрывает все возможности интерферирующих многочленов.
Основываясь на вышеупомянутых параметрах, верхняя граница стоимости C сложности оптимизации методом полного перебора составляет: 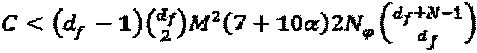 .
.
В порядке примера отметим, если 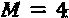 ,
, 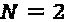 ,
,  ,
, 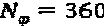 , и
, и 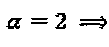
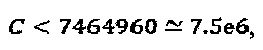 что может быть вычислено за короткое время на обычном процессоре с тактовой частотой 2 ГГц. Отметим, что все это представляет собой вычисления в автономном (несетевом) режиме работы только для оптимизации SCMA-кодирования. На этой стадии, у нас имеется являющееся кандидатом множество
что может быть вычислено за короткое время на обычном процессоре с тактовой частотой 2 ГГц. Отметим, что все это представляет собой вычисления в автономном (несетевом) режиме работы только для оптимизации SCMA-кодирования. На этой стадии, у нас имеется являющееся кандидатом множество 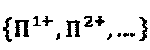 перестановок и их соответствующие операторы и оптимальные расстояния, которые задаются как:
перестановок и их соответствующие операторы и оптимальные расстояния, которые задаются как: 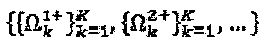 и
и 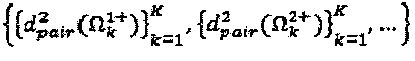 и (соответственно).
и (соответственно).
Наилучшее множество перестановок может быть легко выбрано на основе нижеследующего критерия: 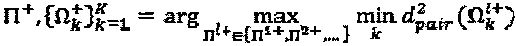 , и если имеется больше чем одно решение
, и если имеется больше чем одно решение 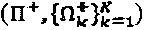 для вышеописанной задачи, то среди их выбирается то решение, у которого максимальное суммарное минимальное расстояние, то есть
для вышеописанной задачи, то среди их выбирается то решение, у которого максимальное суммарное минимальное расстояние, то есть 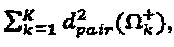 является наибольшим.
является наибольшим.
В качестве альтернативы попарному критерию оптимизации операторов, упомянутому выше, для оптимизации оператора вводится также критерий суперпозиции. Критерий суперпозиции определяется нижеследующим образом: 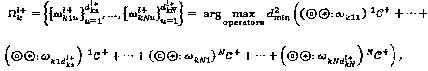
в котором для любых двух множеств 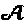 и
и 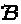 мы определяем
мы определяем 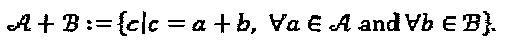 Критерии суперпозиции и попарный сравниваются ниже.
Критерии суперпозиции и попарный сравниваются ниже.
После оптимизации операторов и определения оптимального 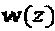 , непосредственно следующий за этим вопрос заключается в том, как распределить оптимальных операторы различным интерферирующим слоям. В качестве простого примера, соответствующим оператором интерферирующего многочлена
, непосредственно следующий за этим вопрос заключается в том, как распределить оптимальных операторы различным интерферирующим слоям. В качестве простого примера, соответствующим оператором интерферирующего многочлена 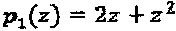 является
является 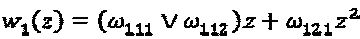 . В соответствии
. В соответствии 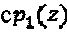 , два интерферирующих слоя - из первого измерения. На Фиг. 11 проиллюстрирован фактор-граф 1100,
, два интерферирующих слоя - из первого измерения. На Фиг. 11 проиллюстрирован фактор-граф 1100, 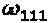 и
и 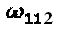 могут быть распределены любому из интерферирующих слоев. Здесь общее количество вариантов выбора распределения составляет 2.
могут быть распределены любому из интерферирующих слоев. Здесь общее количество вариантов выбора распределения составляет 2.
Как общее правило, для интерферирующего многочлена формы 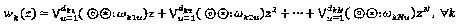 . Следует отметить, что операторы могут быть распределены SCMA-коду
. Следует отметить, что операторы могут быть распределены SCMA-коду 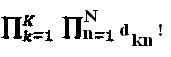 различными способами. Как показано позже, влияние распределения операторов на рабочих характеристиках окончательного SCMA-кода является незначительным. Причина этого заключается в том, что независимо от того, какие операторы распределены каким интерферирующим слоям, объединенная интерференция в данной вершине-ресурсе не изменяется. Основываясь на этом наблюдении, для создания окончательного SCMA-кода можно распределять оптимизированные операторы интерферирующим слоям каждой вершины-ресурса случайным образом (или в некотором заданном порядке).
различными способами. Как показано позже, влияние распределения операторов на рабочих характеристиках окончательного SCMA-кода является незначительным. Причина этого заключается в том, что независимо от того, какие операторы распределены каким интерферирующим слоям, объединенная интерференция в данной вершине-ресурсе не изменяется. Основываясь на этом наблюдении, для создания окончательного SCMA-кода можно распределять оптимизированные операторы интерферирующим слоям каждой вершины-ресурса случайным образом (или в некотором заданном порядке).
В некоторых случаях, LDS-сигнатура в качестве частного случая SCMA. Модулятор LDS-сигнатур определен его матрицей 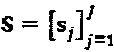 сигнатур и точками
сигнатур и точками 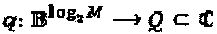 "созвездия" QAM-модуляции, где q=q(b). Полный модулятор LDS-сигнатур представлен как:
"созвездия" QAM-модуляции, где q=q(b). Полный модулятор LDS-сигнатур представлен как: 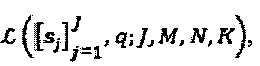 в котором К представляет собой длину, a N, представляет собой количество ненулевых элементов каждой сигнатуры. Модулятор LDS-сигнатур может быть переопределен на основе структуры SCMA-кода, в соответствии с
в котором К представляет собой длину, a N, представляет собой количество ненулевых элементов каждой сигнатуры. Модулятор LDS-сигнатур может быть переопределен на основе структуры SCMA-кода, в соответствии с 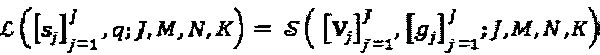 , в котором
, в котором 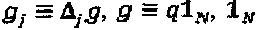 представляет собой вектор, состоящий из одних единиц, размера N,
представляет собой вектор, состоящий из одних единиц, размера N, 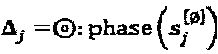 ,
, 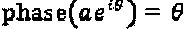 для любого неотрицательный
для любого неотрицательный 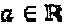 и
и 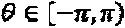 ,
, 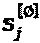 представляет собой N-мерный комплексный вектор ненулевых элементов
представляет собой N-мерный комплексный вектор ненулевых элементов 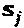 ,
, 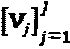 построен на фактор-графовой матрице F, и
построен на фактор-графовой матрице F, и 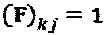 в том случае, и только в том случае, если
в том случае, и только в том случае, если 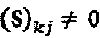 . Следовательно, модулятор LDS-сигнатур представляет собой специальный SCMA-код с простым многомерным материнским "созвездием", созданным посредством повторения точек "созвездия" QAM-модуляции и следовательно
. Следовательно, модулятор LDS-сигнатур представляет собой специальный SCMA-код с простым многомерным материнским "созвездием", созданным посредством повторения точек "созвездия" QAM-модуляции и следовательно 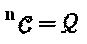 , ∀n=1, …, N. В дополнение к этому, оператор "созвездия" ограничен фазовым поворотом без каких бы то ни было операций сопряжения или перестановки. Перестановка не оказывает влияния в том случае, когда все измерения материнского "созвездия" являются идентичными. Следуя за процедурой проектирования SCMA-кода, попарная оптимизация LDS-сигнатур для некоторого данного множества
, ∀n=1, …, N. В дополнение к этому, оператор "созвездия" ограничен фазовым поворотом без каких бы то ни было операций сопряжения или перестановки. Перестановка не оказывает влияния в том случае, когда все измерения материнского "созвездия" являются идентичными. Следуя за процедурой проектирования SCMA-кода, попарная оптимизация LDS-сигнатур для некоторого данного множества 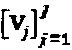 матриц отображения формализуется следующим образом:
матриц отображения формализуется следующим образом: 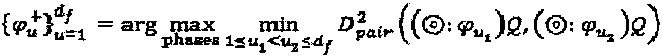 , в котором один оператор установлен в ноль, например,
, в котором один оператор установлен в ноль, например, 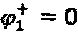 . Кроме того, критерий суперпозиции для оптимизации LDS-сигнатур выражается как:
. Кроме того, критерий суперпозиции для оптимизации LDS-сигнатур выражается как:
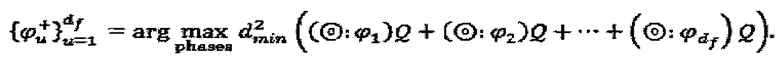
Аналогично SCMA-коду, операторы вершины-ресурса могут быть распределены интерферирующим слоям 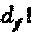 различными способами. Операторы фазы SCMA-кода эквивалентны поворотам фазы сигнатур в модуляторе LDS-сигнатур. Для случая, при котором Q является М-PSK "созвездием", решение вышеупомянутой задачи попарной оптимизации является прямым:
различными способами. Операторы фазы SCMA-кода эквивалентны поворотам фазы сигнатур в модуляторе LDS-сигнатур. Для случая, при котором Q является М-PSK "созвездием", решение вышеупомянутой задачи попарной оптимизации является прямым: 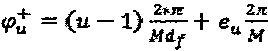 ,
, 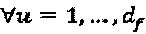 , где еu где представляет собой любой произвольный член Z. На Фиг. 12 проиллюстрирована диаграмма, на которой показан пример оптимальных поворотов фазы, при которых N=2, М=4, и
, где еu где представляет собой любой произвольный член Z. На Фиг. 12 проиллюстрирована диаграмма, на которой показан пример оптимальных поворотов фазы, при которых N=2, М=4, и 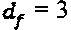 оптимальные повороты фазы представляют собой
оптимальные повороты фазы представляют собой 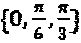 .
.
Каждая вершина-ресурс имеет 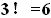 вариантов выбора для распределения фаз интерферирующим слоям. Общее количество вариантов выбора для всего множества сигнатур при 4 вершинах-ресурсах составляет 64=1296.
вариантов выбора для распределения фаз интерферирующим слоям. Общее количество вариантов выбора для всего множества сигнатур при 4 вершинах-ресурсах составляет 64=1296.
Система LDS-сигнатур может быть смоделирована как: y=diag(h)Su+n. Отметим, что для смежных ресурсов h является почти постоянным. Производим замену 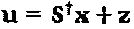 , где
, где 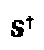 представляет собой псевдоинверсию матрицы S, а x должен представлять основной сигнал, передаваемый по ресурсам, что приводит к самой низкой мощности постобработки для z, которая составляет
представляет собой псевдоинверсию матрицы S, а x должен представлять основной сигнал, передаваемый по ресурсам, что приводит к самой низкой мощности постобработки для z, которая составляет 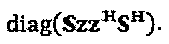 При выборе х=Su, проекция мощности шума постобработки на измерения S, ассоциативно связанные с z, составляет
При выборе х=Su, проекция мощности шума постобработки на измерения S, ассоциативно связанные с z, составляет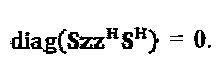 Окончательное отношение "сигнал-шум" для основного сигнала является функцией первоначального отношения "сигнал-шум" и мощности для и, которая является постоянной с учетом ограничения на проектирование матрицы сигнатур. Однако, мощность постобработки каждого слоя является функцией мощности для z, которая задается формулой, при допущении, что полная мощность переданного сигнала
Окончательное отношение "сигнал-шум" для основного сигнала является функцией первоначального отношения "сигнал-шум" и мощности для и, которая является постоянной с учетом ограничения на проектирование матрицы сигнатур. Однако, мощность постобработки каждого слоя является функцией мощности для z, которая задается формулой, при допущении, что полная мощность переданного сигнала 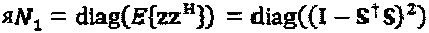 вляется нормализованной. Можно заметить, что
вляется нормализованной. Можно заметить, что 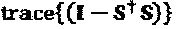 является постоянной, следовательно, для того, чтобы минимизировать полный шум преобразования, и используя неравенство Коши-Шварца, все значения в векторе N1 являются одинаковыми. Кроме того, различные слои отличаются
является постоянной, следовательно, для того, чтобы минимизировать полный шум преобразования, и используя неравенство Коши-Шварца, все значения в векторе N1 являются одинаковыми. Кроме того, различные слои отличаются 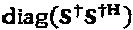 . Другими словами, без учета нелинейного эффекта МРА-алгоритма окончательное отношением "сигнал-шум" для всех слоев задается формулой:
. Другими словами, без учета нелинейного эффекта МРА-алгоритма окончательное отношением "сигнал-шум" для всех слоев задается формулой: 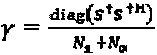 .
.
Выше, N0 представляет собой эффективный шум постобработки, и разделение выполняется поэлементно. Следует отметить, что все вышеприведенные вычисления предназначены только для понимания сути, и нелинейность МРА-алгоритма будет оказывать влияние на точность вычисления. Когда МРА-алгоритм пытается декодировать слои, он фактически пытается уменьшить влияние шума N1 преобразования на основной передаваемый сигнал. Для того, чтобы МРА-алгоритм лучше сходился, следует попробовать сделать мощности сигналов и мощности шумов во всех слоях близкими друг к другу, но не одинаковыми. Сильно различающиеся значения приводят к сильно различающимся рабочим характеристикам для различных слоев, а очень близкие значения приводит к трудности для надлежащей сходимости МРА-алгоритма. После схождения МРА-алгоритма, доминирующий фактор, различающий эффективность различных слоев, представляет собой их мощности, измеренные посредством  . Вышеприведенные вычисления показывают три фактора: (1) Основное усиление шума, вызванное сигнатурой, должно быть уменьшено для того, чтобы улучшить эффективность всех слоев; (2) на эффективность индивидуальных слоев воздействует эффективная мощность постобработки, обозначенная как
. Вышеприведенные вычисления показывают три фактора: (1) Основное усиление шума, вызванное сигнатурой, должно быть уменьшено для того, чтобы улучшить эффективность всех слоев; (2) на эффективность индивидуальных слоев воздействует эффективная мощность постобработки, обозначенная как  ; и (3) полную пропускную способность кода получают тогда, когда значения вектора шума преобразования близки друг к другу (но не очень близки), и эффективная мощность, приходящаяся на слой, также является одинаковой. Для максимизации полной пропускной способности можно применять различные кодовые скорости упреждающей коррекции ошибок к различным слоям, основываясь на их эффективной мощности сигнала.
; и (3) полную пропускную способность кода получают тогда, когда значения вектора шума преобразования близки друг к другу (но не очень близки), и эффективная мощность, приходящаяся на слой, также является одинаковой. Для максимизации полной пропускной способности можно применять различные кодовые скорости упреждающей коррекции ошибок к различным слоям, основываясь на их эффективной мощности сигнала.
Что касается эффективности SCMA, то эффективность SCMA-кода может быть оценена посредством моделирования на уровне звена. Однако, в качестве альтернативного подхода, для оценки SCMA-кода также принимается технология EXIT-диаграммы (Диаграммы передачи внешней информации). EXIT-диаграмма также используется для того, чтобы подтвердить действенность предложенной методологии проектирования для SCMA-кодов. EXIT-диаграмма используется как инструмент проектирования и прогнозирования относительной эффективности SCMA-кодов.
Что касается методологии оценки посредством EXIT-диаграммы, то алгоритмы распространения "убеждений" полагаются на сходимость "разумности" среди различных вершин, где фактически невозможно оптимальный декодер. LDPC, турбокоды, LDS-сигнатуры и SCMA представляют собой примеры систем, где распространение "убеждений" является единственным жизнеспособным решением для декодирования. Эти системы описываются множественными вершинами одинаковых или различных типов, которые обмениваются информацией и при каждой итерации пытаются использовать лежащие в их основе свойства кода. Например, турбокод моделируется двумя составляющими кодами, которые передают большой набор информации. Осуществляется перемежение/расперемежение информации для сохранения некоторого уровня независимости среди смежных позиций. Для LDPC, код описывается двудольным графом, где контрольные вершины и переменные вершины обмениваются информацией, и граф спроектирован таким образом, что короткие петли являются редкими/несуществующими, что сохраняет независимость информации среди ребер, соединенных с одной и той же вершиной.
EXIT-диаграмма (Диаграмма передачи внешней информации) представляет собой очень интересный и мощный инструмент для проектирования и прогнозирования эффективности таких кодов. Для очень длинного кода и с независимостью информации в каждой вершине, можно смоделировать каждый компонент как функцию, в которой он объединяет информацию, данную другими вершинами, со своей внутренней информацией и возвращает информацию назад этим вершинам. Каждая вершина может быть описана некоторой передаточной функцией, где средняя внешняя выходная информация представляет собой функцию ее средней внешней входной информации. Exit-диаграмма в таком случае прогнозирует то, вероятна ли сходимость декодера после разумного количества итераций между этими двумя вершинами. При изображении передаточной функции одной вершины и зеркальной передаточной функции другой вершины относительно линии Y=X, код, вероятно, сходится в том случае, если эти две передаточных функции не перекрываются. Кроме того, чем шире промежуток между двумя кривыми во всей его полноте, тем быстрее и вероятнее сходимость декодера.
SCMA-код представляет собой пример таких кодов, которые могут быть представлены двудольным графом, где вершины-слои обмениваются информацией с вершинами-ресурсами. Для этого кода, изучим его EXIT-диаграмму для того, чтобы спрогнозировать эффективность и изучить критерии проектирования. К сожалению, поскольку кодовый граф очень мал по сравнению с его аналогами в LDPC, то EXIT-диаграмма не очень точна в прогнозировании сходимости, так как (i) информация не является полностью независимой вследствие коротких размеров петель, и (ii) длина кода является малой, и закон больших чисел не применим. Однако, изучение EXIT-диаграммы для этих кодов может навести нас на сравнение различных проектов, так же как и на некоторый инструмент для проектирования таких кодов.
Что касается EXIT-диаграммы для SCMA, то SCMA состоит из двух составляющих его вершин: вершины-слоя и вершин-ресурсов. В каждой вершине-слое переносимая информация представляет вершину того же самого "созвездия", а в каждой вершине-ресурсе точки "созвездия", ассоциативно связанные с множественными слоями, интерферируют друг с другом. Вершина-ресурс использует свою внутреннюю информацию, которая представляет собой принятый комплексный сигнал, со своей внешней информацией по другим слоям для того, чтобы оценить выводимую внешнюю информацию по каждому из слоев. В вершине-слое внутренняя информация, которая является априорной информацией о слоях, задаваемой кодером, или от декодера внешнего цикла, сочетается с внешней информацией для того, чтобы определить информацию о слое, так же как и внешнюю информацию, возвращаемую вершинам-ресурсам. В Приложении описывается то, как моделировать входную и выходную информацию. Такое моделирование не является единственным в своем роде, и разумный выбор должен сымитировать динамику обмена информацией в этом коде. Каждое звено в SCMA может переносить вплоть до максимального количества информации в "созвездии", которое в нашем исследовании, задано как два бита. Можно отметить, что в отличие от LDPC и турбокодов, где роль кода заключается в обеспечении того, чтобы все биты информации сошлись, у SCMA нет ни требования, ни возможности сделать это. Причина кроется в каждой вершине-ресурсе: даже если имеется полная 2-битовая внешняя информация для всех других ребер, шум по-прежнему существует и приводит к менее чем полной внешней информации на выходе вершин-ресурсов. Однако, это не проблема, поскольку за SCMA-декодером следует декодер (следуют декодеры) упреждающей коррекции ошибок, и он требует входной информации, которая немного выше, чем его кодовая скорость. Например, при кодовой скорости 1/2, для того чтобы удовлетворить декодер упреждающей коррекции ошибок (FEC-декодер), на выходе требуется только 1 бит информации, приходящейся на вершину-слой.
Для достижения этого, могут быть использованы три составляющих: (i) моделирование EXIT-передачи в вершине-слое, (ii) EXIT-передача в вершине-ресурсе и (iii) выходная информация в каждом слое. Здесь, предлагается алгоритм для того, чтобы генерировать вышеупомянутую информацию и прогнозировать эффективность кода.
Нижеследующее относится к генерированию EXIT-диаграммы для SCMA. Сохраняя степень общность алгоритма, мы используем пример SCMA с четырьмя ресурсами и шестью слоями, где каждый слой соединен с двумя вершинами-ресурсами, а каждая вершина-ресурс представляет собой суперпозицию четырех слоев. Мы предполагаем, что количество точек в "созвездии" составляет четыре, что означает, что на каждое ребро приходится до двух битов переносимой информации. Для генерирования EXIT-диаграммы для вершин-ресурсов мы используем канал, имеющий один вход и один выход, с аддитивным белым гауссовым шумом (канал SISO AWGN). Для данного SCMA-кода с данными фактор-графом, множеством "созвездий" и множеством операторов, процедура создания EXIT-диаграммы для вершин-ресурсов является следующей: (1) Задают уровень (N0) шума в вершине-ресурсе в соответствии с рабочим значением отношения "сигнал-шум". На это значение влияет кодовая скорость упреждающей коррекции ошибок; (2) В каждой из вершин-ресурсов (4 в этом конкретном примере), задают уровень мощности для каждого ребра в фактор-графе, основываясь на задании мощности вершины-слоя, связанной с этим узлом-ресурсом. Подробности того, как задаются уровни мощности, объясняются в приложении; (3) Задают вспомогательный диапазон (N1) уровня шума для того, чтобы моделировать различные уровни входной внешней информации. Когда N1 является очень большим, никакая внешняя информация недоступна. Очень малые вспомогательные уровни шума, означают, что на входе ребра имеется полная внешняя информация (2 бита в этом примере). Осуществляют квантование диапазона вспомогательного уровня шума в вектор. Процедуру продолжают с первым элементом в векторе; (4) Для каждого слоя, выбирают одно из множества "созвездий" в соответствии с вероятностью "созвездия" (1/4 для каждой из 4 точек в "созвездии" в этом примере); (5) Для каждой вершины-ресурса, генерируют принимаемый гауссов шум, основанный на уровне N0 шума в канале; (6) Для каждого ребра в каждой вершине-ресурсе, используя настройки мощности на этапе (2) и выбранный вспомогательный уровень N1 шума, генерируют 4-местный кортежный набор вероятностей, как это объяснено в приложении; (7) Находят среднюю входную внешнюю информацию для всех ребер в фактор-графе, затем ее сохраняют как X; (8) Выполняют 4-кратный вывод внешней вероятности для каждого из ребер в фактор-графе. В этом примере, генерируется 12 выходных внешних информаций; (9) Находят выходную внешнюю информацию, задаваемую каждой из этих вероятностей из 4-местного кортежа, затем сохраняют ее как информацию: с Y1 по 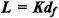 представляет собой количество ребер в фактор-графе (12 в этом примере); (10) Повторяют этапы: с 4 по 9 много раз (1000 как в примере); (11) Усредняют входную информацию (X) и выходную информацию (Y) по всем повторениям. Сохраняют ее в информации
представляет собой количество ребер в фактор-графе (12 в этом примере); (10) Повторяют этапы: с 4 по 9 много раз (1000 как в примере); (11) Усредняют входную информацию (X) и выходную информацию (Y) по всем повторениям. Сохраняют ее в информации  и информации: с
и информации: с 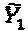 по
по 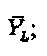 (12) Для каждой из переменных вершин, объединяют входную внешнюю информацию (как это объяснено в приложении) для того, чтобы найти выходную внешнюю информацию: с Z1 по ZI, где I представляет собой количество слоев; (13) Повторяют этапы: с 4 по 12, для всех значений вспомогательного вектора шума.
(12) Для каждой из переменных вершин, объединяют входную внешнюю информацию (как это объяснено в приложении) для того, чтобы найти выходную внешнюю информацию: с Z1 по ZI, где I представляет собой количество слоев; (13) Повторяют этапы: с 4 по 12, для всех значений вспомогательного вектора шума.
Значения Y по отношению к X представляют то, как вершина-ресурс может использовать внешнюю информацию. Более высокая кривая прогнозирует более быструю и более надежную сходимость информации. Значения Z прогнозируют то, как различные слои ведут себя при схождении МРА-алгоритма.
Нижеследующая процедура может быть использована для того, чтобы оценить передаточные функции для вершин-слоев. В простом примере вершин-слоев с двумя вершинами и отсутствием априорной информации, передаточная функция представляет собой просто линию Y=X: (1) В каждой из вершин-слоев (6 в этом примере) задают уровень мощности для каждого ребра в фактор-графе, основываясь на задании мощности вершины-слоя, связанной с этой вершиной-ресурсом. Подробности того, как задавать уровни мощности, объясняются в приложении; (2) Задают вспомогательный диапазон (N1) уровня шума для того, чтобы моделировать различные уровни входной внешней информации. Когда N1 является очень большим, никакая внешняя информация недоступна. Очень малые вспомогательные уровни шума означают, что на входе ребра имеется полная внешняя информация (2 бита в этом примере). Осуществляют квантование диапазона вспомогательного уровня шума в вектор. Процедуру продолжают с первым элементом в векторе; (3) Для каждого слоя, выбирают одно из множества "созвездий" в соответствии с вероятностью "созвездия" (1/4 для каждой из 4 точек в "созвездии" в этом примере); (4) Для каждого ребра в каждой вершине-слое, используя настройки мощности на этапе (2) и выбранный вспомогательный уровень N1 шума, генерируют 4-местный кортежный набор вероятностей, как это объяснено в приложении; (5) Находят среднюю входную внешнюю информацию для всех ребер в фактор-графе, и затем ее сохраняют как X; (6) Выполняют 4-кратный вывод внешней вероятности для каждого из ребер в фактор-графе. В этом примере, генерируется 12 выходных внешних информаций; (7) Находят выходную внешнюю информацию, задаваемую каждой из этих вероятностей из 4-местного кортежа, затем сохраняют ее как информацию: с Y1 по YL. 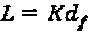 представляет собой количество ребер в фактор-графе (12 в этом примере); (8) Повторяют этапы: с 3 по 7 много раз (1000 как в примере); (9) Усредняют входную информацию (X) и выходную информацию (Y) по всем повторениям. Сохраняют ее в информации
представляет собой количество ребер в фактор-графе (12 в этом примере); (8) Повторяют этапы: с 3 по 7 много раз (1000 как в примере); (9) Усредняют входную информацию (X) и выходную информацию (Y) по всем повторениям. Сохраняют ее в информации  и информации: с
и информации: с 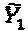 по
по 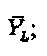 (10) Повторяют этапы: с 3 по 9 для всех значений вспомогательного вектора шума.
(10) Повторяют этапы: с 3 по 9 для всех значений вспомогательного вектора шума.
Значения Y по отношению к X представляют то, как вершина-слой передает информацию между ребрами в той же самой вершине-слое. Более высокая кривая прогнозирует более быструю и более надежную сходимость информации. Поскольку входная внешняя информация для вершины-слоя является выходной для вершины-ресурса и наоборот, то обычно, EXIT-диаграмма для этих вершин является зеркальной относительно линии Y=X..
Что касается оценки посредством EXIT-диаграммы и прогнозирования эффективности, то нижеследующее описание относится к методологии оценки посредством EXIT-диаграммы, а в некоторых случаях к методологии оценки посредством EXIT-диаграммы для простого кода с приводимым в качестве примера фактор-графом. В нижеследующем, канал предполагается каналом, имеющим один вход и один выход, с аддитивным белым гауссовым шумом (каналом SISO AWGN) с отношением "сигнал-шум", составляющим 8 децибел.
Что касается EXIT-диаграммы для LDS-сигнатур, то в LDS-сигнатурах точки "созвездия" берутся просто из точек QPSK (квадратурной фазовой манипуляции), и сигнатуры представляют собой следующее: 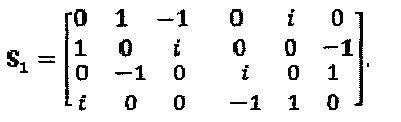
Для сигнатуры (1) кода, внешние передаточные функции для вершин-ресурсов для LDS показаны на нижеследующих кривых. Как можно увидеть на Фиг. 13, выходная информация во всех вершинах является одной и той же. Это не удивительно, поскольку все ребра в LDS имеют дело с одним и тем же "созвездием" и уровнем мощности. Как было упомянуто ранее, передаточная функция для вершины-слоя с двумя ребрами представляет собой просто обмен информацией (то есть линию Y=X). Эта кривая пересекает линию Y=X приблизительно на 1,2 бита, что предполагает, что при очень большой LDS-сигнатуре, код будет сходиться приблизительно к 1,2 бита информации на ребро. Сходимость информации показана стрелками на EXIT-диаграмме, поскольку осуществляется обмен информацией между узлами функции и слоя. Следует отметить, что такое предположение не соблюдается для кода, состоящего только из 4 ресурсов и 6 слоев. На Фиг. 14 показана выходная информации для той же самой внешней информации.
Фиг. 14 показывает выходную информацию на выходе вершин-слоев. Для очень большой LDS-сигнатуры, внешняя информация на ребрах поднялась бы до 1,2 бита, что предполагает, что информация на выходе была бы для отношения сигнал-шум, составляющего 8 децибел, настолько высокой, как 1,6 бита, и, следовательно, кодовой скорости меньше чем 0,8 должно быть достаточно для декодирования. Отметим, что при отношении "сигнал-шум", составляющем 8 децибел, пропускная способность для каждого звена составляет 1,9132 бита, что только на 20% выше, чем скорость, спрогнозированная посредством EXIT диаграммы. Снова отметим, что такое предположение здесь не соблюдается.
Для LDS с сигнатурой 2, имеющей следующий вид:
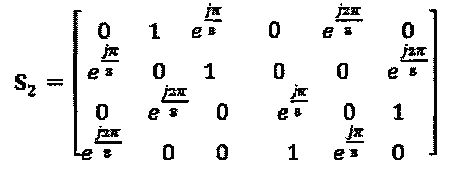
Кривые на Фигурах 15-16 выражают EXIT-диаграммы. Можно заметить, что EXIT-диаграмма прогнозирует то, что внешняя информация вырастет приблизительно до 1,5 бита на ребро, а выходная информация - приблизительно до 1,8 битов, что отстоит на 6% от пропускной способности. Как было упомянуто ранее, предположения о большом коде и независимых потоках данных здесь не соблюдаются.
Что касается EXIT-диаграммы для SCMA, то имеется много параметров, воздействующих на эффективность SCMA. Они включают в себя выбор комплексного "созвездия", эффект фазовой оптимизации, выбор правильной перестановки, назначения различных вершин-ресурсов вершинам-слоям и так далее. В нижеследующем мы изучаем влияние этих элементов.
Что касается влияния операторов фазы и сопряжения, то в нижеследующем для оценки EXIT диаграммы используется оптимизированное многомерное "созвездие". Для каждой вершины-ресурса с тремя ребрами возможны четыре варианта выбора: (i) все три ребра выбираются из первой строки в матрице "созвездий", (ii) два ребра выбираются из первой строки и одно от второй строки, (iii) два ребра - из второй строки и одно из первой, и (iv) всех три ребра - из второй строки. Здесь мы представляем эти вершины-ресурсы типами Т1, …, T4.
Передаточные функции внешней информации для этих четырех типов вершин-ресурсов без оптимизаций фазы/сопряжения или с этими оптимизациями показаны, соответственно, на Фиг. 17 и Фиг. 18.
Из этих фигур могут быть сделаны следующие выводы: (1) выходная внешняя информация на выходе вершин-ресурсов выше в том случае, когда операторы фазы/сопряжения оптимизированы. Это даже в еще большей степени можно наблюдать в том случае, когда имеется небольшая внешняя информация, доступная для других слоев (то есть левая часть кривых); (2) Это приводит к лучшей сходимости МРА-алгоритма с оптимизированной фазой и сопряжением; (3) Для вершин, у которых все точки "созвездий" - из одной и той же строки (то есть типов Т1 и T4, разница более высокая; (4) выходная внешняя информация для ребер, использующих первую строку "созвездий", выше, чем для других. Это объясняется тем фактом, что по этим звеньям передается больше мощности; (5) В правой части кривых, где имеется полная информация об интерференции в вершине-ресурсе, значение имеет только мощность, назначенная этому звену.
Что касается оценки на уровне звена, то показаны результаты моделирования на уровне звена, подтверждающие предложенную методологию проектирования для SCMA и LDS. В дополнение к этому, эффективность спроектированного SCMA- и LDS-кодов сравнивается с наилучшими LDS-сигнатурами, которые уже существуют. Во всех результатах моделирования, представленных ниже, основные параметры задаются следующим образом: N=2, К=4, J=6, 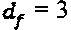 .
.
Что касается влияния "созвездия" для SCMA, то на Фигурах 19а-b, для некоторого данного многомерного "созвездия" в вещественной области, показано влияние вариации мощности измерения "созвездия" в комплексной области. Как показано на Фигурах 19а-b, более высокая вариация мощности повышает общую эффективность.
Что касается влияния оператора перестановки на SCMA, то влияние оператора перестановки на эффективность SCMA-кода представлено на Фиг. 20. Эти результаты подтверждают то, что интерферирующие многочлены должны иметь такое количество одночленов, сколько возможно, для того, чтобы воспользоваться преимуществом вариации мощности измерения материнского "созвездия", увеличивая эффект "близко-далеко" в вершинах-ресурсах.
Что касается влияния операторов фазы/сопряжения для SCMA, то на Фиг. 21 проиллюстрировано влияние операторов фазы/сопряжения на эффективность SCMA -кода. Обычно, влияние оптимизации оператора является положительным, но для этого конкретного случая выигрыш не слишком велик.
Как было объяснено ранее, имеется два подхода к оптимизации операторов фазы/сопряжения: (i) попарная оптимизация и (ii) оптимизации суперпозиции. На Фиг. 22 эти два критерия сравниваются. В соответствии с этой фигурой, два подхода могли бы иметь тенденцию к различному поведению спроектированных кодов. Код, который спроектирован на основе попарного критерия, демонстрирует более равномерную эффективность в отношении различных мультиплексированных пользователей.
Что касается влияния распределения операторов для SCMA, то распределение оптимизированных операторов по интерферирующим слоям вершины-ресурса представляет собой проблему, которая не может быть четко исследована. Для лежащего в основе SCMA-кода имеется 16 различных вариантов выбора распределения. На Фиг. 23 сравниваются эффективности этих 16 вариантов выбора в отношении полной полезной пропускной способности. К счастью, распределение операторов демонстрирует незначительное влияние на окончательную эффективность SCMA-кода. Как было упомянуто ранее, оптимизированные операторы фазы/сопряжения могут быть распределенном интерферирующим слоям случайным образом или в ручном порядке.
Что касается влияния унитарной операции в вещественной области, оказываемого на SCMA, то унитарная матрица может быть применена к многомерному "созвездию" в вещественной области для того, чтобы изменить свойства измерений точек, сохраняя при этом многомерные свойства "созвездия" (такие как минимальное расстояние точек "созвездия") неизменными. Вариация мощности измерения представляет собой пример свойства измерения многомерного "созвездия". Кроме того, другим свойством измерения является минимальное расстояние точек по каждому множеству измерений. В примере, показанном на Фиг. 24, вещественная унитарная матрица применяется к многомерному "созвездию" в вещественной области для того, чтобы максимизировать максимальное расстояние точек в каждом множестве измерений, сохраняя при этом минимальное расстояние каждого множества измерений большим, чем 0,1. Унитарная матрица оптимизирована методом случайного поиска. Ясно, что унитарный матричный оператор может повысить общую эффективность SCMA-кода.
Что касается сравнения SCMA-кодов в терминах полной полезной пропускной способности, то полная суммарная полезная пропускная способность SCMA-кодов и влияние различных параметров оптимизации показаны на Фиг. 25. Сравнение кривых полезной пропускной способности подтверждает действенность подхода многоступенчатой оптимизации, предложенной в этом отчете.
Что касается оптимизации сигнатуры для LDS (Сигнатур низкой плотности), то один пример традиционных LDS-сигнатур может быть найден в работе "Multiple Access with Low-Density Signatures" ("Множественный доступ с сигнатурами низкой плотности"), Huawei Technologies Sweden (Швеция), IEEE GLOBECOM 2009 (Институт инженеров по электротехнике и электронике (США), Глобальная система связи, 2009 г.), которая включена в данную заявку посредством ссылки так, как если бы она была воспроизведена здесь во всей своей полноте. Характеристика полезной пропускной способности для оптимизированных LDS-сигнатур (этого раскрываемого изобретения) и традиционных LDS-сигнатур (найденных в вышеупомянутой статье Института инженеров по электротехнике и электронике (США)) сравниваются на Фиг. 26. В противоположность SCMA, при сравнении влияния распределения для попарных оптимизированных фаз влияние распределения фаз очевидным образом огромно. При хорошем распределении операторов, критерии оптимизации: как суперпозиционный, так и попарный, демонстрируют почти идентичную эффективность.
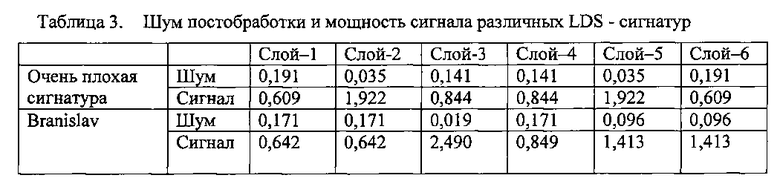
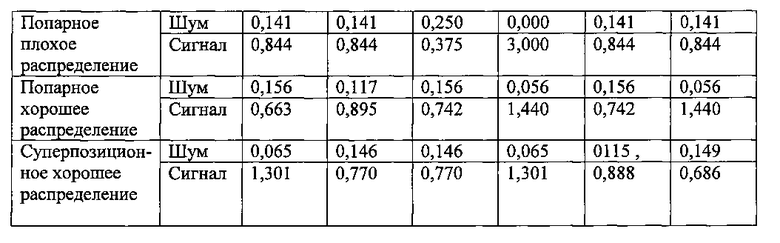
Причину, лежащую за этим поведением сигнатур, можно объяснить, основываясь на их соответствующей обработке "шум/сигнал", которая показана в списке в Таблице 3. Эта таблица может прогнозировать относительную эффективность для пользователей матрицы сигнатур. Например, для первого множества сигнатур с плохой эффективностью, анализ "шум/сигнал" прогнозирует то, что UE (пользовательское оборудование) 2 и 5 имеют наилучшую эффективность с самой высокой мощностью сигнала постобработки и самой низкой мощностью шума. Между тем, пользовательское оборудование (1) и (6) должно иметь низкую эффективность вследствие их самого низкого отношения "сигнал-шум". Это прогнозирование может быть подтверждено результатами моделирования на уровне звена, показанными на Фиг. 27(а).
В соответствии с таблицей, сигнатуры Branislav имеют более однородное распределение "сигнал/шум" по слоям, но все-таки пользовательское оборудование (3), превосходит другое пользовательское оборудование, что также можно увидеть на Фиг. 27 (b). Сравнивая эти два множества сигнатур, можно прийти к выводу, что множество сигнатур обеспечивает более хорошую характеристику полезной пропускной способности в том случае, если нет большие разницы между уровнями мощности "сигнал/шум" для слоев. В качестве общей концепции обнаружения SIC (кода идентификации станции), малое различие между слоями может помочь улучшать эффективность обнаружения SIC, но большое различие имеет тенденцию к снижению эффективности, как это показано для первого множества сигнатур.
Влияние распределения фаз на эффективность LDS-сигнатур можно увидеть в Таблице 3 и на Фигурах 28(а)-(b) для попарно оптимизированных фаз. При хорошем распределении операторов фазы, уровни мощности "сигнал/шум" постобработки для множества сигнатур сбалансированы и, следовательно, рабочая эффективность повышается.
Что касается эффективности SCMA по отношению к LDS, то в теории способ SCMA должен превосходить LDS, вследствие выигрыша в формировании сигналов при многомерном созвездии. Однако, потенциальный выигрыш достижим в том случае, если оптимальный или субоптимальный SCMA-код достижим при разумном подходе к проектированию. На Фиг. 29 сравниваются эффективности LDS-сигнатур "Branislav", взятых в качестве линии отсчета, с нашим наилучшим SCMA и наилучшими LDS-сигнатурами. Наши как LDS-сигнатуры, так и SCMA-решение превосходят эту линию отсчета, но выигрыш SCMA по отношению к наилучшим LDS-сигнатурам не является заметным, для этого конкретного примера. SCMA поддерживается как новый подход к модуляции для множественного доступа, который имеет преимущества CDMA (Множественного доступа с кодовым разделение каналов) и LDS (Сигнатур низкой плотности), так же как и некоторый потенциальный выигрыш, относящийся к выигрышу при кодировании в комплексной области. Даже при том, что структура кода хорошо определена, проектирование и оптимизация кода является частью формирования канала передачи данных. Здесь предложена методология субоптимального проектирования, основанная на подходе многоступенчатой оптимизации. В дополнение к этому, для проектирования SCMA-кодов разработана быстрая и эффективная методология оценки, основанная на технологии EXIT-диаграммы.
Показано, что LDS-сигнатуры являются упрощенным случаем SCMA-структуры. Следовательно, разработанная методология проектирования SCMA повторно используется для того, чтобы проектировать LDS-сигнатуры систематическим образом. Предоставленные результаты моделирования иллюстрируют действенность этого подхода к проектированию как для SCMA, так и для LDS-сигнатур.
Что касается моделирования посредством EXIT-диаграммы, то алгоритм распространения "убеждений" полагается на сходимость "убеждения" между вершинами по мере того, как информация передает туда и обратно между вершинами в графе, таком как LDPC, турбокод, LDS-сигнатуры и так далее. Диаграмма передачи внешней информации (EXIT-диаграмма) предложена Стивеном тен Бринком (Stephen ten Brink) (в 2001 г.) и развита многими другими для проектирования, прогнозирования эффективности и сравнения различных кодов. В EXIT-диаграмме, описывается среднее "убеждение" после каждой вершины, как функция среднего "убеждения", введенного в ту же самую вершину за данной внутренней информацией, и делается прогноз в отношении того, приводит ли итерация к лучшему пониманию закодированной информации.
Что касается моделирования посредством EXIT-диаграммы для нахождения передаточной функции для любой вершины, то необходимо посредством некоторой приемлемой статистической модели смоделировать внешнюю информацию, приходящую в эту вершину, и затем исследовать статистику выходной информации на выходе из этой вершины. SCMA-декодер состоит из вершин-слоев и вершин-ресурсов. Вершины-ресурсы также принимают внутреннюю информацию вследствие принятого комплексного сигнала, прошедшего через канал. Эта внешняя информация приходящая в каждую вершину, как для вершин-слоев, так и для вершин-ресурсов состоит из N-местных кортежей вероятностей (где N=4 для 2-битовых вершин). Выходы имеют ту же самую структуру, и информация, которую несут эти вероятности (во многих N-местных кортежах), представляет собой просто энтропию, определенную этими вероятностями. В нижеследующем исследуется процедура для получения EXIT-диаграммы для каждого компонента. Для простоты мы фокусируемся на SCMA-матрице, состоящей из четырех вершин-ресурсов и шести вершин-слоев. Мы предполагаем, что каждая вершина-ресурс содержит три символа, и каждая вершина-слой соединена с двумя вершинами-ресурсами. Мы также ограничиваем получение EXIT-диаграммы случаем канала с аддитивным белым гауссовым шумом, имеющего один вход и один выход (канала AWGN SISO. Такие ограничения не ограничивают степень общности этого подхода.
Что касается моделирования внутренней информации в вершинах-ресурсах, то входная информация в вершину-ресурс, как внешняя информация, представляет собой принимаемый комплексный сигнал, который содержит суперпозицию трех переданных сигналов плюс аддитивный белый гауссов шум (AWGN). Чтобы смоделировать это, для каждого случая входа, случайным образом генерируются три входных кортежа размером 2 бита. После этого, предполагая некоторое заданное отношение "сигнал-шум", вычисляют принимаемый сигнал. Вариация шума составляет N0=P/SNR, где p представляет собой полную передаваемую мощность, а отношение "сигнал-шум" представляет собой это заданное постоянное отношение "сигнал-шум".
Что касается внешних вероятностей из четырехместных кортежей для вершин-ресурсов при моделировании посредством EXIT-диаграммы, то внешняя информация для вершин-ресурсов состоит из четырех вероятностей, ограниченных при суммировании единицей и коррелированных с фактической передаваемой точкой. Здесь, для каждой точки в "созвездии" мы моделируем ее вероятность посредством вероятности при передаче методом BPSK (двухпозиционной фазовой манипуляции) по модели с аддитивным белым гауссовым шумом. С этой целью, мы предполагаем, что имеем канал с аддитивным белым гауссовым шумом, имеющий мощность p передачи, связанную с мощностью поступающей внешней информации и мощностью N1 шума. Следует отметить, что значение N1 не имеет никакого отношения к фактической мощности шума в канале и является только инструментом для того, чтобы сгенерировать N-местные кортежи отношения "сигнал-шум" с различными уровнями информации. Что касается передаваемой мощности p, то мы обсудим его позже. Более высокая мощность шума в модели приводит к более низкому уровню информации на входе и наоборот.
Для всех N точек в "созвездии" мы генерируем двоичную передачу по каналу с аддитивным белым гауссовым шумом. Для фактической передаваемой точки (одной точки, которая передается при моделировании внутренней информации), мы принимаем, что передается +1, а для всех других N-1 точек мы принимаем, что передается -1. Следовательно, LLR-отношение (логарифмическое отношение правдоподобия), следующее из фактической передаваемой точки, составляет = 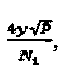 где y представляет собой
где y представляет собой 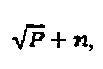 для фактической передаваемой точки и
для фактической передаваемой точки и 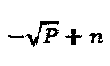 для всех других точек. Это дает нам вектор LLR-отношений, имеющий размер N. Каждое LLR может затем быть преобразовано в вероятность, которая =
для всех других точек. Это дает нам вектор LLR-отношений, имеющий размер N. Каждое LLR может затем быть преобразовано в вероятность, которая = 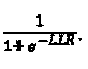 Результирующие вероятности затем нормируется для того, чтобы удовлетворить ограничению по сумме. Энтропия, представленная этими вероятностями, описывается формулой
Результирующие вероятности затем нормируется для того, чтобы удовлетворить ограничению по сумме. Энтропия, представленная этими вероятностями, описывается формулой 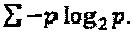 Наконец, посредством повторения этой процедуры на протяжении многих реализаций вероятностей, определяется средняя внешняя информация на входе вершин-ресурсов. Средняя внешняя информация в таком случае составляет
Наконец, посредством повторения этой процедуры на протяжении многих реализаций вероятностей, определяется средняя внешняя информация на входе вершин-ресурсов. Средняя внешняя информация в таком случае составляет 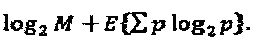 Пожалуйста обратите внимание на то, что для вершины-ресурса, связанной с тремя вершинами-слоями, уровень внешней информации не обязательно является одним и тем же, и можно задавать описанной здесь модели различные уровни (N1) шума. Однако, поскольку внешняя информация для одного звена не является функцией информации, поступающей из того же самого звена, то фокусируясь на одном звене как выходе, мы должны сгенерировать внешний вход только для двух других. Другими словами, EXIT-диаграмма для одного конкретного выхода для некоторого заданного отношения "сигнал-шум" в канале является функцией с двумя входами и одним выходом. Однако, для простоты визуализации EXIT-диаграммы мы используем один и тот же уровень шума на входе, а в качестве средней входной информации используем среднюю информацию входов.
Пожалуйста обратите внимание на то, что для вершины-ресурса, связанной с тремя вершинами-слоями, уровень внешней информации не обязательно является одним и тем же, и можно задавать описанной здесь модели различные уровни (N1) шума. Однако, поскольку внешняя информация для одного звена не является функцией информации, поступающей из того же самого звена, то фокусируясь на одном звене как выходе, мы должны сгенерировать внешний вход только для двух других. Другими словами, EXIT-диаграмма для одного конкретного выхода для некоторого заданного отношения "сигнал-шум" в канале является функцией с двумя входами и одним выходом. Однако, для простоты визуализации EXIT-диаграммы мы используем один и тот же уровень шума на входе, а в качестве средней входной информации используем среднюю информацию входов.
Что касается внешних вероятностей из четырехместных кортежей для вершин-слоев при моделировании посредством EXIT-диаграммы, то вершины-слои в SCMA не имеют внутренней информации, если только не используется неравномерное распределение вероятности "созвездия". Помимо этого, генерация входной информации является такой же, как только что была описана для вершин-ресурсов. Однако, сама структура вершин-слоев делает прогнозирование их поведения проще. В вершине-слое с М звеньями, каждое звено на выходе объединяет информацию на входе всех других звеньев. Для гауссова входа, это просто сводится к MRC, что означает, что выходное отношение "сигнал-шум" в каждом звене представляет собой сумму входного отношения "сигнал-шум" на каждом звене. Другими словами, можно предположить, что мощность на выходе каждой вершины представляет собой сумму входной мощности для всех других вершин. Этот феномен используется для задания мощности на входе модели для вершин-ресурсов.
С этой моделью нам не нужно явным образом описывать EXIT-диаграмму вершины-слоя, и для вершины-слоя с 2 звеньями выходная внешняя информация для каждой вершины представляет собой входную внешнюю информацию для другой вершины и наоборот.
Что касается модели для задания мощности для входа вершины-ресурса, то, как было описано ранее, полная EXIT-диаграмма для каждой вершины является многомерной функцией. Для того чтобы представить ее одномерной функцией, следует принять некоторое соотношение между различными входами в вершину. Здесь, мы используем задание мощности для различных звеньев для того, чтобы провести различие между ними. Например, если различные пользователи имеют различные мощности сигнала, то это может быть отражено в задании мощности для входов в вершину-ресурс. Ранее было упомянуто, что вход в вершину-ресурс является выходом вершины-слоя, и EXIT-функция для этого представляет собой сумму мощности для всех других компонентов в сигнатуре для этого пользователя. Следовательно, можно задавать мощность передачи для различных входов, основываясь на мощности, распределенной для всех других точек "созвездия" для этого потока (не включая сюда рассматриваемую точку), и провести различие между пользователями в одной и той же вершине-ресурсе.
Что касается модели для задания мощности для входа вершины-слоя, то внешняя информация, выходящая из вершины-ресурса, является функцией многих вещей, но наиболее важным фактором является ее мощность, приходящаяся на этот слой в этом ресурсе. Следовательно, распределение мощности для входа вершины-слоя просто пропорционально мощности этого слоя в соответствующем ресурсе.
Что касается объединения вероятности в вершинах-слоях, то результат МРА-алгоритма для SCMA представляет собой N-местный кортеж вероятностей в вершинах-слоях. Это делается посредством умножения всех вероятностей внешней информации в вершине-слое и нормирования этого до суммы, составляющей единицу. Для моделировать этого, мы моделируем систему с параллельными двоичными симметричными каналами. Для каждого звена, ведущего к вершине-слою, внешняя информация моделируется информацией, получаемой от М=log2(N) параллельных двоичных симметричных каналов с пропускной способностью, равной 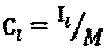 , где
, где 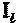 , представляет собой полную информацию на выходе l-х соответствующих вершин-ресурсов, прикрепленных к этой вершине-слою. В случае, когда вершина-слой соединена с множественными звеньями, мы моделируем ее наличием параллельных независимых двоичных симметричных каналов. Пропускная способность этого канала задается следующим образом: предполагая, что имеется L параллельных звеньев, каждое из которых имеет вероятность ошибки, составляющую
, представляет собой полную информацию на выходе l-х соответствующих вершин-ресурсов, прикрепленных к этой вершине-слою. В случае, когда вершина-слой соединена с множественными звеньями, мы моделируем ее наличием параллельных независимых двоичных симметричных каналов. Пропускная способность этого канала задается следующим образом: предполагая, что имеется L параллельных звеньев, каждое из которых имеет вероятность ошибки, составляющую 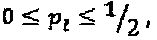 l=1, …, L, где
l=1, …, L, где 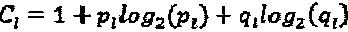 и
и 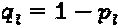
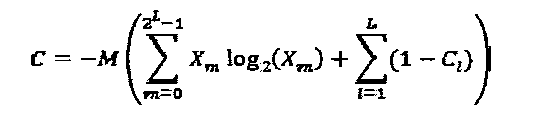
где
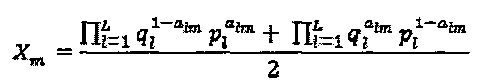
и  представляет собой бит в l-й позиции L-битового двоичного представления
представляет собой бит в l-й позиции L-битового двоичного представления 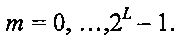
Фиг. 30 представляет собой структурную схему системы обработки данных, которая может быть использована для реализации раскрытых здесь устройств и способов. В конкретных устройствах могут быть использованы все из показанных компонентов, или только некоторое подмножество этих компонентов, и уровни интеграции могут варьироваться от устройства к устройству. Кроме того, устройство может содержать множественные экземпляры компонента, такие как множественные блоки обработки данных, процессоры, запоминающие устройства, передатчики, приемники и так далее. Эта система обработки данных может содержать блок обработки данных, оснащенный одним или более устройствами ввода/вывода, такими как громкоговоритель, микрофон, "мышь", сенсорный экран, малая клавиатура, клавиатура, принтер, устройство отображения и тому подобное. Блок обработки информации может включать в себя центральный процессор (CPU), память, запоминающее устройство большой емкости, видеоадаптер и интерфейс ввода/вывода, соединенные с шиной.
Шина может представлять собой одну или более шин любого типа из нескольких шинных архитектур, включающих в себя шину памяти или контроллер памяти, шину периферийных устройств, шину видеосигналов или тому подобное. Центральный процессор может содержать любой тип электронного процессора данных. Память может содержать любой тип системной памяти, такой как статическое оперативное запоминающее устройство (SRAM), динамическое оперативное запоминающее устройство (DRAM), синхронное динамическое оперативное запоминающее устройство (SDRAM), постоянное запоминающее устройство (ROM), их сочетание или тому подобное. В одном варианте реализации изобретения, память может включать в себя постоянное запоминающее устройство для использования при начальной загрузке, и динамическое оперативное запоминающее устройство для программ и хранения данных для использования при исполнении программ.
Запоминающее устройство большой емкости может содержать любой тип запоминающего устройства, сконфигурированного для того, чтобы хранить данные, программы и другую информацию и делать эти данные, программы и другую информацию доступными через шину. Запоминающее устройство большой емкости может содержать, например, один или более накопителей из числа: твердотельного накопителя, накопителя на жестких магнитных дисках, накопителя на магнитных дисках, накопителя на оптических дисках или тому подобного.
Видеоадаптер и интерфейс ввода-вывода обеспечивают интерфейсы для подсоединения, к этому блоку обработки данных, внешних устройств ввода и вывода. Как проиллюстрировано на фигуре, примеры устройств ввода и вывода включают в себя устройство отображения, соединенное с видеоадаптером, и "мышь"/клавиатуру/принтер, соединенную к интерфейсу ввода-вывода. К блоку обработки данных могут быть подсоединены и другие устройства, и могут быть использованы дополнительные, или меньшее количество интерфейсных плат. Например, для обеспечения интерфейса для принтера может быть использован последовательный интерфейс, такой как Универсальная последовательная шина (USB), (не показанный на фигуре).
Блок обработки данных также включает в себя один или более сетевых интерфейсов, которые могут содержать проводные каналы передачи данных, такие как кабель Ethernet или тому подобное, и/или беспроводные каналы передачи данных, предназначенные для доступа к узлам или другим сетям. Сетевой интерфейс позволяет блоку обработки данных поддерживать связь с удаленными устройствами через сети. Например, сетевой интерфейс может обеспечивать беспроводную связь через один или более передатчиков/передающих антенн и один или более приемников/приемных антенн. В одном варианте реализации изобретения, блок обработки данных подсоединен к локальной сети или глобальной сети для обработки данных и связи с удаленными устройствами, такими как другие блоки обработки данных, Интернет, удаленные установки для хранения информации или тому подобное.
На Фиг. 31 проиллюстрирована структурная схема одного варианта реализации устройства (3100) связи, которое может быть эквивалентно одному или более устройствам (например, пользовательскому оборудованию, NB и так далее) рассматриваемым выше. Устройство 3100 связи может включать в себя процессор 3104, память 3106, интерфейс 3110 сотовой связи, дополнительный интерфейс 3112 беспроводной связи и дополнительный интерфейс 3114, который может (или может не) иметься, которые показаны на Фиг. 31. Процессор 3104 может представлять собой любой компонент, способный к выполнению вычислений и/или других задач, связанных с обработкой данных, а память 3106 может представлять собой любой компонент, способный к хранению программ и/или команд для процессора 3104. Интерфейс 3110 сотовой связи может представлять собой любой компонент или набор компонентов, который позволяет устройству 3100 связи поддерживать связь с использованием сигнала сотовой связи и может быть использован для приема и/или передачи информации по сотовому соединению в сети сотовой связи. Дополнительный интерфейс 3112 беспроводной связи может представлять собой любой компонент или набор компонентов, который позволяет устройству 3100 связи поддерживать связь посредством протокола несотовой беспроводной связи, такого как протокол Wi-Fi или Bluetooth, или протокола управления. Устройство 3100 может использовать интерфейс 3110 сотовой связи и/или дополнительный интерфейс 3112 беспроводной связи для того, чтобы поддерживать связь с любым компонентом, наделенным способностью к беспроводной связи, например с базовой станцией, ретранслятором, мобильным устройством и так далее. Дополнительный интерфейс 3114 может представлять собой любой компонент или набор компонентов, который позволяет устройству 3100 связи поддерживать связь посредством некоторого дополнительного протокола, включающего в себя протоколы проводной линии связи. В вариантах реализации изобретения, дополнительный интерфейс 3114 может позволять устройству 3100 поддерживать связь с другим компонентом, таким как компонент ретрансляционной сети.
Настоящее раскрываемое изобретение также описывает следующие примеры
Пример 1. Способ проектирования кода Множественного доступа с разреженным кодом (SCMA-кода), содержащий этапы, на которых:
генерируют множество кодовых книг многомерной модуляции; и
генерируют из указанного множества кодовых книг многомерной модуляции множество разреженных кодовых книг.
Пример 2. Способ по примеру 1, в котором каждая из множества разреженных кодовых книг содержит множество разреженных кодовых слов и в котором различные разреженные кодовые слова в разреженной кодовой книге ассоциированы с различными двоичными значениями.
Пример 3. Способ по примеру 1, в котором каждое кодовое слово в множестве разреженных кодовых книг содержит низкую плотность ненулевых значений, так что соответствующее кодовое слово может быть обнаружено в пределах мультиплексированных кодовых слов в соответствии с алгоритмом передачи сообщений (МРА-алгоритмом).
Пример 4. Способ по примеру 1, в котором каждая из множества кодовых книг многомерной модуляции назначена отличному от других мультиплексируемому слою.
Пример 5. Способ проектирования кода Множественного доступа с разреженным кодом (SCMA-кода), содержащий этапы, на которых:
генерируют множество матриц отображения;
генерируют по меньшей мере одно многомерное "созвездие";
оптимизируют одно или более из: перестановки, оператора фазы и оператора сопряжения; и
генерируют кодовые слова SCMA в соответствии с указанными матрицами отображения по меньшей мере одним многомерным "созвездием" и одним или более из: перестановки, оператора фазы и оператора сопряжения.
Пример 6. Способ проектирования кода с сигнатурами низкой плотности (LDS-сигнатурами), содержащий этапы, на которых:
генерируют множество матриц отображения;
оптимизируют один или более операторов фазы; и
генерируют LDS-сигнатуры в соответствии с этими матрицами отображения, одним или более операторами фазы, и некоторым "созвездием".
Пример 7. Способ по примеру 6, в котором каждая из LDS-сигнатур назначена отличному от других мультиплексируемому слою.
Хотя варианты реализации этого раскрываемого изобретения были описаны со ссылкой на иллюстративные варианты его реализации, это описание не предназначено для толкования в ограничительном смысле. При обращении к описанию специалистам в данной области техники будут очевидны различные модификации и сочетания иллюстративных вариантов реализации, так же как и другие варианты реализации этого раскрываемого изобретения. Следовательно, предполагается, что прилагаемая формула изобретения охватывает любые такие модификации или варианты реализации изобретения.
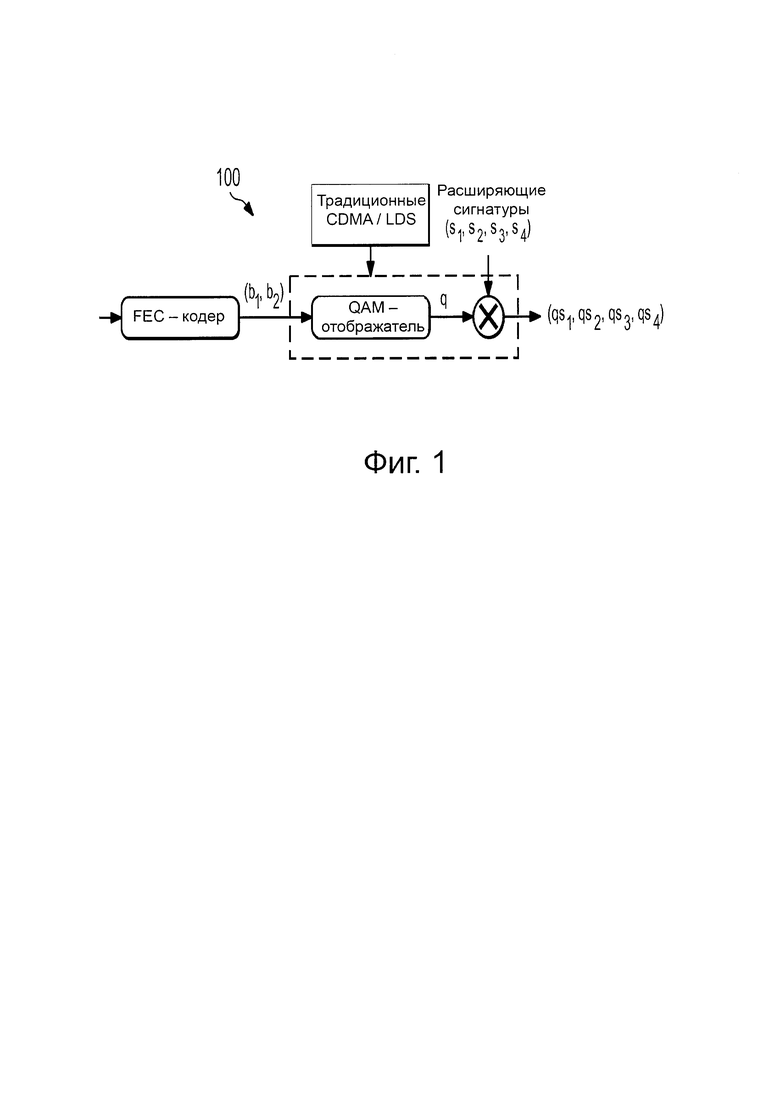
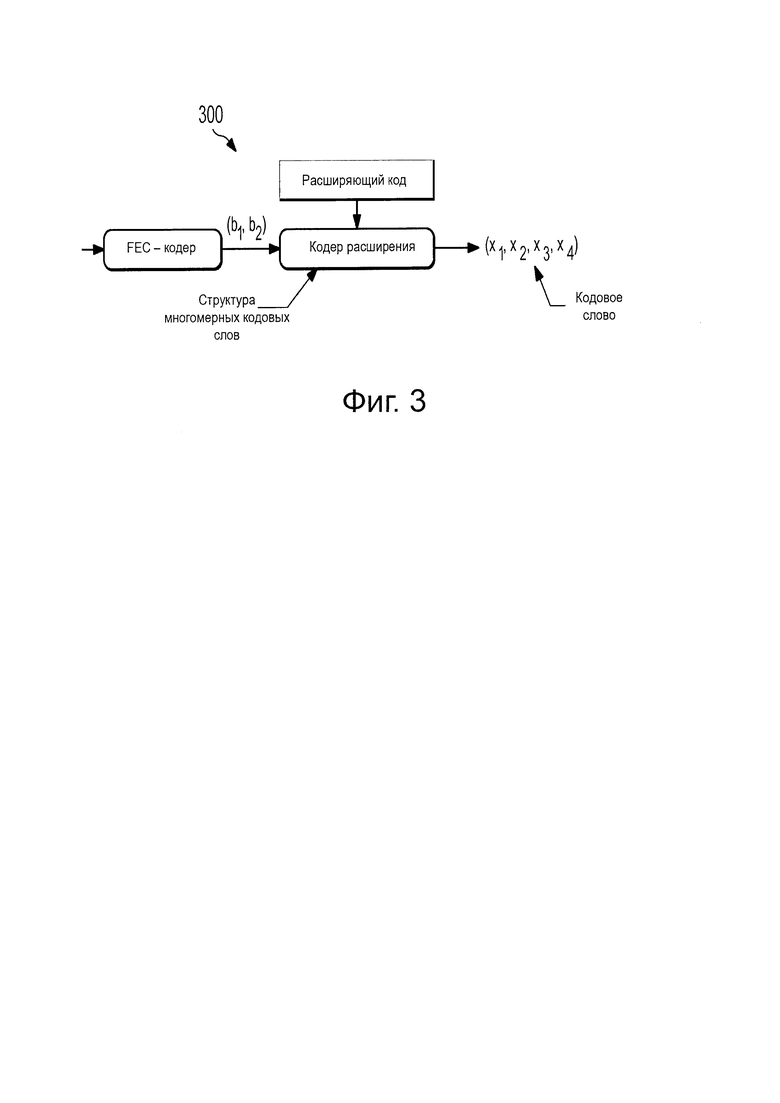
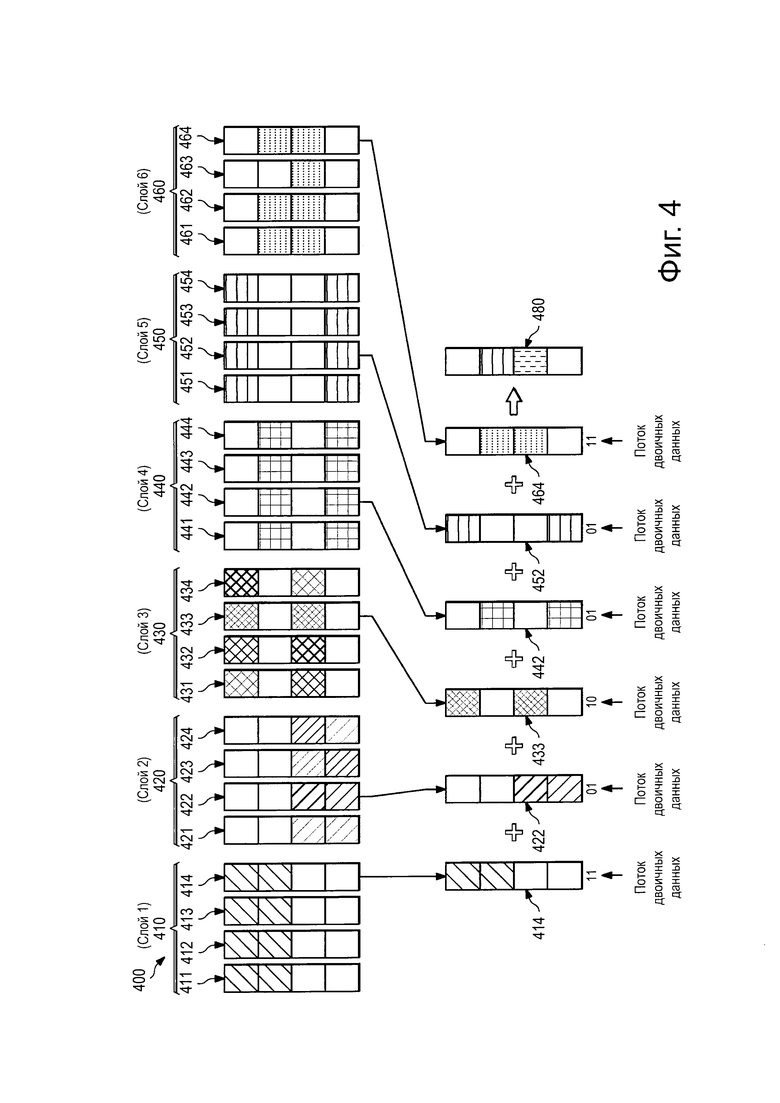

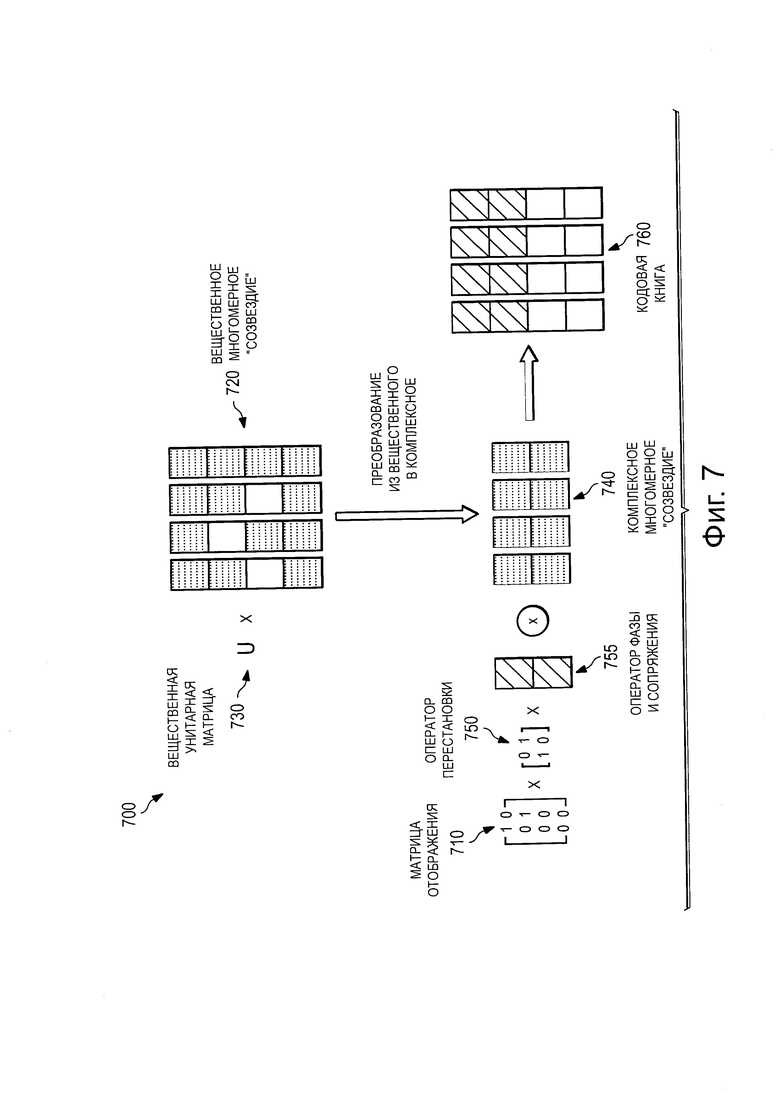
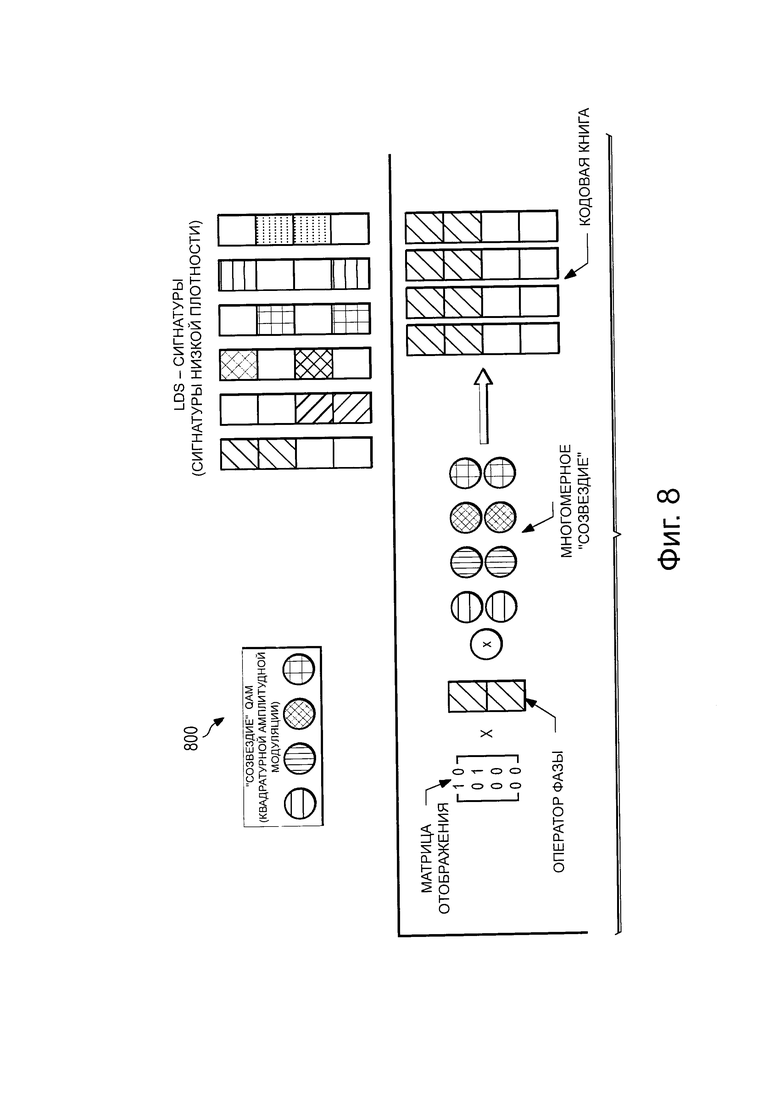
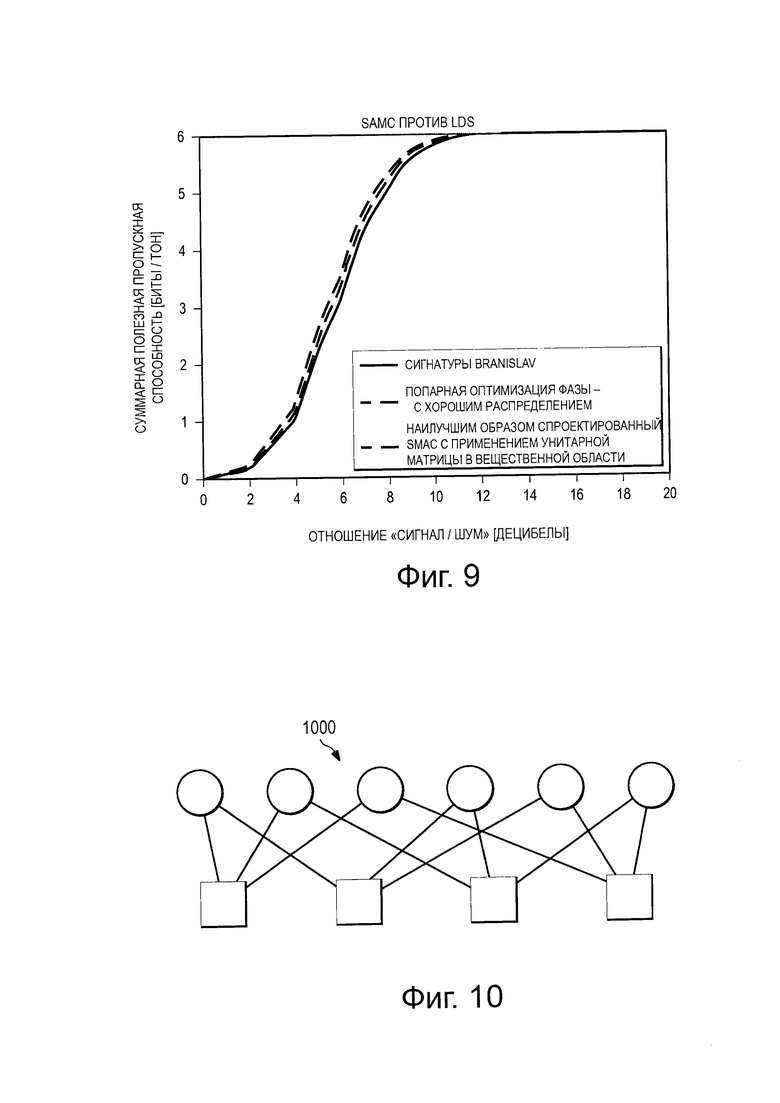
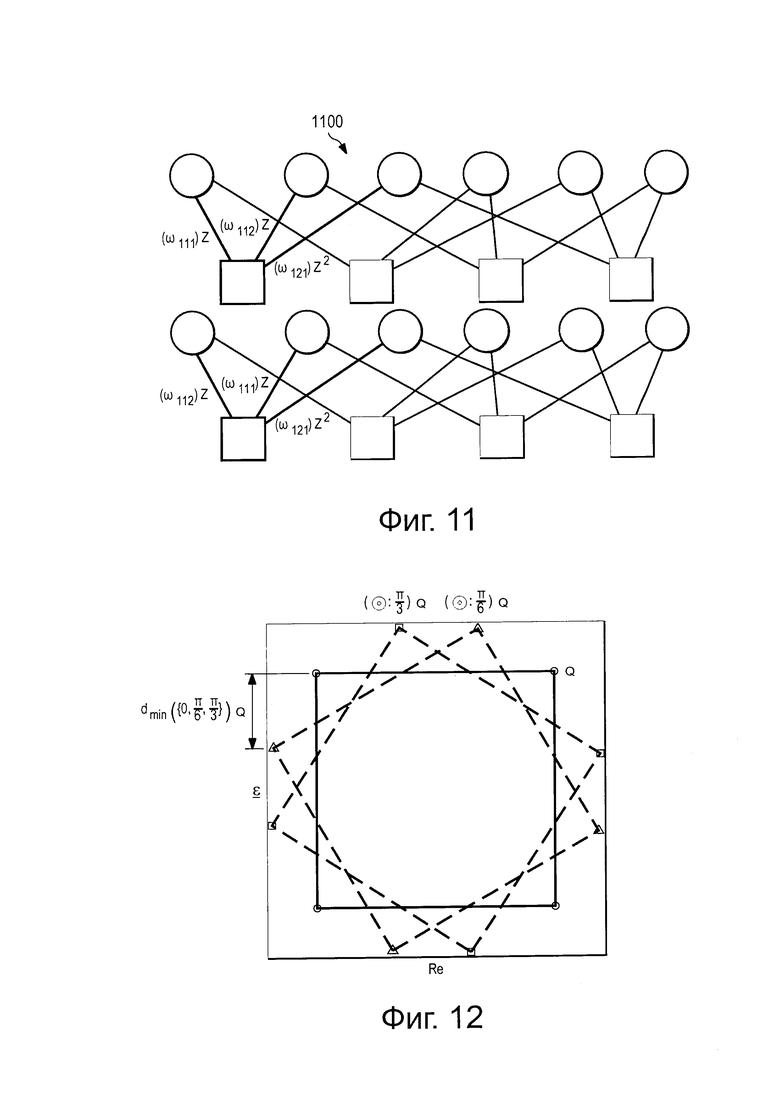
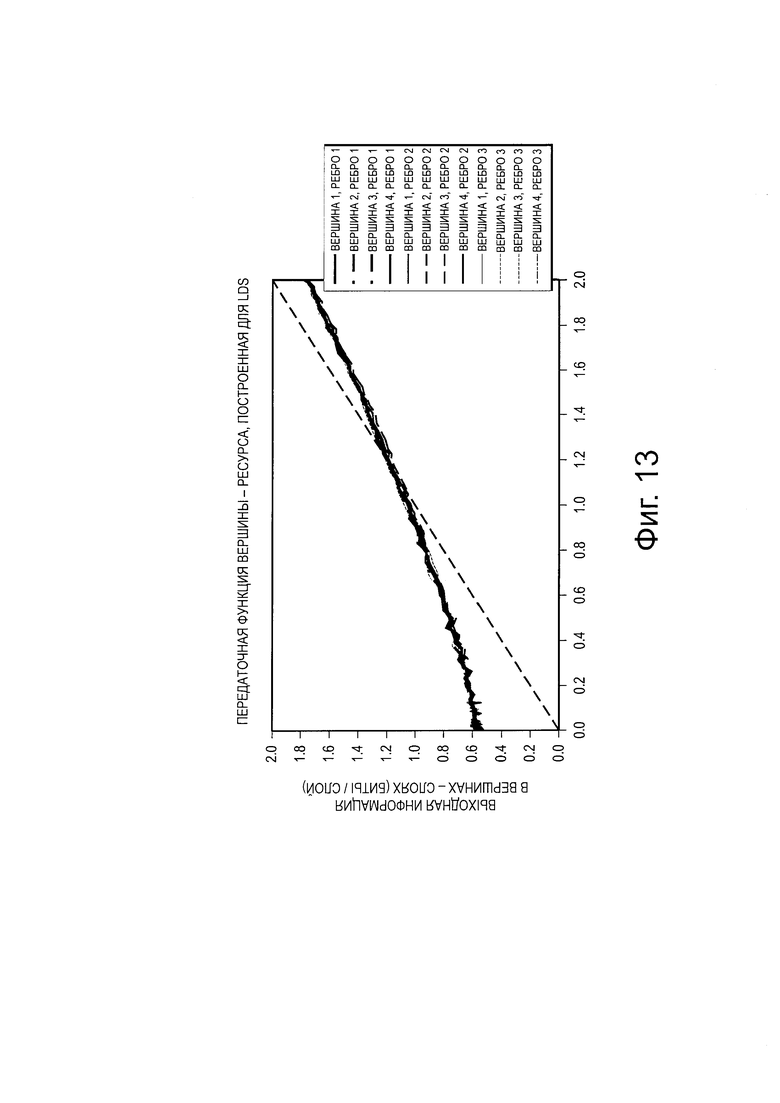
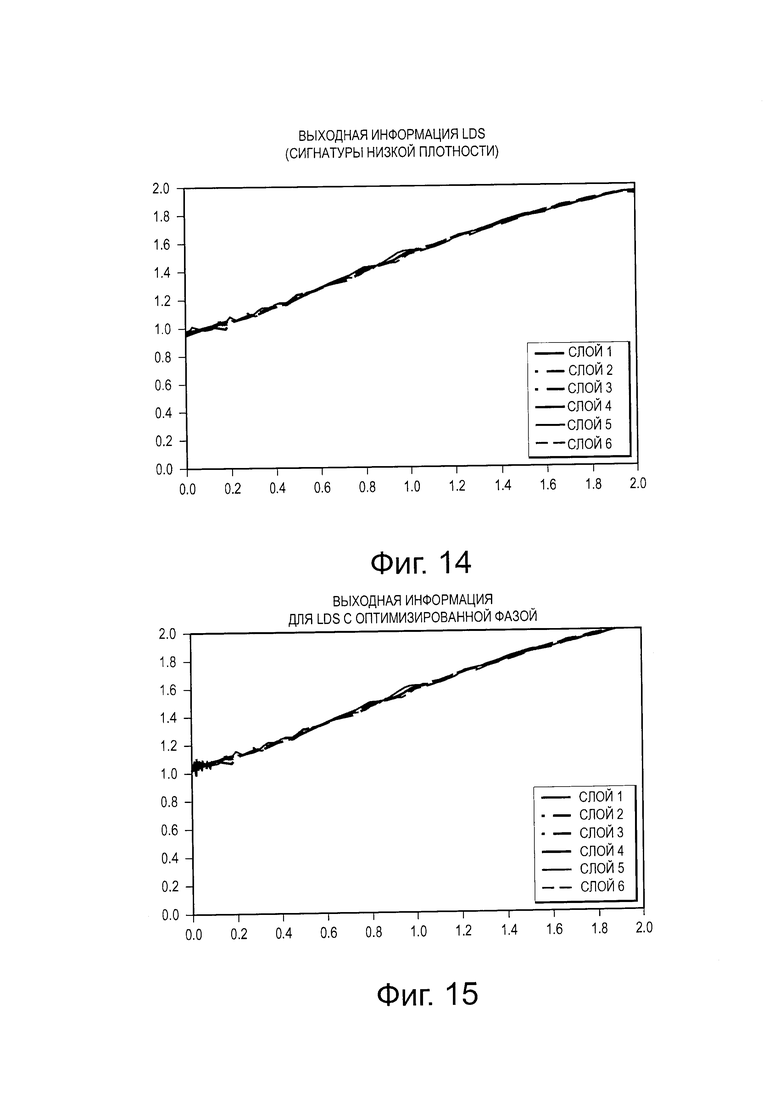
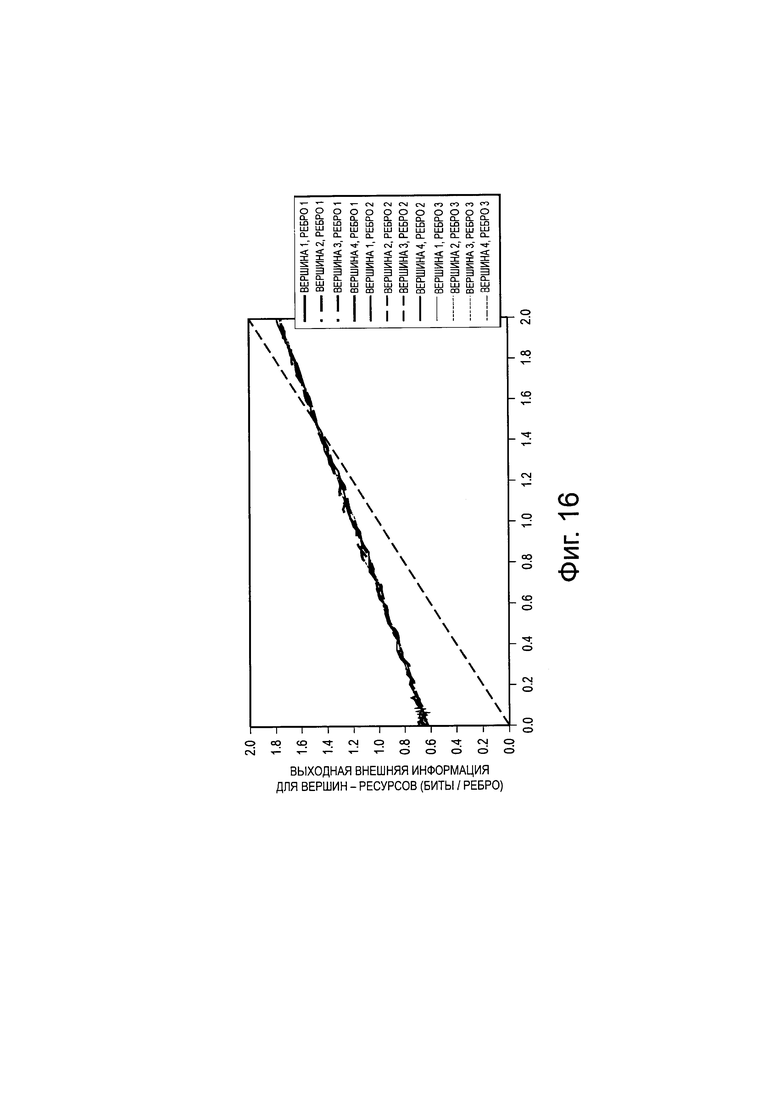
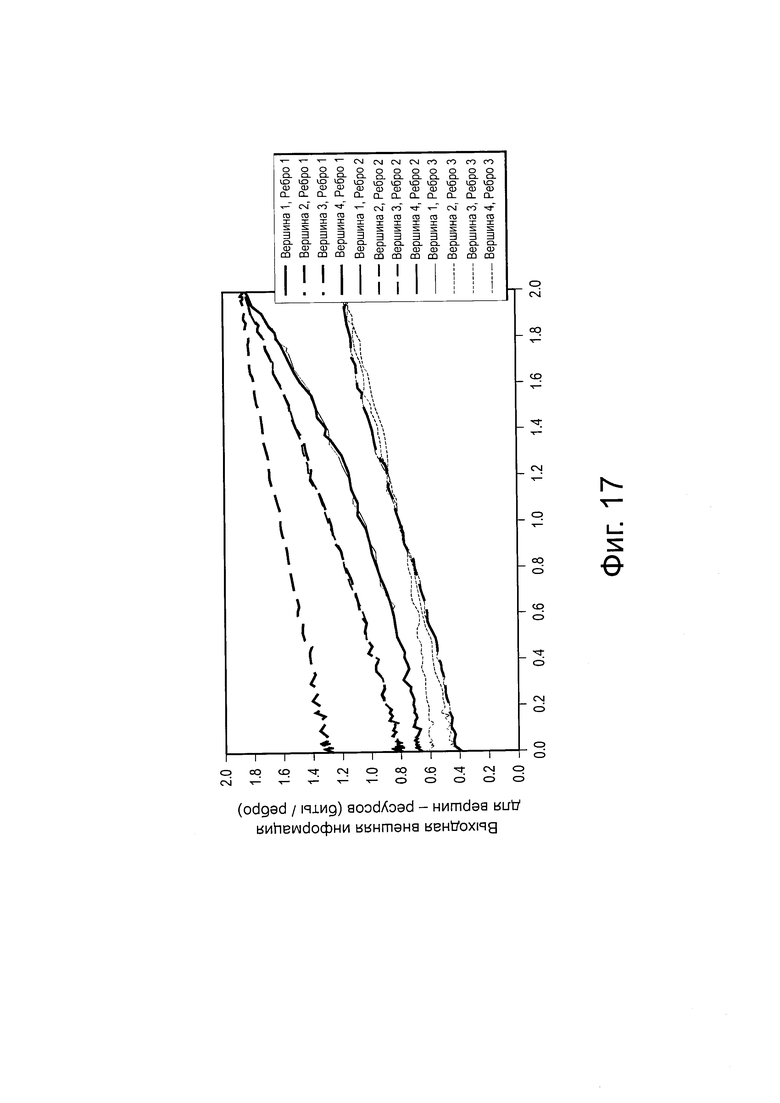
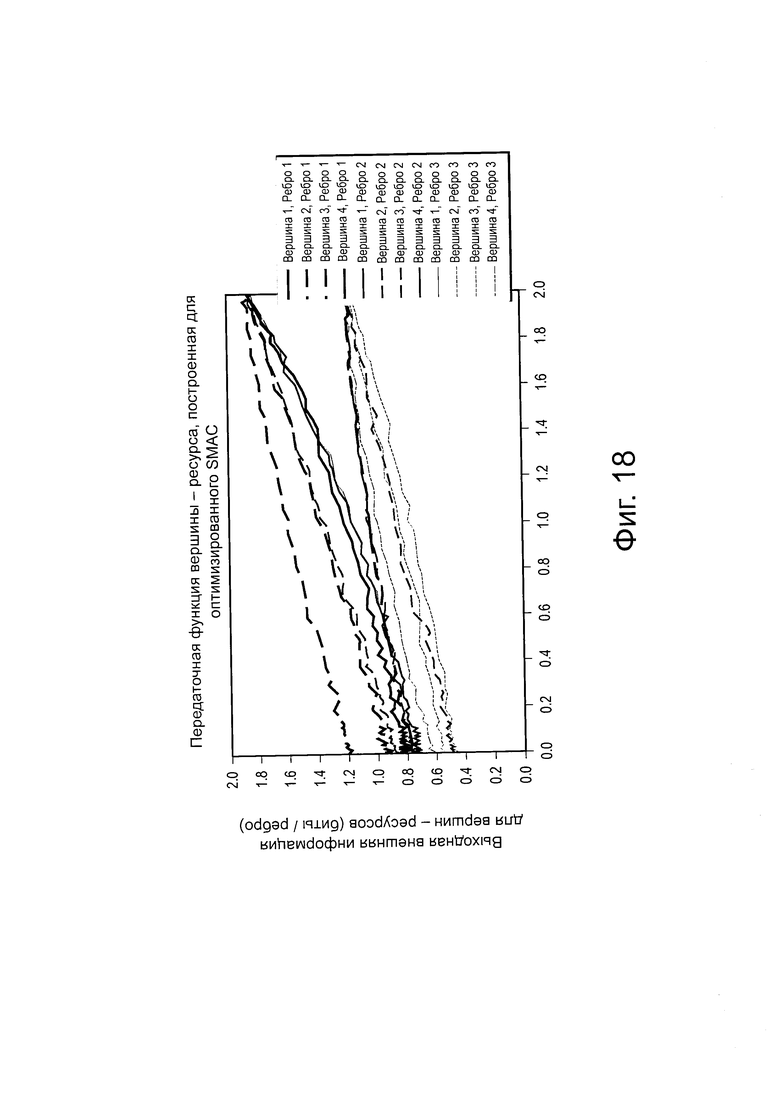
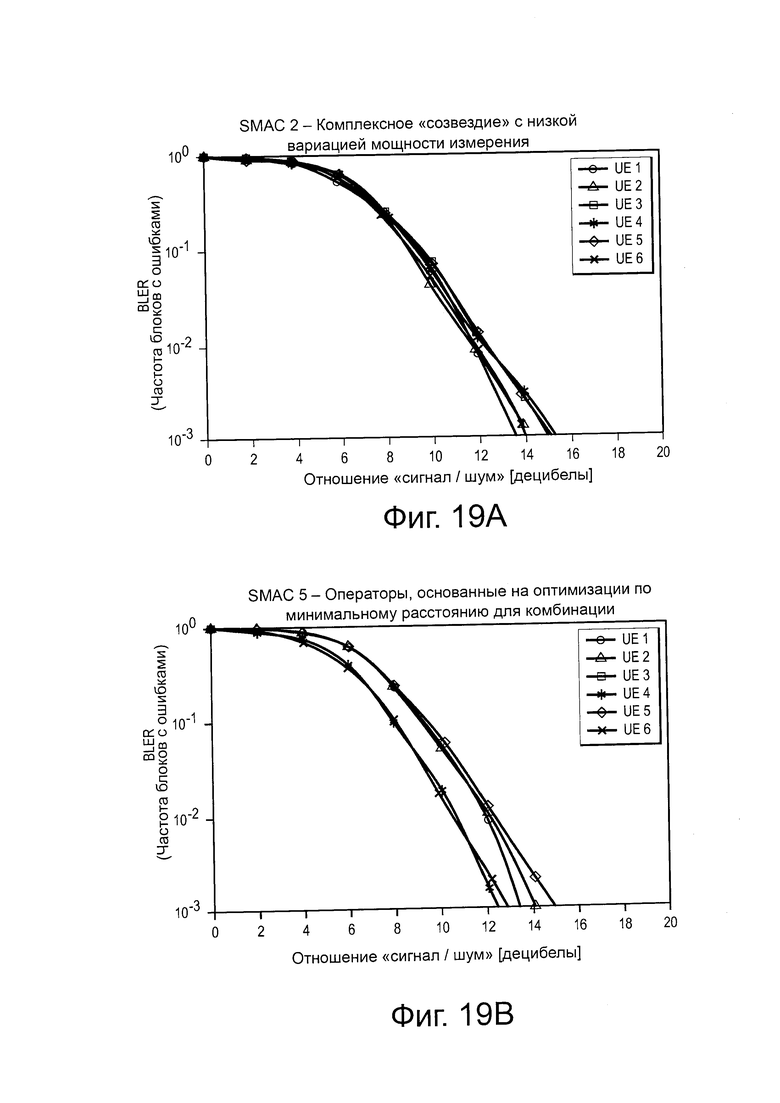
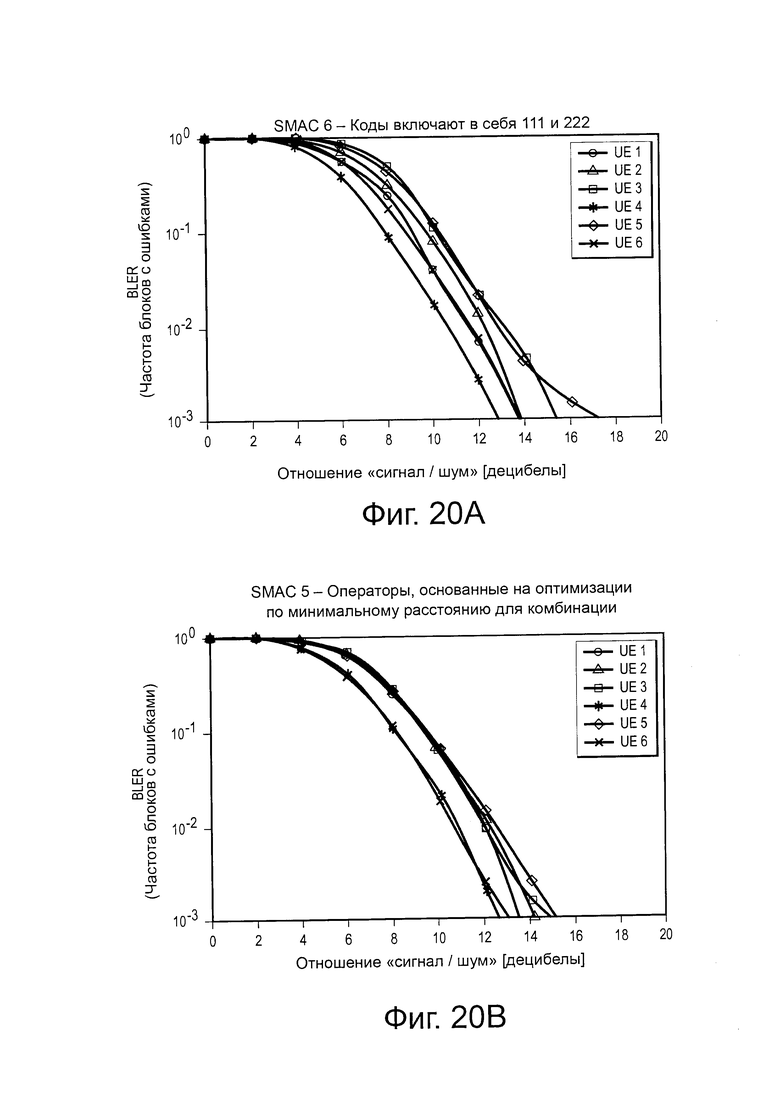
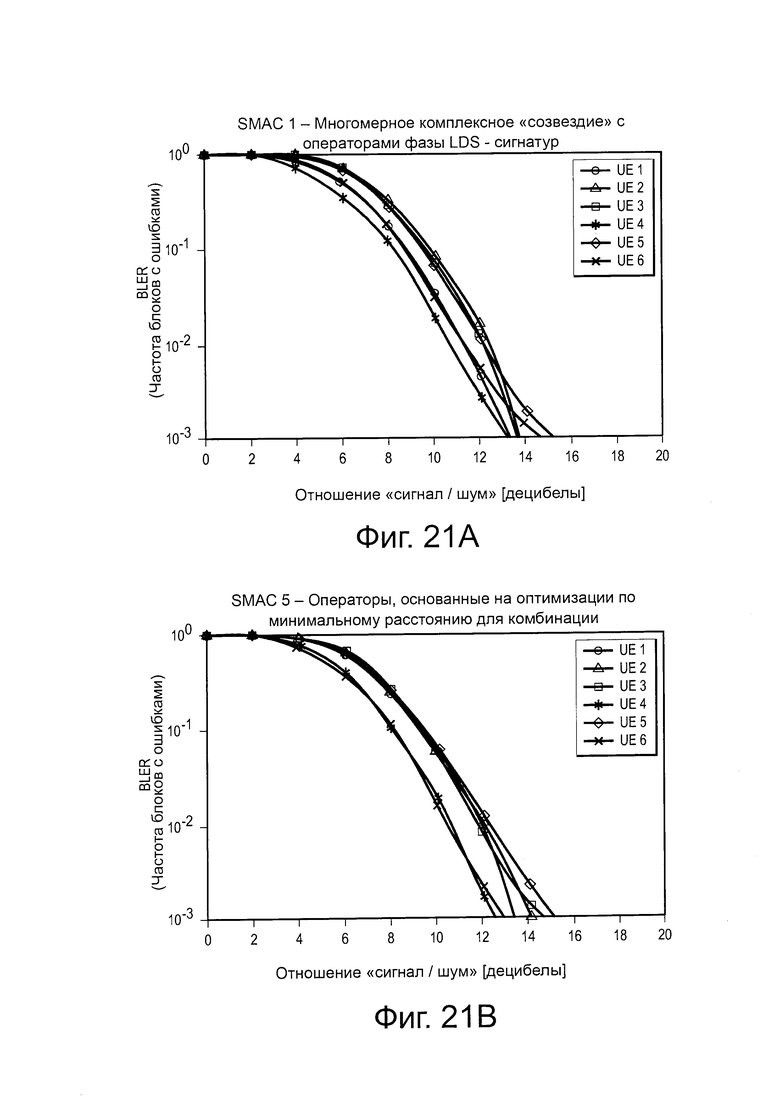
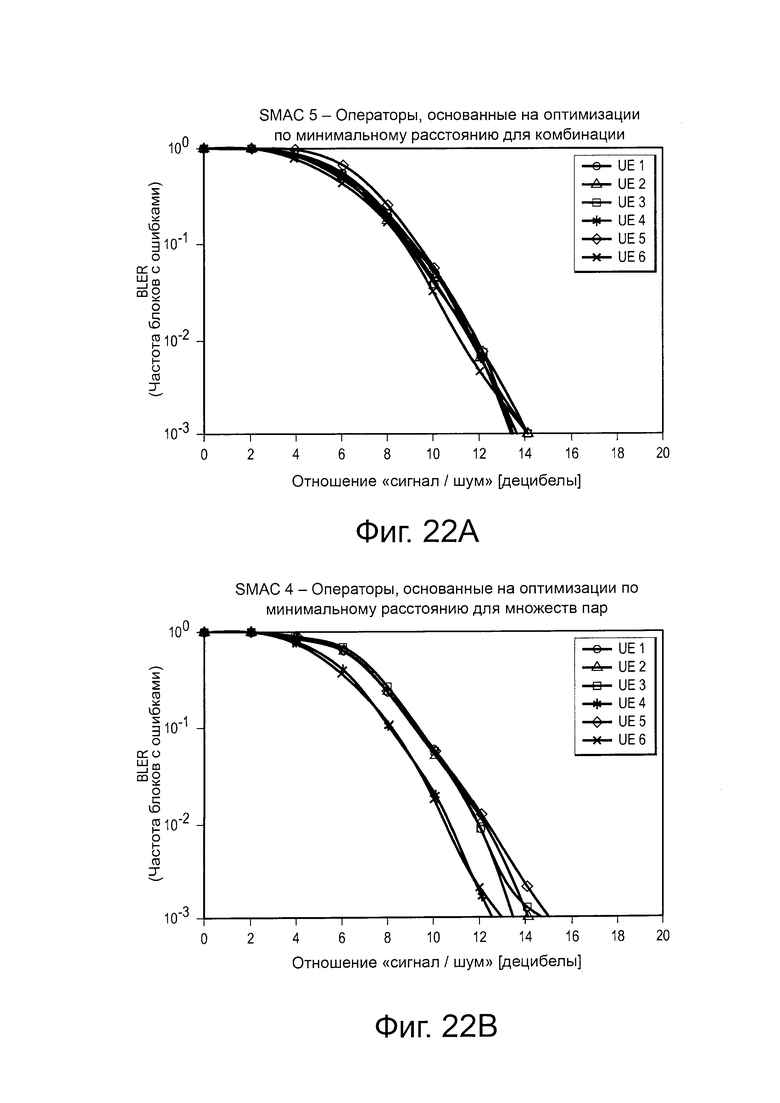
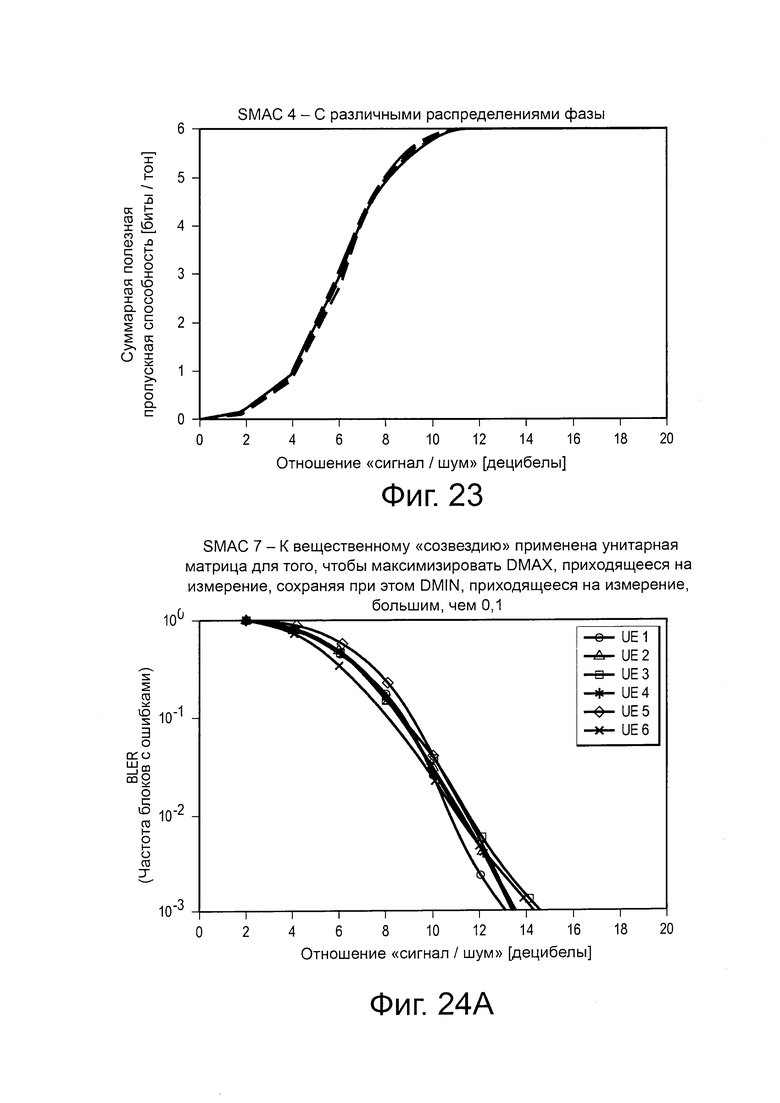
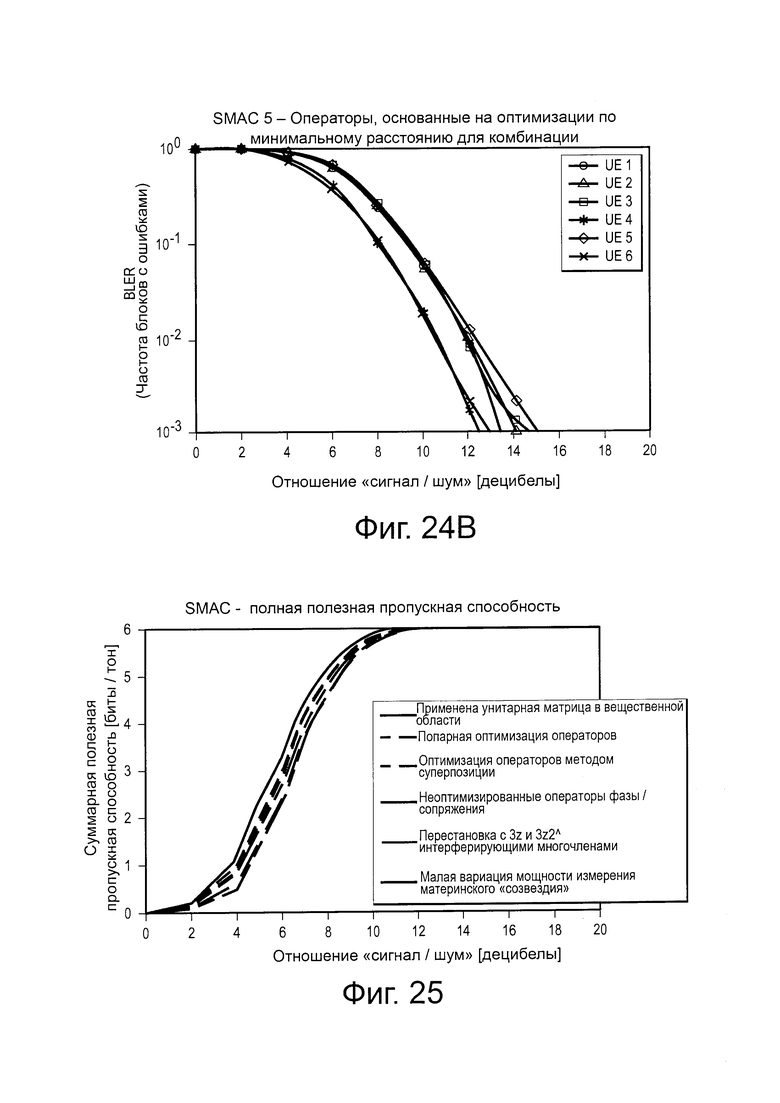
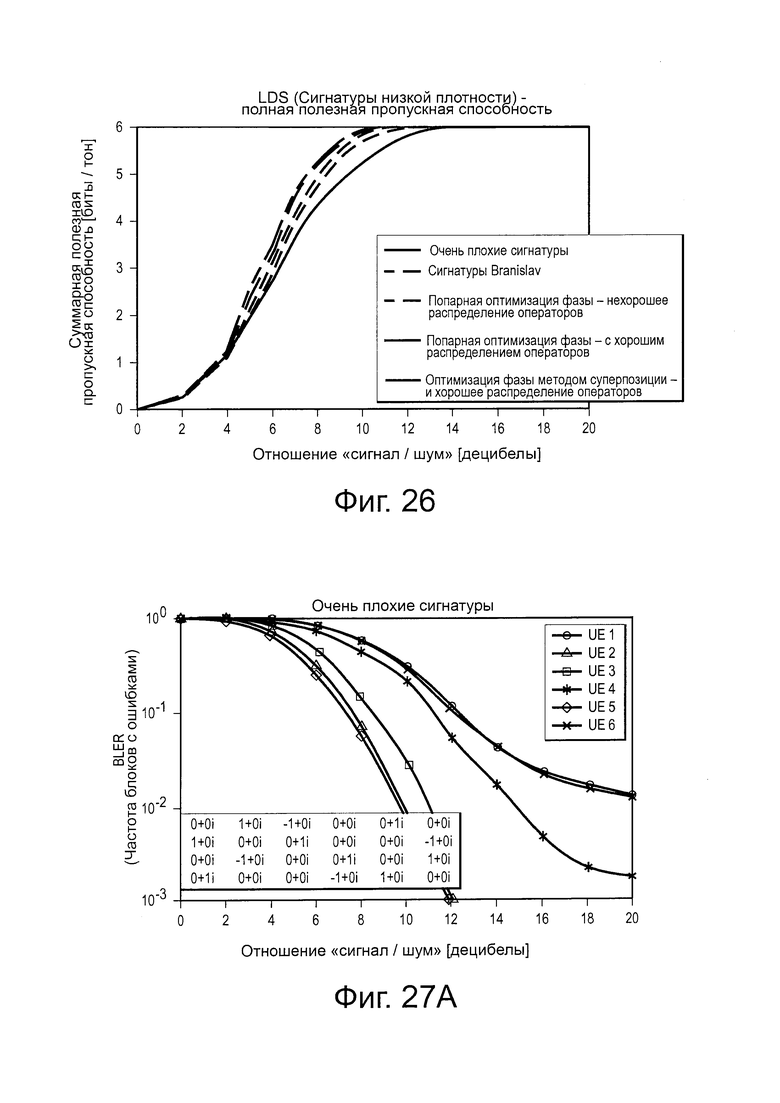
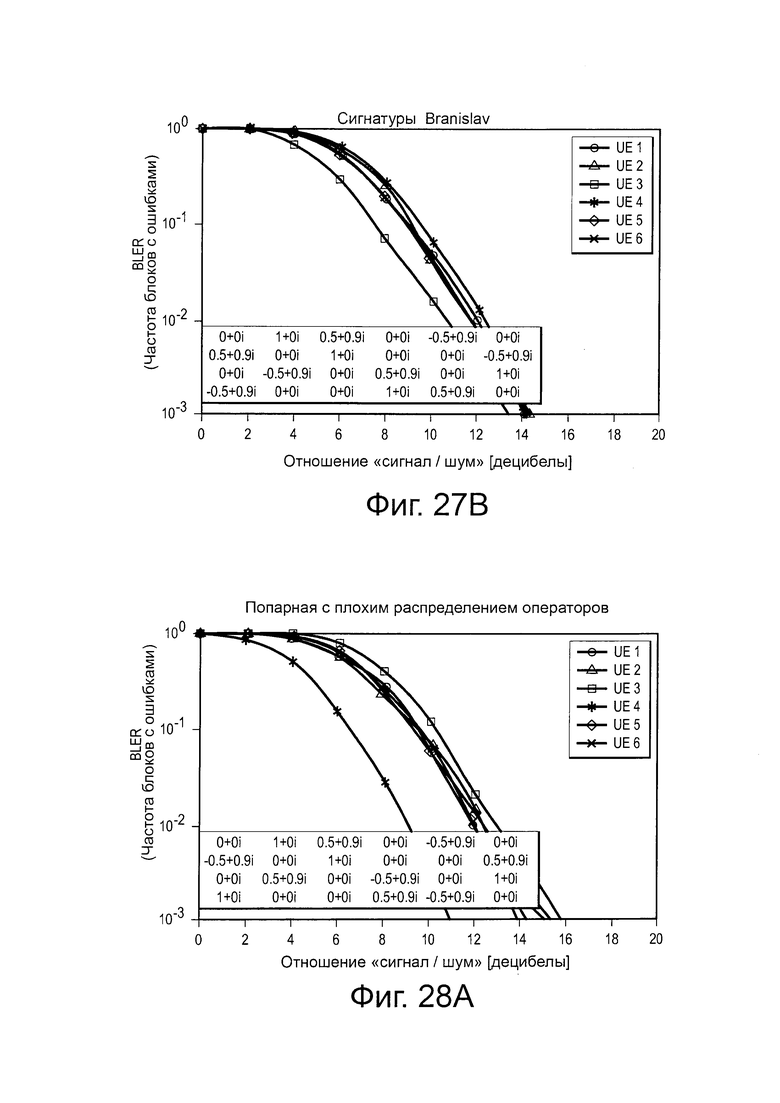
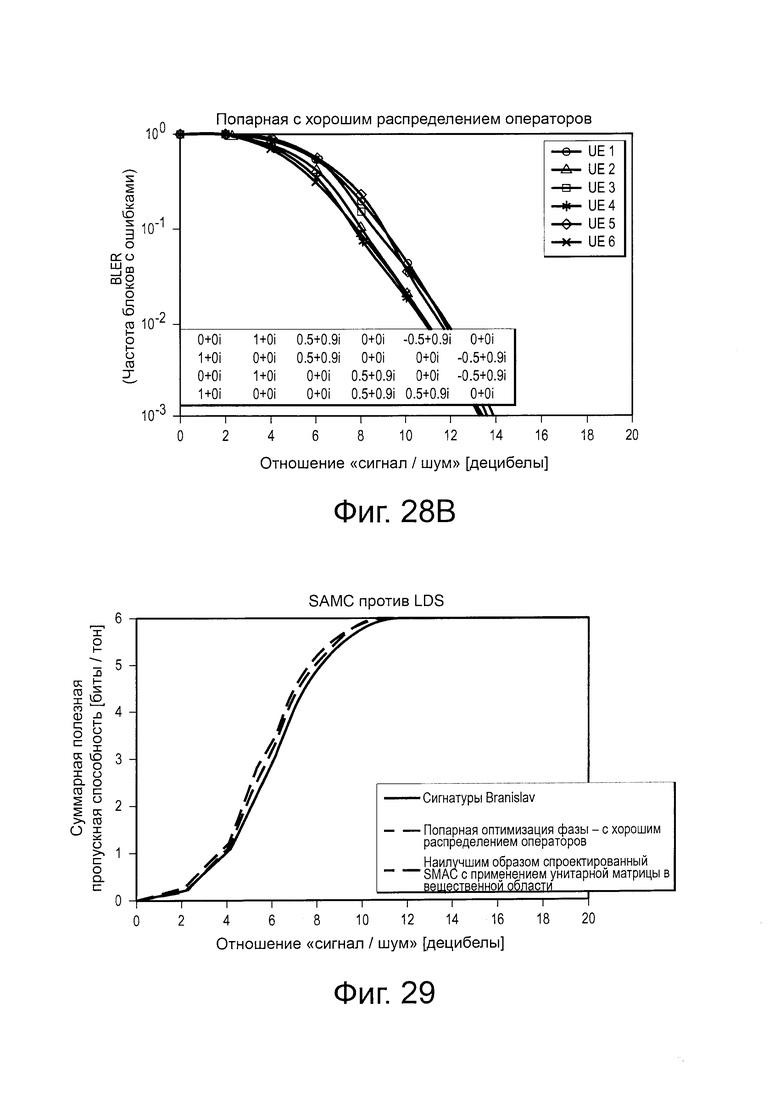
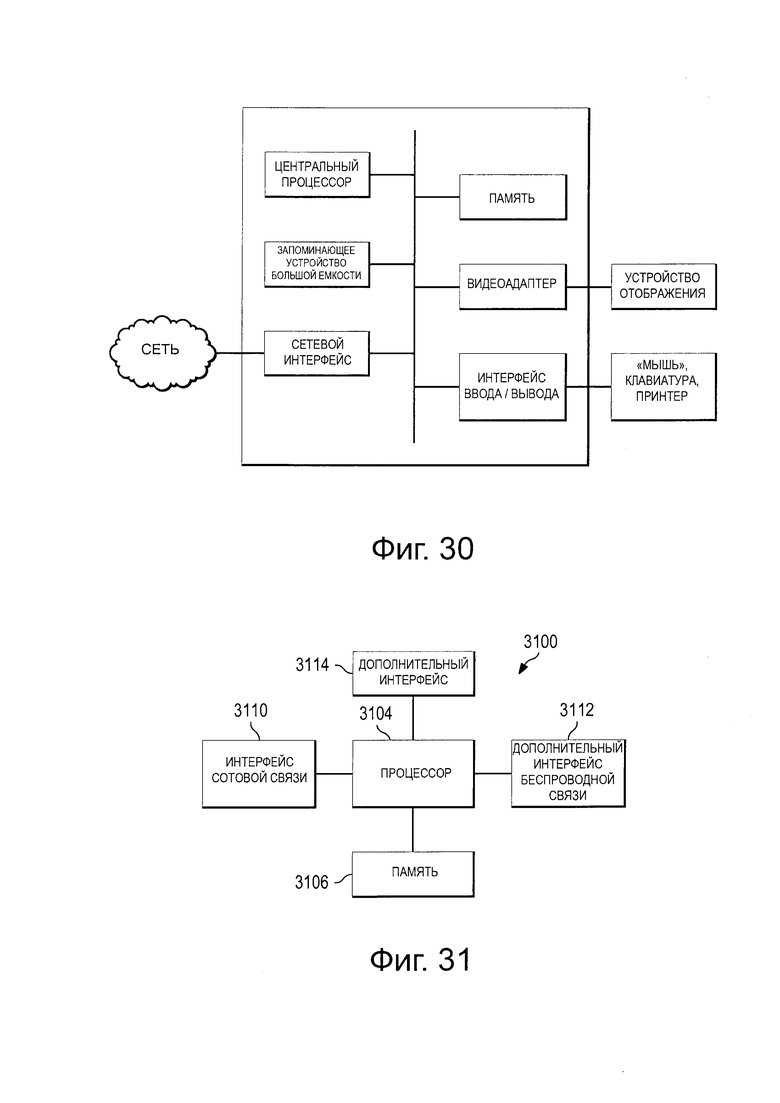
Изобретение относится к области системы связи множественного доступа с кодовым разделением каналов. Преимущества в кодировании могут быть достигнуты посредством кодирования двоичных данных напрямую в многомерные кодовые слова, что обходится без отображения на QAM-символы (символы квадратурной амплитудной модуляции), используемые в традиционных технологиях CDMA-кодирования. Кроме того, множественный доступ может быть достигнут посредством назначения различных кодовых книг различным мультиплексируемым слоям. Кроме того, разреженные кодовые слова могут быть использованы для уменьшения сложности обработки основополосного сигнала на стороне приемника в сети, поскольку разреженные кодовые слова могут быть обнаружены среди мультиплексированных кодовых слов в соответствии с алгоритмами передачи сообщений (MPА). 4 н. и 10 з.п. ф-лы, 38 ил., 3 табл.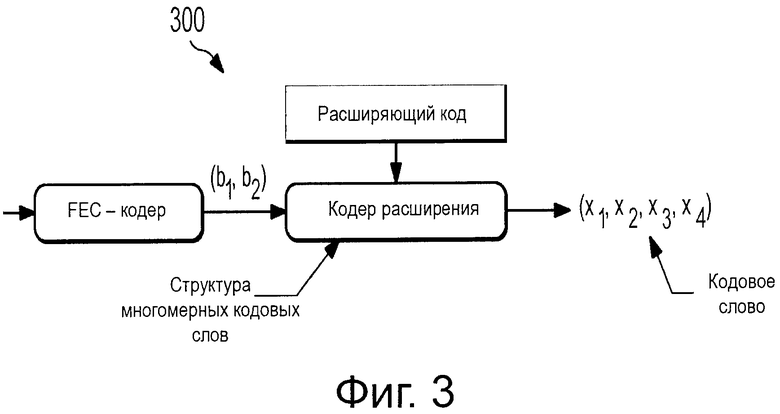
1. Способ мультиплексирования данных, содержащий этапы, на которых:
принимают первые двоичные или M-ичные данные, ассоциированные с первым мультиплексируемым слоем;
кодируют первые двоичные или M-ичные данные посредством выбора первого кодового слова из первой кодовой книги, при этом первая кодовая книга назначена исключительно первому мультиплексируемому слою;
мультиплексируют первое кодовое слово с по меньшей мере одним вторым кодовым словом из второй кодовой книги для получения мультиплексированных кодовых слов, при этом вторая кодовая книга назначена исключительно второму мультиплексируемому слою; и
передают мультиплексированные кодовые слова по совместно используемым ресурсам сети.
2. Способ по п. 1, в котором этап кодирования первых двоичных или M-ичных данных посредством выбора первого кодового слова содержит подэтап, на котором:
выбирают первое кодовое слово из первого набора кодовых слов в первой кодовой книге в соответствии с двоичным или М-ичным значением первых двоичных или M-ичных данных, при этом каждое кодовое слово в первом наборе кодовых слов ассоциативно связано с отличным от других двоичным или М-ичным значением.
3. Способ по п. 2, в котором каждое кодовое слово в первом наборе кодовых слов содержит низкую плотность ненулевых значений, так что соответствующее кодовое слово может быть обнаружено в пределах мультиплексированных кодовых слов в соответствии с алгоритмом передачи сообщений (MPА).
4. Способ по п. 1, в котором первый мультиплексируемый слой ассоциирован с первым пользователем, а второй мультиплексируемый слой ассоциирован со вторым пользователем.
5. Способ по п. 1, в котором первый мультиплексируемый слой и второй мультиплексируемый слой выполнены с возможностью переноса отдельных потоков данных, ассоциированных с общим.
6. Способ по п. 5, в котором первый мультиплексируемый слой и второй мультиплексируемый слой занимают различные пространственные слои системы с множественными входами и множественными выходами (MIMO).
7. Способ по п. 5, в котором первый мультиплексируемый слой и второй мультиплексируемый слой занимают различные тоны Множественного доступа с ортогональным частотным разделением каналов (OFDMA).
8. Передатчик, содержащий:
процессор; и
машиночитаемый носитель информации, хранящий программы для исполнения процессором, причем программы включают в себя команды, вызывающие осуществление способа по любому из пп. 1-7.
9. Способ приема данных, содержащий этапы, на которых:
принимают сигнал, несущий мультиплексированные кодовые слова, причем мультиплексированные кодовые слова включают в себя множество кодовых слов, переданных по совместно используемым ресурсам сети, при этом каждое из этого множества кодовых слов принадлежит отличной от других кодовой книге из множества кодовых книг, при этом каждая из указанного множества кодовых книг ассоциирована с отличным от других мультиплексированным слоем из множества мультиплексированных слоев;
идентифицируют с помощью приемника первое кодовое слово из указанного множества кодовых слов в пределах мультиплексированных кодовых слов, причем первое кодовое слово принадлежит первой кодовой книге из указанного множества кодовых книг, назначенной исключительно первому мультиплексированному слою из указанного множества мультиплексированных слоев, при этом приемник ассоциирован с первым мультиплексированным слоем; и
декодируют первое кодовое слово для получения первых двоичных или M-ичных данных.
10. Способ по п. 9, в котором этап идентификации первого кодового слова в пределах мультиплексированных кодовых слов содержит подэтап, на котором применяют алгоритм передачи сообщений (MPА) для обнаружения первого кодового слова из множества кодовых слов, входящих в число мультиплексированных кодовых слов.
11. Способ по п. 10, в котором этап декодирования первого кодового слова для получения первых двоичных или M-ичных данных содержит подэтап, на котором:
отображают первое кодовое слово напрямую в двоичное или M-ичное значение первых двоичных или M-ичных данных, при этом каждое кодовое слово в первой кодовой книге ассоциировано с отличным от других двоичным или М-ичным значением.
12. Способ по п. 10, в котором различные мультиплексированные слои указанного множества мультиплексированных слоев занимают различные пространственные слои системы с множественными входами и множественными выходами (MIMO).
13. Способ по п. 9, в котором различные мультиплексированные слои указанного множества мультиплексированных слоев занимают различные тоны Множественного доступа с ортогональным частотным разделением каналов (OFDMA).
14. Приемник, содержащий:
процессор; и
машиночитаемый носитель информации, хранящий программы для исполнения процессором, причем программы включают в себя команды, вызывающие выполнение способа по любому из пп. 9-13.
| US 2011274123 A1, 10.11.2011 | |||
| US 2011170625 A1, 14.07.2011 | |||
| US 2011087933 A1, 14.04.2011 | |||
| Приспособление для суммирования отрезков прямых линий | 1923 |
|
SU2010A1 |
| RU 2008106942 А, 27.08.2009 . | |||
Авторы
Даты
2016-11-27—Публикация
2013-11-18—Подача