Перекрестная ссылка на родственную заявку
Эта заявка является родственной по отношению к заявке на патент США № 12/166883, поданной 2 июля 2008 г. и озаглавленной "Reduced Peak-to-RMS Ratio Multicode Signal" (номер дела в досье поверенного № P25701). Содержимое этого документа настоящим заключено в это описание посредством ссылки.
Область техники, к которой относится изобретение
Настоящее изобретение относится, в целом, к области беспроводной связи и, в частности, к передатчику и способу генерирования радиосигнала с уменьшенным отношением пиковой амплитуды к среднеквадратической амплитуде, что способствует улучшению эффективности передачи усилителя мощности передатчика. Кроме того, настоящее изобретение относится к приемнику, который может декодировать этот радиосигнал.
Уровень техники
В этом документе заданы следующие сокращения, по меньшей мере, некоторые из которых упоминаются в пределах нижеследующего описания предшествующего уровня техники и настоящего изобретения.
В данной области техники известно, что можно считать, что сигнал связи, например радиосигнал, имеет мгновенное комплексное значение на двумерной комплексной плоскости, где координата по одному измерению равна амплитуде со знаком синусоидальной компоненты радиосигнала, а координата по второму измерению равна амплитуде со знаком косинусоидальной компоненты радиосигнала. Так как косинусоида и синусоида являются взаимно ортогональными функциями, то их корреляция равна нулю, что означает, что эти два измерения расположены под прямым углом друг к другу. Эти два измерения обычно обозначают I и Q, что означает "Синфазное" и "Квадратурное". Других ортогональных измерений не существует в этом пространстве сигналов, которое является плоскостью. Также хорошо известно, что символы, представляющие группы битов, могут быть расположены на плоскости I, Q так, что любые два символа достаточно отделены друг от друга, чтобы избежать путаницы, до тех пор, пока отношение сигнал/шум находится на довольно высоком уровне. Например, 16 символов могут быть расположены на решетке 4×4, известной как 16QAM, и причем каждой точке назначаются четыре двоичных бита. В 64QAM, 64 символа могут быть расположены на решетке 8×8, и причем каждой точке назначаются 6 двочиных битов. Также может использоваться непрямоугольное созвездие точек, например, 16-PSK (манипуляция сдвигом фазы), в которой 16 точек равномерно расположены по окружности, на равных углах, и для каждой из точек распределяются 4 двоичных бита.
В предшествующем уровне техники, обычно считается желательным и известным, что группы битов распределяются для точек символа согласно схеме кодирования Грея, так что биты, назначенные соседним точкам в пространстве сигналов, отличаются как можно меньшим количеством позиций бита, предпочтительно только одной позицией бита. Далее предоставлено краткое обсуждение некоторых из этих известных схем, а также их недостатки, которые связаны с предшествующим уровнем техники.
В патенте США № 4084337, поданном 24 августа 1976 г., описывается четырехмерная схема модуляции, в которой используются обе поляризации радиоволн для предоставления двух независимых каналов, где каждый канал может переносить двумерный сигнал. В этом патенте существует ссылка на статью в IEEE, озаглавленную "Digital Transmission with Four Dimensional modulation" (Trans IEEE on Information Theory, июль 1974, стр. 497-502), в которой описана четырехмерная схема модуляции, которая создана с ограничением пиковой энергии. Ограничение пиковой энергии описано в упомянутой статье и означает, что сумма мощностей в двух поляризациях не должна превышать некоторое максимальное значение. Например, если (I1,Q1) являются синфазной и квадратурной фазовой компонентами на одной поляризации, и (I2,Q2) являются синфазной и квадратурной фазовой компонентами на другой поляризации, то общая энергия или мощность, которая является ограниченной, задается I12+Q12+I22+Q22. Это ограничение является уместным и подходящим, когда (I1,Q1) и (I2,Q2) генерируются отдельно и применяются к физически независимым каналам, например, ортогонально поляризованным антеннам. Однако, если (I1,Q1) и (I2,Q2) генерируются не отдельно и применяются к физически не отдельным каналам, а, наоборот, применяются к одному и тому же физическому каналу, то передаваемым сигналом является (I1+I2, Q1+Q2), и его энергия или мощность будет пропорциональной (I1+I2)2+(Q1+Q2)2, что не является ограниченным одной и той же метрикой. Соответственно, в последнем случае для ограничения пиковой энергии требуется другая схема.
В патенте США № 4597090, поданном 14 апреля 1983 г., раскрыта схема модуляции для одного физического канала, в котором считается, что два измерения в пространстве сигналов (I,Q) на m последовательных выборках сигналов формируют 2m-мерное пространство, и где mN битов данных кодируются в 2m измерений так, чтобы получить выигрыш кодирования посредством ограничения выбора значения I, Q одной выборки сигнала, зависящего от выбора значений I, Q для других выборок сигналов. Это является одним видом решетчатого кодирования и относится к получению выигрыша кодирования, но в нем отсутствует упоминание о получении уменьшения отношения пиковой к среднеквадратической (rms) амплитуде радиосигнала, что является предметом, который относится к настоящему обсуждению.
В системе сотовой связи 3-го Поколения, известной как WCDMA или UMTS, в настоящее время существует способ согласно спецификации, известной как HSPA, который обеспечивает возможность передачи данных с более высокой скоростью из мобильного телефона в сеть (или базовую станцию). Передача HSPA использует подход, называемый "Multi-code CDMA" ("Многокодовый CDMA"). В этой системе Multi-code CDMA, каждый символ данных расширяется по времени и спектру посредством комбинирования его с кодом расширения. На нисходящей линии связи (от базовой станции к мобильному телефону) коды, используемые для передачи сигналов из базовой станции, координируются так, чтобы они были взаимно ортогональными. В отличие от этого на восходящей линии связи (от мобильного телефона к базовой станции) координация, требуемая между различными мобильными телефонами для достижения ортогональности, считается слишком трудной для реализации, поэтому каждый мобильный телефон использует отличную случайную кодовую последовательность.
Однако в каждом мобильном телефоне, тем не менее, можно генерировать несколько случайных кодовых последовательностей, которые скоординированы между собой для взаимной ортогональности. Каждый из этих ортогональных кодов может затем переносить подпоток символов так, что скорость комбинированного потока символов увеличивается. Но, в этом случае, доступная мощность передатчика мобильного телефона должна делиться между различными кодами, что означает, что диапазон, в котором каждый подпоток может успешно приниматься и декодироваться без ошибок, должен уменьшаться. Фактически, уменьшение мощности для каждого подпотока в сигнале с многокодовой модуляцией, передаваемом из мобильного телефона, является большим, чем можно ожидать при простом делении мощности передатчика на общее количество подпотоков. Это происходит не столько из-за средней мощности, которая ограничивается напряжением батареи, сколько из-за пиковой амплитуды сигнала, которая оказывается ограниченной напряжением батареи.
Соответственно, в системе сотовой связи 3-го Поколения существует потребность в схеме модуляции, которая создает наибольшую среднюю мощность для каждого подпотока в пределах ограничения составной пиковой амплитуды сигнала всех подпотоков. Например, если мобильный телефон использует трехкодовую многокодовую схему с тремя кодами с длиной=4, где каждый код переносит подпоток символов 16QAM с аналогичной амплитудой, то общая средняя мощность, которая передается в пределах данного ограничения пиковой амплитуды, на 7,32 дБ ниже пика до фильтрации, ограничивающей спектр, и средняя мощность для каждого подпотока на 12,1 дБ ниже пика. Фильтрация в общем дополнительно увеличивает отношение пиковой к среднеквадратической амплитуде. Стандарт HSPA описывает улучшение по сравнению со схемой с тремя кодами расширения с длиной=4, т.к. он специфицирует код с длиной=2 в два раза большей мощности (√2 умножить на амплитуду), который переносит два символа в такой же период времени, в какой наложенный и ортогональный код с длиной=4 переносит третий символ, в котором эффективно достигается такая же символьная скорость, как при трех кодах с длиной=4. Эта конфигурация 4+(2,2) может создавать общую среднюю мощность, которая на 5,44 дБ ниже пиковой, и на 1,88 дБ более эффективная, чем конфигурация 4+4+4, которая связана со схемой с тремя кодами расширения с длиной=4.
Однако при конфигурации 4+(2,2) существует уменьшение коэффициента расширения, что является движением не в направлении расширения, при котором также достигается малое отношение пиковой к среднеквадратической амплитуде, но получающийся в результате радиосигнал очень трудно декодировать, когда существует значительное количество искажений, обусловленных многолучевым распространением в канале. Принимая во внимание вышеизложенное, видно, что существовала и все еще существует потребность в передатчике и способе, которые могут разрешать проблемы, связанные с вышеупомянутыми недостатками и другими недостатками, связанными с предшествующим уровнем техники. Эти и другие потребности удовлетворяются с передатчиком и способом настоящего изобретения.
Сущность изобретения
Согласно одному аспекту настоящее изобретение предоставляет способ для уменьшения отношения пиковой к среднеквадратической амплитуде в передаваемом радиосигнале при наложении ограничения на пиковую составную амплитуду символа при использовании многомерной модуляции. Этот способ включает в себя этапы: (a) кодирование информации в поток двоичных битов, (b) формирование множества групп битов из потока двоичных битов, причем это множество групп битов представляет множество символов данных, (c) представление каждого символа данных набором координат в многомерном пространстве, причем количество измерений в этом многомерном пространстве соответствует количеству, равному, по меньшей мере, трем ортогональным компонентам, которые в итоге содержат передаваемый радиосигнал, и (d) выбор координат для каждого символа данных, так что каждый символ данных расположен на минимальном расстоянии от ближайшего другого символа данных в многомерном пространстве, а также так, что отношение пиковой составной амплитуды символа к среднеквадратической амплитуде передаваемого радиосигнала является минимальным. Этот способ генерирования радиосигнала с уменьшенным отношением пиковой амплитуды к среднеквадратической амплитуде способствует улучшению эффективности передачи усилителя мощности передатчика.
Согласно другому аспекту настоящее изобретение предоставляет способ передачи символов данных, в результате которого получается передаваемый сигнал с уменьшенным отношением пиковой амплитуды к среднеквадратической амплитуде. Этот способ включает в себя этапы: (a) одновременное использование множества аддитивно комбинированных кодов расширения спектра, причем каждый переносит синфазное или действительное значение сигнала и квадратурное фазовое или мнимое значение сигнала, для предоставления, по меньшей мере, трех независимых модуляционных измерений, причем каждое измерение переносит значение координаты, и (b) задание набора точек созвездия, которые должны быть связаны с символами данных, причем эти точки созвездия распределены в пределах пространства, содержащего, по меньшей мере, три измерения, так что евклидово расстояние между любыми двумя точками созвездия не меньше желаемого минимума, и так что желаемое значение пиковой амплитуды не превышается любой точкой, причем это пиковое значение определяется посредством любого из следующих показателей: (i) сумма абсолютных значений координат любой точки созвездия, соответствующих измерениям, предоставляемым действительными значениями сигнала, переносимыми множеством аддитивно комбинированных кодов расширения спектра, (ii) сумма абсолютных значений координат любой точки созвездия, соответствующих измерениям, предоставляемым мнимыми значениями сигнала, переносимыми множеством аддитивно комбинированных кодов расширения спектра, и (iii) сумма квадратов (a) суммы абсолютных значений координат любой точки созвездия, соответствующих измерениям, предоставляемым действительными значениями сигнала, переносимыми множеством аддитивно комбинированных кодов расширения спектра, и (b) суммы абсолютных значений координат созвездия любой точки, соответствующих измерениям, предоставляемым мнимыми значениями сигнала, переносимыми множеством аддитивно комбинированных кодов расширения спектра. Этот способ генерирования радиосигнала с уменьшенным отношением пиковой амплитуды к среднеквадратической амплитуде способствует улучшению эффективности передачи усилителя мощности передатчика.
Согласно еще одному аспекту настоящее изобретение предоставляет передатчик, который уменьшает отношение пиковой к среднеквадратической амплитуде в радиосигнале при наложении ограничения на пиковую составную амплитуду символа при использовании многомерной модуляции. Передатчик включает в себя: (a) кодер, который делит группы битов данных на первую подгруппу и вторую подгруппу, (b) кодер использует первую подгруппу битов для выбора одной из определенного количества точек созвездия, которые распределены в пределах первого многомерного пространства, где местоположение точек созвездия определяется так, что сумма их координат меньше желаемого максимального значения, где координаты выбранной точки созвездия используются для установки значений действительных частей соответствующих комплексных чисел, (c) кодер использует вторую подгруппу битов для выбора другой одной из определенного количества точек созвездия, которые распределены в пределах второго многомерного пространства, где местоположение точек созвездия определяется так, что сумма их координат меньше желаемого максимального значения, где координаты выбранной точки созвездия тогда используются для установки значений мнимых частей соответствующих комплексных чисел, (d) кодер соединяет попарно одну действительную и одну мнимую часть для формирования комплексного числа, и аналогично соединяются попарно остальные действительные и мнимые части для получения набора комплексных чисел, (e) кодер назначает комплексные числа, которые должны быть умножены на связанный с ними один из определенного количества ортогональных кодов множества элементарных сигналов, где произведение каждого комплексного числа на его код впоследствии суммируется по элементарным сигналам для получения многокодового символа, (f) фильтр, который принимает поток многокодовых символов и фильтрует их для ограничения передаваемого спектра, (g) модулятор, который модулирует отфильтрованный сигнал с радиочастотной несущей, и (h) антенну, которая передает модулированный радиосигнал. Соответственно, посредством генерирования радиосигнала с уменьшенным отношением пиковой амплитуды к среднеквадратической амплитуде эффективность передачи усилителя мощности передатчика улучшается.
Согласно еще одному аспекту настоящее изобретения предоставляет приемник, который декодирует радиосигнал с уменьшенным отношением пиковой к среднеквадратической амплитуде и ограниченной пиковой составной амплитудой символа. В одном варианте осуществления, приемник включает в себя декодер с процессором, который реализует исполнимые процессором команды из памяти для декодирования радиосигнала посредством: (a) определения грани ромбовидного созвездия, на которой или в пределах которой лежит символ данных радиосигнала, (b) определения поднабора точек на грани, в пределах которой лежит символ данных радиосигнала, (c) определения точки в поднаборе точек, которая находится ближе всех к значениям координат символа данных, и (d) определение символа данных из комбинации грани, поднабора точек и ближайшей точки.
Согласно еще одному аспекту настоящее изобретение предоставляет приемник, который декодирует радиосигнал с уменьшенным отношением пиковой к среднеквадратической амплитуде и ограниченной пиковой составной амплитудой символа. В одном варианте осуществления, приемник включает в себя декодер с процессором, который реализует исполнимые процессором команды из памяти для декодирования радиосигнала посредством: (a) формирования гипотезы о первой из множества точек созвездия на первом ромбовидном созвездии, где эта первая точка созвездия связана с символом данных радиосигнала, (b) установления, с учетом гипотетической первой точки созвездия, второй точки созвездия на втором ромбовидном созвездии, где эта вторая точка созвездия связана с символом данных радиосигнала, (c) установление метрики, описывающей то, насколько точно гипотетическая первая точка созвездия и связанная с ней установленная вторая точка созвездия предсказывают принятый радиосигнал, и (d) сравнение метрики для всех возможных гипотез о первой точке созвездия и выбор гипотезы с наилучшей метрикой в качестве правильной гипотезы, тем самым декодируя радиосигнал.
Дополнительные аспекты изобретения будут изложены, частично, в нижеследующих подробном описании, чертежах и пунктах формулы изобретения, а частично, будут выведены из подробного описания, или о них можно узнать посредством применения изобретения на практике. Должно быть понятно, что как вышеизложенное краткое описание, так и нижеследующее подробное описание являются только иллюстративными и поясняющими, и они не ограничивают раскрытое изобретение.
Краткое описание чертежей
Более полное понимание настоящего изобретения можно получить при обращении к нижеследующему подробному описанию и в совокупности с прилагаемыми чертежами:
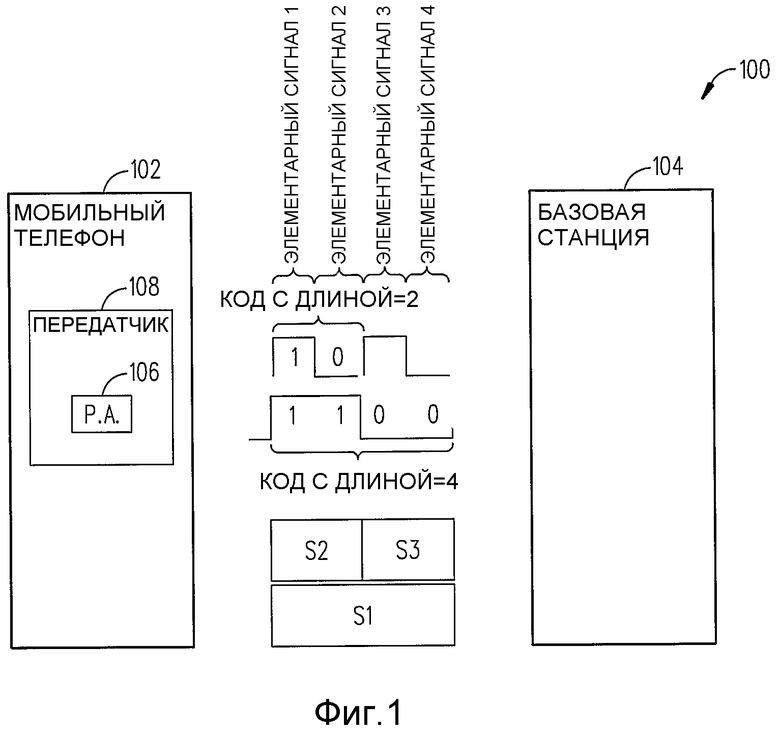
Фиг.1 - схема традиционной многокодовой системы сотовой связи HSPA 4+(2,2), которая используется для содействия пониманию настоящего изобретения.
Фиг.2 - схема, на которой изображены 16 точек созвездия 16QAM, которая используется для содействия пониманию настоящего изобретения.
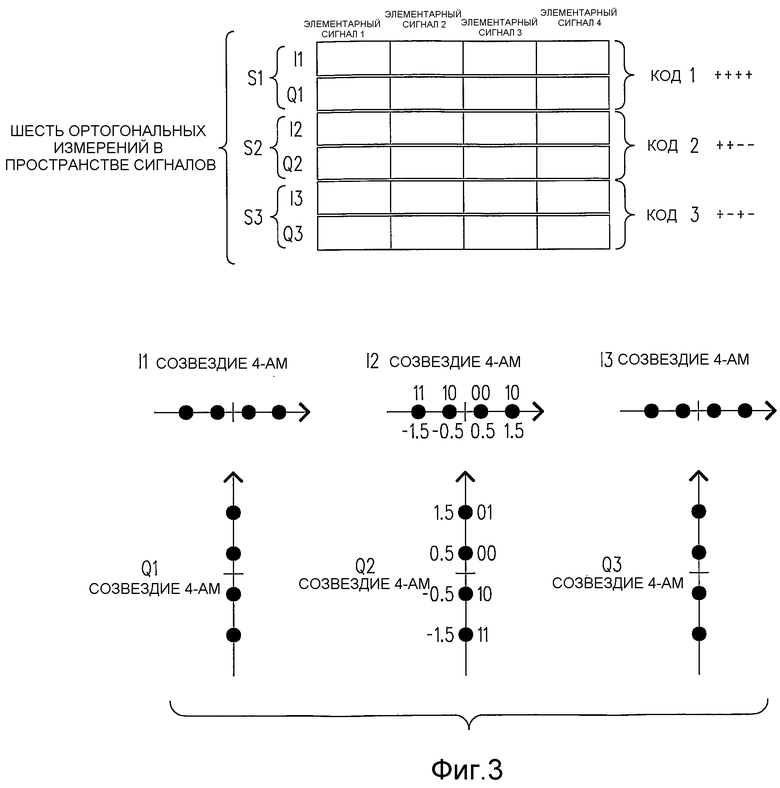
На фиг.3 изображены схемы, связанные с традиционной многокодовой системой сотовой связи 4+4+4, которые используются для содействия пониманию настоящего изобретения.
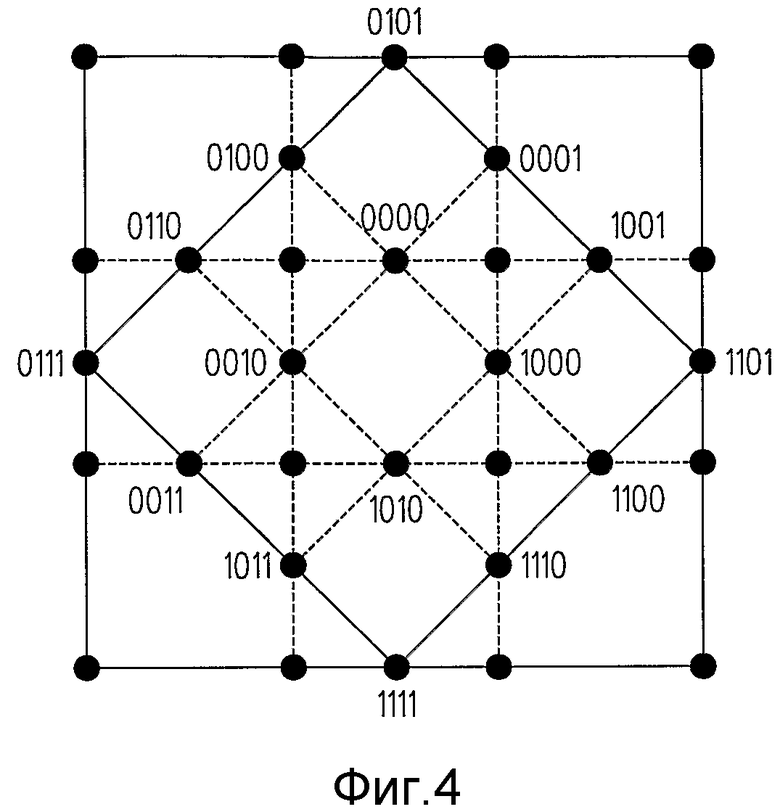
Фиг.4 - схема, на которой наглядно изображен фазовый поворот на 45 градусов символов 16QAM, модулированных на коде с длиной=4, относительно символов 16QAM, модулированных на коде с длиной=2 двойной мощности (√2 умножить на амплитуду), которая используется для содействия пониманию настоящего изобретения.
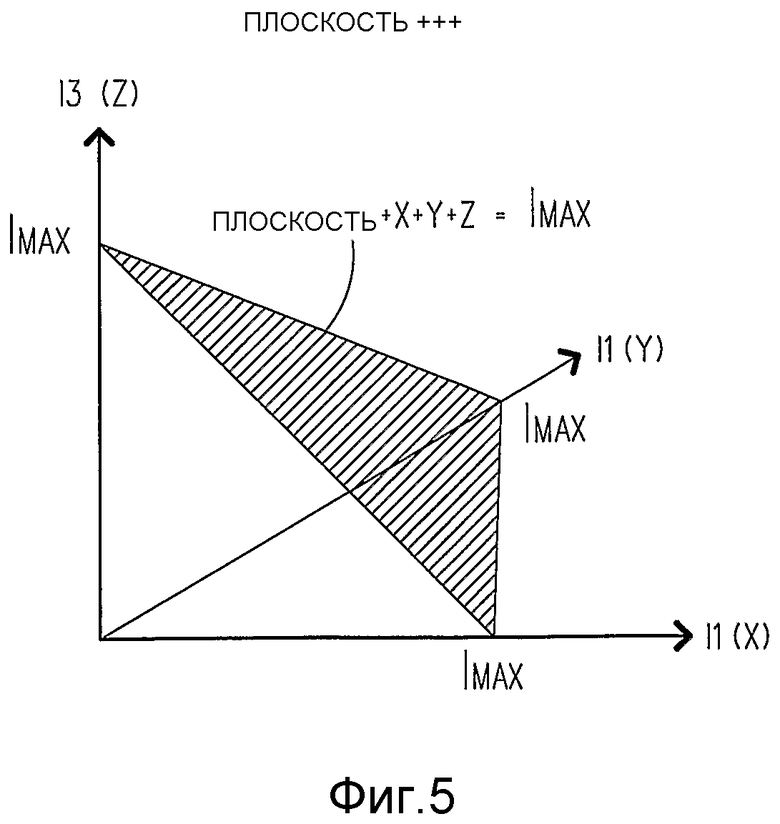
Фиг.5 - график, на котором изображена плоскость для I1, I2, I3 при I1+I2+I3=1, который используется для содействия пониманию настоящего изобретения.
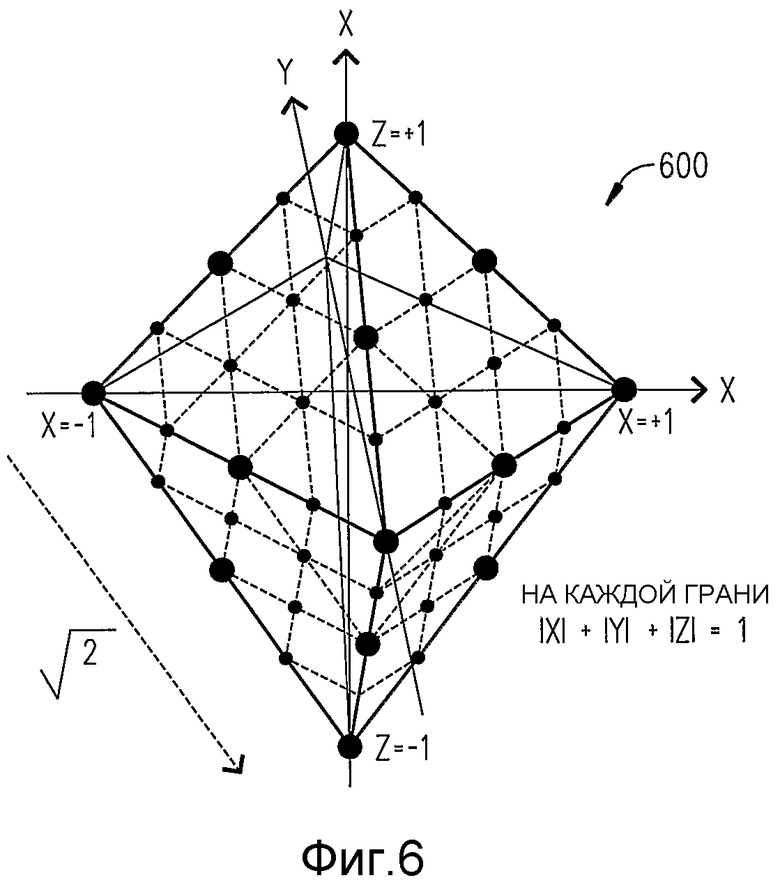
Фиг.6 - схема, на которой изображено ромбовидное созвездие, которая используется для содействия пониманию настоящего изобретения.
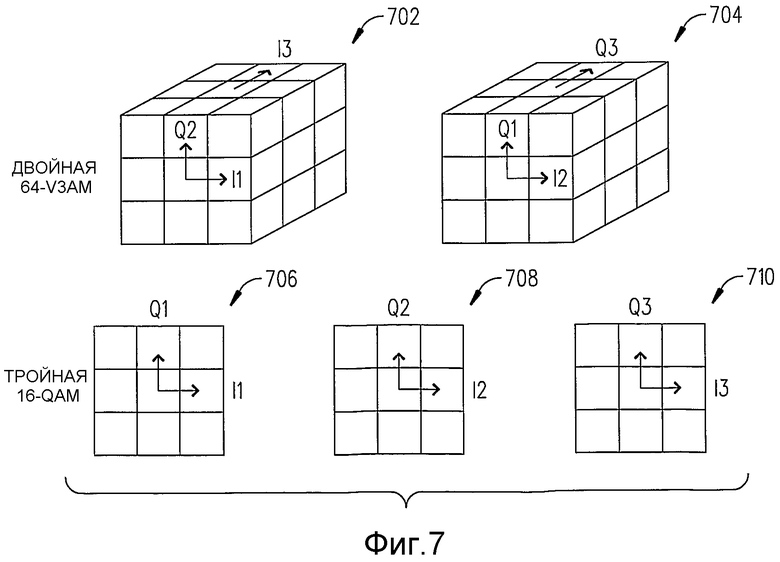
Фиг.7 - схемы, которые иллюстрируют различные пути, которыми можно сгруппировать шесть измерений I1, Q1, I2, Q2, I3 и Q3 для формирования многомерных символов, которые используются для содействия пониманию настоящего изобретения.
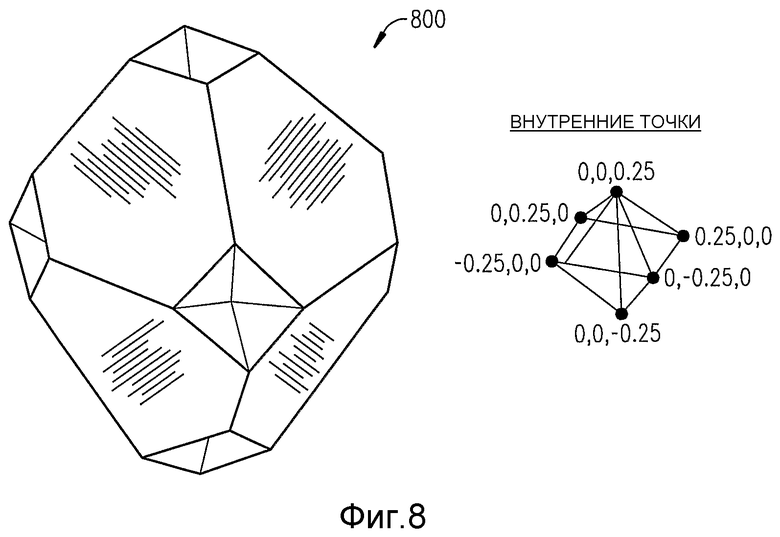
Фиг.8 - схема, на которой изображено ромбовидное созвездие с вогнутыми вершинами, которая используется для содействия пониманию настоящего изобретения.
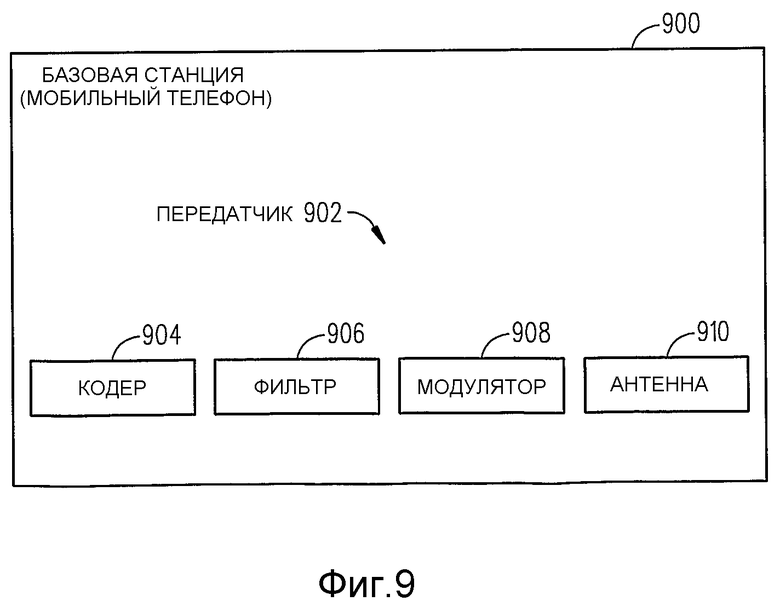
Фиг.9 - блок-схема мобильного телефона с передатчиком, который выполнен согласно одному варианту осуществления настоящего изобретения.
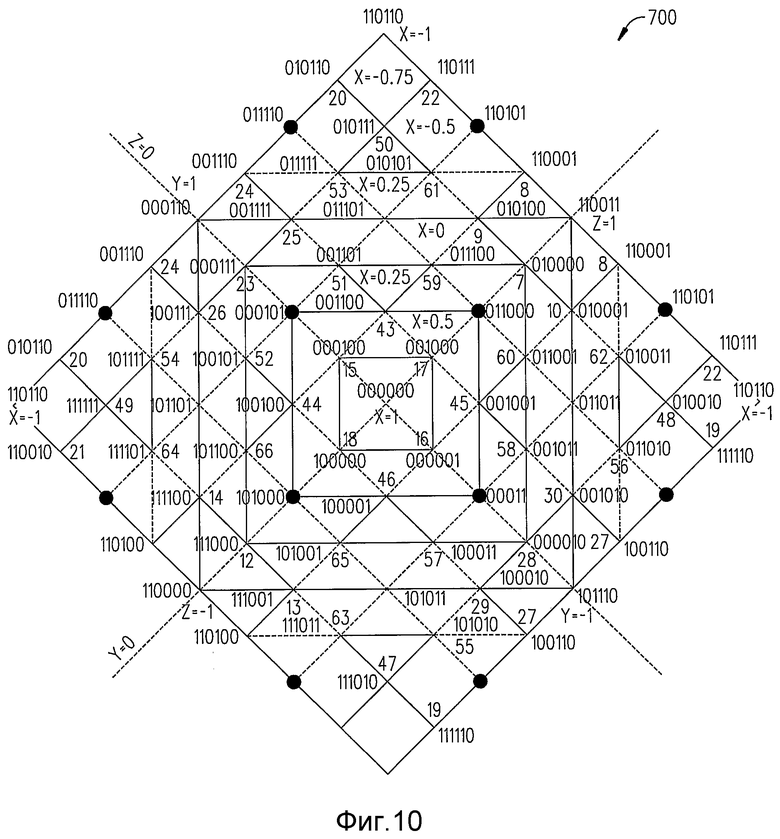
Фиг.10 - схема, на которой изображено назначение кода Грея из 6-битовых групп ромбовидному созвездию, изображенному на фиг.8, которая используется для содействия пониманию настоящего изобретения.
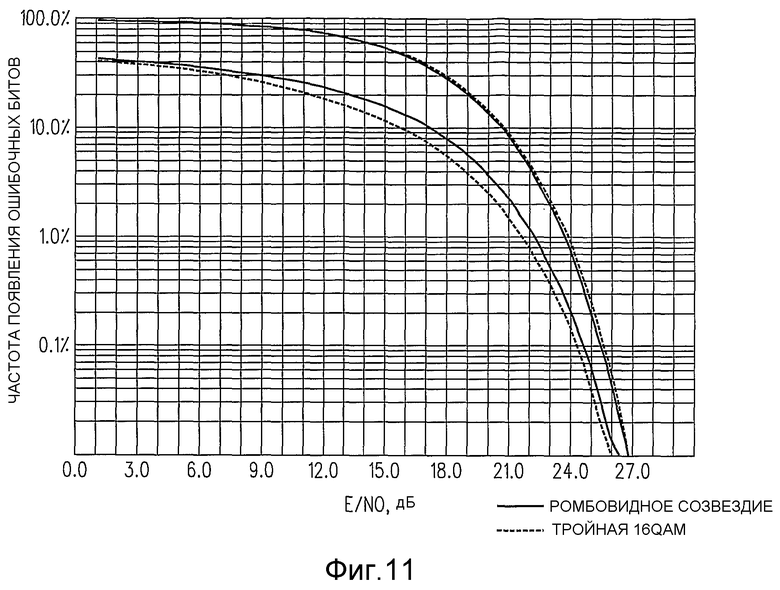
Фиг.11 - график, на котором изображена частота появления ошибок в зависимости от отношения общей передаваемой мощности сигнала к шуму, который используется для содействия пониманию настоящего изобретения.
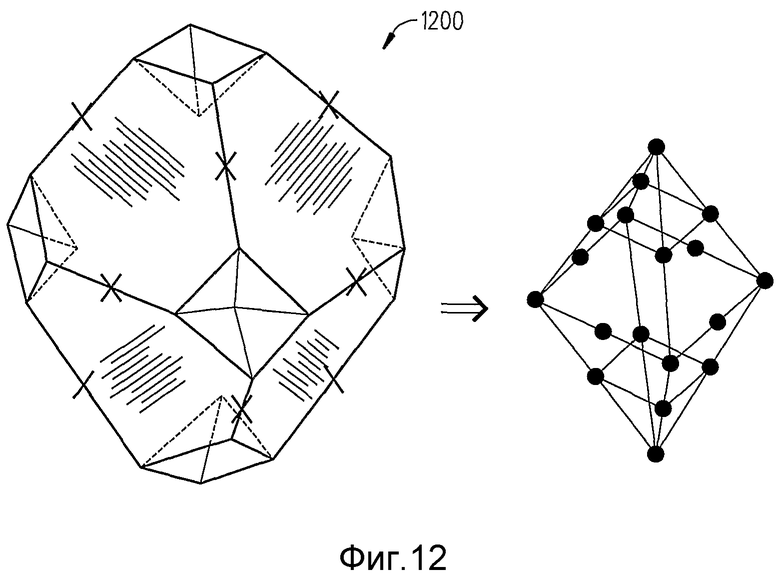
Фиг.12 - схема, на которой изображено ромбовидное созвездие с выемками, которая используется для содействия пониманию настоящего изобретения.
Фиг.13 - блок-схема базовой станции с приемником, которая выполнена согласно одному варианту осуществления настоящего изобретения.
Фиг. 14-16 - схемы, которые используются для содействия пониманию того, как приемник, изображенный на фиг.13, декодирует радиосигнал согласно одному варианту осуществления настоящего изобретения.
Фиг.17 - блок-схема базовой станции с приемником, которая выполнена согласно другому варианту осуществления настоящего изобретения.
Подробное описание
Настоящее изобретение включает в себя передатчик (например, заключенный в пределах мобильного телефона) и способ, который уменьшает отношение пиковой к среднеквадратической амплитуде в радиосигнале при наложении ограничения на пиковую составную амплитуду символа при использовании многомерной модуляции. В частности, передатчик кодирует информацию в поток двоичных битов, и группы битов комбинируются для представления символами данных. Далее, каждый символ данных представляется набором координат в многомерном пространстве, причем количество измерений в этом многомерном пространстве соответствует, по меньшей мере, трем ортогональным компонентам, которые содержат передаваемый радиосигнал. Координаты каждого символа данных выбираются так, что каждый символ данных расположен на минимальном расстоянии от ближайшего другого символа данных в многомерном пространстве, а также так, что отношение пиковой амплитуды к среднеквадратической амплитуде передаваемого радиосигнала является минимальным. После более подробного описания вышеупомянутой традиционной трехкодовой многокодовой схемы с конфигурацией 4+4+4 и вышеупомянутой традиционной трехкодовой многокодовой схемы HSPA с конфигурацией 4+(2,2) обеспечивается подробное описание различных способов, которыми может быть реализовано настоящее изобретение.
Обратимся к фиг.1, на которой представлена блок-схема традиционной трехкодовой многокодовой системы 100 сотовой связи HSPA, в которой мобильный телефон 102 имеет передатчик 108, который передает радиосигнал с тремя символами 16QAM S1, S2 и S3 в каждый период модуляции четырех элементарных сигналов в базовую станцию 104. Как изображено, код с длиной=2 повторяется дважды и используется для переноса двух символов 16QAM S2 и S2 последовательно, в то время как код с длиной=4, ортогональный коду с длиной=2, аддитивно налагается и используется для переноса третьего символа 16QAM S1 в течение такого же периода четырех элементарных сигналов. Созвездие символов 16QAM имеет обычный вид, изображенный на фиг.2. Каждый символ 16QAM S1, S2 и S3 переносит 4 бита, поэтому с тремя символами S1, S2 и S3 переносятся 12 битов в интервале времени четырех элементарных сигналов, представляющем 22=4096 возможностей. Соответственно, декодирование в базовой станции 104 может включать в себя тестирование всех 4096 возможностей (способ решения "в лоб") или может использоваться способ уменьшенной сложности, раскрытый в совместной заявке на патент США № 12/035970, поданной 22 февраля 2008 г. и озаглавленной "Efficient Multicode Detection", содержимое которой заключено в этот документ по ссылке.
Связь с использованием символов 16QAM содержит передачу двух битов на каждой из компонентов I и Q сигнала, причем эти биты равномерно расположены вокруг нуля по каждому из двух измерений комплексной плоскости сигналов. Соответственно, I-компонента может принимать значения +1,5, +0,5, -0,5 и -1,5, в то время как Q-компонента независимо принимает аналогичные значения. На фиг.2 изображены 16 возможных точек сигнала, которые расположены на плоскости I, Q на пересечениях равномерной прямоугольной решетки. Отношение пиковой к среднеквадратической амплитуде одного символа 16QAM может вычисляться посредством определения пиковой амплитуды и среднеквадратического значения. Пиковая амплитуда имеет место, когда и I и Q одновременно принимают свои максимальные значения амплитуды +/-1,5, что дает чистую длину вектора 1,5√2, при этом среднеквадратическое значение вычисляется с усреднением квадрата амплитуды по всем 16 точкам, причем существуют 4 угловые точки, каждая со значением квадрата амплитуды (1,5√2)2=4,5, 8 точек на сторонах, каждая с квадратом амплитуды (1,52+0,52)=2,5, и четыре точки в середине с квадратом амплитуды (0,5√2)2=0,5. Среднее значение этих точек равно (4×4,5+8×2,5+4×0,5)/16=2,5. Соответственно, среднеквадратическое значение равно √2,5 или 1,58. Отношение пиковой к среднеквадратической амплитуде амплитуды равно, соответственно, 1,5√2/√2,5, что в децибелах составляет 2,55 дБ.
Для модуляции по фиг.1, видно, что два значения I и два значения Q накладываются друг на друга в каждом периоде элементарного сигнала. I-значение кода с длиной=4 может быть одним из четырех значений 1,5, 0,5, -1,5, -0,5, но I-значения кода с длиной=2 в √2 раз больше. Q-значения масштабируются аналогично. Соответственно, применение такой же процедуры, как вышеуказанная, для вычисления отношения пиковой к среднеквадратической амплитуде дает решение 5,44 дБ для этого типа многокодовой модуляции, как упоминалось в разделе уровень техники. Если, с другой стороны, используются три кода с длиной=4 традиционной конфигурации 4+4+4, изображенной на фиг.3, то I-значениями для каждого являются любое из значений 1,5, 0,5, -0,5 или 1,5, которые дают пиковое I-значение 4,5 и аналогичное пиковое Q-значение, или пиковую амплитуду комбинированных I и Q 4,5√2. Среднеквадратическое значение, однако, в √3 раз больше среднеквадратического значения одной передачи 16QAM, которое, как было вычислено выше, равно √2,5. Соответственно, отношение пиковой к среднеквадратической амплитуде наложенных трех кодов с длиной=4 равно, соответственно, 4,5√2/(√3×√2,5)=2,32 или 7,32 дБ, как также упоминалось в разделе уровень техники. Следовательно, когда пиковая амплитуда является ограниченной, конфигурация 4+(2,2) по фиг.1 является предпочтительной по сравнению с конфигурацией кода 4+4+4 по фиг.3.
Передатчик 108 мобильного телефона также имеет усилитель 106 мощности, который генерирует среднюю выходную мощность без искажения, которая наряду с другими факторами зависит от отношения пиковой к среднеквадратической амплитуде сигнала. Для усилителя 106 мощности класса B, максимальная эффективность без искажения имеет место, когда он генерирует максимальную мощность, причем максимальная эффективность определяется следующим образом:
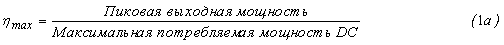
и при нормализации к единичному сопротивлению нагрузки максимальная эффективность может быть задано следующим образом:
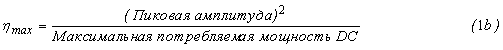
С другой стороны, средняя эффективность с сигналом с переменной амплитудой задано следующим образом:
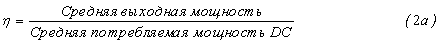
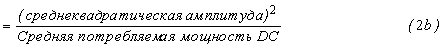
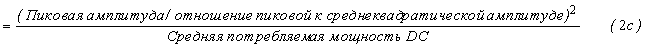
Кроме того, потребляемая мощность усилителя 106 мощности класса B с нулевым смещением в состоянии покоя оказывается пропорциональной амплитуде выходного сигнала. Следовательно, средняя потребляемая мощность DC равна пиковой потребляемой мощности, умноженной на отношение средней амплитуды к пиковой амплитуде, что с нормализацией к единичному сопротивлению нагрузки дает следующее:

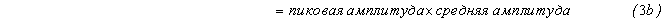
В результате комбинирования уравнений 1b, 2c и 3b получаем следующее:
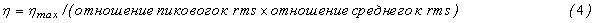
В то время как 
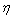
Снова обратимся к тройной модуляции 16QAM HSPA, изображенной на фиг.1, одним способом получения небольшого (0,5 дБ) уменьшения отношения пиковой к среднеквадратической амплитуде без изменения эффективности связи является поворот созвездия 16QAM на коде с длиной=4 на 45 градусов относительно созвездия на коде с длиной=2, как изображено на фиг.4. Эта конкретная схема поворота была раскрыта в вышеупомянутой заявке на патент США № 12/166883, которая озаглавлена "Reduced Peak-to-RMS Ratio Multicode Signal" (номер поверенного в книге записей P25701). В вышеупомянутой заявке на патент США № 12/166883 (номер поверенного в книге записей P25701), также было показано, что улучшения в отношении пиковой к среднеквадратической амплитуде различных схем/способов модуляции, определенные до спектрально ограничивающей фильтрации, как правило, давали такое же улучшение после фильтрации, несмотря на то, что спектральное ограничение увеличивало отношение пиковой к среднеквадратической амплитуде для всех тестируемых модуляций. Принимая это во внимание, настоящее изобретение ориентировано на способ для достижения уменьшения отношений пиковой к среднеквадратической амплитуде, которое определяется до спектрально ограничивающей фильтрации, с ожиданием того, что это преобразуется в аналогичное уменьшение отношений пиковой к среднеквадратической амплитуде при сравнении форм сигнала, при условии спектрально ограничивающей фильтрации. Целью нового способа является устранение уменьшения коэффициента эффективности связи dmin/rms, а также устранение уменьшения коэффициента расширения, чтобы сохранять хорошую устойчивость к искажениям, обусловленным многолучевым распространением, при использовании эквалайзеров передатчика приемлемой сложности. Ниже предоставлено подробное описание того, как этот новый способ может быть реализован, в соответствии с различными вариантами осуществления настоящего изобретения.
Обратимся снова к трехкодовой многокодовой схеме, изображенной на фиг.3, на которой можно увидеть, что три символа 16QAM S1, S2 и S3 можно рассматривать как шесть символов 4-AM, причем каждый символ 4-AM переносит два бита информации посредством своих четырех возможных точек сигнала и занимает одно из шести измерений I1, Q1, I2, Q2, I3 и Q3. Как изображено, пары измерений (I, Q) являются ортогональными в силу не совпадения по фазе на 90 градусов, в то время как использование ортогональных кодов обеспечивает возможность переносить три таких пары значений I, Q с использованием всех шести измерений I1, Q1, I2, Q2, I3 и Q3, которые являются ортогональными друг к другу, когда коды являются взаимно ортогональными. В отсутствие искажения сигнала при передаче шесть измерений I1, Q1, I2, Q2, I3 и Q3 действительно являются независимыми, так как они не создают помехи друг другу, а также шум приемника имеет номинально равное среднеквадратическое значение, которое является номинально некоррелированным между любой парой измерений I1, Q1, I2, Q2, I3 или Q3. Однако эти шесть измерений I1, Q1, I2, Q2, I3 и Q3 не являются независимыми для передатчика 108 мобильного телефона, так как значения I1, I2, I3, а также значения Q1, Q2, Q3 суммируются линейно, а не квадратично. Соответственно, передаваемая амплитуда сигнала равна, как задано ниже (см. код 1, код 2 и код 3 на фиг.3):
сигнал 2
сигнал 3
сигнал 4
Выше показано, что так как все комбинации знаков I1, I2 и I3 тестируются по четырем элементарным сигналам, в некотором элементарном сигнале какие-нибудь их знаки в результате сложения дадут пиковое значение в этом элементарном сигнале. Если не наложены другие ограничения, то наихудшим случаем является случай, когда в одном элементарном сигнале встречаются пик I и пик Q.
Если сигналы I и Q имеют одну и ту же форму, то из этого следует, что отношение пиковой к среднеквадратической амплитуде передачи является таким же, как отношение пиковой к среднеквадратической амплитуде I или Q отдельно, причем комбинирование I и Q просто одинаково увеличивает как пиковое так и среднеквадратическое значение на √2 по сравнению с этим отношением для I или Q отдельно. Следовательно, в результате поиска схемы модуляции с наименьшим отношением пиковой к среднеквадратической амплитуде на I и Q можно получить наименьшее отношение пиковой к среднеквадратической амплитуде для комбинированного сигнала передачи. Соответственно, желательно, чтобы ни одно из I1+I2+I3, I1+I2-I3, I1-I2+I3 и I1-I2-I3 не превышало некоторого желаемого пикового значения, которое может произвольно выбираться, чтобы равняться 1,0. Эти четыре ограничения можно выразить через |I1|+|I2|+|I3|< или =1, причем граница устанавливается в 1.
Эта граница содержит 8 плоскостей, соответствующих каждому из двух возможных знаков + или -, которые могут иметь каждое из трех значений I1, I2 и I3. Например, плоскость +++ для I1, I2, I3, когда все они положительные, задается +I1+I2+I3=1 и изображена на фиг.5. На фиг.5, также представлен переход от представления I1, I2, I3 к обычным трехмерным координатам X, Y, Z.
Если начертить 8 плоскостей, соответствующих всем 8 комбинациям знаков, то в результате получим ромбовидную форму 600, которая изображена на фиг.6. Для представления трех пар битов, переносимых тремя сигналами I1, I2 и I3, принадлежащими первоначальным трем символам 16QAM, необходимо определить местоположение общего количества из 64 возможных точек на ромбовидной форме 600 или в пределах нее. Пример равномерного расположения, в результате которого получается общее количество из 66 точек, изображен на ромбовидной форме 600, где две точки, следовательно, могут быть пропущены. Эти 66 точек включают в себя:
- 6 вершин, у которых одна координата равна +/-1, а остальные две координаты равны нулю (всего 6 точек).
- 12 ребер, у которых одна координата равна нулю, а остальные две являются + или -. Центральные точки ребра имеют ненулевые координаты +/-0,5, в то время как остальные две точки на каждом ребре имеют ненулевые координаты (+/-0,25, +/-0,75) или наоборот, всего получается 36 точек.
- 8 граней, соответствующих плоскостям |X|+|Y|+|Z|=1, причем в центре каждой треугольной грани существует треугольник из трех точек. Координаты этих точек имеют координаты 0,5, 0,25, 0,25 (сумма которых равна единице), переставляемые всеми способами между X, Y и Z и со всеми возможными знаками +/- для общего количества из 24 точек.
Минимальное расстояние dmin этого созвездия равно 0,25√2=0,3535.
Среднеквадратическое значение для этого конкретного созвездия может быть вычислено таким же путем, как тот, который выполнялся выше с созвездием 16QAM (см. фиг.3). Однако для возможности сравнения этой характеристики с характеристикой 16QAM сначала должны быть сгруппированы шесть измерений по фиг.6 для формирования двух трехмерных символов, сравнимых с двумя трехмерными символами 702 и 704, которые изображены на фиг.7.
На фиг.7 предлагается, чтобы шесть измерений I1, Q1, I2, Q2, I3 и Q3 могли быть, по существу, сгруппированы любым желаемым путем, например, как шесть символов 4-AM (фиг.3), как три символа 706, 708 и 710 16QAM, или как вышеупомянутые два трехмерных символа 702 и 704, для чего используется терминология V3AM, что означает амплитудная модуляция вдоль каждой оси трехмерного пространства (V3). В принципе, эти шесть измерений I1, Q1, I2, Q2, I3 и Q3 могут, в качестве альтернативы, быть сгруппированы как один символ V4БM и один символ QAM. Соответственно, когда количество точек вдоль каждой из трех осей равно 4, тогда общее количество точек в трехмерном символе равно 43=64, поэтому может быть использовано обозначение 64-V3AM. Аналогично, четыре точки вдоль каждого измерения V4 дают в результате 256-V4AM, а пять точек вдоль каждого измерения V5 могут дать 1024-V5AM, а шесть точек вдоль каждого измерения V6 могут дать 4096-V6AM.
Нижеследующая Таблица 1 содержит свойства созвездия 64-V3AM (I1, I2, I3) с ромбовидным созвездием 600 по фиг.6, причем две точки были опущены.
Можно увидеть, что ромбовидное созвездие 600 достигает желаемого уменьшения 4,57 дБ в отношении пиковой к среднеквадратической амплитуде и улучшения 2 дБ в эффективности усилителя мощности (PA) за счет небольшого уменьшения 0,44 дБ в минимальном расстоянии. Последнее, однако, можно снизить посредством вдавливания вершин ромба от ненулевой координаты 1,0 до ненулевой координаты +/-0,25 (например) с нижеследующими результатами:
При вдавливании вершин, среднеквадратическое значение уменьшается, что улучшает dmin, однако пиковое значение остается таким же, поэтому отношение пиковой к среднеквадратической амплитуде только незначительно повышается. Это является более желательным результатом, так как средняя потребляемая мощность передатчика для одной и той же частоты появления ошибочных символов будет меньше. Форма трехмерного созвездия 800 с вогнутыми вершинами изображена на фиг.8. Другие модификации ромбовидного созвездия 600, а также другие ромбовидные созвездия, которые находятся в пределах такого же семейства, подробно обсуждаются ниже после обсуждения одного варианта осуществления передатчика мобильного телефона в соответствии с настоящим изобретением.
Согласно фиг.9 изображен мобильный телефон 900 с передатчиком 902, который уменьшает отношение пиковой к среднеквадратической амплитуде в радиосигнале при наложении ограничения на пиковую составную амплитуду символа при использовании многомерной модуляции, в соответствии с одним вариантом осуществления настоящего изобретения (примечание: в этом документе описаны только компоненты-функции передатчика, которые относятся к настоящему изобретению). По существу, передатчик 902 (например, многокодовый передатчик 902) может реализовать уменьшенное отношение пиковой к среднеквадратической амплитуде с ограниченной пиковой составной амплитудой символа с использованием:
(i) Кодера 904, который делит группы битов данных, например, 12 битов, на первую подгруппу (например, 6 битов) и вторую подгруппу (например, 6 битов).
(ii) Кодера 904, который принимает первую подгруппу битов и выбирает одну из определенного количества точек созвездия, которые распределены в пределах первого многомерного пространства (например, трехмерного пространства X, Y, Z), причем местоположение точек созвездия определено так, что сумма их координат меньше желаемого максимального значения. Координаты выбранной точки созвездия далее используются для установки значений действительных частей соответствующих комплексных чисел, соответственно, действительная часть каждого комплексного числа соответствует значению связанной с ним координаты.
(iii) Кодера 904, который принимает вторую подгруппу битов и выбирает еще одну из определенного количества точек созвездия, которые распределены в пределах второго многомерного пространства (например, трехмерного пространства X, Y, Z), причем местоположение точек созвездия определено так, что сумма их координат меньше желаемого максимального значения. Координаты выбранной точки созвездия далее используются для установки значений мнимых частей соответствующих комплексных чисел, соответственно, мнимая часть каждого комплексного числа соответствует значению связанной с ним координаты.
(iv) Кодера 904, который соединяет попарно одну действительную и одну мнимую часть для формирования комплексного числа, и аналогично соединяются попарно остальные действительные и мнимые части для получения набора комплексных чисел. Если у одного многомерного пространства больше измерений, чем у другого, то одна или несколько действительных или мнимых частей могут не соединяться попарно, в результате чего получится одно или несколько некомплексных чисел, которые являются или только действительными, или только мнимыми.
(v) Кодера 904, который назначает числа, полученные выше, которые должны быть умножены на связанный с ними один из определенного количества ортогональных кодов множества элементарных сигналов. Далее произведение каждого числа с его кодом суммируется по элементарным сигналам для получения многокодового символа, содержащего последовательность, в большинстве случаев, комплекснозначных элементарных сигналов.
(vi) Фильтра 906 (например, фильтра 906 Найквиста с извлечением корня), который принимает поток многокодовых символов и фильтрует их для ограничения передаваемого спектра.
(vii) Модулятора 908, который модулирует отфильтрованный сигнал с радиочастотной несущей.
(viii) Антенны 910, которая передает модулированный радиосигнал.
Считается желательным связывать группы битов с точками созвездия на этапах (ii) и (iii) так, чтобы соседние точки созвездия отличались как можно меньшим количеством позиций бита, предпочтительно только одной. Это так называемое кодирование Грея хорошо действует для 4-AM, 16QAM, 64V3-AM и т.д., так как в каждом измерении пары битов распределены в порядке 00, 01, 11, 10 так, что при движении вдоль любого одного измерения последовательно встречающиеся битовые комбинации отличаются только одним битом. Существуют другие ситуации, в которых может быть желательно противоположное, например, при выполнении Решетчатого кодирования по символам, поэтому кодирование Грея не всегда является желательным выбором. Например, если для передачи букв, чисел и других литер языка назначено 66-точечное ромбовидное созвездие 600 или 800, как в коде ASCII, то оптимальное назначение не имеет ничего общего с битовыми комбинациями, а имеет отношение к жесткости самопроизвольной подстановки символов относительно распознаваемости обычного текста. Оптимальное назначение может тогда быть таким, что при ошибке будет тенденция замены одной гласной буквы сходной гласной буквой (например, e, i, y), одной согласной буквы сходной согласной буквой (например, t, d или p, b), одного знака препинания сходным знаком препинания (например, пробел, -, /) и т.д. Другая схема, которая отличается от схемы кодирования Грея, которая может быть выбрана, включает в себя использование 6-битового символа для переноса 6-битового слова речи PCM. В этом случае, битовый код мог бы быть распределен по спирали вниз по созвездию сверху вниз в порядке по численному значению 6-битового слова PCM так, что слова, отстоящие далеко друг от друга по значению, также отстоят далеко друг от друга в созвездии. Однако кодирование Грея желательно, когда целью модуляции является перенос произвольных потоков двоичных битов, например, зашифрованной речи или данных с минимальной частотой появления ошибочных битов.
Совершенное кодирование Грея не всегда возможно, но пример попытки назначения кода Грея из 6-битовых групп ромбовидному созвездию 800 изображен на фиг.10. Фиг.10 следует просматривать вниз по ромбовидному созвездию 800 с одной вершиной (X=1), которой назначен код 000000, в середине, и видна проекция четырех треугольных граней с центральной точкой (код 000000) в качестве общей вершины. Четыре грани с обратной стороны от наблюдателя были разложены и их проекции формируют внешний квадрат, все углы которого являются той же самой точкой, которой назначен код 110110, и которая является диаметрально противоположной вершиной по отношению к вершине 000000 в центре схемы. Из-за развертывания граней с обратной стороны, некоторые ребра (например, линия, содержащая коды 000110, 001110, 011110, 010110, 110110), соответственно, повторяются дважды с зеркальным отображением вдоль сторон внешнего квадрата.
В этом примере, шестибитовые группы рассматриваются как 3+3-битовые группы, и каждая подгруппа из трех битов может увеличиваться в порядке кода Грея вдоль одного набора линий, и причем другая 3-битовая группа увеличивается в порядке кода Грея вдоль набора линий под прямыми углами к первому набору. Посредством этого достигается совершенное кодирование Грея, если ромбовидное созвездие 800 является прямоугольной решеткой 8×8, но из-за зеркального отображения сторон развернутых граней, как описано выше, на ребрах имеют место некоторые негреевские конфликты.
Например, несмотря на то что код 011110 на ребре отличается только одним битом от соседнего кода 011101 в точке 53, он отличается тремя битами от кода 101111 в точке 54. Это происходит потому, что когда грани с обратной стороны свернуты в соответствующие им положения, код 011110 является смежным к обеим точкам 53 и 54, и не может отличаться только одним битом от обоих назначенных им кодов. Однако так как существует небольшая доля от общего количества пар соседних точек, то влияние на среднее расстояние Хемминга является небольшим.
Пробное распределение битов кода Грея, которое выполнено, как описано выше, изображено на фиг.10. Это конкретное распределение битового кода символу использовано для вычисления частоты появления ошибочных битов исходя из частоты появления ошибочных символов при передаче и приеме данных во время шума (см. фиг.11). Как изображено на фиг.11, кривые частоты появления ошибочных символов и частоты появления ошибочных битов для ромбовидного созвездия 800 с выемками по фиг.8 и распределения битового кода по фиг.10 сравниваются с кривой 64-V3AM, которая имела такую же характеристику как тройная 16QAM с использованием любой вышеупомянутой конфигурации 4+4+4 или 4+(2,2) с такой же общей передаваемой мощностью. На фиг.11, частота появления ошибок наносится на график в зависимости от отношения общей передаваемой мощности сигнала к шуму. Этот график иллюстрирует то, что ромбовидное созвездие 800 с выемками дает в результате незначительно меньшую частоту появления ошибочных символов, чем тройная 16QAM, с отражением своего незначительно лучшего отношения dmin к rms, несмотря на то, что имеет незначительно большую частоту появления ошибочных битов из-за того, что среднее количество ошибочных битов для каждого ошибочного символа примерно в 1,5 раза больше для каждого события ошибки ближайшего соседа. Однако эта потеря примерно 0,4 дБ значительно компенсируется возможностью функционирования усилителя мощности передатчика с эффективностью на 0,9 дБ больше, чем тройная 16QAM созвездия 4+(2,2). Ниже в Таблице 3 приведены координаты созвездия и численное значение назначений им псевдогреевского (pseudo-Grey) битового кода.
Если желательно, то в ромбовидном созвездии 600 могут быть образованы выемки по-другому посредством вставки не только вершин, но также 12 центров ребер. Точки вставки формируют внутреннее ромбовидное созвездие порядка 2, как описано ниже, в то время как 48 точек остаются на поверхности большего ромбовидного созвездия 1200 с выемками, которое изображено на фиг.12 (примечание: знаком + отмечены центры кромок, которые были вставлены). Для передачи 6 битов для каждого символа, любые две точки могут быть пропущены, например, две из 48 точек, в интересах минимизации средней передаваемой мощности для такого же dmin. Ниже представлено более подробное описание ромбовидного созвездия после подробного описания того, как приемник декодирует радиосигнал, в соответствии с несколькими разными вариантами осуществления настоящего изобретения.
Согласно фиг.13 изображена базовая станция 1300 с приемником 1302, который декодирует радиосигнал в соответствии с одним вариантом осуществления настоящего изобретения (примечание: в этом документе описаны компоненты-функции приемника, которые относятся к настоящему изобретению). Если желательно, то приемник 1302 может применять декодер 1304 (имеющий процессор 1306, который реализует исполнимые процессором команды из памяти 1308), который является подобным декодеру, описанному в вышеупомянутой заявке на патент № 12/035970 за исключением того, что декодер 1304 выполнен с возможностью декодирования ромбовидного созвездия, как более подробно описано ниже согласно фиг.14-фиг.16.
В одном варианте осуществления, приемник 1302 принимает радиосигнал и снижает влияние многолучевого распространения между ним и передатчиком 902 посредством вычитания воздействия ранее декодированных символов с использованием методики управляющей обратной связи вместе с методикой прямой связи эквалайзера для снижения межсимвольных помех, вызываемых на данный момент недекодируемыми символами в радиосигнале (этапы 1320 и 1322). В результате оставшийся радиосигнал зависит от двух символов ромбовидного созвездия, которые закодированы в действительной и мнимой частях, с шумом и другими потенциальными ухудшениями. Далее, скомпенсированный сигнал декодируется посредством формирования гипотезы сначала об одном из двух символов ромба, поиском его координат X, Y, Z и вычитанием его воздействия из выборок сигналов (этап 1324). Модифицированные выборки сигнала после вычитания гипотетического символа тогда содержат определенное количество комплексных значений, которые линейно зависят от координат X, Y, Z второго символа. Разбиение действительной и мнимой частей на отдельные уравнения дает в результате существенно большее количество уравнений, чем три неизвестные величины X, Y и Z, и эти уравнения, следовательно, могут быть решены в смысле наименьших квадратов для получения значений X, Y и Z, которые лучше всего объясняют все значения модифицированного сигнала (этап 1326). Получающееся в результате решение для координат X, Y и Z квантуется до ближайшего символа в созвездии, что может быть быстро выполнено согласно следующей методике:
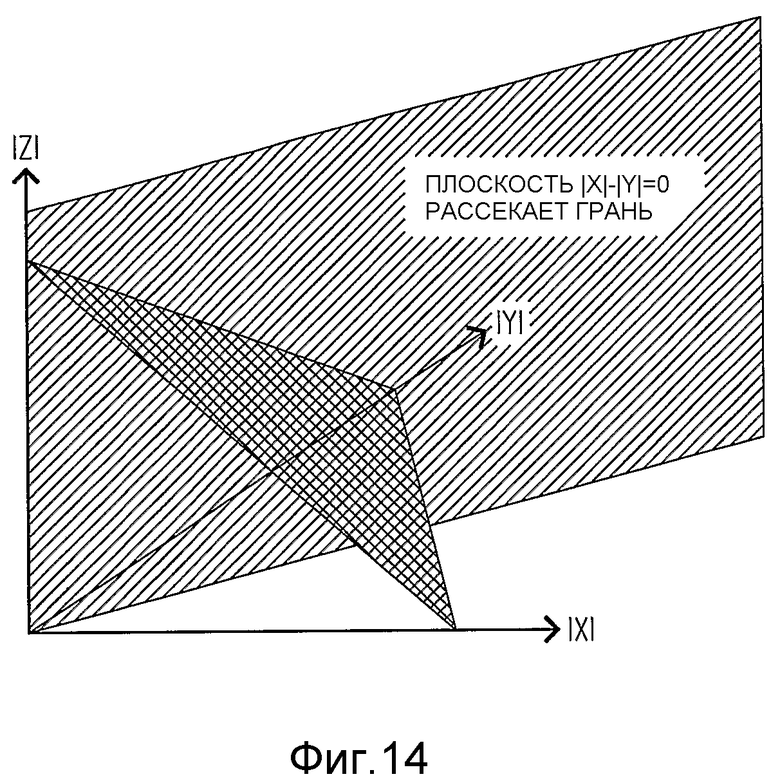
1. Формирование модулей X, Y и Z, которые равны |X|, |Y| и |Z|, и сохранение знаков Sx, Sy, Sz. Знаки определяют то, на какой из 8 граней лежит символ, в то время как |X|, |Y| и |Z| идентифицируют точку на грани так, как если бы она была гранью +++ (этап 1328).
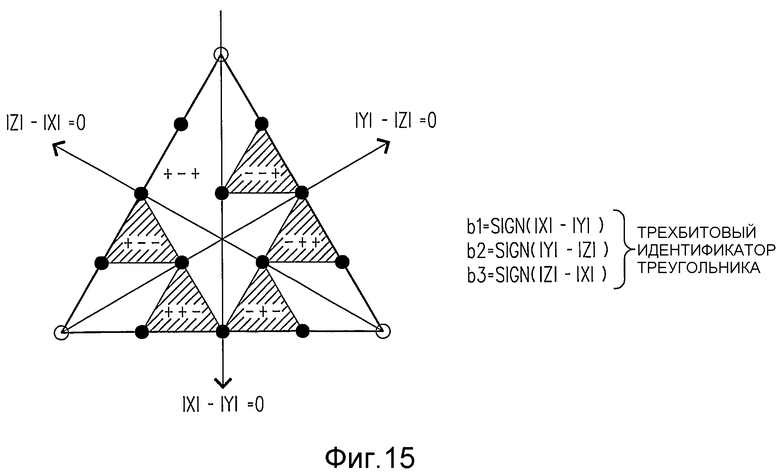
2. На фиг.14 изображено то, что плоскость |X|-|Y|=0 разбивает грань от одной вершины до центра противоположной стороны, наряду с тем, что плоскости |Y|-|Z|=0 и |Z|-|X|=0 аналогично разбивают грань через соответствующие вершины. Соответственно, знаки |X|-|Y|, |Y|-|Z| и |Z|-|X| сужают декодирование до одного из шести треугольников из трех точек на грани, как изображено на фиг.15 (этап 1330).
3. В зависимости от треугольника, определенного на этапе 2, к |X|, |Y|, |Z| применяется сдвиг dX, dY, dZ для центрирования треугольника вокруг середины грани и получения сдвинутых значений X', Y', Z'. Значения сдвига dX, dY, dZ выбираются из небольшой справочной таблицы, к которой обращаются посредством трехбитового идентификатора треугольника, задаваемого тремя знаками, установленными на этапе 2 (этап 1332).
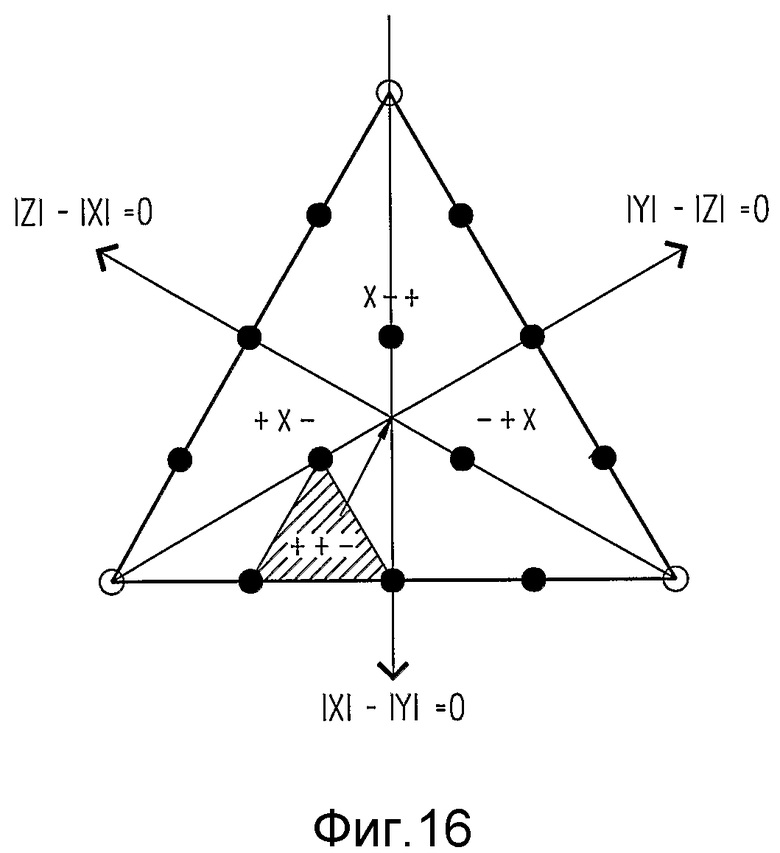
4. Различие между тремя точками центрированного треугольника проводится посредством знаков X'-Y', Y'-Z' и Z'-X', как изображено на фиг.16.
Соответственно, знаки X'-Y', Y'-Z' и Z'-X' идентифицируют точку как одну из трех точек, обозначенных (x-+), (+x-) и (-+x) на фиг.16, где x означает "безразлично" (этап 1334).
Этапы 1-4 не вмещают в себя умножений, а только несколько вычитаний. Квантование значения X, Y, Z до ближайшей из 64 точек созвездия, соответственно, не является существенно более трудным, чем для вышеупомянутого случая тройной 16QAM.
После того как второй символ определен, как описано выше, вместе с гипотетическим символом он формирует кандидата декодирования. Соответственно, каждая гипотеза о первом символе дает в результате кандидата декодирования, и выбор между кандидатами декодирования осуществляется посредством сравнения метрик. Метрики получаются с использованием обоих символов кандидата для вычисления ожидаемых значений сигнала, и вычисления метрики как (суммы квадрата ошибки) между ожидаемым и фактическим значениями сигнала. Когда шум на разных значениях сигнала коррелирован, в вышеупомянутом решении в смысле наименьших квадратов и при вычислении метрики это принимается во внимание, например, посредством взвешиванием уравнений с квадратным корнем обратной матрицы корреляции (см. также вышеупомянутую заявку на патент № 12/035970).
Количество выборок сигналов, используемых для декодирования сигнала передачи, зависит от профиля задержки многолучевого канала и от результатов введения предыскажений. Обычно количество используемых выборок сигналов должно, по меньшей мере, быть равным длине кода. В качестве альтернативы, должно быть понятно, что существует даже большее количество выборок сигналов и, соответственно большее количество уравнений, которые могут решаться, когда радиосигнал понимается более, чем одной разнесенной антенной в приемнике. Это может быть желательно, так как чем больше сверхразмерности решаемых уравнений, тем, вероятно, большая помехоустойчивость получится в результате.
Самой простой методикой декодирования является, посредством корреляции четырех выборок сигналов с каждым из трех кодов с длиной=4, получить три комплексных корреляции. Это в результате приводит к шести действительным уравнениям, которые представляют сверхразмерность 2:1, когда речь идет о решении для координат X, Y, Z символа ромба. Однако, когда существует многолучевое распространение, использование корреляций только с тремя кодами может в результате привести к потере информации, так как сдвиг во времени сигнала из-за задержанного луча при многолучевом распространении в результате приводит к присутствию энергии в 4-ом коде. Однако корреляция со всеми 4 кодами приносит мало пользы по сравнению с просто обработкой всех четырех выборок сигналов и решением восьми действительных уравнений для X, Y и Z. Фактически, многолучевое распространение, вероятно, в результате приведет к присутствию информации в более, чем четырех элементарных сигналах, поэтому количество обрабатываемых выборок сигналов может быть больше четырех. Кроме того, когда шум не является белым, или иначе коррелируется от одной выборки сигнала к следующей, то может быть полезным обрабатывать выборки сигнала, которые не зависят от искомых значений X, Y, Z. Все это объясняется следующим образом.
Принятые выборки сигналов
R1=I1+jQ1
R2=I2+jQ2
R3=I3+jQ3
R4=I4+jQ4
(по меньшей мере, и, вероятно, дополнительные выборки) линейно связаны с координатами X, Y, Z символа 1 ромба и символа 2 ромба такими уравнениями, как (ниже обобщенно называемыми уравнением 5):
A11.X1+ A12.Y1+A13.Z1+A14.X2+A15.Y2+A16.Z2=I1
A21.X1+A22.Y1+A23.Z1+A24.X2+A25.Y2+A26.Z2=Q1
A31.X1+A32.Y1+A33.Z1+A34.X2+A15.Y2+A16.Z2=I2
A41.X1+A42.Y1+A43.Z1+A44.X2+A45.Y2+A46.Z2=Q2
A51.X1+A52.Y1+A53.Z1+A54.X2+A55.Y2+A56.Z2=I3
A61.X1+A62.Y1+A63.Z1+A64.X2+A65.Y2+A66.Z2=Q3
A71.X1+A72.Y1+A73.Z1+A74.X2+A75.Y2+A76.Z2=I4
A81.X1+A82.Y1+A83.Z1+A84.X2+A85.Y2+A86.Z2=Q4
Дополнительно могут существовать уравнения, которые аналогичны этим уравнениям, если большее количество элементарных сигналов зависит от любого значения X, Y или Z. Также могут существовать дополнительные наборы этих уравнений для каждой разнесенной антенны, которая используется для приема. В матричном представлении, вышеуказанные уравнения могут быть сокращены до нижеследующего вида (уравнение 6):
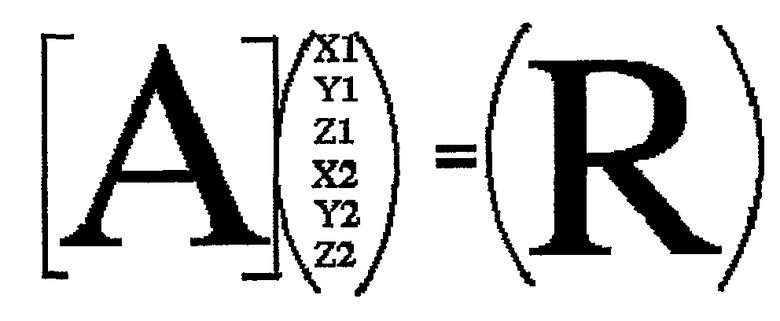
И наконец, для получения очень эффективной обработки, желательно найти пару символов (X1,Y1,Z1), (X2,Y2,Z2), которые удовлетворяют этим уравнениям с минимальной среднеквадратической ошибкой, с ограничением на то, что координаты символа должны быть равны координатам одной из допустимых точек ромбовидного созвездия. Это может называться результатом Максимального правдоподобия. Результат Максимального правдоподобия можно найти с использованием способа решения "в лоб" перебором всех 64×64 комбинаций, однако можно использовать методику пониженной сложности, которая включает в себя формирование гипотезы об одном символе, решение для неограниченных значений другого символа и затем квантование их до ближайшего символа (см. также вышеупомянутую заявку на патент США № 12/035970). Соответственно, будут выявлены только 64 пары символов кандидатов для тестирования и нахождения кандидата, который лучше всего соответствует вышеупомянутым уравнениям в смысле наименьших квадратов. Однако решение методом наименьших квадратов является Максимальным правдоподобием только тогда, когда шум на каждом из принятых значений I1, Q1, I2, Q2, I3, Q3, I4, Q4... является некоррелированным и имеет такую же дисперсию. Если это не так, то может потребоваться решение методом взвешенных наименьших квадратов, при котором взвешивается квадрат ошибки из каждого уравнения по-разному или линейно комбинируется ошибка из двух уравнений до возведения в квадрат. Например, корректное взвешивание может быть достигнуто при умножении обеих сторон ранее упомянутого матричного уравнения на корень квадратный из обратной корреляционной матрицы шума.
Корреляционная матрица шума содержит элементы ij, которые являются ожидаемыми или средними значениями шум(i) × шум(j), и она является квадратной матрицей размера 8×8, если существует восемь уравнений. Квадратный корень корреляционной матрицы шума можно найти с представлением ее в виде: [E][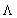

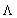
Теперь рассмотрим использование дополнительных выборок сигналов, которые не зависят от какой-либо координаты X, Y или Z, которая должна быть найдена, но которые искажены шумом, коррелированным с шумом на других принятых выборках. Это может быть представлено нижеследующими уравнениями, например (ниже обобщенно называемыми уравнением 7):
A11.X1+A12.Y1+A13.Z1+A14.X2+A15.Y2+A16.Z2=I1
A21.X1+A22.Y1+A23.Z1+A24.X2+A25.Y2+A26.Z2=Q1
A31.X1+A32.Y1+A33.Z1+A34.X2+A15.Y2+A16.Z2=I2
A41.X1+A42.Y1+A43.Z1+A44.X2+A45.Y2+A46.Z2=Q2
A51.X1+A52.Y1+A53.Z1+A54.X2+A55.Y2+A56.Z2=I3
A61.X1+A62.Y1+A63.Z1+A64.X2+A65.Y2+A66.Z2=Q3
A71.X1+A72.Y1+A73.Z1+A74.X2+A75.Y2+A76.Z2=I4
A81.X1+A82.Y1+A83.Z1+A84.X2+A85.Y2+A86.Z2=Q4
0.X1+0.Y1+0.Z1+0.X2+0.Y2+0.Z2=In
Видно, что результат в уравнении 7 присоединяет одну или более нулевых строк к A-матрице с расширением ее от 8×6 до 9×6, например. Теперь корреляционная матрица шума также расширяется до 9×9, и дополнительные элементы являются ненулевыми. Когда расширенную A-матрицу умножают на обратный квадратный корень корреляционной матрицы шума, тогда нулевая строка становится ненулевой строкой, в результате чего увеличивается количество уравнений, которые теперь должны быть решены в смысле наименьших квадратов. Одним желаемым решением является использование всех выборок сигналов, которые каким-либо образом зависят от координат X, Y, Z двух символов, которые должны быть декодированы, плюс всех выборок сигналов, которые не зависят от координат X, Y, Z любой другой неизвестной величины, которая должна быть найдена, но которые могут нести в себе шум или ухудшение, коррелированное с шумом или ухудшением на выборках, которые зависят от символов, которые должны быть найдены. С использованием этого полного набора уравнений фактически используется вся доступная информация в принятом сигнале.
Должно быть понятно, что матричные операции, описанные выше, не должны выполняться для каждой из 64 гипотез о символе, а вместо этого могут быть выполнены только один раз для получения (уравнение 8):
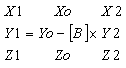
где (X2,Y2,Z2) - гипотетический символ, который должен вычитаться, (Xo, Yo, Zo) предварительно вычисляется исходя из первых трех столбцов расширенной A-матрицы, обозначаемых Adim, и принятый вектор R сигнала обозначается (уравнение 9):
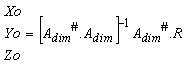
и матрица B 3х3 задается (уравнение 10):
[B]=[Adim #.Adim]-1Adim #.A' dim
где A' dim - последние три столбца расширенной A-матрицы.
Соответственно, только уравнение 8 вычисляется для каждой гипотезы о символе (X2, Y2, Z2). Кроме того, матричные операции, необязательно, должны вычисляться в каждом периоде кода, если элементы A-матрицы и корреляционная матрица шума изменяются медленнее, чем один раз за символ. В случае, когда матрица A одна и та же для многих символов, то это одинаково справедливо для B-матрицы, и, соответственно, умножение B на 64 гипотезы о символе может выполняться один раз, а сохраненные результаты могут использоваться для нескольких периодов кода.
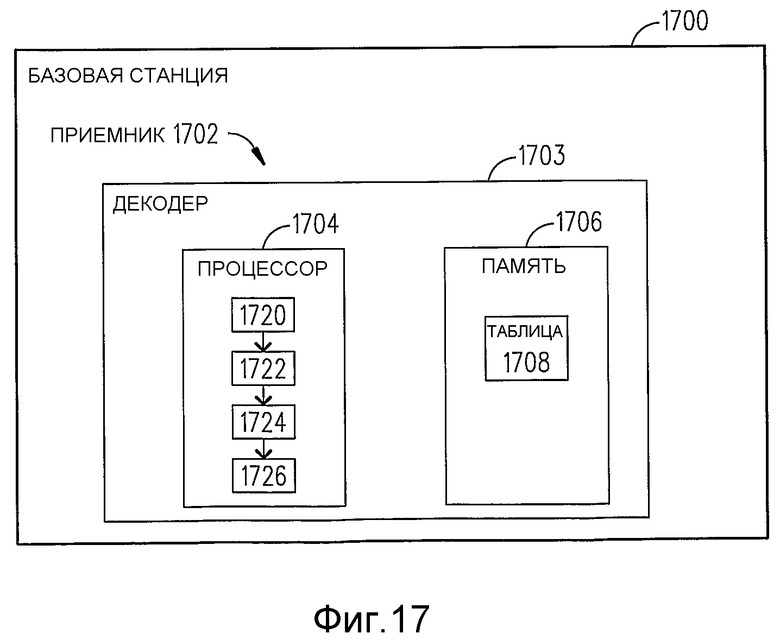
Обратимся к фиг.17, на которой изображена базовая станция 1700 с приемником 1702, который декодирует радиосигнал в соответствии с еще одним вариантом осуществления настоящего изобретение (примечание: в этом документе описаны компоненты-функции приемника, которые относятся к настоящему изобретению). В этом варианте осуществления, предположим, что передатчик 902 мобильного телефона генерирует радиосигнал с использованием методики, в которой большинство точек созвездия находятся на поверхности ромбовидного созвездия, которое задано в трехмерном пространстве с осями координат X, Y и Z, разделенной граничным уравнением |x|+|y|+|z|=1. Приемник 1702 содержит декодер 1703 с процессором 1704, который реализует исполнимые процессором команды из памяти 1706 для декодирования принятого радиосигнала посредством: (a) определения грани ромбовидного созвездия, на которой или в пределах которой лежит передаваемый символ данных (см. этап 1720), (b) определения поднабора точек на грани, в пределах которой лежит символ (этап 1722), (c) определение точки в пределах поднабора, которая лежит ближе всего к принятым значениям координат переданного символа (этап 1724), и (d) определение переданного символа из комбинации грани, упомянутого поднабора и ближайшей точки (этап 1726). В одном случае, переданный символ может быть определен с использованием справочной таблицы 1708, к которой обращаются с использованием номера грани, номера поднабора и номера ближайшей точки.
Для сравнения этого приемника 1702 с вышеупомянутым приемником 1302, ранее обсуждаемый приемник 1302 обычно используется, когда передатчик 902 мобильного телефона генерирует радиосигнал с использованием любой одной из следующих методик кодирования:
(1) Передаваемый радиосигнал содержит символы данных, которые связаны с парой точек созвездия, причем первая точка созвездия выбирается из первого набора точек созвездия, большинство из которых лежит на поверхности первого ромбовидного созвездия, которое задано в трехмерном пространстве с осями координат I1, I2 и I3 граничным уравнением |I1|+|I2|+|I3|=1, а вторая точка созвездия выбирается из второго набора точек созвездия, большинство из которых лежит на поверхности второго ромбовидного созвездия, которое задано в трехмерном пространстве с осями координат Q1, Q2 и Q3 уравнениями |Q1|+|Q2|+|Q3|=1.
(2) Передаваемый радиосигнал содержит символы данных, которые связаны с парой точек созвездия, причем первая точка созвездия выбирается из первого набора точек созвездия, большинство из которых лежит на поверхности первого ромбовидного созвездия, заданного в трехмерном пространстве с осями координат I1, I2 и I3 граничным уравнением |I1|+|I2|+|I3|=A, а вторая точка созвездия выбирается из второго набора точек созвездия, большинство из которых лежит на поверхности второго ромбовидного созвездия, заданного в трехмерном пространстве с осями координат Q1, Q2 и Q3 уравнениями |Q1|+|Q2|+|Q3|=B, причем сумма квадратов A и B меньше или равна желаемому максимальному значению.
Далее, приемник 1302 может декодировать принятый радиосигнал с использованием процессора 1306, который реализует исполнимые процессором команды из памяти 1308 для выполнения следующих этапов: (a) формирование гипотезы о первой из точек созвездия и определение второй точки созвездия с учетом гипотетической точки созвездия, (b) определение метрики, описывающей то, насколько точно гипотетическая точка созвездия и связанная с ней определенная вторая точка созвездия предсказывают принятый сигнал, и (c) сравнение метрики для всех возможных гипотез о первой точке созвездия и выбор гипотезы с наилучшей метрикой в качестве правильной гипотезы, тем самым декодируя радиосигнал. Более подробное описание этой конкретной методики декодирования предоставлено выше согласно фиг.13-фиг.16.
Далее описываются дополнительные варианты ромбовидного созвездия, которые можно рассматривать или для уменьшения частоты появления ошибочных битов, или для дальнейшего уменьшения отношения пиковой к среднеквадратической амплитуде, или для увеличения количества передаваемых битов. Ромбовидную комбинацию можно создать посредством укладки в стопку последовательных квадратных слоев из сфер сверху друг на друга, причем радиус сферы равен половине желаемого минимального расстояния. Количество сфер в каждом слое увеличивается как квадрат целого числа, то есть 1, 4, 9, 16, 25..... Соответственно, начиная с прямоугольного массива 5×5=25 сфер, слой из 4×4=16 укладывается в стопку выше и ниже его, за ним следует слой из 3×3=9 сфер, далее 2×2 и, наконец, 1. Общее количество сфер в этой ромбовидной комбинации равно, соответственно, 1+4+9+16+25+16+9+4+1=66, как изображено на фиг.6. Однако ромбовидное созвездие других размеров можно создать, как указано в нижеследующей таблице, с предположением о радиусе сферы 0,25/√2.
Видно, что созвездие порядка N содержит внутри себя созвездие порядка N-2, и они являются отличными точками с отличными координатами от созвездия порядка N-1.
Первое ромбовидное созвездие 600, которое описано выше, имеет комбинацию точек 85/66 порядка 4, причем используются только 66 точек поверхности с исключением любых двух. Далее обсуждалось то, когда предпочтительно исключать шесть точек поверхности, например, шесть вершин, и заменять их шестью точками созвездия порядка 1, которые содержатся внутри внешних точек и не нарушают требований к минимальному расстоянию. Соответственно, в результате получено ромбовидное созвездие 800 с вогнутыми вершинами, как изображено на фиг.8. На фиг.12 изображено еще одно ромбовидное созвездие 1200 с выемками, в котором вершины и точки центров ребер вставлены, в результате чего получается созвездие порядка 2, которое включает в себя 18 внутренних точек.
Для определения отношений характеристики dmin к rms и пиковой к среднеквадратической амплитуде могут рассматриваться и тестироваться многие другие модификации ромбовидного созвездия. Однако некоторые полезные комбинации могут быть найдены с пониманием того, что более общим показателем пиковой амплитуды передатчика, который должен быть ограничен, является квадрат амплитуды (I1+I2+I3)2+(Q1+Q2+Q3)2. Соответственно, при использовании ромбовидного созвездия с порядком=4 для обоих символов, в котором как сумма I-значений, так и сумма Q-значений являются ограниченными и меньше или равны единице, то квадрат амплитуды является ограниченным и меньше или равен 2. Если, с другой стороны, один из символов выбирается из ромбовидного созвездия с порядком=3, а один - из ромбовидного созвездия с порядком=5, то квадрат амплитуды меньше или равен 1,252+0,752=2,125, что является пиковым значением, которое только на 0,25 дБ больше, чем два ромбовидных созвездия с порядком=4. Количество доступных отдельных точек тогда равно 44×146+102×44=10192, что на 2720 больше, чем 8192, требуемое для кодирования 13 битов. В связи с этим для первого набора 13-битовых комбинаций, первая точка выбирается из ромбовидного созвездия с порядком=3 вместе со второй точкой из ромбовидного созвездия с порядком=5, и наоборот для остальных 13-битовых комбинаций, при этом устраняется вычисление дважды в случае, когда обе точки выбираются из внутренних 44 ромбовидного созвездия с порядком=5. Фактически, существует достаточно точек для кодирования 13 битов, если одна точка выбирается из ромбовидного созвездия с порядком=3 (внутренние 44 ромбовидного созвездия с порядком=5), а другая точка выбирается из 102 точек поверхности ромбовидного созвездия с порядком=5.
В еще одном варианте, 12 битов могут быть закодированы посредством выбора одной точки из 32 ромбовидного созвездия с порядком=3, а другая точка - из 64 ромбовидного созвездия с порядком=4, или наоборот, соответственно с получением 32×64+64×32 отдельных комбинаций. Для этого случая, пиковый квадрат амплитуды равен 1+0,752=1,5625, что на 1,07 дБ меньше, чем выбор обоих точек из ромбовидного созвездия с порядком=4. Можно создать и смоделировать много различных вариантов, после распределения кодирования Грея как можно лучше с учетом созвездия или распределения символов данным некоторым другим способом, в зависимости от приложения (например, PCM, речь, текст ASCII и т.д.). Все такие варианты могут быть разработаны для ограничения отношения пиковой к среднеквадратической амплитуде при сохранении эффективности связи в соответствии с настоящим изобретением.
Из вышеизложенного должно быть понятно, что настоящее изобретение относится к передатчику и способу генерирования радиосигнала с уменьшенным отношением пиковой амплитуды к среднеквадратической амплитуде, что способствует улучшению эффективности передачи усилителя мощности передатчика. В одном варианте осуществления, способ передачи символов данных, в результате которого получается передаваемый сигнал с уменьшенным отношением пиковой амплитуды к среднеквадратической амплитуде, включает в себя этапы: (a) одновременное использование множества аддитивно комбинированных кодов расширения спектра, причем каждый переносит синфазное или действительное значение сигнала и квадратурное фазовое или мнимое значение сигнала, для предоставления, по меньшей мере, трех независимых модуляционных измерений, причем каждое измерение переносит значение координаты, и (b) задание набора точек созвездия, которые должны быть связаны с символами данных, причем эти точки созвездия распределены в пределах пространства, содержащего, по меньшей мере, три измерения, так что евклидово расстояние между любыми двумя точками созвездия не меньше желаемого минимума, и так что желаемое значение пиковой амплитуды не превышается любой точкой, причем это пиковое значение определяется посредством любого из следующих показателей: (i) сумма абсолютных значений координат любой точки созвездия, соответствующих измерениям, предоставляемым действительными значениями сигнала, переносимыми множеством аддитивно комбинированных кодов расширения спектра, (ii) сумма абсолютных значений координат любой точки созвездия, соответствующих измерениям, предоставляемым мнимыми значениями сигнала, переносимыми множеством аддитивно комбинированных кодов расширения спектра, и (iii) сумма квадратов (a) суммы абсолютных значений координат любой точки созвездия, соответствующих измерениям, предоставляемым действительными значениями сигнала, переносимыми множеством аддитивно комбинированных кодов расширения спектра, и (b) суммы абсолютных значений координат созвездия любой точки, соответствующих измерениям, предоставляемым мнимыми значениями сигнала, переносимыми множеством аддитивно комбинированных кодов расширения спектра. Как описано в этом документе, передатчик передает сигнал, который содержит линейную сумму, по меньшей мере, трех ортогональных компонент. В одной реализации три ортогональные компоненты содержат три ортогональные битовые комбинации, в еще одной реализации, три ортогональные компоненты содержат первый и второй взаимно ортогональные коды, причем второй код передается как на синфазной несущей, так и на квадратурной фазовой несущей.
Несмотря на то что несколько вариантов осуществления настоящего изобретения изображены в прилагаемых чертежах и описаны в вышеизложенном подробном описании, должно быть понятно, что изобретение не ограничено раскрытыми вариантами осуществления, а, наоборот, также возможны многочисленные изменения структуры, модификации и замены, не отступая от сути изобретения, изложенной и заданной посредством нижеследующей формулы изобретения.

Заявленное изобретение относится к области беспроводной связи. Технический результат - генерирование радиосигнала с уменьшенным отношением пиковой амплитуды к среднеквадратической амплитуде, что способствует улучшению эффективности передачи усилителя мощности передатчика. Для этого, в частности, передатчик кодирует информацию в поток двоичных битов, и группы битов комбинируются для представления символами данных. Далее, каждый символ данных представляется набором координат в многомерном пространстве, причем количество измерений в этом многомерном пространстве соответствует, по меньшей мере, трем ортогональным компонентам, которые содержат передаваемый радиосигнал. Координаты каждого символа данных выбираются так, что каждый символ данных расположен на минимальном расстоянии от ближайшего другого символа данных в многомерном пространстве, а также так, что отношение пиковой амплитуды к среднеквадратической амплитуде передаваемого радиосигнала является минимальным. 5 н. и 16 з.п. ф-лы, 17 ил., 5 табл.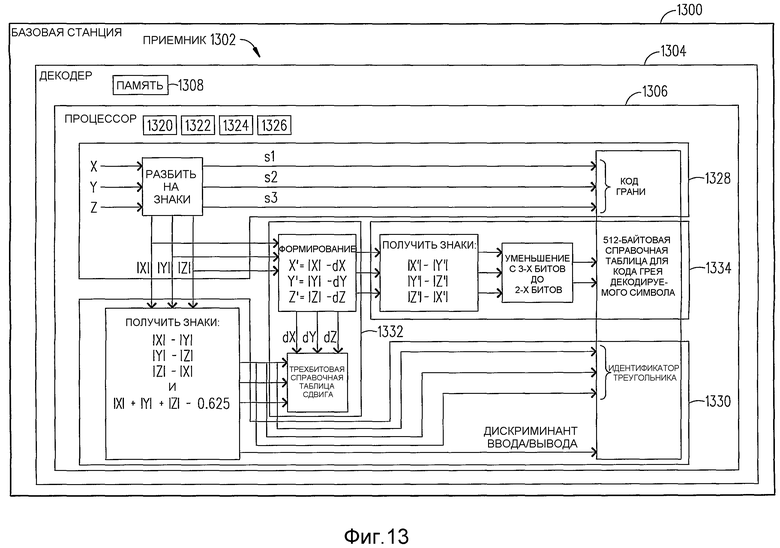
1. Способ передачи символов данных, в результате которого получается передаваемый радиосигнал с уменьшенным отношением пиковой амплитуды к среднеквадратической амплитуде, причем упомянутый способ содержит этапы, на которых:
одновременно используют множество аддитивно комбинированных кодов расширения спектра, каждый из которых переносит синфазное или действительное значение сигнала и квадратурное фазовое или мнимое значение сигнала, для предоставления, по меньшей мере, трех независимых модуляционных измерений, причем каждое измерение переносит значение координаты,
задают набор точек созвездия, которые должны быть связаны с символами данных, точки созвездия распределены в пределах пространства, содержащего, по меньшей мере, три измерения, так что Евклидово расстояние между любыми двумя точками созвездия не меньше желаемого минимума, и так что желаемое значение пиковой амплитуды не превышается любой точкой, пиковое значение определяют посредством любого из следующих показателей:
сумма абсолютных значений координат любой точки созвездия, соответствующих измерениям, предоставляемым действительными значениями сигнала, переносимыми множеством аддитивно комбинированных кодов расширения спектра,
сумма абсолютных значений координат любой точки созвездия, соответствующих измерениям, предоставляемым мнимыми значениями сигнала, переносимыми множеством аддитивно комбинированных кодов расширения спектра, и
сумма квадратов (а) суммы абсолютных значений координат любой точки созвездия, соответствующих измерениям, предоставляемым действительными значениями сигнала, переносимыми множеством аддитивно комбинированных кодов расширения спектра, и (b) суммы абсолютных значений координат созвездия любой точки, соответствующих измерениям, предоставляемым мнимыми значениями сигнала, переносимыми множеством аддитивно комбинированных кодов расширения спектра.
2. Способ по п.1, в котором большинство точек созвездия находятся на внешней поверхности ромбовидного созвездия, заданного в трехмерном пространстве с осями X, Y и Z координат, внешняя поверхность ромбовидного созвездия задана граничным уравнением |x|+|y|+|z|=1.
3. Способ по п.2, дополнительно содержащий этапы, на которых принимают и декодируют упомянутый радиосигнал, включающие в себя этапы, на которых:
определяют грань ромбовидного созвездия, на которой или в пределах которой лежит передаваемый символ данных,
определяют поднабор точек на грани, в пределах которой лежит передаваемый символ данных,
определяют точку в пределах поднабора точек, которая находится ближе всех к принятым значениям координат передаваемого символа данных, и
определяют передаваемый символ данных из комбинации грани, поднабора точек и ближайшей точки.
4. Способ по п.3, в котором упомянутый этап определения передаваемого символа данных дополнительно включает в себя этап, на котором используют справочную таблицу, к которой обращаются по номеру грани, номеру поднабора точек и номеру ближайшей точки.
5. Способ по п.1, в котором упомянутые символы данных связаны с парой точек созвездия, первую точку созвездия выбирают из первого набора точек созвездия, большинство из которых лежит на поверхности первого ромбовидного созвездия, задаваемого в трехмерном пространстве с осями координат I1, I2 и I3 граничным уравнением |I1|+|I2|+|I3|=1, a вторую точку созвездия выбирают из второго набора точек созвездия, большинство из которых лежит на поверхности второго ромбовидного созвездия, задаваемого во втором трехмерном пространстве с осями координат Q1, Q2 и Q3 граничным уравнением |Q1|+|Q2|+|Q3|=1.
6. Способ по п.5, дополнительно содержащий этапы, на которых принимают и декодируют упомянутый радиосигнал, включающий в себя этапы, на которых:
формируют гипотезу о первой из упомянутых точек созвездия и определяют вторую точку созвездия с учетом гипотетической точки созвездия,
определяют метрику, описывающую то, насколько точно гипотетическая точка созвездия и связанная с ней определенная вторая точка созвездия предсказывают принятый радиосигнал,
сравнивают метрику для всех возможных гипотез о первой точке созвездия и выбирают гипотезу с наилучшей метрикой в качестве правильной гипотезы, тем самым декодируя упомянутый радиосигнал.
7. Способ по п.1, в котором упомянутые символы данных связаны с парой точек созвездия, первую точку созвездия выбирают из первого набора точек созвездия, большинство из которых лежит на поверхности первого ромбовидного созвездия, задаваемого в трехмерном пространстве с осями координат I1, I2 и I3 граничным уравнением |I1+|I2|+|I3|=A, a вторую точку созвездия выбирают из второго набора точек созвездия, большинство из которых лежит на поверхности второго ромбовидного созвездия, задаваемого во втором трехмерном пространстве с осями координат Q1, Q2 и Q3 граничным уравнением |Q1+|Q2|+|Q3|=B, причем сумма квадратов А и В меньше или равна желаемому максимальному значению.
8. Способ по п.7, дополнительно содержащий этапы, на которых принимают и декодируют упомянутый радиосигнал, включающие в себя этапы, на которых:
формируют гипотезу о первой из упомянутых точек созвездия и определяют вторую точку созвездия с учетом гипотетической точки созвездия,
определяют метрику, описывающую то, насколько точно гипотетическая точка созвездия и связанная с ней определенная вторая точка созвездия предсказывают принятый радиосигнал,
сравнивают метрику для всех возможных гипотез о первой точке созвездия и выбирают гипотезу с наилучшей метрикой в качестве правильной гипотезы, тем самым декодируя упомянутый радиосигнал.
9. Способ уменьшения отношения пиковой к среднеквадратической амплитуде в передаваемом радиосигнале при наложении ограничения на пиковую составную амплитуду символа при использовании многомерной модуляции, упомянутый способ содержит этапы, на которых:
кодируют информацию в поток двоичных битов,
формируют множество групп битов из потока двоичных битов, причем множество групп битов представляет множество символов данных,
представляют каждый символ данных набором координат в многомерном пространстве, причем количество измерений в многомерном пространстве соответствует количеству, равному, по меньшей мере, трем ортогональным компонентам, которые в итоге содержат передаваемый радиосигнал,
выбирают координаты для каждого символа данных, так что каждый символ данных расположен на минимальном расстоянии от ближайшего другого символа данных в многомерном пространстве, а также так, что отношение пиковой составной амплитуды символа к среднеквадратической амплитуде передаваемого радиосигнала является минимальным.
10. Способ по п.9, в котором многомерное пространство задано ромбовидным созвездием.
11. Способ по п.9, в котором многомерное пространство задано ромбовидным созвездием с вогнутыми вершинами.
12. Способ по п.9, в котором многомерное пространство задано ромбовидным созвездием с выемками.
13. Передатчик, который уменьшает отношение пиковой к среднеквадратической амплитуде в радиосигнале при наложении ограничения на пиковую составную амплитуду символа при использовании многомерной модуляции, упомянутый передатчик содержит:
кодер, который делит группы битов данных на первую подгруппу и вторую подгруппу,
упомянутый кодер использует первую подгруппу битов для выбора одной из определенного количества точек созвездия, которые распределены в пределах первого многомерного пространства, причем местоположение точек созвездия определено так, что сумма их координат меньше желаемого максимального значения, и координаты выбранной точки созвездия используются для установки значений действительных частей соответствующих комплексных чисел,
упомянутый кодер использует вторую подгруппу битов для выбора еще одной из определенного количества точек созвездия, которые распределены в пределах второго многомерного пространства, причем местоположение точек созвездия определено так, что сумма их координат меньше желаемого максимального значения, и координаты выбранной точки созвездия тогда используются для установки значений мнимых частей соответствующих комплексных чисел,
упомянутый кодер соединяет попарно одну действительную и одну мнимую часть для формирования комплексного числа, и аналогично соединяют попарно остальные действительные и мнимые части для получения набора комплексных чисел,
упомянутый кодер назначает комплексные числа, которые должны быть умножены на связанный с ними один из определенного количества ортогональных кодов множества элементарных сигналов, причем произведение каждого комплексного числа на его код впоследствии суммируют по элементарным сигналам для получения многокодового символа,
фильтр, который принимает поток многокодовых символов и фильтрует их для ограничения передаваемого спектра,
модулятор, который модулирует отфильтрованный сигнал с радиочастотной несущей, и
антенну, которая передает модулированный радиосигнал.
14. Передатчик по п.13, в котором каждое многомерное пространство задано ромбовидным созвездием.
15. Передатчик по п.13, в котором каждое многомерное пространство задано ромбовидным созвездием с вогнутыми вершинами.
16. Передатчик по п.13, в котором каждое многомерное пространство задано ромбовидным созвездием с выемками.
17. Приемник, который декодирует радиосигнал, который имеет уменьшенное отношение пиковой к среднеквадратической амплитуде и ограниченную пиковую составную амплитуду символа, упомянутый приемник содержит:
декодер с процессором, который реализует исполнимые процессором команды из памяти для декодирования радиосигнала посредством:
определения грани ромбовидного созвездия, на которой или в пределах которой лежит символ данных радиосигнала,
определения поднабора точек на грани, в пределах которой лежит символ данных радиосигнала,
определения точки в пределах поднабора точек, которая находится ближе всех к значениям координат символа данных, и
определения символа данных из комбинации грани, поднабора точек и ближайшей точки.
18. Приемник по п.17, в котором ромбовидное созвездие задано в трехмерном пространстве с осями координат X, Y и Z, и внешняя поверхность упомянутого ромбовидного созвездия задана граничным уравнением |x|+|y|+|z|=1.
19. Приемник, который декодирует радиосигнал, который имеет уменьшенное отношение пиковой к среднеквадратической амплитуде и ограниченную пиковую составную амплитуду символа, упомянутый приемник содержит:
декодер с процессором, который реализует исполнимые процессором команды из памяти для декодирования радиосигнала посредством:
формирования гипотезы о первой из множества точек созвездия на первом ромбовидном созвездии, причем первая точка созвездия связана с символом данных радиосигнала,
с учетом гипотетической первой точки созвездия, определения второй точки созвездия на втором ромбовидном созвездии, причем эта вторая точка созвездия связана с символом данных радиосигнала,
определения метрики, описывающей то, насколько точно упомянутая гипотетическая первая точка созвездия и связанная с ней определенная вторая точка созвездия предсказывают принятый радиосигнал, и
сравнения упомянутой метрики для всех возможных гипотез об упомянутой первой точке созвездия и выбора гипотезы с наилучшей метрикой в качестве правильной гипотезы, тем самым декодируя упомянутый радиосигнал.
20. Приемник по п.19, в котором упомянутое первое ромбовидное созвездие задано в трехмерном пространстве с осями координат I1, I2 и I3, ограничено граничным уравнением |I1|+|I2|+|I3|=А, а упомянутое второе ромбовидное созвездие задано во втором трехмерном пространстве с осями координат Q1, Q2 и Q3, ограничено граничным уравнением |Q1|+|Q2|+|Q3|=B.
21. Приемник по п.19, в котором упомянутое первое ромбовидное созвездие задано в трехмерном пространстве с осями координат I1, I2 и I3, ограничено граничным уравнением |I1|+|I2|+|I3|=А, а упомянутое второе ромбовидное созвездие задано во втором трехмерном пространстве с осями координат Q1, Q2 и Q3, ограничено граничным уравнением |Q1|+|Q2|+|Q3|=B, причем сумма квадратов А и В меньше или равна желаемому максимальному значению.
| УСТРОЙСТВО И СПОСОБ ПРИЕМА СИГНАЛОВ В СИСТЕМЕ МОБИЛЬНОЙ СВЯЗИ, ИСПОЛЬЗУЮЩЕЙ ТЕХНОЛОГИЮ АДАПТИВНОЙ АНТЕННОЙ РЕШЕТКИ | 2004 |
|
RU2313906C2 |
| СПОСОБ И СИСТЕМА МОДЕЛИРОВАНИЯ РАДИОПОМЕХ, ПРИНИМАЕМЫХ АБОНЕНТСКИМИ АППАРАТАМИ В СИСТЕМЕ СВЯЗИ С РАСШИРЕННЫМ СПЕКТРОМ | 1995 |
|
RU2189114C2 |
| Способ и приспособление для нагревания хлебопекарных камер | 1923 |
|
SU2003A1 |
| Способ обработки целлюлозных материалов, с целью тонкого измельчения или переведения в коллоидальный раствор | 1923 |
|
SU2005A1 |
| US 7142582 B2, 28.11.2006. | |||
Авторы
Даты
2013-07-20—Публикация
2009-06-30—Подача