Изобретение относится к учебным приборам и может быть использовано в лабораторном практикуме в высших и средних специальных учебных заведениях по курсу физики для получения и углубления знаний физических законов и явлений.
Известна установка для исследования движения жидкости, основанная на уравнении Бернулли (Т.К. Трофимова. Сборник задач по курсу физики для втузов. - М.: «ОНИКС 21 век», 2003, с. 64, рис. 32). Она содержит горизонтальную трубу переменного сечения, по которой протекает вода. На данной установке определяется массовый расход воды с применением уравнения Бернулли. На ней можно провести натурный эксперимент, но эта установка сложна в эксплуатации и не мобильна, ее нельзя применить для дистанционного обучения при заочной форме обучения.
Известна установка для моделирования процессов гидродинамики с применением стационарного электрического поля на электропроводящей бумаге (ЭПБ) (Г.А. Рязанов. Опыты и моделирование при изучении электромагнитного поля. - М.:«Наука», 1966, с. 48, рис. 36). На этой установке моделируют обтекание судна в опытном бассейне, обтекание крыла самолета в аэродинамической трубе и т.п. Эта установка позволяет заменить сложное исследование с применением уравнения Бернулли простым экспериментом на ЭПБ, удобным для дистанционного обучения. Моделирование с применением стационарного электрического поля на ЭПБ отличается большой наглядностью и возможностью построения всей картины поля. При этом не уменьшается познавательная результативность обучения. На этой установке можно продемонстрировать электрическое поле и процесс огибания потока жидкости (газа), но нельзя измерить потенциалы на ЭПБ, а по ним величины, характеризующие движение жидкости (газа).
Наиболее близкой к предлагаемой установке является установка (прототип), где моделируется электрическое поле на ЭПБ (Г.А. Рязанов. Опыты и моделирование при изучении электромагнитного поля. М.:«Наука», 1966, с. 75, рис. 71). Она содержит прямоугольный планшет; прямоугольный лист ЭПБ без выреза, который может быть установлен на прямоугольном планшете; источник постоянного тока и двойной зонд.
На этой установке используется только прямоугольный лист ЭПБ без выреза и несъемные электроды, подключенные к источнику постоянного тока. Измерения потенциалов электрического поля проводятся с помощью компенсационной схемы, которая требует затрат значительного времени при проведении эксперимента и обладает низкой точностью измерений.
Техническим результатом изобретения является расширение функциональных возможностей, моделирование уравнения Бернулли на электропроводящей бумаге и повышение точности проведения эксперимента.
Указанный технический результат достигается тем, что в известную установку для моделирования движения жидкости или газа на электропроводящей бумаге, содержащую прямоугольный планшет, съемный прямоугольный лист электропроводящей бумаги без выреза, который установлен на прямоугольном планшете, источник постоянного тока и двойной зонд, согласно изобретению, введены набор съемных прямоугольных листов электропроводящей бумаги с вырезами по форме поперечного сечения исследуемых тел, каждый лист которого в отдельности имеет возможность размещения на прямоугольном планшете, набор съемных лекал, изготовленных из диэлектрика с цифровой разметкой по периметру лекала и совпадающих по размеру и форме с вырезами на соответствующих листах набора съемных прямоугольных листов электропроводящей бумаги с вырезами, при этом каждое лекало в отдельности имеет возможность установки на соответствующий вырез электропроводящей бумаги на прямоугольном планшете, съемные электроды, расположенные на противоположных сторонах съемного прямоугольного листа электропроводящей бумаги и соединенные с источником постоянного тока, вольтметр с большим входным сопротивлением, вводы которого соединены с иглами двойного зонда, крепления съемных электродов и крепления съемных лекал, установленные на прямоугольном планшете.
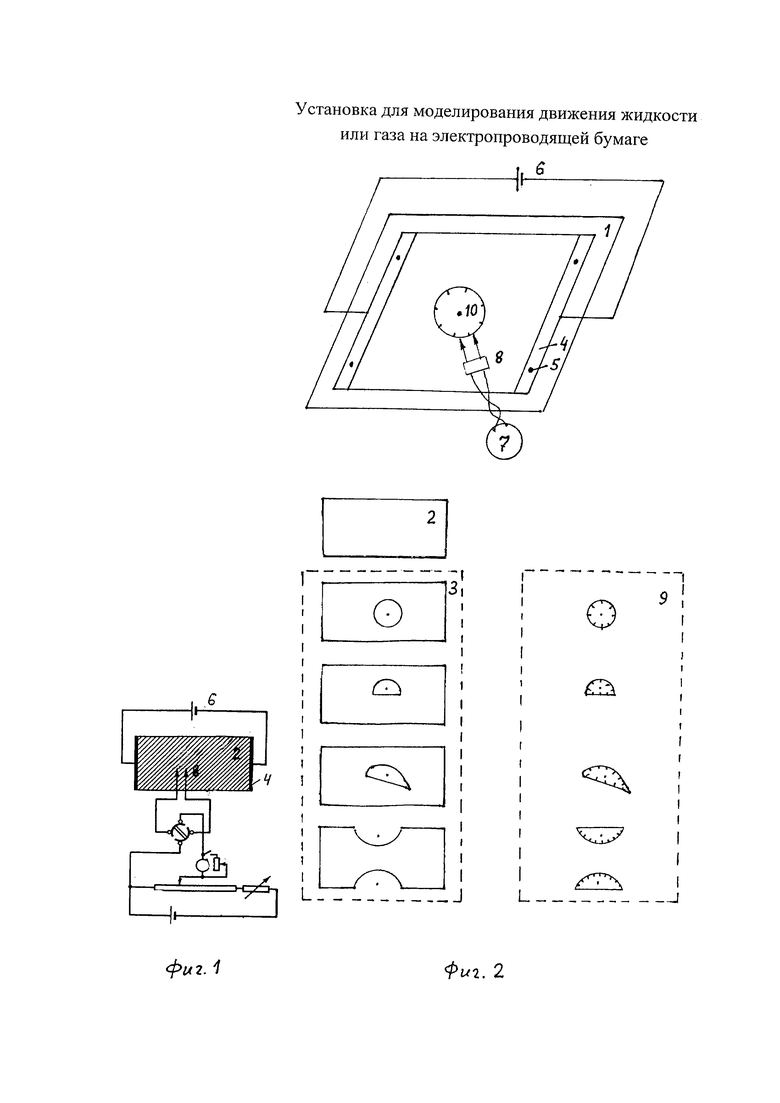
На фиг. 1 изображен прототип; на фиг. 2 - общий вид предлагаемой установки, на фиг. 3-8 - чертежи, поясняющие принцип ее работы.
Предлагаемая установка содержит: 1 - прямоугольный планшет; 2 - съемный прямоугольный лист электропроводящей бумаги без выреза; 3 - набор съемных прямоугольных листов электропроводящей бумаги с вырезами; 4 - съемные электроды; 5 - крепления съемных электродов; 6 - источник постоянного тока; 7 - вольтметр с большим входным сопротивлением; 8 - двойной зонд; 9 - набор съемных лекал; 10 - крепления съемных лекал.
Рассмотрим теоретические положения, которые легли в основу при создании предлагаемой установки. Она позволяет изучить уравнение Бернулли путем моделирования на ЭПБ стационарного электрического поля.
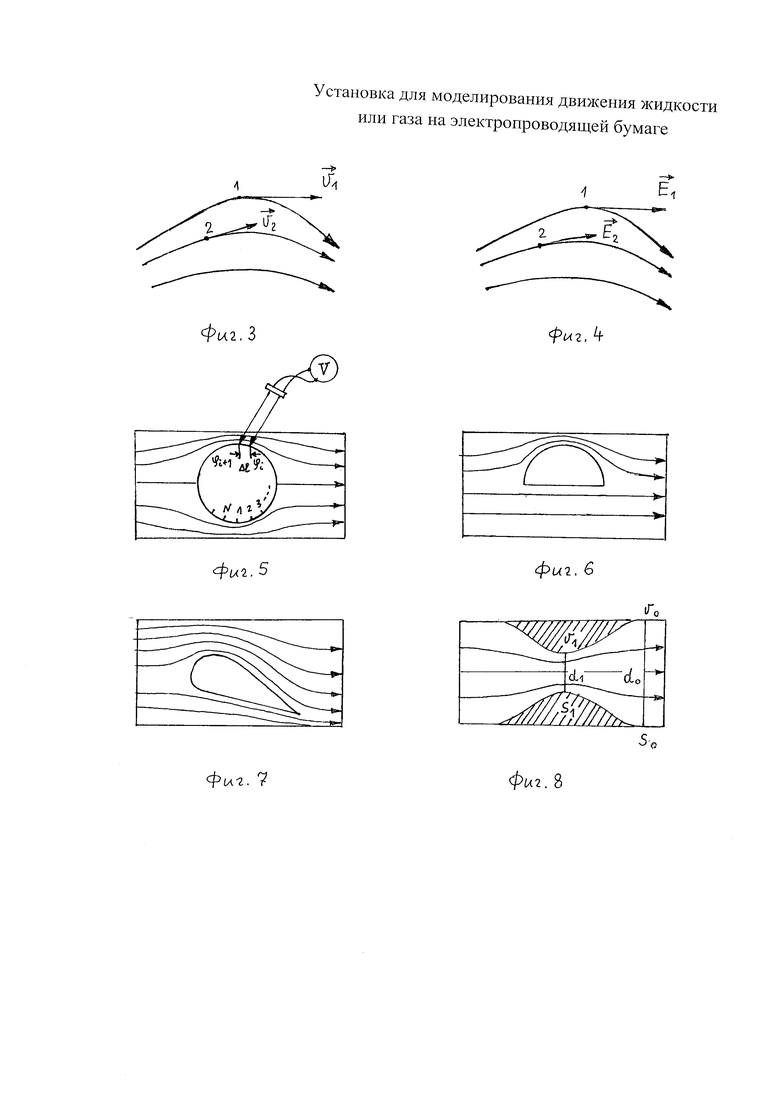
При определенных условиях поле вектора скорости 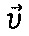 (фиг. 3) в идеальной жидкости или газе (далее - жидкости) аналогично полю вектора
(фиг. 3) в идеальной жидкости или газе (далее - жидкости) аналогично полю вектора 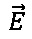 (фиг. 4) стационарного электрического поля на ЭПБ. Наличие этой математической аналогии позволяет изучать поле вектора скорости в потоке жидкости на электрических моделях. Будем полагать, что исследуемое тело находится в неподвижном состоянии, а жидкость движется.
(фиг. 4) стационарного электрического поля на ЭПБ. Наличие этой математической аналогии позволяет изучать поле вектора скорости в потоке жидкости на электрических моделях. Будем полагать, что исследуемое тело находится в неподвижном состоянии, а жидкость движется.
Если пренебречь гидростатическим давлением, тогда давление pi жидкости на поверхности исследуемого тела определяется по уравнению Бернулли:

где ρ - плотность жидкости; υi - скорость течения жидкости в i-х точках на поверхности тела; υ0 и р0 - соответственно скорость и давление в невозмущенном потоке; i=1, 2,..., N; N - число точек на контуре поперечного сечения тела.
Введем безразмерное избыточное давление 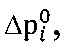 которое получим из выражения (1):
которое получим из выражения (1):
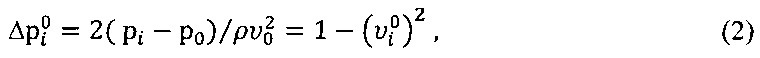
где 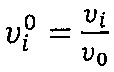 - относительная скорость.
- относительная скорость.
Значения величин 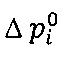 в соответствующих точках геометрически подобных тел будут равны.
в соответствующих точках геометрически подобных тел будут равны.
Так как твердое тело непроницаемо для жидкости, то на его поверхности нормальная составляющая вектора скорости жидкости 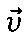 равна нулю
равна нулю 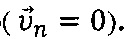 Это соответствует стационарному электрическому полю на поверхности раздела между проводящей средой и диэлектриком
Это соответствует стационарному электрическому полю на поверхности раздела между проводящей средой и диэлектриком 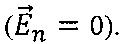
Моделью плоского течения жидкости может служить стационарное электрическое поле в прямоугольном листе ЭПБ, имеющем отверстие, геометрически подобное профилю этого тела. Линии вектора 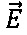 обходят контур тела так же, как струи идеальной жидкости огибают погруженное в нее тело.
обходят контур тела так же, как струи идеальной жидкости огибают погруженное в нее тело.
На фиг. 5-8 изображены в качестве примера листы ЭПБ с вырезами. На фиг. 5 показана картина модели обтекания симметричного тела, на фиг. 6 - модель потока для несимметричного тела, на фиг. 7 показана модель для тела каплевидной формы. На фиг. 8 показана модель горизонтальной трубы переменного сечения, на которой заштрихованная площадь также показывает вырез. На этой модели можно экспериментально проверить теорему о неразрывности струи.
Чтобы установить количественно соответствие между натурой и моделью, воспользуемся безразмерными величинами. При этом скорости частиц жидкости 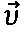 нужно отнести к скорости набегающего потока
нужно отнести к скорости набегающего потока 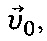 а значения вектора
а значения вектора 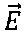 - к напряженности невозмущенного стационарного электрического поля
- к напряженности невозмущенного стационарного электрического поля 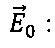
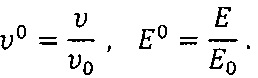
Значения соответственных безразмерных величин в соответственных точках модели и натуры будут равны υ0=Е0 и, следовательно, измерения на электрической модели позволяют находить скорость в соответственных точках потока, причем и размеры тела, и скорости набегающего потока могут быть произвольными: υ=υ0υ0=E0υ0.
Таким образом, по данным, полученным на электрической модели, можно найти распределение избыточного давления на поверхности исследуемого тела:
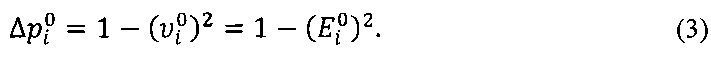
Выражение (3) можно представить в другом виде. Для этого заменим напряженность невозмущенного электрического поля приближенной формулой
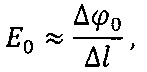
где Δϕ0 - разность потенциалов на ЭПБ, соответствующая области невозмущенного электрического поля; Δl - расстояние между иглами двойного зонда.
Обозначим напряженность электрического поля в i-й точке контура исследуемого тела (фиг. 5) 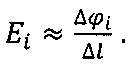 Здесь Δϕt=ϕi+1-ϕi, при i=1, 2,..., N-1; ΔϕN=ϕ1-ϕN. Тогда относительная напряженность электрического поля в i-й точке будет:
Здесь Δϕt=ϕi+1-ϕi, при i=1, 2,..., N-1; ΔϕN=ϕ1-ϕN. Тогда относительная напряженность электрического поля в i-й точке будет:
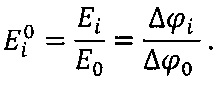
Подставляя последнее выражение в формулу (3), получим окончательное выражение для определения избыточного давления на поверхности исследуемого тела:
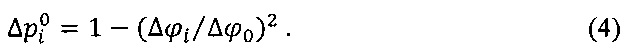
Таким образом, для вычисления избыточного давления на поверхности исследуемого тела необходимо с помощью двойного зонда измерить в i-х точках разности потенциалов и разделить их на разность потенциалов Δϕ0, соответствующую области невозмущенного электрического поля.
На фиг. 8 показаны все величины, необходимые для экспериментального подтверждения теоремы о неразрывности струи:

Учитывая, что υ1=Е1, υ0=Е0, а также площадь поперечного сечения трубы 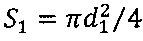 и
и 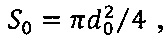 получим экспериментальную формулу для проверки теоремы о неразрывности струи:
получим экспериментальную формулу для проверки теоремы о неразрывности струи:

Здесь Δϕ1 и Δϕ0 - разности потенциалов, измеренные соответственно в первой и нулевой точках трубы, а d1 и d0 - диаметры соответственно в первой и нулевой точках трубы.
Рассмотрим взаимодействие элементов в предлагаемой установке (фиг. 2). Она включает прямоугольный планшет 1, на котором может быть установлен съемный прямоугольный лист ЭПБ без выреза 2 или произвольный лист из набора съемных прямоугольных листов ЭПБ с вырезами 3. Вырезы сделаны на каждом листе по форме поперечного сечения исследуемого тела.
На противоположных сторонах съемного прямоугольного листа ЭПБ без выреза 2 или произвольного листа из набора съемных прямоугольных листов ЭПБ с вырезами 3 установлены съемные электроды 4, которые плотно прижимают лист ЭПБ 2 или произвольный лист из набора 3 с помощью креплений съемных электродов 5 к прямоугольному планшету 1. Съемные электроды 4 соединены с источником постоянного тока 6, под действием которого в листе ЭПБ 2 или в произвольном листе из набора 3 протекает ток и в них создается стационарное электрическое поле.
Для измерения разности потенциалов электрического поля в нужных точках листа ЭПБ, установленного на прямоугольном планшете 1, установка содержит вольтметр с большим входным сопротивлением 7, вводы которого соединены с иглами двойного зонда 8. Иглы двойного зонда 8 расположены на расстоянии Δl друг от друга (см. фиг. 5). Большое входное сопротивление вольтметра необходимо для того, чтобы при касании двойным зондом 8 к листу ЭПБ не было ответвления тока в вольтметр и, соответственно, искажения строения электрического поля.
Установка содержит набор съемных лекал 9, изготовленных из диэлектрика с цифровой разметкой по периметру лекала. Каждое лекало совпадает по размеру и форме с вырезами на соответствующих листах из набора съемных прямоугольных листов ЭПБ с вырезами 3. Цифровая разметка на лекале сделана в соответствии с расстоянием Δl между иглами двойного зонда 8.
Измерение разности потенциалов в требуемых точках установленного лекала осуществляется прикосновением игл двойного зонда 8 к соответствующему листу ЭПБ рядом с цифровой разметкой на лекале (см. фиг. 5).
Установленное лекало прижимается к прямоугольному планшету 1 с помощью креплений съемных лекал 10.
Рассмотрим, каким образом на предлагаемой установке определяется избыточное давление 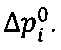 Для этого выбираем из набора трех съемных прямоугольных листов ЭПБ с вырезами требуемый лист, устанавливаем его на прямоугольном планшете 1 и прижимаем с помощью креплений съемных электродов 5 съемные электроды 4 к прямоугольному планшету 1. Из набора съемных лекал 9 выбираем лекало, соответствующее исследуемому телу и вырезу на выбранном листе ЭПБ. Устанавливаем лекало на вырез и прижимаем его к прямоугольному листу ЭПБ 1 с помощью крепления съемных лекал 10. С помощью двойного зонда 8 с подключенным к нему вольтметром 7 измеряем сначала разность потенциалов Δϕ0 в области невозмущенного электрического поля (например, вблизи съемных электродов 4). Затем в каждой точке лекала находим разности потенциалов Δϕi (i=1, 2,..., N), где N - число точек на лекале. И, наконец, по формуле (4) рассчитываем избыточное давление
Для этого выбираем из набора трех съемных прямоугольных листов ЭПБ с вырезами требуемый лист, устанавливаем его на прямоугольном планшете 1 и прижимаем с помощью креплений съемных электродов 5 съемные электроды 4 к прямоугольному планшету 1. Из набора съемных лекал 9 выбираем лекало, соответствующее исследуемому телу и вырезу на выбранном листе ЭПБ. Устанавливаем лекало на вырез и прижимаем его к прямоугольному листу ЭПБ 1 с помощью крепления съемных лекал 10. С помощью двойного зонда 8 с подключенным к нему вольтметром 7 измеряем сначала разность потенциалов Δϕ0 в области невозмущенного электрического поля (например, вблизи съемных электродов 4). Затем в каждой точке лекала находим разности потенциалов Δϕi (i=1, 2,..., N), где N - число точек на лекале. И, наконец, по формуле (4) рассчитываем избыточное давление 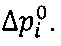
Экспериментальную проверку теоремы о непрерывности струи жидкости проводим следующим образом. Устанавливаем на прямоугольный планшет 1 лист из набора 3 и лекала из набора съемных лекал 9, которые соответствуют трубе разного диаметра d0 и d1 (см. фиг. 8). С помощью линейки измеряем на листе ЭПБ величины d0 и d1. С помощью двойного зонда 8 с подключенным к нему вольтметром 7 измеряем на ЭПБ разности потенциалов Δϕ0 и Δϕ1 соответственно в окрестности диаметров d0 и d1. По результатам измерений по формуле (6) проверяем равенство.
| название | год | авторы | номер документа |
|---|---|---|---|
| Установка для исследования электроёмкости проводников на модели из электропроводящей бумаги | 2016 |
|
RU2621599C1 |
| УСТАНОВКА ДЛЯ ИССЛЕДОВАНИЯ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ МЕТОДОМ МОДЕЛИРОВАНИЯ | 2012 |
|
RU2507590C1 |
| УСТАНОВКА ДЛЯ РЕШЕНИЯ ТРЕТЬЕГО УРАВНЕНИЯ МАКСВЕЛЛА | 2016 |
|
RU2644098C2 |
| УСТАНОВКА ДЛЯ ИССЛЕДОВАНИЯ СТАЦИОНАРНОГО ЭЛЕКТРИЧЕСКОГО ПОЛЯ | 2013 |
|
RU2534979C1 |
| УСТАНОВКА ДЛЯ ИССЛЕДОВАНИЯ СТАЦИОНАРНОГО ЭЛЕКТРИЧЕСКОГО ПОЛЯ | 2011 |
|
RU2479868C1 |
| УСТАНОВКА ДЛЯ МОДЕЛИРОВАНИЯ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ НА ГРАНИЦЕ РАЗДЕЛА ДВУХ ДИЭЛЕКТРИКОВ | 2015 |
|
RU2616915C2 |
| УСТАНОВКА ДЛЯ ИССЛЕДОВАНИЯ ПАССИВНЫХ ЭЛЕМЕНТОВ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ | 2012 |
|
RU2507591C1 |
| УСТАНОВКА ДЛЯ ИССЛЕДОВАНИЯ ВИХРЕВОГО ЭЛЕКТРИЧЕСКОГО ПОЛЯ | 2012 |
|
RU2504016C2 |
| УСТАНОВКА ДЛЯ ИССЛЕДОВАНИЯ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ | 2012 |
|
RU2504017C2 |
| УСТАНОВКА ДЛЯ ИССЛЕДОВАНИЯ СТАЦИОНАРНОГО ЭЛЕКТРИЧЕСКОГО ПОЛЯ | 2005 |
|
RU2284581C1 |
Изобретение относится к учебным приборам и может быть использовано в лабораторном практикуме по курсу физики. Съемный прямоугольный лист электропроводящей бумаги без выреза или произвольный лист из набора съемных прямоугольных листов электропроводящей бумаги с вырезами по форме поперечного сечения исследуемого тела раздельно установлены на прямоугольном планшете. На вырез в листе электропроводящей бумаги устанавливается соответствующее лекало из набора съемных лекал, изготовленных из диэлектрика с цифровой разметкой по периметру и совпадающих по размеру и форме с соответствующими вырезами на съемных прямоугольных листах электропроводящей бумаги. Съемный прямоугольный лист электропроводящей бумаги прижимается съемными электродами, расположенными на противоположных сторонах прямоугольного листа и соединенными с источником постоянного тока. Измерение потенциалов на электропроводящей бумаге в соответствующих точках цифровой разметки лекала осуществляется вольтметром с большим входным сопротивлением, вводы которого соединены с иглами двойного зонда. Техническим результатом изобретения является моделирование уравнения Бернулли на электропроводящей бумаге. 8 ил.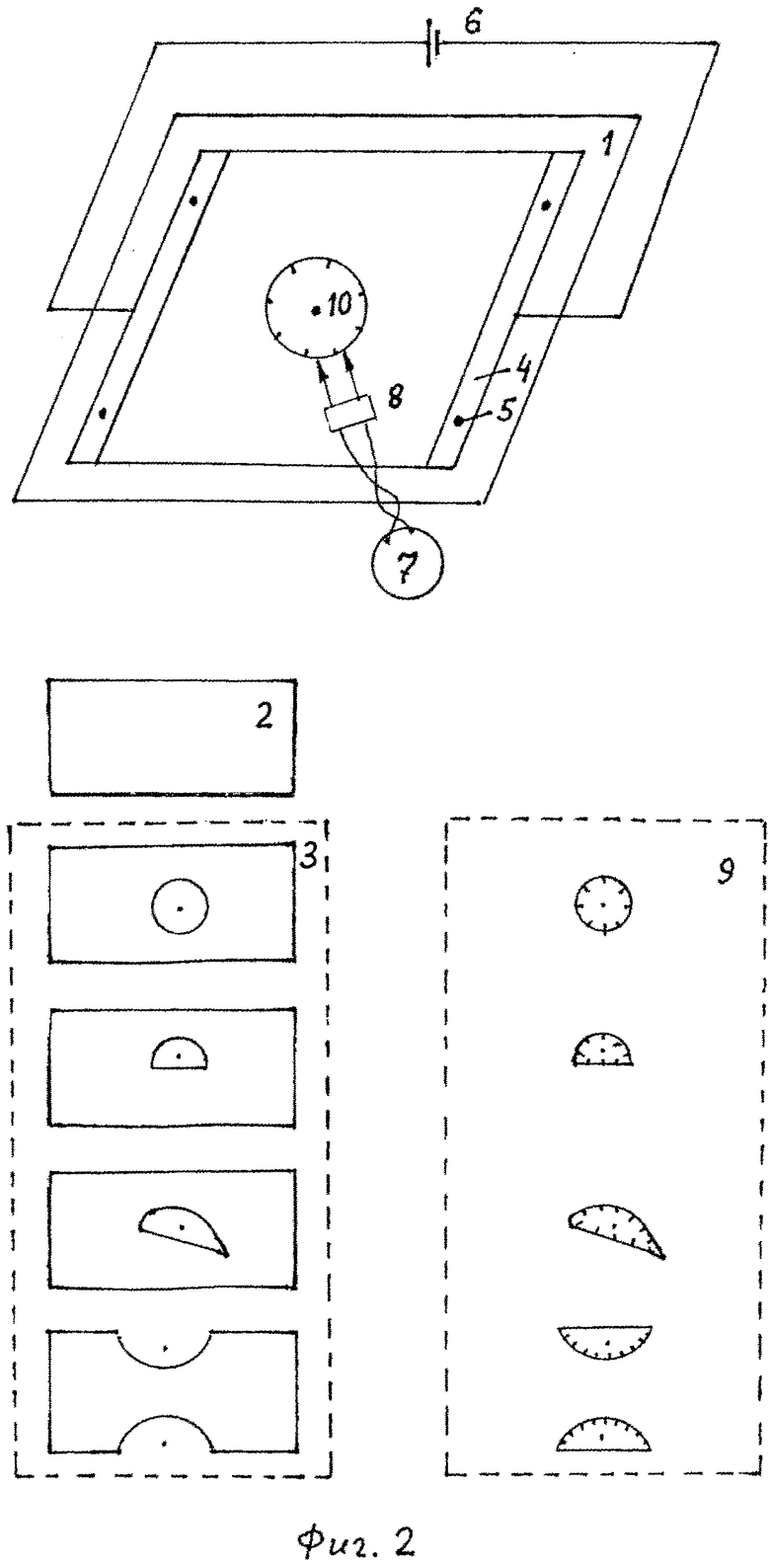
Установка для моделирования движения жидкости или газа на электропроводящей бумаге, содержащая прямоугольный планшет, съемный прямоугольный лист электропроводящей бумаги без выреза, который установлен на прямоугольном планшете, источник постоянного тока и двойной зонд, отличающаяся тем, что в нее введены набор съемных прямоугольных листов электропроводящей бумаги с вырезами по форме поперечного сечения исследуемых тел, каждый лист которого в отдельности имеет возможность размещения на прямоугольном планшете, набор съемных лекал, изготовленных из диэлектрика с цифровой разметкой по периметру лекала и совпадающих по размеру и форме с вырезами на соответствующих листах набора съемных прямоугольных листов электропроводящей бумаги с вырезами, при этом каждое лекало в отдельности имеет возможность установки на соответствующий вырез электропроводящей бумаги на прямоугольном планшете, съемные электроды, расположенные на противоположных сторонах съемного прямоугольного листа электропроводящей бумаги и соединенные с источником постоянного тока, вольтметр с большим входным сопротивлением, вводы которого соединены с иглами двойного зонда, крепления съемных электродов и крепления съемных лекал, установленные на прямоугольном планшете.
| РЯЗАНОВ Г.А | |||
| "Опыты и моделирование при изучении электромагнитного поля", Москва, изд | |||
| "Наука", 1966, с.75, рис.71 | |||
| УСТАНОВКА ДЛЯ ИССЛЕДОВАНИЯ СТАЦИОНАРНОГО ЭЛЕКТРИЧЕСКОГО ПОЛЯ | 2005 |
|
RU2284581C1 |
| УСТАНОВКА ДЛЯ ИССЛЕДОВАНИЯ СТАЦИОНАРНОГО ЭЛЕКТРИЧЕСКОГО ПОЛЯ | 2011 |
|
RU2479868C1 |
| УСТРОЙСТВО для МОДЕЛИРОВАНИЯ ПОСТУПАТЕЛЬНО- ЦИРКУЛЯЦИОННОГО ОБТЕКАНИЯ РЕШЕТОК ПРОФИЛЕЙ | 0 |
|
SU321828A1 |
| УСТАНОВКА ДЛЯ ИССЛЕДОВАНИЯ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ МЕТОДОМ МОДЕЛИРОВАНИЯ | 2012 |
|
RU2507590C1 |
Авторы
Даты
2017-01-10—Публикация
2015-01-26—Подача