Изобретение относится к учебным приборам и может быть использовано в лабораторном практикуме в высших и средних специальных учебных заведениях по курсу физики для получения и углубления знаний физических законов и явлений.
Известно устройство для демонстрации нарастания тока в цепи с индуктивностью (Н.М. Шахмаев, С.Е. Каменецкий Демонстрационные опыты по электродинамике. М.: Просвещение, 1973, с.256). На этой установке можно только продемонстрировать влияние индуктивности на скорость нарастания тока в цепи, но нельзя измерить величину индуктивности и ее исследовать. Здесь используется для объяснения индуктивности только такие физические понятия как индуцированное электрическое поле, ЭДС самоиндукции, но не применяется фундаментальная теорема Гаусса для магнитного поля, не используется численный метод нахождения индуктивности при моделировании на электропроводящей бумаге (ЭПБ).
Известно также устройство для исследования электроемкости плоского конденсатора (там же на с.78), на котором можно измерить величину емкости и ее исследовать. Здесь используются для объяснения емкости такие понятия как заряд, напряжение между обкладками конденсатора, но не применяются такие фундаментальные понятия как поток вектора электрического смещения, теорема Гаусса для электростатического поля, не используется численный метод нахождения емкости при моделировании на ЭПБ.
Известно также устройство для исследования сопротивления (там же на с.112). Однако на этом устройстве не рассматривается сопротивление проводника в самом общем случае, т.к. не используются законы Ома в дифференциальной и интегральной формах, понятие потока вектора напряженности электрического поля. Не используется численный метод определения удельного электрического сопротивления.
Известно устройство, которое предназначено только для измерения емкости конденсаторов и индуктивности катушек с помощью мостов переменного тока (Руководство к лабораторным занятиям по физике. Под ред. Л.Л. Гольдина. М.: Наука, 1973, с.269).
Известно устройство, которое предназначено только для измерения сопротивления с помощью моста Уинстона с использованием правил Кирхгофа (Т.Н. Трофимова Курс физики. М.: Высшая школа, 1994, с.188).
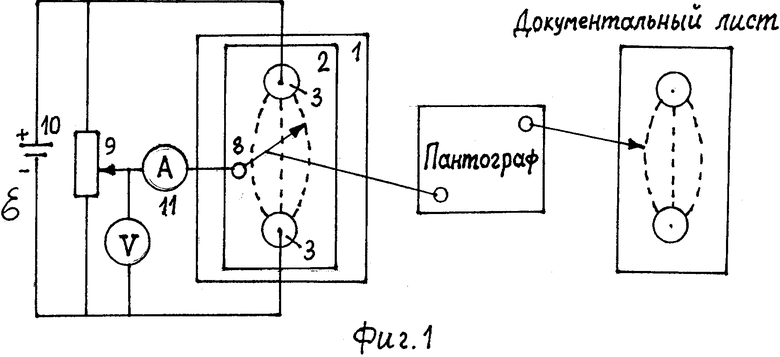
Наиболее близкой к предлагаемой установке является установка для исследования электростатических полей методом моделирования (прототип, фиг.1. Лабораторный практикум по физике. Под ред. К.А. Барсукова и Ю.Н. Уханова. М.: Высшая школа, 1988, с.109, рис.38). Она содержит: зонд; потенциометр, соединенный двумя концевыми контактами с источником постоянного тока; планшет; большой лист электропроводящей бумаги прямоугольной формы, уложенный на планшете; пару электродов круглого сечения, электроды которой установлены на противоположных сторонах большого листа электропроводящей бумаги, при этом, второй электрод круглого сечения соединен с одним из концевых контактов потенциометра; амперметр, первый ввод которого соединен с движком потенциометра.
На этой установке методом моделирования на ЭПБ определяются только погонные емкость и индуктивность системы двух бесконечно длинных проводников. Для этого в необходимых точках ЭПБ измеряются потенциалы с помощью зонда, включенного в мостовую схему, что требует значительного времени для проведения эксперимента и получается невысокая точность измерения потенциалов. На этой установке не используется возможность по полученным измерениям потенциалов на ЭПБ определить удельное электрическое сопротивление р электропроводящей бумаги, а затем рассчитать сопротивление листов ЭПБ различной конфигурации и исследовать зависимость сопротивления не только от свойств материала ЭПБ, но и от геометрических параметров листа ЭПБ. При определении ρ ЭПБ по измеренным потенциалам могут быть использованы фундаментальные законы Ома в дифференциальной и интегральной формах, а также понятие потока вектора плотности тока.
Таким образом, используя все возможности прототипа (фиг.1), на предлагаемой установке можно исследовать все три пассивные элементы электрических цепей: емкость, индуктивность и сопротивление.
Техническим результатом изобретения является упрощение конструкции установки и повышение точности измерений.
Указанный технический результат достигается тем, что в известную установку для исследования пассивных элементов электрических цепей, содержащую зонд, потенциометр, соединенный двумя концевыми контактами с источником постоянного тока, планшет, большой лист электропроводящей бумаги прямоугольной формы, уложенный на планшете, пару электродов круглого сечения, электроды которой установлены на противоположных сторонах большого листа электропроводящей бумаги, при этом второй электрод круглого сечения соединен с одним из концевых контактов потенциометра, амперметр, первый ввод которого соединен с движком потенциометра, согласно изобретению, введены малые листы электропроводящей бумаги прямоугольной формы, создающие сопротивление R/2, R, 2R и уложенные на планшете, пары электродов прямоугольного сечения для каждого малого листа электропроводящей бумаги, электроды которых установлены на противоположных сторонах этих листов, криволинейный четырехугольный лист электропроводящей бумаги, образованный пересечением двух концентрических окружностей и двух радиальных прямых, уложенный на планшете, пара электродов прямоугольного сечения для криволинейного четырехугольного листа электропроводящей бумаги, электроды которой установлены на противоположных сторонах этого листа вдоль радиальных прямых, вольтметр с большим входным сопротивлением, первый ввод которого соединен со вторым вводом амперметра, а второй его ввод - с зондом, переключатель, общий контакт которого соединен со вторым вводом амперметра, а другие контакты его соединены с первыми электродами соответственно большого, малых и криволинейного четырехугольного листов электропроводящей бумаги, при этом вторые электроды малых и криволинейного четырехугольного листов электропроводящей бумаги соединены со вторым электродом круглого сечения большого листа электропроводящей бумаги, круговое кольцо, изготовленное из диэлектрика с нанесенной разметкой на внутреннем и наружном контурах, которое насажено на один из электродов круглого сечения и уложено на большом листе электропроводящей бумаги, полоски, изготовленные из диэлектрика с нанесенной разметкой с обеих сторон и уложенные симметрично между электродами на всех листах электропроводящей бумаги.
На фиг.1 изображен прототип; на фиг.2 - общий вид предлагаемой установки; на фиг.3-12 - чертежи, поясняющие принцип ее работы.
Предлагаемая установка (фиг.2) содержит: 1 - планшет; 2 - большой лист электропроводящей бумаги; 3 - пара электродов круглого сечения; 4.1 - малый лист электропроводящей бумаги с сопротивлением R/2; 4.2 - малый лист электропроводящей бумаги с сопротивлением R; 4.3 - малый лист электропроводящей бумаги с сопротивление 2R; 5.1 - пара электродов для малого листа электропроводящей бумаги с сопротивление R/2; 5.2 - пара электродов для малого листа электропроводящей бумаги с сопротивлением R; 5.3 - пара электродов для малого листа электропроводящей бумаги с сопротивлением 2R; 6 - криволинейный четырехугольный лист электропроводящей бумаги; 7 - пара электродов для криволинейного четырехугольного листа электропроводящей бумаги; 8 - зонд; 9 - потенциометр; 10 - источник постоянного тока; 11 - амперметр; 12 - вольтметр с большим входным сопротивлением; 13 - переключатель; 14 - круговое кольцо; 15.1 - полоска для большого листа электропроводящей бумаги; 15.2 - полоска для малого листа электропроводящей бумаги с сопротивлением R/2; 15.3 - полоска для малого листа электропроводящей бумаги с сопротивлением R; 15.4 - полоска для малого листа электропроводящей бумаги с сопротивлением 2R; 15.5 - полоска для криволинейного четырехугольного листа электропроводящей бумаги.
Рассмотрим теоретические положения, которые легли в основу предлагаемой установки для исследования пассивных элементов электрических цепей. Параметром электрической цепи, определяющим связанное с цепью электрическое поле, является емкость С. Определение емкости будем проводить методом моделирования на ЭПБ открытой двухпроводной линии.
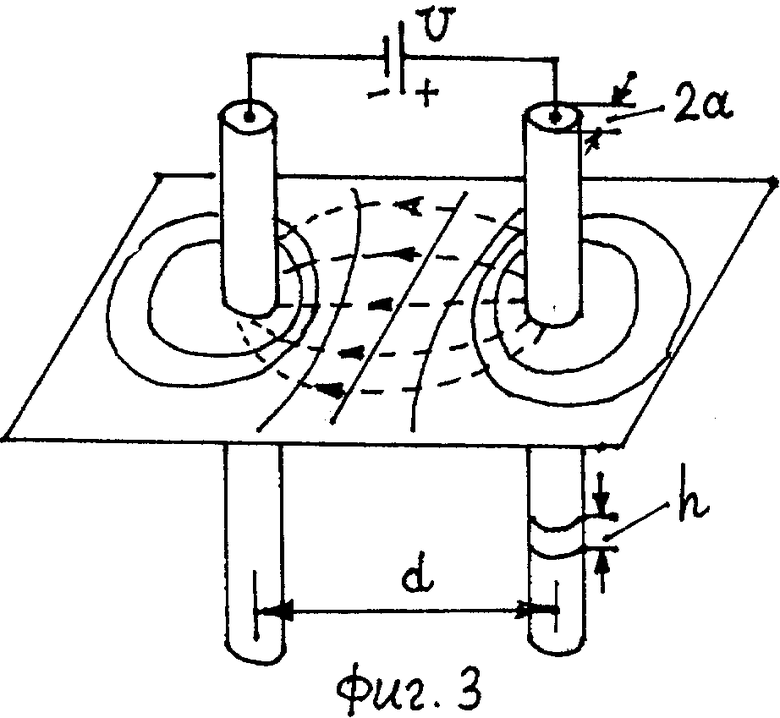
На фиг.3 показаны силовые линии электрического поля (пунктирные) и линии равного потенциала (сплошные) этого поля, создаваемого в вакууме двумя бесконечно длинными параллельными проводниками круглого сечения. Проводники заряжены, т.к. они соединены с источником постоянного тока U. Поскольку тока нет, то вокруг проводников образуется электростатическое поле.
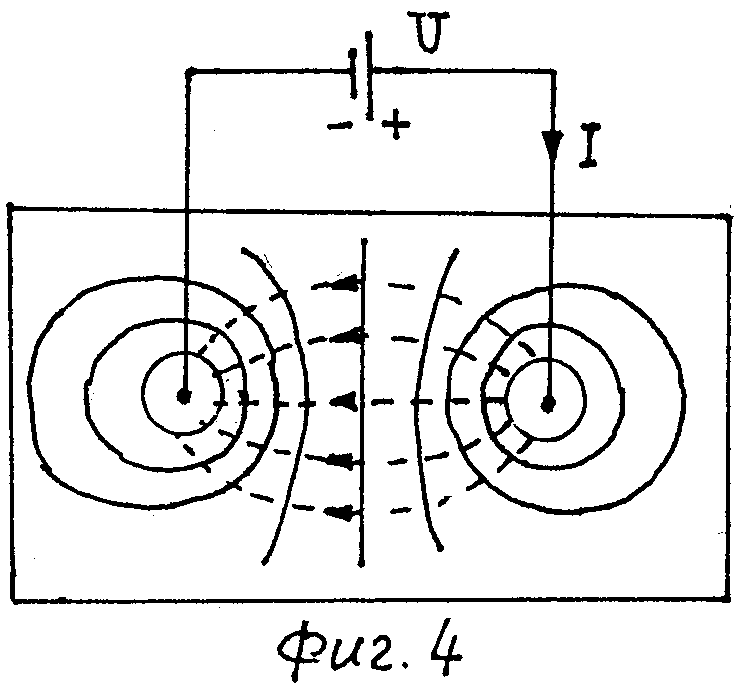
На фиг.4 показано стационарное электрическое поле, создаваемое электродами такого же сечения на ЭПБ с плотно прижатыми к ней электродами. В этом случае при наличии источника постоянного тока U образуется замкнутая электрическая цепь и в цепи течет ток I.
Из фиг.3 и фиг.4 видно, что электростатическое (фиг.3) и стационарное (фиг.4) электрические поля в указанных условиях аналогичны по распределению силовых линий и потенциалов. Это обстоятельство используем для моделирования электростатических полей соответствующими стационарными полями на ЭПБ. Заметим, что экспериментальное исследование стационарного электрического поля технически несколько проще, чем исследование электростатического поля.
Емкость С, исследуемой модели двухпроводной линии, можно найти, если измерить распределение потенциалов на ЭПБ и вычислить по ним напряженность электрического поля. Расчетная формула для определения емкости получается, если в определении емкости C=q/U заменить заряд q по теореме Гаусса для электростатического поля потоком вектора электрического смещения 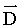

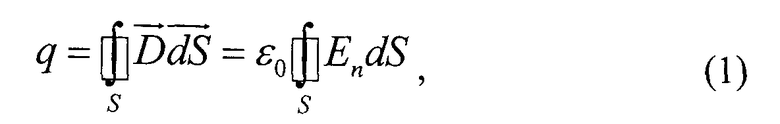
где ε0 - электрическая постоянная, En - проекция вектора 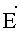
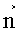
Тогда емкость 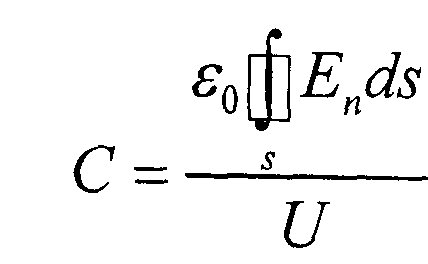
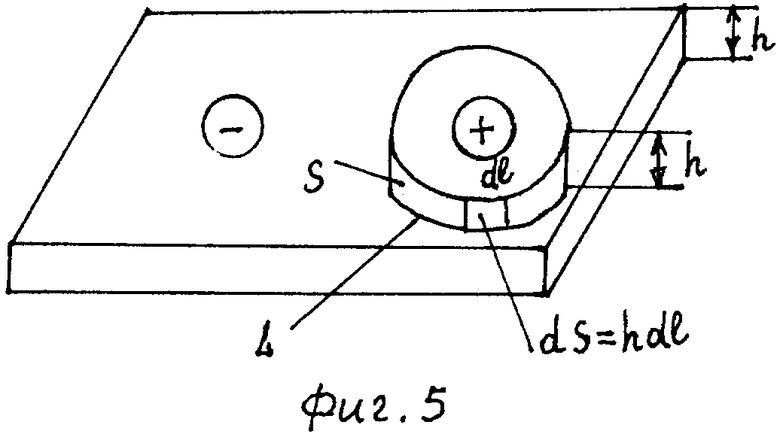
Определим интеграл в выражении (1). Для этого используем круговое кольцо из диэлектрика и разметкой, уложенное на планшет с ЭПБ так, чтобы внутренний и наружный контур кольца охватывали один из электродов, например, положительный электрод (фиг.5). В этом случае используемое кольцо моделирует замкнутую поверхность, охватывающую заряд. Вокруг электрода (фиг.5) формируется плоскопараллельное электрическое поле. Проведем две плоскости вектора 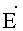
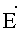
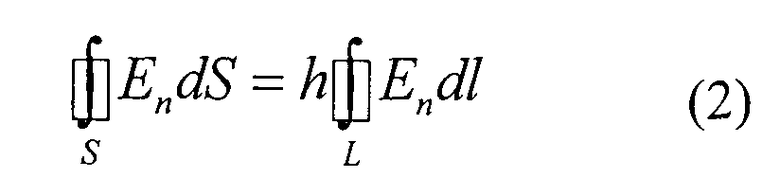
Стационарный заряд q, определяемый соотношением (1), реально существует и расположен на поверхности электрода (фиг.5), граничащей с листом ЭПБ. При моделировании можно считать, что поле в толщине ЭПБ создано не внешним стационарным зарядом, расположенным на поверхности электрода, а воображаемым стационарным зарядом, существующим внутри листа ЭПБ в окрестности электрода.
Для определения интеграла (2) численным методом, заменим точную формулу (2) ее приближением:
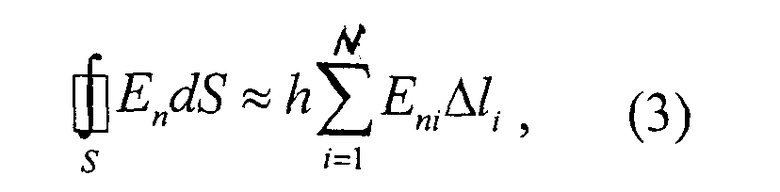
где Еni - проекция вектора 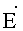
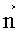
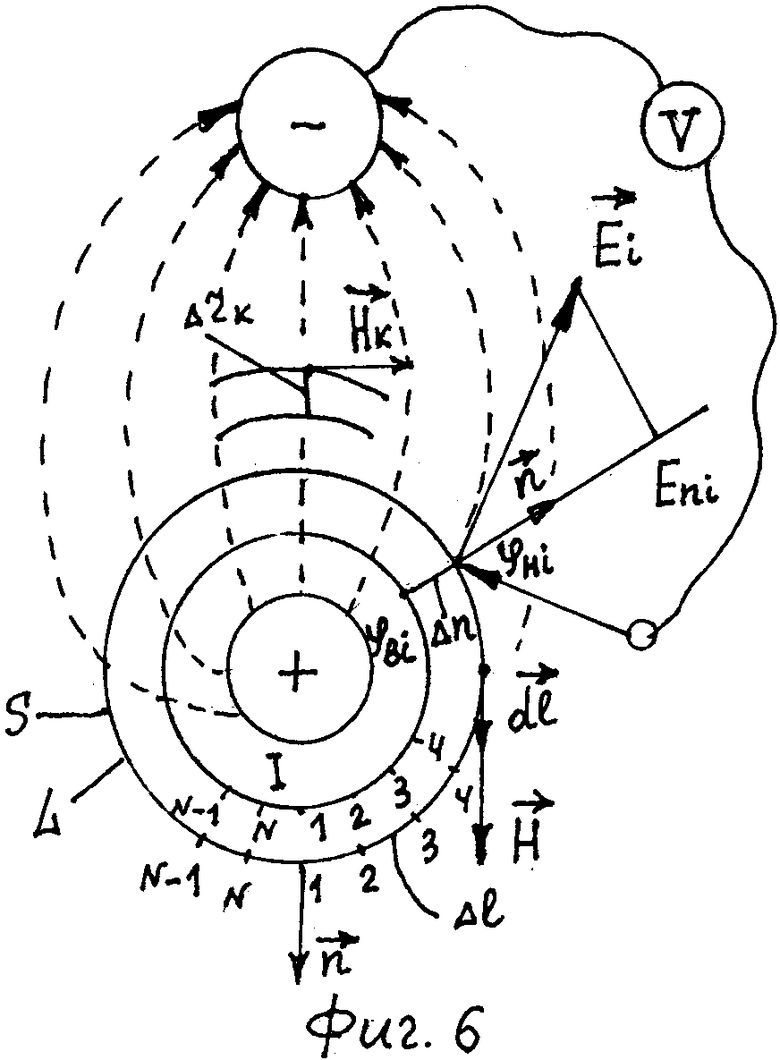
Для определения Еni применяем круговое кольцо, изготовленное из тонкого диэлектрика с нанесенной разметкой на его внутреннем и наружном контурах (фиг.6). Наружный (основной) контур кольца соответствует контуру L, а внутренний (вспомогательный) контур кольца расположен на одинаковом расстоянии Δn=Δni, от наружного контура кольца. Наружный контур кольца разбиваем на равные отрезки длинной Δl=Δli, такой величины, чтобы поле в пределах его было однородным и они лежали на контуре L. Образующиеся точки отрезков нумеруем против часовой стрелки (фиг.6) i=1,2,…,N. В каждой i-й точке проводим нормаль 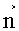
Если нормаль 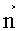
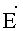
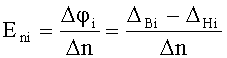

где i=1,2,…,N; φBi - потенциал, измеряемый в i-й точке внутреннего контура кругового кольца; φHi - потенциал, измеряемый в i-й точке наружного контура кругового кольца; N - число точек на контуре L.
С учетом последнего выражения формула (3) приобретает другой вид:
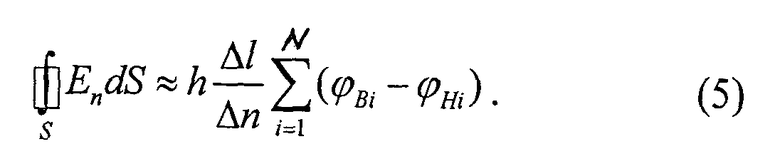
Можно подобрать наружный и внутренний контуры таким образом, чтобы Δl=Δn, тогда окончательное выражение (5) имеет вид:
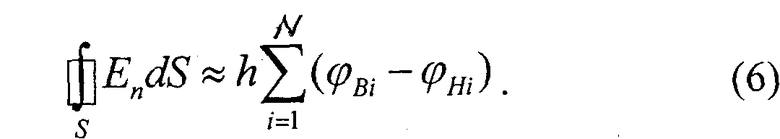 .
.
Емкость бесконечно малого отрезка h двухпроводной линии определяем по формуле:
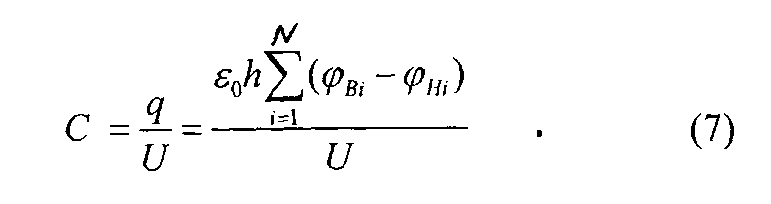
Погонную емкость этой линии определяем по формуле:
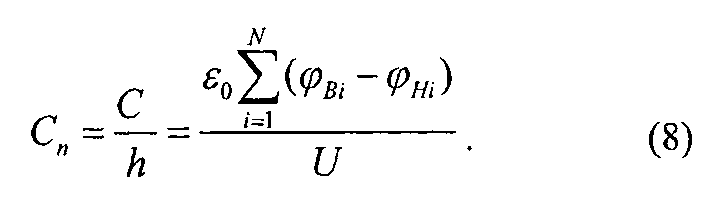
Полученное экспериментальным путем значение емкости Сn можно сравнить с теоретическим значением, которое определяется по формуле:
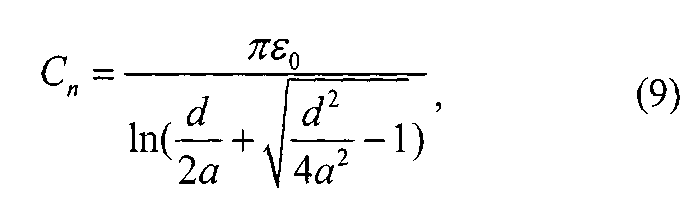
где a - радиус провода, d - расстояние между проводами.
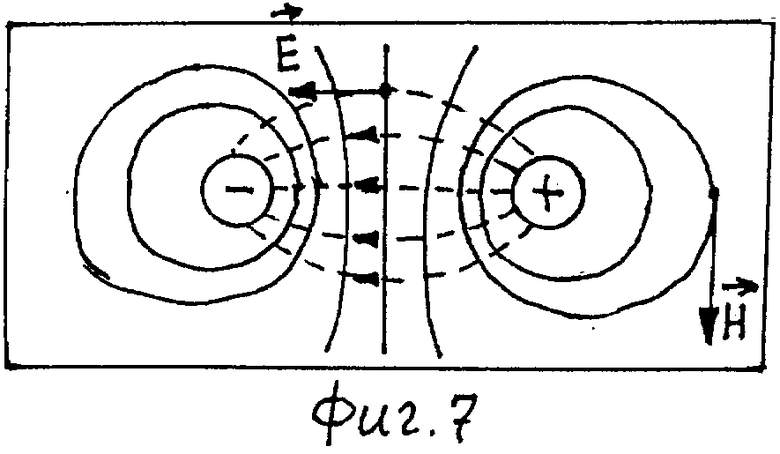
Параметром, количественно характеризующим связанное с электрической цепью магнитное поле, является индуктивность L. На фиг.7 показаны силовые линии электрического (пунктирные) и магнитного (сплошные) полей в двухпроводной линии. Как видно из фиг.7, эти поля в плоскости поперечного сечения аналогичны по структуре соответствующему электростатическому полю (фиг.4). Следовательно, картину магнитного поля системы открытой двухпроводной линии с током I можно получить, если воспользоваться моделью электростатического поля, представленной на фиг.4. Для этого нужно перейти в систему отсчета, равномерно движущуюся с такой скоростью 

где 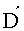
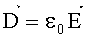
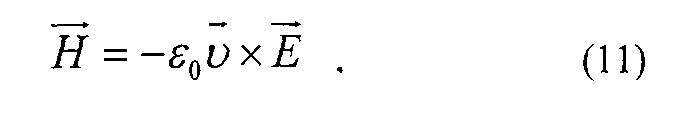
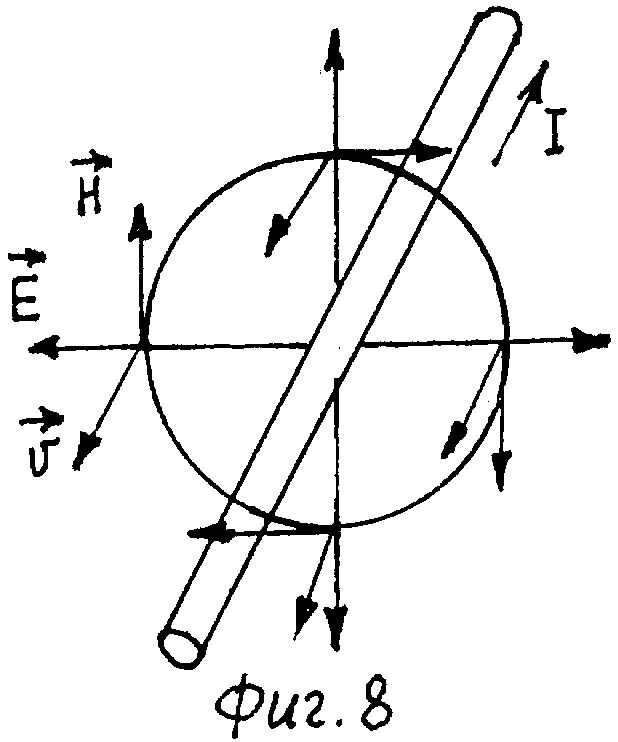
Если точка наблюдения скользит по эквипотенциальной поверхности электрического поля параллельно проводникам, то вектор Н направлен по касательной к эквипотенциальной линии электростатического поля (фиг.8). Напряженность

Из основного соотношения, связывающего напряженность электростатического поля с потенциалом

видно, что лини электростатического поля перпендикулярны поверхности равного потенциала. С учетом выражения (13) формула (12) имеет вид:

где φ - потенциал электростатического поля; производная 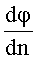
Определим постоянный множитель К=ε0υ в выражении (14). Для этого воспользуемся теоремой о циркуляции вектора 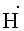
Для вычисления напряженности магнитного поля определяем циркуляцию вектора 
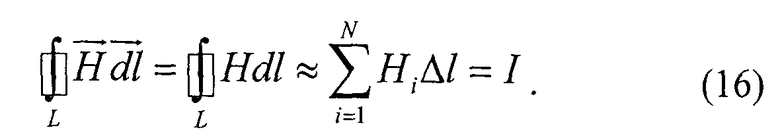
Подставим в формулу (16) выражение (15), тогда
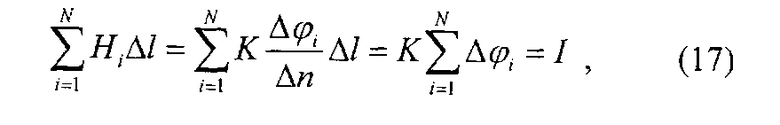
где Δφi=φBi-φHi, φHi - потенциалы i-x точек наружного контура L, φBi - потенциалы i-х точек вспомогательного внутреннего контура.
Из формулы (17) можно определить множитель К модели, если задать значение тока I моделируемой системы равным 1А, т.е.

С помощью выражения (15) и множителя (18) можно определить напряженность магнитного поля на каждом i-ом участке контура L для произвольного тока I:

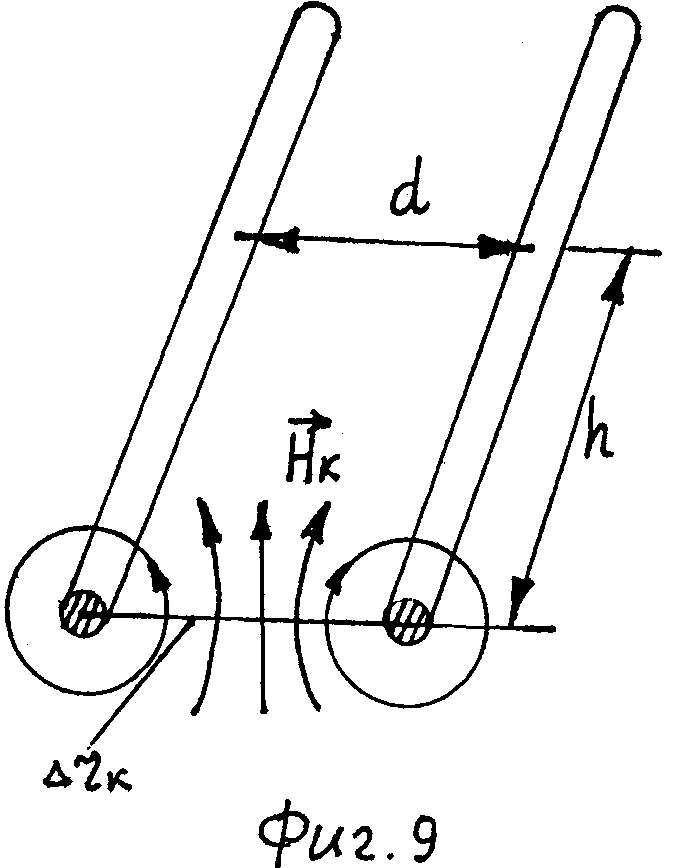
Предлагаемая установка позволяет найти индуктивность бесконечно малого отрезка h моделируемой системы проводников. Для этого следует воспользоваться определением индуктивности L=Ф/I, где Ф - магнитный поток через площадь S=hd (фиг.9) между проводниками с током I.
Магнитный поток
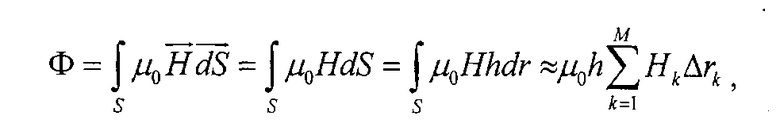
где Hk - значения напряженностей магнитного поля в точках, лежащих на линии, соединяющей центры проводников; Δrk - расстояние между соответствующими линиями напряженностей (фиг.9).
Формулу для вычисления Нk можно получить из выражения (19):
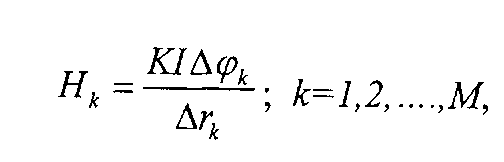
тогда магнитный поток Ф через площадь S=hd
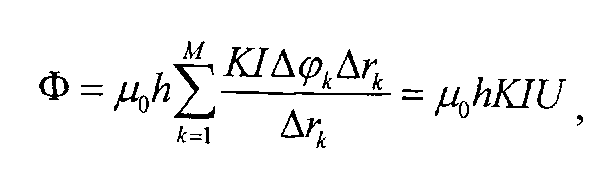
где 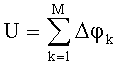
Таким образом, индуктивность бесконечно малого отрезка h открытой двухпроводной линии
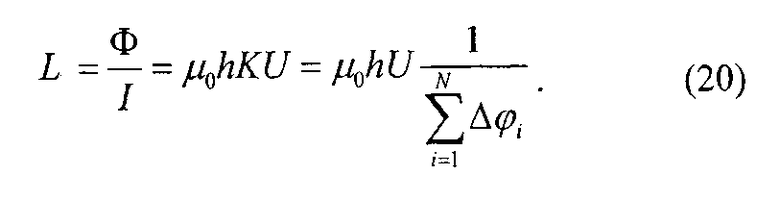
Погонная индуктивность, рассчитываемая на единицу длинны,
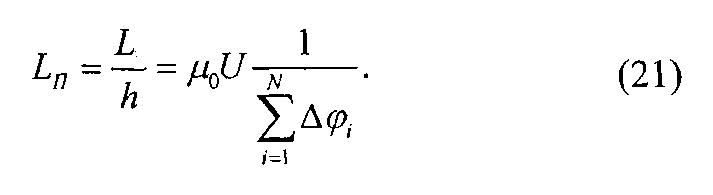
Полученное экспериментальным путем значение индуктивности Ln можно сравнить с теоретическим значением, которое определяется по формуле:
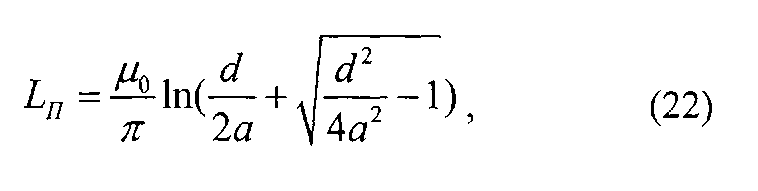
где µ0 - магнитная постоянная, а - радиус провода, d - расстояние между проводами.
Параметром, определяющим потери энергии, связанные с прохождением в электрической цепи тока проводимости, является сопротивление R. В простейшем случае проводника длинной l и с постоянным сечением S его сопротивление будет:

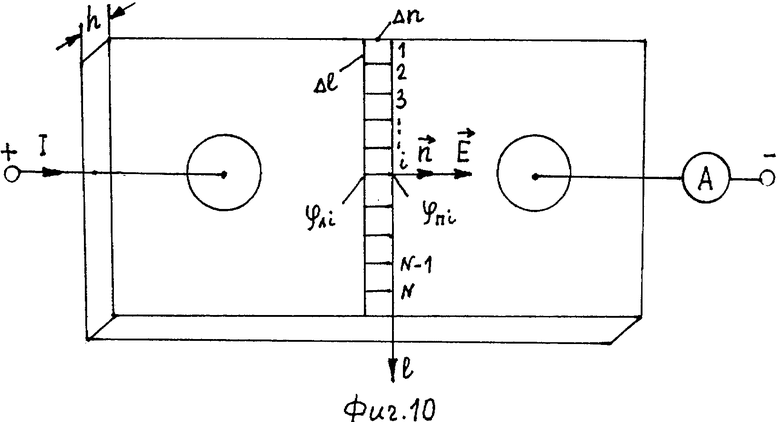
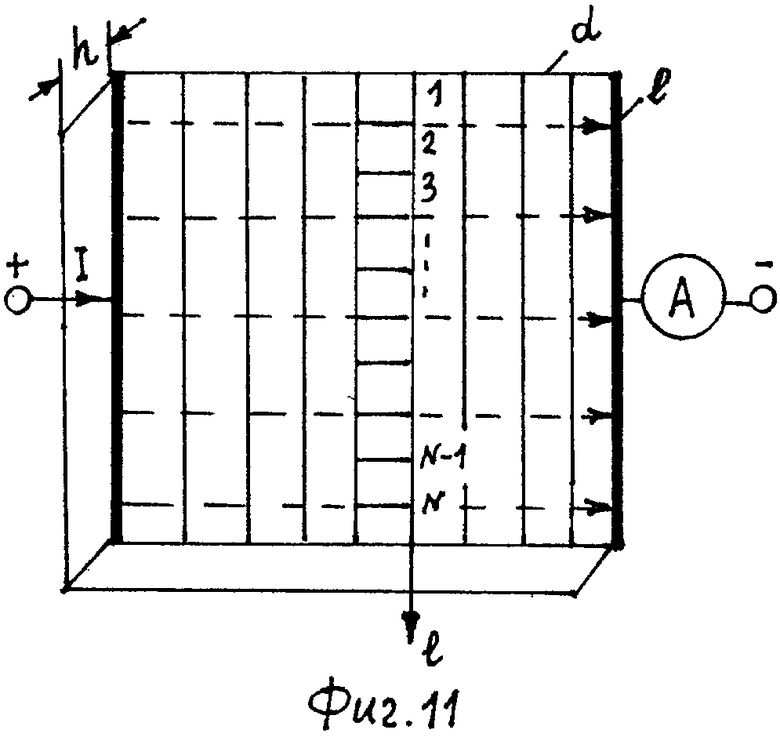
Будем рассматривать сопротивление системы двух электродов, моделирующих двухпроводную линию разделенных листом ЭПБ толщиной h с удельным электрическим сопротивлением ρ, значительно большим сопротивления материала электродов (фиг.10). Для нахождения сопротивления листа ЭПБ по формуле (23) необходимо предварительно рассчитать ее удельное электрическое сопротивление ρ. Для этого воспользуемся законами Ома в дифференциальной и интегральной формах. Сила тока I через замкнутую поверхность S равна потоку через эту поверхность вектора плотности тока 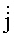
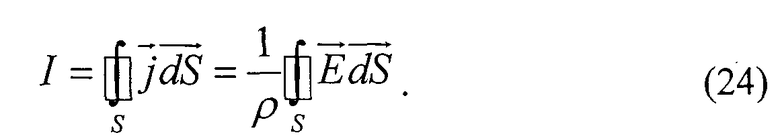
Отсюда 
где En - проекция вектора 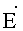
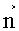
Интеграл в выражении (25) был ранее найден численным методом и определялся по формуле (6), тогда окончательная формула (25) для определения удельного электрического сопротивления имеет вид:
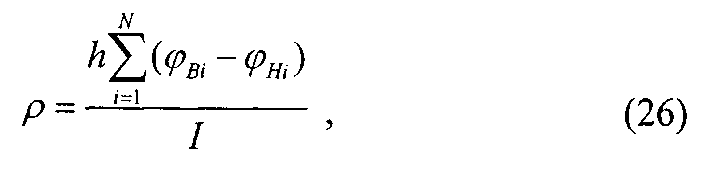
где φBi - потенциал, измеряемый в i-й точки внутреннего контура кругового кольца; φHi - потенциал, измеряемый в i-й точки наружного контура кругового кольца; N - число точек на контуре L; h - толщина ЭПБ; I - ток, протекающий по листу ЭПБ, который может быть измерен амперметром.
Таким образом, при определении емкости С (7) и индуктивности L (20), погонной емкости СП (8) и индуктивности LП (21), а также удельного электрического сопротивления ρ (26) вычисляем с помощью кругового кольца сумму 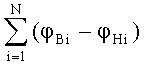
Ток, протекающий через поперечное сечение любого листа ЭПБ, зависит от отношения 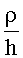
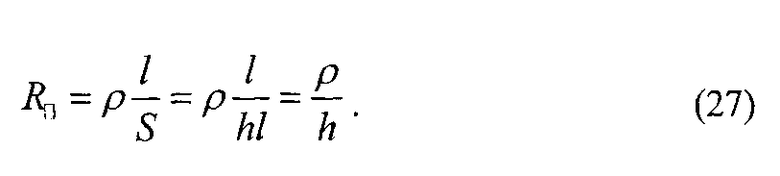
На фиг.11 сплошными линиями показаны линии равного потенциала, а пунктирными линиями - силовые линии. Так как напряженность поля направлена перпендикулярно к изопотенциальным линиям и в сторону убывания потенциала, то, зная расположение изопотенциальных линий, можно сразу представить, как направлен вектор 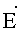
Для построения полной сетки поля в однородном поле, где изопотенциальные линии параллельны друг другу, достаточно провести ряд прямых, перпендикулярных к изопотенциальным линиям, отстоящих друг от друга на равных расстояниях.
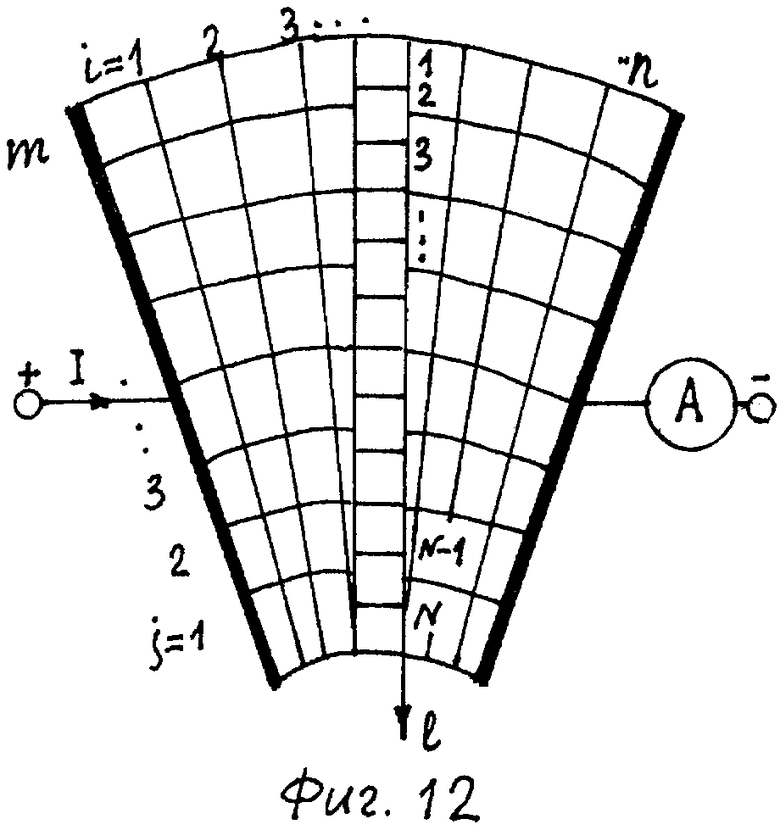
В неоднородном поле построение полной сетки поля сложнее. На фиг.12 изображен криволинейный четырехугольный лист ЭПБ. Он образован пересечением двух концентрических окружностей и двух радиальных прямых, вдоль которых расположены электроды. С помощью дополнительных окружностей и прямых криволинейный лист можно разбить на более мелкие квадраты (фиг.12).
Пусть интервал потенциала, с которым построены изопотенциальные линии, составляет U/n, где n - число равных интервалов потенциала, U - напряжение, приложенное к электродам. Тогда каждая трубка равного тока будет состоять из n квадратов с сопротивлением R⌷ соединенных последовательно, и ее сопротивление будет равно n R⌷.
Если число трубок равного тока, соединенных между собой параллельно, равно т, то общее сопротивление криволинейного листа (фиг.12) составит:

Таким образом, для определения сопротивления криволинейного листа (фиг.12) нужно знать числа n и m. Число n выбираем заранее. Нет необходимости строить сетку поля на всем криволинейном листе и даже не нужно проводить все изопотенциальные линии. Достаточно найти расположение двух соседних изопотенциальных линий, одной из которых может служить питающий электрод и разбить ограниченную ими полоску на квадраты. Очевидно, что число этих квадратов будет равно m. В случае любой прямоугольной фигуры ЭПБ отношения n/m равно отношению длинны l к ее ширине d и получим формулу:

При исследовании сетки поля становится ясным, что сопротивление листа ЭПБ определяется строением поля, которое в свою очередь зависит от его формы. Построив сетку поля, легко установить, какие именно участки листа ЭПБ в основном определяют его сопротивление и каких изменений сопротивления листа ЭПБ можно ожидать при том или ином изменении его формы.
При обсуждении связи между сопротивлением листа ЭПБ и сеткой поля следует подчеркнуть, что эта связь позволяет понять физический смысл зависимости сопротивления проводника от его формы в самом общем случае. С этой точки зрения, изучения сеток поля имеет практическое значение.
На листах ЭПБ произвольной формы можно снять зависимости напряженности электрического поля от расстояния вдоль стороны прямолинейной полоски, содержащей N точек. Напряженность электрического поля в i-x точках определяем численным методом по формуле:

где i=1,2,…,N; Δφi=φЛi-φПi; φЛi, φПi - потенциалы соответственно левой и правой сторон прямолинейной полоски шириной Δn в i-й точке (фиг.10).
На листах ЭПБ любой формы можно определить подвижность электронов по формуле:

где 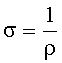
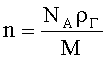
На листах электропроводящей бумаги любой формы можно также определить в i-м объеме прямоугольного параллелепипеда (малого объема ΔVi=hΔlΔn, фиг.10-12) скорость дрейфа электронов:

плотность тока:

ток:
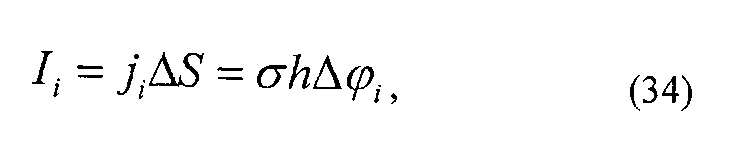 удельную тепловую мощность тока (по закону Джоуля-Ленца в дифференциальной форме):
удельную тепловую мощность тока (по закону Джоуля-Ленца в дифференциальной форме):

и тепловую мощность тока:

Результирующий ток, протекающий по листам электропроводящей бумаги любой формы, можно вычислить по формуле:
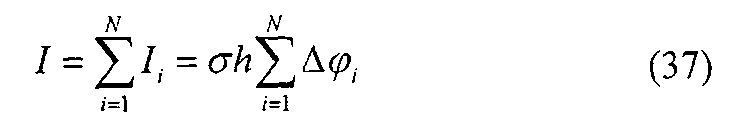
и сравнить с показаниями амперметра установки.
Рассмотрим состав и работу предлагаемой установки (фиг.2). Она включает в себя планшет 1, на части площади которого уложен большой лист электропроводящей бумаги 2 и на котором установлена пара электродов круглого сечения 3. Электроды 3 расположены на противоположных сторонах большого листа 2. На планшете 1 уложены малые листы электропроводящей бумаги 4.1, 4.2 и 4.3, создающие сопротивления R/2, R и 2R. На эти листы установлены пары электродов прямоугольного сечения 5.1, 5.2 и 5.3 соответственно для каждого малого листа электропроводящей бумаги 4.1, 4.2 и 4.3. Электроды каждой пары установлены на противоположных сторонах этих листов.
На планшете 1 также уложен криволинейный четырехугольный лист электропроводящей бумаги 6. Он образован пересечением двух концентрических окружностей и двух радиальных прямых. На листе 6 установлена пара электродов прямоугольного сечения 7, электроды которой расположены на противоположных сторонах листа 6 вдоль радиальных прямых.
Установка содержит зонд 8, потенциометр 9, соединенный двумя концевыми контактами с источником постоянного тока 10, амперметр 11, первый ввод которого соединен с движком потенциометра 9.
Для измерения потенциалов на электропроводящей бумаге введен вольтметр с большим входным сопротивлением 12, первый ввод которого соединен со вторым вводом амперметра 11, а второй его ввод - с зондом 8.
Для подключения вольтметра с большим входным сопротивлением 12, а также амперметра 11 через зонд 8 к соответствующим листам электропроводящей бумаги 2, 4.1, 4.2, 4.3 и 6 служит переключатель 13, общий контакт которого соединен со вторым вводом амперметра 11, а другие контакты его соединены с первыми электродами соответственно большого листа электропроводящей бумаги 2, малых листов электропроводящей бумаги 4.1, 4.2, 4.3 и криволинейного четырехугольного листа электропроводящей бумаги 6, при этом, вторые электроды листов электропроводящей бумаги 2, 4.1, 4.2, 4.3 и 6 соединены с одним из концевых контактов потенциометра 9.
При измерении потенциалов в требуемых точках большого листа электропроводящей бумаги 2 применяется круговое кольцо 14, изготовленное из диэлектрика с нанесенной разметкой на его внутреннем и наружном контурах. Круговое кольцо 14 насажено на один из пары электородов круглого сечения 3 и уложено на большом листе электропроводящей бумаги 2.
На всех листах электропроводящей бумаги 2, 4.1, 4.2, 4.3 и 6 уложены симметрично между электродами прямолинейные полоски соответственно 15.1, 15.2, 15.3, 15.4 и 15.5, изготовленные из диэлектрика с нанесенной разметкой с обеих сторон. Они применяются при измерении потенциалов в требуемых точках на всех листа электропроводящей бумаги.
Рассмотрим работу предлагаемого устройства (фиг.2) в первом положении «L,C» переключателя 13. В этом положении проводим исследование емкости и индуктивности системы двух бесконечно длинных проводников. Эта система моделируется с помощью пары электродов круглого сечения 3, плотно прижатых винтами к большому листу электропроводящей бумаги 2. С помощью потенциометра 9 устанавливаем напряжение U между парой электродов круглого сечения 3, которое измеряем с помощью вольтметра с большим входным сопротивлением 12, прикасаясь зондом 8 ко второму электроду круглого сечения 3. С помощью амперметра 11 измеряем величину тока I, протекающего по листу электропроводящей бумаги 2.
Прикасаясь зондом 8 в i-х точках кругового кольца 14 измеряем вольтметром с большим входным сопротивлением 12 потенциалы внутреннего контура кругового кольца 14 φBi и потенциалы наружного контура кругового кольца φHi. По формулам (7) и (8) соответственно рассчитываем емкость С бесконечно малого отрезка моделируемой двухпроводной линии равного толщине электропроводящей бумаги и погонную емкость Сn этой линии. По формулам (20) и (21) соответственно рассчитываем индуктивность L и погонную индуктивность Ln этой линии. Полученные экспериментальным путем значения Сn и Ln сравниваем с теоретическими значениями, которые определяются по формулам (9) и (22).
Во втором «R/2»; третьем «R»; четвертом «2R» положениях переключателя 13 исследуем сопротивление соответственно малых листов электропроводящей бумаги, создающих сопротивления R/2, R и 2R. В пятом <<K>> положении переключателя 13 исследуем сопротивление криволинейного четырехугольного листа электропроводящей бумаги 6. Во всех случаях используем значение удельного электрического сопротивления ρ, полученного в первом положении «L,C» переключателя 13 и рассчитанное по формуле (26). По формуле (27) определяем сопротивление квадратного листа. Сопротивление криволинейного четырехугольного листа электропроводящей бумаги 6 определяем по формуле (28). Сопротивления малых листов электропроводящей бумаги 4.1, 4.2 и 4.3, создающих сопротивление R/2, R и 2R, рассчитываем по формуле (29).
На листах электропроводящей бумаги любой формы определяем по формуле (31) подвижность электронов. На всех листах электропроводящей бумаги 2, 4.1, 4.2, 4.3 и 6 снимаем зависимости напряженностей электростатического поля от расстояния вдоль соответствующих прямолинейных полосок 15.1, 15.2, 15.3, 15.4 и 15.5. Напряженности электрического поля в i-x точках применяемых полосок определяем по формуле (30).
На листах электропроводящей бумаги любой формы определяем в i-м малом объеме ΔVi скорость дрейфа электронов υдрi по формуле (32), плотность тока ji по формуле (33), ток Ii по формуле (34), удельную тепловую мощность тока Рудi, по формуле (35) и тепловую мощность тока Р по формуле (36). Результирующий ток, протекающий по листу электропроводящей бумаги во всех положениях переключателя 13, рассчитываем по формуле (37) и сравниваем с показаниями амперметра 11.
| название | год | авторы | номер документа |
|---|---|---|---|
| Установка для исследования электроёмкости проводников на модели из электропроводящей бумаги | 2016 |
|
RU2621599C1 |
| УСТАНОВКА ДЛЯ РЕШЕНИЯ ТРЕТЬЕГО УРАВНЕНИЯ МАКСВЕЛЛА | 2016 |
|
RU2644098C2 |
| УСТАНОВКА ДЛЯ ИССЛЕДОВАНИЯ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ МЕТОДОМ МОДЕЛИРОВАНИЯ | 2012 |
|
RU2507590C1 |
| УСТАНОВКА ДЛЯ ИССЛЕДОВАНИЯ СТАЦИОНАРНОГО ЭЛЕКТРИЧЕСКОГО ПОЛЯ | 2013 |
|
RU2534979C1 |
| УСТАНОВКА ДЛЯ ИССЛЕДОВАНИЯ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ | 2012 |
|
RU2504017C2 |
| УСТАНОВКА ДЛЯ МОДЕЛИРОВАНИЯ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ НА ГРАНИЦЕ РАЗДЕЛА ДВУХ ДИЭЛЕКТРИКОВ | 2015 |
|
RU2616915C2 |
| УСТАНОВКА ДЛЯ МОДЕЛИРОВАНИЯ ДВИЖЕНИЯ ЖИДКОСТИ ИЛИ ГАЗА НА ЭЛЕКТРОПРОВОДЯЩЕЙ БУМАГЕ | 2015 |
|
RU2606335C2 |
| УСТРОЙСТВО ДЛЯ ОПРЕДЕЛЕНИЯ ЦИРКУЛЯЦИИ ВЕКТОРА НАПРЯЖЕННОСТИ ЭЛЕКТРИЧЕСКОГО И МАГНИТНОГО ПОЛЯ | 1998 |
|
RU2137209C1 |
| УСТАНОВКА ДЛЯ ИССЛЕДОВАНИЯ ВИХРЕВОГО ЭЛЕКТРИЧЕСКОГО ПОЛЯ | 2012 |
|
RU2504016C2 |
| УСТАНОВКА ДЛЯ ИССЛЕДОВАНИЯ СТАЦИОНАРНОГО ЭЛЕКТРИЧЕСКОГО ПОЛЯ | 2011 |
|
RU2479868C1 |
Изобретение относится к учебным приборам по физике. Малые листы электропроводящей бумаги создают сопротивления R/2, R, 2R и уложены на планшете. Пары электродов прямоугольного сечения для каждого малого листа электропроводящей бумаги установлены на противоположных сторонах этих листов. Криволинейный четырехугольный лист электропроводящей бумаги образован пересечением двух концентрических окружностей и двух радиальных прямых и уложен на планшете. Первый ввод вольтметра с большим входным сопротивлением соединен со вторым вводом амперметра, в второй его ввод - с зондом. Общий контакт переключателя соединен со вторым вводом амперметра, а другие контакты его соединены с первыми электродами соответственно большого, малого и криволинейного четырехугольного листов электропроводящей бумаги. Вторые электроды всех названных листов электропроводящей бумаги соединены с одним из концевых контактов потенциометра. Круговое кольцо изготовлено из диэлектрика с нанесенной разметкой на внутреннем и наружном контурах, насажено на один из электродов круглого сечения и уложено на большом листе электропроводящей бумаги. Полоски, изготовленные из диэлектрика с нанесенной разметкой с обеих сторон, уложены симметрично между электродами на всех листах электропроводящей бумаги. Техническим результатом изобретения является упрощение конструкции и повышение точности измерений. 12 ил.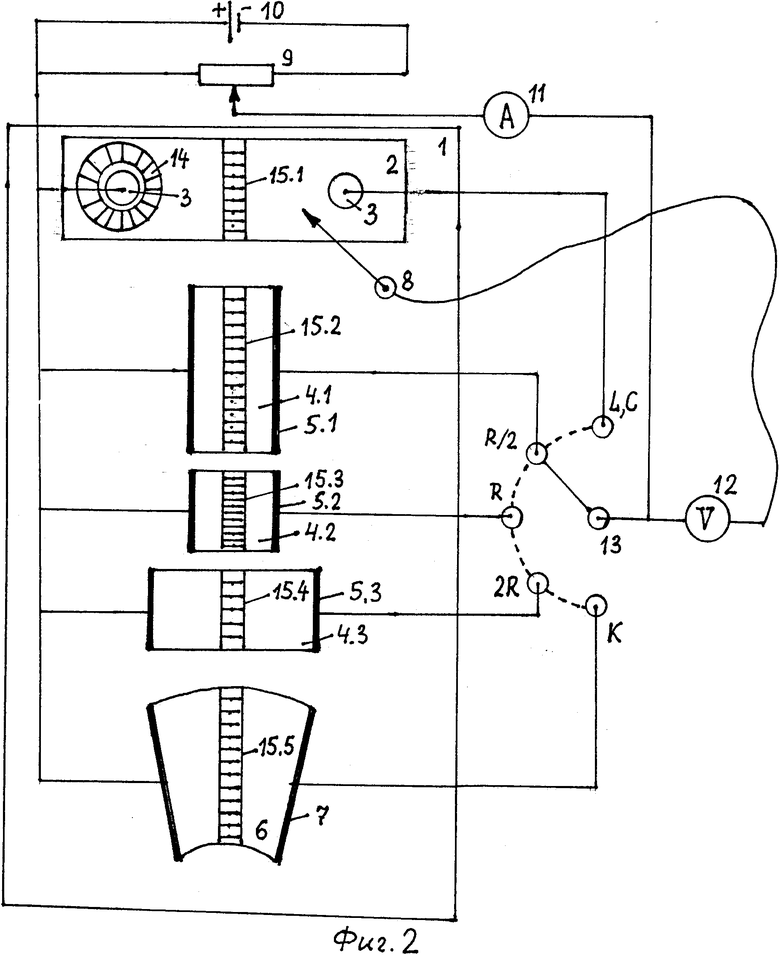
Установка для исследования пассивных элементов электрических цепей, содержащая зонд, потенциометр, соединенный двумя концевыми контактами с источником постоянного тока, планшет, большой лист электропроводящей бумаги прямоугольной формы, уложенный на планшете, пару электродов круглого сечения, электроды которой установлены на противоположных сторонах большого листа электропроводящей бумаги, при этом второй электрод круглого сечения соединен с одним из концевых контактов потенциометра, амперметр, первый ввод которого соединен с движком потенциометра, отличающаяся тем, что в нее введены малые листы электропроводящей бумаги прямоугольной формы, создающие сопротивление R/2, R, 2R и уложенные на планшете, пары электродов прямоугольного сечения для каждого малого листа электропроводящей бумаги, электроды которых установлены на противоположных сторонах этих листов, криволинейный четырехугольный лист электропроводящей бумаги, образованный пересечением двух концентрических окружностей и двух радиальных прямых, уложенный на планшете, пара электродов прямоугольного сечения для криволинейного четырехугольного листа электропроводящей бумаги, электроды которой установлены на противоположных сторонах этого листа вдоль радиальных прямых, вольтметр с большим входным сопротивлением, первый ввод которого соединен со вторым вводом амперметра, а второй его ввод - с зондом, переключатель, общий контакт которого соединен со вторым вводом амперметра, а другие контакты его соединены с первыми электродами соответственно большого, малых и криволинейного четырехугольного листов электропроводящей бумаги, при этом вторые электроды малых и криволинейного четырехугольного листов электропроводящей бумаги соединены со вторым электродом круглого сечения большого листа электропроводящей бумаги, круговое кольцо, изготовленное из диэлектрика с нанесенной разметкой на внутреннем и наружном контурах, которое насажено на один из электродов круглого сечения и уложено на большом листе электропроводящей бумаги, полоски, изготовленные из диэлектрика с нанесенной разметкой с обеих сторон и уложенные симметрично между электродами на всех листах электропроводящей бумаги.
| Лабораторный практикум по физике / Под ред | |||
| К.А | |||
| Барсукова и Ю.И | |||
| Уханова | |||
| - М.: Высшая школа, 1988, с.109, рис.38 | |||
| УСТАНОВКА ДЛЯ ИЗУЧЕНИЯ ВИХРЕВОГО ЭЛЕКТРИЧЕСКОГО ПОЛЯ | 2005 |
|
RU2284580C1 |
| УСТАНОВКА ДЛЯ ИССЛЕДОВАНИЯ НАГРУЗОЧНЫХ ХАРАКТЕРИСТИК ИСТОЧНИКА ТОКА | 2006 |
|
RU2308095C1 |
| УСТАНОВКА ДЛЯ ИССЛЕДОВАНИЯ СТАЦИОНАРНОГО ЭЛЕКТРИЧЕСКОГО ПОЛЯ | 2005 |
|
RU2284581C1 |
| US 4971562 A, 20.11.1990. | |||
Авторы
Даты
2014-02-20—Публикация
2012-07-10—Подача