Задача изобретения
Настоящее изобретение относится к способу для кодирования первого потока данных, имеющему результатом второй кодированный поток данных, и способу для декодирования этого второго потока данных, при этом кодирование является результатом сравнения первого потока данных с третьим потоком данных, сформированным псевдослучайной последовательностью посредством операции сравнения Исключающее ИЛИ (XOR). В частности, изобретение относится к способам, основанным на способах гиперхаотического кодирования для генерирования псевдослучайных последовательностей, используемых при кодировании и декодировании.
Уровень техники
Настоящее изобретение охватывается областью кодирования потоков информации в безопасной связи. В частности, оно охватывается областью способов, основанных на гиперхаотических системах, некоторые из которых известны в области техники.
В простом случае связи, когда сообщение отправляют от передатчика A приемнику B, сообщение кодируется таким способом, что A и B могут выполнять кодирование и декодирование, соответственно.
Кодированную информацию называют шифром или зашифрованным сообщением и отправляют через канал связи. Сообщение сформировано битовым потоком любой длины, и A и B генерируют двоичную последовательность для кодирования и декодирования, соответственно. Эти двоичные последовательности представляют собой последовательности шифрования.
Если сообщение от A зашифровано посредством выполнения двоичной операции XOR, таблица которой показана в таблице 1, с помощью последовательности шифрования для A, исходное сообщение восстанавливается в B, если последовательность шифрования, примененная в A, является такой же, как последовательность шифрования, примененная в B.
Таблица XOR
Изобретение основано на материалах, опубликованных в диссертации этого же автора "Vidal, G. Sincronización y control de sistemas dinamicos en régimen de caos espacio-temporal (Синхронизация и управление динамическими системами в пространственно-временном хаосе) (докторская диссертация, университет Navarra, Испания, 2010)", подробно описывающей способ для получения случайных последовательностей на основе гиперхаотических систем и последовательностей, генерируемых из динамической системы.
Динамическая система - это система, состояние которой меняется с течением времени. Поведение в упомянутом состоянии может быть смоделировано посредством определения уравнений поведения системы после идентификации включенных в нее элементов и их отношений. Динамическая система, смоделированная посредством дифференциального уравнения или системы дифференциальных уравнений, позволяет описывать ее с точки зрения ее поведения через решение упомянутого уравнения или системы уравнений. В частности, возможно выразить задачу дифференциального уравнения первого порядка с начальными условиями в виде x'(t)=f(t, x(t)), где x(t) - решение системы как функция времени t, и где начальные условия представляют собой x(t0)=x0. Если вместо обычного дифференциального уравнения система требует использование большего количества переменных, тогда x является векторной переменной, принадлежащей пространству Rn, где n - размерность системы уравнений, и где каждый компонент вектора x является переменной как функция времени.
Хаотическая криптография основана на использовании теории хаоса в безопасных системах связи. Теория хаоса изучает детерминированные системы с высокой чувствительностью ответа к малому изменению в начальных условиях.
Системы A и B синхронизируются, когда начинается кодирование. Это означает, что в них обеих генерируется одна и та же случайная последовательность, чтобы позволить кодировать и декодировать сообщение с использованием оператора XOR на обоих концах связи. Если эта синхронизация не происходит, то декодированное сообщение не будет являться первоначально кодированным сообщением.
Способ, описанный в упомянутом выше документе диссертации, предлагает способ для генерирования случайных последовательностей, в котором обе системы A и B решают соответствующие системы дифференциальных уравнений. Цель состоит в том, чтобы отыскать некоторое шифрование, подчиняющееся теоретическому подходу К.Э.Шеннона "Shannon, C. E. [1949] "Communication Theory of Secrecy Systems" ("Теория связи в секретных системах") Bell System Technical Journal 28, pp. 656-715", формулирующему, что необходимое и достаточное условие того, чтобы сообщение подчинялось требованию "совершенной криптостойкости", состоит в том, чтобы шифрование вероятностно не зависело от сообщения, и поэтому вероятностный подход не может быть использован для обнаружения свойств сообщения. Другое важное заключение, сделанное Шенноном, состоит в том, что если длина ключа не представляет неудобства, шифр Вернама является самым подходящим. Шифр Вернама имеет 3 фундаментальных особенности:
1. Ключ, в данном случае последовательность шифрования, должен иметь такую же длину, как сообщение, которое должно быть зашифровано.
2. Когда ключ был использован, он не может использоваться снова. По этой причине шифр Вернама также называют "схемой одноразовых блокнотов".
3. Ключ составлен из списка случайных однородно распределенных символов.
Первое свойство требует, чтобы ключ был достаточно длинным. Теоретически при использовании хаотической динамической системы траектории могут быть настолько длинными, насколько необходимо, никогда не становясь периодическими. Невозможно иметь последовательность бесконечной длины в компьютере, но с достаточной точностью может быть реализовано интегрирование по периодам времени без ошибок округления, влияющих на способ, и чтобы эти периоды времени были достаточно длинны, как требуется в рассматриваемых случаях.
Второе свойство может быть легко достигнуто посредством программного обеспечения, запрещающего повторение значений начальных условий.
Особый случай методики шифрования и дешифрования, описанный в документе диссертации, устанавливает две спаренные системы дифференциальных уравнений, связанные с задачей с начальными условиями. Эти системы уравнений, одна из которых используется для генерирования ключа шифрования, и другая для генерирования ключа дешифрования, являются такими, что даже если они исходят из разных начальных условий, они заканчивают изменение в соответствии с одним и тем же решением после их интегрирования по определенному периоду времени вследствие спаренных членов.
Имеется два варианта для выполнения спаривания, гарантирующего аутентичность концов связи: либо значения спаривающих параметров динамической системы являются открытыми, и имеется третий объект для обеспечения возможности аутентификации приемника сообщения, либо значениями динамических параметров обмениваются через безопасный канал, например, с использованием ключей RSA (Rivest, Shamir and Adleman) или ключей Диффи-Хеллмана.
Второе свойство также может быть достигнуто программным обеспечением, запрещающим повторение спаривающих коэффициентов.
В большинстве известных случаев в области техники эти два свойства влекут за собой пересылку громоздких ключей через каналы связи, и затраты слишком высоки. Однако в примере, описанном в документе диссертации, передается только одно множество параметров. Эти параметры обеспечивают доступ к множеству ключей, количество которых равно количеству "дискретных" точек, найденных в фазовом пространстве, в котором заключены траектории. Однако, чтобы знать конкретный ключ, необходимо выполнить процесс синхронизации между системами A и B; то есть, необходимо интегрировать обе системы достаточно долго, чтобы полагать, что решения, полученные в обеих системах как функция времени, являются одинаковыми, или их различие ниже очень небольшого порогового значения или значения, известного как "машинная ошибка", если работа выполняется с помощью компьютера.
Третье свойство требует случайных сигналов; однако начальная точка является детерминированной системой. Динамические свойства системы и процесс отбеливания (“whitening”) сигнала используются для выполнения этого процесса. Одна из основных проблем непрерывных детерминированных сигналов, и даже гиперхаотических сигналов, состоит в том, насколько легко они могут быть отслежены. Это означает, что шпион может более или менее правильно оценить следующие значения сигнала, обладая знанием о предыдущих моментах. Поэтому возможный шпион может ограничить возможные начальные условия, пока наконец не раскроет ключ. Процесс отбеливания используется для предотвращения такой атаки. Документ диссертации описывает процесс отбеливания, который позволяет преобразовывать непрерывный сигнал в двоичный сигнал. Для начала требуются очень некоррелированные непрерывные сигналы, минимизирующие статистическую информацию зашифрованного сообщения.
Документ диссертации описывает способ, который основан на факте, что гиперхаотические системы имеют непрерывные сигналы, временная автокорреляция которых быстро теряется. С другой стороны, также требуется, чтобы генерирующая последовательность система была системой высокой размерности, поэтому периодическим орбитам труднее появиться в решении решаемой системы уравнений, что является типичной проблемой при работе с компьютерным хаосом. Если в решении для системы уравнений имеется периодичность, это помогает работе шпиона, поскольку он/она будет иметь временную опорную информацию для измерения статистики системы.
Другое требование, которому должен подчиняться способ для кодирования, состоит в том, чтобы гарантировать, что между зашифрованным сообщением и исходным сообщением нет биективной функции, или что известно в криптографии как проблема обратной функции. С этой целью используется способ отбеливания сигнала, устраняющий большую часть информации фазы и амплитуды. Таким образом, функция, связывающая сообщение и шифр, больше не будет биективной, и поэтому один и тот же зашифрованный поток битов может иметь разные значения. Однако, поскольку две системы синхронизированы, они всегда будет иметь одно и то же незашифрованное сообщение.
Основной технической проблемой способа отбеливания сигнала, предложенного документом диссертации, являются высокие вычислительные затраты в дополнение к факту, что абсолютно некоррелированная псевдослучайная последовательность не генерируется.
Описание изобретения
Настоящее изобретение решает описанную выше проблему посредством способа для генерирования псевдослучайной последовательности по пункту 1, способа для кодирования потока данных или декодирования кодированного потока данных по пункту 11, кодера сообщений по пункту 14, декодера зашифрованных сообщений по пункту 15 и системы связи по пункту 16 формулы изобретения. Зависимые пункты определяют предпочтительные варианты осуществления изобретения.
Первым аспектом изобретения является способ для генерирования псевдослучайной последовательности, который содержит следующие этапы, на которых:
a) обеспечивают дифференциальное уравнение с начальным значением x'=f(x, t),
b) обеспечивают начальное значение для дифференциального уравнения x0=x(t0),
c) обеспечивают шаг интегрирования δt для дифференциального уравнения для временной дискретизации tk=t0+k⋅δt, k=1, 2, 3, …,
d) выполняют численное интегрирование дифференциального уравнения от начального значения и с шагом δt для получения приближения для решения xk=x(tk),
e) генерируют первую последовательность значений посредством выборки значений xk, представимую в числовой форме с плавающей запятой в виде 0,d0d1d2d3d4...dr...dw⋅10e, где e - показатель степени, w - длина мантиссы, d0 - старший разряд мантиссы, и dr - некоторый разряд, который вместе с разрядами слева от него в приближении для решения xk совпадает с точным значением решения дифференциального уравнения,
f) генерируют псевдослучайную последовательность с разрядами di...dr из набора последовательности значений xk, где i - предопределенное целочисленное значение, удовлетворяющее 0<i≤r.
Первым этапом для начала генерирования псевдослучайной последовательности является установление динамической системы, которая будет использоваться для генерирования псевдослучайной последовательности для шифрования. Динамическая система определяется дифференциальным уравнением с решением x(t), сокращенно x. После обеспечения начального значения и этапа интегрирования, полученного в результате временной дискретизации для интегрирования задачи с начальными условиями, дифференциальное уравнение от начального значения численно интегрируется для вычисления решения x(t). Другими словами, последовательность фактических значений xk получается посредством вычисления численного решения x(t) уравнения x'=f(x, t) при условии начального значения x0=x(t0) для каждого момента tk=t0+k⋅δt, k=1,2,3,...
Значения последовательности xk могут быть представлены с плавающей запятой, причем упомянутое представление может быть выражено как xk=0,d0d1d2d3d4...dr...dw⋅10e, где e - показатель степени, w - длина мантиссы, d0 - старший разряд мантиссы, и dr - некоторый разряд, который вместе с разрядами слева от него в приближении для решения xk совпадает с точным значением решения дифференциального уравнения. Когда это сделано, генерируется псевдослучайная последовательность с разрядами di...dr из набора последовательности значений xk, где i - предопределенное целочисленное значение, удовлетворяющее условию 0<i≤r; то есть, используются разряды фактического числа, которые соответствуют следующим требованиям:
- они принадлежат мантиссе,
- они являются разрядами, совпадающими с точным решением xk,
- они не являются старшими.
Выбор из набора xk имеет результатом совокупность значений, которые будут более некоррелированными, когда они будут больше разнесены на временной шкале.
Последнее свойство - не являться старшими разрядами фактического числа xk - обеспечивает преимущество генерирования последовательности значений, которые не коррелированы относительно друг друга, в самое короткое возможное время. После устранения зависимости между старшими разрядами получается последовательность, значения которой являются некоррелированными.
В соответствии с уровнем техники, чтобы уменьшить степень корреляции среди выборок, расстояние межу элементами набора xk увеличивается. Дистанцирование элементов части xk включает в себя оценку многих промежуточных точек посредством численного интегрирования до получения новой выборки xk. В свою очередь интегрирование на каждом из этапов влечет за собой высокие вычислительные затраты вследствие требуемого количества промежуточных функций и вычислений.
Напротив, даже при том, что изобретение сокращает количество разрядов, используемых для генерирования потока данных для кодирования или декодирования, оно позволяет радикально уменьшить расстояние в функции времени между выборками xk набора. Другими словами, для одного и того же интегрирования используется большее количество выборок, что значительно увеличивает объем случайных некоррелированных разрядов, генерируемых при тех же самых вычислительных затратах.
Вторым аспектом изобретения является способ для кодирования потока данных для передачи упомянутых данных посредством кодированного потока, в котором кодирование является результатом сравнения потока данных со вторым потоком данных, сформированным с помощью псевдослучайной последовательности посредством операции сравнения Исключающее ИЛИ (XOR), или способ для декодирования кодированного потока данных, в котором декодирование является результатом сравнения кодированного потока данных со вторым потоком данных, сформированным с помощью псевдослучайной последовательности посредством операции сравнения Исключающее ИЛИ (XOR), отличающийся тем, что генерирование псевдослучайной последовательности выполняется посредством способа в соответствии с первым аспектом изобретения.
Как разъяснено выше, последовательности, генерируемые в системах A и B, должны быть одинаковыми, чтобы после применения операции XOR на обеих сторонах связи в B было получено исходное сообщение. Посредством решения одного и того же дифференциального уравнения в обеих системах и генерирования псевдослучайной последовательности после одинаковых этапов это условие выполняется с одинаковыми преимуществами.
Третьим аспектом изобретения является кодер сообщений, подходящий для выполнения способа для кодирования потока данных для передачи упомянутых данных посредством кодированного потока, в котором кодирование является результатом сравнения потока данных со вторым потоком данных, сформированным псевдослучайной последовательностью посредством операции сравнения Исключающее ИЛИ (XOR), отличающийся тем, что генерирование псевдослучайной последовательности выполняется посредством способа в соответствии с первым аспектом изобретения.
Четвертым аспектом изобретения является декодер зашифрованных сообщений для выполнения способа для декодирования кодированного потока данных, в котором декодирование является результатом сравнения кодированного потока данных со вторым потоком данных, сформированным псевдослучайной последовательностью посредством операции сравнения Исключающее ИЛИ (XOR), отличающийся тем, что генерирование псевдослучайной последовательности выполняется посредством способа в соответствии с первым аспектом изобретения.
Пятым аспектом изобретения является система связи, включающая в себя по меньшей мере один кодер в соответствии с третьим аспектом изобретения и по меньшей мере один декодер в соответствии с четвертым аспектом изобретения.
В конкретном варианте осуществления системой связи является система мобильной связи. Начальное значение x0 обеспечивается обеим системам от центра связи. Например, если A и B являются мобильными терминалами, этот центр связи может быть основан на базовой приемопередающей станции (BTS). В этом варианте осуществления одинаковые случайные последовательности генерируются на обоих концах системы, чтобы обеспечить возможность восстановления исходного сообщения посредством применения оператора XOR. Эти последовательности являются одинаковыми, поскольку решается одно и то же дифференциальное уравнение с одним и тем же начальным значением.
Описание чертежей
Упомянутые выше и другие преимущества и признаки изобретения будут лучше понятны на основе последующего подробного описания предпочтительного варианта осуществления со ссылкой на приложенные чертежи, представленные посредством иллюстративного и не ограничивающего примера.
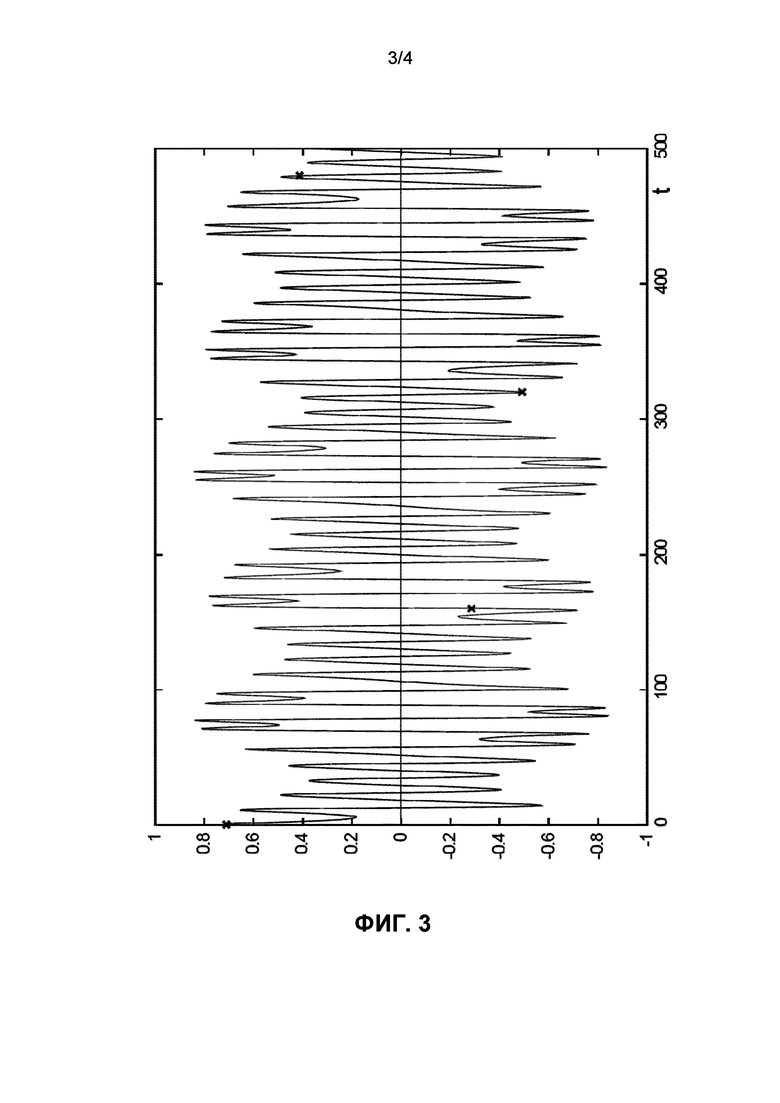
Фиг. 1 иллюстрирует вариант осуществления связи между двумя терминалами A и B и элементы, участвующие в кодировании.
Фиг. 2 изображает вариант осуществления решения дифференциального уравнения x'=f(x, t).
Фиг. 3 изображает дискретизированные и некоррелированные значения, отмеченные посредством X.
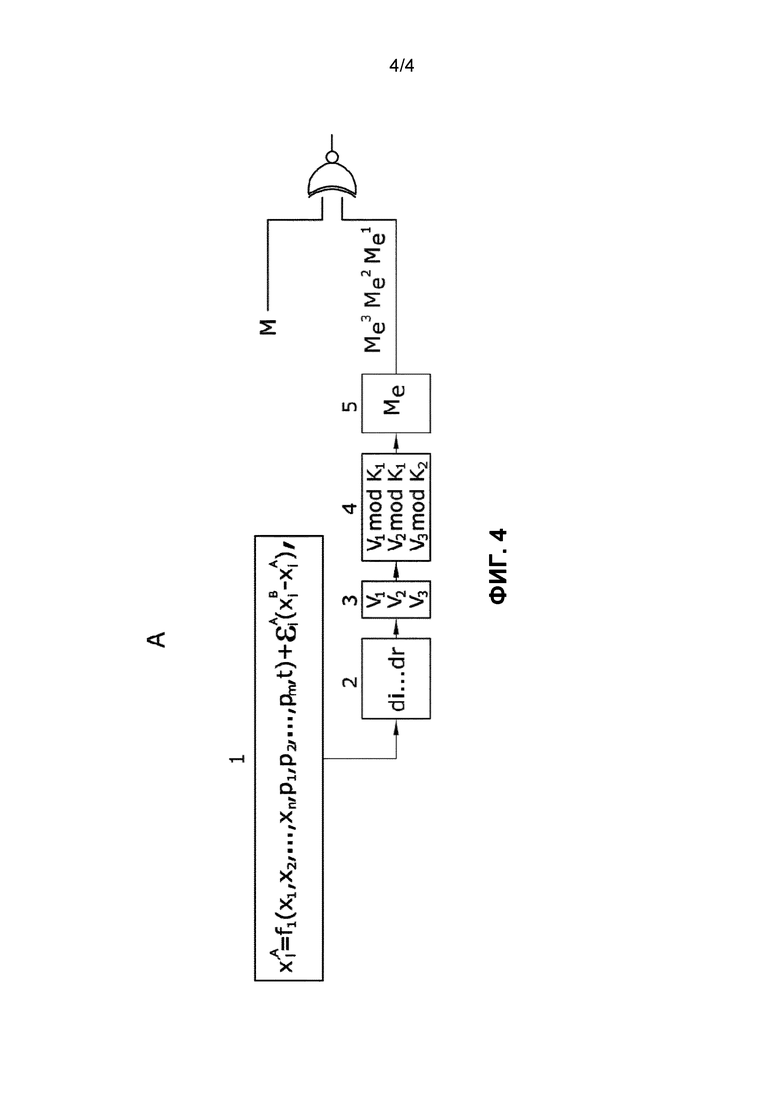
Фиг. 4 изображает конкретный вариант осуществления системы, в котором среди других проиллюстрированы разные функциональные элементы, такие как модуль, решающий систему дифференциальных уравнений, которые могут быть выражены в форме x's=fs(x1, x2,..., xn, p1, p2,..., pm, t), s=1,..., n, модуль, выбирающий диапазон разрядов каждого xk и модуль генератора, генерирующий строки матрицы, известной как матрица расширения Me.
Подробное описание изобретения
Настоящее изобретение применяется в процессах для кодирования сообщений при передаче между двумя концами в системе связи. Таким образом, как проиллюстрировано на фиг. 1, сообщение (M) кодируется в первом конце связи (A) с использованием оператора XOR с помощью последовательности шифрования (S). Зашифрованное сообщение (M XOR S) отправляют через канал передачи. Зашифрованное сообщение декодируется на противоположном конце связи (B) посредством применения оператора XOR снова. Изобретение сосредоточено на генерировании кодирующих последовательностей (S), которые идентичны на каждом конце связи, чтобы обеспечить возможность получения сообщения (M) посредством применения оператора XOR в B. Кодирующая последовательность (S) является псевдослучайной последовательностью.
Изобретение представляет способ для кодирования потока данных для передачи упомянутых данных посредством кодированного потока, в котором кодирование является результатом сравнения потока данных со вторым потоком данных, сформированным псевдослучайной последовательностью посредством операции сравнения Исключающее ИЛИ (XOR), отличающийся тем, что генерирование псевдослучайной последовательности содержит следующие этапы, на которых:
a) обеспечивают дифференциальное уравнение с начальным значением x'=f(x, t),
b) обеспечивают начальное значение для дифференциального уравнения x0=x(t0),
c) обеспечивают шаг интегрирования δt для дифференциального уравнения для временной дискретизации tk=t0+k⋅δt, k=1, 2, 3, …,
d) выполняют численное интегрирование дифференциального уравнения от начального значения и с шагом δt для получения приближения для решения xk=x(tk),
e) генерируют первую последовательность значений посредством выборки значений xk, представимую в числовой форме с плавающей запятой в виде 0,d0d1d2d3d4...dr...dw⋅10e, где e - показатель степени, w - длина мантиссы, d0 - старший разряд мантиссы, и dr - некоторый разряд, который вместе с разрядами слева от него в приближении для решения xk совпадает с точным значением решения дифференциального уравнения,
f) генерируют псевдослучайную последовательность с разрядами di...dr из набора последовательности значений xk, где i - предопределенное целочисленное значение, удовлетворяющее 0<i≤r.
Изобретение также представляет способ для декодирования кодированного потока данных посредством способа в соответствии с первым аспектом изобретения, в котором декодирование является результатом сравнения кодированного потока данных со вторым потоком данных, сформированным псевдослучайной последовательностью посредством операции сравнения Исключающее ИЛИ (XOR), отличающийся тем, что генерирование псевдослучайной последовательности содержит этапы a)-f) способа в соответствии с первым аспектом изобретения.
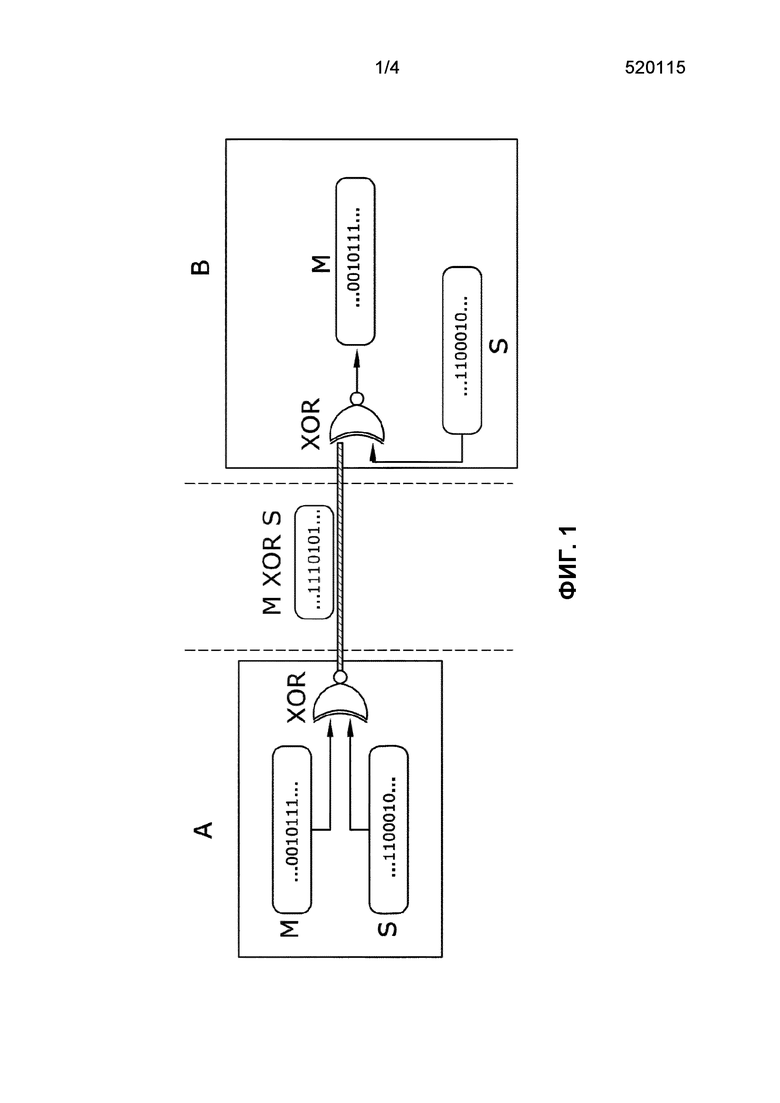
Иллюстрация на фиг. 2 используется в качестве варианта осуществления для описания описанных преимуществ, причем решение дифференциального уравнения x'=f(x, t) для некоторого конкретного начального значения изображено посредством непрерывной кривой. После выбора шага интегрирования получается численная аппроксимация посредством метода для интегрирования задач с начальными условиями, например, с использованием метода вычислений в явном виде.
Даже в этом случае значения решения между последовательными шагами являются высоко коррелированными, и необходимо выполнить много шагов интегрирования, чтобы позволить принять упомянутое значение для использования его разрядов для генерирования последовательности шифрования или дешифрования.
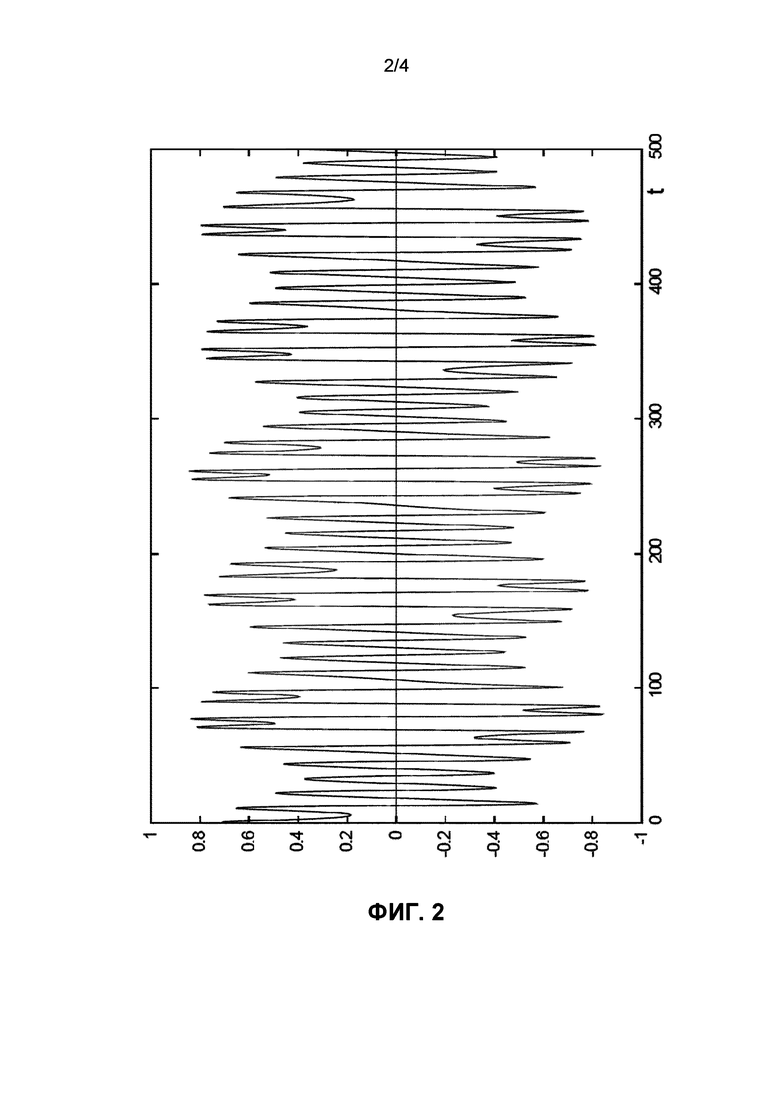
Одним примером является интегрирование задачи с начальными условиями, которая позволяет получить псевдослучайное решение, такое как показанное на фиг. 2, где проиллюстрировано временное пространство от 0 до 500 секунд. Выбраны три значения, извлеченные из значений, полученных в результате численного метода интегрирования, они выделены на фиг. 3 на кривой решения, полученного посредством того же самого метода интегрирования. Мантиссы этих трех значений следующее:
0,71(11)76 (для t=0 с)
-0,28(60)51 (для t=160 с)
-0,49(14)38 (для t=320 с).
Показатели степени каждого из трех значений были приняты во внимание только для того, чтобы установить, что первый разряд справа от десятичной запятой является первым ненулевым разрядом мантиссы.
В этой последовательности значений в круглые скобки были выделены разряды, слева от которых остаются старшие разряды, и справа от которых остаются разряды, на которые могут влиять ошибки округления вследствие архитектуры компьютера, на котором исполняется интегрирование.
Этот выбор менее значимых разрядов устраняет временную зависимость между значениями.
Хотя фактическое число может быть представлено во многих формах, способ рассматривает разряды, полученные в результате этого конкретного представления (независимо от показателя степени).
Способ, который использует множество разрядов, отбрасывая:
- старшие разряды и
- разряды, соответствующие ошибкам округления,
представляет собой метод выполнения изобретения с конкретным способом представления фактических значений (значений, принадлежащих к основной части фактических чисел), поскольку они также могут быть представлены в форме, указанной в этапе e) способа для кодирования потока данных, как описано выше.
Круглая скобка слева и круглая скобка справа находятся в позиции, оставляющей внутри них разряды di...dr, соответствующие этапу f) способа по пункту 1 формулы изобретения. В зависимости от каждого примера позиции круглых скобок, и поэтому диапазон разрядов di...dr, будут отличаться и будут предустановлены перед применением интегрирования.
Конкатенация разрядов в круглых скобках будет иметь результатом последовательность: 116014. Учитывая, что одно из преимуществ заявленного способа позволяет брать более близкие по времени выборки, возможно использовать больше значений, обеспечивающих разряды для генерирования последовательности для одного и того же диапазона времени, всегда проверяя свойства отсутствия корреляции.
В одном варианте осуществления изобретения в способах для кодирования и декодирования численное интегрирование на этапе d) выполняется не для дифференциального уравнения, а для системы из n дифференциальных уравнений с n неизвестными; то есть, x's=fs(x1, x2,..., xn, p1, p2,..., pm, t), s=1,..., n, где n - количество неизвестных, и содержащий m параметров pj, j=1,..., m, так что псевдослучайная последовательность на этапе f) генерируется из одной из n переменных, предварительно выбранных из системы дифференциальных уравнений. Система уравнений обеспечивает преимущество в том, что рассматриваемая переменная зависит от изменчивости других переменных, и поэтому менее вероятно, что шпион сможет успешно воспроизвести ту же самую псевдослучайную последовательность, чтобы дешифровать кодированное сообщение во время передачи от A к B.
В одном варианте осуществления способов выполняются следующие этапы, на которых:
- определяют время интегрирования T,
- предлагают возмущенную систему уравнений, которая может быть выражена следующим образом:
x'A1=f1(x1, x2,..., xn, p1, p2,..., pm, t)+εA1(xB1-xA1),
x'A2=f2(x1, x2,..., xn, p1, p2,..., pm, t)+εA2(xB2-xA2),
...
x'An = fn(x1, x2,..., xn, p1, p2,..., pm, t)+εAn(xBn-xAn),
для генерирования кодирующей последовательности, а также начальные значения; и,
- предлагают возмущенную систему уравнений, которая может быть выражена следующим образом:
x'B1=f1(x1, x2,..., xn, p1, p2,..., pm, t)+εB1(xA1-xB1),
x'B2=f2(x1, x2,..., xn, p1, p2,..., pm, t)+εB2(xA2-xB2),
...
x'Bn=fn(x1, x2,..., xn, p1, p2,..., pm, t)+εBn(xAn-xBn),
для генерирования декодирующей последовательности, а также начальные значения, не обязательно совпадающие с начальными значениями, предложенными для генерирования кодирующей последовательности,
- перед кодированием и декодированием данных генерируют первую кодирующую последовательность и первую декодирующую последовательность посредством интегрирования обеих возмущенных систем уравнений в течение времени T, причем обе системы спарены посредством членов, умноженных на εAs, εBs, s=1,..., n, где εAs, εBs - такие положительные значения, из которых по меньшей мере одно значение в системе, ассоциированной с кодированием, и другое значение в системе, ассоциированной с декодированием, является ненулевым значением, так что обмен по меньшей мере значениями переменных x1, x2,..., xn, которые умножены на ненулевое значение εAs, εBs, s=1, …, n, выполняется во время интегрирования через канал обмена до схождения обеих систем,
- обеспечивают кодирующую и декодирующую данные последовательность посредством интегрирования одинаковых уравнений от значений, достигнутых при интегрировании, выполненном на предыдущем этапе, независимо используемых в качестве начального условия без обмена спаривающими значениями и без включения членов с εAs, εBs, s=1, …, n.
Преимущество использования возмущенной системы уравнений состоит в том, что посредством введения спаривающих коэффициентов εAs, εBs, s=1, …, n, сходимость обеих систем достигается без необходимости выбора начальных условий для интегрирования в течение времени T для совпадения в обеих системах A и B. Спаривающие члены, которые выражены как εAi(xBi-xAi), могут быть интерпретированы как сигналы обратной связи. Когда системы находятся в режиме полной синхронизации, эти члены взаимно компенсируются. Тогда две системы A и B воспроизводят одну и ту же траекторию. Измерение разности (xBi-xAi) по сравнению с небольшим предустановленным пороговым значением является примером критерия для определения, синхронизированы ли системы.
Это означает, что если значение xBi достигает систему A, и xAi=xBi в течение некоторого времени, системы будут синхронизированы. Поэтому нет необходимости делиться информацией перед интегрированием, в результате чего достигается безопасная связь без обмена информацией, восприимчивой к перехвату шпионом. Это случай симметричного шифрования.
Эта ситуация означает, что для обеих систем необходимо передавать свои переменные через канал общего пользования таким образом, чтобы на обоих концах связи A и B было известно, когда настала синхронизация, и это происходит, когда переменные в обеих системах имеют одинаковое значение. Этот обмен переменными выполняется во временных интервалах, которые не обязательно должны совпадать со временем интегрирования T. Когда обнаружено, что схождение в значениях переменных было достигнуто, в A начинается кодирование сообщения, и последующая передача кодированного сообщения берет в качестве начального значения значение решения в некоторый момент времени, так что оно принадлежит решению, полученному после удостоверения, что системы синхронизированы; и в любом случае в один и тот же момент в обеих системах. В одном варианте осуществления это значение представляет собой последнее значение интегрирования, достигнутое в обеих системах.
В конкретном варианте осуществления изобретения обмен переменными выполняется по каналу обмена, зашифрованному посредством открытого ключа. Это обеспечивает преимущество обеспечения безопасности для системы связи, поскольку даже если значения переменных, которыми обмениваются, известны, невозможно вывести решение, поскольку система уравнений не известна, даже в случае, в котором этот секрет был раскрыт, будет невозможно знать изменение решения с учетом того, что параметры, которыми обмениваются, зашифрованы.
В конкретном варианте осуществления изобретения посредством реализации способов для кодирования и декодирования после этапа f) каждый разряд d изображается в двоичном виде с предустановленным размером слова D1, подвергая его конкатенации к двоичной последовательности.
Этот способ представления фактического числа обеспечивает техническое преимущество использования внутреннего представления компьютера, чтобы непосредственно генерировать псевдослучайную последовательность. Таким образом, в этом варианте осуществления были получены результаты, демонстрирующие преимущество экономии вычислительных затрат, если брать разряды di...dr значений, выбранных из xk=x(tk). Таким образом, имеется два некоррелированных значения, взятых из xk, и xk+1, в намного более короткое время, чем необходимо, чтобы найти два некоррелированных значения, если брать все разряды без применения способа в соответствии с изобретением. В конкретном варианте осуществления используется эмпирическое значение di, значения которого, как известно, являются некоррелированными в половине времени.
Способ в соответствии с изобретением подразумевает выбор множества разрядов для каждой выборки и позволяет одновременно использовать больше выборок в один и тот же период интегрирования. Было доказано, что большее количество выборок компенсирует сокращение разрядов, и полученный в результате способ более эффективен, чем описанные в области техники.
С другой стороны, технический эффект, внедренный посредством устранения битов, состоит в том, что усложняется исполнение статистических атак для того, чтобы дешифровать псевдослучайную последовательность и таким образом сообщение.
В конкретном варианте осуществления после этапа f) каждый разряд d сопоставляется с двоичным выражением с размером слова D1, подвергая его конкатенации к двоичной последовательности.
В качестве иллюстративного примера взяты D1=5, xk=0,563124, xk+1=0,648521, r=6, i=4, таким образом, часть псевдослучайной последовательности:
- d4... d6 из xk: 124 → двоичное представление каждого разряда с помощью 5 битов: 000010001000100,
- d4... d6 из xk+1: 521 → двоичное представление каждого разряда с помощью 5 битов: 001010001000001,
таким образом, часть псевдослучайной последовательности, сгенерированной из набора значений xk и xk+1, является конкатенацией: 124521 → (и в двоичном формате) 000010001000100001010001000001.
В одном варианте осуществления предварительно установлен размер слова D2, и целочисленные разряды формируются из двоичной последовательности взятием слов из D2 битов.
Возвращаясь к варианту осуществления, если D2=3, то из последовательности, сгенерированной выше, формируются группы по 3 бита, и получается их представление в десятичных разрядах:
000010001000100001010001000001 → 0210412101
В одном варианте осуществления перед применением операции сравнения Исключающее ИЛИ (XOR) псевдослучайная последовательность расширяется в последовательность с большим числом элементов в соответствии со следующими этапами, на которых:
- предварительно устанавливают положительное целочисленное значение,
- строят два вектора V1 и V2 целых чисел с размерностью DIM из сгенерированной псевдослучайной последовательности, например, беря DIM значений для заполнения V1 и следующие DIM значений последовательности для заполнения V2; и,
- строят матрицу расширения Me с размерностью DIM×DIM из произведения V1⋅V2T, где V2T обозначает транспонированный вектор V2,
- генерируют расширенную последовательность посредством конкатенации строк матрицы Me.
Возвращаясь к варианту осуществления, если псевдослучайная последовательность представляет собой 02104121..., тогда если DIM=3:
- V1=021 (вектор-столбец)
- V2=041 (вектор-столбец)
- 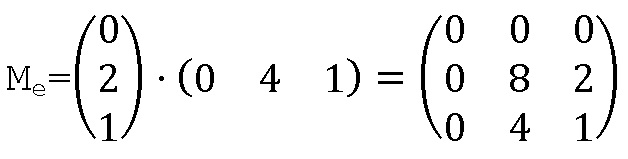
- расширенная последовательность = 000082041,
таким образом, в этом конкретном варианте осуществления, исходя из двух векторов по 3 разряда предпочтительно получается совокупность из 9 разрядов, имеющая результатом новый вектор после ее построчного извлечения, посредством чего, в частности, подтверждается отсутствие корреляции или отношения между переданной последовательностью и начальными уравнениями, и увеличивается степень случайности, чтобы усложнить работу шпиона. Кроме того, увеличивается вычислительная эффективность, поскольку получается "увеличенное" количество разрядов относительно начального количества разрядов, таким образом, требуется меньше входных битов для генерирования последовательности с заданным количеством битов.
В конкретном варианте осуществления после генерирования матрицы расширения выполняется следующее:
- предварительно устанавливается значение K1,
- перед генерированием расширенной последовательности каждый элемент матрицы Me заменяется значением, полученным в результате вычисления его остатка от деления по модулю K1.
Возвращаясь к примеру, если матрица расширения представляет собой
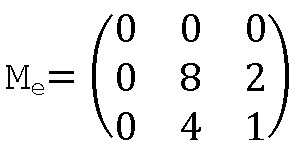
и K1=3,
тогда если операция остатка от деления по модулю K является операцией, результат которой использует остаток от деления первого целого числа на второе число, получается следующее:
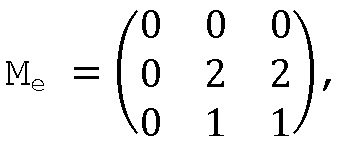 тогда псевдослучайная последовательность:
тогда псевдослучайная последовательность:
S=000022011.
Этот принцип работы, в котором операция остатка от деления по модулю K применяется для значений K в диапазоне [1,10], обеспечивает преимущество возможности работать с числами с единственным разрядом в десятичной системе счисления в диапазоне [0..9]. Это дает преимущество, когда имеются матрицы, элементы которых имеют очень большие значения порядка сотен, поскольку матрица Me является результатом произведения, и поэтому работа с ними является более затратной.
В конкретном варианте осуществления дополнительно выполняются следующие этапы:
- в дополнение к векторам V1 и V2 строится вектор V3 целых чисел с размерностью DIM из сгенерированной псевдослучайной последовательности,
- для каждой из строк матрицы Me перед генерированием расширенной последовательности посредством конкатенации строк матрицы Me каждая из строк Me подвергается круговому повороту целое число раз в предустановленном направлении в соответствии с целочисленным значением, установленным этой же самой строкой вектора V3.
Если в качестве примера использовать приведенную выше иллюстрацию в конкретных вариантах осуществления, начальная псевдослучайная последовательность должна быть s=0210412101.
Таким образом,
- V1=021 (вектор-столбец)
- V2=041 (вектор-столбец)
- V3=210 (вектор-столбец с размерностью DIM=3)
- 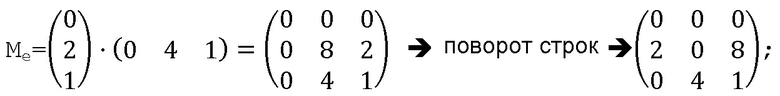
Таким образом, первая строка повернута два раза по часовой стрелке, вторая строка повернута один раз, и третья строка не повернута. Снова преимущество состоит в том, что степень случайности и отсутствие корреляции увеличиваются, предотвращая возможность шпиона вывести начальную последовательность и, таким образом, дифференциальные уравнения, используемые для генерирования случайной последовательности.
В конкретном варианте осуществления после генерирования вектора V3 дополнительно выполняются следующие этапы, на которых:
- предварительно устанавливают значение K2, предпочтительно значение DIM,
- перед выполнением кругового поворота заменяют каждый элемент вектора V3 значением, полученным в результате вычисления его остатка от деления по модулю K2.
Это предотвращает наличие больших значений элементов в V3, что привело бы к повороту строк матрицы Me много раз, даже больше чем размерность самой матрицы, приводя в результате к избыточным задачам. Эта операция оптимизирует вычислительные затраты.
Если рассмотреть иллюстративный пример, в котором значения элементов V3 являются большими, получается следующее:
- начальная псевдослучайная последовательность s=0210418971,
Таким образом,
- V1=021 (вектор-столбец)
- V2=041 (вектор-столбец)
- V3=897 (вектор-столбец с размерностью DIM=3)
- 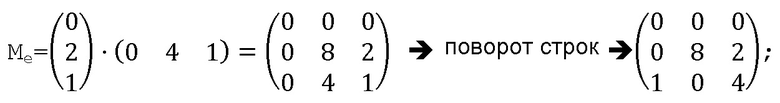
Если строки поворачиваются такое количество раз, которое продиктовано строками вектора V3, то тот же самый результат будет получен, если бы каждая строка V3 mod была повернута 3 раза или 2, 0 и 1 раз, соответственно.
В конкретном варианте осуществления, вместо полного вычисления матрицы Me для начала работы с псевдослучайной последовательностью и с оператором XOR вычисляются строки матрицы, и работа выполняется с ними. Не является необходимым сначала создать матрицу и затем извлечь поток данных. Таким образом, как указано на фиг. 4, система работает быстрее, и нет необходимости сохранять всю матрицу в памяти, только строку подлежащую извлечению, с которой непосредственно выполняется работа. Это обеспечивает эффективность всей системы. Преимущественно с помощью матрицы расширения возможно снизить требования для системы, которая реализует способ, и в процессоре, и в памяти, имея возможность реализовать ее в аппаратных средствах, которые не являются очень мощными.
Фиг. 4 показывает систему с функциональными элементами, генерирующими псевдослучайную последовательность (S), с помощью которой кодируется сообщение (m). Эта же фигура иллюстрирует систему A с другими элементами.
Выделяют первый модуль (1), решающий систему уравнений:
x'A1=f1(x1, x2,..., xn, p1, p2,..., pm, t)+εA1(xB1-xA1),
x'A2=f2(x1, x2,..., xn, p1, p2,..., pm, t)+εA2(xB2-xA2),
...
x'An=fn(x1, x2,..., xn, p1, p2,..., pm, t)+εAn(xBn-xAn),
Также выделяют следующее:
- Второй модуль (2), укорачивающий решение xk до его разрядов d1…dr.
Этот второй модуль (2) позволяет извлекать для каждой выборки xk разряды, имеющие результатом псевдослучайную последовательность, которая будет впоследствии обрабатываться. В одном варианте осуществления модуль может являться сегментом кода компьютерной программы, подходящим для выполнения способа, который выбирает соответствующие разряды из значений фактических чисел, внутренне представленных в компьютере.
- Третий модуль (3), получающий векторы V1, V2 и V3.
Этот третий модуль (3) использует конкатенацию разрядов из второго модуля (2) и представляет их таким образом, что он генерирует векторы V1, V2 и V3 с учетом размерности DIM. В одном варианте осуществления третий модуль (3) является сегментом кода компьютерной программы, подходящим для выполнения способа, который генерирует векторы V1, V2 и V3, с учетом предустановленной размерности DIM и последовательности целочисленных значений, обеспеченной вторым модулем (2).
- Четвертый модуль (4), получающий V1 mod K1, V2 mod K1 и V3 mod K2.
Четвертый модуль (4) работает с каждым элементом векторов V1, V2 и V3 таким образом, что он делит значения элементов на значения K1, K1 и K2 и получает остаток в каждом элементе. Результат представляет собой три вектора, элементы которых являются остатками, полученными от деления, примененного четвертым модулем (4). В одном варианте осуществления четвертый модуль (4) является сегментом кода компьютерной программы, подходящим для выполнения способа, который работает, как описано, и получает векторы V1, V2 и V3 от модуля, такого как третий модуль (3), и значения K1 могут быть предварительно установлены.
- Пятый модуль, генерирующий строки матрицы Me, каждая строка является: Me1 - первая строка, Me2 - вторая строка, и Me3 - третья строка в иллюстрированном варианте осуществления.
В одном варианте осуществления пятый модуль (5) является сегментом компьютерной программы, работающим с векторами V1, V2 и V3 следующим образом. Сначала выполняется векторное произведение V1⋅V2T. Это произведение может быть выполнено по строкам без необходимости вычислять всю матрицу и хранить ее полностью. i-я строка матрицы будет сформирована значениями V1i. V2j, где V1i - i-й компонент вектора V1, и V2j - j-й компонент вектора V2, причем j охватит все столбцы матрицы и вектора V2. После того, как модуль получает первую строку, он поворачивает строку несколько раз, количество которых равно значению первого элемента V3, и обеспечивает результат. Он работает таким образом последовательно с каждой из строк до завершения операции (V1⋅V2T) rot V3.
Сгенерированная псевдослучайная последовательность (последовательности) является конкатенацией строк в порядке их генерирования. Эта последовательность (последовательности) обрабатывается посредством оператора XOR с исходным сообщением (M), и результат передается через канал связи.
Конкретный вариант осуществления
Конкретный вариант осуществления начинается с сигнала xk, сгенерированного из хаотической динамической системы. Конкретные значения, которые являются не коррелированными относительно друг друга, принимаются из этого сигнала:
m1=0,98754213
m2=0,98214356
m3=0,61102348
m4=0,62021309
m5=0,41102441
m6=0,35000227
Старшие разряды и разряды, имеющие результатом ошибки округления вследствие архитектуры компьютера, используемого для интеграции, устраняются из каждой выборки, в результате чего получается следующее:
s1=75421
s2=21435
s3=10234
s4=02130
s5=10244
s6=00022
Следующий этап состоит в группировании этих значений для формирования двух векторов V1, V2:
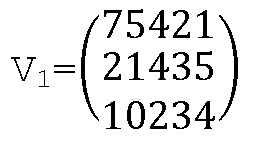
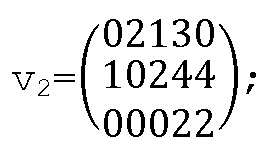
Матрица расширения генерируется с помощью этих двух векторов:

Остаток от деления по модулю K1, 90107, получается из каждого элемента матрицы.
Затем из начального сигнала берутся выборки m7, m8, m9, и генерируется вектор V3, к которому применяется операция остатка деления по модулю K2=3, и получается вектор:
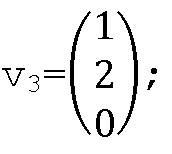
Таким образом, посредством поворота строк матрицы Me получается следующее:

Каждый элемент матрицы затем преобразовывается в двоичный формат посредством преобразования десятичных элементов в двоичные числа. Например, получается псевдослучайная последовательность (из которой показана только часть, соответствующая первым двум числам) посредством конкатенации элементов матрицы в двоичный формат:
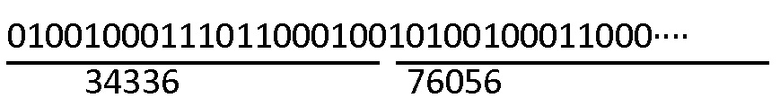
и эта последовательность представляет собой последовательность, которая микшируется посредством операции XOR с сообщением для получения зашифрованного потока данных.
Этот тот же самый набор операций, выполненный на стороне приемника, позволит дешифровать сообщение.
Изобретение относится к области кодирования и декодирования потока данных. Технический результат – эффективная защита потока данных. Кодер сообщений, подходящий для выполнения способа для кодирования потока данных для передачи упомянутых данных посредством кодированного потока, в котором кодирование является результатом сравнения потока данных со вторым потоком данных, сформированным псевдослучайной последовательностью посредством операции сравнения Исключающее ИЛИ (XOR), при этом генерирование псевдослучайной последовательности выполняется посредством способа для генерирования псевдослучайной последовательности, выполняющего этапы, на которых: a) обеспечивают дифференциальное уравнение с начальным значением x'=f(x, t), b) обеспечивают начальное значение для дифференциального уравнения x0=x(t0), c) обеспечивают шаг интегрирования δt для дифференциального уравнения для временной дискретизации tk=t0+k⋅δt, k=1, 2, 3, …, d) выполняют численное интегрирование дифференциального уравнения от начального значения и с шагом δt для получения приближения для решения xk=x(tk), e) генерируют первую последовательность значений посредством выборки значений xk, представимую в числовой форме с плавающей запятой в виде 0,d0d1d2d3d4...dr...dw⋅10e, где e - показатель степени, w - длина мантиссы, d0 - старший разряд мантиссы и dr - некоторый разряд, который вместе с разрядами слева от него в приближении для решения xk совпадает с точным значением решения дифференциального уравнения, f) генерируют псевдослучайную последовательность с разрядами di...dr из набора последовательности значений xk, где i - предопределенное целочисленное значение, удовлетворяющее 0<i≤r, g) псевдослучайная последовательность расширяется в последовательность с большим количеством элементов в соответствии со следующими этапами, на которых: предварительно устанавливают положительное целочисленное значение DIM, строят два вектора V1 и V2 целых чисел с размерностью DIM из псевдослучайной последовательности, строят матрицу расширения Me с размерностью DIM⋅DIM из произведения V1⋅V2T, где V2T - транспонированный вектор V2, генерируют расширенную последовательность посредством конкатенации строк матрицы Me. 5 н. и 10 з.п. ф-лы, 4 ил., 1 табл.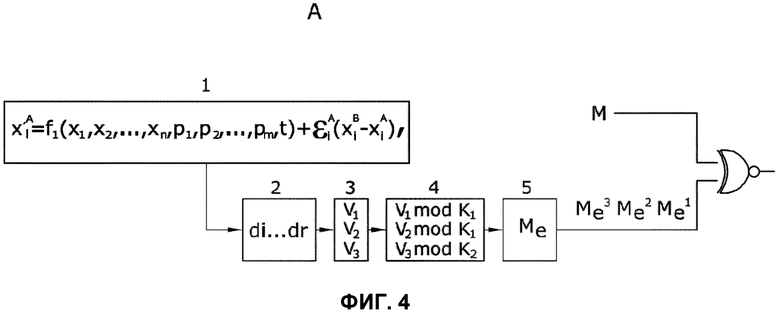
1. Способ для генерирования псевдослучайной последовательности, отличающийся тем, что он содержит следующие этапы, на которых:
a) обеспечивают дифференциальное уравнение с начальным значением x'=f(x, t),
b) обеспечивают начальное значение для дифференциального уравнения x0=x(t0),
c) обеспечивают шаг интегрирования δt для дифференциального уравнения для временной дискретизации tk=t0+k⋅δt, k=1, 2, 3, …,
d) выполняют численное интегрирование дифференциального уравнения от начального значения и с шагом δt для получения приближения для решения xk=x(tk),
e) генерируют первую последовательность значений посредством выборки значений xk, представимую в числовой форме с плавающей запятой в виде 0,d0d1d2d3d4...dr...dw⋅10e, где e - показатель степени, w - длина мантиссы, d0 - старший разряд мантиссы и dr - некоторый разряд, который вместе с разрядами слева от него в приближении для решения xk совпадает с точным значением решения дифференциального уравнения,
f) генерируют псевдослучайную последовательность с разрядами di...dr из набора последовательности значений xk, где i - предопределенное целочисленное значение, удовлетворяющее 0<i≤r,
g) псевдослучайная последовательность расширяется в последовательность с большим количеством элементов в соответствии со следующими этапами, на которых:
- предварительно устанавливают положительное целочисленное значение DIM,
- строят два вектора V1 и V2 целых чисел с размерностью DIM из псевдослучайной последовательности,
- строят матрицу расширения Me с размерностью DIM⋅DIM из произведения V1⋅V2T, где V2T - транспонированный вектор V2,
- генерируют расширенную последовательность посредством конкатенации строк матрицы Me.
2. Способ по п. 1, в котором численное интегрирование системы из n дифференциальных уравнений x's=fs(x1, x2,..., xn, p1, p2,..., pm, t), s=1,..., n, выполняется на этапе d), n также является количеством неизвестных, и содержащий m параметров pj, j=1,..., m, так что псевдослучайная последовательность на этапе f) генерируется из одной из n переменных, предварительно выбранных из системы дифференциальных уравнений.
3. Способ по любому из пп. 1, 2, в котором после этапа f) каждый разряд d изображен в двоичной форме с предустановленным размером слова D1, конкатенация разрядов формирует двоичную последовательность.
4. Способ по любому из пп. 1, 2, в котором после этапа f) каждый разряд d сопоставляется с двоичным выражением, конкатенация разрядов формирует двоичную последовательность.
5. Способ по любому из пп. 1, 2, в котором размер слова D2 предварительно установлен, и целочисленные разряды формируются из двоичной последовательности с использованием слов из D2 битов.
6. Способ по любому из пп. 1, 2, в котором:
- значение K1 предварительно установлено,
- перед генерированием расширенной последовательности каждый элемент матрицы Me заменяется значением, полученным в результате вычисления его остатка от деления по модулю K1.
7. Способ по любому из пп. 1, 2, в котором:
- в дополнение к векторам V1 и V2 строится вектор V3 целых чисел с размерностью DIM из сгенерированной псевдослучайной последовательности,
- для каждой из строк матрицы Me перед генерированием расширенной последовательности посредством конкатенации строк матрицы Me каждая из строк матрицы Me подвергается круговому повороту целое число раз в предустановленном направлении в соответствии с целочисленным значением, установленным этой же самой строкой вектора V3.
8. Способ по любому из пп. 1, 2, в котором:
- предварительно устанавливается значение K2,
предпочтительно значение DIM,
- каждый элемент вектора V3 заменяется на значение, полученное в результате вычисления остатка от его деления по модулю K2.
9. Способ по любому из пп. 1, 2, в котором для генерирования расширенной последовательности посредством конкатенации строк матрицы Me вычисляются только значения каждой строки, чтобы избежать хранения полной матрицы Me.
10. Способ для кодирования потока данных для передачи упомянутых данных посредством кодированного потока, в котором кодирование является результатом сравнения потока данных со вторым потоком данных, сформированным с помощью псевдослучайной последовательности посредством операции сравнения Исключающее ИЛИ (XOR), или способ для декодирования кодированного потока данных, в котором декодирование является результатом сравнения кодированного потока данных со вторым потоком данных, сформированным с помощью псевдослучайной последовательности посредством операции сравнения Исключающее ИЛИ (XOR), отличающийся тем, что генерирование псевдослучайной последовательности выполняется посредством способа по любому из предшествующих пунктов.
11. Способ по п. 10, в котором выполняются следующие этапы, на которых:
- определяют время интегрирования T,
- предлагают возмущенную систему уравнений, которая может быть выражена следующим образом:
x'A1 = f1(x1, x2,..., xn, p1, p2,..., pm, t)+εA1(xB1-xA1),
x'A2 = f2(x1, x2,..., xn, p1, p2,..., pm, t)+ εA2(xB2-xA2),
x'An = fn(x1, x2,..., xn, p1, p2,..., pm, t)+ εAn(xBn-xAn),
для генерирования кодирующей последовательности, а также начальные значения; и,
- предлагают возмущенную систему уравнений, которая может быть выражена следующим образом:
x'B1 = f1(x1, x2,..., xn, p1, p2,..., pm, t)+ εB1(xA1-xB1),
x'B2 = f2(x1, x2,..., xn, p1, p2,..., pm, t)+ εB2(xA2-xB2),
x'Bn = fn(x1, x2,..., xn, p1, p2,..., pm, t)+ εBn(xAn-xBn),
для генерирования декодирующей последовательности, а также начальные значения, необязательно совпадающие с начальными значениями, предложенными для генерирования кодирующей последовательности,
- перед кодированием и декодированием данных генерируют первую кодирующую последовательность и первую декодирующую последовательность посредством интегрирования обеих возмущенных систем уравнений в течение времени T, причем обе системы спарены посредством членов, умноженных на εAs, εBs, s=1,..., n, где εAs, εBs - такие положительные значения, из которых по меньшей мере одно значение в системе, ассоциированной с кодированием, и другое значение в системе, ассоциированной с декодированием, является ненулевым значением, так что обмен по меньшей мере значениями переменных x1, x2,..., xn, которые умножены на ненулевое значение εAs, εBs, s=1, …, n, выполняется во время интегрирования через канал обмена до схождения обеих систем,
- обеспечивают кодирующую и декодирующую данные последовательности посредством интегрирования одинаковых уравнений от значений, достигнутых при интегрировании, выполненном на предыдущем этапе, независимо используемых в качестве начального условия без обмена спаривающими значениями и без включения членов с εAs, εBs, s=1, …, n.
12. Способ по п. 11, в котором канал обмена зашифрован посредством открытого ключа.
13. Кодер сообщений, подходящий для выполнения способа для кодирования потока данных для передачи упомянутых данных посредством кодированного потока, в котором кодирование является результатом сравнения потока данных со вторым потоком данных, сформированным псевдослучайной последовательностью посредством операции сравнения Исключающее ИЛИ (XOR), отличающийся тем, что генерирование псевдослучайной последовательности выполняется посредством способа по любому из пп. 1-9.
14. Декодер зашифрованных сообщений, подходящий для выполнения способа для декодирования кодированного потока данных, в котором декодирование является результатом сравнения кодированного потока данных со вторым потоком данных, сформированным псевдослучайной последовательностью посредством операции сравнения Исключающее ИЛИ (XOR), отличающийся тем, что генерирование псевдослучайной последовательности выполняется посредством способа по любому из пп. 1-9.
15. Система связи, включающая в себя по меньшей мере один кодер по п. 13 и по меньшей мере один декодер по п. 14.
| EP 0467239 A2, 22.01.1992 | |||
| Способ приготовления мыла | 1923 |
|
SU2004A1 |
| Изложница с суживающимся книзу сечением и с вертикально перемещающимся днищем | 1924 |
|
SU2012A1 |
| US 7218733 B2, 15.05.2007 | |||
| US 7526084 B2, 28.04.2009. | |||
Авторы
Даты
2017-01-30—Публикация
2013-05-23—Подача