Область техники, к которой относится изобретение
Настоящее изобретение относится к устройству обработки информации, способу обработки информации и программе.
Уровень техники
По мере быстрого развития технологий обработки информации и технологий связи, происходит интенсивный процесс преобразования документов в цифровую форму независимо от того, являются ли эти документы открытыми для общего пользования или частными. В связи с переводом таких документов в цифровую форму многие - как отдельные люди, так и компании, в значительной степени заинтересованы в обеспечении и управлении безопасностью электронных документов. В связи с увеличением такой заинтересованности сейчас ведутся активные исследования мер противодействия несанкционированному вмешательству, перехвату, взлому и фальсификации электронных документов в различных областях. Что касается перехвата и "прослушивания" электронных документов, безопасность обеспечивается, например, посредством шифрования электронных документов. Далее, что касается фальсификации электронных документов, безопасность обеспечивается, например, посредством использования цифровых подписей. Однако если способы шифрования или цифровой подписи, которые предполагается использовать, не обладают высокой степенью устойчивости против взлома, достаточный уровень безопасности не обеспечивается.
Цифровая подпись используется для идентификации автора электронного документа. Соответственно, эта цифровая подпись должна быть такой, чтобы ее мог генерировать только автор электронного документа. Если какая-либо злонамеренная третья сторона сможет генерировать такую же самую цифровую подпись, такая третья сторона сможет выдать себя за автора электронного документа. Иными словами, электронный документ может быть фальсифицирован такой злонамеренной третьей стороной. Были высказаны самые разнообразные точки зрения относительно обеспечения защиты такой цифровой подписи с целью предотвращения подобной фальсификации. Сегодня широко используются такие алгоритмы цифровой подписи, как, например, RSA-алгоритм подписи и DSA-алгоритм подписи.
Указанный RSA-алгоритм подписи принимает за основу обеспечения безопасности принцип «трудности разложения большого составного числа на простые множители» (в последующем, проблема разложения на простые множители). Кроме того, DSA-алгоритм подписи принимает за основу обеспечения безопасности принцип «трудности решения проблемы дискретного логарифмирования». Эти принципы базируются на том факте, что не существуют алгоритмы, позволяющие эффективно решать проблему разложения на простые множители и проблему дискретного логарифмирования с использованием классического компьютера. Иными словами, упомянутые выше трудности предполагают вычислительные сложности для классического компьютера. Однако считается, что решения проблемы разложения на простые множители и проблемы дискретного логарифмирования могут быть эффективно вычислены с использованием квантового компьютера.
Аналогично RSA-алгоритму подписи и DSA-алгоритму подписи многие другие применяемые сегодня алгоритмы цифровой подписи и алгоритмы аутентификации с открытым ключом также опираются на трудности решения проблемы разложения на простые множители и проблемы дискретного логарифмирования как на основу обеспечения безопасности. Таким образом, если квантовые компьютеры войдут в сферу практического применения, безопасность таких алгоритмов цифровой подписи и алгоритмов аутентификации с открытым ключом больше обеспечена не будет. Соответственно появляется потребность в реализации новых алгоритмов цифровой подписи и алгоритмов аутентификации с открытым ключом, где основой безопасности будут являться проблемы, отличные от таких проблем, как проблема разложения на простые множители и проблема дискретного логарифмирования, которые могут быть легко решены с помощью квантового компьютера. В качестве задачи, решить которую квантовому компьютеру будет нелегко, можно указать задачу, относящуюся к многочленам от нескольких переменных.
Например, в качестве алгоритмов цифровой подписи, использующих проблему многочленов от нескольких переменных в качестве основы безопасности, известны такие алгоритмы, как алгоритмы на основе криптографии Мацумото-Имаи (Matsumoto-Imai (MI)), криптографии с использованием уравнений скрытого поля (Hidden Field Equation (HFE)), алгоритмы подписи типа Oil-Vinegar (OV) signature и криптографии с использованием ручного преобразования (Tamed Transformation Method (TTM)). Например, алгоритм цифровой подписи на основе HFE-криптографии рассмотрен в следующей непатентной литературе 1 и 2.
Список литературы
Непатентная литература
Непатентная литература 1: Жак Патарен, "Асимметричная криптография со скрытым одночленом" (Jacques Patarin, Asymmetric Cryptography with a Hidden Monomial, CRYPTO 1996, pp. 45-60).
Непатентная литература 2: Патарен Ж., Куртуа Н. и Губин Л., "КВАРЦ, Цифровые подписи длиной 128 бит", (Patarin, J., Courtois, N., and Goubin, L., QUARTZ, 128-Bit Long Digital Signatures, In Naccache, D., Ed.). Topics in Cryptology - CT-RSA 2001 (San Francisco, CA, USA, April 2001), vol. 2020 of Lecture Notes in Computer Science, Springer-Verlag., pp. 282-297.
Раскрытие изобретения
Техническая проблема
Как указано выше, задача многочленов от нескольких переменных представляет собой пример так называемой НП-трудной (NP-hard) проблемы, которую трудно решить даже при использовании квантового компьютера. Обычно алгоритм аутентификации с открытым ключом, использующий проблему многочлена от нескольких переменных, описываемую уравнениями HFE или аналогичным способом, использует уравнение множества порядков с несколькими переменными с потайным входом. Например, используют уравнение F(x1,…,xn)=y множества порядков с несколькими переменными x1, …, xn и линейные преобразования А и В, управляемые секретным образом. В таком случае, уравнение F множества порядков с несколькими переменными и линейные преобразования А и В являются потайными входами.
Объект, знающий потайные входы F, А и В, может решить уравнение B(F(A(x1,…,xn)))=y′ относительно переменных x1, …, xn. С другой стороны, уравнение B(F(A(x1,…,xn)))=y′ относительно переменных xi,..., Хп не может быть решено субъектом, который не знает потайных входов F, А и В. Используя этот механизм, можно реализовать алгоритм аутентификации с открытым ключом и алгоритм цифровой подписи, использующие трудности решения уравнения множества порядков с несколькими переменными в качестве основы для обеспечения безопасности.
Как описано выше, для реализации алгоритма аутентификации с открытым ключом или алгоритма цифровой подписи необходимо подготовить специальную систему уравнений множества порядков с несколькими переменными, удовлетворяющую условию B(F(A(x1,…,xn)))=y. Далее, в момент генерации подписи необходимо решить систему уравнений F множества порядков с несколькими переменными. По этой причине совокупность доступных систем уравнений F множества порядков с несколькими переменными до сих пор ограничивалась относительно легко решаемыми системами уравнений. Таким образом, ранее в известных схемах использовались только системы B(F(A(x1,…,xn)))=y уравнений множества порядков с несколькими переменными на основе сочетания трех функций (потайных входов) В, F и А, которые можно относительно решить, вследствие чего трудно обеспечить достаточную степень безопасности.
Соответственно, в свете изложенных выше обстоятельств, авторы настоящего изобретения разработали эффективные и в высокой степени защищенные алгоритм аутентификации с открытым ключом и алгоритм цифровой подписи с использованием систем уравнений множества порядков с несколькими переменными, для которых отсутствуют или присутствуют в недостаточном количестве средства для эффективного решения (потайные входы) (Коити Сакумото, Тайдзо Сираи и Харунага Хиватари, «Алгоритмы идентификации с открытым ключом на основе квадратичных полиномов от нескольких переменных» (Koichi Sakumoto, Taizo Shirai and Harunaga Hiwatari, "Public-Key Identification Schemes Based on Multivariate Quadratic Polynomials", CRYPTO 2011, LNCS 6841, pp. 706 to 723,2011.)).
Однако многочлены от нескольких переменных, используемые в алгоритме аутентификации открытого ключа и алгоритме цифровой подписи, имеют много коэффициентов. Таким образом, для использования многочлена от нескольких переменных в качестве открытого ключа необходимо определить способ эффективного назначения коэффициентов для доказывающей стороны и для проверяющей стороны (верификатора). Предлагаемая технология разработана для создания нового и усовершенствованного устройства обработки информации, нового и усовершенствованного способа обработки информации и новой и усовершенствованной программы, способных эффективно подставлять коэффициенты в многочлен от нескольких переменных.
Решение проблемы
Согласно одному из вариантов настоящего изобретения предложено устройство обработки информации, содержащее модуль генерации чисел, выполненный с возможностью генерации чисел, используемых в коэффициентах членов, входящих в пару многочленов F=(f1, …, fm) множества порядков с несколькими переменными, с использованием заданной функции на основе информации, совместно используемой объектами, исполняющими алгоритм аутентификации с открытым ключом или алгоритм цифровой подписи, применяющий открытый ключ, содержащий указанную пару многочленов F множества порядков с несколькими переменными, и модуль назначения, выполненный с возможностью назначения чисел, генерируемых посредством модуля генерации чисел, коэффициентам многочленов множества порядков с несколькими переменными, составляющими элементами которых является указанная пара многочленов F множества порядков с несколькими переменными. Модуль назначения группирует коэффициенты членов, имеющих идентичное сочетание переменных, из совокупности коэффициентов многочленов множества порядков с несколькими переменными, составляющими элементами которых является пара многочленов F множества порядков с несколькими переменными, и выполняет процедуру назначения в блоках групп.
Согласно другому варианту настоящего изобретения предложено устройство обработки информации, содержащее модуль генерации чисел, выполненный с возможностью генерации чисел, используемых в коэффициентах членов, входящих в пару многочленов F=(f1, …, fm) множества порядков с несколькими переменными, с использованием заданной функции на основе информации, совместно используемой объектами, исполняющими алгоритм аутентификации с открытым ключом или алгоритм цифровой подписи, применяющий открытый ключ, содержащий указанную пару многочленов F множества порядков с несколькими переменными, и модуль назначения, выполненный с возможностью назначения чисел, генерируемых посредством модуля генерации чисел, коэффициентам многочленов множества порядков с несколькими переменными, составляющими элементами которых является указанная пара многочленов F множества порядков с несколькими переменными. Модуль назначения группирует матрицу коэффициентов в каждой строке или столбце, когда многочлены множества порядков с несколькими переменными, составляющими элементами которых является указанная пара многочленов F множества порядков с несколькими переменными, выражены в квадратичной форме, при этом модуль назначения выполняет процедуру назначения в блоках групп.
Согласно другому варианту настоящего изобретения предложено устройство обработки информации, содержащее модуль генерации чисел, выполненный с возможностью генерации чисел, количество которых идентично количеству коэффициентов членов, входящих в пару многочленов F=(f1, …, fm) множества порядков с несколькими переменными, с использованием заданной функции на основе информации, совместно используемой объектами, исполняющими алгоритм аутентификации с открытым ключом или алгоритм цифровой подписи, применяющий открытый ключ, содержащий указанную пару многочленов F множества порядков с несколькими переменными, и модуль назначения, выполненный с возможностью назначения чисел, генерируемых посредством модуля генерации чисел, коэффициентам многочленов множества порядков с несколькими переменными, составляющими элементами которых является указанная пара многочленов F множества порядков с несколькими переменными, в последовательности, заранее определенной между доказывающей стороной и проверяющей стороной.
Согласно другому варианту настоящего изобретения предложен способ обработки информации, содержащий этап генерации чисел, используемых в коэффициентах членов, входящих в пару многочленов F=(f1, …, fm) множества порядков с несколькими переменными, с использованием заданной функции на основе информации, совместно используемой объектами, исполняющими алгоритм аутентификации с открытым ключом или алгоритм цифровой подписи, применяющий открытый ключ, содержащий указанную пару многочленов F множества порядков с несколькими переменными, и этап назначения генерируемых чисел коэффициентам многочленов множества порядков с несколькими переменными, составляющими элементами которых является указанная пара многочленов F множества порядков с несколькими переменными. На этапе назначения чисел группируют коэффициенты членов, имеющих идентичное сочетание переменных, из совокупности коэффициентов многочленов множества порядков с несколькими переменными, составляющими элементами которых является указанная пара многочленов F множества порядков с несколькими переменными, и выполняют процедуру назначения в блоках групп.
Согласно другому варианту настоящего изобретения предложен способ обработки информации, содержащий этап генерации чисел, используемых в коэффициентах членов, входящих в пару многочленов F=(f1, …, fm) множества порядков с несколькими переменными, с использованием заданной функции на основе информации, совместно используемой объектами, исполняющими алгоритм аутентификации с открытым ключом или алгоритм цифровой подписи, применяющий открытый ключ, содержащий указанную пару многочленов F множества порядков с несколькими переменными, и этап назначения генерируемых чисел коэффициентам многочленов множества порядков с несколькими переменными, составляющими элементами которых является указанная пара многочленов F множества порядков с несколькими переменными входит в составляющие элементы. На этапе назначения чисел группируют матрицу коэффициентов в каждой строке или столбце, когда многочлены множества порядков с несколькими переменными, составляющими элементами которых является указанная пара многочленов F множества порядков с несколькими переменными, выражены в квадратичной форме, и выполняют процедуру назначения в блоках групп.
Согласно другому варианту настоящего изобретения предложен способ обработки информации, содержащий этап генерации чисел, количество которых идентично количеству коэффициентов членов, входящих в пару многочленов F=(f1, …, fm) множества порядков с несколькими переменными, с использованием заданной функции на основе информации, совместно используемой объектами, исполняющими алгоритм аутентификации с открытым ключом или алгоритм цифровой подписи, применяющий открытый ключ, содержащий указанную пару многочленов F множества порядков с несколькими переменными, и этап назначения чисел, генерируемых посредством модуля генерации чисел, коэффициентам многочленов множества порядков с несколькими переменными, составляющими элементами которых является указанная пара многочленов F множества порядков с несколькими переменными, в последовательности, заранее определенной между доказывающей стороной и проверяющей стороной.
Согласно другому варианту настоящего изобретения предложена программа, вызывающая выполнение компьютером функции генерации чисел для генерации чисел, используемых в коэффициентах членов, входящих в пару многочленов F=(f1, …, fm) множества порядков с несколькими переменными, с использованием заданной функции на основе информации, совместно используемой объектами, исполняющими алгоритм аутентификации с открытым ключом или алгоритм цифровой подписи, применяющий открытый ключ, содержащий указанную пару многочленов F множества порядков с несколькими переменными, и функции назначения для назначения чисел, генерируемых посредством функции генерации чисел, коэффициентам многочленов множества порядков с несколькими переменными, составляющими элементами которых является указанная пара многочленов F множества порядков с несколькими переменными. Функция назначения группирует коэффициенты членов, имеющих идентичное сочетание переменных, из совокупности коэффициентов многочленов множества порядков с несколькими переменными, составляющими элементами которых является указанная пара многочленов F множества порядков с несколькими переменными, и выполняет процедуру назначения в блоках групп.
Согласно другому варианту настоящего изобретения предложена программа, вызывающая выполнение компьютером функции генерации чисел для генерации чисел, используемых в коэффициентах членов, входящих в пару многочленов F=(f1, …, fm) множества порядков с несколькими переменными, с использованием заданной функции на основе информации, совместно используемой объектами, исполняющими алгоритм аутентификации с открытым ключом или алгоритм цифровой подписи, применяющий открытый ключ, содержащий указанную пару многочленов F множества порядков с несколькими переменными, и функции назначения для назначения чисел, генерируемых посредством функции генерации чисел, коэффициентам многочленов множества порядков с несколькими переменными, составляющими элементами которых является указанная пара многочленов F множества порядков с несколькими переменными. Функция назначения группирует матрицу коэффициентов в каждой строке или столбце, когда многочлены множества порядков с несколькими переменными, составляющими элементами которых является указанная пара многочленов F множества порядков с несколькими переменными, выражены в квадратичной форме, при этом функция назначения выполняет процедуру назначения в блоках групп.
Согласно другому варианту настоящего изобретения предложена программа, вызывающая выполнение компьютером функции генерации чисел для генерации количества чисел, идентичного количеству коэффициентов членов, входящих в пару многочленов F=(f1, …, fm) множества порядков с несколькими переменными, с использованием заданной функции на основе информации, совместно используемой объектами, исполняющими алгоритм аутентификации с открытым ключом или алгоритм цифровой подписи, применяющий открытый ключ, содержащий указанную пару многочленов F множества порядков с несколькими переменными, и функции назначения чисел, генерируемых посредством модуля генерации чисел, коэффициентам многочленов множества порядков с несколькими переменными, составляющими элементами которых является указанная пара многочленов F множества порядков с несколькими переменными, в последовательности, заранее определенной между доказывающей стороной и проверяющей стороной.
Согласно другому варианту настоящего изобретения предложен компьютерный носитель записи, выполненный с возможностью записи описанной выше программы.
Полезные результаты изобретения
Согласно настоящему изобретению, как описано выше, можно эффективно подставлять коэффициенты многочлена от нескольких переменных.
Краткое описание чертежей
Фиг. 1 представляет пояснительную схему для описания структуры алгоритма аутентификации с открытым ключом.
Фиг. 2 представляет пояснительную схему для описания структуры алгоритма цифровой подписи.
Фиг. 3 представляет пояснительную схему для описания структуры алгоритма,
относящейся к n-проходной схеме аутентификации с открытым ключом.
Фиг. 4 представляет пояснительную схему для описания эффективного 3-проходного алгоритма аутентификации с открытым ключом.
Фиг. 5 представляет пояснительную схему для описания параллелизации эффективного 3-проходного алгоритма аутентификации с открытым ключом.
Фиг. 6 представляет пояснительную схему для описания эффективного 3-проходного алгоритма аутентификации с открытым ключом.
Фиг. 7 представляет пояснительную схему для описания примера структуры эффективного 5-проходного алгоритма аутентификации с открытым ключом.
Фиг. 8 представляет пояснительную схему для описания параллелизации эффективного 5-проходного алгоритма аутентификации с открытым ключом.
Фиг. 9 представляет пояснительную схему для описания параллелизации эффективного 5-проходного алгоритма аутентификации с открытым ключом.
Фиг. 10 представляет пояснительную схему для описания способа модификации эффективного 3-проходного алгоритма аутентификации с открытым ключом для преобразования его в алгоритм цифровой подписи.
Фиг. 11 представляет пояснительную схему для описания способа модификации эффективного 5-проходного алгоритма аутентификации с открытым ключом для преобразования его в алгоритм цифровой подписи.
Фиг. 12 представляет пояснительную схему для описания примера структуры хэш-функции.
Фиг. 13 представляет пояснительную схему для описания способа верификации подписи (нормальный способ установки), относящегося к алгоритму цифровой подписи на основе 3-проходной схеме.
Фиг. 14 представляет пояснительную схему для описания способа верификации подписи (способ уменьшения объема памяти), относящегося к алгоритму цифровой подписи на основе 3-проходной схемы.
Фиг. 15 представляет пояснительную схему для описания способа верификации подписи (нормальный способ установки), относящегося к алгоритму цифровой подписи на основе 5-проходной схеме.
Фиг. 16 представляет пояснительную схему для описания способа верификации подписи (способ уменьшения объема памяти), относящегося к алгоритму цифровой подписи на основе 5-проходной схемы.
Фиг. 17 представляет пояснительную схему для описания способа (способ #1 выделения) выделения троичных случайных чисел из двоичных случайных чисел.
Фиг. 18 представляет пояснительную схему для описания способа (способ #2 выделения) выделения троичных случайных чисел из двоичных случайных чисел.
Фиг. 19 представляет пояснительную схему для описания способа (способ #3 выделения) выделения троичных случайных чисел из двоичных случайных чисел.
Фиг. 20 представляет пояснительную схему для описания способа (способ #3 выделения) выделения троичных случайных чисел из двоичных случайных чисел.
Фиг. 21 представляет пояснительную схему для описания способа (способ #3 выделения) выделения троичных случайных чисел из двоичных случайных чисел.
Фиг. 22 представляет пояснительную схему для описания способа структурирования данных (способ #1 структурирования) для эффективной подстановки коэффициентов многочленов от нескольких переменных.
Фиг. 23 представляет пояснительную схему для описания способа структурирования данных (способ #1 структурирования) для эффективной подстановки коэффициентов многочленов от нескольких переменных.
Фиг. 24 представляет пояснительную схему для описания способа структурирования данных (способ #1 структурирования) для эффективной подстановки коэффициентов многочленов от нескольких переменных.
Фиг. 25 представляет пояснительную схему для описания способа структурирования данных (способ #1 структурирования) для эффективной подстановки коэффициентов многочленов от нескольких переменных.
Фиг. 26 представляет пояснительную схему для описания способа структурирования данных (способ #1 структурирования) для эффективной подстановки коэффициентов многочленов от нескольких переменных.
Фиг. 27 представляет пояснительную схему для описания способа структурирования данных (способ #2 структурирования) для эффективной подстановки коэффициентов многочленов от нескольких переменных.
Фиг. 28 представляет пояснительную схему для описания примера конфигурации аппаратуры в устройстве для обработки информации, способном исполнять алгоритм согласно каждому из вариантов настоящего изобретения.
Осуществление изобретения
Далее, предпочтительные варианты настоящего изобретения будут описаны подробно со ссылками на прилагаемые чертежи. Отметим, что в настоящем описании и на чертежах элементам, имеющим по существу такие же функции, присвоены одинаковые позиционные обозначения, а повторные пояснения опущены.
Порядок описания
Здесь будет коротко изложен порядок описания вариантов настоящего изобретения, которое будет приведено ниже. Сначала, структура алгоритма аутентификации с открытым ключом будет рассмотрена со ссылками на Фиг. 1. Далее, структура алгоритма цифровой подписи будет рассмотрена со ссылками на Фиг. 2. Затем, n-проходный алгоритм аутентификации с открытым ключом будет рассмотрен со ссылками на Фиг. 3.
Далее, 3-проходный алгоритм аутентификации с открытым ключом будет рассмотрен со ссылками на Фиг. 4-6. Затем, 5-проходный алгоритм аутентификации с открытым ключом будет рассмотрен со ссылками на Фиг. 7-9. Далее, способ модификации эффективных 3-проходных и 5-проходных алгоритмов аутентификации с открытым ключом для преобразования этих алгоритмов в алгоритмы цифровой подписи будет рассмотрен со ссылками на Фиг. 10-11.
Затем, способы уменьшения объемов памяти, необходимых для верификации подписи во время выполнения алгоритмов цифровой подписи, относящихся к описанным здесь вариантам, будут рассмотрены со ссылками на Фиг. 12-16. Далее, способы эффективного выделения троичных случайных чисел из двоичных случайных чисел будут рассмотрены со ссылками Фиг. 17-21. Затем, способы эффективной подстановки коэффициентов многочленов от нескольких переменных будут рассмотрены со ссылками Фиг. 22-27. Далее, пример конфигурации аппаратуры в устройстве для обработки информации, способном реализовать каждый алгоритм согласно вариантам настоящего изобретения будет рассмотрен со ссылками Фиг. 28. Наконец, будет кратко изложено резюме технических принципов вариантов настоящего изобретения и преимуществ, обеспечиваемых этими техническими принципами.
Содержание
1. Введение
1-1: Алгоритм аутентификации с открытым ключом
1-2: Алгоритмы цифровой подписи
1-3: N-проходный алгоритм аутентификации с открытым ключом
2. Структуры 3-проходных алгоритмов аутентификации с открытым ключом
2-1: Пример конкретной структуры алгоритма
2-2: Пример структуры параллелизованного алгоритма
2-3: Пример структуры алгоритма на основе кубического многочлена от нескольких переменных
3: Структура 5-проходного алгоритма аутентификации с открытым ключом
3-1: Пример конкретной структуры алгоритма
3-2: Пример структуры параллелизованного алгоритма
3-3: Пример структуры алгоритма на основе кубического многочлена от нескольких переменных
4: Модификация алгоритма цифровой подписи
4-1: Модификация 3-проходного алгоритма аутентификации с открытым ключом и преобразование его в алгоритм цифровой подписи
4-2: Модификация 5-проходного алгоритма аутентификации с открытым ключом и преобразование его в алгоритм цифровой подписи
5: Способ уменьшения объема памяти, необходимого для верификации подписи
5-1: Структура хэш-функции
5-2: Пример применения 3-проходного алгоритма цифровой подписи
5-3: Пример применения 5-проходного алгоритма цифровой подписи
6: Способ выделения последовательности троичных случайных чисел из последовательности двоичных случайных чисел
6-1: Способ #1 выделения (2-битовое группирование)
6-2: Способ #2 выделения (нет группирования)
6-3: Способ #3 выделения (k-битовое группирование)
6-3-1: Базовая структура
6-3-2: Дополнительный способ выделения
7: Способ эффективной подстановки коэффициентов в многочлены от нескольких переменных
7-1: Базовое определение
7-2: Структурирование данных
7-2-1: Способ #1 структурирования
7-2-2: Способ #2 структурирования
7-2-3: Способ #3 структурирования
8: Пример конфигурации аппаратуры
9: Резюме
1. Введение
Предложенные здесь варианты относятся к алгоритму аутентификации с открытым ключом и алгоритму цифровой подписи, безопасность которых основана на трудности решения системы уравнений множества порядков с несколькими переменными. Однако предложенные здесь варианты отличаются от известных способов, таких как алгоритмы цифровой подписи на основе уравнений HFE, и относятся к алгоритму аутентификации с открытым ключом и алгоритму цифровой подписи, использующих системы уравнений множества порядков с несколькими переменными, для которых не хватает средств и способов эффективного решения (функций с потайными ходами). Сначала будут кратко обобщены алгоритмы аутентификации с открытым ключом, алгоритмы цифровой подписи и n-проходные алгоритмы аутентификации с открытым ключом.
1-1: Алгоритм аутентификации с открытым ключом
Сначала, обзор алгоритмов аутентификации с открытым ключом будет рассмотрен со ссылками на Фиг. 1. Фиг. 1 представляет пояснительную схему для описания структуры алгоритма аутентификации с открытым ключом.
Аутентификация с открытым ключом используется, когда человек (доказывающая сторона) подтверждает другому человеку (проверяющей стороне), что это он сам, с использованием открытого ключа pk и секретного ключа sk. Например, открытый ключ ркд доказывающей стороны А делают известным проверяющей стороне В. С другой стороны, доказывающая сторона А сохраняет свой секретный ключ skA в секрете. Согласно принципу алгоритма аутентификации с открытым ключом человек, который знает секретный ключ skA, соответствующий открытому ключу pkA, рассматривается как сама доказывающая сторона А.
Для того чтобы доказывающая сторона А доказала проверяющей стороне В, что она действительно является доказывающей стороной А, с использованием процедуры алгоритма аутентификации с открытым ключом, эта доказывающая сторона А предоставляет проверяющей стороне В доказательство, что она знает секретный ключ skA, соответствующий открытому ключу pkA. Тогда проверяющей стороне В представляют доказательство, указывающее, что доказывающая сторона А знает секретный ключ skA, и если проверяющая сторона В способна подтвердить это доказательство, достоверность доказывающей стороны А (факт, что она действительно является доказывающей стороной А) считается и является доказанной.
Однако установление процедуры аутентификации с открытым ключом требует выполнения следующих условий для обеспечения безопасности.
Первое условие формулируется так: «уменьшить насколько это возможно вероятность фальсификации со стороны фальсификатора, не имеющего секретного ключа sk, во время выполнения интерактивного протокола». Состояние, когда это первое условие выполняется, называется «корректность» (soundness). Другими словами, корректность означает, что «фальсификатор, с большой вероятностью не обладающий секретным ключом sk, ничего не фальсифицировал во время выполнения интерактивного протокола». Второе условие формулируется так: «даже при выполнении интерактивного протокола совсем не происходит утечки информации о секретном ключе skA доказывающей стороны А к проверяющей стороне В». Состояние, когда это второе условие выполняется, называется «нулевое разглашение» (zero knowledge).
Обеспечение безопасности с использованием алгоритма аутентификации с открытым ключом включает применение интерактивного протокола (далее - протокол взаимодействия), обладающего и корректностью, и нулевым разглашением. Если, гипотетически, процедура аутентификации осуществляется с использованием протокола взаимодействия, не обладающего корректностью и нулевым разглашением, появится конечная (ненулевая) вероятность фальшивой верификации и конечная вероятность разглашения информации секретного ключа, так что в результате достоверность доказывающей стороны не будет доказана, даже если сама процедура будет завершена успешно. Следовательно, вопрос о том, как обеспечить корректность и нулевое разглашение сеансового протокола, является очень важным.
Модель
В модели алгоритма аутентификации с открытым ключом присутствуют два субъекта - а именно доказывающая сторона и проверяющая сторона, как показано на Фиг. 1. Доказывающая сторона генерирует пару из открытого ключа pk и секретного ключа sk с использованием алгоритма Gen генерации ключей. Затем доказывающая сторона выполняет протокол взаимодействия с проверяющей стороной с использованием пары из секретного ключа sk и открытого ключа pk, сформированных посредством алгоритма Gen генерации ключей. В этот момент доказывающая сторона выполняет протокол взаимодействия с использованием алгоритма Р доказывающей стороны. Как описано выше, в рамках протокола взаимодействия доказывающая сторона предоставляет проверяющей стороне доказательства, что она обладает секретным ключом sk, с использованием алгоритма Р доказывающей стороны.
С другой стороны, проверяющая сторона выполняет протокол взаимодействия с использованием алгоритма V проверяющей стороны и тем самым проверяет, обладает ли доказывающая сторона секретным ключом, соответствующим открытому ключу, который опубликовала доказывающая сторона. Иными словами, проверяющая сторона представляет собой субъект, проверяющий, обладает ли доказывающая сторона секретным ключом, соответствующим открытому ключу. Как описано здесь, модель алгоритма аутентификации с открытым ключом конфигурирована из двух субъектов, а именно - доказывающей стороны и проверяющей стороны, и трех алгоритмов, а именно - алгоритма Gen генерации ключей, алгоритма Р доказывающей стороны и алгоритма V проверяющей стороны.
Кроме того, термины «доказывающая сторона» ("prover") и «проверяющая сторона» ("verifier") используются в последующем описании, но они везде обозначают строго «субъекты». Таким образом, субъект, выполняющий алгоритм Gen генерации ключей и алгоритм Р доказывающей стороны, представляет собой устройство для обработки информации, соответствующее субъекту «доказывающая сторона». Аналогично, субъект, выполняющий алгоритм V проверяющей стороны, представляет собой устройство для обработки информации. Пример аппаратной конфигурации устройства для обработки информации показан на Фиг. 28, например. Иными словами, алгоритм Gen генерации ключей, алгоритм Р доказывающей стороны и алгоритм V проверяющей стороны реализуются центральным процессором CPU 902 на основе программы, записанной в постоянном запоминающем устройстве (ПЗУ ROM) 904, в запоминающем устройстве с произвольной выборкой (ЗУПВ RAM) 906, в модуле 920 памяти, на сменном носителе 928 записи или на аналогичном носителе.
Алгоритм Gen генерации ключей
Указанный алгоритм Gen генерации ключей, используется доказывающей стороной. Этот алгоритм Gen генерации ключей представляет собой алгоритм, генерирующий пару и открытого ключа pk и секретного ключа sk, уникальную для соответствующей доказывающей стороны. Открытый ключ pk, сформированный алгоритмом Gen генерации ключей, публикуется. После этого опубликованный открытый ключ pk используется проверяющей стороной. С другой стороны, доказывающая сторона сохраняет секретность сформированного алгоритмом Gen генерации ключей секретного ключа sk. Секретный ключ sk, с которым доказывающая сторона обращается секретно, используется для доказательства проверяющей стороне, что доказывающая сторона обладает секретным ключом sk, соответствующим открытому ключу pk. Формализованно, алгоритм Gen генерации ключей представлен формулой (1) ниже в качестве алгоритма, получающего на вход параметр защищенности 1λ (λ - целое число, равное 0 или больше) и генерирующего на выходе секретный ключ sk и открытый ключ pk.
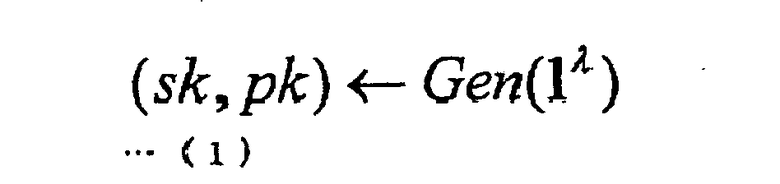
Алгоритм Р доказывающей стороны
Рассматриваемый алгоритм Р доказывающей стороны используется доказывающей стороной. Алгоритм Р доказывающей стороны представляет собой алгоритм для доказывания проверяющей стороне, что доказывающая сторона обладает секретным ключом sk, соответствующим открытому ключу pk. Другими словами, алгоритм Р доказывающей стороны представляет собой алгоритм, использующий открытый ключ pk и секретный ключ sk в качестве входных данных и выполняющий протокол взаимодействия.
Алгоритм V проверяющей стороны
Рассматриваемый алгоритм V проверяющей стороны используется проверяющей стороной. Алгоритм V проверяющей стороны представляет собой алгоритм для проверки, обладает ли доказывающая сторона секретным ключом sk, соответствующим открытому ключу pk, во время выполнения сеансового протокола. Алгоритм V проверяющей стороны представляет собой алгоритм, который получает на вход открытый ключ pk и генерирует на выходе 0 или 1 (1 бит) в соответствии с результатами выполнения сеансового протокола. В этот момент, проверяющая сторона принимает решение, что доказывающая сторона является недостоверной, если алгоритм V проверяющей стороны генерирует на выходе 0, и признает достоверность доказывающей стороны, если алгоритм V проверяющей стороны генерирует на выходе 1. Формализованно алгоритм V проверяющей стороны представлен следующей формулой (2).
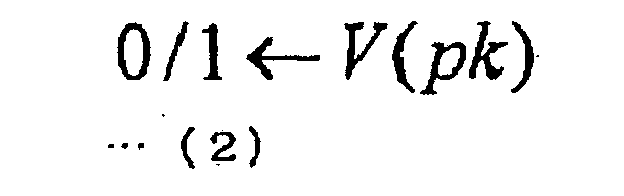
Как описано выше, реализация значимой аутентификации с открытым ключом включает обладание протоколом взаимодействия, удовлетворяющим двум условиям - корректности и нулевого разглашения. Однако доказательство того факта, что доказывающая сторона владеет секретным ключом sk включает выполнение этой доказывающей стороной процедуры, зависящей от этого секретного ключа sk, и затем сообщение проверяющей стороне результата, после чего проверяющая сторона осуществляет верификацию на основе содержания полученного сообщения. Для обеспечения корректности выполняют процедуру, зависящую от секретного ключа sk. В то же время нельзя передавать проверяющей стороне никакой информации о секретном ключе sk. По этой причине, упомянутые выше алгоритм Gen генерации ключей, алгоритм Р доказывающей стороны и алгоритм V проверяющей стороны грамотно построены так, чтобы удовлетворять этим требованиям.
Изложенное выше, таким образом, суммирует принципы алгоритма аутентификации с открытым ключом
1-2: Алгоритмы цифровой подписи
Далее, обзор алгоритмов цифровой подписи будет рассмотрен со ссылками на Фиг. 2. Фиг. 2 представляет пояснительную схему для обзора алгоритмов цифровой подписи.
В отличие от бумажных документов, нет необходимости физически подписывать или скреплять печатью данные в цифровой форме. По этой причине, доказательство достоверности создателя данных в цифровой форме предусматривает использование электронного механизма, создающего эффекты, аналогичные физическому подписанию бумажного документа или скреплению документа печатью. Этот механизм представляет собой цифровые подписи. Цифровая подпись обозначает механизм, ассоциирующий конкретные данные с данными подписи, известными только создателю данных, передающий данные подписи получателю и проверяющий эти данные подписи на стороне получателя.
Модель
Как показано на Фиг. 2, в модели алгоритма цифровой подписи присутствуют два субъекта - подписывающая сторона и проверяющая сторона. Кроме того, модель алгоритма цифровой подписи построена из трех алгоритмов: алгоритма Gen генерации ключей, алгоритма Sig генерации подписи и алгоритма Ver верификации подписи.
Подписывающая сторона использует алгоритм Gen генерации ключей для формирования пары из ключа sk подписи и проверочного ключа pk, уникальной для этой подписывающей стороны. Подписывающая сторона использует также алгоритм Sig генерации подписи с целью генерации цифровой подписи q для присоединения к сообщению М. Другими словами, подписывающая сторона является субъектом, прикрепляющим цифровую подпись к сообщению М. В то же время, проверяющая сторона использует алгоритм Ver верификации подписи для проверки цифровой подписи, прикрепленной к сообщению М. Другими словами, проверяющая сторона - это субъект, проверяющий цифровую подпись q с целью подтвердить, является ли создатель сообщения М подписывающей стороной.
Отметим, что где бы термины «подписывающая сторона» ("signer") и «проверяющая сторона» ("verifier") ни использовались в последующем описании, они в конечном счете обозначают субъектов. Следовательно, агент, выполняющий алгоритм Gen генерации ключей и алгоритм Sig генерации подписи, представляет собой устройство для обработки информации, соответствующее субъекту «подписывающая сторона». Аналогично, агент, выполняющий алгоритм Ver верификации подписи, представляет собой устройство для обработки информации. Вариант аппаратной конфигурации устройства для обработки информации показан на Фиг. 28, например. Иными словами, алгоритм Gen генерации ключей, алгоритм Sig генерации подписи и алгоритм Ver верификации подписи реализуются устройством, таким как центральный процессор CPU 902, на основе программы, записанной в постоянном запоминающем устройстве (ПЗУ ROM) 904, в запоминающем устройстве с произвольной выборкой (ЗУПВ RAM) 906, в модуле 920 памяти или на сменном носителе 928 записи.
Алгоритм Gen генерации ключей
Указанный алгоритм Gen генерации ключей, используется подписывающей стороной. Этот алгоритм Gen генерации ключей представляет собой алгоритм, генерирующий пару из ключа sk подписи и проверочного ключа pk, уникальную для соответствующей подписывающей стороны. Проверочный ключ pk, сформированный алгоритмом Gen генерации ключей, делается общедоступным (публикуется). В то же время, подписывающая сторона сохраняет секретность ключа sk подписи, сформированного алгоритмом Gen генерации ключей. Этот ключ sk подписи затем используется для генерации цифровой подписи q с целью прикрепления ее к сообщению М. Например, алгоритм Gen генерации ключей получает на вход параметр 1p защищенности (где p - целое число, равное или больше 0), и передает на выход ключ sk подписи и проверочный ключ pk. В таком случае алгоритм Gen генерации ключей может быть формализован и выражен следующей формулой (3).
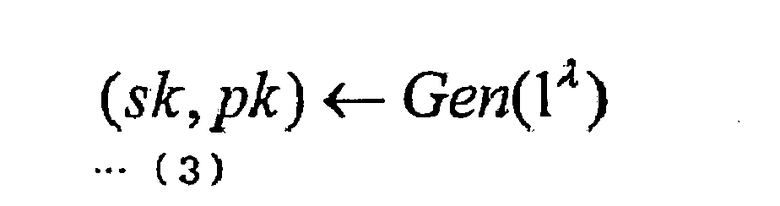
Алгоритм Sig генерации подписи
Указанный алгоритм Sig генерации подписи используется подписывающей стороной. Алгоритм Sig генерации подписи представляет собой алгоритм для генерации цифровой подписи q с целью прикрепления ее к сообщению М. Алгоритм Sig генерации подписи представляет собой алгоритм, получающий ключ sk подписи и сообщение М в качестве входных данных и передающий на выход цифровую подпись q. Формализованно указанный алгоритм Sig генерации подписи представлен следующей формулой (4).
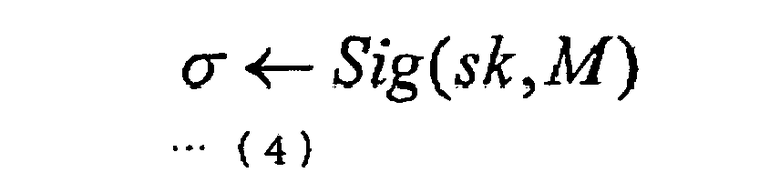
Алгоритм Ver верификации подписи
Указанный алгоритм Ver верификации подписи используется проверяющей стороной. Алгоритм Ver верификации подписи представляет собой алгоритм для проверки, является ли цифровая подпись q действительной и цифровой подписью для сообщения М. Этот алгоритм Ver верификации подписи представляет собой алгоритм, получающий проверочный ключ pk подписывающей стороны, сообщение М и цифровую подпись q в качестве входных данных и передающий на выход 0 или 1 (1 бит). Формализованно указанный алгоритм Ver верификации подписи представлен следующей формулой (5). В этот момент, проверяющая сторона принимает решение, что цифровая подпись q является недостоверной, если алгоритм Ver верификации подписи генерирует на выходе 0 (если проверочный ключ pk отклоняет сообщение М и цифровую подпись q), и признает достоверность цифровой подписи q, если алгоритм Ver верификации подписи генерирует на выходе 1 (если проверочный ключ pk принимает сообщение М и цифровую подпись q).
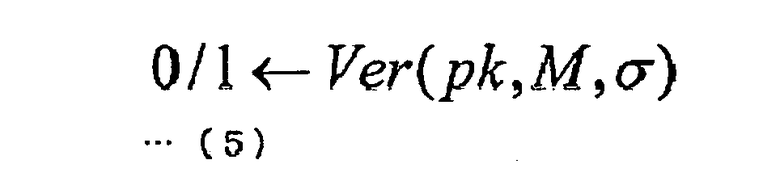
Изложенное выше, таким образом, суммирует принципы алгоритма цифровой подписи.
1-3: N-проходный алгоритм аутентификации с открытым ключом
Далее, n-проходныи алгоритм аутентификации с открытым ключом будет рассмотрен со ссылками на Фиг. 3. Фиг. 3 представляет поясняющую схему, иллюстрирующую пример n-проходного алгоритма аутентификации с открытым ключом.
Как описано выше, алгоритм аутентификации с открытым ключом представляет собой алгоритм аутентификации, доказывающий проверяющей стороне, что доказывающая сторона обладает секретным ключом sk, соответствующим открытому ключу pk, во время выполнения протокола взаимодействия. Кроме того, протокол взаимодействия должен удовлетворять двум условиям - корректности и нулевого разглашения. По этой причине во время выполнения протокола взаимодействия обе стороны - доказывающая сторона и проверяющая сторона, обмениваются информацией п раз в ходе осуществления соответствующих процедур, как показано на Фиг. 3.
В случае n-проходного алгоритма аутентификации с открытым ключом доказывающая сторона выполняет процедуру с использованием алгоритма Р доказывающей стороны (операция #1) и передает информацию T1 проверяющей стороне. После этого проверяющая сторона выполняет процедуру с использованием алгоритма V проверяющей стороны (операция #2) и передает информацию Т2 доказывающей стороне. Такое выполнение процедур и передачу информации Tk осуществляют последовательно для k=3-n, и, наконец, осуществляет процедуру (операция #n+1). Передача и прием информации таким способом п раз называется, таким образом, «п-проходной» схемой аутентификации с открытым ключом.
Изложенное выше, таким образом, описывает n-проходный алгоритм аутентификации с открытым ключом
2. Структуры 3-проходных алгоритмов аутентификации с открытым ключом
Далее будут рассмотрены алгоритмы, относящиеся к классу 3-проходных алгоритмов аутентификации с открытым ключом. Отметим, что в последующем описании 3-проходный алгоритм аутентификации с открытым ключом может быть также назван в некоторых случаях «3-проходной схемой» или «3-проходным алгоритмом».
2-1: Пример конкретной структуры алгоритма (Фиг. 4)
Сначала, пример конкретной структуры алгоритма, относящейся к 3-проходной схеме, будет рассмотрен со ссылками на Фиг. 4. Фиг. 4 представляет пояснительную схему для описания конкретной структуры алгоритма, относящейся к 3-проходной схеме. Здесь будет описан случай использования пары квадратичных многочленов (f1(x), …, fm(x)) в качестве части открытого ключа pk. Здесь предполагается, что квадратичный многочлен fi(x) представлен следующей формулой (6). Кроме того, вектор (x1, …, xn) обозначен x, а пара квадратичных многочленов (f1(x), …, fm(x)) от нескольких переменных обозначены как многочлены F(x) от нескольких переменных.
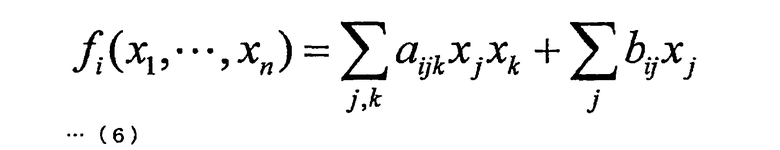
Кроме того, указанная пара квадратичных многочленов (f1(x), …, fm(x)) может быть представлена следующей формулой (7). В дополнение к этому, A1, …, Am представляет собой матрицу n × n. Далее, каждый из b1, …, bm представляет собой вектор n × 1.
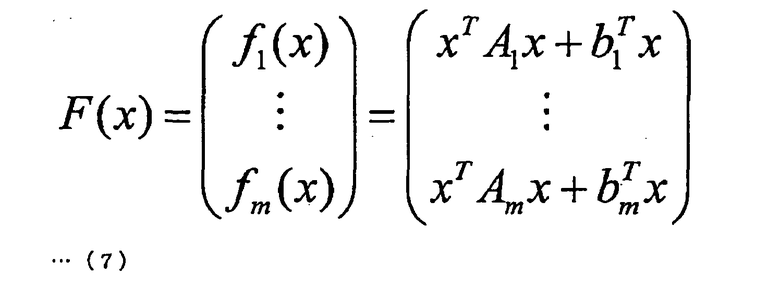
При использовании этих формул многочлен F может быть выражен следующими формулой (8) и формулой (9). На основе следующей формулы (10) можно легко подтвердить, что это выражение удовлетворяется.
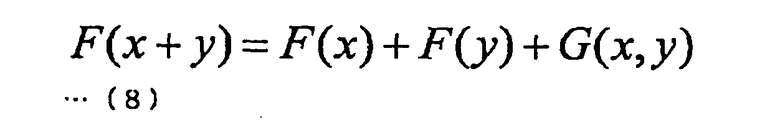
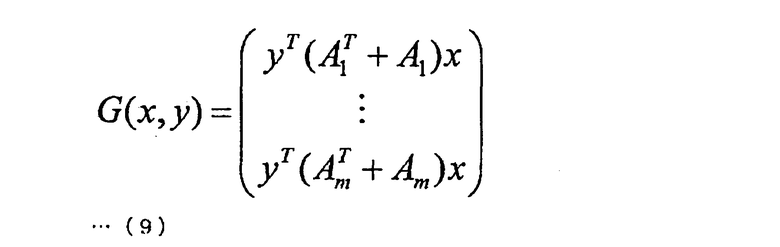
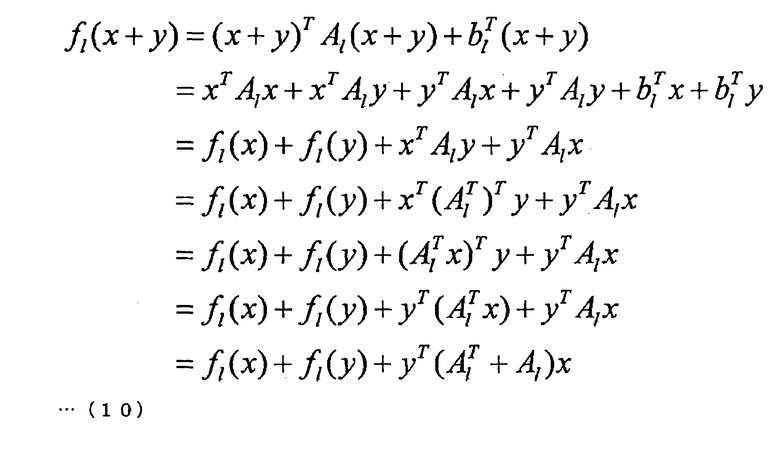
Если F(x+y) разбить на первую часть, зависящую только от х, вторую часть, зависящую только от y, и третью часть, зависящую и от х, и от y, тогда член G(x, y), соответствующий третьей части, становится билинейным относительно х и y. В последующем этот член G(x, y) будет также называться билинейным членом. Использование этого свойства позволяет построить эффективный алгоритм.
Например, используйте вектор t0, являющийся элементом множества Kn, и вектор ео, являющийся элементом множества Km, для представления многочлена F1(x) от нескольких переменных, служащего для маскирования многочленов F(x+r) от нескольких переменных, в виде F1(x)=G(x, t0)+e0. В этом случае сумма многочленов F(x+r0) и G(x) от нескольких переменных, представлена формулой (11) ниже. Здесь, если t1=r0+t0, e1=F(r0)+e0, многочлен F2(x)=F(x+r0)+F1(x) от нескольких переменных может быть представлен вектором t1, являющимся элементом множества Kn, и вектором e1, являющимся элементом множества Km. По этой причине, когда задан многочлен F1(x)=G(x, t0)+e0, многочлены F1 и F2 могут быть выражены с использованием вектора из множества Kn и вектора из множества Km, и, следовательно, можно реализовать эффективный алгоритм, которому для связи и обмена информацией необходим лишь небольшой объем данных.
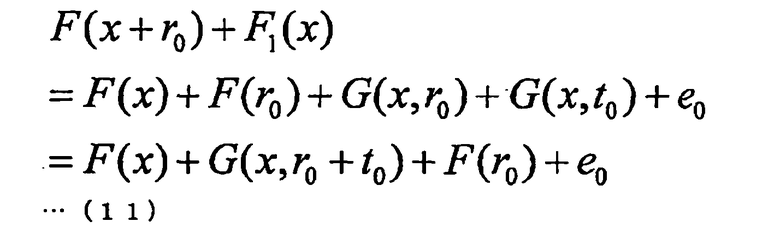
Кроме того, из многочлена F2 (или F1) совсем нет утечки информации относительно r0. Например, даже если даны e1 и t1 (или e0 и t0), информация относительно го остается совсем неизвестной до тех пор, пока неизвестны e0 и t0 (или e1 и t1). Соответственно, обеспечивается нулевое разглашение. Далее будут описаны алгоритмы, относящиеся к классу 3-проходных алгоритмов и построенные на основе изложенной выше логики. Алгоритм по 3-проходной схеме, который будет описан здесь ниже, построен из алгоритма Gen генерации ключей, алгоритма Р доказывающей стороны и алгоритма V проверяющей стороны.
Алгоритм Gen генерации ключей
Алгоритм Gen генерации ключей формирует m многочленов f1(x1, …, xn), …, fm(x1, …, xn) от нескольких переменных, определенных в кольце k, и вектор s=(s1, …, sn), являющийся элементом множества Kn. Далее алгоритм Gen генерации ключей вычисляет y=(y1, …, ym) ← (f1(s), …, fm(s)). Кроме того, алгоритм Gen генерации ключей задает (f1(x1, …, xn), …, fm(x1, …, xn), y) в открытом ключе pk и задает s в качестве секретного ключа. В последующем, вектор (x1, …, xn) обозначен х, а пара многочленов (f1(x), …, fm(x)) от нескольких переменных обозначена как F(x).
Алгоритм Р доказывающей стороны, алгоритм V проверяющей стороны
В дальнейшем, процедура, выполняемая алгоритмом Р доказывающей стороны, и процедура, выполняемая алгоритмом V проверяющей стороны, в ходе работы по протоколу взаимодействия будут описаны со ссылками на Фиг. 4. Во время исполнения протокола взаимодействия доказывающая сторона совсем не допускает утечки информации о секретном ключе s и сообщает проверяющей стороне, что «она сама знает величину s, удовлетворяющую уравнению y=F(s)». С другой стороны, проверяющая сторона осуществляет проверку, действительно ли доказывающая сторона знает величину s, удовлетворяющую уравнению y=F(s). Предполагается, что открытый ключ pk, сформированный алгоритмом Gen генерации ключей, публикуется. Кроме того, предполагается, что доказывающая сторона сохраняет секретность своего секретного ключа s. В дальнейшем описание будет дано со ссылками на логическую схему, изображенную на Фиг. 4.
Операция #1:
Как показано на Фиг. 4, алгоритм Р доказывающей стороны сначала случайным образом генерирует вектор r0, t0, являющийся элементом множества Kn, и вектор е0, являющийся элементом множества Km. После этого алгоритм Р доказывающей стороны вычисляет r1<-s-r0. Эти расчеты эквивалентны маскированию секретного ключа s с использованием вектора r0. Кроме того алгоритм Р доказывающей стороны вычисляет t1<-r0-t0. После этого алгоритм Р доказывающей стороны вычисляет e1<-F(r0) -e0.
Операция #1 (продолжение):
После этого алгоритм Р доказывающей стороны вычисляет с0<-H(r1, G(t0, r1)+e0). После этого алгоритм Р доказывающей стороны вычисляет c1<-H(t0, e0). После этого алгоритм Р доказывающей стороны вычисляет c2<-H(t1, e1). Сообщение (с0, c1, с2), генерируемое в ходе операции #1 посылают алгоритму V проверяющей стороны.
Операция #2:
После приема сообщения (с0, c1, c2) алгоритм V проверяющей стороны выбирает, какую схему использовать, из совокупности трех схем верификации. Например, алгоритм V проверяющей стороны может выбрать числовую величину из совокупности трех числовых величин {0, 1, 2}, представляющих схемы верификации, и задает выбранную числовую величину в качестве параметра Запрос (challenge) Ch. Этот запрос Ch передают алгоритму Р доказывающей стороны.
Операция #3:
По получении запроса Ch алгоритм Р доказывающей стороны генерирует ответ Rsp для передачи алгоритму V проверяющей стороны в ответ на принятый запрос Ch. Если Ch=0, алгоритм Р доказывающей стороны генерирует ответ Rsp=(r0, t1, e1). Если Ch=1, алгоритм Р доказывающей стороны генерирует ответ Rsp=(r1, t0, e0). Если Ch=2, алгоритм Р доказывающей стороны генерирует ответ Rsp=(r1, t1, e1). Ответ Rsp, генерируемый в ходе операции #3, посылают алгоритму V проверяющей стороны.
Операция #4:
После приема ответа Rsp алгоритм V проверяющей стороны выполняет следующую процедуру верификации с использованием принятого ответа Rsp.
Если Ch=0, алгоритм V проверяющей стороны проверяет, выполняется ли равенство c1=Н(r0-t1, F(r0)-e1). Кроме того, алгоритм V проверяющей стороны проверяет, выполняется ли равенство c2=H(t1, e1). Алгоритм V проверяющей стороны передает на выход величину 1, чтобы указать на успех аутентификации, если все эти процедуры верификации завершились успешно, и передает на выход величину 0, чтобы указать на неудачу аутентификации, если какая-либо процедура верификации закончилась неудачей.
Если Ch=1, алгоритм V проверяющей стороны проверяет, выполняется ли равенство с0=H(r1, G(t0, r1)+e0). Кроме того, алгоритм V проверяющей стороны проверяет, выполняется ли равенство c1=H(t0, e0). Алгоритм V проверяющей стороны передает на выход величину 1, чтобы указать на успех аутентификации, если все эти процедуры верификации завершились успешно, и передает на выход величину 0, чтобы указать на неудачу аутентификации, если какая-либо процедура верификации закончилась неудачей.
Если Ch=2, алгоритм V проверяющей стороны проверяет, выполняется ли равенство с0=H(r1, y-F(r1)-G(t1, r1)-e1). Кроме того, алгоритм V проверяющей стороны проверяет, выполняется ли равенство с2=H(t1, e1). Алгоритм V проверяющей стороны передает на выход величину 1, чтобы указать на успех аутентификации, если все эти процедуры верификации завершились успешно, и передает на выход величину 0, чтобы указать на неудачу аутентификации, если какая-либо процедура верификации закончилась неудачей.
Выше был описан пример структуры эфективного алгоритма, относящегося к 3-проходной схеме.
2-2: Пример структуры параллелизованного алгоритма (Фиг. 5)
Далее, способ параллелизации алгоритма, относящегося к 3-проходной схеме, показанной на Фиг. 4, будет описан со ссылками на Фиг. 5. Однако дальнейшее описание структуры алгоритма Gen генерации ключей будет опущено.
На деле, применение описанного выше сеансового протокола делает возможным сохранение вероятности успешной фальсификации на уровне 2/3 или меньше. Следовательно, выполнение этого сеансового протокола дважды делает возможным сохранение вероятности успешной фальсификации на уровне (2/3)2 или меньше. Более того, если рассматриваемый сеансовый протокол выполнить N раз, вероятность успешной фальсификации становится не больше (2/3)N, а если в качестве N задать достаточно большое число (N=140, например), вероятность успешной фальсификации становится пренебрежимо малой.
В качестве способов многократного выполнения протокола взаимодействия можно представить себе последовательный способ, в соответствии с которым последовательно и многократно производят операции обмена сообщениями, передачи запроса и получения ответа, и параллельный способ, когда большим числом сообщений, запросов и ответов обмениваются в единственном цикле обмена, например. Кроме того, можно также представить себе гибридный способ, сочетающий последовательный способ и параллельный способ. Здесь алгоритмы, выполняющие описанный выше протокол взаимодействия, относящийся к 3-проходной схеме, параллельно (далее называемые параллелизованными алгоритмами) будут теперь описаны со ссылками на Фиг. 5.
Операция #1:
Как показано на Фиг. 5, алгоритм Р доказывающей стороны сначала выполняет следующие процессы с (1) по (6) для i=1-N.
Процесс (1): Алгоритм Р доказывающей стороны генерирует векторы r0i, t0i, являющиеся элементами множества Kn, и вектор e0i, являющийся элементом множества Km.
Процесс (2): Алгоритм Р доказывающей стороны вычисляет r1i<-s-r0i. Эти расчеты эквивалентны маскированию секретного ключа s с использованием вектора r0i. Кроме того алгоритм Р доказывающей стороны вычисляет t1i<-r0i+t0i.
Процесс (3): Алгоритм Р доказывающей стороны вычисляет e1i<-F(r0i)-e0i.
Процесс (4): Алгоритм Р доказывающей стороны вычисляет c0i<-Н(r1i, G(r1i, t0i)+e0i).
Процесс (5): Алгоритм Р доказывающей стороны вычисляет c1i<-H(t0i, e0i).
Процесс (6): Алгоритм Р доказывающей стороны вычисляет c2i<-H(t1i, e1i).
Операция #1 (продолжение):
После выполнения описанных выше процессов с (1) по (6) для i=1-N, алгоритм Р доказывающей стороны вычисляет Cmt<-H(c01, с11, с21, …, c0N, c1N, c2N). Хэш-величину Cmt, генерируемую в ходе операции #1, передают алгоритму V проверяющей стороны. Таким путем сообщение (c01, с11, с21, …, c0N, c1N, c2N) преобразуют в хэш-величину, передаваемую алгоритму V проверяющей стороны, тем самым позволяя уменьшить объем обмена информацией в процессе связи.
Операция #2:
После приема хэш-величины Cmt алгоритм V проверяющей стороны выбирает схему верификации для использования из совокупности трех схем верификации для каждого из i=1-N. Например, алгоритм V проверяющей стороны может, для каждого из i=1-N, выбрать числовую величину из совокупности трех цифровых величин {0, 1, 2}, представляющих схемы верификации, и задать выбранную числовую величину в качестве параметра запроса Chi. Параметры запросов Ch1, …, ChN передают алгоритму Р доказывающей стороны.
Операция #3:
По получении запросов Ch1, …, ChN алгоритм Р доказывающей стороны генерирует ответы Rsp1, …, RspN для передачи алгоритму V проверяющей стороны в ответ на каждый из принятых запросов Ch1, …, ChN. Если Chi=0, алгоритм Р доказывающей стороны генерирует ответ Rspi=(r0i, t1i, e1i, c0i). Если Chi=1, алгоритм Р доказывающей стороны генерирует ответ Rspi=(r1i, t0i, e0i, c2i). Если Chi=2, алгоритм Р доказывающей стороны генерирует ответ Rspi=(r1i, t1i, e1i, c1i).
Ответы Rsp1, …, RspN, генерируемые в ходе операции #3, посылают алгоритму V проверяющей стороны.
Операция #4:
После приема ответов Rsp1, …, RspN алгоритм V проверяющей стороны выполняет следующие процессы с (1) по (3) для i=1-N с использованием принятых ответов Rsp1, …, RspN. Здесь алгоритм V проверяющей стороны выполняет процесс (1) для случая Chi=0, процесс (2) для случая Chi=1 и процесс (3) для случая Chi=2.
Процесс (1): Если Chi=0, алгоритм V проверяющей стороны выделяет (r0i, t1i, e1i, c0i) на основе Rspi. После этого, алгоритм V проверяющей стороны вычисляет c1i=Н(r0i-t1i, F(r0i)-e1i). Кроме того, алгоритм V проверяющей стороны вычисляет c2i=H(t1i, e1i). Затем алгоритм V проверяющей стороны сохраняет (c0i, c1i, c2i).
Процесс (2): Если Chi=1, алгоритм V проверяющей стороны выделяет (r1i, t0i, e0i, c2i) на основе Rspi. После этого, алгоритм V проверяющей стороны вычисляет c0i=Н(r1i, G(t0i, r1i)+e0i). Кроме того, алгоритм V проверяющей стороны вычисляет c1i=H(t0i, e0i). Затем алгоритм V проверяющей стороны сохраняет (c0i, c1i, c2i).
Процесс (3): Если Chi=2, алгоритм V проверяющей стороны выделяет (r1i, t1i, e1i, c1i) на основе Rspi. После этого, алгоритм V проверяющей стороны вычисляет Н(r1i, y-F(r1i)-G(t1i, r1i)-e1i). Кроме того, алгоритм V проверяющей стороны вычисляет c2i=Н(t1i, e1i). Затем алгоритм V проверяющей стороны сохраняет (c0i, c1i, c2i).
После выполнения описанных выше процессов с (1) по (3) для i=1-N, алгоритм V проверяющей стороны проверяет, выполняется ли равенство Cmt=H(c01, с11, c21, …, c0N, c1N, C2N). Алгоритм V проверяющей стороны передает на выход величину 1, чтобы указать на успех аутентификации, если процедуры верификации завершились успешно, и передает на выход величину 0, чтобы указать на неудачу аутентификации, если процедура верификации закончилась неудачей.
Выше был описан пример структуры параллелизованного эффективного алгоритма, относящегося к 3-проходной схеме.
2-3: Пример структуры алгоритма на основе кубического многочлена от нескольких переменных
Здесь будет рассмотрен способ построения эффективного алгоритма с использованием кубического многочлена f1 для кольца R, выраженного следующей формулой (12). Многочлен F=(f1, …, fm) от нескольких переменных, выраженный с применением пары кубических многочленов f1 удовлетворяет следующей формуле (13). Здесь, Gx(x, y) представляет линейный член от х. Кроме того, Gy(x, y) представляет линейный член от y. Когда выражены Gx=(gx1,…, gxm) и Gy=(gy1, …, gym), можно вывести параметры gx1 и gy1 согласно следующим формуле (14) и формуле (15), соответственно. Здесь, поскольку второй член справа в составе gx1 также является линейным по одной из переменных x и y, этот второй член справа может содержать gy1.
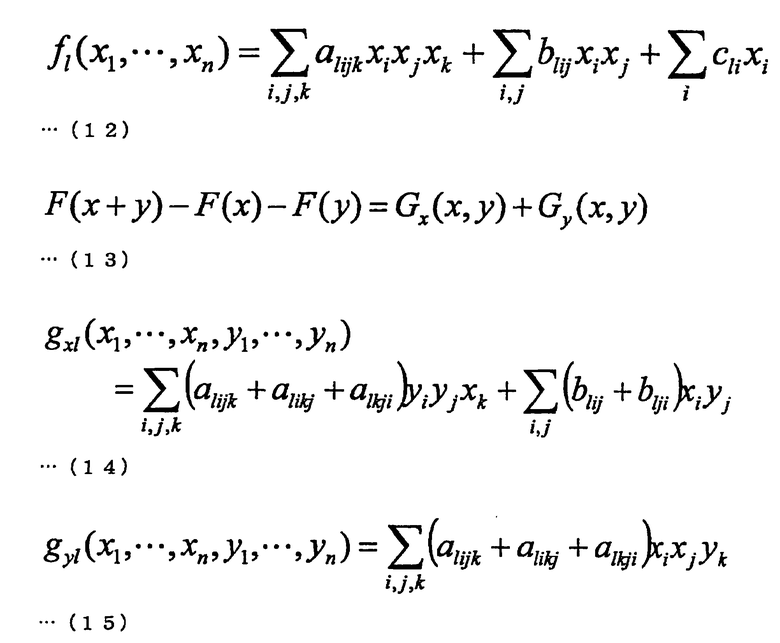
Как понятно из приведенных выше формулы (14) и формулы (15), многочлены Gx(x, y) и Gy(x, y) становятся аддитивно гомоморфными по x и y. Таким образом, с использованием этого свойства открытый ключ F(s) разделен путем введения новых переменных r0, r1, t0, u0 и е0, как в способе построения эффективного алгоритма с использованием квадратичного многочлена fi.
Поскольку многочлены Gx и Gy являются аддитивно гомоморфными, взаимосвязи между формулами с (16) по (19) установлены с использованием переменных r0, r1, t0, u0 и е0. Следующие формулы с (16) по (19) могут быть разделены на первую часть, воспроизводимую с использованием (r0, t0, u0, е0), вторую часть, воспроизводимую с использованием (r0, u1, e1), третью часть, воспроизводимую с использованием (r1, t0, е0), и четвертую часть, воспроизводимую с использованием (r1, t1, u1, e1).
Например, "r0, t0", включенные в следующую формулу (17), "u0", включенный в следующую формулу (18), и "F(r0), Gy(r0, u0), е0", включенные в следующую формулу (19) являются первой частью. Кроме того, "Gy(r0, u1), e1", включенные в следующую формулу (19), являются второй частью. Кроме того, "е0, Gx(r0, r1)", включенные в следующую формулу (16), являются третьей частью. Кроме того, "e1, F(r1), Gx(t1, r1)", включенные в следующую формулу (16), "t1", включенный в следующую формулу (17), и "u1", включенный в следующую формулу (18), составляют четвертую часть.
Другими словами, следующая формула (16) включает третью и четвертую части, следующая формула (17) и следующая формула (18) включают первую и четвертую части и следующая формула (19) включает первую и вторую части. Таким образом, каждая из следующих формул с (16) по (19) включает два вида частей.
Само определение секретного ключа s и взаимосвязь между следующими формулами (16)-(19) обеспечивают, что секретный ключ s невозможно получить, даже если используется какая-либо из групп (r0, t0, u0, е0), (r0, u1, e1), (r1, t0, е0) и (r1, t1, u1, e1). Использование этого свойства позволяет, например, построить эффективный алгоритм (далее именуемый - расширенный алгоритм) с использованием кубического многочлена f1 на кольце R.
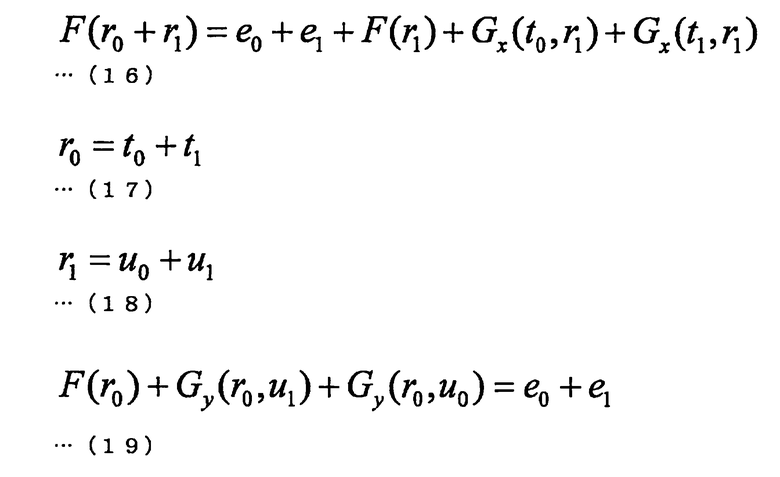
Далее будет описан пример структуры конкретного расширенного алгоритма. К работе расширенного алгоритма относятся два базовых момента, а именно - проверяющей стороне направляют сообщение, выраженное одной из следующих формул (20)-(22), и проверяют одну из указанных частей с первой по четвертую. Однако только такая проверка может и не позволить проверить, что параметр "r1", входящий в состав третьей части, идентичен параметру "r1", входящему в состав четвертой части. Аналогично, может оказаться невозможно проверить, что параметр "r0", входящий в состав первой части, идентичен параметру "r0", входящему в состав второй части, или что параметры "t0, e0", входящие в состав первой части, идентичны параметрам "t0, e0", входящим в состав третьей части. Кроме того, может оказаться невозможно проверить, что параметры "u1, e1", входящие в состав второй части, идентичны параметрам "u1, e1", входящим в состав четвертой части. Соответственно, ниже будет приведен пример структуры, позволяющей осуществить такую проверку.
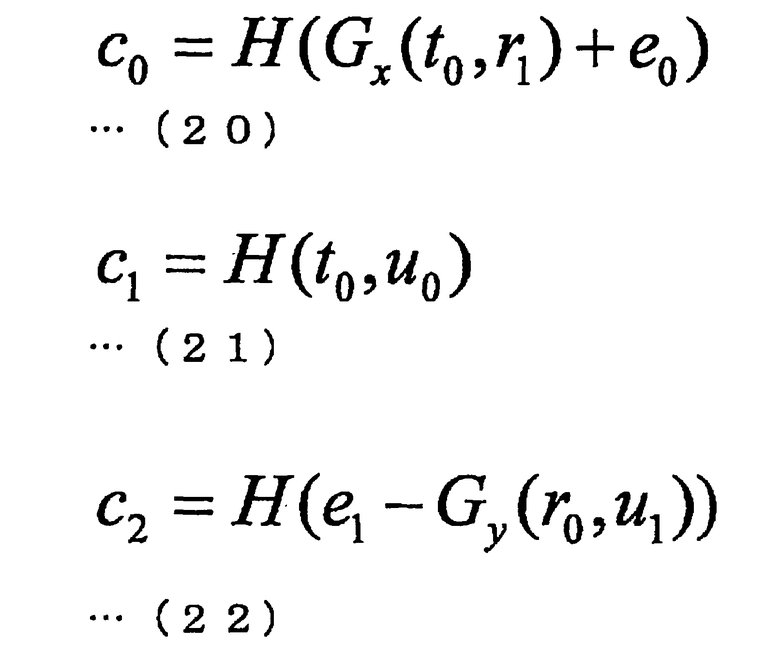
2-3-1: Базовая структура (Фиг. 7)
Далее, пример конфигурации расширенного алгоритма, относящегося к 3-проходной схеме, будет рассмотрен со ссылками на Фиг. 6. Однако дополнительное описание структуры алгоритма Gen генерации ключей будет опущено.
Операция #1:
Как показано на Фиг. 6, алгоритм Р доказывающей стороны случайным образом генерирует векторы r0, t0, u0, являющиеся элементами множества Kn, и вектор е0, являющийся элементом множества Km. После этого алгоритм Р доказывающей стороны вычисляет r1<-s-r0. Эти расчеты эквивалентны маскированию секретного ключа s с использованием вектора го. После этого алгоритм Р доказывающей стороны вычисляет t1<-r0+t0. После этого алгоритм Р доказывающей стороны вычисляет u1<-r1+u0. После этого алгоритм Р доказывающей стороны вычисляет e1<-F(r0)-е0.
Операция #1 (продолжение):
После этого алгоритм Р доказывающей стороны вычисляет c0<-H(r1, Gx(t0, r1)+е0). После этого алгоритм Р доказывающей стороны вычисляет c1<-Н(r0-t0, u0). После этого алгоритм Р доказывающей стороны вычисляет с2<-Н(r0, e1-Gy(r0, u1)). После этого алгоритм Р доказывающей стороны вычисляет c3<-H(t0, е0). После этого алгоритм Р доказывающей стороны вычисляет c4<-H(u1, e1). Сообщения (с0, c1, c2, c3, c4), генерируемые в ходе операции #1 посылают алгоритму V проверяющей стороны.
Операция #2:
После приема сообщений (с0, c1, c2, с3, c4) алгоритм V проверяющей стороны выбирает, какую схему использовать, из совокупности четырех схем верификации. Например, алгоритм V проверяющей стороны может выбрать числовую величину из совокупности четырех числовых величин {0, 1, 2, 3}, представляющих схемы верификации, и задает выбранную числовую величину в качестве параметра Запрос Ch. Этот запрос Ch передают алгоритму Р доказывающей стороны.
Операция #3:
По получении запроса Ch алгоритм Р доказывающей стороны генерирует ответ Rsp для передачи алгоритму V проверяющей стороны в ответ на принятый запрос Ch. Если Ch=0, алгоритм Р доказывающей стороны генерирует ответ Rsp=(r0, t0, u0, е0). Если Ch=1, алгоритм Р доказывающей стороны генерирует ответ Rsp=(r0, u1, e1). Если Ch=2, алгоритм Р доказывающей стороны генерирует ответ Rsp=(r1, t0, е0). Если Ch=3, алгоритм Р доказывающей стороны генерирует ответ Rsp=(r1, t1, u1, e1). Ответ Rsp, генерируемый в ходе операции #3, посылают алгоритму V проверяющей стороны.
Операция #4:
После приема ответа Rsp алгоритм V проверяющей стороны выполняет следующую процедуру верификации с использованием принятого ответа Rsp.
Если Ch=0, алгоритм V проверяющей стороны проверяет, выполняется ли равенство c1=H(r0-t0, u0). После этого, алгоритм V проверяющей стороны проверяет, выполняется ли равенство c2=H(r0, F(r0)+Gy(r0, u0)-е0). После этого, алгоритм V проверяющей стороны проверяет, выполняется ли равенство с3=H(t0, е0). Алгоритм V проверяющей стороны передает на выход величину 1, чтобы указать на успех аутентификации, если все эти процедуры верификации завершились успешно, и передает на выход величину 0, чтобы указать на неудачу аутентификации, если какая-либо процедура верификации закончилась неудачей.
Если Ch=1, алгоритм V проверяющей стороны проверяет, выполняется ли равенство с2=H(r0, e1-Gy(r0, u1)). После этого, алгоритм V проверяющей стороны проверяет, выполняется ли равенство c4=H(u1, e1). Алгоритм V проверяющей стороны передает на выход величину 1, чтобы указать на успех аутентификации, если все эти процедуры верификации завершились успешно, и передает на выход величину 0, чтобы указать на неудачу аутентификации, если какая-либо процедура верификации закончилась неудачей.
Если Ch=2, алгоритм V проверяющей стороны проверяет, выполняется ли равенство с0=H(r1, e0-Gx(t0, r1)). После этого, алгоритм V проверяющей стороны проверяет, выполняется ли равенство с3=H(t0, e0). Алгоритм V проверяющей стороны передает на выход величину 1, чтобы указать на успех аутентификации, если все эти процедуры верификации завершились успешно, и передает на выход величину 0, чтобы указать на неудачу аутентификации, если какая-либо процедура верификации закончилась неудачей.
Если Ch=3, алгоритм V проверяющей стороны проверяет, выполняется ли равенство с0=H(r1, y-F(r1)-e1-Gx(t1, r1)). После этого, алгоритм V проверяющей стороны проверяет, выполняется ли равенство c1=H(t1, r1, u1). После этого, алгоритм V проверяющей стороны проверяет, выполняется ли равенство c4=H(u1, e1). Алгоритм V проверяющей стороны передает на выход величину 1, чтобы указать на успех аутентификации, если все эти процедуры верификации завершились успешно, и передает на выход величину 0, чтобы указать на неудачу аутентификации, если какая-либо процедура верификации закончилась неудачей.
Выше был описан пример структуры расширенного алгоритма, относящегося к 3-проходной схеме. Использование кубического многочлена позволяет реализовать более высокую степень защищенности.
3: Структура 5-проходного алгоритма аутентификации с открытым ключом
Далее будут рассмотрены алгоритмы, относящиеся к классу 5-проходных алгоритмов аутентификации с открытым ключом. Отметим, что в последующем описании 5-проходный алгоритм аутентификации с открытым ключом может быть также в некоторых случаях назван «5-проходной схемой» или «5-проходным алгоритмом».
В случае 3-проходной схемы вероятность ложной верификации составляет 2/3 на каждый цикл выполнения протокола взаимодействия. Однако в случае 5-проходной схемы вероятность ложной верификации составляет 1/2+1/q на каждый цикл выполнения протокола взаимодействия. Здесь q обозначает порядок кольца, которое нужно использовать. Соответственно, когда порядок кольца достаточно велик, вероятность ложной верификации на один цикл 5-проходной схемы можно уменьшить, и, таким образом, вероятность ложной верификации может быть значительно уменьшена при выполнении протокола взаимодействия небольшое число раз.
Например, если нужно, чтобы вероятность ложной верификации была не больше 1/2n, протокол взаимодействия в 3-проходной схеме нужно выполнить не меньше n/(log3-1)=1.701n раз. С другой стороны, если нужно, чтобы вероятность ложной верификации была не больше 1/2n, протокол взаимодействия в 5-проходной схеме нужно выполнить не меньше n/(1-log(1+1/q)) раз. Соответственно, когда q=24, объем информации связи, необходимый для обеспечения одного и того же уровня защищенности, в 5-проходной схеме меньше, чем в 3-проходной схеме.
3-1: Пример конкретной структуры алгоритма (Фиг. 7)
Сначала, пример конкретной структуры алгоритма, относящейся к 5-проходной схеме, будет рассмотрен со ссылками на Фиг. 7. Фиг. 7 представляет пояснительную схему для описания конкретной структуры алгоритма, относящейся к 5-проходной схеме. Здесь будет описан случай использования пары квадратичных многочленов (f1(x), …, fm(x)), как части открытого ключа pk. Здесь предполагается, что квадратичный многочлен fi(x) представлен приведенной выше формулой (6). Кроме того, вектор (x1, …, xn) обозначен x, а пара квадратичных многочленов (f1(x), …, fm(x)) от нескольких переменных обозначены как многочлены F(x) от нескольких переменных.
Как в эффективных алгоритмах, относящихся к 3-проходной схеме, два вектора, а именно вектор t0, являющийся элементом множества Kn, и вектор е0, являющийся элементом множества Km, используют для представления многочлена F1(x) от нескольких переменных, служащего для маскирования многочленов F(x+r0) от нескольких переменных, в виде F1(x)=G(x, t0)+е0. При использовании этих формул можно для многочлена F(x+r0) от нескольких переменных получить соотношение, выраженное следующей формулой (23).
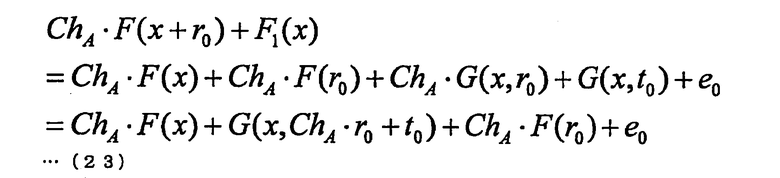
По этой причине, когда t1=ChA·r0+t0, e1=ChA·F(r0)+е0, многочлен F2(x)=ChA·F(x+r0)+F1(x) от нескольких переменных после маскирования также может быть выражен двумя векторами, а именно вектором t1, который является элементом множества Kn, и вектором e1, который является элементом множества Km. По этой причине, когда задан многочлен F1(x)=G(x, t0)+е0, многочлены F1 и F2 могут быть выражены с использованием вектора из множества Kn и вектора из множества Km, и, следовательно, можно реализовать эффективный алгоритм, которому для связи необходим лишь небольшой объем данных.
Кроме того, из многочлена F2 (или F1) совсем нет утечки информации относительно r0. Например, даже если даны e1 и t1 (или е0 и t0), информация относительно r0 остается совсем неизвестной до тех пор, пока неизвестны е0 и t0 (или e1 и t1). Соответственно, обеспечивается нулевое разглашение. Далее будут описаны алгоритмы, относящиеся к классу 5-проходных алгоритмов и построенные на основе изложенной выше логики. Алгоритм по 5-проходной схеме, который будет описан здесь, построен из алгоритма Gen генерации ключей, алгоритма Р доказывающей стороны и алгоритма V проверяющей стороны.
Алгоритм Gen генерации ключей
Алгоритм Gen генерации ключей формирует многочлены f1(x1, …, xn), …, fm(x1, …, xn) от нескольких переменных, определенные в кольце k и вектор s=(s1, …, sn), являющийся элементом множества Kn. Далее алгоритм Gen генерации ключей вычисляет y=(y1, …, ym)<-(f1(s), …, fm(s)). Кроме того, алгоритм Gen генерации ключей задает (f1 …, fm, y) в открытом ключе pk и задает s в качестве секретного ключа. В последующем, вектор (x1, …, xn) обозначен x, а пара многочленов (f1(x), …, fm(x)) от нескольких переменных обозначена как F(x).
Алгоритм Р доказывающей стороны, алгоритм V проверяющей стороны
В дальнейшем, процедура, выполняемая алгоритмом Р доказывающей стороны, и процедура, выполняемая алгоритмом V проверяющей стороны, в ходе работы по протоколу взаимодействия будут описаны со ссылками на Фиг. 7. Во время исполнения протокола взаимодействия доказывающая сторона совсем не допускает утечки информации о секретном ключе s и сообщает проверяющей стороне, что «она сама знает величину s, удовлетворяющую уравнению y=F(s)». С другой стороны, проверяющая сторона осуществляет проверку, действительно ли доказывающая сторона знает величину s, удовлетворяющую уравнению y=F(s). При этом, предполагается, что открытый ключ pk сделан известным проверяющей стороне. Кроме того, предполагается, что доказывающая сторона сохраняет секретность своего секретного ключа s. В дальнейшем описание будет дано со ссылками на логическую схему, изображенную на Фиг. 7.
Операция #1:
Как показано на Фиг. 7, алгоритм Р доказывающей стороны случайным образом генерирует вектор r0, являющийся элементом множества Kn, вектор t0, являющийся элементом множества Kn, и вектор е0, являющийся элементом множества Km. После этого алгоритм Р доказывающей стороны вычисляет r1<-s-r0. Эти расчеты эквивалентны маскированию секретного ключа s с использованием вектора r0. После этого алгоритм Р доказывающей стороны вычисляет хэш-величину со для векторов r0, t0, е0. Иными словами, алгоритм Р доказывающей стороны вычисляет с0<-H(r0, t0, е0). После этого алгоритм Р доказывающей стороны вычисляет G(t0, r1)+е0 и хэш-величину c1 от r1. Иными словами, алгоритм Р доказывающей стороны вычисляет с0<-H(r1, G(t0, r1)+е0). Сообщения (с0, c1), генерируемые в ходе операции #1, посылают алгоритму V проверяющей стороны.
Операция #2:
После приема сообщений (с0, c1), алгоритм V проверяющей стороны случайным образом выбирает одно число ChA из совокупности q колец K и передает выбранное число ChA алгоритму Р доказывающей стороны.
Операция #3:
После приема числа ChA, алгоритм Р доказывающей стороны вычисляет t1<-ChA·r0-t0. Кроме того, алгоритм Р доказывающей стороны вычисляет e1<-ChA·F(r0)-е0. Алгоритм Р доказывающей стороны передает t1 и e1 алгоритму V проверяющей стороны.
Операция #4:
После приема t1 и e1 алгоритм V проверяющей стороны выбирает, какую схему верификации использовать, из совокупности двух схем верификации. Например, алгоритм V проверяющей стороны может выбрать числовую величину из совокупности двух числовых величин {0, 1}, представляющих схемы верификации, и задает выбранную числовую величину в качестве параметра запроса Ch. Этот запрос ChB передают алгоритму Р доказывающей стороны.
Операция #5:
По получении запроса ChB алгоритм Р доказывающей стороны генерирует ответы Rsp для передачи алгоритму V проверяющей стороны в ответ на принятый запрос ChB. Если ChB=0, алгоритм Р доказывающей стороны генерирует ответ Rsp=r0. Если ChB=1, алгоритм Р доказывающей стороны генерирует ответ Rsp=r1. Ответ Rsp, генерируемый в ходе операции #5, посылают алгоритму V проверяющей стороны.
Операция #6:
После приема ответа Rsp алгоритм V проверяющей стороны выполняет следующую процедуру верификации с использованием принятого ответа Rsp.
Если ChB=0, алгоритм V проверяющей стороны выполняет r0<-Rsp. Затем, алгоритм V проверяющей стороны проверяет, выполняется ли равенство с0=Н(r0, ChA·r0-t1, ChA·F(r0)-e1). Алгоритм V проверяющей стороны передает на выход величину 1, чтобы указать на успех аутентификации, если все эти процедуры верификации завершились успешно, и передает на выход величину 0, чтобы указать на неудачу аутентификации, если какая-либо процедура верификации закончилась неудачей.
Если ChB=1, алгоритм V проверяющей стороны выполняет r1<-Rsp. Затем алгоритм V проверяющей стороны проверяет, выполняется ли равенство c1=H1(r1, ChA·(y-F(r1)-G(t1, r1)-e1)). Алгоритм V проверяющей стороны передает на выход величину 1, чтобы указать на успех аутентификации, если все эти процедуры верификации завершились успешно, и передает на выход величину 0, чтобы указать на неудачу аутентификации, если какая-либо процедура верификации закончилась неудачей.
Выше был описан пример структуры эффективного алгоритма, относящегося к 5-проходной схеме.
3-2: Пример структуры параллелизованного алгоритма (Фиг. 8)
Далее, способ параллелизации алгоритма, относящегося к 5-проходной схеме, показанной на Фиг. 7, будет описан со ссылками на Фиг. 8. Однако дальнейшее описание структуры алгоритма Gen генерации ключей будет опущено.
Как описано выше, применение рассмотренного выше протокола взаимодействия, относящегося к 5-проходной схеме, делает возможным сохранение вероятности успешной фальсификации на уровне (1/2+1/q) или меньше. Следовательно, выполнение этого протокола взаимодействия дважды делает возможным сохранение вероятности успешной фальсификации на уровне (1/2+1/q)2 или меньше. Более того, если рассматриваемый протокол взаимодействия выполнить N раз, вероятность успешной фальсификации становится не больше (1/2+1/q)N, а если в качестве N задать достаточно большое число (N=80, например), вероятность успешной фальсификации становится пренебрежимо малой.
В качестве способов многократного выполнения протокола взаимодействия можно представить себе последовательный способ, в соответствии с которым последовательно и многократно производят операции обмена сообщениями, передачи запроса и получения ответа, и параллельный способ, когда большим числом сообщений, запросов и ответов обмениваются в единственном цикле обмена, например. Кроме того, можно также представить себе гибридный способ, сочетающий последовательный способ и параллельный способ. Здесь алгоритмы, выполняющие описанный выше протокол взаимодействия, относящийся к 5-проходной схеме, параллельно (далее называемые параллелизованными алгоритмами) будут теперь описаны.
Операция #1:
Как показано на Фиг. 8, алгоритм Р доказывающей стороны сначала выполняет следующие процессы с (1) по (4) для i=1-N.
Процесс (1): Алгоритм Р доказывающей стороны генерирует векторы r0i, t0i, являющиеся элементами множества Kn, и вектор e0i, являющийся элементом множества Km.
Процесс (2): Алгоритм Р доказывающей стороны вычисляет r1i<-s-r0i. Эти расчеты эквивалентны маскированию секретного ключа s с использованием вектора r0i.
Процесс (3): Алгоритм Р доказывающей стороны вычисляет c0i<-Н(r0i, t0i, e0i).
Процесс (4): Алгоритм Р доказывающей стороны вычисляет c1i<-Н(r1i, G(t0i, r1i)+e0i).
После выполнения описанных выше процессов с (1) по (4) для i=1-N, алгоритм Р доказывающей стороны вычисляет хэш-величину Cmt<-Н(с01, с11, …, c0N, c1N). Хэш-величину Cmt, генерируемую в ходе операции #1, посылают алгоритму V проверяющей стороны.
Операция #2:
После приема хэш-величины Cmt, алгоритм V проверяющей стороны случайным образом выбирает одно число ChAi из совокупности q колец K для i=1-N и передает выбранное число ChAi (i=1-N) алгоритму Р доказывающей стороны.
Операция #3:
После приема числа ChAi(i=1-N), алгоритм Р доказывающей стороны вычисляет t1i<-ChAi·r0i-t0i для i=1-N. Кроме того, алгоритм Р доказывающей стороны вычисляет e1i<-ChAi·F(r0i)-e0i для i=1-N. Далее, алгоритм Р доказывающей стороны вычисляет хэш-величины d<-H(t011, е11, …, t1N, e1N). Затем, алгоритм Р доказывающей стороны передает полученную хэш-величину алгоритму V проверяющей величины.
Операция #4:
После приема хэш-величины алгоритм V проверяющей стороны выбирает схему верификации для использования из совокупности двух схем верификации для каждого из i=1-N. Например, алгоритм V проверяющей стороны может, для каждого из i=1-N, выбрать числовую величину из совокупности двух цифровых величин {0, 1}, представляющих схемы верификации, и задать выбранную числовую величину в качестве параметра запроса ChBi. Этот запрос ChBi(i=1-N) передают алгоритму Р доказывающей стороны.
Операция #5:
По получении запроса ChBi (i=1-N) алгоритм Р доказывающей стороны генерирует ответ Rspi для передачи алгоритму V проверяющей стороны в ответ на принятый запрос ChBi для i=1-N. Если ChBi=0, алгоритм Р доказывающей стороны генерирует ответ Rspi=(r0i, c1i). Если ChBi=1, алгоритм Р доказывающей стороны генерирует ответ Rspi=(r0i, t0i, e0i, c1t1i, e1i, c0i). Ответ Rspi (i=1-N), генерируемый в ходе операции #5, посылают алгоритму V проверяющей стороны.
Операция #6:
После приема ответов Rspi (i=1-N) алгоритм V проверяющей стороны выполняет следующие процессы (1) и (2) с использованием принятого ответа Rspi (i=1-N).
Процесс (1): Если ChBi=0, алгоритм V проверяющей стороны выполняет (r0i, t0i, e0i, c1i)<-Rspi. Алгоритм V проверяющей стороны вычисляет c0i=H(r0i, t0i, e0i). Далее, алгоритм V проверяющей стороны вычисляет t1i<-ChAi·r0i+t0i, и e1i<-ChAi·F(r0i)-e0i. Затем алгоритм V проверяющей стороны сохраняет (c0i, c1i, t1i, e1i).
Процесс (2): Если ChBi=1, алгоритм V проверяющей стороны выполняет (r1i, t1i, e1i, c0i)<-Rspi. После этого, алгоритм V проверяющей стороны вычисляет c1i=Н(r1i-ChAi·(y-F(r1i))-G(t1i, r1i)-e1i). Затем алгоритм V проверяющей стороны сохраняет (c0i, c1i, t1i, e1i).
После вьшолнения процессов с (1) по (2) для i=1-N, алгоритм V проверяющей стороны проверяет, выполняется ли равенство Cmt=H(c0i, с11, …, c0N, c1N). После этого, алгоритм V проверяющей стороны проверяет, выполняется ли равенство d=H(t11, е11, …, t1N, e1N). Затем, алгоритм V проверяющей стороны передает на выход величину 1, чтобы указать на успех аутентификации, если все эти процедуры верификации завершились успешно, и передает на выход величину 0, чтобы указать на неудачу аутентификации, если какая-либо процедура верификации закончилась неудачей.
Выше был описан пример структуры параллелизованного эффективного алгоритма, относящегося к 5-проходной схеме.
3-3: Пример структуры алгоритма на основе кубического многочлена от нескольких переменных
Здесь будет рассмотрен способ построения эффективного алгоритма с использованием кубического многочлена f1 для кольца R, как в случае 3-проходной схемы. Когда кубический многочлен f1 выражен, как в приведенной выше формуле (12), из формулы (14) и формулы (15) можно понять тот факт, что Gx(x, y) и Gy(x, y) становятся линейными по x и y.
Таким образом, используя описанное выше свойство, открытый ключ F(s) разделен на член, кратный ChA, путем введения новых переменных r0, r1, t0, u0 и е0. Поскольку многочлены Gx и Gy являются линейными по x и y, взаимосвязи между формулами с (24) по (27) установлены с использованием переменных r0, r1, t0, u0 и е0. Следующие формулы с (24) по (27) могут быть разбиты на первую часть, зависящую от ChA, и вторую часть, не зависящую от ChA. Здесь первую часть можно воспроизвести с использованием (r1, t1, u1, e1). Вторую часть можно воспроизвести с использованием (r0, t1, u1, e1).
Например, "е0, Gx(t0, r1)", включенные в следующую формулу (32), "t0", включенный в следующую формулу (33), "u0" включенный в следующую формулу (26), и "е0, Gy(r0, u0)", включенные в следующую формулу (27) являются первыми частями. С другой стороны, "ChAi·F(r0+r1), e1, ChA·F(r1), Gx(t1, r1)", включенные в следующую формулу (24), "ChA·r0, t1", включенные в следующую формулу (25), "ChA·r1, u1", включенные в следующую формулу (34), и "ChA·F(r0), Gy(r0, u1), e1", включенные в следующую формулу (27), являются вторыми частями.
Само определение секретного ключа s и взаимосвязь между следующими формулами (24)-(27) обеспечивают, что секретный ключ s невозможно получить, даже если используется какая-либо из групп (r1, t1, u1, e1) или (r0, t1, u1, e1). Использование этого свойства позволяет, например, построить эффективный алгоритм (далее именуемый - расширенный алгоритм) с использованием кубического многочлена f1 на кольце R.
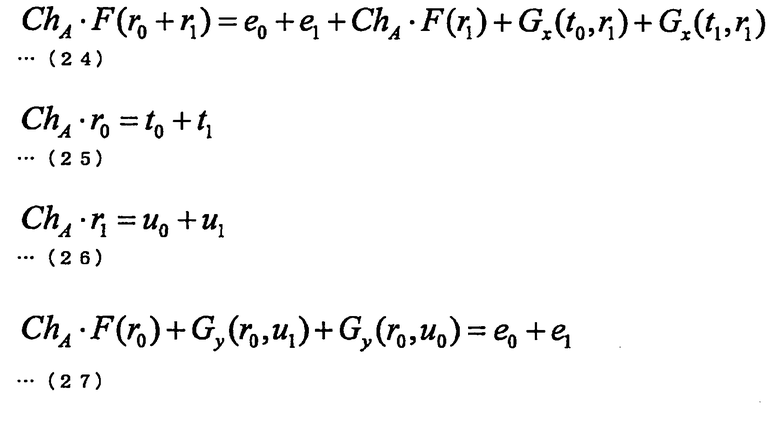
Далее будет описан пример структуры конкретного расширенного алгоритма. К работе расширенного алгоритма относятся два базовых момента, а именно - проверяющей стороне направляют сообщение, выраженное одной из следующих формул (28)-(29), и проверяют часть, зависящую от параметра от ChA, для величины этого параметра ChA, выбранной проверяющей стороной. Здесь, поскольку «векторы r0 и r1, используемые в момент генерации сообщения, нельзя в момент верификации заменить другими векторами r0 и r1», ниже будет приведен пример структуры, в которую добавлена верификация по r0 и r1.
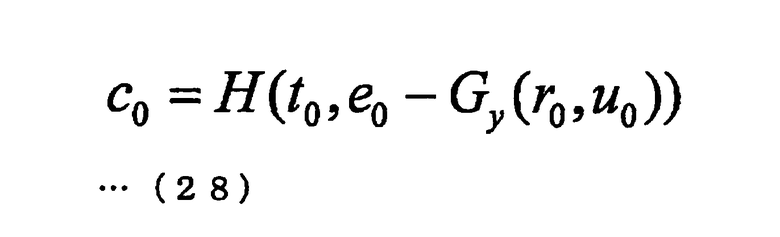
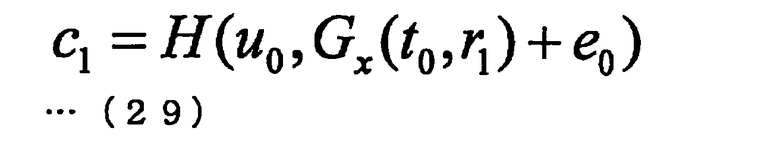
Далее, базовая конфигурация расширенного алгоритма, относящегося к 5-проходной схеме, будет рассмотрена со ссылками на Фиг. 9. Однако дальнейшее описание структуры алгоритма Gen генерации ключей будет опущено.
Операция #1:
Как показано на Фиг. 9, алгоритм Р доказывающей стороны случайным образом генерирует векторы r0, t0, u0, являющиеся элементами множества Kn, и вектор е0, являющийся элементом множества Km. После этого алгоритм Р доказывающей стороны вычисляет r1<-s-r0. Эти расчеты эквивалентны маскированию секретного ключа s с использованием вектора r0. После этого алгоритм Р доказывающей стороны вычисляет c0<-H(r0, t0, е0-Gy(r0, u0)). После этого алгоритм Р доказывающей стороны вычисляет c1<-H(r1, u0, Gx(t0, r1)+е0). Сообщения (с0, c1), генерируемые в ходе операции #1, посылают алгоритму V проверяющей стороны.
Операция #2:
После приема сообщений (с0, c1) алгоритм V проверяющей стороны случайным образом выбирает число ChA. Это число ChA передают алгоритму Р доказывающей стороны.
Операция #3:
После приема числа ChA, алгоритм Р доказывающей стороны вычисляет t1<-ChA·r0-t0. После этого, алгоритм Р доказывающей стороны вычисляет u1<-ChA·r1-u0. После этого, алгоритм Р доказывающей стороны вычисляет e1<-ChA·F(r0)+ChA·Gy(r0, r1)-е0. Затем, (t1, u1, e1), генерируемые в ходе операции #3, посылают алгоритму V проверяющей стороны.
Операция #4:
После приема (t1, u1, e1) алгоритм V проверяющей стороны выбирает, какую схему верификации использовать, из совокупности двух схем верификации. Например, алгоритм V проверяющей стороны может выбрать числовую величину из совокупности двух числовых величин {0, 1}, представляющих схемы верификации, и задает выбранную числовую величину в качестве параметра запроса ChB. Этот запрос ChB передают алгоритму Р доказывающей стороны.
Операция #5:
По получении запроса ChB алгоритм Р доказывающей стороны генерирует ответ Rsp для передачи алгоритму V проверяющей стороны в ответ на принятый запрос ChB. Если ChB=0, алгоритм Р доказывающей стороны генерирует ответ Rsp=r0. Если ChB=1, алгоритм Р доказывающей стороны генерирует ответ Rsp=r1. Ответ Rsp, генерируемый в ходе операции #5, посылают алгоритму V проверяющей стороны.
Операция #6:
После приема ответа Rsp алгоритм V проверяющей стороны выполняет следующую процедуру верификации с использованием принятого ответа Rsp.
Если ChB=0, алгоритм V проверяющей стороны проверяет, выполняется ли равенство с0=Н(r0, ChA·r0-t1, ChA·F(r0)+Gy(r0, u1)-e1). Алгоритм V проверяющей стороны передает на выход величину 1, чтобы указать на успех аутентификации, если все эти процедуры верификации завершились успешно, и передает на выход величину 0, чтобы указать на неудачу аутентификации, если какая-либо процедура верификации закончилась неудачей.
Если ChB=1, алгоритм V проверяющей стороны проверяет, выполняется ли равенство c1=H(r1, ChA·r1-u1, ChA·(y-F(r1))-Gx(t1, r1)-e1). Алгоритм V проверяющей стороны передает на выход величину 1, чтобы указать на успех аутентификации, если все эти процедуры верификации завершились успешно, и передает на выход величину 0, чтобы указать на неудачу аутентификации, если какая-либо процедура верификации закончилась неудачей.
Выше был описан пример структуры расширенного алгоритма, относящегося к 5-проходной схеме. Кроме того, использование кубического многочлена позволяет реализовать более высокую степень защищенности.
4: Модификация алгоритма цифровой подписи
Далее, будет рассмотрен способ модификации изложенного выше алгоритма аутентификации с открытым ключом для преобразования его в алгоритм цифровой подписи.
Когда доказывающая сторона в модели алгоритма аутентификации с открытым ключом совпадает с подписывающей стороной в случае алгоритма цифровой подписи, аппроксимация модели алгоритма цифровой подписи может быть легко понята, если только доказывающая сторона может обращаться к проверяющей стороне. На основе этого подхода будет рассмотрен способ модификации изложенного выше алгоритма аутентификации с открытым ключом для преобразования его в алгоритм цифровой подписи.
4-1: Модификация 3-проходного алгоритма аутентификации с открытым ключом и преобразование его в алгоритм цифровой подписи (Фиг. 10)
Сначала будет рассмотрен способ модификации 3-проходного алгоритма аутентификации с открытым ключом для преобразования его в алгоритм цифровой подписи.
На Фиг. 10 показан эффективный алгоритм (например, см. Фиг. 5), относящийся к 3-проходной схеме с интерактивностью три раза и четырьмя операциями, т.е. с операции #1 по операцию #4.
Операция #1 содержит процесс (1) генерации ai=(r0i, t0i, e0i, r1i, t1i, e1i, c0i, c1i, c2i) и процесс (2) вычисления Cmt<-H(c0i, с11, c21, …, c0N, c1N, c2N). Параметр Cmt, генерируемые алгоритмом Р доказывающей стороны в ходе операции #1, посылают алгоритму V проверяющей стороны.
Операция #2 содержит процедуру выбора параметра Ch1, …, ChN. Параметр Ch1, …, ChN, выбранный в ходе операции #2 посредством алгоритма V проверяющей стороны, посылают алгоритму Р доказывающей стороны.
Операция #3 содержит процедуру генерации ответов Rsp1, …, RspN с использованием Ch1, …, ChN и a1 …, aN. Этот процесс выражен в виде Rspi<-Select (Chi, ai). Ответы Rsp1, …, RspN, генерируемые алгоритмом Р доказывающей стороны в ходе операции #3, посылают алгоритму V проверяющей стороны.
Операция #4 содержит процесс (1) воспроизведения c01, с11, с21, …, c0N, c1N, c2N с использованием Ch1, …, ChN и Rsp1, …, RspN и процесс (2) верификации Cmt=H(c01, с11, c21, …, c0N, c1N, c2N) с использованием воспроизведенных c01, c11, c21, …, c0N, c1N, c2N.
Алгоритм аутентификации с открытым ключом, представленный в виде операций с операции #1 по операцию #4 модифицирован для преобразования в алгоритм Sig генерации подписи и алгоритм Ver верификации подписи, изображенные на Фиг. 10.
(Алгоритм Sig генерации подписи)
Сначала будет описана алгоритма Sig генерации подписи. Алгоритм Sig генерации подписи содержит процессы с (1) по (5),
Процесс (1): Алгоритм Sig генерации подписи генерирует ai=(r0i, t0i, e0i, r1i, t1i, e1i, c0i, c1i, c2i).
Процесс (2): Алгоритм Sig генерации подписи вычисляет Cmt<-H(c01, с11, c21, …, c0N, c1N, c2N).
Процесс (3): Алгоритм Sig генерации подписи вычисляет (Ch1, …, ChN)<-Н(М, Cmt). Здесь М обозначает документ, к которому прикрепляют подпись.
Процесс (4): Алгоритм Sig генерации подписи вычисляет Rspi<-Select (Chi, ai).
Процесс (5): Алгоритм Sig генерации подписи задает (Cmt, Rsp1, …, RspN) в качестве подписи.
Алгоритм Ver верификации подписи
Далее будет описана структура алгоритма Ver верификации подписи. Алгоритм Ver верификации подписи содержит следующие процессы с (1) по (3),
Процесс (1): Алгоритм Ver верификации подписи вычисляет (Ch1, …, chN)<-Н(М, Cmt).
Процесс (2): Алгоритм Ver верификации подписи генерирует с01, с11, с21, …, c0N, c1N, c2N с использованием Ch1, …, ChN и Rsp1, …, RspN.
Процесс (3): Алгоритм Ver верификации подписи проверяет Cmt=Н(с01, с11, c21, …, c0N, c1N, c2N) с использованием воспроизведенных c01, с11, с21, …, c0N, c1N, c2N.
Как описано выше, если совместить доказывающую сторону в модели алгоритма аутентификации с открытым ключом с подписывающей стороной в случае алгоритма цифровой подписи, алгоритм аутентификации с открытым ключом может быть модифицирован и преобразован в алгоритм цифровой подписи.
4-2: Модификация 5-проходного алгоритма аутентификации с открытым ключом и преобразование его в алгоритм цифровой подписи (Фиг. 11)
Далее будет рассмотрен способ модификации 5-проходного алгоритма аутентификации с открытым ключом для преобразования его в алгоритм цифровой подписи.
На Фиг. 11 показан эффективный алгоритм (например, см. Фиг. 8), относящийся к 5-проходной схеме с интерактивностью пять раз и шестью операциями, т.е. с операции #1 по операцию #6.
Операция #1 содержит процесс (1) генерации ai=(r0i, t0i, e0i, r1i, t1i, e1i, c0i, c1i) для i=1-N и процесс (2) вычисления Cmt<-H(c01, с11, …, c0N, c1N). Параметр Cmt, генерируемый алгоритмом Р доказывающей стороны в ходе операции #1, посылают алгоритму V проверяющей стороны.
Операция #2 содержит процедуру выбора параметра ChA1, …, ChAN. Параметр ChA1, …, ChAN, выбранный в ходе операции #2 посредством алгоритма V проверяющей стороны, посылают алгоритму Р доказывающей стороны.
Операция #3 содержит процедуру генерации bi=(t1i, e1i) и процедуру генерации d=Н (t11, е11, …, t1N, e1N) для i=1-N. Здесь параметры d, генерируемые алгоритмом Р доказывающей стороны в ходе операции #3, посылают алгоритму V проверяющей стороны.
Операция #4 содержит процедуру выбора параметра ChB1, …, ChBN. Параметры ChB1, …, ChBN, выбранные в ходе операции #4 посредством алгоритма V проверяющей стороны, посылают алгоритму Р доказывающей стороны.
Операция #5 содержит процедуру генерации ответов Rsp1, …, RspN с использованием ChB1, …, ChBN, a1, …, aN, b1, …, bN. Этот процесс выражен в виде Rspi<-Select (ChBi, ai, bi). Ответы Rsp1, …, RspN, генерируемые алгоритмом Р доказывающей стороны в ходе операции #5, посылают алгоритму V проверяющей стороны.
Операция #6 содержит процесс воспроизведения с01, с11, …, c0N, c1N, t11, е11, …, t1N, e1N с использованием ChA1, …, ChAN, ChB1, …, ChBN, Rsp1, …, RspN, процесс верификации Cmt=H(c01, с11, …, c0N, c1N) с использованием воспроизведенных c01, c11, …, c0N, c1N и процесс верификации d=H(t11, е11, …, t1N, e1N).
Алгоритм аутентификации с открытым ключом, представленный в виде операций с операции #1 по операцию #6 модифицирован для преобразования в алгоритм Sig генерации подписи и алгоритм Ver верификации подписи, изображенные на Фиг. 11.
(Алгоритм Sig генерации подписи)
Сначала будет описана структура алгоритма Sig генерации подписи. Алгоритм Sig генерации подписи содержит процессы с (1) по (7).
Процесс (1): Алгоритм Sig генерации подписи генерирует ai=(r0i, t0i, e0i, r1i, t1i, e1i, c0i, c1i).
Процесс (2): Алгоритм Sig генерации подписи вычисляет Cmt<-H(c01, с11, …, c0N, c1N).
Процесс (3): Алгоритм Sig генерации подписи вычисляет (ChA1, …, ChAN)<-Н(М, Cmt). Здесь М обозначает документ, к которому прикрепляют подпись.
Процесс (4): Алгоритм Sig генерации подписи осуществляет генерацию bi=(t1i, e1i) для i=1-N. Далее, алгоритм Sig генерации подписи вычисляет d=Н (t11, е11, …, t1N, e1N).
Процесс (5): Алгоритм Sig генерации подписи вычисляет (ChB1, …, ChBN)<-H(M, Cmt, ChA1, …, ChAN, d). Кроме того можно осуществить модификацию для преобразования в (ChB1, …, ChBN)<-H(ChA1, …, ChAN, d).
Процесс (6): Алгоритм Sig генерации подписи вычисляет Rspi<-Select (ChBi, ai, bi).
Процесс (7): Алгоритм Sig генерации подписи задает (Cmt, d, Rsp1, …, RspN) в качестве цифровой подписи.
Алгоритм Ver верификации подписи
Далее будет описана структура алгоритма Ver верификации подписи. Алгоритм Ver верификации подписи содержит следующие процессы с (1) по (4).
Процесс (1): Алгоритм Ver верификации подписи вычисляет (ChA1, …, ChAN)=Н(М, Cmt).
Процесс (2): Алгоритм Ver верификации подписи вычисляет (ChB1, …, ChBN)=H(M, Cmt, ChA1, …, ChAN, d). Когда осуществляется модификация для преобразования в (ChB1, …, ChBN)=H(ChA1, …, ChAN, d) в ходе выполнения процесса (5), осуществляемого алгоритмом Ver верификации подписи, этот алгоритм Ver верификации подписи вычисляет (ChB1, …, ChBN)=H(ChA1, …, ChAN, d).
Процесс (3): Алгоритм Ver верификации подписи генерирует t11, е11, …, t1N, e1N, c01, с11, …, c0N, c1N с использованием ChA1, …, ChAN, ChB1, …, ChBN, Rsp1, …, RspN.
Процесс (4): Алгоритм Ver верификации подписи проверяет Cmt=H(c01, с11, …, c0N, c1N) с использованием воспроизведенных c01, с11, …, c0N, c1N, и d=Н (t11, е11, …, t1N, e1N).
Как описано вьппе, если совместить доказывающую сторону в модели алгоритма аутентификации с открытым ключом с подписывающей стороной в случае алгоритма цифровой подписи, алгоритм аутентификации с открытым ключом может быть модифицирован и преобразован в алгоритм цифровой подписи.
5: Способ уменьшения объема памяти, необходимого для верификации подписи
В частности, согласно описанному выше алгоритму цифровой подписи процедура верификации подписи выполнялась после того, как алгоритм Ver верификации подписи получит все цифровые подписи. Однако в случае описанного выше алгоритма цифровой подписи объем данных цифровой подписи относительно велик. По этой причине при выполнении аутентификации с использованием такого устройства, как радио идентификационное устройство (Radio Frequency IDentification (RFID)), имеющее память небольшого объема, необходимо всегда обращать внимание на свободный объем памяти, коэффициент использования памяти в процессе аутентификации или другой подобный показатель. Кроме того, при использовании устройства, обладающего недостаточно большой памятью, предполагается, что в некоторых случаях аутентификация не производится. Соответственно, авторы настоящего изобретения разработали способ уменьшения объема памяти, необходимого для верификации подписи.
5-1: Структура хэш-функции (Фиг. 12)
Сначала авторы настоящего изобретения сосредоточились на структуре хэш-функции. Во многих случаях, хэш-функция имеет структуру, группирующую входные данные в блоки и обрабатывающую эти данные в единицах блоков. Например, в случае SHA-1, хэш-функция имеет структуру, показанную на Фиг. 12. Хэш-функция, показанная на Фиг. 12, генерирует хэш-величину путем группирования заполненных входных данных М в Z блоков m1, …, mZ и работает с блоками mj с применением заданной функции CF вместе с начальной величиной IV или промежуточной величиной CVj, последовательно увеличивая индекс j. Таким образом, когда получена промежуточная величина CVj, ранее использованные блоки становятся ненужными. Соответственно, на основе этих характеристик была разработана структура (далее именуемая способ уменьшения требований к памяти) для уменьшения объема памяти, требуемого для реализации алгоритма. Далее будет рассмотрен способ применения этой структуры к описанному выше алгоритму цифровой подписи.
5-2: Пример применения 3-проходного алгоритма цифровой подписи (Фиг. 14)
Сначала, будет описан способ применения указанного выше подхода для уменьшения необходимого объема памяти к алгоритму цифровой подписи по 3-проходной схеме, изображенному на Фиг. 10.
Нормальный способ установки: Фиг. 13
Обычно, как показано на Фиг. 13, алгоритм Ver верификации подписи, относящийся к описанному выше алгоритму цифровой подписи, принимает (Cmt, Rsp1, …, RspN), входящие в состав цифровой подписи, за один раз (S101). После этого, алгоритм Ver верификации подписи выполняет (Ch1, …, ChN)<-Н(М, cmt) (S102). После этого, алгоритм Ver верификации подписи выполняет (с01, с11, с21, …, c0N, c1N, c2N)<- Reproduce (Ch1, …, ChN; Rsp1, …, RspN) (S103). После этого, алгоритм Ver верификации подписи проверяет Cmt=H(c01, с11, с21, …, c0N, c1N, c2N) (S104) и завершает последовательность операций, относящихся к верификации подписи.
Способ уменьшения объема памяти: Фиг. 14
В случае нормального способа установки, когда цифровые подписи принимают за один раз, как на этапе S101, изображенном на Фиг. 13, необходимо использовать память для сохранения (Rsp1, …, RspN) до завершения процедуры этапа S103. Однако, как понятно из структуры алгоритма, показанной на Фиг. 5, для воспроизведения (c0i, c1i, c2i), осуществляемого на этапе S103, не используется никакая информация, кроме (Chi; Rspi). Кроме того, если рассматривать структуру хэш-функции, показанную на Фиг. 12, понятно, что при вычислении хэш-функции на этапе S104 осуществляют группирование и обработку в единицах блоков. Соответственно, структура, относящаяся к верификации подписи оказывается усовершенствована и преобразована в структуру, показанную на Фиг. 14.
В случае структуры, показанной на Фиг. 14, алгоритм Ver верификации подписи сначала принимает только параметр Cmt, входящий в состав цифровой подписи (S111). После этого, алгоритм Ver верификации подписи выполняет (Ch1, …, ChN)<-H(M, cmt) (S112). После этого, алгоритм Ver верификации подписи последовательно выполняет процедуры этапов c S113 по S115, увеличивая i от i=1 до N.
На этапе S113 алгоритм Ver верификации подписи принимает Rspi (S113). После этого, алгоритм Ver верификации подписи выполняет (c0i, c1i, c2i)<- Reproduce (Chi; Rspi) с использованием принятого Rspi (S114). После выполнения процедуры этапа S114 параметры Chi и Rspi становятся ненужными. Соответственно, алгоритм Ver верификации подписи стирает эти параметры Chi и Rspi из памяти после выполнения процедуры этапа S114.
После этого, алгоритм Ver верификации подписи выполняет tmpi<-Hi (tmpi-1; c0i, c1i, c2i) (этап S115). Кроме того, хэш-функдия Hi представляет собой функцию, передающую на выход промежуточную величину, генерируемую при вычислении до c0i, c1i, c2i посредством хэш-функции H. На практике, поскольку размер входных данных функции Hj отличается в зависимости от выбранной функции, выполняют при необходимости подходящую коррекцию длины входных данных, такую как добавление битов. При использовании функции Hi, хэш-функция Н выражена в виде алгоритма, содержащего процессы с (1) по (3), которые будут описаны ниже. Тогда величина tmpN является конечной выходной величиной (хэш-величиной) хэш-функции Н. На практике, на конечной стадии выполняют дополнительную операцию заполнения в соответствии со спецификацией хэш-функции.
Процесс (1): tmp0<- нулевая строка символов
Процесс (2):
для i=1-N
tmpi<-Hi (tmpi-1; c0i, c1i, c2i)
end for
Процесс (3): передача tmpN на выход
После выполнения процедур этапов с S113 по S115 для i=1-N, алгоритм V проверяющей стороны проверяет (S116), выполняется ли равенство Cmt=tmpN и завершает последовательность процедур, относящихся к верификации плоскости. Как описано выше, алгоритм Ver верификации подписи стирает информацию, которая становится ненужной во время многократного выполнения процедур этапов с S113 по S115. из памяти. По этой причине объем памяти, необходимый для верификации подписи, оказывается уменьшен до минимально возможного уровня. Вследствие этого, описанная выше процедура верификации подписи может быть выполнена даже в устройстве, имеющем память лишь небольшого объема.
5-3: Пример применения 5-проходного алгоритма цифровой подписи (Фиг. 16)
Далее, будет описан способ применения указанного выше подхода для уменьшения необходимого объема памяти к алгоритму цифровой подписи по 5-проходной схеме, изображенному на Фиг. 11.
Нормальный способ установки: Фиг. 15
Обычно, как показано на Фиг. 15, алгоритм Ver верификации подписи, относящийся к описанному выше алгоритму цифровой подписи, принимает (Cmt, d, Rsp1, …, RspN), входящие в состав цифровой подписи, за один раз (S121). После этого, алгоритм Ver верификации подписи выполняет (ChA1, …, ChAN)<- Н(М, cmt) (S122). После этого, алгоритм Ver верификации подписи выполняет (ChB1, …, ChBN)<- Н(М, Cmt, ChA1, …, ChAN, d) (S123). После этого, алгоритм Ver верификации подписи выполняет (c01, с11, …, c0N, c1N, d11, е11, …, d1N, e1N)<- Reproduce (ChA1, …, ChAN, ChB1, …, ChBN; Rsp1, …, RspN) (S124). После этого, алгоритм Ver верификации подписи проверяет Cmt=H(c01, с11, …, c0N, c1N) и d=H(d11, е11, …, d1N, e1N) (S125) и завершает последовательность операций, относящихся к верификации подписи.
Способ уменьшения объема памяти: Фиг. 16
Когда цифровые подписи принимают за один раз, как на этапе S121, изображенном на Фиг. 15, необходимо использовать память для сохранения (Rsp1, …, RspN) до завершения процедуры этапа S124. Однако, как понятно из структуры алгоритма, показанной на Фиг. 8, для воспроизведения (c0i, c1i, d1i, e1i), осуществляемого на этапе S124, не используется никакая информация, кроме (ChAi, ChBi; Rspi). Кроме того, если рассматривать структуру хэш-функции, показанную на Фиг. 12, понятно, что при вычислении хэш-функции на этапе S125 осуществляют группирование и обработку в единицах блоков. Соответственно, структура, относящаяся к верификации подписи. оказывается усовершенствована и преобразована в структуру, показанную на Фиг. 16.
В случае структуры, показанной на Фиг. 16, алгоритм Ver верификации подписи сначала принимает только параметр Cmt, входящий в состав цифровой подписи (S131). После этого, алгоритм Ver верификации подписи выполняет (ChA1, …, ChAN)<- Н(М, cmt) (S132).
После этого, алгоритм Ver верификации подписи принимает параметр d (S133). После этого, алгоритм Ver верификации подписи выполняет (ChB1, …, ChBN)<- Н(М, Cmt, ChA1, …, ChAN, d) с использованием принятого параметра d (S134). После выполнения процедуры этапа S134 параметр d становится ненужным. Соответственно, алгоритм Ver верификации подписи стирает параметр d из памяти после выполнения процедуры этапа S134. После этого, алгоритм Ver верификации подписи последовательно выполняет процедуры этапов с S135 по S137, увеличивая i от i=1 до N.
На этапе S135 алгоритм Ver верификации подписи принимает Rspi (S135). После этого, алгоритм Ver верификации подписи выполняет (c0i, c1i, t1i, e1i)<- Reproduce (ChAi, ChBi; Rspi) с использованием принятого Rspi (S136). После выполнения процедуры этапа S133 параметры ChAi, ChBi, и Rspi становятся ненужными. Соответственно, алгоритм Ver верификации подписи стирает эти параметры ChAi, ChBi и Rspi из памяти после выполнения процедуры этапа S136.
После этого, алгоритм Ver верификации подписи выполняет tmpi<- Hi (tmpi-1; c0i, c1i) и tmpi′<- Hi (tmpi-1′; t1i, e1i) (этап S137). После выполнения процедур этапов с S135 по S137 для i=1-N, алгоритм V проверяющей стороны проверяет (S138), выполняются ли равенства Cmt=tmpN и d=tmpN′ и завершает последовательность процедур, относящихся к верификации плоскости. Как описано выше, алгоритм Ver верификации подписи стирает информацию, которая становится ненужной во время многократного выполнения процедур этапов с S135 по S137, из памяти. По этой причине объем памяти, необходимый для верификации подписи, оказывается уменьшен до минимально возможного уровня. Вследствие этого, описанная выше процедура верификации подписи может быть выполнена даже в устройстве, имеющем память лишь небольшого объема.
Выше были описаны способы уменьшения объема памяти, необходимого для верификации подписи.
6: Способ выделения последовательности троичных случайных чисел из последовательности двоичных случайных чисел
В частности, возможна ситуация, когда алгоритм аутентификации с открытым ключом по 3-проходной схеме генерирует N или более троичных случайных чисел с равномерным распределением. Однако высококачественный генератор случайных чисел, способный генерировать троичные случайные числа с равномерным распределением, не являются обычными. По этой причине необходимо рассмотреть способ генерации троичных случайных чисел с равномерным распределением с использованием высококачественного генератора случайных чисел, который генерирует двоичные случайные числа с равномерным распределением. Соответственно, авторы настоящего изобретения разработали способы эффективной генерации троичных случайных чисел с равномерным распределением на основе двоичных случайных чисел с равномерным распределением. Далее, эти способы будут описаны подробно. В последующем описании предполагается, что одно число, представленное по основанию 1 (где 1 равно 2 или 3), будет считаться 1 символом.
6-1: Способ #1 выделения (2-битовое группирование) (Фиг. 17)
Сначала, способ (далее именуемый способ #1 выделения) группирования двоичных чисел из М бит по два бита каждое и выделения троичных чисел будет рассмотрен со ссылками на Фиг. 17. Как показано Фиг. 17, когда строку случайных чисел в двоичном представлении группируют по два бита каждое, можно получить М/2 2-битовых двоичных чисел. Например, если "00" соответствует троичному числу "0", "01" соответствует троичному числу "1" и "10" соответствует троичному числу "2", из случайного числа, представленного в двоичном виде в единицах по 2 бит, можно получить строку троичных случайных чисел. Однако 2-битовая величина "11" исключена. Иными словами, способ #1 выделения представляет способ выделения 31 элементов, выраженных 1 троичным символом, и 22 элементов, выраженных 2 двоичными символами. Таким образом, вероятность P1 того, что N или более троичных чисел выделить невозможно представлена следующей формулой (30).
Математическое выражение 16
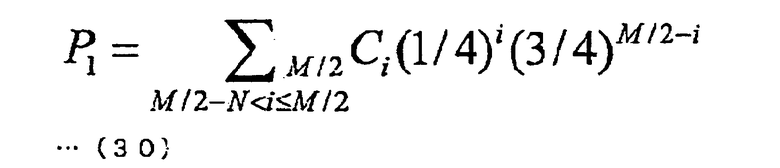
6-2: Способ #2 выделения (нет группирования) (Фиг. 18)
Затем, способ (далее именуемый способ #2 выделения) выделения случайных чисел из L троичных символов с использованием случайных чисел из М двоичных символов без группирования будет рассмотрен со ссылками на Фиг. 18. Здесь, L максимальное целое число, удовлетворяющее соотношению 3L≤2M. Имеется 2M чисел, которые могут быть выражены посредством М двоичных символов. С другой стороны, имеется только 3L чисел, которые могут быть выражены посредством L троичных символов. По этой причине, из 2M чисел, которые могут быть выражены посредством М двоичных символов, 2M-3L чисел не используются в качестве случайных чисел в троичном представлении. Таким образом, вероятность P2 того, что N или более троичных чисел выделить невозможно, представлена следующей формулой (31).
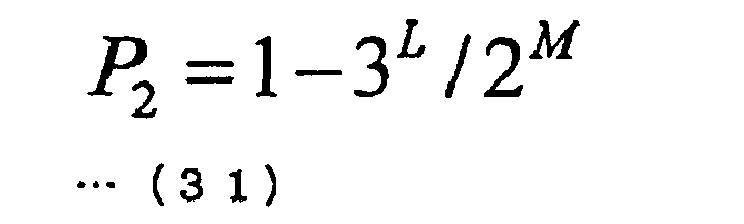
6-3: Способ #3 выделения (k-битовое группирование) (Фиг. 19) Описанный выше способ #1 выделения представляет собой способ группирования строки случайных чисел в двоичном представлении для получения совокупности групп минимального размера. С другой стороны, описанный выше способ #2 выделения представляет собой способ группирования строки случайных чисел в двоичном представлении для получения совокупности групп максимального размера (поскольку рассматривается М-битовое группирование). Как понятно из приведенных выше формул (30) и (31), вероятность того, что N или более троичных чисел будет невозможно выделить, различна в зависимости от длины группирования. Кроме того, когда строку случайных чисел из М двоичных символов группируют в единичные блоки по k бит, как показано на Фиг. 19, вероятность Р3 того, что N или более троичных чисел выделить невозможно, представлена следующей формулой (32).
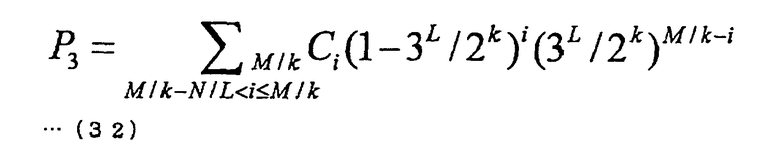
Таким образом, вероятность Р3 того, что N или более троичных чисел выделить невозможно, можно минимизировать, и можно более эффективно выделить строку случайных чисел в троичном представлении. Например, если М=512 и N=140, вероятность Р3 оказывается минимальной при k=8.
6-3-1: Базовая структура (Фиг. 20)
Здесь порядок процедуры выделения строки случайных чисел, содержащей L троичных символов, из строки случайных чисел, содержащей М двоичных символов, будет рассмотрен со ссылками на Фиг. 20. Как показано на Фиг. 20, сначала генерируют строку случайных чисел из М двоичных символов (S201). После этого, строку случайных чисел из М двоичных символов группируют в единичные блоки по k бит (S202). После этого, выделяют битовую строку, удовлетворяющую условию X2k≤3L, из битовых строк X2k, сгруппированных в единичные блоки по k бит (S203). После этого, выделенную битовую строку передают на выход в троичном представлении (S204) и выполнение последовательности процедур завершается.
6-3-2: Дополнительный способ выделения (Фиг. 21)
Вычисляя длину k группирования, при которой вероятность Р3, выраженная приведенной выше формулой (15), является минимальной, и, выполняя алгоритм, показанный на Фиг. 20, можно эффективно выделить строку случайных чисел в троичном представлении из строки случайных чисел в двоичном представлении. Однако авторы настоящего изобретения разработали способ выделения строки случайных чисел в троичном представлении более эффективно, сосредоточившись на том факте, что битовая строка, удовлетворяющая соотношению X2k>3L, не используется на этапе S204, показанном на Фиг. 20. Этот способ будет описан ниже со ссылками на Фиг. 21.
Этот способ представляет собой способ выделения строки символов в троичном представлении с использованием битовых строк, не выделенных на этапе S204, показанном на Фиг. 20. Как показано на Фиг. 21, сначала выделяют множество битовых строк, не выделенных на этапе S204, показанном на Фиг. 20, и удовлетворяющих соотношению X;k>З1' (например, когда множество битовых строк выражено как y1y2 … yN, и каждая индивидуальная битовая строка yi удовлетворяет соотношению 3L≤yi<2k) (S211). После этого, вычитают 3L из каждой выделенной битовой строки у; и вычисляют множество новых битовых строк (например, когда множество новых битовых строк выражено как z1z2…zN′, и каждая индивидуальная битовая строка zi=yi-3L удовлетворяет соотношению 0≤zi<2k-3L) (S212).
После этого, выделяют битовую строку X, удовлетворяющую условию Х<3L, из множества новых битовых строк (S213). Здесь, L′ максимальное целое число, удовлетворяющее соотношению 3L′≤2k-3L. После этого, битовую строку, выделенную на этапе S213, передают на выход в троичном представлении (S214) и выполнение последовательности процедур завершается. Применяя этот алгоритм, можно выделить L′ новых троичных чисел с вероятностью 3L′/(2k-3L). Кроме того, рекурсивно используя этот способ, можно выделить больше троичных чисел. Иными словами, на этапе S213 можно аналогичным образом выделить троичные числа из битовых строк, удовлетворяющих соотношению Х≥3L′.
Выше был описан способ эффективной генерации троичных случайных чисел с равномерным распределением на основе двоичных случайных чисел с равномерным распределением.
7: Способ эффективной подстановки коэффициентов в многочлены от нескольких переменных
Однако выше не был специально описан способ совместного использования многочленов от нескольких переменных между доказывающей стороной (или подписывающей стороной) и проверяющей стороной. Можно представить себе способ совместного использования многочленов, в состав которого входит способ совместного использования начального числа, применяемого в момент генерации коэффициентов (случайных чисел) для многочленов от нескольких переменных, между доказывающей стороной и проверяющей стороной. Однако многочлены от нескольких переменных не могут быть использованы совместно, если последовательность, посредством которой генерируют случайные числа с применением совместно используемого начального числа, не используется совместно доказывающей стороной и проверяющей стороной.
7-1: Базовое определение
Соответственно, выполняют базовое определение последовательности, посредством которой строку случайных чисел, генерируемую с применением начального числа, совместно используемого доказывающей стороной (или подписывающей стороной) и проверяющей стороной, применяют к многочленам от нескольких переменных. Тогда, если используются многочлены от нескольких переменных, строку случайных чисел применяют к таким многочленам от нескольких переменных в соответствии с этим базовым определением. При применении этого способа многочлены от нескольких переменных совместно используются доказывающей стороной (или подписывающей стороной) и проверяющей стороной.
7-2: Структурирование данных
Однако число коэффициентов в многочленах от нескольких переменных является значительным. Когда один коэффициент выражен в единицах по 1 бит, данные в объеме по меньшей мере несколько десятков тысяч бит необходимы для представления многочлена от нескольких переменных. По этой причине нагрузка при подстановке чисел для коэффициентов многочлена от нескольких переменных очень велика. Соответственно, авторы настоящего изобретения разработали способы (способы #1 и #2 структурирования) для реализации эффективности процесса подстановки чисел для коэффициентов путем структурирования коэффициентов многочлена от нескольких переменных в виде совокупности заданных единиц (единичных блоков). Кроме того, авторы настоящего изобретения разработали способ (способ #3 структурирования) для повышения эффективности обработки данных, когда процедура подстановки осуществляется несколько раз применительно к коэффициентам одного и того же многочлена от нескольких переменных. Ниже эти способы будут описаны подробно.
7-2-1: Способ #1 структурирования (Фиг. 22-26)
Сначала будет описан способ #1 структурирования. Как показано на Фиг. 22 и 23, способ #1 структурирования представляет собой способ сбора коэффициентов членов одного рода, входящих в состав многочлена от нескольких переменных, в качестве одной структуры данных. В-примере, показанном на Фиг. 22, коэффициенты с a1IJ по aMIJ многочлена F от нескольких переменных собирают в качестве структуры А данных, а коэффициенты с b1I по bMI собирают в качестве структуры В данных. Кроме того, как показано на Фиг. 23, этот же способ применим к многочлену G от нескольких переменных. В этом случае, коэффициенты с (a1IJ+a1JI) по (aMIJ+aMJI) собирают в качестве структур данных.
Когда способ #1 структурирования не применяется, вычисление многочлена F от нескольких переменных, содержащего М многочленов от N переменных каждый осуществляется посредством алгоритма, показанного в (примере 1). В случае (примера 1), необходимо выполнять 1-битовую операцию "И" (AND) (&) 2×N×(N+1)×M/2 раз. Кроме того, необходимо выполнить 1-битовую операцию "исключающее-ИЛИ" (XOR) (∧) 1×N×(N+1)×M/2 раз. Здесь предполагается, что входные данные x содержат N бит.
(пример 1)
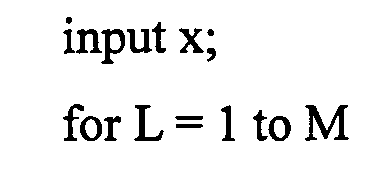
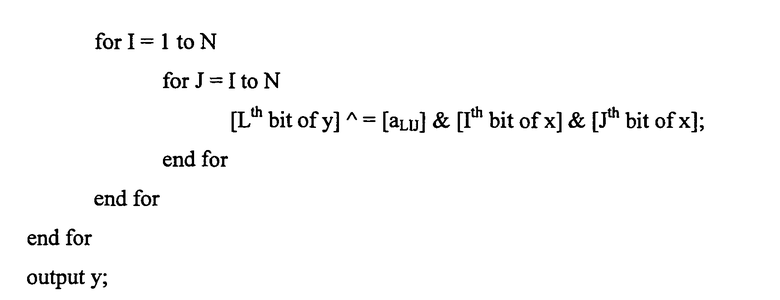
С другой стороны, как показано на Фиг. 22, когда коэффициенты структурированы, а генерируемые случайные числа применяют последовательно по несколько за раз в качестве коэффициентов многочлена F от нескольких переменных, алгоритм подстановки коэффициентов выражен как в (примере 2). В случае (примера 2), выполняют М-битовую операцию "И" (AND) (&) только 2×N×(N+1)/2 раз и выполняют М-битовую операцию "исключающее ИЛИ" (XOR) (∧) только N×(N+1)/2 раз. Кроме того, в каждом цикле генерируют а(1-M)IJ. Коэффициенты могут быть использованы в обратном порядке. Например, когда цикл выполняется N(N-1)/2 раз, можно не генерировать коэффициенты [a(1-M)IJ] каждый раз, а формировать их только однажды на каждые М раз. Кроме того, в цикле из М раз можно использовать коэффициенты [a(1-M)IJ], поворачивая их бит за битом.
(пример 2)

Как показано Фиг. 22, когда коэффициенты структурированы, промежуточные результаты, получаемые в результате применения этих коэффициентов к многочлену F от нескольких переменных, могут быть сохранены в таблице. В этом случае применяется следующий алгоритм, представленный как в (примере 3). Кроме того, aIJ[x1, …, xk] [z1, …, zk]=(a(k(I-1)+1)(k(J-1)+1)&x1&z1) ∧…∧ (a(k(I-1)+1)(k(J-1)+k)&x1&zk) ∧...∧ (a(k(I-1)+k)(k(J-1)+1)&xk&z1) ∧...∧ (a(k(I-1)+k)(k(J-1)+k)&xk&zk) сохраняют в массивах с aIJ [0] [0] по aIJ [2k-1], соответственно. В случае (примера 3), выполняют М-битовую операцию "исключающее ИЛИ" (XOR) (∧) только (N/k)(N/k+1)/2 раз. Однако необходимый объем памяти равен произведению 22k/k2 на объем памяти, требуемый для алгоритма из (примера 2).
Например, когда k=1, М-битовую операцию "исключающее-ИЛИ" (XOR) вьшолняют 120*119/2=7140 раз, необходимый объем памяти в 22=4 раз больше объема памяти для (примера 2), а число циклов не изменяется. Кроме того, когда k=2, М-битовую операцию "исключающее-ИЛИ" (XOR) вьшолняют 60*59/2=1770 раз, необходимый объем памяти в 24=4 раз больше, а число циклов составляет 1/4. Когда k=4, М-битовую операцию "исключающее-ИЛИ" (XOR) вьшолняют 30*29/2=435 раз, необходимый объем памяти в 28/42=16 раз больше, а число циклов составляет 1/16,4. Когда k=6, М-битовую операцию "исключающее-ИЛИ" (XOR) выполняют 20*19/2=190 раз, необходимый объем памяти в 212/62=114 раз больше, а число циклов составляет 1/37,6. Когда k=8, М-битовую операцию "исключающее-ИЛИ" (XOR) вьшолняют 15*14/2=135 раз, необходимый объем памяти в 216/82=1024 раз больше, а число циклов составляет 1/52,9. (пример 3)
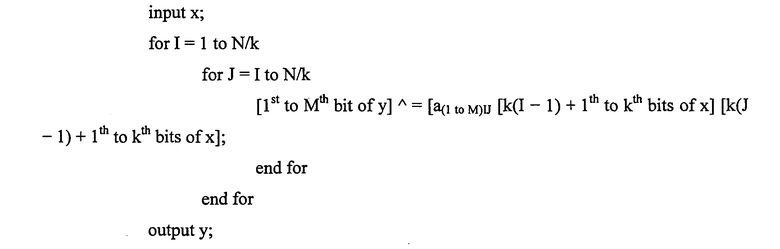
Способ, описанный в (примере 3) может содержать вычисление заранее величин FIJ(…) согласно следующей формуле (33) и сохранение результатов в виде массива.
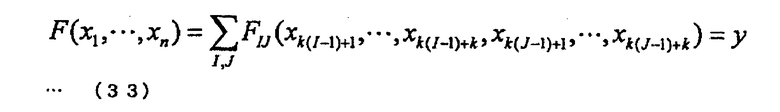
Здесь, FIJ(xk(I-1)+1, …, xk(I-1)+k, xk(J-1)+1, …, xk(J-1)+k) обозначает часть, определяемую посредством [xk(I-1)+1, …, xk(I-1)+k] и [xk(J-1)+1, …, xk(J-1)+k] в F(x1, …, xn).
Приведенные здесь конкретные алгоритмы представляют собой примеры случаев применения способа #1 структурирования к многочлену F от нескольких переменных. В такой структуре можно ожидать, что процесс выполнения этого алгоритма будет проходить с высокой скоростью.
(Применение к G)
Выше алгоритм для вычисления многочлена F от нескольких переменных с применением способа #1 структурирования был описан со ссылками на Фиг. 22. С другой стороны, каждый элемент многочлена G от нескольких переменных выражен в квадратичной форме. Поэтому, как показано на Фиг. 23, описанный выше способ #1 структурирования аналогичным образом применим к вычислению многочлена G от нескольких переменных без изменений.
Например, когда описанный выше способ #1 структурирования не применяется, алгоритм для вычисления многочлена G выражен в следующем (примере 1′). Здесь предполагается, что входные данные x и y содержат каждые по N бит.
(пример 1′)
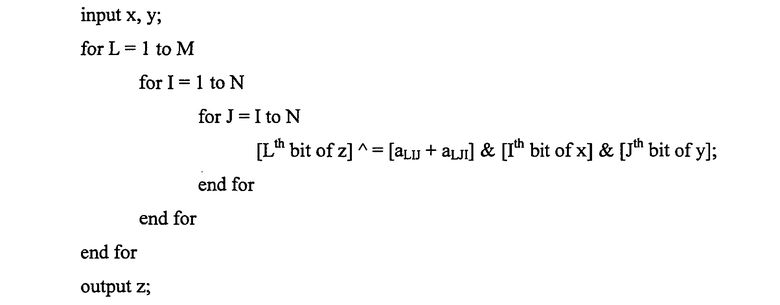
Когда описанный выше способ #1 структурирования применяется в описанном выше (примере 1′), алгоритм для вычисления многочлена G выражен в следующем (примере 2′).
(пример 2′)
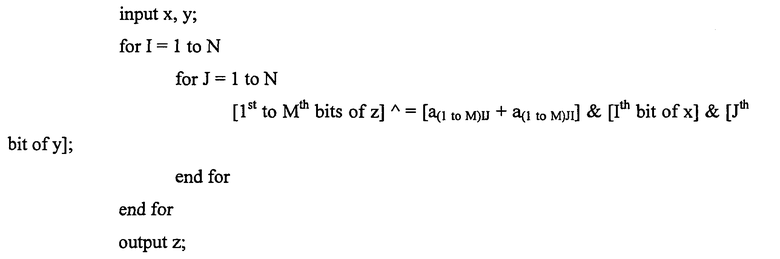
В случае способа сохранения промежуточного результата, полученного путем применения коэффициентов многочлена G от нескольких переменных, в таблице, алгоритм для вычисления многочлена G от нескольких переменных выражен в следующем (пример 3′) в соответствии с указанным выше (пример 3). Кроме того, aIJ[x1, …, xk] [y1, …, yk]=(a(k(I-1)+1)(k(J-1)+1)&x1&y1) ∧…∧ (a(k(I-1)+1)(k(J-1)+k)&x1&yk) ∧...∧ (a(k(I-1)+k)(k(J-1)+1)&xk&y1) ∧...∧ (a(k(I-1)+k)(k(J-1)+k)&xk&yk) сохраняют в массивах с aIJ [0] [0] по aIJ [2k-1] [2k-1], соответственно.
В случае (примера 3′), выполняют М-битовую операцию "исключающее ИЛИ" (XOR) (∧) только (N/k)2 раз. Однако необходимый объем памяти равен произведению 22k/k2 на объем памяти, требуемый для алгоритма из (примера 2′).
Например, когда k=1, М-битовую операцию "исключающее-ИЛИ" (XOR) выполняют 1202=14400 раз, необходимый объем памяти в 22=4 раз больше объема памяти для (примерп 2′), а число циклов не изменяется. Кроме того, когда k=2, М-битовую операцию "исключающее-ИЛИ" (XOR) выполняют 602=3600 раз, необходимый объем памяти в 24=4 раз больше, а число циклов составляет 1/4. Когда k=4, М-битовую операцию "исключающее-ИЛИ" (XOR) выполняют 302=900 раз, необходимый объем памяти в 28/42=16 раз больше, а число циклов составляет 1/16. Когда k=6, М-битовую операцию "исключающее-ИЛИ" (XOR) выполняют 202=400 раз, необходимый объем памяти в 212/62=114 раз больше, а число циклов составляет 1/36. Когда k=8, М-битовую операцию "исключающее-ИЛИ" (XOR) выполняют 152=225 раз, необходимый объем памяти в 216/82=1024 раз больше, а число циклов составляет 1/64.
(пример 3′)
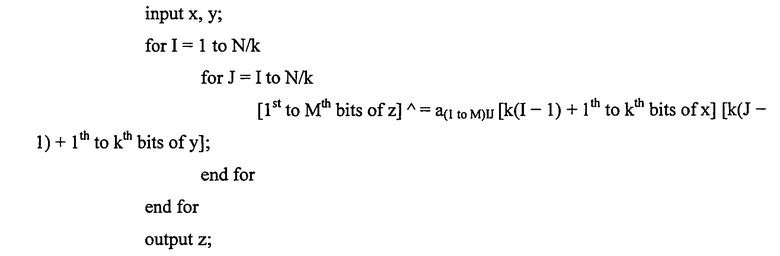
Способ, описанный в (примере 3′) может, в частности, представлять собой способ вычисления заранее величин GIJ(…) согласно следующей формуле (34) и сохранение результатов в виде массива.
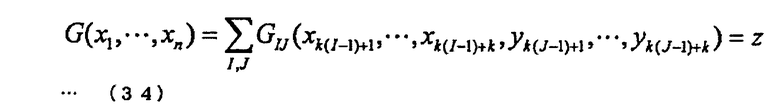
Здесь, GIJ(xk(I-1)+1, …, xk(I-1)+k, xk(J-1)+1, …, xk(J-1)+k) обозначает часть, определяемую посредством [xk(I-1)+1, …, xk(I-1)+k] и [xk(J-1)+1, …, xk(J-1)+k] в G(x1, …, xn, y1, …, yN).
Конкретные структуры алгоритма, относящегося к способу #1 структурирования, были описаны на примере случая вычисления многочлена G от нескольких переменных. В такой структуре можно ожидать, что процесс выполнения этого алгоритма будет проходить с высокой скоростью.
Применение к кубическому многочлену F от нескольких переменных Способы структурирования коэффициентов квадратичного многочлена от нескольких переменных были рассмотрены выше в качестве конкретных примеров способа #1 структурирования. Аналогично можно структурировать также коэффициенты кубического многочлена от нескольких переменных. В примере, показанном на Фиг. 24, коэффициенты с a1IJL по aMIJL собирают в качестве структуры А данных, а коэффициенты с b1IJ по bMIJ собирают в качестве структуры В данных и коэффициенты с c1I по cMI собирают в качестве структуры С данных. Благодаря структурированию коэффициентов таким способом можно эффективно вычислять многочлен от нескольких переменных.
Например, будут конкретно рассмотрены вычисления, относящиеся к структуре А данных. Когда коэффициенты не структурированы, алгоритм для вычислений, относящихся к структуре А данных, выражен в следующем (примере 4).
(пример 4)
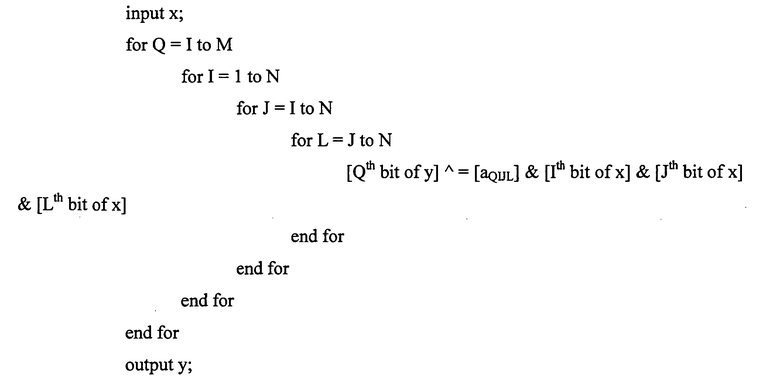
С другой стороны, когда коэффициенты структурированы, алгоритм выражен в следующем (примере 5). В случае (примера 5), М-битовую операцию "И" (AND) (&) выполняют только 2×N×(N+1)×(N+2)/6 раз и М-битовую операцию "исключающее ИЛИ" (XOR) (∧) выполняют только 1×N×(N+1)×(N+2)/6 раз. Кроме того, в каждом цикле генерируют a(1-M)IJL. Коэффициенты могут быть использованы в обратном порядке. Например, когда цикл выполняется, можно не генерировать коэффициенты [a(1-M)IJL] каждый раз, а формировать их только однажды на каждые М раз. Кроме того, в цикле из М раз можно использовать коэффициенты [a(1-M)IJ], поворачивая их бит за битом.
(пример 5)
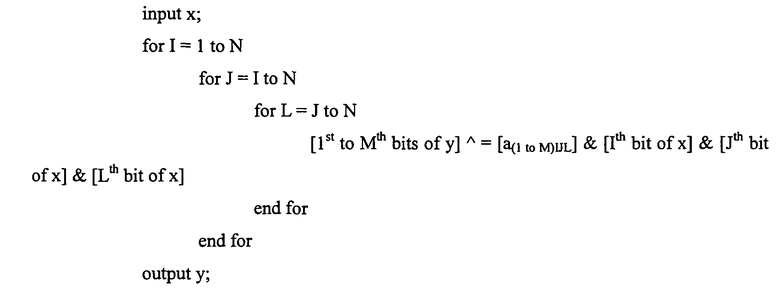
Когда коэффициенты структурированы, промежуточные результаты, получаемые в результате применения этих коэффициентов к многочлену F от нескольких переменных, могут быть сохранены в таблице. В этом случае применяется следующий алгоритм, представленный как в (примере 6). Кроме того, aIJL[x1, …, xk][z1, …, zk][w1, …, wk]=∑1≤α,β,γ≤k (a(k(I-1)+α)(k(J-1)+β)(k(L-1)+γ) &xα &zβ &wγ) сохраняют в массивах с aIJL [0] [0] [0] по aIJL [2k-1] [2k-1] [2k-1], соответственно. В случае (примера 6), выполняют М-битовую операцию "исключающее ИЛИ" (XOR) (∧) только (N/k)(N/k+1)(N/k+2)/6 раз. Однако необходимый объем памяти равен произведению 22k/k3 на объем памяти, требуемый для алгоритма из (примера 4).
Например, когда k=1, М-битовую операцию "исключающее-ИЛИ" (XOR) выполняют 120*121*122/6=295240 раз, необходимый объем памяти в 23=8 раз больше объема памяти для (примера 4), а число циклов не изменяется. Кроме того, когда k=2, М-битовую операцию "исключающее-ИЛИ" (XOR) выполняют 60*61*62/6=37820 раз, необходимый объем памяти в 26/8=8 раз больше, а число циклов составляет 1/7.8. Когда k=4, М-битовую операцию "исключающее-ИЛИ" (XOR) выполняют 30*31*32/6=4960 раз, необходимый объем памяти в 212/43=64 раз больше, а число циклов составляет 1/59,5. Когда k=6, М-битовую операцию "исключающее-ИЛИ" (XOR) выполняют 20*21*22/6=1540 раз, необходимый объем памяти в 218/63=1214 раз больше, а число циклов составляет 1/192.
(пример 6)
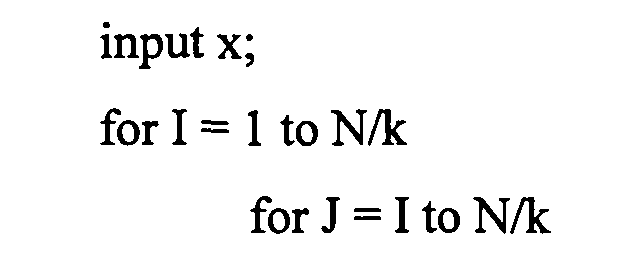
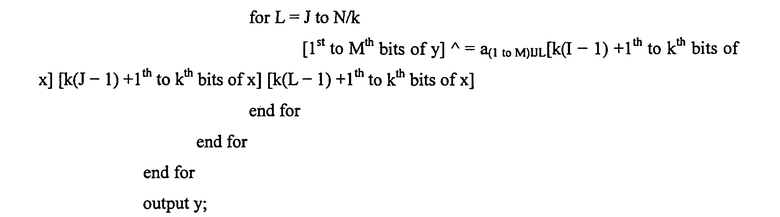
Способ, описанный в (примере 6) может, в частности, представлять собой способ вычисления заранее величин FIJ(…) согласно следующей формуле (35) и сохранения величин в виде массива.
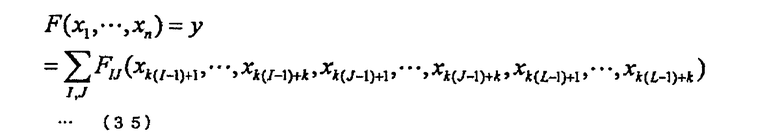
Здесь, FIJ(xk(I-1)+1, …, xk(I-1)+k, xk(J-1)+1, …, xk(J-1)+k, xk(L-1)+1, …, xk(L-1)+k) обозначает часть, определяемую посредством [xk(I-1)+1, …, xk(I-1)+k], [xk(J-1)+1, …, xk(J-1)+k], и [xk(L-1)+1, …, xk(L-1)+k] в F(x1, …, xn).
Выше были описаны случаи применения способа #1 структурирования к кубическому многочлену F от нескольких переменных. В такой структуре можно ожидать, что процесс выполнения этого алгоритма будет проходить с высокой скоростью.
(Применение к кубическим многочленам Gx и Gy от нескольких переменных) Как и в предыдущих (примере 5) и (примере 6) способ #1 структурирования также применим к многочленам Gx и Gy, как показано на Фиг. 25 и 26. Когда способ #1 структурирования не применяется, вычисления, относящиеся к структуре А данных кубического многочлена Gx от нескольких переменных, осуществляются, например, посредством следующего алгоритма (пример 4′Х).
(пример 4′Х)
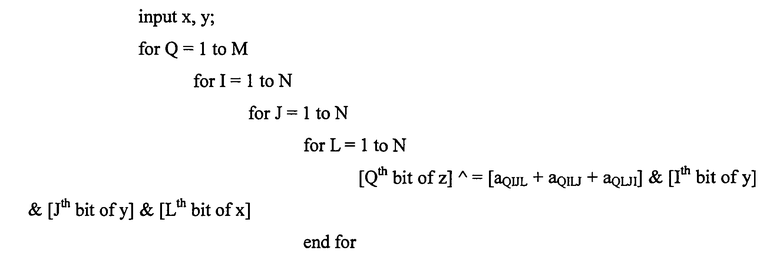

Когда описанный выше способ #1 структурирования применяется в описанном выше (примере 4′Х), алгоритм для вычисления многочлена Gx от нескольких переменных выражен в следующем (примере 5′Х). Кроме того, в описанном выше (примере 6) промежуточные результаты, получаемые в результате применения этих коэффициентов к многочлену Gx от нескольких переменных, могут быть сохранены в таблице.
(пример 5′Х)
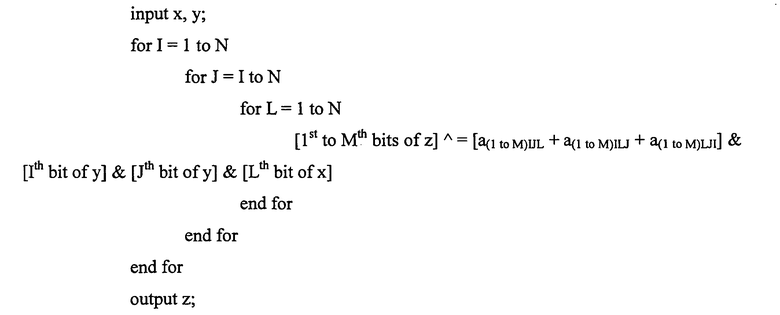
Когда способ #1 структурирования не применяется, вычисления кубического многочлена Gy от нескольких переменных, осуществляются, например, посредством следующего алгоритма из (примера 4′Y).
(пример 4′Y)
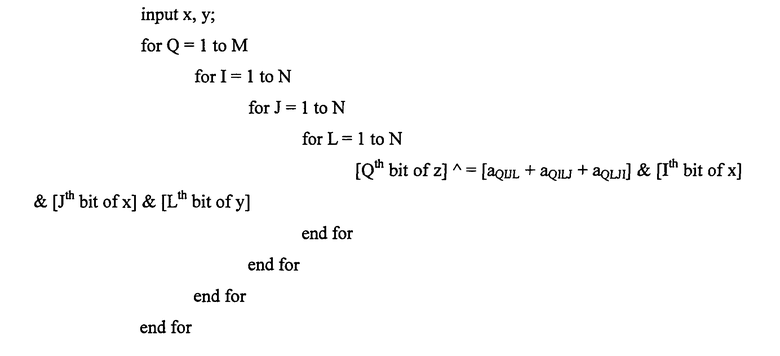
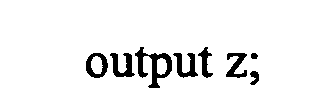
Когда описанный выше способ #1 структурирования применяется в описанном выше (примере 4′Y), алгоритм для вычисления многочлена Gy от нескольких переменных выражен в следующем (примере 5′Y). Кроме того, в описанном выше (примере 6) промежуточные результаты, получаемые в результате применения этих коэффициентов к многочлену Gy от нескольких переменных, могут быть сохранены в таблице.
(пример 5′Y)
Выше были описаны случаи применения способа #1 структурирования к кубическим многочленам Gx и Gy от нескольких переменных. В такой структуре можно ожидать, что процесс выполнения этого алгоритма будет проходить с высокой скоростью. 7-2-2: Способ #2 структурирования (Фиг. 27)
Далее будет описан способ #2 структурирования. Как показано на Фиг. 27, способ #2 структурирования представляет собой способ представления многочлена от нескольких переменных в квадратичной форме и сбора строк и столбцов этой квадратичной формы в качестве одной структуры данных. В примере, показанном на Фиг. 27, структура данных собрана в направлении строк.
Как показано на Фиг. 27, когда коэффициенты структурированы, а генерируемые случайные числа применяют последовательно по несколько за раз в качестве коэффициентов многочлена от нескольких переменных, алгоритм подстановки коэффициентов выражен как в (примере 4). В случае примера 4, выполняют N-битовую операцию "И" (AND) (&) только (N+1)×М раз, выполняют N-битовую операцию "исключающее ИЛИ" (XOR) (∧) только N×М раз и выполняют операцию функции Q только М раз.
(пример 4)

Как показано на Фиг. 27, когда коэффициенты структурированы, промежуточные
результаты, получаемые в результате применения этих коэффициентов к многочлену от нескольких переменных, могут быть сохранены в таблице. В этом случае применяется алгоритм подстановки коэффициентов, представленный как в (примере 5). Кроме того, AI [x1, …, xk]=(A(k(I-1)+1)&x1) ∧…∧ (A(k(I-1)+k)&xk) сохраняют в массивах с AI [0] по AI [2k-1], соответственно. В случае примера 5, выполняют N-битовую операцию "исключающее ИЛИ" (XOR) (∧) только (N/k)×M раз и выполняют N-битовую операцию функции Q только М раз. Однако необходимый объем памяти равен произведению 2k/k на объем памяти, требуемый для алгоритма из (примера 4).
Например, когда k=1, N-битовую операцию "исключающее-ИЛИ" (XOR) выполняют 120 раз, необходимый объем памяти в два раза больше объема памяти для (примера 4), а число циклов не изменяется. Кроме того, когда k=4, N-битовую операцию "исключающее-ИЛИ" (XOR) выполняют 30 раз, необходимый объем памяти в 24/4=4 раз больше, а число циклов составляет 1/4. Когда k=8, N-битовую операцию "исключающее-ИЛИ" (XOR) выполняют 15 раз, необходимый объем памяти в 28/8=32 раз больше, а число циклов составляет 1/8. Когда k=16, N-битовую операцию "исключающее-ИЛИ" (XOR) выполняют 8 раз, необходимый объем памяти в 216/16=4096 раз больше, а число циклов составляет 1/15.
(пример 5)
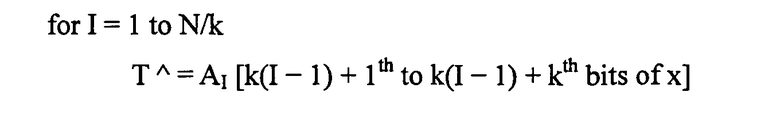
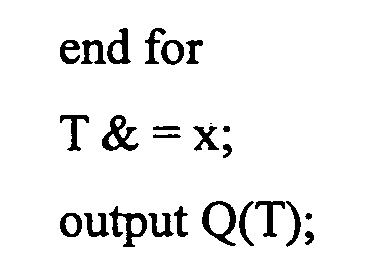
Выше были описаны конкретные алгоритмы подстановки коэффициентов, относящиеся к способу #2 структурирования. В такой структуре можно ожидать, что процесс выполнения этого алгоритма будет проходить с высокой скоростью.
7-2-3: Способ #3 структурирования
Далее будет описан способ #3 структурирования. Способ #3 структурирования представляет собой способ последовательного выполнения процедуры N раз (где N≥2) параллельно путем выполнения сегмента «для генерации нескольких коэффициентов и выполнения процедуры подстановки нескольких коэффициентов N раз» в единичных блоках вместо того, чтобы генерировать многочлен из случайных чисел N раз и выполнять процедуру подстановки в одном и том же многочлене от нескольких переменных N раз. При использовании этого способа повышается производительность всех процессов, выполняемых N раз, в случае, когда стоимость генерации случайных чисел не является пренебрежимо малой.
Например, в алгоритме, представленном на Фиг. 5, вычисление многочленов F и G от нескольких переменных осуществляется многократно N раз, и при этом происходит обновление факторов операции #1. Соответственно, в таком вычислительном сегменте процедура вычислений конфигурирована для многократного выполнения с использованием одних и тех же коэффициентов. Когда многочлен F(r0i) (где i=1-N) от нескольких переменных вычисляют с использованием описанного выше алгоритма из (примера 2), все из N векторов r0i конфигурированы для применения к однажды сформированному массиву [aIJL], а затем выполняется процедура относительно следующего массива [aIJL]. В такой конфигурации один и тот же массив [aIJL] коэффициентов, в конечном итоге, не генерируют N раз.
Выше был описан конкретный алгоритм подстановки коэффициентов, относящийся к способу #3 структурирования. В такой конфигурации производительность повышается для всех процессов, выполняемых N раз, в целом.
8: Пример конфигурации аппаратуры (Фиг. 28)
Каждый алгоритм, описанный выше, может быть выполнен с использованием, например, конфигурации аппаратуры устройства для обработки информации, представленного на Фиг. 28. Иными словами, выполнение каждого алгоритма может быть реализовано посредством управления аппаратурой, показанной на Фиг. 28 с использованием компьютерной программы. Кроме того, характер аппаратуры может быть произвольным - это может быть персональный компьютер, мобильный информационный терминал, такой как мобильный телефон, PHS или PDA, игровой автомат, контактный или бесконтактный кристалл интегральной схемы, контактная или бесконтактная электронная карточка с встроенной интегральной схемой или разнообразная информационная аппаратура. Здесь PHS представляет собой сокращение от Personal Handy-phone System, т.е. персональный миниатюрный радиотелефон. Кроме того, PDA представляет собой сокращение от Personal Digital Assistant, т.е. персональный цифровой помощник.
Как показано на Фиг. 28, эта аппаратура содержит главным образом процессор CPU 902, ПЗУ ROM 904, ЗУПВ RAM 906, главную шину 908 и мост 910. Кроме того, эта аппаратура содержит внешнюю шину 912, интерфейс 914, модуль 916 ввода, модуль 918 вывода, модуль 920 памяти, привод 922 носителя записи, соединительный порт 924 и модуль 926 связи. Здесь CPU представляет собой сокращение от Central Processing Unit, т.е. центральный процессор. Кроме того, ROM представляет собой сокращение от Read Only Memory, т.е. постоянное запоминающее устройство (ПЗУ). Далее, RAM представляет собой сокращение от Random Access Memory, т.е. запоминающее устройство с произвольной выборкой (ЗУПВ).
Центральный процессор CPU 902 служит арифметическим модулем или модулем управления, например, и управляет всей работой или частью работы каждого из структурных элементов на основе различных программ, записанных в ПЗУ ROM 904, в ЗУПВ RAM 906, в модуле 920 памяти или на сменном носителе 928 записи. ПЗУ ROM 904 служит для сохранения программы, подлежащей загрузке в процессор CPU 902, или данных или другой подобной информации, используемой при выполнении арифметических операций. ЗУПВ RAM 906 служит для временного или постоянного хранения программы, подлежащей загрузке в процессор CPU 902, или различных параметров или другой подобной информации, произвольно изменяющейся в ходе выполнения программы.
Эти структурные элементы соединены один с другим посредством, например, главной шины 908, способной передавать данные с высокой скоростью. Со своей стороны главная шина 908 соединена через мост 910 с внешней шиной 912, имеющей относительно низкую скорость передачи данных, например. Модуль 916 ввода представляет собой, например, мышь, клавиатуру, сенсорную панель, кнопки, переключатель или джойстик. Кроме того, модуль 916 ввода может представлять собой пульт дистанционного управления, который может передавать сигнал управления с использования инфракрасного излучения или радиоволн.
Модуль 918 вывода представляет собой, например, дисплей, такой как CRT, LCD, PDP или ELD, выходное аудио устройство, такое как громкоговоритель или наушники, принтер, мобильный телефон или факсимильный аппарат, который может визуально или акустически сообщать пользователю о полученной информации. Здесь CRT представляет собой сокращение от Cathode Ray Tube, т.е. электронно-лучевая трубка. Кроме того, LCD представляет собой сокращение от Liquid Crystal Display, т.е. жидкокристаллический дисплей. Кроме того, PDP представляет собой сокращение от Plasma Display Panel, т.е. панель плазменного дисплея. Кроме того, ELD представляет собой сокращение от Electro-Luminescence Display, т.е. электролюминесцентный дисплей.
Модуль 920 памяти представляет собой устройство для хранения разнообразных данных. Указанный модуль 920 памяти представляет собой, например, магнитное запоминающее устройство, такое как накопитель HDD, полупроводниковое запоминающее устройство, оптическое запоминающее устройство или магнитооптическое запоминающее устройство. Здесь, HDD представляет собой сокращение от Hard Disk Drive, т.е. накопитель на жестком диске.
Привод 922 носителя записи представляет собой устройство, считывающее информацию, записанную на сменном носителе 928 записи, таком как магнитный диск, оптический диск, магнитооптический диск или полупроводниковое запоминающее устройство, или записывает информацию на сменном носителе 928 записи. Этот сменный носитель 928 записи может представлять собой, например, диск DVD, диск Блю-рей, диск HD-DVD, разнообразные полупроводниковые запоминающие устройства или аналогичные компоненты. Безусловно, сменный носитель 928 записи может представлять собой, например, электронное устройство или электронную карточку, на которой смонтирован бесконтактный кристалл интегральной схемы. Здесь 1C представляет собой сокращение от Integrated Circuit, т.е. интегральная схема.
Соединительный порт 924 представляет собой порт, такой как USB-порт, порт IEEE 1394, порт SCSI, порт RS-232C или порт для присоединения внешнего устройства 930, такого как оптический аудио терминал. Указанное внешнее устройство 930 представляет собой принтер, мобильный музыкальный плеер, цифровой фотоаппарат, цифровая видеокамера или записывающее устройство на основе интегральной схемы. Более того, USB представляет собой сокращение от Universal Serial Bus, т.е. универсальная последовательная шина. Кроме того, SCSI представляет собой сокращение от Small Computer System Interface, т.е. интерфейс малых вычислительных систем.
Модуль 926 связи представляет собой устройство связи для соединения с сетью 932 связи и может быть, например, картой связи для взаимодействия с кабельной ли радио сетью LAN, карту стандарта Bluetooth (зарегистрированная торговая марка) или WUSB, оптическим маршрутизатором связи, маршрутизатором ADSL или устройством для контактной или бесконтактной связи. Сеть 932 связи, соединяемая с модулем 926 связи, конфигурирована по принципу кабельной или беспроводной ста связи и может быть, например, сетью Интернет, домашней сетью LAN, сетью инфракрасной связи, сетью оптической связи в видимом диапазоне, сетью вещания или сетью спутниковой связи. Здесь, LAN представляет собой сокращение от Local Area Network, т.е. локальная сеть связи. Кроме того, WUSB представляет собой сокращение от Wireless USB, т.е. радио USB. Далее, ADSL представляет собой сокращение от Asymmetric Digital Subscriber Line, т.е. асимметричная цифровая абонентская линия.
9: Резюме
Наконец, далее будет вкратце изложено техническое содержание рассмотренного варианта настоящего изобретения. Изложенное здесь техническое содержание может быть применено в различных устройствах для обработки информации, таких как персональный компьютер, мобильный телефон, игровой терминал, информационный терминал, информационная аппаратура, автомобильный навигатор или другое подобное устройство. Кроме того, функции устройства для обработки информации, описанные ниже, могут быть реализованы с использованием одного устройства для обработки информации или нескольких устройств для обработки информации. Далее, устройства для хранения данных и арифметические процессоры, используемые для выполнения обработки данных в устройстве для обработки информации, описанном ниже, могут быть смонтированы в самом устройстве для обработки информации или могут быть смонтированы в каком-либо устройстве, соединенном с рассматриваемым устройством для обработки информации через сеть связи.
Функциональная конфигурация устройства для обработки информации, описанного выше, реализована следующим образом. Например, устройство для обработки информации, описанное в следующем п. (1), имеет функцию выполнения алгоритма, относящегося к эффективным алгоритмам аутентификации с открытым ключом или к эффективным алгоритмам цифровой подписи, защищенность которых базируется на трудности решения систем уравнений множества порядков с несколькими переменными.
(1) Устройство обработки информации, содержащее:
модуль генерации чисел, выполненный с возможностью генерации чисел, используемых в коэффициентах членов, входящих в пару многочленов F=(f1, …, fm) множества порядков с несколькими переменными, с использованием заданной функции на основе информации, совместно используемой объектами, исполняющими алгоритм аутентификации с открытым ключом или алгоритм цифровой подписи, применяющий открытый ключ, содержащий указанную пару многочленов F множества порядков с несколькими переменными; и
модуль назначения, выполненный с возможностью назначения чисел, генерируемых посредством модуля генерации чисел, коэффициентам многочленов множества порядков с несколькими переменными, составляющими элементами которых является указанная пара многочленов F множества порядков с несколькими переменными,
при этом модуль назначения выполнен с возможностью группирования коэффициентов членов, имеющих идентичное сочетание переменных, из совокупности коэффициентов многочленов множества порядков с несколькими переменными, составляющими элементами которых является указанная пара многочленов F множества порядков с несколькими переменными, и выполнения процедуры назначения в единицах групп.
(2) Устройство обработки информации, содержащее:
модуль генерирования чисел, выполненный с возможностью генерации чисел, используемых в коэффициентах членов, входящих в пару многочленов F=(f1, …, fm) множества порядков с несколькими переменными, с использованием заданной функции на основе информации, совместно используемой объектами, исполняющими алгоритм аутентификации с открытым ключом или алгоритм цифровой подписи, применяющий открытый ключ, содержащий указанную пару многочленов F множества порядков с несколькими переменными; и
модуль назначения, выполненный с возможностью назначения чисел, генерируемых посредством модуля генерации чисел, коэффициентам многочленов множества порядков с несколькими переменными, составляющими элементами которых является указанная пара многочленов F множества порядков с несколькими переменными,
при этом модуль назначения выполнен с возможностью группирования матрицы коэффициентов в каждой строке или столбце, когда многочлены множества порядков с несколькими переменными, составляющими элементами которых является указанная пара многочленов F множества порядков с несколькими переменными, выражены в квадратичной форме, причем модуль назначения выполнен с возможностью выполнения процедуры назначения в единицах групп.
(3) Устройство обработки информации согласно (1) или (2), в котором модуль генерации чисел выполнен с возможностью генерации чисел по количеству коэффициентов, принадлежащих одной группе, при выполнении модулем назначения процедуры назначения в указанной одной группе.
(4) Устройство обработки информации согласно (3), в котором модуль генерации чисел выполнен с возможностью генерации одного числа при генерации чисел по количеству коэффициентов, принадлежащих одной группе, и генерации необходимого количества чисел путем поворота генерируемых чисел на каждый бит.
(5) Устройство обработки информации согласно (1) или (2), дополнительно содержащее:
модуль хранения таблицы, выполненный с возможностью хранения в виде таблицы значений, получаемых путем назначения коэффициентов члену какого-либо вида, соответствующего каждой группе, и подстановки данного числа для переменных соответствующих членов.
(6) Устройство обработки информации, содержащее:
модуль генерации чисел, выполненный с возможностью генерации чисел в количестве, идентичном количеству коэффициентов членов, входящих в пару многочленов F=(f1, …, fm) множества порядков с несколькими переменными, с использованием заданной функции на основе информации, совместно используемой объектами, исполняющими алгоритм аутентификации с открытым ключом или алгоритм цифровой подписи, применяющий открытый ключ, содержащий указанную пару многочленов F множества порядков с несколькими переменными; и
модуль назначения, выполненный с возможностью назначения чисел, генерируемых посредством модуля генерации чисел, коэффициентам многочленов множества порядков с несколькими переменными, составляющими элементами которых является указанная пара многочленов F множества порядков с несколькими переменными, в последовательности, согласованной заранее между доказывающей стороной и проверяющей стороной.
(7) Устройство обработки информации согласно любому из (1)-(7),
в котором указанная информация является начальным числом для генерации случайного числа, а
указанная заданная функция является генератором случайных чисел, выполненным с возможностью генерации случайного числа с использованием указанного начального числа.
(8) Устройство обработки информации согласно любому из (1)-(7), содержащее:
модуль генерации сообщений, выполненный с возможностью генерации сообщения на основе указанной пары многочленов F=(f1, …, fm) множества порядков от нескольких переменных, определенных в кольце K, и вектора s, являющегося элементом множества Kn;
модуль передачи сообщений, выполненный с возможностью передачи указанного сообщения проверяющей стороне, хранящей указанную пару многочленов F множества порядков от нескольких переменных и векторы y=(y1, …, ym)=(f1(s), …, fm(s)); и
модуль передачи ответа, выполненный с возможностью передачи проверяющей стороне ответной информации, соответствующей схеме верификации, выбранной проверяющей стороной из совокупности k схем верификации, где k≥3,
при этом вектор s представляет собой секретный ключ,
указанная пара многочленов F множества порядков от нескольких переменных и вектор у являются открытыми ключами,
ответная информация представляет собой информацию, выбранную из пары случайных чисел, и указанное сообщение согласно схеме верификации, и
причем указанное сообщение представляет собой информацию, полученную путем вычислений, выполненных заранее для схемы верификации, соответствующей ответной информации, на основе открытых ключей и ответной информации.
(9) Устройство обработки информации согласно любому из (1)-(7), содержащее:
модуль хранения информации, выполненный с возможностью хранения указанной пары многочленов F=(f1, …, fm) множества порядков от нескольких переменных, определенных в кольце K, и векторов y=(y1, …, ym)=(f1(s), …, fm(s));
модуль получения сообщений, выполненный с возможностью получения сообщения, генерируемого на основе указанной пары многочленов F множества порядков от нескольких переменных и вектора s, являющегося элементом множества Kn;
модуль передачи информации о схеме, выполненный с возможностью передачи проверяющей стороне, передавшей сообщение, информации о схеме верификации, выбранной случайным образом из совокупности k схем верификации, где k≥3;
модуль получения ответа, выполненный с возможностью получения от доказывающей стороны ответной информации, соответствующей выбранной схеме верификации; и
модуль верификации, выполненный с возможностью проверки, хранит ли доказывающая сторона вектор s, основанный на сообщении, указанной паре многочленов F множества порядков с несколькими переменными, векторов у и ответной информации,
при этом вектор s представляет собой секретный ключ,
пара многочленов F множества порядков от нескольких переменных и векторы у являются открытыми ключами, а
указанное сообщение представляет собой информацию, получаемую путем вычислений, выполненных заранее для схемы верификации, соответствующей информации ответа, на основе открытых ключей и информации ответа.
(10) Устройство обработки информации согласно любому из (1)-(7), содержащее:
модуль генерации сообщений, выполненный с возможностью генерации сообщения на основе указанной пары многочленов F=(f1, …, fm) множества порядков от нескольких переменных, определенных в кольце К, и вектора s, являющегося элементом множества Kn;
модуль передачи сообщений, выполненный с возможностью передачи указанного сообщения проверяющей стороне, хранящей указанную пару многочленов F множества порядков от нескольких переменных и векторы y=(y1, …, ym)=(f1(s), …, fm(s));
модуль генерации промежуточной информации, выполненный с возможностью генерации третьей информации с использованием первой информации, выбранной случайным образом проверяющей стороной, и второй информации, полученной в момент генерации сообщения;
модуль передачи промежуточной информации, выполненный с возможностью передачи третьей информации проверяющей стороне; и
модуль передачи ответа, выполненный с возможностью передачи проверяющей стороне ответной информации, соответствующей схеме верификации, выбранной проверяющей стороной из совокупности k схем верификации, где k≥2,
при этом вектор s представляет собой секретный ключ,
пара многочленов F множества порядков от нескольких переменных и векторы у являются открытыми ключами,
ответная информация представляет собой информацию, выбранную из сообщений согласно указанной схеме верификации, а
указанное сообщение представляет собой информацию, полученную путем вычислений, выполненных заранее для схемы верификации, соответствующей ответной информации, на основе открытых ключей, первой информации, третьей информации и ответной информации.
(11) Устройство обработки информации согласно любому из (1)-(7), содержащее:
модуль хранения информации, выполненный с возможностью хранения пары многочленов F=(f1, …, fm) множества порядков от нескольких переменных, определенных в кольце K, и векторов y=(y1, …, ym)=(f1(s), …, fm(s));
модуль получения сообщений, выполненный с возможностью получения сообщения, генерируемого на основе указанной пары многочленов F множества порядков от нескольких переменных и вектора s, являющегося элементом множества Kn;
модуль передачи информации, выполненный с возможностью передачи доказывающей стороне, передавшей указанное сообщение, выбранной случайным образом первой информации;
модуль получения промежуточной информации, выполненный с возможностью получения третьей информации, генерируемой доказывающей стороной на основе указанной первой информации, и второй информации, получаемой в момент генерации сообщения;
модуль передачи информации о схеме, выполненный с возможностью передачи доказывающей стороне информации о схеме верификации, выбранной случайным образом из совокупности k схем верификации, где k≥3;
модуль получения ответа, выполненный с возможностью получения от доказывающей стороны ответной информации, соответствующей выбранной схеме верификации; и
модуль верификации, выполненный с возможностью проверки, сохраняет ли доказывающая сторона вектор s, на основе сообщения, первой информации, третьей информации, пары многочленов F множества порядков с несколькими переменными и ответной информации,
при этом вектор s представляет собой секретный ключ,
пара многочленов F множества порядков от нескольких переменных и векторы у являются открытыми ключами,
причем указанное сообщение представляет собой информацию, полученную путем вычислений, выполненных заранее для схемы верификации, соответствующей ответной информации, на основе открытых ключей, первой информации, третьей информации и ответной информации.
(12) Устройство обработки информации согласно (1) или (2), в котором при повторном выполнении алгоритма множество раз модуль генерации чисел выполнен с возможностью генерации чисел только один раз, а модуль назначения выполнен с возможностью выполнения процедуры назначения только один раз,
причем алгоритм многократно использует коэффициенты, назначаемые посредством модуля назначения.
(13) Устройство обработки информации согласно любому из (1)-(7), содержащее:
модуль генерации подписи, выполненный с возможностью генерации цифровой подписи для документа М с использованием указанной пары многочленов F=(f1, …, fm) множества порядков от нескольких переменных, определенных в кольце K, и ключа подписи, являющегося элементом множества Kn; и
модуль передачи подписи, выполненный с возможностью передачи цифровой подписи проверяющей стороне, хранящей пару многочленов F множества порядков от нескольких переменных и векторы y=(f1(s), …, fm(s));
(14) Способ обработки информации, содержащий:
этап генерации чисел, используемых в коэффициентах членов, входящих в пару многочленов F=(f1, …, fm) множества порядков с несколькими переменными, с использованием заданной функции на основе информации, совместно используемой объектами, исполняющими алгоритм аутентификации с открытым ключом или алгоритм цифровой подписи, применяющий открытый ключ, содержащий указанную пару многочленов F множества порядков с несколькими переменными; и
этап назначения сгенерированных чисел коэффициентам многочленов множества порядков с несколькими переменными, составляющими элементами которых является указанная пара многочленов F множества порядков с несколькими переменными,
при этом на этапе назначения чисел группируют коэффициенты членов, имеющих идентичный тип сочетания переменных, из совокупности коэффициентов многочленов множества порядков с несколькими переменными, составляющими элементами которых является указанная пара многочленов F множества порядков с несколькими переменными, и выполняют процедуру назначения в блоках групп.
(15) Способ обработки информации, содержащий:
этап генерации чисел, используемых в коэффициентах членов, входящих в пару многочленов F=(f1, …, fm) множества порядков с несколькими переменными, с использованием заданной функции на основе информации, совместно используемой объектами, исполняющими алгоритм аутентификации с открытым ключом или алгоритм цифровой подписи, применяющий открытый ключ, содержащий указанную пару многочленов F множества порядков с несколькими переменными; и
этап назначения генерируемых чисел коэффициентам многочленов множества порядков с несколькими переменными, составляющими элементами которых является указанная пара многочленов F множества порядков с несколькими переменными,
при этом на этапе назначения чисел группируют матрицу коэффициентов в каждой строке или столбце, когда многочлены множества порядков с несколькими переменными, составляющими элементами которых является указанная пара многочленов F множества порядков с несколькими переменными, выражены в квадратичной форме, и выполняют процедуру назначения в блоках групп.
(16) Способ обработки информации, содержащий:
этап генерации чисел в количестве, идентичном количеству коэффициентов членов, входящих в пару многочленов F=(f1, …, fm) множества порядков с несколькими переменными, с использованием заданной функции на основе информации, совместно используемой объектами, исполняющими алгоритм аутентификации с открытым ключом или алгоритм цифровой подписи, применяющий открытый ключ, содержащий указанную пару многочленов F множества порядков с несколькими переменными; и
этап назначения чисел, сгенерированных посредством модуля генерации чисел, коэффициентам многочленов множества порядков с несколькими переменными, составляющими элементами которых является указанная пара многочленов F множества порядков с несколькими переменными, в последовательности, определенной заранее между доказывающей стороной и проверяющей стороной.
(17) Программа, вызывающая выполнение компьютером:
функции генерации чисел для генерации чисел, используемых в коэффициентах членов, входящих в пару многочленов F=(f1, …, fm) множества порядков с несколькими переменными, с использованием заданной функции на основе информации, совместно используемой объектами, исполняющими алгоритм аутентификации с открытым ключом или алгоритм цифровой подписи, применяющий открытый ключ, содержащий указанную пару многочленов F множества порядков с несколькими переменными; и
функции назначения для назначения чисел, генерируемых посредством функции генерации чисел, коэффициентам многочленов множества порядков с несколькими переменными, составляющими элементами которых является указанная пара многочленов F множества порядков с несколькими переменными,
при этом функция назначения группирует коэффициенты членов, имеющих идентичный тип сочетания переменных, из совокупности коэффициентов многочленов множества порядков с несколькими переменными, составляющими элементами которых является указанная пара многочленов F множества порядков с несколькими переменными, и выполняет процедуру назначения в блоках групп.
(18) Программа, вызывающая выполнение компьютером:
функции генерации чисел для генерации чисел, используемых в коэффициентах членов, входящих в пару многочленов F=(f1, …, fm) множества порядков с несколькими переменными, с использованием заданной функции на основе информации, совместно используемой объектами, исполняющими алгоритм аутентификации с открытым ключом или алгоритм цифровой подписи, применяющий открытый ключ, содержащий указанную пару многочленов F множества порядков с несколькими переменными; и
функции назначения для назначения чисел, генерируемых посредством функции генерации чисел, коэффициентам многочленов множества порядков с несколькими переменными, составляющими элементами которых является указанная пара многочленов F множества порядков с несколькими переменными,
при этом функция назначения группирует матрицу коэффициентов в каждой строке или столбце, когда многочлены множества порядков с несколькими переменными, составляющими элементами которых является указанная пара многочленов F множества порядков с несколькими переменными, выражены в квадратичной форме, при этом функция назначения выполняет процедуру назначения в блоках групп.
(19) Программа, вызывающая выполнение компьютером:
функции генератора чисел, осуществляющую генерацию чисел в количестве, идентичном количеству коэффициентов членов, входящих в пару многочленов F=(f1, …, fm) множества порядков от нескольких переменных, с использованием заданной функции на основе информации, совместно используемой объектами, исполняющими алгоритм аутентификации с открытым ключом или алгоритм цифровой подписи, применяющий открытый ключ, содержащий пару многочленов F множества порядков от нескольких переменных; и
функцию назначения для назначения чисел, генерируемых посредством модуля генерации чисел, коэффициентам многочленов множества порядков от нескольких переменных, составляющими элементами которых является указанная пара многочленов F множества порядков от нескольких переменных, в последовательности, определенной заранее между доказывающей стороной и проверяющей стороной.
(20) Компьютерный носитель записи, на котором записана программа согласно (19).
Замечание
Описанные выше алгоритм Р доказывающей стороны, алгоритм V проверяющей стороны, алгоритм Sig генерации подписи и алгоритм Ver верификации подписи являются примерами модуля генератора чисел, модуля назначения и модуля хранения таблиц. Описанный выше алгоритм Р доказывающей стороны представляет собой пример модуля генератора сообщений, модуля передачи сообщений, модуля передачи ответа, модуля генератора промежуточной информации и модуля передачи промежуточной информации. Кроме того, описанный выше алгоритм V проверяющей стороны представляет собой пример модуля хранения информации, модуля получения сообщений, модуля передачи информации схемы, модуля получения ответа и модуля получения промежуточной информации.
Предпочтительные варианты настоящего изобретения были описаны выше со ссылками на прилагаемые чертежи, тогда как это изобретение, безусловно, приведенными выше примерами не ограничивается. Специалист в рассматриваемой области может найти разнообразные изменения или модификации в пределах объема прилагаемой Формулы изобретения, и должно быть понятно, что такие изменения и модификации естественным образом попадают в пределы технического объема настоящего изобретения.
В приведенном выше описании были предложены алгоритмы, использующие хэш-функцию Н, однако здесь может быть также применена функция фиксации (commitment function СОМ) вместо хэш-функции Н. Функция фиксации СОМ представляет собой функцию, входными данными которой являются строка S символов и случайное число ρ. Одним из примеров функции фиксации является алгоритм, предложенный Шаи Галеви и Сильвио Микали (Shai Halevi and Silvio Micali) на международной конференции CRYPTO 1996.
Список позиционных обозначений
Gen алгоритм генерации ключей
Р алгоритм доказывающей стороны
V алгоритм проверяющей стороны
Sig алгоритм генерации подписи
Ver алгоритм верификации подписи
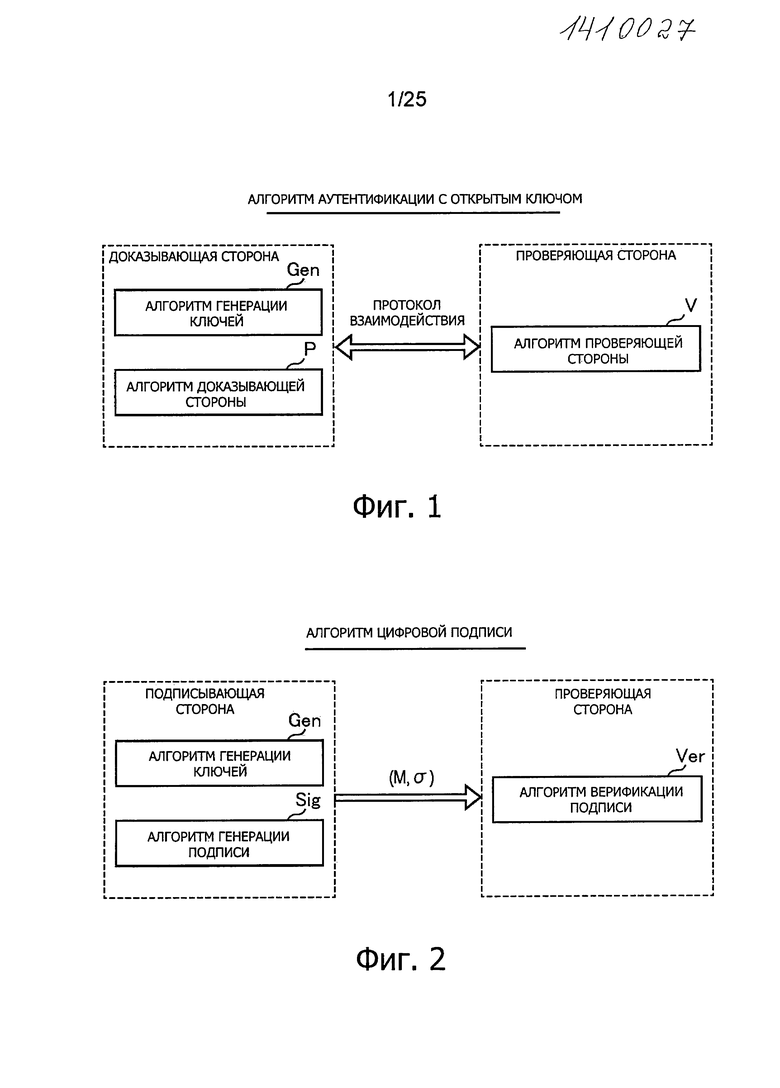
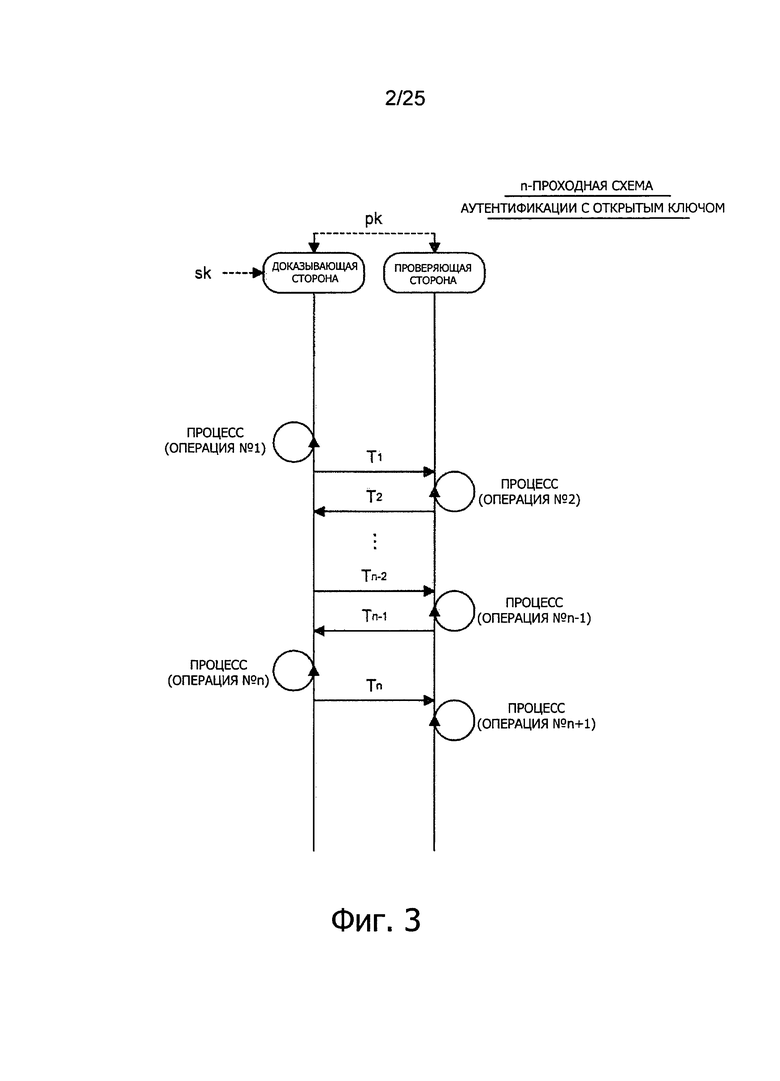
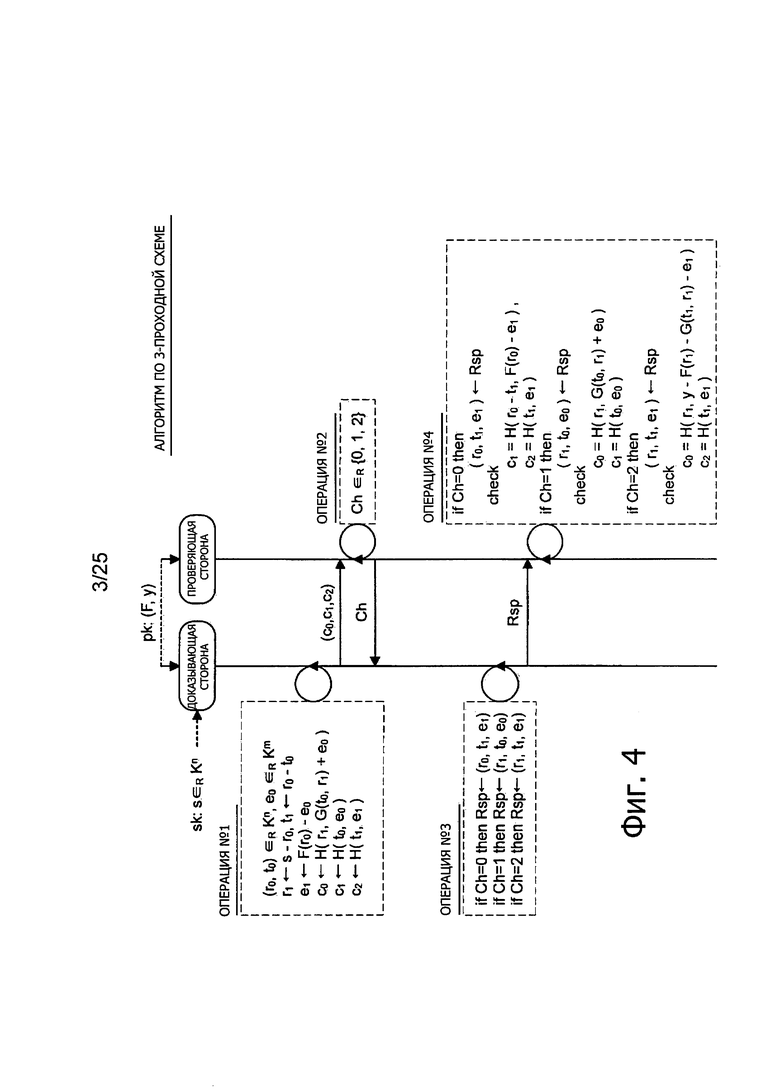
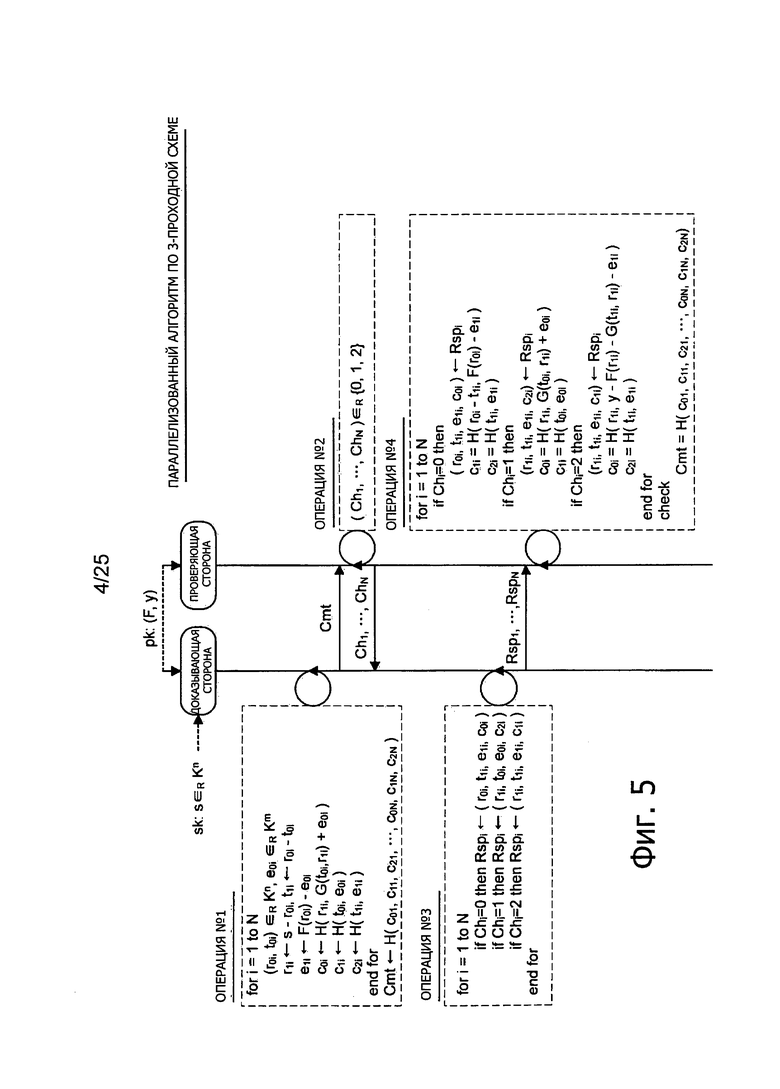
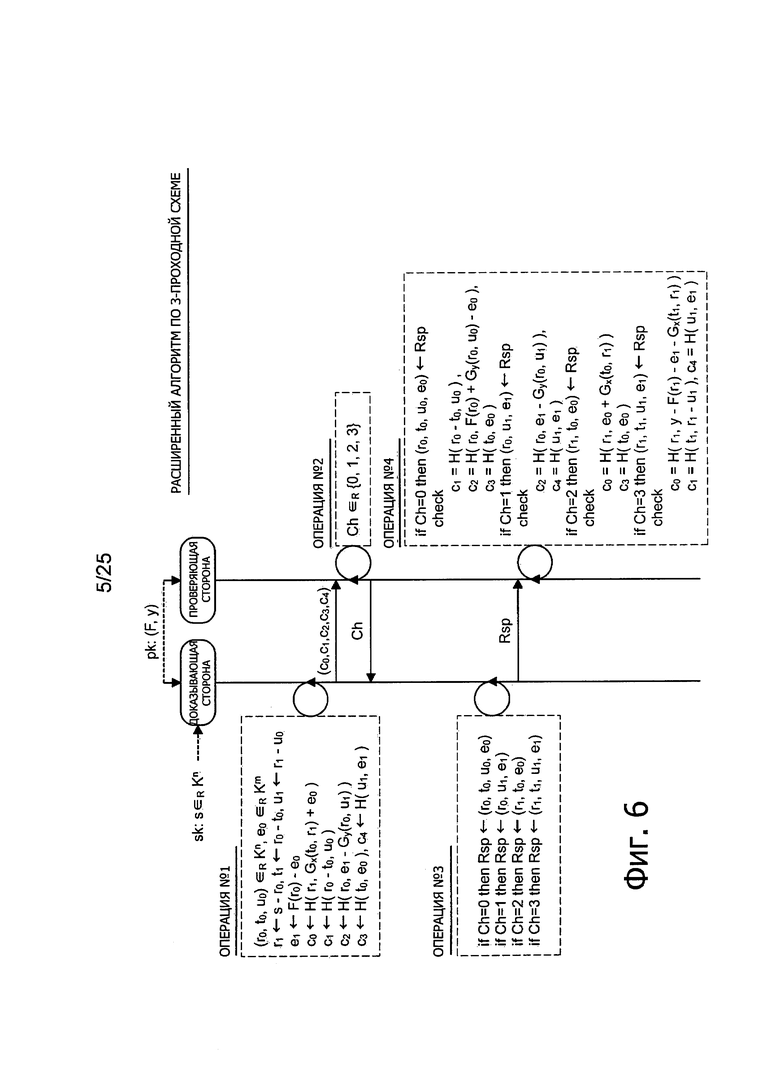
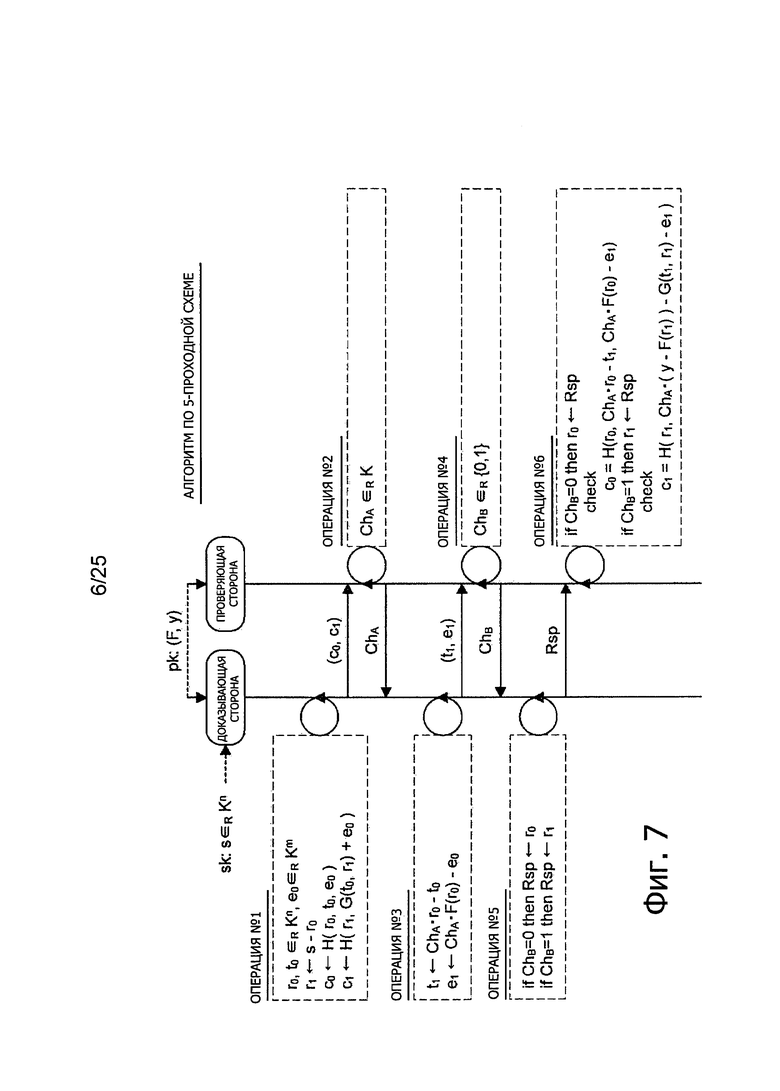
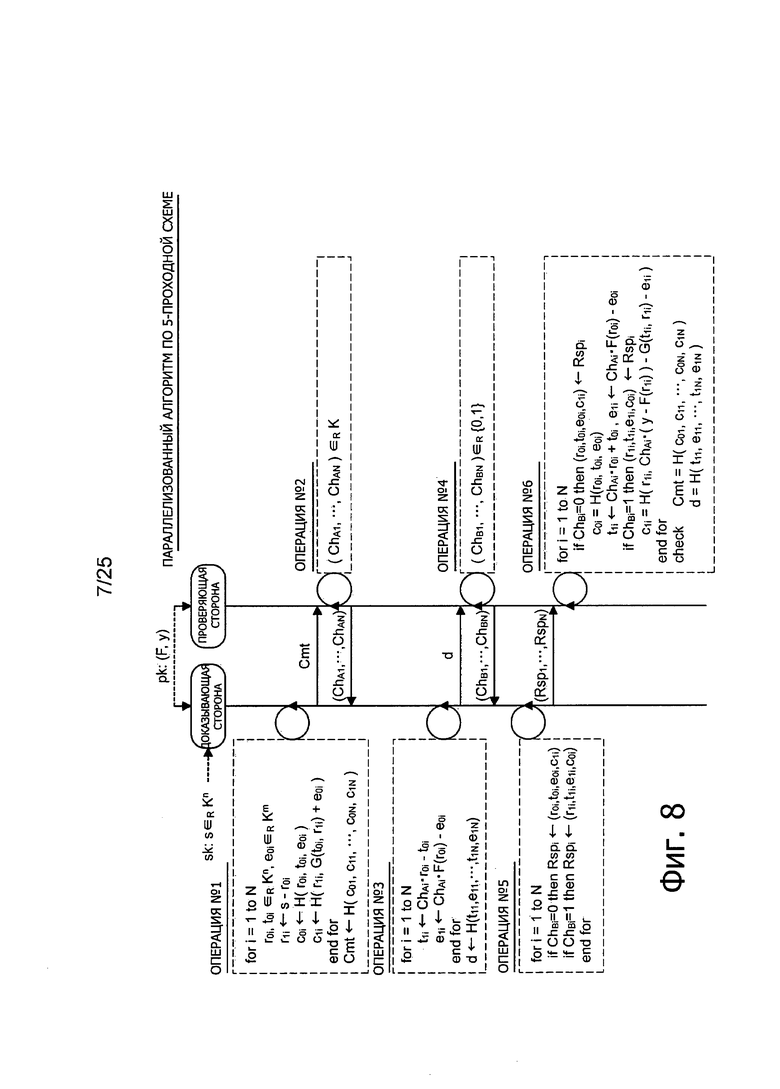
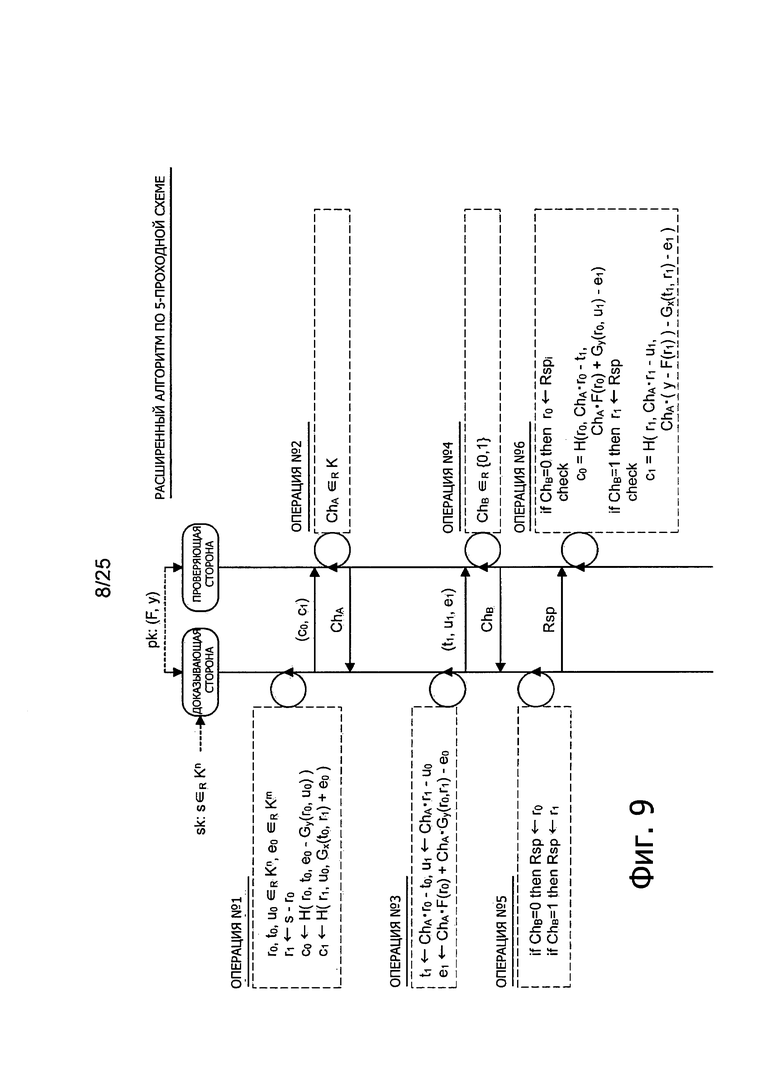
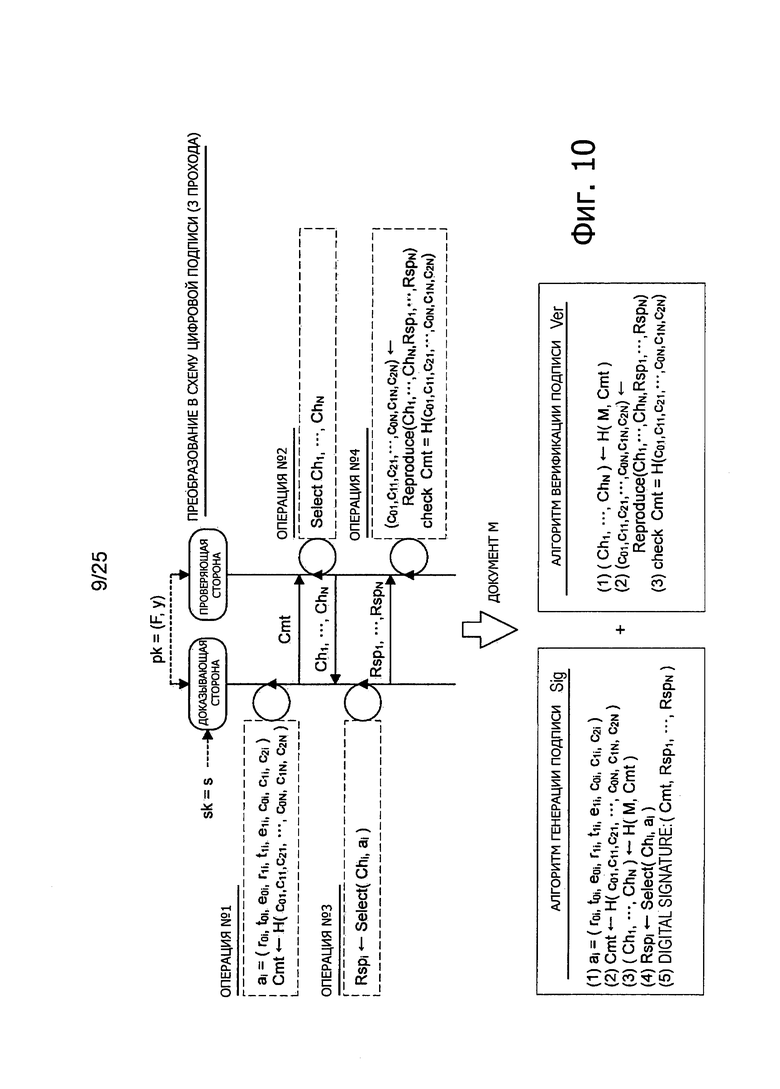
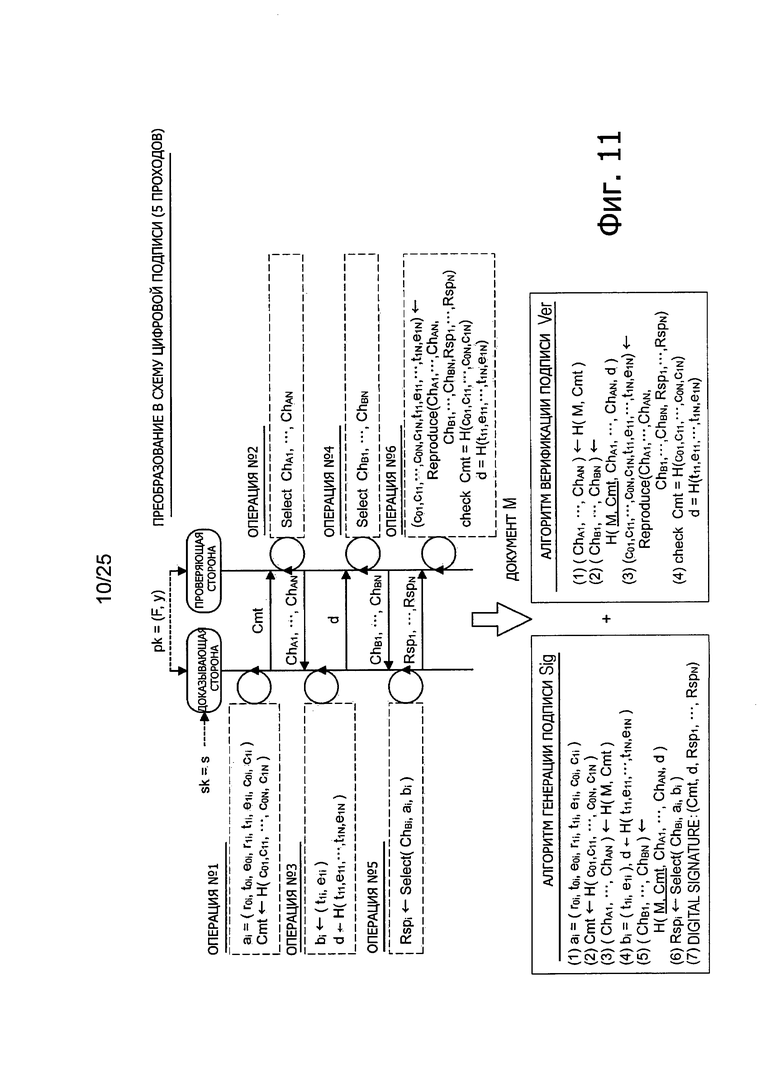
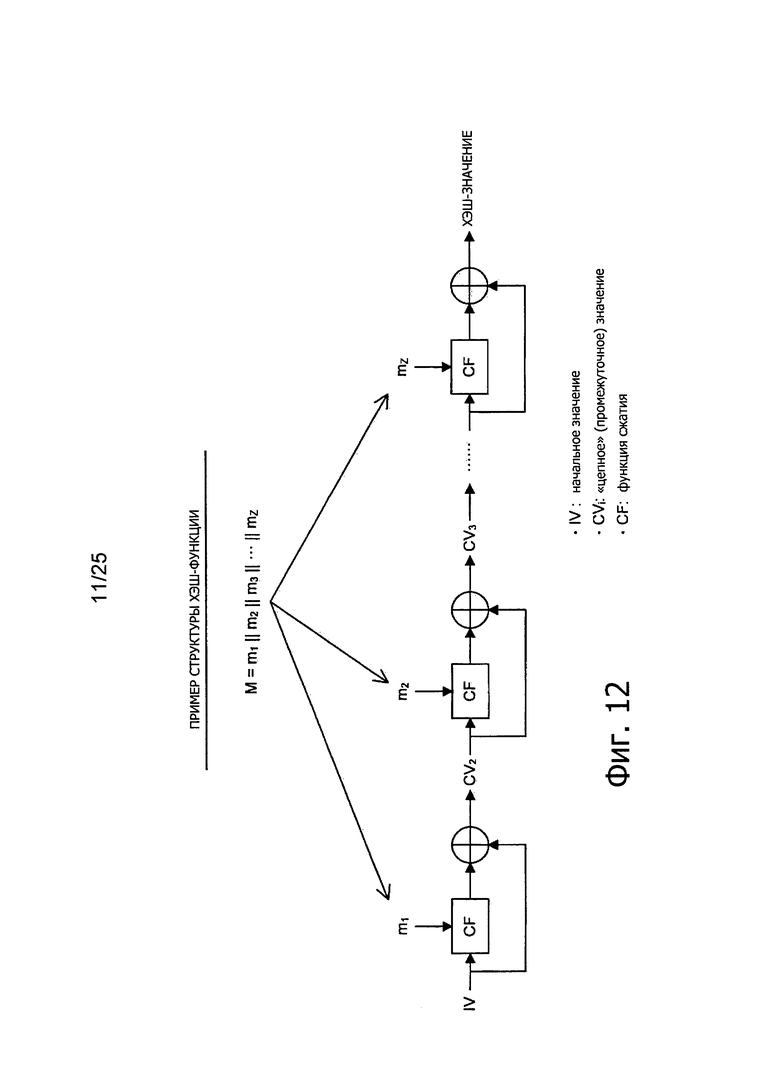
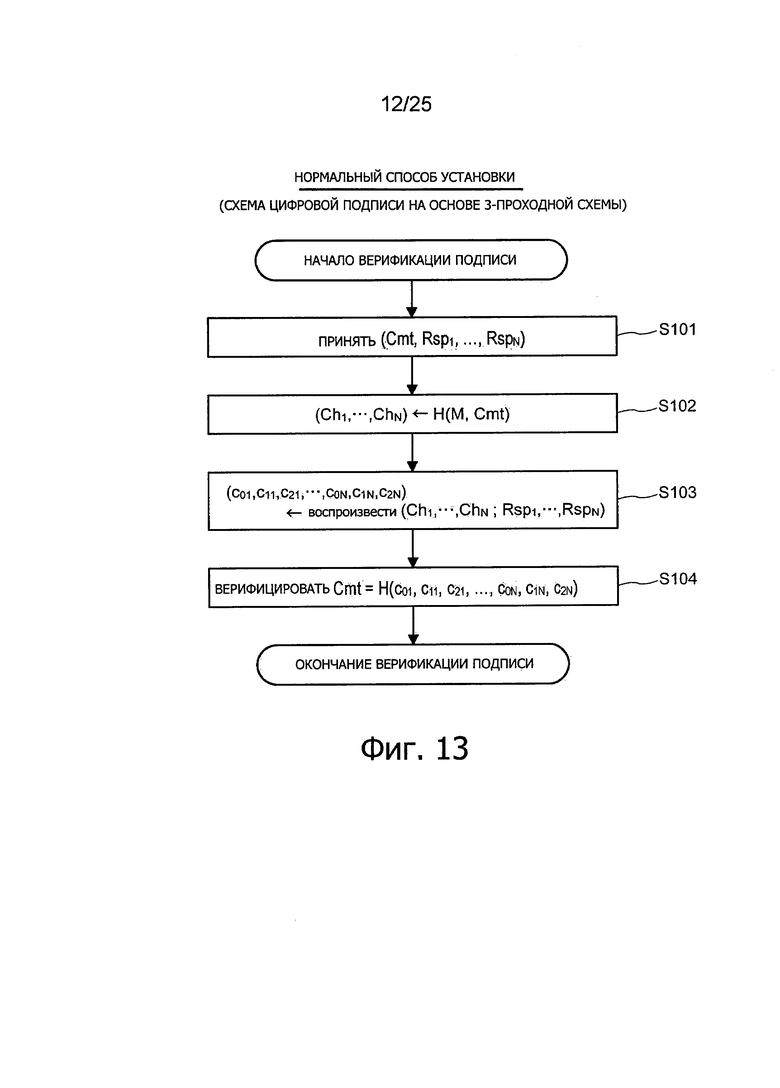
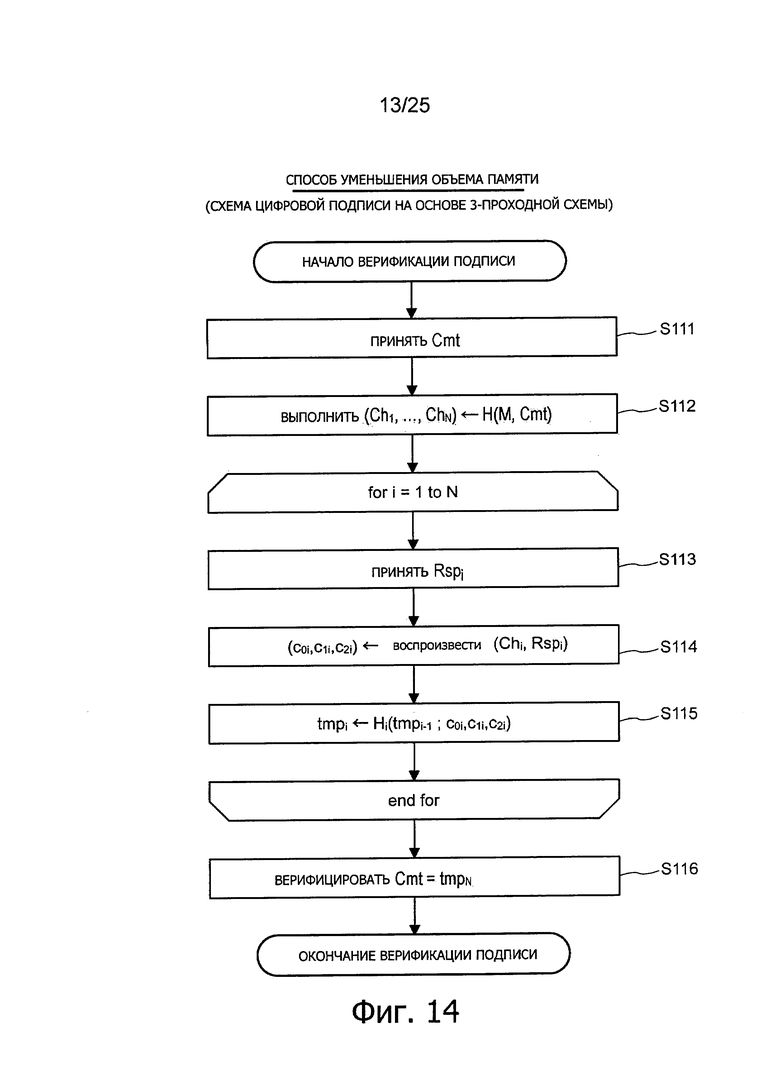
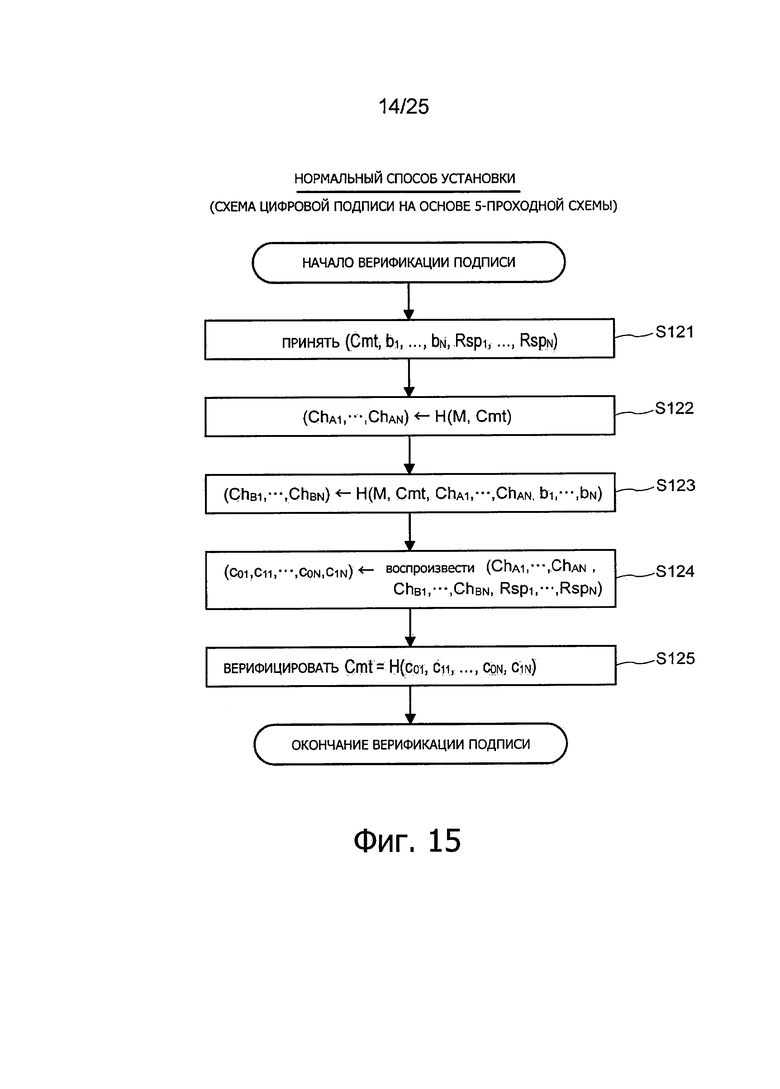
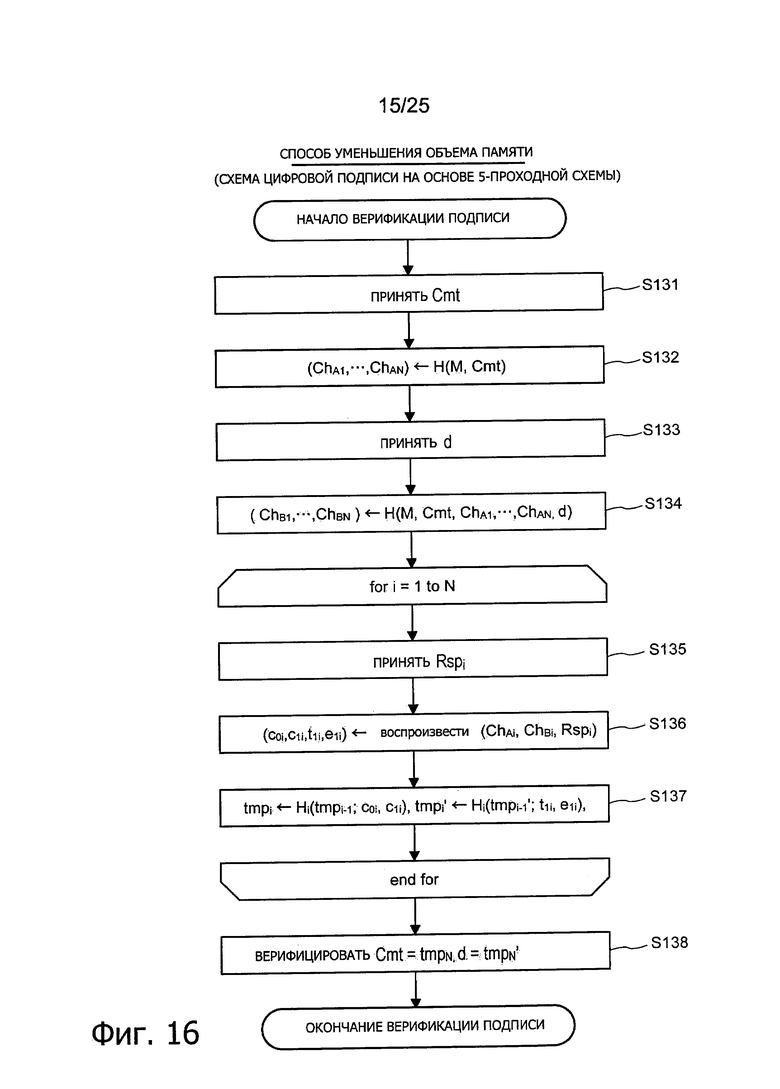

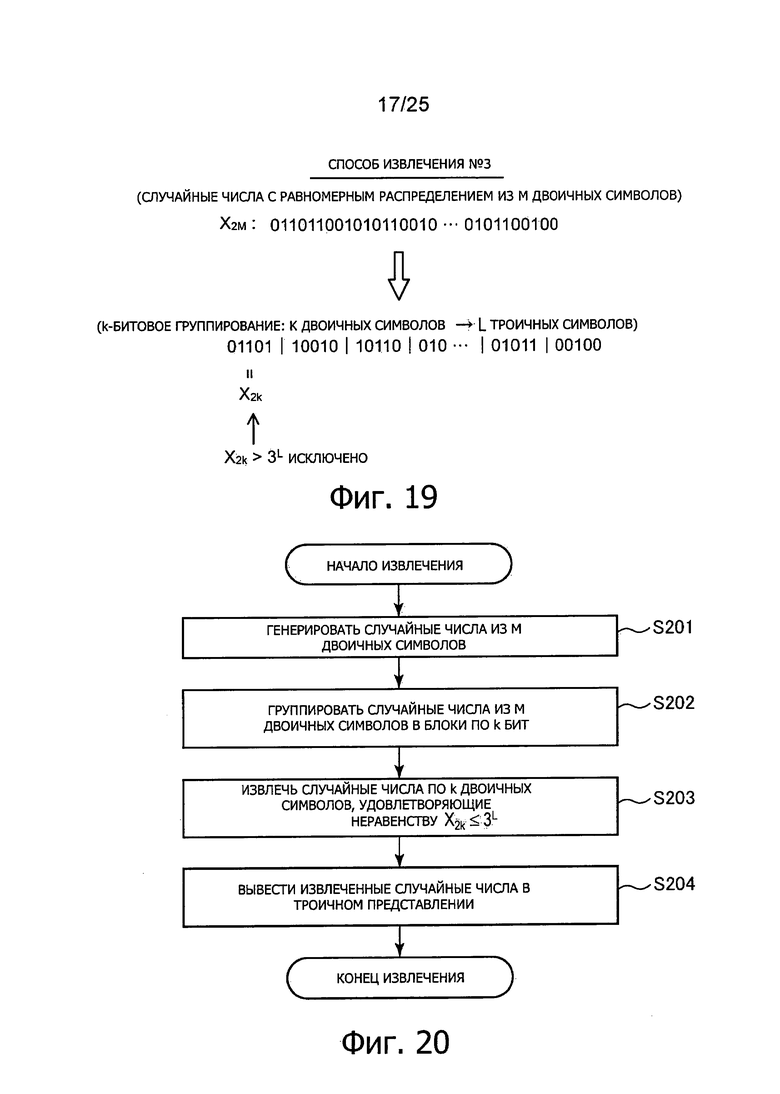
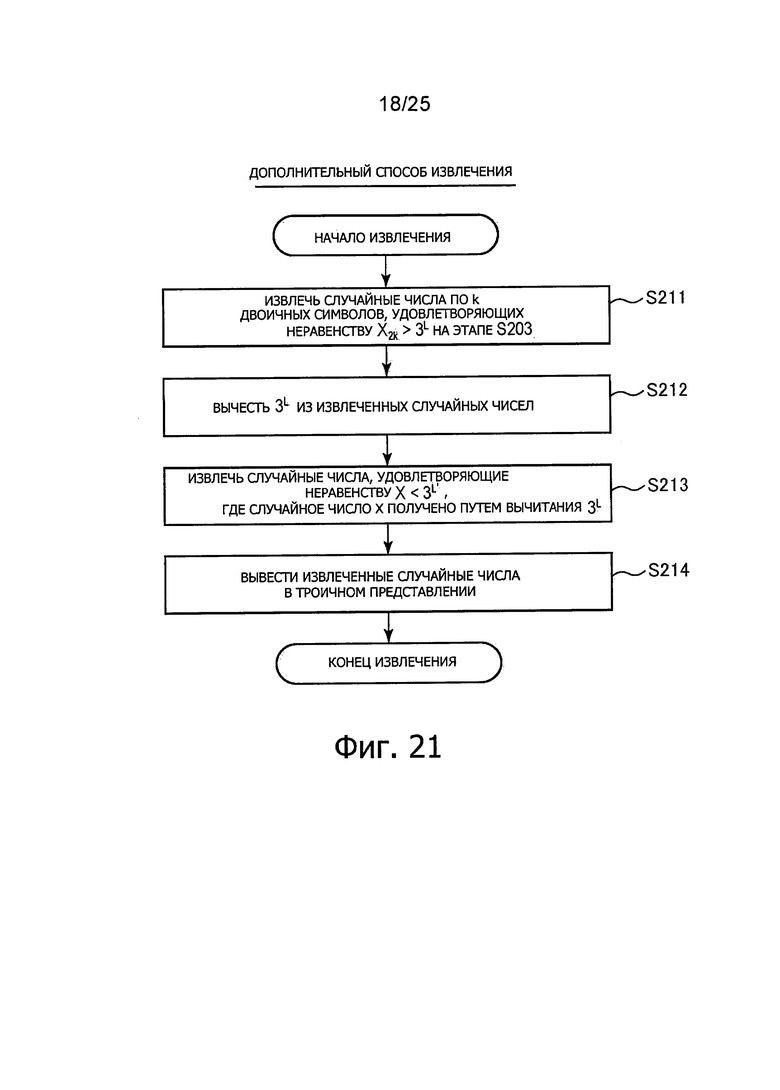

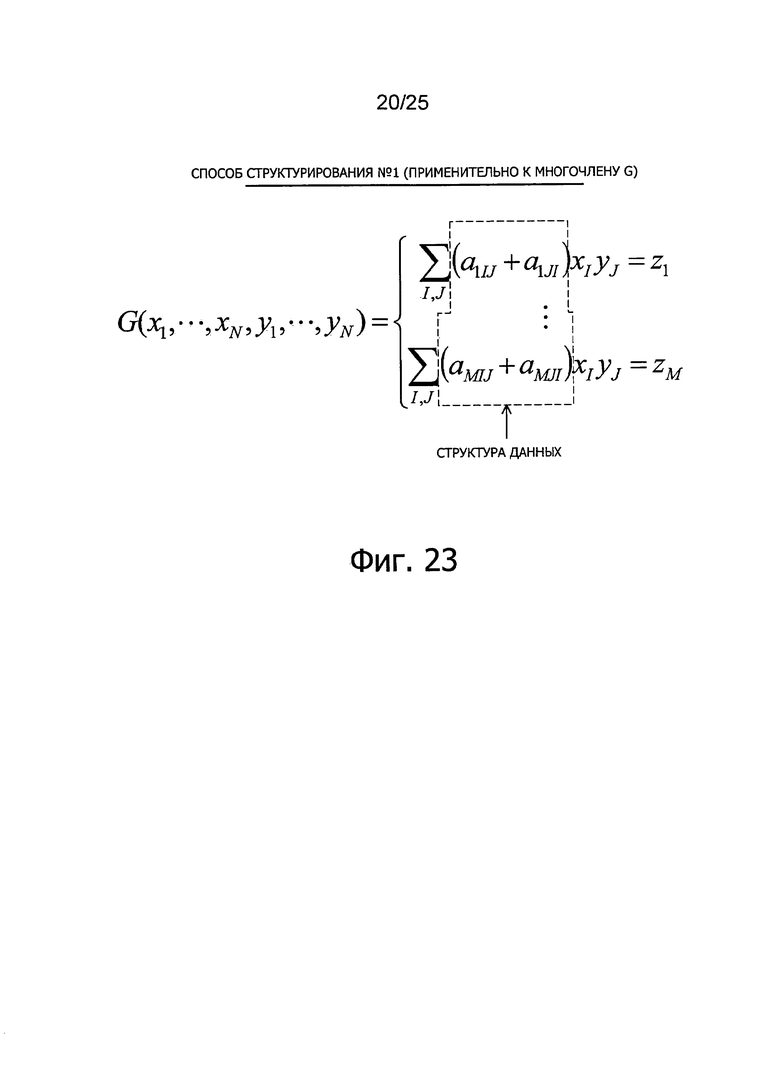
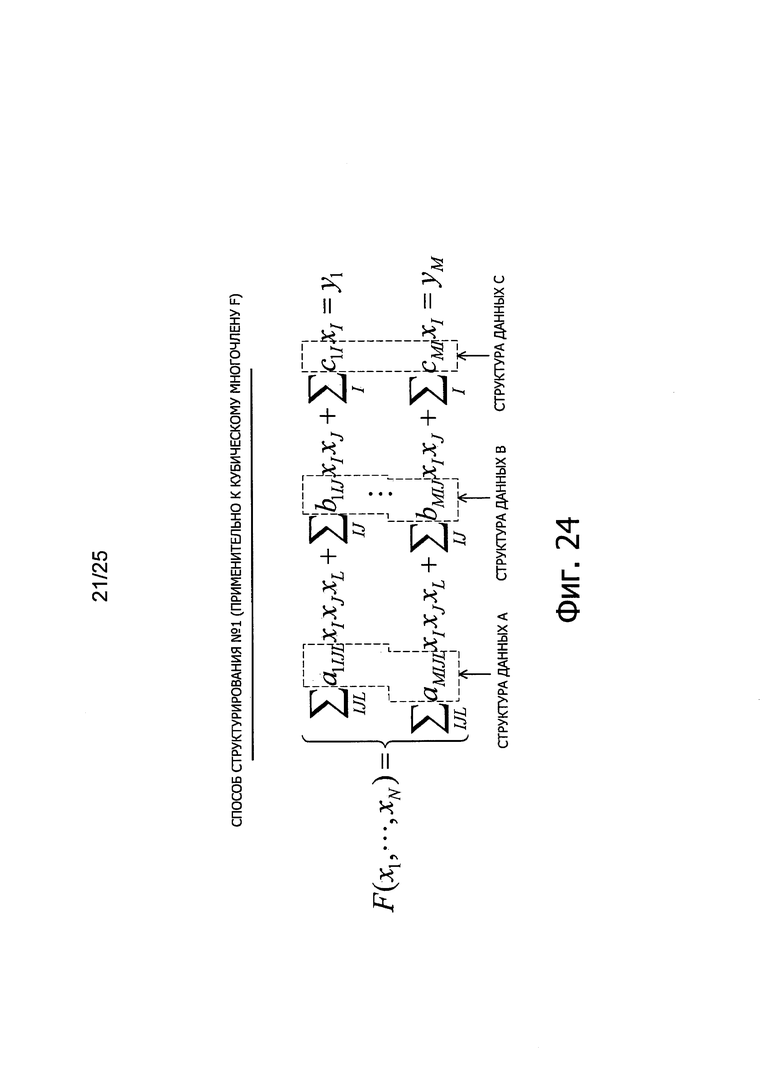
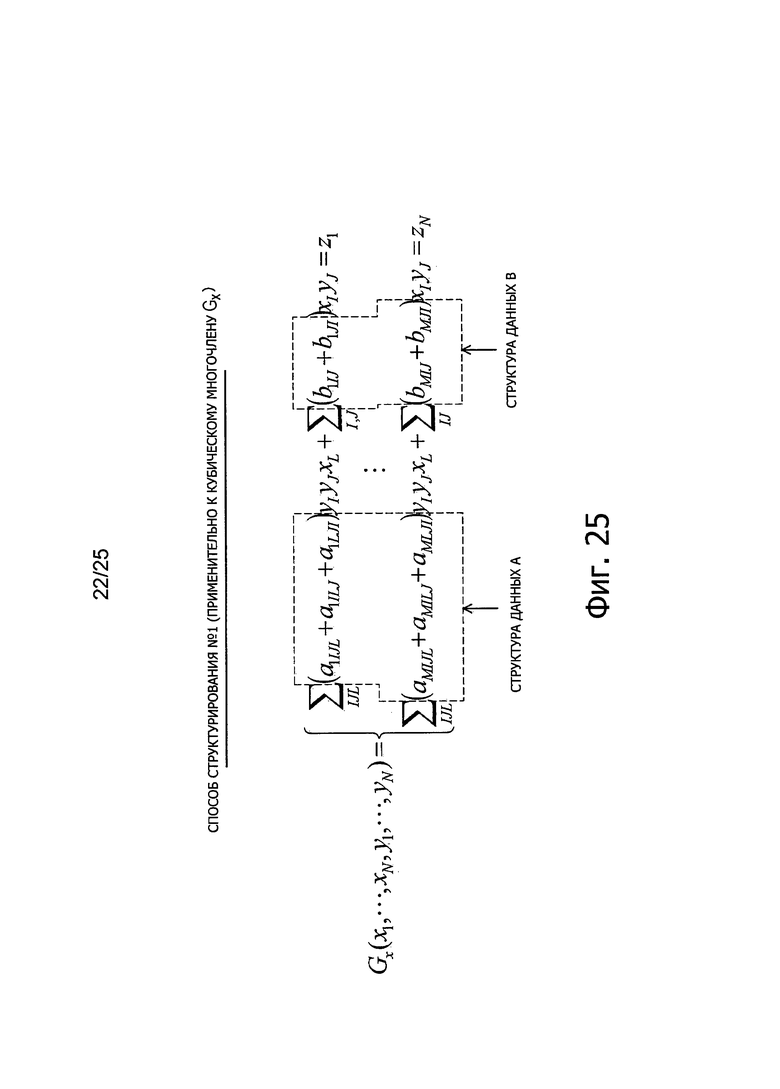
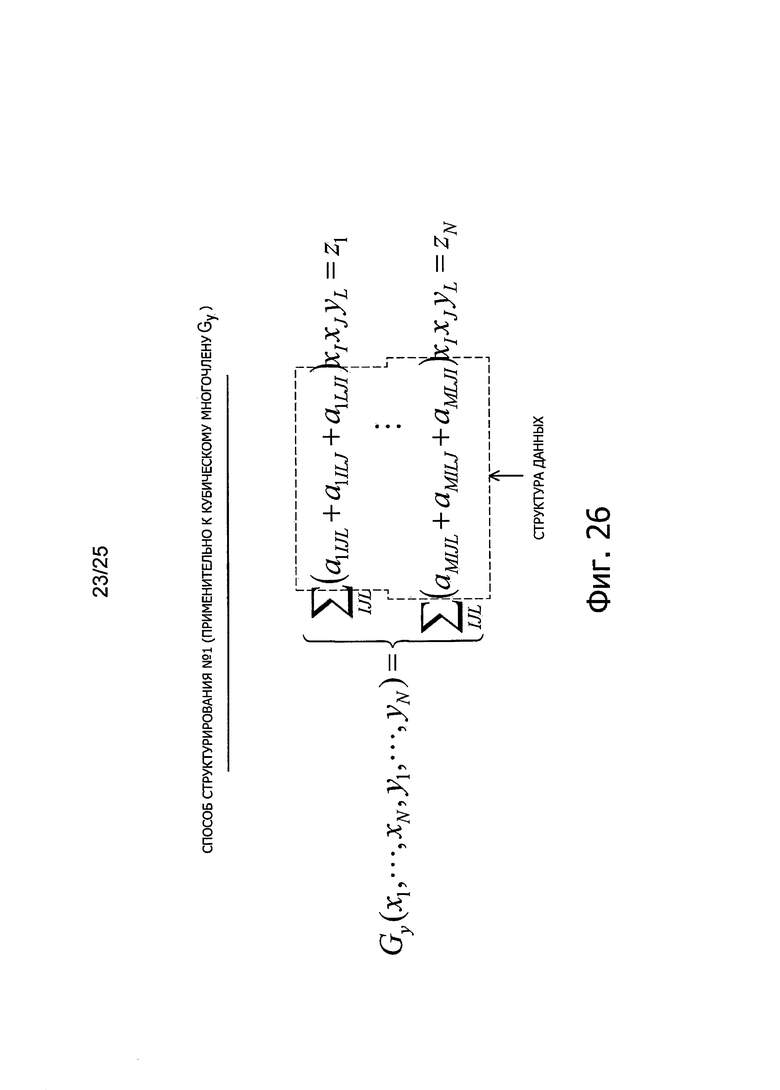
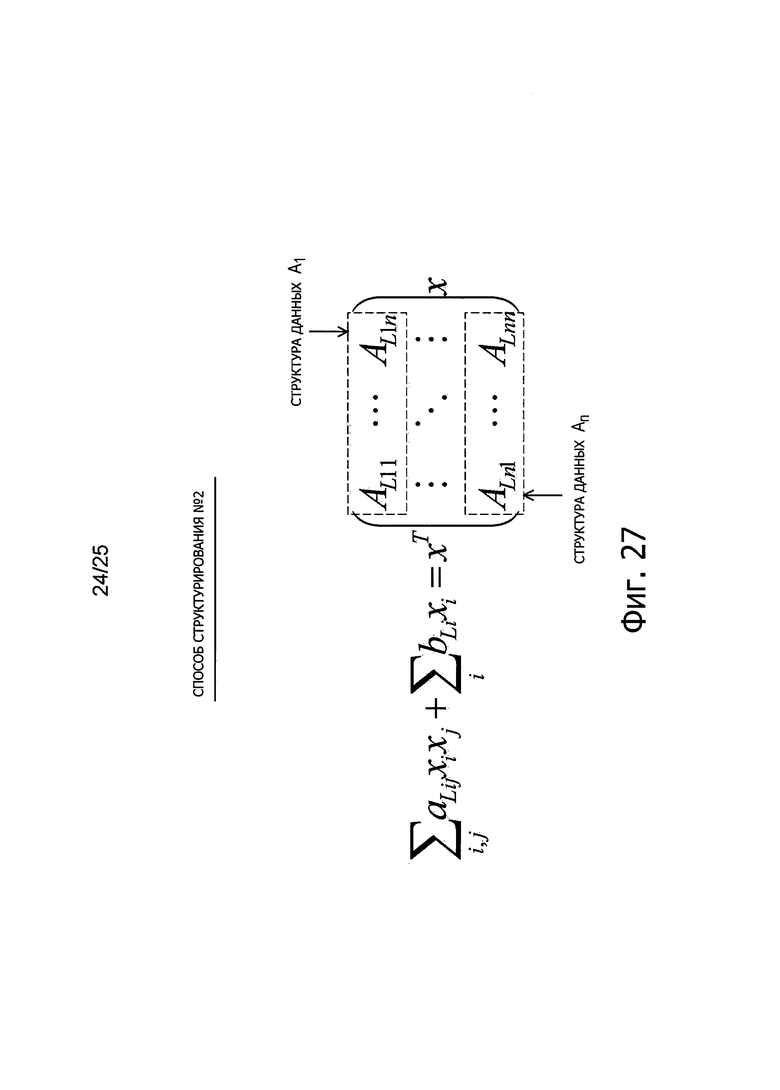
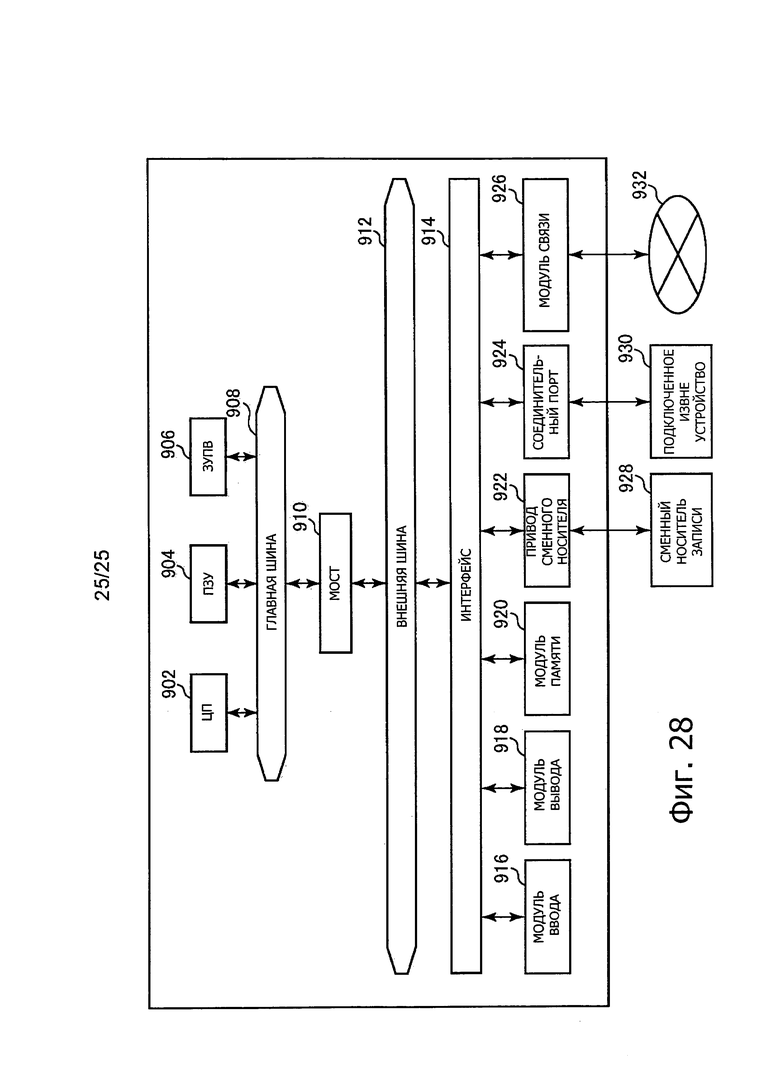
Изобретение относится к технологии обработки информации и технологии связи. Технический результат - обеспечение эффективной безопасности электронных документов. Устройство обработки информации, содержащее модуль генерации чисел, выполненный с возможностью генерации чисел, используемых в коэффициентах членов, входящих в пару многочленов F=(f1, …, fm) множества порядков от нескольких переменных, с использованием заданной функции на основе информации, совместно используемой объектами, исполняющими алгоритм аутентификации с открытым ключом или алгоритм цифровой подписи, применяющий открытый ключ, содержащий указанную пару многочленов F множества порядков от нескольких переменных, и модуль назначения, выполненный с возможностью назначения чисел, генерируемых посредством модуля генерации чисел, коэффициентам многочленов множества порядков от нескольких переменных, составляющими элементами которых является указанная пара многочленов F множества порядков от нескольких переменных. 9 н. и 10 з.п. ф-лы, 28 ил.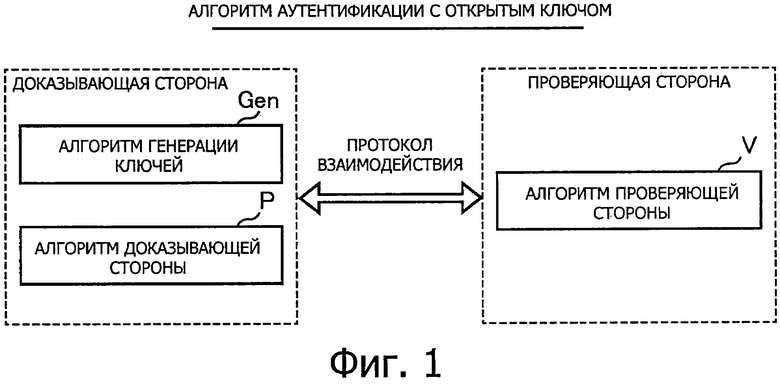
1. Устройство обработки информации, содержащее:
модуль генерации чисел, выполненный с возможностью генерации чисел, используемых в коэффициентах членов, входящих в пару многочленов F=(f1, …, fm) множества порядков с несколькими переменными, с использованием заданной функции на основе информации, совместно используемой объектами, исполняющими алгоритм аутентификации с открытым ключом или алгоритм цифровой подписи, применяющий открытый ключ, содержащий указанную пару многочленов F множества порядков с несколькими переменными; и
модуль назначения, выполненный с возможностью назначения чисел, генерируемых посредством модуля генерации чисел, коэффициентам многочленов множества порядков с несколькими переменными, составляющими элементами которых является указанная пара многочленов F множества порядков с несколькими переменными,
при этом модуль назначения выполнен с возможностью группировать коэффициенты членов, имеющих идентичный тип сочетания переменных, из множества коэффициентов многочленов множества порядков с несколькими переменными, составляющими элементами которых является указанная пара многочленов F множества порядков с несколькими переменными, и выполнять процедуру назначения в блоках групп.
2. Устройство обработки информации, содержащее:
модуль генерации чисел, выполненный с возможностью генерирования чисел, используемых в коэффициентах членов, входящих в пару многочленов F=(f1, …, fm) множества порядков с несколькими переменными, с использованием заданной функции на основе информации, совместно используемой объектами, исполняющими алгоритм аутентификации с открытым ключом или алгоритм цифровой подписи, применяющий открытый ключ, содержащий указанную пару многочленов F множества порядков с несколькими переменными; и
модуль назначения, выполненный с возможностью назначения чисел, генерируемых посредством модуля генерации чисел, коэффициентам многочленов множества порядков с несколькими переменными, составляющими элементами которых является указанная пара многочленов F множества порядков с несколькими переменными,
при этом модуль назначения выполнен с возможностью группировать матрицу коэффициентов в каждой строке или столбце, когда многочлены множества порядков с несколькими переменными, составляющими элементами которых является указанная пара многочленов F множества порядков с несколькими переменными, выражены в квадратичной форме, причем модуль назначения выполнен с возможностью выполнять процедуру назначения в блоках групп.
3. Устройство обработки информации по п. 1, в котором модуль генерации чисел выполнен с возможностью генерировать числа по количеству коэффициентов, принадлежащих одной группе, при выполнении модулем назначения процедуры назначения в указанной одной группе.
4. Устройство обработки информации по п. 3, в котором модуль генерации чисел выполнен с возможностью генерировать одно число при генерировании чисел по количеству коэффициентов, принадлежащих одной группе, и генерировать необходимое количество чисел путем поворота генерируемых чисел на каждый бит.
5. Устройство обработки информации по п. 1, дополнительно содержащее:
модуль хранения таблиц, выполненный с возможностью хранения в виде таблицы значений, получаемых путем назначения коэффициентов члену какого-либо типа, соответствующего каждой группе, и подстановки данного числа для переменных соответствующих членов.
6. Устройство обработки информации, содержащее:
модуль генерации чисел, выполненный с возможностью генерации чисел в количестве, идентичном количеству коэффициентов членов, входящих в пару многочленов F=(f1, …, fm) множества порядков с несколькими переменными, с использованием заданной функции на основе информации, совместно используемой объектами, исполняющими алгоритм аутентификации с открытым ключом или алгоритм цифровой подписи, применяющий открытый ключ, содержащий пару многочленов F множества порядков с несколькими переменными; и
модуль назначения, выполненный с возможностью назначения чисел, генерируемых посредством модуля генерации чисел, коэффициентам многочленов множества порядков с несколькими переменными, составляющими элементами которых является указанная пара многочленов F множества порядков с несколькими переменными, в последовательности, согласованной заранее между доказывающей стороной и проверяющей стороной.
7. Устройство обработки информации по п. 1, в котором указанная информация является начальным числом для генерации случайного числа, а указанная заданная функция является генератором случайных чисел, выполненным с возможностью генерации случайного числа с использованием указанного начального числа.
8. Устройство обработки информации по п. 1, содержащее:
модуль генерации сообщений, выполненный с возможностью генерации сообщения на основе указанной пары многочленов F=(f1, …, fm) множества порядков от нескольких переменных, определенных в кольце K, и вектора s, являющегося элементом множества Kn;
модуль передачи сообщений, выполненный с возможностью передачи указанного сообщения проверяющей стороне, хранящей указанную пару многочленов F множества порядков от нескольких переменных и векторы y=(y1, …, ym)=(f1(s), …, fm(s)); и
модуль передачи ответа, выполненный с возможностью передачи проверяющей стороне ответной информации, соответствующей схеме верификации, выбранной проверяющей стороной из k схем верификации, где k≥3,
при этом s представляет собой секретный ключ,
указанная пара многочленов F множества порядков от нескольких переменных и векторы у являются открытыми ключами,
ответная информация представляет собой информацию, выбранную из пары случайных чисел и указанного сообщения согласно схеме верификации,
причем указанное сообщение представляет собой информацию, полученную путем вычислений, выполненных заранее для схемы верификации, соответствующей ответной информации, на основе указанных открытых ключей и ответной информации.
9. Устройство обработки информации по п. 1, содержащее:
модуль для хранения информации, выполненный с возможностью хранения пары многочленов F=(f1, …, fm) множества порядков от нескольких переменных, определенных в кольце K, и векторов y=(y1, …, ym)=(f1(s), …, fm(s));
модуль получения сообщений, выполненный с возможностью получения сообщения, генерируемого на основе указанной пары многочленов F множества порядков от нескольких переменных и вектора s, являющегося элементом множества Kn;
модуль передачи информации о схеме, выполненный с возможностью передачи проверяющей стороне, передавшей сообщение, информации о схеме верификации, выбранной случайным образом из k схем верификации, где k≥3
модуль получения ответа, выполненный с возможностью приема ответной информации, соответствующей выбранной схеме верификации, от доказывающей стороны; и
модуль верификации, выполненный с возможностью проверки, хранит ли доказывающая сторона вектор s на основе указанного сообщения, указанной пары многочленов F множества порядков с несколькими переменными, векторов у и ответной информации,
при этом вектор s представляет собой секретный ключ,
указанная пара многочленов F множества порядков от нескольких переменных и векторы у являются открытыми ключами, а
указанное сообщение представляет собой информацию, полученную путем вычислений, выполненных заранее для схемы верификации, соответствующей информации ответа, на основе открытых ключей и ответной информации.
10. Устройство обработки информации по п. 1, содержащее:
модуль генерации сообщений, выполненный с возможностью генерации сообщения на основе указанной пары многочленов F=(f1, …, fm) множества порядков от нескольких переменных, определенных в кольце K, и вектора s, являющегося элементом множества Kn;
модуль передачи сообщений, выполненный с возможностью передачи указанного сообщения проверяющей стороне, хранящей указанную пару многочленов F множества порядков от нескольких переменных и векторы y=(y1, …, ym)=(f1(s), …, fm(s));
модуль генерации промежуточной информации, выполненный с возможностью генерации третьей информации с использованием первой информации, выбранной случайным образом проверяющей стороной, и второй информации, полученной во время генерации сообщения;
модуль передачи промежуточной информации, выполненный с возможностью передачи третьей информации проверяющей стороне; и
модуль передачи ответа, выполненный с возможностью передачи проверяющей стороне ответной информации, соответствующей схеме верификации, выбранной проверяющей стороной из k схем верификации, где k≥2
при этом вектор s представляет собой секретный ключ,
указанная пара многочленов F множества порядков от нескольких переменных и векторы у являются открытыми ключами,
ответная информация представляет собой информацию, выбранную из совокупности сообщений согласно схеме верификации, а
указанное сообщение представляет собой информацию, полученную путем вычислений, выполненных заранее для схемы верификации, соответствующей ответной информации, на основе открытых ключей, первой информации, третьей информации и ответной информации.
11. Устройство обработки информации по п. 1, содержащее:
модуль хранения информации, выполненный с возможностью хранения указанной пары многочленов F=(f1, …, fm) множества порядков от нескольких переменных, определенных в кольце K, и векторов y=(y1, …, ym)=(f1(s), …, fm(s));
модуль получения сообщений, выполненный с возможностью получения сообщения, генерируемого на основе указанной пары многочленов F множества порядков от нескольких переменных и вектора s, являющегося элементом множества Kn;
модуль передачи информации, выполненный с возможностью передачи выбранной случайным образом первой информации доказывающей стороне, передающей сообщение;
модуль получения промежуточной информации, выполненный с возможностью получения третьей информации, генерируемой доказывающей стороной на основе указанной первой информации и второй информации, полученной во время генерации сообщения;
модуль передачи информации о схеме, выполненный с возможностью передачи доказывающей стороне информации о схеме верификации, выбранной случайным образом из k схем верификации, где k≥2,
модуль получения ответа, выполненный с возможностью получения от доказывающей стороны информации, соответствующей выбранной схеме верификации; и
модуль верификации, выполненный с возможностью проверки, хранит ли доказывающая сторона вектор s, на основе указанного сообщения, первой информации, третьей информации, указанной пары многочленов F множества порядков с несколькими переменными и ответной информации,
при этом вектор s представляет собой секретный ключ,
указанная пара многочленов F множества порядков от нескольких переменных и векторы у являются открытыми ключами,
причем указанное сообщение представляет собой информацию, получаемую путем вычислений, выполненных заранее для схемы верификации, соответствующей ответной информации, на основе открытых ключей, первой информации, третьей информации и ответной информации.
12. Устройство обработки информации по п. 1, в котором
при многократном исполнении алгоритма модуль генерации чисел выполнен с возможностью генерировать числа только один раз, а модуль назначения выполнен с возможностью выполнения процедуры назначения только один раз,
при этом алгоритм многократно использует коэффициенты, назначаемые посредством модуля назначения.
13. Устройство обработки информации по п. 1, содержащее:
модуль генерации подписи, выполненный с возможностью генерации цифровой подписи для документа М с использованием пары многочленов F=(f1, …, fm) множества порядков от нескольких переменных, определенных в кольце K, и ключа подписи, являющегося элементом множества Kn; и
модуль передачи подписи, выполненный с возможностью передачи цифровой подписи проверяющей стороне, хранящей указанную пару многочленов F множества порядков от нескольких переменных и векторы y=(f1(s), …, fm(s)).
14. Способ обработки информации, содержащий:
этап генерации чисел, используемых в коэффициентах членов, входящих в пару многочленов F=(f1, …, fm) множества порядков с несколькими переменными, с использованием заданной функции на основе информации, совместно используемой объектами, исполняющими алгоритм аутентификации с открытым ключом или алгоритм цифровой подписи, применяющий открытый ключ, содержащий указанную пару многочленов F множества порядков с несколькими переменными; и
этап назначения сгенерированных чисел коэффициентам многочленов множества порядков с несколькими переменными, составляющими элементами которых является указанная пара многочленов F множества порядков с несколькими переменными,
при этом на этапе назначения чисел группируют коэффициенты членов, имеющих идентичный тип сочетания переменных, из множества коэффициентов многочленов множества порядков с несколькими переменными, составляющими элементами которых является указанная пара многочленов F множества порядков с несколькими переменными, и выполняют процедуру назначения в блоках групп.
15. Способ обработки информации, содержащий:
этап генерации чисел, используемых в коэффициентах членов, входящих в пару многочленов F=(f1, …, fm) множества порядков с несколькими переменными, с использованием заданной функции на основе информации, совместно используемой объектами, исполняющими алгоритм аутентификации с открытым ключом или алгоритм цифровой подписи, применяющий открытый ключ, содержащий указанную пару многочленов F множества порядков с несколькими переменными; и
этап назначения сгенерированных чисел коэффициентам многочленов множества порядков с несколькими переменными, составляющими элементами которых является указанная пара многочленов F множества порядков с несколькими переменными,
при этом на этапе назначения чисел группируют матрицу коэффициентов в каждой строке или столбце, когда многочлены множества порядков с несколькими переменными, составляющими элементами которых является указанная пара многочленов F множества порядков с несколькими переменными, выражены в квадратичной форме, и выполняют процедуру назначения в блоках групп.
16. Способ обработки информации, содержащий:
этап генерации чисел в количестве, идентичном количеству коэффициентов членов, входящих в пару многочленов F=(f1, …, fm) множества порядков с несколькими переменными, с использованием заданной функции на основе информации, совместно используемой объектами, исполняющими алгоритм аутентификации с открытым ключом или алгоритм цифровой подписи, применяющий открытый ключ, содержащий указанную пару многочленов F множества порядков с несколькими переменными; и
этап назначения чисел, генерируемых посредством модуля генератора чисел, коэффициентам многочленов множества порядков с несколькими переменными, составляющими элементами которых является указанная пара многочленов F множества порядков с несколькими переменными, в последовательности, определенной заранее между доказывающей стороной и проверяющей стороной.
17. Считываемый компьютером носитель записи, содержащий записанную на нем программу, вызывающую выполнение компьютером:
функции генерации чисел для генерации чисел, используемых в коэффициентах членов, входящих в пару многочленов F=(f1, …, fm) множества порядков с несколькими переменными, с использованием заданной функции на основе информации, совместно используемой объектами, исполняющими алгоритм аутентификации с открытым ключом или алгоритм цифровой подписи, применяющий открытый ключ, содержащий указанную пару многочленов F множества порядков с несколькими переменными; и
функции назначения для назначения чисел, генерируемых посредством функции генерации чисел, коэффициентам многочленов множества порядков с несколькими переменными, составляющими элементами которых является указанная пара многочленов F множества порядков с несколькими переменными,
при этом функция назначения группирует коэффициенты членов, имеющих идентичный тип сочетания переменных, из множества коэффициентов многочленов множества порядков с несколькими переменными, составляющими элементами которых является указанная пара многочленов F множества порядков с несколькими переменными, и выполняет процедуру назначения в блоках групп.
18. Считываемый компьютером носитель записи, содержащий записанную на нем программу, вызывающую выполнение компьютером:
функции генерации чисел для генерации чисел, используемых в коэффициентах членов, входящих в пару многочленов F=(f1, …, fm) множества порядков с несколькими переменными, с использованием заданной функции на основе информации, совместно используемой объектами, исполняющими алгоритм аутентификации с открытым ключом или алгоритм цифровой подписи, применяющий открытый ключ, содержащий указанную пару многочленов F множества порядков с несколькими переменными; и
функции назначения для назначения чисел, генерируемых посредством функции генерации чисел, коэффициентам многочленов множества порядков с несколькими переменными, составляющими элементами которых является указанная пара многочленов F множества порядков с несколькими переменными,
при этом функция назначения группирует матрицу коэффициентов в каждой строке или столбце, когда многочлены множества порядков с несколькими переменными, составляющими элементами которых является указанная пара многочленов F множества порядков с несколькими переменными, выражены в квадратичной форме, при этом функция назначения выполняет процедуру назначения в блоках групп.
19. Считываемый компьютером носитель записи, содержащий записанную на нем программу, вызывающую выполнение компьютером:
функции генерации чисел для генерации чисел в количестве, идентичном количеству коэффициентов членов, входящих в пару многочленов F=(f1, …, fm) множества порядков с несколькими переменными, с использованием заданной функции на основе информации, совместно используемой объектами, исполняющими алгоритм аутентификации с открытым ключом или алгоритм цифровой подписи, применяющий открытый ключ, содержащий указанную пару многочленов F множества порядков с несколькими переменными; и
функции назначения чисел для назначения чисел, генерируемых посредством модуля генерации чисел, коэффициентам многочленов множества порядков с несколькими переменными, составляющими элементами которых является указанная пара многочленов F множества порядков с несколькими переменными, в последовательности, согласованной заранее между доказывающей стороной и проверяющей стороной.
| US 7961876 B2, 14.06.2011 | |||
| Колосоуборка | 1923 |
|
SU2009A1 |
| Колосоуборка | 1923 |
|
SU2009A1 |
| Приспособление для суммирования отрезков прямых линий | 1923 |
|
SU2010A1 |
| Станок для изготовления деревянных ниточных катушек из цилиндрических, снабженных осевым отверстием, заготовок | 1923 |
|
SU2008A1 |
| Приспособление для суммирования отрезков прямых линий | 1923 |
|
SU2010A1 |
Авторы
Даты
2016-08-27—Публикация
2012-08-14—Подача