Область техники
Изобретение относится к области генерации случайных чисел для прикладного использования в криптографии, численном моделировании и других областях науки и техники.
Предшествующий уровень техники
Генераторы случайных чисел, основанные на регистрации отдельных элементарных частиц, например фотонов, привлекают большой интерес со стороны исследователей, так как квантовая природа явлений, заложенная в их основу, не позволяет предсказывать получаемую последовательность чисел даже после сколь угодно точных измерений системы. Квантовые генераторы случайных чисел на данный момент являются наиболее приближенными к идеальным.
В предлагаемом квантовом генераторе случайных чисел используется метод измерения временных интервалов между событиями регистрации фотонов, излучаемых постоянным источником фотонов, подходящим однофотонным детектором. Получаемая случайная последовательность формируется исключительно преобразованием множества результатов измерения указанных интервалов в множество выходных значений с заданным распределением вероятностей по детерминистическому алгоритму.
Из уровня техники известна общая схема построения генераторов случайных чисел, основанных на измерении временных интервалов между событиями регистрации фотонов, раскрытая в заявке на изобретение US 2006/0010182, опубликованной 12.01.2006. Указанная схема определяет общую концепцию семейства квантовых генераторов случайных чисел, к которому относится и настоящее изобретение, однако не определяет конкретный механизм преобразования измеренной последовательности временных интервалов в выходную случайную последовательность. В данной схеме предлагается использовать стандартные хэш-функции для устранения влияния неравновероятности полученных значений длин временных интервалов, которые, жертвуя частью исходной цифровой информации, должны обеспечить несмещенность и независимость значений в выходной последовательности.
Известны конкретные реализации указанной общей схемы квантовых генераторов случайных чисел, в которых используются универсальные хэш-функции типа SHA-256 (М.А. Wayne, Е.R. Jeffrey, G.М. Akselrod and P.G. Kwiat. "Photon arrival time quantum random number generation", Journal of Modern Optics, 56, 4, pp. 516-522 (2009); M.A. Wayne and P.G. Kwiat. "Low-bias high-speed quantum random number generator via shaped optical pulses". Optics Express 18, 9, pp. 9351-9357 (2010)).
Недостатками указанных алгоритмов преобразования результатов измерений временных интервалов между событиями регистрации фотонов в выходную случайную последовательность являются:
1. Эмпирическая сущность известных хэш-функций и недоказанность правомерности их использования для экстракции случайных чисел.
2. Зависимость способа применения хэш-функции (коэффициента сжатия последовательности) от энтропии исходной последовательности, которую невозможно точно измерить за конечное время. Оценка энтропии последовательности - сложная задача, не имеющая достоверных практически применимых решений.
3. Нечувствительность такого алгоритма экстракции к изменениям энтропии исходной последовательности. При ухудшении качества исходной последовательности вплоть до полного исчезновения какой-либо случайности хэш-функция неизменно будет выдавать последовательность, похожую на случайную, но фактически не пригодную для задач, требующих истинную случайность.
Известны другие универсальные методы экстракции случайных чисел, такие как использование матриц Тёплица и экстракция по Тревисану (см., например, X. Ma, F. Xu, Н. Xu, X. Tan, В. Qi, and Н.-К. Lo. "Postprocessing for quantum random-number generators: Entropy evaluation and randomness extraction", Physical Review A 87, 062327 (2013); W. Mauerer, C. Portmann and V.B. Scholz. "A modular framework for randomness extraction based on Trevisan's construction", arXiv: 1212.0520 [cs. IT] (2012)), также обладающие ранее указанными недостатками 2 и 3 и вдобавок требующие дополнительного источника случайности. Кроме того, данные методы являются вычислительно сложными для реализации автономных генераторов случайных чисел, работающих в реальном времени со скоростью генерации порядка мегабит в секунду.
Раскрытие изобретения
Технической задачей, решаемой настоящим изобретением, является устранение указанных недостатков и обеспечение генерации случайных чисел высокого качества с высокой степенью надежности и высокой скоростью.
Техническим результатом, достигаемым при реализации заявленного изобретения, является повышение качества, степени надежности и скорости генерации случайных чисел.
Поставленная задача решается с помощью применения детерминистического экстрактора случайности и использования блока постоянного запоминающего устройства (ПЗУ) с сохраненной заранее вычисленной таблицей преобразования исходных данных в выходную случайную последовательность.
Указанный технический результат достигается за счет того, что в генераторе случайных чисел, содержащем источник фотонов, однофотонный детектор, реагирующий на отдельные фотоны, создаваемые источником фотонов, и схему оцифровки и последующей обработки сигнала детектора, схема оцифровки выполнена с возможностью преобразования длительности временных интервалов между последующими срабатываниями однофотонного детектора в цифровые значения, а также произведения перекодировки и буферизации полученной последовательности для формирования адреса в постоянном запоминающем устройстве (ПЗУ) генератора, с возможностью в дальнейшем получения цифровой информации из ячейки ПЗУ с данным адресом, заложенной в него при изготовлении генератора, и попадания на выход генератора случайных чисел после обработки.
Указанный технический результат достигается также за счет того, что схема оцифровки и последующей обработки может содержать связанный с детектором измеритель времени, выполненный с возможностью измерения временных интервалов между соседними по времени зарегистрированными детектором частицами, причем измеритель времени связан с дискриминатором, выполненным с возможностью окончательной оцифровки временных интервалов и отнесения их длительности к набору целых чисел, при этом дискриминатор связан с процессором, выполненным с возможностью генерации из цифровой информации, переданной из дискриминатора, выходной случайной последовательности, подаваемой на выход генератора. При этом процессор может содержать блок перекодировки, выполненный с возможностью входной последовательности в конечный алфавит и связанный с цифровом буфером, выполненным с возможностью буферизации полученной после перекодировки последовательности для получения битовой строки фиксированной длины, кроме того, цифровой буфер выполнен с возможностью передачи битовой строки в формирователь адреса, преобразующий полученную битовую строку в адрес ячейки ПЗУ, причем процессор также содержит блок дополнительной постобработки, связанный с ячейками ПЗУ и выполненный с возможностью формирования окончательной последовательности по данным, полученным из ПЗУ или цифрового буфера.
Кроме того, блок дополнительной постобработки может быть выполнен с возможностью буферизации данных, полученных из ПЗУ или цифрового буфера, для выдачи на выход генератора в виде блоков требуемой длины.
Применение детерминистического алгоритма экстракции обеспечивает устранение негативного эффекта неравновероятности измеренных длительностей временных интервалов, гарантированное простой математической моделью, условия применимости которой легко проверяются на эксперименте. Следствием такой работы алгоритма экстракции является адаптивность скорости генерации выходной случайной последовательности в зависимости от энтропии исходной последовательности, то есть количества «случайности», содержащейся в ней. Таким образом, даже при ухудшении энтропийных свойств исходной последовательности можно гарантировать высокое качество генерируемых случайных чисел.
Использование заранее вычисленной таблицы преобразования исходных данных в выходную последовательность, заложенной в ПЗУ генератора, позволяет реализовать такой детерминистический алгоритм экстракции с минимальными вычислительными затратами. Это дает возможность использовать простые и надежные процессоры небольшой мощности для реализации квантовых генераторов случайных чисел со скоростью генерации в десятки мегабит в секунду и более.
Краткое описание чертежей
Сущность изобретения поясняется чертежами, где:
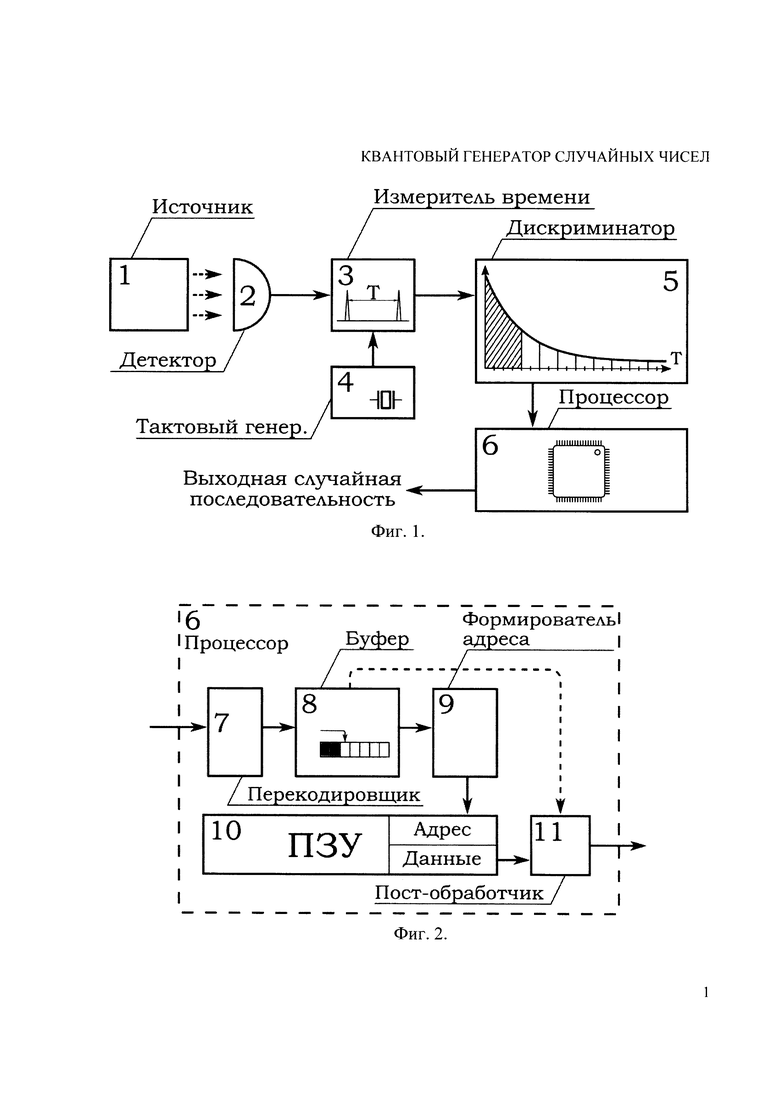
на фиг. 1 представлена общая схема квантового генератора случайных чисел;
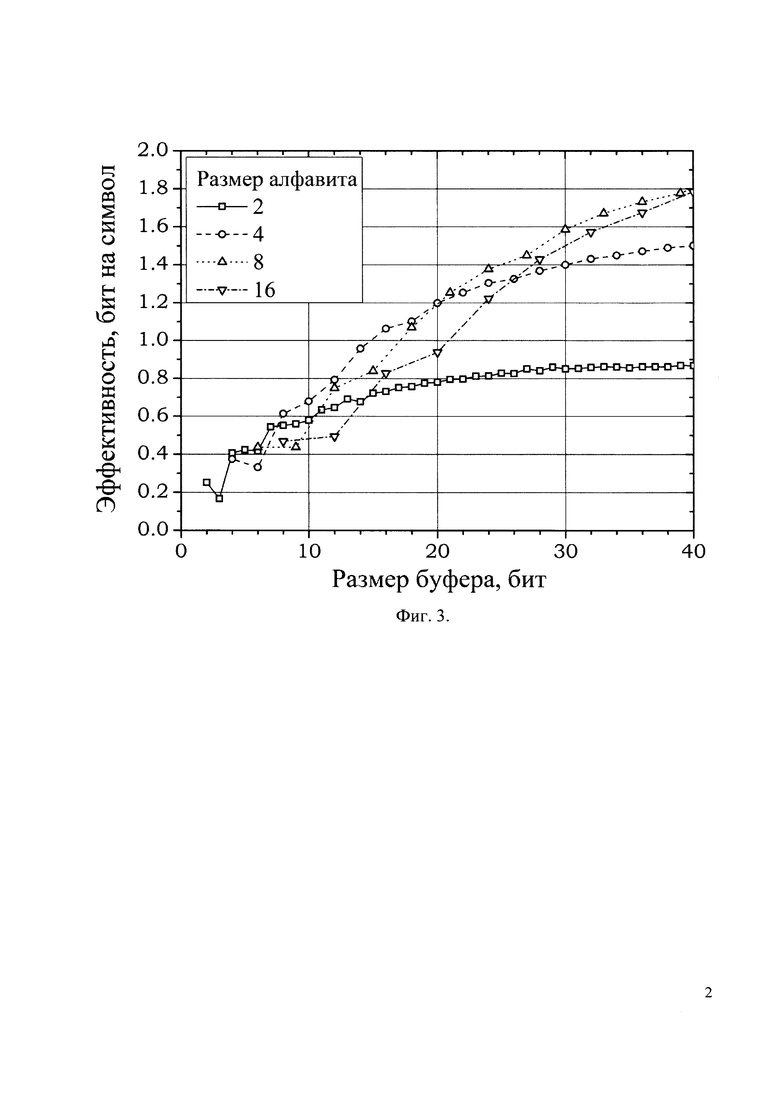
на фиг. 2 показана схема работы процессора;
на фиг. 3 представлен график эффективности алгоритма экстракции в зависимости от размера буфера 8 для различных размеров алфавита перекодировщика 7.
Квантовый генератор случайных чисел состоит из источника фотонов или других элементарных частиц 1, генерирующего постоянный во времени поток частиц подходящей интенсивности. Данный поток или его часть попадает на детектор 2, который способен детектировать отдельные частицы. Электрический сигнал с детектора попадает на измеритель времени 3, который измеряет временные интервалы между соседними по времени зарегистрированными частицами. Данный измеритель времени может являться цифровым счетчиком числа тактов задающего тактового генератора 4. Альтернативно, он может быть выполнен с помощью аналоговой схемотехники, например как преобразователь времени в напряжение. Измеренные интервалы времени передаются на дискриминатор 5, выполняющий функцию окончательной оцифровки временных интервалов и отнесения их длительности к набору целых чисел. Все интервалы короче определенного значения отбрасываются, так как могут содержать корреляции, связанные с неидеальностью детектора.
После оцифровки в дискриминаторе 5 цифровая информация попадает в процессор 6, для генерации выходной случайной последовательности, подаваемой на выход генератора. Схема работы процессора показана на фиг. 2. Входная целочисленная последовательность поступает на блок перекодировки 7, в котором она перекодируется в конечный алфавит из, например, 4 различных символов. Перекодировка осуществляется так, чтобы вероятности получения каждого из символов были по возможности близки между собой. Полученная после перекодировки последовательность буферизуется в цифровом буфере 8 для получения битовой строки фиксированной длины. После заполнения буфера, его содержимое передается на формирователь адреса 9, а сам буфер сбрасывается. Формирователь адреса преобразует полученную битовую строку в адрес ячейки ПЗУ 10, в которой заложена правильная перекодированная информация. В некоторых реализациях данное преобразование не нужно, и сама битовая строка из буфера уже является адресом в ПЗУ 10. Цифровая информация из соответствующей ячейки ПЗУ 10 поступает в блок дополнительной постобработки 11, который окончательно формирует выходную последовательность по данным, полученным из ПЗУ 10 и, возможно, сырых данных из буфера 8. При необходимости в блоке дополнительной постобработки производится буферизация выходных данных для выдачи на выход квантового генератора случайных чисел в виде блоков требуемой длины.
На фиг. 3 представлен график зависимости эффективности предлагаемого алгоритма экстракции (в битах на символ перекодировщика 7) от размера буфера 8 для алфавита перекодировщика 7 размером 2, 4, 8 и 16. Как следует из графика, для приемлемых размеров ПЗУ эффективность алгоритма составляет 1-1,6 бит на символ (на каждое выходное значение дискриминатора 5).
Осуществление изобретения
Квантовая механика открывает возможность генерации истинно случайных последовательностей, благодаря фундаментальной непредсказуемости простейших квантовых измерений. В отличие от классических стохастических систем, тщательное измерение которых, в принципе, позволяет предсказывать их дальнейшую эволюцию, квантовые измерения принципиально непредсказуемы, что позволяет использовать их как источник истинной случайности.
Настоящее изобретение кладет в основу генератора случайных чисел измерение временных интервалов между событиями детектирования отдельных фотонов детектором. Данная схема обладает рядом преимуществ по сравнению с другими известными: позволяет использовать всего один однофотонный детектор; обеспечивает независимость измеренных значений между собой; предоставляет возможность генерировать существенно больше одного бита случайной информации на принятый фотон.
Источник фотонов 1 генерирует слабый поток фотонов, постоянный по времени. При этом, если этот поток достаточно многомодовый (по пространству, или по времени, или по обоим параметрам) вне зависимости от типа источника (когерентный, тепловой, смешанный) статистика детектирования фотонов является Пуассоновской. В качестве источника предполагается использовать светодиод, что автоматически обеспечивает необходимую многомодовость потока фотонов. Источник также может быть выполнен как лазер, лампа накаливания, люминесцентная лампа или другой светоизлучающий элемент. Для обеспечения требуемой интенсивности потока фотонов в источнике может быть использован оптический ослабитель. Также для ослабления потока фотонов может использоваться геометрический фактор, т.е. расположение детектора так, что на него попадет лишь часть генерируемого потока фотонов.
Однофотонный детектор 2 должен обеспечивать возможность детектирования отдельных фотонов, генерируемых источником фотонов 1. Желательно, чтобы он также обладал малым «мертвым временем» tD, т.е. временем, в течение которого после детектирования фотона детектор становится неактивным и не может зарегистрировать другие приходящие на него фотоны; малым временным джиттером Δt, т.е. неопределенностью по времени получения выходного сигнала при известном моменте прихода фотона. Данные два параметра непосредственно ограничивают максимальную скорость генерации случайной последовательности и поэтому должны быть минимизированы. В качестве однофотонного детектора может использоваться однофотонный лавинный фотодиод, работающий в режиме счетчика Гейгера. Также может применяться фотоэлектронный умножитель (ФЭУ) или другой тип однофотонного детектора. Типичные значения «мертвого времени» и временного джиттера составляют около 100 нс и 1 нс соответственно.
Сигнал с однофотонного детектора 2 попадает на блок измерителя временных интервалов 3, который измеряет длительность временных интервалов между последовательными событиями регистрации фотонов. Данный блок может быть выполнен как цифровой счетчик, работающий с частотой, задаваемой тактовым генератором 4. При приходе сигнала с однофотонного детектора 2 значение счетчика передается на дискриминатор 5, после чего счетчик сбрасывается для измерения следующего временного интервала. Тактовый генератор может быть выполнен на базе кварцевого или другого стабильного генератора частоты. Частота тактового генератора F определяет точность измерения временных интервалов, равную τ=1/F. Следовательно, чем больше F, тем выше может быть скорость генерации случайных чисел. При этом F должно быть существенно меньше 1/Δt, так как в противном случае существенная доля случайности будет определяться классическим временным джиттером, что приведет к снижению качества генерируемой последовательности. В одной из возможных реализаций настоящего изобретения используется F=50 МГц, что соответствует τ=20 нс. Также измеритель временных интервалов 3 может быть реализован как аналоговый преобразователь временных интервалов, например, в напряжение, которое затем оцифровывается в дискриминаторе 5. Наилучшая разумная точность оцифровки τ также должна быть существенно меньше Δt. Измеритель временных интервалов может быть основан и на других принципах, требуется лишь его способность измерять данные интервалы с известной точностью τ и передавать полученные значения на дискриминатор 5.
Работа дискриминатора 5 осуществляет две функции: окончательное преобразование длительностей временных интервалов в цифровую форму и устранение неидеальностей статистики временных интервалов. Если величины длительностей временных интервалов передаются на дискриминатор в аналоговой форме, производится их оцифровка, соответствующая дискрету времени τ. Таким образом, с настоящего момента считаем, что длительность каждого временного интервала описывается неотрицательным целым числом n, так что исходная длительность интервала лежит в диапазоне от nτ до (n+1)τ.
Для истинно Пуассоновского процесса с интенсивностью λ распределение вероятностей получения различных значений n описывается экспоненциальным распределением и пропорционально ехр(-λτn). Для удобства будем использовать безразмерную величину  , обозначающую среднее значение временного интервала между соседними зарегистрированными фотонами, выраженную в количестве временных дискретов τ. Следовательно, вероятность получения значения n пропорциональна ехр(-n/T). Однако на практике из-за неидеальности однофотонного фотодетектора данное распределение вероятностей существенно нарушается при n<k, где k соответствует тому минимальному размеру интервала, с которого распределение вероятностей величины n является экспоненциальным. Значение k определяется экспериментально для конкретного однофотонного детектора и схемы оцифровки временных интервалов. В одной из реализаций настоящего изобретения используется значение k=16. Отклонение распределения от идеального на малых временах связано в основном с двумя эффектами - наличием «мертвого времени» однофотонного детектора и так называемым афтерпалсингом (от англ. afterpulsing), т.е. возможностью однофотонного детектора сгенерировать выходной импульс без поглощения фотона вскоре после успешной регистрации (поглощение фотона становится причиной генерации еще одного, второго, выходного импульса). Учет данной особенности необходим для генерации случайной последовательности высокого качества. В настоящем изобретении предлагается использовать только временные интервалы, для которых n≥k, остальные значения (меньшие k) исключаются дискриминатором. Таким образом, на выходе дискриминатора генерируется последовательность целых чисел, не меньших k, распределение вероятности которых с высокой точностью описывается экспоненциальным распределением с показателем -1/Т, причем все значения в получаемой последовательности независимы между собой. В одной из реализаций настоящего изобретения оптимальная интенсивность Пуассоновского процесса соответствует Т=17, т.е. среднее расстояние между срабатываниями однофотонного детектора равняется 17τ.
, обозначающую среднее значение временного интервала между соседними зарегистрированными фотонами, выраженную в количестве временных дискретов τ. Следовательно, вероятность получения значения n пропорциональна ехр(-n/T). Однако на практике из-за неидеальности однофотонного фотодетектора данное распределение вероятностей существенно нарушается при n<k, где k соответствует тому минимальному размеру интервала, с которого распределение вероятностей величины n является экспоненциальным. Значение k определяется экспериментально для конкретного однофотонного детектора и схемы оцифровки временных интервалов. В одной из реализаций настоящего изобретения используется значение k=16. Отклонение распределения от идеального на малых временах связано в основном с двумя эффектами - наличием «мертвого времени» однофотонного детектора и так называемым афтерпалсингом (от англ. afterpulsing), т.е. возможностью однофотонного детектора сгенерировать выходной импульс без поглощения фотона вскоре после успешной регистрации (поглощение фотона становится причиной генерации еще одного, второго, выходного импульса). Учет данной особенности необходим для генерации случайной последовательности высокого качества. В настоящем изобретении предлагается использовать только временные интервалы, для которых n≥k, остальные значения (меньшие k) исключаются дискриминатором. Таким образом, на выходе дискриминатора генерируется последовательность целых чисел, не меньших k, распределение вероятности которых с высокой точностью описывается экспоненциальным распределением с показателем -1/Т, причем все значения в получаемой последовательности независимы между собой. В одной из реализаций настоящего изобретения оптимальная интенсивность Пуассоновского процесса соответствует Т=17, т.е. среднее расстояние между срабатываниями однофотонного детектора равняется 17τ.
Дальнейшей задачей, возлагаемой на процессор 6, является преобразование полученной случайной последовательности с экспоненциальным распределением вероятностей в случайную бинарную или другую последовательность с заданным распределением вероятностей. Данная задача затрагивает проблему экстракции случайности из набора данных, являющихся случайными лишь частично. В настоящем изобретении предлагается использовать детерминистические экстракторы, то есть те, которые не требуют дополнительной случайности для их осуществления.
В общем случае реализация экстрактора случайных чисел представляет собой достаточно сложную вычислительную задачу, в связи с чем ее реализация в реальном времени на скоростях в мегабиты в секунду представляется крайне затруднительной. Решение данной проблемы в настоящем изобретении осуществляется с помощью блока ПЗУ, в который заложена вычисленная заранее таблица преобразования сырых данных в выходные. Таким образом, вместо трудоемкого непосредственного вычисления выходных данных по полученному блоку входных данных, система обращается к ячейке ПЗУ с адресом, формируемым из блока входных данных, и считывает записанную там информацию - требуемые выходные данные. Благодаря дешевизне блоков ПЗУ на мегабайты и десятки мегабайт данных такой подход представляется практичным в реализации генераторов случайных чисел, работающих в реальном времени.
Предлагаемая схема работы процессора 6 представлена на фиг. 2. Поясним ее действие на примере генератора случайной несмещенной бинарной последовательности. Перекодировщик 7 преобразует входной поток данных, состоящий из бесконечного набора цифр, в конечный набор, называемый алфавитом перекодировщика. Одна из возможных реализаций данного изобретения использует алфавит из 4 символов. Простейшее осуществление данного перекодирования - взятие остатка по модулю 4. Любое входящее целое число и преобразуется в одно из 4 различных значений - букв алфавита: 0, 1, 2 и 3. Для большей эффективности работы дальнейшего алгоритма желательно получать как можно более близкие вероятности для каждой из букв алфавита. Ввиду этого возможной реализацией перекодировщика является следующее правило перекодировки:

и так далее, с периодом, равным 8. В общем случае увеличение размера алфавита приводит к увеличению эффективности алгоритма экстракции, однако усложняет его техническую реализацию. Для дальнейшей работы алгоритма удобно использовать алфавит длиной в степень двойки т.е. 2, 4, 8, 16, 32, …
После перекодировки данные поступают в буфер 8. Одна из возможных реализаций использует значения полученного алфавита в двоичном коде и записывает их в последовательные ячейки памяти. Размер буфера составляет, например, 20 бит, таким образом, он вмещает 10 двухбитных значений, соответствующих алфавиту из 4 символов. Аналогичный подход может использоваться для алфавита, размер которого является степенью двойки, т.е. 8-символьный алфавит дает 3-битные значения, 16-символьный - 4-битные и так далее.
Полученное значение буфера, например строка из 20 бит, передается на формирователь адреса 9, после чего значение буфера сбрасывается и он становится готов к приему следующих значений из перекодировщика. Основная задача формирователя адреса - сопоставить входной битовой строке адрес ячейки ПЗУ 10, по которому находится требуемая перекодированная информация. В одной возможной реализации настоящего изобретения формирователь адреса добавляет к полученной битовой строке, т.е. 20-разрядному двоичному числу, смещение, соответствующее адресу ячейки ПЗУ с номером ноль. При отсутствии такого смещения формирователь просто передает значение буфера 8 на ПЗУ 10. Также формирователь адреса может умножать данные на входе на константу, например, если выходные данные преобразования занимают по нескольку ячеек памяти.
ПЗУ 10 получает на вход адрес ячейки памяти и выдает на выход данные из указанной ячейки или нескольких ячеек памяти, например 8-битовое число. Полученное число поступает в блок постобработки, необходимый для преобразования содержимого ячейки памяти в корректную выходную информацию. Поскольку различным строкам из буфера 8 может соответствовать различное число бит выходной информации, используется дополнительное кодирование информации в ПЗУ. Одним из возможных вариантов является кодирование следующего типа: для представления бинарной строки к ней слева добавляется единица и требуемое число нулей, соответствующее размеру блока данных из ПЗУ. Например, для 8-битовых блоков бинарное число ABCD записывается как 0001ABCD, число XYZ - как 00001XYZ, а семибитное число KLMNOPR-как 1KLMNOPR. Соответственно, алгоритм постобработки удаляет слева все нули (если они присутствуют) и следующую за этим единицу. Оставшиеся биты информации и есть результат преобразования входной сырой последовательности в выходную.
В рекомендуемом варианте реализации по сырым входным данным формируется несмещенная бинарная последовательность. Если требуется другой тип выходной случайной последовательности, его формирование также реализуется в блоке постобработки 11. Рассмотрим для примера генерацию случайной последовательности из трех символов А, В и С с соотношением вероятностей 1:2:3 соответственно. Абсолютные значения вероятностей равняются 1/6, 2/6 и 3/6. Для реализации такой последовательности исходная бинарная последовательность группируется по 3 бита, дающих 8 уникальных значений. Значению 0 сопоставляется символ А, значениям 1 и 2 - символ В, значениям 3, 4 и 5 - символ С, а оставшиеся значения 6 и 7 выбрасываются. Как легко понять специалисту, такая схема преобразования гарантирует генерацию независимых значений с требуемым распределением вероятности. Генерация любых требуемых распределений вероятности с произвольным числом выходных значений может быть реализована аналогично.
Последняя задача, выполняемая блоком постобработки, - это буферизация выходной информации, если она необходима. В зависимости от варианта использования получаемой случайной последовательности может требоваться как появление значений по мере их генерации, так и их выдача по запросу после необходимой буферизации. Реализация буферизации зависит от конкретного протокола передачи получаемых случайных значений и должна быть понятна специалисту, проектирующему всю схему, использующую настоящий генератор случайных чисел.
Алгоритм преобразования, реализуемый процессором 6 с помощью ПЗУ 10, является реализацией идей, частично изложенных в работе P. Elias "The efficient construction of an unbiased random sequence", Ann. of Math. Statistics, v. 43, no. 3, pp.865-870 (1972). Простейшая реализация данного алгоритма соответствует конструкции, приписываемой фон Нейману: перекодировщик 7 формирует два различных значения 0 и 1. Буфер 8 группирует такие значения в пары. В зависимости от значения полученных двухбитных значений формируется выходная информация, согласно следующей таблице:

Как легко понять, даже при различных вероятностях возникновения исходных нулей и единиц результат преобразования будет несмещенной бинарной последовательностью, так как вероятность появления пары 0-1 в точности равна вероятности появления пары 1-0. Пары 00 и 11 выбрасываются, так как к ним не существует равновероятных пар.
Эффективность такого алгоритма сравнительно невелика. Даже для случая относительно малого смещения исходной последовательности алгоритм в среднем извлекает 1 случайный бит из четырех исходных. Для увеличения эффективности экстракции следует увеличивать число выходных значений перекодировщика 7 и размер буфера 8.
Рассмотрим для примера реализацию с алфавитом перекодировщика размером в 4 символа и буфером 8 в 20 бит. Выходные значения перекодировщика будем представлять виде символов А, Б, В и Г. Буфер 8 формирует «слова» из 10 таких символов. Рассмотрим, например, слово АББГАВБАГВ. Вероятность появления такого слова в точности равна вероятности появления любого слова, являющегося перестановкой данных символов, т.е. любое слово из 3 символов А, 3 символов Б, двух символов В и двух символов Г. Число таких перестановок, как очевидно специалисту, равно 10!/(3!3!2!2!)=25200. Таким образом, появление такого слова является одним из 25200 равновероятных событий. Присвоив каждой такой перестановке порядковый номер, мы получаем численное значение данного результата (число от 0 до 25199). Преобразование его в несмещенную бинарную последовательность детально описано в работе P. Elias "The efficient construction of an unbiased random sequence", Ann. of Math. Statistics, v. 43, no. 3, pp. 865-870 (1972). Алгоритм заключается в следующем. Число равновероятных событий, т.е. 25200 в данном примере, представляется в виде разложения по степеням двойки: 25200=16384+8192+512+64+32+16. Значениям от 0 до p1=16384 приписывается 14-битное значение, равное двоичному представлению конкретного входного значения p. Значениям от p1 до p2=p1+8192 приписывается 13-битное значение, равное двоичному представлению числа p-p1. Значениям от р2 до p3=р2+512 - 9-битное значение, соответствующее двоичному представлению числа p-р2. И так далее. Значениям от 25184 до 25199 приписывается 4-битное двоичное представление числа p-25184. Таким образом, в зависимости от p получаем от 4 до 13 бит в выходной последовательности. Аналогичным образом обрабатываются другие выпадающие «слова». Данный алгоритм гарантирует генерацию несмещенной последовательности независимых бинарных значений. Кроме того, он обеспечивает адаптивность скорости генерации выходной последовательности в зависимости от распределения вероятностей на выходе перекодировщика 7.
Приведенный для примера алгоритм обеспечивает генерацию приблизительно 1,2 бит информации на один входной символ (при близких вероятностях выпадения символов А-Г). Для сравнения, на фиг. 3 приведен график зависимости эффективности предлагаемого алгоритма экстракции (в битах на символ перекодировщика 7) от размера буфера 8 для алфавита перекодировщика 7 размером 2, 4, 8 и 16. Как следует из графика, взятый для примера алгоритм является наиболее эффективным при размере буфера 8 не более 20 бит, что соответствует размеру ПЗУ в 1 048 576 ячеек.
Изобретение относится к квантовым генераторам случайных чисел и может быть использовано в криптографии. Техническим результатом является повышение качества, степени надежности и скорости генерации. Устройство содержит источник фотонов, однофотонный детектор, измеритель времени, задающий тактовый генератор, дискриминатор, процессор. 3 з.п. ф-лы, 3 ил.
1. Генератор случайных чисел, содержащий источник фотонов, однофотонный детектор, реагирующий на отдельные фотоны, создаваемые источником фотонов, и схему оцифровки и последующей обработки сигнала детектора, отличающийся тем, что схема оцифровки выполнена с возможностью преобразования длительности временных интервалов между последующими срабатываниями однофотонного детектора в цифровые значения, а также произведения перекодировки и буферизации полученной последовательности для формирования адреса в постоянном запоминающем устройстве (ПЗУ) генератора, с возможностью в дальнейшем получения цифровой информации из ячейки ПЗУ с данным адресом, заложенной в него при изготовлении генератора, и попадания на выход генератора случайных чисел после обработки.
2. Генератор случайных чисел по п. 1, отличающийся тем, что схема оцифровки и последующей обработки содержит связанный с детектором измеритель времени, выполненный с возможностью измерения временных интервалов между соседними по времени зарегистрированными детектором частицами, причем измеритель времени связан с дискриминатором, выполненным с возможностью окончательной оцифровки временных интервалов и отнесения их длительности к набору целых чисел, при этом дискриминатор связан с процессором, выполненным с возможностью генерации из цифровой информации, переданной из дискриминатора, выходной случайной последовательности, подаваемой на выход генератора.
3. Генератор случайных чисел по п. 2, отличающийся тем, что процессор содержит блок перекодировки, выполненный с возможностью входной последовательности в конечный алфавит и связанный с цифровом буфером, выполненным с возможностью буферизации полученной после перекодировки последовательности для получения битовой строки фиксированной длины, кроме того, цифровой буфер выполнен с возможностью передачи битовой строки в формирователь адреса, преобразующий полученную битовую строку в адрес ячейки ПЗУ, причем процессор также содержит блок дополнительной постобработки, связанный с ячейками ПЗУ и выполненный с возможностью формирования окончательной последовательности по данным, полученным из ПЗУ или цифрового буфера.
4. Генератор случайных чисел по п. 3, отличающийся тем, что блок дополнительной постобработки выполнен с возможностью буферизации данных, полученных из ПЗУ или цифрового буфера, для выдачи на выход генератора в виде блоков требуемой длины.
| WO 2008077833 A1, 03.07.2008 | |||
| WO 2015070284 A1, 21.05.2015 | |||
| US 2006010182 A1, 12.01.2006 | |||
| US 2015193207 A1, 09.07.2015 | |||
| ГЕНЕРАТОР СЛУЧАЙНЫХ ЧИСЕЛ | 2007 |
|
RU2331916C1 |
Авторы
Даты
2017-03-14—Публикация
2015-10-02—Подача