Предлагаемое решение относится к сейсмологии и может быть использовано для технического контроля состояния разломной структуры литосферы по инструментальной регистрации землетрясений и обработке данных.
Согласно Б. Мандельброта [Мандельброт Б. Фрактальная геометрия природы. М: ИКИ, 2002. 656 с.], фрактальная размерность, как показатель самоподобия, является основной характеристикой структуры многих природных объектов. Фрактальные объекты обладают масштабной инвариантностью, или скейлингом (scaling), когда части объекта подобны целому, и обычно характеризуются фрактальной размерностью (как показателем самоподобия), которая выражается нецелым числом. Однако при ограниченных выборках данных фрактальная размерность может зависеть от степени заполнения фракталами структуры объекта, и по этой причине отличаться от показателя самоподобия.
Одним из основных фрактальных объектов литосферы Земли являются пространственные структуры разломов, генерирующих землетрясения. Установлено, что распределение эпицентров землетрясений самоподобно на исследуемых масштабных уровнях [Садовский М.А., Голубева Т.В., Писаренко В.Ф., Шнирман М.Г. Характерные размеры горной породы и иерархические свойства сейсмичности // Физика Земли. 1984. №2. С. 3-15]. Величина фрактальной размерности поля эпицентров землетрясений лежит в пределах 1≤D<2: значение 1 указывает на цельную, упорядоченную структуру среды без разрывов-землетрясений, промежуточное значение - на частично разрушенную разрывами среду, значения, приближающиеся к 2, указывают на сильно разрушенную среду. В Байкальской рифтовой зоне (БРЗ) самоподобие эпицентрального поля землетрясений подтверждено в работе [Солоненко А.В., Штейман Е.А. Самоподобие поля сейсмичности Байкальского рифта // Доклады РАН. 1994. Т. 337. №2. С. 253-257]. В БРЗ фрактальные размерности разломов Df≈1.68 и сейсмичности Ds≈1.68 совпадают, что указывает на сбалансированность разломообразования и сейсмичности [Sherman S.I., Gladkov A.S. Fractals in studies of faulting and seismicity in the Baikal rift zone // Tectonophysics. 1999. V. 308. P. 133-142]. Таким образом, фрактальные размерности распределения эпицентров землетрясений позволяют охарактеризовать структуру сети разломов, что дает возможность сопоставления разломообразования и сейсмичности и может быть использовано для мониторинга и технического контроля состояния разломной структуры литосферы по инструментальной регистрации землетрясений и обработке данных.
Способы определения фрактальной размерности однотипны - это скейлинг с последующей параметризацией степенного распределения результатов скейлинга в виде наклона линейной аппроксимации в билогарифмической системе координат.
Аналогом является способ определения фрактальной размерности поверхности твердого электрода (патент RU 2436069), содержащий этапы на которых:
- выполняют электрорастворение осажденной монослойной пленки малорастворимого вещества на поверхности,
- регистрируют количество вещества, образующего монослой, используют молекулы малорастворимого неорганического вещества,
- рассчитывают количество вещества в монослое и площади поверхности электрода, занимаемой одной молекулой осажденного на электроде вещества,
- строят в логарифмических координатах зависимость количества вещества в монослое от площади поверхности электрода, занимаемой одной молекулой осажденного вещества,
- по тангенсу угла наклона аппроксимации полученной зависимости прямой линией судят о величине фрактальной размерности.
Недостатки решения
- произвольность выбора диапазона скейлинга площади поверхности электрода, что приводит к снижению точности, неоднозначности и множественности решения и, как следствие, к ограниченности технологических возможностей использования данного решения.
Аналогом применения фрактальной размерности в сейсмологии является способ прогнозирования параметров землетрясений (Патент RU 2255356).
В способе аналога измеряют характеристики магнитного H и электрического Ε полей околоземного космического пространства раздельными датчиками, установленными на космическом аппарате, на восходящем и нисходящем витках. Формируют синтезированную Н×Е матрицу измерений и вычисляют дисперсию σ2 результирующего вектора R и его фрактальную размерность D. Отслеживают изменение фрактальной размерности до серии измерений. Определяют начальные условия отслеживаемого процесса, постоянную времени Τ и установившееся значение D0. Прогнозируют параметры землетрясения: время удара ty=4.7T, магнитуду lg ty[сут]
Недостатком данного решения следует считать:
- неопределенность типа магнитуды M прогнозируемого землетрясения;
- неоднозначность разбиения синтезированной Н×Е матрицы измерений, что понижает точность и приводит к некорректности решения.
Наиболее близким по технической сущности (прототипом) является способ обнаружения аномалий подстилающей поверхности (Патент RU 2160912).
В способе-прототипе получают изображение подстилающей поверхности в виде цифровой функции яркости I(х,у) от пространственных координат, разбивают изображение на сравнительно однородные участки на основе априорных данных, вычисляют функции фрактальной размерности каждого участка, составляют матрицу эталонов из коэффициентов фрактальной размерности каждого участка, а аномалию фиксируют по выходу разности между текущими и эталонным значениями фрактальной размерности за пороговый уровень для анализируемого участка.
Недостатком способа-прототипа являются:
- априорная неопределенность разбиения матрицы изображения на участки, искажающая числовые характеристики фрактальной размерности в пограничных областях;
- неоднозначность разбиения матрицы изображения, что понижает точность и приводит к множественности решения.
Задачей предлагаемого изобретения является устранение вышеуказанных недостатков - решение задачи заявляемым способом однозначно и направлено на повышение точности определения показателя самоподобия поля эпицентров землетрясений при ограниченных выборках данных, обусловленных малой продолжительностью инструментальной регистрации землетрясений.
Поставленная задача решается предлагаемым способом определения показателя самоподобия поля эпицентров землетрясений, при котором на основе экспериментальных материалов пространственное поле эпицентров представительных землетрясений разделяют на сравнительно однородные участки, выполняют разбиение каждого участка на площадки (скейлинг), строят в двойных логарифмических координатах функцию количества площадок с землетрясениями от линейного размера площадок и аппроксимируют функцию прямой линией, при этом определяют коэффициент корреляции линейной аппроксимации функции и выбирают диапазон размеров площадок, на котором линейная аппроксимация имеет максимальное значение коэффициента корреляции, а показатель самоподобия поля эпицентров землетрясений находят по наклону линейной аппроксимации функции в этом диапазоне размеров площадок.
Иными словами, по заявленному способу определяют параметры очагов представительных, зарегистрированных без пропусков, землетрясений. Формируют карту распределения эпицентров этих землетрясений по территории исследуемого региона и выбирают сравнительно однородные участки. Затем выполняют скейлинг карты выбранного участка и по углу наклона линейной аппроксимации функции логарифма количества площадок с землетрясениями от логарифма линейного размера площадок определяют клеточную размерность D0 поля эпицентров землетрясений. Находят диапазон размеров площадок, на котором линейная аппроксимация функции имеет максимальное значение коэффициента корреляции, и в этом диапазоне определяют клеточную размерность как показатель самоподобия поля эпицентров землетрясений. В основе предлагаемого способа определения показателя самоподобия лежит фундаментальное свойство самоподобных объектов - масштабная инвариантность в плотно заполненной фракталами части объекта. Поскольку решение соответствует наилучшей аппроксимации функции прямой линией, имеющей место только при максимальном значении коэффициента корреляции, то оно единственно. При таком решении повышается достоверность, точность и объективность результатов, обеспечивается их устойчивость при ограниченных выборках данных.
Изобретение поясняется чертежами.
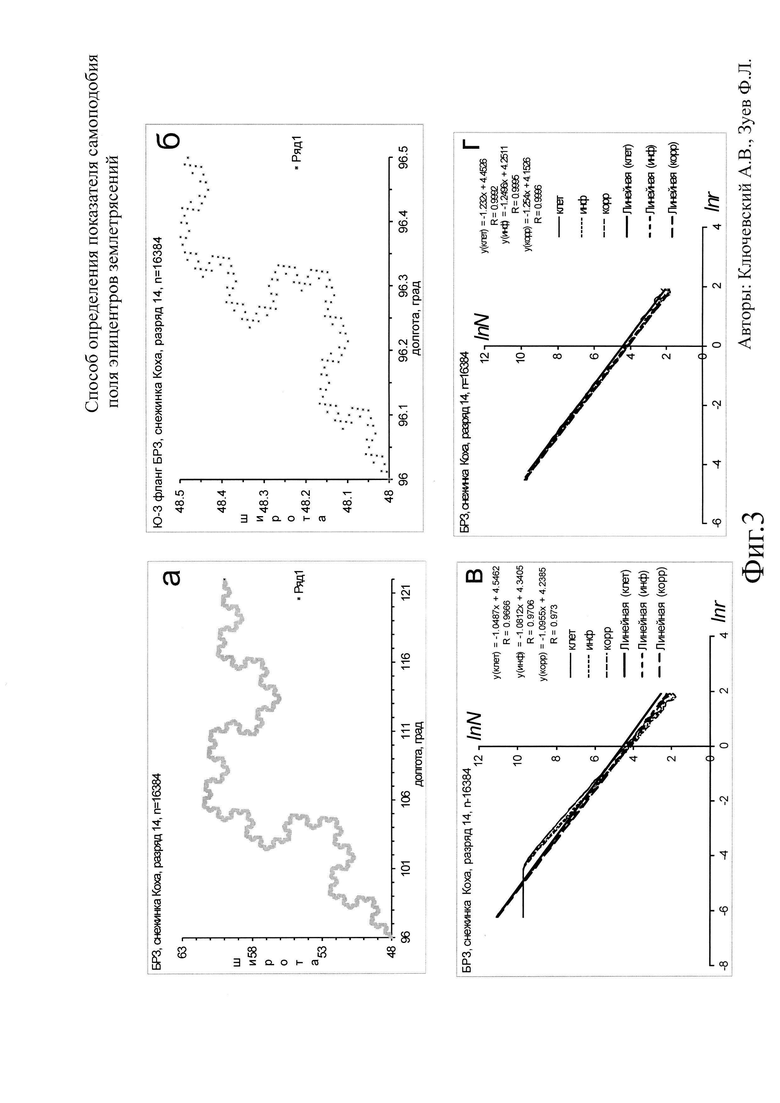
Фиг. 1. Фрактальная структура "снежинки Коха" в масштабе Байкальского региона для 64 точек-эпицентров синтезированных "землетрясений" (разряд 6).
а. Распределение точек-эпицентров синтезированных "землетрясений" по территории Байкальского региона;
б. Результаты скейлинга в полном диапазоне размеров: отражены в виде функций lnN=f(lnr) и линейной аппроксимации функций клеточной D0 (клет), информационной D1 (инф) и корреляционной D2 (корр) размерности. Для каждой размерности приведены уравнения корреляционной связи и коэффициенты корреляции R.
в. Результаты скейлинга наклонной линейной части функций (без "полочки"): отражены в виде функций lnN=f(lnr) и линейной аппроксимации функций клеточной D0 (клет), информационной D1 (инф) и корреляционной D2 (корр) размерности. Для каждой размерности представлены уравнения корреляционной связи и коэффициенты корреляции R.
Фиг. 2. Фрактальная структура "снежинки Коха" в масштабе Байкальского региона для 1024 точек-эпицентров синтезированных "землетрясений" (разряд 10).
Подписи к Фиг. 2 аналогичны подписям к Фиг. 1.
Фиг. 3. Фрактальная структура "снежинки Коха" в масштабе Байкальского региона для 16384 точек-эпицентров синтезированных "землетрясений" (разряд 14) и в масштабе юго-западного фланга БРЗ. Подписи к Фиг. 3а, в, г аналогичны подписям к Фиг. 1a, б, в соответственно.
б. Распределение точек-эпицентров синтезированных "землетрясений" по территории юго-западного фланга БРЗ.
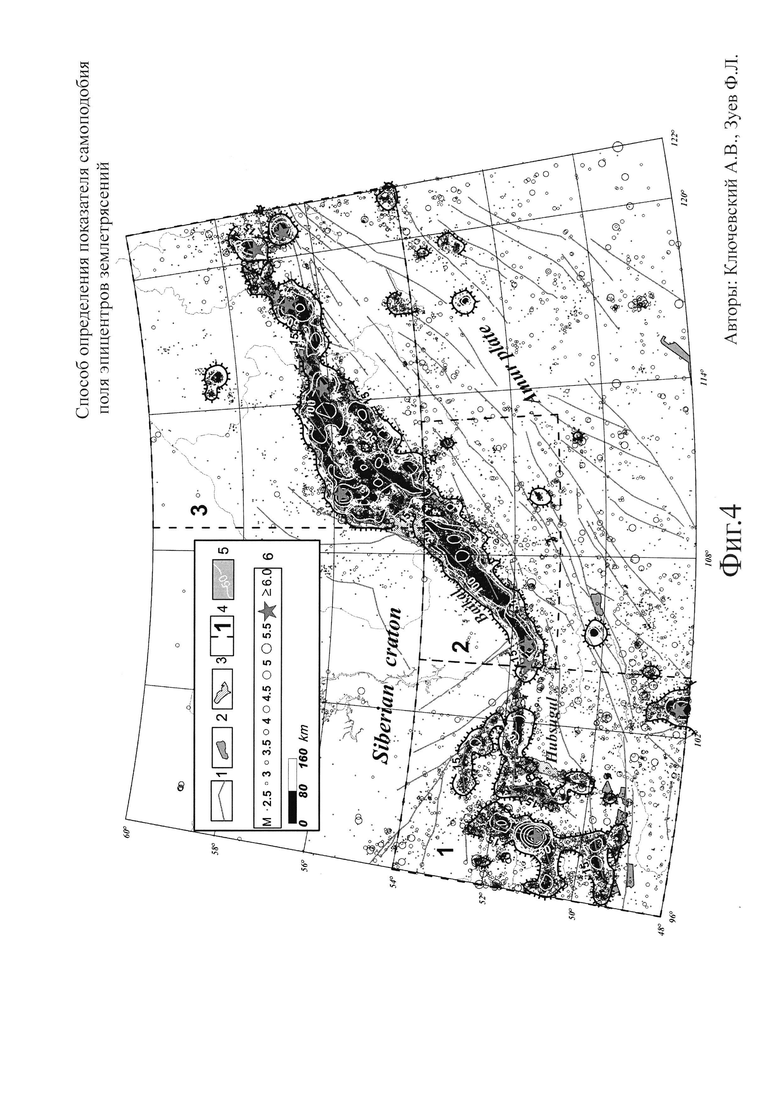
Фиг. 4. Карта эпицентров и изолиний плотности эпицентров землетрясений Байкальского региона (1964-2013 г.).
1 - разломы, 2 - впадины, 3 - озера, 4 - границы и номера районов, 5 - изолинии плотности эпицентров, 6 - эпицентры землетрясений с магнитудой MLH≥2.5 (энергетический класс KP≥8).
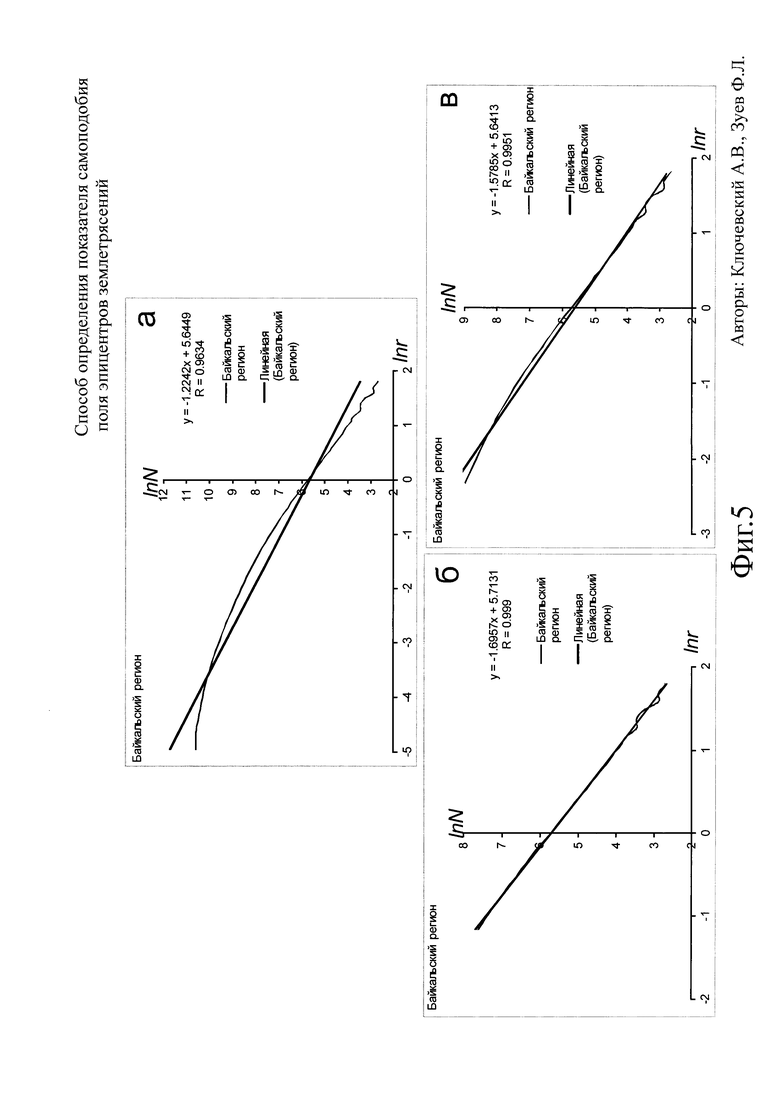
Фиг. 5. Результаты определения клеточной размерности поля эпицентров землетрясений Байкальского региона за 1964-2013 гг.
а. Графики и результаты определения клеточной размерности для всех размеров площадок;
б. Графики и результаты определения показателя самоподобия;
в. Графики и результаты определения клеточной размерности при минимальном размере клетки rk=10 км.
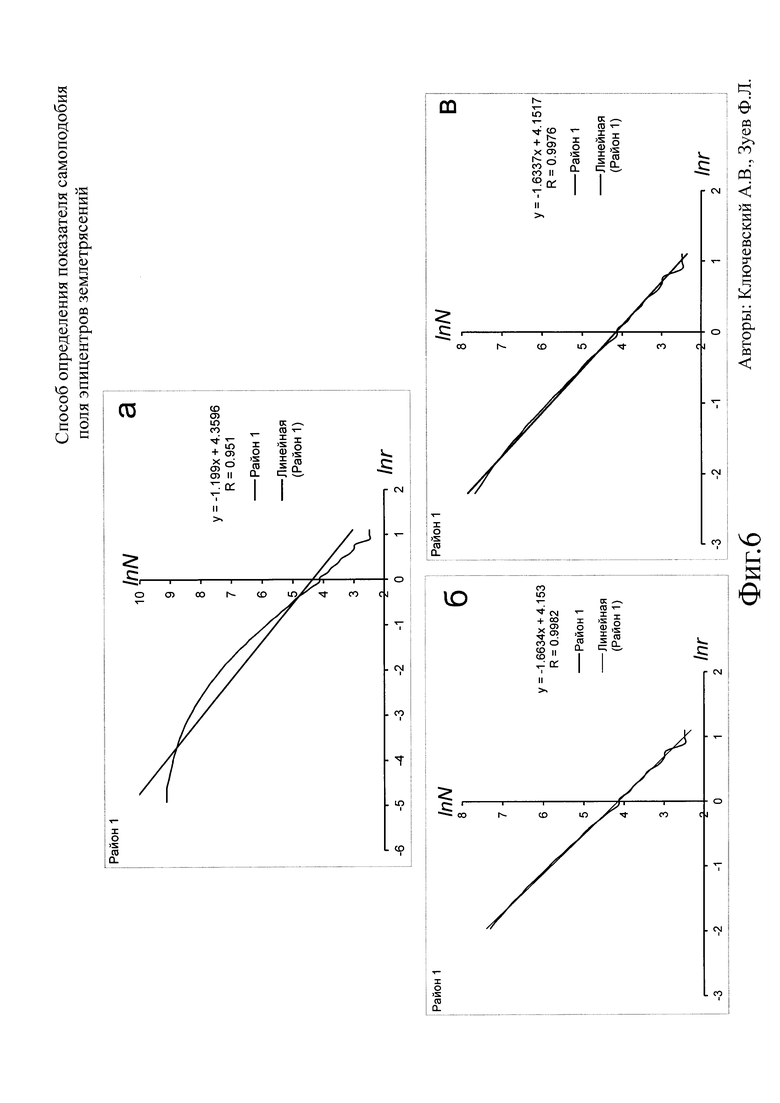
Фиг. 6. Результаты определения клеточной размерности поля эпицентров землетрясений района 1 за 1964-2013 гг.
Подписи к Фиг. 6 аналогичны подписям к Фиг. 5.
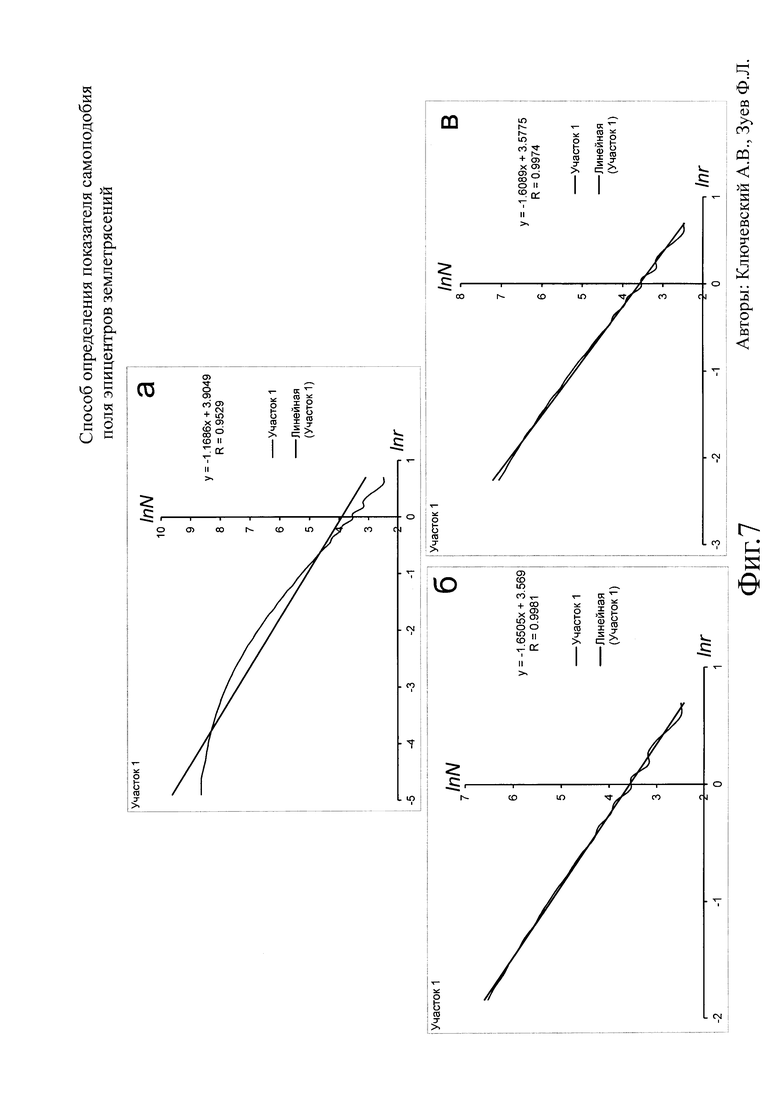
Фиг. 7. Результаты определения клеточной размерности поля эпицентров землетрясений участка 1 за 1964-2013 гг.
Подписи к Фиг. 7 аналогичны подписям к Фиг. 5.
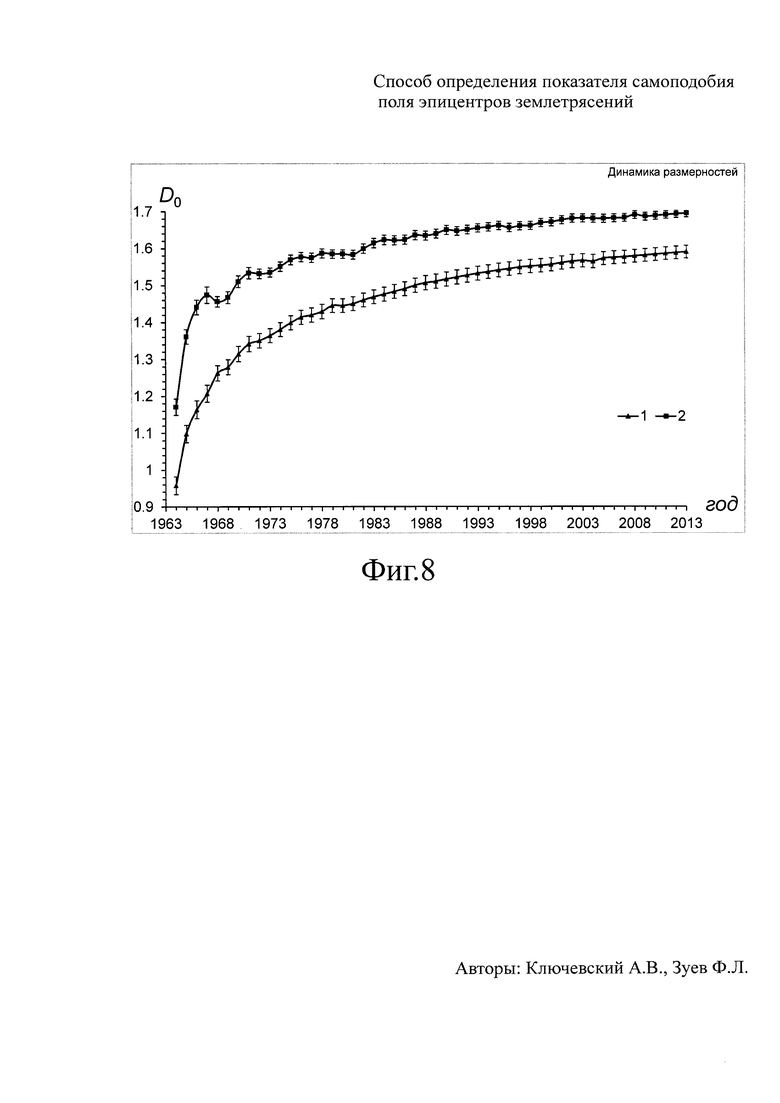
Фиг. 8. Динамика фрактальной структуры поля эпицентров землетрясений как критерий заполнения толчками территории Байкальского региона с 1964 по 2013 гг.
1 - клеточная размерность определена при минимальных размерах клетки rk=10 км; 2 - показатель самоподобия определен по предлагаемому способу.
Техническая сущность способа состоит в следующем:
При определении фрактальной размерности распределения эпицентров землетрясений на поверхности Земли форма и размер максимальной первой клетки обычно соответствуют таковым территории исследования. Например, при исследовании эпицентров землетрясений Байкальского региона они соответствуют территории, ограниченной координатами мониторинга землетрясений сетью сейсмических станций Прибайкалья (ϕ=48.0-60.0° с.ш., λ=96.0-122.0° в.д.). Размер минимальной клетки задается исходя из физических соображений величиной погрешности определения координат эпицентров землетрясений. В Байкальском регионе погрешность обычно принимается равной 10 км, таковы и размеры минимальной клетки (rk=10 км) [Sherman S.I., Gladkov A.S. Fractals in studies of faulting and seismicity in the Baikal rift zone // Tectonophysics. 1999. V. 308. P. 133-142; Ключевский A.B., Зуев Ф.Л. Структура поля эпицентров землетрясений Байкальского региона // Доклады Академии наук. 2007. Т. 415. №5. С. 682-687]. Однако плотность сейсмических станций, от которой зависит в целом погрешность определения координат эпицентров землетрясений, меняется по территории - наиболее высока плотность станций в центральной части БРЗ; на флангах она понижается. Возникающие при этом различия в погрешности определения координат эпицентров землетрясений и, следовательно, разные величины возможных размеров минимальных клеток при скейлинге, создают неоднозначность и понижают точность определения фрактальной размерности.
Основной характеристикой фрактальных объектов является их фрактальная размерность, которая отражает самоподобие иерархической структуры включенных в анализ элементов объекта, но зависит от степени заполнения структуры объекта этими элементами. Понятие фрактальной размерности обычно сводят к простой геометрической интерпретации - насколько фрактальные элементы заполняют пространство, в котором они определены. В таком представлении величина фрактальной размерности эпицентрального поля землетрясений зависит от того, как заполнено сейчас и как будет заполняться пространство в последующие годы. Заполнение территории эпицентрами происходит поступательно во времени - каждое зарегистрированное землетрясение дополняет картину заполнения и приводит к изменению, обычно к росту, фрактальной размерности [Ключевский А.В., Зуев Ф.Л. Структура поля эпицентров землетрясений Байкальского региона // Доклады Академии наук. 2007. Т. 415. №5. С. 682-687]. Территория заполняется эпицентрами землетрясений полностью за сейсмический цикл, продолжительность которого для Байкальского региона составляет около 220 лет [Ключевский А.В., Демьянович В.М., Баяр Г. Оценка рекуррентных интервалов и вероятности сильных землетрясений Байкальского региона и Монголии // Геология и геофизика. 2005. Т. 46. №.7. С. 746-762]. Примерно такая же длительность цикла и на других территориях с высокой сейсмической активностью. На слабоактивных территориях сейсмический цикл может существенно увеличиваться, вплоть до тысяч лет. Следовательно, чтобы корректно определить показатель самоподобия эпицентрального поля землетрясений необходимо осуществить мониторинг сейсмичности продолжительностью в сотни лет, а инструментальная регистрация землетрясений на планете немного превышает 100 лет. Согласно "Каталога землетрясений Прибайкалья" инструментальная регистрация землетрясений сетью сейсмических станций Прибайкалья началась в 1960-х годах, т.е. поле эпицентров землетрясений, включенных в "Каталог землетрясений Прибайкалья", заполнено не полностью, а самоподобно сформировано лишь на какой-то доле территории. Такое поле эпицентров близко отражает самоподобие в наиболее заполненной землетрясениями доле территории региона, и некорректно отражает самоподобие на территории всего региона. Следует отметить, что этот недостаток является артефактом инструментального мониторинга: на самом деле все поля эпицентров землетрясений самоподобны, так как они формируется тысячелетиями непрерывного сейсмотектонического деформирования литосферы с постоянной генерацией землетрясений. Артефакт возникает из-за недостаточного объема данных в каталогах землетрясений и обусловлен малой продолжительностью периода инструментальной регистрации землетрясений.
Модельный пример. В качестве модельного примера такого артефакта приведем результаты вычисления и определения клеточной (D0), информационной (D1) и корреляционной (D2) размерности синтезированного поля точек-эпицентров "землетрясений" для классической самоподобной структуры "снежинка Коха", фрактальная размерность которой (в смысле показателя самоподобия) равна D≈1.26. Синтезирование толчков проведено для территории Байкальского региона (ϕ=48.0-60.0° с.ш., λ=96.0-122.0° в.д.), а расчеты размерностей выполнены по следующим формулам:
Клеточная (Хаусдорфа) размерность D0. Клеточная размерность - наиболее часто используемая из фрактальных метрик. Она выражается формулой
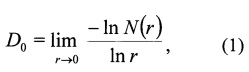
где n(r) - количество непустых, содержащих хотя бы одну точку, клеток сетки с длиной стороны r, накрывающей изучаемое множество. Геометрический смысл метрики - показатель изменения покрываемой множеством области в зависимости от единицы измерения и характерного масштаба. Алгоритм вычисления достаточно прост. На множество накладываются сетки с последовательно уменьшающимся размером ячейки rk, до тех пор, пока rk не станет меньше точности измерения (rk=10 км в Байкальском регионе). Поскольку точность "определения" координат точек-эпицентров синтезированных "землетрясений" очень высока, то для модельных примеров это ограничение не применяется. В билогарифмической системе координат функция lnN=f(lnr) аппроксимируется прямой линией по методу наименьших квадратов, а среднеквадратичное отклонение берется как оценка погрешности метода.
Информационная размерность D1. Информационная размерность имеет формулу
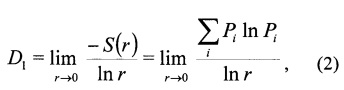
где 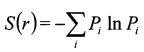 - информационная энтропия по Шеннону.
- информационная энтропия по Шеннону.
Геометрический смысл метрики - показатель изменения информации, необходимой для определения положения точек в зависимости от единицы измерения. Алгоритм вычисления аналогичен вычислению клеточной размерности, с тем различием, что вместо ln N(r) вычисляется S(r).
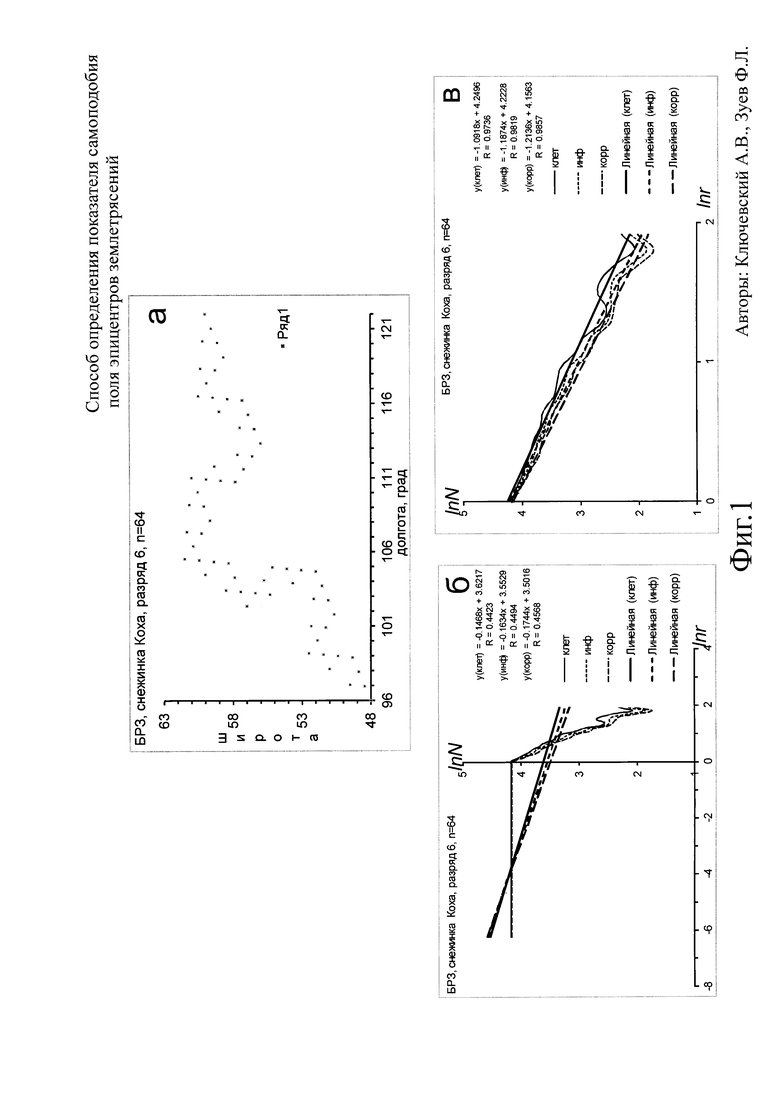
Корреляционная размерность D2. Корреляционная размерность имеет формулу
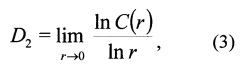
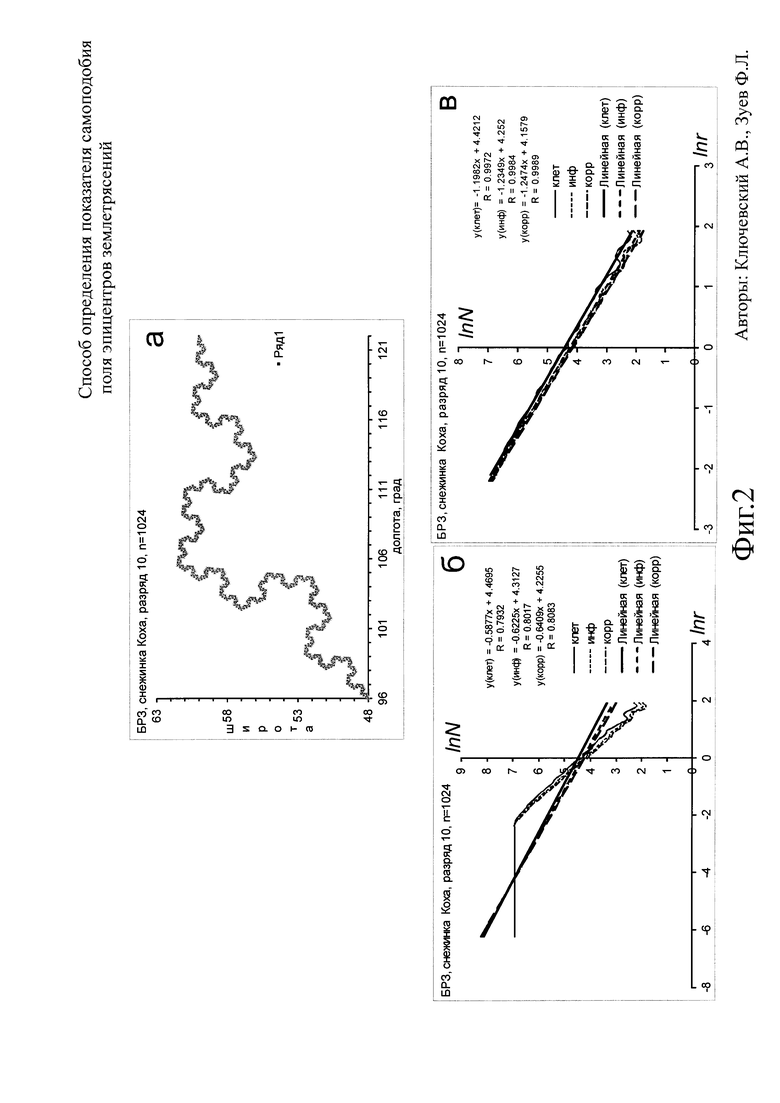
где C(r) - корреляционный интеграл, то есть вероятность того что расстояние между двумя произвольными точками множества меньше r. Интеграл может быть записан через функцию Хевисайда как
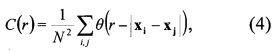
где суммирование проводится по всем парам точек xi, xj изучаемого множества. Для геометрической прогрессии масштабов rk рассчитываются значения С(rk), затем выполняется аппроксимация аналогично предыдущему.
На Фиг. 1а представлена структура самоподобного фрактала "снежинка Коха", построенная в масштабе Байкальского региона по 64 синтезированным точкам-эпицентрам "землетрясений" (разряд 6, 26=64 точки, которые будем интерпретировать условно как количество "землетрясений" в течение t=1 год). На Фиг. 1б результаты определений клеточной D0 (клет), информационной D1 (инф) и корреляционной D2 (корр) размерности в полном диапазоне размеров r отражены в виде функций lnN=f(lnr) и их линейных аппроксимаций. Также представлены уравнения корреляционной связи и коэффициенты корреляции R. Выделяется наклонная часть графика в масштабах 0≤lnr≤2 и полочка для lnr≤0, которая вносит главное искажение в функции lnN=f(lnr) и графики линейной аппроксимации функций. Видно, что линии аппроксимации не соответствуют графикам функций lnN=f(lnr), коэффициенты корреляции низки (менее 0.5), а значения размерностей (D0≈0.15; D1≈0.16 и D2≈0.17) сильно отличаются от показателя самоподобия фрактала "снежинка Koxa" (D≈1.26). На Фиг. 1в результаты представлены только для наклонных частей функций (устранены полочки), а уравнения корреляционной связи получены при максимальных коэффициентах корреляции, т.е. для наилучшего описания функций линейной аппроксимацией. Видно, что графики линейной аппроксимации достаточно близко соответствуют функциям lnN=f(lnr), максимальные коэффициенты корреляции высоки (выше 0.97), а значения показателей самоподобия (D0≈1.09; D1≈1.19 и D2≈1.21) существенно приблизились к величине D≈1.26.
На Фиг. 2а представлена структура "снежинка Коха", построенная по 1024 синтезированным точкам-эпицентрам "землетрясений" (разряд 10, 210=1024 точки, которые можно интерпретировать как количество землетрясений за t=24=16 лет). Этот рисунок, в отличие от Фиг. 1а, достаточно заполнен точками-эпицентрами и структурирован - в масштабе рисунка уже не видны разрывы между маркерами. На Фиг. 2б результаты определений клеточной D0 (клет), информационной D1 (инф) и корреляционной D2 (корр) размерности в полном диапазоне размеров г отражены в виде функций lnN=f(lnr) и их линейных аппроксимаций. Видно, что, несмотря на значительное увеличение наклонной части графика, прямые аппроксимации не соответствуют графикам функций lnN=f(lnr). Наклонная часть графиков расширена до диапазона -2≤lnr≤2, а полочка уменьшилась (lnr≤-2), и небольшие положительные изменения в уравнениях корреляционной связи обусловлены именно этими факторами. Коэффициенты корреляции несколько выросли (R≈0.8), значения определенных размерностей (D0≈0.59; D1≈0.62 и D2≈0.64) существенно отличаются от величины D≈1.26. На Фиг. 2в представлены результаты только для наклонных частей функций, и уравнения корреляционной связи получены при максимальных коэффициентах корреляции. Видно, что прямые аппроксимации хорошо соответствуют функциям lnN=f(lnr), максимальные коэффициенты корреляции высоки (выше 0.99), а значения показателей самоподобия (D0≈1.20; D1≈1.23 и D2≈1.25) близки к величине D≈1.26.
Продолжая, на Фиг. 3 структура "снежинка Коха" построена по 16384 синтезированным точкам-эпицентрам "землетрясений" (разряд 14, 214=16384 точки, t=28=256 лет). В масштабе всего Байкальского региона детали распределения точек-эпицентров уже не наблюдаются, видны только общие контуры. Поэтому мы увеличили масштаб и привели небольшой участок (0.5×0.5°) юго-западного фланга БРЗ (Фиг. 3б). На нем отчетливо повторяются детали самоподобного фрактала структуры "снежинка Коха", заполненной уже достаточно полно. В полном диапазоне размеров г наклонные части функций расширены до -4≤lnr≤2, а полочки уменьшились (lnr≤-4). Видно, что, несмотря на значительное увеличение наклонных частей функций, линейная аппроксимация все-таки не соответствует полностью графикам функций lnN=f(lnr), коэффициенты корреляции существенно выросли (R≈0.97), но значения вычисленных размерностей (D0≈1.05; D1≈1.08 и D2≈1.10) отличаются от величины D≈1.26. На Фиг. 3г представлены результаты только для наклонных частей функций. Видно, что графики линейной аппроксимации хорошо соответствуют функциям lnN=f(lnr), максимальные коэффициенты корреляции высоки (близки к 1), а значения показателей самоподобия (D0≈1.23; D1≈1.25 и D2≈1.25) почти сравнялись с величиной D≈1.26.
Заполнение структуры "снежинка Коха" выполнено до 65536 точек-эпицентров "землетрясений" (разряд 16, 216=65536 точки, t=210=1024 условных года). Поскольку вид карт и поведение графиков аналогично предыдущим построениям, просто опишем полученные для такой выборки данных результаты. В полном диапазоне размеров г наклонные части функций расширены до -6≤lnr≤2, а полочки уменьшились (lnr≤-6). Коэффициенты корреляции высоки (R≈0.99), значения вычисленных размерностей (D0≈1.20; D1≈1.22 и D2≈1.23) немного отличаются от величины D≈1.26. Графики линейной аппроксимации хорошо соответствуют наклонным частям функций lnN=f(lnr), максимальные коэффициенты корреляции высоки (близки к 1.00), а значения показателей самоподобия (D0≈1.24; D1≈1.25 и D2≈1.26) соответствуют величине D≈1.26.
Не приводятся промежуточные построения для других выборок данных, так как совершенно отчетливо видно, что с ростом количества используемых точек-эпицентров "землетрясений" структура "снежинка Коха" полностью заполняется на определенных размерах, характеризуемых максимальным коэффициентом корреляции, и это приводит значения фрактальной размерности в соответствие с показателем самоподобия. Построения и определения, выполненные для очень сложной структуры самоподобного фрактала "ковер Серпинского" (показатель самоподобия D≈1.89), приводят к точно таким же выводам, а именно: использование максимального коэффициента корреляции для выделения области полного заполнения точками-эпицентрами "землетрясений" дает возможность повысить точность определения показателя самоподобия даже при небольшом количестве точек-эпицентров.
Сравнение предлагаемого технического решения с другими известными решениями в области сейсмологии показывает следующее. Все известные решения основаны на ограничении скейлинга величиной погрешности определения координат эпицентров землетрясений [Голубева Т.В., Писаренко В.Ф., Шнирман М.Г. Самоподобие сейсмических процессов в пространстве // Современные геофизические исследования. 4.1. М.: ИФЗ АН, 1993. С. 61-69; Потанина М.Г., Смирнов В.Б., Бернар П. Особенности сейсмической роевой активности в Коринфском рифте в 2000-2005 гг.// Физика Земли. 2011. №7. С. 54-66; Ключевский А.В., Зуев Ф.Л. Структура поля эпицентров землетрясений Байкальского региона // Доклады Академии наук. 2007. Т. 415. №5. С. 682-687]. Однако погрешность определения зависит от числа сейсмических станций, использованных в расчетах координат землетрясений данной территории, и может изменяться во времени, так как не все сейсмические станции этой территории могут быть использованы по техническим и другим причинам. Следовательно, введение априори заданного предела скейлинга, равного такой погрешности, не позволяет соотнести этот теоретический предел с реальным пределом, формируемым пространственно-временными факторами мониторинга.
Недостатки применяемых методов:
- не учитываются пространственно-временные вариации реальной погрешности определения координат эпицентров землетрясений;
- априори принято, что поле эпицентров землетрясений заполнено и самоподобно сформировано в полном диапазоне размеров клеток.
Предлагаемый способ позволяет исключить эти недостатки, обеспечивает единственность решения и повышает точность определения показателя самоподобия даже при небольшом количестве используемых землетрясений.
Не выявлено в результате поиска и сравнительного анализа технических решений, характеризующихся аналогичной с предлагаемым решением совокупностью признаков, обеспечивающих при использовании достижения аналогичных результатов, что позволяет сделать вывод о соответствии предлагаемого технического решения условию патентоспособности изобретения "изобретательский уровень".
Пример реализации способа.
Предлагаемое техническое решение осуществлено для реальной сейсмичности Байкальского региона следующим образом: сетью сейсмических станций региона осуществляется запись землетрясений, определяются кинематические и динамические параметры толчков, и по этим данным формируется "Каталог землетрясений Прибайкалья". На Фиг. 4 представлена карта эпицентров 52700 представительных землетрясений с магнитудой MLH≥2.5 (энергетический класс KP≥8) и изолиний их плотности в площадках 0.2×0.3°, зарегистрированных в Байкальском регионе с 1964 по 2013 гг. Можно отметить, что землетрясений такого класса регистрируются в пределах региона без пропусков, т.е. являются представительными. Анализ карты показывает, что эпицентры землетрясений локализуются в области БРЗ, за ее пределами сейсмичность рассеяна и минимальна на Сибирской платформе. Изолинии плотности эпицентров в площадках 0.2×0.3° позволяют установить особенности распределения землетрясений по территории БРЗ и выбрать сравнительно однородные районы и участки. По внешнему контуру изолинии n=15 (линия типа "hachure") рифтовую зону можно разделить на три района. На юго-западном фланге БРЗ (район 1, ϕ=48.0-54.0° с.ш., λ=96.0-104.0° в.д.) эпицентры формируют полосы преимущественно субширотной и субмеридиональной ориентировки, в результате чего сейсмичность рассеяна по территории. В центральной части БРЗ (район 2, ϕ=51.0-54.0° с.ш., λ=104.0-113.0° в.д.) эпицентры толчков создают одну широкую полосу северо-восточного простирания. На северо-восточном фланге БРЗ (район 3, ϕ=54.0-60.0° с. ш., λ=109.0-122.0° в.д.) эпицентральное поле землетрясений имеет форму "треугольника", основание которого на западе составляют несколько полос эпицентров северо-восточного и восточного направления, а вершина формируется одной узкой полосой на востоке района. Такие особенности распределения эпицентров землетрясений были изучены методами фрактального анализа [Ключевский А.В., Зуев Ф.Л. Структура поля эпицентров землетрясений Байкальского региона // Доклады Академии наук. 2007. Т. 415. №5. С. 682-687]. Районы разделены пополам по долготе λ=100.0°, λ=108.0° и λ=116.0° на шесть участков, которым даны номера 1-6, начиная отсчет с юго-западной границы региона. Такая схема деления территории региона обычно применяется при исследовании сейсмичности и напряженно-деформированного состояния на трех иерархических уровнях литосферы БРЗ [Ключевский А.В. Напряжения и сейсмичность на современном этапе эволюции литосферы Байкальской рифтовой зоны // Физика Земли. 2007. №12. С. 14-26; Ключевский А.В., Демьянович В.М., Джурик В.И. Иерархия сильных землетрясений Байкальской рифтовой системы // Геология и геофизика. 2009. Т. 50. №3. С. 279-288]. В практике изучения сейсмичности БРЗ мы использовали три размерности - клеточную D0, информационную D1 и корреляционную D2 [Ключевский А.В., Зуев Ф.Л. Исследование динамики сейсмичности в Байкальском регионе // Доклады Академии наук. 2006. Т. 409. №2. С. 248-253; Ключевский А.В., Зуев Ф.Л. Структура поля эпицентров землетрясений Байкальского региона // Доклады Академии наук. 2007. Т. 415. №5. С. 682-687; Ключевский А.В., Зуев Ф.Л. Оценки фрактальной структуры поля эпицентров землетрясений Байкальского региона // Современная геодинамика Центральной Азии и опасные природные процессы: результаты исследований на количественной основе. Иркутск: ИЗК СО РАН, 2012. Т. 2. С. 36-39; Ключевский А.В., Демьянович В.М., Ключевская А.А., Зуев Ф.Л. Соотношение случайной и систематической составляющих сейсмичности в районе Бусийнгольской впадины на юго-западе Байкальской рифтовой зоны // Разломообразование в литосфере и сопутствующие процессы: тектонофизический анализ. Иркутск, ИЗК СО РАН, 2014. С. 109]. Было установлено, что с ростом объема выборки данных размерность D0 возрастает монотонно, слабо реагирует на афтершоки сильных землетрясений и адекватно характеризует структуру распределения эпицентров землетрясений. Размерности D1 и D2 подвержены влиянию афтершоков сильных землетрясений и резко уменьшаются при мощных сериях афтершоков, отражая локализацию эпицентров. Так как используемый нами "Каталог землетрясений Прибайкалья" (http://www.seis-bykl.ru/) не очищен от афтершоков и роевых землетрясений, то при обработке реальных землетрясений в заявке на патент мы используем только клеточную размерность D0. Определения клеточной размерности выполнены с использованием формулы (1) по результатам скейлинга карт эпицентров землетрясений региона, трех районов и шести участков.
На Фиг. 5 результаты определений клеточной размерности эпицентров землетрясений Байкальского региона отражены в виде функций lnN=f(lnr), их линейных аппроксимаций, уравнений корреляционной связи и коэффициентов корреляции. На Фиг. 5а показаны результаты определений в тех пределах размеров r площадок, на которых имеются эпицентры землетрясений. График функции lnN=f(lnr) имеет выпуклый вид: прямолинейная наклонная часть графика на крупных масштабах -2≤lnr≤2 и изогнутая часть при lnr≤-2. Видно, что линейная аппроксимация слабо соответствуют функции lnN=f(lnr), хотя коэффициент корреляции достаточно высок (R~0.963), но значение вычисленной размерности D0≈1.22. На Фиг. 5б результаты представлены только для прямолинейной наклонной части, а уравнение корреляционной связи получено для максимального коэффициента корреляции, т.е. для наилучшего соответствия функции lnN=f(lnr) линейной аппроксимации. Видно, что график линейной аппроксимации близко соответствует функции lnN=f(lnr), максимальный коэффициент корреляции очень высок (R-0.999), а значение показателя самоподобия высоко D0≈1.70. На Фиг. 5в результаты представлены для прямолинейной наклонной части, но до размера минимальной клетки в rk=10 км. Видно, что график линейной аппроксимации достаточно близко соответствует функции lnN=f(lnr), коэффициент корреляции высок (R-0.995), а значение клеточной размерности равно D0≈1.58. Таким образом, использование максимального коэффициента корреляции для определения самоподобия поля эпицентров землетрясений Байкальского региона позволяет значимо уточнить величину показателя самоподобия - отличие показателя самоподобия (Фиг. 5б) от клеточной размерности (Фиг. 5в) существенно превышает 3 стандартных отклонения.
Аналогичные процедуры были осуществлены для выборок землетрясений трех районов и шести участков. В качестве примера на Фиг. 6 результаты определений клеточной размерности поля эпицентров землетрясений района 1 (юго-западный фланг БРЗ) отражены в виде функций lnN=f(lnr), их линейных аппроксимаций, уравнений корреляционной связи и коэффициентов корреляции. На Фиг. 6а представлены результаты определений в пределах размеров площадок, на которых выделяются эпицентры землетрясений. График функции lnN=f(lnr) имеет выпуклый вид: прямолинейна наклонная часть графика на крупных масштабах -2≤lnr≤2 и изогнута часть при lnr≤-2. Видно, что прямая аппроксимации слабо соответствуют графику функции lnN=f(lnr), хотя коэффициент корреляции достаточно высок (R~0.951), но величина D0≈1.20. На Фиг. 6б результаты представлены для прямолинейной наклонной части, а уравнения корреляционной связи получены при максимальном коэффициенте корреляции. Видно, что график линейной аппроксимации близко соответствует функции lnN=f(lnr), максимальный коэффициент корреляции высок (R~0.998), значение показателя самоподобия D0≈1.66. На Фиг. 6в результаты представлены для прямолинейной наклонной части до размера минимальной клетки rk=10 км. Видно, что график линейной аппроксимации достаточно близко соответствует функции lnN=f(lnr), коэффициент корреляции высок (R~0.997), значение размерности равно D0≈1.63 и отличается от показателя самоподобия почти на три стандартных отклонения. Таким образом, использование максимального коэффициента корреляции для оценки самоподобия поля землетрясений района 1 позволяет значимо уточнить величину показателя самоподобия.
На Фиг. 7 результаты анализа распределения эпицентров землетрясений по территории участка 1 (юго-западный фланг БРЗ) отражены в виде функций lnN=f(lnr), их линейной аппроксимации, уравнений корреляционной связи и коэффициентов корреляции. На Фиг. 7а представлены результаты определений в пределах размеров площадок, на которых выделяются эпицентры землетрясений. График зависимости lnN=f(lnr) имеет выпуклый вид: имеется прямолинейная наклонная часть графика на крупных масштабах -2≤lnr≤1 и изогнутая часть при lnr≤-2. Видно, что линия аппроксимации слабо соответствуют функции lnN=f(lnr), хотя коэффициент корреляции достаточно высок (R~0.953), но значение вычисленной размерности D0≈1.17. На Фиг. 7б результаты представлены для прямолинейной наклонной части, а уравнения корреляционной связи получены при максимальном коэффициенте корреляции. Видно, что график линейной аппроксимации близко соответствует функции lnN=f(lnr), максимальный коэффициент корреляции высок (R~0.998), а значение показателя самоподобия D0≈1.65. На Фиг. 7в показаны результаты для прямолинейной наклонной части до размера минимальной клетки rk=10 км. Видно, что график линейной аппроксимации достаточно близко соответствует функции lnN=f(lnr), коэффициент корреляции высок (R~0.997), а размерность равна D0≈1.61 и отличается от показателя самоподобия на уровне трех стандартных отклонений.
Таким образом, на всех трех уровнях иерархии литосферы БРЗ использование максимального коэффициента корреляции для определения самоподобия поля эпицентров землетрясений позволяет значимо уточнить величину показателя самоподобия и получить более точные параметры состояния разломной структуры литосферы.
Чтобы показать, как процесс заполнения эпицентрами землетрясений территории Байкальского региона влияет на определение фрактальной размерности и показателя самоподобия, на Фиг. 8 представлены графики изменения клеточной размерности региона, полученные при использовании ограничения rk=10 км (график 1) и по максимальному значению коэффициента корреляции (график 2). На Фиг. 8 видно, что уровни графиков увеличиваются со временем, отражая процесс заполнения территории Байкальского региона землетрясениями. Графики на Фиг. 8 и их аппроксимация полиномом 6 степени показывают, что первые 5 лет кривая 2 растет быстрее, чем график 1, затем повышение уровня происходит примерно одинаково. На рис. 8 видно, что стандартные отклонения на графике 2 значительно меньше, чем на кривой 1. Следовательно, использование максимального коэффициента корреляции для оценки самоподобия эпицентрального поля землетрясений дает возможность оперативного и более точного определения показателя самоподобия фрактальной структуры поля эпицентров землетрясений региона даже при небольших выборках данных.
Получаемую по предлагаемому техническому решению информацию по контролю состояния разломной структуры литосферы можно использовать для характеристики сейсмической обстановки и опасности на территориях возможного промышленного и гражданского строительства, т.е. предлагаемое решение соответствует условию патентоспособности изобретения "промышленная применимость".
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ОЦЕНКИ ПОГРЕШНОСТИ В ОПРЕДЕЛЕНИИ КООРДИНАТ ЭПИЦЕНТРОВ ЗЕМЛЕТРЯСЕНИЙ СИСТЕМОЙ СЕЙСМИЧЕСКОГО МОНИТОРИНГА | 2017 |
|
RU2660363C1 |
| Способ определения индекса сейсмомиграционной активности в эпицентральном поле сейсмичности | 2018 |
|
RU2698559C1 |
| Способ определения цепочек землетрясений в эпицентральном поле сейсмичности зоны разлома | 2018 |
|
RU2701191C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ПАРАМЕТРОВ СТРУКТУРЫ РАЗЛОМНОЙ ТРЕЩИНОВАТОСТИ ЛИТОСФЕРЫ | 2018 |
|
RU2698551C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ЦЕПОЧЕК ЗЕМЛЕТРЯСЕНИЙ В ЭПИЦЕНТРАЛЬНОМ ПОЛЕ СЕЙСМИЧНОСТИ | 2017 |
|
RU2659334C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ УПРУГИХ ДЕФОРМАЦИЙ В ОЧАГАХ ЗЕМЛЕТРЯСЕНИЙ | 2016 |
|
RU2639267C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ПАРАМЕТРОВ СТРУКТУРЫ РАЗЛОМНОЙ ТРЕЩИНОВАТОСТИ ЛИТОСФЕРЫ | 2016 |
|
RU2625615C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ КИНЕМАТИЧЕСКОГО ТИПА ПОДВИЖЕК В ОЧАГАХ ЗЕМЛЕТРЯСЕНИЙ | 2018 |
|
RU2698549C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ВЕРОЯТНОСТИ ЗЕМЛЕТРЯСЕНИЯ | 2003 |
|
RU2244324C1 |
| Способ определения эффективной глубины заполненного флюидами разлома | 2019 |
|
RU2722971C1 |
Изобретение относится к области сейсмологии и может быть использовано для определения показателя самоподобия поля эпицентров землетрясений. Сущность: на основе полученных экспериментальных материалов пространственное поле эпицентров землетрясений разделяют на сравнительно однородные участки. Разбивают каждый участок на площадки (скейлинг). Строят в двойных логарифмических координатах функцию зависимости количества площадок с землетрясениями от линейного размера площадок. Аппроксимируют функцию прямой линией. Определяют коэффициент корреляции линейной аппроксимации функций. Выбирают диапазон размеров площадок, на котором линейная аппроксимация функции имеет максимальное значение коэффициента корреляции. Показатель самоподобия поля эпицентров землетрясений находят по наклону линейной аппроксимации функции в указанном диапазоне размеров площадок. Технический результат: повышение точности определения показателя самоподобия поля эпицентров землетрясений при ограниченных выборках данных. 8 ил.
Способ определения показателя самоподобия поля эпицентров землетрясений, при котором на основе полученных экспериментальных материалов пространственное поле эпицентров землетрясений разделяют на сравнительно однородные участки, выполняют разбиение каждого участка на площадки (скейлинг), строят в двойных логарифмических координатах функцию зависимости количества площадок с землетрясениями от линейного размера площадок и аппроксимируют функцию прямой линией, отличающийся тем, что определяют коэффициент корреляции линейной аппроксимации функции и выбирают диапазон размеров площадок, на котором линейная аппроксимация функции имеет максимальное значение коэффициента корреляции, а показатель самоподобия поля эпицентров землетрясений находят по наклону линейной аппроксимации функции в этом диапазоне размеров площадок.
| Ф.Л.Зуев, А.В.Ключевский | |||
| Вычислительные аспекты характеристик самоподобия сейсмичности / Вестник ИрГТУ, 2015, N3(98), стр.71-75 | |||
| А.В.Ключевский, Ф.Л.Зуев | |||
| Фрактальные оценки сейсмического процесса в литосфере Байкальского региона / Литосфера, 2011, N1, стр.143-149 | |||
| RU 2160912 C1, 20.12.2000. |
Авторы
Даты
2017-07-17—Публикация
2016-01-28—Подача