Изобретение относится к сейсмологии и может быть использовано для технического контроля системы сейсмического мониторинга по инструментальной регистрации землетрясений и обработке данных.
В настоящее время землетрясения являются основным источником информации о структуре и напряженно-деформированном состоянии литосферы Земли и протекающих в ней геодинамических процессах. Так системой сейсмического мониторинга Байкальского региона ежегодно регистрируются тысячи подземных толчков, информация о которых аккумулируется в "Каталоге землетрясений Прибайкалья". В указанном "Каталоге…" каждый толчок характеризуется пятью основными динамическими (энергетический класс или магнитуда) и кинематическими (координаты гипоцентра и время в очаге) параметрами, определенными по результатам обработки записей землетрясений системой сейсмического мониторинга - сетью из 25 региональных сейсмических станций Байкальского филиала Геофизической службы Сибирского отделения Российской академии наук (БФ ГС СО РАН) (Фиг. 1, треугольники, май 2017 года [http://www.seis-bykl.ru/modules.php?name=Network]). Параметры толчков и их среднеквадратические (стандартные) отклонения вычисляются по статистике определенных на каждой сейсмической станции значений. Низкая плотность и вытянутость сети сейсмических станций вдоль структур Байкальской рифтовой зоны (БРЗ), а также неопределенности скоростной модели литосферы и линейные приближения в распространении сейсмических волн оказывают существенное влияние на точность и погрешность определения координат эпицентров землетрясений Байкальского региона [Golenetsky S.I. Problems of seismicity of the Baikal rift zone // Journal of Geodynamics. 1990. V. 11. P. 293-307]. Имея статус основного источника информации о структуре и динамике состояний литосферы, землетрясения имеют низкую точность определения координат эпицентров землетрясений.
Исследованиями установлено [Sato Y., Skoko D. Optimum Distribution of Seismic Observation Points. II. // Bull, of the Earthquake Research Institute. 1965. V. 43. Pp. 451-457], что погрешности в определении координат эпицентров землетрясений минимизируются, если три сейсмические станции расположены в углах треугольника станций, а две дополнительные станции и эпицентр находятся внутри этого треугольника. Наилучшее определение координат достигается, когда три станции формируют треугольник, четвертая станция расположена на одной из сторон треугольника, а пятая станция приближена к эпицентру. О существенной роли плотности сейсмических станций в определения координат эпицентров толчков говорит такой факт: среднее отклонение эпицентров землетрясений, зарегистрированных редкой сетью региональных сейсмических станций Алтае-Саянского региона и плотной локальной сетью временных станций, установленных для регистрации афтершоков Чуйского землетрясения, составило 17.2 км [Арефьев С.С., Аптекман Ж.Я., Быкова В.В., Матвеев И.В., Михин А.Г., Молотков С.Г., Плетнев К.Г., Погребченко В.В. Очаг и афтершоки Алтайского (Чуйского) землетрясения 2003 года // Физика Земли. 2006. №2. С. 85-96].
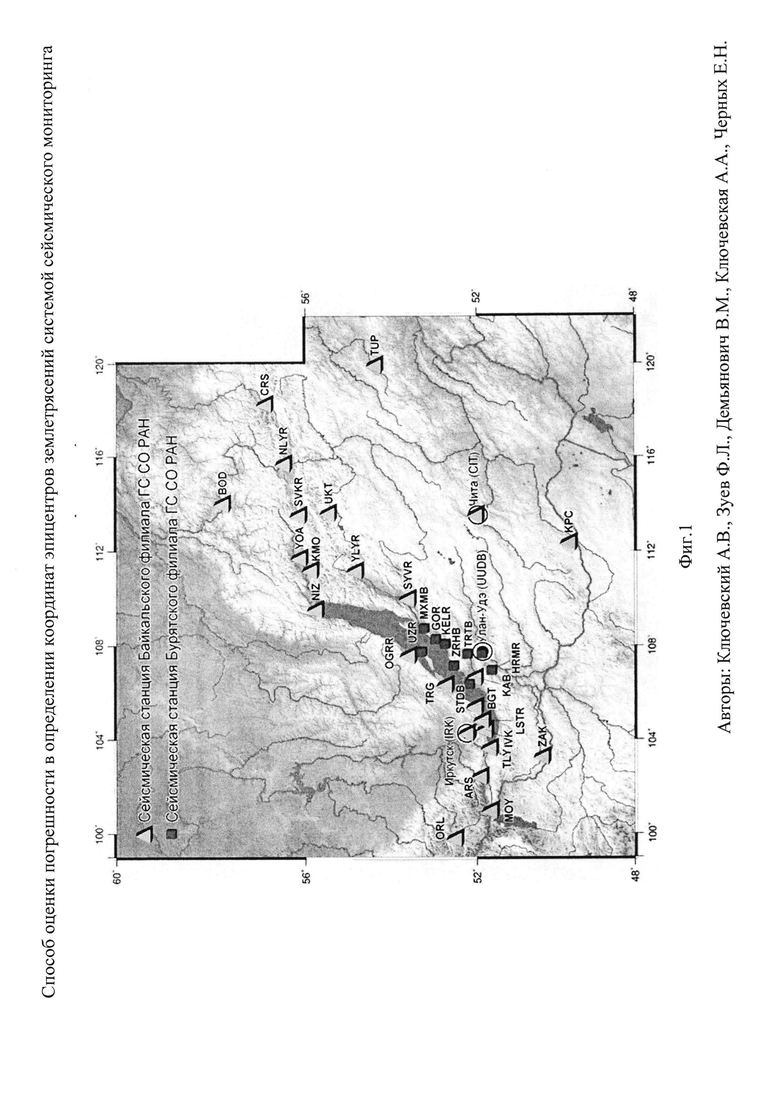
В целом высокая точность в определении координат эпицентров землетрясений может быть достигнута при оптимальной конфигурации плотной сетевой иерархической системы сейсмического мониторинга и хорошо подобранной скоростной модели среды. Мониторинговая система из 25 региональных сейсмических станций БФ ГС СО РАН растянута вдоль БРЗ почти на 2000 км (см. Фиг. 1, треугольники), на Сибирской платформе расположена одна сейсмическая станция "Бодайбо" (сокращенное название на рис. 1 "BOD"), а в Забайкалье - три ("Чита" (CIT), "Тупик (TUP)" и "Хапчеранга (КРС)"). При таком расположении станций координаты эпицентров толчков, происходящих за пределами рифтовой зоны, определяются обычно со значительными стандартными отклонениями, которые формально приняты за меру погрешности в определении координат. Если сопоставить минимальное, среднее и максимальное стандартное отклонение в определении координат эпицентров 735 землетрясений Байкальского региона с энергетическим классом KP≥8, представленных в сборнике "Землетрясения России в 2012 году" [Землетрясения России в 2012 году. Обнинск: ГС РАН, 2014. 224 с.], то можно увидеть отличие более чем на порядок: σmin≈1.4 км, σav≈4.6 км, σmax≈86.3 км соответственно. Гистограмма стандартных отклонений для этой выборки землетрясений имеет близкую к логнормальному распределению форму, с достаточно длинным "хвостом" (Фиг. 2). Для основной массы землетрясений стандартное отклонение варьирует в пределах σ≈2÷5 км, мода распределения равна σmod≈3.6 км. Отсюда следует, что проблема точности и погрешности в определении координат эпицентров землетрясений Байкальского региона (как и многих других сейсмоактивных территорий) пока не решена и требует дополнительных исследований и инновационных разработок.
Точность - одно из понятий логики и методологии науки, характеризующее меру соответствия полученного научного результата и знания реальности, регулирующее процессы и степень достоверности воспроизведения объекта в рамках научной теории. Следует различать точность средства измерений - степень совпадения показаний измерительного прибора с истинным значением измеряемой величины, и точность результата измерений - одну из характеристик качества измерений, отражающую близость к нулю погрешности результата измерений. Точность результата измерений не может быть выше точности средства измерений, но даже при высокой точности измерительного прибора точность результата измерений может быть низкой из-за комплексности его формирования. Погрешность измерения - оценка отклонения измеренного значения величины от ее истинного значения - является мерой точности измерения. Поскольку выяснить с абсолютной точностью истинное значение какой-либо величины невозможно, то и величину отклонения измеренного значения от истинного (погрешность) можно указать только в некотором приближении.
По этим причинам, а также потому, что точность определения координат эпицентров каждого землетрясения зависит от имеющих случайное распределение соотношений входных параметров сейсмических станций и землетрясения, имеется необходимость оценки погрешности в определении координат эпицентров совокупности всех землетрясений, зарегистрированных конкретной системой сейсмического мониторинга. Перед нами стоит задача оценки погрешности в определении координат эпицентров землетрясений, как меры точности инструментальных наблюдений региональной сетью сейсмических станций (например, сети сейсмических станций Байкальского региона за период времени 1964-2013 гг.). Систему мониторинга землетрясений, как и отдельную сейсмическую станцию, можно рассматривать как средство измерения кинематических и динамических параметров очагов землетрясений и производных от них величин. Точность измерений системы мониторинга землетрясений определяется функциональными возможностями и аппаратурным оснащением сейсмических станций, как совокупности отдельных измерительных приборов (как на сейсмической станции: сейсмодатчики, усилители, фильтры, записывающие устройства и пр.). Погрешности при измерениях на станциях могут варьировать в значительных пределах в зависимости от внутренних (эталонов калибровки сейсмографа и вспомогательной аппаратуры, квалификации персонала и пр.) и, особенно, от внешних условий (взаиморасположение станции и эпицентров землетрясений, энергетических классов события, принятой скоростной модели среды и пр.) [Аппаратура и методика сейсмометрических наблюдений в СССР. М.: Наука, 1974. 243 с.]. Погрешность в результатах измерений системы мониторинга землетрясений зависит от плотности, расстановки и чувствительности сейсмических станций и по этой причине может изменяться для различных территорий. Она характеризует точность системы сейсмического мониторинга на исследуемой территории в целом за время наблюдений и является квазиустойчивой величиной. Этим она отличается от погрешностей определения сетью сейсмических станций координат эпицентров отдельных землетрясений, которые имеют стохастический характер, неустойчивый по пространству и времени.
Для оценки погрешности в определении координат эпицентров землетрясений системой сейсмического мониторинга по предлагаемому способу нами используются методы фрактального анализа, позволяющие определить фрактальную размерность и показатель самоподобия пространственной структуры распределения эпицентров землетрясений на поверхности литосферы. Согласно Б. Мандельброту [Мандельброт Б. Фрактальная геометрия природы. М.: ИКИ, 2002. 656 с.], фрактальная размерность, как показатель самоподобия, является фундаментальной характеристикой структуры многих природных объектов. Фрактальные объекты обладают масштабной инвариантностью, или скейлингом (scaling), когда части объекта подобны целому, и обычно характеризуются фрактальной размерностью (как показателем самоподобия), которая выражается нецелым числом. Изменение структуры фрактального объекта влечет за собой изменение фрактальной размерности и обычно имеет объясняемую физическую или техническую причину. Так, изменения фрактальной размерности при переходе от полных к ограниченным выборкам данных об эпицентрах землетрясений объясняется разной степенью заполнения фракталами (землетрясениями) структуры объекта (поверхности литосферы), что приводит к отличию от показателя самоподобия сейсмичности [Ключевский А.В., Зуев Ф.Л., Ключевская А.А. Способ определения показателя самоподобия поля эпицентров землетрясений. Патент на изобретение №2625627. Заявка №2016102935. Приоритет изобретения 28 января 2016 г.].
Установлено, что распределение эпицентров землетрясений самоподобно на исследуемых масштабных уровнях [Садовский М.А., Голубева Т.В., Писаренко В.Ф., Шнирман М.Г. Характерные размеры горной породы и иерархические свойства сейсмичности // Физика Земли. 1984. №2. С. 3-15]. В БРЗ самоподобие эпицентрального поля землетрясений подтверждено в работе [Солоненко А.В., Штейман Е.А. Самоподобие поля сейсмичности Байкальского рифта // Доклады РАН. 1994. Т. 337. №2. С. 253-257]. Величина фрактальной размерности поля эпицентров землетрясений лежит в пределах 1≤D<2: значение 1 указывает на цельную, упорядоченную структуру среды без разрывов-землетрясений, промежуточное значение - на частично разрушенную разрывами среду, значения, приближающиеся к 2, указывают на сильно разрушенную среду. Таким образом, фрактальные размерности распределения эпицентров землетрясений позволяют количественно охарактеризовать структуру расположения землетрясений на территории, что дает возможность использования размерности для целей мониторинга и технического контроля состояния разломной структуры литосферы [Ключевский А.В., Зуев Ф.Л., Ключевская А.А. Способ определения показателя самоподобия поля эпицентров землетрясений. Патент на изобретение №2625627. Заявка №2016102935. Приоритет изобретения 28 января 2016 г.].
Способы определения фрактальной размерности однотипны - это масштабирование с последующей параметризацией степенного распределения результатов скейлинга в виде линейной аппроксимации в билогарифмической системе координат.
Аналогом является способ определения фрактальной размерности поверхности твердого электрода (патент RU 2436069), содержащий этапы на которых:
- выполняют электрорастворение осажденной монослойной пленки малорастворимого вещества на поверхности,
- регистрируют количество вещества, образующего монослой, используют молекулы малорастворимого неорганического вещества,
- рассчитывают количество вещества в монослое и площади поверхности электрода, занимаемой одной молекулой осажденного на электроде вещества,
- строят в логарифмических координатах зависимость количества вещества в монослое от площади поверхности электрода, занимаемой одной молекулой осажденного вещества,
- по тангенсу угла наклона аппроксимации полученной зависимости прямой линией судят о величине фрактальной размерности.
Недостатки решения: произвольность выбора диапазона скейлинга площади поверхности электрода, что приводит к снижению точности, неоднозначности и множественности решения и, как следствие, к ограниченности технологических возможностей использования данного решения.
Аналогом применения фрактальной размерности в сейсмологии является способ прогнозирования параметров землетрясений (Патент RU 2255356).
В способе-аналоге измеряют характеристики магнитного Н и электрического Е полей околоземного космического пространства раздельными датчиками, установленными на космическом аппарате, на восходящем и нисходящем витках. Формируют синтезированную Н×Е матрицу измерений и вычисляют дисперсию σ2 результирующего вектора R и его фрактальную размерность D. Отслеживают изменение фрактальной размерности до серии измерений. Определяют начальные условия отслеживаемого процесса, постоянную времени Т и установившееся значение D0. Прогнозируют параметры землетрясения: время удара ty=4.7T, магнитуду lg ty[сут]≅0.54M-3.37 и гипотетический центр как точку пересечения векторов R нисходящего и восходящего витков.
Недостатком данного решения следует считать:
- неопределенность типа магнитуды М прогнозируемого землетрясения;
- неоднозначность разбиения синтезированной Н×Е матрицы измерений, что понижает точность и приводит к некорректности решения.
Наиболее близким по технической сущности (прототипом) является способ определения показателя самоподобия поля эпицентров землетрясений (Патент RU 2625627).
В способе-прототипе на основе экспериментальных материалов пространственное поле эпицентров представительных землетрясений разделяют на сравнительно однородные участки. Выполняют разбиение каждого участка на площадки (скейлинг). Строят в двойных логарифмических координатах функцию количества площадок с землетрясениями от линейного размера площадок и аппроксимируют функцию прямой линией. Определяют коэффициент корреляции линейной аппроксимации функции и выбирают диапазон размеров площадок, на котором линейная аппроксимация имеет максимальное значение коэффициента корреляции. По наклону линейной аппроксимации функции в этом диапазоне размеров площадок определяют показатель самоподобия поля эпицентров землетрясений.
Недостатком способа-прототипа являются неопределенности выделения однородных участков полей эпицентров землетрясений, искажающие числовые характеристики фрактальной размерности в пограничных областях.
Задачей предлагаемого изобретения является устранение вышеуказанных недостатков. Решение задачи заявляемым способом направлено на оценку погрешности в определении координат эпицентров землетрясений системой сейсмического мониторинга.
Поставленная задача решается предлагаемым способом оценки погрешности в определении координат эпицентров землетрясений системой сейсмического мониторинга, при котором строят карту распределения эпицентров землетрясений по территории исследуемого региона, карту распределения эпицентров землетрясений территории разбивают на площадки уменьшающихся размеров, строят в двойных логарифмических координатах функцию количества площадок с землетрясениями от линейного размера площадок, аппроксимируют функцию прямой линией, выделяют диапазон размеров площадок с максимальным коэффициентом корреляции линейной аппроксимации функции, при этом в выделенном диапазоне определяют размер площадок, на котором линейная аппроксимация имеет локальный максимум коэффициента корреляции, фиксируют этот размер как погрешность определения координат эпицентров землетрясений системой сейсмического мониторинга.
Иными словами, по заявленному способу строят карту распределения эпицентров землетрясений по территории исследуемого региона и выполняют скейлинг карты. Получают в двойных логарифмических координатах функцию количества площадок с землетрясениями от линейного размера площадок и аппроксимируют эту функцию прямой линией. Выделяют диапазон размеров площадок, на котором линейная аппроксимация функции имеет максимальное значение коэффициента корреляции. В этом диапазоне определяют размер площадок, при котором линейная аппроксимация имеет локальный максимум коэффициента корреляции. Фиксируют этот размер как погрешность определения координат эпицентров землетрясений системой сейсмического мониторинга.
Технический результат: повышение точности определения координат эпицентров землетрясений системой сейсмического мониторинга.
Изобретение поясняется чертежами, где показано:
Фиг. 1. Расположение сейсмических станции на территории Байкальского региона [http://www.seis-bykl.ru/modules.php?name=Network]).
Фиг. 2. Гистограмма стандартных отклонений в определении координат эпицентров землетрясений с энергетическим классом KP≥8, зарегистрированных в Байкальском регионе за 2012 г.
Исходные данные для построения гистограммы получены по материалам работы [Землетрясения России в 2012 году. Обнинск: ГС РАН, 2014. 224 с.].
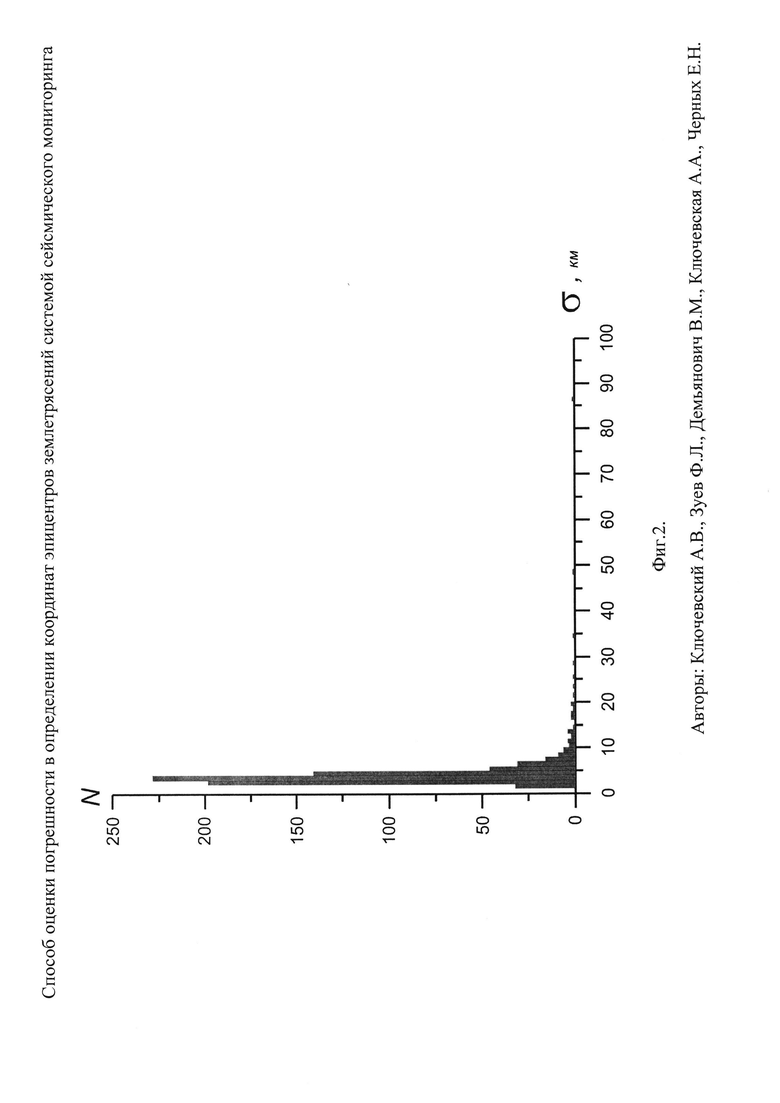
Фиг. 3. Фрактальная структура "снежинка Коха" в масштабе Байкальского региона для 16384 точек-эпицентров синтезированных "землетрясений" (разряд 14, 214=16384) и в масштабе юго-западного фланга БРЗ:
а. Распределение точек-эпицентров синтезированных "землетрясений" на территории Байкальского региона;
б. Распределение точек-эпицентров синтезированных "землетрясений" на территории юго-западного фланга БРЗ.
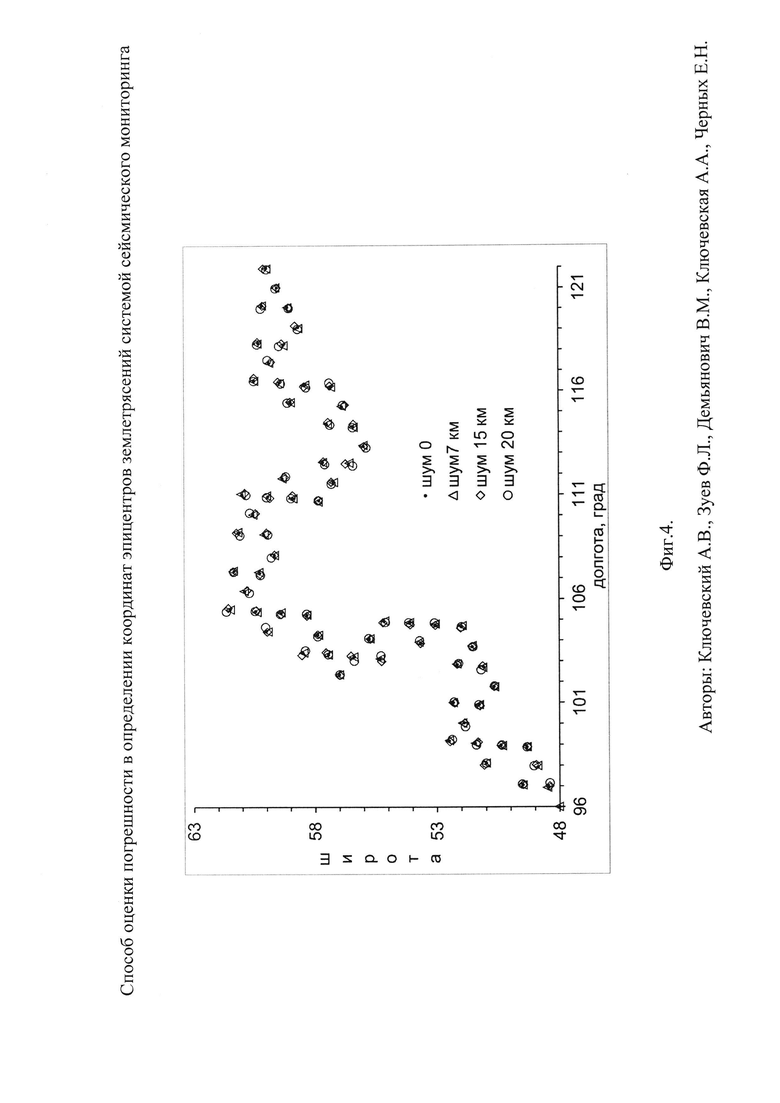
Фиг. 4. Фрактальная структура "снежинка Коха" в масштабе Байкальского региона для 64 точек-эпицентров синтезированных "землетрясений" (разряд 6, 26=64) при разных значениях "координатного шума": "Шум 0" - идеальная самоподобная структура "снежинка Коха"; "Шум 7" - точки-эпицентры смещены относительно положения "Шум 0" на 7 км в случайно выбранном с постоянной плотностью вероятности в диапазоне 0÷360 градусов азимуте;
"Шум 15" - точки-эпицентры смещены относительно положения "Шум 0" на 15 км в случайно выбранном с постоянной плотностью вероятности в диапазоне 0÷360 градусов азимуте;
"Шум 20" - точки-эпицентры смещены относительно положения "Шум 0" на 20 км в случайно выбранном с постоянной плотностью вероятности в диапазоне 0÷360 градусов азимуте.
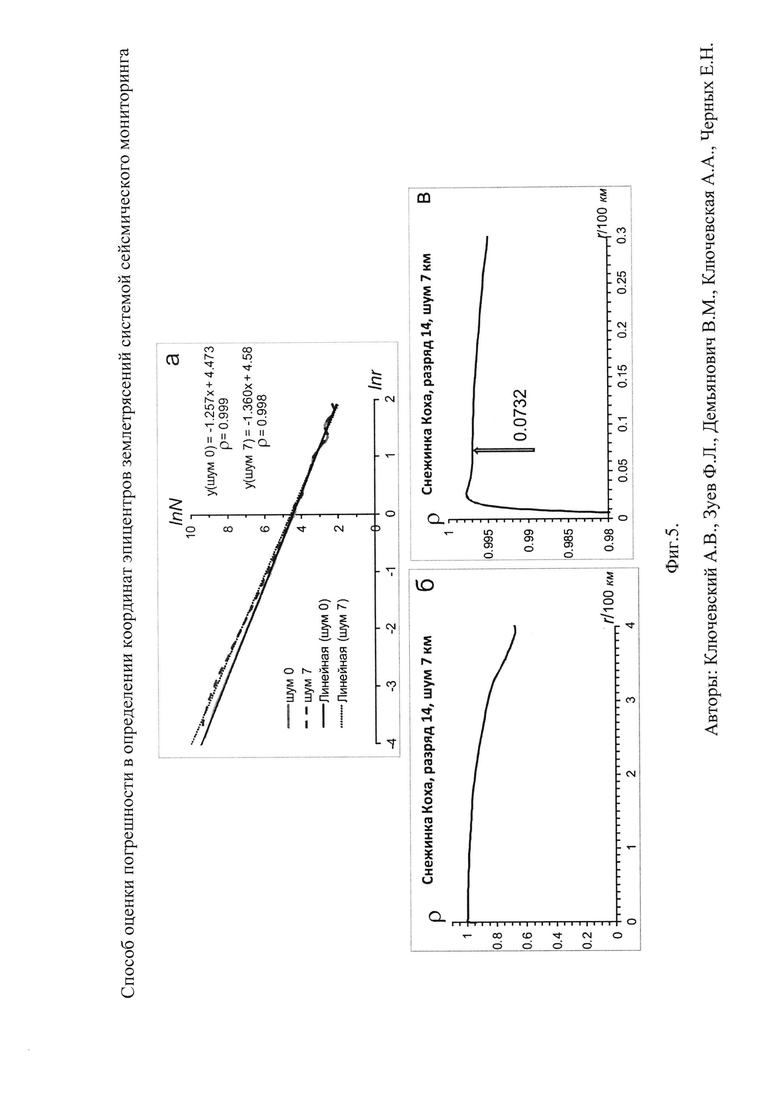
Фиг. 5. Результаты скейлинга фрактальной структуры "снежинка Коха" для образа "Шум 7":
а. Результаты скейлинга для образа "Шум 0" и "Шум 7" отражены в виде функций lnN=ƒ[lnr) и линейной аппроксимации функций. Для каждого образа приведены уравнения корреляционной связи и коэффициенты корреляции ρ;
б. График изменения коэффициента корреляции ρ линейной аппроксимации функции lnN=ƒ(lnr) в широком диапазоне размеров площадок r (0.7÷400 км), полученный для образа "Шум 7";
в. Детальный график изменения коэффициента корреляции ρ линейной аппроксимации функции lnN=ƒ(lnr) в узком диапазоне размеров площадок r (0.7÷30 км), полученный для образа "Шум 7". Стрелкой показано положение локального максимума ρ при размере площадки r≈7.3 км.
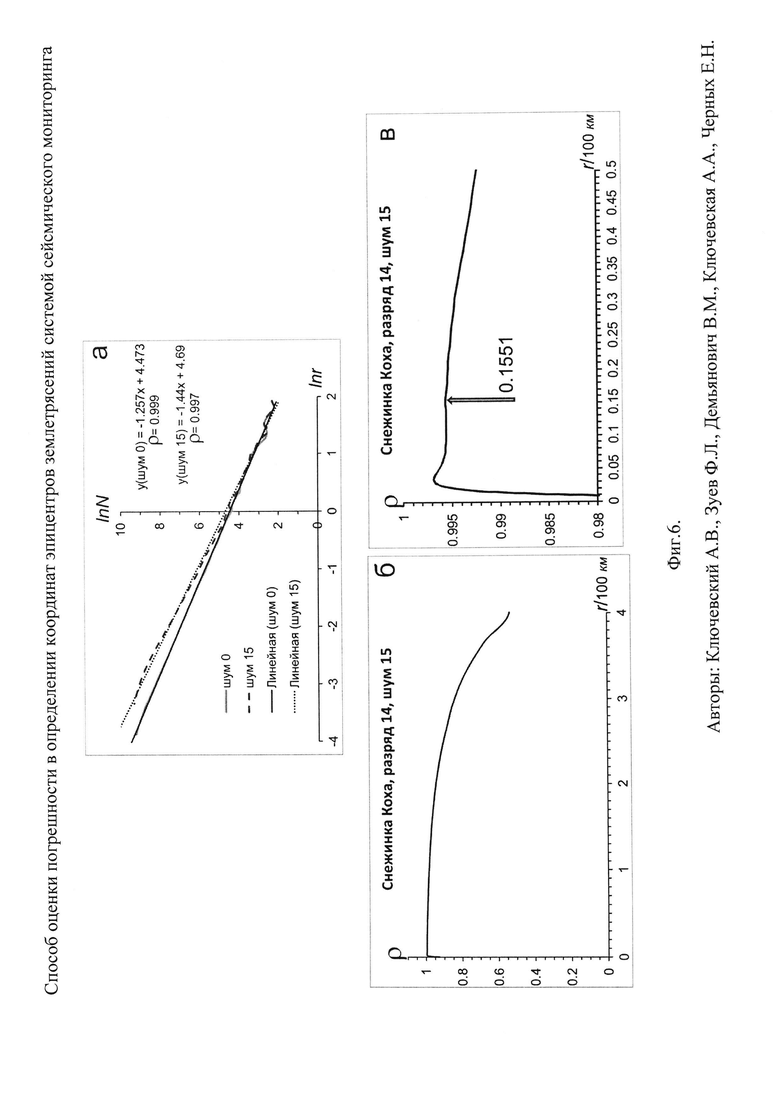
Фиг. 6. Результаты скейлинга фрактальной структуры "снежинка Коха" для образа "Шум 15":
а. Результаты скейлинга для образа "Шум 0" и "Шум 15" отражены в виде функций lnN=ƒ(lnr) и линейной аппроксимации функций. Для каждого образа приведены уравнения корреляционной связи и коэффициенты корреляции ρ;
б. График изменения коэффициента корреляции ρ линейной аппроксимации функции lnN=ƒ(lnr) в широком диапазоне размеров площадок r (0.8÷400 км), полученный для образа "Шум 15";
в. Детальный график изменения коэффициента корреляции линейной аппроксимации функции lnN=ƒ(lnr) в узком диапазоне размеров площадок r (0.8÷50 км), полученный для образа "Шум 15". Стрелкой показано положение локального максимума ρ при размере площадки r≈15.5 км.
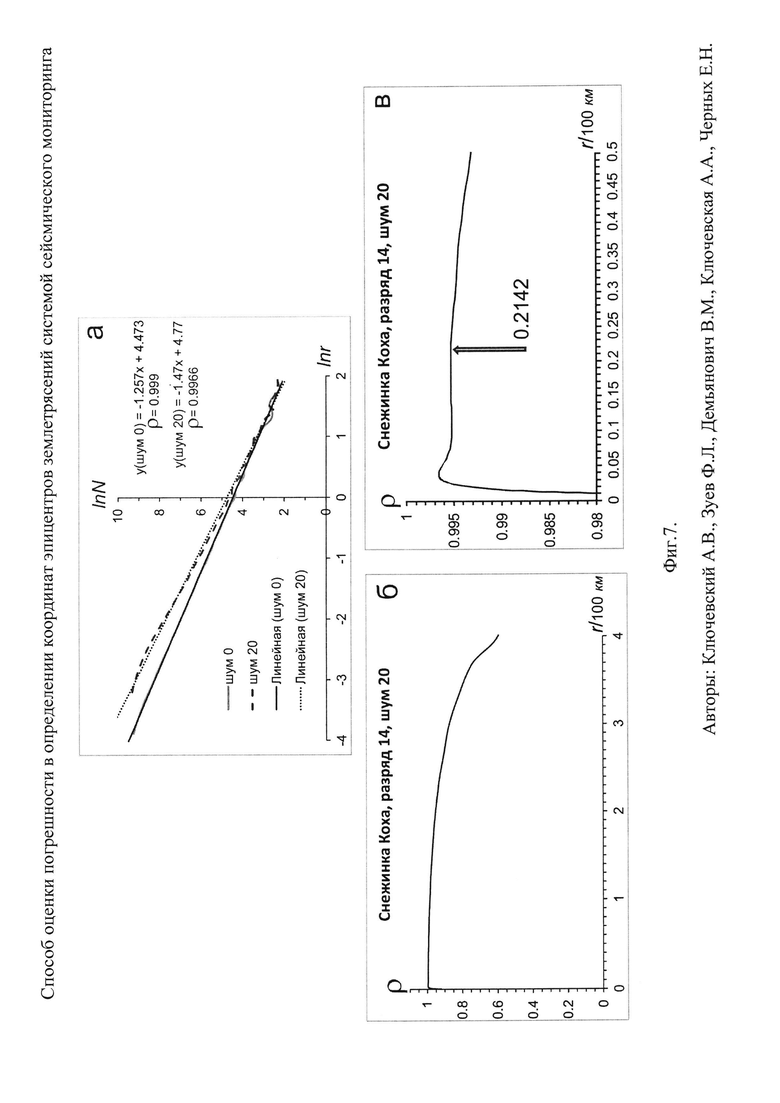
Фиг. 7. Результаты скейлинга фрактальной структуры "снежинка Коха" для образа "Шум 20":
а. Результаты скейлинга для образа "Шум 0" и "Шум 20" отражены в виде функций lnN=ƒ(lnr) и линейной аппроксимации функций. Для каждого образа приведены уравнения корреляционной связи и коэффициенты корреляции ρ;
б. График изменения коэффициента корреляции ρ линейной аппроксимации функции lnN=ƒ(lnr) в широком диапазоне размеров площадок r (1+400 км), полученный для образа "Шум 20";
в. Детальный график изменения коэффициента корреляции ρ линейной аппроксимации функции lnN=ƒ(lnr) в узком диапазоне размеров площадок r (1÷50 км), полученный для образа "Шум 20". Стрелкой показано положение локального максимума ρ при размере площадки r≈21.4 км.
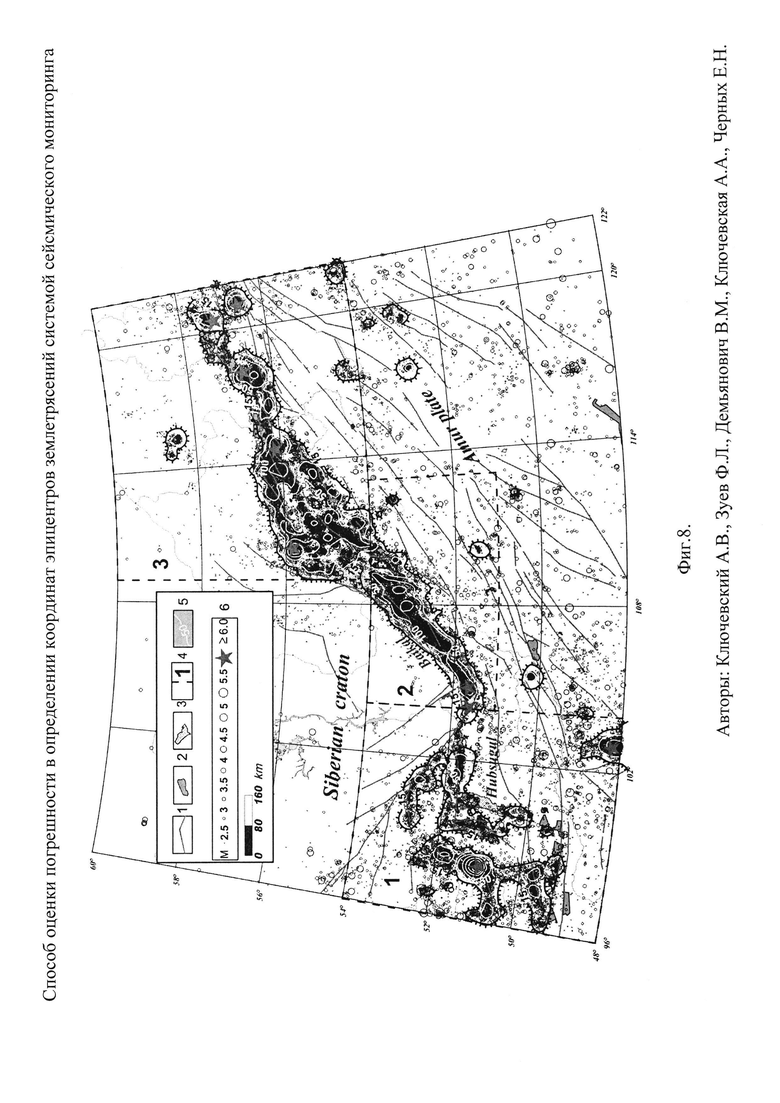
Фиг. 8. Карта эпицентров и изолиний плотности эпицентров землетрясений Байкальского региона (1964-2013 гг.):
1 - разломы, 2 - впадины, 3 - озера, 4 - границы и номера районов, 5 -изолинии плотности эпицентров, 6 - эпицентры землетрясений с магнитудой MLH≥2.5 (энергетический класс KP≥8).
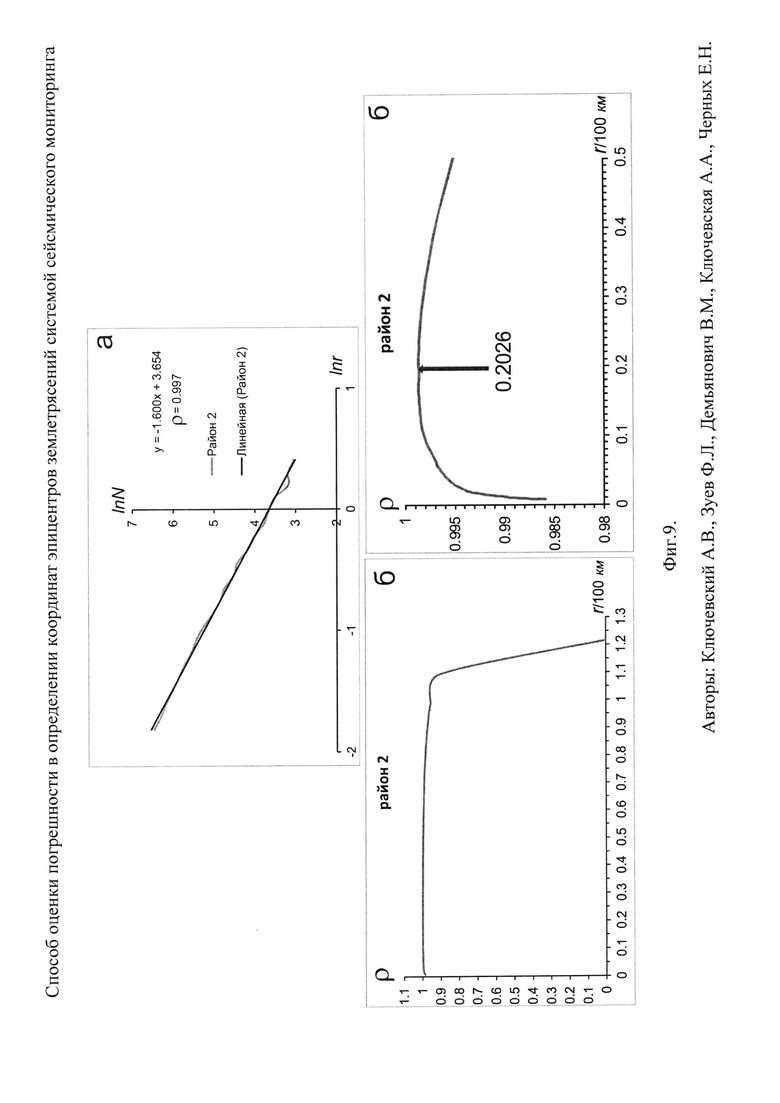
Фиг. 9. Результаты скейлинга фрактальной структуры землетрясений района 2:
а. Результаты скейлинга отражены в виде функции lnN=ƒ(lnr) и линейной аппроксимации функции. Приведено уравнение корреляционной связи и коэффициент корреляции ρ;
б. График изменения коэффициента корреляции ρ линейной аппроксимации функции lnN=ƒ(lnr) в широком диапазоне размеров площадок r (1÷120 км);
в. Детальный график изменения коэффициента корреляции ρ линейной аппроксимации функции lnN=ƒ(lnr) в узком диапазоне размеров площадок r (1÷50 км). Стрелкой показано положение локального максимума ρ при размере площадки r≈20.3 км.
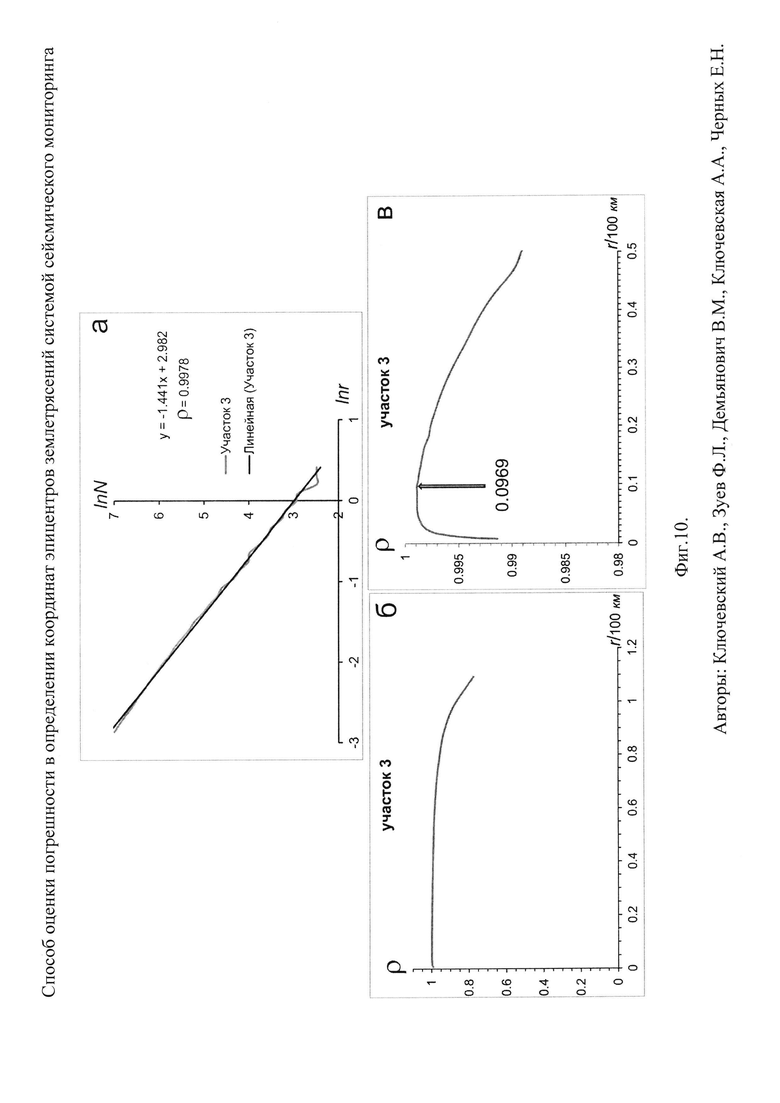
Фиг. 10. Результаты скейлинга фрактальной структуры землетрясений участка 3:
а. Результаты скейлинга отражены в виде функции lnN=ƒ(lnr) и линейной аппроксимации функции. Приведено уравнение корреляционной связи и коэффициент корреляции ρ;
б. График изменения коэффициента корреляции ρ линейной аппроксимации функции lnN=ƒ(lnr) в широком диапазоне размеров площадок r (1÷120 км);
в. Детальный график изменения коэффициента корреляции ρ линейной аппроксимации функции lnN=ƒ(lnr) в узком диапазоне размеров площадок r (1÷50 км). Стрелкой показано положение локального максимума ρ при размере площадки r≈8.7 км.
Техническая сущность способа состоит в следующем.
В основе предлагаемого способа лежит фундаментальное свойство самоподобных объектов - масштабная инвариантность в плотно заполненном фракталами объекте. Для оценки погрешности использован метод, техническая суть которого заключается в том, что ошибки в определении координат эпицентров создают локальное искажение структуры самоподобного распределения эпицентров землетрясений и приводят к нарушению естественного закона самоподобия в монофрактальном распределении эпицентров землетрясений. Выделяемое нами локальное искажение структуры эпицентрального поля землетрясений обусловлено наличием "координатного шума", который приводит к разбросу координат эпицентров толчков около величины погрешности системы мониторинга землетрясений. Эта погрешность определяется нами как размер площадки, при котором формируется локальный максимум коэффициента корреляции линейной аппроксимации функции lnN=ƒ(lnr).
Согласно Б. Мандельброту [Мандельброт Б. Фрактальная геометрия природы. М: ИКИ, 2002. 656 с.], клеточная размерность D0 характеризует самоподобие исследуемого объекта в определенном интервале масштабов - от максимального, близкого к размеру самого объекта, до минимального размера площадки, при котором самоподобие исчезает по техническим или естественным причинам. В задаче оценки самоподобия поля эпицентров землетрясений минимальный размер площадки технически обусловлен количеством используемых толчков (из-за ограниченного времени сейсмического мониторинга часто не хватает землетрясений для заполнения площадок минимального размера) и разбросом координат эпицентров землетрясений (погрешностью определения), технически обусловленным ошибками системы мониторинга землетрясений. Если количество землетрясений позволяет плотно заполнить площадки (зависимость lnN=ƒ(lnr) линейно возрастает на всем диапазоне площадок), тогда погрешности в определении координат эпицентров землетрясений будут приводить к локальному искажению монофрактального самоподобного распределения. Для решения задачи определения погрешности нужно найти локальный максимум коэффициента корреляции линейного в двойном логарифмическом масштабе распределения занятых землетрясениями площадок n от величины размера площадки r (функции lnN=ƒ(lnr)) и присвоить данному размеру статус погрешности системы сейсмического мониторинга.
При определении клеточной размерности распределения эпицентров землетрясений на поверхности Земли форма и размер максимальной первой площадки обычно соответствуют таковым территории исследования. Например, при исследовании эпицентров землетрясений Байкальского региона они соответствуют территории, ограниченной координатами мониторинга землетрясений сетью сейсмических станций Прибайкалья (ϕ=48.0°-60.0° с.ш., λ=96.0°-122.0° в.д.). Размер минимальной площадки задается исходя из физических соображений величиной средней погрешности определения координат эпицентров землетрясений. В Байкальском регионе эта погрешность обычно принимается априори равной 10 км, таковы и размеры минимальной площадки (r=10 км) [Sherman S.I., Gladkov A.S. Fractals in studies of faulting and seismicity in the Baikal rift zone // Tectonophysics. 1999. V. 308. P. 133-142; Ключевский A.B., Зуев Ф.Л. Структура поля эпицентров землетрясений Байкальского региона // Доклады Академии наук. 2007. Т. 415. №5. С. 682-687]. Однако плотность сейсмических станций, от которой зависит в целом погрешность определения координат эпицентров землетрясений, меняется по территории - наиболее высока плотность станций в центральной части БРЗ (см. Фиг. 1), но на флангах она понижается. Возникающие при этом различия в погрешности определения координат эпицентров землетрясений и, следовательно, разные величины возможных размеров минимальных площадок при скейлинге, создают неоднозначности и понижают точность определения клеточной размерности. Устранение недостатков определения показателя самоподобия, имеющих место из-за неполноты выборки данных в поле эпицентров землетрясений, осуществлено в изобретении по патенту №2625627 [Ключевский А.В., Зуев Ф.Л., Ключевская А.А. Способ определения показателя самоподобия поля эпицентров землетрясений. Патент на изобретение №2625627. Заявка №2016102935. Приоритет изобретения 28 января 2016 г.]. Ниже представлено решение задачи оценки погрешности в определении координат эпицентров землетрясений системой сейсмического мониторинга по предлагаемому способу, полученное для модельного и реального примеров.
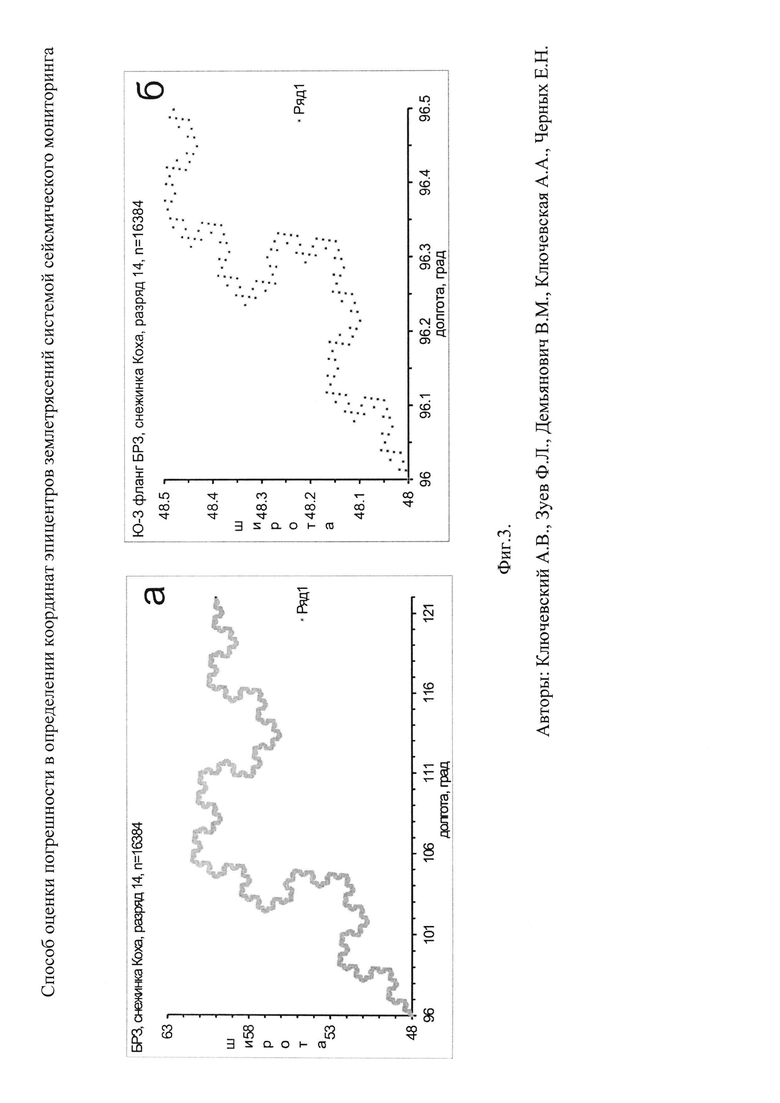
Модельный пример. В качестве модельного примера приведем результаты оценки погрешности в синтезированном поле точек-эпицентров "землетрясений" для классической монофрактальной самоподобной структуры "снежинка Коха", клеточная размерность которой, как и показатель самоподобия, равна D0≈1.26. Такая структура достаточно близко соответствует паттерну распределения эпицентров землетрясений вдоль БРЗ. Синтезирование толчков проведено для территории Байкальского региона, а расчеты клеточной (Хаусдорфа) размерности выполнены по формуле
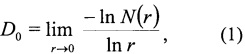
где n(r) - количество непустых, содержащих хотя бы одну точку, площадок сетки с длиной стороны r, накрывающей изучаемое множество. Геометрический смысл этой метрики - показатель изменения покрываемой множеством области в зависимости от единицы измерения и характерного масштаба. Алгоритм вычисления достаточно прост. На множество накладываются сетки с последовательно уменьшающимся размером площадки rk. В билогарифмической системе координат функция lnN=ƒ(lnr) аппроксимируется прямой линией по методу наименьших квадратов, а среднеквадратичное отклонение берется как оценка погрешности метода.
Нужно отметить, что условие плотного заполнения клеток эпицентрами должно выполняться с перекрытием величины погрешности определения координат, иначе размеры погрешности просто не попадут в диапазон функции lnN=ƒ(lnr) (будут за пределами интервала размеров площадок, используемых для определения клеточной размерности D0). Поэтому на Фиг. 3,а представлена структура самоподобного фрактала "снежинка Коха", построенная в масштабе Байкальского региона по 16384 синтезированным точкам-эпицентрам "землетрясений" (разряд 14, 214=16384 точки), при которой минимальные размеры "координатного шума" (см. ниже "шум 7 км") попали в интервал размеров площадок, используемых для определения клеточной размерности D0. Для выборок меньших объемов эта величина не попала в нужный интервал размеров площадок. На Фиг. 3а детали распределения точек-эпицентров не наблюдаются, видны только общие контуры. Поэтому мы изменили масштаб и привели небольшой участок (0.5°×0.5°) юго-западного фланга БРЗ (Фиг. 3,б). На нем отчетливо повторяются детали самоподобного фрактала структуры "снежинка Коха", заполненной достаточно полно, но с видимым разделение точек-эпицентров.
В эту структуру распределения синтезированных точек-эпицентров "землетрясений" были внесены изменения (добавлен "координатный шум"), в результате которого положение точек-эпицентров изменилось. Каждому синтезированному "землетрясению" были приписаны новые координаты точек-эпицентров. Новые координаты точек-эпицентров задавались следующим образом (см. Фиг. 4):
1. "Новая точка-эпицентр" располагалась на расстоянии L от координат "старой точки-эпицентра" (структуры идеального самоподобного фрактала "снежинка Коха", "шум 0 км") в случайно выбранном с постоянной плотностью вероятности в диапазоне 0÷360 градусов азимуте;
2. Расстояние L задавалось в трех вариантах определений величинами:
1. L1=1 км ("шум 7 км");
2. L2=15 км ("шум 15 км");
3. L3=20 км ("шум 20 км").
Таким образом, при L1=l км смещение "новых эпицентров" относительно старых ("шум 0") осуществлялось по случайно выбранным азимутам на 7 км. Аналогично, для L2=15 км и L3=20 км смещение "новых эпицентров" относительно старых ("шум 0") выполнено на 15 и 20 км соответственно. Такое изменение выбрано потому, что оно достаточно близко отражает локальность максимума гистограммы стандартных отклонений на Фиг. 2 и соответствует стандартным погрешностям в определении координат эпицентров землетрясений Байкальского региона. В качестве картины внесения "координатного шума" на Фиг. 4 представлены координаты синтезированных точек-эпицентров 64 событий структуры "снежинка Коха" для четырех вариантов распределений - "шум 0" (без шума), "шум 7" (L1=7 км), "шум 15" (L2=15 км) и "шум 20" (L3=20 км). Небольшое количество использованных событий (64 точки) позволяет хорошо визуализировать изменения положения эпицентров: видно, что с ростом L смещение маркеров от положения "шум 0" увеличивается.
На Фиг. 5,а результаты скейлинга для образа "шум 0" и "шум 7" отражены в виде функций lnN=ƒ(lnr) и линейной аппроксимации функций в полном диапазоне размеров площадок r. Для каждого образа приведены уравнения корреляционной связи и коэффициенты корреляции ρ. Видно, что внесение шума значительно изменяет клеточную размерность: из D0≈1.257 ("шум 0") она трансформировалась в D0≈1.360 ("шум 7"). Также немного понизился коэффициент корреляции. На Фиг. 5,б представлен график изменения коэффициента корреляции ρ линейной аппроксимации функции lnN=ƒ(lnr) в широком диапазоне размеров площадок r (0.7÷400 км), полученный для образа "шум 7". В этом диапазоне размеров виден монотонный рост коэффициента корреляции с уменьшением размеров площадки и резкое падение при минимальных размерах площадки. На Фиг. 5,в график изменения коэффициента корреляции ρ линейной аппроксимации функции lnN=ƒ(lnr) показан увеличено и детально в узком диапазоне минимальных размеров площадок r (0.7÷30 км). В этом диапазоне установлен локальный максимум при размере площадки r≈7.3 км, на который показывает стрелка. Как мы видим, размер этой площадки почти совпадает со значением внесенного "координатного шума" в 7 км.
На Фиг. 6,а результаты скейлинга для образа "шум 0" и "шум 15" отражены в виде функций lnN=ƒ(lnr) и линейной аппроксимации функций в полном диапазоне размеров площадок r. Как и в предыдущем случае, для каждого образа приведены уравнения корреляционной связи и коэффициенты корреляции ρ. Также видно, что внесение шума значительно изменяет клеточную размерность: из D0≈1.257 ("шум 0") она трансформировалась в D0≈1.44 ("шум 15") и немного понизился коэффициент корреляции. На Фиг. 6,б представлен график изменения коэффициента корреляции ρ линейной аппроксимации функции lnN=ƒ(lnr) в широком диапазоне размеров площадок r (0.8÷400 км) для образа "шум 15". Виден монотонный рост коэффициента корреляции с уменьшением размеров площадки и резкое падение при минимальных размерах площадки. На Фиг. 6,в график изменения коэффициента корреляции показан увеличено и детально в узком диапазоне минимальных размеров площадок r (0.8÷50 км) для образа "шум 15". В этом диапазоне локальный максимум установлен при размере площадки r≈15.5 км, на который показывает стрелка. Видно, что размер этой площадки почти совпадает со значением внесенного "координатного шума" в 15 км.
На Фиг. 7,а результаты скейлинга для образа "шум 0" и "шум 20" отражены в виде функций lnN=ƒ(lnr) и линейной аппроксимации функций в полном диапазоне размеров площадок r. Для каждого образа приведены уравнения корреляционной связи и коэффициенты корреляции ρ. Видно, что внесение шума значительно изменяет клеточную размерность: из D0≈1.257 ("шум 0") она трансформировалась в D0≈1.47 ("шум 20"). Также немного понизился коэффициент корреляции. На Фиг. 7,б представлен график изменения коэффициента корреляции линейной аппроксимации функции lnN=ƒ(lnr) в широком диапазоне размеров площадок r (1÷400 км) для образа "шум 20". Виден монотонный рост коэффициента корреляции с уменьшением размеров площадки и резкое падение при минимальных размерах площадки. На Фиг. 7,в график изменения коэффициента корреляции показан увеличено и детально в узком диапазоне минимальных размеров площадок r (1÷50 км) для образа "шум 20". В этом диапазоне установлен локальный максимум при размере площадки r≈21.4 км, на который показывает стрелка. Видно, что размер площадки близко соответствует значению внесенного "координатного шума" в 20 км.
Таким образом, проведенные расчеты показывают, что в модельных фрактальных структурах величина внесенного "координатного шума" однозначно определяется по размеру площадки, которому соответствует локальный максимум коэффициента корреляции линейной аппроксимации функции lnN=ƒ(lnr). Имеющееся небольшое различие "координатного шума" и выделенных размеров площадки обусловлено тем, что шаг скейлинга в этом диапазоне размеров площадки немного превышает один километр. Полученные результаты дают теоретическое обоснование для применения способа к оценке погрешности в определении координат эпицентров реальных землетрясений системой сейсмического мониторинга.
Сравнение предлагаемого технического решения с другими известными решениями в области сейсмологии показывает следующее.
Проблема точности и оценки погрешностей в определении координат эпицентров землетрясений является одной из наиболее сложных в сейсмологической практике. В имеющихся публикациях международных и национальных служб, а также отдельных авторов, такие оценки либо отсутствуют, либо в качестве таковых приводятся величины среднеквадратичной погрешности определения координат эпицентров землетрясений. Последние рассчитываются при решении системы уравнений, основанной на соответствии наблюденных времен пробега сейсмических волн теоретическим, полученным при заданной скоростной модели среды. Было показано, что подобные оценки не отражают реальной погрешности определения эпицентра землетрясения, а указывают лишь на меру сходимости данных [Aichele Н., Gorbunova I.V., Kondorskaya N.V. et al. Improvements of seismogram readings of standard and array processing and determination of main foci parameters (on the basis of selected EUROPEAN earthquakes). Recent seismological investigations in Europe. M.: Nayka. 1988. P. 344-353]. Если учесть, что во многих случаях малая величина среднеквадратичной погрешности является следствием отбраковки данных отдельных станций (как правило, близких к эпицентру), то приводимые оценки погрешностей определения положения эпицентров и, в особенности глубин землетрясений, в международных и национальных публикациях оказываются неоправданно заниженными. Это обстоятельство приводит к целому ряду ошибок при использовании полученных таким образом оценок для геолого-геофизической интерпретации и практической реализации [Кондорская Н.В., Горбунова И.В., Киреев И.А., Вандышева Н.В. О составлении унифицированного каталога сильных землетрясений Северной Евразии по инструментальным данным (1901-1990 гг.)// Сейсмичность и сейсмическое районирование Северной Евразии, Вып. 1. М.: ИФЗ РАН. 1993. С. 70-79].
Большинство известных решений по определению фрактальной размерности основаны на ограничении скейлинга величиной погрешности в определении координат эпицентров землетрясений [Голубева Т.В., Писаренко В.Ф., Шнирман М.Г. Самоподобие сейсмических процессов в пространстве // Современные геофизические исследования. Ч. 1. М.: ИФЗ АН, 1993. С. 61-69; Потанина М.Г., Смирнов В.Б., Бернар П. Особенности сейсмической роевой активности в Коринфском рифте в 2000-2005 гг.// Физика Земли. 2011. №7. С. 54-66; Ключевский А.В., Зуев Ф.Л. Структура поля эпицентров землетрясений Байкальского региона // Доклады Академии наук. 2007. Т. 415. №5. С. 682-687]. Однако погрешность в определении координат зависит от числа сейсмических станций, использованных в расчетах координат землетрясений данной территории, и может изменяться как во времени, так и в пространстве, поскольку не все сейсмические станции этой территории могут быть использованы по техническим или другим причинам. Следовательно, введение априори заданного предела скейлинга, равного погрешности, не позволяет соотнести этот теоретический предел с реальным пределом, формируемым пространственно-временными факторами мониторинга. В этом аспекте возникает ассоциация с понятием представительного энергетического класса землетрясений, широко применяемым в сейсмологии [Ризниченко Ю.В. Проблемы сейсмологии. М.: Наука, 1985. 405 с.]. Под этим термином понимается энергетический класс землетрясений, которые учитываются в энергетической составляющей сейсмического мониторинга и регистрируются данной системой "без существенных пропусков". Погрешности в определении координат эпицентров землетрясений системой сейсмического мониторинга характеризуют пространственную составляющую сейсмического мониторинга - точность определения координат землетрясений, которые регистрируются данной системой "без существенных разбросов".
Недостатки применяемых методов:
- не учитываются пространственно-временные вариации реальной погрешности в определении координат эпицентров землетрясений;
- априори принято, что поле эпицентров землетрясений заполнено и самоподобно сформировано в полном диапазоне размеров клеток.
Предлагаемый способ позволяет исключить эти недостатки, обеспечивает решение и позволяет оценить погрешности в определении координат эпицентров землетрясений системой сейсмического мониторинга.
Не выявлено в результате поиска и сравнительного анализа технических решений, характеризующихся аналогичной с предлагаемым решением совокупностью признаков, обеспечивающих при использовании достижения аналогичных результатов, что позволяет сделать вывод о соответствии предлагаемого технического решения условию патентоспособности изобретения "изобретательский уровень".
Пример реализации способа
Предлагаемое техническое решение осуществлено для реальной сейсмичности Байкальского региона следующим образом: сетью сейсмических станций региона осуществляется запись землетрясений, определяются кинематические и динамические параметры толчков, и по этим данным формируется "Каталог землетрясений Прибайкалья". На Фиг. 8 представлена карта эпицентров 52700 представительных землетрясений с магнитудой MLH≥2.5 (энергетический класс KP≥8) и изолиний их плотности в площадках 0.2°×0.3°, зарегистрированных в Байкальском регионе с 1964 по 2013 г. Можно отметить, что землетрясений такого класса регистрируются в пределах региона без пропусков, т.е. являются представительными. Анализ карты показывает, что эпицентры землетрясений локализуются в области БРЗ, за ее пределами сейсмичность рассеяна и минимальна на Сибирской платформе. Изолинии плотности эпицентров в площадках 0.2°×0.3° позволяют установить особенности распределения землетрясений по территории БРЗ. По внешнему контуру изолинии n=15 (линия типа "hachure") рифтовую зону можно разделить на три района. На юго-западном фланге БРЗ (район 1, ϕ=48.0°-54.0° с.ш., λ=96.0°-104.0° в.д.) эпицентры формируют полосы преимущественно субширотной и субмеридиональной ориентировки, в результате чего сейсмичность рассеяна по территории. В центральной части БРЗ (район 2, ϕ=51.0°-54.0° с.ш., λ=104.0°-113.0° в.д.) эпицентры толчков создают одну широкую полосу северо-восточного простирания. На северо-восточном фланге БРЗ (район 3, ϕ=54.0°-60.0° с.ш., λ=109.0°-122.0° в.д.) эпицентральное поле землетрясений имеет форму "треугольника", основание которого на западе составляют несколько полос эпицентров северо-восточного и восточного направления, а вершина формируется одной узкой полосой на востоке района. Районы разделены пополам по долготе λ=100.0°, λ=108.0° и λ=116.0° на шесть участков, которым даны номера 1-6, начиная отсчет с юго-западной границы региона. Такая схема деления территории региона обычно применяется при исследовании сейсмичности и напряженно-деформированного состояния на трех иерархических уровнях литосферы БРЗ [Ключевский А.В. Напряжения и сейсмичность на современном этапе эволюции литосферы Байкальской рифтовой зоны // Физика Земли. 2007. №12. С. 14-26; Ключевский А.В., Демьянович В.М., Джурик В.И. Иерархия сильных землетрясений Байкальской рифтовой системы // Геология и геофизика. 2009. Т. 50. №3. С. 279-288]. В практике изучения сейсмичности БРЗ мы использовали три размерности - клеточную D0, информационную D1 и корреляционную D2 [Ключевский А.В., Зуев Ф.Л. Исследование динамики сейсмичности в Байкальском регионе // Доклады Академии наук. 2006. Т. 409. №2. С. 248-253; Ключевский А.В., Зуев Ф.Л. Структура поля эпицентров землетрясений Байкальского региона // Доклады Академии наук. 2007. Т. 415. №5. С. 682-687; Ключевский А.В., Зуев Ф.Л. Оценки фрактальной структуры поля эпицентров землетрясений Байкальского региона // Современная геодинамика Центральной Азии и опасные природные процессы: результаты исследований на количественной основе. Иркутск: ИЗК СО РАН, 2012. Т. 2. С. 36-39; Ключевский А.В., Демьянович В.М., Ключевская А.А., Зуев Ф.Л. Соотношение случайной и систематической составляющих сейсмичности в районе Бусийнгольской впадины на юго-западе Байкальской рифтовой зоны // Разломообразование в литосфере и сопутствующие процессы: тектонофизический анализ. Иркутск, ИЗК СО РАН, 2014. С. 109]. Было установлено, что с ростом объема выборки данных размерность D0 возрастает монотонно, слабо реагирует на афтершоки сильных землетрясений и адекватно характеризует структуру распределения эпицентров землетрясений. Так как используемый нами "Каталог землетрясений Прибайкалья" [http://www.seis-bykl.ru/] не очищен от афтершоков и роевых землетрясений, то при обработке реальных землетрясений в заявке на патент мы используем только клеточную размерность D0. Определения клеточной размерности выполнены с использованием формулы (1) по результатам скейлинга карт эпицентров землетрясений региона, трех районов и шести участков.
Следует отметить, что в некоторых территориях (как и при модельных построениях) локальные максимумы на графиках изменения коэффициента корреляции ρ линейной аппроксимации функции lnN=ƒ(lnr) не выделяются. Это обусловлено тем, что в пределах этих территорий имеются незаполненные землетрясениями площадки, размеры которых превышают погрешности определения эпицентров толчков. В этом случае локальный максимум не успевает сформироваться (не достигается размер площадок, соответствующий погрешностям в определении координат), имеется только общий максимум, отражающий размеры площадок минимальных размеров, в которых произошли землетрясения. На Фиг. 8 видно, что плотность распределения толчков по территории Байкальского региона неоднородна, на территории региона, первого, третьего районов, первого, второго, четвертого и шестого участков имеются существенные пробелы в распределении эпицентров землетрясений, преимущественно за пределами рифтовой зоны (Сибирская платформа, Забайкалье). Тем не менее, во втором районе, третьем и пятом участках при построениях нам удалось выделить локальные максимумы на графиках изменения коэффициента корреляции ρ линейной аппроксимации функции lnN=ƒ(lnr)). На этих территориях количество зарегистрированных землетрясений и их распределение удовлетворяет условию плотного заполнения площадок, имеющих размеры меньше погрешности в определении координат эпицентров.
На Фиг. 9 результаты определения клеточной размерности эпицентров землетрясений района 2 отражены в виде функции lnN=ƒ(lnr) и ее линейной аппроксимации, уравнения корреляционной связи и коэффициента корреляции ρ. Видно, что функция lnN=ƒ(lnr) хорошо аппроксимируется линейной зависимостью, коэффициент корреляции высок, а величина клеточной размерности равна D0≈1.60. На Фиг. 9,б представлен график изменения коэффициента корреляции ρ линейной аппроксимации функции lnN=ƒ(lnr) в широком диапазоне размеров площадок r (1÷120 км). В этом диапазоне размеров видно резкое повышение ρ при r≈110 км, затем следует монотонный рост коэффициента корреляции с уменьшением размеров площадки и достаточно резкое падение при минимальных размерах площадки. На Фиг. 9,в график изменения коэффициента корреляции ρ линейной аппроксимации функции lnN=ƒ(lnr) показан увеличено и детально в узком диапазоне минимальных размеров площадок r (1÷50 км). В этом диапазоне установлен локальный максимум при размере площадки r≈20.3 км, на который показывает стрелка. Таким образом, погрешность в определении координат эпицентров землетрясений района 2 системой сейсмического мониторинга Байкальского региона за время инструментальной регистрации с 1964 по 2013 г. равна примерно 20 км.
На Фиг. 10 результаты определения клеточной размерности эпицентров землетрясений участка 3 отражены в виде функции lnN=ƒ(lnr) и ее линейной аппроксимации, уравнения корреляционной связи и коэффициента корреляции ρ. Видно, что функция lnN=ƒ(lnr) хорошо аппроксимируется линейной зависимостью, коэффициент корреляции высок, а величина клеточной размерности равна D0≈1.44. На Фиг. 10,б представлен график изменения коэффициента корреляции ρ линейной аппроксимации функции lnN=ƒ(lnr) в широком диапазоне размеров площадок r (1÷110 км). В этом диапазоне размеров видно повышение ρ при r≈105 км, затем следует монотонный рост коэффициента корреляции с уменьшением размеров площадки и достаточно резкое падение при минимальных размерах площадки. На Фиг. 10,в график изменения коэффициента корреляции ρ линейной аппроксимации функции lnN=ƒ(lnr) показан увеличено и детально в узком диапазоне минимальных размеров площадок r (1÷50 км). В этом диапазоне установлен локальный максимум при размере площадки r≈9.7 км, на который показывает стрелка. Таким образом, погрешность в определении координат эпицентров землетрясений участка 3 системой сейсмического мониторинга Байкальского региона за время инструментальной регистрации с 1964 по 2013 г. равна примерно 10 км. Уменьшение величины погрешности на участке 3 обусловлено, очевидно, расположением здесь дополнительно локальной сети сейсмических станций Бурятского филиала ГС СО РАН (см. Фиг. 1, квадраты).
Аналогичные построения показали, что величина погрешности в определении координат эпицентров землетрясений участка 5 системой сейсмического мониторинга Байкальского региона за время инструментальной регистрации с 1964 по 2013 г. равна примерно 11 км. Это объясняется тем, что с 1977 г. по середину 1990-х гг. здесь функционировала локальная сеть сейсмических станций Северо-Муйского сейсмологического полигона, которая повысила точность регистрации землетрясений [Ангараканский рой землетрясений в Байкальской рифтовой зоне. Новосибирск: Наука, 1987. 81 с.; Аниканова Г.В., Боровик Н.С. Новые данные о глубинах очагов землетрясений Прибайкалья // Геология и геофизика. 1981. №2. С. 157-161].
Для остальных территорий имеющиеся данные пока не позволяют осуществить оценку погрешностей. Можно отметить, что в настоящее время предельный размер минимальной площадки в Байкальском регионе равен 31 км, в районе 1-14 км, в районе 3-27 км, в участке 1-15 км, в участке 2-18 км, в участке 4-20 км, в участке 6-16 км. В лучшем случае, погрешности в определении координат эпицентров землетрясений этих территорий системой сейсмического мониторинга Байкальского региона за время инструментальной регистрации с 1964 по 2013 г. не превышают этих значений.
Получаемую по предлагаемому техническому решению информацию по контролю системы сейсмического мониторинга можно использовать для характеристики сейсмической обстановки и опасности на территориях возможного промышленного и гражданского строительства, т.е. предлагаемое решение соответствует условию патентоспособности изобретения "промышленная применимость".
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ОПРЕДЕЛЕНИЯ ПОКАЗАТЕЛЯ САМОПОДОБИЯ ПОЛЯ ЭПИЦЕНТРОВ ЗЕМЛЕТРЯСЕНИЙ | 2016 |
|
RU2625627C1 |
| Способ определения индекса сейсмомиграционной активности в эпицентральном поле сейсмичности | 2018 |
|
RU2698559C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ЦЕПОЧЕК ЗЕМЛЕТРЯСЕНИЙ В ЭПИЦЕНТРАЛЬНОМ ПОЛЕ СЕЙСМИЧНОСТИ | 2017 |
|
RU2659334C1 |
| Способ определения цепочек землетрясений в эпицентральном поле сейсмичности зоны разлома | 2018 |
|
RU2701191C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ПАРАМЕТРОВ СТРУКТУРЫ РАЗЛОМНОЙ ТРЕЩИНОВАТОСТИ ЛИТОСФЕРЫ | 2016 |
|
RU2625615C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ВЕРОЯТНОСТИ ЗЕМЛЕТРЯСЕНИЯ | 2003 |
|
RU2244324C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ПАРАМЕТРОВ СТРУКТУРЫ РАЗЛОМНОЙ ТРЕЩИНОВАТОСТИ ЛИТОСФЕРЫ | 2018 |
|
RU2698551C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ УПРУГИХ ДЕФОРМАЦИЙ В ОЧАГАХ ЗЕМЛЕТРЯСЕНИЙ | 2016 |
|
RU2639267C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ КИНЕМАТИЧЕСКОГО ТИПА ПОДВИЖЕК В ОЧАГАХ ЗЕМЛЕТРЯСЕНИЙ | 2018 |
|
RU2698549C1 |
| ГЛОБАЛЬНАЯ СИСТЕМА ОПРЕДЕЛЕНИЯ ВЕРОЯТНОСТИ ПРЕДСТОЯЩЕГО ЗЕМЛЕТРЯСЕНИЯ | 2003 |
|
RU2247412C2 |
Изобретение относится к области сейсмологии и может быть использовано для оценки погрешности при определении координат эпицентров землетрясений. Сущность: строят карту распределения эпицентров землетрясений на территории исследуемого региона. Разбивают полученную карту на площадки уменьшающихся размеров. Строят в двойных логарифмических координатах функцию зависимости количества площадок с землетрясениями от линейного размера площадок. Аппроксимируют указанную функцию прямой линией. Выделяют диапазон размеров площадок с максимальным коэффициентом корреляции линейной аппроксимации функции. В выделенном диапазоне определяют размер площадок, на котором линейная аппроксимация имеет локальный максимум коэффициента корреляции. Фиксируют указанный размер площадок как погрешность определения координат эпицентров землетрясений системой сейсмического мониторинга. Технический результат: повышение точности определения координат эпицентров землетрясений. 10 ил.
Способ оценки погрешности в определении координат эпицентров землетрясений системой сейсмического мониторинга, при котором строят карту распределения эпицентров землетрясений по территории исследуемого региона, карту распределения эпицентров землетрясений территории разбивают на площадки уменьшающихся размеров, строят в двойных логарифмических координатах функцию количества площадок с землетрясениями от линейного размера площадок, аппроксимируют функцию прямой линией, выделяют диапазон размеров площадок с максимальным коэффициентом корреляции линейной аппроксимации функции, отличающийся тем, что в выделенном диапазоне определяют размер площадок, на котором линейная аппроксимация имеет локальный максимум коэффициента корреляции, и фиксируют этот размер как погрешность определения координат эпицентров землетрясений системой сейсмического мониторинга.
| СПОСОБ ОПРЕДЕЛЕНИЯ ПОКАЗАТЕЛЯ САМОПОДОБИЯ ПОЛЯ ЭПИЦЕНТРОВ ЗЕМЛЕТРЯСЕНИЙ | 2016 |
|
RU2625627C1 |
| А.В.Ключевский, Ф.Л.Зуев | |||
| Оценки показателя самоподобия поля эпицентров землетрясений Байкальского региона / Сборник трудов конференции "Геодинамическая эволюция литосферы Центрально-Азиатского подвижного пояса (от океана к континенту)", г | |||
| Иркутск: Институт земной коры Сибирского отделения РАН, 2016, стр.112, 113. | |||
Авторы
Даты
2018-07-05—Публикация
2017-09-11—Подача