Изобретение относится к области волоконной оптики и может быть использовано при создании волоконно-оптических гироскопов и других фазовых интерферометрических датчиков физических величин, построенных по схеме интерферометра Саньяка.
Общая структурная схема волоконно-оптического гироскопа (ВОГ) с закрытым контуром описана в ряде патентов (патент РФ №2444704, МПК G01С 19/72, от 26.10.2010, патент РФ №2522147, МПК G01С 19/64, от 13.11.2012). Для реализации предлагаемого способа повышения точности пригодны любые ВОГ компенсационного типа, содержащие схему формирования ступенчатого модулирующего фазового сигнала.
Известен способ модуляции сигнала волоконно-оптического гироскопа с закрытым контуром, обеспечивающий повышение точности работы прибора по сравнению с волоконно-оптическогим гироскопом с открытым контуром, где в качестве вспомогательного сигнала используют фазовый квадратурный сигнал (Pavlath G.A. Closed-loop fiber optic gyros. SPIE v. 2837, 1996, pp. 46-60). Для расширения динамического диапазона измерения угловых скоростей и получения высокой линейности выходной характеристики ВОГ в оптоэлектронной схеме обработки сигнала применяют компенсационный метод: одновременно с напряжением вспомогательной фазовой модуляции подают компенсирующее разность фаз Саньяка пилообразное ступенчатое напряжение. При достижении пилообразным сигналом границы диапазона фазовой модуляции сигнал сбрасывают на величину напряжения, эквивалентную фазовой разности между интерферирующими лучами, равной 2π радиан, тем самым обеспечивая расширение динамического диапазона. Перепад уровня сигнала на фотоприемном устройстве в момент сброса сигнала фазовой модуляции используют в качестве сигнала обратной связи для компенсации отклонений величины масштабного коэффициента (МК) путем подстройки коэффициента усиления генератора модулирующего сигнала.
Одним из недостатков известного способа является зависимость эффективности алгоритма стабилизации значения масштабного коэффициента от величины сигнала вращения. Недостаток объясняется тем, что различным угловым скоростям ВОГ соответствуют различные углы наклона пилообразного ступенчатого сигнала компенсации. Временной интервал между моментами сброса сигнала модуляции, а значит и моментами получения сигнала обратной связи, также зависит от угловой скорости, что может привести к дестабилизации МК при малых скоростях вращения.
Наиболее близким к предлагаемому и принятым за прототип является способ повышения точности устройств на основе кольцевого интерферометра Саньяка (патент US №5141316, МПК G01C 19/72, опубл. 25.08.1992). Суть известного способа состоит в следующем: сигнал представляет собой последовательность уровней длительностью 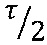 , где - собственное время контура. Исходную форму сигнала Фm на модулирующем устройстве подбирают таким образом, чтобы сигнал фазовой разности лучей на интерферометре имел следующую форму: нечетные по счету уровни должны содержать квадратурную модуляцию с амплитудами ±Ф0, четные - с амплитудами ±aФ0, причем:
, где - собственное время контура. Исходную форму сигнала Фm на модулирующем устройстве подбирают таким образом, чтобы сигнал фазовой разности лучей на интерферометре имел следующую форму: нечетные по счету уровни должны содержать квадратурную модуляцию с амплитудами ±Ф0, четные - с амплитудами ±aФ0, причем:
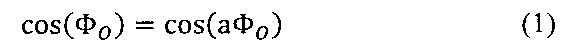
В этом случае линейные комбинации Хр и Хg выходных уровней х1…х4, последовательно регистрируемых на фотоприемном устройстве, помимо информации о величине невзаимного фазового сдвига, будут содержать также информацию об эффективности фазовой модуляции:
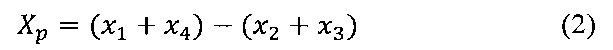
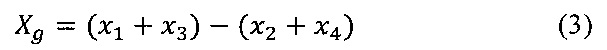
Как и в случае использования квадратурной модуляции с длительностью уровня τ (Pavlath G.A. Closed-loop fiber optic gyros. SPIE v. 2837, 1996, pp. 46-60), предлагаемый в прототипе подход позволяет регистрировать величину фазового сдвига Саньяка с периодом τ, в то время как проблему, связанную с дестабилизацией масштабного коэффициента на малых скоростях, решают за счет включения в модулирующий сигнал вспомогательного сигнала постоянной частоты, предназначенного для оценки величины отклонения МК, и соответствующей подстройки коэффициента усиления генератора модулирующего сигнала.
Недостатком прототипа является то, что при формировании предлагаемой в прототипе фазоразностной последовательности с использованием серродинной модуляции (Pavlath G.A. Closed-loop fiber optic gyros. SPIE v. 2837, 1996, pp. 46-60) на модулирующем устройстве с диапазоном фазовой модуляции -π…+π радиан возможно возникновение режима, при котором х1=х4 и х2=х3, поэтому вычисление величины Хg (3) приводит к получению нулевого результата даже при наличии погрешности масштабного коэффициента. Другими словами, предложенный в прототипе способ модуляции в некоторых режимах фактически приводит к временному размыканию дополнительного контура обратной связи, что, в свою очередь, может стать причиной накопления погрешности масштабного коэффициента и снижения точности измерительной системы.
Изобретение решает задачу повышения точности выходного сигнала волоконно-оптического гироскопа за счет устранения зависимости частоты формирования вспомогательного сигнала, предназначенного для оценки отклонения величины масштабного коэффициента, от величины текущей угловой скорости ВОГ, устранения зависимости величины указанного вспомогательного сигнала от величины действующего на ВОГ углового ускорения, что позволяет использовать приборы, в которых реализован предлагаемый в заявке способ, в условиях жестких динамических нагрузок и исключения возможности возникновения режимов вращения ВОГ, нарушающих работу алгоритма стабилизации масштабного коэффициента
Поставленная задача решается следующим образом. Путем подачи на фазовый модулятор ступенчатого импульсного сигнала напряжения формируют модулирующий фазовый сигнал, состоящий из двух чередующихся последовательностей 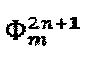 и
и 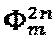 , каждая из которых включает в себя уровни длительностью
, каждая из которых включает в себя уровни длительностью  , где τ - время обхода оптоволоконного контура, m - именной индекс, указывающий на использование сигнала в качестве модуляционного, n - порядковый номер уровня в общем модулирующем фазовом сигнале, являющимся суперпозицией двух указанных чередующихся последовательностей, в обозначенных последовательностях чередуют сигнал компенсации фазового сдвига Саньяка
, где τ - время обхода оптоволоконного контура, m - именной индекс, указывающий на использование сигнала в качестве модуляционного, n - порядковый номер уровня в общем модулирующем фазовом сигнале, являющимся суперпозицией двух указанных чередующихся последовательностей, в обозначенных последовательностях чередуют сигнал компенсации фазового сдвига Саньяка 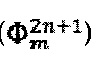 и вспомогательный диагностический сигнал
и вспомогательный диагностический сигнал 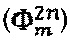 , вызывающие соответственно интерференционные отклики
, вызывающие соответственно интерференционные отклики 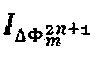 и
и 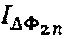 , регистрацией которых на фотоприемном устройстве и их последующей демодуляцией получают, соответственно, величину действующей на прибор угловой скорости и сигнал ошибки, с помощью которого оценивают величину отклонения масштабного коэффициента и стабилизируют его значение путем замыкания дополнительного контура обратной связи. В последовательности
, регистрацией которых на фотоприемном устройстве и их последующей демодуляцией получают, соответственно, величину действующей на прибор угловой скорости и сигнал ошибки, с помощью которого оценивают величину отклонения масштабного коэффициента и стабилизируют его значение путем замыкания дополнительного контура обратной связи. В последовательности 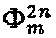 , содержащей вспомогательный диагностический сигнал, его отдельные отсчеты формируют как дискретизированные на интервале τ значения гармонической функции с амплитудой С' и частотой
, содержащей вспомогательный диагностический сигнал, его отдельные отсчеты формируют как дискретизированные на интервале τ значения гармонической функции с амплитудой С' и частотой 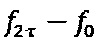 , где
, где 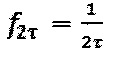 - собственная частота гироскопа и
- собственная частота гироскопа и 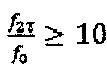 , а регистрируемый на фотоприемном устройстве соответствующий интерференционный отклик
, а регистрируемый на фотоприемном устройстве соответствующий интерференционный отклик 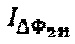 имеет полигармоническую структуру. Демодуляцию полученного интерференционного отклика
имеет полигармоническую структуру. Демодуляцию полученного интерференционного отклика 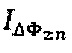 осуществляют следующим образом: на основе зарегистрированного значения
осуществляют следующим образом: на основе зарегистрированного значения 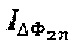 вычисляют дополнительный сигнал
вычисляют дополнительный сигнал  путем умножения последовательных дискретных отсчетов отклика
путем умножения последовательных дискретных отсчетов отклика 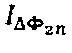 на значения последовательности {1, -1,1, -1,1, …}, из полученных сигналов
на значения последовательности {1, -1,1, -1,1, …}, из полученных сигналов 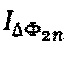 и
и 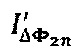 выделяют, соответственно, мгновенные значения
выделяют, соответственно, мгновенные значения 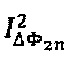 и
и  амплитуд первых двух четных спектральных компонент с частотами 2ƒ0 и 4ƒ0 и мгновенные значения
амплитуд первых двух четных спектральных компонент с частотами 2ƒ0 и 4ƒ0 и мгновенные значения 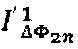 и
и 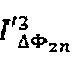 амплитуд первых двух нечетных спектральных компонент с частотами ƒ0 и 3ƒ0, затем формируют сигнал ошибки ΔFB, величину которого вычисляют по формуле
амплитуд первых двух нечетных спектральных компонент с частотами ƒ0 и 3ƒ0, затем формируют сигнал ошибки ΔFB, величину которого вычисляют по формуле 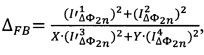 где
где 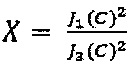 ,
, 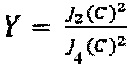 , где
, где 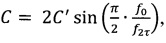 JN - функция Бесселя первого рода N-го порядка.
JN - функция Бесселя первого рода N-го порядка.
Сущность заявляемого способа поясняется следующим: сигнал фазовой модуляции содержит в себе две чередующиеся последовательности  и
и 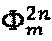 , каждая из которых содержит в себе уровни длительностью
, каждая из которых содержит в себе уровни длительностью  .
.
Уровни 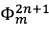 формируют на основании базового уровня пилообразного сигнала с предыдущей итерации
формируют на основании базового уровня пилообразного сигнала с предыдущей итерации 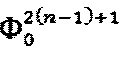 , величины сигнала обратной связи
, величины сигнала обратной связи 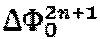 , а также сигнала квадратурной сдвигающей модуляции ±Фb.
, а также сигнала квадратурной сдвигающей модуляции ±Фb.
Уровни 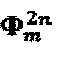 формируются при помощи дискретизации на интервале τ гармонической функции с амплитудой С' и частотой
формируются при помощи дискретизации на интервале τ гармонической функции с амплитудой С' и частотой 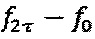 , где
, где 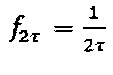 - собственная частота гироскопа, и
- собственная частота гироскопа, и 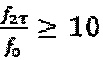 . Зависимость величины уровня от его порядкового номера в последовательности приводится в формуле 1.
. Зависимость величины уровня от его порядкового номера в последовательности приводится в формуле 1.
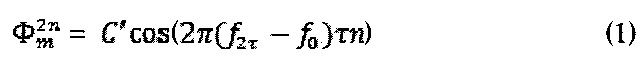
Результатом подачи на модулирующее устройство сигнала предлагаемой структуры является формирование фазоразностного сигнала, содержащего последовательно чередующиеся четные и нечетные уровни длительностью  каждый. Нечетные уровни ΔФ2n+1 соответствуют таковым в случае использования известного алгоритма квадратурной сдвигающей модуляции (Pavlath G.A. Closed-loop fiber optic gyros. SPIE v. 2837, 1996, pp. 46-60) и несут в основном информацию о величине невзаимного фазового сдвига Саньяка. В четных уровнях
каждый. Нечетные уровни ΔФ2n+1 соответствуют таковым в случае использования известного алгоритма квадратурной сдвигающей модуляции (Pavlath G.A. Closed-loop fiber optic gyros. SPIE v. 2837, 1996, pp. 46-60) и несут в основном информацию о величине невзаимного фазового сдвига Саньяка. В четных уровнях 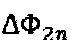 содержатся отсчеты дискретизированной на интервале τ гармонической функции с амплитудой С, частотой
содержатся отсчеты дискретизированной на интервале τ гармонической функции с амплитудой С, частотой 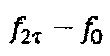 и фазовым сдвигом ϕC. Зависимость между С и С', в силу того, что волоконная катушка представляет собой линию задержки длительностью τ, выражается формулой 2:
и фазовым сдвигом ϕC. Зависимость между С и С', в силу того, что волоконная катушка представляет собой линию задержки длительностью τ, выражается формулой 2: 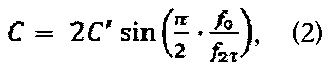
Согласно (2) с приближением 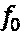 к
к 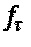 наблюдается приближение значения С к 2С,' иными словами происходит усиление модулирующего сигнала. Величина интерференционного отклика, регистрируемого фотоприемным устройством, соответствующего четным уровням фазоразностного сигнала
наблюдается приближение значения С к 2С,' иными словами происходит усиление модулирующего сигнала. Величина интерференционного отклика, регистрируемого фотоприемным устройством, соответствующего четным уровням фазоразностного сигнала 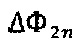 описывается формулой 3:
описывается формулой 3:
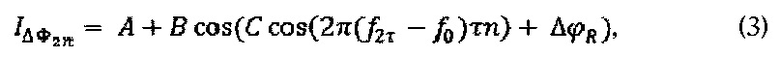
где A - некоторый постоянный уровень, В - видность интерференционной картины, 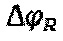 - фаза Саньяка. Величина С в рамках предлагаемого способа в дальнейшем называется глубиной модуляции. Сигнал
- фаза Саньяка. Величина С в рамках предлагаемого способа в дальнейшем называется глубиной модуляции. Сигнал 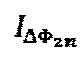 является полигармоническим и состоит из двух подмножеств спектральных составляющих (4), зависимости которых от порядкового номера K, видности интерференционной картины В, глубины модуляции С и фазы Саньяка
является полигармоническим и состоит из двух подмножеств спектральных составляющих (4), зависимости которых от порядкового номера K, видности интерференционной картины В, глубины модуляции С и фазы Саньяка 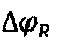 приводятся в формулах (5) и (6) соответственно:
приводятся в формулах (5) и (6) соответственно:
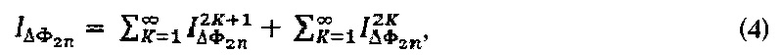
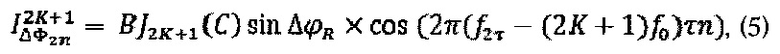
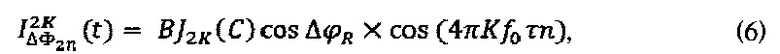
где 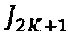 ,
, 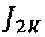 - функции Бесселя первого рода (2К+1)-го и 2К-го порядка.
- функции Бесселя первого рода (2К+1)-го и 2К-го порядка.
Перемножение последовательных дискретных отсчетов сигнала интерференционного отклика 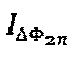 с дискретным сигналом единичной амплитуды на собственной частоте гироскопа
с дискретным сигналом единичной амплитуды на собственной частоте гироскопа 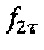 (общий вид подобного сигнала {1, -1,1, -1,1, …}) позволяет получить дополнительный сигнал
(общий вид подобного сигнала {1, -1,1, -1,1, …}) позволяет получить дополнительный сигнал 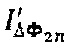 , нечетные спектральные компоненты которого описываются зависимостью, обозначенной в формуле 7:
, нечетные спектральные компоненты которого описываются зависимостью, обозначенной в формуле 7:
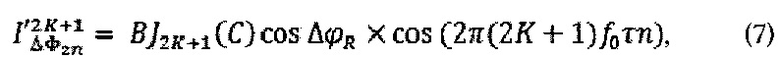
Сигналом обратной связи для системы стабилизации значения масштабного коэффициента выступает сигнал ΔFB, формируемый на основе значений мгновенной амплитуды отдельных спектральных компонент 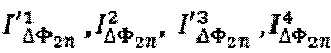 , выделенных из сигналов
, выделенных из сигналов 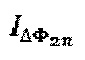 и
и 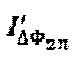 в соответствии с алгоритмом гомодинной демодуляции (Dandridge A., Tveten А.В., Gialloronzi T.G. Homodyne demodulation scheme for fiber optic sensors using phase generated carrier. IEEE Journal of Quantum Electronics, v. 18, n. 10, pp. 1647-1653). Соотношение для определения сигнала обратной связи
в соответствии с алгоритмом гомодинной демодуляции (Dandridge A., Tveten А.В., Gialloronzi T.G. Homodyne demodulation scheme for fiber optic sensors using phase generated carrier. IEEE Journal of Quantum Electronics, v. 18, n. 10, pp. 1647-1653). Соотношение для определения сигнала обратной связи 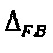 приводится в формуле 8:
приводится в формуле 8:
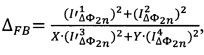 (8)
(8)
где 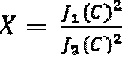 ,
, 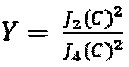 , где
, где 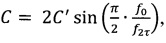
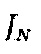 - функция Бесселя первого рода N-го порядка.
- функция Бесселя первого рода N-го порядка.
В случае аппаратной реализации подобной системы сигнал обратной связи используют для подстройки коэффициента усиления выходного сигнала модуляции (Pavlath G.A. Closed-loop fiber optic gyros. SPIE v. 2837, 1996, pp. 46-60). При использовании единого цифрового блока обработки сигналов более простым является способ программного масштабирования модулирующего сигнала.
Сущность заявляемого изобретения поясняется чертежами.
На Фиг. 1a - общий вид модулирующего фазового сигнала, состоящего из двух чередующихся последовательностей 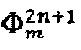 (выделены черной линией базовой толщины) и
(выделены черной линией базовой толщины) и 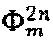 (выделены утолщенной черной линией). Для упрощения понимания уровни последовательности
(выделены утолщенной черной линией). Для упрощения понимания уровни последовательности 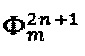 показаны без учета сигнала квадратурной сдвигающей модуляции
показаны без учета сигнала квадратурной сдвигающей модуляции 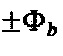 т.е. при их формировании были использованы только два сигнала - значение базового уровня пилообразного сигнала с предыдущей итерации
т.е. при их формировании были использованы только два сигнала - значение базового уровня пилообразного сигнала с предыдущей итерации 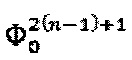 и величина сигнала обратной связи
и величина сигнала обратной связи 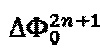 . Уровни последовательности
. Уровни последовательности 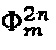 сформированы как дискретизированные на интервале τ значения гармонической функции с амплитудой С' и частотой ƒ0 при условии выполнения неравенства
сформированы как дискретизированные на интервале τ значения гармонической функции с амплитудой С' и частотой ƒ0 при условии выполнения неравенства 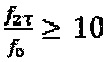 . Использование гармонической функции с относительно низкой частотой недопустимо из-за низкого коэффициента пропускания волоконного контура (см. (2), однако, для облегчения понимания структуры модулирующего сигнала данный рисунок был включен в описание заявляемого способа. Единицы измерения по горизонтали - временные интервалы длительностью τ, по вертикали - радианы.
. Использование гармонической функции с относительно низкой частотой недопустимо из-за низкого коэффициента пропускания волоконного контура (см. (2), однако, для облегчения понимания структуры модулирующего сигнала данный рисунок был включен в описание заявляемого способа. Единицы измерения по горизонтали - временные интервалы длительностью τ, по вертикали - радианы.
На Фиг. 1б - общий вид модулирующего фазового сигнала, состоящего из двух чередующихся последовательностей 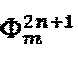 (выделены черной линией базовой толщины) и
(выделены черной линией базовой толщины) и 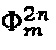 (выделены утолщенной черной линией). Фигура аналогична предыдущей (Фиг. 1а) за исключением частоты гармонической функции, используемой при формировании уровней последовательности
(выделены утолщенной черной линией). Фигура аналогична предыдущей (Фиг. 1а) за исключением частоты гармонической функции, используемой при формировании уровней последовательности 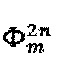 - значение частоты составляет
- значение частоты составляет 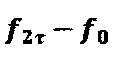 при условии выполнения неравенства
при условии выполнения неравенства 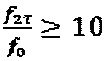 . Приведенный модулирующий фазовый сигнал соответствует фактически используемому в приборе.
. Приведенный модулирующий фазовый сигнал соответствует фактически используемому в приборе.
На Фиг. 2а - дискретный спектр для сигнала, заключенного в последовательности 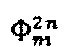 модулирующего фазового сигнала (структура которого приведена на Фиг. 1б).
модулирующего фазового сигнала (структура которого приведена на Фиг. 1б).
На Фиг. 2-б показан дискретный спектр для сигнала интерференционного отклика 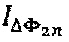 . Два подмножества спектральных составляющих (см. (4)) показаны соответственно сплошными линиями и заштрихованными линиями. На фигуре отмечены значения интересующих спектральных компонент
. Два подмножества спектральных составляющих (см. (4)) показаны соответственно сплошными линиями и заштрихованными линиями. На фигуре отмечены значения интересующих спектральных компонент 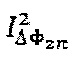 и
и 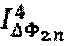 .
.
На Фиг. 2в показан дискретный спектр для дополнительного сигнала 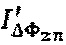 , получаемого перемножением последовательных дискретных отсчетов сигнала интерференционного отклика
, получаемого перемножением последовательных дискретных отсчетов сигнала интерференционного отклика 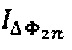 с дискретным сигналом единичной амплитуды на собственной частоте гироскопа
с дискретным сигналом единичной амплитуды на собственной частоте гироскопа 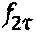 . На фигуре отмечены значения интересующих спектральных компонент
. На фигуре отмечены значения интересующих спектральных компонент 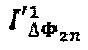 и
и 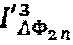 . Как видно, спектр, приведенный на фигуре, является перевернутой слева направо копией спектра, приведенного на Фиг. 2б.
. Как видно, спектр, приведенный на фигуре, является перевернутой слева направо копией спектра, приведенного на Фиг. 2б.
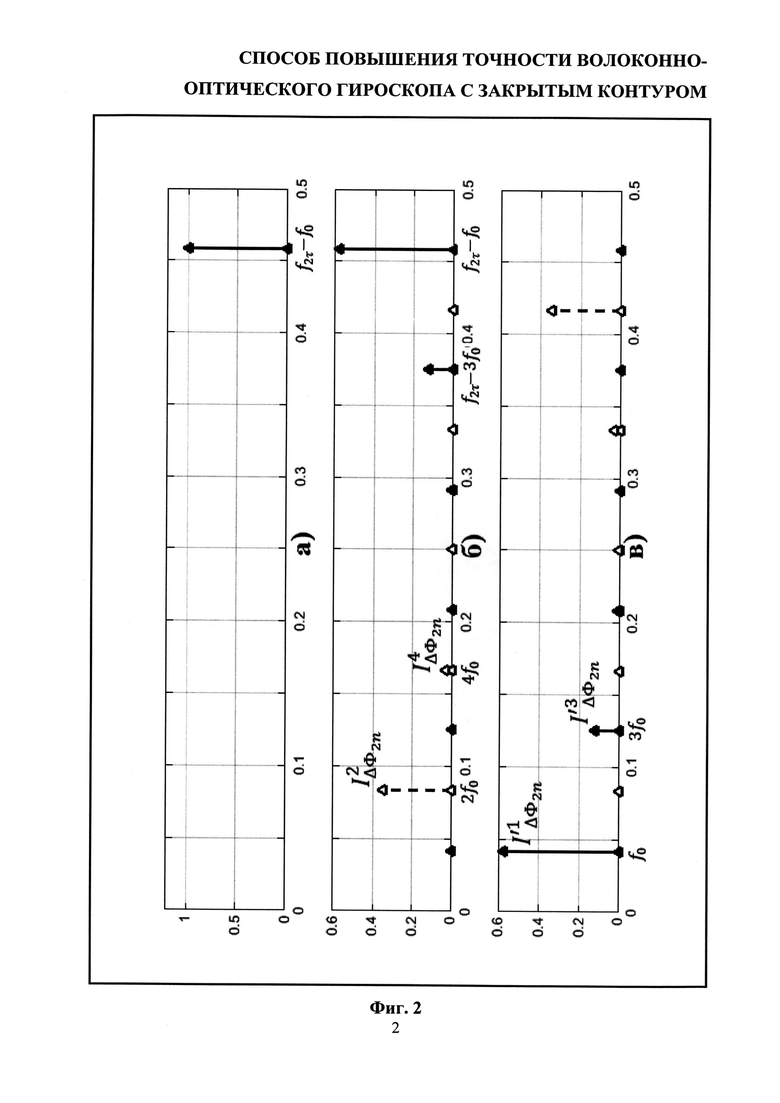
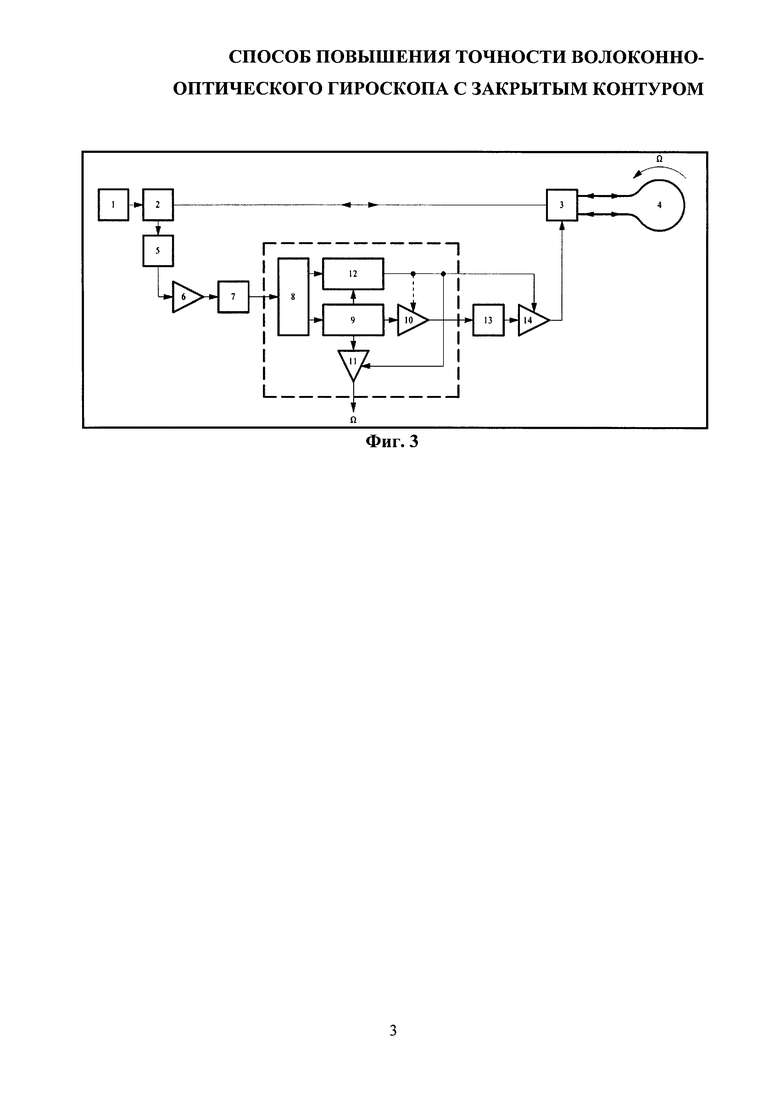
На Фиг. 3, структурная схема волоконно-оптического гироскопа с закрытым контуром, дополненная системой стабилизации масштабного коэффициента.
Предлагаемый способ может быть реализован с помощью устройства, представленного на Фиг. 3. Волоконно-оптический гироскоп с закрытым контуром содержит источник широкополосного оптического излучения 1, волоконный Х-разветвитель 2, многофункциональную интегрально-оптическую схему 3 (МИОС) на основе монокристаллической пластины ниобата лития (LiNbO3), совмещающую Y-разветвитель, поляризатор и фазовый модулятор. Чувствительным элементом ВОГ является кольцевой оптоволоконный интерферометр 4. Цепь регистрации оптического сигнала ВОГ содержит фотоприемное устройство 5, электрическую схему усиления 6 и аналого-цифровой преобразователь 7. Схему цифровой обработки ВОГ, реализованную, как правило, на единой интегральной микросхеме, можно условно разделить на следующие программные блоки: блок цифровой демодуляции 8, блок генерации модулирующего сигнала 9 (цифровой генератор сигналов сложной формы), блок программного усиления модулирующего сигнала 10 (программный умножитель), блок программного усиления выходного сигнала ВОГ 11 (программный умножитель), блок подстройки масштабного коэффициента 12 (цифровой регулятор). Контур обратной связи замыкают цифро-аналоговый преобразователь 13 и электрическая схема усиления 14.
Излучение от источника 1 поступает на вход Х-разветвителя 2 и далее на вход схемы МИОС 3, где Y-разветвитель обеспечивает разделение входящего излучения на два луча равной интенсивности, каждый из которых далее обходит кольцевой интерферометр 4. После прохождения интерферометра лучи вновь объединяются в Y-разветвителе МИОС, суммарный луч проходит через Х-разветвитель 2, после чего поступает на фотоприемное устройство 5, регистрирующее две чередующихся последовательности сигналов интенсивности 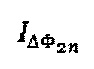 и
и 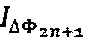 , соответствующих чередующимся последовательностям в фазоразностном сигнале
, соответствующих чередующимся последовательностям в фазоразностном сигнале 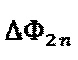 и
и 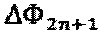 . Ток фотоприемного устройства 5 проходит через схему усиления 6 и попадает на аналого-цифровой преобразователь 7. Цифровой сигнал далее поступает в блок цифровой демодуляции 8, который обеспечивает регистрацию отдельных уровней интенсивности интерференционного сигнала и формирование дополнительного сигнала
. Ток фотоприемного устройства 5 проходит через схему усиления 6 и попадает на аналого-цифровой преобразователь 7. Цифровой сигнал далее поступает в блок цифровой демодуляции 8, который обеспечивает регистрацию отдельных уровней интенсивности интерференционного сигнала и формирование дополнительного сигнала 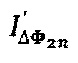 путем перемножения последовательных дискретных отсчетов сигнала интерференционного отклика
путем перемножения последовательных дискретных отсчетов сигнала интерференционного отклика 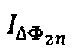 с дискретным сигналом единичной амплитуды на собственной частоте гироскопа
с дискретным сигналом единичной амплитуды на собственной частоте гироскопа 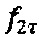 . Блок генерации модулирующего сигнала 9 формирует несколько сигналов:
. Блок генерации модулирующего сигнала 9 формирует несколько сигналов:
- Представленный двумя чередующимися последовательностями 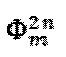 и
и 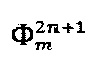 импульсный модулирующий сигнал, в состав которого входят пилообразный сигнал компенсации, совмещенный с сигналом вспомогательной квадратурной модуляции, (уровни
импульсный модулирующий сигнал, в состав которого входят пилообразный сигнал компенсации, совмещенный с сигналом вспомогательной квадратурной модуляции, (уровни 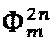 , а также вспомогательный сигнал, предназначенный для оценки величины отклонения МК (уровни
, а также вспомогательный сигнал, предназначенный для оценки величины отклонения МК (уровни 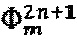 ).
).
- Выходной сигнал вращения, пропорциональный угловой скорости ВОГ и равный по величине фазовому сдвигу Саньяка.
Выходной сигнал модуляции масштабируется блоком программного усиления модулирующего сигнала 10 и поступает на цифро-аналоговый преобразователь 13, после чего проходит через электрическую схему усиления 14 и подается на входящий в состав МИОС фазовый модулятор, замыкая таким образом главный контур обратной связи ВОГ. Блок подстройки масштабного коэффициента 12 осуществляет регулирование коэффициента программного усиления блока 10 или коэффициент усиления электрической схемы усиления 14 на основе сигнала ошибки 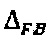 , получаемого с использованием значений мгновенной амплитуды отдельных спектральных компонент
, получаемого с использованием значений мгновенной амплитуды отдельных спектральных компонент 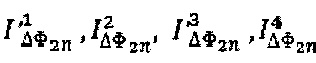 , выделенных из сигналов
, выделенных из сигналов 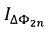 и
и 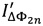 , с целью стабилизации текущего значения масштабного коэффициента. Блок программного усиления выходного сигнала 11 приводит выходной сигнал вращения с блока генерации модулирующего сигнала 9 к необходимым единицам измерения угловой скорости.
, с целью стабилизации текущего значения масштабного коэффициента. Блок программного усиления выходного сигнала 11 приводит выходной сигнал вращения с блока генерации модулирующего сигнала 9 к необходимым единицам измерения угловой скорости.
Таким образом, заявляемое решение приводит к повышению точности выходного сигнала ВОГ за счет устранения зависимости частоты формирования вспомогательного сигнала, предназначенного для оценки величины отклонения масштабного коэффициента, от текущего значения угловой скорости, устранения зависимости величины указанного вспомогательного сигнала от величины действующего на ВОГ углового ускорения, что приводит к возможности исключения влияния последнего на точность определения масштабного коэффициента и исключения возможности возникновения режимов вращения ВОГ, нарушающих работу алгоритма стабилизации масштабного коэффициента.

Изобретение относится к области волоконной оптики и может быть использовано при создании волоконно-оптических гироскопов и других фазовых интерферометрических датчиков физических величин, построенных по схеме интерферометра Саньяка. Технический результат – повышение точности волоконно-оптического гироскопа достигается путем компенсации отклонений значения масштабного коэффициента за счет временного мультиплексирования основного сигнала компенсации фазового сдвига Саньяка со вспомогательным диагностическим сигналом. Указанный дополнительный диагностический сигнал обеспечивает возникновение соответствующего интерферометрического отклика со сложной полигармонической структурой, регистрация которого на фотоприемном устройстве и последующий анализ соотношений отдельных спектральных компонент позволяют оценить величину отклонения масштабного коэффициента. Техническим результатом является повышение точности волоконно-оптического гироскопа без снижения частоты формирования сигнала вращения. 3 ил.
Способ повышения точности волоконно-оптического гироскопа с закрытым контуром, заключающийся в том, что путем подачи на фазовый модулятор ступенчатого импульсного сигнала напряжения формируют модулирующий фазовый сигнал, состоящий из двух чередующихся последовательностей 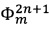 и
и 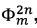 каждая из которых включает в себя уровни длительностью
каждая из которых включает в себя уровни длительностью 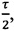 где τ - время обхода оптоволоконного контура, m - именной индекс, указывающий на использование сигнала в качестве модуляционного, n - порядковый номер уровня в общем модулирующем фазовом сигнале, являющемся суперпозицией двух указанных чередующихся последовательностей, в обозначенных последовательностях чередуют сигнал компенсации фазового сдвига Саньяка
где τ - время обхода оптоволоконного контура, m - именной индекс, указывающий на использование сигнала в качестве модуляционного, n - порядковый номер уровня в общем модулирующем фазовом сигнале, являющемся суперпозицией двух указанных чередующихся последовательностей, в обозначенных последовательностях чередуют сигнал компенсации фазового сдвига Саньяка 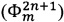 и вспомогательный диагностический сигнал
и вспомогательный диагностический сигнал 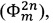 вызывающие соответственно интерференционные отклики
вызывающие соответственно интерференционные отклики 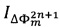 и
и  регистрацией которых на фотоприемном устройстве и их последующей демодуляцией получают соответственно величину действующей на прибор угловой скорости и сигнал ошибки, с помощью которого оценивают величину отклонения масштабного коэффициента и стабилизируют его значение путем замыкания дополнительного контура обратной связи, отличающийся тем, что в последовательности
регистрацией которых на фотоприемном устройстве и их последующей демодуляцией получают соответственно величину действующей на прибор угловой скорости и сигнал ошибки, с помощью которого оценивают величину отклонения масштабного коэффициента и стабилизируют его значение путем замыкания дополнительного контура обратной связи, отличающийся тем, что в последовательности 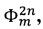 содержащей вспомогательный диагностический сигнал, его отдельные отсчеты формируют как дискретизированные на интервале т значения гармонической функции с амплитудой С' и частотой ƒ2τ - ƒ0, где
содержащей вспомогательный диагностический сигнал, его отдельные отсчеты формируют как дискретизированные на интервале т значения гармонической функции с амплитудой С' и частотой ƒ2τ - ƒ0, где 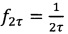 - собственная частота гироскопа и
- собственная частота гироскопа и 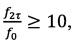 регистрируемый на фотоприемном устройстве соответствующий интерференционный отклик
регистрируемый на фотоприемном устройстве соответствующий интерференционный отклик 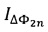 имеет полигармоническую структуру, а его демодуляцию осуществляют следующим образом: на основе зарегистрированного значения
имеет полигармоническую структуру, а его демодуляцию осуществляют следующим образом: на основе зарегистрированного значения 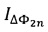 вычисляют дополнительный сигнал
вычисляют дополнительный сигнал 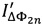 путем умножения последовательных дискретных отсчетов отклика
путем умножения последовательных дискретных отсчетов отклика 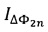 на значения последовательности {1, -1,1, -1,1, …}, из полученных сигналов
на значения последовательности {1, -1,1, -1,1, …}, из полученных сигналов 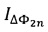 и
и 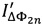 выделяют соответственно мгновенные значения
выделяют соответственно мгновенные значения 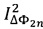 и
и 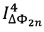 амплитуд первых двух четных спектральных компонент с частотами 2ƒ0 и 4ƒ0 и мгновенные значения
амплитуд первых двух четных спектральных компонент с частотами 2ƒ0 и 4ƒ0 и мгновенные значения 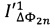 и
и 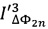 амплитуд первых двух нечетных спектральных компонент с частотами ƒ0 и 3ƒ0, затем формируют сигнал ошибки ΔFB, величину которого вычисляют по формуле
амплитуд первых двух нечетных спектральных компонент с частотами ƒ0 и 3ƒ0, затем формируют сигнал ошибки ΔFB, величину которого вычисляют по формуле 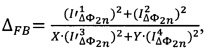
где 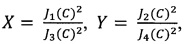
где 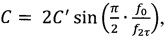 JN - функция Бесселя первого рода N-го порядка.
JN - функция Бесселя первого рода N-го порядка.
| US 5141316 A, 25.08.1992 | |||
| СПОСОБ ПОВЫШЕНИЯ ТОЧНОСТИ ВОЛОКОННО-ОПТИЧЕСКОГО ГИРОСКОПА С ЗАКРЫТЫМ КОНТУРОМ | 2012 |
|
RU2512599C1 |
| US 20120239329 A1, 20.09.2012 | |||
| WO 1999035467 A2, 15.07.1999. | |||
Авторы
Даты
2017-07-24—Публикация
2016-07-13—Подача