Область техники, к которой относится изобретение
Изобретение относится к электричеству, к электрофизике и теплопроводности материалов, к явлению нулевого электрического сопротивления, то есть к гиперпроводимости, а также к явлению нулевого теплового сопротивления, то есть к сверхтеплопроводности материалов при околокомнатных и более высоких температурах.
Гиперпроводимость представляет собой состояние материала с нулевым электрическим сопротивлением. Такое состояние, состояние гиперпроводимости или гиперпроводящее состояние возникает и существует в содержащих электронно-колебательные центры (ЭКЦ) полупроводниковых материалах между электродами при температурах гиперпроводящего перехода (Тh) и при более высоких температурах [1-16]. Материалы, в которых наблюдается гиперпроводимость и сверхтеплопроводность при их нагревании выше температуры Th, являются гиперпроводниками или гиперпроводящими материалами.
Сверхтеплопроводность представляет собой состояние материала с нулевым тепловым сопротивлением. Такое состояние, состояние сверхтеплопроводности или сверхтеплопроводное состояние возникает и существует в содержащих ЭКЦ полупроводниковых материалах между электродами при температуре гиперпроводящего перехода Тh и при более высоких температурах.
Электронно-колебательными центрами или ЭКЦ являются такие локальные центры, равновесные положения или частоты упругих колебаний которых зависят от их электронного состояния в материалах [17-20]. В работе [20] "О влиянии деформации решеток электронами на оптические и электрические свойства кристаллов" на стр. 207 в параграфе 3 приведено определение электронно-колебательных переходов локального центра:
"3. Фотопереходы электронов10
В этом параграфе будут рассмотрены фотопереходы слабо связанных электронов локального "центра" с дискретного на дискретный энергетический уровень. Рассмотрим переход из состояния s1…nχ… в состояние 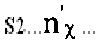 . При этом переходе изменяются не только квантовые числа электронов s, но и квантовые числа колебаний nχ т.е. выделяется теплота. Частота света, поглощаемого при таком переходе, равна
. При этом переходе изменяются не только квантовые числа электронов s, но и квантовые числа колебаний nχ т.е. выделяется теплота. Частота света, поглощаемого при таком переходе, равна

где ω0 - частота, поглощаемая "чисто электронным переходом", при котором  .
.
Вероятность фотоперехода вычисляется при помощи обычного квантовомеханического рассмотрения10.
Энергию света, поглощаемого упомянутым электронно-колебательным переходом за секунду в единице объема диэлектрика, можно записать в виде…"
В данной выдержке из указанной работы С.И. Пекара дано определение электронно-колебательных переходов локальных центров. Локальные центры, в которых происходят электронно-колебательные переходы, т.е. центры электронно-колебательной природы называют электронно-колебательными центрами или ЭКЦ.
Электронные или дырочные переходы на энергетические уровни ЭКЦ или с этих уровней сопряжены с неизбежным участием значительного числа квантов упругих колебаний материала из-за чего их называют электронно-колебательными переходами. Среднее число участвующих в таких переходах фононов численно равно константе электрон-фононной связи Пекара-Хуана-Риса (S). Константа электрон-фононного взаимодействия на ЭКЦ обычно значительно превышает 1 и по теоретическим данным может достигать 150. Известны экспериментальные значения S=22 в широкозонном материале, в диэлектрике. В типичных полупроводниках величина S обычно составляет несколько единиц. Так, в кремнии на А-центрах, представляющих собой ассоциации примесных атомов кислорода с вакансиями, константа S близка к 5, хотя при отсутствии ЭКЦ в материале S≤0,25. Известно, что упругое взаимодействие ЭКЦ друг с другом вызывает уменьшение S. Благодаря участию фононов в электронно-колебательных переходах и их взаимодействию с движениями атомных ядер в материалах открыты принципиально новые, считавшиеся ранее невозможными технические эффекты, такие как колебания атомных ядер в атомах материалов, СВЧ излучение при электронно-колебательных переходах, увлечение электронов фононами при дебаевых температурах фононов, а также гиперпроводимость и сверхтеплопроводность.
Гиперпроводимость и сверхтеплопроводность практически осуществлены в широкозонных материалах и в узкозонных материалах. Примесные атомы кислорода в материалах практически важны для осуществления гиперпроводимости и сверхтеплопроводности поскольку кислород содержится в коре Земли (28%) и присутствует в полупроводниковых материалах. Так в промышленном кремнии концентрация примесных атомов кислорода может быть близка к 1018 см-3 и не поддается существенному уменьшению при современных способах очистки. Часть примесных атомов кислорода в материале переводят в состав ЭКЦ без легирования материала другими примесями для создания ЭКЦ. Используют такие ЭКЦ для осуществления гиперпроводимости и сверхтеплопроводности.
Гиперпроводимость и сверхтеплопроводность являются взаимно связанными состояниями материалов и не могут быть осуществлены порознь, отдельно друг от друга. Это обусловлено тем, что при наличии в материале электронно-колебательных центров электроны и фонононы оказываются сильно связанными друг с другом на электронно-колебательных энергетических уровнях ЭКЦ. В таких условиях электроны и фононы совместно осуществляют переходы, которые получили название электронно-колебательных переходов. Среди таких переходов есть электронно-колебательные переходы с энергетических уровней одного ЭКЦ на энергетические уровни другого ЭКЦ, например, при наличии градиента концентрации ЭКЦ или градиента электрического потенциала, электрического поля или градиента температуры. Такие электронно-колебательные переходы являются квантовыми переходами, они сопровождаются пространственным переносом в материале электрических зарядов электронов и дырок, а также пространственным переносом связанных с электронами и дырками фононов и собственных (Inherent, I-) колебаний атомных ядер в атомах материала, чем обусловлено возникновение и существование гиперпроводимости и сверхтеплопроводности.
Собственные (Inherent, I-) колебания представляют собой упругие периодические колебательные смещения атомных ядер относительно электронных оболочек атомов или ионов материала, то есть I-колебания являются колебательными движениями атомных ядер в потенциальных полях электронных оболочек атомов или ионов материала.
Известны также волны I-колебаний, представляющие собой пространственное распространение I-колебаний в материале, из-за которых кинетические эффекты в материалах приобретают важные особенности.
Электроны, дырки, фононы, I-колебания взаимно связаны друг с другом на ЭКЦ посредством сильного электрон-фононного взаимодействия. При этом система атомных ядер обменивается энергией с системой электронов в материале. Такой энергетический обмен в материалах противоречит адиабатическому приближению Борна-Оппенгеймера [21] которое лежит в основе доминирующей сейчас адиабатической электроники материалов.
Действительно, теоретической основой современной твердотельной электроники является квантовое уравнение Шредингера для кристалла, включающее операторы кинетической энергии электронов (Те), кинетической энергии атомных ядер (Tz), операторы потенциальных энергий кулоновского расталкивания электронов (Vee), кулоновского расталкивания ядер (Vzz) и кулоновского притяжения электронов к ядрам (Vez):
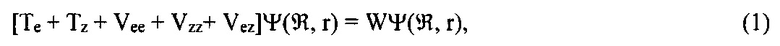
где W - полная энергия кристалла. Решением этого уравнения является волновая функция Ψ(ℜ, r), зависящая от совокупности координат атомных ядер (ℜ) и от совокупности координат электронов (r). Известно, что точное решение уравнения (1) затруднено по принципиальным и техническим причинам.
В 1926 году М. Борн и П. Оппенгеймер предложили приближенный метод решения уравнения (1) положив Ψ(ℜ, r)=ϕ(r, ℜ)⋅Ф(ℜ) и представили его в виде двух следующих уравнений:


где кристаллический потенциал Vкр=Vкp(ℜ, r)=Vee+Vzz+Vze; ϕ(r, ℜ) - волновая функция, описывающая движение системы электронов; Е - полная энергия системы электронов; Ф(ℜ) - волновая функция, описывающая движение системы атомных ядер, Е - энергия системы электронов,
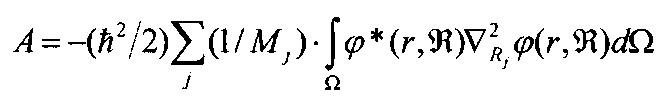
- адиабатический потенциал, j - номер атома в материале, Ω - объем материала. По существу, величина потенциала A определяется зависимостью электронной волновой функции ϕ(r, ℜ) от смещений атомных ядер. М. Борн и П. Оппенгеймер [21] исключили потенциал А из уравнения (3) считая его вклад в энергию материала несущественным. Этот приближенный метод решения уравнения (1) с помощью уравнений (2) и (3) при условии A≡0 получил название адиабатического приближения Борна-Оппенгеймера, поскольку при таком условии, систему электронов представляли отделенной от системы ядер адиабатической оболочкой, препятствующей обмену энергией между этими системами. Полагали, что в этом приближении обмен энергией между электронами и ядрами атомов в материалах невозможен. Очевидно, что адиабатическое приближение, адиабатический принцип Борна-Оппенгеймера является приближенным способом решения уравнения Шредингера для материала и, как выяснилось, применение адиабатического приближения Борна-Оппенгеймера ограничивает круг доступных для исследования и использования физических процессов в материалах.
В 1930 году нобелевский лауреат, один из основателей волновой квантовой механики и создателей ее математического аппарата П. Дирак впервые показал, что адиабатическое приближение Борна-Оппенгеймера в общем случае обосновать нельзя [22]. Тем не менее, приближение Борна-Оппенгеймера получило широкое распространение и сейчас оно лежит в основе электронной теории материалов, в основе доминирующей современной электроники. В связи с этим существующую сейчас в науке и технике твердотельную, в том числе, полупроводниковую электронику, можно обоснованно называть адиабатической электроникой, электроникой Борна-Оппенгеймера. Эта электроника в силу ее приближенного характера не дает исчерпывающего ответа на многие вопросы о природе материалов и о физических явлениях в них, например, таких как сверхпроводимость, сверхтекучесть, гиперпроводимость, сверхтеплопроводность, увлечение электронов фононами при температурах Дебая фононов отчасти в силу ограниченности адиабатического приближения Борна-Оппенгеймера. Дальнейшие исследования упрочили понимание ограниченности адиабатического приближения при его использовании в решении проблем материалов вообще и проблем твердотельной электроники в частности.
Установлено, что даже в адиабатическом приближении Борна-Оппенгеймера, когда потенциал А≡0 и поэтому обмен энергией между ярами и электронами локальных центров якобы отсутствует, тем не менее, такой энергетический обмен все же происходит. Обмен энергией между системой электронов и системой атомных ядер в материалах происходит постоянно, поскольку кристаллический потенциал Vкp в уравнении (2) зависит и от совокупности координат ядер (ℜ) и от совокупности координат электронов (r) из-за чего решения уравнений (2, 3) и их собственные значения, вообще говоря, зависят от совокупностей координат ℜ и r. Таким образом, адиабатическое приближение Борна-Оппенгеймера оказалось адиабатическим только условно, приближенно. Реальность такова, что обмен энергией между системой электронов и системой атомных ядер является принципиальным и неотъемлемым свойством материалов: молекул, жидкостей, твердых тел. Однако, колебания ядер в атомах материалов, их взаимодействие с электронами и фононами почти не изучали с самого основания квантовой науки о материалах, т.е. последние сто лет. В связи с этими данными следует отметить, что утвердившиеся в физике представления о куперовских парах и теория сверхпроводимости Бардина-Купера-Шриффера (БКШ) используют обмен энергией между электронами, используют обмен электронов фононами, представляющими собой упругие колебания атомов кристаллической решетки, колебания атомов или ионов материала. Иначе говоря, теория куперовских пар и связанная с ней теория сверхпроводимости БКШ в принципе используют обмен энергией между системой электронов и системой атомов (ионов) в материале. Это соответствует адиабатическому приближению Борна-Оппенгеймера, поскольку атомы и ионы в этих теориях рассматриваются как материальные точки. В этом приближении не предполагаются ни самостоятельные смещения атомных ядер, ни обмен энергиями между электронами и ядрами, не смотря на то, что движения атомных ядер и движения электронов представлены в уравнении Шредингера для материала (1) отдельными, независимыми друг от друга операторами кинетических энергий.
Заявленное изобретение относится к новой развивающейся неадиабатической электронике. В отличие от существующей традиционной и доминирующей сейчас адиабатической электроники Борна-Оппенгеймера неадиабатическая электроника усиливает с помощью ЭКЦ обмен энергией между атомными ядрами, фононами и электронами в материалах и использует такой энергетический обмен для научных и технических применений.
Таким образом, неадиабатическая электроника представляет собой новое научно-техническое направление, основанное на неотвратимом, но не учитывавшимся ранее обмене энергией между электронами и ядрами атомов в молекулах, газах, жидкостях, в конденсированных материалах и материальных структурах. Особенно интенсивно и ярко эффекты неадиабатической электроники проявляются в полупроводниковых материалах и структурах в виде собственных (I-, Inherent) α-, β- и γ-типов колебаний ядер внутри атомов материалов; в виде глубоких электронно-колебательных уровней в запрещенной энергетической зоне полупроводников (и диэлектриков); в процессах генерирования, усиления, детектирования и преобразования частот СВЧ колебаний и волн на ЭКЦ; в виде увлечения электронов фононами при дебаевых температурах фононов; в виде явлений гиперпроводимости и сверхтеплопроводности, а также в виде отрицательного электрического сопротивления; в явлении электрического управления тепловыми потоками; в оптических, электрических и магнитных способах регулирования оптических свойств материалов; в возможности создавать неохлаждаемые низкошумящие твердотельные электронные и отоэлектронные приборы и устройства.
Открытие I-колебаний и волн в материалах увеличило количество физически важных степеней свободы для частиц, образующих материал; увеличило количество каналов обмена энергией, т.е. взаимодействий между частицами материала. Новые взаимодействия проявляются в виде принципиально новых технических эффектов и в виде новых особенностей известных эффектов.
При определенных условиях в ограниченных областях материала I-колебания и волны становятся когерентными, то есть приобретают одинаковые частоты и фазы колебаний. Такие области материала с одинаковыми фазами упругих колебаний получили название когерентных областей. Когерентность упругих колебаний является условием нулевого электрического сопротивления и нулевого теплового сопротивления материала в когерентных областях, то есть условием гиперпроводимости и сверхтеплопроводности когерентных областей материала является именно когерентность I-колебаний и связанных с ними фононов. Геометрические размеры когерентных областей могут иметь размеры от десятков ангстрем до десятков и сотен микрон при различных технических условиях. Если когерентная область занимает весь материал на протяжении между электродами, то электрическое и тепловое сопротивления материала между электродами становятся нулевыми, тем самым реализуются гиперпроводимость и сверхтеплопроводность материала между электродами.
Переход материала в гиперпроводящее состояние происходит при его нагревании до температуры гиперпроводящего перехода Th или до более высоких температур и представляет собой явление гиперпроводимости, технический эффект гиперпроводимости. Состоянию гиперпроводимости материала сопутствует состояние сверхтеплопроводности. Явление перехода материала в состояние с нулевым тепловым сопротивлением, в состояние сверхтеплопроводности представляет собой технический эффект сверхтеплопроводности. Явления, эффекты гиперпроводимости и сверхтеплопроводности возникают вблизи температуры гиперпроводящего перехода Тh и существуют при более высоких температурах. Гиперпроводимость и сверхтеплопроводность являются взаимно связанными техническими эффектами, они не могут быть отделены друг от друга, возникают и существуют совместно, могут быть осуществлены и практически использованы при температурах выше Тh.
Данное изобретение обеспечивает увеличение эффективности известного способа осуществления гиперпроводимости и сверхтеплопроводности [16]. В заявленном способе реализован технический механизм формирования нулевого электрического сопротивления и нулевого теплового сопротивления материалов между электродами, то есть гиперпроводимости и сверхтеплопроводности при околокомнатных и более высоких температурах за счет использования электронно-колебательных центров и характерного для ЭКЦ сильного электрон-фононного взаимодействия в условиях вывода из материала избыточной колебательной энергии.
Изобретение может быть использовано в наноэлектронике, микроэлектронике, радиотехнике, электротехнике и радиоэлектронике.
Уровень техники
Переход материалов в состояние с нулевым электрическим сопротивлением при низких температурах известен как открытое в 1911 году явление сверхпроводимости [23]. На фиг. 1 приведена типичная температурная зависимость электрического сопротивления (R) сверхпроводникового материала. Из фиг. 1 видно, что его электрическое сопротивление R обращается в ноль при охлаждении материала ниже температуры сверхпроводящего перехода (Тс). Сверхпроводимость наблюдается только у некоторых материалов и только при известных условиях, а именно, если температура материала ниже температуры сверхпроводящего перехода, а плотность электрического тока и напряженность магнитного поля в материале ниже критических значений Jк и Нк [24-26]. Наличие критических значений Tc, Jк и Нк ограничивает технические применения сверхпроводимости вблизи комнатных и при более высоких температурах, поскольку значения Jк и Нк зависят от температуры материала и стремятся к нулю при повышении и приближении температуры к Tc.
Первые сверхпроводники имели малые значения Tc: 4,1 К (ртуть), 7,3 K (свинец). В 1967 г. была обнаружена сверхпроводимость в сплаве соединений ниобия, алюминия и германия с Tc≅20К. В 1986 г. Ж.Г. Беднорцем и К.А.З. Мюллером был обнаружен класс металлооксидов с Tc≅40К [27] в связи с чем им была присуждена Нобелевская премия. Позже было открыто много классов высокотемпературных сверхпроводников, а максимальная температура сверхпроводящего перехода достигла 133К-134К. В соединении HgBa2Ca2Cu3O8 под давлением в десятки Гигапаскалей обнаружен сверхпроводящий переход при температурах от 156К до 164К. Обнаружена сверхпроводимость при температурах около 200К в соединении SrRuO3 подвергнутом лазерной обработке [28]. Полученный в работе [29] материал (Sn5In)Ba4Ca2Cu10OY, демонстрирует сверхпроводимость при температурах до Tc=212K, предположительно до Tc=250K.
Нужно отметить, что сверхпроводимость во всех классах сверхпроводящих материалов была обнаружена экспериментально, без теоретического прогноза, практически "вслепую", а доминирующие представления о сверхпроводимости нередко основываются на неподходящем для этих целей адиабатическом приближении Борна-Оппенгеймера. Экспериментальные поиски сверхпроводящих материалов с высокими значениями Tc все еще продолжаются. Эта важная задача более ста лет решается путем подбора химического состава и технологических обработок материалов, то есть по-прежнему "поиском вслепую", напоминающим средневековую алхимию, новых сверхпроводящих материалов с высокими значениями Tc. Считается определенным и несомненным, что при температуре меньше Tc сверхпроводниковый материал может быть сверхпроводящим, может обладать нулевым электрическим сопротивлением. Ожидания сверхпроводимости именно при температуре Т<Тс традиционно основаны на имеющихся эмпирических данных. Известные физические модели явления сверхпроводимости также ориентированы на существование сверхпроводящего состояния материала при температуре меньше Tc.
Полноценной теории сверхпроводников пока не создано, но выдвинуто несколько физических механизмов, призванных объяснить явление сверхпроводимости. Среди этих механизмов доминирующее положение занимает фононный механизм, объясняющий попарное притяжение электронов проводимости из-за обмена электронов друг с другом виртуальными кристаллическими фононами, сопровождающееся образованием "электронных пар", так называемых «пар Купера» или «куперовских электронных пар». Энергия связи электронов в "электронной паре" определяет величину Tc. Данный механизм лежит в основе общеизвестной теории сверхпроводимости Ж. Бардина, Н. Купера, Ж. Шриффера (БКШ) [30], в которой температура сверхпроводящего перехода Tc зависит от энергии связанного с электронами упругого колебания материала (Екол):

где k - постоянная Больцмана, V* - энергия связи упругого колебания материала с электроном, N(F) - плотность электронных состояний при энергии Ферми, F - энергия Ферми. Например, в сверхпроводящих металлах V*N(F)<<1, Екол≤17 мэВ и поэтому Tc не превышает 20К. Казалось, что теория БКШ не объяснила наблюдаемые на опыте высокие экспериментальные значения Tc. Это давало повод полагать, что данная теория верна только для низкотемпературных сверхпроводников.
Однако, основываясь на теории БКШ [30] в работах [31, 32] была сформулирована принципиальная возможность увеличения температуры сверхпроводящего перехода (Тс) за счет использования фононов с большими энергиями. Эти работы в принципе объясняют высокие значения Tc практически наблюдаемые при осуществлении технических эффектов гиперпроводимости и сверхтеплопроводности, в которых используются I-колебания ядер в атомах материалов, содержащих электронно-колебательные центры (ЭКЦ) кванты упругих колебаний которых многократно превышают энергии оптических и акустических фононов. Именно поэтому гиперпроводимость и сверхтеплопроводность осуществляются в содержащих ЭКЦ материалах.
Для увеличения Tc ранее предлагали использовать в куперовских парах более энергичные фононы, с большими энергиями, с волновыми векторами, пронизывающими несколько зон Бриллюэна (Ларкин А.И.). Однако данное предложение технически не было реализовано.
Б.Д. Джозефсон открыл два технических эффекта [33] подтвержденные экспериментально, отмеченные Нобелевскими премиями и проявляющиеся в структурах, состоящих из двух сверхпроводников, разделенных туннельно тонким диэлектрическим слоем, а именно: стационарный эффект Джозефсона и нестационарный высокочастотный эффект Джозефсона.
Стационарный эффект Джозефсона проявляется в виде постоянного электрического тока (I0), протекающего сквозь туннельно тонкий слой диэлектрика, разделяющего сверхпроводники, даже если между сверхпроводниками не приложено электрическое напряжение. Этот ток объяснили туннелированием куперовских пар электронов сквозь диэлектрик. Величина и направление туннельного тока сквозь диэлектрический слой толщиной порядка десятка ангстрем зависит от разности фаз колебаний куперовских пар в сверхпроводниках. На фиг. 2 приведена вольтамперная характеристика джозефсоновского туннельного контакта двух одинаковых сверхпроводников из работы [24]. Из фиг. 2 видно, что при нулевом напряжении между сверхпроводниками сквозь диэлектрический слой течет постоянный ток I0, представляющий стационарный эффект Джозефсона.
Нестационарный высокочастотный эффект Джозефсона проявляется в виде переменного электрического тока, протекающего сквозь туннельно тонкий слой диэлектрика, разделяющего сверхпроводники, если между сверхпроводниками приложено постоянное электрическое напряжение величиной V. Циклическая частота этого переменного тока

где е - заряд электрона. Квант энергии таких колебаний  . Частота ω/2π обычно соответствует СВЧ диапазону.
. Частота ω/2π обычно соответствует СВЧ диапазону.
В сверхпроводниках действует эффект Мейснера [24] состоящий в том, что материал в сверхпроводящем состоянии, в состоянии с нулевым электрическим сопротивлением, выталкивает из своего объема внешнее магнитное поле. При этом возникают и действуют значительные механические силы, расталкивающие материал и магнит. Эффект Мейснера практически используется в устройствах магнитной подвески, в которых сверхпроводниковые материалы охлаждают до температур ниже Tc, что технически неудобно и затратно.
В невырожденных и слабо вырожденных полупроводниках и полупроводниковых содержащих ЭКЦ структурах, то есть в гиперпроводниках, спонтанно возникают и существуют области когерентности с характерным размером Λ (с длиной когерентности Λ) от десятков ангстрем до десятков микрон, которые обладают нулевым электрическим (и нулевым тепловым) сопротивлением. Благодаря нулевому сопротивлению когерентных областей гиперпроводники и гиперпроводниковые структуры выталкивают из своего объема внешнее магнитное поле, проявляя действие эффекта Мейснера. То есть эффект Мейснера является характерным и для сверхпроводников, и для гиперпроводников вследствие нулевого электрического сопротивления существующих в них когерентных областей.
Эффект Мейснера в гиперпроводниках проявляется практически при температурах спонтанного формирования когерентных областей и усиливается при увеличении объема когерентных областей в материале, например, при увеличении температуры материала. Эффект Мейснера проявляется в материале между электродами при температурах ниже температуры гиперпроводящего перехода Тh, при температуре Тh и выше Тh. Таким образом, технический эффект Мейснера и его технические приложения вполне осуществимы с помощью гиперпроводников при низких, околокомнатных и более высоких температурах. Для усиления эффекта Мейснера в гиперпроводниках целесообразно увеличивать суммарный объем когерентных областей, например, увеличивая их количество, характерный размер, т.е. длину когерентности Λ, например, используя технические средства, предложенные в заявленном изобретении.
Эффект Мейснера проявляется в виде силы, выталкивающей материал с нулевым электрическим сопротивлением из магнитного поля, т.е. эффект Мейснера характеризуют вектором силы: модулем вектора, представляющим величину эффекта, и направлением вектора силы. Изменение эффекта Мейснера состоит из изменения величины (модуля) силы и из изменения направления этой силы.
До 2000 года осуществление нулевого электрического сопротивления материала при околокомнатных и более высоких температурах представляла нерешенную научно-техническую проблему. Более того, не была доказана сама возможность осуществления сверхпроводимости при комнатной температуре и тем более, выше комнатной температуры. Не было доказано и отсутствие такой возможности. Теперь установлено, что в определенных условиях в полупроводниковых материалах между электродами возникает состояние с нулевым электрическим сопротивлением при околокомнатных и более высоких температурах, получившее название гиперпроводимости, сопровождающееся возникновением нулевого теплового сопротивления материала, получившего название сверхтеплопроводности.
Экспериментальное осуществление гиперпроводимости и сверхтеплопроводности стало возможным в результате открытия и исследования нового типа упругих колебаний и волн в материалах, Inherent, I-колебаний и волн [1, 4, 7-15, 34-38]. I-колебания и волны представляют собой упругие колебания ядер в атомах материалов. Оказалось, что I-колебания и волны эффективно взаимодействуют с электронами, дырками, и фононами обеспечивая тем самым сильное электрон-фононное взаимодействие, сильную электрон-фононную связь, благодаря которой возникает гиперпроводимость и сверхтеплопроводность. Были определены α-, β- и γ-типы I-колебаний и волн, вычислены элементарные кванты таких колебаний (EZ) в атомах материалов в зависимости от атомного номера (Z), различными экспериментальными методами измерены кванты таких колебаний в ряде атомов. На фиг. 3 светлыми кружками указаны вычисленные энергии элементарных квантов этих типов I-колебаний в атомах с атомными номерами Z от 1 до 80, а темными кружками указаны соответствующие значения квантов, измеренные различными экспериментальными методами. Из фиг. 3 видно, что наибольшие величины квантов таких колебаний и волн соответствуют колебаниям α-типа, при которых ядро атома осциллирует относительно его электронной оболочки в окрестности ее центра, вблизи равновесного положения ядра в атоме, совпадающего с положением минимума потенциала, создаваемого электронами оболочки атома. Величина квантов I-колебаний α-типа монотонно уменьшается от 0,519 эВ до 0,22 эВ при увеличении Z от 1 до 8 и затем монотонно увеличивается до 0,402 эВ при дальнейшем увеличении Z до 80 и более. Такие кванты I-колебаний взаимодействуя с электронами и дырками согласно формуле (4) способны обеспечить нулевое электрическое и нулевое тепловое сопротивления материалов, гиперпроводящее состояние, при температурах от Тh до 2500 K и выше, то есть температура сверхпроводящего перехода Tc в данном случае может превышать 2500 K. Иначе говоря, сверхпроводимость, сверхпроводящее состояние в принципе может существовать в материалах до температуры их плавления и вероятно в расплавах материалов, когда в расплаве обеспечивается достаточная связь электронов с I-колебаниями атомных ядер.
I-колебания атомного ядра в атоме определенного сорта характеризуются вполне определенной величиной элементарного кванта таких колебаний и набором колебательных термов существенно отличающихся от энергии квантов I-колебаний и набора колебательных термов атомов другого сорта. Экспериментальное определение квантов I-колебаний атомных ядер в газообразных, жидких и твердотельных материалах позволяет надежно идентифицировать такие атомы по величине и набору колебательных термов, что может быть положено в основу действия приборов, определяющих атомный состав материалов.
I-колебания проявляют незначительную ангармоничность. Профиль сферически симметричного потенциального поля в окрестности центра электронной оболочки, в котором движется ядро атома, отличается от параболической зависимости, из-за чего возникают ангармонические поправки к энергии гармонических колебаний. Поправки для одномерных колебаний α-типа (ΔEαν) с колебательными числами ν=0, 1, 2 и 3 вычислены в первом и втором порядках стационарной теории возмущений согласно [39, стр. 93]. Как и следовало ожидать, наибольшие значения поправок относятся к колебательным состояниям с ν=3, соответствующим наибольшим смещениям ядер из равновесных положений в центрах электронных оболочек. На фиг. 4 графически представлены поправки к энергии I-колебаний α-типа в состояниях с ν=0, 1, 2, 3 для атомов в зависимости от атомного номера Z. На вставке фиг. 4 поправки представлены в другом масштабе для атомов с Z>10. Представленные на фиг. 4 данные выявили незначительную ангармоничность I-колебаний.
Согласно имеющимся экспериментальным данным I-колебания являются одномерными, их колебательные энергии описываются формулой линейного гармонического квантового осциллятора:

где EZ - элементарный квант колебаний, а колебательное квантовое число ν принимает значения 0, 1, 2, 3, …
В экспериментах проявляются электронно-колебательные переходы с колебательных уровней ЭКЦ в минимум осцилляторного потенциала с полной потерей энергии I-колебаний. Возможны электронно-колебательные переходы даже с потерей энергии так называемых «нулевых колебаний», равной EZ/2. Это не соответствует свободному квантовому гармоническому осциллятору, для которого согласно квантовой теории состояние в минимуме параболического потенциала в центре электронной оболочки недопустимо. Однако для классического осциллятора такое состояние разрешено. В этом состоит дуализм свойств ЭКЦ, проявляющих квантовые и классические свойства. Иначе говоря, ЭКЦ, I-колебания не являются свободными (идеальными) и обмениваются энергией (кристаллических фононов различных типов) с окружающей средой. Учитывая это, следует полагать, что осцилляторы, описывающие I-колебания ЭКЦ, являются линейными, одномерными гармоническими осцилляторами, проявляющими и квантовые и классические свойства, а стационарные колебательные энергии I-колебаний атомных ядер в ЭКЦ описываются формулой (6), включая еще энергию Екол=0, соответствующую минимуму осцилляторного потенциала.
Величина Екол в полупроводниках может превышать ширину запрещенной зоны материала, если значение ν достаточно велико. Соответствующая температура сверхпроводящего перехода Tc, согласно (4) может превышать десятки тысяч градусов. Такие температуры, несомненно, относятся не к материалу в целом, а только к участвующим в I-колебаниях локальным центрам.
Описываемые формулой (6) электронно-колебательные энергетические уровни ЭКЦ проявляются в полупроводниках в виде так называемых глубоких энергетических уровней, преимущественно лежащих в запрещенной зоне полупроводника. Согласно данным о рекомбинации электронов и дырок на ЭКЦ, об энергиях активации сопротивления содержащих ЭКЦ материалов, большинство из электронно-колебательных уровней ЭКЦ действительно лежат в запрещенной зоне полупроводника, как показано на фиг. 5. В центре фиг. 5 изображена энергетическая схема полупроводника, где Ес и Ev обозначают энергии дна зоны проводимости и потолка валентной зоны, F - уровень Ферми. Рассматриваемые электронно-колебательные центры расположены в объеме полупроводника, в точках с координатами r0 и 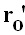 . Параболические потенциалы, удерживающие атомное ядро вблизи центра электронной оболочки ЭКЦ, представлены слева и справа на фиг. 5 параболами V(r-r0) и
. Параболические потенциалы, удерживающие атомное ядро вблизи центра электронной оболочки ЭКЦ, представлены слева и справа на фиг. 5 параболами V(r-r0) и  . Энергетические уровни ЭКЦ с различными значениями колебательного квантового числа ν=0, 1, 2, … показаны пунктирными горизонтальными линиями. Электронные переходы из зоны проводимости на колебательные уровни ЭКЦ с ν>0 показаны вертикальными направленными вниз от Ес стрелками. Переходы дырок на колебательные уровни ЭКЦ изображены вертикальными направленными вверх от Ev стрелками. Для этого ветви параболы V(r-r0) обращены вниз, а ветви параболы
. Энергетические уровни ЭКЦ с различными значениями колебательного квантового числа ν=0, 1, 2, … показаны пунктирными горизонтальными линиями. Электронные переходы из зоны проводимости на колебательные уровни ЭКЦ с ν>0 показаны вертикальными направленными вниз от Ес стрелками. Переходы дырок на колебательные уровни ЭКЦ изображены вертикальными направленными вверх от Ev стрелками. Для этого ветви параболы V(r-r0) обращены вниз, а ветви параболы  обращены вверх, как показано на фиг. 5. Именно такие положения потенциальных кривых V(r-r0) и
обращены вверх, как показано на фиг. 5. Именно такие положения потенциальных кривых V(r-r0) и  соответствуют возбуждению I-колебаний ЭКЦ за счет энергии электронных или дырочных переходов. Эти переходы преимущественно происходят с испусканием или поглощением нескольких кристаллических фононов, возбуждают I-колебания атомных ядер в атомах ЭКЦ и поэтому они являются электронно-колебательными переходами. Электронно-колебательный процесс на ЭКЦ можно представить как последовательное, периодическое чередование электронно-колебательного перехода из зоны проводимости (или из валентной зоны) на ЭКЦ и последующего перехода с ЭКЦ электрона в зону проводимости (дырки в валентную зону) за счет энергии I-колебаний атомного ядра и кристаллических фононов. Каждый атом, ядро которого выполняет свободные или вынужденные I-колебания, целесообразно рассматривать как I-осциллятор, энергии колебаний которого описываются формулой (6).
соответствуют возбуждению I-колебаний ЭКЦ за счет энергии электронных или дырочных переходов. Эти переходы преимущественно происходят с испусканием или поглощением нескольких кристаллических фононов, возбуждают I-колебания атомных ядер в атомах ЭКЦ и поэтому они являются электронно-колебательными переходами. Электронно-колебательный процесс на ЭКЦ можно представить как последовательное, периодическое чередование электронно-колебательного перехода из зоны проводимости (или из валентной зоны) на ЭКЦ и последующего перехода с ЭКЦ электрона в зону проводимости (дырки в валентную зону) за счет энергии I-колебаний атомного ядра и кристаллических фононов. Каждый атом, ядро которого выполняет свободные или вынужденные I-колебания, целесообразно рассматривать как I-осциллятор, энергии колебаний которого описываются формулой (6).
Благодаря сильной электрон-фононной связи ЭКЦ обладают большим сечением захвата электронов и дырок из-за чего электроны и дырки локализуются на указанных электронно-колебательных уровнях ЭКЦ. Причем один из уровней с квантовым числом ν=ν* доминирует в процессах захвата и удержания носителей зарядов. В результате электрические заряды накапливаются на данном уровне и, именно вблизи него фиксируется уровень Ферми F≅E(ν*)=Е*. Плотность электронно-колебательных состояний на уровне Ферми N(F)=N*⋅δ(E*-F), где N* - плотность состояний с энергией Е*, δ(E*-F) - дельта функция Дирака. Очевидно, что N* превышает среднюю плотность состояний, равную N/EZ, где N - концентрация ЭКЦ, а из фиг. 5 видно, что V*=(ЕC-Е*)≥EZ. Если на каждом центре в среднем локализован хотя бы один электрон, то для любого единичного объема материала (1 см3) произведение V*N(F)≥N≥1012. Поэтому входящая в выражение (4) экспонента имеет близкое к единице значение, а вычисленная температура сверхпроводящего перехода Tc≅1,13TD, где температура Дебая I-колебаний TD=V*/k. Например, для содержащего А-центры кремния даже при ν=1 получается Tc>2500 K, то есть выше температуры плавления материала. Соответствующая, ожидаемая по теории БКШ температурная зависимость электрического сопротивления (R) гиперпроводника, т.е. содержащего ЭКЦ полупроводника, качественно показана на фиг. 6. сплошной линией. Она совпадает с нулевым значением сопротивления на температурном участке от Тh до Tc, при этом температура Tc может превышать температуру плавления материала (Тпл). Из фиг. 6 видно, что сопротивление гиперпроводника становится нулевым при температурах выше температуры гиперпроводящего перехода Тh, а при Т<Тh оно имеет конечное, ненулевое значение. Вообще говоря, в гиперпроводнике может возникнуть традиционная сверхпроводимость при низких температурах, ниже  , как это качественно показано пунктирной линией на фиг. 6.
, как это качественно показано пунктирной линией на фиг. 6.
Характерный размер когерентной области (длина когерентности Λ) зависит от температуры материала. При нагревании материала между электродами когерентные области вначале увеличиваются в размерах и при температуре Тh они занимают весь материал на протяжении от одного электрода до другого электрода электрически замыкая электроды друг с другом, что соответствует гиперпроводимости и сверхтеплопроводности. Если температура материала превысит Th, то соответствующее увеличение размера когерентных областей не нарушает гиперпроводимости и сверхтеплопроводности материала между электродами при нагревании. Однако, приближение температуры материала к Tc вызывает уменьшение размера когерентных областей (длины когерентности Λ). При температуре Tc когерентные области хотя и занимают еще весь материал на протяжении от одного электрода до другого электрода электрически замыкая электроды друг с другом, тем не менее, нагревание материала выше Tc вызывает появление слоев материала не относящихся к когерентным областям. В результате электрическое и тепловое сопротивления материала между электродами отличаются от нулевых значений и увеличиваются при дальнейшем нагревании. Таким образом гиперпроводимость и сверхтеплопроводность могут существовать в интервале температур от Th до Tc. При этом расстояние между электродами (D) следует установить не более размера материала, занятого когерентными областями между электродами. Уменьшение D позволяет уменьшить Тh и увеличить Tc, т.е. расширить необходимый для гиперпроводимости и свертеплопроводности интервал температур от Тh до Тc. Увеличение D вызывает сужение этого интервала, уменьшение разности (Тс-Тh) вплоть до нулевого значения из-за чего при увеличенных значениях D осуществление гиперпроводимости и сверхтеплопроводности требует применения дополнительных мер, из которых некоторые предложены в данном изобретении.
Определен диапазон концентраций ЭКЦ допустимых для осуществления электронно-колебательных процессов и гиперпроводимости от минимальной (Nmin=2⋅1012 см-3) до максимальной (Nmax=6⋅1017 см-3).
Для осуществления гиперпроводимости и сверхтеплопроводности следует обеспечить связь I-колебаний с движениями электронов. Такую связь обеспечивают ЭКЦ посредством фононов. Однако необходимые для этого фононы возникают в достаточном количестве только вблизи температур Дебая фононов (Тm). Поэтому при нагревании гиперпроводника состояние гиперпроводимости возникает и может существовать при сравнительно высокой температуре гиперпроводящего перехода Тh, которая близка к дебаевой температуре связанного с ЭКЦ типа кристаллических фононов, и при более высоких температурах.
Гиперпроводимость может существовать при температурах между Тh и Tc, причем Тh<Тс, в то время как сверхпроводимость может существовать при температурах ниже  . В связи с этим очевидно, что механизм формирования гиперпроводимости вообще говоря отличается от механизма формирования сверхпроводимости. Поэтому новому состоянию с нулевым электрическим и тепловым сопротивлением содержащих ЭКЦ материалов было дано иное название: гиперпроводимость, а сопутствующему гиперпроводимости состоянию с нулевым тепловым сопротивлением (RT=0) было дано название - сверхтеплопроводность.
. В связи с этим очевидно, что механизм формирования гиперпроводимости вообще говоря отличается от механизма формирования сверхпроводимости. Поэтому новому состоянию с нулевым электрическим и тепловым сопротивлением содержащих ЭКЦ материалов было дано иное название: гиперпроводимость, а сопутствующему гиперпроводимости состоянию с нулевым тепловым сопротивлением (RT=0) было дано название - сверхтеплопроводность.
Определена связь между температурой гиперпроводящего перехода T=Тh и параметрами материала. Действительно, согласно теории электронно-колебательных переходов [17-20] в таком переходе на ЭКЦ участвуют в среднем S фононов. В стационарном состоянии электроны (дырки) преимущественно локализуются на энергетическом уровне Е* (см. фиг. 5) и материал имеет проводимость, близкую к собственной проводимости. Скорость тепловой генерации электронов и дырок в материале равна скорости их рекомбинации на ЭКЦ. Из этого условия получается следующее выражение (7), связывающее концентрацию электронно-колебательных центров N, температуру гиперпроводящего перехода Т=Тh и константу электрон-фононной связи S на ЭКЦ:

где NC и NV - эффективные значения плотностей электронных и дырочных состояний в зоне проводимости и в валентной зоне, соответственно, Eg - ширина запрещенной зоны полупроводника, E(ν) - колебательная энергия, равная Е*.
На фиг. 7 приведены экспериментально измеренные значения температур гиперпроводящего перехода в различных материалах, содержащих различные концентрации ЭКЦ, в зависимости от среднего значения атомного номера Zcpeдн. Наклонные прямые линии а и б представляют вычисленные по формуле (7) значения Th, при максимальной (Nmax) и минимальной (Nmin) концентрациях ЭКЦ. Из фиг. 7 видно, что экспериментальные значения Тh лежат между прямыми а и б, являющимися пределами области ожидаемых из расчета значений Тh, что подтверждает согласие экспериментальных и вычисленных результатов в условиях термодинамического равновесия.
Известно, что в кристаллах могут существовать и распространяться упругие акустические (А), оптические (О) [40], а также I-колебания и волны I-колебаний [1, 4, 7-15, 34-38]. Акустические колебания представляют собой периодические во времени смещения элементарных ячеек кристалла друг относительно друга и могут существовать как в простых кристаллах, когда элементарная ячейка материала содержит один атом, так и в сложных кристаллах, элементарная ячейка которых содержит несколько атомов. Оптические колебания представляют собой периодические во времени смещения атомов друг относительно друга внутри элементарной ячейки и могут существовать в кристаллах, имеющих в ячейке два или более двух атомов. Собственные (Inherent, I-) колебания (α, β и γ типов) представляют собой периодические во времени смещения ядра атома или иона относительно его электронной оболочки и могут существовать в любых молекулах и материалах. Элементарные кванты акустических и оптических колебаний и волн называют фононами, I-колебания также квантованы. Энергия кванта I-колебаний значительно (в 5-10 раз) превышает максимальную энергию акустического фонона и превышает (в 4-5 раз) максимальную энергию оптического фонона. Эти типы колебаний обычно описываются в приближении линейной связи между смещениями составляющих кристалл частиц и возникающими при этом силами. Соответственно каждый атом в кристалле можно представить как два связанных осциллятора. Один из этих осцилляторов представляет колебания атома с частотами фононов (р), а второй осциллятор это - собственный (Inherent), I-осциллятор представляет периодические смещения ядра в атоме с циклической частотой I-колебаний (ω).
Чаще всего полагают, что колебательные смещения атомов в кристалле и вызываемые такими смещениями упругие силы связаны друг с другом линейно, из-за чего колебания являются гармоническими. В таком приближении классическое уравнение движения атома в узле кристаллической решетки в общем виде модно записать следующим образом:

где x - смещение атома из положения равновесия, М - масса атома, коэффициент g>0, F' - амплитуда силы, возникающей вследствие смещения ядра атома относительно электронной оболочки с циклической частотой I-колебаний (ω). Поделив обе части уравнения (8) на М и обозначив r=g/2M, р2=k/M,  , F=F'/М запишем его в виде
, F=F'/М запишем его в виде

Если r, p и F не зависят от времени, то данное уравнение с постоянными коэффициентами описывает вынужденные колебания затухающего гармонического осциллятора [41, с. 15-22, с. 183-210], а его решение можно записать следующим образом:

где амплитуда вынужденных колебаний
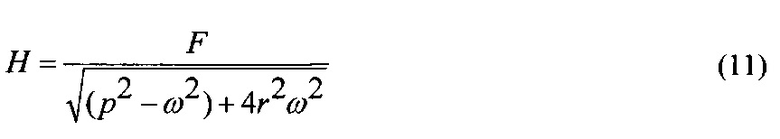
зависит от затухания r, от частоты свободных колебаний p и от частоты вынуждающей силы со. Коэффициент r описывает затухание колебаний или потерю осциллятором колебательной энергии, p - циклическая частота акустической волны, т.е. частота фонона в нашем случае, ω - частота I-колебаний ядра в атоме материала.
Изменение фазы (δ) вынужденных колебаний относительно фазы внешней силы описываются следующими соотношениями:

Из выражения (10) следует, что с течением времени (t) при r>0, свободные колебания, описываемые слагаемым, содержащим множитель e-rt, затухают и прекращаются, однако возникают, и будут существовать только вынужденные колебания с фазой, описываемой выражениями (12). Сдвиг фазы вынужденных колебаний относительно фазы вынуждающей силы (δ) жестко определяется циклической частотой свободных колебаний ЭКЦ (ω), циклической частотой связанных с ЭКЦ фононов (p) и затуханием колебаний (r). Таким образом, имеется реальная техническая возможность создавать вынужденные колебания ЭКЦ с заданной фазой, определяемой амплитудой и фазой внешнего вынуждающего воздействия на ЭКЦ и затуханием колебаний ЭКЦ, т.е. величиной коэффициента r. Для этого следует создавать в материале вынуждающий, синхронизирующий сигнал с определенной частотой и фазой.
Если циклические частоты колебаний ЭКЦ (ω) и фононов (р) в формулах (12) поменять местами, то физический смысл формул не измениться. Следовательно, техническую функцию синхронизирующего сигнала могут выполнять и собственные, т.е. I-колебания ЭКЦ, по отношению к фононам и фононы по отношению к колебаниям атомных ядер в ЭКЦ. Поэтому амплитуду и фазу вынужденных колебаний ЭКЦ можно изменять, изменяя либо амплитуду и фазу собственных колебаний ЭКЦ, либо изменяя амплитуду и фазу связанных с ЭКЦ фононов.
Было установлено, что в состоянии гиперпроводимости материал обладает нулевым электрическим сопротивлением и нулевым тепловым сопротивлением, то есть гиперпроводимость сосуществует с сверхтеплопроводностью [13, 16]. Кроме того, установлено, что материалы в гиперпроводящем состоянии являются неоднородными, в них возникают области когерентности с характерным размером Λ, который имеет смысл длины когерентности. Так в изотропном материале область когерентности имеет форму шара с радиусом Λ. Рассеяние энергии электронами в объеме когерентной области невозможно из-за когерентности, идентичности, неразличимости электронно-колебательных состояний атомов, входящих в когерентные области. Электроны испытывают рассеяние энергии только в пределах слоя материала, прилежащего к когерентной области, имеющего толщину, равную средней длине рассеяния энергии  .
.
В науке о сверхпроводниках используют понятие длины когерентности. B.Л. Гинзбург и Л.Д. Ландау [42] ввели понятие зависящей от температуры Т длины когерентности ξ(Т). Величина ξ(Т) определяет расстояние, на котором волновая функция электронов может изменяться без существенного изменения их энергии.
Понятие длины когерентности применительно к сверхпроводникам также ввел А.Б. Пиппард [43]. Длина когерентности Пиппарда (ξ0) представляет собой минимальный размер волновых пакетов, которые могут образовывать сверхпроводящие носители заряда в чистом (бездефектном) материале, когда нет рассеяния электронов, а при наличии рассеяния длина когерентности  , где
, где  - средняя длина свободного пробега электрона.
- средняя длина свободного пробега электрона.
Волновые функции в этих теориях имеют разный смысл. Длины когерентности в этих теориях также имеют разный смысл и относятся к сверхпроводящим электронам в зоне проводимости сверхпроводника.
Напротив, в заявленном изобретении гиперпроводимость и сверхтеплопроводность обусловлены электронами локальных центров и их когерентными колебаниями, а не электронами зоны проводимости материала как в серхпроводнике. Известные в сверхпроводниковой науке длины когерентности нельзя обоснованно применить для описания характерных размеров участков гиперпроводника с когерентными колебаниями. В связи с этим необходима длина когерентности Λ, которая представляет характерный размер области материала с когерентными колебаниями и поэтому имеющей нулевые электрическое и тепловое сопротивления.
Гиперпроводимость и сверхтеплопроводность обусловлены взаимодействием электронов, фононов и I-колебаний на ЭКЦ и этим принципиально отличаются от сверхпроводимости, обусловленной электронами проводимости связанными фононами в куперовские пары. Видимо в природе есть много механизмов формирования нулевого электрического сопротивления (с наборами различных свойств) из которых нам пока известны только сверхпроводимость и гиперпроводимость. Однако нельзя механически распространять на гиперпроводники свойства сверхпроводников только потому, что сверхпроводники стали известны раньше. Поэтому целесообразно уточнить смысл длины когерентности Λ.
Длину когерентности Λ для отдельной когерентной области в термодинамически равновесных условиях, когда она не взаимодействует с другими когерентными областями или с границами однородного материала, можно определить количественно. По соображениям минимума поверхностной энергии область когерентности в изотропном материале должна иметь форму шара с радиусом, равным длине когерентности Λ. На фиг. 8 изображено сечение материала плоскостью (XY) проходящей через центр сферической области когерентности. Граница области когерентности на фиг. 8 показана пунктирной окружностью с радиусом Λ. Рассеяние энергии I-колебаний происходит в прилежащей к когерентной области части кристалла, являющейся областью рассеяния энергии, которая имеет форму сферического слоя с толщиной, равной средней длине рассеяния энергии электрона 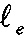 и объем
и объем 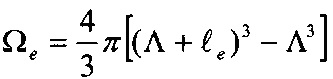 . В области рассеяния имеется
. В области рассеяния имеется 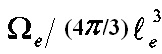 центров рассеяния. За среднее время рассеяния энергии (τе) на этих центрах в среднем рассеивается энергия, равная
центров рассеяния. За среднее время рассеяния энергии (τе) на этих центрах в среднем рассеивается энергия, равная 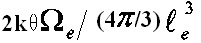 . С другой стороны, за это же время те колебательная энергия (Екол) уменьшается в е раз то есть на (1-1/е)Екол. Если приравнять эти энергии друг к другу и положить
. С другой стороны, за это же время те колебательная энергия (Екол) уменьшается в е раз то есть на (1-1/е)Екол. Если приравнять эти энергии друг к другу и положить 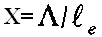 , то получается алгебраическое уравнение:
, то получается алгебраическое уравнение:

которое имеет следующее решение:

где 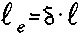 , δ - доля энергии, рассеиваемой в одном акте рассеяния,
, δ - доля энергии, рассеиваемой в одном акте рассеяния,  - средняя длина свободного пробега,
- средняя длина свободного пробега,

и величина

не зависит от температуры материала Т. В формуле (15) приняты следующие обозначения: m* - эффективная масса носителя заряда, k - постоянная Больцмана, ζ - доля энергии, рассеиваемой носителем заряда в одном акте рассеяния, М - масса и Ω - объем элементарной ячейки материала,  - интеграл по объему элементарной ячейки кристалла, Uk - амплитуда электронной волновой функции Блоха, Vзв - скорость звука в материале,
- интеграл по объему элементарной ячейки кристалла, Uk - амплитуда электронной волновой функции Блоха, Vзв - скорость звука в материале,  - постоянная Дирака, θ - параметр гауссова распределения температурной зависимости интенсивности I(Т) электронно-колебательных переходов [17-20]:
- постоянная Дирака, θ - параметр гауссова распределения температурной зависимости интенсивности I(Т) электронно-колебательных переходов [17-20]:

где Тm - температура материала при максимальной интенсивности электронно-колебательных переходов, т.е. maxI(T)=I(Tm). Установлено, что температура Тm совпадает с температурами Дебая связанных на ЭКЦ фононов. Параметр θ имеет размерность температуры, но его величина не зависит от температуры материала и для многих материалов θ обычно имеет постоянное значение, лежащее в примерных пределах от 2 K до 6 K.
Из (13) видно, что длина когерентности зависит от колебательной энергии когерентной области Екол, которая обычно увеличивается при увеличении температуры материала, а образование когерентной области возможно при X>0, когда Екол>0,79kθ, т.е. при температурах около 1,5 K и выше.
На фиг. 9 показано сечение материала между электродами плоскостью, проходящей через центр области когерентности радиусом Λ=D/2 расположенной между электродами 1 и 2, разделенными расстоянием D. Из фиг. 9 видно, что для осуществления гиперпроводимости и сверхтеплопроводности в материале между электродами 1 и 2 следует установить расстояние D между электродами не более 2Λ, D≤2Λ, или обеспечить увеличение Λ до величины D/2 или более. Тогда электроды 1 и 2 будут соединены одной когерентной областью с нулевым сопротивлением, и на всем протяжении в материале между электродами будет существовать гиперпроводимость и сверхтеплопроводность.
В реальном материале при нагревании от низких температур (≈1,5K) увеличивается концентрация и размеры когерентных областей, расстояния между когерентными областями уменьшаются, они могут смыкаться друг с другом при температуре Th и выше, обеспечивая гиперпроводимость и сверхтеплопроводность в материале между электродами вплоть до температуры Tc. Однако при нагревании взаимно перекрываются и уменьшаются размеры областей рассеяния колебательной энергии, уменьшаются размеры самих когерентных областей в соответствии с обратной температурной зависимостью в (14). В результате возникшие в материале между электродами гиперпроводимость и сврхтеплопроводность прекращаются, исчезают выше некоторой температуры (Т*), электрическое и тепловое сопротивления отклоняются от нулевого значения и увеличиваются при дальнейшем нагревании материала. Реальная температурная зависимость электрического сопротивления материала между электродами качественно представлена на фиг. 10. В области низких температур, ниже  , возможна традиционная сверхпроводимость. Гиперпроводимость (и сверхтеплопроводность) существует между Th и T*.
, возможна традиционная сверхпроводимость. Гиперпроводимость (и сверхтеплопроводность) существует между Th и T*.
Уменьшение расстояния между электродами D позволяет уменьшить температуру Th и увеличить температуру T*, т.е. позволяет увеличить температурный интервал существования гиперпроводимости между электродами. Увеличение расстояния между электродами D до величин более 4Λ препятствует осуществлению гиперпроводимости и сверхтеплопроводности в условиях прототипа [16], но это препятствие может быть устранено за счет дополнительного, альтернативного отвода колебательной энергии из материала. Возможные способы отвода колебательной энергии из материала предложены в данном изобретении.
Эффекты Джозефсона, происходящие в сверхпроводниковых туннельных контактах и состоящих в туннелировании куперовских электронных пар сквозь зазор между сверхпроводниками, отличаются от процессов туннелирования электронов, происходящих между когерентными областями в туннельных гиперпроводниковых структурах, в связи с чем электрические эффекты, происходящие в гиперпроводниковых туннельных структурах, являются аналогами эффектов Джозефсона. Установлено, что при наличии между когерентными областями туннельно тонкого для электронов зазора (вакуумного, диэлектрического или состоящего из атомов основного или иного вещества) между этими когерентными областями возникают и существуют аналоги эффектов Джозефсона, вызванные туннелированием электронов когерентных областей сквозь туннельно тонкий зазор. В отличие от эффектов Джозефсона, обусловленных туннелированием куперовских пар электронов и происходящих при температурах ниже температуры сверхпроводящего перехода, аналоги эффектов Джозефсона обусловлены туннелированием электронов сквозь туннельно тонкий зазор между соседними когерентными областями при околокомнатных и более высоких температурах. Участия куперовских электронных пар в аналогах эффектов Джозефсона не выявлено.
Аналог стационарного эффекта Джозефсона проявляется в виде постоянного электрического тока (I0) протекающего между когерентными областями или в виде разности напряжений между когерентными областями, разделенными туннельно тонким зазором толщиной d, даже если между когерентными областями не приложено внешнее электрическое напряжение. Полярность (направление тока) стационарного эффекта Джозефсона определяется знаком разности фаз когерентных колебаний этих областей. Ток I0 образован теми электронами, которые туннелируют между электронно-колебательными состояниями соседних когерентных областей при участии связанных с ними фононов и I-колебаний.
Аналог высокочастотного нестационарного эффекта Джозефсона проявляется в виде переменного (ВЧ или СВЧ) электрического тока с циклической частотой  , протекающего между когерентными областями, если между этими когерентными областями приложено внешнее постоянное напряжение V.
, протекающего между когерентными областями, если между этими когерентными областями приложено внешнее постоянное напряжение V.
Отличительные признаки заявленного изобретения близки к отличительным признакам известного способа [16] который целесообразно принять в качестве прототипа заявленного изобретения. В прототипе используют образец полупроводникового материала с выпрямляющими электродами 1 и 2, разделенными расстоянием D, вводят в материал ЭКЦ. В прототипе, как и в заявленном изобретении, используют электронно-колебательные переходы между различными ЭКЦ и возникающие при этом электрические токи и тепловые потоки. В прототипе указаны пределы допустимой концентрации ЭКЦ (N) (от 2⋅1012 см-3 до 6⋅1017 см-3), установленные путем анализа экспериментальных данных о туннелировании электронов сквозь тонкие диэлектрические слои в контактах металл-диэлектрик-полупроводник и особенности зонной структуры встречно включенных контактов Шоттки [44-46]. Характерные данные о таких процессах туннелирования электронов сквозь диэлектрический слой толщиной h в структурах на основе InP приведены на фиг. 11. Из представленных на фиг. 11 данных видно, что максимальная концентрация ЭКЦ для электронно-колебательных процессов достигает Nmax=6⋅1017 см-3. Минимальная концентрация ЭКЦ близка к Nmin=2⋅1012 см-3, что вытекает из теоретической оценки и соответствует современным технологическим и метрологическим возможностям уменьшать N до таких значений и измерять такие концентрации ЭКЦ с приемлемой точностью. Известное правило «1/3», определяющее высоту потенциального барьера Шоттки в контакте металл-полупроводник, изложено в [47, стр. 287].
В прототипе выбирают D<<L, где L - глубина проникновения в материал электрического поля, вызванного контактной разностью потенциалов, Dmin=10 нанометров, Dmax=30 мкм. Однако в заявленном изобретении показано, что возможности выбора величины D существенно изменяются в зависимости от внешних по отношению к материалу между электродами условий, в частности, от интенсивности вывода из материала колебательной энергии вследствие чего величина D может существенно превышать указанную в прототипе Dmax.
Критика прототипа изобретения. Использование прототипа изобретения при осуществлении гиперпроводимости и сверхтеплопроводности в различных полупроводниковых материалах выявило его низкую эффективность. Говоря техническим языком, применение прототипа обеспечивает достижение цели изобретения, но выход годных к техническому применению приборов, демонстрирующих гиперпроводимость и сверхтеплопроводность, является небольшим, то есть эффективность прототипа невелика, нередко она составляет процент или менее процента. В связи с этим необходим способ, обеспечивающий существенное увеличение эффективности прототипа, необходим способ эффективного осуществления гиперпроводимости и сверхтеплопроводности.
Целью данного изобретения является создание способа эффективного осуществления гиперпроводимости и сверхтеплопроводности.
Сущность изобретения
Указанная цель изобретения достигается тем, что применяют заявленный способ эффективного осуществления гиперпроводимости и сверхтеплопроводности согласно пункту 1 формулы которого, как и в прототипе, используют невырожденный или слабо вырожденный полупроводниковый материал, размещают на его поверхности или в его объеме электроды 1 и 2, образующие выпрямляющие контакты с материалом, такие как контакты металл-полупроводник, контакты Шоттки, отличающийся тем, что расстояние между электродами (D) выбирают не более 4Λ, D≤4Λ, где Λ - длина когерентности; характерный размер контактной области каждого электрода с материалом выбирают не более четверти длины ВЧ или СВЧ волны в материале  , где с - скорость света в вакууме, ε - относительная диэлектрическая проницаемость материала, F - характерная резонансная частота замедляющего устройства; устанавливают и поддерживают тепловой контакт материала с термостатом; устанавливают и поддерживают согласованную электромагнитную связь части материала, примыкающей к электроду 1, или (и) части материала, примыкающей к электроду 2, или материала, или части материала расположенного между электродами 1 и 2, с высокочастотным (высокочастотными, ВЧ) и (или) сверхвысокочастотным (сверхвысокочастотными) (СВЧ) замедляющим устройством (замедляющими устройствами) таким (такими) как коаксиальная линия, волноводная линия, полосковая линия, резонатор, колебательный контур, которые характеризуются резонансными частотами (F) в диапазоне от 106 Гц до 3⋅1015 Гц и добротностями Q≥10; материал нагревают до температуры (Т), равной или превышающей температуру гиперпроводящего перехода (Th), до температур существования гиперпроводимости и свертеплопроводности (Тh≤Т≤Т*), в результате электрическое сопротивление и тепловое сопротивление материала между электродами обращаются в ноль, то есть осуществляется гиперпроводимость и сверхтеплопроводность, усиливается эффект Мейснера; измеряют электрическое и (или) тепловое сопротивление материала между электродами, и (или) Th, и (или) Λ,, или (и) эффект Мейснера, или (и) уровень внутренних (собственных) шумов.
, где с - скорость света в вакууме, ε - относительная диэлектрическая проницаемость материала, F - характерная резонансная частота замедляющего устройства; устанавливают и поддерживают тепловой контакт материала с термостатом; устанавливают и поддерживают согласованную электромагнитную связь части материала, примыкающей к электроду 1, или (и) части материала, примыкающей к электроду 2, или материала, или части материала расположенного между электродами 1 и 2, с высокочастотным (высокочастотными, ВЧ) и (или) сверхвысокочастотным (сверхвысокочастотными) (СВЧ) замедляющим устройством (замедляющими устройствами) таким (такими) как коаксиальная линия, волноводная линия, полосковая линия, резонатор, колебательный контур, которые характеризуются резонансными частотами (F) в диапазоне от 106 Гц до 3⋅1015 Гц и добротностями Q≥10; материал нагревают до температуры (Т), равной или превышающей температуру гиперпроводящего перехода (Th), до температур существования гиперпроводимости и свертеплопроводности (Тh≤Т≤Т*), в результате электрическое сопротивление и тепловое сопротивление материала между электродами обращаются в ноль, то есть осуществляется гиперпроводимость и сверхтеплопроводность, усиливается эффект Мейснера; измеряют электрическое и (или) тепловое сопротивление материала между электродами, и (или) Th, и (или) Λ,, или (и) эффект Мейснера, или (и) уровень внутренних (собственных) шумов.
Согласно п. 2 формулы в способе по п. 1 с целью стабилизации гиперпроводящего перехода материал между электродами нагревают от температуры ≈1,5K или от более высокой температуры до температур существования гиперпроводимости (Th≤Т≤T*), прекращают нагрев или (и) создают в материале поперечное к току магнитное поле с индукцией до 2 Тесла на время до 60 секунд, поддерживают температуру материала в диапазоне между Th и T*; в результате электрическое сопротивление и тепловое сопротивление материала между электродами обращаются в ноль и тем самым осуществляется гиперпроводимость и сверхтеплопроводность, усиливается эффект Мейснера.
Согласно п. 3 формулы в способе по п. 1 с целью уменьшения температуры гиперпроводящего перехода Th за счет увеличения длины когерентности Λ и с целью усиления эффекта Мейснера размер материала (b) выбирают не менее двух длин когерентности (2Λ), (b≥2Λ), например выбирают толщину пластины материала не менее 2Λ или толщину слоя материала не менее 2Λ на полупроводниковой, полуизолирующей или диэлектрической подложке; измеряют Тh, и (или) Λ, и (или) величину эффекта Мейснера.
Согласно п. 4 формулы в способе по п. 3 с целью осуществления гиперпроводимости и сверхтеплопроводности в объеме материала с размерами, многократно превышающими 2Λ, а также с целью усиления эффекта Мейснера на поверхности или (и) в объеме материала размещают вкрапления частиц, образующих выпрямляющие контакты с материалом, например, вкрапления металлических частиц с размерами (с) не более Λ, (с≤Λ), в концентрации от (2Λ)-3 до (2с)-3 или (и) частиц из которых каждая в отдельности или группа (группы) частиц образуют замедляющую систему (замедляющие системы) или (и) является (являются) частью (частями) замедляющей системы (замедляющих систем); измеряют температуру гиперпроводящего перехода Th и (или) длину когерентности Λ, и (или) величину эффекта Мейснера.
Согласно п. 5 формулы в способе по п. 3 с целью осуществления аналога стационарного эффекта Джозефсона устанавливают расстояние между электродами превышающее четыре длины когерентности (4Λ) на величину туннельно прозрачного зазора величиной d между областями когерентности, (D=4Λ+d), (10А°≤d≤50 микрон); измеряют постоянный ток в материале между электродами 1 и 2 и (или) его направление, полярность, или (и) измеряют постоянную разность потенциалов между электродами 1 и 2 и (или) ее полярность; результаты измерений интерпретируют как величину аналога стационарного эффекта Джозефсона и его полярность, соответственно.
Согласно п. 6. в способе по п. 5 с целью осуществления аналога нестационарного высокочастотного эффекта Джозефсона между электродами 1 и 2 прикладывают постоянное напряжение произвольной полярности величиной менее напряжения пробоя данной структуры; измеряют величину переменного напряжения между электродами и (или) измеряют частоту (частоты) переменного напряжения или (и) измеряют величину переменного тока в материале между электродами и (или) измеряют частоту (частоты) переменного тока в материале между электродами и (или) измеряют фазу напряжения и (или) фазу тока; результаты измерений, соответственно, идентифицируют как величину, частоту и фазу аналога высокочастотного нестационарного эффекта Джозефсона.
Согласно п. 7 формулы в способе по п. 5 с целью осуществления аналогов эффектов Джозефсона используют два материала отделенных друг от друга туннельно тонким диэлектрическим слоем толщиной d, размер каждого материала выбирают не менее четырех длин когерентности (4Λ), на внешней поверхности или в объеме каждого материала размещают электрод (электроды), образующий (образующие) выпрямляющий контакт (выпрямляющие контакты) с материалом, например, контакт (контакты) металл-полупроводник; измеряют постоянный ток между электродами 1 и 2 в данной структуре (электрод 1 - материал 1 - диэлектрик - материал 2 - электрод 2); измеряют постоянную разность потенциалов между этими электродами; результаты измерений интерпретируют как аналог стационарного эффекта Джозефсона; прикладывают постоянное напряжение между электродами величиной, не достигающей напряжения электрического пробоя данной структуры, измеряют переменное напряжение между электродами 1 и 2 и (или) переменный ток в материале между электродами, а результаты измерений идентифицируют как аналог высокочастотного нестационарного эффекта Джозефсона; измеряют частоту (частоты) переменного напряжения между электродами и (или) переменного тока в материале между электродами и (или) фазы тока и напряжения; результаты измерений идентифицируют как величину, частоту (частоты) и фазу аналога высокочастотного нестационарного эффекта Джозефсона.
Согласно п. 8 формулы в способе по п. 5 с целью осуществления эффектов Джозефсона используют два различных материала образующих гетероструктуру; на внешней поверхности или в объеме каждого материала устанавливают электрод, образующий выпрямляющий контакт с материалом, например, контакт металл-полупроводник; измеряют постоянный ток в материале между электродами 1 и 2 или (и) измеряют напряжение между электродами и его полярность и идентифицируют результаты измерений как величину и полярность стационарного эффекта Джозефсона; между электродами 1 и 2 прикладывают постоянное напряжение величиной не более напряжения пробоя данной гетероструктуры, измеряют величину и (или) частоту и (или) фазу напряжения между электродами и (или) тока в материале между электродами и идентифицируют их как величину, частоту, фазу аналога высокочастотного нестационарного эффекта Джозефсона.
Согласно п. 9 формулы в способе по п. 6 с целью регулирования величины, частоты, фазы высокочастотного нестационарного эффекта Джозефсона и (или) величины эффекта Мейснера посредством электрического напряжения между электродами 1 и 2, между этими электродами прикладывают постоянное или низкочастотное  переменное напряжение величиной V не более напряжения пробоя данной структуры; изменяют полярность и (или) фазу этого напряжения и (или) его величину; измеряют полярность и (или) фазу и (или) частоту аналога высокочастотного нестационарного эффекта Джозефсона и (или) измеряют изменения величины эффекта Мейснера.
переменное напряжение величиной V не более напряжения пробоя данной структуры; изменяют полярность и (или) фазу этого напряжения и (или) его величину; измеряют полярность и (или) фазу и (или) частоту аналога высокочастотного нестационарного эффекта Джозефсона и (или) измеряют изменения величины эффекта Мейснера.
Согласно п. 10 формулы в способе по п. 5 с целью регулирования температуры гиперпроводящего перехода Тh, величины эффектов Джозефсона, частоты и фазы высокочастотного нестационарного эффекта Джозефсона, а также величины эффекта Мейснера с помощью электромагнитного излучения в материал между электродами 1 и 2 направляют электромагнитное излучение интенсивностью до  квантов⋅с-1см-2, где N* - эффективное число электронных состояний в разрешенной энергетической зоне материала, ζ - коэффициент оптического поглощения и τ - время жизни электронов (дырок), в спектральном диапазоне собственного, основного, фундаментального поглощения материала или (и) в спектральном диапазоне электронно-колебательных переходов ЭКЦ или (и) в спектральном диапазоне упругих колебаний с частотами фононов локализованных на ЭКЦ электронов; измеряют вызванные излучением изменения мощности (мощностей) рассеивающихся в нагрузках связанных с материалом замедляющих устройств или (и) измеряют изменения величины (величин) аналогов эффектов Джозефсона или (и) измеряют изменение частоты (частот) и фазы (фаз) аналога высокочастотного эффекта Джозефсона или (и) измеряют изменение температуры гиперпроводящего перехода (Тh) или (и) измеряют изменения величины эффекта Мейснера; по результатам измерений делают вывод о свойствах излучения, например, о интенсивности регулирующего излучения, о его поляризации, о его частоте, о его когерентности.
квантов⋅с-1см-2, где N* - эффективное число электронных состояний в разрешенной энергетической зоне материала, ζ - коэффициент оптического поглощения и τ - время жизни электронов (дырок), в спектральном диапазоне собственного, основного, фундаментального поглощения материала или (и) в спектральном диапазоне электронно-колебательных переходов ЭКЦ или (и) в спектральном диапазоне упругих колебаний с частотами фононов локализованных на ЭКЦ электронов; измеряют вызванные излучением изменения мощности (мощностей) рассеивающихся в нагрузках связанных с материалом замедляющих устройств или (и) измеряют изменения величины (величин) аналогов эффектов Джозефсона или (и) измеряют изменение частоты (частот) и фазы (фаз) аналога высокочастотного эффекта Джозефсона или (и) измеряют изменение температуры гиперпроводящего перехода (Тh) или (и) измеряют изменения величины эффекта Мейснера; по результатам измерений делают вывод о свойствах излучения, например, о интенсивности регулирующего излучения, о его поляризации, о его частоте, о его когерентности.
Согласно п. 11 формулы в способе по п. 10 с целью стабилизации гиперпроводящего и сверхтеплопроводного состояния, стабилизации температуры гиперпроводящего перехода Тh, величин эффектов Джозефсона и частоты высокочастотного нестационарного эффекта Джозефсона, а также с целью изменения величины эффекта Мейснера толщину полупроводниковой пластины, или толщину полупроводникового слоя на подложке, или толщину подложки, или общую толщину полупроводникового слоя и подложки, или расстояние (расстояния) между взаимно параллельными границами материала или материала и подложки выбирают равным (равными) или кратным (кратными) W=ПVзв/2, где Vзв - скорость звука, распространяющегося между взаимно параллельными границами полупроводника, подложки, или полупроводника и подложки; в материале между электродами создают переменное электрическое поле с напряженностью до SEz/e, где S - константа электрон-фононного взаимодействия и Ez - элементарный квант I-колебаний ядер в атомах, но не более напряжения пробоя, и (или) постоянное и (или) переменное магнитное поле с индукцией В≤2 Тл с периодом П; измеряют температуру гиперпроводящего перехода Th, величину и (или) полярность аналога стационарного эффекта Джозефсона, величину и (или) частоту и (или) фазу высокочастотного нестационарного эффекта Джозефсона, величину или (и) изменение величины эффекта Мейснера.
Согласно п. 12 формулы в способе по п. 5, с целью получения электрического тока посредством аналога стационарного эффекта Джозефсона обеспечивают приток тепла к материалу; направляют постоянный ток в материале между электродами, представляющий аналог стационарного эффекта Джозефсона или аналогичные токи от нескольких таких структур последовательно или параллельно в стационарное или мобильное потребляющее (потребляющие) электрический ток устройство (устройства).
Согласно п. 13 формулы в способах по п. 6 с целью получения электрического тока (электрической энергии) посредством аналога высокочастотного нестационарного эффекта Джозефсона обеспечивают приток тепла к материалу, между электродами 1 и 2 поддерживают постоянную разность потенциалов величиной до SEz/e, но не более напряжения пробоя структуры; высокочастотный ток, протекающий между электродами и представляющий аналог высокочастотного нестационарного эффекта Джозефсона направляют в потребляющие этот ток устройства, при необходимости этот ток детектируют (выпрямляют), а полученный в результате детектирования постоянный ток направляют в стационарное или мобильное потребляющее (потребляющие) электроэнергию устройство (устройства).
Согласно п. 14 формулы в способе по п. 8 с целью регулирования температуры материала между электродами изменяют величины токов, представляющих аналог стационарного эффекта Джозефсона или (и) аналог высокочастотного нестационарного эффекта Джозефсона изменяя величину нагрузочного сопротивления (импеданса) для этих токов; измеряют температуру материала между электродами.
Согласно п. 15 формулы в способе по п. 7 с целью регулирования величин аналогов эффектов Джозефсона, частоты аналога высокочастотного эффекта Джозефсона, величины эффекта Мейснера изменяют температуру материала между электродами в температурной области выше Th, то есть в области существования гиперпроводимости и сверхтеплопроводности, измеряют величину аналога стационарного эффекта Джозефсона и (или) величину аналога высокочастотного нестационарного эффекта Джозефсона, и (или) частоту аналога высокочастотного эффекта Джозефсона, и (или) величину эффекта Мейснера.
Согласно п. 16 формулы в способе по п. 7 с целью регулирования температуры гиперпроводящего перехода Th, величины эффектов Джозефсона и частоты высокочастотного нестационарного эффекта Джозефсона, а также величины эффекта Мейснера используют полевой электрод, образующий выпрямляющий контакт или контакт металл-диэлектрик-полупроводник (МДП) с материалом между электродами, или используют несколько таких полевых электродов; к полевому электроду (к полевым электродам) подводят постоянные, переменные или импульсные внешние напряжения прямой или обратной полярности относительно материала величиной менее напряжения (напряжений) пробоя или разрушения структуры; измеряют изменение температуры гиперпроводящего перехода Th или (и) изменения величин эффектов Джозефсона или (и) изменение частоты высокочастотного нестационарного эффекта Джозефсона или (и) изменение величины эффекта Мейснера вызванные действием напряжений на полевом электроде (на полевых электродах) относительно материала.
Согласно п. 17 формулы в способе по п. 10 с целью упрощения способа используют образец материала с одним электродом (с номером 1 или 2); постоянное или модулированное по амплитуде, или (и) по частоте или (и) по фазе или (и) по поляризации или (и) по направлению распространения и подлежащее регистрации излучение направляют в примыкающую к электроду часть материала; измеряют вызванные излучением изменения тока или (и) частоты тока в примыкающей к электроду части материала или (и) изменения величины и (или) частоты (частот) модуляции мощности, рассеивающейся в согласованной нагрузке связанного (связанных) с материалом замедляющего устройства (замедляющих устройств); по результатам измерений судят о свойствах регистрируемого излучения, например, о интенсивности и (или) о частоте и (или) о спектре модуляции, и (или) о поляризации, и (или) о направлении распространения регистрируемого излучения.
Согласно п. 18 формулы в способе по п. 17 с целью увеличения чувствительности при оптическом регулировании величины, частоты, фазы (полярности) аналогов эффектов Джозефсона на примыкающий к электроду материал наносят просветляющее в спектральной области регулирующего излучения покрытие или (и) устанавливают параллельно поверхности материала на расстоянии (h) кратном половине длины волны излучения зеркало, обращенное рабочей поверхностью к материалу; излучение направляют в примыкающий к электроду материал под острым углом не более arctg[2Λ/(h⋅i)] к направлению нормали к поверхностям материала и зеркала, где i - число отражений луча излучения от поверхности материала или зеркала; измеряют величину и (или) частоту и (или) фазу (полярность) эффекта (эффектов) Джозефсона и (или) величину или (и) изменение величины эффекта Мейснера.
Согласно п. 19 формулы в способе по п. 3 с целью регулирования длины когерентности Λ, величин аналогов эффектов Джозефсона, частоты высокочастотного нестационарного аналога эффекта Джозефсона, а также величины эффекта Мейснера изменяют добротность Q связанного (связанных) с материалом между электродами замедляющего устройства (замедляющих устройств) или (и) изменяют коэффициент (коэффициенты) связи замедляющего устройства (замедляющих устройств) с материалом между электродами; измеряют длину или изменения длины когерентности Λ или (и) изменения величины эффектов Джозефсона или (и) изменения частоты или (и) фазы высокочастотного эффекта Джозефсона или (и) изменение эффекта Мейснера.
Согласно п. 20 формулы в способе по п. 3 с целью регулирования температуры гиперпроводящего перехода Th, величины эффектов Джозефсона и эффекта Мейснера, частоты высокочастотного нестационарного эффекта Джозефсона, а также с целью улучшения стабильности гиперпроводящего состояния и уменьшения внутренних шумов в материале между электродами создают постоянное, переменное или импульсное магнитное поле с индукцией (В) до 2 Тесла; изменяют направление индукции по отношению к направлению электронно-колебательного тока между электродами или (и) изменяют частоту индукции или изменяют величину, направление и частоту индукции; измеряют температуру гиперпроводящего перехода Th, или (и) величину (величины) или (и) частоту или (и) фазу (полярность) эффектов Джозефсона, или (и) эффект Мейснера, или (и) уровень внутренних шумов.
Согласно п. 21 формулы в способе по п. 11 с целью регулирования температуры гиперпроводящего перехода Th, величины аналогов эффектов Джозефсона, частоты аналога высокочастотного нестационарного эффекта Джозефсона, а также эффекта Мейснера с помощью упругих волн в материал между электродами направляют упругую волну (упругие волны), то есть поток звука, инфразвука, ультразвука или гиперзвука с частотой F и с объемной плотностью мощности до  , где S - константа электрон-фононного взаимодействия, N - концентрация ЭКЦ, τ - время жизни электронов (дырок) в материале между электродами; изменяют частоту, направление распространения или (и) поляризацию упругой волны относительно направления между электродами; измеряют изменения температуры гиперпроводящего перехода Th или (и) величину стационарного или (и) величину, частоту и фазу высокочастотного нестационарного эффекта Джозефсона или (и) эффект Мейснера или его изменение.
, где S - константа электрон-фононного взаимодействия, N - концентрация ЭКЦ, τ - время жизни электронов (дырок) в материале между электродами; изменяют частоту, направление распространения или (и) поляризацию упругой волны относительно направления между электродами; измеряют изменения температуры гиперпроводящего перехода Th или (и) величину стационарного или (и) величину, частоту и фазу высокочастотного нестационарного эффекта Джозефсона или (и) эффект Мейснера или его изменение.
Сопоставительный анализ изобретения с прототипом показывает, что заявленный способ отличается применением теплового контакта материала с термостатом, использованием согласованной электромагнитной связи материала между электродами 1 и 2 или прилежащих к электродам частей материала с коаксиальной линией, волноводной линией, полосковой линией, с резонатором, колебательным контуром или другими замедляющими устройствами, имеющими резонансные частоты в диапазоне от 106 Гц до 3⋅1015 Гц и добротностями Q≥10, изменением добротностей, изменением коэффициента связи замедляющих устройств с материалом, нагреванием материала от начальных температур (≈1,5K), выбором определенных размеров электродов образующих выпрямляющие контакты с материалом, выбором величины расстояния D между электродами, выбором размера образца материала не менее 4Λ, изменением температуры материала между электродами в температурной области существования эффектов Мейснера, введением в материал вкраплений частиц определенных размеров и в определенной концентрации, образующих выпрямляющие контакты с материалом, в том числе вкраплений являющихся частями замедляющих систем или образующих замедляющие системы, выбором толщины d туннельно тонкого зазора между областями когерентности, измерением постоянного тока в материале между электродами 1 и 2 или постоянной разности потенциалов между электродами 1 и 2 и идентификацией результатов этих измерений как аналога стационарного эффекта Джозефсона, приложением постоянного электрического напряжения (V) между электродами 1 и 2 и измерением переменного тока в материале между электродами 1 и 2, измерением переменного напряжения между электродами 1 и 2 и идентификацией результатов измерений как аналога высокочастотного нестационарного эффекта Джозефсона, измерением частоты переменного тока в материале между электродами 1 и 2 и измерением частоты напряжения между электродами и идентификацией этих измерений как частоты аналога высокочастотного нестационарного эффекта Джозефсона, созданием постоянных или переменных электрических, магнитных, а также тепловых полей в материале между электродами, определенными изменениями и направлениями этих полей, освещением материала или его частей внешним электромагнитным излучением определенной интенсивности и спектрального состава, направлением в материал между электродами упругих волн: звуковых, ультразвуковых, гиперзвуковых, выбором размеров материала и структуры на подложке в соответствии с условием акустоэлектрического синхронизма, а также измерением эффекта Мейснера.
Анализ аналогов и прототипа изобретения не выявил таких же совокупностей отличительных признаков.
В заявленном изобретении впервые использована возможность изменения, увеличения длины когерентности Λ, за счет высокочастотного электромагнитного отвода колебательной энергии из материала посредством замедляющих устройств. Это позволяет изменить потоки энергии и термодинамическое равновесие электронно-колебательных процессов в материале, обеспечить увеличение Λ и соответственно увеличить эффективность прототипа, что соответствует цели изобретения.
Таким образом, заявленный способ эффективного осуществления гиперпроводимости и сверхтеплопроводности соответствует критерию изобретения "новизна".
Сравнение заявленного способа эффективного осуществления гиперпроводимости и сверхтеплопроводности с прототипом и другими техническими решениями в данной области техники не выявило технических решений, обладающих сходными совокупностями отличительных признаков. Это позволяет сделать обоснованный вывод о соответствии заявленного технического решения критерию изобретения "существенные отличия".
Действительно:
Данное изобретение основано на использовании технической возможности регулирования длины когерентности Λ, являющейся характерным размером области когерентности. В однородном изотропном материале в условиях термодинамического равновесия величина Λ определена применительно к отдельной, изолированной когерентной области. Соответствующие формулы (13-15) приведены и в описании заявленного изобретения. Они связывают величину Λ с длиной рассеяния энергии электронами  , где
, где 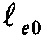 не зависит от температуры, с колебательной энергией когерентной области материала Екол, с температурой материала T, и с величиной θ, имеющей размерность температуры, принимающей для различных материалов и типов ЭКЦ фиксированное, независящее от температуры материала значение от 2 K до 10 K, обычно 4 K≤0≤6 K. Процесс рассеяния энергии электронами представлен величиной
не зависит от температуры, с колебательной энергией когерентной области материала Екол, с температурой материала T, и с величиной θ, имеющей размерность температуры, принимающей для различных материалов и типов ЭКЦ фиксированное, независящее от температуры материала значение от 2 K до 10 K, обычно 4 K≤0≤6 K. Процесс рассеяния энергии электронами представлен величиной 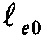 , взаимодействие ЭКЦ с окружающей его кристаллической средой представлен величиной θ. Величины
, взаимодействие ЭКЦ с окружающей его кристаллической средой представлен величиной θ. Величины 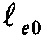 и θ определяются только микроскопическими взаимодействиями внутри материала и не поддаются регулированию за счет изменения внешних условий по отношению к материалу. Регулирование длины когерентности Λ посредством изменения температуры материала T, как это следует из формул (13-15) не обеспечивает увеличение Λ, необходимое для увеличения эффективности прототипа [16]. Следует учесть, что формула (13) верна только в условиях термодинамического равновесия.
и θ определяются только микроскопическими взаимодействиями внутри материала и не поддаются регулированию за счет изменения внешних условий по отношению к материалу. Регулирование длины когерентности Λ посредством изменения температуры материала T, как это следует из формул (13-15) не обеспечивает увеличение Λ, необходимое для увеличения эффективности прототипа [16]. Следует учесть, что формула (13) верна только в условиях термодинамического равновесия.
Известно, что в материалах могут существовать α, β, γ-типы собственных (Inherent, I-) упругих колебаний и волн, обусловленных упругими смещениями ядер в атомах, а также смещениями внутри атомов электронов K и L электронных орбиталей совместно с атомными ядрами. Собственные колебания α-типа представляют собой колебания ядер относительно электронной оболочки атома в материале. Собственные колебания β-типа представляют собой совместные колебания ядер и электронов K электронных орбиталей. Собственные колебания γ-типа представляют собой совместные колебания ядра и электронов K и L орбиталей относительно остальной части электронной оболочки атома материала. Существуют также упругие I-колебания и волны, обусловленные смещениями электронов М, N и одноэлектронных орбиталей совместно с ядром атома относительно остальной части электронной оболочки атома в материале. Кванты колебательных энергий таких I-колебаний с участием электронов М, N и O электронных орбиталей невелики, соответствующие частоты попадают в область частот акустических фононов. Такие упругие I-колебания с частотами от 106 Гц до 3⋅1013 Гц обеспечивают взаимодействие между ЭКЦ, осуществляют обмен энергией между центрами, благодаря чему устанавливаются одинаковые частоты и фазы когерентных колебаний атомов, а также определенная величина длины когерентности.
Спектр упругих колебаний ЭКЦ в материале можно описывать уравнением (8), но его решения не поддаются полному анализу. Согласно [41] выделяют периодические колебания:
а) Гармонические колебания. Решение x(t) имеет период, совпадающий с периодом возмущающей силы 2π/ω, и зависящую от p и от ω амплитуду колебаний  .
.
б) Субгармонические колебания. Решение x(t) имеет наименьший период 2π/p, равный периоду свободных колебаний осциллятора, который в n раз больше периода внешней силы 2π/pn. Частота p=ω/n, n - любое целое число, не равное 1.
в) Ультрагармонические колебания. Решение x(t) имеет период 2πm/p, равный периоду внешней силы. Частота p=mω, m - любое целое число, не равное 1.
г) Ультрасубгармонические колебания. Решение x(t) имеет период 2πm/p, а внешняя сила имеет период 2πm/np, т.е. период колебаний в n раз больше периода внешней силы и в m раз больше периода свободных колебаний, p=mω/n, n и m - целые, простые числа.
В соответствии с пунктом а) кроме общеизвестных оптических и акустических колебаний в содержащем ЭКЦ кристалле имеются гармонические колебания с частотами возмущающей силы, т.е. с частотами собственных (I-) колебаний ядер. Набор этих частот описывается формулой гармонического квантового 1-осциллятора (6): ω(ν)=ω⋅(1/2+ν), где ω - классическая частота данного осциллятора, колебательное квантовое число ν=0, 1, 2, … Наименьшая из этих частот ω/2 значительно превышает максимальную частоту акустических и оптических колебаний. В соответствии с согласующимися вычисленными и экспериментальными данными, представленными на фиг. 3 элементарные кванты I-колебаний α-типа (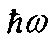 ) в атомах с атомными номерами Z≤80 лежат между 220 мэВ для атома кислорода с Z=8 и ≈400 мэВ для атомов с Z→80. Для сравнения: наибольший квант оптических колебаний обычно не превышает 60 мэВ, наибольший квант акустических колебаний обычно не превышает 25 мэВ.
) в атомах с атомными номерами Z≤80 лежат между 220 мэВ для атома кислорода с Z=8 и ≈400 мэВ для атомов с Z→80. Для сравнения: наибольший квант оптических колебаний обычно не превышает 60 мэВ, наибольший квант акустических колебаний обычно не превышает 25 мэВ.
В соответствии с пунктом б) среди упругих колебаний содержащего ЭКЦ кристалла имеются субгармонические колебания, частоты которых в n=2, 3, 4, … раз меньше частоты возмущающей силы ω.
В соответствии с пунктом в) среди упругих колебаний содержащего ЭКЦ кристалла имеются ультрагармонические колебания, частоты которых в m=2, 3, 4, … раз выше частоты I-колебаний ω. Эти частоты смещены на ω/2 относительно частот, описанных в пункте а).
В соответствии с пунктом г) среди упругих колебаний содержащего ЭКЦ кристалла имеются ультрасубгармонические колебания с частотами mω/n, которые при m<n могут совпасть с частотами оптических, акустических фононов или с частотами I-колебаний.
При субгармонических колебаниях возможны частоты ω/n при n=2, 3, …, при ультрасубгармонических колебаниях возможны частоты (m/n)ω, при n=2, 3, … и m=1, 2, … Среди указанных частот важны те частоты, которые меньше ω. Многие из этих частот попадают в спектр разрешенных фононных частот р. Особенно важны такие частоты, которые совпадают с частотами фононов имеющих наибольшую плотность в кристалле. Такие колебания эффективно усиливаются за счет энергии собственных колебаний и имеют возможность распространяться по кристаллу, участвовать в электронно-колебательных переходах ЭКЦ, определять физические свойства материалов и возникновение разнообразных технических эффектов.
Соотношение квантов упругих колебаний различных частот и типов на ЭКЦ и соответственно в когерентных областях определяется исходным уравнением движения (8). В термодинамически равновесных условиях эти соотношения выражаются гауссовым распределением интенсивности электронно-колебательных переходов (16), где вместо температур можно использовать частоты гармонических упругих колебаний  Уменьшение или увеличение концентрации квантов того или иного типа колебаний вызывает установление нового динамического равновесия. В виду нелинейности уравнений движения системы ЭКЦ и когерентных областей новое динамическое равновесие может качественно и количественно описываться новыми параметрами или новыми значениями прежних параметров. Эта возможность использована в данном изобретении для увеличения длины когерентности и увеличения эффективности известного способа осуществления гиперпроводимости и сверхтеплопроводности (прототипа) [16].
Уменьшение или увеличение концентрации квантов того или иного типа колебаний вызывает установление нового динамического равновесия. В виду нелинейности уравнений движения системы ЭКЦ и когерентных областей новое динамическое равновесие может качественно и количественно описываться новыми параметрами или новыми значениями прежних параметров. Эта возможность использована в данном изобретении для увеличения длины когерентности и увеличения эффективности известного способа осуществления гиперпроводимости и сверхтеплопроводности (прототипа) [16].
В отношении длины когерентности в термодинамически равновесных условиях можно сказать, что в кремнии с А-центрами при  и T=300 K величина Λ≅10 мкм, а размер (диаметр) области когерентности составляет 2Λ≅20 мкм. Получается, что область когерентности содержит Ncog=4πΛ3/3Ω≅2,62⋅1018 атомов. Если же
и T=300 K величина Λ≅10 мкм, а размер (диаметр) области когерентности составляет 2Λ≅20 мкм. Получается, что область когерентности содержит Ncog=4πΛ3/3Ω≅2,62⋅1018 атомов. Если же  , то при этой же температуре T=300 K величина 2Λ≅16 мкм, а при
, то при этой же температуре T=300 K величина 2Λ≅16 мкм, а при  величина 2Λ≅10 мкм и область когерентности содержит примерно Ncog=2,62⋅1015 атомов. Таким образом, изменение размера области когерентности означает изменение частоты и фазы I-колебаний тысяч атомов вещества, а время изменения размера области когерентности превышает среднее время рассеяния энергии электронами (τе). При этом положение области когерентности в кристалле существенно не изменяется, то есть области когерентности малоподвижны. Таким образом, области когерентности характеризуются одной (общей) частотой и фазой вынужденных I-колебаний всех атомов из-за чего эти области обладают нулевым электрическим и нулевым тепловым сопротивлениями, то есть являются гиперпроводящими и сверхтеплопроводными.
величина 2Λ≅10 мкм и область когерентности содержит примерно Ncog=2,62⋅1015 атомов. Таким образом, изменение размера области когерентности означает изменение частоты и фазы I-колебаний тысяч атомов вещества, а время изменения размера области когерентности превышает среднее время рассеяния энергии электронами (τе). При этом положение области когерентности в кристалле существенно не изменяется, то есть области когерентности малоподвижны. Таким образом, области когерентности характеризуются одной (общей) частотой и фазой вынужденных I-колебаний всех атомов из-за чего эти области обладают нулевым электрическим и нулевым тепловым сопротивлениями, то есть являются гиперпроводящими и сверхтеплопроводными.
Структура гиперпроводника представляется такой, что отдельные области когерентности с нулевым электрическим и тепловым сопротивлением размещены в объеме материала и отделены друг от друга обычным материалом (материалом в обычном, нормальном состоянии).
Иначе говоря, каждая пара когерентных областей представляет собой когерентную гетероструктуру, а материал заполнен системой таких когерентных гетероструктур. Когерентные гетероструктуры ранее не были известны и являются новым типом герероструктур.
Можно выделить два типа когерентных гетероструктур. Один тип когерентных гетероструктур представляет синхронные гетероструктуры в которых когерентные области имеют одинаковые частоты, но разные и отличающиеся на постоянную величину фазы колебаний. Другой тип когерентных гетероструктур представляет асинхронные гетероструктуры в которых когерентные области имеют разные частоты колебаний.
Расстояние между ближайшими друг к другу когерентными областями может принимать значения от межатомного расстояния в материале до десятков и сотен микрон и в зависимости от внешних условий изменяться в этих пределах. Электрическое и тепловое сопротивление материала в целом определяются сопротивлением материала за пределами областей когерентности и вызвано известными механизмами рассеяния носителей зарядов, а также возможно дополнительным рассеянием на границах областей когерентности и на электрических контактах к материалу, то есть на границе материала и токовых электродов 1 и 2, если толщина разделяющего когерентные области материала превышает длину свободного пробега электронов. Если же толщина разделяющего когерентные области материала является туннельно тонкой, то возможны эффекты, аналогичные эффектам Джозефсона, влияющие на электрические и тепловые свойства каждой гетероструктуры и материала в целом. Так в синхронных когерентных гетероструктурах с туннельно малыми расстояниями между когерентными областями возможен аналог стационарного эффекта Джозефсона в виде постоянного электрического тока или в виде постоянного электрического напряжения между когерентными областями. Полярность тока и напряжения аналога эффекта Джозефсона в гиперпроводниковой гетероструктуре, как и эффекта Джозефсона в сверхпроводниковой гетероструктуре, определяются разностью фаз колебаний по обе стороны туннельно тонкого слоя, которая постоянна в синхронных когерентных гетероструктурах. Частоты колебаний когерентных областей в асинхронных когерентных гетероструктурах различны. В таких структурах происходит непрерывное изменение относительного значения фаз колебаний. Благодаря непрерывному периодическому знакопеременному изменению относительных фаз колебаний когерентных областей оказывается возможным аналог высокочастотного нестационарного эффекта Джозефсона в виде высокочастотного электрического тока в материале или напряжения между когерентными областями.
Максимальный размер когерентной области (2Λmax) в термодинамически равновесных условиях в значительной мере определяется энергией колебаний Екол когерентной области которая, как мы видели, может быть больше в полупроводниках с большей шириной запрещенной зоны. Так в материалах с Eg≈2 эВ возможно Екол≥2 эВ. Тогда при комнатной температуре 2Λmax≈18 мкм, а при 200K значение 2Λmax≈27…30 мкм. Следовательно, когерентные области в типичных полупроводниках вблизи комнатной температуры могут иметь размеры в примерных пределах от 15 до 30 микрон. Так в кремнии при околокомнатной температуре 2Λmax составляет примерно 20 мкм.
Не представляется возможным осуществить гиперпроводимость и сверхтеплопроводность в материале между электродами, используя прототип при больших расстояниях между электродами 1 и 2. Поскольку в прототипе не приняты меры для отвода из материала избыточной колебательной энергии и необходимое увеличение длины когерентности до Λ≥D/4 невозможно, то нулевое сопротивление материала между электродами не может быть достигнуто. Но и в таких условиях электронно-колебательные энергетические уровни когерентных областей проявляются в температурных зависимостях электрического сопротивления материала как глубокие энергетические уровни, в виде энергий активации сопротивления и согласуются с зависимостью (6).
На фиг. 12 приведена типичная температурная зависимость электрического сопротивления материала между электродами 1 и 2 при D=50 мкм, измеренная на германиевом образце с почти собственной проводимостью без отвода избыточной колебательной энергии, как в прототипе, и не достигающая нулевого значения. На вставке фиг. 12 показан участок этой зависимости при высоких температурах. Данная зависимость содержит участки, отмеченные касательными стрелками к кривой, со следующими энергиями активации сопротивления: 0,22 эВ; 0,55 эВ; 0,68 эВ,0,77 эВ, 1,1 эВ;1,65 эВ; 22,2 эВ и 194,65 эВ, из которых пять последних энергий активации превышают ширину запрещенной зоны материала (≈0,68 эВ). Энергии активации менее ширины запрещенной зоны материала объясняются наличием в материале ЭКЦ и когерентных областей, включающих примесные атомы кислорода с элементарным квантом I-колебаний EZ=E8=0,22 эВ и участвующих в колебаниях с энергиями, совпадающими с вычисленными энергиями по формуле (6). Эти колебания возбуждаются за счет уменьшения потенциальной энергии локализующихся на этих уровнях электронов. Однако энергии активации, значительно и многократно превышающие ширину запрещенной зоны материала нельзя объяснить процессами рекомбинации. Такие энергии активации сопротивления представляют принципиально новый процесс увеличения размеров когерентных областей, предшествующий переходу материала между электродами в гиперпроводящее состояние. На вставке фиг. 12 показан высокотемпературный участок этой зависимости, из которой видно, что сопротивление материала между электродами не достигает нулевой величины, т.е. гиперпроводимость и сверхтеплопроводность в данном случае не осуществляются.
На фиг. 13 приведена типичная температурная зависимость электрического сопротивления материала между электродами в образце на основе GaAs, D=20 мкм. Верхняя кривая измерена при нагревании образца, а нижняя - при охлаждении образца. В этом случае, как и в образцах на основе ряда других полупроводников, проявляются энергии активации сопротивления, характерные для ЭКЦ, многократно превышающие ширину запрещенной зоны полупроводника. Однако нулевого значения сопротивления материала между электродами не достигается, а при дальнейшем нагревании сопротивление достигает некоторого минимального ненулевого значения и затем увеличивается по мере роста температуры, т.е. гиперпроводимость и сверхтеплопроводность в материале между электродами в данном случае не осуществляются.
На фиг. 14 приведена характерная для образцов на основе кремния температурная зависимость электрического сопротивления (R) измеренная в соответствии с прототипом и также не достигающая нулевого значения сопротивления.
Эти данные, представленные на фигурах 12, 13, 14, демонстрируют ограниченные возможности прототипа, невысокую эффективность прототипа, не обеспечивающего надежного осуществления гиперпроводимости и сверхтеплопроводности даже при сравнительно небольших расстояниях между электродами. Эта ограниченность прототипа определяется тем, что избыточная колебательная энергия не выводится из материала и тем самым ограничивается увеличение размера когерентной области, величины Λ.
Если же осуществляется отвод избыточной колебательной энергии из материала между электродами, например высокочастотным или СВЧ способом, как предложено в заявленном изобретении, то с высокой эффективностью обеспечивается достижение нулевого электрического и нулевого теплового сопротивления материала между электродами даже при значительно больших расстояниях между электродами 1 и 2, чем в прототипе даже при нагревании материала от сравнительно высоких температур, в частности от околокомнатных температур. Тем самым в заявленном изобретении обеспечивается эффективное осуществление гиперпроводимости и сверхтеплопроводности, что соответствует цели заявленного изобретения.
К п. 1 формулы. В публикациях предшествовавших прототипу изобретения и в прототипе показано, что гиперпроводимость и сверхтеплопроводность могут быть осуществлены в материале между электродами в результате введения ЭКЦ в материал в концентрации от Nmin=2⋅1012 см-3 до Nmax=6⋅1017 см-3. С другой стороны, в материале вблизи выпрямляющего контакта, например, вблизи поверхности, вблизи границы с другим материалом, вблизи контакта Шоттки возникают и существуют ЭКЦ с объемной концентрацией от 2⋅1014 см-3 до 6⋅1015 см-3 в различных полупроводниках. Эти значения концентрации попадают в указанный допустимый диапазон от Nmin=2⋅1012 см-3 до Nmax=6⋅1017 см-3. В полупроводниковых выпрямляющих контактах ЭКЦ возникают независимо от нашей воли и желания, в связи с нарушением регулярной структуры материала вблизи контакта с другим материалом. Поэтому нет целесообразности и необходимости, как в прототипе, дополнительно вводить в материал ЭКЦ, применяя те или иные технологические процессы. В случае использования выпрямляющего контакта достаточная для достижения цели изобретения концентрация ЭКЦ возникнет в материале вблизи контакта. Поэтому, в отличие от прототипа, в п. 1 формулы заявленного изобретения процесс введения ЭКЦ в материал не предусматривается.
В качестве электродов 1 и 2 можно применять «прижимные» электроды, зонды, образующие выпрямляющие контакты с материалом и обеспечивать тем самым упрощение способа. Действительно, применение прижимных электродов не связано с использованием, например, термического распыления металлов в вакууме. В то же время в материале вблизи контакта прижимного электрода с материалом, как и вблизи нанесенного на поверхность или в объем материала возникают локальные состояния электронно-колебательной природы, ЭКЦ. Поэтому в контактах металл-полупроводник имеется потенциальный барьер, высота которого определяется эмпирическим «правилом 1/3» [47], именно благодаря ЭКЦ возникающим в материале вблизи контакта. Вблизи таких выпрямляющих контактов концентрация ЭКЦ обычно составляет от 2⋅1014 см-3 до 6⋅1015 см-3, что вполне достаточно для осуществления заявленного изобретения. При этом оказывается, что нет необходимости стремиться, как это делают в традиционной адиабатической полупроводниковой электронике, с помощью сложных технологических приемов уменьшить «плотность поверхностных электронных состояний». Допустимый для осуществления данного изобретения диапазон концентраций ЭКЦ довольно велик. Таких центров в материалах вблизи контактов вполне достаточно для осуществления изобретения. Более того, для целей данного изобретения нет каких-либо особых требований к подготовке поверхности материала перед размещением электродов, например, прижимных электродов или зондов, или перед напылением металлических электродов. Эксперименты, выполненные на различных полупроводниках, показали, что электроды можно размещать на чистых шлифованных или полированных поверхностях. Это значительно упрощает подготовку полупроводниковых образцов для осуществления заявленного изобретения. Такое упрощение вообще характерно для неадиабатической полупроводниковой электроники, к которой относится данное изобретение, в отличие от традиционной адиабатической электроники, в которой технологически приходится обеспечивать теоретически определенные предельные значения технических параметров, например, малые значения «плотности поверхностных состояний».
В материале вблизи электродов вследствие взаимодействия между отдельными ЭКЦ и атомами материала самопроизвольно, спонтанно возникают и существуют области когерентности малого размера 4Λ<D. Эти когерентные области являются гиперпроводящими и сверхтеплопроводными участками материала. Иначе говоря, гиперпроводимость и сверхтеплопроводность в материале вблизи электродов возникают самопроизвольно, спонтанно и существуют в результате взаимодействия вынужденных I-колебаний ЭКЦ и атомов основного вещества в ограниченных участках материала, в пределах когерентных областей. Однако, когерентные области обычно занимают не весь материал на протяжении между электродами. В связи с этим технической задачей прототипа и заявленного изобретения является увеличение размера когерентных областей, чтобы обеспечить перекрытие материала одной когерентной областью на всем протяжении между электродами. В таком случае гиперпроводимость и сверхтеплопроводность в материале между электродами будет осуществлена, т.е. цель изобретения будет достигнута. Увеличение длины когерентности Λ в прототипе осуществляют одним способом, нагреванием материала до температур Т≥Тh. Однако возможности прототипа ограничены по нескольким причинам:
- возможность увеличения длины когерентности Λ за счет увеличении температуры материала T ограничена, что видно из формулы (13). Действительно, увеличение колебательной энергии Екол замедляется или прекращается при увеличении T, а множитель 1/Т делает возможным увеличение Λ только при увеличении Т до некоторой критической температуры (Т2) превышение которой вызывает уменьшение Λ и увеличение сопротивления материала между электродами;
- электрический ток, протекающий в материале между электродами при измерении электрического сопротивления, является электронно-колебательным током, состоящим из электронов и связанных с ними I-колебаний атомных ядер и фононов. При протекании этого тока происходит пространственный перенос не только электрических зарядов электронов, но и I-колебаний атомных ядер и фононов, т.е. тепла. В результате протекания этого тока возникает "омическое падение напряжения" в материале между когерентными областями, а также разность температур когерентных областей и, как следствие, возникает дифференциальная термоЭДС в слое материала между когерентными областями, полярность которой противоположна полярности "омического падения напряжения". При этом надо иметь в виду, что дифференциальная термоЭДС включает увлечение электронов фононами (УЭФ), которое многократно усиливается в окрестности дебаевых температур Тm;
- толщина слоя материала между когерентными областями при увеличении температуры может стать туннельно тонкой. В результате становятся возможными аналоги стационарного и нестационарного высокочастотного эффектов Джозефсона, которые совместно с "омическим падением напряжения" и термоЭДС создают разнообразные условия перехода к гиперпроводимости.
Перечисленные особенности определяют нелинейный характер перехода к гиперпроводимости и сверхтеплопроводности материала между электродами. Кроме того, сформировавшиеся вблизи различных электродов и сближающиеся при нагревании когерентные области вообще говоря имеют разные колебательные фазы. При образовании гиперпроводимости и сверхтеплопроводности между электродами эти когерентные области должны слиться в одну когерентную область с новой фазой I-колебаний. Гиперпроводящий переход аналогичен рассеянию одной когерентной области на другой когерентной области и протекает с выделением, рассеянием в окружающий материал "избыточной" колебательной энергии. Величина этой "избыточной" энергии примерно равна колебательной энергии одной когерентной области. В связи с этими особенностями актуальным оказываются:
- отвод "избыточной" колебательной энергии из материала и
- внешние воздействия на материал в виде изменения скорости нагревания, изменения электрического или магнитного поля.
Эти воздействия стимулируют перестройку когерентных областей и их слияние в одну когерентную область, что соответствует меньшей колебательной энергии и соответственно большей устойчивости такого динамического состояния материала.
Образованию одной когерентной области, замыкающей электроды 1 и 2, способствует использование одного замедляющего устройства, связанного со всем материалом между электродами. В таком случае I-колебания во всех частях материала будут однотипными, с одинаковыми колебательными квантами, а поле замедляющего устройства способствует синхронизации поляризации, частоты и фазы колебаний в материале между электродами, что соответствует когерентному состоянию и осуществлению гиперпроводимости и сверхтеплопроводности в материале между электродами.
Из двух контактов 1 и 2 есть возможность использовать один выпрямляющий контакт, а второй - невыпрямляющий и выбрать расстояние между электродами В≤2Λ. В таком случае когерентные области возникают только вблизи выпрямляющего контакта, а второй, невыпрямляющий контакт не препятствует распространению когерентной области от первого контакта до второго и тем самым способствует осуществлению гиперпроводимости и сверхтеплопроводности в материале между электродами.
Увеличение размера (2Λ) области когерентности происходит за счет присоединения к ней соседних атомов материала, общая колебательная энергия которых уменьшается. Уменьшение колебательной энергии этих атомов предложено осуществлять, используя ВЧ или СВЧ электромагнитное поле, которое существует в материале благодаря колебаниям электрических зарядов. Энергию такого электромагнитного поля желательно выводить из материала во внешнюю среду. Преодолевая внешнюю границу материала с электродом ВЧ и СВЧ поле, ток испытывают частичное отражение, из-за чего часть ВЧ и СВЧ энергии возвращается от границы обратно в материал. Для уменьшения возвращающейся в материал электромагнитной мощности, высвобождающейся при увеличении области когерентности, характерный размер контактной области каждого электрода с материалом выбирают не более четверти длины ВЧ или СВЧ волны в материале 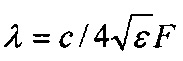 , где с - скорость света в вакууме, ε - относительная диэлектрическая проницаемость материала, F - характерная резонансная частота замедляющего устройства.
, где с - скорость света в вакууме, ε - относительная диэлектрическая проницаемость материала, F - характерная резонансная частота замедляющего устройства.
Гиперпроводимость и сверхтеплопроводность материала между электродами возможны, когда размер двух областей когерентности, расположенных вблизи контактов 1 и 2, становится равным расстоянию между электродами или превышает его, когда 4Λ≥D, и области когерентности занимают весь материал между электродами, электрически соединяют их друг с другом. Из формулы (13) видно, что увеличение Λ возможно при превышении колебательной энергии Екол некоторой минимальной величины  , для θ обычно лежащих между 2 K и 6 K в различных полупроводниках с известными ЭКЦ в таких материалах. Из этого следует также, что нагревание материала между электродами при осуществлении гиперпроводимости и сверхтеплопроводности можно начинать с соответствующих минимальных температур. Минимальные значения длины когерентности при низких температурах в термодинамически равновесных условиях могут составлять десятки ангстрем. Нагревание материала выше минимальной температуры вызывает увеличение колебательной энергии и, несмотря на содержащуюся в (13) обратную температурную зависимость, длина когерентности увеличивается до определенного предела. Например, в кремнии (Z=14) при комнатной температуре величина 2Λ может достигать 20 микрон, а в германии (Z=32) она больше чем в кремнии почти в b раз. Согласно (14, 15)
, для θ обычно лежащих между 2 K и 6 K в различных полупроводниках с известными ЭКЦ в таких материалах. Из этого следует также, что нагревание материала между электродами при осуществлении гиперпроводимости и сверхтеплопроводности можно начинать с соответствующих минимальных температур. Минимальные значения длины когерентности при низких температурах в термодинамически равновесных условиях могут составлять десятки ангстрем. Нагревание материала выше минимальной температуры вызывает увеличение колебательной энергии и, несмотря на содержащуюся в (13) обратную температурную зависимость, длина когерентности увеличивается до определенного предела. Например, в кремнии (Z=14) при комнатной температуре величина 2Λ может достигать 20 микрон, а в германии (Z=32) она больше чем в кремнии почти в b раз. Согласно (14, 15)

где МZ1 и MZ2 - массы ядер атомов основного вещества с атомными номерами Z1 и Z2, а 
 - эффективные массы носителей зарядов в образованных этими атомами материалах. Поэтому в материалах, состоящих из многоэлектронных атомов с большими атомными номерами и с большими эффективными массами основных носителей зарядов можно ожидать значительно больших значений длины когерентности при одинаковых температурах.
- эффективные массы носителей зарядов в образованных этими атомами материалах. Поэтому в материалах, состоящих из многоэлектронных атомов с большими атомными номерами и с большими эффективными массами основных носителей зарядов можно ожидать значительно больших значений длины когерентности при одинаковых температурах.
Такой результат верен, если в материале имеются свободные, невзаимодействующие друг с другом, с границами и иными неоднородностями материала когерентные области. Объем материала, в котором рассеивается энергия когерентных колебаний изолированной когерентной области, имеет форму шарового слоя толщиной 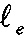 . Этот шаровой слой окружает сферическую когерентную область с радиусом Λ. Увеличение Λ по мере увеличения Екол при повышении температуры характеризуется переходом значительного числа расположенных вблизи когерентной области атомов из колебательного состояния с произвольной частотой и фазой гармонических собственных I-колебаний в колебательное состояние с общей частотой и фазой, в состояние когерентных I-колебаний. Такой переход к когерентным колебаниям дополнительно требует рассеяния избыточной энергии некогерентных колебаний. Действительно, колебательная энергия N атомов осуществляющих независимые 1-колебания с различными фазами за пределами когерентной области близка к сумме колебательных энергий этих атомов
. Этот шаровой слой окружает сферическую когерентную область с радиусом Λ. Увеличение Λ по мере увеличения Екол при повышении температуры характеризуется переходом значительного числа расположенных вблизи когерентной области атомов из колебательного состояния с произвольной частотой и фазой гармонических собственных I-колебаний в колебательное состояние с общей частотой и фазой, в состояние когерентных I-колебаний. Такой переход к когерентным колебаниям дополнительно требует рассеяния избыточной энергии некогерентных колебаний. Действительно, колебательная энергия N атомов осуществляющих независимые 1-колебания с различными фазами за пределами когерентной области близка к сумме колебательных энергий этих атомов 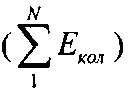 . С другой стороны в составе когерентной области все атомы имеют общую колебательную энергию
. С другой стороны в составе когерентной области все атомы имеют общую колебательную энергию 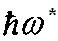 . Поскольку число присоединяющихся к когерентной области атомов может достигать нескольких тысяч, то оказывается, что при увеличении размеров области когерентности необходимо рассеять значительную колебательную энергию, примерно равную
. Поскольку число присоединяющихся к когерентной области атомов может достигать нескольких тысяч, то оказывается, что при увеличении размеров области когерентности необходимо рассеять значительную колебательную энергию, примерно равную  .
.
Рассеяние избыточной энергии некогерентных колебаний за пределами когерентной области частично может обеспечиваться увеличением объема рассеяния энергии при увеличении Λ. Однако следует учесть, что объем когерентной области и соответствующее число когерентно колеблющихся атомов увеличивается пропорционально Λ3, а объем рассеяния колебательной энергии увеличивается «медленнее», пропорционально Λ2. Поэтому возможность увеличения рассеяния избыточной энергии некогерентных колебаний, присоединяющихся к когерентным колебаниям атомов, ограничена. Кроме того, в реальных условиях увеличение Λ приводит к сближению различных когерентных областей друг к другу и к соответствующему уменьшению тех объемов материала, в которых за пределами областей когерентности колебательная энергия может быть рассеяна. Это приводит к ограничению рассеиваемой мощности колебаний и даже к ее уменьшению. Соответственно наступает насыщение увеличения Λ и даже возможно уменьшение Λ, в частности, за счет обратной температурной зависимости (14).
Таким образом, при нагревании материала выше минимальной температуры (≈1.5K) в нем происходят следующие процессы:
1i. Увеличение колебательной энергии и соответствующее увеличение длины когерентности;
2i. Уменьшение длины когерентности из-за обратной температурной зависимости длины рассеяния энергии;
3i. Сближение частот и фаз колебаний атомов когерентной области и присоединяющихся к этой области атомов, увеличение когерентной области, увеличение длины когерентности;
4i. Рассеяние избыточной колебательной энергии атомов, переходящих в состояние когерентных колебаний.
Процессы 1i и 2i имеют противоположные тенденции, они "конкурируют" друг с другом, определяются микроскопическими процессами, которые практически не оставляют нам возможностей влиять на изменение длины когерентности, регулировать длину когерентности за счет изменения внешних по отношению к материалу условий. Изменение колебательной энергии, соответствующее процессу 1i вызывает изменение длины когерентности на фоне монотонной зависимости (Т-1) соответствующей процессу 2i. Конкуренция процессов 1i и 2i вызывает ступенчатые температурные зависимости длины когерентности и размеров когерентных областей, а также гистерезисные явления в температурных зависимостях электрического и теплового сопротивления материала между электродами вследствие дискретности, квантованности I-колебаний.
Процесс 3i описывается формулами (9-12), учитывающими взаимодействие между ЭКЦ, участвующими в гармонических колебаниях с различными частотами и фазами. Взаимодействие, обмен фононами между когерентной областью и окружающими ее атомами создает вынужденные колебания всех атомов на одной частоте и с определенной фазой, что необходимо для присоединения атомов к области когерентности. Процессы установления одинаковых вынужденных частот и одинаковых фаз колебаний происходят самопроизвольно, согласно решениям уравнения движения. Мы имеем возможность интенсифицировать этот процесс, используя ВЧ и (или) СВЧ способ отвода колебательной энергии из материала между электродами. Для этого устанавливают согласованную электромагнитную связь материала между электродами с колебательным контуром, резонатором, волноводом, полосковой линией или с другим замедляющим, резонансным устройством (с другими замедляющими, резонансными устройствами) с добротностью Q. В таких условиях колебания электрических зарядов когерентной области возбуждают переменные электрические (ВЧ или СВЧ) токи в связанном с материалом замедляющем устройстве, усиливая их в Q раз на резонансной частоте замедляющего устройства. Протекание этих токов сопряжено с рассеянием энергии в виде Джоулева тепла в замедляющем устройстве, а также в нагрузке замедляющего устройства. Рассеивающаяся в замедляющем устройстве ВЧ или СВЧ энергия поступает из материала между электродами по согласованной электромагнитной связи. Таким образом, энергия некогерентных I-колебаний выводится из материала, что обеспечивает увеличение длины когерентности и соответствует цели изобретения.
Электрические поля, возникающие в замедляющем устройстве под действием колебаний электрических зарядов в материале, действуют на материал. В материале они выполняют функцию вынуждающего воздействия на колебания всех атомов, способствуют возникновению и существованию их вынужденных колебаний с одной частотой и общей фазой согласно (9-12), то есть выполняют синхронизацию I-колебаний, что необходимо для увеличения длины когерентности и достижения цели изобретения. Чтобы данный процесс был эффективным, выбирают резонансную частоту колебательного контура, резонатора, другого связанного с материалом замедляющего устройства в диапазоне частот фононов, обеспечивающих взаимодействие колебаний атомов, а именно в диапазоне частот от 106 Гц до 3⋅1015 Гц.
Данный процесс может быть использован для увеличения длины когерентности только совместно с процессом 4i, так как переход от колебаний атомов с произвольной фазой к колебаниям с одинаковой фазой, переход к когерентным колебаниям возможен при уменьшении общей энергии колебаний атомов, присоединяющихся к когерентной области.
Процесс 4i допускает влияние на него извне и может быть использован для регулирования длины когерентности за счет изменения внешних условий в отношении материала между электродами. Излучательный механизм (с испусканием электромагнитных квантов) рассеяния энергии некогерентных колебаний атомов, присоединяющихся к когерентным областям, оказывается маловероятным и неэффективным из-за сильной связи электронов с фононами. Поэтому важными остаются процессы рассеяния энергии с участием фононов, связанных с электронами. Связанные с фононами электроны осциллируют на частотах фононов и создают соответствующие переменные электрические поля в материале, вообще говоря, с различными произвольными фазами. Эти поля возбуждают в связанных и согласованных с материалом замедляющих устройствах электрические колебания за счет энергии, поступающей из материала. Тем самым обеспечивается отвод энергии колебаний из материала в замедляющие устройства.
Электрические колебания, возбуждаемые в связанных с материалом замедляющих устройствах вблизи их резонансной частоты, усиливаются примерно в Q>>1 раз и оказываются по отношению к материалу в роли внешнего воздействия, выполняющего синхронизирующую роль согласно формулам (9-12). В результате I-колебания многих атомов становятся когерентными, такие атомы присоединяются к когерентным областям, увеличивая их размер и длину когерентности Λ.
Два процесса (3i и 4i) синхронизации частот колебаний и отвод энергии некогерентных колебаний в заявленном изобретении выполняются контактным или бесконтактным высокочастотным способом. Для этого устанавливают согласованную электромагнитную связь материала между электродами с коаксиальной линией, волноводной линией, полосковой линией, нагруженные на согласованные нагрузки, с резонатором, колебательным контуром или другим (другими) замедляющим (замедляющими) устройством (устройствами), (например, с оптическими микрорезонаторами [48]), имеющими большие добротности и резонансные частоты в диапазоне от 106 Гц до 3⋅1015 Гц. В таких условиях колебательная энергия связанных с фононами электронов затрачивается на создание электрических колебаний и волн в перечисленных устройствах и рассеивается в этих устройствах в виде джоулевых потерь или в их нагрузке. С другой стороны, электрические колебания в указанных замедляющих устройствах оказывают синхронизирующее влияние на I-колебания в материале, обеспечивая их монохроматичность и когерентность. Тем самым с помощью замедляющих устройств с добротностью Q≥10 обеспечивается выполнение двух основных задач:
- синхронизации частот и фаз I-колебаний;
- отвод колебательной энергии из материала между электродами.
Собственно, I-осцилляторы характеризуются параболической связью между энергией и смещениями атомных ядер в атомах или ионах материала. В связи с этим ЭКЦ и области когерентности являются почти идеальными преобразователями частот электрических и акустических сигналов. Их колебания подчиняются зависимостям а, б, в и г (см. стр. 33), описывающим частоты гармонических, субгармоническиех ультрагармонических и ультрасубгармонических колебаний. При любой резонансной частоте замедляющего устройства в указанном диапазоне всегда найдутся такие значения произвольных чисел тип, при которых преобразованная частота попадет в полосу пропускания замедляющего устройства. Это обеспечивает отвод колебательной энергии из материала в замедляющее устройство, увеличение длины когерентности, что в итоге соответствует цели изобретения.
На фиг. 15 схематично показано бесконтактное подключение материала между электродами к колебательному контуру, состоящему из электродов 3 и 4, обеспечивающими емкостную связь материала с колебательным контуром, включающим индуктивность 5. Добротность колебательного контура  , где Рполная - мощность электрических колебаний в контуре, Рпотерь - мощность потерь в контуре. С одной стороны, Рпотерь=(Рполная/Q). С другой стороны, в стационарных условиях Рпотерь равна энергии, поступающей из материала между электродами, которую можно записать как G⋅Ωген⋅δ⋅E*, где G - скорость рекомбинации носителей зарядов, генерирующих I-колебания в объеме материала (Ωген), δ - доля колебательной энергии, рассеиваемая электроном за один акт рассеяния, Е* - энергия колебаний, возникающих в одном акте рекомбинации. Приравняв эти энергии приходим к условию δ⋅Q=Pполн/(G⋅Ωген⋅E*)=1, поскольку вся мощность генерируемых колебаний должна быть рассеяна. Учитывая типичное значение δ≈(10-1…10-2), получаем условие Q≥10.
, где Рполная - мощность электрических колебаний в контуре, Рпотерь - мощность потерь в контуре. С одной стороны, Рпотерь=(Рполная/Q). С другой стороны, в стационарных условиях Рпотерь равна энергии, поступающей из материала между электродами, которую можно записать как G⋅Ωген⋅δ⋅E*, где G - скорость рекомбинации носителей зарядов, генерирующих I-колебания в объеме материала (Ωген), δ - доля колебательной энергии, рассеиваемая электроном за один акт рассеяния, Е* - энергия колебаний, возникающих в одном акте рекомбинации. Приравняв эти энергии приходим к условию δ⋅Q=Pполн/(G⋅Ωген⋅E*)=1, поскольку вся мощность генерируемых колебаний должна быть рассеяна. Учитывая типичное значение δ≈(10-1…10-2), получаем условие Q≥10.
Для отвода избыточной колебательной энергии из материала между электродами можно располагать образец материала между обкладками конденсатора включенного в колебательный контур, включать образец в длинную, например, полосковую или коаксиальную линию, или располагать образец в СВЧ резонатор или волновод.
Внешние электромагнитное и акустическое излучения, магнитные поля влияют на величину длины когерентности и на величину Th. Поэтому материалы между выпрямляющими электродами, проявляющие гиперпроводящие переходы, могут быть применены в качестве бесконтактных прерывателей, реле, выключателей электрического и теплового токов, не имеющих подвижных механических деталей, управляемых с помощью внешних излучений и магнитных полей. И наоборот, они могут быть применены в качестве датчиков, чувствительных к действию внешних излучений и магнитных полей.
Экспериментальная проверка изобретения показала близкую к 100% эффективность, выход приборов на основе различных полупроводников (Ge, Si, GaAs, InAs, InSb, CdHgTe,), демонстрирующих переход в состояние гиперпроводимости и сверхтеплороводности при достижении и превышении соответствующих температур Th, (Тh≤Т≤Т*).
К пункту 2 формулы. Целесообразно начинать нагрев образцов с температур ≈1,5 K поскольку это обеспечивает уменьшение нестабильности сопротивления материалов при нагревании до температуры гиперпроводящего перехода, способствует ускоренному формированию доминирующей моды I-колебаний, уменьшению температур гиперпроводящего перехода, к сужению температурного интервала в котором происходит такой переход и к расширению температурного интервала существования гиперпроводимости и сверхтеплопроводности (Тh, Т*), т.е. к уменьшению Th и к увеличению T*.
Из фиг. 7 видно, что при значениях концентрации ЭКЦ в заявленном изобретении от 2⋅1014 см-3 до 6⋅1015 см-3 существенно сужается температурный диапазон для осуществления цели изобретения, но это относится только к условиям прототипа, когда не осуществляется отвод колебательной энергии из материала. В отличие от прототипа, в заявленном изобретении применяется высокочастотный или СВЧ способ отвода энергии из материала между электродами, который позволяет расширить температурный диапазон осуществления гиперпроводящего перехода. Более того, даже если начинать нагрев образцов не с температур ≈1,5K, а с более высоких температур, например, с околокомнатной температуры, то можно осуществлять гиперпроводимость и сверхтеплопроводность, обеспечивая достижение цели изобретения с высокой эффективностью благодаря примененному высокочастотному способу отвода из материала избыточной колебательной энергии.
Эксперименты с различными полупроводниками показали, что в таких случаях переход к гиперпроводимости и свертеплопроводности обычно оказывается более «плавным», занимает более широкий температурный интервал и при дальнейшем нагревании образцов в определенных условиях такие состояния могут разрушаться из-за уменьшения Λ согласно обратной температурной зависимости (13).
На фиг. 16 приведены температурные зависимости электрического сопротивления арсенида галлия, измеренные при различных расстояниях D=10; 20 и 40 мкм между электродами 1 и 2 в условиях отвода колебательной энергии с помощью колебательных контуров. На вставке фиг. 16 схематически показано подключение колебательных контуров с выводами для подсоединения к измерительной аппаратуре. Колебательные контуры содержат индуктивный элемент 5 и емкостной элемент с диэлектрическим слоем в виде сапфировой пластины, имеют резонансные частоты в диапазоне от 8 Ггц до 10 Ггц. Температуры гиперпроводящих переходов (Th) на рисунке указаны вертикальными стрелками. Для каждой кривой указаны расстояния между электродами в микронах (10 мкм, 20 мкм и 40 мкм). Представленные на фиг. 16 кривые проявляют характерную тенденцию увеличения Th при увеличении D, что соответствует представлениям о формировании гиперпроводимости и сверхтеплопроводности в материале между электродами.
На фиг. 17 представлена характерная температурная зависимость электрического сопротивления материала между электродами (D=50 мкм) в образце на основе германия с почти собственной проводимостью, когда поддерживается электромагнитная связь материала с колебательным контуром, связанным с материалом вблизи одного электрода. Верхняя кривая 6 на фиг. 17 соответствует нагреванию, а нижняя кривая 7 соответствует охлаждению образца. В примерной области температур от 325 K до 425 K на верхней кривой наблюдается неустойчивость величины сопротивления, которая характерна также для образцов на основе различных полупроводников при нагревании от комнатной температуры. Из фиг. 17 видно, что по мере нагревания образца сопротивление материала между электродами достигает нулевого значения при температуре 474,5 K, т.е. при этой температуре достигается гиперпроводимость, что соответствует цели заявленного изобретения. При охлаждении образца гиперпроводимость сохраняется до 449,6 K. Гиперпроводимости сопутствует сверхтеплопроводность. Температурная зависимость теплового сопротивления RT этого же германиевого образца представлена на фиг. 18 кривыми 8 и 9. В температурной зависимости электрического и теплового сопротивлений наблюдается «гистерезис», при охлаждении образца нулевые значения электрического и теплового сопротивлений отличаются от соответствующих температур, измеренных при нагревании образца, что связано с нелинейностью электронно-колебательных процессов в материале. При нагревании данного образца (фиг. 18) тепловое сопротивление обращается в ноль при температурах выше 466 K, а при охлаждении - при 450,4 K оно исчезает.
Нелинейные зависимости длины когерентности Λ от температуры T и от колебательной энергии Eкол, которая также зависит от T, проявляются в виде «гистерезисных» особенностей температурных зависимостей электрического и теплового сопротивлений гиперпроводников (как видно из фиг. 17 и 18) и нередко вызывают спонтанные колебательные процессы, «неустойчивости» сопротивлений обусловленные одновременным участием нескольких мод упругих колебаний в формировании когерентных областей при нагревании от комнатной температуры. Если нагревание образцов начинать с низких температур, то «неустойчивости» ослабевают и переход к гиперпроводящему состоянию занимает меньший температурный интервал.
Неустойчивость сопротивления при нагревании образцов и неустойчивость температуры образцов усиливается, если избыточная колебательная энергия из материала не отводится и если температуру образца не стабилизируют. Эти результаты отвечают представлениям о нелинейных электрон-фононных взаимодействиях на ЭКЦ в гиперпроводниках.
Прототип [16] позволяет осуществлять гиперпроводимость и сверхтеплопроводность в кремниевом материале между электродами, отстоящими друг от друга не более чем на D=20 мкм при нагревании от низких температур. В отличии от прототипа заявленный способ позволяет достигать цели изобретения при больших значениях D даже при нагревании от околокомнатной температуры. На фиг. 19 приведена характерная температурная зависимость электрического сопротивления кремниевого материала между электродами при D=22 мкм из которого видно, что при нагревании образца от комнатной температуры благодаря увеличению длины когерентности Λ его электрическое сопротивление уменьшается до нулевого значения при температуре T1=Тh=459 K и в материале между электродами 1 и 2 осуществляется гиперпроводимость и сверхтеплопроводность. При дальнейшем нагревании образца до температуры Т2=469 K в материале между электродами сохраняется гиперпроводимость и сверхтеплопроводность. Увеличение температуры от T1 до Т2 вызывает увеличение длины когерентности и и 4Λ≥D. При дальнейшем нагревании Λ уменьшается до 4Λ≤D и соответственно гиперпроводимость и сверхтеплопроводность в материале между электродами разрушаются. Нагревание образца выше Т2 соответствует уменьшению Λ. В соответствии с формулами (13-15) при температурах в окрестности выше Т2 приближенно можно записать Λ=Λ0/Т, где Λ0 независящая от температуры величина, и при Т>Т2 температурное изменение длины когерентности (ΔΛ) следует зависимости (1/Т-1/Т2). Величина ΔΛ представляет увеличивающуюся с ростом температуры толщину слоя материала, расположенную между когерентными областям. Этот слой находится в обычном, негиперпроводящем состоянии. В этом слое верен закон Ома и поэтому величина электрического сопротивления материала между электродами примерно следует зависимости R(T)=R0(1/Т2-1/Т), где R0 - не зависит от температуры Т. Эта формула удовлетворительно описывает наблюдаемое увеличение электрического сопротивления материала между электродами 1 и 2 при превышении температуры Т2.
Температурные зависимости сопротивления материала между электродами в образцах на основе InP имеют такие же особенности. Характерная температурная зависимость электрического сопротивления материала между электродами (D=40 мкм) представлена на фиг. 20 где верхняя кривая измерена при нагревании, а нижняя кривая - при охлаждении образца. Нулевое сопротивление при нагревании достигается между температурами T1=Тh=540 K и Т2=542 K, а при охлаждении нулевое сопротивление сохраняется между температурами 542 K и 482 K.
Идентичные температурные зависимости проявляют различные полупроводниковые материалы между выпрямляющими электродами. Таким образом, видно, что температурный диапазон существования гиперпроводимости и сверхтеплопроводности в материалах между электродами существенно зависит от расстояния между электродами D. При уменьшении D температура T1=Тh уменьшается, а температура Т2 увеличивается и может превысить температуру плавления материала или электродов, если нагревание начинать с низких температур. Увеличение D ведет к сближению температур Th и T*, к сужению или к исчезновению температурного интервала (Т*-Th), что вообще делает невозможным осуществление гиперпроводимости и сверхтеплопроводности.
Осуществлению гиперпроводимости и сверхтеплопроводности при больших значениях D способствуют любые способы увеличения длины когерентности Λ. Некоторые способы увеличения Λ и управления величиной Λ содержатся в заявленном изобретении. Если величина D близка к 4Λ, то при нагревании образцов электрическое и тепловое сопротивления материала между электродами значительно уменьшаются, уменьшается также падение напряжения в материале между электродами 1 и 2, вызванные протекающим от внешнего источника током носителей зарядов при измерении сопротивления. Однако протекающий электрический ток связан с потоком I-колебаний и фононов посредством электрон-фононного взаимодействия, которые изменяют температуры материалов вблизи электродов. В результате в материале между электродами 1 и 2 возникает градиент температуры и термоЭДС, УЭФ, которая по величине может быть сравнима с падением напряжения в материале от тока внешнего источника или превышать его. Кроме того, расстояние между когерентными областями (d=D-4Λ) при нагревании материала до высоких температур становится достаточно тонким для туннелирования электронов между когерентными областями и возникают аналоги эффектов Джозефсона величина и полярность которых определяются соотношением фаз колебаний когерентных областей. Поэтому из-за наложения омического падения напряжения, напряжений от термоЭДС и УЭФ и от аналогов эффектов Джозефсона в материале между когерентными областями вблизи температуры перехода к гиперпроводимости возможно нелинейное поведение вольтамперных характеристик образцов и их температурных зависимостей.
В частности, прекращение нагревания образцов способствует усилению рассеяния колебательной, тепловой энергии из когерентных областей и соответствующему увеличению длины когерентности, завершающемуся возникновением гиперпроводимости и сверхтеплопроводности в материале между электродами, как это показано на примере германиевого образца на фиг. 21.
В условиях сильного электрон-фононного взаимодействия термоЭДС совместно с аналогами эффектов Джозефсона может превысить падение напряжения, создаваемого протекающим электрическим током в материале и тогда возникает отрицательное электрическое сопротивление в материале между электродами 1 и 2, что можно видеть из температурной зависимости сопротивления германиевого образца, представленной на фиг. 22. Измеренное отрицательное сопротивление и соответствующий электрический ток возникает и существует за счет колебательной, тепловой энергии когерентных областей в материале и сохраняется, пока существует достаточный для этого градиент температуры в материале между когерентными областями. Время существования отрицательного сопротивления определяется временем рассеяния колебательной энергии когерентными областями и сближения температур когерентных областей. Из фиг. 22 видно, что это время может составлять десятки секунд. Отрицательное сопротивление достигает наибольшего значения, если температура перехода к гиперпроводимости Th близка к любой из дебаевых температур фононов материала Тm или лежит в интервале (Tm±3θ), где термоЭДС, а именно ее составляющая - увлечение электронов фононами (УЭФ), оказывается максимальной.
Известно, что отрицательное электрическое сопротивление возникает в материалах, находящихся в неравновесном состоянии, в неравновесных системах [49].
В нашем случае отрицательное электрическое сопротивление в образцах с сильным электрон-фононным взаимодействием проявляется из-за пространственного, межцентрового переноса I-колебаний, электронов и фононов, сопровождающегося возникновением градиента температуры, термоЭДС (УЭФ) и аналогов эффектов Джозефсона. Нужно отметить, что если электрическое сопротивление материала под влиянием термоЭДС становится отрицательным, то тепловое сопротивление материала изменяет свою полярность. В результате стабилизации нулевого электрического сопротивления, гиперпроводимости и сверхтеплопроводности, в материале между электродами исчезают градиенты электрического потенциала и градиенты температуры. Отрицательное электрическое сопротивление (если оно существовало) также исчезает, устанавливаются стационарные нулевые значения электрического сопротивления и теплового сопротивления материала между электродами, то есть достигается цель изобретения.
Аналогичный результат можно получить при температурах между Th и Т*, создав в материале между электродами поперечное к току между электродами кратковременное (действующее до 50 секунд) магнитное поле с индукцией до 2 Тесла. Действительно, если температура материала между электродами превышает Th, а гиперпроводимость не достигнута, поскольку когерентные области вблизи электродов 1 и 2 не слились в единую когерентную область, то магнитное поле исключит участие кристаллических фононов в электронно-колебательных переходах, по существу магнитное поле сделает невозможными электронно-колебательные переходы. Тем самым приостановливается приток энергии в когерентные области, что обеспечивает увеличение длины когерентности Λ, т.е. размеров когерентных областей, и их неизбежное слияние в единую когерентную область, замыкающую друг с другом электроды 1 и 2.
Кратковременное нарушение термодинамического равновесия в материале между электродами для формирования единой когерентной области, замыкающей собой электроды 1 и 2 и тем самым обеспечивающее осуществление гиперпроводимости и сверхтеплопроводности между электродами можно достичь и прекращением нагрева материала в магнитном поле.
К пункту 3 формулы. Размер материала (b) выбирают не менее четырех длин когерентности (4Λ), (b≥4Λ). Выбирают толщину пластины материала не менее 4Λ или толщину слоя материала не менее 4Λ на полупроводниковой, полуизолирующей или диэлектрической подложке. Данное условие определяется тем, что для размещения когерентной области в материале необходим объем с характерным размером не менее 2Λ. Кроме того, необходим объем материала для размещения области рассеяния энергии колебаний в виде сферического слоя толщиной 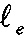 , которая существенно превышает 2Λ. В случае вывода из материала колебательной энергии с помощью замедляющих, резонансных устройств, как предусмотрено п. 1 формулы, размер области рассеяния энергии колебаний может быть существенно уменьшен. Поэтому размер (b) полупроводникового материала целесообразно выбирать не менее четырех длин когерентности (4Λ), (b>4Λ), как это сформулировано в данном пункте формулы.
, которая существенно превышает 2Λ. В случае вывода из материала колебательной энергии с помощью замедляющих, резонансных устройств, как предусмотрено п. 1 формулы, размер области рассеяния энергии колебаний может быть существенно уменьшен. Поэтому размер (b) полупроводникового материала целесообразно выбирать не менее четырех длин когерентности (4Λ), (b>4Λ), как это сформулировано в данном пункте формулы.
К пункту 4 формулы. Для осуществления гиперпроводимости и сверхтеплопроводности в объеме материала с характерным размером, значительно превышающим учетверенную длину когерентности (4Λ), в этот объем материала вводят вкрапления частиц с характерными размерами (с) меньше Λ, с≤Λ, образующих выпрямляющие контакты с материалом. Это могут быть полупроводниковые или металлические вкрапления. При указанных размерах вкрапленных частиц возникающие вблизи них области когерентности целиком окружают частицы. Далее, если концентрации вкрапленных частиц лежат в пределах от (2Λ)-3 до (2с)-3, то охватывающие их когерентные области касаются друг друга или отделены друг от друга тонкими или туннельно тонкими слоями материала, из-за чего в материале между электродами возникает гиперпроводимость и сверхтеплопроводность.
Вкрапленные в материал частицы сами могут образовывать замедляющие системы. При этом избыточная колебательная энергия при увеличении когерентных областей будет преобразовываться такими замедляющими системами в тепло, т.е в фононы, которые не связаны с ЭКЦ. Тем самым обеспечивается осуществление гиперпроводимости и сверхтеплопроводности в значительном объеме материала по размерам, превышающим 2Λ, пригодном для разнообразных технических применений, например, для гиперпроводящих магнитных подвесок в транспорте, для протяженных проводников электрического тока с нулевым сопротивлением, для протяженных проводников тепла с нулевым тепловым сопротивлением.
К пункту 5 формулы. Этот пункт формулы посвящен осуществлению аналога стационарного эффекта Джозефсона. Если расстояние D между электродами 1 и 2 превышает 4Λ на величину d=D-4Λ, то когерентная область размером 2Λ, расположенная, например, у электрода 1, как схематично показано на фиг. 23, может взаимодействовать, обмениваться частицами и квазичастицами, с аналогичной когерентной областью, расположенной вблизи электрода 2, посредством туннельных электронно-колебательных переходов, если d не слишком велико.
Для областей когерентности характерны гармонические колебания с частотами, описываемыми формулой гармонического осциллятора (6) из-за чего эти области представляют собой гармонические осцилляторы с дискретным набором электронно-колебательных уровней. Соответственно, взаимодействия когерентных областей друг с другом можно рассматривать как взаимодействия друг с другом гармонических осцилляторов, относящихся к различным когерентным областям. Упругие взаимодействия осцилляторов количественно описываются формулами (9-12). Приложение этих формул к описанию взаимодействия между различными когерентными областями позволяет сделать обоснованный вывод о том, что между когерентными областями, расположенными вблизи электродов 1 и 2, протекает туннельный электронно-колебательный ток. Частоты этого тока соответствуют разности энергий исходного и конечного состояний электронно-колебательных переходов. Переходы между состояниями с одинаковыми энергиями соответствуют нулевой частоте, т.е. образуют постоянный ток, представляющий аналог стационарного эффекта Джозефсона.
Спектры частот колебаний обеих когерентных областей, расположенных вблизи электродов 1 и 2, одинаковы. Колебания когерентных областей на одинаковой частоте ω* согласно формуле (11) имеют амплитуды колебаний Н=F/2rω*, где F - амплитуда периодического воздействия одной когерентной области на другую когерентную область и r - коэффициент затухания колебаний. Из формулы (11) видно, что величину амплитуды Н можно регулировать за счет изменения амплитуды F, например, изменяя концентрацию ЭКЦ, изменяя скорость тепловой генерации носителей зарядов в материале или изменяя внешнее освещение. Величину Н можно регулировать, изменяя коэффициент затухания, изменяя добротности или коэффициенты связи замедляющих устройств с материалом. Согласно формулам (12) фазы колебаний взаимодействующих когерентных областей определяются выражениями: cosδ=0, sinδ=1, т.е. δ=π/2±2π⋅m, где m - положительное целое число. Видно, что колебания взаимодействующих когерентных областей взаимно поляризованы, они ортогональны друг другу, а туннелирующие между ними электроны изменяют поляризацию своих упругих колебаний на той же частоте ω* и создают постоянный ток, представляющий аналог стационарного эффекта Джозефсона.
Кроме того, I-колебания связаны с локализованными на ЭКЦ фононами из-за чего дискретные линии спектра колебаний, описываемого формулой (6), уширяются в полосы контуры которых подчиняются Гауссовому распределению (16) с параметром θ. Становятся возможными так называемые "непрямые" туннельные переходы с испусканием и с поглощением фононов, т.е с уменьшением и с увеличением энергии туннелирующих частиц, т.е с разными частотами туннелирования. В результате преобразования частот на I-осцилляторах выделяются частоты равные сумме и разности частот туннелирования. Разностная частота соответствует нулевой частоте туннелирования, т.е. соответствует постоянному току в диэлектрическом зазоре между когерентными областями. Этот ток представляет вклад в аналог стационарного эффекта Джозефсона. При этом протекают и переменные токи с разностными и комбинационными частотами туннелирования, образующими аналог высокочастотного нестационарного эффекта Джозефсона. Таким образом оказывается, что аналог стационарного эффекта Джозефсона и аналог нестационарного высокочастотного эффекта Джозефсона проявляются, существуют одновременно, они неразделимы и различить их можно только по частоте и фазе (полярности).
Аналогичное взаимодействие посредством туннельных электронно-колебательных переходов возможно и в общем случае, когда развитой до размера 2Λ оказывается только когерентная область вблизи одного из контактов. В таком случае, вблизи другого контакта существуют спонтанно сформировавшиеся когерентные области, которые определяют его выпрямляющие свойства. Поэтому электронно-колебательные переходы происходят между когерентной областью с размером 2Λ и когерентными областями меньших размеров, расположенными вблизи другого электрода.
На фиг. 24 представлена энергетическая схема двух когерентных областей отделенных друг от друга туннельно тонким зазором толщиной d=D-4Λ при отсутствии разности напряжений между электродами 1 и 2, например, когда электроды электрически замкнуты внешним проводником. Горизонтальными стрелками здесь показаны туннельные электронно-колебательные переходы без изменения колебательного числа ν. Направление соответствующих переходов и токов определяется разностью фаз I-колебаний когерентных областей. Величина результирующего постоянного тока, представляющего аналог стационарного эффекта Джозефсона, определяется суммой токов (Iν) образованных туннельными переходами куперовских пар между состояниями с одинаковыми значениями ν: 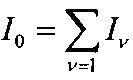 . Основной вклад в эту сумму вносит один из переходов с энергией вблизи уровня Ферми F=Е*, а интенсивность и ее температурная и энергетическая зависимость электронно-колебательных переходов подчиняется гауссовой зависимости (16). При вычислении I0 необходимо определять Iν с учетом интенсивностей переходов с испусканием и поглощением в среднем S фононов различных типов.
. Основной вклад в эту сумму вносит один из переходов с энергией вблизи уровня Ферми F=Е*, а интенсивность и ее температурная и энергетическая зависимость электронно-колебательных переходов подчиняется гауссовой зависимости (16). При вычислении I0 необходимо определять Iν с учетом интенсивностей переходов с испусканием и поглощением в среднем S фононов различных типов.
Если электроды 1 и 2 электрически разомкнуты, то устанавливается вызванная туннельными токами разность потенциалов электродов 1 и 2, при которой ток I0 равен нулю. Эта разность потенциалов также представляет аналог стационарного эффекта Джозефсона, а ее величина определяется величинами квантов упругих колебаний. Энергии меньших из таких квантов лежат в пределах от 0 до  и соответствуют милливольтовым напряжениям между электродами 1 и 2. Энергии максимальных квантов соответствуют зачению ν=ν* в формуле гармонических колебаний (6) и могут составлять доли и даже единицы электрон-вольта.
и соответствуют милливольтовым напряжениям между электродами 1 и 2. Энергии максимальных квантов соответствуют зачению ν=ν* в формуле гармонических колебаний (6) и могут составлять доли и даже единицы электрон-вольта.
К п. 6 формулы. Данный пункт формулы посвящен осуществлению аналога нестационарного высокочастотного эффекта Джозефсона. Аналог нестационарного высокочастотного эффекта Джозефсона возникает, если между электродами 1 и 2 приложено постоянное электрическое напряжение величиной V. В таком случае энергетическая схема двух когерентных областей между электродами имеет вид, представленный на фиг. 25, где электронно-колебательные энергетические уровни когерентных областей, расположенных у электродов 1 и 2 смещены друг относительно друга на величину eV и возможны так называемые «непрямые» туннельные переходы, показанные наклонными стрелками. Энергии электронов в таких переходах уменьшаются на eV. В соответствии с законом сохранения энергии в условиях сильного электрон-фононного взаимодействия аналогично эффекту Джозефсона туннелирующие электроны осциллируют с циклической частотой  . В результате в материале между электродами возникает переменный электрический ток такой же циклической частоты
. В результате в материале между электродами возникает переменный электрический ток такой же циклической частоты  . Этот переменный ток представляет собой аналог нестационарного высокочастотного эффекта Джозефсона. Фаза нестационарного высокочастотного эффекта Джозефсона определяется разностью фаз когерентных упругих колебаний когерентных областей.
. Этот переменный ток представляет собой аналог нестационарного высокочастотного эффекта Джозефсона. Фаза нестационарного высокочастотного эффекта Джозефсона определяется разностью фаз когерентных упругих колебаний когерентных областей.
Постоянное электрическое напряжение между электрически разомкнутыми электродами 1 и 2 возникает в результате протекания джозефсоновского тока I0, т.е. в результате стационарного эффекта Джозефсона, величина которого (в Вольтах) может составлять доли и даже единицы Вольта. Тем самым создаются условия для возникновения аналога нестационарного высокочастотного эффекта Джозефсона. Иначе говоря, аналоги стационарного и высокочастотного нестационарного эффектов Джозефсона оказываются взаимно связанными, различающимися только частотами.
При изменении напряжения V электронно-колебательные уровни соседних когерентных областей с различными значениями колебательных чисел ν, разделенных диэлектрическим туннельно тонким слоем, приобретают одинаковые энергии и на энергетической схеме размещаютс друг против друга. В таких условиях становится возможным аналог стационарного эффекта Джозефсона за счет туннелирования зарядов между этими уровнями с различными ν. Поэтому осуществление аналога нестационарного эффекта Джозефсона оказывается связанным с осуществлением аналога стационарного эффекта Джозефсона. Вообще говоря, эти эффекты различимы только по частоте.
Туннельные переходы между электронно-колебательными состояниями различных когерентных областей, разделенных в материале расстоянием d, пока изучены слабо и в полной мере не описаны количественно. Однако представляется возможным определить допустимый диапазон туннельно тонких толщин d. Так высоты потенциальных барьеров, разделяющих когерентные области, согласно энергетической схеме гиперпроводника, изображенной на фиг. 5, равна разности Ес-Екол и может превышать 1 электронвольт, частота колебаний в этих состояниях может превышать 1015 Герц. При таких данных эффективное туннелирование электронов в полупроводниках возможно сквозь потенциальные барьеры толщиной от 10 A° до 50 микрон [40]. Известно и то, что на электронно-колебательных энергетических уровнях локализованы электроны, дырки и различные фононы, обеспечивающие электрон-фононное взаимодействие. На ЭКЦ есть локализованные фононы с малой энергией и с длинами волн в десятки микрон. Следует отметить, что туннельные переходы происходят практически без изменения энергии туннелирующих частиц. Этому условию при электронно-колебательном туннелировании удовлетворяют переходы с участием малоэнергичных фононов с большими длинами волн, достигающими десятков микрон. В случае электронно-колебательного туннелирования именно малоэнергичные связанные на ЭКЦ фононы с длиной волны достигающей нескольких десятков микрон, определяют наибольшую толщину туннельно прозрачного зазора d достигающего десятков микрон, так как эти фононы пронизывают такой потенциальный барьер. Поэтому толщина туннельно тонкого зазора между когерентными областями d в типичных полупроводниках может принимать значения в примерных пределах от 10 Ангстрем до 50 микрон.
Реальные процессы, определяющие возникновение аналогов стационарного эффекта Джозефсона и нестационарного высокочастотного эффекта Джозефсона в гиперпроводниковых туннельных структурах значительно сложнее, чем рассмотренные электронно-колебательные переходы между когерентными областями и сложнее, чем в сверхпроводниковых туннельных структурах. Эта сложность определяется наличием у когерентных областей большого количества разрешенных электронно-колебательных энергетических уровней, т.е. большого количества гармонических I-осцилляторов (с различными значениями ν=0, 1, 2, см. формулу (6)) и широкого набора колебательных частот, соответствующих участию в электронно-колебательных переходах среднего числа (р≅S>>1) фононов) различных типов.
Огромное количество допустимых разнообразных колебательных состояний когерентных областей в гиперпроводниках, в отличие от единственного колебательного состояния куперовской электронной пары в сверхпроводниках, приводит к качественно новым свойствам аналогов эффектов Джозефсона в гиперпроводниковых туннельных структурах в отличие от эффектов Джозефсона в сверхпроводниковых структурах. Действительно, если совокупность гармонических осцилляторов, характеризующих одну из когерентных областей взаимодействует с совокупностью гармонических осцилляторов, характеризующих другую когерентную область, то взаимодействие когерентных областей можно представить как наложение попарных взаимодействий между осцилляторами обеих областей. Для каждой пары взаимодействующих осцилляторов согласно гармоническим решениям уравнения (8) возникают гармонические, субгармонические, ультрагармонические и ультрасубгармонические колебания (см. стр. 33) и при независящих от нас произвольных значениях целых положительных чисел тип получается широкий спектр колебательных частот каждой когерентной области. Важными оказываются равные и близкие друг к другу колебательные частоты, одинаковые электронно-колебательные уровни взаимодействующих когерентных областей. Именно между равными друг другу уровнями происходит туннелирование куперовских электронных пар между когерентными областями, проявляющееся в виде аналога стационарного эффекта Джозефсона. В этих же условиях "непрямое туннелирование" проявляется в виде аналога нестационарного высокочастотного эффекта Джозефсона. Аналоги стационарного и нестационарного высокочастотного эффектов Джозефсона возникают и существуют в одинаковых условиях. Они одновременно сосуществуют друг с другом и могут быть разделены по частоте. Для аналога стационарного эффекта Джозефсона циклическая частота ω≡0, а для аналога нестационарного высокочастотного эффекта Джозефсона циклическая частота ω>0 и может принимать значения между 0 и  . Обычно эти частоты соответствуют СВЧ диапазону, но в принципе возможны и электронные переходы с частотами оптического диапазона. Тогда можно наблюдать ИК или видимое свечение. Такое свечение живых объектов, которые, как известно, являются полупроводниками, наблюдают в виде ауры.
. Обычно эти частоты соответствуют СВЧ диапазону, но в принципе возможны и электронные переходы с частотами оптического диапазона. Тогда можно наблюдать ИК или видимое свечение. Такое свечение живых объектов, которые, как известно, являются полупроводниками, наблюдают в виде ауры.
Аналоги стационарного и нестационарного эффектов Джозефсона могут проявляться одновременно. Энергия аналога нестационарного высокочастотного эффекта Джозефсона может преобразовываться в энергию аналога стационарного эффекта Джозефсона и обратно, энергия аналога стационарного эффекта Джозефсона может преобразовываться в энергию аналога нестационарного высокочастотного эффекта Джозефсона в зависимости от внешних условий, которые мы можем изменять. Поэтому величины аналогов эффектов Джозефсона можно изменять, изменяя внешние по отношению к материалу туннельной структуры физические условия.
В виду широкого спектра частот колебаний когерентных областей оказываются несущественными конкретные значения резонансных частот, связанных с материалом замедляющих устройств, поскольку всегда найдется колебание электрических зарядов с частотой, попадающей в полосу частотного пропускания этих устройств. Необязательным оказывается и совпадение или даже близость друг к другу резонансных частот замедляющих устройств, связанных с материалом вблизи электродов 1 и 2. Резонансные частоты этих устройств могут существенно отличаться друг от друга, однако они обеспечивают отвод избыточной колебательной энергии из материала, что необходимо для увеличения размера когерентных областей, длины когерентности Λ.
Из-за использования замедляющих устройств аналог нестационарного высокочастотного эффекта Джозефсона можно наблюдать на частотах в пределах полосы пропускания замедляющего устройства. Для определения спектра частот аналога нестационарного высокочастотного эффекта изменяют резонансную частоту связанного с материалом замедляющего устройства.
К пункту 7 формулы. Данный пункт формулы посвящен осуществлению аналогов эффектов Джозефсона при наличии диэлектрического слоя между когерентными областями. При этом используют два гиперпровдниковых материала, каждый из которых выбирают толщиной не менее четырех длин когерентности (4Λ), чтобы в нем могла расположиться область когерентности диаметром 2Λ, разделенных туннельно тонким диэлектрическим слоем толщиной d. На внешней поверхности каждого из образцов или в их объеме, на нормали к границам раздела материалов с диэлектрическим слоем размещают электроды (1 и 2), образующие выпрямляющие контакты с материалами, например контакты металл-полупроводник, как показано на фиг. 26. Измеряют постоянный ток в данной структуре (металл 1 - гиперпроводник 1 - диэлектрик - гиперпроводник 2 - металл 2), протекающий между электродами 1 и 2, а результаты измерений интерпретируют как аналог стационарного эффекта Джозефсона. Между электродами 1 и 2 прикладывают постоянное напряжение от внешнего источника величиной не более напряжения электрического пробоя данной структуры; измеряют переменное напряжение и (или) переменный ток в материале между электродами, а результаты измерений идентифицируют как аналог высокочастотного нестационарного эффекта Джозефсона, измеряют частоту переменного тока в материале между электродами или (и) переменного напряжения между электродами и идентифицируют ее как частоту аналога высокочастотного нестационарного эффекта Джозефсона. Таким образом осуществляют аналоги стационарного эффекта Джозефсона и высокочастотного нестационарного эффекта Джозефсона в гиперпроводниковой туннельной структуре.
Ввиду периодического расположения электронно-колебательных уровней когерентных областей наблюдается периодическая зависимость аналогов эффектов Джозефсона от величины напряжения смещения V с периодами, кратными энергии «нулевых колебаний»: Ez/e.
Туннелирование электронов сквозь зазор толщиной d между когерентными областями возможно с поглощением фононов (когда энергия конечного состояния электронов больше энергии исходного состояния) и с испусканием фононов (когда энергия конечного состояния электронов меньше энергии исходного состояния). В первом случае материал между электродами охлаждается, а во втором случае он нагревается при включении напряжения V.
Изучение аналога стационарного эффекта Джозефсона и аналога высокочастотного нестационарного эффекта Джозефсона, осуществленных в гиперпроводниковых туннельных структурах с многими электронно-колебательными энергетическими уровнями когерентных областей, позволяет глубже понять природу эффектов Джозефсона в сверхпроводниках где такая возможность ограничена, поскольку фактически имеется только одна запрещенная для электронов энергетическая зона шириной 2Δ вблизи уровня Ферми (F±Δ) и величина Δ определяется малоэнергичными фононами связывающими электроны в куперовские пары. В отличие от сверхпроводников в гиперпроводниках имеются упругие I-колебания с энергиями квантов многократно превышающими энергии фононов в сверхпроводниках, что обеспечивает возможность осуществлять, изучать и применять аналоги эффектов Джозефсона при околокомнатных и более высоких температурах и в более широком частотном диапазоне.
К пункту 8 формулы. Данный пункт формулы посвящен осуществлению аналогов эффектов Джозефсона в гетероструктурах, образованных различными гиперпроводниками.
Аналоги эффектов Джозефсона проявляются в гетероструктурах, которые образованы контактирующими друг с другом разнородными гиперпроводниками.
С целью осуществления аналогов эффектов Джозефсона в гетероструктуре используют два различных гиперпровдниковых материала толщиной не менее 4Λ. На внешней поверхности или в объеме каждого из гиперпроводников устанавливают электрод, образующий выпрямляющий контакт с материалом, например, контакт металл-полупроводник. Между этими электродами (1 и 2) прикладывают постоянное или переменное напряжение величиной не более напряжения пробоя данной гетероструктуры, изменяют полярность и (или) фазу этого напряжения и (или) его величину. Тем самым изменяют толщину обедненного слоя в гетероструктуре, который в данном случае представляет собой туннельно тонкий зазор между гиперпроводниками. Сквозь этот зазор туннелируют электронно-колебательные состояния, состоящие из электронов, I-колебаний и фононов. Измеряют величину и (или) полярность аналога стационарного эффекта Джозефсона или (и) измеряют величину и (или) частоту, и (или) фазу аналога высокочастотного нестационарного эффекта Джозефсона.
На фиг. 27 приведены из книги [50] энергетические диаграммы анизотипных гетероструктур n(+)p; n(-)p; n(-)n и p(+)p типов с учетом положительно (+) и отрицательно (-) заряженных локальных дефектов на границе раздела материалов, учитывающих реальное наличие дефектов. Латинские цифры I, II, III и IV относятся к группам гетероконтактов с определенным соотношением электронного сродства и ширины запрещенной зоны материалов. По вертикали на фиг. 27 отложена энергия электрона, а по горизонтали - расстояние, координата вдоль направления между контактирующими материалами. Горизонтальные пунктирные прямые представляют уровни Ферми. Благодаря дефектам на границе раздела энергетические диаграммы гетероструктур подобны диаграммам для сендвичей «полупроводник-металл-полупроводник». Из этих диаграмм видно, что гетероструктуры действительно содержат обедненные основными носителями слои у границы между материалами. Эти слои являются высокоомными и в нашем случае являются теми туннельно тонкими зазорами между двумя гиперпроводниками, сквозь которые туннелируют электроны, связанные с ними фононы и I-колебания, создавая аналоги эффектов Джозефсона.
К пункту 9 формулы. Данный пункт формулы посвящен регулированию величины, частоты и фазы аналога высокочастотного, нестационарного эффекта Джозефсона с помощью электрического напряжения, прикладываемого между электродами. Прикладываемое между электродами 1 и 2 постоянное электрическое напряжение V вызывает смещение электронных колебательных уровней когерентных областей друг относительно друга на величину eV, как показано на фиг. 25. В результате электронно-колебательное туннелирование между различными когерентными областями сопряжено с рассеянием энергии eV. Благодаря сильному электрон-фононному взаимодействию указанная энергия рассеивается в виде фононов, вызывающих осцилляции зарядов с соответствующей циклической частотой  , что создает в материале между электродами переменный электрический ток с этой же частотой, который можно регистрировать во внешней по отношению к материалу с электродами цепи. Можно также регистрировать высокочастотное напряжение между электродами 1 и 2. Область допустимых изменений напряжения V состоит из участков по размеру кратных Ez/e с границами Vгр=(Ez/e)⋅ν, где v=0, 1, 2, … На границах между этими участками напряжений, когда энергетические термы когерентных областей в материалах по обе стороны туннельного зазора совпадают, доминирует аналог стационарного эффекта Джозефсона, а при относительном смещении энергетических термов когерентных областей возникает и усиливается аналог высокочастотного, нестационарного эффекта Джозефсона.
, что создает в материале между электродами переменный электрический ток с этой же частотой, который можно регистрировать во внешней по отношению к материалу с электродами цепи. Можно также регистрировать высокочастотное напряжение между электродами 1 и 2. Область допустимых изменений напряжения V состоит из участков по размеру кратных Ez/e с границами Vгр=(Ez/e)⋅ν, где v=0, 1, 2, … На границах между этими участками напряжений, когда энергетические термы когерентных областей в материалах по обе стороны туннельного зазора совпадают, доминирует аналог стационарного эффекта Джозефсона, а при относительном смещении энергетических термов когерентных областей возникает и усиливается аналог высокочастотного, нестационарного эффекта Джозефсона.
Если между электродами 1 и 2 прикладывают переменное напряжение V с циклической частотой Ω (меньшая из значений  ;
;  ), то возникает аналог высокочастотного, нестационарного эффекта Джозефсона с частотами, определенными в пп. а), б), в), г) на стр. 29-30 величина которого зависит от амплитуды внешнего переменного напряжения, что согласуется с формулой (11). Таким образом, высокочастотный, нестационарный эффект Джозефсона в туннельных структурах гиперпроводников можно использовать для преобразования частот электрических сигналов, причем одновременно можно преобразовывать исходный сигнал в сигналы с определенными фазами на нескольких частотах, а также осуществлять частотное управление фазами частотно преобразованных сигналов согласно формулам (12). Тем самым предоставляется возможность управлять работой, например, излучателей фазовых антенных решеток на нескольких частотах с определенными фазами одновременно.
), то возникает аналог высокочастотного, нестационарного эффекта Джозефсона с частотами, определенными в пп. а), б), в), г) на стр. 29-30 величина которого зависит от амплитуды внешнего переменного напряжения, что согласуется с формулой (11). Таким образом, высокочастотный, нестационарный эффект Джозефсона в туннельных структурах гиперпроводников можно использовать для преобразования частот электрических сигналов, причем одновременно можно преобразовывать исходный сигнал в сигналы с определенными фазами на нескольких частотах, а также осуществлять частотное управление фазами частотно преобразованных сигналов согласно формулам (12). Тем самым предоставляется возможность управлять работой, например, излучателей фазовых антенных решеток на нескольких частотах с определенными фазами одновременно.
В данном пункте формулы предложено использовать эти зависимости для регулирования величины и частоты аналога высокочастотного нестационарного эффекта Джозефсона за счет изменения величины и частоты внешнего напряжения между электродами 1 и 2.
К пункту 10 формулы. Данный пункт формулы посвящен осуществлению аналогов эффектов Джозефсона и эффекта Мейснера в условиях освещения материала между электродами электромагнитным излучением. Освещение материала между электродами электромагнитными квантами, вообще говоря, вызывает изменение длины когерентности Λ, температуры гиперпроводящего перехода Th, величины, частоты и фазы эффектов Джозефсона, а также величины эффекта Мейснера. Величина и знак таких изменений зависят от используемых материалов, от конкретных свойств излучения, от условий освещения образцов и от свойств ЭКЦ, имеющихся в материале.
Несомненно, что температура гиперпроводящего перехода и технические параметры аналогов эффектов Джозефсона изменяются под действием той доли излучения, которая поглощается в материале, приносит в материал дополнительную энергию, создает изменения концентрации фононов и носителей зарядов на электронно-колебательных уровнях. В связи с этим целесообразно выделить спектральные области, соответствующие важным механизмам поглощения электромагнитного излучения в материалах.
Собственное, основное, фундаментальное или зонно-зонное поглощение вызывает в материале биполярную генерацию подвижных носителей зарядов в результате электронных переходов через запрещенную зону. Соответствующая спектральная полоса поглощения расположена при энергиях квантов  , прямозонного полупроводника и при
, прямозонного полупроводника и при  , где ширина запрещенной зоны материала Eg=Ес-Ev, Еех - энергия связи экситона, Ефoн - энергия кристаллического фонона, участвующего в межзонном электронном переходе,
, где ширина запрещенной зоны материала Eg=Ес-Ev, Еех - энергия связи экситона, Ефoн - энергия кристаллического фонона, участвующего в межзонном электронном переходе,  - постоянная Дирака и h - постоянная Планка, ω - циклическая частота поглощаемого излучения, Ес и Ev - дно зоны проводимости и потолок валентной зоны полупроводникового материала, соответственно. Длина волны электромагнитных волн
- постоянная Дирака и h - постоянная Планка, ω - циклическая частота поглощаемого излучения, Ес и Ev - дно зоны проводимости и потолок валентной зоны полупроводникового материала, соответственно. Длина волны электромагнитных волн  , где с - скорость света в вакууме. В этой полосе коэффициент поглощения обычно особенно велик и достигает (105…106) см-1, а полоса поглощения простирается до энергий квантов в несколько электронвольт. Генерируемые в данном случае электроны и дырки рекомбинируют на энергетических уровнях ЭКЦ, вызывают изменение длины когерентности Λ, поскольку или увеличивают колебательную энергию или дополняют энергию, подлежащую рассеянию. Соответственно изменяются условия для осуществления гиперпроводимости и сверхтеплопроводности, изменяется величина эффекта Джозефсона.
, где с - скорость света в вакууме. В этой полосе коэффициент поглощения обычно особенно велик и достигает (105…106) см-1, а полоса поглощения простирается до энергий квантов в несколько электронвольт. Генерируемые в данном случае электроны и дырки рекомбинируют на энергетических уровнях ЭКЦ, вызывают изменение длины когерентности Λ, поскольку или увеличивают колебательную энергию или дополняют энергию, подлежащую рассеянию. Соответственно изменяются условия для осуществления гиперпроводимости и сверхтеплопроводности, изменяется величина эффекта Джозефсона.
Примесное поглощение вызывает монополярные, электронные или дырочные переходы между примесным уровнем и разрешенной энергетической зоной и последующую рекомбинацию на ЭКЦ. Ввиду монополярной генерации зарядовое состояние первоначального доминирующего рекомбинационного уровня Е* (и возможно его энергия) изменяются, вызывая изменение Λ, Th, и величин характеризующих эффекты Джозефсона. Рекомбинация носителей зарядов на электронно-колебательных уровнях в стационарных условиях поддерживает электронейтральность этих уровней, из-за чего стабилизируется состояние уровня Ферми в положении на Eg/3 выше потолка валентной зоны (известное «правило 1/3» [45]), а фотопроводимость оказывается отрицательной.
Вообще говоря, в заявленном изобретении могут использоваться и полосы ИК поглощения, связанные с электронными, дырочными переходами между энергетическим уровнем примесных центров Еt1, Et2, …Eti, это - так называемые межцентровые переходы, которые изменяют колебательное и зарядовое состояния доминирующего рекомбинационного уровня Е*, вызывая изменение Λ, Th, и величины эффектов Джозефсона и Мейснера.
Практически важным является действие излучения в спектральных участках с длинами волн:
- вблизи 0,9 мкм 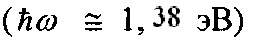 . В этой области спектра переходы типа А можно осуществить, например, в кремнии (Eg=1.12 эВ), переходы типа В можно осуществить, используя материалы: Se (Eg=1,8 эВ), AlSb (Eg=1,6 эВ), CdSe (Eg=1,7 эВ), HgS (Eg=1,7 эВ) переходы типа C можно осуществить в AlN (Eg=3,8 эВ), в АlP (Eg=3,0 эВ);
. В этой области спектра переходы типа А можно осуществить, например, в кремнии (Eg=1.12 эВ), переходы типа В можно осуществить, используя материалы: Se (Eg=1,8 эВ), AlSb (Eg=1,6 эВ), CdSe (Eg=1,7 эВ), HgS (Eg=1,7 эВ) переходы типа C можно осуществить в AlN (Eg=3,8 эВ), в АlP (Eg=3,0 эВ);
- вблизи 1,06 мкм  . В этой области спектра переходы типа А можно осуществить в кремнии (Eg=1.12 эВ), переходы типа В можно осуществить, используя материалы: Se (Eg=1,8 эВ), CdSe (Eg=1,7 эВ), Sb2S3 (Eg=1,7 эВ), переходы типа с) можно осуществить в ZnS (Eg=3,58 эВ), в GaN (Eg=3,3 эВ);
. В этой области спектра переходы типа А можно осуществить в кремнии (Eg=1.12 эВ), переходы типа В можно осуществить, используя материалы: Se (Eg=1,8 эВ), CdSe (Eg=1,7 эВ), Sb2S3 (Eg=1,7 эВ), переходы типа с) можно осуществить в ZnS (Eg=3,58 эВ), в GaN (Eg=3,3 эВ);
- в области от 3 до 5 мкм (с  от 0,41 эВ до 0,25 эВ). Переходы типа А можно осуществить, используя InSb (Eg=0,23 эВ), PbS (Eg=0,37 эВ), InAs (Eg=0,36 эВ), Те (Eg=0,32 эВ), PbSe (Eg=0,26 эВ), Bi2Se3 (Eg=0,28 эВ), переходы типа В можно осуществить в Те (Eg=0,32 эВ), InAs (Eg=0,36 эВ), PbS (Eg=0,37 эВ), переходы типа С можно осуществить используя растворы германия с кремнием GeSi (0,68 эВ≤Eg≤1,12 эВ), а также материалы GaSb (Eg=0,68 эВ), Mg2Si (Eg=0,77 эВ), Mg2Ge (Eg=0,74 эВ);
от 0,41 эВ до 0,25 эВ). Переходы типа А можно осуществить, используя InSb (Eg=0,23 эВ), PbS (Eg=0,37 эВ), InAs (Eg=0,36 эВ), Те (Eg=0,32 эВ), PbSe (Eg=0,26 эВ), Bi2Se3 (Eg=0,28 эВ), переходы типа В можно осуществить в Те (Eg=0,32 эВ), InAs (Eg=0,36 эВ), PbS (Eg=0,37 эВ), переходы типа С можно осуществить используя растворы германия с кремнием GeSi (0,68 эВ≤Eg≤1,12 эВ), а также материалы GaSb (Eg=0,68 эВ), Mg2Si (Eg=0,77 эВ), Mg2Ge (Eg=0,74 эВ);
- в области от 8 мкм до 12 мкм (с  от 0,155 эВ до 0,104 эВ) переходы типа А можно осуществить используя Cd3As2 (Eg=0,13 эВ), Вi2Te3 (Eg=0,13 эВ), переходы типа В можно осуществить используя InSb (Eg=0,18 эВ), PbSe (Eg=0,2 эВ), переходы типа С можно осуществить используя Те (Eg=0,32 эВ), InAs (Eg=0,36 эВ), PbS (Eg=0,37 эВ), Mg2Sn (Eg=0,36 эВ), SbTe3 (Eg=0,3 эВ), CdSb (Eg=0,46 эВ), Ga2Pb (Eg=0,46 эВ).
от 0,155 эВ до 0,104 эВ) переходы типа А можно осуществить используя Cd3As2 (Eg=0,13 эВ), Вi2Te3 (Eg=0,13 эВ), переходы типа В можно осуществить используя InSb (Eg=0,18 эВ), PbSe (Eg=0,2 эВ), переходы типа С можно осуществить используя Те (Eg=0,32 эВ), InAs (Eg=0,36 эВ), PbS (Eg=0,37 эВ), Mg2Sn (Eg=0,36 эВ), SbTe3 (Eg=0,3 эВ), CdSb (Eg=0,46 эВ), Ga2Pb (Eg=0,46 эВ).
Поглощение I-колебаниями атомных ядер в ЭКЦ существенно в данном изобретении, так как в нем используются материалы, содержащие ЭКЦ. Кванты таких колебаний α-, β- и γ-типа известны, их значения можно определить с помощью фиг.3 или вычислить по следующей формуле, верной для атомов с различными атомными номерами Z>8:
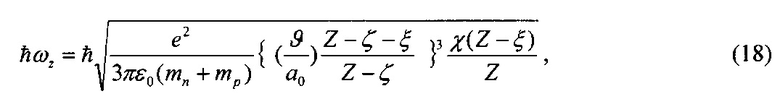
где ζ=5/16 и ξ=ηZ1/3, η изменяется от 1 до 1,15 при изменении Z от 8 до 80, χ=1,2 (для α-типа I-колебаний) учитывает вклад в электронную плотность от орбиталей K, L, М, N, ϑ=0,88534, ε0 - электрическая постоянная, mn и mp - массы нейтрона и протона, а0 - диаметр первой боровской электронной орбиты в атоме водорода. Элементарные кванты собственных колебаний β-типа могут быть аналогично определены по этой формуле при χ=0,2. Элементарные кванты собственных колебаний γ-типа могут быть определены при χ=0,056. Вычисленные величины квантов I-колебаний ( ) и экспериментальные значения квантов I-колебаний для некоторых атомов представлены на фиг. 3 в зависимости от атомного номера Z.
) и экспериментальные значения квантов I-колебаний для некоторых атомов представлены на фиг. 3 в зависимости от атомного номера Z.
Известно также, что с оптическим возбуждением I-колебаний связаны широкие ИК полосы отражения и поглощения. Ширина полос определяется энергиями участвующих в электронно-колебательных переходах фононов и I-колебаний. Контуры спектров отражения описываются теорией отражения заряженным гармоническим осциллятором.
Классическая теория оптического отражения заряженным гармоническим осциллятором [51] вполне применима и для описания оптических полос отражения, локализованными посредством фононов на ЭКЦ электронам, когда электроны действительно локализованы на ЭКЦ, не свободны, и поэтому могут взаимодействовать с ИК излучением. Локализованные на ЭКЦ электроны связаны с фононами, осциллируют с частотами фононов и представляют собой заряженные гармонические осцилляторы. Эти осцилляторы обладают затуханием, поскольку их колебания разрушаются, а энергия рассеивается. Колебания этих осцилляторов поддерживаются за счет энергии внешнего по отношению к ЭКЦ воздействия, например, за счет энергии внешнего электромагнитного излучения. Вынужденные колебательные движения локализованного на ЭКЦ электрона описывают уравнением вынужденных колебаний гармонического заряженного осциллятора

где x - обобщенная, главная или конфигурационная координата осциллятора, m - масса и е - заряд электрона, r - коэффициент затухания, Ω - собственная частота осциллятора, Е - амплитуда и ω - циклическая частота электрической компоненты оптической волны. Решение этого уравнения, соответствующее вынужденным смещениям, колебаниям электрона на ЭКЦ можно записать в следующем виде:

Смещение электрона вызывает появление дипольного момента и поляризации P, которая связана с электрическим вектором E оптической волны: εε0Е=ε0Е+Р. Здесь ε=(n-ik)2 - комплексная диэлектрическая проницаемость, n - оптический коэффициент преломления, k - показатель поглощения (экстинция) и ε0 - электрическая постоянная. Если концентрация собственных осцилляторов равна N, то дипольный момент единицы объема вещества можно записать следующим образом:
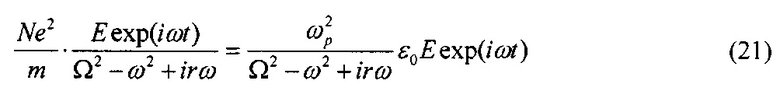
Из этих данных определяют  , где εопт - оптическая, высокочастотная диэлектрическая проницаемость. Далее, воспользовавшись известными соотношениями Крамерса-Кронига, выделяют действительную и мнимую части комплексной диэлектрической проницаемости:
, где εопт - оптическая, высокочастотная диэлектрическая проницаемость. Далее, воспользовавшись известными соотношениями Крамерса-Кронига, выделяют действительную и мнимую части комплексной диэлектрической проницаемости:


где ωp - наибольшая из частот упругих колебаний электронов ЭКЦ.
Из этих выражений можно определить коэффициент преломления и экстинцию:
 и
и  ,
,
где εr и εi - действительная и мнимая части комплексной диэлектрической проницаемости и записать коэффициент оптического отражения в следующем виде:

где R∞ имеет смысл коэффициента оптического отражения от плоской поверхности монолитного материала, занимающего полупространство (половину пространства).
Квантовая теория оптического отражения линейным заряженным гармоническим осциллятором представляет наложение его классических спектров отражения, связанных с каждым из квантовых колебательных уровней, соответствующих значениям колебательного квантового числа ν=0, 1, 2, …
Особенности спектра отражения заряженным гармоническим осциллятором можно видеть на вычисленном спектре осциллятора, представленном на фиг. 28. Спектральное положение полосы оптического отражения осциллятора определяется частотами Ω и ωР. Наибольшего значения R∞ достигает на оптических частотах между Ω и ωР. На частоте осциллятора Ω имеется характерный узкий и поэтому обычно трудно разрешимый минимум отражения, а минимальное значение R∞ располагается вблизи ωР.
Спектр отражения заряженным квантовым гармоническим осциллятором представляет собой сумму спектров отражения (24) осцилляторов с частотами квантовых колебаний.
На фиг. 29 представлен типичный экспериментальный ИК спектр отражения ЭКЦ, которые образованы примесными атомами Al в монокристалле GaP (кривая 11). Приведены вычисленные компоненты этого спектра: 12, 13, 14 и 15, соответствующие заполнению различных колебательных состояний ЭКЦ с энергиями кратными половине энергии кванта колебаний ядра в примесном атоме алюминия. Сумма этих вычисленных спектров совпадает с экспериментальной кривой 11. Характерные энергии ИК квантов в компонентах спектра (ωР) соответственно равны 0,5Е11, Е11, 1,5Е11, 2Е11, то есть они кратны половине энергии элементарного колебательного кванта осциллятора, равной EZ=Е11=0,283 эВ, описывающего колебания ядра в атоме Al. Минимальные энергии квантов в этих компонентах спектра (Ω) совпадают с энергией квантов β- и γ-типов I-колебаний ядра в примесном атоме Al из-за чего обычно узкий минимум отражения вблизи коротковолнового края полосы отражения оказывается уширенным и поэтому хорошо оптически разрешен. Аналогичные результаты были получены при исследовании спектров отражения ЭКЦ, которые в GaP образованны примесными атомами серы с элементарным квантом собственных колебаний α-типа I-колебаний ядра (EZ=0,301 эВ). Минимальные энергии квантов в этих компонентах спектра одинаковы и совпадают с энергиями квантов β- и γ-типов I-колебаний атомных ядер серы. Следовательно, ЭКЦ в данных образцах были образованы именно атомами Al и S, соответственно.
Спектры отражения углеродных нанотрубных пленок, выращенных на различных подложках, также имеют широкие спектры с характерными для I-колебаний ядер в атомах углерода энергиями. Эти пленки впервые были выращены путем распыления высокочистого графита электронным пучком в вакууме и осаждения распыленных атомов углерода на проводящие, полупроводниковые или диэлектрические подложки [52]. Такие пленки представляют собой регулярно и плотно друг к другу расположенные углеродные трубки нанометрового диаметра и высотой около 0,1 мкм стоящие вдоль нормали к поверхности подложки или под острым углом к нормали. Известно, что нанотрубки объединены в жгуты, а жгуты объединены в банделы, которые регулярно и плотно расположены на подложке и образуют регулярную структуру, характерную для монокристаллов.
Типичный спектр ИК отражения углеродной нанотрубной пленки выращенной на кварцевой подложке представлен на фиг. 30. Этот спектр содержит черты спектров отражения осцилляторов, представляющих колебания ядер в атомах кислорода и углерода. Энергия собственных колебаний данного осциллятора совпадает с половиной элементарного кванта кислородного осциллятора (0,11 эВ). Максимальная энергия в данном спектре совпадает с энергией колебаний ядра в атоме углерода. Анализ спектра позволяет связывать его с вынужденными колебаниями ЭКЦ двух типов, из которых один тип ЭКЦ образован атомами кислорода, а второй - атомами углерода. Иначе говоря, в данном спектре проявляется обмен энергией между разными типами ЭКЦ, образованными атомами кислорода и атомами углерода, т.е. атомами подложки и атомами пленки на подложке.
Типичный спектр ИК отражения углеродной нанотрубной пленки, выращенной на молибденовой подложке и представленный на фиг. 31 также является спектром ИК отражения заряженным гармоническим осциллятором с собственной частотой Ω, совпадающей с частотой β-типа колебаний ядра в атоме углерода. В данном случае ЭКЦ образованы атомами углерода.
Типичный спектр ИК отражения углеродной нанотрубной пленки выращенной на медной подложке, представленный на фиг. 32, также является спектром ИК отражения гармоническим осциллятором с собственной частотой Ω, совпадающей с частотой β-типа колебаний ядра в атоме углерода. В этом случае ЭКЦ также образованы атомами углерода.
Анализ спектров отражения на ЭКЦ в различных материалах и структурах на их основе показал, что в них происходит интенсивное поглощение излучения, энергия которого затрачивается на возбуждение I-колебаний ЭКЦ, на возбуждение упругих гармонических колебаний атомных ядер в атомах с участием кристаллических фононов. Именно такие колебания определяют природу гиперпроводимости и сверхтеплопроводности. Поглощаемое колебаниями излучение изменяет величину колебательной энергии Екол, влияет на Λ, Th, на величины эффектов Джозефсона и на величину эффекта Мейснера.
Разогрев электронов ЭКЦ путем разогрева всего материала в целом является малоэффективным. В этом случае затрачиваемая на разогрев участка материала энергия только частично передается электронам локального центра, участвующим в необходимых нам электронно-колебательных токах. Большая часть поступающей в материал энергии передается кристаллической решетке и непроизводительно расходуется на решеточную теплопроводность, на излучательные переходы, которые не дают вклад в электронно-колебательный ток.
В неадиабатической электронике, к которой относится заявленное изобретение, можно повысить эффективность использования подводимой в материал ИК энергии и использовать ее для разогрева именно электронов ЭКЦ, без изменения температуры кристаллической решетки материала. Эффект разогрева преимущественно электронов (дырок) на ЭКЦ достижим, если энергию направлять в материал в виде электромагнитного излучения в определенном спектральном диапазоне длин волн от λmin до λmax. Пределы этого спектрального диапазона вполне определенным образом связаны с электронно-колебательными токами (16) и с температурными границами полос увлечения электронов фононами (УЭФ), расположенными вблизи температур Дебая фононов Tm, между Tm-3θ и Tm+3θ. Общеизвестно, что в кристаллах, содержащих 2 или более атомов в элементарной ячейке, могут существовать акустические и оптические фононы, которые сгруппированы в дисперсионные ветви. Эти дисперсионные ветви достигают максимума, вообще говоря, при различных частотах которым ставят в соответствие температуры Дебая (Tm). Поэтому для кристаллов, содержащих не менее двух атомов в элементарной ячейке, характерны, по крайней мере, четыре температуры Дебая фононов, соответствующих ветвям продольных акустических и оптических фононов, а также - ветвям поперечных акустических и оптических фононов. Согласно закону сохранения энергии этим температурам соответствуют следующие длины электромагнитных волн: 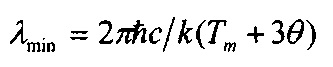 и
и 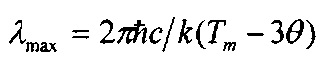 . Таким образом, электромагнитное ИК излучение в полосе с энергиями квантов от
. Таким образом, электромагнитное ИК излучение в полосе с энергиями квантов от  до
до  , соответствующим длинам ИК волн от λmin до λmax затрачивается на возбуждение колебаний связанных на ЭКЦ электронов с частотами фононов. Циклические частоты колебаний электронов совпадают с циклическим частотами локализованных фононов в диапазоне от
, соответствующим длинам ИК волн от λmin до λmax затрачивается на возбуждение колебаний связанных на ЭКЦ электронов с частотами фононов. Циклические частоты колебаний электронов совпадают с циклическим частотами локализованных фононов в диапазоне от 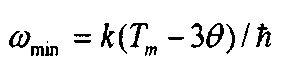 до
до  . При этом энергия ИК квантов передается непосредственно локализованным на ЭКЦ электронам, и не расходуется на непроизводительное нагревание кристаллической решетки. Это позволяет уменьшить затраты ИК энергии на создание электронно-колебательного тока в материале и повысить фоточувствительность при регистрации изучения данным способом в том числе и в длинноволновой части ИК спектра, где ИК кванты и без того мало энергичны. Указанные полосы поглощения электромагнитного излучения, соответствующие различным температурам Дебая, лежат в ИК диапазоне. ИК поглощение, соответствующее акустическим фононам в различных материалах по литературным данным [51] наблюдали в диапазоне длин волн от 15 мкм до 60 мкм.
. При этом энергия ИК квантов передается непосредственно локализованным на ЭКЦ электронам, и не расходуется на непроизводительное нагревание кристаллической решетки. Это позволяет уменьшить затраты ИК энергии на создание электронно-колебательного тока в материале и повысить фоточувствительность при регистрации изучения данным способом в том числе и в длинноволновой части ИК спектра, где ИК кванты и без того мало энергичны. Указанные полосы поглощения электромагнитного излучения, соответствующие различным температурам Дебая, лежат в ИК диапазоне. ИК поглощение, соответствующее акустическим фононам в различных материалах по литературным данным [51] наблюдали в диапазоне длин волн от 15 мкм до 60 мкм.
Приведенные выражения, связывающие значения λmin, λmax, ωmax и ωmin и дебаевы температуры Tm являются взаимно однозначными, то есть, используя эти выражения можно по значениям параметров спектров ИК отражения (λmin, λmax, ωmax и ωmin) определить Tm и θ температурную ширину полосы УЭФ, т.е. θ. И наоборот, по данным о величинах Tm и θ можно определить параметры ИК спектра (λmin, λmax, ωmax и ωmin), связанного с возбуждением колебаний электронов на ЭКЦ с частотами соответствующих фононов.
Таким образом, увеличивать энергию колебаний электронов на ЭКЦ, а значит увеличивать колебательную энергию когерентных областей, можно за счет энергии ИК излучения. В материале с дебаевыми температурами акустических продольных  , акустических поперечных
, акустических поперечных  , оптических продольных
, оптических продольных  , оптических поперечных
, оптических поперечных  , а также с дебаевыми температурами I-колебаний α-, β-, γ - типов в содержащих ЭКЦ материалах имеются соответствующие оптические полосы поглощения и отражения, заключенные между λmin и λmax для каждого из этих типов упругих колебаний материала в которых энергия ИК излучения передается локализованным на ЭКЦ, локализованным в когерентных областях электронам. Положение этих полос в пределах спектрального диапазона зависит от значений температур Tm и θ, от угла падения излучения на поверхность материала и его поляризации, от кристаллографической ориентации материала относительно направления между электродами 1 и 2. Учитывая эти особенности, выбирают материал и его кристаллографическую ориентацию, а также поляризацию и угол падения регистрируемого излучения на материал, осуществляют детектирование ИК квантов с низкими внутренними шумами без охлаждения материала в узкой полосе от
, а также с дебаевыми температурами I-колебаний α-, β-, γ - типов в содержащих ЭКЦ материалах имеются соответствующие оптические полосы поглощения и отражения, заключенные между λmin и λmax для каждого из этих типов упругих колебаний материала в которых энергия ИК излучения передается локализованным на ЭКЦ, локализованным в когерентных областях электронам. Положение этих полос в пределах спектрального диапазона зависит от значений температур Tm и θ, от угла падения излучения на поверхность материала и его поляризации, от кристаллографической ориентации материала относительно направления между электродами 1 и 2. Учитывая эти особенности, выбирают материал и его кристаллографическую ориентацию, а также поляризацию и угол падения регистрируемого излучения на материал, осуществляют детектирование ИК квантов с низкими внутренними шумами без охлаждения материала в узкой полосе от  до
до  по данным о вызываемом этим излучением изменении длины когерентности Λ, или (и) изменении температуры гиперпроводящего перехода Th, или (и) величин, или (и) частот или (и) фаз (полярности) эффектов Джозефсона.
по данным о вызываемом этим излучением изменении длины когерентности Λ, или (и) изменении температуры гиперпроводящего перехода Th, или (и) величин, или (и) частот или (и) фаз (полярности) эффектов Джозефсона.
Экспериментально подтверждена связь между температурными полосами электронно-колебательных токов I в интервале от Tm-3θ до Tm+3θ и полосой ИК отражения ЭКЦ, расположенной между длинами ИК волн Λmin и Λmax. Так, на фиг. 33 изображена характерная температурная зависимость электронно-колебательного тока в монокристалле GaP, содержащего ЭКЦ, которые образованны примесными атомами Al. Ширина наиболее интенсивной полосы тока I, измеренная на ее полувысоте, лежит в пределах от 442 K до 502,3 K, величина θ≅5 K, Tm=693,15 K. Границы этой полосы на 3θ отстоят от значения Tm:Tm-3θ=427 K; Tm+3θ=517,26 K. Учитывая, что тепловая энергия 1 K=8,616562⋅10-5 эВ, определяем энергии, соответствующие температурам Tm-3θ и Tm+3θ, равные 36,79⋅10-3 эВ и 44,57⋅10-3 эВ. Эти энергии соответствуют следующим длинам волн ИК излучения: 33,7 мкм и 27,82 мкм, ширина полосы ≅6 мкм. На фиг. 34 приведена экспериментальная полоса ИК отражения GaP и вычисленный спектр отражения осциллятора из работы [51] расположенный между 31 мкм и 25 мкм, ширина полосы ≅6 мкм. На фиг. 35 приведен измеренный нами спектр отражения GaP, который практически совпадает со спектром на фиг. 34. Вычисленное и экспериментальное положение полос ИК отражения согласуются друг с другом и имеют примерно одинаковую ширину, но несколько смещены друг относительно друга вследствие различных кристаллографических ориентации образцов материала в этих двух экспериментах, а также из-за падения ИК излучения на поверхность материала под разными углами в этих экспериментах.
На фиг. 36 изображена характерная температурная зависимость электронно-колебательного тока в GaAs, содержащем ЭКЦ, образованные примесными атомами кислорода. Данная зависимость представлена экспериментальными точками и сплошной кривой, проведенной по этим точкам. Пунктирные кривые представляют гауссову зависимость (16) контуров этих полос, для которых одинаковое, независящее от температуры значение θ=3,5 K. Максимумы наиболее интенсивных полос в данной зависимости на фиг. 36 расположены вблизи Tm=439 K, Tm=404 K и Tm=347 K,. Эти полосы обусловлены участием в электронно-колебательном токе различных типов фононов материала. Участие этих фононов в процессах ИК отражения ограничивается различными правилами отбора для различных кристаллографических ориентации материала, различных углов падения ИК излучения на материал, поляризации излучения относительно кристаллографических осей материала. Поэтому в одном эксперименте не представляется возможным измерить спектры отражения с участием всех типов фононов, создающих электронно-колебательные токи. Так спектр ИК отражения GaAs, представленный на фиг. 37 из книги [53], связан с двумя взаимно перекрывающимися полосами электронно-колебательного тока, расположенными на фиг. 36 при температурах Tm, равных 404 K и 439 K. В связи с этим полоса ИК отражения GaAs, показанная на фиг. 37 представляет собой наложение, перекрытие двух полос отражения с участием тех же типов фононов, которые вызвали электронно-колебательные токи с максимумами при температурах 404 K и 439 K, что проявляется в особенности профиля полосы. Ожидаемые пределы полосы ИК отражения в данном случае определяются температурами (404 K-3θ)=393,5 K и (439 K+3θ)=449,5 K. Эти температуры соответствуют следующим энергиям кантов и длинам волн ИК излучения: (33,91⋅10-3 эВ; ≅36,6 мкм) и (38,73⋅10-3 эВ; ≅32 мкм). Экспериментальная ИК полоса отражения GaAs на фиг. 35 расположена между значениями волновых векторов и соответствующих им длин ИК волн: (296 см-1; ≅34,5 мкм) и (260 см-1; ≅32,21 мкм). Сравнение приведенных результатов выявило согласие вычисленных из температурной зависимости электронно-колебательного тока и экспериментальных данных о спектральных положениях полос ИК отражения ЭКЦ в GaAs.
На фиг. 38 приведена типичная температурная зависимость электронно-колебательного тока I в углеродной нанотрубной пленке на кварцевой подложке. Данная зависимость содержит несколько максимумов. Максимум при температуре Tm=593 K принадлежит наиболее интенсивной полосе УЭФ, лежащей между температурами Tm-3θ=555,5 K и Тm+3θ=630,5 K. Эти температуры соответствуют следующим энергиям ИК квантов и их оптическим длинам волн: (47,86⋅10-3 эВ; 25,91 мкм) и (54,32⋅10-3 эВ; 22,8 мкм) при которых расположены экспериментальные полосы отражения и поглощения (22,6 мкм - 27,5 мкм) данных структур, представленные на фиг. 39.
На фиг. 40 приведена температурная зависимость термоЭДС, содержащая узкие пики увлечения электронов фононами в монокристалле Ge при дебаевых температурах фононов 314 K; 359,9 K и 414 K. Гауссова пунктирная кривая аппроксимирует контур наиболее интенсивной полосы УЭФ при 314 K с θ=2,5 K. Ожидаемые из установленной зависимости полосы отражения и поглощения лежат между 25,96 мкм и 26,38 мкм. В спектре поглощения Ge [53] действительно содержится такая сравнительно давно известная узкая полоса поглощения, связанная с участием фононов, которая становится ярче на фоне ослабевающего при охлаждении образца поглощения свободными носителями, но не изменяющая своей ширины, что характерно для электронно-колебательных спектров. Соответствующие спектры приведены на фиг. 41 из работы [53]. Данная полоса поглощения имеется также в спектрах работы [54]. Поглощение свободными носителями не влияет на электронно-колебательные спектры и на данную полосу ИК поглощения.
Таким образом, установлено соответствие температурных зависимостей электронно-колебательных токов I или температурных зависимостей увлечения электронов фононами (УЭФ) со спектральным положением ИК полос отражения ЭКЦ. Это соответствие характерно не только для соединений А3В5, но и для других содержащих ЭКЦ материалов и структур и представляется закономерным.
Выявленное соответствие между температурными зависимостями электронно-колебательных переходов в слоях материалов на подложках с их спектрами ИК отражения позволяет использовать слои материалов на подложках для регистрации ИК излучения в диапазоне от 1 мкм до более 1000 мкм по данным о влиянии такого излучения на температуру гиперпроводящего перехода. Для регистрации ИК изучения определенной длины волны выбирают подложку с соответствующей энергией фононов (температурой Дебая фононов), наносят на подложку слой материала толщиной не менее 4Λ, устанавливают электроды 1 и 2, направляют регистрируемое ИК изучение в материал между электродами, измеряют вызванное излучением изменение величины Th или изменение сопротивления материала между электродами при температуре вблизи Th. Целесообразна стабилизация температуры материала вблизи Th. По результатам измерений делают вывод об интенсивности регистрируемого ИК излучения. При этом не требуется охлаждения материала даже при регистрации длинноволнового ИК излучения, а уровень внутренних, собственных, шумов определяется величиной θ<<Th, из-за чего заявленный способ регистрации обладает преимуществом по уровню внутренних, собственных шумов перед аналогами, в которых материал охлаждают до низких температур.
В данном пункте формулы предложено использовать установленные закономерности для регистрации ИК излучения с низкими внутренними шумами без охлаждения фоточувствительных материалов и приборов.
К пункту 11 формулы. Температура гиперпроводящего перехода Th, величины эффектов Джозефсона и частота высокочастотного нестационарного эффекта Джозефсона, а также величина эффекта Мейснера зависят от формы материала, от расстояний между плоскопараллельными границами материала, поскольку при изменении формы образца материала изменяются условия распространения фононов и электронно-колебательных токов. В связи с этим важным оказывается условие акустоэлектрического синхронизма, согласно которому расстояния между взаимно параллельными границами материала выбирают равными или кратными W=Пv/2, где v - скорость звука, распространяющегося между взаимно параллельными границами материала и П - период тока в материале между электродами. При этом условии значительная часть испускаемых фононов возвращается в область их генерации, что оказывает влияние на Th и на эффекты Джозефсона и Мейснера. Влияние акустоэлектрического синхронизма на указанные эффекты и на Th проявляется, если в материале действует периодическое электрическое поле с периодом П. Периодическое с таким же периодом П магнитное поле с индукцией не более 2 Тл в материале подавляет осцилляции электронов на ЭКЦ с частотами локализованных фононов. В связи с этим для стабилизации гиперпроводящго и сверхтеплопроводного состояния, стабилизации температуры гиперпроводящего перехода Th, величин эффектов Джозефсона и частоты высокочастотного нестационарного эффекта Джозефсона, а также с целью изменения величины эффекта Мейснера толщину полупроводниковой пластины, или толщину полупроводникового слоя на подложке, или толщину подложки, или общую толщину полупроводникового слоя и подложки, или расстояние (расстояния) между взаимно параллельными границами полупроводника выбирают равным (равными) или кратным (кратными) W=Пv/2, где v - скорость звука, распространяющегося между взаимно параллельными границами полупроводника, подложки, или полупроводника и подложки, в материале между электродами создают переменное электрическое поле и (или) переменное магнитное поле с индукцией В≤2 Тл с временными периодами П, измеряют температуру гиперпроводящего перехода Th, величины аналогов эффектов Джозефсона и (или) частоту аналога высокочастотного нестационарного эффекта Джозефсона, а также величину или изменение величины эффекта Мейснера.
К пункту 12 формулы. Данный пункт формулы посвящен использованию аналога стационарного эффекта Джозефсона для преобразования тепловой энергии в энергию постоянного электрического тока. Аналог стационарного эффекта Джозефсона по существу предоставляет возможность преобразовывать упругие колебания электрически заряженных частиц в составе когерентных областей в энергию постоянного электрического тока. Упругие колебания когерентных областей происходят благодаря рекомбинации электронов (дырок) на электронно-колебательных энергетических уровнях. Рекомбинирующие электроны (дырки) возникают в материале под действием тепловой генерации, за счет тепла, поступающего в материал из внешней среды. Следовательно, аналог стационарного эффекта Джозефсона осуществляется за счет тепловой энергии, поступающей в материал из внешней среды. Поэтому предусмотрен подвод тепла к материалу между электронами для обеспечения постоянного электрического тока.
Электронно-колебательные переходы между одинаковыми колебательными состояниями взаимодействующих осцилляторов, между колебательными состояниями с одинаковыми значениями колебательных квантовых чисел ν и колебательных частот, образуют токи с нулевой частотой, т.е. постоянные токи, сумма которых по колебательным состояниям ν представляет собой аналог стационарного эффекта Джозефсона. Эти токи протекают в материале между электродами 1 и 2 и могут быть измерены во внешней цепи между этими электродами, а при разорванной внешней цепи аналог стационарного эффекта Джозефсона проявляется в виде постоянного электрического напряжения определенной полярности между электродами 1 и 2.
Тепловая энергия расходуется в материале на генерацию свободных, подвижных электронов и дырок, которые локализуются преимущественно на энергетическом уровне Е* когерентных областей и тем самым поддерживают существование I-колебаний и аналога джозевсоновского тока (I0). Для поддержания постоянного тока I0 обеспечивают приток тепла к материалу извне при температуре не менее температуры Дебая фононов, при температуре материала T=Th или при более высокой температуре. Таким образом, аналог эффекта Джозефсона в гиперпроводниковой структуре с туннельно тонким зазором толщиной d, также как эффект Джозефсона в структуре сверхпроводников, разделенных туннельно тонким диэлектриком, осуществляет преобразование тепловой энергии в электрическую энергию Джозефсоновского тока I0. В этом состоит общее свойство стационарного эффекта Джозефсона в структуре сверхпроводников и аналога стационарного эффекта Джозефсона в структуре гиперпроводников. Между стационарным эффектом Джозефсона и аналогом стационарного эффекта Джозефсона, однако, существует важное различие. Действительно, ширина энергетической щели сверхпроводника (2Δ) обычно составляет несколько миллиэлектронвольт и напряжение «холостого хода» стационарного эффекта Джозефсона не превышает нескольких милливольт. Эта особенность препятствует техническому использованию стационарного эффекта Джозефсона для получения электроэнергии за счет тепла. Напротив, в гиперпроводниковых туннельных структурах энергетическая щель между различными электронно-колебательными состояниями кратна половине кванта I-колебаний, может достигать ширины запрещенной зоны материала и даже превышать ее. Поэтому в гиперпроводниковых туннельных структурах величина напряжения «холостого хода» аналога стационарного эффекта Ждозефсона может составлять величину Е*/е.
Аналог стационарного эффекта Ждозефсона в гиперпроводниковых структурах можно успешно применять для технического преобразования тепловой энергии в электрическую энергию.
С целью получения электрической энергии с помощью аналога стационарного эффекта Джозефсона обеспечивают приток тепла к материалу между электродами 1 и 2, а постоянный ток в материале между электродами, представляющий аналог стационарного эффекта Джозефсона, или аналогичные токи от нескольких таких структур, последовательно или параллельно направляют в стационарное или мобильное потребляющее (потребляющие) электроэнергию устройство (устройства).
Целесообразно использовать аналог стационарного эффекта Джозефсона на основе гиперпроводниковых туннельных структур для преобразования энергии окружающего тепла в энергию постоянного электрического тока. Аналог стационарного эффекта Джозефсона в гиперпроводниковых структурах на основе типичных полупроводников позволяет получать на нагрузке во внешней цепи напряжения, составляющие доли Вольта (Е*/е). При использовании гиперпроводников с ЭКЦ содержащих атомы кислорода, напряжения между электродами кратны половине элементарного кванта I-колебания ядра в атоме кислорода, отнесенного к заряду электрона (0,22 эВ/2е). В образцах на основе Si и Ge при разных температурах эти напряжения практически составляют 0,33; 0,44; 0,55 или 0,66 Вольт, то есть превышают напряжения стационарного эффекта Джозефсона в сверхпроводниках в десятки раз, что обеспечивает аналогу стационарного эффекта Джозефсона значительные технические преимущества по сравнению с общеизвестным стационарным эффектом Джозефсона в сверхпроводниках.
На фиг. 42 приведена характерная температурная зависимость величины аналога стационарного эффекта Джозефсона (V*) в гиперпроводниковой структуре на основе Si. Электронно-колебательные центры образованы примесными атомами кислорода. Величина аналога стационарного эффекта Джозефсона V* практически постоянна при нагревании образца от комнатной температуры, но при 384 K она резко уменьшается на 0,22 В и остается неизменной до 570 K. Оба этих напряжения соответствуют туннелированию электронов между электронно-колебательными состояниями когерентных областей с энергиями 0,33 эВ и 0,22 эВ, которые входят в спектр квантовых разрешенных энергий I-колебаний характерных для примесных атомов кислорода.
На фиг. 43 приведена температурная зависимость величины аналога стационарного эффекта Джозефсона в структуре на основе Ge в условиях рассогласования импедансов материала между электродами и связанного с ним замедляющего устройства. В таких условиях возникают релаксационные колебания из-за последовательных изменений положения уровня Ферми от одного к другому электронно-колебательному уровню и обратно.
Нужно сказать, что атомы кислорода составляют около 28% имеющегося в коре Земли вещества и обычно присутствуют в виде примеси в полупроводниковых материалах. Так в промышленном кремнии концентрация примесных атомов кислорода может превышать 1018 атомов/см3 и ее не удается существенно уменьшить современными средствами очистки. При отсутствии других сортов примесных атомов именно атомы кислорода образуют ЭКЦ и определяют формирование когерентных областей. Температурные зависимости аналога стационарного эффекта Джозефсона в туннельных структурах на основе других типичных полупроводников являются ступенчатыми, что указывает на температурную зависимость вероятности туннелирования электронов сквозь зазор между когерентными областями и на переход уровня Ферми при некоторых температурах от одного электронно-колебательного энергетического уровня к другому электронно-колебательному энергетическому уровню.
Эксперименты подтвердили ожидаемые из расчета величины аналога стационарного эффекта Джозефсона, составляющие доли электрон-вольта. В принципе (в широкозонных материалах) возможны величины аналогов эффектов Джозефсона, превышающие 1 Вольт.
Преобразователи тепловой энергии в электрическую энергию на основе аналога стационарного эффекта Джозефсона можно встраивать, например, в мобильные электронные устройства, в сотовые телефоны, ноутбуки для непрерывной подзарядки аккумуляторов электропитания за счет тепловой энергии окружающей среды, в том числе за счет выделяемого процессорами устройств тепла. Такие преобразователи позволят избавить стационарные и мобильные электронные устройства от периодической подзарядки аккумуляторов, от необходимости подключения к внешней электросети для зарядки, что важно на космических, подводных, авиационных транспортных средствах и в полевых условиях. Преобразователи тепловой энергии в электрическую энергию с помощью аналога стационарного эффекта Джозефсона можно использовать для электропитания светильников, световая энергия которых в итоге преобразуется в тепло окружающей среды, которое гиперпроводниковые туннельные структуры преобразуют в электрический ток I0. Таким образом можно осуществить круговорот и преобразование одного вида энергии в другой вид энергии: тепло-электричество-свет-тепло, что обеспечивает снижение затрат на энергетическое снабжение жизнедеятельности и техники.
В настоящее время промышленное производство постоянно действующих необслуживаемых источников электрического тока с длительным сроком службы с выходной мощностью от 1 до 50 миллиВатт и с выходным напряжением около 1 Вольта осуществляют фирмы США: Widetronix (Firefli-T, Firefli-N), City Labs (ERDIP, LCC) и BetaBatt (Trench, Fill-Jelli-Roll). Продукция этих фирм с 2014 года не может быть импортирована в Российскую Федерацию из-за санкций, ограничивающих поставку в РФ продукции двойного назначения. Действие таких элементов электропитания основано на преобразовании энергии ионизирующего бета-излучения (электроны) радиоактивного изотопа никель-63 в энергию электрического тока. Кремниевые преобразователи в условиях бета облучения способны работать не более года, хотя требуется их работоспособность в течение 20 лет и более. Для импортозамещения до 2018 года в России сейчас выполняется программа исследований, разработок и создания производств радиационно стимулированных элементов электропитания, в частности включающих преобразователи энергии радиационного излучения в энергию электротока на основе радиационно-стойких широкозонных полупроводников (синтетический алмаз, GaN) общим объемом в десятки млн. руб. Очевидно, что производимые и планируемые к разработке и производству элементы питания уступают по техническим параметрам и затратам на их производство преобразователям тепловой энергии в электрическую энергию, работающих на использовании аналогов эффектов Джозефсона в гиперпроводящих туннельных структурах. Действительно, применение аналогов эффетов Джозефсона в гиперпроводящих туннельных контактах для этих целей не требует использования источников радиационного излучения. Это позволяет конструировать и использовать преобразователи энергии окружающего тепла в энергию электрического тока на основе кремния, непосредственно в составе кремниевых интегральных схем для их питания и охлаждения без значительных затрат в микроэлектронном производстве таких микросхем, обеспечивая их работоспособность в автономном режиме без технического обслуживания и замены в течение десятилетий.
К пункту 13 формулы. Данный пункт формулы посвящен использованию аналога высокочастотного нестационарного эффекта Джозефсона для преобразования тепловой энергии в электрическую энергию. Аналог высокочастотного нестационарного эффекта Джозефсона, так же, как и стационарный эффект Джозефсона, осуществляется за счет имеющейся в материале тепловой энергии и за счет электрической энергии, вводимой в материал между электродами от источника внешнего электрического смещения. По существу, аналог высокочастотного нестационарного эффекта Джозефсона позволяет преобразовывать внутреннюю энергию материала, энергию упругих колебаний когерентных областей в энергию высокочастотного электрического тока. Для непрерывного получения высокочастотной электроэнергии обеспечивают постоянный доступ тепла из внешней среды к материалу между электродами и поддерживают определенное внешнее электрическое смещение между электродами 1 и 2.
Согласно закону сохранения энергии, частоты электронно-колебательных переходов определяются разностью энергий электронно-колебательных термов туннельно связанных осцилляторов когерентных областей. На фиг. 25 представлена энергетическая схема когерентных областей, расположенных вблизи контактов 1 и 2 с материалом при подведенном извне напряжении V между электродами. Здесь горизонтальные пунктирные линии обозначают положения электронно-колебательных уровней при V≡0. Если V=0, то электронно-колебательные состояния электронов и дырок с соответствующими значениями колебательного квантового числа ν совпадают с этими пунктирными горизонтальными линиями. Ели между электродами 1 и 2 приложено внешнее напряжение величиной V, то энергетическая схема изменяется и происходит смещение электронно-колебательных уровней относительно друг друга на величину eV. На фиг. 25 наклонными сплошными стрелками показаны туннельные электронно-колебательные переходы из когерентной области вблизи электрода 1 в когерентную область вблизи электрода 2 с уменьшением потенциальной энергии туннелирующего заряда (е) на eV. Результирующее уменьшение потенциальной энергии равно 2eV, поскольку переход осуществляется куперовскими парами электронов. В принципе возможны туннельные переходы и с увеличением энергии, когда энергия конечного состояния превышает энергию исходного состояния. Это увеличение энергии туннелирующих электронов возможно за счет поглощения энергии фононов и I-колебаний и вызывает охлаждение материала.
Электронно-колебательные переходы между различными колебательными состояниями взаимодействующих осцилляторов, между состояниями с различными значениями колебательных квантовых чисел ν и колебательных частот взаимодействующих осцилляторов, образуют переменные токи с циклическими частотами 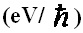 , соответствующими разности энергий этих колебательных состояний, сумма которых представляет аналог нестационарного эффекта Джозефсона. Эти частоты преобразуются на ЭКЦ в частоты, попадающие в полосу пропускания замедляющего устройства, и СВЧ токи соответствующей частоты могут быть измерены. В заявленном изобретении частота аналога нестационарного эффекта Джозефсона преобразуется на ЭКЦ и может быть измерена в пределах частотной полосы пропускания связанного с материалом замедляющего устройства. Для измерения частотного спектра аналога нестационарного эффекта Джозефсона в более широком диапазоне применяют широкополосные замедляющие устройства или изменяют резонансную частоту замедляющих устройств.
, соответствующими разности энергий этих колебательных состояний, сумма которых представляет аналог нестационарного эффекта Джозефсона. Эти частоты преобразуются на ЭКЦ в частоты, попадающие в полосу пропускания замедляющего устройства, и СВЧ токи соответствующей частоты могут быть измерены. В заявленном изобретении частота аналога нестационарного эффекта Джозефсона преобразуется на ЭКЦ и может быть измерена в пределах частотной полосы пропускания связанного с материалом замедляющего устройства. Для измерения частотного спектра аналога нестационарного эффекта Джозефсона в более широком диапазоне применяют широкополосные замедляющие устройства или изменяют резонансную частоту замедляющих устройств.
Мощности аналога высокочастотного нестационарного эффекта Джозефсона на частоте от 8 Ггц до 10 Ггц, поступающей из материала (Ge) между электродами в нагрузку связанного с материалом замедляющего устройства достигают нескольких миллиВатт. Для получения большей мощности целесообразно применять батареи туннельных гиперпроводниковых структур.
В научно-технической литературе предложено применение нестационарного эффекта Джозефсона в туннельных контактах сверхпроводников при низких температурах [55, стр. 72], когда высокочастотный ток Джозефсона подают на диодный выпрямитель и преобразуют в постоянный ток, пригодный для технических применений. В таком случае туннельный контакт Джозефсона с выпрямителем обеспечивает преобразование тепловой энергии, поступающей из внешней среды в контакт Джозефсона, в энергию постоянного электрического тока, выделяющуюся в нагрузке выпрямителя. Такой преобразователь малоинтересен, так как способен создавать на нагрузке милливольтовые напряжения, требует охлаждения Джозефсоновских туннельных контактов до низких температур, что технически неудобно и нерентабельно.
С другой стороны, источники тока на основе аналога нестационарного высокочастотного эффекта Джозефсона позволяют получать напряжение между электродами 1 и 2 величиной сотни милливольт. Такие источники тока можно встраивать, например, в мобильные электронные устройства, в сотовые телефоны, ноутбуки для непрерывной подзарядки аккумуляторов электропитания за счет тепловой энергии окружающей среды, в том числе за счет тепла, выделяемого процессорами устройства, что позволяет охлаждать процессоры. Применение таких источников тока позволяет избавить стационарные и мобильные электронные устройства от периодической подзарядки аккумуляторов, от необходимости подключения к внешней электросети для зарядки, что важно на космических, подводных, авиационных транспортных средствах и в полевых условиях. Электроэнергию, получаемую за счет аналога высокочастотного эффекта Джозефсона, можно также использовать для электропитания светильников, световая энергия которых в итоге преобразуется в тепло окружающей среды, которую контакты аналогов джозефсоновских туннельных структур снова преобразуют в электрическую энергию. Таким образом осуществляется круговорот и преобразование одного вида энергии в другой вид: тепло - электричество - свет - тепло, что обеспечивает снижение затрат на энергетическое снабжение процессов жизнедеятельности и техники.
Поэтому с целью получения электрической энергии посредством аналога высокочастотного нестационарного эффекта Джозефсона обеспечивают приток тепла к материалу между электродами 1 и 2, протекающий между электродами высокочастотный ток направляют в потребляющие этот ток устройства, при необходимости этот ток детектируют, выпрямляют, а полученный постоянный ток последовательно или параллельно направляют в стационарное или мобильное потребляющее (потребляющие) электроэнергию устройство (устройства).
В преобразователях тепловой энергии в электрическую энергию на основе аналогов эффектов Джозефсона (пп. 12, 13 формулы) не требуется создавать и поддерживать в материале разность температур, необходимую обычно для работы тепловых машин и преобразователей энергии, работающих на иных эффектах, что обеспечивает заявленному способу несомненные преимущества. Тем не менее, термодинамическая формула для коэффициента полезного действия (КПД=[T2-T1]/T1) остается верной и в заявленном способе. Разность температур [Т2-Т1] также как в известных тепловых машинах и преобразователях энергии имеется и определяется разностью энергий электрона в исходном (E1) и конечном (Е2) состоянии электронно-колебательного перехода: T1=E1/k и Т2=Е2/k, где k - постоянная Больцмана. Эта разность температур велика, она сосредоточена в ЭКЦ, мало влияет на среднюю температуру материала и преобразование тепловой энергии в электрическую энергию можно осуществлять с высоким КПД.
К пункту 14 формулы. Данный пункт формулы посвящен регулированию температуры материала между электродами в туннельной гиперпроводниковой структуре за счет изменения токов между электродами 1 и 2. Температура материала в туннельных гиперпроводниковых структурах зависит от величины токов аналогов эффектов Джозефсона, поскольку энергия материала затрачивается на поддержание этих токов. Такая зависимость проявляется в области околокомнатных и более высоких температур, т.е. в температурной области существования гиперпроводимости и сверхтеплопроводности и усиливается, если приток тепла к материалу ограничен.
Изменения температуры материала между электродами может достигать нескольких десятков и даже сотен градусов.
Если приток тепла к материалу извне невозможен или ограничен, то значительная часть внутреннего тепла материала в туннельной структуре затрачивается на поддержание токов I0 и высокочастотного тока аналога нестационарного эффекта Джозефсона. В результате температура материала между электродами уменьшается, пока не станет меньше температуры Дебая фононов материала, когда гиперпроводящее состояние материала и туннельные токи исчезнут.
Поэтому такие структуры можно использовать как охлаждающие элементы с регулируемой температурой за счет регулирования величин токов в них, представляющих аналоги стационарного и нестационарного высокочастотного эффектов Джозефсона. Диапазон регулируемых температур совпадает с температурным диапазоном существования гиперпроводимости и сверхтеплопроводности. Температура джозефсоновской туннельной структуры становится меньше, если джозефсоновский ток увеличивается, поскольку этот ток переносит часть энергии колебаний когерентных областей в электрическую нагрузку замедляющего устройства. При этом джозефсоновские структуры могут иметь температуру ниже комнатной, вблизи комнатной температуры или существенно выше комнатной температуры, что технически удобно, т.к. не требует дополнительных мер для охлаждения или поддержания определенной температуры материала туннельной гиперпроводниковой структуры. В определенных условиях аналоги эффектов Джозефсона можно использовать для охлаждения материала между электродами 1 и 2, т.е в качестве принципов действия охлаждающих устройств без движущихся конструктивных элементов, бесшумных и экологически безопасных, обладающих несомненным преимуществом даже по сравнению с перспективными сейчас холодильными процессами на основе ферроиков.
К пункту 15 формулы. Данный пункт формулы посвящен регулированию величин аналогов эффектов Джозефсона и эффекта Мейснера за счет изменения температуры материала между электродами. В области температур выше Th, в температурной области существования гиперпроводимости и сверхтеплопроводности, величины эффектов Джозефсона, частота высокочастотного эффекта Джозефсона, величина эффекта Мейснера зависят от температуры материала между электродами. Эту зависимость предложено использовать для регулирования величин эффектов Джозефсона, частоты аналога высокочастотного эффекта Джозефсона, величины эффекта Мейснера. При этом изменяют температуру материала между электродами в пределах температурной области существования нулевого электрического сопротивления и нулевого теплового сопротивления, выше Th, и измеряют величины эффектов Джозефсона, частоту высокочастотного эффекта Джозефсона, величину эффекта Мейснера или измеряют изменения этих технических эффектов.
К пункту 16 формулы. Данный пункт формулы посвящен регулированию температуры гиперпроводящего перехода Th, величины эффектов Джозефсона и частоты высокочастотного нестационарного эффекта Джозефсона, а также величины эффекта Мейснера с помощью дополнительного полевого электрода, образующего выпрямляющий контакт или контакт металл-диэлектрик-полупроводник (МДП) с материалом между электродами. К дополнительному полевому электроду подводят внешнее напряжение относительно материала. При необходимости используют несколько дополнительных полевых электродов. К дополнительным полевым электродам подводят постоянные, переменные или импульсные внешние напряжения прямой или обратной полярности величиной менее напряжения (напряжений) пробоя или разрушения структуры. Прикладываемые к полевым электродам напряжения изменяют потенциальное поле в объеме материала и тем самым влияют на протекание электронно-колебательных токов между электродами 1 и 2. Это отражается на изменении температуры гиперпроводящего перехода Th, и на величинах эффектов Джозефсона, на длине когерентности и соответственно на величине эффекта Мейснера. В итоге измеряют изменение температуры гиперпроводящего перехода Th или (и) изменения величин эффектов Джозефсона или (и) изменение частоты высокочастотного нестационарного эффекта Джозефсона или (и) изменение величины эффекта Мейснера, вызванные действием напряжений на дополнительном полевом электроде (на дополнительных полевых электродах) относительно материала.
К пункту 17 формулы. Техническое применение гиперпроводимости и сверхтеплопроводности в отдельных случаях возможно без применения двух или большего числа электродов. В данном пункте формулы изложен способ регистрации излучения, в котором с целью упрощения из электродов 1 и 2 используют только один электрод, образующий выпрямляющий контакт с материалом. Постоянное или модулированное по амплитуде, или (и) по частоте или (и) по фазе или (и) по поляризации или (и) по направлению распространения и подлежащее регистрации излучение направляют в примыкающую к электроду часть материала; измеряют вызванные излучением изменения тока или (и) частоты тока в примыкающей к электроду части материала или (и) изменения величины и (или) частоты (частот) модуляции мощности, рассеивающейся в согласованной нагрузке связанного (связанных) с материалом замедляющего устройства (замедляющих устройств); по результатам измерений судят о свойствах, например, о интенсивности и (или) о частоте и (или) о спектре модуляции, и (или) о поляризации, и (или) о направлении распространения регистрируемого излучения.
Вблизи контакта существует хотя бы одна когерентная область. Регистрируемое излучение поглощается в материале и влияет на колебательное состояние когерентной области и на ее размер и, соответственно, изменяются колебания связанных с фононами электронов. В результате изменяется мощность и частота (частоты, спектр) электрических сигналов, поступающих из материала в связанное с ним замедляющее устройство и в его нагрузку. Измерение и анализ этих изменений позволяют судить о свойствах регистрируемого излучения.
К пункту 18 формулы. Известно, что гиперпроводники имеют характерные оптические полосы интенсивного поглощения. В соответствии с электродинамикой в этих же спектральных участках расположены полосы их оптического отражения. Величины коэффициента отражения в таких полосах нередко превышают 50%-90%. Иначе говоря, только незначительная часть регистрируемого излучения проникает в объем материала, а существенная доля регистрируемого излучения отражается от материала и безвозвратно утрачивается, не оказывая влияния на полезный выходной сигнал фотоприемного устройства. В связи с этим целесообразно применять просветляющие покрытия в рабочей спектральной области или использовать широкополосный способ возвращения отраженного излучения в материал с помощью зеркала, расположенного параллельно поверхности материала. Просветляющие покрытия и зеркала позволяют уменьшить непроизводительные потери на отражение регистрируемого излучения до уровня менее 10%, т.е. в несколько раз.
Способы регистрации излучения по данному пункту формулы обеспечивают возможность регистрации излучения в узких спектральных участках, расположенных в диапазоне ИК длин волн от долей микрона, соответствующих собственному поглощению материала, до десятков и сотен микрон, соответствующих энергиям локализованных на электронно-колебательных уровнях фононов.
Имеется принципиальная возможность распространить рабочий спектральный диапазон данных способов детектирования излучения в длинноволновую ИК область, что нередко оказывается предпочтительным. При этом используют слой материала на подложке, а подложку выбирают с Дебаевой температурой соответствующей энергии подлежащих регистрации ИК квантов. В таком случае в слое материала на подложке возникают электронно-колебательные переходы с участием фононов подложки и связанные с ними полосы оптического поглощения в материале на частотах фононов подложки. Для увеличения длины волны регистрируемого излучения 2πс/р, где с - скорость света в вакууме и p - циклическая частота фонона подложки, выбирают материал подложки с меньшими фононными частотами p. Это позволяет расширить спектральный диапазон фоточувствительности рассматриваемого способа регистрации излучения до сотен микрон (примерно до 2500 мкм) без охлаждения материала и регистрировать длинноволновое ИК излучение. При этом обеспечивается пониженный уровень собственных, внутренних шумов при высоком быстродействии.
К пункту 19 формулы. Данный пункт формулы посвящен изменению величины аналогов эффектов Джозефсона, а также регулированию частоты и фазы аналога высокочастотного нестационарного эффекта Джозефсона и величины, направления эффекта Мейснера за счет изменения добротности и (или) коэффициента связи замедляющих устройств, связанных с материалом между электродами. Длина когерентности, величины аналогов эффектов Джозефсона, частота высокочастотного нестационарного аналога эффекта Джозефсона, а также величина и направление эффекта Мейснера зависят от величины отводимой из материала между электродами высокочастотной мощности, которая определяется величиной добротности связанного с материалом замедляющего устройства и от коэффициента связи этого устройства с материалом между электродами. Поэтому можно регулировать величину длины когерентности, изменять величины аналогов эффектов Джозефсона и эффект Мейснера изменяя добротность и коэффициент связи замедляющего устройства с материалом между электродами.
В связи с этим с целью регулирования длины когерентности Λ, частоты высокочастотного нестационарного аналога эффекта Джозефсона и эффекта Мейснера, а также с целью изменения величин аналогов эффектов Джозефсона, изменяют добротность Q связанного (связанных) с материалом между электродами замедляющего устройства (замедляющих устройств) или (и) изменяют коэффициент связи этих замедляющих устройств с материалом между электродами или изменяют добротность (добротности) и коэффициент (коэффициенты) связи замедляющего устройства (замедляющих устройств) с материалом, измеряют длину или изменения длины когерентности Λ или (и) величины аналогов эффектов Джозефсона или (и) изменения частоты высокочастотного эффекта Джозефсона или (и) эффекта Мейснера.
К пункту 20 формулы. Данный пункт формулы посвящен регулированию температуры гиперпроводящего перехода Th, частоты аналога нестационарного эффекта Джозефсона, а также регулированию величин аналогов эффектов Джозефсона и эффекта Мейснера и уменьшению внутренних шумов при гиперпроводящем переходе с помощью магнитного поля, которое создают в материале между электродами. Температура гиперпроводящего перехода Th, величины аналогов эффектов Джозефсона и эффект Мейснера, частота высокочастотного нестационарного эффекта Джозефсона, а также стабильность гиперпроводящего состояния и уровень внутренних шумов при гиперпроводящем переходе зависят от направления и величины индукции магнитного поля В≤2 Тесла в материале между электродами. Эти зависимости объясняются тем, что электронно-колебательные процессы в материале происходят при участии осциллирующих с частотами фононов электрических зарядов.
Магнитное поле, как известно согласно эффекту Мейснера, выталкивается из когерентных областей гиперпроводника по причине их нулевого электрического сопротивления. Однако за пределами когерентных областей, в областях рассеяния энергии, магнитное поле с индукцией В≤2 Тесла действует на осциллирующие с частотами фононов электроны, подавляет осцилляции зарядов и процессы рассеяния энергии и тем самым влияет на технические характеристики гиперпроводимости и сверхтеплопроводности. Поэтому с целью регулирования температуры гиперпроводящего перехода Th, величины эффектов Джозефсона и эффекта Мейснера, частоты высокочастотного нестационарного эффекта Джозефсона, а также с целью улучшения стабильности гиперпроводящего состояния и уменьшения внутренних шумов при гиперпроводящем переходе в материале между электродами создают постоянное, переменное или импульсное магнитное поле с индукцией В до 2 тесла, изменяют направление индукции по отношению к направлению электронно-колебательного тока между электродами 1 и 2, изменяют частоту индукции или изменяют величину, направление и частоту индукции; измеряют температуру гиперпроводящего перехода Th или (и) величины эффектов Джозефсона или (и) частоту высокочастотного нестационарного эффекта Джозефсона и (или) эффект Мейснера и (или) уровень внутренних шумов при гиперпроводящем переходе.
К пункту 21 формулы. Данный пункт формулы посвящен регулированию температуры гиперпроводящего перехода Th, частоты аналога высокочастотного нестационарного эффекта Джозефсона и эффекта Мейснера, а также изменения аналогов эффектов Джозефсона и Мейснера за счет упругих волн, направляемых в материал извне. Температура гиперпроводящего перехода Th, величины аналогов эффектов Джозефсона, частота аналога высокочастотного нестационарного эффекта Джозефсона, а также эффект Мейснера зависят от концентрации фононов и направления их распространения в материале между электродами. Эту зависимость используют для регистрации и определения свойств, направляемых в материал между электродами упругих волн. Поэтому, с целью регулирования температуры гиперпроводящего перехода Th, величин аналогов эффектов Джозефсона, частоты аналога высокочастотного нестационарного эффекта Джозефсона, а также эффекта Мейснера, в материал между электродами направляют упругую волну (упругие волны), поток звука, ультразвука или гиперзвука с частотой F и с объемной плотностью мощности до  , где S - константа электрон-фононного взаимодействия, N - концентрация ЭКЦ, τ - время жизни электронов (дырок) в материале между электродами. Указанная плотность упругих волн соответствует невырожденному материалу, что соответствует п. 1 формулы. Изменяют частоту, направление распространения упругой волны относительно направления тока между электродами, измеряют изменения температуры гиперпроводящего перехода Th или (и) величину стационарного или (и) высокочастотного нестационарного эффекта Джозефсона (или) и частоты высокочастотного нестационарного эффекта Джозефсона или (и) эффекта Мейснера и по этим данным судят о свойствах направляемой в материал упругой волны (направляемых в материал упругих волн), например, о ее (их) интенсивности (интенсивностях). Данный пункт формулы позволяет регистрировать акустическое излучение различных частот с низкими собственными шумами без охлаждения чувствительных элементов акустического приемника.
, где S - константа электрон-фононного взаимодействия, N - концентрация ЭКЦ, τ - время жизни электронов (дырок) в материале между электродами. Указанная плотность упругих волн соответствует невырожденному материалу, что соответствует п. 1 формулы. Изменяют частоту, направление распространения упругой волны относительно направления тока между электродами, измеряют изменения температуры гиперпроводящего перехода Th или (и) величину стационарного или (и) высокочастотного нестационарного эффекта Джозефсона (или) и частоты высокочастотного нестационарного эффекта Джозефсона или (и) эффекта Мейснера и по этим данным судят о свойствах направляемой в материал упругой волны (направляемых в материал упругих волн), например, о ее (их) интенсивности (интенсивностях). Данный пункт формулы позволяет регистрировать акустическое излучение различных частот с низкими собственными шумами без охлаждения чувствительных элементов акустического приемника.
Заявленное изобретение обеспечивает высокую радиационную стойкость использующих его устройств. Действительно, внешняя радиация создает в материале дополнительные к имеющимся (в концентрации от 2⋅1014 см-3 до 6⋅1015 см-3) радиационные дефекты электронно-колебательной природы (ЭКЦ). Однако, работоспособность устройств сохраняется, пока концентрация ЭКЦ в материале не достигнет 6⋅1017 см-3. Таким образом, работоспособность основанных на использовании заявленного изобретения устройств сохраняется до очень высоких доз радиационного облучения, при которых полупроводниковые приборы традиционной адиабатической электроники неработоспособны.
Использование данного изобретения обеспечит значительный научный и технико-экономический эффект за счет применения гиперпроводимости и сверхтеплопроводности в технике, в приборах и устройствах, в социальной сфере.
Перечень чертежей
Изобретение иллюстрируется чертежами.
На фиг. 1 приведена типичная температурная зависимость электрического сопротивления (R) сверхпроводникового материала.
На фиг. 2 приведена вольтамперная характеристика джозефсоновского туннельного контакта двух одинаковых сверхпроводников из книги [24]. I0 - ток, представляющий стационарный эффект Джозефсона. Пунктирная прямая - туннельный ток электронов в нормальном состоянии материалов, при температуре Т>Тс.
На фиг. 3 светлыми кружками указаны вычисленные значения элементарных квантов I-колебаний α-, β- и γ-типов в атомах с различными значениями атомного номера Z. Темными кружками указаны экспериментальные значения квантов I-колебаний для некоторых атомов.
На фиг. 4 графически представлены вычисленные в первом и втором прядке стационарной теории возмущений поправки к энергиям α-типа колебаний атомных ядер (ΔEαν) в состояниях со значениями колебательного квантового числа ν=0, 1, 2, 3 в зависимости от атомного номера Z. На вставке представлены поправки в другом масштабе для атомов с Z>10.
На фиг. 5 приведена энергетическая схема гиперпроводника. В центре изображена энергетическая схема полупроводника, где Ес и Eν обозначают энергии дна зоны проводимости и потолка валентной зоны, F - уровень Ферми. Электронно-колебательные центры расположены в объеме полупроводника, в точках с координатами ro и ro'.
На фиг. 6 сплошной кривой качественно изображена ожидаемая по теории БКШ температурная зависимость электрического сопротивления (R) гиперпроводника, т.е. содержащего ЭКЦ полупроводника. Пунктирная кривая соответствует возможному переходу материала в сверхпроводящее состояние при низких температурах.
На фиг. 7 указаны экспериментальные значения температур гиперпроводящего перехода (Th) в материалах со средним значением атомного номера Zсредн и содержащих различные концентрации ЭКЦ. Наклонные прямые а и б представляют вычисленные по формуле (7) значения Th при максимальной (Nmax) и минимальной (Nmin) концентрациях ЭКЦ.
На фиг. 8 изображено сечение образца материала плоскостью (XY) проходящей через центр области когерентности. Пунктирная окружность радиусом Λ соответствует границе области когерентности, которая окружена шаровым слоем, толщина которого равна средней длине рассеяния энергии  .
.
На фиг. 9 показано сечение материала между разделенными расстоянием D электродами 1 и 2 плоскостью, проходящей вдоль направления между электродами через центр сферической когерентной области радиусом Λ=D/2.
На фиг. 10 качественно показана температурная зависимость электрического сопротивления гиперпроводника между электродами с учетом температурной зависимости длины когерентности (13).
На фиг. 11 представлены данные о туннелировании электронов сквозь диэлектрический слой толщиной h в структурах на основе InP с концентрацией электронов проводимости N.
На фиг. 12 представлена характерная температурная зависимость электрического сопротивления материала между электродами (D=50 мкм), измеренная на германиевом образце с почти собственной проводимостью без отвода избыточной колебательной энергии, как в прототипе. На вставке показан высокотемпературный участок данной зависимости.
На фиг. 13 приведена типичная температурная зависимость электрического сопротивления материала между электродами в образце на основе GaAs, D=20 мкм без отвода избыточной колебательной энергии, как в прототипе. Верхняя кривая измерена при нагревании, а нижняя кривая измерена при охлаждении образца.
На фиг. 14 приведена характерная для образцов на основе кремния (КЭФ4,5) температурная зависимость электрического сопротивления R, измеренная без отвода избыточной колебательной энергии, как в прототипе.
На фиг. 15 приведены типичные вольт-фарадные характеристики контакта Шоттки GaAs-Al, демонстрирующие особенности их частотной зависимости из-за наличия ЭКЦ в приконтактной области полупроводника.
На фиг. 16 приведены вольт-фарадные зависимости контактов Шоттки Si-Al демонстрирующие минимум емкости на различных частотах акусто-электрического синхронизма (fc) и немонотонное увеличение емкости при увеличении измерительной частоты.
На фиг. 17 приведена зависимость обратного квадрата дифференциальной емкости контакта GaAs-Au, демонстрирующая высоту барьера Шоттки в этом контакте высотой ≈0,96 эВ.
На фиг. 18 приведены температурные зависимости сопротивления германиевого материала между электродами (D=40 мкм). Верхняя кривая на этой фигуре измерена в условиях прототипа изобретения, нижняя кривая измерена с использованием замедляющего устройства, связанного и согласованного с материалом между электродами.
На фиг. 19 изображена схема бесконтактного подключения материала между электродами 1 и 2 к колебательному контуру, состоящему из двух емкостей связи, образованных электродами 3 и 4, и из индуктивного элемента 5.
На фиг. 20 приведены типичные температурные зависимости электрического сопротивления материала (GaAs) между электродами при различных расстояниях (D=10, 20 и 40 мкм) между ними. На вставке показано включение колебательных контуров к материалу вблизи электродов 1 и 2.
На фиг. 21 представлена характерная температурная зависимость электрического сопротивления германия с почти собственной проводимостью между электродами при использовании электромагнитной связи материала с колебательным контуром при межэлектродном расстоянии D=50 мкм. Верхняя кривая измерена при нагревании, а нижняя - при охлаждении образца.
На фиг. 22 приведена типичная температурная зависимость теплового сопротивления (RТ) материала между электродами германиевого образца с D=50 мкм. Кривая 8 измерена при нагревании образца, а кривая 9 измерена при охлаждении образца.
На фиг. 23 приведены типичные температурные зависимости электрического сопротивления материала (Si) при расстоянии D=22 мкм между электродами 1 и 2. На вставке показаны высокотемпературные участки этих зависимостей.
На фиг. 24 приведены температурные зависимости сопротивления материала InP между электродами 1 и 2 с D=40 мкм. Верхняя кривая измерена при нагревании, а нижняя - при охлаждении образца. На вставке показаны высокотемпературные участки данных зависимостей.
На фиг. 25 представлена характерная температурная зависимость электрического сопротивления германия между электродами, измеренная при токе 5 мкА. Верхняя часть кривой измерена при нагревании образца, нижняя часть кривой измерена при охлаждении, после прекращения нагрева образца при температуре ≈510 К.
На фиг. 26 приведена типичная температурная зависимость электрического сопротивления германия между электродами, измеренная при токе 0,5 мкА. Верхняя кривая измерена при нагревании образца, нижняя кривая измерена при охлаждении, после прекращения нагрева образца при температуре ≈560 К.
На фиг. 27 показано сечение материала между разделенными расстоянием D электродами плоскостью, проходящей через центры когерентных областей, расположенных вблизи электродов 1 и 2. Границы когерентных областей обозначены пунктирными окружностями с диаметрами 2Λ. Расстояние, зазор между когерентными областями d=D-4Λ.
На фиг. 28 приведена энергетическая схема когерентных областей, разделенных туннельно тонким зазором толщиной d в материале между электродами 1 и 2 с равными электрическими потенциалами. Пунктирными стрелками показаны туннельные переходы электронов.
На фиг. 29 приведена энергетическая схема когерентных областей, разделенных туннельно тонким зазором толщиной d в материале между электродами 1 и 2, при внешнем напряжении величиной V между этими электродами.
На фиг. 30 приведено сечение структуры, состоящей из двух материалов (с электродами) разделенными диэлектрическим слоем толщиной d, плоскостью, проходящей через центры когерентных областей диаметрами 2Λ.
На фиг. 31 приведены энергетические диагаммы гетероструктур, образованных двумя контактирующими друг с другом материалами. Латинские цифры I, II, III и IV обозначают комбинации материалов, различающихся электронным сродством, работой выхода и шириной запрещенной зоны из работы [50].
На фиг. 32 показан вычисленный спектр отражения заряженным гармоническим осциллятором с собственной частотой Ω и с наибольшей частотой связанных фононов ωmax=ωр.
На фиг. 33 приведен характерный экспериментальный спектр ИК отражения 11 монокристалла GaP, содержащего ЭКЦ, образованные примесными атомами Al. Кривые 12, 13, 14 и 15 представляют вычисленные компоненты спектра, соответствующие различным колебательным состояниям ЭКЦ, а их сумма совпадает со спектром 11.
На фиг. 34 показан типичный экспериментальный спектр ИК отражения углеродной нанотрубной пленки, выращенной на кварцевой подложке - 15. Вычисленный спектр 16 относится к компоненте поглощения с участием упругих I-колебаний с энергией  .
.
На фиг. 35 показан типичный экспериментальный спектр ИК отражения углеродной нанотрубной пленки, выращенной на молибденовой подложке - 17. Вычисленный спектр 18 относится к компоненте спектра с максимальной энергией I-колебаний.
На фиг. 36 показан типичный экспериментальный спектр ИК отражения углеродной нанотрубной пленки выращенной на медной подложке - 19. Спектр 20 - вычисленный спектр отражения I-колебаний ядра в атоме углеродной нанотрубной пленки.
На фиг. 37 изображена характерная температурная зависимость коэффициента термоЭДС в монокристалле GaP содержащем ЭКЦ, образованные примесными атомами серы. Заглавными латинскими буквами обозначены существенные особенности данного спектра.
На фиг. 38 сплошной кривой показан экспериментальный спектр ИК отражения монокристалла GaP - 22, из работы [48]. Светлыми кружками обозначен вычисленный спектр ИК отражения гармонического осциллятора - 21.
На фиг. 39 приведен характерный спектр отражения GaP, измеренный нами при падении ИК излучения под углом 45° к поверхности образца.
На фиг. 40 изображена характерная температурная зависимость коэффициента термоЭДС в GaAs, содержащем ЭКЦ, образованные примесными атомами кислорода.
На фиг. 41 приведены спектры ИК отражения полупроводников, в том числе спектр отражения монокристалла GaAs, из работы [53].
На фиг. 42 приведена типичная температурная зависимость коэффициента термоЭДС в углеродной нанотрубной пленке на кварцевой подложке.
На фиг. 43 приведен типичный спектр ИК отражения углеродной нанотрубной пленки на кварцевой подложке содержащий полосу отражения, лежащую между 22,6 мкм и 26,5 мкм.
На фиг. 44 приведена типичная температурная зависимость коэффициента термоЭДС в монокристалле Ge, содержащая полосы увлечения электронов фононами при дебаевых температурах фононов.
На фиг. 45 представлены спектры отражения монокристаллов Ge из работы [53], измеренные при различных температурах.
На фиг. 46 приведена типичная температурная зависимость напряжения V*, представляющего аналог стационарного эффекта Джозефсона в туннельной структуре на основе Si.
На фиг. 47 приведена температурная зависимость величины аналога стационарного эффекта Джозефсона в структуре на основе Ge в условиях рассогласования импедансов материала между электродами и связанного с ним замедляющего устройства.
БИБЛИОГРАФИЧЕСКИЕ ДАННЫЕ ИСТОЧНИКОВ ИНФОРМАЦИИ
1. Vdovenkov V.A. Superconductivity at very high temperatures - hyperconductivity \\ ArXiv: cond-mat/0003190, 2000 г.
2. Вдовенков В.А. Сверхпроводимость при очень высоких температурах в полупроводниках с электронно-колебательными центрами. Тезисы докладов 2-й международной конф. «Радиационотермические эффекты и процессы в неорганических материалах» Томск, 2000, стр. 252-254.
3. Вдовенков В.А. Сверхпроводимость в полупроводниках, обусловленная электронно-колебательными центрами. Тезисы 3 Международн. научно-техн. конф. «электроника и информатика - XXI век», стр. 37-38, Москва, 2000.
4. Вдовенков В.А. Сверхпроводимость, обусловленная электронно-колебательными центрами - гиперпроводимость. Межотраслевой сборник научных трудов МИРЭА "Тепловидение", стр. 33-39, Москва, 2000.
5. Вдовенков В.А. Фазовый переход материала в гиперпроводящее состояние. Материалы Международной научно-технической конф. «Полиматериалы-2001», Москва, 2001, стр. 268-269.
6. Вдовенков В.А. Собственные колебания и сверхпроводимость кристаллов. Тезисы докладов школы-семинара «Актуальные проблемы физической и функциональной электроники», Ульяновск, 2001, стр. 18.
7. Вдовенков В.А. Исследования локальной термоЭДС и гиперпроводимости. Наукоемкие технологии, №4, 2002, с. 55-60.
8. Вдовенков В.А. Электронно-колебательные центры в кристаллах и структурах полупроводниковой электроники. Материалы Международн. Н.-т. конф. «Тонкие пленки и слоистые структуры», 26-30 ноября 2002 г., МИРЭА, часть 2, стр. 38-40.
9. Вдовенков В.А. Электронно-колебательные центры в полупроводниковых элементах микросистемной техники. Микросистемная техника, №12, Москва, 2002 г., стр. 17-22.
10. Вдовенков В.А. Влияние собственных колебаний ядер атомов на электрические и оптические свойства. Известия Вузов, Материалы электронной техники, №1, 2003, с. 57-62.
11. Вдовенков В.А. Межфазная релаксация электрических зарядов в материалах, содержащих электронно-колебательные центры. Материалы Международной научно-практической конференции «Полиматериалы - 2003, Межфазная релаксация в полиматериалах», Москва, 2003 г., 25-29 ноября, с. 111-112.
12. Вдовенков В.А. Адиабатическая и неадиабатическая электроника материалов. Материалы Международной научной конференции «Тонкие пленки и наноструктуры», 2005 г., Москва, часть 2, стр. 99-104.
13. Вдовенков В.А. Очевидность гиперпроводимости и тепловой сверхпроводимости. Материалы Международной научной конференции «Тонкие пленки и нанотруктуры», 2005 г., Москва, часть 2, стр. 99-104.
14. Vdovenkov V.A. Adiabatic and Nonadiabatic Electronics of Materials. ArXiv: cond-mat\0610828.
15. Vdovenkov V.A. Evidence for hyperconductivity and Thermal superconductivity. ArXiv: cond-mat\0801.4212v1.
16. Method of realization of hyperconductivity and super Thermal conductivity. Intern, patent application PCT/IB 2009/005723, WO 2010136834 A1. To же: патент Ru 2497236.
17. Пекар С.И. Исследования по электронной теории кристаллов. - М., Гостехиздат, 1951. 204 с.
18. Huang К. and Rhys A. Proc. Roy. Soc. 1950. V. A204. P. 406.
19. Пекар С.И. ЖЭТФ. 1952. Т. 22, вып. 6, с. 641.
20. Пекар С.И. УФН. 1953. Т. L, вып. 2, с. 197.
21. M. Born, R. Oppenheimer. Ann. D. Phys. v. 84, N4, 1927, p. 457.
22. Dirac P.A.M. Proc. Cambridge Phil. Soc. 1930. V. 26. p 376.
23. Kamerling Onnes H. Leiden. Comm., 1911, p. 120b, 122b.
24. Тинкхам M., Введение в сверхпроводимость. M., Атомиздат, 1980.
25. Проблема высокотемпературной сверхпроводимости под ред. В.Л. Гинзбурга и Д.А. Киржница. М., Наука, 1977, 400 с.
26. Гинзбург В.Л., Максимов Е.Г. О возможных механизмах высокотемпературной сверхпроводимости. Сверхпроводимость. Физика, химия, техника. 1992, т. 5, №9, с. 1543-1596.
27. Bednorz J.G., Muller K.A.Z. Phys. B64, 1986, p. 189.
28. A.M. Gulian, K.S. Wood, D. Van. Vechten, J. Classen, R.J. Soulen, Jr, S. Qadry, M. Osovsky, A. Lucarelly,  , R.G. Badalian, V.S. Kuzanyan, A.S. Kuzanyan, V.R. Nicoghosyan. Evidence for high temperature superconductivity in doped laser processed Sr-Ru-O. ArXiv: cond-mat/0509313.
, R.G. Badalian, V.S. Kuzanyan, A.S. Kuzanyan, V.R. Nicoghosyan. Evidence for high temperature superconductivity in doped laser processed Sr-Ru-O. ArXiv: cond-mat/0509313.
29. http://www.superconductors.org/212K.htm; E. Joe Eck 2008 Superconductors.ORG, Patent Pending #61/199, 804.
30. Bardeen J., Cooper L.N., Schrieffer J.R. Phys. Rev., v. 108, 1957, p. 1175.
31. W.A. Little, Phys. Rev. A134, p. 1416, 1964.
32. L. Ginzburg, Phys. Lett. 13, p. 101, 1964; то же: ЖЭТФ 47, с. 2318, 1964.
33. B.D. Josephson. Phys. Lett., v. 1, 1962, p. 251.
34. Вдовенков B.A. Туннелирование электронов в МОП-структурах. Сборник научн. Трудов под ред. акад. Евтихиева Н.Н., Москва, МИРЭА, 1995, с. 41-44.
35. Вдовенков В.А. Новый тип упругих колебаний и волн в кристаллах. Сборник научн. Трудов МИРЭА «Радиоэлектронные устройства и системы обработки сигналов», 1996, с. 148-150.
36. Vdovenkov V.A., Kosakovskaya Z.Ya., Serebryakova N.V., Mokerov V.G. Connection of IR-reflection with electrical properties carbon nanotube films. Abstracts of invited lectures and contributed papers of The 3-rd international worcshop in Russia "Fullerens and atomic clusters", IWFAC'97, June 30-July 4, 1997, St. Petersburg, Russia.
37. Вдовенков B.A. ИК-поглощение в γ-облученном кварце. Сборник тезисов докладов Международн. конф. Радиационно-термические эффекты и процессы в неорганических материалах. Томск, 22-25 сентября 1998 г., с. 112-113.
38. Вдовенков В.А. Влияние динамических неоднородностей на свойства полупроводниковых структур и приборов радиоэлектроники. Сборник научных трудов «Теория и методы приема и обработки радиотехнических сигналов», МИРЭА, 1998, с. 109-120.
39. З. Флюгге. Задачи по квантовой механике. М., Мир, 1974, том 1, с. 93. (Sigfried Flugge. Practical Quantum Mechanics I. Springer-Verlag, 1971.).
40. К.В.Шалимова. Физика полупроводников. - M: Энергия, 1976, 416 с.
41. Дж. Стокер. Нелинейные колебания в механических и электрических системах. - М: Иностранная литература, 1953, 256 с.
42. В.Л. Гинзбург, Л.Д. Ландау. ЖЭТФ, 1950 г., т. 20, с. 1064.
43. А.Б. Пиппард. Proc. Roy. Soc. (London.), 1955, v. A213, p. 336.
44. В.А. Вдовенков. Особенности полупроводниковых структур микроэлектроники с центрами Яна-Теллера. Техника средств связи. Научно-технический сборник, серия Локальные оптические системы связи, вып. 2, Москва 1990, с. 14-19.
45. В.А. Вдовенков. Туннелирование электронов в МОП-структурах. Сборник научных трудов МИРЭА «Информатика и радиотехника», 1995 г., с. 41-43.
46. В.А. Вдовенков, В.Н. Лукъянов, С.П. Прокофьева, Е.С. Печникова, Т.Н. Усачева, С.Д. Якубович. Фотоэлектрические свойства быстродействующих полупроводниковых фотоприемников. Тезисы 13 Всесоюзной н.т. конференции «Высокоскоростная фотография, фотоника и метрология быстропротекающих процессов», Москва, 1987, с. 83.
47. S. Zi. Physics of semiconductor devices. Mir, Moscow, 1984, v. 1. Имеется перевод: С.Зи. Физика полупроводниковых приборов. М. Мир, 1984, т. 1.
48. М.Л. Городецкий. Оптические микрорезонаторы с гигантской добротностью. Физматлит, 2011,416 с.
49. В.Ф. Елесин. Явления абсолютной отрицательной проводимости в неравновесных трехмерных полупроводниках // Успехи физических наук (2005), http://ufn.ru/ru/articles/2005/2/i/; DOI: 10.3367/UFNr.0175.200502i.0197.
50. B.L. Sharma, R.K. Purohit. Semiconductors heterojunctions. Pergamon Press, 1974. Имеется перевод: Б.Л. Шарма, Р.К. Пурохит. Полупроводниковые гетеропереходы. М., «Советское Радио», 1979.
51. Semiconductors and semimetals. Edited by R.K. Willardson, F.C. Beer, Volume 3. Optical properties of III-V compounds. Academic Press, New York and London, 1967. Имеется перевод: Оптические свойства полупроводников (полупроводниковые соединения типа AIIIBV) под ред. Р. Уиллардсона и А. Бира, перевод под редакцией члена-корреспондента АН СССР Е.Ф. Гросса. Издательство «Мир», Москва, 1970 г., гл. 1: М. Хесс. Решеточное отражение.
52. З.Я. Косаковская, Л.А. Чернозатонский, Е.А. Федоров. Письма в ЖЭТФ. 1992, т. 56, вып. 1, с. 26-30.
53. F.A. Johnson. Progress in Semiconductors. 9, 180 (1965).
54. R.J. Collins, H.Y. Fan. Phys. Rev., v. 93, p. 674 (1954).
55. О.Г. Верин. Энергия. Вещество и поле. М.: Контур-М, 2006 г.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ОСУЩЕСТВЛЕНИЯ ГИПЕРПРОВОДИМОСТИ И СВЕРХТЕПЛОПРОВОДНОСТИ | 2009 |
|
RU2497236C2 |
| СПОСОБ ОСУЩЕСТВЛЕНИЯ УВЛЕЧЕНИЯ ЭЛЕКТРОНОВ ФОНОНАМИ | 2006 |
|
RU2349990C2 |
| СПОСОБ ГЕНЕРАЦИИ СВЕРХВЫСОКОЧАСТОТНЫХ ЭЛЕКТРОМАГНИТНЫХ КОЛЕБАНИЙ | 2007 |
|
RU2356128C2 |
| СВЕРХПРОВОДЯЩИЙ ПРИБОР ДЖОЗЕФСОНА И СПОСОБ ЕГО ИЗГОТОВЛЕНИЯ | 2012 |
|
RU2504049C2 |
| СПОСОБ ИЗГОТОВЛЕНИЯ УСТРОЙСТВА С СУБМИКРОННЫМ ДЖОЗЕФСОНОВСКИМ π-КОНТАКТОМ | 2015 |
|
RU2599904C1 |
| Детектор субтерагерцового излучения на основе графена | 2019 |
|
RU2697568C1 |
| Сверхпроводящий акустический детектор ионизирующего излучения | 1979 |
|
SU820438A1 |
| ПЕРЕСТРАИВАЕМЫЙ КРИОГЕННЫЙ ГЕНЕРАТОР ГЕТЕРОДИНА СУБТЕРАГЕРЦОВОГО ДИАПАЗОНА НА ОСНОВЕ РАСПРЕДЕЛЕННОГО ТУННЕЛЬНОГО ПЕРЕХОДА ДЛЯ ИНТЕГРАЛЬНЫХ ПРИЕМНЫХ СИСТЕМ | 2012 |
|
RU2522711C2 |
| ФОТОКОНВЕРТОР | 2001 |
|
RU2217783C2 |
| СВЕРХПРОВОДНИКОВЫЙ БОЛОМЕТР | 2006 |
|
RU2321921C1 |
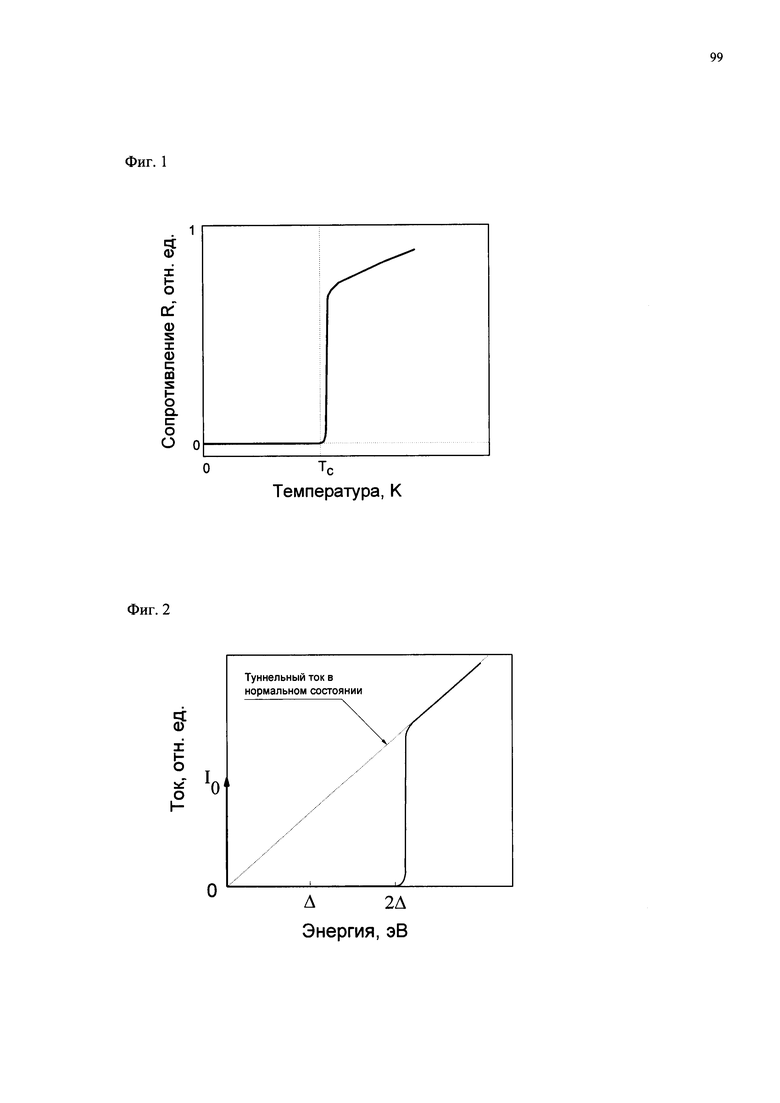
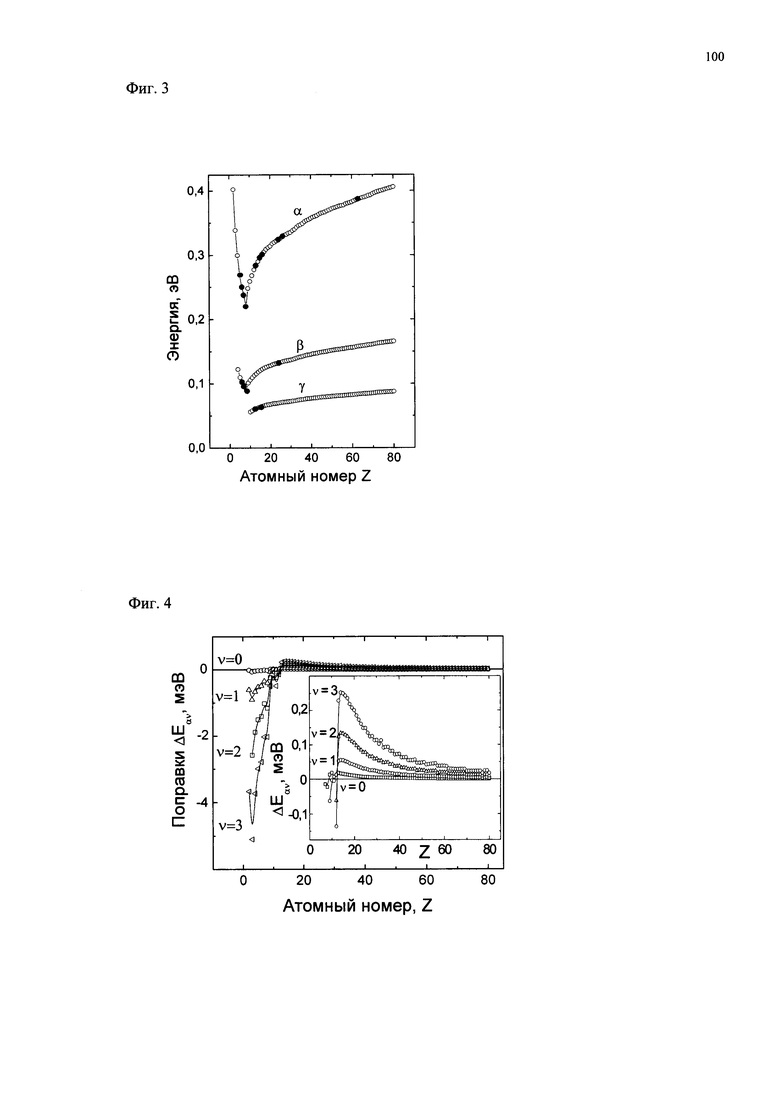




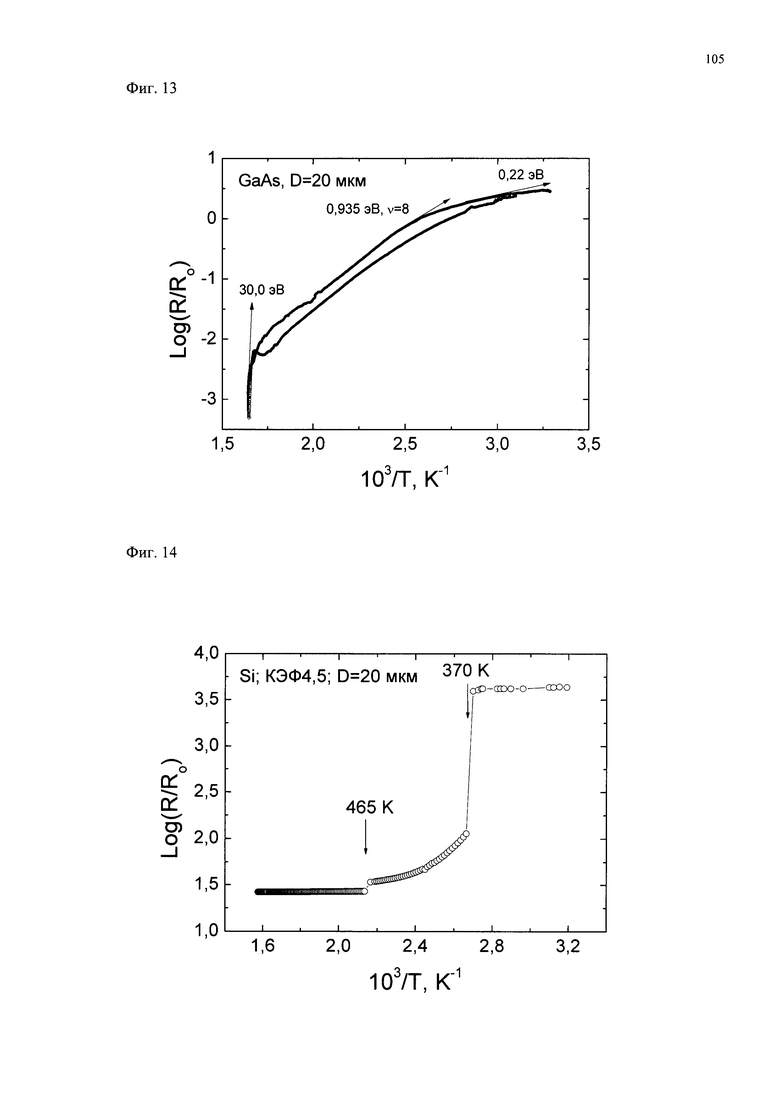







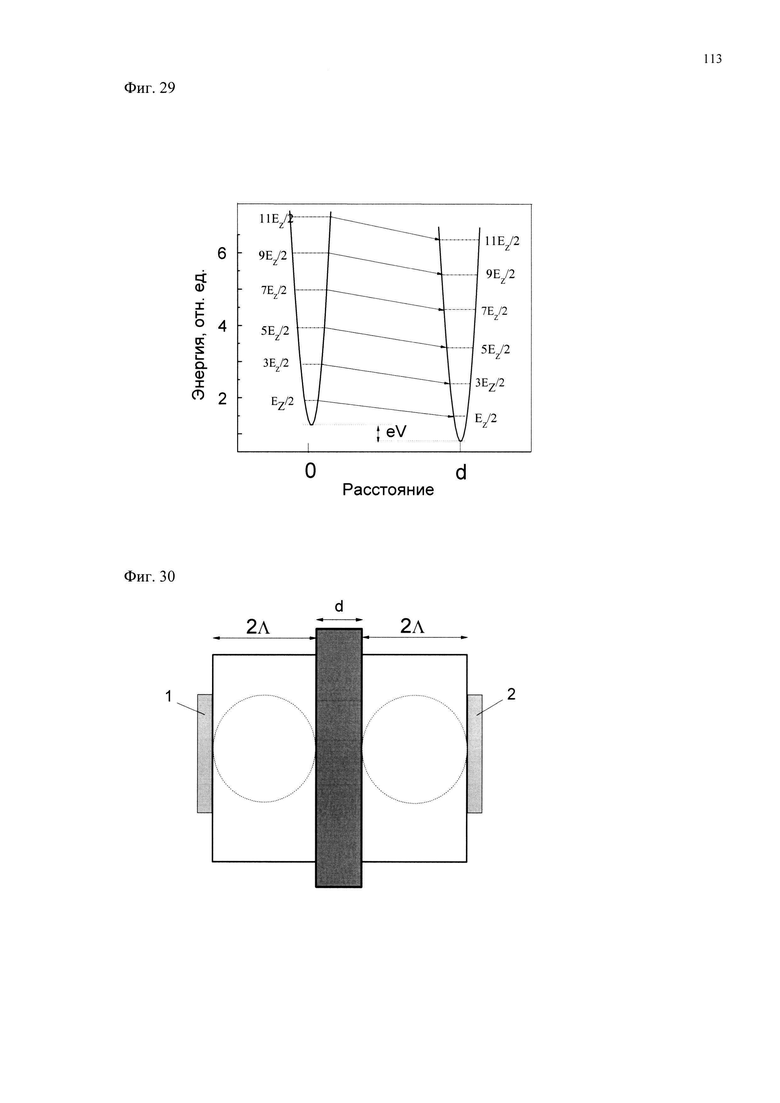




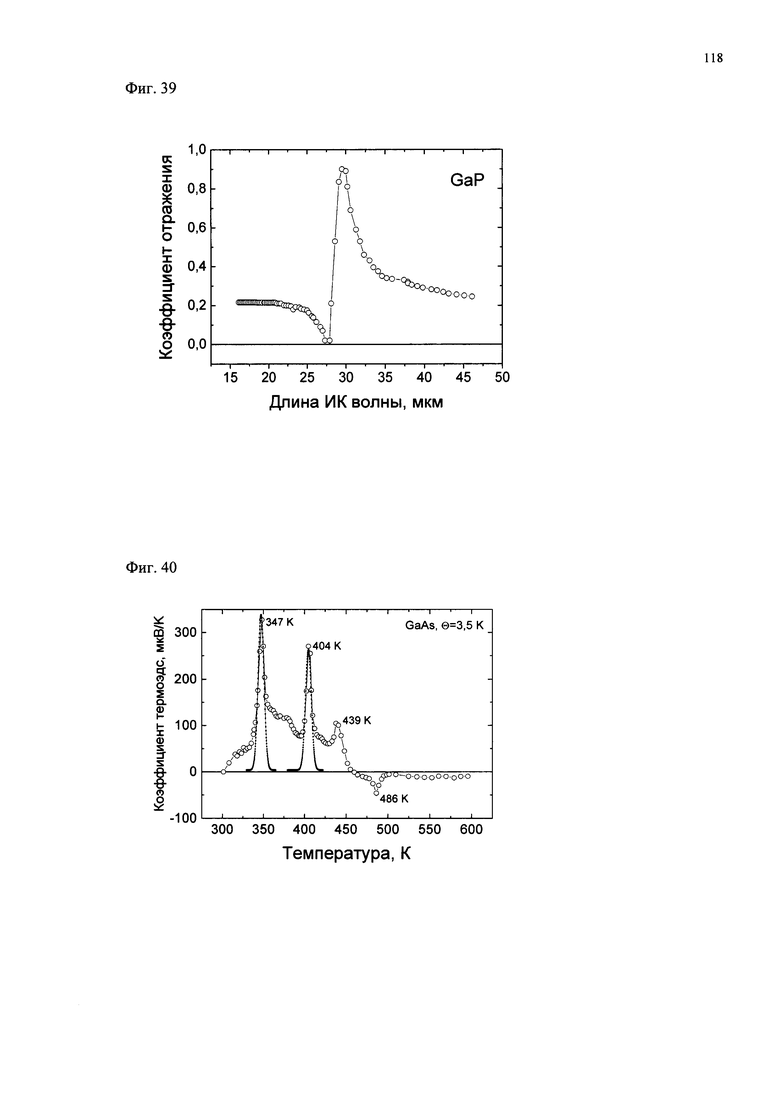




Использование: для осуществления гиперпроводимости и сверхтеплопроводности материалов. Сущность изобретения заключается в том, что используют невырожденный или слабовырожденный полупроводниковый материал, размещают на его поверхности или в его объеме электроды 1 и 2, образующие выпрямляющие контакты с материалом, такие как контакты металл-полупроводник, контакты Шоттки, при этом расстояние между электродами D выбирают не более 4Λ, D≤4Λ, где Λ - длина когерентности; размер площади контакта электрода с материалом а выбирают не более четверти длины упругой волны в материале а≤λ/4, λ=V/F, где V - скорость упругой волны в материале с частотой F=108 Гц; устанавливают и поддерживают согласованную электромагнитную связь части материала, примыкающей к электроду 1, или (и) части материала, примыкающей к электроду 2, или материала или части материала, расположенного между электродами 1 и 2, с высокочастотным (высокочастотными) (ВЧ) и (или) сверхвысокочастотным (сверхвысокочастотными) (СВЧ) замедляющим устройством (замедляющими устройствами), таким (такими) как коаксиальная линия, волноводная линия, полосковая линия, резонатор, колебательный контур, которые характеризуются резонансными частотами f в диапазоне от 106 Гц до 3⋅1015 Гц и добротностями Q≥10; материал нагревают до температуры Т, равной или превышающей температуру гиперпроводящего перехода Th, Th≤Т≤Т*; измеряют электрическое и (или) тепловое сопротивление материала между электродами и (или) эффект Мейснера; в результате электрическое сопротивление и тепловое сопротивление материала между электродами обращаются в ноль, то есть осуществляется гиперпроводимость и сверхтеплопроводность в материале между электродами 1 и 2, усиливается эффект Мейснера. Технический результат: обеспечение возможности увеличения эффективности. 20 з.п. ф-лы, 47 ил.
1. Способ эффективного осуществления гиперпроводимости и сверхтеплопроводности в материале между электродами, в котором используют невырожденный или слабовырожденный полупроводниковый материал, размещают на его поверхности или в его объеме электроды 1 и 2, образующие выпрямляющие контакты с материалом, такие как контакты металл-полупроводник, контакты Шоттки, отличающийся тем, что расстояние между электродами D выбирают не более 4Λ, D≤4Λ, где Λ - длина когерентности; размер площади контакта электрода с материалом а выбирают не более четверти длины упругой волны в материале а≤λ/4, λ=V/F, где V - скорость упругой волны в материале с частотой F=108 Гц; устанавливают и поддерживают согласованную электромагнитную связь части материала, примыкающей к электроду 1, или (и) части материала, примыкающей к электроду 2, или материала или части материала, расположенного между электродами 1 и 2, с высокочастотным (высокочастотными) (ВЧ) и (или) сверхвысокочастотным (сверхвысокочастотными) (СВЧ) замедляющим устройством (замедляющими устройствами), таким (такими) как коаксиальная линия, волноводная линия, полосковая линия, резонатор, колебательный контур, которые характеризуются резонансными частотами f в диапазоне от 106 Гц до 3⋅1015 Гц и добротностями Q≥10; материал нагревают до температуры Т, равной или превышающей температуру гиперпроводящего перехода Th, Th≤Т≤Т*; измеряют электрическое и (или) тепловое сопротивление материала между электродами и (или) эффект Мейснера; в результате электрическое сопротивление и тепловое сопротивление материала между электродами обращаются в ноль, то есть осуществляется гиперпроводимость и сверхтеплопроводность в материале между электродами 1 и 2, усиливается эффект Мейснера.
2. Способ эффективного осуществления гиперпроводимости и сверхтеплопроводности в материале между электродами по п. 1, отличающийся тем, что материал между электродами нагревают от температур ≈1,5 K или от более высокой температуры до температур существования гиперпроводимости и сверхтеплопроводности, Th≤Т≤Т*, прекращают нагрев или (и) создают в материале поперечное к току между электродами 1 и 2 магнитное поле с индукцией до 2 Тл на время до 60 с, поддерживают температуру материала в диапазоне между Th и Т*; в результате электрическое сопротивление и тепловое сопротивление материала между электродами обращаются в ноль, т.е. осуществляется гиперпроводимость и сверхтеплопроводность, усиливается эффект Мейснера.
3. Способ эффективного осуществления гиперпроводимости и сверхтеплопроводности в материале между электродами по п. 1, отличающийся тем, что размер материала b выбирают не менее четырех длин когерентности 4Λ, b≥4Λ, например выбирают толщину пластины материала не менее 4Λ или толщину слоя материала не менее 4Λ на полупроводниковой, полуизолирующей или диэлектрической подложке; измеряют Th, и (или) Λ, и (или) величину эффекта Мейснера.
4. Способ эффективного осуществления гиперпроводимости и сверхтеплопроводности в материале между электродами по п. 3, отличающийся тем, что на поверхности или (и) в объеме материала размещают вкрапления частиц, образующих выпрямляющие контакты с материалом, например металлических частиц с размерами с не более Λ, с≤Λ, в концентрации от 2Λ-3 до 2с-3, или (и) частиц, из которых каждая в отдельности или группа (группы) частиц образуют замедляющую систему (замедляющие системы) или (и) является (являются) частью (частями) замедляющей системы (замедляющих систем); измеряют температуру гиперпроводящего перехода Th, и (или) длину когерентности Λ, и (или) величину эффекта Мейснера.
5. Способ эффективного осуществления гиперпроводимости и сверхтеплопроводности в материале между электродами по п. 3, отличающийся тем, что устанавливают расстояние между электродами, превышающее четыре длины когерентности 4Λ на величину туннельно прозрачного зазора величиной d между областями когерентности, D=4Λ+d, 10 Ao≤d≤50 мкм; измеряют постоянный ток в материале между электродами 1 и 2 и (или) его направление, полярность, или (и) измеряют постоянную разность потенциалов между электродами 1 и 2 и (или) ее полярность; результаты измерений интерпретируют как величину аналога стационарного эффекта Джозефсона и его полярность соответственно.
6. Способ эффективного осуществления гиперпроводимости и сверхтеплопроводности в материале между электродами по п. 5, отличающийся тем, что между электродами 1 и 2 прикладывают постоянное напряжение произвольной полярности величиной менее напряжения пробоя данной структуры; измеряют величину переменного напряжения между электродами, и (или) измеряют частоту (частоты) переменного напряжения, или (и) измеряют величину переменного тока в материале между электродами, и (или) измеряют частоту (частоты) переменного тока в материале между электродами, и (или) измеряют фазу напряжения и (или) фазу тока; результаты измерений соответственно идентифицируют как величину, частоту и фазу аналога высокочастотного нестационарного эффекта Джозефсона.
7. Способ эффективного осуществления гиперпроводимости и сверхтеплопроводности в материале между электродами по п. 5, отличающийся тем, что используют два материала, отделенных друг от друга туннельно тонким диэлектрическим слоем толщиной d, размер каждого материала выбирают не менее четырех длин когерентности 4Λ, на внешней поверхности или в объеме каждого материала размещают электрод (электроды), образующий (образующие) выпрямляющий контакт (выпрямляющие контакты) с материалом, например контакт (контакты) металл-полупроводник; измеряют постоянный ток между электродами 1 и 2 в данной структуре (электрод 1 - материал 1 - диэлектрик - материал 2 - электрод 2); измеряют постоянную разность потенциалов между этими электродами; результаты измерений интерпретируют как аналог стационарного эффекта Джозефсона; прикладывают постоянное напряжение между электродами 1 и 2 величиной, не достигающей напряжения электрического пробоя данной структуры, измеряют переменное напряжение между электродами 1 и 2 и (или) переменный ток в материале между электродами, а результаты измерений идентифицируют как аналог высокочастотного нестационарного эффекта Джозефсона; измеряют частоту (частоты) переменного напряжения между электродами, и (или) переменного тока в материале между электродами, и (или) фазы тока и напряжения; результаты измерений идентифицируют как величину, частоту (частоты) и фазу аналога высокочастотного нестационарного эффекта Джозефсона.
8. Способ эффективного осуществления гиперпроводимости и сверхтеплопроводности в материале между электродами по п. 5, отличающийся тем, что используют два различных материала, образующих гетероструктуру; на внешней поверхности или в объеме каждого материала устанавливают электрод, образующий выпрямляющий контакт с материалом, например контакт металл-полупроводник; измеряют постоянный ток в материале между электродами 1 и 2 или (и) измеряют напряжение между электродами и его полярность и идентифицируют результаты измерений как величину и полярность стационарного эффекта Джозефсона; между электродами 1 и 2 прикладывают постоянное напряжение величиной не более напряжения пробоя данной гетероструктуры, измеряют величину, и (или) частоту, и (или) фазу напряжения между электродами и (или) тока в материале между электродами и идентифицируют их как величину, частоту, фазу аналога высокочастотного нестационарного эффекта Джозефсона.
9. Способ эффективного осуществления гиперпроводимости и сверхтеплопроводности в материале между электродами по п. 6, отличающийся тем, что между электродами 1 и 2 прикладывают постоянное или низкочастотное (с меньшими из циклических частот  ;
;  ) переменное напряжение величиной V не более напряжения пробоя данной структуры; изменяют полярность и (или) фазу этого напряжения и (или) его величину; измеряют полярность, и (или) фазу, и (или) частоту аналога высокочастотного нестационарного эффекта Джозефсона и (или) измеряют изменения величины эффекта Мейснера.
) переменное напряжение величиной V не более напряжения пробоя данной структуры; изменяют полярность и (или) фазу этого напряжения и (или) его величину; измеряют полярность, и (или) фазу, и (или) частоту аналога высокочастотного нестационарного эффекта Джозефсона и (или) измеряют изменения величины эффекта Мейснера.
10. Способ эффективного осуществления гиперпроводимости и сверхтеплопроводности в материале между электродами по п. 5, отличающийся тем, что в материал между электродами 1 и 2 направляют электромагнитное излучение интенсивностью до 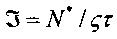 квант⋅с-1⋅см-2, где N* - эффективное число электронных состояний в разрешенной энергетической зоне материала, ς - коэффициент оптического поглощения и τ - время жизни электронов (дырок), в спектральном диапазоне собственного, основного, фундаментального поглощения материала, или (и) в спектральном диапазоне электронно-колебательных переходов ЭКЦ, или (и) в спектральном диапазоне упругих колебаний с частотами фононов локализованных на ЭКЦ электронов; измеряют вызванные излучением изменения мощности (мощностей), рассеивающейся в нагрузках, связанных с материалом замедляющих устройств, или (и) измеряют изменения величины (величин) аналогов эффектов Джозефсона, или (и) измеряют изменение частоты (частот) и фазы (фаз) аналога высокочастотного эффекта Джозефсона, или (и) измеряют изменение температуры гиперпроводящего перехода (Th), или (и) измеряют изменения величины эффекта Мейснера; по результатам измерений делают вывод о свойствах излучения, например о интенсивности регулирующего излучения, о его поляризации, о его частоте, о его когерентности.
квант⋅с-1⋅см-2, где N* - эффективное число электронных состояний в разрешенной энергетической зоне материала, ς - коэффициент оптического поглощения и τ - время жизни электронов (дырок), в спектральном диапазоне собственного, основного, фундаментального поглощения материала, или (и) в спектральном диапазоне электронно-колебательных переходов ЭКЦ, или (и) в спектральном диапазоне упругих колебаний с частотами фононов локализованных на ЭКЦ электронов; измеряют вызванные излучением изменения мощности (мощностей), рассеивающейся в нагрузках, связанных с материалом замедляющих устройств, или (и) измеряют изменения величины (величин) аналогов эффектов Джозефсона, или (и) измеряют изменение частоты (частот) и фазы (фаз) аналога высокочастотного эффекта Джозефсона, или (и) измеряют изменение температуры гиперпроводящего перехода (Th), или (и) измеряют изменения величины эффекта Мейснера; по результатам измерений делают вывод о свойствах излучения, например о интенсивности регулирующего излучения, о его поляризации, о его частоте, о его когерентности.
11. Способ эффективного осуществления гиперпроводимости и сверхтеплопроводности в материале между электродами по п. 10, отличающийся тем, что толщину полупроводниковой пластины, или толщину полупроводникового слоя на подложке, или толщину подложки, или общую толщину полупроводникового слоя и подложки, или расстояние (расстояния) между взаимно параллельными границами материала или материала и подложки выбирают равным (равными) или кратным (кратными) W=ПVзв/2, где Vзв - скорость звука, распространяющегося между взаимно параллельными границами полупроводника, подложки или полупроводника и подложки; в материале между электродами создают переменное электрическое поле с напряженностью до SEz/e, где S - константа электрон-фононного взаимодействия и Ez - элементарный квант I-колебаний ядер в атомах, но не более напряжения пробоя, и (или) постоянное и (или) переменное магнитное поле с индукцией В≤2 Тл с периодом Π; измеряют температуру гиперпроводящего перехода Th, величину и (или) полярность аналога стационарного эффекта Джозефсона, величину, и (или) частоту, и (или) фазу высокочастотного нестационарного эффекта Джозефсона, величину или (и) изменение величины эффекта Мейснера.
12. Способ эффективного осуществления гиперпроводимости и сверхтеплопроводности в материале между электродами по п. 5, отличающийся тем, что обеспечивают приток тепла к материалу; направляют постоянный ток в материале между электродами, представляющий аналог стационарного эффекта Джозефсона, или аналогичные токи от нескольких таких структур последовательно или параллельно в стационарное или мобильное потребляющее (потребляющие) электрический ток устройство (устройства).
13. Способ эффективного осуществления гиперпроводимости и сверхтеплопроводности в материале между электродами по п. 6, отличающийся тем, что обеспечивают приток тепла к материалу, между электродами 1 и 2 создают разность потенциалов величиной до SEz/e, но не более напряжения пробоя структуры; высокочастотный ток, протекающий между электродами и представляющий аналог высокочастотного нестационарного эффекта Джозефсона, направляют в потребляющие этот ток устройства, при необходимости этот ток детектируют (выпрямляют), а полученный в результате детектирования постоянный ток направляют в стационарное или мобильное потребляющее (потребляющие) электроэнергию устройство (устройства).
14. Способ эффективного осуществления гиперпроводимости и сверхтеплопроводности в материале между электродами по п. 8, отличающийся тем, что изменяют величины токов, представляющих аналог стационарного эффекта Джозефсона или (и) аналог высокочастотного нестационарного эффекта Джозефсона, например, изменяя величину нагрузочного сопротивления (импеданса) для этих токов; измеряют температуру материала между электродами.
15. Способ эффективного осуществления гиперпроводимости и сверхтеплопроводности в материале между электродами по п. 7, отличающийся тем, что изменяют температуру материала между электродами в температурной области выше Th, то есть в области существования гиперпроводимости и сверхтеплопроводности; измеряют величину аналога стационарного эффекта Джозефсона, и (или) величину аналога высокочастотного нестационарного эффекта Джозефсона, и (или) частоту аналога высокочастотного эффекта Джозефсона, и (или) величину эффекта Мейснера.
16. Способ эффективного осуществления гиперпроводимости и сверхтеплопроводности в материале между электродами по п. 3, отличающийся тем, что используют полевой электрод, образующий выпрямляющий контакт или контакт металл-диэлектрик-полупроводник (МДП) с материалом между электродами, или используют несколько таких полевых электродов; к полевому электроду (к полевым электродам) подводят постоянные, переменные или импульсные внешние напряжения прямой или обратной полярности относительно материала величиной менее напряжения (напряжений) пробоя или разрушения структуры; измеряют изменение температуры гиперпроводящего перехода Th, или (и) изменения величин эффектов Джозефсона, или (и) изменение частоты высокочастотного нестационарного эффекта Джозефсона, или (и) изменение величины эффекта Мейснера, вызванные действием напряжений на полевом электроде (на полевых электродах) относительно материала.
17. Способ эффективного осуществления гиперпроводимости и сверхтеплопроводности в материале между электродами по п. 10, отличающийся тем, что используют образец материала с одним электродом (с номером 1 или 2); постоянное или модулированное по амплитуде, или (и) по частоте, или (и) по фазе, или (и) по поляризации, или (и) по направлению распространения и подлежащее регистрации излучение направляют в примыкающую к электроду часть материала; измеряют вызванные излучением изменения тока или (и) частоты тока в примыкающей к электроду части материала, или (и) изменения величины и (или) частоты (частот) модуляции мощности, рассеивающейся в согласованной нагрузке связанного (связанных) с материалом замедляющего устройства (замедляющих устройств); по результатам измерений судят о свойствах регистрируемого излучения, например о интенсивности, и (или) о частоте, и (или) о спектре модуляции, и (или) о поляризации, и (или) о направлении распространения регистрируемого излучения.
18. Способ эффективного осуществления гиперпроводимости и сверхтеплопроводности по п. 17, отличающийся тем, что на примыкающий к электроду материал наносят просветляющее в спектральной области регулирующего излучения покрытие или (и) устанавливают параллельно поверхности материала на расстоянии h, кратном половине длины волны излучения, зеркало, обращенное рабочей поверхностью к материалу; излучение направляют в примыкающий к электроду материал под острым углом не более arctg[2Λ/(h⋅i)] к направлению нормали к поверхностям материала и зеркала, где i - число отражений луча излучения от поверхности материала или зеркала; измеряют величину, и (или) частоту, и (или) фазу (полярность) эффекта (эффектов) Джозефсона и (или) измеряют величину или (и) изменение эффекта Мейснера.
19. Способ эффективного осуществления гиперпроводимости и сверхтеплопроводности в материале между электродами по п. 3, отличающийся тем, что изменяют добротность Q связанного (связанных) с материалом между электродами замедляющего устройства (замедляющих устройств) или (и) изменяют коэффициент (коэффициенты) связи замедляющего устройства (замедляющих устройств) с материалом между электродами; измеряют длину или изменения длины когерентности Λ, или (и) изменения величины эффектов Джозефсона, или (и) изменения частоты высокочастотного эффекта Джозефсона, или (и) изменение величины эффекта Мейснера.
20. Способ эффективного осуществления гиперпроводимости и сверхтеплопроводности в материале между электродами по п. 3, отличающийся тем что, в материале между электродами создают постоянное, переменное или импульсное магнитное поле с индукцией (В) до 2 Тл; изменяют направление индукции по отношению к направлению электронно-колебательного тока между электродами или (и) изменяют частоту индукции или изменяют величину, направление и частоту индукции; измеряют температуру гиперпроводящего перехода Th, или (и) величину (величины), или (и) частоту, или (и) фазу (полярность) эффектов Джозефсона, или (и) эффект Мейснера, или (и) уровень внутренних шумов.
21. Способ эффективного осуществления гиперпроводимости и сверхтеплопроводности в материале между электродами по п. 11, отличающийся тем, что в материал между электродами направляют упругую волну (упругие волны), то есть поток звука, инфразвука, ультразвука или гиперзвука с частотой F и с объемной плотностью мощности до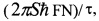 где S - константа электрон-фононного взаимодействия, N - концентрация ЭКЦ, τ - время жизни электронов (дырок) в материале между электродами; изменяют частоту, направление распространения или (и) поляризацию упругой волны относительно направления между электродами; измеряют изменения температуры гиперпроводящего перехода Th, или (и) величины стационарного, или (и) величины, частоты или (и) фазы высокочастотного нестационарного эффекта Джозефсона, или (и) величины эффекта Мейснера, вызванные упругой волной (упругими волнами).
где S - константа электрон-фононного взаимодействия, N - концентрация ЭКЦ, τ - время жизни электронов (дырок) в материале между электродами; изменяют частоту, направление распространения или (и) поляризацию упругой волны относительно направления между электродами; измеряют изменения температуры гиперпроводящего перехода Th, или (и) величины стационарного, или (и) величины, частоты или (и) фазы высокочастотного нестационарного эффекта Джозефсона, или (и) величины эффекта Мейснера, вызванные упругой волной (упругими волнами).
| СПОСОБ ГЕНЕРАЦИИ СВЕРХВЫСОКОЧАСТОТНЫХ ЭЛЕКТРОМАГНИТНЫХ КОЛЕБАНИЙ | 2007 |
|
RU2356128C2 |
| СПОСОБ ОСУЩЕСТВЛЕНИЯ УВЛЕЧЕНИЯ ЭЛЕКТРОНОВ ФОНОНАМИ | 2006 |
|
RU2349990C2 |
| СПОСОБ ОСУЩЕСТВЛЕНИЯ ГИПЕРПРОВОДИМОСТИ И СВЕРХТЕПЛОПРОВОДНОСТИ | 2009 |
|
RU2497236C2 |
| US 8204564 B2, 19.06.2012 | |||
| US 5231295 A1, 27.07.1993. | |||
Авторы
Даты
2017-07-24—Публикация
2016-04-26—Подача