Область техники, к которой относится изобретение.
Изобретение относится к электронике конденсированных материалов, к способам осуществления и применения термоэлектрического эффекта увлечения электронов (дырок) фононами при температурах Дебая фононов в твердотельных материалах и структурах между электродами. Оно может быть использовано в микроэлектронике, радиотехнике и электротехнике в качестве принципа действия твердотельных электронных и оптоэлектронных приборов с пониженным уровнем собственных шумов без охлаждения. Изобретение реализует новый физический механизм увлечения электронов фононами при дебаевых температурах фононов в твердотельных материалах и структурах между электродами. Оно основано на использовании собственных (Inherent, I-) колебаний и волн, источником которых являются электронно-колебательные центры (ЭКЦ), а именно на взаимодействии I-колебаний и волн с электронами, дырками и кристаллическими фононами в полупроводниковых материалах и структурах.
Теоретические основы современной твердотельной электроники включают общеизвестное адиабатическое приближение Борна-Оппенгеймера [1], обычно используемое при решении уравнения Шредингера для кристалла. В этом приближении исключают возможность обмена энергией между электронами и ядрами атомов в кристаллах. Очевидно, что адиабатический принцип Борна-Оппенгеймера ограничивает круг доступных для исследования и применения физических процессов в материалах. Действительно, П.Дирак впервые показал [2], что данный принцип, вообще говоря, не выполняется, а дальнейшие исследования [3] упрочили понимание ограниченности адиабатического подхода к проблеме твердых тел вообще и к твердотельной электронике в частности. В связи с этим существующую, доминирующую в науке и технике твердотельную (полупроводниковую) электронику можно обоснованно называть адиабатической электроникой. Эта электроника не дает ответа на многие вопросы о природе кристаллов и физических явлениях в них, например, таких как сверхпроводимость, гиперпроводимость, сверхтеплопроводность, что, в частности, связано с использованием адиабатического подхода и ограничивает применение кристаллов.
С другой стороны, заявленное изобретение основано на использовании принципиальной возможности обмена энергией между электронами и ядрами атомов в материалах. Такая электроника лежит за пределами адиабатического принципа (адиабатического приближения). Ее можно обоснованно называть неадиабатической твердотельной электроникой. К этой неадиабатической электронике относится заявленное изобретение и некоторые уже известные технические решения, в которых нарушения адиабатического принципа обеспечивают ЭКЦ. Эти центры в кристаллах создают канал обмена энергией между электронами и ядрами атомов, а технические решения, использующие такой энергетический обмен, представляют собой принципиально новую неадиабатическую твердотельную электронику.
Уровень техники.
Эффект увлечения электронов фононами может проявляться при наличии градиента температуры в материале в виде дополнительного вклада в термоэдс (в эффект Зеебека). Он отличается от известного диффузионного (дрейфового) механизма тем, что увлечение электронов фононами возникает благодаря связи электронов с потоком фононов, благодаря увлечению электронов потоком фононов.
Открытое в 1821 году явление дифференциальной термоэдс (эффект Зеебека) наблюдается при наличии градиента температуры в материалах и характеризуется коэффициентом термоэдс α=dE/dT, где Е - термоэдс и Т - температура. Это явление связывали с диффузией подвижных носителей зарядов, концентрации и подвижности которых определяют величину этой диффузионной (дрейфовой) термоэдс Ed. Коэффициент диффузионной (дрейфовой) термоэдс (αd) в невырожденных полупроводниковых материалах выражается следующей формулой:

где


n и p - концентрации, μn и μp - дрейфовые подвижности электронов и дырок, k - постоянная Больцмана, е - элементарный заряд, r - параметр рассеяния, Fn и Fp - квазиуровни Ферми электронов и дырок в невырожденном материале [4, 5].
Величина α равна потоку энтропии, приходящемуся на единичный электрический ток в термоэлектрической цепи [6].
Было установлено экспериментально, что термоэдс в монокристаллах германия увеличивается при понижении температуры от 200 К до 15 К [6-9], значительно превышает вычисленную с помощью формул (1, 2) величину и для ее описания необходимо привлечь дополнительный физический эффект [10], который получил название эффекта увлечения электронов фононами (УЭФ или Phonon drag).
В 1945 г. Л.Гуревич впервые теоретически предсказал существование такого дополнительного к диффузионной термоэдс нового термоэлектрического эффекта (Eф), вызванного увлечением электронов потоком фононов в металлах [11] и отметил возможность его существования в полупроводниках. Г.Пикус в 1951 г. вывел формулу для коэффициента УЭФ в полупроводниках:

где m* - эффективная масса электрона и ν - скорость звука в материале, τф и τe - время релаксации фононов и электронов (сломанные скобки здесь обозначают усредненные величины), но пришел к выводу о якобы несущественной величине данного эффекта. Вывод формулы (3) можно найти в [4, 12]. Таким образом, термоэдс в материале является суммой диффузионной термоэдс и эффекта УЭФ: Е=Еd+Eф, а коэффициент термоэдс α=αd+αф.
Аналогичная теория, учитывающая взаимодействие между фононами и электронами в материале, была успешно применена к анализу экспериментальной термоэдс в легированном Ge [13, 14]. Оказалось, что вклад эффекта увлечения электронов фононами в термоэдс представляет собой полосу, в которой Eф достигает максимума, расположенного между 15 К и 30 К. Эта полоса может быть предсказана по данным о теплопроводности материала [14], но сама теплопроводность почти не зависит от увлечения электронов фононами [11]. Именно данная полоса получила интерпретацию как эффект увлечения электронов фононами (УЭФ), вызванный потоком только тех фононов, которые связаны с электронами. Соответствующее формуле (3) уменьшение УЭФ при повышении температуры выше 30 К дало основание полагать, что УЭФ существует только при низких температурах [15]. Однако, термоэдс в связках углеродных нанотрубок в диапазоне от 4.2 К до 300 К, измеренная в лаборатории Нобелевского лауреата Р.Е.Смолли, предположительно была объяснена именно эффектом УЭФ [16], что возможно при сильной электрон-фононной связи.
Эффективную связь электронов с фононами могут обеспечить введенные в материал электронно-колебательные центры (ЭКЦ). Электронные переходы внутри ЭКЦ или переходы извне на энергетические уровни ЭКЦ сопряжены с участием значительного числа фононов, а равновесные положения и частоты колебаний ЭКЦ зависят от их электронного состояния и могут изменяться при электронно-колебательных переходах. Именно поэтому такие центры и электронные переходы получили название электронно-колебательных центров и электронно-колебательных переходов соответственно. Мерой связи электронов с фононами на ЭКЦ является константа электрон-фононной связи S, имеющая смысл среднего числа участвующих в электронно-колебательном переходе фононов. Для ЭКЦ она может достигать 150, а экспериментальные значения S в некоторых образцах превышают 22 [17-19], хотя при отсутствии ЭКЦ величина S<<1 [20].
Вероятность электронно-колебательного перехода зависит от числа (p) поглощаемых или испускаемых фононов [17-19]. Если важны фононы одной частоты, то спектры переходов состоят из дискретных линий, соответствующих участию р=0, 1, 2, ... фононов, а энергии соседних линий различаются на энергию фонона. Наибольшая вероятность переходов соответствует p≅S, из-за чего возникает (стоксово) смещение максимума спектра на S энергий фонона относительно энергии бесфононного перехода (соответствующего р=0) на один из энергетических уровней собственных колебаний ЭКЦ. Если в электронно-колебательном переходе кроме фононов одной частоты участвуют более 3% фононов других частот, то линии спектра уширяются. Если же в электронно-колебательных переходах участвуют фононы различных типов и частот, то спектр превращается в сплошную полосу, расположенную между энергиями α-, β-, γ-типов собственных (Inherent, I-) колебаний, представляющих собой упругие колебания ядер атомов (α-тип), ядер совместно с K-электронами (β-тип) или ядер атомов совместно с K- и L-электронами (γ-тип) относительно остальной части электронной оболочки или, что одно и то же, относительно центра масс кристалла [21-23]. Собственные колебания в атомах основного вещества возможны при наличии ЭКЦ. При этом обеспечивается сильное электрон-фононное взаимодействие в материале.
Введение ЭКЦ в материалы оказывает значительное влияние на их физические свойства благодаря сильной электрон-фононной связи. Например, связанная с ЭКЦ фотопроводимость является отрицательной. В присутствии ЭКЦ подвижные электроны и дырки локализуются на центрах, их дрейфовые подвижности и описываемая формулами (1, 2) диффузионная термоэдс уменьшаются или практически становятся нулевыми, а эффект УЭФ, обусловленный электронно-колебательными переходами между ЭКЦ, получает возможность доминировать.
Теория [17-19] описывает как излучательные, так и важные для УЭФ безызлучательные электронно-колебательные переходы (происходящие без участия фононов), вызванные упругими колебаниями кристалла с частотой ω. Эта теория применима и для переходов между ЭКЦ, поскольку в каждом материале центры подобны друг другу и неразличимы. Скорость безызлучательных переходов центра υ(ω) из состояния а в состояние b достигает максимума на частоте  , где ωj - частота фононов типа j, участвующих в переходе, и согласно [11] выражается следующей формулой:
, где ωj - частота фононов типа j, участвующих в переходе, и согласно [11] выражается следующей формулой:
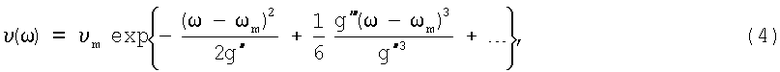
где υm - максимальное значение υ(ω),

 (qja-qjb) - изменение равновесных координат центра,
(qja-qjb) - изменение равновесных координат центра,  - среднее значение колебательного (квантового) числа. Вблизи максимума функции (4) величина (ω-ωm) мала, степенной ряд в показателе экспоненты сходится быстро и можно ограничиться первым квадратичным членом ряда.
- среднее значение колебательного (квантового) числа. Вблизи максимума функции (4) величина (ω-ωm) мала, степенной ряд в показателе экспоненты сходится быстро и можно ограничиться первым квадратичным членом ряда.
П.Дебай в 1912 г. ввел в рассмотрение температуры  где
где 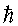 - постоянная Планка, ωl - максимальная частота колебаний кристалла, индекс l обозначает тип колебаний. По этому правилу стали вводить температуры Дебая для акустических (А), оптических (О), продольных (L) и поперечных (Т) колебаний кристаллических решеток и для квантов таких колебаний - фононов [4, 5]. Температуры Дебая удобны для описания взаимодействия фононов с локальными (примесными) центрами и мы воспользуемся этими температурами. Определив по правилу Дебая температуру материала
- постоянная Планка, ωl - максимальная частота колебаний кристалла, индекс l обозначает тип колебаний. По этому правилу стали вводить температуры Дебая для акустических (А), оптических (О), продольных (L) и поперечных (Т) колебаний кристаллических решеток и для квантов таких колебаний - фононов [4, 5]. Температуры Дебая удобны для описания взаимодействия фононов с локальными (примесными) центрами и мы воспользуемся этими температурами. Определив по правилу Дебая температуру материала  , температуру материала при максимальной скорости переходов
, температуру материала при максимальной скорости переходов  , а также температуру
, а также температуру  , полагая, что величина эффекта УЭФ пропорциональна скорости переходов υ(ω) и учитывая только первый член ряда в показателе экспоненты в (4), то можно записать температурную зависимость коэффициента αф в виде функции Гаусса:
, полагая, что величина эффекта УЭФ пропорциональна скорости переходов υ(ω) и учитывая только первый член ряда в показателе экспоненты в (4), то можно записать температурную зависимость коэффициента αф в виде функции Гаусса:

где const - независящая от температуры величина. Функция αф(Т) достигает максимума при температуре Tm и симметрична относительно Тm. Если учесть два первых члена ряда в (4), то αф(T) может стать асимметричной. Функцию (5) мы использовали для аппроксимации полос эффекта УЭФ в температурных зависимостях термоэдс экспериментальных образцов материалов и структур.
Для изучения температурных зависимостей термоэдс мы использовали образцы различных материалов и структур толщиной около 200 мкм и площадью 14×8 мм2, содержащие ЭКЦ с S>1. Значения S были определены из анализа электронно-колебательных ИК-спектров поглощения, отражения или фотопроводимости образцов. ЭКЦ вводили в исследуемые материалы различными способами. Так, образцы Si, InSb, InAs и слои таких материалов толщиной от 2 до 60 мкм с концентрациями электронов проводимости от 6·1012 см-3 до 1,68·1015 см-3 на подложках из полуизолирующего GaAs облучали потоком электронов ˜1018 см-2 с энергией 1 мэВ. По данным вольт-фарадных измерений концентрация ЭКЦ в различных образцах была в пределах от 1014 см-3 до 1016 см-3. Образцы становились частично компенсированными после облучения их быстрыми электронами, что объясняется введением в материалы ЭКЦ, которые были образованы преимущественно примесными атомами кислорода. Образцы GaP с концентрацией примесей алюминия или серы около 1015 см-3 подвергали термообработке для активации ЭКЦ, которые были образованы этими примесными атомами. Были также исследованы высокоориентированные монокристаллы пиролитического графита, эпитаксиальные слои кремния толщиной 0,4 мкм на сапфировых подложках, а также углеродные нанотрубные пленки толщиной примерно 0,1 мкм с поверхностным сопротивлением около 103 Ом/□ на подложках из кварца, флюорита и иттрий алюминиевого граната (YAIG), изготовленные распылением графита электронным пучком в вакууме. Согласно данным о спектрах ИК-отражения и энергиях активации удельного сопротивления ЭКЦ в графите и углеродных нанотрубных пленках были образованы атомами углерода [21-23].
Температурные зависимости термоэдс измеряли традиционным способом. Схема включения образца показана на вставке фиг.1, слева. Выпрямляющие контакты к образцам создавали с помощью электродов 1 и 2, которые наносили на поверхность материала термическим распылением золота или алюминия в вакууме. В обоих случаях получали совпадающие результаты измерений. Исследуемые образцы мы помещали в вакуумный криостат или в термостат с атмосферой азота при нормальном давлении. Между электродами образца создавали разность температур 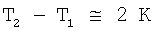 . Температуры измеряли с помощью термопар медь-константан с точностью 0,2 К. Температуру образца T=(T2+T1)/2 изменяли монотонно в течение 2-3 часов в криостате от 15 К, а в термостате - от 77 К до сотен градусов по шкале Кельвина. Величину термоэдс (Е) измеряли между контактами 1 и 2 с точностью 1 мкВ. Зависимость α(Т) измеряли "по точкам", вычисляя значение коэффициента термоэдс (УЭФ) при разных температурах образца, заменяя дифференциалы dE и dT конечными приращениями этих величин: α(T)=dE/dT=Е/(Т2-Т1). Зависимость α(Т) вблизи ее экстремумов аппроксимировали функцией (5).
. Температуры измеряли с помощью термопар медь-константан с точностью 0,2 К. Температуру образца T=(T2+T1)/2 изменяли монотонно в течение 2-3 часов в криостате от 15 К, а в термостате - от 77 К до сотен градусов по шкале Кельвина. Величину термоэдс (Е) измеряли между контактами 1 и 2 с точностью 1 мкВ. Зависимость α(Т) измеряли "по точкам", вычисляя значение коэффициента термоэдс (УЭФ) при разных температурах образца, заменяя дифференциалы dE и dT конечными приращениями этих величин: α(T)=dE/dT=Е/(Т2-Т1). Зависимость α(Т) вблизи ее экстремумов аппроксимировали функцией (5).
На фиг.1 представлена типичная температурная зависимость термоэдс в содержащих ЭКЦ монокристаллах кремния, имеющая сравнительно узкие полосы со сложными контурами. Было замечено, что экстремумы полос В, С и D расположены при температурах Дебая акустических и оптических фононов, определенных из данных о фононах кремния [24]. Учитывая этот факт и полярности полос, полосы В и С были объяснены эффектом увлечения электронов акустическими, а полоса D - эффектом увлечения дырок оптическими фононами [25, 26].
Типичные температурные зависимости термоэдс в монокристаллах InAs представлены на фиг.2, а в GaP - на вставке фиг.2, слева, и содержат ряд полос [27]. Температуры в максимумах полос в GaP и полос G, Н, I, К в InAs совпадают с температурами Дебая различных фононов. В отдельных образцах InAs наблюдается слабая полоса вблизи температуры 424 К, совпадающей с суммой дебаевых температур двух LA фононов. В образцах InSb кроме полос при дебаевых температурах различных LA и LO фононов имеются полосы при температурах 134 К и 430 К, которые равны суммам температур Дебая двух фононов (2ТА и 2ТО).
Полоса А в Si (см. фиг.1), имеющая максимум вблизи 55 К, а также полоса F в InAs (см. фиг.2) с максимумом при 45 К более всего соответствуют интерпретации как эффект УЭФ. Однако, в этих бездефектных материалах нет фононов с такими температурами Дебая. Такие фононы могут возникнуть в результате введения ЭКЦ в материалы. Действительно, дисперсионные ветви акустических фононов под влиянием собственных колебаний ядер атомов в материале существенно изменяются [21, 25]. Для одномерной модели кристалла эти изменения качественно показаны на вставке фиг.2, справа. Коэффициент δ описывает взаимодействие между акустическими (А) и собственными (I) колебаниями. При δ<0 возникает высокая плотность фононных состояний с малыми значениями волнового вектора, а дебаевы температуры этих фононов могут достигать нескольких десятков градусов. Такие низкочастотные фононы, видимо, способны создавать наблюдаемые на опыте низкотемпературные полосы УЭФ (например, полосы А и F).
На фиг.3 приведена характерная температурная зависимость термоэдс монокристалла графита, измеренная вдоль нормали к атомным плоскостям графитового "паркета". Она содержит полосы с максимумами при температурах Дебая LO фононов и, по-видимому, при температуре Дебая двух (LO+LO) фононов, энергии которых определенны из дисперсионных ветвей фононов графита [28].
В тонких эпитаксиальных слоях материалов на подложках также наблюдаются полосы термоэдс, однако они расположены при дебаевых температурах фононов подложки. Температуры максимумов полос М, N и О в слое InAs на GaAs подложке (см. фиг.4) не совпадают с дебаевыми температурами фононов в InAs, а расположены при дебаевых температурах LA, LO и ТО фононов в GaAs. На вставке фиг.4 приведена характерная температурная зависимость термоэдс в слое InSb на GaAs подложке. Эта зависимость имеет полосы с максимумами при температурах Дебая фононов в GaAs подложке или при температурах 383 К, 440 К, 486 К и 523 К, которые равны суммам дебаевых температур пар ТО, LO и LA фононов в GaAs или пар аналогичных фононов в InSb.
На фиг.5 и на вставке фиг.5 приведены типичные температурные зависимости термоэдс в слое кремния на сапфировой подложке и в углеродной нанотрубной пленке на кварцевой подложке, имеющие полосы УЭФ, максимумы которых лежат при температурах Дебая фононов подложек.
Узкие полосы УЭФ наблюдаются только в содержащих ЭКЦ материалах. Они расположены при температурах Дебая фононов, поэтому несомненно вызваны электронно-колебательными переходами между ЭКЦ и определенно представляют собой эффект УЭФ. Мы аппроксимировали контуры полос зависимостью (5), используя измеренные нами значения Тm и подбирая величины θ и const.
Температура Тm имеет смысл стоксова смещения максимума полосы УЭФ на температуру Дебая одного (р=1) или на сумму температур Дебая нескольких (p>1) фононов относительно бесфононного перехода (р=0, Тm=0 К). Наиболее интенсивную полосу согласно теории нужно ожидать при температуре, совпадающей с суммой температур Дебая p≅S фононов. Однако в экспериментах наблюдаются температуры Тm, равные дебаевым температурам одного (р=1) или суммам дебаевых температур пары фононов (р=2), хотя константа электрон-фононного взаимодействия на ЭКЦ в Si может достигать значений S≥5, в InSb - S≥3, в GaP - S≥4, в графите и углеродных нанотрубных пленках на подложках - S>10. Этот результат можно объяснить известным уменьшением величины S до значений близких к 1 за счет усиления взаимодействия между ЭКЦ при сближении центров друг с другом по мере увеличения их концентрации (выше 1016 см-3). Такое уменьшение S объясняет отсутствие полос эффекта УЭФ с участием трех и более фононов (p>2) при высоких концентрациях ЭКЦ.
Температура θ является дисперсией функции Гаусса (5). Она имеет смысл полуширины полосы эффекта УЭФ на ее полувысоте и представляет особенности электронно-колебательных переходов в конкретном материале. Наиболее точная аппроксимация полос УЭФ функцией (5) достигается, если температура θ имеет одно определенное значение для всех полос УЭФ в материале. Так, значение θ=5,8 К было определено для полос УЭФ в Si. При этом выяснилось, что полоса С на фиг.1 является наложением трех гауссовых полос с температурами Тm, соответствующими дебаевым температурам различных LA фононов. Каждая из полос В и D состоит из двух гауссовых полос с температурами Тm, соответствующими дебаевым температурам ТА, LA и LO фононов. Полоса L в графите (см. фиг.3) состоит из трех гауссовых полос с температурами Тm, расположенными при дебаевых температурах различных LO фононов со значением θ=5 К. Полосы в InAs и в InSb имеют полуширину θ=4 К, в графите θ=5 К.
В слоях InAs на GaAs подложках полосы УЭФ имеют характерное для InAs значение θ=4 К. Профиль полосы М в слое InAs (см. фиг.4) состоит из двух гауссовых кривых с θ=5 К. Каждая из полос N и О является суммой полос с θ=4 К и 25 К, θ=4 К и 20К. Наличие гауссовых компонент некоторых полос с температурами θ>10 К в узкозонных материалах, таких как графит, InAs и InSb, можно предположительно объяснить частичным вкладом диффузионной термоэдс. Температуры θ имеют характерные для каждого материала значения, приведеные в Таблице 1.
Значения температур θ в монокристаллах и монокристаллических слоях материалов на полуизолирующих или диэлектрических подложках
Из таблицы 1 видно, что температуры θ для монокристаллов совпадают с соответствующими температурами для слоев этих же материалов на подложках (за исключением субмикронных слоев Si на сапфире). Величины θ одинаковы для всех полос УЭФ в каждом материале [29] и отражают свойства внутрикристаллических процессов, которые не зависят от внешних условий. По-видимому, это - осциллирующие процессы обмена энергией между системами электронов и ядер атомов в кристалле, которые происходят даже в бездефектных материалах, что показано теоретически на примере монокристалла Si [30].
Таким образом, установлено, что в каждом содержащем ЭКЦ материале температурные зависимости термоэдс имеют узкие полосы УЭФ с гауссовым профилем и одинаковой шириной, расположенные при температурах Дебая фононов материала, а в слоях материала на подложке - при температурах Дебая фононов подложки. Эти полосы вызваны электронно-колебательными переходами между ЭКЦ и представляют собой эффект увлечения электронов фононами. Полученные результаты важны потому, что ранее эффект УЭФ наблюдали только при низких температурах в виде полосы с максимумом между 15 К и 39 К и только в монокристаллах германия. Новые данные об эффекте УЭФ в различных материалах при температурах Дебая фононов открывают возможности применения этого технического эффекта без охлаждения материалов.
Аналогами заявленного изобретения являются известные способы осуществления (создания) термоэдс. В аналогах изобретения обычно используют полупроводниковый или металлический твердотельный материал с электродами, образующими электрические невыпрямляющие контакты к материалу, создают между контактами разность температур не более 1 К ... 2 К, измеряют термоэдс, возникающую в материале между контактами [4, 5].
Известен также способ, раскрытый в работах [13,14], в котором используют полупроводниковый монокристалл Ge, размещают на его поверхности электроды, образующие невыпрямляющие контакты к материалу, создают между электродами разность температур величиной ≈1 К, нагревают материал от температуры ниже 30 К и измеряют температурную зависимость термоэдс, возникающей между электродами. Эта термоэдс в основном представляет собой эффект увлечения электронов фононами (при температурах не выше 70 К).
Аналоги изобретения не позволяют осуществить эффект увлечения электронов фононами при температурах выше 70 К и тем более при температурах Дебая фононов, которые обычно превышают 200 К, а в некоторых материалах они достигают 800 К ... 1000 К.
В качестве прототипа можно указать способ, раскрытый в публикации: В.А.Вдовенков, "Увлечение электронов фононами, обусловленное электронно-колебательными переходами в материалах", Известия ВУЗов, Материалы электронной техники, 2005, №1, с.65-70. В известном способе использованы образцы полупроводниковых материалов или слои таких материалов толщиной до 50 мкм на полуизолирующих или диэлектрических подложках с электродами. В образцы были введены электронно-колебательные центры (ЭКЦ). Между электродами образца создавали разность температур и измеряли термоэдс. Однако в известном способе не раскрыты все условия, необходимые для осуществления эффекта увлечения электронов фононами при околокомнатных и более высоких температурах (по существу, при дебаевых температурах кристаллических фононов).
Сущность изобретения.
Целью данного изобретения является создание способа осуществления технического эффекта увлечения электронов фононами при околокомнатных и более высоких температурах (по существу, при дебаевых температурах кристаллических фононов) в полупроводниковых твердотельных материалах и структурах между электродами, а также способов регулирования величины этого эффекта.
Такие способы могут быть пригодны для создания новых твердотельных электронных приборов с пониженным уровнем собственных шумов без охлаждения приборов.
Важной является и задача создания электрических контактов к материалу, не препятствующих существованию и измерению термоэдс и позволяющих пропускать через материал определенный ток или изменять электрический потенциал материала в приборах и устройствах.
Важной также является задача создания и регулирования разности температур в материале с помощью увлечения электронов фононами на основе использования межцентровых электронно-колебательных переходов.
Согласно пункту 1 формулы изобретения с целью осуществления эффекта увлечения электронов фононами (УЭФ) в полупроводниковых материалах или в слоях таких материалов толщиной до 50 мкм на полуизолирующих или диэлектрических подложках на поверхности или в объеме материала размещают электроды, образующие выпрямляющие контакты с материалом, например контакты Шоттки, выбирают расстояние между электродами (D) значительно меньше глубины проникновения в материал электрического поля (L), (D<<L), вызванного контактной разностью потенциалов, минимальное расстояние между электродами DMIN=20 мкм, максимальное расстояние между электродами DMAX=300 мкм, до, после или во время размещения электродов или до, после или во время создания зазора шириной D между электродами в материал вводят электронно-колебательные центры (ЭКЦ) в концентрации (N) от 2·1012 см-3 до 3·1017 см-3, доводят температуру материала до температуры Дебая фононов материала, а в слое материала на подложке ее доводят до температуры Дебая фононов подложки, между электродами создают разность температур ΔT=(T2-T1), такую, чтобы большая из температур T1 и Т2 не достигала температуры плавления электродов, материала или подложки, а меньшая из этих температур должна быть меньше Тm-2θ, где θ - полуширина полосы температурной зависимости увлечения электронов фононами, измеряют термоэдс между электродами, которая в данных условиях представляет собой эффект увлечения электронов фононами (УЭФ) в материале между электродами.
Согласно пункту 2 формулы изобретения электронно-колебательные центры вводят только в обедненную область материала или в примыкающие к электродам части обедненной области материала между электродами.
Согласно пункту 3 формулы изобретения в способе по пп.1, 2 с целью определения температур Дебая и частот Дебая кристаллических фононов материала выбирают ΔТ<θ, измеряют температурную зависимость УЭФ, определяют температуры максимумов этой зависимости (Тm) и приравнивают их температурам Дебая кристаллических фононов, а частоты Дебая кристаллических фононов материала вычисляют по формуле 
Согласно пункту 4 формулы изобретения с целью регулирования величины УЭФ в способах по п.2 устанавливают разность температур электродов (T2-T1) менее θ, (T2-T1)<θ, изменяют температуру материала между электродами как минимум в пределах Тm±3θ.
Согласно пункту 5 формулы изобретения в способах по п.2 с целью регулирования величины эффекта УЭФ материал или часть материала между электродами освещают в спектральной области поглощения ЭКЦ или материала или в спектральной области поглощения и ЭКЦ, и материала и изменяют плотность освещения (I) в пределах от I=0 до I=Nс/(ατ), где Nc - эффективное число электронных состояний в зоне проводимости, α - коэффициент оптического поглощения, τ - время жизни электронов в материале между электродами.
Согласно пункту 6 формулы изобретения в способах по п.2 с целью регулирования величины эффекта УЭФ, что используют дополнительный полевой электрод или несколько полевых электродов, образующих выпрямляющие контакты к материалу между электродами (р-n переходы, контакты металл-полупроводник или металл-диэлектрик-полупроводник), прикладывают постоянные напряжения смещения между материалом и различными полевыми электродами или между различными полевыми электродами, изменяют величины напряжений смещения и манипулируют полярностями напряжений смещения.
Согласно пункту 7 формулы изобретения с целью регулирования величины термоэдс в способе по п.2 между материалом и одним или несколькими дополнительными электродами или между дополнительными электродами прикладывают переменное электрическое напряжение с амплитудой менее полувысоты потенциального барьера для электрона в контакте, выраженной в Вольтах, и с частотой акустоэлектрического синхронизма f=V/2W, где V - скорость звука в материале и W - толщина пластины материала, или V - скорость звука в слое материала на подложке и W - толщина слоя на подложке, или V - скорость звука в подложке и W - общая толщина слоя и подложки, изменяют частоту переменного напряжения в пределах от f/2 до 2f или изменяют амплитуду переменного напряжения, или изменяют частоту и амплитуду переменного напряжения.
Согласно пункту 8 формулы изобретения в способах по п.2 с целью регулирования величины УЭФ и уменьшения внутренних шумов в материале между электродами создают поперечное по отношению к линиям тока магнитное поле, напряженность которого выбирают в пределах от 0 до  ,
,
где m - эффективная масса носителя заряда (электрона) в материале, k - постоянная Больцмана,  - постоянная Планка, р - номер электронно-колебательного уровня ЭКЦ, переходы на который используют для осуществления УЭФ (р=1, 2, 3, ..., S).
- постоянная Планка, р - номер электронно-колебательного уровня ЭКЦ, переходы на который используют для осуществления УЭФ (р=1, 2, 3, ..., S).
Согласно пункту 9 формулы изобретения в способе по п.8 изменяют величину или направление или величину и направление индукции магнитного поля.
Согласно пункту 10 формулы изобретения в способах по пп.1, 2, 4, 5, 6, 8 с целью уменьшения уровня внутренних шумов УЭФ и увеличения эффекта УЭФ в материале между электродами создают постоянное магнитное поле с напряженностью от 0 до 2 Тесла, направленное параллельно линиям тока в материале между электродами.
Согласно пункту 11 формулы изобретения в способе по пп.1, 2, 7 с целью регулирования величины УЭФ в материале создают переменное магнитное поле и изменяют его частоту в пределах от f/2 до 2f, где f - частота акустоэлектрического синхронизма, или изменяют направление его индукции, или изменяют и частоту, и направление индукции.
Согласно пункту 12 формулы изобретения в способах по любому из пп.1, 2, 5, 6, 7, 8, 9 с целью получения дополнительной к ΔT разности температур между электродами создают вдоль линий тока в материале между электродами разность концентраций электронно-колебательных центров (ΔN) или разность концентраций электрически активных электронно-колебательных центров, измеряют величину УЭФ, измеряют дополнительную к ΔТ разность температур.
Заявленное изобретение характеризуется совокупностью отличительных признаков, а именно введением в материал определенной концентрации ЭКЦ, использованием выпрямляющих контактов к материалу, выбором допустимых расстояний между электродами, образующими эти контакты с материалом, размещением электродов на материале или в его объеме, выбором рабочей температуры материала, равной температуре Дебая одного из типов фононов материала или подложки, выбором разности температур электродов, возможностью регулирования величины эффекта УЭФ вплоть до его устранения за счет освещения материала или части материала между электродами, а также за счет наложения магнитного поля определенной величины и ориентации и изменением величины его индукции, использованием дополнительных полевых электродов, образующих выпрямляющие контакты с материалом между электродами, и манипуляциями напряжениями смещения, подаваемыми на полевые электроды относительно материала, изменением температуры материала, приложением между материалом и электродами электрического напряжения с определенной амплитудой и частотой.
Таким образом, заявленный способ осуществления эффекта увлечения электронов фононами соответствует критерию изобретения "новизна".
Сравнение заявленного способа осуществления эффекта увлечения электронов фононами с прототипом и другими техническими решениями в данной области техники не выявило технических решений, обладающих указанной совокупностью отличительных признаков. Это позволяет сделать обоснованный вывод о соответствии заявленного технического решения критерию изобретения "существенные отличия".
Действительно:
Заявленный способ позволяет осуществлять эффект увлечения электронов фононами в узких температурных интервалах вблизи температур Дебая фононов, которые в соответствии с общеизвестными данными о температурах Дебая различных типов фононов в различных материалах могут лежать в пределах от 200 К до (800...1000) К. Таким образом, эффект УЭФ может быть осуществлен в материалах вблизи комнатных и при более высоких температурах, что соответствует цели изобретения.
К п.1 формулы изобретения.
Толщину слоя на подложке согласно экспериментальным данным устанавливают не более 50 микрон. При большей толщине слоя материала наблюдается существенное уменьшение величины УЭФ, в основном за счет шунтирования прилежащего к границе с подложкой слоя материала остальной частью материала, лежащей за пределами этого приграничного слоя, которая оказывается пассивной в УЭФ. Это возможно, поскольку фононы подложки проникают в слой материала не далее, чем на несколько длин акустических волн, что соответствует ожидаемому из расчетов и наблюдаемому на опыте затуханию фононов подложки в слое материала. При толщинах слоя (≈50 мкм) наблюдается ослабление полосы УЭФ при температуре Дебая фононов подложки, а при увеличении толщины слоя (более 50 мкм) происходит возникновение и усиление полосы УЭФ при температуре Дебая фононов материала, а вклад фононов подложки в УЭФ становится несущественным при увеличении толщины слоя материала.
Контакты и расстояния между ними.
Важным является условие, касающееся конструкции электрических контактов к материалу и их положения относительно друг друга. В этом можно убедиться, рассмотрев физические процессы вблизи контактов. На фиг.6 представлена энергетическая зонная диаграмма структуры с контактами металл-полупроводник (контактами Шоттки) в условиях термодинамического равновесия. Здесь Fм и Fпп обозначают уровни Ферми в металле и полупроводнике соответственно. Полупроводник имеет электронный тип проводимости и Fпп близок к дну зоны проводимости Еc. Ev - потолок валентной зоны, а ширина запрещенной зоны полупроводника Еg=Eс-Еv. Высота встроенного потенциального барьера еφk определяется правилом "2/3", согласно которому положение уровня Ферми на границе металл-полупроводник располагается ниже дна зоны проводимости на 2/3 ширины запрещенной зоны полупроводника, то есть на 1/3 ширины запрещенной зоны полупроводника выше потолка валентной зоны [31]. Из фиг.6 видно, что расстояние между электродами D значительно превышает глубину проникновения в полупроводник электрического поля, вызванного контактной разностью потенциалов, т.е.

где ε - относительная диэлектрическая проницаемость полупроводника, ε0 - электрическая постоянная, е - заряд электрона, φk - контактный потенциал, n - концентрация свободных носителей зарядов в разрешенной энергетической зоне (электронов в зоне проводимости n-полупроводника или дырок в валентной зоне p-полупроводника) в состоянии "плоских зон". В таком случае при измерении термоэдс между электродами электроны будут рассеиваться на приконтактных потенциальных барьерах. То есть имеющиеся потенциальные барьеры высотой еφk препятствуют измерению термоэдс в материале между электродами. Этот нежелательный эффект можно устранить выбрав D значительно меньше L. Соответствующая зонная энергетическая диаграмма изображена на фиг.7. Из фиг.7 видно, что при D значительно меньше L (D<<L) встроенный потенциальный барьер может быть уменьшен до незначительной величины. При этом высота барьера может быть не более kT. Для этого следует уменьшать D. При D значительно меньше L (D<<L) полупроводник в материале между электродами имеет дырочный тип проводимости и отделен от остального объема полупроводника физическим p-n переходом, а встроенные потенциальные барьеры не способны рассеивать электроны, которые беспрепятственно могут проникать в металл, и термоэдс в материале между электродами может быть зарегистрирована путем измерения разности потенциалов между электродами. При этом барьер Шоттки препятствует проникновению электронов из металла в материал между электродами и тем самым исключает их влияние на УЭФ.
Аналогичные энергетические диаграммы можно рассмотреть и в случае полупроводника с дырочной проводимостью, полагая, что УЭФ в материале между электродами будет возникать в результате переходов дырок между ЭКЦ. Однако регистрация термоэдс между электродами неизбежно сопряжена с протеканием тока через приконтактные области и, следовательно, неизбежен процесс рекомбинации дырок на границе с металлом, что эквивалентно процессу рассеяния дырок, который не способствует увеличению УЭФ. Кроме того, в данном случае не возникает физический p-n переход и подвижные дырки способны поступать из объема полупроводника в материал между электродами и влиять на УЭФ. Тем не менее, материал с дырочной проводимостью в принципе пригоден для осуществления данного изобретения. Таким образом, условием осуществления эффекта УЭФ в межэлектродном зазоре является условие значительной малости D по сравнению с L (D<<L).
Кроме того, исследования зависимости УЭФ от величины D показали, что УЭФ при температурах Дебая достигает максимума во всех исследованных материалах, если D лежит в пределах от 20 мкм до 300 мкм, а за пределами этих значений D величина УЭФ практически затухает, что можно видеть из фиг.8, где представлены соответствующие данные для некоторых материалов. Эти данные соответствуют связи эффекта УЭФ именно со свойствами ЭКЦ и его слабой зависимости от типа кристаллической решетки материала и от вида материала.
Концентрации ЭКЦ.
Очевидно, что для осуществления УЭФ при рассматриваемом механизме, предусматривающем участие собственных колебаний (и волн таких колебаний), в материал должна быть введена, по крайней мере, минимальная концентрация (Nmin) электронно-колебательных центров. Эти центры с одинаковым успехом можно вводить до, после или во время нанесения электродов на материал или, что одно и то же, до, во время или после создания зазора между электродами шириной D. Минимальную величину концентрации центров Nmin можно оценить исходя из того, что взаимодействие между электронными оболочками электронно-колебательных центров осуществляется посредством акустических кристаллических фононов и такое взаимодействие может оказаться эффективным на расстоянии длины соответствующей акустической волны H=U/F, где U - скорость волны (скорость звука) и F - частота волны. В таком случае N=H-3. Минимальные частоты фононов, эффективно взаимодействующих с ЭКЦ в кристаллах, близки к 1,25·1010 с-1. Исходя из максимальной скорости звука U=9,79·105 см/с и указанной частоты упругой волны для акустических волн (в кремнии), получаем Nmin=2,6·1012 см-3. Приведенная оценка величины N справедлива для любого кристалла, так как кристаллы имеют мало различающиеся постоянные кристаллических решеток и скорости звука в них. Анализ экспериментальных спектров фотопроводимости образцов кремния, содержащих ЭКЦ (А-центры, представляющие собой ассоциации примесных атомов кислорода с вакансиями кремния), позволил определить минимальную концентрацию А-центров (от 2·1012 см-3 до 3·1012 см-3), способную влиять на электрические свойства кремния. Максимальная концентрация ЭКЦ, оказывающих влияние на электрофизические свойства материалов, близка к 3·1017 см-3, что подтверждается экспериментальными данными о фотопроводимости и туннелировании электронов сквозь потенциальные барьеры при электронно-колебательных переходах.
Выбор величины ΔТ=(T2-Т1).
Очевидно, что наибольшая допустимая величина разности температур двух электродов ΔТ=(T2-T1) при измерении контура полосы эффекта УЭФ должна быть как можно меньше и не превышать θ, так как при больших ΔТ она превысит полуширину полосы эффекта на ее полувысоте, составляющую 2θ, измеренный контур полосы УЭФ будет сильно искажен. Эти условия измерения УЭФ соблюдаются в прототипе. В нашем изобретении стоит другая задача, не просто измерить профиль полосы УЭФ, а измерить наибольшую величину УЭФ при наименьших внутренних шумах. Очевидно, что величина УЭФ пропорциональна интегралу от контура полосы УЭФ по интервалу температур. Она будет максимальна, если интервал ΔТ охватывает всю температурную область полосы УЭФ, в основном расположенную между температурами Тm-2θ и Тm+2θ. Поэтому температуры T1 и Т2 должны удовлетворять условиям Т1≥Тm-2θ и Т2≤Тm+2θ2, где Тm - температура в максимуме полосы, равная температуре Дебая фонона, а θ - полуширина полосы на ее полувысоте. На фиг.9 показана такая ситуация. Фиг.9а представляет собой график зависимости температуры материала между электродами от расстояния между ними. Температуры электродов равны T1 и Т2 соответственно, температура Дебая равна Тm. Контур соответствующей полосы УЭФ изображен на фиг.9б при указанных условиях его измерения: Т1≥Tm-2θ и T2≤Tm+2θ с максимумом при Т=Тm. Из фиг 9а и 9б видно, что вклад в УЭФ дает только область материала толщиной ΔХ. Видно, если интервал температур охватывает температуры Тm-2θ и Тm+2θ и превышает его, то интеграл от контура полосы будет стремиться к постоянному значению, а при изменениях температуры в более широких пределах он будет оставаться постоянным. Следовательно, флуктуации температуры в таком случае не вызовут изменения сигнала УЭФ, что обеспечивает понижение уровня внутренних (тепловых) шумов при измерении УЭФ.
Более того, в нашем случае тепловые шумы могут существовать из-за флуктуации температуры только в полосе примерно (Тm-2θ, Тm+2θ). Поэтому температурная полоса (тепловых шумов) в нашем случае не превышает 3θ...4θ, что в несколько раз меньше ширины традиционной температурной полосы тепловых шумов, равной Тm. На фиг.10 приведена ожидаемая (вычисленная) зависимость величины УЭФ от ширины температурного интервала ΔТ, измеренного в единицах θ, и показаны точки соответствующей экспериментальной зависимости для GaAs при D=50 мкм. Из фиг.10 видно, что величина УЭФ достигает «насыщения» и практически не зависит от температуры при ΔT>4θ, что соответствует пониженным (тепловым) шумам и цели изобретения. При этом температуры T1 и Т2 не должны достигать другой температуры Дебая, а также температуры плавления материала или подложки, а наименьшая из этих температур должна быть меньше Tm-2θ.
Важно отметить, что способ измерения УЭФ по п.1 формулы изобретения можно использовать для контроля однородности термоэлектрических свойств материала между электродами. Действительно, при этом изменяют температуры T1 и Т2 таким образом, чтобы слой толщиной ΔX, в котором возникает УЭФ, перемещался от одного электрода к другому (см. фиг.9). При определенных значениях температур T1 и Т2 легко определить положение слоя ΔX. Поэтому сканируя слоем ΔX и измеряя УЭФ можно определить зависимость УЭФ от координаты слоя. В неоднородном материале на зависимости, представленной на фиг.10, в области «плато» появятся отклонения от величины «насыщения» УЭФ, отражающие неоднородность термоэлектрических свойств материала (вызванные, например, неоднородностью распределения концентрации ЭКЦ в материале между электродами). В случае однородного материала отклонений от величины «насыщения» УЭФ не будет наблюдаться. Важно отметить, что увеличение градиента температуры (Т2-T1)/D способствует увеличению разрешающей способности способа контроля однородности материала, т.к. способствует уменьшению ΔX.
Если величина ΔT достигнет и превысит разность дебаевых температур фононов, то на зависимости УЭФ от ΔТ по мере увеличения ΔТ можно обнаружить две (или более) области нарастания УЭФ и два (три или более) «плато», соответствующих вкладам двух (или большего числа) полос УЭФ.
К п.2 формулы. Заявленный способ может быть осуществлен и в тех случаях, когда ЭКЦ вводят только в части материала между электродами, прилежащие к электродам, поскольку взаимодействие между размещенными в этих частях ЭКЦ осуществляется путем обмена фононами. Эту возможность предложено использовать в п.2 формулы изобретения.
К п.3 формулы. Установленное соответствие температур максимумов узких полос УЭФ в содержащих ЭКЦ материалах температурам Дебая кристаллических фононов предложено использовать для определения температур и частот Дебая фононов материалов. Это могут быть монолитные полупроводниковые материалы или слои материалов на подложках, а также полупроводниковые и диэлектрические подложки. Таким образом, доступным, простым и недорогим термоэлектрическим методом, измеряя температурную зависимость УЭФ, можно определять температуры и частоты Дебая в полупроводниковых и диэлектрических материалах, что важно для исследования новых материалов и структур, без применения сложных и дорогостоящих экспериментальных методов, таких как обычно применяемое для таких целей рассеяние медленных нейтронов. Эта простая возможность определения дебаевых параметров колебательного спектра кристаллических решеток различных материалов предложена для использования в п.14 формулы изобретения.
К п.4 формулы. Если разность температур электродов (Т2-T1)<θ, то отклонение температуры материала между электродами от температуры максимума УЭФ (Тm), совпадающей с температурой Дебая фононов, вызывающих данный термоэлектрический эффект, на величину до 3θ и более сопровождается значительным уменьшением УЭФ, что видно из температурных зависимостей УЭФ, приведенных на фиг.1-5. В п.4 формулы изобретения предложено использовать эту температурную зависимость для регулирования величины УЭФ.
К п.5 формулы. Освещение материала между электродами или части материала между электродами в спектральной области поглощения ЭКЦ или материала создает дополнительные электронные и электронно-колебательные переходы, влияющие на величину УЭФ, что предложено использовать в п.5 формулы изобретения. Наибольшую плотность (интенсивность) освещения можно определить, считая, что освещение существенно не изменит положение уровня Ферми (квазиуровня Ферми для электронов) в материале. Согласно теории рекомбинации электронов и дырок в полупроводниках [4, 5] это соответствует концентрации электронов в зоне проводимости материала n не более эффективной плотности электронных состояний в зоне проводимости 
где  - эффективная масса для плотности состояний,
- эффективная масса для плотности состояний,  , n=αIτ≤Nс, где α (см-1) - коэффициент оптического поглощения материала, I (фотонов·см-2·с-1) - плотность освещения, τ(с) - время жизни электронов. Поэтому допустимую плотность освещения можно определить из следующего соотношения I≤Nс/ατ.
, n=αIτ≤Nс, где α (см-1) - коэффициент оптического поглощения материала, I (фотонов·см-2·с-1) - плотность освещения, τ(с) - время жизни электронов. Поэтому допустимую плотность освещения можно определить из следующего соотношения I≤Nс/ατ.
Следует отметить, что часто используемая для регистрации излучения фотопроводимость, в нашем случае связанная с ЭКЦ, является отрицательной, то есть проводимость материала между электродами уменьшается при увеличении интенсивности регистрируемого излучения, в то время как в известных фотоприемниках фотопроводимость положительная. При этом, однако, УЭФ увеличивается с ростом интенсивности регистрируемого освещения, так как практически все носители зарядов (и электроны и дырки, как установлено экспериментально) локализуются на ЭКЦ и участвуют в электронно-колебательных межцентровых переходах, увеличивая УЭФ. Кроме того, температурный диапазон УЭФ не более 4θ<<Тm, θ неизменна для каждого материала, что обеспечивает пониженный уровень внутренних шумов УЭФ по сравнению с уровнем шумов известных фотоприемников [32, 33, 34], в которых величина шумов связана с полосой температур, лежащей между 0 К и рабочей температурой материала Т К, ширина которой совпадает с рабочей температурой материала. Поэтому в заявленном способе величина шумов меньше, поскольку определяется величиной θ, которая меньше рабочей температуры материала Т=Тm и не зависит от нее.
Способ по п.5 формулы изобретения может быть использован для регистрации оптического излучения, обеспечивающей пониженный уровень собственных (внутренних) шумов фотоприемного устройства, работающего в окрестности температуры Дебая фононов. Желаемую рабочую температуру такого фотоприемника можно задать путем выбора и применения полупроводника (подложки) с соответствующей температурой Дебая фононов, а область спектральной чувствительности можно выбрать, выбрав полупроводник с соответствующей шириной запрещенной зоны. Область спектральной чувствительности такого фотоприемника складывается из области собственного (основного, фундаментального) поглощения примененного полупроводника и полос электронно-колебательного поглощения центрами (ЭКЦ), расположенными при энергиях оптических квантов меньше ширины запрещенной зоны, что соответствует теории электронно-колебательных переходов и подтверждается экспериментально.
Интенсивность освещения целесообразно выбирать в пределах от I=0 до I=Nс/(ατ), где Nс - эффективное число состояний в разрешенной энергетической зоне материала, α - коэффициент оптического поглощения материала, τ - время жизни. Действительно, при большей интенсивности света концентрация носителей в материале настолько велика (αIτ>>Nс), что изменение ее уже не влияет на электронно-колебательные переходы и на величину УЭФ.
К п.6 формулы. Использование дополнительного полевого электрода или нескольких полевых электродов, образующих выпрямляющие контакты металл-полупроводник или металл-диэлектрик-полупроводник к материалу между электродами, приложение между материалом и различными полевыми электродам, вообще говоря, различных напряжений смещения и манипулирование величинами и полярностями этих напряжений позволяет изменять длину и форму линии тока между электродами, что эквивалентно изменению расстояния между электродами и вызывает изменение величины УЭФ. Такая возможность регулирования УЭФ использована в п.6 формулы изобретения.
Использование двух (или более) дополнительных полевых электродов позволяет осуществлять более широкий (например, в сравнении с традиционным полевым транзистором) диапазон изменений величины УЭФ в зависимости от напряжений на полевых электродах.
Очевидно, что величина напряжения смещения обратной полярности на любом из дополнительных электродов не должна достигать напряжения его пробоя, а величина прямого смещения не должна достигать высоты потенциального барьера в контакте (φк), измеренной в Вольтах.
Способ по п.6 формулы изобретения может быть использован для создания аналога полевого транзистора с той разницей, что вместо разности электрических потенциалов между истоком и стоком полевого транзистора в изобретении прикладывают разность температур между электродами. Кроме того, используя способ по п.12 формулы, аналогичный прибор может быть реализован и без разности температур электродов, а создавая неоднородное распределение концентраций (электрически активных ЭКЦ). Не исключено и скептическое отношение к данным способам (по пп.6 и 12) в связи со сравнительно невысокими величинами УЭФ, обычно составляющим от единиц до сотен милливольт, однако, например, клетки живого мозга работают примерно при таких же напряжениях, обеспечивают завидную надежность, стабильность, низкое энергопотребление в течение всей жизни организмов. Правда, эта жизнедеятельность организмов сохраняется в узком температурном диапазоне (шириной 2θ градусов) вблизи характерных дебаевых температур органических полупроводниковых структур, клеток, молекул. Такой сравнительно узкий температурный диапазон жизнедеятельности организмов является своеобразной платой за высокую надежность, долговечность и низкий уровень собственных шумов, а также за высокую помехоустойчивость по отношению к действию внешних электрических, магнитных и электромагнитных полей.
К п.7 формулы. В современной технологии изготовления полупроводниковых приборов обычно используются полупроводниковые пластины толщиной W=200...300 мкм. На одной (лицевой, рабочей) плоской поверхности формируют приборы, а другой - тыльной поверхностью кристалл припаивается к держателю (теплоотводу). Такие пластины материалов с плоскопараллельными поверхностями представляют собой для фононов (для звука в кристалле) резонатор, аналогичный оптическому резонатру Фабри-Перо. Для этого звукового (фононного) резонатора характерна определенная частота акустоэлектрического синхронизма f=1/t, где t - время пролета звуковой волны (звука) от лицевой поверхности до тыльной поверхности пластины и обратно со скоростью звука V. Время пролета t=2W/V. Соответствующая частота акустоэлектрического синхронизма f=V/2W. Если между электродом и полупроводником приложить напряжение с частотой акустоэлектрического синхронизма f, то из-за модуляции этим напряжением высоты потенциального барьера контакта при наличии ЭКЦ и повышенной плотности фононов в области контакта изменяется скорость электронно-колебательных переходов и соответственно изменяется величина УЭФ. Это свойство акустоэлектрического синхронизма в п.5 формулы изобретения предложено использовать для регулирования величины УЭФ. В слоистых структурах важными оказываются и другие частоты акустоэлектрического синхронизма, такие, когда V - скорость звука в подложке и W - общая толщина слоя и подложки, а также когда V - скорость звука в слое и W - толщина слоя на подложке. Эти виды акустоэлектрического синхронизма практически осуществляются и являются важными, так как влияют на электронно-колебательные переходы и на величину УЭФ.
Амплитуда напряжения акустоэлектрического синхронизма не должна достигать примерной величины φк/2, где φк - высота потенциального барьера в контакте, выраженная в Вольтах. В противном случае возникают инжекционные токи, способные нарушить акустоэлектрический синхронизм. На практике оказалось, что достаточно напряжения акустоэлектрического синхронизма с амплитудой от 1 до 500 микровольт.
К п.8 формулы. Магнитное поле. Можно оценить индукцию магнитного поля, если исходить из частоты акустического фонона 1,25·1010 с-1, участвующего в электронно-колебательных переходах ЭКЦ. Действительно, ЭКЦ можно представить как заряженный осциллятор с массой m и зарядом электрона е. Уравнение движения осциллятора, учитывающее действие силы Лоренца в магнитном поле, можно записать так:

где Х - обобщенная (конфигурационная) координата, ω - циклическая частота осцилляции, В - проекция индукции магнитного поля на направление нормали к скорости носителя заряда. Слагаемое, содержащее скорость  , учитывает действие силы Лоренца, когда скорость и индукция В взаимно ортогональны. Данное уравнение допускает осциллирующее решение при условии
, учитывает действие силы Лоренца, когда скорость и индукция В взаимно ортогональны. Данное уравнение допускает осциллирующее решение при условии

Другими словами, колебательные движения осциллятора с частотой ω возможны, когда В не слишком велико. Если частота колебаний связанного с ЭКЦ электрона фиксирована и определяется свойствами электронно-колебательного центра, то при увеличении В до некоторого значения, определяемого указанным неравенством, колебания центра станут невозможными. Если электрон участвует в сложном колебании центра с несколькими независимыми частотами, то, по мере увеличения В, последовательно окажутся подавленными магнитным полем колебания с частотами в порядке их возрастания. В принципе можно подобрать такую величину В, при которой будут подавлены колебания электронно-колебательных центров с любой частотой. Таким представляется механизм подавления осцилляции ЭКЦ в магнитном поле. Полагая m равной эффективной массе электрона и ω=2π·1,25·1010 с-1, из неравенства (6) получаем минимальное значение критической напряженности магнитного поля для кремния ≈0,25 Тл. Критическая индукция магнитного поля будет принимать значения, кратные минимальному критическому значению, что соответствует участию р=1, 2, 3, ..., S или более фононов в эффекте УЭФ.
На фиг.11 приведена типичная зависимость термоэдс при температуре Дебая LA фонона в монокристалле кремния, содержащего А-центры (≈1014 см-3), от индукции магнитного поля, на которой видны минимумы, расположенные при вычисленных значениях В. Кроме того, из фиг.11 видно, что влияние на УЭФ оказывают магнитные поля с индукцией не более 1,8 Тл, что соответствует участию в УЭФ примерно (S +2) фононов. Учитывая единый для всех ЭКЦ механизм взаимодействия с фононами и магнитным полем в полупроводниках и неравенство (7), можно определить наибольшую индукцию, необходимую для подавления УЭФ в любом материале.
Согласно формуле (6) направленное по нормали к линии тока в материале между электродами постоянное магнитное поле с индукцией не менее  подавляет участие фононов с циклической частотой
подавляет участие фононов с циклической частотой  в однофононных электронно-колебательных переходах и вызывает уменьшение УЭФ вблизи соответствующих значений индукции магнитного поля. Переходы ЭКЦ с участием одного фонона с частотой ω возможны на электронно-колебательные уровни энергии
в однофононных электронно-колебательных переходах и вызывает уменьшение УЭФ вблизи соответствующих значений индукции магнитного поля. Переходы ЭКЦ с участием одного фонона с частотой ω возможны на электронно-колебательные уровни энергии  , где номер уровня р=1, 2, 3, ..., подавляются магнитным полем с индукцией
, где номер уровня р=1, 2, 3, ..., подавляются магнитным полем с индукцией  . Кроме того, на эти же электронно-колебательные уровни ЭКЦ, вообще говоря, возможны переходы электронов с участием 2-х, 3-х, 4-х, ... фононов и связанные с ними вклады в УЭФ. Из фиг.11 видно, что минимумы зависимости УЭФ от индукции В почти достигают нуля при вычисленных значениях В. Следовательно, вклад в УЭФ 2-х, 3-х, 4-х, ..., фононных процессов является незначительным. Следовательно, для подавления вклада в УЭФ электронно-колебательных переходов с участием фононов частоты ω на p-й энергетический уровень необходима индукция магнитного поля
. Кроме того, на эти же электронно-колебательные уровни ЭКЦ, вообще говоря, возможны переходы электронов с участием 2-х, 3-х, 4-х, ... фононов и связанные с ними вклады в УЭФ. Из фиг.11 видно, что минимумы зависимости УЭФ от индукции В почти достигают нуля при вычисленных значениях В. Следовательно, вклад в УЭФ 2-х, 3-х, 4-х, ..., фононных процессов является незначительным. Следовательно, для подавления вклада в УЭФ электронно-колебательных переходов с участием фононов частоты ω на p-й энергетический уровень необходима индукция магнитного поля  . Выбирая индукцию между 0 и
. Выбирая индукцию между 0 и  можно изменить величину УЭФ, уменьшить шум УЭФ от переходов на уровни с меньшими значениями p, что предусмотрено п.8 формулы изобретения.
можно изменить величину УЭФ, уменьшить шум УЭФ от переходов на уровни с меньшими значениями p, что предусмотрено п.8 формулы изобретения.
Кроме того, на фиг.11 видны минимумы зависимости УЭФ от В числом p=S+2, где S=5 - константа электрон-фононной связи на А-центрах в кремнии. Видно, что активными являются электронно-колебательные уровни до р=7. Следовательно, для подавления колебаний электронов на ЭКЦ достаточна индукция магнитного поля  Эта оценка Bmax верна и в других (кроме кремния) полупроводниках, так как значения S в них мало различаются, а при сравнительно высоких концентрациях ЭКЦ в них S близко к 1. Поэтому максимальное значение индукции В, необходимое для полного подавления колебаний ЭКЦ и соответственно УЭФ, можно принять раной 2 Тл.
Эта оценка Bmax верна и в других (кроме кремния) полупроводниках, так как значения S в них мало различаются, а при сравнительно высоких концентрациях ЭКЦ в них S близко к 1. Поэтому максимальное значение индукции В, необходимое для полного подавления колебаний ЭКЦ и соответственно УЭФ, можно принять раной 2 Тл.
К п.9 формулы. Зависимость скорости электронно-колебательных переходов и соответственно величины УЭФ от величины и направления магнитного поля относительно направления линий тока в материале между электродами, что определяется действием силы Лоренца на движущиеся заряды, предложена к использованию для регулирования величины УЭФ в п.9 формулы изобретения.
К п.10 формулы. Магнитное поле с индукцией в от 0 до 2 Тл, направленное вдоль линий тока в материале между электродами, подавляет осциллирующие с частотой фононов движения электронов при электронно-колебательных переходах по нормали к линиям тока. Это оставляет электронам только одну степень свободы движения вдоль линий тока. Согласно общеизвестной теореме термодинамики о равнораспределении кинетической энергии по степеням свободы у электрона остается энергия только kT/2 (вместо 3kT/2 при отсутствии магнитного поля), где k - постоянная Больцмана, что соответствует значительно меньшим термодинамическим флуктуациям, следовательно, и меньшим шумам электронно-колебательных переходов, и, следовательно, меньшим шумам УЭФ, а также способствует увеличению УЭФ. Эта возможность снижения внутренних шумов и увеличения УЭФ предложена к использованию в п.10. формулы изобретения.
К п.11 формулы. Зависимость УЭФ от величины и направления переменного магнитного поля с частотами от f/2 до 2f в материале между электродами предложено использовать для регулирования величины УЭФ в п.11 формулы изобретения. Такое регулирование величины УЭФ возможно, поскольку магнитное поле (посредством силы Лоренца) с частотой в указанной окрестности частоты f оказывает влияние на акустоэлектрический синхронизм и на УЭФ за счет того, что возбуждаемые при этом акустические волны стимулируют акустоэлектрический синхронизм и электронно-колебательные переходы в зависимости от величины, частоты и направления магнитного поля относительно линий тока в материале между электродами.
К п.12 формулы. При наличии разности концентраций электронно-колебательных центров вдоль линий тока в материале между электродами возникают дополнительные межцентровые электронно-колебательные переходы, вызывающие дополнительный вклад в эффект увлечения электронов фононами и в разность температур между электродами. Необходимую разность концентраций ЭКЦ можно создать при введении центров. Можно также создать соответствующую разность концентраций электрически активных ЭКЦ, например, инжектируя электроны в часть материала между электродами извне или неоднородно освещая материал между электродами.
Изобретение иллюстрируется чертежами.
На фиг.1 показана температурная зависимость термоэдс в Si. На вставке слева показана схема включения образца материала при измерениях термоэдс (Е). T1 и Т2 - температуры материала вблизи электродов 1 и 2. На вставке справа приведены пунктирные гауссовы кривые 3, 4, 5, сумма которых, показанная сплошной кривой, описывает контур полосы С.
На фиг.2. приведена температурная зависимость термоэдс в InAs. Пунктиром показаны гауссовы кривые, аппроксимирующие наиболее яркие полосы. На вставке слева приведена температурная зависимость термоэдс в легированном серой GaP. На вставке справа приведена дисперсионная кривая собственных колебаний ядер в атомах (I) и дисперсионные кривые акустических колебаний при δ<0, δ=0, δ>0, где δ - параметр, описывающий связь между собственными колебаниями ядер атомов с акустическими колебаниями.
На фиг.3. приведена температурная зависимость термоэдс в пиролитическом графите, измеренная вдоль нормали к атомным плоскостям. На вставке показана аппроксимация полосы L сплошной кривой, являющейся суммой трех пунктирных гауссовых кривых (6, 7, 8).
На фиг.4. показана типичная температурная зависимость термоэдс в слое InAs на полуизолирующей GaAs подложке. Кривая 9 измерена при нагревании образца, кривая 10 - при его охлаждении. На вставке - аналогичная зависимость термоэдс в слое InSb на GaAs подложке. Пунктиром показаны аппроксимирующие гауссовы кривые.
На фиг.5 приведена характерная температурная зависимость термоэдс в слое кремния на сапфировой подложке. На вставке приведена температурная зависимость термоэдс в углеродной нанотрубной пленке на кварцевой подложке. Пунктиром показаны аппроксимирующие гауссовы кривые.
На фиг.6 изображена энергетическая зонная диаграмма структуры металл-полупроводник-металл при расстоянии между контактами D (вдоль направления Х по нормали к границе раздела металл-полупроводник, вдоль электрической силовой линии в полупроводнике), превышающем глубину (L) проникновения электрического поля, вызванного контактной разностью потенциалов, в материал (D>>L).
На фиг.7 изображена энергетическая зонная диаграмма структуры металл-полупроводник-металл при расстоянии между контактами D значительно меньше глубины проникновения электрического поля L в материал (D<<L).
На фиг.8 приведены типичные зависимости термоэдс, измеренные между контактами Шоттки в содержащих ЭКЦ (˜5·1015 см-3) материалах Si, Ge, InAs, GaAs, GaP, InP и представляющие эффект УЭФ при температурах Дебая LA фононов, в зависимости от расстояния между контактами D<<L.
На фиг.9а зависимость 11 представляет распределение температуры в материале между электродами. На фиг.9б приведен профиль полосы УЭФ с максимумом при температуре Тm. Пунктирными линиями показано как ширина полосы УЭФ определяет толщину слоя ΔX, в котором возникает эффект УЭФ. Зависимость 12 представляет иное распределение температуры в материале между электродами (при других значениях T1 и Т2), соответствующее другому положению слоя ΔX в котором возникает эффект УЭФ.
На фиг.10 светлыми квадратами обозначена ожидаемая (вычисленная) зависимость величины УЭФ от разности температур между электродами, измеренной в единицах θ: ΔT/θ=(T2-T1)/θ, из которой видно, что при ΔT>4θ имеется «плато», т.е. достигается «насыщение» величины УЭФ. Темными кружками показаны экспериментальные результаты для эффекта УЭФ, вызванного LA фононами в GaAs при D=50 мкм.
На фиг.11 приведена типичная зависимость термоэдс, представляющая эффект УЭФ в кремнии, при температуре Дебая LA фононов (D=50 мкм << L), от индукции магнитного поля (В), направленного по нормали к линиям тока в материале между электродами.
Использование заявленного изобретения позволяет улучшить свойства известных полупроводниковых приборов (например, фотоприемников) и обеспечить функционирование принципиально новых электронных приборов с пониженными собственными (внутренними) шумами за счет того, что они активны только в узких температурных интервалах шириной (3...4θ) вблизи Тm. Собственные шумы приборов, основанных на эффекте УЭФ и работающих при дебаевой температуре (как правило, превышающей 200 К), определяются не рабочей температурой Тm, а шириной температурного интервала ≅4θ<<Tm и оказываются значительно меньше, чем в известных приборах. Действительно, наиболее типичные виды шумов, таких как радиационный (фотонный), температурный, джонсоновский, генерационно-рекомбинационный зависят от ширины температурного интервала между 0 К и рабочей температурой Т К, представленного в шумовых характеристиках в виде зависимости от Т [32, 33, 34]. Для уменьшения шумов обычно прибегают к охлаждению приборов, т.е. к сужению температурного интервала (0...Т). Поэтому использование эффекта УЭФ в качестве принципа работы приборов обеспечивает достижение пониженных внутренних шумов по сравнению с шумами известных приборов за счет сужения шумового температурного интервала до ширины примерно 4θ<<Tm, то есть в несколько раз по сравнению с рабочей температурой Тm. Такая новая техническая ситуация возможна благодаря тому, что электронно-колебательные переходы между ЭКЦ, вызывающие эффект УЭФ, жестко сопряжены с обменом энергией между ядрами атомов и системой электронов в кристаллах. Этот осциллирующий обмен энергией характеризуется температурой θ, определяется природой атомов кристалла и не зависит от температуры кристалла. Именно поэтому шумовая температура эффекта УЭФ 4θ<<Тm и соответственно шумы приборов, работающих на основе данного эффекта, существенно ниже шумов дрейфовых и диффузионных токов, используемых в известных приборах. Это обеспечивает новым приборам, основанным на использовании эффекта УЭФ при дебаевых температурах фононов, существенные шумовые и функциональные преимущества.
Более того, известен и другой способ снижения внутренних шумов за счет уменьшения числа степеней свободы у носителей зарядов (у электронов и дырок). Этот принцип реализуется в полупроводниковых квантово-размерных структурах (КРС), которые также называют полупроводниками со сверхрешетками [35, 36], где движение носителей зарядов возможно только в тонких двумерных слоях вещества и носители имеют не три, а только две степени свободы. В соответствии с общеизвестной теоремой термодинамики о равном распределении кинетической энергии по степеням свободы частиц, образующих термодинамическую систему при температуре Т, на каждую степень свободы в среднем приходится энергия kT/2. В КРС каждый носитель заряда имеет только две степени свободы (двумерный электронный газ, 2D - газ) и обладает меньшей средней энергией, равной 2·(kT/2)=kT. Поэтому флуктуации энергии и соответствующие внутренние шумы токов в КРС значительно ниже, чем в объемных монокристаллах. Использование структур с одномерным движением электронов (с одной степенью свободы носителей зарядов), так называемых квантовых нитей, позволяет обеспечить еще меньшие внутренние шумы приборов.
В заявленном изобретении используются межцентровые электронно-колебательные переходы, которые по своей природе являются одномерными и, следовательно, позволяют уменьшить внутренние шумы до более низкого уровня, чем в КРС, и даже ниже, чем в приборах на квантовых нитях. Были проведены экспериментальные исследования энергий активации удельного сопротивления полупроводников, содержащих электронно-колебательные центры, а также спектров их оптического поглощения (спектров электронно-колебательных переходов) [22]. Исследования показали, что энергетические уровни ЭКЦ описываются формулой линейного (одномерного) гармонического осциллятора: Е(ν)=Е0(ν+1/2), где ν - колебательное квантовое число, принимающее значения 0, 1, 2, .... В экспериментах определены уровни «нулевых колебаний» ЭКЦ, соответствующих ν=0 и равные Е0/2, где Е0 - квант собственных (I-) колебаний ЭКЦ. В случае двумерных и трехмерных колебаний «нулевые» энергии были бы равны 2·E0/2=E0 и 3·E0/2. Таким образом, было показано, что ЭКЦ представляют собой одномерные осцилляторы, имеющие одну степень свободы. В связи с этим, электронно-колебательные переходы между ЭКЦ также являются одномерными (направленными вдоль градиента температуры, что следует и из теории таких переходов [11, 17-19]). Это соответствует наименьшим шумам. Таким образом, оказывается, что содержащие ЭКЦ полупроводники обеспечивают пониженный уровень шумов в приборах, основанных на увлечении электронов фононами по сравнению с приборами на основе КРС или на квантовых нитях. Так, внутренние шумы инфракрасных фотоприемников на основе содержащих ЭКЦ материалов (Ge, Si, InSb, InP, InAs, GaAs) оказались меньше шумов приборов на основе КРС и на квантовых нитях. Если же учесть очень сложную и дорогостоящую технологию изготовления КРС и квантовых нитей, а также приборов на их основе, по сравнению с приборами на основе объемных полупроводников или полупроводниковых слоев, содержащих ЭКЦ на подложках, то преимущество заявленного изобретения представляется несомненным.
Оценим частотные свойства приборов, использующих электронно-колебательные переходы. Для оценки примем, что прибор работает на полосе УЭФ, вызванной акустическими фононами, энергия которых, например в кремнии, равна примерно 22 мэВ (Тm около 265 К), что соответствует частоте акустических фононов f=5·1012 c-1. B каждом электронно-колебательном переходе участвует в среднем S фононов. Вероятность участия S фононов в одном процессе меньше вероятности участия одного фонона примерно в S! раз. Следовательно, ожидаемая рабочая частота может достигать f/S!. Для кремния S≤5. Поэтому рабочая частота прибора может достигать 42 ГГц. Если же прибор работает на полосе УЭФ, вызванной оптическими фононами, то рабочая частота может достигать 85 ГГц. Учитывая, что в материале с высоким содержанием ЭКЦ (более 1015 см-3) величина константы S уменьшается до 1, то рабочие частоты могут достигать сотен ГГц при низких уровнях собственных шумов, при простой и дешевой технологии изготовления приборов, основанных на использовании эффекта УЭФ в материалах, содержащих электронно-колебательные центры. Таким образом, быстродействие приборов, использующих электронно-колебательные переходы ЭКЦ, в принципе ограничивается не пролетным временем носителей заряда, как в известных приборах, а частотами фононов и степенью их связи с центрами, что обеспечивает приборам улучшенные характеристики.
Электронно-колебательные центры вводят в материалы различными известными способами (используя термообработки, легирование, радиационные обработки). Радиационное облучение материалов является одним из наиболее технологичных способов введения ЭКЦ в полупроводниковые материалы и структуры. В связи с этим при работе приборов, использующих ЭКЦ и электронно-колебательные переходы, в условиях радиационного облучения в материал будут вводиться ЭКЦ, что не нарушит работоспособность таких приборов в широком диапазоне доз облучения. Поэтому приборы, основанные на использовании электронно-колебательных переходов, в принципе, обладают повышенной радиационной стойкостью по сравнению с известными приборами.
ИСТОЧНИКИ ИНФОРМАЦИИ
1. Born М., Oppenheimer. Ann. D. Phys. 1927. V.84, №4. Р.457.
2. Dirac P.A.M. Proc. Cambridge Phil. Soc. 1930. V.26. P. 376.
3. Doltsinis N.L., Marx D. Journ. of Theor. and Camput. Chem. 2002. V.1, №2. P.319-349.
4. Ансельм А.И. Введение в теорию полупроводников. - М.: Наука, 1978. - С.557-564.
5. Зеегер К. Физика полупроводников. - М.: Мир, 1977. - С.113.
6. Herring С. // Phys. Rev. 1941. V.59. P.889. - То же.: Herring С., Nichols M.H. // Revs. Modern Phys. 1949. V.21. P.185.
7. Lark-Horovitz К., Middleton A.E., Miller P., Scanlon W.W. and Wallerstein J. // Phys. Rev. 1946. V.69. P.259.
8. Frederikse H.P.R. // Phys. Rev. 1952. V.86. P.647. - To же.: Phys. Rev. 1953. V.91. P.491. - To же.: Phys. Rev. 1953. V.92. P.248.
9. Johnson V.A., Lark-Horowitz K. // Bull. Am. Phys. Soc. 1953. V.28, №2. P.32.
10. Geballe H.H. // Phys. Rev. 1953. V.92, №3. P.857.
11. Gurevich L. // Journ. Of Phys. 1945. V.9. P.477; 1946. V.10. P.67. - То же.: ЖЭТФ. 1946. Т.16. С.193-228.
12. Стльбанс Л.С. // Физика полупроводников. - М.: Сов. Радио, 1967. - С.299-304.
13. Herring С. // Phys. Rev. 1953. V.92. P.857. - To же: Phys. Rev. 1954. V.96. P.1163.
14. Geballe Т.Н. and Hull G.W. // Phys. Rev. 1954. V.94. P.1134.
15. Цидилковский И.М., Матвеев В.А. // В кн.: Физическая энциклопедия. - М.: Сов. Энциклопедия, 1990. - Т.2. С.76-77.
16. Hone J., Ellwood I., Muto М., Mizel A., Cohen M.L., Zettl A., Rinzler A.G., Smally R.E. // Phys. Rev. Lett. 1998. V.80, №5, p.1042.
17. Пекар С.И. Исследования по электронной теории кристаллов. - М., Гостехиздат, 1951. 204 С.
18. Huang К. and Rhys A. // Proc. Roy. Soc. 1950. V.A204. P.406.
19. Пекар С.И. // ЖЭТФ. 1952. Т.22, вып.6, с.641. - То же.: УФН. 1953. т.L, вып.2, с.197.
20. Toyazawa Т. // Techn. Report of ISSP (Tokyo). 1961. Ser. A, №16.
21. Вдовенков В.А., Косаковская З.Я., Колосов В.В., Мокеров В.Г. // ДАН. 1999. Т.365, №5, С.611-613.
22. Вдовенков В.А. // Изв. Вузов. Материалы электрон. техники. 2003. №1. С.57-62.
23. Vdovenkov V.A. // arXiv:cond-mat\9904299; arXiv:cond-mat\0207215.
24. Stierwalt D.L. and Potter R.F. // Phys. Rev. 1965. V.137. С.А1007.
25. Vdovenkov V.A. // arXiv:cond-mat\0207218. - To же: Наукоемкие технологии. 2002. №4. С.55-60. - То же: Микросистемная техника. 2002. №12. С.17-22.
26. Вдовенков В.А. // Материалы Междунар. научно-практич. конф. Интерматик-2003 «Фундаментальные проблемы радиоэлектронного приборостроения». М., 2003. С.69-70.
27. Вдовенков В.А. // Материалы Междунар. научно-технич. конф. «Тонкие пленки и слоистые структуры». М., 2002, ч.2. С.33-40. - То же.: Материалы Междунар. нуаучно-практич. конф. Полиматериалы-2003 «Межфазная релаксация в полиматериалах». М., 2003. Ч.2. С.111-112. 25.
28. Смит Г., Вакабаяси Н. Динамические свойства твердых тел и жидкостей. - М.: Мир, 1970. С.144-146.
29. Вдовенков В.А. Температурная ширина полос эффекта увлечения электронов фононами в материалах. Материалы Международной научно-практической конф. ИНТЕРМАТИК-2004, «Фундаментальные проблемы радиоэлектронного приборостроения», стр.102-105, Москва, 2004 г. То же: В.А.Вдовенков. Увлечение электронов фононами, обусловленное электронно-колебательными переходами в материалах. Известия ВУЗОВ Материалы электронной техники, №1, 2005, с.65-70.
30. Pastore G., Smargiassi E., Buda F. // Phys. Rev. A. 1991. V.44. №10. P.6334-6347.
31. Зи. С. Физика полупроводниковых приборов. Москва, Мир, 1984, т.1, с.283.
32. Марков М.Н. Приемники инфракрасного излучения. М., «Наука», 1968 г., с.40-48.
33. Анисимова И.Д., Викулин И.М., Заитов Ф.А., Курмашев Ш.Д. (под ред. В.И.Стафеева). Полупроводниковые фотоприемники: Ультрафиолетовый, видимый и ближний инфракрасный диапазоны спектра. - М.: Радио и связь, 1984. - 214 с.
34. Ван дер Зил А. Шумы при измерениях. М.: Мир, 1979 г., с.69-112, 129-220.
35. М.Херман. Полупроводниковые сверхрешетки. М.: Мир, 1989 г., 238 с.
36. Басе Ф., Булгаков А.А., Тетервов А.П.. Высокочастотные свойства полупроводников со сверхрешетками. М.: Наука, 1989 г., 287 с.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ЭФФЕКТИВНОГО ОСУЩЕСТВЛЕНИЯ ГИПЕРПРОВОДИМОСТИ И СВЕРХТЕПЛОПРОВОДНОСТИ | 2016 |
|
RU2626195C1 |
| СПОСОБ ГЕНЕРАЦИИ СВЕРХВЫСОКОЧАСТОТНЫХ ЭЛЕКТРОМАГНИТНЫХ КОЛЕБАНИЙ | 2007 |
|
RU2356128C2 |
| СПОСОБ ОСУЩЕСТВЛЕНИЯ ГИПЕРПРОВОДИМОСТИ И СВЕРХТЕПЛОПРОВОДНОСТИ | 2009 |
|
RU2497236C2 |
| Лютеций-марганцевый сульфид с гигантским продольным эффектом Нернста - Эттингсгаузена | 2021 |
|
RU2787206C1 |
| ТЕРМОЭЛЕКТРИЧЕСКИЙ ЭЛЕМЕНТ | 2008 |
|
RU2376681C1 |
| СВЕРХПРОВОДЯЩАЯ ПОЛУПРОВОДНИКОВАЯ НАНОСТРУКТУРА С КВАНТОВЫМИ ЯМАМИ | 2002 |
|
RU2227346C1 |
| СВЕРХПРОВОДНИКОВЫЙ БОЛОМЕТР | 2006 |
|
RU2321921C1 |
| ПОЛУПРОВОДНИКОВАЯ ГЕТЕРОЭПИТАКСИАЛЬНАЯ СТРУКТУРА С ВЫСОКИМ ВРЕМЕНЕМ ЖИЗНИ | 1993 |
|
RU2045106C1 |
| СПОСОБ УПРАВЛЕНИЯ ФОТОЧУВСТВИТЕЛЬНОСТЬЮ ДЕТЕКТОРА ЛАЗЕРНОГО ИЗЛУЧЕНИЯ В ИК-ДИАПАЗОНЕ | 2009 |
|
RU2418344C1 |
| ПОЛУПРОВОДНИКОВАЯ ГЕТЕРОЭПИТАКСИАЛЬНАЯ СТРУКТУРА ДЛЯ ФОТОПРИЕМНОЙ ЯЧЕЙКИ | 1993 |
|
RU2065224C1 |


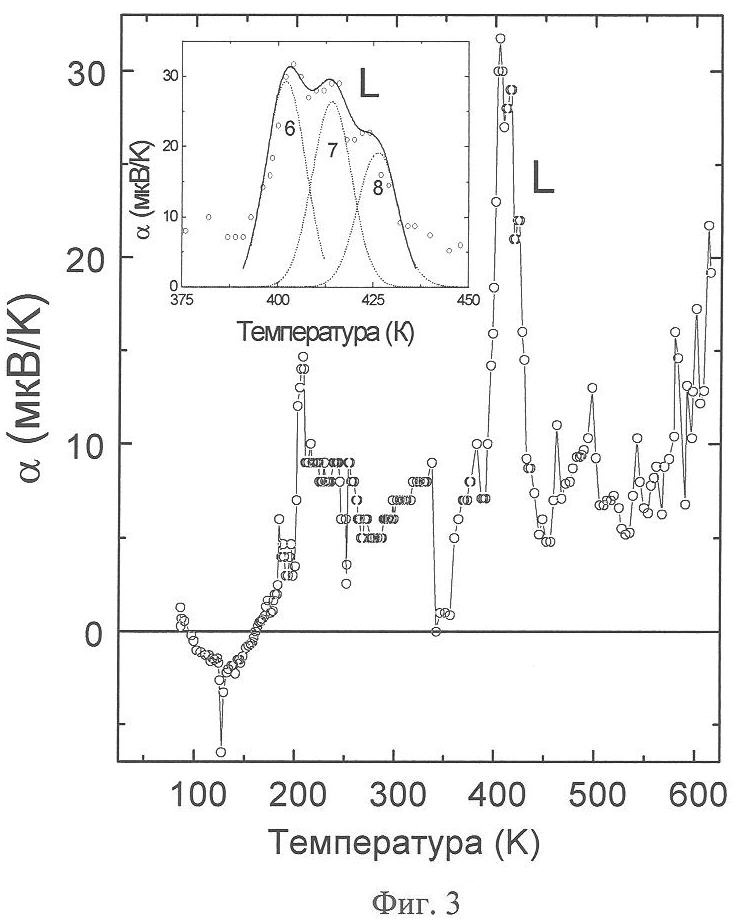








Изобретение относится к термоэлектричеству. Сущность: на поверхности или в объеме полупроводникового материала или слоя материала на полуизолирующей или диэлектрической подложке размещают электроды, образующие выпрямляющие контакты с материалом. При этом выбирают расстояние между электродами (D) значительно меньше глубины проникновения в материал электрического поля (L), (D<<L), вызванного контактной разностью потенциалов. Минимальное расстояние между электродами DMIN=20 мкм, максимальное расстояние между электродами DMAX=300 мкм. До, после или во время размещения электродов или до, после или во время создания зазора между электродами в материал вводят электронно-колебательные центры (ЭКЦ) в концентрации (N) от 2·1012 см-3 до 3·1017 см-3. Доводят температуру материала до температуры Дебая фононов материала, а в слое материала на подложке - до температуры Дебая фононов подложки. Между электродами создают разность температур ΔT=(T2-T1), такую, чтобы большая из температур T1 и Т2 не достигала температуры плавления электродов, материала или подложки, а меньшая из этих температур должна быть меньше Тm-2θ, где θ - полуширина полосы температурной зависимости увлечения электронов фононами. Технический результат: возможность осуществления эффекта при дебаевых температурах кристаллических фононов и возможность регулирования величины эффекта. 11 з.п. ф-лы, 1 табл., 11 ил.

 где m - эффективная масса носителя заряда (электрона) в материале, k - постоянная Больцмана,
где m - эффективная масса носителя заряда (электрона) в материале, k - постоянная Больцмана,  - постоянная Планка, р - номер электронно-колебательного уровня ЭКЦ, переходы на который используют для осуществления УЭФ.
- постоянная Планка, р - номер электронно-колебательного уровня ЭКЦ, переходы на который используют для осуществления УЭФ.
| ТЕРМОЭЛЕКТРИЧЕСКИЙ ПРЕОБРАЗОВАТЕЛЬ | 1998 |
|
RU2131156C1 |
| ТЕРМОЭЛЕКТРИЧЕСКИЙ ПРЕОБРАЗОВАТЕЛЬ И СПОСОБ ПРЕОБРАЗОВАНИЯ ТЕПЛОВОЙ ЭНЕРГИИ | 2001 |
|
RU2275713C2 |
| Способ обработки целлюлозных материалов, с целью тонкого измельчения или переведения в коллоидальный раствор | 1923 |
|
SU2005A1 |
| ВДОВЕНКОВ В.А | |||
| Увлечение электронов фононами, обусловленное электронно-колебательными переходами в материалах | |||
| - Известия ВУЗов, Материалы электронной техники, 2005, №1, с.65-70. | |||
Авторы
Даты
2009-03-20—Публикация
2006-11-07—Подача