Изобретение относится к области измерительной техники и может быть использовано для определения параметра оптической анизотропии кубических кристаллов, относящихся к классу m3m, 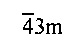 или 432 симметрии.
или 432 симметрии.
В оптических элементах твердотельных лазеров неизбежно возникают тепловые потери, которые приводят к таким негативным эффектам, как возникновение тепловой линзы и термонаведенной деполяризации излучения. Термонаведенная деполяризация в оптических элементах является одним из главных факторов, сдерживающих увеличение средней мощности твердотельных лазеров. Термонаведенное двулучепреломление, вызванное в оптических элементах фотоупругим эффектом, приводит к тому, что исходно оптически изотропная среда становится анизотропной. Термонаведенные собственные поляризации линейны и ортогональны друг другу, однако различны в различных точках поперечного сечения элемента. Разность фаз термонаведенного двулучепреломления также является функцией поперечных координат. В результате изначально поляризованное излучение после прохождения элемента становится деполяризованным.
Под деполяризованным излучением понимается излучение, у которого поляризация постоянна во времени, но изменяется от точки к точке поперечного сечения. Под локальной степенью деполяризации излучения Г понимается отношение интенсивности деполяризованной компоненты излучения к суммарной интенсивности излучения в двух поляризациях в каждой точке поперечного сечения. Интегрирование распределения Г по поперечному сечению с учетом формы пучка, либо измерение отношения мощности в деполяризованной компоненте к суммарной мощности в двух поляризациях дает величину интегральной степени деполяризации излучения γ.
Негативные последствия термонаведенного двулучепреломления очевидны. Прежде всего, это потери мощности, равные интегральной степени деполяризации в поляризованном излучении. Кроме того, исходное поляризованное излучение получает в процессе прохождения оптического элемента модуляцию, связанную с тем, что распределение локальной степени деполяризации существенно неоднородно по поперечному сечению. Таким образом, вызванные двулучепреломлением потери мощности в исходной пространственно-поляризационной моде, например, в линейно-поляризованном гауссовом пучке, заметно больше, чем интегральная степень деполяризации γ.
Одной из важнейших характеристик кубических монокристаллических оптических сред, является параметр оптической анизотропии ξ. Он представляет собой комбинацию компонент пьезо-упругого тензора π (R.Е. Joiner, J. Marburger, and W.H. Steier, "Elimination of stress-induced birefringence effects in single crystal high-power laser windows," Appl. Phys. Lett. 30 (9), 485-486 (1977)):

и определяет направления осей термонаведенного двулучепреломления в образце кубического монокристалла заданной ориентации. Это свойство имеет ряд важных следствий: величина ξ, задает оптимальную ориентацию кристаллографических осей оптического элемента, выполненного из кубического монокристалла, определяет возможности компенсации деполяризации, кроме того, ξ характеризует астигматизм термолинзы. Знак параметра оптической анизотропии также имеет большое значение. Известно, что при отрицательных значениях ξ имеется выделенная ориентация кристаллографических осей оптического элемента [[С]], при которой направления осей термонаведенного двулучепреломления не зависят от точки поперечного сечения, т.е. термонаведенной деполяризации не возникает (Ilya Snetkov, Anton Vyatkin, Oleg Palashov, and Efim Khazanov "Drastic reduction of thermally induced depolarization in CaF2 crystals with [111] orientation", OPTICS EXPRESS, 20 (12), pp. 13357-13367, 2012). Вдобавок отрицательное значение параметра ξ позволяет реализовывать схемы компенсации деполяризации, которые не могут быть реализованы при положительных ξ, (A.G. Vyatkin, I.L. Snetkov, O.V. Palashov, and E.A. Khazanov, "Self-compensation of thermally induced depolarization in CaF2 and definite cubic single crystals", Opt. Express, 21 (19), 22338-22352 (2013)).
Исследование термонаведенного двулучепреломления в изоляторах Фарадея показало, что параметр ξ, сохраняет свою универсальность и уникальность в магнитооптических средах (см. E. Khazanov, N. Andreev, O. Palashov, A. Poteomkin, A. Sergeev, O. Mehl, and D. Reitze, Applied Optics 41, 483 (2002)), в том числе и керамических (см. M.A. Kagan and E.A. Khazanov, Applied Optics 43, 6030 (2004)).
В связи с этим знание величины ξ для кубических монокристаллов, используемых в лазерах с высокой средней мощностью, является принципиально важным.
В последнее время в связи с развитием технологий производства оптических материалов появляется много новых перспективных лазерных и магнитооптических сред, термооптические характеристики которых требуют изучения.
Если известны компоненты пьезооптического тензора πij, то значение ξ вычисляется по формуле (1). Для измерения πij требуется специальное лабораторное оборудование, отработанная методика измерения и калибровки, без которых точность измерения невелика. Из-за этого для многих кубических монокристаллов значения πij на нужной длине волны излучения и при необходимой температуре кубического монокристалла неизвестны, а для других в разных работах приводятся различные значения. Они могут давать различные ξ, существенно отличающиеся не только по величине, но и по знаку.
Наиболее близким к предложенному техническому решению является способ определения параметра оптической анизотропии, основанный на измерении распределения локальной степени деполяризации, возникающей при прохождении мощного лазерного излучения через цилиндрический образец кристалла с ориентацией [001] с последующим его анализом (Ilya Snetkov, Anton Vyatkin, Oleg Palashov, and Efim Khazanov "Drastic reduction of thermally induced depolarization in CaF2 crystals with [111] orientation", OPTICS EXPRESS, 20 (12), pp. 13357-13367, 2012). Распределение локальной степени деполяризации в данном случае представляет собой "мальтийский крест". Измеряют зависимость угла наклона "мальтийского креста" Φ относительно плоскости поляризации лазерного излучения от угла поворота кристалла θ вокруг оси, совпадающей с направлением распространения излучения. По зависимости Φ(θ), добившись максимального совпадения снятой зависимости с построенной теоретически, определяют величину параметра ξ (т.е. как знак параметра ξ, так и его абсолютное значение).
Основным недостатком способа-прототипа является необходимость использования образцов кубических монокристаллов только с ориентацией [001], т.е. когда ось образца совпадает с направлением одной из кристаллографических осей. В случае отклонения ориентации от этой требуется вырезание соответствующего образца из имеющегося, что ведет к сокращению его объема, длины и световой апертуры. Экспериментальные образцы новых сред зачастую бывают выращены с ориентацией, отличной от [001] и, как правило, небольших размеров, не позволяющих изготовить из них новые образцы с желаемой ориентацией [001].
Задачей, на решение которой направлено настоящее изобретение, является разработка способа определения величины параметра оптической анизотропии ξ в цилиндрическом образце кубического монокристалла, относящегося к классу симметрии m3m, 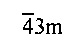 или 432, с произвольной известной ориентацией кристаллографических осей.
или 432, с произвольной известной ориентацией кристаллографических осей.
Технический результат в разработанном способе достигается за счет того, что, как и в способе-прототипе, измеряют распределение локальной степени деполяризации лазерного излучения, прошедшего через цилиндрический образец кубического монокристалла с известной ориентацией кристаллографических осей.
Новым разработанном способе является то, что для измерения используют образец с произвольной ориентацией кристаллографических осей, приводят образец в положение, при котором распределение локальной степени деполяризации в образце представляет собой «мальтийский крест», измеряют угол наклона «мальтийского креста» Φ относительно плоскости поляризации лазерного излучения, и величину параметра оптической анизотропии кубического монокристалла определяют из величины этого угла и известной ориентации кристаллографических осей образца.
Способ поясняется следующими чертежами.
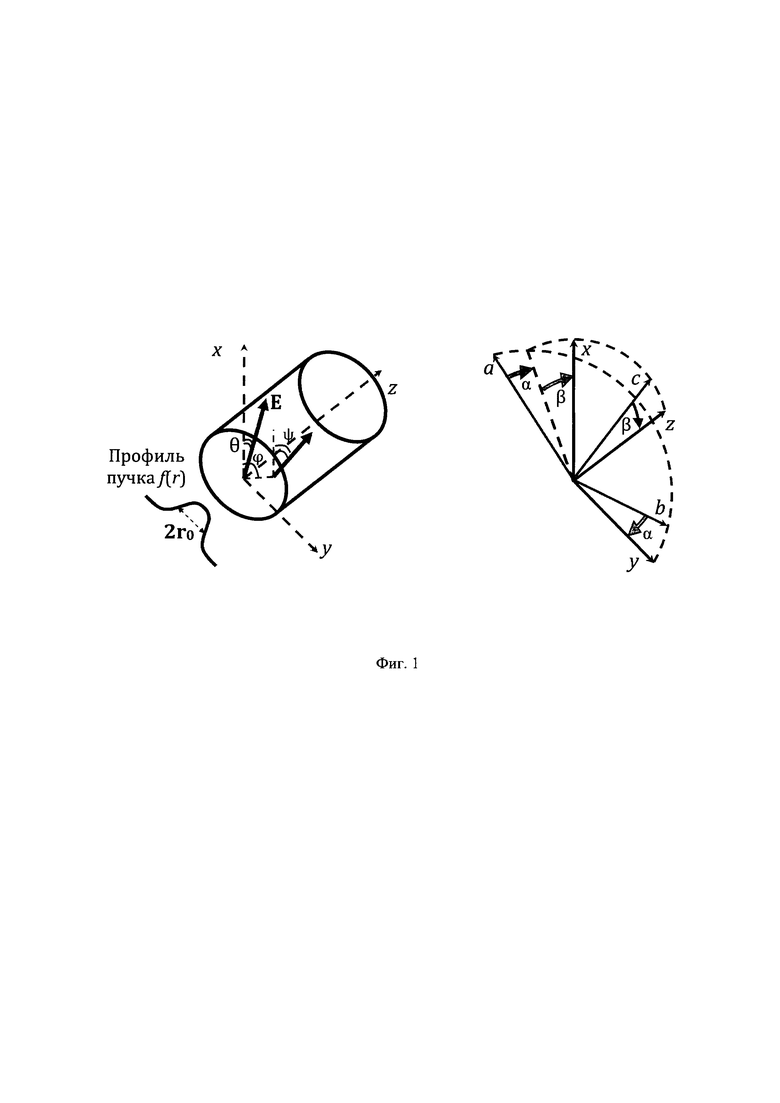
На Фиг. 1 представлены геометрия цилиндрического образца кубического монокристалла (слева) с произвольной ориентацией кристаллографических осей и переход от системы координат (abc), связанной с кристаллической решеткой, в лабораторную (xyz) (справа).
На Фиг. 2 представлены типичный вид распределения локальной степени деполяризации, наводимой в образце кубического монокристалла с произвольной ориентацией (слева), и распределение в виде "мальтийского креста" (справа).
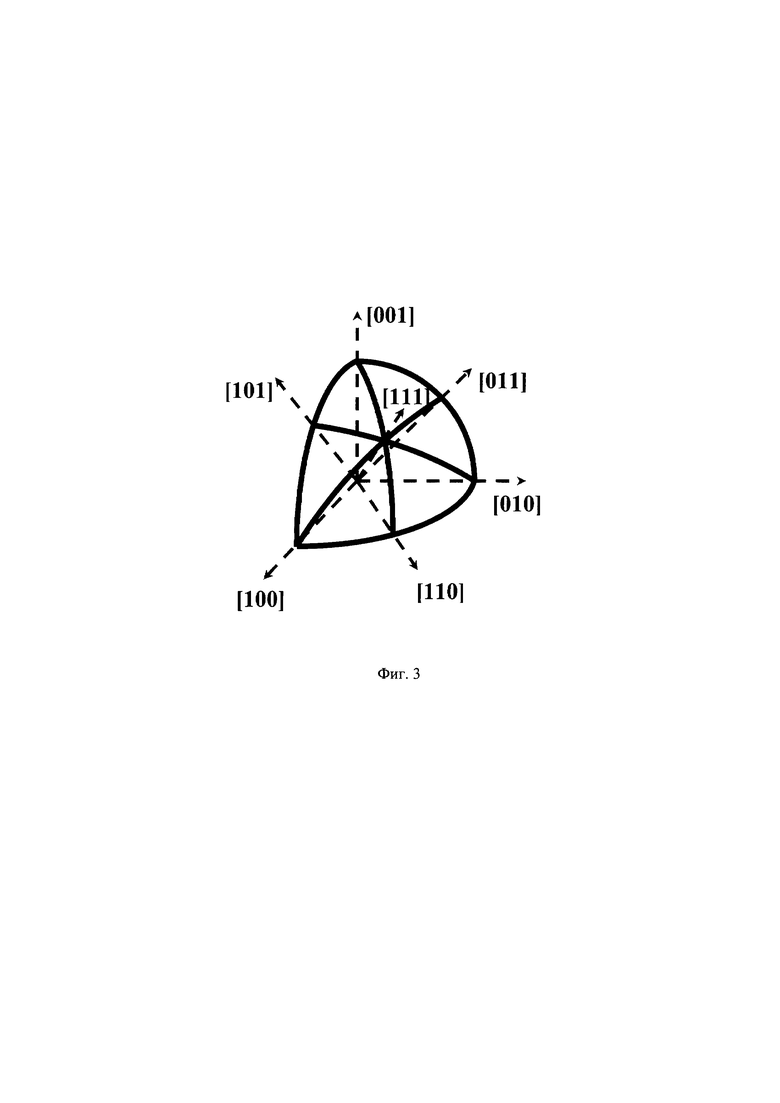
На Фиг. 3 представлены ориентации кристаллографических осей образца кубического монокристалла, непригодные для определения параметра оптической анизотропии предлагаемым методом.
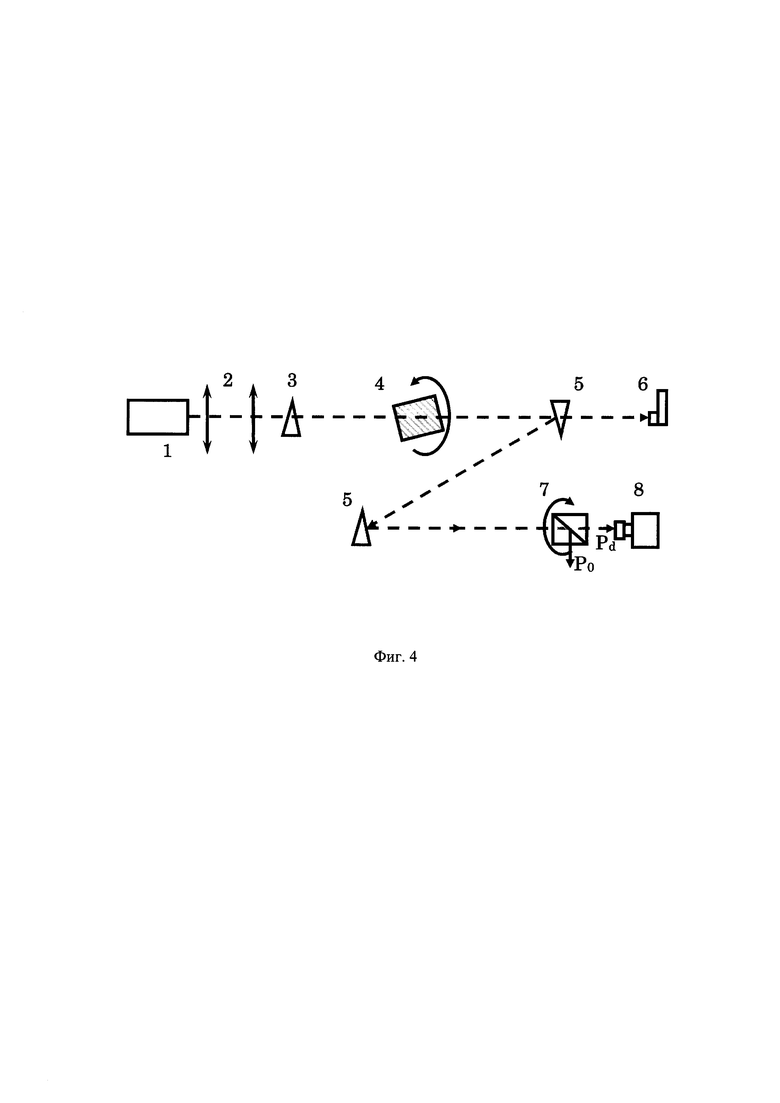
На Фиг. 4 представлена схема измерения локальной степени деполяризации излучения, прошедшего через цилиндрический образец кубического монокристалла с известной ориентацией кристаллографических осей.
Термонаведенное двулучепреломление может быть описано с помощью добавки ΔВ к тензору диэлектрической непроницаемости В (J.F. Nye, Physical Properties of Crystals (Oxford UniversityPress, 1964)). Произвольная ориентация образца кубического монокристалла может быть задана при помощи двух углов Эйлера α и β (W. Koechner and D.К. Rice, "Birefringence of YAG:Nd laser rods as a function of growth direction," J. Opt. Soc. Am. 61, 758-766 (1971)). Для перехода из системы координат (abc), связанной с кристаллической решеткой, в лабораторную систему координат (xyz) необходимо сначала повернуть систему на угол α вокруг оси c, а затем на угол β вокруг оси b (см. Фиг. 1). Варьируя значения α и β, можно получить любую ориентацию кристалла. Угол наклона оси наведенного двулучепреломления ψ относительно оси x (см. Фиг. 1) и разность фаз собственных поляризаций δ выражаются через ΔВij следующим образом:

где n0 - показатель преломления в образце в отсутствие напряжений.
Выражения для элементов тензора ΔВ для цилиндрического образца кубического монокристалла произвольной ориентации, заданной углами Эйлера α и β, с длиной L, много большей радиуса R0, были получены в (Е. Khazanov, N. Andreev, О. Palashov, A. Poteomkin, А. Sergeev, О. Mehl, and D.H. Reitze, "Effect of terbium gallium garnet crystal orientation on the isolation ratio of a Faraday isolator at high average power," Appl. Opt. 41 (3), 483-492 (2002)) в случае аксиально симметричного профиля пучка и бокового теплоотвода:
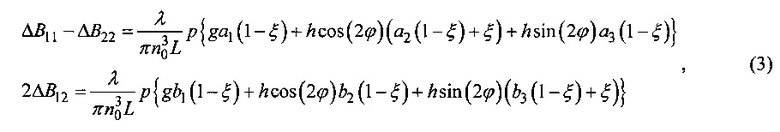
где
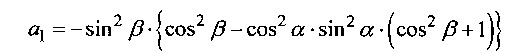 ,
,
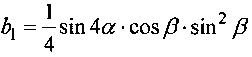 ,
,
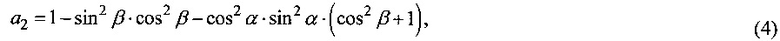
b2=а3,
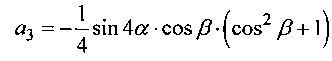 ,
,
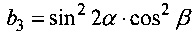 ,
,
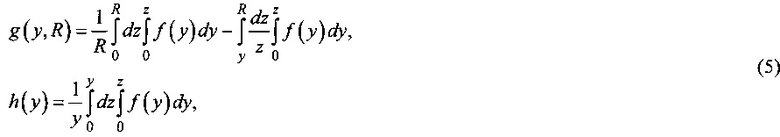
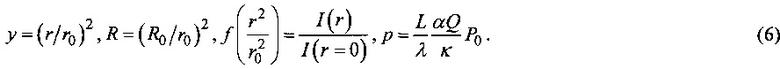
Здесь I(r) - распределение интенсивности излучения лазерного пучка, а r0 и  - его радиус и профиль соответственно. Обозначение p, которое мы будем использовать в дальнейшем, называется нормированной мощностью излучения.
- его радиус и профиль соответственно. Обозначение p, которое мы будем использовать в дальнейшем, называется нормированной мощностью излучения.
Локальная степень деполяризация Г в случае слабого двулучепреломления задается известным выражением (А.V. Mezenov, L.N. Soms, and A.I. Stepanov, Termooptika tverdotel'nykh lazerov [Thermooptics of solid-state lasers] (Mashinostroenie, Leningrad, 1986)):

В этом случае типичная картина распределения локальной степени деполяризации для кристалла произвольной ориентации имеет вид, изображенный на Фиг. 2 слева. При этом при определенном значении угла θ между плоскостью поляризации и осью x эта картина принимает вид так называемого "мальтийского креста" (Фиг. 2 справа)
В выделенных ориентациях [001] и [111] структура распределения локальной степени деполяризации принимает вид креста при любом значении угла θ, в случае же произвольной ориентации только при определенных значениях. Стоит также отметить, что крест в общем случае отклонен от плоскости поляризации проходящего излучения на некоторый угол.
Условием возникновения картины распределения локальной степени деполяризации, изображенной на Фиг. 2 справа, является равенство нулю локальной степени деполяризации в центре лазерного пучка: Г(r=0)=0. Как следует из формулы (7), это условие выполняется, когда ось наведенного двулучепреломления в центре цилиндрического образца кубического монокристалла либо лежит в плоскости поляризации проходящего излучения, либо ортогональна ей, т.е. на углы между осью x и осью двулучепреломления ψ(r=0) и плоскостью поляризации θ* соответственно накладывается условие:

Угол, на который отклонена ось двулучепреломления относительно оси x может быть найден из (2) после подстановки в него выражений (3). Поскольку при r=0 в формулах (5) величина h принимает значение равное нулю, то этот угол определяется простым выражением:

т.е. он определяется только ориентацией цилиндрического образца кубического монокристалла и не зависит ни от материальных характеристик среды, ни от параметров лазерного пучка.
Анализируя выражение (7), можно найти угол наклона "мальтийского креста", выразив его через углы Эйлера и параметр оптической анизотропии. Этот угол соответствует такой угловой координате ϕ на графике распределения локальной степени деполяризации (Фиг. 2 справа), при которой последняя отсутствует для любого значения радиальной компоненты: Г(r, ϕ=Φ)=0. После всех подстановок получим:
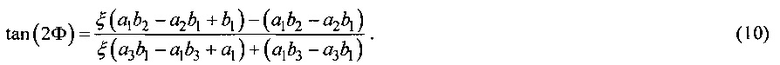
Как видно, этот угол зависит только от ориентации кристалла и параметра оптической анизотропии. Таким образом, получив картину распределения локальной степени деполяризации, аналогичную изображенной на Фиг. 2 справа, и измерив угол наклона креста Φ, мы можем в цилиндрического образце кубического монокристалла с известной ориентацией определить ξ. Из формулы (10) получаем:
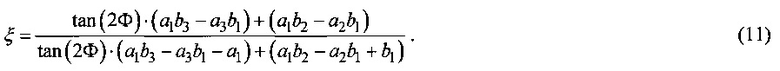
Угол наклона креста Φ задается в лабораторной системе координат, связанной с кристаллической решеткой образца. На практике удобнее измерять угол наклона креста в системе координат, не связанной с кристаллической решеткой, поскольку обычно плоскость поляризации излучения фиксирована, а угол θ варьируется вращением образца вокруг своей оси. В этом случае в неподвижной системе угловые координаты ϕ' могут быть выражены через координаты лабораторной системы ϕ соотношением ϕ'=ϕ-θ. Таким образом, на камере, регистрирующей распределение деполяризованной компоненты излучения, наблюдаемый угол наклона креста Φobs будет равен:

Тогда для экспериментального определения значения ξ, в формулу (11) вместо угла Φ необходимо подставить значение Φobs+0* после чего получим окончательную формулу для определения параметра оптической анизотропии кубического монокристалла, относящегося к классу симметрии m3m,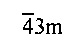 или 432, с произвольной известной ориентацией кристаллографических осей:
или 432, с произвольной известной ориентацией кристаллографических осей:
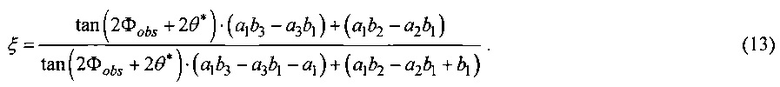
Однако измерение параметра оптической анизотропии описанным методом возможно не при любой ориентации кристаллографических осей в исследуемом цилиндрическом образце кубического монокристалла. Анализ выражения (10) помогает определить эти «невыгодные ориентации». Перепишем (10) в виде:

Коэффициенты mi определяются только ориентацией цилиндрического образца кубического монокристалла и одновременное попарное равенство некоторых из них нулю приводит к тому, что угол Φ перестает зависеть от ξ. Как можно видеть, зависимость Φ от ξ исчезает, если равны нулю пары коэффициентов: m1 и m2, m1 и m3, m2 и m4, m3 и m4. Подставляя в mi, коэффициенты ai и bi, определенные в системе (4) и решая системы уравнений

получим значения углов Эйлера для ориентации, при которых провести измерение ξ описанным методом невозможно:

При выполнении хотя бы одного из условий (16) измерить ξ, не удастся. Если учесть все эквивалентные ориентации, получим распределение ориентаций, непригодных для проведения измерений (см. Фиг. 3)
Сплошные линии на Фиг. 3 задают ориентации, соответствующие (16) и эквивалентные им. Для примера пунктирными стрелками указаны частные случаи таких ориентаций. При попадании ориентации исследуемого образца кубического монокристалла в область непригодных проблема может быть решена контролируемым заклонением оси образца относительно направления лазерного пучка, проходящего через образец. Таким образом, направление распространения пучка в образце кубического монокристалла будет выведено из области непригодных и будет известным, тогда дальнейшее измерение может быть проведено вышеописанным способом.
Способ определения величины параметра оптической анизотропии ξ по п. 1 формулы осуществляют следующим образом. Для определения необходим цилиндрический образец кубического монокристалла с известной ориентацией кристаллографических осей. Образец помещают в схему измерения термонаведенной деполяризации.
Схема измерения представлена на Фиг. 4. Излучение мощного лазера 1 направляют через телескоп 2 и шпатовый клин 3, после чего линейно поляризованное излучение пропускают через исследуемый цилиндрический образец кубического монокристалла 4 с известной ориентацией кристаллографических осей, а затем осуществляют его деление клиньями, выполненными из плавленого кварца 5. Основную порцию излучения направляют в поглотитель 6, а ослабленную в ~103 раз часть направляют на призму Глана 7, плоскость пропускания которой скрещена с плоскостью поляризации исходного излучения. Через нее проходит деполяризованная компонента излучения Рd, которую регистрируют CCD камерой 8. Далее вращением цилиндрического образца кубического монокристалла 4 вокруг направления распространения излучения добиваются его положения, при котором картина распределения локальной степени деполяризации представляет собой "мальтийский крест". Затем измеряют величину угла наклона "мальтийского креста" относительно плоскости поляризации исходного излучения и из этого значения и информации об ориентации кристаллографических осей цилиндрического образца кубического монокристалла 4 находят величину параметра оптической анизотропии кубического монокристалла согласно (13).
Таким образом, предлагаемый способ по п. 1 формулы позволяет определить величину параметра оптической анизотропии ξ в цилиндрическом образце кубического монокристалла, относящегося к классу симметрии m3m, 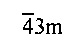 или 432, с произвольной известной ориентацией кристаллографических осей.
или 432, с произвольной известной ориентацией кристаллографических осей.
Такой подход может быть востребован наряду с существующими отработанными методиками измерений, поскольку обладает двумя важными преимуществами. Во-первых, позволяет проводить измерения, не разрушая имеющиеся элементы с ориентацией отличной от [001]. Во-вторых, может оказаться безальтернативным при измерениях уникальных новых оптических сред, существующих в малом (иногда единственном) числе экземпляров небольшого объема и произвольной ориентации.
Как правило, кристаллы для оптических элементов лазера, которые обычно выращивают методом вытягивания из раствора либо расплава, имеют цилиндрически симметричную форму и доводятся до цилиндрической формы последующей обработкой. Поэтому предлагаемое техническое решение обладает большой актуальностью.
| название | год | авторы | номер документа |
|---|---|---|---|
| ОПТИЧЕСКИЙ ВЕНТИЛЬ С КОМПЕНСАЦИЕЙ ТЕРМОНАВЕДЕННОЙ ДЕПОЛЯРИЗАЦИИ В МАГНИТНОМ ПОЛЕ | 2015 |
|
RU2619357C2 |
| КОМПЕНСАТОР ТЕРМОНАВЕДЕННОЙ ДЕПОЛЯРИЗАЦИИ В ПОГЛОЩАЮЩЕМ ОПТИЧЕСКОМ ЭЛЕМЕНТЕ ЛАЗЕРА | 2013 |
|
RU2527257C1 |
| ОПТИЧЕСКИЙ ВЕНТИЛЬ С МОНОКРИСТАЛЛИЧЕСКИМ МАГНИТООПТИЧЕСКИМ ЭЛЕМЕНТОМ ДЛЯ ЛАЗЕРОВ БОЛЬШОЙ МОЩНОСТИ | 2015 |
|
RU2601390C1 |
| Изолятор Фарадея с кристаллическим магнитооптическим ротатором для лазеров большой мощности | 2016 |
|
RU2637363C2 |
| УСТРОЙСТВО ДЛЯ КОМПЕНСАЦИИ ТЕРМОНАВЕДЕННОЙ ДЕПОЛЯРИЗАЦИИ В ПОГЛОЩАЮЩЕМ ОПТИЧЕСКОМ ЭЛЕМЕНТЕ ЛАЗЕРА | 2011 |
|
RU2465698C2 |
| ОПТИЧЕСКИЙ ВЕНТИЛЬ С КОМПЕНСАЦИЕЙ ТЕРМОНАВЕДЕННОЙ ДЕПОЛЯРИЗАЦИИ ДЛЯ ЛАЗЕРОВ БОЛЬШОЙ МОЩНОСТИ | 2011 |
|
RU2458374C1 |
| ИЗОЛЯТОР ФАРАДЕЯ ДЛЯ ЛАЗЕРНЫХ ПУЧКОВ С КВАДРАТНЫМ ПОПЕРЕЧНЫМ ПРОФИЛЕМ РАСПРЕДЕЛЕНИЯ ИНТЕНСИВНОСТИ | 2014 |
|
RU2589754C2 |
| Изолятор Фарадея для лазеров с высокой средней мощностью излучения | 2017 |
|
RU2690037C2 |
| ИЗОЛЯТОР ФАРАДЕЯ НА ПОСТОЯННЫХ МАГНИТАХ ДЛЯ ЛАЗЕРОВ БОЛЬШОЙ МОЩНОСТИ | 2013 |
|
RU2559863C2 |
| ИЗОЛЯТОР ФАРАДЕЯ ДЛЯ НЕПОЛЯРИЗОВАННОГО ЛАЗЕРНОГО ИЗЛУЧЕНИЯ | 2015 |
|
RU2603229C1 |

Способ определения параметра оптической анизотропии кубического монокристалла, относящегося к классу симметрии m3m, 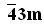 или 432, в котором производят измерение распределения локальной степени деполяризации лазерного излучения, прошедшего через цилиндрический образец кубического монокристалла с произвольной известной ориентацией кристаллографических осей. При реализации способа приводят образец в положение, при котором распределение локальной степени деполяризации в образце представляет собой «мальтийский крест», измеряют угол наклона «мальтийского креста» относительно плоскости поляризации лазерного излучения. Величину параметра оптической анизотропии кубического монокристалла определяют из величины этого угла и известной ориентации кристаллографических осей образца. Технический результат заключается в разработке способа определения величины параметры оптической анизотропии в цилиндрическом образце кубического монокристалла с произвольной известной ориентацией кристаллографических осей. 4 ил.
или 432, в котором производят измерение распределения локальной степени деполяризации лазерного излучения, прошедшего через цилиндрический образец кубического монокристалла с произвольной известной ориентацией кристаллографических осей. При реализации способа приводят образец в положение, при котором распределение локальной степени деполяризации в образце представляет собой «мальтийский крест», измеряют угол наклона «мальтийского креста» относительно плоскости поляризации лазерного излучения. Величину параметра оптической анизотропии кубического монокристалла определяют из величины этого угла и известной ориентации кристаллографических осей образца. Технический результат заключается в разработке способа определения величины параметры оптической анизотропии в цилиндрическом образце кубического монокристалла с произвольной известной ориентацией кристаллографических осей. 4 ил.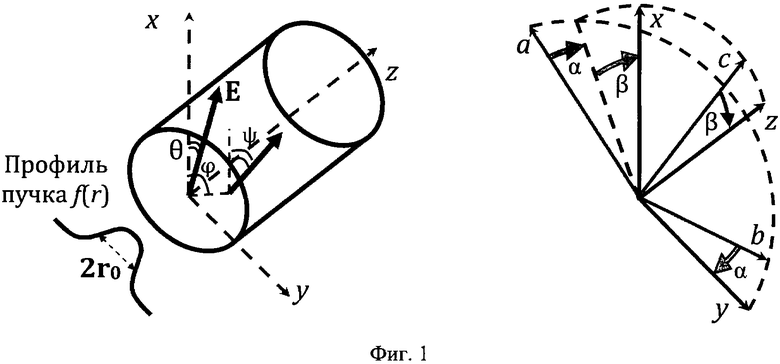
Способ определения параметра оптической анизотропии кубического монокристалла, относящегося к классу симметрии m3m, 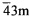 или 432, включающий измерение распределения локальной степени деполяризации лазерного излучения, прошедшего через цилиндрический образец кубического монокристалла с известной ориентацией кристаллографических осей, отличающийся тем, что для измерения используют образец с произвольной ориентацией кристаллографических осей, приводят образец в положение, при котором распределение локальной степени деполяризации в образце представляет собой «мальтийский крест», измеряют угол наклона «мальтийского креста» Ф относительно плоскости поляризации лазерного излучения, и величину параметра оптической анизотропии кубического монокристалла определяют из величины этого угла и известной ориентации кристаллографических осей образца.
или 432, включающий измерение распределения локальной степени деполяризации лазерного излучения, прошедшего через цилиндрический образец кубического монокристалла с известной ориентацией кристаллографических осей, отличающийся тем, что для измерения используют образец с произвольной ориентацией кристаллографических осей, приводят образец в положение, при котором распределение локальной степени деполяризации в образце представляет собой «мальтийский крест», измеряют угол наклона «мальтийского креста» Ф относительно плоскости поляризации лазерного излучения, и величину параметра оптической анизотропии кубического монокристалла определяют из величины этого угла и известной ориентации кристаллографических осей образца.
| RU 2506566 C1, 10.02.2014 | |||
| Способ определения оптических анизотропных параметров кристаллов | 1990 |
|
SU1749784A1 |
| JP 2012103222 A, 31.05.2012 | |||
| US 5838453 A1, 17.11.1998. | |||
Авторы
Даты
2017-08-31—Публикация
2016-10-20—Подача