Предлагаемое изобретение относится к способам исследования локальных параметров плазмы в газоразрядных источниках плазмы, применяемых в составе технологических источников плазмы или ионов, плазменных или ионных двигателей.
Известен способ локальной диагностики максвелловской плазмы газового разряда постоянного тока с помощью одиночного зонда Ленгмюра путем введения в газоразрядное пространство тонкого зондодержателя с зондом на конце, например, в виде отрезка металлической нити, подключенной через источник зондового напряжения к металлическому корпусу газоразрядного устройства или дополнительному опорному электроду, регистрации его вольт-амперной характеристики по точкам изменением зондового напряжения в обе стороны от плавающего потенциала и определения концентрации электронов и их температуры графической обработкой зондовой характеристики на основе теории Ленгмюра и Мотт-Смита [1]. Недостаток данного способа состоит в применяемом виде обработки зондовых характеристик и в предположении максвелловской функции распределения электронов по энергиям (ФРЭЭ), что снижает точность получаемых результатов.
Известен способ локальной диагностики плазмы любого вида с помощью одиночного зонда Ленгмюра путем введения в газоразрядное пространство тонкого зондодержателя с зондом на конце, например, в виде отрезка металлической нити, подключенной через источник пилообразного зондового напряжения к металлическому корпусу газоразрядного устройства или дополнительному опорному электроду с принятием мер по защите зондовой цепи от электрических наводок и очистке собирающей поверхности зонда, автоматизированной регистрации его вольт-амперной характеристики подачей на зонд серии пилообразных импульсов напряжения с последующим усреднением набора характеристик и определения функции распределения электронов по энергиям (ФРЭЭ), концентрации электронов, их температуры и пространственного потенциала плазмы обработкой усредненной зондовой характеристики методом Дрювестейна, пригодным для любой формы реальной ФРЭЭ [2]. Данный способ, как наиболее близкий к заявленному техническому решению, принят в качестве прототипа.
Его недостатком является ограниченность набора измеряемых параметров изучаемой плазмы, в который не входят толщина слоя объемного заряда на собирающей поверхности зонда и масса ионов.
Техническим результатом данного предложения является расширение набора измеряемых параметров изучаемой плазмы определением толщины зондового слоя и массы ионов в том случае, когда ФРЭЭ плазмы близка к функции Максвелла. Первый из дополнительных параметров важен для анализа корректности зондовой теории, применяемой при интерпретации зондовых измерений, а второй - для контроля чистоты плазмообразующего вещества. Максвелловская плазма достаточно широко применяется в технике, например в газоразрядных ионных двигателях и источниках ионов и плазмы, в плазменных двигателях и технологических установках, поэтому дополнительные результаты зондовой диагностики существенно обогатят проведение плазменных исследований.
Заявленный технический результат достигается тем, что в известном способе локальной диагностики максвелловской плазмы с помощью одиночного цилиндрического зонда Ленгмюра путем введения в газоразрядное пространство тонкого зондодержателя с зондом на конце в виде отрезка металлической нити, подключенной через источник зондового напряжения к металлическому корпусу газоразрядного устройства или дополнительному опорному электроду с принятием мер по защите зондовой цепи от электрических наводок и по очистке собирающей поверхности зонда, регистрации его вольт-амперной характеристики изменением зондового напряжения в обе стороны от плавающего потенциала и определения функции распределения электронов по энергиям, концентрации электронов, их температуры и потенциала плазмы, и в случае близости измеренного распределения электронов по энергиям к функции Максвелла, находят плотность тока ионов на зонд под плавающим потенциалом jif по соответствующей потенциалу плазмы плотности электронного тока насыщения на зонд jes, используя формулу Больцмана jif=jes⋅exp(-ΔVf/Te), где ΔVf - разность между потенциалом плазмы и плавающим потенциалом зонда, Te, В - температура электронов, полученную величину jif выражают двояким образом: а) через уравнение Бома jif=СБЦил⋅(R/a)ene(2eTe/Mi)1/2, где СБЦил=1,23 - экспериментально подтвержденный коэффициент Бома для цилиндрического зонда, R - внешний радиус зондового слоя объемного заряда, а - радиус цилиндрического зонда, е - элементарный заряд, ne - концентрация электронов, Mi - масса иона, и б) через уравнение Чайлда-Ленгмюра-Богуславского jif=(4ε0/9)(2e/Mi)1/2(ΔVf3/2/aRAЛ), где ε0 - диэлектрическая постоянная вакуума, АЛ - зависящая от отношения R/a безразмерная константа Ленгмюра, и совместным решением указанных уравнений находят величины R и Mi. Кроме того, при несоответствии реального зондового слоя модели Чайлда-Ленгмюра-Богуславского, исключающей проникновение электронов в зондовый слой, внешний радиус R зондового слоя корректируют по модели зондового слоя, допускающей такое проникновение, например, согласно «ступенчато-фронтальной» модели величину R находят из выражения RСФ=0,692⋅R+0,3816⋅a, где RСФ - радиус зондового слоя, соответствующий «ступенчато-фронтальной» модели.
Экспериментальный коэффициент Бома СБЦил=1,23 был определен в специальном чистом эксперименте с известной величиной массы ионов Mi [3]. Измерения классическим цилиндрическим зондом Ленгмюра были выполнены в высокочастотной (ВЧ) ксеноновой плазме ВЧ индукционного (ВЧИ) разряда на частоте 2 МГц, при давлении 2-10-3 мм рт.ст. и при поглощенной разрядом ВЧ мощности до 175 Вт. Аккуратные измерения с помощью зондовой станции VGPS-12 [2] ФРЭЭ и традиционного набора зондовых параметров плазмы показали, что данная газоразрядная плазма достаточно близко соответствовала максвелловской среде. Эти данные на основе предварительного использования заявленного способа путем решения системы приведенных в нем уравнений позволили определение реальных величин внешнего радиуса зондового слоя R (или толщины этого слоя δ=R-а) и коэффициента Бома СБЦил≈1,23. На этой основе и был построен заявленный способ локальной диагностики плазмы в экспериментах общего характера, в которых средняя величина ионной массы может отличаться от паспортных данных по плазмообразующему газу.
Выражение для определения скорректированного радиуса зондового слоя RСФ было получено аппроксимацией поправочных данных, приведенных в работе [4]. В экспериментальной физике применяются различные методы обработки зондовых характеристик: графический метод Ленгмюра, метод наложения на зондовый потенциал ВЧ компоненты малой амплитуды, методы Лафрамбуаза, орбитальный, Дрювестейна и др. Последний не требует каких-либо априорных предположений о форме ФРЭЭ и начинается с прямого измерения данной функции, что является его важным достоинством.
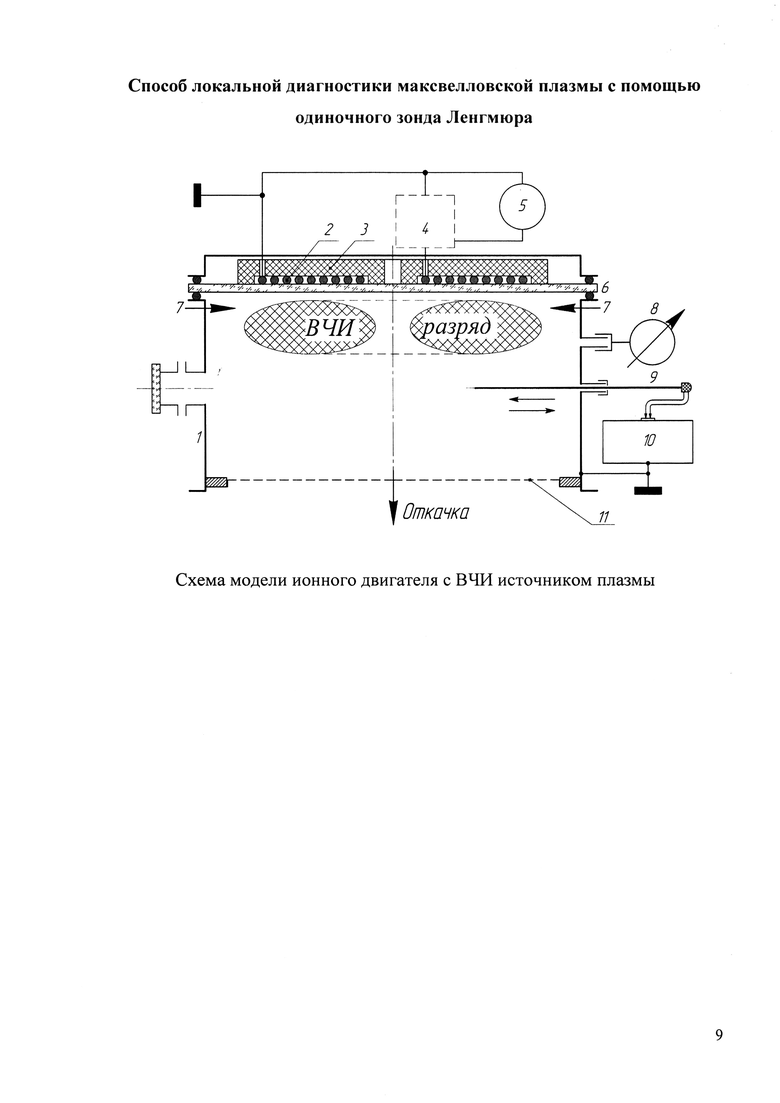
Примером реализации предложенного способа является организация аккуратной зондовой диагностики ксеноновой плазмы в ВЧ индукционном (ВЧИ) газоразрядном узле модельного ВЧ ионного двигателя (ВЧИД) с торцевым плоским индуктором и ферритовым сердечником, схема которого представлена на Фигуре. Здесь 1 - вакуумная камера, 2 - индуктор, 3 - ферритовый сердечник, 4 - согласующее устройство, 5 - ВЧ генератор, 6 - кварцевое окно, отделяющее индуктор от плазмы, 7 - подача рабочего газа - ксенона, 8 - датчик давления, 9 - зонд Ленгмюра, 10 - автоматизированная зондовая станция VGPS-12, 11 - газодинамический имитатор ионно-оптической системы ионного двигателя, обеспечивший давление в газоразрядном пространстве, равное рабочему давлению в модели ВЧИД при номинальном расходе ксенона.
В данном эксперименте зонд Ленгмюра был выполнен в виде вольфрамовой нити диаметра 0,15 мм и длиной 10 мм. Нить была проложена в одном из каналов двухканального керамического капилляра внешнего диаметра 0,88 мм, размещенного в экранирующей трубке из нержавеющей стали внешнего диаметра 1,6 мм. Данный диаметр и представляет собой размер относительно тонкого зондодержателя. В другом канале керамического капилляра находилась такая же вольфрамовая нить, соединенная с электроизолированным отрезком стального экрана длины 10 мм, окружавшего керамический капилляр вблизи его измерительного торца. Эта втулка, подключавшаяся вместе с измерительным зондом к зондовой станции VGPS-12, выполняла роль опорного зонда с развитой собирающей поверхностью, устранявшего ВЧ искажения зондовой характеристики [2]. Такое исполнение зонда Ленгмюра обеспечило практически нулевые возмущения параметров изучавшейся плазмы ксенона, погрешности измерений температуры и концентрации электронов имели размах порядка ±10% при гораздо меньших погрешностях измерений зондовых потенциалов. Статистика обработки набора полученных экспериментальных данных показала, что размах значений коэффициента Бома СБЦил=1,23 охватил диапазон порядка ±7% [3], поэтому полную погрешность его определения вполне можно принять равной ±10%.
Насколько авторам известно, заявленные возможности зондовой диагностики плазмы, широко применяемой в экспериментальной физике, ранее не использовались. Отсюда следует, что данное техническое предложение ново и полезно, обеспечив эффективное расширение области применения локальной диагностики плазмы цилиндрическими зондами Ленгмюра.
Источники информации
1. Langmuir I., Mott-Smith Н., General Electric Review, 1924, v. 27, p. 449.
2. Godyak V.A., Demidov V.I., Probe measurements of electron-energy distributions in plasmas: what can we measure and how can we achieve reliable results? J. Phys. D. Appl. Phys., 2011, v. 44, paper No. 233001 (30 pp.).
3. P.E. Masherov, V.A. Riaby, V.K. Abgaryan, Note: Refined possibilities for plasma probe diagnostics, Rev. of Sci. Instrum., 2016, v. 87, 086106 (опубликовано 06.08.2016).
4. Piejak R.B., Godyak V.A., Garner R., Alexandrovich B.M., The hairpin resonator: A plasma density measuring technique revisited, J. Appl. Phys., 2004, v. 95, No. 7, p. 3785-3791.
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ определения плотности ионного тока на контактирующую с плазмой стенку и устройство для его осуществления | 2016 |
|
RU2660465C2 |
| СПОСОБ ДИАГНОСТИКИ ПЛАЗМЫ ЗОНДАМИ ЛЕНГМЮРА С ВЫВОДАМИ, ЗАЩИЩЁННЫМИ НЕИЗОЛИРОВАННЫМИ СНАРУЖИ ЭКРАНАМИ, И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2017 |
|
RU2671948C1 |
| СПОСОБ ИЗМЕРЕНИЯ ПЛАВАЮЩЕГО ПОТЕНЦИАЛА В ПЛАЗМЕ | 2013 |
|
RU2555495C2 |
| СПОСОБ ИЗМЕРЕНИЯ ПОТЕНЦИАЛА ПЛАЗМЫ | 2013 |
|
RU2556298C2 |
| СПОСОБ ДИАГНОСТИКИ ПЛАЗМЫ И ЗОНД ЛЕНГМЮРА С ЗАЩИТНЫМ КОЛЬЦОМ ДЛЯ ЕГО РЕАЛИЗАЦИИ | 2021 |
|
RU2777900C2 |
| СПОСОБ ДЕТЕКТИРОВАНИЯ МОМЕНТА ОКОНЧАНИЯ КОНДИЦИОНИРОВАНИЯ РЕАКТОРА УСТАНОВКИ ПЛАЗМОХИМИЧЕСКОГО ТРАВЛЕНИЯ | 2024 |
|
RU2832004C1 |
| СПОСОБ ИЗМЕРЕНИЯ ТЕМПЕРАТУРЫ ЛАЗЕРНОЙ ПЛАЗМЫ | 2000 |
|
RU2178156C1 |
| СПОСОБ УПРАВЛЕНИЯ ТОКОМ ПЛАЗМЕННОГО ЭМИТТЕРА БОЛЬШОЙ ПЛОЩАДИ | 1991 |
|
RU2012945C1 |
| БИБЛИОТЕКА ' 'Б. Н. Маков | 1971 |
|
SU304489A1 |
| ЛЕНТОЧНЫЙ ПЛАЗМЕННЫЙ ЭМИТТЕР ИОНОВ | 2005 |
|
RU2294578C1 |
Изобретение относится к способам исследования локальных параметров плазмы в газоразрядных источниках плазмы. В заявленном способе локальной диагностики максвелловской плазмы с помощью одиночного цилиндрического зонда Ленгмюра предусмотрено введение в газоразрядное пространство тонкого зондодержателя с зондом на конце в виде отрезка металлической нити, подключенной через источник зондового напряжения к металлическому корпусу газоразрядного устройства или дополнительному опорному электроду. При этом принимаются меры по защите зондовой цепи от электрических наводок и по очистке собирающей поверхности зонда, регистрации его вольт-амперной характеристики изменением зондового напряжения в обе стороны от плавающего потенциала и определения функции распределения электронов по энергиям, концентрации электронов, их температуры и потенциала плазмы обработкой зондовой характеристики одним из известных методов. Затем находят плотность тока ионов на зонд под плавающим потенциалом, используемую в дальнейшем для контроля чистоты рабочего газа или состояния экспериментальной вакуумной техники. Технический результат - расширение набора измеряемых параметров изучаемой плазмы определением толщины зондового слоя и массы ионов в том случае, когда функция распределения электронов по энергиям плазмы близка к функции Максвелла. 1 з.п. ф-лы, 1 ил.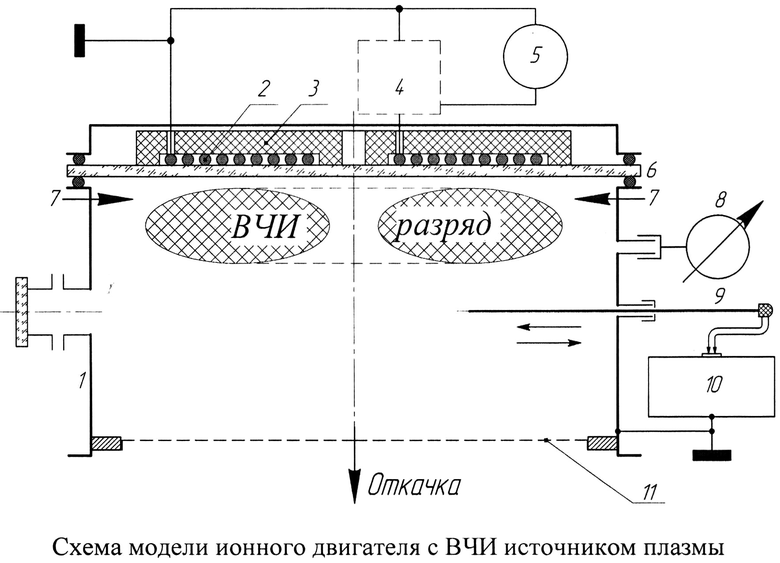
1. Способ локальной диагностики максвелловской плазмы с помощью одиночного цилиндрического зонда Ленгмюра путем введения в газоразрядное пространство тонкого зондодержателя с зондом на конце в виде отрезка металлической нити, подключенной через источник зондового напряжения к металлическому корпусу газоразрядного устройства или дополнительному опорному электроду с принятием мер по защите зондовой цепи от электрических наводок и по очистке собирающей поверхности зонда, регистрации его вольт-амперной характеристики изменением зондового напряжения в обе стороны от плавающего потенциала и определения функции распределения электронов по энергиям, концентрации электронов, их температуры и потенциала плазмы обработкой зондовой характеристики одним из известных методов, отличающийся тем, что, в случае близости измеренного распределения электронов по энергиям к функции Максвелла, находят плотность тока ионов на зонд под плавающим потенциалом jif по соответствующей потенциалу плазмы плотности электронного тока насыщения на зонд jes, используя формулу Больцмана jif=jes⋅exp(-ΔVf/Te), где ΔVf - разность между потенциалом плазмы и плавающим потенциалом зонда, Tе, В - температура электронов, полученную величину jif выражают двояким образом: а) через уравнение Бома jif=CБЦил⋅(R/a)ene(2eTe/Mi)1/2, где СБЦил=1,23 - экспериментально подтвержденный коэффициент Бома для цилиндрического зонда, R - внешний радиус зондового слоя объемного заряда, а - радиус цилиндрического зонда, е - элементарный заряд, nе - концентрация электронов, Мi - масса иона, и б) через уравнение Чайлда-Ленгмюра-Богуславского jif(4ε0/9)(2e/Mi)1/2(ΔVf3/2/aRAЛ), где ε0 - диэлектрическая постоянная вакуума, AЛ - зависящая от отношения R/a безразмерная константа Ленгмюра, и совместным решением указанных уравнений находят величины R и Мi.
2. Способ по п. 1, отличающийся тем, что при несоответствии реального зондового слоя модели Чайлда-Ленгмюра-Богуславского, исключающей проникновение электронов в зондовый слой, внешний радиус R зондового слоя корректируют по модели зондового слоя, допускающей такое проникновение, например, согласно «ступенчато-фронтальной» модели величину R находят из выражения RСФ=0,692⋅R+0,3816⋅a, где RСФ - радиус зондового слоя, соответствующий «ступенчато-фронтальной» модели.
| Godyak V.A., Demidov V.I | |||
| Probe measurements of electron-energy distributions in plasmas: what can we measure and how can we achieve reliable results, J | |||
| Phys | |||
| D | |||
| Appl | |||
| Phys., 2011, v | |||
| Приспособление для плетения проволочного каркаса для железобетонных пустотелых камней | 1920 |
|
SU44A1 |
| Токоприемник электроподвижного состава | 1968 |
|
SU233001A1 |
| RU 2015110801 A, 10.10.2016 | |||
| RU 2015115585 A, 20.11.2016 | |||
| KR 1020160134074 A, 23.11.2016. | |||
Авторы
Даты
2018-01-25—Публикация
2016-11-03—Подача