Изобретение относится к способам оценки внешних и внутренних параметров узлов трения тормозных устройств в стендовых условиях, в частности пар трения ленточно-колодочных тормозов буровых лебедок.
Известен способ определения эксплуатационных параметров при квазилинейной закономерности их изменения в ленточно-колодочных тормозах буровых лебедок заключающийся в том, что при вращении тормозного шкива от установившегося значения до нуля при спуске загруженного элеватора определение эксплуатационных параметров, сведенных в первую группу ленточно-колодочного тормоза выполняют в следующей последовательности: оценивают режим вращения тормозного шкива, затем определяют время торможения, натяжение набегающей ветви тормозной ленты, максимальные и минимальные удельные нагрузки в парах трения, тормозной момент, развиваемый фрикционными узлами; коэффициент запаса тормозного момента, энергоемкость фрикционных узлов, усилия, прикладываемые бурильщиком к рычагу управления тормозом; коэффициент полезного действия тормоза. Затем последовательно производят определение эксплуатационных параметров, сведенных во вторую (коэффициент запаса прочности поперечного сечения тормозной ленты и деформации ее ветвей; деформации фрикционной накладки; общую деформацию элементов тормозной системы), третью (теплоту, температуры и их распределение по толщине обода тормозного шкива; интенсивность теплообмена; коэффициент распределения тепловых потоков между элементами трибосопряжения; тепловые деформации обода тормозного шкива и фрикционной накладки) и четвертую (износо-фрикционные свойства пар трения) группы применительно к ленточно-колодочному тормозу буровой лебедки. Достигается возможность определения эксплуатационных параметров при квазилинейной закономерности их изменения в ленточно-колодочных тормозах с взаимосвязанными силовыми, тепловыми и износо-фрикционными свойствами их пар трения и лимитирующими допустимыми ограничениями скоростного, динамического и теплового режимов, обеспечивающих работоспособное состояние тормозной системы буровой лебедки (1, аналог, патент России №2507423 С2, кл. F16D 49/08 за 20.02.2014 г).
Недостатком данного способа является то, что в нем не были рассмотрены внутренние параметры фрикционных пар трения, а именно: работа выхода электронов и ионов; уровни Ферми; плотность зарядов; дебаевская длина экранирования; различного рода электрические токи, сродство к электрону, различные типы контактов и т.д.
Известно, что для моделирования внешнего трения использован метод анализа размерностей и теории подобия, в которые внесены ряд существенных уточнений. Были рассмотрены четыре подмодели:
- макроконтактирования с учетом КВЗ (коэффициента взаимного перекрытия);
- макротеплообразования, теплопроводности и теплопередачи;
- микроконтактирование пятен выступов пар трения;
- теплообразование на шероховатых поверхностях.
При этом введен в рассмотрение основной параметр - комплекс геометрических размеров Кг, через который определялись все режимные параметры модельных испытаний. Показано, что размеры элементов пары трения и пути трения микровыступов воздействуют на процесс трения различно и характеризовать их необходимо конкретной размерностью. Показано также, что одноименные размерные величины для первого, второго элемента и окружающей среды должны быть учтены. В результате было получено ряд критериев (теплофизический, теплопередачи, физико-механический), соблюдение которых обеспечивает при сухом трении идентичность процессов трения и износа на модели и в натуре (2, прототип, Чичинадзе А.В. Практическая реализация тепловой динамики и моделирования трения и износа при сухом и граничном трении / А.В. Чичинадзе // Практическая трибология. Мировой опыт. Том I. - М.: Центр: Наука и техника. - 1994. - С. 67-72).
Предложенный способ моделирования внешнего трения имеет тот недостаток, что в подмодели входят параметры, которые относятся к различным полям фрикционного взаимодействия с существенно отличающейся природой. Кроме того, такие комплексные критерии, имеющие различную физическую сущность из-за входящих в них параметров, значительно искажает возникающие поля при электротермомеханическом трении и не дают возможность сформировать их в единое поле фрикционного взаимодействия в трибосистеме.
По сравнению с аналогом и прототипом предложенное техническое решение имеет следующие преимущества:
- задекларировано контактно-импульсное электротермомеханическое трение, в котором закономерности изменения нормального усилия во времени исследовались методом импульсных пар при колебательных процессах микровыступов обода шкива для схем импульсных моментов, т.е. "отрицательный-положительный" и "положительный - отрицательный";
- установлено закономерности изменения линий токов силового, электрического, теплового и химического полей, характеризующиеся внутренними и внешними параметрами, во взаимодействии с линиями токов скоростного поля омывающих сред, подчиняющиеся волновой природе по фазе и описываемые как симплексами так и критериями, входящими в функциональные зависимости;
- рассмотрено несколько разных стандартных критериев на микроуровне, на основании которых получен один из основных "нестандартных" критериев, устанавливающих связь между теплофизическими параметрами элементов трения и омывающих их скоростными токами воздуха и смеси не только в газообразном, но и в жидком состоянии;
- введены статический и динамический коэффициенты взаимного перекрытия многопарных узлов трения ленточно-колодочного тормоза, позволяющие управлять импульсными удельными нагрузками на набегающей и сбегающей поверхности его тормозного шкива;
- введены понятия темпов нагревания и вынужденного охлаждения поверхностных и подповерхностных слоев ободов тормозных шкивов при импульсном и длительном подводе теплоты и определить поверхностные и объемные температурные градиенты;
- установлено, что электротермическое сопротивление дискретных контактов с различной энергетической активностью микро-конденсаторов и - термоэлектробатарей с мгновенным их переключением при изменении как площадей пятен так и самих типов контактов микровыступов и градиента механических свойств, а также темпа проникновения взаимодействующих между собой импульсов электрического и теплового токов влияют на интенсивность износа микровыступов при переполяризации, ведущей к дестабилизации динамического коэффициента трения металлополимерных пар трения;
- определены суммарные термонапряжения, действующие на обод тормозного шкива, с учетом его конструктивных параметров и особенности крепежного выступа сопряженного с нерабочей поверхностью обода.
Целью настоящего изобретения является повышение достоверности результатов определения внешних и внутренних эксплуатационных параметров металлополимерных пар трения ленточно-колодочных тормозов буровых лебедок в стендовых условиях.
Поставленная цель достигается тем, что закономерности изменения линий токов силового, электрического, теплового и химического полей, характеризующиеся внутренними и внешними параметрами, во взаимодействии с линиями токов скоростного поля омывающих сред подчиняется волновой природе со сдвигом по фазе и описываются отвечающими ей зависимостями при соблюдении следующих отношений:
- отношение высоты микровыступов фрикционных поверхностей объекта (Н) и модели (h) равно H/h=CH=1,0;
- отношение длины микровыступов фикционных поверхностей объекта (Lм) и модели (lм) равно LM/lM=CLм=1,0;
- отношение площадей пятен контактов микровыступов фрикционных поверхностей объекта (Ао) и модели (Ам) равно Ao/Aм=САо=1,0;
- отношение импульсных нормальных усилий объекта (N) и модели (n) равно N/n=CN=1,0;
- отношение линейных скоростей скольжения объекта (VCK) и модели (vск) равно VCK/vск=CV=1,0;
- отношение импульсных сил трения объекта (Fт) и модели (fт) равно Fт/fт=СFт=1,0;
- отношение импульсных динамических коэффициентов трения объекта (fo) и модели (fм) равно fo/fм=Cfo=1,0;
- отношение импульсных удельных нагрузок объекта (ро) и модели (рм) равно ро/рм=СРо=1,0;
- отношение импульсных тормозных моментов объекта (Мо) и модели (Мм) равно Мо/Мм=СМо=1,0;
- отношение податливости стыков подсистемы "тормозная лента - нерабочие поверхности накладок" объекта (По1) и модели (По2) равно Пo1/По2=CПo1=1,0;
- отношение амплитуд колебаний связей механических подсистем и деформаций микронеровностей объекта (А) и модели (а) равно А/а=СА=1,0;
- отношение энергетических уровней приповерхностных слоев объекта (Э'о) и модели (Э'м) равно Э'о/Э'м=СЭ'о=1,0;
- отношение токов скоростей омывающего воздуха объекта (VB) и модели (vB) равно VB/vB=CVт=1>0;
- отношение токов скоростей компонентов омывающих сред объекта (Vc) и модели (vc) равно Vc/vc=CVc=1,0 и при этом соблюдается в открытой термодинамической системе трибосопряжения равенство не только поверхностных температур, но и равенств химических потенциалов при вынужденном конвективном теплообмене его подсистем:
- «наружная поверхность обода шкива - скоростные токи охлаждающего воздуха»;
- «внутренняя поверхность обода шкива - скоростные токи компонентов омывающей среды»;
- «поверхностный и приповерхностный слой полимерной накладки -скоростные токи компонентов омывающей среды», а взаимодействие подсистемы «обод тормозного шкива - крепежный выступ - фланец барабана лебедки» осуществляется кондуктивным теплообменом за счет переменных температурных градиентов по их толщине, после чего производятся измерения и определение параметров трибосопряжения с одновременным контролем и фиксацией площадей пятен контактов микровыступов в реальном масштабе времени поскольку электротермическое сопротивление дискретных контактов с различной энергетической активностью микроконденсаторов и термобатарей с мгновенным их переключением при изменении площадей пятен контакта микровыступов при соблюдении условий на первой стадии фрикционного взаимодействя (Аф<Ан), исходя из того, что фактическая площадь контактирования (Аф) мала по сравнению с номинальной (Ан) и при этом производится суммирование составляющих генерируемых токов, а при условии Ан=Аф фиксируется трибоЭДС в сопряжении с переменным градиентов механических свойств его материалов. Темп проникновения взаимодействующих между собой импульсов электрического и теплового токов влияет на интенсивность износа микровыступов при переполяризации, а величины тепловых токов на поверхностях пятен контактов микровыступов определяются с помощью гипотезы суммирования температур на поверхности с учетом генерируемых электрических токов

В теле металлического фрикционного элемента формируется объемная температура (ϑv1), вызванная действием первых двух составляющих температур, а также от джоулевой теплоты; температура ϑv1 определяется из условия действия двух источников теплоты (электрического и фрикционного) в зоне трения
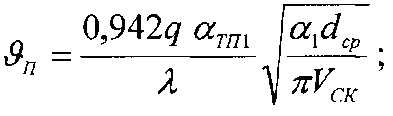
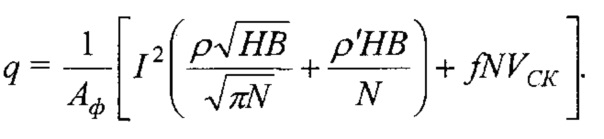
Температуру вспышки ϑвсп определяют по зависимости вида:
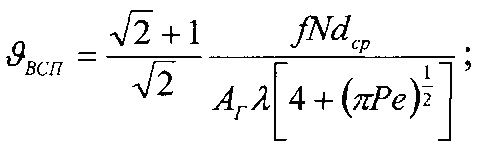
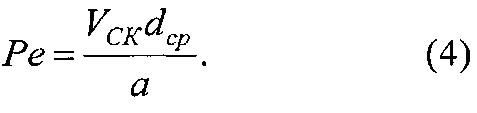
Объемная температура металлического фрикционного элемента (ϑv1) определяется из условия равенства тепловых потоков на контактной поверхности с учетом фрикционной и электрической составляющей, а также с учетом отводимой от его полированной поверхности к скоростным токам омывающей среды:

В дальнейшем по приведенным выше температурам и оцениваются энергетические уровни поверхностных и подповерхностных слоев элементов трибосопряжения. После чего аналитическим путем определяются максимальные сжимающие напряжения σ1max в ободе шкива

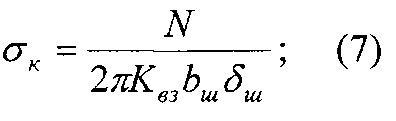
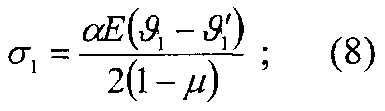
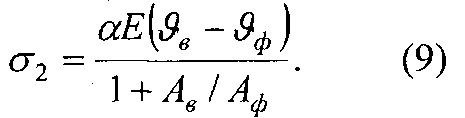
Но при этом для более точного определения составляющих σ1 и σ2 в зависимость вместо (ϑ1-ϑ'1) подставляем слагаемое 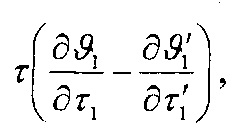 которое характеризует темп нагревания обода шкива, а в зависимость вместо
которое характеризует темп нагревания обода шкива, а в зависимость вместо 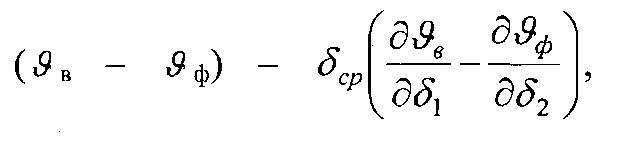 которая характеризует температурные градиенты по толщине рассматриваемых элементов, а зарождение и развитие трещин на рабочей поверхности ободов тормозных шкивов оценивается коэффициентом сопротивления тепловому удару
которая характеризует температурные градиенты по толщине рассматриваемых элементов, а зарождение и развитие трещин на рабочей поверхности ободов тормозных шкивов оценивается коэффициентом сопротивления тепловому удару

На фиг. 1 приведена схема контактирования металлополимерных пар трения: 1 - фрикционная накладка; 2 - тормозной шкив; на фиг. 2 проиллюстрирована классификация микронеровностей по высоте h и шагу Sм микровыступов металлополимерных пар трения: 1 - макроотклонения; 2 - волнистость; 3 - шероховатость; 4 - субшероховатость; на фиг. 3 показаны типовые опорные кривые, построенные в относительных (I) и абсолютных (II) координатах (распределение материалов [а, б, в] по высоте шероховатого слоя) по методу Аббота (А); на фиг. 4 представлена схема иллюстрирующая переход к временно постоянной скорости (Аф1) элементарных площадок контактов при прирабатывании (I) и установившемся (II) режиме; на фиг. 5а, б, в приведено контактно-импульсное взаимодействие микровыступов пары трения «полимер (1) - металл (2)» при различной нагруженности микровыступов: а - 0,1N; б - 0,5N; в - 1,0N; на фиг. 6 проиллюстрированы расчетные модели для оценки характеристик взаимодействия пятен контактов с различными диаметрами (an, an1, an2) пары «металл (1) - полимер (2)» при генерировании: а - импульсных электрических токов; б, в - импульсных температурных токов: вспышки; поверхностные; на фиг. 7а, б показано изменение электрохимического потенциала металлической (а) и неметаллической (б) поверхностей трения при нагружении фрикционной пары в области: I, II - естественных пленок окислов (первичных структур) и их разрушения; IV - динамического равновесия и автоматического регулирования процессов образования и разрушения вторичных структур; I - закономерности для металлического элемента трения; 2, 3, 3' - закономерности для поверхностных и приповерхностных слоев фрикционных накладок до, в зоне и выше допустимой температуры для их материалов; на фиг. 8 представлены закономерности изменения токов электризации во времени (τ) прямой ("колодочка - диск") (а) и обратной ("диск - колодочка") (б) пары трения при разных скоростях скольжения (VCK) и удельных нагрузок (р): а-VCK=0,3 м/с (1); VCK=0,8 м/с (2); VCK=1,5 м/с (3); VCK=2,0 м/с (4) при р=0,15 МПа; ↑ - обозначены моменты разрушения поверхностей полимерных колодок; на фиг. 9а, б, в изображено температурное поле поверхностного слоя металлического (1) элемента (а) и изменение теплового тока (2) и эпюр температур в нем (б) и в приповерхностном слое полимерного (3) элемента (в): на фиг. 10а, б показано распределение поверхностной температуры ϑn и теплового потока q на пятне контакта при: а-ϑn=const; б-q=const; на фиг. 11а, б проиллюстрировано линии электрического поля между разноименными (а) и одноименными (б) зарядами; на фиг. 12а, б, в, г показаны закономерности изменения поверхностной температуры (ϑn, кривая 1) в интервале температур ниже и выше допустимой (ϑд) для материалов полимерной накладки и работы выхода электронов (кривая 2) и ионов (кривая 3) с робочих поверхностей металлополимерных пар трения (WM, WП) от удельных нагрузок (р) во время фрикционного взаимодействия различных типов контактов: а - блокирующего (WM>WП); б - нейтрального (WM=WП); в, г - омического при ϑд<ϑn и ϑд>ϑn (WM<WП); I, II, III - области деформации поверхностных слоев элементов трения: упругого и пластического; на фиг. 13а, б, в, г проиллюстрированы термаграммы изменения температуры по слоям фрикционной накладки при ее толщине ϑн=25 мм в интервалах: а - 253,2-78,9°С; б - 330,5-92,6°С, в - 450,1-98,6°С; г - 535,6-160,0°С; на фиг. 14а, б, в, г показаны термограммы изменения температуры по слоям обода шкива (1) и его крепежного выступа (2) в интервалах: а - 1 - 253,2-235,9°С; 2 - 204,8-136,6°С; б - 1 - 329,5-310,2°С, в - 1 - 450,4-432,5°С; 2 - 400,8-295,7°С; г - 1 - 535,2-52,2°С; 2 - 492,6-403,7°С; на фиг. 15а, б, в проиллюстрированы энергетические уровни различных типов контактов при фрикционном взаимодействии пятен микровыступов металлополимерных пар трения: а - нейтрального; б - омического; в - блокирующего; на фиг. 16 показана энергетическая диаграмма пары трения «металл - полимер»; на фиг. 17а, б представлена качественная картина энергетических зон в системе «металл - полимер» при импульсных нормальных усилиях, действующих на полимерную пленку: а - N<NC; б - N>NC; на фиг. 18 проиллюстрирована зонная диаграмма трехслойной структуры «металл 1 - полимер - металл 2»; на фиг. 18 проиллюстрирована зонная диаграмма трехслойной структуры металл 1 - полимер - металл 2»; на фиг. 19а, б, в, г, д, е представлены схемы направлений составляющих электрических токов в металлополимерных парах трения при температурах до (а) и выше (б-д) допустимой для материалов полимерной накладки; е - векторная диаграмма электрических токов и направлений в приповерхностных слоях полимерной накладки; на фиг. 20а, б показана эквивалентная схема (а) и векторная диаграмма (б) параллельного замещения поверхностного слоя полимерной накладки; на фиг. 21а, б проиллюстрирована поляризация рабочей поверхности полимерной накладки при быстрых (а) и медленных (б) частотах воздействия на процессы; на фиг. 22а, б приведена кинематическая схема ленточно-колодочных тормозов (а, б) и их фрикционный узел (в) буровой лебедки У2-5-5: 1 - рычаг управления; 2, 4 - тормозные ленты и шкивы; 3 - фрикционные накладки; 5 - барабан; 6, 9, 10 - мотылевые шейки коленчатого вала; 7 - кран бурильщика; 8 - пневматический цилиндр; 11 - балансир; на фиг. 23а, б, в, г изображен общий вид стенда с модельным ленточно-колодочным тормозом (а), нагрузочным устройством (б), двигателями постоянного и переменного тока (в) и тормозной лентой с фрикционными накладками (г): 1 - двутавровые балки; 2 - тормозная лента; 3 - фрикционные накладки; 4 - тормозной шкив; 5 - вал с подшипниками; 6 - опоры вала; 7, 8 и 9 - электродвигатели: постоянного и переменного тока; 10 - пальцевая муфта; 11 - нагрузочное устройство; 12 - вал электродвигателя; на фиг. 24а, б, в, г, д приведен энергетический баланс деталей ленточно-колодочного тормоза с различными фрикционными характеристиками: а - линейной (1) и нелинейной (2); б - перемещение деталей при колебаниях; в, г - диаграммы работы деталей в колебательном процессе; д - зависимость энергии колебания деталей от амплитуды; на фиг. 25 представлена зависимость динамического коэффициента трения от поверхностной температуры для фрикционной пары ФК-24А - сталь 35ХНЛ; на фиг. 26 изображены диаграммы работы пары трения ФК-24А - сталь 35ХНЛ в интервале температур: 1 - до 200°С; 2 - 200-350°С; 3 - 350-500°С; на фиг. 27 проиллюстрированы зависимости натяжения набегающей ветви тормозной ленты от амплитуды радиальной вибростойкости наладок для набегающей (1) и сбегающей (2) ветви ленты; на фиг. 28а, б представлены амплитудные спектры радиальной вибростойкости фрикционных пар: а - при удельной нагрузке 0,2 и 2,0 МПа (кривые 3,4, и 1,2) и скорости скольжения 5 и 15 м/с (кривые 3,4, и 1,2); б - от сбегающей ветви ленты к набегающей (цифры соответствуют порядочному номеру накладки) при удельной нагрузке 2,0 МПа на сбегающей ветви ленты; на фиг. 29а, б, в показаны схемы сил, действующие: в узле «накладка-лента» (а); на участке ленты над i-той накладкой (б); при определении деформаций участков ленты (в); 2 - тормозная лента; 3 - фрикционная накладка; на фиг. 30 изображены закономерности изменения относительных деформаций участков тормозной ленты при расположении на дуге ее обхвата фрикционных накладок с постоянным (1, 1') и переменными (2, 2') шагом: расчетные (1, 2) и экспериментальные (1', 2') данные: 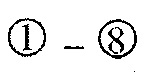 и
и 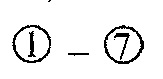 - нумерация зазоров между накладками; на фиг. 31 представлена классификации податливости фрикционных стыков при формировании их контактно-импульсного взаимодействия; на фиг. 32а, б проиллюстрирована зависимость импульсной нормальной нагрузки, вызывающей деформации микровыступов фрикционной накладки при их параллельном соединении в блок (а) и их модель (б): 1 - участок фрикционной накладки: Пп -податливости микровыступов (2); 3 - металлическая пленка на рабочей поверхности шкива; на фиг. 33 изображена закономерность изменения деформаций микровыступов металлополимерных пар трения ленточно-колодочного тормоза от импульсных удельных нагрузок при разных площадях пятен их контактирования; на фиг. 34а, б, в, г, д, е проиллюстрировано влияние коэффициентов перекрытия Квз (б, в, г, д) и температурного градиента по поверхности (∂ϑn/∂l) [а, г, е] на динамический коэффициент трения f (а, б), интенсивность изнашивания ир.п. (д, е) и среднюю температуру поверхностей трения ϑ (в); на фиг. 35а, б показана схема модельного ленточно-колодочного тормоза с подвижными фрикционными накладками, установленными с постоянным (а) и переменным (б) шагами (бандаж составленный из четырех накладок): 1 - тормозной шкив; 2 - тормозная лента; 3 - фрикционные накладки: 4 - кольцевые цилиндрические стержни; 5 - цилиндрические пружины; 6 - стопорная планка; на фиг. 36 показаны зависимости динамического (а, б) и статического (в, г) коэффициентов взаимного перекрытия внешних (1) и внутренних (2) пар трения фрикционных узлов тормоза с подвижными накладками на первой и третей стадиях торможения; на фиг. 37 проиллюстрирован фрагмент изменения нормального усилия в контакте пары трения «шкив-накладка» при импульсном взаимодействии (1 - положительном: 2 - отрицательном) ленточно-колодочного тормоза буровой лебедки по времени торможения; на фиг. 38а, б изображены закономерности изменения нормального усилия во времени, исследуемого методом импульсных пар, при колебательных процессах микровыступов обода тормозного шкива для схем моментов: а - «отрицательный-положительный» б - «положительный-отрицательный»; на фиг. 39 показана расчетная схема фрикционного узла тормоза для определения усилий растяжения в тормозной ленте; на фиг. 40 изображена расчетная схема для определения усилий растяжения участка ленты и нормального контактного усилия на поверхности трения шкива; на фиг. 41 показаны закономерности изменения импульсных нормальных усилий N по длине фрикционной накладки Lн при скоростях скольжения Vck=2,5 м/с в модельном ленточно-колодочном тормозе; на фиг. 42 представлена расчетная схема фрикционного узла ленточно-колодочного тормоза: 1 - тормозная лента; 2 - фрикционная накладка; 3 - тормозной шкив; на фиг. 43 проиллюстрированы закономерности изменения тормозных моментов по длине ленты ленточно-колодочного тормоза буровой лебедки (Rш=0,725м; ϕ=9,8°; Sc=50,0кH) при разных динамических коэффициентах трения в паре «тормозной шкив - фрикционная накладка»: 1 - f=0,2; 2 - f=0,25; 3 - f=0,3; 4 - f=0,35; на фиг. 44 приведена зависимость изменения динамического коэффициента трения фрикционного узла «шкив-накладка» (материал 35ХНМ - ФК-24А) в стендовых условиях при удельных нагрузках 0,6 МПа и поверхностных температурах 200°С (кривая 1) и 400°С (кривая 2) от скорости скольжения; на фиг. 45 представлена схема узла трения в сборе с барабаном лебедки при торможении во взаимодействии со скоростными токами омывающего воздуха: 1, 2, 3 - тормозной шкив с крепежным выступом и с ребордами; 4 - тормозная лента; 5 - фрикционная накладка; 6, 7 - фланец барабана лебедки; 8 - подъемный вал; на фиг. 46а, б показана зависимость коэффициентов теплоотдачи (α) лучеиспусканием матовых (а) и полированных (б) поверхностей металлических фрикционных элементов от температуры нагревания (ϑ) при различных значениях отношения диаметров поверхности трения к площадям поверхностей (d/A); на фиг. 47 проиллюстрировано зависимость напряжений сопротивлению трещинообразования (σ0) от объемной температуры обода шкива (ϑоб) и величины сопротивления тепловому удару (КС); на фиг. 48а, б, в, г приведены закономерности изменения величин безразмерных термонапряжений обода тормозного шкива от относительного времени торможения: фрикционного нагревания (а, б) и естественного охлаждения (в, г) при различных значениях критерия Био: а,
- нумерация зазоров между накладками; на фиг. 31 представлена классификации податливости фрикционных стыков при формировании их контактно-импульсного взаимодействия; на фиг. 32а, б проиллюстрирована зависимость импульсной нормальной нагрузки, вызывающей деформации микровыступов фрикционной накладки при их параллельном соединении в блок (а) и их модель (б): 1 - участок фрикционной накладки: Пп -податливости микровыступов (2); 3 - металлическая пленка на рабочей поверхности шкива; на фиг. 33 изображена закономерность изменения деформаций микровыступов металлополимерных пар трения ленточно-колодочного тормоза от импульсных удельных нагрузок при разных площадях пятен их контактирования; на фиг. 34а, б, в, г, д, е проиллюстрировано влияние коэффициентов перекрытия Квз (б, в, г, д) и температурного градиента по поверхности (∂ϑn/∂l) [а, г, е] на динамический коэффициент трения f (а, б), интенсивность изнашивания ир.п. (д, е) и среднюю температуру поверхностей трения ϑ (в); на фиг. 35а, б показана схема модельного ленточно-колодочного тормоза с подвижными фрикционными накладками, установленными с постоянным (а) и переменным (б) шагами (бандаж составленный из четырех накладок): 1 - тормозной шкив; 2 - тормозная лента; 3 - фрикционные накладки: 4 - кольцевые цилиндрические стержни; 5 - цилиндрические пружины; 6 - стопорная планка; на фиг. 36 показаны зависимости динамического (а, б) и статического (в, г) коэффициентов взаимного перекрытия внешних (1) и внутренних (2) пар трения фрикционных узлов тормоза с подвижными накладками на первой и третей стадиях торможения; на фиг. 37 проиллюстрирован фрагмент изменения нормального усилия в контакте пары трения «шкив-накладка» при импульсном взаимодействии (1 - положительном: 2 - отрицательном) ленточно-колодочного тормоза буровой лебедки по времени торможения; на фиг. 38а, б изображены закономерности изменения нормального усилия во времени, исследуемого методом импульсных пар, при колебательных процессах микровыступов обода тормозного шкива для схем моментов: а - «отрицательный-положительный» б - «положительный-отрицательный»; на фиг. 39 показана расчетная схема фрикционного узла тормоза для определения усилий растяжения в тормозной ленте; на фиг. 40 изображена расчетная схема для определения усилий растяжения участка ленты и нормального контактного усилия на поверхности трения шкива; на фиг. 41 показаны закономерности изменения импульсных нормальных усилий N по длине фрикционной накладки Lн при скоростях скольжения Vck=2,5 м/с в модельном ленточно-колодочном тормозе; на фиг. 42 представлена расчетная схема фрикционного узла ленточно-колодочного тормоза: 1 - тормозная лента; 2 - фрикционная накладка; 3 - тормозной шкив; на фиг. 43 проиллюстрированы закономерности изменения тормозных моментов по длине ленты ленточно-колодочного тормоза буровой лебедки (Rш=0,725м; ϕ=9,8°; Sc=50,0кH) при разных динамических коэффициентах трения в паре «тормозной шкив - фрикционная накладка»: 1 - f=0,2; 2 - f=0,25; 3 - f=0,3; 4 - f=0,35; на фиг. 44 приведена зависимость изменения динамического коэффициента трения фрикционного узла «шкив-накладка» (материал 35ХНМ - ФК-24А) в стендовых условиях при удельных нагрузках 0,6 МПа и поверхностных температурах 200°С (кривая 1) и 400°С (кривая 2) от скорости скольжения; на фиг. 45 представлена схема узла трения в сборе с барабаном лебедки при торможении во взаимодействии со скоростными токами омывающего воздуха: 1, 2, 3 - тормозной шкив с крепежным выступом и с ребордами; 4 - тормозная лента; 5 - фрикционная накладка; 6, 7 - фланец барабана лебедки; 8 - подъемный вал; на фиг. 46а, б показана зависимость коэффициентов теплоотдачи (α) лучеиспусканием матовых (а) и полированных (б) поверхностей металлических фрикционных элементов от температуры нагревания (ϑ) при различных значениях отношения диаметров поверхности трения к площадям поверхностей (d/A); на фиг. 47 проиллюстрировано зависимость напряжений сопротивлению трещинообразования (σ0) от объемной температуры обода шкива (ϑоб) и величины сопротивления тепловому удару (КС); на фиг. 48а, б, в, г приведены закономерности изменения величин безразмерных термонапряжений обода тормозного шкива от относительного времени торможения: фрикционного нагревания (а, б) и естественного охлаждения (в, г) при различных значениях критерия Био: а, 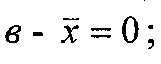 б,
б, 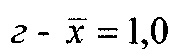 ; на фиг. 49а, б, в, г, д, е представлены усовершенствованные модели электротермомеханического трения и износа фрикционных материалов (первоначально разработанные А.В. Чичинадзе и Э.Д. Брауном) применительно к типичному трибологическому сопряжению; на фиг. 50 показана структурная развивающаяся модель реального сложного многоуровневого трибологического сопряжения фрикционного узла тормоза; на фиг. 51 представлена трибосистема (фрикционного узла) ленточно-колодочного тормоза и ее подсистемы различного порядка; на фиг. 52а, б, в, г, д, е, ж представлены общий вид ленточно-колодочного тормоза с многопарными фрикционными узлами и их графические модели: 1 - тормозная лента; 2, 4 - фрикционные накладки с отверстиями; 3 - тормозной шкив; 5, 6 - цилиндрические стержни и пружины; физические модели сцепления внешних («внутренняя поверхность тормозной ленты - внешние поверхности фрикционных накладок») (б, в, г) и внутренних («внутренние поверхности фрикционных накладок - рабочая поверхность тормозного шкива») (д, е, ж) пар трения его фрикционных узлов; на фиг. 53 приведена блок-схема основного расчетного модуля; на фиг. 54 проиллюстрированны закономерности изменения во времени (τ) динамического коэффициента трения (f) для пары «металл - полимер» (при р=0,3 МПа, VCK=0,6 м/с); 1,2 - высокочастотная и низкочастотная составляющие «сухого» трения; 3 - кривая при «мокром» трении; 4 - систематизированная синусоидальная кривая; на фиг. 55 показан массоперенос материала между фрикционными накладками и рабочей поверхностью обода тормозного барабана при поляризации рабочих поверхностей накладок: 1 - анодной; 2 - катодной; на фиг. 56 представлена связь между режимами разряда и износом пары трения «полимер - металл»: 1 - тлеющий разряд; 2 - искровой; на фиг. 57 проиллюстрированы этапные изменения динамического коэффициента трения материала «Ретинакс» ФК-24А в функции температуры поверхности трения по зонам: I - 200-250°С; II - 250-400°С; III - 400-550°С; IV - 550-800°С; V - 800-1000°С.
; на фиг. 49а, б, в, г, д, е представлены усовершенствованные модели электротермомеханического трения и износа фрикционных материалов (первоначально разработанные А.В. Чичинадзе и Э.Д. Брауном) применительно к типичному трибологическому сопряжению; на фиг. 50 показана структурная развивающаяся модель реального сложного многоуровневого трибологического сопряжения фрикционного узла тормоза; на фиг. 51 представлена трибосистема (фрикционного узла) ленточно-колодочного тормоза и ее подсистемы различного порядка; на фиг. 52а, б, в, г, д, е, ж представлены общий вид ленточно-колодочного тормоза с многопарными фрикционными узлами и их графические модели: 1 - тормозная лента; 2, 4 - фрикционные накладки с отверстиями; 3 - тормозной шкив; 5, 6 - цилиндрические стержни и пружины; физические модели сцепления внешних («внутренняя поверхность тормозной ленты - внешние поверхности фрикционных накладок») (б, в, г) и внутренних («внутренние поверхности фрикционных накладок - рабочая поверхность тормозного шкива») (д, е, ж) пар трения его фрикционных узлов; на фиг. 53 приведена блок-схема основного расчетного модуля; на фиг. 54 проиллюстрированны закономерности изменения во времени (τ) динамического коэффициента трения (f) для пары «металл - полимер» (при р=0,3 МПа, VCK=0,6 м/с); 1,2 - высокочастотная и низкочастотная составляющие «сухого» трения; 3 - кривая при «мокром» трении; 4 - систематизированная синусоидальная кривая; на фиг. 55 показан массоперенос материала между фрикционными накладками и рабочей поверхностью обода тормозного барабана при поляризации рабочих поверхностей накладок: 1 - анодной; 2 - катодной; на фиг. 56 представлена связь между режимами разряда и износом пары трения «полимер - металл»: 1 - тлеющий разряд; 2 - искровой; на фиг. 57 проиллюстрированы этапные изменения динамического коэффициента трения материала «Ретинакс» ФК-24А в функции температуры поверхности трения по зонам: I - 200-250°С; II - 250-400°С; III - 400-550°С; IV - 550-800°С; V - 800-1000°С.
На первом этапе моделирования рассматриваются геометрические параметры микровыступов, энергетические уровни пятен контактов и их поверхностных и подповерхностных слоев при электротермомеханическом фрикционном взаимодействии в металлополимерных парах трения на нано- и микроуровнях.
В процессе фрикционного взаимодействия металлополимерных пар трения, т.е. при скольжении микровыступов, металлический фрикционный элемент получает микроимпульсы со стороны микровыступов неподвижного контртела, которым является рабочая поверхность полимерной накладки (прямая пара трения). В обратных парах трения все происходит наоборот. В многопарных фрикционных узлах ленточно-колодочного тормоза на разных стадиях торможения наблюдаются сначала обратные пары трения, а затем прямые. Импульсные колебания величины нормального усилия, действующего со стороны тормозной ленты, определяются жесткостью фрикционного стыка.
На фиг. 1а, б проиллюстрировано контактно-импульсное взаимодействие микровыступов на различной стадии торможения парой трения «полимер - металл» при ее нагружении нормальной силой N. Различная величина N на каждой из стадий торможения пропорциональна площади контакта. На первой стадии контактирования (фиг. 1а) происходит импульсное взаимодействие микровыступов, способствующее генерированию элементарного электрического тока. В дальнейшем, на второй стадии (фиг. 1б) электрический ток якобы гасится, и превращается в аккумулируемую теплоту. На третьей стадии взаимодействия микровыступов импульсная нормальная сила N является максимальной (фиг. 1в), площадь контактирующих поверхностей увеличивается, а, следовательно, наблюдается рост трибоэффекта, т.е. поверхностной температуры контакта. Суммирование элементарных электротоков, генерируемых на микровыступах (первая стадия торможения), позволило сформировать электрическое поле на взаимодействующих поверхностях контактов. Формируемое тепловое поле на второй и третьей стадииразвивается с ростом, и как следствие, приводит к увеличению тепловых токов.
Между участками фактического касания расположены микро- и макрополости, соединяющиеся между собой и заполненные жидкостью, образовавшиеся за счет выгорания связующих компонентов полимерных накладок, продуктами износа. Указанные полости имеют сужения и расширения по высоте. При вращении металлического фрикционного элемента промежуточная среда увлекается его скользящей поверхностью и в местах сужения образуются гидродинамические клинья. Действие последних суммируется и может привести к всплыванию или подъему одной поверхности над другой.
По мере всплывания тел микронеровностей уменьшается контактная деформация и часть импульсной нормальной нагрузки, воспринимаемой суммарными опорными поверхностями микровыступов, способствует одновременному увеличению части импульсной нормальной нагрузки, приходящейся на жидкостной слой накладки.
Наблюдаемая упругопластическая деформация поверхностных слоев на площадках фактического контакта, приводящая к их постепенному охрупчиванию за счет электроимпульсного прошивания волнистости и шероховатости поверхностей, а также к диспергированию, позволяет представить процесс изнашивания в виде малоцикловой усталости материалов поверхностных слоев, расположенных в зоне деформирования.
В течение незначительного времени не наблюдается разрушение поверхности трения и отделения частиц износа, т.е. имеет место существование латентной фазы, но при этом происходит накопление энергии, микродефектов, развитие и эволюция вторичных структур. При достижении предельного состояния материалов поверхностного слоя, обусловленного появлением определенной концентрации микроповреждений, наступает стадия разрушения поверхностного слоя.
Под влиянием импульсной нормальной нагрузки в касание входят отдельные микровыступы (фиг. 2а, б). Последние представляют собой микронеровности, которые расположены на вершинах волн контактирующих пятен. В связи с этим выделяют следующие площади контакта: номинальную, контурную и фактическую.
Номинальная площадь контакта (Ан) - это геометрическое место всех возможных фактических участков контакта. Эта площадь ограничена размерами взаимодействующих металлополимерных пар трения.
Контурная площадь контакта (Ак) - образуется в результате деформаций микронеровностей взаимодействующих пятен контактов. На контурной площади размещены фактические участки контакта. В зависимости от рельефа контактирующих поверхностей металлополимерных пар трения и внешнего действия на каждую из них импульсной нормальной силы, величина контурной площади может составлять до десяти процентов от всей номинальной площади контакта. Площадь отдельных контурных участков изменяется от единицы до десятков квадратных миллиметров. При взаимодействии двух волнистых поверхностей трения контурные площади контактов изменяются во времени. Это обусловлено изменением микрорельефа поверхностей; действием импульсных нормальных сил и импульсных удельных нагрузок; теплофизических и физико-механических свойств материалов, находящихся в напряженно-деформируемом состоянии; нестабильностью термоупругого контакта под действием импульсных удельных нагрузок, импульсных электрических и тепловых токов, изнашивания и других факторов. Классификацию микронеровностей по высоте h и шагу Sм металлополимерных пар трения ленточно-колодочного тормоза проиллюстрировано на фиг. 3.
Номинальную, контурную и фактическую площадь взаимодействия в металлополимерных парах трения ленточно-колодочного тормоза с учетом формы сечения можно привести к геометрической фигуре (квадрату, кругу, прямоугольнику и др.). В данном случае, площади пятен контактирования поверхностей взаимодействия приведено к кругу, что позволяет определить их соотношения через отношение квадратов радиусов, Так, например, 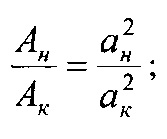
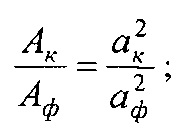
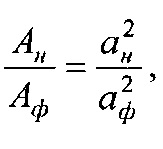 при этом возможны и другие комбинации отношений площадей контакта взаимодействующих металлополимерных пар трения.
при этом возможны и другие комбинации отношений площадей контакта взаимодействующих металлополимерных пар трения.
Микровыступы, приведенные на фиг. 4а, б, в имели следующие геометрические характеристики для материала ФК-24А (в масштабе): a-h=32,5 мм; z1=10 мм; z=17,0 мм; l=60,0 мм; б-h=32,5 мм; l=61,0 мм; в-h=31,0 мм; lS=60,0 мм.
Топография поверхностей микровыступов, оценивалась на основе обработки ограниченного числа профилограмм (zi=10). Для построения кривой опорной поверхности для трех типов характерных микровыступов использовался метод, предложенный Абботом.
Фактическая площадь контакта (АФ) образована воздействием микровыступов поверхностей трения и представляет наибольший интерес в связи с тем, что на фактических участках контактах происходит деформация микровыступов и генерирование электрических токов, а как следствие, образуются тепловые токи и происходит износ. Фактическая площадь контакта указанных пар трения изменяется в широком интервале: от сотых долей до единиц процентов от номинальной площади поверхности трения.
Опорные кривые (I, I', I''), состоящие из трех участков (1, 2 и 3), приведенные на фиг. 4 имеют переменный характер. При этом функция tp(εmax) в интервале от 0 до 1,0 показывает, какая доля материала находится выше заданного уровня. Физический смысл полученной каждой опорной кривой выражает вероятность того, что материал профиля находится выше уровня εmax, т.е. она характеризует распределение материала по высоте шероховатого слоя.
Построенные в относительных величинах опорные кривые позволяют оценить не только топографию поверхности, но и ее площадь согласно табл. 1.
Суммирование площадей элементарных контактов и достижение установившегося значения Аф1 проиллюстрировано на фиг. 5.

Данный процесс протекает постепенно и охватывает по времени несколько часов в зависимости от условий эксплуатации пар трения ленточно-колодочного тормоза. Величина А1 определяется электро- и термодинамическими режимами трения и может находиться в достаточно широких пределах в зависимости от интенсивности удельных нагрузок (уровня активации) и состава омывающих сред (уровень пассивации) при контактно-импульсном взаимодействии металлополимерных пар трения тормоза.
При взаимодействии металлополимерных пар трения тормозных устройств контакт носит дискретный характер из-за постоянной смены его элементарных участков. Последние представляют собой очаги «электрических» и «термических» неровностей. «Электрические» очаги способствуют генерированию электрических токов с помощью сформированных микротермобатарей с различными свойствами материалов и поэтому они работают в режиме микротермоэлектрогенератора и микротермоэлектрохолодильника. Одни участки нагреваются, а другие - охлаждаются. «Термические» очаги нагреваются за счет трибоэффекта. В дальнейшем, более разогретые участки поверхности трения в результате термического расширения и податливости приподнимаются над остальной поверхностью и начинают вследствие этого воспринимать всю приложенную нагрузку. Так будет продолжаться до тех пор, пока локальный износ этого участка не приведет к понижению его уровня, после чего опять произойдет перераспределение нагрузки, которая окажется приложенной к другим участкам поверхности.
Поверхностный слой необходимо рассматривать как синергетическую саморегулирующую систему, которая способна к внутренним перестройкам при достижении внутренней энергией системы определенного порогового значения - энергии активации.
Изучение процессов взаимодействия, протекающих на нано-, микро- и макроскопических уровнях позволяет установить связи возникновения циклов изнашивания с кинетическими фазовыми переходами механизмов диссипации энергии, происходящей в результате самоорганизации и эволюции диссипативно-дислокационных субструктур.
На фиг. 6а, б, в показаны предложенные расчетные модели для оценки характеристик взаимодействия пятен контактов с различными диаметрами пары трения «металл-полимер» при генерировании электрических и аккумулировании тепловых токов.
Следует заметить, что с увеличением площади пятен контактов микровыступов наблюдается рост заряженных частиц на их поверхностях.
Образование двойных электрических слоев происходит на межфазной границе двух сред с различными характеристиками проводимости электронной (металлический элемент трения) и ионной (поверхностный и приповерхностные слои накладки, находящиеся в различных термодинамических состояниях). Поверхностный и приповерхностный слои фрикционных накладок являются многокомпонентными структурами, т.е. гетерогенной системой, в которой рассмотрение их моделей необходимо вести с точки зрения химической кинетики колебания реакций. Химический потенциал зависит от концентрации компонентов в накладке. На фиг. 7а, б проиллюстрировано изменение электрохимического потенциала металлической (а) и неметаллической (б) поверхностей при нагружении пары трения в области их различного структурного и теплового состояния. Установлено, что химпотенциал (кривая 3', см. фиг. 7а) увеличивается в зоне температур, превышающих допустимую для материалов накладки, т.к. на ее поверхности имеются островки электролита.
Наличие химпотенциала сопровождается накоплением зарядов противоположного знака и проявлением в контактной зоне особенностей каждой фазы: ионов в поверхностных и приповерхностных слоях накладки и электронов (дырок) в металлическом элементе трения. Иными словами, физический контакт между указанными выше средами приводит к возникновению и формированию двойного электрического слоя.
В последнем заряды локализуются на очень маленьком расстоянии, толщина слоя в большинстве случаев которого находится в пределах 4,0-7,0 А.
Возникновение электрохимического цилиндрического конденсатора возможно при условиях, обеспечивающих надежное пространственное разделение зарядов на его обечайках и поляризацию объемного заряда в приповерхностных слоях фрикционных накладок. Такие условия являются «идеально поляризованными», а соответствующая обечайка в заданных электролитических системах и определенных пределах потенциалов - поляризованной. Их природа такова, что при поляризации рабочей поверхности металлического элемента трения на ней не происходят фарадеевские процессы, которые связаны с массопереносом материала накладок через границу раздела фаз.
Рассмотрим на нанотрибологическом уровне генерируемые электрические токи в парах трения разных типов.
Диаграмма изменения тока в прямой ("колодочка-диск") паре трения (фиг. 8а), полученная на машине трения и износа СМЦ-2 в лабораторных условиях, показала, что токи являются нестабильными (кривые 1 и 2). Указанные кривые берут начало при одинаковом отрицательном направлении токов, а потом кривая 2 при нагружении в 2,0 Н переходит в зону положительного направления тока. Вид кривой 3 существенно отличается от кривых 1 и 2. Указанная кривая начинается при максимальном значении отрицательного направления тока (- 9,7 нА), пересекает ось абсцисс системы координат при нагрузке в 1,35 Н и подымается к максимальному значению положительного направления тока (5,2 нА). В диапазоне нагружения от 4,5 Н до 7,3 Н имеет место почти одинаковое апериодическое изменение направление тока. При 7,3 Н значение с положительного направления тока (4,5 нА) изменяется к отрицательному (-11,75 нА). Изменение направления тока (кривая 3) происходит при скорости скольжения VCK=1,5 м/с.
С диаграммы кинетики в обратной паре трения (фиг. 7б) видно, что при низких скоростях трения (кривая 1) величина тока электризации в начальный период трения увеличивается, а потом остается практически неизменной. Можно считать, что система находится в нестабильном состоянии. С увеличением скорости скольжения (кривые 2-4) происходит изменение направления (инверсия) тока электризации (соответственно, при силе F, которая равнялась 10,5; 3,0 и 2,0 Н), при этом она имела характер множественного проявления. С увеличением скорости скольжения число инверсий тока тоже увеличивается и при этом для прямой и обратной пар трения (см. фиг. 8а и б) показывает, что в обоих случаях наблюдаются как положительные, так и отрицательные значения токов электризации в зависимости от режима торможения.
Проанализируем теплонагруженность поверхностного и приповерхностного слоев элементов трения металлополимерных пар.
Согласно классической теории в непосредственной близости от точек контакта пары трения «металл (1) - полимер (2)» (фиг. 9а) образуются отдельные полусферические изотермические поверхности, сливающиеся в общую поверхность на некоторой глубине материалов. Расположение изотермических поверхностей характеризуется величиной температурного градиента. В общем случае температурное поле в металлическом и полимерном фрикционных элементах, относящихся, соответственно, к поверхностному и приповерхностному их слоям, представлено на фиг. 9б, в. Из последнего видно, что в зоне взаимодействия имеют место следующие температуры: трения, возникающая в зоне деформации микроучастков рабочей поверхности; контактная, возникающая в точках контакта; поверхностная, возникает на макроучастках поверхностей трения; объемная, возникает в теле элемента трения ниже зоны деформации.
На фиг. 10 приведено распределение температуры (ϑп) и теплового потока (q) на пятне контакта при: а-ϑn=const; б-q=const. Однако такое идеальное распределение температуры (ϑ) и теплового потока (q) на пятне контакта в парах трения невозможно из-за инверсии токов между взаимодействующими зонами, а также линий электрического поля между разноименными (а) и одноименными (б) зарядами (см. фиг. 11а, б).
При контактно-импульсном взаимодействии микровыступов поверхностей трения металлополимерных пар тормозных устройств элементы трения испытывают электротермомеханическое напряженно-деформируемое состояние и при этом происходит распределение электрических и тепловых полей возле зоны контактного взаимодействия. На макроуровне (внешние параметры) - это эксплуатационные параметры (скорость скольжения; податливость элементов пары трения и ее контактного стыка; коэффициенты (статического и динамического) взаимного перекрытия; нормальные усилия; удельные нагрузки; динамический коэффициент трения; тормозной момент; температуры: вспышки, поверхностные, объемные и др.), которые определяются с учетом известных условий взаимодействия и микроформы трущихся поверхностей. На микроуровне (внутренние параметры) - это фактически импульсно действующие: нормальные силы, удельные нагрузки, деформации, механические и термические напряжения, электрические и тепловые токи и порождаемые ими поля, температуры в приповерхностных слоях и др., которые определяются на основании теории единого поля взаимодействия. На наноуровне - рассматриваются условия равновесия на энергетических уровнях при работе полимерной накладки (ее рабочего поверхностного слоя) в зоне температур, ниже и выше допустимой для ее материалов; потенциальные барьеры в условиях равновесия при контактно-импульсном взаимодействии термоэлементов микротермобатарей в парах трения; контакты между микровыступами металлического элемента трения и полупроводниковыми пленками полимерной накладки; переходы типа р-n в микротермобатареях металлического элемента трения и полупроводниковыми пленками полимерных накладок; взаимодействия электрических и тепловых полей и др.
Понятие состояния взаимодействия пятен контактов микровыступов металлополимерных пар трения включает в себя напряженно-деформированное состояние и генерируемые электрические и аккумулированные тепловые токи на их поверхностях и в приповерхностных слоях.
На макроуровне - это номинальные характеристики, определенные с учетом известных условий взаимодействия в макроформе поверхностей. На микроуровне - это фактические импульсные удельные нагрузки, фактические механические электрические, тепловые и химические поля в поверхностных и приповерхностных слоях, омываемых скоростными токами, в которых растет абсолютная величина тока электризации в начальный период работы. При этом необходимо производить анализ токовых диаграмм компонентов сред, возникшие на поверхностях пятен контактов микровыступов при их взаимодействии.
Разрушение материалов при трении обусловлено контактно-импульсным взаимодействием, сопровождающимся совместным действием механической, электрической и тепловой нагрузки. Это вызывает рост поверхностных температур и температурных градиентов, что приводит к значительным термическим напряжениям в металлическом элементе трения.
Тепловые напряжения, возникающие в элементах пары трения тормозов, являются следствием теплового удара, вызванного быстрым нарастанием температуры. Это явление сопровождается структурными изменениями в материалах пары трения.
Электротермомеханическое трение в высоконагруженных металлополимерных парах ленточно-колодочного тормоза буровой лебедки осуществляется при переменных скоростях скольжения и удельных нагрузках, в условиях генерируемых электрических и аккумулируемых тепловых токов с неравномерностью нагревания приповерхностных слоев пар трения «металл-полимер». При этом процессы, явления и эффекты, протекающие в приповерхностных слоях пар трения отличаются большой сложностью. Так, для поверхности каждого из тел в паре характерен высокий уровень неоднородности материалов и дефектов структур, масштабы которых соизмеримы с размерами пятен касания, что оказывает влияние на электротермомеханическое трение. Оценка энергонагруженности поверхностей трения и ее влияние на основные процессы, явления и эффекты необходимы при решении задач обеспечения надежности фрикционных узлов путем увеличения ресурса как полимерных накладок, так и рабочих поверхностей металлических элементов.
Работа выхода частиц с микровывступов металлополимерного сопряжения. Остановимся на работе выхода электронов и ионов с поверхностей фрикционного взаимодействия металлополимерного сопряжения.
Рассмотрим связь работы выхода электронов и ионов с рабочих поверхностей металополимерних пар трения и их поверхностной температуры от импульсных удельных нагрузок, действующих на пятна контактов микровыступов (фиг. 12а, б, в, г). При этом поверхностные температуры полимерных накладок были ниже (фиг. 12а, б, в) и выше (фиг. 12г) допустимой для их материалов, несмотря на то, что в контактах взаимодействия температуры были одинаковыми.
Проведем анализ температур, возникающих на поверхностях пятен микровыступов при различных типах контакта в процессе фрикционного взаимодействия (фиг. 12). Участок I соответствует, в основном, области упругой деформации поверхностных слоев материалов элементов трения, а участки II и III - преимущественно, области пластических деформаций процессов без и с насыщенной плотностью дислокаций.
Участок I на фиг. 12в смещен влево, а на рис. 12г участок I вообще отсутствует, расширяясь при этом на участке II. Объясняется это тем, что в первом случае начинаются деструктивные процессы выгорания связующих компонентов материалов в поверхностных слоях полимерной накладки и имеет место образование пятен жидкости на ее поверхности, а во втором случае - деструктивные процессы заканчивающиеся увеличением количества пятен жидкости на рабочей поверхности полимерной накладки. Третий участок на всех рисунках характеризуется динамическим равновесием между процессами размножения и ангиляции дефектов с образованием микропар и микротрещин в поверхностных слоях металлополимерных пар трения. При этом толщина теплового слоя при больших импульсных удельных нагрузках в металлополимерных парах трения на один-два порядка превышает толщину поверхностного и подповерхностного слоев их элементов.
Проиллюстрируем как влияют указанные выше три участка на изменение поверхностной температуры, удельных нагрузок и работу выхода электронов и ионов с рабочих поверхностей металлополимерных пар трения. Последний параметр является определяющим и в значительной мере влияет на первых два параметра. На участке I (фиг. 12а) наблюдается увеличение работы выхода как электронов, так и ионов с ростом удельных импульсных нагрузок. В результате изменений, которые происходят на рабочих поверхностях металлополимерных пар трения, работа выхода электронов и ионов с поверхностей трения уменьшается (фиг. 12а). Что касается графических зависимостей, представленных на фиг. 12в, г, то наличие жидкой фазы вызывает увеличение удельных нагрузок в парах трения. Работа выхода ионов на них больше работы выхода электронов в связи с эффектом сродственности к электрону (преобразование электронов в ионы). Как видно из фиг. 12а, б, в, г поверхностная температура монотонно увеличивается в данном диапазоне удельных нагрузок, не имеет экстремумов и корреллируется с работой выхода электронов и ионов.
Однако на III-их участках (фиг. 12б, г) при WM=WП и WM<WП в интервале температур, соответственно, ниже и выше допустимой для материалов полимерной накладки имели место постоянная и термостабилизационная температура. Первая возникает тогда, когда кратковременно количества теплоты, генерируемая на поверхностях трения, отводится от матовых поверхностей металлического фрикционного элемента в окружающую среду. Термостабилизационное состояние металлического фрикционного элемента наступает на продолжительное время тогда, когда градиент температуры минимальный по толщине его полированной поверности. Для подтверждения выше сказанного на фиг. 13а, б, в, г и 14а, б, в, г приведены термограммы изменения температуры по слоям, соответственно, фрикционной накладки (ϑН=25,0 мм) и тормозного шкива (δН=20,0 мм) в интервале их теплового состояния, соответственно, от 535,6 до 160,0°С и от 535,2 до 52,2°С.
Энергетические уровни различных типов контактов микровыступов металлополимерных пар трения. В полимерных накладках, составленных из неоднородных материалов, существуют аморфные и кристаллические фазы, возникает захват иного рода - на межфазных границах. Накапливание зарядов на границах обусловлено разницей в проводимостях рассматриваемых фаз (эффект Максвелла - Вагнера). При электризации такого материала носители будут собираться вблизи данной межфазной границы или наоборот, уходить с нее в зависимости от того, какой из двух токов проводимости больше: притекающий к границе зарядов или уходящий от нее. Различия в локальных токах проводимости приводят также к диссипации зарядов при последующем проведении термостимулированного разряда, так как в этом случае токи текут уже в противоположном направлении.
Для процессов нейтрализации зарядов немаловажную роль играют также свойства рабочей поверхности металлического фрикционного элемента. Взаимосвязь между энергетическими уровнями определяется посредством фрикционного контактного взаимодействия микровыступов пар трения.
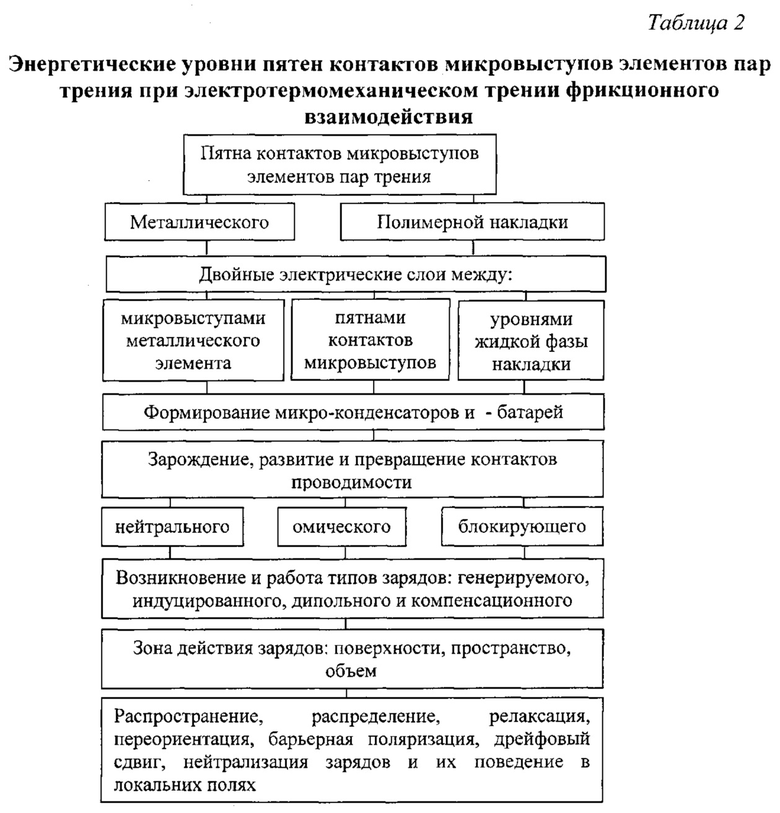
В табл. 2 проиллюстрирован детальный подход к энергетическим уровням пятен контактов микровыступов элементов пар трения при электротермомеханическом фрикционном взаимодействии.
На фиг. 15а, б, в условно показано различие между нейтральным, омическим и блокирующим контактами.
Рассмотрим случаи возникновения нейтральных контактов на микровыступах металлополимерных пар трения согласно фиг. 15а.
Первый случай относится к поверхностным температурам полимерной накладки, которые имеют их величины ниже допустимой для ее материалов. Согласно фиг. 15а работа выхода электронов и ионов из металлического и неметаллического фрикционного элементов равны между собой. Большую прибавку к работе выхода ионов из поверхностного слоя накладки дает сродство к электрону. Последнее является способностью некоторых атомов и молекул присоединять добавочный электрон и превращаться в положительные ионы. Мерой сродства к электрону служит выделяющаяся при этом энергия. Целенаправленная переориентация электронов в ионы и позволяет тем самым за счет данного эффекта достичь равенства работ выхода частиц.
Второй случай. При достижении рабочей поверхностью полимерной накладки температуры выше допустимой для ее материалов происходит выгорание в поверхностных и подповерхностных слоях связующих компонентов, что ведет к образованию жидкостных островков на поверхности накладки. При контакте рабочей поверхности металлического фрикционного элемента с жидкостью наблюдается явления перехода ионов из металла в жидкость (см. фиг. 15а, кривая 1).
Металл входит в раствор в виде либо положительных ионов, либо комплексных отрицательных ионов, если он взаимодействует с раствором жидкости. При этом поверхность металла приобретает некоторый специфический потенциал, устанавливающий равновесие между процессом выделения и осаждения ионов. Этот потенциал зависит как от природы металла, так и от концентрации ионов в жидкости. При некотором значении кислотности (рН) металл не посылает в раствор ионы, а наоборот, принимает их из раствора, приобретая заряды до наступления электрического равновесия.
Как известно, металлы располагаются в электрохимический ряд по отношению к положительному иону водорода Н+. При погружении в жидкость двух различных металлов, каждый из них имеет определенный потенциал по отношению к жидкости. При контакте металлов возникает электрический ток до тех пор, пока в растворе не будут исчерпаны все ионы металлов или раствора. Электрические токи могут протекать и между различными точками одной металлической поверхности, если она заряжена и неоднородна.
Кроме химического механизма электрических явлений в контакте металла и жидкости возможен и другой механизм - электризация поверхностей металла и жидкости при движении последней, т.к. слой жидкости, перемещаясь, уносит с собой ионный заряд. Расчеты показывают, что значительное накопление зарядов при движении жидкости происходит при удельном ее сопротивлении выше 109 Ом⋅см. Считается, что при этом на поверхности металла, соприкасающейся с жидкостью, образуется двойной электрический слой. Поверхность металла в результате потерь или захвата ионов приобретает незначительный химический потенциал, и по ней распределяется некоторый заряд. Противоположный по знаку заряд находится в жидкости. Распределение зарядов в жидкости может характеризоваться потенциалом ϕэ, который меняется с расстоянием от поверхности в соответствии с электростатическими силами и распределением Больцмана (фиг. 15а). Аналитическое выражение для расчета величины потенциала ϕэ получаем решением уравнения Пуассона в предположении о существовании экранирующего двойного слоя [3]:
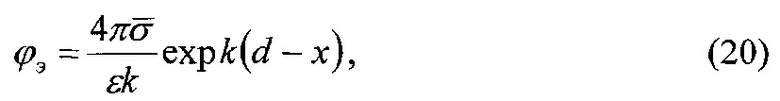
Таким образом, в условиях электротермомеханического трения металлополимерных пар трения энергонагруженность рабочей поверхности полимерной накладки играет решающую роль в формировании нейтрального контакта в зоне фрикционного взаимодействия.
Наиболее часто в металлополимерных парах трения [применительно к двухслойным («металл - полимер»)] структурам тормозных устройств встречается омический (инжектирующий) контакт (фиг. 15в).
На фиг. 16 приведена зонная диаграмма контакта «металл - электропроводящий полимер» [3]. Особенностью этой диаграммы является наличие узкой электропроводящей зоны в середине щели полимера. Согласно одной из гипотез, именно подобная узкая зона может отвечать за транспортные свойства тонких диэлектрических пленок. Изменения положения уровня Ферми металла в области его фазового перехода относительно узкой зоны в полимере обеспечивает условия инжекции из металла в полимер и тем самым характеризует изменение проводимости системы в целом.
На фиг. 17а, б представлена модель энергетических зон в системе «металл - полимер» стимулированной импульсными нормальными усилиями инжекцию носителей тока из металла в зону проводимости полимера. Согласно этой модели сжатие полимера вызывает распад поверхностных состояний, играющих роль акцепторов электронов. Не исключено также, что из-за увеличения поляризуемости поверхностей фрикционного взаимодействия одновременно происходит понижение дна зоны проводимости полимера. В результате при некотором значении N=NC структура энергетических зон вблизи границы раздела «металл - полимер» оказывается благоприятной для инжекции носителей, хотя при N<NC этот процесс либо вообще не реализуется, либо имеет крайне низкую эффективность.
На фиг. 18 представлена упрощенная зонная диаграмма трехслойной структуры "металл 1 - полимер - металл 2". Сплошной жирной линией в слое полимера показана форма потенциального барьера для заряда, когда d больше глубины проникновения поверхностного заряда, пунктирная кривая соответствует случаю, когда d меньше глубины проникновения поверхностного заряда, штриховкой обозначены электронные состояния. Выбран вариант контакта, в котором оба металла одинаковы, работы выхода электрона из металла и полимера также одинаковы. Это так называемый случай прямых зон, и при использовании полимера в такой структуре чаще всего можно получить омический контакт. При этом не будем останавливаться на деталях механизма установления электрического контакта. Констатируем только факт, что наличие между двумя металлическими электродами диэлектрика с большой шириной запрещенной зоны может препятствовать протеканию заряда между электродами в случае, когда толщина диэлектрической прослойки велика. При этом слой диэлектрика играет роль потенциального барьера прямоугольной формы, высота которого определяется разностью между работой выхода металла и энергией электронного сродства полимера.
При уменьшении толщины полимерной пленки может возникнуть ситуация, когда заряды, сосредоточенные вблизи противоположных границ рассматриваемого контакта, начнут взаимодействовать между собой, приводя к искажению формы потенциального барьера. Наибольшей толщиной пленки, при которой начинается взаимодействие граничных зарядов, может считаться удвоенная величина такого параметра контакта, как глубина проникновения поверхностного заряда. Взаимодействие приповерхностных зарядов может привести к тому, что в середине барьера начнет формироваться локальный минимум, который в принципе может привести к пересечению кривой, описывающей огибающую потенциального барьера с уровнем Ферми.
При таком гипотетическом варианте в середине барьера на уровне Ферми могут возникнуть новые электронные состояния, которые увеличивают его проницаемость для электронов. Если научиться управлять такими состояниями, то фактически это будет означать создание принципиально нового электронного гибридного наноструктированного металлополимерного материала.
При этом весомой важности приобретает вопрос управления системой «металл 1 - полимер - металл 2» путем переключений в полимерной пленке эффекта индуцирования зарядов, при которых области изменения электропроводности в ней пространственно разделены. Для исследований были выбраны переключения в системе за счет изменения граничных условий в трехслойной структуре «металл - полимер - металл», что привело к плавлению одного из электродов. В результате чего происходит перераспределение поверхностного заряда в приконтактной области полимера вследствие резкого изменения эффективной работы выхода электронов металла вблизи критической температуры. Таким образом, переход полимера в высокопроводящее состояние вызван изменением положения уровня Ферми металла (эффективной работы выхода электронов) в точке фазового перехода. Аналогичного результата можно достичь, если между металлом, претерпевающем фазовый переход и полимерной пленкой поместить другой металл, стабильный в заданном интервале температур, в такой ситуации все структурно - механические изменения (изменение агрегатного состояния, стрикционные явления и т.п.) в первом металле могут быть подавлены с помощью второго металла, т.е. путем технологического решения. Необходимо отметить еще одну важную особенность омического (инжектирующего) контакта на микровыступах металлического элемента, поведение которого напоминает нагретый катод, уже в отсутствие поля на поверхности, можно спонтанно инжектировать носители внутрь поверхностного слоя полимерной накладки. Возникающее перед электродом облако пространственного заряда в конце концов полностью запирает эмиссию с электрода, если, конечно, облако не рассасывается действием приложенного поля. Граничные условия на инжектирующем электроде сводятся к Е (0, t)=0 и плотности зарядов ρЗ (0)=±∞, причем полярность определяется знаком инжектируемых носителей.
Поведение микровыступов полимерной накладки в сильной степени зависит от материала микровыступов металлического фрикционного элемента. Обычно пятна контактов последних микровыступов покрытые пленками, при слабых и промежуточных напряженностях поля являются блокирующими контактами (фиг. 15а). Такой контакт препятствует передаче носителей заряда от электрода внутрь поверхностного и подповерхностного слоя полимерной накладки в то же время сам он может принимать носители из вышеперечисленных слоев.
В диэлектрике с блокирующими контактами, вообще не содержащем носителей заряда, протекание стационарного тока, очевидно, невозможно. Если же в диэлектрике имеются носители обоих знаков, причем с сильно отличающимися значениями их подвижностей, то вблизи пятен контактов микровыступов металлического фрикционного элемента, знак которого совпадает со знаком более подвижных носителей, образуется барьер Шоттки. Возникающая в этих условиях поляризация пятен контактов микровыступов накладки обусловлена как раз наличием электродов. Эта ситуация довольно легко объясняется в том предельном случае, когда отсутствует подвижность у носителей какой-то одной полярности (например, электронов) и не происходит дальнейшей генерации свободных носителей. Приложенное поле в этом случае удаляет положительные носители от пятен контактов микровыступов накладки (анодов, расположенных, скажем при х=0).
Так как этот электрод не в состоянии передавать материалам положительные заряды, вблизи него в слое толщиной δs между плоскостями х=0 и х=δs образуется облако отрицательного пространственного заряда с плотностью ρ. После того как слой пространственного заряда будет полностью сформирован, напряжение u, первоначально подаваемое по всей толщине металлического микровыступа, теперь станет приложенным к слоя толщиной δs. В результате ток обратится в нуль. Протяженность слоя определяется формулой  и не зависит от приложенного электрического поля.
и не зависит от приложенного электрического поля.
Например, при плотности неподвижных (захваченных) носителей ρз=110-4 Кл/см3, ε=2⋅10-13 Ф/см и u=1,0 В. Толщина слоя δs составляет 1,25⋅10-3 см. Итак, использование блокирующих контактов препятствует полному удалению подвижных носителей из диэлектрика, причем вне зависимости от значения их подвижности.
Наличие непроводящей прослойки конечной толщины между диэлектриком и электродом может вызвать образование барьерной поляризации. Правда, молекулярные размеры образующегося двойного слоя положительных и отрицательных носителей не позволяют обнаружить его в обычных внешних измерениях, например компенсационных зарядов на электроде. Кроме того, образование двойного электрического слоя не приводит к блокирующему эффекту.
Таким образом, если контакты заблокированы, нейтрализация должна протекать внутри металлического элемента трения независимо от типа контакта (является он инжектирующим электроны или блокирующим). Это зависит лишь от того, какая из работ выхода электронов или ионов больше: металлического или полимерного фрикционного элемента. Если работа выхода из первого элемента больше, чем со второго образуется блокирующий барьер. Наличие последнего позволяет изучать методом термостимулированного разряда полуизоляторы и полупроводники, которым свойственны большие токи проводимости. Блокирующие контакты действуют противоположным образом: они препятствуют как инжекции, так и нейтрализации зарядов.
Контактно-импульсное взаимодействие микровыступов узлов трения с различными градиентами электрического потенциала и температуры. Градиентная теория твердых тел и на границах межфазных слоев в интервале поверхностных температур ниже и выше допустимой для материала полимерной накладки позволит дать ответ на вопрос обеспечения положительного градиента механических свойств в поверхностных слоях металлополимерных пар трения тормозных устройств. Однако при этом существенное влияние оказывают градиенты электрического потенциала и температуры на взаимодействующих поверхностях пятен контактов микровыступов пар трения «полимер-металл» и по их глубине.
В табл. 3 показано шесть случаев контактно-импульсного взаимодействия микровыступов поверхностей трения с различными градиентами электрического потенциала и температуры при заданных граничных условиях.
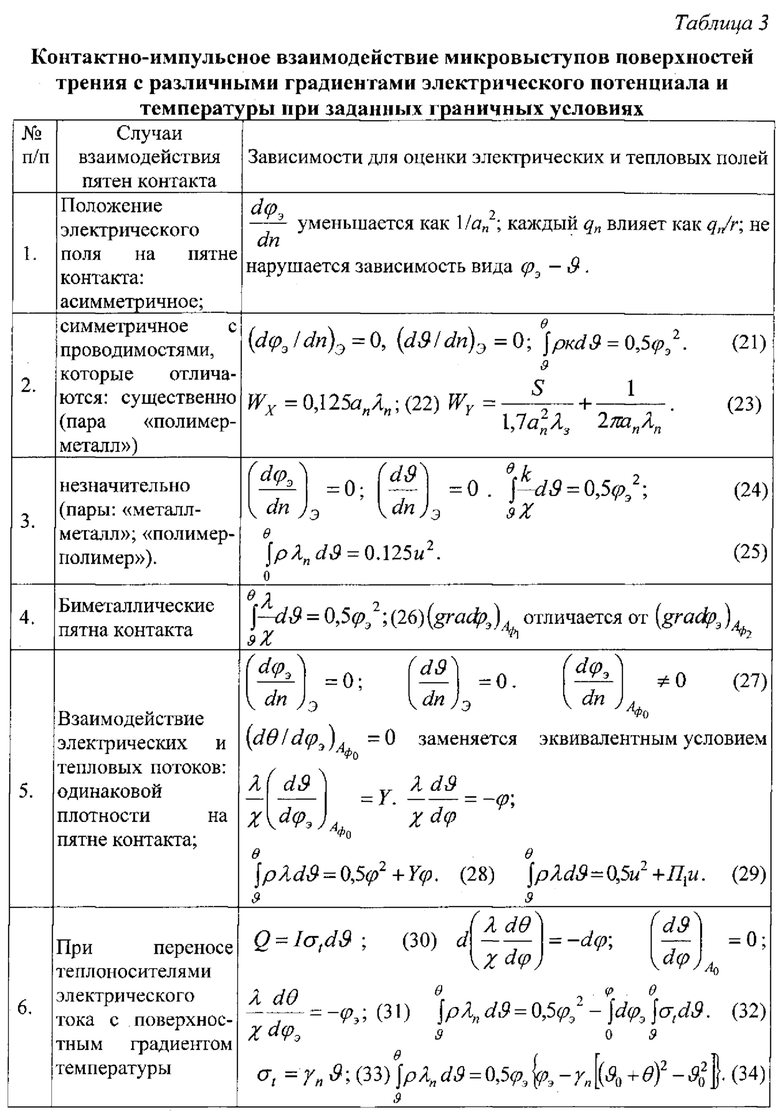
Кратко проанализируем каждый из случаев, представленных в табл. 3.
Первый случай. Асимметрия наблюдается в отдельных зонах там, где расстояние r от контакта велико по сравнению с радиусом an контактного пятна микровыступов Ак, которое в данном случае имеет форму круга.
Установлено, что градиент потенциала в зоне стягивания уменьшается по мере увеличения расстояния от контакта, примерно как 1/aтn2. При этом общий пространственный заряд в отдельных зонах стягивания по величине почти такой же, как и заряды в непосредственной близости от пятна контакта (см. фиг. 11а, б). Следовательно, влияние удельных зарядов на электрическое поле в зоне стягивания пренебрежимо мало. Аналогичные рассуждения справедливы и в отношении теплового поля.
Таким образом, асимметрия не нарушает закона зависимости вида ϕэ-ϑ в наиболее узких частях стягивания, так как градиенты температуры и напряжения в них велики, а асимметрия в отдельных зонах не отражается на общем напряжении и стягивания и на разности температур в контактной поверхности пятна взаимодействия.
Второй случай характерен для металлополимерных пар трения. При нагревании микровыступов поверхности контакта условия (dϕэ/dn)Э=0 и (dϑ/dn)Э=0 не соблюдаются, поскольку имеется разность температур между взаимодействующими пятнами контактов. При этом тепловой поток делится на две части: продольную (часть X) и поперечную (часть Y). Тепловой поток вдоль Y вызовет отклонение результатов расчета по зависимости (23) (см. табл. 3) примерно на величину (WX/WY)100, %. Составляющие уравнения (23) определяются по зависимостям (21) и (22). После выполненных расчетов на основе значений параметров получили величину отклонения теплового потока WX/WY<0,05, которой можно пренебрегать.
Третий случай характерен для интенсивного массопереноса от микровыступов контактирующих поверхностей по схеме «полимер-металл» и наоборот. Он определяет энергетические уровни взаимодействия микровыступов пятен контактов согласно зависимостям (24) и (25).
Четвертый случай отличается от третьего градиентами (gradϕэ)Aф1 и (gradϕэ)Aф2, так как энергетические уровни металлов, входящих в биметалл, различны.
Пятый случай. Поверхность пятна контакта микровыступов Аф0 удовлетворяет граничным условиям, но не удовлетворяет условию (dϕэ/dn)Аф0, так как Аф0 пересекается тепловым потоком, плотность которого пропорциональна плотности электрического тока j. Вследствие этого получаем Yj, где Y имеет единицу измерения напряжения. Поскольку тепловой поток пропорционален j, он не вносит изменений в систему элементарных линий тока.
В результате преобразований ряда зависимостей получили выражение (28) для оценки теплового потока в интервале температур 0-ϑ и при изменении температур от ϑ до θ [выражение (29)]. Часть теплоты Пельтье (П1) уходит в исследуемое пятно контакта и составляет тепловой поток П1J, а и является напряжением зоны стягивания на нем.
Анализ зависимости (29) показывает, что при небольших величинах и, характерных для металлополимерных пар трения, эффект Пельтье вызывает заметное отклонение u от зависимости вида ϕэ-ϑ.
Шестой случай характеризуется переносом теплоносителями электрического тока из более в менее нагретую зону пятна контакта, лежащую на пути его движения. Это осуществляется посредством эффекта Томпсона, интенсивность которого зависит от коэффициента Томпсона (σt). Записав количество теплоты (30), поступающей от сечения микровыступа с температурой ϑ+dϑ к соседнему сечению с температурой 3 с учетом граничных условий, и использовав зависимость вида (32), после окончательного интегрирования получили выражение (33).
В дальнейшем применив условие, что при больших температурах металлического элемента трения σt пропорционален Т в окончательном виде получаем зависимость (34). Последняя связывает между собой параметры электрического и теплового полей, токи которых пронизывают пятна контакта микровыступов трущихся поверхностей.
При кратковременных торможениях при отсутствии теплоотдачи от матовых поверхностей шкива происходит интенсивное аккумулирование теплоты, которое может привести его к предельному тепловому состоянию его обода. Для упрощенного рассмотрения задачи теплопроводности пренебрегаем теплоотдачей в окружающую среду.
Темпы протекания импульсов электрического и теплового токов в микровыступах пар трения. Рассмотрим темпы протекания импульсов электрического и теплового токов в микровыступах поверхностей трения металлополимерных пар.
Остановимся на электрических и тепловых токах, возникающих в металлополимерных парах трения. В табл. 4 приведены расчетные зависимости, описывающие электрические и теплообменные процессы при работе металлополимерных пар трения [4].

В зависимости (36), касающейся теплопроводности, применен темп протекания теплового тока 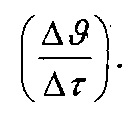 Темп накопления и рассеивания теплоты
Темп накопления и рассеивания теплоты 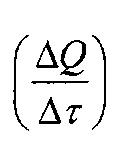 использован в зависимостях: (35), описывающей протекание электрического тока; (37) и (38), относящихся к конвективному и излучательному вынужденному охлаждению.
использован в зависимостях: (35), описывающей протекание электрического тока; (37) и (38), относящихся к конвективному и излучательному вынужденному охлаждению.
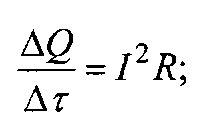
Электродинамика контактного взаимодействия в трибосопряжении. Вольченко А.И. предложен метод определения составляющих генерированных электрических токов в металлополимерных парах трения базирующийся на экспериментально-расчетных данных, реализуемого в пять этапов на каждом из которых определяли [5]:
- суммарный термический ток (IT);
- суммарный ток, который возникает за счет трения скольжения и контакта взаимодействующих макроучастков поверхностей (ICK);
- составляющую суммарного тока, который возникает за счет трения скольжения (ITC);
- составляющую суммарного тока, образованного движением заряженных частиц массопереноса (IM);
- суммарный ток, обусловленный сорбционно-десорбционными процессами в приповерхностных слоях накладки, которые находятся при температуре выше допустимой для ее материалов (IД).
Составляющие вышеперечисленных токов в зависимости от направления вращения тормозного шкива представлены в виде векторной диаграммы на фиг. 19а.
Метод определения направлений составляющих генерируемых электрических токов в парах трения "полимер-металл", опирающийся на зависимости выхода электронов и ионов, соответственно, из металлического и полимерного фрикционного элемента заключается в следующем [6]. В конечном итоге, экспериментально регистрируемый суммарный ток (IC) электризации с учетом направлений составляющих токов имеет вид при
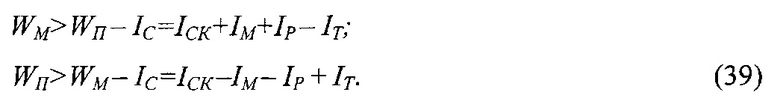
На фиг. 19б, в, г, д проиллюстрированы схемы направлений составляющих электрических токов в металлополимерных парах трения при температуре выше допустимой для материалов полимерной накладки. На фиг. 19б, е показаны токи IM1 и IM2, вызванные движения заряженных частиц массопереноса по схеме "полимер-металл" и "металл-полимер".
Остановимся на электродинамике поверхностного слоя полимерной накладки. Поскольку в приповерхностном слое полимерной накладки протекают активный Ia и реактивный Ir токи (фиг. 20б), которые заменены эквивалентной электрической схемой, содержащей идеальные сопротивления R' и емкость Ср, обеспечивающих протекание указанных токов. Идеальные R' и Ср соединены параллельно (фиг. 20а).
Условиями эквивалентности схемы замещения реальному приповерхностному слою полимерной накладки является равенство [7]:
- сдвига фаз между током I и напряжением u в реальном слое и в схеме замещения;
- мощности, выделяемой в схеме замещения, потерям в приповерхностном слое в реальной полимерной накладке.
Рассмотрим параллельную схему замещения, поскольку при оценке податливости фрикционного стыка металлополимерной пары трения микровыступы соединены между собой параллельно. Векторная диаграмма токов и напряжений для параллельной схемы замещения (фиг. 20б) позволяет рассчитывать tgδ1 и мощность, теряемую в приповерхностном слое полимерной накладки.
Согласно векторной диаграмме (фиг. 20б) для параллельной схемы замещения имеем
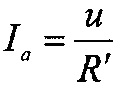 ,
, 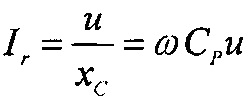 и
и 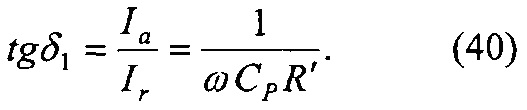
Из(40)следует

Поскольку мощность, теряемая в приповерхностном слое накладки, определяется только активной составляющей тока, то с учетом (41) получаем
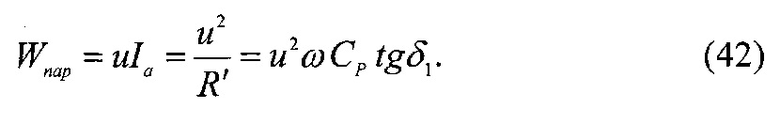
Из (42) следует, что для данной схемы замещения мощность потерь пропорциональна tgδ1, ω и u2. Следовательно, правомерно характеризовать потери в приповерхностном слое в полимерной накладке количественным параметром tgδ1. Для слоев с малым значением сопротивления R, т.е. с большими токами утечки и, следовательно, большими потерями необходимо использовать неравенство tgδ1<5,0-10-2.
При нахождении приповерхностных слоев полимерных накладок в переменном электрическом поле векторная диаграмма имеет вид, показанный на фиг. 20б.
Согласно векторной диаграммы реактивный ток Ir=Io+IPr опережает напряжение u на 90°. Активный ток Ia=Icn+IPa совпадает по фазе с напряжением u. Полный ток I достигнут относительно приложенного напряжения со сдвигом на угол ϕ. Угол δ1, дополняющий угол сдвига фаз ϕ между током и напряжением 90°, называется углом диэлектрических потерь. Тангенс угла диэлектрических потерь характеризирует потери в приповерхностном слое полимерной накладки, которые легко понять из векторной диаграммы tgδ1=Ia/Ir. Чем больше активный ток Ia, нагревающий приповерхностный слой полимерной накладки, тем больше δ1 и tgδ1 и, следовательно, больше потери. По значению tgδ1 оценивается качество приповерхностного слоя полимерной накладки: чем он выше, тем больше будет разогрев приповерхностного слоя накладки, а следовательно, больше площади пятен контактно-импульсного взаимодействия и меньшие импульсные удельные нагрузки на пятнах контакта. Рациональные величины должны быть при условии tgδ1≤10-4.
Явления проводимости в приповерхностных слоях полимерной накладки. Процессами внутренней релаксации заряда в полимерной накладке управляют явлениями проводимости. Последние определяются такими характеристиками: подвижностью носителей и их концентрацией; условиями инжекции зарядов на пятнах контакта и т.д.
В полимерных материалах, способных длительно удерживать заряд, присутствуют центры захвата носителей, подвижность которых подавляется процессами захвата. Захват оказывает воздействие и на процессы проводимости. Помимо собственных носителей заряда в полимерном материале присутствуют и посторонние носители, инжектируемые электроны в тело микровыступа контакта металлополимерной пары трения.
При исследовании контактной проводимости необходимо отличать переходные процессы от стационарных на пятне фрикционного взаимодействия. Это вызвано тем, что при исследовании проводимости или подвижности носителей не удается осуществлять одновременный контроль во времени за распределениями зарядов как в теле полимерной накладки, так и на ее рабочей поверхности. Отпечаток на проблему проводимости полимерного материала накладывает отсутствие его структурной однородности и чистоты.
На подвижность носителей заряда в полимерном материале оказывает влияние наличие в нем различных состояний - свободных (делокализованных) и связанных на мелких и глубоких уровнях захвата, расположенных по толщине накладки. Движение ионов с энергией вблизи поверхности пятна контакта (зоны проводимости) представляет собой квантово-механическое туннелирование между делокализованными состояниями, расположенными на шкале энергии выше края подвижности. Этот процесс происходит без какой-либо термической активации, и отвечающие ему подвижности зарядов оказываются относительно высокими - около 10 см3/(В⋅с). Для движения заряда, захваченного мелким уровнем, расположенным по энергии ниже края подвижности, необходимо определенное количество тепловой энергии, превращенной из электроимпульсной энергии при трении. Процесс движения таких зарядов становится термоактивационным и сводится к последовательным перескокам между локализованными состояниями. В этом случае подвижность зарядов меньше [около 102 см2/(В⋅с)], нежели в первом случае. Наконец, время захвата носителей на глубоком уровне оказывается очень большим, а их подвижность с учетом такого захвата становится чрезвычайно малой [10-10-10-17 см2/(В⋅с)] [3].
Во многих полимерных материалах, не обладающих энергетически сильными носителями, их можно создать посредством инжекции через пятно контакта из металлического фрикционного элемента. Если приток носителей вследствие инжекции превышает поток частиц, переносимых через пленку полимера накладки, то происходит ограничение токов полем образующего пространственного заряда. В обратном случае токи определяются интенсивностью инжекции с металлических пленок пятна контакта.
Энергетический баланс приповерхностного слоя полимерной накладки в формировании режима металлополимерной пары трения.
Диэлектрические потери в приповерхностном слое полимерной накладки, находящемся в переменном электрическом поле при трении, представляет собой рассеиваемую мощность, т.е. энергию, генерируемую электрическим полем.
Различают две причины необратимых потерь энергии электрического поля в приповерхностном слое полимерной накладки на счет:
- нагревание токами сквозной проводимости;
- замедленных видов поляризации.
Согласно закона Джоуля-Ленца протекание тока сквозной проводимости приводит к выделению теплоты в приповерхностном слое накладки, и при этом имеют место необратимые потери энергии внешнего поля.
Поляризационные процессы характеризуются поляризованностью РП и также приводят к необратимым потерям энергии внешнего поля. Поляризованность РП численно равна электрическому дипольному моменту Мд единицы объема приповерхностного слоя накладки.
Если поляризационные процессы успевают следить за изменением внешнего поля, то сдвиг фаз между напряженностью поля ξ и поляризованностью РП отсутствует (фиг. 21а). В этом случае в течение первой четверти периода поле ориентирует связанные заряды по направлению, совершая работу. Направления поля ξ и электрического дипольного момента Мд совпадают. Кинетическая энергия связанных зарядов растет, что равносильно повышению их температуры, т.е. нагреванию приповерхностного слоя полимерной накладки, а вместе с ним и металлополимерной пары трения, что свойственно единичному режиму торможения.
Во второй четверти периода направление поля ξ остается прежним, а поляризованность РП уменьшается, т.е. связанные заряды за счет уменьшения ξ начинают возвращаться в исходное состояние, отдавая накопленную кинетическую энергию, что ведет к понижению их температуры, т.е. охлаждению приповерхностного слоя полимерной накладки.
В течение периода, нагревание компенсируется охлаждением и, таким образом, необратимые потери энергии отсутствуют. Такое состояние приповерхностного слоя полимерной накладки носит название установившегося за счет быстрых видов поляризации.
В случае медленных видов поляризации наблюдается отставание поляризации от изменения внешнего поля (фиг. 21б). За счет сдвига фаз между напряженностью ξ и поляризованностью РП время нагревания приповерхностного слоя полимерной накладки оказывается большим (длительный режим торможения), т.е., время накопления кинетической энергии больше времени ее отвода в металлополимерные пары трения.
Следовательно, приповерхностный слой полимерной накладки нагревается, или в нем наблюдаются необратимые потери энергии внешнего поля. Потери энергии на ориентацию связанных зарядов равносильны тому, что в поверхностном слое как бы протекает активный ток, обусловленный поляризационными процессами, отстающими от изменений внешнего поля.
На втором этапе анализируется динамическое и тепловое подобие подсистемы пар трения ленточно-колодочного тормоза.
При фрикционном взаимодействии, имеющего контактно-импульсный характер, рабочих поверхностей металлополимерных пар трения протекают сложные нелинейные процессы, явления и эффекты, способствующие оказать влияние на их подповерхностные слои, а также на состояние металлического фрикционного элемента. При электротермомеханическом трении металлополимерных пар трения процессы, явления и эффекты оказывают внешнее и внутреннее воздействие на их поверхностные и подповерхностные слои, способствуя тем самым возникновению механических, электрических, тепловых и химических полей.
Перечисленные поля взаимодействуют между собой, находясь при этом в едином энергетическом поле, и для их описания необходимо использовать неоднородную систему нелинейных функциональных зависимостей. Вид дифференциальных уравнений зависит не только от того какие фрикционные материалы используются в узле трения, при каких импульсных нагрузках и скоростях скольжения они контактируют друг с другом, какой подвод теплоты реализуется в парах трения, какое долевое распределение теплоты между фрикционными элементами, какое внешнее управляющее воздействие реализуется в трибосистеме, но и в каком механическом и тепловом поле функционирует узел трения. Теоретический динамический и тепловой расчет трибосистем - очень сложный процесс, так как по данным А.В. Чичинадзе включает в себя более 50-ти параметров, с многими допущениями, упрощениями и линеаризацией динамических и тепловых процессов. В результате этого зачастую получаются результаты расчета, неадекватные реальным условиям эксплуатации из-за нестыковки различных оценочных методик, опирающиеся на огромное количество моделей (до миллиона и более) и несоответствие их результатам экспериментальных исследований в лабораторных (стендовых) и эксплуатационных (промышленных) условиях. Однако все выше сказанное в конечном счете невозможно вследствие нарушения принципа суперпозиции («механическое растяжение – механическое сжатие», «тепловое расширение - тепловое сжатие», «поляризация - деполяризация», «нагревание - охлаждение», «восстановление - разрушение» и т.д.) для нелинейных трибосистем.
Таким образом, произвести эффективную оптимизацию конструктивных и эксплуатационных параметров пар трения теоретическим путем является практически не решаемая задача. Наиболее целесообразно путем реализации оптимизации пар трения ленточно-колодочного тормоза является использование экспериментальных данных, полученных в лабораторных условиях на тормозных стендах, базирующимися на методах физического подобия и моделирования с привлечением элементов теории системного подхода.
Корректная физическая модель металлополимерной пары трения доступнее для исследования, чем реальный объект. При этом модель должна достаточно точно отражать поведение трибосистемы при определенных ограничениях, что позволит получить решение, которое отражает ее адекватное состояние по отношению к реальной трибосистеме.
В качестве объекта исследований выступают фрикционные узлы ленточно-колодочного тормоза буровой лебедки У2-5-5.
Серийный ленточно-колодочный тормоз.
Согласно кинематической схеме (см. фиг. 22а, б) фрикционные накладки 3 установлены на тормозных лентах 2, которые одним концом [со стороны сбегаюшей ветви (II) ленты] прикреплены к балансиру 11, а другим [со стороны набегающей ее ветви (I)] - к мотылевым шейкам 6 и 9 коленчатого вала 10.
Серийные ленточно-колодочные тормоза буровой лебедки работают следующим образом. Перемещением рукоятки 1 осуществляется поворот коленчатого вала 10, в результате которого бурильщик затягивает тормозные ленты 2 с фрикционными накладками 3 и они садятся на тормозные шкивы 4. Процесс торможения ленточно-колодочным тормозом характеризуется следующими стадиями: начальной (первой), промежуточной (второй) и заключительной (третьей). Остановимся на каждой из стадий в отдельности.
На начальной стадии торможения фрикционные накладки 3, размещенные в средней части тормозной ленты 2, взаимодействуют с рабочей поверхностью тормозного шкива 4. Фронт взаимодействия расширяется в сторону фрикционных накладок 3 набегаюшей ветви (I) тормозной ленты 2.
Промежуточная стадия торможения характеризуется дальнейшим распространением фронта взаимодействия в сторону фрикционных накладок 3 сбегаюшей ветви (II) тормозной ленты 2.
Конечная стадия торможения характеризуется тем, что почти все неподвижные накладки 3 тормозной ленты 2 взаимодействуют с рабочей поверхностью вращающегося шкива 4. Во время притормаживаний последовательность вхождения поверхностей трения в контакт повторяется. Полный цикл торможения завершается остановкой тормозных шкивов 4 с барабаном 5. Управление тормозом буровой лебедки осуществляют также подачей сжатого воздуха через кран 7 бурильщика в пневматический цилиндр 8, шток которого соединен с одной из мотылевых шеек коленчатого вала 10 тормоза. Величину давления сжатого воздуха в пневмоцилиндре 8 регулируется поворотом крана 7 бурильщика.
При неравномерном изнашивании фрикционных накладок 3, установленных на лентах 2, балансир 11 в момент торможения несколько отклоняется от горизонтального положения и выравнивает нагрузки на сбегающей ветви (II) тормозных лент 2, обеспечивая при этом равномерный и одновременный обхват ими тормозных шкивов 4. Благодаря шаровым шарнирам реализация нагрузок от тормозных лент 2 к балансиру 11 при этом не изменяется.
Наиболее слабым звеном в тормозном узле являются фрикционные накладки. Они изготавливаются в виде отдельных деталей, которые могут крепиться различными способами (например, с помощью усиков) к относительно гибкой стальной ленте. По дуге обхвата тормозной лентой шкива устанавливают фрикционные накладки с постоянным и переменным шагом. При установке на ленте накладок с постоянным шагом их количество всегда четное (12; 16; 18; 20; 22; 26) (см. фиг. 23г). При переменном шаге это число может быть и нечетным.
Общее количество фрикционных накладок на тормозной ленте зависит от их геометрических параметров, а также от того, какой угол обхвата тормозной лентой рабочей поверхности тормозного шкива реализуется в данном ленточно-колодочном тормозе буровой лебедки.
Модельный ленточно-колодочный тормоз. Основные узлы тормозного стенда смонтированы на двух двутавровых балках 4 (фиг. 23а, б, в), которые, в свою очередь, анкерными болтами прикреплены к бетонному основанию. Модельный тормоз имеет тормозную ленту 2. При этом один конец тормозной ленты 2 закреплен неподвижно, а на втором ее конце находится нагрузочное устройство 11. С нерабочими поверхностями полимерных накладок 3 взаимодействует внутренняя поверхность ленты 2. Накладки 3 крепятся к ленте 2. Тормозной шкив 4 установлено на валу 5 с подшипниками, которые находятся в опорах 6. Вал 5 через упругую пальцевую муфту 10 связан с валом 12 двигателя постоянного тока 7. При этом использован двигатель постоянного тока марки 2ПН225МУ4 мощностью 15,0 кВт. Применение двигателя этой марки позволило плавно регулировать вращательный момент на приводном валу 12 и поддерживать его стабильным при изменении частоты вращения вала 5. Усилие прижатия нерабочих и рабочих поверхностей фрикционных накладок 3, соответственно, к внутренней поверхности тормозной ленты 2 и рабочей поверхности тормозного шкива 4 регулировалось нагрузочным устройством 11.
Тяговой двигатель 7 тормозного шкива 4 (ДПТ) питается постоянным током с номинальным напряжением обмотки якоря (ЯД) 110В, в качестве источника ее питания было использовано аналогичный двигатель постоянного тока 8 (ГПТ), который работал в генераторном режиме. Вал 10 генератора вращался асинхронным трехфазным двигателем переменного тока 9 (ДПТ). На обмотки возбуждения генератора (ОВГ) и двигателя (ОЗД) подавались постоянные токи, которые выпрямлялись на диодных мостах, составленных из диодов VD1-VD4 и VD5-VD8, и регулировались лабораторными автотрансформаторы ЛАТР-1M и ЛАТР-2М.
В табл. 5 приведены основные параметры пар трения модельного ленточно-колодочного тормоза.

Задачи исследования, условия проведения испытаний и реальные возможности определили объект испытаний - физическую модель ленточно-колодочных тормозов буровой лебедки с масштабом:
- геометрического подобия для ее основного размерного параметра - радиуса тормозного шкива

ml=2, 2,45 i 2,9 для Rш=500, 612,5 i 725 мм, соответственно,
где lH и lM - радиусы тормозного шкива натуры и модели (lH=Rш, lм=250 мм);
- динамического сходства
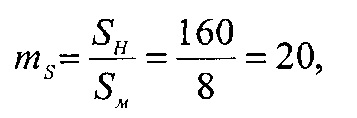
где SH и Sм - усилие натяжения набегающих участков тормозной ленты натуры и модели, кН.
Заметим, что масштабы сходства изменяются, если изменяются параметры натуры или модели, например, натяжения ветви ленты.
Для проведения испытаний модель оборудовалась:
- тормозными лентами из стали 50,0 шириной 200,0 мм 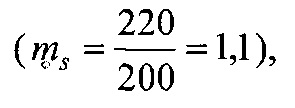 толщиной δЛ=2,0, 3,0 и 3,7 мм (mδ=2,0, 1,67 и 1,62 для толщины ленты натуры 4,0, 5,0 i 6,0 мм, соответственно), с длиной промежутка 2Ln участка ленты между накладками (Ln=30,0-90,0 мм, mLn=1,0);
толщиной δЛ=2,0, 3,0 и 3,7 мм (mδ=2,0, 1,67 и 1,62 для толщины ленты натуры 4,0, 5,0 i 6,0 мм, соответственно), с длиной промежутка 2Ln участка ленты между накладками (Ln=30,0-90,0 мм, mLn=1,0);
- фрикционными накладками из ретинакса ФК-24А толщиной δH=15,0 мм 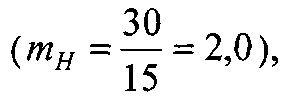 шириной BH=230,0 мм
шириной BH=230,0 мм 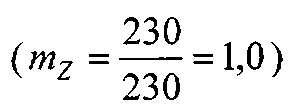 и длиной L=120 мм
и длиной L=120 мм 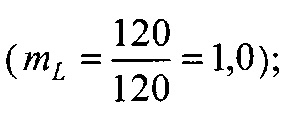
- тормозной шкив вращался с наибольшей частотой 200 мин-1, которая обеспечивала наибольшую линейную скорость перемещения шкива относительно накладок VШ=5,236 м/с (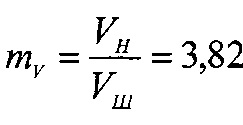 при VH=20,0 м/с; при других значениях скорости на тормозных шкивах буровых лебедок mV уточняется).
при VH=20,0 м/с; при других значениях скорости на тормозных шкивах буровых лебедок mV уточняется).
Энергетический баланс фрикционных узлов тормоза. Колебания основных деталей ленточно-колодочного тормоза приводят к возникновению дополнительных динамических нагрузок, что сказывается на стабильности его выходных параметров и, как следствие, ведет к неравномерному износу сопряженных поверхностей трения.
Как известно, возникновение вибраций деталей ленточно-колодочного тормоза обусловлено рабочими процессами в фрикционных узлах, т.е. изменением закономерностей контактирования микровыступов пар трения, а также неодинаковыми деформациями ветвей тормозных лент.
На фиг. 24а, б представлены линейная и нелинейная фрикционные характеристики в зависимости от импульсной удельной нагрузки, действующей в парах трения тормоза. Принимаем, что при возникновении колебаний участки контактирования накладок будут перемещаться по синусоидальному закону (фиг. 24б) и на основании графических зависимостей (фиг. 24а, б) построим диаграммы работы возмущающей силы.
В случае совпадения фазы вынужденных колебаний с возмущающей силой диаграмма работы возмущающей силы представляет собой прямую линию (прямая 1) при линейном изменении силы трения импульсной удельной нагрузки (фиг. 24в) и кривую в случае нелинейного изменения (кривая 2) [фиг. 24в], а работа возмущающей силы в последнем случае равна нулю.
Однако фазы вынужденных колебаний и действия возмущающей силы могут и не совпадать. При резонансе, когда наблюдается наибольшая амплитуда колебаний, разность фаз составляет величину π/2. Этот случай изображен на фиг. 24в, г, кривые 2, т.е. диаграмма работы изображается в виде эллипса.
Так как энергия, сообщаемая колебательной системе возмущающей силой пропорциональна площади диаграммы, она изменяется за один цикл по линейному закону. С другой стороны энергия, рассеиваемая колебательной системой пропорциональна квадрату амплитуды.
Таким образом, вносимая энергия и энергия рассеяния будут равны только в точке пересечения кривых функций для обоих видов энергии и характеризуют установившееся состояние трибосистемы.
На фиг. 24д приведены графические зависимости, характеризующие изменение вносимой колебательной энергии на сбегающей (Ес) и набегающей (Ен) ветви ленты и энергии, демпфирующей колебания Re и Rн указанными ветвями ленты.
Поскольку нагруженность набегающей ветви ленты больше сбегающей, вносимая энергия на набегающей ветви ленты будет больше, чем на сбегающей. Однако и энергия рассеивания на набегающей ветви больше, чем на сбегающей, причем растет энергия рассеивания быстрее, чем вносимая энергия. В результате амплитуда колебаний на сбегающей ветви ленты оказывается больше, чем на набегающей.
Рассмотрим изменение величины возмущающей энергии и энергии рассеивания при колебании поверхностной температуры пар трения. На фиг. 25 изображена зависимость динамического коэффициента трения от поверхностной температуры для пары трения ретинакс ФК-24А - сталь 35ХНЛ. Из рисунка видно, что в интервале температур до 200°С динамический коэффициент трения указанной пары изменяется незначительно. На диаграмме работы (фиг. 26, кривая 1) этому случаю соответствует наибольшая сила трения и наименьшая амплитуда колебаний.
В интервале температур 200°С-350°С наблюдается падение динамического коэффициента трения вследствие интенсивного развития пластической деформации фрикционного материала накладки. При этом имело место снижение энергии рассеивания, в то время как величина возмущающей энергии оставалась практически постоянной. В результате точка пересечения кривых Rн,с и Ен,с (фиг. 24д) сместилась вправо как для набегающей, так и для сбегающей ветвей ленты, т.е. амплитуда колебаний возросла. Однако за счет размягчения поверхностного слоя накладок улучшаются демпфирующие свойства ветвей лент и рост амплитуды колебаний замедляется (фиг. 26, кривая 2).
В области температур 350°С-450°С динамический коэффициент трения стабилизируется, в то время как амплитуда колебаний продолжает снижаться за счет дальнейшего размягчения поверхностного слоя накладок (фиг. 26, кривая 3).
В интервале поверхностных температур 450°С-600°С наблюдалось дальнейшее снижение амплитуды колебаний, вызванное некоторым повышением динамического коэффициента трения (см. фиг. 25).
Таким образом, наибольшие вибрации возникают на сбегающей ветви тормозной ленты из-за действия намного меньших импульсных удельных нагрузок в паре трения по сравнению с набегающей ветвью, что способствует, в свою очередь, развитию нелинейных характеристик пар трения трибосистем.
Проанализируем колебания, развивающиеся в металлополимерных парах трения ленточно-колодочного тормоза. На фиг. 27а, б приведены закономерности изменения натяжения набегающей ветви ленты при изменении амплитуды радиальной виброскорости накладок на сбегающей (а) и набегающей (б) ветвях ленты и усилий на нагрузочном устройстве 100 Н и 300 Н.
Анализ графических зависимостей показал, что с увеличением амплитуды радиальной виброскорости натяжение набегающей ветви ленты уменьшается при постоянном натяжении ее сбегающей ветви. Увеличение амплитуды радиальной виброскорости на сбегающей ветви ленты приводит к уменьшению натяжения ее набегающей ветви всего на 2-3% независимо от усилия натяжения сбегающей ветви. Увеличение амплитуды радиальной виброскорости на набегающей ветви ленты приводит к более значительному (5-8%) падению натяжения ее сбегающей ветви независимо от натяжения.
Это объясняется тем, что создаваемый за счет разности натяжений набегающей и сбегающей ветви суммарный импульсный тормозной момент, реализуемый фрикционными накладками на сбегающей ветви ленты, в 2- 4 раза больше суммарного импульсного тормозного момента на набегающей ветви ленты. При этом установлено, что уменьшение импульсной силы в результате динамических процессов в фрикционных парах приблизительно на одну и ту же величину на набегающей и сбегающей ветвях ленты вызывает различное уменьшение усилия натяжения их ветвей.
Таким образом, в процессе экспериментальных исследований установлено, что амплитуда радиальной виброскорости участков накладок на сбегающей ветви ленты в среднем в 1,5-2 раза больше, чем на ее набегающей ветви. Однако увеличение радиальной виброскорости участков накладок на набегающей ветви ленты приводит к уменьшению усилия натяжения в 3-5 раз больше, чем аналогичное увеличение на сбегающей ее ветви.
На фиг. 28а, б приведены амплитудные спектры участков лент с накладками, полученные при различных видах импульсного нагружения и скорости вращения тормозного шкива. Анализ полученных спектров показал, что фрикционные колебания возникали на участках во всех парах трения независимо от режима работы. Максимальные амплитуды колебаний наблюдались в полосе частот 300-1000 Гц в зависимости от режима нагружения и степени изношенности участков накладок. Наибольшее видоизменение спектров происходило при изменении импульсных удельных нагрузок. Если при минимальной импульсной удельной нагрузке (0,1-0,2 МПа) наблюдался один ярко выраженный пик в области частот 800-1000 Гц, то с увеличением импульсной удельной нагрузки амплитуда виброскорости на этих частотах падала, в то же время относительно возрастала низкочастотная составляющая виброскорости в диапазоне частот 300-500 Гц, причем при максимальной нагрузке амплитуда виброскорости на этих частотах достигала максимального значения. Такая тенденция наблюдалась от сбегающей к набегающей ветви ленты при постоянном усилии их нагружения. Таким образом, наибольшая амплитуда колебаний при небольших импульсных удельных нагрузках наблюдалась на первой фрикционной накладке (сбегающий конец тормозной ленты) лежала в диапазоне частот 800-1000 Гц, а при максимальных импульсных удельных нагрузках - на набегающем конце ленты (восьмая фрикционная накладка) в диапазоне частот 250-500 Гц. При замене неизношенных накладок изношенными указанная тенденция роста низкочастотной составляющей виброскорости при увеличении импульсной удельной нагрузки изменялась, за счет увеличения амплитуды колебаний в среднем на 20-30%.
Увеличение скорости скольжения с 5,0 до 15,0 м/с привело к смещению максимальных амплитуд колебаний в более высокочастотную область приблизительно на 10-30%. При этом несколько возросли (в среднем на 9-15%) максимальные амплитуды колебаний как в высокочастотной, так и в низкочастотной областях. Так, если при скорости скольжения 5,0 м/с и импульсной удельной нагрузке 0,2 МПа на сбегающем конце ленты максимальная амплитуда виброскорости наблюдалась на частоте 810 Гц и составляла 11,1 мм/с, то при увеличении скорости скольжения до 15,0 м/с максимум амплитуды виброскорости сместился по частотной оси до 1050 Гц и составил 12,7 мм/с.
Аналогичная картина наблюдалась при больших импульсных удельных нагрузках в области частот 250-500 Гц. Если для скорости скольжения 5,0 мм/с и импульсной удельной нагрузки 1,0 МПа на набегающей ветви ленты была зарегистрирована максимальная амплитуда радиальной виброскорости 9,4 мм/с на частоте 260 Гц, то при увеличении скорости скольжения до 15,0 м/с максимальная амплитуда виброскорости составила 11,6 мм/с на частоте 380 Гц.
Коэффициент запаса прочности поперечного сечения тормозной ленты. Коэффициент запаса прочности (nT) поперечного сечения тормозной ленты определяют по зависимости вида [8]
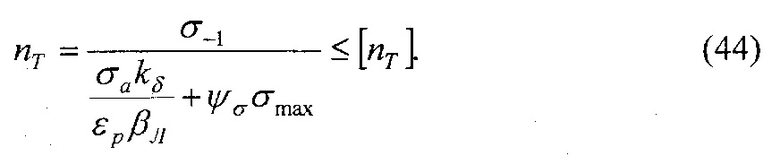
Максимальное напряжение в поперечном сечении тормозной ленты определяют по зависимости вида
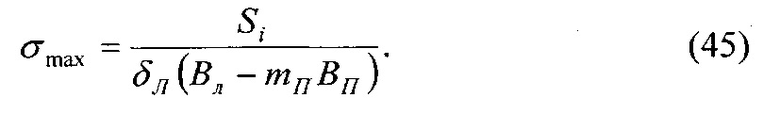
При этом допустимое значение коэффициента запаса прочности тормозной ленты составило [nT]=2.
Деформации тормозной ленты. Выражение для определения полного удлинения тормозной ленты при расположении на дуге ее обхвата фрикционных накладок с переменным шагом имеет следующий вид [1]
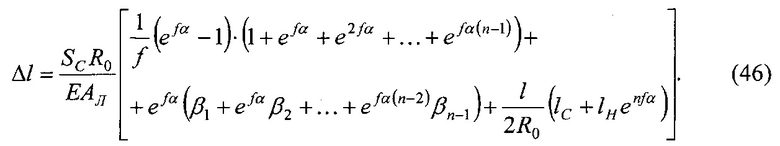
Для тормозной ленты с равномерным шагом расположения накладок, когда β1=β2=…=βn-1=β уравнение (46) принимает следующий вид [1]
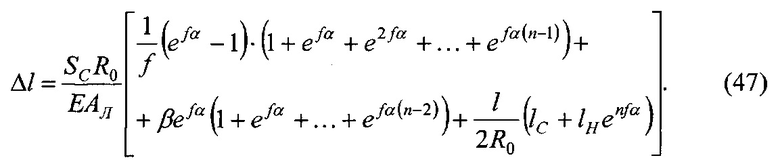
На фиг. 29а, б, в показаны схемы сил, действующие: в узле накладка-лентана участке ленты над i-ой накладкой; при определении деформаций участков ленты; 1 - тормозная лента; 2 - фрикционная накладка.
Закономерности изменения относительных деформаций участков тормозной ленты при расположении по дуге ее обхвата фрикционных накладок с постоянным (1, 1') и переменным (2, 2') шагом: расчетные (1, 2) и экспериментальные (1', 2') данные,  и
и  - нумерация зазоров между накладками представлены на фиг 30.
- нумерация зазоров между накладками представлены на фиг 30.
Податливость фрикционного стыка металлополимерных пар трения. Под податливостью фрикционного стыка понимаем циклический процесс контактно-импульсного взаимодействия его микровыступов, включающий в себя упругую деформацию элементов и возвращение их в некоторое начальное положение в паузах между указанными взаимодействиями (фиг. 31).
Податливость стыков пар трения в значительной степени зависит от упругости микровыступов полимерной накладки. Величина податливости микровыступов во время процесса торможения является переменной. Податливость Пn упругих элементов, которыми являются микровыступы, находящиеся под действием импульсных нормальных нагрузок, действующих на микроконтактах, т.е. на пятнах контакта, характеризует предел отношения приращения деформации к изменению импульсной нормальной нагрузки, вызвавшему это приращение:
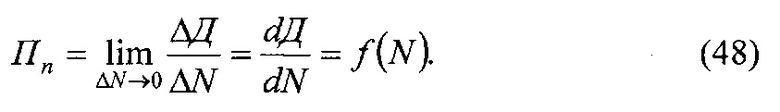
Зависимость импульсной нормальной нагрузки, вызывающей деформации микровыступов фрикционной накладки при их параллельном соединении в блок показана на фиг. 32а.
В зависимости от высоты микровыступа и расположения между соседствующими с ним микровыступов на рабочей поверхности фрикционной накладки считаем, что каждый из них нагружен переменной импульсной нормальной силой, а, следовательно, имеет также переменную податливость.
При параллельном соединении в блоки упругих элементов с различными характеристиками (фиг. 32б) учитывая, что их деформации разные и равны общей деформации, имеем
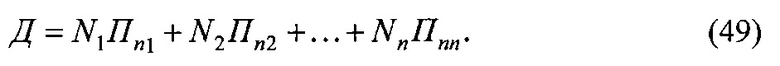
Следовательно, силы, действующие на каждый упругий элемент в параллельном блоке, обратно пропорциональны их податливости
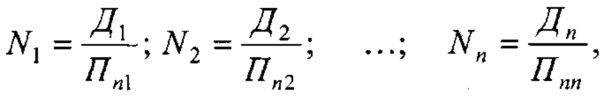
откуда 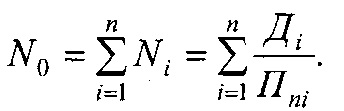
В этом случае податливость блока составит

Таким образом, при параллельном соединении упругих элементов в блоки их суммарная податливость уменьшается по мере износа микровыступов, а общая жесткость блока равна сумме их жесткостей

Однако, на податливость стыков металлополимерных прямых и обратных пар трения, в ленточно-колодочных тормозах, влияют особенности их конструкции и деформации элементов, в частности, тормозных лент.
Результаты исследований, устанавливающие закономерности изменения деформаций микровыступов металлополимерных пар трения ленточно-колодочного тормоза от импульсных удельных нагрузок при разных площадях пятен их контактирования представлены на фиг. 33.
Коэффициент взаимного перекрытия металлополимерных пар трения. Исследованиями установлено, что геометрия микро- и макроконтактирования оказывает существенное влияние на температурное поле при фрикционном взаимодействии пар трения. А.В. Чичинадзе ввел в рассмотрение коэффициент взаимного перекрытия Квз для однопарных узлов трения. Этот коэффициент представляет собой отношение произведения контактных площадей трения обеих фрикционных элементов пары Ак1 и Ак2 к квадрату общей площади A0.

Данный коэффициент существенно влияет на величины: импульсных нормальных нагрузок N в зоне контакта микровыступов, генерируемых электрических и аккумулируемых тепловых токов, динамических коэффициентов трения, скоростей скольжения, продольных (на поверхности) и поперечных (по толщине) температурных градиентов, термонапряжений в телах трения, интенсивности износа рабочих поверхностей трения, импульсного тормозного момента. Кроме того, этот параметр наряду с перечисленными выше факторами учитывает условия теплопередачи при определении коэффициентов распределения тепловых потоков между парами трения.
Величина Квз определяет среднюю температуру поверхности трения ϑn1,2, объемную температуру ϑv1,2, и температурные градиенты 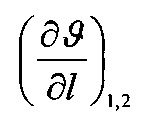 и
и 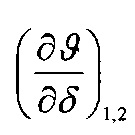 , соответственно, на поверхности обода шкива и по его толщине.
, соответственно, на поверхности обода шкива и по его толщине.
В экспериментах по изучению температурного поля при трении торцами использовалась универсальная машина трения «Унитриб». При этом применялись стандартные модельные кольцевые образцы (dн=28,0 мм, dвн=20,0MM, hн=15,0 мм), отвечающие фрикционному полимерному материалу и серому чугуну СЧ15. В результате исследований взаимосвязи коэффициента перекрытия Квз с параметрами процесса трения было установлено: снижение Квз приводит к снижению средней температуры поверхности ϑn и возрастанию градиента температуры 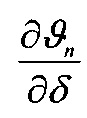 . Этот эффект достигается при нормальной удельной нагрузке p=const и скорости скольжения Vck=const. Следствием этих изменений является возрастание динамического коэффициента трения f и снижение интенсивности изнашивания up.n [9]. В данных исследованиях не было четкого разграничения температурных градиентов по поверхности пары трения и по толщине цилиндрического кольца. Такие исследования следует отнести к выполненным на микроуровне.
. Этот эффект достигается при нормальной удельной нагрузке p=const и скорости скольжения Vck=const. Следствием этих изменений является возрастание динамического коэффициента трения f и снижение интенсивности изнашивания up.n [9]. В данных исследованиях не было четкого разграничения температурных градиентов по поверхности пары трения и по толщине цилиндрического кольца. Такие исследования следует отнести к выполненным на микроуровне.
На реальных физических моделях в промышленных и стендовых условиях (материал пары трения «сталь 35ХНЛ - ФК-24А») при изучении температурного поля при электротермомеханическом трении с соблюдением условия, что Δϑn>Δϑv на серийном и модельном ленточно-колодочном тормозе в результате исследований коэффициента взаимного перекрытия Квз с параметрами процесса трения, из которых выделено импульсное нормальное усилие N, в зависимости от термосостояния обода тормозного шкива было установлено (фиг. 34а, б, в, г, д, е):
- снижение Квз приводит к снижению средней поверхностной температуры ϑn, и как следствие, объемной температуры ϑv и уменьшению 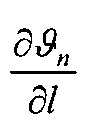 и
и 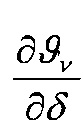 ; увеличение Квз способствует возрастанию
; увеличение Квз способствует возрастанию 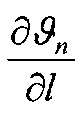 и
и 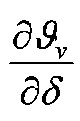 ;
;
- снижение Квз вызывает увеличение динамического коэффициента трения; что касается динамического коэффициента трения то он увеличивается (f) в связи с уменьшением Квз и 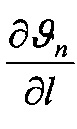 ;
; 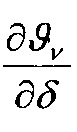 ;
;
- увеличение Квз и 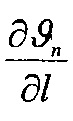 ;
; 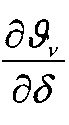 способствует увеличению интенсивности износа up.n.
способствует увеличению интенсивности износа up.n.
Для фрикционных пар ленточно-колодочного тормоза (в стендовых условиях) уменьшение Квз при работе трения WT=const приводит к высокому и стабильному динамическому коэффициенту трения, а также к минимальному износу только при условии, когда функции 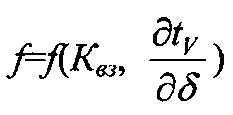 и
и 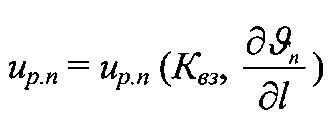 изменяются больше от Квз, чем от
изменяются больше от Квз, чем от 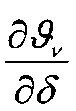 и
и 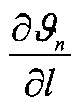 :
:
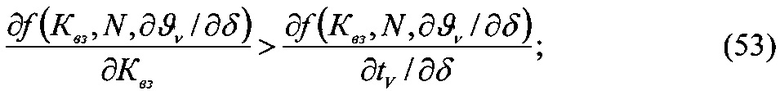
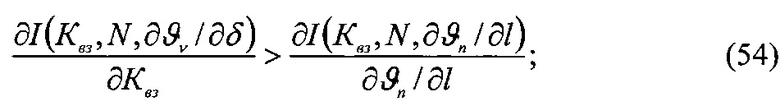
А.И. Вольченко ввел в рассмотрение статический и динамический коэффициенты взаимного перекрытия Квз для многопарных узлов трения.
На фиг. 35а, б, в изображена схема ленточно-колодочного тормоза с подвижными фрикционными накладками, установленными с постоянным (а) и переменным (б) шагами (бандаж составленный из четырех накладок) [10].
В тормозе накладки 3 соединены между собой пружинами 5 в гибкое кольцо - бандаж, который с натягом посажен на рабочую поверхность тормозного шкива 1. При этом образуются внешние и внутренние фрикционные узлы. В связи с этим различают следующие стадии торможения: начальную (I), когда внутренняя поверхность тормозной ленты 2 взаимодействует с внешней поверхностью накладок 3, неподвижных относительно шкива 1; промежуточную (II), когда работа трения выполняется внешними и внутренними поверхностями накладок 3, движущихся относительно шкива 1 и ленты 2. Во время этой стадии нагрузка передается от внешних к внутренним фрикционных узлов тормоза, и она является переходной и продолжается весьма малый промежуток времени; и конечную (III), в течение которой происходит взаимодействие внутренних поверхностей неподвижных накладок 3 с рабочей поверхностью тормозного шкива 1. Именно во время третьей стадии тормоз выполняет свою основную работу.
Две поверхности одной фрикционной накладки, внешняя поверхность которой является подвижной при взаимодействии с внутренней поверхностью тормозной ленты (на первой стадии торможения имеет место переменный коэффициент взаимного перекрытия) с увеличением силы затягивания тормозной ленты. Коэффициент взаимного перекрытия внешних пар трения все время увеличивается и достигает своего максимального значения до завершения первой стадии торможения. После чего остается постоянным даже при дальнейшем увеличении силы затягивания тормозной ленты. На третьей стадии торможения происходит взаимодействие квазинеподвижных внутренних поверхностей накладок с подвижной рабочей поверхностью тормозного шкива. При этом коэффициент взаимного перекрытия увеличивается до тех пор, пока не произойдет срыва натяга между внутренней поверхностью последней накладки бандажа и шкивом. В дальнейшем коэффициент взаимного перекрытия внутренних пар трения фрикционных узлов является постоянным до конца третьей стадии торможения. В связи с тем, что фрикционные узлы ленточно-колодочного тормоза с подвижными накладками работают поочередно, т.е. сначала внешние, а затем внутренние, а также для четкого понимания стадий торможения введем понятие «статический» и «динамический» коэффициенты взаимного перекрытия для их пар трения.
Итак, на первой стадии торможения динамический коэффициент взаимного перекрытия внешних фрикционных узлов (фиг. 36, прямая 1а) является величиной переменной во времени, а статический коэффициент взаимного перекрытия внутренних фрикционных узлов (фиг. 36, прямая 2г) - является постоянным во времени. На третьей стадии торможения статический коэффициент взаимного перекрытия внешних фрикционных узлов (фиг. 36, прямая 1, в) является величиной постоянной во времени, а динамический коэффициент взаимного перекрытия внутренних фрикционных узлов (фиг. 36, прямая 2б) - величина переменная во времени до тех пор, пока не произойдет срыва натяга последней накладки бандажа. После чего динамический коэффициент взаимного перекрытия внутренних фрикционных узлов становится статическим (фиг. 36, прямая 2г) и держится постоянным во времени до завершения третьей стадии торможения. На фиг. 36 штриховыми линиями изображены возможные изменения статических и динамических коэффициентов взаимного перекрытия внешних и внутренних пар трения во времени на первой и третьей стадии торможения.
Динамика процесса торможения неразрывно связана с фрикционными свойствами материалов прямых (внутренних) и обратных (внешних) пар трения, которые, в свою очередь, зависят от скоростного, нагрузочного и температурного режимов фрикционных контактов, а также воздействия окружающей среды.
Влияние этих факторов на динамический коэффициент трения для различных материалов осуществляется по-разному. Это связано с физико-механическими свойствами материалов, характером и интенсивностью процессов, явлений и эффектов, происходящих на фрикционных контактах и в объемах материалов.
Знание коэффициентов взаимного перекрытия в парах трения тормозных устройств позволяет регулировать статические удельные нагрузки в сопряжениях. Особенно, это очевидно в работах Д.А. Вольченко применительно к ленточно-колодочным тормозам, компонуя фрикционные накладки с переменным и постоянным шагом на ветвях тормозной ленты.
Импульсная природа изменения нормальных усилий при фрикционном взаимодействии узлов. В энергетическом аспекте трение представляет собой процесс трансформирования поступающей в систему механической энергии в электрическую, тепловою и другие виды энергии. Перераспределение энергетических потоков на поверхностях пар трения тормозных устройств наблюдаются только в процессах самого трения и поэтому необходимо развивать и использовать in-situ методы исследований.
Контактно-импульсное взаимодействие металлополимерных пар трения ленточно-колодочного тормоза, выражающееся закономерностью изменения нормального усилия по времени торможения, представлено на фиг. 37. Из последнего следует, что закономерность изменения импульсного нормального усилия по времени имеет волновую природу и приближается к квазисинусоидальному закону его изменения.
Взаимодействие микровыступов в паре трения «металл-полимер» носит дискретный характер, из-за различной высоты микронеровностей реализуется одновременно по уровням и по времени. Возникающие при этом импульсы характеризуются амплитудой (высотой), длительностью (шириной), апериодическим повторением и положением импульса внутри периода (временной сдвиг или фаза импульса).
Известно, что перемещение микровыступов массой mм обода шкива под действием переменной нормальной силы N, заданной в виде функции времени τ, определяется следующей зависимостью
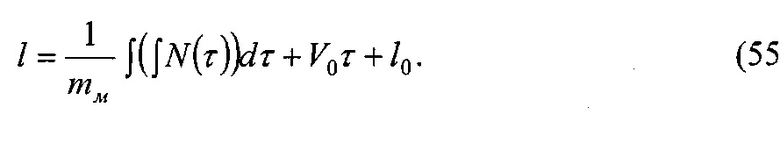 )
)
Принимая пределы интегрирования от 0 до T и, пользуясь формулой Коши для преобразования n-кратного интеграла в однократный, запишем уравнение для проекции пути, пройденного за время Т:
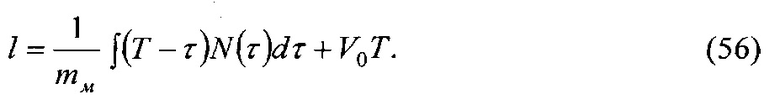
Интеграл в этом выражении является статическим моментом площади импульсов, образованной силой N(t) в промежутке времени от 0 до T относительно прямой, положение которой определяется уравнением
t=T.
В данном случае под статическим моментом подразумевается алгебраическая сумма статических моментов положительных и отрицательных площадей относительно упомянутой прямой, поэтому уравнение (56)записываем в следующем виде
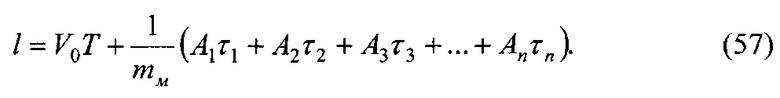
Раскрыв скобки в уравнении (47), получаем
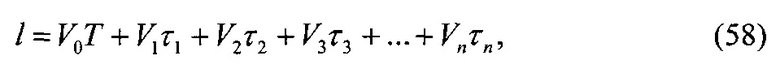
где 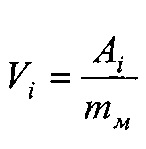 - мгновенное изменение скорости i-ой массы mм микровыступов под действием импульсов Ai.
- мгновенное изменение скорости i-ой массы mм микровыступов под действием импульсов Ai.
Для колебательных процессов обычно характерно чередование положительных и отрицательных импульсов. В работе [11] изложен метод анализа таких колебательных движений с помощью импульсных пар, сущность которого заключается в следующем. Кривую нормальной силы N(τ) разбиваем на участки, для которых справедливо равенство

Следовательно, на каждом пятне контакта микровыступов «металл-полимер» действуют два импульса (импульсная пара), причем модули импульсов равны. Заменив действительные импульсы равновеликими фиктивными, приложенными в центрах тяжести площадей микроконтактов, получаем импульсные пары, образованные мгновенными импульсами 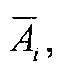 которые назовем приведенными импульсными парами. Тогда путь массы mм микровыступа обода шкива согласно выражениям (46) и (47) можно изобразить в виде ломаной линии, абсциссы точек излома которой будут соответствовать точкам приложения фиктивных мгновенных импульсов, а ординаты определяются из уравнения, которое показывает абсолютное изменение величины пути микровыступа обода шкива под действием приведенной импульсной пары, т.е.
которые назовем приведенными импульсными парами. Тогда путь массы mм микровыступа обода шкива согласно выражениям (46) и (47) можно изобразить в виде ломаной линии, абсциссы точек излома которой будут соответствовать точкам приложения фиктивных мгновенных импульсов, а ординаты определяются из уравнения, которое показывает абсолютное изменение величины пути микровыступа обода шкива под действием приведенной импульсной пары, т.е.

Представленный метод оценки колебательных процессов с помощью импульсных пар использовался при изучении микровыступов «металл-пролимер» при взаимодействии их контактных пятен в процессе торможения.
Принимая во внимание импульсы Ау и A0, действующие на микровыступ обода шкива в момент его взаимодействия с микровыступами полимерной накладки записываем
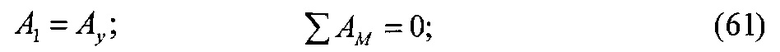
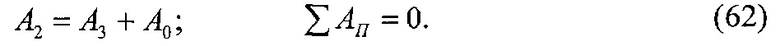
Отсюда следует, что ось О-О (фиг. 38а, б, взяты фрагменты из фиг. 37) делит цикл нагружения микроконтактов на две зоны, удовлетворяющие условию (61 и 62). В данном случае имеем две импульсные пары, одна из которых действует со стороны микровыступов «металл-полимер», а вторая - со стороны микровыступов «полимер-металл». При взаимодействии указанных пар наблюдается явление смещения микровыступов. Импульсные пары заменяем приведенными. Тогда путь микровыступа обода шкива, пройденный за время действия приведенной импульсной пары (при V0=0), равен моменту пары, деленному на массу микровыступа обода шкива

График пути микровыступа обода шкива, построенный по методу импульсных пар, изобразился ломаной линией 0-1-2-3-4, которая совпадает с действительным графиком пути в точках, представляющих наибольший интерес. В промежутках между ними действительная кривая строится приближенно путем скругления углов ломаной. Каждой импульсной паре соответствует характерный для колебательных процессов участок графика пути. Точки с нулевой скоростью А', В' и 4 (0, А'' и В'') соответствуют границам импульсных пар. В данном случае максимальная скорость микровыступа обода шкива достигается в момент перемены знака при смещении микровыступа накладки и действия силы реакции (точка Б на графике пути).
Таким образом, при взаимодействии микровыступов «металл-полимер» образуются два одинаковых по величине, но различных по направлению момента. Вследствие этого взаимодействие микровыступов пар трения «металл-полимер» являются как бы уравновешенными. Из зависимостей (61) и (62) следует, что сумма площадей положительных импульсов равна сумме площадей отрицательных импульсов, а центр тяжести площади положительных импульсов лежит на одной вертикали с общим центром тяжести всех площадей отрицательных импульсов.
Импульсная природа взаимодействия микровыступов пар трения «металл-полимер» накладывает отпечаток на изменение импульсных нормальных сил на их пятнах контакта, и как следствие, на закономерностях изменения импульсных удельных нагрузок.
Одним из основных эксплуатационных параметров ленточно-колодочного тормоза является натяжение ветвей тормозной ленты. Разность между натяжениями набегающей и сбегающей ветви тормозной ленты определяет импульсную силу трения, действующую в парах трения тормоза.
Известно, что эффективность и долговечность металлополимерных пар трения ленточно-колодочного тормоза зависит от его конструктивных параметров. Последние, в свою очередь, влияют на эксплуатационные параметры тормоза. Перейдем к их определению. На фиг. 39 приведена схема ленточно-колодочного тормоза для определения усилий натяжения в тормозной ленте.
Составляем уравнение равновесия элементарного участка ленты с накладкой 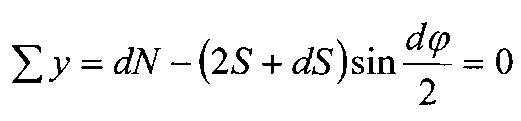 . Считаем
. Считаем 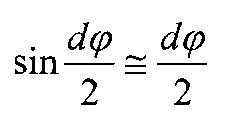 и, пренебрегая величиной второго порядка малости
и, пренебрегая величиной второго порядка малости 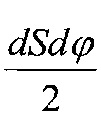 , получаем
, получаем

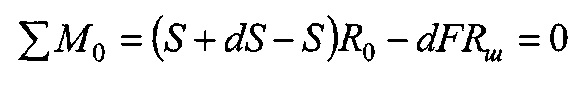 ; откуда
; откуда 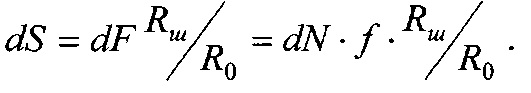 (65)
(65)
Из (64) и (65) получаем 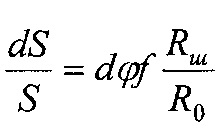 ; или
; или 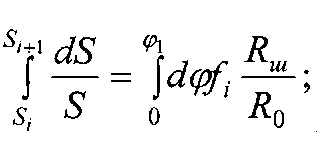 откуда
откуда

При этом 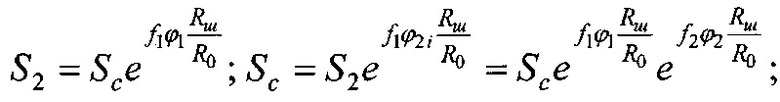
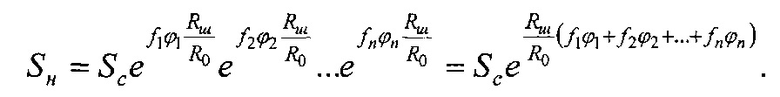
Определение натяжения набегающей ветви тормозной ленты через задание величины натяжения сбегающей ветви позволяет перейти к оценке определения нормального, импульсного контактного усилия в паре трения «накладка-шкив».
Сначала рассмотрим контактную задачу взаимодействия со шкивом системы фрикционных накладок, шарнирно соединенных со стальной лентой при действии на концах ленты статических сил Sн и Sc. Следуя работе [12], накладки заменим точками, а центральные углы примем переменными (фиг. 40), исходя из того, что равномерное расположение накладок по дуге обхвата ленты приводит к неравномерному распределению импульсной нормальной нагрузки на них, и как следствие, к неравномерного изнашиванию их рабочих поверхностей.
Составим уравнение равновесия i-ой накладки. Обозначим через Fi и Ni, силу трения и нормальное усилие точки контакта, действующие на ленту, через Si-1, Si, Si+1 силы натяжения участков ленты, действующие на трех выбранных накладках вдоль хорд. Проектируя эти силы вдоль касательной и нормали, получаем:
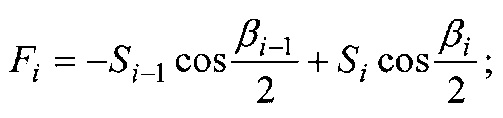
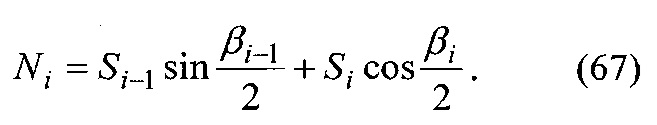
При наличии скольжения в точке контакта выполняется условие трения Кулона (f - динамический коэффициент трения)

Пользуясь условием (68), получаем
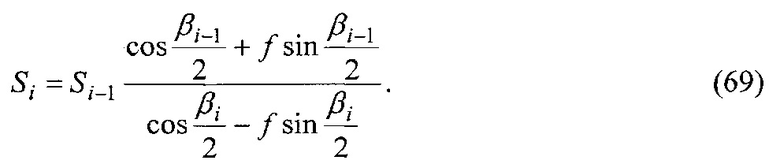
В формулах (67, 69) Si, β0, и βn считаются заданными величинами. В частности, если положить β0=β1=β2=…=βn=β, то из соотношения (69) (после исключения Si (i=1, 2, 3…n-1), получаем формулу, использованную в [10]:
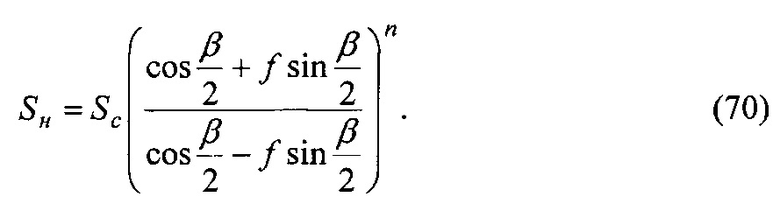
При выводе соотношения (70) было принято, что во всех контактных точках накладок со шкивом имеет место скольжение, т.е. выполняется условие (68).
С помощью зависимостей (69)-(70) можно найти величины натяжения тормозной ленты и выбрать углы βj таким образом, чтобы нормальные усилия по точкам контакта накладок со шкивом было распределено равномерно. В этом случае фрикционные материалы накладок будут использоваться более рационально.
Результаты расчетов импульсных нормальных усилий по зависимости (67) проиллюстрированы на фиг. 41.
Закономерности импульсного изменения контактного нормального усилия в паре трения «шкив-накладка» ленточно-колодочного тормоза по длине накладки в различных зонах ее ширины (а) взаимодействия показали следующее. Накладка по ширине была разбита на три зоны: первая (а1=30,0 мм); вторая (a2=60,0 мм) и третья (a3=90,0 мм). Первая и вторая зоны накладки находились на ее набегающей части, а третья зона располагалась на сбегающей части накладки. Максимальные нормальные усилия имели место в первой и второй зоне (кривые 1 и 2), а минимальные - в третьей зоне (кривая 3). Если рассматривать изменение нормальных усилий по длине фрикционной накладки, то со стороны незащемленного края обода шкива примерно на одной третьей его длины наблюдалось квазивыравнивание нормальных усилий.
Тормозной момент, развиваемый фрикционными узлами тормоза.
В большинстве случаев, очень трудно детально проанализировать и оценить динамические параметры металлополимерных пар трения ленточно-колодочного тормоза буровой лебедки в процессе торможения из-за контактно-импульсного их взаимодействия. Импульсная природа взаимодействия микровыступов металлополимерных пар трения накладывает отпечаток на закономерности изменения в контакте нормальных сил, динамического коэффициента трения, сил трения и других эксплуатационных параметров, и как следствие, на один из важнейших параметров - тормозной момент, развиваемый ленточно-колодочным тормозом буровой лебедки.
Расчетная схема фрикционного узла тормоза приведена на фиг 42.
Тормозной момент, развиваемый парами трения тормоза
«накладки-шкив»
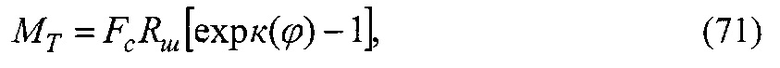
«накладки-лента»
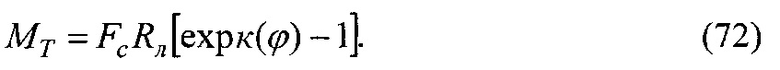
Зависимость (72) используется для определения тормозного момента в том случае, когда фрикционные накладки посажены с натягом на рабочую поверхность тормозного шкива и вместе с ним вращаются. При этом тормозная лента свободна от фрикционных накладок.
Проанализируем закономерности изменения тормозных моментов по длине ленты тормоза, которая разбита на три зоны: с 1-ой до 7-ой; с 7-ой до 15-ой; с 15-ой до 22-ой накладки (фиг. 43). В каждой из зон наблюдаются всплески тормозных моментов, которые имеют максимальные значения на третей, одиннадцатой (при f=0,2 максимум смещен на 12-ую накладку) и девятнадцатой накладках. Относительно последней накладки смещение максимальных величин тормозных моментов при значениях f=0,2; 0,25 и 0,3 приходится на двадцатую накладку.
В табл. 6 приведены моментные характеристики накладок ленты тормоза при их минимальных и максимальных значениях.
Приведем анализ величин тормозных моментов отдельно по каждой зоне участка тормозной ленты по конкретным фрикционным накладках при изменении динамического коэффициента трения от 0,2 до 0,35. Определим сначала соотношения динамических коэффициентов трения 0,25/0,2=1,25; 0,3/0,25=1,2 и 0,35/0,3=1,16, т.е. их величины уменьшаются. При этом при минимальных значениях тормозных моментов их соотношения в зонах тормозной ленты составляют: в первой - 1,564; 3,23 и 2,27; во второй - 1,16; 1,8 и 1,08; в третей - 1,27; 1,22 и 1,19 (при вышеуказанных соотношениях динамических коэффициентах трения). Наиболее стабильными являются соотношения минимальных тормозных моментов в третьей зоне, поскольку они почти равны соотношениям динамических коэффициентов трения. Во второй зоне соотношения минимальных тормозных моментов изменяются от 1,08 до 1,8, а в первой зоне - от 2,24 до 15,6.
Что касается соотношений максимальных тормозных моментов, то они изменяются в зонах тормозных лент следующим образом: в первой - 2,68; 1,40 и 1,211; во второй - 0,745; 2,02 и 1,25; в третьей - 1,25; 1,69 и 1,49. Наиболее близкими по величине соотношения применительно к динамическим коэффициентам трения являются соотношения максимальных тормозных моментов, развиваемых накладками третьей зоны ленты.
Таким образом, соотношение минимальных и максимальных тормозных моментов, развиваемых третьей зоной тормозной ленты (находится на набегающей ветви ленты), являются квазистабильными величинами.
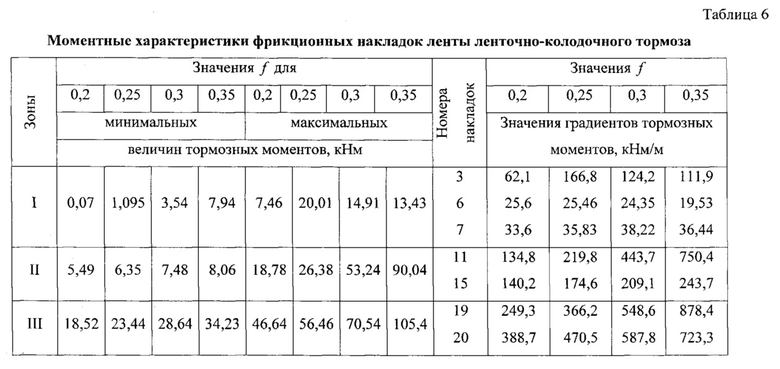
Анализ величин градиентов тормозных моментов, развиваемых третьей накладкой (первая зона ленты), согласно табл. 6, показывает что имеет место колебание их значений от 62,1 до 166,8 кНм/м, а соотношения изменяются от 0,745 до 2,686. Наиболее стабильные величины соотношений имеют градиенты тормозных моментов, развиваемые двадцатой накладкой (третья зона ленты), которые составляют 1,21; 1,25 и 1,23 при соотношениях динамических коэффициентов трения 1,25; 1,2 и 1,16.
Использование нового эксплуатационного параметра, которым является градиент тормозных моментов, развиваемых парами трения «тормозной шкив - фрикционная накладка» позволяет давать оценку их величин по каждой фрикционной накладке тормозной ленты.
Скорость скольжения пар трения тормоза. При реализуемой удельной мощности трения fpVck парами трения ленточно-колодочного тормоза удельные нагрузки р и динамический коэффициент трения f, развиваемые на пятнах контактов их микровыступов, в значительной степени зависят от скорости скольжения Vck. Так, на начальной стадии торможения при высокой скорости скольжения Vck при взаимодействии микровыступов пар трения происходит генерирование электрических токов на их вершинах при больших удельных нагрузках р на пятнах контактов при заметно сниженных величинах динамического коэффициента трения f. При дальнейшем увеличении площадей пятен контактов микровыступов из-за их деформации и износа происходит снижение скорости скольжения Vck и импульсных удельных нагрузок р, и как следствие, увеличение динамического коэффициента трения f. При этом наблюдается увеличение поверхностной температуры ϑn на пятнах контактов микровыступов пар трения.
Таким образом, изменение скорости скольжения Vck и импульсных удельных нагрузок р значительно меньше влияет на изменение динамического коэффициента трения f и интенсивность износа, чем воздействие температуры поверхности трения ϑn.
Между скоростью скольжения и температурой поверхностного слоя металлического фрикционного элемента, при прочих равных условиях, существует зависимость согласно формуле Егера, прирост температуры пропорционален корню из скорости скольжения. При температуре в 100…200°С, когда поверхностные и подповерхностные слои металлического фрикционного элемента являются прогретыми, вследствие дискретности контакта их микровыступов в общем напряженно-деформированном состоянии поверхностей возрастают и контактные импульсные удельные нагрузки уменьшаются. Подплавление микровыступов пятен контактов, т.е. поверхностей активного массопереноса приводит к изменению их формы, что в общем случае сопровождается увеличением фактической площади пятен контактов и пропорциональным снижением контактных импульсных удельных нагрузок. В месте с тем температура при электротермомеханическом трении от этого не изменяется, т.е. глубинный градиент температуры в ободе металлического фрикционного элемента не зависит от импульсных удельных нагрузок и вполне определяется скоростью скольжения и выполненной работой трения. Пики температур практически полностью реализуются в активном микрообъеме микровыступов металлического фрикционного элемента. При температуре на пятнах контактов микровыступов в 800…1000°С объемная температура остального материала обода металлического фрикционного элемента будет составлять 200…250°С и существенно отличается от окружающей среды (20…40°С). Это позволяет говорить о большом поверхностном температурном градиенте, а также о температурном градиенте активного микрообъема микровыступов. Продолжительность температурного пика и периода перехода от нагревания к охлаждению и наоборот согласно принципа суперпозиции оценивается темпами нагревания и охлаждения.
Величина активного микрообъема микровыступов пары трения «металл-полимер» зависит от физико-механических характеристик, а также от параметра pVck (произведения скорости относительного скольжения на импульсную удельную нагрузку) и ограничивается глубиной проникновения теплового импульса, на которой влияние температуры на физико-механические свойства материала обода металлического фрикцинного элемента являются ощутимым.
На рис. 44 приведены результаты экспериментальных исследования пары трения «шкив-накладка» (материал сталь 35ХНЛ-ФК-24А) в стендовых условиях при удельных нагрузках 0,6МПа и поверхностных температурах 200°С и 400°С зависимости динамического коэффициента трения от скорости скольжения. Анализ приведенных графических зависимостей указывает на следующее: с увеличением скорости скольжения пар трения при уровнях ниже (крива 1) и выше (кривая 2) допустимой температуры материалов накладки изменение динамического коэффициента трения выражается падающими криволинейными зависимостями. При этом отклонение величин значений динамических коэффициентов трения составляет 0,015 при Vck=1,0 м/с и 0,041 при Vck=6,0 м/с, т.е. при увеличении скорости скольжения в шесть раз, а поверхностная температура увеличивается только в два раза при постоянных удельных нагрузках p=0,6МПа. Что касается динамического коэффициента трения, то его величина изменения увеличилась в 2,8 раза.
Важнейшим параметром температурного режима трения и изнашивания является поверхностный и глубинный градиенты температуры металлического фрикционного элемента. Температурные градиенты влияют на градиент механических свойств контактирующих материалов, а следовательно, на динамический коэффициент трения и износ.
Энергонагруженность металлополимерных пар трения тормозов.
Ленточно-колодочные тормоза имеют тяжелонагруженные узлы трения, в которых температура в контактных зонах может достигать 1000°С и выше, что приводит к расплавлению металлических пятен контактов микровыступов и разложению поверхностного слоя полимерной накладки. Интенсивность деформации и температура поверхностных и подповерхностных слоев уменьшаются, а температурные градиенты в таких условиях могут достигать по поверхности 800-1000°С/см и по глубине 80-100°С/мм.
Если гармонические колебания температуры в рабочем слое обода тормозного шкива ленточно-колодочного тормоза выразить синусоидой, то получим уравнение
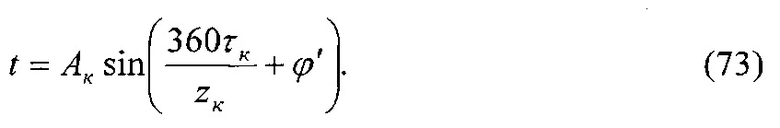
Для заданной кривой угол ϕ' зависит от начального момента отсчета времени; для этого момента (τ=0) из уравнения (73) следует

Максимум температуры получим при τк равном

Уравнение (74) описывает колебание температуры с течением времени около некоторой постоянной температуры, принимаемой при отсчете колебаний в качестве нулевой.
Гармонические колебания тепловых потоков (кВт/м2) выражаются аналогичным уравнением. При своих колебаниях тепловые потоки имеют направления либо в сторону движения волны, либо в обратную сторону. Считаем первое направление положительным, а второе - отрицательным.
При гармонических колебаниях положительный тепловой поток в течении полупериода переносит теплоту в сторону движения волны, а в течение следующего полупериода - столько же теплоты в обратную сторону.
Распространение теплового потока в материале пар трения тормозных устройств определяется по зависимости

Перепад температур на участке поверхности длиной lуч определяется как
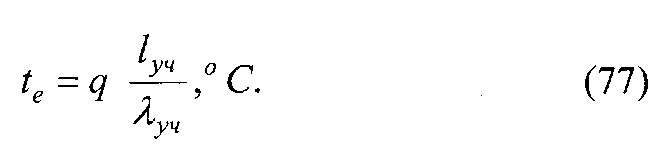
С учетом (77) перепад температур на участке поверхности определяется как
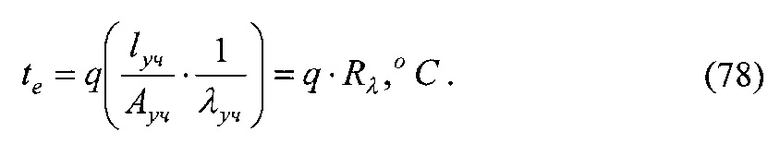
Параметр Rλ (78) называется термическим сопротивлением участка поверхности
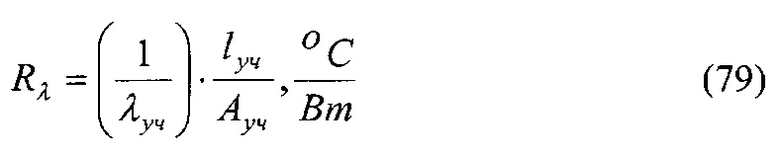
В формулах (78) и (79) наблюдается аналогия из соотношений для линейных электрических цепей, в частности, формула (78) представляет собой аналог закона Ома, где в качестве падения напряжения выступает перепад температур на участке поверхности ϑl. Температуре ϑl отвечает электрический потенциал, а аналогом тока является тепловой поток q. Формула (79) является аналогом известной формулы оммического сопротивления, в которой в роли удельного сопротивления выступает величина 1/λуч [13].
Тепловой поток, проходящий через любой участок взаимодействующих поверхностей пар трения тормоза, определяем из выражения

Последний параметр определяется по формуле
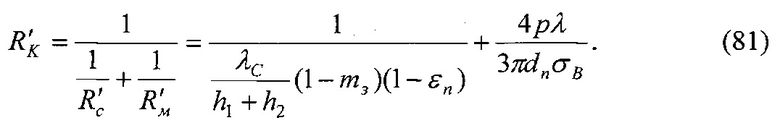
В основу приведенной формулы (81) заложена расчетная модель контакта, базирующаяся на общепринятых допущениях теории механического контактирования поверхностей. Данную теорию разработал Н.М. Демким, согласно которой предполагается определение общей проводимости контакта 1/R'K в виде суммы проводимостей фактического контакта 1/R'λ и межконтактной среды 1/R'C. Особенно важно знать последнее слагаемое при попадании обода тормозного барабана в термостабилизационное состояние.
Проникновение теплоты в тело обода шкива и фрикционной накладки при длительном и импульсном режимах их нагружения.
Результаты расчетов по вышеприведенным зависимостям с учетом изменения коэффициентов температуропроводности при температурах 150; 300 и 450°С позволили произвести анализ полученных данных при импульсном и длительном режимах подведения теплоты, которые свидетельствуют о следующем:
импульсном (обод шкива)
- при изменении аш в пределах (0,87-1,08)10-5, м2/с - глубина проникновения теплоты колебалась от 0,051 мм до 0,22 мм, т.е. прогретым был приповерхностный слой обода шкива;
длительном (обод шкива)
- при изменении аш в пределах (0,87-1,08)10-5, м2/с глубина проникновения теплоты колебалась от 5,1 мм до 22,02 мм, - т.е. была прогрета полностью толщина обода шкива;
импульсном (накладка)
- при изменении ан в пределах (0,2-0,6)10-6, м2/с глубина проникновения теплоты составила от 0,008 мм до 0,052 мм, т.е. прогретым был поверхностный слой накладки;
длительном (накладка)
- при изменении ан в пределах (0,2-0,6)10-6, м2/с глубина проникновения теплоты составила от 0,77 мм до 5,19 мм, т.е. прогретым был рабочий слой накладки.
При расчетах время изменялось следующим образом: при подведении теплоты: импульсном - от 0,0001 с до 0,0015 с; длительном - от 1,0 с до 14,0 с.
Таким образом, энергонагруженность обода тормозного шкива таковая, что эффективная глубина проникновения тепловых токов заведомо больше его номинальной толщины при длительном тепловом режиме нагрузки.
Энергонагруженность металлополимерных пар трения тормозных устройств в значительной степени зависит от их вынужденного охлаждения.
На фиг. 45 проиллюстрирована схема теплообмена от поверхностей фрикционных узлов ленточно-колодочного тормоза буровой лебедки. В теплообмене принимают участие: тормозной шкив 1 с ребордами 3 и выступом 2; тормозная лента 4 с фрикционными накладками 5. Аккумулятором тепловой энергии в данном виде тормоза является шкив 1. Фрикционные накладки 5 являются своего рода теплоизолятором между тормозным шкивом 1 и тормозной лентой 4. Интенсивность теплообмена от поверхностей последней незначительна и поэтому ее эффективностью можно пренебречь. Полированной поверхностью тормозного шкива 1 является его рабочая (наружная) поверхность. Матовыми поверхностями тормозного шкива 1 являются; внутренние и торцевые поверхности его обода, а также его наружная поверхность, которая контактирует с фланцем 6 барабана лебедки 7. Полированная поверхность тормозного шкива 1 является нагреваемой, а его матовые поверхности - охлаждаемые.
При поверхностных температурах металлических фрикционных элементов, которыми являются тормозные шкивы и барабаны, изготовленные из различных материалов, выше 150-200°С интенсивность вынужденного конвективного теплообмена резко падает, а заметно увеличивается теплообмен лучеиспусканием. Согласно закону Стефана-Больцмана, коэффициент теплоотдачи лучеиспусканием [14]
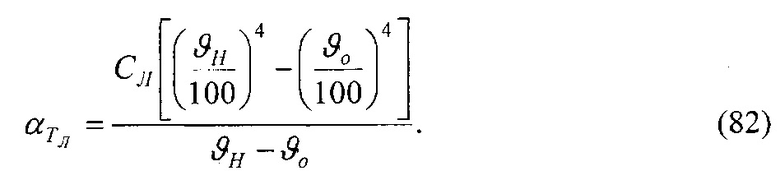
На фиг. 46а, б представлены результаты расчетов по формуле (82) коэффициентов теплоотдачи лучеиспусканием матовых и полированных поверхностей металлических фрикционных элементов от температуры их нагревания.
Однако имеется особенность в том, что коэффициенты излучения для матовой и полированной поверхности для чугуна и стали имеют различное значение. Кроме того, по отношению к коэффициентам излучения матовой поверхности к полированной, которое равно отношению площади охлаждаемой поверхности к площади нагреваемой поверхности металлического фрикционного элемента можно судить о наступлении установившегося теплового состояния металлического фрикционного элемента. В виде соотношений получаем:
для барабанно-колодочного тормоза
(тормозной барабан изготовлен из чугуна)
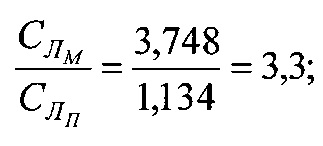
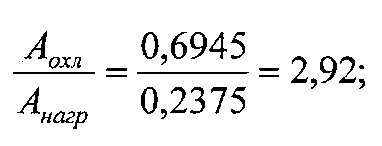
для ленточно-колодочного тормоза
(тормозной шкив изготовлен из стали)
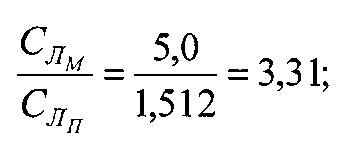
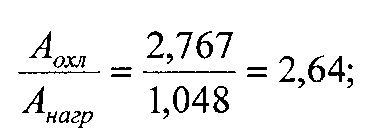
В данном случае рассматриваются площади поверхностей теплообмена: заднего тормозного барабана автотранспортного средства КрАЗ-250 (табл. 7) и тормозного шкива ленточно-колодочного тормоза буровой лебедки У2-5-5 (табл. 8). Процентное расхождение между величинами отношений для различных видов тормозных устройств составляет: 11,5% - для первого случая; 23,0% - для второго.
Если предположить, что 15,5% теплоты компенсируют вынужденный конвективный и кондуктивный теплообмены от поверхностей тормозного барабана автотранспортного средства, то такой вариант установившегося теплового состояния возможен в интервале небольших температур, т.е. 15-125°С. Для шкива ленточно-колодочного тормоза вариант установившегося его теплового состояния не возможен до допустимой температуры материала фрикционной накладки.
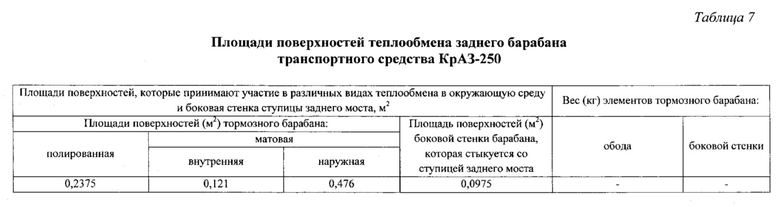

Таким образом, предложен способ определения площадей поверхностей металлических фрикционных элементов при различной их энергоемкости в тормозных устройствах.
Температурные градиенты в металлическом фрикционном элементе трибосопряжения. Процесс электротермомеханического трения, реализуемый тормозным устройством (ленточно-дисково-барабанно-колодочным), может быть как непродолжительным (единичное торможение) так продолжительным и длительным (циклическое и длительное торможение). От продолжительности процесса зависят генерируемые токи на поверхности трения фрикционных узлов, количество аккумулируемой теплоты и глубина проникновения тепловых волн по толщине металлического элемента трения. Исходя из вышеизложенного и предлагается к рассмотрению импульсный и длительный подвод теплоты к элементам трибосопряжения.
Взаимосвязь между темпом нагревания обода шкива и градиентом температуры по его толщине устанавливаем с помощью управляющей функции [4]
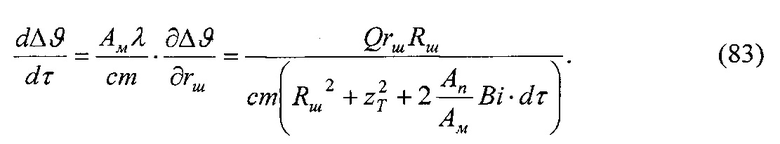
Однако, в зависимости (83) необходимо ввести величину δ, т.е. толщину поверхностного и приповерхностного слоев фрикционных элементов для более точной их оценки нагретости. Для этого воспользуемся подстановкой а=λ/(сρ) (где ρ - плотность фрикционных материалов) и ν=Амδш (где ν - объем фрикционного материала). В результате подстановок и преобразований получаем
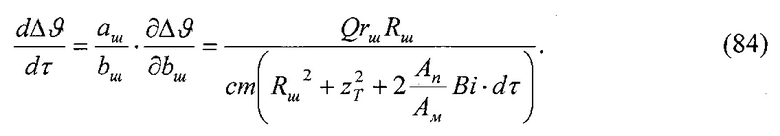
Проведем анализ зависимости (84) по параметрам. Увеличение рабочей (полированной) площади обода шкива способствует росту его металлоемкости, так как увеличивается и его толщина, и как следствие, момент инерции. При этом толщина обода (δш) тормозного шкива определяется через регламентируемый его момент инерции (Iин Ш)

Диаметр тормозного шкива определяется из условия достижения ленточно-колодочным тормозом момента, обеспечивающего спуск колонны бурильных труб максимального веса, а также возможности удержании их на весу.
Увеличение коэффициента теплопроводности, а в месте с ним и температуропроводности материалов обода шкива вызывает быстрый прогрев по его толщине, и как следствие, уменьшение температурного градиента. Если обозначить постоянное слагаемое 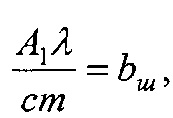 то можно установить связь между темпом нагревания
то можно установить связь между темпом нагревания 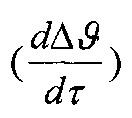 и градиентом температуры
и градиентом температуры 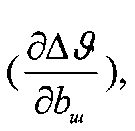 имеющим место на рабочей поверхности обода шкива.
имеющим место на рабочей поверхности обода шкива.
Что касается зависимости (84), то здесь несколько инная картина. Значение закономерности изменения коэффициента температуропроводности материалов обода шкива от температуры, а также времени проникновения теплоты в слои обода шкива позволяет более точно, нежели в первом случае, определять отношение (аш/bш). При этом используется зависимость, предложенная А.В. Чичинадзе, вида  (для обода шкива) и
(для обода шкива) и 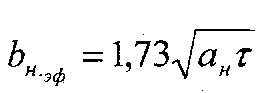 (для полимерной накладки) для определения эффективной глубины проникновения теплоты в тело обода и накладки при длительном и импульсном режимах.
(для полимерной накладки) для определения эффективной глубины проникновения теплоты в тело обода и накладки при длительном и импульсном режимах.
Термические напряжения в ободе тормозного шкива. Остановимся на определении составляющих сжимающих напряжений, действующих на рабочую поверхность обода шкива в процессе спускоподъемных операций. Максимальные сжимающие напряжения σ1max в ободе шкива будут на его рабочей поверхности и они равны алгебраической сумме составляющих

Оценим величины термонапряжений, возникающих в ободе тормозного шкива, являющихся результатом особенностей его тепловой нагруженности.
Согласно энергетической теории прочности максимальное эквивалентное напряжение, возникающее в ободе шкива в месте соединения его с крепежным выступом, определяем по зависимости вида

Обработка статистических данных по разрезке краев трех новых ободов тормозных шкивов показала, что они сходились на 1,0-2,0 мм, т.е. имело место действие в них сжимающих напряжений. После разрезки 12-ти отработанных шкивов их края расходились на 40,0-50,0 мм. Следовательно, значительные остаточные растягивающие напряжения в ободе тормозного шкива образовались только в процессах фрикционного взаимодействия пар трения тормоза при их нагревании и вынужденном охлаждении при спускоподъемных операциях.
Как видно из табл. 9 сжимающие напряжения в ободе тормозного шкива создаются, в основном, за счет напряжений от значительного температурного градиента на поверхностях обода, составляющего более 74,0% суммарных напряжений, а также от расположения крепежного выступа на середине обода (см. фиг. 22в). Из табл. 9 и формул (7-9) следует, что такие сжимающие напряжения в шкиве σ1 могли образоваться при перепаде температур свыше 38,5°С; перепад температур ниже 22,5°С не приводит к образованию остаточных напряжений.
В процессе остывания элементов тормозного шкива после спуска инструмента вследствие различной интенсивности теплоотдачи от 
полированной и матовых его поверхностей происходит перераспределение токов тепловых потоков в результате чего возникают температурные градиенты обратного знака по толщине слоев обода из-за их подпитки тепловыми потоками, идущими от крепежного выступа, а также вследствие деструкционных процессов, происходящих в поверхностных и подповерхностных слоях фрикционной накладки, которые вынужденно охлаждают рабочую поверхность обода шкива. В этом случае поверхностная температура последнего и становится меньше температуры слоев обода (см. фиг. 22а, в). Напряжения на поверхности обода тормозного шкива при этом совпадают с остаточными напряжениями. Величину их определяем по зависимости

Для исследуемой конструкции тормозного шкива даже при самых неблагоприятных условиях, т.е. при работе на серийных парах трения на всем протяжении спуска инструмента до забоя, эти напряжения составили менее 5% остаточных растягивающих напряжений. Температурный градиент обратного знака при этом составлял 10°С.
Полученные данные дают возможность определить максимальное эквивалентное напряжение, возникающее в ободе шкива от сопряжения с ним крепежного выступа в результате действия температурного градиента по их толщине, используя зависимость (8). В данном случае при торможении для обода шкива градиент температуры по отношению к крепежному выступу составляет 65,0°С, а расчетное напряжение при этом достигает σ0=147,5 МПа.
Следовательно, температурные напряжения в ободе шкива могут достигать нерегламентированных величин особенно летом, когда поверхностный температурный градиент большой. Неоднократное приложение импульсных нормальных сил, электрических и тепловых токов приводит к появлению в теле обода шкива остаточных напряжений. В тормозных шкивах при эксплуатации возникает усадка, образующая на центрирующей поверхности усилие, вызывающее растягивающее напряжения. Этим и объясняется тот факт, что отработанные шкивы из сталей всех марок, при условии отсутствия в них трещин, при демонтаже приходилось разрезать автогеном, при этом концы в местах реза расходятся на 40-50 мм.
Решающим фактором в зарождении и развитии трещин на рабочей поверхности ободов является отношение сопротивления трещинообразованию (σ0) к максимальному тепловому напряжению (σ')

Если KC>1,0 поверхностный и подповерхностный слой материала обода шкива не разрушается.
На фиг. 47 проиллюстрирована зависимость напряжений сопротивления трещинообразованию (σ0) от объемной температуры обода шкива (ϑоб) и величины сопротивления тепловому удару (KC). В интервале объемных температур от 50,0 до 200,0°С обода шкива суммарные остаточные термические напряжения изменяются от 100,8 до 299,0 МПа и при KC=1,0 они равны напряжениям сопротивления трещинообразованию (σ0). При KC=0,2-0,8 напряжения сопротивления трещинообразованию изменяются от 20,2 до 239,2 МПа, которые будут способствовать зарождению и развитию микротрещин на рабочей поверхности обода шкива.
Исходя из вышеизложенного, повышение работоспособности ободов шкивов ленточно-колодочного тормоза буровой лебедки достигается за счет:
- снижения остаточных термических напряжений в ободе шкива, как путем уменьшения поверхностных допустимых температур для материалов фрикционной накладки для предохранения возникновения деструктивных процессов и сетки трещин на рабочих поверхностях ободов шкивов;
- снижения металлоемкости ободов тормозных шкивов путем: уменьшения их толщины; выполнение разборными или их устранением с процесса электротермомеханического трения.
Для оценки относительного напряжения на любой толщине (по нормали к поверхности трения) обода тормозного шкива, работающего в апериодическом циклическом режиме, используем полученные соотношения при:
нагревании когда 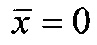 , т.е. на поверхности обода тормозного шкива
, т.е. на поверхности обода тормозного шкива
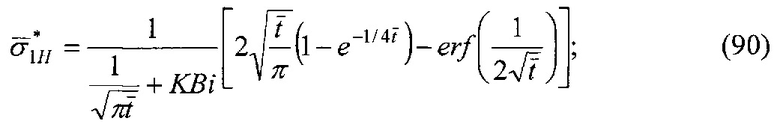
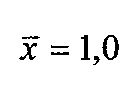
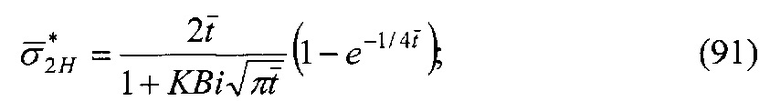
естественном охлаждении когда 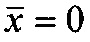
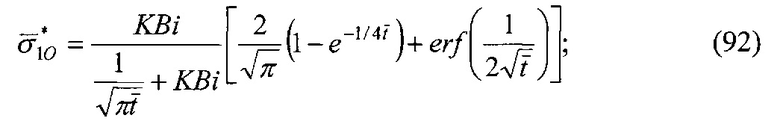
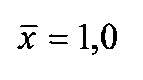
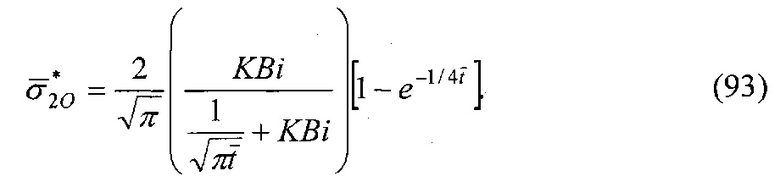
На основании полученных выражений (90)-(93) построены графические зависимости относительных термических напряжений при нагревании и естественном охлаждении для одного цикла подвода теплоты (фиг. 48а, б, в, г).
Анализ графических зависимостей (см. фиг. 48а, б, в, г) показывают, что относительные термонапряжения (при нагревании) на рабочей поверхности обода шкива почти в десять раз превышают значение термонапряжений, возникающих в его слоях. Относительные напряжения достигают максимума, когда процесс происходит при теплоизолированных матовых поверхностях шкива (Bi=0) и приравниваются к нулю, когда теплообмен бесконечен (Bi→∞). Существенное влияние оказывает на естественное охлаждение критерий Bi. Причем с увеличением продолжительности процесса торможения влияние его на естественное охлаждение возрастает.
Из анализа графических зависимостей (см. фиг. 48а, б, в, г) следует, что при естественном охлаждении относительных термических напряжений на полированной поверхности, являющейся источником радиационного теплообмена, почти в пять раз больше, чем по слоям обода шкива. Причем относительные напряжения достигают максимума, когда происходит интенсивный теплообмен (Bi→∞) и имеет максимальное значение, когда матовые поверхности теплоизолированы (Bi=0).
Выполненные расчеты показали, что наибольшие термические напряжения испытывают полированные поверхности обода шкива из-за больших поверхностях температурных градиентов. Кроме того, проявляется действие принципа суперпозиции при процессах «нагревание - охлаждение» слоев обода шкива, способствующих их тепловому как расширению так и сжатию, поскольку имеет место неравномерного прогрева слоев обода шкива.
Скоростные токи сред и их компонентов омывающие фрикционные узлы. Качественный и количественный состав токов омывающих сред в зазорах между микровыступами металлополимерных пар трения значительно влияет на их трибологические характеристики. Установлено, что состав токов омывающих сред также оказывает значительное влияние и на процессы, явления и эффекты, происходящие на пятнах контактов микровыступов пар трения и их изнашивание, в особенности фрикционных материалов на основе Fe, работающих в паре с металлическим контртелом. При работе в таких омывающих средах, содержащих в своем составе О2, на пятнах контактов трения происходит образование окисных пленок, обеспечивающих работу во фрикционных контактах в режиме окислительного износа, что исключает схватывание.
Токи омывающих сред необходимо рассматривать с позиций газовой динамики, нестационарной диффузии и химической кинетики и потреблении активных компонентов среды как между микровыступами не взаимодействующими в данный момент так и боковыми поверхностями микровыступов, находящихся в контактировании при условии, что коэффициент взаимного перекрытия Квз<1,0.
Площадь зоны трения, свободная от непосредственного контакта и доступная для химического взаимодействия с активными компонентами омывающей среды определяется по зависимости

Газодинамическая модель контактного зазора представляет собой полость, в которой имеет место течение токов омывающей среды, содержащей активные компоненты. Характер течения токов омывающей среды оценивается критерием Кнудсона

Контактный зазор высотой hэф необходимо рассматривать как химический нанореактор, на стенках которого протекают гетерогенные химические реакции с образованием окисных пленок. В процессы трения (при торможении) регенерация окисных пленок взамен изношенных осуществляется путем нестационарного химического потребления активных компонентов токов омывающей среды стенками микровыступов с последующей их доставкой извне в межконтактный зазор.
Однако при этом необходимо учитывать условие теплового равновесия, которое требует, как известно, наряду с постоянством температуры также и постоянства вдоль среды суммы μxn+U. В данном случае речь идет о равновесии по отношению к электронам, так что под μxn надо понимать их химический потенциал, a U=-еϕэ. Соответственно, этому электрический ток j1 и диссипативный поток энергии q' обращаются одновременно в нуль лишь при условиях q1=const, μ-eϕэ=const, т.е. при ∇ϑ1=0, ∇μxn+еЕе=0. Выражение для j1 и q' записывают в виде следующих соотношений, удовлетворяющих указанному условию
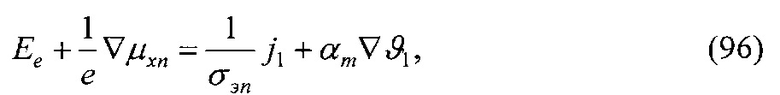
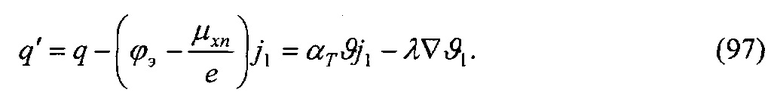
Соотношение между коэффициентами ∇ϑ1 в (96) и j1 в (97) - следствие принципа Онсагера. Величина  , вычтенная из полного потока энергии, представляет собой плотность конвективного потока энергии. Последнюю и необходимо учитывать при оценке термостабилизационного состояния металлического фрикционного элемента в тормозных устройствах.
, вычтенная из полного потока энергии, представляет собой плотность конвективного потока энергии. Последнюю и необходимо учитывать при оценке термостабилизационного состояния металлического фрикционного элемента в тормозных устройствах.
Указанное стабилизационное тепловое состояние обода шкива поддерживается возникновением в элементарных объемах приповерхностных слоев фрикционных элементов множества микротермобатарей, создающих внешние и внутренние электрические поля с различными двойными электрическими слоями, и работающими в режимах микротермоэлектрогенераторов и микротермоэлектрохолодильников, а при преобладании внутреннего электрического поля происходит инверсия токов от приповерхностного слоя шкива в приповерхностные слои накладок.
На третьем этапе моделирования рассматриваются: трибосопряжение, трибосистема, критерии подобия и основные эксплуатационные параметры узла трения тормозного устройства [11; 15-19].
Под трибосопряжением подразумевается фрикционное взаимодействие двух тел, имеющими различные механофизические свойства.
Общая модель трибологического сопряжения имеет следующие подмодели на нано-, микро- и миллиуровнях: кинематическую; электротепловую; контактирования; электрообразования и поведения контактирующих слоев материалов с учетом дискретной природы контакта; многослойное образование на поверхности вследствие фрикционного взаимодействия; дефекты в материалах элементов пары трения (см. фиг. 49а, б, в, г, д, е).
Остановимся кратко на подмоделях, которые обязательно учитываются при декомпозиции общей модели и моделировании процессов электротермомеханического трения и изнашивания на различных испытательных установках:
1) кинематическую подмодель (см. фиг. 49а), воспроизводящую коэффициент взаимного перекрытия натурного объекта и направление движения элементов пары трения, параметрами которой являются коэффициент взаимного перекрытия Квз<1, нагрузка р, площади: номинальных (Aн1,2) и вентилируемых (Aσ1,2) поверхностей трения; масса элементов пары трения mc1,2; объемы пары трения ν1,2; работы трения WТП; скорость скольжения Vck; угловая скорость ω; ускорение w и время τ (продолжительность трения);
2) макротепловую модель (фиг. 49б), учитывающую распределение тепловых потоков, параметрами которой являются объемные температуры элементов пары трения ϑv1,2; коэффициенты внешней теплоотдачи αТ1,2; температура окружающей среды ϑ0; коэффициенты теплопроводности материалов λ1,2; удельные теплоемкости материалов c1,2; плотности материалов пары трения и окружающей среды ρм1,2,3; динамическая вязкость окружающей среды η3;
3) подмодель контактирования (рис. 49в), в которой наглядно представлены соотношения между номинальной, контурной и фактическими площадями контакта;
4) микромодель электротеплообразования и поведения контактирующих слоев материала с учетом дискретной природы контакта (фиг. 49г), параметрами которой являются среднестатистические радиусы единичных выступов шероховатых поверхностей элементов пары трения r1,2, высоты единичных неровностей h1,2, сопротивление сдвигу тонких поверхностных элементов (пленок) пары трения τn1,2, генерируемые импульсные электрические токи I, объемные температуры элементов пары трения ϑv1,2, температура вспышки на фактическом пятне касания ϑвсп, коэффициенты теплопроводности λ1,2, удельные теплоемкости c1,2 и плотности ρм1,2 материалов пары трения, модуля упругости Е1,2 и твердость HB1,2 материалов, динамическая вязкость η1,2 материалов пары трения;
5) многослойное образование на поверхности (фиг. 49д) вследствие фрикционного взаимодействия с шестью слоями - адсорбированным, граничным, смазочного материала, оксидов, текстурированного и исходного материалов;
6) дефекты в материале элемента пары трения, возникающие при трении (рис. 49е) (1 - дислокации, 2 и 3 микро- и макротрещины).
Общая модель внешнего трения полностью учитывает две основополагающие триады внешнего трения, предложенные И.В. Крагельским и А.В. Чичинадзе, а также основные положения совместимости трибосистем, разработанные Н.А. Буше [9].
Моделируемость - возможность представления системы конечным множеством моделей, каждая из которых отражает определенную грань ее сущности.
Последнее свойство нашло применение при разработке рационального цикла триботехнических испытаний. Вместо создания полной модели для сложного триботехнического сопряжения применяют ряд последовательных моделей, которые дают возможность установить границы применения пары трения. Затем внутри этих границ применительно к заданному режиму эксплуатации выявляют выходные характеристики трибосопряжения (температура ϑ, динамический коэффициент трения f, интенсивность износа up.n и) и, наконец устанавливают степень влияния конструкции узлов трения машины на эти же характеристики.
Создание полной модели для сложного трибосопряжения вообще бесполезно, так как согласно теореме Тьюринга, такая модель будет такой же сложной, как и само трибосопряжение и малопригодное для подробного изучения.
При разработке конечного множества следует учитывать (или понимать), какие свойства подсистемы подавляют или усиливают общесистемные свойства, например, недостаточная жесткость подсистемы способствует проявлению фреттинга.
Иерархическая модель, соответствующая графической модели, показанной на фиг. 49 приведена на фиг. 50. Графическая модель трибологического сопряжения - фрикционного узла имеет пять уровней: геометрический, электрический, тепловой, силовой и информационный, кроме этих уровней учитываются исходные свойства материалов и функциональные свойства системы.
Следует иметь в виду, что вследствие тепловыделения, которое усиливается генерируемыми токами (уровень три) происходит изменение исходных свойств материалов, геометрического и силового уровня. Обо всех этих изменениях исследователь получает сведение на информационном уровне: в динамические эффекты входят динамический коэффициент трения, нестабильность трения и фрикционного разогрева, а в локальные разрушения материала - износ в отдельных точках поверхности.
Моделирование рассматривается как процесс сопоставления результатов модельного и натурного опыта на основе подобных преобразований (анализа подобия). Таким образом, моделирование означает осуществление каким-либо способом отображения или воспроизведения действительности для изучения имеющихся в ней объективных закономерностей. Под подобием понимается взаимно-однозначное соответствие между двумя объектами, при котором функции перехода от параметров, характеризующих один из объектов, к другим параметрам -известны, а математическое описание этих объектов могут быть преобразованы в тождественные.
На фиг. 51 проиллюстрирована трибосистема, в качестве которой представлено ленточно-колодочный тормоз буровой лебедки У2-5-5, при этом трибосистема рассмотрена от подсистемы первого порядка до подсистемы восьмого порядка.
На фиг. 52а, б, в, г, д, е, ж показан общий вид ленточно-колодочного тормоза с многопарными фрикционными узлами и их графическими моделями.
Критерии подобия при моделировании процессов трибосистемы.
Критерий гомохронности, характеризующий однородность процессов во времени Vck⋅τ/l=idem, в реализованном моделировании получаем, если 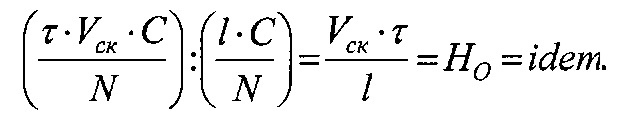 Критерий гомохронности сформирован из параметров Vck, τ и l, то даже если не один из них не входит в число базисных, имеем основные параметры фрикционного взаимодействия микровыступов металлополимерных пар трения.
Критерий гомохронности сформирован из параметров Vck, τ и l, то даже если не один из них не входит в число базисных, имеем основные параметры фрикционного взаимодействия микровыступов металлополимерных пар трения.
Остальные критерии, используемые при моделировании, были получены таким же путем как и критерий HO. При этом их толкование отвечает нано- и микроуровням развития трибологии.
Рассмотрим несколько разных "стандартных" критериев на основании которых получим один из основных "нестандартных" критериев, устанавливающих связь между теплофизическими параметрами пар трения и омывающих их скоростные токи воздуха, и смеси не только в газообразном, но и в жидком состоянии.
Критерий Био

Критерий Био можно рассматривать как отношение процессов охлаждения при омывании скоростными токами компонентами смеси среды к процессам кондуктивного нагревания слоев тормозного шкива при достижении тепловыми токами заданной глубины его обода.
Критерий Фурье

Критерий Фурье можно рассматривать как отношение времени протекания торможения τ к времени перестройки энергонагруженности рабочих слоев тормозного шкива b2ш.эф/а, пропорциональному квадрату их толщины и обратно пропорциональному коэффициенту температуропроводности материала его обода.
Критерий Нуссельта

Полученное выражение можно рассматривать как отношение величины плотности теплового потока, переданного в процессе теплоотдачи от полированной и матовых поверхностей тормозного шкива при их омывании скоростными токами смеси среды к величине плотности теплового тока через ее слои толщиной h вследствие их теплопроводности.
Критерий Пекле

В числителе находится величина теплового потока, переносимого омывающими скоростными потоками компонентов смеси среды, циркулирующего в зазорах с переменными сечениями между микровыступами пар трения, а в знаменателе величина теплового потока, прошивающая слой толщиной hC вследствие их температуропроводности. В таком виде критерий Пекле можно рассматривать как меру относительной роли молярного и молекулярного переноса теплоты.
Отношение критериев
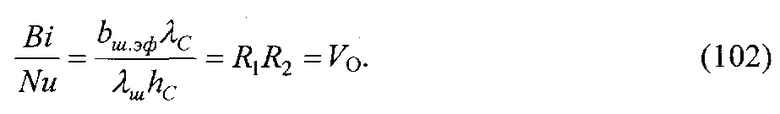
Анализ соотношения критериев с концептуального подхода с позиции синергетики и фракталов в трибологии [20] позволил предложить критерий Вольченко для оценки состояния охлаждаемой рабочей поверхности обода тормозного шкива и энергонагруженности его поверхностных и подповерхностных слоев.
Полученное соотношение можно рассматривать как произведение термического сопротивления поверхностного и подповерхностного слоев обода тормозного шкива к поверхности которого якобы "прилипают" слои омывающего воздуха при поверхностной температуре полимерной накладки ниже допустимой для ее фрикционноых материалов. В случае попадания поверхности полимерной накладки в зону выше допустимой температуры происходит выгорание связующих компонентов из ее материалов. Компоненты последних смешиваются с циркулирующими слоями воздуха. В дальнейшем на поверхности накладки появляются островки жидкости, которые якобы прилипают к рабочей поверхности обода шкива. Таким образом, управляющим воздействием для термического сопротивления поверхностного слоя полимерной накладки является ее состояние (твердое, жидкое, газообразное). Для поверхностных и подповерхностных слоев обода тормозного шкива управляющим воздействием для термического сопротивления является их энергонагруженность. Знание величин составляющих критерия Вольченко позволяет прогнозировать энергонагруженность поверхностных и подповерхностных слоев микровыступов металлополимерных пар трения.
Особенности компьютерного моделирования энергонагруженности металлополимерных пар трения тормозов. Исходные предпосылки модели следующие: материалы пятна контакта микровыступов однородны и изотропны; контакт носит дискретный характер и происходит по вершинам отдельных микровыступов шероховатостей, деформация микровыступов имеет упругий характер и описывается зависимостью Герца для контакта двух криволинейных гладких тел с первоначальным касанием в точке; размеры единичных пятен контакта малы по сравнению с размерами зоны взаимодействия и радиусами кривизны микровыступов в точке касания; в зоне контакта действуют только импульсные нормальные силы и силы трения; распределение пятен контакта по поверхности пар трения равномерное. Исходными данными для расчета являются характеристики микрогеометрии поверхностей - максимальная высота выступов над средней линией профиля hмax и максимальный радиус закругления выступов rmax; физико-механические характеристики материала - модуль упругости (модуль Юнга) Е, коэффициент Пуассона μ, удельное электрическое сопротивление материала ρ; эксплуатационные характеристики, импульсная нормальная сила, сжимающая контакт.
Компьютерная модель практически реализована в виде windows - приложения, написана на языке С++ с использованием библиотеки классов Borland. Програмно модель входит в основной расчетный модуль, в который включена оценка внешних и внутренних параметров металлополимерных пар трения на макро-, микро- и наноуровнях.
Кроме основного, есть дополнительный модуль, отвечающий за удобство представления данных и пользовательский интерфейс. Результатом работы являются эксплуатационные характеристики контакта, представленные в виде таблицы. Для большей наглядности на основе предложенных формул предусмотрена возможность строить графики зависимостей характеристик контакта от внешних факторов, которыми являются токи омывающего воздуха и компонентов смесей.
В табл. 10 представлены основные зависимости для расчета характеристик единичного контакта двух сферических микровыступов пятна контакта [21].
В рамках компьютерной модели расчет характеристик контакта происходит следующим образом. Генерируется пара случайных чисел, распределенных по заданному закону, соответствующих высоте и радиусу выступа шероховатой поверхности. Логику работы программы иллюстрирует блок-схема основного расчетного модуля для параметров механического, электрического и теплового полей (фиг. 53).

Программа связана с базой данных MS Access, состоящей из двух таблиц, каждая из которых включает в себя 33 поля. Первая таблица содержит значения исходных промежуточных данных, а вторая - значения результатов. Таблицы используются для построения графиков.
При этом первое поле каждой таблицы зарезервировано для проверенной начальной комбинации исходных параметров и используется только в начале работы и только для чтения. Прежде всего программа считывает начальную комбинацию исходных параметров из базы данных и дополняет этими значениями поля исходных данных. Затем пользователь редактирует их, выполняет расчет, после чего заполняется таблица значений и по ней строится график.
Адекватность модели проверялась путем сравнения результатов моделирования с данными работ других авторов, полученными на основании аналитических моделей для некоторых частных случаев.
Посредством компьютерного моделирования определяли:
- закономерности изменения твердости металлического и неметаллического материала от удельных нагрузок и относительной величины отношения 2an/l;
- закономерности изменений микротоков на пятне контактов микровыступов трибосопряжения в зависимости от поверхностной температуры и ее градиента по длине пятна контактов, и при различной импульсной нормальной нагрузке;
- закономерности изменения деформаций микровыступов металлополимерных пар трения ленточно-колодочного тормоза буровой лебедки от импульсных удельных нагрузок при разных площадях поверхностей пятен их контактирования;
- закономерности изменения площадей пятен контактов металлических микровыступов и их количества от действующих импульсных нормальных усилий.
Программное обеспечение модельного тормозного стенда включает специальную программу записи и обработки сигналов с датчиков микровыступов металлополимерных пар трения трибосистемы.
В программе задается:
- частота дискретизации - максимальная частота зависит от тактовой частоты компьютера, технической характеристики аналогового цифрового преобразователя (АЦП) и подбирается экспериментально (например, 1,2 кГц);
- длительность выборки - задает время записи в секундах. Запись начинается с момента нажатия на клавишу СТАРТ и продолжается до истечения времени, заданного в данном пункте или до нажатия на клавишу СТОП. Длительность записи ограничена только размером жесткого диска компьютера;
- калибровка - уровни, которые установлены в данный момент, считаются нулевыми (выбирается смещение нуля).
Записанные сигналы используются для их программной обработки, например, MATLAB. Система. MATLAB разработана фирмой The Math Works, Inc. (США, г. Нейтик, шт. Массачусетс) и является интерактивной системой для выполнения инженерных и научных расчетов, ориентированной на работу с массивами данных. Система использует математический сопроцессор и допускает возможность обращения к программам, написанным на языках FORTRAN, С и С++.
Программное обеспечение определяет частотную функцию передачи по результатам обработки сигналов импульсных нормальных нагрузок и силы трения и на основе анализа частотной функции передачи производится анализ динамического состояния пятен контактов микровыступов трибосистемы, а также проверку ее устойчивости по критериям устойчивости Найквиста, Ляпунова и пр. [22].
Приведем некоторые теоретические сведения.
Пусть выходной сигнал узла трения у(k) представляет сумму (с весовыми коэффициентами) некоторого количества предыдущих выходных отсчетов, зависящих от некоторого количества входных отсчетов u(k) (включая последний). Если сгруппировать полученные слагаемые так, чтобы с одной стороны от знака равенства были только входные отсчеты, а с другой -только выходные, то получим форму записи, называемую разностным уравнением:
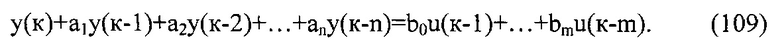
Структура разностного уравнения похожа на структуру дифференциального уравнения аналоговой системы, только вместо операции дифференцирования в формуле фигурируют задержки дискретных последовательностей сигнала.
Выходной сигнал, исходя из линейности и стационарности рассматриваемой системы, должен представлять собой линейную комбинацию импульсных характеристик, т.е. нормальной и трения силы
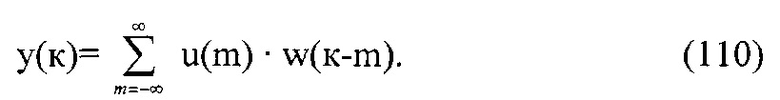
Удобным анализом дискретных последовательностей является z-преобразование (z-transform). Смысл его заключается в том, что последовательность чисел {u(к)} ставится в соответствие функции комплексной переменной z.

Знание импульсной характеристики дискретной системы позволяет проанализировать прохождение через нее любого сигнала и найти ее внутреннее состояние. Применив z-преобразование к уравнениям дискретной системы (111), получим ее системную функцию или функцию передачи (transfer function)
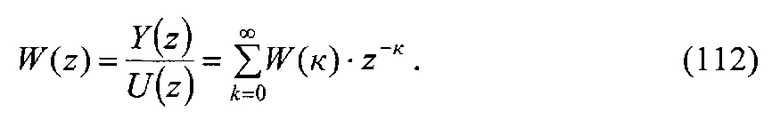
Применив z - преобразование к обеим частям разностного уравнения (112), получим
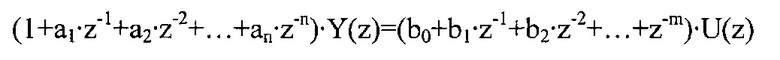
Отсюда легко получить вид функции передачи дискретной системы:
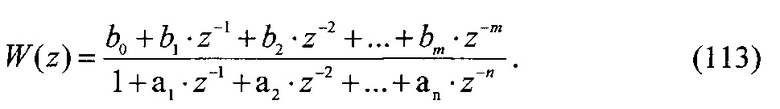
Таким образом, функция передачи физически реализуемой дискретной системы показывает, как изменяется при прохождении через систему комплексная амплитуда синусоиды с частотой со и может быть представлена в виде отношения полиномов по отрицательным степеням переменной z. Полином числителя характеризует внешнее воздействие на узел трения, а полином знаменателя (характеристический полином) - результат этого воздействия на пятна контактов микровыступов трибосистемы.
Зная спектры * (* спектр - форма представления анализируемого сигнала не во временной области исследования, а в частотной), и преобразования сигнала из временного домена исследований в частотный осуществляется алгоритмом быстрого преобразования Фурье согласно выражения 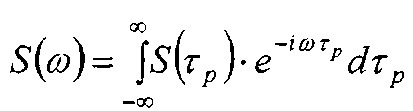 входного и выходного сигналов, дальше рассчитывается взаимный спектр входного и выходного сигналов, представляющий собой произведение их спектральных функций, одна из которых подвергнута комплексному сопряжению:
входного и выходного сигналов, дальше рассчитывается взаимный спектр входного и выходного сигналов, представляющий собой произведение их спектральных функций, одна из которых подвергнута комплексному сопряжению:
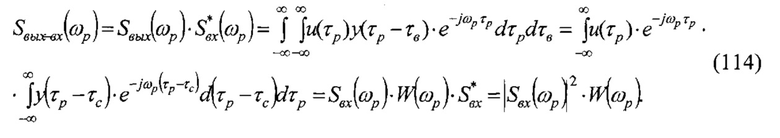
Если сигнал u(τр-τс) - четная функция, то спектр будет чисто вещественным (будет являться четной функцией). Если u(τр-τс) - функция нечетная, то спектральная функция S(ω) будет чисто мнимой (и нечетной).
Таким образом, если спектры сигналов не перекрываются, то их взаимный спектр равен нулю на всех частотах и взаимная корреляционная функция этих сигналов будет также равна нулю при любых временных сдвигах τ. Следовательно, сигналы с неперекрывающимися спектрами являются некоррелированными.
Из полученного выражения (114) определяется комплексный коэффициент передачи дискретной системы
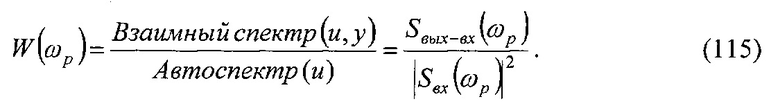
Математические модели динамики реальных трибосистем являются, в основном, нелинейными и во многих случаях не могут быть линеаризованы из-за возможности потерять характерные динамические свойства, обусловленные принципиальной нелинейностью уравнений динамики. Однако, с некоторыми ограничениями, частотную передаточную функцию трибологии линеаризовывают по критерию минимума дисперсии выходного сигнала импульсной функции Дирака. Оптимальным порядком полиномов числителя и знаменателя является такой порядок полиномов числителя (m) и знаменателя (n) функции передачи (115), при котором дисперсия выходного импульсного сигнала будет минимальна.
Результатом анализа амплитудно-фазочастотных характеристик (АФЧХ) является, возможность проверки устойчивости внутреннего пространства состояний системы и значения комплексного динамического коэффициента трения, действующего в зоне фрикционного нагружения пятен контактов микровыступов металлополимерных пар трения
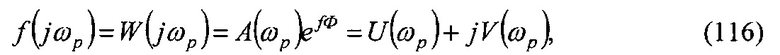
где 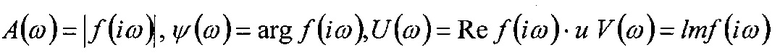 - характеристики динамического коэффициента трения: амплитудно-частотная; фазочастотная; вещественная частотная и мнимая частотная.
- характеристики динамического коэффициента трения: амплитудно-частотная; фазочастотная; вещественная частотная и мнимая частотная.
Рассмотрим процесс изменения динамического коэффициента трения при электротермомеханическом фрикционном взаимодействии пятен контактов микровыступов металлополимерных пар трения во времени (фиг. 54).
Исследование этого динамического процесса выполнялось на модельном ленточно-колодочном тормозе при импульсной нормальной нагрузке N=0,3 кН на восьмой накладке набегающей ветви тормозной ленты при отношении линейных размеров ободов шкивов
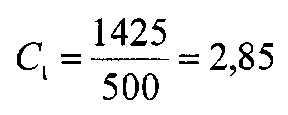
и масштабном факторе нормальной нагрузки CN=C1=8,12 кН и скорости скольжения Vcк=0,6 м/с и объекта исследований V=1,71 м/с.
Структурные изменения и перераспределение энергетических потоков на поверхностях пятен контактов микровыступов металлополимерных пар трения ленточно-колодочного тормоза можно наблюдать только в процессах самого электротермомеханического трения, которые необходимо развивать и использовать in-situ методы исследования.
Износофрикционные свойства пар трения «полимер - металл» в тормозных устройствах.
Изучение во времени зависимостей динамического коэффициента трения фрикционных узлов тормозных устройств (фиг. 55) позволяет констатировать о динамической картине общего баланса подведенной и отведенной к трибосистеме энергии.
Внешняя работа, подводимая к трибосистеме, затрачивается на упругое и пластическое деформирование поверхностных слоев и на образование микротермобатарей, которые работают в режимах микротермоэлектрогенераторов и микротермохолодильников, и, как следствие, прямого нагревания и охлаждения поверхностных и приповерхностных слоев пар трения тормозных устройств. Другие виды трансформации механической энергии при низких скоростях скольжения пар трения тормозов являются несущественными (например, излучение). Работа трения зависит от площади фактического контакта и от физико-механических и химических свойств поверхностных и подповерхностных слоев материалов пар трения тормозных устройств, которые упрочняются и разупрочняются в процессе трения сравнительно медленно. Поэтому часть кривой 2 (фиг. 54) динамического коэффициента трения, которая описывается низкочастотной составляющей, связанная с поступающей в трибосистему механической энергией. Последняя затрачивается на ее перераспределение и обеспечение работы микротермобатарей, которые генерируют электрическую энергию с последующим ее превращением в тепловую в приповерхностных слоях элементов фрикционных узлов тормозных устройств.
Природа высокочастотной составляющей (кривая 1 на фиг. 54), связана с дискретностью контакта, а высокочастотные пики динамического коэффициента трения отвечают мгновенно происходящим энергетическим процессам в контактируемых поверхностным слоях, которые являются источником теплоты и холода, за счет генерирования в них прямых и обратных токов. Кривые 1, 2 и 3 (фиг. 54) содержат информацию о влиянии направления тока, генерируемого в парах трения «полимер - металл», на величину динамического коэффициента трения. При прохождении прямых микротоков от контактирующих поверхностей обода тормозного шкива к рабочим поверхностям полимерных накладок (анодно-поляризованные поверхности накладок) f оказывается всегда больше (см. фиг. 54 интервалы времени (510-520) с и (550-570) с для кривых 1 и 2), чем у катодно-поляризованных участках поверхностей накладок ленты, материал которых находится при температурах выше допустимой температуры, и при этом возникают обратные микротоки (см. фиг. 54 интервал времени (510-580) с для кривой 3). Причем во всех случаях f снижается с увеличением плотности тока j на контакте пар трения тормозных устройств. Динамический коэффициент трения катодно-поляризованных участков полимерных накладок всегда меньше динамического коэффициента трения их анодно-поляризованных участков, т.е. (fa>fk), при возрастании j изменяется для фрикционных материалов по-разному.
Таким образом, переполяризация участков фрикционных накладок в парах трения тормозных устройств вызывает инверсию микротоков и изменение их величин, и как следствие, изменение динамического коэффициента трения, характеризующего энергетические процессы в их поверхностных и приповерхностных слоях пар трения.
Характеристика износа определяет долговечность и многие другие эксплуатационные параметры пар трения тормозных устройств. Если работа пар трения происходит при температурах ниже допустимой для материалов фрикционной накладки, то можно утверждать, что износ их рабочих поверхностей и металлических фрикционных элементов является суммой механического (усталостного) up.n.м и электрического (эрозионного) ир.n.э износов (фиг. 55).
Оценка вклада up.n.м в общий износ дает от 1/2 до 3/4 в зависимости от полярности рабочих поверхностей полимерных накладок. Механический износ рабочей поверхности обода металлического фрикционного элемента составляет 5-10% от износа рабочей поверхности полимерных накладок.
Расчет электрической компоненты износа up.n.э зависит от совокупности факторов (направления тока, режима разряда между элементами контакта). Количество переносимого вещества с рабочих поверхностей ободов металлического фрикционного элемента, а следовательно, и износ зависят от направления тока, его величины. Зависимость количества переносимого вещества с неодинаково поляризованных участков поверхностей полимерных накладок на рабочую поверхность обода металлического фрикционного элемента, полученная методом радиоактивных изотопов, показана на фиг. 55. Видно, что перенос с анодно-поляризованных участков поверхностей полимерных накладок является более интенсивным.
Схема зависимости, позволяющая оценить влияние режима разрядов при работе участков рабочих поверхностей накладок с искрообразованием на износ, показана на фиг. 56. Любая форма самостоятельного разряда в ионизированных газах, находящихся между парами трения при их взаимодействии, сопровождается эрозией микроучастков. При тлеющем разряде преобладает износ рабочей поверхности обода металлического фрикционного элемента, а искровой разряд приводит к изнашиванию рабочих поверхностей полимерных накладок. Переход разряда из одной формы в другую всегда сопровождается инверсией электрической составляющей износа взаимодействующих микроучастков поверхностей трения.
Энергонагруженность дискретного контакта микровыступов металлополимерных пар трения трибосистемы выполнена на основании фиг. 57 с привлечением процентного соотношения компонентов газовой смеси, образованной в межконтактном пространстве пары трения (табл. 11). Энергонагруженность дискретного контакта микровыступов металлополимерных пар трения трибосистем приведена в табл. 12.
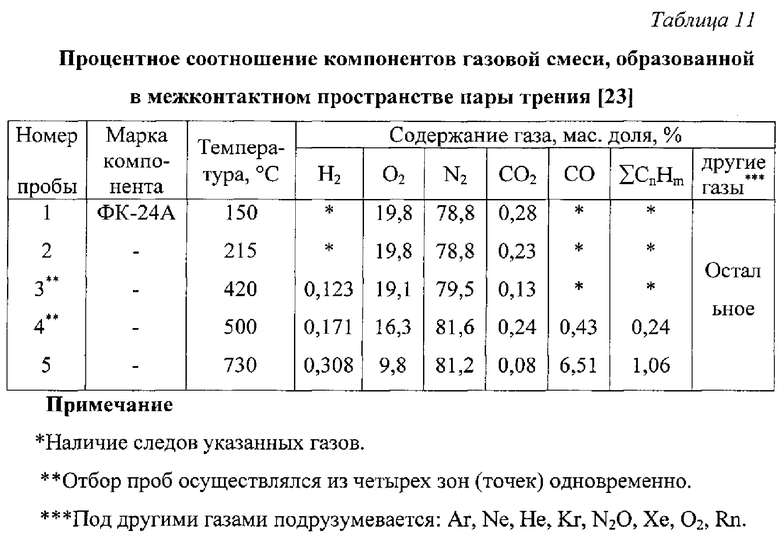
Таким образом, на примере изменения динамического коэффициента трения в зависимости от энергонагруженности пятен контактов микровыступов металлополимерных пар трения во взаимной связи их внешних и внутренних параметров проиллюстрирована реализация различных энергетических уровней поверхностных и подповерхностных слоев фрикционных узлов.
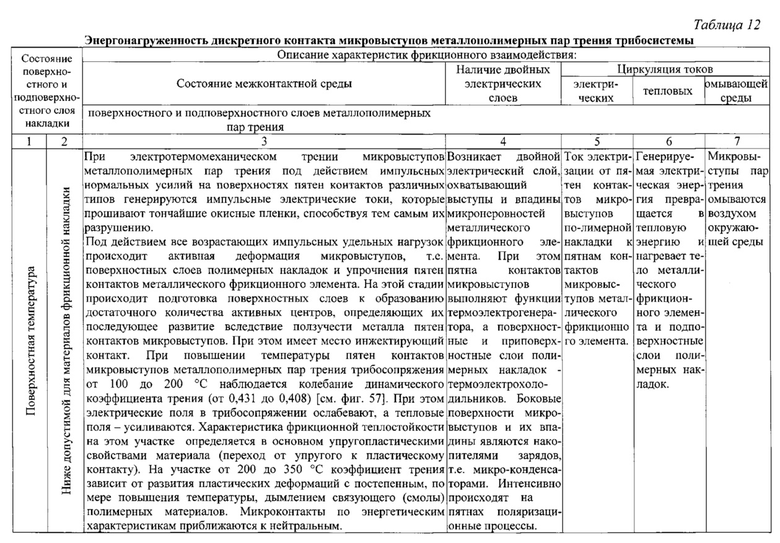
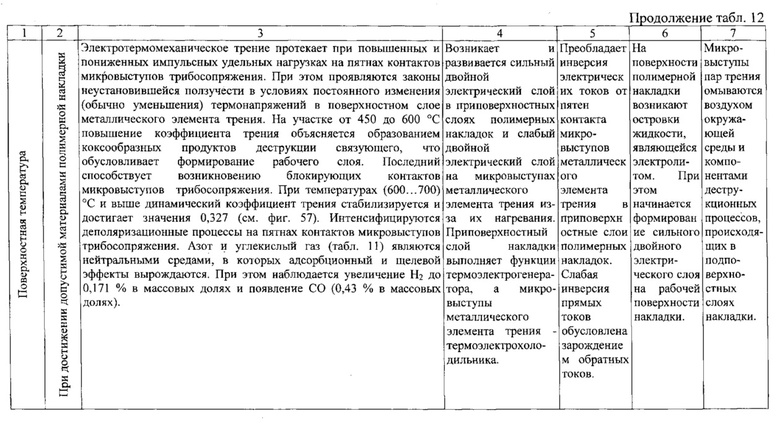

УСЛОВНЫЕ ОБОЗНАЧЕНИЯ
Размеры
Аф, Ак, Ан - площади фрикционного взаимодействия: фактическая; контурная; номинальная, мм2;
ΔАф, ΔАк - элементарная площадь: единичного фактического пятна касания; контурной площади трения, мм2;
Аα1, Аα2, Аα3 - площади поверхностей теплоотдачи, м2;
Aq - площадь сечения, через которую проходит тепловой поток Qλ, м2
ηr - относительная фактическая площадь контакта; ηr=Аф/Ан;
А1, А2, - площади положительных и отрицательных импульсов, мм2;
А3…An
Ав, Аф - площади поперечных сечений крепежных выступов обода и фланца барабана, м2;
An, Ам - площади поверхностей металлического элемента: полированная, матовые трения, м2;
dcp, dn - диаметр пятна контакта: средний, приведенный, мм;
bш, δш - ширина и толщина обода шкива, м;
Lн, ВН и δН - размеры фрикционной накладки: длина, ширина и толщина, м;
δ1, δ2, δср - толщина: крепежного выступа; фланца барабана; их средняя величина, м;
δЛ, Вл, ВП, - конструктивные параметры тормозной ленты: толщина,
АЛ, Rл и R0 ширина, ширина паза, площадь поперечного сечения, радиус ленты и ее срединной поверхности, м;
Rш, RB и rш - радиусы обода шкива: наружный, внутренней и текущий, м;
a n - радиус пятна контакта, мкм;
ν1, 2, 3 - объемы, м3;
е' - зазор между наружными поверхностями фрикционных накладок и внутренней поверхностью тормозной ленты в разомкнутом фрикционном узле тормоза, мм;
h, hmax, rmax и Sм - выступ микронеровности: текущая и наибольшая высота, радиус закругления, шаг, мкм;
hC - толщина слоев скоростных токов омывающей среды, м;
d - толщина слоя, прочно связанного с поверхностью полимерной накладки, мм;
lk - длина контакта, мм;
r - расстояние от пятна контакта, мкм;
hэф - высота контактного зазора, мкм;
s - воздушный зазор между пятнами контактов, мкм;
lC и lH - длина сбегающей и набегающей ветвей ленты, м;
l0 - величина пройденного пути микровыступа обода шкива к началу его движения, мкм;
ln - длина свободного пробега молекул токов омывающих сред, мкм;
l - путь трения микровыступа, мм;
z - некоторое расстояние от линии микровыступов относительно сечения профиля линий, параллельных средней, мкм;
tp=li/l - отношение опорной длины микровыступа к его базовой длине;
ε - усредненное значение относительного сближения поверхностей;
zT - координата по ширине обода шкива, мм;
lci - плечо статического момента, создаваемого действием приведенной импульсной пары, мкм;
ϕ - центральный угол накладки, °;
βi - угол между торцами соседних фрикционных накладок, °.
Масса, энергия
mc, mм - масса: слоев элемента трения, микровыступа, кг;
m - масса обода тормозного шкива, кг;
g - ускорение свободного падения, м/с2
γ, ρ* - удельный вес материала обода шкива, кг/м3;
G - вес колонны бурильных труб, Н;
up.n - износ рабочих поверхностей, мг;
EC, FM (EF) - энергетические уровни: критического движения, металла и FП (Ферми), полимера;
ЕС1, ЕП1 - энергии зон: дна проводимости и валентного потолка полимера, Дж;
WM, WП - работы выхода электронов и ионов из металла и полимера, Дж;
ΔQ - изменение тепловой энергии, Дж;
δ0 - толщина обагащенного и обедненного электронного слоев, мкм;
Ес, Ен - энергия от колебания на ветвях ленты: сбегающей, набегающей, Дж;
Iин - момент инерции тормозного шкива, кг⋅м2;
U - энергия частиц во внешнем электрическом поле, Дж.
Динамические параметры
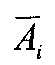 - значение мгновенного фиктивного импульса, Н;
- значение мгновенного фиктивного импульса, Н;
ΣAM, ΣАП - суммарные импульсы, создаваемые микровыступами пары трения «металл-полимер»;
N, dN - импульсное нормальное усилие и его приращение, кН;
F, dF - импульсная сила трения и ее приращение, кН;
∂N - нормальная реакция обода шкива, кН;
∂FT - элементарная сила трения в паре «накладка-шкив», кН;
Qp - реакция металлического микровыступа, кН;
S, S+ΔS - натяжения концов участка ленты, кН
SH, SC - натяжение набегающей и сбегающей ветви тормозной ленты, кН;
р - импульсная удельная нагрузка, МПа;
Миз, Mиз+dMиз - изгибающие моменты в сечениях накладки и их приращение, кНм;
МТ - тормозной момент, кНм;
С - жесткость фрикционного стыка;
Пn - податливости микровыступов, мкм;
Д - деформация полимерного микровыступа, мкм;
εД - относительная деформация участков тормозной ленты;
σ1max, σк, σ1, σ2 - максимальные сжимающие напряжения и напряжения в ободе шкива от действия: удельных нагрузок в парах трения; температурных градиентов рабочей поверхности; объемной температуры: крепежного выступа (ϑв) и обода шкива (ϑоб) при условии (ϑоб>ϑв), МПа;
σ0, σ' - напряжения: сопротивления трещинообразованию; максимальное тепловое, МПа;
σа, σmax - амплитуда и максимальные напряжения цикла, МПа;
τкн - касательные напряжения, МПа
σ-1 - предел выносливости материала при симметрическом цикле нагружения, МПа;
σB - предел прочности при сжатии пластически деформируемого материала, МПа;
Е - модуль упругости (Юнга), МПа;
НВ - твердость по Бринеллю контактных материалов, МПа.
Термодинамические параметры
Q - количество теплоты, аккумулируемое на поверхностях металлополимерных пар трения тормоза, кДж;
П1 - теплота Пельтье;
q - тепловой поток на контактной поверхности с учетом электрической и фрикционной составляющей, Вт/м2;
Wx, WY - тепловые сопротивления частей потоков, отнесенные к осям координат X и Y
bш.эф - эффективная глубина проникновения теплоты в тело обода шкива, м;
ϑ1, ϑ'1 и ϑ2 - температуры обода шкива: рабочей и внутренней поверхности, приповерхностного слоя, °С;
ϑП, ΔϑП1, ϑν1 и ϑвсп - температуры: поверхностная и ее приращение, объемная и вспышки, °С;
ϑв, ϑоб, ϑф - объемная температура: крепежного выступа; обода шкива, °С; объемная температура фланца барабана, °С;
Δϑ, Δϑυ - разность температур: поверхностных на исследуемом участке; объемных между ободом шкива и его крепежным выступом, °С;
ϑf, ϑк, ϑn, ϑν, ϑд - температуры: пар трения, контактная, поверхностная на микроучастках взаимодействия; объемная ниже зоны деформации; допустимая для материалов полимерной накладки, °С;
ϑmax - максимальная температура на пятне контакта микровыступов, °С.
θ, ϑ и ϑ0 - температуры: разности на пятне контакта; металлической поверхности и окружающей среды, °С;
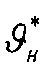 ,
, 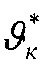 - температуры поверхностей трения: номинальной; контурного участка, °С;
- температуры поверхностей трения: номинальной; контурного участка, °С;
ϑН - температура нагревания поверхности металлического элемента трения, °К;
ϕк - начальный фазовый угол колебаний температуры, град; ϕ'=90-ϕк;
Ак - амплитуда температурных колебаний, °С;
dϑ/dn - градиент температуры, °С/мм
ΔQ/Δτ и Δϑ/Δτ - темпы изменения количества теплоты (Дж/с) и температуры (°С/с);
WТД - уровень тепловых деформаций и напряжений;
с - теплоемкость, Дж/(кг°С);
R'К, R'c, R'м - термическое сопротивление: контакта; межконтактной среды; фактического контакта, °С/Вт;
R1, R2 - термическое сопротивление: слоев обода шкива; слоев циркулирующей среды или находящейся в жидком состоянии между микровыступами пятен контактов, °С/Вт;
μxn - химический потенциал частиц, Дж/кг.
Электрические параметры
I - генерируемый ток на микровыступах пар трения, мА;
Io и IPr, Icn, IPa - токи: реактивные, обусловленные быстрым и замедленными видами поляризации; сквозной проводимости; медленный, обусловленный замедленными видами поляризации, мА;
IT, ICK, IД - суммарные токи: термический; возникающие за счет трения скольжения и контактного взаимодействия; обусловленные сорбционно-десорбционными процессами в приповерхностных слоях накладки при температуре выше допустимой для ее материалов, мА;
ITC, IM - составляющие суммарного тока: возникающие за счет трения скольжения; образованные движением заряженных частиц массопереноса, мА;
IP, Ia, Ir - токи: импульсный (разрядный), активный, реактивный, мА;
j - плотность электрического тока, мА/мм2;
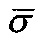 - плотность заряда поверхностного слоя, Кл/мм2;
- плотность заряда поверхностного слоя, Кл/мм2;
qn - общий пространственный заряд, Кл/мм3;
u - общее напряжение стягивания, мВ;
ϕэ - потенциал электрического поля, мВ;
dϕ/dn - градиенты электрического потенциала, мВ/мм;
РП - поляризованность поверхностей фрикционного взаимодействия, (Кл⋅м)/м3;
R' - электрическое сопротивление контактов микровыступов, Ом;
ρ, ρ' - удельное сопротивление: контактных материалов; пленок на контакте, (Ом⋅мм2)/м;
σэn - электрическая проводимость среды, Ом-1;
ε - диэлектрическая проницаемость жидкости, Ф/м;
ξ - напряженность электрического поля, В/м;
М∂ - электрический дипольный момент, Кл⋅м;
Ср - емкость электрического тока, Ф.
Критерии подобия
Но - критерий гомохронности;
Ре - критерий Пекле;
Bi - критерий Био;
FO - критерий Фурье;
Nu - критерий Нуссельта;
VO - критерий Вольченко.
Математические параметры
G(x) - распределение инжектированных электронов в полимерной пленке;
N(τ) - переменная во времени и величине импульсной нормальной силы, действующая за время τ;
w(к) - импульсная характеристика дискретной динамической системы;
z-к - элемент памяти дискретного фильтра, осуществляющий задержку дискретной последовательности тактов (z-к=е-рТ);
u(к) - отсчеты входного сигнала;
U(z)-z - преобразование входного сигнала;
Y(z) и - преобразование выходного и входного сигналов;
U(z) - z
W(к) - импульсная характеристика системы от k-го отсчета входного сигнала;
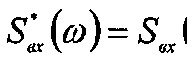 - комплексное сопряжение спектральной плотности входного сигнала;
- комплексное сопряжение спектральной плотности входного сигнала;
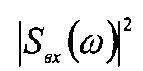 - энергетический спектр входного сигнала, автоспектр;
- энергетический спектр входного сигнала, автоспектр;
W(ω) - комплексный коэффициент передачи системы;
u(τр) - входной сигнал, поступающий на узел трения (изменение импульсной нормальной нагрузки), Н;
у(τр) - выходной сигнал, полученный в результате трения (импульсная тангенциальная сила трения), Н;
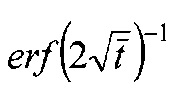 - основная функция ошибки.
- основная функция ошибки.
Коэффициенты
Квз - коэффициента взаимного перекрытия внешних и внутренних поверхностей;
f - динамический коэффициент трения;
αТП1 - коэффициент распределения тепловых потоков;
λуч, λ, λЗ, λС - коэффициент теплопроводности: участка поверхности, материалов пар трения, воздушного зазора между контактами, слоев скоростных токов омывающей среды, Вт/(м⋅°С);
а, аС - коэффициент температуропроводности: материалов пар трения, слоев смеси среды, м2/с;
α - коэффициент линейного расширения;
αm - термоэлектрический коэффициент.
μ - коэффициент Пуассона;
KC - коэффициент сопротивления тепловому удару;
αT - коэффициент теплоотдачи, Bт/(м2⋅°C);
l/k - коэффициент экранирования Дебая;
χ - коэффициент электропроводности контактирующих материалов;
σt, γ - коэффициенты: Томпсона, пропорциональности;
kδ - эффективный коэффициент концентрации напряжений;
Ψσ - коэффициент, зависящий от материала тормозной ленты;
εp и βЛ - коэффициенты, учитывающие размеры поперечного сечения ленты и класс чистоты ее рабочей поверхности.
mЗ - коэффициент заполнения профиля неровностей материалами при различных видах механической обработки;
СЛ - коэффициент излучения (постоянная Стефана-Больцмана), Вт/(м2⋅К4);
aj, bi - вещественные коэффициенты.
Разные
к - номер отсчета;
е1 - безразмерное число, изменяющееся от 0 до 1,0;
mП - количество пазов в поперечном сечении тормозной ленты;
z1 - минимальное количество микровыступов;
εmax=z/Hmax - относительный уровень микровыступов;
τ, τ1 и τ'1 - время: торможения; достижения температур ϑ1 и ϑ'1, с;
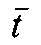 - относительное время торможения;
- относительное время торможения; 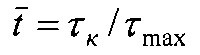 - отношение времени цикла к максимально возможной его величине;
- отношение времени цикла к максимально возможной его величине;
τ1, τ2, τ3…τn - отрезки времени, определяющие положения центров тяжести площадей импульсов до прямой, относительно которой находится алгебраическая сумма статических моментов, с;
τк - время, отсчитываемое от некоторого заданного начального момента, с;
zк - период колебаний, с;
τр - регистрируемое время, с;
τс - временной сдвиг выходного сигнала относительно входного, с;
Aν - амплитуда радиальной виброскорости ветвей тормозной ленты, мм/с;
V0 - начальная скорость движения микровыступа обода шкива, м/с;
VCK, V - скорость: скольжения; токов омывающей смеси, м/с;
ωр - регистрируемая частота сигналов (0…0,5 fЛ), Гц;
tД - частота дискретизации аналого-цифрового преобразователя.
Источники информации
1. Патент РФ №2507423 С2, кл. F16D 49/08 Способ определения эксплуатационных параметров при квазилинейной закономерности их изменения в ленточно-колодочных тормозах буровых лебедок. - 20.02.2014. Бюл. №5. - 39 с. (аналог).
2. Чичинадзе А.В. Практическая реализация тепловой динамики и моделирования трения и износа при сухом и граничном трении / А.В. Чичинадзе // Практическая трибология, мировой опыт. Том 1. - М.: Центр: наука и техника. - 1994. - С. 67-72 (прототип).
3. Фрикционное взаимодействие в электрических и тепловых полях металлополимерных пар трения / А.Х. Джанахмедов, А.И. Вольченко, Э.С. Пирвердиев [и др.] // Вестник Азербайджанской инженерной академии. - Баку. - 2014. - №6(2). - С. 30-54.
4. Темпы нагревания металлополимерных пар трения при импульсном и длительном подводе теплоты в ленточно-колодочном тормозе / А.Х. Джанахмедов, А.И. Вольченко, Д.А. Вольченко, Н.А. Вольченко, Н.М. Стебелецкая // Научно-техн. журнал / - Киев: НАУ. - №2(61). - 2013. - С. 20-30.
5. Патент 2459986 С2 РФ F16D 65/82, F16D 51/10. Способ определения составляющих электрических токов в парах трения «полимер-металл» барабанно-колодочного тормоза при их нагревании в стендовых условиях (варианты). / Вольченко А.И., Вольченко Н.А., Вольченко Д.А., Бачук И.В., Горбей А.Н., Поляков П. А.; заявитель и патентообладатель Ивано-Франковск, национал, техн. ун-т нефти и газа. - №2010107170/11; заявл. 26.02.2010; опубл. 27.08.2012, Бюл.№25. - 14 с.
6. Патент 2462628 С2 РФ F16D 65/82, F16D 51/10. Способ определения направлений составляющих электрических токов в парах трения «полимер-металл» барабанно-колодочного тормоза при их нагревании в стендовых условиях / Вольченко А.И., Вольченко Н.А., Вольченко Д.А., Бачук И.В., Горбей А.Н., Поляков П. А.; заявитель и патентообладатель Ивано-Франковск, национал, техн. ун-т нефти и газа. - №2010115528/11; заявл. 19.04.2010; опубл. 27.10.2011, Бюл. №30. - 27 с.
7. Патент 2502900 С2 РФ F16D 49/08. Способ электродинамического исследования закономерностей изменения эксплуатационных параметров металлополимерных пар трения ленточно-колодочных тормозов буровой лебедки. / Вольченко А.И., Вольченко Н.А., Вольченко Д.А., Поляков П.А., Возный А.В.; заявитель и патентообладатель Ивано-Франковск, национал, техн. ун-т нефти и газа. - №20125664/11; заявл. 20.02.2012; опубл. 27.12.2013, Бюл. №36. - 11 с.
8. Тимошенко С.П. Механика материалов / С.П. Тимошенко, Дж. Гере. - М.: Мир, 1976. - 669 с.
9. Трение, износ и смазка (трибология и триботехника) / Под общ. редакцией А.В. Чичинадзе. - М.: Машиностроение, 2003. - 575 с.
10. Вольченко Н.А. Динамика многопарных фрикционных узлов / Н.А. Вольченко. - Ростов-на-Дону: Северо-Кавказский науч. центр, высш. школы, 2005. - 238 с.
11. Браун Э.Д. Модели трения и изнашивания в машинах / Э.Д. Браун, Ю.А. Евдокимов, А.В. Чичинадзе. - М.: Машиностоение, 1982, - 191 с.
12. Ленточно-колодочные тормозные устройства. Монография (научное издание) в 2 т. Т. 2 / [Н.А. Вольченко, Д.А. Вольченко, С.И. Крыштопа, Д.Ю. Журавлев, А.В. Возный]. - Кубанск. государств, технолог, ун-т. - Краснодар - Ивано-Франковск, 2013. - 441 с.
13. Шлыков Ю.П. Контактное термическое сопротивление / Ю.П. Шлыков, Е.А. Ганин, СИ. Царевский. - М.: Энергия, 1977. - 328 с.
14. Трибология (электротермомеханические основы, анализ и синтез на нано-, микро- и миллиуровнях и технические приложения): учеб. пособие. [А.И. Вольченко, М.В. Киндрачук, Д.А. Вольченко и др.]. - Киев - Краснодар, 2015. - 371 с.
15. Бердинских В.А. Статическое моделирование процессов фрикционно-контактного взаимодействия при внешнем трении / В.А. Бердинских, В.В. Запорожец // Надежность и долговечность машин и сооружений, - М, 1984, №5. С. 80-84.
16. Гухман А.А. Введение в теорию подобия / А.А. Гухман. - М.: Высшая школа, 1963, 254 с.
17. Седов Л.И. Методы подобия и размерностей в механике / Л.И. Седов. - М.: Наука, 1967, 438 с.
18. Шаповалов В.В. Комплексное моделирование динамических нагруженных узлов трения машин / В.В. Шаповалов // Трение и износ. - М., 1985. №3. С. 451-457.
19. Бакли Д. Поверхностные явления при адгезии и фрикционном взаимодействии / Д. Бакли: Пер. с англ. / Под ред. А. И. Свериденка. М.: Мир, 1986, 294 с.
20. Джанахмедов А.Х. Синергетика и фракталы в трибологии / А.Х. Джанахмедов, О.А. Дышин, М.Я. Джавадов // Баку: Апостроф: 2014. - 504 с.
21. Компьютерное моделирование энергонагруженности металлополимерных пар трения ленточно-колодочного тормоза буровых лебедок (часть первая) / Д.Ю. Журавлев, С.И. Крыштопа, И.О. Бекиш и др. // Научно-техн. журнал. - Киев: НАУ. - №4(65). - 2014. - С. 47-59.
22. Патент 2343450 С2 РФ, МПК G01N 3/56. Способ испытаний узлов трения / Шаповалов В.В., Челохьян А.В., Лубягов A.M. и др.; заявитель и патентообладатель Шаповалов Владимир Владимирович. - №2006121024/28; заявл. 13.06.06; опубл. 10.01.09, Бюл. №1. - 31 с.
23. Чичинадзе А.В. Износостойкость фрикционных полимерных материалов / Чичинадзе А.В., Белоусов В.Я., Богатчук И.М. / Львов. - Высшая школа, 1989. - 114 с.
24. Диплом №444 на открытие «Явление тепловой стабилизации в металлополимерных парах трения» от 18.01.2013 г. авторов А.И. Вольченко, М.В. Киндрачук, Д.А. Вольченко, Н.А. Вольченко. - М.: Международ, акад. авторов научн. открыт, и изобрет. - Экспертиза заявки на открытие № А-588 от 05.09.2012 г.
| название | год | авторы | номер документа |
|---|---|---|---|
| УСТРОЙСТВО И СПОСОБ СНИЖЕНИЯ ТЕМПЕРАТУРНЫХ ГРАДИЕНТОВ В ЛЕНТОЧНО-КОЛОДОЧНОМ ТОРМОЗЕ | 2015 |
|
RU2585364C1 |
| ЛЕНТОЧНО-КОЛОДОЧНЫЙ ТОРМОЗ С "ТЕПЛОВЫМИ МОСТИКАМИ" В ОБОДЕ ШКИВА | 2014 |
|
RU2561646C1 |
| СПОСОБ ЭЛЕКТРОДИНАМИЧЕСКОГО УСТАНОВЛЕНИЯ ЗАКОНОМЕРНОСТЕЙ ИЗМЕНЕНИЯ ЭКСПЛУАТАЦИОННЫХ ПАРАМЕТРОВ МЕТАЛЛОПОЛИМЕРНЫХ ПАР ТРЕНИЯ ЛЕНТОЧНО-КОЛОДОЧНЫХ ТОРМОЗОВ БУРОВОЙ ЛЕБЕДКИ | 2012 |
|
RU2502900C2 |
| УСТРОЙСТВО И СПОСОБ ОПРЕДЕЛЕНИЯ ТЕПЛОВОГО РЕЖИМА МЕТАЛЛОПОЛИМЕРНЫХ ПАР ТРЕНИЯ БАРАБАННО-КОЛОДОЧНОГО ТОРМОЗА ПРИ ИХ НАГРУЖЕНИИ В СТЕНДОВЫХ УСЛОВИЯХ | 2012 |
|
RU2514385C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ КОЭФФИЦИЕНТОВ РАСПРЕДЕЛЕНИЯ ТЕПЛОВЫХ ПОТОКОВ МЕЖДУ ПАРАМИ ТРЕНИЯ РАЗЛИЧНЫХ ВИДОВ ФРИКЦИОННЫХ УЗЛОВ В ЛЕНТОЧНО-КОЛОДОЧНЫХ ТОРМОЗАХ БУРОВЫХ ЛЕБЕДОК (ВАРИАНТЫ) | 2007 |
|
RU2386061C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ПЛОЩАДЕЙ ПОВЕРХНОСТЕЙ МЕТАЛЛИЧЕСКИХ ДИСКОВ ПРИ РАЗЛИЧНОЙ ИХ ЭНЕРГОЕМКОСТИ В ДИСКОВО-КОЛОДОЧНЫХ ТОРМОЗНЫХ УСТРОЙСТВАХ | 2015 |
|
RU2594044C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ГЕОМЕТРИЧЕСКИХ ПАРАМЕТРОВ ТОРМОЗНЫХ ШКИВОВ ЛЕНТОЧНО-КОЛОДОЧНЫХ ТОРМОЗОВ БУРОВЫХ ЛЕБЕДОК (ВАРИАНТЫ) | 2012 |
|
RU2534158C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ПЛОЩАДЕЙ ПОВЕРХНОСТЕЙ МЕТАЛЛИЧЕСКИХ ФРИКЦИОННЫХ ЭЛЕМЕНТОВ ПРИ РАЗЛИЧНОЙ ИХ ЭНЕРГОЕМКОСТИ В ТОРМОЗНЫХ УСТРОЙСТВАХ | 2011 |
|
RU2561415C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ НАПРАВЛЕНИЙ СОСТАВЛЯЮЩИХ ЭЛЕКТРИЧЕСКИХ ТОКОВ В ПАРАХ ТРЕНИЯ "ПОЛИМЕР-МЕТАЛЛ" БАРАБАННО-КОЛОДОЧНОГО ТОРМОЗА ПРИ ИХ НАГРЕВАНИИ В СТЕНДОВЫХ УСЛОВИЯХ (ВАРИАНТЫ) | 2010 |
|
RU2459986C2 |
| Способ определения градиентов коэффициентов теплопередачи при оценке интенсивности теплообмена принудительного воздушно-жидкостного охлаждения трибосистемы ленточно-колодочного тормоза | 2017 |
|
RU2677428C1 |
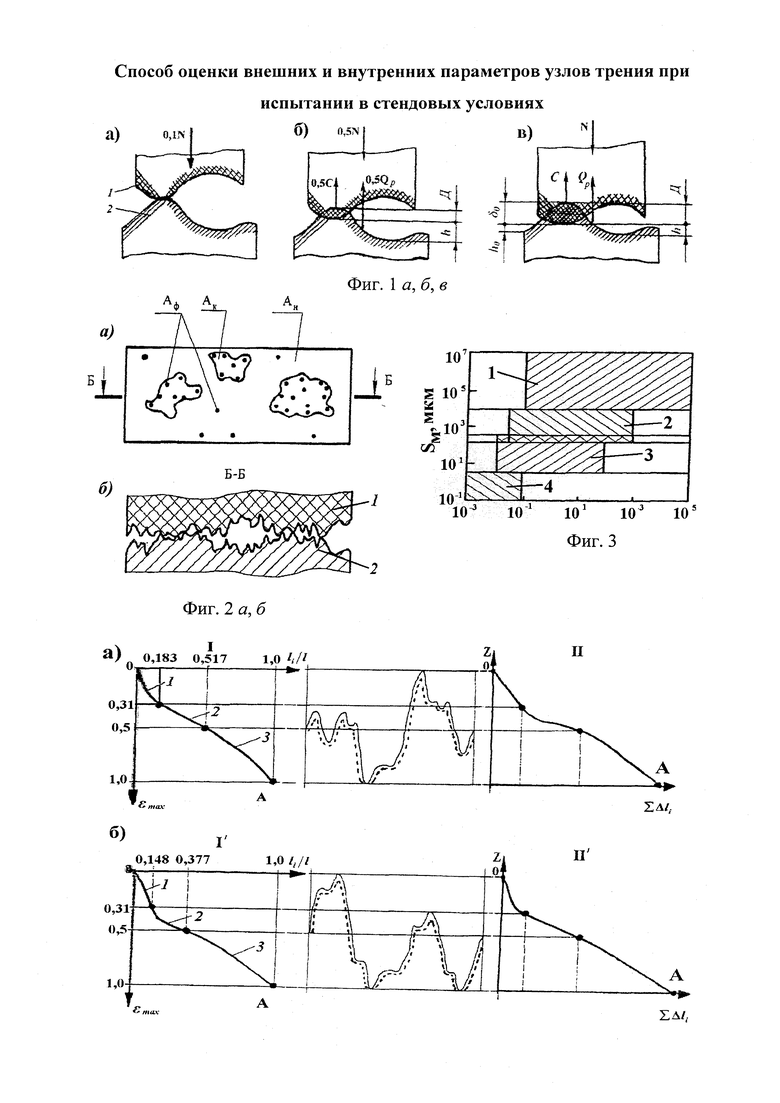
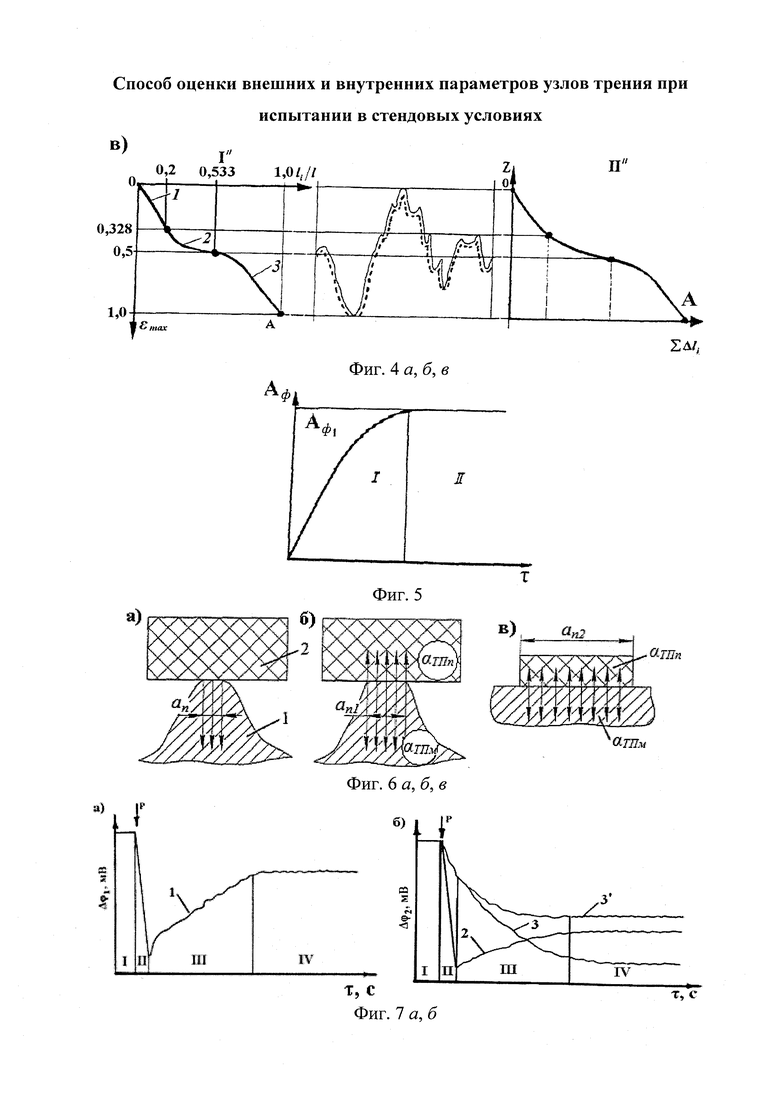
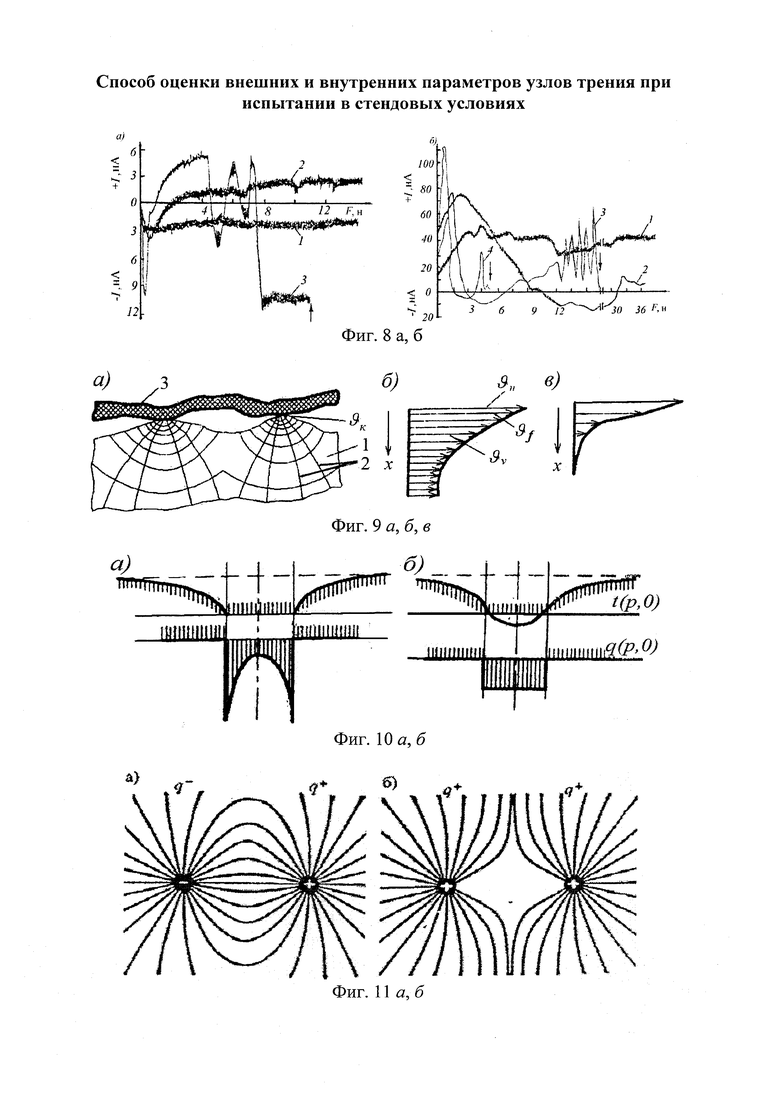
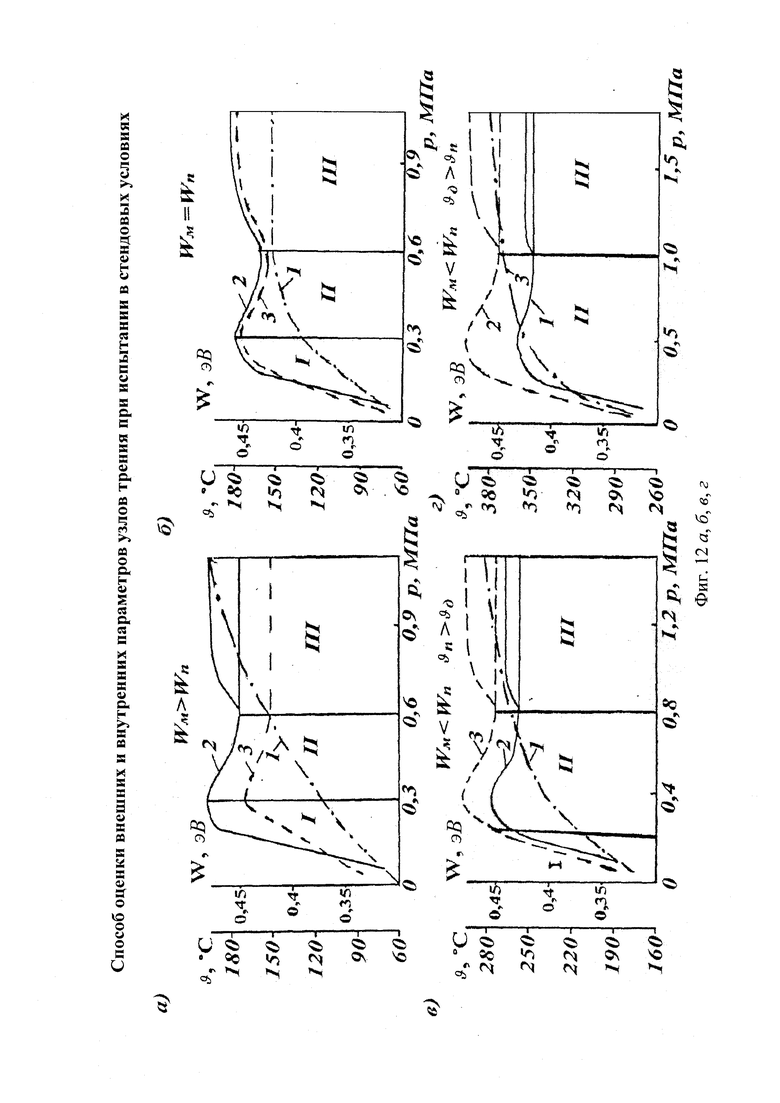
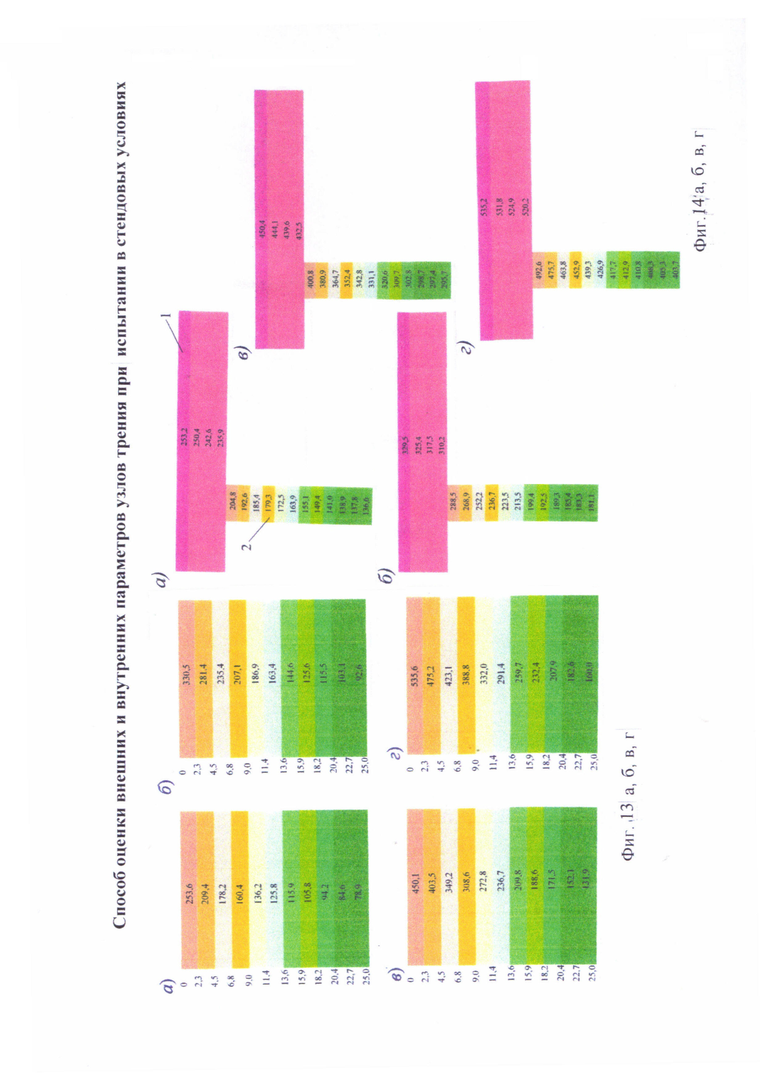
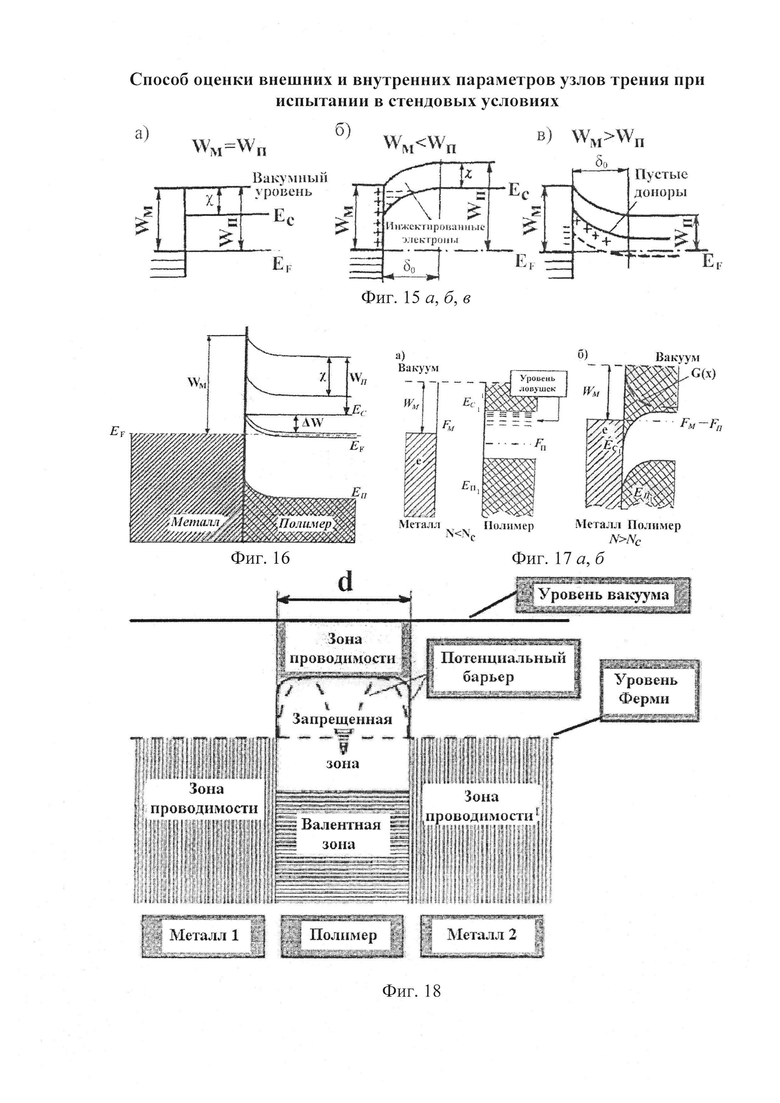
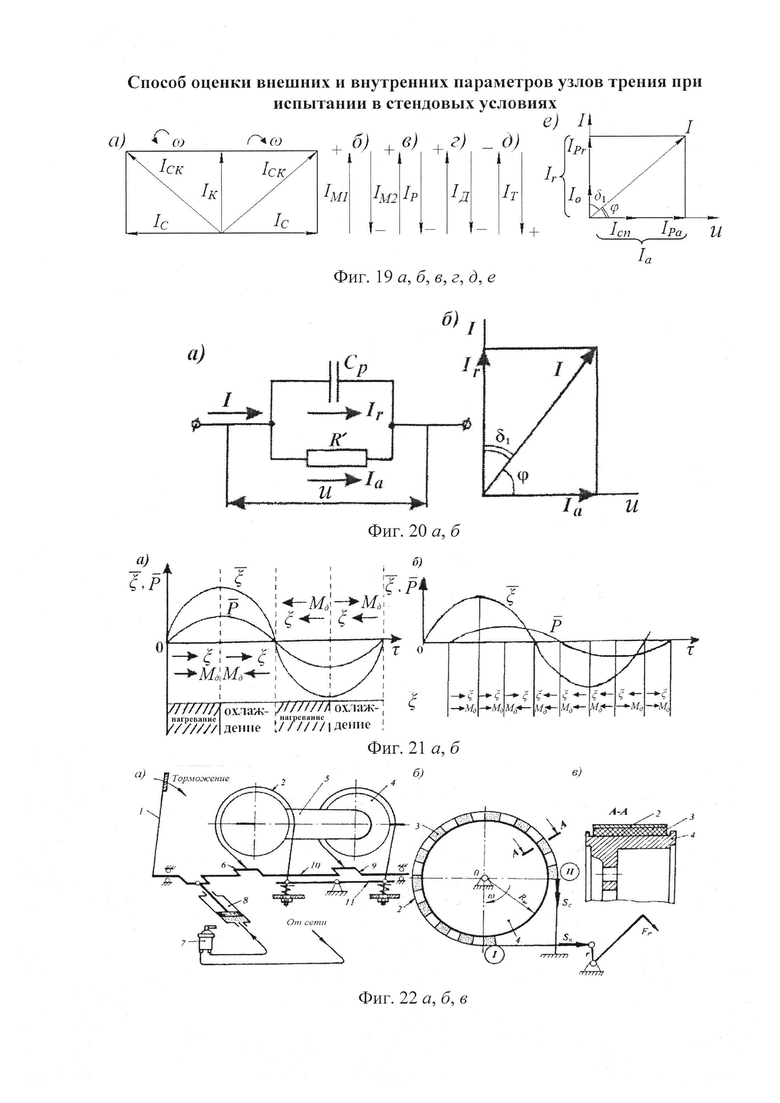

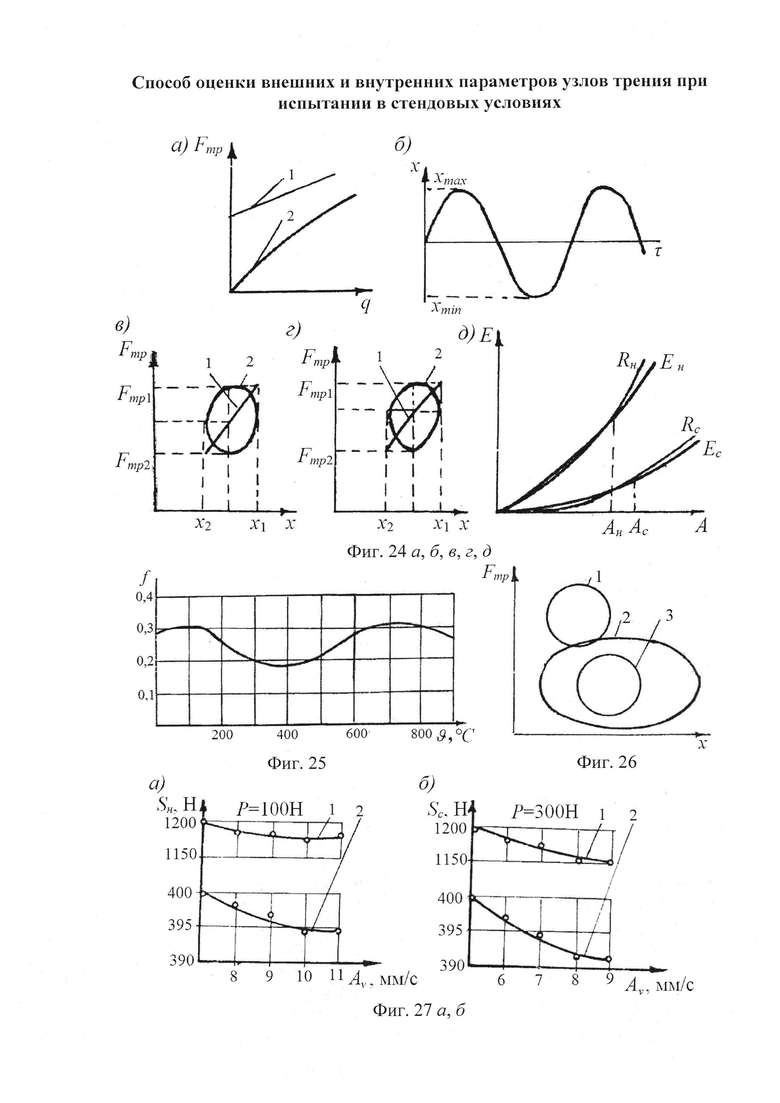
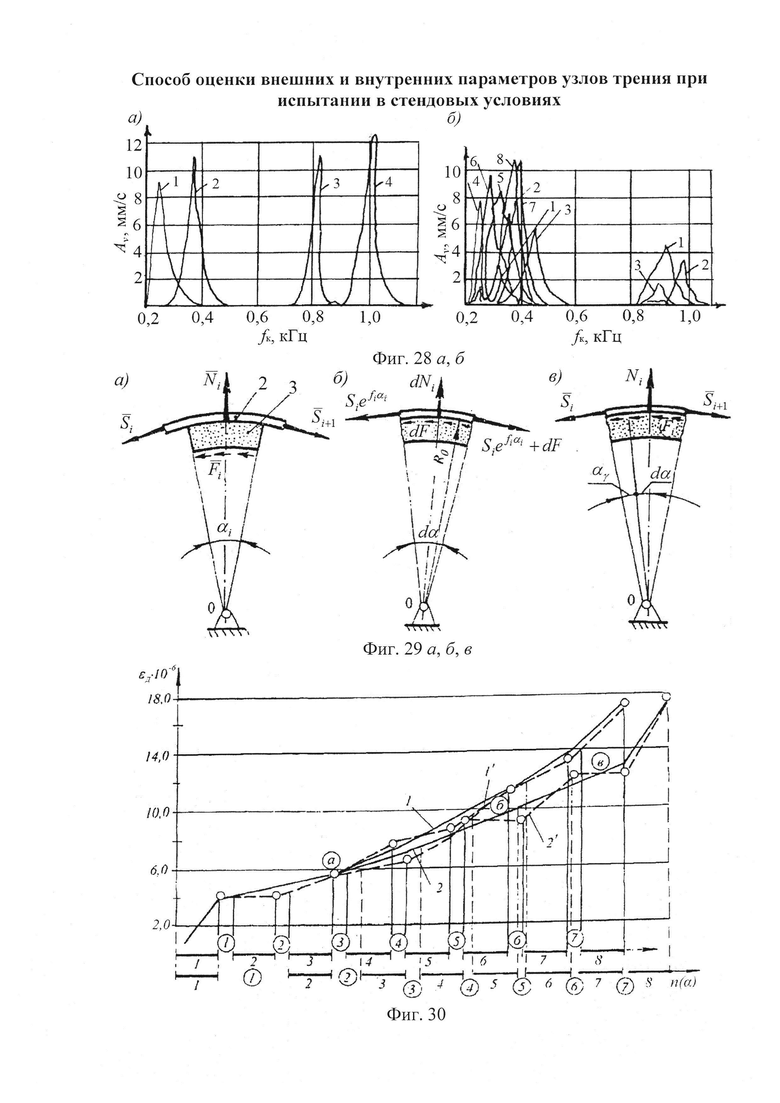
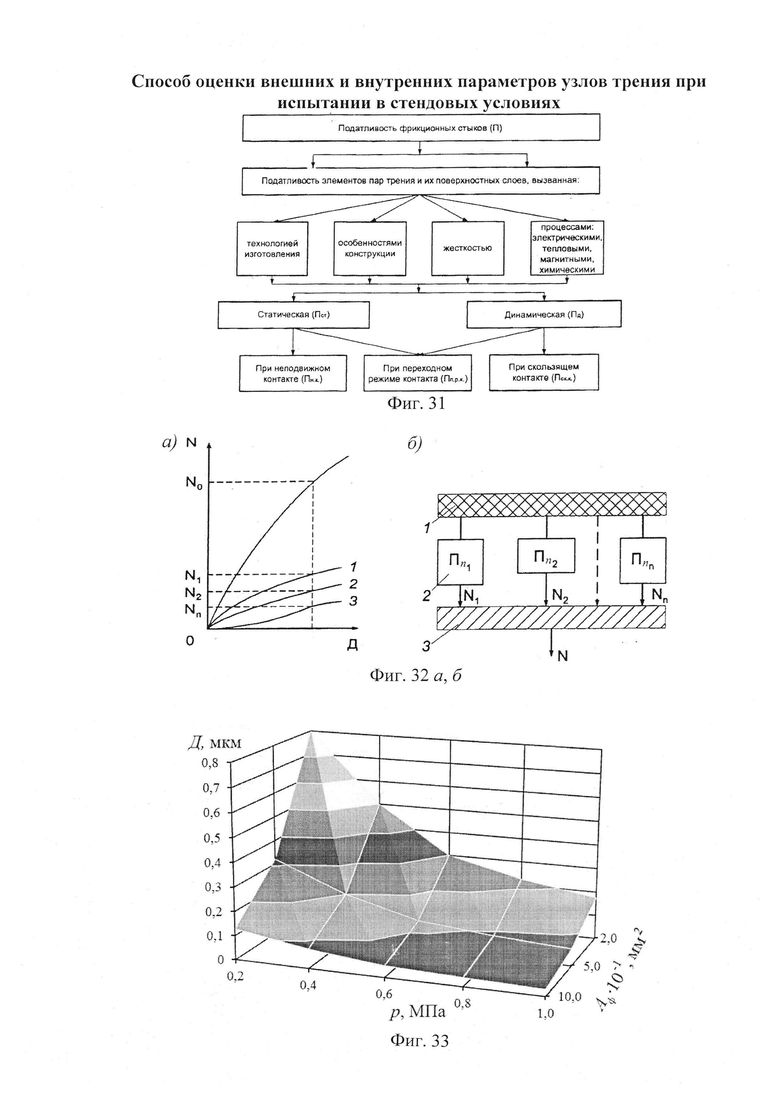
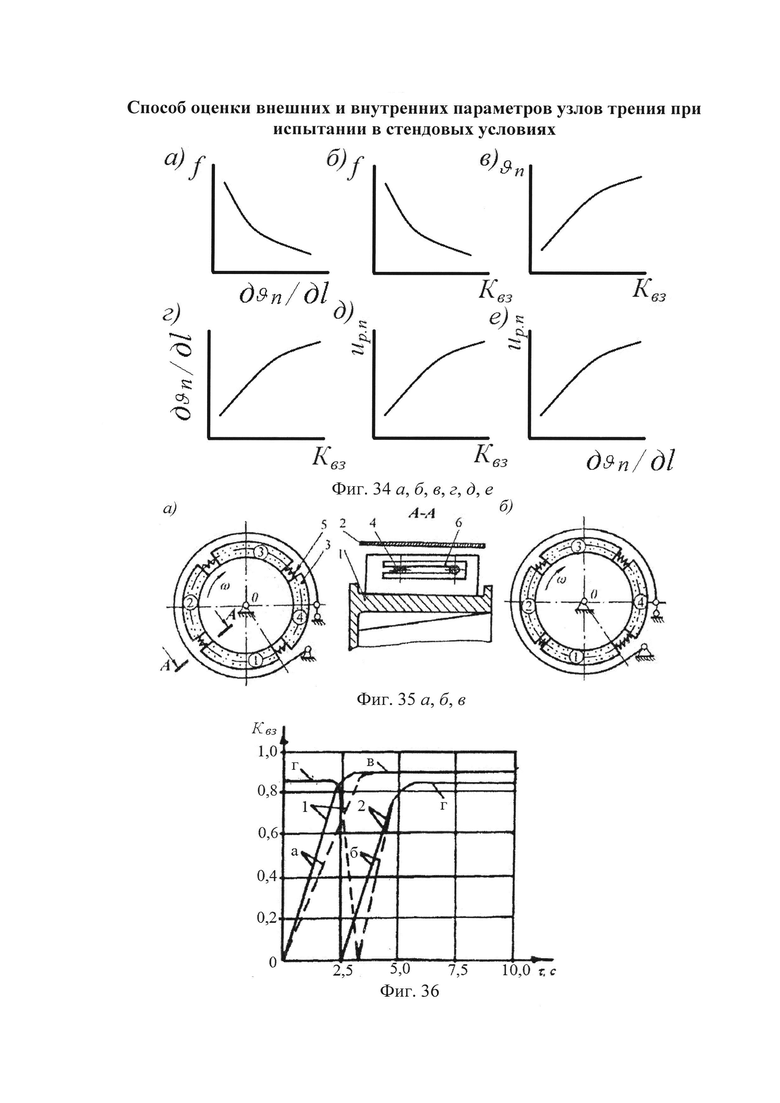
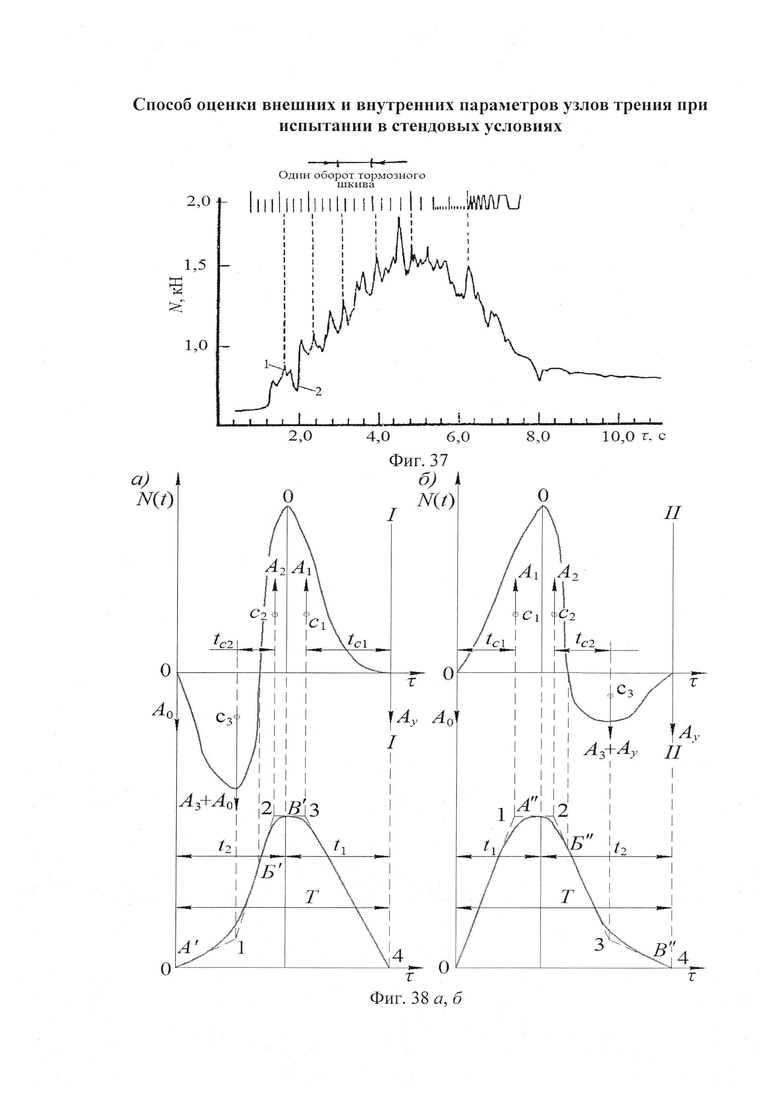
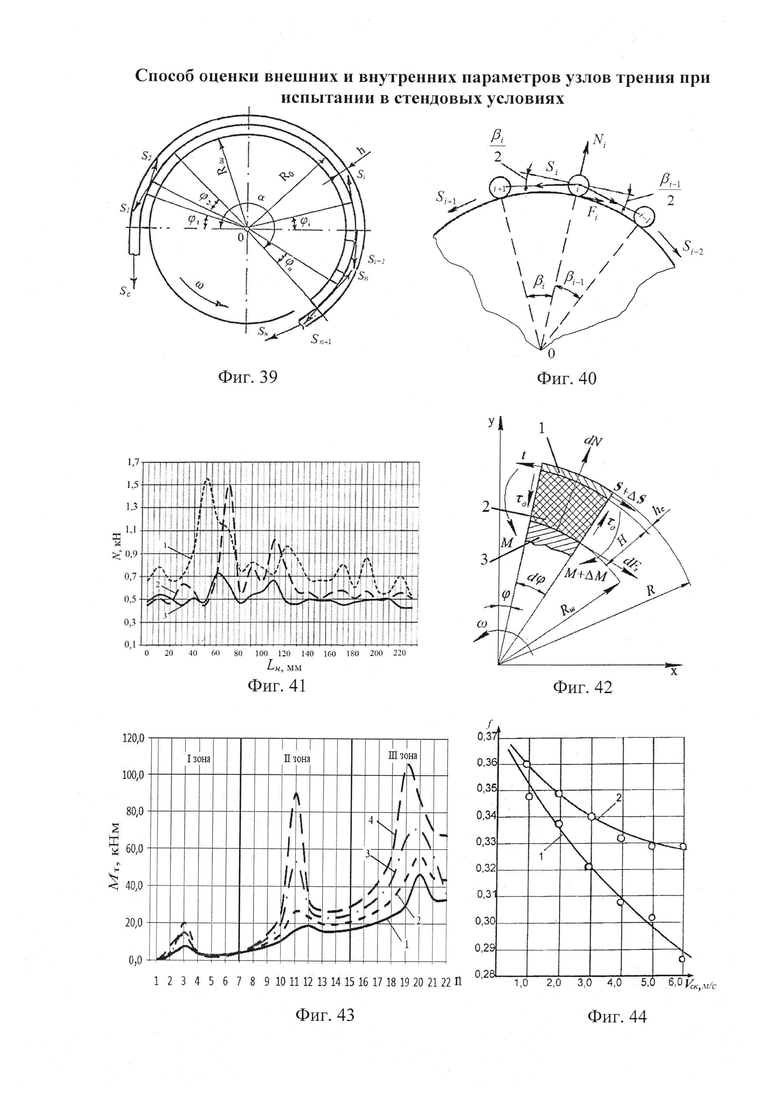
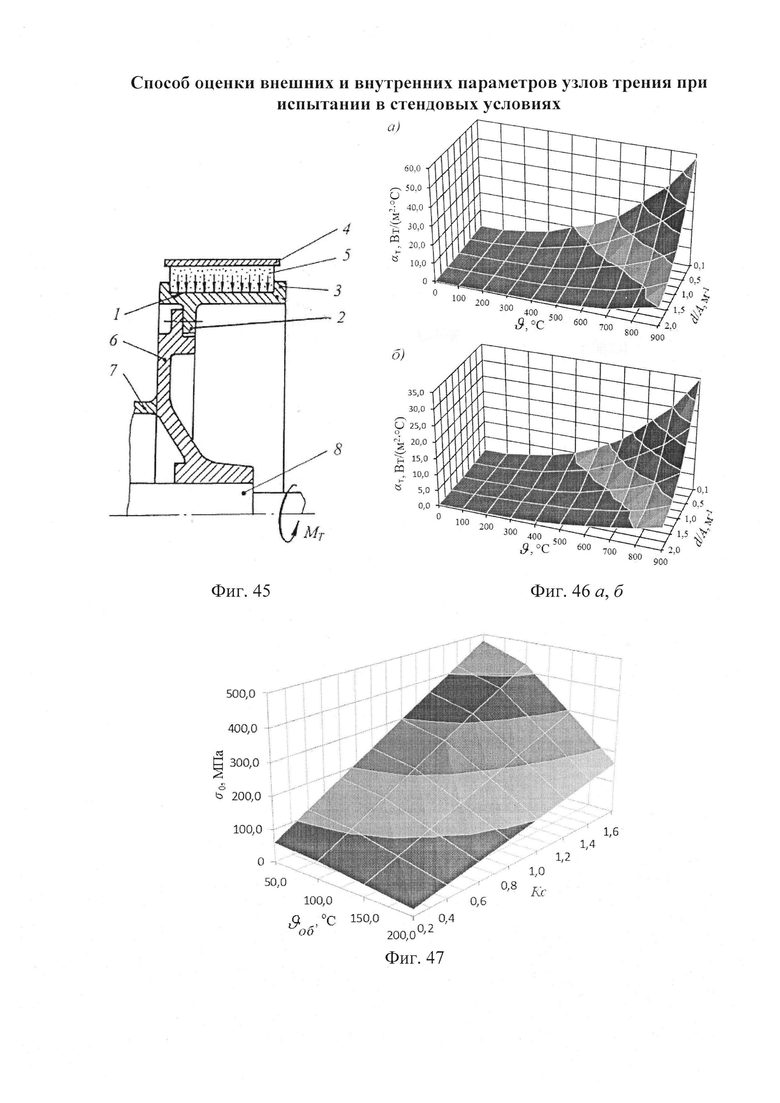
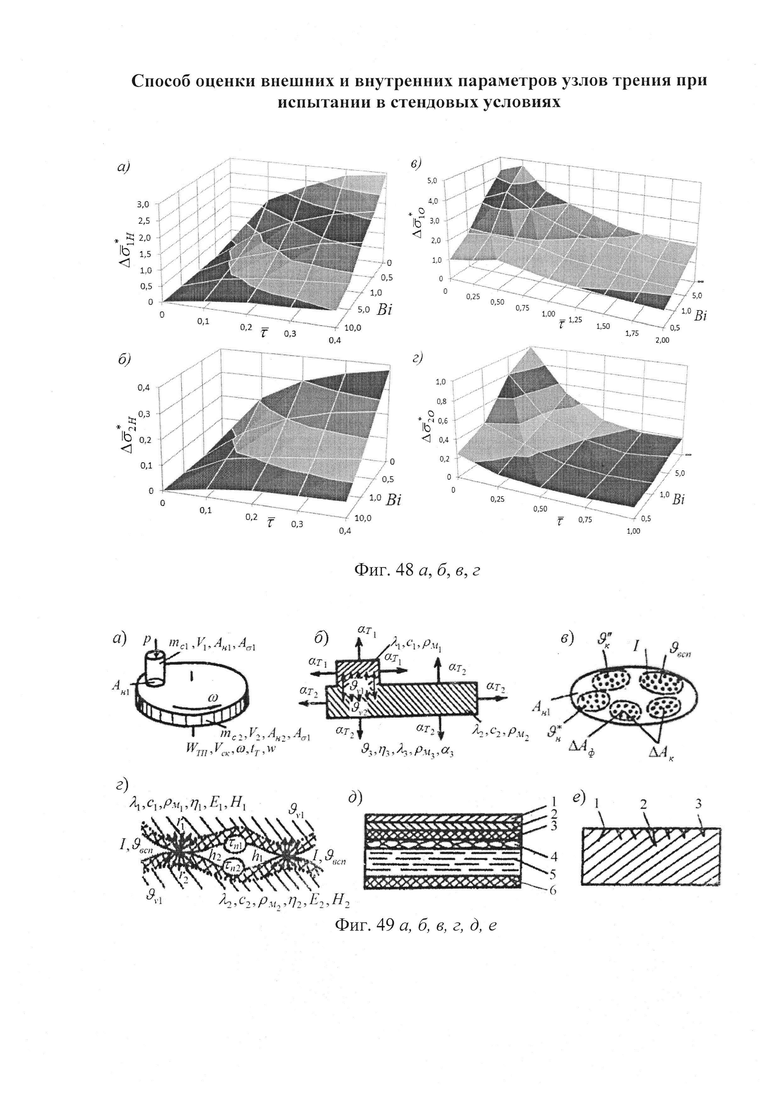
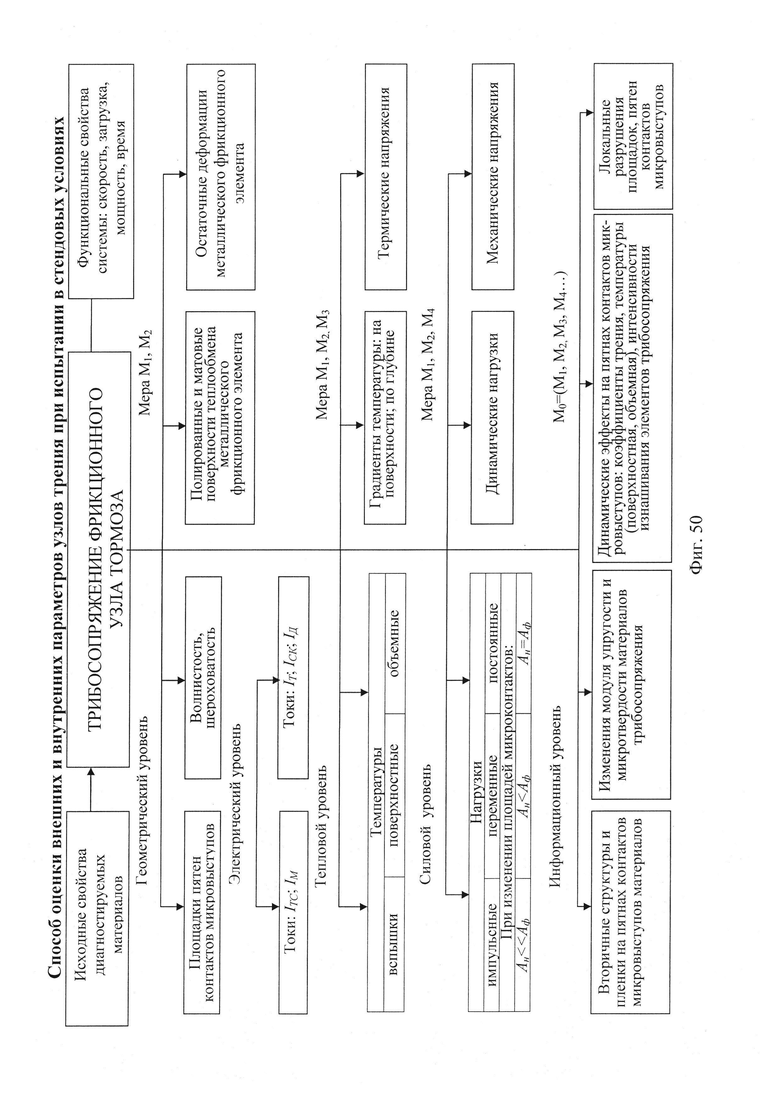
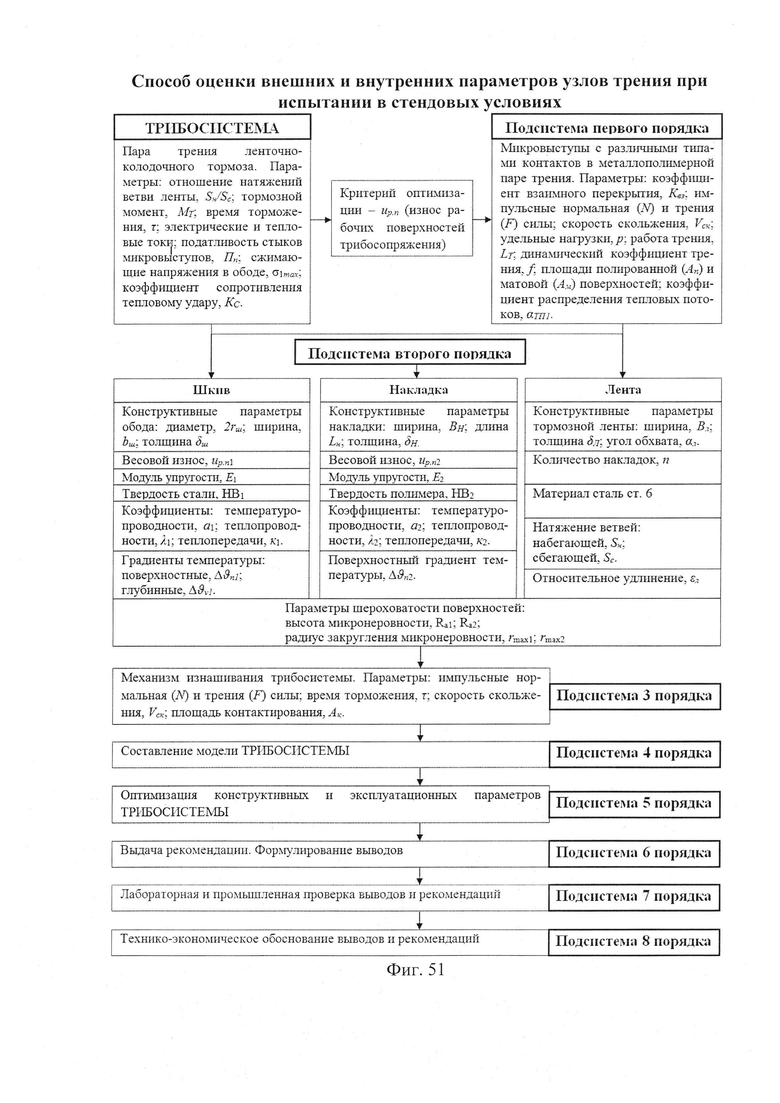
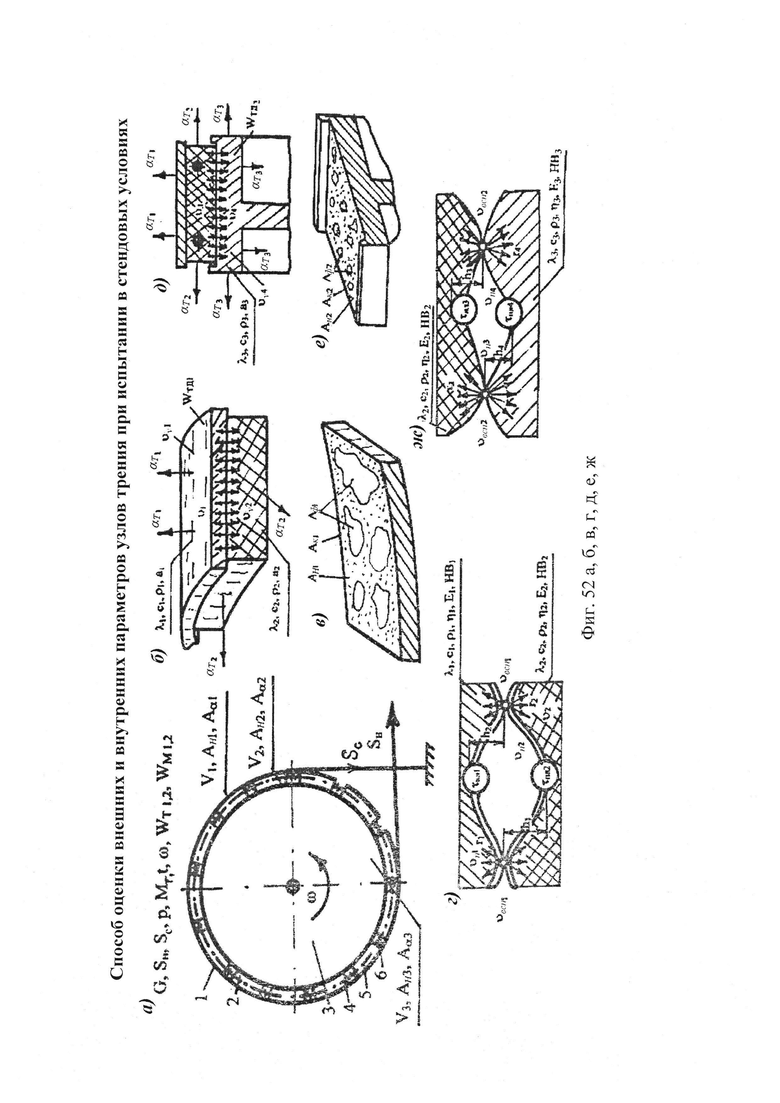
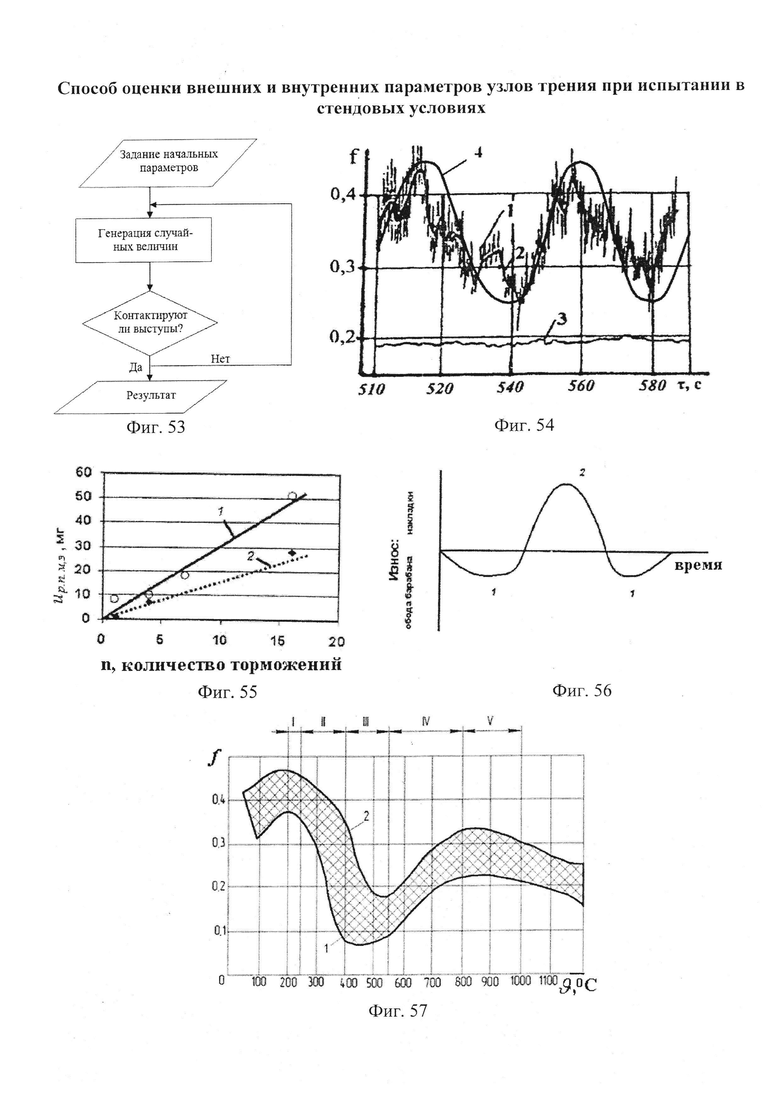
Изобретение относится к способам оценки внешних и внутренних параметров узлов трения тормозных устройств в стендовых условиях, в частности пар трения ленточно-колодочных тормозов буровых лебедок. Предложен способ оценки внешних и внутренних параметров узлов трения при испытании в стендовых условиях, при которой механические системы объектной и модельной структуры, состоящие из подсистем, при их контактно-импульсном электротермомеханическом фрикционном взаимодействии подсистем, находящемся во взаимодействии с конструктивными особенностями, линейным или полиноминальным законами изменения тахограмм металлического фрикционного элемента пары трения, а также со скоростной, силовой, электрической, тепловой и химическими характеристиками узла трения, составляющими его единое поле энергетического взаимодействия при условии, что между внешними и внутренними параметрами «объекта» и «модели» обеспечивают необходимые соотношения. Достигается повышение достоверности результатов определения эксплуатационных параметров пар трения. 12 табл., 57 ил.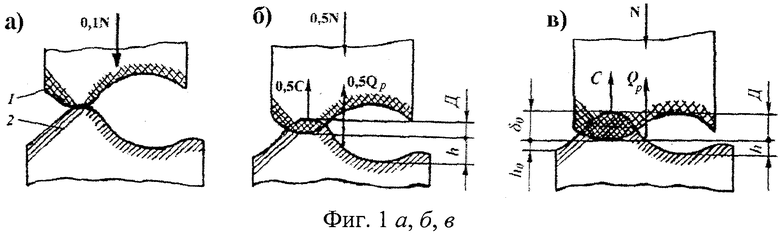
Способ оценки внешних и внутренних параметров узлов трения при испытании в стендовых условиях, при которой механические системы объектной и модельной структуры, состоящие из подсистем, при их контактно-импульсном электротермомеханическом фрикционном взаимодействии, находящемся во взаимодействии с конструктивными особенностями, линейным или полиноминальным законами изменения тахограмм металлического фрикционного элемента пары трения, а также со скоростной, силовой, электрической, тепловой и химическими характеристиками узла трения, составляющими его единое поле энергетического взаимодействия при условии, что между внешними и внутренними параметрами «объекта» и «модели» обеспечивают следующие соотношения:
- отношения масс объекта (М) и модели (m) равно М/m=См=C2L;
- отношение линейных размеров объекта (L) и модели 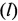 равно геометрическому масштабному подобию
равно геометрическому масштабному подобию 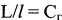 ;
;
- отношение полированных площадей объекта (Sп) и модели (sп) равно Sп/sп=CSп=С2Lп;
- отношение матовых площадей объекта (Sм) и модели (sм) равно Sм/sм=CSм=С2Lм,
- отношение физико-механических параметров материалов: коэффициентов теплопроводности и температуропроводности, температур и их градиентов, коэффициентов теплоотдачи; твердости, модуля упругости, предела прочности, сопротивления срезу объекта (Ф) и модели (ф) равно Ф/ф=Сф=1,0;
- отношение внешних сил, действующих на элементы пары трения, объекта (F) и модели (f) равно F/f=CF=C2L;
- отношение времени протекания исследуемых процессов, явлений и эффектов в объекте (ζ) и модели (τ) равно ζ/τ=Сτ=1,0, которые соблюдают при следующих допустимых внешних параметрах:
- отношение натяжений набегающей ветви (SH) и натяжение сбегающей ветви (SC) тормозной ленты составляет SH/SC≤[n];
- удельные нагрузки (р) не превышают допустимой величины для материалов фрикционной накладки;
- изменение динамического коэффициента трения (f) колеблется от 0,2 до 0,5;
- поверхностные температуры фрикционной накладки не превышают допустимой для ее материалов;
- обод шкива не попадает в зону термостабилизационного состояния,
отличающийся тем, что закономерности изменения линий токов силового, электрического, теплового и химического полей характеризуются внутренними и внешними параметрами, во взаимодействии с линиями токов скоростного поля омывающих сред подчиняются волновой природе со сдвигом по фазе и описываются отвечающими ей симплексами при соблюдении следующих отношений:
- отношение высоты микровыступов фрикционных поверхностей объекта (Н) и модели (h) равно H/h=CH=1,0;
- отношение длины микровыступов фрикционных поверхностей объекта (Lм) и модели 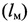 равно
равно 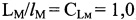 ;
;
- отношение площадей пятен контактов микровыступов фрикционных поверхностей объекта (Ао) и модели (Ам) равно Ао/Ам=САо=1,0;
- отношение импульсных нормальных усилий объекта (N) и модели (n) равно N/n=CN=1,0;
- отношение линейных скоростей скольжения объекта (VСК) и модели (vск) равно VСК/vск=CV=1,0;
- отношение импульсных сил трения объекта (Fт) и модели (fт) равно Fт/fт=CFт=1,0;
- отношение импульсных динамических коэффициентов трения объекта (fо) и модели (fм) равно fо/fм=Cfо=1,0;
- отношение импульсных удельных нагрузок объекта (ро) и модели (рм) равно ро/рм=СРо=1,0;
- отношение импульсных тормозных моментов объекта (Мо) и модели (Мм) равно Мо/Мм=СМо=1,0;
- отношение податливости стыков подсистемы "тормозная лента - нерабочие поверхности накладок" объекта (По1) и модели (По2) равно По1/По2=СПо1=1,0;
- отношение податливости стыков подсистемы «рабочая поверхность накладки - поверхность обода шкива» объекта (По3) и модели (По4) равно По3/По4=СПо3=1,0;
- отношение амплитуд колебаний связей механических подсистем и деформаций микронеровностей объекта (А) и модели (а) равно А/а=СА=1,0;
- отношение частот колебаний объекта (Ω) и модели (ω) равно Ω/ω=CΩ=1,0;
- отношение энергетических уровней подповерхностных слоев объекта (Э'о) и модели (Э'м) равно Э'о/Э'м=СЭ'о=1,0;
- отношение токов скоростей омывающего воздуха объекта (Vв) и модели (vв) равно Vв/vв=CVт=1,0;
- отношение токов скоростей компонентов омывающих сред объекта (Vc) и модели (vc) равно Vc/vc=СVс=1,0 и при этом соблюдают в открытой термодинамической системе трибосопряжения равенство не только поверхностных температур, но и равенство химических потенциалов при вынужденном конвективном теплообмене его подсистем:
- «наружная поверхность обода шкива - скоростные токи охлаждающего воздуха»;
- «внутренняя поверхность обода шкива - скоростные токи компонентов омывающей среды»;
- «поверхностный и подповерхностный слой полимерной накладки - скоростные токи компонентов омывающей среды», а взаимодействие подсистемы «обод тормозного шкива - крепежный выступ - фланец барабана лебедки» осуществляют кондуктивным теплообменом за счет температурных градиентов по их толщине, после чего производят измерение и определение параметров трибосопряжения с одновременным контролем и фиксацией площадей пятен контактов микровыступов в реальном масштабе времени, поскольку электротермическое сопротивление дискретных контактов с различной энергетической активностью микроконденсаторов и -термобатарей с мгновенным их переключением при изменении площадей пятен контакта микровыступов при соблюдении условий на первой стадии фрикционного взаимодействия (Аф<Ан), что фактическая площадь контактирования (Аф) мала по сравнению с номинальной (Ан), производят суммирование составляющих генерируемых токов, а при Ан=Аф фиксируют трибоЭДС в сопряжении с переменным градиентов механических свойств его материалов и при этом темп проникновения взаимодействующих между собой импульсов электрического и теплового токов влияет на интенсивность износа микровыступов при переполяризации, а величины тепловых токов на поверхностях пятен контактов микровыступов определяют с помощью гипотезы суммирования температур на поверхности с учетом генерируемых электрических токов

где ϑП - поверхностная температура от трения и контактного сопротивления, вызванная генерируемыми токами на пятнах контактов микровыступов, а также фрикционной составляющей; ΔϑП1 - прирост поверхностной температуры от температуры вспышки, вызванной разрядными токами между микровыступами; ϑвсп - температура вспышки, вызванная разрядными токами между микровыступами;
при этом в теле металлического фрикционного элемента формируется объемная температура (ϑυ1), вызванная действием первых двух составляющих, определяют из условия действия двух источников теплоты (электрического и фрикционного) в зоне трения
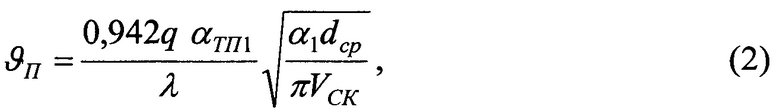
где 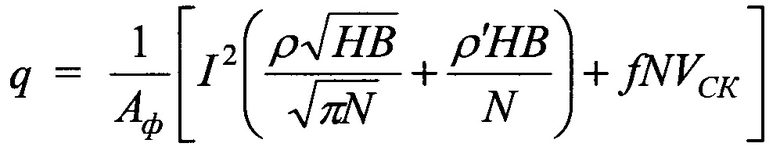 - тепловой поток на контактной поверхности с учетом электрической и фрикционной составляющей, Вт/м2; Аф - фактическая площадь касания, мм2; I - генерируемый ток в парах трения, А; ρ - удельное сопротивление контактных материалов, (Ом⋅мм2)/м; HB - твердость по Бринеллю контактных материалов, МПа; N - импульсное нормальное усилие, действующее в зоне контакта материалов, Н; ρ' - удельное сопротивление пленок на контакте, (Ом⋅мм2)/м; ƒ - динамический коэффициент трения; VСК - скорость скольжения, м/с; αТП1 - коэффициент распределения тепловых потоков; λ - приведенный коэффициент теплопроводности материалов пар трения, Вт/(м⋅°С); dcp - средний диаметр пятна контакта, определяют с учетом реальной его шероховатости, мм; температуру вспышки ϑвсп определяют по зависимости вида
- тепловой поток на контактной поверхности с учетом электрической и фрикционной составляющей, Вт/м2; Аф - фактическая площадь касания, мм2; I - генерируемый ток в парах трения, А; ρ - удельное сопротивление контактных материалов, (Ом⋅мм2)/м; HB - твердость по Бринеллю контактных материалов, МПа; N - импульсное нормальное усилие, действующее в зоне контакта материалов, Н; ρ' - удельное сопротивление пленок на контакте, (Ом⋅мм2)/м; ƒ - динамический коэффициент трения; VСК - скорость скольжения, м/с; αТП1 - коэффициент распределения тепловых потоков; λ - приведенный коэффициент теплопроводности материалов пар трения, Вт/(м⋅°С); dcp - средний диаметр пятна контакта, определяют с учетом реальной его шероховатости, мм; температуру вспышки ϑвсп определяют по зависимости вида
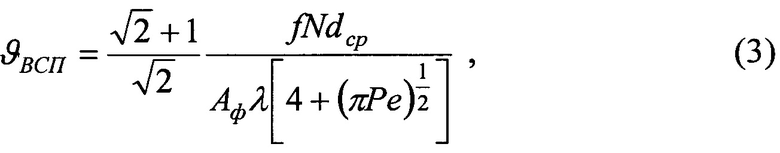
где Ре=(VСКdcp)/а - критерий Пекле; а - приведенный коэффициент температуропроводимости материалов пар трения, м/с2, а объемную температуру металлического фрикционного элемента (ϑν1) определяют из условия равенства тепловых потоков на контактной поверхности с учетом фрикционной и электрической составляющей и которая отводится от его полированной поверхности к скоростным токам омывающей среды:

в дальнейшем по приведенным выше температурам и оценивают энергетические уровни поверхностных и подповерхностных слоев элементов трибосопряжения, после чего аналитическим путем оценивают максимальные сжимающие напряжения σ1max в ободе шкива по зависимости вида

где σк, σ1, σ2 - напряжение в ободе шкива от действия: удельных нагрузок в парах трения; температурных градиентов на его рабочей поверхности; объемной температуры: крепежного выступа (ϑв) и обода шкива (ϑоб) при условии (ϑоб>ϑв),

где Квз - коэффициент взаимного перекрытия пар трения; bш, δш - ширина и толщина обода шкива,

где α - коэффициент линейного расширения; Е - модуль упругости; ϑ1, ϑ'1 - температуры рабочей и внутренней поверхности обода шкива; μ - коэффициент Пуассона,

где ϑв, ϑф - объемная температура крепежного выступа и фланца барабана; Ав, Аф - площади поперечных сечений крепежных выступов обода и фланца барабана;
но при этом для более точного определения составляющих σ1 и σ2 в зависимость вместо (ϑ1-ϑ'1) подставляют слагаемое 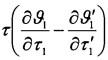 (где τ - время торможения; τ1, τ'1 - время достижения температур ϑ1 и ϑ'1), которое характеризует темп нагревания обода шкива, а в зависимость вместо
(где τ - время торможения; τ1, τ'1 - время достижения температур ϑ1 и ϑ'1), которое характеризует темп нагревания обода шкива, а в зависимость вместо 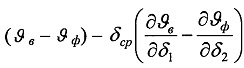 (где δ1, δ2, δср - толщины: крепежного выступа; фланца барабана; их средняя величина), которое характеризует температурные градиенты по толщине рассматриваемых элементов, а зарождение и развитие трещин на рабочей поверхности ободов тормозных шкивов оценивают коэффициентом сопротивления тепловому удару
(где δ1, δ2, δср - толщины: крепежного выступа; фланца барабана; их средняя величина), которое характеризует температурные градиенты по толщине рассматриваемых элементов, а зарождение и развитие трещин на рабочей поверхности ободов тормозных шкивов оценивают коэффициентом сопротивления тепловому удару

где σ0, σ' - напряжения: сопротивления трещинообразованию; максимальное тепловое.
| СПОСОБ ОПРЕДЕЛЕНИЯ ЗОНЫ ПЕРВОНАЧАЛЬНОГО ВЗАИМОДЕЙСТВИЯ ПАР ТРЕНИЯ ЛЕНТОЧНО-КОЛОДОЧНЫХ ТОРМОЗОВ БУРОВОЙ ЛЕБЕДКИ | 2007 |
|
RU2357131C2 |
| СПОСОБ УПРАВЛЕНИЯ УДЕЛЬНЫМИ НАГРУЗКАМИ НА ВЕТВЯХ ТОРМОЗНОЙ ЛЕНТЫ ЛЕНТОЧНО-КОЛОДОЧНОГО ТОРМОЗА БУРОВОЙ ЛЕБЕДКИ | 2007 |
|
RU2357130C2 |
| СПОСОБ НАГРЕВАНИЯ И ОХЛАЖДЕНИЯ ТОРМОЗНЫХ ШКИВОВ ЛЕНТОЧНО-КОЛОДОЧНОГО ТОРМОЗА БУРОВОЙ ЛЕБЕДКИ ПРИ ОЦЕНКЕ ИХ ТЕПЛОВОГО БАЛАНСА | 2004 |
|
RU2279579C2 |
| АККУМУЛЯТОРНАЯ БАТАРЕЯ И СНАБЖЕННАЯ ЕЮ РУЧНАЯ МАШИНА | 2008 |
|
RU2516292C2 |
| US 3450242 A, 17.06.1969. | |||
Авторы
Даты
2018-03-15—Публикация
2015-06-11—Подача