Изобретение относится к области цифровой обработки и анализа данных и предназначено для определения относительного размера синхронных кластеров в сетях нелинейных элементов со сложной топологией связи по их макропараметрам. В частности, изобретение может быть эффективно использовано в задачах автоматического выделения размеров синхронных кластеров в нейронных сетях головного мозга человека и животных по анализу временных биологических цифровых данных электроэнцефалограмм (ЭЭГ) и магнитоэнцефаллограмм (МЭГ), а также при исследовании динамики техногенных (транспортных, энергетических, информационных) и социальных сетей.
Выделение синхронных кластеров в сетях связанных осцилляторов важно в задачах различных областей жизни и науки, включая нейрофизиологию, инженерные науки, транспорт, информатику, социальные науки. Например, в настоящее время инструменты и методы теории сложных сетей все шире применяются для анализа активности нейронной сети головного мозга [Valencia, М., et al. Phys. Rev. Е 77 (5), 050905 (2008); Sitnikova, Е., et al. Brain Research 1436, 147-156 (2012)]. Эта задача тесно связана с проблемами диагностики и детального изучения патологий головного мозга, а также с развитием технологий создания интерфейса мозг-компьютер [Santhanam, G., et al. Nature Letters, 442, 195 (2006)]. Сложный процесс взаимодействия отдельных нейронов приводит к образованию локальных синхронных мод в различных отделах нейронной сети головного мозга, а в некоторых случаях и к установлению глобальной синхронизации. Известно, что формирование локальных и глобальных кластеров синхронной активности нейронов отражает различные типы когнитивной активности головного мозга [Uhlhaas, P., et al. Frontiersin Integrative Neuroscience 3, 17 (2009)] и является биомаркером возникновения различной патологической активности, в частности эпилепсии [Panayiotopoulos, С.Р., 2005. Idiopathic generalised epilepsies. In: Panayiotopoulos, C.P. (Ed.), The Epilepsies: Seizures, Syndromes and Management. Bladon Medical Publishing, Oxford, pp. 271-348.].
Основными инструментами для экспериментального исследования электрической и магнитной активности нейронной сети головного мозга являются электроэнцефалография (ЭЭГ) и магнитоэнцефалография (МЭГ). Развитие измерительной техники ЭЭГ и МЭГ позволяет регистрировать пространственно-временную электрическую и магнитную активность нейронов головного мозга с высоким разрешением [Dale, A.M. et al. Neuron, V. 26 (1), P. 55-67 (2000); Waldert S. et al. J. Neurosci. V. 28 (4) P. 1000-1008 (2008); Ball, Т., et al. Neuro Image, 46, 708 (2009);]. Таким образом, получаемые данные дают исследователям широкие возможности по выделению различных паттернов активности нейронной сети и контролю ее динамикой (например, прерывание патологической активности в течение пик-волнового разряда). Кроме того, анализ ЭЭГ и МЭГ данных позволит переводить нейронную активность на язык двигательных команд при помощи интерфейса мозг-компьютер [Beronyi, A., et al. Science, 37, 735 (2012); Ovchinnikov, А.А., et al. Journal of Neuroscience Methods 194, 172-178 (2010)].
При анализе колебательной активности нейронной сети головного мозга важно изучить динамику и параметры конкретных популяций нейронов, вовлеченных в ту или иную активность головного мозга. Существуют проблемы изучения процессов формирования кластеров в нейронной сети головного мозга по экспериментальным данным, поскольку сигналы, регистрируемые ЭЭГ и МЭГ, являются интегральными сигналами усредненными по некоторому нейронному ансамблю области головного мозга и представляют собой суммарную активность нейронной подсети в окрестности регистрирующего электрода. Поэтому вопрос эффективного использования ЭЭГ и МЭГ данных, как макроскопических параметров активности нейронов, для анализа процессов кластеризации нейронной сети до последнего момента оставался открытым.
В настоящее время известны и широко используются способы частотно-временного анализа сигналов ЭЭГ и МЭГ, которые позволяют достаточно эффективно выделять те или иные колебательные паттерны активности нейронной сети головного мозга [Carmonia, A. Practicaltime-frequencyanalysis. – Academic Press, (1998); Hramov, A.E., et al. Wavelets in Neuroscience, Springer Heidelberg New York Dordrecht London, (2015)]. Такие подходы основываются, как правило, на известных методах спектрального Фурье и вейвлетного преобразования, а диагностика колебательных паттернов происходит за счет анализа энергии спектра, приходящейся на частотные диапазоны, соответствующие характерным колебательным ритмам. К недостаткам существующих методик частотно-временного анализа сигналов применительно к задачам исследования коллективной временной динамики элементов сложной сети можно отнести, главным образом, невозможность определения размеров синхронных кластеров сети, вовлеченных в ту или иную колебательную активность. В то же время отличием заявляемого способа от известных подходов для спектрального анализа является возможность точного вычисления относительной численности элементов, формирующих синхронные кластеры, образующие паттерны колебательной активности сети.
Таким образом, проблема настоящего изобретения заключается в необходимости разработки универсального способа, позволяющего проводить автоматическую диагностику синхронных кластеров сети нелинейных элементов со сложной топологией связи и определять их относительные размеры посредством анализа регистрируемых цифровых интегральных сигналов сети со сложной топологией связей.
Техническим результатом изобретения является возможность идентификации и определения относительных размеров отдельных синхронных кластеров сложной сети по усредненным по ансамблю макропараметрам активности сети со сложной топологией связей.
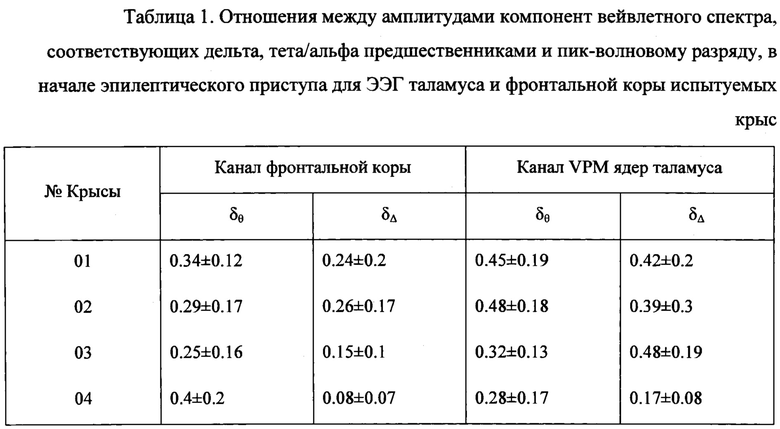
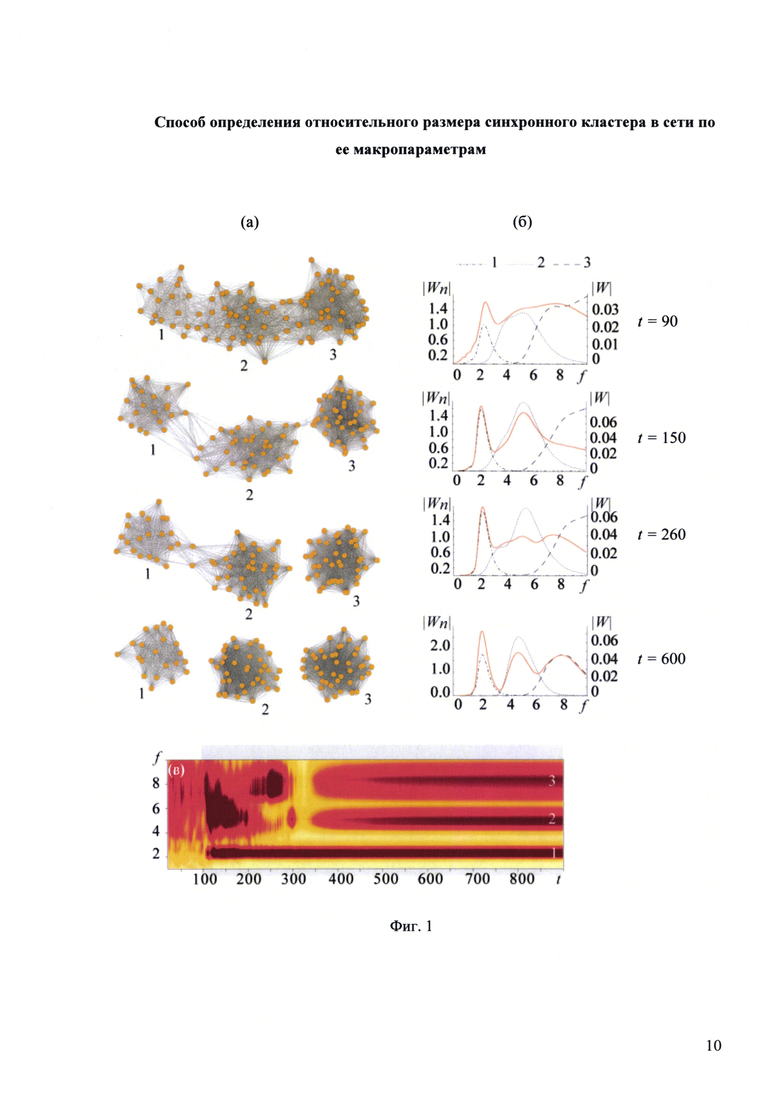
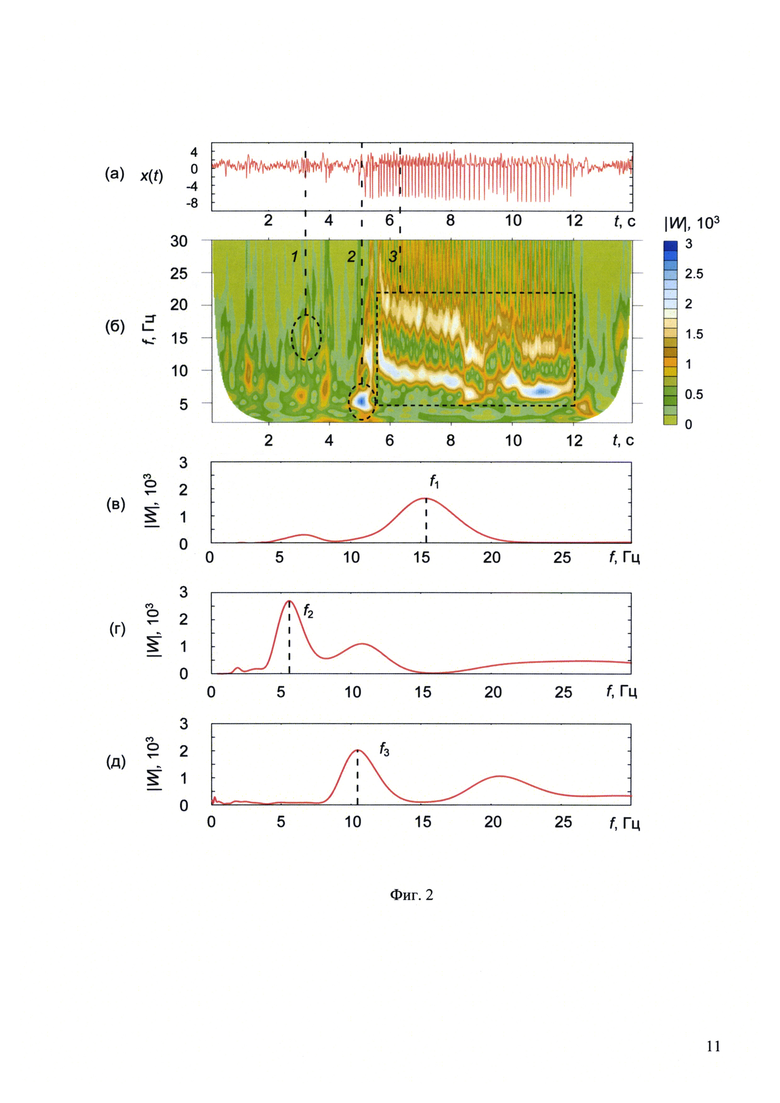
Предлагаемое изобретение поясняется чертежами: на Фиг. 1 изображено графическое представление сети связанных колебательных элементов и процесса ее кластеризации на примере временной эволюции модельной сети связанных осцилляторов Курамото с адаптивными связями. В левой колонке (а) представлена временная эволюция топологии сети в процессе адаптации связей и формировании кластеров, в правой колонке (б) представлены мгновенные спектры, полученные в ходе вейвлетного преобразования интегрального сигнала сети, в соответствующие моменты времени. В начальный момент времени и до завершения переходного процесса (t=90) связь между элементами распределена случайным образом. Благодаря адаптации связей между элементами сети, в ходе их временной эволюции в сети возникают кластеры синхронных элементов (t=100÷900). Процесс адаптации связей приводит к формированию трех колебательных кластеров, содержащих синхронные элементы, демонстрирующие близкую колебательную динамику (t=600). Макропараметром сети является аддитивная сумма сигналов узлов сети. Его частотно-временное представление изображено на Фиг. 1 (в). На Фиг. 2 представлен пример сигнала ЭЭГ, регистрируемого во фронтальной коре головного мозга крысы WAG/Rij, содержащего паттерн пик-волнового разряда (а). Для соответствующего отрезка сигнала ЭЭГ приведена вейвлетная поверхность (б), полученная путем применения процедуры вейвлетного преобразования к исходному временному ряду. Эллипсом и пунктирной линией с цифрой 1 отмечен тета/альфа предшественник, а эллипсом и пунктирной линией с цифрой 2 отмечен дельта предшественник. Прямоугольник и пунктирная линия с цифрой 3 выделяют область пик-волнового разряда. Для указанных паттернов, наблюдаемых в исходном сигнале, приведены соответствующие мгновенные спектры (в)-(д), построенные в моменты времени t=3.2 с, t=5.0 с, t=6.2 с.
Под сетью понимают совокупность связанных колебательных элементов с различными топологиями связи друг с другом (Фиг. 1, а), например компьютерные сети, где в роли элементов выступают персональные компьютеры, городские энергетические сети, содержащие связанные узлы выработки и потребления энергии, сети линейных и нелинейных радиотехнических осцилляторов, а также нейронные сети, представляющие собой соединенные друг с другом сложным образом простейшие элементы - нейроны. Временная эволюция сети связанных элементов приводит к образованию кластеров - групп связанных между собой элементов сети, чья колебательную активность определяется близкими характерными для данного кластера параметрами колебаний (Фиг. 1, а, б), например частотой колебаний, в случае сетей радиотехнических осцилляторов или нейронных ансамблей головного мозга.
При исследовании сети связанных колебательных элементов проводят анализ макропараметра изучаемой сети, полученный путем сложения и усреднения выходных сигналов всех элементов сети. По макропараметру определяют относительные размеры синхронных кластеров в сложной сети связанных нелинейных элементов с помощью применения процедуры вейвлетного преобразования [Hramov А.Е., Koronovskii А.А., Makarov V.A., Pavlov A.N., Sitnikova E. Yu. Wavelets in Neuroscience. Springer Heidelberg New York Dordrecht London, 2015] к анализируемой временной зависимости макропараметра сети, содержащей различные колебательные паттерны, соответствующие характерным типам колебательной активности сформировавшихся в сети синхронных кластеров (Фиг. 1, в). Затем проводят анализ амплитуд наиболее ярко выраженных компонент вейвлетного спектра.
Пусть X(t) - макропараметр исследуемой сети, представляющий суммарную активность ее элементов, усредненную по ансамблю. К сигналу X(t) применяется процедура непрерывного вейвлетного преобразования:
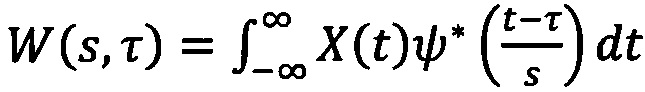 ,
,
где X(t) - исходный макропараметр, "*" обозначает комплексное сопряжение, а ψ(s,τ) - вейвлетная функция, определенная для временного масштаба s как
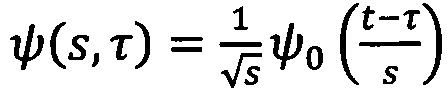 .
.
Здесь ψ0 - материнская вейвлетная функция, τ - параметр временного сдвига, s - временной масштаб, определяющий ширину вейвлетной функции. В рамках заявленного способа в качестве материнской вейвлетной функции выбран Морле вейвлет, наиболее эффективный для задач частотно-временного анализа и выделения паттернов во временных рядах. Морле вейвлет представляется в форме:
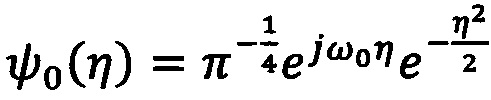 ,
,
где ω0 - центральная частота, которая была выбрана равной 2π.
Далее производят анализ модуля комплексной величины |W(s,τ)|, которая пропорциональна энергии сигнала. Количество кластеров соответствует количеству пиков в вейвлетном спектре на частотах ƒi, i=1…n, n - количество кластеров. Каждый синхронный кластер характеризуется частотой ƒi, дисперсией распределения фаз σi и амплитудой 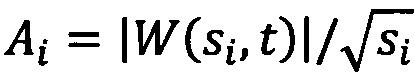 , где si=1/ƒi. Коэффициент
, где si=1/ƒi. Коэффициент 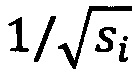 нормирует амплитуду вейвлет-коэффициентов [Короновский А.А., Храмов А.Е. Непрерывный вейвлетный анализ и его приложения. М.: Физматлит, 2003]. Таким образом, отношение нормированных амплитуд вейвлетного спектра можно рассматривать как относительное число элементов сети, входящих в состав различных синхронных кластеров, другими словами Ai/Aj~Ni/Nj. В итоге, относительный размер синхронного кластера 8 определяется соотношением:
нормирует амплитуду вейвлет-коэффициентов [Короновский А.А., Храмов А.Е. Непрерывный вейвлетный анализ и его приложения. М.: Физматлит, 2003]. Таким образом, отношение нормированных амплитуд вейвлетного спектра можно рассматривать как относительное число элементов сети, входящих в состав различных синхронных кластеров, другими словами Ai/Aj~Ni/Nj. В итоге, относительный размер синхронного кластера 8 определяется соотношением:
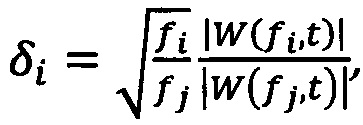
где индекс i соответствует рассматриваемому кластеру, а индекс j соответствует некоторому кластеру, относительно которого определяется размер i-го синхронного кластера сложной сети.
Рассмотрим пример конкретной реализации заявляемого способа. Проводился анализ образования синхронных кластеров в головном мозге крыс породы WAG/Rij во время приступа эпилепсии. В качестве макропараметра нейронной сети головного мозга выступает сигнал ЭЭГ, регистрирующий суммарную электрическую активность элементов сети - нейронов.
Заявляемый способ был апробирован на данных ЭЭГ крыс породы WAG/Rij, имеющих врожденную предрасположенность в абсенс эпилепсии. Запись сигналов ЭЭГ производилась у 8 особей крыс WAG/Rij мужского пола, выращенных в лаборатории Биологической психологии в Donders Institute for Brain, Cognition and Behavior of Radboud University Nijmegen (Нидерланды). Записывающие электроды были эпидурально внедрены во фронтальную кору и VPM ядра таламуса мозга крысы. Сигнал ЭЭГ фильтровался в частотном диапазоне от 0.5 до 100 Гц с временным разрешением 1024 Гц.
Был проведен анализ сигналов ЭЭГ с двух областей мозга крысы (фронтальная кора и VPM ядер таламуса) во время приступов абсенс эпилепсии. Записи ЭЭГ таламуса и фронтальной коры изучались за 5 с до пик-волнового разряда и в течение пик-волнового разряда. Применение непрерывного вейвлетного преобразования показало, что пик-волновому разряду непосредственно предшествуют два колебательных паттерна с характерными частотами в области 3-5 и 7-12 Гц -дельта и тета/альфа предшественники соответственно (Фиг. 2).
Для определения числа популяции нейронов, вовлеченных в образование того или иного колебательного паттерна в сигнале ЭЭГ, применялся заявляемый способ с учетом двух важных предположений. Во-первых, активность предшественников и пик-волновой разряд связаны с образованием синхронных кластеров в нейронной сети головного мозга, в подсетях коры и ядер таламуса. Во-вторых, предполагалось, что распределение фаз тех или иных синхронных кластеров характеризуется примерно одинаковым значением дисперсии. В рамках указанных предположений число популяций синхронных нейронов, вовлеченных в процесс образования тета/альфа, дельта и пик-волновой активностей головного мозга, определялось оценкой амплитуды вейвлетного спектра на соответствующих частотах в вейвлетном спектре сигналов ЭЭГ, регистрируемых в VPM ядрах таламуса и фронтальной коре головного мозга. Относительный размер синхронного кластера тета/альфа и дельта при этом определялся отношением амплитуд вейвлетного спектра, соответствующих тета/альфа и дельта ритмам, к амплитуде вейвлетного спектра, соответствующей пик-волновому разряду:
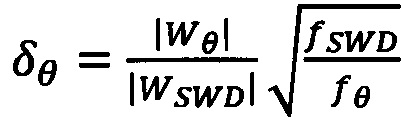 ,
,
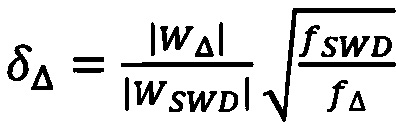 ,
,
где δθ, δΔ - относительные размеры кластеров нейронной сети, вовлеченных в тета/альфа и дельта активность соответственно, |Wθ| - усредненная амплитуда вейвлетного спектра тета/альфа предшественника, |WΔ| - усредненная амплитуда вейвлетного спектра дельта предшественника, |WSWD| - усредненная амплитуда вейвлетного спектра в начале пик-волнового разряда, ƒSWD, ƒθ, ƒΔ - характерные частоты колебаний пик-волнового разряда, тета/альфа и дельта предшественников соответственно. Результаты применения заявленного способа для определения относительных размеров синхронных кластеров нейронной сети головного мозга животного на примере записей ЭЭГ мозга крыс породы WAG/Rij приведены в таблице 1.
Использование заявляемого способа показало, что размер нейронного ансамбля, задействованного в образовании активности дельта предшественника во фронтальной коре головного мозга крысы породы WAG/Rij, составляет 8-25% от числа нейронов, входящих в синхронный кластер в течение пик-волнового разряда, а в активности тета/альфа предшественника принимают участие 25-40%. Характерные цифры получаются и для синхронных нейронных ансамблей в VPM ядрах таламуса - 17-48% и 28-44% для дельта и тета/альфа предшественников соответственно.
Таким образом, техническим результатом заявляемого способа определения относительного размера синхронных кластеров сети по ее макропараметрам является возможность точной идентификации и определения относительных размеров отдельных синхронных кластеров сложной сети по усредненным по ансамблю макропараметрам активности сети со сложной топологией связей. Данный способ, в частности, обеспечит возможность более детального анализа активности нейронной сети головного мозга по записям ЭЭГ и МЭГ.
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ классификации сигналов ЭЭГ при воображении двигательной активности у нетренированного оператора | 2018 |
|
RU2682492C1 |
| СПОСОБ ВЫДЕЛЕНИЯ ВЕРЕТЕНОПОДОБНЫХ ПАТТЕРНОВ ПО ВРЕМЕННЫМ ДАННЫМ ЭЛЕКТРОЭНЦЕФАЛОГРАММ | 2014 |
|
RU2565993C1 |
| СПОСОБ АВТОМАТИЧЕСКОГО ВЫДЕЛЕНИЯ ФИЗИОЛОГИЧЕСКИХ СОСТОЯНИЙ МЕЛКИХ ЛАБОРАТОРНЫХ ЖИВОТНЫХ | 2020 |
|
RU2751744C1 |
| Способ определения уровня концентрации внимания по временным данным электроэнцефалограмм | 2018 |
|
RU2675340C1 |
| Способ идентификации состояния сомнений человека по данным активности головного мозга | 2018 |
|
RU2688320C1 |
| СПОСОБ ВЫДЕЛЕНИЯ СИГНАЛОВ ИМПУЛЬСНОГО ТИПА ПО ВРЕМЕННЫМ ДАННЫМ | 2014 |
|
RU2552183C1 |
| СПОСОБ ИССЛЕДОВАНИЯ ЭЛЕКТРОЭНЦЕФАЛОГРАММЫ ЧЕЛОВЕКА И ЖИВОТНЫХ | 2012 |
|
RU2543275C2 |
| Способ классификации двигательной активности человека | 2020 |
|
RU2751816C1 |
| СПОСОБ РАННЕЙ ЭЛЕКТРОЭНЦЕФАЛОГРАФИЧЕСКОЙ ДИАГНОСТИКИ БОЛЕЗНИ ПАРКИНСОНА | 2012 |
|
RU2484766C1 |
| СПОСОБ ДИАГНОСТИКИ НАРУШЕНИЙ ФУНКЦИОНАЛЬНОЙ АКТИВНОСТИ МОЗГА У БОЛЬНЫХ С ОПУХОЛЯМИ ГОЛОВНОГО МОЗГА | 2011 |
|
RU2473302C1 |
Изобретение относится к области цифровой обработки и анализа данных. Технический результат заключается в расширении арсенала технических средств определения относительных размеров отдельных синхронных кластеров сложной сети. Способ определения относительных размеров синхронных кластеров сетей со сложной топологией связей, заключающийся в том, что с помощью датчиков снимают сигналы узлов сети, получают интегральный сигнал сети, представляющий собой аддитивную сумму сигналов узлов сети, определяют коэффициенты вейвлет-преобразования интегрального сигнала, определяют максимальные значения вейвлет-коэффициентов, соответствующие различным синхронным кластерам, определяют частоты ƒi и энергии |W(si, t)| колебаний каждого синхронного кластера по максимальным значениям вейвлет-коэффициентов, вычисляют размер i-го синхронного кластера δi относительно размера j-го синхронного кластера, вычисляют отношение частот, соответствующих синхронным кластерам, извлекают квадратный корень из соотношения частот, нормируют отношение энергий колебаний синхронных кластеров на квадратный корень соотношения частот кластеров, определяющее относительный размер кластера. 2 ил., 1 табл.
Способ определения относительных размеров синхронных кластеров сетей со сложной топологией связей, заключающийся в том, что с помощью датчиков снимают сигналы узлов сети, получают интегральный сигнал сети, представляющий собой аддитивную сумму сигналов узлов сети, определяют коэффициенты вейвлет-преобразования интегрального сигнала, определяют максимальные значения вейвлет-коэффициентов, соответствующие различным синхронным кластерам, определяют частоты ƒi и энергии |W(si,t)| колебаний каждого синхронного кластера по максимальным значениям вейвлет-коэффициентов, вычисляют размер i-го синхронного кластера δi относительно размера j-го синхронного кластера по формуле:
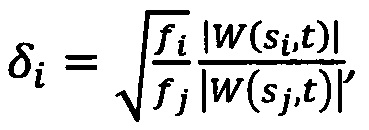
где вычисляют отношение частот, соответствующих синхронным кластерам, извлекают квадратный корень из соотношения частот, нормируют отношение энергий колебаний синхронных кластеров на квадратный корень соотношения частот кластеров, определяющее относительный размер кластера.
| US 20090059827 A1, 05.03.2009 | |||
| US 20020181799 A1, 05.12.2002 | |||
| US 20070083730 A1, 12.04.2007 | |||
| ВЫБОР СИНХРОНИЗИРУЮЩИХ СТАНЦИЙ В ОДНОРАНГОВОЙ СЕТЕВОЙ СРЕДЕ | 2013 |
|
RU2595611C2 |
| US 7512271 B2, 31.03.2009. | |||
Авторы
Даты
2018-03-16—Публикация
2017-01-10—Подача