Изобретение относится к области микро- и наноэлектронике, а именно к определению физических параметров полупроводниковых приборов, в частности к определению температурной зависимости распределения потенциала в двухзатворных симметричных полностью обедненных полевых транзисторах со структурой «кремний на изоляторе» с гауссовым вертикальным профилем легирования рабочей области и может быть использовано при моделировании и разработке интегральных схем в специализированных программах.
Для решения задач нового научного направления - высокотемпературная электроника, в полной мере подходят микросхемы, изготовленные по тонкопленочной технологии «кремний на изоляторе» (далее КНИ), которые являются идеальными высокотемпературными устройствами. К одним из основных компонентов элементной базы КНИ цифровых микросхем по праву относят двухзатворные полевые КМОП транзисторы [1], которые находят широкое применение в вооруженных силах, нефтегазовой, ядерной и других отраслях.
Здесь следует отметить, что на современном этапе развития технологии реальные двухзатворные симметричные КНИ КМОП транзисторы характеризуются наличием гауссова профиля распределения легирующей примеси в рабочей области транзистора из-за требования ряда операций имплантации и диффузии во время процесса изготовления [2]. В рассматриваемом случае профиль описывается функцией Гаусса:  где Npick - максимальная концентрация легирующей примеси (в дальнейшем - пиковая концентрация), Rd - глубина залегания уровня максимальной концентрации (в дальнейшем - характерная глубина), σd - крутизна профиля легирования.
где Npick - максимальная концентрация легирующей примеси (в дальнейшем - пиковая концентрация), Rd - глубина залегания уровня максимальной концентрации (в дальнейшем - характерная глубина), σd - крутизна профиля легирования.
Для наноэлектронных устройств проведение макетных исследований в высоко температурной области становится не постижимо дорогостоящей задачей [3]. С целью сокращения расходов разрабатываются методы схемотехнического моделирования, с помощью которых получают прогноз, сообразуясь с которым и разрабатывают микросхемы. Главенствующая роль в методах схемотехнического моделирования отводится определению распределения потенциала, поскольку оно определяет ключевые электрофизические характеристики транзистора. Следует отметить, что моделирование основных характеристик транзистора, в частности распределение потенциала в рабочей области, с учетом гауссова профиля легирования может обеспечить более адекватные его электрофизические характеристики [3].
Для экстракции физических параметров профиля легирования необходимо измерять концентрацию легирующей примеси по глубине. Измерение концентрации легирующей примеси производится методом, схожим со способом, который представлен в работе [4]. В данном случае определение концентрации легирующей примеси производится путем многократного проведения блока операций - измерений высокочастотных вольт-фарадных характеристик (ВЧ ВФХ) и последующего электрохимического растворения части приповерхностного слоя образца. Воспроизведение блока таких операций проводится более 10 раз, что является очень трудоемким процессом. Повышение достоверности измерений достигается за счет вычитания емкости плотности состояний, локализованных вблизи поверхности образца, из результатов измерений ВЧ ВФХ. Определение температурной зависимости двумерного распределения потенциала в двухзатворных симметричных полностью обедненных полевых транзисторах со структурой «кремний на изоляторе» с гауссовым вертикальным профилем легирования рабочей области основывается на численном решении уравнения Пуассона, реализованном в коммерчески доступном программном пакете ATLAS™, который предназначен для 2D моделирования транзисторных структур [5].
Недостаток такого способа состоит в больших трудозатратах на измерение параметров, низком быстродействии и в использовании больших вычислительных ресурсов.
Техническим результатом изобретения является снижение трудозатрат на измерение параметров, повышение быстродействия для вычисления температурной зависимости распределения потенциала и в использовании меньших вычислительных ресурсов.
Технический результат достигается способом определения температурной зависимости двумерного распределения потенциала в двухзатворных симметричных полностью обедненных полевых транзисторах со структурой «кремний на изоляторе» с гауссовым вертикальным профилем легирования рабочей области, включающим не более шести измерений концентрации легирующей примеси по глубине рабочей области транзистора и экстракцию из экспериментальных данных физических параметров профиля: крутизны, характерной глубины, пиковой концентрации, - с последующим вычислением по ним температурной зависимости двумерного распределения потенциала из следующего выражения:
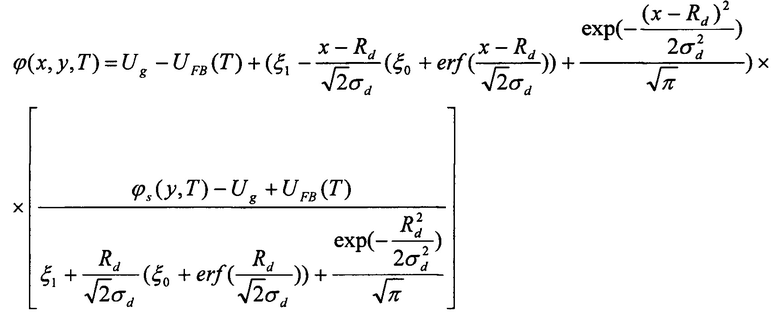
где ϕ(х,у,Т) - распределение потенциала в рабочей области транзистора при фиксированной температуре, х - координата по глубине рабочей области, у - координата вдоль рабочей области, Т - температура, ϕs(y, T) - поверхностный потенциал, Ug - напряжение на затворах, UFB(T) - напряжение плоских зон, Rd - характерная глубина профиля легирования, σd - крутизна профиля легирования, erƒ (χ) - специальная функция - интеграл ошибок,
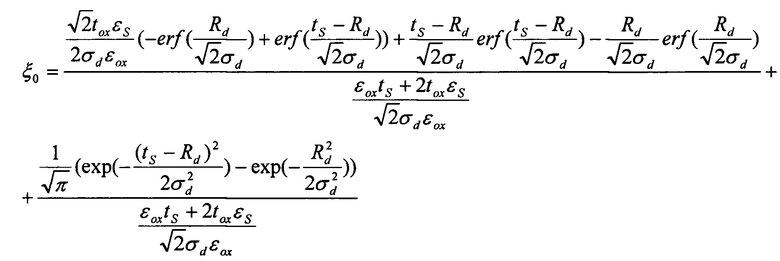
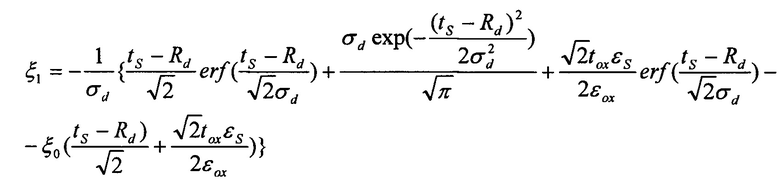
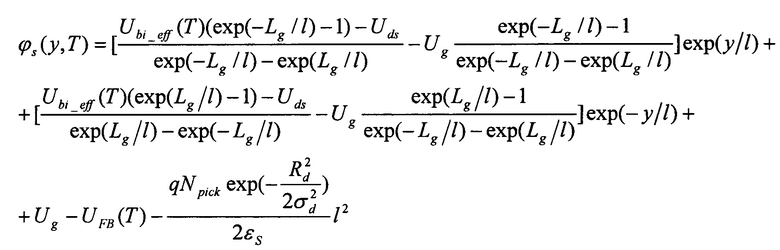
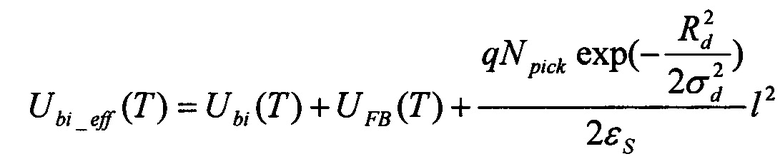
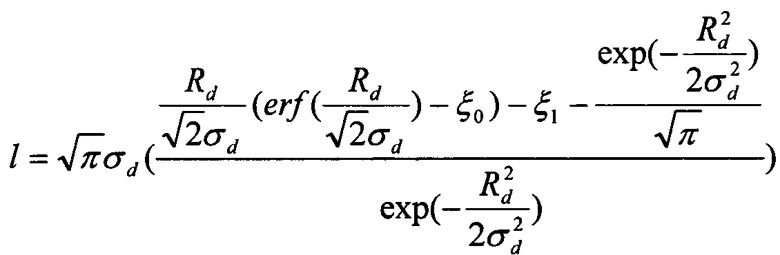
где q - заряд электрона, εs - диэлектрическая проницаемость рабочей области, εох - диэлектрическая проницаемость подзатворного окисла, tox - толщина подзатворного окисла, Ubi(T) - контактная разность потенциалов, ts - толщина рабочей области транзистора, Lg - длина затвора, Uds - напряжение сток-исток, Npick - пиковая концентрация легирования.
На фиг. 1 изображена схема двухзатворной симметричной КНИ транзисторной структуры с гауссовым вертикальным профилем легирования рабочей области.
На фиг. 2 - распределение профиля легирования по глубине рабочей области транзистора при tS=8 нм для разной крутизны профиля, где 1 - σd=1 нм, 2 - σd=2 нм, 3 - σd=3 нм, 4 - σd=5 нм.
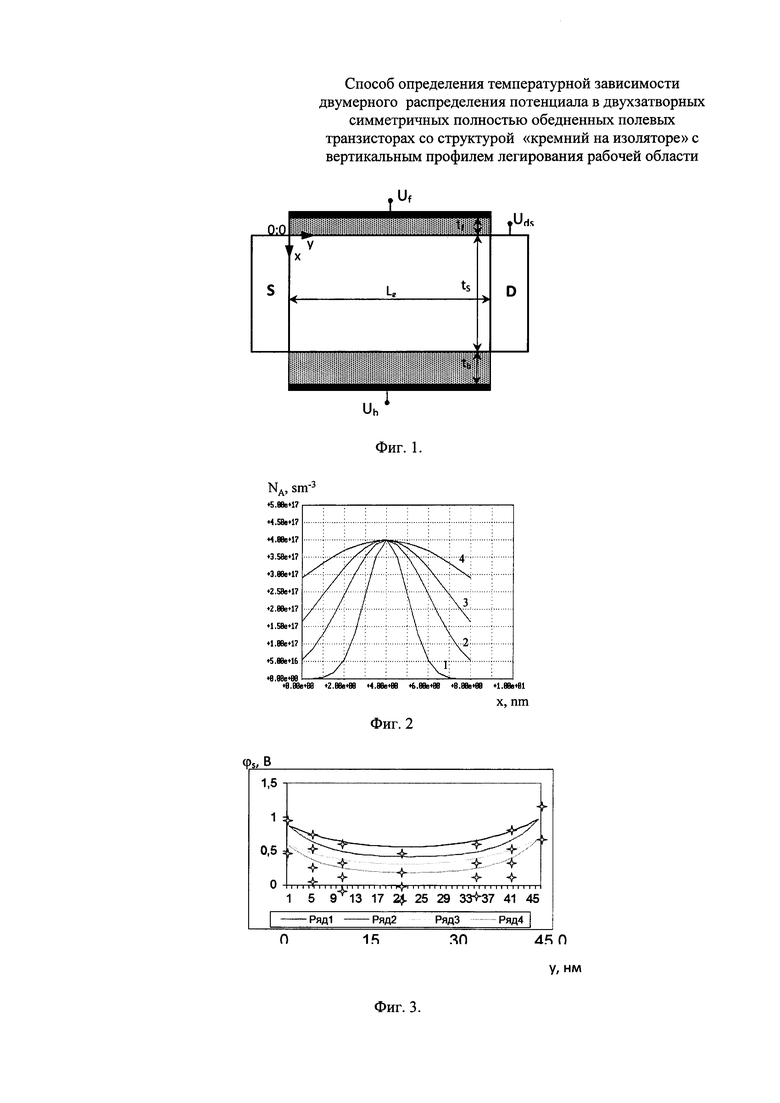
На фиг. 3 - распределение поверхностного потенциала по длине рабочей области при разных значениях Т и σd при напряжении на затворах Ug=0.1 В и напряжении между стоком и истоком Uds=0.1 В, где верхняя кривая σd=10 нм, Т=300 К, ниже - σd=3 нм, Т=300 К, следующая - σd=10 нм, Т=500 К, самая нижняя - σd=3 нм, Т=500 К. Символами отмечены результаты расчетов, полученные при помощи программы ATLAS™.
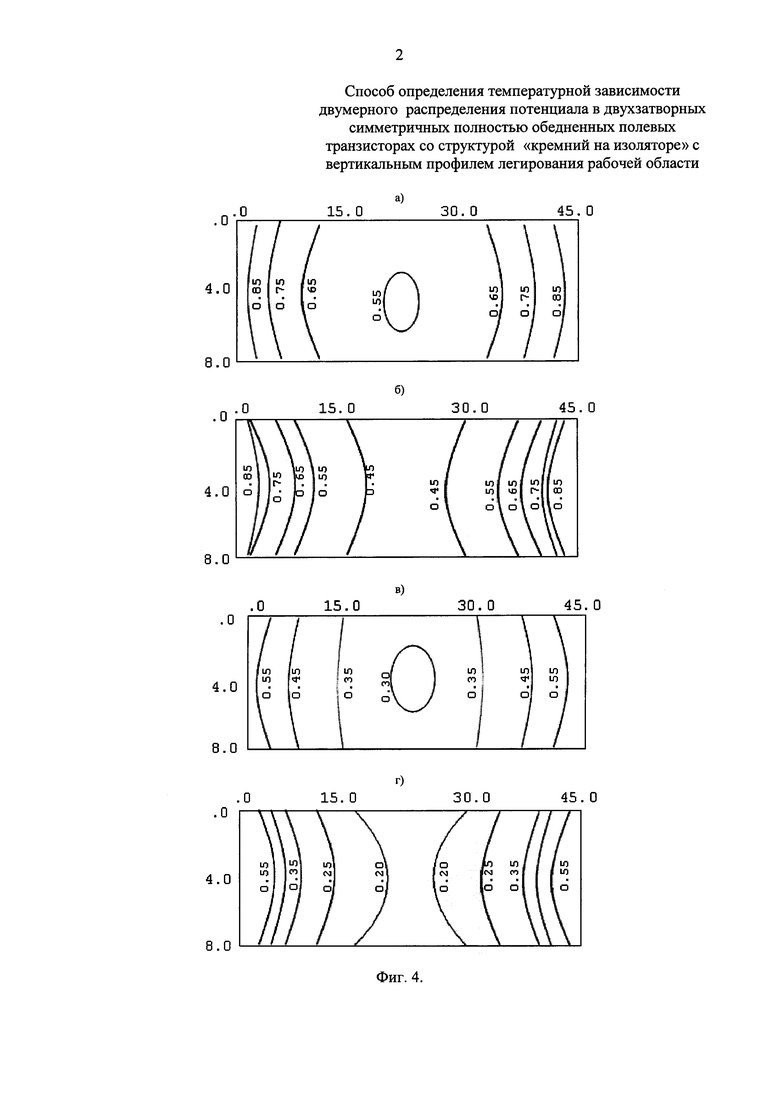
На фиг 4. Двумерное распределение потенциала по рабочей области при тех же напряжениях, что и на фиг. 3, где а) - σd=10 нм, Т=300 К, б) σd=3 нм, Т=300 К, в) σd=10 нм, Т=500 К, г) σd=3 нм, Т=500 К.
Способ осуществляется следующим образом.
Первоначально измеряется концентрация легирующей примеси по глубине рабочей области транзистора. Подготовленный тестовый образец помещается в электрохимическую ячейку в электролит, проводят измерение высокочастотной дифференциальной емкости при заданном изменении электродного потенциала и фиксированной температуре в области потенциалов, соответствующих обеднению приповерхностного слоя рабочей области транзистора носителями заряда. Затем проводится электрохимическое растворение части приповерхностного слоя образца. По измеренным зависимостям дифференциальной емкости от электродного потенциала с учетом величины падения потенциала в электролите определяют зависимость концентрации примеси по глубине рабочей области транзистора. Таких измерений необходимо провести минимум 4, что будет пояснено ниже.
Для экстракции параметров профиля легирования используется известный метод - нелинейный метод наименьших квадратов (НМНК), реализованный в программной среде Maple. Цель НМНК заключается в обработке данных по формуле, которая нелинейно зависит от определяемых параметров. В нашем случае необходимо описать экспериментальную зависимость концентрации легирования по глубине в виде гауссовой функции:

где Npick - пиковая концентрация легирования, Rd - характерная глубина профиля легирования, σd - крутизна профиля легирования - параметры, которые необходимо определить из условия, чтобы сумма квадратов отклонений величин, рассчитанных по этой формуле, от экспериментальных значений была минимальной.
Способ решения задачи НМНК носит название широко применяемого метода Гаусса-Ньютона. Он обладает квадратичной сходимостью. Так, при обработке данных по формуле 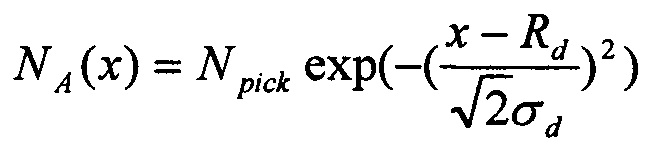 параметры Npick, Rd, σd обычно перестают изменяться уже через 4-6 шагов. При этом минимум суммы квадратов отклонений обращается в ноль. Необходимым условием применимости НМНК является то, что число экспериментальных точек должно превышать количество определяемых параметров. В нашем случае минимальное число измерений составляет 4. Для валидности проводится еще одно дополнительное измерение. Итоговое значение измерений составляет 5. Время экстракции параметров не превышает 6 с.
параметры Npick, Rd, σd обычно перестают изменяться уже через 4-6 шагов. При этом минимум суммы квадратов отклонений обращается в ноль. Необходимым условием применимости НМНК является то, что число экспериментальных точек должно превышать количество определяемых параметров. В нашем случае минимальное число измерений составляет 4. Для валидности проводится еще одно дополнительное измерение. Итоговое значение измерений составляет 5. Время экстракции параметров не превышает 6 с.
Заключительный этап - вычисление по вышепредставленной формуле температурной зависимости двумерного распределения потенциала в двухзатворных симметричных полностью обедненных полевых транзисторах со структурой «кремний на изоляторе» с гауссовым вертикальным профилем легирования рабочей области, параметры которого (профиля) определены на предыдущем этапе.
1. Обоснование математического выражения, используемого для вычисления температурной зависимости распределения потенциала.
Для вычисления температурной зависимости распределения потенциала в рабочей области двухзатворного симметричного полностью обедненного КНИ КМОП нанотранзистора с вертикальным профилем легирования рабочей области, структурная схема которого представлена на фиг. 1, рассмотрим квазиклассическую задачу в диффузионно-дрейфовом приближении. Ищется аналитическое решение двумерного (2D) уравнения Пуассона, которое, как известно, используется для анализа распределения потенциала в рабочей области транзистора. Для вышеуказанных условий 2D уравнение Пуассона имеет вид:
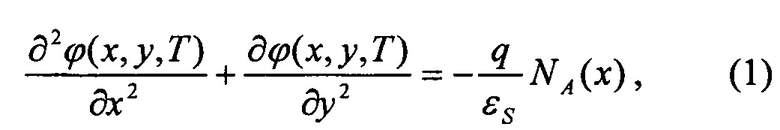
где q - заряд электрона, ϕ(х,у,Т) - распределение потенциала в рабочей области транзистора при температуре Т, εS - диэлектрическая проницаемость рабочей области, Т - температура, NA(x) - распределение концентрации легирующей примеси в рабочей области, где в рассматриваемом случае форма NА(х) описывается функцией Гаусса: 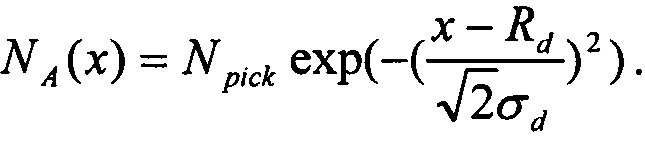
Фиг. 2 иллюстрирует вид профиля легирования для разных случаев.
Для аналитического решения уравнения (1) используются следующие граничные условия
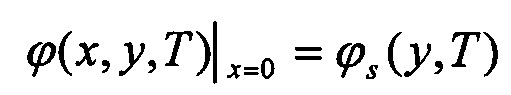
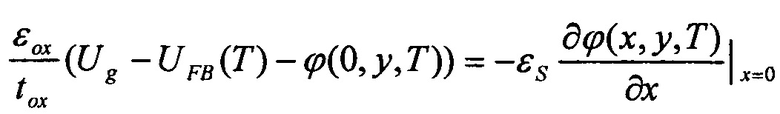
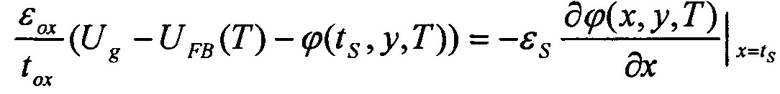
ϕ(x,0,T)=Ubi(T)
ϕ(x,Lg,T)=Ubi(T)+Uds
где ϕs(y,T) - поверхностный потенциал, εох - диэлектрическая проницаемость подзатворного окисла, tox - толщина подзатворного окисла, Ug - напряжение на затворах, UFB(T) - напряжение плоских зон, Ubi(Т) - контактная разность потенциалов, tS - толщина рабочей области транзистора, Lg - длина затвора, Uds - напряжение сток-исток, UFB(T) - напряжение плоских зон, где 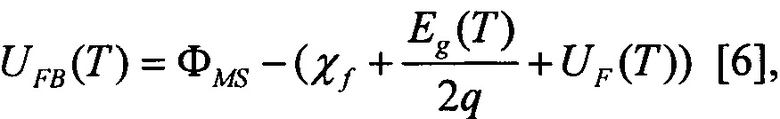 здесь ФMS - работа выхода затвора, χƒ - сродство электрона, Eg(Т) - ширина запрещенной зоны, UF(T) - уровень Ферми. Температурная зависимость ширина запрещенной зоны
здесь ФMS - работа выхода затвора, χƒ - сродство электрона, Eg(Т) - ширина запрещенной зоны, UF(T) - уровень Ферми. Температурная зависимость ширина запрещенной зоны 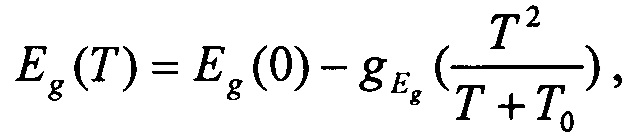 где Eg(0) - ширина запрещенной зоны при 0 К,
где Eg(0) - ширина запрещенной зоны при 0 К, 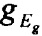 - температурный градиент ширины запрещенной зоны, Т0 - начальная температура. Температурная зависимость уровня Ферми
- температурный градиент ширины запрещенной зоны, Т0 - начальная температура. Температурная зависимость уровня Ферми
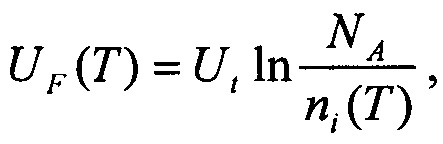 где
где 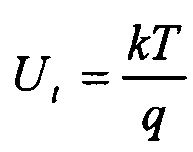 - тепловой потенциал, k - константа Больцмана,
- тепловой потенциал, k - константа Больцмана, 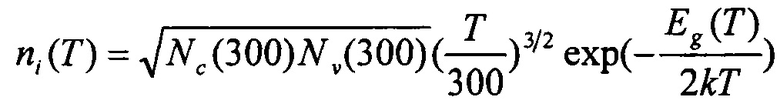 - собственная концентрация носителей, Nc (300) и Nv (300) - плотность поверхностных состояний в зоне проводимости и валентной зоне при температуре 300 К соответственно,
- собственная концентрация носителей, Nc (300) и Nv (300) - плотность поверхностных состояний в зоне проводимости и валентной зоне при температуре 300 К соответственно,  - контактная разность потенциалов, Nds - концентрация легирования областей стока и истока.
- контактная разность потенциалов, Nds - концентрация легирования областей стока и истока.
2. Метод решения уравнения Пуассона
Для решения уравнения (1) вводится новая переменная  для более компактных математических выкладок. В результате получаем следующее уравнение Пуассона:
для более компактных математических выкладок. В результате получаем следующее уравнение Пуассона:
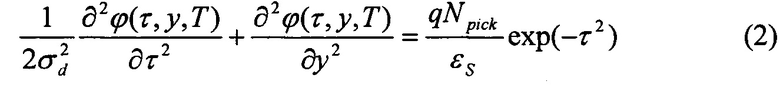
и новые граничные условия
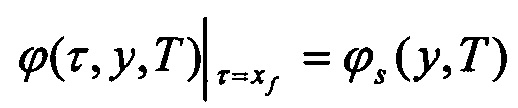
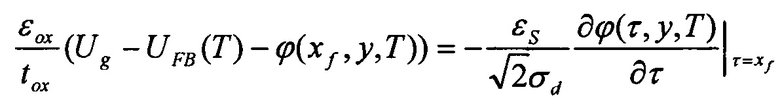
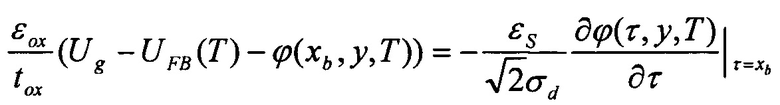
ϕ(τ,0,T)=Ubi(T)
ϕ(τ,Lg,T)=Ubi(T)+Uds
где 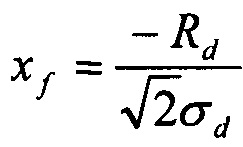 и
и 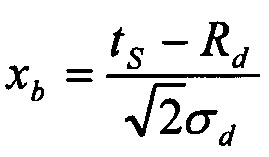 - масштабирующие параметры.
- масштабирующие параметры.
Решение уравнения Пуассона ищем в виде:
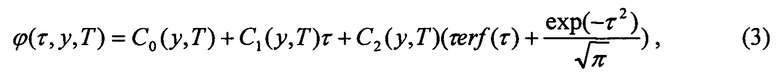
где С0(у,Т), С1(у,Т), С2(у,Т) - произвольные функции, для определения которых необходимо использовать уже новые граничные условия. Функция 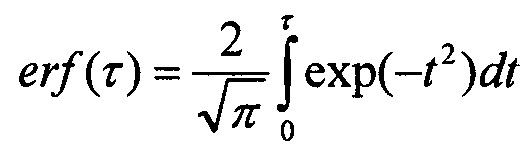 - интеграл вероятности (интеграл ошибок) является, как известно, одной из наиболее используемых в теории и практике специальных функций.
- интеграл вероятности (интеграл ошибок) является, как известно, одной из наиболее используемых в теории и практике специальных функций.
Из условий (2)-(3) вытекают следующие выражения для функций С0(у,Т), С1(у,T), С2(у,Т):
C0(y,T)=Ug-UFB(T)+ξ1C2(y,T)
С1(у,Т)=-ξ0С2(у,Т)
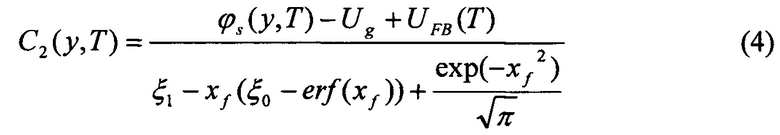
где 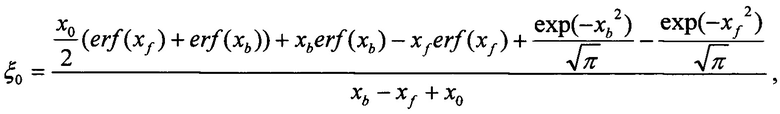

Для определения температурной зависимости поверхностного потенциала ϕs(y,T) необходимо решить уравнение Пуассона (2) на границе кремний-окисел, которое можно представить в виде:
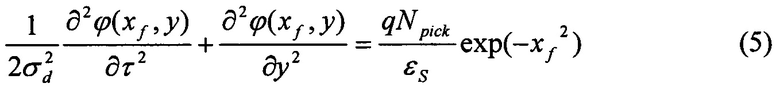
Решение уравнения (5) можно представить так
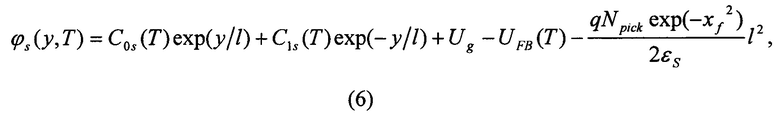
где С0s(T) и С1s(Т) - произвольные константы, 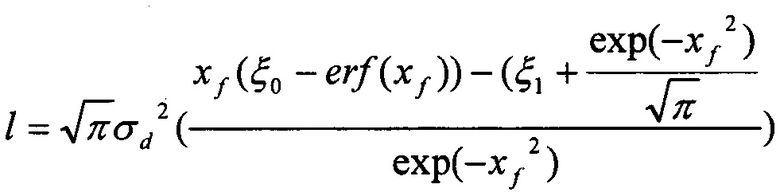 - характеристическая длина.
- характеристическая длина.
Используя граничные условия и подставив их в (6), выражение для С0s(T) и С1s(T) можно получить в виде

где
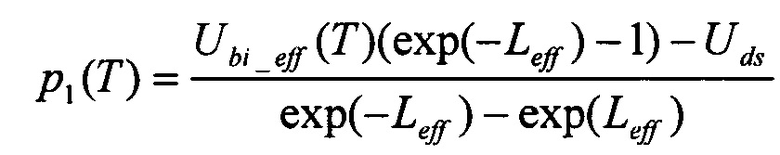 ,
, 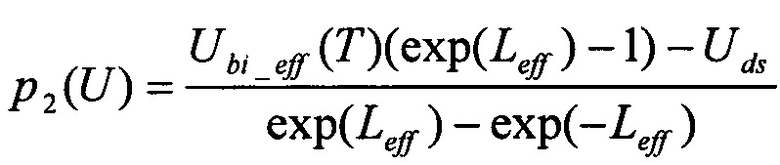 ,
,
 ,
, 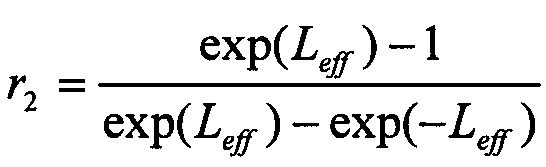 ,
,
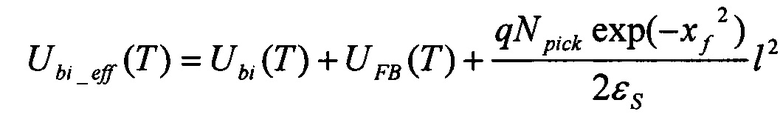 ,
,
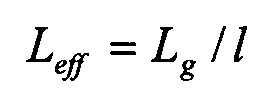
Из (3-7) следует итоговое выражение в принятых выше сокращениях для вычисления температурной зависимости распределения потенциала ϕ(τ,у,Т):
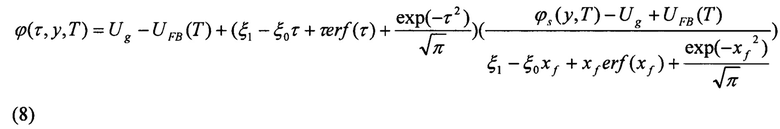
3. Примеры расчетов
Для иллюстрации представленного способа приведем результаты вычисления распределения потенциала при разной температуре для прототипа симметричного двухзатворного КНИ КМОП нанотранзистора с параметрами: Lg=45 нм, tS=8 нм, tox=2.5 нм, Npick=1×1016 см-3, Nds=5×1018 см-3.
На фиг. 3 приведены расчетные зависимости распределения поверхностного потенциала при разных значениях крутизны профиля легирования и фиксированными напряжениями на затворах и стоком и истоком.
Результаты вычислений по выражению (6) хорошо согласуются с данными моделирования, полученными при помощи коммерчески доступного для 2D моделирования транзисторных структур программного пакета ATLAS™ [5]. При этом время, затраченное на проведение расчетов, более чем в 1000 раз меньше по сравнению с использованием программы ATLAS™.
На фиг. 4 представлены результаты вычисления распределения потенциала в рабочей области транзистора при тех же условиях.
Патентуемый способ может быть реализован с использованием любых типов компьютеров и даже в виде специализированного процессора.
Время, затраченное на проведение расчетов, более чем в 1000 раз меньше по сравнению с использованием программы ATLAS™.
Точность вычислений патентуемого способа проверяется при помощи сравнения с данными моделирования, полученными при помощи программного пакета ATLAS™.
По совокупности патентуемый способ является очень актуальным и будет востребованным в ближайшем будущем.
Список источников информации:
1. International technology roadmap for semiconductor 2014 edition. - [Электронный ресурс] - Режим доступа: http://public.itrs.net.
2. Zhang G., Zhibiao S., Kai Z. Threshold voltage model of short-channel FD-SOI MOSFETs with vertical gaussian profile. IEEE Trans. Electron Devices. 2008, vol. 55, № 3, p. 803-809.
3. Масальский H.B. Двухзатворные неравномерно легированные полевые нанотранзисторы. 2016. LAP LAMBERT Academic Publishing GmbH & Co, 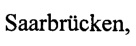 Germany.
Germany.
4. Патент SU 1304674.
5. URL: http://www.silvaco.com/ Silvaco Int. 2004: ATLAS User's Manual A 2D numerical device simulator (дата обращения 22.10.2015).
6. Зи С. Физика полупроводниковых приборов. М.: Мир, 1984.
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ контроля профиля примеси во встроенном канале МДП - транзистора | 1990 |
|
SU1777189A1 |
| ПОЛЕВОЙ НАНОТРАНЗИСТОР | 2003 |
|
RU2250535C1 |
| СПОСОБ ИЗГОТОВЛЕНИЯ САМОСОВМЕЩЕННОГО ПЛАНАРНОГО ДВУХЗАТВОРНОГО МОП-ТРАНЗИСТОРА НА КНИ ПОДЛОЖКЕ | 2003 |
|
RU2312422C2 |
| Мощный полевой транзистор СВЧ на полупроводниковой гетероструктуре на основе нитрида галлия | 2021 |
|
RU2782307C1 |
| Мощный полевой транзистор СВЧ на полупроводниковой гетероструктуре на основе нитрида галлия | 2024 |
|
RU2827690C1 |
| МДП-транзистор | 1990 |
|
SU1762342A1 |
| ПОЛЕВОЙ ТРАНЗИСТОР | 1993 |
|
RU2120155C1 |
| СПОСОБ УВЕЛИЧЕНИЯ РАДИАЦИОННОЙ СТОЙКОСТИ ЭЛЕМЕНТОВ КМОП-СХЕМ НА КНИ ПОДЛОЖКЕ | 2003 |
|
RU2320049C2 |
| СПОСОБ ИЗГОТОВЛЕНИЯ МОП-ТРАНЗИСТОРА НА СТРУКТУРЕ "КРЕМНИЙ НА ИЗОЛЯТОРЕ" | 2022 |
|
RU2784405C1 |
| ПОЛЕВОЙ ТРАНЗИСТОР НА ГЕТЕРОСТРУКТУРЕ | 1993 |
|
RU2093924C1 |
Изобретение относится к области микро- и наноэлектроники, а именно к определению физических параметров полупроводниковых приборов, в частности к определению температурной зависимости распределения потенциала в двухзатворных симметричных полностью обедненных полевых транзисторах со структурой «кремний на изоляторе» с гауссовым вертикальным профилем легирования рабочей области, и может быть использовано при моделировании и разработке интегральных схем в специализированных программах. Техническим результатом изобретения является снижение трудозатрат на измерение параметров, повышение быстродействия для вычисления температурной зависимости распределения потенциала и использование меньших вычислительных ресурсов. Технический результат достигается способом определения температурной зависимости двумерного распределения потенциала в двухзатворных симметричных полностью обедненных полевых транзисторах со структурой «кремний на изоляторе» с гауссовым вертикальным профилем легирования рабочей области, включающим не более шести измерений концентрации легирующей примеси по глубине рабочей области транзистора и экстракцию из экспериментальных данных физических параметров профиля: крутизны, характерной глубины, пиковой концентрации, - с последующим вычислением по ним температурной зависимости двумерного распределения потенциала по определенной зависимости. 4 ил.
Способ определения температурной зависимости двумерного распределения потенциала в двухзатворных симметричных полностью обедненных полевых транзисторах со структурой «кремний на изоляторе» с гауссовым вертикальным профилем легирования рабочей области, включающий не более шести измерений концентрации легирующей примеси по глубине рабочей области транзистора, экстракцию из экспериментальных данных физических параметров профиля: крутизны, характерной глубины, пиковой концентрации, с последующим вычислением по ним температурной зависимости двумерного распределения потенциала из следующего выражения:
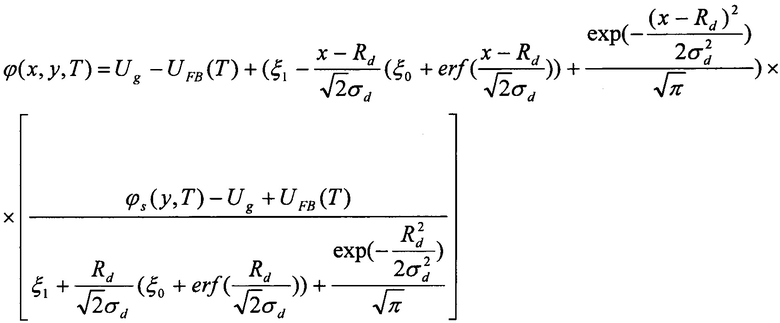
где ϕ(х,у,Т) - распределение потенциала в рабочей области транзистора при фиксированной температуре, x - координата по глубине рабочей области, у - координата вдоль рабочей области, T - температура, ϕs(у,T) - поверхностный потенциал, Ug - напряжение на затворах, UFB(T) - напряжение плоских зон, Rd - характерная глубина профиля легирования, σd - крутизна профиля легирования,  - специальная функция - интеграл ошибок,
- специальная функция - интеграл ошибок,
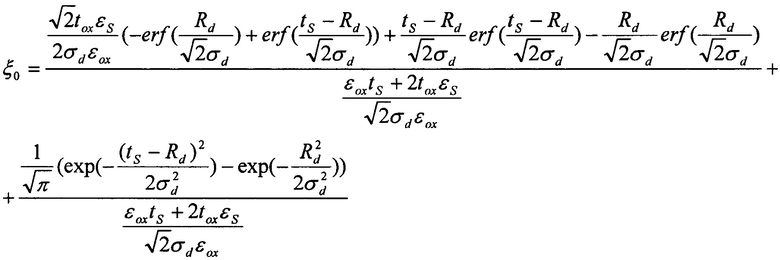
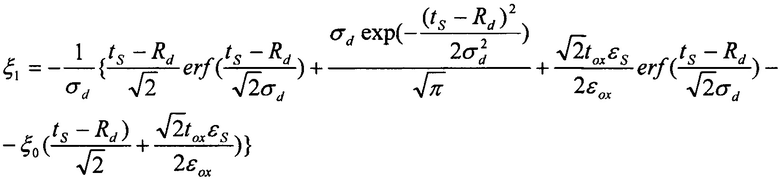
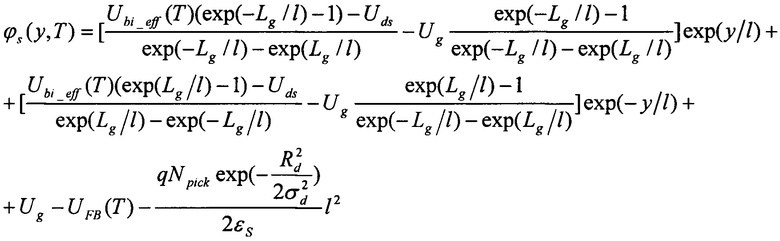
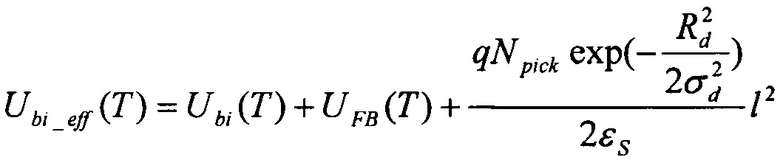
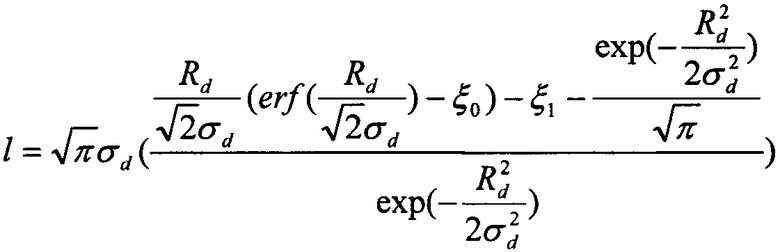
где q - заряд электрона, εS - диэлектрическая проницаемость рабочей области, εox - диэлектрическая проницаемость подзатворного окисла, tox - толщина подзатворного окисла, Ubi(T) - контактная разность потенциалов, tS - толщина рабочей области транзистора, Lg - длина затвора, Uds - напряжение сток-исток, Npick - пиковая концентрация легирования.
| Масальский Н.В | |||
| Температурная модель тока симметричного двухзатворного КНИ КМОП нанотранзистора | |||
| Материалы Международной научно-технической конференции, 1-5 декабря 2015 г | |||
| Масальский Н.В | |||
| Моделирование характеристик логических элементов на двухзатворных полевых нанотранзисторах с Гауссовым вертикальным профилем легирования | |||
| Материалы Международной научно-технической конференции, 21-25 ноября 2016 г | |||
| Масальский Н.В | |||
| Пороговые характеристики двухзатворных симметричных полевых нанотранзисторов с Гауссовым вертикальным профилем легирования | |||
| Наноматериалы и наноструктуры XXI век: международный научно-технический и теоретический журнал | |||
| Токарный резец | 1924 |
|
SU2016A1 |
| Железобетонный фасонный камень для кладки стен | 1920 |
|
SU45A1 |
| Шестаков А.К., Журавлев К.С | |||
| Влияние профиля легирования на характеристики ионно-легированного полевого GaAs транзистора с затвором Шоттки | |||
| Физика и техника полупроводников | |||
| Способ приготовления лака | 1924 |
|
SU2011A1 |
| Шкив для канатных передач | 1924 |
|
SU1652A1 |
Авторы
Даты
2018-04-17—Публикация
2017-04-04—Подача