ИНФОРМАЦИЯ О РОДСТВЕННОЙ ЗАЯВКЕ
[0001] Эта заявка заявляет приоритет по предварительной заявки на патент США № 62/008082 поданной 5 июня 2014, описание которой включено в данный документ в полном объеме.
ОБЛАСТЬ ТЕХНИКИ
[0002] Данное изобретение имеет отношение к области геомеханики и механики гидравлического разрыва пласта. Также оно имеет отношение к интенсификации нефтегазоносного продуктивного пласта, осуществляемой посредством гидравлического разрыва породы из ствола скважины, включая предоставление методики для прогнозирования развития высоты трещины гидроразрыва пласта в породе, которая определенной ранее существовавшими слабыми механическими горизонтальными границами, такими как плоскости напластования, слоистые границы, границы проскальзывания и другие.
УРОВЕНЬ ТЕХНИКИ
[0003] Для контекста, демонстрируются результаты моделирования двух случаев распространения трещины с различной структурой границ породы по отношению к горизонтальной скважине. В обоих примерах, одна трещина гидроразрыва пласта образуется в горизонтальной скважине и распространяется в вертикальном и горизонтальном направлениях. Свойства породы и напряжения в пласте одинаковы в разных слоях, разделенных заданными границами для обоих приведенных примеров. Границы являются несвязными, но фрикционными плоскостями ослабления.
Случай симметричных границ по отношению к стволу скважины
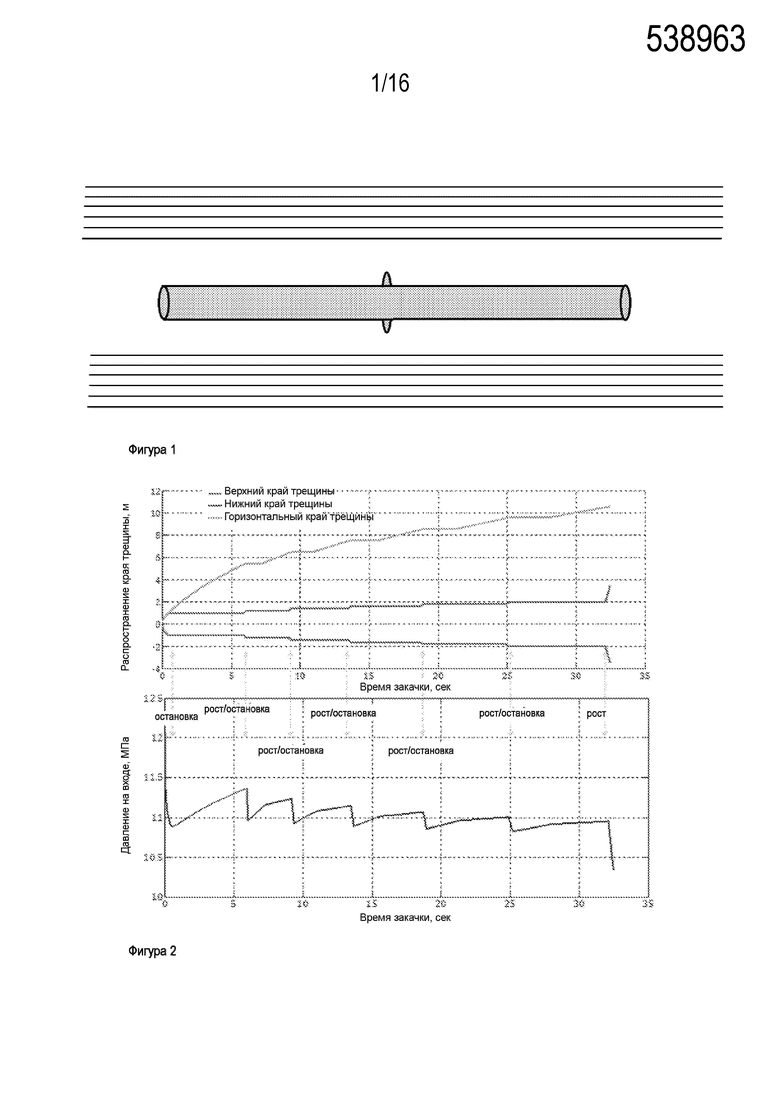
[0004] В первом примере, горизонтальные границы расположены симметрично по отношению к горизонтальному стволу скважины. Трещина гидроразрыва пласта образуется и распространяется через эти границы, а также вдоль них в горизонтальном направлении, как проиллюстрировано на Фигуре 1. На Фигуре 1 проиллюстрировано распространение трещины гидроразрыва пласта из горизонтального ствола скважины, в случае симметричного расположения горизонтальных границ по отношению к стволу скважины.
[0005] Распространение двух вертикальных краев трещины гидроразрыва пласта через границы относительно медленное, по причине непрерывных остановок в каждой из этих границ. В то же время, боковые края трещины гидроразрыва пласта распространяются без взаимодействия с границами (параллельно им). В результате, длина трещины гидроразрыва пласта кажется гораздо длиннее, чем высота (Фигура 2).
[0006] На Фигуре 2 проиллюстрировано распространение верхнего, нижнего и бокового края трещины во время закачки флюида (верхний график), и соответствующий отклик давления на входе трещины (нижний график) для симметричного расположения границ.
Случай несимметричных границ по отношению к стволу скважины
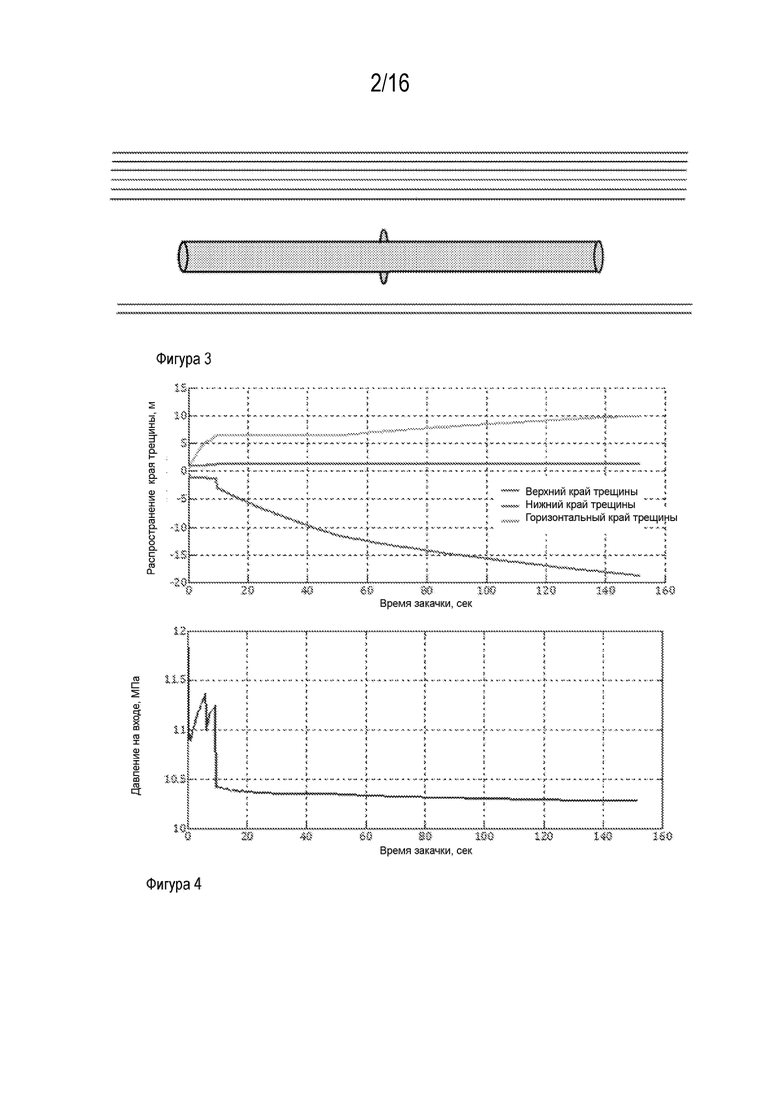
[0007] Во втором случае моделирования, несвязные горизонтальные границы расположены несимметрично по отношению к стволу скважины. Количество границ ниже ствола скважины меньше, чем то, количество границ выше ствола скважины (см. Фигуру 3). План-график накачивания, интервал между границами, и все другие параметры породы и трещины остаются такими же, как в первом примере. На Фигуре 3 проиллюстрировано распространение трещины гидроразрыва пласта из горизонтального ствола скважины в случае несимметричного расположения горизонтальных границ по отношению к стволу скважины.
[0008] Моделирование иллюстрирует, что в этом случае после пересечения двух границ ниже ствола скважины, трещина гидроразрыва пласта полностью останавливается в одной из верхних границ, и вместе с тем свободно распространяется вниз (Фигура 4). На Фигуре 4 проиллюстрировано распространение верхнего, нижнего и бокового края трещины во время закачки флюида (верхний график), и соответствующий отклик давления на входе трещины (нижний график) для несимметричного расположения границ.
[0009] Эти два примера показывают, что предварительное измерение плоскостей ослабления в породе и грамотное моделирование распространения трещины в слоистом пласте необходимы, чтобы грамотно определить сдерживание распространения высоты трещины в слоистой породе. И напротив, отсутствие информации о неоднородном профиле крепости породы в вертикальном направлении и основных границах может привести к ошибочным результатам при прогнозировании сдерживания распространения высоты трещины, обусловленного взаимодействием трещины гидроразрыва пласта с плоскостями ослабления.
[00010] Гидравлический разрыв пласта используется с целью интенсификации продуктивного пласта, как правило, направлен на распространение достаточно длинных трещин в продуктивном пласте. Трещина может быть длиной до нескольких сотен метров в горизонтальном направлении. При такой протяженности трещины, структура слоистой породы показывает сильную неоднородность по вертикали. В зависимости от типа породы, осадочные тонкие слоистости или напластования могут иметь толщину в диапазоне от нескольких миллиметров до метров. Неравномерное изменение свойств пород в вертикальном и горизонтальном направлениях приводит к заметному ограничению роста высоты трещины по отношению к распространению боковой трещины. С начала эры гидроразрыва пласта, внимание к сдерживанию распространения высоты трещины гидроразрыва пласта всегда было общепризнанным.
[00011] Подповерхностное трехмерное распространение трещин гидроразрыва пласта (далее трещин ГРП), как правило, предполагает одновременный рост трещины в горизонтальном и вертикальном направлениях. Протяженность типовой горизонтальной трещины ГРП в процессе обработки месторождения варьируется от десятков до сотен метров вдоль намеченного слоя пласта. В противоположность этому, протяженность вертикальной трещины кажется значительно короче по размеру по причине большого различия свойств породы и тектонических напряжений, а также уже существующих горизонтального напластования и тонкой слоистости границ. Существует несколько признанных механизмов, контролирующих вертикальный рост трещины ГРП (вверх или вниз) в геологических пластах: (1) изменение минимальных горизонтальных напряжений, как функция от глубины (здесь и далее называется "сравнение напряжения" или "механизм 1"), (2) сравнение модулей упругости между смежными и разными литологическими слоями (здесь и далее называется "сравнение упругости" или "механизм 2"), и (3) неустойчивая механическая граница между аналогичными или разными слоями в литологическом разрезе (здесь и далее называется "неустойчивая граница" или "механизм 3"). ʺНеустойчивая механическая границаʺ или ʺнеустойчивая границаʺ или ʺплоскость ослабленияʺ относится к любым механическим прерывистостям пласта, которые имеют низкую прочность связывания (сдвиг, растяжение, интенсивность напряжения, трение) относительно прочности скелета породы. Неустойчивая граница представляет потенциальный барьер для распространения трещины следующим образом: если трещина ГРП достигает неустойчивой границы, то она создает зону проскальзывания вблизи контакта, как проиллюстрировано посредством обоих исследований: аналитического и числового. Проскальзывание вблизи зоны контакта может задержать распространение трещины и привести к обширному просачиванию флюида или даже гидравлическому вскрытию границы посредством образования так называемых Т-образных трещин. Такие Т-образные трещины неоднократно наблюдались в различных разработках пластов каменного угля.
[00012] В настоящее время, механизм "сравнение напряжения" является основным используемым в большинстве кодов моделирования трещины ГРП для того, чтобы контролировать вертикальный рост высоты, как для псевдо 3D, так и плоских 3D-моделей. Механизм "сравнение упругости", как правило, явно не моделируется в большинстве кодов моделирования трещины ГРП, но в некотором роде, адресуется посредством механизма "сравнение напряжения", поскольку вертикальный профиль напряжения минимального горизонтального напряжения часто получается из калиброванной упругодеформируемой модели и перегруженного профиля напряжения (можно интерпретировать изотропную и трансверсальную изотропию), которые зависят от упругости пласта. Механизм "неустойчивая граница" привлекает меньше внимания в сообществе гидроразрыва до сих пор, хотя он был хорошо известен из работ по гидроразрыву пластов месторождений и обсуждался в литературе еще в 1980-е годы. Это отсутствие интереса может быть вызвано отсутствием описания расположения неустойчивых границ в глубоких слоях и/или отсутствием замеров их механических свойств (сопротивление сдвигу и растяжению, трещиностойкость, коэффициент трения и проницаемость). В то же время механизм "неустойчивой границы" является чуть ли не единственным из вышеперечисленных механизмов, который может полностью остановить трещину ГРП от дальнейшего распространения вверх или вниз в пластах. Основными причинами для завершения края трещины в неустойчивых границах являются проскальзывание границы, повышение давления посредством проникшего флюида для гидроразрыва, или даже механическое вскрытие границы. В отличие от этого, первые два механизма могут лишь временно остановить трещину ГРП, до тех пор, пока полезное давление не увеличится в трещине ГРП до порогового уровня, который позволит трещине ГРП развиваться далее. Механизм сдерживания распространения "неустойчивая граница" может быть более важен, чем механизмы "напряжение" или "сравнение упругости" и возможна причина, почему трещины ГРП часто хорошо локализуются в вертикальной протяженности, несмотря на очевидное отсутствие какого-либо наблюдаемого "напряжения" или "сравнения упругости". В любом случае, необходимы более эффективные способы для описания пласта, влияния существующих трещин на разработку новых трещин, а также описания образования трещин.
КРАТКОЕ ОПИСЕНИЕ ГРАФИЧЕСКИХ МАТЕРИАЛОВ
[00013] На Фигуре 1 проиллюстрировано распространение трещины гидроразрыва пласта из горизонтального ствола скважины, в случае симметричного расположения горизонтальных границ по отношению к стволу скважины.
[00014] Фигура 2. иллюстрирует распространение верхнего, нижнего и бокового края трещины во время закачки флюида (верхний график), и соответствующий отклик давления на входе трещины (нижний график) для симметричного расположения границ.
[00015] Фигура 3. иллюстрирует распространение трещины гидроразрыва пласта из горизонтального ствола скважины в случае несимметричного расположения горизонтальных границ по отношению к стволу скважины.
[00016] На Фигуре 4 проиллюстрировано распространение верхнего, нижнего и бокового края трещины во время закачки флюида (верхний график), и соответствующий отклик давления на входе трещины (нижний график) для несимметричного расположения границ.
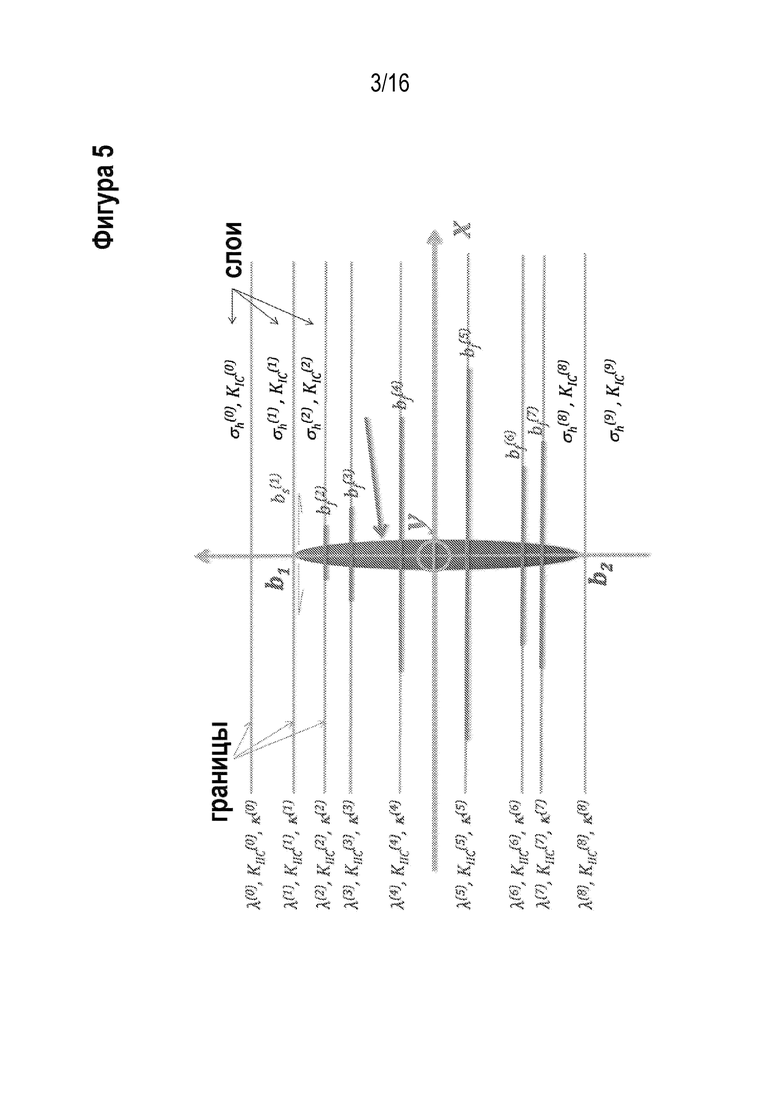
[00017] На Фигуре 5 проиллюстрировано схематическое изображение вертикального роста трещины гидроразрыва пласта (трещины ГРП) в подземной слоистой породе с горизонтальными границами.
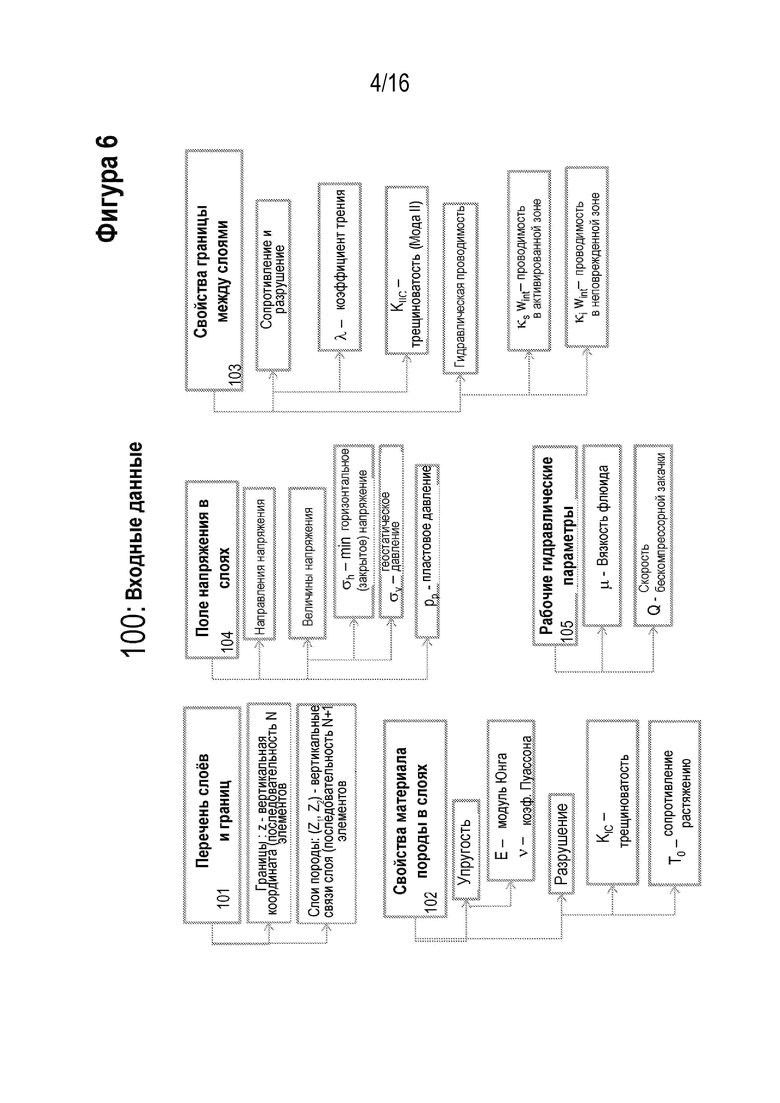
[00018] На Фигуре 6 проиллюстрирована блок-схема с указанием информации, которая может быть использована для варианта реализации в контексте настоящего изобретения.
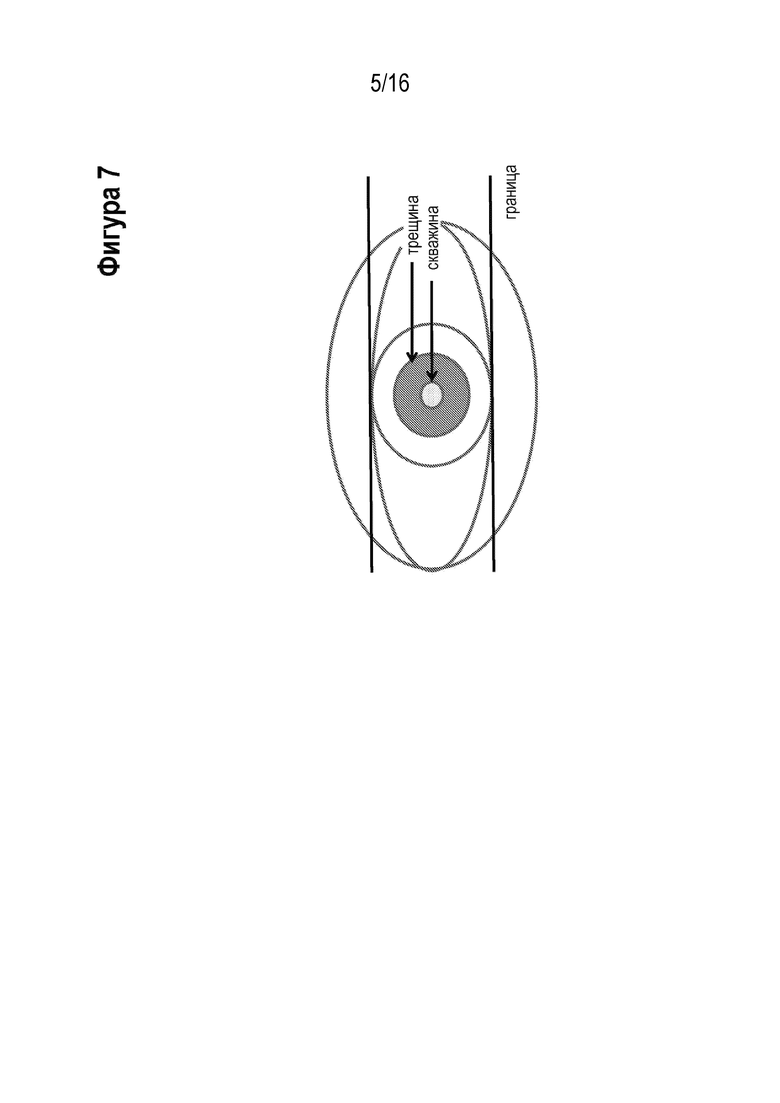
[00019] На Фигуре 7 проиллюстрированы примеры этапов для 3D развития трещин гидроразрыва через плоскости ослабления.
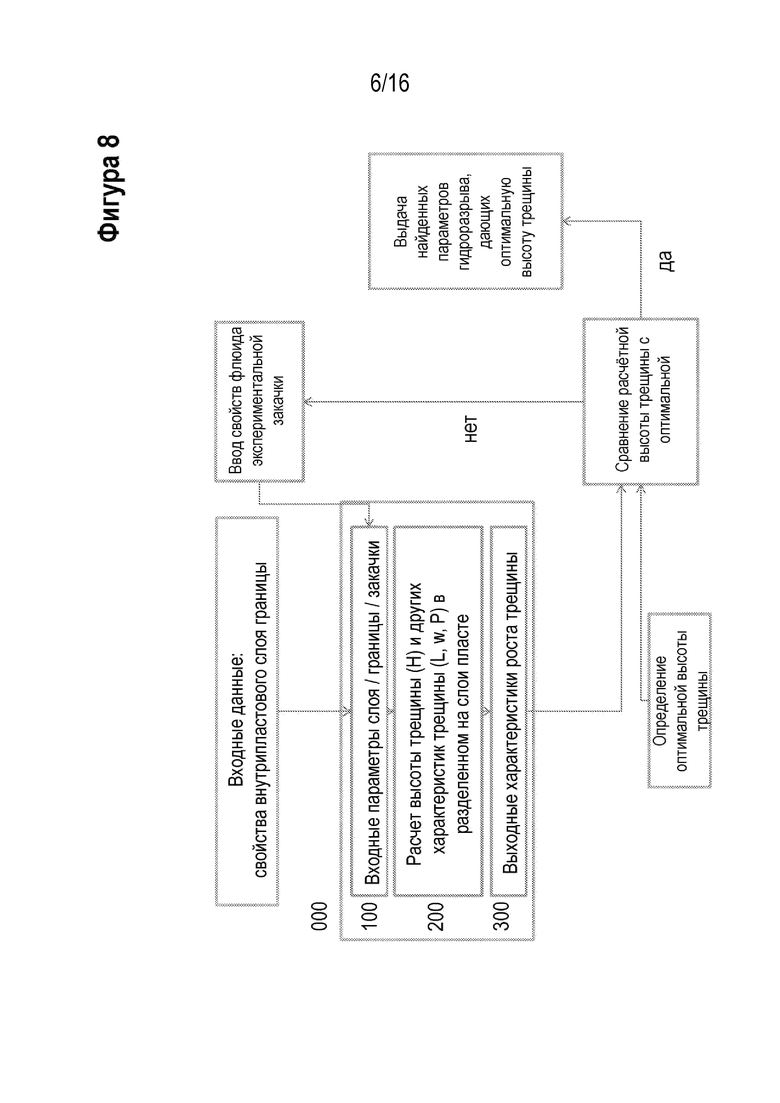
[00020] На Фигуре 8 проиллюстрирована блок-схема способов для одного из вариантов реализации настоящего изобретения.
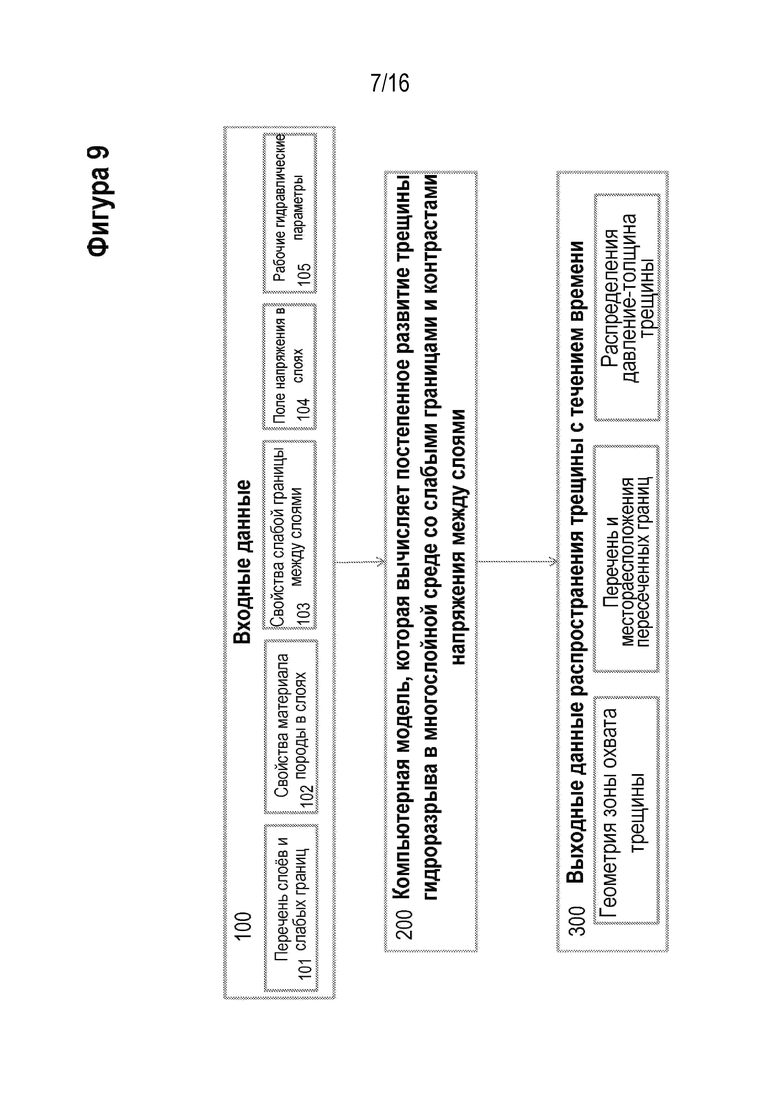
[00021] На Фигуре 9 проиллюстрирована блок-схема компонента способа для одного из вариантов реализации настоящего изобретения.
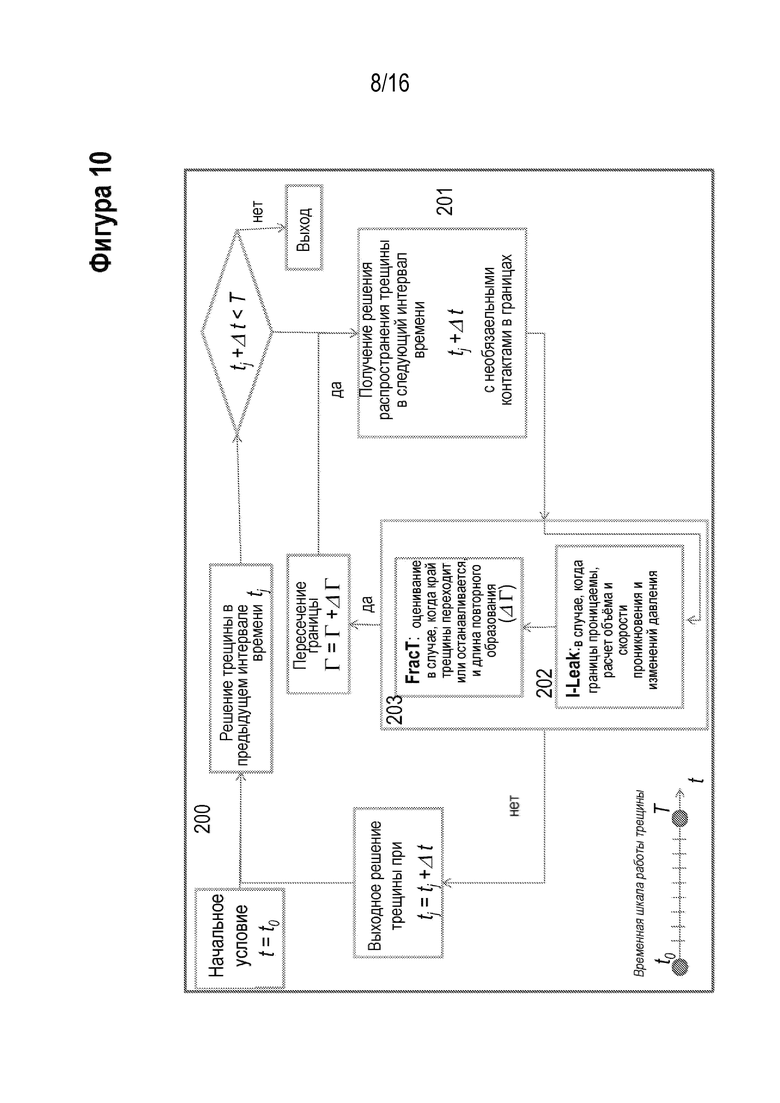
[00022] На Фигуре 10 проиллюстрирован вариант реализации алгоритма последовательности выполняемых действий компьютерной модели (200) трещины ГРП от начала операции по гидроразрыву пласта t0 до конца T.
[00023] На Фигуре 11 проиллюстрирована горизонтальная граница, пересеченная вертикальной трещиной гидроразрыва пласта (вверху), и схематическое распределение давления просочившегося флюида вдоль границы (внизу).
[00024] На Фигуре 12 проиллюстрирован профиль давления флюида вдоль границы для режимов просачивания ʺпри проскальзыванииʺ (верхний) и ʺвне проскальзыванияʺ (нижний).
[00025] На Фигуре 13 проиллюстрирован ряд схематических диаграмм, чтобы показать распространение трещины гидроразрыва пласта вверх и вниз в геометрии плоской деформации (вертикальное поперечное сечение).
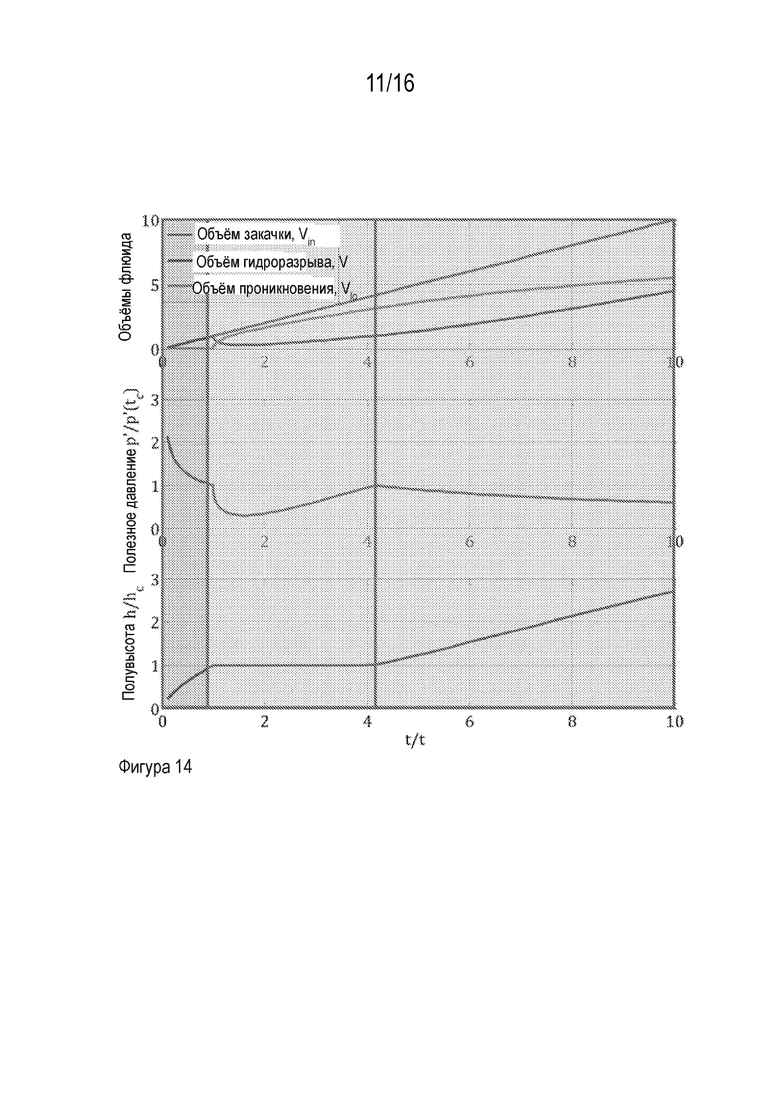
[00026] На Фигуре 14 проиллюстрированы графики объемов закачиваемого, разрывающего и утекающего флюида (вверху), полезного давления (посредине), и полувысоты трещины гидроразрыва пласта (внизу) в процессе всего цикла закачки флюида в трещину.
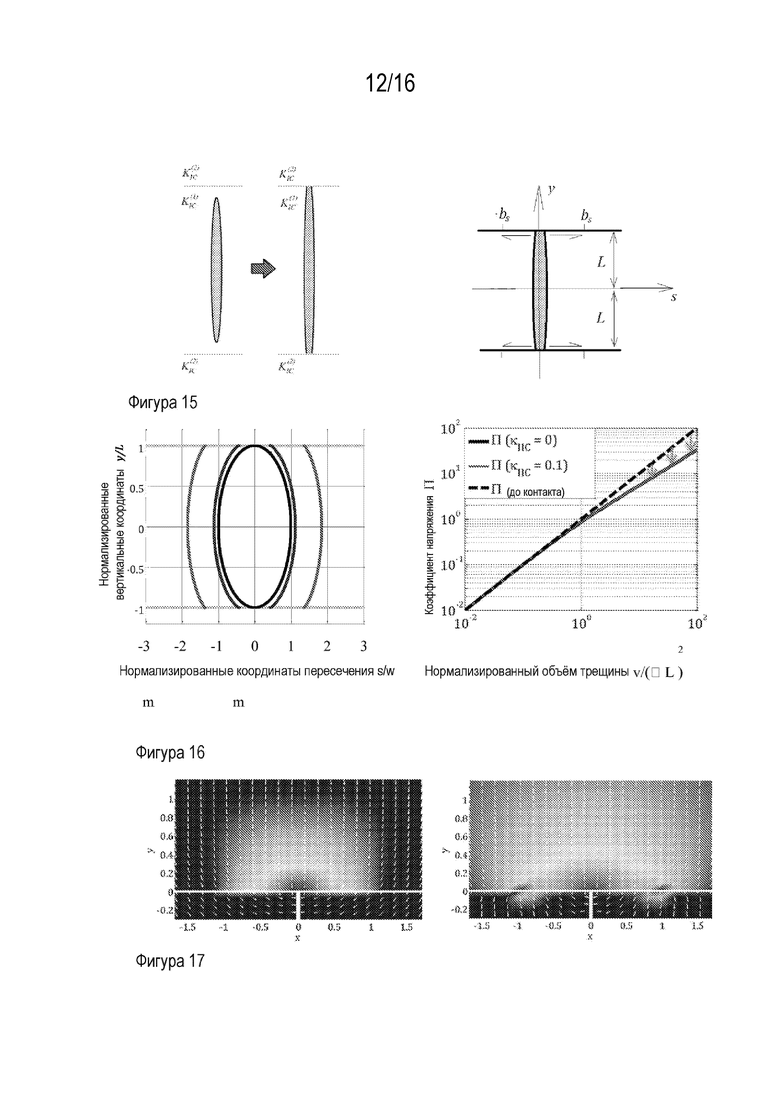
[00027] На Фигуре 15 проиллюстрирован двухсторонний контакт вертикально растущей трещины с неустойчивыми горизонтальными границами (слева), активация границ, и затупление края трещины в результате контакта с границами (справа).
[00028] На Фигуре 16 проиллюстрированы профили раскрытия вертикальной трещины (слева) при контакте с двумя несвязными границами и нормализированный объем трещины в зависимости от коэффициента напряжения (справа).
[00029] На Фигуре 17 проиллюстрирован компонент максимального напряжения при растяжении, сгенерированный на противоположной стороне несвязной (слева) и связной границы с 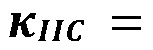
 (справа).
(справа).
[00030] На Фигуре 18 проиллюстрировано распространение края трещины (вверху) и снижение давления на входе (внизу) в случае эллиптической трещины с использованием ньютоновской жидкости с вязкостью 1 сПз (слева) и 10000 сПз (справа), соответственно.
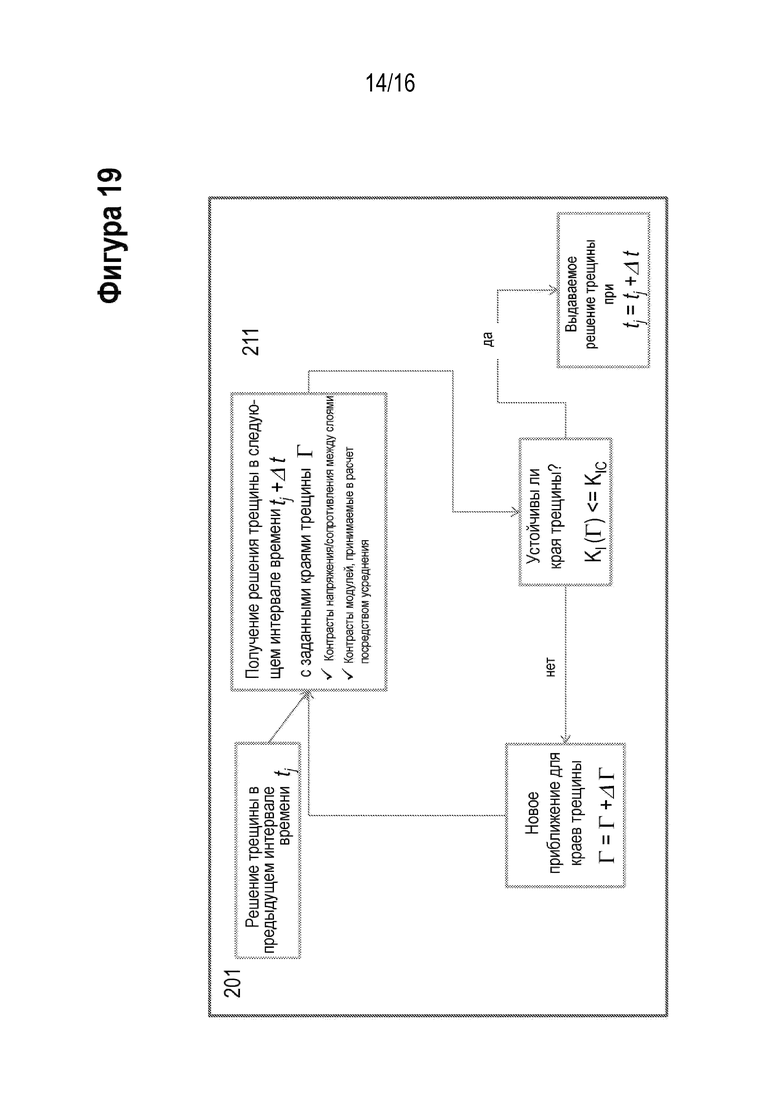
[00031] На Фигуре 19 проиллюстрирована блок-схема компонента способа для одного из вариантов реализации настоящего изобретения (алгоритм решения для распространения края трещины гидроразрыва пласта при отсутствии границ).
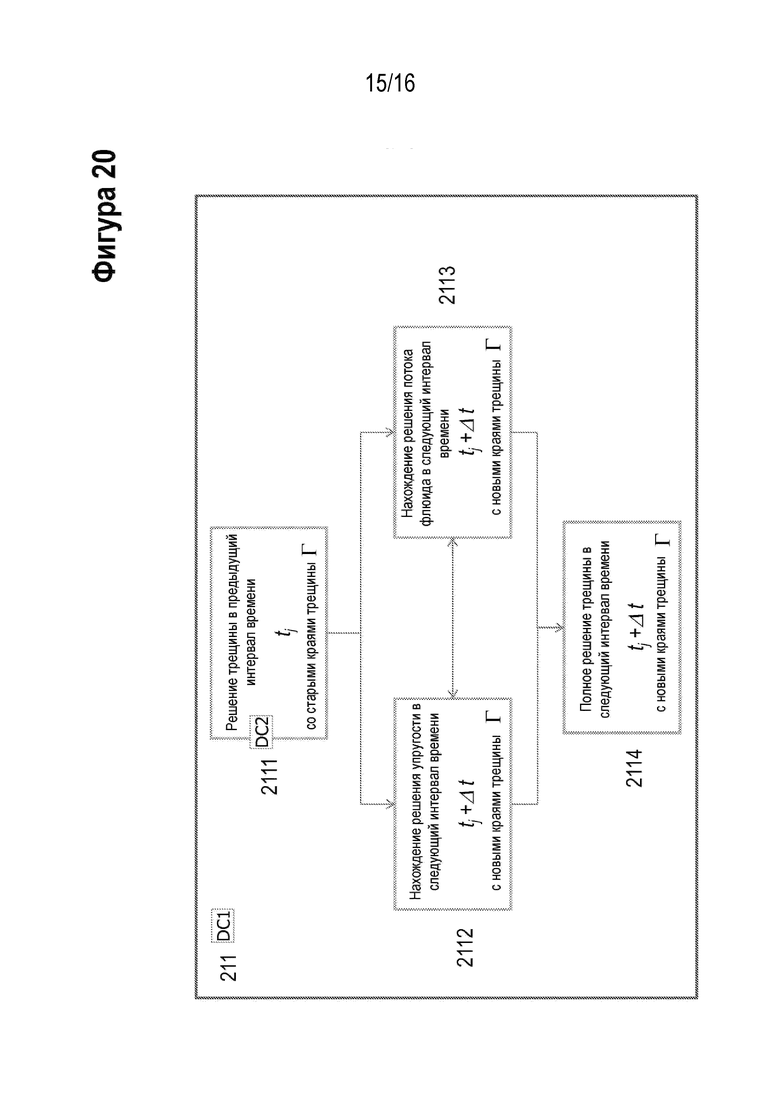
[00032] На Фигуре 20 проиллюстрирована блок-схема компонента способа для одного из вариантов реализации настоящего изобретения (подкомпонент из вышеизложенного: сопряженный алгоритм решения твердая порода - флюид для трещины гидроразрыва пласта с заданным положением края трещины).
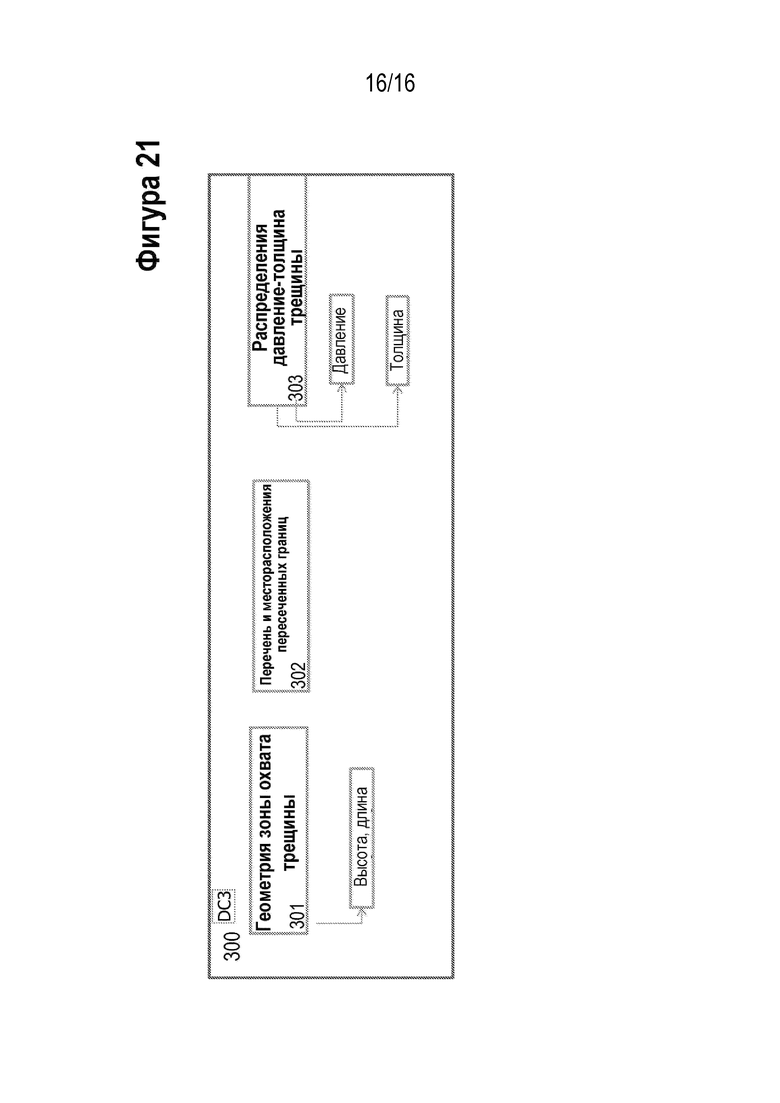
[00033] На Фигуре 21 проиллюстрирована блок-схема выходных данных для одного из вариантов реализации способа.
СУЩНОСТЬ ИЗОБРЕТЕНИЯ
[00034] Варианты реализации в контексте настоящего изобретения относятся к способу гидравлического разрыва подземного пласта, пройденного стволом скважины, включающему получение характеристик данного пласта с использованием измеренных характеристик пласта, включая механические характеристики геологических границ, идентификация высоты трещины в пласте, при этом идентификация включает расчет поверхности контакта трещины гидроразрыва пласта с геологическими границами, и гидравлический разрыв пласта, при этом вязкость флюида или скорость потока флюида либо и то, и другое выбираются с применением расчетов. Варианты реализации в контексте настоящего изобретения также относятся к способу гидравлического разрыва подземного пласта, пройденного стволом скважины, включающему проведение замеров пласта, содержащих механические характеристики геологических границ, получение характеристик пласта с использованием замеров, расчет высоты трещины пласта с использованием характеристик пласта, расчет оптимальной высоты трещины с использованием замеров, и сравнение оптимальной высоты трещины с высотой трещины пласта.
ПОДРОБНОЕ ОПИСАНИЕ ИЗОБРЕТЕНИЯ
[00035] В контексте настоящего изобретения предлагается подход, чтобы спрогнозировать рост высоты трещины гидроразрыва пласта в породах, имеющих слоистую структуру. Данный способ включает (i) предварительное получение характеристик вертикальных механических свойств породы, насыщенной флюидами, механических прерывистостей пласта и напряжения в пласте, и (ii) запуск вычислительной модели распространения 3D или псевдо 3D трещины гидроразрыва пласта в заданной слоистой породе пласта и принимая во внимание взаимодействие с заданными неустойчивыми механическими и/или проницаемыми горизонтальными границами. Способы в контексте настоящего изобретения для получения характеристик породы и самые современные способы моделирования трещины дают более точный прогноз роста высоты трещины, проникновения флюида гидроразрыва вдоль неустойчивых границ, образования T-образной трещины, контактирующей с горизонтальными границами, и изменения направления трещины от вертикальной ориентации к горизонтальной.
Ниже более подробно описаны 3 механизма, контролирующие рост высоты.
1. Механизм 1 (стандартный): изменение минимального горизонтального напряжения как функция от глубины, называемое ʺсравнение напряженияʺ
2. Механизм 2 (стандартный): сравнение модулей упругости между смежными и разными литологическими слоями, называемый ʺсравнение упругостиʺ
3. Механизм 3 (наиболее важный, является новшеством данной заявки): неустойчивая механическая граница между аналогичными или разными слоями в литологическом разрезе, называемая ʺнеустойчивая границаʺ
a. Подмеханизм 3а: упругое взаимодействие, критерий пересечения, и повторное образование позади границы
b. Подмеханизм 3b: повышенное проникновение флюида гидроразрыва через границу
Описание вертикальной текстуры породы
[00036] Для того, чтобы сделать точный прогноз роста высоты трещины, требуется информация о свойствах породы, о механических прерывистостях пласта, и о напряжении в пласте. Информация о породе содержит подробное вертикальное распределение механических свойств толщи породы, включая изменение крепости породы, с точки зрения, например, прочности на разрыв, прочности на сжатие (например, временное сопротивление породы одноосному сжатию или UCS) и трещиностойкости, которое должно предоставить информацию о расположении плоскости ослабления в породе посредством свойств упругости (например, модуль Юнга и коэффициент Пуассона). Замер напряжений породы должен донести информацию о вертикальном напряжении и минимальном горизонтальном напряжении в условиях нормального напряжения, когда компонент вертикального напряжения является наибольшим сжимающим компонентом напряжения (или условия удар-проскальзывание, когда вертикальное напряжение является промежуточным сжимающим компонентом напряжения).
[00037] Существуют доступные инструменты получения характеристик свойств породы, которые могут быть использованы для механического измерения свойств породы. Таковыми являются ультразвуковой сканер и наклонограммы (например, REW: FMI, UBI; OBMI; например, LWD: MicroScope, geoVISION, EcoScope, PathFinder Density Imager), которые могут предоставить информацию о свойствах упругости и о расположениях существовавших ранее границ. В случае, когда доступны образцы керна, в исследовательской лаборатории можно выполнить гетерогенный анализ породы (HRA) на образцах керна, извлеченных из данной толщи породы, а также склерометрическое испытание, которое предоставляет информацию о статистическом распределении плоскости ослабления на шкале образцов керна и их свойствах (сопротивление растяжению и сжатие, трещиностойкость).
[00038] Таким образом, входными свойствами, которые следует охарактеризовать, являются:
- Плотность (т.е. инверсия разряженности) и ориентация (в основном горизонтальная) неустойчивых границ как функция от глубины
- Механические и гидравлические свойства неустойчивых границ (соответственно, трение, связность, сопротивление растяжению, и трещиностойкость, а также проницаемость и заполнение)
- Вертикальное напряжение (Sv) как функция от глубины
- Минимальное горизонтальное напряжение (Sh) как функция от глубины
- Упругость породы, насыщенной флюидами (например, модуль Юнга и коэффициент Пуассона) как функция от глубины
В Таблице 1 приводится классификация источников данных и параметры модели для данного типа породы и продуктивного пласта. Инструменты SONICSCANNERTM и ISOLATION SCANNERTM имеются в продаже от Schlumberger Technology Corporation из Sugar Land, штат Техас.
[00039] На Фигуре 5 проиллюстрировано схематическое изображение вертикального роста трещины гидроразрыва пласта (трещины ГРП) в подземной слоистой породе. Трещина ГРП распространяется вертикально (в плоскости проскальзывания) и в боковом направлении (поперек плоскости проскальзывания) посредством накачки флюида для гидроразрыва (серый цвет) из скважины. Вертикальное распространение происходит вверх и вниз и характеризуется координатами b1 и b2 соответственно. На рост высоты с обеих сторон оказывают влияние механические свойства слоев породы там, где есть края трещины (например трещиностойкость), ограничение напряжений породы, и гидромеханические свойства границ между смежными слоями (например коэффициент трения, трещиностойкость, гидравлическая проводимость). Распространение трещины ГРП связано с проникновением флюида гидроразрыва из трещины ГРП вдоль гидравлически проводящих границ.
[00040] На Фигуре 6 представлен подробный обзор семейств входных параметров и наименования каждого параметра в семействе, требуемого для компьютерной модели трещины ГРП.
[00041] Далее приводится обсуждение основных принципов. Существуют три основных механизма, относящихся к ограничению развития трещины ГРП в высоту: (i) сравнения напряжений породы и прочностей между смежными слоями породы (ʺмеханизм 1ʺ, представленный выше), (201), (ii) повышенное проникновение флюида гидроразрыва через плоскости напластования, представленное в контексте настоящего изобретения физической моделью ILeak (202) (подмеханизм ʺмеханизма 3ʺ, представленный выше), и (iii) упругое взаимодействие со слабо связными скользящими границами, представленное в контексте настоящего изобретения физической моделью FracT (203) (подмеханизм ʺмеханизма 3ʺ, представленный выше).
[00042] На Фигуре 7 представлен пример последовательного роста трещины ГРП в высоту, на который оказывает влияние взаимодействие со слабо связными и проводящими границами. Равномерный рост трещины ГРП временно задерживается посредством непосредственного контакта краев трещины с верхней и нижней границами, тем временем продолжается ее распространение в боковом направлении. После некоторой задержки краев трещины ГРП в границах, трещина ГРП повторно начинает свой вертикальный рост через них. Этапы следующие.
Радиальная трещина: равное распространение во всех направлениях
Края достигают границы
Вертикальные края временно задержаны, горизонтальные края продолжают распространяться
Трещина разрывает границу и распространяется вертикально
[00043] На Фигуре 8 продемонстрирована последовательность выполняемых действий при планировании роста высоты трещины ГРП, не вдаваясь в подробности. Она включает ввод предварительно заданных измеренных или рассчитанных свойств породы и границы с одной стороны, и ввод контролирующих параметров трещины ГРП по плану-графику накачивания, с другой стороны. Ими заполняется модель для моделирования роста трещины ГРП (000), которая описана ниже. Результаты моделирования поступают в модуль сравнения, чтобы выявить отклонение моделируемой высоты трещины по отношению к оптимальной. В зависимости от допуска роста высоты трещины, полученного при моделировании, он регулирует параметры накачки флюида для следующего цикла моделирования трещины ГРП или выдает используемые параметры накачки, которые производят оптимальную высоту трещины ГРП в данной породе.
[00044] Далее будет рассмотрено моделирование распространения трещины в вертикально неоднородной слоистой среде. Подразумевается, что модель трещины должна обеспечить решение сопряженной системы уравнений для механического отклика породы, окружающей трещину, и вязкого потока флюида, закачиваемого в трещину. Следует предположить, что определимая прочность породы и непрерывное протекание флюида в трещину будет приводить к распространению краев трещины (контур в 3D геометрии) и закачиваемому внутрь толщи породы флюиду. Используемые уравнения, описывающие механику отклика как твердой породы, так и потока флюида внутри трещины, должны быть преимущественно трехмерными для того, чтобы рассчитывать рост трещины в горизонтальном и вертикальном направлениях. Взаимодействие распространения трещины в обоих направлениях с объемом закачиваемого флюида позволит оценить сдерживание распространения высоты трещины в породе для промышленных объемов закачиваемого флюида.
[00045] Модель трещины должна учитывать не только разные напряжения и свойства породы в различных слоях породы, но и взаимодействие краев трещины с плоскостями ослабления, такими как плоскости напластования и границы с тонкой слоистостью. Следует предположить, что механическое взаимодействие трещины гидроразрыва пласта с этими границами может неизбежно привести к созданию зон повышенной гидравлической проницаемости вдоль этих границ и существенному проникновению флюида гидроразрыва. Влияния плоскостей ослабления и повышенной проницаемости границы должны быть ключевыми компонентами предполагаемой расчетной модели распространения трещины в слоистых пластах.
[00046] В контексте настоящего изобретения разработана обширная аналитическая модель взаимодействия трещины гидроразрыва пласта, пересечения и последующего роста через неустойчивые горизонтальные границы в предельном случае низковязкого трения флюида (доминирует режим трещиностойкости). Последнее подтверждается при условии, что скорость распространения вертикального края трещины уменьшается. Также оцениваются модифицированные механические характеристики трещины, такие как полезное давление, раскрытие (ширина) и протяженность зоны проскальзывания, когда трещина отклоняется посредством границы. Оценка состояния для пересечения границы обуславливает обнаружение запаздывания завершения трещины в границе. Общая картина прерывистого характера роста трещины через ряд плоскостей ослабления в дальнейшем используется в сопряженном с флюидом получении характеристик распространения трещины в высоту в обеих геометриях эллиптической трещины: деформация в одной плоскости и трехмерная.
[00047] Построение эффективной модели распространения трещины в тонко расслоенной среде приводит к модели анизотропной среды с различной трещиностойкостью в вертикальном и горизонтальном направлениях. Оценивается соотношение длины и высоты эллиптической трещины в такой среде при заданных свойствах трения и связности границ. Другие механизмы сдерживания распространения трещины, вызванные сравнениями напряжения и свойств породы между слоями, могут применяться поверх этой модели, чтобы использовать ее в современных инструментах моделирования трещины.
[00048] На Фигуре 9 объясняется концептуальная структура компьютерной модели (000) трещины ГРП. Она содержит входные данные (100), более подробно описанные выше, спецпроцессор моделирования (200) и выходные данные (300). Спецпроцессор моделирования и выходные данные более подробно описаны ниже. На Фигуре 10 проиллюстрирован вариант реализации последовательности выполняемых действий алгоритма компьютерной модели трещины ГРП (200) от начала операции по гидроразрыву пласта t0 до конца T. В каждом последующим интервале времени проблема распространения трещины решается обычным способом (201), чтобы не было взаимодействия с границами в породе. Далее, при условии, что трещина ГРП имела контакт с или пересекла какие-либо границы породы, вызывается модуль проникновения флюида гидроразрыва ILeak (202) для обновления объема флюида трещины ГРП, скорости потока, и колебаний давления флюида внутри трещины ГРП и в пропитанных границах. Далее в случае, когда край трещины ГРП достигает какой-либо границы, модуль FracT (203) оценивает потенциальную задержку края трещины или пересечение границы в заданный интервал времени. В случае, когда край трещины задерживается, она остается нераспространяющейся в течение следующего интервала времени. В противном случае, когда трещина ГРП пересекает границу или не контактирует, модуль увеличивает ее длину и переходит к следующему интервалу времени.
[00049] Модуль ILeak (202) будет описан более подробно ниже. Вводимая информация содержит границу, давление в зоне контакта, вязкость флюида, и интервал времени. Модуль работает при каждом изменении времени для всех контактирующих или пересеченных границ. Модуль не воспринимает упругого взаимодействия и существования проникновения флюида гидроразрыва в границах. Модуль вычисляет возрастание просачивания флюида с использованием заданной границы для изменения во времени и предлагает фронт флюида, проникновение из объема, и скорость потока в границу.
[00050] Рассмотрим ортогональный стык вертикальной трещины гидроразрыва пласта и горизонтальной границы. Граница конечной мощности 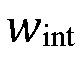 заполняется проницаемым материалом. Собственной проницаемостью заполняющего материала в неповрежденных частях границ является
заполняется проницаемым материалом. Собственной проницаемостью заполняющего материала в неповрежденных частях границ является 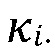 . Предположим, что определенный сегмент границы,
. Предположим, что определенный сегмент границы, 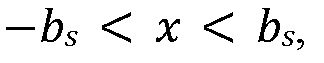 поблизости стыка активируется посредством сдвигового смещения в результате механического взаимодействия с трещиной гидроразрыва пласта. Это приводит к повреждению заполняющего материала в этом сегменте и изменению его проницаемости до
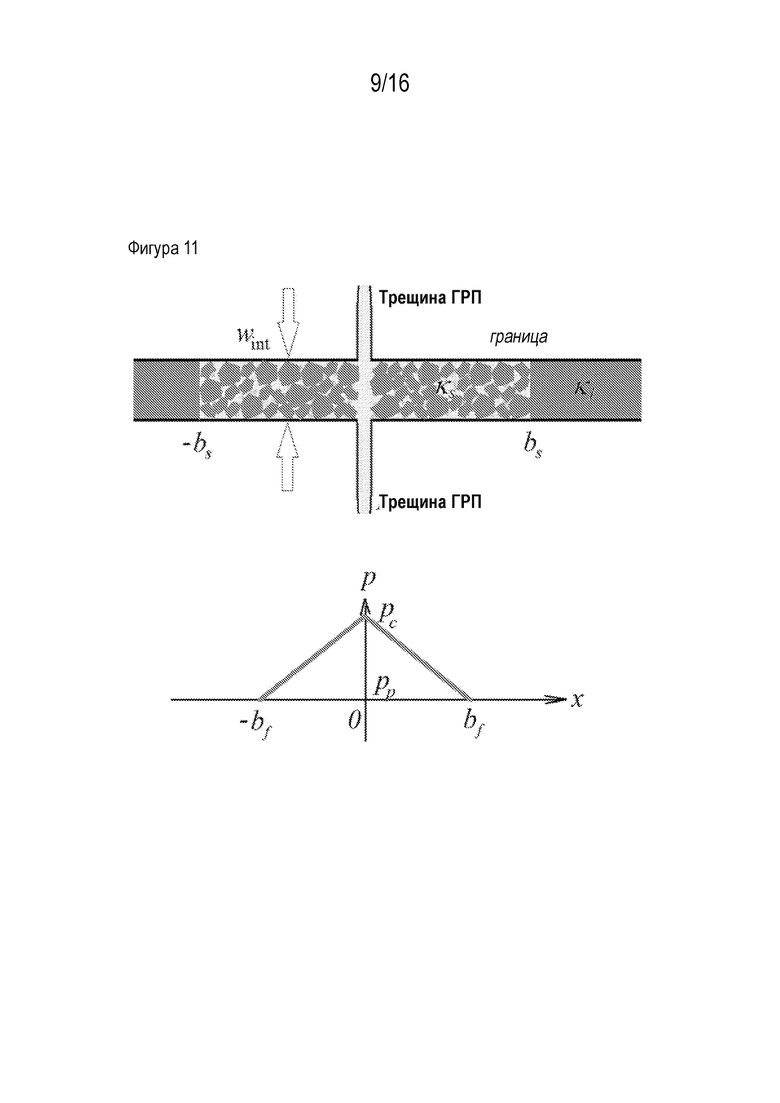
поблизости стыка активируется посредством сдвигового смещения в результате механического взаимодействия с трещиной гидроразрыва пласта. Это приводит к повреждению заполняющего материала в этом сегменте и изменению его проницаемости до 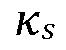 (Фигура 11). На Фигуре 11 проиллюстрирована горизонтальная граница, пересеченная вертикальной трещиной гидроразрыва пласта (вверху), и схематическое распределение давления просочившегося флюида вдоль границы (внизу).
(Фигура 11). На Фигуре 11 проиллюстрирована горизонтальная граница, пересеченная вертикальной трещиной гидроразрыва пласта (вверху), и схематическое распределение давления просочившегося флюида вдоль границы (внизу).
[00051] В малопроницаемых пластах 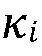 может быть пренебрежимо мало. Это условие
может быть пренебрежимо мало. Это условие 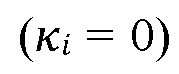 может быть использовано позже, чтобы упростить модель проникновения. С другой стороны, участок активации границы может быть существенно более проницаемым, чем внутренний участок, посредством измельченных зерен заполняющего материала или сдвига растяжений. Активация проскальзывания минерализованных границ может быть доминирующим механизмом для проникновения флюида гидроразрыва в малопроницаемые породы с ультра-низкой проницаемостью.
может быть использовано позже, чтобы упростить модель проникновения. С другой стороны, участок активации границы может быть существенно более проницаемым, чем внутренний участок, посредством измельченных зерен заполняющего материала или сдвига растяжений. Активация проскальзывания минерализованных границ может быть доминирующим механизмом для проникновения флюида гидроразрыва в малопроницаемые породы с ультра-низкой проницаемостью.
[00052] Допустим, что поток флюида для гидроразрыва вдоль проницаемой границы является одномерным, устойчивым и потенциальным. В этих условиях можно описать следующим законом Дарси
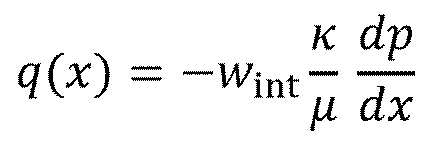 (1)
(1)
где 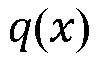 представляет собой 2D скорость просачивания флюида внутрь материала проницаемости
представляет собой 2D скорость просачивания флюида внутрь материала проницаемости 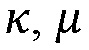 представляет собой вязкость флюида, и
представляет собой вязкость флюида, и 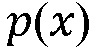 представляет собой распределение давления флюида вдоль границы (Фиг. 11, внизу). Иногда оказывается удобным заменить результат
представляет собой распределение давления флюида вдоль границы (Фиг. 11, внизу). Иногда оказывается удобным заменить результат 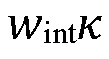 гидравлической проводимостью границы
гидравлической проводимостью границы 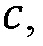 как правило, измеряемой в лаборатории (и использовать
как правило, измеряемой в лаборатории (и использовать 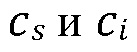 обозначения далее, соответственно).
обозначения далее, соответственно).
[00053] Общая скорость проникновения флюида гидроразрыва из трещины гидроразрыва пласта в конкретную границу в точке стыка 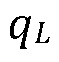 удваивается посредством симметричного отклонения флюида в обе стороны от границы
удваивается посредством симметричного отклонения флюида в обе стороны от границы
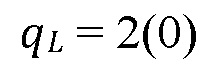 (2)
(2)
Посредством симметрии просачивания флюида в обе стороны от границы, в дальнейшем получается решение только для положительного направления 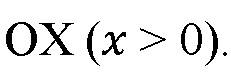 Закон Дарси (1) устанавливает связь между локальной скоростью потока q и соответствующим падением давления флюида
Закон Дарси (1) устанавливает связь между локальной скоростью потока q и соответствующим падением давления флюида 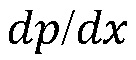 в каждой точке проницаемого материала, пропитанного флюидом. Запишем этот закон сначала для скорости потока
в каждой точке проницаемого материала, пропитанного флюидом. Запишем этот закон сначала для скорости потока 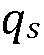 и падения давления
и падения давления 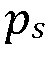 в пределах (сдвинутого) участка активации как
в пределах (сдвинутого) участка активации как
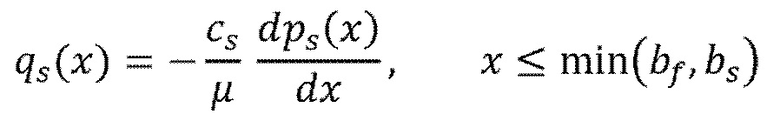 (3)
(3)
и для скорости флюида 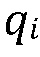 и давления
и давления 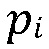 в пределах неповрежденного участка границы
в пределах неповрежденного участка границы
 (4)
(4)
где 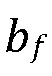 представляет собой фронт просочившегося флюида. Вне зоны проникшего флюида предполагается условие внутрипластового давления, т.е.
представляет собой фронт просочившегося флюида. Вне зоны проникшего флюида предполагается условие внутрипластового давления, т.е.
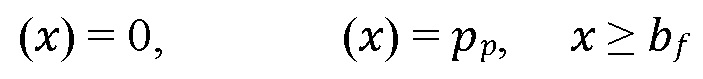 (5)
(5)
Решение должно включать положение просачившегося фронта флюида  и профиль давления (x) в каждый момент времени процесса проникновения.
и профиль давления (x) в каждый момент времени процесса проникновения.
Из уравнения массового равновесия флюида, написанного для несжимаемого флюида в пределах границы с непроницаемыми стенками (за исключением точки стыка)
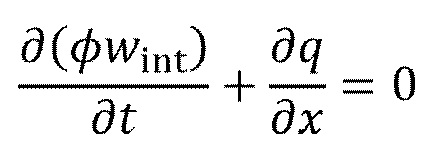 (6)
(6)
где 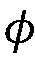 представляет собой пористость заполняющего материала или естественные шероховатости границы,
представляет собой пористость заполняющего материала или естественные шероховатости границы, 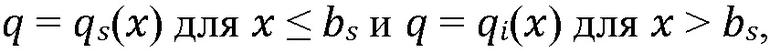 отсюда следует, что в случае, когда ширина
отсюда следует, что в случае, когда ширина 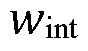 является константой
является константой 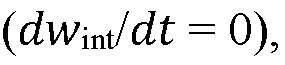 скорость потока q имеет равномерное значение вдоль координат границы, являясь лишь функцией от времени, т.е.
скорость потока q имеет равномерное значение вдоль координат границы, являясь лишь функцией от времени, т.е.
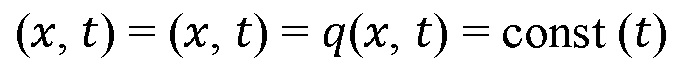 (7)
(7)
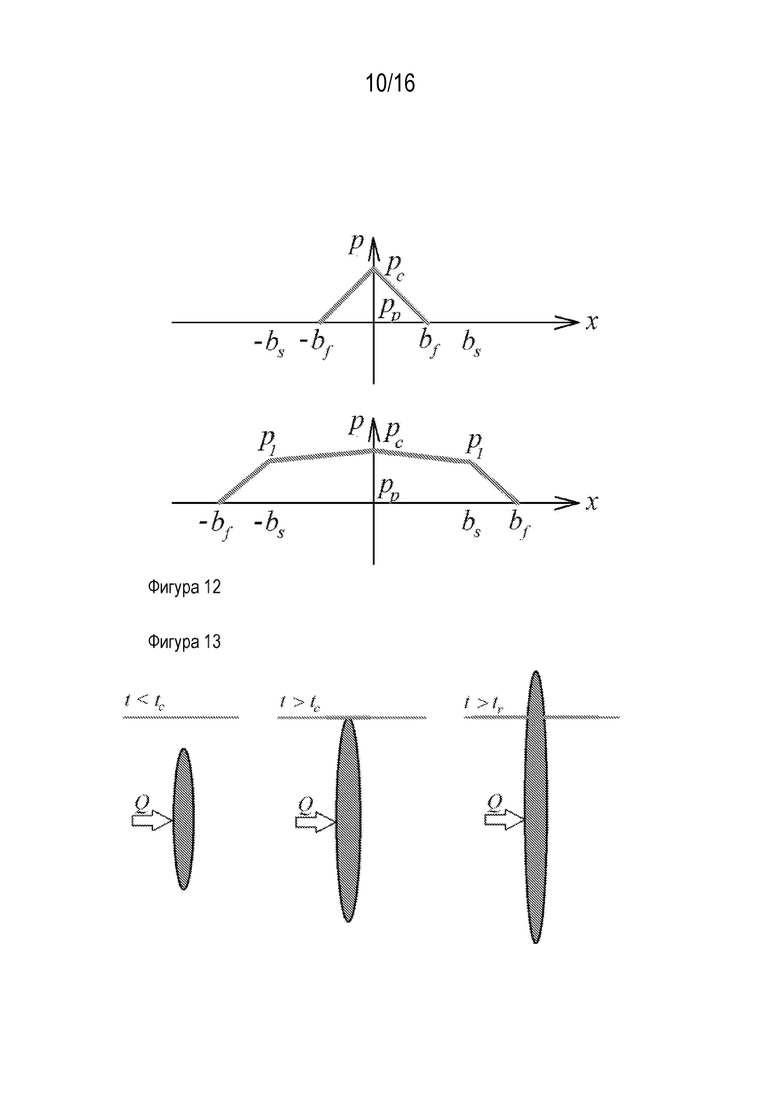
С учетом (7) и граничного условия (5) при 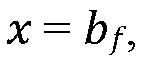 решение (3) - (4) для распределения давления просочившегося флюида (x) вдоль границы указывает на линейное затухание, проиллюстрированное на Фигуре 12. На Фигуре 12 проиллюстрирован профиль давления флюида вдоль границы для режимов просачивания ʺпри проскальзыванииʺ (верхний) и ʺвне проскальзыванияʺ (нижний).
решение (3) - (4) для распределения давления просочившегося флюида (x) вдоль границы указывает на линейное затухание, проиллюстрированное на Фигуре 12. На Фигуре 12 проиллюстрирован профиль давления флюида вдоль границы для режимов просачивания ʺпри проскальзыванииʺ (верхний) и ʺвне проскальзыванияʺ (нижний).
Решение для профиля давления записывается отдельно для двух режимов просачивания флюида в границу: просачивание ʺпри проскальзыванииʺ, когда просочившийся флюид полностью содержится в пределах зоны проскальзывания границы, т.e. 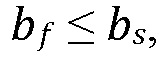 и просачивание ʺвне проскальзыванияʺ в зону неповрежденной границы также, т.e.
и просачивание ʺвне проскальзыванияʺ в зону неповрежденной границы также, т.e. 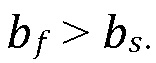 Для проникновения ʺпри проскальзыванииʺ (Фиг. 12, верхняя), получается следующий линейный профиль давления
Для проникновения ʺпри проскальзыванииʺ (Фиг. 12, верхняя), получается следующий линейный профиль давления
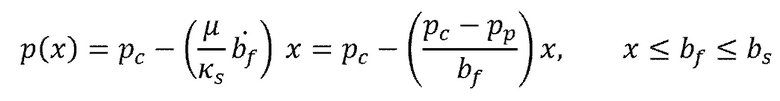 (8)
(8)
где 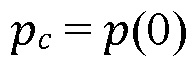 представляет собой давление флюида в ʺконтактеʺ с трещиной гидроразрыва пласта, т.e. р=0. Для проникновения "вне проскальзывания" (Фиг. 12, нижняя), получается следующий ломанный линейный профиль
представляет собой давление флюида в ʺконтактеʺ с трещиной гидроразрыва пласта, т.e. р=0. Для проникновения "вне проскальзывания" (Фиг. 12, нижняя), получается следующий ломанный линейный профиль
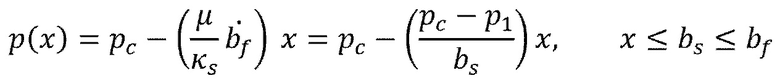 (9)
(9)
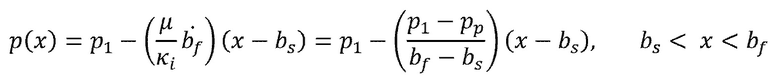 (10)
(10)
где 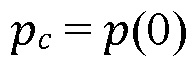 представляет собой давление флюида в вершине зоны проскальзывания. В (8)-(10) принимается во внимание, что
представляет собой давление флюида в вершине зоны проскальзывания. В (8)-(10) принимается во внимание, что
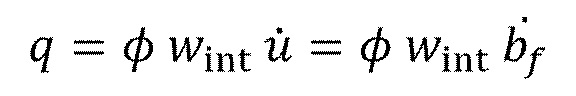 (11)
(11)
где 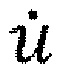 представляет собой продольную скорость флюида (верхняя точка означает дифференцирование по времени), равную скорости распространения просачиваемого флюида
представляет собой продольную скорость флюида (верхняя точка означает дифференцирование по времени), равную скорости распространения просачиваемого флюида 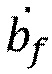 Таким образом, из (8) - (10) получим следующие обыкновенные дифференциальные уравнения для распространения фронта флюида (t) сразу после контакта
Таким образом, из (8) - (10) получим следующие обыкновенные дифференциальные уравнения для распространения фронта флюида (t) сразу после контакта  для проникновения флюида ʺпри проскальзыванииʺ:
для проникновения флюида ʺпри проскальзыванииʺ:
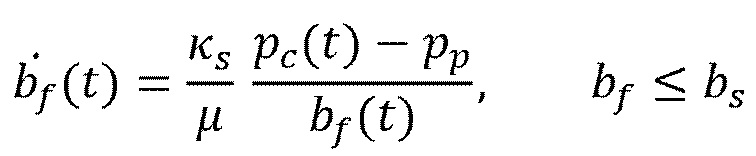 (12)
(12)
и для проникновения "вне проскальзывания":
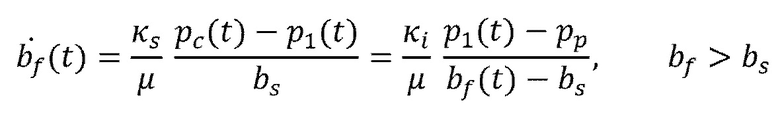 (13)
(13)
где давление флюида на вершине зоны проскальзывания 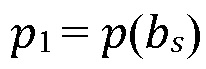 находится как
находится как
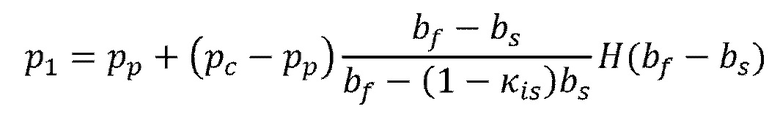 (14)
(14)
где 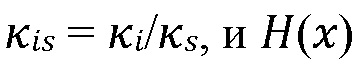 является ступенчатой функцией Хевисайда (ноль для отрицательных, и единица для положительных аргументов соответственно).
является ступенчатой функцией Хевисайда (ноль для отрицательных, и единица для положительных аргументов соответственно).
[00054] Решение уравнений (12) - (13) находится для обоих режимов проникновения флюида следующим образом
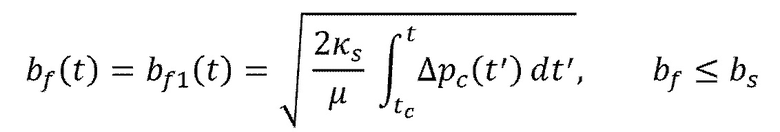 (15)
(15)
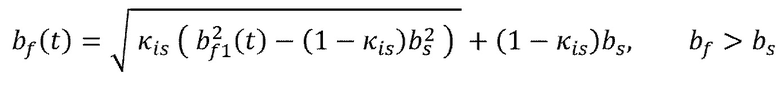 (16)
(16)
где 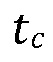 представляет собой время в начале контакта трещина-граница,
представляет собой время в начале контакта трещина-граница, 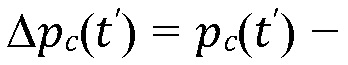
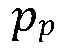 представляет собой перепад давления флюида на границе. Постепенное изменение перепада давления со временем, таким образом, обуславливает процесс проникновения через данную контактирующую границу.
представляет собой перепад давления флюида на границе. Постепенное изменение перепада давления со временем, таким образом, обуславливает процесс проникновения через данную контактирующую границу.
[00055] Рассмотрим вертикальную трещину плоской деформации, накачиваемую с постоянной скоростью закачки, и распространяющуюся симметрично вверх и вниз в однородной породе. Пусть проницаемая граница расположена на некотором расстоянии y=ℎc от точки закачки y=0. После того, как высота трещины достигает ℎ=ℎc, флюид начинает просачиваться в границу. В момент времени 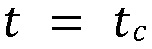 трещина может остановиться или продолжить расти с некоторым проникновением, как проиллюстрировано на Фигуре 13. На Фигуре 13 проиллюстрирована трещина гидроразрыва пласта, распространяющаяся вверх и вниз в геометрии плоской деформации (вертикальное поперечное сечение). Существуют три различных этапа: (слева) предварительный контакт с растущей трещиной без проникновения, (посредине) ранний контакт с нерастущей трещиной с проникновением, и (справа) поздний контакт с растущей трещиной с проникновением.
трещина может остановиться или продолжить расти с некоторым проникновением, как проиллюстрировано на Фигуре 13. На Фигуре 13 проиллюстрирована трещина гидроразрыва пласта, распространяющаяся вверх и вниз в геометрии плоской деформации (вертикальное поперечное сечение). Существуют три различных этапа: (слева) предварительный контакт с растущей трещиной без проникновения, (посредине) ранний контакт с нерастущей трещиной с проникновением, и (справа) поздний контакт с растущей трещиной с проникновением.
[00056] Допустим, что до прямого контакта с границей при 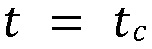 гидравлическая трещина распространяется без какого-либо упругого или гидравлического взаимодействия. Удаленно размещенная проницаемая граница не активируется механически из-за приближающейся трещины и, таким образом, она не меняет состояние напряжения вокруг. Перед контактом, закачиваемый флюид полностью содержится внутри трещины в качестве среды, как предполагается, не проницаемой. Сразу после контакта с границей (
гидравлическая трещина распространяется без какого-либо упругого или гидравлического взаимодействия. Удаленно размещенная проницаемая граница не активируется механически из-за приближающейся трещины и, таким образом, она не меняет состояние напряжения вокруг. Перед контактом, закачиваемый флюид полностью содержится внутри трещины в качестве среды, как предполагается, не проницаемой. Сразу после контакта с границей (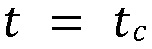 ), флюид протекает внутрь границы и приводит к потере объема флюида, наполняющего трещину гидроразрыва. Трещина продолжает расти, как только потеря объема флюида компенсируется посредством закачиваемого объема в более позднее время
), флюид протекает внутрь границы и приводит к потере объема флюида, наполняющего трещину гидроразрыва. Трещина продолжает расти, как только потеря объема флюида компенсируется посредством закачиваемого объема в более позднее время 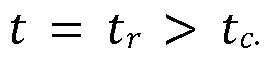 Далее предоставляется подробный пример механики распространения трещины, зависимой от присутствия гидравлически проводящей границы на пути роста ее высоты по Фигуре 14.
Далее предоставляется подробный пример механики распространения трещины, зависимой от присутствия гидравлически проводящей границы на пути роста ее высоты по Фигуре 14.
[00057] Фигура 14. Объемы закачиваемого, разрывающего и утекающего флюида (вверху), полезное давление (посредине), и полувысота трещины гидроразрыва пласта (внизу) в процессе всего цикла закачки флюида в трещину. Диапазон времени слева, закрашенный синим цветом, является этапом предварительного контакта. Средний диапазон времени, закрашенный оранжевым цветом, является этапом раннего контакта. Диапазон времени справа, закрашенный зеленым цветом, является этапом позднего контакта. В самом начале (в диапазоне времени, закрашенном синим цветом) трещина гидравлического разрыва распространяется без взаимодействия и проникновения. Понижение полезного давления и рост высоты трещины следуют ожидаемому поведению. Сразу же после контакта с проницаемой плоскостью (в диапазоне времени, закрашенном желтым цветом), начинается проникновение, следующее известному асимптотическому поведению. Первоначально оно доминирует над закачкой, как было спрогнозировано из уравнения просачивания выше, а объем флюида разрыва 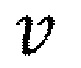 частично падает. Скорость проникновения через границу постепенно уменьшается со временем просачивания. В процессе этапа раннего контакта скорость проникновения становится меньше, чем скорость закачки в трещину. Это возобновляет увеличение объема флюида внутри трещины гидроразрыва пласта, потерянного в момент контакта. Когда потри объема флюида из-за проникновения полностью компенсируются посредством постконтактной закачки в трещину, тогда снова достигается критическое полезное давление внутри трещины, и она повторно начинает свой вертикальный рост (диапазон времени, закрашенный зеленым цветом). На поздней стадии контакта, рост трещины происходит с постоянным проникновением. Скорость накачивания объема, занятого трещиной, вследствие этого, меньше, чем она была до контакта, таким образом падение полезного давления и скорость роста высоты трещины также меньше. В случае, когда проникновение происходит только через одну границу, скорости роста трещины будут возвращаться к первоначальным значениям со временем, когда проникновение становится пренебрежимо малым, и им полностью можно пренебречь в моделированиях.
частично падает. Скорость проникновения через границу постепенно уменьшается со временем просачивания. В процессе этапа раннего контакта скорость проникновения становится меньше, чем скорость закачки в трещину. Это возобновляет увеличение объема флюида внутри трещины гидроразрыва пласта, потерянного в момент контакта. Когда потри объема флюида из-за проникновения полностью компенсируются посредством постконтактной закачки в трещину, тогда снова достигается критическое полезное давление внутри трещины, и она повторно начинает свой вертикальный рост (диапазон времени, закрашенный зеленым цветом). На поздней стадии контакта, рост трещины происходит с постоянным проникновением. Скорость накачивания объема, занятого трещиной, вследствие этого, меньше, чем она была до контакта, таким образом падение полезного давления и скорость роста высоты трещины также меньше. В случае, когда проникновение происходит только через одну границу, скорости роста трещины будут возвращаться к первоначальным значениям со временем, когда проникновение становится пренебрежимо малым, и им полностью можно пренебречь в моделированиях.
[00058] Далее будут рассмотрены способы, входные данные и выходные данные модуля FracT (203). Входные данные содержат верхнюю или нижнюю координаты края, профиль давления, слои пласта и границы, в также индекс границы при T-образном контакте. Модуль предлагает границу скольжения, остаточное скольжение, и состояние неповрежденной границы, Т-образной, или пересеченной. Модуль FracT обращается к подпрограмме для каждой границы при Т-образном контакте с краем трещины и содержит упругое взаимодействие и критерий пересечения, а также повторное образование позади границы.
[00059] Рассмотрим вертикальное поперечное сечение трещины гидроразрыва пласта, распространяющейся в высоту (Фигура 15, слева). Предположим, что оба края трещины одновременно достигают две ранее существовавшие горизонтальные границы выше и ниже. После контакта, границы проскальзывают и задерживают дальнейшее распространение края трещины в вертикальном направлении (Фигура 15). На Фигуре 15 проиллюстрирован двухсторонний контакт вертикально распространяющейся трещины с неустойчивыми горизонтальными границами (слева), активация границы, и затупление края трещины в результате контакта с границами (справа).
[00060] В точке контакта возникает проблема с одним из: ортогональным контактом между трещиной под давлением и двумя неустойчивыми границами, проиллюстрированная на Фигуре 15 (справа). Чтобы решить эту проблему, сначала необходимо получить измененные характеристики трещины, такие как объем трещины, раскрытие (ширина), характеристики затупления края, протяженность межфазной зоны скольжения 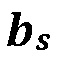 , и связанное с этим падение полезного давления внутри трещины после контакта. Далее, нам необходимо оценить минимальное повышение полезного давления, необходимого для пересечения границ. Этот критерий пересечения границы затем может быть использован, например, в точных 3D моделях распространения трещины, где он будет количественно выражать временную задержку роста высоты трещины из-за межфазных контактов (т.e. с момента контакта трещины с границей и ее задержки, чтобы в последующем пересечь границу для продолжения распространения).
, и связанное с этим падение полезного давления внутри трещины после контакта. Далее, нам необходимо оценить минимальное повышение полезного давления, необходимого для пересечения границ. Этот критерий пересечения границы затем может быть использован, например, в точных 3D моделях распространения трещины, где он будет количественно выражать временную задержку роста высоты трещины из-за межфазных контактов (т.e. с момента контакта трещины с границей и ее задержки, чтобы в последующем пересечь границу для продолжения распространения).
[00061] Проблема упруго-фрикционного контакта трещины может быть решена в очной числовой форме. В данном документе используется приближенное аналитическое решение этой проблемы, описанное более подробно в SPE-173337, ʺHydraulic Fracture Height Containment by Weak Horizontal Interfaces,ʺ февраль 2015 года, авторами Dimitry Chuprakov и Romain Prioul, которое включено в настоящее описание посредством ссылки. Аналитическая модель облегчает параметрическое понимание проблемы контакта трещины. Происходит ориентировка на следующие характеристики контакта трещина-граница: (i) протяженность активации границы в сдвиге 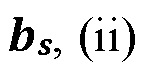 связанное с трещиной гидроразрыва пласта раскрытие
связанное с трещиной гидроразрыва пласта раскрытие 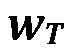 (ширина) в стыке с границей, и (iii) постконтактный объем трещины V в вертикальном поперечном сечении. Эти характеристики оказываются функциями от полезного давления трещины p′, критического напряжения сдвига в участке проскальзывания горизонтальной границы
(ширина) в стыке с границей, и (iii) постконтактный объем трещины V в вертикальном поперечном сечении. Эти характеристики оказываются функциями от полезного давления трещины p′, критического напряжения сдвига в участке проскальзывания горизонтальной границы 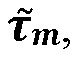 трещиностойкости границы
трещиностойкости границы 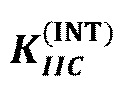 , и полувысоты вертикальной трещины под давлением L. Для облегчения формулирования проблемы в безразмерном виде, вводятся относительная длина активации границы
, и полувысоты вертикальной трещины под давлением L. Для облегчения формулирования проблемы в безразмерном виде, вводятся относительная длина активации границы 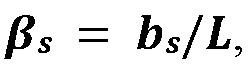 модифицированное раскрытие трещины при контакте
модифицированное раскрытие трещины при контакте 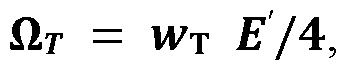 и модифицированный объем трещины
и модифицированный объем трещины 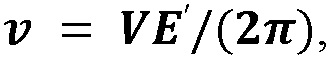 где
где 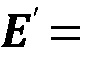
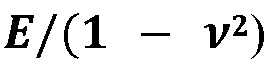 представляет собой модифицированный модуль Юнга плоской деформации, и они могут быть выражены как
представляет собой модифицированный модуль Юнга плоской деформации, и они могут быть выражены как
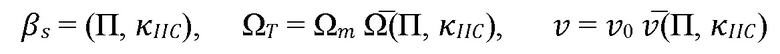 (17)
(17)
где 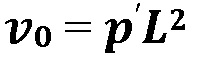 представляет собой модифицированный объем трещины, а
представляет собой модифицированный объем трещины, а 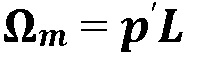 представляет собой максимальное модифицированное раскрытие трещины посередине трещины до контакта. Двумя безразмерными параметрами являются относительное полезное давление
представляет собой максимальное модифицированное раскрытие трещины посередине трещины до контакта. Двумя безразмерными параметрами являются относительное полезное давление 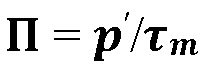 и безразмерная трещиностойкость границы
и безразмерная трещиностойкость границы 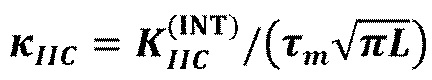 , где
, где 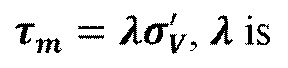 представляет собой коэффициент трения и
представляет собой коэффициент трения и 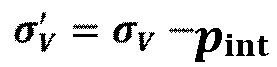 представляет собой эффективное вертикальное напряжение в границы с интерстициальным давлением флюида
представляет собой эффективное вертикальное напряжение в границы с интерстициальным давлением флюида  . Изначально,
. Изначально,  равно внутрипластовому давлению; проникновение флюида в границу после гидроразрыва представляет давление проникшего флюида.
равно внутрипластовому давлению; проникновение флюида в границу после гидроразрыва представляет давление проникшего флюида.
[00062] Величина относительного полезного давления Π определяет величину этих характеристик. Объем активации границы монотонно возрастает с Π. Он мал, когда полезное давление p′ мало или напряжение трения 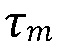 велико. В более конкретных случаях, когда полезное давление мало по отношению к напряжению трения
велико. В более конкретных случаях, когда полезное давление мало по отношению к напряжению трения 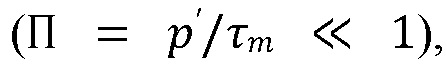 зона активации подчиняется следующему асимптоту
зона активации подчиняется следующему асимптоту
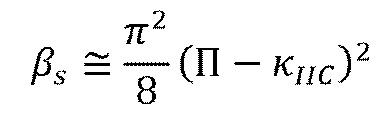 (18)
(18)
В противоположном ограничении относительно высоких полезных давлений (Π>>1), мы приходим к следующей линейной асимптоте
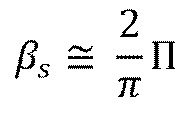 (19)
(19)
Аналогичная тенденция наблюдается и для раскрытия трещины (ширина)  в стыке. Трещина имеет склонность к закрытию при контакте с границей в случае, когда
в стыке. Трещина имеет склонность к закрытию при контакте с границей в случае, когда 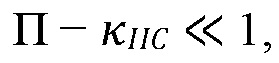 после асимптоты
после асимптоты
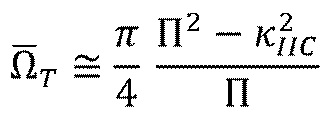 (20)
(20)
В противоположном ограничении (Π>>1), раскрытие на стыке имеет тот же порядок величины, что и максимальное раскрытие, Ωm. Оно изменяется логарифмически вместе с П следующим образом
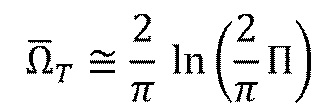 (21)
(21)
[00063] В случае одновременного контакта трещины с двумя слабыми границами, профиль раскрытия трещины расширяется как функция от Π, как проиллюстрировано на Фигуре 16 (слева). На Фигуре 16 проиллюстрированы профили вертикального раскрытия трещины в контакте с двумя несвязными границами (серый) для относительного полезного давления Π, равного 0,1 (черный), 1 (синий), и 10 (красный) (слева), и относительного полезного давления Π в трещине до (пунктирная линия) и после (сплошные линии) контакта с границами по сравнению с нормализированным объемом трещины 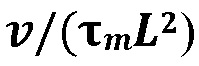 для случая двустороннего контакта трещины (справа). Черные линии иллюстрируют нормализированную трещиностойкость вдоль границ
для случая двустороннего контакта трещины (справа). Черные линии иллюстрируют нормализированную трещиностойкость вдоль границ 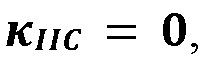 а красные линии для
а красные линии для 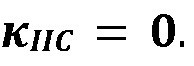 1. Синие стрелки обозначают соответствующее падение давления в трещине в момент контакта с границами.
1. Синие стрелки обозначают соответствующее падение давления в трещине в момент контакта с границами.
[00064] Чем больше относительное полезное давление Π, тем шире трещина открывается вдоль всего вертикального поперечного сечения, как и следовало ожидать. Влияние границ на раскрытие упругой трещины напоминает внезапное изменение упругой податливости породы. Действительно, плоскости ослабления представляют собой две совместимые плоскости в жесткой породе. Когда трещина устанавливает контакт с ними, то очевидно, что упругий отклик трещины должен стать более согласующимся. Этот эффект резкого расширения трещины в момент контакта со слабыми границами может привести к резкому падению давления гидравлического разрыва. Быстрое увеличение объема трещины должно приводить к соответствующему быстрому уменьшению давления в флюиде. Были проведены дополнительные исследования перепада полезного давления в момент контакта трещины с двумя слабыми границами. На Фигуре 16 (справа) проиллюстрирована величина перепада относительного полезного давления для данного объема закачиваемого флюида в трещине непосредственно перед контактом с границами. В случае если относительное полезное давление невелико (Π<1), перепад давления невелик и не обнаруживается. Для больших значений относительного полезного давления (Π >1) давление внутри трещины заметно падает. В контексте настоящего изобретения, профиль открытия трещины находится как часть решения проблемы.
Проблема повторного образования трещины: пересечение границ.
[00065] Активация границы генерирует локализованное поле напряжения при растяжении на противоположной стороне границы (Фигура17). Высокие напряжения растяжения сосредоточены близко к точке стыка и могут превышать предел прочности на разрыв пласта. В наиболее возмущенной области напряжений, компонент максимального основного напряжения при растяжении параллелен границе. Контакт-индуцированные напряжения способствуют образованию нового раскола растяжения в неповрежденной породе в направлении нормали к границе (см. стрелки на Фигуре17). Аналогичная проблема решается аналитически, если предположить равномерное раскрытие трещины. На Фигуре 17 проиллюстрирован компонент максимального напряжения при растяжении, сгенерированный на противоположной стороне несвязной (слева) и связной границы с 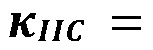
 (справа). Вертикальные и горизонтальные белые сплошные линии изображают трещину и границу, соответственно. Белые стрелки указывают на локальные направления максимального основного напряжения при сжатии (перпендикулярно максимальному основному напряжению при растяжении). Координатные шкалы все нормализованы по протяженности зоны скольжения
(справа). Вертикальные и горизонтальные белые сплошные линии изображают трещину и границу, соответственно. Белые стрелки указывают на локальные направления максимального основного напряжения при сжатии (перпендикулярно максимальному основному напряжению при растяжении). Координатные шкалы все нормализованы по протяженности зоны скольжения 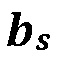 .
.
[00066] Для образования нового раскола и пересечения границы, в горной породе также должно быть накоплено достаточное количество энергии упругой деформации. Критическое напряжение и высвобождение критической энергии упругости необходимы для образования раскола в твердых породах. Для того, чтобы использовать этот смешанный критерий напряжение-и-энергия для повторного образования трещины, получается и оценивается инициирующий коэффициент интенсивности напряжений 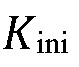 в пределах зоны критического напряжения как функцию от параметров проблемы. Затем вводится следующая функция пересечения, Cr, как соотношение инициирующего коэффициента интенсивности напряжений
в пределах зоны критического напряжения как функцию от параметров проблемы. Затем вводится следующая функция пересечения, Cr, как соотношение инициирующего коэффициента интенсивности напряжений 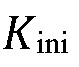 и трещиностойкости горной породы позади границы
и трещиностойкости горной породы позади границы 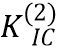 , где должен начаться раскол:
, где должен начаться раскол:
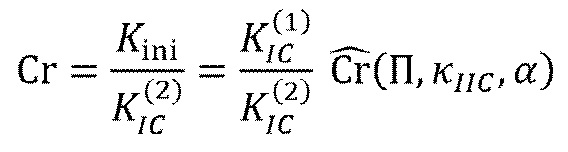 (22)
(22)
где
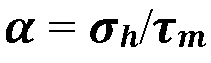 представляет собой относительное минимальное горизонтальное напряжение
представляет собой относительное минимальное горизонтальное напряжение
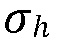 в слое позади границы. Функция пересечения Cr больше 1 в случае, когда критерий пересечения выполняется, в противном случае трещина задерживается на границе. Сравнение трещиностойкости с обеих сторон границы,
в слое позади границы. Функция пересечения Cr больше 1 в случае, когда критерий пересечения выполняется, в противном случае трещина задерживается на границе. Сравнение трещиностойкости с обеих сторон границы,
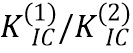 , играет важную роль, как и ожидалось. Рост трещины в более слабом пласте менее устойчив по сравнению с ростом в более сильной породе. Далее будет рассмотрен конкретный случай одинаковой трещиностойкости пород по обе стороны границы
, играет важную роль, как и ожидалось. Рост трещины в более слабом пласте менее устойчив по сравнению с ростом в более сильной породе. Далее будет рассмотрен конкретный случай одинаковой трещиностойкости пород по обе стороны границы
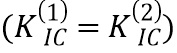 . Для того, чтобы понять возможную задержку роста края трещины на границе, будет исследована зависимость модифицированной функции пересечения Cr=Cr̂ от безразмерных параметров проблемы:
. Для того, чтобы понять возможную задержку роста края трещины на границе, будет исследована зависимость модифицированной функции пересечения Cr=Cr̂ от безразмерных параметров проблемы:
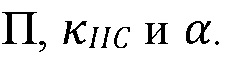
[00067] Рассмотрим первоначальный момент контакта с границей. Оказывается, что при всех значениях безразмерных параметров проблемы, функция пересечения изначально меньше, чем 1. Это означает, что граница никогда не может быть пересечена сразу же в ходе процесса непрерывного распространения трещины. Край трещины задерживается посредством границы до тех пор, пока не накапливается достаточно полезного давления, чтобы значение функции пересечения выросло до 1. Это можно понять с точки зрения механической работы разрушения. Невзаимодействующему краю трещины для распространения требуется дополнительная энергия закачиваемого флюида. После установления контакта с границей, часть энергии разрушения расходуется на энергию, необходимую для проскальзывания границы. Таким образом, при пересечении границы требуется больше энергии, чем это необходимо в случае отсутствия взаимодействия. Это объясняет внезапную остановку края трещины в слабой границе.
[00068] Приведенные выше результаты на пересечении границы относятся к проблеме двухстороннего контакта трещины гидроразрыва пласта. В рассмотренных примерах, полувысота трещины L поэтому предполагается фиксированной после контакта. В общем случае, трещина может взаимодействовать только с одной границей, в то время как другой вертикальный край трещины продолжает распространяться. Это общий случай был решен с использованием аналогичной методики и показывает, что сдерживание распространения на границах будет следовать тем же тенденциям в поведении полезного давления.
[00069] Прерывистое распространение трещины через поверхности границы (модель LamiFrac)
[00070] Далее исследуется влияние предыдущего механизма на планарное 3D распространение трещины гидравлического разрыва из горизонтальной скважины в многослойном пласте с горизонтальными слабыми границами по обеим сторонам скважины (мы рассмотрим симметричный случай для простоты, хотя методология носит общий характер). В пределах каждого слоя, напряжения, упругость породы и прочностные свойства не изменяются, но они могут изменяться между слоями. Распространение трещины начинается с небольшой круговой трещины. Обратитесь, пожалуйста, к Фигуре 1, которая иллюстрирует геометрию слоев и границы, а также трещину гидравлического разрыва пласта.
[00071] Изначально трещина гидроразрыва пласта развивается в равной степени в верхнем вертикальном, нижнем вертикальном, и горизонтальном направлениях (т.e., как радиальная трещина в начале). Затем, после контакта с границами, распространение в горизонтальном и вертикальном направлениях становится разным. В целях демонстрации, в контексте настоящего изобретения используется приближенное решение проблемы 3D трещины, основываясь на решении для эллиптического раскола. Геометрия трещины сохраняет эллиптическую форму, учитывая неодинаковый рост в трех направлениях (два вертикальных и одно горизонтальное). Алгоритм моделирования состоит из трех вычислительных компонентов. Первый из них вычисляет отклик упругого разрушения на давление закачиваемого флюида и внутрипластовое напряжение. Он учитывает взаимодействие трещины с границами, как представлено выше. Второй компонент решает проблему для одновременного развития края трещины во всех трех направлениях. Третий компонент находит давление жидкости внутри трещины и всех контактирующих границ, принимая во внимание условия для скорости закачки флюида, проникновение вдоль проводящих границ, и трение вязкого флюида внутри трещины. Последнее подчиняется известному закону смазывания для ньютоновских жидкостей.
[00072] При моделировании сначала задаются параметры породы и закачки флюида в скважину. Затем вычисляется геометрия постепенного распространения трещины для заданных условий, что позволяет исследовать влияние ранее существующих горизонтальных границ на сдерживание распространения трещины.
[00073] Качественная картина распространения трещины выглядит аналогично во всех моделированиях и может быть описана следующим образом. После того, как вертикальные края достигают верхних и нижних границ, их распространение прекращается на некоторое время. Трещина по-прежнему продолжает распространяться в горизонтальном направлении. На данном этапе, в трещине накапливается полезное давление (аналогично тому, как можно было наблюдать в трещине PKN-типа). После того, как полезное давление увеличилось до критического значения, трещина имеет достаточно энергии, чтобы разорвать границы. После пересечения границ, трещина тотчас же контактирует со следующими границами. Поскольку трещина резко переходит по вертикали от одной границы к другой, полезное давление падает. В результате, рост трещины временно прекращается во всех направлениях. При дальнейшем увеличении давления, трещина снова продолжает расти в горизонтальном направлении до тех пор, пока она не прекратит задержку в вертикальном направлении, и этот рост приводит к дополнительному повышению давления. Пересечение границ и следующий цикл падения давления повторяется. Такое прерывистое распространение трещины продолжается до тех пор, пока трещина взаимодействует с горизонтальными границами.
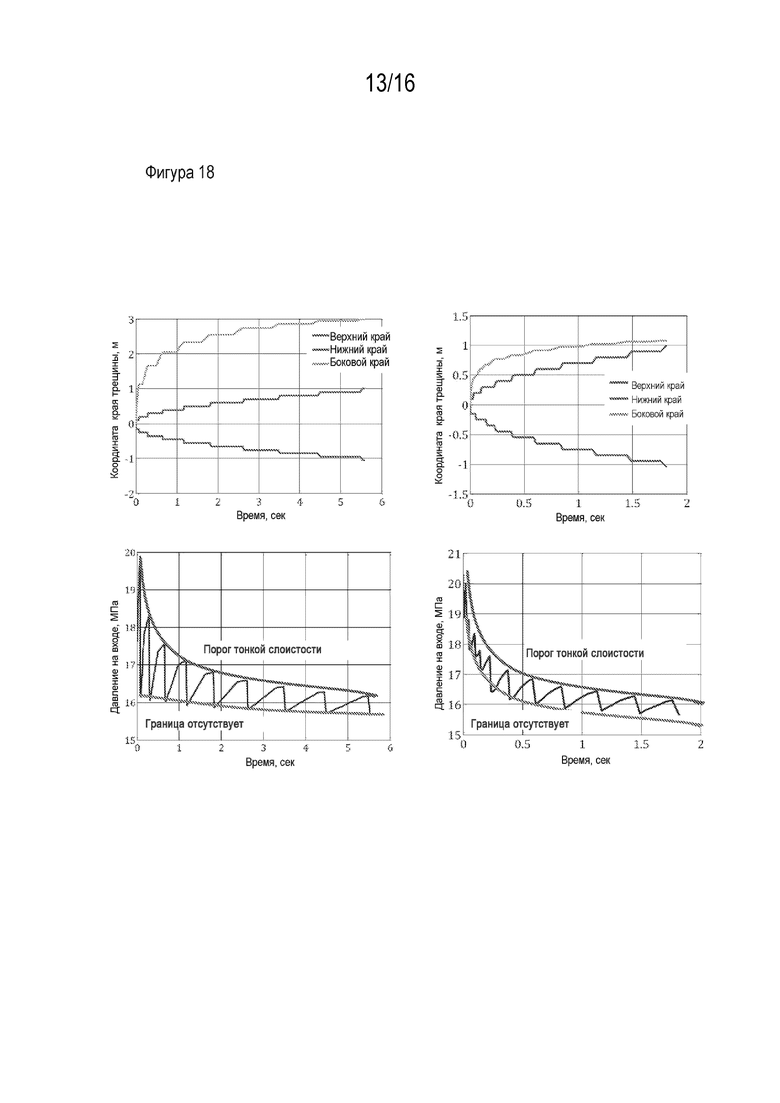
[00074] На Фигуре 18 проиллюстрирована описанная механика распространения края трещины и колебаний давления. На ней показаны результаты двух моделирований с небольшой и большой вязкостью закачиваемого флюида (1 сПз и 10000 сПз, соответственно). Интервал между границами составляет 0,1 м. Для простоты, свойства породы и границ в пределах каждого слоя в этих опытах одинаковы. Эти моделирования показывают (Фиг. 18, вверху) что вертикальный рост трещины гидроразрыва тормозится из-за присутствия слабых границ.
[00075] В результате, трещина растет преимущественно в горизонтальном направлении. Повышенная вязкость закачиваемого в трещину флюида способствует пересечению границы, что хорошо известно. Это объясняет, почему эффект сдерживания распространения является менее заметным с большей вязкостью флюида (Фигура 18, вверху справа). На Фигуре 18 проиллюстрировано распространение края трещины (вверху) и снижение давления на входе (внизу) в случае эллиптической трещины с использованием ньютоновской жидкости с вязкостью 1 сПз (слева) и 10000 сПз (справа), соответственно. Постоянная скорость закачки флюида в трещину составляет 0,001 м2/сек. Радиус первоначальной трещины составляет 1 см. Пространственный интервал между горизонтальными поверхностями составляет 0,1 м. Границы являются несвязными с коэффициентом трения 0,6 и внутрипластовым давлением 12 МПа. Вертикальное внутрипластовое напряжение составляет 20 МПа, минимальное горизонтальное внутрипластовое напряжение составляет 15 МПа. Трещиностойкость породы составляет 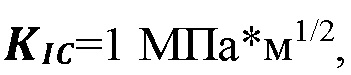 сопротивление растяжению 5 МПа,
сопротивление растяжению 5 МПа, 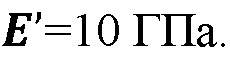
[00076] В предельном случае тонкослоистой структуры, колебания давления и резкие переходы края становятся исчезающе малы. Затем рост трещины представляет собой непрерывный процесс. Получение характеристик распространения трещины в этих породах может быть аналогичным получению характеристик распространения в однородной породе, с той лишь разницей, что трещиностойкость в вертикальном направлении через границы имеет увеличенное "эффективное" значение. Огибающие кривых давления для «эффективной» тонкослоистой структуры со слабыми границами и непрерывной однородной породой без границ графически представлены на Фиг. 18 (красная и зеленая кривые, соответственно). Эти кривые давления уточняют разницу между действием трещиностойкости через многослоистый/ многослойный пласт и пласт без границ.
[00077] Используя модель выше, получается "эффективная" трещиностойкость для слоистых пластов. Устойчивый критерий распространения трещины требует, чтобы коэффициент интенсивности напряжений 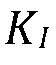 на краю равнялся трещиностойкости породы
на краю равнялся трещиностойкости породы 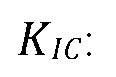
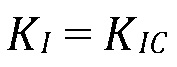 (23)
(23)
В слоистом пласте, устойчивый рост в высоту означает, что вертикальный край постоянно пересекает бесконечно близкие границы, так что 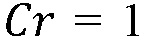 (Уравнение 22). Переписывая это уравнение с учетом коэффициента интенсивности напряжений в вертикальном крае, имеется
(Уравнение 22). Переписывая это уравнение с учетом коэффициента интенсивности напряжений в вертикальном крае, имеется
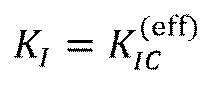 (24)
(24)
где 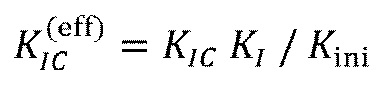 представляет собой ʺэффективнуюʺ трещиностойкость. Она всегда больше, чем
представляет собой ʺэффективнуюʺ трещиностойкость. Она всегда больше, чем 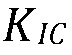 и зависит от механических свойств границ, таких как связность, коэффициент трения и гидравлическая проводимость. Этот результат согласуется с лабораторными измерениями трещиностойкости в слое и при пересечении слоя, используемыми в предыдущих моделях.
и зависит от механических свойств границ, таких как связность, коэффициент трения и гидравлическая проводимость. Этот результат согласуется с лабораторными измерениями трещиностойкости в слое и при пересечении слоя, используемыми в предыдущих моделях.
[00078] На Фигуре 19 выстроена последовательность действий для алгоритма решения (201) обычного распространения трещины ГРП, например, если не существует никакого взаимодействия с границами породы (но он включает механизм 1 сравнения напряжения и прочности). Сопряженный алгоритм решения (211) для трещины ГРП твердая порода-флюид вызывается для каждого предположенного прироста края трещины для того, чтобы выдать решение для коэффициента интенсивности напряжений (SIF) KI в крае трещины ГРП. Затем SIF сравнивается с трещиностойкостью имеющегося слоя породы KIC, чтобы выяснить, является ли край трещины устойчивым или нет. Цикл возобновляется каждый раз в случае, когда текущий прирост края трещины ГРП не стабилизируется, и выводит найденное решение.
[00079] На Фигуре 20 выстроена последовательность действий для подкомпонента (211) алгоритма решения (201) распространения трещины ГРП выше. Она представляет собой сопряженный алгоритм решения твердая порода-флюид трещины ГРП для данного размещения краев трещины ГРП. Алгоритм принимает решение для трещины ГРП в предыдущем интервале времени (2111), обнаруживает сопряженное решение упругости (2112) и потока флюида (2113) в следующем новом интервале времени и новые края трещины, и выводит его (2114). Сопряженное решение для упругости (2112) и потока флюида (2113) требует дополнительных итераций (горизонтальная стрелка между 2112 и 2113).
[00080] На Фигуре 21 показаны выходные подмодули основной последовательности выполняемых действий (300 на Фиг.9). Они являются геометрическими (301), например, высота и длина трещины ГРП, содержащими информацию о подвергшихся воздействию границах породы (302), например, координаты пересеченных границ и сгенерированные проскальзывания на каждой из них, а также механическими (303), например, давление флюида и толщина трещины.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ГИДРОРАЗРЫВА ПЛАСТА | 2021 |
|
RU2772626C1 |
| Способ определения геометрии трещин ГРП с учетом разделения и взаимодействия потоков жидкости ГРП между трещинами | 2022 |
|
RU2786303C1 |
| СПОСОБ ФОРМИРОВАНИЯ ПРОВОДЯЩИХ ТРЕЩИН В ПРОДУКТИВНОЙ ПОРОДЕ ЗА ОБСАДНОЙ КОЛОННОЙ СКВАЖИНЫ | 2015 |
|
RU2601341C1 |
| СПОСОБ ПОИНТЕРВАЛЬНОГО ГИДРАВЛИЧЕСКОГО РАЗРЫВА КАРБОНАТНОГО ПЛАСТА В ГОРИЗОНТАЛЬНОМ СТВОЛЕ СКВАЖИНЫ С ПОДОШВЕННОЙ ВОДОЙ | 2014 |
|
RU2558058C1 |
| Способ гидроразрыва пласта в условиях высокорасчлененного высокопроводимого коллектора с низким контрастом напряжений перемычек | 2019 |
|
RU2737455C1 |
| СПОСОБ ДОБЫЧИ ТРУДНОИЗВЛЕКАЕМОГО ТУРОНСКОГО ГАЗА | 2020 |
|
RU2743478C1 |
| Способ разработки низкопроницаемого коллектора с поочередной инициацией трещин авто-ГРП | 2020 |
|
RU2745058C1 |
| СИСТЕМА И СПОСОБ ВЫПОЛНЕНИЯ РАБОТ ПО СТИМУЛЯЦИИ НЕДР | 2013 |
|
RU2591857C1 |
| СПОСОБ ПРОГНОЗИРОВАНИЯ ГИДРОРАЗРЫВА ПЛАСТА, СПОСОБ ГИДРОРАЗРЫВА ПЛАСТА, СПОСОБЫ ПРОГНОЗИРОВАНИЯ РИСКОВ ГИДРОРАЗРЫВА ПЛАСТА | 2017 |
|
RU2730576C1 |
| Способ увеличения нефтеотдачи керогенсодержащих сланцевых пластов | 2023 |
|
RU2802297C1 |
Варианты реализации в контексте настоящего изобретения относятся к способу гидравлического разрыва подземного пласта, пересекаемого стволом скважины, включающему получение характеристик данного пласта с использованием измеренных характеристик пласта, включая механические характеристики геологических границ, идентификацию высоты трещины пласта, при этом идентификация включает расчет поверхности контакта трещины гидроразрыва пласта с геологическими границами, и гидравлический разрыв пласта, при этом вязкость флюида или скорость потока флюида или же оба выбираются с применением расчетов. Варианты реализации в контексте настоящего изобретения также относятся к способу гидравлического разрыва подземного пласта, через который проходит ствол скважины, включающему проведение замеров пласта, содержащих механические свойства геологических границ, получение характеристик пласта с использованием замеров, расчет высоты трещины пласта с использованием характеристик пласта, расчет оптимальной высоты трещины с использованием замеров и сравнение оптимальной высоты трещины с высотой трещины пласта. 2 н. и 18 з.п. ф-лы, 21 ил.
1. Способ гидравлического разрыва подземного пласта, пройденного стволом скважины, включающий:
получение характеристик пласта с использованием измеренных свойств пласта, включая механические свойства геологических границ;
идентификацию высоты трещины в пласте, при этом идентификация включает в себя вычисление поверхности контакта трещины гидроразрыва пласта с геологическими границами; и
гидравлический разрыв пласта, при этом вязкость флюида или скорость потока флюида либо и то, и другое выбираются с использованием вычислений.
2. Способ по п. 1, отличающийся тем, что идентификация включает в себя получение характристик неустойчивой механической границы между смежными литологическими слоями.
3. Способ по п. 2, отличающийся тем, что определение неустойчивой границы включает в себя упругое взаимодействие, критерий пересечения и повторное образование позади границы.
4. Способ по п. 2, отличающийся тем, что неустойчивая граница содержит повышенное проникновение флюида гидроразрыва через границу.
5. Способ по п. 1, отличающийся тем, что идентификация включает в себя изменение минимального горизонтального напряжения как функцию глубины.
6. Способ по п. 1, отличающийся тем, что идентификация включает в себя сравнение модулей упругости между смежными и разными литологическими слоями.
7. Способ по п. 1, отличающийся тем, что для получения характеристик используются вертикальные границы слоя породы, вертикальная координата, направления напряжений, величины напряжений, упругость, трещиностойкость, сопротивление растяжению, коэффициент трения, трещиностойкость, гидравлическая проводимость или их комбинация.
8. Способ по п. 1, отличающийся тем, что получение характеристик дополнительно включает в себя использование эксплуатационных гидравлических параметров.
9. Способ по п. 8, отличающийся тем, что параметры включают в себя вязкость флюида или скорость закачки либо и то, и другое.
10. Способ по п. 1, отличающийся тем, что идентификация включает в себя получение характеристик роста трещины.
11. Способ по п. 1, отличающийся тем, что идентификация включает в себя получение характеристик края трещины.
12. Способ по п. 1, отличающийся тем, что идентификация включает в себя определение объема проникновения внутрь пласта или изменение давления либо и то, и другое.
13. Способ по п. 1, отличающийся тем, что идентификация включает в себя решение задачи распространения трещины.
14. Способ по п. 1, отличающийся тем, что идентификация включает в себя определение оптимальной высоты трещины.
15. Способ по п. 14, отличающийся тем, что идентификация включает в себя сравнение расчетной высоты трещины с оптимальной высотой трещины.
16. Способ гидравлического разрыва подземного пласта, пересекаемого стволом скважины, включающий:
проведение измерений пласта, содержащих механические свойства геологических границ;
получение характеристик пласта с использованием измерений;
вычисление высоты трещины пласта с использованием характеристик пласта;
вычисление оптимальной высоты трещины с использованием измерений;
и сравнение оптимальной высоты трещины с высотой трещины пласта.
17. Способ по п. 16, отличающийся тем, что идентификация включает в себя определение объема проникновения внутрь существовавших ранее проницаемых геологических прерывистостей пласта.
18. Способ по п. 16, отличающийся тем, что идентификация включает себя получение характеристик неустойчивой механической границы между смежными литологическими слоями.
19. Способ по п. 18, отличающийся тем, что определение неустойчивой границы включает в себя упругое взаимодействие, критерий пересечения и повторное образование позади границы.
20. Способ по п. 8, отличающийся тем, что неустойчивая граница определяет повышенное проникновение флюида гидроразрыва через границу.
| СОСТАВ МУЛЬЧИРУЮЩЕГО ПОКРЫТИЯ (ВАРИАНТЫ) | 2012 |
|
RU2497900C1 |
| СПОСОБ И УСТРОЙСТВО ДЛЯ ОПРЕДЕЛЕНИЯ ФОРМЫ ТРЕЩИН В ГОРНЫХ ПОРОДАХ | 2003 |
|
RU2324813C2 |
| СПОСОБ ГИДРОРАЗРЫВА ПОДЗЕМНОГО ПЛАСТА (ВАРИАНТЫ) | 2006 |
|
RU2404359C2 |
| US 20100250216 A1, 30.09.2010 | |||
| WO 2013067363 A1, 10.05.2013. | |||
Авторы
Даты
2018-04-23—Публикация
2015-06-05—Подача