Изобретение относится к технике проектирования и изготовления антенных обтекателей.
Известен способ оптимизации радиотехнических характеристик антенного обтекателя, в котором авторы выбирают определенную толщину стенки однослойного обтекателя [Каплун В.А. Обтекатели антенн СВЧ. М., Советское радио, 1974 г., 238 с., стр. 93. Гуртовник И.Г., Соколов В.Н., Трофимов Н.Н., Шалгунов С.Г. Радиопрозрачные изделия из стеклопластиков. - М.: Мир, 2002. - 368 с., стр 117].
Так как при выборе материала для конструкции обтекателя кроме радиотехнических оцениваются теплофизические и прочностные свойства, то при проектировании антенного обтекателя выбор диэлектрических свойств связывается с выбором косвенного параметра, электрической или фазовой толщина слоя (ϕ), связывающего диэлектрические свойства, геометрическую толщину стенки (d) и частоту электромагнитных колебаний падающего поля (f0) в приближении геометрической оптики для плоского слоя:

где 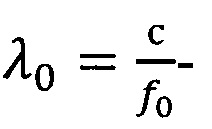 длина волны падающего электромагнитного поля в свободном пространстве,
длина волны падающего электромагнитного поля в свободном пространстве,
с - скорость света,
α - угол падения плоской волны на диэлектрический слой.
Формулу (1) используют для определенной априорно диэлектрической проницаемости материала стенки обтекателя, применяя в качестве значения угла падения величину среднего угла падения падающей волны на внешнюю поверхность обтекателя, составляющую величину от 60 до 70 град в зависимости от формы внешнего контура оболочки. Толщина стенки обтекателя выбирается кратной половине длины волны рабочего диапазона:

С увеличением толщины стенки улучшаются теплофизические и прочностные характеристики конструкции, но радиотехнические требования не позволяют выбирать любые величины толщины стенки, а только те, которые кратны половине длины волны.
Оптимальные радиотехнические характеристики обтекателя реализуются только для резонансной толщины стенки, достигая высоких уровней коэффициента прохождения, выше 0,9, и малых уровней пеленгационных ошибок. Подобрать по формуле (2) оптимальную толщину можно для априорно известной диэлектрической проницаемости однородной стенки, которая измеряется с помощью специальных приборов, как для монолитного однородного материала.
Определить толщину стенки из многокомпонентного материала по формуле (2) для оптимизации радиотехнических характеристик антенного обтекателя не представляется возможным. В представленном способе не учитывается, что материал является смесью многих компонентов, а эффективная диэлектрическая проницаемость не соответствует структуре стенки.
Наиболее близким является способ определения толщины стенки антенного обтекателя из многокомпонентного материал, включающий определение толщины стенки, настроенной на рабочий частотный диапазон обтекателя, его изготовление и измерение радиотехнических характеристик на стенде, в котором при определении толщины стенки материал моделируется однородным материалом с эффективной диэлектрической проницаемостью, рассчитываемой на основе моделирования материала, как смеси [Гуртовник И.Г., Спортсмен В.Н. Стеклопластики радиотехнического назначения. - М.: Химия, 1987. 160 с., стр. 149].
Эвристические модели электродинамического моделирования многокомпонентного материала в виде однослойного материала с расчетной эффективной диэлектрической проницаемостью базируются на представлении слоя в виде квазирегулярной структуры с распределением компонентов по слоям, описывая свойства материала в рамках модели двухслойного конденсатора Максвелла-Вагнера и расчетным определением эффективной диэлектрической проницаемости. При этом определение толщины стенки антенного обтекателя производится по эффективной диэлектрической проницаемости смеси, как для монолитной однородной стенки. По найденной толщине стенки изготавливают и проверяют его радиотехнические характеристики на измерительном стенде, моделирующем реальные взаимные положения антенны и обтекателя при эксплуатации. Если измеренные радиотехнические характеристики антенного обтекателя не удовлетворяют заданным требованиям, то обтекатель доводится с применением профилирования стенки изменением её толщины.
Недостатком способа оптимизации радиотехнических характеристик антенного обтекателя по прототипу является неточность определения толщины стенки для многокомпонентного материала. При расчете по формулам толщины стенки материал представляют однородным, но для многокомпонентного материала это не так. При определении, по представленным алгоритмам, эффективной диэлектрической проницаемости пренебрегают свойством некоммутируемости произведения матриц в матричном методе расчета прохождения волны через плоскую пластину [Хиппель А.Р. Диэлектрики и волны. - М.: Изд-во иностранной литературы. 1960. - 439 с., стр. 355, Борн М., Вольф Э. Основы оптики. - М.: Наука, 1973. - 720 с., стр. 72], в результате чего возникают неточности при расчете величины коэффициента прохождения плоской волны через плоский слой многослойного материала и ошибки в определении толщины стенки антенного обтекателя с оптимальными радиотехническими характеристиками.
Другим недостатком является также то, что по этому способу при определении толщины стенки не учитываются тангенсы углов диэлектрических потерь материалов, входящих в состав многокомпонентного материала, которые отсутствует в формулах (1 и 2).
Ещё одним недостатком является то, что по этому способу при определении толщины стенки не учитывается поляризация падающей волны, для которой коэффициент прохождения падающей волны при среднем угле падения может значительно различаться.
В таблице 1 приведены различные приближенные формулы расчета эффективной диэлектрической проницаемости многокомпонентного материала, заимствованные из оптики. Очевидно, что моделирование многокомпонентного материала плоской пластины однородным слоем с эффективной диэлектрической проницаемостью при нахождении коэффициента прохождения прошедшей волны не будет давать точные результаты, потому что при таком моделировании не учитывается распределение диэлектрической проницаемости по толщине пластины с учетом его конструкционной структуры.
Целью изобретения является улучшение радиотехнических характеристик антенного обтекателя за счет непосредственного определения толщины стенки антенного обтекателя из многокомпонентного материала по коэффициенту прохождения.
Это достигается тем, что в заявляемом способе оптимизации радиотехнических характеристик антенного обтекателя со стенкой из многокомпонентного материала, включающий определение толщины стенки, настроенной на рабочий частотный диапазон обтекателя, его изготовление и измерение радиотехнических характеристик на стенде, отличающийся тем, что измеряют диэлектрические проницаемости и тангенсы углов диэлектрических потерь, объемы и плотности всех компонентов, входящих в состав материала стенки обтекателя, определяют по максимуму коэффициента прохождения прошедшей волны для среднего угла падения на обтекатель в рабочем диапазоне частот толщину стенки, представляя её одномерной стопкой из одинаковых последовательно расположенных пластин со структурой в виде однородных последовательно расположенных стопкой слоев, равных числу компонентов материала с толщиной, равной объемной доли каждого материала, поделенной между числом пластин относительно полной объемной доли компонента в материале, составляющей структуру в виде суммы объемных долей компонентов и равной полному объему материала.

Авторы установили, что только для оптимизации радиотехнических характеристик антенного обтекателя толщину стенки из многокомпонентного материала можно определить только непосредственно из коэффициента прохождения без использования промежуточных процедур нахождения эффективных параметров стенки и расчета по формулам, представляя стенку выполненной из однородного материала.
По сравнению с известными решениями в предлагаемом способе исключается процедура определения эффективной диэлектрической проницаемости смеси, а определение толщины стенки антенного обтекателя со стенкой из многокомпонентного материала с оптимальными радиотехническими характеристиками производится непосредственно по измеренным диэлектрическим проницаемостям и тангенсам углов диэлектрических потерь, объемам и плотностям всех компонентов, входящих в состав материала стенки обтекателя.
Вместо формул (1 и 2) для определения толщины стенки антенного обтекателя в предлагаемом способе используется непосредственный расчет амплитуды и фазы коэффициента прохождения и отражения плоской электромагнитной волны через стенку антенного обтекателя из многокомпонентного материала. В расчете стенка антенного обтекателя из многокомпонентного материала толщиной D=n⋅Δd моделируется одномерной стопкой из imax=n, одинаковых последовательно расположенных пластин каждая толщиной 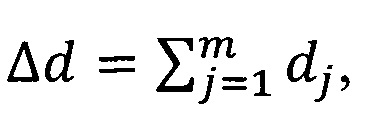 где Δd<<λ, λ - длина волны, со структурой в виде однородных последовательно расположенных стопкой слоев по числу jmax = m компонентов материала, каждый с диэлектрической проницаемостью εj и тангенсом угла диэлектрических потерь tgδj, а объемная доля j материала поделена между числом пластин относительно полной объемной доли компонента в материале, равной υj=n⋅dj, %, составляющей структуру в виде полного объема материала
где Δd<<λ, λ - длина волны, со структурой в виде однородных последовательно расположенных стопкой слоев по числу jmax = m компонентов материала, каждый с диэлектрической проницаемостью εj и тангенсом угла диэлектрических потерь tgδj, а объемная доля j материала поделена между числом пластин относительно полной объемной доли компонента в материале, равной υj=n⋅dj, %, составляющей структуру в виде полного объема материала 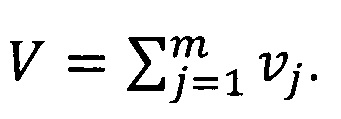
С помощью современных вычислительных машин не представляет сложности произвести определение толщины стенки антенного обтекателя, используя квазирегулярную модель в матричном методе расчета коэффициента прохождения и представляя многокомпонентный материал в виде чередующихся пластин с многослойной структурой тонких плоских слоев, без приближений, примененных при нахождении эффективной диэлектрической проницаемости смеси компонентов по прототипу, представленных в таблице 1, и определением с её помощью толщины стенки антенного обтекателя с оптимальными радиотехническими характеристиками по формулам (1 и 2).
Известно, что наилучшие радиотехнические характеристики имеют узкополосные антенные монолитные обтекатели с толщиной стенки, кратной половине длины волны на рабочей частоте. Поэтому рассмотрим применение предлагаемого способа в сравнении с прототипом на примере определения толщины стенки антенного обтекателя из многокомпонентного материала для оптимизации радиотехнических характеристик такого антенного обтекателя.
Для кварцевой керамики, как двухкомпонентного материала, состоящего из кварцевого стекла с диэлектрической проницаемостью ε0 при наличии пор, эффективная диэлектрическая проницаемость εэфф рассчитывается по эмпирической формуле: 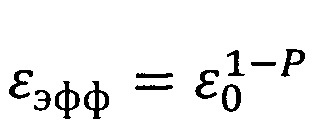 [Суздальцев Е.И. Свойства кварцевой керамики. Огнеупоры и техническая керамика. №7-8, 2009, С. 21-34]. Диэлектрическую проницаемость материала, как некую интегральную величину, определяют экспериментальными измерениями образцов материала на специальных установках, например, резонаторным способом. Авторы установили, что для определения оптимальной толщины стенки из кварцевой керамики, как двухкомпонентного материала, антенного обтекателя, оптимизируя коэффициент прохождения волны через плоскую пластину, недостаточно знания величины, а важны дифференциальные значения диэлектрической проницаемости материала структуры стенки антенного обтекателя в виде распределения диэлектрической проницаемости по объему материала.
[Суздальцев Е.И. Свойства кварцевой керамики. Огнеупоры и техническая керамика. №7-8, 2009, С. 21-34]. Диэлектрическую проницаемость материала, как некую интегральную величину, определяют экспериментальными измерениями образцов материала на специальных установках, например, резонаторным способом. Авторы установили, что для определения оптимальной толщины стенки из кварцевой керамики, как двухкомпонентного материала, антенного обтекателя, оптимизируя коэффициент прохождения волны через плоскую пластину, недостаточно знания величины, а важны дифференциальные значения диэлектрической проницаемости материала структуры стенки антенного обтекателя в виде распределения диэлектрической проницаемости по объему материала.
Авторы провели сравнительные расчеты зависимости коэффициентов прохождения плоской волны от угла падения α для ТЕ (вектор Е перпендикулярен плоскости падения) и ТМ (вектор Е параллелен плоскости падения) волн через плоскую пластину (по мощности |ТTM|2(α), |ТTE|2(α) и фазе δTM(α), δТЕ(α)) для εэфф=3,2, соответствующей пористости Р=13%, для трех модельных вариантов структуры материала:
- для первого, как в способе по аналогу, представляя пластину однородной монолитной с эффективной диэлектрической проницаемостью εэфф=3,2(|TTM1|2(α), |ТТЕ1|2(α) и фазе δТМ1(α), δТE1(α));
- для второго, как в способе по прототипу, по двуслойной модели для слоя из кварцевого стекла составляющую 0,87 от общей толщины и слоя воздуха толщиной 0,13 от общей (|ТТМ2|2(α), |ТТЕ2|2(α) и δТМ2(α), δТЕ2(α));
- для третьего, как по предлагаемому способу, по описанной выше многослойной модели структуры материала, чередуя пластины в виде тонких слоев из кварцевого стекла и воздуха (|ТTM3|2(α), |ТTE3|2(α) и δTM3(α), δТЕ3(α)).
Последняя модель наиболее точно описывает структуру материала с учетом состава компонент и их равномерное распределение по толщине пластины.
На Фиг. 1 и 2 представлены результаты различия в расчетах мощности коэффициентов прохождения при различных вариантах моделирования материала в зависимости от толщины пластины для нулевого угла падения ТЕ волны при α=0° и среднем угле падения для обтекателя α=70°:
- для первой кривой (ΔКП1=|ТТЕ1|2(α)-|ТТЕ2|2(α));
- для второй кривой (ΔКП2=|ТТЕ1|2(α)-|ТТЕ3|2(α)).
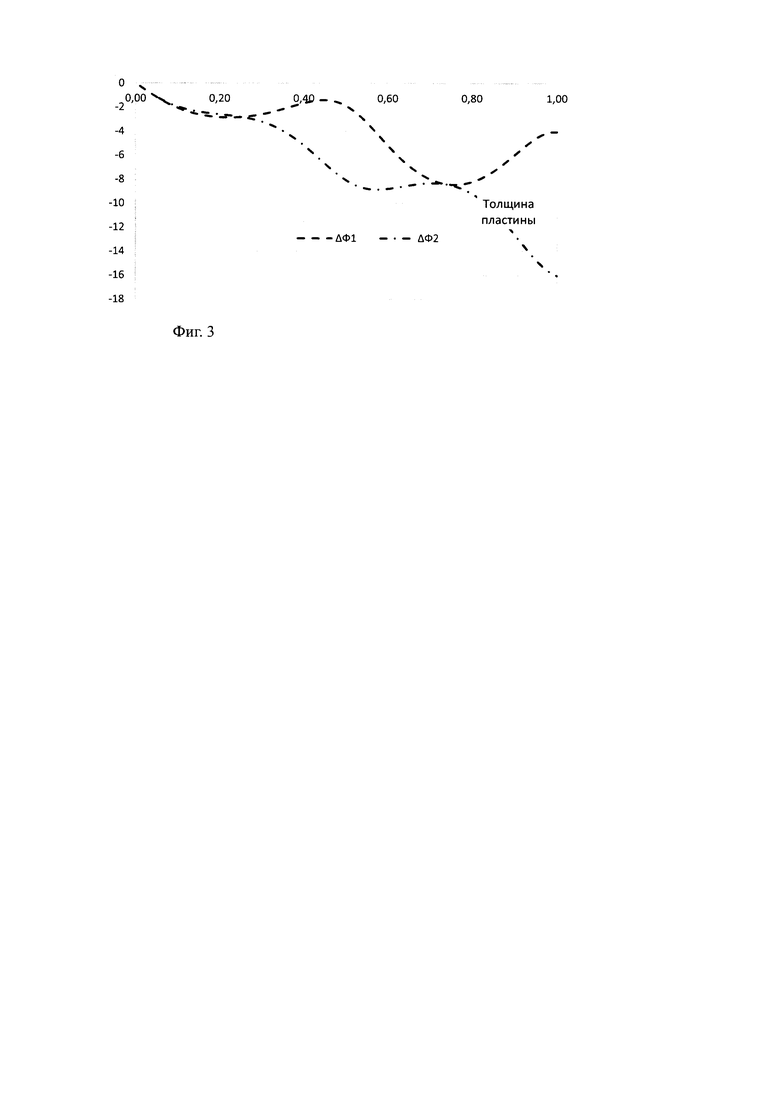
На Фиг. 3 и 4 представлены результаты различия в расчетах фазы коэффициентов прохождения для различных вариантов моделирования материала в зависимости от толщины пластины для нулевого угла падения ТЕ волны при α=0° и среднем угле падения для обтекателя α=70°:
- для первой кривой (Δϕ1=δТЕ1(α)-δТЕ2(α);
- для второй кривой (Δϕ2=δТЕ1(α)-δТЕ3(α).
Из сравнения кривых на Фиг. 1-4 видно, что расчет коэффициента прохождения, проведенный для монолитной стенки с эффективной диэлектрической проницаемостью, дает отклонение по мощности до 18%, а по фазе до 22°. Видно, что для повышения точности расчетов даже двух компонентных материалов происходит при моделировании структуры материала в пластине с учетом распределения компонент.
Для оценки влияния использования различных моделей на точность определения толщины стенки из многокомпонентного материала проведем расчет оболочки по электродинамической модели на основе физической оптики для трех вариантов, описанных выше способов. Для системы «антенна-обтекатель», с пеленгующей антенной диаметром 300 мм, проведен расчет для оболочки оживальной формы с удлинением 2,5 из кварцевой керамики в диапазоне F1-3=10±0,3 ГГц для вариантов моделирования материала с полуволновой толщиной с диэлектрической проницаемостью εэфф=3,2 при нулевом угле падения, Е поляризации падающей линейно-поляризованной волне:
1 - для монолитной стенки с εэфф=3,2 h=8,38 мм для F2=10 ГГц;
2 - для двухслойной стенки с первым слоем ε1=3,81, толщиной h1=7,29 мм и вторым слоем с ε2=1,00, толщиной h2=1,089 мм, моделируя содержание компонентов материала пропорционально их объемному распределению по формулам расчета смеси;
3 - для многослойной стенки, моделируя равномерное распределение пор по толщине, чередуя 200 двухслойных пластин с ε1=3,81, толщиной h1=0,03664 мм и с ε2=1,00, толщиной h2 =0,00545 мм.
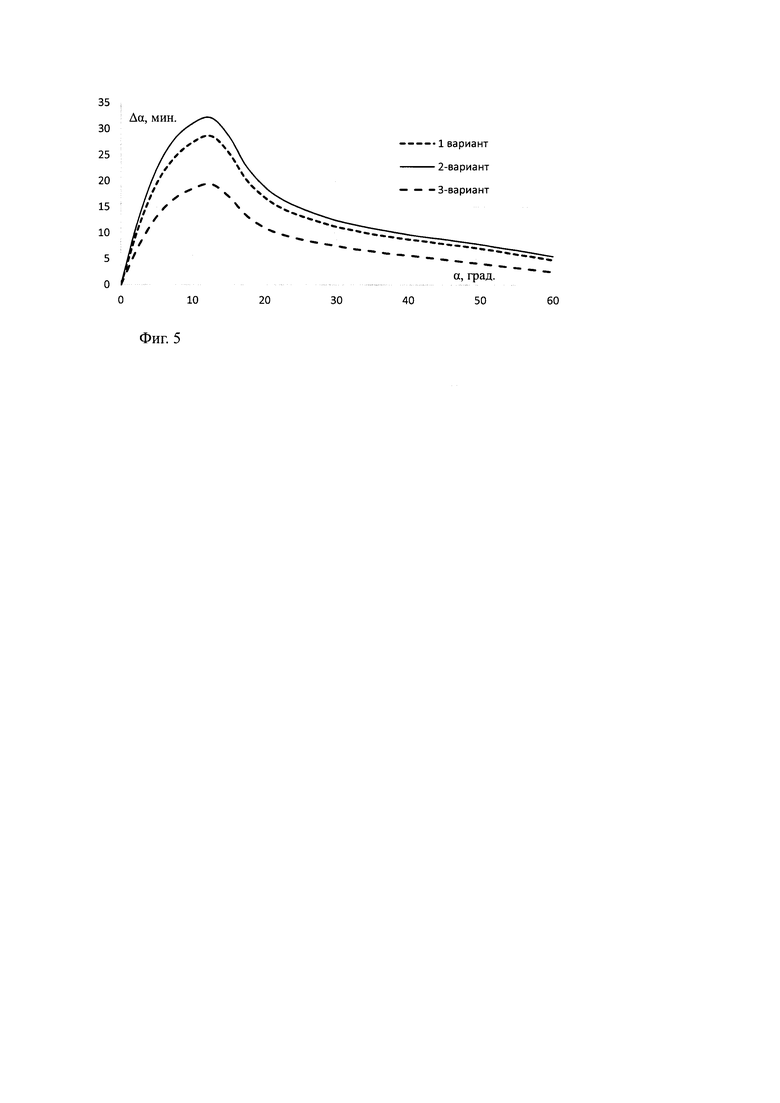
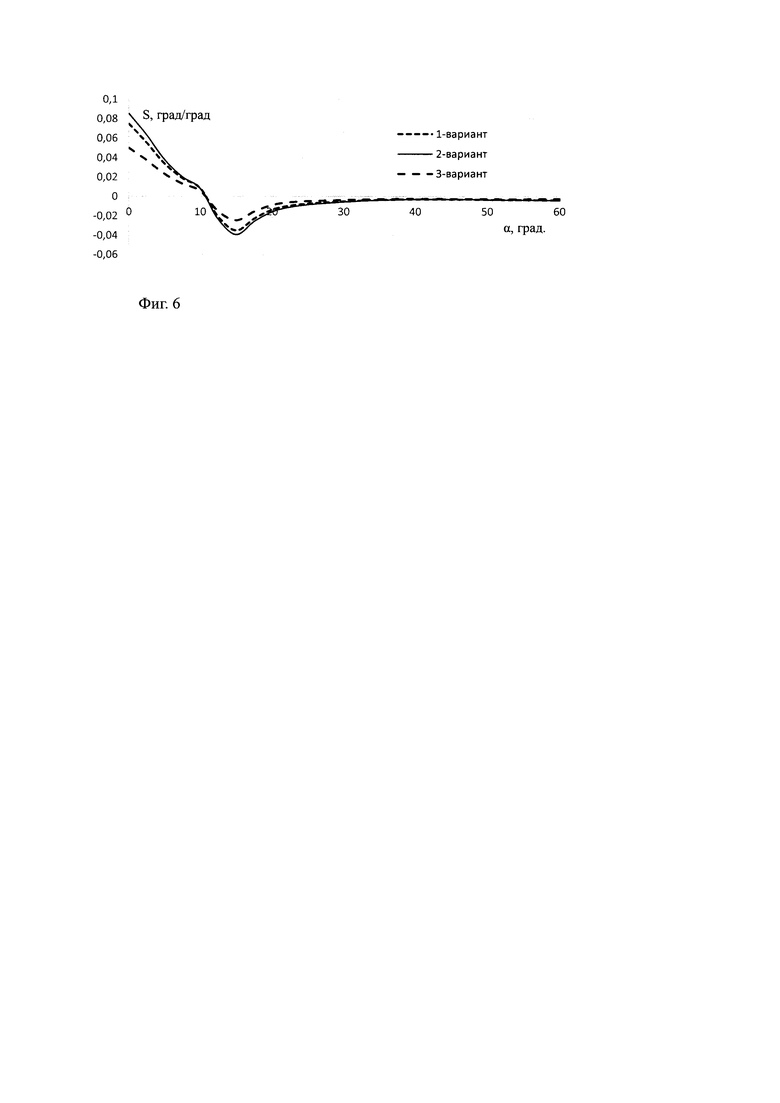
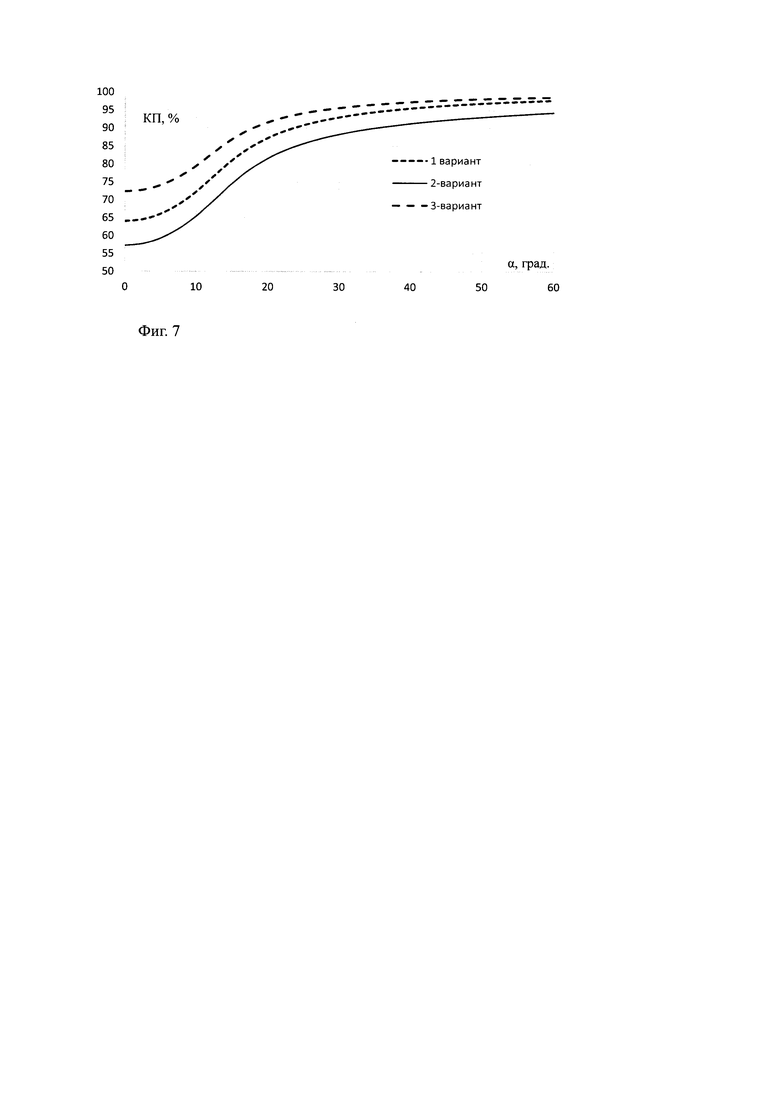
На Фиг. 5-7 приведены рассчитанные зависимости от угла поворота антенны пеленгационных ошибок, крутизны пеленгационных ошибок и коэффициента прохождения системы «антенна-обтекатель» из кварцевой керамики для трех вариантов электродинамического моделирования структуры материала. Толщина стенки рассчитывалась как для пластины при нулевом угле падения и при расчете системы «антенна-обтекатель» была не оптимальной.
Из Фиг. 5-7 видно значительное различие в результатах расчетов для различных вариантов моделирования материала: отличие в максимальной ошибке до 10 мин, 0,03 град/град по крутизне и до 15% по коэффициенту прохождения.
Из проведенного анализа видно, что при оптимизации радиотехнических характеристик поиск стенки антенного обтекателя из многокомпонентных материалов нужно проводить с использованием в физической модели «антенна обтекатель» электродинамического расчета прохождения волны через многослойную стенку, моделируя материал, как соединенные вместе чередующиеся равномерно распределенные плоские пластины, внутри состоящие из однородных слоев для каждого компонента материала, соединенных в единую пластину.
Рассмотрим состав материала из кварцевой ткани с алюмофосфатным связующим, который состоит из 50 % весовых частей связующего с 35% окиси алюминия, остальное 56% объемной части кварцевой ткани с Р=35% воздушных пор в связующем (таблица 2). Тангенсы углов диэлектрических потерь компонентов в таблице 2 не указаны.
Эффективная диэлектрическая проницаемость материала из кварцевой ткани с алюмофосфатным связующим, определенная на специальных установках по измерению диэлектрической проницаемости, равняется εэфф=3,2±0,1.
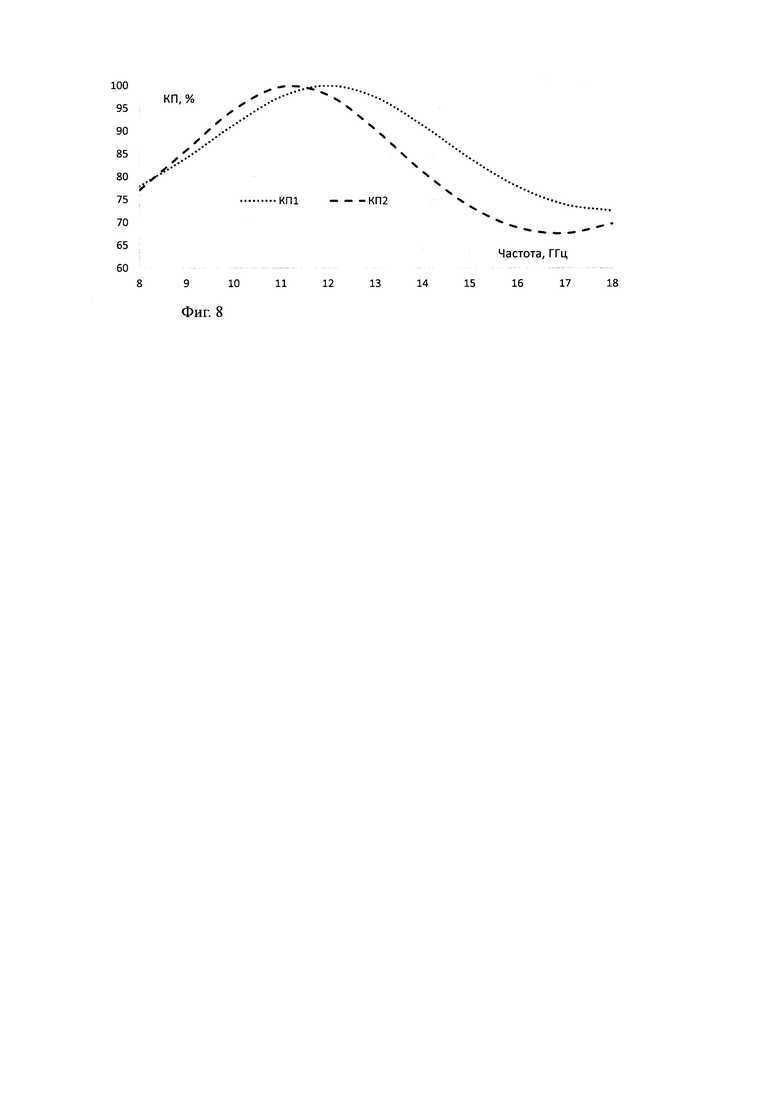
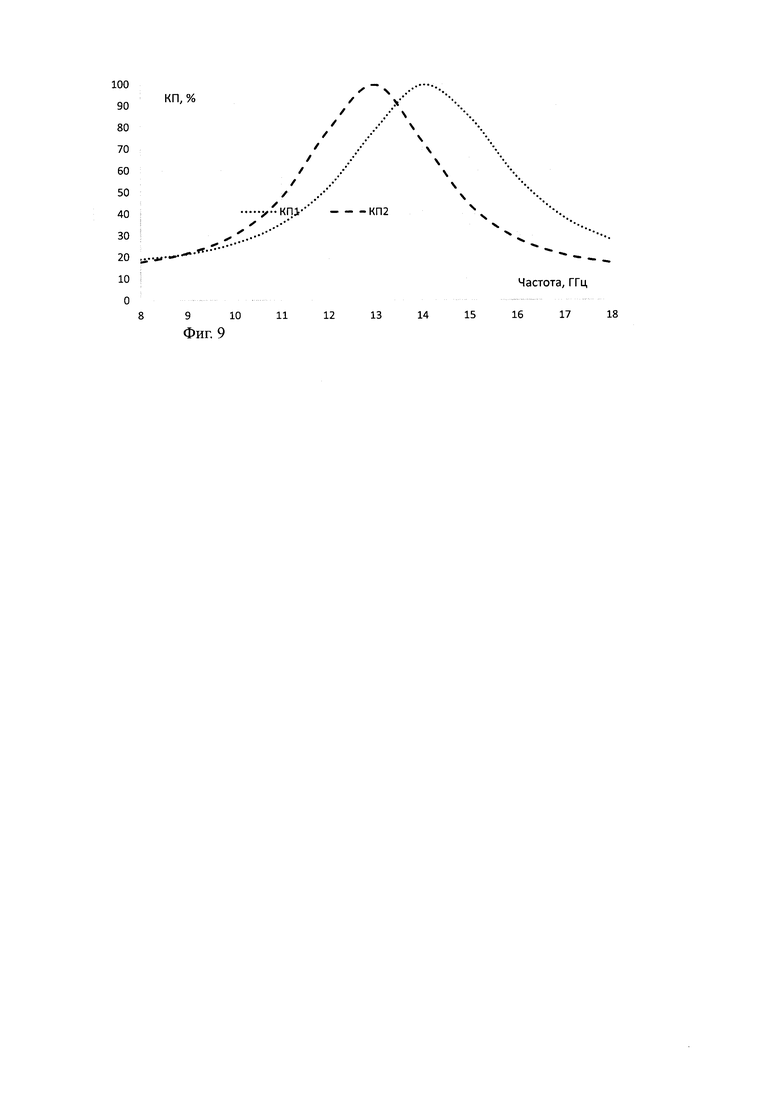
На Фиг. 8-9 представлены сравнительные расчетные частотные зависимости мощности коэффициента прохождения для ТЕ поляризации падающей волны при моделировании пластины из композиционного материала монолитным однородным слоем с εэфф=3,2 (КП1) и, представляя материал в виде многослойной структуры слоев толщиной, пропорциональной объемному содержанию компонентов (КП2).
Из Фиг. 8, 9 видно, что результаты расчетов различаются в зависимости от применяемой расчетной модели структуры материала и для них не совпадают максимумы кривых на частотной оси.
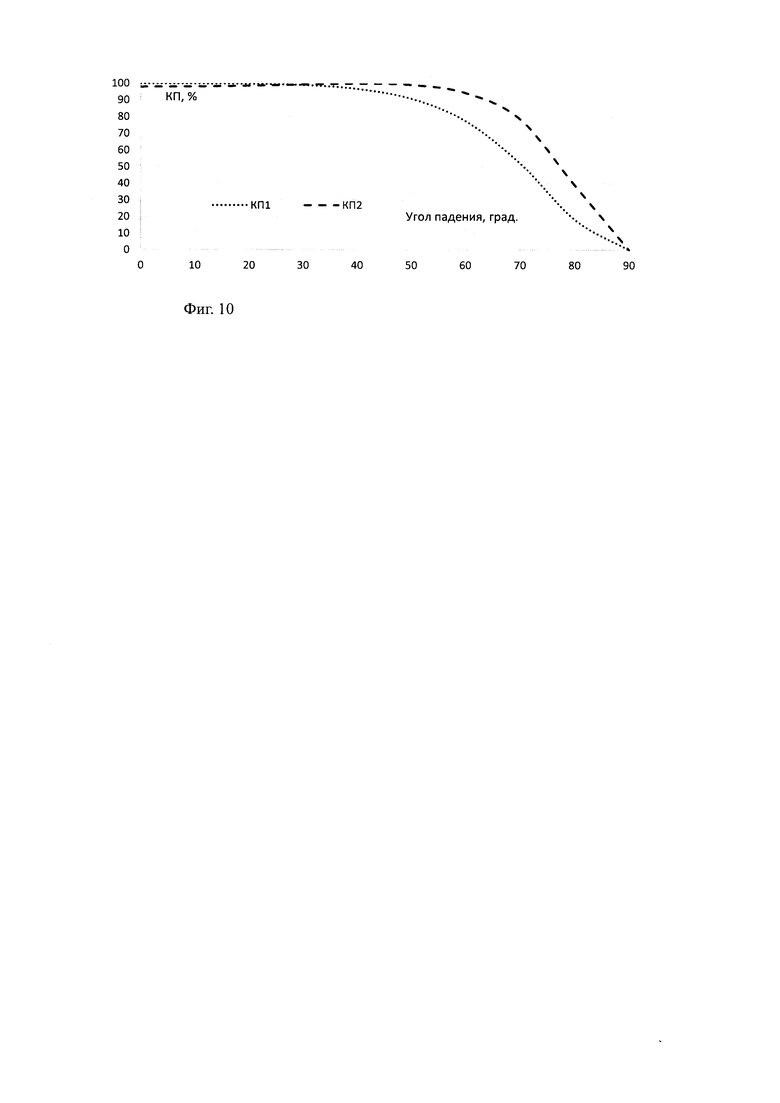
На Фиг. 10 представлены сравнительные расчетные угловые зависимости мощности коэффициента прохождения для ТЕ поляризации для пластины, настроенной на частоту 12 ГГц при моделировании пластины из композиционного материала монолитным однородным слоем с εэфф=3,2 (КП1), и представляя материал в виде многослойной структуры слоев толщиной, пропорциональной объемному содержанию компонентов (КП2).
Из Фиг. 10 видно, что результаты расчетов отличаются в зависимости от применяемой расчетной модели структуры материала и увеличиваются с ростом величины угла падения.
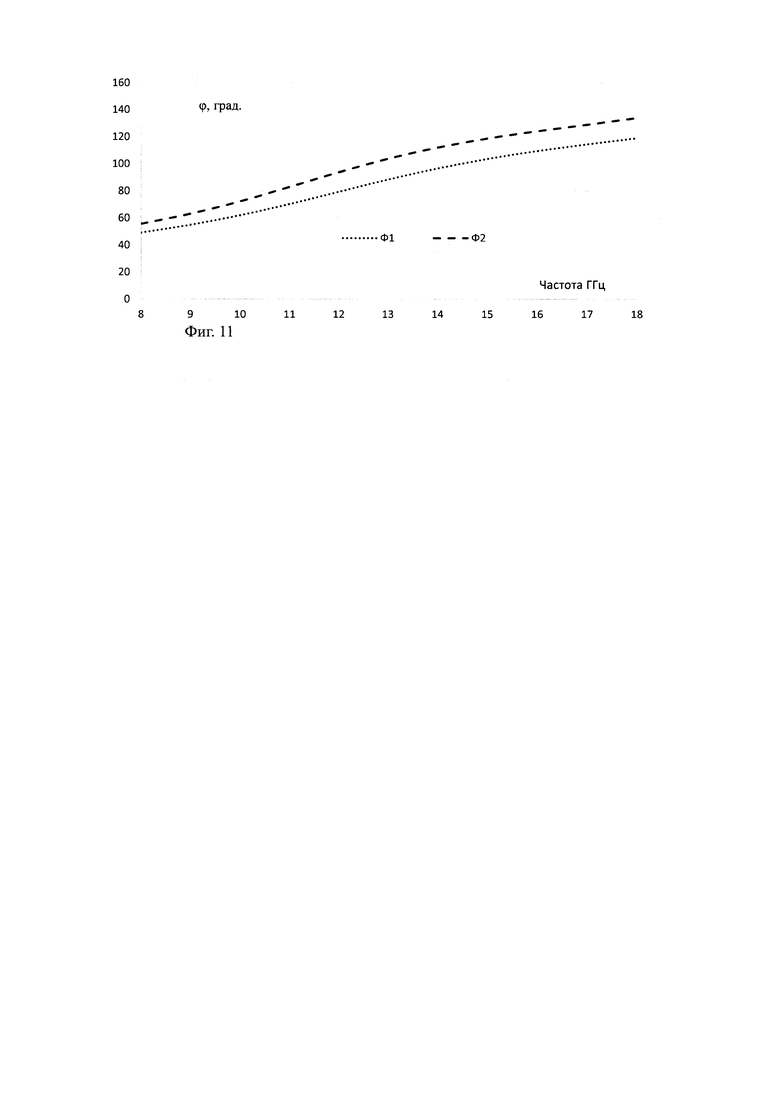
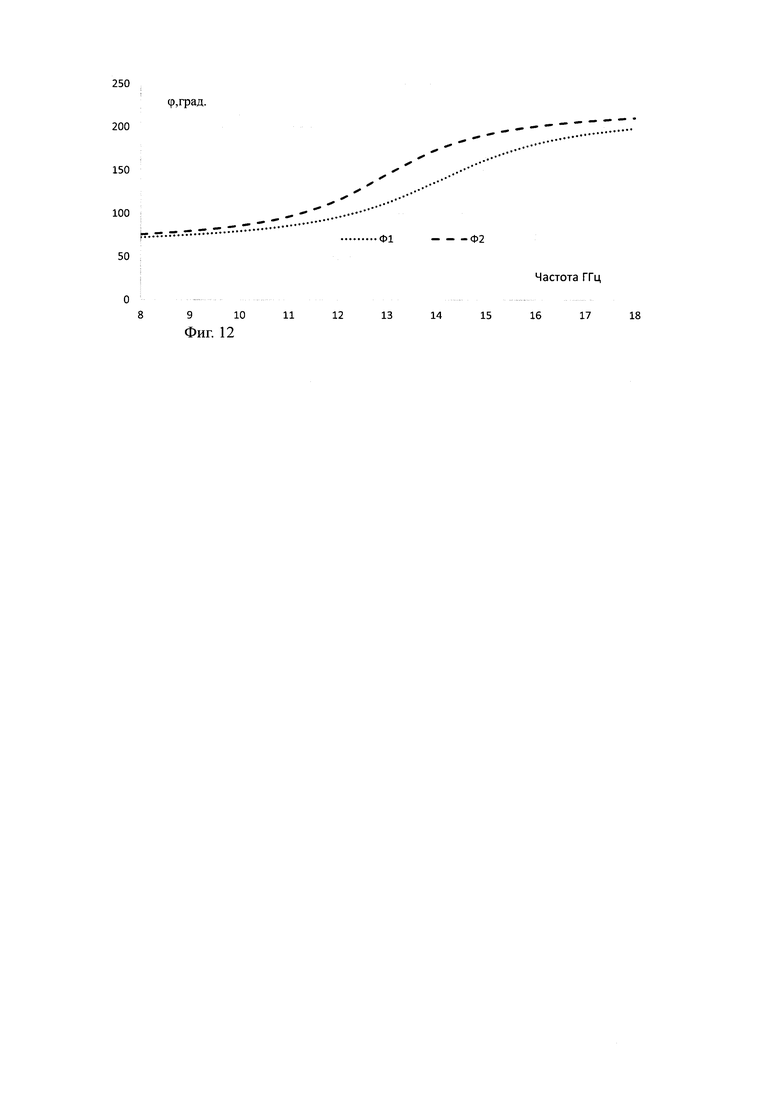
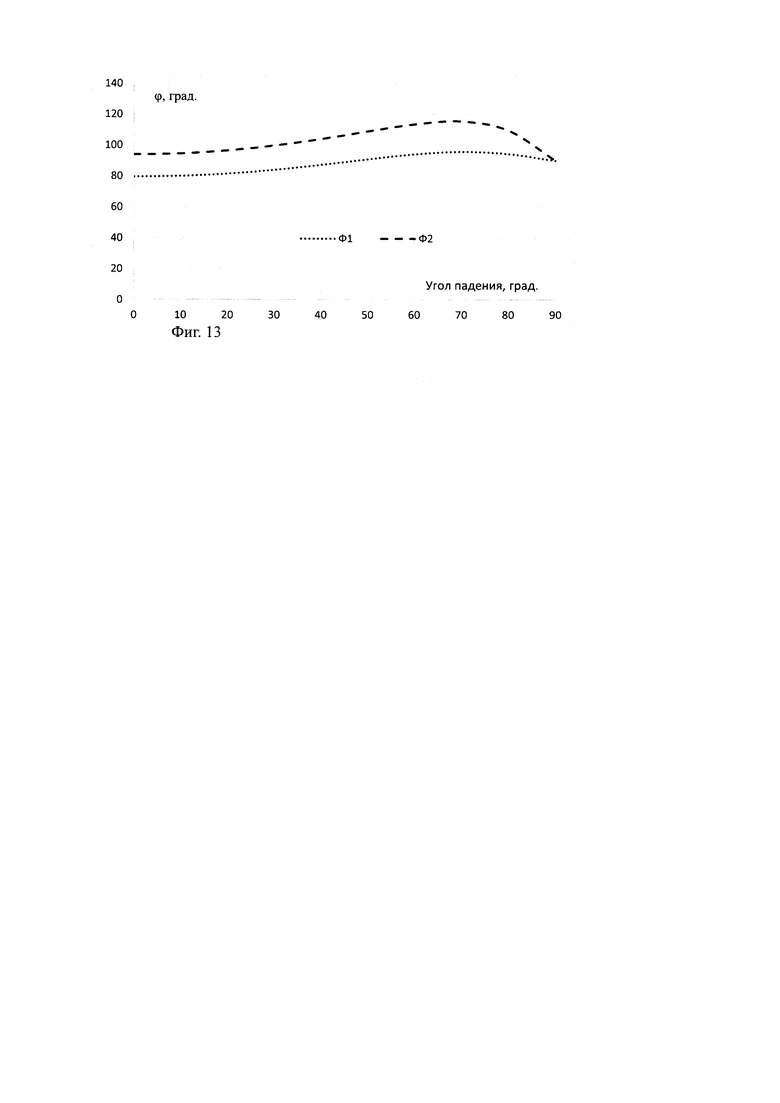
Заметны также изменения в фазе прошедшей волны на Фиг. 11-13 в зависимости от модели представления структуры многослойного композиционного материала для ТЕ поляризации при моделировании пластины монолитным однородным слоем с εэфф=3,2 (Ф1) и, представляя материал в виде многослойной структуры слоев толщиной, пропорциональной объемному содержанию компонентов (Ф2).
При расчете радиотехнических характеристик системы «антенна обтекатель» с использованием электродинамической модели на основе физической оптики поле на внутренней поверхности оболочки находится решением задачи прохождения полны через бесконечную пластину, поэтому точность определения величины амплитуды и фазы прошедшего поля существенно сказывается на точности расчетов выходных характеристик системы.
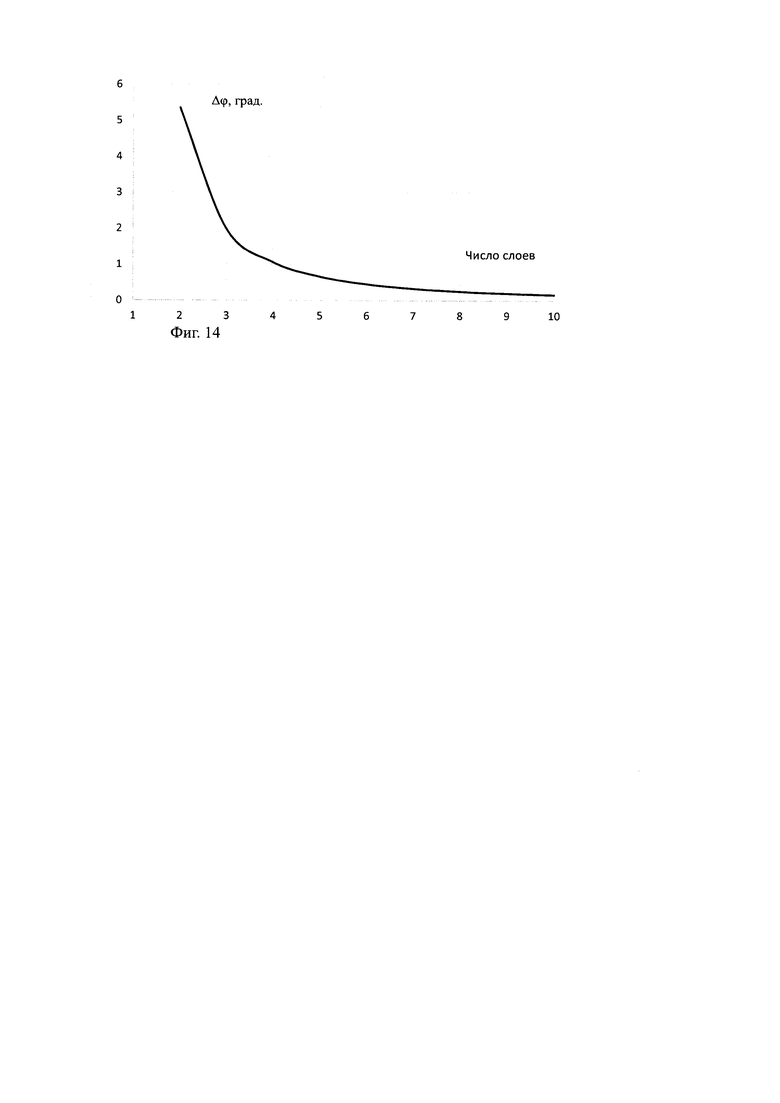
На Фиг. 14 показано отклонение рассчитанной фазы при падении волны прошедшего поля на пластину под углом 70 град, при моделировании стенки из многокомпонентного материала композиционного стеклопластикового материала (пять компонент) в зависимости от числа пластин многокомпонентной комбинации. Из Фиг. 14 видно, что для достижения достаточной для практики точности определения фазы в расчете стенка разбивается более чем на 10 пластин многокомпонентной комбинации в стопке толщины стенки.
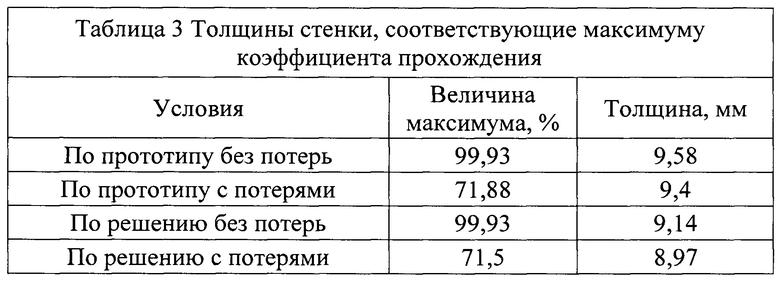
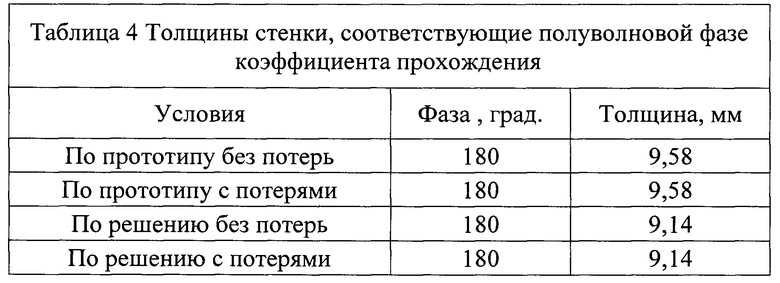
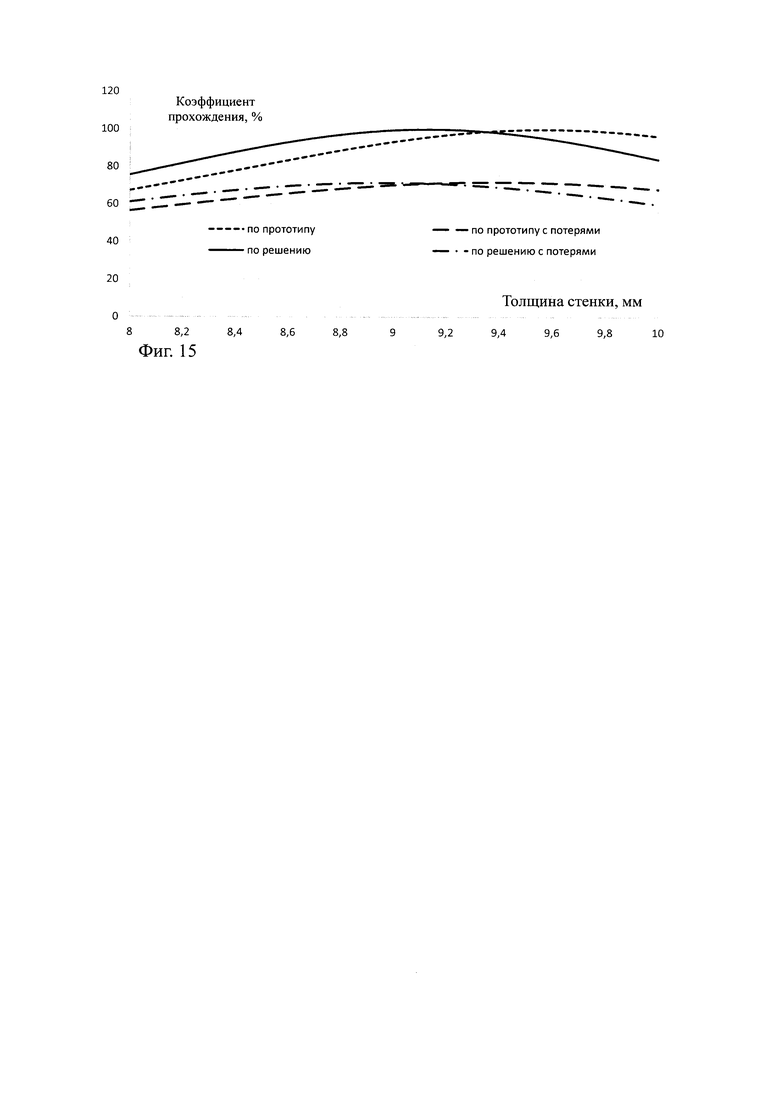
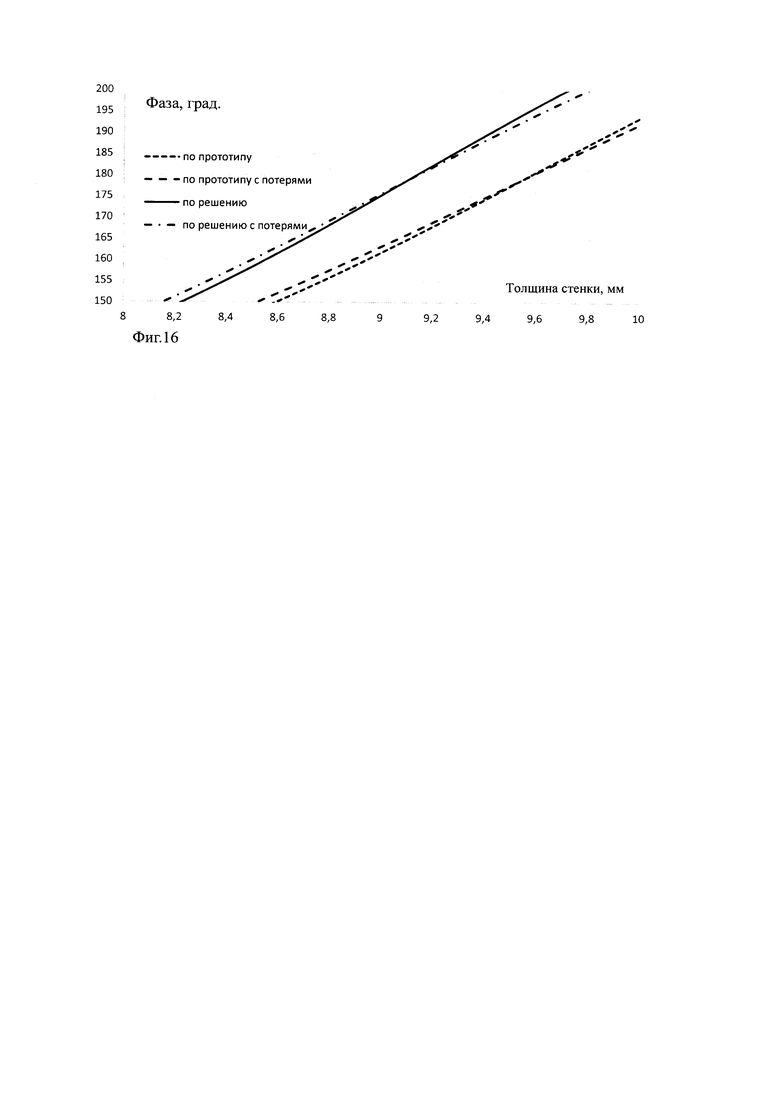
На фиг. 15 и 16 представлены расчеты зависимости коэффициента прохождения (мощности и фазы) от толщины стенки из кварцевой керамики антенного обтекателя для среднего угла падения 60 град, на частоте ƒ0=10 ГГц с эффективной диэлектрической проницаемостью εэфф=3,2 и пористостью 13% по прототипу и по решению с потерями в материале (tgδ=0,0500) и без них. Видно, что отличие в определении толщины резонансной толщины стенки различными способами по прототипу и по предлагаемому решению составляет 0,4 мм. Это большое отличие в толщине стенки, которое существенно повлияет на качество радиотехнических характеристик антенного обтекателя.
В таблицах 3 и 4 приведены результаты обработки приведенных данных на фиг. 15 и 16. Из которых видно, что тангенс угла диэлектрических потерь существенно влияет на настройку толщины стенки антенного обтекателя в резонанс и также должен учитываться при определении толщины стенки антенного обтекателя.
Заявляемый способ оптимизации радиотехнических характеристик антенного обтекателя со стенкой из многокомпонентного материала включает необходимые признаки, обеспечивающие преимущество по сравнению с известными способами.
| название | год | авторы | номер документа |
|---|---|---|---|
| Широкополосная система "антенна-обтекатель" | 2017 |
|
RU2647563C1 |
| ШИРОКОПОЛОСНАЯ СИСТЕМА "АНТЕННА-ОБТЕКАТЕЛЬ" | 2012 |
|
RU2513718C2 |
| ШИРОКОПОЛОСНЫЙ ОБТЕКАТЕЛЬ | 2008 |
|
RU2364998C1 |
| Стенка широкополосного обтекателя | 2020 |
|
RU2755584C1 |
| ШИРОКОПОЛОСНАЯ СИСТЕМА "АНТЕННА-ОБТЕКАТЕЛЬ" | 2011 |
|
RU2446520C1 |
| Широкополосная система "антенна-обтекатель" | 2018 |
|
RU2688034C1 |
| Способ измерения диэлектрических свойств материала и устройство для его осуществления | 2017 |
|
RU2665593C1 |
| АНТЕННЫЙ ОБТЕКАТЕЛЬ | 1993 |
|
RU2054763C1 |
| РАДИОПРОЗРАЧНАЯ СТЕНКА ОБТЕКАТЕЛЯ | 2000 |
|
RU2168816C1 |
| Пеленгационная система "антенна-обтекатель" | 2020 |
|
RU2749384C1 |



Способ оптимизации радиотехнических характеристик антенного обтекателя со стенкой из многокомпонентного материала, включающий определение толщины стенки, настроенной на рабочий частотный диапазон обтекателя, его изготовление и измерение радиотехнических характеристик на стенде, отличающийся тем, что измеряют диэлектрические проницаемости и тангенсы углов диэлектрических потерь, объемы и плотности всех компонентов, входящих в состав материала стенки обтекателя, определяют по максимуму коэффициента прохождения прошедшей волны для среднего угла падения на обтекатель в рабочем диапазоне частот толщину стенки, представляя ее одномерной стопкой из одинаковых последовательно расположенных пластин со структурой в виде однородных последовательно расположенных стопкой слоев, равных числу компонентов материала с толщиной, равной объемной доле каждого материала, поделенной между числом пластин относительно полной объемной доли компонента в материале, составляющей структуру в виде суммы объемных долей компонентов и равной полному объему материала. По сравнению с известными решениями в предлагаемом способе исключается процедура определения эффективной диэлектрической проницаемости смеси, а определение толщины стенки антенного обтекателя со стенкой из многокомпонентного материала с оптимальными радиотехническими характеристиками производится непосредственно по измеренным диэлектрическим проницаемостям и тангенсам углов диэлектрических потерь, объемам и плотностям всех компонентов, входящих в состав материала стенки обтекателя. 4 табл., 16 ил.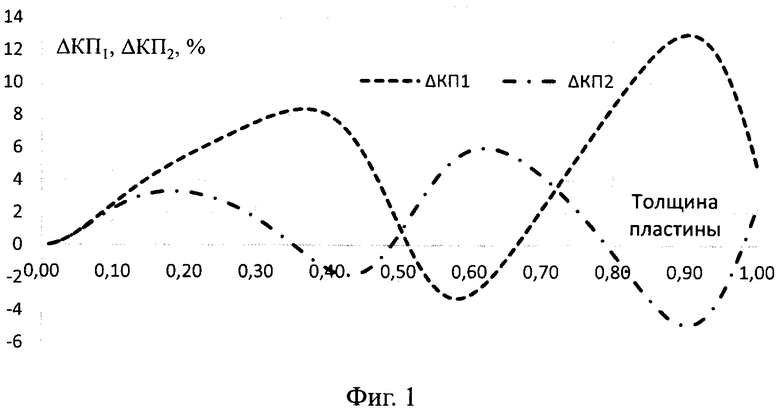
Способ оптимизации радиотехнических характеристик антенного обтекателя со стенкой из многокомпонентного материала, включающий определение толщины стенки, настроенной на рабочий частотный диапазон обтекателя, его изготовление и измерение радиотехнических характеристик на стенде, отличающийся тем, что измеряют диэлектрические проницаемости и тангенсы углов диэлектрических потерь, объемы и плотности всех компонентов, входящих в состав материала стенки обтекателя, определяют по максимуму коэффициента прохождения прошедшей волны для среднего угла падения на обтекатель в рабочем диапазоне частот толщину стенки, представляя ее одномерной стопкой из одинаковых последовательно расположенных пластин со структурой в виде однородных последовательно расположенных стопкой слоев, равных числу компонентов материала с толщиной, равной объемной доле каждого материала, поделенной между числом пластин относительно полной объемной доли компонента в материале, составляющей структуру в виде суммы объемных долей компонентов и равной полному объему материала.
| Басков К.М | |||
| Современное электродинамическое сопровождение проектирования и изготовления систем антенна-радиопрозрачное укрытие | |||
| Диссертация на соискание ученой степени кандидата технических наук | |||
| Москва, 2016 | |||
| И.Г | |||
| Гуртовник, В.Н | |||
| Спортсмен | |||
| Стеклопластики радиотехнического назначения | |||
| Москва, Химия, 1987, стр.146-151 | |||
| ГОЛОВКОВ А.А | |||
| Комплексированные радиоэлектронные устройства | |||
| -М: Радио и связь, 1996, 114-120 | |||
| СПОСОБ УМЕНЬШЕНИЯ ЧАСТОТНОЙ ЗАВИСИМОСТИ ОСЛАБЛЕНИЯ ПРИ ПРОХОЖДЕНИИ ЭЛЕКТРОМАГНИТНОЙ ВОЛНЫ ЧЕРЕЗ ДИЭЛЕКТРИЧЕСКУЮ ОБОЛОЧКУ ОДНОВРЕМЕННО ДЛЯ ПАРАЛЛЕЛЬНОЙ И ПЕРПЕНДИКУЛЯРНОЙ ПОЛЯРИЗАЦИЙ И УСТРОЙСТВО ДЛЯ ЕГО РЕАЛИЗАЦИИ (ВЕКТОРНЫЙ АНТЕННЫЙ ОБТЕКАТЕЛЬ) | 2007 |
|
RU2334315C1 |
| УСТРОЙСТВО УМЕНЬШЕНИЯ ЭФФЕКТИВНОЙ ПОВЕРХНОСТИ РАССЕЯНИЯ АНТЕНН | 2006 |
|
RU2304329C1 |
| ВАКЦИННЫЕ КОМПОЗИЦИИ, СОДЕРЖАЩИЕ ВИРУС БЫЧЬЕЙ ВИРУСНОЙ ДИАРЕИ 1В ТИПА, И СПОСОБЫ ИХ ПОЛУЧЕНИЯ И ПРИМЕНЕНИЯ | 2011 |
|
RU2595873C2 |
Авторы
Даты
2018-05-07—Публикация
2017-05-30—Подача