Изобретение относится к технике измерения диэлектрической проницаемости в свободном пространстве.
Известные методы измерения диэлектрической проницаемости в волноводе и резонаторе, имея высокую точность и чувствительность обладают существенным недостатком: узкополосностью в частотном диапазоне [Егоров В.Н. Резонансные методы исследования диэлектриков на С.В.Ч. Приборы и техника эксперимента. №2, 2007 с. 5-38.].
Диэлектрические свойства материала в свободном пространстве определяют сравнительными измерениями мощности и фазы волны, распространяющейся между передающей и приемной антеннами без образца материала и проходящей через образец материала или отражающейся от него [Брандт А.А. Исследование диэлектриков на сверхвысоких частотах М., Физматгиз, 1963, 404 стр. А.А. Беляев, А.М. Романов, В.В. Широков, Е.М. Шульдешов. Измерение диэлектрической проницаемости стеклосотопласта в свободном пространстве. Электронный научный журнал «ТРУДЫ ВИАМа», №5, 2014, с. 1-8. Валеев Г.Г. Способ измерения относительной комплексной диэлектрической проницаемости материала с потерями в СВЧ диапазоне. Патент РФ №2613810. От 06.10.2015. Воробьев Е.А. Радиоволновой контроль судовых радиотехнических конструкций и материалов. - Л., Судостроение, 1986, 84 стр, (22 стр). Федюнин П.А., Каберов С.Р., Дмитриев Д.А., Федоров Н.П. СВЧ-способ определения комплексной диэлектрической проницаемости и толщины диэлектрических пластин. Патент РФ №2249178. От 10.09.2004. Приборы для неразрушающего контроля материалов и изделий. В 2-х книгах. Кн. 1 / Под ред. В.В. Клюева. - 2-е изд., перераб. и доп. - М: Машиностроение. 1986, 488 с.].
В работе [Воробьев Е.А. Радиоволновой контроль судовых радиотехнических конструкций и материалов. - Л., Судостроение, 1986, 84 стр, (22 стр).] описаны способы определения диэлектрической проницаемости материала по мощности и фазе прошедшей волны и отраженной волны, а также применение СВЧ-измерителя в качестве приемной аппаратуры.
В работах [Валеев Г.Г. Способ измерения относительной комплексной диэлектрической проницаемости материала с потерями в СВЧ диапазоне. Патент РФ №2613810. От 06.10.2015. Федюнин П.А., Каберов С.Р., Дмитриев Д.А., Федоров Н.П. СВЧ-способ определения комплексной диэлектрической проницаемости и толщины диэлектрических пластин. Патент РФ №2249178. От 10.09.2004.] описаны способы определения диэлектрической проницаемости материала по мощности и фазе отраженной волны от пластины, расположенной под углом Брюстера.
Для получения расширенной информации о физической и химической структуре исследуемого материала требуется исследования материалов в широкой частотной области с увеличением граничных частот, где размеры резонансных систем становятся сравнимыми в длиной волны, поэтому направление развития методов исследований свойств диэлектрических материалов связано с использованием в радиодиапазоне оптических методов в свободном пространстве для которых, с созданием СВЧ-измерителей в виде широкополосных анализаторов цепей, достигнут прогресс в приборном обеспечении.
Вместе с тем методы измерения в свободном пространстве обладают многими методическими недостатками, которые приводят к погрешности производимых измерений до уровня 10% по диэлектрической проницаемости и не высокой точностью определения тангенса угла диэлектрических потерь.
Недостатком метода измерения диэлектрической проницаемости в свободном пространстве является требование к высокой точности изготовления образцов пластин протяженных размеров на уровне 0,05 мм, что с технологической точки зрения при больших размерах образцов трудно выполнимо. Высокие требования предъявляются также к радиотехническому качеству измерительного полигона и точности измерительной аппаратуры. При всех недостатках присущих методу измерения диэлектрических материалов в свободном пространстве его важное преимущество состоит в возможности получения зависимостей диэлектрической проницаемости от частоты в широкой полосе.
Наиболее близкими техническим решением является способ измерения диэлектрической проницаемости материала [Nicolson A.M. and Ross G.F. // IEEE Trans. Instrum. Meas. - 1970. - v. l9 - p. 377-382.].
Описан способ измерения диэлектрических свойств материала, включающий измерение мощности и фазы прошедшей волны через образец материала, измерение мощности и фазы отраженной волны от образца материала, вычисление изменения мощности и фазы, с образцом материала и без него, определение по изменениям величин мощности и фаз диэлектрических свойств образца материала.
Наиболее близким является устройство для измерения диэлектрической проницаемости материала [А.А. Беляев, А.М. Романов, В.В. Широков, Е.М. Шульдешов. Измерение диэлектрической проницаемости стеклосотопласта в свободном пространстве. Электронный научный журнал «ТРУДЫ ВИАМа», №5, 2014, с. 1-8.], включающее СВЧ-измеритель, генераторный выход которого соединен с передающей антенной, а приемный вход с приемной антенной, подставка под образец расположенная между антеннами, управляющий компьютер, соединенный с СВЧ-измерителем.
Определение величины изменения диэлектрической проницаемости и тангенса угла диэлектрических потерь в свободном пространстве производится динамическим методом сравнения мощностей и фаз прошедшей или отраженной волн без и с образцом материала при его помещении в область испытательного полигона. В качестве измерительных устройств применяются приемная и передающая антенны, настроенные специальным образом, так чтобы уменьшить искажения, вносимые вторичными волнами рассеяния и интерференции, возникающие на краях образца испытуемого материала.
Недостатком представленных способа и устройства является низкая точность измерения диэлектрической проницаемости в полосе частот.
Целью изобретения является повышение точности измерения в свободном пространстве частотной зависимости диэлектрической проницаемости образца материала в широкой полосе частот.
Цель достигается тем, что предложен способ измерения диэлектрических свойств материала, включающий измерение на СВЧ измерителе мощности и фазы прошедшей волны без образца материала, расположение образца материала на подставке в центре полигона между передающей антенной, приемной антенной, измеряющей прошедшую волну, и приемной антенной, измеряющей отраженную волну, измерение мощности и фазы прошедшей волны через образец материала, измерение угловой зависимости мощности и фазы отраженной волны от образца материала, определение угла Брюстера по минимуму угловой зависимости сигнала отраженного от образца материала, вычисление изменения мощности и фазы прошедшей и отраженной волн, с расположенным образцом материала и без него, определение по изменению мощности и фазы прошедшей и отраженных волн диэлектрической проницаемости образца материала, отличающийся тем, что образец материала располагают и поворачивают относительно падающей волны и по максимуму мощности прошедшей волны в диапазоне частот находят угол Брюстера, затем образец материала на подставке устанавливают под найденным углом Брюстера, измеряют мощность и фазу прошедшей волны и по изменению фазы прошедшей волны в полосе частот по формуле рассчитывают предварительную частотную зависимость величины диэлектрической проницаемости образца материала, выбирают ряд частот внутри частотного диапазона, последовательно устанавливая на СВЧ-измерителе, а по предварительно определенной величине диэлектрической проницаемости на каждой установленной частоте рассчитывают угол Брюстера, после чего поворачивают образец материала на подставке, устанавливая рассчитанный угол Брюстера, по изменению фазы прошедшей волны, измеренной СВЧ-измерителем, вновь рассчитывают диэлектрическую проницаемость материала образца на установленной частоте, затем на каждой частоте вращают образец материала вблизи угла Брюстера и синхронно с ним приемную антенну, принимающую отраженную волну, записывают зависимость изменения фазы отраженной волны от угла падающей волны на образец материала и по градиенту угловой зависимости фазы отраженной волны расчетом по формуле определяют тангенс угла диэлектрических потерь материала образца, проведя определение диэлектрической проницаемости и тангенса угла диэлектрических потерь на всех выбранных частотах, записывают частотные зависимости диэлектрической проницаемости и тангенса угла диэлектрических потерь.
Для достижения цели изобретения предложено устройство для измерения диэлектрических свойств материала, включающее передающую антенну, приемную антенну, принимающую прошедшую волну через образец материала, приемную антенну, принимающую отраженную волну от образца материала, подставку для крепления образца материала, СВЧ-измеритель, соединенный с управляющим компьютером, отличающееся тем, что антенны установлены так, что электрические векторы антенн лежат в горизонтальной плоскости падения волны на образец материала, приемная антенна, принимающая отраженную волну, расположена на платформе, установленной соосно с подставкой для образца материала, с возможностью их вращения вокруг оси, причем платформа и подставка снабжены датчиками угла поворота и двигателями с блоками управления, подключенными к управляющему компьютеру, а приемные антенны подключены к СВЧ-измерителю через коммутатор, соединенный с управляющим компьютером.
Как установили авторы, изменение фазы, прошедшей или отраженной волн, для любой частоты и при обеих поляризациях и любых углов падения волны на плоскую пластину при взаимодействии падающей и отраженной волн в зависимости от электрической толщины пластины имеют гармонический вид, кроме случая при падения плоской волны с параллельной поляризацией под углом Брюстера, для которой зависимость изменения фазы от толщины пластины линейна из-за отсутствия отраженной волны. Это приводит к тому, что методы определения диэлектрической проницаемости в свободном пространстве, основанные на измерениях фазы прошедшей или отраженной волн, для несогласованной по электрической толщине стенки, имеют значительную погрешность. Для определения величины погрешности определения диэлектрической проницаемости методом свободного пространства при нулевом угле падения волны на плоскую пластину промоделируем условия эксперимента определив зависимость диэлектрической проницаемости от частоты по схеме рисунка 4.2.1. в полосе частот от 1 до 20 ГГц, считая пластину однородной и изготовленной из однородного материала толщиной d=9 мм, например, из диоксида кремния (кварцевого стекла) с диэлектрической проницаемостью ε=3,81 и тангенсом угла диэлектрических потерь tgδ=0,0001, которые измерены на частоте 10 ГГц по ГОСТ Р 8.623-2015 резонаторным методом. На первом этапе рассчитаем мощность и фазу прошедшей волны (Δϕ(f)) для параллельной поляризации падающей волны в диапазоне частот от 1 до 20 ГГц, а затем из этих расчетных данных определим величину диэлектрической проницаемости по формуле:
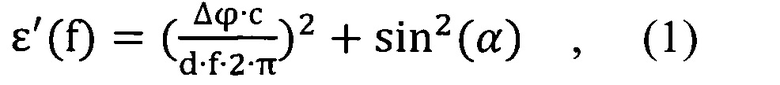
где с - скорость света.
Расчетная модель, описывающая представленный эксперимент, основывается на матричном методе расчета прохождения плоской волны через пластину диэлектрического материала [Борн М., Вольф Э. Основы оптики. - М.: Наука, 1973. - 720 с.]. При использовании алгоритма расчетной модели в виде программного продукта исчезает необходимость вывода аналитических формул, связывающих косвенные параметры, полученные в ходе эксперимента с диэлектрическими свойствами, как это сделано, например, в [Брандт А.А. Исследование диэлектриков на сверхвысоких частотах М., Физматгиз, 1963, 404 стр.], достаточно, моделируя в программе условия эксперимента, рассчитывать выходные данные.
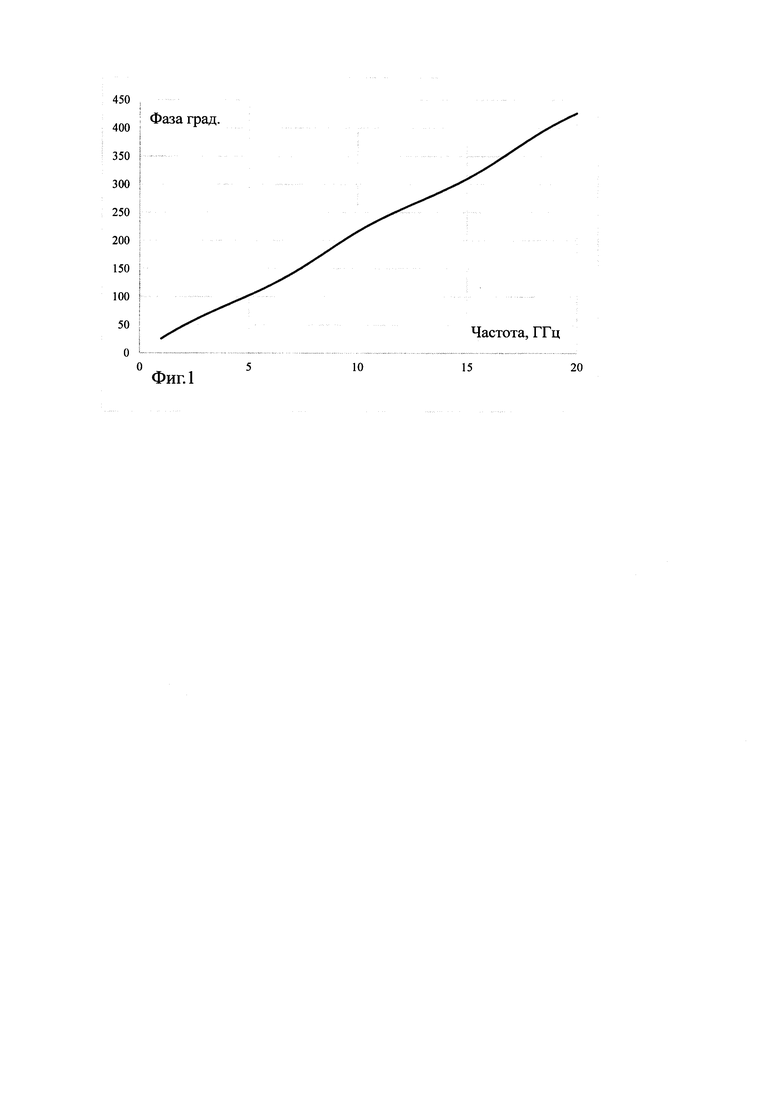
Результаты расчета частотной зависимости фазы прошедшей волны по модели эксперимента представлены на Фиг. 1.
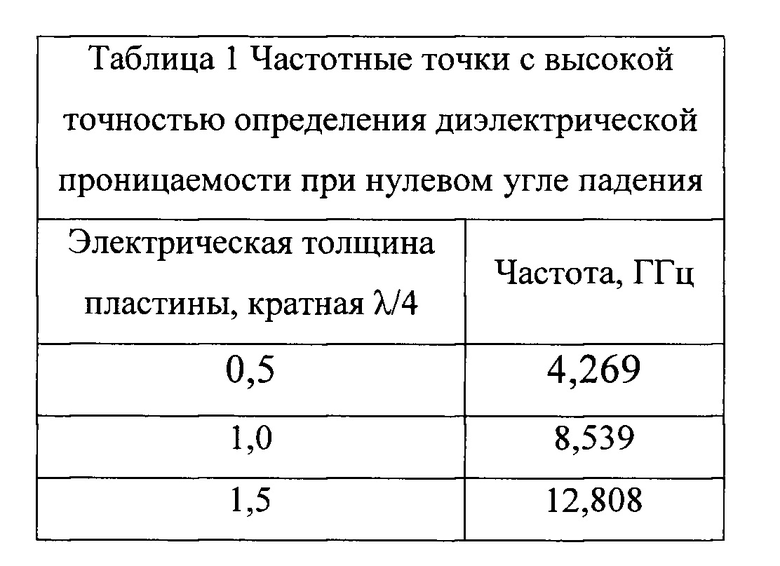
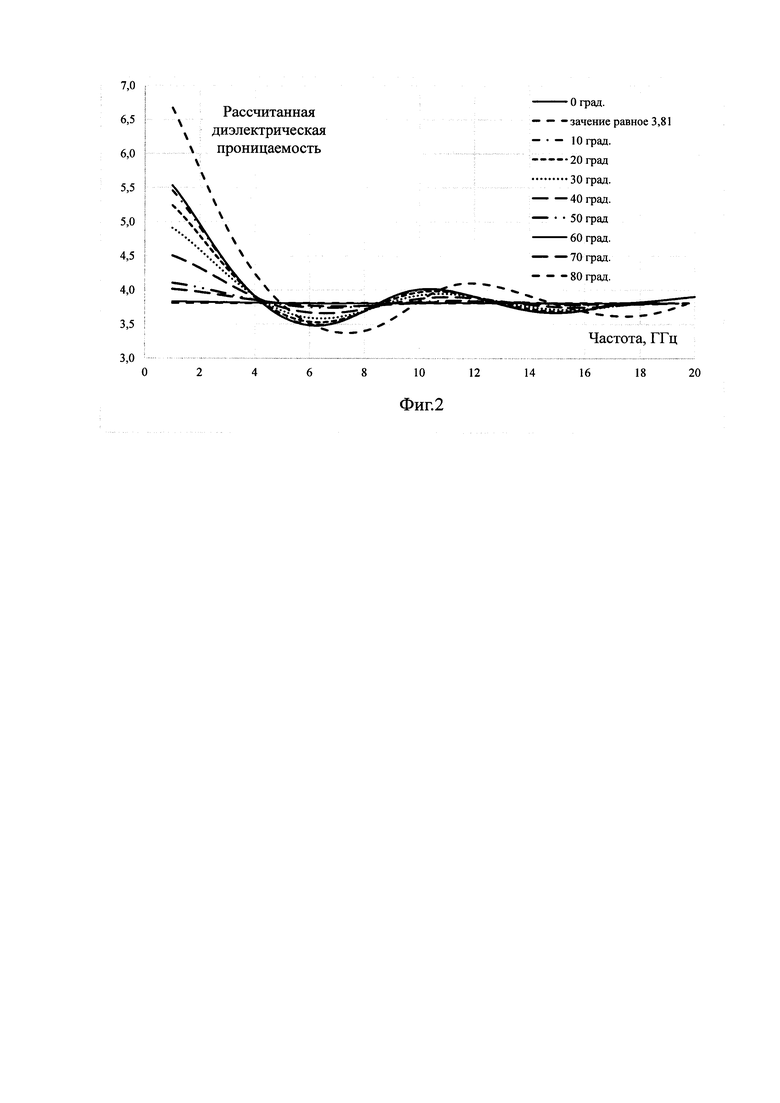
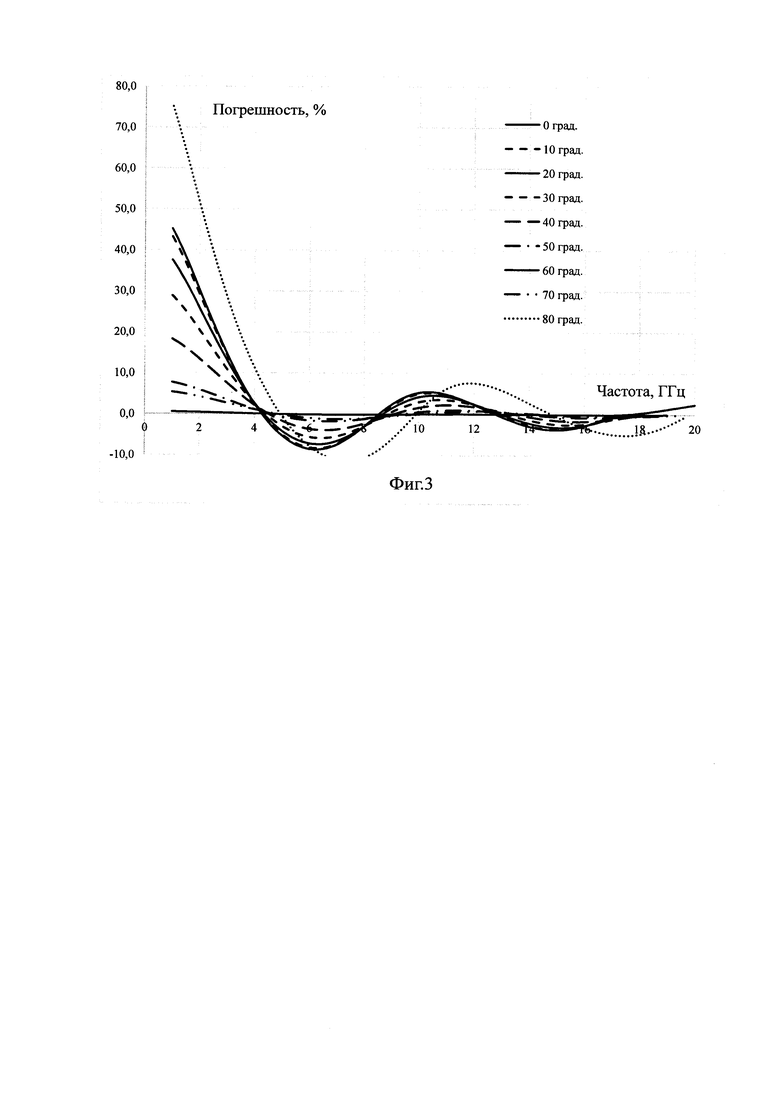
Из Фиг. 1 видно, что частотная зависимость фазы имеет гармонический вид. Используя частотные зависимости фазы прошедшей волны по формуле (1) проведены расчеты диэлектрической проницаемости в зависимости от частоты, результаты которых представлены на Фиг. 2, а на Фиг. 3 представлены частотные зависимости величин погрешности определения диэлектрической проницаемости материала пластины по фазе прошедшей волны для различных углов падения.
Из Фиг. 3 видно, что для радиочастотного диапазона точность определения диэлектрической проницаемости материала пластины методом свободного пространства существенно зависит от электрической толщины пластины и становится приемлемой, когда она кратна четверть длине волны, как видно из сравнения Фиг. 3 и таблицы 1, так как при четверть волновой электрической толщине пластины уменьшается величина отраженной волны и в этих точках зависимость фазы от электрической толщины становится линейной.

Из проведенного анализа видно, что в области радиодиапазона реализовать метод определения диэлектрической проницаемости в свободном пространстве в широкой полосе для малых величин угла падения с приемлемой для практики точностью не представляется возможным. Как показывают проведенные расчеты, основной причиной высокой погрешности определения диэлектрической проницаемости в методе свободного пространства является интерференция волн подающей и отраженной от образца материала. При отсутствии отраженной волны методическая погрешность определения диэлектрической проницаемости в свободном пространстве отсутствует.
При проведении расчетов изменения фазы прошедшей волны авторами было установлено, что для параллельной поляризации при падении волны под углом Брюстера зависимость фазы прошедшей волны линейна и не зависит от электрической и геометрической толщин, а также от частоты электромагнитной волны.
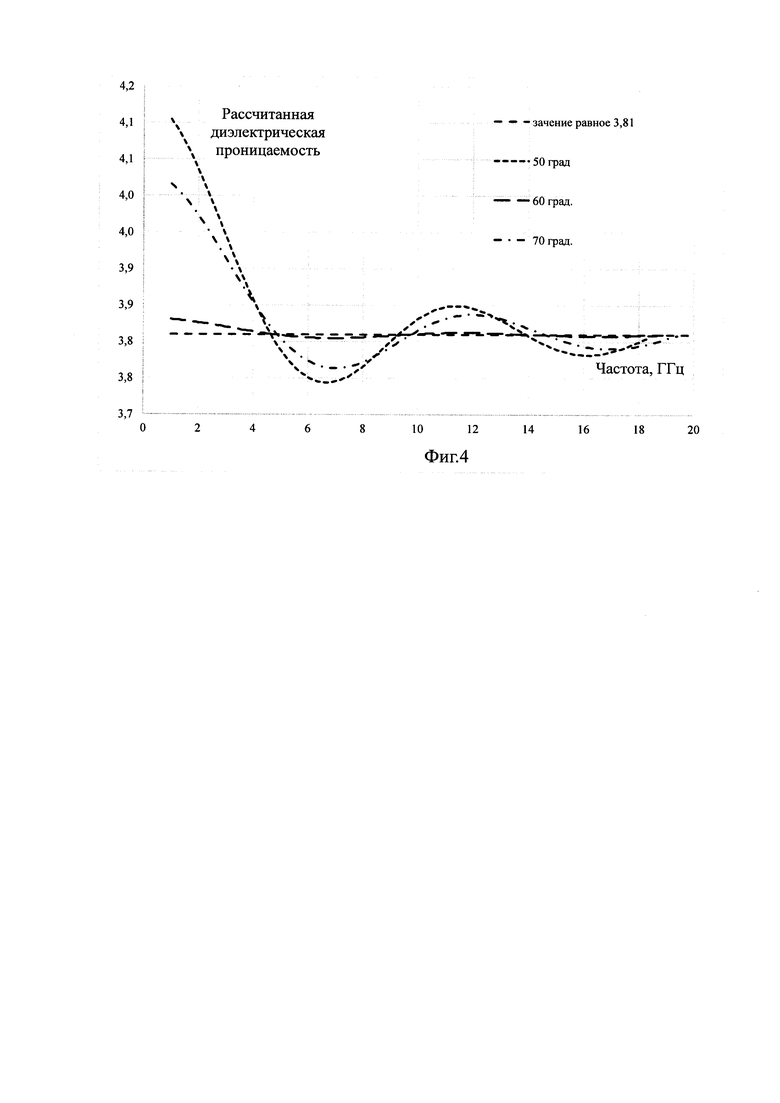
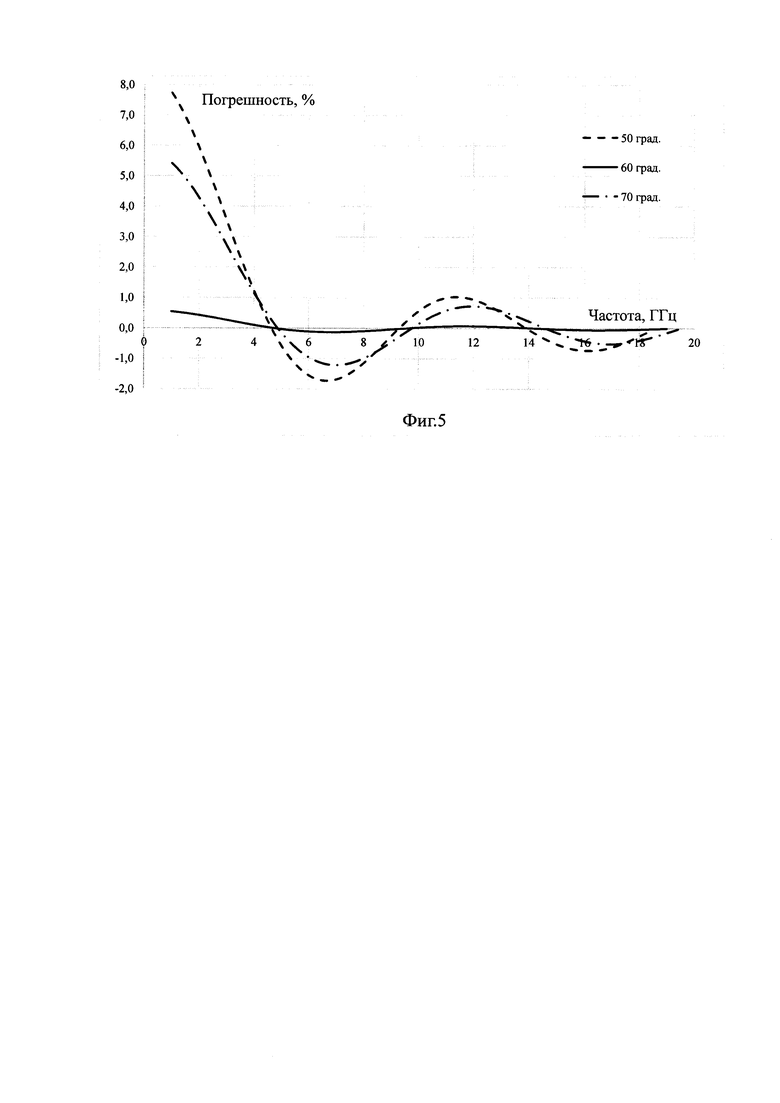
Из частотных зависимостей фазы прошедшей волны по формуле (1) проведены расчеты зависимостей диэлектрической проницаемости от частоты, результаты которых представлены на Фиг. 4. На Фиг. 5 представлены частотные зависимости величин погрешности определения диэлектрической проницаемости по фазе прошедшей волны для различных углов падения близи угла Брюстера для диэлектрической проницаемости пластины равной ε'=3,81.
Из Фиг. 4 и 5 видно, что при реализации угла падения близкого к величине угла Брюстера погрешность определения диэлектрической проницаемости по фазе прошедшей волны резко падает, а при угле падения равного углу Брюстера методическая погрешность определения зависимости диэлектрической проницаемости образца материала в методе свободного пространства равна нулю.
Авторы определили основные операции в реализации метода определения частотной зависимости диэлектрической проницаемости образца материала пластины в свободном пространстве по результатам измерения:
1. Определение предварительного значения диэлектрической проницаемости образца материала на одной фиксированной частоте, f=10 ГГц, сначала по найденному углу падения волны, соответствующего одновременно максимуму прошедшей волны и минимуму отраженной, определяют угол Брюстера, например, для кварцевого стекла αБрюстера=62,873° толщина пластины d=5 мм;
2. Вычисление по формуле: ε’=tan2αБрюстера диэлектрической проницаемости, ε'(10 ГГц)=3,81 на фиксированной частоте;
3. Устанавливают пластину испытуемого материала под углом поворота для падающей волны, равного αБрюстера=62,873°;
4. Измеряют фазу прошедшей волны в полосе частот Δϕ(f);
5. По формуле:
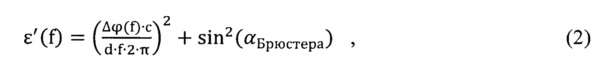
определяют частотную зависимость эффективной диэлектрической проницаемости материала пластины.
Определение диэлектрической проницаемости по фазе прошедшей волны через образец материала, установленный под углом Брюстера, позволяет устранить неопределенность, связанную с кратностью резонансных электрических толщин и производить измерение образцов с различными толщинами (с толщинами значительной толщины по сравнению с длиной волны) с более высокой точностью, чем в известных способах.
Для анализа преимуществ предложенного способа и для определения методической погрешности способа определения диэлектрической проницаемости образца материала в полосе частот проведем моделирование схемы эксперимента, рассчитывая фазу прошедшей волны для пластины с расположенной под углом αБрюстера=62,873°, соответствующему углу Брюстера для ε'(10 ГГц)=3,81 при параллельной поляризации падающей волны для различных значений диэлектрической проницаемости пластины, которая может наблюдаться в эксперименте ε'(1-20 ГГц)=2,0÷5,0, а затем по формуле (2) определим из рассчитанной фазы в полосе частот априорно заданную диэлектрическую проницаемость пластины.
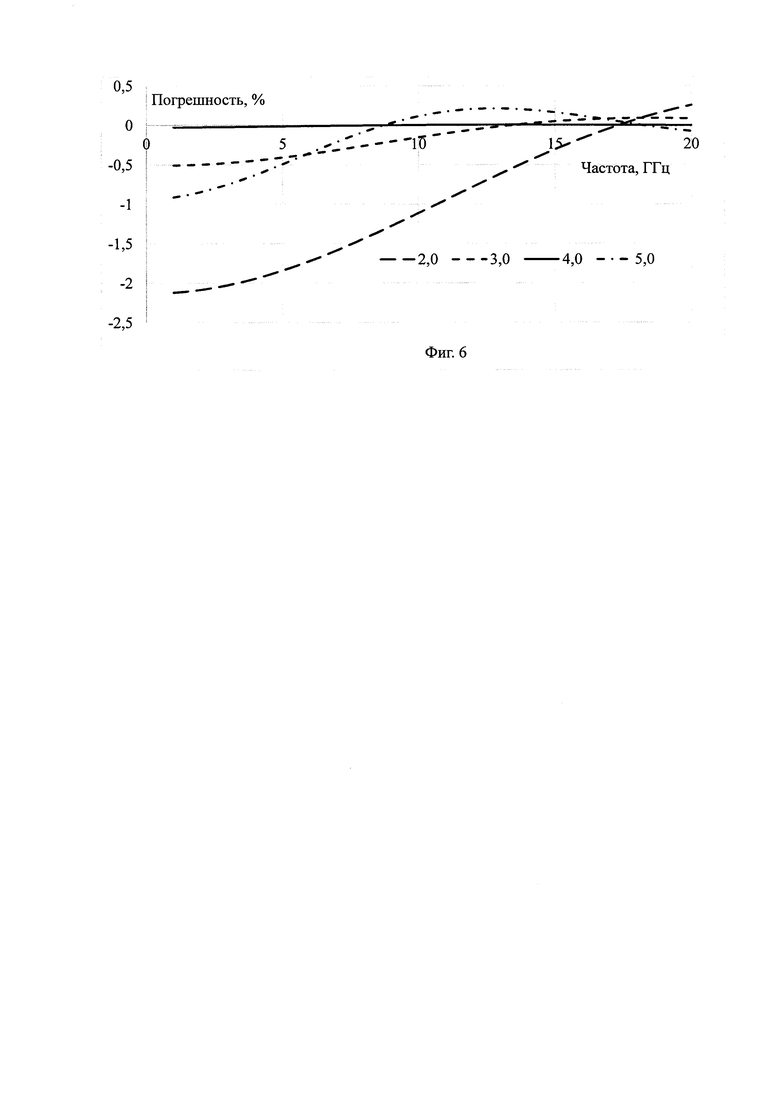
На Фиг. 6 представлены результаты расчета погрешности определения частотной зависимости диэлектрической проницаемости пластины относительно ее априорных значений в диапазоне возможных изменений: 2,0; 3,0; 4,0; 5,0.
Из Фиг. 6 видно, что методическая погрешность определения диэлектрической проницаемости от 2 до 5 в полосе частот от 1 до 20 ГГц не превосходит 2,2%.
При уменьшении интервала изменения диэлектрической проницаемости в полосе частот погрешность снижается так, что, как видно из Фиг. 6, при уменьшении интервала возможного изменения диэлектрической проницаемости материала испытуемой пластины от 3 до 5 в полосе частот от 1 до 20 ГГц методическая погрешность не превосходит 1%.
Рассчитаем инструментальную погрешность определения диэлектрической проницаемости предложенным способом. Прологарифмируем выражение (2):
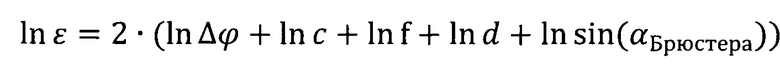 ,
,
Запишем:
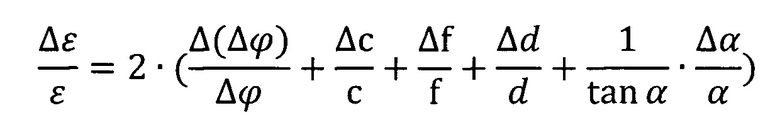
Абсолютная погрешность определения диэлектрической проницаемости равна:
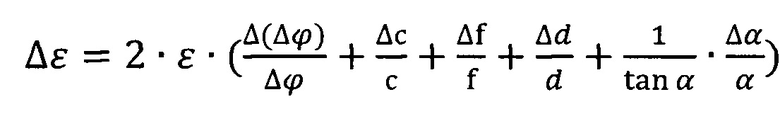 ,
,
где Δϕ - погрешность определения фазы которая при настройке и при применении компенсации изменения фазы в тракте СВЧ-измерителя составляет 1,5 град,
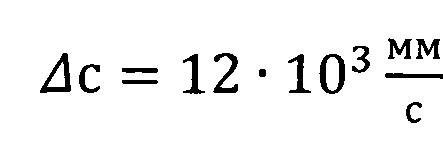 - погрешность определения скорости света
- погрешность определения скорости света 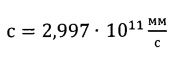 ,
,
Δf=10⋅103 Гц - погрешность определения частоты для f=10⋅109 Гц,
Δd=0,01 мм - погрешность изготовления толщины образца для d=5 мм,
Δα=0,012° - погрешность установки угла для αБрюстера=62,873°, соответствующего диоксиду кремния с ε=3,81.
Основным источником аппаратных ошибок в определении диэлектрической проницаемости является погрешность измерения фазы прошедшей волны, так расчеты показывают, что инструментальная погрешность 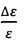 при использовании в расчете погрешностей составляющих, входящих в формулу (2), и со значениями, указанными выше, составит 3%.
при использовании в расчете погрешностей составляющих, входящих в формулу (2), и со значениями, указанными выше, составит 3%.
Основанием для введения операции по определению диэлектрической проницаемости образца материала по фазе прошедшей волны является то, что для параллельной поляризации при падении волны под углом Брюстера зависимость фазы прошедшей волны линейна и не зависит от электрической и геометрической толщин, а также от частоты электромагнитной волны, что значительно снижает погрешность определения диэлектрической проницаемости в полосе частот.
Основанием для введения операции по определению диэлектрической проницаемости образца материала по фазе прошедшей волны для параллельной поляризации при падении волны под углом Брюстера является то, что для предложенного способа в полосе частот методическая погрешность мала.
Известно, что для материала с потерями задача прохождения волны через плоский слой становится неоднородной, тем не менее, так как в окончательных выражениях формулы Френеля зависят только от вещественного угла падения, а комплексный угол преломления исчезает, то моделирование задачи прохождения волны через слой с потерями заключается в решении классической задачи с использованием комплексного значения диэлектрической проницаемости материала.
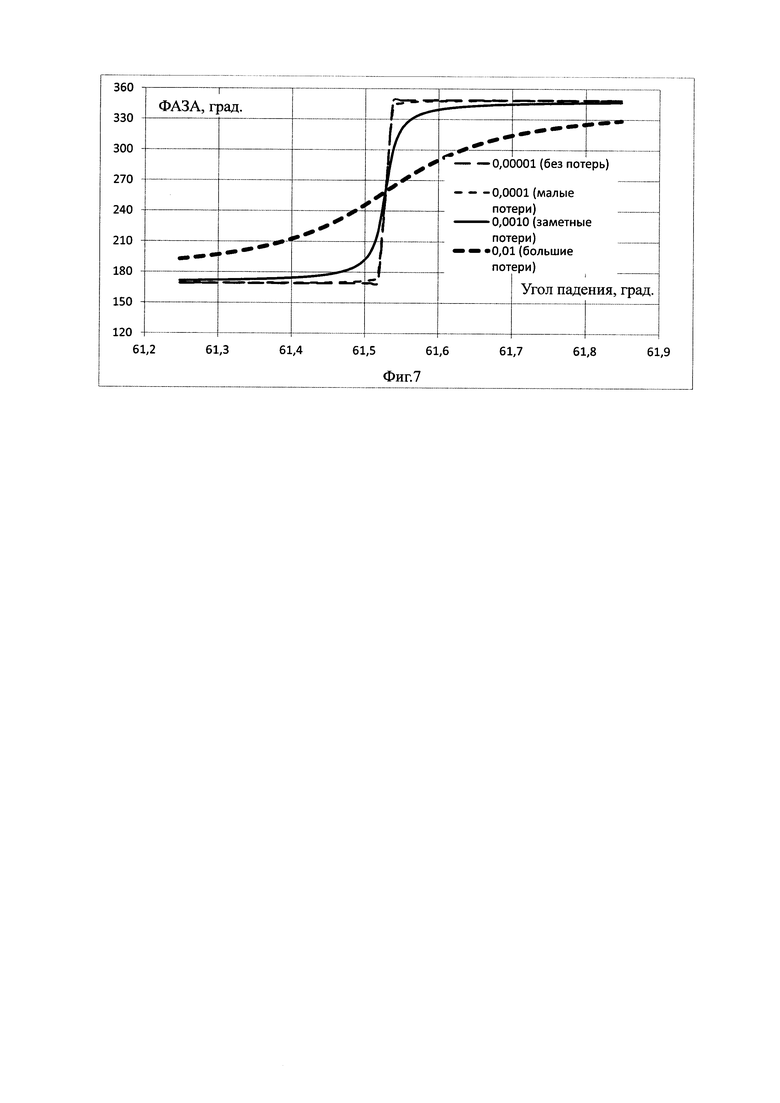
Например, наблюдающееся отличие величины разности фаз между падающей и отраженной волнами в теоретических расчетах и экспериментальных измерениях вблизи угла Брюстера, могут быть смоделированы в расчете введением диэлектрических потерь в материале пластины.
На Фиг. 7 представлены расчетные зависимости разности фаз между отраженной и падающей плоскими волнами вблизи угла Брюстера. Видно, что наличие потерь в материале образца вызывает плавное, соответствующее экспериментальным наблюдениям изменение фазы, и только в расчете для материала без потерь наблюдается скачок фазы на π, соответствующий теоретическим представлениям [Хиппель А.Р. Диэлектрики и волны - М.: Из-во иностранной литературы. 1960. - 439 с. 3], поэтому в предлагаемом способе, по измеренным угловым зависимостям фазы отраженной волны, вблизи угла Брюстера, относительно падающей волны, по градиенту угловой фазовой характеристики S в точке, соответствующей углу Брюстера определяется тангенс угла диэлектрических потерь.
Для подтверждения применимости в способе определения тангенса угла диэлектрических потерь по градиенту угловой зависимости фазы отраженной волны, проведем модельный расчет для образца материала из плавленого кварца с диэлектрической проницаемостью с ε=3,81, толщиной пластины d=5 мм, при изменении тангенса угла диэлектрических потерь в пределах tgδ=0,00001÷1,0.
Для определения тангенса угла диэлектрических потерь авторами предложена формула:
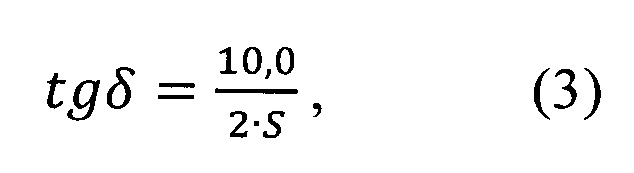
где S - градиент угловой фазовой характеристики отраженной волны при падении волны на образец материала под углом Брюстера. Градиент угловой фазовой характеристики определяется измерением фазы отраженной волны в двух угловых точках поворота образца материала относительно угла Брюстера:
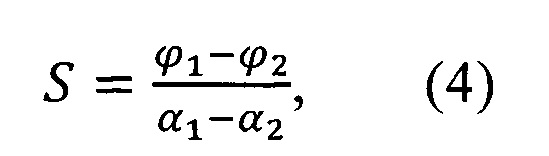
где ϕ1 - фаза измеренная в угловой точке α1, ϕ2 - фаза измеренная в угловой точке α2. Угловые точки для измерения выбираются симметрично относительно угла Брюстера или точки изменения фазы на величину π.
В таблице 2 приведены результаты расчета тангенса угла диэлектрических потерь материала образца, выполненные по формуле (3) с использованием модельных расчетов.
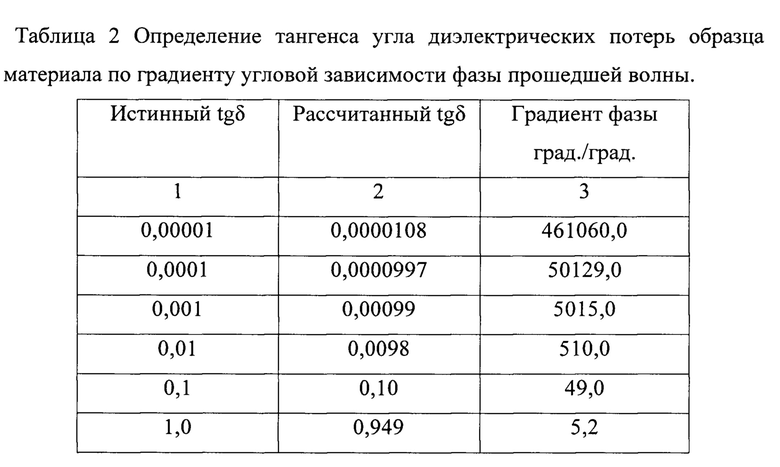
Основанием для введения операции по определению угла диэлектрических потерь по наклону угловой зависимости фазы отраженной волны образца материала для параллельной поляризации при падении волны под углом Брюстера является то, что для предложенной операции определение тангенса угла диэлектрических потерь по изменению фазы производится с большей точностью, чем по изменению мощностных характеристик, как в известных решениях, а так как в предложенном способе определение тангенса угла диэлектрических потерь не зависит от частоты и толщины образца материала, то аппаратурная погрешность определения так же ниже.
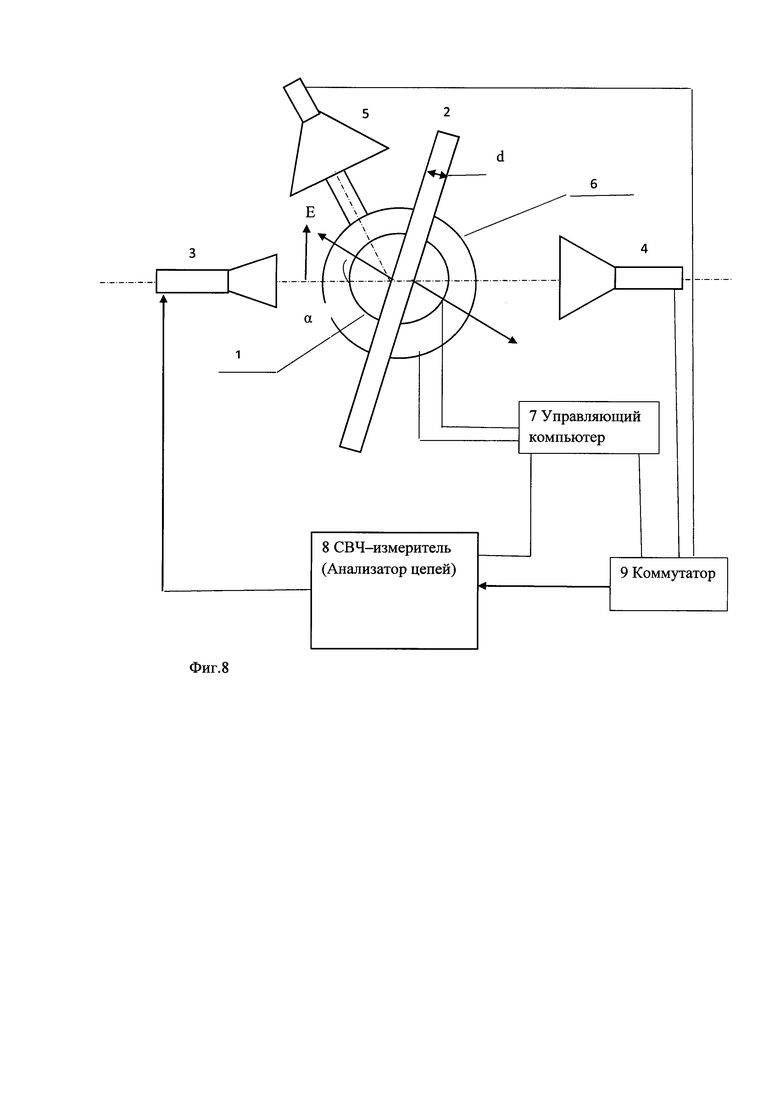
Предлагаемое устройство для измерения диэлектрических свойств образца материала в свободном пространстве представлено на фиг. 8.
На Фиг. 8 представлено устройство для измерения диэлектрических свойств материала в полосе частот.
В устройстве подставка 1 для образца 2 установлена в центре между линейно-поляризованной передающей антенной 3, линейно-поляризованной приемной антенной 4, измеряющей прошедшую волну, и линейно-поляризованной приемной антенной 5, измеряющей отраженную волну. Раскрыв антенн ориентирован так, что вектор электрического поля лежит в плоскости падения волны на образец материала (в горизонтальной плоскости). Антенны 3 и 4 закреплены соосно и неподвижно, а антенна 5 на платформе 6, установленной соосно с подставкой под образец 1. Подставка 1 и платформа 6 оборудованы моторами с блоками управления и датчиками угла поворота, которые входят в их конструкции и на чертеже не показаны. Моторы, через блоки управления, и угловые датчики соединены с управляющим компьютером 7, который позволяет устанавливать взаимные угловые положения между антеннами 3, 4, 5 и образцом материала 2. В качестве СВЧ-измерителя 8 в схеме представлен анализатор цепей, который позволяет реализовать основное преимущество методов измерения в свободном пространстве диэлектрических свойств материала, измерение в широкой полосе частот. Дополнительно в схему введен коммутатор 9, который соединен с управляющим компьютером 7 и позволяет производить измерение мощности и фазы, прошедшей и отраженной волн, используя один вход СВЧ-измерителя.
Основанием для введения в устройство для измерения диэлектрической проницаемости образца материала в свободном пространстве дополнительно платформы 6 с закрепленной антенной, принимающей отраженную волну, моторов с блоками управления и датчиками угла поворота является необходимость проведения высокоточных измерений угловых зависимостей мощности и фазы отраженной волны для определения тангенса угла диэлектрических потерь образца материала по градиенту угловой зависимости фазы отраженной волны и для высокоточной установки величины угла Брюстера падающей волны для точного измерения диэлектрической проницаемости образца материала по измерению угловой зависимости мощности и фазе прошедшей волны.
С использованием в качестве СВЧ измерителя векторный анализатор цепей, появляется возможность перекрыть единым приборным измерительным комплексом весь используемый в настоящее время радиочастотный диапазон для исследования диэлектрических материалов.
Для решения методических вопросов применения метода измерения диэлектрических свойств материалов в широкой полосе частот рассмотрим модель измерительного полигона с расположением линейно-поляризованных рупорных антенн в ближней зоне по схеме, представленной на Фиг. 8.
На Фиг. 8 представлены измерительные антенны в виде линейно-поляризованных рупоров, расположенных для измерения в совпадающих поляризациях так, что вектора Е рупоров лежат в плоскости падения электромагнитной волны на пластину из испытуемого материала толщиной d. Приемный и передающий рупор соединены с анализатором цепей. Излучаемая передающим рупором электромагнитная волна, проходя через пластину попадает в приемный рупор. На рисунке пластина повернута на угол α, равный углу падения плоской волны, в модели, с помощью которой описывается данный измерительный эксперимент. Элементы радиоизмерительного тракта хорошо разработаны и имеют погрешность определения фазы в СВЧ диапазоне от 1,5 град до 2 град. [Воробьев Е.А., Калашников B.C., Негурей А.В., Харитонов А.А. Измеритель радиотехнического качества диэлектрических материалов и изделий на СВЧ. - Дефектоскопия. - №9, 1993, - С. 45-49].
При повороте подставки 1 с образцом материала 2 на угол α относительно падающей волны платформа 6 с приемной антенной 5, принимающей отраженную волну, поворачивается на угол 2⋅α. Величины углов, а также мощность и фаза отраженной волны фиксируются в управляющем компьютере 7. Сканируя угловым положением приемной антенны 5 в области угла 2⋅α производится определение тангенса угла диэлектрических потерь материала образца по предложенному алгоритму. Величины мощности и фазы прошедшей волны, измеряемые приемной антенной 4, запоминаются в управляющем компьютере 7 в котором по предложенному алгоритму производится определение диэлектрической проницаемости материала образца.
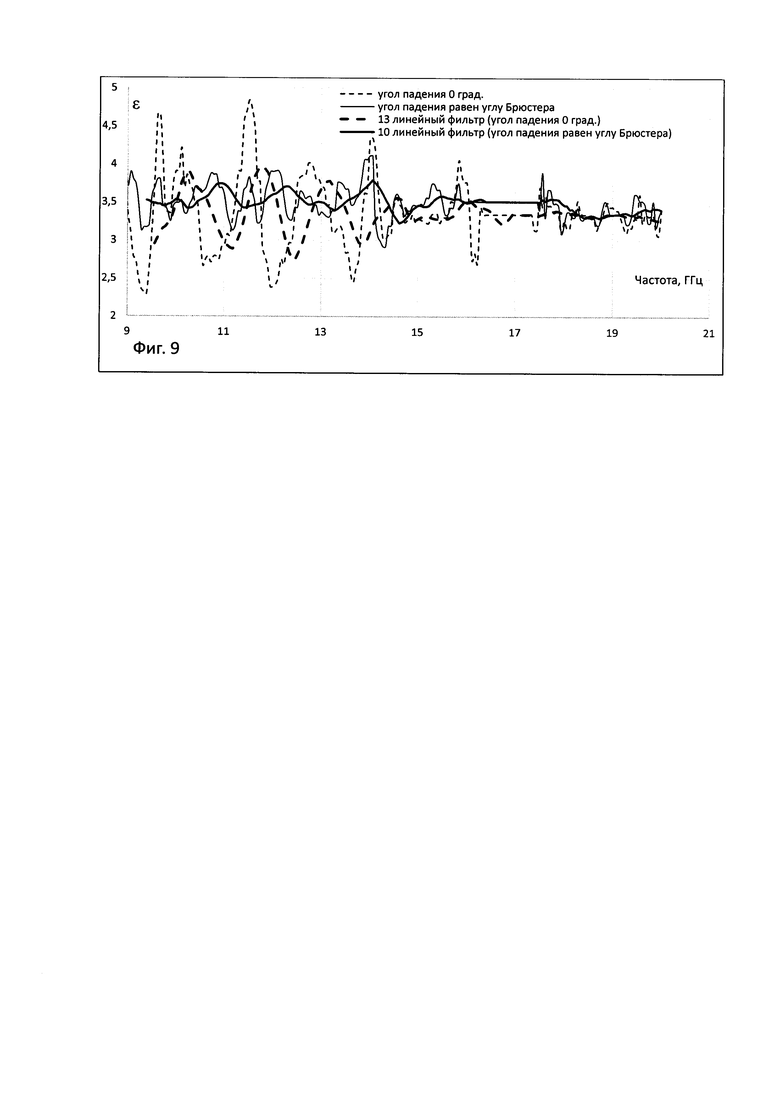
Для оценки предложенного технического решения проведены экспериментальные измерения мощности и фазы прошедшей волны через пластину из кварцевой керамики с диэлектрической проницаемостью ε=3,45 толщиной d=4,51 мм в полосе частот от 9 до 20 ГГц по которым расчетом определена частотная зависимость диэлектрической проницаемости для углов падения волны 0 градусов и для угла падения близкого к углу Брюстера, которые приведены на фиг. 9.
Из фиг. 9 видно, что погрешность определения частотной зависимости диэлектрической проницаемости в эксперименте с углом падения 0 градусов больше, чем в эксперименте с углом падения близким к углу Брюстера, для которого отсутствует гармоническая зависимость измерения фазы от частоты или толщины пластины, что позволяет получить высокую точность определения частотной зависимости диэлектрической проницаемости в широкой полосе частот при использовании для измерения пластин со значительной толщиной.
Таким образом, использование в способе измерения диэлектрической проницаемости материала в широкой полосе частот падение волны под углом близким к углу Брюстера по анализу фазы прошедшей волны по процедуре изложенной в предлагаемом техническом решении позволяет определить частотную зависимость диэлектрической проницаемости с более высокой точностью, чем при использовании известных способов, а анализируя по предложенному техническому решению фазы отраженной волны с более высокой разрешающей способностью определить частотную зависимость тангенса угла диэлектрических потерь по сравнению с известными способами.
Предложенное устройство, реализующее способ для измерения диэлектрических свойств материала, позволяет производить измерение в широкой частотной полосе с точностью более высокой, чем в известных устройствах.
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ определения сверхвысокочастотных параметров материала в полосе частот и устройство для его осуществления | 2018 |
|
RU2688588C1 |
| Способ определения диэлектрической проницаемости материала | 2019 |
|
RU2713162C1 |
| Способ измерения относительной комплексной диэлектрической проницаемости материала с потерями | 2022 |
|
RU2789626C1 |
| УСТРОЙСТВО ДЛЯ ОПРЕДЕЛЕНИЯ ДИЭЛЕКТРИЧЕСКОЙ ПРОНИЦАЕМОСТИ ОБРАЗЦА МАТЕРИАЛА ПРИ ВОЗДЕЙСТВИИ ВНЕШНИХ ФАКТОРОВ | 2011 |
|
RU2453856C1 |
| СПОСОБ ДИСТАНЦИОННОГО ИЗМЕРЕНИЯ КОМПЛЕКСНОЙ ДИЭЛЕКТРИЧЕСКОЙ ПРОНИЦАЕМОСТИ ПЛОСКОСЛОИСТЫХ ДИЭЛЕКТРИКОВ ЕСТЕСТВЕННОГО ПРОИСХОЖДЕНИЯ | 2022 |
|
RU2790085C1 |
| Способ пеленгации и широкополосный пеленгатор для его осуществления | 2018 |
|
RU2699079C1 |
| Способ измерения комплексной диэлектрической проницаемости материала в диапазоне СВЧ | 2022 |
|
RU2797142C1 |
| Способ измерения относительной комплексной диэлектрической проницаемости материала с потерями в СВЧ диапазоне | 2015 |
|
RU2613810C1 |
| НЕРАЗРУШАЮЩИЙ СВЧ-СПОСОБ КОНТРОЛЯ ВЛАЖНОСТИ ТВЕРДЫХ МАТЕРИАЛОВ И УСТРОЙСТВО ДЛЯ ЕГО РЕАЛИЗАЦИИ | 2004 |
|
RU2269763C2 |
| СВЧ-СПОСОБ ИЗМЕРЕНИЯ ПОВЕРХНОСТНОЙ ВЛАЖНОСТИ ТВЕРДЫХ МАТЕРИАЛОВ, ВЛАЖНОСТИ ПО ОБЪЕМУ ВЗАИМОДЕЙСТВИЯ, НОРМАЛЬНОГО К ПОВЕРХНОСТИ ГРАДИЕНТА ВЛАЖНОСТИ, И УСТРОЙСТВО ЕГО РЕАЛИЗАЦИИ | 2004 |
|
RU2294533C2 |
Изобретение относится к измерению диэлектрической проницаемости и тангенса угла диэлектрических потерь материалов. В свободном пространстве образец материала располагают под углом Брюстера, в диапазоне частот измеряют мощность и фазу прошедшей волны и по изменению фазы прошедшей волны в полосе частот по формуле рассчитывают частотную зависимость величины диэлектрической проницаемости образца материала, по диэлектрической проницаемости на каждой установленной частоте рассчитывают угол Брюстера, после чего поворачивают образец материала на подставке, устанавливая рассчитанный угол Брюстера, по градиенту угловой зависимости фазы отраженной волны определяют тангенс угла диэлектрических потерь материала образца. Устройство для осуществления преимуществ способа для измерения диэлектрических свойств материала, включающее передающую антенну, приемную антенну, принимающую прошедшую волну через образец материала, приемную антенну, принимающую отраженную волну от образца материала, подставку для крепления образца материала, СВЧ-измеритель, соединенный с управляющим компьютером, отличающееся тем, что приемная антенна, принимающая отраженную волну, расположена на платформе, установленной соосно с подставкой для образца материала, с возможностью их вращения вокруг оси, причем платформа и подставка снабжены датчиками угла поворота и двигателями с блоками управления, подключенными к управляющему компьютеру, а приемные антенны подключены к СВЧ-измерителю через коммутатор, соединенный с управляющим компьютером. Технический результат заключается в повышении точности проведения измерения диэлектрических свойств материалов в широкой полосе частот. 2 н.п. ф-лы, 9 ил.
1. Способ измерения диэлектрических свойств материала, включающий измерение на СВЧ измерителе мощности и фазы прошедшей волны без образца материала, расположение образца материала на подставке в центре полигона между передающей антенной, приемной антенной, измеряющей прошедшую волну, и приемной антенной, измеряющей отраженную волну, измерение мощности и фазы прошедшей волны через образец материала, измерение угловой зависимости мощности и фазы отраженной волны от образца материала, определение угла Брюстера по минимуму угловой зависимости сигнала отраженного от образца материала, вычисление изменения мощности и фазы прошедшей и отраженной волн, с расположенным образцом материала и без него, определение по изменению мощности и фазы прошедшей и отраженных волн диэлектрической проницаемости образца материала, отличающийся тем, что образец материала располагают и поворачивают относительно падающей волны и по максимуму мощности прошедшей волны в диапазоне частот находят угол Брюстера, затем образец материала на подставке устанавливают под найденным углом Брюстера, измеряют мощность и фазу прошедшей волны и по изменению фазы прошедшей волны в полосе частот по формуле рассчитывают предварительную частотную зависимость величины диэлектрической проницаемости образца материала, выбирают ряд частот внутри частотного диапазона, последовательно устанавливая на СВЧ-измерителе, а по предварительно определенной величине диэлектрической проницаемости на каждой установленной частоте рассчитывают угол Брюстера, после чего поворачивают образец материала на подставке, устанавливая рассчитанный угол Брюстера, по изменению фазы прошедшей волны, измеренной СВЧ-измерителем, вновь рассчитывают диэлектрическую проницаемость материала образца на установленной частоте, затем на каждой частоте вращают образец материала вблизи угла Брюстера и синхронно с ним приемную антенну, принимающую отраженную волну, записывают зависимость изменения фазы отраженной волны от угла падающей волны на образец материала и по градиенту угловой зависимости фазы отраженной волны расчетом по формуле определяют тангенс угла диэлектрических потерь материала образца, проведя определение диэлектрической проницаемости и тангенса угла диэлектрических потерь на всех выбранных частотах, записывают частотные зависимости диэлектрической проницаемости и тангенса угла диэлектрических потерь.
2. Устройство для измерения диэлектрических свойств материала, включающее передающую антенну, приемную антенну, принимающую прошедшую волну через образец материала, приемную антенну, принимающую отраженную волну от образца материала, подставку для крепления образца материала, СВЧ-измеритель, соединенный с управляющим компьютером, отличающееся тем, что антенны установлены так, что электрические векторы антенн лежат в горизонтальной плоскости падения волны на образец материала, приемная антенна, принимающая отраженную волну, расположена на платформе, установленной соосно с подставкой для образца материала, с возможностью их вращения вокруг оси, причем платформа и подставка снабжены датчиками угла поворота и двигателями с блоками управления, подключенными к управляющему компьютеру, а приемные антенны подключены к СВЧ-измерителю через коммутатор, соединенный с управляющим компьютером.
| Измерительная ячейка для измерения параметров диэлектриков на СВЧ | 1987 |
|
SU1741088A1 |
| Способ измерения диэлектрических характеристик твердых материалов | 1985 |
|
SU1439478A1 |
| Устройство для промежуточного останова рамы кегельбана | 1976 |
|
SU657733A3 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ДИЭЛЕКТРИЧЕСКОЙ ПРОНИЦАЕМОСТИ КРИВОЛИНЕЙНОГО СЛОЯ МАТЕРИАЛА И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2008 |
|
RU2365926C1 |
| Измеритель диэлектрических свойств материалов | 1979 |
|
SU783712A1 |
Авторы
Даты
2018-08-31—Публикация
2017-09-27—Подача