FIELD: water supply systems.
SUBSTANCE: invention relates to the field of water supply and wastewater systems and can be used to optimize their operation in dry weather and rainy periods. Method comprises the following stages: a) receive data parameters values of the system streams, transmit them to the control block and write it into the computer's main memory; b) solve on a computer the problem of mathematical programming, using as initial data of the parameters values of the system streams, and obtain as a solution the values of the optimal parameters of the streams; c) transmit to the automated control blocks the values of their position settings ensuring the redistribution of the optimum parameters of the sewage streams in accordance with the solution of the mathematical programming problem. Prior to step a), the entire sewage disposal system is divided into a finite number of n independent drainage basins, each contains at least the surface runoff networks connected to the transport main, which, with the help of the main pumping station, is connected to the treatment facilities with the release of treated sewage into the environment, at least one discharge of wastewater into the environment connected with the main transport route and configured to discharge untreated sewage into the environment when the main transport route is full. As the parameters of the flows of the surface runoff system, the surface runoff volumes are accepted νi, i = 1, 2, ..., n, for each i-th independent surface runoff basin for a period of time Δt. As automated control bodies, inter-basin pumping stations and / or inter-basin transport routes with shut-off and regulating bodies connecting the transport routes of independent basins are adopted. Determine the maximum system flow parameters νimax=νicot(t0)+νiwell(t0)+νinetworks(t0)+qiMPS*Δt for each i-th independent surface runoff basin for a period of time Δt without emissions of untreated sewage into the environment, where νicot(t0), νiwell(t0), νinetworks(t0) – free volumes of collectors and wells,main transport route and surface runoff networks at the moment of t0 solving the problem of mathematical programming, qiMPS – the maximum supply of the MPS of the i-th independent surface runoff basin. Form the maximum productivity matrix of  automated controls that characterizes the limits of possible surface runoff inflows from the i-th independent surface runoff basin into the j-th independent surface runoff basin, where the values for the principal diagonal and non-existent elements are zero. Experimentally determine for each i-th independent surface runoff basin for a period of time Δt the experimental dependence vi=f(Hi) of the flow parameters of the system vi at least from the predicted values of precipitation volumes Hi. Receive data on the forecast values of precipitation volumes Hi, i = 1, 2, ..., n, for each i-th independent surface runoff basin for a period of time Δt. Receive parameters values data of the system streams by calculating the value of the parameters of the streams of the system vi for each i-th independent surface runoff basin for the forecast period Δt from the experimental dependence vi=f(Hi). In step b) the mathematical programming problem is solved by the criterion of minimum payments for pumping water, i.e. as a solution, they form a matrix of optimal productivity of
automated controls that characterizes the limits of possible surface runoff inflows from the i-th independent surface runoff basin into the j-th independent surface runoff basin, where the values for the principal diagonal and non-existent elements are zero. Experimentally determine for each i-th independent surface runoff basin for a period of time Δt the experimental dependence vi=f(Hi) of the flow parameters of the system vi at least from the predicted values of precipitation volumes Hi. Receive data on the forecast values of precipitation volumes Hi, i = 1, 2, ..., n, for each i-th independent surface runoff basin for a period of time Δt. Receive parameters values data of the system streams by calculating the value of the parameters of the streams of the system vi for each i-th independent surface runoff basin for the forecast period Δt from the experimental dependence vi=f(Hi). In step b) the mathematical programming problem is solved by the criterion of minimum payments for pumping water, i.e. as a solution, they form a matrix of optimal productivity of 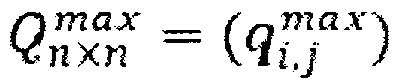 automated management bodies, in the implementation of which the total payment for the power consumption of independent water drainage basins and inter-basin pumping stations will be minimal and νimax–vi+Σnk=1 qik–Σnk=1 qki≥0, i=1, 2, …, n, i≠k,
automated management bodies, in the implementation of which the total payment for the power consumption of independent water drainage basins and inter-basin pumping stations will be minimal and νimax–vi+Σnk=1 qik–Σnk=1 qki≥0, i=1, 2, …, n, i≠k, 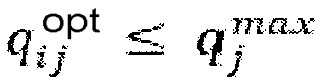 . In the absence of such a result, a decision is taken to solve the problem of mathematical programming by the criterion of minimum discharges of sewage into the environment, i.e. as a solution, a matrix of optimal productivity of
. In the absence of such a result, a decision is taken to solve the problem of mathematical programming by the criterion of minimum discharges of sewage into the environment, i.e. as a solution, a matrix of optimal productivity of 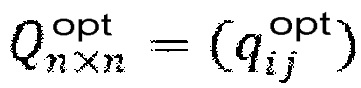 automated control bodies is formed, in the implementation of which the total discharge of sewage into the environment will be minimal, i.e. Σni=1(νi–νimax+Σnk=1 qik–Σnk=1 qki)→min for i = 1, 2, …, n, i≠k,
automated control bodies is formed, in the implementation of which the total discharge of sewage into the environment will be minimal, i.e. Σni=1(νi–νimax+Σnk=1 qik–Σnk=1 qki)→min for i = 1, 2, …, n, i≠k, 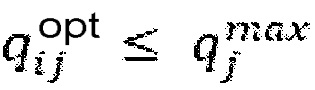 .
.
EFFECT: provides a reduction in capital costs and expansion of functionality.
1 cl, 3 dwg
| Title | Year | Author | Number |
|---|---|---|---|
| METHOD FOR OPTIMAL CONTROL OF WATER DISPOSAL SYSTEM | 2017 |
|
RU2669873C2 |
| WATER DISPOSAL SYSTEM FOR MEGAPOLIS | 2010 |
|
RU2438984C1 |
| WASTE REDISTRIBUTION UNIT | 2019 |
|
RU2699119C1 |
| REGULATED SYSTEM OF WATER DISPOSAL | 2017 |
|
RU2655931C1 |
| CONTROLLED WATER DISPOSAL SYSTEM | 2017 |
|
RU2650908C1 |
| WATER DRAINAGE SYSTEM | 2017 |
|
RU2655930C1 |
| SELF-REGULATED WATER DISCHARGE SYSTEM | 2017 |
|
RU2655320C1 |
| OPTIMIZED WATER TREATMENT SYSTEM | 2017 |
|
RU2646064C1 |
| MEGACITY WASTE WATERS SLUDGE SALVAGING SYSTEM | 2005 |
|
RU2300503C2 |
| METHOD OF DETERMINING RAIN WASTE WATER CONSUMPTION | 2018 |
|
RU2716209C1 |
Authors
Dates
2018-09-24—Published
2017-08-07—Filed