Область техники
Изобретение относится к критическим реально-временным многозадачным системам, таким как системы контроля-управления, используемые в отраслях транспорта (автомобильного, железнодорожного, морского, авиационного), промышленных автоматов, энергетики, а также другие системы, для которых важное значение имеет контролируемое распределение ресурсов, например, в коммуникационных сетях. Изобретение относится как к реально-временным системам, для которых необходим высокий уровень эффективности в применении, так и к критическим системам, от которых требуется высокий уровень гарантии в том, что касается использования материальных исполнительных ресурсов, выделяемых для каждой задачи системы.
Уровень техники
В критических реально-временных системах, то есть в системах, которые не могут допускать никакого нарушения сроков из-за задержки в выполнении операции, задачи часто выполняют в соответствии с методами статического планирования. При этом автономно составляют статическое временное распределение потребности в использовании исполнительных ресурсов, что позволяет выявить временную независимость задач между собой в том, что касается использования ресурсов и, в частности, процессора. Такой подход описан, например, в статье [“A method and a technique to model and ensure timeliness in safety critical real time systems”, C. Aussaguès, V. David, Fourth IEEE International Conference on Engineering of Complex Computer Systems, 1998] и в патентных заявках WO2006-050967 и
US2010-0199280.
Однако такой тип подхода предполагает рассматривать только единый план задания последовательности, то есть рассматривать только одну шкалу времени для определения сроков. Это затрудняет выполнение задач без помех на одном и том же процессоре с невзаимосвязанными шкалами времени, таких как задача, использующая один синхрогенератор для определения своих сроков, и задача, использующая положение объекта с переменной скоростью для определения своих сроков. Для этого понадобилось бы составить два плана задания последовательности при помощи одной шкалы времени, чтобы иметь возможность объединить их в один план задания последовательности без помех между задачами. На практике это можно реализовать, только если исполнительные ресурсы предусмотрены с избыточными параметрами с целью прогнозирования наихудшего развития каждой ситуации.
В высокоэффективных реально-временных системах, которые не называют «критическими», так как они могут допускать нарушения сроков в определенных пределах, составление двух планов задания последовательности, рассчитываемых по разным шкалам времени, осуществляют при помощи динамических алгоритмов планирования. Такие алгоритмы описаны, например, в [“Scheduling algorithms for multiprogramming in a hard real-time environment”, C. Liu, J. Layland, Journal of the ACM, vol. 20, no. 1, pp. 46-61] и [Foundations of Real-Time Computing: Scheduling and Resource Management”, André M. Van Tilborg, Gary M. Koob, 1991, Kluwer Academic Publishers], а также в [“A method and a technique to model and ensure timeliness in safety critical real time systems”, C. Aussaguès, V. David, Fourth IEEE International Conference on Engineering of Complex Computer Systems, 1998].
С этими алгоритмами неизбежны преобладающие приоритеты, то есть система может прерывать текущую операцию для исполнения более срочной операции. Поскольку планирование является динамическим, невозможно определить число и продолжительность приоритетных перерывов, и каждый перерыв расходует время системы для внесения изменения контекста. Это создает помехи между задачами, поэтому затрудняется параметризация систем, они являются менее предсказуемыми и не воспроизводимыми на сложных архитектурах процессоров. Кроме того, разработчики этих систем сталкиваются с трудностями в правильной регулировке приоритетов задач или сроков в системе с двумя разными шкалами времени. Выбираемые опции, такие как изменение исполнительных потребностей в зависимости от значения прикладных параметров, делает разрабатываемые таким образом системы очень сложными и не контролируемыми.
Раскрытие изобретения
Таким образом, существует потребность в технологии, позволяющей исполнять без помех с разделением времени два плана задания последовательности, даже если шкалы времени двух планов являются разными.
Эту потребность можно удовлетворить, предложив способ выполнения двух задач с разделением времени, содержащий этапы, на которых каждую задачу автономно раскладывают на повторяющуюся последовательность последовательных фреймов, в которой каждый фрейм связан с атомарной операцией, имеющей одну исполнительную потребность, и определяет дату начала, с которой операцию можно начать, и дату конечного срока, к которой операцию необходимо завершить, при этой каждый фрейм определяет запас времени, в течение которого можно запустить операцию; для каждого фрейма первой из повторяющихся последовательностей проверяют, что соответствующую операцию можно исполнить между двумя любыми последовательными операциями из группы фреймов второй повторяющейся последовательности с перекрыванием фрейма (Fai) первой повторяющейся последовательности и с соблюдением дат начала и сроков операций; и, если проверка оказалась удовлетворительной, разрешают выполнение обеих задач.
При этом операции обеих задач планируют в зависимости от следующих случаев, оцениваемых по каждой ключевой дате, когда одна ключевая дата наступает при каждом истечении срока исполнения, по каждой дате начала и по каждому концу исполнения операции: если можно запустить две операции, выполняют ту операцию, которая имеет более короткий срок исполнения; и, если, можно запустить только одну операцию, ее выполняют только, если исполнительная потребность меньше времени, остающегося до даты начала следующего фрейма другой последовательности и увеличенного на запас времени, связанный с указанным следующим фреймом другой последовательности.
Согласно варианту осуществления, каждый фрейм дополнительно содержит интервал резервного времени, который может быть нулевым, находящийся после срока исполнения фрейма или перед датой начала фрейма, при этом можно брать интервалы резервного времени любой одной из повторяющихся последовательностей для выполнения операции другой повторяющейся последовательности.
Согласно варианту осуществления, этап проверки содержит следующие этапы:
• для каждого фрейма Fai первой повторяющейся последовательности оценивают следующие условия для каждого фрейма Fbj второй повторяющейся последовательности:
[A.1] Dai ≤ Tbj+1
[B.1] Dai ≤ Rbj +Tbj+1 и Dbj ≤ Tai, и
[C.1] Dbj ≤ Tai,
где D, T и R обозначают исполнительную потребность, запас времени и резервное время, индексированные идентификатором повторяющейся последовательности и номером фрейма в последовательности;
• повторяют оценки условий, переставляя местами фреймы Fai и Fbj;
• разрешают выполнение задач, если для любой пары (i, j) удовлетворены все три условия [A.1], [B.1] и [C.1].
Согласно варианту осуществления, этап проверки содержит следующие этапы:
• если условие [A.1] является ошибочным, оценивают следующие условия:
[A.2] Dai ≤ Tbj+1 + Rbj + Tbj+2
и Dai + Dbj+1 ≤ Tai + Tbj+1
• если условие [B.1] является ошибочным, оценивают следующие условия:
[B.2] Dai ≤ Tbj+1 + Rbj+1 + Tbj+2
и Dbj + Dai + Dbj+1 ≤ Tai + Tbj+1
• если условие [C.1] является ошибочным, оценивают следующее условие:
[С.2] Dbj ≤ Tai + min[Tbj-Dai, Rai, Rai-1]
• разрешают выполнение задач, если условия [A.1] или [A.2], и [В.1] или [В.2], и [С.1] или [С.2] удовлетворены для любой пары (i,j).
Согласно варианту осуществления, шкалы времени, определяющие продолжительность фреймов, могут изменяться таким образом, что запас времени Т и резервное время R меняются на коэффициент от 1 до za для фреймов Fa и на коэффициент от 1 до zb для фреймов Fb, при этом этап проверки содержит следующие этапы:
• если условие [A.1] является ошибочным, оценивают следующее условие:
[A.2] Dai ≤ Tbj+1 + Rbj+1 + Tbj+2
и min[q1(zb⋅(Tbj+Rbj) + (zb-1)Dbj),Dai] + Dbj+1 ≤ Tai
где q1 = (Dai-Tbj+1)/(Tbj+Rbj);
• если условие [B.1] является ошибочным, оценивают следующее условие:
[B.2] Dai ≤ Tbj+1 + Rbj+1 + Tbj+2
и Dbj + min[q1(zb⋅Tbj + (zb-1)Dbj) + zb⋅Rbj, Dai] + Dbj+1 ≤ Tai
где q1 = (Dai - Rbj - Tbj+1)/Tbj;
• если условие [C.1] является ошибочным, оценивают следующее условие:
[С.2] Dbj ≤ Tai + min[Tbj-Dai, Rai, Rai-1]
• разрешают выполнение задач, если условия [A.1] или [A.2], и [В.1] или [В.2], и [С.1] или [С.2] удовлетворены для любой пары (i,j).
Согласно варианту осуществления, этап проверки содержит следующие этапы:
• если условие [B.1] является ошибочным, перед условием [В.2] оценивают следующее условие:
[B.1.1] Dai ≤ Tbj + Rbj + Tbj+1
и Dbj-1 ≤ T1 + min[Tbj-1 + Dbj-1 + Rbj-1 - T1 - Dai-1, Rai-2]
где q1 = (Dai - Rbj - Tbj+1)/Tbj и T1 = Tai-1 - (1-q1)Tbj + Rai-1
• разрешают выполнение задач, если условия [A.1] или [A.2], и [В.1] или [В.2], и [С.1] или [С.2] удовлетворены для любой пары (i,j).
Краткое описание чертежей
Варианты осуществления изложены в нижеследующем описании, представленном в качестве не ограничительного примера со ссылками на следующие прилагаемые фигуры:
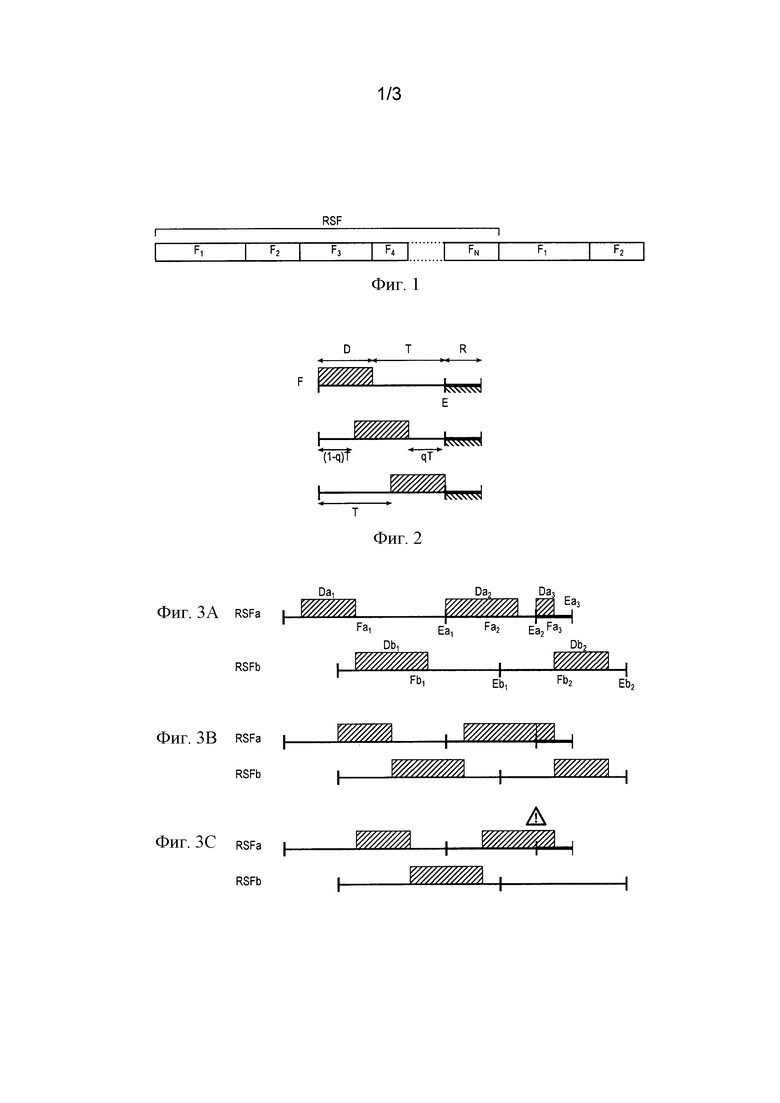
Фиг. 1 - пример повторяющейся последовательности фреймов, предназначенной для составления плана задания последовательности задачи.
Фиг. 2 - состав фрейма повторяющейся последовательности и различные возможности запуска операции в фрейме.
Фиг. 3А-3С иллюстрируют различные возможности процесса развертывания с разделением времени двух повторяющихся последовательностей фреймов, при этом на фиг.3С представлена ситуация ошибки.
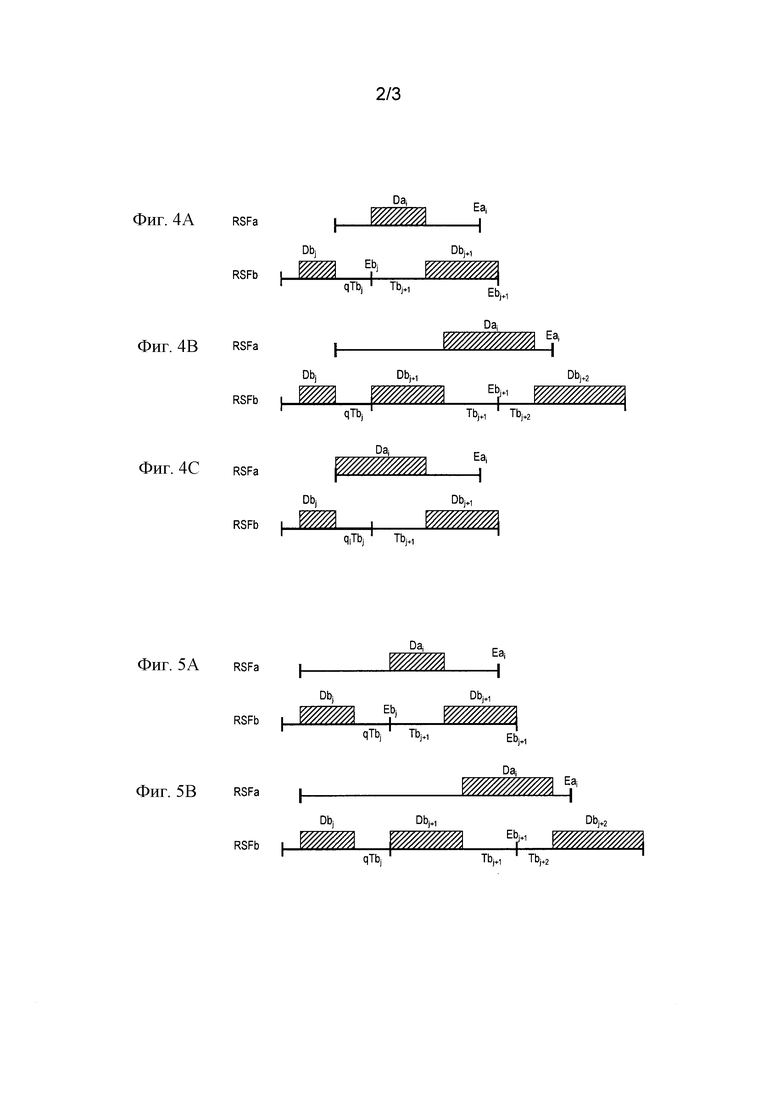
Фиг. 4А-4С иллюстрируют случаи процесса развертывания с разделением времени двух последовательностей в соответствии с первым предположением в разработке критериев подтверждения состава двух последовательностей.
Фиг. 5А 5В иллюстрируют случаи процесса развертывания с разделением времени двух последовательностей в соответствии с вторым предположением в разработке критериев подтверждения состава двух последовательностей.
Фиг. 6 иллюстрирует случай процесса развертывания с разделением времени двух последовательностей в соответствии с третьим предположением в разработке критериев подтверждения состава двух последовательностей.
Фиг. 7 - пример последовательности фреймов, предназначенной для установления другого условия достоверности в ситуации, показанной на фиг. 5А.
Фиг. 8 - дополнительный случай процесса развертывания двух последовательностей в соответствии с третьим предположением, позволяющих разработать альтернативные условия достоверности.
Описание варианта осуществления изобретения
Реально-временную задачу можно рассматривать как последовательность обработок или исполняемых друг за другом элементарных операций, где каждая операция имеет срок исполнения в шкале времени, связанной с задачей. В критической реально-временной системе сроки являются императивными, то есть операция, превысившая свой срок исполнения, приводит, например, к условию ошибки и к остановке системы. Описанные ниже методы применимы к такой системе и позволяют, несмотря ни на что, повысить уровень эффективности за счет того, что в системе можно выполнять с разделением времени несколько задач, даже имеющих невзаимосвязанные между собой шкалы времени.
На фиг. 1 представлено разложение задачи на повторяющуюся последовательность фреймов RSF, где каждый фрейм F связан с одной последовательной операцией задачи. Задачу выполняют посредством цикличного исполнения повторяющейся последовательности RSF.
На фиг. 2 представлена временная структура фрейма F. Начало фрейма соответствует дате, начиная с которой можно начать операцию. Фрейм определяет конечный срок Е, к которому операция должна завершиться. Предполагается, что операция является атомарной, то есть ее нельзя приостановить для исполнения другой операции. Срок Е может быть отделен от конца фрейма интервалом резервного времени R, который является факультативным, то есть может быть нулевым. Интервал времени D является исполнительной потребностью операции, связанной с фреймом. Исполнительная потребность D соответствует, например, числу циклов тактового генератора процессора, необходимому для исполнения операции, и ее можно выразить в фиксированном времени в зависимости от характеристик процессора целевой системы. Интервал Т соответствует запасу времени между началом фрейма и конечным сроком Е исполнения операции.
Как показано на фиг. 2, операция D может начаться в любой момент между началом фрейма, когда интервал Т разделяет конец операции и конечный срок, и временем Т после начала фрейма, когда операция заканчивается точно в срок Е. Для промежуточных ситуаций qT обозначает интервал между концом операции и конечным сроком при 0≤q≤1, и (1-q)Т обозначает дополнительный интервал между началом фрейма и началом операции.
Сумма резервных интервалов R соответствует, например, времени, которое программист выделяет системе для осуществления не реально-временных операций, таких как вводы/выводы.
Таким образом, две задачи, которые необходимо выполнить с разделением времени на критической реально-временной системе, разбивают на повторяющиеся последовательности фреймов. Чтобы можно было выполнять задачи без помех, последовательности составляют таким образом, чтобы каждую операцию одной последовательности можно было в любой момент выполнить между двумя последовательными операциями другой последовательности, соблюдая при этом условия фреймов обеих последовательностей, то есть конечные сроки и моменты начала фрейма.
На фиг. 3А-3С представлены различные ситуации, которые могут встречаться в процессе развертывания двух последовательностей RSFa и RSFb. Для упрощения пояснений предполагается, что резервные интервалы R являются нулевыми.
Например, на фиг. 3А последовательность RSFa содержит три фрейма Fa1-Fa3 с соответствующими параметрами (Da1 = 3, Ta1 = 6), (Da2 = 4, Ta2 = 1) и (Da3 = 1, Ta3 = 1), где значения времени выражены в нормализованных единицах. Последовательность RSFb начинается спустя 3 единицы после начала фрейма Fa1 и содержит два фрейма Fb1 и Fb2 с соответствующими параметрами (Db1 = 4, Tb1 = 5) и (Db2 = 3, Tb2 = 4).
Операция Da1 начинается спустя одну единицу после начала соответствующего фрейма. В конце операции Da1 пока нельзя запустить операцию Da2, но уже можно запустить операцию Db1. В конце операции Db1 ни одна операция пока не готова для исполнения. Выжидают начала фрейма Fa2, в данном случае срок Еа1, чтобы начать операцию Da2. В конце операции Da2 операция Db2 готова для исполнения, но ее нельзя запустить. Действительно, если операцию Db2 запустить сразу, она закончится точно в срок Еа3, поэтому до этого срока нельзя исполнить операцию Da3. В этом случае ожидают начало фрейма Fa3, чтобы запустить операцию Da3. Наконец, после завершения операции Da3 можно запустить операцию Db2.
На фиг. 3В сохранены те же параметры, за исключением того, что операция Da1 начинается спустя три единицы после начала фрейма. Операции Db1 и Da2 оказываются задержанными на две единицы по сравнению с фиг. 3А, но с соблюдением условий соответствующих фреймов. Операция Da2 завершается точно в свой срок Еа2.
На фиг. 3С сохранены те же параметры, за исключением того, что операция Da1 начинается спустя четыре единицы после начала фрейма. Операции Db1 и Da2 оказываются задержанными на три единицы по сравнению с фиг. 3А. Операцию Db1 можно еще исполнить с соблюдением ее конечного срока Eb1, но операция Da2 нарушает свой срок Ea2.
Первым этапом, общим для рассматриваемых в данном случае методов, является составление, - для двух задач, предназначенных для выполнения с разделением времени, - двух повторяющихся последовательностей RSFa и RSFb, которые могут проходить в условиях фиг. 3А или 3В, независимо от временного смещения между моментами начала последовательностей. Это составление является статическим, то есть происходит автономно для программиста.
Второй этап представляет собой проверку совместимости двух любых последовательностей, то есть проверяют, что они могут проходить таким образом, чтобы каждую операцию можно быть исполнять с соблюдением ее условий, как на фиг. 3А и 3В.
Эту проверку совместимости можно осуществлять в инструменте разработки, позволяющем программисту составлять последовательности для последовательных испытаний. Предпочтительно ее осуществляют также непосредственно в самой реально-временной системе при загрузке для исполнения планов задания последовательности, определенных двумя повторяющимися последовательностями. При этом систему можно конфигурировать таким образом, чтобы запрещать запуск, если обнаруживается, что последовательности являются несовместимыми.
Третьим этапом является планирование операций двух последовательностей на реально-временной системе. Как показано на фигурах, недостаточно чередовать операции первой последовательности с операциями второй последовательности или запускать операцию, как только она оказывается готовой к исполнению. Планирование осуществляют в зависимости от следующих случаев, оцениваемых для каждой ключевой даты. Ключевыми датами являются моменты начала фреймов двух последовательностей, конечные сроки и концы операции. Если интервалы резервного времени R (фиг. 2) являются нулевыми, как в представленных примерах, конечные сроки совпадают с началами фрейма. Для данной ключевой даты, связанной с первой из последовательностей, текущий фрейм второй последовательности называют «параллельным фреймом».
1) Ни одну операцию нельзя запустить. Этот случай возникает, когда одна операция уже находится в ходе исполнения (как в момент конечного срока Еb1 на фиг. 3А) или в конце операции, которая исполнялась между операцией параллельного фрейма и ее конечным сроком, как в случае операции Db1 на фиг. 3А.
2) Можно запустить две операции. Как правило, этот случай возникает, когда начинается фрейм и когда одна операция находится в стадии выжидания в параллельном фрейме, как в момент конечного срока Еа2 на фиг. 3А и 3В. В этом случае исполняют операцию с самым коротким сроком (Da3 на фиг. 3А и 3В). Такой случай возникает также, когда два параллельных фрейма начинаются одновременно.
3) Можно запустить только одну операцию. Как правило, этот случай встречается в конце операции (Da1) или в начале фрейма, когда операция параллельного фрейма завершилась (Еа1, фиг. 3А). При этом операцию исполняют, только если ее исполнительная потребность меньше или равна времени, оставшемуся до начала следующего параллельного фрейма, увеличенному на запас времени, связанный с этим параллельным фреймом. Например, на фиг. 3А операция Da2 готова к запуску в срок Еа1, до начала фрейма Fb2 остается 3 единицы, и Тb2 = 4. Операцию Da2 запускают, так как Da2 = 4 < 3 + 4.
В противном случае выжидают следующую ключевую дату для повторной оценки ситуации. Например, на фиг. 3А операция Db2 готова к исполнению в конце операции Da2. Однако остается одна единица до начала фрейма Fа3, и Та3 = 1, отсюда Db2 = 3 > 1 + 1.
Далее определим критерии совместимости между двумя любыми повторяющимися последовательностями RSFa и RSFb, используемыми для определения планов задания последовательности для реально-временной системы.
При избыточной проверке совместимости необходимо было бы рассмотреть все возможные комбинации положений операций в их фреймах и все возможные положения одной из последовательностей относительно другой с грануляцией цикла тактового генератора, чтобы оценить, можно ли исполнять параллельные операции в соответствии с заданными требованиями.
Такую избыточную проверку трудно осуществить в разумные сроки. Необходимо найти упрощенные критерии, которые можно оценивать «онлайн» на реально-временной системе в момент загрузки планов задания последовательности, сопровождающих исполнительный код задач. Для этого предусматривают три общих предположения позиционирования каждого фрейма одной из последовательностей относительно каждого фрейма другой последовательности. Для каждого предположения проверяют, чтобы операцию рассматриваемого фрейма Fаi можно было исполнить в свободный интервал, оставленный параллельными фреймами Fbj, Fbj-1,…, перекрывающими фрейм Fаi. Оба фрейма Fаi и Fbj считаются совместимыми, если проверка является удовлетворительной для каждого из трех предположений.
• Предположение (А): рассматриваемый фрейм Fаi начинается, тогда как операция Dbj первого фрейма Fbj исполнена.
• Предположение (В): операция первого параллельного фрейма находится в стадии исполнения.
• Предположение (С): операция параллельного фрейма не запущена.
Для каждого предположения определяют критерии, не зависящие от относительного положения фреймов. Для этого оценивают снизу неизвестные интервалы времени, служащие для нахождения свободных промежутков для исполнения операций, и оценивают сверху неизвестные интервалы времени, служащие для проверки соблюдения сроков.
На фиг. 4А-4С представлены примеры фреймов, которые могут служить для разработки критериев совместимости в соответствии с предположением (А). Рассматриваемый фрейм Fаi начинается в ходе параллельного фрейма Fbj, тогда как операция Dbj этого параллельного фрейма завершена. Фрейм Fаi перекрывает следующий параллельный фрейм Fbj+1. Все, что известно о начале фрейма Fаi, это то, что он находится в интервале qTbj, следующем за концом операции Dbj, где 0 ≤ q ≤ 1.
На фиг. 4А фрейм Fаi заканчивается перед фреймом Fbj+1. Операцию Dai можно было бы запустить сразу по завершении операции Dbj в интервале qTbj + Tbj+1. Однако, поскольку q не известно и является любым, рассматривают наихудший из случаев при q=0, то есть когда операция Dai стартует в начале фрейма Fbj+1. Таким образом, операцию Dai можно исполнить, если:
Dai < Tbj+1. [A.1]
На фиг. 4В операция Dai не удовлетворяет условию А.1. Тогда предусматривают исполнение операции Dai с перекрыванием фреймов Fbj+1 и Fbj+2, то есть фрейм Fаi перекрывает все три фрейма от Fbj до Fbj+2. Это требует удовлетворения одновременно условия, чтобы сумма интервалов Тbj+1 и Тbj+2 была гарантированно достаточной, и условия гарантированного соблюдения срока Еаi:
Dai ≤ Тbj+1 + Тbj+2
И
qTbj + Dbj+1 + Dai ≤ Dai + Тai, то есть qTbj + Dbj+1 ≤ Тai
Наихудшим случаем при соблюдении срока является q = 1 с переоценкой левого члена неравенства. Таким образом, срок Еаi соблюдается во всех случаях, если:
Тbj + Dbj+1 ≤ Тai
Однако было бы нереально предусматривать в одном и том же контексте ситуации наихудшего случая с использованием двух предельных значений одной переменной. В реальности, можно исключить определенный диапазон значений для переменной q, если рассматривать поведение реальной системы в ситуации, представленной на фиг. 4А.
На фиг. 4С показано поведение реальной системы в ситуации фиг. 4А. Поскольку операция Dbj завершена, система, зная параметры фреймов «онлайн», запускает операцию Dai с самого начала фрейма Fаi, поскольку:
Dai ≤ qTbj + Тbj+1
то есть если соблюдены условия 3) способа планирования.
Обозначим q1 предельное значение q для достижения равенства в вышеупомянутом неравенстве:
Dai ≤ q1Tbj + Тbj+1, то есть q1 = (Dai - Tbj+1)/ Tbj
Если q ≥ q1, то можно с уверенностью сказать, что исполнение на реальной системе происходит в соответствии с фиг. 4С и что нет необходимости рассматривать ситуацию, показанную на фиг. 4В. При этом наихудшим случаем для фиг. 4В является q = q1, поэтому:
qTbj + Dbj+1 ≤ Тai, то есть, если заменить q1 на его значение, Dai - Тbj+1 + Dbj+1 ≤ Тai, или Dai + Dbj+1 ≤ Тai + Тbj+1
Выражение, используемое для вычисления значения q1, не ограничено значением 1. Если оно превышает 1, это не имеет практического смысла. Поэтому потолочным значением для q1 считается 1.
Следовательно, условиями, вытекающими из ситуации фиг. 4В, являются:
Dai ≤ Тbj+1 + Тbj+2
И [A.2]
qTbj + Dbj+1 ≤ Тai
Условие А.1 проверяется в ситуации, когда фрейм Fаi перекрывает по меньшей мере два последовательных фрейма Fb. Условие А.2 проверяется в ситуации, когда фрейм Fаi перекрывает по меньшей мере три последовательных фрейма Fb. Аналогично можно найти условия А.3 и следующие, проверяемые в ситуациях, когда фрейм Fаi перекрывает по меньшей мере четыре последовательных фрейма Fb или более, но удовлетворение таких условий становится все менее вероятным. Условия А.1 и А.2 (и, в случае необходимости, А.3 и следующие) являются альтернативными, что есть достаточно, чтобы любое из этих условий проверялось, чтобы можно было продолжить подтверждение других предположений.
На фиг. 5А и 5В представлены примеры фреймов, которые могут служить для разработки критериев совместимости в соответствии с предположением (В). Рассматриваемый фрейм Fаi стартует в ходе параллельного фрейма Fbj, тогда как операция Dbj этого параллельного фрейма находится в стадии исполнения. В наихудшем случае, как было указано, операция Dbj стартует. Ситуации являются аналогичными ситуациям на фиг.4А и 4В за исключением того, что для проверки соблюдения срока Еаi учитывают время Dbj.
В соответствии с фиг. 5А:
Dai ≤ Тbj+1 и для соблюдения срока Еаi: Dbj + Dai ≤ Dai + Тai, то есть Dbj ≤ Тai
Следовательно, условиями, вытекающими из ситуации на фиг. 4В, являются:
Dai ≤ Тbj+1
И [В.1]
Dbj ≤ Тai
В соответствии с фиг. 5В и следуя такому же рассуждению, что и для фиг. 4В, получаем:
Dai ≤ Тbj+1 + Тbj+2
И [В.2]
Dbj + qTbj + Dbj+1 ≤ Тai
Как и для условия А.1, условие В.1 проверяется в ситуации, когда фрейм Fаi перекрывает по меньшей мере два последовательных фрейма Fb. Условие В.2 проверяется в ситуации, когда фрейм Fаi перекрывает по меньшей мере три последовательных фрейма Fb. Аналогично можно найти условия В.3 и следующие, проверяемые в ситуациях, когда фрейм Fаi перекрывает по меньшей мере четыре последовательных фрейма Fb или более, но удовлетворение таких условий становится все менее вероятным. Условия В.1 и В.2 (и, в случае необходимости, В.3 и следующие) являются альтернативными, что есть достаточно, чтобы любое из этих условий проверялось, чтобы можно было продолжить подтверждение других предположений.
На фиг. 6 представлен пример фреймов, которые могут служить для разработки критериев совместимости в соответствии с предположением (С). В рамках предположения (С) считается, что операция Dbj еще не исполнена. Если конечный срок фрейма Fаi наступает после конечного срока фрейма Fbj, встречаются те же ситуации, что и ситуации на фиг. 5А и 5В, когда операция Dbj как раз только начинается. Таким образом, в рамках предположения (С) рассматривают только случай, когда конечный срок фрейма Fаi наступает до конечного срока фрейма Fbj.
Обе операции Dai и Dbj готовы для исполнения в начале фрейма Fаi. Можно предположить, что операция Dbj не была запущена в начале своего фрейма, так как условия 3) планирования не были соблюдены, например, как было указано выше, когда операция Dai-1 завершается в свой срок в начале фрейма Fаi. Поскольку срок Еаi является более коротким, сначала запускают операцию Dai. Операцию Dbj запускают по окончании операции Dai. В наихудшем случае в пределах предположения (С) сроки фреймов Fаi и Fbj совпадают, и в этом случае получаем:
Dbj ≤ Таi [C.1]
Это же неравенство получаем, предположив, что операция Dbj стартует в начале фрейма Fаi, хотя способ планирования этого не предусматривает. Чтобы операция Dai завершилась до ее срока исполнения, проверяют Dbj + Dai ≤ Dai + Тai, то есть неравенство, которое было указано выше.
Таким образом, каждый фрейм Fаi сравнивают с каждым фреймом Fbj, проверяя, чтобы соблюдались сроки фреймов Fаi, но не проверяя соблюдение сроков фреймов Fbj. Это является первым прогоном проверки. Второй прогон проверки для дополнения проверки состоит в этом случае в повторении вышеупомянутых операций, сравнивая каждый фрейм Fbj с каждым фреймом Fаi и проверяя тем самым соблюдение сроков фреймов Fbj.
Проверку совместимости двух повторяющихся последовательностей RSFa и RSFb, соответственно содержащих Na и Nb фреймов, можно выразить в виде нижеследующего псевдокода. В этом псевдокоде альтернативные условия сгруппированы в выражениях min(x,y) с левой стороны неравенств и max(x,y) с правой стороны неравенств, а необходимые условия сгруппированы в выражениях min(x,y) с правой стороны неравенств и max(x,y) с левой стороны неравенств. Предусмотрены вышеупомянутые условия А.3 и В.3, чтобы учитывать возможность того, что фрейм Fаi может перекрыть четыре фрейма от Fbj до Fbj+3. Разумеется операции на индексах i и j осуществляют по модулю максимального значения индекса (Na для i и Nb для j), так как последовательности фреймов можно повторять бесконечно.
Для каждого i между 0 и Na-1 рассматривают:
Для каждого j между 0 и Nb-1 рассматривают:
[A.1]
если Dai ≤ Tbj+1, то продолжают при [В.1]
[A.2]
q1: = (Dai - Тbj+1)/ Тbj
если q1 > 1 или Тbj = 0, то q1: = 1
если Dai ≤ Tbj+1 + Tbj+2
и q1Tbj + Dbj+1 ≤ Таi
то продолжают при [В.1]
[A.3]
если Dai ≤ Tbj+2 + Tbj+3
и q1Tbj + Dbj+1 + Dbj+2 + min[Tbj+1, Dai] ≤ Таi
то продолжают при [В.1]
неудачное завершение цикла
[В.1]
если Dai ≤ Tbj+1
и Dbj ≤ Таi
то продолжают при [D]
[В.1.1]
q1: = (Dai - Тbj+1)/ Тbj
если q1 > 1 или Тbj = 0, то q1: = 1 и продолжают при [В.2]
Т1: Таi-1 - (1 - q1) Tbj
если Dbj-1 ≤ Т1
то продолжают при [С.1]
[В.2]
если Dai ≤ Tbj+1 + Tbj+2
и Dbj + qTbj + Dbj+1 ≤ Таi
то продолжают при [С.1]
[В.3]
если Dai ≤ Tbj+2 + Tbj+3
и Dbj + q1Tbj + Dbj+1 min[Tbj+1, Dai] + Dbj+2 ≤ Таi
то продолжают при [С.1]
неудачное завершение цикла
[С.1]
если Dbj ≤ Таi
то продолжают при [D]
неудачное завершение цикла
[D] Переходят к следующему j
Переходят к следующему i
Для дополнения проверки, как было указано выше, этот цикл повторяют, поменяв местами Fa и Fb.
В этом цикле, согласно варианту, по сравнению с тем, что было изложен выше, прежде чем перейти к оценке условия В.2, оценивают условие В.1.1.
На фиг. 7 представлен пример последовательности фреймов, служащей для определения условия В.1.1. Фреймы Fаi и Fbj находятся в тех же условиях, что и на фиг. 4А, но вместо запуска операции в начале фрейма Fbj+1, предполагается, что ее можно запустить сразу после операции Dbj, и в предыдущих фреймах Fаi-1 и Fbj-1 выявляют общие условия, которые позволяют это сделать при q = q1. Условие В.1.1, как и условие В.1, основано на предположении, что фрейм Fаi перекрывает два фрейма (Fbj и Fbj+1), что соответствует более вероятной ситуации, которую можно встретить, чем ситуацию, в которой фрейм Fаi перекрывает три фрейма или более.
Как было указано выше, фреймы могут включать в себя резервное время R, которое может брать система для осуществления не реально-временных задач. Такое резервное время можно брать для исполнения реально-временных операций. Его добавляют к запасам времени Т одной последовательности, чтобы способствовать исполнению операций D другой последовательности, но оно может ужесточить условия соблюдения сроков.
Не равные нулю значения резервного времени R могут, в частности, смягчить условие С.1.
На фиг. 8 представлен пример последовательности фреймов, служащей для определения смягченного условия в случае, когда условие С.1 не удовлетворено, то есть если Dbj > Тai. В рамках предположения С предполагают, что операция Dbj еще не запущена в начале фрейма Fаi. В самом начале фрейма Fаi запускают операцию Dai, которая имеет самый короткий конечный срок исполнения. Фрейм Fbj начинается до фрейма Fаi, предположительно во время интервала Rai-1 фрейма Fаi-1. Обозначим kRai-1 интервал между началом фрейма Fbj и началом фрейма Fаi, при 0 ≤ k ≤ 1.
Если операция Dbj не была запланирована в начале фрейма Fbj, это значит, что:
Dbj > kRai-1 + Tаi.
Обозначим k1 предельное значение k, при котором Dbj = k1Rai-1 + Tаi, то есть k1=(Dbj-Tаi)/Rai-1. Если k > k1, операцию Dbj можно с уверенностью планировать до начала фрейма Fаi, и этот случай не рассматривается, так как он не соответствует предположению С. В этом случае рассматривают только значения k в пределах от 0 до k1.
Чтобы можно было исполнить Dai, необходимо, чтобы Dai ≤ Tbj - kRai-1. Наихудшим случаем является k = k1, когда получаем:
Dai ≤ Tbj - k1Rai-1, то есть при замене k1 на его значение:
Dai ≤ Tbj - (Dbj - Tаi), или
Dbj ≤ Tаi + Tbj - Dai
Коэффициент k1 не превышает 1, что можно выразить, как:
Dbj - Tаi ≤ Rai-1, то есть
Dbj ≤ Tаi + Rai-1
В конечном итоге, чтобы не влиять на исполнение операции Dai+1, операция Dbj не должна переходить на фрейм Fаi+1. Это соблюдается, если:
Dbj ≤ Tаi + Rai.
Таким образом, подходим к следующему условию, которое является альтернативным условию С.1:
Dbj ≤ Tаi + Tbj - Dai
И
Dbj ≤ Tаi + Rai-1 [С.2]
И
Dbj ≤ Tаi + Rai
Следующий псевдокод учитывает резервы времени R.
Для каждого i между 0 и Na-1 рассматривают:
Для каждого j между 0 и Nb-1 рассматривают:
[A.1]
если Dai ≤ Tbj+1, то продолжают при [В.1]
[A.2]
q1: = (Dai - Тbj+1)/ Тbj + Rbj)
если q1 > 1 или Тbj + Rbj = 0, то q1: = 1
если Dai ≤ Tbj+1 + Rbj+1 + Tbj+2
и q1 (Tbj + Rbj) + Dbj+1 ≤ Таi
то продолжают при [В.1]
[A.3]
если Dai ≤ Tbj+2 + Rbj+2 + Tbj+3
и Dbj+1 + q1 (Tbj + Rbj+1) + Dbj+2 + min[Tbj+1 + Rbj+1, Dai] ≤ Таi
то продолжают при [В.1]
неудачное завершение цикла
[В.1]
если Dai ≤ Rbj + Tbj+1
и Dbj ≤ Таi
то продолжают при [C.2]
q1:= (Dai - Rbj - Tbj+1)/ Tbj
если q1 > 1 или Tbj = 0, то q1:= 1 и продолжают при [В.2]
[В.1.1]
Т1:= Tаi-1 - (1 - q1) Tbj + Rаi-1
если Dbj-1 ≤ Т1 + min[Tbj-1 + Dbj-1 + Rbj-1 - T1 - Dai-1, Ra1-2)
то продолжают при [С.1]
[В.1.2]
если Dbj-1 + Rbj-1 ≤ Т1
и Dai-1 ≤ Tbj-2 + Rbj-2 + Tbj-1
и Tbj-2 + Dbj-2 + Rbj-2 + Tbj-1 + Dbj-1 + Rbj-1 ≤ Rai-2 + T1 + Dai-1
то продолжают при [С.1]
[В.2]
если Dai ≤ Tbj+1 + Rbj+1 + Tbj+2
и Dbj + q1Tbj + Rbj + Dbj+1 ≤ Tаi
то продолжают при [С.1]
[В.3]
если Dai ≤ Tbj+2 + Rbj+2 + Tbj+3
и Dbj + q1Tbj + Rbj + Dbj+1 + min[Tbj+1 + Rbj+1, Dai] + Dbj+2 ≤ Tаi
то продолжают при [С.1]
неудачное завершение цикла
[С.1]
если Dbj ≤ Таi
то продолжают при [D]
[С.2]
если Dbj ≤ Tаi + min[Tbj -Dai, Rai, Rai-1]
то продолжают при [D]
неудачное завершение цикла
[D] Переходят к следующему j
Переходят к следующему i
Условие В.1.2, которое появляется в этом псевдокоде, устанавливают так же, как и условие В.1.1, продолжив исследования на фреймах Fаi-2 и Fbj-2.
До сих пор предполагалось, что шкалы времени, позволяющие упорядочить во времени обе задачи, были изохронными, то есть время интервалов одной из последовательностей не менялось относительно времени интервалов другой последовательности. На практике иногда приходится составлять две задачи с использованием не взаимосвязанных шкал времени, таких как задачи, связанные с положениями подвижных элементов, движущихся с переменным скоростями.
Для рассмотрения этого случая вводят коэффициент изменчивости z ≥ 1 для каждой повторяющейся последовательности, соответственно za и zb для последовательностей RSFa и RSFb. Коэффициенты za и zb являются фиксированными и выражают максимальное замедление, которым подвергаются интервалы Т и R в обеих последовательностях. Предположив, что обозначения, используемые в предыдущих отношениях, выражают минимальные значения интервалов, каждое из значений Т и R может принимать два значения: Т или zT и R или zR. Исполнительные потребности D являются фиксированными, так как они зависят только от тактового генератора системы.
В предыдущих отношениях, если интервал служит для нахождения свободного промежутка для исполнения операции, сохраняют его недооцененное значение Т или R. Если интервал служит для проверки соблюдения срока, берут его переоцененное значение zT или zR. При этом получают следующий псевдокод:
Для каждого i между 0 и Na-1 рассматривают:
Для каждого j между 0 и Nb-1 рассматривают:
[A.1]
если Dai ≤ Tbj+1, то продолжают при [В.1]
[A.2]
q1: = (Dai - Тbj+1)/ Тbj + Rbj)
если q1 > 1 или Тbj + Rbj = 0, то q1: = 1
если Dai ≤ Tbj+1 + Rbj+1 + Tbj+2
и min[ q1 (zb⋅(Tbj + Rbj) + (zb-1) Dbj), Dai] + Dbj+1 ≤ Таi
то продолжают при [В.1]
[A.3]
если Dai ≤ Tbj+2 + Rbj+2 + Tbj+3
и Dbj+1 + min[ q1 (zb⋅(Tbj + Rbj) + (zb-1) Dbj, Dai] + Dbj+2 + min[ zb⋅(Tbj+1 + Rbj+1)
+ (zb-1) Dbj+1, Dai] ≤ Таi
то продолжают при [В.1]
неудачное завершение цикла
[В.1]
если Dai ≤ Rbj + Tbj+1
и Dbj ≤ Таi
то продолжают при [C.2]
[В.1.1]
q1:= (Dai - Rbj - Tbj+1)/ Tbj
если q1 > 1 или Tbj = 0, то q1:= 1 и продолжают при [В.2]
Т1:= Tаi-1 - (1 - q1) Tbj + Rаi-1
если Dbj-1 ≤ Т1 + min[Tbj-1 + Dbj-1 + Rbj-1 - T1 - Dai-1, Ra1-2)
то продолжают при [С.1]
[В.1.2]
если Dbj-1 + zb⋅Rbj-1 ≤ Т1
и Dai-1 ≤ Tbj-2 + Rbj-2 + Tbj-1
и zb⋅(Tbj-2 + Dbj-2 + Rbj-2 + Tbj-1 + Dbj-1 + Rbj-1) ≤ Rai-2 + T1 + Dai-1
то продолжают при [С.1]
[В.2]
если Dai ≤ Tbj+1 + Rbj+1 + Tbj+2
и Dbj + min[ q1 (zb⋅Tbj + (zb-1) Dbj) + zb⋅Rbj, Dai ] + Dbj-1 ≤ Tаi
то продолжают при [С.1]
[В.3]
если Dai ≤ Tbj+2 + Rbj+2 + Tbj-3
и Dbj + min[ q1 (zb⋅Tbj + (zb-1) Dbj)+ zb⋅Rbj, Dai] + Dbj+1 + min[zb⋅(Tbj+1 + Rbj+1)
+ (zb-1) Dbj+1, Dai] + Dbj+2 ≤ Tаi
то продолжают при [С.1]
неудачное завершение цикла
[С.1]
если Dbj ≤ Таi
то продолжают при [D]
[С.2]
если Dbj ≤ Tаi + min[Tbj - Dai, Rai, Rai+1]
то продолжают при [D]
неудачное завершение цикла
[D] Переходят к следующему j
Переходят к следующему i
Для случая 3) описанного выше способа планирования рассматриваемый запас времени является минимальным значением, то есть Т, а не zT.
Представленные принципы были описаны в отношении двух выполняемых с разделением времени задач, но их можно применять для любого числа задач. Действительно, описанный способ позволяет на практике составлять единый план задания последовательности для двух совместимых задач. Полученный таким образом план задания последовательности можно составить опять, используя те же методы, вместе с планом задания последовательности третьей совместимой задачи, и так далее.
| название | год | авторы | номер документа |
|---|---|---|---|
| Разностно-дальномерный способ определения координат источника радиоизлучения (варианты) и устройство для их реализации | 2020 |
|
RU2740640C1 |
| Разностно-дальномерный способ определения координат источника радиоизлучения | 2019 |
|
RU2717231C1 |
| ОПРЕДЕЛЕНИЕ РАЗМЕРА ШИФРОВАЛЬНОЙ КНИГИ HARQ/ACK | 2013 |
|
RU2604432C2 |
| СПОСОБ ИЗМЕРЕНИЯ ЦВЕТА В ПРОИЗВОЛЬНОЙ СИСТЕМЕ КООРДИНАТ | 2012 |
|
RU2491521C1 |
| Разностно-дальномерный способ определения координат источника радиоизлучения и устройство для его реализации | 2019 |
|
RU2719770C1 |
| СПОСОБ ОСНОВАННОГО НА ОКОНЕЧНОМ УСТРОЙСТВЕ РАСПОЗНАВАНИЯ ДОМАШНИХ БАЗОВЫХ СТАНЦИЙ В СОТОВОЙ СИСТЕМЕ МОБИЛЬНОЙ РАДИОСВЯЗИ ПОСРЕДСТВОМ ПОДДЕРЖКИ СЕТЬЮ МОБИЛЬНОЙ РАДИОСВЯЗИ | 2008 |
|
RU2454829C2 |
| МУЛЬТИПЛЕКСИРОВАНИЕ УПРАВЛЯЮЩЕЙ ИНФОРМАЦИИ И ИНФОРМАЦИИ ДАННЫХ ОТ ПОЛЬЗОВАТЕЛЬСКОГО ОБОРУДОВАНИЯ В РЕЖИМЕ ПЕРЕДАЧИ MIMO | 2011 |
|
RU2575414C2 |
| Разностно-дальномерный способ определения местоположения объектов | 2022 |
|
RU2790347C1 |
| ПОДАВЛЕНИЕ ПОМЕХ В ТРАФИКЕ | 2005 |
|
RU2369964C2 |
| СПОСОБ И АППАРАТ ОПТИМИЗАЦИИ ИНФОРМАЦИИ, УСТРОЙСТВО И НОСИТЕЛЬ ДАННЫХ | 2020 |
|
RU2795154C1 |

Изобретение относится к области вычислительной техники. Технический результат заключается в возможности исполнения без помех двух задач с разделением времени, даже если шкалы времени двух задач являются разными. Раскрыт способ выполнения без помех двух задач с разделением времени, даже если шкалы времени двух задач являются разными, содержащий этапы, на которых: каждую задачу автономно раскладывают на соответствующую повторяющуюся последовательность последовательных неоднородных фреймов на шкале времени, связанной с соответствующей задачей, причем каждый фрейм связан с элементарной операцией, имеющей одну исполнительную потребность, и определяет дату начала, после которой операция начинается, дату конечного срока, до которой операция завершается, и запас времени, равный длительности фрейма за вычетом исполнительской потребности элементарной операции; для каждого текущего фрейма повторяющихся последовательностей первой из двух задач выполняют этап проверки, содержащий подэтапы, на которых: определяют группу последовательных фреймов повторяющейся последовательности второй из двух задач, причем каждый фрейм указанной группы перекрывает текущий фрейм, и проверяют, что элементарная операция текущего фрейма может быть исполнена между двумя последовательными элементарными операциями указанной группы последовательных фреймов, соблюдая при этом даты начала и конечного срока элементарной операции текущего фрейма и элементарных операций указанной группы последовательных фреймов; если на этапе проверки определено, что элементарная операция текущего время может быть исполнена, разрешают выполнение обеих задач и элементарные операции обеих задач планируют в зависимости от следующих случаев, оцениваемых по каждой дате из группы ключевых дат, содержащих сроки исполнения, даты начала и концы элементарных операций: если можно запустить элементарную операцию каждой задачи, выполняют ту элементарную операцию, которая имеет более короткий срок исполнения; и если можно запустить элементарную операцию только одной из двух задач, ее выполняют только в том случае, если ее исполнительная потребность меньше времени, остающегося до даты начала следующего фрейма повторяющейся последовательности другой из двух задач и увеличенного на запас времени, связанный с указанным следующим фреймом. 2 н. и 8 з.п. ф-лы, 13 ил.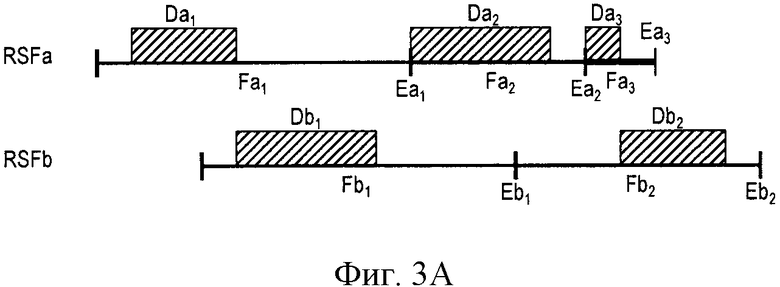
1. Способ выполнения без помех двух задач с разделением времени, даже если шкалы времени двух задач являются разными, содержащий этапы, на которых:
каждую задачу автономно раскладывают на соответствующую повторяющуюся последовательность последовательных неоднородных фреймов на шкале времени, связанной с соответствующей задачей, причем каждый фрейм связан с элементарной операцией, имеющей одну исполнительную потребность, и определяет дату начала, после которой операция начинается, дату конечного срока, до которой операция завершается, и запас времени, равный длительности фрейма за вычетом исполнительской потребности элементарной операции;
для каждого текущего фрейма повторяющихся последовательностей первой из двух задач выполняют этап проверки, содержащий подэтапы, на которых:
определяют группу последовательных фреймов повторяющейся последовательности второй из двух задач, причем каждый фрейм указанной группы перекрывает текущий фрейм, и
проверяют, что элементарная операция текущего фрейма может быть исполнена между двумя последовательными элементарными операциями указанной группы последовательных фреймов, соблюдая при этом даты начала и конечного срока элементарной операции текущего фрейма и элементарных операций указанной группы последовательных фреймов;
если на этапе проверки определено, что элементарная операция текущего времени может быть исполнена, разрешают выполнение обеих задач и элементарные операции обеих задач планируют в зависимости от следующих случаев, оцениваемых по каждой дате из группы ключевых дат, содержащих сроки исполнения, даты начала и конца элементарных операций:
если можно запустить элементарную операцию каждой задачи, выполняют ту элементарную операцию, которая имеет более короткий срок исполнения; и
если можно запустить элементарную операцию только одной из двух задач, ее выполняют только в том случае, если ее исполнительная потребность меньше времени, остающегося до даты начала следующего фрейма повторяющейся последовательности другой из двух задач и увеличенного на запас времени, связанный с указанным следующим фреймом.
2. Способ по п. 1, в котором каждый фрейм дополнительно содержит интервал резервного времени, который может быть нулевым, находящийся после конечного срока фрейма или перед датой начала фрейма, при этом интервалы резервного времени повторяющейся последовательности любой из двух задач добавляются к запасам времени для исполнения элементарных операций повторяющейся последовательности другой из двух задач.
3. Способ по п. 2, в котором этап проверки содержит этапы, на которых:
для каждого фрейма Fai повторяющейся последовательности первой задачи оценивают следующие условия для каждого фрейма Fbj повторяющейся последовательности второй задачи:
[A.1] Dai ≤ Tbj+1,
[B.1] Dai ≤ Rbj +Tbj+1 и Dbj ≤ Tai и
[C.1] Dbj ≤ Tai,
где D, T и R обозначают соответственно исполнительную потребность, запас времени и резервное время, индексированные идентификатором повторяющейся последовательности и номером фрейма в последовательности;
повторяют предыдущий этап, переставив местами фреймы Fai и Fbj;
разрешают выполнение задач, если для любой пары (i, j) соблюдены все три условия [A.1], [B.1] и [C.1].
4. Способ по п. 3, в котором этап проверки содержит этапы, на которых:
если условие [A.1] не соблюдается, оценивают следующее условие:
[A.2] Dai ≤ Tbj+1 + Rbj + Tbj+2
и Dai + Dbj+1 ≤ Tai + Tbj+1,
если условие [B.1] не соблюдается, оценивают следующее условие:
[B.2] Dai ≤ Tbj+1 + Rbj+1 + Tbj+2
и Dbj + Dai + Dbj+1 ≤ Tai + Tbj+1,
если условие [C.1] не соблюдается, оценивают следующее условие:
[С.2] Dbj ≤ Tai + min[Tbj-Dai, Rai, Rai-1],
разрешают выполнение задач, если условия [A.1] или [A.2], и [В.1] или [В.2], и [С.1] или [С.2] соблюдены для любой пары (i,j).
5. Способ по п. 3, в котором шкалы времени, определяющие продолжительность фреймов, являются переменными, так что запас времени Т и резервное время R изменяются на коэффициент от 1 до za для фреймов Fa и на коэффициент от 1 до zb для фреймов Fb, при этом этап проверки содержит этапы, на которых:
если условие [A.1] не соблюдается, оценивают следующее условие:
[A.2] Dai ≤ Tbj+1 + Rbj+1 + Tbj+2
и min[q1(zb⋅(Tbj+Rbj) + (zb-1)Dbj),Dai] + Dbj+1 ≤ Tai,
где q1 = (Dai-Tbj+1)/(Tbj+Rbj);
если условие [B.1] не соблюдается, оценивают следующее условие:
[B.2] Dai ≤ Tbj+1 + Rbj+1 + Tbj+2
и Dbj + min[q1(zb⋅Tbj + (zb-1)Dbj) + zb⋅Rbj, Dai] + Dbj+1 ≤ Tai,
где q1 = (Dai - Rbj - Tbj+1)/Tbj;
если условие [C.1] не соблюдается, оценивают следующее условие:
[С.2] Dbj ≤ Tai + min[Tbj-Dai, Rai, Rai-1];
разрешают выполнение задач, если условия [A.1] или [A.2], и [В.1] или [В.2], и [С.1] или [С.2] соблюдены для любой пары (i,j).
6. Способ по п. 5, в котором этап проверки содержит этапы, на которых:
если условие [B.1] не соблюдается, перед условием [В.2] оценивают следующее условие:
[B.1.1] Dai ≤ Tbj + Rbj + Tbj+1
и Dbj-1 ≤ T1 + min[Tbj-1 + Dbj-1 + Rbj-1 - T1 - Dai-1, Rai-2],
где q1 = (Dai - Rbj - Tbj+1)/Tbj и T1 = Tai-1 - (1-q1)Tbj + Rai-1,
разрешают выполнение задач, если условия [A.1] или [A.2], и [В.1] или [В.1.1], и [С.1] или [С.2] соблюдены для любой пары (i,j).
7. Способ выполнения без помех двух задач с разделением времени, даже если шкалы времени двух задач являются разными, содержащий этапы, на которых:
каждую задачу автономно раскладывают на соответствующую повторяющуюся последовательность последовательных фреймов на шкале времени, связанной с соответствующей задачей, причем каждый фрейм связан с элементарной операцией, имеющей одну исполнительную потребность, и определяет дату начала, после которой операция начинается, дату конечного срока, до которой операция завершается, запас времени, равный длительности фрейма за вычетом исполнительской потребности элементарной операции, и интервал резервного времени, который может быть нулевым, находящийся после конечного срока или перед датой начала;
для каждого фрейма Fai повторяющейся последовательности первой из двух задач оценивают следующие условия для каждого фрейма Fbj повторяющейся последовательности второй из двух задач:
[A.1] Dai ≤ Tbj+1,
[B.1] Dai ≤ Rbj +Tbj+1 и Dbj ≤ Tai и
[C.1] Dbj ≤ Tai,
где D, T и R обозначают соответственно исполнительную потребность, запас времени и резервное время, индексированные идентификатором повторяющейся последовательности и номером фрейма в последовательности;
повторяют предыдущий этап, переставив местами фреймы Fai и Fbj;
разрешают выполнение задач, если для любой пары (i, j) соблюдены все три условия [A.1], [B.1] и [C.1]; и
планируют элементарные операции обеих задач, разрешенных для выполнения, в зависимости от следующих случаев, оцениваемых по каждой дате из группы ключевых дат, содержащих сроки исполнения, даты начала и конца элементарных операций:
если можно запустить элементарную операцию каждой задачи, выполняют ту элементарную операцию, которая имеет более короткий срок исполнения; и
если можно запустить элементарную операцию только одной из двух задач, ее выполняют только в том случае, если ее исполнительная потребность меньше времени, остающегося до даты начала следующего фрейма повторяющейся последовательности другой из двух задач и увеличенного на запас времени, связанный с указанным следующим фреймом.
8. Способ по п. 7, в котором этап проверки содержит этапы, на которых:
если условие [A.1] не соблюдается, оценивают следующее условие:
[A.2] Dai ≤ Tbj+1 + Rbj + Tbj+2
и Dai + Dbj+1 ≤ Tai + Tbj+1,
если условие [B.1] не соблюдается, оценивают следующее условие:
[B.2] Dai ≤ Tbj+1 + Rbj+1 + Tbj+2
и Dbj + Dai + Dbj+1 ≤ Tai + Tbj+1,
если условие [C.1] не соблюдается, оценивают следующее условие:
[С.2] Dbj ≤ Tai + min[Tbj-Dai, Rai, Rai-1],
разрешают выполнение задач, если условия [A.1] или [A.2], и [В.1] или [В.2], и [С.1] или [С.2] соблюдены для любой пары (i,j).
9. Способ по п. 7, в котором шкалы времени, определяющие продолжительность фреймов, являются переменными, так что запас времени Т и резервное время R изменяются на коэффициент от 1 до za для фреймов Fa и на коэффициент от 1 до zb для фреймов Fb, при этом этап проверки содержит этапы, на которых:
если условие [A.1] не соблюдается, оценивают следующее условие:
[A.2] Dai ≤ Tbj+1 + Rbj+1 + Tbj+2
и min[q1(zb⋅(Tbj+Rbj) + (zb-1)Dbj),Dai] + Dbj+1 ≤ Tai,
где q1 = (Dai-Tbj+1)/(Tbj+Rbj);
если условие [B.1] не соблюдается, оценивают следующее условие:
[B.2] Dai ≤ Tbj+1 + Rbj+1 + Tbj+2
и Dbj + min[q1(zb⋅Tbj + (zb-1)Dbj) + zb⋅Rbj, Dai] + Dbj+1 ≤ Tai,
где q1 = (Dai - Rbj - Tbj+1)/Tbj;
если условие [C.1] не соблюдается, оценивают следующее условие:
[С.2] Dbj ≤ Tai + min[Tbj-Dai, Rai, Rai-1];
разрешают выполнение задач, если условия [A.1] или [A.2], и [В.1] или [В.2], и [С.1] или [С.2] соблюдены для любой пары (i,j).
10. Способ по п. 9, в котором этап проверки содержит этапы, на которых:
если условие [B.1] не соблюдается, перед условием [В.2] оценивают следующее условие:
[B.1.1] Dai ≤ Tbj + Rbj + Tbj+1
и Dbj-1 ≤ T1 + min[Tbj-1 + Dbj-1 + Rbj-1 - T1 - Dai-1, Rai-2],
где q1 = (Dai - Rbj - Tbj+1)/Tbj и T1 = Tai-1 - (1-q1)Tbj + Rai-1,
разрешают выполнение задач, если условия [A.1] или [A.2], и [В.1] или [В.1.1], и [С.1] или [С.2] соблюдены для любой пары (i,j).
| Пломбировальные щипцы | 1923 |
|
SU2006A1 |
| Колосоуборка | 1923 |
|
SU2009A1 |
| Колосоуборка | 1923 |
|
SU2009A1 |
| РЕАЛИЗАЦИЯ КОМПЬЮТЕРНОЙ МНОГОЗАДАЧНОСТИ ЧЕРЕЗ ВИРТУАЛЬНУЮ ОРГАНИЗАЦИЮ ПОТОЧНОЙ ОБРАБОТКИ | 2001 |
|
RU2286595C2 |
Авторы
Даты
2019-01-29—Публикация
2014-11-27—Подача