Изобретение относится к области техники связи и может быть использовано для моделирования дискретного канала связи с независимыми и группирующимися ошибками.
Способ настоящей заявки может применяться для моделирования двоичного симметричного канала связи и позволяет формировать побитный поток ошибок, требуемый для испытания аппаратуры передачи данных.
Во многих случаях канал связи определяют блочной статистикой ошибок канала связи. Под блочной статистикой ошибок канала связи понимают распределение P(t,n) вероятностей t ошибок в блоке длиной n бит для различных значений t и n, при этом t≤n. Например, модель канала связи по Пуртову задается блочной статистикой ошибок канала связи [В.Г. Морозов, Л.П. Пуртов, А.С. Замрий. Обобщение экспериментальных данных по вероятности и показателю группирования ошибок // Техника средств связи. - Сер. ТПС - Вып. 4. - 1981. - С. 53-60].
Также известен способ моделирования канала связи с группирующимися ошибками по Марковской модели канала, заключающийся в том, что сначала определяют множество состояний канала связи S0, S1, …, Sm-1 и вычисляют условные вероятности P(e|Si) возникновения ошибки в каждом состоянии Si канала связи, где i=0, …, m-1. При этом следующее состояние канала связи определяется переходными вероятностями P(Sj|Si), соответствующими переходу из текущего состояния Si в следующее состояние Sj [Блох Э.Л., Попов О.В., Турин В.Я. Модели источника ошибок в каналах передачи цифровой информации. М.: 1971, стр. 64].
Недостатком этого способа является высокая сложность моделирования канала связи по блочной статистике ошибок канала связи, поскольку при построении Марковской модели по блочной статистике ошибок канала связи необходим большой объем вычислений для определения параметров Марковской модели. Во многих случаях для получения приемлемой точности Марковская модель будет иметь большое число состояний, что усложняет получение побитной статистики канала связи. Кроме того, этот способ имеет низкое быстродействие, обусловленное тем, что в каждом состоянии канала связи генерируется только один бит потока ошибок, а затем принимается решение о переходе в следующее состояние.
Наиболее близким к предлагаемому способу (прототип) является способ моделирования канала связи, заключающийся в том, что определяют множество состояний канала связи S0, S1, …, Sm-1 и вычисляют условные вероятности P(e|Si) возникновения ошибки в каждом состоянии Si канала связи, где i=0, …, m-1, и, в соответствии с условной вероятностью ошибки для текущего состояния канала связи, получают ошибки в канале связи, при этом определяют вероятность появления безошибочного интервала Р(0i) длиной i бит по значению р - средней вероятности ошибки на бит и значению α - коэффициенту группирования ошибок, затем, используя значение вероятности безошибочных интервалов, по рекуррентным правилам вычисляют условные вероятности Р(0i1|11), Р(0i1|01) для безошибочных интервалов длиной i бит только для двух состояний канала связи, составляющих комбинации ошибок 11 или 01, затем генерируют равномерно распределенное в интервале от 0 до 1 случайное число L и при этом, суммируя условные вероятности Р(0i1|11) или Р(0i1|01), которым соответствуют ошибки в канале в виде 0i1, начиная с i=0, определяют последовательность 0k1, которая составляет побитный поток ошибок канала связи [Патент №2254675 МПК H03M 13/01. Квашенников В.В., Яковлев В.Г. Способ моделирования канала связи. Приор. 05.09.2002, опубл. 20.06.2005. Бюл. 17].
Последовательность 0k1, которая составляет побитный поток ошибок канала связи, выбирают по правилу
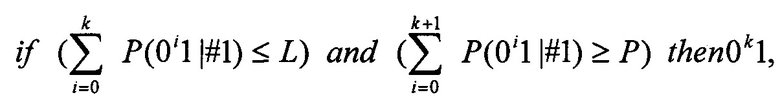
где символ # может принимать значение 0 или 1.
Этот способ имеет простую реализацию и высокое быстродействие. Однако, не достаточно точно соответствует модифицированной модели канала связи по Пуртову [В.М. Самойлов. Обобщенная аналитическая модель канала с групповым распределением ошибок. // Вопросы радиоэлектроники. - Сер ОВР. - Вып. 6 - 1990. - С. 152-156].
Цель предлагаемого способа - повысить при моделировании точность соответствия модифицированной модели канала связи по Пуртову.
Для достижения цели предложен способ, заключающийся в том, что заданную длину сообщения из N бит разбивают на более короткие сообщения из n бит, при этом 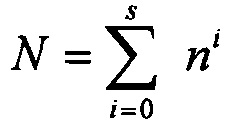 ,
,
где s - число сообщений из n бит в сообщении из N бит.
Для сообщения из n бит вычисляют вероятности безошибочных интервалов Р(0i) длиной i бит, где i=0, …, n, по значению p - средней вероятности ошибки на бит и значению α - коэффициенту группирования ошибок. Далее, используя значения вероятности безошибочных интервалов Р(0i), вычисляют условные вероятности Р(0i1|11), Р(0i1|01) для двух состояний канала связи, составляющих комбинации 01 и 11, которым соответствуют ошибки в канале в виде 0i1.
Новым является то, что для сообщения из n бит вводят коэффициент коррекции для коэффициента группирования ошибок, и вычисляют условные вероятности Р(0i1|00), P(0i1|11), Р(0i1|01) для трех состояний канала связи, составляющих комбинации 00, 11, 01, которым соответствуют ошибки в канале в виде 0i1, и Р(0n|00), Р(0n|01), Р(0n|11), которым соответствуют безошибочные интервалы в виде 0n, что повышает при моделировании точность соответствия предлагаемого способа модифицированной модели канала связи по Пуртову.
Реализацию предлагаемого способа рассмотрим на примере модифицированной модели канала связи по Пуртову, где вероятность t и более ошибок t≥2 в блоке длиной n бит выражается формулой:
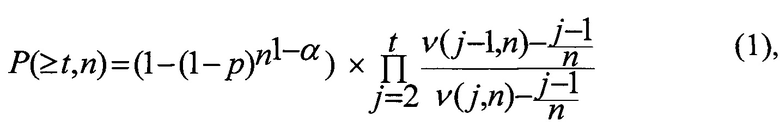
где p - средняя вероятность ошибки на бит (p<0,5),
α - коэффициент группирования ошибок (0≤α≤1).
Значение α=0 приближенно соответствует каналу с независимыми ошибками. Значение α=1 соответствует каналу, когда все ошибки сосредоточены в одной группе.
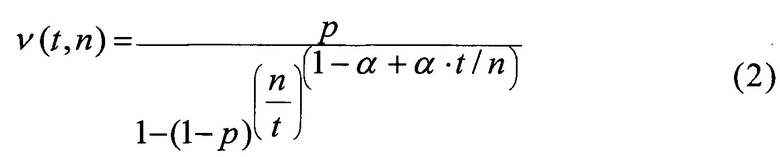
Вероятность искажения кодовой комбинации из n бит равна

Пусть Р(0i) - вероятность появления безошибочного интервала длиной i бит, i=0, 1, …. Вероятность Р(0i) вычисляют по формуле, которая следует из (3)
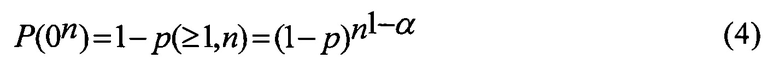
Если сообщение из N бит содержит большой объем бит, например более одного Мбайта, то для такого сообщения невозможно «в лоб» реализовать поток ошибок по модели Пуртова. Это сообщение необходимо разбить на более короткие сообщения из n бит, поток ошибок для которых позволяет реализовать современный уровень вычислительной техники. Ограничение связано с тем, что надо различать вероятности последовательностей Р(0k) и Р(0k+1) при k+1=n.
Пусть сообщение содержит n=104 бит, средняя вероятность ошибки на бит равна p=5⋅10-2, значение α=0. Тогда вероятности P(0k) и Р(0k+1) будут
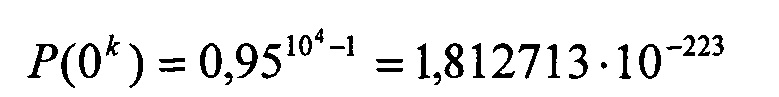
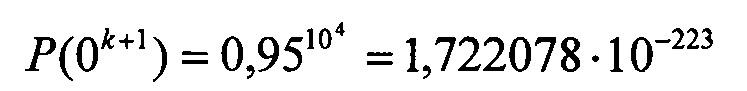
Очевидно, что требуется генератор псевдослучайных чисел с диапазоном 10224, чтобы различить эти последовательности.
Если сообщение содержит n=104 бит, средняя вероятность ошибки на бит равна p=10-1, значение α=0. Тогда вероятности Р(0k) и Р(0k+1) будут
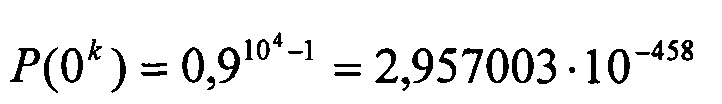
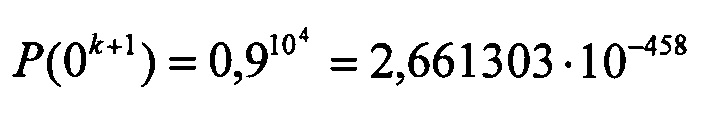
Требуется генератор псевдослучайных чисел с диапазоном 10459, чтобы различить эти последовательности.
Чтобы уменьшить диапазон генератора псевдослучайных чисел, надо сократить длину последовательности в виде 0i1.
Пусть сообщение содержит n=103 бит, средняя вероятность ошибки на бит равна p=5⋅10-2, значение α=0. Тогда вероятности Р(0k) и Р(0k+1) будут
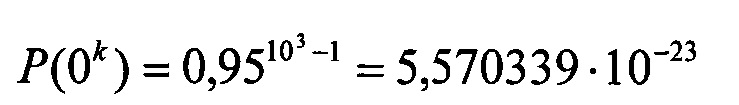
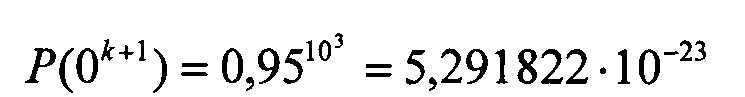
Очевидно, что требуется генератор псевдослучайных чисел с диапазоном 1024, чтобы различить эти последовательности.
Если сообщение содержит n=103 бит, средняя вероятность ошибки на бит равна p=10-1, значение α=0. Тогда вероятности Р(0k) и Р(0k+1) будут
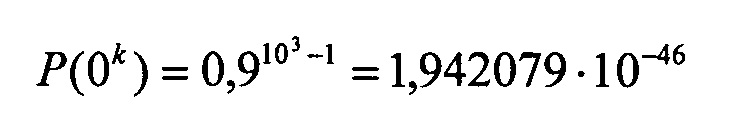
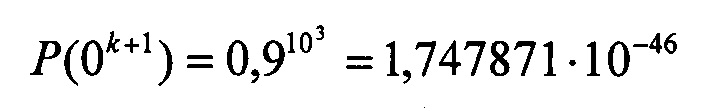
Требуется генератор псевдослучайных чисел с диапазоном 1046, чтобы различить эти последовательности.
В ЭВМ типа Intel Core Duo Е 8400 с операционной системой Astra Linux содержится генератор псевдослучайных чисел с диапазоном 231=2147482648≅2⋅109.
Если брать по четыре значения такого генератора псевдослучайных чисел, то диапазон чисел составит 8⋅1036≅1037 и при n=103 бит позволит различить эти последовательности при средней вероятности ошибки на бит до p=8⋅10-2 при значении α=0.
Возможно группирование ошибок, поэтому при приеме информационная последовательность наряду со словами с большим числом ошибок может содержать безошибочные слова или слова с малым числом ошибок даже для каналов с высоким уровнем помех.
Для сообщения из N бит вероятность P(0N) вычисляется по формуле
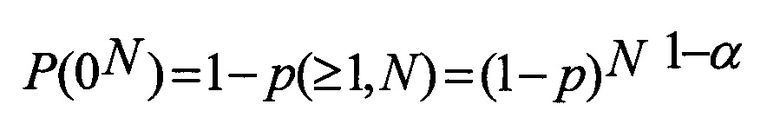
Сообщение 0N больше сообщения 0n в N/n раз. Однако P(0n)N/n≠P(0N), т.е. повторение N/n раз последовательностей 0n не соответствует вероятности P(0N) последовательности 0N.
Введем и определим коэффициент коррекции для коэффициента группирования ошибок для выполнения равенства
P(0n)N/n=P(0N)
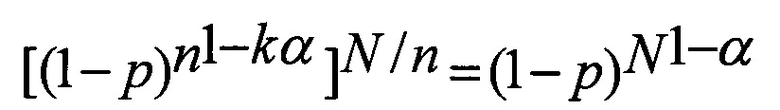
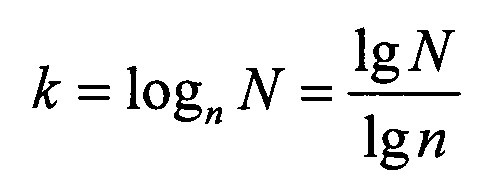
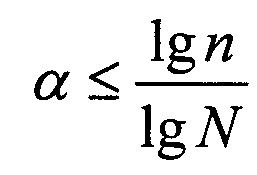
В таблице 1 приведены границы значений коэффициента группирования α для точного моделирования последовательности из N бит последовательностями из n бит
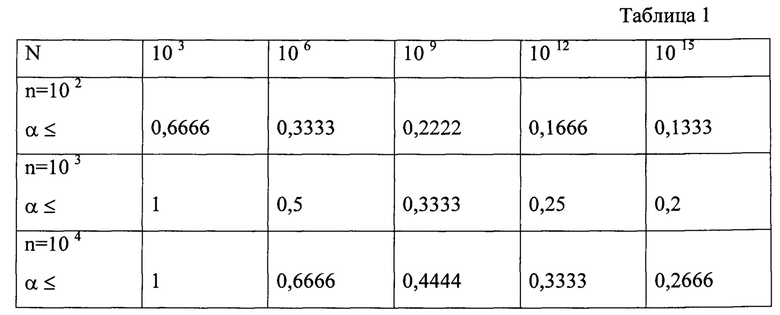
Чем меньше коэффициент группирования для последовательности из N бит, тем меньшей последовательностью из n бит можно смоделировать последовательность из N бит
Начальный интервал сообщения из n бит для потока ошибок может иметь следующий вид:
0n (n - следующих подряд нулей)
0i1 i=1, …, (n-1)
10i1 i=0, …, (n-2)
10n-1
Вычисление вероятностей начального интервала производится по следующим формулам:


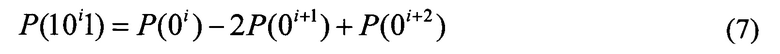
Сумма всех вероятностей вариантов начальных интервалов для сообщения из n бит равна единице, то есть
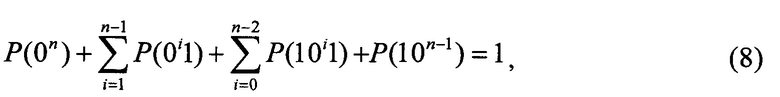
что проверяется подстановкой (6) и (7) в (8).
Присвоим по адресам оперативного запоминающего устройства (ОЗУ) значения вероятностей начального интервала. Чтобы не проводить операции суммирования вероятностей, запишем в ОЗУ по этим адресам результат
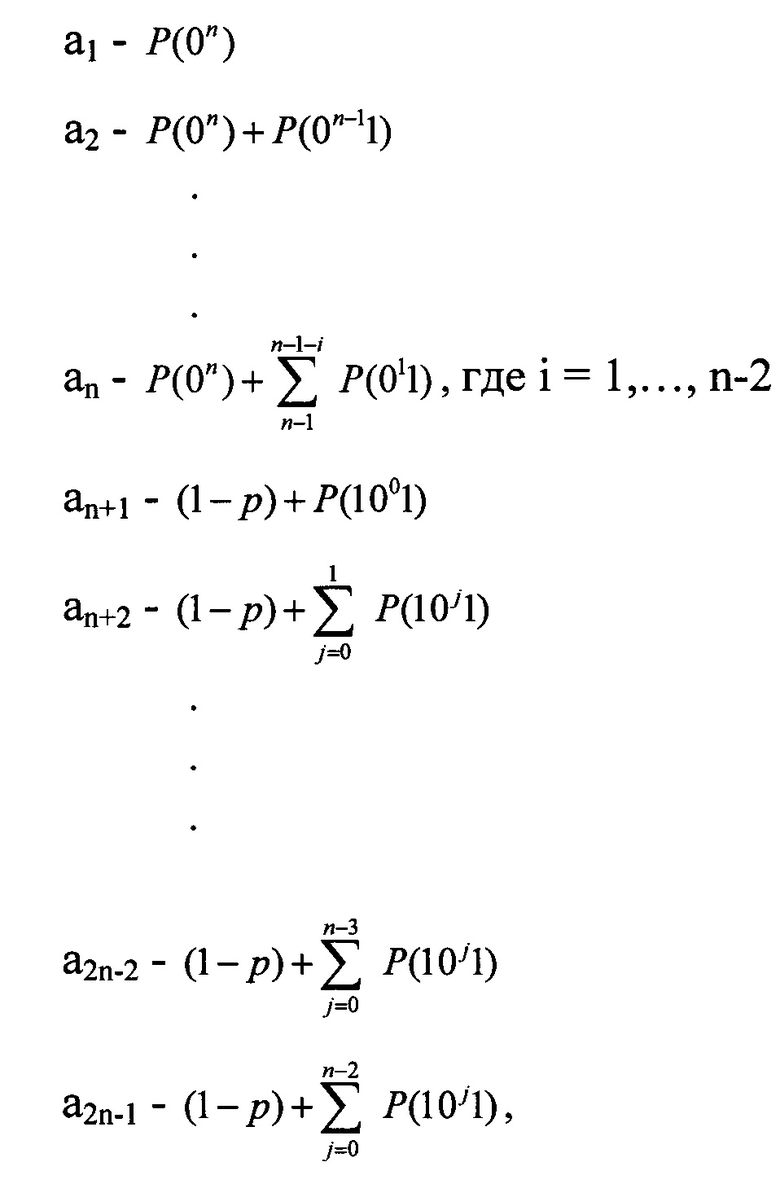
где j=0, …, n-2;
p - средняя вероятность ошибки на бит.
Каждому адресу данного ОЗУ соответствует другой адрес ОЗУ, по которому записано значение потока, который кроме первого и последнего адреса заканчивается единицей. Начальный интервал выбирается перебором адресов ОЗУ, начиная с а1 и до a2n-1, и, при сравнении значений вероятностей в ОЗУ с L, определяют вероятность и соответствующий ей адрес, а по нему другой адрес с видом последовательности по правилам
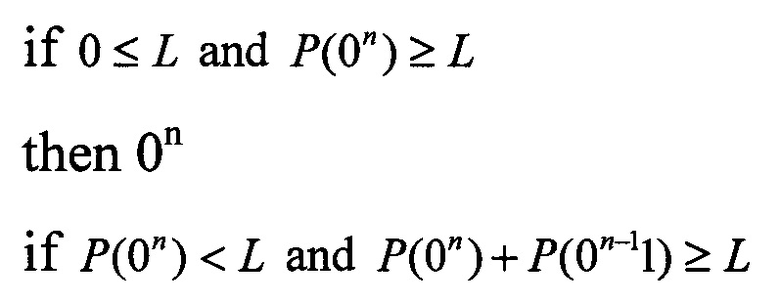
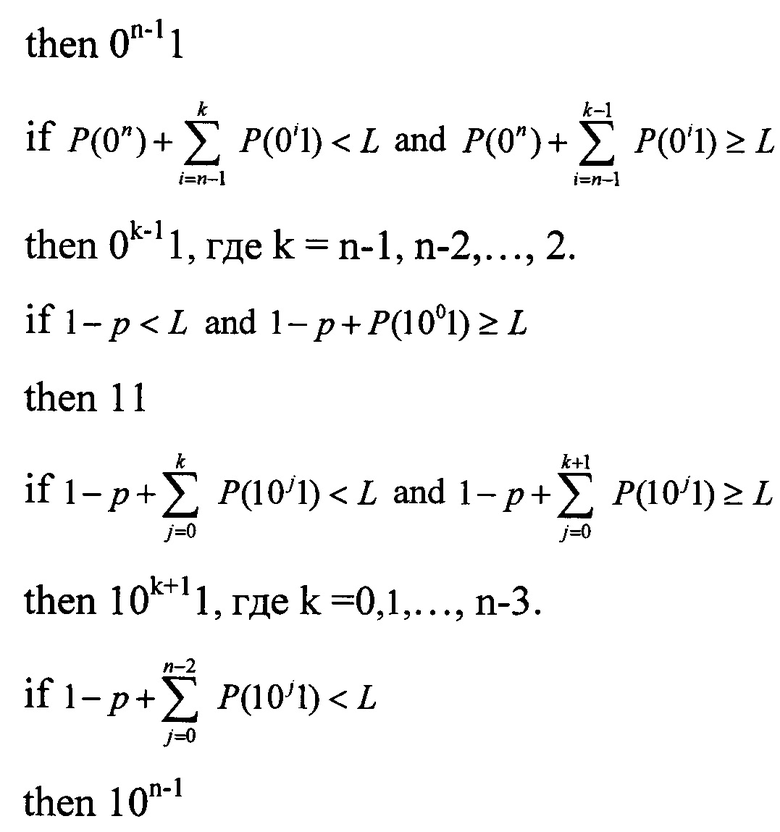
Второй и последующие интервалы, входящие в сообщение из n бит, имеют следующий вид:
0n-m, где m - суммарная длина предыдущих интервалов,
0i1, где i=0, …, n-m-1
Вычисление вероятностей производится по следующим формулам:
P(0i|11)=Р(110i)/Р(11)
Р(110i)=Р(0i)-2Р(0i+1)+Р(0i+2)
Р(11)=1-2Р(01)+Р(02)
Р(0i|01)=Р(0i|10)
Р(0i|01)=Р(0i+11)/Р(01)
P(0i+11)=P(0i+1)-P(0i+2)
Р(01)=Р(01)-Р(02)
Р(0i|00)=Р(0i+2)/Р(02)
Р(0i1|00)=Р(0i+21)/Р(02)
Р(0i+21)=Р(0i+2)-Р(0i+3)
Р(0i1|11)=Р(110i1)/Р(11)
P(110i1)=P(01)-3P(0i+1)+3P(0i+2)-P(0i+3)
P(0i1|01)=P(10i+11)/P(01)
P(10i+11)=P(0i+1)-2P(0i+2)+P(0i+3)
Аналогично начальному интервалу для последующих интервалов используются по два ОЗУ для каждого из состояний канала связи 00,01,11. Поскольку анализируют три состояния канала связи, то для определения количества бит в каждой последовательности 0n или 0i1 потребуется шесть ОЗУ.
Присвоим по адресам ОЗУ значения вероятностей для последующих интервалов. Чтобы не проводить операции суммирования вероятностей, запишем в ОЗУ по этим адресам результат
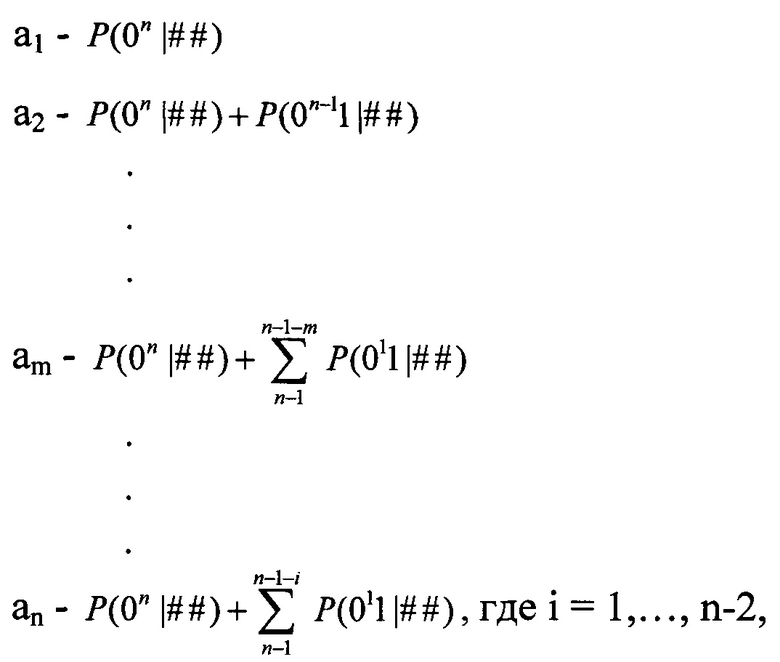
где ## могут принимать значения 00, 01 или 11.
Интервалы второго и последующих сообщений из n бит выбирают перебором адресов, начиная с а1, и по L определяют вероятность, а по ней соответствующую последовательность для трех состояний канала связи, составляющих комбинации 00, 01, 11, по следующим правилам
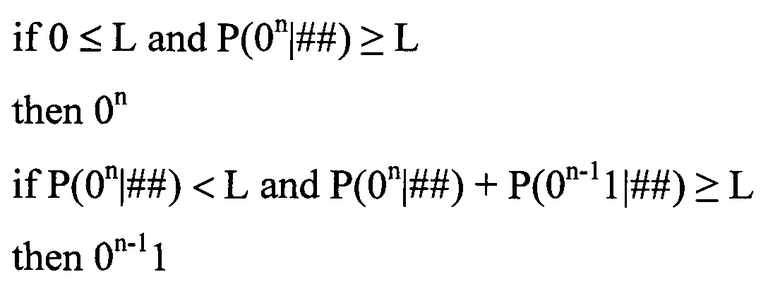
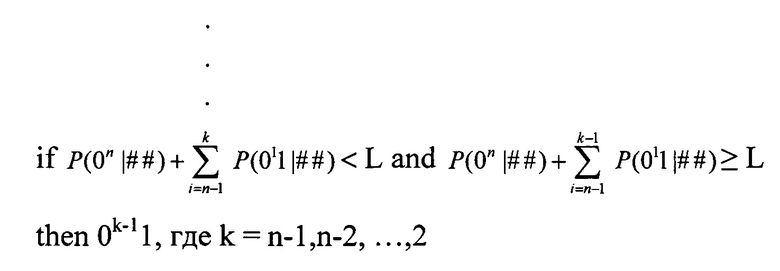
Адресам первого ОЗУ соответствуют значения условных вероятностей последовательностей, а адресам второго ОЗУ - количество бит в каждой последовательности 0i. Предварительно проводят расчет условных вероятностей последовательностей для каждого из трех состояний канала связи 00, 01, 11 до длины n бит. После определения по случайному числу L последовательности m0 бит начального интервала остается длина сообщения (n-m0) бит. После выбора m1 последовательности в интервале (n-m0) остается длина сообщения (n-m0-m1). Такой выбор проводится до тех пор, пока 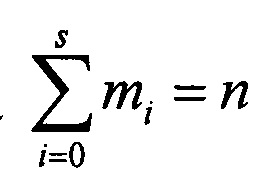 , где s - число выбранных последовательностей.
, где s - число выбранных последовательностей.
Покажем, что сумма вероятностей вариантов интервалов для конечных длин n-mi, где 0≤mi≤n равна единице, то есть
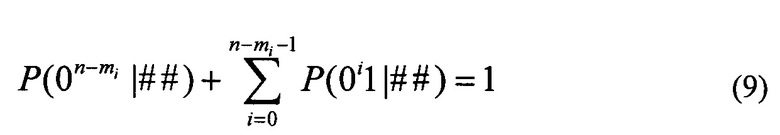
При α≠0
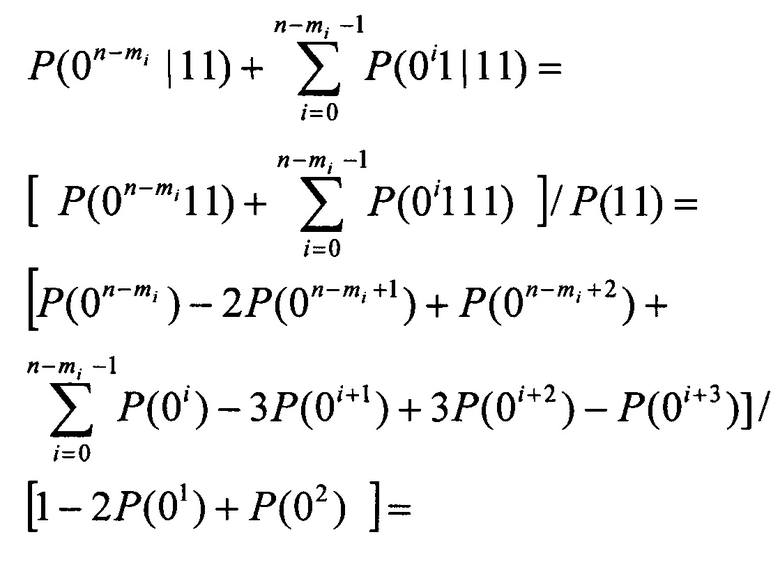
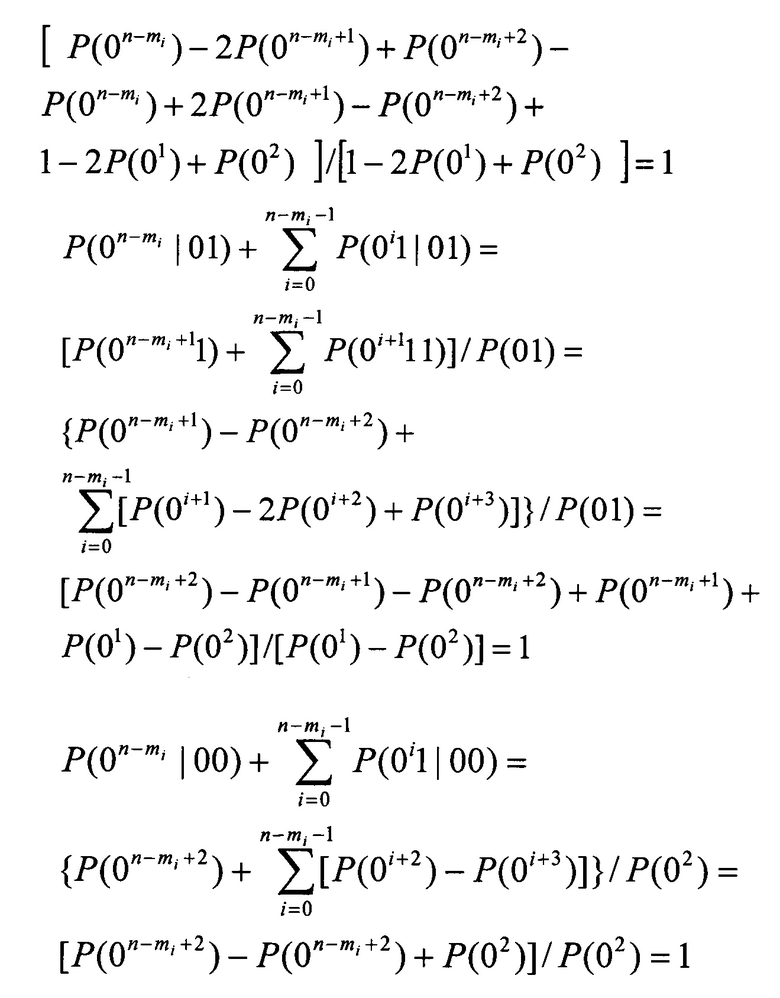
При α=0
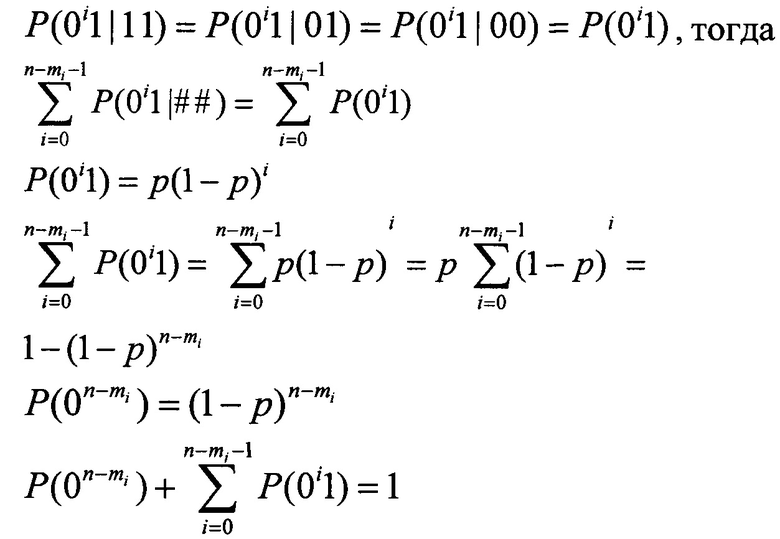
Из (9) следует, что
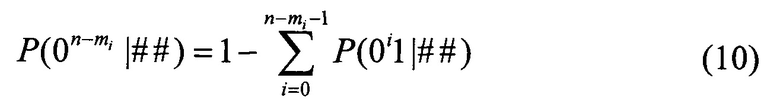
Очевидно, что пространство псевдослучайного генератора равно единице для последовательностей n бит. Однако из (9) следует, что и для последовательностей менее n бит пространство псевдослучайного генератора также равно единице. Из (10) следует, что в таких случаях для сообщения из n-mi бит числам L псевдослучайного генератора, определяющим адреса ОЗУ с последовательностями равными или более n-mi бит, будет соответствовать только одна последовательность 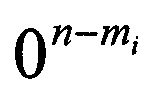 бит. Таким образом, для сообщения n-mi бит всем псевдослучайным числам
бит. Таким образом, для сообщения n-mi бит всем псевдослучайным числам
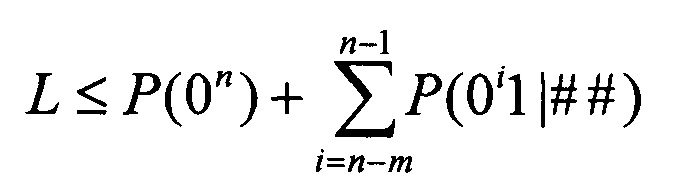
соответствуют последовательности 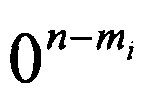 .
.
Вероятность 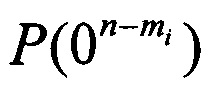 с увеличением mi возрастает, поэтому сообщения из n бит могут заканчиваться не только состояниями 01 или 11, но и состоянием 00, что, в отличие от прототипа, учтено в предлагаемом способе.
с увеличением mi возрастает, поэтому сообщения из n бит могут заканчиваться не только состояниями 01 или 11, но и состоянием 00, что, в отличие от прототипа, учтено в предлагаемом способе.
Сообщение N бит больше в несколько раз сообщения n бит, поэтому для него поток ошибок формируется из нескольких потоков ошибок сообщений из n бит. Для последующих интервалов состояние канала связи 00,01,11 берется из предыдущих интервалов сообщений.
Чтобы обеспечить непрерывный многобайтный поток ошибок, необходимо применить два ОЗУ. Сначала в одном ОЗУ формируют поток ошибок для сообщения n бит. Затем с началом вывода потока ошибок из этого ОЗУ происходит переключение на другое ОЗУ для записи в него следующего потока ошибок, и с его выводом опять идет подключение к исходному ОЗУ для формирования потока ошибок для сообщения n бит и так далее. При этом необходимо для самого медленного случая обеспечить время формирования потока ошибок меньше времени передачи в канале потока ошибок для сообщения из n бит.С увеличением скорости передачи в канале вышеприведенное требование труднее выполнить, а при превышении пороговой скорости передачи это требование нельзя выполнить и обеспечить непрерывный многобайтный поток ошибок.
Пусть средняя вероятность ошибки на бит в канале 5⋅10-2. Тогда каждое сообщение в 1000 бит в среднем должно содержать примерно 50 ошибок. Последовательность 0i1 содержит всего одну ошибку. Для сообщения в 1000 бит, содержащего примерно 50 ошибок, длина таких последовательностей в среднем составит 20 бит.Таким образом, в среднем необходимо проанализировать 1000 адресов для каждой последовательности в 1000 бит с примерно 50 ошибками. Пусть на обработку одного адреса, то есть на увеличение его значения на единицу, выбор числа, соответствующего границе интервала, определение по псевдослучайному числу генератора последовательностей потребуется 10 мкс. Тогда на обработку одного сообщения в 1000 бит потребуется 10 мс, что соответствует максимальной скорости передачи в канале 100 кГц. Чтобы обеспечить скорость передачи выше 100 кГц, например, для ускоренных испытаний аппаратуры, можно сгенерировать поток ошибок для всего сообщения N бит и записать его в ОЗУ. ОЗУ должно обеспечить считывание потока ошибок в соответствии с заданной скоростью тестирования. Однако между сообщениями из N бит будут паузы на время формирования следующих потоков ошибок.
Для исключения пауз между сообщениями можно заготавливать в ОЗУ сообщение, состоящее из нескольких сообщений по N бит каждое, которые затем считывать с требуемой скоростью тестирования.
Процесс моделирования потока ошибок носит псевдослучайный характер и его надо проконтролировать для сообщения из N бит, определив реальные значения параметров p и α. Среднюю вероятность ошибки на бит сначала вычисляют для каждого сообщения из ni бит
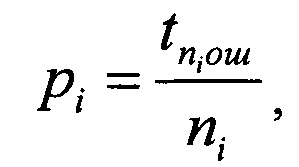
где 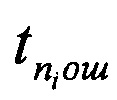 - число ошибок в сообщении из n бит.
- число ошибок в сообщении из n бит.
Затем определяют среднюю вероятность ошибки на бит pN для сообщения из N бит
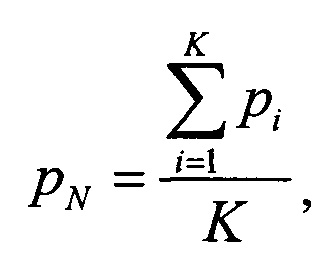
где 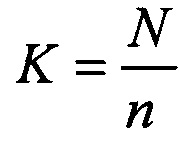
Коэффициент группирования ошибок αN для сообщения из N бит определяют по вероятности приема безошибочных слов из k бит.
Сначала определяют qi - число безошибочных слов из k бит для сообщения из ni бит.
Затем определяют qN - число безошибочных слов из k бит для сообщения из N бит.
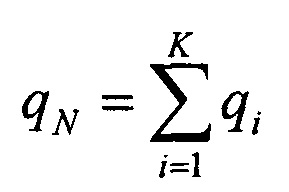
Вероятность безошибочных слов из k бит для сообщения из N бит при моделировании можно рассчитать по статистике

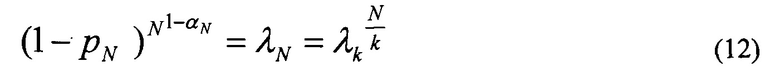
Затем из(11)и(12) определяют коэффициент группирования ошибок αN для сообщения из N бит
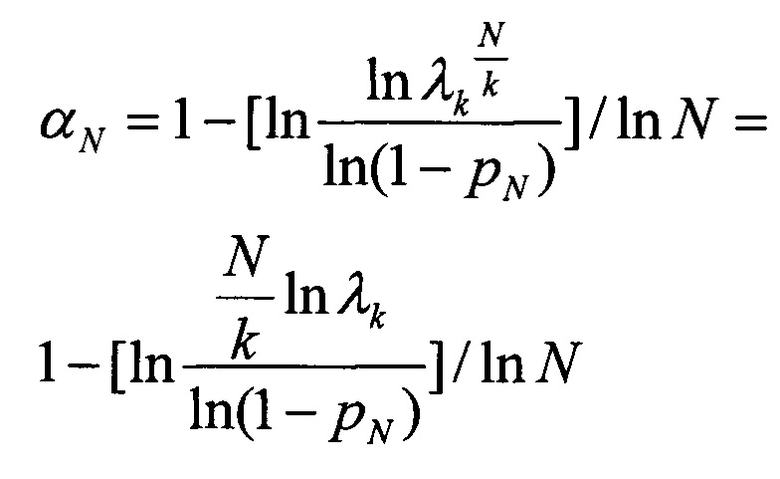
Определение реальных значений параметров p и α при контроле позволяет оценить точность моделирования потока ошибок и отобрать требуемую модель независимых и группирующихся ошибок канала связи для сообщения из N бит для проведения тестирования оборудования.
В предлагаемом способе в отличие от прототипа вводят коэффициент коррекции для коэффициента группирования ошибок и дополнительно вычисляют условные вероятности Р(0i1|00), P(0i1|01), P(0i1|11), которым соответствуют ошибки в канале в виде 0i1 и Р(0n|00), Р(0n|01), Р(0n|11), которым соответствуют безошибочные интервалы в виде 0n, что повышает при моделировании точность соответствия предлагаемого способа модифицированной модели канала связи по Пуртову.
Достигаемым техническим результатом предлагаемого способа моделирования независимых и группирующихся ошибок канала связи является повышение при моделировании точности соответствия модифицированной модели канала связи по Пуртову.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ МОДЕЛИРОВАНИЯ КАНАЛА СВЯЗИ | 2002 |
|
RU2254675C2 |
| УСТРОЙСТВО МОДЕЛИРОВАНИЯ КАНАЛА СВЯЗИ | 2006 |
|
RU2319301C2 |
| Генератор последовательности ошибок | 1982 |
|
SU1077044A1 |
| СПОСОБ ПЕРЕДАЧИ СООБЩЕНИЙ В СИСТЕМЕ С ОБРАТНОЙ СВЯЗЬЮ | 2004 |
|
RU2259636C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ТАКТОВОГО ИНТЕРВАЛА СЛУЧАЙНОГО ПОТОКА ИМПУЛЬСОВ С ДИСКРЕТНЫМ ВРЕМЕНЕМ | 2002 |
|
RU2230331C2 |
| Устройство для моделирования системы связи | 1985 |
|
SU1256043A1 |
| СПОСОБ ПЕРЕДАЧИ ИНФОРМАЦИИ С ИСПОЛЬЗОВАНИЕМ АДАПТИВНОГО ПОМЕХОУСТОЙЧИВОГО КОДИРОВАНИЯ | 2004 |
|
RU2276837C1 |
| СПОСОБ АДАПТИВНОГО ПОМЕХОУСТОЙЧИВОГО КОДИРОВАНИЯ | 2007 |
|
RU2375824C2 |
| СПОСОБ КОНТРОЛЯ КАЧЕСТВА КАНАЛА СВЯЗИ | 2008 |
|
RU2380836C1 |
| Способ кодовой цикловой синхронизации для каскадного кода при применении жестких решений | 2016 |
|
RU2633148C2 |
Изобретение относится к способу моделирования независимых и группирующихся ошибок канала связи. Технический результат заключается в повышении быстродействия модифицированной модели канала связи. Способ заключается в том, что заданную длину сообщения N бит разбивают на более короткие сообщения из n бит, при этом сумма бит сообщений из n бит равна числу бит в сообщении из N бит, для сообщений из n бит вводят коэффициент коррекции для коэффициента группирования ошибок и с учетом этой коррекции для трех состояний канала - связи, составляющих комбинации 11, 01, 00, вычисляют условные вероятности Р(0i1|11), Р(0i1|01), Р(0i1|00), которым соответствуют ошибки в канале в виде 0i1, и Р(0n|00), Р(0n|01), Р(0n|11), которым соответствуют безошибочные интервалы в виде 0n, генерируют равномерно распределенное в интервале от 0 до 1 случайное число L, для которого по условным вероятностям Р(0i1|11), Р(0i1|01), Р(0i|00), Р(0n|00), Р(0n|01), Р(0n|11) определяют последовательности 0k1 или 0k, которые для сообщений из n бит составляют побитные потоки ошибок, из которых последовательно формируется побитный поток ошибок для каждого сообщения из N бит. 1 з.п. ф-лы.
1. Способ моделирования независимых и группирующихся ошибок канала связи, заключающийся в том, что определяют множество состояний канала связи S0, S1, …, Sm-1 и вычисляют условные вероятности P(e|Si) возникновения ошибки в каждом состоянии Si канала связи, где i=0, …, m-1, и в соответствии с условной вероятностью ошибки для текущего состояния канала связи получают ошибки в канале связи, при этом определяют вероятность появления безошибочного интервала Р(0i) длиной i бит по значению р - средней вероятности ошибки на бит и значению α - коэффициенту группирования ошибок, затем, используя значение вероятности безошибочных интервалов, по рекуррентным правилам вычисляют условные вероятности Р(0i|11), Р(0i1|01) для безошибочных интервалов длины i бит только для двух состояний канала связи, составляющих комбинации ошибок 11 или 01, генерируют равномерно распределенное в интервале от 0 до 1 случайное число L при этом суммируют условные вероятности P(0i1|11) или Р(0i1|01), и определяют последовательность 0k1, которая составляет побитный поток ошибок канала связи, отличающийся тем, что заданную длину сообщения N бит разбивают на более короткие сообщения из n бит, при этом сумма бит сообщений из n бит равна числу бит в сообщении из N бит, для сообщений из n бит вводят коэффициент коррекции для коэффициента группирования ошибок и с учетом этой коррекции для трех состояний канала связи, составляющих комбинации 11, 01, 00, вычисляют условные вероятности Р(0i1|11), Р(0i|01), Р(0i1|00), которым соответствуют ошибки в канале в виде 0i1, и Р(0n|00), Р(0n|01), Р(0n|11), которым соответствуют безошибочные интервалы в виде 0n, генерируют равномерно распределенное в интервале от 0 до 1 случайное число L, для которого по условным вероятностям Р(0i1|11), Р(0i1|01), Р(0i1|00), Р(0n|00), Р(0n|01), Р(0n|11) определяют последовательности 0k1 или 0k, которые для сообщений из n бит составляют побитные потоки ошибок, из которых последовательно формируют побитный поток ошибок для каждого сообщения из N бит.
2. Способ по п. 1, отличающийся тем, что для отбора требуемой модели определяют реальные значения р и α для смоделированных сообщений.
| СПОСОБ МОДЕЛИРОВАНИЯ КАНАЛА СВЯЗИ | 2002 |
|
RU2254675C2 |
| US 6088678 A, 11.07.2000 | |||
| US 5802446 A, 01.09.1998 | |||
| Парашют для клетей шахтного подъема | 1948 |
|
SU78383A1 |
Авторы
Даты
2019-11-11—Публикация
2019-03-27—Подача