Изобретение относится к области вычислительной техники, в частности к способам и устройствам обработки статистических данных, и может быть использовано при определении длительности элементарных посылок разведываемых многопозиционных (многочастотных) сигналов, а также при определении параметров сигналов с программной перестройкой рабочих частот.
Известен способ определения постоянного тактового интервала потоков импульсов с дискретным временем tn=nT, n=1, 2,..., для которых тактовая вероятность появления импульса равна единице рп=р=1, включающий измерение временного интервала τ 0N между моментами прихода первого (опорного) t0 и последнего tN импульса в наблюдаемой реализации потока, подсчет числа NИ=N+1 импульсов входного потока и определение тактового интервала по формуле
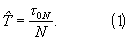
[1. Мирский Г.Я. Радиоэлектронные измерения. Изд. 3-е. М.: Энергия, 1975, с.223-226].
Дисперсия ошибок определения параметра Т известным способом с использованием формулы (1) в N2 раз меньше дисперсии ошибок измерения 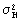 временного интервала
временного интервала 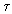 0N [1]:
0N [1]:
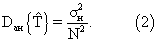
Недостатком известного способа определения тактового интервала является ограниченная область его применения периодическими потоками импульсов, для которых тактовая вероятность появления импульса равна единице, при невысокой точности определения тактового интервала.
Наиболее близким по технической сущности к предложенному способу определения постоянного тактового интервала Т случайного потока импульсов с дискретным временем является статистический способ, включающий измерение независимых временных интервалов τ k=tk- tk-1,
tk-1, 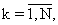 между моментами t0<t1<...<tN появления импульсов в наблюдаемой реализации потока и определение с привлечением априорных данных о статистической модели наблюдаемых временных интервалов τ k,
между моментами t0<t1<...<tN появления импульсов в наблюдаемой реализации потока и определение с привлечением априорных данных о статистической модели наблюдаемых временных интервалов τ k, 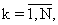 тактового интервала как параметра соответствующего распределения случайных величин [Левин Б.Р. Теоретические основы статистической радиотехники, кн.2. М.: Советское радио, 1968, с. 122].
тактового интервала как параметра соответствующего распределения случайных величин [Левин Б.Р. Теоретические основы статистической радиотехники, кн.2. М.: Советское радио, 1968, с. 122].
Рассмотрим возможности известного статистического способа определения тактового интервала Т случайного потока импульсов с дискретным временем на конкретном примере при двух облегчающих решение данной задачи условиях:
тактовая вероятность появления импульсов постоянна pn=p=const;
ошибки наблюдения (измерения) временных интервалов равны нулю (σ н=0).
При данных условиях выборочные временные интервалы (ВВИ) τ k являются дискретными случайными величинами, распределенными по смещенному на единицу геометрическому закону:
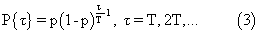
с математическим ожиданием и дисперсией соответственно
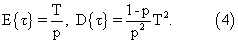
Для совместной оценки двух постоянных параметров р и Т распределения (3) воспользуемся в соответствии с известными рекомендациями критерием максимального правдоподобия [Левин Б.Р. Теоретические основы статистической радиотехники, кн.3. М.: Советское радио, 1976, с.16]. С этой целью запишем функцию правдоподобия выборки временных интервалов размера N в виде произведения N вероятностей (3):
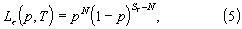
где 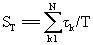 - сумма длин (кратностей) N величин τ k в единицах Т.
- сумма длин (кратностей) N величин τ k в единицах Т.
Уравнение для оценки параметра р находим дифференцированием логарифма от функции правдоподобия (5):
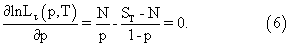
Уравнение для оценки параметра Т имеет вырожденный вид:
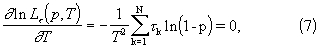
поскольку Т - масштабный коэффициент ВВИ.
Из уравнения (6) находим
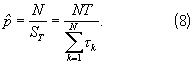
Таким образом, оценка тактовой вероятности существует, если известен тактовый интервал, и наоборот. В тех немногих случаях, когда параметр p априори известен, оценку Т находят из соотношения (8):
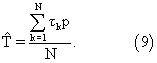
Поскольку сумма 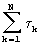 равна τ 0N, то достаточно измерять временной интервал τ 0N и определять параметр Т по формуле
равна τ 0N, то достаточно измерять временной интервал τ 0N и определять параметр Т по формуле
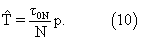
Найдем точность определения параметра T с помощью статистики (10) при наличии ошибок измерения интервала τ 0N. Дисперсия суммарного интервала τ 0N по сравнению с дисперсией (4) одного интервала возрастает в N раз:
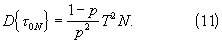
С учетом независимых ошибок измерения (σ н&λτ;&λτ;Т) дисперсия измеренного временного интервала τ 0N составит
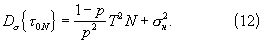
Применяя известное правило изменения дисперсии случайной величины τ 0N, умноженной на неслучайную величину p/N, находим дисперсию ошибок определения тактового интервала с помощью известного способа (10) при наличии априорной информации о тактовой вероятности (0<p≤ 1):
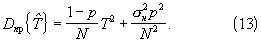
Отметим, что при р=1 формулы (9) и (13) совпадают с (1) и (2) соответственно.
Из (13) следует, что при σ н≤T (на практике в большинстве случаев σ н&λτ;&λτ;Т) основная доля погрешности при оценке параметра Т, определяемая первым слагаемым, обусловлена случайным характером длин ВВИ. Так, при р=0,5 и σ н=Т вклад первого слагаемого в 2N раз превышает вклад, вносимый ошибками измерения ВВИ. Очевидно, что при p<0,5 и σ н<Т относительное влияние первого слагаемого в (13) на точность определения тактового интервала Т возрастает. Поэтому при ограниченном размере выборки N добиться существенного повышения точности определения параметра Т с помощью известного статистического способа за счет повышения точности наблюдения ВВИ не удается.
С учетом изложенного существенным недостатком известного статистического способа является его невысокая точность определения тактового интервала и невозможность его применения при отсутствии априорных данных о величине тактовой вероятности появления импульсов входного потока.
Задачей данного изобретения является повышение точности определения тактового интервала случайного потока импульсов с дискретным временем при неизвестной тактовой вероятности появления импульсов с одновременным расширением области применения способа.
Поставленная задача решается за счет того, что в известном способе, включающем измерение временного интервала между моментами появления первого и последнего импульсов в наблюдаемой реализации потока, дополнительно измеряют временные интервалы от момента появления первого до моментов появления каждого промежуточного по времени появления импульса в наблюдаемой реализации потока, причем по совокупности измеренных временных интервалов путем организованного перебора возможных значений целочисленных кратностей временных интервалов тактовому интервалу определяют оценки их общих делителей в виде угловых коэффициентов прямых регрессии, проходящих через начало координат с одинаковыми наименьшими суммами квадратов уклонений собственных точек, при этом за величину тактового интервала принимают максимальный угловой коэффициент прямой регрессии из числа указанных.
В предложенном способе повышение точности определения тактового интервала случайного потока импульсов с дискретным временем обеспечено благодаря более полному извлечению информации о тактовом интервале, содержащейся в совокупности перекрывающихся (зависимых) случайных временных интервалов с независимыми дискретными приращениями по модулю за счет использования избирательных свойств взаимно простых чисел, реализованных в статистике "наибольшего общего делителя" дискретных случайных величин, и выравнивающих (по отношению к измеренным временным интервалам) свойств прямой регрессии, проходящей через начало координат с непрерывными значениями измеренных временных интервалов по оси ординат и целочисленными значениями их кратностей тактовому интервалу T по оси абсцисс.
Сущность предложенного способа определения тактового интервала случайного потока импульсов с дискретным временем заключается в следующем.
Вначале предположим, что ошибки измерения временных интервалов равны нулю (σ H=0). Тогда при постоянном тактовом интервале Т имеем систему из N≥ 2 линейных уравнений
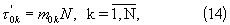
где τ '0k - дискретный временной интервал между моментами появления опорного (первого) и k-го импульса;
m01<m02<...<m0N - неизвестные случайные кратности (целые числа) временных интервалов τ 0k в единицах Т.
Система уравнений (14) является недоопределенной (количество неизвестных N+1) и при отсутствии ограничений на область значений Т имеет счетное множество решений. Однако фактор стохастичности целочисленных кратностей m0k позволяет решать систему (14) относительно неизвестного Т с вероятностью, отличной от нуля. Из системы (14) следует, что оцениваемый параметр Т является общим делителем (ОД) нескольких N≥ 2 дискретных величин τ '0k. Счетное множество ОД включает и наибольший общий делитель (НОД), для вычисления которого применим, например, алгоритм Евклида [Бронштейн И.Н., Семендяев К.А. Справочник по математике. Изд. 8, - М.: Физматгиз, 1959, с.129]. Все множество решений, удовлетворяющих системе уравнений (14), находим следующим образом:
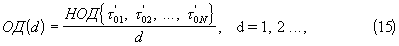
где d - порядковый номер ОД.
С учетом (15) и случайного характера элементов выборки для определения интервала Т существует счетное множество статистик
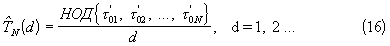
Статистики (16) характеризуются различными вероятностями правильного определения интервала 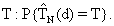 Наибольшей вероятностью правильного определения Т обладает первая (d=1) статистика
Наибольшей вероятностью правильного определения Т обладает первая (d=1) статистика
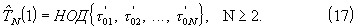
Статистика (17) правильно определяет T, если среди N кратностей m0k ВВИ (14) имеется хотя бы одна пара взаимно простых чисел, НОД которых, по определению, равен единице. Очевидно, что с увеличением размера N выборки вероятность выполнения этого условия возрастает. Статистики (16) с параметрами d=2, 3,... правильно определяют интервал Т, если НОД {m01, m02,..., m0N}=2, 3,... соответственно, с парциальными вероятностями, общая сумма которых является дополнением вероятности правильного определения T по статистике (17) до единицы:
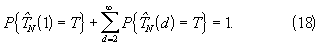
Определение дискретных составляющих суммы (18) аналитическим путем является довольно трудоемкой задачей.
По результатам эксперимента на ЭВМ в таблице приведены оценки вероятностей появления хотя бы одной пары взаимно простых чисел в выборке размером N=2, 3, 4, 5 кратностей m0k образованных из кратностей mk с геометрическим распределением с параметром 0<р<1.
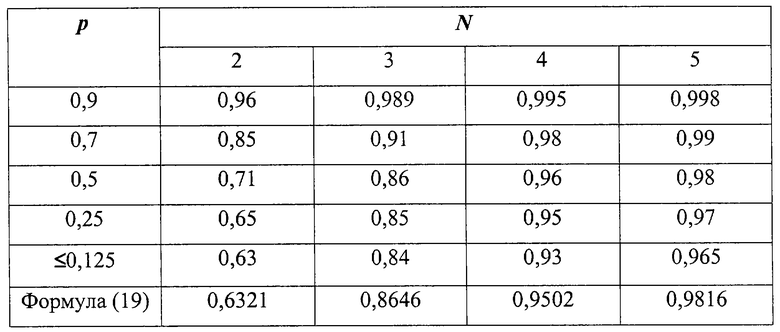
На основании данных таблицы нижняя граница значений вероятности правильного определения постоянного параметра Т с помощью статистики (17) как функция размера N≥ 2 выборки с приемлемой для практики точностью δ р=1...3% может быть аппроксимирована дискретной экспонентой при любой величине тактовой вероятности (0<р≤ 1):
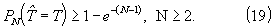
Таким образом, при отсутствии ошибок наблюдения временных интервалов τ '0k дисперсия условной (с вероятностью (19)) оценки параметра Т с помощью статистики (17) равна нулю. Сопоставляя этот результат с (13) при σ H=0, приходим к выводу о том, что мешающий в (10) фактор стохастичности дискретных величин обращен в статистике (17) в фактор, обеспечивающий новое качество оценок параметра Т.
Формула (19) определяет потенциальные возможности предложенного способа при σ н(ρ)0 в зависимости от размера N выборки.
В реальных условиях ВВИ (14) наделяются случайными ошибками наблюдения Δ k с параметрами: Е(Δ k)=0, D(Δ k)=σ
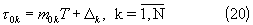
Очевидно, что НОД нескольких дискретных величин со структурой (14) является максимальным угловым коэффициентом прямой, проходящей через начало координат с нулевой суммой уклонений от узловых точек прямоугольной дискретной решетки {mkТ, m}, 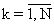 , m=1, 2,... Поэтому при наличии ошибок наблюдения (σ н≠0) поиск оценок НОД в предложенном способе реализован в рамках предписаний метода наименьших квадратов с использованием прямых регрессии вида у=bх, где x - целочисленный аргумент.
, m=1, 2,... Поэтому при наличии ошибок наблюдения (σ н≠0) поиск оценок НОД в предложенном способе реализован в рамках предписаний метода наименьших квадратов с использованием прямых регрессии вида у=bх, где x - целочисленный аргумент.
Угловой коэффициент b=Т(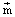 0) прямой регрессии по измеренным ВВИ (20) при произвольно заданном (либо известном) N-мерном векторе кратностей
0) прямой регрессии по измеренным ВВИ (20) при произвольно заданном (либо известном) N-мерном векторе кратностей 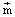 0 определяется из условия минимальной суммы квадратов уклонений:
0 определяется из условия минимальной суммы квадратов уклонений:
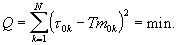
Приравнивая нулю производную
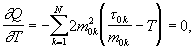
находим угловой коэффициент прямой регрессии
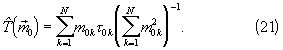
Если истинные кратности временных интервалов (20) известны, то дисперсия оценки (21) тактового интервала Т составит [Линник Ю.В. Метод наименьших квадратов и основы теории обработки наблюдений. - М.: Физматгиз, 1962, с.124, формула (5.2.7), в которой веса рi заменяем на веса m
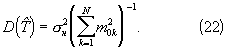
Для поиска неизвестного целочисленного вектора кратностей  0 заявленный способ включает процедуру перебора его целочисленных компонент с целью нахождения линии регрессии с наименьшей (нулевой при σ н=0) суммой квадратов уклонений собственных точек {τ 0k, m0k,},
0 заявленный способ включает процедуру перебора его целочисленных компонент с целью нахождения линии регрессии с наименьшей (нулевой при σ н=0) суммой квадратов уклонений собственных точек {τ 0k, m0k,}, 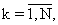
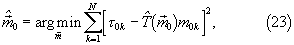
где 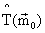 - пробная оценка (21) параметра Т по текущему вектору кратностей при переборе возможных значений его N целочисленных компонент.
- пробная оценка (21) параметра Т по текущему вектору кратностей при переборе возможных значений его N целочисленных компонент.
Так как суммы квадратов уклонений в (23) (в том числе наименьшие) повторяются для векторов кратностей 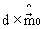 , d=1, 2,..., то в соответствии со статистикой (17), для которой d=1, максимально правдоподобную оценку НОД "в шумах" находят по формуле (21) при векторе кратностей
, d=1, 2,..., то в соответствии со статистикой (17), для которой d=1, максимально правдоподобную оценку НОД "в шумах" находят по формуле (21) при векторе кратностей 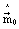 , выбранном по правилу (23) с наименьшей суммой его компонент:
, выбранном по правилу (23) с наименьшей суммой его компонент:
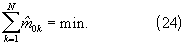
Другими словами, за величину тактового интервала принимают максимальный угловой коэффициент прямой регрессии, проходящей через начало координат с наименьшей суммой квадратов уклонений собственных точек.
Для реализации процедуры (23) целесообразен организованный перебор целочисленных компонент N-мерного вектора кратностей. Дерево перебора их возможных значений, назначаемых с учетом относительных величин ВВИ, формируют следующим образом.
Первому временному интервалу τ 01 назначают возможные значения кратности m01=1, 2,... На каждое значение кратности m01 назначают другим временным интервалам выборки по (2v+1) возможных значений кратностей:
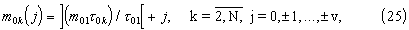
где ]· [ - целая часть числа;
v - параметр разветвленности дерева поиска, определяемый эмпирическим путем и зависящий от относительного уровня ошибок наблюдения σ H/Т. В диапазоне уровней ошибок наблюдения 0<(σ н/T)≤ 0,2 параметр v≤ 2.
Отметим, что при σ н=0 процедура (23, 24) сводится к алгоритму вычисления НОД нескольких N≥ 2 дискретных величин (чисел).
Предложенный способ является новым, поскольку из общепринятых сведений не известен способ определения тактового интервала случайного потока импульсов в условиях отсутствия априорной информации о величине тактовой вероятности, включающий измерение N≥ 2 перекрывающихся временных интервалов от момента появления первого до момента появления каждого последующего импульса входного потока, организованный перебор возможных значений их кратностей тактовому интервалу с целью нахождения оценок общих делителей в виде угловых коэффициентов прямых регрессии, проходящих через начало координат с одинаковыми наименьшими суммами квадратов уклонений собственных точек, при этом за величину тактового интервала принимают максимальный угловой коэффициент прямой регрессии из числа указанных.
Предложенный способ имеет изобретательский уровень, поскольку из опубликованных научных данных и известных технических решений явным образом не следует, что заявленная последовательность операций с импульсным сигналом по формированию выборки перекрывающихся временных интервалов между опорным (первым) и каждым последующим импульсом входного потока и вскрытию их дискретной структуры за счет совместного использования избирательных свойств взаимно простых чисел, какими являются случайные кратности временных интервалов тактовому интервалу, и выравнивающих (по отношению к измеренным временным интервалам) свойств прямых регрессии приведет к повышению точности определения тактового интервала в условиях отсутствия априорной информации о величине тактовой вероятности.
Предложенный способ промышленно применим, так как для его технической реализации могут быть использованы типовые логические и структурные элементы дискретной и вычислительной техники.
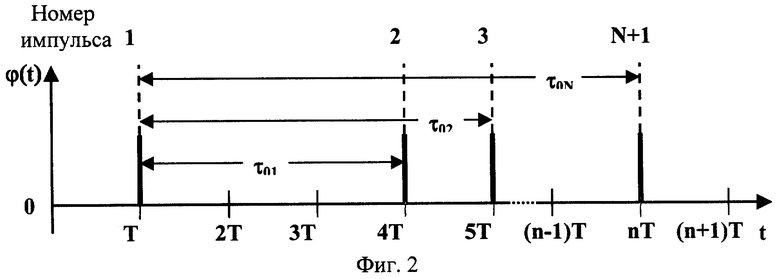
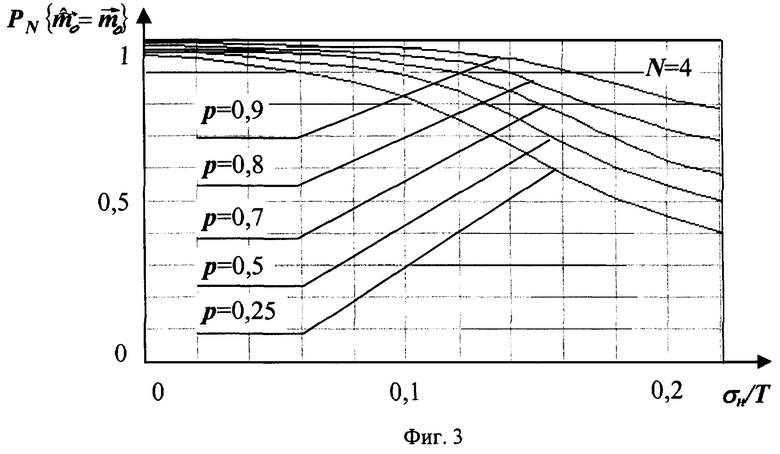
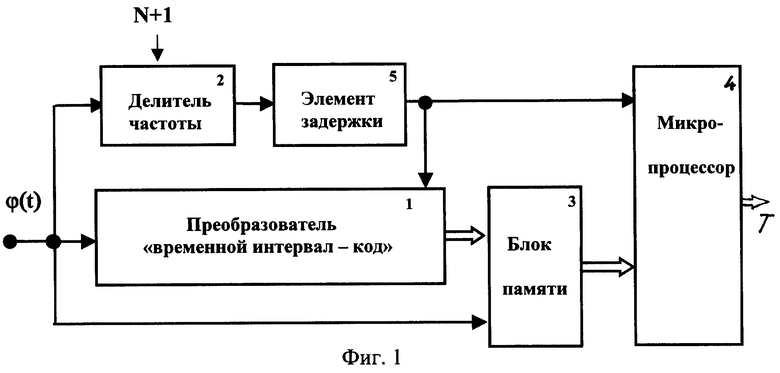
На фиг.1 приведена укрупненная структурная схема возможного варианта технической реализации способа, на фиг.2 - реализация случайного потока импульсов с дискретным временем, на фиг.3 - экспериментальные зависимости вероятностей правильного определения вектора кратностей временных интервалов предложенным способом от параметров потока импульсов и ошибок их наблюдения для размера выборки N=4.
Структурная схема возможного варианта реализации предложенного способа (фиг.1) содержит преобразователь временной интервал - код 1, делитель частоты 2, блок памяти 3, микропроцессор 4 и элемент задержки 5; вход преобразователя 1, объединенный с входом записи блока памяти 3 и входом делителя частоты 2, является входом случайного потока импульсов ϕ (t) с дискретным временем (фиг.2), выход делителя 2 через элемент задержки 5 соединен с входом запуска микропроцессора 4 и входом "сброс" преобразователя 1, разрядный выход которого соединен с разрядным входом блока памяти 3, разрядный выход последнего соединен с разрядным входом микропроцессора 4.
Схема работает следующим образом. В исходном состоянии элементы памяти блоков 1 и 2 находятся в нулевом состоянии. Первый импульс входного потока ϕ (t), реализация которого приведена на фиг.2, записывает нулевой код исходного состояния преобразователя 1 в блок памяти 3 в качестве маркера начала серии из N значений выборочных временных интервалов, одновременно разрешает работу преобразователя 1 и увеличивает состояние делителя частоты 2 на единицу. К моменту появления второго импульса входного потока на выходе преобразователя 1 присутствует кодовый эквивалент величины первого временного интервала τ 01 с общей ошибкой наблюдения (включающей и ошибки преобразователя 1), который этим же импульсом записывается в блок памяти 3. К моменту прихода третьего импульса входного потока на выходе преобразователя 1, работающего нарастающим итогом, будет присутствовать кодовый эквивалент величины второго временного интервала τ 02 с аналогичными первому интервалу τ 01 ошибками наблюдения, который этим же (третьим) импульсом записывается в блок памяти 3 и т.д. Каждый импульс входного потока увеличивает состояние делителя частоты 2 на единицу. К моменту прихода (N+1)-го импульса входного потока на выходе преобразователя 1 будет находиться кодовый эквивалент величины N-го временного интервала τ 0N, который этим же импульсом входного потока заносится в блок памяти 3. С выхода делителя частоты 2 (N+1)-й импульс, задержанный элементом задержки 5, устанавливает исходное (нулевое) состояние преобразователя 1, прерывает его работу и одновременно переносит кодовые эквиваленты величин временных интервалов τ 0k, 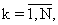 из блока памяти 3 в оперативную память микропроцессора 4, который запрограммирован на вычисление тактового интервала T по формуле
из блока памяти 3 в оперативную память микропроцессора 4, который запрограммирован на вычисление тактового интервала T по формуле
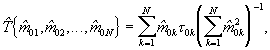
где τ 0k, 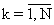 - измеренные временные интервалы входного потока импульсов;
- измеренные временные интервалы входного потока импульсов;
{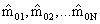 } - оценка вектора кратностей временных интервалов τ 0k,
} - оценка вектора кратностей временных интервалов τ 0k, 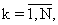 тактовому интервалу Т, удовлетворяющая системе их двух требований:
тактовому интервалу Т, удовлетворяющая системе их двух требований:
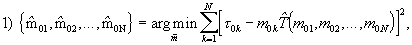
где 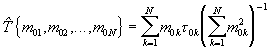 - пробная оценка параметра Т для текущего вектора кратностей при переборе его целочисленных компонент: {m01=1, 2,..., m02=2, 3,... m0N=N, N+1,...} с учетом условия m0l&λτ;m02<...<m0N;
- пробная оценка параметра Т для текущего вектора кратностей при переборе его целочисленных компонент: {m01=1, 2,..., m02=2, 3,... m0N=N, N+1,...} с учетом условия m0l&λτ;m02<...<m0N;
Началу нового цикла работы схемы (фиг.1) предшествует пауза, равная величине (N+1)-го временного интервала, по окончании которой в блок памяти 3 (N+2)-м импульсом будет занесен нулевой код исходного состояния преобразователя 1, разделяющий отдельные выборки из N временных интервалов. Далее работа схемы повторяется.
Экспериментальные зависимости вероятностей правильного определения векторов кратностей 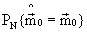 четырех временных интервалов N=4 от относительного уровня ошибок наблюдения σ н/Т для различных величин тактовых вероятностей р, полученные методом статистических испытаний разработанного способа на ЭВМ, приведены на фиг.3. Число испытаний для каждой точки Nисп=1000. Из анализа этих зависимостей следует, что влияние уровня ошибок наблюдения на вероятность правильного определения вектора кратностей снижается с увеличением тактовой вероятности р и тактового интервала Т при постоянном уровне ошибок σ н=const.
четырех временных интервалов N=4 от относительного уровня ошибок наблюдения σ н/Т для различных величин тактовых вероятностей р, полученные методом статистических испытаний разработанного способа на ЭВМ, приведены на фиг.3. Число испытаний для каждой точки Nисп=1000. Из анализа этих зависимостей следует, что влияние уровня ошибок наблюдения на вероятность правильного определения вектора кратностей снижается с увеличением тактовой вероятности р и тактового интервала Т при постоянном уровне ошибок σ н=const.
Повышение точности определения тактового интервала случайного потока импульсов с дискретным временем при неизвестной величине тактовой вероятности по сравнению с прототипом достигается в предложенном способе за счет более полного использования информации об измеренных перекрывающихся временных интервалах N≥ 2 с независимыми дискретными приращениями по модулю, в то время как в прототипе измеряют только один максимальный временной интервал между первым и (N+1)-м (последним) импульсом входного потока.
Для случаев правильного определения вектора кратностей найдем среднюю по случайным реализациям ВВИ дисперсию ошибок определения тактового интервала 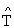 с учетом схемы образования ВВИ и геометрического распределения их независимых дискретных приращений по модулю.
с учетом схемы образования ВВИ и геометрического распределения их независимых дискретных приращений по модулю.
Используя (4) при Т=1, найдем математическое ожидание квадрата случайных кратностей 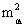 ВВИ в виде начального момента второго порядка:
ВВИ в виде начального момента второго порядка:
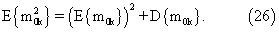
В соответствии со схемой образования временных интервалов τ 0k=τ 1+τ 2+...τ k, 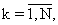 математические ожидания и дисперсии их кратностей параметру T равны соответственно
математические ожидания и дисперсии их кратностей параметру T равны соответственно
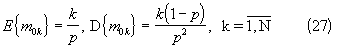
Подставляя (27) в (26), находим математическое ожидание квадрата кратностей отдельных временных интервалов τ 0k, 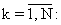
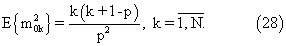
С учетом (22) и (28) при правильно определенном векторе кратностей средняя дисперсия ошибок определения тактового интервала Т составляет
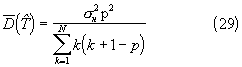
и не зависит от величины Т.
В сравнении со способом-прототипом с дисперсией ошибок (13) заявленный способ с дисперсией ошибок (29) обеспечивает выигрыш по величине среднеквадратической ошибки (СКO) определения тактового интервала, равный
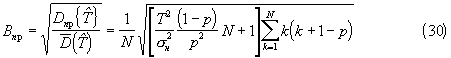
при условии правильного вскрытия структуры (вектора кратностей) временных интервалов.
Например, при тактовой вероятности р=0,9, относительной ошибке измерения временных интервалов σ н/Т=0,1 и размере выборки N=4 предложенный способ обеспечивает вероятность правильного вскрытия структуры временных интервалов, близкую к единице (см. фиг.3), при этом величина выигрыша по СКО при определении тактового интервала составляет Впр∀10 раз.
Кроме того, предложенный способ позволяет определять тактовый интервал и периодического потока импульса (р=1). В этом случае кратности временных интервалов τ 0k, k, k=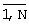 , известны: m01=1, m02=2,..., mоN=N и в соответствии с формулой (30) безусловный выигрыш по сравнению с аналогом составит
, известны: m01=1, m02=2,..., mоN=N и в соответствии с формулой (30) безусловный выигрыш по сравнению с аналогом составит
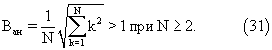
В частности, для размеров выборки: N=4, 8, 12 величина выигрыша (31) составляет Ван=1,37; 1,78; 2,13 соответственно.
Другим, не менее важным, достоинством заявленного способа определения тактового интервала Т является то обстоятельство, что он позволяет преодолеть априорную недостаточность данных о величине тактовой вероятности, что по сравнению с прототипом расширяет область его применения и разрешает проблему оценивания (с привлечением формулы (8)) второго определяющего параметра р стационарного (p=const) случайного потока событий с дискретным временем.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ОБНАРУЖЕНИЯ ПЕРИОДИЧЕСКИХ ИМПУЛЬСНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ И ОЦЕНКИ ИХ ПЕРИОДА | 2003 |
|
RU2251704C2 |
| СПОСОБ СТАТИСТИЧЕСКОЙ ОБРАБОТКИ СЛУЧАЙНЫХ ПОТОКОВ ИМПУЛЬСОВ С ДИСКРЕТНЫМ ВРЕМЕНЕМ | 2005 |
|
RU2289140C2 |
| Способ моделирования независимых и группирующихся ошибок канала связи | 2019 |
|
RU2705771C1 |
| СПОСОБ АНАЛОГО-ЦИФРОВОЙ ОБРАБОТКИ СИГНАЛА РАДИОМЕТРИЧЕСКОГО ДАТЧИКА | 2009 |
|
RU2386209C1 |
| СПОСОБ БОРЬБЫ С ГАРМОНИЧЕСКОЙ ПОМЕХОЙ ПРИ АВТОКОРРЕЛЯЦИОННОМ МЕТОДЕ ПРИЕМА ИНФОРМАЦИИ С ИСПОЛЬЗОВАНИЕМ ШУМОПОДОБНЫХ СИГНАЛОВ | 2014 |
|
RU2569554C1 |
| СПОСОБ РЕГИСТРАЦИИ И ВОССТАНОВЛЕНИЯ ПОСЫЛОК В КАНАЛАХ СВЯЗИ С МЕЖСИМВОЛЬНЫМИ ИСКАЖЕНИЯМИ | 2024 |
|
RU2835375C1 |
| УСТРОЙСТВО для МОДЕЛИРОВАНИЯ КАНАЛОВ ПЕРЕДАЧИ , ДИСКРЕТНОЙ ИНФОРМАЦИИ | 1972 |
|
SU326591A1 |
| СПОСОБ ДЕМОДУЛЯЦИИ РАДИОСИГНАЛОВ С ФАЗОРАЗНОСТНОЙ МОДУЛЯЦИЕЙ | 2011 |
|
RU2469488C1 |
| Генератор последовательности ошибок | 1982 |
|
SU1077044A1 |
| Устройство контроля дискретных каналов | 1989 |
|
SU1626406A1 |
Способ относится к вычислительной технике и может быть использован при определении длительности элементарных посылок разведываемых многопозиционных (многочастотных) сигналов, а также при определении параметров сигналов с программной перестройкой рабочих частот. Измеряют временные интервалы от момента появления первого импульса входного потока до моментов появления каждого импульса в наблюдаемой реализации потока. Организуют перебор возможных значений целочисленных кратностей временных интервалов тактовому интервалу. Определяют оценки их общих делителей в виде угловых коэффициентов прямых регрессии, проходящих через начало координат с одинаковыми наименьшими суммами квадратов уклонений собственных точек. За величину тактового интервала принимают максимальный угловой коэффициент прямой регрессии. Способ позволит повысить точность определения тактового интервала случайного потока импульсов при априорной неопределенности тактовой вероятности их появления. 1 табл., 3 ил.
Способ определения тактового интервала случайного потока импульсов с дискретным временем, включающий измерение временного интервала между моментами появления первого и последнего импульсов в наблюдаемой реализации потока, отличающийся тем, что дополнительно измеряют временные интервалы от момента появления первого до моментов появления каждого промежуточного по времени появления импульса в наблюдаемой реализации потока, причем по совокупности измеренных временных интервалов путем организованного перебора возможных значений целочисленных кратностей временных интервалов тактовому интервалу определяют оценки их общих делителей в виде угловых коэффициентов прямых регрессии, проходящих через начало координат с одинаковыми наименьшими суммами квадратов уклонений собственных точек, при этом за величину тактового интервала принимают максимальный угловой коэффициент прямой регрессии из числа указанных.
| ЛЕВИН Б.Р | |||
| Теоретические основы статистической радиотехники | |||
| Кн | |||
| Аппарат для очищения воды при помощи химических реактивов | 1917 |
|
SU2A1 |
| - М.: Советское радио, 1968, с.122 | |||
| МИРСКИЙ Г.Я | |||
| Радиоэлектронные измерения | |||
| Изд | |||
| Переносная печь для варки пищи и отопления в окопах, походных помещениях и т.п. | 1921 |
|
SU3A1 |
| - М.: Энергия, 1975, с.223-226 | |||
| US 5835530 А, 10.11.1998 | |||
| US 5506577 A, 09.04.1996. | |||
Авторы
Даты
2004-06-10—Публикация
2002-07-08—Подача