[0001] Настоящее изобретение относится к респираторной терапии, мониторингу дыхания и родственным областям техники.
[0002] При респираторной терапии различных типов используют механический аппарат искусственной вентиляции легких. При лечении пассивных пациентов пациент не может дышать, а аппарат искусственной вентиляции легких работает в режиме вентиляции, управляемой по давлению, в котором аппарат искусственной вентиляции легких осуществляет всю работу дыхания (work of breathing, WoB). При лечении активных пациентов пациент может осуществлять часть необходимой работы, но не может самостоятельно удовлетворить свою потребность в дыхании. В таком случае аппарат искусственной вентиляции легких работает в режиме поддержки давлением для обеспечения давления, необходимого, чтобы устранить дыхательную недостаточность пациента. Также известны режимы работы аппарата искусственной вентиляции легких с регулируемым объемом, при которых вместо регулировки давления (хотя настройки пределов давления могут быть также применены для предотвращения баротравмы легких) регулируемым параметром является скорость потока или объем, и которые в основном используются для лечения пассивных пациентов.
[0003] При определении настроек аппарата искусственной вентиляции легких и последующего мониторинга механически вентилируемого пациента предпочтительным может быть измерение различных параметров дыхания. В случае вентиляции в режиме поддержки давлением (ВПД) оценка работы дыхания пациента, которая является клиническим параметром, обычно используемым для заключения об усилиях пациента на вдохе, обеспечивается путем оценки давления дыхательной мускулатуры, Pmus(t), за дыхательный цикл. Более конкретно, работу дыхания вычисляют путем интегрирования Pmus(t) по вдыхаемому объему. Для вентиляции пассивных пациентов предпочтительной может быть проверка того, что Pmus~0 по всему дыхательному циклу (что указывает на отсутствие наблюдаемой работы дыхания, осуществляемой пациентом). Параметры дыхания, такие как сопротивление (R) и растяжимость (С) дыхательных путей, также могут быть важны, или их определение может быть необходимо для оценки других параметров.
[0004] Оценка Pmus(t) в режимах поддержки механической вентиляции обеспечивает возможность установки аппарата искусственной вентиляции легких таким образом, что пациент и аппарат искусственной вентиляции легких разделяют механическую работу, выполняемую в дыхательной системе. Количественная оценка Pmus(t) может быть использована для выбора подходящего уровня поддержки вентиляции для предотвращения как атрофии, так и утомления дыхательной мускулатуры пациента. Давление Pmus(t) дыхательной мускулатуры обычно оценивают посредством измерения пищеводного давления (Pes) посредством введения баллонного катетера в пищевод пациента. Предполагается, что измеренное Pes(t) является хорошим приблизительным значением плеврального давления (Ppl) и может быть использовано в сочетании с оценкой растяжимости Ccw стенки грудной клетки для вычисления работы дыхания через так называемую диаграмму Кэмпбелла или посредством отдельного вычисления Pmus(t), а затем работы дыхания, что является эквивалентным способом вычисления.
[0005] Оценки параметров дыхания R и С являются важными сами по себе, так как они предоставляют лечащему врачу количественную информацию о механических свойствах дыхательной системы пациента и могут быть использованы для диагностики заболеваний органов дыхания и для выбора подходящих режимов вентиляции и способов лечения. Кроме того, R и С также могут быть использованы для оценки Pmus(t) в качестве неинвазивной альтернативы использованию пищеводного катетера. При условии, что R и С являются известными, Pmus(t) подходящим образом вычисляют посредством следующего уравнения (известного как уравнение движения легких):
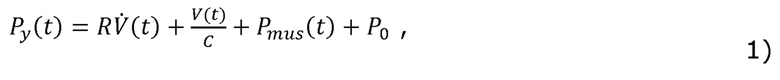
[0006] где Py(t) выражает давление, измеренное на Y-образной детали аппарата искусственной вентиляции легких (также известное как давление у рта пациента), 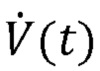 выражает поток воздуха, проходящего в дыхательную систему пациента и выходящего из нее, (также измеряемый на Y-образной детали), V(t) выражает чистый объем воздуха, подаваемый пациенту (измеренный путем интегрирования сигнала
выражает поток воздуха, проходящего в дыхательную систему пациента и выходящего из нее, (также измеряемый на Y-образной детали), V(t) выражает чистый объем воздуха, подаваемый пациенту (измеренный путем интегрирования сигнала 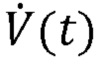 потока по времени), а Р0 выражает постоянный член для учета давления в конце выдоха.
потока по времени), а Р0 выражает постоянный член для учета давления в конце выдоха.
[0007] В случае с пассивным пациентом, не прикладывающим дыхательных усилий, получается, что Pmus(t)=0 по всему дыхательному циклу, а уравнение (1) сокращается до 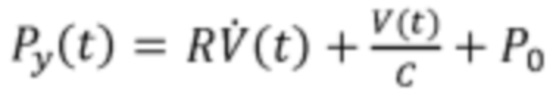 . Для пассивного пациента кривые Py(t),
. Для пассивного пациента кривые Py(t), 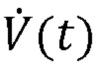 и V(t) полностью определены выбранными настройками аппарата искусственной вентиляции легких и являются непосредственно измеримыми, так что обеспечена возможность непосредственной генерации достаточного набора данных для определения R и С. В отличие от этого, в случае с активным пациентом, осуществляющим некоторую работу дыхания, значение Pmus(t) варьируется со временем на протяжении дыхательного цикла, а уравнение (1) имеет непростое решение.
и V(t) полностью определены выбранными настройками аппарата искусственной вентиляции легких и являются непосредственно измеримыми, так что обеспечена возможность непосредственной генерации достаточного набора данных для определения R и С. В отличие от этого, в случае с активным пациентом, осуществляющим некоторую работу дыхания, значение Pmus(t) варьируется со временем на протяжении дыхательного цикла, а уравнение (1) имеет непростое решение.
[0008] Для активных пациентов уравнение (1) в основном применялось для неинвазивной оценки Pmus(t) с использованием двухшагового метода, в котором сначала оценивают R и С, а затем уравнение (1) применяют для вычисления Pmus(t) с использованием вычисленных значений R и С. Оценка R и С может быть осуществлена посредством применения метода прерывания потока (также именуемого паузой в конце вдоха (End Inspiratory Pause, «EIP»). Однако метод прерывания потока имеет недостаток, который заключается во вмешательстве в вентиляционный паттерн, подаваемый пациенту. Кроме того, для того, чтобы вычисления параметров R и С были достоверными, дыхательная мускулатура пациента должна быть полностью расслаблена во время процедуры паузы в конце вдоха, что не всегда может быть так. Еще одна сложность заключается в том, что значения для R и С, оцененные посредством процедуры паузы в конце вдоха, могут отличаться от значений R и С, полученных во время вентиляционного паттерна, для которого требуется определение Pmus(t). Процедуру паузы в конце вдоха осуществляют в определенном режиме вентиляции (ассистируемая вентиляция с управлением по объему (Volume Assisted Control, «VAC»)), а полученные в результате значения R и С могут быть не показательными в отношении соответствующих значений, определяющих динамику легочной механики при других режимах вентиляции, таких как вентиляция с поддержкой давлением, потенциально приводя к ошибке в Pmus(t), вычисляемом впоследствии.
[0009] Другой подход к оценке параметров R и С в случае с активным пациентом заключается в применении аппроксимации наименьших квадратов уравнения (1) к измерениям потока и давления при определенных условиях, для которых предполагается, что член Pmus(t) равен нулю. Некоторые условия, для которых предполагается, что Pmus(t) приближается к нулю, включают: (1) периоды парализации пациента, во время которых применяют непрерывную принудительную вентиляцию (Continuous Mandatory Ventilation, «CMV»); (2) периоды высоких уровней вентиляции с поддержкой давлением; (3) определенные части каждого дыхательного движения с поддержкой давлением, которые присутствуют во время фаз вдоха и выдоха; и (4) части выдоха дыхательных движений с поддержкой давлением, в которых сигнал потока удовлетворяет определенным условиям, указывающим на отсутствие усилий пациента на вдохе. Однако условия (1) и (2) являются нежелательными клиническими состояниями, и не могут быть надлежащим образом вызваны в качестве способа измерения й и С. Предположение того, что Pmus(t)~0 для условия (3) является сомнительным, в частности во время фазы вдоха. Условие (4) предоставляет лишь ограниченное количество данных для процедуры аппроксимации наименьших квадратов. В целом, добиться клинически пригодного периода времени достаточной продолжительности, для которого у активных пациентов достоверно достигается Pmus(t)~0 с целью оценки R и С, затруднительно.
[00010] Следующее описание предоставляет новые и улучшенные систему и способ, которые преодолевают эти и другие проблемы.
[00011] Медицинский аппарат искусственной вентиляции легких реализует способ, включающий: прием измеренных значений давления воздуха, вдыхаемого или выдыхаемого вентилируемым пациентом, функционально соединенным с медицинским аппаратом искусственной вентиляции легких; прием измеренных значений потока воздуха, проходящего в вентилируемого пациента или выходящего из вентилируемого пациента, функционально соединенного с медицинским аппаратом искусственной вентиляции легких; разделение интервала времени дыхания на множество областей аппроксимации и одновременное оценивание сопротивления и растяжимости или эластичности дыхательной системы и давления дыхательной мускулатуры путем аппроксимации по временным рядам образцов давления и потока воздуха в каждой области. Согласно одному способу аппроксимация включает в себя параметризацию давления дыхательной мускулатуры непрерывной дифференцируемой функцией, такой как полиномиальная функция, по области аппроксимации. Согласно другому способу аппроксимацию осуществляют к уравнению движения легких в каждой области с применением в каждой области ограничений монотонности давления дыхательной мускулатуры и доменных ограничений параметров дыхания.
[00012] Одно преимущество заключается в обеспечении неинвазивной оценки параметров дыхания, включающих сопротивление, растяжимость и давление дыхательной мускулатуры.
[00013] Другое преимущество заключается в обеспечении аппарата искусственной вентиляции легких с улучшенной вычислительной надежностью анализа данных.
[00014] Другие преимущества настоящего изобретения будут понятны специалистам в данной области техники после прочтения и понимания следующего подробного описания.
[00015] Изобретение может быть реализовано в различных компонентах и конфигурациях компонентов, и в различных этапах и конфигурациях этапов. Чертежи предоставлены исключительно для иллюстрации предпочтительных вариантов реализации, и не ограничивают изобретение.
[00016] На фиг. 1 схематично показана система искусственной вентиляции легких.
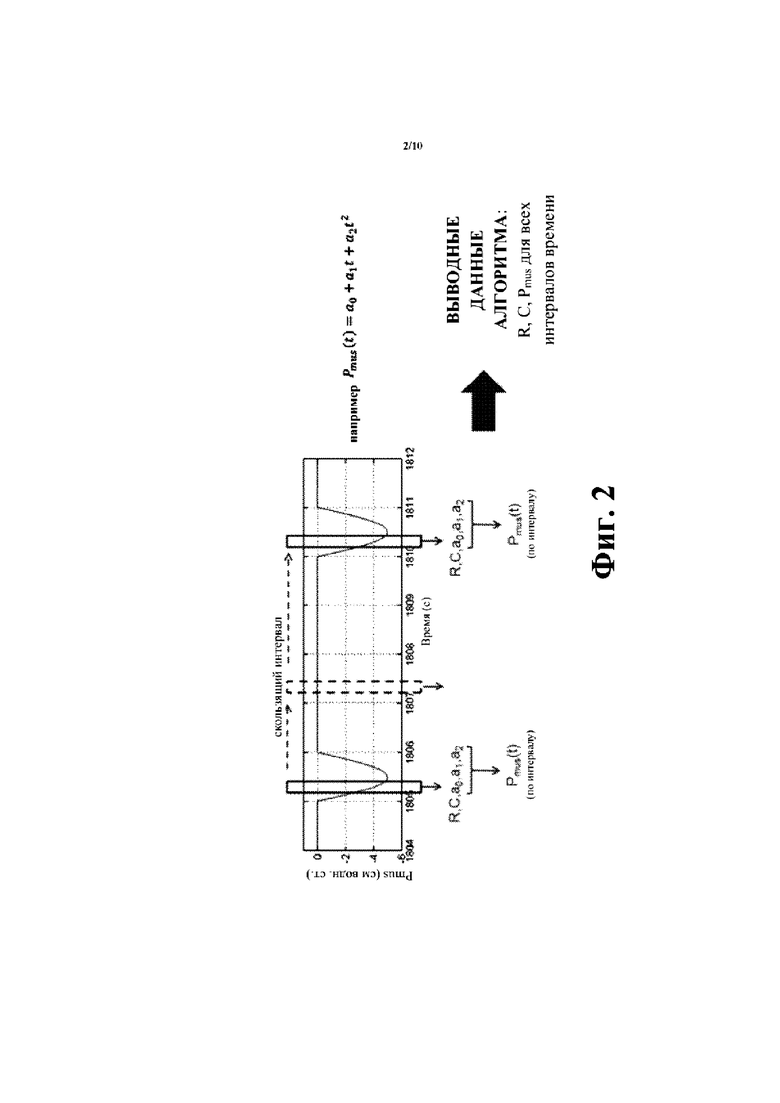
[00017] На фиг. 2 схематично показан раскрытый в настоящем документе алгоритм анализа данных, который одновременно оценивает несколько параметров дыхания путем аппроксимации давления Pmus(t) дыхательной мускулатуры полиномиальной функцией низкого порядка.
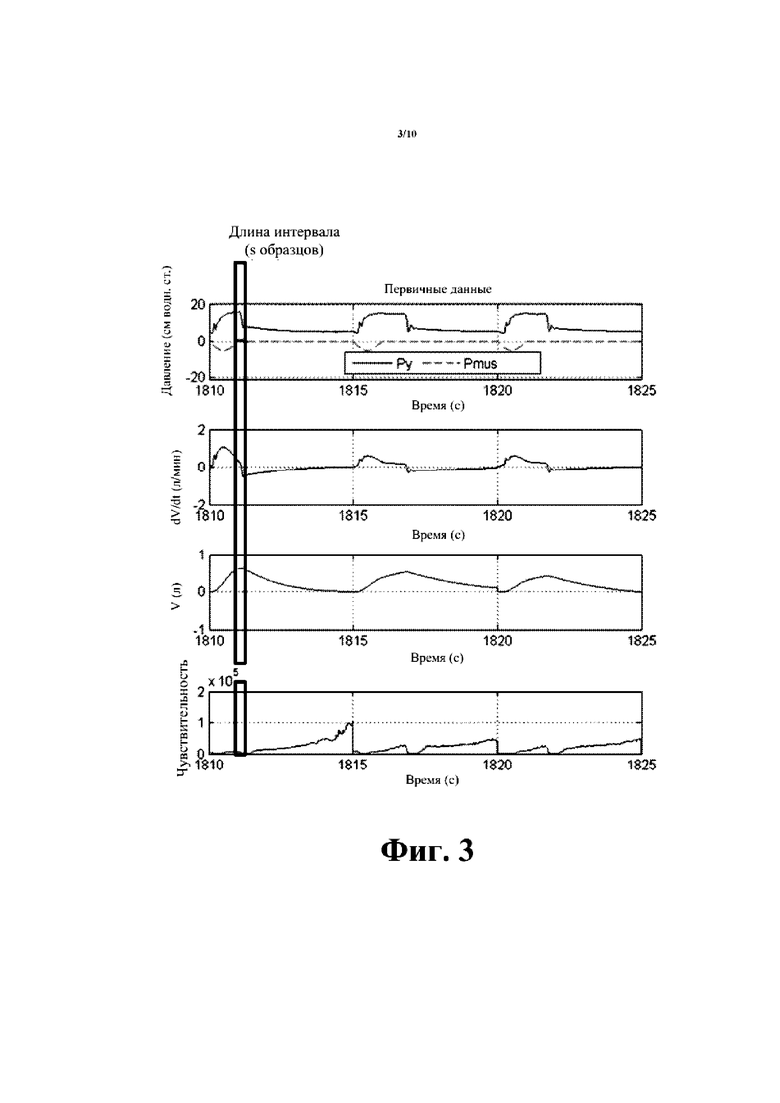
[00018] На фиг. 3 показан график моделированных кривых дыхания на протяжении приблизительно трех вдохов с чувствительностью матрицы параметров, изображенной на нижнем графике фиг. 3.
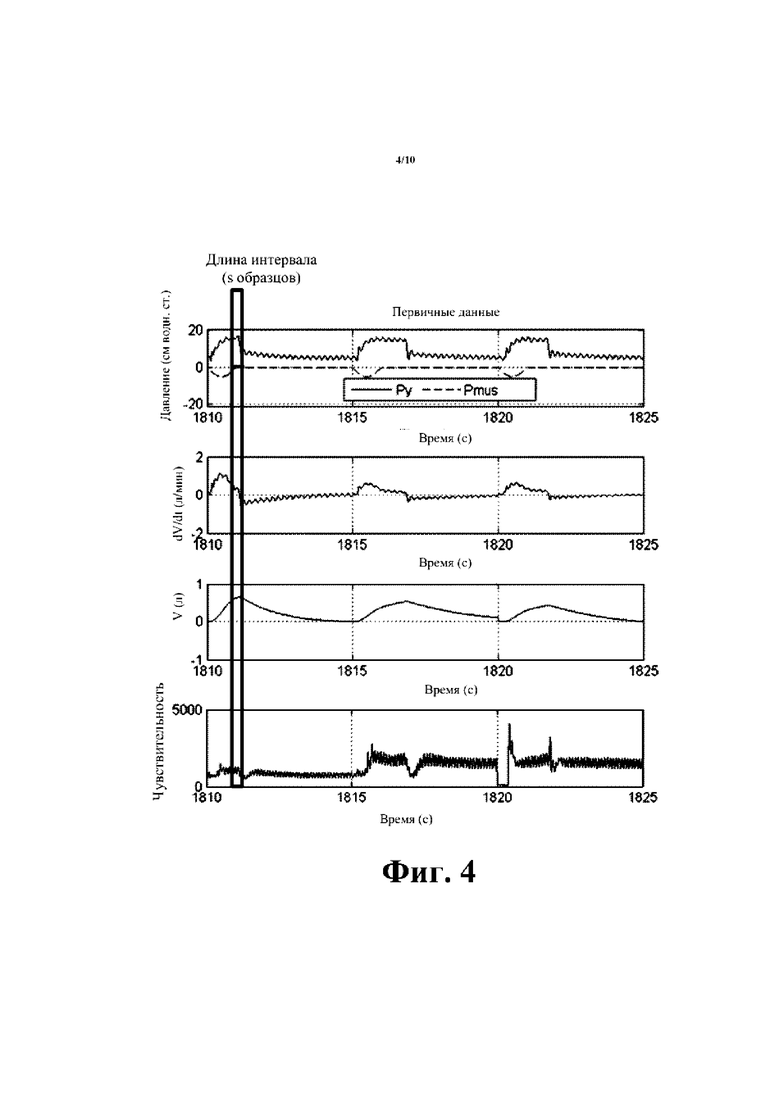
[00019] На фиг. 4 показаны графики моделированных кривых дыхания на протяжении приблизительно трех вдохов, причем сигнал ΔP(t) давления с малой амплитудой и высокой частотой наложен на давление, прикладываемое аппаратом искусственной вентиляции легких, с чувствительностью матрицы параметров, изображенной на нижнем графике фиг. 4.
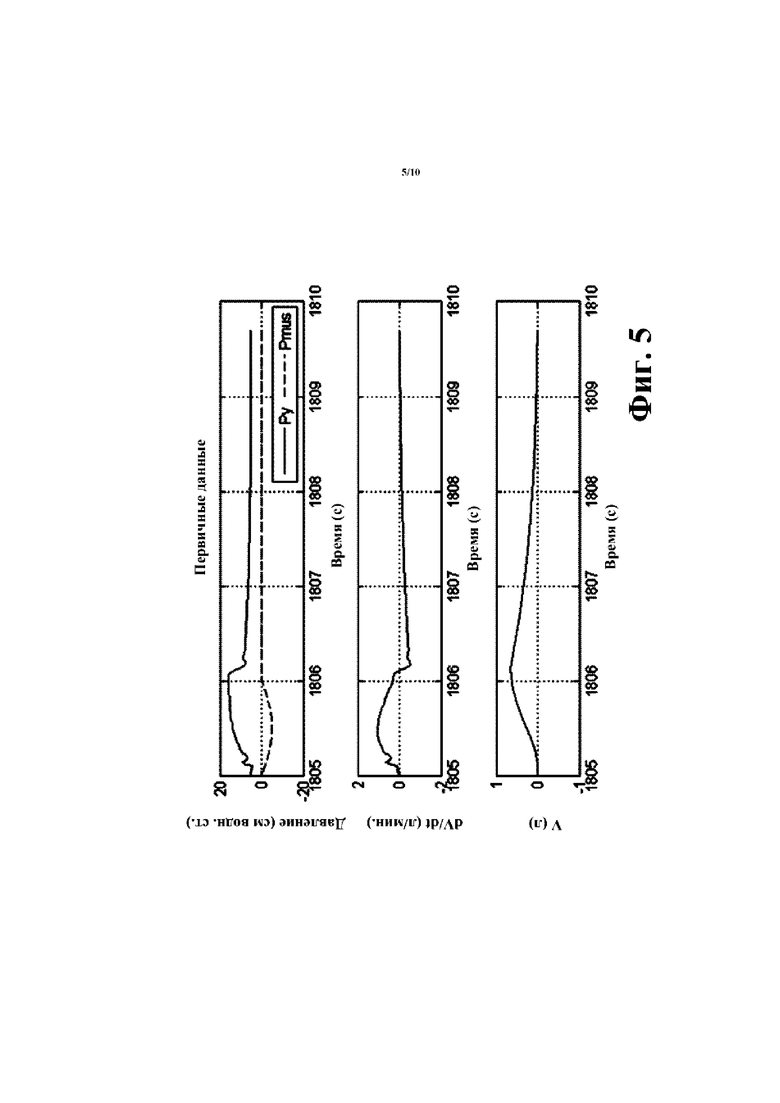
[00020] На фиг. 5 показаны графики нормального взаимодействия между аппаратом искусственной вентиляции легких и пациентом, эмулированным с помощью смоделированного на компьютере эмулятора легких, работающего с идеальной схемой R, С и с отсутствием шума.
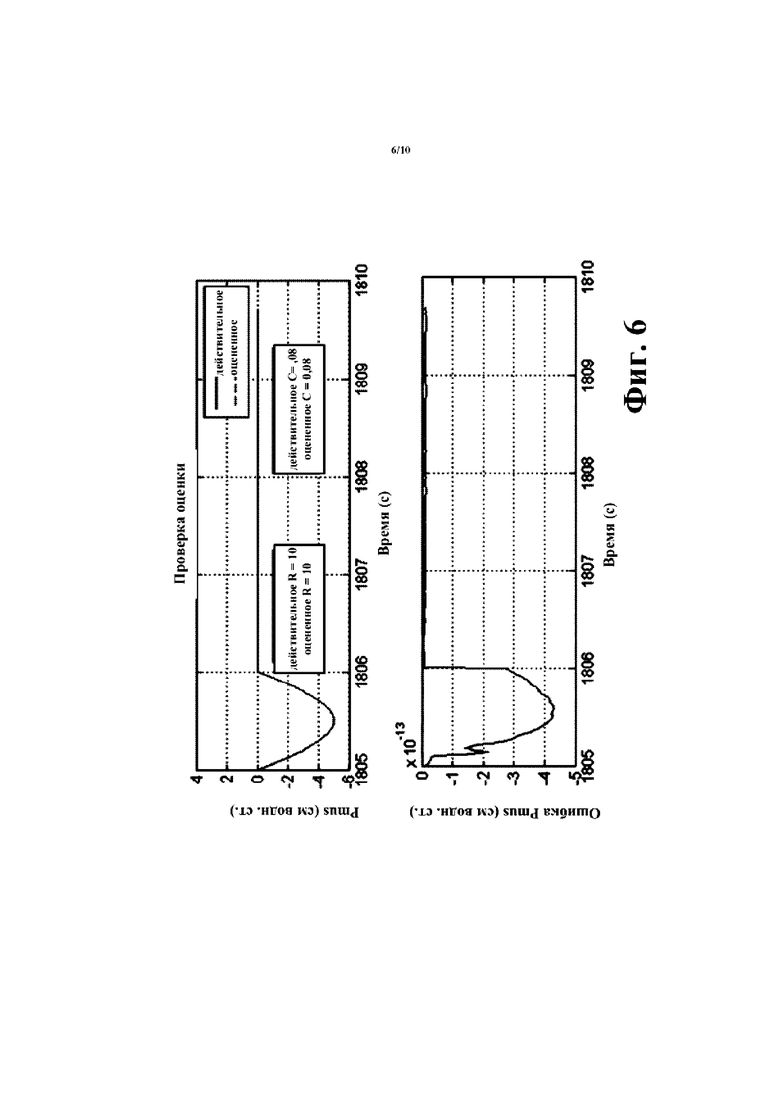
[00021] На фиг. 6 показаны графики выводимых данных раскрытого алгоритма оптимизации с применением ограничений (верхний график) и ошибки (нижний график) для данных по фиг. 5.
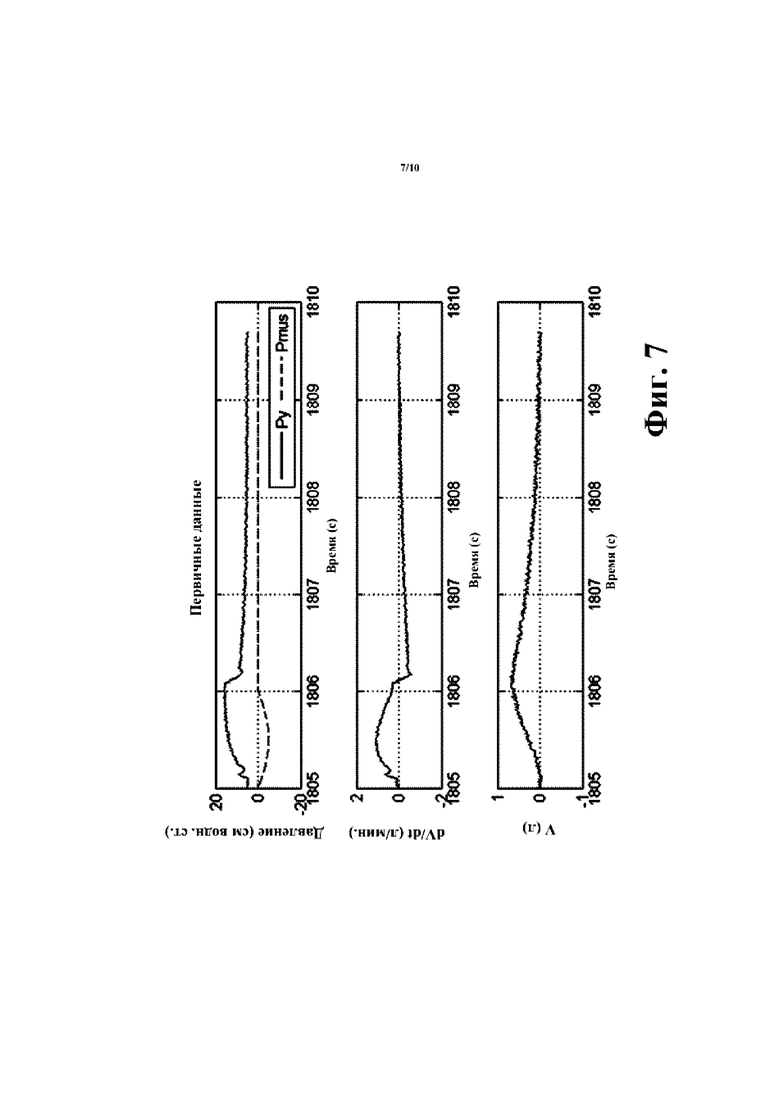
[00022] На фиг. 7 показаны графики нормального взаимодействия между аппаратом искусственной вентиляции легких и пациентом, эмулированным с помощью смоделированного на компьютере эмулятора легких, работающего с идеальной схемой R, С и с программно добавленным шумом.
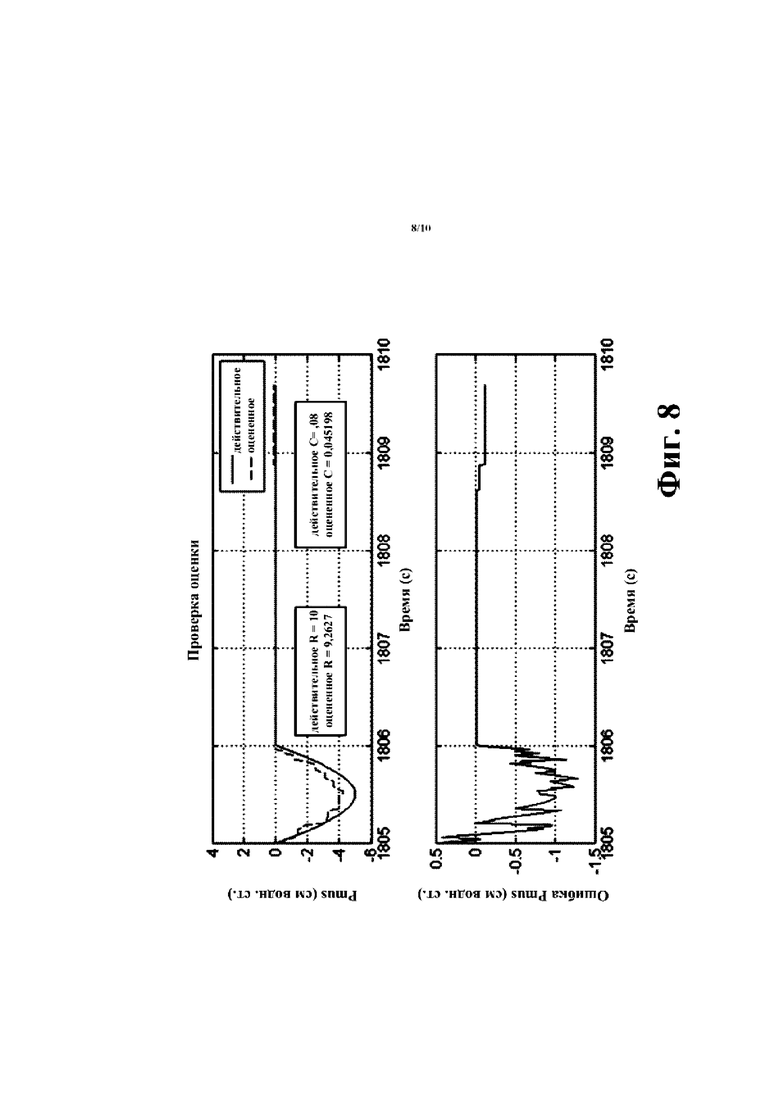
[00023] На фиг. 8 показаны графики выводимых данных раскрытого алгоритма оптимизации с применением ограничений (верхний график) и ошибки (нижний график) для данных по фиг.7.
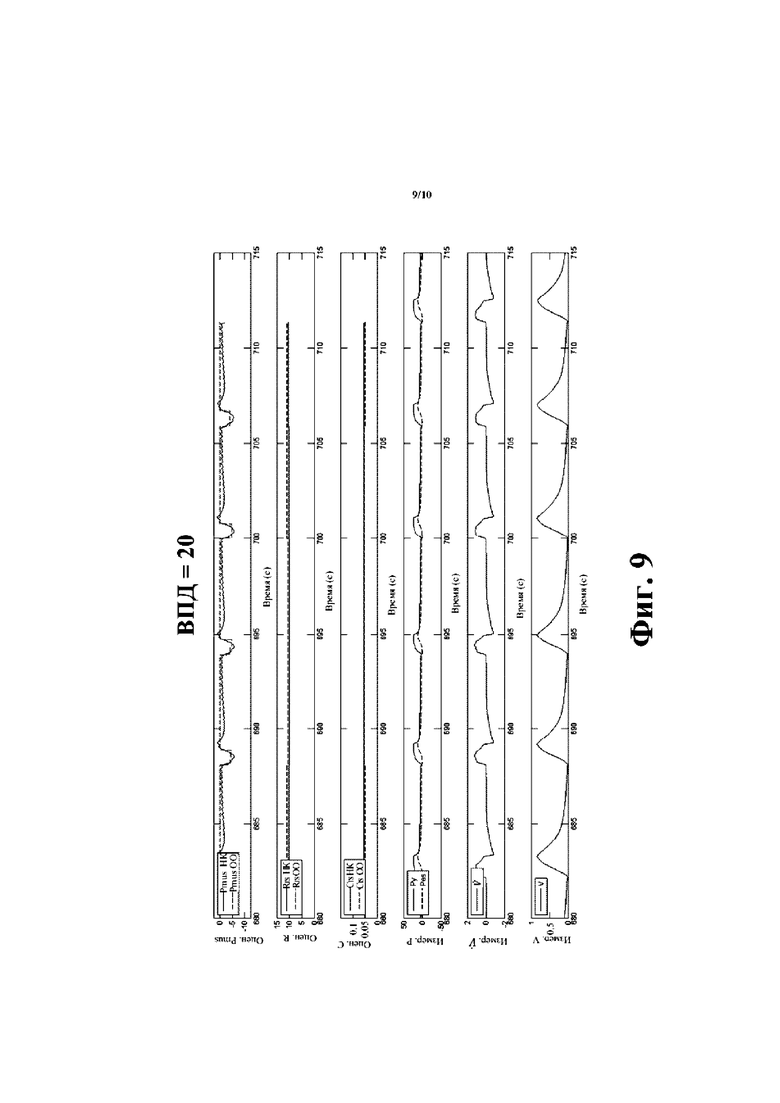
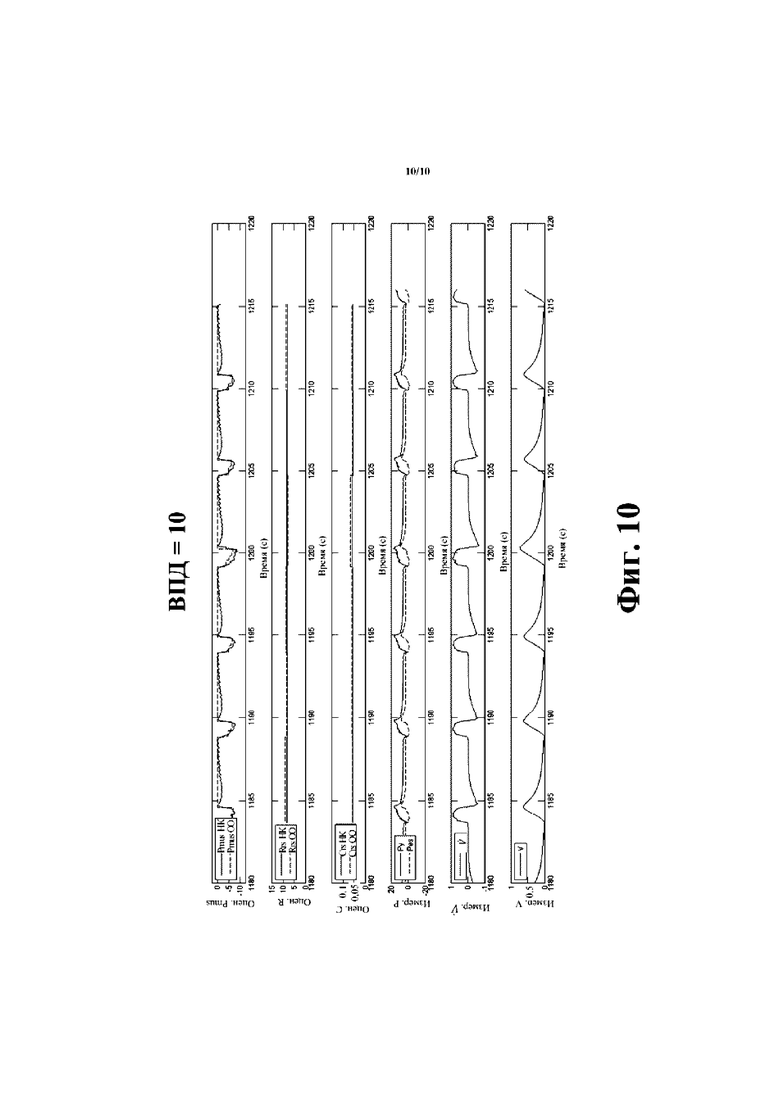
[00024] На фиг. 9 и 10 показаны графики оценки R, С и Pmus(t) из выводимых данных раскрытого алгоритма оптимизации с применением ограничений для настоящей свиньи (экспериментальные данные) в различных условиях вентиляции с поддержкой давлением (ВПД): ВПД=20 (фиг. 9) и ВПД=10 (фиг. 10).
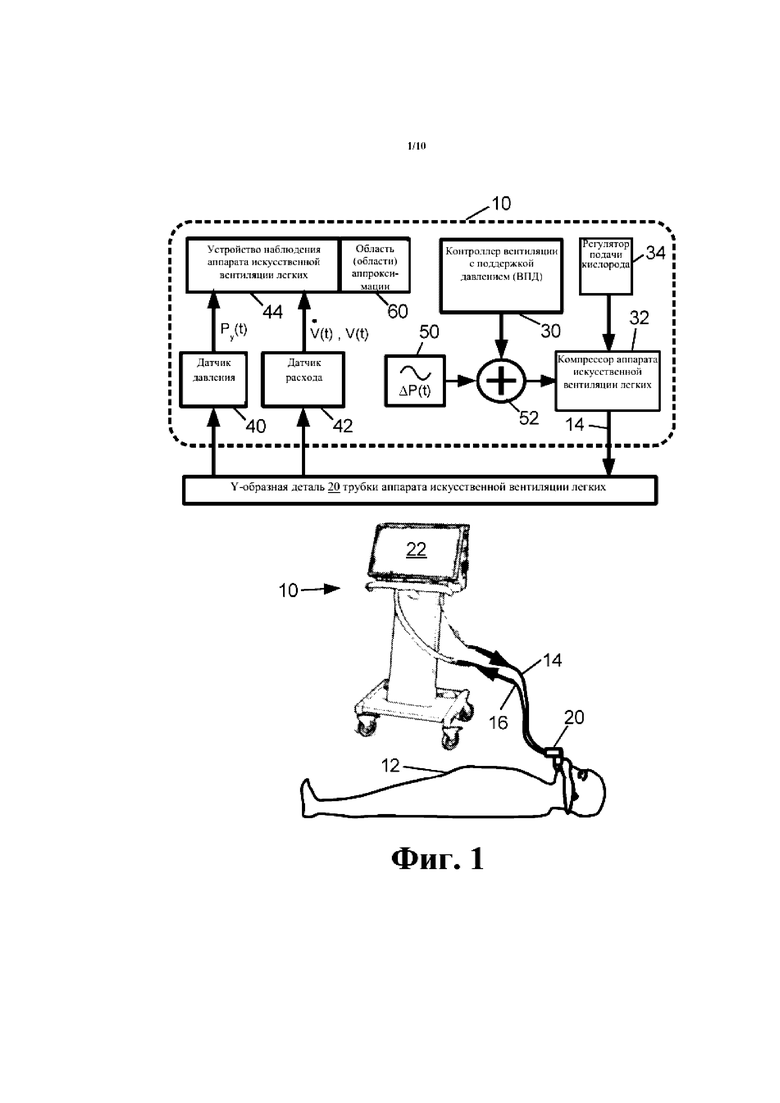
[00025] Со ссылкой на фиг. 1, медицинская система искусственной вентиляции легких включает в себя медицинский аппарат 10 искусственной вентиляции легких, подающий поток воздуха с положительным давлением пациенту 12 через впускной воздушный шланг 14. Выдыхаемый воздух возвращается в аппарат 10 искусственной вентиляции легких через выпускной воздушный шланг 16. Y-образная деталь 20 системы искусственной вентиляции легких обеспечивает направление воздуха из выпускного конца впускного воздушного шланга 14 к пациенту во время вдоха и обеспечивает направление выдыхаемого воздуха от пациента в выпускной воздушный шланг 16 во время выдоха. Следует отметить, что Y-образную деталь иногда именуют другими терминами, например Т-образная деталь 20. На фиг. 1 не показаны многие другие вспомогательные компоненты, которые могут быть предоставлены в зависимости от респираторной терапии, получаемой пациентом 12. В качестве иллюстрации такие вспомогательные компоненты могут включать: кислородный баллон или другой медицинский источник кислорода для подачи управляемого уровня кислорода в поток воздуха (обычно контролируемого таким параметром аппарата искусственной вентиляции легких, как фракция кислорода во вдыхаемой смеси (Fraction of Inspired Oxygen, «FiO2»), устанавливаемым лечащим врачом или другим медицинским персоналом); увлажнитель, подключенный во впускную линию 14; назогастральный зонд для обеспечения пациента 12 питательными веществами; и т.п. Аппарат 10 искусственной вентиляции легких включает в себя интерфейс пользователя, в иллюстративном примере включающий в себя компонент 22 дисплея с сенсорным экраном, посредством которого лечащий врач, специалист по заболеваниям органов дыхания или другой медицинский персонал может настраивать работу аппарата искусственной вентиляции легких и наблюдать измеренные физиологические сигналы и рабочие параметры аппарата 10 искусственной вентиляции легких. Дополнительно или альтернативно интерфейс пользователя может включать в себя физические устройства ввода пользователя (кнопки, ручки регулирования, переключатели и т.д.), клавиатуру, мышь, устройство (устройства) звукового оповещения, световой индикатор (световые индикаторы) или т.п.
[00026] Также со ссылкой на фиг. 1, в виде блок схемы в верхней части схематически изображены некоторые дополнительные значимые аспекты системы искусственной вентиляции легких, включая аппарат 10 искусственной вентиляции легких, изображенный как упрощенная блок-схема, и Y-образная деталь 20, изображенная как схематический четырехугольник, причем функциональные соединения обозначены соединительными стрелками. В иллюстративном примере аппарат 10 искусственной вентиляции легких работает в режиме вентиляции с поддержкой давлением, реализуемым контроллером 30. Вентиляция с поддержкой давлением является подходящим режимом вентиляции для активного пациента, способного осуществлять по меньшей мере некоторую работу дыхания, то есть диафрагма и другие мышцы грудной клетки которого прикладывают усилия по меньшей мере для способствования работе легких для осуществления дыхания. В режиме вентиляции с поддержкой давлением давление, обеспечиваемое аппаратом 10 искусственной вентиляции легких через впускной воздушный шланг 14, функционирует совместно с работой дыхания пациента для осуществления дыхания. В более широком смысле, контроллер 30 может реализовать различные режимы вентиляции в зависимости от состояния пациента и применяемой терапии. Например, в случае с пассивным пациентом, который не осуществляет работу дыхания, контроллер 30 может управлять аппаратом 10 искусственной вентиляции легких в режиме вентиляции, управляемой по давлению (ВУД). (Следует отметить, что в некоторых схемах классификации вентиляцию с поддержкой давлением рассматривают как тип режима вентиляции с поддержкой давлением, так как в вентиляции, управляемой по давлению, и вентиляции с поддержкой давлением давление, прикладываемое аппаратом 10 искусственной вентиляции легких, является контролируемым параметром). Также иногда применяют режимы вентиляции с регулируемым объемом, хотя в вентиляции с регулируемым объемом могут быть также применены настройки пределов давления для предотвращения баротравмы легких. В целом контроллер 30 аппарата искусственной вентиляции легких реализован в форме микропроцессора с вспомогательными электронными устройствами, такими как постоянное запоминающее устройство (ПЗУ), электронно-стираемое программируемое постоянное запоминающее устройство (ЭСППЗУ), флэш-память или другой компонент энергонезависим запоминающего устройства, хранящий программное обеспечение или прошивка, выполняемое микропроцессором, микросхемой (микросхемами) оперативного запоминающего устройства (ОЗУ) для предоставления оперативной памяти и т.п.В случае использования электронно-стираемого программируемого постоянного запоминающего устройства, флэш-памяти или другой обновляемого запоминающего устройства для хранения программного обеспечения или прошивки, возможности аппарата 10 искусственной вентиляции легких могут быть преимущественно обновляемыми (в пределах его аппаратных компонентов) путем обновления программного обеспечения или прошивки.
[00027] Контроллер 30 вентиляции с поддержкой давлением выводит сигнал желаемой вентиляции, управляемой по давлению, как функцию времени, который используют для управления компрессором 32 аппарата искусственной вентиляции легких (например, пневматическим насосом, турбонасосом и т.п.), образующим поток воздуха под управляемым положительным давлением, воздействующим на Y-образную деталь 20 через впускной воздушный шланг 14. В зависимости от выбранной респираторной терапии регулятор 34 подачи кислорода может добавлять контролируемую фракцию кислорода в поток воздуха для достижения фракции кислорода во вдыхаемой смеси, установленной лечащим врачом, специалистом по заболеваниям органов дыхания или другим медицинским работником, который устанавливает конфигурацию аппарата 10 искусственной вентиляции легких для пациента 12. Давление паттерна вентиляции может варьироваться в зависимости от дыхательного цикла для обеспечения вдоха, обусловленного давлением или ассистируемого давлением, и для уменьшения давления для способствования выдоху.
[00028] Система искусственной вентиляции легких обычно также включает в себя датчики мониторинга физиологических показателей, такие как иллюстративный датчик 40 давления и иллюстративный датчик 42 расхода. Датчик 40 давления измеряет давление на Y-образной детали 20 (также известное как давление у рта пациента), в настоящем документе обозначенное как Py(t). Датчик 42 расхода измеряет скорость потока воздуха в и из Y-образной детали 20, в настоящем документе обозначенный как 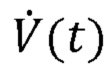 . Датчик 42 расхода также непосредственно или опосредованно предоставляет чистый объем воздуха, поданного пациенту, в настоящем документе обозначенный как V(t), который может быть непосредственно измерен или может быть выведен путем интегрирования скорости
. Датчик 42 расхода также непосредственно или опосредованно предоставляет чистый объем воздуха, поданного пациенту, в настоящем документе обозначенный как V(t), который может быть непосредственно измерен или может быть выведен путем интегрирования скорости 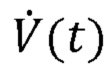 потока по времени. Эти измеренные значения Py(t),
потока по времени. Эти измеренные значения Py(t), 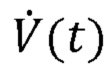 , V(t), при необходимости совместно с другой информацией, такой как настройки аппарата искусственной вентиляции легких (например, фракция кислорода во вдыхаемой смеси, профиль давления, доставляемого устройством управления вентиляции с поддержкой давлением и т.д.), могут быть по-разному использованы устройством 44 мониторинга аппарата искусственной вентиляции легких для эффективности механической вентиляции, для обнаружения ухудшения состояния пациента 12, для обнаружения любой неисправности аппарата 10 искусственной вентиляции легких или т.п. Аналогично контроллеру 30 аппарата искусственной вентиляции легких, устройство 44 мониторинга аппарата искусственной вентиляции легких реализовано как микропроцессор с вспомогательными электронными устройствам, и может быть обновляемым посредством обновления программного обеспечения или прошивки. В некоторых вариантах реализации контроллер 30 аппарата искусственной вентиляции легких и устройство 44 мониторинга аппарата искусственной вентиляции легких могут быть реализованы одним микропроцессором, а функции контроллера и устройства мониторинга могут быть встроены на разных уровнях - например, предусмотрено обеспечение управления вентиляцией на основании обратной связи на основании измеренных значений Py(t),
, V(t), при необходимости совместно с другой информацией, такой как настройки аппарата искусственной вентиляции легких (например, фракция кислорода во вдыхаемой смеси, профиль давления, доставляемого устройством управления вентиляции с поддержкой давлением и т.д.), могут быть по-разному использованы устройством 44 мониторинга аппарата искусственной вентиляции легких для эффективности механической вентиляции, для обнаружения ухудшения состояния пациента 12, для обнаружения любой неисправности аппарата 10 искусственной вентиляции легких или т.п. Аналогично контроллеру 30 аппарата искусственной вентиляции легких, устройство 44 мониторинга аппарата искусственной вентиляции легких реализовано как микропроцессор с вспомогательными электронными устройствам, и может быть обновляемым посредством обновления программного обеспечения или прошивки. В некоторых вариантах реализации контроллер 30 аппарата искусственной вентиляции легких и устройство 44 мониторинга аппарата искусственной вентиляции легких могут быть реализованы одним микропроцессором, а функции контроллера и устройства мониторинга могут быть встроены на разных уровнях - например, предусмотрено обеспечение управления вентиляцией на основании обратной связи на основании измеренных значений Py(t),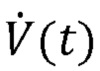 , V(t) или параметров, выведенных из них. Такое программное обеспечение или прошивка может быть предоставлено в форме некратковременного носителя данных, хранящего команды, выполненные с возможностью чтения и выполнения микропроцессором устройства 44 мониторинга аппарата искусственной вентиляции легких с целью осуществления функций мониторинга. Некратковременный носитель данных, например, может включать в себя флэш-память, оптический диск, накопитель на жестком диске или другой носитель данных.
, V(t) или параметров, выведенных из них. Такое программное обеспечение или прошивка может быть предоставлено в форме некратковременного носителя данных, хранящего команды, выполненные с возможностью чтения и выполнения микропроцессором устройства 44 мониторинга аппарата искусственной вентиляции легких с целью осуществления функций мониторинга. Некратковременный носитель данных, например, может включать в себя флэш-память, оптический диск, накопитель на жестком диске или другой носитель данных.
[00029] Особо следует выделить оценку работы дыхания или ее производной - давления Pmus(t) дыхательной мускулатуры. В целом работа дыхания может быть вычислена посредством интегрирования Pmus(t) по вдыхаемому объему. В подходах, описанных в настоящем документе, в оценке используется уравнение движения легких, приведенное в уравнении (1) в настоящем документе, и, следовательно, сопротивление R и растяжимость С дыхательной системы также являются значимыми целевыми параметрами. Уравнение (1) вычисляют относительно совокупности данных N точек данных, измеренных на протяжении одного или более дыхательных циклов. Формально задача может быть выражена следующим образом:

[00030] где:

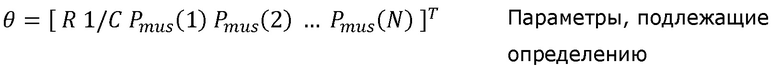
[00031] а матрица X является матрицей (N+2) × N, полученной из 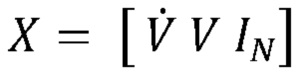 , где IN является N×N матрицей тождественности. Путем решения системы уравнений Y=Хθ для вектора θ параметров, могут быть выведены сопротивление Р, растяжимость С и давление Pmus(t) дыхательной мускулатуры. Однако система уравнений, раскрытая в уравнении (2), содержит больше неизвестных (N+2 неизвестных), чем уравнения (уравнения N), и, следовательно, является недоопределенной задачей, которая не может быть решена, так как содержит неограниченное количество решений, только одно из которых является верным «фактическим» решением.
, где IN является N×N матрицей тождественности. Путем решения системы уравнений Y=Хθ для вектора θ параметров, могут быть выведены сопротивление Р, растяжимость С и давление Pmus(t) дыхательной мускулатуры. Однако система уравнений, раскрытая в уравнении (2), содержит больше неизвестных (N+2 неизвестных), чем уравнения (уравнения N), и, следовательно, является недоопределенной задачей, которая не может быть решена, так как содержит неограниченное количество решений, только одно из которых является верным «фактическим» решением.
[00032] Вследствие своей недоопределенности, система уравнений, выраженная матричным уравнением (2), является очень чувствительной к шуму в измерениях, неизвестным помехам и немоделируемым динамическим характеристикам. Проблематично, шум находится в одном масштабе времени с изменениями в измеренных сигналах Py(t),  , V(t) и в аппроксимированном давлении Pmus(t) дыхательной мускулатуры. Следовательно, даже в случае преодоления недоопределенной сущности задачи одновременного оценивания каким-то образом, значения параметров, полученные в результате, характеризуются шумами и, следовательно, имеют ограниченное клиническое значение.
, V(t) и в аппроксимированном давлении Pmus(t) дыхательной мускулатуры. Следовательно, даже в случае преодоления недоопределенной сущности задачи одновременного оценивания каким-то образом, значения параметров, полученные в результате, характеризуются шумами и, следовательно, имеют ограниченное клиническое значение.
[00033] Также со ссылкой на фиг. 1, в настоящем документе раскрыто произвольное противодействие эффекту шума путем накладывания сигнала давления с относительно высокой частотой и малой амплитудой, обозначенного как ΔP(t) в настоящем документе, генерируемого генератором 50 сигнала, на нормальный профиль давления, предоставляемый аппаратом 10 искусственной вентиляции легких. Как показано на фиг. 1, это может быть осуществлено путем добавления малоамплитудного синусоидального ΔP(t) к сигналу управляемого давления, выводимого контроллером 30, с использованием объединителя 52 сигналов перед его вводом в компрессор 32 аппарата искусственной вентиляции легких. Амплитуду ΔP(t) предпочтительно выбирают таким образом, что она достаточна низкая для наблюдаемого влияния на терапевтическое значение сигнала вентиляции в режиме поддержки давлением, выводимого контроллером 30. Частота ΔP(t) предпочтительно является достаточно высокой для существенного превышения частоты дыхания (например, обычно несколько вдохов в минуту соответствуют частоте, приблизительно составляющей, например, 0,2 Гц для 5 секундного дыхания).
[00034] Также со ссылкой на фиг. 1, недоопределенность системы уравнений, выраженных матричным уравнением (2), решена в вариантах реализации, раскрытых в настоящем документе (с произвольным наложением ΔP(t) или без него), путем решения уравнения (2) в области (областях) 60 аппроксимации, для которой с достаточными основаниями предполагается, что давление Pmus(t) дыхательной мускулатуры, без предположения его равенства нулю, имеет некоторую ограничительную характеристику (характеристики), обеспечивающую возможность уменьшения количества параметров, достаточного для того, чтобы сделать уравнение (2) переопределенным. Одновременная оценка R, С и Pmus(t), характеризующих одно дыхательное движение (без утраты обобщенности выраженное зарегистрированными N образцами моментов времени) через уравнение (2), является недоопределенной задачей, так как она требует вычисления N+2 неизвестных (значения N для N образцов моментов времени Pmus(t), плюс дополнительное неизвестное для Р и дополнительное неизвестное для С) из N уравнений, соответствующих N образцам времени. Однако в настоящем документе учтено, что N уравнений не являются независимыми. Вместо этого, можно предполагать, что значение Pmus(t) для соседних образцов должно быть непрерывным. В некоторых областях с достаточными основаниями может быть предположено, что Pmus(t) монотонно увеличивается, является ровным или монотонно уменьшается.
[00035] В одном варианте реализации, раскрытом в настоящем документе, осуществляется локальная (то есть на небольшом количестве образцов s<N) аппроксимация Pmus(t) полиномиальной функцией n-порядка, подходящим образом выраженная как 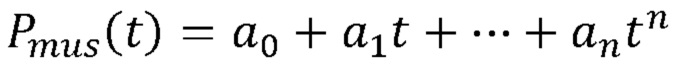 . Эту аппроксимацию используют для образования задачи наименьших квадратов (least squares, «LS») от временного интервала s образцов (где s<N), в которой неизвестными являются R, С и а0, …, an. Недоопределенность преодолевается посредством удержания n+3<s (а в некоторых вариантах реализации n<<s). Локальная аппроксимация Pmus(t) полиномиальной функцией подтверждается физиологическим пониманием того, что Pmus(t) является плавным сигналом без резких прерываний.
. Эту аппроксимацию используют для образования задачи наименьших квадратов (least squares, «LS») от временного интервала s образцов (где s<N), в которой неизвестными являются R, С и а0, …, an. Недоопределенность преодолевается посредством удержания n+3<s (а в некоторых вариантах реализации n<<s). Локальная аппроксимация Pmus(t) полиномиальной функцией подтверждается физиологическим пониманием того, что Pmus(t) является плавным сигналом без резких прерываний.
[00036] В другом варианте реализации временной интервал, занимаемый N образцами разделен на области аппроксимации, в которых Pmus(t) монотонно увеличивается, монотонно уменьшается или является ровным по всей области аппроксимации. В пределах каждой области может быть разработана квадратичная программа, использующая известную монотонность в области. Это обеспечивает эффективное определение единственного решения.
[00037] Со ссылкой на фиг. 2, первый иллюстративный способ преодоления неопределенности матричного уравнения (2) описан более подробно. Согласно этому способу области 60 аппроксимации выбирают таким образом, что они достаточно малы для хорошей аппроксимации Pmus(t) посредством полиномиальной аппроксимации. Оценку R, С и Pmus(t) в каждый момент времени 1,…,N получают путем решения проблемы наименьших квадратов по интервалу длины s. Для обычного случая, в котором s<N, интервал перемещен вперед по времени (то есть интервал ширины s применяют к последовательным прибавляемым величинам ширины s во временном ряде образцов 1,…,N). При мониторинге пациента в реальном времени это может быть осуществлено посредством скользящего интервала, при получении каждой последующей группы s образов аппроксимацию осуществляют таким образом, чтобы предоставлять одновременную оценку для R, С, Pmus(t) в реальном времени. Интервалы ширины s могут не перекрываться; альтернативно, предусмотрено, что смежные интервалы ширины s перекрываются, что может обеспечить выравнивающий эффект. На фиг. 2 изображен случай, в котором полиномиальная аппроксимация Pmus(t) по временному интервалу ширины s имеет порядок n=2, то есть полиномиальный: Pmus(t)=а0+a1t+a2t2. Матричное уравнение (2), решенное для интервала ширины s, имеет такую же форму, как и уравнение (2), за исключением отличающегося вектора параметров. Для различения, вектор параметров выражен как φ (в отличие от вектора θ параметров уравнения (2)), матрица X заменена матрицей χ, а остальная система уравнений выглядит следующим образом:

[00038] где:

[00039] а матрица χ является матрицей s × (n+3), заданной
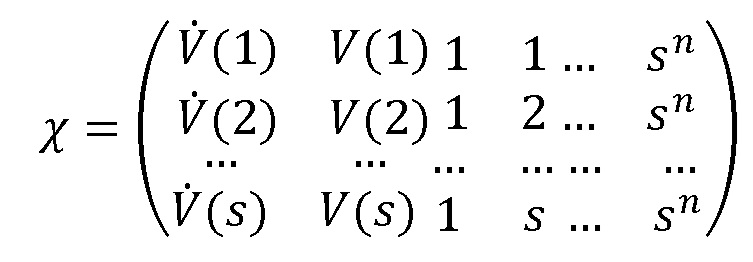
[00040] В указанной ранее системе обозначений первый образец в интервале ширины s обозначен без утраты обобщенности как образец t=1 таким образом, что последний образец в интервале обозначен как образец t=s. Следовательно, матричное уравнение (2а) выражает систему s уравнений с n+3 неизвестными, и является переопределенным, при условии, что s>(n+3). Более типично, s >> n. Например, в одном иллюстративном примере n=2 (квадратичная аппроксимация для Pmus(t)) интервал выборки составляет 100 Гц, а длина интервала составляет 0,6 с в соответствии с s=60.
[00041] При условии переопределенной системы уравнений, матричное уравнение (2а) может быть решено в смысле наименьших квадратов в соответствии с:

[00042] Альтернативно, итеративный метод аппроксимации наименьших квадратов, такой как градиентный спуск или алгоритм Левенберга-Марквардта, может быть использован для решения уравнения (3) для параметров φ.
[00043] Указанный иллюстративный способ использует полиномиальную аппроксимацию Pmus(t) порядка n по временному интервалу ширины s. Порядок n выбран, чтобы соответствовать n≥2. Выбор более высокого порядка обеспечивает полиномиальную аппроксимацию с большей гибкостью для отображения изменений в Pmus(t) по временному интервалу ширины s; однако он также добавляет дополнительные параметры (общее количество параметров составляет n+3), что приводит к меньшей надежности аппроксимации наименьших квадратов. Предполагается, что n=2, n=3 или n=4 будет достаточным в большинстве случаев, хотя также предусмотрено n>4. Кроме того, следует понимать, что способ может быть обобщен до аппроксимации Pmus(t) по временному интервалу ширины s любой непрерывной функцией, плавной по интервалу ширины s (т.е. дифференцируемой по интервалу ширины s). Другие предусмотренные непрерывные и плавные функции аппроксимации включают сплайн-функции, например, кубические сплайн-функции.
[00044] Со ссылкой на фиг. 3 и 4, нормальное взаимодействие между аппаратом искусственной вентиляции легких и пациентом эмулируется с использованием смоделированного на компьютере эмулятора легких. Это нормальное взаимодействие образует кривые потока и объема, изображенные на графике на фиг. 3, что делает матрицу данных плохо обусловленной. Следовательно, параметры, вычисленные через уравнение (3), являются чувствительными к шуму или ошибке в измеренных данных. На фиг. 3 чувствительность матрицы параметров изображена нижнем на графике на фиг. 3. Следует отметить, что на этом графике ордината чувствительности находится в пределах [0, 200,000]. Как описано ранее, при необходимости осуществляется противодействие этому шуму посредством наложения компонента ΔP(t) с низкой амплитудой и высокой частотой. Для иллюстрации на фиг. 4 показано, как наложение синусоидального сигнала ΔP(t) малой амплитуды (в этом примере 1 сантиметр водного столба) и относительно высокой частоты (в этом примере 5 Гц) существенно уменьшает чувствительность (коэффициент переноса) матрицы параметров, таким образом улучшая устойчивость к шуму. Следует отметить, что на фиг. 4 диапазон ординат чувствительности крайнего нижнего графика составляет всего [0, 5000]. Для реализации ΔP(t) генератор 50 сигнала и объединитель 52 сигнала (см. фиг. 1) могут быть реализованы в программном обеспечении или прошивке как часть программного обеспечения или прошивки контроллера 30 аппарата искусственной вентиляции легких, или генератор 50 сигнала и объединитель 52 сигнала могут являться компонентами, отдельными от контроллера 30 аппарата искусственной вентиляции легких, например, схемой управляемого напряжением осциллятора (voltage-controlled oscillator, «VCO»), выводящей сигнал ΔP(t), и объединителем сигнала на основе операционного усилителя или другим объединителем сигнала, реализованным в аппаратных средствах.
[00045] Способ аппроксимации Pmus(t) до плавной непрерывной функции (например, полиномиальной функции порядка n≥2), как описано со ссылкой на фиг. 2, имеет дополнительное преимущество работы в области времени, и, следовательно, позволяет оперативно использовать нелинейные модели механики легких в анализе данных параметров дыхания. Например, необязательно предполагать, что R и С являются постоянными значениями на протяжении дыхательного цикла. В одном иллюстративном способе для учета возможных нелинейностей в сопротивлении R и растяжимости С, уравнение (1) может быть изменено для содержания квадратичных характеристик, как указано далее:
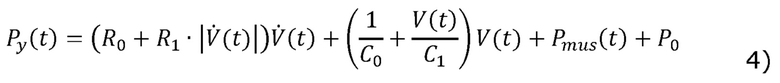
[00046] Уравнение (4) характеризуется зависимым от потока сопротивлением 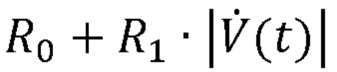 и зависимой от объема эластичностью
и зависимой от объема эластичностью 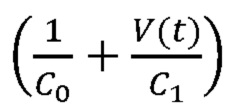 . Теперь параметрами, подлежащими вычислению, являются R0, R1, C0, С1 и Pmus(t). Задача наименьших квадратов, подлежащая решению (с полиномиальной аппроксимацией Pmus(t), т.е. в соответствии с уравнением (2а)), выражается следующим образом:
. Теперь параметрами, подлежащими вычислению, являются R0, R1, C0, С1 и Pmus(t). Задача наименьших квадратов, подлежащая решению (с полиномиальной аппроксимацией Pmus(t), т.е. в соответствии с уравнением (2а)), выражается следующим образом:

[00047] где:
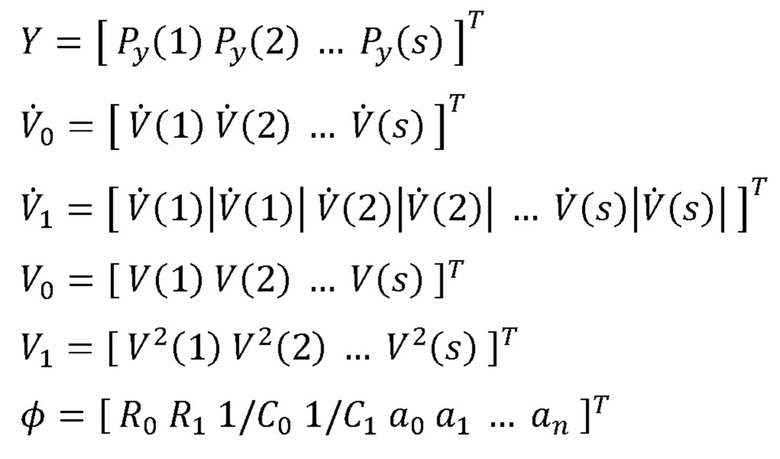
[00048] а матрица χ является s × (n+5) матрицей, полученной из:
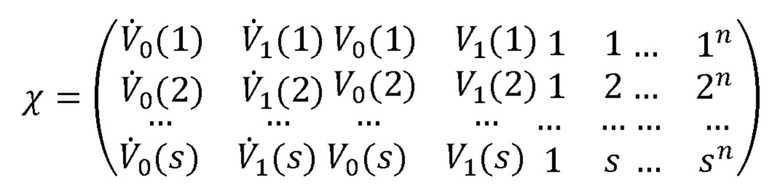
[00049] При условии переопределенной системы уравнений, матричное уравнение (5) может быть решено в смысле наименьших квадратов в соответствии с:
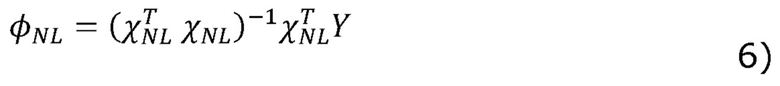
[00050] Альтернативно, итеративный метод аппроксимации наименьших квадратов, такой как градиентный спуск или алгоритм Левенберга-Марквардта, может быть использован для решения уравнения (5) для параметров φNL.
[00051] Далее дополнительно описан второй иллюстративный способ для преодоления недоопределенности матричного уравнения (2). Согласно этому способу каждую область 60 аппроксимации выбирают таким образом, что Pmus(t) является монотонным (монотонно увеличивается или монотонно уменьшается) во всей области аппроксимации. Согласно этому способу ограничения в виде неравенства возможных значений Pmus(t) и ограничения интервала, возможные для R и С, вводят на основании физиологических факторов таким образом, что решение наименьших квадратов становится единственным. В подходящем способе ограничения вычисляют в линейной форме и определяют подлежащую минимизации целевую функцию типа наименьших квадратов таким образом, что математическая формулировка задачи на оптимизацию относится к категории квадратичного программирования. Таким образом не только гарантируется единственность решения, но также операция решения программы может быть очень эффективной, так как квадратичное программирование является развитой математической технологией.
[00052] При необходимости, надежность полученного в результате способа оценки R, С и Pmus(t) дополнительно усовершенствуется введением ограничения в виде неравенства. Надежность является преимущественной для практических применений вследствие неопределенностей и неидеальных факторов, которые могут влиять на применение (шум в измерениях, неизвестные помехи, нелинейности, немоделируемые динамические характеристики). Ограничения в виде неравенства значений Pmus(t) используют для уменьшения количества неизвестных для выражения Pmus(t), таким образом обеспечивая большую надежность общей оценки.
[00053] Со ссылкой на фиг. 5, нормальное взаимодействие между аппаратом искусственной вентиляции легких и пациентом эмулируют с использованием смоделированного на компьютере эмулятора легких. Как показано на верхнем графике фиг. 5, на протяжении одного вдоха (соответствующему времени 1805-1806 с на иллюстративной фиг. 5), Pmus(i) сначала монотонно уменьшается (по направлению к более отрицательным значениям при работе диафрагмы и мышц грудной клетки с целью создания отрицательного давления дыхательной мускулатуры для нагнетания воздуха в легкие), а затем Pmus(t) переходит в область монотонного увеличения при постепенном уменьшении отрицательного давления дыхательной мускулатуры до Pmus(t)=0 при завершении вдоха. Как показано на верхнем графике фиг. 5, Pmus(t)=0 в общем удерживается между вдохами, так как выдох обуславливается расслаблением расширенных легких.
[00054] Вследствие этих наблюдений, способ включает в себя определение области монотонного уменьшения и области монотонного увеличения, и трансформацию монотонности в математические неравенства для ограничения оптимизации методом наименьших квадратов. Целевая подлежащая минимизации функция, обозначенная в настоящем описании как/, легко вычисляется из уравнения (1):
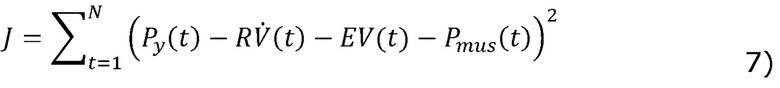
[00055] В целевой функции J уравнения (7) растяжимость С дыхательной системы заменена на эластичность Е в соответствии с соотношением 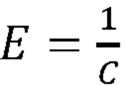 . Целевая функция J минимизирована относительно параметров R, С (или Е) и Pmus(1), …, Pmus(N), подчиняющихся ограничениям в виде неравенства, захватывающим известные области монотонности Pmus(t). Эта задача может быть вычислена как квадратичная программа посредством минимизации J, подчиняющейся следующим ограничениям в виде неравенства:
. Целевая функция J минимизирована относительно параметров R, С (или Е) и Pmus(1), …, Pmus(N), подчиняющихся ограничениям в виде неравенства, захватывающим известные области монотонности Pmus(t). Эта задача может быть вычислена как квадратичная программа посредством минимизации J, подчиняющейся следующим ограничениям в виде неравенства:
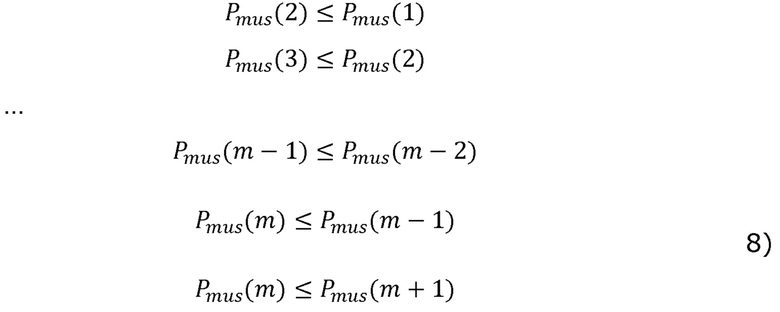
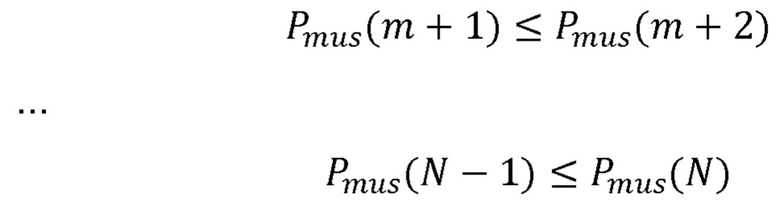
[00056] где время t=m является «поворотным моментом», то есть точкой, на которой Pmus(t) переходит от монотонного уменьшения (для t=1, …,m) до монотонного увеличения (для t=m+1,…,N). Другими словами, Pmus(m) является моментом времени, в который Pmus(t) достигает своего минимального значения. При необходимости квадратичная программа может включать в себя дополнительные ограничения на основании физиологических знаний. Например, при наличии некоторого известного минимального давления Pmax дыхательной мускулатуры и/или некоторого известного максимального давления Pmax дыхательной мускулатуры (например, в некоторых случаях можно предположить, что Pmax = 0, так как диафрагма и мышцы грудной клетки не могут функционировать для приложения положительного давления к легким), могут быть добавлены следующие неравенства:
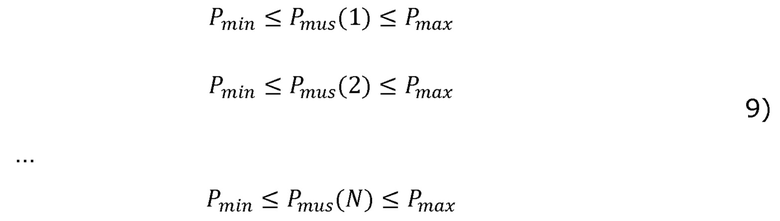
[00057] Аналогичные ограничения пределов (интервала) могут быть при необходимости применены к R и С:

[00058] Разложение квадратной матрицы, которая не может быть составлена из целевой функции с использованием действительных данных, по собственным значениям указывает на то, что задача полностью определена под ограничениями (8)-(10). Все собственные значения являются отрицательными, кроме двух, которые равны нулю. Для того чтобы задача квадратичного программирования имела единственное решение, все собственные значения строго должны быть отрицательными. Однако собственные векторы, соответствующие нулевым собственным значениям, минимизируют направления, запрещенные данными ограничениями, таким образом, чтобы преодолевать неопределенность одновременной оценки R, С и Pmus(t) методом наименьших квадратов.
[00059] В предшествующем выражении предположено, что t=m, причем монотонность переключения Pmus(t) является известной. Однако это не так в действительных применениях. Для определения времени m переключения может быть осуществлен поиск оптимального переключения монотонности путем решения квадратичной программы, определенной целевой функцией J (уравнение (7)) и ограничениями (8)-(10) для каждого подходящего минимального момента времени, и выбора подходящего минимального момента времени, обеспечивающего наименьшее значение для J в качестве минимального момента т времени.
[00060] Предусмотрены ограничения в дополнение к ограничениям (8)-(10) или вместо них. Ввод в алгоритм является системой измеренных Py(t), 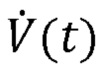 и V(t) за полный вдох, где V(t) также подходящим образом определено посредством интегрирования
и V(t) за полный вдох, где V(t) также подходящим образом определено посредством интегрирования 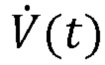 . Выводимые данные включают в себя значение для каждого из R, С (или Е) и кривую Pmus(t) для всего вдоха.
. Выводимые данные включают в себя значение для каждого из R, С (или Е) и кривую Pmus(t) для всего вдоха.
[00061] Со ссылкой на фиг. 5-8, испытания на данных параметров моделированного дыхания указывают то, что указанный ранее алгоритм квадратичной программы обеспечивает подходящие оценки R, С и Pmus(t), когда данные давления и потока поступают от идеальной схемы R, C с аддитивным шумом, вносящим искажения в измеренные значения, и без него. На фиг. 5 изображены данные параметров моделированного дыхания для симулятора идеальной схемы R, С без шума в сигналах, а на фиг. 6 изображены выводимые данные алгоритма квадратичной программы (верхний график) и ошибка (нижний график; следует отметить, что ордината графика ошибки имеет диапазон [0,10-13] таким образом, что пренебрежимая ошибка наблюдается по всему графику). На фиг. 7 и 8 показано такое же испытание, как на фиг. 5 и 6, но с количественно добавленным шумом. Несмотря на наблюдение некоторой степени ошибки вследствие шума, аппроксимация остается достаточно точной.
[00062] Для предоставления дополнительного улучшения, раскрытые способы могут быть совмещены, например, квадратичная программа (уравнение (7) с применением ограничений (8)-(10)) может быть применена в сочетании с такой параметризацией Pmus(t), например, как описанная со ссылкой на фиг. 2, или некоторой другой параметризацией.
[00063] Со ссылкой на фиг. 9 и 10, представлена оценка R, С и Pmus(t) Для настоящей свиньи (экспериментальные данные) в различных условиях вентиляции с поддержкой давлением: ВПД=20 (фиг. 9) и ВПД=10 (фиг. 10). Эти данные иллюстрируют, как алгоритм квадратичной программы может неинвазивно воссоздавать значения сопротивления и растяжимости, оцененные инвазивно на свинье через пищеводный катетер. Прерывистые линии выражают оценки, полученные квадратичной программой с дополнительной параметризацией, в которой Pmus(t) параметризирован через четыре области, три из которых характеризуются подлежащим оценке наклоном, а четвертая область содержит ограничение монотонности и максимальное отрицательное значение, подлежащее оценке. Непрерывные линии выражают оценки способом наименьших квадратов R и С, полученные посредством измерения Pes(t), что требует инвазивного катетера (знание Pes(t) обеспечивает возможность оценки сопротивления и растяжимости дыхательной системы посредством способа наименьших квадратов без проблем с неопределенностью). Следовательно, алгоритм квадратичной программы обеспечивает возможность неинвазивного предоставления идентичных оценок R и С, которые на данном уровне техники получают инвазивно.
[00064] Изобретение было описано со ссылкой на предпочтительные варианты реализации. Модификации и изменения и могут быть понятны после прочтения и понимания предшествующего подробного описания. Подразумевается, что изобретения включает все такие модификации и изменения, находящиеся в пределах объема прилагаемой формулы изобретения или ее эквивалентов.
| название | год | авторы | номер документа |
|---|---|---|---|
| АППАРАТ ДЛЯ МЕХАНИЧЕСКОЙ ИСКУССТВЕННОЙ ВЕНТИЛЯЦИИ ЛЕГКИХ И МОНИТОРИНГА ДЫХАНИЯ | 2017 |
|
RU2737295C2 |
| КОМПЕНСАЦИЯ ДЛЯ ИСКУССТВЕННОГО ДЫХАНИЯ | 2012 |
|
RU2639853C2 |
| СИСТЕМА И СПОСОБ ОЦЕНКИ СИЛЫ ДЫХАНИЯ В РЕАЛЬНОМ ВРЕМЕНИ И КОНТРОЛЛЕР ЗАМКНУТОГО КОНТУРА | 2013 |
|
RU2641516C2 |
| СИСТЕМЫ И СПОСОБЫ ОПТИМИЗАЦИИ ИСКУССТВЕННОЙ ВЕНТИЛЯЦИИ ЛЕГКИХ НА ОСНОВАНИИ МОДЕЛИ | 2015 |
|
RU2712749C2 |
| НЕИНВАЗИВНАЯ ОЦЕНКА ВНУТРИПЛЕВРАЛЬНОГО ДАВЛЕНИЯ И/ИЛИ ВЫЧИСЛЕНИЕ РАБОТЫ ДЫХАНИЯ НА ОСНОВАНИИ НЕИНВАЗИВНОЙ ОЦЕНКИ ВНУТРИПЛЕВРАЛЬНОГО ДАВЛЕНИЯ | 2014 |
|
RU2700981C2 |
| Устройство для регистрации параметров дыхания | 1980 |
|
SU944537A1 |
| Симулятор спонтанной дыхательной активности пациента | 2021 |
|
RU2763657C1 |
| СПОСОБ ДИАГНОСТИКИ НАРУШЕНИЙ ОКСИГЕНАЦИИ КРОВИ В ПРОЦЕССЕ ИСКУССТВЕННОЙ ВЕНТИЛЯЦИИ ЛЕГКИХ | 2011 |
|
RU2457781C1 |
| СПОСОБ И УСТРОЙСТВО ИСКУССТВЕННОЙ ВЕНТИЛЯЦИИ ЛЕГКИХ ПАЦИЕНТА | 2017 |
|
RU2745966C2 |
| СПОСОБ ПРОВЕДЕНИЯ ИСКУССТВЕННОЙ ВЕНТИЛЯЦИИ ЛЕГКИХ, РЕГУЛИРУЕМОЙ ПО ОБЪЕМУ | 2001 |
|
RU2207159C2 |
Группа изобретений относится к медицинской технике, а именно к медицинской системе искусственной вентиляции легких, некратковременному носителю данных и способу оценки давления дыхательной мускулатуры во время дыхания. Система содержит аппарат (10) искусственной вентиляции легких для подачи потока воздуха под положительным давлением вентилируемому пациенту (12). Система включает датчик (40) давления для измерения давления Py(t) воздуха, вдыхаемого или выдыхаемого вентилируемым пациентом (12). Система имеет датчик (42) расхода для измерения потока 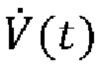 воздуха, проходящего в вентилируемого пациента или выходящего из него. Система содержит устройство (44) мониторинга аппарата искусственной вентиляции легких. Устройство содержит микропроцессор для оценки давления дыхательной мускулатуры во время дыхания посредством разделения интервала времени дыхания на области (60) аппроксимации и одновременной оценки сопротивления R и растяжимости С или эластичности Е дыхательной системы и давления Pmus(t) дыхательной мускулатуры в каждой области посредством аппроксимации к временному ряду образцов Py(t) и
воздуха, проходящего в вентилируемого пациента или выходящего из него. Система содержит устройство (44) мониторинга аппарата искусственной вентиляции легких. Устройство содержит микропроцессор для оценки давления дыхательной мускулатуры во время дыхания посредством разделения интервала времени дыхания на области (60) аппроксимации и одновременной оценки сопротивления R и растяжимости С или эластичности Е дыхательной системы и давления Pmus(t) дыхательной мускулатуры в каждой области посредством аппроксимации к временному ряду образцов Py(t) и 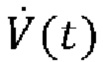 в этой области. Некратковременный носитель данных, хранящий инструкции для чтения и исполнения одним или более микропроцессорами медицинского аппарата (10) искусственной вентиляции легких, для обеспечения выполнения медицинским аппаратом искусственной вентиляции легких способа оценки давления дыхательной мускулатуры во время дыхания. Способ оценки давления дыхательной мускулатуры во время дыхания включает прием измеренных значений давления Py(t) воздуха, вдыхаемого или выдыхаемого вентилируемым пациентом (12). Способ содержит прием измеренных значений потока
в этой области. Некратковременный носитель данных, хранящий инструкции для чтения и исполнения одним или более микропроцессорами медицинского аппарата (10) искусственной вентиляции легких, для обеспечения выполнения медицинским аппаратом искусственной вентиляции легких способа оценки давления дыхательной мускулатуры во время дыхания. Способ оценки давления дыхательной мускулатуры во время дыхания включает прием измеренных значений давления Py(t) воздуха, вдыхаемого или выдыхаемого вентилируемым пациентом (12). Способ содержит прием измеренных значений потока 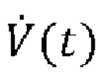 воздуха, проходящего в вентилируемого пациента или выходящего из вентилируемого пациента. Способ включает разделение интервала времени дыхания на области (60) аппроксимации и в каждой области аппроксимации решение уравнения:
воздуха, проходящего в вентилируемого пациента или выходящего из вентилируемого пациента. Способ включает разделение интервала времени дыхания на области (60) аппроксимации и в каждой области аппроксимации решение уравнения: 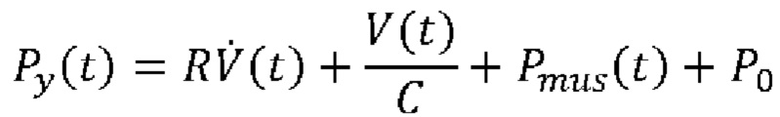 или
или 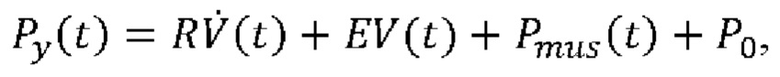 где V(t) выражает чистый объем воздуха, поданный пациенту, вычисленный посредством интегрирования указанного потока
где V(t) выражает чистый объем воздуха, поданный пациенту, вычисленный посредством интегрирования указанного потока 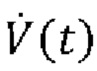 воздуха, Р0 является постоянной, для одновременной оценки сопротивления R и растяжимости С или эластичности Е дыхательной системы и давления Pmus(t) дыхательной мускулатуры в каждой области аппроксимации посредством аппроксимации к временному ряду образцов Py(t) и
воздуха, Р0 является постоянной, для одновременной оценки сопротивления R и растяжимости С или эластичности Е дыхательной системы и давления Pmus(t) дыхательной мускулатуры в каждой области аппроксимации посредством аппроксимации к временному ряду образцов Py(t) и 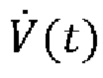 в этой области аппроксимации. Техническим результатом является обеспечение неинвазивной оценки параметров дыхания с улучшенной вычислительной надёжностью анализа данных. 3 н. и 12 з.п. ф-лы, 10 ил.
в этой области аппроксимации. Техническим результатом является обеспечение неинвазивной оценки параметров дыхания с улучшенной вычислительной надёжностью анализа данных. 3 н. и 12 з.п. ф-лы, 10 ил.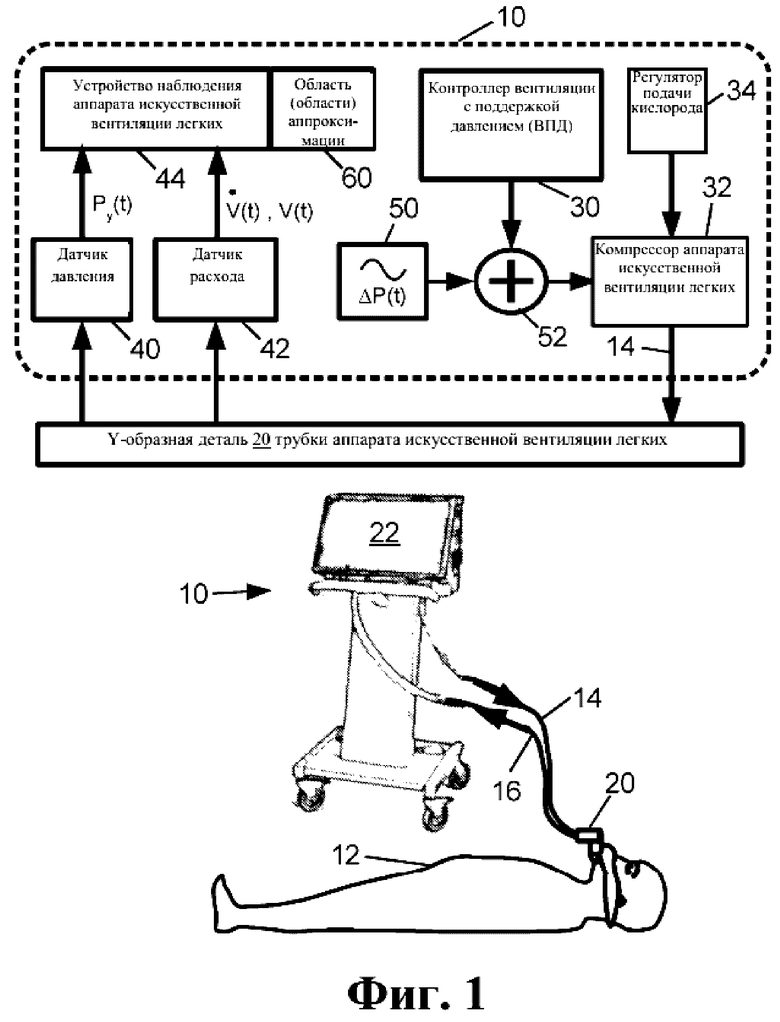
1. Медицинская система искусственной вентиляции легких, содержащая:
аппарат (10) искусственной вентиляции легких, выполненный с возможностью подачи потока воздуха под положительным давлением вентилируемому пациенту (12);
датчик (40) давления, выполненный с возможностью измерения давления Py(t) воздуха, вдыхаемого или выдыхаемого вентилируемым пациентом (12);
датчик (42) расхода, выполненный с возможностью измерения потока 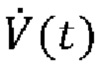 воздуха, проходящего в вентилируемого пациента или выходящего из него; и
воздуха, проходящего в вентилируемого пациента или выходящего из него; и
устройство (44) мониторинга аппарата искусственной вентиляции легких, содержащее микропроцессор, запрограммированный для оценки давления дыхательной мускулатуры во время дыхания посредством разделения интервала времени дыхания на области (60) аппроксимации и одновременной оценки сопротивления R и растяжимости С или эластичности Е дыхательной системы и давления Pmus(t) дыхательной мускулатуры в каждой области посредством аппроксимации к временному ряду образцов Py(t) и 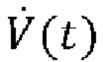 в этой области.
в этой области.
2. Медицинская система искусственной вентиляции легких по п. 1, в которой устройство (44) мониторинга аппарата искусственной вентиляции легких запрограммировано для одновременной оценки сопротивления и растяжимости или эластичности дыхательной системы и давления дыхательной мускулатуры в каждой области аппроксимации посредством операций, включающих в себя:
аппроксимацию давления Pmus(t) дыхательной мускулатуры, параметризованного непрерывной дифференцируемой функцией по области аппроксимации.
3. Медицинская система искусственной вентиляции легких по п. 2, в которой непрерывная дифференцируемая функция является полиномиальной или сплайн-функцией.
4. Медицинская система искусственной вентиляции легких по п. 2, в которой непрерывная дифференцируемая функция является полиномиальной функцией следующей формы:
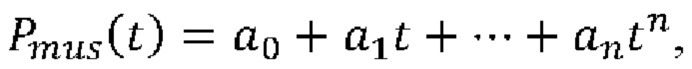
а одновременная аппроксимация включает в себя оценку параметров а0, a1, …, an.
5. Медицинская система искусственной вентиляции легких по п. 1, в которой устройство (44) мониторинга аппарата искусственной вентиляции легких запрограммировано для одновременной оценки сопротивления и растяжимости или эластичности дыхательной системы и давления дыхательной мускулатуры в каждой области аппроксимации посредством операций, включающих в себя:
аппроксимацию уравнения движения легких в каждой области аппроксимации с применением в каждой области ограничений монотонности давления Pmus(t) дыхательной мускулатуры.
6. Медицинская система искусственной вентиляции легких по п. 5, в которой области аппроксимации включают в себя первую область, в пределах которой применено ограничение монотонного уменьшения давления Pmus(t) дыхательной мускулатуры, и вторую область, которая следует после первой области по времени и в пределах которой применено ограничение монотонного увеличения.
7. Медицинская система искусственной вентиляции легких по любому из пп. 5, 6, в которой аппроксимация с применением ограничений монотонности содержит решение квадратичной программы, включающей в себя целевую функцию, выражающую уравнение движения легких, и систему неравенств, относящуюся к образцам давления Pmus(t) дыхательной мускулатуры, которые определяют ограничения монотонности.
8. Медицинская система искусственной вентиляции легких по п. 7, в которой квадратичная программа включает в себя дополнительные неравенства, не определяющие ограничения монотонности.
9. Медицинская система искусственной вентиляции легких по п. 8, в которой дополнительные неравенства, не определяющие ограничения монотонности, включают в себя неравенства, связанные по меньшей мере с давлением Pmus(t) дыхательной мускулатуры и сопротивлением R и растяжимостью С дыхательной системы.
10. Медицинская система искусственной вентиляции легких по любому из пп. 1-9, в которой одновременная оценка сопротивления R и растяжимости С или эластичности Е дыхательной системы и давления Pmus(t) дыхательной мускулатуры в каждой области аппроксимации посредством аппроксимации по временным рядам образцов Py(t) и 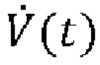 содержит решение уравнения движения легких в каждой области аппроксимации, полученного из:
содержит решение уравнения движения легких в каждой области аппроксимации, полученного из:
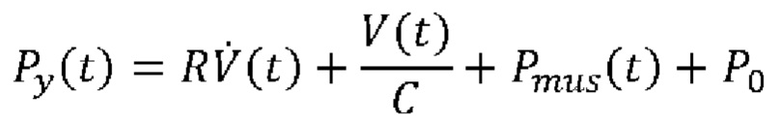
или
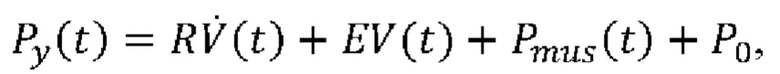
где V(t) выражает чистый объем воздуха, поданный пациенту, вычисленный посредством интегрирования потока 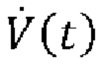 воздуха, a P0 является постоянной.
воздуха, a P0 является постоянной.
11. Медицинская система искусственной вентиляции легких по любому из пп. 1-9, в которой одновременная оценка сопротивления R и растяжимости С или эластичности Е дыхательной системы и давления Pmus(t) дыхательной мускулатуры в каждой области аппроксимации посредством аппроксимации по временным рядам образцов Py(t) и 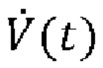 содержит решение уравнения движения легких в каждой области аппроксимации, полученного из:
содержит решение уравнения движения легких в каждой области аппроксимации, полученного из:
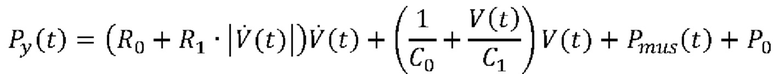
или
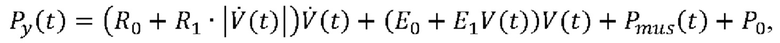
где V(t) выражает чистый объем воздуха, поданный пациенту, вычисленный посредством интегрирования указанного потока 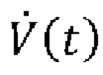 воздуха, Р0 является постоянной, сопротивление дыхательной системы составляет
воздуха, Р0 является постоянной, сопротивление дыхательной системы составляет 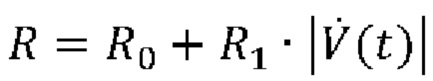 и растяжимость дыхательной системы составляет
и растяжимость дыхательной системы составляет 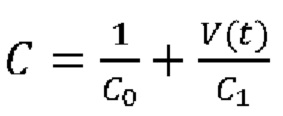 или эластичность стенки грудной клетки составляет Е=Е0+E1V(t).
или эластичность стенки грудной клетки составляет Е=Е0+E1V(t).
12. Некратковременный носитель данных, хранящий инструкции, выполненные с возможностью чтения и исполнения одним или более микропроцессорами медицинского аппарата (10) искусственной вентиляции легких для обеспечения выполнения медицинским аппаратом искусственной вентиляции легких способа оценки давления дыхательной мускулатуры во время дыхания, включающего:
прием измеренных значений давления Py(t) воздуха, вдыхаемого или выдыхаемого вентилируемым пациентом (12), функционально соединенным с медицинским аппаратом искусственной вентиляции легких;
прием измеренных значений потока 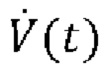 воздуха, проходящего в вентилируемого пациента или выходящего из вентилируемого пациента, функционально соединенного с медицинским аппаратом искусственной вентиляции легких;
воздуха, проходящего в вентилируемого пациента или выходящего из вентилируемого пациента, функционально соединенного с медицинским аппаратом искусственной вентиляции легких;
разделение интервала времени дыхания на области (60) аппроксимации и
одновременную оценку сопротивления R и растяжимости С или эластичности Е дыхательной системы и давления Pmus(t) дыхательной мускулатуры в каждой области аппроксимации посредством аппроксимации к временному ряду образцов Py(t) и 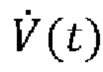 в этой области аппроксимации.
в этой области аппроксимации.
13. Некратковременный носитель данных по п. 12, в котором одновременная аппроксимация включает:
аппроксимацию давления Pmus(t) дыхательной мускулатуры, параметризированного непрерывной дифференцируемой функцией по указанной области аппроксимации.
14. Некратковременный носитель данных по п. 12, в котором одновременная аппроксимация включает:
аппроксимацию параметров a0, a1, …, an давления Pmus(t) дыхательной мускулатуры, параметризованных в соответствии с полиномиальной аппроксимацией:
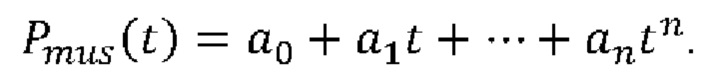
15. Способ оценки давления дыхательной мускулатуры во время дыхания, включающий:
прием измеренных значений давления Py(t) воздуха, вдыхаемого или выдыхаемого вентилируемым пациентом (12);
прием измеренных значений потока 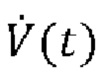 воздуха, проходящего в вентилируемого пациента или выходящего из вентилируемого пациента;
воздуха, проходящего в вентилируемого пациента или выходящего из вентилируемого пациента;
разделение интервала времени дыхания на области (60) аппроксимации и в каждой области аппроксимации решение уравнения:
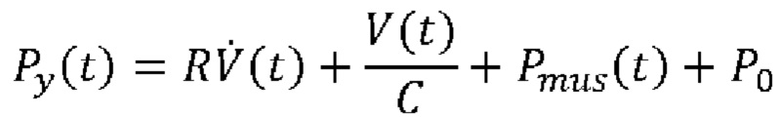
или
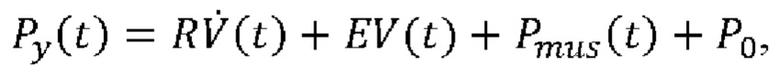
где V(t) выражает чистый объем воздуха, поданный пациенту, вычисленный посредством интегрирования указанного потока 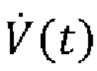 воздуха, Р0 является постоянной, для одновременной оценки сопротивления R и растяжимости С или эластичности Е дыхательной системы и давления Pmus(t) дыхательной мускулатуры в каждой области аппроксимации посредством аппроксимации к временному ряду образцов Py(t) и
воздуха, Р0 является постоянной, для одновременной оценки сопротивления R и растяжимости С или эластичности Е дыхательной системы и давления Pmus(t) дыхательной мускулатуры в каждой области аппроксимации посредством аппроксимации к временному ряду образцов Py(t) и 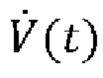 в этой области аппроксимации.
в этой области аппроксимации.
| US2003010339 A1, 16.01.2003 | |||
| US2011237970 A1, 29.09.2011 | |||
| JP2008000436 A, 10.01.2008 | |||
| US2010071696 A1, 25.03.2010 | |||
| АППАРАТ ИСКУССТВЕННОЙ ВЕНТИЛЯЦИИ ЛЕГКИХ С БЫСТРОЙ ОТВЕТНОЙ РЕАКЦИЕЙ НА СОСТОЯНИЕ РЕСПИРАТОРНОГО ЗАБОЛЕВАНИЯ | 2007 |
|
RU2449814C2 |
Авторы
Даты
2020-01-24—Публикация
2016-01-12—Подача