Изобретение относится к вычислительной технике, в частности, к способам контроля, и может быть использовано в опытно-конструкторских работах и практике эксплуатации, где требуется определять оптимальную периодичность контроля сложных объектов.
Ускоряющиеся темпы развития технологий во всех направлениях жизнедеятельности человека приводит к постоянному усложнению окружающих его объектов. Сегодня в повседневную жизнь и хозяйство активно внедряются «умные» вещи, автомобили, дома, заводы – развивается интернет вещей [режим доступа: https://iot.ru/ Дата обращения: 01.12.2019 г.]. Практически в любом виде техники, от телефона и кофемашины до ракеты и сети связи, имеется автоматизированная система управления. Количество и функциональные возможности объектов растут, что снижает их надежность в целом, особенно с учетом внешних деструктивных факторов [Матвеевский В.Р. Надежность технических систем. Учебное пособие – Московский государственный институт электроники и математики. М., 2002 г. – 113 с.]. Поэтому такие сложные объекты требуют своевременного обслуживания и, следовательно, контроля их состояния.
Сложные объекты имеют множество параметров, значения которых определяют их состояние (варианты штатного функционирования, предкритическое, критическое, закритическое состояния и др.). Последствия нахождения сложных объектов, особенно объектов критической инфраструктуры в критическом состоянии, могут иметь разрушающие последствия как для самого объекта, так и для окружающей его среды [режим доступа: https://www.1tv.ru/news/2019-08-04/369823-v_amurskoy_oblasti_nachata_evakuatsiya_lyudey_iz_za_ugrozy_razrusheniya_damby_na_reke_zeya Дата обращения: 01.12.2019 г.]. Это подчеркивает актуальность контроля параметров сложных объектов.
Непрерывный контроль всех параметров сложного объекта требует привлечения больших измерительных и вычислительных ресурсов, а время реакции на изменения параметров и, следовательно, состояния объекта должно быть максимально высоким. Стоимость систем контроля и автоматизации управления объектом в этом случае может быть неприемлема. Поэтому необходима разработка способов определения оптимальной периодичности контроля параметров (состояний) сложных объектов, которые должны учитывать информативность параметров объекта и дестабилизирующих факторов для определения его состояния, взаимосвязи параметров между собой, интенсивность изменения параметров в различных фазах функционирования элементов объекта и объекта в целом, ресурсы системы контроля и автоматизации управления объектом и др.
Из существующего уровня техники известны различные способы, направленные на определение периодичности контроля состояния объектов.
Известен способ определения периодичности контроля оперативного запоминающего устройства при функционировании в радиационных условиях космического пространства на солнечно-синхронной орбите [Патент РФ № 2438163 C1, класс G06F 11/00, опубл. 27.12.2011 г.].
Способ заключается в следующей последовательности действий: оценивают условия функционирования оперативного запоминающего устройства, определяют интенсивность отказов, определяют периодичность контроля. Недостатком данного способа является ограниченная область применения. Кроме того, результаты контроля указывают только на критические значения параметров. Восстановление контролируемого процесса с заданной точностью невозможно.
Известен способ определения оптимальной периодичности контроля состояния технических средств и систем при минимальном времени получения результата [Патент РФ № 2659374 C1, класс G05B 23/00, G06F 19/00, опубл. 29.06.2018].
Способ заключается в том, что в качестве исходных данных задают множество периодических функций аппроксимации, пределы и шаг измерения аппроксимирующих функций, формируют множество данных о времени и характере воздействия различных дестабилизирующих факторов, фиксируют значения параметров дестабилизирующих факторов, разделяют их на однородные группы, аппроксимируют значения параметров дестабилизирующих факторов каждой из однородных групп аппроксимирующими функциями, определяют оптимальный период контроля, задают алгоритмы вычисления аппроксимирующих функций, вычисляют минимально возможную для заданных исходных данных точность аппроксимации, записывают в память ЭВМ результаты измерения, выделяют аппроксимирующую функцию с минимальным временем вычисления, выбирают алгоритм по критерию использования минимального объема памяти, используемой в процессе вычисления алгоритма, вычисляют период следования аппроксимирующей функции, вычисляют значение частоты полученной функции для определения оптимального периода контроля.
Недостатком данного способа является высокая нагрузка на средства контроля и автоматизации управления сложного объекта, обусловленная реализуемым подходом контроля всех параметров в течение всего времени функционирования объекта с периодом контроля, соответствующим наихудшему варианту деструктивных воздействий.
Наиболее близким по своей технической сущности к заявленному является способ определения оптимальной периодичности контроля состояния процессов [патент РФ № 2623791 C1, G06F 19/00, G05B 23/00, опубл. 29.06.2017 г.].
В способе-прототипе определения оптимальной периодичности контроля оценивают условия функционирования объекта контроля, определяют интенсивность отказов, задают в качестве элементов исходных данных множество аппроксимирующих функций, удовлетворяющих заданным требованиям, задают точность аппроксимации, пределы и шаг изменения параметров аппроксимирующих функций, формируют множество данных о времени и характере воздействия различных дестабилизирующих факторов, фиксируют их и разделяют на однородные группы, аппроксимируют значения параметров дестабилизирующих факторов каждой из однородных групп аппроксимирующими функциями с заданной точностью, определяют частоту каждой полученной функции, строят вариационный ряд значений частот всех полученных функций, определяют наибольшее значение частоты, определяют оптимальный период контроля.
Недостатком способа-прототипа является высокая нагрузка на средства контроля и автоматизации управления сложного объекта, обусловленная реализуемым подходом контроля параметров по наихудшему варианту деструктивных воздействий в течение всего времени функционирования объекта.
Технической проблемой, на решение которой направлено предлагаемое решение, является высокая нагрузка на средства контроля и автоматизации управления сложного многопараметрического объекта, что ведет к задержкам восстановления при его сбоях и усложнению средств контроля и автоматизации управления.
Техническая проблема решается за счет последовательного и обоснованного определения перечня и оптимальной периодичности контроля базовых параметров сложного объекта, достаточных для контроля с сохранением степени информированности о его состоянии.
Техническим результатом заявленного способа является снижение нагрузки на средства контроля и автоматизации управления сложного объекта за счет минимизации количества измеряемых параметров с сохранением степени информированности о состоянии сложного объекта и определения оптимальной периодичности контроля этих параметров в различных фазах функционирования объекта.
Технический результат достигается тем, что в известном способе определения оптимальной периодичности контроля состояния сложного объекта, заключающийся в том, что оценивают условия функционирования сложного объекта, задают множество аппроксимирующих функций, удовлетворяющих заданным требованиям, точность аппроксимации εтр, пределы и шаг изменения параметров аппроксимирующих функций, дополнительно задают N состояний сложного объекта, M параметров, которые определяют его состояние, R возможных дестабилизирующих факторов и K характеризующих их параметров, время tоц, в течение которого проводится оценка условий и процесса функционирования сложного объекта и период ∆t проверки M параметров сложного объекта, оценивают процесс функционирования сложного объекта, для чего измеряют и запоминают значения M параметров сложного объекта в течение tоц, при этом в течение tоц объект должен находится к каждом из N возможных состояний под воздействием K дестабилизирующих факторов, определяют взаимозависимости M параметров сложного объекта между собой, определяют перечень базовых L параметров, позволяющих вычислить остальные H параметры, аппроксимируют значения каждого из L параметров сложного объекта множеством аппроксимирующих функций с заданной точностью εтр, рассчитывают оптимальный период контроля каждой аппроксимирующей функции каждого из L параметров.
Из уровня техники не выявлено решений, касающихся способов определения периодичности контроля сложных объектов, характеризующихся заявленной совокупностью признаков, что, следовательно, указывает на соответствие заявленного способа условию патентоспособности «новизна».
Результаты поиска известных решений в данной и смежной областях техники с целью выявления признаков, совпадающих с отличительными от прототипов признаками заявленного изобретения, показали, что они не следуют явным образом из уровня техники. Из определенного заявителем уровня техники не выявлена известность влияния предусматриваемых существенными признаками заявленного изобретения на достижение указанного технического результата. Следовательно, заявленное изобретение соответствует условию патентоспособности «изобретательский уровень».
«Промышленная применимость» способа обусловлена наличием элементной базы, на основе которой могут быть выполнены устройства, реализующие способ.
Заявленный способ поясняется чертежами, на которых показаны:
фиг. 1 – обобщенная блок-схема способа определения оптимальной периодичности контроля состояния сложного объекта;
фиг. 2 – блок-схема способа определения оптимальной периодичности контроля состояния сложного объекта;
фиг. 3 – обобщенная схема измерения сложного объекта;
фиг. 4 – структура модельного времени оценки сложного объекта;
фиг. 5 – примеры аппроксимации значений m-го параметра сложного объекта аппроксимирующими функциями вида 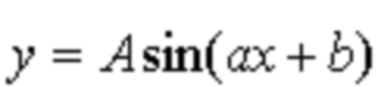 .
.
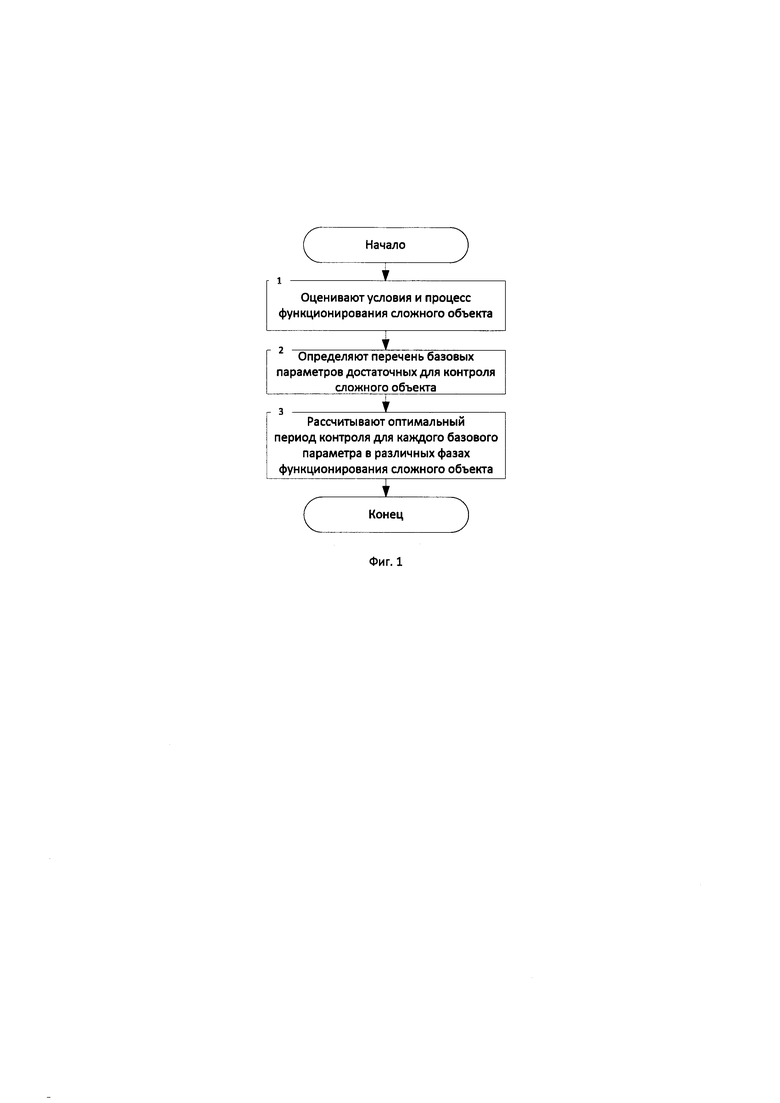
Основные этапы способа определения оптимальной периодичности контроля состояния сложного объекта представлены на фиг.1.
В блоке 1 оценивают условия и процесс функционирования сложного объекта в течение времени, достаточного для сбора данных об объекте во всех возможных состояниях под воздействием всех возможных дестабилизирующих факторов. При этом при осуществлении оценки условий функционирования сложного объекта формируют множество данных о времени и характере воздействия различных K дестабилизирующих факторов путем измерения значений соответствующих R параметров, записи значений
в ПЗУ ЭВМ [патент РФ № 2623791 C1, G06F 19/00, G05B 23/00, опубл. 29.06.2017 г.]; при оценке процесса функционирования сложного объекта измеряют и осуществляют запись в ПЗУ ПЭВМ значения M параметров непосредственно самого сложного объекта.
В блоке 2 определяют перечень базовых L параметров достаточных для контроля сложного объекта, т.е. из всех параметров определяют наиболее информативные – достаточные для контроля сложного объекта базовые параметры, контроль характеристик которых позволяет вычислить все остальные параметры сложного объекта.
В блоке 3 рассчитывают оптимальный период контроля для каждого базового параметра в различных фазах функционирования сложного объекта. Для этого полученные по результатам набора статистики характеристики каждого базового параметра аппроксимируют множеством заданных гармонических аппроксимирующих функций с заданной точностью. При этом время аппроксимации каждой функцией должно соответствовать отдельной фазе функционирования сложного объекта по данному параметру; аппроксимирующие функции должны меняться при нарушении требований к точности аппроксимации. Далее для каждой фазы функционирования определяется период контроля в соответствии с частотой аппроксимирующей функции.
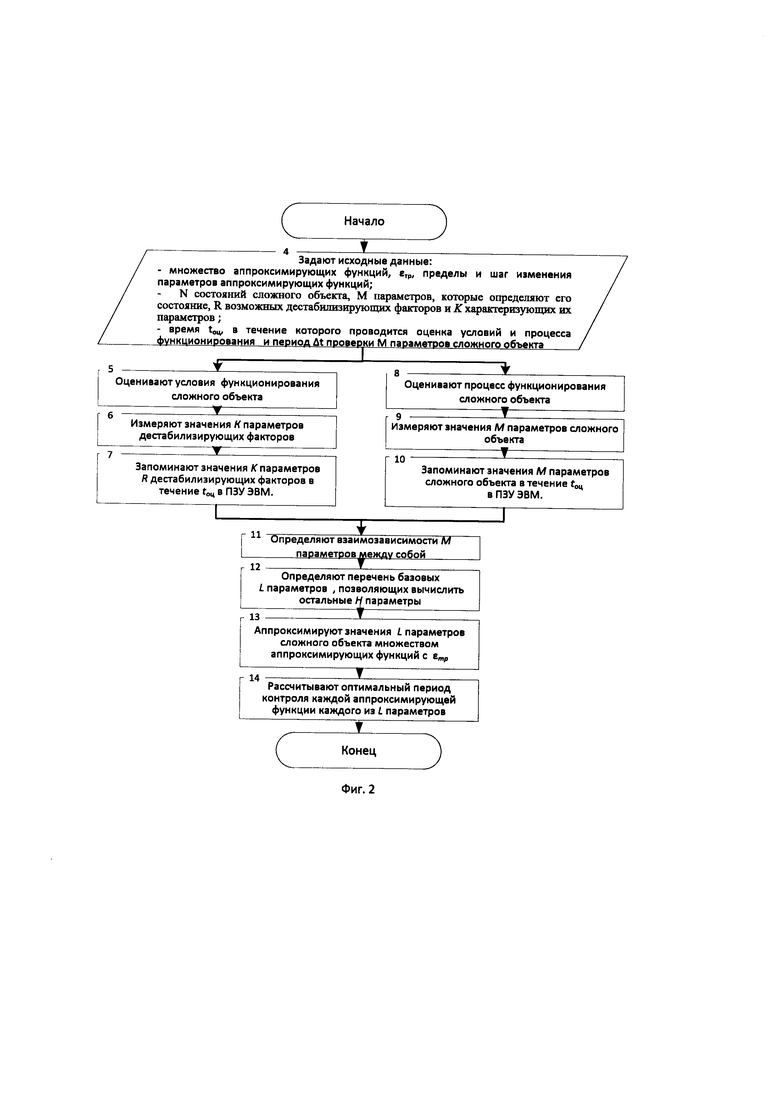
Заявленный способ реализован в виде блок-схемы, представленной на фиг. 2.
В блоке 4 фиг. 2 предварительно задают в качестве исходных данных:
– множество аппроксимирующих функций, удовлетворяющим заданным требованиям (а именно, функции должны быть гармоническими);
– точность аппроксимации εтр, которая определяет возможность применения гармонических функций для аппроксимации характеристики параметра сложного объекта на временном промежутке, а также является критерием для смены аппроксимирующей функции при аппроксимации характеристики параметра в целом [В.И.Смирнов. Курс высшей математики, Т.2.: Изд-во "Наука". 1974. – 479 с., стр. 435-451; Савельев И. В. Курс общей физики, т. 1. Механика. Молекулярная физика: Учебное пособие. – 2-е изд., перераб. – М.: Наука. Главная редакция физико-математической литературы, 1982. – 432 с., стр. 190-195];
– пределы и шаг изменения параметров аппроксимирующих функций [В.И.Смирнов. Курс высшей математики, Т.2.: Изд-во "Наука". 1974. – 479 с., стр. 435-451; Савельев И. В. Курс общей физики, т. 1. Механика. Молекулярная физика: Учебное пособие. – 2-е изд., перераб. – М.: Наука. Главная редакция физико-математической литературы, 1982. – 432 с., стр. 190-195];
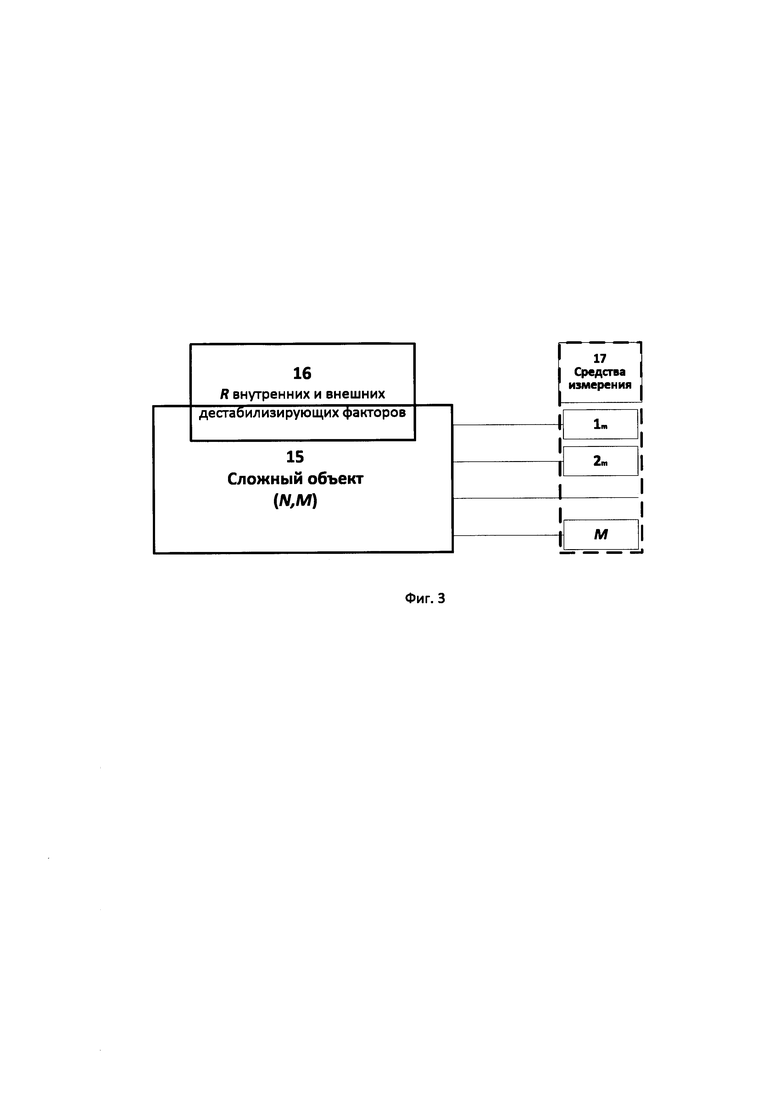
– N состояний сложного объекта и M параметров (бл. 17, фиг. 3), характеризующих его состояние; задание состояний и параметров сложных объектов возможно исходя из результатов их моделирования, проектирования и производства, а также исходя из опыта их эксплуатации; при этом значения параметров сложного объекта должны определять состояние, в котором он находится [например: сложный объект – сеть связи; состояния – выключена, функционирует штатно, функционирует в час наибольшей нагрузки, функционирует под предкритической нагрузкой, находится в критическом состоянии (возможно восстановление), находится в закритическом состоянии (невозможно восстановление); тогда параметрами, характеризующими ее состояние могут выступать пропускная способность, задержка передачи информации, уровень деградации оптического волокна, загруженность вычислительного ресурса автоматизированной системы управления и др. ];
– R возможных внутренних и внешних дестабилизирующих факторов и K характеризующих их параметров (бл. 16, фиг. 3). Например, дестабилизирующим фактором для сети электросвязи является физический или технологический процесс внутреннего или внешнего по отношению к сети электросвязи характера, приводящее к выходу из строя элементов сети [ГОСТ Р 53111-2008: Устойчивость функционирования сети связи общего пользования. Требования и методы проверки]. Согласно [ГОСТ Р 53111-2008: Устойчивость функционирования сети связи общего пользования. Требования и методы проверки] воздействие дестабилизирующих факторов на сети электросвязи разделяется на воздействие внутренних и внешних дестабилизирующих факторов. Под внешними дестабилизирующими факторами по отношению к сети электросвязи понимаются такие дестабилизирующие факторы, источники которых расположены вне сети электросвязи. В зависимости от характера воздействия на элементы сети электросвязи внешние дестабилизирующие факторы делятся на классы: механические (сейсмический удар, ударная волна взрыва, баллистический удар); электромагнитные (низкочастотное излучение, высокочастотное излучение, сверхвысокочастотное излучение, электромагнитный импульс); ионизирующие (альфа-излучение, бета-излучение, гамма-излучение, нейтронное излучение); термические (световое излучение взрыва). Под внутренними дестабилизирующими факторами по отношению к сети электросвязи понимаются дестабилизирующие факторы, источники воздействия которых находятся внутри сети электросвязи и имеется достаточная информация о характеристиках их воздействий, позволяющая принимать эффективные решения по их локализации и проведению соответствующих профилактических и ремонтно-восстановительных мероприятий на всех этапах, от разработки и производства средств электросвязи до проектирования и эксплуатации сетей электросвязи. Наиболее распространенными источниками внутренних дестабилизирующих факторов являются: качество электрических контактов; старение электро-радиоэлементов (изменение со временем их характеристик); нарушение электромагнитной совместимости (нарушение экранирования, заземлений, фильтрации) и, вследствие этого, ухудшение устойчивости оборудования электросвязи к воздействию электромагнитных помех; перебои в электроснабжении. Параметрами, характеризующими дестабилизирующий фактор, могут выступать: например, для сейсмической волны (механические внешние дестабилизирующие факторы) - амплитуда волны, ее скорость (ускорение), продолжительность импульса (число фаз в импульсе) и т.д. [Геологический словарь. Т.2. М.: Недра, 1973. - 456 с., стр. 135]; для электромагнитного импульса (электромагнитные внешние дестабилизирующие факторы) - изменения напряженностей электрического и магнитного полей во времени (форма импульса) и их ориентация в пространстве, а также величина максимальной напряженности поля (амплитуда импульса) [Электромагнитный импульс. Электронный ресурс www://http://gochs.info/p0967.htm. Дата последнего обращения 08.12.2019; Лоборев В.М. (ред.) Физика ядерного взрыва. Том 1. М.: Наука, 1997. - 528 с., стр.85 - 120], основными параметрами электромагнитных излучений – частота, напряженность электрического и магнитного полей [Богуш В.А., Торботько Т.В., Гусинский А.В и др. Электромагнитные излучения методы и средства защиты. Под ред. Л. М. Лынькова. - Мн.: Бестпринт, 2003. - 406 с., стр. 11- 54] и т.д.
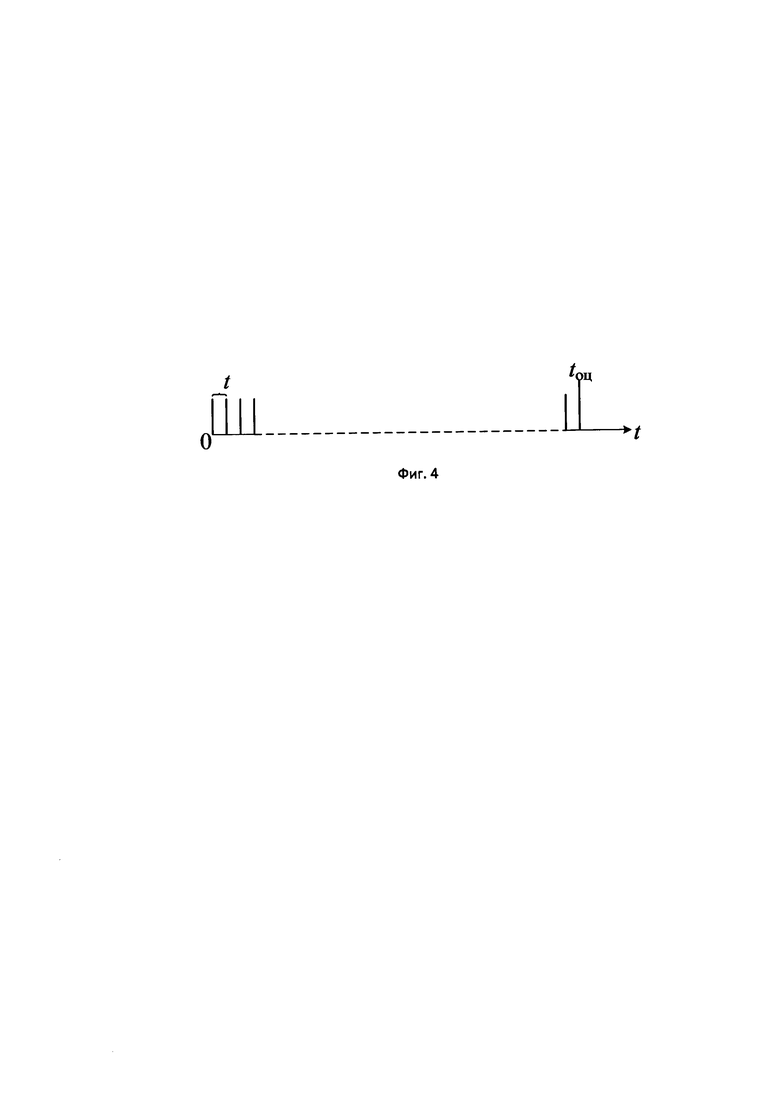
– время tоц, в течение которого проводится оценка условий и процесса функционирования сложного объекта (фиг. 4), при этом в течение tоц объект должен находится к каждом из N возможных состояний под воздействием R дестабилизирующих факторов; например, оценка сложного объекта – самолета, проводимая согласно отраслевого стандарта (ОСТ) в течение tоц, установленной программой и методиками испытаний, в ходе которой самолет подвергается всем возможным деструктивным воздействиям внутреннего и внешнего характера (попадание молнии, град, боковой ветер, выход из строя узлов и агрегатов и др.) в различных состояниях (разгон по взлетной полосе, посадка, набор высоты, автоматическое и ручное управление и т.д.) [режим доступа: https://rg.ru/2016/12/07/kak-ispytyvali-rossijskij-lajner-sukhoi-superjet.html. Дата обращения: 01.12.2019 г.].
– период ∆t проверки M параметров сложного объекта (фиг. 4); на этапе оценки может задаваться наихудший случай, определяемый согласно [патент РФ № 2623791 C1, G06F 19/00, G05B 23/00, опубл. 29.06.2017 г.].
Исходные данные могут быть заданы путем их записи в постоянное запоминающее устройство (ПЗУ) электронно-вычислительной машины (ЭВМ).
В блоке 5 фиг. 2 оценивают условия функционирования сложного объекта. При этом при осуществлении оценки условий функционирования сложного объекта формируют множество данных о времени и характере воздействия различных R дестабилизирующих факторов (бл.16 фиг. 3) путем измерения значений соответствующих K параметров (бл. 17 фиг. 3), записи их в ПЗУ ЭВМ в течение времени оценки tоц (бл. 6, 7 фиг. 2) [патент РФ № 2623791 C1, G06F 19/00, G05B 23/00, опубл. 29.06.2017 г.].
В блоке 8 фиг. 2 оценивают процесс функционирования сложного объекта, для чего:
В блоке 9 фиг. 2 измеряют значения M параметров сложного объекта в течение tоц. При этом в течение tоц объект должен находится к каждом из N возможных состояний под воздействием R дестабилизирующих факторов
Для измерения параметров могут использоваться как отдельные средства измерения (бл. 17, фиг. 3), так и измерительные комплексы. Так, для волоконно-оптической системы передачи используются: рефлектометр для измерения характеристик линейного тракта (оптического волокна) [режим доступа: https://skomplekt.com/solution/reflekt.htm/. Дата обращения: 01.12.2019 г.], когерентные измерители рассеянных сигналов для поиска виброакустических (деструктивных) воздействий на оптический кабель и повреждений [режим доступа: https://t8-sensor.ru/, https://fibertop.ru/poisk_i_ustranenie_neispravnostey_na_vols_s_pom_reflectometra_930XC.htm/ . Дата обращения: 01.12.2019 г.], микроскоп для определения качества торцов оптического волокна [режим доступа: https://skomplekt.com/tovar/1/1/52/. Дата обращения: 01.12.2019 г.], измерители оптической мощности для определения параметров сигнала [режим доступа: https://skomplekt.com/solution/optm.htm/. Дата обращения: 01.12.2019 г.], анализаторы транспортных сетей для тестирования канального оборудования [режим доступа: https://skomplekt.com/tovar/1/3/31/. Дата обращения: 01.12.2019 г.] и т.д.
В блоке 10 фиг. 2 запоминают значения M параметров сложного объекта в течение tоц в ПЗУ ЭВМ.
В блоке 11 фиг. 2 определяют взаимозависимости M параметров между собой. Получение взаимозависимостей, например, возможно на основе корреляционного анализа с получением различных корреляционных коэффициентов (линейный, множественный, ранговый Спирмена, ранговый Кендалла и т.д.) между различными параметрами [Гмурман В. Е. Теория вероятностей и математическая статистика: Учебное пособие для вузов. - 10-е издание, стереотипное. - Москва: Высшая школа, 2004. - 479 с.; Елисеева И. И., Юзбашев М. М. Общая теория статистики: Учебник / Под ред. И. И. Елисеевой. - 4-е издание, переработанное и дополненное. - Москва: Финансы и Статистика, 2002. - 480 с.]. При этом часть взаимозависимостей параметров может быть известна.
Определение взаимозависимости M параметров между собой возможно при помощи известных программных средств, например Statistica, MicroSoft Excel, SPSS, позволяющие выполнить корреляционный анализ на ЭВМ [Бараз В.Р. Корреляционно-регрессионный анализ связи показателей коммерческой деятельности с использованием программы Excel : учебное пособие / В.Р. БАРАЗ. – Екатеринбург : ГОУ ВПО «УГТУ–УПИ», 2005. – 102 с., стр. 1- 102; Расчет коэффициента корреляции в SPSS. Электронный ресурс: https://statpsy.ru/correlation/correlation-spss/. Дата обращения 23.12.2019 г.].
В блоке 12 фиг. 2 определяют перечень базовых L параметров, позволяющих вычислить остальные H параметры, при этом M ≤ L + H.
Перечень базовых параметров должен быть достаточен для вычисления остальных, не вошедших в перечень, параметров и, одновременно, не быть избыточным, т.е. при выполнении условия, при котором, если при определении L базовых параметров посредством измерений и вычислений контролируются все параметры сложного объекта из множества M, недопустимо измерять остальные вычисляемые параметры (т.е. увеличивать нагрузку на средства контроля и автоматизации управления сложного объекта). К базовым относят параметры с максимальной информативностью – параметры, установленные взаимосвязи которых (блок 11, фиг. 2) позволяют вычислить максимальное количество других параметров). В этих целях строят вариационный ряд параметров в соответствии с количеством вычисляемых взаимосвязей с другими параметрами и выбирают минимальное, достаточное для вычисления остальных параметров, количество старших членов вариационного ряда [Вариационные ряды и их характеристики / И.Г. Венецкий. М.: Статистика, 1970 – 160 с.; Теория вероятностей / Е.С. Вентцель. М.: Государственное издательство физико-математической литературы, 1962 – 564 с.]. Вариационный ряд может быть построен по известным алгоритмам при помощи ЭВМ.
В блоке 13 фиг. 2 аппроксимируют значения каждого из L параметров сложного объекта множеством аппроксимирующих функций с заданной точностью εтр.
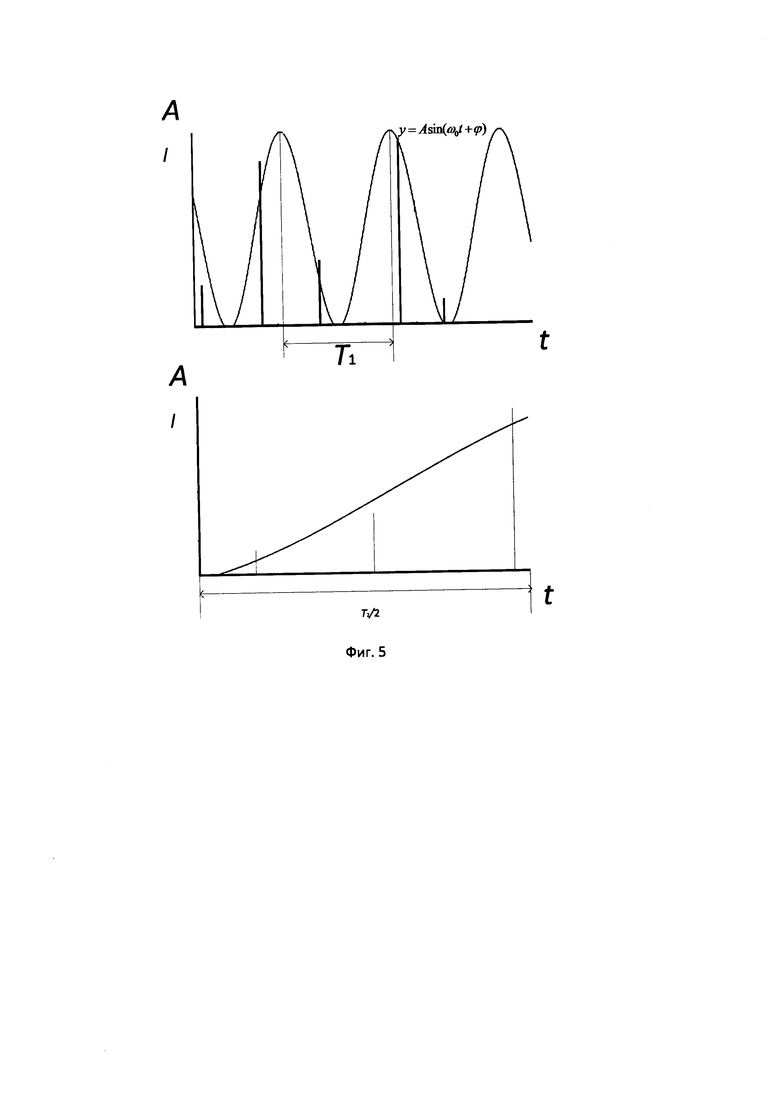
Полученные значения параметров аппроксимируют с заданной точностью εтр непрерывными периодическими функциями (например, простыми гармоническими кривыми вида 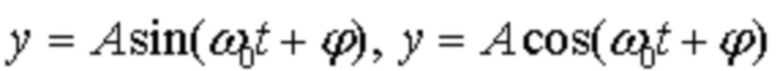 , где A – амплитуда колебания,
, где A – амплитуда колебания, 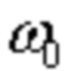 - круговая (циклическая) частота,
- круговая (циклическая) частота, 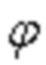 - начальная фаза колебания [В.И.Смирнов Курс высшей математики, Т.1.: Изд-во «Наука». 1974. - 479 с., стр. 43 – 48; Сканави М.И. Элементарная математика. 2-е изд., перераб. и доп., М.: 1974г. – 592 с., стр. 273 – 338; Энциклопедический словарь юного математика/Сост. Э-68 А. П. Савин. – М.: Педагогика, 1989. - 352 с., стр. 301 – 305; В.И.Смирнов. Курс высшей математики, Т.2.: Изд-во «Наука». 1974. – 479 с., стр. 435 – 451; Савельев И. В. Курс общей физики, т. 1. Механика. Молекулярная физика: Учебное пособие. – 2-е изд., перераб. – М.: Наука. Главная редакция физико-математической литературы, 1982. – 432 с., стр. 190-195] и др., удовлетворяющими заданным требованиям (бл. 2.1 фиг. 2)). На фиг. 5 представлен пример аппроксимации значений параметра Аl функциями вида
- начальная фаза колебания [В.И.Смирнов Курс высшей математики, Т.1.: Изд-во «Наука». 1974. - 479 с., стр. 43 – 48; Сканави М.И. Элементарная математика. 2-е изд., перераб. и доп., М.: 1974г. – 592 с., стр. 273 – 338; Энциклопедический словарь юного математика/Сост. Э-68 А. П. Савин. – М.: Педагогика, 1989. - 352 с., стр. 301 – 305; В.И.Смирнов. Курс высшей математики, Т.2.: Изд-во «Наука». 1974. – 479 с., стр. 435 – 451; Савельев И. В. Курс общей физики, т. 1. Механика. Молекулярная физика: Учебное пособие. – 2-е изд., перераб. – М.: Наука. Главная редакция физико-математической литературы, 1982. – 432 с., стр. 190-195] и др., удовлетворяющими заданным требованиям (бл. 2.1 фиг. 2)). На фиг. 5 представлен пример аппроксимации значений параметра Аl функциями вида 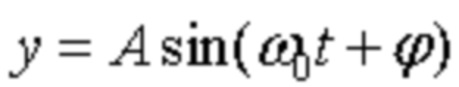 в различных фазах функционирования сложного объекта по l-му параметру.
в различных фазах функционирования сложного объекта по l-му параметру.
Согласно [Савельев И. В. Курс общей физики, т. 1. Механика. Молекулярная физика: Учебное пособие. – 2-е изд., перераб. – М.: Наука. Главная редакция физико-математической литературы, 1982. – 432 с., стр. 190-195], поскольку косинус (синус) – периодическая функция с периодом 2π, ее период T может быть определен как 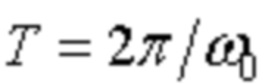 .
.
Число колебаний в единицу времени называется частотой колебания f. Очевидно, что частота f связана с продолжительностью одного колебания Т следующим соотношением: 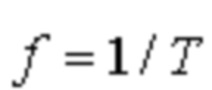 .
.
Аппроксимация – это представление сложных функций s(x) или дискретных выборок из этих функций s(xi) простыми и удобными для практического использования функциями аппроксимации f(x) таким образом, чтобы отклонение f(x) от s(x) в области ее задания было наименьшим по определенному критерию приближения [Давыдов А.В. Цифровая обработка сигналов. Лекции и практикум на ПК. Тема 14. Аппроксимация сигналов и функций. Режим доступа: http://www.geoin.org/dsp/dsp14.htm. Дата обращения: 01.12.2019 г.].
Точность аппроксимации εтр может оцениваться различными критериями приближения [Андреев В.С. Теория нелинейных электрических цепей: Учебное пособие для ВУЗов. – М.: Радио и связь, 1982. – 280 с., стр. 40; Калиткин Н. Н. Численные методы. - М.: Наука, 1978. - 512 стр., стр. 51 - 69].
Наибольшее распространение имеют:
– среднеквадратичное приближение, при котором требуют, чтобы среднее значение квадрата отклонения аппроксимирующей зависимости 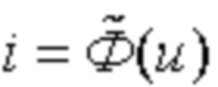 от действительной
от действительной 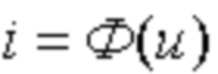 не превышало некоторой допустимой величины δ:
не превышало некоторой допустимой величины δ:
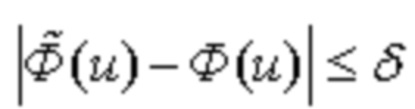
в интервале 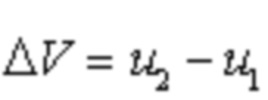 значений u, в пределах которого производится аппроксимация;
значений u, в пределах которого производится аппроксимация;
– равномерное приближение, при котором требуют, чтобы при любом значении u интервала 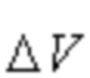 величина отклонения
величина отклонения 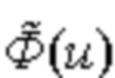 от
от 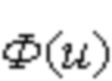 не превышало δ, т.е.
не превышало δ, т.е.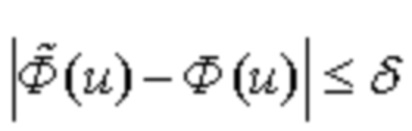 .
.
Точности аппроксимации и множество аппроксимирующих функций, удовлетворяющих заданным требованиям, задаются в исходных данных (бл. 2.1 фиг. 2).
Согласно [Хандрос М.Я. Тригонометрическая аппроксимация экспериментальных последовательностей. Вычисление естественных спектров. Электронный ресурс http://perviydoc.ru/. Дата обращения 03.12.2019 г.], как правило, достаточно точности аппроксимации – 0,05. Уменьшение допустимой точности приводит к значительному усложнению аппроксимирующей функции.
Алгоритмы нахождения аппроксимирующих функций, в том числе тригонометрических, известны. Например, в [Хандрос М.Я. Тригонометрическая аппроксимация экспериментальных последовательностей. Вычисление естественных спектров. Электронный ресурс http://perviydoc.ru/. Дата обращения 03.12.2019 г.] предлагается следующий многоступенчатый алгоритм нахождения тригонометрического полинома:
– задается допустимая погрешность (точность аппроксимации) ε;
– задаются величины вариаций параметров;
– определяется частота (выбор частоты осуществляется в соответствии с методом статистических испытаний; в заданном интервале генерируется некоторое количество j1 равномерно распределённых случайных чисел. Из этого набора последовательно выбираются частоты);
– для каждой частоты вычисляются вариации для отдельных составляющих;
– выполняется проверка значения критерия.
В результате будет найдена частота и значения составляющих функции, которая обеспечивает минимальную погрешность при аппроксимации.
При нарушении требований к точности аппроксимации для описания значений l-го параметра сложного объекта находят другую аппроксимирующую функцию из заданного множества. Таким образом, значения каждого из L параметров сложного объекта в течение tоц аппроксимируют Gl гармоническими функциями из множества заданных функций аппроксимации, а время аппроксимации каждой функцией соответствует отдельной фазе функционирования сложного объекта по l-му параметру.
В блоке 14 рассчитывают оптимальный период контроля каждой аппроксимирующей функции каждого из L параметров.
После определения всех аппроксимирующих функций, для получения значений оптимального периода контроля каждого из L параметров в каждой фазе, определяют частоты соответствующих аппроксимирующих функций.
Данный этап реализации способа базируется на одном из фундаментальных положений теоретической радиотехники – теореме Котельникова. [Баскаков С.И. Радиотехнические цепи и сигналы. М.: Высшая школа, 2-е издание. – 446 с., стр. 116-117; Теория передачи сигналов: Учебник для вузов/Зюко А. Г., Кловский Д. Д., Назаров М. В., Финк Л. М.— М.: Связь, 1980. — 288 с., стр. 68; Хургин Я.И., Яковлев В.П. Методы теории целых функций в радиофизике, теории связи и оптике. – М., 1962. – 220 с., стр. 107].
Согласно теореме Котельникова, произвольный сигнал, спектр которого не содержит частот выше fв, может быть полностью и однозначно восстановлен, если известны отсчетные значения этого сигнала, взятые через равные промежутки времени 1/(2 fв).
Таким образом, если контроль будет проводиться через промежутки времени, равные отношению Тконтр=1/(2 fв), где fв – наибольшее значение частоты аппроксимирующей функции, то значения параметров контролируемого процесса могут быть однозначно восстановлены на заданном интервале времени. Поскольку все аппроксимирующие функции равномерные и гармонические, то fв = f, где f – частота аппроксимирующей функции.
Согласно выражению Тконтр = 1/(2 f) определяется оптимальный период для осуществления контроля каждого из L параметров в каждой фазе в условиях воздействия различных дестабилизирующих факторов.
Таким образом, за счет минимизации количества измеряемых параметров с сохранением степени информированности о состоянии сложного объекта и определения оптимальной периодичности контроля этих параметров в различных фазах функционирования объекта, снижается вычислительная нагрузка на его средства контроля и автоматизации управления. Технический результат достигнут.
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ контроля многопараметрического объекта | 2021 |
|
RU2764389C1 |
| Способ определения оптимальной периодичности контроля состояния технических средств и систем при минимальном времени получения результата | 2017 |
|
RU2659374C1 |
| СПОСОБ УПРАВЛЕНИЯ СОСТОЯНИЕМ СЛОЖНОГО ОБЪЕКТА | 2020 |
|
RU2748778C1 |
| Способ определения оптимальной периодичности контроля состояния процессов | 2016 |
|
RU2623791C1 |
| Способ мониторинга состояния электрических сетей и сетей связи | 2017 |
|
RU2646321C1 |
| СПОСОБ РЕЗЕРВНОГО КОПИРОВАНИЯ СОСТОЯНИЯ СЛОЖНОГО ОБЪЕКТА | 2020 |
|
RU2726318C1 |
| СПОСОБ ПОВЫШЕНИЯ УСТОЙЧИВОСТИ СЕТИ СВЯЗИ С ПАМЯТЬЮ | 2020 |
|
RU2734103C1 |
| Способ моделирования виртуальной сети | 2020 |
|
RU2741262C1 |
| Способ моделирования оптимального варианта топологического размещения множества информационно взаимосвязанных абонентов на заданном фрагменте сети связи общего пользования | 2018 |
|
RU2690213C1 |
| СПОСОБ ИДЕНТИФИКАЦИИ ЭЛЕМЕНТОВ СЛОЖНОЙ СИСТЕМЫ В ПЕРЕМЕННЫХ УСЛОВИЯХ | 2020 |
|
RU2726027C1 |
Изобретение относится к вычислительной технике, в частности к способам контроля, и может быть использовано в опытно-конструкторских работах и практике эксплуатации, где требуется определять оптимальную периодичность контроля сложных объектов. Технический результат заключается в снижении нагрузки на средства контроля и автоматизации управления сложного объекта. Технический результат достигается за счет минимизации количества измеряемых параметров с сохранением степени информированности о состоянии сложного объекта и определения оптимальной периодичности контроля этих параметров в различных фазах функционирования объекта. 5 ил.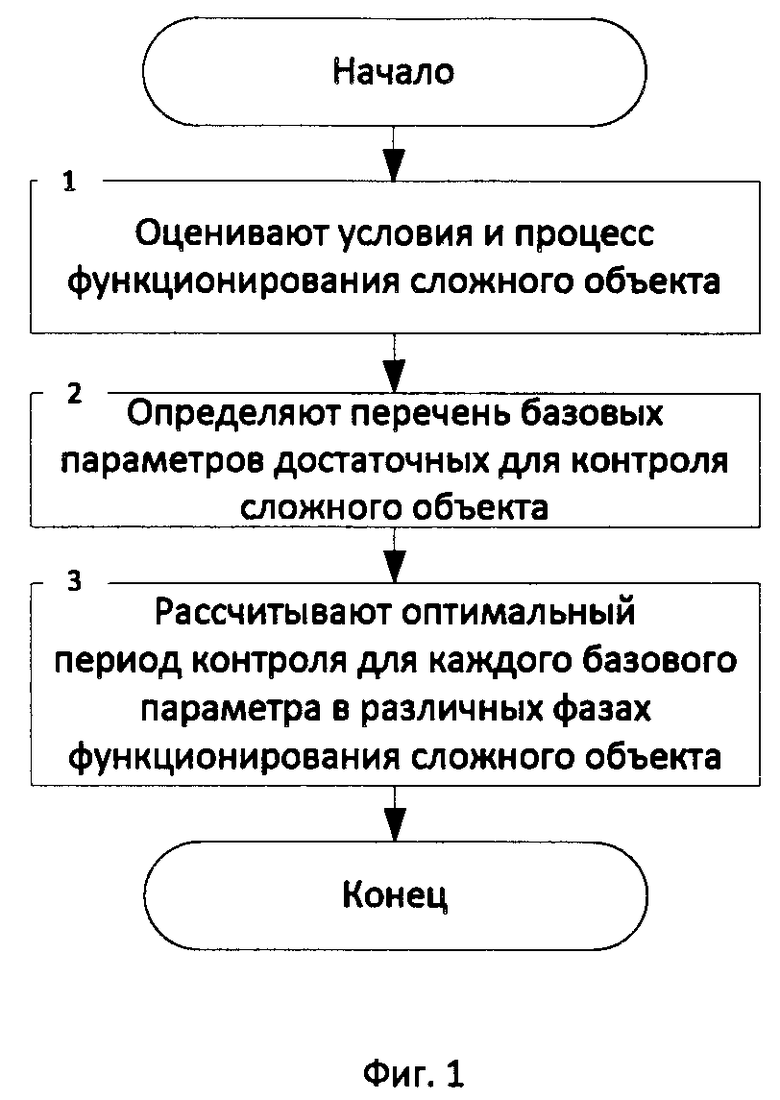
Способ определения оптимальной периодичности контроля состояния сложного объекта, заключающийся в том, что оценивают условия функционирования сложного объекта, задают множество аппроксимирующих функций, удовлетворяющих заданным требованиям, точность аппроксимации εтр, пределы и шаг изменения параметров аппроксимирующих функций, отличающийся тем, что дополнительно задают N состояний сложного объекта, M параметров, которые определяют его состояние, R возможных дестабилизирующих факторов и K характеризующих их параметров, время tоц, в течение которого проводится оценка условий и процесса функционирования сложного объекта и период ∆t проверки M параметров сложного объекта, оценивают процесс функционирования сложного объекта, для чего измеряют и запоминают значения M параметров сложного объекта в течение tоц, при этом в течение tоц объект должен находиться к каждом из N возможных состояний под воздействием K дестабилизирующих факторов, определяют взаимозависимости M параметров сложного объекта между собой, определяют перечень базовых L параметров, позволяющих вычислить остальные H параметры, аппроксимируют значения каждого из L параметров сложного объекта множеством аппроксимирующих функций с заданной точностью εтр, рассчитывают оптимальный период контроля каждой аппроксимирующей функции каждого из L параметров.
| Способ определения оптимальной периодичности контроля состояния процессов | 2016 |
|
RU2623791C1 |
| СПОСОБ КОНТРОЛЯ СОСТОЯНИЯ МНОГОПАРАМЕТРИЧЕСКОГО ОБЪЕКТА | 2007 |
|
RU2373650C2 |
| СПОСОБ КОНТРОЛЯ И ДИАГНОСТИКИ СОСТОЯНИЯ СЛОЖНЫХ ОБЪЕКТОВ | 2016 |
|
RU2641322C2 |
| УСТРОЙСТВО ДЛЯ КОНТРОЛЯ СОСТОЯНИЯ УДАЛЕННЫХ ОБЪЕКТОВ | 1999 |
|
RU2174084C2 |
| US 8725677 B1, 13.05.2014. | |||
Авторы
Даты
2020-03-30—Публикация
2019-12-24—Подача