Изобретение относится к вычислительной технике, в частности, к способам контроля, и может быть использовано в опытно-конструкторских работах и практике эксплуатации, где требуется определять оптимальную периодичность контроля сложных многопараметрических объектов.
Ускоряющиеся темпы развития технологий во всех направлениях жизнедеятельности человека приводит к постоянному усложнению окружающих его объектов. Сегодня в повседневную жизнь и хозяйство активно внедряются «умные» вещи, автомобили, дома, заводы – развивается интернет вещей [режим доступа: https://iot.ru/ Дата обращения: 01.12.2019 г.]. Практически в любом виде техники, от телефона и кофемашины до ракеты и сети связи, имеется автоматизированная система управления. Количество и функциональные возможности объектов растут, что снижает их надежность в целом, особенно с учетом внешних деструктивных факторов [Матвеевский В.Р. Надежность технических систем. Учебное пособие – Московский государственный институт электроники и математики. М., 2002 г. – 113 с.]. Поэтому такие сложные объекты требуют своевременного обслуживания и, следовательно, контроля их состояния.
Сложные объекты имеют множество параметров, значения которых определяют их состояние (варианты штатного функционирования, предкритическое, критическое, закритическое состояния и др.). Последствия нахождения сложных объектов, особенно объектов критической инфраструктуры в критическом состоянии, могут иметь разрушающие последствия как для самого объекта, так и для окружающей его среды [режим доступа: https://www.1tv.ru/news/2019-08-04/369823-v_amurskoy_oblasti_nachata_evakuatsiya_lyudey_iz_za_ugrozy_razrusheniya_damby_na_reke_zeya Дата обращения: 01.12.2019 г.]. Это подчеркивает актуальность контроля параметров сложных объектов.
В настоящее время для контроля и диспетчеризации состояния сложных объектов применяется два подхода [1. ГОСТ Р МЭК 60870-5-1-95 Устройства и системы телемеханики. Часть5. Протоколы передачи. Раздел 1. Форматы передаваемых кадров. 2.ГОСТ Р МЭК 60870-5-104-2004 Устройства и системы телемеханики. Часть5. Протоколы передачи. Раздел104. Доступ к сети для ГОСТ Р МЭК 870-5-101 с использованием стандартных транспортных профилей. 3. IEC 61850-5 Communication networks and system sinsubstations-Part5: Communication requirements for functions and device models. 4. IEC 61850-7-2 Communication networks and systems in substations-Part7-2: Basic communication structure for substation and feeder equipment-Abstract communication service interface(ACSI)]:
- непрерывная передача данных о состоянии объекта с заданным периодом обновления, при этом данные содержат значения измеряемого параметра и содержат или не содержат метку времени;
- формирование событий при обнаружении изменения состояния объекта (выход измеряемого значения за заданный порог, изменение текущего измеряемого значения относительно предыдущего на заданную величину и т.п.), при этом события содержат значения измеряемого параметра и метку времени события.
Первый подход позволяет получить высокую степень детализации измеряемых параметров. Однако непрерывный контроль всех параметров сложного объекта требует привлечения больших измерительных и вычислительных ресурсов, что приводит к увеличению времени реакции на изменения параметров объекта. Данные о результатах контроля обладают большой избыточностью. Следовательно, объем передаваемых данных о результатах измерений требует наличия канала связи с объектом контроля с достаточно высокой пропускной способностью. Стоимость систем контроля и автоматизации управления объектом в этом случае может быть неприемлема.
Второй подход обеспечивает обнаружение изменений состояния объекта при уменьшении, по сравнению с первым подходом, объема данных с объекта контроля, но обладает низкой степенью детализации измеряемых параметров, вплоть до пропуска быстро протекающих процессов.
Следовательно, необходима разработка способов контроля сложных многопараметрических объектов, которые позволят обеспечить требуемый уровень информированности о состоянии объекта, а также восстановление контролируемого процесса с заданной точностью при уменьшении количества измерений, а, следовательно, и сокращении ресурсов (сил и средств), затрачиваемых на контроль.
Из существующего уровня техники известны различные способы контроля состояния объектов.
Так, известен способ непрерывного пассивного контроля параметров телефонных линий, реализованный в устройстве типа ЛСТ-1007 [Лысов А.В. Телефон и безопасность. Проблемы защиты информации в телефонных сетях / А.В. Лысов, А.Н. Остапенко. - СПб.: Политехника, 1995. - 109 с. (Лаборатория ППШ)], при котором предварительно проверяют телефонную линию на отсутствие повреждений и несанкционированных подключений, задают контролируемые параметры телефонной линии, измеряют контролируемые параметры, запоминают их в качестве эталонов, непрерывно измеряют и сравнивают текущие значения контролируемых параметров с эталонными, формируют сигнал тревоги при несовпадении измеренных значений параметров с эталонными, продолжают измерения при их совпадении с эталонными значениями контролируемых параметров.
Недостатками данного способа являются низкая экономическая эффективность системы контроля, обусловленная значительными временными и материальными затратами (контроль ведется непрерывно), а также необходимость наличия канала связи с объектом контроля с достаточно высокой пропускной способностью, что ограничивает область применения способа.
Известны также способы контроля состояния объектов, включающих большое число контролируемых параметров [Патент РФ № 2210112 C2 «Унифицированный способ Чернякова/Петрушина для оценки эффективности больших систем», класс G06F 17/00, опубл. 10.08.2003; Патент РФ № 2364926 С2, класс G06F 17/00, опубл. 20.08.2009 г.]. Способы основаны на представлении большой системы в виде иерархии ее структурных элементов, задании контролируемых параметров и осуществлении их периодического контроля. Однако значение периода контроля в данных способах не определяется, что приводит к невысокой точности и оперативности оценки состояния объекта контроля. Кроме того, состояние объекта контроля определяют по значениям показателей состояния, при вычислении которых используются предварительно заданные на эмпирическом уровне неизменные весовые коэффициенты, что также оказывает негативное влияние на точность, достоверность оценки состояния объекта контроля и ограничивает область применения способов.
Известен способ определения периодичности контроля оперативного запоминающего устройства при функционировании в радиационных условиях космического пространства на солнечно-синхронной орбите [Патент РФ № 2438163 C1, класс G06F 11/00, опубл. 27.12.2011 г.].
Способ заключается в следующей последовательности действий: оценивают условия функционирования оперативного запоминающего устройства, определяют интенсивность отказов, определяют периодичность контроля. Недостатком данного способа является ограниченная область применения. Кроме того, результаты контроля указывают только на критические значения параметров. Восстановление контролируемого процесса с заданной точностью невозможно.
Известен способ определения оптимальной периодичности контроля состояния процессов [Патент 2623791 Российская Федерация, МПК G05B 23/00 (2006.01), G06Q 10/04 (2012.01). Способ определения оптимальной периодичности контроля состояния процессов / Синев С.Г., Сорокин М.А., Стародубцев П.Ю., Сухорукова Е.В.; заявитель и патентообладатель Стародубцев П.Ю.– 2015108734; заявл. 25.01.2016; опубл 29.06.2017, бюл. № 19. – 13 с.]. В способе определения оптимальной периодичности контроля оценивают условия функционирования объекта контроля, определяют интенсивность отказов, задают в качестве элементов исходных данных множество аппроксимирующих функций, удовлетворяющих заданным требованиям, задают точность аппроксимации, пределы и шаг изменения параметров аппроксимирующих функций, формируют множество данных о времени и характере воздействия различных дестабилизирующих факторов, фиксируют их и разделяют на однородные группы, аппроксимируют значения параметров дестабилизирующих факторов каждой из однородных групп аппроксимирующими функциями с заданной точностью, определяют частоту каждой полученной функции, строят вариационный ряд значений частот всех полученных функций, определяют наибольшее значение частоты, определяют оптимальный период контроля.
Недостатком способа является высокая нагрузка на средства контроля и автоматизации управления сложного объекта, обусловленная реализуемым подходом контроля параметров по наихудшему варианту деструктивных воздействий в течение всего времени функционирования объекта.
Известен способ определения оптимальной периодичности контроля состояния технических средств и систем при минимальном времени получения результата [Патент 2659374 Российская Федерация, G05B 23/00, G06F 19/00. Способ определения оптимальной периодичности контроля состояния технических средств и систем при минимальном времени получения результата/ Алашеев В.В., Вершенник А.В., Вершенник Е.В., Карпов А.В., Латушко Н.А., Чеснаков М.Н., Стародубцев Ю.И.,; заявитель и патентообладатель Алашеев В.В., Вершенник А.В., Карпов А.В., Латушко Н.А., Чеснаков М.Н. – 2017137312; заявл. 24.10.2017; опубл 29.06.2018. бюл. № 19 – 14 с.].
Способ заключается в том, что в качестве исходных данных задают множество периодических функций аппроксимации, пределы и шаг измерения аппроксимирующих функций, формируют множество данных о времени и характере воздействия различных дестабилизирующих факторов, фиксируют значения параметров дестабилизирующих факторов, разделяют их на однородные группы, аппроксимируют значения параметров дестабилизирующих факторов каждой из однородных групп аппроксимирующими функциями, определяют оптимальный период контроля, задают алгоритмы вычисления аппроксимирующих функций, вычисляют минимально возможную для заданных исходных данных точность аппроксимации, записывают в память ЭВМ результаты измерения, выделяют аппроксимирующую функцию с минимальным временем вычисления, выбирают алгоритм по критерию использования минимального объема памяти, используемой в процессе вычисления алгоритма, вычисляют период следования аппроксимирующей функции, вычисляют значение частоты полученной функции для определения оптимального периода контроля.
Недостатком данного способа является высокая нагрузка на средства контроля и автоматизации управления сложного объекта, обусловленная реализуемым подходом контроля всех параметров в течение всего времени функционирования объекта с периодом контроля, соответствующим наихудшему варианту деструктивных воздействий.
Наиболее близким по технической сущности к заявленному способу и принятому за прототип является способ определения оптимальной периодичности контроля состояния сложного объекта [Патент 2718152 Российская Федерация, G06F 17/10 (2006.01), G05B 23/00 (2006.01). Способ определения оптимальной периодичности контроля состояния сложного объекта / Стародубцев Ю.И., Иванов С.А., Вершенник Е.В., Вершенник А.В., Закалкин П.В., Шевчук А.Л., Карасенко А.О. – 2019143358; заявл. 24.12.2019; опубл. 30.03.2020. бюл. № 10 – 19 с.]. Способ заключается в том, что оценивают условия функционирования сложного объекта, задают множество аппроксимирующих функций, удовлетворяющих заданным требованиям, точность аппроксимации εтр, пределы и шаг изменения параметров аппроксимирующих функций, дополнительно задают N состояний сложного объекта, M параметров, которые определяют его состояние, R возможных дестабилизирующих факторов и K характеризующих их параметров, время tоц, в течение которого проводится оценка условий и процесса функционирования сложного объекта и период ∆t проверки M параметров сложного объекта, оценивают процесс функционирования сложного объекта, для чего измеряют и запоминают значения M параметров сложного объекта в течение tоц , при этом в течение tоц объект должен находиться к каждом из N возможных состояний под воздействием K дестабилизирующих факторов, определяют взаимозависимости M параметров сложного объекта между собой, определяют перечень базовых L параметров, позволяющих вычислить остальные H параметры, аппроксимируют значения каждого из L параметров сложного объекта множеством аппроксимирующих функций с заданной точностью εтр, рассчитывают оптимальный период контроля каждой аппроксимирующей функции каждого из L параметров.
Недостатком способа-прототипа является избыточность результатов контроля, высокая нагрузка на средства контроля и автоматизации управления сложного объекта, большой объем передаваемых данных о результатах контроля, и, как следствие, увеличение нагрузки на сеть связи, обусловленные проведением измерений в заданные временные интервалы всего множества базовых L параметров.
Технической проблемой, на решение которой направлено предлагаемое решение, является высокая нагрузка на средства контроля и автоматизации управления сложного многопараметрического объекта, что ведет к задержкам восстановления при его сбоях и усложнению средств контроля и автоматизации управления, а также большой объем передаваемых данных о результатах контроля, что обуславливает увеличение нагрузки на сеть связи.
Техническая проблема решается за счет последовательного и обоснованного определения перечня и периодичности контроля параметров сложного объекта в заданные временные интервалы, достаточных для контроля многопараметрического объекта с сохранением степени информированности о его состоянии.
Техническим результатом заявленного способа является снижение избыточности результатов контроля, снижение нагрузки на средства контроля и автоматизации управления сложного объекта, снижение объема передаваемых данных о результатах контроля, а следовательно, и снижение нагрузки на сеть связи за счет минимизации количества измеряемых параметров в заданных временных интервалах, а также снижения информационной избыточности дискретных измерений непрерывно изменяющихся параметров путем поинтервального определения периодичности измерений каждого контролируемого параметра с сохранением степени информированности о состоянии сложного объекта.
Технический результат достигается тем, что в известном способе, заключающемся в том, что задают М параметров, характеризующих состояние многопараметрического объекта, время tоц, в течение которого проводится оценка функционирования многопараметрического объекта, оценивают процесс функционирования сложного объекта, для чего измеряют и запоминают значения М параметров многопараметрического объекта в течение времени tоц, отличающийся тем, что дополнительно задают множество состояний объекта, критерии стационарности состояний объекта, общее время контроля Т и интервалы определения периодичности контроля множества параметров Δt, максимальное практически значимое значение коэффициента корреляции Ккор max, критерии ранжирования параметров, осуществляют статистическую обработку результатов измерений, при этом определяют и запоминают функцию распределения значений каждого параметра, а также математическое ожидание, дисперсию и среднеквадратическое отклонение частоты изменения значений каждого из параметров М, строят вариационный ряд параметров по заданному критерию от большего значения к меньшему, формируют матрицу коэффициентов корреляции, попарно, начиная со старшего члена вариационного ряда, определяют коэффициент корреляции между частотами изменения М параметров многопараметрического объекта и запоминают его в соответствующей ячейке матрицы, сравнивают определенные значения коэффициента корреляции с заданным максимальным значением коэффициента корреляции Ккор max, если определенное значение коэффициента корреляции больше или равно заданному практически значимому значению коэффициента корреляции Ккор max, то удаляют из матрицы параметр, который в данной паре параметров является младшим членом вариационного ряда, разбивают оставшиеся параметры на I подмножеств, для чего сравнивают функции распределения значений каждого параметра, параметры с функциями распределения, подчиненными одному закону, относят к отдельному подмножеству, параметры с функциями распределения, не подчиненными одному закону, относят к отдельным подмножествам, в каждом подмножестве, на каждом интервале Δt в соответствии с заданными критериями определяют и запоминают состояние объекта, определяют количество характеризующих его на данном временном интервале параметров, если в подмножестве количество параметров больше или равно двум, то определяют и запоминают математическое ожидание частоты изменения значений каждого из параметров подмножества, строят вариационный ряд параметров по значению математического ожидания от меньшего значения к большему, выбирают параметр, соответствующий старшему члену вариационного ряда, определяют и запоминают периодичность контроля по верхнему значению частоты изменения выбранного параметра, если подмножество состоит только из одного параметра, то для всех данных подмножеств определяют и запоминают периодичность контроля по верхнему значению частоты изменения выбранного параметра, при дальнейшем функционировании многопараметрического объекта осуществляют его контроль, для чего с интервалом Δt в соответствии с заданными критериями определяют состояние объекта и измеряют значения выбранных в каждом подмножестве параметров с определенной периодичностью.
Достижение технического результата обусловлено следующим.
Описанные аналоги [Патент 2623791 Российская Федерация, МПК G05B 23/00 (2006.01), G06Q 10/04 (2012.01). Способ определения оптимальной периодичности контроля состояния процессов / Синев С.Г., Сорокин М.А., Стародубцев П.Ю., Сухорукова Е.В.; заявитель и патентообладатель Стародубцев П.Ю. – 2015108734; заявл. 25.01.2016; опубл. 29.06.2017, бюл. № 19. – 13 с.; Патент 2659374 Российская Федерация, G05B 23/00, G06F 19/00. Способ определения оптимальной периодичности контроля состояния технических средств и систем при минимальном времени получения результата/ Алашеев В.В., Вершенник А.В., Вершенник Е.В., Карпов А.В., Латушко Н.А., Чеснаков М.Н., Стародубцев Ю.И.,; заявитель и патентообладатель Алашеев В.В., Вершенник А.В., Карпов А.В., Латушко Н.А., Чеснаков М.Н. – 2017137312; заявл. 24.10.2017; опубл. 29.06.2018. бюл. № 19 – 14 с.] и прототип [Патент 2718152 Российская Федерация, G06F 17/10 (2006.01), G05B 23/00 (2006.01). Способ определения оптимальной периодичности контроля состояния сложного объекта / Стародубцев Ю.И., Иванов С.А., Вершенник Е.В., Вершенник А.В., Закалкин П.В., Шевчук А.Л., Карасенко А.О. – 2019143358; заявл. 24.12.2019; опубл. 30.03.2020. бюл. № 10 – 19 с.] базируются на одном из фундаментальных положений теоретической радиотехники – теореме Котельникова [Баскаков С.И. Радиотехнические цепи и сигналы. М.: Высшая школа, 2-е издание. - 446 с., стр. 116-117, Теория передачи сигналов: Учебник для вузов/Зюко А. Г., Кловский Д.Д., Назаров М. В., Финк Л. М. - М.: Связь, 1980. - 288 с., стр. 68, Хургин Я.И., Яковлев В.П. Методы теории целых функций в радиофизике, теории связи и оптике. – М., 1962. – 220 с., стр. 107]. Согласно данной теореме, произвольный сигнал, спектр которого не содержит частот выше fв, может быть полностью и однозначно восстановлен, если известны отсчетные значения этого сигнала, взятые через равные промежутки времени 1/(2 fв).
Таким образом, для восстановления значений параметров контролируемого процесса на заданном интервале времени в представленных аналогах и прототипе период контроля всех параметров в течение всего времени функционирования составлял Тконтр=1/(2fв), где fв - наибольшее значение частоты изменения параметров.
Однако такой подход обуславливает существенную избыточность результатов контроля.
Предлагаемый способ основан на следующем.
Многопараметрические объекты, по сравнению с объектами, состояние которых может быть представлено одним параметром, позволяют получить больше данных о состоянии объекта. При этом контроль всех параметров на заданном интервале времени в целях определения состояния объекта будет избыточным. Множество параметров объекта можно разделить на группы взаимозависимых, т.е. коррелированных с некоторым уровнем между собой, параметров. Следовательно, зная зависимости коррелированных параметров, можно своевременно вычислять значения одного параметра по значениям другого, и наоборот, что позволить уменьшить количество измерений и объем передаваемых данных о результатах контроля.
Таким образом, на каждом из {I} временных интервалов необходимо отдельно выбирать параметр для последующей дискретизации, преобразования и передачи по каналу связи с последующим восстановлением на приемной стороне всех необходимых зависимых от него параметров на определенном временном интервале. Критерием выбора параметра на интервале является минимальное математическое ожидание его частоты изменения. По сути на i-ом временном интервале выбирается параметр с минимальным значением верхней частоты его изменения, но на общий случай, целесообразнее использовать математическое ожидание при допущении о том, что изменение всех параметров статистически подчинено одному закону распределения.
На фиг. 1 показано графическое представление характеристики частот изменения параметров сигнала F(t), записанных в память:
fA(t), находящейся в диапазоне значений от fAн до fAв, параметра A(t);
fB(t), находящейся в диапазоне значений от fBн до fBв, параметра B(t).
Общее время контроля T обоих параметров сигнала разбито на I интервалов по Δt, таким образом, что
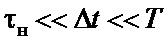 , (1)
, (1)
где τн=1/(2 fн).
Тогда получим количество I интервалов:
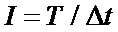 . (2)
. (2)
При достаточно большом T найдется хотя бы один i-й интервал, в котором значение математического ожидания 

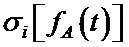
математическим ожиданием 
дисперсией 

множеством значений математического ожидания, включающим каждое из 
множеством значений дисперсии (среднеквадратического отклонения), включающим каждое 
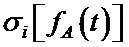
Частота изменения параметра B(t) (фиг. 1) характеризуется подобными показателями.
При выполнении условия 

Выберем все интервалы, удовлетворяющие условию (3). В полученном множестве 


Если пара параметров не полностью коррелированы:
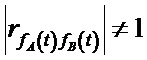
то на достаточно большом T найдется хотя бы один i-й интервал, для которого выполняется условие:

В оставшемся множестве интервалов 


С учетом выполнения условия (6) можно утверждать, что справедливо неравенство:


где 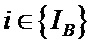
Количество необходимых интервалов для передачи всей функции F(t) определяется в соответствии с (2), при этом периодичность следования отсчетов в интервалах, не вошедших в множества 



С учетом (7) справедливо неравенство:

Таким образом, имея хотя бы один интервал ∆t, в котором выполняется условие (7) при справедливости (5) можно утверждать, что чем меньше корреляция частот изменения параметров непрерывного сигнала 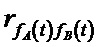
Даже при необходимости передачи одного параметра сигнала практическая реализация представленных выше утверждений позволит обеспечить снижение информационной нагрузки на канал связи по сравнению с теоремой Котельникова за счет представления непрерывного сигнала дискретными отсчетами в соответствии с минимальным значением верхней частоты изменения параметра (fвi min), выбираемого из всех взаимозависимых параметров на каждом i-ом временном интервале.
Таким образом, совокупность действий предлагаемого способа, обеспечивающая использование меньшего числа параметров для контроля состояния сложного объекта на заданном временном интервале за счет учета их корреляции, а также обеспечивающая снижение информационной нагрузки на канал связи за счет уменьшения количества отсчетов при дискретизации сигнала, приводит к достижению технического результата, а именно позволяет уменьшить избыточность результатов контроля, снизить нагрузку на средства контроля и автоматизации управления сложного многопараметрического объекта, уменьшить объем передаваемых данных о результатах контроля, снизить нагрузку на сеть связи, а также снизить информационную избыточность дискретных измерений непрерывно изменяющихся параметров путем поинтервального определения периодичности измерений каждого контролируемого параметра с сохранением степени информированности о состоянии сложного объекта.
Из уровня техники не выявлено решений, касающихся способов определения периодичности контроля сложных объектов, характеризующихся заявленной совокупностью признаков, что, следовательно, указывает на соответствие заявленного способа условию патентоспособности «новизна».
Результаты поиска известных решений в данной и смежной областях техники с целью выявления признаков, совпадающих с отличительными от прототипов признаками заявленного изобретения, показали, что они не следуют явным образом из уровня техники. Из определенного заявителем уровня техники не выявлена известность влияния предусматриваемых существенными признаками заявленного изобретения на достижение указанного технического результата. Следовательно, заявленное изобретение соответствует условию патентоспособности «изобретательский уровень».
«Промышленная применимость» способа обусловлена наличием элементной базы, на основе которой могут быть выполнены устройства, реализующие способ.
Заявленный способ поясняется чертежами, на которых показаны:
фиг. 1 – Графическое представление частоты изменения параметров A(t) и B(t) непрерывного сигнала F(t);
фиг. 2 – обобщенная схема контроля многопараметрического объекта;
фиг. 3 – блок-схема способа контроля многопараметрического объекта;
фиг. 4 – пример матрицы коэффициентов корреляции;
фиг. 5 – графическое представление эффективности представленного решения по сравнению с решением.
Основные этапы способа контроля многопараметрического объекта представлены на фиг.2.
В блоке 1 фиг. 2 оценивают условия и процесс функционирования многопараметрического объекта в течение времени, достаточного для сбора данных об объекте во всех возможных состояниях под воздействием всех возможных дестабилизирующих факторов. При этом измеряют и запоминают значения М параметров многопараметрического объекта в течение времени tоц, осуществляют их статистическую обработку.
В блоке 2 фиг. 2 определяют перечень параметров, достаточных для контроля многопараметрического объекта. В этих целях попарно вычисляют коэффициенты корреляции между частотами изменения всех параметров объекта, на их основании определяют наиболее значимые (в соответствии с заданными критериями) параметры, по значениям которых можно вычислять значения зависимых параметров.
В блоке 3 фиг. 2 рассчитывают оптимальный период контроля на каждом заданном интервале Δt. В этих целях в соответствии с заданными критериями определяют и запоминают состояние объекта, определяют количество характеризующих его на данном временном интервале параметров, если в подмножестве количество параметров больше или равно двум, то определяют и запоминают математическое ожидание частоты изменения значений каждого из параметров подмножества, определяют и запоминают периодичность контроля по верхнему значению частоты изменения параметра с наибольшим значением математического ожидания частоты изменения его значений, если подмножество состоит только из одного параметра, то для всех данных подмножеств определяют и запоминают периодичность контроля по верхнему значению частоты изменения выбранного параметра.
В блоке 4 осуществляют контроль многопараметрического объекта, для чего с интервалом Δt в соответствии с заданными критериями определяют состояние объекта и измеряют значения выбранных в каждом подмножестве параметров с определенной периодичностью.
Заявленный способ реализован в виде блок-схемы, представленной на фиг. 3.
В блоке 5 фиг. 3 предварительно задают в качестве исходных данных:
- N состояний сложного объекта;
- критерии стационарности состояний объекта;
- M параметров, характеризующих его состояние; задание состояний и параметров сложных объектов возможно исходя из результатов их моделирования, проектирования и производства, а также исходя из опыта их эксплуатации; при этом значения параметров сложного объекта должны определять состояние, в котором он находится [например: сложный объект - сеть связи; состояния - выключена, функционирует штатно, функционирует в час наибольшей нагрузки, функционирует под предкритической нагрузкой, находится в критическом состоянии (возможно восстановление), находится в закритическом состоянии (невозможно восстановление); тогда параметрами, характеризующими ее состояние, могут выступать пропускная способность, задержка передачи информации, уровень деградации оптического волокна, загруженность вычислительного ресурса автоматизированной системы управления и др.];
- время tоц, в течение которого проводится оценка условий и процесса функционирования сложного объекта, при этом в течении tоц объект должен находиться к каждом из N возможных состояний под воздействием R дестабилизирующих факторов; например, оценка сложного объекта – самолета, проводимая согласно отраслевого стандарта (ОСТ) в течении tоц, установленной программой и методиками испытаний, в ходе которой самолет подвергается всем возможным деструктивным воздействиям внутреннего и внешнего характера (попадание молнии, град, боковой ветер, выход из строя узлов и агрегатов и др.) в различных состояниях (разгон по взлетной полосе, посадка, набор высоты, автоматическое и ручное управление и т.д.) [режим доступа:https://rg.ru/2016/12/07/kak-ispytyvali-rossijskij-lajner-sukhoi-superjet.html. Дата обращения: 01.12.2019 г.].
общее время контроля Т и интервалы определения периодичности контроля множества параметров Δt,
максимальное практически значимое значение коэффициента корреляции Ккор max,
критерии ранжирования параметров.
Исходные данные могут быть заданы путем их записи в постоянное запоминающее устройство (ПЗУ) электронно-вычислительной машины (ЭВМ).
В блоке 6 фиг. 3 оценивают процесс функционирования сложного объекта, для чего:
В блоке 7 фиг. 3 измеряют значения M параметров сложного объекта в течении tоц. При этом в течении tоц объект должен находиться к каждом из N возможных квазистационарных состояний.
Для измерения параметров могут использоваться как отдельные средства измерения, так и измерительные комплексы. Так, например, для измерения параметров волоконно-оптической системы передачи используются: рефлектометр для измерения характеристик линейного тракта (оптического волокна) [режим доступа: https://skomplekt.com/solution/reflekt.htm/. Дата обращения: 20.03.2021 г.], когерентные измерители рассеянных сигналов для поиска виброакустических (деструктивных) воздействий на оптический кабель и повреждений [режим доступа: https://t8-sensor.ru/, https://fibertop.ru/poisk_i_ustranenie_neispravnostey_na_vols_s_pom_reflectometra_930XC.htm/ . Дата обращения: 20.03.2021 г.], микроскоп для определения качества торцов оптического волокна [режим доступа: https://skomplekt.com/tovar/1/1/52/. Дата обращения: 20.03.2021 г.], измерители оптической мощности для определения параметров сигнала [режим доступа: https://skomplekt.com/solution/optm.htm/. Дата обращения: 20.03.2021 г.], анализаторы транспортных сетей для тестирования канального оборудования [режим доступа: https://skomplekt.com/tovar/1/3/31/. Дата обращения: 20.03.2021 г.] и т.д.
В блоке 8 фиг. 3 запоминают значения M параметров сложного объекта в течении tоц в ПЗУ ЭВМ.
В блоке 9 фиг. 3 осуществляют статистическую обработку результатов измерений, при этом определяют и запоминают функцию распределения значений каждого параметра, а также математическое ожидание, дисперсию и среднеквадратическое отклонение частоты изменения значений каждого из параметров М.
Статистическая обработка результатов измерений может быть проведена при помощи известных программных средств, например STATGRAPHICS [Катранов А.Г. Компьютерная обработка данных экспериментальных исследований: Учебное пособие/ А.Г. Катранов, А.В. Самсонова; СПб ГУФК им. П.Ф. Лесгафта. – СПб.: изд-во СПб ГУФК им. П.Ф. Лесгафта, 2005. – 131 с.], MathCad [В. И. Губин, В. Н. Осташков. Статистические методы обработки экспериментальных данных: Учеб. пособие для студентов технических вузов.— Тюмень: Изд-во «ТюмГНГУ», 2007. - 202 с.; Медведева, Л.И. Статистическая обработка экспериментальных данных [Электронный ресурс] : учебно-методическое пособие / Л.И. Медведева, В.И. Капля; ВПИ (филиал) ВолгГТУ. – Электрон. текстовые дан. (1 файл: 8,76 МБ). – Волжский, 2018. – Режим доступа: http://lib.volpi.ru], Statistica [В.В. Веременюк, Е.А. Крушевский, О.А. Мороз. Cтатистическая обработка экспериментальных данных. Минск: БНТУ. - 2015. 80 с.; Ю.Я. Кацман. Методические указания к лабораторным работам (цикл лабораторных работ) по дисциплине "Статистическая обработка экспериментальных данных". Томск: Изд. ТПУ, 2008. – 37c], MicroSoft Excel, SPSS, позволяющие выполнить статистическую обработку результатов измерений на ЭВМ [Бараз В.Р. Корреляционно-регрессионный анализ связи показателей коммерческой деятельности с использованием программы Excel : учебное пособие / В.Р. БАРАЗ. – Екатеринбург : ГОУ ВПО «УГТУ–УПИ», 2005. – 102 с., стр. 1- 102].
В блоке 10 фиг. 3 строят вариационный ряд параметров по заданному критерию от большего значения к меньшему.
В блоке 11 фиг. 3 формируют матрицу коэффициентов корреляции. Пример матрицы коэффициентов корреляции представлен на фиг. 4. Матрица коэффициентов корреляции представляет собой квадратную таблицу M Х M, где M – количество параметров многопараметрического объекта, в которую на пересечении соответствующей i-той строки и j-го столбца записывают коэффициент корреляции между соответствующими Mi и Mj параметрами.
В блоке 12 фиг. 3 попарно, начиная со старшего члена вариационного ряда, определяют коэффициент корреляции между частотами изменения М параметров многопараметрического объекта и запоминают его в соответствующей ячейке матрицы.
Коэффициент корреляции представляет собой:
1. Количественную мера силы и направления вероятностной взаимосвязи двух переменных; принимает значения в диапазоне от -1 до +1.
2. Мера прямой или обратной пропорциональности между двумя переменными.
3. Количественную меру взаимосвязи (совместимой изменчивости) двух переменных [Наследов А.Д. Математические методы психологического исследования. Анализ и интерпретация данных [Текст] / А. Д. Наследов. – СПб.: Речь, 2012. – 392 с. С. 64, 67, 147].
Метод вычисления коэффициента корреляции зависит от вида шкалы, которой относятся переменные [Тема 4. Корреляционный анализ Электронный ресурс: https://pandia.ru/text/80/158/20893.php 7/30. Дата обращения 22.03.2021 г.]:
– переменные с интервальной и с номинальной шкалой: коэффициент корреляции Пирсона (корреляция моментов произведений);
– по меньшей мере, одна из двух переменных имеет порядковую шкалу либо не является нормально распределённой: ранговая корреляция по Спирману или Кендала;
– одна из двух переменных является дихотомической: точечная двухрядная корреляция;
– обе переменные являются дихотомическими: четырёхполевая корреляция.
Расчет различных корреляционных коэффициентов (линейный, множественный, ранговый Спирмена, ранговый Кендалла и т.д.) между различными параметрами возможен при помощи известных программных средств, например Statistica, MicroSoft Excel, SPSS, позволяющие выполнить корреляционный анализ на ЭВМ [Бараз В.Р. Корреляционно-регрессионный анализ связи показателей коммерческой деятельности с использованием программы Excel : учебное пособие / В.Р. БАРАЗ. – Екатеринбург : ГОУ ВПО «УГТУ–УПИ», 2005. – 102 с., стр. 1- 102; Расчет коэффициента корреляции в SPSS. Электронный ресурс: https://statpsy.ru/correlation/correlation-spss/. Дата обращения 23.12.2019 г.].
В блоке 13 фиг. 3 сравнивают определенные значения коэффициента корреляции с заданным максимальным практически значимым значением коэффициента корреляции Ккор max. Ккор >Ккор max.
Для оценки силы связи коэффициента корреляции используются различные шкалы. Например, шкала Чеддока имеет вид:
Значение коэффициента корреляции:
от 0 до 0,3 - очень слабая;
от 0,3 до 0,5 – слабая;
от 0, 5 до 0,7 – средняя;
от 0,7 до 0, 9 – высокая;
от 0,9 до 1 – очень высокая.
Максимальное возможное абсолютное значение коэффициента корреляции равно 1 (параметры полностью взаимосвязаны). Чем ближе значение коэффициента корреляции к 1, тем больше коррелируют между собой параметры объекта. Однако на практике такой результат встречается крайне редко.
Поэтому в качестве максимального целесообразно задавать практически значимый коэффициент корреляции, который выбирается исходя из затрат ресурсов на измерение и передачу данных о параметре и затрат ресурсов на его вычисление по значениям взаимозависимого параметра.
Если определенное значение коэффициента корреляции больше или равно заданному практически значимому значению коэффициента корреляции Ккор max, то в блоке 14 фиг. 3 удаляют из матрицы параметр, который в данной паре параметров является младшим членом вариационного ряда. Таким образом, путем сокращения матрицы, выбирают множество некоррелированных параметров объекта для контроля. Остальные параметры могут быть вычислены по имеющимся взаимосвязям.
В блоке 15 фиг. 3 разбивают оставшиеся параметры на K подмножеств, для чего в блоке 16 сравнивают функции распределения значений каждого параметра.
В блоке 17 фиг. 3 параметры с функциями распределения, подчиненными одному закону, относят к отдельному подмножеству. Параметры с функциями распределения, не подчиненными одному закону, относят к отдельным подмножествам (бл. 18 фиг. 2)
Далее в каждом подмножестве на каждом интервале Δt:
в блоке 19 фиг. 3 в соответствии с заданными критериями определяют и запоминают состояние объекта;
в блоке 20 фиг. 3 определяют количество характеризующих его на заданном интервале времени параметров;
если в подмножестве количество параметров больше или равно двум (бл. 21 фиг. 3), то
в блоке 22 фиг. 3 определяют и запоминают математическое ожидание частоты изменения значений каждого из параметров подмножества;
блоке 23 фиг. 3 строят вариационный ряд параметров по значению математического ожидания от меньшего значения к большему;
в блоке 24 фиг. 3 выбирают параметр, соответствующий старшему члену вариационного ряда;
В блоке 25 фиг. 3 определяют и запоминают периодичность контроля по верхнему значению частоты изменения выбранного параметра:

Если подмножество состоит только из одного параметра, то для всех данных подмножеств в блоке 25 фиг. 3 определяют и запоминают периодичность контроля по верхнему значению частоты изменения выбранного параметра:

При дальнейшем функционировании многопараметрического объекта осуществляют его контроль, для чего в блоке 26 фиг. 3 с интервалом Δt в соответствии с заданными критериями определяют состояние объекта и измеряют значения выбранных в каждом подмножестве параметров с определенной периодичностью.
Таким образом, благодаря совокупности действий способа достигается снижение избыточности результатов контроля, снижение нагрузки на средства контроля и автоматизации управления сложного объекта, снижение объема передаваемых данных о результатах контроля, а, следовательно, и снижение нагрузки на сеть связи за счет минимизации количества измеряемых параметров в заданных временных интервалах, а также снижение информационной избыточности дискретных измерений непрерывно изменяющихся параметров путем поинтервального определения периодичности измерений каждого контролируемого параметра с сохранением степени информированности о состоянии сложного объекта.
Для наглядного представления выигрыша в снижении информационной нагрузки представленного решения по сравнению с решением (1) представим их соотношение в графической форме (фиг. 5).
На фиг. 5 представлены две фигуры. Первая фигура соответствует прямоугольнику со сторонами T и f1 (верхняя частота изменения параметра сигнала постоянна для всего времени его дискретизации). Вторая фигура характеризуется площадью под кривой, описываемой нормальным законом распределения верхней частоты изменения параметра непрерывного сигнала fв. Статистически известно, что распределение случайных (квазислучайных) величин в телекоммуникационных системах подчинено нормальному распределению [Замятина О.М. Моделирование сетей: учебное пособие / О.М. Замятина: Томский политехнический университет. – Томск: Изд-во Томского политехнического университета, 2011. – 168 с.], поэтому он принят в качестве распределения fв.
В физическом смысле, площадь фигур отображает информационную нагрузку непрерывного сигнала на канал связи за время T при его представлении дискретными отсчетами. Соотношение площадей наглядно демонстрирует возможную эффективность представленного решения. В математической форме соотношение результатов можно представить коэффициентом в следующем виде:

где S1 – площадь фигуры (прямоугольника), соответствующая информационной нагрузке непрерывного сигнала на канал связи за время T при его представлении дискретными отсчетами по решению (1); S1 – площадь фигуры (под функцией плотности распределения), соответствующая информационной нагрузке непрерывного сигнала на канал связи за время T при его представлении дискретными отсчетами на основе представленного решения; fв(t) – функция верхней частоты изменения параметра непрерывного сигнала; fв ср – среднее значение верхней частоты изменения параметра непрерывного сигнала за время T; σ – среднеквадратическое отклонение верхней частоты изменения параметра непрерывного сигнала за время T.
Фиг. 5 отображает выигрыш в снижении информационной нагрузки при представлении непрерывного сигнала отсчетами одного параметра. Наличие в сигнале нескольких параметров с некоторой степенью корреляции повысят эффективность решения за счет выбора параметра с минимальным значением верхней частоты изменения (fвi min) на каждом i-ом временном интервале.
Технический результат достигнут.
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ определения оптимальной периодичности контроля состояния сложного объекта | 2019 |
|
RU2718152C1 |
| СПОСОБ УПРАВЛЕНИЯ СОСТОЯНИЕМ СЛОЖНОГО ОБЪЕКТА | 2020 |
|
RU2748778C1 |
| Способ оценки информированности об источнике деструктивных воздействий на структуру корпоративной системы управления | 2020 |
|
RU2764390C1 |
| СПОСОБ ИДЕНТИФИКАЦИИ ЭЛЕМЕНТОВ СЛОЖНОЙ СИСТЕМЫ В ПЕРЕМЕННЫХ УСЛОВИЯХ | 2020 |
|
RU2726027C1 |
| СПОСОБ ПЕРЕДАЧИ ДАННЫХ В СЕТЯХ СВЯЗИ С НЕСТАБИЛЬНЫМИ ХАРАКТЕРИСТИКАМИ ЭЛЕМЕНТОВ | 2020 |
|
RU2747092C1 |
| Способ мониторинга состояния электрических сетей и сетей связи | 2017 |
|
RU2646321C1 |
| СПОСОБ МОДЕЛИРОВАНИЯ ВИРТУАЛЬНОЙ СЕТИ СВЯЗИ НА ОСТАТОЧНЫХ РЕСУРСАХ ФИЗИЧЕСКОЙ СЕТИ | 2020 |
|
RU2749444C1 |
| СПОСОБ ПОВЫШЕНИЯ УСТОЙЧИВОСТИ ВИРТУАЛЬНОЙ СЕТИ СВЯЗИ КОРПОРАТИВНОЙ СИСТЕМЫ УПРАВЛЕНИЯ | 2020 |
|
RU2750950C1 |
| Способ моделирования подключения мобильных элементов корпоративной системы управления к стационарной сети связи | 2020 |
|
RU2746670C1 |
| Способ трансформации исходной физической структуры сети связи для повышения устойчивости представления информационных ресурсов органам управления корпоративной системы управления | 2022 |
|
RU2788672C1 |




Изобретение относится к вычислительной технике, в частности, к способам контроля. Технический результат изобретения заключается в снижении избыточности результатов контроля, нагрузки на средства контроля и автоматизации управления сложного объекта и объема передаваемых данных о результатах контроля. Технический результат достигается за счет последовательного и обоснованного определения перечня и периодичности контроля параметров сложного объекта в заданные временные интервалы, достаточных для контроля многопараметрического объекта с сохранением степени информированности о его состоянии. 5 ил.
Способ контроля многопараметрического объекта, заключающийся в том, что задают М параметров, характеризующих состояние многопараметрического объекта, время tоц, в течение которого проводится оценка функционирования многопараметрического объекта, оценивают процесс функционирования сложного объекта, для чего измеряют и запоминают значения М параметров многопараметрического объекта в течение времени tоц, отличающийся тем, что дополнительно задают множество состояний объекта, критерии стационарности состояний объекта, общее время контроля Т и интервалы определения периодичности контроля множества параметров Δt, максимальное практически значимое значение коэффициента корреляции Ккор max, критерии ранжирования параметров, осуществляют статистическую обработку результатов измерений, при этом определяют и запоминают функцию распределения значений каждого параметра, а также математическое ожидание, дисперсию и среднеквадратическое отклонение частоты изменения значений каждого из параметров М, строят вариационный ряд параметров по заданному критерию от большего значения к меньшему, формируют матрицу коэффициентов корреляции, попарно, начиная со старшего члена вариационного ряда, определяют коэффициент корреляции между частотами изменения М параметров многопараметрического объекта и запоминают его в соответствующей ячейке матрицы, сравнивают определенные значения коэффициента корреляции с заданным максимальным значением коэффициента корреляции Ккор max, если определенное значение коэффициента корреляции больше или равно заданному практически значимому значению коэффициента корреляции Ккор max, то удаляют из матрицы параметр, который в данной паре параметров является младшим членом вариационного ряда, разбивают оставшиеся параметры на I подмножеств, для чего сравнивают функции распределения значений каждого параметра, параметры с функциями распределения, подчиненными одному закону, относят к отдельному подмножеству, параметры с функциями распределения, не подчиненными одному закону, относят к отдельным подмножествам, в каждом подмножестве, на каждом интервале Δt в соответствии с заданными критериями определяют и запоминают состояние объекта, определяют количество характеризующих его на данном временном интервале параметров, если в подмножестве количество параметров больше или равно двум, то определяют и запоминают математическое ожидание частоты изменения значений каждого из параметров подмножества, строят вариационный ряд параметров по значению математического ожидания от меньшего значения к большему, выбирают параметр, соответствующий старшему члену вариационного ряда, определяют и запоминают периодичность контроля по верхнему значению частоты изменения выбранного параметра, если подмножество состоит только из одного параметра, то для всех данных подмножеств определяют и запоминают периодичность контроля по верхнему значению частоты изменения выбранного параметра, при дальнейшем функционировании многопараметрического объекта осуществляют его контроль, для чего с интервалом Δt в соответствии с заданными критериями определяют состояние объекта и измеряют значения выбранных в каждом подмножестве параметров с определенной периодичностью.
| Способ определения оптимальной периодичности контроля состояния сложного объекта | 2019 |
|
RU2718152C1 |
| СПОСОБ И СИСТЕМА ДЛЯ ДИАГНОСТИРОВАНИЯ ПРОМЫШЛЕННОГО ОБЪЕКТА | 2018 |
|
RU2707423C2 |
| СПОСОБ КОНТРОЛЯ СОСТОЯНИЯ МНОГОПАРАМЕТРИЧЕСКОГО ОБЪЕКТА | 2007 |
|
RU2373650C2 |
| СПОСОБ КОМПЛЕКСНОГО КОНТРОЛЯ СОСТОЯНИЯ МНОГОПАРАМЕТРИЧЕСКОГО ОБЪЕКТА ПО РАЗНОРОДНОЙ ИНФОРМАЦИИ | 2019 |
|
RU2719467C1 |
| Станок для придания концам круглых радиаторных трубок шестигранного сечения | 1924 |
|
SU2019A1 |
Авторы
Даты
2022-01-17—Публикация
2021-04-06—Подача