Изобретение относится к транспортному машиностроению и может быть использовано при разработке и модернизации транспортных машин, оснащенных гидромеханическими трансмиссиями с фрикционами управления переключением передач.
В процессе испытаний опытных гидромеханических трансмиссий (ГМТ) и эксплуатации некоторых серийных наблюдается малоизученное явление - разрыв фрикционных дисков элементов управления после ограниченного срока эксплуатации. Металлографический анализ разрушенных дисков показывает, что трещины носят усталостный характер. Это является следствием резонансных режимов работы, возникающих при совпадении одной из собственных частот фрикционных дисков с частотой возмущающего воздействия, формируемого двигателем, гидродинамическими процессами в гидротрансформаторе, пульсацией давления рабочей жидкости в системе его подпитки или нелинейностью характеристики упругого взаимодействия фрикционных дисков с ведущим барабаном. Для исследования динамической нагруженности фрикционных дисков и определения путей исключения резонансных режимов необходимо определить спектр их собственных частот. Аналитически определить значения частот можно по приближенным формулам, справедливым для кругового кольца, выполненного из однородного материала. В волновой теории колебания кругового кольца описываются дифференциальными уравнениями в частных производных, решением которых является равенство [Тимошенко, Янг Д.Х., Уивер У. Колебания в инженерном деле. Изд-во: М.: Машиностроение, 1985, с. 435]:
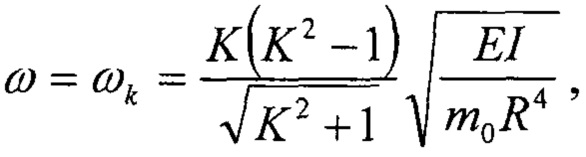
где K - целое число, определяющее количество волн z длиной λ, укладывающихся на длине кольца 2πR (K=1, 2, …N, 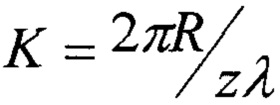 ) и форму колебаний диска; Е - модуль упругости второго рода; J - момент инерции прямоугольного сечения кольца
) и форму колебаний диска; Е - модуль упругости второго рода; J - момент инерции прямоугольного сечения кольца 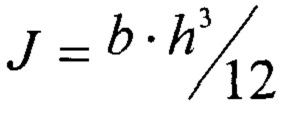 размером b⋅h; m0 - погонная масса; R - средний радиус кольца.
размером b⋅h; m0 - погонная масса; R - средний радиус кольца.
Однако конструкция фрикционных дисков может быть многокомпонентной, сочетающей в себе металлический диск, металлокерамические или целлюлозные накладки, адгезионные слои, то есть разнородные материалы с различными нелинейными физико-механическими свойствами. Кроме того, на одной из торцевых поверхностей фрикционных дисков выполняется зубчатый венец. Собственные частоты дисков, состоящих из неоднородных материалов и имеющих сложную форму, могут быть рассчитаны на основе определения реакции конечно-разностной модели фрикционного диска на гармоническое воздействие регулируемой частоты при численном моделировании, например, в программном пакете NASTRAN (аналог - Басов К.А., Мовчан Д.А. ANSYS. Справочник пользователя / Издательство: ДМК-Пресс, 2011 г., 640 с.). Однако достоверность построения модели ограничивается точностью описания нелинейного адгезионного взаимодействия между элементами фрикционного диска (стальным кольцом и металлокерамическими или целлюлозными накладками). В связи с этим, результаты численной оценки собственных частот фрикционных дисков необходимо корректировать с учетом экспериментальных данных, полученных при испытаниях на специальном стенде с использованием метода неразрушающего контроля - по реакции диска на гармонический сигнал регулируемой частоты [Патент РФ на ПМ №122171 от 20.11.2012 «Стенд для определения спектра собственных частот металлокерамических дисков гидромеханических трансмиссий», патент РФ на ПМ №157159 от 30.10.2015 «Стенд для определения пространственных модальных характеристик фрикционных дисков гидромеханических трансмиссий»]. Вероятность возбуждения резонансных режимов определяется по равенству частот возмущения и собственных кольца. Исключение резонанса в литературе предлагается обеспечить варьированием собственных частот металлокерамического диска в соответствии с приведенным уравнением. Однако физико-механические свойства (модуль упругости F, плотность материала ρ определяющая погонную массу m0, соответственно и скорость звука в материале Е/ρ) для используемых материалов диска стабильны, а варьирование геометрическими параметрами (J,R) ограничено условиями компоновки фрикционных дисков в картере трансмиссии.
Известен способ исключения резонансных режимов во фрикционных дисках гидромеханических трансмиссий заключающийся в аналитическом или экспериментальном определении спектра частот возмущения двигателя и спектра собственных частот металлокерамического диска, а также вероятности возбуждения резонансных режимов при равенстве частот возмущения и собственных (Зайцев В.А., Жучков М.Г., Крюков А.П. Виброударные процессы в дисковых фрикционных муфтах // Вестник бронетанковой техники. - 1968. - №6. - с. 33-36, аналог). Спектр частот возмущений двигателя определяется аналитически на основе расчета полигармонической функции момента двигателя по индикаторной диаграмме одного цилиндра с учетом порядка работы и особенностей конструкции, на основе спектрального анализа полученной функции. Другим способом определения частот возмущения двигателя является спектральный анализ момента двигателя по данным завода изготовителя и определения основных моторных гармоник.
Суть известного метода заключается в следующем:
1. Определение спектра собственных частот фрикционных дисков по аналитической зависимости.
2. Расчет функции полигармонического возмущения момента двигателя по индикаторной диаграмме одного цилиндра с учетом порядка работы и особенностей конструкции; на основе спектрального анализа полученной функции определяются моторные гармоники.
3. Определение вероятности возбуждения резонансного режима по равенству собственных частот диска и моторных гармоник двигателя.
При выполнении условий возбуждения резонансных режимов из-за ограниченных возможностей корректировки частот возмущения двигателя или собственных частот диска предусматривается снижение концентрации напряжения в основании зубьев дисков и повышение несущей способности конструкторско-технологическими мероприятиями (упрочнение поверхностной твердости у основания зуба на основе нанотехнологий, лазерное насыщение карбидами тугоплавких металлов - WC, TiC и др.). Однако при этом резонансный режим не исключается, происходит разрушение сложных элементов трансмиссии, взаимодействующих с дисками.
Следует отметить, что в рассмотренном способе при прогнозировании резонансных режимов не учитывается генерация частот возмущения гидродинамическими процессами в межлопаточном пространстве и пульсацией давления рабочей жидкости в системе подпитки гидротрансформатора.
Выполненными авторами исследованиями установлено, что возбуждение резонанса в не рассматриваемом ранее частотном диапазоне происходит при работе гидротрансформатора (ГТ) в режиме гидромуфты при незначительном, 10…15%, проскальзывании турбины относительно насоса. При блокировке гидротрансформатора спектральная плотность является «белым шумом», т.е. колебания происходят в широком спектре частот без резонансов. На основе имитации гидродинамических потоков в межлопаточном пространстве при относительном движении рабочих колес широко применяемого и энергоемкого гидротрансформатора ГТК-XV с числом лопаток рабочих колес насосного kн=28, турбинного km=22 установлено, что в переходе насос-турбина при относительном проскальзывании 30…200 об/мин происходит одновременное взаимодействие двух пар лопаток насосного и турбинного колес. При этом формируются гидродинамические импульсы с частотой 703 Гц, что соответствует частоте колебаний, фиксируемых в ходе экспериментальных исследований ГМТ (700-730 Гц).
Эффективным способом коррекции спектра собственных частот колебаний диска является «разрушение» числа волн, длина которых соответствует длине окружности среднего радиуса диска. Однако в анализируемых источниках это не реализуется. Таким образом, известные способы исключения резонансных режимов колебаний фрикционных дисков обладают следующими недостатками:
1. При прогнозировании резонансного режима не учитывается генерация частот возмущения, формируемая гидродинамическими процессами в межлопаточном пространстве и пульсацией давления рабочей жидкости в системе подпитки гидротрансформатора.
2. Способы коррекции спектра собственных частот фрикционных дисков имеют ограниченные возможности, снижают прочность конструкции, кроме того, диск теряет упругую устойчивость, когда скорость распространения волны по диску становится равной скорости вращения.
Из-за приведенных недостатков существующий способ прогнозирования и исключения резонансных режимов колебаний фрикционных дисков обладает ограниченными возможностями.
Наиболее близким по технической сути является способ исключения резонансных режимов колебаний фрикционных дисков гидромеханической трансмиссии транспортной машины, заключающийся в аналитическом или экспериментальном определении спектра частот возмущений двигателя и спектра собственных частот фрикционных дисков, оценке возможности возбуждения резонансных режимов по равенству частот возмущений и собственных (патент на изобретение RU №2012136760 от 23.07.2013 г. «Способ исключения резонансных режимов колебаний металлокерамических дисков гидромеханической трансмиссии транспортной машины»). В этом способе дополнительно определяют и сравнивают со спектром собственных частот металлокерамического диска спектр частот возмущений, формируемый гидродинамическими процессами в межлопаточном пространстве гидротрансформатора и пульсациями давления рабочей жидкости в системе его подпитки, определяют возможность резонансного режима по равенству собственных частот фрикционного диска и частот возмущений двигателя, частот возмущений, формируемых гидродинамическими процессами в межлопаточном пространстве гидротрансформатора и пульсациями давления рабочей жидкости в системе его подпитки. При выполнении условия возбуждения резонанса осуществляют корректировку спектра собственных частот фрикционного диска разрушением кратности числа волн, сумма длин которых соответствует длине окружности среднего радиуса фрикционного диска, выполнением на этой окружности пар симметрично расположенных отверстий, изменяющих спектр частот фрикционного диска.
Известный способ (прототип) осуществляется выполнением следующих операций:
1. Определяют спектр собственных частот фрикционных дисков по аналитической зависимости, численным моделированием по твердотельным чертежам или по результатам экспериментального исследования при облучении диска звуковой волной регулируемой частоты.
2. Определяют функцию полигармонического возмущения момента двигателя по индикаторной диаграмме одного цилиндра с учетом порядка работы и особенностей конструкции; на основе спектрального анализа полученной функции определяют моторные гармоники.
3. Рассчитывают спектр частот, возбуждаемых гидродинамическими процессами в гидротрансформаторе при формировании парных импульсов по известным значениям числа лопаток колес.
4. Определяют экспериментально или рассчитывают по зависимости ωп=F(zш, C, mп) спектр частот, возбуждаемых системой подпитки гидротрансформатора и зависящий от числа зубьев шестеренчатого насоса zш, жесткости пружины С, массы mп поршня золотника.
5. Определяют возможность возбуждения резонансного режима по равенству собственных частот фрикционных дисков и частот моторных гармоник двигателя, частот возмущений, возбуждаемых гидродинамическими процессами гидротрансформатора или системой его подпитки.
6. При выполнении условия возбуждения резонанса осуществляют корректировку спектра собственных частот диска разрушением кратности числа волн, сумма длин которых соответствует длине окружности среднего радиуса диска. Для этого выполняют на окружности среднего радиуса диска пары симметричных расположенных отверстий, изменяющих спектр его частот. Число пар отверстий определяют в зависимости от требуемого смещения спектра собственных частот диска.
Основной недостаток известного способа состоит в том, что он применим для механических систем, упругая характеристика которых является линейной. В реальных конструкциях ведущий барабан элементов планетарных рядов (эпицикл, солнечная шестерня или водило) трансмиссии соединяется с дисками по подвижной посадке, обеспечивающей осевое перемещение дисков в процессе включения-выключения фрикционов. Раскрытие зазора в зубчатом соединении приводит к нелинейности характеристики упругого взаимодействия ведущего барабана с диском. Исследованием установлено, что высокочастотное ударное взаимодействие диска с барабаном порождает колебания в широком спектре частот (от 0 до 6000 Гц) со значительной мощностью. Этот спектр частот перекрывает диапазон собственных частот колебаний диска как системы с распределенной массой. При этом возрастает вероятность возникновения параметрических колебаний диска и резонансов. Параметрический резонанс отличается от обычного тем, что происходит не на определенных частотах, а в области частот. Известный способ не позволяет исключать параметрические резонансы. В связи с эти предлагается способ исключения параметрических резонансов в дисках гидромеханических трансмиссий транспортных машин. Новизна способа состоит в том, что в нелинейной системе «барабан - диск» прогнозируются условия возбуждения параметрических резонансов, определяется область устойчивости и синтезируется низкочастотный фильтр, обеспечивающий отстройку высокочастотных резонансов и расширение области устойчивости.
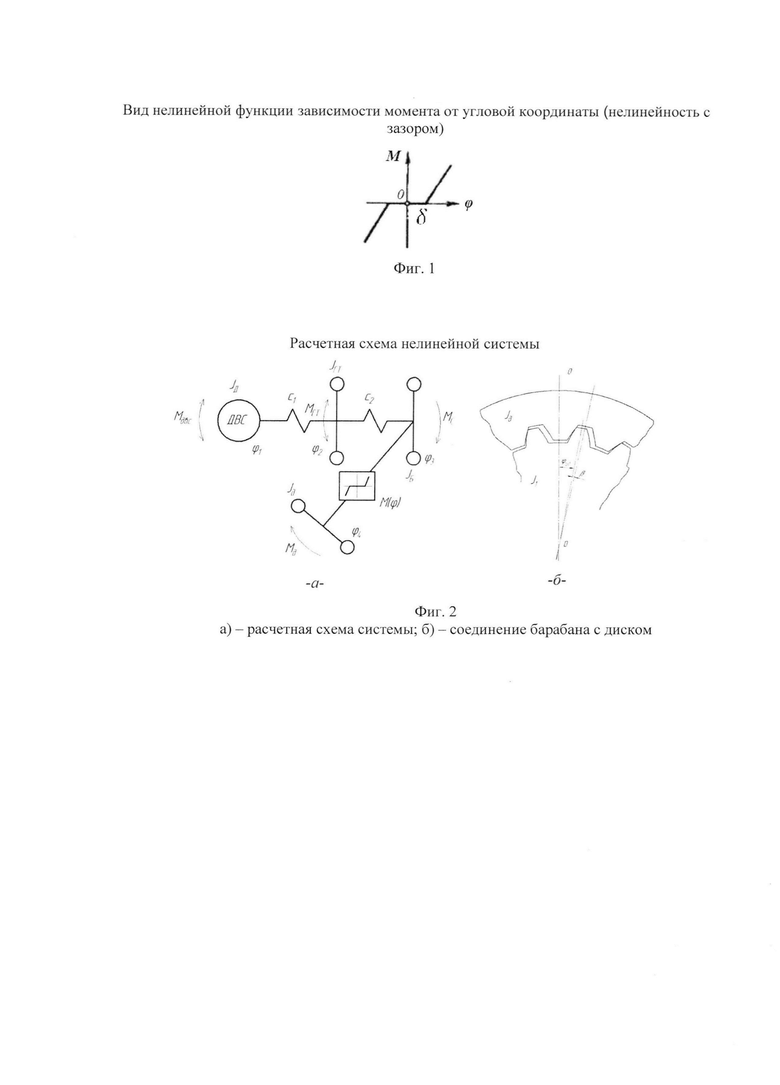
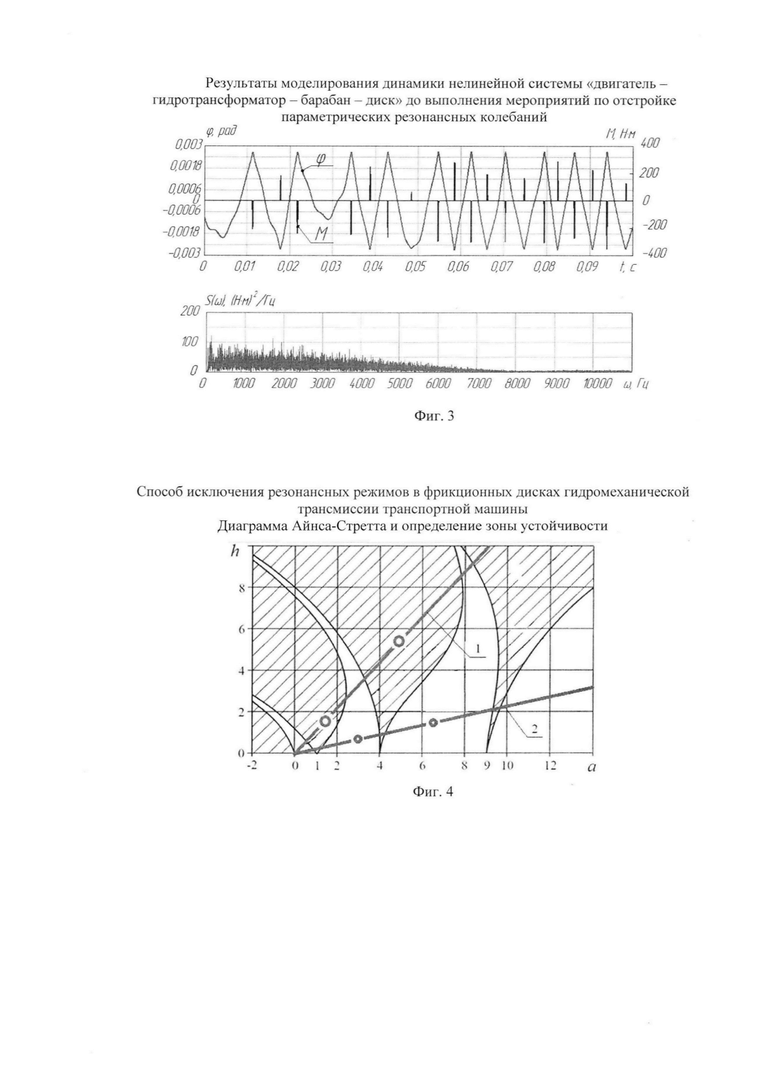
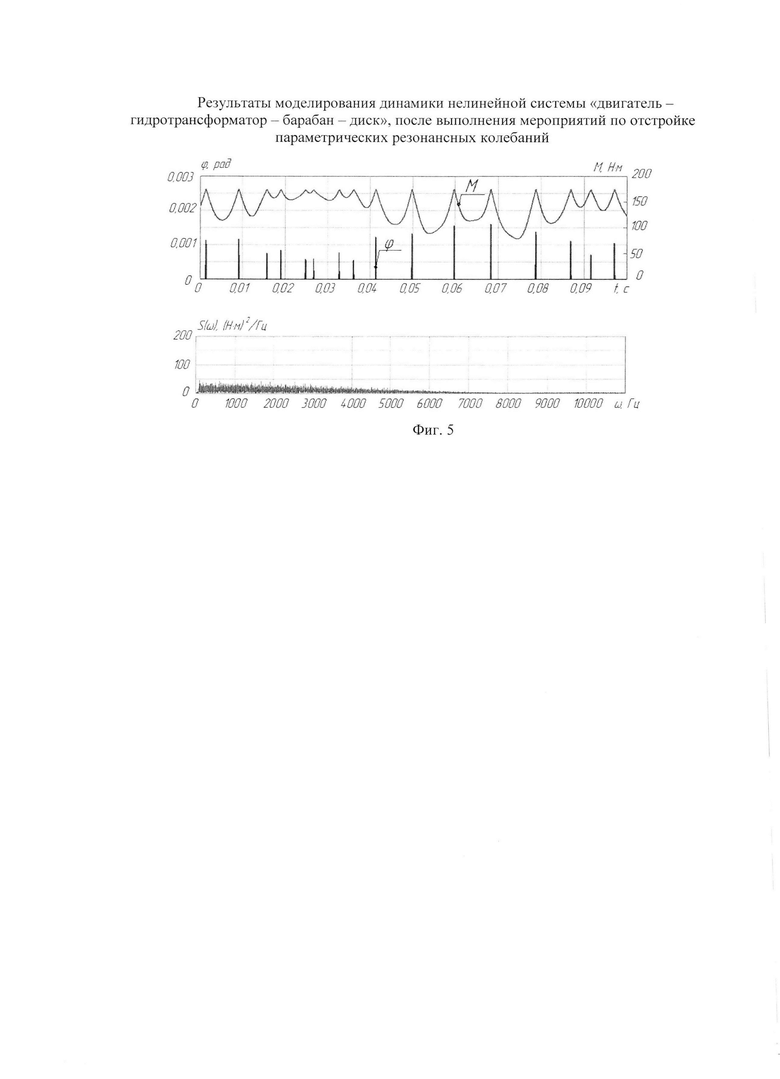
Ниже приведена блок-схема алгоритма последовательности действий, реализующей предлагаемый способ, а на фиг. 1, 2, 3, 4, 5 приведены поясняющие графики. (Фиг. 1 - вид нелинейной функции зависимости момента от угловой координаты (нелинейность с зазором); фиг. 2 - расчетная схема системы; фиг. 3 - результаты моделирования и спектральная плотность процесса генерируемых колебаний; фиг. 4 -диаграмма Айнса-Стретта, определение зоны устойчивости и требуемых параметров системы, исключающих резонанс, а фиг. 5 - результаты моделирования и спектральная плотность возмущения после отстройки параметрического резонанса, т.е. эффективность предлагаемого способа).
Предлагаемый способ исключения и параметрических резонансов в фрикционных дисках гидромеханической трансмиссии транспортной машины осуществляется выполнением следующих операций:
1. Определение спектра собственных частот фрикционных дисков по аналитической зависимости, численным моделированием по твердотельным чертежам или по результатам экспериментального исследования при облучении диска звуковой волной регулируемой частоты.
2. Дополнительное определение параметров нелинейной функции упругого взаимодействия «барабан - диск» (величин зазора δ и угловой жесткости с, фиг. 1), входящих в зависимость момента от угловой координаты М(ϕ):
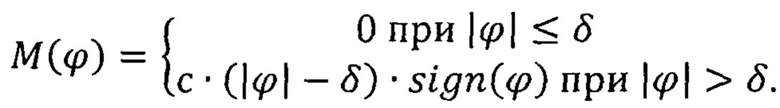
3. Идентификация параметров расчетной схемы системы «двигатель-гидротрансформатор-барабан-диск» - матриц моментов инерции J; коэффициентов диссипации b; характеристик жесткости упругого взаимодействия элементов с(ϕ) и внешних моментов M(t) (расчетная динамическая схема системы приведена на фиг. 2).
4. Выполнение имитационного моделирования динамики нелинейной системы 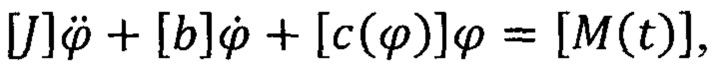 расчет спектральной плотности процесса колебаний, установление порогового значения частоты спектра, колебания с частотами выше которой не пропускаются фильтром (образец результатов моделирования и спектральной плотности процесса приведены на фиг. 3).
расчет спектральной плотности процесса колебаний, установление порогового значения частоты спектра, колебания с частотами выше которой не пропускаются фильтром (образец результатов моделирования и спектральной плотности процесса приведены на фиг. 3).
5. Математическая модель относительного движения двухмассовой нелинейной системы «барабан - диск» 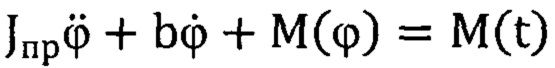 приводится к форме дифференциального уравнения Матье
приводится к форме дифференциального уравнения Матье 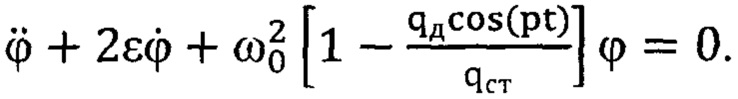 Определяются параметры, входящие в уравнение. В этом уравнении
Определяются параметры, входящие в уравнение. В этом уравнении 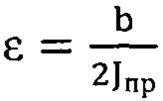 - параметр диссипации;
- параметр диссипации; 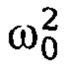 - квадрат частот свободных колебаний нелинейной системы, соответствующий значению коэффициента гармонической линеаризации qст, р - частота внешнего возмущения.
- квадрат частот свободных колебаний нелинейной системы, соответствующий значению коэффициента гармонической линеаризации qст, р - частота внешнего возмущения.
Определяются глубина модуляции жесткости 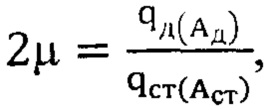 где числитель представляет собой жесткость упругого взаимодействия «барабан-диск» при амплитуде Ад колебаний барабана, определяемой по расчету либо по экспериментальным данным, а знаменатель представляет собой жесткость упругого взаимодействия «барабан-диск» при амплитуде, соответствующей моменту ведения вращающихся дисков Аст. Для данных амплитуд коэффициенты qд и qст определяются по формуле, полученной методом гармонической линеаризации.
где числитель представляет собой жесткость упругого взаимодействия «барабан-диск» при амплитуде Ад колебаний барабана, определяемой по расчету либо по экспериментальным данным, а знаменатель представляет собой жесткость упругого взаимодействия «барабан-диск» при амплитуде, соответствующей моменту ведения вращающихся дисков Аст. Для данных амплитуд коэффициенты qд и qст определяются по формуле, полученной методом гармонической линеаризации.
6. Вычисляются координаты диаграммы Айнса-Стретта (фиг. 4) и анализируются область устойчивости параметрических колебаний
Вводя параметры глубину модуляции жесткости μ и частоту ее изменения р, уравнение Матье без учета диссипации (как показал выполненный расчет это несущественно сужает область неустойчивости) приводится к виду
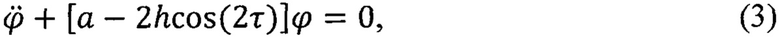
В этом уравнении а и h параметры (абсцисса и ордината) диаграммы Айнса-Стретта 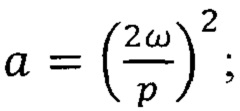 h=аμ; 2τ=pt. Такое представление позволяет анализировать устойчивость параметрических колебаний по диаграмме Айнса-Стретта (фиг. 4) по расположению на диаграмме точек с известными координатами a и h (область устойчивости не заштрихована). Для рассматриваемой системы с параметром глубины модуляции μ=1,3 на диаграмме приведена зависимость h(a) - график 1. По его расположению на диаграмме устанавливается, что параметрические резонансы возможны в широком диапазоне параметра a, определяемого соотношением частот собственных и возмущения.
h=аμ; 2τ=pt. Такое представление позволяет анализировать устойчивость параметрических колебаний по диаграмме Айнса-Стретта (фиг. 4) по расположению на диаграмме точек с известными координатами a и h (область устойчивости не заштрихована). Для рассматриваемой системы с параметром глубины модуляции μ=1,3 на диаграмме приведена зависимость h(a) - график 1. По его расположению на диаграмме устанавливается, что параметрические резонансы возможны в широком диапазоне параметра a, определяемого соотношением частот собственных и возмущения.
7. Устанавливаются требуемые значение параметра глубины модуляции и коэффициента отстройки системы, обеспечивающие расширение области устойчивости. Для рассматриваемой системы снижение параметра глубины модуляции μ до значения 0,1 (график 2 на фиг. 4) позволяет существенно сузить диапазон частот возникновения параметрических резонансных колебаний. Вариация параметра глубины модуляции μ реализуется введением фильтра низкочастотных колебаний, который осуществляет фильтрацию высокочастотных возмущений, генерируемых в системе и виброзащиту барабана.
8. Синтезируется низкочастотный фильтр, обеспечивающий гашение (непрохождение) колебаний с частотами выше установленного порога.
9. Результаты синтеза реализуются в зависимости от требуемого снижения угла наклона линии 1 до линии 2 (фиг. 4), например, в виде разработки упруго-фрикционного гасителя (пружинный демпфер, торсионный вал, эластичная муфта и др.), устанавливаемого на участке между турбинным колесом гидротрансформатора и барабаном, на который устанавливается пакет фрикционных дисков.
На фиг. 5 приведены результаты моделирования динамики нелинейной системы «двигатель - гидротрансформатор - барабан - диск», после выполнения мероприятий по отстройке параметрических резонансных колебаний в соответствии с предлагаемым способом. Из сопоставления результатов моделирования (фиг. 3 и фиг. 5) видно, что мощность спектральной плотности возмущения генерируемого нелинейной системой сокращается по сравнению с исходной в 2,5 раза, а амплитуда момента снижается до 3 раз.
Изобретение относится к области машиностроения. Определяют спектр собственных частот диска и спектр возмущений, формируемых системой. Идентифицируют параметры расчетной схемы системы. Рассчитывают спектральную плотность процесса возбуждаемых в нелинейной системе колебаний. Математическую модель относительного движения двухмассовой нелинейной системы приводят к дифференциальному уравнению параметрических колебаний Матье. Вычисляют параметры системы в координатах диаграммы Айнса-Стретта. Определяют области устойчивости колебаний, требуемые значения параметра глубины модуляции и собственной частоты системы. Устанавливают пороговое значение частоты спектра. Синтезируют низкочастотный фильтр в виде упругофрикционного гасителя. Гаситель размещают на участке между турбинным колесом гидротрансформатора и барабаном, на который устанавливается пакет фрикционных дисков. Достигается расширение области устойчивости. 5 ил.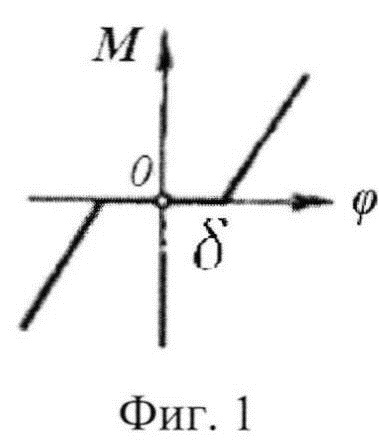
Способ исключения резонансных режимов в металлокерамических дисках гидромеханической трансмиссии транспортной машины, заключающийся в аналитическом или экспериментальном определении спектра собственных частот диска и спектра возмущений, формируемых системой, отличающийся тем, что дополнительно идентифицируют параметры расчетной схемы системы «двигатель - гидротрансформатор - барабан - диск», в том числе параметры нелинейной функции жесткости упругого взаимодействия «барабан - диск», рассчитывают спектральную плотность процесса возбуждаемых в нелинейной системе колебаний, математическую модель относительного движения двухмассовой нелинейной системы «барабан - диск» приводят к дифференциальному уравнению параметрических колебаний Матье, вычисляют параметры системы в координатах диаграммы Айнса-Стретта, по их расположению на диаграмме определяют области устойчивости колебаний, требуемые значения параметра глубины модуляции и собственной частоты системы, обеспечивающие расширение области устойчивости, в которых исключается параметрический резонанс, устанавливают пороговое значение частоты спектра, колебания с частотами выше которой необходимо устранить, синтезируют низкочастотный фильтр в виде упругофрикционного гасителя, выполненного в виде пружинного демпфера, или торсионного вала, или эластичной муфты, размещаемого на участке между турбинным колесом гидротрансформатора и барабаном, на который устанавливается пакет фрикционных дисков, обеспечивающий гашение колебаний, с частотами выше порогового значения.
| СПОСОБ ИСКЛЮЧЕНИЯ РЕЗОНАНСНЫХ РЕЖИМОВ КОЛЕБАНИЙ МЕТАЛЛОКЕРАМИЧЕСКИХ ДИСКОВ ГИДРОМЕХАНИЧЕСКОЙ ТРАНСМИССИИ ТРАНСПОРТНОЙ МАШИНЫ | 2012 |
|
RU2499927C1 |
| WO 2013125050 A1, 29.08.2013 | |||
| DE 10024191 A1, 30.11.2000 | |||
| Демпфер роторных вибраций | 1985 |
|
SU1252570A1 |
Авторы
Даты
2020-07-30—Публикация
2019-06-05—Подача