Изобретение относится к области масс-спектрометрии и может быть использовано для совершенствования аналитических, эксплуатационных и коммерческих характеристик приборов микроанализа вещества, использующих движение ионов в квадрупольных высокочастотных ВЧ электрических полях. Техническая задача изобретения состоит в усовершенствовании конструкции ионно-оптической системы (ИОС) квадрупольных масс-анализаторов с возбуждением колебаний ионов и повышении их разрешающей способности и чувствительности. Известными приборами этого типа являются линейные ионные ловушки или с квадрупольными анализаторами [1], или с планарными дискретными электродами [2, 3] с дипольным возбуждением колебаний ионов. Их аналитические возможности ограничены сложной структурой функции возбуждения и низкой скоростью ее нарастания в процессе возбуждения колебаний [4].
Предлагаемое устройство, реализуемое с помощью ИОС с планарными дискретными электродами в полупространстве у≥0, позволяет усовершенствовать аналитические, конструктивные и эксплуатационные параметры масс-спектрометров этого класса.
В известных квадрупольных масс-анализаторах с резонансным возбуждением колебаний ионов ИОС состоят из 4-х гиперболических [1] или из 2-х планарных дискретных [2] электродов. Они образуют суперпозиции квадрупольных ВЧ и однородных гармонических электрических полей в двухполярной рабочей области -уа≤у≤уа в плоскости X0Y, где уа - размер ИОС по оси возбуждения Y. Для возбуждения колебаний в этих случаях используется однородное гармоническое поле и ионы в процессе масс-анализа совершают в рабочей области анализатора двухполярные колебания [1, 2].
В предлагаемом устройстве резонансное возбуждение колебаний ионов в квадрупольных ВЧ полях происходит под действием суперпозиции квазистатических квадрупольных и статических однородных полей, при этом колебания по оси возбуждения Y оказываются однополярными y(t)>0 [5]. Поэтому рабочая область анализатора по оси Y также может быть монополярной.
Предлагаемое устройство масс-анализа ионов, содержащее ионно-оптическую систему для образования в плоскости X0Y суперпозиции квадрупольных и однородных электрических полей и возбуждения в них резонансных колебаний отличается тем, что его ИОС с размерами 2ха, уа и 2za по осям X, Y, Z монополярная, расположена в полупространстве у≥0 и состоит из 2-х в плоскостях х=±ха, с размерами уа>>ха, 2za>>ха по осям Y, Z, дискретных с шагом Δуа<<уа по оси Y электродов (I) и (II) с дискретно-линейным по оси Y распределениями ВЧ, квазистатических и статических потенциалов u(I)i=ΔUy(t)i+ΔVyicosωt+ΔUвi, u(II)i=-ΔUy(t)i-ΔVyicosωt+ΔUвi, где i=1, 2, 3, …, n - номер дискретных элементов электродов, n=ya/Δy, ΔUy(t)=U(t)/n, U(t)=Ut/T - квазистатический (медленно изменяющийся при развертке масс) потенциал, Т - длительность развертки масс, ΔUв=Uв/n, Uв - потенциал однородного возбуждающего поля, одного в плоскости y=0, с размерами 2ха, 2za по осям X, Y, заземленного электрода (IV), и одного в плоскости у=уа с размерами 2ха, 2za по осям X и Z, дискретного с шагом Δх<<ха по оси X электрода (III) с суперпозицией дискретно-линейных распределений высокочастотного и квазистатического потенциалов и статического возбуждающего потенциала u(III)j=ΔUx(t)j+ΔVxjcosωt+ΔUв, где j=-m, …, - 2, - 1, 0, 1, 2, …, m - номер дискретного элемента электрода, m=ха/Δх, ΔUx(t)=U(t)/m, ΔVx=V/m. Для вывода ионов из анализатора на регистрацию электрод (III) выполняется полупрозрачным.
Схема ИОС предлагаемого устройства приведена на Фиг. 1. Ионно-оптическая система в плоскости X0Y замкнутая, поэтому точность распределения суперпозиции электрических полей в ней зависит только от шага дискретности электродов I, II, III. При оптимизации режимов резонансного возбуждения ионов размеры рабочей области анализатора ха и уа, и их соотношения, могут выбираться в широких пределах.
Питание анализатора осуществляется ВЧ напряжением с постоянными параметрами V и ω, что обеспечивает их высокую точность установки и стабильность. Монополярная схема ИОС возбуждает колебания ионов в одном направлении оси Y, что в 2 раза увеличивает чувствительность анализатора.
Таким образом предлагаемое решение позволяет усовершенствовать конструкцию ИОС масс-анализаторов с резонансным возбуждением ионов, осуществлять оптимизацию ее параметров, повысить аналитические и эксплуатационные характеристики масс-спектрометров такого типа, а также повысить эффективность систем их ВЧ питания и развертки.
Литература
1. D.J. Douglas, N.V. Konenkov. Mass selectivity of dipolar resonant excitation in a linear quadrupole ion trap // Rapid Communications in Mass Spectrometry. 2014, V. 28, p. 430-438.
2. E.В. Мамонтов. Способ масс-анализа с резонансным возбуждением ионов и устройство для его осуществления. Патент на изобретение RU 2634614, 11.02.2017. Заявка №2016149722 от 16.12.2016.
3. Е.В. Мамонтов. Способ образования двумерного линейного высокочастотного электрического поля и устройство для его осуществления. Патент РФ №2497226, 2012 г.
4. Мамонтов Е.В., Судаков М.Ю., Дятлов Р.Н. Свободные и вынужденные колебания заряженных частиц в инерционно-нестационарных быстроосциллирующих квадрупольных электрических полях. Радиотехника и электроника. 2020, том 65, №2, с. 197-202.
5. Е.В. Мамонтов. Способ масс-анализа ионов в квадрупольных полях с возбуждением колебаний на границы устойчивости. Заявка на патент, 2020 г.

Изобретение относится к области масс-спектрометрии и может быть использовано для совершенствования аналитических, эксплуатационных и коммерческих характеристик приборов микроанализа вещества, использующих движение ионов в квадрупольных высокочастотных электрических полях. Технический результат - повышение разрешающей способности и чувствительности квадрупольных масс-анализаторов. Устройство содержит ионно-оптическую систему из планарных электродов с дискретно-линейными распределениями на них суперпозиций квадрупольных ВЧ и квазистатических и однородных статических потенциалов. В процессе развертки масс изменением постоянной составляющей квадрупольного поля под действием однородного статического поля происходит возбуждение на границе устойчивости однополярных колебаний ионов. При этом ионы поочередно, в порядке убывания их массы выводятся из анализатора на регистрацию. 1 ил.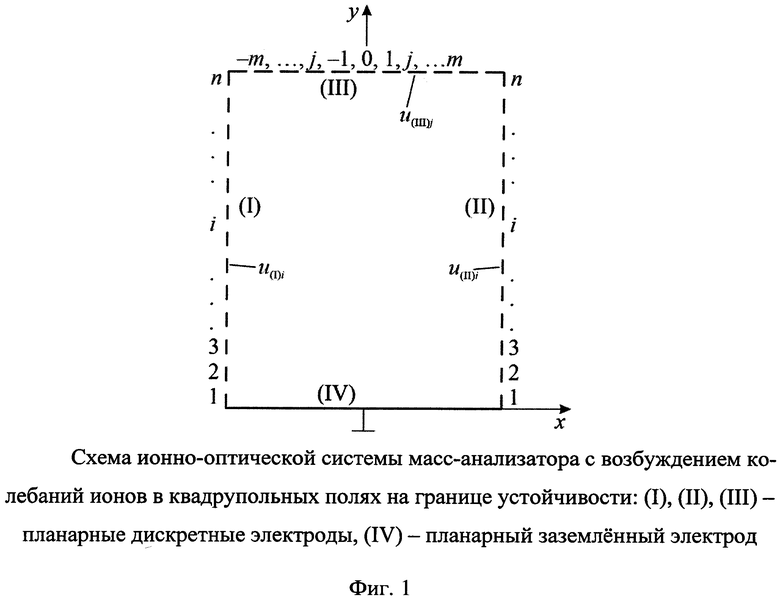
Устройство масс-анализа ионов, содержащее ионно-оптическую систему для образования в плоскости X0Y суперпозиций квадрупольных и однородных электрических полей и возбуждения в них резонансных колебаний, отличается тем, что его монополярная ионно-оптическая система с размерами 2ха, уа и za по осям X, Y и Z расположена в полупространстве у≥0 и состоит из двух в плоскостях х=±ха, с размерами уа>>ха, 2za>>ха по осям Y, Z, дискретных с шагом Δуа<<уа по оси Y, электродов (I) и (II) с дискретно-линейными по оси Y распределениями высокочастотных, квазистатических и статических потенциалов u(I)i=ΔUy(t)i+ΔVyicosωt+ΔUвi, u(II)i=-ΔUy(t)i-ΔVyicosωt+ΔUвi, где i=1, 2, 3, …, n - номер дискретного элемента электрода, n=уа/Δу, ΔUy(t)=U(t)/n, U(t)=Ut/T - квазистатический (медленно изменяющийся при развертке масс) потенциал, T - длительность развертки масс, ΔUв=Uв/n, Uв - потенциал возбуждающего однородного поля, одного в плоскости у=0, с размерами 2ха, 2za по осям X, Z, заземленного электрода (IV), и одного в плоскости у=уа, с размерами 2ха, 2za по осям X, Z, дискретного с шагом Δх<<ха по оси X, электрода (III) с суперпозицией дискретно-линейных распределений высокочастотного и квазистатического потенциалов и статического возбуждающего потенциала u(III)j=ΔUx(t)j+ΔVxjcosωt+ΔUв, где j = -m, …, - 2, - 1, 0, 1, 2, …, m - номер дискретного элемента электрода, m=ха/Δх, ΔUx(t)=U(t)/m, ΔVx=V/m, причем для вывода ионов из анализатора на регистрацию электрод (III) выполняется полупрозрачным.
| Способ масс-анализа ионов в квадрупольных высокочастотных полях с дипольным возбуждением колебаний на границах стабильности | 2017 |
|
RU2683018C1 |
| Способ масс-анализа с резонансным возбуждением ионов и устройство для его осуществления | 2016 |
|
RU2634614C1 |
| СПОСОБ МАСС-СЕЛЕКТИВНОГО АНАЛИЗА ИОНОВ ПО ВРЕМЕНИ ПРОЛЕТА И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2006 |
|
RU2327245C2 |
| WO 2006075189 A2, 20.07.2006 | |||
| WO 2015007165 A1, 22.01.2015 | |||
| JP 2020021602 A, 06.02.2020. | |||
Авторы
Даты
2021-06-15—Публикация
2020-07-14—Подача