Изобретение относится к антенной технике, а именно, к способам построения системы диаграммообразования приемных цифровых антенных решеток (ЦАР) для систем радиосвязи, радиолокации и т.д.
Известен способ построения системы диаграммообразования активных фазированных антенных решеток (АФАР) [1 - Активные фазированные антенные решетки /под ред. Д.И. Воскресенского, А.И. Канащенкова. М.: Радиотехника. 2004. С. 113, рис. 6.2. - 488 с.], при котором принятый каждым антенным элементом сигнал усиливают и делят на число, равное числу формируемых диаграмм. В канале каждой диаграммы устанавливают управляемые фазовращатель и аттенюатор, с помощью которых для каждой формируемой диаграммы направленности (ДН) устанавливается оптимальный весовой коэффициент. Далее сигналы каналов, соответствующих каждой ДН, суммируют с помощью сумматоров.
Недостатком известного способа является значительный рост потерь в энергетике АФАР при формировании большого числа лучей.
Известен способ цифрового диаграммообразования в приемной цифровой антенной решетке (ЦАР) [2 - Григорьев Л.Н. Цифровое формирование диаграммы направленности в фазированных антенных решетках. - М.: Радиотехника, 2010. С. 22.-144 с.], состоящий в том, что осуществляют прием сигналов со всех направлений пространства антенными элементами приемных каналов антенной решетки, в каждом приемном канале принятые сигналы усиливают, переносят на промежуточную частоту, преобразуют в цифровую форму в виде последовательности цифровых отсчетов, формируют выходной сигнал путем последовательного суммирования цифровых отсчетов, полученных от предыдущего приемного канала со взвешенными значениями отсчетов сигнала следующего приемного канала, а весовые коэффициенты задают из условия синфазного приема сигнала с заданного направления.
Недостатком данного способа являются пониженные функциональные возможности из-за ограничений на скорость передачи данных между процессорами и наличие физической и логической задержек. Физическая задержка обусловлена ограниченной скоростью передачи данных, а логическая - невозможностью для следующего процессора начать обработку данных до того, как эти данные будут обработаны предыдущим процессором.
Известен способ построения системы диаграммообразования АФАР [3 - Пат. 2516683, RU. Способ цифрового формирования диаграммы направленности активной фазированной антенной решетки при излучении и приеме линейно-частотно-модулированного сигнала / Гуськов Ю.Н., Жибурдович Н.Ю., Абраменков В.В. и др. МКИ H01Q 21/00. Опубл. 20.05.2014. Бюл. №14; 2 -, с. 23], заключающийся в том, что принятый каждым антенным элементом сигнал усиливают, преобразуют по частоте, фильтруют в полосовом фильтре и с помощью аналого-цифрового преобразователя (АЦП) превращают в цифровую последовательность. Формируют ДН путем взвешенного сложения отсчетов, соответствующих одним и тем же моментам квантования.
Недостаток способа состоит в сложности его технической реализации, поскольку для этого потребуется ввод большого количества кабельных соединений с оцифрованными данными в единственный процессор от каждого приемного модуля и обеспечения параллельной обработки этих данных путем взвешенного сложения матриц данных большой размерности при сохранении высокого быстродействия.
Наиболее близким по технической сущности к изобретению является способ построения системы диаграммообразования АФАР [4 - Пат. 2731604, RU. Способ построения системы диаграммообразования активной фазированной антенной решетки / Косогор А.А., Задорожный В.В., Ланкин А.С., Ларин А.Ю., Омельчук И.С., Васильев А.В., Чернышев М.И. МКИ G01S 13/26. Опубл. 04.09.2020, Бюл. №25], взятый за прототип, в соответствии с которым принятый каждым антенным элементом сигнал усиливают, преобразуют по частоте, фильтруют в полосовом фильтре и с помощью АЦП превращают в цифровую последовательность. Формируют ДН путем весового суммирования последовательностей отсчетов входных сигналов, соответствующих одним и тем же моментам квантования. Формируют антенное полотно из М N - канальных приемопередающих модулей, объединенных в L подрешеток, формируют последовательность отсчетов парциальных ДН первого уровня во встроенных в приемопередающие модули процессорах формирования ДН первого уровня путем весового суммирования последовательности отсчетов N входных сигналов, соответствующих одним и тем же моментам квантования, формируют парциальные ДН второго уровня в процессорах формирования ДН второго уровня путем весового суммирования последовательностей отсчетов с выходов процессоров формирования ДН первого уровня из состава подрешетки, формируют результирующие ДН в процессорах формирования ДН последнего уровня, используя последовательности отсчетов парциальных ДН с выходов процессоров формирования ДН предыдущего уровня, при этом число уровней формирования ДН определяют по формуле, учитывающей число приемопередающих модулей и число процессоров формирования ДН на первом уровне, а для передачи данных между процессорами формирования ДН используют линии связи с последовательной передачей данных.
Достоинством способа является упрощение аппаратной реализации. Основной недостаток - снижение функциональных возможностей, состоящее в ограничении числа формируемых лучей из-за ограниченной пропускной способности линии связи. В качестве линий связи с последовательной передачей данных используют волоконно-оптические линии связи (ВОЛС), пропускная способность которых без частотного уплотнения составляет 11…16 Гбит/с [5 - Скляров O.K. Современные волоконно-оптические системы передачи, аппаратура и элементы. - М.: СОЛОН-Р, 2001. - 237 с.]. Если частота дискретизации сигнала выбрана равной 100 МГц, а разрядность одного отсчета квадратурной составляющей сигнала - 32 бита, то требуемая скорость передачи комплексных отсчетов для одного луча ДН составляет 6.4 Гбит/с. Это означает, что по ВОЛС без частотного уплотнения для рассматриваемого примера можно передать данные только для двух лучей. На практике для увеличения числа формируемых ДН уменьшают разрядность АЦП, снижают частоту дискретизации или осуществляют децимацию отсчетов. При этом число параллельно формируемых лучей остается ограниченным, вследствие ограниченной пропускной способности линий связи с последовательной передачей данных.
Технической проблемой, на решение которой направлено заявляемое изобретение, является расширение функциональных возможностей ЦАР, состоящее в увеличении числа формируемых лучей при сохранении технически обеспечиваемой скорости передачи данных по линиям связи.
Для решения указанной технической проблемы предлагается способ построения системы диаграммообразования приемной цифровой антенной решетки, при котором формируют антенное полотно из М приемных модулей по N каналов в каждом, объединенных в L подрешеток, в каждом канале приемного модуля принимают входной сигнал антенным элементом, усиливают входной сигнал, в случае выполнения приемной цифровой антенной решетки по супергетеродинной схеме выполняют преобразование частоты входного сигнала, фильтруют входной сигнал в полосовом фильтре, выполняют его дискретизацию с помощью аналого-цифрового преобразования в виде последовательностей комплексных отсчетов сигналов каналов приемных модулей.
Согласно изобретению из последовательностей комплексных отсчетов сигналов каналов приемных модулей формируют прямоугольные комплексные матрицы сигналов размером N×Nst, в каждом приемном модуле выполняют двумерное симметричное косинусное преобразование комплексных матриц сигналов размером N×Nst, формируя косинусные спектры комплексных матриц сигналов, при помощи заданных базисных функций аппроксимируют соответствующую матрицу косинусного спектра комплексных матриц сигналов М' выходными коэффициентами каждого приемного модуля, формируют векторы данных подрешеток путем объединения М' выходных коэффициентов каждого приемного модуля, переданных последовательно по линиям связи в L подрешетках, формируют общую последовательность данных длиной М⋅М' путем объединения векторов данных подрешеток, переданных последовательно по линиям связи, из общей последовательности данных восстанавливают выходные коэффициенты каждого приемного модуля, формируют косинусные спектры комплексных матриц сигналов путем взвешенного сложения базисных функций с выходными коэффициентами каждого приемного модуля, выполняют обратное симметричное косинусное преобразование косинусного спектра комплексных матриц сигналов и восстанавливают комплексные матрицы сигналов размером N×Nst, формируют необходимое число результирующих диаграмм направленности путем весового суммирования восстановленных комплексных матриц сигналов размером N×Nst, соответствующих одним и тем же моментам квантования.
Таким образом, заявленный способ имеет следующие отличительные признаки и последовательность его реализации от способа-прототипа, которые приведены в таблице 1.
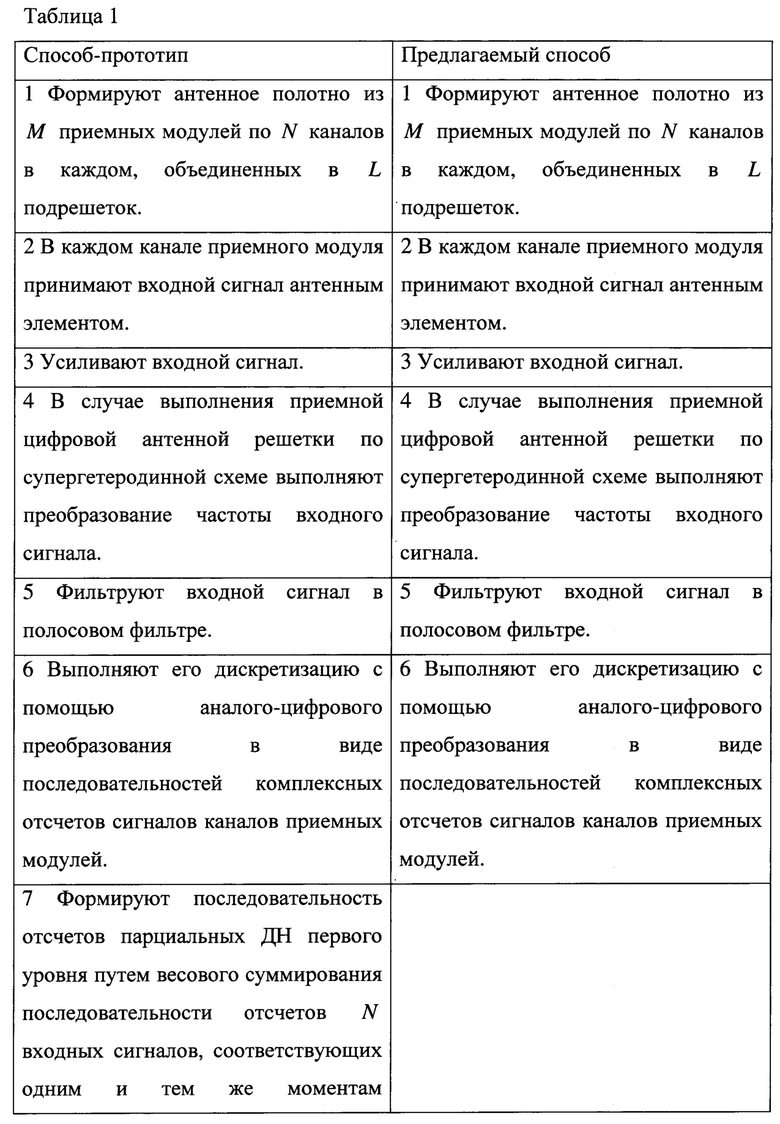
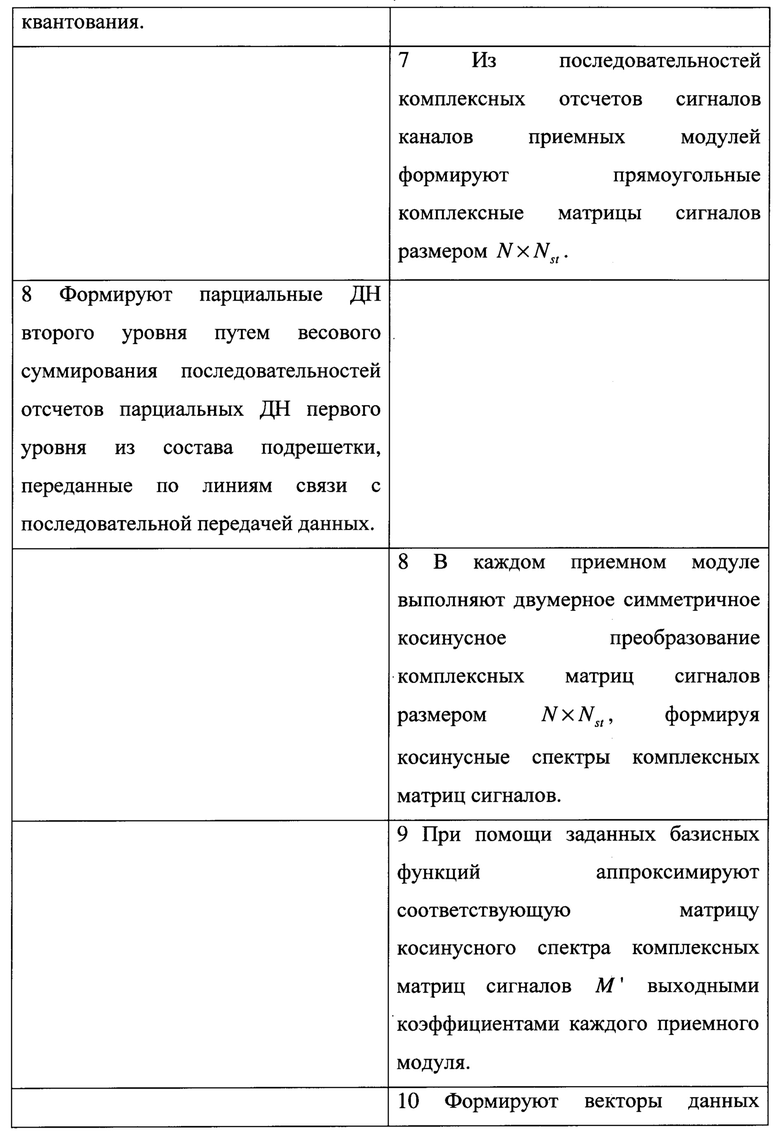
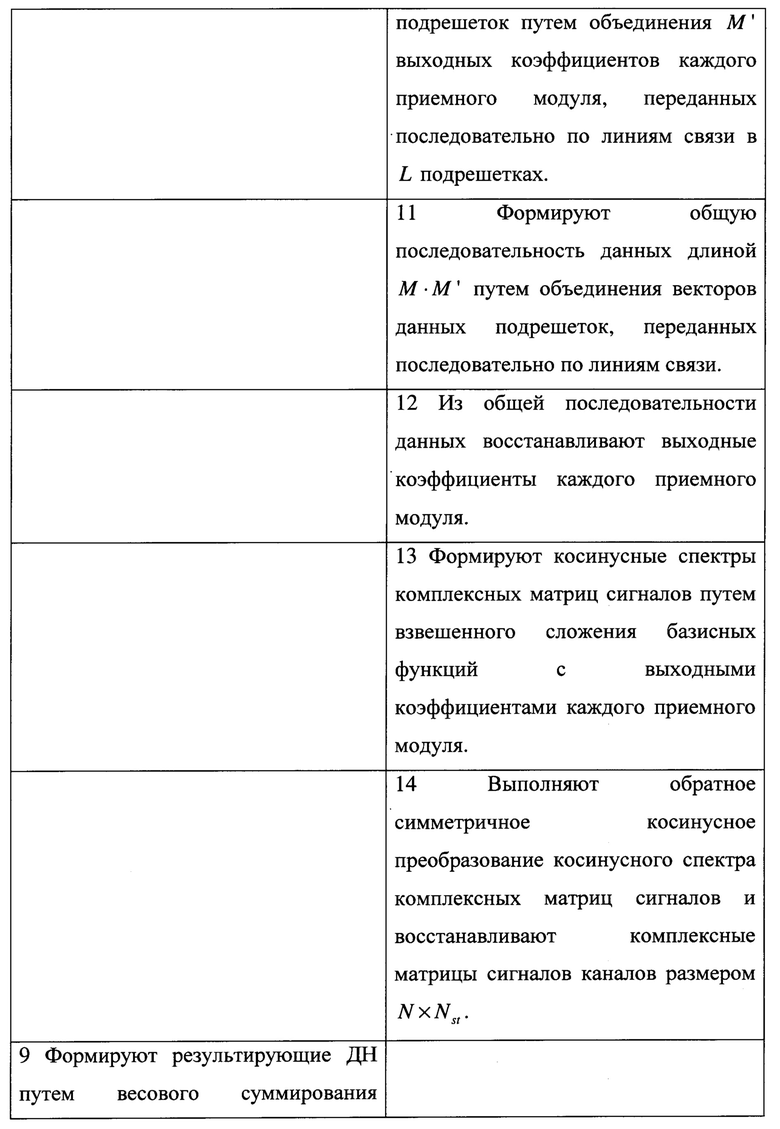

Из представленной таблицы сравнения последовательностей реализации способа-прототипа и заявленного способа видно, что введены следующие новые операции:
7 Из последовательностей комплексных отсчетов сигналов каналов приемных модулей формируют прямоугольные комплексные матрицы сигналов размером N×Nst.
8 В каждом приемном модуле выполняют двумерное симметричное косинусное преобразование комплексных матриц сигналов размером N×Nst, формируя косинусные спектры комплексных матриц сигналов.
9 При помощи заданных базисных функций аппроксимируют соответствующую матрицу косинусного спектра комплексных матриц сигналов М' выходными коэффициентами каждого приемного модуля.
10 Формируют векторы данных подрешеток путем объединения М' выходных коэффициентов каждого приемного модуля, переданных последовательно по линиям связи в L подрешетках.
11 Формируют общую последовательность данных длиной М⋅М' путем объединения векторов данных подрешеток, переданных последовательно по линиям связи.
12 Из общей последовательности данных восстанавливают выходные коэффициенты каждого приемного модуля.
13 Формируют косинусные спектры комплексных матриц сигналов путем взвешенного сложения базисных функций с выходными коэффициентами каждого приемного модуля.
14 Выполняют обратное симметричное косинусное преобразование косинусного спектра комплексных матриц сигналов и восстанавливают комплексные матрицы сигналов каналов размером N×Nst.
15 Формируют необходимое число результирующих диаграмм направленности путем весового суммирования восстановленных комплексных матриц сигналов размером N×Nst, соответствующих одним и тем же моментам квантования.
Изменение совокупности действий, связанных с организацией процесса обработки последовательностей отсчетов входных сигналов и введением девяти операций, позволяет по сравнению со способом-прототипом обеспечить технический результат, заключающийся в расширении функциональных возможностей ЦАР за счет увеличения числа формируемых лучей при сохранении технически обеспечиваемой скорости передачи данных по линиям связи.
Проведенный анализ уровня техники позволил установить, что аналоги, характеризующиеся совокупностью признаков, тождественных всем признакам заявленного технического решения, отсутствуют, что указывает на соответствие заявленного способа построения системы диаграммообразования приемной цифровой антенной решетки условию патентоспособности "новизна".
Результаты поиска известных решений в данной и смежных областях для выявления признаков, совпадающих с отличительными от прототипа признаками заявленного способа построения системы диаграммообразования приемной цифровой антенной решетки, показали, что они не следуют явным образом из уровня техники. Из уровня техники также не выявлена известность влияния предусматриваемых существующими признаками заявленного изобретения преобразований на достижение указанного технического результата. Следовательно, заявленное изобретение соответствует условию патентоспособности "изобретательский уровень".
Сущность заявленного способа раскрывается фигурами 1-10.
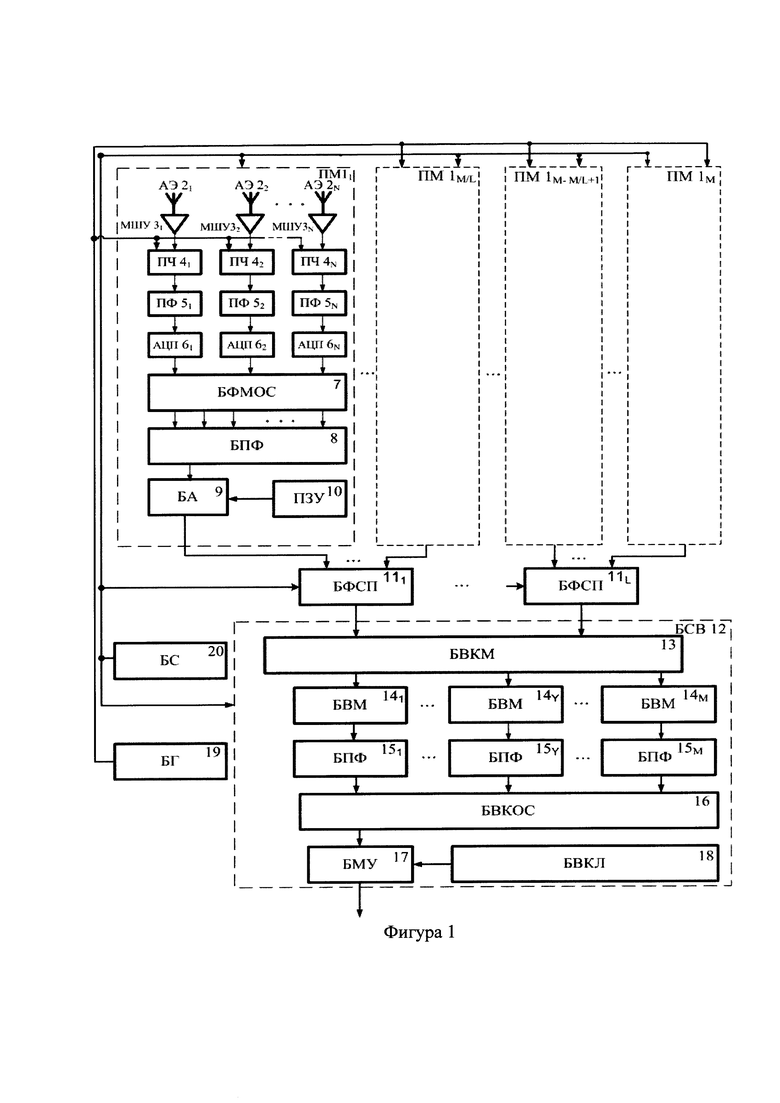
На фиг.1 приведена структурная схема устройства, обеспечивающего реализацию заявленного способа.
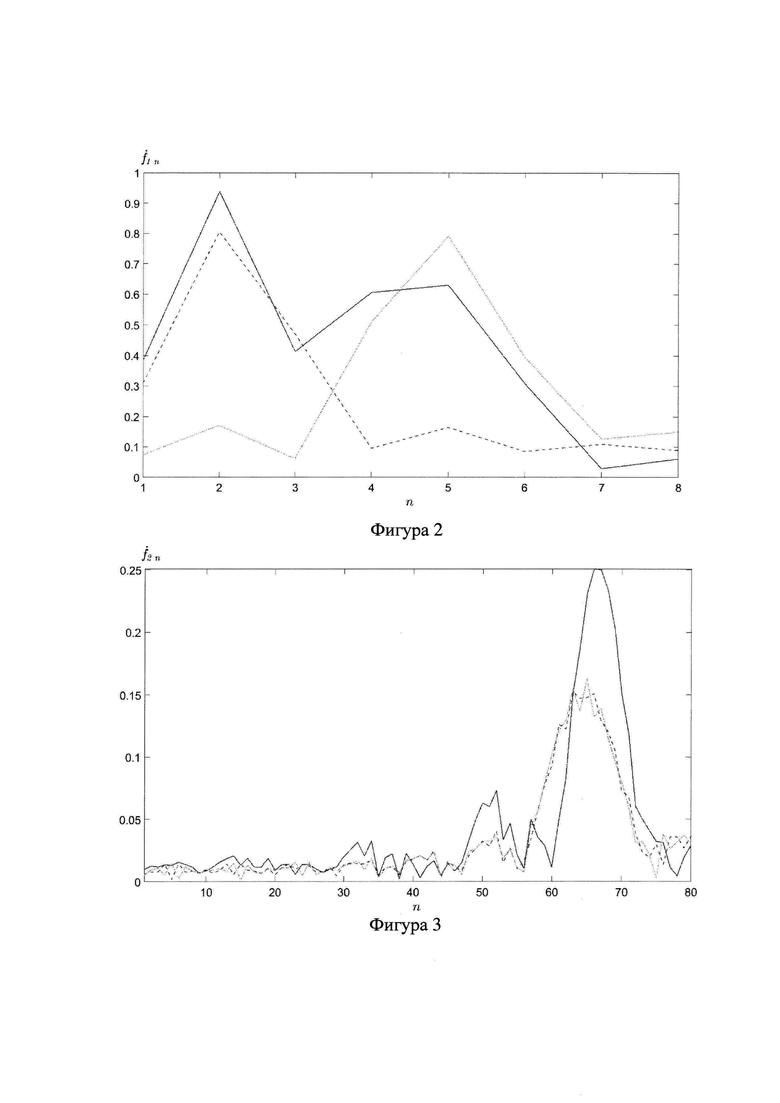
На фиг.2 приведено распределение амплитуд гармоник суммы двух спектров одномерного симметричного косинусного преобразования вдоль пространственной координаты для двух разнесенных в пространстве источников (сплошная кривая) и распределения амплитуд гармоник аналогичных спектров при приеме сигналов каждого из источников по отдельности (штриховая и штрих-пунктирная кривые соответственно).
На фиг.3 представлено распределение амплитуд гармоник спектра одномерного симметричного косинусного преобразования вдоль временной координаты, соответствующего приему двух эхо-сигналов в случае использования зондирующего сигнала с линейной частотной модуляцией: при совместном приеме эхо-сигналов (сплошная кривая) и при приеме эхо-сигналов по отдельности (штриховая и штрих-пунктирная кривые).
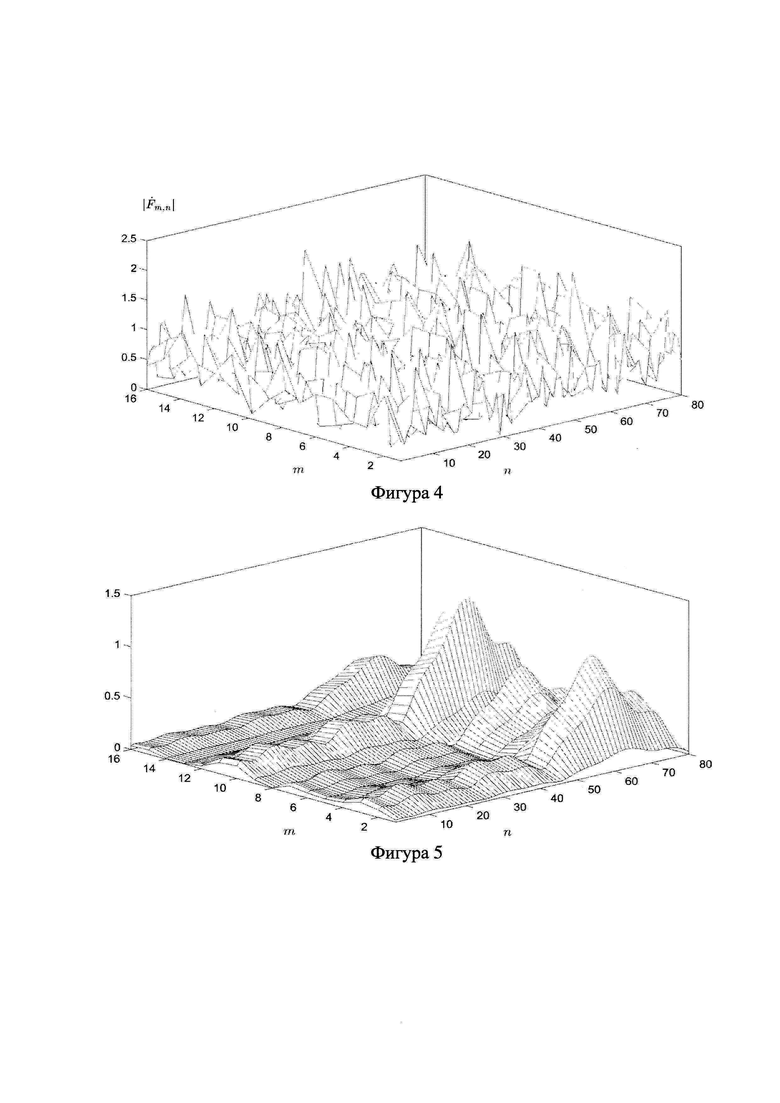
На фиг.4 приведено распределение амплитуд гармоник спектра двумерного симметричного косинусного преобразования (по пространству и времени), соответствующего выборке данных, содержащей принимаемые сигналы и шум.
На фиг.5 показано распределение амплитуд гармоник двумерного спектра симметричного косинусного преобразования при отсутствии шумов и при наличии сигнальной составляющей.
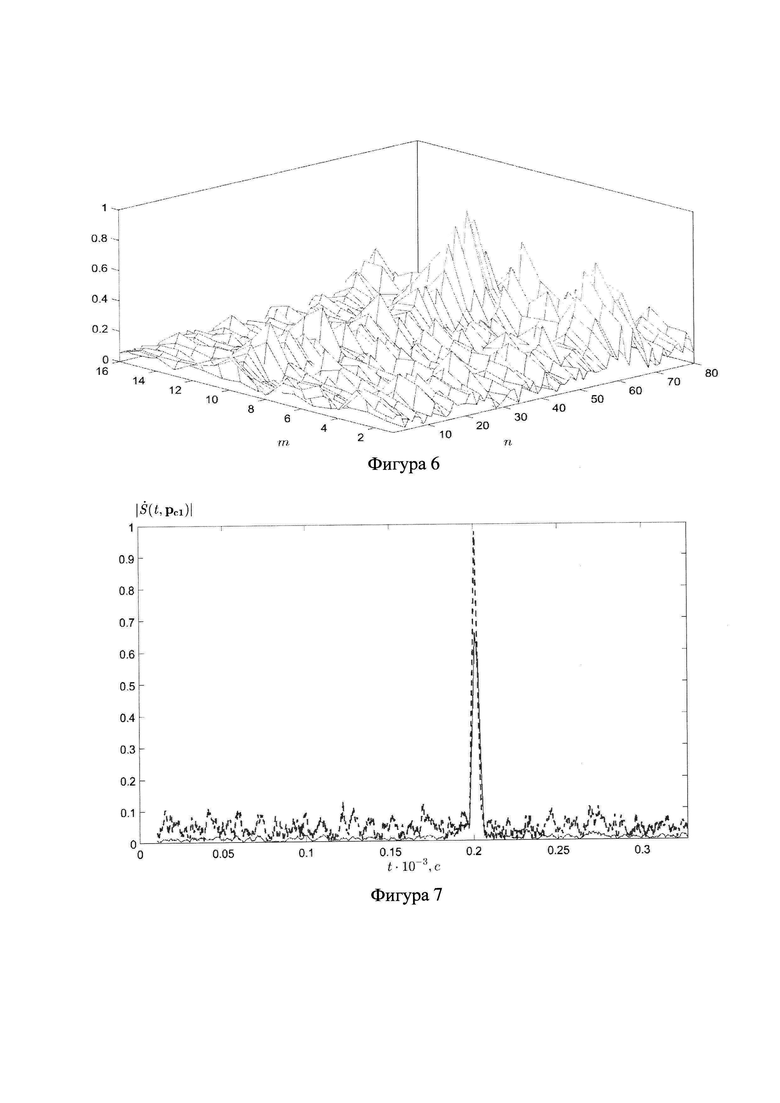
На фиг.6 приведено распределение амплитуд гармоник спектра, полученное при реализации алгоритма аппроксимации при наличии шумов.
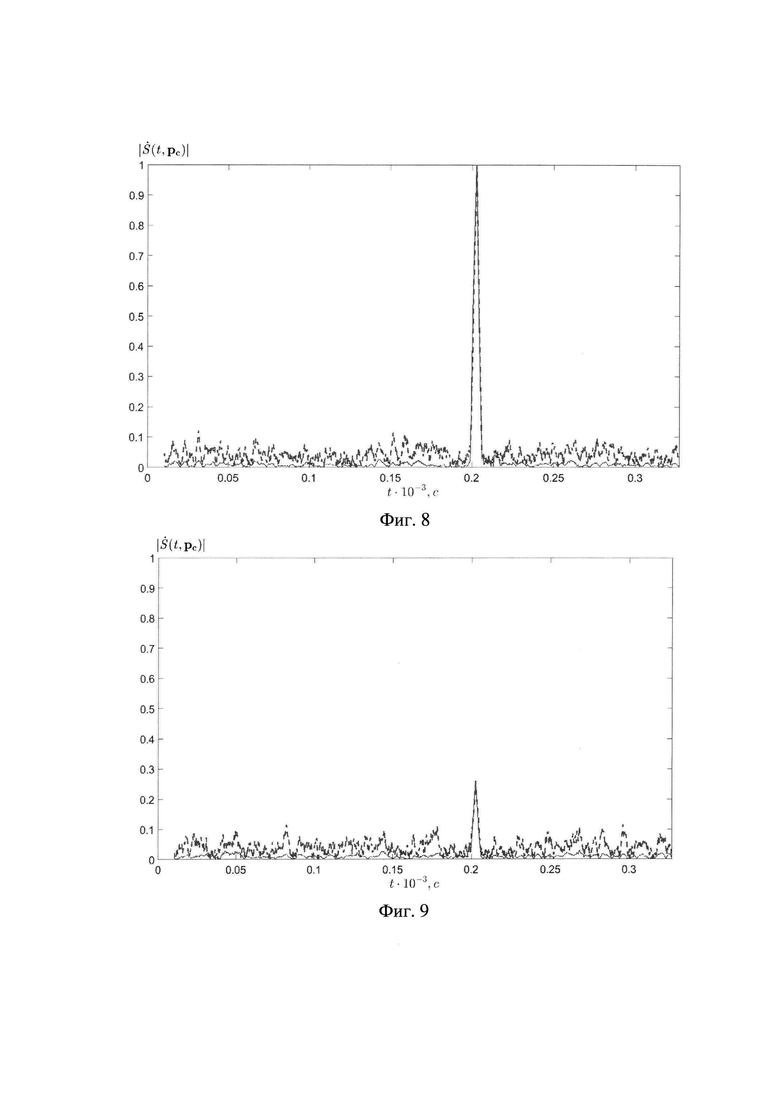
На фиг.7-9 представлены временные диаграммы, полученные в результате согласованной фильтрации в трех лучах, соответственно ориентированных на первый, второй источники сигналов и по нормали к раскрыву (для заявленного способа - сплошная кривая, для прототипа -штриховая кривая).
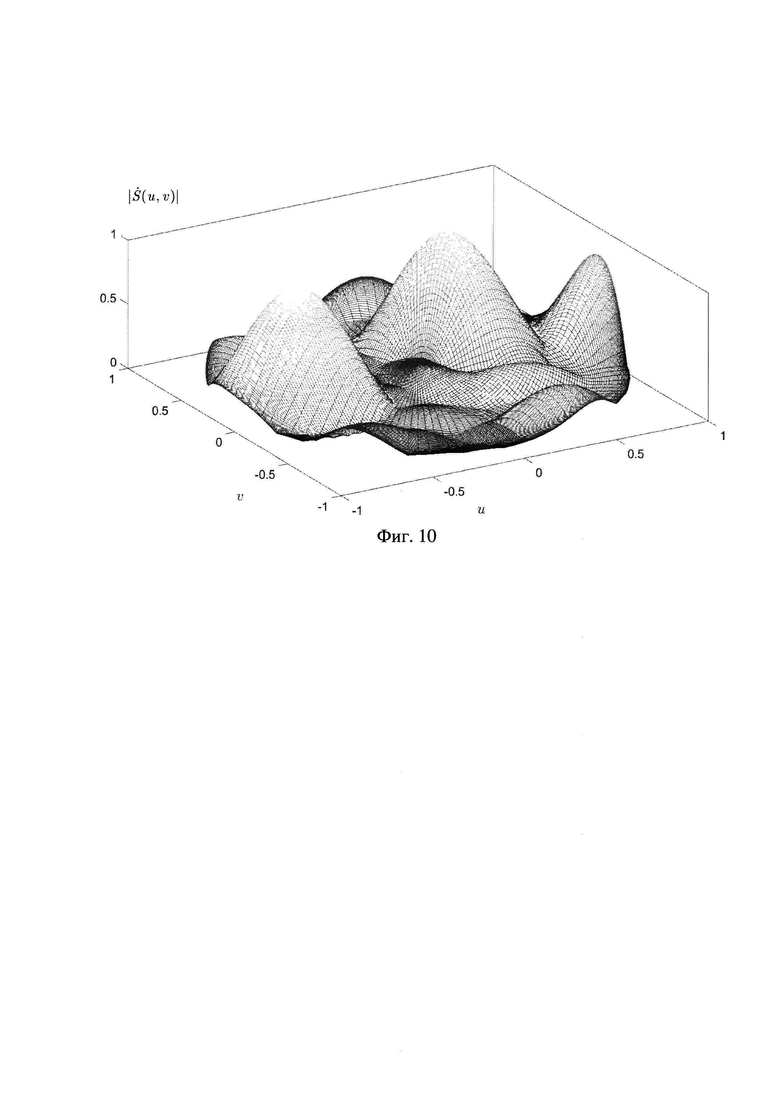
На фиг.10 показан пространственный пеленгационный рельеф.
При реализации заявленного способа построения системы диаграммообразования приемной цифровой антенной решетки выполняется следующая последовательность операций:
- формируют антенное полотно из М приемных модулей по N каналов в каждом, объединенных в L подрешеток - 1;
- в каждом канале приемного модуля принимают входной сигнал антенным элементом - 2;
- усиливают входной сигнал - 3;
- в случае выполнения приемной цифровой антенной решетки по супергетеродинной схеме выполняют преобразование частоты входного сигнала - 4;
- фильтруют входной сигнал в полосовом фильтре - 5;
- выполняют его дискретизацию с помощью аналого-цифрового преобразования в виде последовательностей комплексных отсчетов сигналов каналов приемных модулей - 6;
- из последовательностей комплексных отсчетов сигналов каналов приемных модулей формируют прямоугольные комплексные матрицы сигналов размером N×Nst - 7;
- в каждом приемном модуле выполняют двумерное симметричное косинусное преобразование комплексных матриц сигналов размером N×Nst, формируя косинусные спектры комплексных матриц сигналов - 8;
- при помощи заданных базисных функций аппроксимируют соответствующую матрицу косинусного спектра комплексных матриц сигналов М' выходными коэффициентами каждого приемного модуля - 9;
- формируют векторы данных подрешеток путем объединения М' выходных коэффициентов каждого приемного модуля, переданных последовательно по линиям связи в L подрешетках - 10;
- формируют общую последовательность данных длиной М⋅М' путем объединения векторов данных подрешеток, переданных последовательно по линиям связи - 11;
- из общей последовательности данных восстанавливают выходные коэффициенты каждого приемного модуля - 12;
- формируют косинусные спектры комплексных матриц сигналов путем взвешенного сложения базисных функций с выходными коэффициентами каждого приемного модуля - 13;
- выполняют обратное симметричное косинусное преобразование косинусного спектра комплексных матриц сигналов и восстанавливают комплексные матрицы сигналов каналов размером N×Nst - 14;
- формируют необходимое число результирующих диаграмм направленности путем весового суммирования восстановленных комплексных матриц сигналов размером N×Nst, соответствующих одним и тем же моментам квантования - 15.
Реализация заявленного способа построения системы диаграммообразования приемной цифровой антенной решетки в случае выполнения каналов приемных модулей по супергетеродинной схеме возможна, например, с помощью устройства, приведенного на фиг.1.
Устройство, приведенное на фиг.1, включает М приемных модулей (ПМ) 11-1M. Каждый ПМ 11-1M (фиг.1) включает в свой состав N каналов, содержащих антенные элементы (АЭ) 21-2N, с каждым из которых последовательно соединены малошумящие усилители (МШУ) 31-3N, преобразователи частоты (ПЧ) 41-4N, полосовые фильтры (ПФ) 51-5N и аналого - цифровые преобразователи (АЦП) 61-6N. Выходы АЦП 61-6N подключены ко входам блока формирования матрицы комплексных отсчетов сигналов (БФМОС) 7. Выход БФМОС 7 подключен к блоку преобразования Фурье (БПФ) 8. К выходу БПФ 8 присоединен блок аппроксимации (БА) 9, управляющие входы которого соединены с выходами постоянного запоминающего устройства (ПЗУ) 10. Выход БА 9 является выходом каждого ПМ 11-1M. Выходы ПМ 11-1M с учетом объединения по подрешеткам посредством линий связи с последовательной передачей данных подключены ко входам соответствующих L блоков формирования сигналов подрешеток (БФСП) 111-11L. Выходы БФСП 111-11L посредством линий связи с последовательной передачей данных подключены к L входам блока специализированного вычислителя (БСВ) 12, в частности, ко входам блока восстановления аппроксимирующих коэффициентов модулей (БВКМ) 13. Суммарное число выходов БВКМ 13 равно числу М ПМ 11-1M. Каждый из М выходов БДМП 13 последовательно связан с соответствующим блоком восстановления матриц (БВМ) 141-14M и блоком преобразования Фурье (БПФ) 151-15M. Выходы каждого БПФ 151-15M соединены с соответствующими номеру модуля входами блока восстановления комплексных отсчетов сигнала (БВКОС) 16. Выход БВКОС 16 соединен с входом блока матричного умножения (БМУ) 17, к управляющим входам которого подключен блок весовых коэффициентов лучей (БВКЛ) 18. Выход БМУ 17 является выходом БСВ 12 и выходом устройства.
Синхронизация всех активных блоков производится с помощью блока синхронизации 19, а формирование гетеродинного сигнала для преобразования входного сигнала на промежуточную частоту - с помощью блока гетеродинирования 20.
Устройство, реализующее заявленный способ, работает следующим образом.
В каждом приемном модуле ПМ 11-1M сигналы, принятые АЭ 21-2N, (см. фиг.1) усиливают в МШУ 31-3N, преобразуют с помощью сигнала гетеродина 19 частоты Fгет в ПЧ 41-4N, фильтруют в ПФ 51-5N и передают на АЦП 61-6N. С помощью АЦП 61-6N принимаемый сигнал преобразуют в последовательность комплексных отсчетов сигналов каналов приемных модулей, следующих с установленной тактовой частотой. Полученные отсчеты передают на входы БФМОС 7, где из последовательностей комплексных отсчетов сигналов длиной Nst, соответствующих ДН каналов каждого первого уровня, формируют прямоугольные комплексные матрицы сигналов размером N×Nst. В БПФ 8 из сформированных матриц выполняют двумерное симметричное косинусное преобразование комплексных матриц сигналов размером N×Nst, формируя косинусные спектры комплексных матриц сигналов. В БА 9 с учетом информации, поступающей из ПЗУ 10, аппроксимируют соответствующую матрицу косинусного спектра комплексных матриц сигналов М' выходными коэффициентами каждого приемного модуля.
Последовательно передают М' выходных коэффициентов приемных модулей по линиям связи на входы БФСП 111-11L, в которых объединяют М' выходных коэффициентов каждого приемного модуля в векторы данных L подрешеток.
С выходов БМП 111-11L последовательно передают по линиям связи сформированные векторы данных L подрешеток в БСВ 12, а именно в БВКМ 13 (общем процессоре формирования диаграмм направленности), в котором объединяют векторы данных L подрешеток, формируя общую последовательность данных длиной М⋅М'.
Из общей последовательности данных в БВМ 141-14M восстанавливают выходные коэффициенты каждого приемного модуля, которые затем передают в БПФ 151-15М, в которых формируют косинусные спектры комплексных матриц сигналов каждого приемного модуля путем взвешенного сложения базисных функций с выходными коэффициентами каждого приемного модуля.
Сформированные косинусные спектры комплексных матриц сигналов приемных модулей передают на соответствующие номеру приемного модуля входы блока БВКОС 16, в котором выполняют обратное симметричное косинусное преобразование косинусного спектра комплексных матриц сигналов и восстанавливают комплексные матрицы сигналов размером N×Nst. Восстановленные комплексные матрицы сигналов размером N×Nst передают в БМУ 17, в котором формируют необходимое число результирующих диаграмм направленности путем весового суммирования восстановленных комплексных матриц сигналов размером N×Nst, соответствующих одним и тем же моментам квантования, с использованием весовых коэффициентов лучей, хранящихся в БВКЛ 18.
Рассмотрим теоретическое обоснование заявленного способа.
В результате взаимодействия зондирующего сигнала с движущейся целью в направлении, заданном единичным вектором рс, спектр отраженного сигнала сдвигается на величину ±Ωс доплеровского смещения частоты и запаздывает на время tc. Комплексную огибающую эхо-сигнала, принимаемого m-ым антенным элементом РЛС на фоне комплексной огибающей шума в канале ξm(t) в дискретные моменты времени tα, можно представить в виде [6 - Черняк B.C. Многопозиционная радиолокация. - М.: Радио и связь, 1993. С. 81-416 с.]
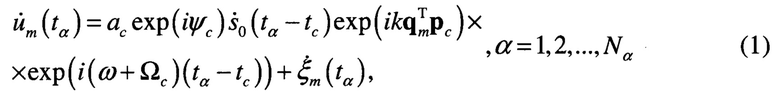
где ас и ψс - эффективная амплитуда эхо-сигнала и его фаза;
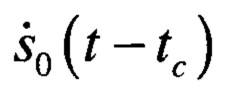 - нормированная комплексная огибающая зондирующего сигнала;
- нормированная комплексная огибающая зондирующего сигнала;
i - мнимая единица;
tc - запаздывание сигнала, пропорциональное наклонной дальности цели;
k - волновое число;
qm - вектор координат фазового центра антенного элемента m-го канала ЦАР;
Т - символ;
Nα - число временных отсчетов, соответствующих времени ожидания эхо-сигналов со всех направлений пространства.
Если зондирующий сигнал является импульсным, то его огибающую можно задать в виде прямоугольного импульса единичной амплитуды и длительностью τ с высокочастотным заполнением.
Как следует из выражения (1), комплексная огибающая эхо-сигнала (без учета шумов) может быть представлена в виде произведения двух сомножителей: пространственного exp 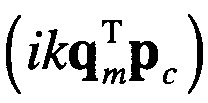 и временного. Первый из них связан с направлением на источник эхо-сигнала, а второй - с запаздыванием эхо-сигнала относительно зондирующего сигнала.
и временного. Первый из них связан с направлением на источник эхо-сигнала, а второй - с запаздыванием эхо-сигнала относительно зондирующего сигнала.
Пусть обработку данных в приемном модуле начинают после записи Nst временных отсчетов. В результате принимаемые радиолокационные данные приемных модулей из N каналов по времени разбивают на Nα/Nst выборок комплексных отсчетов в виде комплексных матриц
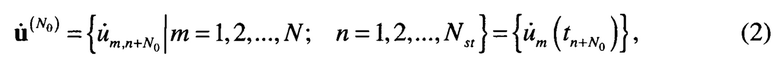
где N0=1,Nst+1,…,Nα-Nst+1 - номер начального значения временного отсчета в комплексной матрице комплексных отсчетов.
Задача состоит в том, чтобы передать данные комплексные матрицы 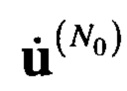 сигналов размером N×Nst в общий процессор формирования ДН без потери содержащейся в них полезной информации о целях на фоне шумов.
сигналов размером N×Nst в общий процессор формирования ДН без потери содержащейся в них полезной информации о целях на фоне шумов.
Известно, что эффективность сжатия данных без потерь весьма ограничена [7 - Дворкович А.В., Дворкович В.П., Зубарев Ю.Б. и др. Цифровая обработка телевизионных и компьютерных изображений. - М.: МЦНТИ, 1997. С. 123.-212 с.]. В монографиях [7, 8 - Прэт У. Цифровая обработка изображений. М.: Мир, Кн.1, 1987. - 312 с.] приведен ряд унитарных дискретных преобразований, которые используются для сжатия графических данных.
Наиболее известным из дискретных преобразований, используемых для обработки сигналов и изображений, является дискретное преобразование Фурье. Недостаток обычного преобразования Фурье был указан в [8, с. 245]: если значения данных преобразуемого массива в крайних строках и столбцах не совпадают, то при выполнении прямого и обратного преобразований Фурье возникают ошибки. Косинусные симметричные преобразования лишены этого недостатка, что оправдывает выбор в пользу последних. В монографии [7, с. 136] указывается, что нечетное симметричное косинусное преобразование может быть реализовано путем выполнения операций с векторами, а четное - с векторами и матрицами. При этом эффективность последнего выше, что определяет его более широкое распространение.
Выполним двумерное симметричное четное косинусное преобразование сигнала (1) без составляющей шума в окне из Nst отсчетов. В результате получили
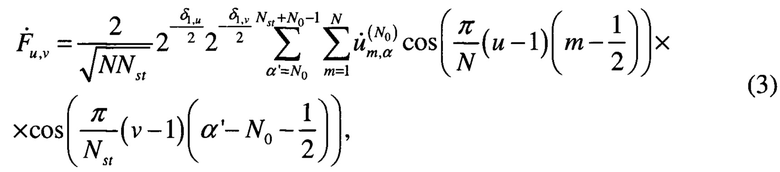
где δ1,u, δ1,v - символы Кронекера (δ1,1=1; δ1,u>1=0; δ1,u>1=0); u=1,2,…,N; v=1,2,…,Nst.
Подставим в выражение (3) выражение (1). Результат будет иметь следующий вид
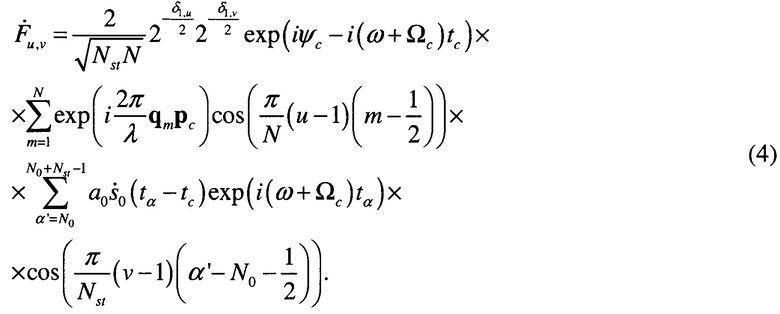
Изображение, соответствующее двумерному четному симметричному косинусному преобразованию, не обладает симметрией. Однако выражение (4) может быть записано в матричном виде

где векторы-строки 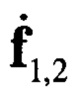 соответствуют преобразованиям по пространству и времени соответственно:
соответствуют преобразованиям по пространству и времени соответственно:
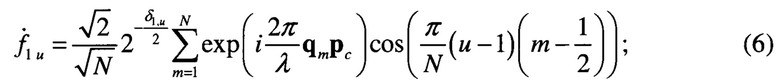
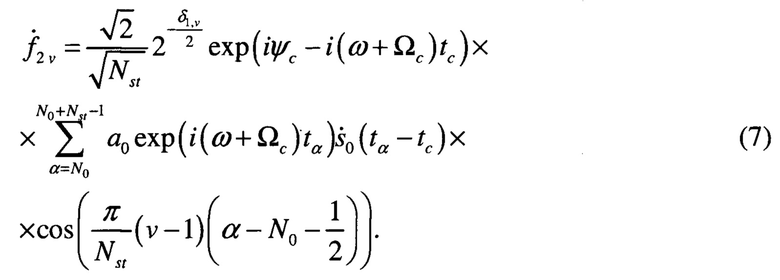
Спектр нормированной огибающей зондирующего радиолокационного сигнала ограничен. В связи с этим и энергия косинусных спектров (6) и (7) концентрируется в ограниченной области.
Если рассматривается выборка данных, в которой присутствует один источник, то область концентрации энергии спектра (6) определяется пространственным положением источника. При наличии нескольких источников, разнесенных в пространстве, спектр может содержать несколько областей, в которых гармоники Фурье будут иметь значительные амплитуды.
В качестве примера на фиг.2 приведено амплитудное распределение суммы двух спектров вида (6) для двух разнесенных в пространстве источников при приеме равноамплитудных синфазных сигналов линейной эквидистантной антенной решеткой из восьми приемных каналов (сплошная кривая) и амплитудные распределения спектров симметричного косинусного преобразования при приеме сигналов каждого из источников по отдельности (штриховая и штрих-пунктирная кривые).
Для спектра вида (7) можно утверждать, что возможный интервал значений tα-tc в пределах рассматриваемой выборки ограничен. Для временной выборки из нескольких десятков отсчетов этот интервал превышает шаг дискретизации не более, чем в 100 раз. Также относительно малы изменения несущей частоты, обусловленные эффектом Доплера. В результате получим, что спектр (7) для каждой цели будет соответствовать младшим гармоникам спектра комплексной огибающей зондирующего сигнала 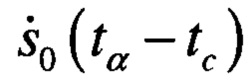 . При этом положение максимальной гармоники спектра будет для каждой цели отличаться несущественно и, главным образом, определяться видом модуляции и параметрами зондирующего сигнала, в частности, выбором шага дискретизации и длительностью зондирующего импульса.
. При этом положение максимальной гармоники спектра будет для каждой цели отличаться несущественно и, главным образом, определяться видом модуляции и параметрами зондирующего сигнала, в частности, выбором шага дискретизации и длительностью зондирующего импульса.
В качестве примера на фиг.3 приведен пример амплитудного распределения спектра вида (8), соответствующего приему двух эхо-сигналов при использовании зондирующего сигнала с линейной частотной модуляцией. Длительность импульса была выбрана равной 3.5 мкс, частота дискретизации - 5 МГц. Число отсчетов в выборке было равно 80, время запаздывания первого эхо-сигнала было равно 10 мкс, а второго - 11.25 мкс. Радиальные скорости цели были равны 100 м/с и - 100 м/с соответственно. На данной фигуре сплошная кривая соответствует спектру при совместном приеме эхо-сигналов, а штриховая и штрих-пунктирная кривые - приему сигналов по отдельности.
Из анализа результатов на фигурах 2 и 3 следует, что положение области спектра (7) с максимальными амплитудами гармоник может быть спрогнозировано заранее, а соответствующие области спектра (6) определяются расположением источников эхо-сигналов.
Если антенна одновременно принимает несколько эхо-сигналов, то матрица 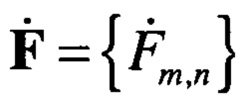 в отличие от выражения (5) будет представлять собой конечную сумму аналогичных слагаемых, каждое из которых можно будет представить в виде произведений одномерных косинусных спектров, например, в виде
в отличие от выражения (5) будет представлять собой конечную сумму аналогичных слагаемых, каждое из которых можно будет представить в виде произведений одномерных косинусных спектров, например, в виде
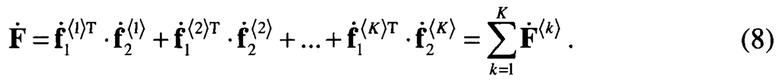
Выражение (8) является ключевым для выполнения операции аппроксимации матрицы коэффициентов косинусного спектра 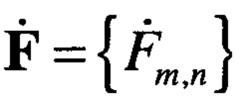 при наличии источника сигнала в рассматриваемом спектре. При отсутствии сигнала источника аппроксимация косинусного спектра
при наличии источника сигнала в рассматриваемом спектре. При отсутствии сигнала источника аппроксимация косинусного спектра 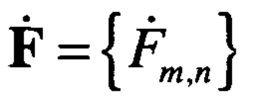 в виде суммы (8) не отражает истинную структуру спектра шума.
в виде суммы (8) не отражает истинную структуру спектра шума.
Рассмотрим сначала задачу поиска векторов 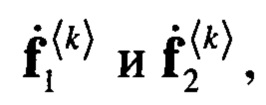 аппроксимирующих матрицу
аппроксимирующих матрицу 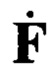 при наличии источника сигнала. Пусть искомые векторы
при наличии источника сигнала. Пусть искомые векторы 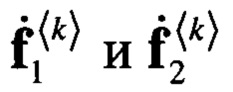 должны обеспечивать минимальное среднеквадратическое отклонение
должны обеспечивать минимальное среднеквадратическое отклонение
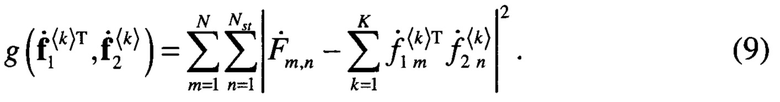
Из анализа выражения (9) следует, что в общем случае задача минимизации выражения (9) является нелинейной. Чтобы задачу преобразовать в линейную, необходимо добавить одно или несколько ограничений вида

где 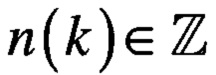 - значение индекса, соответствующее слагаемому с номером к в выражении (9).
- значение индекса, соответствующее слагаемому с номером к в выражении (9).
Наилучшее значение индекса n(k) соответствует столбцу матрицы 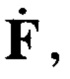 который содержит максимальную амплитуду. Поиск максимальной амплитуды при обработке комплексных отсчетов требует выполнения неудобных математических операций, связанных с вычислением амплитуд и их сортировкой. В связи с этим воспользуемся тем, что в общем случае при наличии источника сигнала значения индекса n0, удовлетворяющего условию
который содержит максимальную амплитуду. Поиск максимальной амплитуды при обработке комплексных отсчетов требует выполнения неудобных математических операций, связанных с вычислением амплитуд и их сортировкой. В связи с этим воспользуемся тем, что в общем случае при наличии источника сигнала значения индекса n0, удовлетворяющего условию
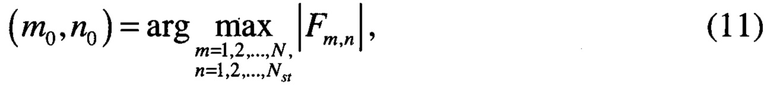
можно приближенно предсказать. Например, из результатов на фиг.3 следует, что n0 ∈ [60,70].
Зададим последовательность отсчетов n(k) таким образом, чтобы входящие в последовательность номера индексов отсчетов соответствовали области с наибольшей концентрацией энергии гармоник спектра вида (7). В этом случае при k=1 целевая функция (9) может быть представлена в виде
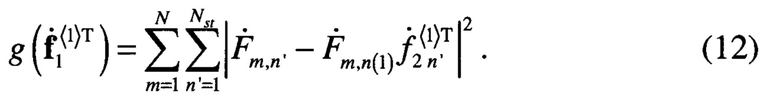
Минимальное значение выражения (12) достигается при
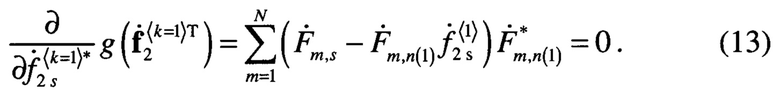
Отсюда следует, что элементы соответствующего вектора 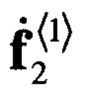 равны
равны
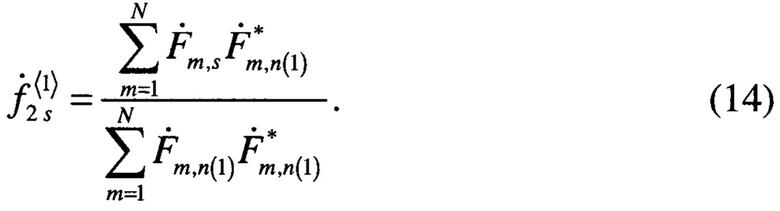
Рассмотрим теперь матрицу 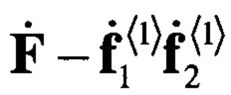 . Если исходная матрица
. Если исходная матрица 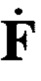 обладала структурой вида (8), то в разностной матрице
обладала структурой вида (8), то в разностной матрице 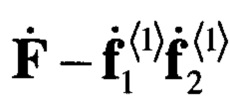 , где
, где 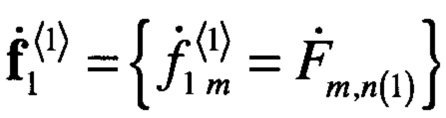 , элементы столбца с номером станут равными нулю, а элементы в строках будут уменьшены в зависимости от корреляции элементов вектора
, элементы столбца с номером станут равными нулю, а элементы в строках будут уменьшены в зависимости от корреляции элементов вектора 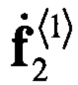 и строк исходной матрицы. Если матрица
и строк исходной матрицы. Если матрица 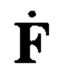 содержит только шум, то корреляция между вектором
содержит только шум, то корреляция между вектором 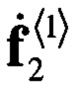 и столбцами матрицы
и столбцами матрицы 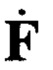 практически отсутствует. В результате выбор нового индекса n(2), задание ограничения
практически отсутствует. В результате выбор нового индекса n(2), задание ограничения 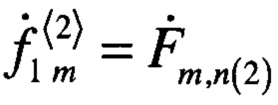 и определение элементов вектора по формуле
и определение элементов вектора по формуле
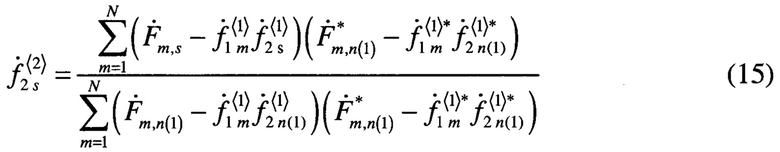
приведет к уточнению аппроксимации матрицы  , если она имеет структуру вида (8).
, если она имеет структуру вида (8).
Далее можно последовательно добавлять ограничения вида (10) и рассчитывать векторы по общей формуле
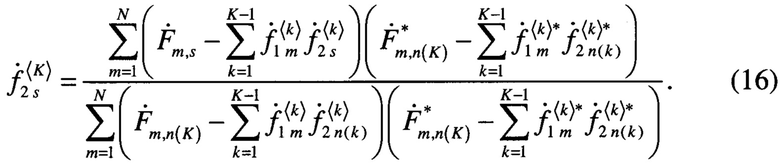
Таким образом, предлагаемый алгоритм аппроксимации является итерационным. Как и во многих алгоритмах сжатия, реализация алгоритма через некоторое число итераций позволяет устранить корреляции между элементами разностной матрицы 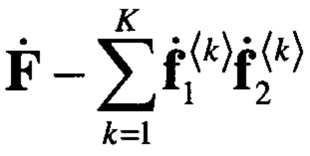 , т.е. увеличить ее энтропию, если спектр матрицы содержит спектр сигнальной составляющей. В противном случае высокая энтропия данных будет сохраняться в ходе итерационного процесса. Это и обеспечивает возможность сжатия передаваемых данных. Очевидно, что коэффициент сжатия H, достигаемый при реализации данного алгоритма, будет равен
, т.е. увеличить ее энтропию, если спектр матрицы содержит спектр сигнальной составляющей. В противном случае высокая энтропия данных будет сохраняться в ходе итерационного процесса. Это и обеспечивает возможность сжатия передаваемых данных. Очевидно, что коэффициент сжатия H, достигаемый при реализации данного алгоритма, будет равен

Дополнительное увеличение коэффициента сжатия можно получить, если векторы аппроксимировать при помощи заданных базисных функций векторами более короткой длиной N'st<Nst соответственно. Аппроксимация векторов 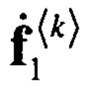 векторами более короткой длины может привести к потере части радиолокационной информации о пространственном положении цели, поскольку приемные модули ЦАР обычно содержат небольшое число приемных каналов.
векторами более короткой длины может привести к потере части радиолокационной информации о пространственном положении цели, поскольку приемные модули ЦАР обычно содержат небольшое число приемных каналов.
Например, рассмотрим базисные функции

у которых v'=1,2,…,N'st<Nst; m=1,2,…,N.
С использованием базисных функций векторы можно представить в виде

Решение задачи аппроксимации может быть получено известным методом, например, при помощи метода наименьших квадратов. В этом случае элементы векторов 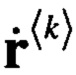 несложно найти по формулам
несложно найти по формулам

При этом коэффициент сжатия будет равен

Здесь М' - общее число отсчетов, передаваемое от одного приемного модуля по линии связи.
Сжатие данных не увеличивает скорость линии связи с последовательной передачей данных. Однако выполнение этой процедуры позволяет в Н раз сократить объем передаваемых данных. Это позволяет уменьшить число уровней формирования ДН, а, следовательно, уменьшить объем аппаратуры, требуемой для построения системы цифрового диаграммообразования.
Естественно, что сжатие данных требует увеличения объема вычислений. Однако все затратные действия, связанные с обращениями матриц, могут быть выполнены заранее. В результате в приемном модуле необходимо реализовать операции умножения комплексных вектора на вектор, вектора на матрицу и разности двух матриц. Все эти операции могут быть реализованы с использованием существующих технологий ПЛИС или многоядерных параллельных вычислителей, реализуемых, например, в видеокартах ПЭВМ.
В прототипе заключительная операция соответствовала формированию сигналов, число которых было пропорционально ограниченному числу формируемых парциальных ДН.
В заявленном способе в вычислительное устройство поступают сигналы, число которых пропорционально числу каналов приемной ЦАР. Это принципиально позволяет формировать любое число ДН, что обеспечивает расширение функциональных возможностей ЦАР.
Положительные эффекты, достигаемые при использовании сжатия данных, вытекают из сокращения потока цифровых данных от одного элемента цифровой диаграммообразующей схемы к другому.
Рассмотрим следующий вычислительный эксперимент.
Зондирующий сигнал представляет собой линейно-частотно-модулированный (ЛЧМ) с несущей частотой ω=2⋅1010 рад/с; девиация частоты Δω=4π⋅106 рад/с; длительность импульса τ=3.5 мкс.
Будем считать, что интервал наблюдения ограничен 1600 отсчетами с частотой дискретизации ωД=π⋅107 рад/с.
Пусть в контролируемой области пространства расположены две цели, которым соответствуют запаздывания сигнала tc1=1.9913⋅10-4 с и tc2=2.0084⋅10-4 с. Эффективные амплитуды целей и их фазы совпадают (положим ac1=1, ас2=1, ψc1=1, ψс2=1). Первая цель приближается к РЛС с радиальной скоростью 100 м/с, а вторая - удаляется с такой же скоростью. Угловые координаты первой цели равны θ01=30°, ϕ01=45° (направляющие косинусы u01=v01=0.3536). Координаты второй цели равны θ02=40°, ϕ02=180° (направляющие косинусы u02=-0.6428, v02=0).
Размер временного окна выбран равным Nst=80.
Для моделирования шумов в квадратурных составляющих сигналов каналов использовался датчик случайных чисел, распределенных по нормальному закону с нулевым математическим ожиданием и дисперсией, равной 0.25.
Пусть прием эхо-сигналов осуществляет N=16-канальный приемный модуль, элементы которого расположены в узлах прямоугольной сетки с горизонтальным и вертикальным шагом, равным 0.55λ. Число горизонтальных линеек приемного модуля равно четырем по четыре приемных канала в каждой.
На фиг.4 показано распределение амплитуд гармоник симметричного косинусного преобразования, соответствующего выборке данных, содержащей принимаемые сигналы. Из анализа данного распределения следует, что информация о структуре данной матрицы визуально не просматривается на фоне шумов.
На фиг.5 представлено аналогичное распределение амплитуд гармоник симметричного косинусного спектра при отсутствии шумов.
Для решения задачи аппроксимации использовалось семь итераций, для которых была установлена последовательность n(k)=61,62,…,67. На первом этапе длины аппроксимирующих векторов 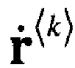 совпадали с длиной векторов
совпадали с длиной векторов 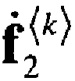 и были равны Nst. При этом для рассматриваемой задачи коэффициент сжатия данных был равен
и были равны Nst. При этом для рассматриваемой задачи коэффициент сжатия данных был равен
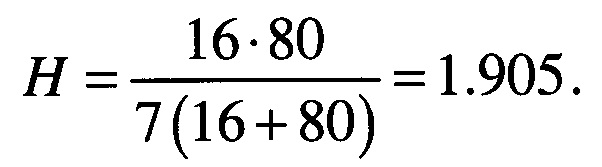
На фиг.6 приведено распределение амплитуд гармоник спектра, которое было получено в результате реализации рассмотренного выше алгоритма аппроксимации на основе соотношений (10) и (16) при наличии шумов. Из этого распределения следует, что в результате решения задачи аппроксимации, несмотря на воздействие шумов, структура спектра, соответствующего сигнальной составляющей, визуально начинает просматриваться.
Далее полученные векторы восстанавливались в последовательности комплексных отсчетов приемных каналов, из них формировались лучи путем линейного фазирования каналов в заданных направлениях наблюдения. В каждом луче выполнялась согласованная фильтрация.
На фиг.7-9 приведены временные диаграммы, полученные в результате согласованной фильтрации в трех лучах:
- ориентированном на первый источник;
- ориентированном на второй источник;
- ориентированном по нормали к раскрыву.
На данных рисунках сплошная кривая соответствует предлагаемому способу, а штриховая получена при обычном способе диаграммообразования, используемом в прототипе.
Из анализа результатов на фиг.7-9 следует, что положения максимумов обнаруживаемых целей на каждой диаграмм для предлагаемого способа и способа-прототипа совпадают. Уровень шумов в заявленном способе снижается по сравнению со способом-прототипом. При ориентации луча по нормали экстремум объясняется тем, что для слабонаправленной диаграммы направленности приемного модуля хотя бы одна из целей может быть видна.
При увеличении запаздывания сигнала второго источника до tc2=2.0613⋅10-4 с наблюдалось смещение максимума на фиг.8 в соответствующую временную позицию на диаграмме, а пеленгационный рельеф не изменяется.
На фиг.10 показан пеленгационный рельеф. Каждой точке поверхности соответствует максимальное значение сигнала на выходе согласованного фильтра при соответствующей ориентации формируемого луча. Положения главных максимумов данной диаграммы соответствуют пространственной ориентации целей. Пеленгационный рельеф аналогичен тому, который может быть сформирован по способу-прототипу.
При уменьшении длины вектора 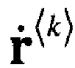 до 60 элементов способ остается работоспособным, а коэффициент сжатия увеличивается до 2.406 раз. При этом в наборе базисных функций (выражение (18)) используются гармоники v'=21,22,…80.
до 60 элементов способ остается работоспособным, а коэффициент сжатия увеличивается до 2.406 раз. При этом в наборе базисных функций (выражение (18)) используются гармоники v'=21,22,…80.
Наконец, работоспособность заявленного способа была проверена при укороченной длине аппроксимирующего вектора 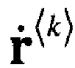 при Nst=60 и n(k)=61,63,65,67,69 (H=3.368). Было установлено, что и в этом случае удалось на фоне шумов полностью восстановить радиолокационную информацию, содержащуюся в выборке данных.
при Nst=60 и n(k)=61,63,65,67,69 (H=3.368). Было установлено, что и в этом случае удалось на фоне шумов полностью восстановить радиолокационную информацию, содержащуюся в выборке данных.
Таким образом, приведенные примеры демонстрируют возможность сокращения потока цифровых данных по линиям связи с последовательной передачей данных от приемных модулей к вычислительному устройству для цифрового диаграммообразования в приемной ЦАР от 1.9 до 3.3 раз. Увеличение сжатия данных будет тем выше, чем большее число каналов содержит приемный модуль. При этом сокращение потока цифровых данных по линиям связи с последовательной передачей не приводит к потере информации об источниках сигнала.
Приведенные выше материалы о возможной реализации способа на основе математического моделирования подтверждают получение выигрыша, заключающегося в сокращении потока цифровых данных по линиям связи с последовательной передачей данных от приемных модулей к вычислительному устройству.
Выполнение устройства, с помощью которого можно реализовать заявленный способ построения системы диаграммообразования приемной цифровой антенной решетки, не вызовет затруднений ввиду того, что его основные блоки и устройства широко используются. Так, в частности, блоки преобразования Фурье, программно реализующие быстрое преобразование Фурье, могут быть выполнены на программируемых логических интегральных схемах (ПЛИС), как и другие основные блоки.
Блок аппроксимации требует реализации известных математических операций с матрицами и векторами, которые также могут быть реализованы по технологии ПЛИС.
Вышеизложенное позволяет сделать вывод о том, что заявленный способ соответствует критерию «промышленная применимость» для изобретения.
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ подавления импульсных помех в N-элементной адаптивной антенной решетке | 2021 |
|
RU2776862C1 |
| Способ диаграммообразования в проемной цифровой антенной решетке | 2021 |
|
RU2766536C1 |
| Способ определения направления на цель цифровой антенной решеткой моноимпульсной радиолокационной станции | 2021 |
|
RU2761106C1 |
| Способ обработки сигналов в модульной адаптивной антенной решетке при приеме коррелированных сигналов и помех | 2015 |
|
RU2609792C1 |
| Способ адаптивной обработки сигналов в модульной фазированной антенной решетке | 2016 |
|
RU2629921C1 |
| СПОСОБ ФОРМИРОВАНИЯ КОМПЕНСАЦИОННОЙ ДИАГРАММЫ НАПРАВЛЕННОСТИ В ПЛОСКОЙ АНТЕННОЙ РЕШЕТКЕ С ЭЛЕКТРОННЫМ УПРАВЛЕНИЕМ ЛУЧОМ | 2023 |
|
RU2810696C1 |
| Способ углового сверхразрешения в приемной цифровой антенной решётке | 2020 |
|
RU2746063C1 |
| Способ формирования диаграммы направленности приемной цифровой антенной решетки | 2021 |
|
RU2769087C1 |
| Способ пеленгации источников радиоизлучения | 2022 |
|
RU2788079C1 |
| СПОСОБ ПОДАВЛЕНИЯ ПОМЕХ ПРИ ПРИЕМЕ ЭЛЕКТРОМАГНИТНОЙ ВОЛНЫ КРУГОВОЙ ПОЛЯРИЗАЦИИ БИОРТОГОНАЛЬНОЙ АНТЕННОЙ СИСТЕМОЙ | 2003 |
|
RU2235392C1 |
Использование: изобретение относится к антенной технике, а именно к способам построения системы диаграммообразования приемных цифровых антенных решеток (ЦАР) для систем радиосвязи, радиолокации. Сущность: согласно способу формируют антенное полотно из М приемных модулей по N каналов в каждом, объединенных в L подрешеток, в каждом канале приемного модуля принимают входной сигнал антенным элементом, усиливают входной сигнал, в случае выполнения приемной цифровой антенной решетки по супергетеродинной схеме выполняют преобразование частоты входного сигнала, фильтруют входной сигнал в полосовом фильтре, выполняют его дискретизацию с помощью аналого-цифрового преобразования в виде последовательностей комплексных отсчетов сигналов каналов приемных модулей. Из последовательностей комплексных отсчетов сигналов каналов приемных модулей формируют прямоугольные комплексные матрицы сигналов размером N×Nst, в каждом приемном модуле выполняют двумерное симметричное косинусное преобразование комплексных матриц сигналов размером N×Nst, формируя косинусные спектры комплексных матриц сигналов. При помощи заданных базисных функций аппроксимируют соответствующую матрицу косинусного спектра комплексных матриц сигналов М' выходными коэффициентами каждого приемного модуля, формируют векторы данных подрешеток путем объединения М' выходных коэффициентов каждого приемного модуля, переданных последовательно по линиям связи в L подрешетках, формируют общую последовательность данных длиной М⋅М' путем объединения векторов данных подрешеток, переданных последовательно по линиям связи. Из общей последовательности данных восстанавливают выходные коэффициенты каждого приемного модуля, формируют косинусные спектры комплексных матриц сигналов путем взвешенного сложения базисных функций с выходными коэффициентами каждого приемного модуля. Выполняют обратное симметричное косинусное преобразование косинусного спектра комплексных матриц сигналов и восстанавливают комплексные матрицы сигналов размером N×Nst. Формируют необходимое число результирующих диаграмм направленности путем весового суммирования восстановленных комплексных матриц сигналов размером N×Nst, соответствующих одним и тем же моментам квантования. Технический результат: расширение функциональных возможностей ЦАР за счет увеличения числа формируемых лучей при сохранении технически обеспечиваемой скорости передачи данных по линиям связи. 10 ил., 1 табл.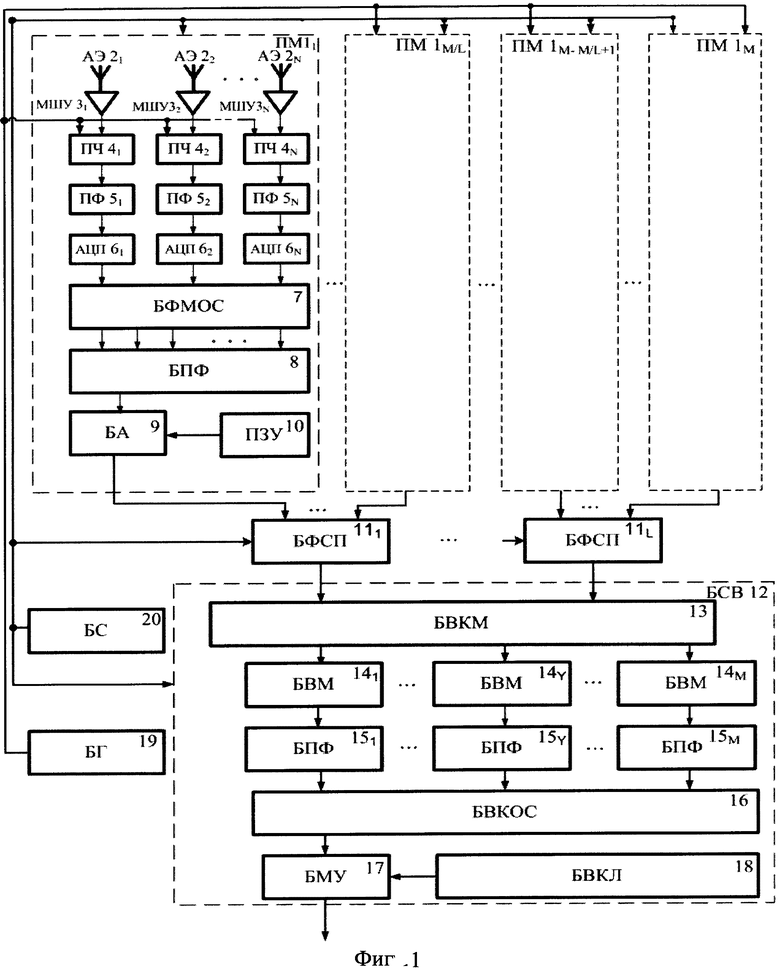
Способ построения системы диаграммообразования приемной цифровой антенной решетки, при котором формируют антенное полотно из М приемных модулей по N каналов в каждом, объединенных в L подрешеток, в каждом канале приемного модуля принимают входной сигнал антенным элементом, усиливают входной сигнал, в случае выполнения приемной цифровой антенной решетки по супергетеродинной схеме выполняют преобразование частоты входного сигнала, фильтруют входной сигнал в полосовом фильтре, выполняют его дискретизацию с помощью аналого-цифрового преобразования в виде последовательностей комплексных отсчетов сигналов каналов приемных модулей, отличающийся тем, что из последовательностей комплексных отсчетов сигналов каналов приемных модулей формируют прямоугольные комплексные матрицы сигналов размером N×Nst, в каждом приемном модуле выполняют двумерное симметричное косинусное преобразование комплексных матриц сигналов размером N×Nst, формируя косинусные спектры комплексных матриц сигналов, при помощи заданных базисных функций аппроксимируют соответствующую матрицу косинусного спектра комплексных матриц сигналов М' выходными коэффициентами каждого приемного модуля, формируют векторы данных подрешеток путем объединения М' выходных коэффициентов каждого приемного модуля, переданных последовательно по линиям связи в L подрешетках, формируют общую последовательность данных длиной М⋅М' путем объединения векторов данных подрешеток, переданных последовательно по линиям связи, из общей последовательности данных восстанавливают выходные коэффициенты каждого приемного модуля, формируют косинусные спектры комплексных матриц сигналов путем взвешенного сложения базисных функций с выходными коэффициентами каждого приемного модуля, выполняют обратное симметричное косинусное преобразование косинусного спектра комплексных матриц сигналов и восстанавливают комплексные матрицы сигналов размером N×Nst, формируют необходимое число результирующих диаграмм направленности путем весового суммирования восстановленных комплексных матриц сигналов размером N×Nst, соответствующих одним и тем же моментам квантования.
| Способ построения системы диаграммообразования активной фазированной антенной решётки | 2019 |
|
RU2731604C1 |
| US 9374145 B2, 21.06.2016 | |||
| Способ построения активной фазированной антенной решетки | 2020 |
|
RU2730120C1 |
| Способ построения радиолокационной станции | 2019 |
|
RU2723299C1 |
| Способ построения активной фазированной антенной решетки | 2019 |
|
RU2717258C1 |
Авторы
Даты
2022-06-16—Публикация
2021-05-31—Подача