Область техники
Группа изобретений относится к информационным технологиям, а именно к способам защиты электронного изображения от подделки на основе аффинных преобразований и проверки подлинности полученной информации. Изобретения могут быть использованы для защиты канала связи между отправителем информации в виде изображения и получателем от попыток третьих сторон отправить получателю информацию под видом информации от отправителя, а также аутентификации полученного изображения или информации, приводимой к виду изображения.
Уровень техники
Одной из главных задач защиты информации при ее автоматизированной (автоматической) обработке является управление доступом. Решение о предоставлении доступа для использования информационных и вычислительных ресурсов средств вычислительной техники, а также ресурсов автоматизированных (информационных) систем, основывается на результатах идентификации и аутентификации.
Как указано в ГОСТ Р 58833-2020, при автоматизированной обработке информации физическому лицу как субъекту доступа соответствуют вычислительные процессы, выполняющие операции с данными. Это создает риски неоднозначного сопоставления вычислительных процессов с конкретным физическим лицом. Аналогичные риски существуют и при автоматической обработке информации. Кроме того, удаленное информационное взаимодействие дополнительно порождает риск ошибочной идентификации удаленного субъекта доступа и, следовательно, риск предоставления доступа злоумышленнику. Наряду с этим существуют риски того, что вычислительный процесс, действующий в интересах злоумышленника, может имитировать объекты (субъекты) доступа, функционирующие как параллельно с легальными, так и существующие независимо от них.
Устанавливая правила управления доступом к информации и сервисам, обеспечивающим ее обработку, для различных категорий субъектов доступа необходимо учитывать не только конфиденциальность защищаемой информации, но и указанные риски. Для снижения рисков должны применяться соответствующие методы идентификации и аутентификации, которые обеспечивают уверенность в подлинности сторон, участвующих в информационном взаимодействии, включая и субъекты доступа, и объекты доступа. Это особенно востребовано в том случае, когда взаимодействующие стороны имеют дефицит взаимного доверия, обусловленный, например, использованием небезопасной среды функционирования.
В настоящее время широко известны такие способы защиты информации как электронная подпись, электронная цифровая подпись, цифровая подпись. Как правило, работа их основывается на использовании функции, для которой при заданном значении аргумента получить значение функции нетрудно, но обратное, т.е. выяснение аргумента, при имеющемся значении функции, связано со значительными вычислительными трудностями.
Из уровня техники известно изобретение по патенту RU2568268C1. Решение относится к области защиты подлинности электронных изображений. Технический результат - эффективная защита подлинного аутентифицированного электронного изображения. В способе аутентификации электронного изображения у отправителя над электронным изображением выполняют вейвлет преобразование, вейвлет коэффициенты квантуют и разделяют на N≥2 кодовых блоков каждый размером n1×n2 коэффициентов, где n1≥2 и n2≥2, квантованные вейвлет коэффициенты n-го, где n=1, 2,…, N, кодового блока преобразуют в L≥2 упорядоченных двоичных последовательностей, изменяют разрядность представления интервала арифметического кодирования по секретному ключу и кодируют с использованием арифметического кодирования в кодированные последовательности, передают кодированное электронное изображение (ЭИ) получателю, где проверяют подлинность принятого получателем ЭИ, для чего разделяют двоичную последовательность принятого получателем ЭИ на двоичные последовательности его принятых блоков, изменяют разрядность представления интервала арифметического декодирования по секретному ключу и декодируют кодированные последовательности с использованием арифметического декодирования, принятое ЭИ считают подлинным, если в каждом принятом кодовом блоке декодировано L×n1×n2 бит.
Недостатком аналога является то, что передают только кодированное изображение без дополнительной защиты. Кроме того, способ кодирования – квантование вейвлет коэффициентов отличается от способа аффинных преобразований.
Из уровня техники также известен патент RU2739059C1, раскрывающий изобретение из области проверки (аутентификации) геометрических кодов, которое может быть использовано при установлении фактов производства и продажи контрафактных товаров, установления подлинности документов. Способ проверки подлинности маркировки включает ряд этапов обработки и сравнения изображений посредством нейросети U-net: этап получения изображений подлинного и проверяемого отпечатков двухмерного кода, этап предварительной локализации изображений, поворот и вырезание изображения двухмерного кода из отпечатка двухмерного кода на основании локализованных краевых точек, этап точного выравнивания изображений двухмерных кодов, этап попиксельного сравнения изображений двухмерных кодов при помощи нейросети U-net с подсчетом количества различающихся пикселов, этап сравнения подсчитанного количества различающихся пикселов с установленным пороговым значением. Причем в случае, когда количество различающихся пикселов превышает установленное пороговое значение, устанавливают, что проверяемый отпечаток двухмерного кода не является подлинным, в противном случае устанавливают, что проверяемый отпечаток двухмерного кода является подлинным. Техническим результатом является повышение точности определения подлинности маркировки при исключении необходимости точного совпадения пространственного расположения двух отпечатков двухмерных кодов.
Достоинством аналога является внедрение нейросети. Недостатком аналога является то, что отпечатки двухмерного кода имеют меньшую степень защиты, чем код, обеспечиваемый при аффинном преобразовании. Кроме того, кодирование точечных изображений для аффинных преобразований качественно лучше, чем пиксельных.
Из зарубежных патентных источников известен аналог EP1113617A2 - Способ передачи права на декодирование сообщений, раскрывающий общедоступный некоммутативный метод кодирования исходного сообщения, передаваемого получателю через лицо, предоставляющее право, при этом способ включает следующие этапы:
- получение зашифрованного сообщения, представляющего исходное сообщение, при этом зашифрованное сообщение было зашифровано открытым ключом, соответствующим лицу, предоставляющему право;
- генерируют открытый ключ-посредник на основе закрытого ключа, соответствующего получателю, при этом с вычислительной точки зрения трудно восстановить закрытый ключ, соответствующий получателю, из открытого ключа-посредника;
- а также применение открытого прокси-ключа для преобразования зашифрованного сообщения в преобразованное сообщение, при этом преобразованное сообщение может быть расшифровано получателем с использованием информации, выбранной из закрытого ключа, соответствующего получателю, и любой общедоступной информации.
Достоинством аналога является эффективное использование ключей, однако общедоступный некоммутативный метод кодирования не обеспечивает необходимую аутентификацию отправителя и не относится к аффинным преобразованиям.
Предлагаемые способ защиты электронного изображения на основе аффинных преобразований и способ аутентификации электронного изображения основан на отличной от известных решений технологий – на аффинных преобразованиях и предназначен для работы с изображениями или с информацией, приводимой к изображениям, при котором обеспечивается лучшая относительно аналогов целостность информации при передаче и повышается уверенность в подлинности сторон.
Раскрытие изобретения
Технический результат, получаемый при использовании изобретений, заключается в повышении защищенности информации при ее передаче по каналам связи, путем формирования на основе аффинных преобразований посылаемой информации механизма, позволяющего точно аутентифицировать подлинность отправителя и, следовательно, в повышении уверенности в подлинности отправленной/полученной информации. Сопутствующим результатом является сохранение целостности информации. Аутентификация отправителя является неотъемлемой частью способа защиты. Раскрытие всех этапов взаимодействия с информацией от ее отправления до проверки получателем и установление аутентичности источника представлено далее.
Эффект повышенной защиты подлинности информации достигается благодаря внедрению аффинных преобразований и проверочных изображений к отправляемым материалам на основе этих преобразований, и благодаря тому, что
- предварительно, у отправителя формируют закрытый ключ безопасности Z в виде электронного точечного изображения,
- формируют из подлинной исходной информации для отправления электронное пиксельное изображение,
- из полученного электронного пиксельного изображения формируют сообщение X в виде электронного точечного изображения,
- кодируют закрытый ключ Z, формируя для получателя открытый ключ – ограниченное множество чисел Qz кода закрытого ключа Z,
- формируют как минимум одно проверочное аффинно-эквивалентное одновременно части закрытого ключа Z и части сообщения X электронное точечное изображение Y у отправителя,
- посылают получателю сообщение X и как минимум одно полученное проверочное электронное точечное изображение Y,
- осуществляют аутентификацию полученного сообщения Х по проверочному изображению Y путем проверки его аффинной эквивалентности части сообщения Х и по открытому ключу Qz.
Раскрытый способ защиты информации относится преимущественно к информации в виде электронных пиксельных изображений или приводимой к виду электронных пиксельных изображений.
Термины, используемые в описании:
Изображение - электронное изображение.
Электронное изображение (ЭИ) -электронное точечное изображение, конечное множество точек на декартовой плоскости.
Электронное пиксельное изображение (ЭПИ) - любое цифровое изображение на экране либо в виде файла.
Подлинная исходная информация – любые данные для отправления, например, фото или документы, которые можно оцифровать.
Краткое описание чертежей
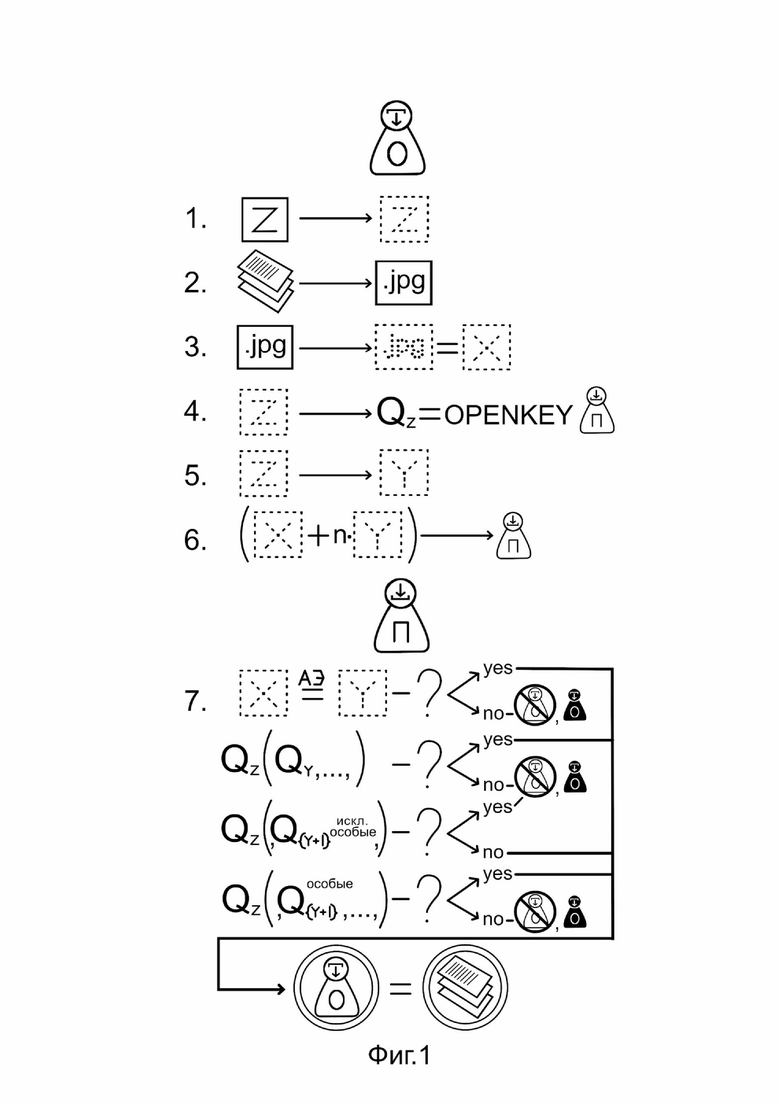
Фиг.1 – Общий вид, схематичная иллюстрация способа и связей.
Осуществление изобретения
Способ защиты информации от подделки на основе аффинных преобразований и аутентификации отправителя представлен в раскрытой последовательности этапов.
1. У отправителя формируют закрытый ключ безопасности Z в виде электронного точечного изображения. Закрытый ключ Z имеется у отправителя исходно и представляет собой преимущественно физический носитель, такой как магнитная карта, листовой документ с магнитными метками, документ с печатными метками, кодом, символами. Таким образом закрытый ключ — это любой объект, содержащий закодированную информацию, эквивалентом которой может быть электронное изображение. Каждая магнитная частица может быть представлена в виде точки и каждый пиксель отсканированного документа также может быть представлен в виде точки или совокупности точек, образовывая электронные изображения в виде конечного множество точек на декартовой плоскости. Для дальнейшей работы необходимо иметь указанное ЭИ. Преобразование пикселя в точку и магнитной частицы в точку осуществляется очевидными простыми алгоритмами. В качестве примера, пусть дано электронное пиксельное чёрно-белое изображение, у пикселей есть градации темноты нуль (белый пиксель) и единица (черный пиксель). В этом случае действуют следующим образом: пиксель — это маленький квадрат, и имея черно-белое изображение, белый пиксель оставляют пустым, а вместо черного пикселя ставят точку. И изображение из пикселей преобразуется в изображение из точек. Если изображение полутоновое чёрно-белое, тогда пиксели имеют градацию темноты от нуля до К без единицы. Преобразовывают это в изображение из точек следующим образом: снова ставят в квадрат точки, если с градацией единица (не белый квадрат) - ставят одну точку, если градация два (уже темнее) ставят 2 точки в этом квадрате и так далее вплоть до К без единицы (до самого темного) и изображение из пикселей превращается в изображение из точек, где разная плотность точек в разных частях изображения обеспечивает светлый или темный тон. Градация определяется тем, что в пиксельных изображениях каждый квадрат уже изначально имеет одну из К–градаций, в этом состоит суть пиксельного изображения, т.е. градации определяются любыми доступными графическими программами.
Предполагается, что магнитные частицы-точки изначально распределены хаотично, неважно откуда – с бумажного носителя или с магнитного. По аналогии с пиксельным преобразованием, если есть частица, в квадрате ставят точку, если нет – оставляют пустой, если есть скопления точек, обращаются к градациям.
Идентичность точечного изображения при копировании (повторении) обусловлена применением аффинных преобразований. Именно базовые свойства этого преобразования обеспечивают повторение изображения точь-в-точь с сохранением градаций.
2. Далее формируют из подлинной исходной информации для отправления электронное пиксельное изображение. Фото, документы, иные материалы для отправления оцифровывают любыми известными аппаратными средствами, например сканируют, так получают электронное пиксельное изображение для следующего этапа. Либо данные для передачи могут быть у отправителя в виде ЭПИ изначально.
3. Из полученного электронного пиксельного изображения формируют сообщение X в виде электронного точечного изображения по аналогии с п.1. ЭИ называем конечное (непустое) множество точек на плоскости. Обосновываем это тем, что любую фигуру можно «аппроксимировать» конечным множеством точек, которые уже сами по себе делают фигуру вполне узнаваемой. При этом если точек много, то такая совокупность точек практически неотличима от исходной фигуры. Так же можно представлять и полутоновые, черно-бело-серые изображения, при этом разная плотность точек в разных частях изображения дает разные оттенки «серого цвета». Множествами точек можно представлять и цветные изображения, тогда необходимо применить преобразование пикселей в точки для каждого из цветных каналов RGB отдельно. Либо преобразовывают изображение в черно-белое, а только затем в точечное.
4. Кодируют закрытый ключ Z, формируя для получателя открытый ключ – ограниченное множество чисел QZ кода закрытого ключа Z. Кодирование осуществляют с помощью алгоритма «парой множеств», а именно:
Пусть задано изображение произвольного вида (с числом точек больше трех). Перенумеруют точки изображения А с единственным условием: разные точки – разные номера. Пусть МА – множество номеров. Пусть Smnu и Sksp – площади треугольников с вершинами в точках с номерами соответственно m, n, u и k, s, p, и пусть ρmnu,ksp = Smnu\Sksp (разумеется, Sksp не равно нулю), и все числа ρ для всех пар троек m, n, u и k, s, p составляют множество ТА. При этом множество ТА — это только числа вида ρmnu,ksp, никакой информации об исходных треугольниках и их площадях уже нет. Пара < МА, ТА> называется кодом точечного изображения А. Доказано (теорема, см. Козлов В.Н., Введение в математическую теорию зрительного восприятия, Изд-во центра прикладных исследований мех.-мат. факультета МГУ, 2007), что код определяет изображение с точностью до аффинных преобразований.
Содержательно аффинные преобразования – это любая комбинация преобразований параллельного переноса, вращений, симметрии, изменений в размерах, сжатий и растяжений по любому направлению. Теорема означает, что любое изображение В, переводимое в А аффинными преобразованиями, имеет тот же (с точностью до перенумерации точек) код, что и А.
И обратное, если восстанавливать изображение по коду <МА, ТА>, то получающееся изображение заведомо переводится в А аффинными преобразованиями.
Следует отметить для корректности, что при доказательстве теоремы из рассмотрения исключены два узких, вырожденных и несущественных для практики класса изображений: когда все точки изображения (именно все) лежат на одной прямой или на двух параллельных прямых.
В рамках алгоритма допускается использование и укороченного кода, когда в ТА присутствуют числа ρmnu,ksp только для четырехточечников, но всех возможных четырехточечников. Это значит, что из исходного ТА отбираются только те числа ρmnu,ksp, у которых тройки m, n, u и k, s, p разнятся только одним номером. Такой код тоже представляет изображение с точностью до аффинных преобразований.
Теперь помимо кода точечного изображения закрытого ключа Z имеется множество QZ чисел, получающихся из чисел множества Т, но с удаленными индексами при них. Назовем QZ стертым кодом для Z. Восстановить по стертому коду QZ изображение Z практически невозможно.
Теорема доказывалась для полного кода, но применима и для сокращенного, просто при кодировании будет меньше элементов. В таком случае для ускорения процесса делается выборка из полного кода. Возможное сокращение состоит еще в том, что, как следует из определения кода, если есть элемент ρmnu,ksp с двумя тройками индекса, то есть и обратный элемент - единица, деленная на ρmnu,ksp в этом полном коде, поэтому берут и оставляют только те элементы, которые меньше единицы, поскольку то, что больше единицы однозначно восстанавливается. Дополнительно, возможно и некое огрубление кода: идеального совпадения чисел, как правило, нет, но всегда есть малый зазор, в пределах которого они совпадают. Поэтому промежуток от нуля до единицы разбивают на N интервалов, где каждый интервал длины 2 Δ, и рассматривают центры интервалов. Все числа из кода попадают каждое в свой интервал. После чего оставляют только числа, являющиеся серединками интервалов (возможно, с учетом кратности, то есть количества попавших в данный интервал элементов исходного кода). Так получается возможный огрубленный открытый ключ. Разумеется, при использовании огрубленного ключа совпадения сравниваемых с ним чисел следует проводить с учетом введенного Δ.
5. Формируют как минимум одно проверочное аффинно-эквивалентное части закрытого ключа Z электронное точечное изображение Y у отправителя. В начале этапа у отправителя есть электронное точечное изображение X, которое он должен отправить получателю. У получателя есть открытый ключ. Ценность этапа состоит в том, что отправитель посылает получателю информацию, и предусмотрено средство, которое не позволит злоумышленнику, даже располагая подробной информацией о модели, получить данные о закрытом ключе и выдать себя за отправителя. Для этого отправляют сообщение Х получателю, но для защиты снабжают его одним или несколькими дополнительными изображениями Y - проверочными. Поэтому в конце этапа у отправителя должны быть изображение X – сообщение, и некоторые изображения Y1-Yk – проверочные, сформированные у отправителя с помощью закрытого ключа, как будет описано ниже. Изображение Y - проверочное, тест и защита, его роль – участвовать в проверке подлинности сообщения Х. Полагаем, изображение Y аффинно-эквивалентно с некоторыми подизображениями (т.е. подмножествами точек) одновременно как в Х, так и в Z, причем это максимальное по количеству точек такое изображение, т.е. при добавлении хотя бы одной точки аффинная эквивалентность нарушится.
Обозначают через Y+1 изображение «с добавленной точкой», т.е. это изображение в сравнении с Y имеет добавленную точку, и оно аффинно-эквивалентно с некоторым подмножеством точек в Х. По построению, Y+1 уже не аффинно-эквивалентное ни с каким подизображением в Z (это и означает максимальность исходного изображения Y). Множество всех таких Y+1 обозначим через {Y+1}. Для каждого Y+1 из {Y+1} проверяем условие: стертый код для Y+1 не является подмножеством стертого кода QZ . Если условие не выполняется, то Y+1 называем особым. Отправителю нет нужды направлять получателю информацию о множестве {Y+1}- оно легко строится по Х и Y, исключая особые изображения, о них получателю сообщается. Здесь описана ситуация с одним проверочным изображением, но их может быть и несколько.
Отметим для корректности, что полагаем исключенными очевидно вырожденные и легко проверяемые случаи, когда X совпадает с Z, или Z является частью X, или X является частью Z.
6. Посылают получателю сообщение X и как минимум одно полученное проверочное электронное точечное изображение Y.
7. Осуществляют аутентификацию полученного сообщения Х по проверочному изображению Y и по стертому коду QZ.
Проверку по аффинной эквивалентности электронного точечного изображения Y подмножеству точек сообщения X и по QZ проводят следующим образом:
1) проверяется, является ли изображение Y аффинно-эквивалентным (АЭ) с некоторыми подизображениями (подмножествами точек) сообщения Х,
2) является ли стертый код QY проверочного изображения Y подмножеством стертого кода QZ закрытого ключа Z (т.е. подмножеством открытого ключа),
3) а) является ли стертый код каждого из изображений из { Y+1}, исключая особые, подмножеством открытого ключа,
б) является ли стертый код каждого из особых изображений в {Y+1} подмножеством открытого ключа.
Ответы «да» на вопросы 1 и 2, «нет» на 3а и «да» на 3б означают, что сообщение Х подлинное и получено именно от авторизованного отправителя.
Пример 1
Способ защиты подлинности информации на основе аффинных преобразований, отличающийся тем, что электронные точечные изображения подлинной исходной информации сообщения X могут быть сжаты в меньшие по объему без потери защиты данных таким образом, что после этапа формирования сообщения X в виде электронного точечного изображения на него накладывают виртуальную сетку из квадратных ячеек, задают каждому квадрату градацию по количеству точек в каждой ячейке и образовывают электронное точечное изображение меньшего объема – сообщение X1, которое используют далее по способу вместо сообщения X, а получателю посылают сообщение X с наложенной виртуальной сеткой и изображение X1.
Пример 2
Способ защиты подлинности информации на основе аффинных преобразований, отличающийся тем, что из цветных электронных пиксельных изображений подлинной исходной информации сообщение X формируют путем преобразования каждого из цветных каналов RGB отдельно. Затем описанное выше для каждого из каналов проделывают отдельно. Возможен и вариант, когда точечные изображения для каждого из каналов объединяют в единое (с пометками для точек о том, к какому каналу они относятся).
Пример 3
Способ защиты подлинности информации на основе аффинных преобразований, отличающийся тем, что цветные электронные пиксельные изображения подлинной исходной информации переводят в градацию черно-серо-белого, а затем формируют сообщение X.
Пример 4
Стертый код Q упрощают и сокращают следующими возможными способами:
а) убирают в нем повторение чисел, т.е. от каждого множества одинаковых чисел (если они есть) оставляют в нем только одно число.
б) оставляют в нем только числа меньшие или равные единице.
в) разбивают сегмент от 0 до 1 на N частей длины 1/N=2Δ.
Затем заменяют каждое число в стертом коде на середину части, в которую он попадает. Обозначают через Q’Z множество получившихся чисел.
Эти три пункта меняют вопрос 2 при проверке аутентификации в преимущественном описании способа выше следующим образом:
2)имеется ли для каждого числа, меньшего или равного единице, из стертого кода QY проверочного изображения Y, число из Q’Z, отличающееся от него не более, чем на Δ.
Вопросы в пункте 3 меняются на следующие:
3) а) имеется ли для каждого числа, меньшего или равного единице, из стертого кода каждого из изображений в {Y+1}, исключая особые, число из Q’Z, отличающееся от него не более, чем на Δ.
б) имеется ли для каждого числа, меньшего или равного единице из кода особого изображения в{Y+1}, число из Q’Z, отличающееся от него не более, чем на Δ.
В целом это дополнение к основному описанию сокращает стертый код (открытый ключ), и упрощает алгоритм проверки сообщения Х на достоверность.
Пример 5
Поиск на изображении Z (закрытом ключе) и Х (сообщении) общего подизображения Y, а также проверка получателем совпадения (разумеется, с точностью до аффинных преобразований) проверочного изображения Y с каждым из некоторого множества частей сообщения Х, имеют нечто общее, заключающееся в том, что нужно определить, является ли некоторое изображение В частью (с точностью до аффинных преобразований) некоторого изображения А. Конечно, это можно сделать тривиальным перебором по всем подизображениям, но это не рационально. Делают так: на изображении А выбирают три точки a1, a2, a3 (произвольные, но не лежащие на одной прямой). Выбирают на В три точки b1, b2, b3 (произвольные, но не лежащие на одной прямой). Совмещают аффинным преобразованием точки b1, b2, b3 с точками соответственно a1, a2, a3, такое преобразование существует и единственно. Если В аффинно-эквивалентно с частью изображения А, причем с соответствием точек b1, b2, b3 точкам a1, a2, a3, то и остальные точки изображения В совместятся с соответствующими точками изображения А. Если нет, то проделывается описанное со всеми тройками точек на А и В и всеми вариантами соответствия между точками в тройках. Либо получается совмещение В с частью А, либо делается вывод, что В аффинно-неэквивалентно никакой части в А.
Пример 6
В предыдущем примере 5 в рамках поиска на изображении Z (закрытом ключе) и Х (сообщении) общего для них подизображения Y, а также проверке получателем совпадения ( с точностью до аффинных преобразований) проверочного изображения Y с каждым из некоторого множества частей сообщения Х, выделялась общая для них подзадача, заключающаяся в том, что нужно определить, является ли некоторое изображение В частью (с точностью до аффинных преобразований) некоторого изображения А. Но может статься, что такого общего подизображения Y, с числом точек больше трех, нет. Тогда для Y, по-прежнему аффинно-эквивалентного части Х, полного аффинного совпадения с частью в Z можно не требовать, а только «приблизительного совпадения», с «зазором ε», и называть это ε-эквивалентностью. Определение, является ли некоторое изображение В частью (с точностью до ε-эквивалентности) некоторого изображения А, выглядит следующим образом.
Выбирают на В три точки b1, b2, b3 (произвольные, но не лежащие на одной прямой), ставят им в соответствие три произвольные (но не на одной прямой) точки a1, a2, a3 изображения А. Берут на В точку х1, сопоставляют ей некоторую точку у1 на А. Если теперь элементы кода изображения из точек b1, b2, b3 и х1 отличаются от соответствующих элементов кода изображения из точек a1, a2, a3 и у1 на А не более, чем на ε, то точку у1 называют приемлемой при соответствии с точкой х1. Если точка у1 оказалась не приемлемой, то берут другую точку из А в качестве точки у1 и повторяют рассуждение. Затем то же делают для точки х2, и т.д. Пусть В состоит из точек b1, b2, b3, х1, …, хk, и для точек х1, …, хk найдены соответствующие приемлемые точки у1,…, уk на А. Тогда для изображения В из точек b1, b2, b3, х1,…, хk и изображения А’ из точек a1, a2, a3, у1,…, уk ( при указанном соответствии) проверяют в целом различие всех соответствующих элементов их кодов не более, чем на ε. При положительном результате проверки подизображение А’ изображения A называют искомым.
Если первоначально выбранные тройки точек a1,a2,a3 и b1,b2,b3не дали возможность для каждой из точек х1,…, хk подобрать приемлемые точки у1,…, уk, то проделывается описанное со всеми тройками точек на А и В и всеми вариантами соответствия между точками в тройках. В результате либо находят искомое изображение, либо делают вывод, что такого изображения нет.
Разумеется, при сравнении чисел из QY с числами из QZ для Y, подобранного в рамках описанной процедуры, нужно учитывать величину ε.
В частном случае при ε=0 процедура с очевидностью превращается в поиск на А части, аффинно-эквивалентной с В, но, в отличие от примера 5, только по коду, без использования геометрических преобразований.
Пример 7
Особые изображения среди изображений множества {Y+1} из пункта 5 описания способа возникают по следующим причинам. Если некоторое изображение B аффинно-эквивалентно части изображения A, то стертый код QB есть подмножество стертого кода QA, но обратное неверно, т.е. стертый код QB может быть подмножеством стертого кода QA, но B при этом не аффинно-эквивалентно части изображения A. Элементы стертых кодов – просто обезличенные числа, поэтому среди большого множества чисел QA могут «разрознено», «случайно» найтись все числа из небольшого QB, хотя вместе они в A не составляли код некоторого подизображения. Такое маловероятно, но возможно, поэтому такое изображение и называется особым.
Далее описаны возможные «атаки» на модель со стороны третьих лиц и ее «реакция» на атаки. Атака может состоять в том, что третье лицо со стороны, не имеющее закрытого ключа, пытается отправить получателю сообщение под видом сообщения от отправителя. Полагаем, он располагает максимально подробной информацией о модели, ее алгоритмах, включая примеры ранее посланных сообщений с проверочными изображениями.
Первый и простой случай состоит в том, что вместе с Х в качестве проверочного отправляется изображение Y, взятое наугад из числа подизображений сообщения Х. Поскольку Y не является подизображением для Z, то проверка на открытом ключе выявит это. Конечно, возможно случайное совпадение Y с подизображением на Z. Однако если, например, Х содержит 100 точек (не очень много), то оценка сверху для числа подизображений – два в степени 100. Это число с тридцатью знаками. Аналогичное и для подизображений в Z.
Более сложный случай – взять одно из ранее посланных проверочных изображений Y, присоединить его как часть к фальшивому изображению, все вместе назвать сообщением Х, и Y сделать при нем проверочным изображением. Тогда Y пройдет проверку и на то, чтобы быть подизображением сообщения, и на то, что его стертый код есть подмножество открытого ключа. Но он не выдержит проверку на максимальность как подизображения в «составном» сообщении Х, то есть проверку на стертые коды изображений из множества {Y+1} на открытом ключе.
Если, наконец, полагать, что это третье лицо, собрав статистику всех ранее посланных проверочных изображений, попытается по ней восстановить закрытый ключ, то оно столкнется с комбинаторной проблемой, некоторым аналогом которой можно считать гипотезу Улама из теории графов. Эта проблема сложна, стоит с 1945 года и до сих пор не решена.
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ защиты электронного изображения на основе аффинных преобразований | 2022 |
|
RU2791834C1 |
| СПОСОБ ФОРМИРОВАНИЯ И ПРОВЕРКИ ЗАВЕРЕННОГО ЦИФРОВЫМ ВОДЯНЫМ ЗНАКОМ ЭЛЕКТРОННОГО ИЗОБРАЖЕНИЯ | 2010 |
|
RU2450354C1 |
| СПОСОБ ФОРМИРОВАНИЯ И ПРОВЕРКИ ЗАВЕРЕННОГО ЦИФРОВЫМ ВОДЯНЫМ ЗНАКОМ ЭЛЕКТРОННОГО ИЗОБРАЖЕНИЯ | 2008 |
|
RU2393538C1 |
| СПОСОБ ФОРМИРОВАНИЯ И ПРОВЕРКИ ЗАВЕРЕННОГО ЦИФРОВЫМ ВОДЯНЫМ ЗНАКОМ ЭЛЕКТРОННОГО ИЗОБРАЖЕНИЯ | 2008 |
|
RU2399953C1 |
| СПОСОБ ФОРМИРОВАНИЯ И ПРОВЕРКИ ЗАВЕРЕННОГО ЦИФРОВЫМ ВОДЯНЫМ ЗНАКОМ ЭЛЕКТРОННОГО ИЗОБРАЖЕНИЯ | 2009 |
|
RU2419149C9 |
| СПОСОБ И УСТРОЙСТВО ДЛЯ ПРОВЕРКИ ПОДЛИННОСТИ ИЛИ ПРАВА С ИСПОЛЬЗОВАНИЕМ РАЗОВЫХ КОДОВ ТРАНЗАКЦИЙ | 2006 |
|
RU2414001C2 |
| ПЕРСОНАЛЬНЫЙ КРИПТОЗАЩИТНЫЙ КОМПЛЕКС | 2002 |
|
RU2300844C2 |
| СПОСОБ СИНХРОНИЗАЦИИ ЦИФРОВОГО ВОДЯНОГО ЗНАКА ЭЛЕКТРОННОГО ИЗОБРАЖЕНИЯ | 2014 |
|
RU2544779C1 |
| СПОСОБ ОБЕСПЕЧЕНИЯ РОБАСТНОСТИ ЦИФРОВОГО ВОДЯНОГО ЗНАКА, ВСТРАИВАЕМОГО В СТАТИЧЕСКОЕ ИЗОБРАЖЕНИЕ, ПЕРЕДАВАЕМОЕ ПО КАНАЛУ СВЯЗИ С ПОМЕХАМИ | 2022 |
|
RU2785832C1 |
| СПОСОБ ДЛЯ ОБМЕНА ЦИФРОВЫМИ СООБЩЕНИЯМИ С АССОЦИАЦИЕЙ СООБЩЕНИЯ С МАТЕРИАЛЬНЫМ ОБЪЕКТОМ | 2018 |
|
RU2752607C2 |
Изобретение относится к вычислительной технике. Технический результат заключается в повышении защищенности информации при ее передаче по каналам связи. Способ аутентификации электронного изображения заключается в том, что формируют у получателя ограниченное множество чисел QY кода электронного точечного изображения Y, проверяют подлинность принятого электронного изображения, для чего устанавливают: является ли изображение Y аффинно-эквивалентным с какими-либо подизображениями сообщения Х; является ли стертый код QY проверочного изображения Y подмножеством стертого кода QZ закрытого ключа Z; является ли стертый код каждого из не особых изображений из {Y+1} подмножеством открытого ключа; является ли стертый код каждого из особых изображений в {Y+1} подмножеством открытого ключа, по результатам электронное изображение считают подлинным при одновременном выполнении следующих условий: изображение Y аффинно-эквивалентно с подизображениями - подмножествами точек сообщения Х, стертый код QY проверочного изображения Y является подмножеством стертого кода QZ закрытого ключа Z, стертый код каждого из изображений в {Y+1}, исключая особые, не является подмножеством открытого ключа, при этом стертый код каждого из особых изображений в {Y+1} является подмножеством открытого ключа. 1 ил.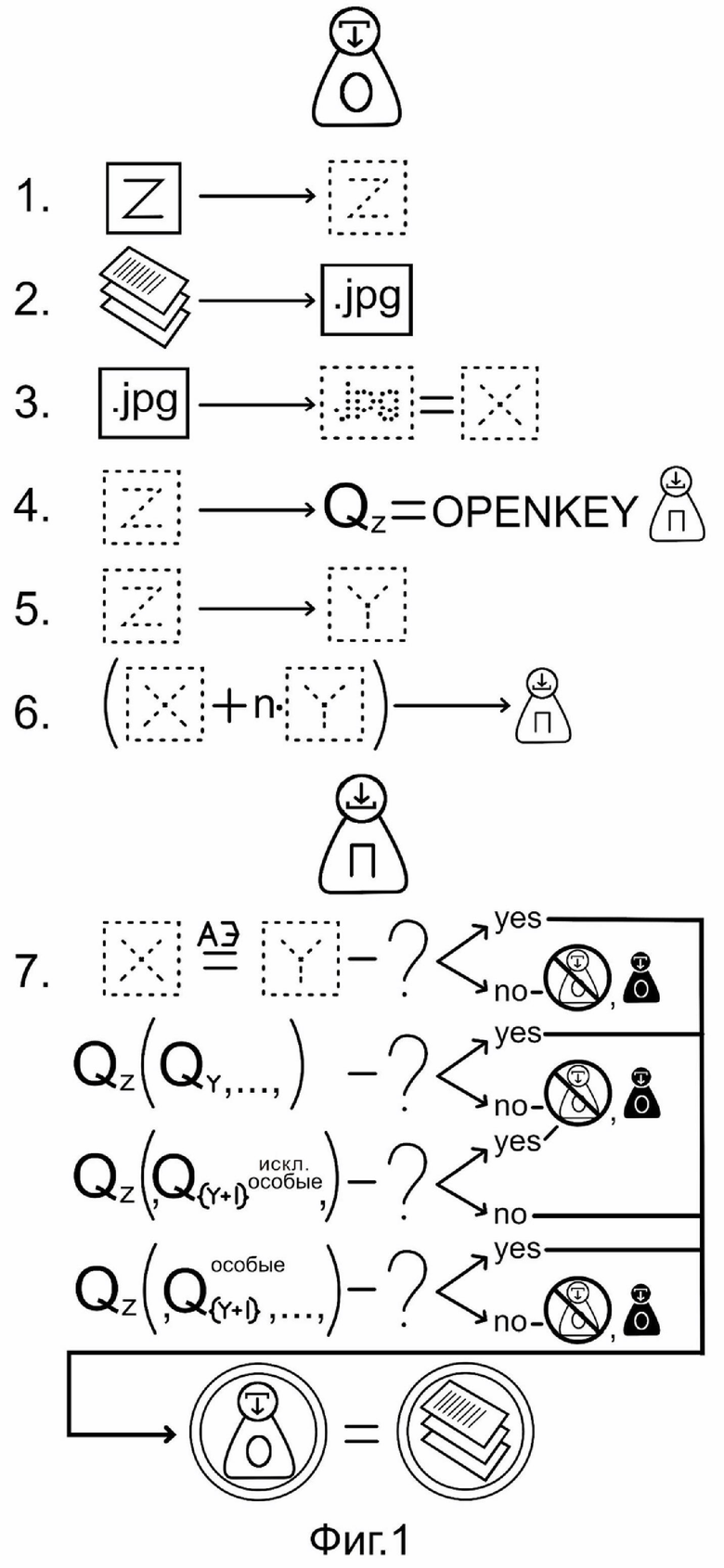
Способ аутентификации электронного изображения, заключающийся в том, что формируют у получателя ограниченное множество чисел QY кода электронного точечного изображения Y, затем проверяют подлинность принятого получателем электронного изображения, для чего устанавливают: является ли изображение Y аффинно-эквивалентным с какими-либо подизображениями сообщения Х; является ли стертый код QY проверочного изображения Y подмножеством стертого кода QZ закрытого ключа Z; является ли стертый код каждого из не особых изображений из {Y+1} подмножеством открытого ключа; является ли стертый код каждого из особых изображений в {Y+1} подмножеством открытого ключа, по результатам электронное изображение считают подлинным при одновременном выполнении следующих условий: изображение Y аффинно-эквивалентно с подизображениями - подмножествами точек сообщения Х, стертый код QY проверочного изображения Y является подмножеством стертого кода QZ закрытого ключа Z, стертый код каждого из изображений в {Y+1}, исключая особые, не является подмножеством открытого ключа, при этом стертый код каждого из особых изображений в {Y+1} является подмножеством открытого ключа.
| Способ проверки подлинности маркировки | 2020 |
|
RU2739059C1 |
| СПОСОБ АУТЕНТИФИКАЦИИ ЭЛЕКТРОННОГО ИЗОБРАЖЕНИЯ | 2014 |
|
RU2568268C1 |
| US 6381375 B1, 30.04.2002 | |||
| US 6215915 B1, 10.04.2001 | |||
| US 5376971 A, 27.12.1994. | |||
Авторы
Даты
2022-09-06—Публикация
2021-08-24—Подача