Изобретение относится к области гидроакустики и может быть использовано для определения комплексной частотной характеристики чувствительности гидрофона по полю, при подборе преобразователей для изготовления антенных решеток, а также при решении задач, связанных с необходимостью восстанавливать форму акустического сигнала.
Известен способ, при использовании которого фазочастотную характеристику (ФЧХ) гидрофона определяют одновременно с измерением его амплитудно-частотной характеристики (АЧХ) чувствительности по методу взаимности с использованием трех преобразователей: излучатель (И), обратимый преобразователь (ОП) и гидрофон (Г) [1]. Из этих преобразователей образуют три пары излучатель-приемник: пару излучатель-гидрофон (И-Г), пару обратимый преобразователь - гидрофон (ОП-Г) и пару излучатель-обратимый преобразователь (И-ОП). Пары преобразователей располагают в резервуаре, заполненном водой. Для каждой пары приемник ориентируют опорным направлением на излучатель и выполняют следующие операции:
- измеряют расстояние d… между излучателем и приемником,
- излучатель возбуждают током, частоту ƒ которого изменяют в требуемом диапазоне измерений,
- сигналом излучателя облучают приемник,
-измеряют частотную зависимость Z…(ƒ) отношения напряжения на выходе приемника к току возбуждения излучателя,
- измеряют частотную зависимость φ… (ƒ) сдвига фаз между напряжением на выходе приемника и током возбуждения излучателя.
АЧХ чувствительности гидрофона вычисляют по формуле:
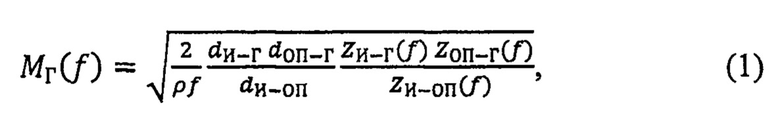
где ρ - плотность воды, dИ-Г, dОП-Г и dИ-ОП расстояния между излучателем и приемником в парах И-Г, ОП-Г и И-ОП соответственно, ZИ-Г(ƒ), ZОП-Г(ƒ) и ZИ-ОП(ƒ) - частотные зависимости отношения напряжения на выходе приемника к току возбуждения излучателя для пар И-Г, ОП-Г и И-ОП соответственно.
ФЧХ гидрофона φГ(ƒ) рассчитывают по формуле:

где φИ-Г(ƒ), φОП-Г(ƒ) и φИ-ОП(ƒ) - частотные зависимости сдвига фаз между напряжением на выходе приемника и током возбуждения излучателя для пар И-Г, ОП-Г и И-ОП соответственно;  - волновое число, с - скорость звука в воде.
- волновое число, с - скорость звука в воде.
Недостаток этого способа - процедура определения ФЧХ значительно более трудоемкая и менее точная в сравнении с определением АЧХ чувствительности гидрофона. Ошибки в расстояниях между преобразователями не входят в число доминирующих составляющих бюджета неопределенностей измерения АЧХ. При измерениях ФЧХ погрешность измерения расстояния становится доминирующей. Важно точно определять расстояния между преобразователями, поскольку любая ошибка в расстоянии приводит к частотно зависимой ошибке фазового угла. С увеличением частоты ошибка фазового угла возрастает пропорционально частоте. Размещение преобразователей в больших испытательных резервуарах и на открытых водоемах с точностью, необходимой для выполнения разумных фазовых измерений, является далеко не тривиальной задачей.
Известен способ определения комплексной частотной характеристики чувствительности Г по методу взаимности, принятый за прототип [1, 2], заключающийся в том, что И, Г и ОП располагают в заполненном водой измерительном бассейне на одной прямой так, чтобы Г находился между И и ОП. Измеряют расстояния dИ-Г, dОП-Г и dИ-ОП. Ориентируют ОП и Г опорным направлением на И. Облучают Г и ОП сигналом И в требуемом диапазоне частот. Измеряют частотные зависимости φИ-Г(ƒ), ZИ-Г(ƒ),φИ-ОП(ƒ) и ZИ-ОП(ƒ). Ориентируют Г опорным направлением на ОП, развернув Г вокруг его оси на 180°. Облучая Г сигналом ОП в требуемом диапазоне частот, измеряют частотные зависимости φОП-Г(ƒ) и ZОП-Г(ƒ). При выполнении эксперимента по такой схеме расстояния между преобразователями dИ-Г, dОП-Г и dИ-ОП остаются неизменными, причем dИ-Г + dОП-Г = dИ-ОП.
АЧХ гидрофона вычисляют по формуле (1). ФЧХ гидрофона φг(ƒ) рассчитывают по формуле:
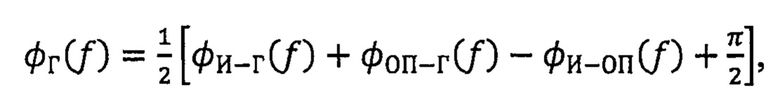
в которую не входят расстояния между преобразователями.
Недостатки прототипа - необходимость обеспечить неизменность расстояний между преобразователями при развороте гидрофона на 180°, сложность и трудоемкость эксперимента по измерению фазочастотных зависимостей.
На практике И, ОП и Г закрепляют на штангах, длина которых определяется глубиной погружения преобразователей и может достигать двух-трех метров. Чтобы при развороте Г не смещался относительно исходного положения он должен лежать на оси вращения. Вследствие смещений штанги при развороте Г, исходное расположение преобразователей нарушается. В результате фазовый угол чувствительности получают не для опорной точки Г, а для некоторой точки, остающейся неподвижной при вращении Г и лежащей на пересечении прямой расположения преобразователей и оси вращения. Смещение опорной точки относительно оси вращения приводят к ошибке в фазовом угле, пропорциональной смещению и частоте измерений.
Чтобы уменьшить влияние этих недостатков положения Г юстируют по лучу лазера с помощью прецизионной 3-D системы позиционирования [3]. Помимо того, что такой подход существенно усложняет процедуру калибровки, его невозможно применить в измерительном бассейне с оптически непрозрачными стенками. Отметим также, что юстировка положения Г не гарантирует точного результата в случае, когда, например, вследствие технологических причин акустический центр гидрофона не совпадает с его геометрическим центром. Смещение положения акустического центра от опорной точки в 1 мм приводит к частотно-зависимой ошибке в измеренной ФЧХ, которая составляет порядка 18° на частоте 150 кГц [3].
Принимаемые меры значительно усложняют как саму процедуру измерений, так и возможность ее автоматизации. 3-D позиционирование по лучам лазера чувствительно к малейшим толчкам и вибрациям, а по сути - осуществляется «на глаз». Измерения ФЧХ трудоемки, методически в значительно меньшей степени отработаны по сравнению с измерениями АЧХ, в силу чего результаты измерения ФЧХ в большой мере зависят от искусства экспериментатора.
Техническим результатом, получаемым от внедрения изобретения, является устранение отмеченных недостатков прототипа, т.е. повышение точности определения ФЧХ чувствительности Г и уменьшение трудоемкости измерительного эксперимента.
Данный технический результат достигают за счет того, что в известном способе определения комплексной частотной характеристики чувствительности гидрофона, заключающемся в том, что в заполненном водой измерительном бассейне излучатель, гидрофон и обратимый преобразователь располагают на одной прямой так, чтобы гидрофон находился между излучателем и обратимым преобразователем, обратимый преобразователь и гидрофон ориентируют опорными направлениями на излучатель, измеряют расстояния dИ-Г, dОП-Г и dИ-ОП между излучателем и гидрофоном, обратимым преобразователем и гидрофоном, излучателем и обратимым преобразователем соответственно, облучают гидрофон и обратимый преобразователь сигналом излучателя в требуемом диапазоне частот, измеряют частотные зависимости ZИ-Г(ƒ) и ZИ-ОП(ƒ) отношения напряжений на выходе гидрофона и обратимого преобразователя соответственно к току излучателя, разворачивают гидрофон вокруг его оси на 180°, облучают гидрофон сигналом обратимого преобразователя в требуемом диапазоне частот, измеряют частотную зависимость ZOП-Г(ƒ) отношения напряжения на выходе гидрофона к току обратимого преобразователя, по полученным данным рассчитывают амплитудно-частотную характеристику чувствительности гидрофона
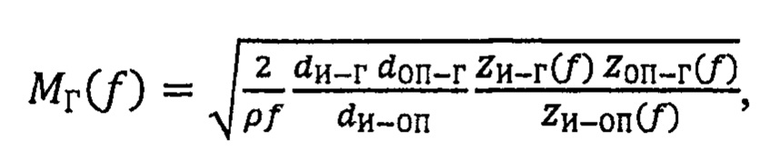
задают расстояние а от поверхности активного элемента гидрофона до опорной точки, фазочастотную характеристику гидрофона φГ(ƒ) для опорной точки рассчитывают по формуле:

где 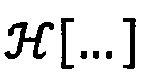 означает преобразование Гильберта,
означает преобразование Гильберта,  - волновое число, с - скорость звука в воде.
- волновое число, с - скорость звука в воде.
В предложенном способе не выполняют прямых измерений фазочастотных зависимостей, поэтому смещения опорной точки относительно оси вращения Г не оказывают влияния на результат.ФЧХ получают по формуле, в которую не входят расстояния между преобразователями, соответственно, погрешность в измерении расстояний также не приводит к ошибке определения ФЧХ.
Изобретение поясняется чертежами. На фиг. 1-фиг. 4 представлены результаты измерительных экспериментов, выполненных на установках Государственного первичного эталона ГЭТ 55-2017, с целью подтверждения применимости предложенного способа для определения ФЧХ гидрофонов с различной конструкцией активных элементов.
Часто используемая математическая модель Г представляет собой совокупность уравнений, описьшающих поведение RLC колебательных контуров и дифракцию звука на активном элементе [4].
Уравнение дифракции описывает уменьшение при возрастании частоты амплитуды и соответствующую этому уменьшению задержку по фазе среднего звукового давления на поверхности Г относительно амплитуды и фазы звукового давления в свободном поле (т.е. в отсутствие Г) в месте расположения опорной точки Г [5]. В теории электрических цепей подобные зависимости характерны для фильтра нижних частот.
Например, дифракцию звука на сферическом активном элементе описывают комплексной функцией [5]:
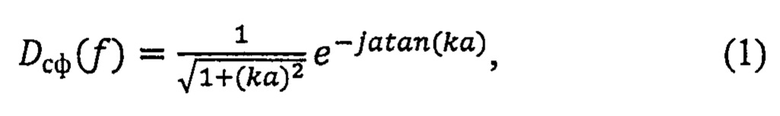
где а - радиус сферы. Переписав выражение (1) в виде комплексной дробно-рациональной функции нетрудно убедиться, что она имеет единственный действительный полюс, расположенный слева от нуля на комплексной плоскости. Следовательно, функцию дифракции (1) можно рассматривать как комплексную передаточную функцию линейной системы, которую в теории линейных цепей принято называть минимально-фазовой [6]. Передаточная функция системы из колебательных RLC контуров не имеет нулей и полюсов в правой части комплексной плоскости и также относится к классу линейных минимально-фазовых систем.
Обычно минимально-фазовую модель применяют для описания систем с сосредоточенными параметрами. В методе взаимности Г также представляют точкой, совпадающей с его опорным центром, в качестве которого обычно принимают геометрический центр активного элемента. Условия, при котором такое представление допустимо, называют дальним полем. Поскольку Г имеет физический размер (не является точкой), его реакция опережает момент прихода звуковой волны в опорную точку. ФЧХ получает дополнительную компоненту ka, равную набегу фазы при распространении звуковой волны на расстояние, равное радиусу активного элемента. Эффект, порождающий эту компоненту, по аналогии с используемым в радиотехнике термином «линия задержки», назовем «линией опережения». Формально, такое опережение реакцией вызвавшего ее воздействия противоречит принципу казуальности, который является одним из непременных условий минимально-фазовости системы [6]. В то же время «линия опережения», как и идеальная линия задержки, не искажают форму принимаемого сигнала, а вызывают лишь его смещение по времени. Это обстоятельство позволяет использовать модель Г, состоящую из двух частей: минимально-фазовой части (дифракция звука на активном элементе и набор колебательных контуров) и «линии опережения».
Использование такой модели позволяет:
- представить ФЧХ Г суммой его минимально-фазовой частотной характеристики (МФЧХ) и фазового набега «линии опережения» ka,
- воспользоваться для определения МФЧХ свойством минимально-фазовой системы - ФЧХ и АЧХ минимально-фазовой системы связаны через преобразование Гильберта.
Преобразование Гильберта натурального логарифма АЧХ, заданной с точностью до постоянного множителя, дает ФЧХ. Применительно к Г словосочетание «АЧХ, заданная с точностью до постоянного множителя» означает, что для получения МФЧХ нет необходимости использовать АЧХ чувствительности Г в силу ее избыточности, достаточно использовать зависимость  которая представляет поведение АЧХ.
которая представляет поведение АЧХ.
На фиг. 1 и 2 с шагом 1 кГц представлены результаты комплексной калибровки на ГЭТ 55-2017 гидрофона ГИ20 (производства ФГУП ВНИИФТРИ) со сферическим активным элементом радиуса а=10 мм. В качестве опорной точки принимали геометрический центр активного элемента. На фиг. 1 приведена АЧХ чувствительности, поведение которой позволяет судить о наличии у гидрофона ГИ 20 трех в разной степени демпфированных резонансов на частотах 65 кГц, 100 кГц и 150 кГц.
Экспериментальная ФЧХ, полученная прямыми измерениями фазочастотньгх зависимостей, и расчетная ФЧХ, полученная предложенным способом с использованием преобразования Гильберта, приведены на фиг. 2 рядами 1 и 2 соответственно. Отклонения ряда 2 от ряда 1 достигают наибольших значений 3,5° и 12° на частотах 150 кГц и 200 кГц соответственно, что меньше погрешностей современных национальных эталонов при измерениях ФЧХ на этих частотах [3].
На фиг. 3 и 4 с шагом 1 кГц представлены результаты комплексной калибровки гидрофона В&K 8103 с цилиндрическим активным элементом. В качестве опорной принимали точку на оси цилиндра на половине его высоты. На фиг. 3 приведена АЧХ чувствительности гидрофона. Экспериментальная и расчетная ФЧХ приведены на фиг. 4 рядами 1 и 2 соответственно. Отклонения ряда 2 от ряда 1 не превосходят 2,5° на частотах ≤250 кГц, и на частотах выше 250 кГц возрастают до 5°.
Полученные результаты подтверждают достижимость заявленного технического результата - повышение точности определения ФЧХ гидрофона и уменьшение трудоемкости измерительного эксперимента.
Разбиение модели гидрофона на «линию опережения» и минимально-фазовую часть, включающую влияние дифракции звука и резонансные свойства активного элемента, позволяет избежать сложностей, связанных с прямыми измерениями фазочастотных зависимостей, и получать ФЧХ значительно менее трудоемким способом - преобразованием Гильберта АЧХ. Ошибка в измерении расстояния между опорными центрами излучателя и приемника входит в число доминирующих составляющих погрешности прямых измерений ФЧХ, однако не оказывает влияния при получении ФЧХ по АЧХ.
Литература:
1. L. D. Luker and A. L. Van Buren. "Phase calibration of hydrophones". J. Acoust. Soc. Am. 70, pp. 516-519. (1981).
2. МЭК 60565-1(2020). Подводная акустика. Гидрофоны. Калибровка гидрофонов. Часть 1. Процедуры калибровки гидрофонов по свободному полю
3. G. Hayman and S. Robinson, "Phase calibration of hydrophones by the free-field reciprocity method," Proc. 11th Europ. Conf. on Underwater Acoustics, Edinburgh (2012), pp. 1437-1444.
4. H.H. Дмитревский, Л.Е. Павлов, С.В. Сильвестров Применение импеданцного метода для определения чувствительности пьезоэлектрических приемников звука. Акустический Журнал, Том XXII, Вып. 3. 1976 г.
5. T.F. Henriquez. Diffraction Constants of Acoustic Transducers. J. Acoust. Soc. Amer., 1964, 36, 12, 267-269.
6. С.Септу, H. Балабанян Анализ линейных цепей. Пер. с англ. И.В. Соловьева; Под ред. проф. Г.И. Атабекова. - Москва; Ленинград: Госэнергоиздат, 1963. - 551 с.


Изобретение относится к области метрологии и гидроакустики. Способ определения фазочастотной характеристики гидрофона по его амплитудно-частотной характеристике чувствительности заключается в том, что в заполненном водой измерительном бассейне излучатель, гидрофон и обратимый преобразователь располагают на одной прямой так, чтобы гидрофон находился между излучателем и обратимым преобразователем, обратимый преобразователь и гидрофон ориентируют опорными направлениями на излучатель, измеряют расстояния dИ-Г, dОП-Г и dИ-ОП между излучателем и гидрофоном, обратимым преобразователем и гидрофоном, излучателем и обратимым преобразователем соответственно, облучают гидрофон и обратимый преобразователь сигналом излучателя в требуемом диапазоне частот, измеряют частотные зависимости ZИ-Г и ZИ-ОП отношения напряжений на выходах гидрофона и обратимого преобразователя соответственно к току излучателя, разворачивают гидрофон вокруг его оси на 180°, облучают гидрофон сигналом обратимого преобразователя в требуемом диапазоне частот, измеряют частотную зависимость ZОП-Г отношения напряжения на выходе гидрофона к току обратимого преобразователя, по полученным данным рассчитывают амплитудно-частотную характеристику чувствительности гидрофона. Затем задают расстояние от поверхности активного элемента гидрофона до его опорной точки, фазочастотную характеристику чувствительности гидрофона φГ(ƒ) для опорной точки рассчитывают с использованием преобразования Гильберта. Технический результат - повышение точности определения фазочастотной характеристики гидрофона и уменьшение трудоемкости измерительного эксперимента. 4 ил.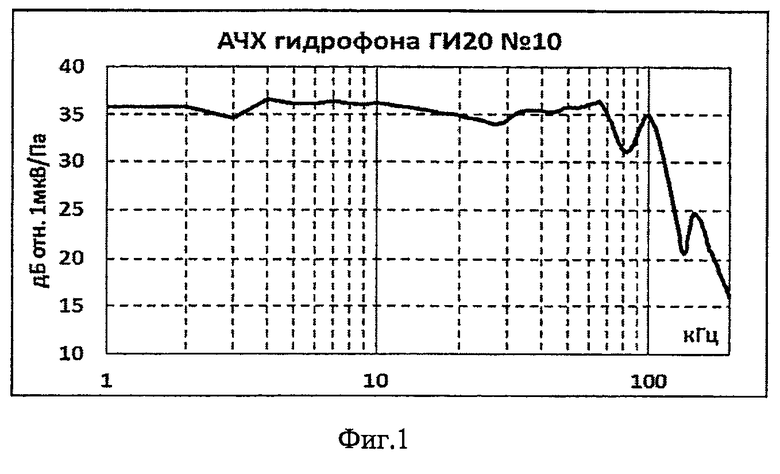
Способ определения фазочастотной характеристики гидрофона по его амплитудно-частотной характеристике чувствительности, заключающийся в том, что в заполненном водой измерительном бассейне излучатель, гидрофон и обратимый преобразователь располагают на одной прямой так, чтобы гидрофон находился между излучателем и обратимым преобразователем, обратимый преобразователь и гидрофон ориентируют опорными направлениями на излучатель, измеряют расстояния dИ-Г, dОП-Г и dИ-ОП между излучателем и гидрофоном, обратимым преобразователем и гидрофоном, излучателем и обратимым преобразователем соответственно, облучают гидрофон и обратимый преобразователь сигналом излучателя в требуемом диапазоне частот, измеряют частотные зависимости ZИ-Г и ZИ-ОП отношения напряжений на выходах гидрофона и обратимого преобразователя соответственно к току излучателя, разворачивают гидрофон вокруг его оси на 180°, облучают гидрофон сигналом обратимого преобразователя в требуемом диапазоне частот, измеряют частотную зависимость ZОП-Г отношения напряжения на выходе гидрофона к току обратимого преобразователя, по полученным данным рассчитывают амплитудно-частотную характеристику чувствительности гидрофона

отличающийся тем, что задают расстояние а от поверхности активного элемента гидрофона до его опорной точки, фазочастотную характеристику чувствительности гидрофона φГ(ƒ) для опорной точки рассчитывают по формуле:
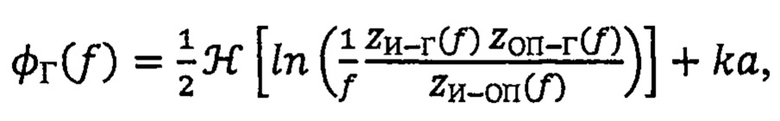
где 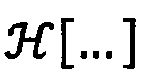 означает преобразование Гильберта,
означает преобразование Гильберта, 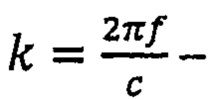 - волновое число, с - скорость звука в воде, ƒ - частота.
- волновое число, с - скорость звука в воде, ƒ - частота.
| Luker, L | |||
| D., & Van Buren, A | |||
| L | |||
| Приспособление для изготовления в грунте бетонных свай с употреблением обсадных труб | 1915 |
|
SU1981A1 |
| Phase calibration of hydrophones | |||
| The Journal of the Acoustical Society of America, 70(2), 516-519 | |||
| Печь-кухня, могущая работать, как самостоятельно, так и в комбинации с разного рода нагревательными приборами | 1921 |
|
SU10A1 |
| Исаев, А | |||
| Е | |||
| Определение фазочастотной характеристики гидрофона по амплитудно-частотной характеристике / А | |||
| Е | |||
| Исаев, Б | |||
| И | |||
| Хатамтаев // Измерительная техника | |||
| Способ регенерирования сульфо-кислот, употребленных при гидролизе жиров | 1924 |
|
SU2021A1 |
| Способ восстановления хромовой кислоты, в частности для получения хромовых квасцов | 1921 |
|
SU7A1 |
| - С | |||
Авторы
Даты
2023-01-09—Публикация
2022-04-25—Подача