Изобретение относится к области радиосвязи и может быть использовано в широкополосных системах для передачи информации, оценки параметров канала распространения и выполнения процедур частотно-временной синхронизации.
В последние годы для увеличения пропускной способности систем радиосвязи в условиях жесткого дефицита радиочастотного спектра большое внимание уделяется разработке новых видов сложных широкополосных сигналов с поляризационным кодированием (ПК) элементов [1, 2].
Известен способ радиосвязи, приведенный в патенте US 6448941, H01Q 1/36 от 10.09.2002 г., в котором осуществляется скачкообразная перестройка поляризации сигнала несущей синхронно с псевдослучайной перестройкой несущей частоты, что достигается использованием на передающей и приемной сторонах идентичных антенн специальной конструкции; поляризационное состояние (поляризационная структура) элементов излучаемого сигнала зависит от частоты питающего напряжения и на длительности сигнала может принимать несколько заданных состояний.
У этого способа можно выделить несколько основных недостатков:
- жесткая связь поляризационного состояния элементов сигнала с частотой несущего колебания, что ограничивает количество возможных сигналов в ансамбле;
- необходимость антенн специальной конструкции, идентичных на передающей и приемной сторонах;
- неиспользование поляризационной избыточности сигнала для улучшения его корреляционных свойств.
В заявке US 2004/0114548 Н04В 7/204 от 17.06.2004 г. предложен способ использования сигнала с поляризационным кодированием, в котором также осуществляется скачкообразная перестройка поляризации сигнала несущей в соответствии с кодом псевдослучайной последовательности (ПСП). Этому способу присущ следующий недостаток - избыточность, которую вносит разнесение элементов сигнала по ортогональным поляризационным состояниям, используется только для разделения абонентов в системах связи и не используется для улучшения корреляционных свойств сигнала.
Вопросам повышения пропускной способности и помехозащищенности систем радиосвязи (СРС), использующих двоичные фазоманипулированные широкополосные сигналы (ФМШПС), без дополнительных затрат радиочастотного и энергетического ресурсов за счет применения метода поляризационного кодирования элементов указанных сигналов и дополнительной инверсной поляризационной манипуляции достаточно большое внимание уделяется в работах [1, 2, 3].
Широко известным является способ формирования двоичного фазоманипулированного широкополосного сигнала с ортогональным ПК, приведенный в статье [4].
Данный способ формирования фазоманипулированных широкополосных сигналов с поляризационным кодированием [4] заключается в следующем.
Известным образом формируют две псевдослучайные М-последовательности одинакового периода N [5], но с разными порождающими полиномами 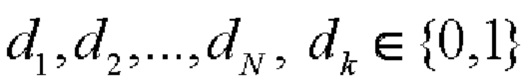 и
и 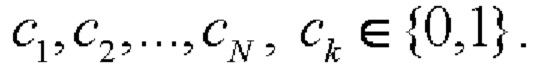
- Строят бинарную последовательность wk=2dk-1, 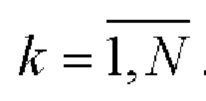
- Формируют последовательность длины N двумерных векторов pk, 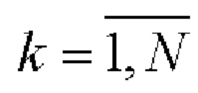 согласно правилу (1):
согласно правилу (1):
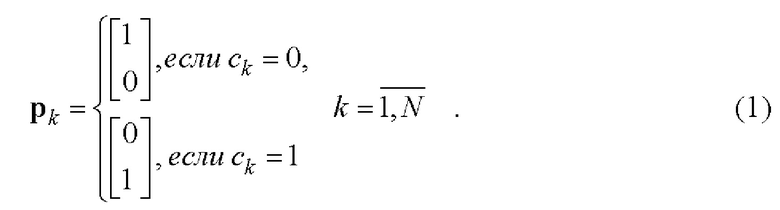
- Последовательности wk и рk, 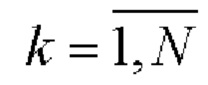 поэлементно перемножают и формируют соответствующую последовательность произведений.
поэлементно перемножают и формируют соответствующую последовательность произведений.
- Для текущего значения времени t из интервала периода 0≤t≤Nτ0 двоичного ФМШПС с ортогональным ПК формируют значение векторной комплексной огибающей. При этом каждый k-й элемент последовательности произведений перемножают на соответствующий сформированный элементарный импульс единичной амплитуды 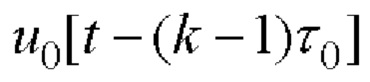 длительностью τ0.
длительностью τ0.
В этом способе используют принцип дополнительной избыточности за счет ортогонального поляризационного кодирования элементов широкополосного фазоманипулированного сигнала в соответствии с двоичной псевдослучайной последовательностью, в том числе М-последовательностью.
Фазоманипулированный широкополосный сигнал с поляризационным кодированием [4] состоит из последовательности элементарных радиоимпульсов с начальными значениями фаз, определяемых кодом первой псевдослучайной последовательности (ПСП), и поляризационными состояниями, определяемыми кодом второй ПСП. При этом обе ПСП имеют одинаковую длину N.
Общее выражение, описывающее один период данного двоичного фазоманипулированного широкополосного радиосигнала с ортогональным ПК и дополнительной инверсной поляризационной манипуляцией, может быть представлено в виде [4]:
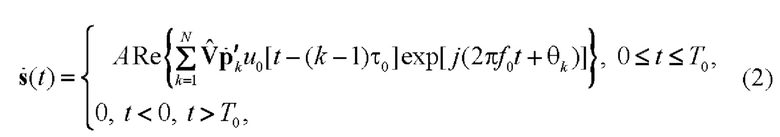
где 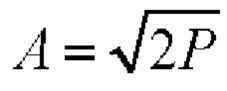 - амплитуда сигнала; Р - средняя мощность сигнала;
- амплитуда сигнала; Р - средняя мощность сигнала;
N - период псевдослучайных последовательностей, используемых в качестве фазового и поляризационного кодов; 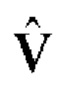 - оператор, описывающий дополнительную инверсную поляризационную манипуляцию;
- оператор, описывающий дополнительную инверсную поляризационную манипуляцию;
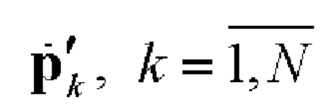 - единичный комплексный вектор-столбец (состоящий из двух элементов) [6], определяющий поляризацию k-го элементарного импульса (чипа) сигнала;
- единичный комплексный вектор-столбец (состоящий из двух элементов) [6], определяющий поляризацию k-го элементарного импульса (чипа) сигнала;
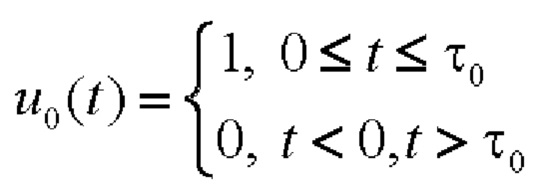 - прямоугольная огибающая элементарного радиоимпульса единичной амплитуды длительностью τ0;
- прямоугольная огибающая элементарного радиоимпульса единичной амплитуды длительностью τ0;
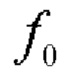 - несущая частота сигнала;
- несущая частота сигнала; 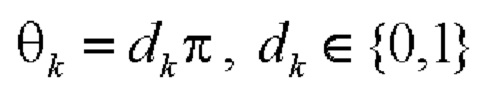 - начальная фаза k-го элементарного импульса (dl, d2, …, dN - код расширяющей спектр сигнала ПСП);
- начальная фаза k-го элементарного импульса (dl, d2, …, dN - код расширяющей спектр сигнала ПСП); 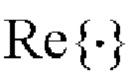 - символ операции взятия реальной части;
- символ операции взятия реальной части;
Т0=Nτ0 - длительность периода ПСП.
Оператор 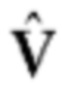 при использовании согласованного поляризационного базиса [2] имеет матричное представление вида
при использовании согласованного поляризационного базиса [2] имеет матричное представление вида 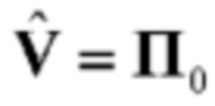 в отсутствие инверсии поляризационных состояний элементарных импульсов сигнала и
в отсутствие инверсии поляризационных состояний элементарных импульсов сигнала и 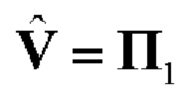 - при ее наличии, где П0, П1 - матрицы Паули [7].
- при ее наличии, где П0, П1 - матрицы Паули [7].
Вектор 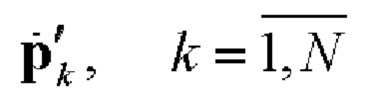 определяет состояние поляризации k-го элементарного импульса двоичного ФМШПС в соответствии с кодом
определяет состояние поляризации k-го элементарного импульса двоичного ФМШПС в соответствии с кодом 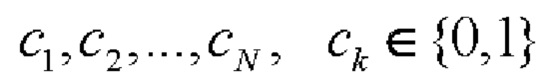 поляризационной ПСП. Причем при использовании согласованного поляризационного базиса [2] это соответствие задается следующим образом:
поляризационной ПСП. Причем при использовании согласованного поляризационного базиса [2] это соответствие задается следующим образом: 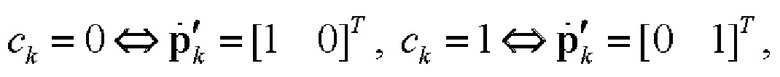
где 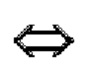 - символ соответствия;
- символ соответствия; 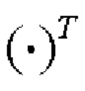 - символ операции транспонирования.
- символ операции транспонирования.
Так как сигнал (2) в радиотехническом смысле является узкополосным 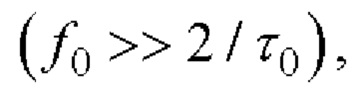 то для упрощения анализа его свойств целесообразно перейти к его комплексной огибающей [8, 9].
то для упрощения анализа его свойств целесообразно перейти к его комплексной огибающей [8, 9].
Полагая А=1 и вводя обозначения 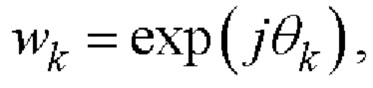
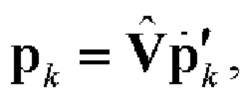 векторную комплексную огибающую одного периода двоичного ФМШПС с ортогональным ПК (2) можно представить в виде
векторную комплексную огибающую одного периода двоичного ФМШПС с ортогональным ПК (2) можно представить в виде
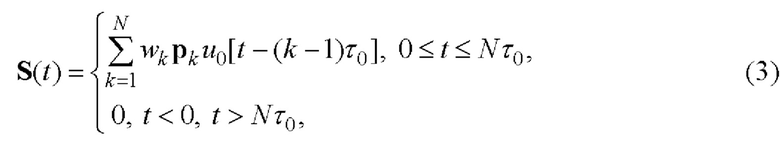
где 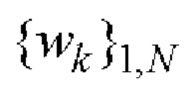 - бинарная кодовая последовательность, задающая закон фазовой манипуляции элементарных радиоимпульсов;
- бинарная кодовая последовательность, задающая закон фазовой манипуляции элементарных радиоимпульсов; 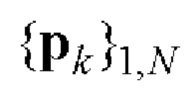 - кодовая последовательность единичных векторов
- кодовая последовательность единичных векторов 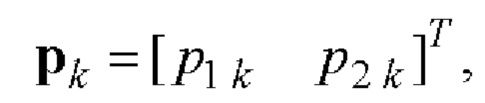
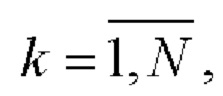 задающая закон поляризационной манипуляции элементарных радиоимпульсов; р1 k и р2 k - компоненты вектора в согласованном поляризационно-ортогональном базисе [2].
задающая закон поляризационной манипуляции элементарных радиоимпульсов; р1 k и р2 k - компоненты вектора в согласованном поляризационно-ортогональном базисе [2].
Решетчатая апериодическая автокорреляционная функция (АКФ) векторной комплексной огибающей S(t) двоичного ФМШПС с ортогональным ПК (3) имеет вид (4):
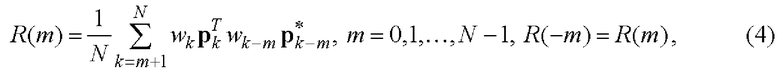
где 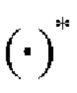 - символ операции комплексного сопряжения.
- символ операции комплексного сопряжения.
Решетчатая апериодическая взаимокорреляционная функция (ВКФ) i-й и j-й комплексных огибающих Si(t) и Sj(t) двоичных ФМШПС с ортогональным поляризационным кодированием с соответствующими кодовыми последовательностями 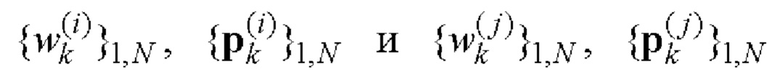 имеет вид (5)
имеет вид (5)
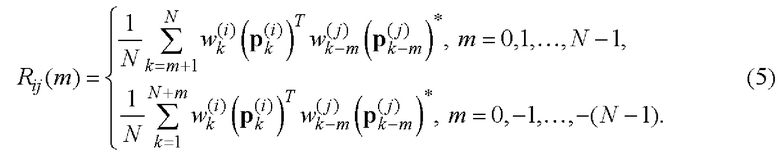
Существенным недостатком данного способа формирования двоичных ФМШПС с ортогональным ПК при фазовом и поляризационных кодах в виде М-последовательностей является то, что апериодические АКФ данных сигналов (4) имеют ненулевые боковые лепестки, а апериодические ВКФ (5) - ненулевые боковые и центральные лепестки.
Наиболее близким аналогом по технической сущности к предлагаемому является способ формирования фазоманипулированных широкополосных сигналов с поляризационным кодированием с оптимальными апериодическими автокорреляционными функциями по патенту RU 2776777, Н04В 7/204 [10], принятый за прототип.
Способ-прототип заключается в следующем.
1. Выбирают длину последовательности N=2Р, где р=1, 2, ….
2. На основе обобщенных символических матриц Адамара [13] формируют последовательность Е-кода Велти [5, 8] длиной N=2P, р=1, 2, …. с элементами алфавита α, β, γ, δ.
Для этого:
3. Строят первообразную квадратную матрицу второго порядка 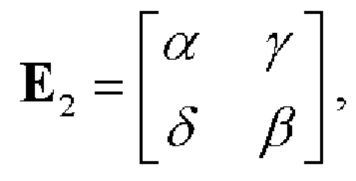 где α, β, γ, δ - элементы алфавита четверичного кода, удовлетворяющие правилу инверсии
где α, β, γ, δ - элементы алфавита четверичного кода, удовлетворяющие правилу инверсии
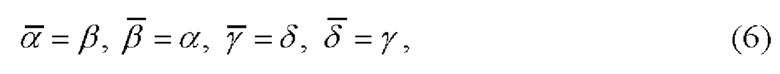
где «-» - символ операции инверсии.
4. С использованием матрицы Е2 строят квадратную блочную матрицу четвертого порядка 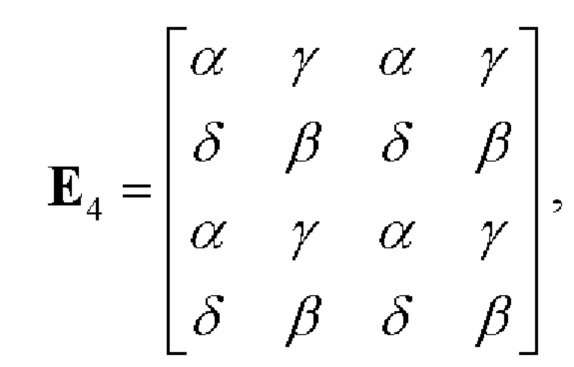 в которой блоками являются матрицы Е2.
в которой блоками являются матрицы Е2.
5. В полученной матрице в соответствии с правилом инверсии в правом верхнем и правом нижнем блоках выполняется инверсия элементов: в верхнем блоке - всех элементов в правой половине блока, а в нижнем блоке - всех элементов в левой половине блока.
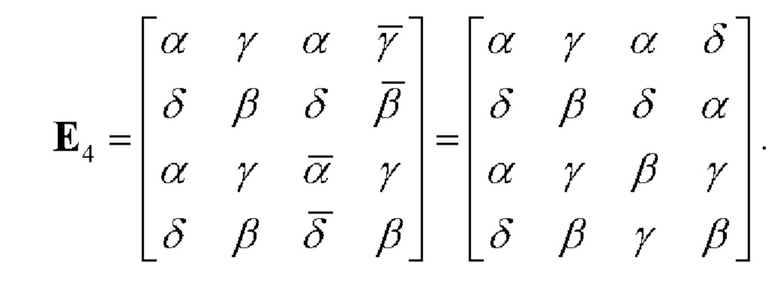
6. При необходимости с использованием в качестве блоков полученной в соответствии с правилом инверсии матрицы Е4 строят квадратную блочную матрицу восьмого порядка

7. В полученной матрице Е8 в соответствии с правилом инверсии в правом верхнем и правом нижнем блоках выполняется инверсия элементов: в верхнем блоке - всех элементов в правой половине блока, а в нижнем блоке -всех элементов в левой половине блока.

8. Описанная процедура рекурсивно повторяется для матриц порядка N=2Р, р=1, 2, …, до тех пор, пока порядок матрицы не совпадет с выбранным значением длины последовательности.
9. При этом строки полученной матрицы являются последовательностями Е-кода Велти с требуемыми корреляционными свойствами.
10. На основе полученной последовательности 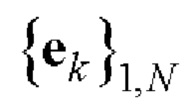 Е-кода Велти с помощью таблицы соответствия 1 находят элементы кодовых последовательностей
Е-кода Велти с помощью таблицы соответствия 1 находят элементы кодовых последовательностей 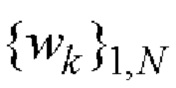 и
и 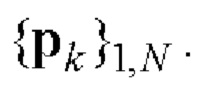
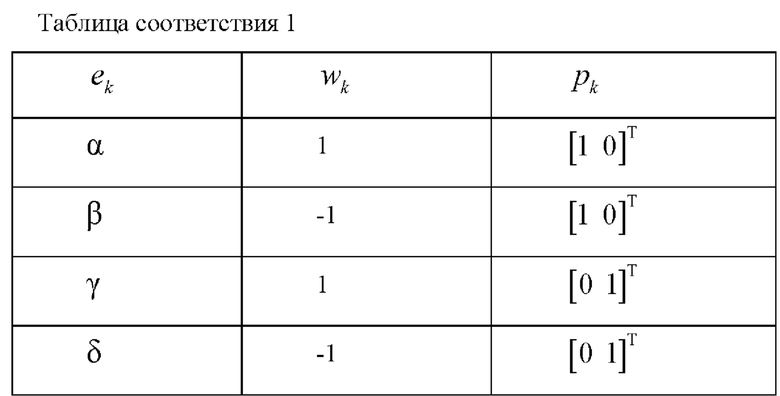
11. Найденные элементы кодовых последовательностей 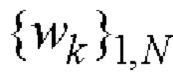 и
и 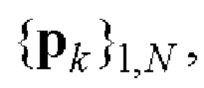
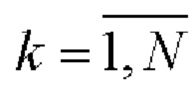 поэлементно перемножают и формируют соответствующую последовательность произведений.
поэлементно перемножают и формируют соответствующую последовательность произведений.
12. Для текущего значения времени t из интервала периода 0≤t≤Nτ0 двоичного ФМШПС с ортогональным ПК формируют значение векторной комплексной огибающей. При этом каждый k-й элемент последовательности произведений перемножают на соответствующий сформированный элементарный импульс единичной амплитуды 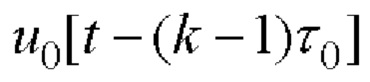 длительностью τ0.
длительностью τ0.
Полученная таким образом векторная комплексная огибающая S(t) двоичного ФМШПС с ортогональным поляризационным кодированием (3) имеет АКФ (4) с нулевыми боковыми лепестками.
Основные недостатки способа-прототипа заключаются в следующем. Во-первых, получаемые множества кодовых последовательностей 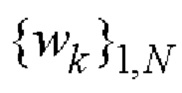 и
и 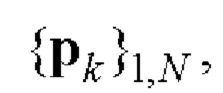
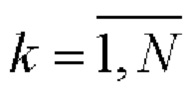 для формирования комплексных огибающих двоичных ФМШПС с ортогональным поляризационным кодированием ограничены периодами
для формирования комплексных огибающих двоичных ФМШПС с ортогональным поляризационным кодированием ограничены периодами 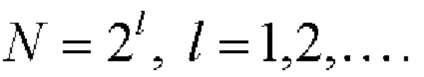 Во-вторых, при данном способе формирования двоичных ФМШПС с ортогональным поляризационным кодированием ВКФ любых пар несовпадающих комплексных огибающих этих сигналов имеют ненулевые боковые и центральные лепестки.
Во-вторых, при данном способе формирования двоичных ФМШПС с ортогональным поляризационным кодированием ВКФ любых пар несовпадающих комплексных огибающих этих сигналов имеют ненулевые боковые и центральные лепестки.
Задача заявляемого способа заключается в разработке процедуры формирования пар двоичных ФМШПС с ортогональным поляризационным кодированием на основе пар дополнительных последовательностей Е-кода Велти с периодами N=2Р⋅10q⋅26r, где числа 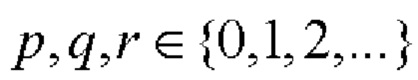 одновременно не равны нулю, у которых боковые лепестки АКФ и боковые и центральные лепестки ВКФ имеют нулевые уровни.
одновременно не равны нулю, у которых боковые лепестки АКФ и боковые и центральные лепестки ВКФ имеют нулевые уровни.
Для решения поставленной задачи в способе формирования пар фазоманипулированных широкополосных сигналов с поляризационным кодированием с оптимальными апериодическими автокорреляционными и взаимокорреляционными функциями, заключающемся в том, что формируют кодовые последовательности 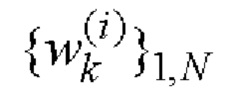 и
и 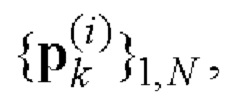 i=1, 2 комплексных огибающих S1(t) и S2(t) двоичных ФМШПС с ортогональным поляризационным кодированием (ПК);
i=1, 2 комплексных огибающих S1(t) и S2(t) двоичных ФМШПС с ортогональным поляризационным кодированием (ПК);
- последовательности 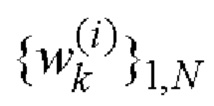 и
и 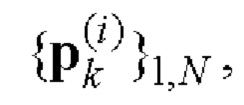 i=1, 2 поэлементно перемножают и формируют соответствующие последовательности произведений
i=1, 2 поэлементно перемножают и формируют соответствующие последовательности произведений 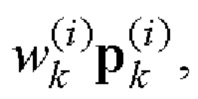
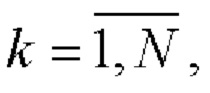 i=1, 2;
i=1, 2;
- для текущего значения времени t из интервала периода 0≤t≤Nτ0 двоичного ФМШПС с ортогональным ПК одновременно формируют значения двух векторных комплексных огибающих, при этом каждый k-й элемент i-й последовательности произведений перемножают на соответствующий сформированный элементарный импульс единичной амплитуды 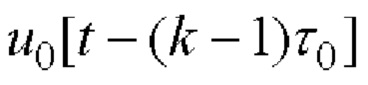 длительностью τ0, согласно изобретению,
длительностью τ0, согласно изобретению,
- выбирают длину последовательностей N, представимую в виде N=2Р⋅10q⋅26r, где числа 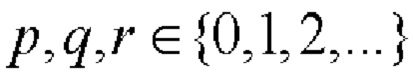 одновременно не равны нулю;
одновременно не равны нулю;
- по выбранному значению числа N путем разложения его на множители 2, 10 и 26 находят числа р, q и r;
- в зависимости от полученных значений параметров р, q и r в соответствии с табличным правилом формирования символической матрицы Е на основе базовых матриц пар дополнительных последовательностей Е-кода Велти с использованием процедуры поблочного формирования символических матриц с элементами четверичного алфавита α, β, γ, δ предварительно формируют вспомогательные символические матрицы А, В и С;
- на основе вспомогательных символических матриц А, В и С с использованием процедуры поблочного формирования символических матриц находят символическую матрицу Е размера 2×N в соответствии с табличным правилом; при этом строки полученной матрицы Е образуют пару дополнительных последовательностей 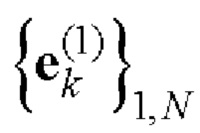 и
и 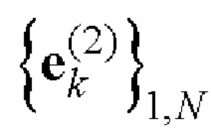 Е-кода Велти с требуемыми корреляционными свойствами;
Е-кода Велти с требуемыми корреляционными свойствами;
- на основе полученных дополнительных последовательностей 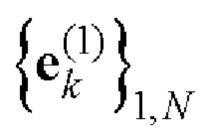 и
и 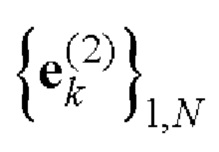 Е-кода Велти с помощью таблицы соответствия однозначно находят элементы кодовых последовательностей
Е-кода Велти с помощью таблицы соответствия однозначно находят элементы кодовых последовательностей 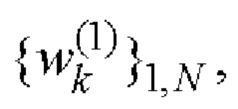
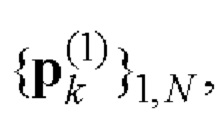 и
и 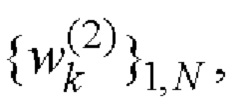
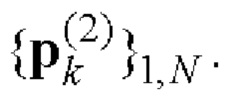
В отличие от способа-прототипа, реализованного на основе процедуры формирования обобщенных символических матриц Адамара [13], для решения поставленной задачи в заявляемом способе кодовые последовательности 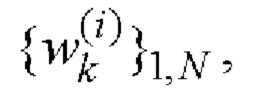
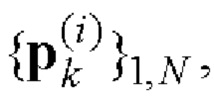 i=1, 2 комплексных огибающих S1(t) и S2(t) двоичных ФМШПС с ортогональным поляризационным кодированием (ПК) формируют следующим образом.
i=1, 2 комплексных огибающих S1(t) и S2(t) двоичных ФМШПС с ортогональным поляризационным кодированием (ПК) формируют следующим образом.
Формируют кодовые последовательности 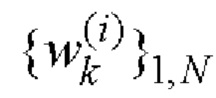 и
и 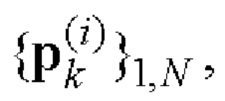 i=1, 2 комплексных огибающих S1(t) и S2(t) двоичных ФМШПС с ортогональным поляризационным кодированием (ПК);
i=1, 2 комплексных огибающих S1(t) и S2(t) двоичных ФМШПС с ортогональным поляризационным кодированием (ПК);
- последовательности 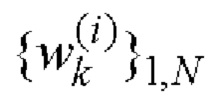 и
и 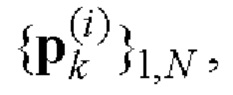 i=1, 2 поэлементно перемножают и формируют соответствующие последовательности произведений
i=1, 2 поэлементно перемножают и формируют соответствующие последовательности произведений 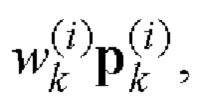
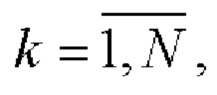 i=1, 2;
i=1, 2;
- для текущего значения времени t из интервала периода 0≤t≤Nτ0 двоичного ФМШПС с ортогональным ПК одновременно формируют значения двух векторных комплексных огибающих, при этом каждый k-й элемент i-й последовательности произведений перемножают на соответствующий сформированный элементарный импульс единичной амплитуды 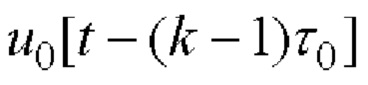 длительностью τ0, выбирают длину последовательностей N, представимую в виде N=2Р⋅10q⋅26r, где числа
длительностью τ0, выбирают длину последовательностей N, представимую в виде N=2Р⋅10q⋅26r, где числа 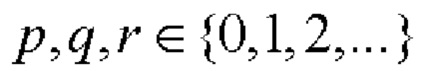 одновременно не равны нулю;
одновременно не равны нулю;
- по выбранному значению числа N путем разложения его на множители 2, 10 и 26 находят числа р, q и r;
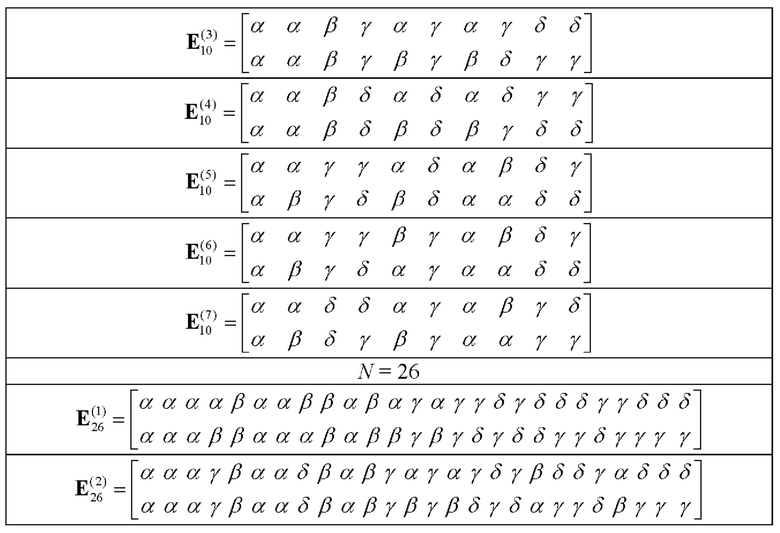
- на основе базовых матриц пар дополнительных последовательностей Е-кода Велти из таблицы 2 с использованием процедуры поблочного формирования символических матриц с элементами четверичного алфавита α, β, γ, δ, ставящей в соответствие символическим матрицам 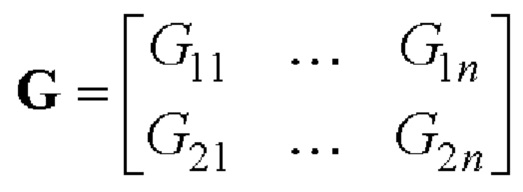 размера 2×n и
размера 2×n и 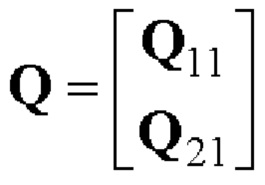 размера
размера 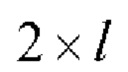 символическую блочную матрицу
символическую блочную матрицу  размера
размера 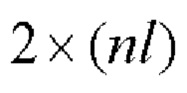 согласно правилу:
согласно правилу:
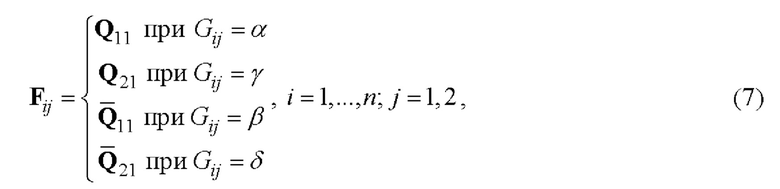
где «-» - символ операции инверсии элементов матрицы в соответствии с правилом (6), и обозначаемой далее как 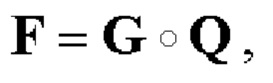 формируют пару дополнительных последовательностей Е-кода Велти длиной N; для этого:
формируют пару дополнительных последовательностей Е-кода Велти длиной N; для этого:
- если 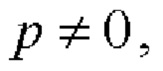 то формируют вспомогательную символическую матрицу А размера 2 х 2Р, для чего из таблицы 2 берут базовую матрицу для N=2
то формируют вспомогательную символическую матрицу А размера 2 х 2Р, для чего из таблицы 2 берут базовую матрицу для N=2 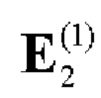 и рекурсивно р-1 раз выполняют процедуру (7):
и рекурсивно р-1 раз выполняют процедуру (7):
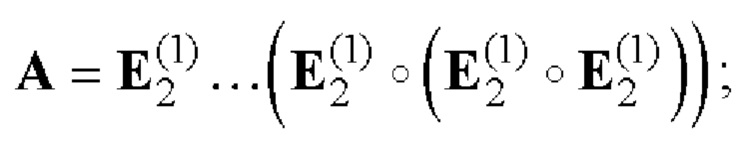 при р=1
при р=1 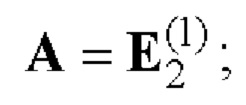
- если q≠0, то формируют вспомогательную символическую матрицу В размера 2×10q, для чего из таблицы 2 берут на каждом шаге произвольные базовые матрицы для N=10 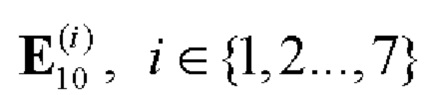 и рекурсивно q-1 раз выполняют процедуру (7):
и рекурсивно q-1 раз выполняют процедуру (7): 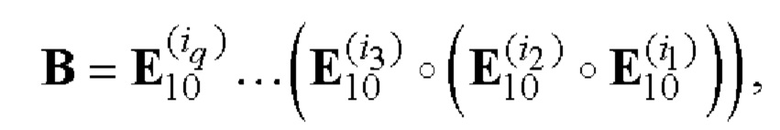
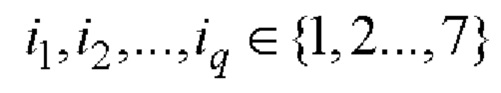 ; при q=1
; при q=1 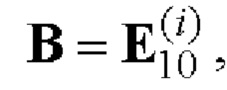
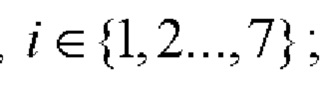
- если r≠0, то формируют вспомогательную символическую матрицу С размера 2×26r, для чего из таблицы 2 берут на каждом шаге произвольные базовые матрицы для N=26 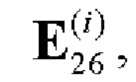
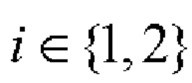 и рекурсивно r-1 раз выполняют процедуру (7):
и рекурсивно r-1 раз выполняют процедуру (7): 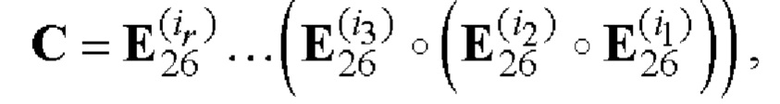
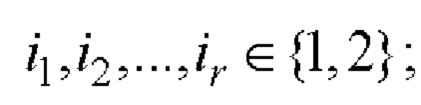 при r=1
при r=1 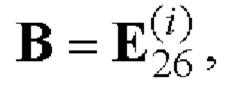
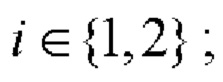
- на основе вспомогательных символических матриц А, В и С с использованием процедуры (7) находят символическую матрицу Е размера 2×N согласно правилу, задаваемому таблицей 3;
- при этом строки полученной матрицы Е образуют пару дополнительных последовательностей 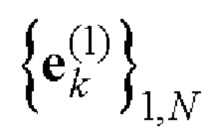 и
и 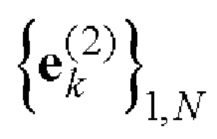 Е-кода Велти с требуемыми корреляционными свойствами;
Е-кода Велти с требуемыми корреляционными свойствами;
- на основе полученных дополнительных последовательностей 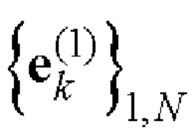 и
и 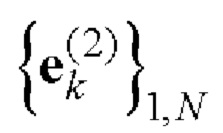 Е-кода Велти с помощью таблицы соответствия 1 однозначно находят элементы кодовых последовательностей
Е-кода Велти с помощью таблицы соответствия 1 однозначно находят элементы кодовых последовательностей 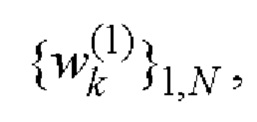
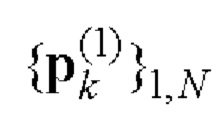 и
и 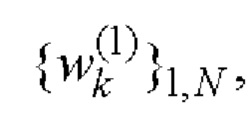
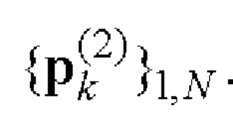


Предварительно строится пара дополнительных четверичных кодовых
последовательностей Е-кода Велти [5, 8] длиной N=2Р⋅10q⋅26r, где числа 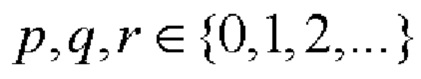 одновременно не равны нулю [14]. Известно [5, 8], что дополнительные кодовые последовательности Е-кода Велти имеют апериодические АКФ с нулевым уровнем боковых лепестков и апериодические ВКФ с нулевым уровнем боковых и центральных лепестков, а все возможные произведения элементов последовательностей
одновременно не равны нулю [14]. Известно [5, 8], что дополнительные кодовые последовательности Е-кода Велти имеют апериодические АКФ с нулевым уровнем боковых лепестков и апериодические ВКФ с нулевым уровнем боковых и центральных лепестков, а все возможные произведения элементов последовательностей 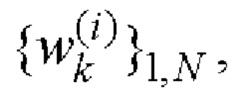
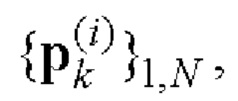 i=1, 2 вида
i=1, 2 вида 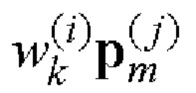 принадлежат алфавиту этого кода [14]. Поэтому построенные на основе пар этих кодовых последовательностей пары ФМШПС с ПК будут обладать необходимыми корреляционными свойствами.
принадлежат алфавиту этого кода [14]. Поэтому построенные на основе пар этих кодовых последовательностей пары ФМШПС с ПК будут обладать необходимыми корреляционными свойствами.
Заявляемый способ формирования пары дополнительных последовательностей Е-кода Велти заключается в следующем.
1. Выбирают длину последовательностей N, представимую в виде N=2Р⋅10q⋅26r, где числа 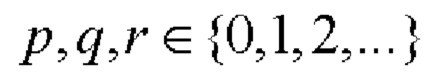 одновременно не равны нулю.
одновременно не равны нулю.
2. По выбранному значению числа N путем разложения его на множители 2, 10 и 26 находят числа р, q и r.
3. На основе базовых матриц пар дополнительных последовательностей Е-кода Велти таблицы 2 с использованием процедуры (7) поблочного формирования символических матриц с элементами четверичного алфавита α, β, γ, δ формируют пару дополнительных последовательностей Е-кода Велти длиной N.
Для этого:
4. Если р≠0, то формируют вспомогательную символическую матрицу А размера 2×2P, для чего из таблицы 2 берут базовую матрицу для N=2 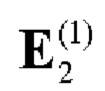 и рекурсивно р-1 раз выполняют процедуру (7):
и рекурсивно р-1 раз выполняют процедуру (7): 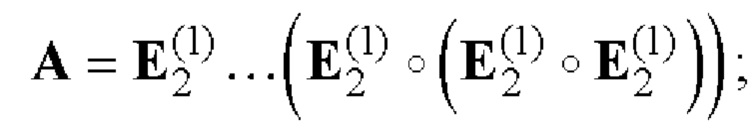 при р=1
при р=1 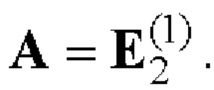
5. Если q≠0, то формируют вспомогательную символическую матрицу В размера 2×10q, для чего из таблицы 2 берут на каждом шаге произвольные базовые матрицы для N=10 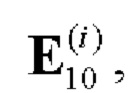
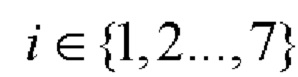 и рекурсивно q-1 раз выполняют процедуру (7):
и рекурсивно q-1 раз выполняют процедуру (7): 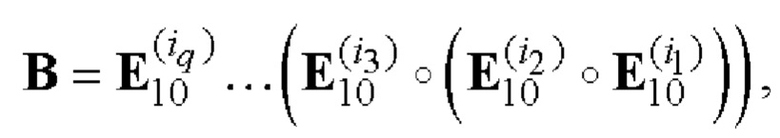
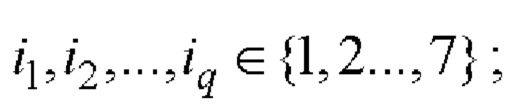 при q=1
при q=1 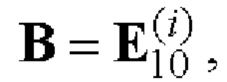
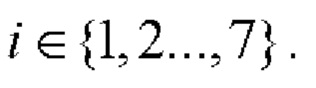
6. Если r≠0, то формируют вспомогательную символическую матрицу С размера 2×26r, для чего из таблицы 2 берут на каждом шаге произвольные базовые матрицы для N=26 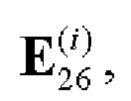
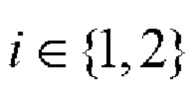 и рекурсивно r-1 раз выполняют процедуру (7):
и рекурсивно r-1 раз выполняют процедуру (7): 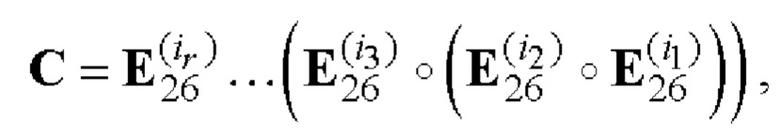
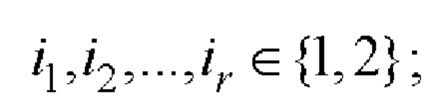 при r=1
при r=1 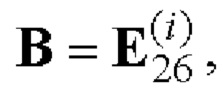
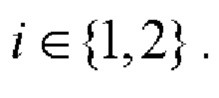
7. На основе вспомогательных символических матриц А, В и С с использованием процедуры (7) находят символическую матрицу Е размера 2×N согласно правилу, задаваемому таблицей 3.
8. При этом строки полученной матрицы Е образуют пару дополнительных последовательностей 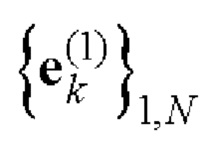 и
и 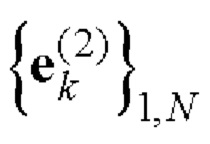 Е-кода Велти с требуемыми корреляционными свойствами.
Е-кода Велти с требуемыми корреляционными свойствами.
9. На основе полученных дополнительных последовательностей 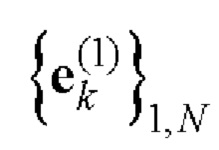 и
и 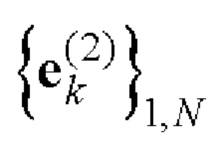 Е-кода Велти с помощью таблицы соответствия 1 однозначно находят элементы кодовых последовательностей
Е-кода Велти с помощью таблицы соответствия 1 однозначно находят элементы кодовых последовательностей 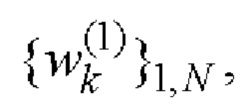
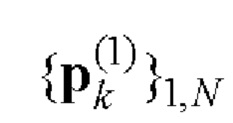 и
и 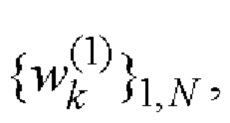
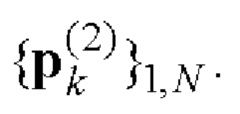
10. Найденные последовательности 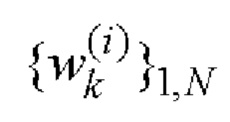 и
и 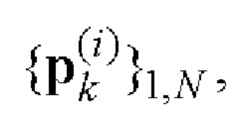 i=1, 2 поэлементно перемножают и формируют соответствующие последовательности произведений
i=1, 2 поэлементно перемножают и формируют соответствующие последовательности произведений 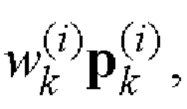
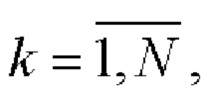 i=1, 2.
i=1, 2.
11. Для текущего значения времени t из интервала периода 0≤t≤Nτ0 двоичного ФМШПС с ортогональным ПК одновременно формируют значения двух векторных комплексных огибающих, при этом каждый k-й элемент i-й последовательности произведений перемножают на соответствующий сформированный элементарный импульс единичной амплитуды 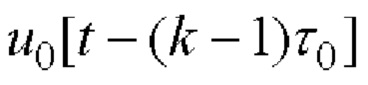 длительностью τ0.
длительностью τ0.
В соответствии с данным правилом для пары двоичных ФМШПС с ортогональным ПК можно построить любую прямоугольную символическую матрицу Е размера 2×N, где N=2Р⋅10q⋅26r, а числа 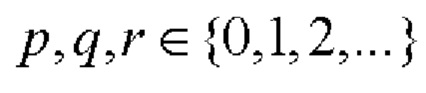 одновременно не равны нулю. Как отмечалось ранее, решетчатые апериодические АКФ и ВКФ векторных комплексных огибающих двоичных ФМШПС с ортогональным ПК данной пары имеют оптимальный вид: АКФ с нулевыми боковыми лепестками, ВКФ - с нулевыми боковыми и центральными лепестками.
одновременно не равны нулю. Как отмечалось ранее, решетчатые апериодические АКФ и ВКФ векторных комплексных огибающих двоичных ФМШПС с ортогональным ПК данной пары имеют оптимальный вид: АКФ с нулевыми боковыми лепестками, ВКФ - с нулевыми боковыми и центральными лепестками.
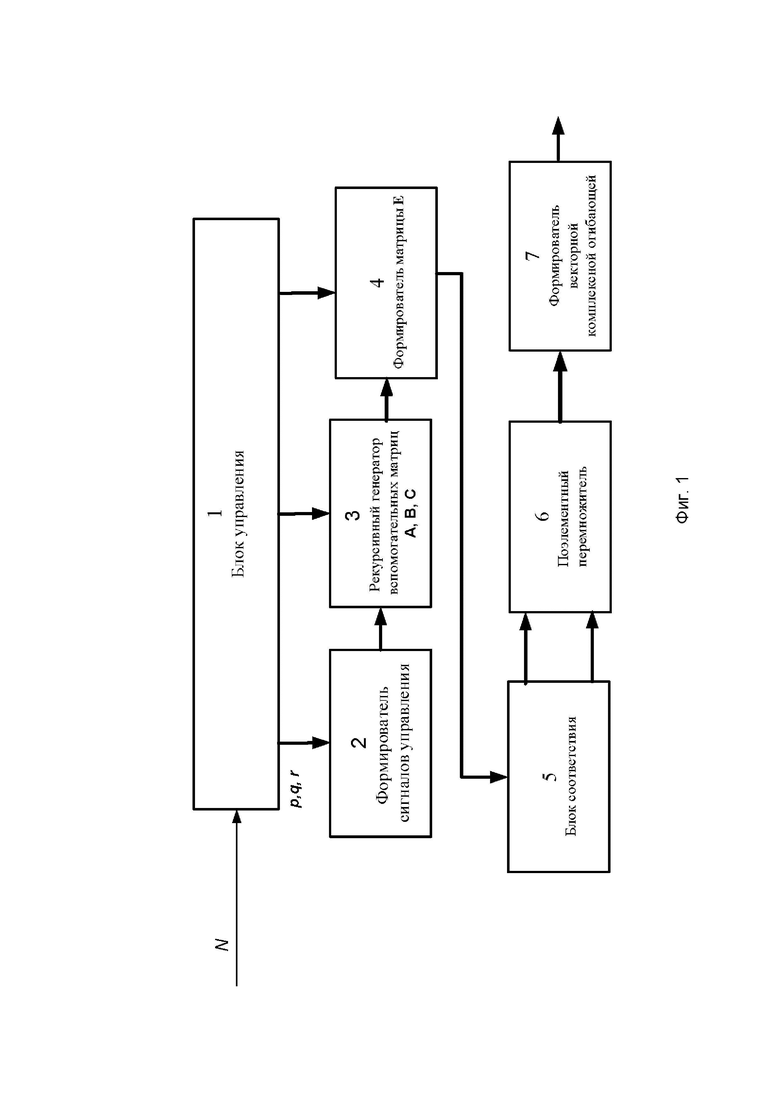
Предлагаемый способ реализуется устройством, структурная схема которого представлена на фиг. 1, где обозначено:
1 - блок управления (БУ);
2. - формирователь сигналов управления;
3. - рекурсивный генератор вспомогательных матриц А, В, С;
4. - формирователь матрицы Е;
5. - блок соответствия;
6. - поэлементный перемножитель;
7 - формирователь векторной комплексной огибающей.
Устройство содержит последовательно соединенные блок управления 1, формирователь сигналов управления 2, рекурсивный генератор вспомогательных матриц А, В, С 3, формирователь матрицы Е 4 и блок соответствия 5, два выхода которого соединены с соответствующими входами поэлементного перемножителя 6, выход которого соединен с входом формирователя векторной комплексной огибающей 7, выход которого является выходом устройства. Второй и третий выходы блока управления 1 соединены со вторыми входами рекурсивного генератора вспомогательных матриц А, В, С 3 и формирователя матрицы Е 4 соответственно. При этом все соединения блоков выполнены шинами. Вход блока управления 1 является входом устройства.
Работает устройство следующим образом.
Предварительно формируют начальные параметры устройства. Для этого выбирают необходимую длину последовательностей N, представимую в виде N=2Р⋅10q⋅26r , где числа 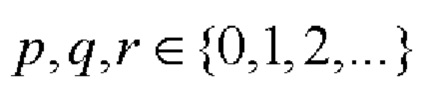 одновременно не равны нулю. Данное значение N в качестве управляющего сигнала подается на вход блока управления 1, в котором по выбранному значению N путем разложения его на множители 2, 10 и 26 находят числа р, q и г, и подают на вход формирователя сигналов управления 2, в котором выполняют их анализ и формируют соответствующие сигналы управления в соответствии с таблицей 3, которые определяют варианты формирования матрицы Е и подаются на первый вход блока 3. Со второго и третьего выходов блока управления 1 на вторые входы блоков 3 и 4 соответственно подаются сигналы управления, определяющие процедуру поблочного формирования символических матриц А, В, С и Е соответственно.
одновременно не равны нулю. Данное значение N в качестве управляющего сигнала подается на вход блока управления 1, в котором по выбранному значению N путем разложения его на множители 2, 10 и 26 находят числа р, q и г, и подают на вход формирователя сигналов управления 2, в котором выполняют их анализ и формируют соответствующие сигналы управления в соответствии с таблицей 3, которые определяют варианты формирования матрицы Е и подаются на первый вход блока 3. Со второго и третьего выходов блока управления 1 на вторые входы блоков 3 и 4 соответственно подаются сигналы управления, определяющие процедуру поблочного формирования символических матриц А, В, С и Е соответственно.
В блоке 1 определяется процедура поблочного формирования в блоке 3 матриц А, В, С с использованием соответствующих матриц таблицы 2. В блоке 1 определяется процедура формирования матрицы Е с учетом сформированных в блоке 3 вспомогательных матриц А, В и С. С выхода блока 3 на первый вход блока 4 поступают сформированные вспомогательные матрицы А, В, С.
С выхода блока 4 сформированная матрица Е подается на вход блока соответствия 5, в котором согласно таблице соответствия 1 на основе полученных дополнительных последовательностей 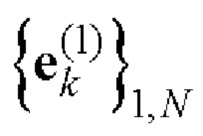 и
и 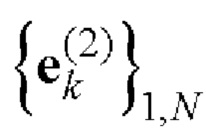 Е-кода Велти, являющихся строками матрицы Е, однозначно находят элементы кодовых последовательностей
Е-кода Велти, являющихся строками матрицы Е, однозначно находят элементы кодовых последовательностей 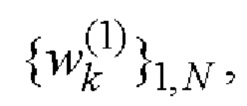
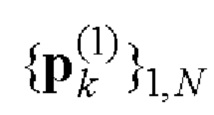 и
и 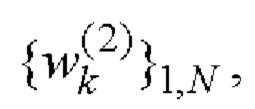
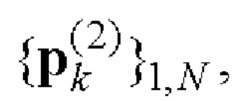 которые подаются на первый и второй входы блока 6 соответственно, где выполняется операция их поэлементного перемножения. Результаты перемножения с выхода блока 6 подаются на вход блока 7, где выполняется операция вычисления векторных комплексных огибающих пар двоичных ФМШПС с ортогональным ПК с оптимальными корреляционными свойствами.
которые подаются на первый и второй входы блока 6 соответственно, где выполняется операция их поэлементного перемножения. Результаты перемножения с выхода блока 6 подаются на вход блока 7, где выполняется операция вычисления векторных комплексных огибающих пар двоичных ФМШПС с ортогональным ПК с оптимальными корреляционными свойствами.
В качестве примера рассмотрим последовательность операций нахождения бинарных кодовых последовательностей 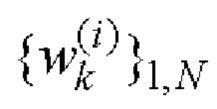 и кодовых последовательностей единичных векторов
и кодовых последовательностей единичных векторов 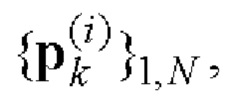 i=1, 2 для N=40.
i=1, 2 для N=40.
В данном случае р=2. q=1 и r=0. Находим вспомогательную символическую матрицу А:
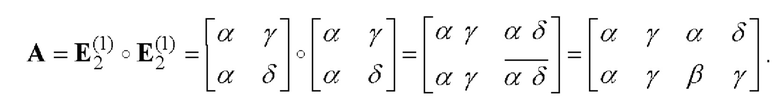
В качестве вспомогательной символической матрицы В выбираем из таблицы 2 матрицу 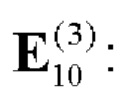
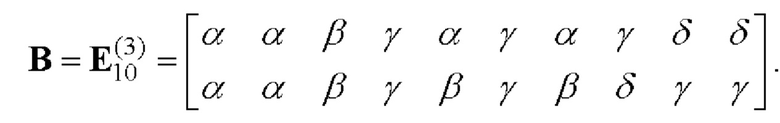
В соответствии с правилом таблицы 3 для набора значений чисел р, q и r для данного случая найдем матрицу Е как 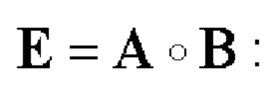

Таким образом, для N=40 получим следующую пару дополнительных кодовых последовательностей Е-кода Велти (первая и вторая строки матрицы Е):
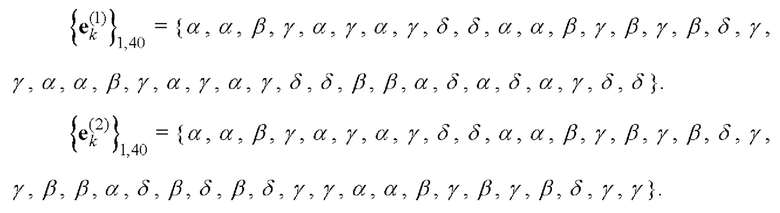
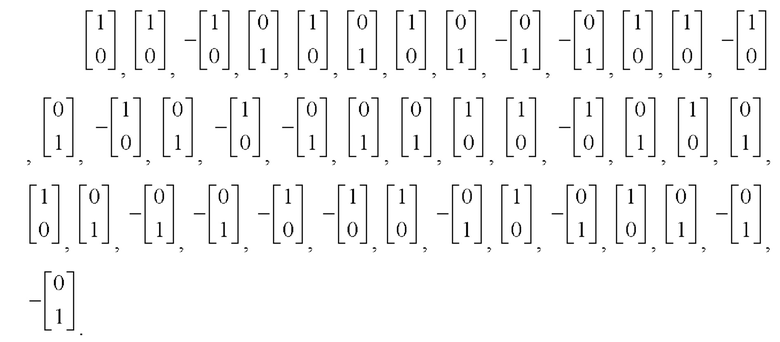
На основании этих последовательностей с помощью таблицы соответствия 1 для произведений элементов 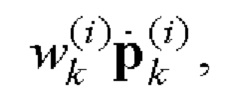
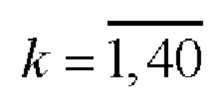 кодовых последовательностей
кодовых последовательностей 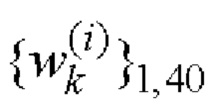 и
и 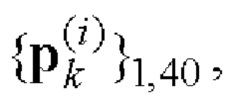 i=1, 2 получаем:
i=1, 2 получаем:
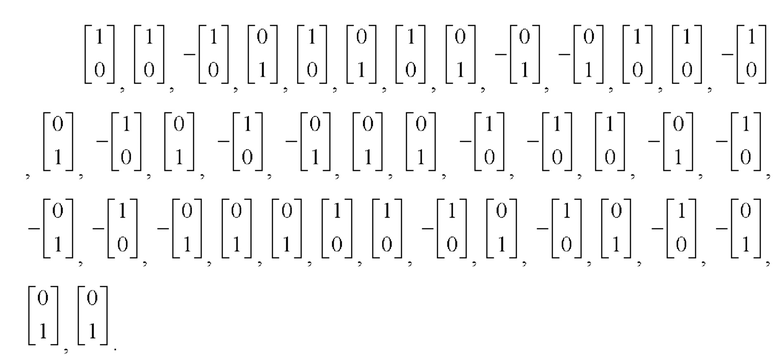
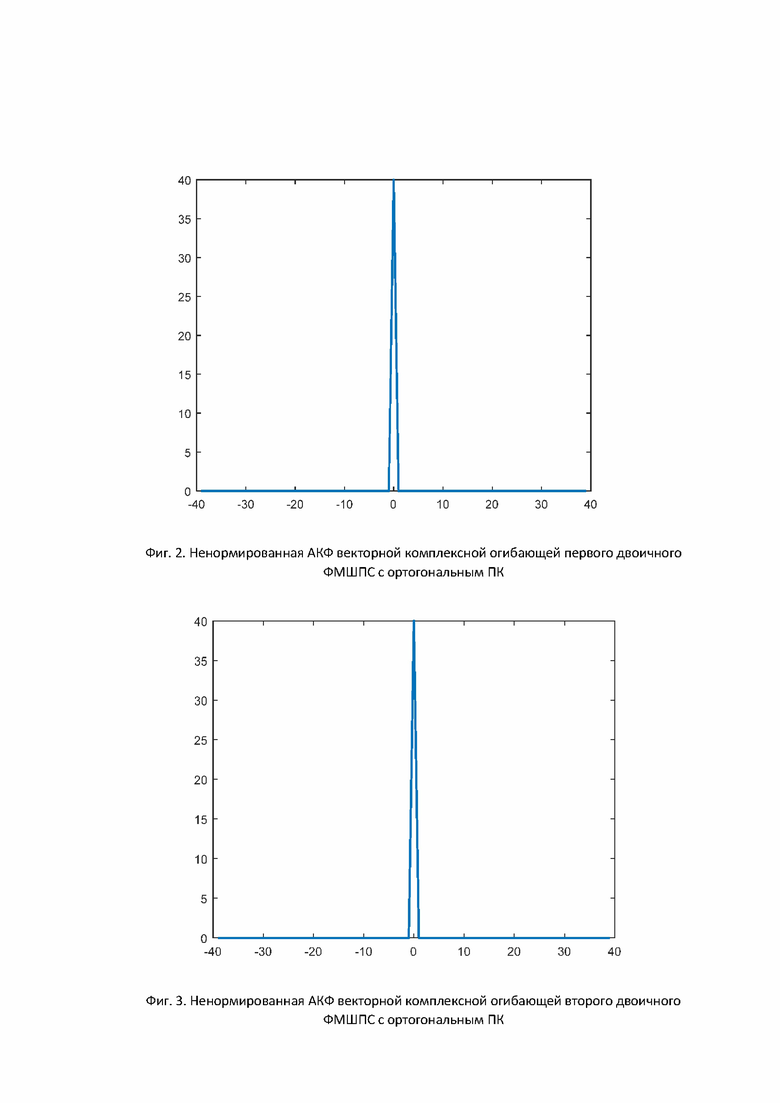
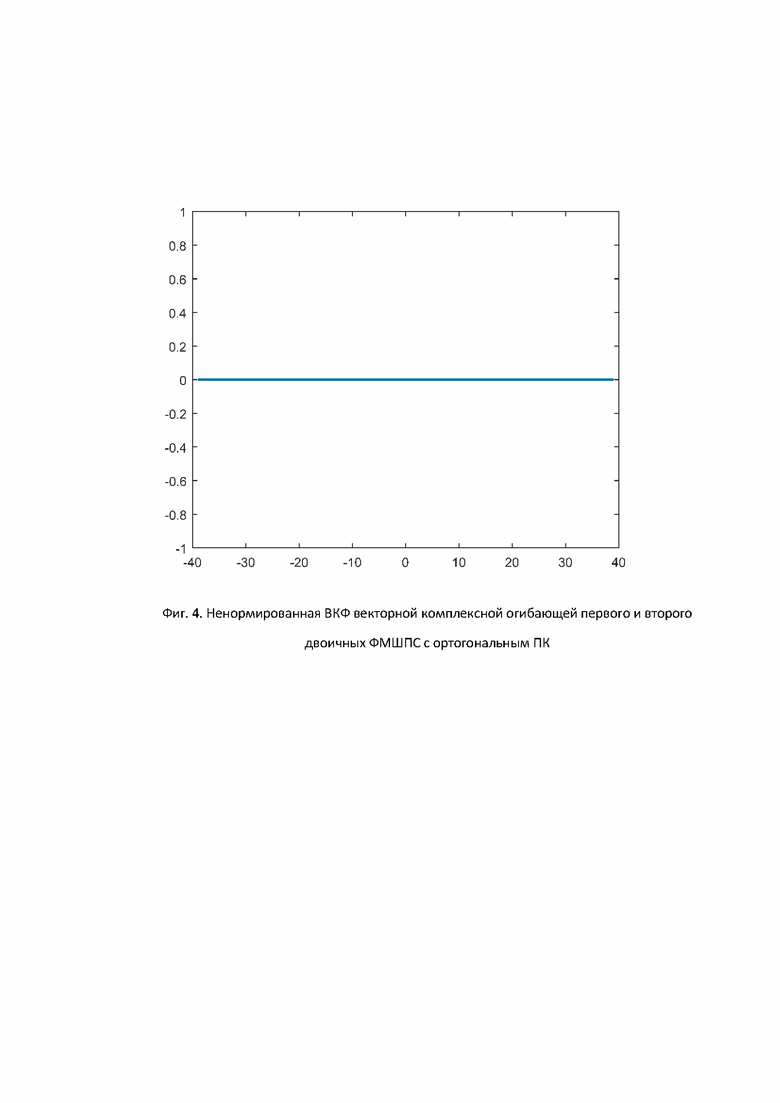
На фиг. 2-4 представлены формы ненормированных решетчатых апериодических АКФ (4) и ВКФ (5) комплексных огибающих двоичных ФМШПС с ортогональным ПК (3) при использовании бинарных кодовых последовательностей и кодовых последовательностей единичных векторов на основе синтезированной в примере пары дополнительных кодовых последовательностей Е-кода Велти.
Видно, что форма АКФ каждой огибающей из пары имеет оптимальный вид. Также видно, что форма ВКФ пары огибающих имеет оптимальный вид.
Таким образом, достигается технический результат - формирование пар двоичных ФМШПС с поляризационным кодированием с оптимальными апериодическими автокорреляционными функциями, имеющими нулевые боковые лепестки, и оптимальными взаимокорреляционными функциями, имеющими нулевые боковые и центральные лепестки.
Сравнение заявляемого способа формирования пар фазоманипулированных широкополосных сигналов с поляризационным кодированием с оптимальными апериодическими автокорреляционными и взаимокорреляционными функциями с другими известными решениями в данной области техники не позволило выявить признаки, заявленные в отличительной части формулы изобретения.
Известно, что в современных радиотехнических системах часто используют цифровые сигналы. Вследствие этого в узлах устройства, реализующего заявляемый способ, целесообразно применять дискретные и цифровые сигналы. Для обработки таких сигналов наряду с аппаратными часто используют программные и вычислительные средства. В данном случае для реализации заявляемого способа разумно использовать стандартные процедуры матричного анализа [11, 15, 16, 17, 18], что позволяет применять высокопроизводительные специализированные цифровые сигнальные процессоры, например, (digital signal processor (DSP)) и быстродействующие программируемые логические интегральные схемы (ПЛИС, Field Programmable Gate Array (FPGA)), например, типов 1892BM3T (Multicore), 1892 ВМ10Я (NVcom), FPGA Virtex-7 и их перспективные версии [19, 20,21].
Литература.
1. Pat. 7310379 US, Int. C1.7 H04В 7/02. Polarization state techniques for wireless communications / S. Sibecas, C. Corral, S. Emami, G. Stratis, G. Rasor; Motorola, Inc. No 10/631430; Filed 31.07.2003; Pub. 18.12.2007.
2. Лукьянчиков В.Д., Ливенцев В.В. Способ повышения пропускной способности систем радиосвязи с шумоподобными сигналами // Изв. ВУЗов. Радиоэлектроника. 2007. Т. 50, №8. С. 22-35.
3. Ливенцев В.В. Анализ эффективности энергетического обнаружения широкополосных сигналов с поляризационным кодированием // Теория и техника радиосвязи: науч.-тех. сб. / АО «Концерн «Созвездие». 2007. Вып. 2. С. 21-29.
4. Зарубин B.C., Ливенцев В.В., Лукьянчиков В.Д., Прибытков Ю.Н. Спектральные характеристики фазоманипулированных широкополосных сигналов с поляризационным кодированием // Теория и техника радиосвязи: науч.-тех. сб. / АО «Концерн «Созвездие». - 2019. - Вып. 2. - С. 55-61.
5. Варакин Л.Е. Системы связи с шумоподобными сигналами / Л.Е. Варакин. - М.: Радио и связь, 1985. - 384 с.
6. Козлов А.И., Логвин А.И., Сарычев В.А. Поляризация радиоволн. Поляризационная структура радиолокационных сигналов. М.: Радиотехника, 2005. 704 с.
7. Гусев К.Г., Филатов А.Д., Сополев А.П. Поляризационная модуляция. М.: Сов. радио, 1974. 288 с.
8. Варакин Л.Е. Теория сложных сигналов. М., изд-во «Советское радио», 1970, 376 с, С.50.
9. Гоноровский И.С. Радиотехнические цепи и сигналы: Учебник для вузов. - М.: Радио и связь, 1986. - 512 с., С. 104.
10. Патент RU 2776777, Н04В 7/204. Способ формирования фазоманипулированных широкополосных сигналов с поляризационным кодированием с оптимальными апериодическими автокорреляционными функциями (Прототип).
11. G.H. Golub, C.F. Van Loan. Matrix computations, The Johns Hopkins University Press, Baltimore, 2013. 756 p.
12. Варакин Л.Е. Теория сложных сигналов. М., изд-во «Советское радио», 1970, 376 с. (С. 257-261).
13. Литюк В.И., Литюк Л.В. Методы цифровой многопроцессорной обработки ансамблей радиосигналов. - М., СОЛОН-ПРЕСС, 2007. - 592 с.: - (серия «Библиотека инженера» (С. 396-398).
14. Luke H.D. Sets of one and higher dimensional Welti codes and complementary codes // IEEE Trans. Aerospace and Electronic Systems. 1985. V. AES-21.N2. P. 170-179.
15. Куприянов M.C., Матюшкин Б.Д. Цифровая обработка сигналов: процессоры, алгоритмы, средства проектирования / М.С. Куприянов, Б.Д. Матюшкин. - Спб: Политехника, 1999. - 592 с.
16. Гантмахер Ф.Р. Теория матриц. 4-е издание. М.: Наука, 1988. - 552 с.
17. Беллман Р. Введение в теорию матриц. 2-е издание: Пер. с англ. М.: Наука, 1976. - 352 с.
18. Хорн Р., Джонсон Ч. Матричный анализ: Пер. с англ. М.: Мир, 1989. - 655 с.
19. Максфилл К. Проектирование на ПЛИС.Курс молодого бойца / К. Максфилл. - М.: Издательский дом «Додэка XXI», 2007. - 408 с.
20. Бродин В.Б., Калинин А.В. Системы на микроконтроллерах и БИС программируемой логики / В.Б. Бродин, А.В. Калинин. - М.: Издательство ЭКОМ, 2002. - 400 с.
21. Грушвицкий Р.И., Мурсаев А.Х., Угрюмов ЕЛ. Проектирование систем на микросхемах программируемой логики / Р.И. Грушвицкий, А.Х. Мурсаев., Е.П. Угрюмов. - СПб: БХВ-Петербург, 2002. - 608 с.
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ формирования фазоманипулированных широкополосных сигналов с поляризационным кодированием с оптимальными апериодическими автокорреляционными функциями | 2020 |
|
RU2734287C1 |
| СПОСОБ АСИНХРОННОЙ АДРЕСНОЙ СВЯЗИ | 2000 |
|
RU2182403C1 |
| ОПТИМАЛЬНЫЙ НЕКОГЕРЕНТНЫЙ ПРИЕМНИК С ФАЗОМАНИПУЛИРОВАННЫМ СИГНАЛОМ | 2021 |
|
RU2760560C1 |
| СПОСОБ ПЕРЕДАЧИ И ПРИЕМА СИГНАЛОВ | 2010 |
|
RU2438250C1 |
| СИСТЕМА ПЕРЕДАЧИ ДАННЫХ С МНОЖЕСТВЕННЫМ ДОСТУПОМ И ВРЕМЕННЫМ РАЗДЕЛЕНИЕМ КАНАЛОВ | 2006 |
|
RU2320084C1 |
| СПОСОБ ПЕРЕДАЧИ И ПРИЕМА ИНФОРМАЦИИ С КОДОВЫМ УПЛОТНЕНИЕМ СИГНАЛОВ | 1991 |
|
RU2014738C1 |
| СИСТЕМА ПЕРЕДАЧИ ДАННЫХ С МНОЖЕСТВЕННЫМ ДОСТУПОМ И ВРЕМЕННЫМ РАЗДЕЛЕНИЕМ КАНАЛОВ | 2005 |
|
RU2305368C2 |
| СИСТЕМА ПЕРЕДАЧИ ДАННЫХ С МНОЖЕСТВЕННЫМ ДОСТУПОМ И ВРЕМЕННЫМ РАЗДЕЛЕНИЕМ КАНАЛОВ | 2023 |
|
RU2819030C1 |
| СПОСОБ РАДИОСВЯЗИ С МНОЖЕСТВЕННЫМ ДОСТУПОМ | 2011 |
|
RU2445732C1 |
| СИСТЕМА ПЕРЕДАЧИ ДАННЫХ С МНОЖЕСТВЕННЫМ ДОСТУПОМ И ВРЕМЕННЫМ РАЗДЕЛЕНИЕМ КАНАЛОВ | 2006 |
|
RU2315428C9 |
Изобретение относится к области радиосвязи и может быть использовано в широкополосных системах для передачи информации, оценки параметров канала распространения и выполнения процедур частотно-временной синхронизации. Техническим результатом является формирование пар двоичных фазоманипулированных широкополосных сигналов (ФМШПС) с поляризационным кодированием с оптимальными апериодическими автокорреляционными функциями, имеющими нулевые боковые лепестки, и оптимальными взаимокорреляционными функциями, имеющими нулевые боковые и центральные лепестки. Упомянутый технический результат достигается тем, что в заявляемый способ включена процедура формирования оригинальных фазовых и поляризационных кодовых последовательностей для двоичных ФМШПС с ортогональным поляризационным кодированием (ПК). Таким образом, сформированные двоичные ФМШПС с ортогональным ПК имеют оптимальные апериодические АКФ и ВКФ. 4 ил.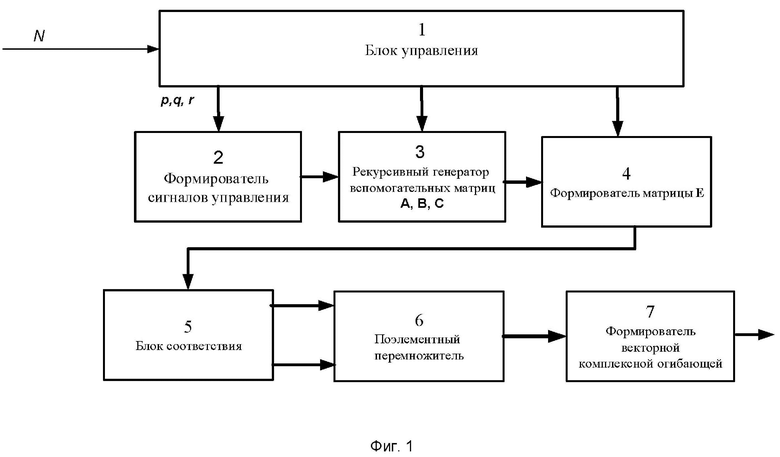
Способ формирования пар фазоманипулированных широкополосных сигналов (ФМШПС) с поляризационным кодированием с оптимальными апериодическими автокорреляционными и взаимокорреляционными функциями, заключающийся в том, что формируют кодовые последовательности 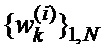 и
и 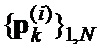 ,
, 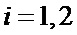 комплексных огибающих
комплексных огибающих 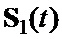 и
и 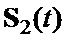 двоичных ФМШПС с ортогональным поляризационным кодированием (ПК);
двоичных ФМШПС с ортогональным поляризационным кодированием (ПК);
- последовательности 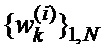 и
и 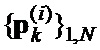 ,
, 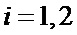 поэлементно перемножают и формируют соответствующие последовательности произведений
поэлементно перемножают и формируют соответствующие последовательности произведений 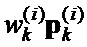 ,
, 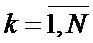 ,
, 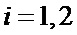 ;
;
- для текущего значения времени 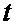 из интервала периода
из интервала периода 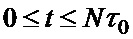 двоичного ФМШПС с ортогональным ПК одновременно формируют значения двух векторных комплексных огибающих, при этом каждый
двоичного ФМШПС с ортогональным ПК одновременно формируют значения двух векторных комплексных огибающих, при этом каждый 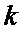 -й элемент
-й элемент 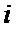 -й последовательности произведений перемножают на соответствующий сформированный элементарный импульс единичной амплитуды
-й последовательности произведений перемножают на соответствующий сформированный элементарный импульс единичной амплитуды 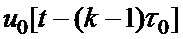 длительностью
длительностью 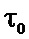 , отличающийся тем, что
, отличающийся тем, что
- выбирают длину последовательностей 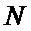 , представимую в виде
, представимую в виде 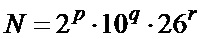 , где числа
, где числа 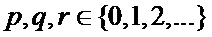 одновременно не равны нулю;
одновременно не равны нулю;
- по выбранному значению числа 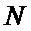 путем разложения его на множители 2, 10 и 26 находят числа
путем разложения его на множители 2, 10 и 26 находят числа 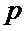 ,
, 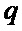 и
и 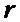 ;
;
- в зависимости от полученных значений параметров 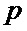 ,
, 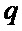 и
и 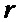 в соответствии с табличным правилом формирования символической матрицы
в соответствии с табличным правилом формирования символической матрицы 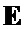 на основе базовых матриц пар дополнительных последовательностей Е-кода Велти с использованием процедуры поблочного формирования символических матриц с элементами четверичного алфавита
на основе базовых матриц пар дополнительных последовательностей Е-кода Велти с использованием процедуры поблочного формирования символических матриц с элементами четверичного алфавита 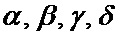 предварительно формируют вспомогательные символические матрицы А, В и С;
предварительно формируют вспомогательные символические матрицы А, В и С;
- на основе вспомогательных символических матриц 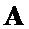 ,
, 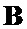 и
и 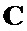 с использованием процедуры поблочного формирования символических матриц находят символическую матрицу
с использованием процедуры поблочного формирования символических матриц находят символическую матрицу 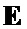 размера
размера 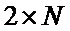 в соответствии с табличным правилом; при этом строки полученной матрицы
в соответствии с табличным правилом; при этом строки полученной матрицы 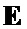 образуют пару дополнительных последовательностей
образуют пару дополнительных последовательностей 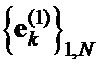 и
и 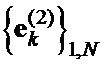 Е-кода Велти с требуемыми корреляционными свойствами;
Е-кода Велти с требуемыми корреляционными свойствами;
- на основе полученных дополнительных последовательностей 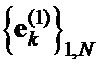 и
и 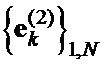 Е-кода Велти с помощью таблицы соответствия однозначно находят элементы кодовых последовательностей
Е-кода Велти с помощью таблицы соответствия однозначно находят элементы кодовых последовательностей 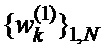 ,
, 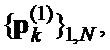 и
и 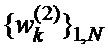 ,
, 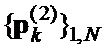 .
.
| RU 2776777 C1, 26.07.2022 | |||
| Способ формирования фазоманипулированных широкополосных сигналов с поляризационным кодированием с оптимальными апериодическими автокорреляционными функциями | 2020 |
|
RU2734287C1 |
| ОПТИМАЛЬНЫЙ НЕКОГЕРЕНТНЫЙ ПРИЕМНИК С ФАЗОМАНИПУЛИРОВАННЫМ СИГНАЛОМ | 2021 |
|
RU2760560C1 |
| СПОСОБ ПОДАВЛЕНИЯ БОКОВЫХ ЛЕПЕСТКОВ АВТОКОРРЕЛЯЦИОННЫХ ФУНКЦИЙ ШУМОПОДОБНЫХ СИГНАЛОВ | 2013 |
|
RU2549163C1 |
| US 7310379 B2, 18.12.2007 | |||
| US 9722651 B2, 01.08.2017 | |||
| Ливенцев В.В | |||
| Алгоритм синтеза ансамблей двоичных фазоманипулированных широкополосных сигналов с поляризационным кодированием с идеальными апериодическими автокорреляционными функциями / | |||
Авторы
Даты
2023-06-07—Публикация
2022-11-11—Подача