Изобретение относится к области радиосвязи и может быть использовано в широкополосных системах для передачи информации, оценки параметров канала распространения и выполнения процедур частотно-временной синхронизации.
В последние годы для увеличения пропускной способности систем радиосвязи в условиях жесткого дефицита радиочастотного спектра большое внимание уделяется разработке новых видов сложных широкополосных сигналов с поляризационным кодированием (ПК) элементов [1, 2].
Известен способ радиосвязи, приведенный в патенте US 6448941 B1, H01Q 1/36 от 10.09.2002 г., в котором осуществляется скачкообразная перестройка поляризации сигнала несущей синхронно с псевдослучайной перестройкой несущей частоты, что достигается использованием на передающей и приемной сторонах идентичных антенн специальной конструкции; поляризационное состояние (поляризационная структура) элементов излучаемого сигнала зависит от частоты питающего напряжения и на длительности сигнала может принимать несколько заданных состояний.
У этого способа можно выделить несколько основных недостатков:
– жесткая связь поляризационного состояния элементов сигнала с частотой несущего колебания, что ограничивает количество возможных сигналов в ансамбле;
– необходимость антенн специальной конструкции, идентичных на передающей и приемной сторонах;
– неиспользование поляризационной избыточности сигнала для улучшения его корреляционных свойств.
В заявке US 2004/0114548 H04B 7/204 от 17.06.2004 г. предложен способ использования сигнала с поляризационным кодированием, в котором также осуществляется скачкообразная перестройка поляризации сигнала несущей в соответствии с кодом псевдослучайной последовательности (ПСП). Этому способу присущ следующий недостаток:
– избыточность, которую вносит разнесение элементов сигнала по ортогональным поляризационным состояниям, используется только для разделения абонентов в системах связи и не используется для улучшения корреляционных свойств сигнала.
Вопросам повышения пропускной способности и помехозащищенности систем радиосвязи (СРС), использующих двоичные фазоманипулированные широкополосные сигналы (ФМШПС), без дополнительных затрат радиочастотного и энергетического ресурсов за счет применения метода поляризационного кодирования элементов указанных сигналов и дополнительной инверсной поляризационной манипуляции достаточно большое внимание уделяется в работах [1, 2, 3].
Наиболее близким аналогом по технической сущности к предлагаемому является способ формирования двоичного фазоманипулированного широкополосного сигнала с ортогональным ПК, приведенный в статье [4], принятый за прототип.
Способ-прототип формирования фазоманипулированных широкополосных сигналов с поляризационным кодированием заключается в следующем:
- Известным образом формируют две псевдослучайные М-последовательности одинакового периода 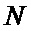 [5], но с разными порождающими полиномами
[5], но с разными порождающими полиномами  ,
, 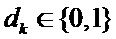 и
и 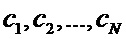 ,
,  .
.
- Строят бинарную последовательность 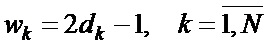 .
.
- Формируют последовательность длины 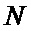 двумерных векторов
двумерных векторов 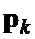 ,
,  согласно правилу :
согласно правилу :
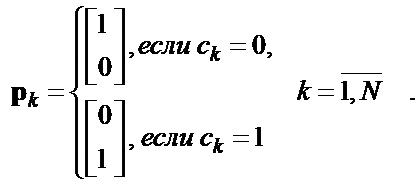
- Последовательности 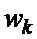 и
и 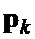 ,
,  поэлементно перемножают и формируют соответствующую последовательность произведений.
поэлементно перемножают и формируют соответствующую последовательность произведений.
- Для текущего значения времени 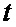 из интервала периода
из интервала периода  двоичного ФМШПС с ортогональным ПК формируют значение векторной комплексной огибающей. При этом каждый
двоичного ФМШПС с ортогональным ПК формируют значение векторной комплексной огибающей. При этом каждый 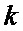 -й элемент последовательности произведений перемножают на соответствующий сформированный элементарный импульс единичной амплитуды
-й элемент последовательности произведений перемножают на соответствующий сформированный элементарный импульс единичной амплитуды 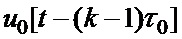 длительностью
длительностью  .
.
В способе-прототипе используют принцип дополнительной избыточности за счет ортогонального поляризационного кодирования элементов широкополосного фазоманипулированного сигнала в соответствии с двоичной псевдослучайной последовательностью, в том числе М-последовательностью.
Фазоманипулированный широкополосный сигнал с поляризационным кодированием [4] состоит из последовательности элементарных радиоимпульсов с начальными значениями фаз, определяемых кодом первой псевдослучайной последовательности (ПСП), и поляризационными состояниями, определяемыми кодом второй ПСП. При этом обе ПСП имеют одинаковую длину 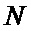 .
.
Общее выражение, описывающее один период данного двоичного фазоманипулированного широкополосного радиосигнала с ортогональным ПК и дополнительной инверсной поляризационной манипуляцией, может быть представлено в виде [4]:

где  – амплитуда сигнала;
– амплитуда сигнала; 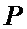 – средняя мощность сигнала;
– средняя мощность сигнала;  – период псевдослучайных последовательностей, используемых в качестве фазового и поляризационного кодов;
– период псевдослучайных последовательностей, используемых в качестве фазового и поляризационного кодов;  – оператор, описывающий дополнительную инверсную поляризационную манипуляцию;
– оператор, описывающий дополнительную инверсную поляризационную манипуляцию; 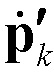 ,
,  – единичный комплексный вектор-столбец (состоящий из двух элементов) [6], определяющий поляризацию k-го элементарного импульса (чипа) сигнала;
– единичный комплексный вектор-столбец (состоящий из двух элементов) [6], определяющий поляризацию k-го элементарного импульса (чипа) сигнала; 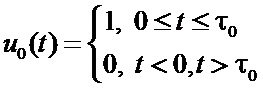 – прямоугольная огибающая элементарного радиоимпульса единичной амплитуды длительностью
– прямоугольная огибающая элементарного радиоимпульса единичной амплитуды длительностью  ;
;  – несущая частота сигнала;
– несущая частота сигнала; 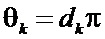 ,
,  – начальная фаза k-го элементарного импульса (
– начальная фаза k-го элементарного импульса ( – код расширяющей спектр сигнала ПСП);
– код расширяющей спектр сигнала ПСП);  – символ операции взятия реальной части;
– символ операции взятия реальной части;  – длительность периода ПСП.
– длительность периода ПСП.
Оператор 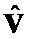 при использовании согласованного поляризационного базиса [2] имеет матричное представление вида
при использовании согласованного поляризационного базиса [2] имеет матричное представление вида  в отсутствие инверсии поляризационных состояний элементарных импульсов сигнала и
в отсутствие инверсии поляризационных состояний элементарных импульсов сигнала и 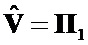 – при ее наличии, где
– при ее наличии, где  ,
, 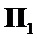 – матрицы Паули [7].
– матрицы Паули [7].
Вектор 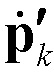 ,
,  определяет состояние поляризации k-го элементарного импульса двоичного ФМШПС в соответствии с кодом
определяет состояние поляризации k-го элементарного импульса двоичного ФМШПС в соответствии с кодом 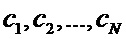 ,
,  поляризационной ПСП. Причем при использовании согласованного поляризационного базиса [2] это соответствие задается следующим образом:
поляризационной ПСП. Причем при использовании согласованного поляризационного базиса [2] это соответствие задается следующим образом: 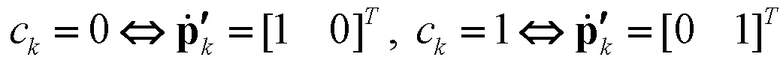 , где
, где  – символ соответствия;
– символ соответствия;  – символ операции транспонирования.
– символ операции транспонирования.
Так как сигнал в радиотехническом смысле является узкополосным  , то для упрощения анализа его свойств целесообразно перейти к его комплексной огибающей [8, 9]
, то для упрощения анализа его свойств целесообразно перейти к его комплексной огибающей [8, 9]
Полагая  и вводя обозначения
и вводя обозначения 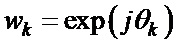 ,
,  , векторную комплексную огибающую одного периода двоичного ФМШПС с ортогональным ПК можно представить в виде
, векторную комплексную огибающую одного периода двоичного ФМШПС с ортогональным ПК можно представить в виде
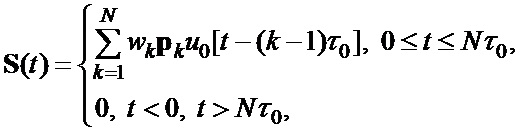
где  – бинарная кодовая последовательность, задающая закон фазовой манипуляции элементарных радиоимпульсов;
– бинарная кодовая последовательность, задающая закон фазовой манипуляции элементарных радиоимпульсов;  – кодовая последовательность единичных векторов
– кодовая последовательность единичных векторов 
 , задающая закон поляризационной манипуляции элементарных радиоимпульсов;
, задающая закон поляризационной манипуляции элементарных радиоимпульсов;  и
и 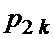 – компоненты вектора
– компоненты вектора 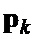 в согласованном поляризационно-ортогональном базисе [2].
в согласованном поляризационно-ортогональном базисе [2].
Решетчатая апериодическая автокорреляционная функция (АКФ) векторной комплексной огибающей 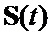 двоичного ФМШПС с ортогональным ПК имеет вид :
двоичного ФМШПС с ортогональным ПК имеет вид :
 .
.
Существенным недостатком способа-прототипа формирования двоичного ФМШПС с ортогональным ПК при фазовом и поляризационных кодах в виде M-последовательностей является то, что апериодическая АКФ данного сигнала имеет ненулевые боковые лепестки.
Задача заявляемого способа – разработка процедуры формирования двоичного ФМШПС с ортогональным ПК, боковые лепестки апериодической АКФ которого имеют нулевые значения.
Для решения поставленной задачи в способе, включающем формирование кодовых последовательностей  и
и  комплексной огибающей
комплексной огибающей  двоичного ФМШПС с ортогональным поляризационным кодированием (ПК);
двоичного ФМШПС с ортогональным поляризационным кодированием (ПК);
– последовательности 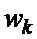 и
и 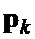 ,
,  поэлементно перемножают и формируют соответствующую последовательность произведений;
поэлементно перемножают и формируют соответствующую последовательность произведений;
– для текущего значения времени 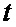 из интервала периода
из интервала периода  двоичного ФМШПС с ортогональным ПК формируют значение векторной комплексной огибающей, при этом каждый
двоичного ФМШПС с ортогональным ПК формируют значение векторной комплексной огибающей, при этом каждый 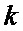 -й элемент последовательности произведений перемножают на соответствующий сформированный элементарный импульс единичной амплитуды
-й элемент последовательности произведений перемножают на соответствующий сформированный элементарный импульс единичной амплитуды 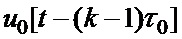 длительностью
длительностью  , согласно изобретению,
, согласно изобретению,
– предварительно формируют вспомогательные дополнительные троичные последовательности 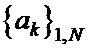 и
и  , при этом длину последовательностей
, при этом длину последовательностей 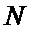 выбирают четной и представимой в виде суммы квадратов двух целых чисел;
выбирают четной и представимой в виде суммы квадратов двух целых чисел;
– векторы-строки  формируют согласно правилу:
формируют согласно правилу:
в первой половине вектора-строки 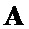 ,
, 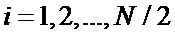 произвольным образом элементам
произвольным образом элементам 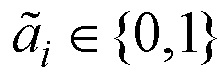 присваивают значения 0 или 1;
присваивают значения 0 или 1;
при этом элементам во второй половине вектора-строки  ,
,  ,
, 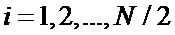 присваивают значения, равные инверсным значениям элементов
присваивают значения, равные инверсным значениям элементов  первой половины вектора-строки
первой половины вектора-строки  ;
;
– векторы-строки  формируют как векторы инверсных элементов
формируют как векторы инверсных элементов  вектора-строки
вектора-строки 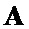 ;
;
– находят матрицы шаблонов  и
и 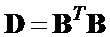 ;
;
– формируют общий вид корреляционных матриц 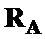 и
и  последовательностей
последовательностей 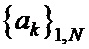 и
и  ;
;
– формируют систему уравнений для определения знаков ненулевых элементов последовательностей  и
и  , для этого, используя матрицы шаблонов
, для этого, используя матрицы шаблонов  ,
, 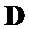 и корреляционные матрицы
и корреляционные матрицы  ,
,  , путем поэлементного произведения корреляционных матриц
, путем поэлементного произведения корреляционных матриц  и
и 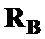 на соответствующие матрицы шаблонов
на соответствующие матрицы шаблонов 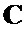 и
и  формируют преобразованные корреляционные матрицы
формируют преобразованные корреляционные матрицы  ;
;
– в преобразованных корреляционных матрицах  выделяют диагонали, лежащие выше главной диагонали и содержащие не менее двух элементов;
выделяют диагонали, лежащие выше главной диагонали и содержащие не менее двух элементов;
– выполняют суммирование элементов в соответствующих диагоналях матриц  , а полученные суммы приравнивают нулю, в результате получают общую систему уравнений для определения знаков ненулевых элементов в последовательностях
, а полученные суммы приравнивают нулю, в результате получают общую систему уравнений для определения знаков ненулевых элементов в последовательностях 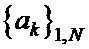 и
и 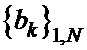 , которая имеет вид
, которая имеет вид  где
где 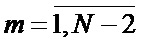 ;
;
– решая систему уравнений, находят знаки ненулевых элементов векторов-строк  и
и  , если же система оказывается несовместной, то изменяют векторы-строки
, если же система оказывается несовместной, то изменяют векторы-строки 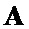 и
и 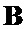 , пока решение не будет найдено или исчерпаны все пары векторов-строк
, пока решение не будет найдено или исчерпаны все пары векторов-строк  и
и  для данной длины
для данной длины  ;
;
– если для данной длины  ни для одной из возможных пар векторов-строк
ни для одной из возможных пар векторов-строк  и
и 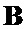 найти решение системы не удается, то переходят к другой длине
найти решение системы не удается, то переходят к другой длине  и осуществляют поиск в соответствии с описанной процедурой;
и осуществляют поиск в соответствии с описанной процедурой;
– по полученным вспомогательным дополнительным троичным последовательностям  и
и 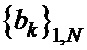 однозначно находят бинарные кодовые последовательности
однозначно находят бинарные кодовые последовательности  и кодовые последовательности единичных векторов
и кодовые последовательности единичных векторов 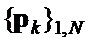 , используя таблицу соответствия.
, используя таблицу соответствия.
Заявляемый способ заключается в следующем.
Кодовые последовательности  и
и  комплексной огибающей
комплексной огибающей  двоичного ФМШПС с ортогональным ПК формируют следующим образом. Предварительно формируют вспомогательные дополнительные троичные последовательности
двоичного ФМШПС с ортогональным ПК формируют следующим образом. Предварительно формируют вспомогательные дополнительные троичные последовательности 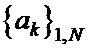 и
и  . При этом длину последовательностей
. При этом длину последовательностей 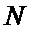 выбирают четной и представимой в виде суммы квадратов двух целых чисел.
выбирают четной и представимой в виде суммы квадратов двух целых чисел.
1. Формируют шаблоны последовательностей 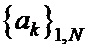 и
и 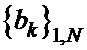 в виде векторов-строк
в виде векторов-строк  и
и  длины
длины  (в поэлементном представлении
(в поэлементном представлении 
2. Векторы-строки  формируют согласно правилу:
формируют согласно правилу:
а) произвольным образом элементам 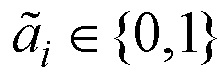 в первой половине вектора-строки
в первой половине вектора-строки 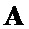 ,
, 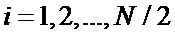 присваивают значения 0 или 1;
присваивают значения 0 или 1;
б) при этом элементам во второй половине вектора-строки  ,
,  ,
, 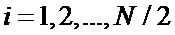 присваивают значения, равные инверсным значениям элементов
присваивают значения, равные инверсным значениям элементов  первой половины вектора-строки
первой половины вектора-строки  .
.
3. Векторы-строки  формируют как векторы инверсных элементов
формируют как векторы инверсных элементов  вектора-строки
вектора-строки 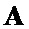 .
.
4. Находят матрицы шаблонов  и
и 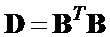 .
.
5. Формируют общий вид корреляционных матриц 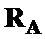 и
и  последовательностей
последовательностей 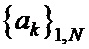 и
и  [8]:
[8]:
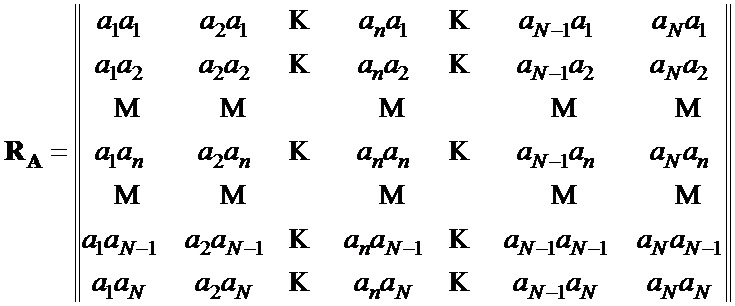 ,
,
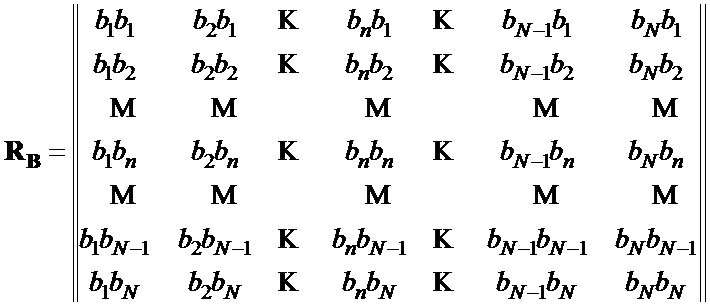
6. Используя матрицы шаблонов  ,
, 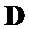 и корреляционные матрицы
и корреляционные матрицы  ,
,  , формируют систему уравнений для определения знаков ненулевых элементов последовательностей
, формируют систему уравнений для определения знаков ненулевых элементов последовательностей  и
и  . Для этого путем поэлементного произведения корреляционных матриц
. Для этого путем поэлементного произведения корреляционных матриц  и
и 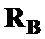 на соответствующие матрицы шаблонов
на соответствующие матрицы шаблонов 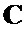 и
и  [10] формируют преобразованные корреляционные матрицы
[10] формируют преобразованные корреляционные матрицы  .
.
7. В преобразованных корреляционных матрицах  выделяют диагонали, лежащие выше главной диагонали и содержащие не менее двух элементов.
выделяют диагонали, лежащие выше главной диагонали и содержащие не менее двух элементов.
8. Выполняют суммирование элементов в соответствующих диагоналях матриц  , а полученные суммы приравнивают нулю. В результате получают общую систему уравнений для определения знаков ненулевых элементов в последовательностях
, а полученные суммы приравнивают нулю. В результате получают общую систему уравнений для определения знаков ненулевых элементов в последовательностях 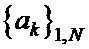 и
и 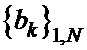 . Общая система уравнений имеет вид:
. Общая система уравнений имеет вид:

где 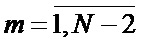 .
.
9. Решая систему уравнений , находят знаки ненулевых элементов векторов-строк  и
и  . Если же система оказывается несовместной, то изменяют векторы-строки
. Если же система оказывается несовместной, то изменяют векторы-строки 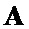 и
и 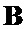 , пока решение не будет найдено или исчерпаны все пары векторов-строк
, пока решение не будет найдено или исчерпаны все пары векторов-строк  и
и  для данной длины
для данной длины  . Если для данной длины
. Если для данной длины  ни для одной из возможных пар векторов-строк
ни для одной из возможных пар векторов-строк  и
и 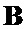 найти решение системы не удается, то переходят к другой длине
найти решение системы не удается, то переходят к другой длине  и осуществляют поиск в соответствии с описанной процедурой.
и осуществляют поиск в соответствии с описанной процедурой.
10. По полученным вспомогательным дополнительным троичным последовательностям  и
и 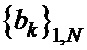 однозначно находят бинарные кодовые последовательности
однозначно находят бинарные кодовые последовательности  и кодовые последовательности единичных векторов
и кодовые последовательности единичных векторов 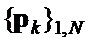 , используя таблицу соответствия 1, которая вытекает из решения дискретной системы уравнений , связывающей элементы
, используя таблицу соответствия 1, которая вытекает из решения дискретной системы уравнений , связывающей элементы  и
и 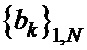 с кодовыми последовательностями
с кодовыми последовательностями  и компонентами единичных векторов кодовой последовательности
и компонентами единичных векторов кодовой последовательности 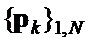 :
:
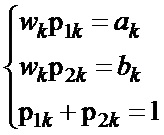 .
.
Таблица соответствия 1

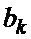






11. Последовательности 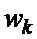 и
и 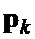 ,
,  поэлементно перемножают и формируют соответствующую последовательность произведений.
поэлементно перемножают и формируют соответствующую последовательность произведений.
12. Для текущего значения времени 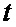 из интервала периода
из интервала периода  двоичного ФМШПС с ортогональным ПК формируют значение векторной комплексной огибающей. При этом каждый
двоичного ФМШПС с ортогональным ПК формируют значение векторной комплексной огибающей. При этом каждый 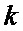 -й элемент последовательности произведений перемножают на соответствующий сформированный элементарный импульс единичной амплитуды
-й элемент последовательности произведений перемножают на соответствующий сформированный элементарный импульс единичной амплитуды 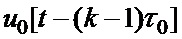 длительностью
длительностью  .
.
Полученная таким образом векторная комплексная огибающая ФМШПС с ортогональным ПК имеет оптимальную апериодическую АКФ .
Предлагаемый способ может быть реализован устройством, структурная схема которого представлена на фиг. 1, где обозначено:
1 – блок управления (БУ);
2 – генератор вектора 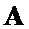 ;
;
3 – формирователь матрицы шаблона для вектора  ;
;
4, 8, 13 – первый, второй и третий поэлементные перемножители;
5 – генератор общей корреляционной матрицы последовательности 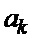 ;
;
6 – генератор вектора 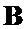 ;
;
7 – формирователь матрицы шаблона для вектора 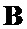 ;
;
9 – генератор общей корреляционной матрицы последовательности  ;
;
10 – блок решения системы уравнений;
11 – формирователь системы уравнений;
12 – блок соответствия;
14 – формирователь векторной комплексной огибающей.
Устройство содержит два параллельных канала, один из которых состоит из последовательно соединенных генератора вектора  2, формирователя матрицы шаблона для вектора
2, формирователя матрицы шаблона для вектора  3 и первого поэлементного перемножителя 4, выход которого соединен с первым входом формирователя системы уравнений 11. Другой канал содержит последовательно соединенные генератор вектора
3 и первого поэлементного перемножителя 4, выход которого соединен с первым входом формирователя системы уравнений 11. Другой канал содержит последовательно соединенные генератор вектора  6, формирователь матрицы шаблона для вектора
6, формирователь матрицы шаблона для вектора  7 и второй поэлементный перемножитель 8, выход которого соединен со вторым входом формирователя системы уравнений 11, выход которого через блок решения системы уравнений 10 соединен с входом блока управления 1, первый управляющий выход которого соединен с первым входом генератора вектора
7 и второй поэлементный перемножитель 8, выход которого соединен со вторым входом формирователя системы уравнений 11, выход которого через блок решения системы уравнений 10 соединен с входом блока управления 1, первый управляющий выход которого соединен с первым входом генератора вектора  2 и входами генератора общей корреляционной матрицы последовательности
2 и входами генератора общей корреляционной матрицы последовательности  5 и генератора общей корреляционной матрицы последовательности
5 и генератора общей корреляционной матрицы последовательности  9. Второй управляющий выход блока управления 1 соединен со вторыми входами генератора вектора
9. Второй управляющий выход блока управления 1 соединен со вторыми входами генератора вектора  2 и генератора вектора
2 и генератора вектора  6, первый вход которого подключен ко второму выходу генератора вектора
6, первый вход которого подключен ко второму выходу генератора вектора  2. При этом выход генератора общей корреляционной матрицы последовательности
2. При этом выход генератора общей корреляционной матрицы последовательности 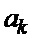 5соединен со вторым входом первого поэлементного перемножителя 4. Выход генератора общей корреляционной матрицы последовательности
5соединен со вторым входом первого поэлементного перемножителя 4. Выход генератора общей корреляционной матрицы последовательности  9 соединен со вторым входом второго поэлементного перемножителя 8. Кроме того, второй выход блока решения системы уравнений 10 подсоединен к входу блока соответствия 12, первый и второй выходы которого соединены с соответствующими входами третьего поэлементного перемножителя 13, выход которого соединен с входом формирователя векторной комплексной огибающей 14, выход которого является выходом устройства.
9 соединен со вторым входом второго поэлементного перемножителя 8. Кроме того, второй выход блока решения системы уравнений 10 подсоединен к входу блока соответствия 12, первый и второй выходы которого соединены с соответствующими входами третьего поэлементного перемножителя 13, выход которого соединен с входом формирователя векторной комплексной огибающей 14, выход которого является выходом устройства.
Работает устройство, реализующее предлагаемый способ, следующим образом. На первом этапе в устройстве предварительно формируют вспомогательные дополнительные троичные последовательности 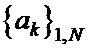 и
и  . Для этого в блоке управления 1 задают длину последовательностей
. Для этого в блоке управления 1 задают длину последовательностей 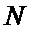 , равную четному числу, представимому в виде суммы квадратов двух целых чисел. Данное значение
, равную четному числу, представимому в виде суммы квадратов двух целых чисел. Данное значение 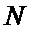 в качестве управляющего сигнала подается на первый вход генератора вектора
в качестве управляющего сигнала подается на первый вход генератора вектора 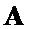 2 и входы генератора общей корреляционной матрицы последовательности
2 и входы генератора общей корреляционной матрицы последовательности  5 и генератора общей корреляционной матрицы последовательности
5 и генератора общей корреляционной матрицы последовательности  9. На вторые входы генератора вектора
9. На вторые входы генератора вектора 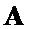 2 и генератора вектора
2 и генератора вектора 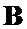 6 со второго управляющего выхода блока управления 1 подается сигнал управления изменения векторов-строк
6 со второго управляющего выхода блока управления 1 подается сигнал управления изменения векторов-строк 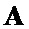 и
и 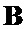 . В соответствии с данными сигналами управления в генераторе вектора
. В соответствии с данными сигналами управления в генераторе вектора 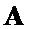 2 формируют шаблоны последовательностей
2 формируют шаблоны последовательностей  согласно правилу: а) произвольным образом элементам
согласно правилу: а) произвольным образом элементам 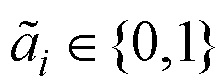 в первой половине вектора-строки
в первой половине вектора-строки  ,
, 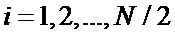 присваивают значения 0 или 1; б) при этом элементам во второй половине вектора-строки
присваивают значения 0 или 1; б) при этом элементам во второй половине вектора-строки  ,
, 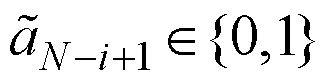 ,
, 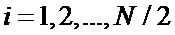 присваивают значения, равные инверсным значениям элементов
присваивают значения, равные инверсным значениям элементов  первой половины вектора-строки
первой половины вектора-строки  . Шаблоны последовательностей
. Шаблоны последовательностей  формируют в генераторе вектора
формируют в генераторе вектора 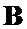 6, как векторы инверсных элементов
6, как векторы инверсных элементов  вектора-строки
вектора-строки 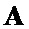 . По сформированным векторам
. По сформированным векторам 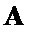 и
и 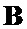 в соответствующих формирователях матриц-шаблонов векторов
в соответствующих формирователях матриц-шаблонов векторов 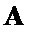 3 и
3 и 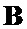 7 находят матрицы-шаблоны
7 находят матрицы-шаблоны  и
и 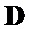 для вектора-строки
для вектора-строки 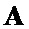 и для вектора-строки
и для вектора-строки 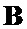 в соответствии с правилом:
в соответствии с правилом:  и
и 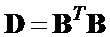 . Одновременно в генераторе общей корреляционной матрицы последовательности
. Одновременно в генераторе общей корреляционной матрицы последовательности 
 5 и в генераторе общей корреляционной матрицы последовательности
5 и в генераторе общей корреляционной матрицы последовательности 
 9 формируют общий вид корреляционных матриц
9 формируют общий вид корреляционных матриц 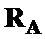 и
и  последовательностей
последовательностей 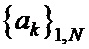 и
и  [8].
[8].
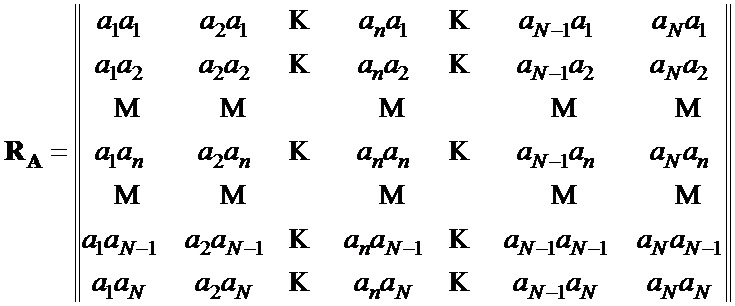 ,
,
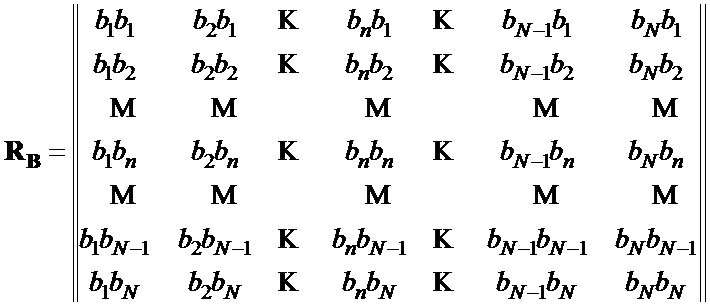 .
.
Используя матрицы шаблоны  ,
, 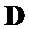 и корреляционные матрицы
и корреляционные матрицы  ,
,  , по результатам их поэлементного перемножения [10] в поэлементных перемножителях 4 и 8 формируют преобразованные корреляционные матрицы
, по результатам их поэлементного перемножения [10] в поэлементных перемножителях 4 и 8 формируют преобразованные корреляционные матрицы  , используя которые в формирователе системы уравнений 11 формируют систему уравнений для определения знаков ненулевых элементов последовательностей
, используя которые в формирователе системы уравнений 11 формируют систему уравнений для определения знаков ненулевых элементов последовательностей  и
и  . Для этого в преобразованных корреляционных матрицах
. Для этого в преобразованных корреляционных матрицах  выделяют диагонали, лежащие выше главной диагонали и содержащие не менее двух элементов. Выполняют суммирование элементов в соответствующих диагоналях матриц
выделяют диагонали, лежащие выше главной диагонали и содержащие не менее двух элементов. Выполняют суммирование элементов в соответствующих диагоналях матриц  , а полученные суммы приравнивают нулю. В результате получают общую систему уравнений для определения знаков ненулевых элементов в последовательностях
, а полученные суммы приравнивают нулю. В результате получают общую систему уравнений для определения знаков ненулевых элементов в последовательностях 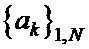 и
и 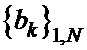 . Общая система уравнений имеет вид:
. Общая система уравнений имеет вид:  где
где 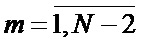 . Решая эту систему уравнений в блоке решения системы уравнений 10, находят знаки ненулевых элементов векторов-строк
. Решая эту систему уравнений в блоке решения системы уравнений 10, находят знаки ненулевых элементов векторов-строк  и
и  . Если же система оказывается несовместной, то по управляющему сигналу с первого управляющего выхода блока решения системы уравнений 10 в блоке управления 1 изменяют пары векторов-строк
. Если же система оказывается несовместной, то по управляющему сигналу с первого управляющего выхода блока решения системы уравнений 10 в блоке управления 1 изменяют пары векторов-строк 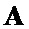 и
и 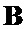 до тех пор, пока решение не будет найдено или исчерпаны все пары векторов для данной длины
до тех пор, пока решение не будет найдено или исчерпаны все пары векторов для данной длины  . Если для данной длины
. Если для данной длины  ни для одной из возможных пар векторов-строк
ни для одной из возможных пар векторов-строк  и
и 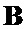 найти решение системы не удается, то по сигналу с первого управляющего выхода блока решения системы уравнений 10 в блоке управления 1 переходят к другой длине
найти решение системы не удается, то по сигналу с первого управляющего выхода блока решения системы уравнений 10 в блоке управления 1 переходят к другой длине  и осуществляют поиск решения в соответствии с описанной процедурой. Далее по полученным в блоке решения системы уравнений 10 вспомогательным дополнительным троичным последовательностям
и осуществляют поиск решения в соответствии с описанной процедурой. Далее по полученным в блоке решения системы уравнений 10 вспомогательным дополнительным троичным последовательностям 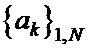 и
и  в блоке соответствия 12, используя заданную таблицу соответствия, однозначно находят бинарные кодовые последовательности
в блоке соответствия 12, используя заданную таблицу соответствия, однозначно находят бинарные кодовые последовательности  и кодовые последовательности единичных векторов
и кодовые последовательности единичных векторов 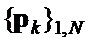 . Полученные последовательности
. Полученные последовательности 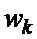 и
и 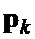 ,
,  поэлементно перемножают в поэлементном перемножителе 13 и формируют соответствующую последовательность произведений, используя которую на выходе формирователя векторной комплексной огибающей 14 для текущего значения времени
поэлементно перемножают в поэлементном перемножителе 13 и формируют соответствующую последовательность произведений, используя которую на выходе формирователя векторной комплексной огибающей 14 для текущего значения времени 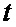 из интервала периода
из интервала периода  двоичного ФМШПС с ортогональным ПК формируют значение векторной комплексной огибающей. При этом каждый
двоичного ФМШПС с ортогональным ПК формируют значение векторной комплексной огибающей. При этом каждый 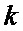 -й элемент последовательности произведений перемножают на соответствующий сформированный элементарный импульс единичной амплитуды
-й элемент последовательности произведений перемножают на соответствующий сформированный элементарный импульс единичной амплитуды 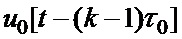 длительностью
длительностью  .
.
В качестве примера рассмотрим последовательность операций нахождения бинарных кодовых последовательностей  и кодовых последовательностей единичных векторов
и кодовых последовательностей единичных векторов  для
для 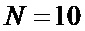 .
.
Формируем шаблон последовательности  в виде вектора-строки
в виде вектора-строки
 .
.
Формируем шаблон последовательности  путем инверсии элементов вектора-строки
путем инверсии элементов вектора-строки  :
:
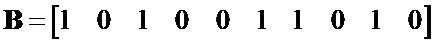 .
.
Находим матрицы-шаблоны 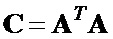 и
и 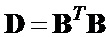 :
:
 ,
,
 .
.
Используя матрицы-шаблоны  и
и  , путем поэлементного произведения с корреляционными матрицами
, путем поэлементного произведения с корреляционными матрицами 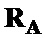 и
и 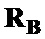 получаем преобразованные корреляционные матрицы
получаем преобразованные корреляционные матрицы  для
для  .
.
 ,
,
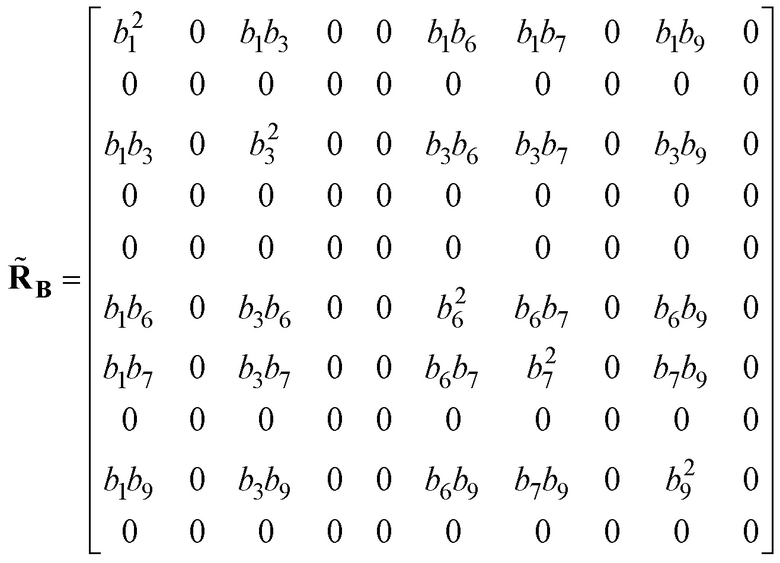
Суммируя в матрицах  элементы вдоль соответствующих диагоналей, лежащих над их главными диагоналями, и приравнивая соответствующие суммы нулю, записываем систему уравнений для определения знаков ненулевых элементов вектор-шаблонов
элементы вдоль соответствующих диагоналей, лежащих над их главными диагоналями, и приравнивая соответствующие суммы нулю, записываем систему уравнений для определения знаков ненулевых элементов вектор-шаблонов  и
и  :
:

Для удобства решения запишем эту систему в мультипликативной форме:

Из-за идентичности второго и шестого уравнений этой системы, их отбрасываем. В пятое уравнение неизвестные  и
и  входят в квадрате, поэтому их исключаем из этого уравнения. Оставшиеся уравнения решаем относительно пар
входят в квадрате, поэтому их исключаем из этого уравнения. Оставшиеся уравнения решаем относительно пар  ,
,  ,
,  ,
,  ,
,  .
.
Имеем два решения этой системы:  ,
,  ,
,  ,
,  ,
,  и
и  ,
,  ,
,  ,
,  ,
, 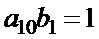 . Далее полученные решения используем в качестве уравнений для определения возможных комбинаций знаков элементов, входящих в пары
. Далее полученные решения используем в качестве уравнений для определения возможных комбинаций знаков элементов, входящих в пары  ,
,  ,
,  ,
, 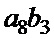 ,
,  . Соответствующие результаты для первого решения преобразованной системы приведены в таблице 2, а для второго – в таблице 3.
. Соответствующие результаты для первого решения преобразованной системы приведены в таблице 2, а для второго – в таблице 3.
Таблица 2. Возможные комбинации знаков элементов, входящих в пары  ,
,  ,
,  ,
, 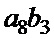 ,
,  , для первого решения
, для первого решения
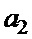

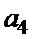


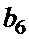
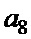
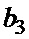

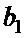
Таблица 3. Возможные комбинации знаков элементов, входящих в пары  ,
,  ,
,  ,
, 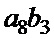 ,
,  , для второго решения
, для второго решения




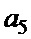
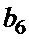

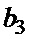


Для каждой из пяти пар существует два варианта выбора знаков и этот выбор независим от выбора знаков в других парах. Поэтому всего можно получить 64 различных комбинации знаков, являющихся решением системы уравнений в мультипликативной форме. Поскольку переход к мультипликативной форме системы уравнений сопровождается появлением лишних решений, то все полученные 64 решения надо подставить в исходную систему уравнений и подвергнуть проверке. После отсеивания лишних решений для заданного шаблона 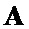 окончательно получим возможные варианты пар последовательностей
окончательно получим возможные варианты пар последовательностей 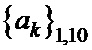 и
и 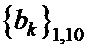 , приведенные в таблице 4.
, приведенные в таблице 4.
Таблица 4. Синтезированные последовательности 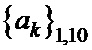 и
и 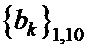
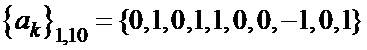 ,
, 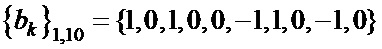
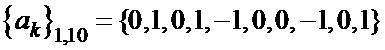 ,
, 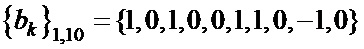
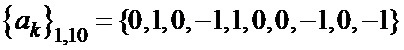 ,
, 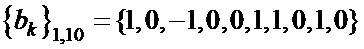
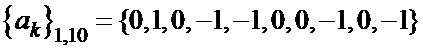 ,
, 
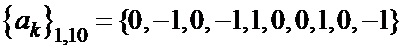 ,
, 
 ,
, 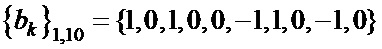
 ,
, 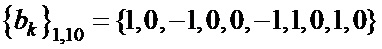
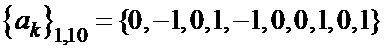 ,
, 
 ,
, 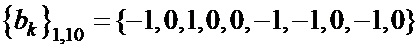
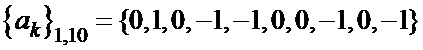 ,
, 
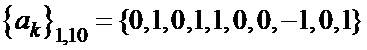 ,
, 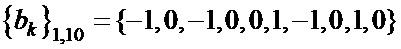
 ,
, 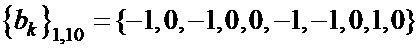
 ,
, 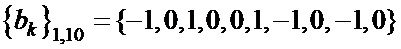
 ,
, 
 ,
, 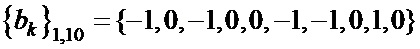
 ,
, 
На фиг. 2 представлена форма решетчатой апериодической АКФ комплексной огибающей двоичного ФМШПС при использовании кода рассмотренного в примере синтезированной последовательности. Видно, что форма АКФ имеет оптимальный вид.
Достигаемый технический результат – увеличение помехозащищенности системы радиосвязи и точности синхронизации.
Сравнение заявляемого способа формирования фазоманипулированных широкополосных сигналов с поляризационным кодированием с оптимальными апериодическими автокорреляционными функциями с другими известными решениями в данной области техники не позволило выявить признаки, заявленные в отличительной части формулы изобретения.
Известно, что в современных радиотехнических системах часто используют цифровые сигналы. Вследствие этого, в узлах устройства, реализующего заявляемый способ, целесообразно применять дискретные и цифровые сигналы. Для обработки таких сигналов наряду с аппаратными часто используют программные и вычислительные средства [11]. В данном случае для реализации заявляемого способа разумно использовать стандартные процедуры матричного анализа [10, 12, 13, 14], что позволяет применять высокопроизводительные специализированные цифровые сигнальные процессоры (digital signal processor (DSP)) и быстродействующие программируемые логические интегральные схемы (ПЛИС, Field Programmable Gate Array (FPGA)), например, типов 1892ВМ3Т (Multicore), 1892ВМ10Я (NVcom), FPGA Virtex-7 и их перспективные версии [15, 16, 17].
Литература.
1. Pat. 7310379 US, Int. Cl.7 H 04 B 7/02. Polarization state techniques for wireless communications / S. Sibecas, C. Corral, S. Emami, G. Stratis, G. Rasor; Motorola, Inc. No 10/631430; Filed 31.07.2003; Pub. 18.12.2007.
2. Лукьянчиков В.Д., Ливенцев В.В. Способ повышения пропускной способности систем радиосвязи с шумоподобными сигналами // Изв. ВУЗов. Радиоэлектроника. 2007. Т. 50, № 8. С. 22–35.
3. Ливенцев В.В. Анализ эффективности энергетического обнаружения широкополосных сигналов с поляризационным кодированием // Теория и техника радиосвязи: науч.-тех. сб. / АО «Концерн «Созвездие». 2007. Вып. 2. С. 21–29.
4. Зарубин В.С., Ливенцев В.В., Лукьянчиков В.Д., Прибытков Ю.Н. Спектральные характеристики фазоманипулированных широкополосных сигналов с поляризационным кодированием // Теория и техника радиосвязи: науч.-тех. сб. / АО «Концерн «Созвездие». – 2019. – Вып. 2. – С. 55–61.
5. Варакин Л.Е. Системы связи с шумоподобными сигналами / Л.Е. Варакин. – М.: Радио и связь, 1985. – 384 с.
6. Козлов А.И., Логвин А.И., Сарычев В.А. Поляризация радиоволн. Поляризационная структура радиолокационных сигналов. М.: Радиотехника, 2005. 704 с.
7. Гусев К.Г., Филатов А.Д., Сополев А.П. Поляризационная модуляция. М.: Сов. радио, 1974. 288 с.].
8. Варакин Л.Ε. Теория сложных сигналов. Μ., изд-во «Советское радио», 1970, 376 с., С. 50.
9. Гоноровский И.С. Радиотехнические цепи и сигналы: Учебник для вузов. – М.: Радио и связь, 1986. – 512 с., С. 104.
10. G.H. Golub, C.F. Van Loan. Matrix computations, The Johns Hopkins University Press, Baltimore, 2013. 756 p.
11. Куприянов М.С., Матюшкин Б.Д. Цифровая обработка сигналов: процессоры, алгоритмы, средства проектирования / М.С. Куприянов, Б.Д. Матюшкин. – Спб.: Политехника, 1999. – 592 с.
12. Гантмахер Ф.Р. Теория матриц. 4-е издание. М.: Наука, 1988. – 552 с.
13. Беллман Р. Введение в теорию матриц. 2-е издание: Пер. с англ. М.: Наука, 1976. – 352 с.
14. Хорн Р., Джонсон Ч. Матричный анализ: Пер. с англ. М.: Мир, 1989. – 655 с.
15. Максфилл К. Проектирование на ПЛИС. Курс молодого бойца / К. Максфилл. – М.: Издательский дом «Додэка XXI», 2007. – 408 c.
16. Бродин В.Б., Калинин А.В. Системы на микроконтроллерах и БИС программируемой логики / В.Б. Бродин, А.В. Калинин. – М.:Издательство ЭКОМ, 2002. – 400 с.
17. Грушвицкий Р.И., Мурсаев А.Х., Угрюмов Е.П. Проектирование систем на микросхемах программируемой логики / Р.И. Грушвицкий., А.Х. Мурсаев., Е.П. Угрюмов. – СПб.: БХВ-Петербург, 2002. – 608 с.
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ формирования пар фазоманипулированных широкополосных сигналов с поляризационным кодированием с оптимальными апериодическими автокорреляционными и взаимокорреляционными функциями | 2022 |
|
RU2797534C1 |
| СПОСОБ РАДИОСВЯЗИ С МНОЖЕСТВЕННЫМ ДОСТУПОМ | 2008 |
|
RU2386212C1 |
| СПОСОБ РАДИОСВЯЗИ С МНОЖЕСТВЕННЫМ ДОСТУПОМ | 2006 |
|
RU2314642C1 |
| СПОСОБ ПЕРЕДАЧИ ИНФОРМАЦИИ НА ОСНОВЕ ХАОТИЧЕСКИ ФОРМИРУЕМЫХ АНСАМБЛЕЙ ДИСКРЕТНЫХ МНОГОУРОВНЕВЫХ ОРТОГОНАЛЬНЫХ СИГНАЛОВ | 2010 |
|
RU2428795C1 |
| СИСТЕМА ПЕРЕДАЧИ ИНФОРМАЦИИ С ПРИМЕНЕНИЕМ СТОХАСТИЧЕСКИХ ОРТОГОНАЛЬНЫХ КОДОВ | 2021 |
|
RU2780418C1 |
| СИСТЕМА НЕПРЕРЫВНОЙ ПЕРЕДАЧИ ИНФОРМАЦИИ АНСАМБЛЯМИ СТОХАСТИЧЕСКИХ ОРТОГОНАЛЬНЫХ КОДОВ | 2022 |
|
RU2801172C1 |
| НЕКОГЕРЕНТНЫЙ ЦИФРОВОЙ ДЕМОДУЛЯТОР "В ЦЕЛОМ" КОДИРОВАННЫХ СИГНАЛОВ С ФАЗОВОЙ МАНИПУЛЯЦИЕЙ | 2014 |
|
RU2556429C1 |
| СИСТЕМА РАДИОСВЯЗИ С МНОЖЕСТВЕННЫМ ДОСТУПОМ | 2007 |
|
RU2327288C1 |
| СПОСОБ АСИНХРОННОЙ АДРЕСНОЙ СВЯЗИ | 2000 |
|
RU2182403C1 |
| СПОСОБ ПРИЕМА ШУМОПОДОБНЫХ СИГНАЛОВ С МИНИМАЛЬНОЙ ЧАСТОТНОЙ МАНИПУЛЯЦИЕЙ | 2006 |
|
RU2307474C1 |


Изобретение относится к области радиосвязи и может быть использовано в широкополосных системах для передачи информации, оценки параметров канала распространения и выполнения процедур частотно-временной синхронизации. Технический результат – увеличение помехозащищенности системы радиосвязи и точности синхронизации. Данный способ включает процедуру формирования фазовых и поляризационных кодовых последовательностей для двоичных фазоманипулированных широкополосных сигналов (ФМШПС) с ортогональным поляризационным кодированием (ПК). Таким образом, сформированные двоичные ФМШПС с ортогональным ПК имеют оптимальные апериодические автокорреляционные функции. 2 ил., 4 табл.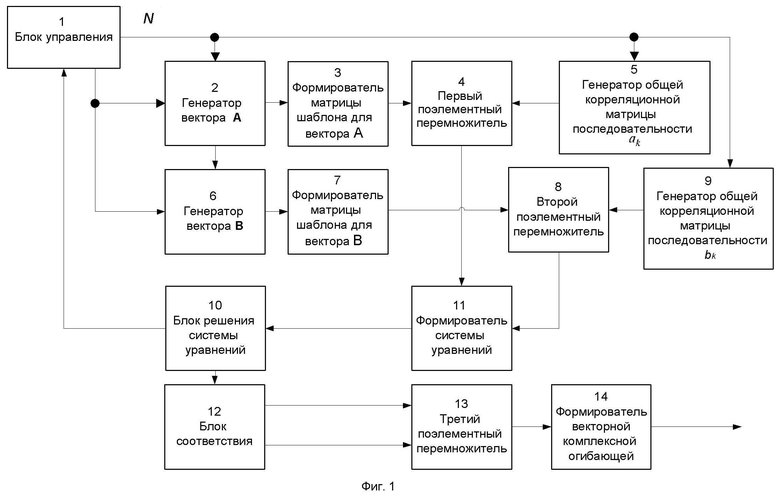
Способ формирования фазоманипулированных широкополосных сигналов (ФМШПС) с поляризационным кодированием с оптимальными апериодическими автокорреляционными функциями, включающий формирование кодовых последовательностей 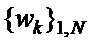 и
и  комплексной огибающей
комплексной огибающей 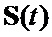 двоичного ФМШПС с ортогональным поляризационным кодированием (ПК);
двоичного ФМШПС с ортогональным поляризационным кодированием (ПК);
последовательности  и
и 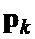 ,
, 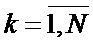 поэлементно перемножают и формируют соответствующую последовательность произведений;
поэлементно перемножают и формируют соответствующую последовательность произведений;
для текущего значения времени  из интервала периода
из интервала периода  двоичного ФМШПС с ортогональным ПК формируют значение векторной комплексной огибающей, при этом каждый
двоичного ФМШПС с ортогональным ПК формируют значение векторной комплексной огибающей, при этом каждый 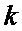 -й элемент последовательности произведений перемножают на соответствующий сформированный элементарный импульс единичной амплитуды
-й элемент последовательности произведений перемножают на соответствующий сформированный элементарный импульс единичной амплитуды 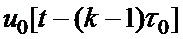 длительностью
длительностью  ,
,
отличающийся тем, что
предварительно формируют вспомогательные дополнительные троичные последовательности  и
и  , при этом длину последовательностей
, при этом длину последовательностей  выбирают четной и представимой в виде суммы квадратов двух целых чисел;
выбирают четной и представимой в виде суммы квадратов двух целых чисел;
векторы-строки 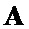 формируют согласно правилу:
формируют согласно правилу:
в первой половине вектора-строки  ,
, 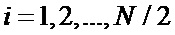 произвольным образом элементам
произвольным образом элементам  присваивают значения 0 или 1;
присваивают значения 0 или 1;
при этом элементам во второй половине вектора-строки 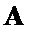 ,
,  ,
, 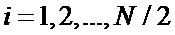 присваивают значения, равные инверсным значениям элементов
присваивают значения, равные инверсным значениям элементов  первой половины вектора-строки
первой половины вектора-строки 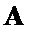 ;
;
векторы-строки  формируют как векторы инверсных элементов
формируют как векторы инверсных элементов  вектора-строки
вектора-строки 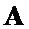 ;
;
находят матрицы шаблонов  и
и 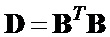 ;
;
формируют общий вид корреляционных матриц 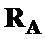 и
и  последовательностей
последовательностей  и
и 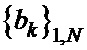 ;
;
формируют систему уравнений для определения знаков ненулевых элементов последовательностей  и
и  , для этого, используя матрицы шаблонов
, для этого, используя матрицы шаблонов  ,
,  и корреляционные матрицы
и корреляционные матрицы 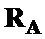 ,
, 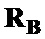 , путем поэлементного произведения корреляционных матриц
, путем поэлементного произведения корреляционных матриц 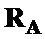 и
и 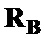 на соответствующие матрицы шаблонов
на соответствующие матрицы шаблонов  и
и  формируют преобразованные корреляционные матрицы
формируют преобразованные корреляционные матрицы  ;
;
в преобразованных корреляционных матрицах 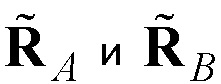 выделяют диагонали, лежащие выше главной диагонали и содержащие не менее двух элементов;
выделяют диагонали, лежащие выше главной диагонали и содержащие не менее двух элементов;
выполняют суммирование элементов в соответствующих диагоналях матриц 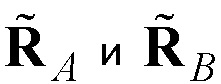 , а полученные суммы приравнивают нулю, в результате получают общую систему уравнений для определения знаков ненулевых элементов в последовательностях
, а полученные суммы приравнивают нулю, в результате получают общую систему уравнений для определения знаков ненулевых элементов в последовательностях 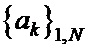 и
и  , которая имеет вид
, которая имеет вид  где
где  ;
;
решая систему уравнений, находят знаки ненулевых элементов векторов-строк 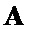 и
и  , если же система оказывается несовместной, то изменяют векторы-строки
, если же система оказывается несовместной, то изменяют векторы-строки  и
и 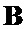 , пока решение не будет найдено или исчерпаны все пары векторов-строк
, пока решение не будет найдено или исчерпаны все пары векторов-строк 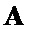 и
и  для данной длины
для данной длины  ;
;
если для данной длины  ни для одной из возможных пар векторов-строк
ни для одной из возможных пар векторов-строк 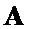 и
и  найти решение системы не удается, то переходят к другой длине
найти решение системы не удается, то переходят к другой длине 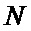 и осуществляют поиск в соответствии с описанной процедурой;
и осуществляют поиск в соответствии с описанной процедурой;
по полученным вспомогательным дополнительным троичным последовательностям  и
и 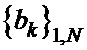 однозначно находят бинарные кодовые последовательности
однозначно находят бинарные кодовые последовательности  и кодовые последовательности единичных векторов
и кодовые последовательности единичных векторов  , используя таблицу соответствия.
, используя таблицу соответствия.
| Зарубин В.С., Ливенцев В.В., Лукьянчиков В.Д., Прибытков Ю.Н., статья: Спектральные характеристики фазоманипулированных широкополосных сигналов с поляризационным кодированием, Теория и техника радиосвязи, научно-технический сборник, АО "Концерн "Созвездие", 2019, выпуск 2, стр | |||
| Устройство двукратного усилителя с катодными лампами | 1920 |
|
SU55A1 |
| Формирователь шумоподобных фазоманипулированных сигналов | 2019 |
|
RU2716217C1 |
| US 7310379 B2, 18.12.2007 | |||
| US | |||
Авторы
Даты
2020-10-14—Публикация
2020-05-28—Подача