Изобретение относится к методам создания термоядерного реактора на основе открытой магнитной ловушки.
Известны способы создания магнитных систем, на основе которых предложены концепции возможных термоядерных реакторов и источников тепловых нейтронов (токамаки, стеллараторы, открытые ловушки). Известно, что реакционная способность альтернативных (не содержащих тритий) топлив: D – D, D – He3, включая p – B11, где реакции синтеза протекают без выделения нейтронов, по меньшей мере в сто раз ниже, чем в дейтерий-тритиевой реакции при сравнимом давлении плазмы. Для поддержания стационарной термоядерной реакции это давление должно уравновешиваться давлением магнитного поля, поэтому важнейшей задачей является создание такой магнитной ловушки, которая могла бы с высокой эффективностью использовать как технологии генерации сильных магнитных полей, так и их применение для удержания плазмы. Для этих целей хорошо подходят осесимметричные линейные системы, такие как открытые ловушки и конфигурации с обращенным полем (field-reversed configurations, FRC).
Известен способ, описанный в работе [1], где были исследованы перспективы использования газодинамической ловушки (ГДЛ) в качестве термоядерного реактора. Реализация чисто газодинамического режима удержания ведет к линейной зависимости коэффициента усиления мощности реактора от его длины: QDT ∝ L, следовательно, реактор с положительным энергетическим выходом на основе ГДЛ теоретически реализуем. Основным недостатком такого реактора является длина реактора, которая даже для предельно достижимых сегодня значений магнитного поля в пробках (Bm ~ 30 Tл) оказывается слишком большой (L > 5 км), а мощность неприемлемо высокой. Чтобы уменьшить длину реактора и его минимальную мощность, необходимо улучшить продольное удержание ионов, то есть уменьшить поток частиц и энергии плазмы через магнитные пробки. Уже в ранней работе [2] было предложено использовать секции с многопробочной конфигурацией магнитного поля, присоединенные к торцам ловушки, для уменьшения продольных потерь. Этот способ улучшения эффективности пробочного удержания теоретически позволяет создать термоядерный реактор на основе газодинамической ловушки. Однако, его параметры не выглядят достаточно привлекательными по сравнению с соответствующими проектами на базе токамаков. Главным недостатком такого реактора является его геометрия. Реактор оказывается длинным и тонким, так как термоядерная мощность прямо пропорциональна объёму плазмы и квадрату её плотности n. В то же время мощность продольных потерь пропорциональна плотности и площади сечения плазмы в магнитных пробках. Плазма заполняет объём трубок магнитного потока, поэтому отношение её сечения в пробке к сечению в центральной плоскости равно пробочному отношению R = Bm / B0, где Bm – магнитное поле в пробках, а B0 – магнитное поле в центральном сечении ловушки. В результате 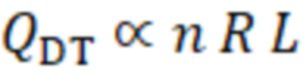 . Максимальная плотность плазмы так же, как и максимальное пробочное отношение, определяется максимально достижимой величиной удерживающего магнитного поля. В параксиальном приближении равновесие плазмы ограничивается величиной относительного давления β, которая определяется как отношение давления плазмы p к давлению вакуумного магнитного поля:
. Максимальная плотность плазмы так же, как и максимальное пробочное отношение, определяется максимально достижимой величиной удерживающего магнитного поля. В параксиальном приближении равновесие плазмы ограничивается величиной относительного давления β, которая определяется как отношение давления плазмы p к давлению вакуумного магнитного поля: 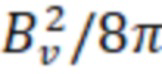 , то есть
, то есть 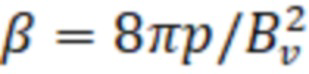 , поэтому
, поэтому 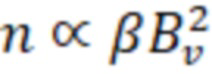 , где
, где 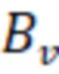 – величина невозмущенного (вакуумного) магнитного поля в зоне удержания, а магнитное поле внутри плазмы уменьшается как
– величина невозмущенного (вакуумного) магнитного поля в зоне удержания, а магнитное поле внутри плазмы уменьшается как
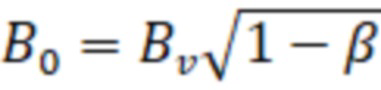 . Таким образом
. Таким образом
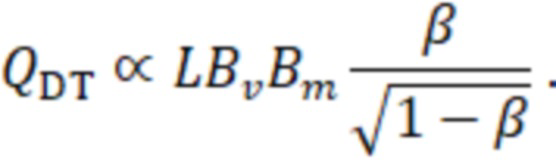
Из этого следует, что поле в зоне удержания и поле в пробках должны быть выбраны настолько большими, насколько это технически реализуемо, в то время как радиус плазмы можно уменьшать до тех пор, пока поперечные потери остаются меньше продольных. Это последнее требование фактически определяет отношение длины оптимизированного реактора к его радиусу: 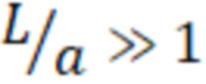 . Когда величина β существенно меньше единицы, зависимость
. Когда величина β существенно меньше единицы, зависимость 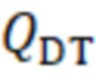 от β близка к линейной. Однако, когда β приближается к единице, эффективное пробочное отношение быстро возрастает за счёт вытеснения магнитного потока из объёма плазмы. Этот эффект был замечен более 50 лет назад для тета-пинчей [4], однако ему не было придано должного значения. В случае же газодинамического удержания этот эффект может иметь определяющее значение ввиду линейной зависимости QDT от R,
от β близка к линейной. Однако, когда β приближается к единице, эффективное пробочное отношение быстро возрастает за счёт вытеснения магнитного потока из объёма плазмы. Этот эффект был замечен более 50 лет назад для тета-пинчей [4], однако ему не было придано должного значения. В случае же газодинамического удержания этот эффект может иметь определяющее значение ввиду линейной зависимости QDT от R, 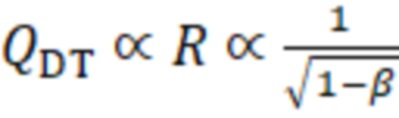 . Увеличение эффективности реактора ядерного синтеза за счёт β можно использовать для соответствующего снижения его длины L.
. Увеличение эффективности реактора ядерного синтеза за счёт β можно использовать для соответствующего снижения его длины L.
Технический результат предлагаемого способа заключается в существенном увеличении коэффициента усиления мощности реактора в сравнении с другими проектами термоядерных реакторов на основе линейных магнитных систем.
Теоретические оценки, сделанные в работе [3], предсказывают значительный прирост времени жизни плазмы, если на оси системы создать так называемый «диамагнитный пузырь» – плазму с высоким относительным давлением. Для этого требуется ввести в ловушку любым известным способом, например, путем инжектирования пучков нейтральных атомов большой мощности, энергию, достаточную для создания плазмы с минимальным относительным давлением β ≈ 2/3, которая за счет собственных диамагнитных токов вытеснит магнитное поле с оси системы.
Результаты изучения равновесия при удержании «диамагнитного пузыря» с β стремящимся к единице в рамках магнитной гидродинамики изложены в работах [4, 5]. Показано, что, если магнитное поле вблизи области своего минимума квазиоднородно, то «диамагнитный пузырь» может иметь приблизительно цилиндрическую форму с радиусом много большим по сравнению с радиусом трубки магнитного потока в вакуумном поле. При этом концы «пузыря» имеют непараксиальную конфигурацию. В этих условиях эффективное пробочное отношение в такой диамагнитной ловушке становится очень большим, а поперечный транспорт возрастает. Показано, что время удержания энергии может быть оценено как 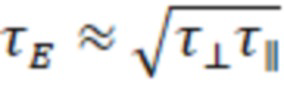 , где
, где 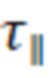 – характерное время продольного удержания, а
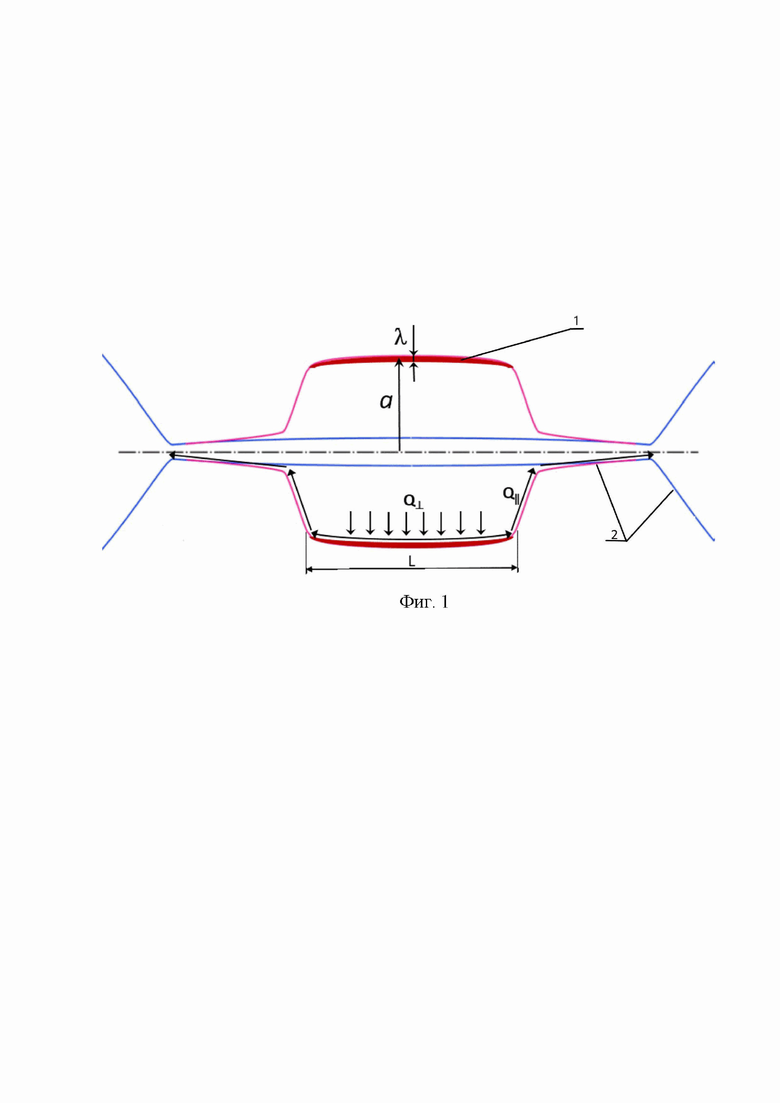
– характерное время продольного удержания, а 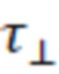 – характерное время диффузии магнитного поля внутрь «пузыря» на глубину его радиуса. Если поперечное удержание не слишком деградирует вследствие турбулентности, то такая оценка, в принципе, позволяет сконструировать относительно компактный реактор ядерного синтеза с длиной в несколько десятков метров. Во многих отношениях такое диамагнитное удержание и соответствующие параметры реактора аналогичны системам с обращённым магнитным полем. Фиг.1 поясняет, как происходит удержание плазмы в диамагнитной ловушке.
– характерное время диффузии магнитного поля внутрь «пузыря» на глубину его радиуса. Если поперечное удержание не слишком деградирует вследствие турбулентности, то такая оценка, в принципе, позволяет сконструировать относительно компактный реактор ядерного синтеза с длиной в несколько десятков метров. Во многих отношениях такое диамагнитное удержание и соответствующие параметры реактора аналогичны системам с обращённым магнитным полем. Фиг.1 поясняет, как происходит удержание плазмы в диамагнитной ловушке.
1 – переходный слой толщиной λ,
2 – граница плазмы,
а – радиус «диамагнитного пузыря»,
Q|| и Q⊥ – продольный и поперечный потоки энергии из ловушки,
L – длина «диамагнитного пузыря».
Внутри диамагнитного пузыря величина магнитного поля пренебрежимо мала, а ионы практически не замагничены. По этой причине поперечный транспорт является доминирующим, а продольный – исчезающе мал, поскольку эффективное пробочное отношение во внутренней области пузыря стремится к бесконечности. Поперечное удержание в этих условиях полностью определяется тонким пограничным слоем с характерной толщиной λ. Магнитное поле в пограничном слое имеет ненулевую величину, поэтому эффективное пробочное отношение здесь также имеет ограниченное значение, определяя продольные потери частиц и энергии из слоя.
Вне слоя снаружи магнитное поле не ослаблено диамагнетизмом плазмы и имеет большое значение, поэтому естественно предположить, что время удержания частиц в слое определяется продольными газодинамическими потерями и может быть оценено как время удержания плазмы в классической газодинамической ловушке 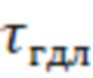 :
:
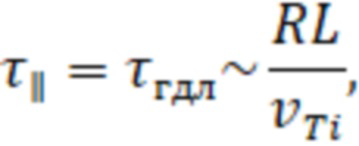
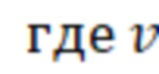 Ti
– тепловая скорость ионов. Поток частиц из области переходного слоя радиусом a, толщиной λ и длиной L вдоль силовых линий магнитного поля можно оценить как:
Ti
– тепловая скорость ионов. Поток частиц из области переходного слоя радиусом a, толщиной λ и длиной L вдоль силовых линий магнитного поля можно оценить как:
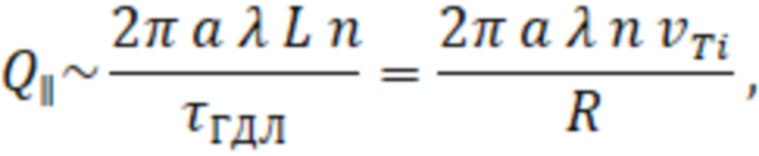
где n – плотность частиц плазмы в переходном слое, которую будем для оценок считать равной плотности во внутренней области ловушки. Характерное время диффузии плазмы из центральной области, где в порядка единицы, на расстояние λ поперёк магнитного поля равно времени диффузии магнитного поля в плазму на глубину λ, поэтому оно может быть оценено как:
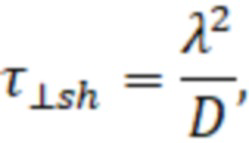
где 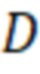 – коэффициент диффузии плазмы поперек магнитного поля. Поток частиц из центральной области в слой через его внутреннюю границу при этом можно оценить следующим образом:
– коэффициент диффузии плазмы поперек магнитного поля. Поток частиц из центральной области в слой через его внутреннюю границу при этом можно оценить следующим образом:
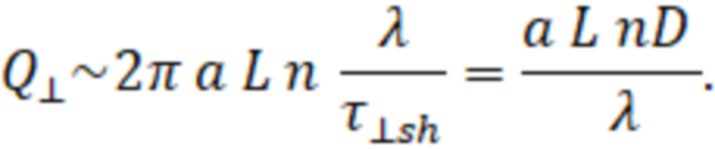
Из условия равенства потоков  найдём λ:
найдём λ:
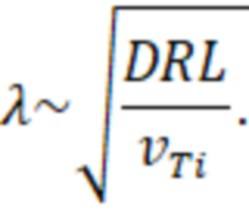
Имея оценки для толщины переходного слоя и потока частиц из ловушки, можно оценить характерное время удержания частиц:
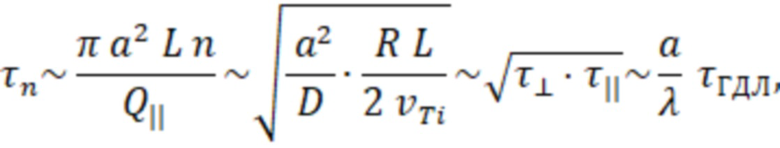
где 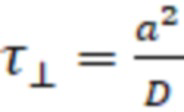 – время, соответствующее времени диффузии магнитного поля на глубину радиуса плазмы.
– время, соответствующее времени диффузии магнитного поля на глубину радиуса плазмы.
Таким образом, можно грубо оценить коэффициент усиления мощности реактора ядерного синтеза на основе диамагнитной ловушки, удержание плазмы в которой происходит в обозначенном выше режиме. Для такой оценки выберем следующие параметры: температура плазмы T = 9 кэВ, длина ловушки L = 30 м, вакуумное магнитное поле 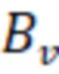 = 10 Тл, пробочное отношение R = 2, радиус плазмы a = 1 м. В случае классической диффузии
= 10 Тл, пробочное отношение R = 2, радиус плазмы a = 1 м. В случае классической диффузии 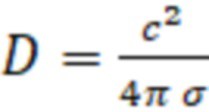 ,
,
где с – скорость света, σ – спитцеровская проводимость плазмы, получим: λ ≈ 2 ⋅ 10-4 м, τГДЛ ≈ 5 ⋅ 10-5 с, а следовательно: τE ≈ 0,1 с (при поле в 10 Тл и плотности плазмы n = 1,4 ⋅ 1022 м-3).
Таким образом получается: nτE ≈ 1.4 ⋅ 1021 м-3 ⋅ с > 1020 м-3 ⋅ с, что на порядок превышает величину, соответствующую критерию Лоусона для DT топлива. Отсюда также следует, что критерий Лоусона будет выполнен, даже если поперечная проводимость плазмы вследствие турбулентных процессов окажется на два порядка выше классической.
Столь значительная величина времени удержания плазмы мотивирует рассмотрение возможности использования диамагнитной ловушки в качестве основы для создания термоядерного реактора с наиболее привлекательным видом топлива, а именно p – B11, при котором реакции должны протекать без выделения нейтронов в основных каналах.
Как отмечалось ранее, внутри пузыря магнитное поле близко к нулю. В этом случае ларморовский радиус и длина свободного пробега достаточно высокоэнергичных частиц может оказаться сравнима или больше характерных размеров неоднородностей магнитного поля. Особенно это актуально для установок, где планируется инжекция атомарных пучков высокой энергии. Бесстолкновительная динамика отдельных частиц в диамагнитной ловушке исследовалась в работах [6, 7]. Показано, что существует два механизма удержания частиц в осесимметричной диамагнитной ловушке: за счет сохранения адиабатического инварианта, связанного с большой разницей в периоде радиальных колебаний и времени пролета от пробки до пробки, и за счет быстрого вращения вокруг оси ловушки (так называемое абсолютное удержание). Из-за малости магнитного поля в диамагнитном пузыре и несохранения магнитного момента часть частиц движется хаотически, при этом возникает новый вид бесстолкновительных продольных потерь, причем время жизни хаотически движущихся частиц оценивается как
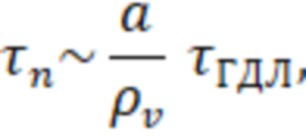
где 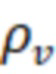 – ларморовский радиус частиц, вычисленный по вакуумному полю в центре. Таким образом, если вакуумное магнитное поле в центре достаточно велико, а ларморовский радиус частиц достаточно мал:
– ларморовский радиус частиц, вычисленный по вакуумному полю в центре. Таким образом, если вакуумное магнитное поле в центре достаточно велико, а ларморовский радиус частиц достаточно мал: 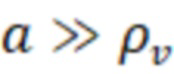 , то в диамагнитном пузыре можно ожидать значительного прироста времени удержания по сравнению с классической газодинамической ловушкой.
, то в диамагнитном пузыре можно ожидать значительного прироста времени удержания по сравнению с классической газодинамической ловушкой.
Для осуществления предложенного способа удержания плазмы необходима открытая магнитная ловушка, состоящая из вакуумной камеры, катушек магнитного поля, системы вакуумной откачки, генератора предварительной плазмы и системы атомарной инжекции.
Генератор плазмы создаёт стартовую мишенную плазму с плотностью 1013-1014 см-3 и температурой до 50 эВ, которая заполняет ловушку вдоль силовых линий магнитного поля. После чего в ловушку инжектируются мощные импульсные водородные пучки для формирования азимутального ионного тока. В результате процессов взаимодействия атомов пучка с электронами и ионами мишенной плазмы происходит накопление ионного азимутального диамагнитного тока. Согласно оценкам, суммарной мощности инжекции порядка 4 МВт при токе частиц 250-300 экв. А и энергии частиц пучка 15 кэВ должно быть достаточно для реализации диамагнитного удержания плазменного образования с характерным размером 20 см и относительным давлением, приближающимся к единице, в магнитном поле величиной порядка 2 кГс.
Источники информации
1. Beklemishev A. D. Diamagnetic “bubble” equilibria in linear traps // Physics of plasmas. - 2016. - Vol. 23. - P. 082506. - DOI: 10.1063/1.4960129.
2. Мирнов В. В., Рютов Д. Д. Газодинамическая линейная ловушка для удержания плазмы // Письма в ЖТФ. - 1979. - Т. 5. - С. 678.
3. Будкер Г. И., Мирнов В. В., Рютов Д. Д. Влияние гофрировки магнитного поля на расширение и остывание плотной плазмы // Письма в ЖЭТФ. - 1971. - Т. 14, 5. - С. 320–322.
4. Taylor J. B. and Wesson J. A. End losses from a theta pinch // Nuclear Fusion. - 1965. - Vol. 5, 2. — P. 159. — DOI: 10.1088/0029-5515/5/2/008.
5. Khristo, M. S., & Beklemishev, A. D. (2022). Two-dimensional MHD equilibria of diamagnetic bubble in gas-dynamic trap. Plasma Physics and Controlled Fusion, 64(9), 095019. https://doi.org/10.1088/1361-6587/ac8616
6. Chernoshtanov, I. (2020). Collisionless particle dynamic in an axi-symmetric diamagnetic trap. Retrieved from http://arxiv.org/abs/2002.03535
7. Chernoshtanov, I. S. (2022). Collisionless dynamics of particles in diamagnetic trap. Plasma physics, 48(2), 99–110. https://doi.org/10.31857/S0367292122020056
Изобретение относится к способу удержания термоядерной плазмы в открытой ловушке и может использоваться. Способ включает создание плазмы с плотностью 1013-1014 см-3 и температурой до 50 эВ в осесимметричной камере и ее нагрев до температуры 9 кэВ с энергетическим временем удержания τE ≈ 0,1 с, отличающийся тем, что в открытую магнитную ловушку путем инжектирования пучков нейтральных атомов с мощностью порядка 4 МВт при токе 250-300 экв.А и энергией частиц пучка 15 кэВ вводят энергию, достаточную для создания плазмы с минимальным относительным давлением β ≈ 2/3. Техническим результатом является увеличение коэффициента усиления мощности реактора. 1 ил.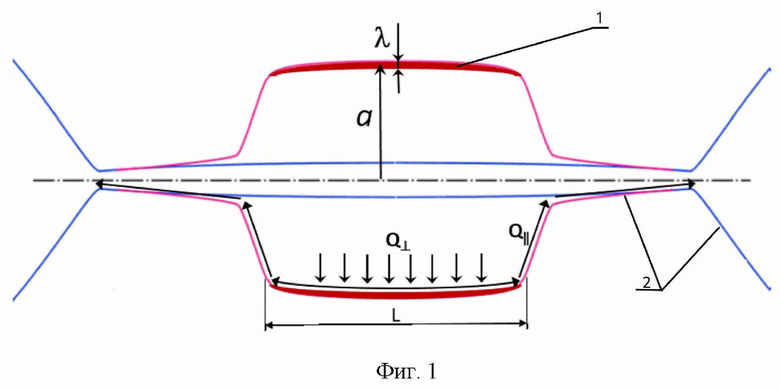
Способ удержания термоядерной плазмы в открытой ловушке, включающий создание плазмы с плотностью 1013-1014 см-3 и температурой до 50 эВ в осесимметричной камере и ее нагрев до температуры 9 кэВ с энергетическим временем удержания τE ≈ 0,1 с, отличающийся тем, что в открытую магнитную ловушку путем инжектирования пучков нейтральных атомов с мощностью порядка 4 МВт при токе 250-300 экв.А и энергией частиц пучка 15 кэВ вводят энергию, достаточную для создания плазмы с минимальным относительным давлением β ≈ 2/3.
| Khristo, M | |||
| S | |||
| и др | |||
| Способ получения продуктов конденсации фенолов с формальдегидом | 1924 |
|
SU2022A1 |
| Two-dimensional MHD equilibria of diamagnetic bubble in gas-dynamic trap | |||
| Plasma Physics and Controlled Fusion, 64(9), 095019 | |||
| Печь-кухня, могущая работать, как самостоятельно, так и в комбинации с разного рода нагревательными приборами | 1921 |
|
SU10A1 |
| Taylor J | |||
| B | |||
| и др | |||
| End losses from a theta pinch // Nuclear Fusion | |||
| Приводный механизм в судовой турбинной установке с зубчатой передачей | 1925 |
|
SU1965A1 |
| - Vol | |||
| Кипятильник для воды | 1921 |
|
SU5A1 |
| - P | |||
| Катодное реле | 1918 |
|
SU159A1 |
| Печь-кухня, могущая работать, как самостоятельно, так и в комбинации с разного рода нагревательными приборами | 1921 |
|
SU10A1 |
| Будкер Г | |||
| и др | |||
Авторы
Даты
2023-11-08—Публикация
2022-11-17—Подача